Article contents
Genetic variability maintained in a finite population due to mutational production of neutral and nearly neutral isoalleles*
Published online by Cambridge University Press: 14 April 2009
Extract
1. The average and the effective numbers of alleles maintained in a finite population due to mutational production of neutral isoalleles were studied by mathematical analysis and computer simulation.
2. The exact formula was derived for the effective number (ne) of alleles maintained in a population of effective size Ne, assuming that there are K possible allelic states and mutation occurs with equal frequency in all directions. If the number of allelic states is so large that every mutation is to a new, not pre-existing, allele, we have ne = 4Neu+1 − 2Neu2, where u is the mutation rate. Thus, the approximation formula, ne = 4Neu+1, given by Kimura & Crow (1964) is valid as long as 2Neu2 ≪ 1.
3. The formula for the average number of alleles (na) maintained in a population of actual size N and effective size Ne was derived by using the method of diffusion approximation. If every mutation is to a new, not pre-existing, allele, we obtain
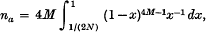
where M = 4Neu. The average number of alleles as a function of M and N is listed in Table 1.
4. In order to check the validity of the diffusion approximations, Monte Carlo experiments were carried out using the computer IBM 7090. The experiments showed that the approximations are satisfactory for practical purposes.
5. It is estimated that among the mutations produced by DNA base substitutions, synonymous mutations, that is, those which cause no alterations of amino acids, amount roughly to 0·2–0·3 in vertebrates. Incompletely synonymous mutations, that is, those which lead to substitution of chemically similar amino acids at a different position of the polypeptide chain from the active site and therefore produce almost no phenotypic effects, must be very common. Together with synonymous mutations, they might constitute at least some 40% of all mutations. These considerations suggest that neutral and nearly neutral mutations must be more common than previously considered.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1968
References
REFERENCES
- 257
- Cited by


