Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T08:26:43.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions to the model of an infinite number of selectively neutral alleles in a finite population

Published online by Cambridge University Press:  14 April 2009

P. J. Avery
P. J. Avery
Affiliation:
Department of Biomathematics, University of Oxford, Pusey St, Oxford 0X1 2JZ
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The model, suggested by Ohta & Kimura, of an infinite number of selectively neutral alleles, in which alleles can only mutate to neighbouring alleles, has been extended to include a migratory pattern. The stepping-stone and island models of migration have been considered. In the latter case, it has been found that as the number of colonies becomes large, the expected number of alleles, ne, becomes approximately equal to

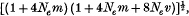
where m is the migration rate, v is the mutation rate and Ne is the effective size of each population. This solution tends to that of Ohta & Kimura as m → 0 but one can see that for any appreciable value of Nem, a large increase in ne is obtained. In order to check the validity of iterative results, models with a finite number of alleles have been considered, and their solutions have been found to converge quickly to those of the infinite case. The results exemplify the great power of migratory structure and neutral alleles to maintain a large amount of heterozygosity. Double step mutation and the finite time solution have also been considered.

Type
Research Article
Information
Genetics Research , Volume 25 , Issue 2 , April 1975 , pp. 145 - 153
Copyright
Copyright © Cambridge University Press 1975

References

REFERENCES

Kimura, M. & Weiss, G. H. (1964). The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics 49, 561–576.CrossRefGoogle ScholarPubMed
Latter, B. D. H. (1973). The island model of population differentiation: a general solution. Genetics 73, 147–157.CrossRefGoogle ScholarPubMed
Ohta, T. & Kimura, M. (1971). Linkage disequilibrium between 2 segregating nucleotide sites under the steady flux of mutations in a finite population. Genetics 68, 571–580.CrossRefGoogle Scholar
Ohta, T. & Kimura, M. (1973). A model of mutation appropriate to estimate the number of electrophoretically detectable alleles in a finite population. Genetical Research 22, 201–4.CrossRefGoogle Scholar
Wehrahn, C. F. (1974). The evolution of selectively similar electrophoretically detectable alleles in finite natural populations. (To be published in Genetics.)Google Scholar