Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T01:29:08.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimating variance effect of QTL: an important prospect to increase the resolution power of interval mapping

Published online by Cambridge University Press:  14 April 2009

A. B. Korol ,
Y. I. Ronin ,
Y. Tadmor ,
A. Bar-Zur ,
V. M. Kirzhner  and
E. Nevo
A. B. Korol*
Affiliation:
Institute of Evolution, University of Haifa, Mount Carmel, Haifa 31905, Israel
Y. I. Ronin
Affiliation:
Institute of Evolution, University of Haifa, Mount Carmel, Haifa 31905, Israel
Y. Tadmor
Affiliation:
Corn Breeding Unit, Neve Yaar Research Center ARO, P.O.B. 90000, Haifa 31900, Israel
A. Bar-Zur
Affiliation:
Corn Breeding Unit, Neve Yaar Research Center ARO, P.O.B. 90000, Haifa 31900, Israel
V. M. Kirzhner
Affiliation:
Institute of Evolution, University of Haifa, Mount Carmel, Haifa 31905, Israel
E. Nevo
Affiliation:
Institute of Evolution, University of Haifa, Mount Carmel, Haifa 31905, Israel
*
*A. B. Korol, Institute of Evolution, University of Haifa, Mount Carmel, Haifa 31905, Israel. Tel. (972)-4240-449, Fax: (972)-4246-554, E-mail: [email protected].
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Equal variances within quantitative trait locus (QTL) groups in the segregating population are a usual simplifying assumption in QTL mapping. The objective of this paper is to demonstrate the advantages of taking into account potential variance effect of QTLs within the framework of standard interval mapping approach. Using backcross case as an example, we show that the resolution power of the analysis may be increased in the presence of variance effect, if the latter is allowed for in the model. 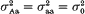For a putative QTL (say, A/a) one can compare two situations, (i) and (ii) 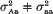. It was found that, if the variance effect of A/a is large enough, then in spite of the necessity to evaluate an increased number of parameters, the more correctly specified model provides an increase in the resolution power, as compared to the situation (i). This is not unexpected, if either 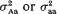in (ii) is lower than 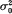from (i). But our conclusion holds even if 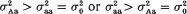. These advantages are illustrated on sweet corn data data (F3 families of F2 genotypes). In particular, the log-likelihood test statistics and the parameter estimates obtained for a QT locus in the distal region of chromosome 2 show that the allele enhancing the trait is recessive over the opposite allele simultaneously for the mean value and variance.

Type
Research Article
Information
Genetics Research , Volume 67 , Issue 2 , April 1996 , pp. 187 - 194
Copyright
Copyright © Cambridge University Press 1996

References

Boehnke, M. & Moll, P. (1989). Identifying pedigrees segregating at a major locus for a quantitative trait: an efficient strategy for linkage analysis. American Journal of Human Genetics 44, 216–224.Google Scholar
Carbonell, E. A., Asins, M. J., Baselga, M., Balansard, E. & Gerig, T. M. (1993). Power studies in the estimation of genetic parameters and the localization of quantitative trait loci for backcross and doubled haploid populations. Theoretical and Applied Genetics 86, 411–416.CrossRefGoogle ScholarPubMed
Carey, G. & Williamson, J. (1991). Linkage analysis of quantitative traits: increased power by using selected samples. American Journal of Human Genetics 49, 786–796.Google ScholarPubMed
Churchill, G. A. & Doegre, R. W. (1994). Empirical threshold values for quantitative trait mapping. Genetics 138, 963–971.CrossRefGoogle ScholarPubMed
Darvasi, A. & Soller, M. (1992). Selective genotyping for determination of linkage between a marker locus and a quantitative trait locus. Theoretical and Applied Genetics 85, 353–359.CrossRefGoogle Scholar
Demenais, E., Lathrop, G. M. & Lalouel, J. M. (1988). Detection of linkage between a quantitative trait and marker locus by the lod scores method: sample size and sampling considerations. Annals of Human Genetics 52, 237–246.CrossRefGoogle ScholarPubMed
Ferguson, J. E., Rhoads, A. M. & Dickinson, D. B. (1978). The genetics of sugary enhancer (se) and independent modifier of sweet corn (su). Journal of Heredity 69, 377–380.CrossRefGoogle Scholar
Jansen, R. C. & Stam, P. (1994). High resolution of quantitative traits into multiple loci via interval mapping. Genetics 136, 1447–1455.CrossRefGoogle ScholarPubMed
Knott, S. A., & Haley, C. S., (1992). Aspects of maximum likelihood methods for mapping of quantitative trait loci in line crosses. Genetical Research 60, 139–151.CrossRefGoogle Scholar
Korol, A. B., Preygel, I. A., & Preygel, S. I., (1994). Recombination Variability and Evolution. London: Chapman & Hall.Google Scholar
Korol, A. B., Ronin, Y. I., & Kirzhner, V. M., (1995). Interval mapping of quantitative trait loci employing correlated trait complexes. Genetics 140, 1137–1147.CrossRefGoogle ScholarPubMed
Korol, A. B., Zhuchenko, A. A., & Samovol, A. P., (1981). Linkage between quantitative trait loci and marker loci. 3. Biasing of estimates resulting from departures from initial assumptions. Genetika (USSR) 17, 1234–1247.Google Scholar
Kullback, S., (1959). Information Theory and Statistics. New York: John Wiley & Sons.Google Scholar
La Bonte, D. R., & Juvik, J. A., (1990). Characterization of sugary (sul) and sugary enhancer (se) kernels in segregating maize (Zea mays L.) populations. Journal of the American Society for Horticultural Science 114, 153–157.CrossRefGoogle Scholar
Lander, E. S., & Botstein, D., (1989). Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121, 185–199.CrossRefGoogle ScholarPubMed
Lebowitz, B. J., Soller, M., & Beckmann, J. S., (1987). Traitbased analyses for the detection of linkage between marker loci and quantitative trait loci in crosses between inbred lines. Theoretical and Applied Genetics 73, 556–562.CrossRefGoogle ScholarPubMed
Lerner, I. M., (1954). Genetic Homeostasis. Edinburgh and London: Oliver & Boyd.Google Scholar
Motro, U., & Soller, M., (1993). Sequential sampling in determining linkage between marker loci and quantitative trait loci. Theoretical and Applied Genetics 85, 658–664.CrossRefGoogle ScholarPubMed
Ronin, Y. I., Kirzhner, V. M., & Korol, A. B., (1995). Linkage between loci of quantitative traits and marker loci: multi-trait analysis with a single marker. Theoretical and Applied Genetics 90, 776–786.CrossRefGoogle ScholarPubMed
Soller, M., & Beckmann, J. S., (1990). Marker-based mapping of quantitative trait loci using replicated progeny. Theoretical and Applied Genetics 80, 205–208.CrossRefGoogle Scholar
Tadmor, Y., Azanza, F., Han, T., Rocheford, T. R., & Juvik, J. A., (1995). RFLP mapping of the sugary enhancer 1 gene in sweet corn. Theoretical and Applied Genetics 88 (in the Press).Google Scholar
Titterington, D. M., Smith, A. F., & Makov, U. E., (1985). Statistical Analysis of Finite Mixture Distributions. Wiley, Chichester, UK.Google Scholar
Weller, J. I., (1986). Maximum likelihood techniques for the mapping and analysis of quantitative trait loci with the aid of genetic markers. Biometrics 42, 627–640.CrossRefGoogle ScholarPubMed
Weller, J. I., (1987). Mapping and analysis of quantitative trait loci in Lycopersicon (tomato) with the aid of genetic markers using approximate maximum likelihood methods. Heredity 59, 413–421.CrossRefGoogle Scholar
Weller, J. I., & Wyler, A., (1992). Power of different sampling strategies to detect quantitative trait loci variance effect. Theoretical and Applied Genetics 83, 582–588.CrossRefGoogle Scholar
Wilks, S. S., (1962). Mathematical Statistics. New York: Wiley.Google Scholar
Zeng, Z.-B., (1994). Precise mapping of quantitative trait loci. Genetics 136, 1457–1468.CrossRefGoogle ScholarPubMed
Zhuchenko, A. A., Samovol, A. P., Korol, A. B., & Andryuschenko, V. K., (1979). Linkage between quantitative trait loci and marker loci. 2. Effects of three tomato chromosomes on the variation for five quantitative characters in backcross generations. Genetika (USSR) 15, 672–683.Google Scholar