Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T06:15:54.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimating the proportion of neutral mutants

Published online by Cambridge University Press:  14 April 2009

G. A. Watterson
G. A. Watterson
Affiliation:
Mathematics Department, Monash University, Clayton, Victoria, 3168, Australia
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kimura used the heterozygosity and the number of low-frequency alleles to estimate that about 14% of mutations are selectively neutral. The method is shown to be subject to biases and to disruption due to bottleneck effects. Let deleterious alleles have selective disadvantage, s, compared with neutral alleles and let Ne denote the effective diploid population size. The estimator, 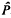, of the proportion of neutral alleles is positively biased if (roughly) 4NeS < 25 or if 4Nes > 200. In the former case, one cannot adequately detect the different influences of deleterious and neutral alleles, whereas in the latter case, deleterious alleles will rarely appear in the sample. These difficulties cause the biases in 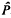, and are likely to cause similar biases for any estimation method based solely on allele frequencies. There is substantial sampling variability in 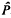in cases of practical interest, when data from 11 loci, or even as many as 31 loci, are pooled. If there has been a recent contraction in population size, 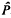will be positively biased, often yielding values greater than 1 or even being infinite. But after a recent expansion in population size, the heterozygosity will not have made as quick an increase and 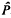will be negatively biased. Population expansion alone can produce 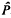values close to those observed by Kimura, even if all alleles are neutral. In an appendix, a new method for simulating samples of neutral and deleterious genes is described.

Type
Research Article
Information
Genetics Research , Volume 50 , Issue 2 , October 1987 , pp. 155 - 163
Copyright
Copyright © Cambridge University Press 1987

References

Ewens, W. J. (1964). The maintenance of alleles by mutation. Genetics 50, 891–898.CrossRefGoogle ScholarPubMed
Ewens, W. J. & Li, W.-H. (1980). Frequency spectra of neutral and deleterious alleles in a finite population. Journal of Mathematical Biology 10, 155–166.Google Scholar
Griffiths, R. C. (1983). Allele frequencies with genetic selection. Journal of Mathematical Biology 17, 1–10.CrossRefGoogle Scholar
Gurland, J. & Tripathi, R. (1975). Estimation of parameters on some extensions of the Katz family of discrete distributions involving hypergeometric functions. In Statistical Distributions in ScientfIc Work, vol. 1 (ed. Patil, G. P., Kotz, S. and Ord, J. K.), pp. 59–79. Boston: Reidel.Google Scholar
Hoppe, F. M. (1984). Polya-like urns and the Ewens sampling formula. Journal of Mathematical Biology 20, 91–94.Google Scholar
Kennedy, W. J. & Gentle, J. E. (1980). Statistical Computing. New York: Marcel Dekker.Google Scholar
Kimura, M. (1983). Rare variant alleles in the light of the neutral theory. Molecular Biology and Evolution 1, 84–93.Google Scholar
Kimura, M. & Crow, J. F. (1964). The number of alleles that can be maintained in a finite population. Genetics 49, 725–738.CrossRefGoogle Scholar
Kingman, J. F. C. (1980). Mathematics of genetic diversity. SIAM CBMS-NSF regional conference series in applied mathematics,34.Google Scholar
Nei, M. (1977). Estimation of mutation rate from rare protein variants. American Journal of Human Genetics 29, 225–232.Google Scholar
Stewart, F. M. (1976). Variability in the amount of heterozygosity maintained in neutral populations. Theoretical Population Biology 9, 188–201.Google Scholar
Watterson, G. A. (1974 a). The sampling theory of selectively neutral alleles. Advances in Applied Probability 6, 463–488.CrossRefGoogle Scholar
Watterson, G. A. (1974 b). Models for the logarithmic species abundance distributions. Theoretical Population Biology 6, 217–250.Google Scholar
Watterson, G. A. (1978). The homozygosity test of neutrality. Genetics 88, 405–417.Google Scholar
Watterson, G. A. (1984). Estimating the divergence time of two species. Statistics Research Report 94, Monash University.Google Scholar
Watterson, G. A. (1988). The neutral alleles model with bottlenecks. In Mathematical Evolutionary Theory (ed. Feldman, M. W.) Princeton: Princeton University Press (in press).Google Scholar