1. Introduction
Characterizing the pattern of genomic diversity is important for insights into genomic evolution in natural or artificial populations. This pattern records the naturally occurring processes that maintain the pattern of genomic diversity along chromosomes, including the relative effects of basic evolutionary forces (mutation, migration, selection and genetic drift) in different chromosomal regions. Historical, ecological and demographical processes are also implicitly recorded underlying this pattern (Oleksyk et al. Reference Oleksyk, Smith and O'Brien2010). In reality, such a pattern can facilitate genomic selection in plant or animal breeding programmes, since individual correlation blocks are easier to manipulate compared to individual single nucleotide polymorphism (SNP) markers. Markers within correlation blocks can be jointly used in breeding value predictions, reinforcing recently extensive explorations of genomic selection (Meuwissen et al. Reference Meuwissen, Hayes and Goddard2001; Hu Reference Hu2007; Hayes et al. Reference Hayes, Bowman, Chamberlain and Goddard2009). Currently, although numerous methods have been proposed to characterize the genomic structure (Percus Reference Percus2002; Hahn Reference Hahn2007; Begun et al. Reference Begun, Holloway and Stevens2007), most of them focus on genome features at the individual level and hence are not suitable for describing the genomic structure at the population level. Theoretical development in this area remains in its infant phase (Hernandez-Sanchez et al. Reference Hernandez-Sanchez, Haley and Woolliams2004; Hill & Weir Reference Hill and Weir2007). One type of genomic structure is the pattern for the correlation of genetic diversities among linked sites along chromosomes and the chromosomal segment within which strong genetic correlations exist and can be broadly termed as a correlation block. For instance, the gametic linkage disequilibria (LDs) block pattern describes the pattern for the correlations between frequencies of non-alleles at different loci (Wright Reference Wright1969; Slatkin Reference Slatkin2008). Here, we examine an alternative correlation block pattern, the correlation of non-allelic identity by descents (IBD) among linked sites, to characterize the genomic structure at the population level.
Three types of descent correlations are possible when a random pair of gametes for two or more sites is considered: IBD between alleles from different gametes at the same site, IBD between non-alleles from the sites on different gametes, and IBD between non-alleles from the sites on the same gametes. Cockerham & Weir (Reference Cockerham and Weir1973) exhaustively described all possible descent correlations/measures and explored their applications to some specific cases. Previous studies mainly lie in developing the method for estimating the correlation of IBD between alleles from different gametes at the same site (Lynch Reference Lynch1988; Rousset Reference Rousset2002; Wang Reference Wang2002), mainly due to its conceptual importance in breeding programme and in population genetics (e.g. inbreeding coefficient; Wright Reference Wright1969; Jacquard Reference Jacquard, Krickeberg, Lewontin, Neyman and Schreiber1974). The second and third types of descent correlations are studied in a limited way, such as IBD among multigene families (Kimura & Ohta Reference Kimura and Ohta1983) and the distribution of surviving blocks of an ancestral genome (Baird et al. Reference Baird, Barton and Etheridge2003). In this study, the method for estimating the third-type correlation is emphasised for describing the genomic structure. We extend the concept of non-allele IBD correlations to a three-site case where multiple IBD correlations among sites can be simultaneously estimated.
The focal IBD correlation block among non-alleles refers to the chromosomal segment within which any pair of non-alleles significantly comes from the same ancestor (different copies of the same ancestral genome). Such a correlation pattern is distinct from the correlation pattern of pairwise relatedness that focuses on the first type of IBD correlation (Hu Reference Hu2005) or from kinship mapping along chromosomes (Morton & Simpson Reference Morton and Simpson1983). Although both types of patterns can be used to characterize the genomic structure at the population level, they differ in relation to the pattern of the recombination rate along a chromosome. The pattern for non-allele IBD correlations along chromosomes is tightly associated with the pattern of the recombination rate. Also, this pattern is more sensitive to LD than the pattern of pairwise relatedness, since the occurrence of recombination immediately changes IBD status between linked non-alleles. LD is the genetic basis for causing the pattern of non-allele IBD correlation.
The purpose of this study is to develop a new method for estimating the IBD correlation based on non-allele descent measures, complementary to the previous IBD correlation study based on the allele descent measures (Hu Reference Hu2005). Two types of descent correlations are estimated: one is the standardized parental disequilibria termed by Cockerham & Weir (Reference Cockerham and Weir1973) ; the other is the standardized IBD segment disequilibria. Similar to the previous studies in pairwise relatedness estimation, the approach of sampling pairwise haploids is employed. Diallelic SNP markers are focused as tri-/tetra-allelic SNP are infrequent in natural or artificial populations. Use of haploid data sets also leads to the method being applicable to specific chromosomes, such as the sex chromosomes, irrespective of the effects of the mating system. However, the use of diploid genotyping data in terms of heterozygosity at different sites produces over parameterization, different from the pairwise relatedness analysis (Hu Reference Hu2005), and thus is not explored here.
In the following sections, we begin by describing the method for the two-site case where only one type of descent correlation is measured. The three-site case is then examined to estimate two types of descent correlations. In each case, Monte Carlo (MC) simulations are used to explore the statistical properties related to the application to real data analysis. Based on the previous study showing a comparable performance between the weighted least square (WLS) method and the maximum likelihood (ML) method (Hu Reference Hu2005), only the WLS method is employed. The application of the proposed method is discussed from the analytical and simulation results.
2. The statistical model
The model is suitable for diallelic SNP marker-based population genomic analysis. Different from Cockerham & Weir (Reference Cockerham and Weir1973), who inclusively analysed the descent measures for two loci in theory, this study emphasizes the statistical estimation of the two- and three-site non-allele descent measures and their correlations on the same chromosome.
(i) Two-site descent correlation
Consider a pair of two linked SNP markers in a natural or artificial population, denoted by A and B, respectively. Let p a and p a′ (=1−p a) be the frequencies of alleles a and a′ at the A site; and p b and p b′ (=1−p b) be the frequencies of alleles b and b′ at the B site. There are four types of two-allele gametes, with gametic frequencies denoted by p ab, p ab′, p a′b and p a′b′ for ab, ab′, a′b, and a′b′, respectively. The two-site gametic frequencies can be expressed in the conventional way in terms of LD, e.g. p ab=p ap b+D AB, where D AB is the LD between the A and B sites. Throughout this study, the gametic and allelic frequencies are assumed to be known beforehand or estimated from the same or different sampling datasets, similar to the previous pairwise relatedness studies (Hu Reference Hu2005).
Following the definition on the two-locus descent measures by Cockerham & Weir (Reference Cockerham and Weir1973), two parameters can be defined with regard to the descent measures between two linked non-alleles. For a pair of non-alleles from two linked sites, let the Kronecker delta variable δ(uv)=1, if u and v are from the copies of non-alleles on an ancestral gamete; and δ(uv)=0, otherwise. Considering a pair of two-site non-alleles (ab, a′b′), let i=δ(ab) and i′=δ(a′b′). Let F i,i′ (0⩽F i,i′⩽1) be the joint probability that IBD occurs between a and b and between a′ and b′. F 1,1 is the same in biological meaning as F 11 of Cockerham & Weir (Reference Cockerham and Weir1973). Figure 1 illustrates these four combinations for a random pair of two-site gametes (F 1,1+F 1,0+F 0,1+F 0,0=1). Only two parameters (F 1,1 and F 1,0 or F 1,1 and F 0,1) are distinguishable, since the equivalence, F 1,0=F 0,1, holds.
Fig. 1. Four combinations of non-allele descents are illustrated for a random pair of gametes at the two-site case. Each site has two alleles, with alleles a and a′ at the A site, and alleles b and b′ at the B site. The thicker solid lines indicate the linked non-alleles that are IBD. F i,j (i,j=0,1) denotes the joint IBD probability for a random pair of gametes.
The approach for estimating F parameters is based on the probabilities of pairwise two-site gametes (haplotypes) sampled from the focal population. This is essentially the same as previous studies on pairwise relatedness (Hu Reference Hu2005), i.e. from the probability of identity by state (IBS) to that of IBD. Let P a′b′ab be the observed probability that a random pair of two-site gametes are ab and a′b′. Non-alleles a and b on one gamete may or may not be identical in state with a′ and b′ on the other gamete, respectively. This type of information is extensively considered in previous pairwise relatedness studies and is not included here. Four types of gametes can generate 16 types of pairwise combinations, but only 10 of them (4×(4+1)/2=10) are distinguishable. Using the same approach as Cockerham & Weir (Reference Cockerham and Weir1973), the observed probability for a random pair of gametes,P a′b′ab, can be decomposed as
where F i,j is the F-parameters at the two-site case. From eqn (1), one randomly sampled gamete probability can be expressed as P ab=∑a′, b′P a′b′ab=F 1.p ab+F 0.p ap b, where F 1.=F 1,1+F 1,0 and F 0.=F 0,1+F 0,0. The expression for P ab is essentially the same as Cockerham & Weir (Reference Cockerham and Weir1973, p. 308) for a random sample from an infinite randomly mating population.
The F-parameters can be estimated from eqn (1). Let c F be the covariance between non-allele descents of ab and a′b′ for two randomly sampled gametes, i.e. c F=cov(F 1.,F .1). Here, F 1. and F .1 are expected to be the same. Cockerham & Weir (Reference Coop and Prezeworski1973) defined c F as the parental descent disequilibrium, since it describes the difference between the joint probability and the product of individual non-allele IBD probabilities from different gametes. Thus, the following expressions can be obtained from the definition of covariance in statistics
Solution to eqns (2a)–(2d) yields 
and 
or 
. To make this estimate comparable among different regions on the same or different chromosomes, the correlation coefficient is standardized, i.e. 
or 
, which ranges from −1 to 1.
(ii) Three-site descent correlation
Now, consider a random pair of three-site SNP markers in a natural or artificial population, denoted by sites A, B, and C, respectively. Notation for allele frequencies at the A and B sites remains the same as in the preceding two-site case. Let p c and p c′(=1−p c) be the frequencies of alleles c and c′ at the C site. There are eight types of three-site gametes, with the frequencies denoted by p abc, p abc′, …, p ab′c′ and p a′b′c′ for gametes abc, abc′, …, ab′c′, and a′b′c′, respectively. According to Bennett (Reference Bennett1954), the three-site gametic frequency, e.g. p abc, can be expressed as p abc=p ap bp c+p aD BC+p bD AC+p cD AB+D ABC, where D ij(=freq.(ij)−freq.(i)×freq.(j)) is the gametic LD at the i and j sites and D ABC is the gametic LD at the A, B and C sites. The two-site gametic frequencies can be readily derived from the three-site gametic frequencies, e.g., p ab=p abc+p abc′ for the frequency of gamete ab.
Sixteen parameters can be defined with regard to the non-allele descent measures in the three-site case, excluding the allele-descent measures at individual sites from separate chromosomes (Hu Reference Hu2005) and the descent measures of non-alleles at different sites from separate chromosomes (recombinant descent coefficients; Cockerham & Weir Reference Cockerham and Weir1973). This may remove the number of parameters that are difficult to estimate simultaneously. For a random pair of non-alleles at two different sites on the same chromosome, let the Kronecker delta variable δ(uv)=1 if u and v come from the copies of the same ancestral gamete, and δ(uv)=0 otherwise. Considering a random pair of three-site non-alleles (abc, a′b′c′), let i=δ(ab), j=δ(bc), i′=δ(a′b′) and j′=δ(b′c′). Let F ij,i′j′ (0⩽F ij,i′j′⩽1) be the joint probability that IBD occurs between a and b, between b and c, between a′ and b′ and between b′ and c′. Figure 2 illustrates different combinations for a random pair of three-site gametes (∑i,j,i′,j′=0,1F ij,i′j′=1). For example, F 11,11 is the probability that IBD occurs among three non-alleles on each chromosome (abc and a′b′c′); F 10,10 is the probability that IBD occurs between non-alleles a and b and between non-alleles a′ and b′, but does not occur between b and c and between b′ and c′ for the random pair of three-site gametes. Note that F 00,..(=∑i′,j′=01F 00,i′j′) or F ..,00(=∑i,j=01F ij.00) contains the probability of the occurrence of double crossovers, where δ(ab)=δ(bc)=0, but δ(ac)=1, or δ(a′b′)=δ(b′c′)=0, but δ(a′c′)=1, and the probability of non-double crossovers where δ(ab)=δ(bc)=0, but δ(ac)=0, or δ(a′b′)=δ(b′c′)=0, but δ(a′c′)=0. This partitioning of F 00,..or F ..,00 is not extended. Because of the symmetry between different random pairs of three-site gametes, there are six equivalences among the 16 F-parameters and hence the 16 parameters can be reduced to nine distinct F-parameters (F 11,11, F 11,10=F 10,11, F 11,01=F 01,11, F 11,00=F 00,11, F 10,10, F 10,01=F 01,10, F 10,00=F 00,10, F 01,00=F 00,01 and F 01,01). The above F-parameters are only related to the IBD between non-alleles on different sites on the same chromosome, and the genetic basis for the occurrence of such IBD is the presence of LD among linked sites.
Fig. 2. Part of 64 combinations of non-allele descents is illustrated for a random pair of gametes at the three-site case. Each site has two alleles, with alleles a and a′ at the A site, alleles b and b′ at the B site and alleles c and c′ at the C site. The thicker solid lines indicate the linked non-alleles that are IBD. F ij,i′j′ (i, j, i′,j′=0, 1)denotes the joint IBD probability for a random pair of gametes.
Let P a′b′c′abc be the observed probability that a random pair of three-site gametes are abc and a′b′c′. Note that non-alleles a, b and c on one gamete may or may not be identical in state with a′, b′, and c′ on the other gamete, respectively. The observed probability is partitioned into different components based on the case of IBS for the random pair of three-site gametes. Using the same approach as Cockerham & Weir (Reference Cockerham and Weir1973), P a′b′c′abc can be expressed as
The relationship F 00,00=1−F 11,11−…−F 01,01 is used in deriving the above expression. In the case of two sites, say the A and B sites, eqn (3) reduces to eqn (1).
Again, accurate allelic and gametic frequencies in eqn (3) are assumed to be known beforehand, which can be estimated by directly using the counting method (ML estimates) when the sample size is not small. The IBD information between alleles at the same site from different gametes and the linkage phases are not necessitated on a prior basis. For the diallelic SNPs, there are eight types of gametes, 64 types of pairwise combinations, but only 36 pairwise combinations (8×(8+1)/2=36) are distinguishable.
The nine unknown F-parameters can be estimated according to the above approach based on haplotype data sets (see the next subsection). When diploid data are considered, eight equations can be produced in terms of various combinations of heterozygosity at individual sites, analogous to eqn (6) in Hu (Reference Hu2005), which is less than the number of F-parameters (=9). Thus, the diploid-based approach in terms of heterozygosity is not applicable to obtain solutions due to over parameterization, different from the case of estimating IBD probabilities between alleles at the same site from different chromosomes.
Two types of correlation coefficients are accordingly calculated in the three-site case. One is the correlation between the IBD probability for the two non-alleles at the A and B sites and the IBD probability for the two non-alleles at the B and C sites, denoted by r segment. The other is the correlation between the IBD probabilities for the two non-alleles at the A and B sites (or at the B and C sites) from different gametes, which is addressed in the preceding section. From the estimates of F-parameters based on eqn (3), we obtain three correlation coefficients:
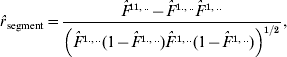
where 
, 
, 
, 
, and 
. 
is the joint probability of IBD between non-alleles at the A and B sites and between non-alleles at the B and C sites on one gamete; 
is the joint probability of IBD between non-alleles at the A and B sites on each of a random pair of gametes; and 
is the joint probability of IBD between non-alleles at the B and C sites on each of the random pair of gametes. 
and 
are the probabilities of IBD between non-alleles at the A and B sites and between non-alleles at the B and C sites on one gamete, respectively. F 11,..−F 1.,..F .1,.. is the covariance of IBD probabilities between two IBD segments on the same chromosomes, i.e. segments AB and BC (Fig. 2). F 1.,1.−F 1.,..F 1.,.. and F .1,.1−F .1,..F .1,.. are the covariances of IBD probabilities for a random pair of segments AB and BC from separate gametes (Fig. 2), respectively, which is the same as that in the two-site case. Standardization of these covariances makes them useful for comparisons among different regions of chromosomes, with the correlation coefficients (r segment, r parent (AB) and r parent (BC)) ranging from −1 to 1.
(iii) Parameter estimation
Several statistical methods can be applied for estimating F-parameters, such as WLS and ML methods. Hu (Reference Hu2005) has compared these two methods and demonstrated that the two methods can yield comparable results in accuracy and precision in pairwise relatedness analysis. However, the iteration approach for the ML method, such as using Newton–Raphson's iterative approach, takes a long time to obtain convergent estimates in the presence of many parameters (e.g. nine F-parameters in the three-site case), especially when the sample size is large. The ML method is inappropriate for analysing large population genomic datasets since it may take an extremely long time, such as the use of human population genome data or 50K SNP panel in beef cattle population. Following, only the WLS method is described due to its fast and efficient calculation.
In the two-site case, let Y be the known vector 
where y a′b′ab=Pa′b′ab−papbpa′pb′
and nAB
=10. Let X be the known matrix with n AB×2 elements, X=(x1 x2), where 
and 
; and F be the parameter vector F=(F 1,1 F 1,0)′. As an approximation, we assume that errors for individual observations of yi
are uncorrelated with each other. This assumption is reasonable when the sample size is not too small (their covariances are small in the case of a large sample size). To include the likely impacts of the uncertainty of each observation, the weight wi
(i=1, …,n AB), the reciprocal of the variance of the ith observation, is assigned to the ith observation. Note that other more sophisticated algorithms for setting weights can also be proposed, which is not emphasized here. Estimation of F-parameters can be derived by minimizing the weighted sum of square residuals, i.e. 
. Expression for F-parameter estimates can be further simplified:
where 1 is the vector 
, W is the weight vector 
with the diagonal element being wa′b′ab=1/Pa′b′ab(1−Pa′b′ab) and zero for non-diagonal elements, and 
is the estimate of the mean of ya′b′ab. Note that the intercept estimate 
is expected to be zero since the original constant term in eqn (1) is removed from each observation (ya′b′ab=Pa′b′ab− papbpa′pb′
). Alternatively, Pa′b′ab can be straightforwardly used as the dependent variable in regression analysis. Under this situation, the intercept is not expected to be zero and its biological meaning refers to the average probability of a random haplotype pair in the absence of non-allele descents.
The analysis is similar to the two-site case, which is applied to the three-site case. Let Y be the known vector 
in which ya′b′c′abc=Pa′b′c′abc− papbpcpa′pb′pc′
and n ABC=36; X be the known matrix with n ABC×9 elements, X=(x1 x2 … x9), where 
, 
, …, and 
; and F be the F-parameter vector, F=(F 11,11F 11,10 … F 01,01)′. F-parameters can be estimated using the same formula as eqn (5) except that 1 is the vector 
, W is the weight vector 
with the diagonal element being wa′b′c′abc=1/Pa′b′c′abc(1−Pa′b′c′abc) and zero for non-diagonal elements, and 
is the estimate of the mean of ya′b′c′abc. Three correlation coefficients can be simultaneously estimated according to eqn (4) once all F-parameters are calculated according to eqn (5).
3. Simulation results
MC simulation is employed to examine the effects of (i) sample size, (ii) allele frequency distribution and (iii) LD. For the effects of allele frequency distribution, two types of distribution are examined: uniform and non-uniform distributions. For the uniform distribution, each allele at a site has equal frequency (=0·5). For the non-uniform allele frequency distribution, one allele frequency is set as 1/3 and the other is set as 2/3 at each site. Other settings of non-uniform allele frequency distribution can also be examined in different cases. The simulation is conducted in a way similar to the previous pairwise relatedness study of Hu (Reference Hu2005).
Simulation data are generated in the following steps. Given a set of parameters, including two- or three-site gametic frequencies, allelic frequencies, and F-parameters, calculate the probabilities for each pair of two- and three-site gametes according to eqns (1) and (3), respectively. All parameter settings are arbitrary as long as these settings are biologically meaningful. Use these calculated probabilities that follow the multinomial distribution for generating random samples. Random numbers with uniform distribution within (0, 1) are generated using the routine of Press et al. (Reference Press, Flannery, Teukolsky and Vetterling1991, pp. 210–211). For a sample of N diploids (2N haploids), it can generate a sample of 2N(2N−1) random gamete pairs. F-parameters are then calculated according to eqn (5) and the correlation coefficients are calculated according to eqn (2) for the two-site case and eqn (4) for the three-site case. Gauss–Jordan elimination method is used to calculate the inverse matrix and F-parameters (Press et al. Reference Press, Flannery, Teukolsky and Vetterling1991, pp. 36–37). Ten thousand independent simulation runs are conducted in each simulation case. These replicates are used to estimate mean and standard deviation of correlation coefficients according to the statistical model detailed in the preceding section. Simulation programs in C are available from Hu upon request.
In the two-site case, Fig. 3(a) shows the changes of average F-parameter estimates with the sample size. Unbiased estimates can be obtained when the sample size is >50 individuals. The precision of estimates in terms of standard deviation slightly increases when the sample size is >50 (Fig. 3b). Simulation results also confirm that the average estimate of intercept is essentially equal to zero, with a very small standard deviation. This is the same case for all other simulations described below.
Fig. 3. Effects of the sample size on F-parameter estimation at the two-site case: (a) average estimates of F 1,1 and F 1,0 and (b) standard deviations of F 1,1 and F 1,0estimates. The results are obtained from 10 000 independent simulation runs under uniform distribution of allele frequencies. The parameter settings are the LD between the two sites=0·1, F 1,1=0·1, F 1,0=0·05, and the correlation coefficient r parent=0·6078. The dashed line represents the truth F-parameter values.
The results that are similar to the pattern of F-parameter estimates can be observed for the accuracy and precision of parental descent correlation coefficient (r parent). Basically, unbiased estimates and small standard deviations can be obtained when the number of individuals is >50 under the uniform distribution of allele frequencies (Fig. 4). The effects of the distribution of allele frequencies (uniform versus non-uniform distribution) on parameter estimation are not significant (results not given here). However, the magnitude of LD can affect the accuracy and precision of F-parameters and r parent. For example, smaller LD can lower the precision of r parent estimate (Fig. 4), indicating that a large sample size is required to obtain a comparable precision with that in case of larger LD.
Fig. 4. Effects of the sample size on estimating the parental descent correlation at the two-site case. The results are obtained from 10 000 independent simulation runs under the non-uniform and uniform distributions of allele frequencies. The dashed lines with opened circles and opened triangles represent the average and standard deviation of parental descent correlations, respectively, with the LD between the two sites=0·05 under the non-uniform distribution of allele frequencies. The lines with closed circles and closed triangles represent the average and standard deviation of parental descent correlations, respectively, with the LD between the two sites=0·1 under the uniform distribution of allele frequencies. The common parameter settings are F 1,1=0·1, F 1,0=0·05, and the correlation coefficient r parent=0·6078. The dashed line represents the truth parental descent correlation coefficient.
In the three-site case, Fig. 5 shows the effects of the sample size on the accuracies and precisions of three correlation coefficients under the assumption of uniform distribution of allele frequency at each site, i.e. ½ for each allele frequency. The average estimates of three correlation coefficients are generally unbiased from their actual values when the number of sample size increases, such as >20 individuals in Fig. 5(a). The standard deviations for estimating the correlation coefficients decrease with the sample size (e.g., Fig. 5b). When the number of individuals is >50, an appropriate estimate can be obtained in terms of both accuracy and precision (Fig. 5).
Fig. 5. Effects of the sample size on estimating correlation coefficients at the three-site case: (a) average estimates of three correlation coefficients; (b) standard deviations for the estimates of correlation coefficients. The results are obtained from 10 000 independent simulation runs under the uniform distribution of allele frequencies at each site. The parameter settings are the LD between the A and B sites=0·12, between the A and C sites=0·10, between B and C sites=0·12, and LD among the three sites=0·05, F 11,11=0·2, F 11,10=0·01, F 11,01=0·01, F 11,00=0·1, F 10,10=0·01, F 10,01=0·02, F 10,00=0·01, F 01,00=0·02 and F 01,01=0·01. The dashed line represents the truth correlation coefficients. The line with closed circles represents the estimate of r segment=0·7655; the line with closed squares represents the estimate of r parent(AB)=0·39994; and the line with closed triangles represents the estimate of r parent(BC)=0·3633.
The preceding result shows the case with a larger IBD segment correlation coefficient (r segment= 0·7655), but smaller parental descent coefficients (the truth r parent(AB)=0·3994, r parent(BC)=0·3633). Similar results can also be obtained in the case of larger parental descent correlation coefficients but smaller IBD segment correlation coefficients (data not shown here). Generally, unbiased estimates of correlation coefficients together with appropriate precisions can be obtained in each case when the number of individuals is >50 in each case.
In the three-site case, the effects of the distribution of allele frequency are not significant when the sample size is not too small, indicating the robustness of this method. Comparable estimates in terms of the unbiased average and the small standard deviation are obtained between the uniform and non-uniform distributions of allele frequencies. Similar results can be observed in various cases with different parameter settings (results not shown here).
Simulation results show that the magnitude of LD among the three linked sites can affect estimation in accuracy and precision. Figure 6 shows that larger sample sizes are needed to obtain unbiased estimates in the case of low LD (the truth r segment=0·5612, r parent (AB)=0·2927 and r parent (BC)=0·4048), compared to the results of the cases with high LD. Large standard deviations exist even with a large sample size (Fig. 6b).
Fig. 6. Effects of low LD on estimating correlation coefficients at the three-site case: (a) average estimates of three correlation coefficients; (b) standard deviations for the estimates of correlation coefficients. The results are obtained from 10 000 independent simulation runs under the uniform distribution of allele frequency. The parameter settings are the LD between the A and B sites=0·05, between the A and C sites=0·01, between the B and C sites=0·05, and the LD among the three sites=0·005, F 11,11=0·02, F 11,10=0·01, F 11,01=0·02, F 11,00=0·04, F 10,10=0·01, F 10,01=0·01, F 10,00=0·01, F 01,00=0·02 and F 01,01=0·02. The dashed line represents the truth values. The line with closed circles represents the estimate of r segment=0·5613; the line with closed squares represent the estimate of r parent(AB)=0·2927; and the line with closed triangles represents the estimate of r parent(BC)=0·4048.
4. Discussion
This study presents a statistical issue for characterizing the structure of genomic diversity in terms of the correlation of non-allele descents along chromosomes. Two types of correlations (standardized parental disequilibrium and standardized IBD segment disequilibrium) can be estimated by partitioning the joint probabilities of a random pair of gametes into the probabilities of non-alleles IBD at two or three sites. These descent correlations are complementary to the previous studies focusing on the correlation of alleles IBD probabilities (pairwise relatedness) at two or three sites (Hu Reference Hu2005). The patterns in terms of allele- or non-allele-descent correlations reflect different aspects of the genomic structure at the population level although a similar statistical approach is employed. The practical significance is that such a pattern of correlation blocks along chromosomes can be broadly utilized for various purposes, including marker-assisted selection in breeding programs, genome-wide association studies and insights into genomic evolution at the population level.
It is important to understand that mechanisms maintaining the gametic LD block pattern can also change the non-allele IBD correlation pattern although concordance or discordance between them remains to be empirically verified. Migration (or infusion of breeders to the plant or animal breeding populations) and drift can cause whole genome changes and hence alter whole genome level of IBD correlation blocks. Selection and mutation, such as selective sweep effects and genetic hitchhiking effects (Hill & Robertson Reference Hill and Robertson1966; Maynard Smith & Haigh Reference Maynard Smith and Haigh1974), can cause regional chromosomal variation in correlation block size. Mating system as an additional agent can shape the correlation block pattern. Non-random distribution of recombination reinforces the regional variation of correlation block sizes (Coop & Prezeworski Reference Coop and Prezeworski2007). Different combinations of these effects provide the basis for generating various correlation patterns in populations of distinct histories.
It is interesting to understand the similarity and difference in biological meaning between LD and IBD disequilibrium, or between their standardizations. Both are directly affected by recombination, but do not have a one-to-one functional relationship. LD itself does not contain any biological meaning since it only measures the non-random association between two alleles. Its biological meaning can be activated only when linked to the effects of ecological and evolutionary processes (Slatkin Reference Slatkin2008). To the contrary, correlation of non-allele descents has an explicit genetic meaning, measuring the joint probability of two connected segments that come from the same ancestor. The correlation pattern directly reflects the effects of various evolutionary and ecological processes on the recombination rate in distinct regions.
To apply the proposed method for constructing the maps of non-allele descent correlation blocks, two steps are needed. First, a sample of the haplotype SNP markers with a certain density is required. When only diploid genotyping data are available, the haplotype marker sequences are needed to estimate, including the information on SNP marker linkage phases. This can be done with the existing software (e.g., Marchini et al. Reference Marchini, Cutler and Patterson2006; Scheet & Stephens, Reference Scheet and Stephens2006). One caution is that the false positive error in inferring genome-wide linkage phases needs to be controlled, which otherwise might likely result in a biased correlation block pattern. The robustness of the proposed method to biased linkage phased remains to be assessed. This is different from the method for estimating the correlation of pairwise relatedness where diploid genotyping data can be directly applied under the assumption of random mating (Hu Reference Hu2005). When the sexual chromosome or the sequence sample based on megagametes is employed, the proposed method can be directly applied. The second step is to use the three conjunctive sites as one unit (an overlapping sliding window) to estimate for correlation of non-allele descents. The individual three-site results are then jointly analysed to construct the correlation block map for the whole chromosome. The thresholds for determining the correlation block size can be set according to statistical tests or some empirical values, similar to the approach of gametic LD block setting in previous studies (Barrett et al. Reference Barrett, Fry, Maller and Daly2005; Tomita et al. Reference Tomita, Hatsumich and Kurihara2008). Those consecutive SNP markers with strong correlations among them are then grouped into one block and such an analysis continues until all SNP markers on one chromosome are examined.
When the linkage map of dense markers with some markers of more than two alleles, instead of the sequence of SNP markers, is applied for constructing correlation block maps, method presented needs to be expanded to a more complicated analysis. One frequent situation is that our regular linkage maps are inappropriate for correlation block mapping due to large physical distances between adjacent markers where strong LD are often present, or due to the low marker density. This case occurs because most linkage maps are family based and a general method is needed for population-based linkage mapping for the population with a mixed mating system (Hu et al. Reference Hu, Goodwillie and Ritland2004). Like the previous studies on pairwise relatedness, this method only uses one-generation data that are randomly sampled from the population with prior unknown genetic pedigree, and thus has a potential of wide applications in future population genomics analysis.
This study only explores the theory for the two- and three-site cases. Use of the two-site case only estimates the parental descent disequilibrium (Cockerham & Weir Reference Cockerham and Weir1973). The correlation among non-allele descent segments, r segemnt, can be estimated with a minimum number of three sites. This is different from the analysis of the correlation block of pairwise relatedness where both two- and three-site methods can be used to estimate the correlation of pairwise relatedness except that the double crossover effects are included in the three-site case (Hu Reference Hu2005). The proposed method can be extended to the case of more than three sites without technical difficulty. For n(≥3) conjunctive diallelic SNP sites on a chromosome, there are n−1 segments. It can produce 2n− 1(2n+1) distinguishable random n−site haplotype pairs (analogous to eqn (3) in the three-site case), 2n− 2 (2n− 1−1)+2n− 1−1 distinguishable F-parameters, n−1 parental descent disequilibrira (r parent's), and (n−1)(n−2)/2 disequilibria between non-allele descent segments (r segment's). The number of joint equations, 2n− 1(2n+1), is much greater than the number of F-parameters, with the difference being 22n− 3(22−1)+ 2n− 2+1. The probability for a random pair of n-site haplotypes can be decomposed in the way similar to eqn (3). The advantage of multiple-site analysis is that all these correlation parameters can be simultaneously estimated in theory although the calculation becomes more complicated. This requires a large sample size so that 2N(2N−1) haplotype pairs are greater than the number of joint equations.
Statistically, the time-consuming step for the WLS method is to calculate the number of haplotype pairs, 2N(2N−1) for sampling N diploids, which increases substantially with the sample size. This is the same case for using the ML method, since the number of haplotype pairs in constructing the likelihood is required in parameter estimation. The advantage for the WLS method over the ML method is its fast calculation to obtain estimates in the later steps (Hu Reference Hu2005). The diagonal elements in matrix 
are non-zeros, resulting in robustness in calculating its inverse matrix (eqn (5)). This property is of significance in population genomics analysis as the number of pairwise correlations increases significantly with a large SNP panel.
Our simulation results suggest the sample sizes of ~100 diploids can produce estimates with appropriate precision under various effects of LD and allele frequency distribution. The proposed sample sizes are much greater than those required for pairwise relatedness analysis (Hu Reference Hu2005). This is attributable to the effects of LD and more number of parameters. However, the proposed sample size can be met in the future with the development of high-throughput genotyping techniques, such as commercially available Illumina Bovine SNP50K BeadChip for genotyping in beef and dairy cattle populations.
One striking result is that our simulations demonstrate a high precision (low standard deviation) for the estimate of the correlation of non-allele descents from the same chromosomes (r segment), compared to the precision of the estimates of the correlation of non-allele descents from different chromosomes (r parent). This is due to the non-uniform distribution for the number of haplotype pairs in the presence of LD that is the genetic basis for the presence of non-allele correlation. Thus, the results imply that the WLS method is effective in practice for estimating the correlation of non-allele descents along chromosomes.
It is necessary to mention briefly the assumption underlying the method presented for estimating the correlation of non-allele descent measures. Like the previous studies on estimating pairwise relatedness, accurate and precise estimates of gamete and allele frequencies are assumed to be available beforehand. These frequencies might be estimated from the same sampling data sets as well. Biased estimates of these frequencies can affect estimates of the correlation coefficients of descent measures in precision and accuracy. The statistical robustness remains to be assessed in the presence of biased estimates of gametic and allelic frequencies. However, this problem might not be serious when large sample sizes, say ~100 diploids, are applied in practice since gametic and allelic frequencies are often estimated accurately.
We sincerely appreciate Graham Plastow, Stephen Moore, Rong-Cai Yang and Changxi Li for discussions during the preparation of this article, and two anonymous reviewers for useful comments that substantially improved the earlier version of this article. This work was financially supported by Alberta Livestock Industry Development Fund Ltd (ALIDF) and Alberta Agricultural Research Institute (AARI) to Z. W.
