1. Introduction
Epistasis – the dependence of the allelic effects at one locus on the genotype at another locus – is an important feature of the genetic architecture of quantitative traits (Anholt & Mackay, Reference Anholt and Mackay2004; Flint & Mackay, Reference Flint and Mackay2009; Mackay et al., Reference Mackay, Stone and Ayroles2009). Assessing the magnitude and nature of epistatic interactions is important from several perspectives. First, epistasis causes bias in estimates of allelic effects from quantitative trait locus (QTL) mapping studies when it is present but not accounted for (Carlborg et al., Reference Carlborg, Jacobsson, Ahgren, Siegel and Andersson2006; Phillips, Reference Phillips2008). Second, epistatic interactions can be used to infer genetic networks affecting complex traits (Phillips, Reference Phillips2008). Finally, epistasis can affect predictions of long-term response to artificial and natural selection (Wright, Reference Wright1977; Carlborg et al., Reference Carlborg, Jacobsson, Ahgren, Siegel and Andersson2006; Phillips, Reference Phillips2008).
Epistasis is not easy to detect in experiments designed to map QTLs. Genome scans for pairwise epistatic interactions with n markers require n(n−1)/2 statistical tests, which impose a severe multiple testing penalty and concomitantly low significance thresholds, such that only very large interactions are detectable. Further, all possible two locus genotypes may not be present unless mapping populations are very large; this is a particular problem for closely linked loci. Nevertheless, epistatic interactions have been reported between QTLs affecting Drosophila bristle number (Long et al., Reference Long, Mullaney, Reid, Fry, Langley and Mackay1995; Gurganus et al., Reference Gurganus, Nuzhdin, Leips and Mackay1999; Dilda & Mackay, Reference Dilda and Mackay2002), wing morphology (Weber et al., Reference Weber, Eisman, Morey, Patty, Sparks, Tausek and Zeng1999, Reference Weber, Eisman, Higgins, Morey, Patty, Tausek and Zeng2001), lifespan (Leips & Mackay, Reference Leips and Mackay2000, Reference Leips and Mackay2002; Mackay et al., Reference Mackay, Roshina, Leips, Pasyukova, Masaro and Austad2006) and startle-induced locomotor behaviour (Jordan et al., Reference Jordan, Morgan and Mackay2006). In mice, epistasis has been documented between QTLs affecting many traits related to growth, body weight and morphometry (Brockmann et al., Reference Brockmann, Kratzsch, Haley, Renne, Schwerin and Karle2000; Cheverud et al., Reference Cheverud, Vaughn, Pletscher, Peripato, Adams, Erikson and King-Ellison2001; Klingenberg et al., Reference Klingenberg, Leamy, Routman and Cheverud2001; Reference Klingenberg, Leamy and Cheverud2004; Workman et al., Reference Workman, Leamy, Routman and Cheverud2002; Yi et al., Reference Yi, Zinniel, Kim, Eisen, Bartolucci, Allison and Pomp2006). Epistasis also features prominently in the genetic architecture of growth rate of chickens (Carlborg et al., Reference Carlborg, Jacobsson, Ahgren, Siegel and Andersson2006), Arabidopsis (Kroymann & Mitchell-Olds, Reference Kroymann and Mitchell-Olds2005) and yeast (Steinmetz et al., Reference Steinmetz, Sinha, Richards, Spiegelman, Oefner, McCusker and Davis2002; Sinha et al., Reference Sinha, David, Pascon, Clauder-Münster, Krishnakumar, Nguyen, Shi, Dean, Davis, Oefner, McCusker and Steinmetz2008). Epistatic effects can be as large as main QTL effects, and can occur in opposite directions between different pairs of interacting loci and between loci without significant main effects on the trait. Epistatic effects can also occur between closely linked QTLs (Steinmetz et al., Reference Steinmetz, Sinha, Richards, Spiegelman, Oefner, McCusker and Davis2002; Kroymann & Mitchell-Olds, Reference Kroymann and Mitchell-Olds2005; Sinha et al., Reference Sinha, David, Pascon, Clauder-Münster, Krishnakumar, Nguyen, Shi, Dean, Davis, Oefner, McCusker and Steinmetz2008) and even between polymorphisms at a single locus (Stam & Laurie, Reference Stam and Laurie1996).
Epistasis is more readily detectable in crosses among lines in which genetic heterogeneity is reduced and the genetic background is controlled precisely. Diallel crosses have revealed extensive epistasis between introgression lines of tomato for yield-associated traits (Eshed & Zamir, Reference Eshed and Zamir1996), and between Drosophila P-element mutations in a common isogenic background affecting olfactory (Fedorowicz et al., Reference Fedorowicz, Fry, Anholt and Mackay1998; Sambandan et al., Reference Sambandan, Yamamoto, Fanara, Mackay and Anholt2006), climbing (van Swinderen & Greenspan, Reference Van Swinderen and Greenspan2005) and startle (Yamamoto et al., Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008) behaviour. Clark & Wang (Reference Clark and Wang1997) constructed all nine possible two-locus genotypes for several pairs of P-elements and identified extensive epistasis affecting metabolic activity in Drosophila.
Other powerful designs for detecting epistatic interactions are to construct a panel of chromosome substitution lines, in which single chromosomes from one strain are each substituted into the homozygous genetic background of a second strain; or even more precisely, to construct segmental introgression lines, in which small genomic segments from one strain are introgressed into the background of a second strain, such that the entire collection of introgression lines tile across the genome. In the presence of epistasis, the sum of the effects of all chromosome substitution lines or introgression lines is greater or less than the difference in the mean value of the trait between the two parental strains. Using these designs, substantial epistasis has been revealed for tomato yield traits (Eshed & Zamir, Reference Eshed and Zamir1996), a battery of quantitative traits in mice (Shao et al., Reference Shao, Burrage, Sinasac, Hill, Ernest, O'Brien, Courtland, Jepsen, Kirby, Kulbokas, Daly, Broman, Lander and Nadeau2008) and Drosophila aggressive behaviour (Edwards & Mackay, Reference Edwards and Mackay2009).
Drosophila melanogaster is an excellent model system for studies of epistasis affecting quantitative traits, due to the ease of constructing the relevant genotypes. Previously, we showed that startle-induced locomotor behaviour is a phenotype that is easily and reproducibly quantified, highly polygenic and exhibits epistasis both at the level of QTLs and P-element mutations in a diallel cross design (Jordan et al., Reference Jordan, Morgan and Mackay2006, Reference Jordan, Carbone, Yamamoto, Morgan and Mackay2007; Yamamoto et al., Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008). Here, we characterize epistatic interactions among homozygous P-element mutations affecting startle-induced locomotion in the Canton-S isogenic background. In addition, we combine mutational analysis with the chromosome substitution design to assess the effects of naturally occurring modifiers of mutations affecting the startle response. We accomplish this by substituting second or third Canton-S chromosomes with or without P-element insertion mutations that impair the startle response into 21 wild-derived inbred genetic backgrounds. We show that epistasis is pervasive both for pairwise combinations of homozygous P-element insertional mutations and for mutations in wild-derived backgrounds; that in all cases the direction of the epistatic effects is to suppress the mutant phenotypes; and that there is variation in the magnitude of epistasis among the wild-derived genetic backgrounds. We discuss the implications of these results for genetic networks affecting startle-induced locomotion, phenotypic robustness and maintenance of genetic variation for the startle response in natural populations.
2. Materials and methods
(i) Drosophila stocks
The 15 P-element insertion mutants affecting locomotor startle response used in this study have been described previously (Yamamoto et al., Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008). They contain single P[GT1] insertions (Lukacsovich et al., Reference Lukacsovich, Asztalos, Awano, Baba, Kondo, Niwa and Yamamoto2001) and were generated in the same isogenic w 1118; Canton-S B background as part of the Berkeley Drosophila Gene Disruption Project (Bellen et al., Reference Bellen, Levis, Liao, He, Carlson, Tsang, Evans-Holm, Hiesinger, Schulze, Rubin, Hoskins and Spradling2004). All P-elements were inserted within or in close proximity to a well-annotated gene: tramtrack (ttk BG01491), extramacrochaetae (emc BG00986), HLHm7 BG02029, longitudinals lacking (lola BG02501), Calreticulin (Crc BG01724), neuralized (neur BG02542), Laminin A (LanA BG01389), roundabout (robo BG01092), Sema-1a BG02570, Sema-5c BG01245, Darkener of apricot (Doa BG02498), Cysteine string protein (Csp BG01863), CG8963 BG02470, mir-279 BG01888 and mir-317 BG01900.
Four of the genes tagged by P[GT1] insertions were on the second chromosome (Sema-1a, CG8963, robo and lola) and 11 were on the third chromosome (ttk, emc, HLHm7, Crc, neur, LanA, Sema-5c, Doa, Csp, mir-279 and mir-317). We created all 44 possible chromosome 2–chromosome 3 double homozygous genotypes of these P-element insertions in the Canton-S background.
Inbred lines were derived by 20 generations of full-sib mating from isofemale lines that were collected from the Raleigh, NC Farmer's Market in 2003 (Ayroles et al., Reference Ayroles, Carbone, Stone, Jordan, Lyman, Magwire, Rollmann, Duncan, Lawrence, Anholt and Mackay2009). We selected 21 Raleigh inbred lines of which males caused no obvious hybrid dysgenesis with Canton-S females when their F1 hybrids were examined for ovarian development at 28·9°C. We chose three P[GT1]-tagged genes on the second chromosome (Sema-1a, robo and lola) and seven on the third chromosome (emc, HLHm7, Crc, neur, Sema-5c, Csp and mir-317) for further analyses, and constructed chromosome substitution lines in which a Canton-S chromosome carrying a P[GT1]-element insertion or its co-isogenic P-element free counterpart was substituted in each of the Raleigh inbred line genetic backgrounds, using balancer chromosomes to prevent recombination, and minimizing any remnant P-element activities by using flies with natural population-derived chromosomes as female progenitors (Supplementary Figures 1 and 2). We were able to generate all homozygous genotypes of combinations between each of the 10 P[GT1]-tagged genes and 21 Raleigh inbred lines except in two cases (RAL-765 and mir-317 and RAL-765 and Crc).
All flies were reared on cornmeal–agar–molasses medium at 25°C under controlled density and aged 3–7 days post-eclosion prior to the behavioural assay.
(ii) Behavioural assay
We measured startle behaviour as described previously (Jordan et al., Reference Jordan, Morgan and Mackay2006, Reference Jordan, Carbone, Yamamoto, Morgan and Mackay2007; Yamamoto et al., Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008). We placed single flies in a plastic culture vial with medium the day before measurement. The next day, we subjected the flies to a mechanical disturbance by a gentle sudden tap of the vial, which was then immediately placed horizontally under a fluorescent lamp. We quantified startle-induced locomotion as the number of seconds each fly was active in the 45 s period immediately following the disturbance. All tests were done at 25°C between 8 am and 12 pm. The sample size for all experiments was N=20 measurements/sex/genotype. For the P-element mutations in the Canton-S background, we measured two males and two females from each of the 44 double homozygous lines, 15 single homozygous parental genotypes and the progenitor Canton-S strain each day for 10 days (N=2400). We measured two males and two females from each of the second chromosome substitution lines (84 genotypes) each day for 10 days (N=3360) and one male and one female from each of the third chromosome substitution lines (166 genotypes) each day for 20 days (N=6640).
(iii) Analysis of epistasis in the Canton-S background
We performed three-way fixed effects analysis of variance (ANOVA) of the startle-induced locomotion scores of the double homozygous genotypes using the model
where Y is the observed value, μ is the overall mean, C2 is the effect of the second chromosome insertions, C3 is the effect of the third chromosome insertions, C2×C3 is the effect of the epistatic interaction between the second and third chromosome insertions, C2×S and C3×S represent the sex interaction terms between the second chromosome and third chromosome effects, respectively, C2×C3×S is the three-way interaction between P-element insertion effects on the second chromosome, the third chromosome and sex, and ε is the error term.
We estimated 2a, the deviation of the mean startle-induced locomotion score of the homozygous mutations from the mean of the Canton-S strain (Falconer & Mackay, Reference Falconer and Mackay1996), for each of the 15 homozygous P-element mutations. We then computed the expected startle-induced locomotion score of the double homozygous genotypes from the deviation of (2ai+2aj) from the mean of the Canton-S strain, where the subscripts i and j denote the respective homozygous genotypes. The estimate of the epistatic effect (I) for each double homozygous genotype is then the difference between the expected and observed scores. We assessed the significance of the C2×C3 epistatic interactions by performing the same ANOVA models described above to the four relevant genotypes (Canton S, second chromosome homozygote P-element insertion, third chromosome homozygous P-element insertion, and the double chromosome 2–chromosome 3 P-element insertion) for each of the 44 double homozygotes.
(iv) Analysis of epistasis in the Raleigh inbred line backgrounds
We estimated the expected effect of the P-element mutants in each wild-derived inbred line background by subtracting the estimate of 2a for each mutation in the pure Canton-S background from the observed startle-induced locomotion score of the chromosome substitution lines with wild-type Canton-S chromosomes. The estimate of the epistatic effects (I) for each inbred line genetic background is thus the difference between the expected effect and the observed startle-induced locomotion score of the line in which the mutant Canton-S chromosome was substituted. We assessed the significance of each of the 208 epistatic interactions by three-way fixed effect performing ANOVAs using the model:
where Y and μ are defined above, G is the effect of the presence or absence of the P-element, S is the effect of sex, R is the effect of Raleigh inbred line versus Canton-S genetic backgrounds, G×R, G×S, R×S and G×R×S are the interaction terms and ε is the environmental variance. Significance of the G×R and/or G×R×S interaction terms indicates significant epistasis. In addition, we determined whether there was variation in epistatic effects among the 21 wild-derived inbred lines by performing the mixed model ANOVAs of the same structure described above across all Raleigh line genotypes, treating the Raleigh genotypes and interactions with Raleigh genotypes as random effects.
3. Results
(i) Epistasis between P[GT1] mutations affecting startle behaviour in the Canton-S-background
Based on our previous observations of extensive epistasis among double heterozygotes (Yamamoto et al., Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008), we predicted that defects in startle-induced locomotor reactivity should be aggravated in double homozygotes and epistatic interactions would also be prevalent. We generated all 44 possible double homozygous combinations of four second chromosomal and 11 third chromosomal P[GT1] insertion lines which had been used in the previous double heterozygote analysis, and measured their startle-induced locomotion.
When all 44 genotypes of the combinations of four P-element-tagged genes on the second chromosome and 11 on the third chromosome were analysed by three-way ANOVA, the main effects of the second and third chromosome insertional mutations were highly significant, as expected (Table 1). The interaction between the second and third chromosome mutations was also highly significant overall (Table 1), which indicates epistatic interactions among these mutations.
Table 1. ANOVA of startle-induced locomotion scores of double homozygous genotypes between P[GT1] insertions in a common isogenic background

d.f., degrees of freedom; MS, mean square.
**** P<0·0001; ** 0·01<P<0·001; ns P>0·05.
The mean startle response scores of homozygous P[GT1] insertional mutations, estimates of 2a (the difference between the mean startle response score of the co-isogenic Canton-S B strain and the P[GT1] mutation), observed and expected double homozygous mutant scores, and estimates of the epistatic interactions between chromosome 2 and chromosome 3 mutations are given in Supplementary Table 1. Since the overall main effect of sex and its interaction terms were not significant (or only marginally significant for the interaction with chromosome 2 mutations, Table 1), we present these data averaged across both sexes. The average startle response of the 15 mutations was 27·59 s, 33% lower than the wild-type Canton-S B score. The average startle response of the 44 double homozygous genotypes was 23·87 s, lower than that of the parental homozygotes from which they were derived, as expected from combining mutations which affect the trait in the same direction, but not as low as predicted from additive combinations of homozygous mutations. Thus, the interactions indicated by the overall ANOVA (Table 1) must predominantly involve suppressing epistasis, such that the double homozygotes are less mutant (i.e. more wild-type) than expected. This trend is clear from the plot of observed versus expected startle response of the 44 double homozygous genotypes (Fig. 1).

Fig. 1. Plot of observed (squares) and expected (diamonds) startle-induced locomotion scores of 44 double homozygous P-element mutations in the Canton-S genetic background.
Widespread suppressing epistasis was indeed confirmed from estimates of individual epistatic effects for each of the 44 pair wise interactions, of which 35 were at least nominally significant and negative, and 20 had P-values (assessed from the significance of the C2×C3 interaction term) that survived a Bonferroni correction for multiple tests (Supplementary Table 1). Graphical depictions of these epistatic interactions are given in Figs 2 and 3. Particularly prominent and abundant epistatic interactions involve robo and Sema-1a on the second chromosome, and emc, Sema-5c, mir-317 and HLHm7 on the third chromosome.

Fig. 2. Epistatic interactions for startle-induced locomotion among 44 double homozygous P-element mutations in the Canton-S genetic background. The plot depicts the estimates of the epistatic effect, I, for each double homozygote genotype. The colours indicate different values of I. Most estimates of I are negative, indicating widespread suppressing epistasis.

Fig. 3. Epistatic interaction network of startle-induced locomotion of double homozygous P-element insertions in a Canton-S genetic background. The approximate locations of P-element insertion sites on the left (L) and right (R) arms of the second and the third chromosomes are illustrated. The colours of lines connecting genes represent significance of epistasis at P<0·05 (teal), P<0·01 (blue), P<0·001 (violet) and P<0·0001 (purple).
(ii) Epistasis between P[GT1] mutations affecting startle behaviour and wild-derived genetic backgrounds
We substituted ten Canton-S chromosomes with P[GT1] mutations that affect startle behaviour as well as the wild-type Canton-S chromosomes into 21 wild-derived Raleigh inbred lines (Supplementary Tables 2 and 3) and measured the startle-induced locomotion behaviour of each of the resulting 250 genotypes. Similarly to the analysis of double homozygous mutations, the observed startle responses of the wild-derived chromosomes in which a P-element mutation had been substituted was much less than predicted based on the estimate of 2a in the Canton-S background (Fig. 4). That is, naturally segregating alleles suppress the mutational effects of the P-element mutations on startle-induced locomotion. We quantified the epistatic effects of each mutant allele in the wild-derived backgrounds (Supplementary Table 4). The loci exhibiting the largest epistatic effects in the wild-derived genetic backgrounds were the same as those showing the greatest epistasis in double homozygotes in the Canton-S genetic background: robo, Sema-1a, mir-317, emc, Sema-5c and HLHm7. However, the lola mutation, which displayed little epistasis in the Canton-S double homozygotes, also had large epistatic effects in the Raleigh inbred line backgrounds.

Fig. 4. Plot of observed (squares) and expected (diamonds) startle-induced locomotion scores of 208 chromosomes with P-element mutations affecting startle response substituted into 21 Raleigh inbred line genetic backgrounds.
When we examined the correlation between main effects and epistatic effects, we found that, remarkably, the magnitude of the epistatic effect in the wild-derived lines is nearly perfectly correlated with the magnitude of the main effect of the mutation in the Canton-S background (r=0·952, t 8=8·8, P<0·0001, Fig. 5). That is, the more extreme the effect of the mutation, the greater the degree of suppression in the Raleigh inbred lines. Suppressing epistasis may be a general mechanism for conferring phenotypic robustness.

Fig. 5. Scatter plot of the relationship between the absolute value of the difference between the mean startle induced locomotion score of the P-element mutations and wild-type in the Canton-S background (|2a|, x-axis) and the estimate of the absolute value of the epistatic interaction in the Raleigh wild-derived inbred lines (|I|, y-axis). The correlation coefficient is r=0·952.
ANOVAs confirmed highly significant variation among the Raleigh inbred line backgrounds for all 10 P[GT1]-tagged genes; the line term was highly significant in all cases (Table 2). Genotype, i.e. absence or presence of a P[GT1]-tagged gene, was also significant for most genes. The one exception was Sema-1a, with an average deviation from the control across all Raleigh inbred lines of only 0·19 s (Supplementary Table 2): the large mutant effect observed in the Canton-S background was eliminated in the wild-derived backgrounds. The Raleigh inbred lines also vary in the extent to which they suppress the effects of mutations (Table 2, Fig. 6), as indicated by the significant G×R and/or G×R×S interactions for most of the genes (Table 2). Thus, there is evolutionary potential for enhancing or suppressing effects of single mutations.

Fig. 6. Landscape of epistatic interactions for startle-induced locomotion among (a) second and (b) third chromosome homozygous P-element mutations in Raleigh inbred line genetic backgrounds. The plots depict the estimates of the epistatic effect, I, of the mutations in the different inbred line backgrounds, colour-coded to indicate different values of I. Most estimates of I are negative, indicating widespread suppressing epistasis.
Table 2. P values from mixed model ANOVAs of the effects of wild-type Canton-S chromosomes and co-isogenic chromosomes with P-element mutations affecting startle response in 21 wild-derived genetic backgrounds
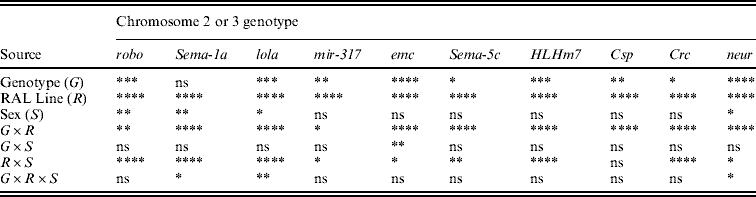
The alleles of the genes are robo BG01092, Sema-1a BG02570, lola BG02501, mir-317 BG01900, emc BG00986, Sema-5c BG01245, HLHm7 BG02029, Csp BG01863, Crc BG01724 and neur BG02542.
**** P<0·0001; *** 0·0001<P<0·001; ** 0·001<P<0·01; * 0·01<P<0·05; ns P>0·05.
4. Discussion
We observed substantial suppressing epistasis among 15 P-element insertion mutations with large homozygous effects on locomotor startle response in the Canton-S genetic background. The only previous evidence for genetic interactions among these loci is our diallel cross analysis of locomotor startle response of all 105 double heterozygotes (Yamamoto et al., Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008) among the 15 mutant lines. The diallel cross analysis implicated both suppressing and enhancing epistatic interactions among these loci, rather than the pervasive suppressing epistasis observed in this study. There are two, non-mutually exclusive, explanations for this discrepancy. First, epistasis in the diallel cross analysis was measured relative to the mean startle response of all 105 double heterozygotes and not relative to the startle response of the Canton-S progenitor strain, as is done in this study. Second, the analysis for double heterozygotes detects dominance by dominance epistasis, and the analysis for double homozygotes detects additive by additive epistasis: the two sources of epistatic interaction are independent (Falconer & Mackay, Reference Falconer and Mackay1996).
Epistasis indicates that the interacting loci affect the same genetic network or pathway leading to the quantitative trait phenotype. Suppressing epistasis occurs when the network is buffered against deleterious mutations, such that the trait phenotype resulting from the combination of two mutations is less than additive. An understanding of the mechanism underlying this buffering, or canalization (Waddington, Reference Waddington1957) is required if we are to predict individual phenotypes from knowledge of their genotypes at loci affecting the trait, as well as to predict the response to artificial and natural selection. Can we derive clues about the underlying network affecting locomotor startle response from knowledge of the molecular functions of the 15 interacting loci in this study? The genes tagged by the P-elements include transcriptional regulators (ttk, emc, HLHm7 and lola), a calcium binding chaperone (Crc), an ubiquitin protein ligase (neur), an extracellular matrix protein (LanA), axon guidance molecules (robo and Sema-1a), a protein threonine/tyrosine kinase (Doa) and microRNAs (mir-279 and mir-317), as well as a gene of unknown function (CG8963). However, with the sole exception of mir-279, all of these genes have been implicated in the development and function of the central and/or peripheral nervous system (Tweedie et al., Reference Tweedie, Ashburner, Falls, Leyland, McQuilton, Marygold, Millburn, Osumi-Sutherland, Schroeder, Seal and Zhang2009), consistent with their role in modulating startle-induced locomotion.
We have shown that suppressing epistasis is prevalent among 15 loci affecting startle response, but have not generated all 105 possible double homozygotes necessary to determine their relationships in the underlying network. Further, locomotor startle response is highly polygenic. Yamamoto et al. (Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008) observed significant effects on startle response for 267 of 720 (37%) P-element insertions tested. This analysis does not approach a saturation mutagenesis screen. Even so, a complete analysis of all of these mutations would require synthesis and testing of 35 511 double homozygous genotypes, which ignores the possibility of higher order interactions. An alternative strategy for dealing with the issue of dimensionality when making inferences about epistasis and networks is to take advantage of the multifactorial perturbations of the network from naturally occurring variation. There is substantial naturally occurring variation for locomotor startle response (Jordan et al., Reference Jordan, Morgan and Mackay2006, Reference Jordan, Carbone, Yamamoto, Morgan and Mackay2007; Ayroles et al., Reference Ayroles, Carbone, Stone, Jordan, Lyman, Magwire, Rollmann, Duncan, Lawrence, Anholt and Mackay2009), and comparison of estimates of genetic variation from realized heritability and variation among inbred lines implicates a large contribution of epistasis to the genetic architecture of this trait (Jordan et al., Reference Jordan, Carbone, Yamamoto, Morgan and Mackay2007). Thus, we should be able to use single P-element mutations as molecular probes to discover interacting loci without fully exploring the universe of potentially interacting mutations.
We substituted 10 chromosomes containing P-element mutations affecting startle response in the Canton-S background and the wild-type Canton-S chromosomes into each of 21 distinct wild-derived inbred backgrounds. On average, the effects of P-element insertions on startle-induced locomotion were nearly five times greater in the Canton-S background than in the introgression lines (13·17 s compared to 2·76 s). Suppressing epistasis was observed for all 10 mutations, but was very strong for robo, Sema-1a, mir-317, emc, Sema-5c, HLHm7 and lola, and weaker for Csp, Crc and neur. Therefore, wild-derived lines harbour modifiers that attenuate the effects of the homozygous P-element insertions on the startle response. More importantly, there is genetic variation among the lines in the extent to which modifiers suppress the mutant effects. The 21 inbred lines used for this study are a subset of the 192 inbred line Drosophila Genetic Reference Panel (DGRP), for which whole genome sequences are being obtained (Mackay et al., Reference Mackay, Richards and Gibbs2008). With the future availability of complete polymorphism data for the DGRP and the ability to construct larger sets of chromosome substitution lines, we will be able to use genome-wide association analysis to map the modifiers suppressing the mutant effects.
Rapid avoidance of sudden and adverse environmental disruptions is essential for survival and, hence, startle-induced locomotion is plausibly associated with fitness. Whereas impairment of startle behaviour may compromise survival, excessive startle behaviour might also be detrimental in that it would interfere with normal behavioural functions, including feeding, mating, and defence of territory; and would be energetically wasteful. Thus, startle behaviour is likely to be under stabilizing selection for an intermediate optimum.
Waddington (Reference Waddington1957) suggested that traits under strong stabilizing selection would be strongly genetically canalized; i.e. the phenotype would be robust to deleterious mutations. The mechanism underlying genetic canalization is suppressing epistasis. There has recently been much theoretical attention to the evolution of genetic canalization in terms of developmental and genetic networks (Siegal & Bergman, Reference Siegal and Bergman2002; Hermisson et al., Reference Hermisson, Hansen and Wagner2003; Hermisson & Wagner, Reference Hermisson and Wagner2004; Proulx & Phillips, Reference Proulx and Phillips2005; Gros et al., Reference Gros, Le Nagard and Tenaillon2009). Indirect evidence for the evolution of suppressing epistasis comes from experiments demonstrating an increase in genetic variance when mutations are introduced into different wild-derived genotypes (Gibson & Wagner, Reference Gibson and Wagner2000; Flatt, Reference Flatt2005), as expected if the mutation is in a gene for which the wild-type allele suppresses the effects of segregating variation at other loci, thus releasing previously hidden cryptic genetic variation. Our observations provide direct experimental support for widespread suppressing epistasis in natural populations, as well as natural variation in the magnitude of epistatic modulation. P-element mutations have pleiotropic effects on multiple quantitative traits (Rollmann et al., Reference Rollmann, Magwire, Morgan, Özsoy, Yamamoto, Mackay and Anholt2006; Sambandan et al., Reference Sambandan, Yamamoto, Fanara, Mackay and Anholt2006; Yamamoto et al., Reference Yamamoto, Zwarts, Callaerts, Norga, Mackay and Anholt2008); therefore, it will be interesting in the future to evaluate a similar panel of chromosome substitution lines for a suite of quantitative traits to determine whether suppressing epistasis is a general feature of the genetic architecture of most traits; and, if so, whether the same modifiers modulate the effects on multiple traits.
Widespread suppressing epistasis has implications for gene mapping studies of common human diseases and more generally for maintenance of quantitative genetic variation in natural populations. The main effects of individual loci will be underestimated if suppressing epistasis exists but is not accounted for in a mapping study. The collective result of many highly powered whole genome association studies for human common diseases and complex traits is that the main effects of significant loci are small, and together explain very little of the estimated heritable variance for these traits (Altshuler et al., Reference Altshuler, Daly and Lander2008). Suppressing epistasis is one of several explanations for this observation. The consequence of genetic variation in suppressing epistasis is that a particular variant affecting the likelihood of developing the disease will have a greater or lesser effect depending on the individual's genetic background with respect to other loci.
An unresolved problem in evolutionary quantitative genetics is the reconciliation of the twin observations of strong stabilizing selection (s~0·01) with large amounts of segregating variation for most quantitative traits, such that heritabilities are of the order of 0·5, and hence genetic variation (V G) is approximately the same as environment variation (V E). Theory predicts that the equilibrium genetic variance maintained by a balance between stabilizing selection and the input of variation from new mutations (V M) is ![]() . Estimates of V M are consistently 0·001V E. However, evaluating the equation for V G=V E and V M=10−3V E, gives s=0·001, which is not a strong stabilizing selection. Alternatively, evaluating the equation for V G=V E and s=0·01 gives V M=10−2V E, which is too large (Falconer & Mackay, Reference Falconer and Mackay1996). However, with suppressing epistasis, it is possible that the strength of stabilizing selection is overestimated, and/or the input of mutational variation is underestimated. Support for this hypothesis comes from long-term mutation accumulation experiments on sensory bristle number in which the divergence among inbred lines (Mackay et al., Reference Mackay, Lyman and Hill1995) or among lines selected for divergent trait values from an inbred base population (Mackay et al., Reference Mackay, Fry, Lyman and Nuzhdin1994) attenuate over time, and the effects of mapped mutations exceed the divergence among lines (Mackay et al., Reference Mackay, Lyman and Lawrence2005), as would be expected if new mutations exhibit suppressing epistasis.
. Estimates of V M are consistently 0·001V E. However, evaluating the equation for V G=V E and V M=10−3V E, gives s=0·001, which is not a strong stabilizing selection. Alternatively, evaluating the equation for V G=V E and s=0·01 gives V M=10−2V E, which is too large (Falconer & Mackay, Reference Falconer and Mackay1996). However, with suppressing epistasis, it is possible that the strength of stabilizing selection is overestimated, and/or the input of mutational variation is underestimated. Support for this hypothesis comes from long-term mutation accumulation experiments on sensory bristle number in which the divergence among inbred lines (Mackay et al., Reference Mackay, Lyman and Hill1995) or among lines selected for divergent trait values from an inbred base population (Mackay et al., Reference Mackay, Fry, Lyman and Nuzhdin1994) attenuate over time, and the effects of mapped mutations exceed the divergence among lines (Mackay et al., Reference Mackay, Lyman and Lawrence2005), as would be expected if new mutations exhibit suppressing epistasis.
This work was supported by grants from the National Institutes of Health (GM059469 to R. R. H. A. and GM45146 to T. F. C. M.).










