Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-03T00:15:32.620Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of unconditionally deleterious mutations: Gaussian approximation and soft selection

Published online by Cambridge University Press:  14 April 2009

Alexey S. Kondrashov
Alexey S. Kondrashov
Affiliation:
Section of Ecology and Systematics, Corson Hall, Cornell University, Ithaca, NY 14853, USA

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper studies the influence of two opposite forces, unidirectional unconditionally deleterious mutations and directional selection against them, on an amphimictic population. Mutant alleles are assumed to be equally deleterious and rare, so that homozygous mutations can be ignored. Thus, a genotype is completely described by its value with respect to a quantitative trait x, the number of mutations it carries, while a population is described by its distribution p(x) with mean M[p] and variance V[p] = σ2[p]. When mutations are only slightly deleterious, so that M » 1, before selection p(x) is close to Gaussian with any mode of selection. I assume that selection is soft in the sense that the fitness of a genotype depends on the difference between its value of x and M, in units of σ. This leads to a simple system of equations connecting the values of M and V in successive generations. 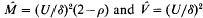This system has a unique and stable equilibrium, where U is the genomic deleterious mutation rate, δ is the selection differential for x in units of σ, and p is the ratio of variances of p(x) after and before selection. Both δ and ρ are parameters of the mode of soft selection, and do not depend on M or V. In an equilibrium population, the selection coefficient against a mutant allele is ŝ = δ2[U(2–ρ)]−1. The mutation load can be tolerable only if the genome degradation rate υ = U/σ is below 2. Other features of mutation-selection equilibrium are also discussed.

Type
Research Article
Information
Genetics Research , Volume 65 , Issue 2 , April 1995 , pp. 113 - 121
Copyright
Copyright © Cambridge University Press 1995

References

Agren, J., & Schemske, D., (1993). Outcrossing rate and inbreeding depression in two annual monoecious herbs, Begonia hirsuta and B. semiovata. Evolution 47, 125–135.CrossRefGoogle ScholarPubMed
Allendorf, F. W., (1979). Rapid loss of duplicate gene expression by natural selection. Heredity 43, 247–258.CrossRefGoogle Scholar
Bulmer, M. G., (1985). The Mathematical Theory of Quantitative Genetics, 2nd edition. Oxford: Oxford University Press.Google Scholar
Charlesworth, B., (1990). Mutation-selection balance and the evolutionary advantage of sex and recombination. Genetical Research 55, 199–221.CrossRefGoogle ScholarPubMed
Charlesworth, B., (1993). Evolutionary mechanisms of senescence. Genetica 91, 11–19.CrossRefGoogle ScholarPubMed
Charlesworth, B., Charlesworth, D., & Morgan, M. T., (1990). Genetic loads and estimates of mutation rates in highly inbred plant populations. Nature 347, 380–382.CrossRefGoogle Scholar
Charlesworth, B., Morgan, M. T., & Charlesworth, D., (1993). The effect of deleterious mutations on neutral molecular variation. Genetics 134, 1289–1303.CrossRefGoogle ScholarPubMed
Crow, J. F., (1958). Some possibilities for measuring selection intensities in man. Human Biology 30, 1–13.Google ScholarPubMed
Crow, J. F., (1970). Genetic loads and the cost of natural selection. In Mathematical Topics in Population Genetics (ed. Kojima, K.), pp. 128–177. Heidelberg: Springer.CrossRefGoogle Scholar
Crow, J. F., (1979). Minor viability mutants in Drosophila. Genetics 92 (Suppl.), s165–s172.Google ScholarPubMed
Crow, J. F., & Kimura, M., (1970). An Introduction to Population Genetics Theory. New York: Harper and Row.Google Scholar
Crow, J. F., & Kimura, M., (1979). Efficiency of truncation selection. Proceedings of the National A cademy of Sciences, USA 76, 396–399.CrossRefGoogle ScholarPubMed
Crow, J. F., & Simmons, M. J., (1983). The mutation load in Drosophila. In The Genetics and Biology of Drosophila, Vol. 3c (ed. Ashburner, M., Carson, H. L., and Thompson, J. N.), pp. 2–35. New York: Academic Press.Google Scholar
Fisher, R. A., (1930). The Genetical Theory of Natural Selection. Oxford: Clarendon Press.CrossRefGoogle Scholar
Haldane, J. B. S., (1927). A mathematical theory of natural and artificial selection. Part V. Selection and mutation. Proceedings of the Cambridge Philosophical Society 23, 838–844.CrossRefGoogle Scholar
Haldane, J. B. S., (1937). The effect of variation on fitness. American Naturalist 71, 337–349.CrossRefGoogle Scholar
Hofbauer, J., (1985). The selection mutation equation. Journal of Mathematical Biology 23, 41–53.CrossRefGoogle ScholarPubMed
Houle, D., (1992). Comparing evolvability and heritability of quantitative traits. Genetics 130, 195–204.CrossRefGoogle ScholarPubMed
Houle, D., Hoffmaster, D. K., Assimacopoulos, S., & Charlesworth, B., (1992). The genomic mutation rate for fitness in Drosophila. Nature 359, 58–60.CrossRefGoogle ScholarPubMed
Karlin, S., & McGregor, J., (1971). On mutation-selection balance for two-locus haploid and diploid populations. Theoretical Population Biology 2, 60–70.CrossRefGoogle ScholarPubMed
Kendall, M. G., & Stuart, A., (1977). The Advanced Theory of Statistics, 4th edition, Vol. 1. London: Charles Griffin and Co.Google Scholar
Kimura, M., & Crow, J. F., (1978). Effect of overall phenotypic selection on genetic change at individual loci. Proceedings of the National Academy of Sciences, USA 75, 6168–6171.CrossRefGoogle ScholarPubMed
Kimura, M., & Maruyama, T., (1966). The mutation load with epistatic gene interactions in fitness. Genetics 54, 1337–1351.CrossRefGoogle ScholarPubMed
Kondrashov, A. S., (1982). Selection against harmful mutations in large sexual and asexual populations. Genetical Research 40, 325–332.CrossRefGoogle ScholarPubMed
Kondrashov, A. S., (1984). Deleterious mutations as an evolutionary factor. I. The advantage of recombination. Genetical Research 44, 199–217.CrossRefGoogle Scholar
Kondreashov, A. S., (1988). Deleterious mutations and the evolution of sexual reproduction. Nature 336, 435–440.CrossRefGoogle Scholar
Kondrashov, A. S., (1993). Classification of hypotheses on the advantage of amphimixis. Journal of Heredity 84, 372–387.CrossRefGoogle ScholarPubMed
Kondrashov, A. S., (1995). Modifiers of mutation-selection balance: general approach and the evolution of mutation rates. Genetical Research, in press.CrossRefGoogle Scholar
Kondrashov, A. S., & Turelli, M., (1992). Deleterious mutations, apparent stabilizing selection and maintenance of quantitative variation. Genetics 132, 603–618.CrossRefGoogle ScholarPubMed
Malmberg, R. L., (1977). The evolution of epistasis and the advantage of recombination in populations of bacteriophage T4. Genetics 86, 607–621.CrossRefGoogle ScholarPubMed
Smith, J. Maynard, (1978). The Evolution of Sex. Cambridge: Cambridge University Press.Google Scholar
Mukai, T., (1964). The genetic structure of natural populations of Drosophila melanogaster. I. Spontaneous mutation rate of polygenes controlling viability. Genetics 50, 1–19.CrossRefGoogle ScholarPubMed
Mukai, T., (1969). The genetic structure of natural populations of Drosophila melanogaster. VII. Synergistic interaction of spontaneous mutant polygenes controlling viability. Genetics 61, 749–761.CrossRefGoogle ScholarPubMed
Mukai, T., Cardellino, R. A., Watanabe, T. K., & Crow, J. F., (1974). The genetic variance for viability and its components in a local population of Drosophila melanogaster. Genetics 78, 1195–1208.CrossRefGoogle Scholar
Mukai, T., Chigusa, S. T., Mettler, L. E., & Crow, J. F., (1972). Mutation rate and dominance of genes affecting viability in Drosophila melanogaster. Genetics 72, 335–355.CrossRefGoogle ScholarPubMed
Muller, H. J., (1950). Our load of mutations. American Journal of Human Genetics 2, 111–176.Google ScholarPubMed
Partridge, L., & Barton, N. H., (1993). Optimality, mutation and the evolution of ageing. Nature 362, 305–311.CrossRefGoogle ScholarPubMed
Shnol, E. E., & Kondrashov, A. S., (1993). Effect of selection on the phenotypic variance. Genetics 134, 995–996.CrossRefGoogle ScholarPubMed
Shnol, E. E., & Kondrashov, A. S., (1994). Some relations between different characteristics of selection. Journal of Mathematical Biology, 32, 835–840.CrossRefGoogle Scholar
Wallace, B., (1975). Hard and soft selection revisited. Evolution 29, 465–473.CrossRefGoogle ScholarPubMed
Wright, S., (1929). Fisher's theory of dominance. American Naturalist 63, 274–279.CrossRefGoogle Scholar
Wright, S., (1977). Evolution and the Genetics of Populations, Vol. 3. Chicago: University of Chicago Press.Google Scholar