1. Introduction
Evolutionary biologists have long acknowledged the importance of identifying the relative contribution of the four different evolutionary processes mutation, selection, random genetic drift and gene flow for understanding the distribution of fitness-related phenotypic variation within and across populations (Hartl & Clark, Reference Hartl and Clark1989; Falconer & Mackay, Reference Falconer and Mackay1996; Lynch et al., Reference Lynch, Pfrender, Spitze, Lehman, Hicks, Allen, Latta, Ottene, Bogue and Colbourne1999; Freeman & Herron, Reference Freeman and Herron2004; Goodnight, Reference Goodnight, Hanski & and Gaggiotti2004; Whitlock, Reference Whitlock, Hanski & and Gaggiotti2004). First, such knowledge will help us understand the mechanisms that have generated the variation present within and among populations today. Equally important, it will enable us to better understand the future direction of evolutionary changes within and across populations (Palo et al., Reference Palo, O'Hara, Laugen, Laurila, Primmer and Merilä2003; Leinonen et al., Reference Leinonen, Cano, Mäkinen and Merilä2006).
Both empirical and theoretical studies suggest that a major force that drives phenotypic population differentiation in natural populations is natural selection (Merilä & Crnokrak, Reference Merilä and Crnokrak2001; Riesenberg et al., Reference Riesenberg, Widmer, Arntz and Burke2002; Saint-Laurent et al., Reference Saint-Laurent, Legault and Bernatchez2003; Leinonen et al., Reference Leinonen, Cano, Mäkinen and Merilä2006, Reference Leinonen, O'Hara, Cano and Merilä2008). When populations are subdivided over a geographical range, local environmental conditions may create spatially and temporally varying selection pressures, thus creating population differentiation (Merilä & Crnokrak, Reference Merilä and Crnokrak2001; Zhan et al., Reference Zhan, Linde, Jürgens, Merz, Steinebrunner and McDonald2005). Although natural selection, creating local adaption, plays a major role in the phenotypic, and hence the underlying quantitative genetic differentiation of populations, genetic differentiation may also be affected by random genetic drift (Zhan et al., Reference Zhan, Linde, Jürgens, Merz, Steinebrunner and McDonald2005).
Small effective population size (N e) increases the importance of genetic drift (Freeman & Herron, Reference Freeman and Herron2004). In addition to natural selection and genetic drift, divergence in quantitative traits is also influenced by migration (i.e. gene flow) (Porcher et al., Reference Porcher, Giraud and Lavigne2006), which will restrain populations from diverging (Freeman & Herron, Reference Freeman and Herron2004). Along with the generation of new genetic variation through mutations, these evolutionary processes act to either generate quantitative genetic and phenotypic divergence between populations through genetic drift, mutation and/or divergent selection, or reduce such divergence by gene flow between populations and/or uniform selection (Whitlock, Reference Whitlock1999).
Neutral genetic variation is on the other hand, by definition, only affected by mutation, genetic drift (increased by small N e) and gene flow (Wright, Reference Wright1951; Kimura, Reference Kimura, Nei and Koehn1983; Hartl & Clark, Reference Hartl and Clark1989; Lande, Reference Lande1992). Hence, it is possible to estimate the relative role of selection and other evolutionary processes, such as genetic drift for differentiation among populations in quantitative genetic variation by comparing the level of inter-population quantitative genetic variation and neutral genetic variation (Morgan et al., Reference Morgan, Evans, Garland, Swallow and Carter2005; Zhan et al., Reference Zhan, Linde, Jürgens, Merz, Steinebrunner and McDonald2005).
This theory of neutrality predicts that the genetic divergence in a quantitative polygenic trait should be identical to that in a marker locus if both are neutral to selection and the quantitative genetic trait has an additive genetic basis (Wright, Reference Wright1951). An analogue to Wright's F ST, the divergence among populations in neutral marker loci (Wright, Reference Wright1922), is Q ST, the genetic differentiation in a quantitative trait, described by Spitze (Reference Spitze1993). The expression of Q ST is analogous to F ST
where σGB2 and σGW2 is the (additive) genetic variance between and within populations, respectively (Spitze, Reference Spitze1993). Using theory for Q ST and F ST one can create a set of hypotheses to test the influence of natural selection on phenotypic differentiation within and among populations (Lynch et al., Reference Lynch, Pfrender, Spitze, Lehman, Hicks, Allen, Latta, Ottene, Bogue and Colbourne1999; Merilä & Crnokrak, Reference Merilä and Crnokrak2001; McKay & Latta, Reference McKay and Latta2002): (1) We expect to observe a level of population differentiation for quantitative traits that exceeds that for differentiation in neutral marker loci when directional selection is favouring different phenotypes in different populations (Q ST>F ST). (2) A lower level of differentiation in quantitative traits than would have been obtained by genetic drift alone (i.e. lower than the level of differentiation in molecular markers) indicates that selection favours the same phenotypes in different populations (Q ST<F ST). (3) If Q ST and F ST estimates are not significantly different, the observed differentiation cannot be rejected as being caused by genetic drift (Q ST=F ST). These interpretations are subject to a number of assumptions underlying the inference based on Q ST and F ST estimates (see e.g. Kimura, Reference Kimura, Nei and Koehn1983; Merilä & Crnokrak, Reference Merilä and Crnokrak2001; Miller et al., Reference Miller, Wood and Hamilton2008; Whitlock, Reference Whitlock2008).
There are, however, three potential problems with such an approach, especially in studies of natural populations. Firstly, because Q ST is based on purely additive genetic variance (Merilä & Crnokrak, Reference Merilä and Crnokrak2001), its calculation is strictly speaking dependent on inter- and intra-population estimates of the additive genetic variance of a trait (Lande, Reference Lande1992; Spitze, Reference Spitze1993; Merilä & Crnokrak, Reference Merilä and Crnokrak2001). Secondly, to assess the additive genetic variance in a population, it is necessary to separate the genetic from the environmental components of the phenotypic variation (Lynch & Walsh, Reference Lynch and Walsh1998). Thirdly, the Q ST estimate can vary both because of sampling error, e.g. due to data from few populations or small samples within populations (Whitlock & Guillaume, Reference Whitlock and Guillaume2009), and inter-population stochastic variation in the evolutionary process (Whitlock, Reference Whitlock2008).
These problems mean that it often is problematic to estimate Q ST in natural populations. Many recent studies have disregarded these problems and used population-specific phenotypic variances as a surrogate for additive genetic variance when estimating Q ST (e.g. Morgan et al., Reference Morgan, Hicks, Spitze, Latta, Pfrender, Weaver, Ottone and Lynch2001). This will either overestimate or underestimate the genetic population divergence, depending on the effect of the environment on the phenotypic variance (Leinonen et al., Reference Leinonen, O'Hara, Cano and Merilä2008; Whitlock, Reference Whitlock2008).
The aim of this study was to explore the relative importance of random genetic drift and selection as causes of population differentiation in different quantitative morphological traits in house sparrow (Passer domesticus) populations along the coast of mid- and northern Norway. The inter-population variability in topography and habitat on islands and mainland along the coast of Norway may result in different environmental conditions, and thus suggest the existence of different selection pressures across the house sparrow populations. Because of the relatively low migration rate of house sparrows (see Blair & Hagemeijer, Reference Blair and Hagemeijer1997; Altwegg et al., Reference Altwegg, Ringsby and Sæther2000; Tufto et al., Reference Tufto, Ringsby, Dhondt, Adriaensen and Matthysen2005; Skjelseth et al., Reference Skjelseth, Ringsby, Tufto, Jensen and Sæther2007; Pärn et al., Reference Pärn, Jensen, Ringsby and Sæther2009) genetic differentiation exists on a relatively small geographic scale among house sparrow populations along the coast of northern Norway (Jensen et al.,Reference Jensen, Moe, Hagen, Kekkonen, Holand, Tufto and Sætherin review). Furthermore, Jensen et al. (Reference Jensen, Sæther, Ringsby, Tufto, Griffith and Ellegren2003, Reference Jensen, Sæther, Ringsby, Tufto, Griffith and Ellegren2004, Reference Jensen, Steinsland, Ringsby and Sæther2008) and Ringsby et al. (Reference Ringsby, Sæther, Berge and Jensen2009) have in a sub-set of these populations identified heritable morphological traits that are associated with individual fitness. Accordingly, some of these traits are therefore acted upon by natural and sexual selection (Jensen et al., Reference Jensen, Steinsland, Ringsby and Sæther2008). Consequently, this study system seems suitable to examine the effects of genetic drift and selection on population differentiation in quantitative traits. We do this by comparing the genetic differences at neutral microsatellite loci with phenotypic variation in fitness-related morphological characters with additive genetic basis in the same populations. We use existing theory on Q ST and a model where the environmental component of population differentiation in natural populations is allowed to vary to estimate Q ST without having estimates of additive genetic variance within each of the sub-populations (under certain assumptions). Furthermore, by combining this with a recent approach that compare the observed Q ST of a trait versus F ST to the distribution of Q ST versus F ST expected under neutrality, we obtain more reliable inference about the relative importance of selection and other evolutionary processes for any observed phenotypic population differentiation (Whitlock, Reference Whitlock2008; Whitlock & Guillaume, Reference Whitlock and Guillaume2009). These methods give us the opportunity to explore the possibilities for population divergence in natural populations.
2. Materials and methods
(i) Study populations and estimates of FST
The study was carried out on 14 island and mainland populations on the coast of mid- and northern Norway, from Gjerøy (67°N, 13°E) to Brattvåg (63°N, 6°E) (see Fig. 1 and Supplementary Table S1 available at http://journals.cambridge.org/grh).

Fig. 1. Map showing sampled house sparrow populations (indicated with numbered dots) along the coast of mid- and northern Norway. Populations are numbered from south to north (see also Supplementary Table S1).
Morphological measurements and blood samples from individual house sparrows were collected from the study populations during summer 2006, and for some island populations during summer 2001 or 2002 (see Jensen et al.,Reference Jensen, Moe, Hagen, Kekkonen, Holand, Tufto and Sætherin review).
Males and females were analysed separately because of the sexual differences previously documented in strength of selection and amount of additive genetic variation of different traits (Jensen et al., Reference Jensen, Sæther, Ringsby, Tufto, Griffith and Ellegren2003, Reference Jensen, Steinsland, Ringsby and Sæther2008).
The sex-specific estimated levels of genetic differentiation among the study populations (see Supplementary Table S1 for populations sizes and sample sizes) on neutral molecular markers, F ST, were estimated with the R package HIERFSTAT (Goudet, Reference Goudet2005) based on 17 presumably neutral microsatellite loci. See Jensen et al. (Reference Jensen, Moe, Hagen, Kekkonen, Holand, Tufto and Sætherin review) for description of genotyping methods.
(ii) Phenotypic traits and heritability (h2)
Morphological characters measured were tarsus length, wing length, bill depth, bill length and body mass (of both sexes) and for males also total and visible badge size. To correct for any differences between field workers in measurement technique, the measurements of each field worker were adjusted to the corresponding measurement of T. H. Ringsby using regression techniques. See Jensen et al. (Reference Jensen, Steinsland, Ringsby and Sæther2008) for further description of measurements.
The sex-specific heritability (h 2) and its standard error (SE) (presented in Table 1) for each of the morphological traits within males and females used in this study had previously been estimated with high precision using animal models and restricted maximum likelihood (REML) methods (Lynch & Walsh, Reference Lynch and Walsh1998; Kruuk, Reference Kruuk2004) with phenotypic information on >3500 individuals in a large genetically determined pedigree from six islands off the coast of northern Norway (Jensen et al., Reference Jensen, Sæther, Ringsby, Tufto, Griffith and Ellegren2003, Reference Jensen, Steinsland, Ringsby and Sæther2008). Three of these populations (Aldra, Gjerøy and Hestmannøy) were also included in the present study (see Supplementary Table S1).
Table 1. Tests of inter-population variation in mean size and heritability (ĥ2) with SE of morphological traits of male and female house sparrows in 14 populations on the coast of mid- and northern Norway

Degrees of freedom is denoted by df. The F statistics and the levels of significance (P) are from separate ANOVAs for each trait within each sex.
3. Statistical analyses
(i) Estimation of Q
ST
( )
)
To estimate Q ST in eqn (1) based on phenotypic measures in a set of populations (under certain assumptions) Sæther et al. (Reference Sæther, Fiske, Kålås, Kuresoo, Luigujõe, Piertney, Sahlman and Höglund2007) (see also Merilä, Reference Merilä1997; Brommer, Reference Brommer2011) suggested including a constant that reflects the proportion of differences between population phenotypes due to genetic differences when estimating Q ST.
The genetic between population variance, σGB2 in eqn (1) was estimated as
where c is the additive genetic proportion of differences between populations, ![]() , allowing for environmental between-population variance in the phenotypic variance between populations,
, allowing for environmental between-population variance in the phenotypic variance between populations, ![]() . If c=0 this means that the environment is causing all the phenotypic variance seen between the populations. On the other hand, c=1 means that all the phenotypic variation seen between populations is determined by genetic variation between them, and thereby that none of the phenotypic differences observed between populations are influenced by environmental differences. Note, however, that c=1 does not exclude the possibility that variation among populations in strength and direction of selection in the past, e.g. because populations have adapted to different population-specific environments, may be the cause of the observed inter-population phenotypic, and hence genetic, variation. The value of c only reflects the relative proportion of any phenotypic between-population differences that is due to environmental conditions per se. In reality c will probably lie somewhere between 0 and 1, and the exact value may vary between traits (e.g. morphological, behavioural and fitness-traits; Crnokrak & Roff, Reference Crnokrak and Roff1995; Merilä & Sheldon, Reference Merilä and Sheldon1999).
. If c=0 this means that the environment is causing all the phenotypic variance seen between the populations. On the other hand, c=1 means that all the phenotypic variation seen between populations is determined by genetic variation between them, and thereby that none of the phenotypic differences observed between populations are influenced by environmental differences. Note, however, that c=1 does not exclude the possibility that variation among populations in strength and direction of selection in the past, e.g. because populations have adapted to different population-specific environments, may be the cause of the observed inter-population phenotypic, and hence genetic, variation. The value of c only reflects the relative proportion of any phenotypic between-population differences that is due to environmental conditions per se. In reality c will probably lie somewhere between 0 and 1, and the exact value may vary between traits (e.g. morphological, behavioural and fitness-traits; Crnokrak & Roff, Reference Crnokrak and Roff1995; Merilä & Sheldon, Reference Merilä and Sheldon1999).
Furthermore, assuming a constant heritability (but allowing for different amounts of additive genetic variance) within populations, the genetic within population variance, σGW2, can be estimated as
where ![]() is the observed within-populations variance and
is the observed within-populations variance and ![]() is the estimated narrow sense heritability. The genetic variance is assumed to have only an additive genetic basis (i.e.
is the estimated narrow sense heritability. The genetic variance is assumed to have only an additive genetic basis (i.e. ![]() ).
).
We now have estimates for σGB2 and σGW2 (see Section 3 (ii) for practical estimation of parameters), and by inserting eqns (2) and (3) into eqn (1) and re-organizing we obtain an equation for estimating Q ST using phenotypic data:
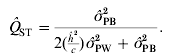
where ![]() is the observed between-populations variance and
is the observed between-populations variance and ![]() is the observed within-populations variance,
is the observed within-populations variance, ![]() is the estimated trait-specific heritability and c is the additive genetic proportion of phenotypic differences between populations. This expression has been rewritten slightly from the expression used by others (see e.g. Sæther et al., Reference Sæther, Fiske, Kålås, Kuresoo, Luigujõe, Piertney, Sahlman and Höglund2007; Brommer, Reference Brommer2011).
is the estimated trait-specific heritability and c is the additive genetic proportion of phenotypic differences between populations. This expression has been rewritten slightly from the expression used by others (see e.g. Sæther et al., Reference Sæther, Fiske, Kålås, Kuresoo, Luigujõe, Piertney, Sahlman and Höglund2007; Brommer, Reference Brommer2011).
(ii) Practical estimation of parameters
Partitioning of the phenotypic variance of a character into σPW2 and σPB2, respectively, was carried out using a single classification analysis of variance with unequal sample sizes, n i (ANOVA Model II; Sokal & Rohlf, Reference Sokal and Rohlf1995). The F-test in the ANOVA permits us to detect any significant differences in average phenotype between populations (Sokal & Rohlf, Reference Sokal and Rohlf1995). σPW2 was estimated by MSW, and σPB2 was estimated by (Storz, Reference Storz2002),
where MSB is the observed mean squares (variance) between sub-populations and MSW is the observed mean squares (variance) within subpopulations given from the ANOVA (Sokal & Rohlf, Reference Sokal and Rohlf1995; Storz, Reference Storz2002).
Because the sample size, i.e. n i, differs among subpopulations (i) (see Supplementary Table S1), we used a kind of average sample size n 0, calculated as

where a is the number of sub-populations and n i the number of individuals in the ith subpopulation sample (Storz, Reference Storz2002).
(iii) Comparing  and
and  across populations
across populations
To test whether ![]() and
and ![]() , based on data from all populations, were significantly different from each other for different values of c, we used the approach proposed by Whitlock & Guillaume (Reference Whitlock and Guillaume2009). This approach tests whether the observed Q ST of a trait falls within the distribution of Q ST expected under neutrality, predicted using the mean F ST
, based on data from all populations, were significantly different from each other for different values of c, we used the approach proposed by Whitlock & Guillaume (Reference Whitlock and Guillaume2009). This approach tests whether the observed Q ST of a trait falls within the distribution of Q ST expected under neutrality, predicted using the mean F ST
![]() and the χ2 distribution of Lewontin & Krakauer (Reference Lewontin and Krakauer1973). Using this approach the problem that a relatively small number of loci often is used when estimating F ST is taken into consideration, as well as the variation in neutral Q ST due to variation in evolutionary history among populations and sampling error due to small sample size (Whitlock, Reference Whitlock2008; Whitlock & Guillaume, Reference Whitlock and Guillaume2009). In addition, this method requires the F ST to be small, which is the case in this study.
and the χ2 distribution of Lewontin & Krakauer (Reference Lewontin and Krakauer1973). Using this approach the problem that a relatively small number of loci often is used when estimating F ST is taken into consideration, as well as the variation in neutral Q ST due to variation in evolutionary history among populations and sampling error due to small sample size (Whitlock, Reference Whitlock2008; Whitlock & Guillaume, Reference Whitlock and Guillaume2009). In addition, this method requires the F ST to be small, which is the case in this study.
Under the null hypothesis of neutrality, the statistic ![]() will have a distribution that is almost independent of the true parameter value of F ST, essentially because F ST is a scale parameter in the distribution of both
will have a distribution that is almost independent of the true parameter value of F ST, essentially because F ST is a scale parameter in the distribution of both ![]() and
and ![]() , when the amount of genetic differentiation is small. This test statistic is thus close to being a so-called pivotal statistic (Shao, Reference Shao2003). This makes it more suitable as test statistic, because the critical values and P values can be determined without the knowledge of the true value F ST than a test based on the test statistic Q ST−F ST (Whitlock & Guillaume, Reference Whitlock and Guillaume2009).
, when the amount of genetic differentiation is small. This test statistic is thus close to being a so-called pivotal statistic (Shao, Reference Shao2003). This makes it more suitable as test statistic, because the critical values and P values can be determined without the knowledge of the true value F ST than a test based on the test statistic Q ST−F ST (Whitlock & Guillaume, Reference Whitlock and Guillaume2009).
We use the parametric simulation approach used in Whitlock & Guillaume (Reference Whitlock and Guillaume2009) to find the sampling distribution of ![]() under the null hypothesis. To simulate the sampling error in estimates of
under the null hypothesis. To simulate the sampling error in estimates of ![]() , we draw randomly from the bootstrap distribution of
, we draw randomly from the bootstrap distribution of ![]() obtained from the R-package HIERFSTAT (Goudet, Reference Goudet2005), bootstrapping loci 10 000 times. To take into account the sampling error of σGW2 and σGB2 when estimating Q ST (eqn 1), we simulated values of σGW2 by multiplying
obtained from the R-package HIERFSTAT (Goudet, Reference Goudet2005), bootstrapping loci 10 000 times. To take into account the sampling error of σGW2 and σGB2 when estimating Q ST (eqn 1), we simulated values of σGW2 by multiplying ![]() with a number drawn randomly from the χ2 distribution with
with a number drawn randomly from the χ2 distribution with ![]() degrees of freedom, where a is the number of populations (see Sections 3 (ii) and 3 (iii)). To account for sampling error in h 2 estimated from field data (accounting for environmental variation), we draw samples of
degrees of freedom, where a is the number of populations (see Sections 3 (ii) and 3 (iii)). To account for sampling error in h 2 estimated from field data (accounting for environmental variation), we draw samples of ![]() from a beta distribution, defined on the interval (0,1), with shape parameters calculated from the h 2 estimate and squared SE of the h 2 estimate as the mean and variance, respectively, in the beta distribution. Whitlock & Guillaume (Reference Whitlock and Guillaume2009) showed that the expected value of σGB2 under neutrality is
from a beta distribution, defined on the interval (0,1), with shape parameters calculated from the h 2 estimate and squared SE of the h 2 estimate as the mean and variance, respectively, in the beta distribution. Whitlock & Guillaume (Reference Whitlock and Guillaume2009) showed that the expected value of σGB2 under neutrality is

Thus, we simulated values of σGB2, as calculated in eqn (7), by multiplying ![]() with a number drawn randomly from the χ2 distribution with a−1 degrees of freedom.
with a number drawn randomly from the χ2 distribution with a−1 degrees of freedom.
We randomly draw values of ![]() ,
, ![]() , σGW2 and
, σGW2 and ![]() (described above), and then calculated
(described above), and then calculated ![]() from these simulated values. A sampling distribution of
from these simulated values. A sampling distribution of ![]() was obtained by repeating this random sampling with 1000 iterations.
was obtained by repeating this random sampling with 1000 iterations.
To compare the test statistics of observed ![]() for different c values with the sampling distribution of
for different c values with the sampling distribution of ![]() under neutrality, we found the 0·025 and 0·975% quantiles of the neutral sampling distribution of
under neutrality, we found the 0·025 and 0·975% quantiles of the neutral sampling distribution of ![]() . If the observed
. If the observed ![]() for a given c-value was smaller or larger than the 95% confidence limits for the neutral sampling distribution,
for a given c-value was smaller or larger than the 95% confidence limits for the neutral sampling distribution, ![]() was defined as significantly smaller or larger than expected by neutrality, respectively (P<0·05) (Manly, Reference Manly2007; Whitlock & Guillaume, Reference Whitlock and Guillaume2009). These c-values are the limits for where
was defined as significantly smaller or larger than expected by neutrality, respectively (P<0·05) (Manly, Reference Manly2007; Whitlock & Guillaume, Reference Whitlock and Guillaume2009). These c-values are the limits for where ![]() .
.
4. Results
(i) Inter-population phenotypic variation
All phenotypic traits showed considerable and significant variation between populations (Table 1). The variation between populations in mean trait sizes was largest in males and for the traits body mass, total and visible badge size.
(ii) Relationship between  and
and  allowing for environmental causes of inter-population variance
allowing for environmental causes of inter-population variance
We found that the mean male ![]() was 0·0246 and mean female
was 0·0246 and mean female ![]() was 0·0240. The 95% confidence intervals for
was 0·0240. The 95% confidence intervals for ![]() were for both males and females quite narrow (males: [0·0216, 0·0279]; females: [0·0218, 0·0278]).
were for both males and females quite narrow (males: [0·0216, 0·0279]; females: [0·0218, 0·0278]).
Assuming that all the phenotypic differences between populations (Table 1) were due to genetic differences (c=1) our results suggest that spatially divergent selection have caused the observed inter-population variance in phenotypic traits in females and males (Table 2 and Figs 2 and 3).

Fig. 2. The relationship between observed and neutral ![]() , indicated with the solid and dashed lines, respectively, when the environmental component of the between-population variance varies between 0% (c=1) and 100% (c=0) (
, indicated with the solid and dashed lines, respectively, when the environmental component of the between-population variance varies between 0% (c=1) and 100% (c=0) (![]() [0,1]) for five morphological traits in female house sparrows in 14 populations in mid- and northern Norway. The critical values for the null sampling distribution of the neutral
[0,1]) for five morphological traits in female house sparrows in 14 populations in mid- and northern Norway. The critical values for the null sampling distribution of the neutral ![]() are indicated with the dotted lines. The different panels correspond to the relationship between
are indicated with the dotted lines. The different panels correspond to the relationship between ![]() and c for different phenotypic traits (a) tarsus length, (b) wing length, (c) bill depth, (d) bill length and (e) body mass.
and c for different phenotypic traits (a) tarsus length, (b) wing length, (c) bill depth, (d) bill length and (e) body mass.
Table 2. Critical values for c where observed ![]() are smaller or larger, respectively, than expected under neutrality (i.e. outside the null sampling distribution
are smaller or larger, respectively, than expected under neutrality (i.e. outside the null sampling distribution ![]() under neutrality) in morphological traits of males and females in 14 house sparrow populations on the coast of mid- and northern Norway
under neutrality) in morphological traits of males and females in 14 house sparrow populations on the coast of mid- and northern Norway
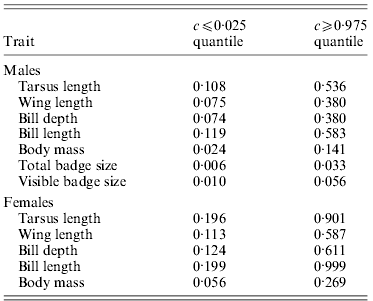
However, allowing for environmental causes of phenotypic inter-population variance, the quantitative genetic divergence, ![]() , for female tarsus length and bill length was not significantly different from neutral expectations for most values of c (Table 2 and Fig. 2). Furthermore, only for large values of c was
, for female tarsus length and bill length was not significantly different from neutral expectations for most values of c (Table 2 and Fig. 2). Furthermore, only for large values of c was ![]() for wing length and bill depth significantly larger than the neutral expectation (Table 2 and Fig. 2).
for wing length and bill depth significantly larger than the neutral expectation (Table 2 and Fig. 2). ![]() for female body mass was on the other hand significantly higher than neutral expectations for most values of c (Table 2 and Fig. 2). If we use
for female body mass was on the other hand significantly higher than neutral expectations for most values of c (Table 2 and Fig. 2). If we use ![]() >critical c value as a reasonable limit for selection, for female traits the critical c is either larger or approximately similar to the
>critical c value as a reasonable limit for selection, for female traits the critical c is either larger or approximately similar to the ![]() (Tables 1 and 2). This indicates (without knowing anything about the effect of environment and hence the true value of c) that we cannot distinguish the effects of genetic drift and selection for the observed spatial phenotypic differentiation in most female traits, but that differences across populations in female body mass may have been caused by spatially divergent selection.
(Tables 1 and 2). This indicates (without knowing anything about the effect of environment and hence the true value of c) that we cannot distinguish the effects of genetic drift and selection for the observed spatial phenotypic differentiation in most female traits, but that differences across populations in female body mass may have been caused by spatially divergent selection.
For males ![]() was significantly higher than the neutral exception for a larger range of values for c for all traits (Table 2 and Fig. 3). Accordingly,
was significantly higher than the neutral exception for a larger range of values for c for all traits (Table 2 and Fig. 3). Accordingly, ![]() for all traits except tarsus length and bill length was significantly higher than neutral expectations for most values of c (Table 2 and Fig. 3), and the critical c value was either larger or approximately similar to the
for all traits except tarsus length and bill length was significantly higher than neutral expectations for most values of c (Table 2 and Fig. 3), and the critical c value was either larger or approximately similar to the ![]() (Tables 1 and 2). For male body mass, total badge size and visible badge size genetic drift could have caused the observed phenotypic inter-population variation for only very small values of c (Table 2 and Fig. 3). Accordingly, for these traits the critical c value was much lower than
(Tables 1 and 2). For male body mass, total badge size and visible badge size genetic drift could have caused the observed phenotypic inter-population variation for only very small values of c (Table 2 and Fig. 3). Accordingly, for these traits the critical c value was much lower than ![]() (Tables 1 and 2). Without knowing anything about the actual environmental influence on the spatial phenotypic variation, and hence the true value of c, it seems that selection has been directional on at least some male traits, favouring different phenotypes in different populations.
(Tables 1 and 2). Without knowing anything about the actual environmental influence on the spatial phenotypic variation, and hence the true value of c, it seems that selection has been directional on at least some male traits, favouring different phenotypes in different populations.

Fig. 3. The relationship between observed and neutral ![]() , indicated with the solid and dashed lines, respectively, when the environmental component of the between-population variance varies between 0% (c=1) and 100% (c=0) (
, indicated with the solid and dashed lines, respectively, when the environmental component of the between-population variance varies between 0% (c=1) and 100% (c=0) (![]() [0,1]) for seven morphological traits in male house sparrows in 14 populations in mid- and northern Norway. The critical values for the null sampling distribution of the neutral
[0,1]) for seven morphological traits in male house sparrows in 14 populations in mid- and northern Norway. The critical values for the null sampling distribution of the neutral ![]() are indicated with the dotted lines. The different panels correspond to the relationship between
are indicated with the dotted lines. The different panels correspond to the relationship between ![]() and c for different phenotypic traits (a) tarsus length, (b) wing length, (c) bill depth, (d) bill length, (e) body mass, (f) total badge size and (g) visible badge size.
and c for different phenotypic traits (a) tarsus length, (b) wing length, (c) bill depth, (d) bill length, (e) body mass, (f) total badge size and (g) visible badge size.
5. Discussion
The estimated level of additive genetic differentiation in morphological traits among 14 house sparrow populations along the coast of Norway suggest that the differentiation may be higher than expected if caused by random genetic drift for some traits (see Figs 2 and 3).
Importantly, this was demonstrated using a model where we can explore and estimate the over-estimation (if no selection on the phenotypic trait) of the degree of genetic differentiation in quantitative traits when using phenotypic data. This method allowed us to vary the effect of the environmental component of the phenotypic between population variance on the observed Q ST estimates. Furthermore, the test of significance for each trait was carried out by comparing the observed additive genetic differentiation to the probability distribution for the trait if it was neutral, improving the type I error rate in this test (Whitlock & Guillaume, Reference Whitlock and Guillaume2009). However, this method, using phenotypic data to approximate Q ST, shows the importance of common garden studies in these types of studies of genetic differentiation. It is not possible to safely conclude anything about the actual inter-population level of additive genetic variation in different types of traits without such studies. Currently, it is unfortunately a problem to infer the likely amount of additive genetic variance between populations in different traits, because few common garden studies actually give these estimates in the results. We ask that common garden studies give these estimates because this will help us infer likely values of c, so that results from methods based on phenotypic data such as the one used here might be interpreted and discussed more reliably.
The phenotypic differentiation observed between the populations for all traits in both sexes (Table 1, see also Supplementary Table S1), might lead one to believe that a spatially varying environment has resulted in local adaption to different optima in different populations (Bürger & Krall, Reference Bürger, Krall, Ferrière, Dieckmann and Couvet2004; Dieckmann & Ferrière, Reference Dieckmann, Ferrière, Ferrière, Dieckmann and Couvet2004). The observed ![]() was, however, not significantly different from the distribution of
was, however, not significantly different from the distribution of ![]() under neutrality for most traits for a wide range of c values (Table 2; Figs 2 and 3). Consequently, we cannot rule out random genetic drift as the cause for the phenotypic differentiation in many morphological traits across house sparrow populations along the coast of Norway (Whitlock, Reference Whitlock1999, Reference Whitlock2008; Whitlock & Guillaume, Reference Whitlock and Guillaume2009).
under neutrality for most traits for a wide range of c values (Table 2; Figs 2 and 3). Consequently, we cannot rule out random genetic drift as the cause for the phenotypic differentiation in many morphological traits across house sparrow populations along the coast of Norway (Whitlock, Reference Whitlock1999, Reference Whitlock2008; Whitlock & Guillaume, Reference Whitlock and Guillaume2009).
Recent reviews on divergence in quantitative traits and neutral markers found that studies in most cases showed that Q ST values were higher than F ST values, suggesting that directional selection is the prevailing evolutionary force in quantitative trait divergence (reviews in Merilä & Crnokrak, Reference Merilä and Crnokrak2001; McKay & Latta, Reference McKay and Latta2002; Leinonen et al., Reference Leinonen, O'Hara, Cano and Merilä2008).
One reason why our results seem to contrast with general findings from other species could be due to the fragmented landscape along the Norwegian coast, where the sea separates house sparrow populations on islands from populations nearby, and populations on the mainland are separated from other populations by fjords or mountains. Combined with relatively short dispersal distances (Blair & Hagemeijer, Reference Blair and Hagemeijer1997; Altwegg et al., Reference Altwegg, Ringsby and Sæther2000; Tufto et al., Reference Tufto, Ringsby, Dhondt, Adriaensen and Matthysen2005; Skjelseth et al., Reference Skjelseth, Ringsby, Tufto, Jensen and Sæther2007; Pärn et al., Reference Pärn, Jensen, Ringsby and Sæther2009) and relatively small population sizes (see Supplementary Table S1) this may lead to increased importance of random genetic drift relative to selection in these house sparrow populations (Hartl & Clark, Reference Hartl and Clark1989; Freeman & Herron, Reference Freeman and Herron2004). In turn, this could increase both (neutral) genetic differentiation of marker loci used to estimate F ST (see e.g. discussion in Kekkonen et al., Reference Kekkonen, Seppä, Hanski, Jensen, Väisänen and Brommer2011) as well as the expected differentiation of additive genetic variation of phenotypic traits (Q ST) under neutrality (Whitlock, Reference Whitlock1999; Whitlock & Guillaume, Reference Whitlock and Guillaume2009).
Despite the possible importance of random genetic drift in the sampled house sparrow populations, the results for body mass of both sexes and in particular the badge size of males suggest (although not knowing the true value of c) that directional selection was likely to have influenced the observed phenotypic divergence between populations in these traits (Table 2, Figs 2 and 3). The badge of male house sparrows is assumed to act as a sexual ornament (Møller, Reference Møller1987; Veiga, Reference Veiga1993), signal dominance (Liker & Barta, Reference Liker and Barta2001; McGraw et al., Reference McGraw, Dale and Mackillop2003) and is thus correlated with the social status of males (Nakagawa et al., Reference Nakagawa, Ockendon, Gillespie, Hatchwell and Burke2007). Accordingly, Jensen et al. (Reference Jensen, Sæther, Ringsby, Tufto, Griffith and Ellegren2004) found that badge size was positively associated with lifetime reproductive success (LRS), showing it is related to male fitness. Furthermore, the results of Jensen et al. (Reference Jensen, Steinsland, Ringsby and Sæther2008) suggest that the total badge of male house sparrows is subject to sexual selection through a positive effect on mating success. In the same study populations the badge size has also been found to increase with the population density in which the males grow up (Jensen et al., Reference Jensen, Svorkmo-Lundberg, Ringsby and Sæther2006). Jointly, these results indicate that social mechanisms, such as sexual selection and dominance, can give different optimal phenotypes in different populations. Furthermore, the results in Jensen et al. (Reference Jensen, Svorkmo-Lundberg, Ringsby and Sæther2006), showing that badge size is partly environmentally dependent, suggest potential for population-specific plastic variation in badge size. This is further supported by the low heritability (![]() ) found for this trait. Body mass is another fitness-related trait (Jensen et al., Reference Jensen, Steinsland, Ringsby and Sæther2008) with moderate heritability in house sparrows (Table 1). In other species, this is also a trait shown to have potential for plastic changes (Larsson, Reference Larsson1993; Madsen & Shine, Reference Madsen and Shine1993; Pelletier et al., Reference Pelletier, Réale, Garant, Coltman and Festa-Bianchet2007). Accordingly, fitness-related traits have been found to be influenced by the environment and thus have low heritability in general (Merilä & Sheldon, Reference Merilä and Sheldon2000). Irrespective of the proximate mechanism causing population differentiation in badge size, the results presented here suggest that despite relatively low heritability and potential for plastic variation of total badge size and body mass, the strength and perhaps direction of directional selection vary sufficiently between populations for the evolutionary consequences of selection to exceed that of random genetic drift. Although we do not know the actual importance of any variation in environmental conditions for phenotypic inter-population variance and hence the value of c for male badge size or body mass in both sexes, our results show that this conclusion, for example, holds even when less than approximately 3·3% of the phenotypic inter-population variation in total badge size is due to genetic differences between populations (Table 2 and Fig. 3).
) found for this trait. Body mass is another fitness-related trait (Jensen et al., Reference Jensen, Steinsland, Ringsby and Sæther2008) with moderate heritability in house sparrows (Table 1). In other species, this is also a trait shown to have potential for plastic changes (Larsson, Reference Larsson1993; Madsen & Shine, Reference Madsen and Shine1993; Pelletier et al., Reference Pelletier, Réale, Garant, Coltman and Festa-Bianchet2007). Accordingly, fitness-related traits have been found to be influenced by the environment and thus have low heritability in general (Merilä & Sheldon, Reference Merilä and Sheldon2000). Irrespective of the proximate mechanism causing population differentiation in badge size, the results presented here suggest that despite relatively low heritability and potential for plastic variation of total badge size and body mass, the strength and perhaps direction of directional selection vary sufficiently between populations for the evolutionary consequences of selection to exceed that of random genetic drift. Although we do not know the actual importance of any variation in environmental conditions for phenotypic inter-population variance and hence the value of c for male badge size or body mass in both sexes, our results show that this conclusion, for example, holds even when less than approximately 3·3% of the phenotypic inter-population variation in total badge size is due to genetic differences between populations (Table 2 and Fig. 3).
Similar results have been found for the sexually selected trait tail white (length of white on the outermost tail feather) (Höglund et al., Reference Höglund, Eriksson and Lindell1990), in the great snipe (Gallinago media) (Sæther et al., Reference Sæther, Fiske, Kålås, Kuresoo, Luigujõe, Piertney, Sahlman and Höglund2007). Furthermore, Chenoweth & Blows (Reference Chenoweth and Blows2008) looked at a set of sexually selected traits in Drosophila serrata, using a multivariate analogue of Q ST, accounting for correlations between traits. Their study suggested that divergent selection acting in a sex-specific direction caused population divergence. Similar results have also been found for other traits that are directly connected to fitness (reviews in Merilä & Crnokrak, Reference Merilä and Crnokrak2001; McKay & Latta, Reference McKay and Latta2002; Leinonen et al., Reference Leinonen, O'Hara, Cano and Merilä2008). That studies of sexually selected traits generally demonstrate higher levels of Q ST than F ST suggests that variation in the strength of sexual selection across populations may be a general pattern. The strength of sexual selection will depend on the social mating system, which in turn may be determined by factors such as the population sex ratio, population density and distribution of males and females due to variation in important ecological resources (Bennett & Owens, Reference Bennett and Owens2002; Kokko & Johnstone, Reference Kokko and Johnstone2002). Furthermore, in birds, it has, for example, been found that the strength of sexual selection may be connected with the degree of sexual dimorphism and occurrence of extra-pair paternity (Petrie & Kempenaers, Reference Petrie and Kempenaers1998; Bennett & Owens, Reference Bennett and Owens2002). Because all these factors may vary in space and time (e.g. Bennett & Owens, Reference Bennett and Owens2002; Engen et al., Reference Engen, Ringsby, Sæther, Lande, Jensen, Lillegård and Ellegren2007) this may also give rise to inter-population variation in strength of sexual selection (Kwiatkowski & Sullivan, Reference Kwiatkowski and Sullivan2002).
In many studies of natural populations, obtaining estimates of additive genetic variation within and among populations is problematic. To estimate the population-specific additive genetic variance σAW2 (see σGW2 eqn 3) from measures of phenotypic variances within populations, we assumed a constant trait-specific heritability (h 2) equal for each population, based on actual estimates from a sub-set of the populations included in the study. The possible sampling error in the h 2 estimates, due to environmental variation in field data, giving lower heritability estimates, were included in the sampling procedure.
Studies suggest that heritability can change over time under different environmental conditions, indicating a higher heritability under more favourable conditions (although h 2 depends on the phenotypic variance, additive genetic variance was also found to be higher under better conditions), indicating genotype-by-environment (G×E) interactions (Kruuk et al., Reference Kruuk, Slate and Wilson2008; Husby et al., Reference Husby, Visser and Kruuk2011). There are also a number of empirical examples where morphological traits in birds show higher additive genetic variance under favourable environmental conditions (Larsson, Reference Larsson1993; Merilä & Sheldon, Reference Merilä and Sheldon2001; Charmantier et al., Reference Charmantier, Kruuk and Lambrechts2004). Studies indicate, however, that life-history traits (traits closely related to fitness) show less change in h 2 in different environmental conditions than morphological (morphometric) traits (Charmantier & Garant Reference Charmantier and Garant2005; Kruuk et al., Reference Kruuk, Slate and Wilson2008). This suggests that the environment may be very important for the response to selection (Kruuk et al., Reference Kruuk, Slate and Wilson2008). If different environmental conditions can create different heritability in the study populations (i.e. that the additive genetic variance is not proportional to phenotypic variance), this means that the estimated Q ST may be lower than the true one. If this is the case in the current study, it follows that ![]() in reality may exceed neutral expectations for a wider range of c values. Hence, the conclusions for the importance of selection for population differences in badge size would hold regardless of this potential bias.
in reality may exceed neutral expectations for a wider range of c values. Hence, the conclusions for the importance of selection for population differences in badge size would hold regardless of this potential bias.
It is important to carefully think of the potential pitfalls when estimating Q ST and to interpret the results with this in mind. Using the simulation method described in Whitlock & Guillaume (Reference Whitlock and Guillaume2009) for estimating the neutral distribution of Q ST, we take into consideration many of the different problems while estimating the error in Q ST and problems related to comparing Q ST to F ST (O'Hara & Merilä, Reference O'Hara and Merilä2005). This includes the sampling error caused by finite samples of individuals and populations, which is a problem in many studies of Q ST where the number of populations is often too low (Miller et al., Reference Miller, Wood and Hamilton2008). Pairwise Q ST were not estimated because of large uncertainties in Q ST due to sampling error (finite sample of individuals and small sample of population).
Another potential bias when comparing ![]() and
and ![]() may be introduced if gene flow is not random with respect to quantitative genetic variation in traits used in the study. In the present study, this may be a possible factor explaining some of the patterns. For example, Skjelseth et al. (Reference Skjelseth, Ringsby, Tufto, Jensen and Sæther2007) found that female dispersers have longer wings. Because wing length is genetically correlated with most other morphological traits within and across sexes (Jensen et al., Reference Jensen, Steinsland, Ringsby and Sæther2008) this means that gene flow might not be random with respect to the genes underlying quantitative morphological traits that are transferred among populations. These effects of gene flow may in addition to the possibly relatively high levels of random genetic drift (see above) be a contributing factor to the low levels of
may be introduced if gene flow is not random with respect to quantitative genetic variation in traits used in the study. In the present study, this may be a possible factor explaining some of the patterns. For example, Skjelseth et al. (Reference Skjelseth, Ringsby, Tufto, Jensen and Sæther2007) found that female dispersers have longer wings. Because wing length is genetically correlated with most other morphological traits within and across sexes (Jensen et al., Reference Jensen, Steinsland, Ringsby and Sæther2008) this means that gene flow might not be random with respect to the genes underlying quantitative morphological traits that are transferred among populations. These effects of gene flow may in addition to the possibly relatively high levels of random genetic drift (see above) be a contributing factor to the low levels of ![]() found for most morphological traits in this study.
found for most morphological traits in this study.
6. Conclusion
The results in this study show that for body mass in both sexes and for badge size in males directional selection may have been a more important evolutionary force than genetic drift in driving phenotypic differentiation among populations. However, we must conclude that for most of the morphological traits in both females and males, we cannot rule out random genetic drift or environmentally induced differences as the cause for the phenotypic differentiation, even with the low to moderate values found for ![]() .
.
The popularity of comparing estimates of Q ST and F ST in order to understand the relative importance of random genetic drift and selection for adaptive population divergence among natural populations will probably increase as the cost decreases and efficiency increases for obtaining good estimates of F ST (e.g. Freeland, Reference Freeland2005). Here, we have used a method that can help us explore the possibilities for population divergence based on phenotypic measurements of individuals in a set of populations and only one estimate of the heritability of the trait(s) of interest. This is the information that is likely to be available for many natural populations. At present, a critical assumption of a constant heritability across populations has to be made. Importantly, this method makes evolutionary biologists able to explore the potential influence of environmental causes of phenotypic differentiation when estimating Q ST based on phenotypic measures. Because population-specific estimates of additive genetic variance are difficult to obtain in natural populations, avoiding the need for this by instead using phenotypic data and being able to quantify the effect of varying environmental contribution to phenotypic differentiation is advantageous. To draw general and reliable conclusions from such analyses, it is, however, necessary to know more about the proportion of any observed phenotypic inter-population variation which is due to additive genetic differences (i.e. the value of c) for different types of traits and species. Consequently, proper common garden experiments are needed for more populations and species. Furthermore, we urge that such studies also present the variance components, so that one can examine whether any general rules about likely values for c for different traits can be generated.
We are grateful to the inhabitants in our study area for their hospitality and friendliness that made this study possible. We thank O.R. Davidsen, J. Gogstad-Thorsen, T. Kolaas, L. K. Larsen, A. Lorås, M. Mørkved, T. H. Ringsby, B. G. Stokke, T. Svorkmo-Lundberg, K. Sørensen and T. Vedal for help with fieldwork. T. H. Ringsby and B.-E. Sæther have contributed to helpful discussions and comments that improved the manuscript. We also thank M. C. Whitlock and four anonymous referees for their valuable comments. This study was supported by grants from the Norwegian Research Council (Storforsk, Strategic University Program (SUP) in Conservation Biology, and grant no. 191847 to H.J.).







