1. Introduction
The departures of genotype frequencies from Hardy–Weinberg proportions (HWP) for a given locus provide relevant information for understanding genetic characteristics of populations, such as deviations from random mating, population subdivision, asymmetric allelic contributions of the sexes, or viability selection. Furthermore, the analysis of deviations from HWP is one of the few ways to identify systematic genotyping errors, so that at present it is a fundamental tool for genotyping quality control in large-scale studies of molecular markers (Hare et al., Reference Hare, Karl and Avise1996; Gomes et al., Reference Gomes, Collins, Lonjou, Thomas, Wilkinson, Watson and Morton1999; Xu et al., Reference Xu, Turner, Little, Bleecker and Meyers2002; Hosking et al., Reference Hosking, Lumsden, Lewis, Yeo, McCarthy, Bansal, Riley, Purvis and Xu2004; Chen et al., Reference Chen, Duan, Single, Mather and Thomson2005; Zou & Donner, Reference Zou and Donner2006; Teo et al., Reference Teo, Fry, Clark, Tai and Seielstad2007). Furthermore, in the context of studies of association between human diseases and molecular markers, the analysis of deviations from HWP is important for distinguishing those deviations in patients and control samples that could be attributed to the underlying genetic disease model at the susceptibility locus from those due to genotyping errors, chance and/or violations of the assumptions of Hardy–Weinberg equilibrium (Wittke-Thompson et al., Reference Wittke-Thompson, Pluzhnikov and Cox2005).
Natural selection operating through differential survival of genotypes is probably one of the most important mechanisms disturbing HWP in random mating populations, particularly when genotypes are recorded at the adult stage of the life cycle. Departures from HWP for a single autosomal locus produced by viability selection have been investigated for the two-allele case, especially as regards statistical tests for detecting natural selection (Lewontin & Cockerham, Reference Lewontin and Cockerham1959; Li, Reference Li1959; Workman, Reference Workman1969; Brown, Reference Brown1970; Hedrick, Reference Hedrick2005, pp. 150–152). However, the study of deviations from HWP caused by viability selection acting on multiple alleles has received very little attention. In contrast, analysis of deviations from HWP for multiple alleles has been performed for models of subdivided populations (Nei, Reference Nei1965; Li, Reference Li1969), inbreeding (Li & Horvitz, Reference Li and Horvitz1953; Yasuda, Reference Yasuda1968; Curie-Cohen, Reference Curie-Cohen1982; Robertson & Hill, Reference Robertson and Hill1984; Hill et al., Reference Hill, Babiker, Ranford-Cartwright and Walliker1995; Rousset & Raymond, Reference Rousset and Raymond1995) and differential selection between the sexes (Purser, Reference Purser1966; Ziehe & Gregorius, Reference Ziehe and Gregorius1981). Consequently, viability selection is the only basic model of deviations from HWP for which the multiple-allele case has not been investigated. This is rather striking given that the classical model of multiallele viability selection has been extensively studied, in particular with respect to conditions for the stability of multiallelic polymorphisms (Mandel, Reference Mandel1959, Reference Mandel1970; Weir, Reference Weir1970; Lewontin et al., Reference Lewontin, Ginzburg and Tuljapurkar1978; Karlin, Reference Karlin1981; Karlin & Feldman, Reference Karlin and Feldman1981). On theoretical grounds, multiallelic polymorphisms are expected to be easily maintained in natural populations by viability selection since, although the proportion of the viability parameter space permitting stable polymorphisms becomes extremely small as the number of alleles increases (Lewontin et al., Reference Lewontin, Ginzburg and Tuljapurkar1978; Karlin, Reference Karlin1981; Karlin & Feldman, Reference Karlin and Feldman1981), models based on Monte Carlo simulations in which a series of new mutations are introduced into the population show that viability selection is capable of maintaining a large number of alleles (up to 38 in some cases) (Spencer & Marks, Reference Spencer and Marks1988, Reference Spencer and Marks1992; Marks & Spencer, Reference Marks and Spencer1991). In the present article, expressions for departures of genotype frequencies from HWP, as measured by means of fixation indices (F IS statistics), are obtained for an autosomal locus with multiple alleles under a deterministic model of constant viability selection and random mating. Special attention is devoted to characterizing the multiallelic pattern of deviations from HWP exhibited by the population when it attains a stable equilibrium due to viability selection.
2. Hardy–Weinberg deviations under the multiallele viability model
(i) Model and notation
An autosomal locus with k alleles (denoted as A 1, A 2, …, A k) is considered, where p i is the frequency of the A i allele at the zygotic stage. Assuming random mating, the frequency of the A iA i homozygote is p i2 and the frequency of the A iA j heterozygote is 2p ip j. Under the standard one-locus multiallele viability selection model, with fitness values w ii for the A iA i homozygote and w ij for the A iA j heterozygote, the adult frequencies for the A iA i and A iA j genotypes, A ii and A ij respectively, are
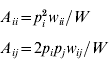
and the allele frequencies in adults are
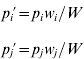
where w i is the marginal fitness of allele A i and W is the mean fitness of the population, given by
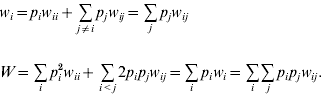
The departures of adult genotype frequencies from HWP for multiple alleles can be expressed in terms of either k f ii fixation indices (F IS statistics) or, alternatively, k(k−1)/2 f ij fixation indices, as
taking into account that f ii and f ij are functionally related by
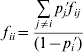
(Weir, Reference Weir1996, p. 94). In this formulation, the f ii coefficients can be considered as allele-specific F IS statistics (Chakraborty & Danker-Hopfe, Reference Chakraborty, Danker-Hopfe, Rao and Chakraborty1991).
(ii) Hardy–Weinberg deviations
Expressions for the f ii and f ij fixation indices under the model of viability selection are obtained by substituting the allele and genotype frequencies in (4) and (5) by their values given by (1) and (2), and they are
In these expressions for the deviations from HWP for multiple alleles, the terms (w iiW−w i2) for the homozygote A iA i and (w iw j−w ijW) for the heterozygote A iA j determine the sign of the deviation. Thus, when the fitness of a particular genotype multiplied by the mean fitness is equal to the product of the marginal fitnesses of the alleles forming that genotype, a deviation from HWP is not expected to occur for that genotype. This is the case for multiplicative or geometric fitnesses where w ii=a i2 and w ij=a ia j since, in this case, marginal and mean fitnesses take the form
and substituting these expressions in (7) and (8), we have
Therefore, under multiplicative viability fitnesses, the genotype frequencies at a multiallelic locus, after the operation of selection, are in accordance with Hardy–Weinberg expectations. This result was demonstrated for a two-allele locus by Lewontin & Cockerham (Reference Lewontin and Cockerham1959) and extended to the three-allele case by Li (Reference Li1959), and here is generalized for a k-allele system.
When the genotype fitnesses do not follow a geometric progression, the pattern of Hardy–Weinberg deviations is difficult to specify since f ii and f ij, as expressed by (7) and (8), are dependent on the marginal and mean fitness which are changing along generations. However, a particular and relatively simple pattern of Hardy–Weinberg departures is expected to occur for a multiallelic locus when a stable equilibrium is attained in the population by the operation of viability selection. At the equilibrium, f ii and f ij, as expressed by (7) and (8), reduce to
where * denotes equilibrium values, since the condition for equilibrium in the multiallele viability model is simply w i=w j=………=W (Lewontin et al., Reference Lewontin, Ginzburg and Tuljapurkar1978). Consequently, the departure from HWP for a given genotype is basically determined, at the stable equilibrium, by the ratio of the genotype fitness to the mean fitness of the population. Given that the homozygote and heterozygote finesses must satisfy two inequalities with respect to the mean fitness of the population as necessary conditions for the existence of a stable multiallele polymorphism, which are W*>w ii for all i=1, 2, …, k and ![]() , where
, where ![]() is the weighted mean fitness of heterozygotes at the equilibrium (Mandel, Reference Mandel1959; Ginzburg, Reference Ginzburg1979), it follows that all homozygotes must present a deficiency with respect to HWP, that is
is the weighted mean fitness of heterozygotes at the equilibrium (Mandel, Reference Mandel1959; Ginzburg, Reference Ginzburg1979), it follows that all homozygotes must present a deficiency with respect to HWP, that is
and an excess must be present in many but not necessarily all heterozygote classes. In the three-allele case, for example, it has been shown that at most one heterozygous viability may fall below that of at most two homozygotes (Mandel, Reference Mandel1959) and therefore, in this case, the f ij* corresponding to that particular heterozygote will be positive.
For a two-allele locus, the expression for departures from HWP under viability selection, obtained by Workman (Reference Workman1969) and Brown (Reference Brown1970), is a particular case of expressions (7) and (8). At equilibrium, the Hardy–Weinberg deviation for a diallelic locus as given by Workman (Reference Workman1969) is a particular case of expressions (9) and (10).
(iii) Estimation of FIS statistics
The model for statistical estimation of deviations from HWP for multiple alleles under viability selection is a model where either k f ii parameters, or alternatively k(k−1)/2 f ij parameters, must be independently estimated, in addition to the allele frequencies. At first sight, this model is more complicated than the model for the estimation of the inbreeding coefficient under regular inbreeding, in which only one f value needs to be estimated in addition to the allelic frequencies, and which has been extensively studied (Li & Horvitz, Reference Li and Horvitz1953; Curie-Cohen, Reference Curie-Cohen1982; Robertson & Hill, Reference Robertson and Hill1984; Hill et al., Reference Hill, Babiker, Ranford-Cartwright and Walliker1995; Rousset & Raymond, Reference Rousset and Raymond1995). However, in the framework of maximum likelihood theory, the estimation of both the set of parameters f and the allele frequencies is straightforward. Consider a random sample of n adults in which the observed numbers of A iA i and A iA j genotypes are n ii and n ij, respectively, and the observed allele frequency of A i is p i′. The likelihood of a sample of n individuals composed of n ii genotypes A iA i and n ij genotypes A iA j can be expressed in terms of a set F of k(k−1)/2 f ij parameters and a set P of k parameters of allele frequencies as

Under this formulation the f ii parameters are not taken into consideration and therefore the number of independent parameters to be estimated equals the number of degrees of freedom in the data, so that Bailey's method (Bailey, Reference Bailey1951; Weir, Reference Weir1996, pp. 63–66) can be applied. Consequently, the maximum likelihood estimates of the parameters are simply their observed values and, therefore, both the f ij obtained from (5) and the allele frequencies computed by gene counting are maximum likelihood estimates. With regard to the f ii fixation indices, their estimates from (4) are also maximum likelihood estimates since each particular f ii corresponds to the f estimate that results from grouping all the alleles into two categories, i versus non-i, and for a diallelic system both f 11=f 12=f 22=f and the allele frequency are maximum likelihood estimates (Li & Horvitz, Reference Li and Horvitz1953; Weir, Reference Weir1996, pp. 64–65). In this way, a k-allele system can be split into k diallelic systems each leading to maximum likelihood estimates of both f ii and p i′. Note that all this estimation procedure is valid not only for the particular case of deviations from HWP produced by viability selection, but for any case where each specific genotype has a specific departure from HWP, as for example population subdivision or different allelic frequencies between the sexes.
3. Hardy–Weinberg deviations for the β-globin locus in human populations from West Africa
The β-globin gene is one of the most thoroughly studied polymorphisms in man, since it is an adaptive polymorphism involved in resistance against Plasmodium falciparum malaria (Cavalli-Sforza & Bodmer, Reference Cavalli-Sforza and Bodmer1971; Vogel & Motulsky, Reference Vogel and Motulsky1997). An analysis of multiallelic deviations from HWP for this locus in human populations has been performed in the present study using published data (Allison, Reference Allison1956; Roberts & Boyo, Reference Roberts and Boyo1962; Modiano et al., Reference Modiano, Luoni, Sirima, Simporé, Verra, Konaté, Rastrelli, Olivieri, Calissano, Paganotti, D'Urbano, Sanou, Sawadogo, Modiano and Coluzzi2001). The populations considered belong to the geographical area of West Africa where this locus presents three alleles with detectable frequencies: the HbA allele that gives rise to the normal haemoglobin, the HbS allele responsible for the sickle haemoglobin, and the HbC responsible for haemoglobin C. Samples of adults and infants from the Jola and Fula populations (The Gambia), and of adults and children from the Yoruba population (Nigeria), were analysed. A very large sample (n=3513) from the Mossi population (Burkina Faso) was also included in the analysis: this is a control sample from a large case–control study performed in Burkina Faso to investigate the protective role against severe malaria of genotypes at the β-globin locus, and was composed mainly of healthy subjects more than 6 years old (87% children aged 6–15 years, and 8·4% individuals more than 15 years old), though a small number of children aged 1–5 years (4·6%) was also included (Modiano et al., Reference Modiano, Luoni, Sirima, Simporé, Verra, Konaté, Rastrelli, Olivieri, Calissano, Paganotti, D'Urbano, Sanou, Sawadogo, Modiano and Coluzzi2001).
Genotype distribution, allele frequencies and deviations from HWP for each of the samples analysed are given in Table 1. Deviations from HWP were measured by means of the f ii estimators of Robertson & Hill (Reference Robertson and Hill1984), giving estimates for the three homozygous genotypes (![]() for the homozygote HbAA,
for the homozygote HbAA, ![]() for HbSS, and
for HbSS, and ![]() for HbCC) and a global estimate of deviation from HWP at the locus (
for HbCC) and a global estimate of deviation from HWP at the locus (![]() ) obtained from the weighted average of the f ii estimates. The variance of f ii estimates equals 1/n for f ii=0 and the ratio of the squared estimate to its variance will be approximately distributed as a chi-square variable with one degree of freedom, leading to a two-tailed test of the null hypothesis H0: f ii=0 (Elandt-Johnson, Reference Elandt-Johnson1971, pp. 355–356; Robertson & Hill, Reference Robertson and Hill1984). One-tailed tests can be performed from the ratio of the estimate to its standard error, which is approximately distributed as a standard normal variable (Elandt-Johnson, Reference Elandt-Johnson1971, pp. 355–356). The two-tailed test of f ii is equivalent to the Hardy–Weinberg test of a single homozygous genotype recently proposed by Chen et al. (Reference Chen, Duan, Single, Mather and Thomson2005), since the chi-square statistic given by Chen et al. (Reference Chen, Duan, Single, Mather and Thomson2005, p. 1440) is simply nf ii2. The analysis of deviation from HWP for multiple alleles by means of f ii fixation indices and/or single genotype tests gives a complete view of the distribution of deviations among particular genotypes at the given locus in contrast to the overall tests such as the chi-square goodness-of-fit test or the exact test (Louis & Dempster, Reference Louis and Dempster1987; Guo & Thompson, Reference Guo and Thompson1992; Chakraborty & Zhong, Reference Chakraborty and Zhong1994; Rousset & Raymond, Reference Rousset and Raymond1995). A very regular pattern of deviations from HWP for the β-globin locus is observed in the adult samples from West Africa populations. First, a global heterozygote excess is found in all adult samples:
) obtained from the weighted average of the f ii estimates. The variance of f ii estimates equals 1/n for f ii=0 and the ratio of the squared estimate to its variance will be approximately distributed as a chi-square variable with one degree of freedom, leading to a two-tailed test of the null hypothesis H0: f ii=0 (Elandt-Johnson, Reference Elandt-Johnson1971, pp. 355–356; Robertson & Hill, Reference Robertson and Hill1984). One-tailed tests can be performed from the ratio of the estimate to its standard error, which is approximately distributed as a standard normal variable (Elandt-Johnson, Reference Elandt-Johnson1971, pp. 355–356). The two-tailed test of f ii is equivalent to the Hardy–Weinberg test of a single homozygous genotype recently proposed by Chen et al. (Reference Chen, Duan, Single, Mather and Thomson2005), since the chi-square statistic given by Chen et al. (Reference Chen, Duan, Single, Mather and Thomson2005, p. 1440) is simply nf ii2. The analysis of deviation from HWP for multiple alleles by means of f ii fixation indices and/or single genotype tests gives a complete view of the distribution of deviations among particular genotypes at the given locus in contrast to the overall tests such as the chi-square goodness-of-fit test or the exact test (Louis & Dempster, Reference Louis and Dempster1987; Guo & Thompson, Reference Guo and Thompson1992; Chakraborty & Zhong, Reference Chakraborty and Zhong1994; Rousset & Raymond, Reference Rousset and Raymond1995). A very regular pattern of deviations from HWP for the β-globin locus is observed in the adult samples from West Africa populations. First, a global heterozygote excess is found in all adult samples: ![]() ranges from −0·103 to −0·052 with an average of −0·070±0·016. This heterozygote excess is statistically significant by one-sided tests in the Yoruba sample. Second, the distribution of Hardy–Weinberg deviations among particular homozygotes is clearly uneven in the adult samples, since homozygotes for the HbA and HbS alleles show a clear deficiency with respect to HWP, whereas the frequency of the homozygote HbCC is very close to Hardy–Weinberg expectations. Specifically,
ranges from −0·103 to −0·052 with an average of −0·070±0·016. This heterozygote excess is statistically significant by one-sided tests in the Yoruba sample. Second, the distribution of Hardy–Weinberg deviations among particular homozygotes is clearly uneven in the adult samples, since homozygotes for the HbA and HbS alleles show a clear deficiency with respect to HWP, whereas the frequency of the homozygote HbCC is very close to Hardy–Weinberg expectations. Specifically, ![]() ranges from −0·165 to −0·105 with a mean value of −0·128±0·019, these deviations being statistically significant in two of the three adult samples analysed; similarly, f SS ranges from −0·144 to −0·091 with a mean value of −0·112±0·016, these deviations being statistically significant in the Yoruba sample. In contrast,
ranges from −0·165 to −0·105 with a mean value of −0·128±0·019, these deviations being statistically significant in two of the three adult samples analysed; similarly, f SS ranges from −0·144 to −0·091 with a mean value of −0·112±0·016, these deviations being statistically significant in the Yoruba sample. In contrast, ![]() ranges from −0·053 to −0·008 with a mean value of −0·024±0·015 and these negative estimates are associated with the absence of HbCC homozygotes in the adult samples due to the low frequency of the HbC allele (see expression (4)). In addition, these deviations are not statistically significant in any of the three adult samples studied. A substantial number of HbCC homozygotes is present in the large sample from the Mossi population which probably represents a partially selected stage since it is composed by individuals older than 6 years and, in this case,
ranges from −0·053 to −0·008 with a mean value of −0·024±0·015 and these negative estimates are associated with the absence of HbCC homozygotes in the adult samples due to the low frequency of the HbC allele (see expression (4)). In addition, these deviations are not statistically significant in any of the three adult samples studied. A substantial number of HbCC homozygotes is present in the large sample from the Mossi population which probably represents a partially selected stage since it is composed by individuals older than 6 years and, in this case, ![]() takes a positive value (
takes a positive value (![]() =0·0004). As a whole, these results do not support the idea that this three-allele polymorphism is at stable equilibrium in the West African populations due to viability selection, since stable equilibrium would require all three homozygotes to present a deficiency with respect to Hardy–Weinberg expectations, as already demonstrated. Obviously, a large number of West African populations must be analysed in order to confirm these results but it is interesting to point out that the analysis of multiallelic deviations from HWP presented here is in accordance with recent evidence based on epidemiological and fitness data which suggests that this three-allele system may be a transient polymorphism in West African populations (Modiano et al., Reference Modiano, Luoni, Sirima, Simporé, Verra, Konaté, Rastrelli, Olivieri, Calissano, Paganotti, D'Urbano, Sanou, Sawadogo, Modiano and Coluzzi2001; Hedrick, Reference Hedrick2004, 2005, pp. 161–163).
=0·0004). As a whole, these results do not support the idea that this three-allele polymorphism is at stable equilibrium in the West African populations due to viability selection, since stable equilibrium would require all three homozygotes to present a deficiency with respect to Hardy–Weinberg expectations, as already demonstrated. Obviously, a large number of West African populations must be analysed in order to confirm these results but it is interesting to point out that the analysis of multiallelic deviations from HWP presented here is in accordance with recent evidence based on epidemiological and fitness data which suggests that this three-allele system may be a transient polymorphism in West African populations (Modiano et al., Reference Modiano, Luoni, Sirima, Simporé, Verra, Konaté, Rastrelli, Olivieri, Calissano, Paganotti, D'Urbano, Sanou, Sawadogo, Modiano and Coluzzi2001; Hedrick, Reference Hedrick2004, 2005, pp. 161–163).
Table 1. Genotype distribution, allele frequencies and Hardy–Weinberg deviations at the β-globin locus in samples from West African populations

1 Allison (Reference Allison1956) ; 2 Roberts & Boyo (Reference Roberts and Boyo1962) ; 3 Modiano et al. (Reference Modiano, Luoni, Sirima, Simporé, Verra, Konaté, Rastrelli, Olivieri, Calissano, Paganotti, D'Urbano, Sanou, Sawadogo, Modiano and Coluzzi2001).
a 2 months to 1 year; b 6 years to 12 years; c 21 months to 6 years; d 4 months to 28 months.
* P<0·05; ** P<0·01; *** P<0·001.
The analysis of deviations from HWP for infants (2 months to 1 year) and very young children (4–28 months) shows that their genotypic frequencies are very close to Hardy–Weinberg expectation and, thus, the pattern of deviations from HWP observed in these age groups is very different from that found in adult samples (Table 1): mean values for ![]() ,
, ![]() ,
, ![]() and
and ![]() are 0·018±0·005, 0·027±0·004, 0·043±0·007 and −0·007±0·004, respectively, in the three samples analysed. These results reveal that the heterozygote excess observed in adult samples is not a consequence of asymmetric allelic contributions of the sexes due to differential selection in the two sexes or to chance, since in this case the heterozygote excess would be present at the zygotic stage (see Section 4). On the contrary, our findings indicate that the heterozygote excess observed in adult samples is probably due to the operation of viability selection. In older children (21 months to 6 years, 6–12 years and >6 years), the pattern of deviations from HWP observed is very close to that seen in the adult samples: mean values for
are 0·018±0·005, 0·027±0·004, 0·043±0·007 and −0·007±0·004, respectively, in the three samples analysed. These results reveal that the heterozygote excess observed in adult samples is not a consequence of asymmetric allelic contributions of the sexes due to differential selection in the two sexes or to chance, since in this case the heterozygote excess would be present at the zygotic stage (see Section 4). On the contrary, our findings indicate that the heterozygote excess observed in adult samples is probably due to the operation of viability selection. In older children (21 months to 6 years, 6–12 years and >6 years), the pattern of deviations from HWP observed is very close to that seen in the adult samples: mean values for ![]() ,
, ![]() ,
, ![]() and
and ![]() in the three older-children samples are −0·056±0·016, −0·094±0·018, −0·095±0·027 and −0·013±0·008, respectively. This heterozygote excess is statistically significant by one-sided tests for both f T and f SS in two of the three samples analysed (Yoruba and Mossi) and for f AA in the Mossi sample. This result is consistent with evidence indicating that differential mortality among genotypes at the β-globin locus due to death from either sickle-cell anaemia or malaria occurs mainly in young children (Allison, Reference Allison1956; Roberts & Boyo, Reference Roberts and Boyo1960; Cavalli-Sforza & Bodmer, Reference Cavalli-Sforza and Bodmer1971, Greenwood et al., Reference Greenwood, Bradley, Greenwood, Byass, Jammeh, Marsh, Tulloch, Oldfield and Hayes1987; Vogel & Motulsky, Reference Vogel and Motulsky1997).
in the three older-children samples are −0·056±0·016, −0·094±0·018, −0·095±0·027 and −0·013±0·008, respectively. This heterozygote excess is statistically significant by one-sided tests for both f T and f SS in two of the three samples analysed (Yoruba and Mossi) and for f AA in the Mossi sample. This result is consistent with evidence indicating that differential mortality among genotypes at the β-globin locus due to death from either sickle-cell anaemia or malaria occurs mainly in young children (Allison, Reference Allison1956; Roberts & Boyo, Reference Roberts and Boyo1960; Cavalli-Sforza & Bodmer, Reference Cavalli-Sforza and Bodmer1971, Greenwood et al., Reference Greenwood, Bradley, Greenwood, Byass, Jammeh, Marsh, Tulloch, Oldfield and Hayes1987; Vogel & Motulsky, Reference Vogel and Motulsky1997).
4. Discussion
The effect of viability selection on the distribution of genotypes for a multiallelic polymorphism in a random mating population is effectively identified through the departures of genotype frequencies from Hardy–Weinberg proportions (HWP) (expressions (7) and (8)). Furthermore, a genetic polymorphism for multiple alleles maintained by balancing viability selection will show, at equilibrium, both a global heterozygote excess and a deficiency of each of the homozygotes (expressions (9) and (10)). This pattern of Hardy–Weinberg deviations is a consequence of the relationship between the genotype fitnesses and the mean fitness when the population reaches stable equilibrium, since, at this point, the mean fitness of the population must be higher than the fitness of each homozygote and lower than the weighted mean fitness of heterozygotes (Mandel, Reference Mandel1959; Ginzburg, Reference Ginzburg1979). This ‘footprint’ of selection on the genotypic distribution may be useful for detecting whether a given multiallele polymorphism is at stable equilibrium in the population due to viability selection, since it can be easily distinguished from other potential causes of deviations from HWP. Inbreeding and subdivision or admixture of populations will give rise to heterozygote deficiency although, under population subdivision for multiple alleles, some particular heterozygote might be in excess due to a positive covariation of allelic frequencies (Nei, Reference Nei1965; Li, Reference Li1969). On the other hand, heterozygote excess can also be caused by differences in allelic frequencies between the sexes. These differences might arise either by chance or by differential selection between the sexes. These two different mechanisms are formally analogous in terms of deviations from HWP, since in both cases the deviation is dependent on the difference in allele frequencies in the two sexes, irrespective of the process generating these differences. Differences in allelic frequencies between sexes may well arise by chance if the number of parents is small, and will cause an excess of heterozygotes in the progeny (Robertson, Reference Robertson1965). Heterozygote excess as a consequence of asymmetric allelic contributions of the sexes due to differential viability or fertility selection in the two sexes has been characterized for the two-allele case (Bundgaard & Christiansen, Reference Bundgaard and Christiansen1972; Andresen, Reference Andresen1978) and for multiallelic systems (Purser, Reference Purser1966; Ziehe & Gregorius, Reference Ziehe and Gregorius1981). For multiple alleles, differential allelic contributions from each sex lead to a deficiency of each homozygote and an excess of the sum of all heterozygotes. Therefore, differences in allelic frequencies between sexes will give rise to a pattern of Hardy–Weinberg deviations very similar, at first sight, to that produced by balancing viability selection at equilibrium. There is, however, a striking difference between these two patterns of Hardy–Weinberg deviations as regards the specific stage of the life cycle in which they originate. Thus, differences in allelic frequencies between sexes will produce deviations from HWP apparent at the zygotic stage; in contrast, under viability selection genotypic frequencies at the zygotic stage are expected to show HWP as a consequence of random mating, and the deviations generated by the operation of the viability selection will be mainly observed in the adult phase of the life cycle. Moreover, under differential selection between the sexes, the deviations of genotype frequencies from HWP become very small after several generations and a strong affinity of these frequencies for HWP is observed at the equilibrium (Ziehe & Gregorius, Reference Ziehe and Gregorius1981). In contrast, under a viability selection model, large deviations from HWP may be seen at the stable equilibrium, at least for those genotypes showing larger departures from the mean fitness of the population (expressions (9) and (10)).
Heterozygote excess has been detected for some multiallelic polymorphisms such as the inversion polymorphism in Drosophila (Dobzhansky & Levene, Reference Dobzhansky and Levene1948; Ruiz et al., Reference Ruiz, Fontdevila, Santos, Seoane and Torroja1986) or the polymorphisms of the human β-globin gene (Cavalli-Sforza & Bodmer, Reference Cavalli-Sforza and Bodmer1971, pp. 161–165) and HLA complex (Hedrick, Reference Hedrick1990; Markov et al., Reference Markov, Hedrick, Zuerlein, Danilovs, Martin, Vyvial and Armstrong1993; Chen et al., Reference Chen, Hollenbach, Trachtenberg, Just, Carrington, Rønningen, Begovich, King, McWeeney, Mack, Erlich and Thomson1999). This excess is thought to be the result of the operation of natural selection. However, analysis of multiallelic deviations from HWP through the estimation of f ii fixation indices has rarely been carried out for such polymorphisms, since until now there was no reference model to interpret the observed patterns of multiallelic deviations generated by selection. Certainly, analysis of the heterozygote excess associated with adaptive polymorphisms in terms of multiallelic deviations may give valuable information on the mechanism of balancing selection responsible for the maintenance of such polymorphisms. As discussed above, the occurrence of a global heterozygote excess associated with a deficiency of each and every one of the homozygotes (f ii*<0, for all i=1, 2......k) is strong evidence suggesting that a multiallelic polymorphism is at equilibrium due to viability selection. Otherwise, when such a pattern of multiallelic deviations is not seen, either the population is not at equilibrium, or some mechanism of balancing selection other than viability selection must be responsible for maintaining the observed multiallelic polymorphism.



