Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T11:40:20.641Z Has data issue: false hasContentIssue false
  • English
  • Français

ZETA ELEMENTS IN DEPTH 3 AND THE FUNDAMENTAL LIE ALGEBRA OF THE INFINITESIMAL TATE CURVE

Part of: Discontinuous groups and automorphic forms Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  05 January 2017

FRANCIS BROWN
FRANCIS BROWN*
Affiliation:
All Souls College, Oxford, Oxford OX1 4AL, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

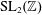This paper draws connections between the double shuffle equations and structure of associators; Hain and Matsumoto’s universal mixed elliptic motives; and the Rankin–Selberg method for modular forms for $\text{SL}_{2}(\mathbb{Z})$. We write down explicit formulae for zeta elements 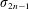$\unicode[STIX]{x1D70E}_{2n-1}$ (generators of the Tannaka Lie algebra of the category of mixed Tate motives over 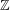$\mathbb{Z}$) in depths up to four, give applications to the Broadhurst–Kreimer conjecture, and solve the double shuffle equations for multiple zeta values in depths two and three.

MSC classification

Primary: 11M32: Multiple Dirichlet series and zeta functions and multizeta values
Secondary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e1
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2017

References

Arbesfeld, N. and Enriquez, B., ‘On a lower central series filtration of the Grothendieck–Teichmüller Lie algebra grt 1 ’, Mosc. Math. J. 15(2) (2015), 205–256, 403.Google Scholar
Belyi, G. V., ‘On Galois extensions of a maximal cyclotomic field’, Math. USSR Izvestiya 14 (1980), 247–256.CrossRefGoogle Scholar
Brown, F., Anatomy of an associator, notes (see also http://www.ihes.fr/∼brown/AnatomyBeamer.pdf).Google Scholar
Brown, F., ‘Mixed Tate motives over ℤ’, Ann. of Math. (2) 175(1) (2012), 949–976.Google Scholar
Brown, F., ‘On the decomposition of motivic multiple zeta values’, inGalois–Teichmüller Theory and Arithmetic Geometry, Advanced Studies in Pure Mathematics, 63 (Math. Soc. Japan, Tokyo, 2012), 31–58.CrossRefGoogle Scholar
Brown, F., ‘Motivic periods and the projective line minus 3 points’, in Proceedings of the ICM, 2014, arXiv:1407.5165.Google Scholar
Brown, F., ‘Depth-graded motivic multiple zeta values’, Preprint, 2013, arXiv:1301.3053.Google Scholar
Brown, F., ‘Multiple modular values for $\text{SL}_{2}(\mathbb{Z})$ ’, Preprint, 2014, arXiv:1407.5167.Google Scholar
Broadhurst, D. and Kreimer, D., ‘Association of multiple zeta values with positive knots via Feynman diagrams up to 9 loops’, Phys. Lett. B 393(3–4) (1997), 403–412.Google Scholar
Blümlein, J., Broadhurst, D. J. and Vermaseren, J. A. M., ‘The multiple zeta value data mine’, Comput. Phys. Comm. 181 (2010), 582–625.Google Scholar
Calaque, D., Enriquez, B. and Etingof, P., ‘Universal KZB equations: the elliptic case’, inAlgebra, Arithmetic, and Geometry: in honor of Yu. I. Manin. Vol. I, Progress in Mathematics, 269 (Birkhäuser Boston, Inc., Boston, MA, 2009), 165–266.Google Scholar
Deligne, P. and Goncharov, A. B., ‘Groupes fondamentaux motiviques de Tate mixte’, Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 1–56.Google Scholar
Drinfeld, V., ‘On quasi-triangular quasi-Hopf algebras and some group closely related with Gal(ℚ/ℚ)’, Algebra i Analiz 2(4) (1990), 149–181.Google Scholar
Ecalle, J., ‘ARI/GARI, la dimorphie et l’arithmétique des multizêtas: un premier bilan’, J. Théor. Nombres Bordeaux 15(2) (2003), 411–478.Google Scholar
Ecalle, J., ‘Multizetas, perinomal numbers, arithmetical dimorphy, and ARI/GARI’, Ann. Fac. Sci. Toulouse Math. (6) 13(4) (2004), 683–708.Google Scholar
Enriques, B. and Lochak, P., ‘Homology of depth-graded motivic Lie algebras and koszulity’, Preprint, 2014, arXiv:1407.4060.Google Scholar
Furusho, H., ‘Double shuffle relation for associators’, Ann. of Math. (2) 174(1) (2011), 341–360.Google Scholar
Gangl, H., Kaneko, M. and Zagier, D., ‘Double zeta values and modular forms’, inAutomorphic Forms and Zeta Functions (World Scientific Publishing, Hackensack, NJ, 2006), 71–106.Google Scholar
Glanois, C., ‘Periods of the motivic fundamental groupoid of $\mathbb{P}^{1}\backslash \{0,\unicode[STIX]{x1D707}_{N},\infty \}$ , PhD Thesis, Université Pierre et Marie Curie, 2016.Google Scholar
Goncharov, A. B., ‘The dihedral Lie algebras and Galois symmetries of 𝜋1 (l)(ℙ1 - ({0, ∞}∪𝜇 N ))’, Duke Math. J. 110(3) (2001), 397–487. (English summary).Google Scholar
Goncharov, A. B., ‘Multiple polylogarithms, cyclotomy and modular complexes’, Math. Res. Lett. 5(4) (1998), 497–516.Google Scholar
Grothendieck, A., ‘Esquisse d’un programme’, 1984. http://matematicas.unex.es/∼navarro/res/esquissefr.pdf.Google Scholar
Hain, R., ‘Notes on the Universal Elliptic KZB Equation’, Preprint, 2013, arXiv:1309.0580.Google Scholar
Hain, R., ‘The Hodge–de Rham theory of modular groups’, inRecent Advances in Hodge Theory, London Mathematical Society Lecture Note Series, 427 (Cambridge University Press, Cambridge, 2016), 422–514.CrossRefGoogle Scholar
Hain, R. and Matsumoto, M., ‘Universal mixed elliptic motives’, Preprint, 2015,arXiv:1512.03975.Google Scholar
Ihara, Y. and Takao, N., Seminar talk (May 1993).Google Scholar
Kohnen, W. and Zagier, D., ‘Modular forms with rational periods’, inModular Forms (Durham, 1983), Ellis Horwood Ser. Math. Appl.: Statist. Oper. Res. (Horwood, Chichester, 1984), 197–249.Google Scholar
Levin, A. and Racinet, G., ‘Towards multiple elliptic polylogarithms’, Preprint, 2007,arXiv:math/0703237.Google Scholar
Manin, Y., ‘Iterated Shimura integrals’, Mosc. Math. J. 5 (2005), 869–881.Google Scholar
Manin, Y., ‘Iterated integrals of modular forms and noncommutative modular symbols’, inAlgebraic Geometry and Number Theory, Progress in Mathematics, 253 (Birkhäuser Boston, Boston, MA, 2006), 565–597.CrossRefGoogle Scholar
McCallum, W. and Sharifi, R., ‘A cup product in the Galois cohomology of number fields’, Duke Math. J. 120(2) (2003), 269–310.Google Scholar
Nakamura, H., ‘Tangential base points and Eisenstein power series’, inAspects of Galois Theory (Gainesville, FL, 1996), London Mathematical Society Lecture Note Series, 256 (Cambridge University Press, Cambridge, 1999), 202–217.Google Scholar
Panzer, E., ‘The parity theorem for multiple polylogarithms’, J. Number Theory 172 (2017), 93–113.Google Scholar
Pollack, A., ‘Relations between derivations arising from modular forms’, Undergraduate Thesis, Duke University, 2009.Google Scholar
Racinet, G., ‘Doubles mélanges des polylogarithmes multiples aux racines de l’unité’, Publ. Math. Inst. Hautes Études Sci. 95 (2002), 185–231.Google Scholar
Tsumura, H., ‘Combinatorial relations for Euler–Zagier sums’, Acta Arith. 111 (2004), 27–42.Google Scholar
Tsunogai, H., ‘On some derivations of Lie algebras related to Galois representations’, Publ. Res. Inst. Math. Sci. 31 (1995), 113–134.Google Scholar
Zagier, D., ‘Periods of modular forms, traces of Hecke operators, and multiple zeta values’, RIMS Kokyuroku 843 (1993), 162–170.Google Scholar
Zagier, D. B., ‘Evaluation of the multiple zeta values 𝜁(2, …, 2, 3, 2, …, 2)’, Ann. of Math. (2) 175(2) (2012), 977–1000.CrossRefGoogle Scholar