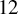1 Introduction
Let k be an algebraically closed field of characteristic
![]() $p> 0$
, and let G be a finite group. Associated to each block b of
$p> 0$
, and let G be a finite group. Associated to each block b of
![]() $kG$
, there is a saturated fusion system
$kG$
, there is a saturated fusion system
![]() $\mathcal {F} = \mathcal {F}_S(b)$
over the defect group S of the block in which the morphisms between subgroups are given by conjugation by elements of G preserving the corresponding Brauer pairs [Reference Aschbacher, Kessar and OliverAKO11, Reference CravenCra11]. Several questions in the modular representation theory of finite groups concern the connection between representation theoretic properties of
$\mathcal {F} = \mathcal {F}_S(b)$
over the defect group S of the block in which the morphisms between subgroups are given by conjugation by elements of G preserving the corresponding Brauer pairs [Reference Aschbacher, Kessar and OliverAKO11, Reference CravenCra11]. Several questions in the modular representation theory of finite groups concern the connection between representation theoretic properties of
![]() $kGb$
and the category
$kGb$
and the category
![]() $\mathcal {F}$
. However, it is known that for many purposes
$\mathcal {F}$
. However, it is known that for many purposes
![]() $\mathcal {F}$
does not, in general, retain enough information about
$\mathcal {F}$
does not, in general, retain enough information about
![]() $kGb$
-mod. For example, it does not determine the number of simple modules in b, in part because it retains too little of the
$kGb$
-mod. For example, it does not determine the number of simple modules in b, in part because it retains too little of the
![]() $p'$
-structure of p-local subgroups. On the other hand, the block b also determines a family of degree 2 cohomology classes
$p'$
-structure of p-local subgroups. On the other hand, the block b also determines a family of degree 2 cohomology classes
![]() $\alpha _Q \in H^2(\operatorname {Aut}_{\mathcal {F}}(Q), k^\times )$
, for
$\alpha _Q \in H^2(\operatorname {Aut}_{\mathcal {F}}(Q), k^\times )$
, for
![]() $Q \in \mathcal {F}^c$
an
$Q \in \mathcal {F}^c$
an
![]() $\mathcal {F}$
-centric subgroup, by work of Külshammer and Puig (see [Reference Aschbacher, Kessar and OliverAKO11, IV.5.5]). This family is expected to supply the missing information away from the prime p. The Külshammer-Puig classes are compatible in the sense that, by [Reference LinckelmannLin19, Theorem 8.14.5], they determine an element
$\mathcal {F}$
-centric subgroup, by work of Külshammer and Puig (see [Reference Aschbacher, Kessar and OliverAKO11, IV.5.5]). This family is expected to supply the missing information away from the prime p. The Külshammer-Puig classes are compatible in the sense that, by [Reference LinckelmannLin19, Theorem 8.14.5], they determine an element
where
![]() $[S(\mathcal {F}^c)]$
is the partially ordered set of
$[S(\mathcal {F}^c)]$
is the partially ordered set of
![]() $\mathcal {F}$
-isomorphism classes of chains
$\mathcal {F}$
-isomorphism classes of chains
![]() $\sigma =(X_0 < X_1 < \cdots < X_n)$
of
$\sigma =(X_0 < X_1 < \cdots < X_n)$
of
![]() $\mathcal {F}$
-centric subgroups, and
$\mathcal {F}$
-centric subgroups, and
![]() $\mathcal {A}_{\mathcal {F}}^2$
is the covariant functor which sends a chain
$\mathcal {A}_{\mathcal {F}}^2$
is the covariant functor which sends a chain
![]() $\sigma $
to
$\sigma $
to
![]() $H^2(\operatorname {Aut}_{\mathcal {F}}(\sigma ), k^\times )$
. Here,
$H^2(\operatorname {Aut}_{\mathcal {F}}(\sigma ), k^\times )$
. Here,
![]() $\operatorname {Aut}_{\mathcal {F}}(\sigma ) \leqslant \operatorname {Aut}_{\mathcal {F}}(X_n)$
is the group of automorphisms in
$\operatorname {Aut}_{\mathcal {F}}(\sigma ) \leqslant \operatorname {Aut}_{\mathcal {F}}(X_n)$
is the group of automorphisms in
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $X_n$
preserving all members
$X_n$
preserving all members
![]() $X_i$
of the chain. For example, if b is the principal block of
$X_i$
of the chain. For example, if b is the principal block of
![]() $kG$
, then
$kG$
, then
![]() $\alpha $
is always the trivial class [Reference Aschbacher, Kessar and OliverAKO11, IV.5.32].
$\alpha $
is always the trivial class [Reference Aschbacher, Kessar and OliverAKO11, IV.5.32].
Thus, by a Külshammer-Puig pair, we mean a pair
![]() $(\mathcal {F},\alpha )$
, where
$(\mathcal {F},\alpha )$
, where
![]() $\mathcal {F}$
is a saturated fusion system on a p-group S and
$\mathcal {F}$
is a saturated fusion system on a p-group S and
![]() $\alpha $
is an element of
$\alpha $
is an element of
![]() $\lim _{[S(\mathcal {F}^c)]} \mathcal {A}_{\mathcal {F}}^2$
. Given such a pair
$\lim _{[S(\mathcal {F}^c)]} \mathcal {A}_{\mathcal {F}}^2$
. Given such a pair
![]() $(\mathcal {F},\alpha )$
arising from a block b, the quantity
$(\mathcal {F},\alpha )$
arising from a block b, the quantity
counts the number of
![]() $kGb$
-weights. Here,
$kGb$
-weights. Here,
![]() $k_{\alpha _Q}\operatorname {Out}_{\mathcal {F}}(Q)$
is the algebra obtained from the group algebra
$k_{\alpha _Q}\operatorname {Out}_{\mathcal {F}}(Q)$
is the algebra obtained from the group algebra
![]() $k\operatorname {Out}_{\mathcal {F}}(Q)$
by twisting with
$k\operatorname {Out}_{\mathcal {F}}(Q)$
by twisting with
![]() $\alpha _Q$
[Reference Aschbacher, Kessar and OliverAKO11, IV.5.36],
$\alpha _Q$
[Reference Aschbacher, Kessar and OliverAKO11, IV.5.36],
![]() $z(-)$
denotes the number of projective simple modules, and the sum is taken over a set of representatives for the conjugacy classes of
$z(-)$
denotes the number of projective simple modules, and the sum is taken over a set of representatives for the conjugacy classes of
![]() $\mathcal {F}$
-centric and
$\mathcal {F}$
-centric and
![]() $\mathcal {F}$
-radical subgroups. Thus, Alperin’s Weight conjecture says that
$\mathcal {F}$
-radical subgroups. Thus, Alperin’s Weight conjecture says that
![]() $\mathbf {w}(\mathcal {F},\alpha )$
is the number of simple
$\mathbf {w}(\mathcal {F},\alpha )$
is the number of simple
![]() $kGb$
-modules [Reference Aschbacher, Kessar and OliverAKO11, IV.5.46].
$kGb$
-modules [Reference Aschbacher, Kessar and OliverAKO11, IV.5.46].
There is always a natural map
![]() $H^{2}(\mathcal {F}^c, k^{\times }) \to \lim _{[S(\mathcal {F}^c)]} \mathcal {A}_{\mathcal {F}}^2$
, and the gluing problem asks whether this map is surjective (see [Reference LinckelmannLin09] and [Reference LibmanLib11] for further details). Linckelmann has shown that Alperin’s conjecture has a structural reformulation in terms of algebras constructed from p-local finite groups, provided the gluing problem always has a solution [Reference LinckelmannLin04]. However, while the weight conjecture has relevance for actual blocks only, the gluing problem is a question about the Külshammer-Puig pair itself and can be considered: (1) when
$H^{2}(\mathcal {F}^c, k^{\times }) \to \lim _{[S(\mathcal {F}^c)]} \mathcal {A}_{\mathcal {F}}^2$
, and the gluing problem asks whether this map is surjective (see [Reference LinckelmannLin09] and [Reference LibmanLib11] for further details). Linckelmann has shown that Alperin’s conjecture has a structural reformulation in terms of algebras constructed from p-local finite groups, provided the gluing problem always has a solution [Reference LinckelmannLin04]. However, while the weight conjecture has relevance for actual blocks only, the gluing problem is a question about the Külshammer-Puig pair itself and can be considered: (1) when
![]() $\mathcal {F}$
is the fusion system of a block, but of no block with the specified compatible family
$\mathcal {F}$
is the fusion system of a block, but of no block with the specified compatible family
![]() $\alpha $
, and (2) when
$\alpha $
, and (2) when
![]() $\mathcal {F}$
is the fusion system of no block at all. Thus, we are interested in investigating such pairs disembodied from an actual block as a way of gauging the degree to which certain questions, and potential answers to those questions, are p-locally determined. A direct study of Külshammer-Puig pairs might reveal, for example, that there is an exotic pair as in (1) or (2) that does not satisfy the gluing problem. At this stage, such a possibility seems unlikely. On the other hand, and conversely, we would be very interested in a structural explanation why the gluing problem should hold in general, and it seems reasonable to expect that such an explanation would apply to all such pairs, exotic or not.
$\mathcal {F}$
is the fusion system of no block at all. Thus, we are interested in investigating such pairs disembodied from an actual block as a way of gauging the degree to which certain questions, and potential answers to those questions, are p-locally determined. A direct study of Külshammer-Puig pairs might reveal, for example, that there is an exotic pair as in (1) or (2) that does not satisfy the gluing problem. At this stage, such a possibility seems unlikely. On the other hand, and conversely, we would be very interested in a structural explanation why the gluing problem should hold in general, and it seems reasonable to expect that such an explanation would apply to all such pairs, exotic or not.
In this paper, we consider Külshammer-Puig pairs associated with the exotic family
![]() $\operatorname {Sol}(q)$
of Benson-Solomon
$\operatorname {Sol}(q)$
of Benson-Solomon
![]() $2$
-fusion systems [Reference Levi and OliverLO02, Reference Aschbacher and ChermakAC10]. Although these are defined for any odd prime power q, the fusion systems
$2$
-fusion systems [Reference Levi and OliverLO02, Reference Aschbacher and ChermakAC10]. Although these are defined for any odd prime power q, the fusion systems
![]() $\operatorname {Sol}(q)$
and
$\operatorname {Sol}(q)$
and
![]() $\operatorname {Sol}(q')$
are isomorphic if
$\operatorname {Sol}(q')$
are isomorphic if
![]() $q^{2}-1$
and
$q^{2}-1$
and
![]() $q^{\prime 2}-1$
have the same
$q^{\prime 2}-1$
have the same
![]() $2$
-part. A Benson-Solomon system is known not to be the fusion system of any genuine block. This is a result of Kessar for the smallest such system [Reference KessarKes06], while Craven extended Kessar’s proof to the general case [Reference CravenCra11, Theorem 9.34]. Thus, there exists no genuine “Benson-Solomon block” of the title. For the purposes of this paper, we simply regard a Külshammer-Puig pair of the form
$2$
-part. A Benson-Solomon system is known not to be the fusion system of any genuine block. This is a result of Kessar for the smallest such system [Reference KessarKes06], while Craven extended Kessar’s proof to the general case [Reference CravenCra11, Theorem 9.34]. Thus, there exists no genuine “Benson-Solomon block” of the title. For the purposes of this paper, we simply regard a Külshammer-Puig pair of the form
![]() $(\mathcal {F},\alpha )$
with
$(\mathcal {F},\alpha )$
with
![]() $\mathcal {F}$
a Benson-Solomon system as an avatar of the nonexistent block, one which allows us still to compute some local invariants, such as the number of weights, that such a block would have if it existed.Footnote 1
$\mathcal {F}$
a Benson-Solomon system as an avatar of the nonexistent block, one which allows us still to compute some local invariants, such as the number of weights, that such a block would have if it existed.Footnote 1
Our first theorem determines the possible Külshammer-Puig classes that these fusion systems support.
Theorem 1.1. Let
![]() $\mathcal {F} = \operatorname {Sol}(q)$
. Then
$\mathcal {F} = \operatorname {Sol}(q)$
. Then
That is, each Benson-Solomon system supports a unique Külshammer-Puig pair.
Theorem 1.1 is shown by explicitly computing the
![]() $\mathcal {F}$
-conjugacy classes of centric radical subgroups along with their outer automorphism groups in
$\mathcal {F}$
-conjugacy classes of centric radical subgroups along with their outer automorphism groups in
![]() $\mathcal {F}$
. The results of [Reference Aschbacher and ChermakAC10, Section 10] go a long way towards accomplishing such a task, but more details are required for the present applications. In Section 2 we refine the results of [Reference Aschbacher and ChermakAC10] to prove the following.
$\mathcal {F}$
. The results of [Reference Aschbacher and ChermakAC10, Section 10] go a long way towards accomplishing such a task, but more details are required for the present applications. In Section 2 we refine the results of [Reference Aschbacher and ChermakAC10] to prove the following.
Theorem 1.2. Let
![]() $\mathcal {F} = \operatorname {Sol}(q)$
. Representatives for the
$\mathcal {F} = \operatorname {Sol}(q)$
. Representatives for the
![]() $\mathcal {F}$
-conjugacy classes of
$\mathcal {F}$
-conjugacy classes of
![]() $\mathcal {F}$
-centric radical subgroups, together with their
$\mathcal {F}$
-centric radical subgroups, together with their
![]() $\mathcal {F}$
-outer automorphism groups, are listed in Tables 1 and 4.
$\mathcal {F}$
-outer automorphism groups, are listed in Tables 1 and 4.
Theorem 1.3. The number of weights in the unique pair of Theorem 1.1 is
independently of q.
The Benson-Solomon systems are finite versions of the simply connected
![]() $2$
-compact group
$2$
-compact group
![]() $DI(4)$
of Dwyer and Wilkerson [Reference BensonBen94]. As such, they have an associated
$DI(4)$
of Dwyer and Wilkerson [Reference BensonBen94]. As such, they have an associated
![]() $2$
-adic reflection group
$2$
-adic reflection group
![]() $W = W(\operatorname {Sol}(q)) \cong C_2 \times \operatorname {GL}_3(2)$
, which in
$W = W(\operatorname {Sol}(q)) \cong C_2 \times \operatorname {GL}_3(2)$
, which in
![]() $\operatorname {Sol}(q)$
, appears as the automorphism group of a finite
$\operatorname {Sol}(q)$
, appears as the automorphism group of a finite
![]() $2$
-torus of rank
$2$
-torus of rank
![]() $3$
, and
$3$
, and
![]() $\mathbf {w}(\operatorname {Sol}(q),0) = 12 = |\operatorname {Irr}(W)|$
. This was later proved for all finite versions of simply connected
$\mathbf {w}(\operatorname {Sol}(q),0) = 12 = |\operatorname {Irr}(W)|$
. This was later proved for all finite versions of simply connected
![]() $\ell $
-compact groups as long as
$\ell $
-compact groups as long as
![]() $\ell $
is “very good” for W [Reference Kessar, Malle and SemeraroKMS20, Theorem 1]. But note that the prime
$\ell $
is “very good” for W [Reference Kessar, Malle and SemeraroKMS20, Theorem 1]. But note that the prime
![]() $2$
is bad for
$2$
is bad for
![]() $W(\operatorname {Sol}(q))$
.
$W(\operatorname {Sol}(q))$
.
We prove Theorem 1.3 in Section 4 by explicitly computing
![]() $z(k\operatorname {Out}_{\mathcal {F}}(Q))$
for each of the groups Q appearing in Tables 1 and 4 of Theorem 1.2.
$z(k\operatorname {Out}_{\mathcal {F}}(Q))$
for each of the groups Q appearing in Tables 1 and 4 of Theorem 1.2.
Beyond the weight conjecture, and assuming its validity, we have in mind other counting questions that can be considered for Külshammer-Puig pairs without reference to a group or a block. For example, Malle and Robinson recently conjectured that if b is a p-block associated to a finite group G, then the number of simple
![]() $kG$
-modules in b should be bounded by
$kG$
-modules in b should be bounded by
![]() $p^{s(S)}$
, where S is a defect group of b and
$p^{s(S)}$
, where S is a defect group of b and
![]() $s(S)$
denotes the sectional rank of S, namely, the largest rank of an elementary abelian section [Reference Malle and RobinsonMR17]. Moreover, they verified their conjecture in a large number of cases where the weight conjecture holds. In Lemma 2.19, we observe that the sectional rank of S is
$s(S)$
denotes the sectional rank of S, namely, the largest rank of an elementary abelian section [Reference Malle and RobinsonMR17]. Moreover, they verified their conjecture in a large number of cases where the weight conjecture holds. In Lemma 2.19, we observe that the sectional rank of S is
![]() $6$
, and so the following conjecture, which was suggested to us by Kessar and Linckelmann, also holds easily for
$6$
, and so the following conjecture, which was suggested to us by Kessar and Linckelmann, also holds easily for
![]() $\operatorname {Sol}(q)$
.
$\operatorname {Sol}(q)$
.
Conjecture 1.4. Let
![]() $(\mathcal {F},\alpha )$
be a Külshammer-Puig pair, where
$(\mathcal {F},\alpha )$
be a Külshammer-Puig pair, where
![]() $\mathcal {F}$
is a saturated fusion system on S. Then
$\mathcal {F}$
is a saturated fusion system on S. Then
![]() $\mathbf {w}(\mathcal {F},\alpha ) \le p^{s(S)}$
.
$\mathbf {w}(\mathcal {F},\alpha ) \le p^{s(S)}$
.
This conjecture is just one small example in a host of other conjectures which are certain purely local analogues of the various local-to-global conjectures in the modular representation theory of finite groups. The local conjectures by their nature do not discriminate between realizable and exotic Külshammer-Puig pairs. They are discussed more fully in a sequel to this paper [Reference Kessar, Linckelmann, Lynd and SemeraroKLLS19].
Outline and notation for the tables
After recalling certain initial results about fusion systems and the
![]() $2$
-local structure of
$2$
-local structure of
![]() $\operatorname {SL}_2(q)$
, we set up in Section 2 notation for working in the Benson-Solomon systems and identify the important subgroups of the Aschbacher-Chermak free amalgamated product which realizes the systems. Section 2.7 provides an initial classification of some centric radical subgroups, namely, the centric radical subgroups lying above the
$\operatorname {SL}_2(q)$
, we set up in Section 2 notation for working in the Benson-Solomon systems and identify the important subgroups of the Aschbacher-Chermak free amalgamated product which realizes the systems. Section 2.7 provides an initial classification of some centric radical subgroups, namely, the centric radical subgroups lying above the
![]() $2$
-torsion in a maximal torus.
$2$
-torsion in a maximal torus.
Section 3 contains the proof of Theorem 1.2, where the smallest Benson-Solomon system is handled separately (Section 3.1) from the larger ones (Section 3.2). The results are summarized in Tables 1 and 4. Those tables give a list of subgroups whose notation was fixed previously in Notation 2.11, Notation 2.12, Section 2.6, (3.1), or Notation 3.3.
Theorem 1.3 is proved in Section 4. Finally, in Section 5, we compute the Schur multipliers of the outer automorphism groups to give a proof of Theorem 1.1.
2 The Benson-Solomon fusion systems
2.1 Fusion system preliminaries
Throughout this paper, our group-theoretic nomenclature is standard and follows [Reference WilsonWil09], and we are usually consistent with the fusion-theoretic terminology and notation of [Reference Aschbacher, Kessar and OliverAKO11]. One exception to this is that we use exponential notation for images of subgroups and elements under a morphism in a fusion system, as described below. A fusion system on a finite p-group S is a category with object set the set of subgroups of S and with morphisms that are injective group homomorphisms, subject to two weak axioms. The standard example of a fusion system is that of a finite group G with Sylow p-subgroup S, where the morphisms are the conjugation homomorphisms between subgroups of S induced by elements of the group G, and which is denoted
![]() $\mathcal {F}_S(G)$
. Due to the validity of Sylow’s theorem in G and its p-local subgroups, the standard example satisfies two additional saturation axioms, the Sylow and Extension axioms [Reference Broto, Levi and OliverBLO03, Definition 1.2]. All fusion systems in this paper are assumed to be (or known already to be) saturated unless otherwise stated, and we will sometimes drop that adjective and speak simply of a fusion system when there is no cause for confusion. For this subsection, we fix a saturated fusion system
$\mathcal {F}_S(G)$
. Due to the validity of Sylow’s theorem in G and its p-local subgroups, the standard example satisfies two additional saturation axioms, the Sylow and Extension axioms [Reference Broto, Levi and OliverBLO03, Definition 1.2]. All fusion systems in this paper are assumed to be (or known already to be) saturated unless otherwise stated, and we will sometimes drop that adjective and speak simply of a fusion system when there is no cause for confusion. For this subsection, we fix a saturated fusion system
![]() $\mathcal {F}$
over the p-group S. By analogy with the standard example, two subgroups of S are said to be
$\mathcal {F}$
over the p-group S. By analogy with the standard example, two subgroups of S are said to be
![]() $\mathcal {F}$
-conjugate if they are isomorphic in the category
$\mathcal {F}$
-conjugate if they are isomorphic in the category
![]() $\mathcal {F}$
. For a morphism
$\mathcal {F}$
. For a morphism
![]() $\varphi \colon P \to Q$
in
$\varphi \colon P \to Q$
in
![]() $\mathcal {F}$
, we write
$\mathcal {F}$
, we write
![]() $P^\varphi $
for the image of
$P^\varphi $
for the image of
![]() $\varphi $
. Similarly,
$\varphi $
. Similarly,
![]() $x^\varphi $
denotes the image of an element x under a morphism whose domain contains x.
$x^\varphi $
denotes the image of an element x under a morphism whose domain contains x.
Definition 2.1. Fix a subgroup
![]() $P \leqslant S$
. We say that P is
$P \leqslant S$
. We say that P is
-
(a) fully
 $\mathcal {F}$
-normalized if
$\mathcal {F}$
-normalized if
 $|N_S(P)| \geqslant |N_S(Q)|$
whenever Q is
$|N_S(P)| \geqslant |N_S(Q)|$
whenever Q is
 $\mathcal {F}$
-conjugate to P,
$\mathcal {F}$
-conjugate to P, -
(b)
 $\mathcal {F}$
-centric if
$\mathcal {F}$
-centric if
 $C_S(Q)=Z(Q)$
for each
$C_S(Q)=Z(Q)$
for each
 $\mathcal {F}$
-conjugate Q of P,
$\mathcal {F}$
-conjugate Q of P, -
(c)
 $\mathcal {F}$
-radical if
$\mathcal {F}$
-radical if
 $O_p(\operatorname {Out}_{\mathcal {F}}(P))=1$
,
$O_p(\operatorname {Out}_{\mathcal {F}}(P))=1$
, -
(d)
 $\mathcal {F}$
-centric radical if it is both
$\mathcal {F}$
-centric radical if it is both
 $\mathcal {F}$
-centric and
$\mathcal {F}$
-centric and
 $\mathcal {F}$
-radical, and
$\mathcal {F}$
-radical, and -
(e) weakly
 $\mathcal {F}$
-closed if P is the only
$\mathcal {F}$
-closed if P is the only
 $\mathcal {F}$
-conjugate of P,
$\mathcal {F}$
-conjugate of P, -
(f) strongly
 $\mathcal {F}$
-closed if each
$\mathcal {F}$
-closed if each
 $\mathcal {F}$
-conjugate of a subgroup of P is contained in P.
$\mathcal {F}$
-conjugate of a subgroup of P is contained in P.
Denote by
![]() $\mathcal {F}^c$
,
$\mathcal {F}^c$
,
![]() $\mathcal {F}^r$
, and
$\mathcal {F}^r$
, and
![]() $\mathcal {F}^{cr}$
the collection of
$\mathcal {F}^{cr}$
the collection of
![]() $\mathcal {F}$
-centric,
$\mathcal {F}$
-centric,
![]() $\mathcal {F}$
-radical, and
$\mathcal {F}$
-radical, and
![]() $\mathcal {F}$
-centric radical subgroups of S, respectively.
$\mathcal {F}$
-centric radical subgroups of S, respectively.
The collections
![]() $\mathcal {F}^c$
,
$\mathcal {F}^c$
,
![]() $\mathcal {F}^{r}$
, and
$\mathcal {F}^{r}$
, and
![]() $\mathcal {F}^{cr}$
are all closed under
$\mathcal {F}^{cr}$
are all closed under
![]() $\mathcal {F}$
-conjugacy. Also, the
$\mathcal {F}$
-conjugacy. Also, the
![]() $\mathcal {F}$
-centric subgroups are closed under passing to overgroups.
$\mathcal {F}$
-centric subgroups are closed under passing to overgroups.
Remark 2.2. Let G be a finite group with Sylow p-subgroup S. A p-subgroup P of G is said to be p-radical in G if
![]() $O_p(N_G(P)/P) = 1$
. By contrast, a subgroup P is
$O_p(N_G(P)/P) = 1$
. By contrast, a subgroup P is
![]() $\mathcal {F}_S(G)$
-radical if and only if
$\mathcal {F}_S(G)$
-radical if and only if
![]() $O_p(N_G(P)/PC_G(P)) = 1$
. The collection of p-radical subgroups of G contained in S does not coincide, in general, with the collection of
$O_p(N_G(P)/PC_G(P)) = 1$
. The collection of p-radical subgroups of G contained in S does not coincide, in general, with the collection of
![]() $\mathcal {F}_S(G)$
-radical subgroups.
$\mathcal {F}_S(G)$
-radical subgroups.
For example, let
![]() $p = 3$
and
$p = 3$
and
![]() $G = G_1 \times G_2$
with
$G = G_1 \times G_2$
with
![]() $G_i \cong D_6$
. The subgroup
$G_i \cong D_6$
. The subgroup
![]() $P = S \cap G_1$
has order
$P = S \cap G_1$
has order
![]() $3$
with
$3$
with
![]() $N_G(P)/P \cong C_2 \times D_6$
, so P is not
$N_G(P)/P \cong C_2 \times D_6$
, so P is not
![]() $3$
-radical in G. However,
$3$
-radical in G. However,
![]() $\operatorname {Out}_{\mathcal {F}_S(G)}(P) = N_G(P)/PC_G(P) \cong C_2$
, so P is
$\operatorname {Out}_{\mathcal {F}_S(G)}(P) = N_G(P)/PC_G(P) \cong C_2$
, so P is
![]() $\mathcal {F}_S(G)$
-radical. Conversely, take
$\mathcal {F}_S(G)$
-radical. Conversely, take
![]() $p = 2$
, but instead
$p = 2$
, but instead
![]() $G = D_{24}$
, and P of order
$G = D_{24}$
, and P of order
![]() $4$
in the cyclic maximal subgroup. Then
$4$
in the cyclic maximal subgroup. Then
![]() $\operatorname {Out}_{\mathcal {F}_S(G)}(P) \cong C_2$
so P is not
$\operatorname {Out}_{\mathcal {F}_S(G)}(P) \cong C_2$
so P is not
![]() $\mathcal {F}_S(G)$
-radical, but
$\mathcal {F}_S(G)$
-radical, but
![]() $N_G(P)/P \cong D_{6}$
, so P is
$N_G(P)/P \cong D_{6}$
, so P is
![]() $2$
-radical in G. This distinction is important in Lemma 2.7 below, where both concepts appear simultaneously. It is also relevant in Chevalley groups
$2$
-radical in G. This distinction is important in Lemma 2.7 below, where both concepts appear simultaneously. It is also relevant in Chevalley groups
![]() $G = G(q)$
with q odd, which have an element in the Weyl group inverting a split maximal torus. When such a torus has a nontrivial odd order normal subgroup (often the case), a Sylow
$G = G(q)$
with q odd, which have an element in the Weyl group inverting a split maximal torus. When such a torus has a nontrivial odd order normal subgroup (often the case), a Sylow
![]() $2$
-subgroup T of such a torus is
$2$
-subgroup T of such a torus is
![]() $2$
-radical in G but not radical in
$2$
-radical in G but not radical in
![]() $\mathcal {F}_S(G)$
, where S is a Sylow
$\mathcal {F}_S(G)$
, where S is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $G(q)$
containing T. This situation occurs, for example, when
$G(q)$
containing T. This situation occurs, for example, when
![]() $G(q) = \operatorname {Spin}_7(q)$
, q odd,
$G(q) = \operatorname {Spin}_7(q)$
, q odd,
![]() $q \neq 3, 5$
.
$q \neq 3, 5$
.
Definition 2.3. Fix a subgroup
![]() $P \leqslant S$
.
$P \leqslant S$
.
-
(a) The normalizer
 $N_{\mathcal {F}}(P)$
of P is the fusion system on
$N_{\mathcal {F}}(P)$
of P is the fusion system on
 $N_S(P)$
consisting of those morphisms
$N_S(P)$
consisting of those morphisms
 $\varphi \colon Q \to R$
in
$\varphi \colon Q \to R$
in
 $\mathcal {F}$
for which there exists an extension
$\mathcal {F}$
for which there exists an extension
 $\tilde {\varphi }\colon PQ \to PR$
of
$\tilde {\varphi }\colon PQ \to PR$
of
 $\varphi $
in
$\varphi $
in
 $\mathcal {F}$
, such that
$\mathcal {F}$
, such that
 $P^{\tilde {\varphi }} = P$
.
$P^{\tilde {\varphi }} = P$
. -
(b) The centralizer
 $C_{\mathcal {F}}(P)$
of P is the fusion system on
$C_{\mathcal {F}}(P)$
of P is the fusion system on
 $C_S(P)$
consisting of those morphisms
$C_S(P)$
consisting of those morphisms
 $\varphi \colon Q \to R$
in
$\varphi \colon Q \to R$
in
 $\mathcal {F}$
for which there exists an extension
$\mathcal {F}$
for which there exists an extension
 $\tilde {\varphi }\colon PQ \to PR$
of
$\tilde {\varphi }\colon PQ \to PR$
of
 $\varphi $
in
$\varphi $
in
 $\mathcal {F}$
, such that the restriction
$\mathcal {F}$
, such that the restriction
 $\tilde {\varphi }|_P$
is the identity on P.
$\tilde {\varphi }|_P$
is the identity on P. -
(c) The subgroup
 $P\leqslant S$
is normal in
$P\leqslant S$
is normal in
 $\mathcal {F}$
if
$\mathcal {F}$
if
 $\mathcal {F} = N_{\mathcal {F}}(P)$
.
$\mathcal {F} = N_{\mathcal {F}}(P)$
. -
(d)
 $\mathcal {F}$
is constrained if
$\mathcal {F}$
is constrained if
 $\mathcal {F}$
has a centric normal subgroup.
$\mathcal {F}$
has a centric normal subgroup.
These centralizer and normalizer fusion systems are not always saturated, but they are both saturated provided P is fully
![]() $\mathcal {F}$
-normalized.
$\mathcal {F}$
-normalized.
Lemma 2.4. If P is
![]() $\mathcal {F}$
-centric, then
$\mathcal {F}$
-centric, then
![]() $C_{\mathcal {F}}(P) = \mathcal {F}_{Z(P)}(Z(P))$
.
$C_{\mathcal {F}}(P) = \mathcal {F}_{Z(P)}(Z(P))$
.
Proof. Assume that P is
![]() $\mathcal {F}$
-centric. The centralizer system
$\mathcal {F}$
-centric. The centralizer system
![]() $C_{\mathcal {F}}(P)$
is a fusion system over the abelian group
$C_{\mathcal {F}}(P)$
is a fusion system over the abelian group
![]() $C_S(P) = Z(P)$
, and
$C_S(P) = Z(P)$
, and
![]() $Z(P)$
is normal in
$Z(P)$
is normal in
![]() $C_{\mathcal {F}}(P)$
from the definitions. As each morphism between subgroups of
$C_{\mathcal {F}}(P)$
from the definitions. As each morphism between subgroups of
![]() $Z(P)$
in
$Z(P)$
in
![]() $C_{\mathcal {F}}(P)$
extends to act as the identity on P, each such morphism is an identity map.
$C_{\mathcal {F}}(P)$
extends to act as the identity on P, each such morphism is an identity map.
Lemma 2.5. Suppose that
![]() $P \leqslant S$
is normal in
$P \leqslant S$
is normal in
![]() $\mathcal {F}$
. Then P is contained in every
$\mathcal {F}$
. Then P is contained in every
![]() $\mathcal {F}$
-centric radical subgroup.
$\mathcal {F}$
-centric radical subgroup.
Proof. Let
![]() $Q \in \mathcal {F}^{cr}$
. Then
$Q \in \mathcal {F}^{cr}$
. Then
![]() $\operatorname {Aut}_{PQ}(Q)$
is normal in
$\operatorname {Aut}_{PQ}(Q)$
is normal in
![]() $\operatorname {Aut}_{\mathcal {F}}(Q)$
, and so
$\operatorname {Aut}_{\mathcal {F}}(Q)$
, and so
![]() $\operatorname {Aut}_{PQ}(Q) \leqslant \operatorname {Inn}(Q)$
since Q is radical. Then
$\operatorname {Aut}_{PQ}(Q) \leqslant \operatorname {Inn}(Q)$
since Q is radical. Then
![]() $P \leqslant PQ \leqslant QC_S(Q) = Q$
with the equality because Q is centric.
$P \leqslant PQ \leqslant QC_S(Q) = Q$
with the equality because Q is centric.
The next two lemmas give applications of the Extension axiom. The second is useful for locating the
![]() $\mathcal {F}$
-centric radicals that contain a given weakly
$\mathcal {F}$
-centric radicals that contain a given weakly
![]() $\mathcal {F}$
-closed subgroup.
$\mathcal {F}$
-closed subgroup.
Lemma 2.6. Let
![]() $P' \leqslant S$
be fully
$P' \leqslant S$
be fully
![]() $\mathcal {F}$
-normalized, and let P be a subgroup of S which is
$\mathcal {F}$
-normalized, and let P be a subgroup of S which is
![]() $\mathcal {F}$
-conjugate to
$\mathcal {F}$
-conjugate to
![]() $P'$
. Then there exists a morphism
$P'$
. Then there exists a morphism
![]() $\alpha \in \operatorname {Hom}_{\mathcal {F}}(N_S(P), N_{S}(P'))$
, such that
$\alpha \in \operatorname {Hom}_{\mathcal {F}}(N_S(P), N_{S}(P'))$
, such that
![]() $P^\alpha = P'$
.
$P^\alpha = P'$
.
Proof. See [Reference Aschbacher, Kessar and OliverAKO11, I.2.6(c)].
Lemma 2.7. Let W be an
![]() $\mathcal {F}$
-centric and weakly
$\mathcal {F}$
-centric and weakly
![]() $\mathcal {F}$
-closed subgroup of S. For any subgroup P of S containing W, restriction induces an isomorphism
$\mathcal {F}$
-closed subgroup of S. For any subgroup P of S containing W, restriction induces an isomorphism
and therefore an isomorphism
Hence, the map
![]() $P \mapsto \operatorname {Out}_P(W)$
is a bijection between the collection of
$P \mapsto \operatorname {Out}_P(W)$
is a bijection between the collection of
![]() $\mathcal {F}$
-centric radical subgroups containing W and the collection of subgroups of
$\mathcal {F}$
-centric radical subgroups containing W and the collection of subgroups of
![]() $\operatorname {Out}_S(W)$
which are p-radical in the group
$\operatorname {Out}_S(W)$
which are p-radical in the group
![]() $\operatorname {Out}_{\mathcal {F}}(W)$
.
$\operatorname {Out}_{\mathcal {F}}(W)$
.
Proof. Consider the restriction map
![]() $\rho \colon \operatorname {Aut}_{\mathcal {F}}(P) \to N_{\operatorname {Aut}_{\mathcal {F}}(W)}(\operatorname {Aut}_P(W))$
, under which
$\rho \colon \operatorname {Aut}_{\mathcal {F}}(P) \to N_{\operatorname {Aut}_{\mathcal {F}}(W)}(\operatorname {Aut}_P(W))$
, under which
![]() $\operatorname {Aut}_W(P)$
maps onto
$\operatorname {Aut}_W(P)$
maps onto
![]() $\operatorname {Inn}(W)$
and under which
$\operatorname {Inn}(W)$
and under which
![]() $\operatorname {Inn}(P)$
maps onto
$\operatorname {Inn}(P)$
maps onto
![]() $\operatorname {Aut}_P(W)$
. Since W is weakly closed, it is fully
$\operatorname {Aut}_P(W)$
. Since W is weakly closed, it is fully
![]() $\mathcal {F}$
-normalized by Lemma 2.6. A direct application of the Extension axiom [Reference Broto, Levi and OliverBLO03, Definition 1.2(II)] then gives that
$\mathcal {F}$
-normalized by Lemma 2.6. A direct application of the Extension axiom [Reference Broto, Levi and OliverBLO03, Definition 1.2(II)] then gives that
![]() $\rho $
is surjective. Since W is
$\rho $
is surjective. Since W is
![]() $\mathcal {F}$
-centric, the centralizer in
$\mathcal {F}$
-centric, the centralizer in
![]() $\mathcal {F}$
of the centric subgroup W is the fusion system of
$\mathcal {F}$
of the centric subgroup W is the fusion system of
![]() $Z(W)$
by Lemma 2.4, so the kernel of
$Z(W)$
by Lemma 2.4, so the kernel of
![]() $\rho $
is
$\rho $
is
![]() $\operatorname {Aut}_{Z(W)}(P)$
, which is contained in
$\operatorname {Aut}_{Z(W)}(P)$
, which is contained in
![]() $\operatorname {Aut}_W(P) \subseteq \operatorname {Inn}(P)$
. The induced map
$\operatorname {Aut}_W(P) \subseteq \operatorname {Inn}(P)$
. The induced map
is an isomorphism, and therefore upon factoring by
![]() $\operatorname {Aut}_P(P)/\operatorname {Aut}_W(P)$
, the induced map
$\operatorname {Aut}_P(P)/\operatorname {Aut}_W(P)$
, the induced map
is an isomorphism.
Observe that W is normal in S because it is weakly
![]() $\mathcal {F}$
-closed. So
$\mathcal {F}$
-closed. So
![]() $\operatorname {Out}_P(W) \cong P/W$
since
$\operatorname {Out}_P(W) \cong P/W$
since
![]() $C_S(W) \leqslant W$
. The map
$C_S(W) \leqslant W$
. The map
![]() $P \mapsto \operatorname {Out}_P(W)$
is therefore a bijection between the subgroups containing W and the subgroups of
$P \mapsto \operatorname {Out}_P(W)$
is therefore a bijection between the subgroups containing W and the subgroups of
![]() $\operatorname {Out}_S(P)$
. By (2.1),
$\operatorname {Out}_S(P)$
. By (2.1),
![]() $\operatorname {Out}_{\mathcal {F}}(P)$
corresponds to
$\operatorname {Out}_{\mathcal {F}}(P)$
corresponds to
![]() $N_{\operatorname {Out}_{\mathcal {F}}(W)}(\operatorname {Out}_P(W))/\operatorname {Out}_P(W)$
under the bijection, so P is
$N_{\operatorname {Out}_{\mathcal {F}}(W)}(\operatorname {Out}_P(W))/\operatorname {Out}_P(W)$
under the bijection, so P is
![]() $\mathcal {F}$
-radical if and only if
$\mathcal {F}$
-radical if and only if
![]() $\operatorname {Out}_P(W)$
is p-radical in the group
$\operatorname {Out}_P(W)$
is p-radical in the group
![]() $\operatorname {Out}_{\mathcal {F}}(W)$
(Remark 2.2). The last statement now follows because the collection of
$\operatorname {Out}_{\mathcal {F}}(W)$
(Remark 2.2). The last statement now follows because the collection of
![]() $\mathcal {F}$
-centric subgroups is closed under passing to overgroups.
$\mathcal {F}$
-centric subgroups is closed under passing to overgroups.
2.2 Quaternion groups and the 2-local structure of
 $\operatorname {SL}_2(q)$
$\operatorname {SL}_2(q)$
It will be convenient to recall here standard facts about the
![]() $2$
-local structure of
$2$
-local structure of
![]() $\operatorname {SL}_2(q)$
, where q is an odd prime power. For reasons that will become apparent in a moment, we set
$\operatorname {SL}_2(q)$
, where q is an odd prime power. For reasons that will become apparent in a moment, we set
![]() $l \geqslant 0$
and take
$l \geqslant 0$
and take
![]() $q = q_l = 5^{2^{l}}$
for simplicity of exposition. Given this notation,
$q = q_l = 5^{2^{l}}$
for simplicity of exposition. Given this notation,
![]() $\operatorname {SL}_2(q)$
has generalized quaternion Sylow
$\operatorname {SL}_2(q)$
has generalized quaternion Sylow
![]() $2$
-subgroups of order
$2$
-subgroups of order
![]() $2^{l+3}$
, and this can be seen as follows. First, the size of a Sylow
$2^{l+3}$
, and this can be seen as follows. First, the size of a Sylow
![]() $2$
-subgroup can be deduced from the order
$2$
-subgroup can be deduced from the order
![]() $q(q-1)(q+1)$
of
$q(q-1)(q+1)$
of
![]() $\operatorname {SL}_2(q)$
, together with the fact that the
$\operatorname {SL}_2(q)$
, together with the fact that the
![]() $2$
-adic valuation
$2$
-adic valuation
![]() $v_2(5^{2^l}-1)$
is
$v_2(5^{2^l}-1)$
is
![]() $l+2$
. By the choice of q, the multiplicative group
$l+2$
. By the choice of q, the multiplicative group
![]() $\mathbb {F}_q^\times $
contains a primitive root of unity
$\mathbb {F}_q^\times $
contains a primitive root of unity
![]() $\omega $
of order
$\omega $
of order
![]() $2^{l+2}$
. Thus,
$2^{l+2}$
. Thus,
generate a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\operatorname {SL}_2(q)$
by order considerations. Since a and b satisfy the relations
$\operatorname {SL}_2(q)$
by order considerations. Since a and b satisfy the relations
we see that
![]() $R:=\langle a,b \rangle $
is a generalized quaternion group of order
$R:=\langle a,b \rangle $
is a generalized quaternion group of order
![]() $2^{l+3}$
. The following lemma records some basic facts about the subgroup structure of a generalized quaternion group.
$2^{l+3}$
. The following lemma records some basic facts about the subgroup structure of a generalized quaternion group.
Lemma 2.8. The following hold:
-
(a) each element of R is of the form
 $a^ib^j$
with
$a^ib^j$
with
 $0 \le i \le 2^{l+2}-1$
and
$0 \le i \le 2^{l+2}-1$
and
 $0 \le j \le 1$
;
$0 \le j \le 1$
; -
(b) each element in
 $R \backslash \langle a \rangle $
is of order 4;
$R \backslash \langle a \rangle $
is of order 4; -
(c)
 $a^ib$
is conjugate to
$a^ib$
is conjugate to
 $a^jb$
if and only if
$a^jb$
if and only if
 $i \equiv j \mod 2$
, where
$i \equiv j \mod 2$
, where
 $0 \le i,j \le 2^{l+2}-1$
;
$0 \le i,j \le 2^{l+2}-1$
; -
(d) the set
 $\mathcal {Q}$
of subgroups of R isomorphic with
$\mathcal {Q}$
of subgroups of R isomorphic with
 $Q_8$
is given by {
$Q_8$
is given by {
 $\langle a^{2^l},a^ib \rangle \mid 0 \le i \le 2^{l+2}-1$
};
$\langle a^{2^l},a^ib \rangle \mid 0 \le i \le 2^{l+2}-1$
}; -
(e) when
 $l> 0$
, there are two R-conjugacy classes, each of size
$l> 0$
, there are two R-conjugacy classes, each of size
 $2^{l-1}$
, of subgroups isomorphic to
$2^{l-1}$
, of subgroups isomorphic to
 $Q_8$
, and
$Q_8$
, and
 $Q:=\langle a^{2^l},b \rangle $
and
$Q:=\langle a^{2^l},b \rangle $
and
 $Q':=\langle a^{2^l},ab \rangle $
are representatives of these classes; and
$Q':=\langle a^{2^l},ab \rangle $
are representatives of these classes; and -
(f) when
 $l> 0$
,
$l> 0$
,
 $N_S(Q)=\langle Q,a^{2^{l-1}} \rangle $
and
$N_S(Q)=\langle Q,a^{2^{l-1}} \rangle $
and
 $N_S(Q')=\langle Q',a^{2^{l-1}} \rangle $
.
$N_S(Q')=\langle Q',a^{2^{l-1}} \rangle $
.
Proof. Part (a) is clear, and (b) follows since, for each i,
has order 2. A general element
![]() $a^jb^m$
as in (a) conjugates
$a^jb^m$
as in (a) conjugates
![]() $a^ib$
to
$a^ib$
to
 $$\begin{align*}b^{-m}a^{-j}a^iba^jb^{m}=(b^{-m}a^{i-2j}b^{m})b= \begin{cases} a^{i-2j}b, \mbox{ if } m=0\\ a^{2j-i}b, \mbox{ if } m=1 \end{cases} \end{align*}$$
$$\begin{align*}b^{-m}a^{-j}a^iba^jb^{m}=(b^{-m}a^{i-2j}b^{m})b= \begin{cases} a^{i-2j}b, \mbox{ if } m=0\\ a^{2j-i}b, \mbox{ if } m=1 \end{cases} \end{align*}$$
from which the claim in (c) follows.
Let
![]() $\mathcal {Q}$
be the set of subgroups of R isomorphic to
$\mathcal {Q}$
be the set of subgroups of R isomorphic to
![]() $Q_8$
as in (d), and fix
$Q_8$
as in (d), and fix
![]() $Q \in \mathcal {Q}$
. As
$Q \in \mathcal {Q}$
. As
![]() $\langle a \rangle $
is cyclic of index
$\langle a \rangle $
is cyclic of index
![]() $2$
in R, we have
$2$
in R, we have
![]() $Q\langle a \rangle = R$
, and so
$Q\langle a \rangle = R$
, and so
![]() $Q \cap \langle a \rangle = \langle a^{2^l} \rangle $
by order considerations. This shows that Q is of the form
$Q \cap \langle a \rangle = \langle a^{2^l} \rangle $
by order considerations. This shows that Q is of the form
![]() $\langle a^{2^l},a^ib \rangle $
for some i. Conversely, for each i, the elements
$\langle a^{2^l},a^ib \rangle $
for some i. Conversely, for each i, the elements
![]() $a^{2^{l}}$
and
$a^{2^{l}}$
and
![]() $a^{i}b$
satisfy the relations (2.2), applied with
$a^{i}b$
satisfy the relations (2.2), applied with
![]() $l=0$
, in place of a and b, respectively. Hence,
$l=0$
, in place of a and b, respectively. Hence,
![]() $\langle a^{2^l},a^ib \rangle \cong Q_8$
, and so
$\langle a^{2^l},a^ib \rangle \cong Q_8$
, and so
![]() $\langle a^{2^l}, a^ib \rangle \in \mathcal {Q}$
. This completes the proof of (d).
$\langle a^{2^l}, a^ib \rangle \in \mathcal {Q}$
. This completes the proof of (d).
Note that exactly four elements of the form
![]() $a^ib$
lie in a given member of
$a^ib$
lie in a given member of
![]() $\mathcal {Q}$
. Since there are
$\mathcal {Q}$
. Since there are
![]() $2^{l+2}$
choices for i,
$2^{l+2}$
choices for i,
![]() $\mathcal {Q}$
has cardinality
$\mathcal {Q}$
has cardinality
![]() $2^{l+2}/4 = 2^l$
. Part (e) now follows from the conjugacy information in (c), while (f) follows from the observation that
$2^{l+2}/4 = 2^l$
. Part (e) now follows from the conjugacy information in (c), while (f) follows from the observation that
![]() $b^a=a^{-2}b$
so that
$b^a=a^{-2}b$
so that
![]() $b^{a^i}=a^{-2i}b$
.
$b^{a^i}=a^{-2i}b$
.
Since
![]() $v_2(q-1)=l+2$
and
$v_2(q-1)=l+2$
and
![]() $\omega $
is a primitive
$\omega $
is a primitive
![]() $2^{l+2}$
root of unity,
$2^{l+2}$
root of unity,
![]() $\sqrt {\omega } \notin \mathbb {F}_{q}^\times $
. So
$\sqrt {\omega } \notin \mathbb {F}_{q}^\times $
. So
![]() $p(t):=t^2-\omega $
is irreducible in
$p(t):=t^2-\omega $
is irreducible in
![]() $\mathbb {F}_q$
, and
$\mathbb {F}_q$
, and
![]() $\mathbb {F}_0:=\mathbb {F}_q[t]/p(t)$
is a finite field of order
$\mathbb {F}_0:=\mathbb {F}_q[t]/p(t)$
is a finite field of order
![]() $q^2$
containing
$q^2$
containing
![]() $\mathbb {F}_q$
. Set
$\mathbb {F}_q$
. Set
![]() $c:=\left ( \begin {smallmatrix} t & 0 \\ 0 & t^{-1} \\ \end {smallmatrix} \right ) \in \operatorname {SL}_2(\mathbb {F}_0).$
Then straightforward computations show that
$c:=\left ( \begin {smallmatrix} t & 0 \\ 0 & t^{-1} \\ \end {smallmatrix} \right ) \in \operatorname {SL}_2(\mathbb {F}_0).$
Then straightforward computations show that
![]() $c^2=a$
(so c has order
$c^2=a$
(so c has order
![]() $2^{l+3}$
) and that
$2^{l+3}$
) and that
![]() $c^{-1}bc=ba$
and
$c^{-1}bc=ba$
and
![]() $cbc^{-1}=ab$
. Hence, by Lemma 2.8 (d),(e), c fuses the two conjugacy classes of subgroups of R isomorphic with
$cbc^{-1}=ab$
. Hence, by Lemma 2.8 (d),(e), c fuses the two conjugacy classes of subgroups of R isomorphic with
![]() $Q_8$
.
$Q_8$
.
Finally, we will need the following lemma, which we will usually use in Section 3 without further comment. For a discussion of (2), see, for example [Reference CravenCra11, Theorem 4.54].
Lemma 2.9. For
![]() $q={5^{2^l}}$
, as above, let
$q={5^{2^l}}$
, as above, let
![]() $\mathcal {F}:=\mathcal {F}_R(\operatorname {SL}_2(q))$
be the
$\mathcal {F}:=\mathcal {F}_R(\operatorname {SL}_2(q))$
be the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $\operatorname {SL}_2(q)$
.
$\operatorname {SL}_2(q)$
.
-
1. If
 $l = 0$
, then
$l = 0$
, then
 $\mathcal {F}$
is constrained with centric normal subgroup R,
$\mathcal {F}$
is constrained with centric normal subgroup R,
 $N_{\operatorname {SL}_2(q)}(R) \cong \operatorname {SL}_2(3)$
, and
$N_{\operatorname {SL}_2(q)}(R) \cong \operatorname {SL}_2(3)$
, and
 $\operatorname {Out}_{\mathcal {F}}(R) \cong C_3$
.
$\operatorname {Out}_{\mathcal {F}}(R) \cong C_3$
. -
2. If
 $l> 0$
, then
$l> 0$
, then
 $\{R,Q,Q'\}$
is a complete set of
$\{R,Q,Q'\}$
is a complete set of
 $\mathcal {F}$
-conjugacy class representatives of
$\mathcal {F}$
-conjugacy class representatives of
 $\mathcal {F}$
-centric radical subgroups. Moreover,
$\mathcal {F}$
-centric radical subgroups. Moreover,
 $N_{\operatorname {SL}_2(q)}(Q) \cong N_{\operatorname {SL}_2(q)}(Q') \cong \operatorname {GL}_2(3)$
,
$N_{\operatorname {SL}_2(q)}(Q) \cong N_{\operatorname {SL}_2(q)}(Q') \cong \operatorname {GL}_2(3)$
,
 $\operatorname {Out}_{\mathcal {F}}(Q) \cong \operatorname {Out}_{\mathcal {F}}(Q') \cong S_3$
, and
$\operatorname {Out}_{\mathcal {F}}(Q) \cong \operatorname {Out}_{\mathcal {F}}(Q') \cong S_3$
, and
 $\operatorname {Out}_{\mathcal {F}}(R) = 1$
.
$\operatorname {Out}_{\mathcal {F}}(R) = 1$
.
2.3
 $\operatorname {Spin}_7(q)$
$\operatorname {Spin}_7(q)$
Let q be an odd prime power, and let V be an odd dimensional vector space over
![]() $\mathbb {F}_q$
. Let
$\mathbb {F}_q$
. Let
![]() $\mathfrak {q}$
be a nondegenerate quadratic form on V and
$\mathfrak {q}$
be a nondegenerate quadratic form on V and
![]() $\mathfrak {b}$
the associated symmetric bilinear form, which determine each other via
$\mathfrak {b}$
the associated symmetric bilinear form, which determine each other via
![]() $\mathfrak {q}(v) = \mathfrak {b}(v,v)$
and
$\mathfrak {q}(v) = \mathfrak {b}(v,v)$
and
![]() $\mathfrak {b}(v,w) = \frac {1}{2}(\mathfrak {q}(v+w)-\mathfrak {q}(v)-\mathfrak {q}(w))$
. Let
$\mathfrak {b}(v,w) = \frac {1}{2}(\mathfrak {q}(v+w)-\mathfrak {q}(v)-\mathfrak {q}(w))$
. Let
![]() $(V,\mathfrak {q})$
be the associated geometric space, and
$(V,\mathfrak {q})$
be the associated geometric space, and
![]() $\mathrm {O}(V) = \mathrm {O}(V,\mathfrak {q})$
the isometry group. There are two such forms
$\mathrm {O}(V) = \mathrm {O}(V,\mathfrak {q})$
the isometry group. There are two such forms
![]() $\mathfrak {b}$
up to equivalence, and the corresponding isometry groups are isomorphic. We may therefore take
$\mathfrak {b}$
up to equivalence, and the corresponding isometry groups are isomorphic. We may therefore take
![]() $\mathfrak {b}$
to be of square discriminant when convenient. We have
$\mathfrak {b}$
to be of square discriminant when convenient. We have
![]() $\mathrm {O}(V) = \{\pm 1\} \times \operatorname {SO}(V)$
. The spinor norm
$\mathrm {O}(V) = \{\pm 1\} \times \operatorname {SO}(V)$
. The spinor norm
![]() $\operatorname {SO}(V) \to \mathbb {F}_q^{\times }/\mathbb {F}_q^{\times 2}$
is defined by writing an element of
$\operatorname {SO}(V) \to \mathbb {F}_q^{\times }/\mathbb {F}_q^{\times 2}$
is defined by writing an element of
![]() $\operatorname {SO}(V)$
as a product of reflections, and then taking the product of the discriminants of the
$\operatorname {SO}(V)$
as a product of reflections, and then taking the product of the discriminants of the
![]() $-1$
-eigenspaces of those reflections. The kernel of the spinor norm is the simple subgroup
$-1$
-eigenspaces of those reflections. The kernel of the spinor norm is the simple subgroup
![]() $\Omega (V)$
. Let
$\Omega (V)$
. Let
![]() $\operatorname {Spin}(V)$
be the perfect double cover of
$\operatorname {Spin}(V)$
be the perfect double cover of
![]() $\Omega (V)$
, and write Z for the center of
$\Omega (V)$
, and write Z for the center of
![]() $\operatorname {Spin}(V)$
. Thus,
$\operatorname {Spin}(V)$
. Thus,
![]() $Z = \langle z \rangle $
is of order
$Z = \langle z \rangle $
is of order
![]() $2$
. We sometimes speak of the action of an element of
$2$
. We sometimes speak of the action of an element of
![]() $\operatorname {Spin}(V)$
on V, we mean the action of the image of the element in
$\operatorname {Spin}(V)$
on V, we mean the action of the image of the element in
![]() $\Omega (V)$
.
$\Omega (V)$
.
We generally refer to [Reference Levi and OliverLO02, Appendix A] and [Reference Aschbacher and ChermakAC10, Section 4] for information on the construction and subgroup structure of the
![]() $\operatorname {Spin}$
groups but record the following basic lemma for use in Section 3.
$\operatorname {Spin}$
groups but record the following basic lemma for use in Section 3.
Lemma 2.10. An involution in
![]() $\Omega (V)$
lifts to an involution in
$\Omega (V)$
lifts to an involution in
![]() $\operatorname {Spin}(V)$
if and only if the dimension of its
$\operatorname {Spin}(V)$
if and only if the dimension of its
![]() $-1$
-eigenspace is a multiple of
$-1$
-eigenspace is a multiple of
![]() $4$
.
$4$
.
Proof. See [Reference Levi and OliverLO02, Lemma A.4(b)].
From now, take V to be of dimension
![]() $7$
. To help motivate some of the definitions in the next subsection, we describe very roughly the structure of the normalizer of a four subgroup containing Z in
$7$
. To help motivate some of the definitions in the next subsection, we describe very roughly the structure of the normalizer of a four subgroup containing Z in
![]() $\operatorname {Spin}_7(q)$
. For more information and proofs, we refer the reader to Proposition 2.5(b) of [Reference Levi and OliverLO02] (which views
$\operatorname {Spin}_7(q)$
. For more information and proofs, we refer the reader to Proposition 2.5(b) of [Reference Levi and OliverLO02] (which views
![]() $\operatorname {Spin}(V)$
classically) or Lemma 4.3(b) of [Reference Henke, Libman and LyndHLL23] (for a Lie theoretic approach). Lemma 2.10 implies that
$\operatorname {Spin}(V)$
classically) or Lemma 4.3(b) of [Reference Henke, Libman and LyndHLL23] (for a Lie theoretic approach). Lemma 2.10 implies that
![]() $\operatorname {Spin}_7(q) := \operatorname {Spin}(V)$
has two classes of involutions, namely, those with representatives given by the central involution
$\operatorname {Spin}_7(q) := \operatorname {Spin}(V)$
has two classes of involutions, namely, those with representatives given by the central involution
![]() $z \in Z(\operatorname {Spin}_7(q))$
and by the preimage of an involution with
$z \in Z(\operatorname {Spin}_7(q))$
and by the preimage of an involution with
![]() $-1$
-eigenspace of dimension
$-1$
-eigenspace of dimension
![]() $4$
. Let
$4$
. Let
![]() $V_1$
be a nondegenerate subspace of dimension
$V_1$
be a nondegenerate subspace of dimension
![]() $4$
(and Witt index
$4$
(and Witt index
![]() $2$
), and let
$2$
), and let
![]() $V_2$
be its orthogonal complement. Let
$V_2$
be its orthogonal complement. Let
![]() $z_1 \in \operatorname {Spin}(V)$
be an element whose image in
$z_1 \in \operatorname {Spin}(V)$
be an element whose image in
![]() $\Omega (V)$
is an involution with
$\Omega (V)$
is an involution with
![]() $-1$
-eigenspace
$-1$
-eigenspace
![]() $V_1$
(thus,
$V_1$
(thus,
![]() $z_1$
is an involution by Lemma 2.10). Setting
$z_1$
is an involution by Lemma 2.10). Setting
![]() $U = \langle z,z_1 \rangle $
, the normalizer
$U = \langle z,z_1 \rangle $
, the normalizer
![]() $B := N_{\operatorname {Spin}(V)}(U)$
contains the normal subgroup
$B := N_{\operatorname {Spin}(V)}(U)$
contains the normal subgroup
![]() $C_B(V_2)C_B(V_1)$
with index
$C_B(V_2)C_B(V_1)$
with index
![]() $4$
, isomorphic to the commuting product
$4$
, isomorphic to the commuting product
There is a four group complementing
![]() $C_B(V_2)C_B(V_1)$
in B, which contains an involution interchanging the first two
$C_B(V_2)C_B(V_1)$
in B, which contains an involution interchanging the first two
![]() $\operatorname {SL}_2(q)$
’s and centralizing the third (and whose image in
$\operatorname {SL}_2(q)$
’s and centralizing the third (and whose image in
![]() $\Omega _7(q)$
acts as
$\Omega _7(q)$
acts as
![]() $-1$
on
$-1$
on
![]() $V_2$
), and which contains an involution acting simultaneously as a diagonal automorphism on each
$V_2$
), and which contains an involution acting simultaneously as a diagonal automorphism on each
![]() $\operatorname {SL}_2(q)$
factor.
$\operatorname {SL}_2(q)$
factor.
All additional information about
![]() $\operatorname {Spin}_7(q)$
that we require directly will be collected later in Lemmas 2.14 through 2.18, in Proposition 3.2, and in the proof of Lemma 3.8.
$\operatorname {Spin}_7(q)$
that we require directly will be collected later in Lemmas 2.14 through 2.18, in Proposition 3.2, and in the proof of Lemma 3.8.
2.4 Construction of
 $\operatorname {Sol}(q)$
$\operatorname {Sol}(q)$
Following work of Solomon [Reference SolomonSol74], the Benson-Solomon systems were predicted to exist by Benson [Reference BensonBen98c], and then later constructed by Levi and Oliver [Reference Levi and OliverLO02, Reference Levi and OliverLO05]. They are exotic in the sense that they are not of the form
![]() $\mathcal {F}_S(G)$
for any finite group G with Sylow
$\mathcal {F}_S(G)$
for any finite group G with Sylow
![]() $2$
-subgroup S. They are also not the fusion system of any
$2$
-subgroup S. They are also not the fusion system of any
![]() $2$
-block of a finite group [Reference KessarKes06], [Reference CravenCra11, Section 9.4], an a priori stronger statement. After Levi and Oliver, Aschbacher and Chermak gave a different construction of the Benson-Solomon systems as the fusion system of a certain free amalgamated product of two finite groups having Sylow 2-subgroup isomorphic to
$2$
-block of a finite group [Reference KessarKes06], [Reference CravenCra11, Section 9.4], an a priori stronger statement. After Levi and Oliver, Aschbacher and Chermak gave a different construction of the Benson-Solomon systems as the fusion system of a certain free amalgamated product of two finite groups having Sylow 2-subgroup isomorphic to
![]() $\operatorname {Spin}_7(q)$
[Reference Aschbacher and ChermakAC10]. We primarily view
$\operatorname {Spin}_7(q)$
[Reference Aschbacher and ChermakAC10]. We primarily view
![]() $\operatorname {Sol}(q)$
through the lens of [Reference Aschbacher and ChermakAC10], so we consider it as the
$\operatorname {Sol}(q)$
through the lens of [Reference Aschbacher and ChermakAC10], so we consider it as the
![]() $2$
-fusion system of an amalgamated product
$2$
-fusion system of an amalgamated product
![]() $G=H *_B K$
, where
$G=H *_B K$
, where
![]() $H:=\operatorname {Spin}_7(q)$
.
$H:=\operatorname {Spin}_7(q)$
.
The isomorphism type of the Benson-Solomon system
![]() $\operatorname {Sol}(q)$
depends not on q, but only (uniquely) on the
$\operatorname {Sol}(q)$
depends not on q, but only (uniquely) on the
![]() $2$
-adic valuation of
$2$
-adic valuation of
![]() $q^2-1$
by [Reference Chermak, Oliver and ShpectorovCOS08, Theorem 3.4]. For reasons of exposition, it will be helpful therefore to fix the following choice of q: unless otherwise specified, for the remainder of this section and the next, we
$q^2-1$
by [Reference Chermak, Oliver and ShpectorovCOS08, Theorem 3.4]. For reasons of exposition, it will be helpful therefore to fix the following choice of q: unless otherwise specified, for the remainder of this section and the next, we
We have described how B arises as a subgroup of H in Subsection 2.3 (but the explicit embedding
![]() $B \hookrightarrow H$
in the amalgam is not the “obvious” one). We now take a more abstract approach to obtain a working description of K in Aschbacher-Chermak free amalgamated product, as follows. Consider the natural inclusion
$B \hookrightarrow H$
in the amalgam is not the “obvious” one). We now take a more abstract approach to obtain a working description of K in Aschbacher-Chermak free amalgamated product, as follows. Consider the natural inclusion
![]() $\operatorname {SL}_2(q) \le \operatorname {SL}_2(q^2)$
induced by an inclusion of fields, and define
$\operatorname {SL}_2(q) \le \operatorname {SL}_2(q^2)$
induced by an inclusion of fields, and define
![]() $N := N_{\operatorname {SL}_2(q^2)}(\operatorname {SL}_2(q))$
so that
$N := N_{\operatorname {SL}_2(q^2)}(\operatorname {SL}_2(q))$
so that
![]() $|N:\operatorname {SL}_2(q)|=2$
and N and
$|N:\operatorname {SL}_2(q)|=2$
and N and
![]() $\operatorname {SL}_2(q)$
both have generalized quaternion Sylow
$\operatorname {SL}_2(q)$
both have generalized quaternion Sylow
![]() $2$
-subgroups, as explained more fully in Subsection 2.2. Form the wreath product
$2$
-subgroups, as explained more fully in Subsection 2.2. Form the wreath product
![]() $W:= N \wr S_3$
, and let
$W:= N \wr S_3$
, and let
![]() $N_0 := N_1 \times N_2 \times N_3$
and
$N_0 := N_1 \times N_2 \times N_3$
and
![]() $X := S_3$
be the base and acting group respectively. Note that
$X := S_3$
be the base and acting group respectively. Note that
![]() $O^2(N_0) \unlhd W$
is a direct product
$O^2(N_0) \unlhd W$
is a direct product
![]() $\widehat {L}_1 \times \widehat {L}_2 \times \widehat {L}_3$
of three copies of
$\widehat {L}_1 \times \widehat {L}_2 \times \widehat {L}_3$
of three copies of
![]() $\operatorname {SL}_2(q)$
permuted transitively by X.
$\operatorname {SL}_2(q)$
permuted transitively by X.
Define
![]() $\widehat {K} := O^2(N_0)C_{N_0}(X)X$
regarded as the group generated by the wreath product
$\widehat {K} := O^2(N_0)C_{N_0}(X)X$
regarded as the group generated by the wreath product
![]() $O^2(N_0) \rtimes X$
, and an element of
$O^2(N_0) \rtimes X$
, and an element of
![]() $N_0 \backslash O^2(N_0)$
acting in the same way simultaneously on each factor
$N_0 \backslash O^2(N_0)$
acting in the same way simultaneously on each factor
![]() $\widehat {L}_i$
of
$\widehat {L}_i$
of
![]() $O^2(N_0)$
. Thus,
$O^2(N_0)$
. Thus,
![]() $Z(O^2(N_0)) = Z(O^2(N_0)C_{N_0}(X)) = \langle (\pm 1, \pm 1, \pm 1) \rangle $
and
$Z(O^2(N_0)) = Z(O^2(N_0)C_{N_0}(X)) = \langle (\pm 1, \pm 1, \pm 1) \rangle $
and
![]() $Z(\widehat {K}) = \langle (-1, -1, -1) \rangle $
. Here, we write
$Z(\widehat {K}) = \langle (-1, -1, -1) \rangle $
. Here, we write
![]() $1$
for the identity matrix. Finally, set
$1$
for the identity matrix. Finally, set
We will write
![]() $[a_1,a_2,a_3]$
, for example, for the image in K of an element
$[a_1,a_2,a_3]$
, for example, for the image in K of an element
![]() $(a_1,a_2,a_3)$
of
$(a_1,a_2,a_3)$
of
![]() $O^2(N_0)C_{N_0}(X)$
.
$O^2(N_0)C_{N_0}(X)$
.
Notation 2.11. We fix the following notation for certain subgroups of K.
-
(a)
 $L_i \cong \operatorname {SL}_2(q)$
for
$L_i \cong \operatorname {SL}_2(q)$
for
 $i = 1, 2, 3$
are the images in K of the subgroups
$i = 1, 2, 3$
are the images in K of the subgroups
 $\widehat {L}_i$
of
$\widehat {L}_i$
of
 $\widehat {K}$
;
$\widehat {K}$
; -
(b)
 $L_0 := L_1L_2L_3$
;
$L_0 := L_1L_2L_3$
; -
(c)
 $X \cong S_3$
is the image in K of the subgroup with the same name;
$X \cong S_3$
is the image in K of the subgroup with the same name; -
(d)
 $\tau \in X$
is the permutation
$\tau \in X$
is the permutation
 $(1,2)$
on the indices of the
$(1,2)$
on the indices of the
 $L_i$
;
$L_i$
; -
(e) S is a Sylow
 $2$
-subgroup of K containing
$2$
-subgroup of K containing
 $\tau $
;
$\tau $
; -
(f)
 $U = Z(L_0) = \langle [\pm 1, \pm 1, \pm 1] \rangle \cong C_2 \times C_2$
; and
$U = Z(L_0) = \langle [\pm 1, \pm 1, \pm 1] \rangle \cong C_2 \times C_2$
; and -
(g)
 $B := L_0S$
.
$B := L_0S$
.
Thus, the subgroup B in Notation 2.11(g) is a subgroup of K of index
![]() $3$
, and
$3$
, and
![]() $B \cap X = \langle \tau \rangle $
. As was shown in [Reference Aschbacher and ChermakAC10], there is a four subgroup
$B \cap X = \langle \tau \rangle $
. As was shown in [Reference Aschbacher and ChermakAC10], there is a four subgroup
![]() $U \leqslant H$
, such that
$U \leqslant H$
, such that
![]() $B \cong N_{H}(U)$
, and a choice of injection
$B \cong N_{H}(U)$
, and a choice of injection
![]() $\iota :B \hookrightarrow H$
, such that the free amalgamated product
$\iota :B \hookrightarrow H$
, such that the free amalgamated product
![]() $G=H *_B K$
has finite Sylow
$G=H *_B K$
has finite Sylow
![]() $2$
-subgroup S and determines a saturated fusion system
$2$
-subgroup S and determines a saturated fusion system
![]() $\operatorname {Sol}(q)$
over S that was constructed by Levi and Oliver by different means [Reference Levi and OliverLO02, Reference Levi and OliverLO05]. An incorrect choice of
$\operatorname {Sol}(q)$
over S that was constructed by Levi and Oliver by different means [Reference Levi and OliverLO02, Reference Levi and OliverLO05]. An incorrect choice of
![]() $\iota $
can lead to a fusion system which is not saturated (see [Reference Aschbacher and ChermakAC10, Section 5] and [Reference Levi and OliverLO05] for more details, but generally, this subtlety will be unimportant in our computations).
$\iota $
can lead to a fusion system which is not saturated (see [Reference Aschbacher and ChermakAC10, Section 5] and [Reference Levi and OliverLO05] for more details, but generally, this subtlety will be unimportant in our computations).
It will be helpful to introduce some more notation. Some of it follows the notation of [Reference Aschbacher and ChermakAC10, Section 10] in preparation for the application in Section 3 of some of the results there.
Notation 2.12. We fix the following additional notation for subgroups and elements of K.
-
(a)
 $R_i \cong Q_{2^{l+3}}$
is a Sylow
$R_i \cong Q_{2^{l+3}}$
is a Sylow
 $2$
-subgroup of
$2$
-subgroup of
 $L_i$
for
$L_i$
for
 $i=1,2,3$
, chosen so that
$i=1,2,3$
, chosen so that
 $X \cong S_3$
acts on the set
$X \cong S_3$
acts on the set
 $\{R_1,R_2,R_3\}$
;
$\{R_1,R_2,R_3\}$
; -
(b)
 $R_0:=R_1R_2R_3 \in \operatorname {Syl}_2(L_0)$
;
$R_0:=R_1R_2R_3 \in \operatorname {Syl}_2(L_0)$
; -
(c)
 $\mathcal {Q}_i$
is the set of subgroups of
$\mathcal {Q}_i$
is the set of subgroups of
 $R_i$
isomorphic to
$R_i$
isomorphic to
 $Q_8$
for
$Q_8$
for
 $i=1,2,3$
; thus,
$i=1,2,3$
; thus,
 $\mathcal {Q}_i = \{R_i\}$
if
$\mathcal {Q}_i = \{R_i\}$
if
 $l = 0$
, while
$l = 0$
, while
 $\mathcal {Q}_i$
is a union of two
$\mathcal {Q}_i$
is a union of two
 $R_i$
-conjugacy classes of subgroups if
$R_i$
-conjugacy classes of subgroups if
 $l> 0$
by Lemma 2.8(e);
$l> 0$
by Lemma 2.8(e); -
(d) when
 $l> 0$
,
$l> 0$
,
 $Q_i,Q_i' \in \mathcal {Q}_i$
are representatives for the two
$Q_i,Q_i' \in \mathcal {Q}_i$
are representatives for the two
 $R_i$
-conjugacy classes of subgroups chosen so that
$R_i$
-conjugacy classes of subgroups chosen so that
 $X \cong S_3$
acts by permuting the sets
$X \cong S_3$
acts by permuting the sets
 $\{Q_1,Q_2,Q_3\}$
and
$\{Q_1,Q_2,Q_3\}$
and
 $\{Q_1',Q_2',Q_3'\}$
;
$\{Q_1',Q_2',Q_3'\}$
; -
(e)
 $\mathbf {c} := [c,c,c]$
, where c is as in Section 2.2, so that
$\mathbf {c} := [c,c,c]$
, where c is as in Section 2.2, so that
 $\mathbf {c}$
acts simultaneously on
$\mathbf {c}$
acts simultaneously on
 $L_i \cong SL_2(q)$
by conjugation in the way described there;
$L_i \cong SL_2(q)$
by conjugation in the way described there; -
(f)
 $\mathbf {d} := [b,b,b]\mathbf {c} \in K$
, where b is as in Section 2.2, an involution commuting with
$\mathbf {d} := [b,b,b]\mathbf {c} \in K$
, where b is as in Section 2.2, an involution commuting with
 $\tau $
; and
$\tau $
; and -
(g)
 $\tau ' = \mathbf {d}\tau $
.
$\tau ' = \mathbf {d}\tau $
.
Note that
![]() $\langle \mathbf {d}, \tau \rangle $
is a four group which intersects
$\langle \mathbf {d}, \tau \rangle $
is a four group which intersects
![]() $R_0$
trivially. Thus, refining Notation 2.11(e), we fix the following Sylow
$R_0$
trivially. Thus, refining Notation 2.11(e), we fix the following Sylow
![]() $2$
-subgroup of K throughout the remainder of this section and in Section 3:
$2$
-subgroup of K throughout the remainder of this section and in Section 3:
Then S is isomorphic with a Sylow
![]() $2$
-subgroup of H,
$2$
-subgroup of H,
![]() $R_0$
is normal in S with complement
$R_0$
is normal in S with complement
![]() $\langle \mathbf {d},\tau \rangle $
,
$\langle \mathbf {d},\tau \rangle $
,
![]() $R_3$
is normal in S, and
$R_3$
is normal in S, and
![]() $\mathbf {d}$
interchanges the two
$\mathbf {d}$
interchanges the two
![]() $R_i$
-conjugacy classes of subgroups isomorphic with
$R_i$
-conjugacy classes of subgroups isomorphic with
![]() $Q_8$
when
$Q_8$
when
![]() $l> 0$
. Finally, we define
$l> 0$
. Finally, we define
We note that
![]() $\mathcal {F}$
is the fusion system generated by
$\mathcal {F}$
is the fusion system generated by
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {K}$
by [Reference SemeraroSem14, Theorem 3.3], namely,
$\mathcal {K}$
by [Reference SemeraroSem14, Theorem 3.3], namely,
![]() $\mathcal {F}$
is the smallest fusion system on S containing all morphisms in
$\mathcal {F}$
is the smallest fusion system on S containing all morphisms in
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
2.5 The torus of
 $\mathcal {F}$
$\mathcal {F}$
The next lemma calls attention to the 2-power torsion subgroup
![]() $T \leqslant S$
in a maximal torus of H. As a subgroup of K, it may be generated by the elements
$T \leqslant S$
in a maximal torus of H. As a subgroup of K, it may be generated by the elements
![]() $[a,1,1], [1,a,1], [c,c,c]$
in the notation of Section 2.2, and it is inverted by the involution
$[a,1,1], [1,a,1], [c,c,c]$
in the notation of Section 2.2, and it is inverted by the involution
![]() $\mathbf {d}$
. In the lemma and elsewhere, we refer to Borel and parabolic subgroups of
$\mathbf {d}$
. In the lemma and elsewhere, we refer to Borel and parabolic subgroups of
![]() $C_2 \times \operatorname {GL}_3(2)$
, as an algebraic group over
$C_2 \times \operatorname {GL}_3(2)$
, as an algebraic group over
![]() $\mathbb {F}_2$
with unipotent radical
$\mathbb {F}_2$
with unipotent radical
![]() $C_2$
. Thus, a Borel subgroup is the stabilizer of a maximal flag in the three-dimensional
$C_2$
. Thus, a Borel subgroup is the stabilizer of a maximal flag in the three-dimensional
![]() $\mathbb {F}_2$
-representation of
$\mathbb {F}_2$
-representation of
![]() $C_2 \times \operatorname {GL}_3(2)$
which is natural for
$C_2 \times \operatorname {GL}_3(2)$
which is natural for
![]() $\operatorname {GL}_3(2)$
and has
$\operatorname {GL}_3(2)$
and has
![]() $C_2$
in its kernel, and the two maximal parabolic subgroups are similarly stabilizers of proper subspaces and isomorphic to
$C_2$
in its kernel, and the two maximal parabolic subgroups are similarly stabilizers of proper subspaces and isomorphic to
![]() $C_2 \times S_4$
.
$C_2 \times S_4$
.
Lemma 2.13. There is a unique subgroup T of S isomorphic to
![]() $(C_{2^{l+2}})^3$
. The centralizer
$(C_{2^{l+2}})^3$
. The centralizer
![]() $C_H(T)$
is a split maximal torus of H; in particular,
$C_H(T)$
is a split maximal torus of H; in particular,
![]() $C_S(T) = T$
. The subgroup T is
$C_S(T) = T$
. The subgroup T is
![]() $\mathcal {F}$
-centric and weakly
$\mathcal {F}$
-centric and weakly
![]() $\mathcal {F}$
-closed. Moreover,
$\mathcal {F}$
-closed. Moreover,
![]() $\operatorname {Out}_S(T) = S/T \cong C_2 \times D_8$
,
$\operatorname {Out}_S(T) = S/T \cong C_2 \times D_8$
,
![]() $\operatorname {Out}_{\mathcal {F}}(T) \cong C_2 \times \operatorname {GL}_3(2)$
, and
$\operatorname {Out}_{\mathcal {F}}(T) \cong C_2 \times \operatorname {GL}_3(2)$
, and
![]() $\operatorname {Out}_{\mathcal {H}}(T) \cong C_2 \times S_4$
is the maximal parabolic in
$\operatorname {Out}_{\mathcal {H}}(T) \cong C_2 \times S_4$
is the maximal parabolic in
![]() $\operatorname {Out}_{\mathcal {F}}(T)$
, lying over the Borel subgroup
$\operatorname {Out}_{\mathcal {F}}(T)$
, lying over the Borel subgroup
![]() $\operatorname {Out}_S(T)$
, given by the stabilizer of Z in the action of
$\operatorname {Out}_S(T)$
, given by the stabilizer of Z in the action of
![]() $\operatorname {Out}_{\mathcal {F}}(T)$
on
$\operatorname {Out}_{\mathcal {F}}(T)$
on
![]() $\Omega _1(T)$
.
$\Omega _1(T)$
.
Proof. By [Reference Aschbacher and ChermakAC10, Lemma 4.9(c)], there is a unique homocyclic subgroup of S of rank
![]() $3$
and exponent
$3$
and exponent
![]() $4$
, T is the centralizer in S of that subgroup, and
$4$
, T is the centralizer in S of that subgroup, and
![]() $C_H(T)$
is a split maximal torus of H. Since T is abelian, this shows that T is the unique subgroup of S of its isomorphism type. Then [Reference Aschbacher and ChermakAC10, Lemmas 4.3 and 4.8] show that
$C_H(T)$
is a split maximal torus of H. Since T is abelian, this shows that T is the unique subgroup of S of its isomorphism type. Then [Reference Aschbacher and ChermakAC10, Lemmas 4.3 and 4.8] show that
![]() $S/T \cong C_2 \times D_8$
, and
$S/T \cong C_2 \times D_8$
, and
![]() $\operatorname {Out}_{\mathcal {H}}(T) \cong C_2 \times S_4$
. The structure of the outer automorphism group
$\operatorname {Out}_{\mathcal {H}}(T) \cong C_2 \times S_4$
. The structure of the outer automorphism group
![]() $\operatorname {Out}_{\mathcal {F}}(T)$
follows from the construction of the Aschbacher-Chermak amalgam in [Reference Aschbacher and ChermakAC10, Lemma 5.2]. All other points follow.
$\operatorname {Out}_{\mathcal {F}}(T)$
follows from the construction of the Aschbacher-Chermak amalgam in [Reference Aschbacher and ChermakAC10, Lemma 5.2]. All other points follow.
2.6 The standard elementary abelian chain in S
We refer to Sections 4 and 7 of [Reference Aschbacher and ChermakAC10] for more discussion on the following items. Set
![]() $z := [-1,-1,1] = [1,1,-1] \in S$
, so
$z := [-1,-1,1] = [1,1,-1] \in S$
, so
![]() $z \in Z(\operatorname {Spin}_7(q))$
as in Section 2.3. There is a chain of elementary abelian subgroups
$z \in Z(\operatorname {Spin}_7(q))$
as in Section 2.3. There is a chain of elementary abelian subgroups
of ranks 1, 2, 3, and 4, respectively, where
![]() $Z = Z(S) = \langle z \rangle $
, U is the unique normal four subgroup of S of Notation 2.11(f),
$Z = Z(S) = \langle z \rangle $
, U is the unique normal four subgroup of S of Notation 2.11(f),
![]() $E = \Omega _1(T)=\langle [-1,1,1],[1,-1,1],[a^{2^l},a^{2^l},a^{2^l}]\rangle $
, and
$E = \Omega _1(T)=\langle [-1,1,1],[1,-1,1],[a^{2^l},a^{2^l},a^{2^l}]\rangle $
, and
![]() $A = E\langle \mathbf {d} \rangle $
. For a member
$A = E\langle \mathbf {d} \rangle $
. For a member
![]() $X_n$
of the above chain of rank n,
$X_n$
of the above chain of rank n,
![]() $\operatorname {Aut}_{\mathcal {F}}(X_n) = \operatorname {Out}_{\mathcal {F}}(X_n) \cong \operatorname {GL}_n(2)$
by [Reference Levi and OliverLO02, Lemma 3.1]. Also,
$\operatorname {Aut}_{\mathcal {F}}(X_n) = \operatorname {Out}_{\mathcal {F}}(X_n) \cong \operatorname {GL}_n(2)$
by [Reference Levi and OliverLO02, Lemma 3.1]. Also,
![]() $\mathcal {H} = C_{\mathcal {F}}(Z)$
and
$\mathcal {H} = C_{\mathcal {F}}(Z)$
and
![]() $\mathcal {K} = N_{\mathcal {F}}(U)$
by [Reference Aschbacher and ChermakAC10, Proposition 9.2].
$\mathcal {K} = N_{\mathcal {F}}(U)$
by [Reference Aschbacher and ChermakAC10, Proposition 9.2].
2.7 Centric radicals containing the torus
In the next five lemmas, we identify, using Lemma 2.7, the outer automorphism groups of the centric radical subgroups that contain the
![]() $2$
-torus T.
$2$
-torus T.
Lemma 2.14. The subgroup
![]() $C_S(E)$
of S is
$C_S(E)$
of S is
![]() $\mathcal {F}$
-centric and weakly
$\mathcal {F}$
-centric and weakly
![]() $\mathcal {F}$
-closed,
$\mathcal {F}$
-closed,
![]() $C_S(E) = T\langle \mathbf {d} \rangle $
, and
$C_S(E) = T\langle \mathbf {d} \rangle $
, and
![]() $C_H(C_S(E)) = Z(C_S(E))) = E$
. Moreover,
$C_H(C_S(E)) = Z(C_S(E))) = E$
. Moreover,
![]() $\operatorname {Out}_S(C_S(E)) = S/C_S(E) \cong D_8$
,
$\operatorname {Out}_S(C_S(E)) = S/C_S(E) \cong D_8$
,
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(E)) \cong \operatorname {GL}_3(2)$
, and
$\operatorname {Out}_{\mathcal {F}}(C_S(E)) \cong \operatorname {GL}_3(2)$
, and
![]() $\operatorname {Out}_{\mathcal {H}}(C_S(E)) \cong S_4$
is the maximal parabolic in
$\operatorname {Out}_{\mathcal {H}}(C_S(E)) \cong S_4$
is the maximal parabolic in
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(E))$
given by the stabilizer of Z under the natural action of
$\operatorname {Out}_{\mathcal {F}}(C_S(E))$
given by the stabilizer of Z under the natural action of
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(E))$
on E.
$\operatorname {Out}_{\mathcal {F}}(C_S(E))$
on E.
Proof. Since
![]() $E = \Omega _1(T)$
, we have
$E = \Omega _1(T)$
, we have
![]() $C_S(E) \geqslant T$
. As T is
$C_S(E) \geqslant T$
. As T is
![]() $\mathcal {F}$
-centric, so is
$\mathcal {F}$
-centric, so is
![]() $C_S(E)$
. Let
$C_S(E)$
. Let
![]() $\varphi \in \operatorname {Hom}_{\mathcal {F}}(C_S(E),S)$
. By Lemma 2.13,
$\varphi \in \operatorname {Hom}_{\mathcal {F}}(C_S(E),S)$
. By Lemma 2.13,
![]() $T^\varphi = T$
, so also
$T^\varphi = T$
, so also
![]() $E^\varphi = E$
. Hence,
$E^\varphi = E$
. Hence,
![]() $C_S(E)^\varphi \leqslant C_S(E^\varphi ) = C_S(E)$
, and so
$C_S(E)^\varphi \leqslant C_S(E^\varphi ) = C_S(E)$
, and so
![]() $C_S(E)$
is weakly
$C_S(E)$
is weakly
![]() $\mathcal {F}$
-closed. From the description of
$\mathcal {F}$
-closed. From the description of
![]() $\operatorname {Out}_{\mathcal {F}}(T)$
in Lemma 2.13, the kernel of the action of
$\operatorname {Out}_{\mathcal {F}}(T)$
in Lemma 2.13, the kernel of the action of
![]() $S/T$
on E is of order
$S/T$
on E is of order
![]() $2$
. Now
$2$
. Now
![]() $\mathbf {d} \in S$
inverts T, so centralizes
$\mathbf {d} \in S$
inverts T, so centralizes
![]() $E = \Omega _1(T)$
. Hence,
$E = \Omega _1(T)$
. Hence,
![]() $\mathbf {d}$
represents the lone nontrivial coset of
$\mathbf {d}$
represents the lone nontrivial coset of
![]() $C_H(T)$
in
$C_H(T)$
in
![]() $C_H(E)$
, whose elements invert the maximal torus
$C_H(E)$
, whose elements invert the maximal torus
![]() $C_H(T)$
of H containing T (see [Reference Aschbacher and ChermakAC10, Lemma 4.3(a,d)]). So
$C_H(T)$
of H containing T (see [Reference Aschbacher and ChermakAC10, Lemma 4.3(a,d)]). So
![]() $C_S(E) = T\langle \mathbf {d} \rangle $
, and
$C_S(E) = T\langle \mathbf {d} \rangle $
, and
![]() $C_H(C_S(E)) \leqslant T$
from Lemma 2.13. Hence, the center
$C_H(C_S(E)) \leqslant T$
from Lemma 2.13. Hence, the center
![]() $Z(C_S(E))$
is
$Z(C_S(E))$
is
![]() $C_H(C_S(E)) = C_{T}(\mathbf {d}) = E$
.
$C_H(C_S(E)) = C_{T}(\mathbf {d}) = E$
.
As
![]() $O_2(\operatorname {Out}_{\mathcal {F}}(T)) = \operatorname {Out}_{C_S(E)}(T)$
, the descriptions of the outer automorphism groups in
$O_2(\operatorname {Out}_{\mathcal {F}}(T)) = \operatorname {Out}_{C_S(E)}(T)$
, the descriptions of the outer automorphism groups in
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {H}$
follow from Lemmas 2.7 and 2.13.
$\mathcal {H}$
follow from Lemmas 2.7 and 2.13.
Lemma 2.15.
![]() $N_H(S) = S$
and
$N_H(S) = S$
and
![]() $\operatorname {Out}_{\mathcal {H}}(S) = \operatorname {Out}_{\mathcal {F}}(S) = \operatorname {Out}_{\mathcal {K}}(S) = 1$
.
$\operatorname {Out}_{\mathcal {H}}(S) = \operatorname {Out}_{\mathcal {F}}(S) = \operatorname {Out}_{\mathcal {K}}(S) = 1$
.
Proof. Since
![]() $C_S(E)$
contains its centralizer in H from Lemma 2.14, so does S. Then as the Sylow
$C_S(E)$
contains its centralizer in H from Lemma 2.14, so does S. Then as the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $S_4$
and
$S_4$
and
![]() $\operatorname {GL}_3(2)$
are self-normalizing, the lemma now follows from Lemmas 2.7 and 2.14.
$\operatorname {GL}_3(2)$
are self-normalizing, the lemma now follows from Lemmas 2.7 and 2.14.
Lemma 2.16. The subgroup
![]() $C_S(U)$
of S is
$C_S(U)$
of S is
![]() $\mathcal {F}$
-centric and weakly
$\mathcal {F}$
-centric and weakly
![]() $\mathcal {F}$
-closed, and
$\mathcal {F}$
-closed, and
![]() $Z(C_S(U)) = U$
. The quotient
$Z(C_S(U)) = U$
. The quotient
![]() $C_S(U)/C_S(E)$
is the unipotent radical of the stabilizer in
$C_S(U)/C_S(E)$
is the unipotent radical of the stabilizer in
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(E))$
of U. Thus,
$\operatorname {Out}_{\mathcal {F}}(C_S(E))$
of U. Thus,
![]() $\operatorname {Out}_S(C_S(U)) = \operatorname {Out}_{\mathcal {H}}(C_S(U)) \cong C_2$
is induced by
$\operatorname {Out}_S(C_S(U)) = \operatorname {Out}_{\mathcal {H}}(C_S(U)) \cong C_2$
is induced by
![]() $\langle \tau \rangle $
, and
$\langle \tau \rangle $
, and
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(U)) \cong S_3$
is induced by X.
$\operatorname {Out}_{\mathcal {F}}(C_S(U)) \cong S_3$
is induced by X.
Proof. From the structure of
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(E))$
in Lemma 2.14,
$\operatorname {Out}_{\mathcal {F}}(C_S(E))$
in Lemma 2.14,
![]() $\operatorname {Out}_{C_S(U)}(C_S(E)) = C_S(U)/C_S(E)$
is the unipotent radical of the stabilizer of U in the action of
$\operatorname {Out}_{C_S(U)}(C_S(E)) = C_S(U)/C_S(E)$
is the unipotent radical of the stabilizer of U in the action of
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(E))$
on E, so, in particular,
$\operatorname {Out}_{\mathcal {F}}(C_S(E))$
on E, so, in particular,
![]() $Z(C_S(U)) = C_{E}(C_S(U)) = U$
. The descriptions of the outer automorphism groups now follow from Lemmas 2.7 and 2.14 and the structure of
$Z(C_S(U)) = C_{E}(C_S(U)) = U$
. The descriptions of the outer automorphism groups now follow from Lemmas 2.7 and 2.14 and the structure of
![]() $\operatorname {GL}_3(2)$
.
$\operatorname {GL}_3(2)$
.
Lemma 2.17. The subgroup
![]() $C_S(E/Z) = \{s \in S \mid [E,s] \leqslant Z\}$
is
$C_S(E/Z) = \{s \in S \mid [E,s] \leqslant Z\}$
is
![]() $\mathcal {F}$
-centric and weakly
$\mathcal {F}$
-centric and weakly
![]() $\mathcal {F}$
-closed, and
$\mathcal {F}$
-closed, and
![]() $Z(C_S(E/Z)) = Z$
. The quotient
$Z(C_S(E/Z)) = Z$
. The quotient
![]() $C_S(E/Z)/C_S(E)$
is the unipotent radical of the stabilizer in
$C_S(E/Z)/C_S(E)$
is the unipotent radical of the stabilizer in
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(E))$
of Z in the natural action on E. Thus,
$\operatorname {Out}_{\mathcal {F}}(C_S(E))$
of Z in the natural action on E. Thus,
![]() $\operatorname {Out}_{\mathcal {H}}(C_S(E/Z)) = \operatorname {Out}_{\mathcal {F}}(C_S(E/Z)) \cong S_3$
.
$\operatorname {Out}_{\mathcal {H}}(C_S(E/Z)) = \operatorname {Out}_{\mathcal {F}}(C_S(E/Z)) \cong S_3$
.
Proof. Observe that,
![]() $C_S(E) \leqslant C_S(E/Z)$
and that
$C_S(E) \leqslant C_S(E/Z)$
and that
![]() $C_S(E/Z)/C_S(E)$
is the group of transvections in
$C_S(E/Z)/C_S(E)$
is the group of transvections in
![]() $\operatorname {Out}_{\mathcal {F}}(C_S(E))$
on E with center Z. So
$\operatorname {Out}_{\mathcal {F}}(C_S(E))$
on E with center Z. So
![]() $C_S(E/Z)/C_S(E)$
is the unipotent radical of the stabilizer of Z. Also, as
$C_S(E/Z)/C_S(E)$
is the unipotent radical of the stabilizer of Z. Also, as
![]() $Z(C_S(E)) = Z$
from Lemma 2.14, we have
$Z(C_S(E)) = Z$
from Lemma 2.14, we have
![]() $Z(C_S(E/Z)) = C_{E}(C_S(E/Z)) = Z$
. Since
$Z(C_S(E/Z)) = C_{E}(C_S(E/Z)) = Z$
. Since
![]() $C_S(E)$
is
$C_S(E)$
is
![]() $\mathcal {F}$
-centric, weakly
$\mathcal {F}$
-centric, weakly
![]() $\mathcal {F}$
-closed, and
$\mathcal {F}$
-closed, and
![]() $\operatorname {Aut}_{\mathcal {H}}(C_S(E)) = C_{\operatorname {Aut}_{\mathcal {F}}(C_S(E))}(Z)$
, all points follow from Lemmas 2.7 and 2.14 as in the previous lemma.
$\operatorname {Aut}_{\mathcal {H}}(C_S(E)) = C_{\operatorname {Aut}_{\mathcal {F}}(C_S(E))}(Z)$
, all points follow from Lemmas 2.7 and 2.14 as in the previous lemma.
Lemma 2.18. The collection of
![]() $\mathcal {F}$
-centric radical subgroups containing T is
$\mathcal {F}$
-centric radical subgroups containing T is
![]() $\{C_S(E), C_S(U), C_S(E/Z), S\}$
. The collection of
$\{C_S(E), C_S(U), C_S(E/Z), S\}$
. The collection of
![]() $\mathcal {H}$
-centric radical subgroups containing T is
$\mathcal {H}$
-centric radical subgroups containing T is
![]() $\{C_S(E/Z),S\}$
.
$\{C_S(E/Z),S\}$
.
2.8 The sectional rank of S
Before continuing, we record the sectional rank of S using the later Proposition 3.2, which locates an extraspecial subgroup of order
![]() $2^7$
in S.
$2^7$
in S.
Lemma 2.19. The sectional rank of S is
![]() $6$
.
$6$
.
Proof. By Lemma 3.2(a) below, S contains an extraspecial subgroup with central quotient of rank
![]() $6$
, and hence
$6$
, and hence
![]() $s(S) \geqslant 6$
. On the other hand, the sectional rank of a group is at most the sum of the sectional ranks of a normal subgroup and corresponding quotient, so Lemma 2.13 shows that
$s(S) \geqslant 6$
. On the other hand, the sectional rank of a group is at most the sum of the sectional ranks of a normal subgroup and corresponding quotient, so Lemma 2.13 shows that
![]() $s(S) \leqslant s(T) + s(S/T) = 3 + 3 = 6$
.
$s(S) \leqslant s(T) + s(S/T) = 3 + 3 = 6$
.
3 Centric radicals in
 $\operatorname {Sol}(q)$
$\operatorname {Sol}(q)$
The aim of this section is to refine the description of the centric radical subgroups of a Benson-Solomon system that results from a combination of [Reference Aschbacher and ChermakAC10, Section 10] and [Reference Chermak, Oliver and ShpectorovCOS08, Section 2]. A starting point is the next result due to Aschbacher and Chermak, which allows us to work in the groups H and K separately. Adopt the notation from Section 2, and, in particular, from Notations 2.11 and 2.12 and Sections 2.5 and 2.6. Recall that G is the Aschbacher-Chermak free amalgamated product, and that
![]() $\mathcal {F} = \mathcal {F}_S(G)$
.
$\mathcal {F} = \mathcal {F}_S(G)$
.
Proposition 3.1. Up to
![]() $\mathcal {F}$
-conjugacy, a subgroup
$\mathcal {F}$
-conjugacy, a subgroup
![]() $P \leqslant S$
is
$P \leqslant S$
is
![]() $\mathcal {F}$
-centric radical if and only if
$\mathcal {F}$
-centric radical if and only if
-
(a)
 $P = A$
is elementary abelian of order
$P = A$
is elementary abelian of order
 $2^4$
and
$2^4$
and
 $\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {GL}_4(2)$
;
$\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {GL}_4(2)$
; -
(b)
 $P=C_S(E)$
and
$P=C_S(E)$
and
 $\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {GL}_3(2)$
;
$\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {GL}_3(2)$
; -
(c) Either:
-
(i)
 $N_G(P) \le K$
and
$N_G(P) \le K$
and
 $P \in \mathcal {K}^{cr}$
; or
$P \in \mathcal {K}^{cr}$
; or -
(ii)
 $N_G(P) \le H$
and
$N_G(P) \le H$
and
 $P \in \mathcal {H}^{cr}$
.
$P \in \mathcal {H}^{cr}$
.
-
Proof. See [Reference Aschbacher and ChermakAC10, Lemma 10.9].
For the smallest Benson-Solomon system, the results of [Reference Chermak, Oliver and ShpectorovCOS08], when combined with Proposition 3.1, supply sufficiently precise information for our needs, as we make clear in Section 3.1. For the larger systems, Proposition 3.2 below yields a sufficiently detailed description for the centric radicals occurring in Proposition 3.1(c)(ii), whose normalizer in G is not contained in K.
Recall that
![]() $(V, \mathfrak {q})$
is the orthogonal space from Section 2.3;
$(V, \mathfrak {q})$
is the orthogonal space from Section 2.3;
![]() $\mathfrak {q}(v)$
is referred to as the norm of the vector v. Following [Reference Aschbacher and ChermakAC10, Section 10], we write
$\mathfrak {q}(v)$
is referred to as the norm of the vector v. Following [Reference Aschbacher and ChermakAC10, Section 10], we write
![]() $\Lambda (V)$
for the collection of all sets of pairwise orthogonal subspaces whose sum is V. For
$\Lambda (V)$
for the collection of all sets of pairwise orthogonal subspaces whose sum is V. For
![]() $\Lambda \in \Lambda (V)$
, the type of
$\Lambda \in \Lambda (V)$
, the type of
![]() $\Lambda $
is the nondecreasing list of dimensions of the members of
$\Lambda $
is the nondecreasing list of dimensions of the members of
![]() $\Lambda $
. Write
$\Lambda $
. Write
![]() $N_H(\Lambda )$
for the subgroup of H which permutes the members of
$N_H(\Lambda )$
for the subgroup of H which permutes the members of
![]() $\Lambda $
, and write
$\Lambda $
, and write
![]() $C_H(\Lambda )$
for the subgroup of H which acts on each member of
$C_H(\Lambda )$
for the subgroup of H which acts on each member of
![]() $\Lambda $
. We use exponential notation for the type, writing, for example,
$\Lambda $
. We use exponential notation for the type, writing, for example,
![]() $1^7$
for
$1^7$
for
![]() $(1,\dots ,1)$
and
$(1,\dots ,1)$
and
![]() $1^52$
for
$1^52$
for
![]() $(1,\dots ,1,2)$
. Also, we write
$(1,\dots ,1,2)$
. Also, we write
![]() $2^{1+2k}_{+}$
and
$2^{1+2k}_{+}$
and
![]() $2^{1+2k}_{-}$
for the extraspecial
$2^{1+2k}_{-}$
for the extraspecial
![]() $2$
-groups of width k and plus and minus type, respectively. Finally, if Y is a finite group and
$2$
-groups of width k and plus and minus type, respectively. Finally, if Y is a finite group and
![]() $\pi $
is a set of primes, we write (as usual)
$\pi $
is a set of primes, we write (as usual)
![]() $O_{\pi }(Y)$
for the unique maximal normal
$O_{\pi }(Y)$
for the unique maximal normal
![]() $\pi $
-subgroup of Y,
$\pi $
-subgroup of Y,
![]() $O_{\pi ,\pi '}(Y)$
for the preimage in Y of
$O_{\pi ,\pi '}(Y)$
for the preimage in Y of
![]() $O_{\pi '}(Y/O_{\pi }(Y))$
, and
$O_{\pi '}(Y/O_{\pi }(Y))$
, and
![]() $O_{\pi ,\pi ',\pi }(Y)$
for the preimage in Y of
$O_{\pi ,\pi ',\pi }(Y)$
for the preimage in Y of
![]() $O_{\pi }(Y/O_{\pi ,\pi '}(Y))$
.
$O_{\pi }(Y/O_{\pi ,\pi '}(Y))$
.
Proposition 3.2. Suppose that
![]() $P \in \mathcal {H}^{cr}$
with
$P \in \mathcal {H}^{cr}$
with
![]() $N_H(P) \nleq K$
. Then, using
$N_H(P) \nleq K$
. Then, using
![]() $*$
to denote a central product, one of the following holds.
$*$
to denote a central product, one of the following holds.
-
(a)
 $P = C_H(\Lambda )$
for some
$P = C_H(\Lambda )$
for some
 $\Lambda \in \Lambda (V)$
of type
$\Lambda \in \Lambda (V)$
of type
 $1^7$
with each member of
$1^7$
with each member of
 $\Lambda $
spanned by a vector of square norm. Moreover,
$\Lambda $
spanned by a vector of square norm. Moreover,
 $P \cong D_8*D_8*D_8 \cong 2^{1+6}_+$
, and
$P \cong D_8*D_8*D_8 \cong 2^{1+6}_+$
, and
 $\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {Out}_{\mathcal {H}}(P) \cong \begin {cases} A_7 \mbox { if } l=0 \\ S_7 \mbox { if } l> 0; \end {cases}$
$\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {Out}_{\mathcal {H}}(P) \cong \begin {cases} A_7 \mbox { if } l=0 \\ S_7 \mbox { if } l> 0; \end {cases}$
-
(b)
 $P = C_H(\Lambda )$
for some
$P = C_H(\Lambda )$
for some
 $\Lambda \in \Lambda (V)$
of type
$\Lambda \in \Lambda (V)$
of type
 $1^7$
with exactly six
$1^7$
with exactly six
 $1$
-spaces spanned by a vector of nonsquare norm. Moreover,
$1$
-spaces spanned by a vector of nonsquare norm. Moreover,
 $P \cong C_4*D_8*Q_8 = C_4*2^{1+4}_- \cong C_4 * 2^{1+4}_{+}$
and
$P \cong C_4*D_8*Q_8 = C_4*2^{1+4}_- \cong C_4 * 2^{1+4}_{+}$
and
 $\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {Out}_{\mathcal {H}}(P) \cong S_6$
;
$\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {Out}_{\mathcal {H}}(P) \cong S_6$
; -
(c)
 $l> 0$
, and
$l> 0$
, and
 $P = O_2(N_H(\Lambda ))\langle t \rangle $
for some
$P = O_2(N_H(\Lambda ))\langle t \rangle $
for some
 $\Lambda \in \Lambda (V)$
of type
$\Lambda \in \Lambda (V)$
of type
 $1^52$
with each
$1^52$
with each
 $1$
-space spanned by a vector of square norm and with the
$1$
-space spanned by a vector of square norm and with the
 $2$
-space a hyperbolic line. Moreover, t acts as
$2$
-space a hyperbolic line. Moreover, t acts as
 $-1$
on the
$-1$
on the
 $1$
-spaces and as a reflection on the line,
$1$
-spaces and as a reflection on the line,
 $P \cong D_8*Q_8 * Q_{2^{l+3}}$
, and
$P \cong D_8*Q_8 * Q_{2^{l+3}}$
, and
 $\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {Out}_{\mathcal {H}}(P) \cong S_5$
;
$\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {Out}_{\mathcal {H}}(P) \cong S_5$
; -
(d)
 $P = C_S(E/Z)$
,
$P = C_S(E/Z)$
,
 $|S:P|=2$
, and
$|S:P|=2$
, and
 $\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {Out}_{\mathcal {H}}(P) \cong S_3$
.
$\operatorname {Out}_{\mathcal {F}}(P) \cong \operatorname {Out}_{\mathcal {H}}(P) \cong S_3$
.
Moreover, there is exactly one
![]() $\mathcal {H}$
-conjugacy class of subgroups of S of each of the given types.
$\mathcal {H}$
-conjugacy class of subgroups of S of each of the given types.
Proof. Except for the last statement and the alternative descriptions of the groups P in (c) and (d), this is proved in [Reference Aschbacher and ChermakAC10, Lemma 10.7] (note each subgroup in (a)–(d) has center Z, so
![]() $\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {Out}_{\mathcal {H}}(P)$
in all cases). To see that
$\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {Out}_{\mathcal {H}}(P)$
in all cases). To see that
![]() $P \cong D_8*Q_8*Q_{2^{l+3}}$
in (c), we recall the setup of Aschbacher and Chermak as follows. Set
$P \cong D_8*Q_8*Q_{2^{l+3}}$
in (c), we recall the setup of Aschbacher and Chermak as follows. Set
![]() $\overline {H} := H/Z \cong \Omega _7(q)$
. The description of the subgroup in part (c) is discussed at and around [Reference Aschbacher and ChermakAC10, p. 937, l.5]. For such a subgroup P as in (c), P preserves a decomposition
$\overline {H} := H/Z \cong \Omega _7(q)$
. The description of the subgroup in part (c) is discussed at and around [Reference Aschbacher and ChermakAC10, p. 937, l.5]. For such a subgroup P as in (c), P preserves a decomposition
![]() $V = V_1 \perp \cdots \perp V_5 \perp W$
, where
$V = V_1 \perp \cdots \perp V_5 \perp W$
, where
![]() $\operatorname {dim} V_i = 1$
and where W is a hyperbolic line. Set
$\operatorname {dim} V_i = 1$
and where W is a hyperbolic line. Set
![]() $V_0 = V_1+\cdots +V_5$
,
$V_0 = V_1+\cdots +V_5$
,
![]() $H_1 = C_{H}(W)$
,
$H_1 = C_{H}(W)$
,
![]() $H_2 = C_H(V_0)$
, and let t be an element which acts as
$H_2 = C_H(V_0)$
, and let t be an element which acts as
![]() $-1$
on the
$-1$
on the
![]() $V_i$
and which induces a reflection on W. The subgroup of H preserving the above decomposition is of the form
$V_i$
and which induces a reflection on W. The subgroup of H preserving the above decomposition is of the form
![]() $H_1H_2\langle t \rangle $
, where
$H_1H_2\langle t \rangle $
, where
![]() $O_2(H_1) \cong D_8*Q_8$
has center Z,
$O_2(H_1) \cong D_8*Q_8$
has center Z,
![]() $H_1/O_2(H_1) \cong S_5$
, and
$H_1/O_2(H_1) \cong S_5$
, and
![]() $H_2$
is cyclic of order
$H_2$
is cyclic of order
![]() $2(q-1)$
. Further,
$2(q-1)$
. Further,
![]() $P = P_1P_2\langle t \rangle $
, where
$P = P_1P_2\langle t \rangle $
, where
![]() $P_1 = O_2(H_1)$
,
$P_1 = O_2(H_1)$
,
![]() $P_2 = O_2(H_2)$
, and
$P_2 = O_2(H_2)$
, and
![]() $[P_1,P_2\langle t \rangle ] = 1$
. The image of t in
$[P_1,P_2\langle t \rangle ] = 1$
. The image of t in
![]() $\overline {H}$
has
$\overline {H}$
has
![]() $-1$
-eigenspace of dimension
$-1$
-eigenspace of dimension
![]() $6$
, so t squares to z in H by Lemma 2.10. Likewise, an element
$6$
, so t squares to z in H by Lemma 2.10. Likewise, an element
![]() $s \in P_2$
acting as
$s \in P_2$
acting as
![]() $-1$
on W and as the identity on
$-1$
on W and as the identity on
![]() $V_0$
squares to z. This shows
$V_0$
squares to z. This shows
![]() $P_2\langle t \rangle = Q_{2^{l+3}}$
and
$P_2\langle t \rangle = Q_{2^{l+3}}$
and
![]() $Z(P_1) = Z = Z(P_2\langle t \rangle )$
, so that P has the structure as claimed in (c). The subgroup in (d) appears in the proof of 10.7 as the only subgroup P satisfying the conditions that contains an elementary abelian normal subgroup
$Z(P_1) = Z = Z(P_2\langle t \rangle )$
, so that P has the structure as claimed in (c). The subgroup in (d) appears in the proof of 10.7 as the only subgroup P satisfying the conditions that contains an elementary abelian normal subgroup
![]() $P_0$
of rank at least 3. Having such
$P_0$
of rank at least 3. Having such
![]() $P_0$
of rank
$P_0$
of rank
![]() $\geqslant 4$
is ruled out on [Reference Aschbacher and ChermakAC10, p. 957, lines 19–22]. Let
$\geqslant 4$
is ruled out on [Reference Aschbacher and ChermakAC10, p. 957, lines 19–22]. Let
![]() $P \in \mathcal {H}^{cr}$
with
$P \in \mathcal {H}^{cr}$
with
![]() $N_H(P) \nleq K$
, and assume that there is an elementary abelian normal subgroup
$N_H(P) \nleq K$
, and assume that there is an elementary abelian normal subgroup
![]() $P_0$
of P of
$P_0$
of P of
![]() $2$
-rank
$2$
-rank
![]() $3$
. Then [Reference Aschbacher and ChermakAC10, p. 973, lines 22–29] shows that
$3$
. Then [Reference Aschbacher and ChermakAC10, p. 973, lines 22–29] shows that
![]() $P_0 = E$
and
$P_0 = E$
and
![]() $C_S(E) \leqslant P$
. As
$C_S(E) \leqslant P$
. As
![]() $N_{H}(S) = S \leqslant K$
from Lemma 2.15, we have
$N_{H}(S) = S \leqslant K$
from Lemma 2.15, we have
![]() $P = C_S(E/Z)$
by Lemma 2.18. Lemma 2.17 then gives
$P = C_S(E/Z)$
by Lemma 2.18. Lemma 2.17 then gives
![]() $\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {Out}_{\mathcal {H}}(P) \cong S_3$
.
$\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {Out}_{\mathcal {H}}(P) \cong S_3$
.
Finally, we must verify the last statement. For P in (a)–(b), this follows from a slight extension of Witt’s lemma, as stated in [Reference Gorenstein, Lyons and SolomonGLS98, Lemma 2.7.2], and induction on dimension. Consider a subgroup satisfying the conditions in (c). From the description of P in the first paragraph, we see that P is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $O_{2',2}(N_H(\Lambda ))$
. By [Reference Gorenstein, Lyons and SolomonGLS98, Lemma 2.7.2] again,
$O_{2',2}(N_H(\Lambda ))$
. By [Reference Gorenstein, Lyons and SolomonGLS98, Lemma 2.7.2] again,
![]() $O_{2',2}(N_H(\Lambda ))$
is uniquely determined up to H-conjugacy, so P is uniquely determined up to H-conjugacy by Sylow’s theorem in
$O_{2',2}(N_H(\Lambda ))$
is uniquely determined up to H-conjugacy, so P is uniquely determined up to H-conjugacy by Sylow’s theorem in
![]() $O_{2',2}(N_{H}(\Lambda ))$
. For uniqueness of the subgroup in (d), there is nothing to do. This completes the proof of the proposition.
$O_{2',2}(N_{H}(\Lambda ))$
. For uniqueness of the subgroup in (d), there is nothing to do. This completes the proof of the proposition.
Notation 3.3. We denote a member of the
![]() $\mathcal {F}$
-conjugacy class of a subgroup appearing in Proposition 3.2 parts (a), (b), and (c) by
$\mathcal {F}$
-conjugacy class of a subgroup appearing in Proposition 3.2 parts (a), (b), and (c) by
![]() $R_{1^7}$
,
$R_{1^7}$
,
![]() $R_{1^7}'$
, and
$R_{1^7}'$
, and
![]() $R_{1^52}$
, respectively, to best indicate their origins. The reader should not confuse these with the generalized quaternion groups
$R_{1^52}$
, respectively, to best indicate their origins. The reader should not confuse these with the generalized quaternion groups
![]() $R_1$
,
$R_1$
,
![]() $R_2$
, and
$R_2$
, and
![]() $R_3$
. When
$R_3$
. When
![]() $l = 0$
, the subgroups
$l = 0$
, the subgroups
![]() $R_{1^7}$
and
$R_{1^7}$
and
![]() $R_{1^7}'$
correspond with the subgroups R and
$R_{1^7}'$
correspond with the subgroups R and
![]() $R^*$
of Section 2 of [Reference Chermak, Oliver and ShpectorovCOS08].
$R^*$
of Section 2 of [Reference Chermak, Oliver and ShpectorovCOS08].
We next describe the centric radical subgroups arising in case (c)(i) of Proposition 3.1. Recall Notations 2.11 and 2.12. In addition, for any subgroup Y of K, we set
![]() $Y_0 = Y \cap L_0$
, and let
$Y_0 = Y \cap L_0$
, and let
![]() $Y_i$
be the projection of
$Y_i$
be the projection of
![]() $Y_0$
in
$Y_0$
in
![]() $L_i$
for
$L_i$
for
![]() $1 \leqslant i \leqslant 3$
. That is,
$1 \leqslant i \leqslant 3$
. That is,
![]() $Y_i$
is the image in
$Y_i$
is the image in
![]() $L_i$
of the projection of the preimage of
$L_i$
of the projection of the preimage of
![]() $Y_0$
in
$Y_0$
in
![]() $\widehat {L}_i$
(cf. Notation 2.11(a)) under the quotient map
$\widehat {L}_i$
(cf. Notation 2.11(a)) under the quotient map
![]() $\widehat {K} \to K$
.
$\widehat {K} \to K$
.
Proposition 3.4. Fix
![]() $P \leqslant S$
. Then
$P \leqslant S$
. Then
![]() $P \in \mathcal {K}^{cr}$
if and only if
$P \in \mathcal {K}^{cr}$
if and only if
-
(a)
 $P \cap L_0 = P_1P_2P_3$
, and for each
$P \cap L_0 = P_1P_2P_3$
, and for each
 $i \in \{1,2,3\}$
, either
$i \in \{1,2,3\}$
, either
 $P_i \in \mathcal {Q}_i$
or
$P_i \in \mathcal {Q}_i$
or
 $P_i = R_i$
; and
$P_i = R_i$
; and -
(b) one of the following holds. Either,
-
(i)
 $P \in \{C_S(U), S\}$
,
$P \in \{C_S(U), S\}$
, -
(ii)
 $P = P_1P_2P_3 \leqslant R_0$
with
$P = P_1P_2P_3 \leqslant R_0$
with
 $P_i \in \mathcal {Q}_i$
for at least two indices i, or
$P_i \in \mathcal {Q}_i$
for at least two indices i, or -
(iii)
 $P = P_0\langle s \rangle $
for some
$P = P_0\langle s \rangle $
for some
 $s \in P \backslash C_P(U)$
, such that
$s \in P \backslash C_P(U)$
, such that-
(1)
 $s^2 \in P_0$
,
$s^2 \in P_0$
, -
(2) either
 $P_3 \in \mathcal {Q}_3$
or
$P_3 \in \mathcal {Q}_3$
or
 $P_i \in \mathcal {Q}_i$
for both
$P_i \in \mathcal {Q}_i$
for both
 $i = 1$
and
$i = 1$
and
 $2$
, and
$2$
, and -
(3) if
 $P_3 \in \mathcal {Q}_3$
, then
$P_3 \in \mathcal {Q}_3$
, then
 $\operatorname {Out}_{L_3}(P)$
is not a
$\operatorname {Out}_{L_3}(P)$
is not a
 $2$
-group.
$2$
-group.
-
-
Proof. This is part of [Reference Aschbacher and ChermakAC10, Lemma 10.2], namely, (c) and (d) of that lemma together with the statement beginning “Conversely”. The requirement here in (b)(iii)(1) that s square into
![]() $P_0$
does not appear in [Reference Aschbacher and ChermakAC10], but it is needed for the “if” part of the proposition to hold in general. A patch for the proof of the “if” part in [Reference Aschbacher and ChermakAC10, Lemma 10.2] is given later in Remark 3.10.
$P_0$
does not appear in [Reference Aschbacher and ChermakAC10], but it is needed for the “if” part of the proposition to hold in general. A patch for the proof of the “if” part in [Reference Aschbacher and ChermakAC10, Lemma 10.2] is given later in Remark 3.10.
3.1 The case
 $l=0$
$l=0$
An important distinguishing feature of the smallest Benson-Solomon system is that
![]() $R_0$
is normal in the fusion system
$R_0$
is normal in the fusion system
![]() $\mathcal {K}$
. When
$\mathcal {K}$
. When
![]() $l = 0$
, this is most naturally seen over
$l = 0$
, this is most naturally seen over
![]() $\mathbb {F}_3$
, where a
$\mathbb {F}_3$
, where a
![]() $Q_8$
Sylow
$Q_8$
Sylow
![]() $2$
-subgroup is normal in
$2$
-subgroup is normal in
![]() $\operatorname {SL}_2(3)$
. Over
$\operatorname {SL}_2(3)$
. Over
![]() $\mathbb {F}_5$
, the normalizer of a quaternion Sylow
$\mathbb {F}_5$
, the normalizer of a quaternion Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\operatorname {SL}_2(5)$
is
$\operatorname {SL}_2(5)$
is
![]() $\operatorname {SL}_2(3)$
, which still controls
$\operatorname {SL}_2(3)$
, which still controls
![]() $2$
-fusion in
$2$
-fusion in
![]() $\operatorname {SL}_2(5)$
(c.f. Lemma 2.9). It will therefore be convenient to treat the cases
$\operatorname {SL}_2(5)$
(c.f. Lemma 2.9). It will therefore be convenient to treat the cases
![]() $l=0$
and
$l=0$
and
![]() $l> 0$
separately. So assume here that
$l> 0$
separately. So assume here that
![]() $l = 0$
. We adopt the previous notation, except that we set
$l = 0$
. We adopt the previous notation, except that we set
in this smallest case so that Q,
![]() $R_{1^7}$
, and
$R_{1^7}$
, and
![]() $R_{1^7}'$
correspond with the groups “Q,” “R,” and “
$R_{1^7}'$
correspond with the groups “Q,” “R,” and “
![]() $R^*$
” considered in [Reference Chermak, Oliver and ShpectorovCOS08, Section 2].
$R^*$
” considered in [Reference Chermak, Oliver and ShpectorovCOS08, Section 2].
The next proposition lists the
![]() $\mathcal {K}$
-centric radicals when
$\mathcal {K}$
-centric radicals when
![]() $l = 0$
, and does not require Proposition 3.4.
$l = 0$
, and does not require Proposition 3.4.
Proposition 3.5. Let
![]() $l = 0$
and
$l = 0$
and
![]() $P \in \mathcal {K}^{cr}$
. Then exactly one of the following holds.
$P \in \mathcal {K}^{cr}$
. Then exactly one of the following holds.
-
(a)
 $P = S$
, and
$P = S$
, and
 $\operatorname {Out}_{\mathcal {K}}(P) = 1$
;
$\operatorname {Out}_{\mathcal {K}}(P) = 1$
; -
(b)
 $P = Q$
, and
$P = Q$
, and
 $\operatorname {Out}_{\mathcal {K}}(P) \cong (C_3)^3 \overset {-1 \times \wr }{\rtimes } (C_2 \times S_3)$
, where here, and in Table 1, the notation
$\operatorname {Out}_{\mathcal {K}}(P) \cong (C_3)^3 \overset {-1 \times \wr }{\rtimes } (C_2 \times S_3)$
, where here, and in Table 1, the notation
 $-1 \times \wr $
indicates that the
$-1 \times \wr $
indicates that the
 $C_2$
factor acts by inversion while
$C_2$
factor acts by inversion while
 $S_3$
acts by wreathing;
$S_3$
acts by wreathing; -
(c)
 $P = Q\langle \tau \rangle $
, and
$P = Q\langle \tau \rangle $
, and
 $\operatorname {Out}_{\mathcal {K}}(P) \cong (C_3 \times C_3) \overset {-1}{\rtimes } C_2$
;
$\operatorname {Out}_{\mathcal {K}}(P) \cong (C_3 \times C_3) \overset {-1}{\rtimes } C_2$
; -
(d)
 $P = Q\langle \tau ' \rangle $
, and
$P = Q\langle \tau ' \rangle $
, and
 $\operatorname {Out}_{\mathcal {K}}(P) \cong S_3$
; or
$\operatorname {Out}_{\mathcal {K}}(P) \cong S_3$
; or -
(e)
 $P = C_S(U) = Q\langle \mathbf {d} \rangle $
, and
$P = C_S(U) = Q\langle \mathbf {d} \rangle $
, and
 $\operatorname {Out}_{\mathcal {K}}(P) \cong S_3$
.
$\operatorname {Out}_{\mathcal {K}}(P) \cong S_3$
.
Proof. As Q is a centric normal
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathcal {K}$
, it is contained in every member of
$\mathcal {K}$
, it is contained in every member of
![]() $\mathcal {K}^{cr}$
by Lemma 2.5. Now
$\mathcal {K}^{cr}$
by Lemma 2.5. Now
![]() $S/Q$
is a four group (the four group
$S/Q$
is a four group (the four group
![]() $\langle \mathbf {d}, \tau \rangle $
is a complement to Q in S), so there are only five possible centric radical subgroups. Since
$\langle \mathbf {d}, \tau \rangle $
is a complement to Q in S), so there are only five possible centric radical subgroups. Since
![]() $O^2(K) \cap S = Q$
, if two distinct subgroups of S containing Q were
$O^2(K) \cap S = Q$
, if two distinct subgroups of S containing Q were
![]() $\mathcal {K}$
-conjugate, then two distinct subgroups of the abelian group
$\mathcal {K}$
-conjugate, then two distinct subgroups of the abelian group
![]() $S/Q$
would be
$S/Q$
would be
![]() $K/O^2(K) \cong S/Q$
-conjugate. Since this is not the case, no two distinct subgroups of S containing Q are
$K/O^2(K) \cong S/Q$
-conjugate. Since this is not the case, no two distinct subgroups of S containing Q are
![]() $\mathcal {K}$
-conjugate. Next, from the definition of U, both Q and
$\mathcal {K}$
-conjugate. Next, from the definition of U, both Q and
![]() $\mathbf {d}$
centralize U while
$\mathbf {d}$
centralize U while
![]() $\tau $
does not, so we must have
$\tau $
does not, so we must have
![]() $Q\langle \mathbf {d} \rangle =C_S(U)$
. This shows the equality in (e).
$Q\langle \mathbf {d} \rangle =C_S(U)$
. This shows the equality in (e).
The structure of the outer automorphism groups are computable from knowledge of
![]() $\operatorname {Out}_{\mathcal {K}}(Q)$
: note that from the structure of K (cf. Lemma 2.9),
$\operatorname {Out}_{\mathcal {K}}(Q)$
: note that from the structure of K (cf. Lemma 2.9),
is a split extension of the wreath product
![]() $C_3 \wr S_3$
by the group generated by the class
$C_3 \wr S_3$
by the group generated by the class
![]() $\left [c_{\mathbf {d}}\right ] \in \operatorname {Out}_{\mathcal {K}}(Q)$
of conjugation by
$\left [c_{\mathbf {d}}\right ] \in \operatorname {Out}_{\mathcal {K}}(Q)$
of conjugation by
![]() $\mathbf {d}$
acting by inversion on the base. As Q is weakly
$\mathbf {d}$
acting by inversion on the base. As Q is weakly
![]() $\mathcal {K}$
-closed and centric,
$\mathcal {K}$
-closed and centric,
![]() $\operatorname {Out}_{\mathcal {K}}(P) \cong N_{\operatorname {Out}_{\mathcal {K}}(Q)}(\operatorname {Out}_P(Q))/\operatorname {Out}_P(Q)$
for each overgroup P of Q in S by Lemma 2.7. From a computation in the group
$\operatorname {Out}_{\mathcal {K}}(P) \cong N_{\operatorname {Out}_{\mathcal {K}}(Q)}(\operatorname {Out}_P(Q))/\operatorname {Out}_P(Q)$
for each overgroup P of Q in S by Lemma 2.7. From a computation in the group
![]() $(C_3)^3 \overset {-1 \times \wr }{\rtimes } (C_2 \times S_3)$
, one sees, for example, that
$(C_3)^3 \overset {-1 \times \wr }{\rtimes } (C_2 \times S_3)$
, one sees, for example, that
where the acting group is given by
![]() $\langle \left [c_{\mathbf {d}} \right ]\rangle \times \langle \left [c_{\tau } \right ]\rangle $
. This shows that
$\langle \left [c_{\mathbf {d}} \right ]\rangle \times \langle \left [c_{\tau } \right ]\rangle $
. This shows that
![]() $\operatorname {Out}_{\mathcal {K}}(Q\langle \tau \rangle ) = N_{\operatorname {Out}_{\mathcal {K}}(Q)}(\langle \left [ c_\tau \right ] \rangle )/\langle \left [ c_\tau \right ] \rangle \cong (C_3 \times C_3) \overset {-1}{\rtimes } C_2$
as claimed. Cases (d) and (e) are handled similarly. Visibly, no resulting outer automorphism group has a nontrivial normal
$\operatorname {Out}_{\mathcal {K}}(Q\langle \tau \rangle ) = N_{\operatorname {Out}_{\mathcal {K}}(Q)}(\langle \left [ c_\tau \right ] \rangle )/\langle \left [ c_\tau \right ] \rangle \cong (C_3 \times C_3) \overset {-1}{\rtimes } C_2$
as claimed. Cases (d) and (e) are handled similarly. Visibly, no resulting outer automorphism group has a nontrivial normal
![]() $2$
-subgroup, so all the candidate subgroups are
$2$
-subgroup, so all the candidate subgroups are
![]() $\mathcal {K}$
-centric radical.
$\mathcal {K}$
-centric radical.
Table 1
![]() $\operatorname {Sol}(5)$
-conjugacy classes of
$\operatorname {Sol}(5)$
-conjugacy classes of
![]() $\operatorname {Sol}(5)$
-centric radical subgroups.
$\operatorname {Sol}(5)$
-centric radical subgroups.

Proposition 3.6. Let
![]() $l = 0$
. Then, up to conjugacy, the
$l = 0$
. Then, up to conjugacy, the
![]() $\mathcal {K}$
-,
$\mathcal {K}$
-,
![]() $\mathcal {H}$
-, and
$\mathcal {H}$
-, and
![]() $\mathcal {F}$
-centric radical subgroups of S together with their orders and automorphism groups appear in Table 1, where a “
$\mathcal {F}$
-centric radical subgroups of S together with their orders and automorphism groups appear in Table 1, where a “
![]() $-$
” indicates that the subgroup is not centric radical in that fusion system.
$-$
” indicates that the subgroup is not centric radical in that fusion system.
Proof. By Proposition 3.5, the column for
![]() $\mathcal {K}$
is correct. By [Reference Chermak, Oliver and ShpectorovCOS08, Lemma 2.1] and [Reference Levi and OliverLO02, Lemma A.11(e,f)], the column for
$\mathcal {K}$
is correct. By [Reference Chermak, Oliver and ShpectorovCOS08, Lemma 2.1] and [Reference Levi and OliverLO02, Lemma A.11(e,f)], the column for
![]() $\mathcal {H}$
is correct. We work up to
$\mathcal {H}$
is correct. We work up to
![]() $\mathcal {F}$
-conjugacy in what follows. Let
$\mathcal {F}$
-conjugacy in what follows. Let
![]() $P \in \mathcal {F}^{cr}$
. By Proposition 3.1, either P is listed in the last two rows of Table 1, or one of the following holds: (1)
$P \in \mathcal {F}^{cr}$
. By Proposition 3.1, either P is listed in the last two rows of Table 1, or one of the following holds: (1)
![]() $P \in \mathcal {K}^{cr}$
and
$P \in \mathcal {K}^{cr}$
and
![]() $\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {Out}_{\mathcal {K}}(P)$
, or (2)
$\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {Out}_{\mathcal {K}}(P)$
, or (2)
![]() $N_G(P) \nleq K$
,
$N_G(P) \nleq K$
,
![]() $P \in \mathcal {H}^{cr}$
, and
$P \in \mathcal {H}^{cr}$
, and
![]() $\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {Out}_{\mathcal {H}}(P)$
. If (1) holds, then P is listed in the first five rows of the table by Proposition 3.5. If (1) does not hold, then (2) holds, P is listed in the next three rows of the table, where the entries follow from Proposition 3.2(a,b,d).
$\operatorname {Out}_{\mathcal {F}}(P) = \operatorname {Out}_{\mathcal {H}}(P)$
. If (1) holds, then P is listed in the first five rows of the table by Proposition 3.5. If (1) does not hold, then (2) holds, P is listed in the next three rows of the table, where the entries follow from Proposition 3.2(a,b,d).
That no additional
![]() $\mathcal {F}$
-conjugacy can occur between these subgroups can be seen in several ways, one of which as follows. Only three subgroups have pairwise equal orders and isomorphic outer automorphism groups in
$\mathcal {F}$
-conjugacy can occur between these subgroups can be seen in several ways, one of which as follows. Only three subgroups have pairwise equal orders and isomorphic outer automorphism groups in
![]() $\mathcal {F}$
, namely,
$\mathcal {F}$
, namely,
![]() $Q\langle \tau ' \rangle $
,
$Q\langle \tau ' \rangle $
,
![]() $C_S(U)$
, and
$C_S(U)$
, and
![]() $C_S(E/Z)$
.
$C_S(E/Z)$
.
By Lemma 2.14,
![]() $C_S(E/Z)$
has center Z. Likewise, since
$C_S(E/Z)$
has center Z. Likewise, since
![]() $Z(Q) = U$
, we have
$Z(Q) = U$
, we have
![]() $Z(Q\langle \tau ' \rangle ) = C_{U}(\tau ')~=~Z$
. So as
$Z(Q\langle \tau ' \rangle ) = C_{U}(\tau ')~=~Z$
. So as
![]() $U \leqslant Z(C_S(U))$
, it follows that
$U \leqslant Z(C_S(U))$
, it follows that
![]() $C_S(U)$
is not
$C_S(U)$
is not
![]() $\mathcal {F}$
-conjugate to either of the other two subgroups.
$\mathcal {F}$
-conjugate to either of the other two subgroups.
Finally, note that
![]() $C_S(E/Z)$
contains the torus T. On the other hand, from the description of T in Section 2.5, we see that
$C_S(E/Z)$
contains the torus T. On the other hand, from the description of T in Section 2.5, we see that
![]() $Q \cap T = \langle [a,1,1],[1,a,1],[c^2,c^2,c^2] \rangle $
is of index
$Q \cap T = \langle [a,1,1],[1,a,1],[c^2,c^2,c^2] \rangle $
is of index
![]() $2$
in T. As each element in the coset
$2$
in T. As each element in the coset
![]() $Q\tau '$
is nontrivial on
$Q\tau '$
is nontrivial on
![]() $Q \cap T$
and T is abelian, it follows that
$Q \cap T$
and T is abelian, it follows that
![]() $Q\langle \tau ' \rangle \cap T$
is still of index
$Q\langle \tau ' \rangle \cap T$
is still of index
![]() $2$
in T. So
$2$
in T. So
![]() $C_S(E/Z)$
contains T, but
$C_S(E/Z)$
contains T, but
![]() $Q\langle \tau ' \rangle $
does not. Since T is weakly
$Q\langle \tau ' \rangle $
does not. Since T is weakly
![]() $\mathcal {F}$
-closed (Lemma 2.13), the subgroups
$\mathcal {F}$
-closed (Lemma 2.13), the subgroups
![]() $C_S(E/Z)$
and
$C_S(E/Z)$
and
![]() $Q\langle \tau ' \rangle $
are not
$Q\langle \tau ' \rangle $
are not
![]() $\mathcal {F}$
-conjugate.
$\mathcal {F}$
-conjugate.
We end this subsection with two lemmas in the case
![]() $l=0$
, which will be needed later.
$l=0$
, which will be needed later.
Lemma 3.7. Each member of
![]() $\mathcal {F}^{cr}-\{A\}$
is weakly
$\mathcal {F}^{cr}-\{A\}$
is weakly
![]() $\mathcal {F}$
-closed when
$\mathcal {F}$
-closed when
![]() $l=0$
.
$l=0$
.
Proof. The subgroup S is clearly weakly closed, and
![]() $C_S(E)$
,
$C_S(E)$
,
![]() $C_S(U)$
, and
$C_S(U)$
, and
![]() $C_S(E/Z)$
were shown to be weakly
$C_S(E/Z)$
were shown to be weakly
![]() $\mathcal {F}$
-closed in Lemmas 2.14, 2.16, and 2.17. Let P be one of the remaining subgroups, but not A. By Proposition 3.6, P is centric and radical in
$\mathcal {F}$
-closed in Lemmas 2.14, 2.16, and 2.17. Let P be one of the remaining subgroups, but not A. By Proposition 3.6, P is centric and radical in
![]() $\mathcal {H}$
, and either
$\mathcal {H}$
, and either
![]() $P = Q$
or
$P = Q$
or
![]() $Z(P) = Z$
. The quotient
$Z(P) = Z$
. The quotient
![]() $P/Z$
is centric and radical in
$P/Z$
is centric and radical in
![]() $\mathcal {H}/Z$
by [Reference Levi and OliverLO02, Lemma A.11(e)]. Hence,
$\mathcal {H}/Z$
by [Reference Levi and OliverLO02, Lemma A.11(e)]. Hence,
![]() $P/Z$
is weakly
$P/Z$
is weakly
![]() $\mathcal {H}/Z$
-closed by [Reference Chermak, Oliver and ShpectorovCOS08, Lemma 2.1]. It follows that P is weakly
$\mathcal {H}/Z$
-closed by [Reference Chermak, Oliver and ShpectorovCOS08, Lemma 2.1]. It follows that P is weakly
![]() $\mathcal {H}$
-closed. Since Q is normal in
$\mathcal {H}$
-closed. Since Q is normal in
![]() $\mathcal {K}$
, it is weakly
$\mathcal {K}$
, it is weakly
![]() $\mathcal {K}$
-closed. Hence, Q is weakly
$\mathcal {K}$
-closed. Hence, Q is weakly
![]() $\mathcal {F}$
-closed since
$\mathcal {F}$
-closed since
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {K}$
are fusion systems over S which generate
$\mathcal {K}$
are fusion systems over S which generate
![]() $\mathcal {F}$
(end of Section 2.4).
$\mathcal {F}$
(end of Section 2.4).
We are reduced to the case in which
![]() $Z(P) = Z$
. Assume on the contrary that P is not weakly
$Z(P) = Z$
. Assume on the contrary that P is not weakly
![]() $\mathcal {F}$
-closed. By Alperin’s Fusion theorem [Reference Broto, Levi and OliverBLO03, Theorem A.10], there is an overgroup
$\mathcal {F}$
-closed. By Alperin’s Fusion theorem [Reference Broto, Levi and OliverBLO03, Theorem A.10], there is an overgroup
![]() $Y \leqslant S$
of P and an automorphism
$Y \leqslant S$
of P and an automorphism
![]() $\alpha \in \operatorname {Aut}_{\mathcal {F}}(Y)$
, such that
$\alpha \in \operatorname {Aut}_{\mathcal {F}}(Y)$
, such that
![]() $P^\alpha \neq P$
. Then
$P^\alpha \neq P$
. Then
![]() $Z(Y) \leqslant Z(P) = Z$
, as P is centric, so that
$Z(Y) \leqslant Z(P) = Z$
, as P is centric, so that
![]() $Z(Y) = Z$
is centralized by
$Z(Y) = Z$
is centralized by
![]() $\alpha $
. That is,
$\alpha $
. That is,
![]() $\alpha \in \mathcal {H}$
. But then
$\alpha \in \mathcal {H}$
. But then
![]() $P^\alpha = P$
by the previous paragraph, a contradiction.
$P^\alpha = P$
by the previous paragraph, a contradiction.
Lemma 3.8.
![]() $QR_{1^7} = Q\langle \tau \rangle $
and
$QR_{1^7} = Q\langle \tau \rangle $
and
![]() $QR_{1^7}' = Q\langle \tau ' \rangle $
when
$QR_{1^7}' = Q\langle \tau ' \rangle $
when
![]() $l = 0$
.
$l = 0$
.
Proof. This is a statement depending on H only. Since
![]() $l=0$
,
$l=0$
,
![]() $q = 5$
. Write
$q = 5$
. Write
![]() $\overline {H}$
for
$\overline {H}$
for
![]() $H/Z$
. Fix a decomposition
$H/Z$
. Fix a decomposition
with the following properties ([Reference Aschbacher and ChermakAC10, cf. Lemmas 4.4, 4.6]):
-
1. each
 $\ell _i = \langle x_{2i-1}, x_{2i} \rangle $
is a hyperbolic line (i.e.,
$\ell _i = \langle x_{2i-1}, x_{2i} \rangle $
is a hyperbolic line (i.e.,
 $\mathfrak {q}(x_{2i-1}) = 0 = \mathfrak {q}(x_{2i})$
,
$\mathfrak {q}(x_{2i-1}) = 0 = \mathfrak {q}(x_{2i})$
,
 $\mathfrak {b}(x_{2i-1}, x_{2i}) = 1$
), and
$\mathfrak {b}(x_{2i-1}, x_{2i}) = 1$
), and
 $\mathfrak {q}(x_7) = 1$
.
$\mathfrak {q}(x_7) = 1$
. -
2.
 $\ell _1 \perp \ell _2 = \langle x_1,x_4 \rangle \oplus \langle x_3,x_2 \rangle $
, with each summand on the right side a natural
$\ell _1 \perp \ell _2 = \langle x_1,x_4 \rangle \oplus \langle x_3,x_2 \rangle $
, with each summand on the right side a natural
 $\mathbb {F}_5L_1$
-module; in particular,
$\mathbb {F}_5L_1$
-module; in particular,
 $[a,1,1]$
and
$[a,1,1]$
and
 $[b,1,1]$
act via the matrices with respect to the basis
$[b,1,1]$
act via the matrices with respect to the basis $$ \begin{align*} [a,1,1] &\mapsto \left[\begin{smallmatrix}2&0&0&0\\0&-2&0&0\\0&0&2&0\\0&0&0&-2\end{smallmatrix}\right] & [b,1,1] &\mapsto \left[\begin{smallmatrix}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{smallmatrix}\right] \end{align*} $$
$$ \begin{align*} [a,1,1] &\mapsto \left[\begin{smallmatrix}2&0&0&0\\0&-2&0&0\\0&0&2&0\\0&0&0&-2\end{smallmatrix}\right] & [b,1,1] &\mapsto \left[\begin{smallmatrix}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{smallmatrix}\right] \end{align*} $$
 $\{x_1,x_2,x_3,x_4\}$
.
$\{x_1,x_2,x_3,x_4\}$
.
-
3.
 $\ell _1 \perp \ell _2 = \langle x_1,x_3 \rangle \oplus \langle x_4,x_2 \rangle $
, with each summand on the right side a natural
$\ell _1 \perp \ell _2 = \langle x_1,x_3 \rangle \oplus \langle x_4,x_2 \rangle $
, with each summand on the right side a natural
 $\mathbb {F}_5L_2$
-module; in particular,
$\mathbb {F}_5L_2$
-module; in particular,
 $[1,a,1]$
and
$[1,a,1]$
and
 $[1,b,1]$
act via the matrices with respect to the basis
$[1,b,1]$
act via the matrices with respect to the basis $$ \begin{align*} [1,a,1] &\mapsto \left[\begin{smallmatrix}2&0&0&0\\0&-2&0&0\\0&0&-2&0\\0&0&0&2\end{smallmatrix}\right] & [1,b,1] &\mapsto \left[\begin{smallmatrix}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{smallmatrix}\right] \end{align*} $$
$$ \begin{align*} [1,a,1] &\mapsto \left[\begin{smallmatrix}2&0&0&0\\0&-2&0&0\\0&0&-2&0\\0&0&0&2\end{smallmatrix}\right] & [1,b,1] &\mapsto \left[\begin{smallmatrix}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{smallmatrix}\right] \end{align*} $$
 $\{x_1,x_2,x_3,x_4\}$
.
$\{x_1,x_2,x_3,x_4\}$
.
-
4.
 $\ell _3 \perp \langle x_7 \rangle $
is the three-dimensional orthogonal module for
$\ell _3 \perp \langle x_7 \rangle $
is the three-dimensional orthogonal module for
 $L_3 \cong \operatorname {Spin}_3(5)$
. We may view it as the module in which
$L_3 \cong \operatorname {Spin}_3(5)$
. We may view it as the module in which
 $L_3$
acts by conjugation on
$L_3$
acts by conjugation on
 $2\times 2$
trace zero matrices
$2\times 2$
trace zero matrices
 $M_2^0(\mathbb {F}_5)$
with quadratic form given by the determinant, via the isometry
$M_2^0(\mathbb {F}_5)$
with quadratic form given by the determinant, via the isometry
 $M_2^0(\mathbb {F}_5) \longrightarrow \ell _3 \perp \{x_7\}$
defined by Under this identification,
$M_2^0(\mathbb {F}_5) \longrightarrow \ell _3 \perp \{x_7\}$
defined by Under this identification, $$\begin{align*}\left\{\left[\begin{smallmatrix}0&0\\2&0\end{smallmatrix}\right], \left[\begin{smallmatrix}0&-1\\0&0\end{smallmatrix}\right], \left[\begin{smallmatrix}2&0\\0&-2\end{smallmatrix}\right]\right\} \longmapsto \{x_5,x_6,x_7\}. \end{align*}$$
$$\begin{align*}\left\{\left[\begin{smallmatrix}0&0\\2&0\end{smallmatrix}\right], \left[\begin{smallmatrix}0&-1\\0&0\end{smallmatrix}\right], \left[\begin{smallmatrix}2&0\\0&-2\end{smallmatrix}\right]\right\} \longmapsto \{x_5,x_6,x_7\}. \end{align*}$$
 $[1,1,a]$
acts via the matrix
$[1,1,a]$
acts via the matrix
 $\operatorname {diag}(-1, -1, 1)$
with respect to the ordered basis
$\operatorname {diag}(-1, -1, 1)$
with respect to the ordered basis
 $\{x_5,x_6,x_7\}$
, and
$\{x_5,x_6,x_7\}$
, and
 $[1,1,b]$
acts via the matrix
$[1,1,b]$
acts via the matrix
 $\left [\begin {smallmatrix}0&2&0\\-2&0&0\\0&0&-1\end {smallmatrix}\right ]$
.
$\left [\begin {smallmatrix}0&2&0\\-2&0&0\\0&0&-1\end {smallmatrix}\right ]$
.
Next, define
![]() $u_{j}$
and
$u_{j}$
and
![]() $v_{j}$
via
$v_{j}$
via
 $$ \begin{align*} u_{2i-1} &= x_{2i-1}-2x_{2i}, & v_{2i-1} &= u_{2i-1}+u_{2i},\\ u_{2i} &= -2x_{2i-1}+x_{2i}, & v_{2i} &= u_{2i-1}-u_{2i},\\ u_7 &= x_7, & v_7 &= u_7. \end{align*} $$
$$ \begin{align*} u_{2i-1} &= x_{2i-1}-2x_{2i}, & v_{2i-1} &= u_{2i-1}+u_{2i},\\ u_{2i} &= -2x_{2i-1}+x_{2i}, & v_{2i} &= u_{2i-1}-u_{2i},\\ u_7 &= x_7, & v_7 &= u_7. \end{align*} $$
Thus,
![]() $\{u_1,\dots ,u_7\}$
is an orthonormal basis for V, and
$\{u_1,\dots ,u_7\}$
is an orthonormal basis for V, and
![]() $\{v_1,\dots ,v_7\}$
is an orthogonal basis, such that
$\{v_1,\dots ,v_7\}$
is an orthogonal basis, such that
![]() $\mathfrak {q}(v_i) = 2 \notin \mathbb {F}_5^{\times 2}$
for each
$\mathfrak {q}(v_i) = 2 \notin \mathbb {F}_5^{\times 2}$
for each
![]() $i = 1,\dots ,6$
. The decompositions
$i = 1,\dots ,6$
. The decompositions
of V are therefore of the type appearing in Proposition 3.2(a) and (b), respectively. The centralizers of the decompositions are
 $$ \begin{align*} C_H(\Lambda) &= \{e \in \operatorname{Spin}_7(5) \mid (u_i)\overline{e} = \pm u_i, i = 1,\dots,7\}, \text{ and}\\ C_{H}(\Lambda') &= \{f \in \operatorname{Spin}_7(5) \mid (v_i)\overline{f} = \pm v_i, i = 1,\dots,7\}. \end{align*} $$
$$ \begin{align*} C_H(\Lambda) &= \{e \in \operatorname{Spin}_7(5) \mid (u_i)\overline{e} = \pm u_i, i = 1,\dots,7\}, \text{ and}\\ C_{H}(\Lambda') &= \{f \in \operatorname{Spin}_7(5) \mid (v_i)\overline{f} = \pm v_i, i = 1,\dots,7\}. \end{align*} $$
Observe from the definition of the
![]() $v_i$
that
$v_i$
that
![]() $C_H(\Lambda ) \leqslant N_H(\Lambda ')$
. Similarly, it is a straightforward computation to see using (2)–(4) that Q acts on the sets
$C_H(\Lambda ) \leqslant N_H(\Lambda ')$
. Similarly, it is a straightforward computation to see using (2)–(4) that Q acts on the sets
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
, that is,
$\Lambda '$
, that is,
![]() $Q \leqslant N_H(\Lambda )$
and
$Q \leqslant N_H(\Lambda )$
and
![]() $Q \leqslant N_H(\Lambda ')$
. It follows that
$Q \leqslant N_H(\Lambda ')$
. It follows that
![]() $QC_H(\Lambda )C_H(\Lambda )'$
is a
$QC_H(\Lambda )C_H(\Lambda )'$
is a
![]() $2$
-subgroup of H. Hence, we may choose
$2$
-subgroup of H. Hence, we may choose
![]() $h \in H$
with
$h \in H$
with
![]() $(QC_H(\Lambda )C_H(\Lambda '))^h \leqslant S$
. But
$(QC_H(\Lambda )C_H(\Lambda '))^h \leqslant S$
. But
![]() $Q \leqslant S$
, and so
$Q \leqslant S$
, and so
![]() $Q^h = Q$
by Lemma 3.7. Likewise, it follows from Lemma 3.7 that
$Q^h = Q$
by Lemma 3.7. Likewise, it follows from Lemma 3.7 that
![]() $C_H(\Lambda )^h = R_{1^7}$
and
$C_H(\Lambda )^h = R_{1^7}$
and
![]() $C_H(\Lambda ')^h = R_{1^7}'$
. Replacing S with
$C_H(\Lambda ')^h = R_{1^7}'$
. Replacing S with
![]() $S^{h^{-1}}$
if necessary, we may assume that
$S^{h^{-1}}$
if necessary, we may assume that
![]() $R_{1^7} = C_H(\Lambda )$
and
$R_{1^7} = C_H(\Lambda )$
and
![]() $R_{1^7}' = C_H(\Lambda ')$
.
$R_{1^7}' = C_H(\Lambda ')$
.
For a subset
![]() $I \subseteq \{1,\dots ,7\}$
, write
$I \subseteq \{1,\dots ,7\}$
, write
![]() $e_I$
for a fixed element of
$e_I$
for a fixed element of
![]() $C_H(\Lambda )$
which maps
$C_H(\Lambda )$
which maps
![]() $u_i \mapsto -u_i$
if
$u_i \mapsto -u_i$
if
![]() $i \in I$
, and which fixes
$i \in I$
, and which fixes
![]() $u_i$
otherwise. When
$u_i$
otherwise. When
![]() $I \subseteq \{1,\dots ,6\}$
, denote by
$I \subseteq \{1,\dots ,6\}$
, denote by
![]() $f_I$
an analogous element of
$f_I$
an analogous element of
![]() $C_H(\Lambda ')$
with respect to the
$C_H(\Lambda ')$
with respect to the
![]() $v_i$
’s. A computation of the action of Q with respect to the bases
$v_i$
’s. A computation of the action of Q with respect to the bases
![]() $\{u_i \mid 1 \leqslant i \leqslant 7\}$
and
$\{u_i \mid 1 \leqslant i \leqslant 7\}$
and
![]() $\{v_i \mid 1 \leqslant i \leqslant 7\}$
using (2)–(4) yields
$\{v_i \mid 1 \leqslant i \leqslant 7\}$
using (2)–(4) yields
 $$ \begin{align*} Q \cap R_{1^7} &= \langle [-1,1,1], [b,ab,1], [ab,b,1], [1,1,a], [1,1,b] \rangle\\ &= \langle e_{1234}, e_{13}, e_{14}, e_{56}, e_{57} \rangle\\ &\cong C_2 \times (Q_8*Q_8), \end{align*} $$
$$ \begin{align*} Q \cap R_{1^7} &= \langle [-1,1,1], [b,ab,1], [ab,b,1], [1,1,a], [1,1,b] \rangle\\ &= \langle e_{1234}, e_{13}, e_{14}, e_{56}, e_{57} \rangle\\ &\cong C_2 \times (Q_8*Q_8), \end{align*} $$
and
 $$ \begin{align*} Q \cap R_{1^7}' &= \langle [-1,1,1], [b,b,1], [ab,ab,1], [1,1,a] \rangle\\ &= \langle f_{1234}, f_{23}, f_{13}, f_{56} \rangle\\ &\cong C_2 \times (Q_8*C_4), \end{align*} $$
$$ \begin{align*} Q \cap R_{1^7}' &= \langle [-1,1,1], [b,b,1], [ab,ab,1], [1,1,a] \rangle\\ &= \langle f_{1234}, f_{23}, f_{13}, f_{56} \rangle\\ &\cong C_2 \times (Q_8*C_4), \end{align*} $$
where here we have used Lemma 2.10 and the identity
![]() $[e,f] = (ef)^2$
to determine the isomorphism types. The order
$[e,f] = (ef)^2$
to determine the isomorphism types. The order
![]() $|Q \cap R_{1^7}| = 2^6$
, and so
$|Q \cap R_{1^7}| = 2^6$
, and so
![]() $|QR_{1^7}| = \frac {|Q||R_{1^7}|}{|Q \cap R_{1^7}|}= 2^9$
. Similarly,
$|QR_{1^7}| = \frac {|Q||R_{1^7}|}{|Q \cap R_{1^7}|}= 2^9$
. Similarly,
![]() $|Q \cap R_{1^7}'| = 2^5$
, so also
$|Q \cap R_{1^7}'| = 2^5$
, so also
![]() $|QR_{1^7}'| = 2^9$
.
$|QR_{1^7}'| = 2^9$
.
We have shown that
![]() $\{QR_{1^7}, QR_{1^7}'\} \subset \{Q\langle \mathbf {d} \rangle , Q\langle \tau \rangle , Q\langle \tau ' \rangle \}$
. The involution
$\{QR_{1^7}, QR_{1^7}'\} \subset \{Q\langle \mathbf {d} \rangle , Q\langle \tau \rangle , Q\langle \tau ' \rangle \}$
. The involution
![]() $e_{4567} \in R_{1^7}-Q$
(Lemma 2.10) acts as
$e_{4567} \in R_{1^7}-Q$
(Lemma 2.10) acts as
![]() $-1$
on
$-1$
on
![]() $\ell _3 \perp \langle x_7 \rangle $
, so centralizes
$\ell _3 \perp \langle x_7 \rangle $
, so centralizes
![]() $L_3$
. It also interchanges the one-dimensional subspaces
$L_3$
. It also interchanges the one-dimensional subspaces
![]() $\langle x_3 \rangle $
and
$\langle x_3 \rangle $
and
![]() $\langle x_4 \rangle $
while centralizing the line
$\langle x_4 \rangle $
while centralizing the line
![]() $\ell _1$
, and hence from (2)–(3), it interchanges
$\ell _1$
, and hence from (2)–(3), it interchanges
![]() $L_1$
and
$L_1$
and
![]() $L_2$
by conjugation. It follows that
$L_2$
by conjugation. It follows that
![]() $QR_{1^7} = Q\langle \tau \rangle $
, since neither
$QR_{1^7} = Q\langle \tau \rangle $
, since neither
![]() $Q\langle \mathbf {d} \rangle $
nor
$Q\langle \mathbf {d} \rangle $
nor
![]() $Q\langle \tau ' \rangle $
have such an element.
$Q\langle \tau ' \rangle $
have such an element.
Finally, we show that
![]() $QR_{1^7}' = Q\langle \tau ' \rangle $
. First, since
$QR_{1^7}' = Q\langle \tau ' \rangle $
. First, since
![]() $f_{1234} \in U-Z$
does not commute with
$f_{1234} \in U-Z$
does not commute with
![]() $f_{45}$
by Lemma 2.10, it follows that
$f_{45}$
by Lemma 2.10, it follows that
![]() $QR_{1^7}'$
is not contained in
$QR_{1^7}'$
is not contained in
![]() $C_S(U) = Q\langle \mathbf {d} \rangle $
. Next, observe that in contrast to the previous case,
$C_S(U) = Q\langle \mathbf {d} \rangle $
. Next, observe that in contrast to the previous case,
![]() $C_{R_{1^7}'}(L_3) = C_{R_{1^7}'}(\ell _3+\langle x_7 \rangle )$
(for example, note that “
$C_{R_{1^7}'}(L_3) = C_{R_{1^7}'}(\ell _3+\langle x_7 \rangle )$
(for example, note that “
![]() $f_{4567}$
” has nontrivial spinor norm). The group
$f_{4567}$
” has nontrivial spinor norm). The group
![]() $C_{R_{1^7}'}(L_3) = \langle f_{12}, f_{13}, f_{14} \rangle $
induces the permutation group
$C_{R_{1^7}'}(L_3) = \langle f_{12}, f_{13}, f_{14} \rangle $
induces the permutation group
![]() $\langle (1,2)(3,4) \rangle $
on
$\langle (1,2)(3,4) \rangle $
on
![]() $\{\langle x_1 \rangle ,\langle x_2 \rangle ,\langle x_3 \rangle ,\langle x_4 \rangle \}$
, and hence
$\{\langle x_1 \rangle ,\langle x_2 \rangle ,\langle x_3 \rangle ,\langle x_4 \rangle \}$
, and hence
![]() $C_{R_{1^7}'}(L_3)$
acts on
$C_{R_{1^7}'}(L_3)$
acts on
![]() $L_1$
and
$L_1$
and
![]() $L_2$
by (2)–(3). Therefore,
$L_2$
by (2)–(3). Therefore,
![]() $QR_{1^7}'$
has no element centralizing
$QR_{1^7}'$
has no element centralizing
![]() $L_3$
and interchanging
$L_3$
and interchanging
![]() $L_1$
and
$L_1$
and
![]() $L_2$
, and so
$L_2$
, and so
![]() $QR_{1^7}' = Q\langle \tau ' \rangle $
.
$QR_{1^7}' = Q\langle \tau ' \rangle $
.
3.2 The case
 $l> 0$
$l> 0$
In this subsection, we determine a set of representatives for the
![]() $\mathcal {D}$
-conjugacy classes of elements in
$\mathcal {D}$
-conjugacy classes of elements in
![]() $\mathcal {D}^{cr}$
for
$\mathcal {D}^{cr}$
for
![]() $\mathcal {D} \in \{\mathcal {K},\mathcal {H},\mathcal {F}\}$
, in the case when
$\mathcal {D} \in \{\mathcal {K},\mathcal {H},\mathcal {F}\}$
, in the case when
![]() $l> 0$
. First, we treat the case
$l> 0$
. First, we treat the case
![]() $\mathcal {D}=\mathcal {K}$
.
$\mathcal {D}=\mathcal {K}$
.
Proposition 3.9. Suppose that
![]() $l> 0$
. There are 11
$l> 0$
. There are 11
![]() $\mathcal {K}$
-conjugacy classes of elements of
$\mathcal {K}$
-conjugacy classes of elements of
![]() $\mathcal {K}^{cr}$
. Representatives of these classes together with their outer automorphism groups in
$\mathcal {K}^{cr}$
. Representatives of these classes together with their outer automorphism groups in
![]() $\mathcal {K}$
are listed in Table 2.
$\mathcal {K}$
are listed in Table 2.
Proof. Let
![]() $P \leqslant S$
be a centric radical subgroup of
$P \leqslant S$
be a centric radical subgroup of
![]() $\mathcal {K}$
, taken up to
$\mathcal {K}$
, taken up to
![]() $\mathcal {K}$
-conjugacy. We proceed through the possibilities in the description of
$\mathcal {K}$
-conjugacy. We proceed through the possibilities in the description of
![]() $\mathcal {K}^{cr}$
given by Proposition 3.4 and refer to the labelings of the three cases given there. If P occurs in (b)(i), then P is listed in the first two rows of the table. By Lemma 2.15,
$\mathcal {K}^{cr}$
given by Proposition 3.4 and refer to the labelings of the three cases given there. If P occurs in (b)(i), then P is listed in the first two rows of the table. By Lemma 2.15,
![]() $\operatorname {Aut}_{\mathcal {K}}(S) = \operatorname {Inn}(S)$
, so that
$\operatorname {Aut}_{\mathcal {K}}(S) = \operatorname {Inn}(S)$
, so that
![]() $\operatorname {Out}_{\mathcal {K}}(S) = 1$
. Also,
$\operatorname {Out}_{\mathcal {K}}(S) = 1$
. Also,
![]() $C_S(U) = R_0\langle \mathbf {d} \rangle $
, so that
$C_S(U) = R_0\langle \mathbf {d} \rangle $
, so that
![]() $\operatorname {Out}_{\mathcal {K}}(C_S(U)) \cong S_3$
is induced by X.
$\operatorname {Out}_{\mathcal {K}}(C_S(U)) \cong S_3$
is induced by X.
Table 2
![]() $\mathcal {K}$
-conjugacy classes of
$\mathcal {K}$
-conjugacy classes of
![]() $\mathcal {K}$
-centric radical subgroups,
$\mathcal {K}$
-centric radical subgroups,
![]() $l> 0$
.
$l> 0$
.

Consider a subgroup P in (b)(ii). First, assume that
![]() $P_i \in \mathcal {Q}_i$
for all i. Upon conjugating in
$P_i \in \mathcal {Q}_i$
for all i. Upon conjugating in
![]() $L_0$
, we may assume that
$L_0$
, we may assume that
![]() $P_i = Q_i$
or
$P_i = Q_i$
or
![]() $Q_i'$
for each i. Conjugating by
$Q_i'$
for each i. Conjugating by
![]() $\mathbf {d}$
, which interchanges
$\mathbf {d}$
, which interchanges
![]() $Q_i$
and
$Q_i$
and
![]() $Q_i'$
for each i, we may assume that there is at most one
$Q_i'$
for each i, we may assume that there is at most one
![]() $Q_i'$
among the
$Q_i'$
among the
![]() $P_i$
’s. Finally, we may conjugate by elements of X to see that P is one of the subgroups in rows 3 and 4 of the table.
$P_i$
’s. Finally, we may conjugate by elements of X to see that P is one of the subgroups in rows 3 and 4 of the table.
To compute
![]() $\operatorname {Out}_{\mathcal {K}}(P)$
, observe that if
$\operatorname {Out}_{\mathcal {K}}(P)$
, observe that if
![]() $t \in L_0X$
, then
$t \in L_0X$
, then
![]() $P^t$
and P have the same number of components
$P^t$
and P have the same number of components
![]() $P_i^t$
which are
$P_i^t$
which are
![]() $L_i$
-conjugate to
$L_i$
-conjugate to
![]() $Q_i$
, while
$Q_i$
, while
![]() $P^{\mathbf {d}}$
has three minus the number for P. This shows that
$P^{\mathbf {d}}$
has three minus the number for P. This shows that
![]() $N_{K}(P) = N_{L_{0}X}(P)$
. Thus, if
$N_{K}(P) = N_{L_{0}X}(P)$
. Thus, if
![]() $P = Q_1Q_2Q_3$
, then
$P = Q_1Q_2Q_3$
, then
![]() $N_K(P) = (N_{L_1}(Q_1)N_{L_2}(Q_2)N_{L_3}(Q_3))X$
, and we see that
$N_K(P) = (N_{L_1}(Q_1)N_{L_2}(Q_2)N_{L_3}(Q_3))X$
, and we see that
![]() $\operatorname {Out}_{\mathcal {K}}(P) \cong S_3 \wr S_3$
by Lemma 2.9. Likewise, if
$\operatorname {Out}_{\mathcal {K}}(P) \cong S_3 \wr S_3$
by Lemma 2.9. Likewise, if
![]() $P = Q_1Q_2Q_3'$
, then
$P = Q_1Q_2Q_3'$
, then
![]() $N_K(P) = N_{L_1}(Q_1)N_{L_2}(Q_2)N_{L_3}(Q_3')\langle \tau \rangle $
, so that
$N_K(P) = N_{L_1}(Q_1)N_{L_2}(Q_2)N_{L_3}(Q_3')\langle \tau \rangle $
, so that
![]() $\operatorname {Out}_{\mathcal {K}}(P) \cong (S_3 \wr C_2) \times S_3$
.
$\operatorname {Out}_{\mathcal {K}}(P) \cong (S_3 \wr C_2) \times S_3$
.
Next, assume that
![]() $P_i \in \mathcal {Q}_i$
for exactly two indices i. Then as before, we may conjugate so that
$P_i \in \mathcal {Q}_i$
for exactly two indices i. Then as before, we may conjugate so that
![]() $P = Q_1Q_2R_3$
or
$P = Q_1Q_2R_3$
or
![]() $Q_1Q_2'R_3$
is on the table. Appealing to Lemma 2.9 again to see that
$Q_1Q_2'R_3$
is on the table. Appealing to Lemma 2.9 again to see that
![]() $\operatorname {Out}_{L_3}(R_3) = 1$
, we have in the former case that
$\operatorname {Out}_{L_3}(R_3) = 1$
, we have in the former case that
![]() $\operatorname {Out}_{\mathcal {K}}(P) \cong S_3 \wr C_2$
with the class of
$\operatorname {Out}_{\mathcal {K}}(P) \cong S_3 \wr C_2$
with the class of
![]() $\tau $
wreathing, while in the latter case, we have a similar situation with the class of
$\tau $
wreathing, while in the latter case, we have a similar situation with the class of
![]() $\tau '$
wreathing. This concludes the case (b)(ii).
$\tau '$
wreathing. This concludes the case (b)(ii).
Consider now a subgroup P in (b)(iii), and recall that
![]() $Z(L_0) = U$
. Thus,
$Z(L_0) = U$
. Thus,
![]() $P = P_0\langle s \rangle $
with
$P = P_0\langle s \rangle $
with
![]() $s \in P-C_P(U)$
normalizing
$s \in P-C_P(U)$
normalizing
![]() $P_0$
. Set
$P_0$
. Set
![]() $N = N_K(P)$
and
$N = N_K(P)$
and
![]() $M = N_K(P_0)$
. Denote quotients modulo
$M = N_K(P_0)$
. Denote quotients modulo
![]() $P_0$
with bars. We set
$P_0$
with bars. We set
![]() $M^+ = \overline {M}/O_{2'}(\overline {M})$
and write quotients modulo
$M^+ = \overline {M}/O_{2'}(\overline {M})$
and write quotients modulo
![]() $O_{2'}(\overline {M})$
with pluses. Thus, for any subgroup
$O_{2'}(\overline {M})$
with pluses. Thus, for any subgroup
![]() $Y \leqslant M$
, we write
$Y \leqslant M$
, we write
![]() $Y^+$
for the image of Y modulo the preimage of
$Y^+$
for the image of Y modulo the preimage of
![]() $O_{3}(\overline {M})$
in M.
$O_{3}(\overline {M})$
in M.
Since
![]() $L_0 \unlhd K$
, we see that
$L_0 \unlhd K$
, we see that
![]() $P_0 = P \cap L_0 \unlhd N$
, so that
$P_0 = P \cap L_0 \unlhd N$
, so that
![]() $N \leqslant M$
. In particular,
$N \leqslant M$
. In particular,
![]() $\overline {N}$
is defined. Also, since
$\overline {N}$
is defined. Also, since
![]() $\overline {s}$
is of order
$\overline {s}$
is of order
![]() $2$
, N is the preimage in M of
$2$
, N is the preimage in M of
![]() $C_{\overline {M}}(\overline {s})$
. As P is radical, we must have
$C_{\overline {M}}(\overline {s})$
. As P is radical, we must have
We consider separately the cases where
![]() $P_0 \notin \mathcal {K}^{cr}$
and where
$P_0 \notin \mathcal {K}^{cr}$
and where
![]() $P_0 \in \mathcal {K}^{cr}$
. Assume first that
$P_0 \in \mathcal {K}^{cr}$
. Assume first that
![]() $P_0 \notin \mathcal {K}^{cr}$
, the easier case. Upon comparing the conditions in (b)(ii) and (b)(iii), we have by our assumption that
$P_0 \notin \mathcal {K}^{cr}$
, the easier case. Upon comparing the conditions in (b)(ii) and (b)(iii), we have by our assumption that
![]() $P_3 \in \mathcal {Q}_3$
and
$P_3 \in \mathcal {Q}_3$
and
![]() $P_i = R_i$
for
$P_i = R_i$
for
![]() $i = 1, 2$
. Thus,
$i = 1, 2$
. Thus,
![]() $\overline {M} = \langle \overline {\tau } \rangle \times \overline {N_{L_3}(P_3)} \cong C_2 \times S_3$
, and so
$\overline {M} = \langle \overline {\tau } \rangle \times \overline {N_{L_3}(P_3)} \cong C_2 \times S_3$
, and so
![]() $P = P_0\langle \tau \rangle $
by (3.2). Hence,
$P = P_0\langle \tau \rangle $
by (3.2). Hence,
![]() $\operatorname {Out}_{\mathcal {F}}(P) \cong S_3$
, and P appears in the last row of the table.
$\operatorname {Out}_{\mathcal {F}}(P) \cong S_3$
, and P appears in the last row of the table.
Assume next that
![]() $P_0 \in \mathcal {K}^{cr}$
, so that
$P_0 \in \mathcal {K}^{cr}$
, so that
![]() $P_0$
is conjugate to a subgroup considered in (b)(ii), rows 3–6 of the table. First, assume that
$P_0$
is conjugate to a subgroup considered in (b)(ii), rows 3–6 of the table. First, assume that
![]() $P_0$
itself appears in rows 3–6. Our description of the normalizer in K of
$P_0$
itself appears in rows 3–6. Our description of the normalizer in K of
![]() $P_0$
in a previous paragraph together with order considerations imply that
$P_0$
in a previous paragraph together with order considerations imply that
![]() $N_{R_0}(P_0)\langle \tau \rangle /P_0$
is a Sylow
$N_{R_0}(P_0)\langle \tau \rangle /P_0$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\operatorname {Out}_{\mathcal {K}}(P_0)$
if
$\operatorname {Out}_{\mathcal {K}}(P_0)$
if
![]() $P_0$
appears in rows 3–5, and that
$P_0$
appears in rows 3–5, and that
![]() $N_{R_{0}}(P_0)\langle \tau ' \rangle /P_0$
is a Sylow
$N_{R_{0}}(P_0)\langle \tau ' \rangle /P_0$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\operatorname {Out}_{\mathcal {K}}(P_0)$
if
$\operatorname {Out}_{\mathcal {K}}(P_0)$
if
![]() $P_0$
appears in row 6. This shows that
$P_0$
appears in row 6. This shows that
![]() $\operatorname {Aut}_{S}(P_0)$
is a Sylow
$\operatorname {Aut}_{S}(P_0)$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\operatorname {Aut}_{\mathcal {K}}(P_0)$
, that is,
$\operatorname {Aut}_{\mathcal {K}}(P_0)$
, that is,
![]() $P_{0}$
is fully
$P_{0}$
is fully
![]() $\mathcal {K}$
-automized [Reference Aschbacher, Kessar and OliverAKO11, I.2.2]. Since
$\mathcal {K}$
-automized [Reference Aschbacher, Kessar and OliverAKO11, I.2.2]. Since
![]() $P_0$
is
$P_0$
is
![]() $\mathcal {K}$
-centric, it is fully
$\mathcal {K}$
-centric, it is fully
![]() $\mathcal {K}$
-centralized ([Reference Aschbacher, Kessar and OliverAKO11, I.3.1]). Hence,
$\mathcal {K}$
-centralized ([Reference Aschbacher, Kessar and OliverAKO11, I.3.1]). Hence,
![]() $P_0$
is fully
$P_0$
is fully
![]() $\mathcal {K}$
-normalized by [Reference Aschbacher, Kessar and OliverAKO11, I.2.6(c)]. Thus, by Lemma 2.6 (and since
$\mathcal {K}$
-normalized by [Reference Aschbacher, Kessar and OliverAKO11, I.2.6(c)]. Thus, by Lemma 2.6 (and since
![]() $P_0 \unlhd P$
), we may in any case replace P by a
$P_0 \unlhd P$
), we may in any case replace P by a
![]() $\mathcal {K}$
-conjugate and assume that
$\mathcal {K}$
-conjugate and assume that
![]() $P_0$
is in rows 3–6 of the table.
$P_0$
is in rows 3–6 of the table.
Case 1. Assume
![]() $P_0 = Q_1Q_2Q_3$
, and recall Lemma 2.8(e).
$P_0 = Q_1Q_2Q_3$
, and recall Lemma 2.8(e).
Here,
![]() $\overline {M} = \overline {N_{L_0}(P_0)}\overline {X} \cong S_3 \wr S_3$
,
$\overline {M} = \overline {N_{L_0}(P_0)}\overline {X} \cong S_3 \wr S_3$
,
![]() $\overline {N_{R_0}(P_0)}^+ = O_{2}(M^+)$
, and
$\overline {N_{R_0}(P_0)}^+ = O_{2}(M^+)$
, and
![]() $\overline {N_{S}(P_0)} = \overline {N_{R_0}(P_0)}\langle \overline {\tau } \rangle $
. By assumption, s is not in
$\overline {N_{S}(P_0)} = \overline {N_{R_0}(P_0)}\langle \overline {\tau } \rangle $
. By assumption, s is not in
![]() $C_P(U)$
, so it is not in
$C_P(U)$
, so it is not in
![]() $R_0$
. Hence,
$R_0$
. Hence,
![]() $\overline {s}$
is not in
$\overline {s}$
is not in
![]() $\overline {N_{R_0}(P_0)}$
. Thus,
$\overline {N_{R_0}(P_0)}$
. Thus,
Write
![]() $\overline {s} = \overline {[t_1,t_2,t_3]}\overline {\tau }$
, where each
$\overline {s} = \overline {[t_1,t_2,t_3]}\overline {\tau }$
, where each
![]() $t_i \in R_i$
, and where we take
$t_i \in R_i$
, and where we take
![]() $t_i = 1$
if
$t_i = 1$
if
![]() $t_i \in P_i$
and
$t_i \in P_i$
and
![]() $t_i = a^{2^{l-1}}$
if
$t_i = a^{2^{l-1}}$
if
![]() $t_i \notin P_i$
. As
$t_i \notin P_i$
. As
![]() $\tau $
acts by swapping
$\tau $
acts by swapping
![]() $R_1$
and
$R_1$
and
![]() $R_2$
and centralizing
$R_2$
and centralizing
![]() $R_3$
, it follows from (3.3) that
$R_3$
, it follows from (3.3) that
![]() $C_{\overline {N_{R_0}(P_0)}}(\overline {s})$
is of order 4 generated by
$C_{\overline {N_{R_0}(P_0)}}(\overline {s})$
is of order 4 generated by
![]() $\overline {[a^{2^{l-1}}, a^{2^{l-1}}, 1]}$
and
$\overline {[a^{2^{l-1}}, a^{2^{l-1}}, 1]}$
and
![]() $\overline {[1,1,a^{2^{l-1}}]}$
.
$\overline {[1,1,a^{2^{l-1}}]}$
.
Note that
![]() $t_1 = t_2$
since
$t_1 = t_2$
since
![]() $\overline {s}$
is of order
$\overline {s}$
is of order
![]() $2$
. We claim that (3.2) and (3.3) imply
$2$
. We claim that (3.2) and (3.3) imply
![]() $t_3 = 1$
. Assume on the contrary that
$t_3 = 1$
. Assume on the contrary that
![]() $t_3 = a^{2^{l-1}}$
. Then
$t_3 = a^{2^{l-1}}$
. Then
![]() $O_{2'}(C_{\overline {M}}(\overline {s})) = C_{O_{2'}(\overline {M})}(\overline {s}) \leqslant \overline {N_{L_1}(Q_1)}\overline {N_{L_2}(Q_2)}$
. By (3.3),
$O_{2'}(C_{\overline {M}}(\overline {s})) = C_{O_{2'}(\overline {M})}(\overline {s}) \leqslant \overline {N_{L_1}(Q_1)}\overline {N_{L_2}(Q_2)}$
. By (3.3),
![]() $C_{O_{2',2,2'}(\overline {M})}(\overline {s}) = C_{O_{2',2}(\overline {M})}(\overline {s})$
. So since
$C_{O_{2',2,2'}(\overline {M})}(\overline {s}) = C_{O_{2',2}(\overline {M})}(\overline {s})$
. So since
![]() $\langle \overline {[1,1,a^{2^{l-1}}]} \rangle $
is a normal
$\langle \overline {[1,1,a^{2^{l-1}}]} \rangle $
is a normal
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\overline {N_S(P_0)}$
, it follows that
$\overline {N_S(P_0)}$
, it follows that
![]() $\langle \overline {[1,1,a^{2^{l-1}}]} \rangle $
is a normal
$\langle \overline {[1,1,a^{2^{l-1}}]} \rangle $
is a normal
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_{\overline {M}}(\overline {s})$
. By (3.2),
$C_{\overline {M}}(\overline {s})$
. By (3.2),
![]() $\overline {s} = \overline {[1,1,a^{2^{l-1}}]}$
. This contradicts (3.3).
$\overline {s} = \overline {[1,1,a^{2^{l-1}}]}$
. This contradicts (3.3).
We conclude that
![]() $\overline {s} = \overline {\tau }$
or
$\overline {s} = \overline {\tau }$
or
![]() $\overline {s} = \overline {[a^{2^{l-1}}, a^{2^{l-1}}, 1]}\overline {\tau }$
, and hence
$\overline {s} = \overline {[a^{2^{l-1}}, a^{2^{l-1}}, 1]}\overline {\tau }$
, and hence
However, since the two possibilities for
![]() $\overline {s}$
are conjugate under
$\overline {s}$
are conjugate under
![]() $\overline {N_{R_1}(Q_1)}$
, we may take
$\overline {N_{R_1}(Q_1)}$
, we may take
![]() $\overline {s} = \overline {\tau }$
, as desired.
$\overline {s} = \overline {\tau }$
, as desired.
Case 2. Assume
![]() $P_0 = Q_1Q_2Q_3'$
. In this case,
$P_0 = Q_1Q_2Q_3'$
. In this case,
![]() $\overline {M} \cong S_3 \wr \langle \overline {\tau } \rangle \times S_3$
. Replacing all occurrences of
$\overline {M} \cong S_3 \wr \langle \overline {\tau } \rangle \times S_3$
. Replacing all occurrences of
![]() $Q_3$
by
$Q_3$
by
![]() $Q_3'$
, we argue verbatim as in Case 1, except that in the present situation, we have
$Q_3'$
, we argue verbatim as in Case 1, except that in the present situation, we have
![]() $O_{2',2,2'}(\overline {M}) = O_{2',2}(\overline {M}) = \overline {M}$
, obviating the need to observe that
$O_{2',2,2'}(\overline {M}) = O_{2',2}(\overline {M}) = \overline {M}$
, obviating the need to observe that
![]() $C_{O_{2',2,2'}(\overline {M})}(\overline {s}) = C_{O_{2',2}(\overline {M})}(\overline {s})$
. Again, we may take
$C_{O_{2',2,2'}(\overline {M})}(\overline {s}) = C_{O_{2',2}(\overline {M})}(\overline {s})$
. Again, we may take
![]() $\overline {s}=\overline {\tau }$
.
$\overline {s}=\overline {\tau }$
.
Case 3. Assume
![]() $P_0 = Q_1Q_2R_3$
. We have
$P_0 = Q_1Q_2R_3$
. We have
![]() $\overline {M} = \overline {N_{L_0}(P_0)}\overline {X} \cong S_3 \wr \langle \overline {\tau } \rangle $
,
$\overline {M} = \overline {N_{L_0}(P_0)}\overline {X} \cong S_3 \wr \langle \overline {\tau } \rangle $
,
![]() $\overline {N_{R_0}(P_0)}^+ = O_{2}(M^+)$
, and
$\overline {N_{R_0}(P_0)}^+ = O_{2}(M^+)$
, and
![]() $\overline {N_{S}(P_0)} = \overline {N_{R_0}(P_0)}\langle \overline {\tau } \rangle $
. By assumption, s is not in
$\overline {N_{S}(P_0)} = \overline {N_{R_0}(P_0)}\langle \overline {\tau } \rangle $
. By assumption, s is not in
![]() $C_P(U)$
, so it is not in
$C_P(U)$
, so it is not in
![]() $R_0$
. Hence,
$R_0$
. Hence,
![]() $\overline {s}$
is not in
$\overline {s}$
is not in
![]() $\overline {N_{R_0}(P_0)}$
. Thus,
$\overline {N_{R_0}(P_0)}$
. Thus,
![]() $\overline {s} \in \overline {N_{R_0}(P_0)}\overline {\tau }.$
As in the previous cases, (3.2) forces
$\overline {s} \in \overline {N_{R_0}(P_0)}\overline {\tau }.$
As in the previous cases, (3.2) forces
![]() $\overline {s} = \overline {\tau }$
or
$\overline {s} = \overline {\tau }$
or
![]() $\overline {[a^{2^{l-1}}, a^{2^{l-1}},1]}\overline {\tau },$
so that
$\overline {[a^{2^{l-1}}, a^{2^{l-1}},1]}\overline {\tau },$
so that
Again, these possibilities for
![]() $\overline {s}$
are conjugate under
$\overline {s}$
are conjugate under
![]() $\overline {N_{R_1}(Q_1)}$
, and we see that we may take
$\overline {N_{R_1}(Q_1)}$
, and we see that we may take
![]() $\overline {s} = \overline {\tau }$
, as needed.
$\overline {s} = \overline {\tau }$
, as needed.
Case 4. Assume
![]() $P_0 = Q_1Q_2'R_3$
. This time, replace
$P_0 = Q_1Q_2'R_3$
. This time, replace
![]() $\tau $
by
$\tau $
by
![]() $\tau '$
, and repeat the argument from the previous case.
$\tau '$
, and repeat the argument from the previous case.
Remark 3.10. The minor omission in the proof of [Reference Aschbacher and ChermakAC10, Lemma 10.2] alluded to in the proof of Proposition 3.4 occurs in the middle of page 953 with the claim “
![]() $|O_3(\overline {N})| = 9$
”. It is possible that
$|O_3(\overline {N})| = 9$
”. It is possible that
![]() $|O_3(\overline {N})| = 3$
under the hypotheses there. More precisely, consider the subgroup
$|O_3(\overline {N})| = 3$
under the hypotheses there. More precisely, consider the subgroup
![]() $P = P_{0}\langle s \rangle $
, where
$P = P_{0}\langle s \rangle $
, where
![]() $P_0 = Q_1Q_2Q_3$
and
$P_0 = Q_1Q_2Q_3$
and
![]() $s = [a^{2^{l-1}},1,1]\tau $
. Then
$s = [a^{2^{l-1}},1,1]\tau $
. Then
![]() $\overline {s}$
centralizes
$\overline {s}$
centralizes
![]() $O_3(\overline {N_{L_3}(Q_3)})$
,
$O_3(\overline {N_{L_3}(Q_3)})$
,
![]() $\overline {s}$
has order
$\overline {s}$
has order
![]() $4$
, and
$4$
, and
![]() $\overline {s}$
squares to
$\overline {s}$
squares to
![]() $\overline {[a^{2^{l-1}}, a^{2^{l-1}}, 1]}$
. As
$\overline {[a^{2^{l-1}}, a^{2^{l-1}}, 1]}$
. As
![]() $\overline {s}$
centralizes no nontrivial element in
$\overline {s}$
centralizes no nontrivial element in
![]() $O_{3}(\overline {N_{L_1L_2}(P_0)}) \cong C_3 \times C_3$
, we have
$O_{3}(\overline {N_{L_1L_2}(P_0)}) \cong C_3 \times C_3$
, we have
![]() $O_3(C_{\overline {M}}(\overline {s})) = O_{3}(\overline {N_{L_3}(Q_3)})$
is of order
$O_3(C_{\overline {M}}(\overline {s})) = O_{3}(\overline {N_{L_3}(Q_3)})$
is of order
![]() $3$
. But in this case,
$3$
. But in this case,
![]() $O_2(N_{\overline {M}}(\langle \overline {s} \rangle )) \cong D_8$
while
$O_2(N_{\overline {M}}(\langle \overline {s} \rangle )) \cong D_8$
while
![]() $\langle \overline {s} \rangle $
is cyclic of index
$\langle \overline {s} \rangle $
is cyclic of index
![]() $2$
in this subgroup, and so
$2$
in this subgroup, and so
![]() $|O_2(\operatorname {Out}_{\mathcal {K}}(P))| = 2$
is generated by the image of
$|O_2(\operatorname {Out}_{\mathcal {K}}(P))| = 2$
is generated by the image of
![]() $\overline {[a^{2^{l-1}},1,1]}$
. Thus,
$\overline {[a^{2^{l-1}},1,1]}$
. Thus,
![]() $P_0\langle s \rangle $
satisfies Proposition 3.4(b)(iii)(2-3), but is not
$P_0\langle s \rangle $
satisfies Proposition 3.4(b)(iii)(2-3), but is not
![]() $\mathcal {K}$
-radical.
$\mathcal {K}$
-radical.
This example also indicates how to patch the proof of [Reference Aschbacher and ChermakAC10, Lemma 10.2]. Paragraph 3 of page 953 gives an argument for the statement that if (b)(iii)(2–3) holds (in our numbering), then P is centric radical. Follow it until line
![]() $-2$
of that paragraph. In particular, one is reduced to the case in which
$-2$
of that paragraph. In particular, one is reduced to the case in which
![]() $P_0 = Q_1Q_2Q_3$
, and
$P_0 = Q_1Q_2Q_3$
, and
![]() $\overline {M} \cong S_3 \wr S_3$
. The Sylow
$\overline {M} \cong S_3 \wr S_3$
. The Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $\overline {N_S(P_0)}$
of
$\overline {N_S(P_0)}$
of
![]() $\overline {M}$
has the structure
$\overline {M}$
has the structure
![]() $D_8 \times C_2$
, and it acts on
$D_8 \times C_2$
, and it acts on
![]() $O_3(\overline {M})$
decomposably with nontrivial summands
$O_3(\overline {M})$
decomposably with nontrivial summands
![]() $O_{3}(\overline {N_{L_1L_2}(P_0)})$
and
$O_{3}(\overline {N_{L_1L_2}(P_0)})$
and
![]() $O_{3}(\overline {N_{L_3}(P_0)})$
. Fix any element
$O_{3}(\overline {N_{L_3}(P_0)})$
. Fix any element
![]() $s \in N_S(P_0)-C_S(U)$
, such that
$s \in N_S(P_0)-C_S(U)$
, such that
![]() $\overline {s}$
is of order
$\overline {s}$
is of order
![]() $4$
in
$4$
in
![]() $\overline {M}$
. Indeed, there are exactly two possibilities for
$\overline {M}$
. Indeed, there are exactly two possibilities for
![]() $\langle \overline {s} \rangle $
and hence for
$\langle \overline {s} \rangle $
and hence for
![]() $P = P_0\langle s \rangle $
, namely,
$P = P_0\langle s \rangle $
, namely,
![]() $\langle \overline {[a^{2^{l-1}},1,1]}\overline {\tau } \rangle $
and
$\langle \overline {[a^{2^{l-1}},1,1]}\overline {\tau } \rangle $
and
![]() $\langle \overline {[a^{2^{l-1}},1,a^{2^{l-1}}]}\overline {\tau } \rangle $
. The latter determines a subgroup
$\langle \overline {[a^{2^{l-1}},1,a^{2^{l-1}}]}\overline {\tau } \rangle $
. The latter determines a subgroup
![]() $P = P_0\langle s \rangle $
that is not
$P = P_0\langle s \rangle $
that is not
![]() $\mathcal {K}$
-radical because it does not satisfy Proposition 3.4(b)(iii)(3), while the first determines a subgroup
$\mathcal {K}$
-radical because it does not satisfy Proposition 3.4(b)(iii)(3), while the first determines a subgroup
![]() $P = P_0\langle s \rangle $
that is also not
$P = P_0\langle s \rangle $
that is also not
![]() $\mathcal {K}$
-radical (from the previous paragraph). Hence, we must have
$\mathcal {K}$
-radical (from the previous paragraph). Hence, we must have
![]() $\overline {s}$
is of order
$\overline {s}$
is of order
![]() $2$
, that is, it is necessary that (b)(iii)(1) also holds.
$2$
, that is, it is necessary that (b)(iii)(1) also holds.
We next determine the set
![]() $\mathcal {H}^{cr}$
up to
$\mathcal {H}^{cr}$
up to
![]() $\mathcal {H}$
-conjugacy in the case
$\mathcal {H}$
-conjugacy in the case
![]() $l> 0$
.
$l> 0$
.
Proposition 3.11. Suppose that
![]() $l> 0$
. There are 18
$l> 0$
. There are 18
![]() $\mathcal {H}$
-conjugacy classes of elements of
$\mathcal {H}$
-conjugacy classes of elements of
![]() $\mathcal {H}^{cr}$
. Representatives for these classes together with their outer automorphism groups in
$\mathcal {H}^{cr}$
. Representatives for these classes together with their outer automorphism groups in
![]() $\mathcal {H}$
are listed in Table 3.
$\mathcal {H}$
are listed in Table 3.
Table 3
![]() $\mathcal {H}$
-conjugacy classes of
$\mathcal {H}$
-conjugacy classes of
![]() $\mathcal {H}$
-centric radical subgroups,
$\mathcal {H}$
-centric radical subgroups,
![]() $l> 0$
.
$l> 0$
.

Proof. Let
![]() $P \in \mathcal {H}^{cr}$
. If
$P \in \mathcal {H}^{cr}$
. If
![]() $N_H(P) \nleq K$
, then using Proposition 3.2(a)–(d), we obtain the groups in the last four rows of Table 3. Hence, for the remainder of the proof, we may assume that
$N_H(P) \nleq K$
, then using Proposition 3.2(a)–(d), we obtain the groups in the last four rows of Table 3. Hence, for the remainder of the proof, we may assume that
By [Reference Levi and OliverLO02, Lemma 3.3(a)], P is
![]() $\mathcal {F}$
-centric, so that P is also
$\mathcal {F}$
-centric, so that P is also
![]() $\mathcal {K}$
-centric.
$\mathcal {K}$
-centric.
Suppose first that P is
![]() $\mathcal {K}$
radical, so that
$\mathcal {K}$
radical, so that
![]() $P \in \mathcal {K}^{cr}$
. In this case, we appeal to Proposition 3.9 to obtain the first 13 entries in Table 3, as follows. A case-by-case check shows that for each
$P \in \mathcal {K}^{cr}$
. In this case, we appeal to Proposition 3.9 to obtain the first 13 entries in Table 3, as follows. A case-by-case check shows that for each
![]() $\mathcal {K}$
-conjugacy class
$\mathcal {K}$
-conjugacy class
![]() $\mathcal {C} = Y^{\mathcal {K}}$
of a subgroup Y listed in Table 2, one of the following holds: either no member of
$\mathcal {C} = Y^{\mathcal {K}}$
of a subgroup Y listed in Table 2, one of the following holds: either no member of
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
![]() $\mathcal {H}$
-radical (
$\mathcal {H}$
-radical (
![]() $Y = C_S(U)$
),
$Y = C_S(U)$
),
![]() $\mathcal {C}$
meets exactly one
$\mathcal {C}$
meets exactly one
![]() $\mathcal {H}$
-radical conjugacy class (
$\mathcal {H}$
-radical conjugacy class (
![]() $Y = S, Q_1Q_2Q_3, Q_1Q_2Q_3\langle \tau \rangle , Q_1Q_2Q_3'\langle \tau \rangle , Q_1Q_2R_3\langle \tau \rangle , Q_1Q_2'R_3\langle \tau ' \rangle $
,
$Y = S, Q_1Q_2Q_3, Q_1Q_2Q_3\langle \tau \rangle , Q_1Q_2Q_3'\langle \tau \rangle , Q_1Q_2R_3\langle \tau \rangle , Q_1Q_2'R_3\langle \tau ' \rangle $
,
![]() $R_1R_2Q_3\langle \tau \rangle $
), or
$R_1R_2Q_3\langle \tau \rangle $
), or
![]() $\mathcal {C}$
is the class of one of the entries in rows
$\mathcal {C}$
is the class of one of the entries in rows
![]() $4$
through
$4$
through
![]() $6$
of Table 2 (
$6$
of Table 2 (
![]() $Y = Q_1Q_2Q_3', Q_1Q_2R_3$
, or
$Y = Q_1Q_2Q_3', Q_1Q_2R_3$
, or
![]() $Q_1Q_2'R_3$
). In this last case,
$Q_1Q_2'R_3$
). In this last case,
![]() $\mathcal {C}$
meets one of two
$\mathcal {C}$
meets one of two
![]() $\mathcal {H}$
-classes of
$\mathcal {H}$
-classes of
![]() $\mathcal {H}$
-radical subgroups, and corresponding representatives of these
$\mathcal {H}$
-radical subgroups, and corresponding representatives of these
![]() $\mathcal {H}$
-classes appear in rows
$\mathcal {H}$
-classes appear in rows
![]() $3$
through
$3$
through
![]() $8$
of Table 3. In each of the three cases,
$8$
of Table 3. In each of the three cases,
![]() $\operatorname {Out}_{\mathcal {H}}(P)$
is computed using (3.4) and the descriptions
$\operatorname {Out}_{\mathcal {H}}(P)$
is computed using (3.4) and the descriptions
![]() $K = C_H(U)X$
and
$K = C_H(U)X$
and
![]() $H \cap K = C_K(Z) = N_H(U) = C_H(U)\langle \tau \rangle = C_H(U)\langle \tau ' \rangle $
.
$H \cap K = C_K(Z) = N_H(U) = C_H(U)\langle \tau \rangle = C_H(U)\langle \tau ' \rangle $
.
We illustrate the argument of the previous paragraph with four examples. First, consider
![]() $Y = C_S(U)$
. As
$Y = C_S(U)$
. As
![]() $C_H(U)$
is normal in K with Sylow
$C_H(U)$
is normal in K with Sylow
![]() $C_S(U)$
, we have
$C_S(U)$
, we have
![]() $C_S(U)$
is strongly
$C_S(U)$
is strongly
![]() $\mathcal {K}$
-closed. In particular,
$\mathcal {K}$
-closed. In particular,
![]() $C_S(U)^{\mathcal {K}} = \{C_S(U)\}$
. Appealing to Lemma 2.16, we see that
$C_S(U)^{\mathcal {K}} = \{C_S(U)\}$
. Appealing to Lemma 2.16, we see that
![]() $\operatorname {Out}_{\mathcal {H}}(C_S(U)) \cong C_2$
, so
$\operatorname {Out}_{\mathcal {H}}(C_S(U)) \cong C_2$
, so
![]() $C_S(U)$
is not
$C_S(U)$
is not
![]() $\mathcal {H}$
-radical.
$\mathcal {H}$
-radical.
Next, consider
![]() $Y = Q_1Q_2Q_3$
. Since X normalizes Y, we have that
$Y = Q_1Q_2Q_3$
. Since X normalizes Y, we have that
![]() $Y^{\mathcal {K}} = Y^{\mathcal {H}}$
, and
$Y^{\mathcal {K}} = Y^{\mathcal {H}}$
, and
![]() $N_H(Y)$
is of index
$N_H(Y)$
is of index
![]() $3$
in
$3$
in
![]() $N_K(Y)$
. Since
$N_K(Y)$
. Since
![]() $N_H(U) = C_H(U)\langle \tau \rangle = C_H(U)\langle \tau ' \rangle $
, it follows that
$N_H(U) = C_H(U)\langle \tau \rangle = C_H(U)\langle \tau ' \rangle $
, it follows that
![]() $\operatorname {Out}_{\mathcal {H}}(Y) \cong S_3 \wr C_2 \times S_3$
is of index
$\operatorname {Out}_{\mathcal {H}}(Y) \cong S_3 \wr C_2 \times S_3$
is of index
![]() $3$
in
$3$
in
![]() $\operatorname {Out}_{\mathcal {K}}(Y) \cong S_3 \wr S_3$
.
$\operatorname {Out}_{\mathcal {K}}(Y) \cong S_3 \wr S_3$
.
Third, consider
![]() $Y = Q_1Q_2'R_3\langle \tau ' \rangle $
. This time, no element of
$Y = Q_1Q_2'R_3\langle \tau ' \rangle $
. This time, no element of
![]() $K-C_K(Z)$
normalizes Y, so
$K-C_K(Z)$
normalizes Y, so
![]() $N_H(Y) = N_K(Y)$
by (3.4). However, we claim that
$N_H(Y) = N_K(Y)$
by (3.4). However, we claim that
![]() $Y^{\mathcal {K}} = Y^{\mathcal {H}}$
. For the proof, assume on the contrary that there is
$Y^{\mathcal {K}} = Y^{\mathcal {H}}$
. For the proof, assume on the contrary that there is
![]() $k \in K$
with
$k \in K$
with
![]() $Y^k \leqslant S$
and
$Y^k \leqslant S$
and
![]() $Y^k$
not H-conjugate to Y. Then
$Y^k$
not H-conjugate to Y. Then
![]() $k \notin K-N_H(U)$
, and k normalizes
$k \notin K-N_H(U)$
, and k normalizes
![]() $R_0 = L_0 \cap S$
, so
$R_0 = L_0 \cap S$
, so
![]() $\langle k \rangle $
permutes the set
$\langle k \rangle $
permutes the set
![]() $\{R_1,R_2,R_3\}$
transitively. It follows that the element
$\{R_1,R_2,R_3\}$
transitively. It follows that the element
![]() $\tau ^{\prime k} \in S$
interchanges
$\tau ^{\prime k} \in S$
interchanges
![]() $R_3$
and some other
$R_3$
and some other
![]() $R_i$
by conjugation. This is a contradiction, as
$R_i$
by conjugation. This is a contradiction, as
![]() $R_3$
is a fixed point in the action of S on
$R_3$
is a fixed point in the action of S on
![]() $\{R_1,R_2,R_3\}$
(see Section 2.4). Hence,
$\{R_1,R_2,R_3\}$
(see Section 2.4). Hence,
![]() $Y^{\mathcal {K}}$
meets exactly one
$Y^{\mathcal {K}}$
meets exactly one
![]() $\mathcal {H}$
-conjugacy class as claimed, and
$\mathcal {H}$
-conjugacy class as claimed, and
![]() $\operatorname {Out}_{\mathcal {H}}(Y) = \operatorname {Out}_{\mathcal {K}}(Y)$
, so Y is
$\operatorname {Out}_{\mathcal {H}}(Y) = \operatorname {Out}_{\mathcal {K}}(Y)$
, so Y is
![]() $\mathcal {H}$
-radical.
$\mathcal {H}$
-radical.
Finally, consider
![]() $Y = Q_1Q_2R_3$
. Then
$Y = Q_1Q_2R_3$
. Then
![]() $N_X(Y) = \langle \tau \rangle $
is of order
$N_X(Y) = \langle \tau \rangle $
is of order
![]() $2$
. As
$2$
. As
![]() $L_3$
is
$L_3$
is
![]() $C_H(U)$
-invariant,
$C_H(U)$
-invariant,
![]() $R_3$
is strongly closed in
$R_3$
is strongly closed in
![]() $C_S(U)$
with respect to
$C_S(U)$
with respect to
![]() $C_H(U)$
, so no element of
$C_H(U)$
, so no element of
![]() $C_H(U)O_3(X)-C_H(U)$
normalizes Y. It follows that
$C_H(U)O_3(X)-C_H(U)$
normalizes Y. It follows that
![]() $N_H(Y) = N_K(Y)$
from (3.4). This also shows that if we fix a nontrivial element
$N_H(Y) = N_K(Y)$
from (3.4). This also shows that if we fix a nontrivial element
![]() $x \in O_3(X)$
, then representatives for the
$x \in O_3(X)$
, then representatives for the
![]() $\mathcal {H}$
-conjugacy classes in
$\mathcal {H}$
-conjugacy classes in
![]() $Y^{\mathcal {K}}$
may be taken as a subset of
$Y^{\mathcal {K}}$
may be taken as a subset of
![]() $\{Y, Y^x, Y^{x^2}\} = \{Q_1Q_2R_3, Q_1R_2Q_3, R_1Q_2Q_3\}$
. As
$\{Y, Y^x, Y^{x^2}\} = \{Q_1Q_2R_3, Q_1R_2Q_3, R_1Q_2Q_3\}$
. As
![]() $\tau \in S$
interchanges
$\tau \in S$
interchanges
![]() $R_1Q_2Q_3$
and
$R_1Q_2Q_3$
and
![]() $Q_1R_2Q_3$
, it follows that
$Q_1R_2Q_3$
, it follows that
![]() $Y^{\mathcal {K}}$
meets two
$Y^{\mathcal {K}}$
meets two
![]() $\mathcal {H}$
-conjugacy classes (at most), with representatives Y and
$\mathcal {H}$
-conjugacy classes (at most), with representatives Y and
![]() $Q_1R_2Q_3$
. From
$Q_1R_2Q_3$
. From
![]() $N_H(Y) = N_K(Y)$
, we have
$N_H(Y) = N_K(Y)$
, we have
![]() $\operatorname {Out}_{\mathcal {H}}(Y) = \operatorname {Out}_{\mathcal {K}}(Y) \cong S_3 \wr C_2$
, while
$\operatorname {Out}_{\mathcal {H}}(Y) = \operatorname {Out}_{\mathcal {K}}(Y) \cong S_3 \wr C_2$
, while
![]() $\operatorname {Out}_{\mathcal {H}}(Q_1R_2Q_3) \cong S_3 \times S_3$
is induced by
$\operatorname {Out}_{\mathcal {H}}(Q_1R_2Q_3) \cong S_3 \times S_3$
is induced by
![]() $N_{L_1}(Q_1)N_{L_3}(Q_3)$
. So indeed
$N_{L_1}(Q_1)N_{L_3}(Q_3)$
. So indeed
![]() $Q_1R_2Q_3$
is
$Q_1R_2Q_3$
is
![]() $\mathcal {H}$
-radical and not
$\mathcal {H}$
-radical and not
![]() $\mathcal {H}$
-conjugate to Y.
$\mathcal {H}$
-conjugate to Y.
It remains to consider the case in which P is not
![]() $\mathcal {K}$
-radical. We claim here that P is
$\mathcal {K}$
-radical. We claim here that P is
![]() $\mathcal {H}$
-conjugate to
$\mathcal {H}$
-conjugate to
![]() $Q_1R_2R_3$
, the last remaining entry of Table 3. Observe first that
$Q_1R_2R_3$
, the last remaining entry of Table 3. Observe first that
![]() $P \leqslant C_S(U) = R_0\langle \mathbf {d} \rangle $
. Indeed, otherwise
$P \leqslant C_S(U) = R_0\langle \mathbf {d} \rangle $
. Indeed, otherwise
![]() $Z(P) \cap U = Z$
would be
$Z(P) \cap U = Z$
would be
![]() $N_K(P)$
-invariant, and so as
$N_K(P)$
-invariant, and so as
![]() $N_H(P) = N_K(P)$
by (3.4), this would yield that
$N_H(P) = N_K(P)$
by (3.4), this would yield that
![]() $\operatorname {Out}_{\mathcal {H}}(P) = \operatorname {Out}_{\mathcal {K}}(P)$
has no nontrivial normal
$\operatorname {Out}_{\mathcal {H}}(P) = \operatorname {Out}_{\mathcal {K}}(P)$
has no nontrivial normal
![]() $2$
-subgroups, contradicting the assumption that P is not
$2$
-subgroups, contradicting the assumption that P is not
![]() $\mathcal {K}$
-radical. Hence,
$\mathcal {K}$
-radical. Hence,
![]() $P \leqslant C_S(U) = R_0\langle \mathbf {d} \rangle $
as claimed, and so
$P \leqslant C_S(U) = R_0\langle \mathbf {d} \rangle $
as claimed, and so
![]() $U \leqslant Z(P)$
since P is centric.
$U \leqslant Z(P)$
since P is centric.
Set
![]() $P_0 = P \cap L_0$
, and for each
$P_0 = P \cap L_0$
, and for each
![]() $i = 1,2,3$
, let
$i = 1,2,3$
, let
![]() $P_i$
be the projection of
$P_i$
be the projection of
![]() $P_0$
in
$P_0$
in
![]() $R_i$
as before; see the remarks just before Proposition 3.4. A reading of the first three paragraphs of the proof of [Reference Aschbacher and ChermakAC10, Lemma 10.2] reveals that the given argument applies to an
$R_i$
as before; see the remarks just before Proposition 3.4. A reading of the first three paragraphs of the proof of [Reference Aschbacher and ChermakAC10, Lemma 10.2] reveals that the given argument applies to an
![]() $\mathcal {H}$
-centric radical
$\mathcal {H}$
-centric radical
![]() $P \leqslant S$
whose normalizer
$P \leqslant S$
whose normalizer
![]() $N_H(P)$
is contained in K, our current situation (3.4). We conclude that
$N_H(P)$
is contained in K, our current situation (3.4). We conclude that
![]() $P_i = P \cap R_i$
and that
$P_i = P \cap R_i$
and that
![]() $P_i \in \mathcal {Q}_i$
or
$P_i \in \mathcal {Q}_i$
or
![]() $P_i = R_i$
for each
$P_i = R_i$
for each
![]() $i = 1,2,3$
. In particular,
$i = 1,2,3$
. In particular,
![]() $P_0 = P_1P_2P_3$
.
$P_0 = P_1P_2P_3$
.
We next claim that
![]() $P = P_0$
. Suppose on the contrary that
$P = P_0$
. Suppose on the contrary that
![]() $P_0 < P = C_P(U)$
, and choose
$P_0 < P = C_P(U)$
, and choose
![]() $d \in P-C_P(U)$
. Then
$d \in P-C_P(U)$
. Then
![]() $d \in R_0\langle \mathbf {d} \rangle -R_0$
, and since
$d \in R_0\langle \mathbf {d} \rangle -R_0$
, and since
![]() $\mathbf {d}$
interchanges the
$\mathbf {d}$
interchanges the
![]() $R_0$
-conjugacy classes of subgroups in
$R_0$
-conjugacy classes of subgroups in
![]() $\mathcal {Q}_i$
for each i (c.f. Notation 2.12(e,f)), d has the same property. On the other hand, as d normalizes
$\mathcal {Q}_i$
for each i (c.f. Notation 2.12(e,f)), d has the same property. On the other hand, as d normalizes
![]() $R_i$
and P, it normalizes
$R_i$
and P, it normalizes
![]() $P_i = P \cap R_i$
. We conclude that
$P_i = P \cap R_i$
. We conclude that
![]() $P_i = R_i$
for each i. But then
$P_i = R_i$
for each i. But then
![]() $P = R_0\langle \mathbf {d} \rangle = C_S(U)$
and
$P = R_0\langle \mathbf {d} \rangle = C_S(U)$
and
![]() $\operatorname {Out}_{\mathcal {H}}(P)$
is of order
$\operatorname {Out}_{\mathcal {H}}(P)$
is of order
![]() $2$
. Thus, P is not
$2$
. Thus, P is not
![]() $\mathcal {H}$
-radical, contrary to the original choice of P.
$\mathcal {H}$
-radical, contrary to the original choice of P.
Finally, conjugating in
![]() $L_0\langle \mathbf {d} \rangle = C_H(U) \leqslant H$
if necessary, we have
$L_0\langle \mathbf {d} \rangle = C_H(U) \leqslant H$
if necessary, we have
![]() $P = Q_1R_2R_3$
or
$P = Q_1R_2R_3$
or
![]() $R_1R_2Q_3$
. But in the latter case,
$R_1R_2Q_3$
. But in the latter case,
![]() $\operatorname {Out}_{\mathcal {H}}(P) \cong C_2 \times S_3$
is induced by
$\operatorname {Out}_{\mathcal {H}}(P) \cong C_2 \times S_3$
is induced by
![]() $\langle \tau \rangle \times N_{L_3}(Q_3)$
, so again, P is not
$\langle \tau \rangle \times N_{L_3}(Q_3)$
, so again, P is not
![]() $\mathcal {H}$
-radical, a contradiction. Thus, up to
$\mathcal {H}$
-radical, a contradiction. Thus, up to
![]() $\mathcal {H}$
-conjugacy,
$\mathcal {H}$
-conjugacy,
![]() $P = Q_1R_2R_3$
and
$P = Q_1R_2R_3$
and
![]() $\operatorname {Out}_{\mathcal {H}}(P) \cong S_3$
is induced by
$\operatorname {Out}_{\mathcal {H}}(P) \cong S_3$
is induced by
![]() $N_{L_1}(Q_1)$
, and this is the only remaining entry in Table 3.
$N_{L_1}(Q_1)$
, and this is the only remaining entry in Table 3.
Table 4
![]() $\mathcal {F}$
-conjugacy classes of
$\mathcal {F}$
-conjugacy classes of
![]() $\mathcal {F}$
-centric radical subgroups,
$\mathcal {F}$
-centric radical subgroups,
![]() $l> 0$
.
$l> 0$
.

Finally, we are able to describe the set of
![]() $\mathcal {F}$
-centric radical subgroups, up to
$\mathcal {F}$
-centric radical subgroups, up to
![]() $\mathcal {F}$
-conjugacy:
$\mathcal {F}$
-conjugacy:
Theorem 3.12. Let
![]() $\mathcal {F}=\operatorname {Sol}(5^{2^l})$
with
$\mathcal {F}=\operatorname {Sol}(5^{2^l})$
with
![]() $l> 0$
. Representatives for the
$l> 0$
. Representatives for the
![]() $\mathcal {F}$
-conjugacy classes of
$\mathcal {F}$
-conjugacy classes of
![]() $\mathcal {F}$
-centric radical subgroups, together with their orders and automorphism groups, are listed in Table 4, where “
$\mathcal {F}$
-centric radical subgroups, together with their orders and automorphism groups, are listed in Table 4, where “
![]() $-$
” indicates that the subgroup is not centric radical in that fusion system.
$-$
” indicates that the subgroup is not centric radical in that fusion system.
Proof. This follows upon combining Propositions 3.1, 3.9, and 3.11. Note that
![]() $Q_1R_2R_3$
appears in Table 3, but it does not appear in Table 4 because it does not satisfy the hypotheses of Proposition 3.1(c)(ii): there is an involution in
$Q_1R_2R_3$
appears in Table 3, but it does not appear in Table 4 because it does not satisfy the hypotheses of Proposition 3.1(c)(ii): there is an involution in
![]() $K \leqslant G$
of the form
$K \leqslant G$
of the form
![]() $\tau ^x$
for a nonidentity
$\tau ^x$
for a nonidentity
![]() $x \in O_3(X)$
which normalizes
$x \in O_3(X)$
which normalizes
![]() $Q_1R_2R_3$
but is not contained in H. Indeed,
$Q_1R_2R_3$
but is not contained in H. Indeed,
![]() $O_{2}(\operatorname {Out}_{\mathcal {F}}(Q_1R_2R_3))$
is of order
$O_{2}(\operatorname {Out}_{\mathcal {F}}(Q_1R_2R_3))$
is of order
![]() $2$
and induced by conjugation by this element, so
$2$
and induced by conjugation by this element, so
![]() $Q_1R_2R_3$
is not
$Q_1R_2R_3$
is not
![]() $\mathcal {F}$
-radical.
$\mathcal {F}$
-radical.
4 Number of projective simple modules
In this section, we calculate the number of projective simple modules for the outer automorphism groups in the various tables of the previous section. Let G be a finite group, and let
![]() $\operatorname {Irr}(G)$
be the set of ordinary irreducible characters of G, that is, those over a splitting field of characteristic
$\operatorname {Irr}(G)$
be the set of ordinary irreducible characters of G, that is, those over a splitting field of characteristic
![]() $0$
. A character
$0$
. A character
![]() $\chi \in \operatorname {Irr}(G)$
is said to be of p-defect d if
$\chi \in \operatorname {Irr}(G)$
is said to be of p-defect d if
![]() $|G|_p/\chi (1)_p = p^d$
, where
$|G|_p/\chi (1)_p = p^d$
, where
![]() $n_p$
denotes the p-part of the integer n.
$n_p$
denotes the p-part of the integer n.
Write
![]() $z(kG)$
for the number of projective simple
$z(kG)$
for the number of projective simple
![]() $kG$
-modules. Any projective simple module is the unique indecomposable module in the block of
$kG$
-modules. Any projective simple module is the unique indecomposable module in the block of
![]() $kG$
in which it lies. Blocks of
$kG$
in which it lies. Blocks of
![]() $kG$
of defect
$kG$
of defect
![]() $0$
are exactly those which contain such a module. Equivalently, blocks of defect
$0$
are exactly those which contain such a module. Equivalently, blocks of defect
![]() $0$
are exactly those which contain a unique ordinary irreducible character of defect
$0$
are exactly those which contain a unique ordinary irreducible character of defect
![]() $0$
. Thus, one can count projective simple
$0$
. Thus, one can count projective simple
![]() $kG$
-modules by looking at the list of irreducible character degrees for G.
$kG$
-modules by looking at the list of irreducible character degrees for G.
Theorem 4.1. Let G be a finite group and p be a prime. Then
![]() $z(kG)$
is the number of ordinary irreducible characters of defect
$z(kG)$
is the number of ordinary irreducible characters of defect
![]() $0$
.
$0$
.
Proof. See [Reference NavarroNav98, Theorem 3.18].
Along with Theorem 4.1, the following result will be used in order to compute the character degrees of various solvable groups.
Theorem 4.2. Let G be a finite group with normal subgroup A, and let
![]() $\Theta = [\operatorname {Irr}(A)/G]$
denote a set of representatives for the G-orbits on
$\Theta = [\operatorname {Irr}(A)/G]$
denote a set of representatives for the G-orbits on
![]() $\operatorname {Irr}(A)$
. Assume that each irreducible character
$\operatorname {Irr}(A)$
. Assume that each irreducible character
![]() $\theta $
of A extends to an irreducible character
$\theta $
of A extends to an irreducible character
![]() $\widehat {\theta }$
of its inertia subgroup
$\widehat {\theta }$
of its inertia subgroup
![]() $I_G(\theta )$
. Then there is a bijection
$I_G(\theta )$
. Then there is a bijection
given by sending
![]() $(\theta , \beta )$
to the induced character
$(\theta , \beta )$
to the induced character
![]() $(\widehat {\theta }\beta )\!\uparrow ^G_{I_G(\theta )}$
, where
$(\widehat {\theta }\beta )\!\uparrow ^G_{I_G(\theta )}$
, where
![]() $\widehat {\theta }$
is any extension of
$\widehat {\theta }$
is any extension of
![]() $\theta $
, and where
$\theta $
, and where
![]() $\beta $
is regarded also as an irreducible character of
$\beta $
is regarded also as an irreducible character of
![]() $I_G(\theta )$
with A in its kernel.
$I_G(\theta )$
with A in its kernel.
Proof. See [Reference Nagao and TsushimaNT89, Chapter 3, Theorem 5.8 and Corollary 5.9].
Proposition 4.3. Each of the groups listed in Table 5 has the stated number of blocks of defect zero.
Table 5 The number of projective simple modules.

Proof. Let G be one of the groups listed in Table 5. It suffices by Theorem 4.1 to compute the number of characters having degree divisible by the
![]() $2$
-part of the group order. The character tables of
$2$
-part of the group order. The character tables of
![]() $G=\operatorname {GL}_3(2),S_5,S_6,A_7,S_7,\operatorname {GL}_4(2) \cong A_8$
can be found in the ATLAS [ Reference ConwayCCN+85]. For those G which split as a direct product
$G=\operatorname {GL}_3(2),S_5,S_6,A_7,S_7,\operatorname {GL}_4(2) \cong A_8$
can be found in the ATLAS [ Reference ConwayCCN+85]. For those G which split as a direct product
![]() $G = G_1 \times G_2$
, we use the fact that the irreducible characters of G are the pairwise tensor products of the irreducible characters of
$G = G_1 \times G_2$
, we use the fact that the irreducible characters of G are the pairwise tensor products of the irreducible characters of
![]() $G_1$
and
$G_1$
and
![]() $G_2$
.
$G_2$
.
In all remaining cases, the character degrees are computed using Theorem 4.2 by taking A to be a normal elementary abelian
![]() $3$
-group which is complemented in G. Each irreducible character of A extends to its stabilizer in G in this case by [Reference Curtis and ReinerCR90, 11.8(ii)], so Theorem 4.2 applies. For a representative
$3$
-group which is complemented in G. Each irreducible character of A extends to its stabilizer in G in this case by [Reference Curtis and ReinerCR90, 11.8(ii)], so Theorem 4.2 applies. For a representative
![]() $\theta $
of an orbit of
$\theta $
of an orbit of
![]() $G/A$
on
$G/A$
on
![]() $\operatorname {Irr}(A)$
, we compute the
$\operatorname {Irr}(A)$
, we compute the
![]() $2$
-parts of the index in G and of the irreducible character degrees
$2$
-parts of the index in G and of the irreducible character degrees
![]() $\beta (1)$
of the inertia subgroup
$\beta (1)$
of the inertia subgroup
![]() $I_G(\theta )$
. The pairs
$I_G(\theta )$
. The pairs
![]() $(\theta , \beta )$
with
$(\theta , \beta )$
with
![]() $\theta (1)_2 \cdot [G:I_G(\theta )]_2 \cdot \beta (1)_2$
equal to the
$\theta (1)_2 \cdot [G:I_G(\theta )]_2 \cdot \beta (1)_2$
equal to the
![]() $2$
-part of the group order are recorded in Table 6. For example, suppose that
$2$
-part of the group order are recorded in Table 6. For example, suppose that
![]() $G=(C_3)^3 \rtimes (C_2 \times S_3)$
and set
$G=(C_3)^3 \rtimes (C_2 \times S_3)$
and set
![]() $A=(C_3)^3 \leqslant G$
. For each
$A=(C_3)^3 \leqslant G$
. For each
![]() $\theta \in \operatorname {Irr}(A)$
, we have
$\theta \in \operatorname {Irr}(A)$
, we have
![]() $\theta = \theta _{i_1} \otimes \theta _{i_2} \otimes \theta _{i_3}$
for some
$\theta = \theta _{i_1} \otimes \theta _{i_2} \otimes \theta _{i_3}$
for some
![]() $1 \le i_j \le 3$
. An
$1 \le i_j \le 3$
. An
![]() $S_3$
factor in
$S_3$
factor in
![]() $G/A \cong S_3 \times C_2$
acts on
$G/A \cong S_3 \times C_2$
acts on
![]() $\operatorname {Irr}(A)$
by permuting the
$\operatorname {Irr}(A)$
by permuting the
![]() $\theta _{i_j}$
, while the
$\theta _{i_j}$
, while the
![]() $C_2$
factor fixes
$C_2$
factor fixes
![]() $\theta _1$
and interchanges
$\theta _1$
and interchanges
![]() $\theta _2$
and
$\theta _2$
and
![]() $\theta _3$
in each coordinate. One computes that there are six orbits on irreducible characters. The pair
$\theta _3$
in each coordinate. One computes that there are six orbits on irreducible characters. The pair
![]() $(\theta , \beta )$
, where
$(\theta , \beta )$
, where
![]() $\theta = \theta _2 \otimes \theta _2 \otimes \theta _2$
and
$\theta = \theta _2 \otimes \theta _2 \otimes \theta _2$
and
![]() $\beta $
is the degree
$\beta $
is the degree
![]() $2$
irreducible character of
$2$
irreducible character of
![]() $I_G(\theta )/A \cong S_3$
, gives rise to the only irreducible character of G of
$I_G(\theta )/A \cong S_3$
, gives rise to the only irreducible character of G of
![]() $2$
-defect
$2$
-defect
![]() $0$
. The remaining cases are summarized in Table 6, where a representative
$0$
. The remaining cases are summarized in Table 6, where a representative
![]() $\theta _{i_1}\otimes \theta _{i_2} \otimes \theta _{i_3}$
is abbreviated to
$\theta _{i_1}\otimes \theta _{i_2} \otimes \theta _{i_3}$
is abbreviated to
![]() $[i_1,i_2,i_3]$
, for example.
$[i_1,i_2,i_3]$
, for example.
Table 6 Characters
![]() $\chi \in \operatorname {Irr}(G)$
of defect
$\chi \in \operatorname {Irr}(G)$
of defect
![]() $0$
.
$0$
.

The dashes mean the group G listed on the line has no irreducible character of defect 0.
Using Tables 1, 3, and 4, we can give a count of the number of weights.
Corollary 4.4. For
![]() $\mathcal {D} \in \{\mathcal {H},\mathcal {F}\}$
and all
$\mathcal {D} \in \{\mathcal {H},\mathcal {F}\}$
and all
![]() $l \ge 0$
, the number of weights associated with the Külshammer-Puig pair
$l \ge 0$
, the number of weights associated with the Külshammer-Puig pair
![]() $(\mathcal {D},0)$
is
$(\mathcal {D},0)$
is
Note that
![]() $\mathbf {w}(\mathcal {H},0)=12$
is known as a consequence of results in [Reference AnAn93].
$\mathbf {w}(\mathcal {H},0)=12$
is known as a consequence of results in [Reference AnAn93].
5 Külshammer-Puig classes
We give here a proof of Theorem 1.1 essentially by direct computation. Throughout this section, we fix an arbitrary nonnegative integer l and set
![]() $q = 5^{2^l}$
. We adopt the notation
$q = 5^{2^l}$
. We adopt the notation
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
![]() $\mathcal {K}$
from Section 2. These systems depend implicitly on q.
$\mathcal {K}$
from Section 2. These systems depend implicitly on q.
Recall that the Schur multiplier of a finite group G is the cohomology group
![]() $M(G) := H^2(G,\mathbb {C}^\times )$
. It is a finite abelian group. Given any algebraically closed field k of characteristic
$M(G) := H^2(G,\mathbb {C}^\times )$
. It is a finite abelian group. Given any algebraically closed field k of characteristic
![]() $2$
, the
$2$
, the
![]() $2'$
-primary part of
$2'$
-primary part of
![]() $M(G)$
is isomorphic to
$M(G)$
is isomorphic to
![]() $H^2(G,k^\times )$
. The approach taken to showing Theorem 1.1 requires the explicit computation of
$H^2(G,k^\times )$
. The approach taken to showing Theorem 1.1 requires the explicit computation of
![]() $H^2(G,k^\times )$
(the values of the functor
$H^2(G,k^\times )$
(the values of the functor
![]() $\mathcal {A}^2$
) for each group G appearing as the outer automorphism group of a centric radical in Section 3. The computation of Schur multipliers of finite groups is typically a delicate task. In our case, the task is simpler for two reasons. First, the outer automorphism groups are relatively small finite groups. Second, the task is simpler because of the following lemma, which allows us in many cases to reduce the computation of the odd part of the Schur multiplier to computations of
$\mathcal {A}^2$
) for each group G appearing as the outer automorphism group of a centric radical in Section 3. The computation of Schur multipliers of finite groups is typically a delicate task. In our case, the task is simpler for two reasons. First, the outer automorphism groups are relatively small finite groups. Second, the task is simpler because of the following lemma, which allows us in many cases to reduce the computation of the odd part of the Schur multiplier to computations of
![]() $H^2(G,\mathbb {F}_p)$
for odd primes p. A finite group is said to be p-perfect if it has no nontrivial p-group as a quotient.
$H^2(G,\mathbb {F}_p)$
for odd primes p. A finite group is said to be p-perfect if it has no nontrivial p-group as a quotient.
Lemma 5.1. Let
![]() $\mathcal {D} \in \{\mathcal {F},\mathcal {H},\mathcal {K}\}$
. Then for each subgroup
$\mathcal {D} \in \{\mathcal {F},\mathcal {H},\mathcal {K}\}$
. Then for each subgroup
![]() $P \in \mathcal {D}^{rc}$
and each odd prime p, the outer automorphism group
$P \in \mathcal {D}^{rc}$
and each odd prime p, the outer automorphism group
![]() $\operatorname {Out}_{\mathcal {D}}(P)$
is p-perfect.
$\operatorname {Out}_{\mathcal {D}}(P)$
is p-perfect.
The next lemma collects various standard results on group cohomology stated in the special cases in which they will be used. We thank the referee for several simplifications in our original arguments.
Lemma 5.2. Let G and H be finite groups, and let k be an algebraically closed field of characteristic
![]() $2$
. Write
$2$
. Write
![]() $|G| = 2^rw$
, where w is odd. The following hold.
$|G| = 2^rw$
, where w is odd. The following hold.
-
(a) For any abelian group A with trivial G-action,
 $H^1(G,A) = \operatorname {Hom}(G,A)$
.
$H^1(G,A) = \operatorname {Hom}(G,A)$
. -
(b) There is a surjective map
which is an isomorphism if G is p-perfect for every odd prime p dividing $$\begin{align*}H^2(G, \mathbb{Z}/w\mathbb{Z}) \to H^2(G,k^\times), \end{align*}$$
$$\begin{align*}H^2(G, \mathbb{Z}/w\mathbb{Z}) \to H^2(G,k^\times), \end{align*}$$
 $|G|$
.
$|G|$
.
-
(c) If
 $H^2(G,\mathbb {F}_p) = 0$
for all odd primes p, then
$H^2(G,\mathbb {F}_p) = 0$
for all odd primes p, then
 $H^2(G,k^\times ) = 0$
.
$H^2(G,k^\times ) = 0$
. -
(d) If p is odd and G is a p-perfect group with cyclic Sylow p-subgroups, then
 $H^2(G,\mathbb {F}_p) = 0$
.
$H^2(G,\mathbb {F}_p) = 0$
. -
(e) If G is a p-perfect group with an elementary abelian Sylow p-subgroup V of order
 $p^2$
, then
$p^2$
, then  $$\begin{align*}H^2(G,\mathbb{F}_p) = \begin{cases} \mathbb{F}_p & \text{ if } \operatorname{Aut}_G(V) \subseteq \operatorname{SL}(V), \text{ and}\\ 0 & \text{ otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}H^2(G,\mathbb{F}_p) = \begin{cases} \mathbb{F}_p & \text{ if } \operatorname{Aut}_G(V) \subseteq \operatorname{SL}(V), \text{ and}\\ 0 & \text{ otherwise.} \end{cases} \end{align*}$$
-
(f) If G and H are p-perfect, then
 $$\begin{align*}H^2(G \times H, \mathbb{F}_p) \cong H^2(G,\mathbb{F}_p) \oplus H^2(H, \mathbb{F}_p). \end{align*}$$
$$\begin{align*}H^2(G \times H, \mathbb{F}_p) \cong H^2(G,\mathbb{F}_p) \oplus H^2(H, \mathbb{F}_p). \end{align*}$$
-
(g) Let p be an odd prime. If G is p-perfect and the p-part
 $M(G)_{p}$
of the Schur multiplier of G is of exponent at most p, then Here,
$M(G)_{p}$
of the Schur multiplier of G is of exponent at most p, then Here, $$\begin{align*}M(G)_{p} = H^2(G,\mathbb{C}^{\times}) \otimes \mathbb{Z}_{(p)} \cong H^2(G,\mathbb{F}_p) \cong H^2(G,k^{\times}) \otimes \mathbb{Z}_{(p)}. \end{align*}$$
$$\begin{align*}M(G)_{p} = H^2(G,\mathbb{C}^{\times}) \otimes \mathbb{Z}_{(p)} \cong H^2(G,\mathbb{F}_p) \cong H^2(G,k^{\times}) \otimes \mathbb{Z}_{(p)}. \end{align*}$$
 $\mathbb {Z}_{(p)}$
denotes the p-local integers.
$\mathbb {Z}_{(p)}$
denotes the p-local integers.
-
(h) (Schur) If
 $M(G)$
has exponent e, then
$M(G)$
has exponent e, then
 $e^2$
divides the order of G.
$e^2$
divides the order of G.
Proof.
-
(a) This follows from the description
 $H^1(G,A)$
as the group of derivations
$H^1(G,A)$
as the group of derivations
 $G \to A$
[Reference WeibelWei94, Corollary 6.4.6].
$G \to A$
[Reference WeibelWei94, Corollary 6.4.6]. -
(b) Fix a Sylow
 $2$
-subgroup S of G. Since
$2$
-subgroup S of G. Since
 $k^{\times }$
has all odd roots of unity, powering by w is a surjective endomorphism with kernel
$k^{\times }$
has all odd roots of unity, powering by w is a surjective endomorphism with kernel
 $\mathbb {Z}/w\mathbb {Z}$
. Thus, there is an exact sequence The last map is multiplication by
$\mathbb {Z}/w\mathbb {Z}$
. Thus, there is an exact sequence The last map is multiplication by $$\begin{align*}H^1(G,k^{\times}) \to H^2(G,\mathbb{Z}/w\mathbb{Z}) \to H^2(G,k^\times) \to H^2(G,k^{\times}). \end{align*}$$
$$\begin{align*}H^1(G,k^{\times}) \to H^2(G,\mathbb{Z}/w\mathbb{Z}) \to H^2(G,k^\times) \to H^2(G,k^{\times}). \end{align*}$$
 $w = |G:S|$
, and so it factors as by [Reference BensonBen98b, Proposition 3.6.17] applied with
$w = |G:S|$
, and so it factors as by [Reference BensonBen98b, Proposition 3.6.17] applied with $$\begin{align*}H^2(G,k^{\times}) \xrightarrow{\operatorname{res}} H^2(S,k^{\times}) \xrightarrow{\operatorname{tr}} H^2(G,k^{\times}) \end{align*}$$
$$\begin{align*}H^2(G,k^{\times}) \xrightarrow{\operatorname{res}} H^2(S,k^{\times}) \xrightarrow{\operatorname{tr}} H^2(G,k^{\times}) \end{align*}$$
 $M = M' = k^{\times }$
. Since
$M = M' = k^{\times }$
. Since
 $H^2(S,k^{\times }) = 0$
, we conclude that the last map is
$H^2(S,k^{\times }) = 0$
, we conclude that the last map is
 $0$
. The middle map is therefore a surjection, and since
$0$
. The middle map is therefore a surjection, and since
 $H^1(G,k^\times ) = \operatorname {Hom}(G,k^{\times })$
by (a), we see that it is an isomorphism if G is p-perfect for every odd prime p dividing
$H^1(G,k^\times ) = \operatorname {Hom}(G,k^{\times })$
by (a), we see that it is an isomorphism if G is p-perfect for every odd prime p dividing
 $|G|$
.
$|G|$
.
-
(c) This follows upon filtering
 $\mathbb {Z}/w\mathbb {Z}$
by subgroups of prime order, considering the corresponding long exact sequences in cohomology, and applying (b).
$\mathbb {Z}/w\mathbb {Z}$
by subgroups of prime order, considering the corresponding long exact sequences in cohomology, and applying (b). -
(d) Let P be a Sylow p-subgroup with p odd. Restriction induces an isomorphism
 $H^*(G,\mathbb {F}_p) \to H^*(N_G(P),\mathbb {F}_p) \cong H^{*}(P,\mathbb {F}_p)^{\operatorname {Aut}_G(P)}$
by [Reference BensonBen98b, Corollary 3.6.19] applied with
$H^*(G,\mathbb {F}_p) \to H^*(N_G(P),\mathbb {F}_p) \cong H^{*}(P,\mathbb {F}_p)^{\operatorname {Aut}_G(P)}$
by [Reference BensonBen98b, Corollary 3.6.19] applied with
 $M = M' = \mathbb {F}_p$
. Now
$M = M' = \mathbb {F}_p$
. Now
 $H^*(P,\mathbb {F}_p) \cong \mathbb {F}_p[x,y]/(x^2)$
with
$H^*(P,\mathbb {F}_p) \cong \mathbb {F}_p[x,y]/(x^2)$
with
 $\deg x = 1$
and
$\deg x = 1$
and
 $\deg y = 2$
[Reference BensonBen98b, Proposition 3.5.5], and the Bockstein
$\deg y = 2$
[Reference BensonBen98b, Proposition 3.5.5], and the Bockstein
 $H^1(P,\mathbb {F}_p) \to H^2(P,\mathbb {F}_p)$
is an isomorphism of
$H^1(P,\mathbb {F}_p) \to H^2(P,\mathbb {F}_p)$
is an isomorphism of
 $N_G(P)$
-modules (cf. [Reference BensonBen98b, p. 132, Example]). As
$N_G(P)$
-modules (cf. [Reference BensonBen98b, p. 132, Example]). As
 $N_G(P)$
has no invariants in
$N_G(P)$
has no invariants in
 $H^1(P,\mathbb {F}_p)$
by assumption, it also has no invariants on
$H^1(P,\mathbb {F}_p)$
by assumption, it also has no invariants on
 $H^2(P,\mathbb {F}_p)$
.
$H^2(P,\mathbb {F}_p)$
. -
(e) Restriction to V again identifies
 $H^*(G,\mathbb {F}_p)$
with the invariants
$H^*(G,\mathbb {F}_p)$
with the invariants
 $H^*(V,\mathbb {F}_p)^{\operatorname {Aut}_G(V)}$
. Now with
$H^*(V,\mathbb {F}_p)^{\operatorname {Aut}_G(V)}$
. Now with $$\begin{align*}H^{*}(V,\mathbb{F}_p) \cong \Lambda_{\mathbb{F}_p}(x_1,x_2) \otimes \mathbb{F}_p[y_1,y_2], \end{align*}$$
$$\begin{align*}H^{*}(V,\mathbb{F}_p) \cong \Lambda_{\mathbb{F}_p}(x_1,x_2) \otimes \mathbb{F}_p[y_1,y_2], \end{align*}$$
 $\deg x_i = 1$
and
$\deg x_i = 1$
and
 $\deg y_i = 2$
by [Reference BensonBen98b, Corollary 3.5.7(ii)], so that Here,
$\deg y_i = 2$
by [Reference BensonBen98b, Corollary 3.5.7(ii)], so that Here, $$\begin{align*}H^1(V,\mathbb{F}_p) = \langle x_1,x_2 \rangle_{\mathbb{F}_p} \quad \text{ and } \quad H^2(V,\mathbb{F}_p) = \langle y_1,y_2, x_1x_2 \rangle_{\mathbb{F}_p}. \end{align*}$$
$$\begin{align*}H^1(V,\mathbb{F}_p) = \langle x_1,x_2 \rangle_{\mathbb{F}_p} \quad \text{ and } \quad H^2(V,\mathbb{F}_p) = \langle y_1,y_2, x_1x_2 \rangle_{\mathbb{F}_p}. \end{align*}$$
 $H^1(V,\mathbb {F}_p)$
is the natural module for
$H^1(V,\mathbb {F}_p)$
is the natural module for
 $\operatorname {Aut}(V) \cong \operatorname {GL}(V)$
, while
$\operatorname {Aut}(V) \cong \operatorname {GL}(V)$
, while
 $H^2(V,\mathbb {F}_p)$
is the direct sum of the natural module
$H^2(V,\mathbb {F}_p)$
is the direct sum of the natural module
 $\langle y_1,y_2 \rangle _{\mathbb {F}_p}$
and
$\langle y_1,y_2 \rangle _{\mathbb {F}_p}$
and
 $\langle x_1x_2 \rangle _{\mathbb {F}_p}$
on which
$\langle x_1x_2 \rangle _{\mathbb {F}_p}$
on which
 $\operatorname {GL}(V)$
acts via the determinant map. By assumption,
$\operatorname {GL}(V)$
acts via the determinant map. By assumption,
 $\operatorname {Aut}_G(V) \leqslant \operatorname {GL}(V)$
has no fixed points on the natural module, so
$\operatorname {Aut}_G(V) \leqslant \operatorname {GL}(V)$
has no fixed points on the natural module, so
 $H^2(V,\mathbb {F}_p)$
is nontrivial generated by
$H^2(V,\mathbb {F}_p)$
is nontrivial generated by
 $x_1x_2$
if and only if every element of
$x_1x_2$
if and only if every element of
 $\operatorname {Aut}_G(V)$
has determinant 1.
$\operatorname {Aut}_G(V)$
has determinant 1.
-
(f) This follows from the Künneth theorem [Reference BensonBen98a, Theorem 2.7.1] and the assumption.
-
(g) Powering by p on
 $\mathbb {C}^{\times }$
gives the exact sequence The assumptions imply that tensoring with
$\mathbb {C}^{\times }$
gives the exact sequence The assumptions imply that tensoring with $$\begin{align*}H^1(G,\mathbb{C}^\times) \to H^2(G,\mathbb{F}_p) \to H^2(G,\mathbb{C}^\times) \xrightarrow{p} H^2(G,\mathbb{C}^{\times}). \end{align*}$$
$$\begin{align*}H^1(G,\mathbb{C}^\times) \to H^2(G,\mathbb{F}_p) \to H^2(G,\mathbb{C}^\times) \xrightarrow{p} H^2(G,\mathbb{C}^{\times}). \end{align*}$$
 $\mathbb {Z}_{(p)}$
kills
$\mathbb {Z}_{(p)}$
kills
 $H^1(G,\mathbb {C}^\times )$
and the last map. Hence,
$H^1(G,\mathbb {C}^\times )$
and the last map. Hence,
 $H^2(G,\mathbb {F}_{p}) \cong H^2(G,\mathbb {C}^\times ) \otimes \mathbb {Z}_{(p)}$
. Since
$H^2(G,\mathbb {F}_{p}) \cong H^2(G,\mathbb {C}^\times ) \otimes \mathbb {Z}_{(p)}$
. Since
 $M_{2'}(G)$
is isomorphic to
$M_{2'}(G)$
is isomorphic to
 $H^{2}(G,k^\times )$
([Reference KarpilovskyKar87, Proposition 2.1.14]) and p is odd, the p-primary part of
$H^{2}(G,k^\times )$
([Reference KarpilovskyKar87, Proposition 2.1.14]) and p is odd, the p-primary part of
 $H^2(G,k^\times )$
is of exponent at most p by assumption. Thus, the exact same argument with
$H^2(G,k^\times )$
is of exponent at most p by assumption. Thus, the exact same argument with
 $k^{\times }$
in place of
$k^{\times }$
in place of
 $\mathbb {C}^{\times }$
shows that
$\mathbb {C}^{\times }$
shows that
 $H^2(G,\mathbb {F}_p) \cong H^2(G,k^{\times }) \otimes \mathbb {Z}_{(p)}$
.
$H^2(G,\mathbb {F}_p) \cong H^2(G,k^{\times }) \otimes \mathbb {Z}_{(p)}$
.
-
(h) We refer to [Reference KarpilovskyKar87, Theorem 2.1.5] for a proof.
We are interested in computing the cohomology of the functor
![]() $H^2(-,k^\times )$
defined on the subdivision category of the full subcategory of the fusion systems
$H^2(-,k^\times )$
defined on the subdivision category of the full subcategory of the fusion systems
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\mathcal {H}$
, and
$\mathcal {H}$
, and
![]() $\mathcal {K}$
, respectively, on the collection of centric subgroups. Let
$\mathcal {K}$
, respectively, on the collection of centric subgroups. Let
![]() $\mathcal {C}$
be any full subcategory of a saturated fusion system. Recall from [Reference LinckelmannLin19, Definition 8.13.2] that the subdivision category
$\mathcal {C}$
be any full subcategory of a saturated fusion system. Recall from [Reference LinckelmannLin19, Definition 8.13.2] that the subdivision category
![]() $S(\mathcal {C})$
of proper inclusions is the category with objects of the chains
$S(\mathcal {C})$
of proper inclusions is the category with objects of the chains
![]() $\sigma = (X_0 < X_1 < \cdots < X_m)$
(of proper inclusions) in
$\sigma = (X_0 < X_1 < \cdots < X_m)$
(of proper inclusions) in
![]() $\mathcal {C}$
; here, m is the length
$\mathcal {C}$
; here, m is the length
![]() $|\sigma |$
of
$|\sigma |$
of
![]() $\sigma $
. Given another object
$\sigma $
. Given another object
![]() $\tau = (Y_0 < Y_1 < \cdots < Y_n) \in S(\mathcal {C})$
, a morphism from
$\tau = (Y_0 < Y_1 < \cdots < Y_n) \in S(\mathcal {C})$
, a morphism from
![]() $\sigma $
to
$\sigma $
to
![]() $\tau $
consists of an order preserving function
$\tau $
consists of an order preserving function
![]() $\beta \colon \{0,1\dots ,m\} \to \{0,1,\dots ,n\}$
together with isomorphisms
$\beta \colon \{0,1\dots ,m\} \to \{0,1,\dots ,n\}$
together with isomorphisms
![]() $\varphi _i \colon X_i \to Y_{\beta (i)}$
in
$\varphi _i \colon X_i \to Y_{\beta (i)}$
in
![]() $\mathcal {C}$
for each
$\mathcal {C}$
for each
![]() $i \in \{0,1,\dots ,m\}$
, which make the evident skewed ladder commute. In particular, the automorphism group of the chain
$i \in \{0,1,\dots ,m\}$
, which make the evident skewed ladder commute. In particular, the automorphism group of the chain
![]() $\sigma $
in
$\sigma $
in
![]() $\mathcal {C}$
may be identified with the group of automorphisms of
$\mathcal {C}$
may be identified with the group of automorphisms of
![]() $X_m$
which preserve
$X_m$
which preserve
![]() $X_i$
for all
$X_i$
for all
![]() $0 \leqslant i \leqslant m$
. We write
$0 \leqslant i \leqslant m$
. We write
![]() $[S(\mathcal {C})]$
for the partially ordered set of isomorphism classes of objects in
$[S(\mathcal {C})]$
for the partially ordered set of isomorphism classes of objects in
![]() $S(\mathcal {C})$
, where
$S(\mathcal {C})$
, where
![]() $[\sigma ] \leqslant [\tau ]$
if there are representatives
$[\sigma ] \leqslant [\tau ]$
if there are representatives
![]() $\sigma ' \in [\sigma ]$
and
$\sigma ' \in [\sigma ]$
and
![]() $\tau ' \in [\tau ]$
and a morphism
$\tau ' \in [\tau ]$
and a morphism
![]() $\sigma ' \to \tau '$
in
$\sigma ' \to \tau '$
in
![]() $S(\mathcal {C})$
.
$S(\mathcal {C})$
.
There is a simpler resolution than the standard bar resolution for computing cohomology of a functor defined on the subdivision category of any EI-category, which was given in [Reference LinckelmannLin05].
Lemma 5.3. Let
![]() $\mathcal {C}$
be any full subcategory of a saturated fusion system, and let
$\mathcal {C}$
be any full subcategory of a saturated fusion system, and let
![]() $F\colon [S(\mathcal {C})] \to \mathcal {A}b$
be a covariant functor. The cohomology groups
$F\colon [S(\mathcal {C})] \to \mathcal {A}b$
be a covariant functor. The cohomology groups
![]() $H^n([S(\mathcal {C})],F)$
, and thus the derived functors of
$H^n([S(\mathcal {C})],F)$
, and thus the derived functors of
![]() $\lim F$
, can be computed via the cochain complex
$\lim F$
, can be computed via the cochain complex
![]() $C^*(F)$
defined as follows:
$C^*(F)$
defined as follows:
whose elements are viewed as functions
![]() $\alpha $
from isomorphism classes of chains of length n, and where
$\alpha $
from isomorphism classes of chains of length n, and where
![]() $|\sigma |$
denotes the length of
$|\sigma |$
denotes the length of
![]() $\sigma $
. The coboundary map
$\sigma $
. The coboundary map
![]() $\delta ^n \colon C^n(F) \to C^{n+1}(F)$
is defined by
$\delta ^n \colon C^n(F) \to C^{n+1}(F)$
is defined by
 $$\begin{align*}\delta^n(\alpha)([\sigma]) = \sum_{i = 0}^n (-1)^{i} F(\iota_{[\sigma(i)], [\sigma]})(\alpha([\sigma(i)])), \end{align*}$$
$$\begin{align*}\delta^n(\alpha)([\sigma]) = \sum_{i = 0}^n (-1)^{i} F(\iota_{[\sigma(i)], [\sigma]})(\alpha([\sigma(i)])), \end{align*}$$
where
![]() $\sigma (i)$
denotes the chain
$\sigma (i)$
denotes the chain
![]() $\sigma $
with its ith term removed and
$\sigma $
with its ith term removed and
![]() $\iota _{[\sigma (i)], [\sigma ]}$
denotes the unique morphism from
$\iota _{[\sigma (i)], [\sigma ]}$
denotes the unique morphism from
![]() $[\sigma (i)]$
to
$[\sigma (i)]$
to
![]() $[\sigma ]$
.
$[\sigma ]$
.
Proof. This is [Reference LinckelmannLin05, Proposition 3.2], applied as in [Reference ParkPar10, Lemma 3.1].
Finally, the aim of the following, highly specialized lemma is to orient the reader to the way in which Lemma 5.3 will be used later in the proof of Theorem 5.6.
Lemma 5.4. Let
![]() $\mathcal {C}$
be a saturated fusion system, and let
$\mathcal {C}$
be a saturated fusion system, and let
![]() $F \colon [S(\mathcal {C}^{cr})] \to \mathcal {A}b$
be a covariant functor. Then
$F \colon [S(\mathcal {C}^{cr})] \to \mathcal {A}b$
be a covariant functor. Then
![]() $\lim _{[S(\mathcal {C}^{cr})]}F = 0$
under either of the following conditions.
$\lim _{[S(\mathcal {C}^{cr})]}F = 0$
under either of the following conditions.
-
(a)
 $F([X]) = 0$
for all subgroups
$F([X]) = 0$
for all subgroups
 $X \in \mathcal {C}^{cr}$
;
$X \in \mathcal {C}^{cr}$
; -
(b) F is zero on all but two distinct chains
 $[X_0]$
and
$[X_0]$
and
 $[X_1]$
of length zero, and there exists a subgroup
$[X_1]$
of length zero, and there exists a subgroup
 $Y \in \mathcal {C}^{cr}$
, such that
$Y \in \mathcal {C}^{cr}$
, such that
 $F([Y])= 0$
,
$F([Y])= 0$
,-
(i)
 $X_0 < X_1> Y$
, and
$X_0 < X_1> Y$
, and -
(ii) the maps
 $F([X_0]) \to F([X_0 < X_1])$
and
$F([X_0]) \to F([X_0 < X_1])$
and
 $F([X_1]) \to F([Y < X_1])$
are injective.
$F([X_1]) \to F([Y < X_1])$
are injective.
-
Proof. We view
![]() $\lim _{[S(\mathcal {C}^{cr})]} F$
as the degree
$\lim _{[S(\mathcal {C}^{cr})]} F$
as the degree
![]() $0$
cohomology of the functor F. As such, it can be computed by using the cochain complex of Lemma 5.3. The coboundary map
$0$
cohomology of the functor F. As such, it can be computed by using the cochain complex of Lemma 5.3. The coboundary map
![]() $\delta ^0 \colon C^0(F) \to C^1(F)$
on
$\delta ^0 \colon C^0(F) \to C^1(F)$
on
![]() $0$
-cochains is obtained by extending linearly from
$0$
-cochains is obtained by extending linearly from
With this in mind, the two parts of the lemma are simply ways of saying that the kernel of
![]() $\delta ^0$
, and thus
$\delta ^0$
, and thus
![]() $\lim _{[S(\mathcal {C}^{cr})]} F$
, is
$\lim _{[S(\mathcal {C}^{cr})]} F$
, is
![]() $0$
. This is trivial in the case of part (a). The assumption in (b) implies that
$0$
. This is trivial in the case of part (a). The assumption in (b) implies that
![]() $C^0(F) = F([X_0]) \oplus F([X_1])$
, and then (i) and (ii) ensure that the composite
$C^0(F) = F([X_0]) \oplus F([X_1])$
, and then (i) and (ii) ensure that the composite
is injective.
We now begin the computation of the higher limits of
![]() $H^2(-,k^\times )$
in the cases of interest.
$H^2(-,k^\times )$
in the cases of interest.
Lemma 5.5. Fix an algebraically closed field k of characteristic
![]() $2$
, and let
$2$
, and let
![]() $\mathcal {D} \in \{\mathcal {F},\mathcal {H},\mathcal {K}\}$
. For each
$\mathcal {D} \in \{\mathcal {F},\mathcal {H},\mathcal {K}\}$
. For each
![]() $P \in \mathcal {D}^{cr}$
, one of the following holds.
$P \in \mathcal {D}^{cr}$
, one of the following holds.
-
(a)
 $H^2(\operatorname {Out}_{\mathcal {D}}(P), k^\times ) = 0$
, or
$H^2(\operatorname {Out}_{\mathcal {D}}(P), k^\times ) = 0$
, or -
(b)
 $l = 0$
,
$l = 0$
,
 $H^2(\operatorname {Out}_{\mathcal {D}}(P), k^\times ) \cong H^2(\operatorname {Out}_{\mathcal {D}}(P), \mathbb {F}_3) \cong C_3$
, and either
$H^2(\operatorname {Out}_{\mathcal {D}}(P), k^\times ) \cong H^2(\operatorname {Out}_{\mathcal {D}}(P), \mathbb {F}_3) \cong C_3$
, and either-
(i)
 $P = QR_{1^7}$
,
$P = QR_{1^7}$
, -
(ii)
 $P = Q$
and
$P = Q$
and
 $\mathcal {D} = \mathcal {H}$
, or
$\mathcal {D} = \mathcal {H}$
, or -
(iii)
 $P = R_{1^7}$
and
$P = R_{1^7}$
and
 $\mathcal {D} = \mathcal {H}$
or
$\mathcal {D} = \mathcal {H}$
or
 $\mathcal {F}$
.
$\mathcal {F}$
.
-
Proof. We first prove the lemma for
![]() $l> 0$
. Fix
$l> 0$
. Fix
![]() $P \in \mathcal {D}^{cr}$
appearing in Tables 2, 3, or 4, and let
$P \in \mathcal {D}^{cr}$
appearing in Tables 2, 3, or 4, and let
![]() $G = \operatorname {Out}_{\mathcal {D}}(P)$
be its outer automorphism group in
$G = \operatorname {Out}_{\mathcal {D}}(P)$
be its outer automorphism group in
![]() $\mathcal {D}$
, for short. In order to show that (a) holds in this case
$\mathcal {D}$
, for short. In order to show that (a) holds in this case
![]() $(l> 0)$
, it suffices to show that
$(l> 0)$
, it suffices to show that
![]() $H^2(G,\mathbb {F}_p) = 0$
for all odd primes p by Lemma 5.2(c). Now G is p-perfect for all odd primes p by Lemma 5.1. An inspection of the tables shows that one of three cases holds: (1) G has cyclic Sylow p-subgroups for all odd primes p, (2) G has cyclic Sylow p-subgroups for all
$H^2(G,\mathbb {F}_p) = 0$
for all odd primes p by Lemma 5.2(c). Now G is p-perfect for all odd primes p by Lemma 5.1. An inspection of the tables shows that one of three cases holds: (1) G has cyclic Sylow p-subgroups for all odd primes p, (2) G has cyclic Sylow p-subgroups for all
![]() $p \geqslant 5$
and elementary Sylow
$p \geqslant 5$
and elementary Sylow
![]() $3$
-subgroups of order
$3$
-subgroups of order
![]() $3^2$
, or (3)
$3^2$
, or (3)
![]() $G \cong S_3 \wr S_3$
. By Lemma 5.2(d), we have
$G \cong S_3 \wr S_3$
. By Lemma 5.2(d), we have
![]() $H^2(G,\mathbb {F}_p)=0$
for all odd primes p in Case (1). Assume (2). Then
$H^2(G,\mathbb {F}_p)=0$
for all odd primes p in Case (1). Assume (2). Then
![]() $G \cong S_6$
,
$G \cong S_6$
,
![]() $S_7$
,
$S_7$
,
![]() $GL_4(2)$
,
$GL_4(2)$
,
![]() $S_3 \times S_3$
, or
$S_3 \times S_3$
, or
![]() $S_3 \wr C_2$
. In all cases,
$S_3 \wr C_2$
. In all cases,
![]() $H^2(G,\mathbb {F}_p) = 0$
for all
$H^2(G,\mathbb {F}_p) = 0$
for all
![]() $p \geqslant 5$
, again by Lemma 5.2(d). For a Sylow
$p \geqslant 5$
, again by Lemma 5.2(d). For a Sylow
![]() $3$
-subgroup V of G, we have
$3$
-subgroup V of G, we have
![]() $\operatorname {Aut}_G(V) \nleq \operatorname {SL}(V)$
by direct computation, and so
$\operatorname {Aut}_G(V) \nleq \operatorname {SL}(V)$
by direct computation, and so
![]() $H^2(G,\mathbb {F}_3) = 0$
in Case (2) as well, by Lemma 5.2(e). Finally, assume Case (3), so that
$H^2(G,\mathbb {F}_3) = 0$
in Case (2) as well, by Lemma 5.2(e). Finally, assume Case (3), so that
![]() $G \cong S_3 \wr S_3$
. Again, we just need to show that
$G \cong S_3 \wr S_3$
. Again, we just need to show that
![]() $H^2(G,\mathbb {F}_3) = 0$
. In this case, one can apply the Lyndon-Hochschild-Serre spectral sequence [Reference WeibelWei94, Lyndon-Hochschild-Serre Spectral Sequence 6.8.2] with respect to the base B of the wreath product. The relevant parts of the
$H^2(G,\mathbb {F}_3) = 0$
. In this case, one can apply the Lyndon-Hochschild-Serre spectral sequence [Reference WeibelWei94, Lyndon-Hochschild-Serre Spectral Sequence 6.8.2] with respect to the base B of the wreath product. The relevant parts of the
![]() $E_2$
-page are
$E_2$
-page are
-
○
 $H^{0}(S_3, H^{2}(B, \mathbb {F}_3)) = 0$
(the coefficients are 0);
$H^{0}(S_3, H^{2}(B, \mathbb {F}_3)) = 0$
(the coefficients are 0); -
○
 $H^{1}(S_3, H^1(B, \mathbb {F}_3)) = 0$
(since the base is
$H^{1}(S_3, H^1(B, \mathbb {F}_3)) = 0$
(since the base is
 $3$
-perfect); and
$3$
-perfect); and -
○
 $H^2(S_3, H^0(B, \mathbb {F}_3)) = 0$
(trivial invariants).
$H^2(S_3, H^0(B, \mathbb {F}_3)) = 0$
(trivial invariants).
Hence,
![]() $H^2(G,\mathbb {F}_3) = 0$
. This completes the proof in the case
$H^2(G,\mathbb {F}_3) = 0$
. This completes the proof in the case
![]() $l> 0$
. We now turn to the case
$l> 0$
. We now turn to the case
![]() $l=0$
. By inspection of Table 1, either it was shown in the previous case that
$l=0$
. By inspection of Table 1, either it was shown in the previous case that
![]() $H^2(\operatorname {Out}_{\mathcal {D}}(P), k^\times ) = 0$
, or else the subgroup P is listed in (b)(i)–(b)(iii) of the lemma. We go through these three cases in turn, and we set
$H^2(\operatorname {Out}_{\mathcal {D}}(P), k^\times ) = 0$
, or else the subgroup P is listed in (b)(i)–(b)(iii) of the lemma. We go through these three cases in turn, and we set
![]() $G = \operatorname {Out}_{\mathcal {D}}(P)$
again for short.
$G = \operatorname {Out}_{\mathcal {D}}(P)$
again for short.
Case 1.
![]() $P = QR_{1^7}$
and
$P = QR_{1^7}$
and
![]() $G \cong (C_3 \times C_3) \overset {-1}{\rtimes } \langle \mathbf {d} \rangle $
:
$G \cong (C_3 \times C_3) \overset {-1}{\rtimes } \langle \mathbf {d} \rangle $
:
Recall that
![]() $M_{2'}(G) \cong H^2(G,k^\times )$
is an abelian group of odd order, so it must be
$M_{2'}(G) \cong H^2(G,k^\times )$
is an abelian group of odd order, so it must be
![]() $M_3(G)$
. Let e be its exponent. From Lemma 5.2(h),
$M_3(G)$
. Let e be its exponent. From Lemma 5.2(h),
![]() $e^2$
divides
$e^2$
divides
![]() $|G| = 3^2\cdot 2$
. Hence,
$|G| = 3^2\cdot 2$
. Hence,
![]() $e = 1$
or
$e = 1$
or
![]() $3$
. By Lemma 5.2(g), we see that
$3$
. By Lemma 5.2(g), we see that
and
![]() $H^2(G, \mathbb {F}_3) \cong \mathbb {F}_3$
by Lemma 5.2(e) (
$H^2(G, \mathbb {F}_3) \cong \mathbb {F}_3$
by Lemma 5.2(e) (
![]() $\mathbf {d}$
acts by minus the identity). This completes the proof of Case 1.
$\mathbf {d}$
acts by minus the identity). This completes the proof of Case 1.
Case 2.
![]() $P = Q$
: Suppose first that
$P = Q$
: Suppose first that
![]() $\mathcal {D} = \mathcal {H}$
. Then
$\mathcal {D} = \mathcal {H}$
. Then
![]() $G := \operatorname {Out}_{\mathcal {D}}(P) \cong C_3^3 \rtimes (C_2 \times C_2)$
with one factor inverting
$G := \operatorname {Out}_{\mathcal {D}}(P) \cong C_3^3 \rtimes (C_2 \times C_2)$
with one factor inverting
![]() $C_3^3$
and the other swapping the first two
$C_3^3$
and the other swapping the first two
![]() $C_3$
factors. We first claim that the exponent of
$C_3$
factors. We first claim that the exponent of
![]() $H^2(G,k^\times )$
is not divisible by
$H^2(G,k^\times )$
is not divisible by
![]() $3^2$
. Indeed, this follows directly from Lemma 5.2(h), as otherwise
$3^2$
. Indeed, this follows directly from Lemma 5.2(h), as otherwise
![]() $|G|$
would be divisible by
$|G|$
would be divisible by
![]() $3^4$
, which is not the case. It follows that
$3^4$
, which is not the case. It follows that
![]() $H^2(G,k^\times ) \cong H^2(G,\mathbb {F}_3)$
by Lemma 5.2(g). Now
$H^2(G,k^\times ) \cong H^2(G,\mathbb {F}_3)$
by Lemma 5.2(g). Now
where the
![]() $y_i$
are polynomial generators and the
$y_i$
are polynomial generators and the
![]() $x_i$
are exterior generators. Further,
$x_i$
are exterior generators. Further,
![]() $H^2(G, \mathbb {F}_3)$
is the invariants under
$H^2(G, \mathbb {F}_3)$
is the invariants under
![]() $\langle \mathbf {d},\tau \rangle $
here. We compute directly that the invariants are spanned by
$\langle \mathbf {d},\tau \rangle $
here. We compute directly that the invariants are spanned by
![]() $x_1x_3 + x_2x_3$
, and so have dimension
$x_1x_3 + x_2x_3$
, and so have dimension
![]() $1$
. Thus,
$1$
. Thus,
![]() $H^2(G, k^\times ) \cong H^2(G,\mathbb {F}_3) \cong C_3$
.
$H^2(G, k^\times ) \cong H^2(G,\mathbb {F}_3) \cong C_3$
.
Now suppose that
![]() $\mathcal {D} = \mathcal {K}$
or
$\mathcal {D} = \mathcal {K}$
or
![]() $\mathcal {F}$
. Then
$\mathcal {F}$
. Then
![]() $G=\operatorname {Out}_{\mathcal {D}}(P) \cong C_3^3 \rtimes (\langle \mathbf {d} \rangle \times S_3)$
with
$G=\operatorname {Out}_{\mathcal {D}}(P) \cong C_3^3 \rtimes (\langle \mathbf {d} \rangle \times S_3)$
with
![]() $\mathbf {d}$
inverting, and we have
$\mathbf {d}$
inverting, and we have
since a Sylow
![]() $3$
-subgroup is normal in G. Let
$3$
-subgroup is normal in G. Let
![]() $W \cong C_3 \wr C_3$
be the Sylow
$W \cong C_3 \wr C_3$
be the Sylow
![]() $3$
-subgroup of G, and write
$3$
-subgroup of G, and write
![]() $W_0$
for the base subgroup of W. By a result of Nakaoka [Reference NakaokaNak61, Theorem 3.3], we have
$W_0$
for the base subgroup of W. By a result of Nakaoka [Reference NakaokaNak61, Theorem 3.3], we have
The middle term above vanishes: by Lemma 5.2(a),
as a
![]() $W/W_0$
-module, so that
$W/W_0$
-module, so that
![]() $H^1(C_3, H^1(W_0, \mathbb {F}_3)) \cong H^1(C_3, \operatorname {Coind}_1^{C_3} \mathbb {F}_3) = 0$
by Shapiro’s Lemma [Reference WeibelWei94, Lemma 6.3.2]. Hence,
$H^1(C_3, H^1(W_0, \mathbb {F}_3)) \cong H^1(C_3, \operatorname {Coind}_1^{C_3} \mathbb {F}_3) = 0$
by Shapiro’s Lemma [Reference WeibelWei94, Lemma 6.3.2]. Hence,
With notation as in (5.1), the first summand is spanned by
![]() $y_1+y_2+y_3$
and
$y_1+y_2+y_3$
and
![]() $x_1x_2+x_2x_3+x_3x_1$
, both being negated by the action of
$x_1x_2+x_2x_3+x_3x_1$
, both being negated by the action of
![]() $\mathbf {d}\tau $
(note that
$\mathbf {d}\tau $
(note that
![]() $\tau $
negates
$\tau $
negates
![]() $x_1x_2+x_2x_3+x_3x_1$
). Similarly, the second summand is also negated by
$x_1x_2+x_2x_3+x_3x_1$
). Similarly, the second summand is also negated by
![]() $\mathbf {d}\tau $
. Hence,
$\mathbf {d}\tau $
. Hence,
![]() $H^2(G,\mathbb {F}_3) = 0$
, and we conclude that
$H^2(G,\mathbb {F}_3) = 0$
, and we conclude that
![]() $H^2(G,k^{\times }) = 0$
by Lemma 5.2(c).
$H^2(G,k^{\times }) = 0$
by Lemma 5.2(c).
Case 3.
![]() $P = R_{1^7}$
: Then
$P = R_{1^7}$
: Then
![]() $\mathcal {D} = \mathcal {H}$
or
$\mathcal {D} = \mathcal {H}$
or
![]() $\mathcal {F}$
, and
$\mathcal {F}$
, and
![]() $\operatorname {Out}_{\mathcal {D}}(P) \cong A_7$
. The odd part of the Schur multiplier is well known to be
$\operatorname {Out}_{\mathcal {D}}(P) \cong A_7$
. The odd part of the Schur multiplier is well known to be
![]() $C_3$
. Alternatively, apply Lemma 5.2(h) to see that the exponent of the odd part of the Schur multiplier is
$C_3$
. Alternatively, apply Lemma 5.2(h) to see that the exponent of the odd part of the Schur multiplier is
![]() $3$
, and then use Lemma 5.2(e,g).
$3$
, and then use Lemma 5.2(e,g).
Theorem 5.6. For q an odd prime power and
![]() $\mathcal {F} = \operatorname {Sol}(q)$
, we have
$\mathcal {F} = \operatorname {Sol}(q)$
, we have
Proof. Let
![]() $(\mathcal {F},\alpha )$
be a Külshammer-Puig pair. When
$(\mathcal {F},\alpha )$
be a Külshammer-Puig pair. When
![]() $l> 0$
, all minimal elements of the partially ordered set
$l> 0$
, all minimal elements of the partially ordered set
![]() $[S(\mathcal {F}^{cr})]$
, namely, the chains
$[S(\mathcal {F}^{cr})]$
, namely, the chains
![]() $\sigma = (R)$
of length one, have
$\sigma = (R)$
of length one, have
![]() $\alpha _{[\sigma ]} = 0$
by Lemma 5.5. Thus, the theorem holds in this case by Lemma 5.4(a).
$\alpha _{[\sigma ]} = 0$
by Lemma 5.5. Thus, the theorem holds in this case by Lemma 5.4(a).
It remains to consider the case
![]() $l = 0$
. Then
$l = 0$
. Then
![]() $H^2(\operatorname {Out}_{\mathcal {F}}(P), k^\times )$
is nonzero (of order
$H^2(\operatorname {Out}_{\mathcal {F}}(P), k^\times )$
is nonzero (of order
![]() $3$
) if and only if
$3$
) if and only if
![]() $P = R_{1^7}$
or
$P = R_{1^7}$
or
![]() $QR_{1^7}$
. For the remainder of the proof, we set
$QR_{1^7}$
. For the remainder of the proof, we set
![]() $R := R_{1^7}$
, for short. Consider the chains
$R := R_{1^7}$
, for short. Consider the chains
![]() $\sigma := (R < QR)$
and
$\sigma := (R < QR)$
and
![]() $\tau := (Q < QR)$
. All three subgroups R, Q, and
$\tau := (Q < QR)$
. All three subgroups R, Q, and
![]() $QR$
are weakly
$QR$
are weakly
![]() $\mathcal {F}$
-closed by Lemma 3.7; hence,
$\mathcal {F}$
-closed by Lemma 3.7; hence,
![]() $\operatorname {Aut}_{\mathcal {F}}(\sigma ) = \operatorname {Aut}_{\mathcal {F}}(QR) = \operatorname {Aut}_{\mathcal {F}}(\tau )$
and the induced map on
$\operatorname {Aut}_{\mathcal {F}}(\sigma ) = \operatorname {Aut}_{\mathcal {F}}(QR) = \operatorname {Aut}_{\mathcal {F}}(\tau )$
and the induced map on
![]() $\mathcal {A}^2$
is the identity in each of these cases. We next prove that the induced map
$\mathcal {A}^2$
is the identity in each of these cases. We next prove that the induced map
is injective. Once this is done, Lemma 5.4(b) then yields that
![]() $\lim _{[S(\mathcal {F}^{cr}])} \mathcal {A}^2 = 0$
.
$\lim _{[S(\mathcal {F}^{cr}])} \mathcal {A}^2 = 0$
.

Figure 1 Hasse diagram for
![]() $[\operatorname {Sol}(q)^{cr}]$
,
$[\operatorname {Sol}(q)^{cr}]$
,
![]() $q \equiv \pm 3 \pmod {8}$
.
$q \equiv \pm 3 \pmod {8}$
.

Figure 2 Hasse diagram for
![]() $[\operatorname {Sol}(q)^{cr}]$
,
$[\operatorname {Sol}(q)^{cr}]$
,
![]() $q \equiv \pm 7 \pmod {16}$
, that is, for
$q \equiv \pm 7 \pmod {16}$
, that is, for
![]() $l = 1$
.
$l = 1$
.
By Lemmas 3.7 and 3.8,
![]() $QR$
contains R as a normal subgroup with index 4, and
$QR$
contains R as a normal subgroup with index 4, and
![]() $QR/R \cong C_2 \times C_2$
. Hence, Lemma 2.7 yields that the restriction map
$QR/R \cong C_2 \times C_2$
. Hence, Lemma 2.7 yields that the restriction map
![]() $\operatorname {Aut}_{\mathcal {F}}(\sigma ) = \operatorname {Aut}_{\mathcal {F}}(QR) \to \operatorname {Aut}_{\mathcal {F}}(R)$
induces an isomorphism
$\operatorname {Aut}_{\mathcal {F}}(\sigma ) = \operatorname {Aut}_{\mathcal {F}}(QR) \to \operatorname {Aut}_{\mathcal {F}}(R)$
induces an isomorphism
This isomorphism identifies
![]() $\operatorname {Aut}_{\mathcal {F}}(QR)/\operatorname {Aut}_{R}(QR)$
with the normalizer in
$\operatorname {Aut}_{\mathcal {F}}(QR)/\operatorname {Aut}_{R}(QR)$
with the normalizer in
![]() $\operatorname {Out}_{\mathcal {F}}(R) \cong A_7$
of the four subgroup
$\operatorname {Out}_{\mathcal {F}}(R) \cong A_7$
of the four subgroup
![]() $QR/R \cong \operatorname {Aut}_{QR}(R)/\operatorname {Aut}_{R}(R)$
.
$QR/R \cong \operatorname {Aut}_{QR}(R)/\operatorname {Aut}_{R}(R)$
.
Since this normalizer contains a Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $A_7$
, we conclude that the restriction map
$A_7$
, we conclude that the restriction map
in
![]() $\mathbb {F}_3$
-cohomology is injective by [Reference BensonBen98b, Corollary 3.6.18]. By [Reference WeibelWei94, Functoriality of H * and Restriction 6.7.6] on the functoriality of restriction, the diagram
$\mathbb {F}_3$
-cohomology is injective by [Reference BensonBen98b, Corollary 3.6.18]. By [Reference WeibelWei94, Functoriality of H * and Restriction 6.7.6] on the functoriality of restriction, the diagram

commutes. Here, the vertical arrows are given by the isomorphisms of Lemma 5.2(g), which applies since
![]() $\operatorname {Aut}_{\mathcal {F}}(R)$
and
$\operatorname {Aut}_{\mathcal {F}}(R)$
and
![]() $\operatorname {Aut}_{\mathcal {F}}(\sigma )$
have Sylow
$\operatorname {Aut}_{\mathcal {F}}(\sigma )$
have Sylow
![]() $3$
-subgroups of order
$3$
-subgroups of order
![]() $3^2$
. Therefore,
$3^2$
. Therefore,
![]() $\rho _{(3)}$
is injective, as claimed. This completes the proof in the case
$\rho _{(3)}$
is injective, as claimed. This completes the proof in the case
![]() $l=0$
and of the theorem.
$l=0$
and of the theorem.
Proof of Theorem 1.1
By [Reference Levi and OliverLO02], there exists a centric linking system associated with
![]() $\mathcal {F}$
. Thus, [Reference LibmanLib11, Theorem 1.2] yields that
$\mathcal {F}$
. Thus, [Reference LibmanLib11, Theorem 1.2] yields that
The result now follows from Theorem 5.6.
Appendix: Hasse diagrams
Displayed without proof are Hasse diagrams for the partially ordered set of isomorphism classes of centric radicals in
![]() $\operatorname {Sol}(q)$
that were computed with the aid of Magma [Reference Bosma, Cannon and PlayoustBCP97].
$\operatorname {Sol}(q)$
that were computed with the aid of Magma [Reference Bosma, Cannon and PlayoustBCP97].
Acknowledgements
We thank Markus Linckelmann and Radha Kessar for encouragement, Geoffrey Robinson for comments on an earlier version, and Dave Benson and Ian Leary for helpful conversations concerning Section 5. We express our gratitude to both referees, whose thorough readings and many suggestions resulted in numerous improvements to the paper. JL was supported by Marie Curie Fellowship No. 707778 and National Science Foundation Grant DMS-1902152 during the preparation of this manuscript. JS acknowledges personal support from the Heilbronn Institute for Mathematical Research and the Engineering and Physical Sciences Research Council (grant EP/W028794/1).
Competing interest
The authors have no competing interest to declare.