Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T00:04:47.714Z Has data issue: false hasContentIssue false
  • English
  • Français

WEIGHTED BESOV AND TRIEBEL–LIZORKIN SPACES ASSOCIATED WITH OPERATORS AND APPLICATIONS

Part of: Distributions, generalized functions, distribution spaces Harmonic analysis in several variables Parabolic equations and systems Groups and semigroups of linear operators, their generalizations and applications Special classes of linear operators

Published online by Cambridge University Press:  26 February 2020

HUY-QUI BUI ,
THE ANH BUI  and
XUAN THINH DUONG
HUY-QUI BUI
Affiliation:
Department of Mathematics, University of Canterbury, Private Bag 4800, Christchurch8140, New Zealand; [email protected], [email protected]
THE ANH BUI
Affiliation:
Department of Mathematics and Statistics, Macquarie University, NSW 2109, Australia; [email protected], [email protected], [email protected]
XUAN THINH DUONG
Affiliation:
Department of Mathematics and Statistics, Macquarie University, NSW 2109, Australia; [email protected], [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

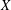Let $X$ be a space of homogeneous type and 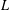$L$ be a nonnegative self-adjoint operator on 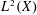$L^{2}(X)$ satisfying Gaussian upper bounds on its heat kernels. In this paper, we develop the theory of weighted Besov spaces 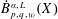${\dot{B}}_{p,q,w}^{\unicode[STIX]{x1D6FC},L}(X)$ and weighted Triebel–Lizorkin spaces 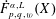${\dot{F}}_{p,q,w}^{\unicode[STIX]{x1D6FC},L}(X)$ associated with the operator 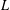$L$ for the full range 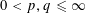$0<p,q\leqslant \infty$, 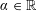$\unicode[STIX]{x1D6FC}\in \mathbb{R}$ and $w$ being in the Muckenhoupt weight class 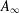$A_{\infty }$. Under rather weak assumptions on 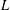$L$ as stated above, we prove that our new spaces satisfy important features such as continuous characterizations in terms of square functions, atomic decompositions and the identifications with some well-known function spaces such as Hardy-type spaces and Sobolev-type spaces. One of the highlights of our result is the characterization of these spaces via noncompactly supported functional calculus. An important by-product of this characterization is the characterization via the heat kernel for the full range of indices. Moreover, with extra assumptions on the operator 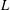$L$, we prove that the new function spaces associated with 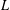$L$ coincide with the classical function spaces. Finally we apply our results to prove the boundedness of the fractional power of 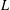$L$, the spectral multiplier of 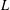$L$ in our new function spaces and the dispersive estimates of wave equations.

MSC classification

Primary: 42B37: Harmonic analysis and PDE
Secondary: 47D08: Schrödinger and Feynman-Kac semigroups 46F05: Topological linear spaces of test functions, distributions and ultradistributions 47B38: Operators on function spaces (general) 35K08: Heat kernel
Type
Differential Equations
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e11
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Aguilera, N. and Segovia, C., ‘Weighted norm inequalities relating the g 𝜆∗ and the area functions’, Studia Math. 61(3) (1977), 293–303.CrossRefGoogle Scholar
Auscher, P., Duong, X. T. and McIntosh, A., ‘Boundedness of Banach space valued singular integral operators and Hardy spaces’, Preprint, 2005 (unpublished).Google Scholar
Auscher, P. and Martell, J. M., ‘Weighted norm inequalities, off–diagonal estimates and elliptic operators. Part III: harmonic Analysis of elliptic operators’, J. Funct. Anal. 241 (2006), 703–746.CrossRefGoogle Scholar
Besov, O. V., ‘On a family of function spaces, embedding theorems and extensions’, Dokl. Akad. Nauk SSSR 126 (1959), 1163–1165 (in Russian).Google Scholar
Besov, O. V., ‘On a family of function spaces in connection with embeddings and extensions’, Tr. Mat. Inst. Steklova 60 (1961), 42–81 (in Russian).Google Scholar
Besov, O. V., II’in, V. P. and Nikol’skii, S. M., Integral Representation of Functions and Embedding Theorems (ed. Winston, V. H.) vol. I (Sons, Washington, DC, 1979), vol. II.Google Scholar
Bui, H.-Q., Bui, T. A. and Duong, X. T., ‘New test distribution spaces, Besov and Triebel–Lizorkin spaces associated to operators and applications to dispersive estimates’, Preprint (unpublished).Google Scholar
Bui, H.-Q. and Candy, T., ‘A characterisation of the Besov–Lipschitz and Triebel–Lizorkin spaces using Poisson like kernels’, Contemp. Maths 693 (2017), 109–141.CrossRefGoogle Scholar
Bui, H.-Q., Duong, X. T. and Yan, L. X., ‘Calderón reproducing formulas and new Besov spaces associated with operators’, Adv. Math. 229 (2012), 2449–2502.CrossRefGoogle Scholar
Bui, H.-Q., Paluszýnski, M. and Taibleson, M. H., ‘A note on the Besov–Lipschitz and Triebel–Lizorkin spaces’, Contemp. Math. 189 (1995), 95–101.CrossRefGoogle Scholar
Bui, H.-Q., Paluszýnski, M. and Taibleson, M. H., ‘A maximal function characterization of weighted Besov–Lipschitz and Triebel–Lizorkin spaces’, Studia Math. 119 (1996), 219–246.Google Scholar
Bui, H.-Q., Paluszýnski, M. and Taibleson, M. H., ‘Characterization of the Besov–Lipschitz and Triebel–Lizorkin spaces. The case q < 1’, J. Fourier Anal. Appl. 3 (1997), 837–846.CrossRefGoogle Scholar
Bui, H.-Q. and Taibleson, M. H., ‘The characterization of the Triebel–Lizorkin spaces for p = ∞’, J. Fourier Anal. Appl. 6 (2000), 537–550.CrossRefGoogle Scholar
Bui, T. A., Cao, J., Ky, L. D., Yang, D. and Yang, S., ‘Musielak–Orlicz–Hardy spaces associated with operators satisfying reinforced off-diagonal estimates’, Anal. Geom. Metr. Spaces 1 (2013), 69–129.CrossRefGoogle Scholar
Bui, T. A., D’Ancona, P., Duong, X. T. and Müller, D., ‘On the flows associated to selfadjoint operators on metric measure spaces’, Math. Ann. 375 (2019), 1393–1426.CrossRefGoogle Scholar
Bui, T. A. and Duong, X. T., ‘Besov and Triebel–Lizorkin spaces associated to Hermite operators’, J. Fourier Anal. Appl. 21(2) (2015), 405–448.CrossRefGoogle Scholar
Bui, T. A. and Duong, X. T., ‘Laguerre operator and its associated weighted Besov and Triebel–Lizorkin spaces’, Trans. Amer. Math. Soc. 369(3) (2017), 2109–2150.CrossRefGoogle Scholar
Bui, T. A. and Duong, X. T., ‘Spectral multipliers of self-adjoint operators on Besov and Triebel–Lizorkin spaces associated to operators’, Int. Math. Res. Not. IMRN (to appear).Google Scholar
Bui, T. A. and Duong, X. T., ‘Weighted BMO spaces associated to operators’, Proceedings of the AMSI/AustMS 2014 Workshop in Harmonic Analysis and its Applications, 725, Proc. Centre Math. Appl. Austral. Nat. Univ., 47 (Center of Mathematics Analysis at ANU, 2017).Google Scholar
Bui, T. A., Duong, X. T. and Hong, Y., ‘Dispersive and Strichartz estimates for the three–dimensional wave equation with a scaling-critical class of potentials’, J. Funct. Anal. 271 (2016), 2215–2246.CrossRefGoogle Scholar
Bui, T. A., Duong, X. T. and Ly, F. K., ‘Maximal function characterizations for new local Hardy type spaces on spaces of homogeneous type’, Trans. Amer. Math. Soc. 370(10) (2018), 7229–7292.CrossRefGoogle Scholar
Calderón, A. P. and Torchinsky, A., ‘Parabolic maximal functions associated with a distribution’, Adv. Math. 16 (1975), 1–64.CrossRefGoogle Scholar
Christ, M., ‘A T (b) theorem with remarks on analytic capacity and the Cauchy integral’, Colloq. Math. 61 (1990), 601–628.CrossRefGoogle Scholar
Coifman, R. R. and Weiss, G., Analyse Harmonique Non-commutative sur Certains Espaces Homogenes, Lecture Notes in Mathematics, 242 (Springer, Berlin–New York, 1971).CrossRefGoogle Scholar
Coulhon, T. and Duong, X. T., ‘Maximal regularity and kernel bounds: observations on a theorem by Hieber and Prüss’, Adv. Differential Equ. 5 (2000), 343–368.Google Scholar
Coulhon, T., Kerkyacharian, G. and Petrushev, P., ‘Heat kernel generated frames in the setting of Dirichlet spaces’, J. Fourier Anal. Appl. 18(5) (2012), 995–1066.CrossRefGoogle Scholar
Coulhon, T. and Sikora, A., ‘Gaussian heat kernel upper bounds via Phragmén–Lindelöf theorem’, Proc. Lond. Math. Soc. (3) 96 (2008), 507–544.CrossRefGoogle Scholar
D’Ancona, P. and Pierfelice, V., ‘On the wave equation with a large rough potential’, J. Funct. Anal. 227(1) (2005), 30–77.CrossRefGoogle Scholar
D’Ancona, P., Pierfelice, V. and Ricci, F., ‘On the wave equation associated to the Hermite and the twisted Laplacian’, J. Fourier Anal. Appl. 16 (2010), 294–310.CrossRefGoogle Scholar
Duong, X. T., Ouhabaz, E. M. and Sikora, A., ‘Plancherel-type estimates and sharp spectral multipliers’, J. Funct. Anal. 196 (2002), 443–485.CrossRefGoogle Scholar
Duong, X. T. and Yan, L. X., ‘New function spaces of BMO type the John–Nirenberg inequality, interpolation and applications’, Comm. Pure Appl. Math. 58 (2005), 1375–1420.CrossRefGoogle Scholar
Duong, X. T. and Yan, L. X., ‘Duality of Hardy and BMO spaces associated with operators with heat kernel bounds’, J. Amer. Math. Soc. 18 (2005), 943–973.CrossRefGoogle Scholar
Duong, X. T., Li, J. and Yan, L. X., ‘A Littlewood–Paley type decomposition and weighted Hardy spaces associated with operators’, J. Geom. Anal. 26(2) (2016), 1617–1646.CrossRefGoogle Scholar
Frazier, M. and Jawerth, B., ‘Decomposition of Besov spaces’, Indiana Univ. Math. J. 34 (1985), 777–799.CrossRefGoogle Scholar
Frazier, M. and Jawerth, B., ‘A discrete transform and decomposition of distribution spaces’, J. Funct. Anal. 93 (1990), 34–170.CrossRefGoogle Scholar
Georgiadis, A. G., Kerkyacharian, G., Kyriazis, G. and Petrushev, P., ‘Homogeneous Besov and Triebel–Lizorkin spaces associated to non-negative self-adjoint operators’, J. Math. Anal. Appl. 449(2) (2017), 1382–1412.CrossRefGoogle Scholar
Georgiadis, A. G., Kerkyacharian, G., Kyriazis, G. and Petrushev, P., ‘Atomic and molecular decomposition of homogeneous spaces of distributions associated to non-negative self-adjoint operators’, J. Fourier Anal. Appl. 25 (2019), 3259–3309.CrossRefGoogle Scholar
Grafakos, L., Liu, L. and Yang, D., ‘Vector-valued singular integrals and maximal functions on spaces of homogeneous type’, Math. Scand. 104 (2009), 296–310.CrossRefGoogle Scholar
Han, Y. S. and Sawyer, E. T., ‘Littlewood–Paley theory on spaces of homogeneous type and the classical function spaces’, Mem. Amer. Math. Soc. 110(530) (1994), vi+126 pp.Google Scholar
Hou, S. X., Yang, D. and Yang, S., ‘Musielak–Orlicz BMO-type spaces associated with generalized approximations to the identity’, Acta Math. Sin. (Engl. Ser.) 30(11) (2014), 1917–1962.CrossRefGoogle Scholar
Hu, G., ‘Littlewood–Paley characterization of weighted Hardy spaces associated with operators’, J. Aust. Math. Soc. 103 (2017), 250–267.CrossRefGoogle Scholar
Han, Y. S., Müller, D. and Yang, D., ‘A theory of Besov and Triebel–Lizorkin spaces on metric measure spaces modeled on Carnot–Caratheodory spaces’, Abstr. Appl. Anal. (2008), Art. ID 893409, 250 pp.CrossRefGoogle Scholar
Heideman, N. J. H., ‘Duality and fractional integration in Lipschitz spaces’, Studia Math. 50 (1974), 65–85.CrossRefGoogle Scholar
Hofmann, S., Lu, G., Mitrea, D., Mitrea, M. and Yan, L., ‘Hardy spaces associated to non-negative self-adjoint operators satisfying Davies–Gaffney estimates’, Mem. Amer. Math. Soc. 214(1007) (2011).Google Scholar
Hofmann, S. and Mayboroda, V., ‘Hardy and BMO spaces associated to divergence form elliptic operators’, Math. Ann. 344 (2009), 37–116.CrossRefGoogle Scholar
Hofmann, S., Mayboroda, V. and McIntosh, A., ‘Second order elliptic operators with complex bounded measurable coefficients in L p, Sobolev and Hardy spaces’, Ann. Sci. Éc. Norm. Supér. (4) 44 (2011), 723–800.CrossRefGoogle Scholar
Jiang, R. and Yang, D., ‘Orlicz–Hardy spaces associated with operators satisfying Davies–Gaffney estimates’, Commun. Contemp. Math. 13(2) (2011), 331–373.CrossRefGoogle Scholar
Keel, M. and Tao, T. T., ‘End point Strichartz estimates’, Amer. J. Math. 120 (1998), 955–980.CrossRefGoogle Scholar
Kenig, C. E., Ponce, G. and Vega, L., ‘Oscillatory integrals and regularity of dispersive equations’, Indiana Math. J. 40 (1991), 33–69.CrossRefGoogle Scholar
Keryacharian, G. and Petrushev, P., ‘Heat kernel based decomposition of spaces of distributions in the framework of Dirichlet spaces’, Trans. Amer. Math. Soc. 367(1) (2015), 121–189.CrossRefGoogle Scholar
Kerkyacharian, G., Petrushev, P., Picard, D. and Xu, Y., ‘Decomposition of Triebel–Lizorkin and Besov spaces in the context of Laguerre expansions’, J. Funct. Anal. 256 (2009), 1137–1188.CrossRefGoogle Scholar
Liu, L., Yang, D. and Yuan, W., ‘Besov-type and Triebel–Lizorkin-type spaces associated with heat kernels’, Collect. Math. 67 (2016), 247–310.CrossRefGoogle Scholar
Müller, D. and Ricci, F., ‘Analysis of second order differential operators on Heisenberg groups. I’, Invent. Math. 101 (1990), 545–582.CrossRefGoogle Scholar
Petrushev, P. and Xu, Y., ‘Decomposition of spaces of distributions induced by Hermite expansions’, J. Fourier Anal. Appl. 14(3) (2008), 372–414.CrossRefGoogle Scholar
Peetre, J., New Thoughts on Besov Spaces, Duke University Mathematica Series (Durham, NC, 1976).Google Scholar
Schlag, W., ‘Dispersive estimates for Schrödinger operators: a survey’, inMathematical Aspects of Nonlinear Dispersive Equations, 255285, Annals of Mathematical Studies, 163 (Princeton University Press, Princeton, NJ, 2007).Google Scholar
Sikora, A., ‘Riesz transform, Gaussian bounds and the method of wave function’, Math. Z. 247 (2004), 643–662.CrossRefGoogle Scholar
Strömberg, J.-O. and Torchinsky, A., Weighted Hardy Spaces (Springer, Berlin, 1989).CrossRefGoogle Scholar
Taggart, R. J., ‘Inhomogeneous Strichartz estimates’, Forum Math. 22(5) (2010), 825–853.CrossRefGoogle Scholar
Triebel, H., Theory of Function Spaces, Monographs in Mathematics, 78 (Birkhäuser, Basel, 1983).CrossRefGoogle Scholar
Triebel, H., Theory of Function Spaces II, Monographs in Mathematics, 84 (Birkhäuser, Basel, 1992).CrossRefGoogle Scholar
Yang, S. and Yang, D., ‘Atomic and maximal function characterizations of Musielak–Orlicz–Hardy spaces associated to non-negative self-adjoint operators on spaces of homogeneous type’, Collect. Math. 70(2) (2019), 197–246.CrossRefGoogle Scholar
Yang, D. and Yuan, W., ‘Pointwise characterizations of Besov and Triebel–Lizorkin spaces in terms of averages on balls’, Trans. Amer. Math. Soc. 369 (2017), 7631–7655.CrossRefGoogle Scholar
Yang, D. and Yang, S., ‘Musielak–Orlicz–Hardy spaces associated with operators and their applications’, J. Geom. Anal. 24(1) (2014), 495–570.CrossRefGoogle Scholar
Yajima, K., ‘The W k, p-continuity of wave operators for Schrödinger operators. III. Even-dimensional cases m⩾4’, J. Math. Sci. Univ. Tokyo 2 (1995), 311–346.Google Scholar
Yuan, W., Sickel, W. and Yang, D., Morrey and Campanato Meet Besov, Lizorkin and Triebel, Lecture Notes in Mathematics, 2005 (Springer, Berlin, 2010).CrossRefGoogle Scholar