Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-07T02:07:15.825Z Has data issue: false hasContentIssue false
  • English
  • Français

UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ARISING FROM HILBERT MODULAR SURFACES

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  23 November 2017

MATTHEW EMERTON ,
DAVIDE REDUZZI  and
LIANG XIAO
MATTHEW EMERTON
Affiliation:
Department of Mathematics, The University of Chicago, 5734 S. University Avenue, Chicago, Illinois 60637, USA; [email protected], [email protected]
DAVIDE REDUZZI
Affiliation:
Department of Mathematics, The University of Chicago, 5734 S. University Avenue, Chicago, Illinois 60637, USA; [email protected], [email protected]
LIANG XIAO
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, 341 Mansfield Road, Storrs, Connecticut 06269, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 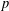$p$ be a prime number and 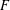$F$ a totally real number field. For each prime 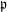$\mathfrak{p}$ of 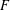$F$ above 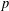$p$ we construct a Hecke operator 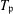$T_{\mathfrak{p}}$ acting on 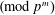$(\text{mod}\,p^{m})$ Katz Hilbert modular classes which agrees with the classical Hecke operator at 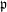$\mathfrak{p}$ for global sections that lift to characteristic zero. Using these operators and the techniques of patching complexes of Calegari and Geraghty we prove that the Galois representations arising from torsion Hilbert modular classes of parallel weight 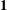$\mathbf{1}$ are unramified at 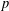$p$ when 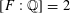$[F:\mathbb{Q}]=2$. Some partial and some conjectural results are obtained when 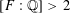$[F:\mathbb{Q}]>2$.

MSC classification

Primary: 11F80: Galois representations
Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 14G35: Modular and Shimura varieties 11G18: Arithmetic aspects of modular and Shimura varieties
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e29
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Andreatta, F. and Goren, E., ‘Hilbert modular forms: mod p and p-adic aspects’, inMemoirs of the American Mathematical Society, Vol. 173 (American Mathematical Society, 2005), 819.Google Scholar
Blickle, M., Schwede, K. and Tucker, K., ‘ F-singularities via alterations’, Amer. J. Math. 137 (2015), 61–109.CrossRefGoogle Scholar
Boeckle, G., Deformations of Galois Representations, Elliptic curves, Hilbert modular forms and Galois deformations, 21–115, Adv. Courses Math. CRM Barcelona (Birkhäuser/Springer, Basel, 2013).Google Scholar
Boxer, G., ‘Torsion in the coherent cohomology of Shimura varieties and Galois representations’, Preprint, 2015, arXiv:1507.05922.Google Scholar
Calegari, F. and Geraghty, D., ‘Modularity liftings beyond the Taylor–Wiles method’, to appear in Inventiones Mathematicae.Google Scholar
Conrad, B., Grothendieck Duality and Base Change, Lecture Notes in Mathematics, 1750 (Springer, Berlin, 2000), vi+296 pp.Google Scholar
Conrad, B., ‘Arithmetic moduli of generalized elliptic curves’, J. Inst. Math. Jussieu 6 (2007), 209–278.Google Scholar
Deligne, P. and Pappas, G., ‘Singularités des espaces de modules de Hilbert en caractéristiques divisant le discriminant’, Compos. Math. 90 (1994), 59–79.Google Scholar
Deligne, P. and Rapoport, M., ‘Les schémas de modules des courbes elliptiques’, inModular Functions of One Variable II, Springer Lecture Notes in Mathematics, 349 (Springer, Berlin, 1973), 143–316.Google Scholar
Deligne, P. and Serre, J.-P., ‘Formes modulaires de poids 1’, Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 507–530.Google Scholar
Dimitrov, M., ‘Compactifications arithmétiques des variétés de Hilbert et formes modulaires de Hilbert pour 𝛤1(c, n)’, inGeometric Aspects of Dwork Theory (Walter de Gruyter, Berlin, 2004), 527–554.Google Scholar
Dimitrov, M. and Tilouine, J., ‘Variétés et formes modulaires de Hilbert arithmétiques pour 𝛤1(c, n)’, inGeometric Aspects of Dwork Theory (Walter de Gruyter, Berlin, 2004), 555–614.Google Scholar
Dimitrov, M. and Wiese, G., ‘Unramifiedness of Galois representations attached to weight one Hilbert modular eigenforms mod p ’, J. Inst. Math. Jussieu (accepted) (2017).Google Scholar
Edixhoven, B., ‘The weight in Serre’s conjecture on modular forms’, Invent. Math. 109 (1992), 563–594.Google Scholar
Emerton, M., Reduzzi, D. and Xiao, L., ‘Galois representations and torsion in the coherent cohomology of Hilbert modular varieties’, J. Reine Angew. Math. 726 (2017), 93–127.CrossRefGoogle Scholar
Gee, T., Modulairty Lifting Theorems (Notes for Arizona Winter School, 2014).Google Scholar
Golding, W. and Kostivirta, J.-S., ‘Strata Hasse invariants, Hecke algebras and Galois representations’, Preprint, 2015, arXiv:1507.05032.Google Scholar
Goren, E., ‘Hasse invariants for Hilbert modular varieties’, Israel J. Math. 122 (2001), 157–174.Google Scholar
Goren, E. and Oort, F., ‘Stratifications of Hilbert modular varieties’, J. Algebraic Geom. 9 (2000), 111–154.Google Scholar
Goren, E. and Kassaei, P., ‘Canonical subgroups over Hilbert modular varieties’, J. Reine Angew. Math. 670 (2012), 1–63.Google Scholar
Gross, B., ‘A tameness criterion for Galois representations associated to modular forms mod p ’, Duke Math. J. 61 (1990), 445–517.Google Scholar
Grothendieck, A., Groupes de Barsotti-Tate et cristaux de Dieudonné, Séminaire de Mathématiques Supérior, 45 (Presses de l’Université de Montréal, Montreal, Que., 1974), 155 pp.Google Scholar
Harris, M., ‘Automorphic forms and the cohomology of vector bundles on Shimura varieties’, inAutomorphic Forms, Shimura Varieties, and L-Functions (Academic Press, New York, 1988), 41–91.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, 52 (Springer, New York-Heidelberg, 1977), xvi+496 pp.Google Scholar
Helm, D., ‘A geometric Jacquet-Langlands correspondence for U (2) Shimura varieties’, Israel J. Math. 187 (2012), 37–80.Google Scholar
Katz, N., ‘A result on modular forms in characteristic p ’, inModular Functions of One Variable, V (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976), Lecture Notes in Mathematics, 601 (Springer, Berlin, 1977), 53–61.CrossRefGoogle Scholar
Katz, N., ‘ p-adic L-functions for CM Fields’, Invent. Math. 49 (1978), 199–297.Google Scholar
Kisin, M. and Lai, K., ‘Overconvergent Hilbert modular forms’, Amer. J. Math. 127 (2005), 735–783.Google Scholar
Lan, K.-W., Arithmetic Compactifications of PEL-type Shimura Varieties, London Mathematical Society Monographs, 36 (Princeton University Press, Princeton, 2013).Google Scholar
Lan, K.-W., ‘Integral models of toroidal compactifications with projective cone decompositions’, Int. Math. Res. Not. IMRN 11 (2017), 3237–3280.Google Scholar
Mazur, B. and Messing, W., Universal Extensions and One-dimensional Crystalline Cohomology, Lecture Notes in Mathematics, 370 (Springer, Berlin-New York, 1974).Google Scholar
Pappas, G., ‘Arithmetic models for Hilbert modular varieties’, Compos. Math. 98 (1995), 43–76.Google Scholar
Pappas, G. and Rapoport, M., ‘Local models in the ramified case. II. Splitting models’, Duke Math. J. 127 (2005), 193–250.Google Scholar
Rapoport, M., ‘Compactifications de l’espace de modules de Hilbert-Blumenthal’, Compos. Math. 36 (1978), 255–335.Google Scholar
Reduzzi, D. and Xiao, L., ‘Partial Hasse invariants on splitting models of Hilbert modular varieties’, Ann. Sci. Éc. Norm. Supér. (4) 50 (2017), 579–607.CrossRefGoogle Scholar
Sasaki, S., ‘Integral models of Hilbert modular varieties in the ramified case, deformations of modular Galois representations, and weight one forms’, Preprint, 2014.Google Scholar
Scholze, P., ‘On torsion in the cohomology of locally symmetric varieties’, Ann. of Math. 182 (2015), 945–1066.Google Scholar
Stamm, H., ‘On the reduction of the Hilbert-Blumenthal-moduli scheme with 𝛤0(p)-level structure’, Forum Math. 9 (1997), 405–455.Google Scholar
Tian, Y. and Xiao, L., ‘On Goren–Oort stratification for quaternionic Shimura varieties’, Compos. Math. 152 (2016), 2134–2220.Google Scholar
Tian, Y. and Xiao, L., ‘ p-adic cohomology and classicality of overconvergent Hilbert modular forms’, Astérisque 382 (2016), 73–162.Google Scholar
Wiese, G., ‘On Galois representations of weight one’, Doc. Math. 19 (2014), 689–707.Google Scholar