Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-23T11:38:10.683Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniformly factoring weakly compact operators and parametrised dualisation

Part of: Normed linear spaces and Banach spaces; Banach lattices Set theory

Published online by Cambridge University Press:  08 March 2021

L. Antunes ,
K. Beanland  and
B. M. Braga
L. Antunes*
Affiliation:
Departamento de Matemática, Universidade Tecnológica Federal do Paraná, Campus Toledo, 85902-490Toledo, PR Brazil; E-mail: [email protected]
K. Beanland
Affiliation:
Department of Mathematics, Washington & Lee University, 204 W. Washington St. Lexington, VA, 24450; E-mail: [email protected]
B. M. Braga
Affiliation:
Department of Mathematics, University of Virginia, 141 Cabell Drive, Kerchof Hall P.O. Box 400137 Charlottesville, VA22904; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This article deals with the problem of when, given a collection 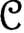$\mathcal {C}$ of weakly compact operators between separable Banach spaces, there exists a separable reflexive Banach space Z with a Schauder basis so that every element in 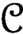$\mathcal {C}$ factors through Z (or through a subspace of Z). In particular, we show that there exists a reflexive space Z with a Schauder basis so that for each separable Banach space X, each weakly compact operator from X to 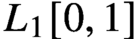$L_1[0,1]$ factors through Z.

We also prove the following descriptive set theoretical result: Let 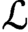$\mathcal {L}$ be the standard Borel space of bounded operators between separable Banach spaces. We show that if 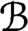$\mathcal {B}$ is a Borel subset of weakly compact operators between Banach spaces with separable duals, then for 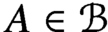$A \in \mathcal {B}$, the assignment 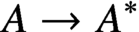$A \to A^*$ can be realised by a Borel map 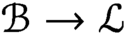$\mathcal {B}\to \mathcal {L}$.

MSC classification

Primary: 46B10: Duality and reflexivity
Secondary: 03E15: Descriptive set theory
Type
Analysis
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e22
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Abramovič, J., ‘Weakly compact sets in topological $K$-spaces’, Teor. Funkciĭ Funkcional. Anal. i Priložen. 15 (1972), 27–35.Google Scholar
Albiac, F. and Kalton, N. J., Topics in Banach Space Theory, Vol. 233 of Graduate Texts in Mathematics (Springer, New York, 2006).Google Scholar
Argyros, S. A. and Dodos, P., ‘Genericity and amalgamation of classes of Banach spaces’, Adv. Math. 209(2) (2007), 666–748.CrossRefGoogle Scholar
Beanland, K. and Causey, R. M., ‘On a generalization of Bourgain’s tree index’, Houston J. Math. 44(1) (2018), 201–208.Google Scholar
Beanland, K. and Causey, R. M., ‘Quantitative factorization of weakly compact, Rosenthal, and $\xi$-Banach-Saks operators’, Math. Scand. 123(2) (2018), 297–319.CrossRefGoogle Scholar
Beanland, K. and Causey, R. M., ‘Genericity and universality for operator ideals’, Q. J. Math. 71(3) (2020), 1081–1129.CrossRefGoogle Scholar
Beanland, K., Causey, R., Freeman, D. and Wallis, B., ‘Classes of operators determined by ordinal indices’, J. Funct. Anal. 271(6) (2016), 1691–1746.CrossRefGoogle Scholar
Beanland, K. and Freeman, D., ‘Ordinal ranks on weakly compact and Rosenthal operators’, Extracta Math. 26(2) (2011), 173–194.Google Scholar
Beanland, K. and Freeman, D., ‘Uniformly factoring weakly compact operators’, J. Funct. Anal. 266(5) (2014), 2921–2943.CrossRefGoogle Scholar
Bossard, B., ‘A .32coding of separable Banach spaces. Analytic and coanalytic families of Banach spaces’, Fund. Math. 172(2) (2002), 117–152.CrossRefGoogle Scholar
Braga, B. M., ‘Duality on Banach spaces and a Borel parametrized version of Zippin’s theorem’, Ann. Inst. Fourier (Grenoble) 65(6) (2015), 2413–2435.CrossRefGoogle Scholar
Causey, R. M. and Navoyan, K. V., ‘$\zeta$-completely continuous operators and $\zeta$-Schur Banach spaces’, J. Funct. Anal. 276(7) (2019), 2052–2102.CrossRefGoogle Scholar
Cúth, M., Doležal, M., Doucha, M. and Ondřej, K., ‘Polish spaces of Banach spaces. Complexity of isometry classes and generic properties’, preprint arXiv:1912.03994.Google Scholar
Cúth, M., Doucha, M. and Ondřej, K., ‘Complexity of distances: reductions of distances between metric and Banach spaces’, preprint arXiv:2004.11752.Google Scholar
Davis, W. J., Figiel, T., Johnson, W. B. and Pełczyński, A., ‘Factoring weakly compact operators’, J. Funct. Anal. 17 (1974), 311–327.CrossRefGoogle Scholar
Dodos, P., Banach Spaces and Descriptive Set Theory: Selected Topics, Vol. 1993 of Lecture Notes in Mathematics (Springer-Verlag, Berlin, 2010).CrossRefGoogle Scholar
Dodos, P., ‘Definability under duality’, Houston J. Math. 36(3) (2010), 781–792.Google Scholar
Dodos, P. and Ferenczi, V., ‘Some strongly bounded classes of Banach spaces’, Fund. Math. 193(2) (2007), 171–179.CrossRefGoogle Scholar
Figiel, T., Johnson, W. B. and Tzafriri, L., ‘On Banach lattices and spaces having local unconditional structure, with applications to Lorentz function spaces’, J. Approx. Theory 13 (1975), 395–412. Collection of articles dedicated to G. G. Lorentz on the occasion of his 65th birthday.CrossRefGoogle Scholar
Godefroy, G. and Saint-Raymond, J., ‘Descriptive complexity of some isomorphism classes of Banach spaces’, J. Funct. Anal. 275(4) (2018), 1008–1022.CrossRefGoogle Scholar
Johnson, W. B., URL: https://mathoverflow.net/questions/240472/davis-figiel-johnson-and-pelczynski-factorization-through-spaces-with-a-bases.Google Scholar
Johnson, W. B., Rosenthal, H. P. and Zippin, M., ‘On bases, finite dimensional decompositions and weaker structures in Banach spaces’, Israel J. Math. 9 (1971), 488–506.CrossRefGoogle Scholar
Johnson, W. B. and Szankowski, A., ‘Complementably universal Banach spaces. II’, J. Funct. Anal. 257(11) (2009), 3395–3408.CrossRefGoogle Scholar
Kechris, A. S., Classical Descriptive Set Theory, Vol. 156 of Graduate Texts in Mathematics (Springer, New York, 1995).CrossRefGoogle Scholar
Kurka, O., ‘Amalgamations of classes of Banach spaces with a monotone basis’, Studia Math. 234(2) (2016), 121–148.Google Scholar
Kurka, O., ‘Zippin’s embedding theorem and amalgamations of classes of Banach spaces’, Proc. Amer. Math. Soc. 144(10) (2016), 4273–4277.CrossRefGoogle Scholar
Pełczyński, A., ‘Universal bases’, Studia Math. 32 (1969), 247–268.CrossRefGoogle Scholar
Szlenk, W., ‘The non-existence of a separable reflexive Banach space universal for all separable reflexive Banach spaces’, Studia Math. 30 (1968), 53–61.CrossRefGoogle Scholar