Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T08:41:32.819Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIFORM BMO ESTIMATE OF PARABOLIC EQUATIONS AND GLOBAL WELL-POSEDNESS OF THE THERMISTOR PROBLEM

Part of: Parabolic equations and systems Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  02 December 2015

BUYANG LI  and
CHAOXIA YANG
BUYANG LI
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China; [email protected]
CHAOXIA YANG
Affiliation:
College of Science, Nanjing University of Posts and Telecommunications, Nanjing 210023, PR China; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove global well-posedness of the time-dependent degenerate thermistor problem by establishing a uniform-in-time bounded mean ocsillation (BMO) estimate of inhomogeneous parabolic equations. Applying this estimate to the temperature equation, we derive a BMO bound of the temperature uniform with respect to time, which implies that the electric conductivity is an 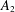$A_{2}$ weight. The Hölder continuity of the electric potential is then proved by applying the De Giorgi–Nash–Moser estimate for degenerate elliptic equations with an 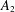$A_{2}$ coefficient. The uniqueness of the solution is proved based on the established regularity of the weak solution. Our results also imply the existence of a global classical solution when the initial and boundary data are smooth.

MSC classification

Primary: 35K20: Initial-boundary value problems for second-order parabolic equations
Secondary: 35Q99: None of the above, but in this section
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e26
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Adams, R. A., Sobolev Spaces, (Academic Press, New York, 1975).Google Scholar
Akrivis, G. and Larsson, S., ‘Linearly implicit finite element methods for the time dependent joule heating problem’, BIT 45 (2005), 429–442.Google Scholar
Allegretto, W. and Xie, H., ‘Existence of solutions for the time-dependent thermistor equations’, IMA J. Appl. Math. 48 (1992), 271–281.Google Scholar
Allegretto, W. and Yan, N., ‘A posteriori error analysis for FEM of thermistor problems’, Int. J. Numer. Anal. Model. 3 (2006), 413–436.Google Scholar
Antontsev, S. N. and Chipot, M., ‘The thermistor problem: existence, smoothness, uniqueness, blowup’, SIAM J. Math. Anal. 25 (1994), 1128–1156.CrossRefGoogle Scholar
Aronson, D. G. and Serrin, J., ‘Local behavior of solutions of quasilinear parabolic equations’, Arch. Ration. Mech. Anal. 25 (1967), 81–122.CrossRefGoogle Scholar
Chen, Y. Z., Parabolic Partial Differential Equations of Second Order, (Peking University Press, Beijing, 2003), (in Chinese).Google Scholar
Cimatti, G., ‘Existence of weak solutions for the nonstationary problem of the joule heating of a conductor’, Ann. Mat. Pura Appl. 162 (1992), 33–42.Google Scholar
Di Fazio, G., Fanciullo, M. S. and Zamboni, P., ‘Harnack inequality and smoothness for quasilinear degenerate elliptic equations’, J. Differential Equations 245 (2008), 2939–2957.Google Scholar
Elliott, C. M. and Larsson, S., ‘A finite element model for the time-dependent joule heating problem’, Math. Comp. 64 (1995), 1433–1453.Google Scholar
Fabes, E. B., Kenig, C. E. and Serapioni, R. P., ‘The local regularity of solutions of degenerate elliptic equations’, Comm. Partial Differential Equations 7 (1982), 77–116.CrossRefGoogle Scholar
Gao, H., Li, B. and Sun, W., ‘Unconditionally optimal error estimates of a Crank–Nicolson Galerkin method for the nonlinear thermistor equations’, SIAM J. Numer. Anal. 52 (2014), 933–954.Google Scholar
Grafakos, L., Classical and Modern Fourier Analysis, (China Machine Press, Beijing, 2005).Google Scholar
Hachimi, A. E. and Ammi, M. R. S., ‘Existence of weak solutions for the thermistor problem with degeneracy’, Electron. J. Differential Equations (2002), 127–137; (Conference 09).Google Scholar
Hömberg, D., Meyer, C., Rehberg, J. and Ring, W., ‘Optimal control for the thermistor problem’, SIAM J. Control Optim. 48 (2009/10), 3449–3481.Google Scholar
Hrynkiv, V., ‘Optimal boundary control for a time dependent thermistor problem’, Electron. J. Differential Equations 83 (2009), 1–22.Google Scholar
Jerison, D. and Kenig, C. E., ‘The inhomogeneous Dirichlet problems in Lipschitz domains’, J. Funct. Anal. 130 (1995), 161–219.CrossRefGoogle Scholar
Kuttler, K. L., Shillor, M. and Fernández, J. R., ‘Existence for the thermoviscoelastic thermistor problem’, Differ. Equ. Dyn. Syst. 17(3) (2009), 217–233.Google Scholar
Li, B. and Sun, W., ‘Error analysis of linearized semi-implicit Galerkin finite element methods for nonlinear parabolic equations’, Int. J. Numer. Anal. Model. 10 (2013), 622–633.Google Scholar
Lieberman, G. M., Second Order Parabolic Differential Equations, (World Scientific Publishing, Singapore, 1996).Google Scholar
Macklen, E. D., Thermistors, (Electrochemical Publications Ltd, Ayr, 1979).Google Scholar
Montesinos, M. T. G. and Gallego, F. Q., ‘Existence of a capacity solution to a coupled nonlinear parabolic-elliptic system’, Commun. Pure Appl. Anal. 6 (2007), 23–42.Google Scholar
Montesinos, M. T. G. and Gallego, F. Q., ‘The evolution thermistor problem under the Wiedemann–Franz law with metallic conduction’, Discrete Contin. Dyn. Syst. Ser. B 8 (2007), 901–923.Google Scholar
Sommerfeld, A., Thermodynamics and Statistical Mechanics, (Academic Press, New York, 1964).Google Scholar
Troianiello, G. M., Elliptic Differential Equations and Obstacle Problems, (Plenum Press, New York, 1987).Google Scholar
Wood, I., ‘Maximal L p-regularity for the Laplacian on Lipschitz domains’, Math. Z. 255 (2007), 855–875.Google Scholar
Xu, X., ‘Partial regularity of solutions to a class of degenerate systems’, Trans. Amer. Math. Soc. 349 (1997), 1973–1992.Google Scholar
Xu, X., ‘On the existence of bounded temperature in the thermistor problem with degeneracy’, Nonlinear Anal. 42 (2000), 199–213.Google Scholar
Yin, H., ‘$L^{2,{\it\mu}}(Q)$-estimates for parabolic equations and applications’, IMA Preprint Series [2209], http://purl.umn.edu/2337.Google Scholar
Yuan, G., ‘Regularity of solutions of the thermistor problem’, Appl. Anal. 53 (1994), 149–156.Google Scholar
Yuan, G. and Liu, Z., ‘Existence and uniqueness of the C 𝛼 solution for the thermistor problem with mixed boundary value’, Appl. Anal. 53 (1994), 149–156.CrossRefGoogle Scholar
Zhou, S. and Westbrook, D. R., ‘Numerical solutions of the thermistor equations’, J. Comput. Appl. Math. 79 (1997), 101–118.Google Scholar
Ziman, J. M., Electrons and Phonons, (Clarendon Press, Oxford, 1960).Google Scholar