Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T05:54:44.106Z Has data issue: false hasContentIssue false
  • English
  • Français

THE TYPICAL STRUCTURE OF MAXIMAL TRIANGLE-FREE GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  09 October 2015

JÓZSEF BALOGH ,
HONG LIU ,
ŠÁRKA PETŘÍČKOVÁ  and
MARYAM SHARIFZADEH
JÓZSEF BALOGH
Affiliation:
Department of Mathematical Sciences, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA; [email protected], [email protected], [email protected], [email protected]
HONG LIU
Affiliation:
Department of Mathematical Sciences, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA; [email protected], [email protected], [email protected], [email protected]
ŠÁRKA PETŘÍČKOVÁ
Affiliation:
Department of Mathematical Sciences, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA; [email protected], [email protected], [email protected], [email protected]
MARYAM SHARIFZADEH
Affiliation:
Department of Mathematical Sciences, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA; [email protected], [email protected], [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, settling a question of Erdős, Balogh, and Petříčková showed that there are at most 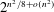$2^{n^{2}/8+o(n^{2})}$$n$-vertex maximal triangle-free graphs, matching the previously known lower bound. Here, we characterize the typical structure of maximal triangle-free graphs. We show that almost every maximal triangle-free graph 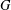$G$ admits a vertex partition 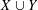$X\cup Y$ such that 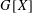$G[X]$ is a perfect matching and 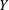$Y$ is an independent set.

Our proof uses the Ruzsa–Szemerédi removal lemma, the Erdős–Simonovits stability theorem, and recent results of Balogh, Morris, and Samotij and Saxton and Thomason on characterization of the structure of independent sets in hypergraphs. The proof also relies on a new bound on the number of maximal independent sets in triangle-free graphs with many vertex-disjoint 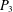$P_{3}$s, which is of independent interest.

MSC classification

Primary: 05C35: Extremal problems 05C30: Enumeration in graph theory 05C69: Dominating sets, independent sets, cliques
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e20
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Alon, N., Balogh, J., Morris, R. and Samotij, W., ‘Counting sum-free sets in Abelian groups’, Israel J. Math. 199(1) (2014), 309–344.Google Scholar
Balogh, J., Bollobás, B. and Simonovits, M., ‘The typical structure of graphs without given excluded subgraphs’, Random Structures Algorithms 34 (2009), 305–318.CrossRefGoogle Scholar
Balogh, J., Bushaw, N., Collares Neto, M., Liu, H., Morris, R. and Sharifzadeh, M., ‘The typical structure of graphs with no large cliques’, Combinatorica, to appear.Google Scholar
Balogh, J. and Butterfield, J., ‘Excluding induced subgraphs: critical graphs’, Random Structures Algorithms 38 (2011), 100–120.Google Scholar
Balogh, J., Das, S., Delcourt, M., Liu, H. and Sharifzadeh, M., ‘Intersecting families of discrete structures are typically trivial’, J. Combin. Theory Ser. A. 132 (2015), 224–245.Google Scholar
Balogh, J., Liu, H., Sharifzadeh, M. and Treglown, A., ‘The number of maximal sum-free subsets of integers’, Proc. Amer. Math. Soc. 143(11) (2015), 4713–4721.Google Scholar
Balogh, J., Liu, H., Sharifzadeh, M. and Treglown, A., ‘Sharp bound on the number of maximal sum-free subsets of integers’, submitted.Google Scholar
Balogh, J., Morris, R. and Samotij, W., ‘Independent sets in hypergraphs’, J. Amer. Math. Soc. 28(3) (2015), 669–709.Google Scholar
Balogh, J., Morris, R., Samotij, W. and Warnke, L., ‘The typical structure of sparse $K_{r+1}$-free graphs’, Trans. Amer. Math. Soc., to appear.Google Scholar
Balogh, J. and Mubayi, D., ‘Almost all triple systems with independent neighborhoods are semi-bipartite’, J. Combin. Theory Ser. A 118 (2011), 1494–1518.Google Scholar
Balogh, J. and Petříčková, Š., ‘Number of maximal triangle-free graphs’, Bull. Lond. Math. Soc. 46(5) (2014), 1003–1006.Google Scholar
Erdős, P., Frankl, P. and Rödl, V., ‘The asymptotic number of graphs not containing a fixed subgraph and a problem for hypergraphs having no exponent’, Graphs Combin. 2 (1986), 113–121.Google Scholar
Erdős, P., Kleitman, D. J. and Rothschild, B. L., ‘Asymptotic enumeration of K n -free graphs’, inColloquio Internazionale sulle Teorie Combinatorie, Tomo II, Atti dei Convegni Lincei, no. 17 (Accad. Naz. Lincei, Rome, 1976), 19–27.Google Scholar
Erdős, P. and Simonovits, M., ‘A limit theorem in graph theory’, Studia Sci. Math. Hungar. 1 (1966), 51–57.Google Scholar
Füredi, Z., ‘The number of maximal independent sets in connected graphs’, J. Graph Theory 11(4) (1987), 463–470.CrossRefGoogle Scholar
Green, B., ‘A Szemerédi-type regularity lemma in abelian groups, with applications’, Geom. Funct. Anal. 15 (2005), 340–376.Google Scholar
Green, B. and Ruzsa, I., ‘Counting sumsets and sum-free sets modulo a prime’, Studia Sci. Math. Hungar. 41 (2004), 285–293.Google Scholar
Hujter, M. and Tuza, Z., ‘The number of maximal independent sets in triangle-free graphs’, SIAM J. Discrete Math. 6(2) (1993), 284–288.Google Scholar
Kolaitis, P. G., Prömel, H. J. and Rothschild, B. L., ‘K ℓ+1 -free graphs: asymptotic structure and a 0-1 law’, Trans. Amer. Math. Soc. 303 (1987), 637–671.Google Scholar
Moon, J. W. and Moser, L., ‘On cliques in graphs’, Israel J. Math. 3 (1965), 23–28.Google Scholar
Osthus, D., Prömel, H. J. and Taraz, A., ‘For which densities are random triangle-free graphs almost surely bipartite?’, Combinatorica 23 (2003), 105–150.Google Scholar
Person, Y. and Schacht, M., ‘Almost all hypergraphs without Fano planes are bipartite’, inProceedings of the Twentieth Annual ACM-SIAM Symposium on Discrete Algorithms (2009), 217–226.Google Scholar
Prömel, H. J. and Steger, A., ‘The asymptotic number of graphs not containing a fixed color-critical subgraph’, Combinatorica 12 (1992), 463–473.Google Scholar
Ruzsa, I. Z. and Szemerédi, E., ‘Triple systems with no six points carrying three triangles’, inCombinatorics (Keszthely, 1976), Coll. Math. Soc. J. Bolyai 18, Volume II939–945.Google Scholar
Saxton, D. and Thomason, A., ‘Hypergraph containers’, Invent. Math. 201(3) (2015), 925–992.Google Scholar
Simonovits, M., Paul Erdős’ Influence on Extremal Raph Theory, The Mathematics of Paul Erdős, II (Springer, Berlin, 1996), 148–192.Google Scholar