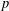Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T11:43:35.108Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSPORT PARALLÈLE ET CORRESPONDANCE DE SIMPSON $p$-ADIQUE

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry Curves

Published online by Cambridge University Press:  19 June 2017

DAXIN XU
DAXIN XU*
Affiliation:
Laboratoire Alexander Grothendieck, ERL 9216 du CNRS, Institut des Hautes Études Scientifiques, 35 route de Chartres, 91440 Bures-sur-Yvette, France; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Deninger et Werner ont développé un analogue pour les courbes 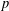$p$-adiques de la correspondance classique de Narasimhan et Seshadri entre les fibrés vectoriels stables de degré 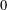$0$ et les représentations unitaires du groupe fondamental topologique pour une courbe complexe propre et lisse. Par transport parallèle, ils ont associé fonctoriellement à chaque fibré vectoriel sur une courbe 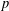$p$-adique, dont la réduction est fortement semi-stable de degré 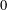$0$, une représentation 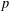$p$-adique du groupe fondamental de la courbe. Ils se sont posé quelques questions : leur foncteur est-il pleinement fidèle ? La cohomologie des systèmes locaux fournis par celui-ci admet-elle une filtration de Hodge-Tate ? Leur construction est-elle compatible avec la correspondance de Simpson 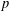$p$-adique développée par Faltings ? Nous répondons à ces questions dans cet article.

Deninger and Werner developed an analogue for 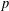$p$-adic curves of the classical correspondence of Narasimhan and Seshadri between stable bundles of degree 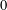$0$ and unitary representations of the topological fundamental group for a complex smooth proper curve. Using parallel transport, they associated functorially to every vector bundle on a 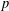$p$-adic curve whose reduction is strongly semi-stable of degree 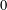$0$ a 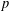$p$-adic representation of the fundamental group of the curve. They asked several questions: whether their functor is fully faithful; whether the cohomology of the local systems produced by this functor admits a Hodge–Tate filtration; and whether their construction is compatible with the 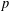$p$-adic Simpson correspondence developed by Faltings. We answer these questions in this article.

MSC classification

Primary: 14H60: Vector bundles on curves and their moduli
Secondary: 11G20: Curves over finite and local fields 14G20: Local ground fields
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e13
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2017

References

Bibliographie

Abbes, A., ‘Réduction semi-stable des courbes d’après Artin, Deligne, Grothendieck, Mumford, Saito, Winters...’, inCourbes semi-stables et groupe fondamental en géométrie algébrique, Progress in Mathematics, 187 (Birkhäuser, Boston, 2000), 59–110.Google Scholar
Abbes, A., Éléments de géométrie rigide : Volume I. Construction et étude géométrique des espaces rigides, (Springer, Berlin, 2010).Google Scholar
Abbes, A. and Gros, M., ‘La suite spectrale de Hodge-Tate’, Preprint, 2015,arXiv:1509.03617.Google Scholar
Abbes, A., Gros, M. and Tsuji, T., The p-adic Simpson Correspondence, Annals of Mathematics Studies, 193 (Princeton University Press, Princeton, 2016).Google Scholar
Achinger, P., ‘ K (𝜋, 1)-neighborhoods and comparison theorems’, Compos. Math. 151(10) (2015), 1945–1964.Google Scholar
Artin, M., Grothendieck, A. and Verdier, J. L., Théorie des topos et cohomologie étale des schémas, SGA 4, Tome 1, LNM, 269 (Springer, Berlin, 1972), Tome 2, LNM, 270 (Springer, Berlin, 1972); Tome 3, LNM, 305 (Springer, Berlin, 1973).Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models, (Springer, Berlin, 1990).Google Scholar
Bourbaki, N., Algèbre commutative, (Hermann, Paris, 1985), chapitres 1–9.Google Scholar
Cartan, H. and Eilenberg, S., Homological Algebra, (Princeton University Press, Princeton, 1956).Google Scholar
Deligne, P. and Milne, J. S., ‘Tannakian categories’, inHodge Cycles, Motives, and Shimura Varieties, LNM, 900 (Springer, Berlin, 1981), 101–228.Google Scholar
Demazure, M. and Grothendieck, A., Schémas en groupes, SGA3, LNM, 151–153 (Springer, Berlin, 1970).Google Scholar
Deninger, C. and Werner, A., ‘Vector bundles and $p$ -adic representations I’, Preprint, 2003,arXiv:0309.273.Google Scholar
Deninger, C. and Werner, A., ‘Vector bundles on p-adic curves and parallel transport’, Ann. Sci. Éc. Norm. Supér. (4) 38(4) (2005), 553–597.Google Scholar
Epp, H. P., ‘Eliminating wild ramification’, Invent. Math. 19(3) (1973), 235–249.Google Scholar
Faltings, G., ‘ p-adic Hodge theory’, J. Amer. Math. Soc. 1 (1988), 255–299.Google Scholar
Faltings, G., ‘Almost étale extensions’, inCohomologies p-adiques et applications arithmétiques. II, Astérisque, 279 (Société mathématique de France, 2002), 185–270.Google Scholar
Faltings, G., ‘A p-adic Simpson correspondence’, Adv. Math. 198 (2005), 847–862.Google Scholar
Gabber, O. and Ramero, L., Almost Ring Theory, LNM, 1800 (Springer, Berlin, 2003).Google Scholar
Gabber, O. and Ramero, L., ‘Foundations for Almost Ring Theory’, Release 6.8, Preprint, 2014, arXiv:math/0409584.Google Scholar
Gabriel, P., ‘Des catégories abéliennes’, Bull. de la S. M. F. 90 (1962), 323–448.Google Scholar
Gieseker, D., ‘Stable vector bundles and the frobenius morphism’, Ann. Sci. Éc. Norm. Supér. (4) 6(1) (1973), 95–101.Google Scholar
Giraud, J., Cohomologie non abélienne, (Springer, Berlin, 1971).Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental, SGA 1, LNM, 224 (Springer, Berlin, 1971).Google Scholar
Grothendieck, A. and Dieudonné, J., ‘Éléments de géométrie algébrique, III Étude cohomologique des faisceaux cohérents’, Publ. Math. Inst. Hautes Études Sci. 11 (1961), 17 (1963).Google Scholar
Grothendieck, A. and Dieudonné, J., ‘Éléments de géométrie algébrique, IV Étude locale des schémas et des morphismes de schémas’, Publ. Math. Inst. Hautes Études Sci. 20 (1964), 24 (1965); 28 (1966); 32 (1967).Google Scholar
Grothendieck, A. and Dieudonné, J. A., Éléments de géométrie algébrique I, Seconde édition, (Springer, Berlin, 1971).Google Scholar
Illusie, L., Complexe cotangente et déformations I, LNM, 239 (Springer, Berlin, 1971).Google Scholar
Illusie, L., ‘Produits orientés’, inTravaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents, Astérisque, 363–364 (Société mathématique de France, 2014).Google Scholar
Kato, K., ‘Logarithmic structures of Fontaine-Illusie’, inAlgebraic Analysis, Geometry, and Number Theory (Baltimore, MD, 1988), 191–224.Google Scholar
Lichtenbaum, S., ‘Curves over discrete valuation rings’, Am. J. Math. 90 (1968), 380–405.Google Scholar
Liu, Q., Algebraic Geometry and Arithmetic Curves, (Oxford University Press, Oxford, 2002).Google Scholar
Liu, Q., ‘Stable reduction of finite covers of curves’, Compos. Math. 142(01) (2006), 101–118.Google Scholar
Milne, J. S., Etale Cohomology, Princeton Mathematical Series, Vol. 33 (Princeton University Press, Princeton, 1980).Google Scholar
Moret-Bailly, L., ‘Métriques permises’, inSéminaire sur les pinceaux arithmétiques: la conjecture de Mordell, Astérisque, 129 (Société mathématique de France, 1985).Google Scholar
Mumford, D., Abelian Variety, (Oxford University Press, Oxford, 1970).Google Scholar
Narasimhan, M. S. and Seshadri, C. S., ‘Stable and unitary vector bundles on a compact Riemann surface’, Ann. of Math. (2) 82 (1965), 540–567.Google Scholar
Raynaud, M., ‘Spécialisation du foncteur de Picard’, Publ. Math. Inst. Hautes Études Sci. 38 (1970), 27–76.Google Scholar
Raynaud, M., ‘ p-groupes et réduction semi-stable des courbes’, inThe Grothendieck Festschrift, vol. III, Progress in Mathematics, 88 (Birkhäuser, Boston, 1990), 179–197.Google Scholar
Raynaud, M. and Gruson, L., ‘Critères de platitude et de projectivité’, Invent. Math. 13(1) (1971), 1–89.Google Scholar
Saito, T., ‘Log smooth extension of a family of curves and semi-stable reduction’, J. Algebraic Geom. 13(2) (2004), 287–322.Google Scholar
Scholze, P., ‘ p-adic Hodge theory for rigid-analytic varieties’, Forum Math., Pi 1(e1) (2013).Google Scholar
Serre, J.-P., Groupes algébriques et corps de classes, (Hermann, Paris, 1975).Google Scholar
Simpson, C., ‘Higgs bundles and local systems’, Publ. Math. Inst. Hautes Études Sci. 75 (1992), 5–95.Google Scholar
Tate, J., ‘ p-divisible groups’, inProc. Conf. Local Fields (Driebergen, 1966) (Springer, Berlin, 1967), 158–183.Google Scholar
Tate, J., ‘Relations between K 2 and Galois cohomology’, Invent. Math. 36 (1976), 257–274.Google Scholar
Tong, J., ‘Application d’Albanese pour les courbes et contractions’, Math. Ann. 338 (2007), 405–420.Google Scholar
Weibel, C. A., An Introduction to Homological Algebra, (Cambridge University Press, Cambridge, 1995).Google Scholar
The Stacks Project Authors, Stacks Project, 2017, http://stacks.math.columbia.edu.Google Scholar