Published online by Cambridge University Press: 01 February 2021
We show that the perfect derived categories of Iyama’s d-dimensional Auslander algebras of type 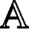 ${\mathbb {A}}$ are equivalent to the partially wrapped Fukaya categories of the d-fold symmetric product of the
${\mathbb {A}}$ are equivalent to the partially wrapped Fukaya categories of the d-fold symmetric product of the 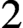 $2$-dimensional unit disk with finitely many stops on its boundary. Furthermore, we observe that Koszul duality provides an equivalence between the partially wrapped Fukaya categories associated to the d-fold symmetric product of the disk and those of its
$2$-dimensional unit disk with finitely many stops on its boundary. Furthermore, we observe that Koszul duality provides an equivalence between the partially wrapped Fukaya categories associated to the d-fold symmetric product of the disk and those of its 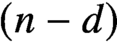 $(n-d)$-fold symmetric product; this observation leads to a symplectic proof of a theorem of Beckert concerning the derived Morita equivalence between the corresponding higher Auslander algebras of type
$(n-d)$-fold symmetric product; this observation leads to a symplectic proof of a theorem of Beckert concerning the derived Morita equivalence between the corresponding higher Auslander algebras of type 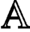 ${\mathbb {A}}$. As a by-product of our results, we deduce that the partially wrapped Fukaya categories associated to the d-fold symmetric product of the disk organise into a paracyclic object equivalent to the d-dimensional Waldhausen
${\mathbb {A}}$. As a by-product of our results, we deduce that the partially wrapped Fukaya categories associated to the d-fold symmetric product of the disk organise into a paracyclic object equivalent to the d-dimensional Waldhausen 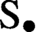 $\text {S}_{\bullet }$-construction, a simplicial space whose geometric realisation provides the d-fold delooping of the connective algebraic K-theory space of the ring of coefficients.
$\text {S}_{\bullet }$-construction, a simplicial space whose geometric realisation provides the d-fold delooping of the connective algebraic K-theory space of the ring of coefficients.