Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-17T05:17:32.520Z Has data issue: false hasContentIssue false
  • English
  • Français

A Symmetric Function of Increasing Forests

Part of: Combinatorics Algebraic combinatorics

Published online by Cambridge University Press:  29 April 2021

Alex Abreu  and
Antonio Nigro
Alex Abreu
Affiliation:
Instituto de Matemática e Estatística, Universidade Federal Fluminense, Rua Prof. M. W. de Freitas, S/N, 24210-201 Niterói, Rio de Janeiro, Brasil; E-mail: [email protected].
Antonio Nigro
Affiliation:
Instituto de Matemática e Estatística, Universidade Federal Fluminense, Rua Prof. M. W. de Freitas, S/N, 24210-201 Niterói, Rio de Janeiro, Brasil; E-mail: [email protected].

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an indifference graph G, we define a symmetric function of increasing spanning forests of G. We prove that this symmetric function satisfies certain linear relations, which are also satisfied by the chromatic quasisymmetric function and unicellular 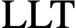$\textrm {LLT}$ polynomials. As a consequence, we give a combinatorial interpretation of the coefficients of the 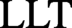$\textrm {LLT}$ polynomial in the elementary basis (up to a factor of a power of 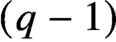$(q-1)$), strengthening the description given in [4].

MSC classification

Primary: 05A05: Permutations, words, matrices
Secondary: 05E05: Symmetric functions and generalizations
Type
Discrete Mathematics
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e35
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Abreu, A. and Nigro, A.. Chromatic symmetric functions from the modular law. J. Combin. Theory Ser. A, 180:105407, 30, 2021.CrossRefGoogle Scholar
Alexandersson, P.. LLT polynomials, elementary symmetric functions and melting lollipops. Journal of Algebraic Combinatorics, Apr 2020.CrossRefGoogle Scholar
Alexandersson, P. and Panova, G.. LLT polynomials, chromatic quasisymmetric functions and graphs with cycles. Discrete Math., 341(12):3453–3482, 2018.CrossRefGoogle Scholar
Alexandersson, P. and Sulzgruber, R.. A combinatorial expansion of vertical-strip LLT polynomials in the basis of elementary symmetric functions, Preprint, 2020, arXiv:2004.09198.CrossRefGoogle Scholar
Athanasiadis, C.A.. Power sum expansion of chromatic quasisymmetric functions. Electron. J. Combin., 22(2):Paper 2.7, 9, 2015.CrossRefGoogle Scholar
Bergeron, F.. Open questions for operators related to rectangular Catalan combinatorics. J. Comb., 8(4):673–703, 2017.Google Scholar
Bergeron, F., Flajolet, P., and Salvy, B.. Varieties of increasing trees. In CAAP ’92 (Rennes, 1992), volume 581 of Lecture Notes in Comput. Sci., pages 24–48. Springer, Berlin, 1992.Google Scholar
Carlsson, E. and Mellit, A.. A proof of the shuffle conjecture. J. Amer. Math. Soc., 31(3):661–697, 2018.CrossRefGoogle Scholar
D’Adderio, M.. $e$-positivity of vertical strip LLT polynomials. J. Combin. Theory Ser. A, 172:105212, 15, 2020.Google Scholar
Garsia, A.M., Haglund, J., Qiu, D., and Romero, M.. $e$-positivity results and conjectures, Preprint, 2019, arXiv:1904.07912.Google Scholar
Garsia, A.M. and Remmel, J.B.. $Q$-counting rook configurations and a formula of Frobenius. J. Combin. Theory Ser. A, 41(2):246–275, 1986.CrossRefGoogle Scholar
Gasharov, V.. Incomparability graphs of $\left(3+1\right)$-free posets are $s$-positive. In Proceedings of the 6th Conference on Formal Power Series and Algebraic Combinatorics (New Brunswick, NJ, 1994), volume 157, pages 193–197, 1996.Google Scholar
Gould, H.W.. The $q$-Stirling numbers of first and second kinds. Duke Math. J., 28:281–289, 1961.CrossRefGoogle Scholar
Hallam, J. and Sagan, B.. Factoring the characteristic polynomial of a lattice. J. Combin. Theory Ser. A, 136:39–63, 2015.CrossRefGoogle Scholar
Kowalski, M.. LLT cumulants of unicellular Young diagrams, parking functions and Schur positivity, 2020. arxiv:2011.15080.Google Scholar
Lascoux, A., Leclerc, B., and Thibon, J.-Y.. Ribbon tableaux, Hall-Littlewood functions, quantum affine algebras, and unipotent varieties. J. Math. Phys., 38(2):1041–1068, 1997.CrossRefGoogle Scholar
Macdonald, I.G.. Symmetric functions and Hall polynomials. Oxford Classic Texts in the Physical Sciences. The Clarendon Press, Oxford University Press, New York, second edition, 2015. With contribution by Zelevinsky, A. V. and a foreword by Richard Stanley, Reprint of the 2008 paperback edition.Google Scholar
Pólya, G.. Gaussian binomial coefficients and the enumeration of inversions. In Proc. Second Chapel Hill Conf. on Combinatorial Mathematics and its Applications (Univ. North Carolina, Chapel Hill, N.C., 1970), pages 381–384. Univ. North Carolina, Chapel Hill, N.C., 1970.Google Scholar
Ram, A.. A Frobenius formula for the characters of the Hecke algebras. Invent. Math., 106(3):461–488, 1991.CrossRefGoogle Scholar
Shareshian, J. and Wachs, M.L.. Chromatic quasisymmetric functions. Adv. Math., 295:497–551, 2016.CrossRefGoogle Scholar
Stanley, R.P.. A symmetric function generalization of the chromatic polynomial of a graph. Adv. Math., 111(1):166–194, 1995.CrossRefGoogle Scholar
Stanley, R.P.. Enumerative combinatorics. Volume 1, volume 49 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge, second edition, 2012.Google Scholar
Stanley, R. P. and Stembridge, J. R.. On immanants of Jacobi-Trudi matrices and permutations with restricted position. J. Combin. Theory Ser. A, 62(2):261–279, 1993.CrossRefGoogle Scholar