Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T08:21:34.976Z Has data issue: false hasContentIssue false
  • English
  • Français

SYMMETRIC AND ASYMMETRIC RAMSEY PROPERTIES IN RANDOM HYPERGRAPHS

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  23 November 2017

LUCA GUGELMANN ,
RAJKO NENADOV ,
YURY PERSON ,
NEMANJA ŠKORIĆ ,
ANGELIKA STEGER  and
HENNING THOMAS
LUCA GUGELMANN
Affiliation:
Institute of Theoretical Computer Science, ETH Zurich, 8092 Zurich, Switzerland; [email protected], [email protected], [email protected], [email protected]
RAJKO NENADOV
Affiliation:
School of Mathematical Sciences, Monash University, VIC 3800, Australia; [email protected]
YURY PERSON
Affiliation:
Institute of Mathematics, Goethe-Universität, 60325 Frankfurt am Main, Germany; [email protected]
NEMANJA ŠKORIĆ
Affiliation:
Institute of Theoretical Computer Science, ETH Zurich, 8092 Zurich, Switzerland; [email protected], [email protected], [email protected], [email protected]
ANGELIKA STEGER
Affiliation:
Institute of Theoretical Computer Science, ETH Zurich, 8092 Zurich, Switzerland; [email protected], [email protected], [email protected], [email protected]
HENNING THOMAS
Affiliation:
Institute of Theoretical Computer Science, ETH Zurich, 8092 Zurich, Switzerland; [email protected], [email protected], [email protected], [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A celebrated result of Rödl and Ruciński states that for every graph 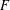$F$, which is not a forest of stars and paths of length 3, and fixed number of colours 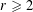$r\geqslant 2$ there exist positive constants 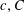$c,C$ such that for 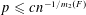$p\leqslant cn^{-1/m_{2}(F)}$ the probability that every colouring of the edges of the random graph 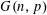$G(n,p)$ contains a monochromatic copy of 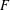$F$ is 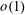$o(1)$ (the ‘0-statement’), while for 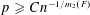$p\geqslant Cn^{-1/m_{2}(F)}$ it is 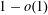$1-o(1)$ (the ‘1-statement’). Here 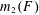$m_{2}(F)$ denotes the 2-density of 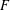$F$. On the other hand, the case where 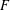$F$ is a forest of stars has a coarse threshold which is determined by the appearance of a certain small subgraph in 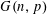$G(n,p)$. Recently, the natural extension of the 1-statement of this theorem to 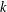$k$-uniform hypergraphs was proved by Conlon and Gowers and, independently, by Friedgut, Rödl and Schacht. In particular, they showed an upper bound of order 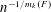$n^{-1/m_{k}(F)}$ for the 1-statement, where 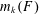$m_{k}(F)$ denotes the 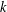$k$-density of 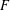$F$. Similarly as in the graph case, it is known that the threshold for star-like hypergraphs is given by the appearance of small subgraphs. In this paper we show that another type of threshold exists if 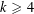$k\geqslant 4$: there are 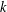$k$-uniform hypergraphs for which the threshold is determined by the asymmetric Ramsey problem in which a different hypergraph has to be avoided in each colour class. Along the way we obtain a general bound on the 1-statement for asymmetric Ramsey properties in random hypergraphs. This extends the work of Kohayakawa and Kreuter, and of Kohayakawa, Schacht and Spöhel who showed a similar result in the graph case. We prove the corresponding 0-statement for hypergraphs satisfying certain balancedness conditions.

MSC classification

Primary: 05C80: Random graphs 05D10: Ramsey theory 05C65: Hypergraphs
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e28
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Alon, N. and Spencer, J. H., The Probabilistic Method (John Wiley & Sons, 2015).Google Scholar
Balogh, J., Morris, R. and Samotij, W., ‘Independent sets in hypergraphs’, J. Amer. Math. Soc. 28(3) (2015), 669–709.CrossRefGoogle Scholar
Bollobás, B., ‘Threshold functions for small subgraphs’, Math. Proc. Cambridge Philos. Soc. 90(2) (1981), 197–206.CrossRefGoogle Scholar
Conlon, D., Dellamonica, D. Jr., La Fleur, S., Rödl, V. and Schacht, M., ‘A note on induced Ramsey numbers’, Preprint (2016), arXiv:1601.01493, https://link.springer.com/chapter/10.1007/978-3-319-44479-6_13.Google Scholar
Conlon, D. and Gowers, W. T., ‘Combinatorial theorems in sparse random sets’, Ann. of Math. (2) 184 (2016), 367–454.CrossRefGoogle Scholar
Conlon, D., Gowers, W. T., Samotij, W. and Schacht, M., ‘On the KŁR conjecture in random graphs’, Israel J. Math. 203(1) (2014), 535–580.CrossRefGoogle Scholar
Friedgut, E., ‘Hunting for sharp thresholds’, Random Structures Algorithms 26(1–2) (2005), 37–51.CrossRefGoogle Scholar
Friedgut, E., Hàn, H., Person, Y. and Schacht, M., ‘A sharp threshold for van der Waerden’s theorem in random subsets’, Discrete Analysis 7 (2016), 20.Google Scholar
Friedgut, E. and Krivelevich, M., ‘Sharp thresholds for certain Ramsey properties of random graphs’, Random Structures Algorithms 17(1) (2000), 1–19.3.0.CO;2-4>CrossRefGoogle Scholar
Friedgut, E., Rödl, V., Ruciński, A. and Tetali, P., ‘A sharp threshold for random graphs with a monochromatic triangle in every edge coloring’, Mem. Amer. Math. Soc. 179(845) (2006), 66.Google Scholar
Friedgut, E., Rödl, V. and Schacht, M., ‘Ramsey properties of random discrete structures’, Random Structures Algorithms 37(4) (2010), 407–436.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A., Random Graphs (Wiley, New York, 2000).CrossRefGoogle Scholar
Kohayakawa, Y. and Kreuter, B., ‘Threshold functions for asymmetric Ramsey properties involving cycles’, Random Structures Algorithms 11(3) (1997), 245–276.3.0.CO;2-0>CrossRefGoogle Scholar
Kohayakawa, Y., Schacht, M. and Spöhel, R., ‘Upper bounds on probability thresholds for asymmetric ramsey properties’, Random Structures Algorithms 44(1) (2014), 1–28.CrossRefGoogle Scholar
Łuczak, T., Ruciński, A. and Voigt, B., ‘Ramsey properties of random graphs’, J. Combin. Theory Ser. B 56(1) (1992), 55–68.CrossRefGoogle Scholar
Marciniszyn, M., Skokan, J., Spöhel, R. and Steger, A., ‘Asymmetric Ramsey properties of random graphs involving cliques’, Random Structures Algorithms 34(4) (2009), 419–453.CrossRefGoogle Scholar
Nenadov, R., Person, Y., Škorić, N. and Steger, A., ‘An algorithmic framework for obtaining lower bounds for random Ramsey problems’, J. Combin. Theory Ser. B 124 (2017), 1–38.CrossRefGoogle Scholar
Nenadov, R. and Steger, A., ‘A short proof of the random Ramsey theorem’, Combin. Probab. Comput. 25(01) (2016), 130–144.CrossRefGoogle Scholar
Nenadov, R., Steger, A. and Stojaković, M., ‘On the threshold for the Maker–Breaker H-game’, Random Structures Algorithms 49(3) (2016), 558–578.CrossRefGoogle Scholar
Rödl, V. and Ruciński, A., ‘Lower bounds on probability thresholds for Ramsey properties’, inCombinatorics, Paul Erdős is eighty, 1, Vol. 1, Bolyai Society Mathematical Studies (János Bolyai Mathematical Society, 1993), 317–346.Google Scholar
Rödl, V. and Ruciński, A., ‘Random graphs with monochromatic triangles in every edge coloring’, Random Structures Algorithms 5(2) (1994), 253–270.CrossRefGoogle Scholar
Rödl, V. and Ruciński, A., ‘Threshold functions for Ramsey properties’, J. Amer. Math. Soc. 8(4) (1995), 917–942.CrossRefGoogle Scholar
Rödl, V. and Ruciński, A., ‘Ramsey properties of random hypergraphs’, J. Combin. Theory Ser. A 81(1) (1998), 1–33.CrossRefGoogle Scholar
Rödl, V., Ruciński, A. and Schacht, M., ‘Ramsey properties of random k-partite, k-uniform hypergraphs’, SIAM J. Discrete Math. 21(2) (2007), 442–460.CrossRefGoogle Scholar
Rödl, V., Ruciński, A. and Schacht, M., ‘An exponential-type upper bound for Folkman numbers’, Combinatorica 37(4) (2017), 767–784.CrossRefGoogle Scholar
Saxton, D. and Thomason, A., ‘Hypergraph containers’, Invent. Math. 201(3) (2015), 925–992.CrossRefGoogle Scholar
Schacht, M. and Schulenburg, F., ‘Sharp thresholds for Ramsey properties of strictly balanced nearly bipartite graphs’, Random Structures Algorithms Preprint (2016), arXiv:1602.02501.Google Scholar
Thomas, H., ‘Aspects of games on random graphs’, PhD Thesis, ETH Zurich, 2013.Google Scholar