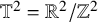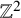1 Introduction
Let
$(M,g)$
be a smooth, compact Riemannian manifold with no boundary, unit mass, and let
$\Delta _g$
denote the Laplace–Beltrami operator. Also, let
$\{ \phi _{\lambda } \}$
be an orthonormal basis of eigenfunctions of
$\Delta _g$
with eigenvalues
$0 \le \lambda _1 \le \lambda _2 \le \ldots $
. For an observable
$f \in C^{\infty }({\mathbb S}^* M)$
, where
${\mathbb S}^* M$
denotes the unit cotangent bundle of M, let
$\operatorname {Op}(f)$
denote its quantization, defined as a pseudo-differential operator (cf. [Reference Dimassi and Sjöstrand9] for details.) A central problem in quantum chaos (cf. [Reference Zelditch52, Problem 3.1]) is to understand the set of possible quantum limits (sometimes called semiclassical measures) describing the distribution of mass of the eigenfunctions
$\{ \phi _{\lambda } \}$
within
${\mathbb S}^* M$
, in the limit as the eigenvalue
$\lambda $
tends to infinity. A cornerstone result in this direction is the quantum ergodicity theorem of Shnirelman [Reference Šnirel'man45], Colin de Verdiére [Reference Colin de Verdière8] and Zelditch [Reference Zelditch51] which states that if the geodesic flow on M is ergodic there exists a density one subsequence of eigenfunctions
$\{ \phi _{\lambda _j}\}$
such that
$$\begin{align*}\mu_{\phi_{\lambda_{j}}}(f) =\langle \operatorname{Op}(f) \phi_{\lambda_j}, \phi_{\lambda_j} \rangle \rightarrow \int_{{\mathbb S}^* M} f(x) d\mu_{L}(x)\\[-15pt] \end{align*}$$
as
$\lambda _j \rightarrow \infty $
, where
$d\mu _{L}$
is the normalized Liouville measure on
${\mathbb S}^* M$
. (Note that any quantum limit, by Egorov’s theorem, is invariant under the classical dynamics.)
While the quantum ergodicity theorem implies that the mass of almost all eigenfunctions equidistributes in
${\mathbb S}^{*} M$
with respect to
$d\mu _{L}$
, it does not rule out the existence of sparse subsequences along which the mass of the eigenfunctions localizes. Whether or not this happens crucially depends on the geometry of M, cf. Section 1.3.
In this article, we study quantum limits of ‘point scatterers’ on
$M=\mathbb T^2=\mathbb R^2/2\pi \mathbb Z^2$
. These are singular perturbations of the Laplacian on M and were used by Šeba [Reference Šeba40] in order to study the transition between integrability and chaos in quantum systems. The perturbation is quite weak and has essentially no effect on the classical dynamics, yet the quantum dynamics ‘feels’ the effect of the scatterer, and an analog of the quantum ergodicity theorem is known to hold [Reference Rudnick and Ueberschär38, Reference Kurlberg and Ueberschär27] (namely, equidistribution holds for a full density subset of the ‘new’ eigenfunctions), even though classical ergodicity does not hold.
The model also exhibits scarring along sparse subsequences of the new eigenfunctions [Reference Kurlberg and Rosenzweig25]. In particular, there exist quantum limits whose momentum push-forwards, which can be viewed as probability measures on the unit circle, are of the form
$c \mu _{\text {sing}} + (1-c) \mu _{\text {uniform}}$
, for some
$c \in [1/2,1]$
. Here, both
$\mu _{\text {uniform}}$
and
$\mu _{\text {sing}}$
are normalized to have mass one, and
$\mu _{\text {sing}}$
can be taken to be a sum of delta measures giving equal mass to the four points
$\pm (1,0), \pm (0,1)$
. We note that
$\mu _{\text {uniform}}$
is the push-forward of the Liouville measure and hence maximally delocalized, whereas
$\mu _{\text {sing}}$
is maximally localized since any quantum limits in this setting must be invariant under a certain eight fold symmetry (cf. equation (1.7)).
Stronger localization, that is, going beyond
$c=1/2$
, is interesting given a number of ‘half delocalization’ results for quantum limits for some other (strongly chaotic) systems, namely quantized cat maps and geodesic flows on manifolds with constant negative curvature
$-1$
. In the former case, Faure and Nonnenmacher showed [Reference Faure and Nonnenmacher12] that if a quantum limit
$\nu $
is decomposed as
$\nu = \nu _{\text {pp}} + \nu _{\text {Liouville}} + \nu _{sc}$
, with
$\nu _{\text {pp}}$
denoting the pure point part and
$\nu _{sc}$
denoting the singular continuous part, then
$\nu _{\text {Liouville}}({\mathbb T}^2) \ge \nu _{\text {pp}}({\mathbb T}^2)$
, and thus
$\nu _{\text {pp}}({\mathbb T}^2) \le 1/2$
. (We emphasize that
${\mathbb T}^{2}$
is the full phase space in this setting.) In the latter case, it was shown that the Kolmogorov-Sinai (KS) entropy with respect to any measure arising as a quantum limit is at least
$1/2$
. We remark that for arithmetic point scatterers, the KS entropy is zero with respect to any flow invariant probability measure, in particular for any measure arising as a quantum limit.
The aim of this paper is to exhibit essentially maximal localization for a quantum ergodic system, namely arithmetic toral point scatterers. In particular, we construct quantum limits (in momentum) corresponding to
$c=1$
in the above decomposition; other interesting examples include singular continuous measures with support, say, on Cantor sets. This can be viewed as a step towards a ‘measure classification’ for quantum limits of quantum ergodic systems.
1.1 Description of the model
Let us now describe the basic properties of the point scatterer. This is discussed in further detail in [Reference Rudnick and Ueberschär38, Reference Rudnick and Ueberschär39, Reference Kurlberg and Ueberschär27, Reference Kurlberg and Rosenzweig25, Reference Šeba40, Reference Shigehara42]. To describe the quantum system associated with the point scatterer, consider
$ -\Delta |_{D_{x_0}}, $
where
$$\begin{align*}D_{x_0}=\{ f \in L^2(\mathbb T^2) : f(x) =0 \text{ in some neighborhood of } x_0 \}. \end{align*}$$
By von Neumann’s theory of self-adjoint extensions (see Appendix A of [Reference Rudnick and Ueberschär38]) there exists a one parameter family of self-adjoint extension of
$-\Delta |_{D_{x_0}}$
parameterized by a phase
$\varphi \in (- \pi , \pi ]$
. Moreover, for
$\varphi \neq \pi $
the eigenvalues of these operators may be divided into two categories. The old eigenvalues which are eigenvalues of
$-\Delta $
, with multiplicity decreased by one, along with new eigenvalues which are solutions to the spectral equation
$$ \begin{align} \sum_{m \ge 1} r(m) \left( \frac{1}{m-\lambda}-\frac{m}{m^2+1} \right)=\tan(\varphi/2)\sum_{m\ge 1} \frac{r(m)}{m^2+1}, \end{align} $$
where
$$\begin{align*}r(m)=\# \{ (a,b) \in \mathbb Z^2 : a^2+b^2=m\}. \end{align*}$$
We will refer to the case when
$\varphi $
is fixed as
$\lambda \rightarrow \infty $
the weak coupling quantization. In this regime work of Shigehara [Reference Shigehara42] suggests that the level spacing of the eigenvalues should have Poisson spacing statistics, and this is supported by work of Rudnick and Ueberschär [Reference Rudnick and Ueberschär39] along with Freiberg, Kurlberg and Rosenzweig [Reference Freiberg, Kurlberg and Rosenzweig14]. In the hope of exhibiting wave chaos, Shigehara proposes the following strong coupling quantization
$$ \begin{align} \sum_{|m-\lambda|\le \lambda^{1/2}} r(m) \left( \frac{1}{m-\lambda}-\frac{m}{m^2+1} \right)=\frac{1}{\alpha}, \end{align} $$
where
$\alpha \in \mathbb R$
is called the physical coupling constant and reflects the strength of the scatterer. The strong coupling quantization restricts the spectral equation to the physically relevant energy levels. Notably, this forces a renormalization of equation (1.1)
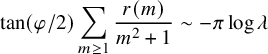$$\begin{align*}\tan(\varphi/2)\sum_{m \ge 1} \frac{r(m)}{m^2+1} \sim -\pi \log \lambda \end{align*}$$
so that
$\varphi $
depends on
$\lambda $
in this case (see [Reference Ueberschär48] equation (3.14)). We note that the weak coupling quantization corresponds to a fixed self-adjoint extension, whereas the strong coupling quantization can be viewed as an energy-dependent, albeit very slowly varying, family of self-adjoint extensions.
From the spectral equation, it follows that new eigenvalues interlace with integers which are representable as the sum of two integer squares. We denote these eigenvalues as follows:
$$\begin{align*}0< \lambda_0 < 1 < \lambda_1 < 2 < \lambda_2 <4 < \lambda_4 < 5< \lambda_5 < \cdots \end{align*}$$
and write
$\Lambda _{new}$
for the set of all such eigenvalues. Also, given
$n=a^2+b^2$
, let
$n^+$
denote the smallest integer greater than n which is also a sum of two squares. Let
$$ \begin{align} {s_n}=\lambda_n-n>0 \end{align} $$
denote the distance between
$\lambda _n$
and the nearest old eigenvalue n to the left. In addition, given
$\lambda \in \Lambda _{new}$
the associated Green’s function is given by
$$ \begin{align} G_{\lambda}(x)=-\frac{1}{4 \pi^2} \sum_{ \xi \in \mathbb Z^2} \frac{ \exp(-i \xi \cdot x_0)}{|\xi|^2- \lambda} e^{i \xi \cdot x}, \qquad g_{\lambda}(x)=\frac{1}{\lVert G_{\lambda} \rVert_2} G_{\lambda}(x) \end{align} $$
(see equation (5.2) of [Reference Rudnick and Ueberschär38]). Also, note that the new eigenvalues interlace between the old eigenvalues; hence,
$G_{\lambda }$
is well defined for
$\lambda \in \Lambda _{new}$
. Since the torus is homogeneous, we may without loss of generality assume that
$x_{0}=0$
. Our main focus will be the behavior of the matrix coefficients
$ \{\langle \operatorname {Op}(f) g_{\lambda }, g_{\lambda } \rangle \}_{\lambda \in \Lambda _{new}}$
as f ranges over the set of pure momentum observables (i.e.,
$f \in C^{\infty } (S^1) \subset C^{\infty }({\mathbb S}^{*}(\mathbb T^2))$
; for such f the matrix coefficients are explicitly given by (cf. equation (5.3))
$$ \begin{align} \langle \operatorname{Op}(f) g_{\lambda}, g_{\lambda} \rangle = \frac{1}{\sum_{n \ge 0} \frac{r(n)}{(n-\lambda)^2}} \left( \frac{f(1)}{\lambda^{2}} + \sum_{ n> 0 }\frac{1}{(n-\lambda)^2} \sum_{ a^2+b^2=n} f\left(\frac{a+ib}{|a+ib|} \right) \right). \end{align} $$
1.2 Results
Our first main result shows that along a zero density, yet relatively large, subsequence of new eigenvalues
$\{\lambda _j\}$
the mass of
$g_{\lambda _j}$
, in momentum space, localizes on measures arising from
${\mathbb Z}^2$
-lattice points on circles (after projecting them to the unit circle). To describe these measures in more detail, consider an integer
$n=a^2+b^2$
, with
$a,b\in {\mathbb Z}$
, and the following probability measure on the unit circle
$S^1 \subset {\mathbb C}$
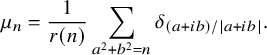$$\begin{align*}\mu_n =\frac{1}{r(n)} \sum_{a^2+b^2=n} \delta_{(a+ib)/|a+ib|}. \end{align*}$$
We remark that
$\mu _n$
can be viewed as the matrix coefficient of the ‘flat’ (old) Laplace eigenfunction
$ \psi _n(x) = \frac {1}{2 \pi \sqrt {r(n)}} \sum _{\xi \in {\mathbb Z}^2 : |\xi |^{2} = n} e^{ -i \xi \cdot x }, $
in the sense that, for f a pure momentum observable, we have
$$ \begin{align} \langle \operatorname{Op}(f) \psi_{n}, \psi_{n}\rangle = \sum_{ a^2+b^2=n} f\left(\frac{a+ib}{|a+ib|} \right) = \mu_n(f).\\[-9pt]\nonumber \end{align} $$
Following Kurlberg and Wigman [Reference Kurlberg and Wigman29], we call a measure
$\mu _{\infty }$
attainable if it is a weak limit point of the set
$\{ \mu _n \}_{n=a^2+b^2}$
. Any such measure is invariant under rotation by
$\pi /2$
, as well as under reflection in the x-axis; for convenience let
$$ \begin{align} \text{Sym}_{8} := \left\{ \left\langle \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \right\rangle \right\} \subset GL_{2}({\mathbb Z})\\[-9pt]\nonumber \end{align} $$
denote the group generated by these transformations.
Theorem 1.1. Let
$m_0=a^2+b^2 \in \mathbb N$
be odd.Footnote
1
In each of the weak and strong coupling quantizations, there exists a subset of eigenvalues
${\mathcal E}_{m_0} \subset \Lambda _{new}$
with
$$\begin{align*}\frac{ \# \{ \lambda \le X : \lambda \in {\mathcal E}_{m_0} \}}{\# \{ \lambda \le X : \lambda \in \Lambda_{\text{new}} \} } \gg \frac{1 }{(\log X)^{1+o(1)}}\\[-9pt] \end{align*}$$
such that for any pure momentum observable
$f \in C^{\infty } (S^1) \subset C^{\infty }(\mathbb S^{*}(\mathbb T^2))$
$$\begin{align*}\langle \operatorname{Op}(f) g_{\lambda}, g_{\lambda} \rangle \xrightarrow{ \substack{\lambda \rightarrow \infty \\ \lambda \in {\mathcal E}_{m_0}}} \frac{1}{r(m_0)} \sum_{a^2+b^2=m_0} f\left(\frac{a+ib}{|a+ib|} \right).\\[-9pt] \end{align*}$$
The key idea of the proof is to show that some new eigenvalues
$\lambda $
lie very close to certain old eigenvalues n, and this implies that
$g_{\lambda }$
is very well approximated by the flat eigenfunction
$\psi _{n}$
(cf. equations (1.5) and (1.6)), and consequently, in momentum space, the mass of
$g_{\lambda }$
completely localizes on the measure
$ \mu _{m_0}$
. Further, for any attainable measure
$\mu _{\infty }$
there exists
$\{m_{0, \ell } \}_{\ell }$
such that
$\mu _{m_{0},\ell }$
weakly converges to
$\mu _{\infty }$
, and this implies the following corollary.
Corollary 1.1. Let
$\mu _{\infty }$
be an attainable measure. Then there exists
$\{\lambda _j\}_{j} \subset \Lambda _{\text {new}}$
such that for any pure momentum observable
$f \in C^{\infty }(S^1) $
$$\begin{align*}\langle \operatorname{Op}(f) g_{\lambda_j}, g_{\lambda_j} \rangle \xrightarrow{j \rightarrow \infty} \int_{S^1} f d\mu_{\infty}.\\[-9pt] \end{align*}$$
We note that the set of attainable measures is much smaller than the set of probability measures on
$S^{1}$
that are
$\text {Sym}_{8}$
-invariant, in particular the set of attainable measures is not convex (cf. [Reference Kurlberg and Wigman29, Section 3.2].) In our next result, we show that in the strong coupling quantization there is a subsequence of new eigenvalues along which the entire mass of
$g_{\lambda }$
localizes on a certain convex combination of two measures arising from lattice points on the circle. In particular, the set of quantum limits, in momentum space, is strictly richer than the set of attainable measures.
Theorem 1.2. Let
$m_0,m_1$
be odd integers which are each representable as a sum of two squares. Then in the strong coupling quantization there exists a subsequence of eigenvalues
$ {\mathcal E}_{m_0,m_1} \subset \Lambda _{\text {new}}$
such that for each
$\lambda \in {\mathcal E}_{m_0,m_1}$
there is an integer
$\ell _{\lambda }$
with
$r(\ell _{\lambda }) \neq 0$
and
$r(\ell _{\lambda }) \ll 1$
such that for pure momentum observables
$f \in C^{\infty }(S^1)$
$$ \begin{align} \begin{aligned} \langle \operatorname{Op}(f) g_{\lambda}, g_{\lambda} \rangle =\,& c_{\lambda} \cdot \frac{1}{r(m_0)} \sum_{a^2+b^2=m_0} f\left( \frac{a+ib}{|a+ib|}\right) \\ & + (1-c_{\lambda}) \cdot \frac{1}{r(m_1\ell_{\lambda})} \sum_{a^2+b^2=m_1 \ell_{\lambda}} f\left( \frac{a+ib}{|a+ib|}\right)+O\left(\frac{1}{(\log \log \lambda)^{1/11}} \right), \end{aligned} \end{align} $$
where
$$\begin{align*}c_{\lambda}=\frac{1}{1+r(m_0)/r(m_1\ell_{\lambda})}. \end{align*}$$
Additionally,
$$\begin{align*}\frac{ \# \{ \lambda \le X : \lambda \in {\mathcal E}_{m_0,m_1} \}}{\# \{ \lambda \le X : \lambda \in \Lambda_{\text{new}} \} } \gg \frac{1 }{(\log X)^{2+o(1)}}. \end{align*}$$
Note that, since
$\sum _{p|\ell _{\lambda }} 1 \ll 1$
, the measure
$\mu _{m_{1} \ell _{\lambda }}$
can be viewed as a fairly small perturbation of
$\mu _{m_{1}}$
.
Remark 1. By removing a further ‘thin’ set of eigenvalues (with spectral counting function of size
$O(x^{1-\epsilon })$
for
$\epsilon>0$
, we can construct quantum limits that are flat in position (for details, cf. [Reference Kurlberg and Rosenzweig25, Remark 4]), in addition to the momentum push-forward properties given in Theorems 1.1 and 1.2. In particular, taking say
$m_{0}=9$
in Theorem 1.1 and noting that
$|z|^{2} = 9$
for
$z \in {\mathbb Z}[i]$
has the four solutions
$\pm 3, \pm 3i$
, this then yields quantum limits that are completely localized on the superposition of two Lagrangian states – essentially two plane waves, one in the horizontal and one in the vertical direction. This phenomenon is sometimes called superscarring (cf. [Reference Bogomolny and Schmit6, Reference Kurlberg and Rosenzweig25]).
Further, assuming a plausible conjecture on the distribution of the prime numbers, we show that given
$m_0,m_1$
as in Theorem 1.2 the quantum limit of
$\langle \operatorname {Op}(f) g_{\lambda }, g_{\lambda } \rangle $
can be made to be any given convex combination of
$\mu _{m_0}$
and
$\mu _{m_1}$
. The conjecture on the distribution of primes concerns obtaining a lower bound on the number solutions
$(u,v)$
in almost primes to the Diophantine equation
$$\begin{align*}aX-bY=4, \end{align*}$$
where
$v=p_1p_2$
,
$u=p_3$
with
$p_j$
a prime satisfying
$p_j=a_j^2+b_j^2$
and
$b_j=o(a_j)$
for
$j=1,2,3$
. The precise formulation of this conjecture, which we call Hypothesis 1, is given in Section 5.5.
Theorem 1.3. Assume Hypothesis 1. Let
$\mu _{\infty _0}, \mu _{\infty _1}$
be attainable measures and
$0\le c \le 1$
. Then in the strong coupling quantization there exists
$\{ \lambda _j \}_{j} \subset \Lambda _{new}$
such that for any
$f \in C^{\infty }(S^1)$
$$\begin{align*}\langle \operatorname{Op}(f) g_{\lambda_j}, g_{\lambda_j} \rangle \xrightarrow{ j \rightarrow \infty} c\int_{S^1} f d\mu_{\infty_0} +(1-c) \int_{S^1} f d\mu_{\infty_1}. \end{align*}$$
Further, assuming a variation of the prime k-tuple conjecture that also allows for prescribing Gaussian angles, we can show (cf. Appendix C) that all
$\text {Sym}_{8}$
-invariant probability measures on
$S^{1}$
arise as quantum limits in momentum space.
1.3 Discussion
For integrable systems it is often straightforward to construct nonuniform quantum limits, for example, ‘whispering gallery modes’ for the geodesic flow in the unit ball, and for linear flows on
${\mathbb T}^2$
, Lagrangian states with maximal localization (i.e., a single plane wave) are easily constructed. We note that strong localization in position for quantum limits on
${\mathbb T}^2$
was ruled out by Jakobson [Reference Jakobson20] – in position, any quantum limit is given by trigonometric polynomials whose frequencies lie on at most two circles (hence absolutely continuous with respect to Lebesgue measure.) Further, for the sphere, Jakobson and Zelditch in fact obtained a full classification – any flow invariant measure on
$S^{*}(S^{2})$
is a quantum limit [Reference Jakobson and Zelditch21].
The quantum ergodicity theorem holds in great generality as long as the key assumption of ergodic classical dynamics holds, but the existence of exceptional subsequence of nonuniform quantum limits (‘scarring’) is subtle. For classical systems given by the geodesic flow on compact negatively curved manifolds, the celebrated quantum unique ergodicity (QUE) conjecture [Reference Rudnick and Sarnak37] by Rudnick and Sarnak asserts that the only possible quantum limit is the Liouville measure. Known results for QUE include Lindenstrauss’ breakthrough [Reference Lindenstrauss30] for Hecke eigenfunctions on arithmetic modular surfaces, together with Soundararajan ruling out ‘escape of mass’ in the noncompact case [Reference Soundararajan46]. On the other hand, for a generic Bunimovich stadium (with strongly chaotic classical dynamics), Hassell [Reference Hassell and Hillairet16] has shown that there exists a subsequence of exceptional eigenstates where the mass localizes on sets of bouncing ball trajectories.
For quantized cat maps, again for Hecke eigenfunctions, QUE is known to hold [Reference Kurlberg and Rudnick26]. However, unlike for arithmetic modular surfaces, where Hecke desymmetrization is believed to be unnecessary, it is essential for quantum cat maps. Namely, Faure, Nonnenmacher and de Bièvre [Reference Faure, Nonnenmacher and De Bièvre13] constructed, in the presence of extreme spectral multiplicities and no Hecke desymmetrization, quantum limits of the form
$\nu = \frac {1}{2} \nu _{\text {pp}} + \frac {1}{2} \nu _{\text {Liouville}}$
; in [Reference Faure and Nonnenmacher12], this was shown to be sharp in the sense that the Liouville component always carries at least as much mass as the pure point one. (We note that, on assuming very weak bounds on spectral multiplicities, Bourgain showed [Reference Bourgain7] that scarring does not occur.) For higher-dimensional analogs of quantum cat maps, Kelmer has for certain maps shown [Reference Kelmer23] ‘super scarring’, even after Hecke desymmetrization, on invariant rational isotropic subspaces. Further, these type of scars persist on adding certain perturbations that destroy the spectral multiplicities [Reference Kelmer24]. Other models where scarring is known to exist include toral point scatterers with irrational aspect ratios [Reference Kurlberg and Ueberschär28, Reference Keating, Marklof and Winn22, Reference Berkolaiko, Keating and Winn3] and quantum star graphs [Reference Berkolaiko, Keating and Winn4], though neither model is quantum ergodic [Reference Kurlberg and Ueberschär28, Reference Berkolaiko, Keating and Winn4].
Classifying the set of possible quantum limits, in particular for quantum ergodic settings, is an interesting question. Here, Anantharaman proved very strong results for geodesic flows on negatively curved manifolds [Reference Anantharaman1]: any quantum limit has positive KS entropy with respect to the dynamics of the geodesic flow. In particular, this rules out localization on a finite number of closed geodesics (for compact arithmetic surfaces this was already known due to Rudnick and Sarnak [Reference Rudnick and Sarnak37].) Moreover, in the case of constant negative curvature, Anantharaman and Nonnenmacher showed [Reference Anantharaman and Nonnenmacher2] that the KS-entropy is at least half of the maximum possible. The measure of maximum entropy is given by the Liouville measure, and thus ‘eigenfunctions are at least half delocalized’. Dyatlov and Jin [Reference Dyatlov and Jin10] consequently showed that any quantum limit must have full support in
$S^{*}(M)$
, for compact hyperbolic surfaces M with constant negative curvature; together with Nonnenmacher this was recently strengthened [Reference Dyatlov, Jin and Nonnenmacher11] to the include the case of surfaces with variable negative curvature.
1.4 Outline of the proofs
Our arguments use the multiplicative structure of the integers to create an imbalance in the spectral equation (1.2) along a zero density, yet relatively large subsequence of new eigenvalues. Through exploiting this imbalance, we control the location of the new eigenvalues in our subsequence and show that they lie close to integers which are sums of two squares (cf. Section 5.3, in particular equation (5.14) for the argument placing full mass at one nearby eigenspace and 5.4, in particular equation (5.18) for placing mass at two nearby eigenspaces.) This greatly amplifies the amount of mass of the corresponding eigenfunctions in momentum space which lies on the terms which correspond to these integers, so much so that the contribution of the remaining terms is negligible in comparison. Consequently, the mass completely localizes on a convex combination of two measures and moreover our construction allows us to completely control the first measure.
In Section 2, we use sieve methods to produce integers
$n=p_1p_2$
, where
$p_j$
,
$j=1,2$
, is a prime with
$p_j=a^2+b^2=(a+ib)(a-ib)$
,
$0< b \le a$
, with
$0\le \arctan (b/a) \le \varepsilon $
, where
$\varepsilon $
is a small parameter, such that
$Q_0p_1p_2+4$
is also a sum of two squares,
$Q_1|Q_0p_1p_2+4$
and
$(Q_0p_1p_2+4)/Q_1$
has a bounded number of prime factors, where
$Q_0,Q_1$
are large integers whose purpose we will describe later. In particular, we exploit special features of the half-dimensional sieve using an ingenious observation of Huxley and Iwaniec [Reference Huxley and Iwaniec18]. Further, in order to find suitable Gaussian primes in narrow sectors we use a classical result of Hecke together with nontrivial bounds on exponential sums over finite fields to control sums of integral lattice points in narrow sectors with norms lying in arithmetic progressions to large moduli.
The subsequence of almost primes
$\{n_{\ell }\}$
constructed as described above creates the imbalance in the spectral equation (1.2) by boosting the contribution of the terms
$m=Q_0n_{\ell }, Q_0n_{\ell }+4$
, without perturbing the target measure(s). The next step in our argument is to show that this imbalance typically overwhelms the contribution of the remaining terms. To do this, we first show in Section 3 that for all new eigenvalues lying outside a small exceptional set the spectral equation (1.2) can be effectively truncated to integers m with essentially
$|m-\lambda | \ll (\log \lambda )^{10}$
. This is done by controlling sums of
$r(n)$
over short intervals and uses a second moment estimate of the Dedekind zeta-function
$\zeta _{\mathbb Q(i)}$
. In Section 4, we apply this result to new eigenvalues which lie between
$Q_0n_{\ell }$
and
$Q_0n_{\ell }+4$
and show that for almost all such new eigenvalues the remaining terms in the spectral sum (i.e.,
$|m-\lambda | \ll (\log \lambda )^{10}, m \neq Q_0n_{\ell }, Q_0n_{\ell }+4)$
is relatively small, provided that we take
$Q_0,Q_1$
sufficiently large thereby boosting the contribution of the closest two terms. This is accomplished by using bounds for sums of multiplicative functions over polynomials due to Henriot [Reference Henriot17]. Crucially, we need good estimates for these sums in terms of the discriminant of the polynomials.
Finally, to get complete control on the first measure in Theorem 1.2 we choose
$Q_0$
so that it is the product of a given fixed integer
$m_0$
and large primes
$p_{k}=a^2+b^2$
with
$0 \le \arctan (b_k/a_k) \le p_k^{-1/10}$
so that the probability measure on
$S^1$
associated with
$Q_0n_{\ell }$
weakly converges to the measure associated with
$m_0$
as
$\ell \rightarrow \infty $
. This last construction uses work of Ricci [Reference Ricci35] on Gaussian primes in narrow sectors.
1.5 Notation
We write
$f(x) \ll g(x)$
provided that
$f(x)=O(g(x))$
. Additionally, if for all x under consideration
$|f(x)| \ge c g(x)$
we write
$f(x) \gg g(x)$
. If we have both
$f(x) \ll g(x)$
and
$f(x) \gg g(x)$
, we write
$f(x) \asymp g(x)$
. For some additional notation related to sieves, see Section 2.1.1.
2 Sieve estimates
Let
$B_0$
be a sufficiently large integer, define
$\varepsilon = (\log \log x)^{-1/11}$
, and let
$$ \begin{align} \begin{aligned} {\mathcal P}_{\varepsilon,x}=\,&\{ p \ge (\log x)^{B_0} : p=a^2+b^2 \, \text{ and } \, 0 < \arctan(b/a) \le \varepsilon \}, \\ {\mathcal P}_{\varepsilon,x}'=\,&\{ p \in {\mathcal P}_{\varepsilon} : p \le x^{1/9}\}. \end{aligned} \end{align} $$
For brevity, we will write
${\mathcal P}_{\varepsilon }$
and
${\mathcal P}_{\varepsilon }'$
for
${\mathcal P}_{\varepsilon ,x}$
and
${\mathcal P}_{\varepsilon ,x}'$
, respectively. Also, given
$f,g : \mathbb N \rightarrow \mathbb C$
we define the Dirichlet convolution of f and g by
$$\begin{align*}(f \ast g)(n)=\sum_{ab=n} f(a)g(b). \end{align*}$$
Also, let
$Q_0,Q_1 \le (\log x)^{1/10}$
be odd coprime integers whose prime factors are all
$\equiv 1\ \pmod 4$
. Moreover, we assume that
$Q_0=f_0^2 e_0 r_0^{a_0}, Q_1=f_1^2e_1 r_1^{a_1}$
, where
$e_0,e_1$
are square-free,
$f_0,f_1 \ll 1$
and
$r_0,r_1$
are primes congruent to
$1\ \pmod 4$
. Throughout, the arithmetic function
$b(n)$
is the indicator function of the set of integers which are representable as a sum of two squares. Also, for
${\mathcal S} \subset \mathbb N$
we define
$$\begin{align*}1_{ {\mathcal S}}(n)=\begin{cases} 1 & \text{ if } n \in {\mathcal S}, \\ 0 & \text{ otherwise,} \end{cases} \end{align*}$$
and let
$\varphi (n)=\#\{ m < n : (m,n)=1\}$
.
Proposition 2.1. Let
$\eta>0$
be sufficiently small, and let
$y=x^{\eta }$
. Suppose
$y>Q_0Q_1$
. Then
$$\begin{align*}\sum_{\substack{x \le n \le 2x \\ Q_1 | Q_0 n+4 \\ (\frac{Q_0n+4}{Q_1},\prod_{p \le y} p)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) b(Q_0n+4) \asymp \frac{ \varepsilon^{2} Q_0}{ \eta^{1/2} \varphi(Q_0)} \cdot \frac{x \log \log x}{ \varphi(Q_1) (\log x)^2}. \end{align*}$$
This proposition builds on a result of Friedlander and Iwaniec [Reference Friedlander and Iwaniec15, Ch. 4]. The main novelty here is that we capture almost primes
$n =p_1p_2$
such that each prime factor
$p=a^2+b^2$
, with
$0 \le b \le a$
, has the property that
$a+ib$
lies within a certain small sector.
We also will require the following result.
Proposition 2.2. We have that
$$\begin{align*}\sum_{\substack{x \le n \le 2x \\ Q_1 | Q_0 n+4 }} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) b(Q_0n+4) \asymp \varepsilon^2 \frac{x \log \log x}{ \varphi(Q_1) (\log x)^{3/2}}. \end{align*}$$
Since Proposition 2.2 follows from a similar, yet simpler argument than the one used to prove Proposition 2.1, we will omit its proof. The rest of this section will be devoted to proving Proposition 2.1.
2.1 The Rosser–Iwaniec sieve
Let us first introduce the Rosser–Iwaniec
$\beta $
-sieve and the classical sieve terminology. We start with a sequence of
$\mathcal A=\{ a_n \}$
of nonnegative real numbers, a set of primes
${\mathcal P}$
and a parameter z. Define
$$ \begin{align} P(z)=\prod_{\substack{p \in {\mathcal P} \\ p < z}} p. \end{align} $$
Our goal is to obtain an estimate for the sieved set
$$\begin{align*}{\mathcal S}(\mathcal A, {\mathcal P}, z):=\sum_{\substack{n \le x \\ (n, P(z))=1}} a_n. \end{align*}$$
This will be accomplished through calculating, for square-free
$d \in \mathbb {N}$
,
$$ \begin{align} A_d(x):=\sum_{\substack{n \le x \\ n \equiv 0\ \ \ \pmod d}} a_n. \end{align} $$
We now make the hypothesis that our estimate for
$A_d(x)$
will be of the form
$$ \begin{align} A_d(x)=g(d)X+r_d, \end{align} $$
where
$g(d)$
is a multiplicative function with
$0 \le g(p)<1$
. The number
$r_d$
should be thought of as a remainder term, so X is an approximation to
$A_1(x)$
, and the function
$g(d)$
can be interpreted as a density.
Let
$$\begin{align*}V(z)=\prod_{p |P(z)}\left(1-g(p) \right). \end{align*}$$
We further suppose for all
$w<z$
that
$$ \begin{align} \frac{V(w)}{V(z)}=\prod_{\substack{w \le p <z \\p \in {\mathcal P}}}(1-g(p))^{-1} \le \left( \frac{\log z}{\log w}\right)^{\kappa}\left( 1+O\left( \frac{1}{\log w}\right)\right) \end{align} $$
for some
$\kappa>0$
. The constant
$\kappa $
is referred to as the dimension of the sieve.
Our arguments also require sieve weights. Let
$\Lambda =\{ \lambda _{d}\}_d$
be a sequence of real numbers, where d ranges over square-free integers. The sequence
$\Lambda $
is referred to as an upper bound sieve provided that
$$ \begin{align} 1_{n=1}=\sum_{d|n} \mu(d) \le \sum_{d|n} \lambda_d, \qquad \forall n \in \mathbb N, \end{align} $$
where
$1_{n=1}$
equals one if
$n=1$
and equals zero otherwise. We call
$\Lambda $
a lower bound sieve if
$$ \begin{align} \sum_{d|n} \lambda_d \le 1_{n=1}, \qquad \forall n \in \mathbb N. \end{align} $$
For a sieve
$\Lambda =\{\lambda _d\}$
, we use the notation
$$ \begin{align} (\lambda \ast 1)(n)=\sum_{d|n} \lambda_d. \end{align} $$
(This will be used to show the existence of primes, or almost primes, with desired properties.) Additionally, we say that the sieve
$\Lambda $
has level D if
$\lambda _d=0$
for
$d>D$
.
Given
$\kappa>0$
, the
$\beta $
-sieve gives both an upper and lower bound for
${\mathcal S}(\mathcal A, {\mathcal P}, z)$
whenever
$s=\log D/\log z$
is sufficiently large in terms of
$\kappa $
. The bounds consist of an error term, which is a sum of the remainder terms
$|r_d|$
for
$d \le D$
and a main term
$XV(z)F(s)$
,
$XV(z)f(s)$
(resp.), where
$F,f$
are certain continuous functions with
$0 \le f(s) < 1 < F(s)$
. For precise definitions, motivation and context, we refer the reader to [Reference Friedlander and Iwaniec15, Chapter 11].
Theorem 2.1 (Cf. [Reference Friedlander and Iwaniec15, Theorem 11.13])
Let
$D \ge z$
, and write
$s=\frac {\log D}{\log z}$
. Then there exists
$\beta $
-sieve weights such that
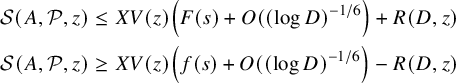$$\begin{align*}\begin{aligned} {\mathcal S}(A, {\mathcal P}, z) \le X V(z)\left( F(s)+O(( \log D)^{-1/6}\right)+R(D,z)\\ {\mathcal S}(A, {\mathcal P}, z) \ge X V(z)\left( f(s)+O(( \log D)^{-1/6}\right)-R(D,z) \end{aligned} \end{align*}$$
for
$s \ge \beta (\kappa )-1$
and
$ s\ge \beta (\kappa )$
(resp.), where
$$\begin{align*}R(D,z) \le \sum_{\substack{d \le D \\ d|P(z)}} |r_d| \end{align*}$$
and
$\beta (\kappa )$
denotes the sifting limit of dimension
$\kappa $
(cf. [Reference Friedlander and Iwaniec15, Ch. 6.4].)
In particular, note that for
$\kappa =1/2$
(which is of particular interest to us since we sieve out by the density
$1/2$
sequence of primes
$ \equiv 3\ \pmod 4 $
to detect sums of two squares), it is well known that
$\beta (\kappa ) =1$
(e.g., see [Reference Friedlander and Iwaniec15, Ch. 14.2]), which will be important for us as the ‘sifting variable’ s (which measures the sifting range relative to the sifting level, for example, smaller s corresponds to a smaller sifting range) only needs to be
$\ge 1$
to provide a lower bound for
${\mathcal S}(A,{\mathcal P},z)$
, whereas for the linear sieve
$\beta (1)=2$
so that one needs
$s \ge 2$
. In our arguments, we will use
$\beta $
-sieve weights, which are as defined in [Reference Friedlander and Iwaniec15] Sections 6.4–6.5. In particular for these weights, we have
$|\lambda _d| \le 1$
. We will sometimes refer to the fundamental lemma of the sieve, by which we mean the following result (see [Reference Friedlander and Iwaniec15, Lemma 6.11].)
Theorem 2.2. Let
$\Lambda ^{\pm }=\{ \lambda _d^{\pm } \}$
be upper and lower bound (resp.)
$\beta $
-sieves of level D with
$\beta \ge 4 \kappa +1$
. Also, let
$s=\log D/\log z$
. Then for any multiplicative function satisfying equation (2.5) and
$s \ge \beta +1$
we have
$$\begin{align*}\sum_{d|P(z)} \lambda_d^{\pm} g(d)=V(z)\left(1+O\left(s^{-s/2} \right) \right). \end{align*}$$
We also require the following estimate for the convolution of two sieves (see equation (5.97) and Theorem 5.9 of [Reference Friedlander and Iwaniec15]).
Theorem 2.3. Let
$\Lambda _1=\{ \lambda _{d} \}$
and
$\Lambda _2=\{ \lambda _{d}^{'} \}$
be upper-bound sieve weights of level
$D_1,D_2$
(resp.). Also, let
$g_1,g_2$
be multiplicative functions satisfying equation (2.5) with
$\kappa =1$
. Then
$$\begin{align*}\bigg|\sum_{\substack{d,e \\ (d,e)=1 }} \lambda_d \lambda_e^{'} g_1(d)g_2(e) \bigg| \le (4 e^{2\gamma}+o(1)) \prod_{p}(1+h_1(p)h_2(p)) \prod_{j=1}^2 \prod_{p < D_j} (1-g_j(p)) \end{align*}$$
as
$\min \{D_1,D_2\} \rightarrow \infty $
, where for
$j=1,2$
,
$ h_j(n)=g_j(n)(1-g_j(n))^{-1} $
and
$\gamma $
is Euler’s constant.
If in addition
$g_1(p), g_2(p) \le 1/p$
so that
$h_1(p)h_2(p) \ll 1/p^2$
, which will be the case for us, then
$$ \begin{align} \bigg| \sum_{\substack{d,e \\ (d,e)=1 }} \lambda_d \lambda_e^{'} g_1(d)g_2(e) \bigg| \le C \prod_{p< D_1}(1-g_1(p))\prod_{p<D_2}(1-g_2(p)), \end{align} $$
where
$C>0$
is an absolute constant.
2.1.1 Notation
We will also use the notation
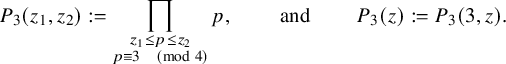$$\begin{align*}P_3(z_1,z_2):=\prod_{\substack{z_1 \le p \le z_2 \\ p \equiv 3\ \ \ \pmod 4}} p, \qquad \text{ and }\qquad P_3(z):=P_3(3,z). \end{align*}$$
Additionally, let
$1(n)=1_{\mathbb N}(n)=1$
denote the identity function and let
$\tau (n)=(1\ast 1)(n)=\sum _{d|n} 1$
. Also, define
$$ \begin{align} \mathcal B(x;q,a,\varepsilon) := \sum_{\substack{ x \le n \le 2x\\ n \equiv a\ \ \ {\pmod q}}} (1_{{{\mathcal P}}_{\varepsilon}} \ast 1_{{{\mathcal P}}_{\varepsilon}'})(n)-\frac{1}{\varphi(q)} \sum_{\substack{x \le n \le 2x \\ (n,q)=1}} (1_{{{\mathcal P}}_{\varepsilon}} \ast 1_{{{\mathcal P}}_{\varepsilon}'}) (n). \end{align} $$
Further,
$\delta> 0$
will denote a small, but fixed real number.
2.2 Preliminary lemmas
We begin by showing that the difference between the upper and lower bound sieves is ‘small’.
Lemma 2.1. Let
$\Lambda ^{\pm }=\{ \lambda _d^{\pm }\}$
be upper and lower bound linear sieves (resp.) each of level
$w=x^{\sqrt {\eta }}$
, where
$\eta>0$
is sufficiently small, whose sieve weights are supported on integers d such that
$d|P(y)$
, where
$y=x^{\eta }$
,
$y>Q_0Q_1$
, and
$(d,2Q_0 f_1r_1)=1$
; in particular,
$$ \begin{align} \lambda_{d}^{\pm} = 0 \text{ if } (d,2Q_0 f_1r_1)> 1.\\[-9pt]\nonumber \end{align} $$
Then
$$\begin{align*}\begin{aligned} &\sum_{\substack{x \le n \le 2x \\ Q_1|Q_0n+4}} \left((\lambda^+ \ast 1)\left(\frac{Q_0n+4}{Q_1}\right)-(\lambda^- \ast 1) \left(\frac{Q_0n+4}{Q_1}\right)\right) (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \\ &\qquad \qquad \qquad \ll \varepsilon^{2} \eta^{1/(4\eta^{1/2})-1} \frac{Q_0}{\varphi(Q_0)} \frac{x \log \log x}{\varphi(Q_1) (\log x)^2}+\frac{x}{(\log x)^{10}}. \end{aligned}\\[-9pt] \end{align*}$$
Remark 2. We imposed the assumption that
$\eta>0$
is sufficiently small so small that the error
$O(\eta ^{1/(4\eta ^{1/2})})$
in equation (2.16) is less than
$1/2$
. The requirement
$y>Q_0Q_1$
is not essential; in the case
$y<Q_0Q_1$
the argument proceeds similarly, but some additional, straightforward estimates are needed to treat the contribution of the primes between y and
$Q_0Q_1$
.
Proof. Switching order of summation, it follows that
$$ \begin{align} \begin{aligned} &\sum_{\substack{x \le n \le 2x \\ Q_1|Q_0n+4}} \left((\lambda^+ \ast 1)\left(\frac{Q_0n+4}{Q_1}\right)-(\lambda^- \ast 1) \left(\frac{Q_0n+4}{Q_1}\right)\right) (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \\ & \qquad \qquad \qquad = \sum_{\pm} \pm \sum_{\substack{d <w \\ d|P(y) \\ (d,2Q_0f_1r_1)=1}}\lambda_d^{\pm} \sum_{\substack{x \le n \le 2x \\ Q_0n+4 \equiv 0\ \ \ {\pmod dQ_1}}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n). \end{aligned}\\[-9pt]\nonumber \end{align} $$
The inner sum on the right-hand side (RHS) of equation (2.12) equals
$$ \begin{align} \begin{aligned} &\frac{1}{\varphi(dQ_1)} \sum_{\substack{x\le n \le 2x \\ (n,dQ_1)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n)+\mathcal B\left(x; dQ_1, \gamma, \varepsilon \right), \end{aligned}\\[-9pt]\nonumber \end{align} $$
where
$\gamma $
is the unique reduced residue
$\pmod {dQ_1}$
satisfying
$\gamma \cdot Q_0 \equiv -4\ \pmod {dQ_1}$
and
$\mathcal B$
is as defined in equation (2.10). Also,
$$ \begin{align} \sum_{\substack{ x\le n \le 2x \\ (n,dQ_1)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n)=\sum_{\substack{x \le n \le 2x }} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n)+O\bigg( \sum_{\substack{p_1p_2 \le 2x \\ (p_1p_2,dQ_1) \neq 1}}1_{ {\mathcal P}_{\varepsilon}}(p_1) 1_{ {\mathcal P}_{\varepsilon}'}(p_2) \bigg).\\[-9pt]\nonumber \end{align} $$
Since
$dQ_1 \le x^{1/9}$
(as
$\eta $
is small) and
$p_2 \le x^{1/9}$
the contribution to the error term from
$p_1p_2 \le x$
with
$p_1|(p_1p_2,dQ_1)$
is
$\ll \sum _{p_2 \le x^{1/9}} \sum _{p_1 \le x^{1/9} } 1 \ll x^{2/9}$
. Also, since
$p_2 \ge (\log x)^{B_0}$
$$ \begin{align} \sum_{\substack{p_1p_2 \le 2x \\ (p_1p_2,dQ_1) = p_2}}1_{ {\mathcal P}_{\varepsilon}}(p_1) 1_{ {\mathcal P}_{\varepsilon}'}(p_2) \le \sum_{\substack{p_2|dQ_1 \\ p_2 \ge (\log x)^{B_0}}} \sum_{p_1 \le 2 x/p_2} 1 \ll \frac{x}{\log x} \sum_{\substack{p_2|dQ_1 \\ p_2 \ge (\log x)^{B_0}}} \frac{1}{p_2} \ll \frac{x (\log \log x)}{(\log x)^{B_0}}. \end{align} $$
Hence, using equations (2.13), (2.14) and (2.15) along with the fundamental lemma of the sieve (see Theorem 2.2 and recall
$|\lambda _d|\le 1$
) with
$g(d)=\varphi (Q_1)/\varphi (Q_1 d)$
,Footnote
2
and
$s=\log w/\log y=\eta ^{-1/2}$
we have that
$$ \begin{align} \begin{aligned} &\sum_{\substack{d <w \\ d|P(y) \\ (d,2Q_0)=1}}\lambda_d^{\pm} \sum_{\substack{x \le n \le 2x \\ Q_0n+4 \equiv 0\ \ \ {\pmod dQ_1}}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n)\\ &=\frac{1}{\varphi(Q_1)} \sum_{\substack{x \le n \le 2x }} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \prod_{\substack{p \le y \\ (p , 2Q_0f_1r_1 )=1}}\left(1-\frac{\varphi(Q_1)}{\varphi(Q_1p)} \right)(1+O(\eta^{1/(4\eta^{1/2})}))\\ & \qquad \qquad \qquad +O\bigg( \sum_{\substack{d < w \\ (d,2)=1}} \left|\mathcal B \left(x; dQ_1, \gamma, \varepsilon \right)\right|\bigg)+O\left( \frac{x \log \log x}{(\log x)^{B_0-1}}\right). \end{aligned}\\[-17pt]\nonumber \end{align} $$
Applying Theorem A.1 from the appendix, since
$w=x^{\sqrt {\eta }} < x^{1/2-o(1)}$
we get that
$$\begin{align*}\sum_{\substack{d < w \\ (d,2)=1}} \left|\mathcal B \left(x; dQ_1, \gamma, \varepsilon \right)\right| \ll \frac{x}{ (\log x)^{10}}.\\[-17pt] \end{align*}$$
Using the two estimates above in equation (2.12) (note the main terms in equation (2.16) are the same for each of the sieves
$\Lambda ^{\pm }$
so they cancel in equation (2.12)) and applying equation (A.3) (with
$q=1$
) from the appendix to estimate the sum over n completes the proof upon noting that
$$\begin{align*}\prod_{\substack{p \le y \\ (p , 2Q_0f_1r_1)=1}}\left(1-\frac{\varphi(Q_1)}{\varphi(Q_1p)} \right) \asymp \frac{Q_0}{\varphi(Q_0) \log y} = \frac{Q_0}{\varphi(Q_0) \eta \log x}.\\[-56pt] \end{align*}$$
We next give a lower bound on the upper bound sieve, which together with Lemma 2.1 is strong enough (given suitable parameter choices) to show the existence of infinitely many integers with exactly two prime factors with the desired properties.
Lemma 2.2. Let
$w = x^{\sqrt {\eta }}$
,
$y=x^{\eta }$
and
$\Lambda ^{+}$
be as in Lemma 2.1. Let
$\delta> 3 \sqrt {\eta }>0$
and
$z=x^{\frac 12-\delta }$
. Then there exists a constant
$C_1>0$
such that
$$\begin{align*}\sum_{\substack{x \le n \le 2x \\ (Q_0n+4, P_3(y,z))=1 \\ Q_1|Q_0n+4}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'}) (n) (\lambda^+ \ast 1)\left(\frac{Q_0n+4}{Q_1}\right) \ge C_1 \frac{\varepsilon^2 \delta^{1/2}}{\eta^{1/2}} \frac{Q_0}{\varphi(Q_0)} \frac{x \log \log x}{\varphi(Q_1)(\log x)^2}.\\[-15pt] \end{align*}$$
Proof. We now implement the sieve as discussed in Section 2. We start with the sifting sequence
$$\begin{align*}\mathcal A=\bigg\{ (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})\bigg(\frac{m-4}{Q_0}\bigg) (\lambda^+ \ast 1)\left(\frac{m}{Q_1}\right) : Q_1|m, Q_0|m-4 \bigg\}\\[-15pt] \end{align*}$$
and primes
${\mathcal P}=\{ p \ge y : p \equiv 3\ \pmod 4 \}$
. With (2.11) in mind, we may choose
$$ \begin{align} \begin{aligned} X :=& \sum_{\substack{e<w \\ e|P(y)}} \frac{\lambda_e^+}{\varphi(eQ_1)} \sum_{\substack{x \le n \le 2x \\ (n, Q_1e)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \\ =&\sum_{\substack{x \le n \le 2x \\ (n, Q_1)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \sum_{\substack{e<w \\ e|P(y) \\ (e,2Q_0f_1r_1n)=1}} \frac{\lambda_e^+}{\varphi(eQ_1)}. \end{aligned} \end{align} $$
Arguing as in the proof of Lemma 2.1, to estimate the inner sum we apply the fundamental lemma of the sieve (see equation (2.16) and take
$D=w$
,
$z=y$
in Theorem 2.2 and note that we then have
$s=\eta ^{-1/2}$
) to get that it is
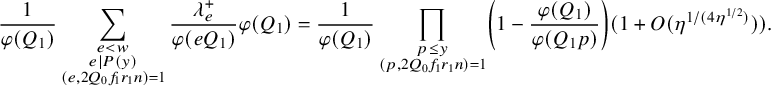$$\begin{align*}\frac{1}{\varphi(Q_1)}\sum_{\substack{e<w \\ e|P(y) \\ (e,2Q_0f_1r_1n)=1}} \frac{\lambda_e^+}{\varphi(eQ_1)} \varphi(Q_1)= \frac{1}{\varphi(Q_1)}\prod_{\substack{p \le y \\ (p , 2Q_0f_1r_1 n )=1}}\left(1-\frac{\varphi(Q_1)}{\varphi(Q_1p)} \right)(1+O(\eta^{1/(4\eta^{1/2})})). \end{align*}$$
For
$n=p_1p_2$
, recalling that
$f_1 \ll 1$
and
$r_1$
is prime, the RHS above is
$$\begin{align*}\asymp \frac{1}{\varphi(Q_1)} \prod_{\substack{p \le y \\ (p,Q_0)=1}}\left(1-\frac{1}{p-1}\right) \asymp \frac{1}{\varphi(Q_1)} \cdot \frac{Q_0}{\varphi(Q_0)} \frac{1}{\log y}. \end{align*}$$
Using equations (2.14) and (2.15) along with the prime number theorem for Gaussian primes in sectors (see equations (A.1) and (A.3) in the appendix, with
$q=1$
) yields
$$\begin{align*}\sum_{\substack{x \le n \le 2x \\ (n, Q_1)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \sim 4 \varepsilon^2 \cdot \frac{x \log \log x}{ \log x}. \end{align*}$$
We conclude that
$$ \begin{align} X \asymp \varepsilon^2 \frac{Q_0}{\varphi(Q_0)} \frac{x \log \log x}{ \varphi(Q_1) (\log y) (\log x)}. \end{align} $$
For
$d|P_3(y,z)$
, note that
$(d, eQ_0 Q_1)=1$
for e such that
$p|e \Rightarrow p< y$
, and
$(1_{ {\mathcal P}_{\varepsilon }} \ast 1_{ {\mathcal P}_{\varepsilon }'})(n)=0$
if
$(d,n) \neq 1$
. To apply the sieve, we require an estimate for
$A_d$
(cf. equations (2.3) and (2.4) for the definition of
$A_{d}$
) and recalling our choice for X and the definition of
$\mathcal B$
in equation (2.10) it follows that
$$ \begin{align} \begin{aligned} A_d(Q_0x+4)&:=\sum_{\substack{x \le n \le 2x \\ Q_1 | Q_0n+4 \\ Q_0n+4 \equiv 0\ \ \ {\pmod d}}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) (\lambda^+ \ast 1)\left(\frac{Q_0n+4}{Q_1}\right) \\ &= \sum_{\substack{e< w \\ e|P(y)}} \lambda_e^{+} \sum_{\substack{ x \le n \le 2x \\ Q_0n+4 \equiv 0\ \ \ {\pmod eQ_1} \\ Q_0n+4 \equiv 0\ \ \ {\pmod d}}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \\ &=\sum_{\substack{e< w \\ e|P(y)}} \frac{\lambda_e^{+}}{\varphi(deQ_1)} \sum_{\substack{x \le n \le 2x \\ (n, Q_1 e)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n)+r_d =\frac{1}{\varphi(d)}X+r_d, \end{aligned} \end{align} $$
where
$$ \begin{align} r_d \ll \sum_{\substack{e<w \\ (e,2)=1}} \left|\mathcal B(x;deQ_1, \gamma, \varepsilon)\right| \end{align} $$
and
$\gamma $
is the unique residue class
$\pmod {deQ_1}$
with
$Q_0 \gamma \equiv -4\ \pmod {eQ_1}$
and
$Q_0\gamma \equiv -4\ \pmod d$
; also note that
$(d,eQ_1)=1$
and
$\mathcal B$
is as in equation (2.10).
Hence, the half-dimensional Rosser–Iwaniec sieve Theorem 2.1 with set of primes
${\mathcal P}=\{ p \equiv 3\ \pmod {4} : p>y\}$
(so that equation (2.21) holds with
$\kappa =1/2$
), gives for any
$D \ge z$
with
$s=\log D/\log z$
$$ \begin{align} \begin{aligned} \sum_{\substack{x \le n \le 2x \\ (Q_0n+4, P_3(y,z))=1 \\ Q_1|Q_0n+4}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'}) (n) (\lambda^+ \ast 1)\left(\frac{Q_0n+4}{Q_1}\right)& \\ \ge X V(z)\left(f(s)+O\left(\frac{1}{(\log D)^{1/6}}\right)\right) &-\sum_{\substack{d < D \\ d|P_3(y,z)}} |r_d|, \end{aligned} \end{align} $$
where
$$ \begin{align} V(z)=\prod_{\substack{y \le p \le z \\ p \equiv 3\ \pmod 4}} \left( 1-\frac{1}{p-1} \right) \asymp \sqrt{\frac{\log y}{\log z}} \asymp \eta^{1/2}. \end{align} $$
Taking
$D=z^{1+\delta }$
, so
$s=1+\delta $
, we have by Theorem A.1, which is proved in the appendix, that (taking
$q=edQ_{1}$
)
$$ \begin{align} \sum_{\substack{d < D \\ d|P_{3}(y,z)}} |r_d| \ll \sum_{ \substack{q < DQ_1w \\ (q,2)=1}}\left( \tau(q) \max_{(a,q)=1} |\mathcal B(x;q,a, \varepsilon)| \right)\ll \frac{x}{(\log x)^3}. \end{align} $$
Here, note that
$DQ_1w < x^{\frac 12-\frac {\delta }{2}+\sqrt {\eta }}< x^{\frac 12-\frac {\delta }{6}}$
, and the contribution of the divisor function is handled by using Cauchy–Schwarz along with the trivial bound
$|\mathcal B(x;q,a, \varepsilon )| \ll x/q $
. Also, note that
$f(t) \sim 2 \sqrt {\frac {e^{\gamma }}{\pi }} \cdot \sqrt {t-1}$
as
$t \rightarrow 1^+$
(see the equation after (14.3) of [Reference Friedlander and Iwaniec15]), so
$f(s)=f(1+\delta ) \gg \sqrt {\delta }$
. Using this along with equations (2.17), (2.22) and (2.23) in equation (2.21) completes the proof.
Sieving as in the previous lemma, we will now deduce the claimed upper bound in Proposition 2.1.
Lemma 2.3. Let
$\eta>0$
be sufficiently small and
$y=x^{\eta }$
, with
$y>Q_0Q_1$
. Then
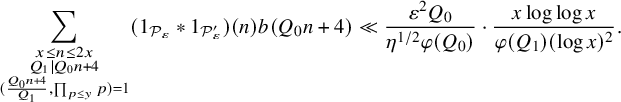$$\begin{align*}\sum_{\substack{x \le n \le 2x \\ Q_1 | Q_0 n+4 \\ (\frac{Q_0n+4}{Q_1},\prod_{p \le y} p)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) b(Q_0n+4) \ll \frac{ \varepsilon^{2} Q_0}{ \eta^{1/2} \varphi(Q_0)} \cdot \frac{x \log \log x}{ \varphi(Q_1) (\log x)^2}. \end{align*}$$
Proof. Write
$Q_0n+4=Q_1 f^2 s$
, where s is square-free and note that since
$((Q_0n+4)/Q_1,P(y))=1$
all the prime divisors of f (and s as well) are
$\ge y$
, in particular f is coprime to
$Q_0Q_1$
. We now note that
$b(s)\le 1_{S}(s)$
for
$S=\{ n : (n,P_3(y,z))=1\}$
and take
$\Lambda ^+$
to be the upper bound sieve from Lemma 2.1, which we use to bound the condition
$((Q_0n+4)/Q_1, \prod _{p \le y} p)=1$
to get that
$$ \begin{align} \begin{aligned} & \sum_{\substack{x \le n \le 2x \\ Q_1 | Q_0 n+4 \\ (\frac{Q_0n+4}{Q_1},\prod_{p \le y} p)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) b(Q_0n+4) \\ & \le \sum_{ \substack{f \le (\log x)^{10} \\ p|f \Rightarrow p>y}} \sum_{\substack{x\le n \le 2x \\ ((Q_0n+4)/f^2, P_3(y,z'))=1 \\ f^2Q_1|Q_0n+4}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'}) (n) (\lambda^+ \ast 1)\left(\frac{Q_0n+4}{Q_1}\right)+O(x/(\log x)^{10}), \end{aligned} \end{align} $$
where the error term arises from the contribution of
$f> (\log x)^{10}$
. The following sieving argument is similar to the previous lemma (in fact we have already handled the case
$f=1$
). For f as above let
$$ \begin{align} X_f:=\sum_{\substack{e<w \\ e|P(y)}} \frac{\lambda_e^+}{\varphi(eQ_1f^2)} \sum_{\substack{x \le n \le 2x \\ (n,f Q_1e)=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \asymp \varepsilon^2 \frac{Q_0}{\varphi(Q_0)} \frac{x \log \log x}{\varphi(Q_1 f^2)(\log y) (\log x)}, \end{align} $$
where the last estimate follows from repeating the argument given in equation (2.18). Similarly, arguing as in equation (2.19) we have for each
$d|P_{3}(y,z)$
with d coprime to f that
$$\begin{align*}A_d(Qx+4;f):=\sum_{\substack{x \le n \le 2x \\ Q_1f^2 | Q_0n+4 \\ Q_0n+4 \equiv 0\ \ \ {\pmod d}}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) (\lambda^+ \ast 1)\left(\frac{Q_0n+4}{Q_1}\right) =\frac{1}{\varphi(d)} X_f+r_{d,f}, \end{align*}$$
where
$$\begin{align*}r_{d,f} \ll \sum_{\substack{e<w \\ (e,2)=1}} \left|\mathcal B(x;def^2 Q_1, \gamma, \varepsilon)\right|. \end{align*}$$
We will now apply an upper bound sieve. For
$D=x^{1/50}$
and
$z'=x^{1/100}$
, Theorem 2.1 with set of primes
${\mathcal P}=\{p \equiv 3\ \pmod 4: (p,f)=1 \, \& \, p>y\}$
gives for each
$f \le (\log x)^{10}$
with prime divisors all
$>y$
that the inner sum on the RHS of equation (2.24) is
$$ \begin{align} \begin{aligned} & \le X_f V_f(z')\left(F(2)+O\left(\frac{1}{(\log D)^{1/6}}\right)\right)+\sum_{\substack{d < D \\ d|P_3(y,z), (d,f)=1}} |r_{d,f}|, \end{aligned} \end{align} $$
where the sum over d is
$O(x^{1/25})$
since
$D = x^{1/50}$
, and
$$ \begin{align} V_f(z')=\prod_{\substack{y \le p \le z' \\ p \equiv 3\ \ \ \pmod 4, \, p\nmid f}} \left(1-\frac{1}{p-1} \right)\ll \frac{f}{\varphi(f) } \eta^{1/2}, \end{align} $$
where the upper bound follows from equation (2.22). Using equations (2.25) and (2.27) in equation (2.26) then applying the resulting estimate in equation (2.24) and summing over f completes the proof.
2.3 The Proof of Proposition 2.1
We first require a Brun–Titchmarsh type bound for primes in narrow sectors.
Lemma 2.4. Let
$Q, q\le x^{2/3-o(1)}$
be odd. Then
$$\begin{align*}\sum_{ \substack{p=a^2+b^2 \le x \\ |\arctan(b/a)| \le \varepsilon \\ qp+4=Q p_1, \, p_1 \text{ prime} }} 1 \ll \varepsilon \frac{q}{\varphi(q)}\frac{x}{\varphi(Q)(\log x)^2}. \end{align*}$$
Remark 3. The point of the lemma is that it holds for large moduli
$Q>x^{1/2}$
. To accomplish this, we use asymptotic estimates for Gaussian integers
$\alpha =a+ib$
with
$N(\alpha ) \le x$
and
$N(\alpha ) \equiv a\ \pmod Q$
and
$|\arg (\alpha )|\le \varepsilon $
, where
$N(\alpha )=\alpha \overline {\alpha }$
is the norm of
$\alpha $
. Details are given in Appendix, cf. section A.2.
The main step in the proof of Proposition 2.1 is the following lemma.
Lemma 2.5. Let
$z=x^{\frac 12-\delta }$
, where
$\delta>0$
is sufficiently small and
$ y = x^{\eta }$
with
$0< \eta < 1/3$
. There exists a constant
$C_2>0$
such that
$$\begin{align*}\sum_{\substack{x \le n \le 2x \\ Q_1|Q_0n+4 \\ (\frac{Q_0n+4}{Q_1},P(y)P_3(y,z))=1}} (1_{{\mathcal P}_{\varepsilon}} \ast 1_{{\mathcal P}_{\varepsilon}'})(n) = \sum_{\substack{x \le n \le 2x \\ Q_1|Q_0n+4 \\ (\frac{Q_0n+4}{Q_1},P(y)) = 1 \\ p|Q_0n+4 \Rightarrow p \equiv 1\ \ \ {\pmod 4}}} (1_{{\mathcal P}_{\varepsilon}}\ast 1_{{\mathcal P}_{\varepsilon}'})(n)+R, \end{align*}$$
where
$$\begin{align*}0 \le R \le C_2 \cdot \varepsilon^2 \cdot \frac{\delta^{3/2}}{\eta^{1/2}} \frac{Q_0}{\varphi(Q_0)} \cdot \frac{x \log \log x}{\varphi(Q_1)(\log x)^2}. \end{align*}$$
Proof. By construction, if
$(1_{\mathcal P_{\varepsilon }} \ast 1_{ {\mathcal P}_{\varepsilon }'})(n) \neq 0$
, then
$Q_0n+4 \equiv 1\ \pmod 4$
and
$Q_1 \equiv 1\ \pmod 4$
so that
$(Q_0n+4)/Q_1 \equiv 1\ \pmod 4$
and must have an even number of prime factors which are congruent to
$3\ \pmod 4$
. Since
$z>x^{1/4}$
the integers which contribute to R must have precisely two such prime factors. Dropping several conditions on the integers n which contribute to R, it follows that R is bounded by the number of integers
$n=p_1p_2 \le 2x$
,
$( 1_{ {\mathcal P}_{\varepsilon }} \ast 1_{ \mathcal P_{\varepsilon }'})(n) \neq 0$
such that
$(Q_0n+4)/Q_1=aq_1q_2$
, where
$b(a)=1$
,
$(a,P(y))=1$
,
$q_1 \equiv q_2 \equiv 3\ \pmod 4$
and
$q_1,q_2$
are primes with
$z< q_1, q_2 \le 4Q_0x/Q_1$
so
$a \le 4Q_0x/(Q_1z^2)$
. By symmetry, it suffices to consider the terms with
$q_1 \le q_2$
. We get that
$$ \begin{align} R \le 2 \sum_{p_2 \le (2x)^{1/9} } 1_{{\mathcal P}_{\varepsilon}'}(p_2) \sum_{\substack{ a \le \frac{4Q_0 x}{Q_{1}z^2} \\ (a,P(y))=1}} b(a) \sum_{z< q_1 \le \sqrt{\frac{4Q_0 x}{aQ_1}}} \sum_{q_1 \le q_2 \le 4Q_0x/Q_1} \sum_{\substack{p_1 \le 2x/p_2 \\ Q_0p_1p_2+4=aq_1q_2Q_1}} 1_{{\mathcal P}_{\varepsilon}}(p_1). \end{align} $$
Applying Lemma 2.4 with
$q=Q_0p_2$
and
$Q=aq_1Q_1$
,
$$ \begin{align} \sum_{\substack{p_1 \le 2x/p_2 \\ Q_0p_1p_2+4=aq_1q_2Q_1}} 1_{{\mathcal P}_{\varepsilon}}(p_1) \ll \varepsilon \frac{Q_0}{\varphi(Q_0)}\frac{x}{ \varphi(aQ_1) q_1p_2 (\log x)^2}. \end{align} $$
Note that
$x/p_2 \ge 2^{-1/9}x^{8/9}$
and
$Q_0p_2, aq_1Q_1 \le \left ( \frac {x}{p_2}\right )^{2/3-o(1)}$
, for
$\delta>0$
sufficiently small, so the application of Lemma 2.4 is valid.
We claim that
$$ \begin{align} \sum_{\substack{a \le \frac{4Q_0x}{Q_1z^2} \\ (a,P(y))=1}} \frac{b(a)}{\varphi(a)} \ll \sqrt{\frac{\log x/z^2}{\log y}}, \end{align} $$
which we will justify below. Additionally,
$$ \begin{align} \sum_{z<q_1 \le \sqrt{\frac{4Q_0 x}{aQ_1}}} \frac{1}{q_1} \sim \log \frac{\log \sqrt{\frac{2Q_0 x}{aQ_1}}}{\log z} \ll \frac{\log \frac{ x}{z^2}}{\log z}+\frac{\log Q_0}{\log z} \ll \frac{\log \frac{ x}{z^2}}{\log z} \ll \delta. \end{align} $$
Therefore, using equations (2.29), (2.30) and (2.31) in equation (2.28) we conclude that
$$\begin{align*}\begin{aligned} R \ll & \varepsilon \cdot \frac{Q_0}{\varphi(Q_0)} \cdot \frac{x \log x/z^2}{\varphi(Q_1) (\log x)^2 \log z} \sqrt{\frac{\log x/z^2}{\log y}} \sum_{p_2 \le (2x)^{1/9} } \frac{ 1_{{\mathcal P}_{\varepsilon}'}(p_2)}{p_2} \\ \ll & \varepsilon^2 \cdot \frac{\delta^{3/2}}{\eta^{1/2}}\cdot \frac{ Q_0}{ \varphi(Q_0)} \cdot \frac{x \cdot \log \log x }{\varphi(Q_1) (\log x)^2} \end{aligned} \end{align*}$$
as desired.
It remains to justify equation (2.30). Let
$F(n)$
be the completely multiplicative function defined by
$F(p)=1$
if
$p \ge y$
and zero otherwise. Then for all
$t \ge y$
, it follows from basic estimates for multiplicative functions (see (1.85) of [Reference Iwaniec and Kowalski19]) that
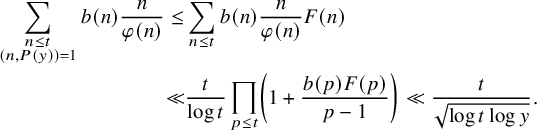$$\begin{align*}\begin{aligned} \sum_{\substack{n \le t \\ (n,P(y))=1}} b(n) \frac{n}{\varphi(n)} \le& \sum_{\substack{n \le t }} b(n) \frac{n}{\varphi(n)} F(n) \\ \ll & \frac{t}{\log t} \prod_{ p \le t} \left(1+ \frac{b(p)F(p)}{p-1} \right) \ll \frac{t}{\sqrt{\log t \log y}}. \end{aligned} \end{align*}$$
For
$1 \le t \le y$
, the sum on the left-hand side (LHS) is empty so the bound is true in that case as well. Hence, equation (2.30) follows from this estimate along with partial summation.
Proof of Proposition 2.1
The upper bound has already been established in Lemma 2.3. It remains to establish the lower bound. Let
$\delta $
be sufficiently small in terms of
$C_1$
and
$C_2$
. Applying the inequality (2.7) for a lower bound sieve (also recall our notation (2.8)) along with Lemmas 2.1 and 2.2, using a lower bound sieve to take care of the condition
$( \frac {Q_0n+4}{Q_1} , P(y)) = 1$
(and recalling that
$z=x^{\frac 12-\delta }$
for
$\delta>0$
), we have that
$$ \begin{align} \begin{aligned} \sum_{\substack{x \le n \le 2x \\ Q_1 |Q_0n+4 \\ (\frac{Q_0n+4}{Q_1},P(y)P_3(y,z))=1 }} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \ge& \sum_{\substack{ x \le n \le 2x \\ Q_1 |Q_0n+4\\ (Q_0n+4,P_3(y,z))=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) (\lambda^- \ast 1)\left(\frac{Q_0n+4}{Q_1}\right) \\ =& \sum_{\substack{ x \le n \le 2x \\ Q_1 |Q_0n+4\\ (Q_0n+4,P_3(y,z))=1}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) (\lambda^+ \ast 1)\left(\frac{Q_0n+4}{Q_1}\right)\\ &\qquad \qquad +O\left(\varepsilon^2 \eta^{1/(4\eta^{1/2})-1} \frac{Q_0}{\varphi(Q_0)} \frac{x \log \log x}{\varphi(Q_1)(\log x)^2} \right) \\ \ge& C_1 \frac{\varepsilon^2 \delta^{1/2}}{\eta^{1/2}} \frac{Q_0}{\varphi(Q_0)} \frac{x \log \log x}{\varphi(Q_1)(\log x)^2}\left(1+O\left( \frac{ \eta^{\frac{1}{4\eta^{1/2}}-\frac12}}{\delta^{1/2}} \right)\right). \end{aligned} \end{align} $$
Choosing
$\eta $
sufficiently small in terms of
$\delta $
(which we choose in a way that only depends on
$C_{1},C_{2}$
; see below) the O-term above is
$ \le 1/2$
in absolute value. Therefore, by equation (2.32) along with Lemma 2.5 it follows that
$$ \begin{align*} \begin{aligned} \sum_{\substack{x \le n \le 2x \\ Q_1 |Q_0n+4 \\ (\frac{Q_0n+4}{Q_1},P(y)P_3(y,z))=1 \\ p|Q_0n+4 \Rightarrow p \equiv 1\ \ \ {\pmod 4 }}} (1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \ge \left(\frac{C_1}{2} \frac{\varepsilon^2 \delta^{1/2}}{\eta^{1/2}}-\frac{C_2 \varepsilon^2 \delta^{3/2}}{\eta^{1/2}} \right) \frac{Q_0}{\varphi(Q_0)} \frac{x \log \log x}{\varphi(Q_1)(\log x)^2}. \end{aligned} \end{align*} $$
The term
$\left (\frac {C_1}{2} \delta ^{1/2}-C_2 \delta ^{3/2} \right )$
is positive for
$\delta $
sufficiently small in terms of
$C_1$
and
$C_2$
. Also,
$b(Q_0n+4) =1$
for n such that all the prime factors of
$Q_0n+4$
are congruent to
$1\ \pmod 4$
. This completes the proof.
3 Truncating the spectral equation
In this section, we show that it is possible to achieve a very short truncation of the spectral equation which holds for almost all new eigenvalues.
Theorem 3.1. Let
$A \ge 1$
. Then for
$B=B(A)$
sufficiently large, we have for every eigenvalue
$\lambda _n \in \Lambda _{new} \cap [1,x]$
except those outside an exceptional set of size
$O(x/(\log x)^A)$
that
$$ \begin{align} \sum_{m:|m-n| \le \frac{n}{x} (\log x)^B} \frac{r(m)}{m-\lambda_n} = \begin{cases} \pi \log \lambda_n+O(1)& \text{ in the weak coupling quantization},\\ \frac{1}{\alpha}+O(1) & \text{ in the strong coupling quantization}. \end{cases} \\[-17pt]\nonumber\end{align} $$
The above theorem is proved by capturing cancellation in the spectral equation even at very small scales for almost all new eigenvalues. This is done by showing that the average behavior of sums of
$r(n)$
over even very short intervals is fairly regular.
Lemma 3.1. Let
$x\ge 3$
and
$3 \le L \le x $
. Then
$$ \begin{align} \frac{1}{x} \sum_{ \ell \le x} \bigg| \sum_{\ell \le n \le \ell+\frac{\ell}{L}} r(n)-\pi \frac{\ell}{L} \bigg|^2 \ll \frac{x}{L} (\log x)^2.\\[-17pt]\nonumber \end{align} $$
Proof. We repeat a classical argument, which was used by Selberg [Reference Selberg41] to study primes in short intervals. Consider
$$\begin{align*}\zeta_{\mathbb Q(i)}:= \frac14 \sum_{n \ge 1} \frac{r(n)}{n^s}=L(s,\chi_4) \zeta(s) \qquad \operatorname{Re}(s)>1,\\[-17pt] \end{align*}$$
where
$L(s,\chi _4)$
is the Dirichlet L-function attached to the nontrivial Dirichlet character
$\pmod 4$
, and
$\zeta (s)$
denotes the Riemann zeta-function. Note
$L(1, \chi _4)=\pi /4$
. Applying Perron’s formula, then shifting contours to
$\operatorname {Re}(s)=1/2$
(which is valid since it is well known that
$\zeta _{\mathbb Q(i)}(\sigma +it) \ll t^{1-\sigma +o(1)}$
, for
$0 \le \sigma \le 1$
) and picking up a simple pole at
$s=1$
we see that for
$v,v+v/L \notin \mathbb Z$
$$\begin{align*}\begin{aligned} \sum_{v \le n \le v+\frac{v}{L}} r(n)& = \frac{1}{2\pi i} \int_{(2)} 4\zeta_{\mathbb Q(i)} (s) \frac{(v+\frac{v}{L})^s-v^s}{s} \, ds \\ & = 4 L(1,\chi_4) \cdot \frac{v}{L}+\frac{v^{1/2}}{2\pi} \int_{\mathbb R} 4 \zeta_{\mathbb Q(i)}(\tfrac12+it) \frac{(1+\frac{1}{L})^{\frac{1}{2}+it}-1}{\frac12+it} \cdot e^{i t \log v} \, dt. \end{aligned}\\[-17pt] \end{align*}$$
Notice that the integral on the RHS is a Fourier transform. Writing
$\nu =\log (1+\frac 1L)$
, making a change of variables
$v=e^{\tau }$
and then applying Plancherel’s theorem yields
$$\begin{align*}\begin{aligned} \frac{1}{x^2} \int_1^{x} \bigg(\sum_{v \le n \le v+\frac{v}{L}} r(n)- \pi \cdot \frac{v}{L} \bigg)^2 \, dv \le & \int_{\mathbb R} \bigg(\sum_{e^{\tau} \le n \le e^{\tau+\nu}} r(n)- \pi \cdot \frac{e^{\tau}}{L} \bigg)^2 \frac{d\tau}{e^{\tau}} \\ =&\frac{8}{\pi} \int_{\mathbb R} |\zeta_{\mathbb Q(i)}(\tfrac12+it)|^2 |w_{\nu}(\tfrac12+it)|^2 \, dt, \end{aligned}\\[-17pt] \end{align*}$$
where
$w_{\nu }(s)=(e^{\nu s}-1)/s \ll \min \{ \nu , 1/(1+|t|) \}$
uniformly for
$\frac 14 \le \operatorname {Re}(s) \le 1$
. To estimate the integral on the RHS, we apply the well-known bound
$$\begin{align*}\int_0^{T} |\zeta_{\mathbb Q(i)} (\tfrac12+it)|^2 \, dt \ll T (\log T)^2 \end{align*}$$
(see the introduction of [Reference Müller32]). Hence, we see that
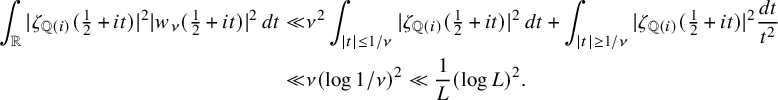$$\begin{align*}\begin{aligned} \int_{\mathbb R} |\zeta_{\mathbb Q(i)}(\tfrac12+it)|^2 |w_{\nu}(\tfrac12+it)|^2 \, dt \ll & \nu^2 \int_{|t| \le 1/\nu} |\zeta_{\mathbb Q(i)} (\tfrac12+it)|^2 \, dt+\int_{|t| \ge 1/\nu} |\zeta_{\mathbb Q(i)} (\tfrac12+it)|^2 \frac{dt}{t^2} \\ \ll & \nu (\log 1/\nu)^2 \ll \frac{1}{L} (\log L)^2. \end{aligned}\\[-9pt] \end{align*}$$
Combining the estimates above, we conclude that
$$ \begin{align} \frac{1}{x} \int_{x}^{2x} \bigg( \sum_{v \le n \le v+\frac{v}{L}} r(n)-\pi \frac{v}{L} \bigg)^2 \, dv \ll \frac{x}{L} (\log x)^2.\\[-9pt]\nonumber \end{align} $$
We will now bound the sum over integers
$ \ell \le x$
on the LHS of equation (3.2) in terms of an integral over
$1 \le v \le x$
. Let
$$\begin{align*}F(v)=\sum_{v \le n \le v+\frac{v}{L}} r(n)- \pi \cdot \frac{v}{L},\\[-9pt] \end{align*}$$
and let
$v_{\ell } \in [\ell , \ell +1]$
be a point where the minimum of
$|F(v)|$
on
$[\ell , \ell +1]$
is achieved. Observe that
$$\begin{align*}F(\ell)=F(v_{\ell})+O\left( r(\ell)+r(\ell^*)+1 \right), \end{align*}$$
where
$\ell ^*=\lfloor \ell +1+(\ell +1)/L \rfloor $
. Hence,
$$\begin{align*}\begin{aligned} \frac{1}{x}\sum_{ \ell \le x} F(\ell)^2 &\ll \frac{1}{x}\sum_{ \ell \le x} F(v_{\ell} )^2+\frac{1}{x}\sum_{\ell \le x }(r^2(\ell)+r^2(\ell^*))+1 \\ & \ll \frac{1}{x}\int_{1}^{x} F(x)^2 \, dx+ \log x \ll \frac{x}{L} (\log x)^2, \end{aligned}\\[-9pt] \end{align*}$$
where the last bound follows from equation (3.3) and the bound
$\sum _{\ell \le x} r(l)^{2} \ll x \log x$
(which in turns follows from a Wirsing type estimate (cf. [Reference Wirsing49]) or by taking
$k=1$
,
$R_{1}(X)=X$
and
$F_{1}(n) = r(n)$
in Lemma 4.1).
Lemma 3.2. Let
$A \ge 3$
and
$x,Y \ge 3$
. Then for all but
$\ll x/(\log x)^{A}$
integers
$m \in [ 1, x]$
we have
$$\begin{align*}\bigg| \sum_{Y \frac{m}{x} < k \le x^{1/2} \frac{m}{x}} \frac{r(m+k)-r(m-k)}{k} \bigg| \le \frac{(\log x)^{3A}}{\sqrt{Y}}. \end{align*}$$
Proof. Let
$$\begin{align*}R_m(t)=\sum_{1 \le k \le t} (r(m+k)-r(m-k)). \end{align*}$$
It suffices to consider
$m \in [x/(\log x)^A,x]$
. Hence, by summation by parts for each integer
$m \in [x/(\log x)^A,x]$
we have that
$$\begin{align*}\begin{aligned} \sum_{Y \frac{m}{x} < k \le x^{1/2} \frac{m}{x}} \frac{r(m+k)-r(m-k)}{k}=&\frac{R_m(x^{1/2} \frac{m}{x})}{x^{1/2} \frac{m}{x}}- \frac{R_m(Y \frac{m}{x})}{Y \frac{m}{x}}+\int_{Y \frac{m}{x}}^{x^{1/2} \frac{m}{x}} \frac{R_m(t)}{t^2} \, dt. \end{aligned} \end{align*}$$
Using this along with Chebyshev’s inequality and the elementary inequality
$(|a|+|b|+|c|)^{2} \le 3^2 (a^2+b^2+c^2)$
, it follows that
$$ \begin{align} \begin{aligned} & \# \left \{ \frac{x}{(\log x)^A} \le m \le x : \bigg| \sum_{Y \frac{m}{x} < k \le x^{1/3} \frac{m}{x}} \frac{r(m+k)-r(m-k)}{k} \bigg| \ge \frac{(\log x)^{3A}}{\sqrt{Y}} \right\} \\ & \le 9 \frac{Y}{(\log x)^{6A}} \sum_{ \frac{x}{(\log x)^A} \le m \le x} \left(\frac{R_m\left(x^{1/2} \frac{m}{x}\right)^2 (\log x)^{2A}}{x}+ \frac{R_m\left(Y \frac{m}{x}\right)^2 (\log x)^{2A}}{Y^2}+ \left(\int_{Y \frac{m}{x}}^{x^{1/2} \frac{m}{x}} \frac{R_m(t)}{t^2} \, dt \right)^2 \right). \end{aligned}\\[-9pt]\nonumber \end{align} $$
In the integral, we make a change of variables and apply the Cauchy–Schwarz inequality to get for each
$m \in [x/(\log x)^A,x]$
that
$$ \begin{align} \left( \int_{Y \frac{m}{x}}^{x^{1/2} \frac{m}{x}} \frac{R_m(t)}{t^2} \, dt \right)^2\le \frac{(\log x)^{2A}}{Y} \int_{Y}^{x^{1/2}} \frac{1}{t^2} R_m\left( t\frac{m}{x}\right)^2 \, dt.\\[-9pt]\nonumber \end{align} $$
Observe that
$$\begin{align*}R_m\left(H \frac{m}{x}\right)=\sum_{m \le n \le m+\frac{m}{x} H} r(n)-\sum_{m-\frac{m}{x} H \le n \le m} r(n).\\[-9pt] \end{align*}$$
Hence, by Lemma 3.1 with
$L=x/H$
(along with an analogue of this lemma for the second sum, which is proved in the same way) we get
$$\begin{align*}\frac{1}{x}\sum_{ m \le x}R_m\left(H \frac{m}{x}\right)^2 \ll H (\log x)^2, \end{align*}$$
for
$1 \le H \le x/3$
. Using this bound and equation (3.5) in equation (3.4) gives
$$\begin{align*}\begin{aligned} &\# \left \{ \frac{x}{(\log x)^A} \le m \le x : \bigg|\sum_{Y \frac{m}{x} < k \le x^{1/2} \frac{m}{x}} \frac{r(m+k)-r(m-k)}{k} \bigg| \ge \frac{(\log x)^{3A}}{\sqrt{Y}} \right\} \\ &\qquad \qquad \ll \frac{Y \cdot x}{(\log x)^{4A}}\left(\frac{(\log x)^2}{x^{1/2}}+\frac{(\log x)^2}{Y}+\frac{(\log x)^3}{Y} \right) \ll \frac{x}{(\log x)^{4A-3}} \end{aligned}\\[-9pt] \end{align*}$$
since we may assume
$Y \le x^{1/2}$
, otherwise the set on the LHS above is empty.
Before proving the main result of this section, we require the following technical lemma.
Lemma 3.3. Let
$u,v$
be sufficiently large positive real numbers such that
$v^{9/10} \le u \le 2v$
. Let
$t> 1$
be a real number that is not expressible as a sum of two squares such that
$|u-t|\le v^{1/3}$
. Then
$$\begin{align*}\sum_{m:|m-u|> v^{\frac12}} r(m) \left(\frac{1}{m-t}-\frac{m}{m^2+1} \right)=-\pi \log t+O(1). \end{align*}$$
Proof. Let
$A(x)=\sum _{1 \le n \le x} r(n)=\pi x+E(x)$
. It is well known that (cf. [Reference Sierpiński43]) that
$E(x) \ll x^{\frac 13}$
. Also, let
$f_t(x)=\log \frac {|x-t|}{(x^2+1)^{1/2}}$
, (so
$f_t(x) \rightarrow 0$
as
$x \rightarrow \infty $
). Since
$|u-t| \le v^{1/3}$
, partial summation gives
$$\begin{align*}\begin{aligned} \sum_{m:|m-u|> v^{\frac12}} r(m) \left(\frac{1}{m-t}-\frac{m}{m^2+1} \right)& = \int_{u+v^{\frac12}}^{\infty} f_t'(x) dA(x)+\int_{1^-}^{(u-v^{\frac12})^{-}} f_t'(x) dA(x) \\ & = \pi \left(f_t(u-v^{\frac12})-f_t(u+v^{\frac12})-\log t\right)\\ &\quad + O\left(1+\max_{\pm} \frac{u^{\frac13}}{|u\pm v^{\frac12}-t|} \right). \end{aligned} \end{align*}$$
The error is
$O(1)$
since we assumed
$|u-t| \le v^{1/3}$
. Also,
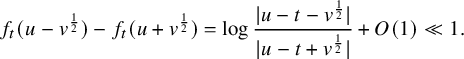$$\begin{align*}f_t(u-v^{\frac12})-f_t(u+v^{\frac12})=\log \frac{|u-t-v^{\frac12}|}{|u-t+v^{\frac12}|}+O(1) \ll 1.\\[-48pt] \end{align*}$$
We are now ready to prove the main result of this section.
Proof of Theorem 3.1
Let
$A \ge 1$
. In the weak coupling quantization, it follows from the spectral equation (1.1) along with Lemma 3.3 that
$$ \begin{align} \sum_{ m : |m-n| \le \frac{n}{x} x^{1/2}} \frac{r(m)}{m-\lambda_n}=\pi \log \lambda_n+O(1) \end{align} $$
for every integer
$\frac {x}{(\log x)^A} \le n \le x$
, which is a sum of two squares. Note that the application of Lemma 3.3 is justified since it is well known that
$\lambda _n-n \le n^+-n \le 10n^{1/4}$
(see for instance [Reference Montgomery and Vaughan31] p. 43).
In the strong coupling quantization, applying Lemma 3.3 twice we get for
$\frac {x}{(\log x)^A} \le n \le x$
that
$$\begin{align*}\bigg| \sum_{m : |m-n|> \frac{n}{x} x^{1/2}} r(m) \left(\frac{1}{m-\lambda_n}-\frac{m}{m^2+1} \right) - \sum_{m :|m-\lambda_n| > \lambda_n^{1/2}} r(m) \left(\frac{1}{m-\lambda_n}-\frac{m}{m^2+1} \right)\bigg| \ll 1. \end{align*}$$
Hence, using this along with the spectral equation (1.2) we have
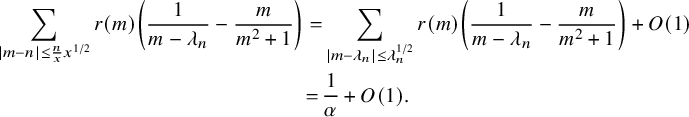$$\begin{align*}\begin{aligned} \sum_{|m-n| \le \frac{n}{x} x^{1/2}} r(m) \left(\frac{1}{m-\lambda_n}-\frac{m}{m^2+1} \right)=&\sum_{|m-\lambda_n| \le \lambda_n^{1/2}} r(m) \left(\frac{1}{m-\lambda_n}-\frac{m}{m^2+1} \right)+O(1) \\ =\,& \frac{1}{\alpha}+O(1). \end{aligned} \end{align*}$$
Hence, in the strong coupling quantization for each
$\frac {x}{(\log x)^A} \le n \le x$
$$ \begin{align} \sum_{ m : |m-n| \le \frac{n}{x} x^{1/2}} \frac{r(m)}{m-\lambda_n} = \frac{1}{\alpha}+O(1). \end{align} $$
For
$\frac {x}{(\log x)^A} \le n \le x$
, we now analyze the sum that appears on the LHS of both equations (3.6) and (3.7). Let
$B \ge 1$
, to be determined later, and consider
$$ \begin{align} \sum_{|m-n|\le \frac{n}{x} x^{1/2}} \frac{r(m)}{m-\lambda_n}= \sum_{|m-n|\le \frac{n}{x}(\log x)^B} \frac{r(m)}{m-\lambda_n}+ \sum_{ \frac{n}{x}(\log x)^B < |k| \le \frac{n}{x} x^{1/2} } \frac{r(n+k)}{k-{s_n}}, \end{align} $$
where recall
${s_n}=\lambda _n-n$
. Note that
$$\begin{align*}\begin{aligned} \sum_{\substack{n \le x \\ {s_n} \ge (\log x)^{B/2}}} b(n) \le & \frac{1}{(\log x)^{B/2}} \sum_{n \le x} b(n){s_n} \\ \le & \frac{1}{(\log x)^{B/2}} \sum_{n \le x} b(n) (n^+-n) \ll \frac{x}{(\log x)^{B/2}}. \end{aligned} \end{align*}$$
Hence, for all but
$O(x/(\log x)^{B/2})$
integers
$n \le x$
which are representable as a sum of two squares,
${s_n} < (\log x)^{B/2}$
. For these integers, the second sum on the RHS of equation (3.8) equals
$$ \begin{align} \sum_{ \frac{n}{x}(\log x)^B \le k \le \frac{n}{x}x^{1/2} } \frac{r(n+k)-r(n-k)}{k}+O\left( (\log x)^{B/2} \sum_{ \frac{n}{x}(\log x)^B \le |k| \le x^{1/2}} \frac{r(n+k)}{k^2} \right). \end{align} $$
Since
$$\begin{align*}\begin{aligned} &\# \bigg\{ \frac{x}{(\log x)^A} \le n \le x : (\log x)^{B/2} \sum_{\frac{n}{x}(\log x)^B \le |k| \le x^{1/2}} \frac{r(n+k)}{k^2} \ge 1 \bigg\}\\ &\le (\log x)^{B/2} \sum_{(\log x)^{B-A} \le |k| \le x^{1/2}} \frac{1}{k^2}\sum_{ n \le x} r(n+k) \ll \frac{x}{(\log x)^{B/2-A}} \end{aligned} \end{align*}$$
the O-term in equation (3.9) is
$\ll 1$
for all but
$O(x/(\log x)^{B/2-A})$
integers
$\frac {x}{(\log x)^A} \le n \le x$
. The first sum in equation (3.9) is estimated using Lemma 3.2, with
$Y=(\log x)^B$
; so for
$B \ge 6A$
, this sum is
$\ll 1$
for all but at most
$\ll x/(\log x)^{A}$
integers
$n \le x$
. Hence, applying the two previous estimates in equation (3.9) and using the resulting bound along with equation (3.8) in equations (3.6) and (3.7) completes the proof upon taking
$B \ge 6A$
.
4 Estimates for new eigenvalues nearby almost primes
In this section, we analyze the location of eigenvalues in
$\Lambda _{\text {new}}$
nearby certain integers which are almost primes. To state the result, let
$$ \begin{align} \begin{aligned} {\mathcal N}_{1,x}=&\{ n \in \mathbb N : (1_{ {\mathcal P}_{\varepsilon,x}} \ast 1_{ {\mathcal P}_{\varepsilon,x}'})(n) \neq 0, \, b(Q_0n+4)=1, \, \& \, \, Q_1 | Q_0n+4\}, \\ {\mathcal N}_{2,x}=&\left\{ n \in {\mathcal N}_{1,x} : \left(\frac{Q_0n+4}{Q_1}, P(y)\right)=1\right\}, \end{aligned} \end{align} $$
where
$y=x^{\eta }$
with
$\eta $
as in Proposition 2.1 and
$Q_0,Q_1, \varepsilon , 1_{{\mathcal P}_{\varepsilon }}$
and
$b(\cdot )$
are as defined in the beginning of Section 2; we will write
${\mathcal N}_{1,x}={\mathcal N}_1, {\mathcal N}_{2,x}={\mathcal N}_2$
for brevity. For
$j=1,2$
, let
${\mathcal N}_{j}(x)={\mathcal N}_{j,x} \cap [x,2x]$
. In particular, for each
$n \in {\mathcal N}_2(x)$
,
$Q_0n+4=Q_1 \mathcal \ell _n$
, where
$\ell _n$
is an integer which is a sum of two squares. Moreover, since every prime divisor of
$\ell _n$
is
$\ge y=x^{\eta }$
, we have for
$n \le x$
that
$ x^{ \eta \cdot \# \{ p| \ell _n\}} \le \ell _n \le 2Q_0x$
and
$$ \begin{align} \# \{ p| \ell_n\} \le \frac{2}{\eta}. \end{align} $$
Note that by Propositions 2.1 and 2.2
$$ \begin{align} \begin{aligned} \# {\mathcal N}_1(x) \asymp & \varepsilon^2 \frac{1}{\varphi(Q_1)} \frac{x \log \log x}{(\log x)^{3/2}}, \\ \# {\mathcal N}_2(x) \asymp & \varepsilon^2 \frac{Q_0}{\varphi(Q_0 Q_1)} \frac{x \log \log x}{(\log x)^2}. \end{aligned} \end{align} $$
The main result of this section is the following proposition.
Proposition 4.1. For all
$n \in {\mathcal N}_j(x)$
,
$j=1,2$
, apart for elements in an exceptional set of size
$$\begin{align*}\ll \frac{\# {\mathcal N}_j(x)}{ \varepsilon^2 (\log \log x)^{1-o(1)}} \end{align*}$$
we have for
$m=Q_0n$
that
$m^+=m+4$
and
$$\begin{align*}\begin{aligned} &\frac{r(m)}{m-\lambda_m}+\frac{r(m^+)}{m^+-\lambda_m} \\ & \qquad \qquad =\begin{cases} \pi \log \lambda_m+O\left( (\log \log x)^5 \right) & \text{ in the weak coupling quantization},\\ O\left( (\log \log x)^5 \right) & \text{ in the strong coupling quantization}. \end{cases} \end{aligned} \end{align*}$$
We also require a sieve estimate for averages of correlations of multiplicative functions. The following result is due to Henriot [Reference Henriot17], which builds on the work of Nair and Tenenbaum [Reference Nair and Tenenbaum33]. See Corollary 1 of [Reference Henriot17] and the subsequent remark therein. Recall that
$\tau (n)=\sum _{d|n}1$
denotes the divisor function, and for a polynomial
$R =\sum a_n X^n \in \mathbb Z[X]$
, let
$\lVert R \rVert _1=\sum |a_n|$
denote the norm of R.
Lemma 4.1. Let
$R_1(X),\ldots , R_k( X) \in \mathbb Z[ X]$
be irreducible, pairwise coprime polynomials, for which each polynomial
$R_j$
does not have a fixed prime divisor.Footnote
3
Let D be the discriminant of
$R=R_1\cdots R_k$
and
$\varrho _{R_j}(n)=\# \{ a\ \pmod n: R_j(a) \equiv 0\ \pmod n\}$
. Then there exist
$C,c_0>0$
such that for any nonnegative multiplicative functions
$F_j$
,
$j=1, \ldots , k$
with
$F_j(n) \le \tau (n)^{{E}}$
for some
${E} \ge 1$
, we have for
$x \ge c_0 \lVert R \rVert _1^{1/10} $
and some
$A \ge 1$
that
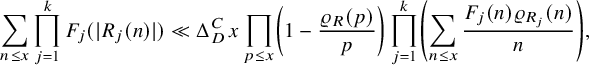$$\begin{align*}\sum_{n \le x} \prod_{j=1}^k F_j(|R_j(n)|) \ll \Delta_D^{C} \, x \prod_{p \le x} \left(1-\frac{\varrho_{R}(p)}{p} \right) \prod_{j=1}^k \left(\sum_{n \le x} \frac{F_j(n) \varrho_{R_j}(n)}{n}\right), \end{align*}$$
where
$$\begin{align*}\Delta_D :=\prod_{p|D}\left(1+\frac{1}{p} \right) \end{align*}$$
and the implicit constant, C and
$c_0$
depend at most on the degree of R and
${E}$
.
We first start with a technical lemma.
Lemma 4.2. Let f be a nonnegative multiplicative function with
$f(n) {\,\le\,} \tau (n)$
and
$f(mn) {\,\le\,} \max \{1,f(n)\} f(m)$
for
$m \in \mathbb N$
and n such that
$b(n)=1$
. Then for
$1 {\,\le\,} |h| {\,\le\,} x^{1/30}$
, with
$h {\,\neq\,} 4$
and
$j=1,2$
, we have
$$ \begin{align} \begin{aligned} \sum_{n \in {\mathcal N}_j(x)} f(Q_0n+h) \ll \frac{1}{\varepsilon^2} \cdot g(h) \prod_{p|Q_0Q_1} \left(1+\frac{1}{p} \right)^C \prod_{p \le x} \left(1+\frac{f(p)-1}{p} \right) \# {\mathcal N}_j(x), \end{aligned} \end{align} $$
where
$C>0$
is an absolute constant and
$$\begin{align*}g(h)=\tau(|h|)\tau(|h-4|)\prod_{p|h} \left(1+\frac{1}{p} \right)^C\prod_{p|h-4} \left(1+\frac{1}{p} \right)^C. \end{align*}$$
Additionally, (for
$h=4$
) there exists
$C>0$
such that
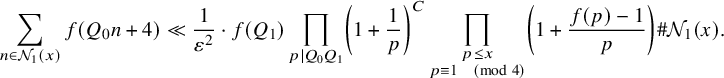$$\begin{align*}\sum_{n \in {\mathcal N}_1(x)} f(Q_0n+4) \ll \frac{1}{\varepsilon^2} \cdot f(Q_1) \prod_{p|Q_0Q_1}\left(1+\frac{1}{p} \right)^C \prod_{\substack{p \le x \\ p \equiv 1\ \ \ {\pmod 4}}} \left(1+\frac{f(p)-1}{p} \right) \# {\mathcal N}_1(x).\\[-9pt] \end{align*}$$
Remark 4. When applying this lemma, we will take
$f(n)=\tfrac 14 \cdot r(n),b(n)$
or
$2^{-\omega _1(n)}$
, where
$\omega _1(n)=\# \{ p|n : p \equiv 1\ \pmod 4\}$
. The hypotheses of the lemma are satisfied for each of these choices.
Proof. Let
$T_j=2$
if
$j=1$
and
$T_j=y=x^{\eta }$
if
$j=2$
. Dropping several of the conditions on
$n \in {\mathcal N}_j$
, we get that (here
$q< p$
denote primes; also recall that
$P(z)$
is defined in equation (2.2))
$$ \begin{align} \begin{aligned} \sum_{n \in {\mathcal N}_j(x/2)} f(Q_0n+h) \le 2 \sum_{\substack{q \le \sqrt{x} \\ q\equiv 1\ \ \ {\pmod 4}}} \sum_{\substack{p \le x/q \\ Q_1 | Q_0pq+4 \\ (\frac{Q_0pq+4}{Q_1}, P(T_j))=1}} b(Q_0qp+4)f(Q_0qp+h). \end{aligned}\\[-12pt]\nonumber \end{align} $$
Let
$K=Q_0q$
and
$Y=x/q$
. Note that the sum above is empty unless
$(K,Q_1)=1$
. Since
$(K, Q_1)=1$
, there exist integers
$\overline {K},\overline Q_1$
with
$1 \le | \overline {K}| < Q_1$
and
$1 \le |\overline {Q_1}| < K$
such that
$K \overline K -Q_1\overline Q_1=1$
. Also, for
$Z \ge 1$
let
$F_Z$
be the totally multiplicative function given by
$F_Z(p)=1$
if
$p \ge Z$
and zero otherwise. The inner sum on the RHS of equation (4.5) is bounded by
$$ \begin{align} \begin{aligned} \ll& \sum_{\substack{n \le Y, Q_1|Kn+4}} F_{\sqrt{Y}}(n)F_{T_j}\left(\frac{Kn+4}{Q_1} \right)b(Kn+4)f(Kn+h)+Y^{1/2+o(1)} \\ =& \sum_{\substack{m \le \frac{Y-4 \overline{K}}{Q_1}}} F_{\sqrt{Y}}(Q_1m-4\overline{K})F_{T_j}\left(Km-4\overline{Q_1} \right)b(KQ_1m-4Q_1\overline{Q_1})f(KQ_1m+h-4K\overline{K})\\ &+O(Y^{1/2+o(1)}) , \end{aligned}\\[-9pt]\nonumber \end{align} $$
where the error term
$Y^{1/2+o(1)}$
accounts for the primes
$p {\,\le\,} \sqrt {Y}$
. First, note
$b(KQ_1n-4Q_1\overline {Q_1})=b(Kn-4\overline {Q_1})$
. Let
$d=(KQ_1,h-4K\overline K)$
, and suppose that
$h \neq 4$
. We have
$$\begin{align*}f(KQ_1m+h-4K\overline{K}) \le \max\{1, f(d)\} f\left(\frac{KQ_1}{d}m+\frac{h-4K\overline{K}}{d}\right).\\[-9pt] \end{align*}$$
Let
$R_1(X)=Q_1 X-4 \overline K$
,
$R_2(X)=K X-4 \overline Q_1$
,
$R_3( X)=\frac {KQ_1}{d} X+\frac {h-4K\overline K}{d}$
and D denote the discriminant of
$R=R_1R_2R_3$
. The polynomials
$R_1,R_2,R_3$
and multiplicative functions
$F_1=F_{\sqrt {Y}}$
,
$F_2=F_{T_j}\cdot b$
and
$F_3=f$
satisfy the assumptions of Lemma 4.1. Also, for
$(p,KQ_1)=1$
we have
$\varrho _R(p)=3$
and
$\varrho _{R_j}(p^k)=1$
for each
$j=1,2,3$
and
$k \ge 1$
, which follows from Hensel’s lemma. Hence, the sum in equation (4.6) is bounded by
$$\begin{align*}\begin{aligned} \ll & \max\{1,f(d)\} \Delta_{D}^{C} \frac{Y}{Q_1} \prod_{p \le Y} \left(1+\frac{F_{\sqrt{Y}}(p)+F_{T_j}(p)b(p)+f(p)-3}{p} \right) \prod_{p|KQ_1}\left( 1+\frac{1}{p}\right)^C \\ \ll & \max\{1,f(d)\} \Delta_{D}^{C} \prod_{p|KQ_1}\left(1+\frac{1}{p} \right)^C \frac{Y}{Q_1(\log Y)^{3/2}(\log T_j)^{1/2}} \prod_{p \le Y} \left( 1+\frac{f(p)-1}{p}\right). \end{aligned} \end{align*}$$
Write
$d=p_1^{a_1} \cdots p_{\ell }^{a_\ell }$
. For each
$j=1, \ldots , \ell $
, we have
$p_j^{a_j}|h$
or
$p_j^{a_j}|h-4$
(depending on whether
$p_j^{a_j}|K$
or
$p_j^{a_j}|Q_1$
, respectively); so
$f(d) \ll \tau (|h|)\tau (|h-4|)$
. Note the discriminant of R equals
$D=16 \frac {K^2Q_1^2}{d^4}h^2(h-4)^2$
so that
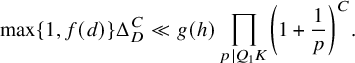$$\begin{align*}\max\{1,f(d)\} \Delta_D^{C} \ll g(h) \prod_{p|Q_1K}\left(1+\frac{1}{p} \right)^C. \end{align*}$$
Also, since
$Y =x/q\ge \sqrt {x}$
,
$\prod _{p \le Y} \left ( 1+\frac {f(p)-1}{p}\right ) \ll \prod _{p \le x} \left ( 1+\frac {f(p)-1}{p}\right ) $
. Hence, applying the estimates above in equation (4.5), summing over q and using equation (4.3) gives the claimed bound for
$h \neq 4$
.
For
$h =4$
, we argue similarly. Only now in order to estimate equation (4.6) we use Lemma 4.1 with
$R_1, R_2$
as before,
$R=R_1R_2$
(so the discriminant is
$D=16$
) and
$F_1=F_{\sqrt {Y}}$
,
$F_2= b \cdot f$
. Also, noting that here
$d=Q_1$
we conclude that equation (4.6) is bounded by
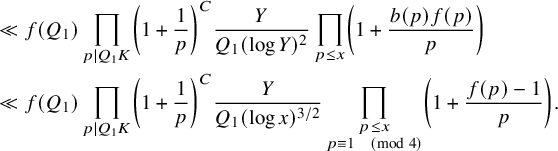$$\begin{align*}\begin{aligned} &\ll f(Q_1) \prod_{p|Q_1K}\left(1+\frac{1}{p} \right)^C \frac{Y}{Q_1 (\log Y)^2} \prod_{p \le x} \left(1+\frac{b(p)f(p)}{p} \right) \\ &\ll f(Q_1) \prod_{p|Q_1K}\left(1+\frac{1}{p} \right)^C \frac{Y}{Q_1 (\log x)^{3/2}} \prod_{\substack{p \le x \\ p \equiv 1\ \ \ {\pmod 4}}} \left(1+\frac{f(p)-1}{p} \right). \end{aligned} \end{align*}$$
Hence, the claim follows in the same way as before.
Lemma 4.3. Let
$(\log \log x)^4 \le U \le \frac {1}{10}(\log x)^{1/2}$
. There exists
$C>0$
such that for all
$n \in {\mathcal N}_j(x)$
,
$j=1,2$
, outside a set of size
$$ \begin{align*}\ll \frac{1}{\varepsilon^2} \cdot \# {\mathcal N}_j(x) \prod_{p|Q_1Q_0}\left( 1+\frac{1}{p}\right)^C \frac{(\log \log x)^4}{U}\end{align*} $$
the following hold:
$$ \begin{align} \sum_{\substack{1 \le |k| \le \frac{1}{U}(\log x)^{1/2} \\ k \neq 4}} b(Q_0n+k)=0, \end{align} $$
$$ \begin{align} \sum_{\substack{ 1 \le |k| \le \frac{n}{2x}(\log x)^{B} \\ k \neq 4}} \frac{r(Q_0n+k)}{|k|} \le U \end{align} $$
and
$$ \begin{align} \sum_{ |k| \ge U } \frac{r(Q_0n+k)}{k^2} \le \frac{1}{\log \log x}. \end{align} $$
Proof. We first establish equation (4.7). By Chebyshev’s inequality
$$ \begin{align} \# \bigg\{ n \in {\mathcal N}_j(x) : \sum_{\substack{1 \le |k| \le \frac{1}{U}(\log x)^{1/2} \\ k \neq 4}} b(Q_0n+k) \ge 1 \bigg\} \le \sum_{\substack{1 \le |k| \le \frac{1}{U}(\log x)^{1/2} \\ k \neq 4}} \sum_{n \in {\mathcal N}_j(x)} b(Q_0n+k). \end{align} $$
Applying Lemma 4.2 to the inner sum and noting that
$$\begin{align*}\prod_{p \le x} \left(1+\frac{b(p)-1}{p} \right)\ll \frac{1}{\sqrt{\log x}},\\[-7pt] \end{align*}$$
we get that the LHS of equation (4.10) is bounded by
$$ \begin{align} \begin{aligned} &\ll\prod_{p |Q_1Q_0} \left(1+\frac{1}{p} \right)^C \frac{\# {\mathcal N}_j(x)}{\varepsilon^2 \sqrt{\log x}} \sum_{\substack{1 \le |k| \le \frac{1}{U}(\log x)^{1/2} \\ k \neq 4}} g(k)\\ &\ll \prod_{p |Q_1Q_0} \left(1+\frac{1}{p} \right)^C \frac{\# {\mathcal N}_j(x)}{\varepsilon^2} \frac{(\log \log x)^2}{U}, \end{aligned}\\[-7pt]\nonumber \end{align} $$
where the second step follows upon using Lemma 4.1.
To prove equation (4.8), we argue similarly and apply Lemmas 4.1 and 4.2 to get
$$ \begin{align*} \begin{aligned} &\# \bigg\{ n \in {\mathcal N}_j(x) : \sum_{\substack{ 1 \le |k| \le \frac{n}{2x}(\log x)^{B} \\ k \neq 4}} \frac{r(Q_0n+k)}{|k|}> U \bigg\} \\ & \qquad \qquad \qquad \le \frac{1}{U} \sum_{\substack{ 1 \le |k| \le (\log x)^{B} \\ k \neq 4}} \frac{1}{|k|}\sum_{n \in {\mathcal N}_j(x)} r(Q_0n+k) \\ & \qquad \qquad \qquad \ll \frac{\# {\mathcal N}_j(x)}{\varepsilon^2 U} \prod_{p|Q_0Q_1}\left(1+\frac{1}{p} \right)^C \sum_{\substack{ 1 \le |k| \le (\log x)^{B} \\ k \neq 4}} \frac{g(k)}{|k|} \\ & \qquad \qquad \qquad \ll \frac{\# {\mathcal N}_j(x)}{\varepsilon^2 U} \prod_{p|Q_0Q_1}\left(1+\frac{1}{p} \right)^C (\log \log x)^3. \end{aligned}\\[-7pt] \end{align*} $$
We will omit the proof of equation (4.9) since it follows similarly.
For almost all
$n \in {\mathcal N}_1(x)$
, it is possible to show that
$r(Q_0n+4) \asymp (\log n)^{\log 2/2\pm o(1)}$
; however, since we do not actually need this estimate we will record the weaker estimate below, which suffices for our purposes and is simpler to prove.
Lemma 4.4. Let
$\nu>0$
be sufficiently small. There exists
$C>0$
such that for all
$n \in {\mathcal N}_1(x)$
outside a set of size
$$ \begin{align*}\ll \frac{r(Q_1)}{\varepsilon^2} \# {\mathcal N}_1(x) \frac{(\log \log x)^C}{(\log x)^{\nu}}\\[-7pt]\end{align*} $$
the following holds
$$ \begin{align} (\log x)^{1/4-\nu} \le r(Q_0n+4) \le (\log x)^{1/2+\nu}. \end{align} $$
Proof. We begin with proving the lower bound stated in equation (4.12). Let
$\omega _1(n)=\sum _{\substack {p |n \\ p \equiv 1\ \pmod 4}} 1$
. For n which is a sum of two squares
$r(n) \ge 2^{\omega _1(n)}$
. Using this with Chebyshev’s inequality and Lemma 4.2, the number of
$n \in {\mathcal N}_1(x)$
which
$r(Q_0n+4)<(\log x)^{1/4-\nu }$
is bounded by
$$\begin{align*}\begin{aligned} (\log x)^{1/4-\nu}\sum_{n \in {\mathcal N}_1(x)} 2^{-\omega_1(Q_0n+4)} \ll & (\log x)^{1/4-\nu} \cdot \frac{(\log \log x)^C}{\sqrt{\log x}} \prod_{\substack{p \le x \\ p \equiv 1\ \ \ {\pmod 4}}}\left(1+\frac{1}{2p} \right) \cdot \frac{1}{\varepsilon^2} \# {\mathcal N}_1(x) \\ \ll & \frac{1}{\varepsilon^2} \# {\mathcal N}_1(x) \frac{(\log \log x)^C}{(\log x)^{\nu}} \end{aligned} \end{align*}$$
using Lemma 4.2.
The proof of the upper bound is similar: The number of
$n \in {\mathcal N}_1(x)$
for which
$r(Q_0n+4)> (\log x)^{1/2+\nu }$
is, again by using Lemma 4.2, bounded by
$$\begin{align*}\begin{aligned} \frac{1}{(\log x)^{1/2+\nu}} \sum_{n \in {\mathcal N}_1(x)} r(Q_0n+4) & \ll \frac{r(Q_1)(\log \log x)^{C} \cdot \# {\mathcal N}_1(x)}{ \varepsilon^{2} \cdot (\log x)^{1/2+\nu}} \prod_{\substack{p \le x \\ p \equiv 1\ \ \ {\pmod 4}}} \left( 1 + \frac{r(p)-1}{p}\right)\\ & \ll \frac{r(Q_1)(\log \log x)^{C}}{ \varepsilon^{2} \cdot(\log x)^{\nu}} \# {\mathcal N}_1(x). \end{aligned} \\[-44pt]\end{align*}$$
Proof of Proposition 4.1
By Theorem 3.1, for say
$A=3$
, we get for all but
$O(x/(\log x)^A)$
new eigenvalues
$ \lambda _{\ell } \le 2x$
that
$$\begin{align*}\sum_{|m-\ell| \le \frac{\ell}{2x}(\log x)^B} \frac{r(m)}{m-\lambda_{\ell}}=\begin{cases} \pi \log \lambda_{\ell}+O(1) & \text{in the weak coupling quantization},\\ \frac{1}{\alpha}+O\left(1 \right) & \text{in the strong coupling quantization}. \end{cases} \end{align*}$$
We now consider integers
$\ell =Q_0n$
with
$n \in {\mathcal N}_j(x)$
,
$j=1,2$
such that the above holds. Writing
$m = \ell + k$
and using Lemma 4.3 with
$U=(\log \log x)^5$
, we find, by equation (4.7), that
$r(\ell +k)/(\ell +k-\lambda _{l})=0$
for
$k \le (\log x)^{1/2}/U$
unless
$k=0,4$
. Further, for
$k \ge (\log x)^{1/2}/U$
, we have
$|r(\ell +k)/(\ell +k-\lambda _{l})| \ll r(\ell +k)/k$
, and it follows (cf. equation (4.8)) that for all but
$O(\# {\mathcal N}_j/(\varepsilon ^2(\log \log x)^{1-o(1)}))$
of these integers
$n \in {\mathcal N}_j(x)$
,
$j=1,2$
, with
$\ell =Q_0n$
that
$\ell ^+=\ell +4$
and
$$\begin{align*}\begin{aligned} \sum_{|m-\ell| \le \frac{\ell }{x}(\log x)^B} \frac{r(m)}{m-\lambda_{\ell}}=\frac{r(\ell)}{\ell-\lambda_{\ell}}+\frac{r(\ell^+)}{\ell^+-\lambda_{\ell}}+O\left((\log \log x)^5 \right). \end{aligned} \end{align*}$$
Combining the two estimates above completes the proof.
5 Proofs of the main theorems
5.1 Quantization of observables
On the unit cotangent bundle
${\mathbb S}^* M \mathbb \cong \mathbb T^2\times S^1$
, a smooth function
$f \in C^{\infty }(T^2\times S^1)$
has the Fourier expansion
$$\begin{align*}f(x, e^{i\phi}) =\sum_{ \zeta \in \mathbb Z^2, k \in \mathbb Z} \widehat f(\zeta,k) e^{i \langle x, \zeta \rangle +i k \phi}. \end{align*}$$
Following Kurlberg and Ueberschär [Reference Kurlberg and Ueberschär27], we quantize our observables as follows. For
$g \in L^2(\mathbb T^2)$
, let
$$ \begin{align} (\operatorname{Op}(f) g)(x)=\sum_{ \xi \in \mathbb Z^2 \setminus 0 }\sum_{ \zeta \in \mathbb Z^2 , k \in \mathbb Z} \widehat f(\zeta,k) e^{ik \arg \xi} \widehat g(\xi) e^{i \langle \zeta+\xi, x \rangle}+\sum_{ \zeta \in \mathbb Z^2 , k \in \mathbb Z} \widehat f(\zeta,k) \widehat g(0) e^{i \langle \zeta, x \rangle}. \end{align} $$
Hence, for pure momentum observables
$f : S^1 \rightarrow \mathbb R$
, one has
$$ \begin{align} (\operatorname{Op}(f)g)(x)=\sum_{\xi \in \mathbb Z^2 } f\left( \frac{\xi}{|\xi|} \right) \widehat g(\xi) e^{i \langle \xi, x\rangle}, \end{align} $$
where for
$\xi =0$
,
$f(\tfrac {\xi }{|\xi |})$
is defined to be
$f(1)$
. (Another option is defining it as the average
$\int _{S^1} f(\theta ) \, \frac {d\theta }{2\pi }$
; a technical point is that some choice must be made to extend f to a smooth observable on the cotangent bundle; for example, see [Reference Yesha50, Section 3]. However, this choice only affects the matrix coefficients in equation (5.3) by
$O(1/(\lVert G_{\lambda } \rVert _2 \cdot \lambda ^{2})$
.)
Let
$g_{\lambda }$
be as given in equation (1.4). Then for f a pure momentum observable it follows from equations (1.4) and (5.2) that
$$ \begin{align} \begin{aligned} \langle \operatorname{Op}(f) g_{\lambda}, g_{\lambda} \rangle =& \frac{1}{16 \pi^4 }\cdot \frac{1}{\lVert G_{\lambda} \rVert_2^2} \sum_{ n \ge 0 }\frac{1}{(n-\lambda)^2} \sum_{ a^2+b^2=n} f\left(\frac{a+ib}{|a+ib|} \right) \\ =&\frac{1}{\sum_{n \ge 0} \frac{r(n)}{(n-\lambda)^2}} \sum_{ n \ge 0 }\frac{1}{(n-\lambda)^2} \sum_{ a^2+b^2=n} f\left(\frac{a+ib}{|a+ib|} \right). \end{aligned} \end{align} $$
5.2 Measures associated to sequences of almost primes in narrow sectors
Let
${\mathcal N}_1, {\mathcal N}_2$
be as in equation (4.1). Before proceeding to the main result of this section, we will specify our choice of
$Q_0,Q_1$
. Consider the set of primes
$$ \begin{align} {\mathcal S}= \{ p : p=a^2+b^2, 0 \le b \le a \text{ and } \, 0 < \arctan(b/a) \le p^{-1/10} \}, \end{align} $$
and let
$q_j$
be the
$jth$
element of
${\mathcal S}$
. It follows from work of Ricci [Reference Ricci35, Th’m 2, p. 21–22] that
$$\begin{align*}\# \{ p \le x : p \in {\mathcal S}\} \asymp \frac{x^{9/10}}{\log x}, \end{align*}$$
so
$q_j \asymp (j \log j)^{10/9}$
. Let
$ T = \lfloor \log \log x \rfloor $
,
$H= \lfloor 100 \log \log \log x\rfloor $
and
$$ \begin{align} Q_0'= \prod_{j=T}^{T+H-1} q_j, \qquad Q_1'=\prod_{j=T+H}^{T+2H-1} q_j. \end{align} $$
Also, let
$r_0, r_1 \in {\mathcal S}$
with
$\tfrac 14 \log \log x \le r_0,r_1 \le \frac 12 \log \log x$
and
$a_0,a_1 \in \mathbb Z$
with
$0 \le a_0,a_1 \le \log \log \log x$
. Let
$m_0,m_1$
be integers, which are fixed (in terms of x), whose prime factors are all congruent to
$1\ \pmod 4$
. Write
$(m_0,m_1)=p_1^{e_1}\cdots p_s^{e_s}$
, and let
$g'=\widetilde p_1^{e_1} \cdots \widetilde p_s^{e_s}$
, where
$\tfrac 12 \log \log x < \widetilde p_j < \log \log x$
,
$\widetilde p_j=c_j^2+d_j^2$
with
$0 \le c_j \le d_j$
and
$\arctan (c_j/d_j)=\arctan (b_j/a_j)+O(1/(\log \log x)^{1/10})$
, where
$a_j^2+b_j^2=p_j$
with
$0 \le b_j \le a_j$
, for each
$j=1, \ldots , s$
. (Note that such primes exist by Ricci’s result on angular equidistribution of Gaussian primes.) We now take
$$ \begin{align} Q_0=Q_0'm_0 r_0^{a_0}, \qquad Q_1=Q_1' \frac{m_1}{(m_0,m_1)} r_1^{a_1}g'. \end{align} $$
Note that
$(Q_0,Q_1)=1$
and that
$Q_0,Q_1 \ll \exp (200 (\log \log \log x)^2) \le (\log x)^{1/10}$
so that this choice of
$Q_0,Q_1$
is consistent with our prior assumption. For
$j=1,2$
, let
$$ \begin{align} \mathcal M_{j}(x)=\{ x \le m \le 2 x : m=Q_0n \text{ and } n \in {\mathcal N}_{j}\}. \end{align} $$
It follows from equation (4.3) that
$$ \begin{align} \# \mathcal M_1(x) \asymp \varepsilon^2 \frac{1}{\varphi(Q_1)} \frac{x \log \log x}{Q_0(\log x)^{3/2}}\\[-10pt]\nonumber \end{align} $$
and
$$ \begin{align} \# \mathcal M_2(x) \asymp \varepsilon^2 \frac{1}{\varphi(Q_0Q_1)} \frac{x \log \log x}{(\log x)^{2}}.\\[-10pt]\nonumber \end{align} $$
Recall that we have chosen
$$\begin{align*}\varepsilon = (\log \log x)^{-1/11}.\\[-10pt] \end{align*}$$
Lemma 5.1. Let
$Q_0,Q_1$
be as in equation (5.6) and
$ \eta>0$
be as in Proposition 2.1. Let
$m \in \mathcal M_j(x)$
,
$j=1,2$
, where
$\mathcal M_j(x)$
is defined as in equation (5.7). Then for
$f\in C^1(S^1)$
with
$|f'| \ll 1$
$$ \begin{align} \frac{1}{r(m)} \sum_{a^2+b^2=m}f\left(\frac{a+ib}{|a+ib|} \right) =\frac{1}{r(m_0)} \sum_{a^2+b^2=m_0}f\left(\frac{a+ib}{|a+ib|} \right)+O\left( \varepsilon \right).\\[-9pt]\nonumber \end{align} $$
Under the same hypotheses, we have for
$m=Q_0n \in {\mathcal N}_2(x) $
that there exists an integer
$\ell _n$
which is a sum of two squares with
$\#\{ p|\ell _n \} \le 2/\eta $
such that
$$ \begin{align} \frac{1}{r(m^+)} \sum_{a^2+b^2=m^+}f\left(\frac{a+ib}{|a+ib|} \right) =\frac{1}{r(m_1 \ell_n)} \sum_{a^2+b^2=m_1\ell_n}f\left(\frac{a+ib}{|a+ib|} \right)+O\left( \varepsilon \right). \end{align} $$
Proof. First, note that, for a unit, u of
$\mathbb Z[i]$
, that is,
$u \in \{\pm 1, \pm i\}$
, for any
$n \in \mathbb N$
$$ \begin{align} \sum_{a^2+b^2=n}f\left(\frac{u(a+ib)}{|a+ib|} \right)=\sum_{a^2+b^2=n}f\left(\frac{a+ib}{|a+ib|} \right). \end{align} $$
For
$m \in \mathcal M_j(x)$
with
$j=1$
or
$j=2$
, write
$m=Q_0'm_0r_0^{a_0}n$
, where
$n \in {\mathcal N}_j(x)$
. The factorizations of the ideals
$(m)=((a+ib)(a-ib))$
in
$\mathbb Z[i]$
are in one-to-one correspondence with factorizations
$(Q_0')=((c+id)(c-id))$
,
$(m_0)=((e+if)(e-if))$
,
$(r_0^{a_0})=((g+ih)(g-ih))$
and
$(n)=((k+il)(k-il))$
since
$Q_0',m_0,n$
are pairwise coprime. Hence, it follows from this and equation (5.12) that
$$ \begin{align} \frac{1}{r(m)}\sum_{a^2+b^2=m} f\left( \frac{a+ib}{|a+ib|}\right) = \frac{1}{r(Q_0')r(m_0)r(r_0^{a_0})r(n)}\sum_{\substack{\alpha \in \mathbb Z[i] \\ \alpha \overline{\alpha}=Q_0'}} \sum_{\substack{ \beta \in \mathbb Z[i] \\ \beta \overline{\beta}=m_0 } } \sum_{\substack{ \gamma \in \mathbb Z[i] \\ \gamma \overline{\gamma}=r_0^{a_0} } } \sum_{\substack{ \delta \in \mathbb Z[i] \\ \delta \overline{\delta}=n } } f\left(\frac{\alpha \beta \gamma \delta}{|\alpha \beta \gamma \delta|} \right). \end{align} $$
Let
${\mathcal S}$
be as in equation (5.4), and write the jth element of
${\mathcal S}$
as
$q_j=a_j^2+b_j^2$
, with
$0 \le b_{j} \le a_{j}$
. By construction, for
$\alpha \in \mathbb Z[i]$
with
$\alpha \overline \alpha =Q_0'$
we can write
$\alpha =u \prod _{j \in J} (a_j+\epsilon _jib_j)$
where
$J = \{ T, T+1, \ldots , T+H_1-1\}$
,
$\epsilon _j\in \{ \pm 1\}$
and u is a unit. It follows that
$$\begin{align*}\begin{aligned} \frac{\alpha}{|\alpha|}& = u\prod_{j \in J}\frac{a_j+\epsilon_jib_j}{|a_j+ib_j|}\\ &= u\left(1+O\left( \sum_{j \in J } |\arctan(b_j/a_j)| \right)\right) =u+O\left( \frac{1}{(\log \log x)^{1/11}}\right), \end{aligned} \end{align*}$$
where the unit u depends on
$\alpha $
. Also, for
$\gamma \in \mathbb Z[i]$
with
$\gamma \overline \gamma =r_0^{a_0}$
, we have
$ \frac {\gamma }{|\gamma |}=u+O(1/(\log \log x)^{1/11}), $
and for
$\delta \in \mathbb Z[i]$
with
$\delta \overline \delta =n$
, we have
$ \frac {\delta }{|\delta |}=u+O(\varepsilon ). $
Hence, by this and equation (5.12)
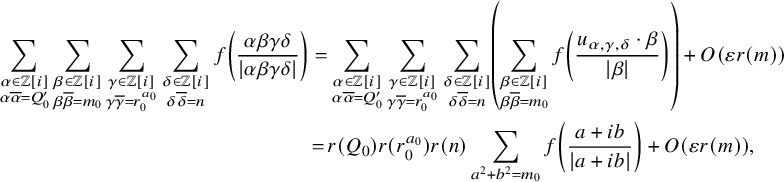$$\begin{align*}\begin{aligned} \sum_{\substack{\alpha \in \mathbb Z[i] \\ \alpha \overline{\alpha}=Q_0'}} \sum_{\substack{ \beta \in \mathbb Z[i] \\ \beta \overline{\beta}=m_0 } } \sum_{\substack{ \gamma \in \mathbb Z[i] \\ \gamma \overline{\gamma}=r_0^{a_0} } } \sum_{\substack{ \delta \in \mathbb Z[i] \\ \delta \overline{\delta}=n } } f\left(\frac{\alpha \beta \gamma \delta}{|\alpha \beta \gamma \delta|} \right)=& \sum_{\substack{\alpha \in \mathbb Z[i] \\ \alpha \overline{\alpha}=Q_0'}} \sum_{\substack{ \gamma \in \mathbb Z[i] \\ \gamma \overline{\gamma}=r_0^{a_0} } } \sum_{\substack{ \delta \in \mathbb Z[i] \\ \delta \overline{\delta}=n } } \left( \sum_{\substack{ \beta \in \mathbb Z[i] \\ \beta \overline{\beta}=m_0 } } f\left(\frac{u_{\alpha, \gamma,\delta} \cdot \beta }{| \beta |} \right) \right)+O(\varepsilon r(m)) \\ =\,&r(Q_0) r(r_0^{a_0})r(n) \sum_{ a^2+b^2=m_0} f\left(\frac{ a+ib}{| a+ib|}\right)+O(\varepsilon r(m)), \end{aligned} \end{align*}$$
thereby proving equation (5.10).
The proof of equation (5.11) follows along the same lines upon noting that for
$m=Q_0n \in \mathcal M_2(x)$
we can write
$m^+=Q_1' r_1^{a_1} \frac {m_1}{(m_1,m_0)} g' \ell _n$
, where
$\ell _n$
is a sum of two squares. Note that
$Q_1',\frac {m_1}{(m_1,m_0)}, r_1^{a_1}, g',\ell _n$
are pairwise coprime by construction since all the prime divisors of
$\ell _n$
are
$\ge y$
; the latter also implies that
$\#\{ p|\ell _n \} \le 2/\eta $
. Also, note that since all primes dividing
$g', Q_{1}', r_{1}$
have very small Gaussian angles (by construction), the set of Gaussian angles associated with
$m^{+}$
is very close to the set of angles associated with
$m_{1} \ell _{n}$
, after taking multiplicities into account.
5.3 Proof of Theorem 1.1
Since Gaussian angles associated with inert primes are trivial, we can without loss of generality assume all the prime factors of
$m_0$
are congruent to
$1\ \pmod 4$
. Let
$Q_0,Q_1$
be as in equation (5.6) and
$\mathcal M_1(x)$
be as in equation (5.7), and recall for
$m \in \mathcal M_1(x)$
that
$m=Q_0n$
, where
$n \in {\mathcal N}_1(x)$
and
${\mathcal N}_1$
is as in equation (4.1). By equation (4.7) and Lemma 4.4 it follows that for all but at most
$o(\# \mathcal M_1(x))$
integers
$m \in \mathcal M_1(x)$
that
$m^+=m+4$
,
$(\log x)^{1/4-\nu } \le r(m^+) \le (\log x)^{1/2+\nu }$
(for any fixed
$\nu>0$
) and
$4 \le r(m) \ll (\log x)^{o(1)}$
. Combining this with Proposition 4.1, we get that for all but
$o(\# \mathcal M_1(x))$
integers
$m \in \mathcal M_1(x)$
that
$\lambda _m-m=o(1)$
and moreover
$$ \begin{align} \lambda_m-m \asymp \begin{cases} \displaystyle \frac{r(m)}{\log \lambda_m} & \text{ in the weak coupling quantization},\\[10pt] \displaystyle \frac{r(m)}{r(m^+)} & \text{ in the strong coupling quantization}. \end{cases} \end{align} $$
Also, note that, for such m as above, we also have
$|\lambda _m-m^+| \ge 3$
. Hence, using the above estimate along with equations (4.7) and (4.9) with
$U= (\log \log x)^5$
we get for all but at most
$o(\# \mathcal M_1(x))$
integers
$m \in \mathcal M_1(x)$
that (in both cases)
$$ \begin{align} \begin{aligned} \sum_{\ell \ge 0} \frac{r(\ell)}{(\ell-\lambda_m)^2} =&\frac{r(m)}{(m-\lambda_m)^2}+\frac{r(m^+)}{(m^+-\lambda_m)^2}+o(1) \\ =&\frac{r(m)}{(m-\lambda_m)^2}\left(1+O\left( \frac{r(m^+)(m-\lambda_m)^2}{r(m)} \right) \right)+o(1)\\ =&\frac{r(m)}{(m-\lambda_m)^2}\left(1+o(1) \right). \end{aligned} \end{align} $$
Similarly, for all but at most
$o(\# \mathcal M_1(x))$
integers
$m \in \mathcal M_1(x)$
$$ \begin{align} \sum_{ \ell \ge 0 }\frac{1}{(\ell-\lambda_m)^2} \sum_{ a^2+b^2=\ell} f\left(\frac{a+ib}{|a+ib|} \right)= \frac{1}{(m-\lambda_m)^2}\sum_{ a^2+b^2=m} f\left(\frac{a+ib}{|a+ib|} \right)+O(r(m^+)). \end{align} $$
Therefore, combining equations (5.3), (5.14), (5.15) and (5.16), it follows for all but at most
$o(\# \mathcal M_1(x))$
integers
$m \in \mathcal M_1(x)$
we have that
$$\begin{align*}\begin{aligned} \langle \operatorname{Op}(f) g_{\lambda_m}, g_{\lambda_m} \rangle=& (1+o(1)) \frac{(m-\lambda_m)^2}{r(m)} \cdot \left( \frac{1}{(m-\lambda_m)^2}\sum_{ a^2+b^2=m} f\left(\frac{a+ib}{|a+ib|} \right)+O(r(m^+))\right) \\ =&(1+o(1))\frac{1}{r(m)} \sum_{ a^2+b^2=m} f\left(\frac{a+ib}{|a+ib|} \right) +o(1)\\ =& (1+o(1)) \frac{1}{r(m_0)} \sum_{a^2+b^2=m_0} f\left(\frac{a+ib}{|a+ib|} \right)+O(\varepsilon), \end{aligned} \end{align*}$$
where the last step follows by equation (5.10). The estimate for the density of this subsequence of eigenvalues follows immediately from equation (5.8), noting that
$Q_0,Q_1 \ll (\log x)^{o(1)}$
.
5.4 Proof of Theorem 1.2
As before, without loss of generality, we can assume all the prime factors of
$m_0,m_1$
are congruent to
$1\ \pmod 4$
. For the sake of brevity, let
$\mathcal L_2=\log \log x$
. Let
$Q_0,Q_1$
be as in equation(5.6) and
$\mathcal M_2(x)$
be as in equation (5.7), and recall for
$m \in \mathcal M_2(x)$
that
$m=Q_0n$
, where
$n \in {\mathcal N}_2(x)$
where
${\mathcal N}_2$
is as in equation (4.1). Note for each
$m \in \mathcal M_2(x)$
that
$r(m) \gg \mathcal L_2^{10}$
. Also, by construction
$r(m)/r(m+4) \asymp \frac {a_0+1}{a_1+1}$
, where
$H,a_0,a_1$
are also as in equation (5.6), and note
$a_0,a_1 \le \log \mathcal L_2$
. Applying Proposition 4.1, we get that for all
$m \in \mathcal M_2(x)$
outside an exceptional set of size
$o(\#\mathcal M_2(x))$
that
$m^+=m+4$
and
$$ \begin{align} \frac{\lambda_m-m}{m^+-\lambda_m}=\frac{r(m)}{r(m^+)}\left(1+O\left(\frac{\mathcal L_2^6}{r(m)}\right)\right)=\frac{r(m)}{r(m^+)}\left(1+O\left(\mathcal L_2^{-4}\right)\right). \end{align} $$
In particular, this implies that
$\lambda _m-m \gg \mathcal L_2^{-1}$
and
$m^+-\lambda _m \gg \mathcal L_2^{-1}$
. As before, using equations (4.7) and (4.9) with
$U= \mathcal L_2^5$
, we get for all but at most
$o(\# \mathcal M_2(x))$
integers
$m \in \mathcal M_2(x)$
that
$$ \begin{align} \begin{aligned} \sum_{\ell \ge 0} \frac{r(\ell)}{(\ell-\lambda_m)^2}=\frac{r(m)}{(m-\lambda_m)^2}+\frac{r(m^+)}{(m^+-\lambda_m)^2}+O(\mathcal L_2^{-1}) \end{aligned} \end{align} $$
and
$$ \begin{align} \begin{aligned} \sum_{ \ell \ge 0 }\frac{1}{(\ell-\lambda_m)^2} \sum_{ a^2+b^2=\ell} f\left(\frac{a+ib}{|a+ib|} \right)=& \frac{1}{(m-\lambda_m)^2}\sum_{ a^2+b^2=m} f\left(\frac{a+ib}{|a+ib|} \right)\\ &+\frac{1}{(m^+-\lambda_n)^2}\sum_{ a^2+b^2=m^+} f\left(\frac{a+ib}{|a+ib|} \right) +O(\mathcal L_2^{-1}). \end{aligned} \end{align} $$
Let
$C_m=\frac {1}{1+r(m)/r(m^+)}$
. Applying equations (5.17),(5.18) and (5.19) equation in (5.3), we get
$$ \begin{align} \begin{aligned} &\langle \operatorname{Op}(f) g_{\lambda_m}, g_{\lambda_m} \rangle=(1+O(\mathcal L_2^{-1})) \left(\frac{r(m)}{(m-\lambda_m)^2}+\frac{r(m^+)}{(m^+-\lambda_m)^2} \right)^{-1} \\ & \qquad \times \left( \frac{1}{(m-\lambda_m)^2}\sum_{ a^2+b^2=m} f\left(\frac{a+ib}{|a+ib|} \right) +\frac{1}{(m^+-\lambda_m)^2}\sum_{ a^2+b^2=m^+} f\left(\frac{a+ib}{|a+ib|} \right)+O(\mathcal L_2^{-1})\right) \\ &\qquad =\frac{C_m}{r(m)} \sum_{ a^2+b^2=m} f\left(\frac{a+ib}{|a+ib|} \right)+\frac{1-C_m}{r(m^+)}\sum_{ a^2+b^2=m^+} f\left(\frac{a+ib}{|a+ib|} \right)+O(\mathcal L_2^{-1}). \end{aligned} \end{align} $$
Applying equation (5.10) to the first sum above, we get
$$ \begin{align} \frac{C_m}{r(m)} \sum_{ a^2+b^2=m} f\left(\frac{a+ib}{|a+ib|} \right)= \frac{C_m}{r(m_0)} \sum_{ a^2+b^2=m_0} f\left(\frac{a+ib}{|a+ib|} \right)+O(\varepsilon). \end{align} $$
Similarly, applying equation (5.11) to the second sum on the RHS of equation (5.20) we get that
$$ \begin{align} \frac{1-C_m}{r(m^+)} \sum_{ a^2+b^2=m^+} f\left(\frac{a+ib}{|a+ib|} \right)= \frac{1-C_m}{r(m_1\ell_n)} \sum_{ a^2+b^2=m_1 \ell_n} f\left(\frac{a+ib}{|a+ib|} \right)+O(\mathcal L_2^{-1/11}), \end{align} $$
for some integer
$\ell _n$
with
$\#\{p: p|\ell _m\} \le 2/\eta $
by equation (4.2). Using equations (5.21) and (5.22) in equation (5.20) completes the proof upon recalling that
$\varepsilon =\mathcal L_2^{-1/11}$
. The estimate for the density of this subsequence of eigenvalues follows from equation (5.9).
5.5 Proof of Theorem 1.3
The proof of Theorem 1.3 relies on the following hypothesis concerning the distribution of primes.
Hypothesis 1. Let
$Q_1,Q_0$
be as in equation (5.6) and
$ \varepsilon \ge (\log \log x)^{-1/2}$
be sufficiently small. Also, let
$y=x^{\eta }$
, where
$\eta>0$
is sufficiently small. Then the number of solutions
$(u,v) \in \mathbb Z^2$
to
$$\begin{align*}Q_1u-Q_0v=4, \end{align*}$$
where
$v=p_1p_2$
and
$u=p_3$
are primes satisfying
$1_{\mathcal P_{\varepsilon }}(p_1)1_{{\mathcal P}_{\varepsilon }'}(p_2)1_{\mathcal P_{\varepsilon }}(p_3)=1$
,
$p_3> y$
such that
$ v \le x$
is
$$\begin{align*}\gg \varepsilon^3 \frac{Q_0}{\varphi(Q_0 Q_1)} \frac{x \log \log x}{(\log x)^2}, \end{align*}$$
where
${\mathcal P}_{\varepsilon }, {\mathcal P}_{\varepsilon }'$
are as in equation (2.1).
Proof of Theorem 1.3
Recall the definition of
${\mathcal N}_2$
given in equation (4.1). Let us define
$$\begin{align*}{\mathcal N}_3=\{ n \in {\mathcal N}_2 : Q_0n+4=Q_1 p , b(p)=1, \, \&\, |\theta_p| \le \varepsilon\}. \end{align*}$$
Following equation (5.7), we also define
$$\begin{align*}\mathcal M_3(x)=\{ m \le x : m=Q_0n \text{ and } n \in {\mathcal N}_3\}.\end{align*}$$
By Hypothesis 1 and equation (5.9), it follows that
$$ \begin{align} \# \mathcal M_3(x) \asymp \varepsilon \# \mathcal M_2(x), \end{align} $$
where we also have used an upper bound sieve to get that
$\# \mathcal M_3(x) \ll \varepsilon \# \mathcal M_2(x)$
. Observe that
$\mathcal M_3(x) \subset \mathcal M_2(x)$
and the exceptional set in Proposition 4.1 is
$o(\# \mathcal M_3(x))$
since we take
$\varepsilon =(\log \log x)^{-1/4}$
. Hence, we get that equation (5.17) holds for
$m \in \mathcal M_3(x)$
outside an exceptional set of size
$o(\# \mathcal M_3(x))$
. Similarly, we can conclude that equations (5.18) and (5.19) also hold for all
$m \in \mathcal M_3(x)$
outside an exceptional set of size
$o(\# \mathcal M_3(x))$
. Therefore, arguing as in equations 5.20–5.22 we conclude that for
$m \in \mathcal M_3(x)$
outside an exceptional set of size
$o(\#\mathcal M_3(x))$
we have that
$$ \begin{align} \langle \operatorname{Op}(f) g_{\lambda_m}, g_{\lambda_m} \rangle =\frac{C_m}{r(m_0)} \sum_{ a^2+b^2=m_0} f\left(\frac{a+ib}{|a+ib|} \right)+ \frac{1-C_m}{r(m_1\ell_n)} \sum_{ a^2+b^2=m_1 \ell_n} f\left(\frac{a+ib}{|a+ib|} \right)+O(\mathcal L_2^{-1/11}), \end{align} $$
where
$m_0,m_1$
are arbitrary, fixed integers whose prime factors are all congruent to
$1\ \pmod 4$
and
$C_m=1/(1+r(m )/r(m+4))$
. By our hypothesis, we have that
$\ell _n=p$
with
$|\theta _p| \le \varepsilon $
and
$(m_1,p)=1$
. Hence, repeating the argument used to prove equation (5.10) it follows that
$$ \begin{align} \frac{1}{r(m_1\ell_n)} \sum_{ a^2+b^2=m_1 \ell_n} f\left(\frac{a+ib}{|a+ib|} \right)=\frac{1}{r(m_1)} \sum_{ a^2+b^2=m_1 } f\left(\frac{a+ib}{|a+ib|} \right)+O(\varepsilon). \end{align} $$
Given
$0 < c <1$
with
$c=d/e \in \mathbb Q$
, we will now specify our choice of
$a_0, a_1$
(from equation (5.5)). Recall we allow
$a_0,a_1$
to grow slowly with x and
$Q_0',Q_1'$
have the same number of prime factors. Also, by construction
$r(\frac {m_1}{(m_0,m_1)} g')=r(m_1)$
. Let
$\mathcal L=\lfloor (\log \log \log x)^{1/2} \rfloor $
. We take
$$\begin{align*}a_0= 2(e-d) r(m_1)\mathcal L \qquad \text{ and } \qquad a_1=dr(m_0) \mathcal L.\end{align*}$$
Hence,
$$ \begin{align} C_m=\frac{1}{1+\frac{8r(m_0)(a_0+1)}{16 r(m_1)(a_1+1)}}=\frac{d}{e}+o(1). \end{align} $$
We are now ready to complete the proof. Given any attainable measures
$\mu _{\infty _0}$
,
$\mu _{\infty _1}$
and
$0 \le c \le 1$
, we can take
$\{m_{0,j}\}_j \ \{m_{1,j}\}$
such that
$\mu _{0,j}$
weakly converges to
$\mu _{\infty _0}$
and
$\mu _{1,j}$
weakly converges to
$\mu _{\infty _1}$
, as
$j \rightarrow \infty $
. We also take
$\{a_{0,j}\}_j,\{a_{1,j}\}_j$
so that
$d_j/e_j \rightarrow c$
as
$j \rightarrow \infty $
. Therefore, by equations (5.24), (5.25) and (5.26) we conclude that there exists
$\{\lambda _{\ell }\}_{\ell } \subset \Lambda _{\text {new}}$
such that
$$\begin{align*}\langle \operatorname{Op}(f) g_{\lambda_{\ell}}, g_{\lambda_{\ell}} \rangle \xrightarrow{\ell \rightarrow \infty} c\int_{S^1} f d\mu_{\infty_0} +(1-c) \int_{S^1} f d\mu_{\infty_1}.\\[-38pt] \end{align*}$$
A Arithmetic over
$\mathbb Q(i)$
Consider the number field
$\mathbb Q(i)$
with the corresponding ring of integers
$\mathbb Z[i]$
. For
$\mathfrak b$
a nonzero integral ideal of
$\mathbb Z[i]$
, the residue classes
$\alpha\ \pmod { \mathfrak b}$
, where
$(\alpha )$
and
$\mathfrak b$
are relatively prime ideals, form the multiplicative group
$(\mathbb Z[i]/\mathfrak b)^*$
. We now summarize some well-known facts, which may be found in [Reference Neukirch, Schappacher and Harder34] or [Reference Iwaniec and Kowalski19]. A Dirichlet character
$\pmod {\mathfrak b}$
is a group homomorphism
$$\begin{align*}\chi : (\mathbb Z[i]/\mathfrak b) ^*\rightarrow S^1. \end{align*}$$
We extend
$\chi $
to all of
$\mathbb Z[i]$
by setting
$\chi (\mathfrak a)=0$
for
$\mathfrak a$
and
$\mathfrak b$
which are not relatively prime. Let I denote multiplicative group of nonzero fractional ideals and
$I_{\mathfrak b}=\{\mathfrak a \in I : \mathfrak a \text { and } \mathfrak b \text { are relatively prime}\}$
. A Hecke Großencharakter
$\pmod {\mathfrak b}$
is a homomorphism
$\psi : I_{\mathfrak b} \rightarrow \mathbb C \setminus \{0\}$
for which there exists a pair of homomorphisms
$$\begin{align*}\chi \, : \, (\mathbb Z[i]/\mathfrak b) ^*\rightarrow S^1, \qquad \chi_{\infty} \, : \, \mathbb C^* \rightarrow S^1 \end{align*}$$
such that for an ideal
$(\alpha )$
with
$\alpha \in \mathbb Z[i]$
$$\begin{align*}\psi((\alpha))=\chi(\alpha)\chi_{\infty}(\alpha). \end{align*}$$
Conversely, given any
$\chi\ \pmod {\mathfrak b}$
and
$\chi _{\infty }$
there exists a Großencharakter
$\psi\ \pmod {\mathfrak b}$
such that
$\psi =\chi \cdot \chi _{\infty }$
provided that
$\chi ( u)\chi _{\infty }( u) = 1$
for each unit
$u \in \mathbb Z[i]$
.
In particular, for
$4|k$
and
$\mathfrak a=(\alpha )$
a nonnegative integer
$$\begin{align*}\psi(\mathfrak a)=\left(\frac{\alpha}{|\alpha|} \right)^{k} \end{align*}$$
is a Hecke Großenchakter
$\pmod 1$
and these Hecke Großencharakteren can be used to detect primes in sectors. Additionally, given a positive rational integer q with
$(4,q)=1$
the homomorphism
$$\begin{align*}\chi \circ N : I_q \rightarrow S^1 \end{align*}$$
given by
$(\chi \circ N)(\mathfrak a)=\chi (N(\mathfrak a))$
is a Dirichlet character
$\pmod q$
, where
$\chi $
is a Dirichlet character
$\pmod q$
for
$\mathbb Z$
, that is
$\chi : (\mathbb Z/(q))^* \rightarrow S^1$
, where
$N \mathfrak a$
is the norm of
$\mathfrak a$
. Hence, for
$4|k$
$$\begin{align*}\psi(\mathfrak a)=(\chi \circ N)( \alpha ) \left( \frac{\alpha}{|\alpha|}\right)^k \end{align*}$$
is a Hecke Großencharakter with modulus q and frequency k, where
$\mathfrak a=(\alpha )$
. (A priori
$\alpha $
is only defined up to multiplication by i, but for these characters the choice does not matter.) The L-function attached to the Großencharakter
$\psi $
given by
$$\begin{align*}L(s, \psi)=\sum_{\mathfrak a} \frac{\psi(\mathfrak a)}{N (\mathfrak a)^s} \end{align*}$$
has a functional equation and admits an analytic continuation to
$\mathbb C\setminus \{1\}$
.
Moreover, if
$\psi $
is not a real character,
$L(s,\psi )$
has a standard zero-free region. That is, we have
$$\begin{align*}L(\sigma+it,\psi) \neq 0 \qquad \text{ for } \qquad \sigma>1-\frac{c}{ \log (q(|t|+1)(|k|+1))} \end{align*}$$
(see [Reference Iwaniec and Kowalski19, Section 5.10]). In particular, if
$k \ne 0$
,
$$\begin{align*}\sum_{N (\pi) \le x } \chi(N(\pi)) \left( \frac{\pi}{|\pi|}\right)^{k} \ll ((|k|+1) q) \cdot x \exp\left( -c \sqrt{\log x}\right), \end{align*}$$
where the summation is over prime ideal
$\mathfrak p=(\pi )$
with norm
$\le x$
.
Furthermore, for
$k =0$
the same estimate holds for any complex
$\chi\ \pmod q$
. However, for
$k=0$
and
$\chi\ \pmod q$
a real character, there may be a possible Siegel zero, and in this case we have Siegel’s estimate (see Section 5.9 of [Reference Iwaniec and Kowalski19])
$$\begin{align*}L(\sigma+it , \chi) \neq0 \qquad \text{for } \qquad \sigma \ge 1- \frac{c(\epsilon)}{q^{\epsilon}} \end{align*}$$
for any
$\epsilon>0$
. Consequently, we have the Siegel–Walfisz type prime number theorem for
$(a,q)=1$
and
$(q,2)=1$
$$ \begin{align} \sum_{\substack{N(\pi) \le x \\ N(\pi) \equiv a\ \ \ {\pmod q} \\ 0 \le \arg \pi \le \varepsilon}} 1=\frac{1}{\varphi(q)} \sum_{\substack{N(\pi) \le x \\ (N(\pi),q)=1 \\ 0 \le \arg \pi \le \varepsilon } } 1+O\left(\frac{x}{(\log x)^A} \right) \end{align} $$
for any
$A \ge 1$
. (After multiplication by
$i^{l}$
for some l, we can ensure that
$\theta = \arg i^{l}\pi \in [0,\pi /2)$
; we will let
$\arg \pi $
denote this angle.)
Recall that a prime
$p \equiv 3\ \pmod 4$
is inert in
$\mathbb Z[i]$
; additionally, a prime
$p \equiv 1\ \pmod 4$
splits in
$\mathbb Z[i]$
so that
$p=\pi \overline {\pi }=a^2+b^2$
, where
$\pi $
is a prime in
$\mathbb Z[i]$
. Writing
$$\begin{align*}\mathcal B(x;q,a,\varepsilon)=\sum_{\substack{n \le x \\ n \equiv a\ \ \ {\pmod q}}} ( 1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) -\frac{ 1}{\varphi(q)} \sum_{\substack{n \le x \\ (n,q)=1}}( 1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n), \end{align*}$$
formula (A.1) gives, for
$(a,q)=1$
and
$(q,2)=1$
, that
$$ \begin{align} |\mathcal B(x;q,a, \varepsilon)| \ll \frac{x}{(\log x)^A}, \end{align} $$
for
$q \le (\log x)^A$
. In addition, it is worth noting that equation (A.1) also implies
$$ \begin{align} \sum_{\substack{ n \le x \\ n \equiv a\ \ \ {\pmod q}}} ( 1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n) \sim \frac{4\varepsilon^2}{\varphi(q)} \frac{x \log \log x}{\log x}. \end{align} $$
We are now ready to state the following result which is an analog of the Bombieri–Vinogradov theorem.
Theorem A.1. There exists
$B_0$
sufficiently large so that
$$\begin{align*}\sum_{ \substack{q \le Q \\ (q,2)=1}} \max_{(a,q)=1} \left|\mathcal B(x;q,a,\varepsilon) \right| \ll \frac{x}{(\log x)^{10}} \end{align*}$$
for
$Q \le x^{1/2}/(\log x)^{B_0}$
.
Let
${\mathcal S} \subset \mathbb N$
. A sequence of complex numbers
$\{ \beta _n\}$
with
$|\beta _n| \le \tau (n)$
satisfies the Siegel–Walfisz property for
${\mathcal S}$
provided that for every
$q \in {\mathcal S}$
and
$A \ge 0$
and
$N \ge 2$
we have
$$\begin{align*}\sum_{\substack{ n \le N \\ n \equiv a\ \ \ \pmod q}} \beta_n=\frac{1}{\varphi(q)}\sum_{\substack{n \le N \\ (n,q)=1}} \beta_n+ O\left( \frac{N}{(\log N)^A}\right) \end{align*}$$
for every
$a \in \mathbb Z$
with
$(a,q)=1$
.
A.1 An application of the large sieve
We next recall a consequence of the large sieve, which follows applying a minor modification of Theorem 9.17 of [Reference Friedlander and Iwaniec15].
Lemma A.1. Let
$A \ge 1$
and
$Q=x^{1/2}(\log x)^{-B}$
, where
$B=B(A)$
is sufficiently large. Suppose
$\{\beta _n\}$
satisfies the Siegel–Walfisz property for all q with
$(q,2)=1$
. Then for any sequence
$\{\alpha _n\}$
of complex numbers such that
$|\alpha _n| \le \tau (n)$
$$\begin{align*}\sum_{\substack{q \le Q \\ (q,2)=1}} \max_{(a,q)=1} \Bigg| \sum_{\substack{mn \le x \\m,n \le \frac{x}{(\log x)^B} \\ mn \equiv a\ \ \ { \pmod q}}} \beta_m \alpha_n- \frac{1}{\varphi(q)} \sum_{\substack{mn \le x \\m,n \le \frac{x}{(\log x)^B} \\ (mn,q)=1}} \beta_m \alpha_n\Bigg| \ll \frac{x}{(\log x)^A}. \end{align*}$$
Proof of Theorem A.1
By equation (A.2), the sequence
$\beta _n=1_{ {\mathcal P}_{\varepsilon }}(n)$
satisfies the Siegel–Walfisz condition for all q with
$(q,2)=1$
. Take
$\alpha _n=1_{ \mathcal P_{\varepsilon }'}(n)$
, and note that (cf. equation (2.1))
$$\begin{align*}\sum_{\substack{n \le x \\ n \equiv a\ \ \ \pmod q}} ( 1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n)=\sum_{ \substack{mn \le x \\ m,n \le \frac{x}{(\log x)^{B_0}} \\ mn \equiv a\ \ \ \pmod q}} 1_{ {\mathcal P}_{\varepsilon}}(m)1_{ {\mathcal P}_{\varepsilon}'}(n) \end{align*}$$
and
$$\begin{align*}\sum_{\substack{n \le x \\ (n,q)=1}} ( 1_{ {\mathcal P}_{\varepsilon}} \ast 1_{ {\mathcal P}_{\varepsilon}'})(n)=\sum_{ \substack{mn \le x \\ m,n \le \frac{x}{(\log x)^{B_0}}\\ (mn,q)=1}} 1_{ {\mathcal P}_{\varepsilon}}(m)1_{ {\mathcal P}_{\varepsilon}'}(n). \end{align*}$$
Hence, applying Lemma A.1 completes the proof.
A.2 Gaussian integers in sectors with norms in progressions
The goal of this section is to show that a result of Smith [Reference Smith44] (also cf. [Reference Tolev47]) holds for Gaussian integers in sectors. We recall that, for
$\alpha \in {\mathbb Z}[i]$
,
$N(\alpha ) = |\alpha |^{2}$
denotes the norm of
$\alpha $
. For
$a,q>0$
, define
$$ \begin{align*}\eta_{a}(q) := |\{ \alpha_1,\alpha_2\ \ \ {\pmod q} : \alpha_1^{2}+\alpha_2^{2} \equiv a \ \ \ {\pmod q} \}|. \end{align*} $$
Proposition A.1. Let
$a, q>0$
be integers, and put
$g = (a,q)$
. Given an angle
$\theta $
and
$\epsilon \in (0,2\pi )$
, let
$S=S_{\epsilon ,\theta }$
denote the set of lattice points
$\alpha \in {\mathbb Z}[i]$
contained in the sector defined byFootnote
4
$ |\arg (\alpha )-\theta | < \epsilon /2 $
. Then, uniformly for
$\epsilon>0$
,
$$ \begin{align*}|\{ \alpha \in S : N(\alpha) \equiv a\ \ \ {\pmod q}, N(\alpha)\le x \}| \end{align*} $$
$$ \begin{align*}= \frac{\epsilon x \eta_{a}(q)}{q^{2}} +O\left( \frac{x^{1-\delta/3}}{q}\right) \end{align*} $$
provided that
$q^{3}g < x^{2(1-2\delta )}$
for
$\delta>0$
.
We begin by showing that solutions to
$\alpha _{1}^{2} + \alpha _{2}^{2} \equiv a\ \pmod q$
is well distributed in fairly small boxes. Given q, let
$f : ({\mathbb Z} /q {\mathbb Z})^{2} \to {\mathbb C}$
denote the characteristic function of the set
$\{ (\alpha _1,\alpha _2) \in ({\mathbb Z} /q {\mathbb Z})^{2} : \alpha _1^{2} + \alpha _2^{2} \equiv a\ \pmod q\}$
. With the modulo q Fourier transform given by
$$ \begin{align} \widehat{f}(\xi_1,\xi_2) := \sum_{\alpha_1,\alpha_2\ \ \ {\pmod q}} f(\alpha_1,\alpha_2) e^{-2 \pi i (\xi_1 \alpha_1 + \xi_2 \alpha_2)/q}, \end{align} $$
we recall the following estimate by Tolev [Reference Tolev47]:
$$ \begin{align} |\widehat{f}(\xi_1,\xi_2)| \ll q^{1/2} \tau(q)^{2} (q,\xi_1,\xi_2)^{1/2} (q,a,\xi_1^{2}+\xi_2^{2})^{1/2} \leq q^{1/2} \tau(q)^{2} (q,\xi_1,\xi_2)^{1/2} (q,a)^{1/2}. \end{align} $$
By the Chinese remainder theorem,
$\eta _{a}(q)$
is multiplicative in q, and we note that
$\widehat {f}(0,0) = \eta _{a}(q)$
.
Let
$B \subset [0,q) \times [0,q)$
be a ‘box’ with side lengths T, and let
$g = g_{B}$
denote the characteristic function of
$B \cap ({\mathbb Z}/q{\mathbb Z})^2$
. By standard estimates (from summing a geometric series), we have, for
$\xi _1, \xi _2 \neq 0$
,
$$ \begin{align} \widehat{g}(\xi_1,\xi_2) \ll q^{2}/|\xi_1\xi_2|, \end{align} $$
for
$\xi _1 \neq 0$
,
$$ \begin{align} \widehat{g}(\xi_1,0) \ll Tq /|\xi_1|, \end{align} $$
(and similarly for
$\xi _2 \neq 0$
) and trivially
$$ \begin{align*}\widehat{g}(0,0) = T^{2}. \end{align*} $$
Lemma A.2. Let
$g = (a,q)$
. Then
$$ \begin{align*}|\{ (\alpha_1,\alpha_2) \in B : \alpha_1^{2}+\alpha_2^{2} \equiv a \ \ \ {\pmod q} \}| = T^{2} \cdot\frac{\eta_{a}(q)}{q^{2}} + O(q^{1/2} \tau(q)^{3} \log(q)^{2} g^{1/2} ). \end{align*} $$
Proof. By Fourier analysis on
$({\mathbb Z}/q{\mathbb Z})^{2}$
(i.e., Plancherel’s theorem for finite abelian groups), we have
$$ \begin{align*}|\{ (\alpha_1,\alpha_2) \in B : \alpha_1^{2}+\alpha_2^{2} \equiv a \ \ \ {\pmod q} \}| = \sum_{ \alpha_1,\alpha_2\ \ \ {\pmod q} } f(\alpha_1,\alpha_2) g(\alpha_1,\alpha_2) \end{align*} $$
$$ \begin{align*}= \frac{1}{q^{2}} \sum_{ \xi_1, \xi_2\ \ \ {\pmod q} } \widehat{f}(\xi_1,\xi_2) \overline{\widehat{g}(\xi_1,\xi_2)}. \end{align*} $$
The main term is given by
$\xi _1=\xi _2=0$
and equals
$$ \begin{align*}\frac{\widehat{f}(0,0) \widehat{g}(0,0)}{q^{2}} = T^{2}\frac{ \eta_a(q)}{q^{2}}. \end{align*} $$
Using equations (A.5) and (A.7), the contribution from (say)
$\xi _1=0$
and
$\xi _2 \neq 0$
is
$$ \begin{align} \ll \frac{1}{q^{2}} \sum_{\xi_2 = 1 }^{q-1} \frac{Tq}{\xi_2} q^{1/2} \tau(q)^{2} (q,\xi_2)^{1/2} g^{1/2} \ll \frac{Tq^{3/2} \tau(q)^{2} g^{1/2}}{ q^{2}} \sum_{d|q} \sum_{0 < \xi_2 < q/d} \frac{d^{1/2} }{d \xi_2} \end{align} $$
$$ \begin{align*}\ll \frac{T \tau(q)^{3} \log(q) g^{1/2}}{ q^{1/2}} = O(q^{1/2}\tau(q)^{3} \log(q) g^{1/2} ). \end{align*} $$
The contribution from terms
$\xi _2=0$
and
$\xi _1 \neq 0$
is bounded similarly.
As for the terms
$\xi _1,\xi _2 \neq 0$
, we have by equation (A.5)
$$ \begin{align*}\frac{1}{q^{2}} \sum_{ \xi_1, \xi_2 \neq 0 } \widehat{f}(\xi_1,\xi_2) \overline{\widehat{g}(\xi_1,\xi_2)} \ll \frac{q^{1/2} \tau(q)^{2}}{q^{2}} \sum_{ \xi_1, \xi_2 \neq 0 } \frac{q^{2}}{\xi_1 \xi_2} (q,\xi_1,\xi_2)^{1/2} g^{1/2} \end{align*} $$
$$ \begin{align*}= q^{1/2} \tau(q)^{2} \sum_{d|q} \sum_{ 0 < \xi_1, \xi_2 \leq q/d } \frac{d^{1/2} g^{1/2}}{d^{2}\xi_1 \xi_2} \ll q^{1/2} \tau(q)^{2} \log(q)^{2} g^{1/2}.\\[-36pt] \end{align*} $$
Concluding the proof of Proposition A.1
Take
$T = x^{(1-\delta )/2}$
. The case
$T>q$
is straightforward using a simple tiling argument, and we only give details for
$T \le q$
.
By a simple geometry of numbers argument, we may ‘tile’ the sector S, intersected with a ball of radius
$x^{1/2}$
, with
$\epsilon x/T^{2} + O(x^{1/2}/T)$
boxes B (with side lengths T) entirely contained in the sector and with
$O(x^{1/2}/T)$
boxes intersecting the boundary. By Lemma A.2, each box B contains
$$ \begin{align*}T^{2} \cdot\frac{\eta_{a}(q)}{q^{2}} + O(q^{1/2} \tau(q)^{2} \log(q)^{2} g^{1/2} ) \end{align*} $$
points satisfying
$ \alpha _1^{2} + \alpha _2^{2} \equiv a\ \pmod q$
.
As
$\eta _{a}(q) < q^{1+o(1)}$
(cf. [Reference Blomer, Brüdern and Dietmann5, Lemma 2.8]), we find that the number of lattice points in the sector is
$$\begin{align*}\begin{aligned} & ( \epsilon x/T^{2} + O(x^{1/2}/T)) ( T^{2} \cdot\frac{\eta_{a}(q)}{q^{2}} + O(q^{1/2} \tau(q)^{3} \log(q)^{2} g^{1/2} ) )\\ &=\frac{\epsilon \eta_a(q) x}{q^2}+O\left(\frac{x^{1-\delta/2}}{q^{1-o(1)}}+ \epsilon g^{1/2} q^{1/2+o(1)} x^{\delta} \right). \end{aligned} \end{align*}$$
For
$q^{3} g < x^{2(1-2\delta )}$
, the error term is
$\ll \frac {x^{1-\delta /3}}{q} $
.
A.3 Proof of Lemma 2.4
We may assume
$(Q,q)=1$
; otherwise, the result is trivial. Let
$\delta>0$
be sufficiently small but fixed, and set
$$\begin{align*}r_{\varepsilon}(n)=\sum_{\substack{a^2+b^2=n \\ |\arg(a+ib)| \le \varepsilon}} 1. \end{align*}$$
Also, for
$n \in \mathbb N$
and
$z>0$
let
$\widetilde P_n(z)=\prod _{2 < p <z} p$
. Let
$\Lambda _1=\{\lambda _d\}$
,
$\Lambda '=\{\lambda _e'\}$
be upper bound sieves of level
$D=x^{\delta }$
with
$(d,2q)=1$
and
$(e,2Q)=1$
. Then for
$z=x^{\delta /2}$
, we have
$$\begin{align*}\begin{aligned} \sum_{ \substack{p=a^2+b^2 \le x \\ |\arg(a+ib)| \le \varepsilon \\ qp+4=Q p_1 \text{where } p_1 \text{ is prime} }} 1 \le& \sum_{m \le qx+4}\sum_{\substack{n \le x \\ qn+4=Qm \\ (m, \widetilde P_q(z))=1 \\ (n,\widetilde P_{Q}(z))=1 }} r_{\varepsilon}(n)+O(x^{\delta/2}) \\ \le& \sum_{m \le qx+4} \sum_{\substack{n \le x \\ qn+4=Qm}} r_{\varepsilon}(n) (\lambda' \ast 1)\left( n \right) (\lambda \ast 1)\left(m\right)+O(x^{\delta/2}). \end{aligned} \end{align*}$$
Switching order of summation, we have that the sum on the LHS above is
$$ \begin{align} \begin{aligned} =&\sum_{\substack{d,e < D \\ (d,e)=1 \\ (d,2q)=1, (e,2Q)=1}} \lambda_d \lambda_e' \sum_{\substack{ n \le x \\ e|n}} r_{\varepsilon}(n) \sum_{\substack{m \le qx+4 \\ d|m \\ qn+4=Qm}} 1 \\ = &\sum_{\substack{d,e < D \\ (d,e)=1 \\ (d,2q)=1, (e,2Q)=1}} \lambda_d \lambda_e' \sum_{\substack{n \le x \\ n \equiv \gamma\ \ \ { \pmod {Qed}}}} r_{\varepsilon}(n) \end{aligned} \end{align} $$
since the inner sum in the first equation above consists of precisely one term provided that
$qn+4 \equiv 0\ \pmod {Qd}$
and is empty otherwise. Also, here
$\gamma =-4e \overline {e} \overline {q}$
, where
$q\overline q \equiv 1\ \pmod {Qd}$
and
$e \overline e \equiv 1\ \pmod {Qd}$
. In particular,
$(\gamma , Qed)=e$
.
Let us note some properties of the function
$\eta _a(q)$
. Recall,
$\eta _a(\cdot )$
is multiplicative. Moreover, for
$p>2$
and
$\ell \ge 1$
$$ \begin{align} \eta_a(p^{\ell})=p^{\ell} \sum_{0 \le j \le \ell} \frac{\chi_4(p)^j}{p^j} c_{p^j}(a) \end{align} $$
and for any
$a,q \ge 1$
$$ \begin{align} \eta_q(q) \ll \frac{q^2}{\varphi(q)} \tau((a,q)) \end{align} $$
(see [Reference Blomer, Brüdern and Dietmann5, Eqn. (2.20) and Lemma 2.8]), where
$$ \begin{align} c_q(a)=\sum_{\substack{b\ \ \ {\pmod q} \\ (b,q)=1}} e\left(\frac{ab}{q} \right)=\frac{\varphi(q)}{\varphi(q/(q,a))} \mu(q/(q,a)) \end{align} $$
is the Ramanujan sum and
$\chi _4$
is the nonprincipal Dirichlet character
$\pmod 4$
. In particular, note that if
$(a,q)=g$
then
$\eta _a(q)=\eta _g(q)$
for odd q.
By Proposition A.1, equations (A.10) and (A.11) and recalling that
$(Qed, \gamma )=e$
, we get the RHS of equation (A.9) equals
$$\begin{align*}\begin{aligned} &2\varepsilon x \sum_{\substack{d,e < D \\ (d,e)=1 \\ (d,2q)=1, (e,2Q)=1}} \frac{\lambda_d \lambda_e'}{(Qed)^2} \eta_{\gamma}(Qed)+O\left(\frac{ x^{1-\delta/4}}{Q}\right)\\ &=\frac{2\varepsilon x \eta_1(Q)}{Q^2}\sum_{\substack{d,e < D \\ (d,e)=1 \\ (d,2q)=1, (e,2Q)=1}} \frac{\lambda_d \lambda_e'}{(ed)^2} \frac{\eta_{1}(Qd) \eta_{e}(e)}{\eta_1(Q)}+O\left( \frac{ x^{1-\delta/4}}{Q}\right) \end{aligned} \end{align*}$$
provided that
$ Q^3 D^7< x^{2(1-2\delta )}$
which we rewrite as
$Q < x^{2/3-11 \delta /3}$
. Using Theorem 2.3 in the form of equation (2.9), and noting that
$\eta _1(Qd)/\eta _1(Q)$
is a multiplicative function, we get that the above sum is
$$ \begin{align} \begin{aligned} &\ll \frac{\varepsilon x \eta_1(Q)}{Q^2} \prod_{\substack{p < D \\ (p,2q)=1}}\left(1-\frac{\eta_1(Qp)}{p^2 \eta_1(Q)}\right) \prod_{\substack{p < D \\ (p,2Q)=1}}\left(1-\frac{\eta_p(p)}{p^2}\right). \end{aligned} \end{align} $$
To evaluate the Euler products we use equation (A.10) to get
$\eta _p(p)=p(1+\chi _4(p)-\frac {1}{p})$
,
$\eta _1(Qp)/\eta _1(Q)=p+O(1)$
and
$\eta _1(Q)=Q\prod _{p|Q}\left (1-\frac {\chi _4(p)}{p} \right )$
. Hence, by these estimates we get that equation (A.13) is
$$\begin{align*}\begin{aligned} \ll & \frac{\varepsilon x \eta_1(Q)}{Q^2 } \prod_{p|Q} \left( 1+\frac{\chi_4(p)+1}{p} \right) \prod_{p|q} \left(1+\frac{1}{p} \right) \cdot \frac{1}{(\log D)^2} \\ \ll & \frac{q}{\varphi(q)} \cdot \frac{\varepsilon x }{Q\delta^2 (\log x)^2 } \prod_{p|Q}\left(1+\frac{1}{p} \right) \ll \frac{q}{\varphi(q) } \cdot \frac{\varepsilon x }{\varphi(Q) \delta^2 (\log x)^2 } \end{aligned} \end{align*}$$
for
$Q < x^{2/3-11\delta /3}$
which completes the proof since
$\delta>0$
is arbitrary.
B Nonattainable quantum limits
Given an integer n such that
$r(n)>0$
, define a probability measure
$\mu _n$
on the unit circle by
$$ \begin{align*}\mu_{n} := \frac{1}{r(n)}\sum_{\lambda \in {\mathbb Z}[i]: |\lambda|^{2}=n} \delta_{\lambda/|\lambda|}, \end{align*} $$
that is,
$\mu _n$
is obtained by projecting the set of
${\mathbb Z}^{2}$
-lattice points on a circle of radius
$n^{1/2}$
to the unit circle and
$\delta $
here denotes the Dirac delta function. A measure
$\mu $
is said to be attainable if
$\mu $
is a weak* limit of some subsequence of measures
$\mu _{n_{i}}$
. A partial classification of the set of attainable measures was given in [Reference Kurlberg and Wigman29] in terms of their Fourier coefficients. Namely, for
$k \in {\mathbb Z}$
, let
$\widehat {\mu }(k) := \int z^{k} \, d\mu (z)$
denote the k-th Fourier coefficient of
$\mu $
. By [Reference Kurlberg and Wigman29, Theorem 1.3], the inequalities
$$ \begin{align*}2 \widehat{\mu}(4)^{2}-1 \le \widehat{\mu}(8) \le \max( \widehat{\mu}(4)^{4}, (2|\widehat{\mu}(4)|-1)^{2}) \end{align*} $$
hold if
$\mu $
is attainable. In particular, for
$\gamma>0$
small and
$\widehat {\mu }(4) = 1-\gamma $
, we must have
$\widehat {\mu }(8) = 1-4\gamma + O(\gamma ^{2})$
.
Now, by Theorem 1.2, there exists quantum limits that are convex combinations
$c \nu _{1} + (1-c) \nu _{2}$
for
$c>0$
arbitrarily small and where
$\nu _1$
is the uniform measure (with
$(\widehat {\nu _{2}}(4), \widehat {\nu _2}(8)) = (0,0)$
), and
$\nu _{2}$
is a Cilleruelo type measure, that is, localized on the four points
$\pm 1, \pm i$
, and with
$(\widehat {\nu _{2}}(4), \widehat {\nu _2}(8)) = (1,1)$
. Clearly, such convex combinations cannot be attainable for c small.
C Convexity assuming a k-prime tuple analog
C.1 Preliminaries
We begin by noting that it is enough to show that any probability measure on the unit circle can be approximated by a convex combination of Dirac measures with uniform weights and similarly for
$\operatorname {Sym}_{8}$
-invariant measures. Namely, by the Krein–Milman theorem (cf. [Reference Rudin36, §3.21]), any measure on the unit circle is in the closed convex hull of its extreme points. Now, the extreme points are exactly the Dirac deltas: If one tries to decompose the measure
$\delta _{0} = c \alpha + (1-c)\beta $
(with
$\alpha ,\beta $
probability measures and
$c \in [0,1]$
) it’s clear that
$\alpha (0)=\beta (0)=1$
(both of them have mass
$\le 1$
at
$0$
, and if
$<1$
, then
$\delta _{0}$
would have too little mass at
$0$
.) On the other hand, if some measure
$\mu $
puts positive mass on two disjoint subsets
$A,B$
whose union is
$S^{1}$
, then as long as we have
$\mu (X) = \mu (X \cap A) + \mu (X \cap B)$
we arrive, after renormalizing, at a convex combination of
$\mu $
in terms of two probability measures. Thus, for Borel probability measures on
$S^{1}$
, the extremal points are exactly the Dirac measures.
We also find that any measure can be approximated by
$k^{-1} \sum _{i \le k} \delta _{\theta _{i}}$
for any subsequence of integers k tending to infinity since a finite convex combination of delta measures can be approximated by a uniformly weighted sum of delta measures. Further, we can also approximate via delta measures whose angles are restricted to come from Gaussian primes by using Hecke’s theorem.
Let
$k>0$
be an even integer. Given collection of angles
$\theta _{1}, \ldots , \theta _{k}$
define a probability measure
$\mu = \frac {1}{k} \sum _{i \le k} \nu _{\theta _{i}}$
on the unit circle, where
$\nu _{\theta }$
denotes the
$\operatorname {Sym}_{8}$
-invariant probability measure
$\nu _{\theta } = \frac {1}{8} \sum _{l=1}^{4} \delta _{\pm \theta + l \pi /2}$
. As explained above, it is enough to show that any such
$\mu $
is a quantum limit.
Assuming a plausible analogue of the prime k-tuple, or the Bateman–Horn, conjectures, we show that there exists an infinite subsequence of new eigenvalues
$\lambda $
so that
$$ \begin{align} \langle \operatorname{Op}(f) g_{\lambda}, g_{\lambda} \rangle = \mu(f) + o(1), \end{align} $$
as
$\lambda \to \infty $
along said subsequence, in the strong coupling limit.
To state our ‘Bateman–Horn type hypothesis’ precisely, we define an ‘admissibility parameter’
$Q_0=\prod _{p \le k} k$
and moduli
$Q_i$
,
$i=1,\ldots , k$
which are square-free and pairwise coprime. Let
$$\begin{align*}Q:= \prod_{i=1}^k Q_i. \end{align*}$$
We also require admissible shifts
$h_i, i=1,\ldots , k$
with
$$\begin{align*}h_i=1+l_i Q_0, \end{align*}$$
where
$l_i$
are distinct integers such that each prime divisor of Q is larger than
$\max _{i,j}|l_j-l_i|$
, and
$h_0\ \pmod Q$
is an integer satisfying
$h_0 \equiv 0\ \pmod {Q_0}$
and
$h_0 \equiv h_i\ \pmod {Q_i}$
,
$i=1, \ldots , k$
(these conditions will ensure admissibility; also such an
$h_0$
with
$|h_{0}| \le Q$
exists by the Chinese remainder theorem by pairwise coprimality of the
$Q_i$
). The point of admissibility is to ensure that there are no local obstructions to certain k-tuples being simultaneously prime (e.g., there are only finitely many prime pairs of the form
$(n,n+1)$
and finitely many prime triples of the form
$(n,n+2,n+4)$
; cf. equation (C.3) for the exact formulation in our setting.) Finally, let
$$\begin{align*}{\mathcal P}_{\varepsilon}=\{ p \text{ prime} : p=a^2+b^2, \, a,b> 0, \, \text{ and } \, 0 < \arctan(b/a) \le \varepsilon \}. \end{align*}$$
We formulate the following conjecture.
Conjecture 1. Let
$\varepsilon>0$
. Suppose
$Q \le x^{o(1)}$
,
$|h_1|,\ldots ,|h_k| \ll _k 1$
and
$\prod _{p|Q}(1+1/p) \ll 1$
. In the notation above, we have
$$ \begin{align*}|\{ n \le x : \frac{Qn - h_{0} + h_{1}}{Q_{1}}, \ldots, \frac{Qn -h_{0}+h_{k}}{Q_{k}} \in {\mathcal P}_{\epsilon} \}| \gg_{\epsilon,k} \frac{x}{ (\log x)^{k}}. \end{align*} $$
To justify this conjecture, we will show in Section C.3 that the polynomial
$$ \begin{align} L(x)=\prod_{i=1}^k L_i(x), \quad L_i(x)=A_ix+B_i, \quad A_i=Q/Q_i, B_i=(h_i-h_0)/Q_i \end{align} $$
has no fixed prime divisor (note by construction that
$B_i \in \mathbb Z$
since
$h_i \equiv h_0\ \pmod {Q_i}$
) so that there are no local obstructions to k-tuples of integers of the form
$$ \begin{align} \left( \frac{Q n - h_{0} + h_{1}}{Q_{1}}, \ldots, \frac{Qn -h_{0} + h_{k}}{Q_{k}} \right) \end{align} $$
being simultaneously prime.
C.2 Proof of equation (C.1), assuming Conjecture 1
C.2.1 The construction and a high-level overview of the argument
Let k be a given even integer. Similar to Section 5.2., given a large value of x choose moduli
$Q_{1}, \ldots , Q_{k}$
as follows: Put
$T = \lfloor \log \log x \rfloor $
,
$H = \lfloor 100 \log \log \log x \rfloor $
, and let
$$ \begin{align*}Q_{i} = q_{i}' \cdot \prod_{j = T+1+(i-1)H}^{T+iH-1} q_{j}, \end{align*} $$
where
$q_{j}$
denotes the j-th element of
$\{ q \in {\mathcal S} : q \equiv 1\ \pmod {Q_{0}}\}$
(cf. equation (5.4); note that
$q_{j} \asymp _{k} (j \log j)^{10/9}$
holds), and
$q_{i}' \asymp T$
is a Gaussian prime with associated angle
$\theta _{i} + o(1)$
as x grows. In particular, note that
$Q_{i} \equiv 1\ \pmod { Q_{0}}$
and that
$$ \begin{align} \mu_{Q_{i}} \to \nu_{\theta_{i}} \end{align} $$
as x grows, where
$\mu _{Q_i}$
is the probability measure with delta masses placed at the angles of lattice points lying on the circle of radius
$\sqrt {Q_i}$
. Let
$\mathcal H = \{ h_{1}, \ldots , h_{k}\}$
, where
$$\begin{align*}h_i=1+l_i Q_0, \qquad i =1,\ldots, k \end{align*}$$
and the integers
$l_i$
are distinct and chosen so that
$$ \begin{align} h_1,\ldots, h_{k/2} \in [-W^3-W,-W^3], \qquad h_{k/2+1},\ldots, h_k \in [W^3,W^3+W],\end{align} $$
where
$W = W_{0} k Q_{0}$
, and
$W_{0} \ge 10$
is a (large) parameter. Observe that
$\max _{i,j} |l_i-l_j|\le 3W^3/Q_0$
, so any prime divisor of Q does not divide
$\max _{i,j} |l_i-l_j|$
for x sufficiently large. We note that we may apply Conjecture 1 with this choice of
$h_1,\ldots , h_k$
,
$Q_1,\ldots , Q_k$
. Let
$$ \begin{align*}{\mathcal N}_{3} := \{ n \in {\mathcal N} : L_{i}(n) \in {\mathcal P}_{\varepsilon} \text{ for } 1 \le i \le k\}. \end{align*} $$
Let us now give an overview of the argument to establish equation (C.1). The basic idea is that for most such values of
$n \in {\mathcal N}_3$
, if we put
$m = Qn-h_{0}$
there exists a corresponding new eigenvalue
$\lambda \in (m+h_{k/2}, m+ h_{k/2+1})$
which satisfies
$\lambda = m + O(W)$
(which we will prove later). In other words, the new eigenvalue
$\lambda $
‘sits in the middle’ of two clusters of k old eigenvalues, where
$k/2$
of them lie in
$[m-W^{3}-W,m-W^{3}]$
, and the remaining
$k/2$
of them lie in
$[m+W^{3}, m+W^{3}+W]$
. Moreover, we will see later that, for most such n in a positive density subset of
${\mathcal N}_3 \cap [x/2,x]$
, essentially all of the
$L^{2}$
-mass is carried by terms arising from the two clusters, in the sense that for f a pure momentum observable,
$$ \begin{align*}\langle \operatorname{Op}(f) G_{\lambda}, G_{\lambda}\rangle = \frac{1}{k} \sum_{i=1}^{k} \sum_{\xi \in {\mathbb Z}[i] : |\xi|^{2} = m+h_{i}} \frac{f(\xi/|\xi|)}{(m+h_{i}-\lambda)^{2}} + o( || G_{\lambda}||^{2}), \end{align*} $$
$$ \begin{align*}= \frac{2^{H}}{kW^{6}} \left( \sum_{i=1}^{k} (\nu_{\theta_{i}}(f) + o(1)) \cdot (1 + O(1/W^{2})) \right) + o( || G_{\lambda}||^{2}), \end{align*} $$
where we have used equation (C.4) in the last step. As this construction also gives
$||G_{\lambda }||_2^{2} = \frac {2^{H}}{W^{6}}(1+o(1))$
, we find that
$$ \begin{align*}\langle \operatorname{Op}(f) g_{\lambda}, g_{\lambda}\rangle = \frac{1}{k} \sum_{i=1}^{k} (\nu_{\theta_{i}}(f) + o(1))\cdot (1+O(1/W^{2})) = (\mu(f) + o(1))\cdot (1+O(1/W^{2})), \end{align*} $$
which completes the argument by taking a sequence of
$W_{0}$
’s tending to infinity.
C.2.2 Restricting to typical
$n \in {\mathcal N}_3$
We also require the following analog of Lemma 4.3, which follows from the techniques used in Section 4 of the paper. A formal proof of this result is given in Section C.4.
Lemma C.1. Let
$U = (\log \log x)^{5}$
. There exists
$C>0$
such that for all
$n \in {\mathcal N}_{3} \cap [x/2,x]$
, outside a set of size
$$ \begin{align*}\ll_{k,W} \frac{x}{(\log x)^{k}} \frac{( \log \log \log \log x)^{2C} \cdot \log \log x}{U}, \end{align*} $$
the following hold:
$$ \begin{align} \sum_{|h| \le (\log x)^{1/2}/U, h \not \in \mathcal H} b(Qn - h_{0} + h) = 0, \end{align} $$
$$ \begin{align} \sum_{|h| \le (\log x)^{B}, h \not \in \mathcal H} \frac{r(Qn - h_{0} + h)}{|h|} \le U \end{align} $$
and
$$ \begin{align} \sum_{|h| \ge U, h \not \in \mathcal H} \frac{r(Qn-h_{0}+h)}{h^{2}} \ll \frac{1}{ \log \log x}. \end{align} $$
Note that Lemma C.1 and Conjecture 1 imply that equations (C.6), (C.7) and (C.8) hold for a full density subset of
$n \in \mathcal N_3 \cap [x/2,x]$
.
C.2.3 Proof of equation (C.1)
By equations (C.6) and (C.7) and Theorem 3.1, we have for
$m = Qn - h_{0}$
and all
$n \in {\mathcal N}_{3} \cap [x/2,x]$
that lie outside a subset of size
$o(x/(\log x)^k)$
, that the new eigenvalue
$\lambda _{*} = \lambda _{m+h_{k/2+1}}$
satisfies the spectral equation
$$ \begin{align} \sum_{i \le k} \frac{r(m+h_{i})}{m+h_{i}-\lambda_{*}} = O( (\log \log x)^{5}). \end{align} $$
Thus, by Conjecture 1 the above holds for a density one subset of
$n \in {\mathcal N}_3 \cap [x/2,x]$
. Letting
$$ \begin{align*}F_{m}(\lambda) := \sum_{i \le k} \frac{1}{m+h_{i}-\lambda},\end{align*} $$
we find, as
$r(m+h_{i}) = 2^{H}$
for
$i=1,\ldots ,k$
, with
$H = [ 100 \log \log \log x ]$
and recalling equation (C.9), that
$$ \begin{align*}F_{m}(\lambda_{*}) = o(1). \end{align*} $$
Recalling equation (C.5), we then note that
$$ \begin{align*}F_{m}(m) = \sum_{i \le k} 1/h_{i} = \frac{k/2}{-(W^{3}+O(W))} + \frac{k/2}{W^{3}+O(W)} = O(k/W^{5}). \end{align*} $$
Further, for
$\lambda \in [m_{h_{k/2}},m_{h_{k/2+1}}]$
, we have
$$ \begin{align*}F_{m}'(\lambda) \ge (k/2) \frac{1}{(W^{3}+O(W))^{2}} \gg k/W^{6}. \end{align*} $$
Thus, combining the previous three assertions and using the mean value theorem gives
$$ \begin{align} \lambda_{*} = m + O(W). \end{align} $$
This tells us that
$\lambda _{*}$
lies essentially at the center of the two clusters of old eigenvalues (which lie of distance
$2W^{3}+O(W)$
apart).
Hence, using equations (C.6) and (C.8) we find that
$$ \begin{align*}||G_{\lambda}||_{2}^{2} = \frac{k 2^{H}}{(W^{3}+O(W))^{2}} + O( 1/\log \log x) \end{align*} $$
and further, recalling
$m+h_i=Qn-h_0+h_i$
,
$n \in {\mathcal N}_{3}$
, and using equations (C.5), (C.4) and (C.10), we have that
$$ \begin{align*}\sum_{i \le k} \sum_{\xi \in {\mathbb Z}[i] : |\xi|^{2} = m+h_{i}} \frac{f(\xi/|\xi|)}{(m+h_{i}-\lambda_{*})^{2}} = \sum_{i \le k} \frac{2^{H}(\nu_{\theta_{i}}(f)+o(1))}{(W^{3}+O(W))^{2}} \end{align*} $$
and consequently
$$ \begin{align*}\langle \operatorname{Op}(f) g_{\lambda_{*}}, g_{\lambda_{*}}\rangle = \frac{2^{H} (\mu(f) + o(1))(1+O(1/W^{2})) } { 2^{H}} = (\mu(f)+o(1)) \cdot (1+O(1/W^{2})). \end{align*} $$
C.3 Admissibility
We need to show that the polynomial
$L(x)$
as above has no fixed prime divisor. That is, for each prime p there exists an integer n with
$L(n) \not \equiv 0\ \pmod {p}$
.
We first consider small primes
$p \le k$
. Since
$Q_iB_{i} = h_{i}-h_{0} \equiv 1\ \pmod { Q_{0}}$
, we find that
$(B_{i},Q_{0}) = 1$
and thus
$L(0) \not \equiv 0\ \pmod p$
for
$p \le k$
.
We next treat large primes
$p> k$
. If p does not divide
$\prod _{i \le k} A_{i}$
,
$L(x)\ \pmod p$
is a polynomial of degree k and hence can have at most k roots in
$\mathbb Z/p\mathbb Z$
, and thus there exists an integer n so that
$L(n) \not \equiv 0\ \pmod p$
.
If
$p | \prod _{i \le k} A_{i}$
, we must rule out
$L(x) \equiv 0\ \pmod p$
for all
$x \in \mathbb Z/p\mathbb Z$
(i.e., that the reduction of L modulo p is the constant trivial polynomial). Since
$Q_{i}$
are coprime and
$p>k$
, p can divide at most one element in
$\{Q_{i}\}_{i=1}^{k}$
; say
$p | Q_{i}$
. As
$A_{i} = Q/Q_{i}$
is coprime to p, we find that
$L_{i}(x)$
mod p is nonconstant and hence has exactly one root. For
$j \neq i$
, we next show
$L_{j}(x)$
mod p has no roots by showing that
$p \nmid B_{j}$
. Assume that
$p|B_{j}$
. Now,
$B_{j} = (h_{j}-h_{0})/Q_{j} \equiv (h_{j}-h_{i})/Q_{j}\ \pmod { Q_{i}}$
, and since
$h_{j}-h_{i} = Q_{0}(l_{j}-l_{i})$
we must have
$p | l_{j}-l_{i}$
; however, since
$p|\prod _{i \le k} A_i$
, we have
$p|Q$
, so this contradicts our assumption that all prime divisors of Q are larger than
$\max _{i,j}|l_i-l_j|$
.
In conclusion, the polynomial
$L(x)$
has no fixed prime divisor, and the linear forms
$L_{1}(x), \ldots , L_{k}(x)$
are indeed admissible.
C.4 Proof of Lemma C.1
We begin with the following simple consequence of the prime number theorem.
Lemma C.2. Given an integer
$D \ge 2$
, we have
$$ \begin{align*}\prod_{p|D}(1+1/p) \ll \log \log D. \end{align*} $$
Proof. First, note that the product will be maximized if
$D= \prod _{p < t} p \asymp e^{t}$
, with t chosen so that
$\pi (t) = \omega (D) \le \log D$
. In this case,
$\prod _{p|D}(1+1/p) \ll \exp ( \sum _{p<t} 1/p) = \exp ( \log \log t) = \log t$
, and the result follows.
Given an integer h with
$|h| \leq x^{1/4}$
and
$ h \not \in \{ h_{1}, \ldots , h_{k}\}$
, define
$$ \begin{align*}L_{0}(x) = L_{0,h}(x) := Q x - h_{0}+h. \end{align*} $$
We next determine the prime divisors of
$D(h)$
, the discriminant of
$$ \begin{align*}L(x) := \prod_{i=0}^{k} L_{i}(x). \end{align*} $$
With
$A= \prod _{i=1}^{k} A_{i}$
and
$r_{i}= -B_{i} /A_{i} = (h_{0}-h_{i})/Q$
for
$i=1,\ldots , k$
and
$r_{0} = (h_{0}-h)/Q$
, the discriminant
$D(h)$
of L equals
$$ \begin{align*}\pm A^{2k} \prod_{0 \le i<j \le k} (r_{i}-r_{j})^{2}. \end{align*} $$
For
$0<i<j \le k$
,
$r_{i}-r_{j} = (h_{i}-h_{j})/Q = Q_{0}(l_{i}-l_{j})/Q$
, whereas
$r_{0}-r_{j} = (h_j-h)/Q$
. In particular, as
$Q|A$
, we find that
$p|D(h)$
implies that
$$ \begin{align*}p | Q_{0}Q \cdot \prod_{1 \le i < j \le k} (l_{i}-l_{j}) \cdot \prod_{i=1}^{k} (h_{i}-h). \end{align*} $$
Lemma C.3. For each fixed
$C>0$
, we have
$$ \begin{align*}\prod_{p|D(h)}(1+1/p)^{C} \ll_{k,W} \prod_{p| \prod_{i=1}^{k}(h-h_{i})}(1+1/p)^{C}. \end{align*} $$
Proof. As we have seen, if
$p|D(h)$
, then
$ p | Q_{0}Q \cdot \prod _{1 \le i < j \le k} (l_{i}-l_{j}) \cdot \prod _{i=1}^{k} (h_{i}-h). $
Since
$\prod _{p | Q} (1+1/p) \ll 1$
and
$\prod _{p|Q_{0}}(1+1/p) \ll _{k} 1$
, together with
$\prod _{1 \le i < j \le k} (l_{i}-l_{j}) \ll _{k,W} 1$
, we find that
$$ \begin{align*}\prod_{p|D(h)} (1+1/p)^{C} \ll_{k,W} \prod_{p| \prod_{i=1}^{k} (h_{i}-h) } (1+1/p)^{C}.\\[-36pt] \end{align*} $$
We also record a useful estimate involving prime divisors of
$$ \begin{align*}D_{2} := \pm \prod_{0 \le i < j \le k} (h_{i}-h_{j})^{2}, \end{align*} $$
the discriminant of the polynomial
$\prod _{i=0}^{k}(x-h_{i})$
.
Lemma C.4. For each fixed
$C>0$
, we have
$$ \begin{align*}\prod_{p|D_{2}}(1+1/p)^{C} \ll_{k,W} (\log \log \log \log x)^{2C}. \end{align*} $$
Proof. For
$i,j>0$
, we have
$h_{i}-h_{j} = Q_{0}(l_{i}-l_{j}) \ll _{k,W}1$
, and thus
$\prod _{1 \le i < j \le k} (h_{i}-h_{j})^{2} \ll _{k,W} 1$
. Further, as
$|h_{0} | \le Q$
and
$h_{1}, \ldots , h_{k} \ll _{k,W} 1$
, we have
$$ \begin{align*}\prod_{i=1}^{k} (h_{i}-h_{0})^{2} \ll_{k,W} Q^{2k}. \end{align*} $$
Since
$Q = \prod _{i=1}^{k} Q_{i}$
and each
$Q_{i} \asymp T^{H}$
, with
$H \ll \log \log \log x$
and
$T \ll \log \log x$
we find that
$$ \begin{align*}\log D_{2} \ll_{k,W} (\log \log \log x)^{2}. \end{align*} $$
The result now follows from Lemma C.2.
C.4.1 Applying Henriot’s result
Recall that
$L_{0}(x) = Qx - h_{0} + h$
. Let
$f_1$
be the characteristic function supported on the set of small angle primes
$p \in {\mathcal P}_{\varepsilon } \cap [x/2,x]$
; putting
$f_{1}(1) = 1$
we may extend
$f_{1}$
to a multiplicative function. In what follows,
$C=C(k)>0$
is the constant in Lemma 4.1; note that we allow C to depend on k. Let g denote the multiplicative function
$$ \begin{align*}g(n) := \prod_{p|n} (1+1/p). \end{align*} $$
Lemma C.5. With
$f(n) = b(n)$
, or
$f(n) = r(n)/4$
, we have
$$ \begin{align*} \sum_{x/2 \le n \le x} f(L_{0}(n)) \prod_{1 \leq i \le k} f_{1}(L_{i}(n)) \ll f((h-h_{0},Q)) g(D(h))^{C+k+1} \frac{x}{(\log x)^{k+1}} \prod_{p \leq x} (1+f(p)/p), \end{align*} $$
where
$D(h)$
is the discriminant of the polynomial
$$ \begin{align*}L(x) = \prod_{i=0}^{k} L_{i}(x). \end{align*} $$
Further, for
$H>(\log x)^{1/4}$
, we have
$$ \begin{align*}\sum_{|h| \le H, h \not \in \mathcal H} f((h-h_{0},Q)) g(D(h))^{C+k+1} \ll_{k,W} H (\log \log \log \log x)^{2C}. \end{align*} $$
Proof. We first assume that
$(h-h_{0},Q)=1$
. Now, for
$p \nmid Q$
, the linear forms
$L_{i}$
are nondegenerate modulo p for
$0 \le i \le k$
, and we have
$\rho _{L_i}(p) = 1$
for
$0 \le i \le k$
. Further, we have
$\rho _L(p) = k+1$
provided p does not divide
$Q_{0} Q \prod _{1 \le i < j \le k}(l_{i}-l_{j}) \cdot \prod _{i=1}^{k}(h_{i}-h)$
.
If
$p|Q_{i}$
for some
$i \in [1,k]$
, since
$p \nmid A_{i}$
, we have
$\rho _{L_{i}}(p) = 1$
. For
$j\neq i$
and
$1 \leq j \le k$
, as
$p | A_{j}$
and
$p \nmid B_{j}$
, we have
$\rho _{L_{j}}(p) = 0$
. Further, as we assume that
$(h-h_{0},Q)=1$
, we also have
$\rho _{L_{0}}(p) = 0$
.
Since
$\rho _{L}(p)=k+1$
for
$p \nmid D(h)$
, we find that
$$ \begin{align*}\prod_{p \leq x} (1-\rho_L(p)/p) \ll_{k} \frac{g(D(h))^{k+1}}{ (\log x)^{k+1}} \end{align*} $$
since
$$ \begin{align*}\prod_{p \leq x} (1-(k+1)/p) \ll 1/(\log x)^{k+1}\end{align*} $$
and the contribution from primes
$p | D(h)$
is of size
$g(D(h))^{k+1}$
.
Finally, noting that
$\sum _{n \leq x} \frac {f_{1}(n)}{n} = 1 + O(\sum _{p \in [x/2,x]} 1/p) = 1 + O(1/\log x)$
and
$$ \begin{align*}\sum_{n \leq x } f(n)/n \ll \prod_{p \leq x} (1+f(p)/p) \end{align*} $$
the result follows for
$(h-h_{0},Q)=1$
.
The case
$(h-h_{0},Q)>1$
is then easily deduced as follows. First, note that
$f(mn) = f(m) f(n)$
if
$mn|Q$
since
$p \equiv 1\ \pmod 4$
for any prime divisor
$p|Q$
, as in our construction we assumed that each prime divisor of
$Q_i$
is
$\equiv 1\ \pmod 4$
, together with Q being square-free, as well as the estimate
$f(p^{k}) \le f(p) \cdot f(p^{k-1})$
. Letting
$\tilde {L_{0}}(x) = (Q/(h-h_{0},Q)) \cdot x + (h-h_{0})/(h-h_{0},Q)$
, we have
$f(L_{0}(n)) \leq f((h-h_{0},Q)) f(\tilde {L_{0}}(n))$
and we may apply the previous argument to the polynomials
$\tilde {L_{0}}, L_{1}, \ldots , L_{k}$
(note that the two linear polynomials
$L_{0}$
and
$\tilde {L_{0}}$
have the same roots).
To bound the h-sum, define
$f_{Q}(n) = \prod _{p | (Q,n)} f(p)$
, and note, again using Lemma 4.1, that
$$ \begin{align*}\sum_{|h|< H} f((h-h_{0},Q)) g(D(h))^{C+k+1} \ll_{k,W} \sum_{|h|< H} f_{Q}(h-h_{0}) \prod_{i=1}^{k}g(h-h_{i})^{C+k+1} \end{align*} $$
$$ \begin{align*}\ll \frac{H \cdot g(D_{2})^{C}}{(\log H)^{k+1}} \prod_{p<H}(1+f_{Q}(p)/p) ( \prod_{p<H} (1+g(p)^{C+k+1}/p))^{k} \end{align*} $$
$$ \begin{align*}\ll_{k} g(D_{2})^{C} H \ll_{k,W} H (\log \log \log \log x)^{2C}.\\[-36pt] \end{align*} $$
C.4.2 Completing the proof of Lemma C.1
We are now ready to prove Lemma C.1.
Proof of Lemma C.1
With
$g(n) := \prod _{p|n}(1+1/p)$
, note that
$\Delta _{D(h)} = g(D(h))^{C}$
. Using Lemma C.5, we find that
$$ \begin{align*}\sum_{n \in {\mathcal N}_{3}(x)} f(Qn-h_{0}+h) \ll f((h-h_{0},Q)) g( D(h))^{C+k+1} \frac{x}{(\log x)^{k+1}} \prod_{p \le x} (1+f(p)/p) \end{align*} $$
and, for
$H \ge (\log x)^{1/4}$
,
$$ \begin{align*}\sum_{|h|< H} f((h-h_{0},Q)) g(D(h))^{C+k+1} \ll H (\log \log \log \log x)^{2C}. \end{align*} $$
Taking
$f=b$
and
$H = \sqrt {\log x}/U$
, together with Chebyshev’s inequality, gives the desired bound for the first sum.
Taking
$f{\,=\,}r/4$
and using that apart from n in a small subset of
${\mathcal N}_{3}$
,
$b(Qn-h_{0}+h){\,=\,}0$
for
$|h| {\,\le\,} (\log x)^{1/2}/U$
and
$h {\,\not \in\,} \mathcal H$
(from the condition in the first sum), the second bound follows from Lemma C.5 if we use a dyadic decomposition of the h-sum, say for intervals of the form
$[ 2^{i}(\log x)^{1/2}/U, 2^{i+i}(\log x)^{1/2}/U]$
, and then using Chebyshev’s inequality.
For the third sum, again we use that
$b(Qn-h_{0}+h)=0$
for
$|h| \le (\log x)^{1/2}/U$
and
$h \not \in \mathcal H$
which gives, for n outside a small exceptional set, that
$$ \begin{align*}\sum_{|h| \ge U, h \not \in \mathcal H} \frac{r(Qn-h_{0}+h)}{h^{2}} = \sum_{|h| \ge (\log x)^{1/2}/U, h \not \in \mathcal H} \frac{r(Qn-h_{0}+h)}{h^{2}}. \end{align*} $$
Summing over n outside this small subset, the result follows from Lemma C.5 by taking
$f=r/4$
, together with Chebyshev’s inequality. (The sum over h is easily treated by splitting into dyadic intervals.)
Acknowledgements
P.K. was partially supported by the Swedish Research Council (2016-03701,2020-04036). S.L. was partially supported by the Engineering and Physical Sciences Research Council (EP/T028343/1). We would also like to thank Dimitris Koukouloupolos, Stéphane Nonnenmacher, Maksym Radziwiłł, Zeév Rudnick and Steve Zelditch for very helpful discussions and suggestions.
Competing interest
The authors have no competing interest to declare.
Open access
