Article contents
Strichartz estimates for orthonormal families of initial data and weighted oscillatory integral estimates
Published online by Cambridge University Press: 11 January 2021
Abstract
We establish new Strichartz estimates for orthonormal families of initial data in the case of the wave, Klein–Gordon and fractional Schrödinger equations. Our estimates extend those of Frank–Sabin in the case of the wave and Klein–Gordon equations, and generalize work of Frank et al. and Frank–Sabin for the Schrödinger equation. Due to a certain technical barrier, except for the classical Schrödinger equation, the Strichartz estimates for orthonormal families of initial data have not previously been established up to the sharp summability exponents in the full range of admissible pairs. We obtain the optimal estimates in various notable cases and improve the previous results.
The main novelty of this paper is our derivation and use of estimates for weighted oscillatory integrals, which we combine with an approach due to Frank and Sabin. Our weighted oscillatory integral estimates are, in a certain sense, rather delicate endpoint versions of known dispersive estimates with power-type weights of the form 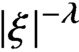 $|\xi |^{-\lambda }$ or
$|\xi |^{-\lambda }$ or 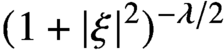 $(1 + |\xi |^2)^{-\lambda /2}$, where
$(1 + |\xi |^2)^{-\lambda /2}$, where 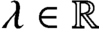 $\lambda \in \mathbb {R}$. We achieve optimal decay rates by considering such weights with appropriate
$\lambda \in \mathbb {R}$. We achieve optimal decay rates by considering such weights with appropriate 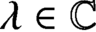 $\lambda \in \mathbb {C}$. For the wave and Klein–Gordon equations, our weighted oscillatory integral estimates are new. For the fractional Schrödinger equation, our results overlap with prior work of Kenig–Ponce–Vega in a certain regime. Our contribution to the theory of weighted oscillatory integrals has also been influenced by earlier work of Carbery–Ziesler, Cowling et al., and Sogge–Stein.
$\lambda \in \mathbb {C}$. For the wave and Klein–Gordon equations, our weighted oscillatory integral estimates are new. For the fractional Schrödinger equation, our results overlap with prior work of Kenig–Ponce–Vega in a certain regime. Our contribution to the theory of weighted oscillatory integrals has also been influenced by earlier work of Carbery–Ziesler, Cowling et al., and Sogge–Stein.
Finally, we provide some applications of our new Strichartz estimates for orthonormal families of data to the theory of infinite systems of Hartree type, weighted velocity averaging lemmas for kinetic transport equations, and refined Strichartz estimates for data in Besov spaces.
- Type
- Differential Equations
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 8
- Cited by



