1 Introduction
1.1 Background
Let k be a field, let G be a p-adic reductive group and let
![]() ${\mathrm {Mod}}_k(G)$
denote the category of smooth k-linear representations of G. The centre
${\mathrm {Mod}}_k(G)$
denote the category of smooth k-linear representations of G. The centre
![]() $\mathfrak {Z}(G)$
of the category
$\mathfrak {Z}(G)$
of the category
![]() ${\mathrm {Mod}}_k(G)$
is called the Bernstein centre of G. When k is the field of complex numbers,
${\mathrm {Mod}}_k(G)$
is called the Bernstein centre of G. When k is the field of complex numbers,
![]() $\mathfrak {Z}(G)$
was studied in detail by Bernstein [Reference Bernstein, Bernstein, Deligne, Kazhdan and VignerasBer] and it plays a fundamental role in the classical local Langlands correspondence. Recently, there has been interest in the case where k is a field of characteristic p motivated by considerations from the p-adic and mod-p Langlands programmes. However, in this case,
$\mathfrak {Z}(G)$
was studied in detail by Bernstein [Reference Bernstein, Bernstein, Deligne, Kazhdan and VignerasBer] and it plays a fundamental role in the classical local Langlands correspondence. Recently, there has been interest in the case where k is a field of characteristic p motivated by considerations from the p-adic and mod-p Langlands programmes. However, in this case,
![]() $\mathfrak {Z}(G)$
turned out to be quite small: In our previous work [Reference Ardakov and SchneiderAS23], we showed that
$\mathfrak {Z}(G)$
turned out to be quite small: In our previous work [Reference Ardakov and SchneiderAS23], we showed that
![]() $\mathfrak {Z}(G)$
only depends on the centre
$\mathfrak {Z}(G)$
only depends on the centre
![]() $Z(G)$
of G and in particular, that
$Z(G)$
of G and in particular, that
![]() $\mathfrak {Z}(G)$
is isomorphic to the finite-dimensional k-algebra
$\mathfrak {Z}(G)$
is isomorphic to the finite-dimensional k-algebra
![]() $k[Z(G)]$
whenever G is assumed to be connected and semisimple.
$k[Z(G)]$
whenever G is assumed to be connected and semisimple.
This situation is reminiscent of the fact that the ring of global regular functions
![]() $\mathcal {O}(X)$
on any projective variety X is also rather small. This observation becomes relevant to the Bernstein centre of G when we recall the work of Gabriel [Reference GabrielGab], who proved that the structure sheaf of a noetherian scheme X can be reconstructed from the category
$\mathcal {O}(X)$
on any projective variety X is also rather small. This observation becomes relevant to the Bernstein centre of G when we recall the work of Gabriel [Reference GabrielGab], who proved that the structure sheaf of a noetherian scheme X can be reconstructed from the category
![]() ${\mathrm {QCoh}}(X)$
of quasi-coherent sheaves on X, by associating with any open subscheme U of X the localising subcategory
${\mathrm {QCoh}}(X)$
of quasi-coherent sheaves on X, by associating with any open subscheme U of X the localising subcategory
![]() $\mathcal {L}_U$
of
$\mathcal {L}_U$
of
![]() ${\mathrm {QCoh}}(X)$
consisting of sheaves supported on the complement of U in X and by showing that the ring
${\mathrm {QCoh}}(X)$
consisting of sheaves supported on the complement of U in X and by showing that the ring
![]() $\mathcal {O}(U)$
can be recovered from
$\mathcal {O}(U)$
can be recovered from
![]() ${\mathrm {QCoh}}(X)$
as the centre of the quotient category
${\mathrm {QCoh}}(X)$
as the centre of the quotient category
![]() ${\mathrm {QCoh}}(X) / \mathcal {L}_U$
. In our recent work [Reference Ardakov and SchneiderAS24], we generalised Gabriel’s construction to the case of an arbitrary Grothendieck category
${\mathrm {QCoh}}(X) / \mathcal {L}_U$
. In our recent work [Reference Ardakov and SchneiderAS24], we generalised Gabriel’s construction to the case of an arbitrary Grothendieck category
![]() $\mathcal {C}$
, as follows.
$\mathcal {C}$
, as follows.
Recall that the localising subcategory
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\mathcal {C}$
is said to be stable if it is stable under essential extensions. The set
$\mathcal {C}$
is said to be stable if it is stable under essential extensions. The set
![]() $\mathbf {L}^{st}(\mathcal {C})$
of stable localising subcategories of
$\mathbf {L}^{st}(\mathcal {C})$
of stable localising subcategories of
![]() $\mathcal {C}$
forms a partially ordered set under reverse inclusion. For
$\mathcal {C}$
forms a partially ordered set under reverse inclusion. For
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {L}_1,\cdots ,\mathcal {L}_n$
in
$\mathcal {L}_1,\cdots ,\mathcal {L}_n$
in
![]() $\mathbf {L}^{st}(\mathcal {C})$
, we call
$\mathbf {L}^{st}(\mathcal {C})$
, we call
![]() $\{\mathcal {L}_i\}_{1 \leq i \leq n}$
a covering of
$\{\mathcal {L}_i\}_{1 \leq i \leq n}$
a covering of
![]() $\mathcal {L}$
if
$\mathcal {L}$
if
![]() $\mathcal {L} = \bigcap _i \mathcal {L}_i$
. This notion makes
$\mathcal {L} = \bigcap _i \mathcal {L}_i$
. This notion makes
![]() $\mathbf {L}^{st}(\mathcal {C})$
into a Grothendieck site, and we proved in [Reference Ardakov and SchneiderAS24] Theorem 1.1 that the presheaf
$\mathbf {L}^{st}(\mathcal {C})$
into a Grothendieck site, and we proved in [Reference Ardakov and SchneiderAS24] Theorem 1.1 that the presheaf
![]() $\mathcal {L} \mapsto Z(\mathcal {C}/\mathcal {L})$
on
$\mathcal {L} \mapsto Z(\mathcal {C}/\mathcal {L})$
on
![]() $\mathbf {L}^{st}(\mathcal {C})$
is in fact a sheaf. When the category
$\mathbf {L}^{st}(\mathcal {C})$
is in fact a sheaf. When the category
![]() $\mathcal {C}$
is additionally assumed to be locally noetherian, we showed that there is an order-reversing bijection
$\mathcal {C}$
is additionally assumed to be locally noetherian, we showed that there is an order-reversing bijection
![]() $U \mapsto \mathcal {L}_U$
between the so-called stable subsets of the injective spectrum
$U \mapsto \mathcal {L}_U$
between the so-called stable subsets of the injective spectrum
![]() $\mathbf {Sp}(\mathcal {C})$
of
$\mathbf {Sp}(\mathcal {C})$
of
![]() $\mathcal {C}$
, and
$\mathcal {C}$
, and
![]() $\mathbf {L}^{st}(\mathcal {C})$
. We showed in [Reference Ardakov and SchneiderAS24] Theorem 1.2 that the corresponding presheaf
$\mathbf {L}^{st}(\mathcal {C})$
. We showed in [Reference Ardakov and SchneiderAS24] Theorem 1.2 that the corresponding presheaf
![]() $U \mapsto Z(\mathcal {C}/\mathcal {L}_U)$
on
$U \mapsto Z(\mathcal {C}/\mathcal {L}_U)$
on
![]() $\mathbf {Sp}(\mathcal {C})$
satisfies the sheaf condition with respect to arbitrary coverings. These results suggest that, even though
$\mathbf {Sp}(\mathcal {C})$
satisfies the sheaf condition with respect to arbitrary coverings. These results suggest that, even though
![]() $Z({\mathrm {Mod}}_k(G))$
may be small and uninteresting, this only reflects the fact that this centre is the ring of global sections of the sheaf formed by the centres of the quotient categories of
$Z({\mathrm {Mod}}_k(G))$
may be small and uninteresting, this only reflects the fact that this centre is the ring of global sections of the sheaf formed by the centres of the quotient categories of
![]() ${\mathrm {Mod}}_k(G)$
. Of course, this sheaf is only interesting if one can write down sufficiently many stable localising subcategories of
${\mathrm {Mod}}_k(G)$
. Of course, this sheaf is only interesting if one can write down sufficiently many stable localising subcategories of
![]() ${\mathrm {Mod}}_k(G)$
.
${\mathrm {Mod}}_k(G)$
.
1.2 Main results
The main goal in this paper is to construct a large family of stable localising subcategories of
![]() ${\mathrm {Mod}}_k(G)$
in the case where
${\mathrm {Mod}}_k(G)$
in the case where
![]() $p \geq 5$
and G is the group
$p \geq 5$
and G is the group
![]() ${\mathrm {SL}}_2(\mathbb {Q}_p)$
. In order to state our results, it will be convenient to introduce an axiomatic framework as follows. Let
${\mathrm {SL}}_2(\mathbb {Q}_p)$
. In order to state our results, it will be convenient to introduce an axiomatic framework as follows. Let
![]() $\mathcal {A}$
be a full abelian subcategory of a locally noetherian Grothendieck category
$\mathcal {A}$
be a full abelian subcategory of a locally noetherian Grothendieck category
![]() $\mathcal {C}$
. We say that
$\mathcal {C}$
. We say that
![]() $\mathcal {C}$
is a thickening of
$\mathcal {C}$
is a thickening of
![]() $\mathcal {A}$
if, roughly speaking,Footnote
1
every noetherian object in
$\mathcal {A}$
if, roughly speaking,Footnote
1
every noetherian object in
![]() $\mathcal {C}$
has a finite filtration all of whose subquotients lie in
$\mathcal {C}$
has a finite filtration all of whose subquotients lie in
![]() $\mathcal {A}$
, and the inclusion functor
$\mathcal {A}$
, and the inclusion functor
![]() $i : \mathcal {A} \to \mathcal {C}$
has a left exact right adjoint
$i : \mathcal {A} \to \mathcal {C}$
has a left exact right adjoint
![]() $r : \mathcal {C} \to \mathcal {A}$
which restricts to the identity functor on
$r : \mathcal {C} \to \mathcal {A}$
which restricts to the identity functor on
![]() $\mathcal {A}$
and which respects nonzero objects in
$\mathcal {A}$
and which respects nonzero objects in
![]() $\mathcal {C}$
. We prove that r induces a bijection
$\mathcal {C}$
. We prove that r induces a bijection
![]() $r : \mathbf {Sp}(\mathcal {C}) \stackrel {\cong }{\longrightarrow } \mathbf {Sp}(\mathcal {A})$
between the corresponding injective spectra and that the map
$r : \mathbf {Sp}(\mathcal {C}) \stackrel {\cong }{\longrightarrow } \mathbf {Sp}(\mathcal {A})$
between the corresponding injective spectra and that the map
![]() $\mathcal {L} \mapsto \mathcal {L} \cap \mathcal {A}$
defines a bijection between the set of localising subcategories of
$\mathcal {L} \mapsto \mathcal {L} \cap \mathcal {A}$
defines a bijection between the set of localising subcategories of
![]() $\mathcal {C}$
and the set of localising subcategories of
$\mathcal {C}$
and the set of localising subcategories of
![]() $\mathcal {A}$
. The bijection
$\mathcal {A}$
. The bijection
![]() $r : \mathbf {Sp}(\mathcal {C}) \stackrel {\cong }{\longrightarrow } \mathbf {Sp}(\mathcal {A})$
respects stable subsets and therefore induces an injective map
$r : \mathbf {Sp}(\mathcal {C}) \stackrel {\cong }{\longrightarrow } \mathbf {Sp}(\mathcal {A})$
respects stable subsets and therefore induces an injective map
![]() $\mathbf {r}: \mathbf {L}^{st}(\mathcal {C}) \to {\mathbf {L}}^{st}(\mathcal {A})$
; however,
$\mathbf {r}: \mathbf {L}^{st}(\mathcal {C}) \to {\mathbf {L}}^{st}(\mathcal {A})$
; however,
![]() $\mathbf {r}$
is in general not surjective.
$\mathbf {r}$
is in general not surjective.
Example 1.2.1. Let
![]() $G = {\mathrm {SL}}_2(\mathbb {Q}_p)$
,and let I be the pro-p Iwahori subgroup of G. Let
$G = {\mathrm {SL}}_2(\mathbb {Q}_p)$
,and let I be the pro-p Iwahori subgroup of G. Let
![]() ${\mathrm {Mod}}_k^I(G)$
denote the full subcategory of
${\mathrm {Mod}}_k^I(G)$
denote the full subcategory of
![]() ${\mathrm {Mod}}_k(G)$
whose objects are generated by their I-fixed vectors, and let
${\mathrm {Mod}}_k(G)$
whose objects are generated by their I-fixed vectors, and let
![]() $r(V) = k[G] \cdot V^I$
for all V in
$r(V) = k[G] \cdot V^I$
for all V in
![]() ${\mathrm {Mod}}_k(G)$
. We show in
${\mathrm {Mod}}_k(G)$
. We show in
![]() $\S $
2.1 below that
$\S $
2.1 below that
![]() ${\mathrm {Mod}}_k(G)$
is a thickening of
${\mathrm {Mod}}_k(G)$
is a thickening of
![]() ${\mathrm {Mod}}_k^I(G)$
and moreover that the compactly induced representation
${\mathrm {Mod}}_k^I(G)$
and moreover that the compactly induced representation
![]() ${\mathrm {ind}}_I^G(k)$
is in fact a noetherian projective generator of
${\mathrm {ind}}_I^G(k)$
is in fact a noetherian projective generator of
![]() ${\mathrm {Mod}}_k^I(G)$
.
${\mathrm {Mod}}_k^I(G)$
.
Returning to our axiomatic framework, we assume in addition that
![]() $\mathcal {A}$
has a noetherian projective generator P. The functor
$\mathcal {A}$
has a noetherian projective generator P. The functor
![]() ${\mathrm {Hom}}_{\mathcal {A}}(P,-):\mathcal {A} \to {\mathrm {Mod}}(H)$
is then an equivalence of categories with quasi-inverse
${\mathrm {Hom}}_{\mathcal {A}}(P,-):\mathcal {A} \to {\mathrm {Mod}}(H)$
is then an equivalence of categories with quasi-inverse
![]() $P \otimes _H - : {\mathrm {Mod}}(H) \to \mathcal {A}$
, where
$P \otimes _H - : {\mathrm {Mod}}(H) \to \mathcal {A}$
, where
![]() $H := {\mathrm {End}}_{\mathcal {A}}(P)^{{\mathrm {op}}}$
, and in Theorem 3.5.8 we show that the image of
$H := {\mathrm {End}}_{\mathcal {A}}(P)^{{\mathrm {op}}}$
, and in Theorem 3.5.8 we show that the image of
![]() $\mathbf {r}$
consists precisely of those localising subcategories of
$\mathbf {r}$
consists precisely of those localising subcategories of
![]() $\mathcal {A}$
that are preserved under the functor
$\mathcal {A}$
that are preserved under the functor
![]() $P \otimes _H {\mathrm {Ext}}^1_{\mathcal {C}}(P,-) : \mathcal {A} \to \mathcal {A}$
. To understand this condition better we introduce the graded
$P \otimes _H {\mathrm {Ext}}^1_{\mathcal {C}}(P,-) : \mathcal {A} \to \mathcal {A}$
. To understand this condition better we introduce the graded
![]() $(H,H)$
-bimodule
$(H,H)$
-bimodule
 $$ \begin{align} {\mathrm{Ext}}_{\mathcal{C}}^*(P,P) := \bigoplus_{i=0}^\infty {\mathrm{Ext}}_{\mathcal{C}}^i(P,P) \end{align} $$
$$ \begin{align} {\mathrm{Ext}}_{\mathcal{C}}^*(P,P) := \bigoplus_{i=0}^\infty {\mathrm{Ext}}_{\mathcal{C}}^i(P,P) \end{align} $$
which is in particular a module for
![]() $Z \otimes Z := Z \otimes _{\mathbb {Z}} Z$
, where
$Z \otimes Z := Z \otimes _{\mathbb {Z}} Z$
, where
![]() $Z := Z(H)$
is the centre of H. We let
$Z := Z(H)$
is the centre of H. We let
![]() $\mathcal {J} := {\mathrm {Ann}}_{Z \otimes Z}({\mathrm {Ext}}_{\mathcal {C}}^*(P,P))$
be its annihilator ideal and
$\mathcal {J} := {\mathrm {Ann}}_{Z \otimes Z}({\mathrm {Ext}}_{\mathcal {C}}^*(P,P))$
be its annihilator ideal and
![]() $\mathcal {R} := V(\mathcal {J}) \subseteq {\mathrm {Spec}}(Z \otimes Z)$
be the corresponding Zariski closed subset. Let
$\mathcal {R} := V(\mathcal {J}) \subseteq {\mathrm {Spec}}(Z \otimes Z)$
be the corresponding Zariski closed subset. Let
![]() $\pi _1, \pi _2 : \mathcal {R} \rightarrow \Xi := {\mathrm {Spec}}(Z)$
denote the restrictions of the two projection maps
$\pi _1, \pi _2 : \mathcal {R} \rightarrow \Xi := {\mathrm {Spec}}(Z)$
denote the restrictions of the two projection maps
![]() ${\mathrm {Spec}}(Z \otimes Z) \rightrightarrows \Xi $
. We then have a coequaliser diagram
${\mathrm {Spec}}(Z \otimes Z) \rightrightarrows \Xi $
. We then have a coequaliser diagram
in the category of locally ringed spaces (cf. [Reference Demazure and GabrielDG] Proposition I.1.1.6). To state our main theorem, we introduce the map
![]() $\tau : \mathbf {Sp}(\mathcal {C}) \to \Xi /\mathcal {R}$
by the commutativity of the following diagram:
$\tau : \mathbf {Sp}(\mathcal {C}) \to \Xi /\mathcal {R}$
by the commutativity of the following diagram:

The first vertical arrow on the left comes from the equivalence
![]() ${\mathrm {Hom}}_{\mathcal {A}}(P,-) : \mathcal {A} \stackrel {\cong }{\longrightarrow } {\mathrm {Mod}}(H)$
, and the map
${\mathrm {Hom}}_{\mathcal {A}}(P,-) : \mathcal {A} \stackrel {\cong }{\longrightarrow } {\mathrm {Mod}}(H)$
, and the map
![]() $\varphi $
is given by
$\varphi $
is given by
![]() $\varphi (P) = P \cap Z$
for all
$\varphi (P) = P \cap Z$
for all
![]() $P \in {\mathrm {Spec}}(H)$
. The second vertical arrow comes from [Reference GabrielGab] V
$P \in {\mathrm {Spec}}(H)$
. The second vertical arrow comes from [Reference GabrielGab] V
![]() $\S $
4; it is a bijection if H is finitely generated as a module over its centre. Our first main result is then the following
$\S $
4; it is a bijection if H is finitely generated as a module over its centre. Our first main result is then the following
Theorem 1.2.2 (Proposition 3.7.4).
Let
![]() $\mathcal {C}$
be a thickening of
$\mathcal {C}$
be a thickening of
![]() $\mathcal {A}$
. Suppose that
$\mathcal {A}$
. Suppose that
![]() $\mathcal {A}$
has a noetherian projective generator P, and let
$\mathcal {A}$
has a noetherian projective generator P, and let
![]() $H = {\mathrm {End}}_{\mathcal {A}}(P)^{{\mathrm {op}}}$
. Assume furthermore that:
$H = {\mathrm {End}}_{\mathcal {A}}(P)^{{\mathrm {op}}}$
. Assume furthermore that:
-
(A1) H is finitely generated as a module over its centre Z,
-
(A2) there is an integer d such that
 ${\mathrm {Ext}}_{\mathcal {C}}^j(P,-)|_{\mathcal {A}} = 0$
for any
${\mathrm {Ext}}_{\mathcal {C}}^j(P,-)|_{\mathcal {A}} = 0$
for any
 $j> d$
and
$j> d$
and -
(A3)
 $Z \otimes Z/\mathcal {J}^{d+1}$
is noetherian.
$Z \otimes Z/\mathcal {J}^{d+1}$
is noetherian.
Then
![]() $\tau : \mathbf {Sp}(\mathcal {C}) \to \Xi /\mathcal {R}$
is continuous with respect to the stable topologies.
$\tau : \mathbf {Sp}(\mathcal {C}) \to \Xi /\mathcal {R}$
is continuous with respect to the stable topologies.
In this generality,
![]() $\Xi /\mathcal {R}$
is just a locally ringed space and
$\Xi /\mathcal {R}$
is just a locally ringed space and
![]() $\tau $
is only a surjective map. Section
$\tau $
is only a surjective map. Section
![]() $\S$
4 of our paper is devoted to the computation of
$\S$
4 of our paper is devoted to the computation of
![]() $\Xi /\mathcal {R}$
in the situation of Example 1.2.1 above, relying crucially on the calculations of [Reference Ollivier and SchneiderOS22] on the structure of the pro-p Iwahori
$\Xi /\mathcal {R}$
in the situation of Example 1.2.1 above, relying crucially on the calculations of [Reference Ollivier and SchneiderOS22] on the structure of the pro-p Iwahori
![]() ${\mathrm {Ext}}$
-algebra (1). Our second main result is then the following
${\mathrm {Ext}}$
-algebra (1). Our second main result is then the following
Theorem 1.2.3 (Theorem 4.5.23, Corollary 4.5.24).
Suppose that
![]() $p \geq 5$
,
$p \geq 5$
,
![]() $G = {\mathrm {SL}}_2(\mathbb {Q}_p)$
,
$G = {\mathrm {SL}}_2(\mathbb {Q}_p)$
,
![]() $\mathcal {C} = {\mathrm {Mod}}_k(G)$
and
$\mathcal {C} = {\mathrm {Mod}}_k(G)$
and
![]() $\mathcal {A} = {\mathrm {Mod}}_k^I(G)$
.
$\mathcal {A} = {\mathrm {Mod}}_k^I(G)$
.
-
a)
 $\Xi /\mathcal {R}$
is a scheme.
$\Xi /\mathcal {R}$
is a scheme. -
b)
 $\Xi /\mathcal {R}$
has two connected components.
$\Xi /\mathcal {R}$
has two connected components. -
c) Each connected component of
 $\Xi /\mathcal {R}$
is a chain of projective lines.
$\Xi /\mathcal {R}$
is a chain of projective lines.
Example 1.2.4. When
![]() $p = 13$
, the scheme
$p = 13$
, the scheme
![]() $\Xi /\mathcal {R}$
looks as follows:
$\Xi /\mathcal {R}$
looks as follows:

In Example 4.5.25 below, we sketch how to obtain this gluing from the scheme
![]() $\Xi $
.
$\Xi $
.
Corollary 1.2.5. Let
![]() $p \geq 5$
, and let
$p \geq 5$
, and let
![]() $G = {\mathrm {SL}}_2(\mathbb {Q}_p)$
. For every Zariski open subset U of
$G = {\mathrm {SL}}_2(\mathbb {Q}_p)$
. For every Zariski open subset U of
![]() $\Xi /\mathcal {R}$
,
$\Xi /\mathcal {R}$
,
![]() $\tau ^{-1}(U)$
is a stable open subset of
$\tau ^{-1}(U)$
is a stable open subset of
![]() $\mathbf {Sp}({\mathrm {Mod}}_k(G))$
.
$\mathbf {Sp}({\mathrm {Mod}}_k(G))$
.
Proof. This follows from Theorem 1.2.2, once we verify its conditions. Note that
![]() $\mathcal {C} = {\mathrm {Mod}}_k(G)$
is a thickening of
$\mathcal {C} = {\mathrm {Mod}}_k(G)$
is a thickening of
![]() $\mathcal {A} = {\mathrm {Mod}}_k^I(G)$
and that
$\mathcal {A} = {\mathrm {Mod}}_k^I(G)$
and that
![]() $P = {\mathrm {ind}}_I^G(k)$
is a noetherian projective generator of
$P = {\mathrm {ind}}_I^G(k)$
is a noetherian projective generator of
![]() $\mathcal {A}$
by Example 1.2.1.
$\mathcal {A}$
by Example 1.2.1.
(A1). The pro-p Iwahori–Hecke algebra
![]() $H = {\mathrm {End}}_{\mathcal {C}}(P)^{{\mathrm {op}}}$
is finitely generated as a module over its centre by [Reference VignérasVig]; see also [Reference Ollivier and SchneiderOS18] Corrollary 3.4 and Remark 3.5.
$H = {\mathrm {End}}_{\mathcal {C}}(P)^{{\mathrm {op}}}$
is finitely generated as a module over its centre by [Reference VignérasVig]; see also [Reference Ollivier and SchneiderOS18] Corrollary 3.4 and Remark 3.5.
(A2). Since
![]() $p \geq 5$
, the group I has no elements of order p and therefore has finite p-cohomological dimension equal to
$p \geq 5$
, the group I has no elements of order p and therefore has finite p-cohomological dimension equal to
![]() $3$
, the dimension of I as a p-adic Lie group. Using Frobenius reciprocity, we see that for all V in
$3$
, the dimension of I as a p-adic Lie group. Using Frobenius reciprocity, we see that for all V in
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
(A3). In view of Remark 3.7.5 below, we may replace
![]() $\textbf {(A3)}$
by the weaker assumption that
$\textbf {(A3)}$
by the weaker assumption that
![]() $Z \otimes _k Z$
is noetherian because
$Z \otimes _k Z$
is noetherian because
![]() $\mathcal {C}$
happens to be a k-linear category. Proposition 4.1.5 and Equation (11) imply that Z is finitely generated as a k-algebra. Hence,
$\mathcal {C}$
happens to be a k-linear category. Proposition 4.1.5 and Equation (11) imply that Z is finitely generated as a k-algebra. Hence,
![]() $Z \otimes _k Z$
is noetherian, by Hilbert’s basis theorem.
$Z \otimes _k Z$
is noetherian, by Hilbert’s basis theorem.
The paper [Reference Dotto, Emerton and GeeDEG] considers, for the group
![]() $G = GL_2(\mathbb {Q}_p)$
, the full subcategory
$G = GL_2(\mathbb {Q}_p)$
, the full subcategory
![]() ${\mathrm {Mod}}_{k,\zeta }(G)$
of those representations in
${\mathrm {Mod}}_{k,\zeta }(G)$
of those representations in
![]() ${\mathrm {Mod}}_k(G)$
which have a fixed central character
${\mathrm {Mod}}_k(G)$
which have a fixed central character
![]() $\zeta $
. They associate with this subcategory a scheme X which is also a chain of projective lines. This scheme is definitively the analogue of a connected component of our quotient space
$\zeta $
. They associate with this subcategory a scheme X which is also a chain of projective lines. This scheme is definitively the analogue of a connected component of our quotient space
![]() $\Xi /\mathcal {R}$
in this situation. But the idea of [Reference Dotto, Emerton and GeeDEG] behind X is completely different: X is viewed as a kind of moduli space of two-dimensional semisimple Galois representations modulo p. From this point of view, the relation between X and the representation theory of G comes from Breuil’s semisimple Langlands correspondence modulo p. Still another approach to the space X is given in [Reference Pépin and SchmidtPS]. The paper [Reference Dotto, Emerton and GeeDEG] also develops a localisation theory for the category
$\Xi /\mathcal {R}$
in this situation. But the idea of [Reference Dotto, Emerton and GeeDEG] behind X is completely different: X is viewed as a kind of moduli space of two-dimensional semisimple Galois representations modulo p. From this point of view, the relation between X and the representation theory of G comes from Breuil’s semisimple Langlands correspondence modulo p. Still another approach to the space X is given in [Reference Pépin and SchmidtPS]. The paper [Reference Dotto, Emerton and GeeDEG] also develops a localisation theory for the category
![]() ${\mathrm {Mod}}_{k,\zeta }(G)$
and shows that the closed points of X parameterize the blocks of the Krull-dimension
${\mathrm {Mod}}_{k,\zeta }(G)$
and shows that the closed points of X parameterize the blocks of the Krull-dimension
![]() $0$
subcategory of
$0$
subcategory of
![]() ${\mathrm {Mod}}_{k,\zeta }(G)$
. We emphasize that in the present paper we work entirely on the representation theoretic side of the full category
${\mathrm {Mod}}_{k,\zeta }(G)$
. We emphasize that in the present paper we work entirely on the representation theoretic side of the full category
![]() ${\mathrm {Mod}}_k(G)$
, and our quotient space
${\mathrm {Mod}}_k(G)$
, and our quotient space
![]() $\Xi /\mathcal {R}$
arises from the nonvanishing (and the structure) of universal
$\Xi /\mathcal {R}$
arises from the nonvanishing (and the structure) of universal
![]() ${\mathrm {Ext}}$
-groups. We therefore like to think that these approaches complement each other in an interesting way.
${\mathrm {Ext}}$
-groups. We therefore like to think that these approaches complement each other in an interesting way.
2 Basic facts about the category
 ${\mathrm {Mod}}_k(G)$
${\mathrm {Mod}}_k(G)$
We fix a field k of characteristic
![]() $p> 0$
. For any locally compact and totally disconnected group
$p> 0$
. For any locally compact and totally disconnected group
![]() $\mathcal {G}$
, we denote by
$\mathcal {G}$
, we denote by
![]() ${\mathrm {Mod}}_k(\mathcal {G})$
the abelian category of smooth
${\mathrm {Mod}}_k(\mathcal {G})$
the abelian category of smooth
![]() $\mathcal {G}$
-representations on k-vector spaces. Let
$\mathcal {G}$
-representations on k-vector spaces. Let
![]() $G = SL_2(\mathbb {Q}_p)$
. We fix the pro-p Iwahori subgroup
$G = SL_2(\mathbb {Q}_p)$
. We fix the pro-p Iwahori subgroup
![]() $I \subseteq SL_2(\mathbb {Z}_p)$
of all matrices which are upper triangular unipotent mod p.
$I \subseteq SL_2(\mathbb {Z}_p)$
of all matrices which are upper triangular unipotent mod p.
2.1 Locally noetherian
Let
![]() ${\mathrm {Mod}}_k^I(G)$
denote the full subcategory of all V in
${\mathrm {Mod}}_k^I(G)$
denote the full subcategory of all V in
![]() ${\mathrm {Mod}}_k(G)$
which are generated by their pro-p Iwahori fixed vectors
${\mathrm {Mod}}_k(G)$
which are generated by their pro-p Iwahori fixed vectors
![]() $V^I$
. Write
$V^I$
. Write
![]() $H := {\mathrm {End}}_{k[G]}(k[G/I])^{{\mathrm {op}}}$
.
$H := {\mathrm {End}}_{k[G]}(k[G/I])^{{\mathrm {op}}}$
.
Theorem 2.1.1. The functor
 $$ \begin{align*} {\mathrm{Mod}}_k^I(G) & \xrightarrow{\;\simeq\;} {\mathrm{Mod}}(H) \\ V & \longmapsto V^I \end{align*} $$
$$ \begin{align*} {\mathrm{Mod}}_k^I(G) & \xrightarrow{\;\simeq\;} {\mathrm{Mod}}(H) \\ V & \longmapsto V^I \end{align*} $$
is an equivalence of categories with quasi-inverse
![]() $M \longmapsto k[G/I] \otimes _{H} M$
. Moreover,
$M \longmapsto k[G/I] \otimes _{H} M$
. Moreover,
![]() $k[G/I]$
is projective and faithfully flat as an H-module.
$k[G/I]$
is projective and faithfully flat as an H-module.
Proof. [Reference KoziolKoz] and [Reference Ollivier and SchneiderOS18] Proposition 3.25 and its proof.
Lemma 2.1.2.
![]() ${\mathrm {Mod}}_k^I(G)$
is an abelian subcategory of
${\mathrm {Mod}}_k^I(G)$
is an abelian subcategory of
![]() ${\mathrm {Mod}}_k(G)$
closed under the formation of subobjects, quotient objects and arbitrary colimits.
${\mathrm {Mod}}_k(G)$
closed under the formation of subobjects, quotient objects and arbitrary colimits.
Proof. Clearly,
![]() ${\mathrm {Mod}}_k^I(G)$
is closed under the formation of arbitrary direct sums. Let
${\mathrm {Mod}}_k^I(G)$
is closed under the formation of arbitrary direct sums. Let
![]() $0 \rightarrow V_0 \rightarrow V_1 \rightarrow V_2 \rightarrow 0$
be an exact sequence in
$0 \rightarrow V_0 \rightarrow V_1 \rightarrow V_2 \rightarrow 0$
be an exact sequence in
![]() ${\mathrm {Mod}}_k(G)$
such that
${\mathrm {Mod}}_k(G)$
such that
![]() $V_1$
lies in
$V_1$
lies in
![]() ${\mathrm {Mod}}_k^I(G)$
. Obviously, then also
${\mathrm {Mod}}_k^I(G)$
. Obviously, then also
![]() $V_2$
lies in
$V_2$
lies in
![]() ${\mathrm {Mod}}_k^I(G)$
. For
${\mathrm {Mod}}_k^I(G)$
. For
![]() $V_0$
, we consider the commutative diagram
$V_0$
, we consider the commutative diagram

The upper horizontal row is exact by the left exactness of the functor
![]() $(-)^I$
and the fact that
$(-)^I$
and the fact that
![]() $k[G/I]$
is flat as a (right) H-module. By the category equivalence in Theorem 2.1.1, the middle and right perpendicular arrows are isomorphisms. Hence, the left one is an isomorphism as well. This shows that
$k[G/I]$
is flat as a (right) H-module. By the category equivalence in Theorem 2.1.1, the middle and right perpendicular arrows are isomorphisms. Hence, the left one is an isomorphism as well. This shows that
![]() $V_0$
lies in
$V_0$
lies in
![]() ${\mathrm {Mod}}_k^I(G)$
.
${\mathrm {Mod}}_k^I(G)$
.
The k-algebra H is finitely generated as a module over its centre, which is a finitely generated k-algebra ([Reference VignérasVig] or, in an explicit form, [Reference Ollivier and SchneiderOS18] Corollary 3.4 and Remark 3.5), and hence noetherian. Therefore, the abelian category
![]() ${\mathrm {Mod}}(H)$
is locally noetherian Grothendieck.
${\mathrm {Mod}}(H)$
is locally noetherian Grothendieck.
Lemma 2.1.3. Let
![]() $\mathcal {G}$
be any locally compact and totally disconnected group with an open pro-p subgroup J. Any finitely generated
$\mathcal {G}$
be any locally compact and totally disconnected group with an open pro-p subgroup J. Any finitely generated
![]() $\mathcal {G}$
-representation V in
$\mathcal {G}$
-representation V in
![]() ${\mathrm {Mod}}_k(\mathcal {G})$
has a finite filtration
${\mathrm {Mod}}_k(\mathcal {G})$
has a finite filtration
![]() $\{0\} \subset V_1 \subset \ldots \subset V_\ell = V$
by subrepresentations such that each subquotient
$\{0\} \subset V_1 \subset \ldots \subset V_\ell = V$
by subrepresentations such that each subquotient
![]() $V_i /V_{i-1}$
, for
$V_i /V_{i-1}$
, for
![]() $0 < i \leq \ell $
, is generated by finitely many J-fixed vectors.
$0 < i \leq \ell $
, is generated by finitely many J-fixed vectors.
Proof. It suffices to consider the case where V is generated by a single vector v. We can then find an open normal subgroup
![]() $N \subseteq J$
such that N fixes v. Then V is a quotient of the
$N \subseteq J$
such that N fixes v. Then V is a quotient of the
![]() $\mathcal {G}$
-representation
$\mathcal {G}$
-representation
![]() $k[\mathcal {G}/N]$
. Hence, it actually suffices to consider the case
$k[\mathcal {G}/N]$
. Hence, it actually suffices to consider the case
![]() $V = k[\mathcal {G}/N]$
. In V, we then have the J-subrepresentation
$V = k[\mathcal {G}/N]$
. In V, we then have the J-subrepresentation
![]() $k[J/N]$
. Let
$k[J/N]$
. Let
![]() $\mathfrak {m}$
denote the augmentation ideal of the ring
$\mathfrak {m}$
denote the augmentation ideal of the ring
![]() $k[J/N]$
. Since
$k[J/N]$
. Since
![]() $J/N$
is a finite p-group, we find an integer
$J/N$
is a finite p-group, we find an integer
![]() $\ell \geq 0$
such that
$\ell \geq 0$
such that
![]() $\mathfrak {m}^\ell = 0$
. Observe that J acts trivially on each subquotient
$\mathfrak {m}^\ell = 0$
. Observe that J acts trivially on each subquotient
![]() $\mathfrak {m}^i / \mathfrak {m}^{i+1}$
. We now define
$\mathfrak {m}^i / \mathfrak {m}^{i+1}$
. We now define
![]() $V_i \subseteq V$
as the
$V_i \subseteq V$
as the
![]() $\mathcal {G}$
-subrepresentation generated by
$\mathcal {G}$
-subrepresentation generated by
![]() $\mathfrak {m}^{\ell - i}$
. The subquotient
$\mathfrak {m}^{\ell - i}$
. The subquotient
![]() $V_i /V_{i-1}$
then is generated by the image of
$V_i /V_{i-1}$
then is generated by the image of
![]() $\mathfrak {m}^{\ell - i} / \mathfrak {m}^{(\ell - i)+1}$
, which is contained in
$\mathfrak {m}^{\ell - i} / \mathfrak {m}^{(\ell - i)+1}$
, which is contained in
![]() $(V_i/V_{i-1})^J$
.
$(V_i/V_{i-1})^J$
.
Proposition 2.1.4. The abelian category
![]() ${\mathrm {Mod}}_k(G)$
is locally noetherian.
${\mathrm {Mod}}_k(G)$
is locally noetherian.
Proof. By Lemma 1(iv) [Reference SchneiderSch],
![]() ${\mathrm {Mod}}_k(G)$
is a Grothendieck category. We have to show that any finitely generated G-representation V in
${\mathrm {Mod}}_k(G)$
is a Grothendieck category. We have to show that any finitely generated G-representation V in
![]() ${\mathrm {Mod}}_k(G)$
is noetherian. Lemma 2.1.3 reduces us to the case that V is generated by finitely many I-fixed vectors. According to Lemma 2.1.2, any increasing chain of G-subrepresentations of V already lies in
${\mathrm {Mod}}_k(G)$
is noetherian. Lemma 2.1.3 reduces us to the case that V is generated by finitely many I-fixed vectors. According to Lemma 2.1.2, any increasing chain of G-subrepresentations of V already lies in
![]() ${\mathrm {Mod}}_k^I(G)$
. By Theorem 2.1.1, it therefore corresponds to a chain in the finitely generated H-module
${\mathrm {Mod}}_k^I(G)$
. By Theorem 2.1.1, it therefore corresponds to a chain in the finitely generated H-module
![]() $V^I$
. Hence, it must become stationary.
$V^I$
. Hence, it must become stationary.
The exact inclusion functor
![]() ${\mathrm {Mod}}_k^I(G) \subseteq {\mathrm {Mod}}_k(G)$
is left adjoint to the left exact functor
${\mathrm {Mod}}_k^I(G) \subseteq {\mathrm {Mod}}_k(G)$
is left adjoint to the left exact functor
 $$ \begin{align*} {\mathrm{Mod}}_k(G) & \longrightarrow {\mathrm{Mod}}_k^I(G) \\ V & \longmapsto V(I) := G\text{-subrepresentation of}\ V\ \text{generated by}\ V^I (\cong k[G/I] \otimes_{H} V^I) . \end{align*} $$
$$ \begin{align*} {\mathrm{Mod}}_k(G) & \longrightarrow {\mathrm{Mod}}_k^I(G) \\ V & \longmapsto V(I) := G\text{-subrepresentation of}\ V\ \text{generated by}\ V^I (\cong k[G/I] \otimes_{H} V^I) . \end{align*} $$
Lemma 2.1.5. The functor
![]() $V \mapsto V(I)$
$V \mapsto V(I)$
-
a) restricts to the identity functor on
 ${\mathrm {Mod}}_k^I(G)$
,
${\mathrm {Mod}}_k^I(G)$
, -
b) respects nonzero objects,
-
c) respects injective objects and
-
d) commutes with arbitrary filtered colimits.
Proof. a) is obvious. b) holds since I is pro-p. c) is a consequence of the functor being right adjoint to a (left) exact functor. For d), let
![]() $V = \varinjlim _j V_j$
be a filtered colimit in
$V = \varinjlim _j V_j$
be a filtered colimit in
![]() ${\mathrm {Mod}}_k(G)$
. Since filtered colimits are exact in the Grothendieck category
${\mathrm {Mod}}_k(G)$
. Since filtered colimits are exact in the Grothendieck category
![]() ${\mathrm {Mod}}_k(G)$
, we have the inclusion
${\mathrm {Mod}}_k(G)$
, we have the inclusion
![]() $\varinjlim _j V_j(I) \subseteq V(I)$
. But
$\varinjlim _j V_j(I) \subseteq V(I)$
. But
![]() $V^I = \varinjlim _j V_j^I$
. Hence, this inclusion is an equality.
$V^I = \varinjlim _j V_j^I$
. Hence, this inclusion is an equality.
2.2 Krull dimension
We briefly recall Gabriel’s notion of a Krull dimension for arbitrary Grothendieck categories
![]() $\mathcal {C}$
. Gabriel’s dimension filtration of
$\mathcal {C}$
. Gabriel’s dimension filtration of
![]() $\mathcal {C}$
is a filtration by localising subcategories
$\mathcal {C}$
is a filtration by localising subcategories
![]() $\mathcal {C}_\alpha $
of
$\mathcal {C}_\alpha $
of
![]() $\mathcal {C}$
indexed by ordinals
$\mathcal {C}$
indexed by ordinals
![]() $\alpha $
. His convention is that
$\alpha $
. His convention is that
![]() $\mathcal {C}_{-1}$
is the subcategory of all zero objects of
$\mathcal {C}_{-1}$
is the subcategory of all zero objects of
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {C}_0$
is the smallest localising subcategory containing all objects of finite length. The
$\mathcal {C}_0$
is the smallest localising subcategory containing all objects of finite length. The
![]() $\mathcal {C}_\alpha $
then are defined successively as follows. If
$\mathcal {C}_\alpha $
then are defined successively as follows. If
![]() $\alpha = \beta + 1$
, then
$\alpha = \beta + 1$
, then
![]() $\mathcal {C}_\alpha $
is the preimage of
$\mathcal {C}_\alpha $
is the preimage of
![]() $(\mathcal {C}/\mathcal {C}_\beta )_0$
under the quotient functor
$(\mathcal {C}/\mathcal {C}_\beta )_0$
under the quotient functor
![]() $q_{\mathcal {C}_\beta } : \mathcal {C} \rightarrow \mathcal {C}/\mathcal {C}_\beta $
; if
$q_{\mathcal {C}_\beta } : \mathcal {C} \rightarrow \mathcal {C}/\mathcal {C}_\beta $
; if
![]() $\alpha $
is a limit ordinal, then
$\alpha $
is a limit ordinal, then
![]() $\mathcal {C}_\alpha $
is the smallest localising subcategory containing all
$\mathcal {C}_\alpha $
is the smallest localising subcategory containing all
![]() $\mathcal {C}_\beta $
for
$\mathcal {C}_\beta $
for
![]() $\beta < \alpha $
. This process terminates as soon as
$\beta < \alpha $
. This process terminates as soon as
![]() $\mathcal {C}_/\mathcal {C}_\alpha $
has no simple objects. But by [Reference GabrielGab] Proposition 7 on p. 387, the latter implies that
$\mathcal {C}_/\mathcal {C}_\alpha $
has no simple objects. But by [Reference GabrielGab] Proposition 7 on p. 387, the latter implies that
![]() $\mathcal {C}_\alpha $
must be equal to
$\mathcal {C}_\alpha $
must be equal to
![]() $\mathcal {C}$
. The Krull dimension
$\mathcal {C}$
. The Krull dimension
![]() $\kappa (\mathcal {C})$
of
$\kappa (\mathcal {C})$
of
![]() $\mathcal {C}$
can now be defined as the smallest
$\mathcal {C}$
can now be defined as the smallest
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathcal {C} = \mathcal {C}_\alpha $
. Similarly, the Krull dimension
$\mathcal {C} = \mathcal {C}_\alpha $
. Similarly, the Krull dimension
![]() $\kappa (Y)$
of an object Y in
$\kappa (Y)$
of an object Y in
![]() $\mathcal {C}$
is defined to be the smallest
$\mathcal {C}$
is defined to be the smallest
![]() $\alpha $
such that Y lies in
$\alpha $
such that Y lies in
![]() $\mathcal {C}_\alpha $
. Correspondingly, the set
$\mathcal {C}_\alpha $
. Correspondingly, the set
![]() $\mathbf {Sp}(\mathcal {C})$
of isomorphism classes of indecomposable injective objects in
$\mathbf {Sp}(\mathcal {C})$
of isomorphism classes of indecomposable injective objects in
![]() $\mathcal {C}$
admits a stratification
$\mathcal {C}$
admits a stratification
by the subsets
![]() $\mathbf {Sp}_\alpha (\mathcal {C})$
of all
$\mathbf {Sp}_\alpha (\mathcal {C})$
of all
![]() $[E] \in \mathbf {Sp}(\mathcal {C})$
such that
$[E] \in \mathbf {Sp}(\mathcal {C})$
such that
![]() $q_{\mathcal {C}_\alpha }(E)$
contains a simple object ([Reference GabrielGab] p. 383). In general, it is not possible to read off the Krull dimension
$q_{\mathcal {C}_\alpha }(E)$
contains a simple object ([Reference GabrielGab] p. 383). In general, it is not possible to read off the Krull dimension
![]() $\kappa (E)$
of an
$\kappa (E)$
of an
![]() $[E] \in \mathbf {Sp}_\alpha (\mathcal {C})$
from the
$[E] \in \mathbf {Sp}_\alpha (\mathcal {C})$
from the
![]() $\alpha $
.
$\alpha $
.
Remark 2.2.1. Let
![]() $\alpha < \kappa (\mathcal {C})$
be an ordinal such that
$\alpha < \kappa (\mathcal {C})$
be an ordinal such that
![]() $\mathcal {C}_{\alpha + 1}$
is a stable localising subcategory; then
$\mathcal {C}_{\alpha + 1}$
is a stable localising subcategory; then
![]() $\kappa (E) = \alpha + 1$
for any
$\kappa (E) = \alpha + 1$
for any
![]() $[E] \in \mathbf {Sp}_\alpha (\mathcal {C})$
.
$[E] \in \mathbf {Sp}_\alpha (\mathcal {C})$
.
Proof. By our assumption, E is
![]() $\mathcal {C}_\alpha $
-closed and contains a nonzero subobject S lying in
$\mathcal {C}_\alpha $
-closed and contains a nonzero subobject S lying in
![]() $\mathcal {C}_{\alpha + 1}$
(cf. [Reference GabrielGab] p. 383). Since E is an essential extension of any of its nonzero subobjects (cf. [Reference GabrielGab] Proposition 11 on p. 361) it follows from the stability of
$\mathcal {C}_{\alpha + 1}$
(cf. [Reference GabrielGab] p. 383). Since E is an essential extension of any of its nonzero subobjects (cf. [Reference GabrielGab] Proposition 11 on p. 361) it follows from the stability of
![]() $\mathcal {C}_{\alpha + 1}$
that E lies in
$\mathcal {C}_{\alpha + 1}$
that E lies in
![]() $\mathcal {C}_{\alpha + 1}$
.
$\mathcal {C}_{\alpha + 1}$
.
Remark 2.2.2. ([Reference GabrielGab] Proposition 7 on p. 387) Suppose that
![]() $\mathcal {C}$
is locally noetherian. Then
$\mathcal {C}$
is locally noetherian. Then
![]() $\mathcal {C}$
has a Krull dimension and, for any nonlimit ordinal
$\mathcal {C}$
has a Krull dimension and, for any nonlimit ordinal
![]() $\alpha $
, the category
$\alpha $
, the category
![]() $\mathcal {C}_\alpha /\mathcal {C}_{\alpha - 1}$
is locally finite.
$\mathcal {C}_\alpha /\mathcal {C}_{\alpha - 1}$
is locally finite.
For the convenience of the reader, we point out the following elementary consequences of the fact that the subcategories
![]() $\mathcal {C}_\alpha $
are localising:
$\mathcal {C}_\alpha $
are localising:
-
– If
 $0 \rightarrow U_1 \rightarrow U_2 \rightarrow U_3 \rightarrow 0$
is a short exact sequence in
$0 \rightarrow U_1 \rightarrow U_2 \rightarrow U_3 \rightarrow 0$
is a short exact sequence in
 $\mathcal {C}$
, then
$\mathcal {C}$
, then  $$ \begin{align*} \kappa(U_2) = \sup(\kappa(U_1),\kappa(U_3)) . \end{align*} $$
$$ \begin{align*} \kappa(U_2) = \sup(\kappa(U_1),\kappa(U_3)) . \end{align*} $$
-
– If U in
 $\mathcal {C}$
is the inductive limit of a family of subobjects
$\mathcal {C}$
is the inductive limit of a family of subobjects
 $U_i$
, then
$U_i$
, then
 $\kappa (U) = \sup _i \kappa (U_i)$
. In particular, for any U, we have
$\kappa (U) = \sup _i \kappa (U_i)$
. In particular, for any U, we have
 $\kappa (U) = \sup _i \kappa (U_i)$
, where the
$\kappa (U) = \sup _i \kappa (U_i)$
, where the
 $U_i$
run over all noetherian subobjects of U.
$U_i$
run over all noetherian subobjects of U.
In [Reference McConnell and RobsonMCR] Chapter 6, the notion of Krull dimension for the category
![]() $\mathcal {C} = {\mathrm {Mod}}(R)$
of modules over a noetherian ring R is introduced using posets. By loc. cit. Lemmas 6.2.4 and 6.2.17, it also has the above two properties. Therefore, it follows, for example, from [Reference Gordon and RobsonGR] Proposition 2.3 (beware that this reference shifts the Gabriel definition by 1) that these two notions of Krull dimension coincide for noetherian rings R.
$\mathcal {C} = {\mathrm {Mod}}(R)$
of modules over a noetherian ring R is introduced using posets. By loc. cit. Lemmas 6.2.4 and 6.2.17, it also has the above two properties. Therefore, it follows, for example, from [Reference Gordon and RobsonGR] Proposition 2.3 (beware that this reference shifts the Gabriel definition by 1) that these two notions of Krull dimension coincide for noetherian rings R.
Proposition 2.2.3. The categories
![]() ${\mathrm {Mod}}_k(G)$
and
${\mathrm {Mod}}_k(G)$
and
![]() ${\mathrm {Mod}}(H)$
have Krull dimension one.
${\mathrm {Mod}}(H)$
have Krull dimension one.
Proof. The computation of
![]() $Z(H)$
in [Reference Ollivier and SchneiderOS18] §3.2.4 (together with [Reference McConnell and RobsonMCR] Corollary 6.4.8) shows that
$Z(H)$
in [Reference Ollivier and SchneiderOS18] §3.2.4 (together with [Reference McConnell and RobsonMCR] Corollary 6.4.8) shows that
![]() $Z(H)$
has Krull dimension one. By [Reference Ollivier and SchneiderOS18] Corollary 3.4, the centre
$Z(H)$
has Krull dimension one. By [Reference Ollivier and SchneiderOS18] Corollary 3.4, the centre
![]() $Z(H)$
contains a polynomial ring
$Z(H)$
contains a polynomial ring
![]() $k[\zeta ]$
over which H is a finitely generated free module. Using [Reference McConnell and RobsonMCR] Corollary 6.5.3, it then follows that H has Krull dimension one as well. Hence,
$k[\zeta ]$
over which H is a finitely generated free module. Using [Reference McConnell and RobsonMCR] Corollary 6.5.3, it then follows that H has Krull dimension one as well. Hence,
![]() ${\mathrm {Mod}}_k^I(G) \simeq {\mathrm {Mod}}(H)$
has Krull dimension one. By the proof of Lemma 2.1.2, the subcategory
${\mathrm {Mod}}_k^I(G) \simeq {\mathrm {Mod}}(H)$
has Krull dimension one. By the proof of Lemma 2.1.2, the subcategory
![]() ${\mathrm {Mod}}_k^I(G)$
is closed under the passage to subobjects in
${\mathrm {Mod}}_k^I(G)$
is closed under the passage to subobjects in
![]() ${\mathrm {Mod}}_k(G)$
. Therefore, the Krull dimensions of an object in
${\mathrm {Mod}}_k(G)$
. Therefore, the Krull dimensions of an object in
![]() ${\mathrm {Mod}}_k^I(G)$
when viewed in
${\mathrm {Mod}}_k^I(G)$
when viewed in
![]() ${\mathrm {Mod}}_k^I(G)$
or in
${\mathrm {Mod}}_k^I(G)$
or in
![]() ${\mathrm {Mod}}_k(G)$
, coincide.
${\mathrm {Mod}}_k(G)$
, coincide.
Since the subcategory
![]() ${\mathrm {Mod}}_k(G)_1$
is closed under extensions, it follows from Lemma 2.1.3 that every finitely generated representation lies in
${\mathrm {Mod}}_k(G)_1$
is closed under extensions, it follows from Lemma 2.1.3 that every finitely generated representation lies in
![]() ${\mathrm {Mod}}_k(G)_1$
. The assertion about
${\mathrm {Mod}}_k(G)_1$
. The assertion about
![]() ${\mathrm {Mod}}_k(G)$
then is immediate from the fact that
${\mathrm {Mod}}_k(G)$
then is immediate from the fact that
![]() ${\mathrm {Mod}}_k(G)_1$
also is closed under inductive limits.
${\mathrm {Mod}}_k(G)_1$
also is closed under inductive limits.
3 Thickenings
It will be useful to axiomatize the situation in the previous section.
3.1 Definitions
For this, we fix a locally noetherian Grothendieck category
![]() $\mathcal {C}$
together with a full abelian subcategory
$\mathcal {C}$
together with a full abelian subcategory
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Definition 3.1.1. The category
![]() $\mathcal {C}$
is called a thickening of
$\mathcal {C}$
is called a thickening of
![]() $\mathcal {A}$
if:
$\mathcal {A}$
if:
-
a)
 $\mathcal {A}$
is closed under the formation of subobjects, quotient objects and arbitrary colimits in
$\mathcal {A}$
is closed under the formation of subobjects, quotient objects and arbitrary colimits in
 $\mathcal {C}$
;
$\mathcal {C}$
; -
b) the inclusion functor
 $\mathcal {A} \subseteq \mathcal {C}$
has a left exact right adjoint functor
$\mathcal {A} \subseteq \mathcal {C}$
has a left exact right adjoint functor
 $r = r_{\mathcal {C}, \mathcal {A}} : \mathcal {C} \rightarrow \mathcal {A}$
such that:
$r = r_{\mathcal {C}, \mathcal {A}} : \mathcal {C} \rightarrow \mathcal {A}$
such that:-
- the functor
 $r : \mathcal {C} \xrightarrow {r} \mathcal {A} \xrightarrow {\subseteq } \mathcal {C}$
is a subfunctor of the identity functor
$r : \mathcal {C} \xrightarrow {r} \mathcal {A} \xrightarrow {\subseteq } \mathcal {C}$
is a subfunctor of the identity functor
 ${\mathrm {id}}_{\mathcal {C}}$
,
${\mathrm {id}}_{\mathcal {C}}$
, -
-
 $r | \mathcal {A} = {\mathrm {id}}_{\mathcal {A}}$
,
$r | \mathcal {A} = {\mathrm {id}}_{\mathcal {A}}$
, -
- r preserves nonzero objects and
-
- r commutes with arbitrary filtered colimits;
-
-
c) every noetherian object V in
 $\mathcal {C}$
has a finite filtration
$\mathcal {C}$
has a finite filtration
 $0 = V_0 \subseteq V_1 \subseteq \ldots \subseteq V_m = V$
such that all subquotients
$0 = V_0 \subseteq V_1 \subseteq \ldots \subseteq V_m = V$
such that all subquotients
 $V_j/V_{j-1}$
, for
$V_j/V_{j-1}$
, for
 $1 \leq j \leq m$
, lie in
$1 \leq j \leq m$
, lie in
 $\mathcal {A}$
.
$\mathcal {A}$
.
In the following, we fix an
![]() $\mathcal {A}$
as in the above definition. Note that
$\mathcal {A}$
as in the above definition. Note that
![]() $\mathcal {A}$
is a strictly full subcategory. For any V in
$\mathcal {A}$
is a strictly full subcategory. For any V in
![]() $\mathcal {C}$
, the subobject
$\mathcal {C}$
, the subobject
![]() $r(V)$
is the largest subobject of V which lies in
$r(V)$
is the largest subobject of V which lies in
![]() $\mathcal {A}$
. The functor r in fact gives rise to a whole sequence of subfunctors
$\mathcal {A}$
. The functor r in fact gives rise to a whole sequence of subfunctors
![]() $r_j : \mathcal {C} \rightarrow \mathcal {C}$
, for
$r_j : \mathcal {C} \rightarrow \mathcal {C}$
, for
![]() $j \geq 0$
, of the identity functor
$j \geq 0$
, of the identity functor
![]() ${\mathrm {id}}_{\mathcal {C}}$
which are defined inductively as follows. We define
${\mathrm {id}}_{\mathcal {C}}$
which are defined inductively as follows. We define
Obviously, we have, for any V in
![]() $\mathcal {C}$
, the increasing filtration by subobjects
$\mathcal {C}$
, the increasing filtration by subobjects
Lemma 3.1.2. For any
![]() $j \geq 0$
, the functor
$j \geq 0$
, the functor
![]() $r_j$
has the following properties:
$r_j$
has the following properties:
-
a)
 $r_j$
is left exact;
$r_j$
is left exact; -
b)
 $r_j \circ r_i = r_i \circ r_j = r_j$
for any
$r_j \circ r_i = r_i \circ r_j = r_j$
for any
 $i \geq j$
;
$i \geq j$
; -
c)
 $r_j$
preserves filtered unions of subobjects.
$r_j$
preserves filtered unions of subobjects.
Proof. In [Reference StenströmSte] VI§1, the functor
![]() $r_0$
is called a left exact idempotent preradical of
$r_0$
is called a left exact idempotent preradical of
![]() $\mathcal {C}$
and the asserted properties of the
$\mathcal {C}$
and the asserted properties of the
![]() $r_j$
can be found in the Exercises 1 and 2 of that Chapter VI.
$r_j$
can be found in the Exercises 1 and 2 of that Chapter VI.
Correspondingly, we introduce, for any
![]() $j \geq 0$
, the strictly full subcategory
$j \geq 0$
, the strictly full subcategory
of
![]() $\mathcal {C}$
. We have
$\mathcal {C}$
. We have
![]() $\mathcal {A}_0 = \mathcal {A}$
, and
$\mathcal {A}_0 = \mathcal {A}$
, and
![]() $\mathcal {A}_j$
is a subcategory of
$\mathcal {A}_j$
is a subcategory of
![]() $\mathcal {A}_{j+1}$
. Each functor
$\mathcal {A}_{j+1}$
. Each functor
![]() $r_j$
may be viewed as a functor
$r_j$
may be viewed as a functor
![]() $r_j : \mathcal {C} \rightarrow \mathcal {A}_j$
.
$r_j : \mathcal {C} \rightarrow \mathcal {A}_j$
.
Lemma 3.1.3. For any
![]() $j \geq 0$
, we have:
$j \geq 0$
, we have:
-
a)
 $\mathcal {A}_j$
is an abelian subcategory of
$\mathcal {A}_j$
is an abelian subcategory of
 $\mathcal {C}$
closed under the formation of subobjects, quotient objects and arbitrary colimits in
$\mathcal {C}$
closed under the formation of subobjects, quotient objects and arbitrary colimits in
 $\mathcal {C}$
;
$\mathcal {C}$
; -
b)
 $r_j : \mathcal {C} \rightarrow \mathcal {A}_j$
is right adjoint to the inclusion functor
$r_j : \mathcal {C} \rightarrow \mathcal {A}_j$
is right adjoint to the inclusion functor
 $\mathcal {A}_j \subseteq \mathcal {C}$
;
$\mathcal {A}_j \subseteq \mathcal {C}$
; -
c)
 $r_j | \mathcal {A}_j = {\mathrm {id}}_{\mathcal {A}_j}$
;
$r_j | \mathcal {A}_j = {\mathrm {id}}_{\mathcal {A}_j}$
; -
d)
 $r_j$
preserves nonzero objects;
$r_j$
preserves nonzero objects; -
e)
 $r_j$
commutes with arbitrary filtered colimits;
$r_j$
commutes with arbitrary filtered colimits; -
f) any object V in
 $\mathcal {A}_j$
has the finite filtration
$\mathcal {A}_j$
has the finite filtration
 $0 \subseteq r_0(V) \subseteq r_1(V) \subseteq \ldots \subseteq r_j(V) = V$
whose subquotients
$0 \subseteq r_0(V) \subseteq r_1(V) \subseteq \ldots \subseteq r_j(V) = V$
whose subquotients
 $r_i(V)/r_{i-1}(V)$
all lie in
$r_i(V)/r_{i-1}(V)$
all lie in
 $\mathcal {A}$
.
$\mathcal {A}$
.
Proof. a) follows from [Reference StenströmSte] Propositions VI.1.2 and VI.1.7. For b) we observe that for any homomorphism
![]() $f : V_0 \rightarrow V_1$
in
$f : V_0 \rightarrow V_1$
in
![]() $\mathcal {C}$
we have
$\mathcal {C}$
we have
![]() $r_j(f) = f|r_j(V_0)$
. c), d) and f) hold by construction. e) We proceed by induction with respect to j. For
$r_j(f) = f|r_j(V_0)$
. c), d) and f) hold by construction. e) We proceed by induction with respect to j. For
![]() $j = 0$
, the claim is part of the Definition 3.1.1. Now, assume that the claim holds for some j. Let
$j = 0$
, the claim is part of the Definition 3.1.1. Now, assume that the claim holds for some j. Let
![]() $V = \varinjlim _i V_i$
be a filtered colimit in
$V = \varinjlim _i V_i$
be a filtered colimit in
![]() $\mathcal {C}$
. We then have
$\mathcal {C}$
. We then have
 $$ \begin{align*} r_{j+1}(V)/r_j(V) & = r_0(V/r_j(V)) = r_0(\varinjlim_i V_i / r_j(\varinjlim_i V_i)) = r_0(\varinjlim_i V_i / \varinjlim_i r_j(V_i)) \\ & = r_0(\varinjlim_i (V_i / r_j(V_i))) = \varinjlim_i r_0(V_i / r_j(V_i)) = \varinjlim_i (r_{j+1}(V_i) / r_j(V_i)) \\ & = \varinjlim_i r_{j+1}(V_i) / \varinjlim_i r_j(V_i) = (\varinjlim_i r_{j+1}(V_i)) / r_j(V) \ , \end{align*} $$
$$ \begin{align*} r_{j+1}(V)/r_j(V) & = r_0(V/r_j(V)) = r_0(\varinjlim_i V_i / r_j(\varinjlim_i V_i)) = r_0(\varinjlim_i V_i / \varinjlim_i r_j(V_i)) \\ & = r_0(\varinjlim_i (V_i / r_j(V_i))) = \varinjlim_i r_0(V_i / r_j(V_i)) = \varinjlim_i (r_{j+1}(V_i) / r_j(V_i)) \\ & = \varinjlim_i r_{j+1}(V_i) / \varinjlim_i r_j(V_i) = (\varinjlim_i r_{j+1}(V_i)) / r_j(V) \ , \end{align*} $$
where we use for Equations
![]() $4$
and
$4$
and
![]() $7$
that filtered colimits in
$7$
that filtered colimits in
![]() $\mathcal {C}$
are exact. It follows that
$\mathcal {C}$
are exact. It follows that
![]() $r_{j+1}(V) = \varinjlim _i r_{j+1}(V_i)$
.
$r_{j+1}(V) = \varinjlim _i r_{j+1}(V_i)$
.
Lemma 3.1.4. Let
![]() $0 \rightarrow X \rightarrow Y \rightarrow Z \rightarrow 0$
be a short exact sequence in
$0 \rightarrow X \rightarrow Y \rightarrow Z \rightarrow 0$
be a short exact sequence in
![]() $\mathcal {C}$
such that X lies in
$\mathcal {C}$
such that X lies in
![]() $\mathcal {A}_j$
for some
$\mathcal {A}_j$
for some
![]() $j \geq 0$
and Z lies in
$j \geq 0$
and Z lies in
![]() $\mathcal {A}$
; then Y lies in
$\mathcal {A}$
; then Y lies in
![]() $\mathcal {A}_{j+1}$
.
$\mathcal {A}_{j+1}$
.
Proof. Since
![]() $r_j$
is left exact by Lemma 3.1.2.a, we have the commutative exact diagram
$r_j$
is left exact by Lemma 3.1.2.a, we have the commutative exact diagram

which exhibits
![]() $Y/r_j(Y)$
as a quotient object of Z. Since
$Y/r_j(Y)$
as a quotient object of Z. Since
![]() $\mathcal {A}$
is closed under quotient objects it follows that
$\mathcal {A}$
is closed under quotient objects it follows that
![]() $r_0(Y/r_j(Y)) = Y/r_j(Y)$
. On the other hand, by construction we have
$r_0(Y/r_j(Y)) = Y/r_j(Y)$
. On the other hand, by construction we have
![]() $r_{j+1}(Y)/r_j(Y) = r_0(Y/r_j(Y))$
. It follows that
$r_{j+1}(Y)/r_j(Y) = r_0(Y/r_j(Y))$
. It follows that
![]() $r_{j+1}(Y) = Y$
.
$r_{j+1}(Y) = Y$
.
Lemma 3.1.5. For any V in
![]() $\mathcal {C}$
, we have
$\mathcal {C}$
, we have
![]() $V = \bigcup _{j \geq 0} r_j(V)$
.
$V = \bigcup _{j \geq 0} r_j(V)$
.
Proof. Write V as a filtered union of noetherian subobjects. Using Lemma 3.1.2.c, we see that it suffices to prove the assertion for a noetherian V. In this case, however, it follows from Definition 3.1.1.c and an iterated application of Lemma 3.1.4 that
![]() $V = r_j(V)$
for sufficiently large j.
$V = r_j(V)$
for sufficiently large j.
Proposition 3.1.6.
![]() $\mathcal {A}_j$
, for any
$\mathcal {A}_j$
, for any
![]() $j \geq 0$
, is a locally noetherian Grothendieck category.
$j \geq 0$
, is a locally noetherian Grothendieck category.
Proof. By [Reference Bazzoni and PositselskiBP] Lemma 3.4, the category
![]() $\mathcal {A}_j$
is Grothendieck. That it is locally noetherian is clear.
$\mathcal {A}_j$
is Grothendieck. That it is locally noetherian is clear.
Remark 3.1.7. Let V be an object in
![]() $\mathcal {A}_j$
for some
$\mathcal {A}_j$
for some
![]() $j \geq 0$
; then the Krull dimensions of V viewed in
$j \geq 0$
; then the Krull dimensions of V viewed in
![]() $\mathcal {A}_j$
and viewed in
$\mathcal {A}_j$
and viewed in
![]() $\mathcal {C}$
coincide.
$\mathcal {C}$
coincide.
Proof. This is immediate from
![]() $\mathcal {A}_j$
being closed under the passage to subobjects in
$\mathcal {A}_j$
being closed under the passage to subobjects in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
3.2 A spectral sequence
The Ext-groups in
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {A}$
are related by the following spectral sequence.
$\mathcal {A}$
are related by the following spectral sequence.
Proposition 3.2.1. For objects A in
![]() $\mathcal {A}$
and V in
$\mathcal {A}$
and V in
![]() $\mathcal {C}$
, we have the Grothendieck spectral sequence
$\mathcal {C}$
, we have the Grothendieck spectral sequence
Proof. We have the adjunction
![]() ${\mathrm {Hom}}_{\mathcal {A}}(A, r(V)) = {\mathrm {Hom}}_{\mathcal {C}}(A,V)$
. Since r, being right adjoint to a (left) exact functor, preserves injective objects, this equation extends to the asserted composed functor spectral sequence.
${\mathrm {Hom}}_{\mathcal {A}}(A, r(V)) = {\mathrm {Hom}}_{\mathcal {C}}(A,V)$
. Since r, being right adjoint to a (left) exact functor, preserves injective objects, this equation extends to the asserted composed functor spectral sequence.
Corollary 3.2.2. Suppose that P is a projective object in
![]() $\mathcal {A}$
. For any object V in
$\mathcal {A}$
. For any object V in
![]() $\mathcal {C}$
and any
$\mathcal {C}$
and any
![]() $j \geq 0$
, we then have
$j \geq 0$
, we then have
3.3 Injective spectra
We first recall some standard notations. For any object Y in a locally noetherian Grothendieck category
![]() $\mathcal {D}$
a choice of injective hull of Y is denoted by
$\mathcal {D}$
a choice of injective hull of Y is denoted by
![]() $E_{\mathcal {D}}(Y)$
or simply
$E_{\mathcal {D}}(Y)$
or simply
![]() $E(Y)$
. The injective spectrum
$E(Y)$
. The injective spectrum
![]() $\mathbf {Sp}(\mathcal {D})$
is the collection of isomorphism classes
$\mathbf {Sp}(\mathcal {D})$
is the collection of isomorphism classes
![]() $[Y]$
of indecomposable injective objects Y of
$[Y]$
of indecomposable injective objects Y of
![]() $\mathcal {D}$
; it is a set, for example, by [Reference HerzogHer] p. 523.
$\mathcal {D}$
; it is a set, for example, by [Reference HerzogHer] p. 523.
In the following, we keep the setting of a thickening
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Lemma 3.3.1. For any V in
![]() $\mathcal {C}$
, we have:
$\mathcal {C}$
, we have:
-
a) The inclusion
 $r(V) \subseteq V$
is an essential extension. In particular, if V is injective, then V is an injective hull of
$r(V) \subseteq V$
is an essential extension. In particular, if V is injective, then V is an injective hull of
 $r(V)$
.
$r(V)$
. -
b) If V is injective in
 $\mathcal {A}$
, then
$\mathcal {A}$
, then
 $V \cong r(E_{\mathcal {C}}(V))$
.
$V \cong r(E_{\mathcal {C}}(V))$
. -
c) If V is injective in
 $\mathcal {C}$
, then V is indecomposable if and only if
$\mathcal {C}$
, then V is indecomposable if and only if
 $r(V)$
is indecomposable.
$r(V)$
is indecomposable.
Proof. a) Let
![]() $U \subseteq V$
be a nonzero subobject. Since r preserves nonzero objects, we then have
$U \subseteq V$
be a nonzero subobject. Since r preserves nonzero objects, we then have
![]() $0 \neq r(U) \subseteq r(V)$
and hence
$0 \neq r(U) \subseteq r(V)$
and hence
![]() $U \cap r(V) \neq 0$
.
$U \cap r(V) \neq 0$
.
b) We obviously have
![]() $V = r(V) \subseteq r(E_{\mathcal {C}}(V)) \subseteq E_{\mathcal {C}}(V)$
. Since r, as a right adjoint of a (left) exact functor, preserves injective objects, both terms in the essential extension
$V = r(V) \subseteq r(E_{\mathcal {C}}(V)) \subseteq E_{\mathcal {C}}(V)$
. Since r, as a right adjoint of a (left) exact functor, preserves injective objects, both terms in the essential extension
![]() $V = r(V) \subseteq r(E_{\mathcal {C}}(V))$
are injective in
$V = r(V) \subseteq r(E_{\mathcal {C}}(V))$
are injective in
![]() $\mathcal {A}$
. Hence, we must have equality.
$\mathcal {A}$
. Hence, we must have equality.
c) Suppose that
![]() $r(V) = U_1 \oplus U_2$
with
$r(V) = U_1 \oplus U_2$
with
![]() $U_i \neq 0$
(and necessarily lying in
$U_i \neq 0$
(and necessarily lying in
![]() $\mathcal {A}$
). Using [Reference StenströmSte] Proposition V.2.6, we see that V, being an injective hull of
$\mathcal {A}$
). Using [Reference StenströmSte] Proposition V.2.6, we see that V, being an injective hull of
![]() $r(V)$
by a), is isomorphic to the direct sum of injective hulls of
$r(V)$
by a), is isomorphic to the direct sum of injective hulls of
![]() $U_1$
and
$U_1$
and
![]() $U_2$
and hence is decomposable. On the other hand, if
$U_2$
and hence is decomposable. On the other hand, if
![]() $V = V_1 \oplus V_2$
with
$V = V_1 \oplus V_2$
with
![]() $V_i \neq 0$
, then
$V_i \neq 0$
, then
![]() $r(V) = r(V_1) \oplus r(V_2)$
with
$r(V) = r(V_1) \oplus r(V_2)$
with
![]() $r(V_i) \neq 0$
.
$r(V_i) \neq 0$
.
The above lemma implies that the map
 $$ \begin{align*} \mathbf{Sp}(\mathcal{C}) & \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}) \\ [E] & \longmapsto r([E]) := [r(E)] \end{align*} $$
$$ \begin{align*} \mathbf{Sp}(\mathcal{C}) & \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}) \\ [E] & \longmapsto r([E]) := [r(E)] \end{align*} $$
is a bijection with inverse
![]() $[U] \longmapsto [E_{\mathcal {C}}(U)]$
. In fact, because of Lemma 3.1.3 all of the above remains valid for each functor
$[U] \longmapsto [E_{\mathcal {C}}(U)]$
. In fact, because of Lemma 3.1.3 all of the above remains valid for each functor
![]() $r_j$
. Hence, we have the bijections
$r_j$
. Hence, we have the bijections
 $$ \begin{align} \mathbf{Sp}(\mathcal{C}) & \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}_j) \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}) \\ [E] & \longmapsto [r_j(E)] \longmapsto [r(E)] . \nonumber \end{align} $$
$$ \begin{align} \mathbf{Sp}(\mathcal{C}) & \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}_j) \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}) \\ [E] & \longmapsto [r_j(E)] \longmapsto [r(E)] . \nonumber \end{align} $$
3.4 Localising subcategories
We recall that a full subcategory
![]() $\mathcal {L}$
of a locally noetherian Grothendieck category
$\mathcal {L}$
of a locally noetherian Grothendieck category
![]() $\mathcal {D}$
is called localising if it is closed under the formation of subobjects, quotient objects, extensions and arbitrary direct sums. In particular, it is strictly full and contains the zero object (as the empty direct sum). It will be technically useful to also recall the following fact. Let
$\mathcal {D}$
is called localising if it is closed under the formation of subobjects, quotient objects, extensions and arbitrary direct sums. In particular, it is strictly full and contains the zero object (as the empty direct sum). It will be technically useful to also recall the following fact. Let
![]() $\mathcal {D}^{noeth}$
denote the full subcategory of all noetherian objects in
$\mathcal {D}^{noeth}$
denote the full subcategory of all noetherian objects in
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Proposition 3.4.1. The map
 $$ \begin{align*} \text{collection of all localising}\, & \xrightarrow{\;\simeq\;} \text{collection of all Serre} \\ \text{subcategories of} \mathcal{D} & \qquad \text{subcategories of}\ \mathcal{D}^{noeth} \\ \mathcal{L} & \longmapsto \mathcal{L} \cap \mathcal{D}^{noeth} \end{align*} $$
$$ \begin{align*} \text{collection of all localising}\, & \xrightarrow{\;\simeq\;} \text{collection of all Serre} \\ \text{subcategories of} \mathcal{D} & \qquad \text{subcategories of}\ \mathcal{D}^{noeth} \\ \mathcal{L} & \longmapsto \mathcal{L} \cap \mathcal{D}^{noeth} \end{align*} $$
is a bijection; its inverse sends a Serre subcategory
![]() $\mathcal {S}$
to the smallest localising subcategory
$\mathcal {S}$
to the smallest localising subcategory
![]() $\langle \mathcal {S} \rangle $
of
$\langle \mathcal {S} \rangle $
of
![]() $\mathcal {D}$
which contains
$\mathcal {D}$
which contains
![]() $\mathcal {S}$
; equivalently,
$\mathcal {S}$
; equivalently,
![]() $\langle \mathcal {S} \rangle $
is the full subcategory of all filtered colimits of objects in
$\langle \mathcal {S} \rangle $
is the full subcategory of all filtered colimits of objects in
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Proof. [Reference HerzogHer] Theorem 2.8.
Lemma 3.4.2. If
![]() $\mathcal {L}$
is a localising subcategory of
$\mathcal {L}$
is a localising subcategory of
![]() $\mathcal {C}$
, then
$\mathcal {C}$
, then
![]() $\mathcal {A} \cap \mathcal {L}$
is localising in
$\mathcal {A} \cap \mathcal {L}$
is localising in
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof. Each of the categories
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {L}$
is closed under subobjects, quotient objects and arbitrary direct sums. Therefore, the same holds for
$\mathcal {L}$
is closed under subobjects, quotient objects and arbitrary direct sums. Therefore, the same holds for
![]() $\mathcal {A} \cap \mathcal {L}$
. It remains to consider extensions. Let
$\mathcal {A} \cap \mathcal {L}$
. It remains to consider extensions. Let
![]() $0 \rightarrow X \rightarrow Y \rightarrow Z \rightarrow 0$
be a short exact sequence in
$0 \rightarrow X \rightarrow Y \rightarrow Z \rightarrow 0$
be a short exact sequence in
![]() $\mathcal {A}$
such that X and Z lie in
$\mathcal {A}$
such that X and Z lie in
![]() $\mathcal {L}$
. Then Y must lie in
$\mathcal {L}$
. Then Y must lie in
![]() $\mathcal {L}$
and hence in
$\mathcal {L}$
and hence in
![]() $\mathcal {A} \cap \mathcal {L}$
.
$\mathcal {A} \cap \mathcal {L}$
.
Proposition 3.4.3. The map
 $$ \begin{align*} \text{collection of all localising}\, & \xrightarrow{\;\simeq\;} \text{collection of all localising} \\ \text{subcategories of}\ \mathcal{C} & \qquad \text{subcategories of}\ \mathcal{A} \\ \mathcal{L} & \longmapsto \mathcal{A} \cap \mathcal{L} \end{align*} $$
$$ \begin{align*} \text{collection of all localising}\, & \xrightarrow{\;\simeq\;} \text{collection of all localising} \\ \text{subcategories of}\ \mathcal{C} & \qquad \text{subcategories of}\ \mathcal{A} \\ \mathcal{L} & \longmapsto \mathcal{A} \cap \mathcal{L} \end{align*} $$
is a bijection; its inverse sends a localising subcategory
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $\mathcal {A}$
to the smallest localising subcategory
$\mathcal {A}$
to the smallest localising subcategory
![]() $\langle \mathcal {K} \rangle $
of
$\langle \mathcal {K} \rangle $
of
![]() $\mathcal {C}$
which contains
$\mathcal {C}$
which contains
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Proof. We obviously have
![]() $\mathcal {A}^{noeth} = \mathcal {A} \cap \mathcal {C}^{noeth}$
. Hence, Proposition 3.4.1 reduces the asserted bijectivity to the bijectivity of the map
$\mathcal {A}^{noeth} = \mathcal {A} \cap \mathcal {C}^{noeth}$
. Hence, Proposition 3.4.1 reduces the asserted bijectivity to the bijectivity of the map
 $$ \begin{align*} \text{collection of all Serre}\, & \xrightarrow{\;\simeq\;} \text{collection of all Serre} \\ \text{subcategories of}\ {\mathcal{C}}^{\text{noeth}} & \qquad \text{subcategories of}\ {\mathcal{A}}^{\text{noeth}} \\ & {\mathcal{S}} \longmapsto {\mathcal{A}} \cap {\mathcal{S}}. \end{align*} $$
$$ \begin{align*} \text{collection of all Serre}\, & \xrightarrow{\;\simeq\;} \text{collection of all Serre} \\ \text{subcategories of}\ {\mathcal{C}}^{\text{noeth}} & \qquad \text{subcategories of}\ {\mathcal{A}}^{\text{noeth}} \\ & {\mathcal{S}} \longmapsto {\mathcal{A}} \cap {\mathcal{S}}. \end{align*} $$
But it follows from Definition 3.1.1.c that any such
![]() $\mathcal {S}$
is the smallest Serre subcategory of
$\mathcal {S}$
is the smallest Serre subcategory of
![]() $\mathcal {C}^{noeth}$
which contains
$\mathcal {C}^{noeth}$
which contains
![]() $\mathcal {A} \cap \mathcal {S}$
. On the other hand, let
$\mathcal {A} \cap \mathcal {S}$
. On the other hand, let
![]() $\mathcal {T}$
be a Serre subcategory of
$\mathcal {T}$
be a Serre subcategory of
![]() $\mathcal {A}^{noeth}$
. We define
$\mathcal {A}^{noeth}$
. We define
![]() $\mathcal {S}$
to be the full subcategory of
$\mathcal {S}$
to be the full subcategory of
![]() $\mathcal {C}^{noeth}$
whose objects V have a finite filtration
$\mathcal {C}^{noeth}$
whose objects V have a finite filtration
![]() $0 = V_0 \subseteq V_1 \subseteq \ldots \subseteq V_m = V$
with
$0 = V_0 \subseteq V_1 \subseteq \ldots \subseteq V_m = V$
with
![]() $V_j/V_{j-1}$
in
$V_j/V_{j-1}$
in
![]() $\mathcal {T}$
for any
$\mathcal {T}$
for any
![]() $1 \leq j \leq m$
. It is straightforward to check that
$1 \leq j \leq m$
. It is straightforward to check that
![]() $\mathcal {S}$
is a Serre subcategory of
$\mathcal {S}$
is a Serre subcategory of
![]() $\mathcal {C}^{noeth}$
and that
$\mathcal {C}^{noeth}$
and that
![]() $\mathcal {A} \cap \mathcal {S} = \mathcal {T}$
.
$\mathcal {A} \cap \mathcal {S} = \mathcal {T}$
.
The above Proposition 3.4.3, of course, holds true correspondingly with
![]() $\mathcal {A}$
replaced with
$\mathcal {A}$
replaced with
![]() $\mathcal {A}_j$
.
$\mathcal {A}_j$
.
For any localising subcategory
![]() $\mathcal {L}$
of a locally noetherian Grothendieck category
$\mathcal {L}$
of a locally noetherian Grothendieck category
![]() $\mathcal {D}$
one defines the subset
$\mathcal {D}$
one defines the subset
of
![]() $\mathbf {Sp}(\mathcal {D})$
. These subsets
$\mathbf {Sp}(\mathcal {D})$
. These subsets
![]() $A(\mathcal {L})$
form the closed subsets of a topology on
$A(\mathcal {L})$
form the closed subsets of a topology on
![]() $\mathbf {Sp}(\mathcal {D})$
which is called the Ziegler topology (cf. [Reference HerzogHer] Theorem 3.4). In fact, by Proposition 3.4.1 and [Reference HerzogHer] Theorem 3.8, the map
$\mathbf {Sp}(\mathcal {D})$
which is called the Ziegler topology (cf. [Reference HerzogHer] Theorem 3.4). In fact, by Proposition 3.4.1 and [Reference HerzogHer] Theorem 3.8, the map
 $$ \begin{align} \text{collection of all localising} & \xrightarrow{\;\simeq\;} \text{set of all Ziegler-closed} \\ \text{subcategories of} \mathcal{D} & \qquad \text{subsets of}\ \mathbf{\text{Sp}}(\mathcal{D}) \nonumber \\ \mathcal{L} & \longmapsto A(\mathcal{L}) \nonumber \end{align} $$
$$ \begin{align} \text{collection of all localising} & \xrightarrow{\;\simeq\;} \text{set of all Ziegler-closed} \\ \text{subcategories of} \mathcal{D} & \qquad \text{subsets of}\ \mathbf{\text{Sp}}(\mathcal{D}) \nonumber \\ \mathcal{L} & \longmapsto A(\mathcal{L}) \nonumber \end{align} $$
is an inclusion reversing bijection. This means that the Ziegler closed subsets of
![]() $\mathbf {Sp}(\mathcal {D})$
classify the Serre subcategories of
$\mathbf {Sp}(\mathcal {D})$
classify the Serre subcategories of
![]() $\mathcal {D}^{noeth}$
as well as the localising subcategories of
$\mathcal {D}^{noeth}$
as well as the localising subcategories of
![]() $\mathcal {D}$
. It also implies that
$\mathcal {D}$
. It also implies that
![]() $\mathcal {L}$
can be reconstructed from
$\mathcal {L}$
can be reconstructed from
![]() $A(\mathcal {L})$
by
$A(\mathcal {L})$
by
Corollary 3.4.4. The maps
![]() $\mathbf {Sp}(\mathcal {C}) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A}_j) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A})$
in Equation +(2) are homeomorphisms for the Ziegler topologies.
$\mathbf {Sp}(\mathcal {C}) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A}_j) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A})$
in Equation +(2) are homeomorphisms for the Ziegler topologies.
Proof. Using [Reference HerzogHer] Proposition 3.2 and Corollary 3.5, we see that Definition 3.1.1.c implies that the sets
 $$ \begin{align*} O_{\mathcal{C}}(U) & := \{[E] \in \mathbf{Sp}(\mathcal{C}) : {\mathrm{Hom}}_{\mathcal{C}}(U,E) \neq 0\} , \\ \text{resp.}\ O_{\mathcal{A}}(U) & := \{[r(E)] \in \mathbf{Sp}(\mathcal{A}) : {\mathrm{Hom}}_{\mathcal{A}}(U,r(E)) \neq 0\}, \end{align*} $$
$$ \begin{align*} O_{\mathcal{C}}(U) & := \{[E] \in \mathbf{Sp}(\mathcal{C}) : {\mathrm{Hom}}_{\mathcal{C}}(U,E) \neq 0\} , \\ \text{resp.}\ O_{\mathcal{A}}(U) & := \{[r(E)] \in \mathbf{Sp}(\mathcal{A}) : {\mathrm{Hom}}_{\mathcal{A}}(U,r(E)) \neq 0\}, \end{align*} $$
for
![]() $U \in {\mathrm {ob}}(\mathcal {A})$
, form a base for the Ziegler-open subsets of
$U \in {\mathrm {ob}}(\mathcal {A})$
, form a base for the Ziegler-open subsets of
![]() $\mathbf {Sp}(\mathcal {C})$
, resp.
$\mathbf {Sp}(\mathcal {C})$
, resp.
![]() $\mathbf {Sp}(\mathcal {A})$
. But, for such U, we have
$\mathbf {Sp}(\mathcal {A})$
. But, for such U, we have
![]() ${\mathrm {Hom}}_{\mathcal {C}}(U,E) = {\mathrm {Hom}}_{\mathcal {A}}(U,r(E))$
since r is right adjoint to the inclusion functor.
${\mathrm {Hom}}_{\mathcal {C}}(U,E) = {\mathrm {Hom}}_{\mathcal {A}}(U,r(E))$
since r is right adjoint to the inclusion functor.
Later on, another topology on
![]() $\mathbf {Sp}(\mathcal {D})$
will be more important for our purposes.
$\mathbf {Sp}(\mathcal {D})$
will be more important for our purposes.
Proposition 3.4.5. For a localising subcategory
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\mathcal {D}$
, the following are equivalent:
$\mathcal {D}$
, the following are equivalent:
-
a) there is a noetherian object C in
 $\mathcal {D}$
such that
$\mathcal {D}$
such that
 $\mathcal {L}$
is the smallest localising subcategory containing C;
$\mathcal {L}$
is the smallest localising subcategory containing C; -
b) there is a noetherian object C in
 $\mathcal {D}$
such that
$\mathcal {D}$
such that  $$\begin{align*}A(\mathcal{L}) = \{ [E] \in \mathbf{Sp}(\mathcal{D}) : {\mathrm{Hom}}_{\mathcal{D}}(C,E) = 0\};\end{align*}$$
$$\begin{align*}A(\mathcal{L}) = \{ [E] \in \mathbf{Sp}(\mathcal{D}) : {\mathrm{Hom}}_{\mathcal{D}}(C,E) = 0\};\end{align*}$$
-
c) the Ziegler open subset
 $\mathbf {Sp}(\mathcal {D}) \setminus A(\mathcal {L})$
is quasi-compact.
$\mathbf {Sp}(\mathcal {D}) \setminus A(\mathcal {L})$
is quasi-compact.
Proof. For the equivalence of a. and b. we consider more generally an arbitrary object of
![]() $\mathcal {D}$
, and we let
$\mathcal {D}$
, and we let
![]() $\langle C \rangle $
denote the smallest localising subcategory containing C. Let E be any injective object in
$\langle C \rangle $
denote the smallest localising subcategory containing C. Let E be any injective object in
![]() $\mathcal {D}$
. If
$\mathcal {D}$
. If
![]() ${\mathrm {Hom}}_{\mathcal {D}}(-,E)$
vanishes on
${\mathrm {Hom}}_{\mathcal {D}}(-,E)$
vanishes on
![]() $\langle C \rangle $
, then obviously
$\langle C \rangle $
, then obviously
![]() ${\mathrm {Hom}}_{\mathcal {D}}(C,E) = 0$
. But the injectivity of E easily implies that the converse holds as well. It follows that
${\mathrm {Hom}}_{\mathcal {D}}(C,E) = 0$
. But the injectivity of E easily implies that the converse holds as well. It follows that
For the equivalence of b. and c., see [Reference HerzogHer] Corollary 3.9.
The topology on
![]() $\mathbf {Sp}(\mathcal {D})$
which has as a base of open subsets the complements of quasi-compact Ziegler-open subsets is called the Gabriel–Zariski topology.
$\mathbf {Sp}(\mathcal {D})$
which has as a base of open subsets the complements of quasi-compact Ziegler-open subsets is called the Gabriel–Zariski topology.
Corollary 3.4.6. The maps
![]() $\mathbf {Sp}(\mathcal {C}) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A}_j) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A})$
in Equation (2) are homeomorphisms for the Gabriel–Zariski topologies.
$\mathbf {Sp}(\mathcal {C}) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A}_j) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A})$
in Equation (2) are homeomorphisms for the Gabriel–Zariski topologies.
3.5 Stability
We recall that a localising subcategory of a locally noetherian Grothendieck category
![]() $\mathcal {D}$
is called stable if it is closed under the passage to essential extensions.
$\mathcal {D}$
is called stable if it is closed under the passage to essential extensions.
Lemma 3.5.1. For any localising subcategory
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\mathcal {D}$
the following are equivalent:
$\mathcal {D}$
the following are equivalent:
-
a)
 $\mathcal {L}$
is stable;
$\mathcal {L}$
is stable; -
b) any indecomposable injective object of
 $\mathcal {D}$
either lies in
$\mathcal {D}$
either lies in
 $\mathcal {L}$
or has no nonzero subobject lying in
$\mathcal {L}$
or has no nonzero subobject lying in
 $\mathcal {L}$
.
$\mathcal {L}$
.
Proof. We argue similarly as in [Reference GolanGol] Proposition 11.3.
![]() $a) \Longrightarrow b)$
: Let E be an indecomposable injective object in
$a) \Longrightarrow b)$
: Let E be an indecomposable injective object in
![]() $\mathcal {D}$
, and let
$\mathcal {D}$
, and let
![]() $t_{\mathcal {L}}(E)$
denote the largest subobject of E contained in
$t_{\mathcal {L}}(E)$
denote the largest subobject of E contained in
![]() $\mathcal {L}$
. Suppose that
$\mathcal {L}$
. Suppose that
![]() $t_{\mathcal {L}}(E) \neq 0$
. Then E is an injective hull of
$t_{\mathcal {L}}(E) \neq 0$
. Then E is an injective hull of
![]() $t (E)$
and hence, by stability, is contained in
$t (E)$
and hence, by stability, is contained in
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
![]() $b) \Longrightarrow a)$
: We write an injective hull
$b) \Longrightarrow a)$
: We write an injective hull
![]() $E(V)$
of an object V lying in
$E(V)$
of an object V lying in
![]() $\mathcal {L}$
as a direct sum
$\mathcal {L}$
as a direct sum
![]() $E(V) = \oplus _{i \in I} E_i$
of indecomposable injective objects
$E(V) = \oplus _{i \in I} E_i$
of indecomposable injective objects
![]() $E_i$
. Since
$E_i$
. Since
![]() $E_i \cap V \neq 0$
lies in
$E_i \cap V \neq 0$
lies in
![]() $\mathcal {L}$
for any
$\mathcal {L}$
for any
![]() $i \in I$
, we see that all
$i \in I$
, we see that all
![]() $E_i$
and hence
$E_i$
and hence
![]() $E(V)$
lie in
$E(V)$
lie in
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
Corollary 3.5.2. Let
![]() $\mathcal {L}$
be a stable localising subcategory of
$\mathcal {L}$
be a stable localising subcategory of
![]() $\mathcal {D}$
; then
$\mathcal {D}$
; then
The following is a straightforward generalization of [Reference LoudenLou] Proposition 4.
Lemma 3.5.3. For a subset
![]() $A \subseteq \mathbf {Sp}(\mathcal {D})$
, the following are equivalent:
$A \subseteq \mathbf {Sp}(\mathcal {D})$
, the following are equivalent:
-
a)
 $A = A(\mathcal {L})$
for a stable localising subcategory
$A = A(\mathcal {L})$
for a stable localising subcategory
 $\mathcal {L}$
of
$\mathcal {L}$
of
 $\mathcal {D}$
;
$\mathcal {D}$
; -
b) if
 $[E] \in \mathbf {Sp}(\mathcal {D})$
satisfies
$[E] \in \mathbf {Sp}(\mathcal {D})$
satisfies
 ${\mathrm {Hom}}_{\mathcal {D}}(E,E') \neq 0$
for some
${\mathrm {Hom}}_{\mathcal {D}}(E,E') \neq 0$
for some
 $[E'] \in A$
, then
$[E'] \in A$
, then
 $[E] \in A$
.
$[E] \in A$
.
Proof.
![]() $a) \Longrightarrow b)$
: Let
$a) \Longrightarrow b)$
: Let
![]() $[E'] \in A(\mathcal {L})$
such that
$[E'] \in A(\mathcal {L})$
such that
![]() ${\mathrm {Hom}}_{\mathcal {D}}(E,E') \neq 0$
. Then E does not lie in
${\mathrm {Hom}}_{\mathcal {D}}(E,E') \neq 0$
. Then E does not lie in
![]() $\mathcal {L}$
. Since
$\mathcal {L}$
. Since
![]() $\mathcal {L}$
is stable, Lemma 3.5.1 applies and tells us that E does not have any nonzero subobject lying in
$\mathcal {L}$
is stable, Lemma 3.5.1 applies and tells us that E does not have any nonzero subobject lying in
![]() $\mathcal {L}$
. Hence,
$\mathcal {L}$
. Hence,
![]() $[E] \in A(\mathcal {L}) = A$
.
$[E] \in A(\mathcal {L}) = A$
.
![]() $b) \Longrightarrow a)$
: Let
$b) \Longrightarrow a)$
: Let
![]() $\mathcal {L}$
be the localising subcategory of
$\mathcal {L}$
be the localising subcategory of
![]() $\mathcal {D}$
cogenerated by the
$\mathcal {D}$
cogenerated by the
![]() $E'$
for
$E'$
for
![]() $[E'] \in A$
. This means that
$[E'] \in A$
. This means that
![]() $\mathcal {L}$
is the full subcategory of those objects V in
$\mathcal {L}$
is the full subcategory of those objects V in
![]() $\mathcal {D}$
which satisfy
$\mathcal {D}$
which satisfy
![]() ${\mathrm {Hom}}_{\mathcal {D}}(V,E') = 0$
for any
${\mathrm {Hom}}_{\mathcal {D}}(V,E') = 0$
for any
![]() $[E'] \in A$
. It is immediate that
$[E'] \in A$
. It is immediate that
![]() $A \subseteq A(\mathcal {L})$
. Consider any
$A \subseteq A(\mathcal {L})$
. Consider any
![]() $[E] \in A(\mathcal {L})$
. Then E cannot lie in
$[E] \in A(\mathcal {L})$
. Then E cannot lie in
![]() $\mathcal {L}$
. Hence, there must exist an
$\mathcal {L}$
. Hence, there must exist an
![]() $[E'] \in A$
such that
$[E'] \in A$
such that
![]() ${\mathrm {Hom}}_{\mathcal {D}}(E,E') \neq 0$
. It follows from (b) that
${\mathrm {Hom}}_{\mathcal {D}}(E,E') \neq 0$
. It follows from (b) that
![]() $[E] \in A$
. This shows that
$[E] \in A$
. This shows that
![]() $A = A(\mathcal {L})$
. To establish that
$A = A(\mathcal {L})$
. To establish that
![]() $\mathcal {L}$
is stable, we use Lemma 3.5.1. We have just seen that the E which do not lie in
$\mathcal {L}$
is stable, we use Lemma 3.5.1. We have just seen that the E which do not lie in
![]() $\mathcal {L}$
must have
$\mathcal {L}$
must have
![]() $[E] \in A(\mathcal {L})$
. By the very definition of
$[E] \in A(\mathcal {L})$
. By the very definition of
![]() $A(\mathcal {L})$
, such E do not have a nonzero subobject lying in
$A(\mathcal {L})$
, such E do not have a nonzero subobject lying in
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
A subset
![]() $A \subseteq \mathbf {Sp}(\mathcal {D})$
will be called stable, resp. stable-open, if it is of the form
$A \subseteq \mathbf {Sp}(\mathcal {D})$
will be called stable, resp. stable-open, if it is of the form
![]() $A = A(\mathcal {L})$
for some stable localising subcategory
$A = A(\mathcal {L})$
for some stable localising subcategory
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\mathcal {D}$
, resp. if it is stable and open for the Gabriel–Zariski topology. It is clear, for example, from Lemma 3.5.3, that arbitrary intersections and unions of stable subsets are stable again. Therefore, the stable, resp. stable-open, subsets are the open subsets for a topology which we call the stable, resp. stable Zariski, topology of
$\mathcal {D}$
, resp. if it is stable and open for the Gabriel–Zariski topology. It is clear, for example, from Lemma 3.5.3, that arbitrary intersections and unions of stable subsets are stable again. Therefore, the stable, resp. stable-open, subsets are the open subsets for a topology which we call the stable, resp. stable Zariski, topology of
![]() $\mathbf {Sp}(\mathcal {D})$
.
$\mathbf {Sp}(\mathcal {D})$
.
Corollary 3.5.4. The bijections
![]() $\mathbf {Sp}(\mathcal {C}) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A}_j) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A})$
in Equation (2) respect stable subsets; in particular, the inverse maps are continuous for the stable topologies.
$\mathbf {Sp}(\mathcal {C}) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A}_j) \xrightarrow {\;\simeq \;} \mathbf {Sp}(\mathcal {A})$
in Equation (2) respect stable subsets; in particular, the inverse maps are continuous for the stable topologies.
Proof. It suffices to consider the map
![]() $\mathbf {Sp}(\mathcal {C}) \rightarrow \mathbf {Sp}(\mathcal {A})$
sending
$\mathbf {Sp}(\mathcal {C}) \rightarrow \mathbf {Sp}(\mathcal {A})$
sending
![]() $[E]$
to
$[E]$
to
![]() $[r(E)]$
. Let
$[r(E)]$
. Let
![]() $S \subseteq \mathbf {Sp}(\mathcal {C})$
be any stable subset and
$S \subseteq \mathbf {Sp}(\mathcal {C})$
be any stable subset and
![]() $[r(E')]$
be any point in the image of S. Now, suppose that we have
$[r(E')]$
be any point in the image of S. Now, suppose that we have
![]() $[U] \in \mathbf {Sp}(\mathcal {A})$
such that
$[U] \in \mathbf {Sp}(\mathcal {A})$
such that
![]() ${\mathrm {Hom}}_{\mathcal {A}}(U,r(E')) \neq 0$
. Then
${\mathrm {Hom}}_{\mathcal {A}}(U,r(E')) \neq 0$
. Then
![]() ${\mathrm {Hom}}_{\mathcal {C}}(U,E') \neq 0$
and hence
${\mathrm {Hom}}_{\mathcal {C}}(U,E') \neq 0$
and hence
![]() ${\mathrm {Hom}}_{\mathcal {C}}(E_{\mathcal {C}}(U),E') \neq 0$
. Using Lemma 3.5.3, we deduce that
${\mathrm {Hom}}_{\mathcal {C}}(E_{\mathcal {C}}(U),E') \neq 0$
. Using Lemma 3.5.3, we deduce that
![]() $[E (U)] \in S$
. But
$[E (U)] \in S$
. But
![]() $U \cong r(E_{\mathcal {C}}(U))$
. It follows that
$U \cong r(E_{\mathcal {C}}(U))$
. It follows that
![]() $[U]$
lies in the image of S. Using again Lemma 3.5.3, we conclude that the image of S is stable.
$[U]$
lies in the image of S. Using again Lemma 3.5.3, we conclude that the image of S is stable.
Lemma 3.5.5. Suppose that
![]() $\mathcal {L}$
is a stable localising subcategory of
$\mathcal {L}$
is a stable localising subcategory of
![]() $\mathcal {C}$
; then the right derived functors
$\mathcal {C}$
; then the right derived functors
![]() $R^j r$
of r, for any
$R^j r$
of r, for any
![]() $j \geq 0$
, map
$j \geq 0$
, map
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathcal {A} \cap \mathcal {L}$
.
$\mathcal {A} \cap \mathcal {L}$
.
Proof. Let V be any object in
![]() $\mathcal {L}$
. Since
$\mathcal {L}$
. Since
![]() $\mathcal {L}$
is stable an injective hull
$\mathcal {L}$
is stable an injective hull
![]() $E(V)$
of V in
$E(V)$
of V in
![]() $\mathcal {C}$
lies already in
$\mathcal {C}$
lies already in
![]() $\mathcal {L}$
. Hence, we find an injective resolution
$\mathcal {L}$
. Hence, we find an injective resolution
![]() $V \xrightarrow {\simeq } I^\bullet $
of V in
$V \xrightarrow {\simeq } I^\bullet $
of V in
![]() $\mathcal {C}$
all of whose terms lie in
$\mathcal {C}$
all of whose terms lie in
![]() $\mathcal {L}$
. The values
$\mathcal {L}$
. The values
![]() $R^j r(V)$
of the right derived functors in question are the cohomology objects of the complex
$R^j r(V)$
of the right derived functors in question are the cohomology objects of the complex
![]() $r(I^\bullet )$
. On the other hand, Definition 3.1.1.b easily implies that r maps
$r(I^\bullet )$
. On the other hand, Definition 3.1.1.b easily implies that r maps
![]() $\mathcal {L}$
to
$\mathcal {L}$
to
![]() $\mathcal {A} \cap \mathcal {L}$
. It follows that the complex
$\mathcal {A} \cap \mathcal {L}$
. It follows that the complex
![]() $r(I^\bullet )$
and then also its cohomology objects lie in
$r(I^\bullet )$
and then also its cohomology objects lie in
![]() $\mathcal {A} \cap \mathcal {L}$
.
$\mathcal {A} \cap \mathcal {L}$
.
For the rest of this section, we impose on our thickening
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\mathcal {A}$
the additional condition that
$\mathcal {A}$
the additional condition that
![]() $\mathcal {A}$
has a noetherian projective generator P. Note that P then also is noetherian as an object in
$\mathcal {A}$
has a noetherian projective generator P. Note that P then also is noetherian as an object in
![]() $\mathcal {C}$
. We let
$\mathcal {C}$
. We let
![]() $H := {\mathrm {End}}_{\mathcal {A}}(P)^{{\mathrm {op}}} = {\mathrm {End}} (P)^{{\mathrm {op}}}$
denote the opposite ring of the endomorphism ring of the generator P. In this situation, one has the equivalence of categories
$H := {\mathrm {End}}_{\mathcal {A}}(P)^{{\mathrm {op}}} = {\mathrm {End}} (P)^{{\mathrm {op}}}$
denote the opposite ring of the endomorphism ring of the generator P. In this situation, one has the equivalence of categories
 $$ \begin{align} \mathcal{A} & \xrightarrow{\;\simeq\;} {\mathrm{Mod}}(H) \\ A & \longmapsto {\mathrm{Hom}}_{\mathcal{A}}(P,A) = {\mathrm{Hom}}_{\mathcal{C}}(P,A) \nonumber \end{align} $$
$$ \begin{align} \mathcal{A} & \xrightarrow{\;\simeq\;} {\mathrm{Mod}}(H) \\ A & \longmapsto {\mathrm{Hom}}_{\mathcal{A}}(P,A) = {\mathrm{Hom}}_{\mathcal{C}}(P,A) \nonumber \end{align} $$
(cf. [Reference PopescuPop] Corollary 5.9.5). In fact, the
![]() ${\mathrm {Ext}}$
-functors
${\mathrm {Ext}}$
-functors
![]() ${\mathrm {Ext}}_{\mathcal {C}}^j(P,-)$
on
${\mathrm {Ext}}_{\mathcal {C}}^j(P,-)$
on
![]() $\mathcal {C}$
, for
$\mathcal {C}$
, for
![]() $j \geq 0$
, can naturally be viewed as functors
$j \geq 0$
, can naturally be viewed as functors
In particular, the natural isomorphism
from Corollary 3.2.2 is an isomorphism of H-modules.
Lemma 3.5.6. Let A and V be objects in
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
-
a) There is a natural exact sequence of abelian groups
 $$ \begin{align*} 0 \rightarrow {\mathrm{Ext}}^1_{\mathcal{A}}(A, V) \rightarrow {\mathrm{Ext}}^1_{\mathcal{C}}(A,V) \xrightarrow{\varphi_{A,V}} {\mathrm{Hom}}_H({\mathrm{Hom}}_{\mathcal{A}}(P,A),{\mathrm{Ext}}_{\mathcal{C}}^1(P,V)) \rightarrow {\mathrm{Ext}}^2_{\mathcal{A}}(A, V) . \end{align*} $$
$$ \begin{align*} 0 \rightarrow {\mathrm{Ext}}^1_{\mathcal{A}}(A, V) \rightarrow {\mathrm{Ext}}^1_{\mathcal{C}}(A,V) \xrightarrow{\varphi_{A,V}} {\mathrm{Hom}}_H({\mathrm{Hom}}_{\mathcal{A}}(P,A),{\mathrm{Ext}}_{\mathcal{C}}^1(P,V)) \rightarrow {\mathrm{Ext}}^2_{\mathcal{A}}(A, V) . \end{align*} $$
-
b) If V is an injective object in
 $\mathcal {A}$
, then
$\mathcal {A}$
, then
 $\varphi _{A,V}$
is a natural isomorphism.
$\varphi _{A,V}$
is a natural isomorphism.
Proof. a) By Proposition 3.2.1, we have the convergent Grothendieck spectral sequence
The exact sequence of low degree terms is
Since V lies in
![]() $\mathcal {A}$
, we have
$\mathcal {A}$
, we have
![]() $r(V) = V$
. Moreover, using Equation (5) for the second equality, we obtain
$r(V) = V$
. Moreover, using Equation (5) for the second equality, we obtain
 $$ \begin{align*} {\mathrm{Hom}}_{\mathcal{A}}(A, R^1r(V)) & = {\mathrm{Hom}}_H({\mathrm{Hom}}_{\mathcal{A}}(P,A),{\mathrm{Hom}}_{\mathcal{A}}(P, R^1 r(V))) \\ & = {\mathrm{Hom}}_H({\mathrm{Hom}} (P,A),{\mathrm{Ext}}_{\mathcal{C}}^1(P,V)) . \end{align*} $$
$$ \begin{align*} {\mathrm{Hom}}_{\mathcal{A}}(A, R^1r(V)) & = {\mathrm{Hom}}_H({\mathrm{Hom}}_{\mathcal{A}}(P,A),{\mathrm{Hom}}_{\mathcal{A}}(P, R^1 r(V))) \\ & = {\mathrm{Hom}}_H({\mathrm{Hom}} (P,A),{\mathrm{Ext}}_{\mathcal{C}}^1(P,V)) . \end{align*} $$
b) Since V is injective, we have
![]() ${\mathrm {Ext}}^1_{\mathcal {A}}(A,V) = {\mathrm {Ext}}^2_{\mathcal {A}}(A,V) = 0$
.
${\mathrm {Ext}}^1_{\mathcal {A}}(A,V) = {\mathrm {Ext}}^2_{\mathcal {A}}(A,V) = 0$
.
Now, let
![]() $\mathcal {L}$
be a localising subcategory of
$\mathcal {L}$
be a localising subcategory of
![]() $\mathcal {C}$
. Then
$\mathcal {C}$
. Then
![]() $\mathcal {L} \cap \mathcal {A}$
is a localising subcategory of
$\mathcal {L} \cap \mathcal {A}$
is a localising subcategory of
![]() $\mathcal {A}$
. We want to investigate how the stability requirements for
$\mathcal {A}$
. We want to investigate how the stability requirements for
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {A} \cap \mathcal {L}$
are related to each other. It is obvious that if
$\mathcal {A} \cap \mathcal {L}$
are related to each other. It is obvious that if
![]() $\mathcal {L}$
is stable in
$\mathcal {L}$
is stable in
![]() $\mathcal {C}$
, then
$\mathcal {C}$
, then
![]() $\mathcal {A} \cap \mathcal {L}$
is stable in
$\mathcal {A} \cap \mathcal {L}$
is stable in
![]() $\mathcal {A}$
. The converse is more subtle. We denote the corresponding localising subcategory of
$\mathcal {A}$
. The converse is more subtle. We denote the corresponding localising subcategory of
![]() ${\mathrm {Mod}}(H)$
by
${\mathrm {Mod}}(H)$
by
Proposition 3.5.7. Suppose that
![]() $\mathcal {A} \cap \mathcal {L}$
is stable in
$\mathcal {A} \cap \mathcal {L}$
is stable in
![]() $\mathcal {A}$
and that
$\mathcal {A}$
and that
![]() ${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
maps
${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
maps
![]() $\mathcal {A} \cap \mathcal {L}$
to
$\mathcal {A} \cap \mathcal {L}$
to
![]() $\mathcal {L}^H$
. Let V in
$\mathcal {L}^H$
. Let V in
![]() $\mathcal {C}$
be a nonzero object such that
$\mathcal {C}$
be a nonzero object such that
-
a)
 $V = r_1(V)$
, and
$V = r_1(V)$
, and -
b)
 $r(V)$
is the largest subobject of V contained in
$r(V)$
is the largest subobject of V contained in
 $\mathcal {L}$
.
$\mathcal {L}$
.
Then
![]() $V = r(V)$
.
$V = r(V)$
.
Proof. We first note that we have
![]() $r(V) \neq 0$
by Definition 3.1.1.b.
$r(V) \neq 0$
by Definition 3.1.1.b.
Let
![]() $E_{\mathcal {C}}(V)$
be an injective hull of V in
$E_{\mathcal {C}}(V)$
be an injective hull of V in
![]() $\mathcal {C}$
, and let
$\mathcal {C}$
, and let
![]() $E = r_1(E_{\mathcal {C}}(V))$
. Then
$E = r_1(E_{\mathcal {C}}(V))$
. Then
![]() $r(E) = r(E_{\mathcal {C}}(V))$
is an injective object in
$r(E) = r(E_{\mathcal {C}}(V))$
is an injective object in
![]() $\mathcal {A}$
, and
$\mathcal {A}$
, and
![]() $r(V) \subseteq r(E)$
. In fact, we have the inclusions
$r(V) \subseteq r(E)$
. In fact, we have the inclusions

By Lemma 3.3.1.a, the extension
![]() $r(V) \subseteq V$
is essential. Hence, the extension
$r(V) \subseteq V$
is essential. Hence, the extension
![]() $r(V) \subseteq r(E)$
is essential as well. Since
$r(V) \subseteq r(E)$
is essential as well. Since
![]() $\mathcal {A} \cap \mathcal {L}$
is stable in
$\mathcal {A} \cap \mathcal {L}$
is stable in
![]() $\mathcal {A}$
and since
$\mathcal {A}$
and since
![]() $r(V)$
lies
$r(V)$
lies
![]() $\mathcal {A} \cap \mathcal {L}$
by assumption b), we see that
$\mathcal {A} \cap \mathcal {L}$
by assumption b), we see that
![]() $r(E)$
lies in
$r(E)$
lies in
![]() $\mathcal {A} \cap \mathcal {L}$
.
$\mathcal {A} \cap \mathcal {L}$
.
Now, because
![]() $r_1$
is left exact,
$r_1$
is left exact,
![]() $V = r_1(V) \subseteq r_1(E_{\mathcal {C}}(V)) = E$
. Next,
$V = r_1(V) \subseteq r_1(E_{\mathcal {C}}(V)) = E$
. Next,
![]() $(r(E) + V)/r(E) \cong V / (V \cap r(E)) = V / r(V)$
because r is left exact. Since
$(r(E) + V)/r(E) \cong V / (V \cap r(E)) = V / r(V)$
because r is left exact. Since
![]() $r(V)$
is the largest subobject of V contained in
$r(V)$
is the largest subobject of V contained in
![]() $\mathcal {L}$
, we see that
$\mathcal {L}$
, we see that
![]() $V/r(V)$
is
$V/r(V)$
is
![]() $\mathcal {L}$
-torsion-free. Also,
$\mathcal {L}$
-torsion-free. Also,
![]() $V = r_1(V)$
means that
$V = r_1(V)$
means that
![]() $V / r(V)$
lies in
$V / r(V)$
lies in
![]() $\mathcal {A}$
. We deduce that
$\mathcal {A}$
. We deduce that
![]() $(r(E) + V)/r(E) \cong V / r(V)$
lies in
$(r(E) + V)/r(E) \cong V / r(V)$
lies in
![]() $\mathcal {A}$
and is
$\mathcal {A}$
and is
![]() $\mathcal {L}$
-torsion-free. Hence, we need to show that
$\mathcal {L}$
-torsion-free. Hence, we need to show that
![]() $V \subseteq r(E)$
.
$V \subseteq r(E)$
.
Consider any intermediate object
![]() $r(E) \subseteq V^{\prime \prime } \subseteq V' := r(E) + V \subseteq E$
in
$r(E) \subseteq V^{\prime \prime } \subseteq V' := r(E) + V \subseteq E$
in
![]() $\mathcal {C}$
. We obtain extension classes
$\mathcal {C}$
. We obtain extension classes
![]() $e' = [0 \rightarrow r(E) \rightarrow V' \rightarrow V'/r(E) \rightarrow 0] \in {\mathrm {Ext}}_{\mathcal {C}}^1(V'/r(E),r(E))$
and analogously
$e' = [0 \rightarrow r(E) \rightarrow V' \rightarrow V'/r(E) \rightarrow 0] \in {\mathrm {Ext}}_{\mathcal {C}}^1(V'/r(E),r(E))$
and analogously
![]() $e^{\prime \prime } \in {\mathrm {Ext}}_{\mathcal {C}}^1(V^{\prime \prime }/r(E),r(E))$
. Note that
$e^{\prime \prime } \in {\mathrm {Ext}}_{\mathcal {C}}^1(V^{\prime \prime }/r(E),r(E))$
. Note that
![]() $V'/r(E)$
,
$V'/r(E)$
,
![]() $V^{\prime \prime }/r(E)$
and
$V^{\prime \prime }/r(E)$
and
![]() $r(E)$
are objects in
$r(E)$
are objects in
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
![]() $V'/r(E)$
and
$V'/r(E)$
and
![]() $V^{\prime \prime }/r(E)$
being
$V^{\prime \prime }/r(E)$
being
![]() $\mathcal {A} \cap \mathcal {L}$
-torsion-free and
$\mathcal {A} \cap \mathcal {L}$
-torsion-free and
![]() $r(E)$
being injective in
$r(E)$
being injective in
![]() $\mathcal {A}$
. Hence, Lemma 3.5.6 applies. We define the H-modules
$\mathcal {A}$
. Hence, Lemma 3.5.6 applies. We define the H-modules
![]() $N^{\prime \prime } := {\mathrm {Hom}}_{\mathcal {A}}(P,V^{\prime \prime }/r(E)) \subseteq N' := {\mathrm {Hom}}_{\mathcal {A}}(P,V'/r(E))$
and obtain the commutative diagram
$N^{\prime \prime } := {\mathrm {Hom}}_{\mathcal {A}}(P,V^{\prime \prime }/r(E)) \subseteq N' := {\mathrm {Hom}}_{\mathcal {A}}(P,V'/r(E))$
and obtain the commutative diagram

with horizontal isomorphisms. Obviously, the left perpendicular arrow maps
![]() $e'$
to
$e'$
to
![]() $e^{\prime \prime }$
. Since
$e^{\prime \prime }$
. Since
![]() $r(E)$
lies in
$r(E)$
lies in
![]() $\mathcal {A} \cap \mathcal {L}$
the H-module
$\mathcal {A} \cap \mathcal {L}$
the H-module
![]() ${\mathrm {Ext}}^1_{\mathcal {C}}(P, r(E))$
lies in
${\mathrm {Ext}}^1_{\mathcal {C}}(P, r(E))$
lies in
![]() $\mathcal {L}^H$
by our assumptions. We have the H-linear map
$\mathcal {L}^H$
by our assumptions. We have the H-linear map
![]() $f' := \varphi '(e') : N' \rightarrow {\mathrm {Ext}}^1_{\mathcal {C}}(P, r(E))$
. Suppose now that
$f' := \varphi '(e') : N' \rightarrow {\mathrm {Ext}}^1_{\mathcal {C}}(P, r(E))$
. Suppose now that
![]() $N' \neq 0$
, and choose a nonzero element
$N' \neq 0$
, and choose a nonzero element
![]() $v \in N'$
. Let
$v \in N'$
. Let
![]() $J := {\mathrm {Ann}}_H(f'(v)) \subseteq H$
be the annihilator left ideal. Then
$J := {\mathrm {Ann}}_H(f'(v)) \subseteq H$
be the annihilator left ideal. Then
![]() $H/J \cong Hf'(v)$
lie in
$H/J \cong Hf'(v)$
lie in
![]() $\mathcal {L}^H$
. We now consider specifically the H-submodule
$\mathcal {L}^H$
. We now consider specifically the H-submodule
![]() $N^{\prime \prime } := Jv \subseteq N'$
. By the category equivalence, there is a unique
$N^{\prime \prime } := Jv \subseteq N'$
. By the category equivalence, there is a unique
![]() $V^{\prime \prime }$
as above such that
$V^{\prime \prime }$
as above such that
![]() $N^{\prime \prime } = {\mathrm {Hom}}_{\mathcal {A}}(P,V^{\prime \prime }/r(E))$
. We first check that
$N^{\prime \prime } = {\mathrm {Hom}}_{\mathcal {A}}(P,V^{\prime \prime }/r(E))$
. We first check that
![]() $N^{\prime \prime } \neq 0$
. Otherwise, we would have
$N^{\prime \prime } \neq 0$
. Otherwise, we would have
![]() $J \subseteq {\mathrm {Ann}}_H(v)$
so that
$J \subseteq {\mathrm {Ann}}_H(v)$
so that
![]() $H/J$
surjects onto
$H/J$
surjects onto
![]() $Hv \subseteq N'$
, which implies that
$Hv \subseteq N'$
, which implies that
![]() $Hv$
lies in
$Hv$
lies in
![]() $\mathcal {L}^H$
. On the other hand the modules
$\mathcal {L}^H$
. On the other hand the modules
![]() $Hv \subseteq N'$
are
$Hv \subseteq N'$
are
![]() $\mathcal {L}^H$
-torsion-free, which is a contradiction. Hence,
$\mathcal {L}^H$
-torsion-free, which is a contradiction. Hence,
![]() $N^{\prime \prime } \neq 0$
. Now,
$N^{\prime \prime } \neq 0$
. Now,
The commutativity of the above diagram then implies that the extension class
![]() $e^{\prime \prime } = 0$
, that is, the short exact sequence
$e^{\prime \prime } = 0$
, that is, the short exact sequence
![]() $0 \rightarrow r(E) \rightarrow V^{\prime \prime } \rightarrow V^{\prime \prime }/r(E) \rightarrow 0$
in
$0 \rightarrow r(E) \rightarrow V^{\prime \prime } \rightarrow V^{\prime \prime }/r(E) \rightarrow 0$
in
![]() $\mathcal {C}$
splits. But then because
$\mathcal {C}$
splits. But then because
![]() $V^{\prime \prime }/r(E) \neq 0$
, we see
$V^{\prime \prime }/r(E) \neq 0$
, we see
![]() $r(E)$
is not essential in E, which contradicts Lemma 3.3.1.a. It follows that
$r(E)$
is not essential in E, which contradicts Lemma 3.3.1.a. It follows that
![]() $N'$
must be zero, that is, that
$N'$
must be zero, that is, that
![]() $r(E) + V = r(E)$
.
$r(E) + V = r(E)$
.
Theorem 3.5.8. Suppose that
![]() $\mathcal {A} \cap \mathcal {L}$
is stable in
$\mathcal {A} \cap \mathcal {L}$
is stable in
![]() $\mathcal {A}$
. Then the following are equivalent:
$\mathcal {A}$
. Then the following are equivalent:
-
a)
 $\mathcal {L}$
is stable in
$\mathcal {L}$
is stable in
 $\mathcal {C}$
,
$\mathcal {C}$
, -
b)
 $R^jr$
maps
$R^jr$
maps
 $\mathcal {L}$
to
$\mathcal {L}$
to
 $\mathcal {A} \cap \mathcal {L}$
for all
$\mathcal {A} \cap \mathcal {L}$
for all
 $j \geq 0$
,
$j \geq 0$
, -
c)
 ${\mathrm {Ext}}^j_{\mathcal {C}}(P,-)$
maps
${\mathrm {Ext}}^j_{\mathcal {C}}(P,-)$
maps
 $\mathcal {L}$
to
$\mathcal {L}$
to
 $\mathcal {L}^H$
for all
$\mathcal {L}^H$
for all
 $j \geq 0$
,
$j \geq 0$
, -
d)
 ${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
maps
${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
maps
 $\mathcal {L}$
to
$\mathcal {L}$
to
 $\mathcal {L}^H$
,
$\mathcal {L}^H$
, -
e)
 ${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
maps
${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
maps
 $\mathcal {A} \cap \mathcal {L}$
to
$\mathcal {A} \cap \mathcal {L}$
to
 $\mathcal {L}^H$
.
$\mathcal {L}^H$
.
Proof. a)
![]() $\Rightarrow $
b). This is Lemma 3.5.5.
$\Rightarrow $
b). This is Lemma 3.5.5.
b)
![]() $\Rightarrow $
c). This follows from Equation (5) and the definition of
$\Rightarrow $
c). This follows from Equation (5) and the definition of
![]() $\mathcal {L}^H$
.
$\mathcal {L}^H$
.
c)
![]() $\Rightarrow $
d)
$\Rightarrow $
d)
![]() $\Rightarrow $
e). These are trivial.
$\Rightarrow $
e). These are trivial.
e)
![]() $\Rightarrow $
a). Let E be an indecomposable injective object in
$\Rightarrow $
a). Let E be an indecomposable injective object in
![]() $\mathcal {C}$
, and let Y be its largest subobject in
$\mathcal {C}$
, and let Y be its largest subobject in
![]() $\mathcal {L}$
. We suppose that
$\mathcal {L}$
. We suppose that
![]() $Y \neq 0$
and will aim to show that
$Y \neq 0$
and will aim to show that
![]() $Y = E$
. Let
$Y = E$
. Let
![]() $E_n := r_n(E)$
for
$E_n := r_n(E)$
for
![]() $n \geq 0$
, and note that
$n \geq 0$
, and note that
![]() $E = \bigcup \limits _{n=0}^\infty E_n$
by Lemma 3.1.5. Correspondingly,
$E = \bigcup \limits _{n=0}^\infty E_n$
by Lemma 3.1.5. Correspondingly,
![]() $Y = \bigcup \limits _{n=0}^\infty Y_n$
with
$Y = \bigcup \limits _{n=0}^\infty Y_n$
with
![]() $Y_n := r_n(Y)$
, and note that
$Y_n := r_n(Y)$
, and note that
![]() $Y_n = Y \cap V_n$
for all
$Y_n = Y \cap V_n$
for all
![]() $n \geq 0$
because each
$n \geq 0$
because each
![]() $r_n$
is left exact.
$r_n$
is left exact.
Since Y is the largest subobject of E contained in
![]() $\mathcal {L}$
,
$\mathcal {L}$
,
![]() $E/Y$
is
$E/Y$
is
![]() $\mathcal {L}$
-torsion free. Hence, for any
$\mathcal {L}$
-torsion free. Hence, for any
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $(E_n + Y)/Y$
is also
$(E_n + Y)/Y$
is also
![]() $\mathcal {L}$
-torsion free. But
$\mathcal {L}$
-torsion free. But
![]() $(E_n + Y)/Y \cong E_n / (E_n \cap Y) = E_n / Y_n$
. Hence, for all
$(E_n + Y)/Y \cong E_n / (E_n \cap Y) = E_n / Y_n$
. Hence, for all
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $E_n / Y_n$
is
$E_n / Y_n$
is
![]() $\mathcal {L}$
-torsion-free, and
$\mathcal {L}$
-torsion-free, and
![]() $Y_n$
is the largest subobject of
$Y_n$
is the largest subobject of
![]() $E_n$
contained in
$E_n$
contained in
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
With
![]() $Y \neq 0$
, also
$Y \neq 0$
, also
![]() $Y_0 = r(Y)$
is nonzero. Since E is an indecomposable injective in
$Y_0 = r(Y)$
is nonzero. Since E is an indecomposable injective in
![]() $\mathcal {C}$
, it follows that
$\mathcal {C}$
, it follows that
![]() $Y_0$
is essential in E.
$Y_0$
is essential in E.
Suppose for a contradiction that
![]() $Y \neq E$
, and let n be minimal such that
$Y \neq E$
, and let n be minimal such that
![]() $Y_n \neq E_n$
. Now,
$Y_n \neq E_n$
. Now,
![]() $Y_0 \subseteq E_0$
is an essential extension in
$Y_0 \subseteq E_0$
is an essential extension in
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
![]() $Y_0$
lying in
$Y_0$
lying in
![]() $\mathcal {A} \cap \mathcal {L}$
; since
$\mathcal {A} \cap \mathcal {L}$
; since
![]() $\mathcal {A} \cap \mathcal {L}$
is stable in
$\mathcal {A} \cap \mathcal {L}$
is stable in
![]() $\mathcal {A}$
, we see that
$\mathcal {A}$
, we see that
![]() $Y_0 = E_0$
. Hence,
$Y_0 = E_0$
. Hence,
![]() $n \geq 1$
, and the minimality of n implies that
$n \geq 1$
, and the minimality of n implies that
![]() $Y_{n-1} = E_{n-1}$
so that
$Y_{n-1} = E_{n-1}$
so that
![]() $E_{n-1} \subseteq Y_n$
.
$E_{n-1} \subseteq Y_n$
.
Now, consider the short exact sequence
in
![]() $\mathcal {A}$
. Note that
$\mathcal {A}$
. Note that
![]() $Y_n / E_{n-1}$
lies in
$Y_n / E_{n-1}$
lies in
![]() $\mathcal {L}$
and that
$\mathcal {L}$
and that
![]() $E_n / Y_n$
is
$E_n / Y_n$
is
![]() $\mathcal {L}$
-torsion-free and nonzero. If
$\mathcal {L}$
-torsion-free and nonzero. If
![]() $Y_n / E_{n-1}$
is also nonzero, then because
$Y_n / E_{n-1}$
is also nonzero, then because
![]() $\mathcal {A} \cap \mathcal {L}$
is stable in
$\mathcal {A} \cap \mathcal {L}$
is stable in
![]() $\mathcal {A}$
, this extension is not essential. This gives us some subobject W of
$\mathcal {A}$
, this extension is not essential. This gives us some subobject W of
![]() $E_n$
containing
$E_n$
containing
![]() $E_{n-1}$
such that
$E_{n-1}$
such that
![]() $W / E_{n-1}$
is isomorphic to a nonzero subobject of
$W / E_{n-1}$
is isomorphic to a nonzero subobject of
![]() $E_n/Y_n$
; thus,
$E_n/Y_n$
; thus,
![]() $W / E_{n-1}$
is also nonzero and
$W / E_{n-1}$
is also nonzero and
![]() $\mathcal {L}$
-torsion-free. If
$\mathcal {L}$
-torsion-free. If
![]() $Y_n = E_{n-1}$
, then we can take
$Y_n = E_{n-1}$
, then we can take
![]() $W = E_n$
to obtain an object with the same properties.
$W = E_n$
to obtain an object with the same properties.
Write
![]() $E_{-1} := 0$
and
$E_{-1} := 0$
and
![]() $X := W/E_{n-2} \subseteq E_n / E_{n-2}$
, and consider the short exact sequence
$X := W/E_{n-2} \subseteq E_n / E_{n-2}$
, and consider the short exact sequence
Since the outer terms in this short exact sequence lie in
![]() $\mathcal {A}$
, we see that
$\mathcal {A}$
, we see that
![]() $r_1(X) = X$
. Also,
$r_1(X) = X$
. Also,
![]() $r(X) \subseteq r(E_n / E_{n-2}) = E_{n-1}/E_{n-2} = r( E_{n-1}/E_{n-2} ) \subseteq r(X)$
, where the left equality uses Lemma 3.1.2.b, shows that
$r(X) \subseteq r(E_n / E_{n-2}) = E_{n-1}/E_{n-2} = r( E_{n-1}/E_{n-2} ) \subseteq r(X)$
, where the left equality uses Lemma 3.1.2.b, shows that
Since
![]() $W / E_{n-1}$
is
$W / E_{n-1}$
is
![]() $\mathcal {L}$
-torsion-free and
$\mathcal {L}$
-torsion-free and
![]() $E_{n-1} / E_{n-2} = Y_{n-1} / E_{n-2}$
is a subquotient of Y, we see that
$E_{n-1} / E_{n-2} = Y_{n-1} / E_{n-2}$
is a subquotient of Y, we see that
![]() $r(X)$
is the largest subobject of X contained in
$r(X)$
is the largest subobject of X contained in
![]() $\mathcal {L}$
. Applying now Proposition 3.5.7 with X leads to a contradiction.
$\mathcal {L}$
. Applying now Proposition 3.5.7 with X leads to a contradiction.
3.6 A ring-theoretic case
In this section, we discuss stability for the category
![]() $\mathcal {C} = {\mathrm {Mod}}(H)$
of left H-modules over a ring H which is assumed to be left noetherian and finitely generated as a module over its centre
$\mathcal {C} = {\mathrm {Mod}}(H)$
of left H-modules over a ring H which is assumed to be left noetherian and finitely generated as a module over its centre
![]() $Z(H)$
. This material will be needed in
$Z(H)$
. This material will be needed in
![]() $\S$
3.7.
$\S$
3.7.
The ring
![]() $Z(H)$
is necessarily noetherian by [Reference McConnell and RobsonMCR] Corollary 10.1.11(ii). The ring H is also right noetherian, and the abelian categories
$Z(H)$
is necessarily noetherian by [Reference McConnell and RobsonMCR] Corollary 10.1.11(ii). The ring H is also right noetherian, and the abelian categories
![]() ${\mathrm {Mod}}(H)$
and
${\mathrm {Mod}}(H)$
and
![]() ${\mathrm {Mod}}(Z(H))$
are locally noetherian Grothendieck categories. Of course,
${\mathrm {Mod}}(Z(H))$
are locally noetherian Grothendieck categories. Of course,
![]() ${\mathrm {Spec}}(H)$
and
${\mathrm {Spec}}(H)$
and
![]() ${\mathrm {Spec}}(Z(H))$
denote the prime ideal spectra of the respective rings equipped with its Zariski topology.
${\mathrm {Spec}}(Z(H))$
denote the prime ideal spectra of the respective rings equipped with its Zariski topology.
Let
![]() $\varrho : {\mathrm {Mod}}(H) \rightarrow {\mathrm {Mod}}(Z(H))$
denote the functor of passing to the underlying
$\varrho : {\mathrm {Mod}}(H) \rightarrow {\mathrm {Mod}}(Z(H))$
denote the functor of passing to the underlying
![]() $Z(H)$
-module. By [Reference GabrielGab] Proposition 10 on p. 428, any localising subcategory of
$Z(H)$
-module. By [Reference GabrielGab] Proposition 10 on p. 428, any localising subcategory of
![]() ${\mathrm {Mod}}(Z(H))$
is stable. We further have the following facts.
${\mathrm {Mod}}(Z(H))$
is stable. We further have the following facts.
Lemma 3.6.1.
-
a) For any localising subcategory
 $\mathcal {L}$
of
$\mathcal {L}$
of
 ${\mathrm {Mod}}(Z(H))$
, the localising subcategory
${\mathrm {Mod}}(Z(H))$
, the localising subcategory
 $\varrho ^{-1}(\mathcal {L})$
of
$\varrho ^{-1}(\mathcal {L})$
of
 ${\mathrm {Mod}}(H)$
is stable.
${\mathrm {Mod}}(H)$
is stable. -
b) For any ordinal
 $\alpha $
, we have
$\alpha $
, we have
 $\varrho ^{-1}({\mathrm {Mod}}(Z(H))_\alpha ) = {\mathrm {Mod}}(H)_\alpha $
, which therefore is stable.
$\varrho ^{-1}({\mathrm {Mod}}(Z(H))_\alpha ) = {\mathrm {Mod}}(H)_\alpha $
, which therefore is stable. -
c) For any ordinal
 $\alpha < \kappa ({\mathrm {Mod}}(H))$
, we have
$\alpha < \kappa ({\mathrm {Mod}}(H))$
, we have  $$ \begin{align*} \mathbf{Sp}_\alpha({\mathrm{Mod}}(H)) = \{[E] \in \mathbf{Sp}({\mathrm{Mod}}(H)) : \kappa(E) = \alpha + 1\}. \end{align*} $$
$$ \begin{align*} \mathbf{Sp}_\alpha({\mathrm{Mod}}(H)) = \{[E] \in \mathbf{Sp}({\mathrm{Mod}}(H)) : \kappa(E) = \alpha + 1\}. \end{align*} $$
Proof. a) [Reference GabrielGab] Proposition 12 on p. 431. b) The equality is [Reference McConnell and RobsonMCR] Corollary 10.1.10, and the stability then follows from a). c) Because of b) this follows from Remark 2.2.1.
Next, we have:
-
(A) The continuous map
 $\varphi : {\mathrm {Spec}}(H) \rightarrow {\mathrm {Spec}}(Z(H))$
sending
$\varphi : {\mathrm {Spec}}(H) \rightarrow {\mathrm {Spec}}(Z(H))$
sending
 $\mathfrak {p}$
to
$\mathfrak {p}$
to
 $\mathfrak {p} \cap Z(H)$
is surjective with finite fibers (cf. [Reference GabrielGab] Proposition 11 on p. 429).
$\mathfrak {p} \cap Z(H)$
is surjective with finite fibers (cf. [Reference GabrielGab] Proposition 11 on p. 429). -
(B) We recall from [Reference StenströmSte] Chapter VII
 $\S $
1 that a prime ideal
$\S $
1 that a prime ideal
 $\mathfrak {p}$
of H is associated to the H-module M if there exists a nonzero submodule L of M such that
$\mathfrak {p}$
of H is associated to the H-module M if there exists a nonzero submodule L of M such that
 $\mathfrak {p} = {\mathrm {Ann}}_H(L')$
for all nonzero H-submodules
$\mathfrak {p} = {\mathrm {Ann}}_H(L')$
for all nonzero H-submodules
 $L'$
of L. The map (6)is a homeomorphism w.r.t. the Gabriel–Zariski and the Zariski topology on the left-hand and right-hand sides, respectively ([Reference StenströmSte] Theorem VII.2.1 recalling the fact that H is fully left and right bounded by [Reference StenströmSte] VII §2 Example 4), [Reference GabrielGab] V §4). Let
$L'$
of L. The map (6)is a homeomorphism w.r.t. the Gabriel–Zariski and the Zariski topology on the left-hand and right-hand sides, respectively ([Reference StenströmSte] Theorem VII.2.1 recalling the fact that H is fully left and right bounded by [Reference StenströmSte] VII §2 Example 4), [Reference GabrielGab] V §4). Let $$ \begin{align} \mathbf{Sp}({\mathrm{Mod}}(H)) & \xrightarrow{\;\sim\;} {\mathrm{Spec}}(H) \\ [J] & \longmapsto\ \text{the unique prime ideal associated to}\ J \nonumber \end{align} $$
$$ \begin{align} \mathbf{Sp}({\mathrm{Mod}}(H)) & \xrightarrow{\;\sim\;} {\mathrm{Spec}}(H) \\ [J] & \longmapsto\ \text{the unique prime ideal associated to}\ J \nonumber \end{align} $$
 $\mathfrak {p} \in {\mathrm {Spec}}(H)$
. Fix an injective hull
$\mathfrak {p} \in {\mathrm {Spec}}(H)$
. Fix an injective hull
 $E(H/\mathfrak {p})$
of
$E(H/\mathfrak {p})$
of
 $H/\mathfrak {p}$
in
$H/\mathfrak {p}$
in
 ${\mathrm {Mod}}(H)$
. From [Reference StenströmSte] Proposition VII.1.9, we know that
${\mathrm {Mod}}(H)$
. From [Reference StenströmSte] Proposition VII.1.9, we know that
 $E(H/\mathfrak {p}) \cong \oplus _{i \in I} E_{\mathfrak {p}}$
for a single indecomposable injective H-module
$E(H/\mathfrak {p}) \cong \oplus _{i \in I} E_{\mathfrak {p}}$
for a single indecomposable injective H-module
 $E_{\mathfrak {p}}$
. Using [Reference StenströmSte] Lemma VII.1.7, we see that the inverse of the bijection (6) is given by
$E_{\mathfrak {p}}$
. Using [Reference StenströmSte] Lemma VII.1.7, we see that the inverse of the bijection (6) is given by
 $\mathfrak {p} \longmapsto [E_{\mathfrak {p}}]$
.
$\mathfrak {p} \longmapsto [E_{\mathfrak {p}}]$
.
First, we describe the stable Zariski topology, where we will always make silently the identification (6). Hence, on
![]() ${\mathrm {Spec}}(Z(H))$
the stable Zariski topology is the Zariski topology. From [Reference GabrielGab] V §4, we know that the Ziegler-open subsets of
${\mathrm {Spec}}(Z(H))$
the stable Zariski topology is the Zariski topology. From [Reference GabrielGab] V §4, we know that the Ziegler-open subsets of
![]() ${\mathrm {Spec}}(H)$
are the possibly infinite unions of Zariski-closed subsets. Hence, the quasi-compact Ziegler-open subsets are the Zariski-closed subsets. Therefore, the open subsets for the stable Zariski topology are the stable Zariski-open subsets.
${\mathrm {Spec}}(H)$
are the possibly infinite unions of Zariski-closed subsets. Hence, the quasi-compact Ziegler-open subsets are the Zariski-closed subsets. Therefore, the open subsets for the stable Zariski topology are the stable Zariski-open subsets.
Lemma 3.6.2.
![]() $A(\varrho ^{-1}(\mathcal {L})) = \varphi ^{-1}(A(\mathcal {L}))$
for any localising subcategory
$A(\varrho ^{-1}(\mathcal {L})) = \varphi ^{-1}(A(\mathcal {L}))$
for any localising subcategory
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() ${\mathrm {Mod}}(Z(H))$
.
${\mathrm {Mod}}(Z(H))$
.
Proof. (Recall the notation
![]() $A(\mathcal {L})$
from
$A(\mathcal {L})$
from
![]() $\S $
3.4.) Using Corollary 3.5.2, we compute
$\S $
3.4.) Using Corollary 3.5.2, we compute
 $$ \begin{align*} A(\varrho^{-1}(\mathcal{L})) & = \{\mathfrak{p} \not\in {\mathrm{Spec}}(H) : E_{\mathfrak{p}} \in {\mathrm{ob}}(\varrho^{-1}(\mathcal{L})) \} \\ & = \{\mathfrak{p} \in {\mathrm{Spec}}(H) : H/\mathfrak{p} \not\in {\mathrm{ob}}(\varrho^{-1}(\mathcal{L})) \} \\ & = \{\mathfrak{p} \in {\mathrm{Spec}}(H) : \varrho(H/\mathfrak{p}) \not\in {\mathrm{ob}}(\mathcal{L}) \} \\ & \supseteq \{\mathfrak{p} \in {\mathrm{Spec}}(H) : Z(H)/\varphi(\mathfrak{p}) \not\in {\mathrm{ob}}(\mathcal{L}) \} \\ & = \varphi^{-1}(A(\mathcal{L})) . \end{align*} $$
$$ \begin{align*} A(\varrho^{-1}(\mathcal{L})) & = \{\mathfrak{p} \not\in {\mathrm{Spec}}(H) : E_{\mathfrak{p}} \in {\mathrm{ob}}(\varrho^{-1}(\mathcal{L})) \} \\ & = \{\mathfrak{p} \in {\mathrm{Spec}}(H) : H/\mathfrak{p} \not\in {\mathrm{ob}}(\varrho^{-1}(\mathcal{L})) \} \\ & = \{\mathfrak{p} \in {\mathrm{Spec}}(H) : \varrho(H/\mathfrak{p}) \not\in {\mathrm{ob}}(\mathcal{L}) \} \\ & \supseteq \{\mathfrak{p} \in {\mathrm{Spec}}(H) : Z(H)/\varphi(\mathfrak{p}) \not\in {\mathrm{ob}}(\mathcal{L}) \} \\ & = \varphi^{-1}(A(\mathcal{L})) . \end{align*} $$
For the reverse inclusion, we suppose that
![]() $Z(H)/\varphi (\mathfrak {p})$
lies in
$Z(H)/\varphi (\mathfrak {p})$
lies in
![]() $\mathcal {L}$
. Being a finitely generated
$\mathcal {L}$
. Being a finitely generated
![]() $Z(H)/\varphi (\mathfrak {p})$
-module
$Z(H)/\varphi (\mathfrak {p})$
-module
![]() $\varrho (H / \varphi (\mathfrak {p}) H)$
also must lie in
$\varrho (H / \varphi (\mathfrak {p}) H)$
also must lie in
![]() ${\mathrm {ob}}(\mathcal {L})$
and hence
${\mathrm {ob}}(\mathcal {L})$
and hence
![]() $H / \varphi (\mathfrak {p}) H \in {\mathrm {ob}}(\varrho ^{-1}(\mathcal {L}))$
. It follows that
$H / \varphi (\mathfrak {p}) H \in {\mathrm {ob}}(\varrho ^{-1}(\mathcal {L}))$
. It follows that
![]() $H/\mathfrak {p}$
, as a quotient of
$H/\mathfrak {p}$
, as a quotient of
![]() $H / \varphi (\mathfrak {p}) H$
, is contained in
$H / \varphi (\mathfrak {p}) H$
, is contained in
![]() ${\mathrm {ob}}(\varrho ^{-1}(\mathcal {L}))$
.
${\mathrm {ob}}(\varrho ^{-1}(\mathcal {L}))$
.
Lemma 3.6.3. For
![]() $\mathfrak {p}, \mathfrak {q} \in {\mathrm {Spec}}(H)$
, we have:
$\mathfrak {p}, \mathfrak {q} \in {\mathrm {Spec}}(H)$
, we have:
-
a) Let
 $z \in Z(H)$
; if
$z \in Z(H)$
; if
 $z \in \mathfrak {p}$
, then z acts locally nilpotently on
$z \in \mathfrak {p}$
, then z acts locally nilpotently on
 $E_{\mathfrak {p}}$
; if
$E_{\mathfrak {p}}$
; if
 $z \not \in \mathfrak {p}$
, then z acts invertibly on
$z \not \in \mathfrak {p}$
, then z acts invertibly on
 $E_{\mathfrak {p}}$
.
$E_{\mathfrak {p}}$
. -
b) If
 ${\mathrm {Hom}}_H(E_{\mathfrak {p}},E_{\mathfrak {q}}) \neq 0$
, then
${\mathrm {Hom}}_H(E_{\mathfrak {p}},E_{\mathfrak {q}}) \neq 0$
, then
 $\mathfrak {p} \cap Z(H) \subseteq \mathfrak {q} \cap Z(H)$
.
$\mathfrak {p} \cap Z(H) \subseteq \mathfrak {q} \cap Z(H)$
.
Proof. a) Let L be a uniform left ideal in
![]() $H/\mathfrak {p}$
so that
$H/\mathfrak {p}$
so that
![]() $E_{\mathfrak {p}}$
is the injective hull
$E_{\mathfrak {p}}$
is the injective hull
![]() $E(L)$
of L.
$E(L)$
of L.
Suppose first that
![]() $z \notin \mathfrak {p}$
. Multiplication by z is an injective H-linear map
$z \notin \mathfrak {p}$
. Multiplication by z is an injective H-linear map
![]() $\ell _z : H/\mathfrak {p} \to H/\mathfrak {p}$
: If
$\ell _z : H/\mathfrak {p} \to H/\mathfrak {p}$
: If
![]() $x + \mathfrak {p} \in H/\mathfrak {p}$
is such that
$x + \mathfrak {p} \in H/\mathfrak {p}$
is such that
![]() $z(x+\mathfrak {p}) = \mathfrak {p}$
, then
$z(x+\mathfrak {p}) = \mathfrak {p}$
, then
![]() $(HzH)(HxH) \subseteq \mathfrak {p}$
since z is central in H, so
$(HzH)(HxH) \subseteq \mathfrak {p}$
since z is central in H, so
![]() $x \in \mathfrak {p}$
since
$x \in \mathfrak {p}$
since
![]() $\mathfrak {p}$
is prime and
$\mathfrak {p}$
is prime and
![]() $z \notin \mathfrak {p}$
. Since L is an H-submodule of
$z \notin \mathfrak {p}$
. Since L is an H-submodule of
![]() $H/\mathfrak {p}$
,
$H/\mathfrak {p}$
,
![]() $\ell _z : L \to L$
is also injective. Hence, it extends to an injective H-linear map
$\ell _z : L \to L$
is also injective. Hence, it extends to an injective H-linear map
![]() $\ell _z : E(L) \to E(L)$
by the injectivity of
$\ell _z : E(L) \to E(L)$
by the injectivity of
![]() $E(L)$
. The image of
$E(L)$
. The image of
![]() $\ell _z$
must admit a complement in
$\ell _z$
must admit a complement in
![]() $E(L)$
since it is itself injective. Since
$E(L)$
since it is itself injective. Since
![]() $E(L) \cong E_{\mathfrak {p}}$
is indecomposable,
$E(L) \cong E_{\mathfrak {p}}$
is indecomposable,
![]() $\ell _z : E(L) \to E(L)$
is an isomorphism, as claimed.
$\ell _z : E(L) \to E(L)$
is an isomorphism, as claimed.
Now, suppose that
![]() $z \in \mathfrak {p}$
and let
$z \in \mathfrak {p}$
and let
![]() $x \in E_{\mathfrak {p}}$
be nonzero. Since L is essential in
$x \in E_{\mathfrak {p}}$
be nonzero. Since L is essential in
![]() $E_{\mathfrak {p}}$
, we see that
$E_{\mathfrak {p}}$
, we see that
![]() $Hx \cap L$
is essential in
$Hx \cap L$
is essential in
![]() $Hx$
. Since H is noetherian and z is central, the ideal
$Hx$
. Since H is noetherian and z is central, the ideal
![]() $zH$
of H satisfies the left Artin–Rees property by [Reference McConnell and RobsonMCR] Proposition 4.2.6. Since
$zH$
of H satisfies the left Artin–Rees property by [Reference McConnell and RobsonMCR] Proposition 4.2.6. Since
![]() $z \in \mathfrak {p}$
kills L, it also kills
$z \in \mathfrak {p}$
kills L, it also kills
![]() $Hx \cap L$
. So
$Hx \cap L$
. So
![]() $z^n$
kills
$z^n$
kills
![]() $Hx$
for some
$Hx$
for some
![]() $n \geq 1$
by the implication (i)
$n \geq 1$
by the implication (i)
![]() $\Rightarrow $
(iii) of [Reference McConnell and RobsonMCR] Theorem 4.2.2.
$\Rightarrow $
(iii) of [Reference McConnell and RobsonMCR] Theorem 4.2.2.
b) Let
![]() $\phi : E_{\mathfrak {p}} \rightarrow E_{\mathfrak {q}}$
be a nonzero map. Suppose that there is a
$\phi : E_{\mathfrak {p}} \rightarrow E_{\mathfrak {q}}$
be a nonzero map. Suppose that there is a
![]() $z \in (\mathfrak {p} \cap Z(H)) \setminus \mathfrak {q}$
. Then, by a), z acts invertibly on
$z \in (\mathfrak {p} \cap Z(H)) \setminus \mathfrak {q}$
. Then, by a), z acts invertibly on
![]() $E_{\mathfrak {q}}$
but locally nilpotently on
$E_{\mathfrak {q}}$
but locally nilpotently on
![]() $E_{\mathfrak {p}}$
. Consider any
$E_{\mathfrak {p}}$
. Consider any
![]() $x \in E_{\mathfrak {p}}$
such that
$x \in E_{\mathfrak {p}}$
such that
![]() $\phi (x) \neq 0$
. We find a
$\phi (x) \neq 0$
. We find a
![]() $t \geq 1$
such that
$t \geq 1$
such that
![]() $z^t x = 0$
. Hence,
$z^t x = 0$
. Hence,
![]() $z^t \phi (x) = \phi (z^t x) = \phi (0) = 0$
, which is a contradiction.
$z^t \phi (x) = \phi (z^t x) = \phi (0) = 0$
, which is a contradiction.
For any subset
![]() $A \subseteq {\mathrm {Spec}}(H)$
, the full subcategory
$A \subseteq {\mathrm {Spec}}(H)$
, the full subcategory
![]() $\mathcal {L}_A$
of all modules U in
$\mathcal {L}_A$
of all modules U in
![]() ${\mathrm {Mod}}(H)$
such that
${\mathrm {Mod}}(H)$
such that
![]() ${\mathrm {Hom}}_H(U,E_{\mathfrak {p}}) = 0$
for any
${\mathrm {Hom}}_H(U,E_{\mathfrak {p}}) = 0$
for any
![]() $\mathfrak {p} \in A$
is a localising subcategory of
$\mathfrak {p} \in A$
is a localising subcategory of
![]() ${\mathrm {Mod}}(H)$
. Obviously, we have
${\mathrm {Mod}}(H)$
. Obviously, we have
![]() $A \subseteq A(\mathcal {L}_A)$
.
$A \subseteq A(\mathcal {L}_A)$
.
We now describe explicitly all localising subcategories of
![]() ${\mathrm {Mod}}(H)$
which are of the form
${\mathrm {Mod}}(H)$
which are of the form
![]() $\rho ^{-1}(\mathcal {L})$
as in Lemma 3.6.1.a.
$\rho ^{-1}(\mathcal {L})$
as in Lemma 3.6.1.a.
Recall that a subset S of a topological space T is called generalization-closed if any point
![]() $y \in T$
whose closure
$y \in T$
whose closure
![]() $\overline {\{y\}}$
contains a point in S also lies in S. Equivalently, S is generalization-closed if and only if it is a (possibly infinite) intersection of open subsets of T.
$\overline {\{y\}}$
contains a point in S also lies in S. Equivalently, S is generalization-closed if and only if it is a (possibly infinite) intersection of open subsets of T.
Before Lemma 3.6.2, we had noted that the Ziegler-open subsets of
![]() ${\mathrm {Spec}}(H)$
are the unions of Zariski-closed subsets. Hence, the Ziegler-closed subsets are the generalization-closed subsets. Therefore, the inverse of the bijection (3) is the map
${\mathrm {Spec}}(H)$
are the unions of Zariski-closed subsets. Hence, the Ziegler-closed subsets are the generalization-closed subsets. Therefore, the inverse of the bijection (3) is the map
 $$ \begin{align*} \text{set of all generalization-closed} & \xrightarrow{\;\simeq\;}\ \ \text{collection of all localising} \\ \text{subsets of}\ {\mathrm{Spec}}(Z(H)) \qquad & \qquad\ \text{subcategories of}\ {\mathrm{Mod}}(Z(H)) \\ W & \longmapsto \mathcal{L}_W^Z := \text{all}\ M\ \text{with}\ {\mathrm{Hom}}_{Z(H)}(M,E) = 0 \\ & \qquad\qquad\qquad\qquad \text{ for any}\ [E]\ \in W. \end{align*} $$
$$ \begin{align*} \text{set of all generalization-closed} & \xrightarrow{\;\simeq\;}\ \ \text{collection of all localising} \\ \text{subsets of}\ {\mathrm{Spec}}(Z(H)) \qquad & \qquad\ \text{subcategories of}\ {\mathrm{Mod}}(Z(H)) \\ W & \longmapsto \mathcal{L}_W^Z := \text{all}\ M\ \text{with}\ {\mathrm{Hom}}_{Z(H)}(M,E) = 0 \\ & \qquad\qquad\qquad\qquad \text{ for any}\ [E]\ \in W. \end{align*} $$
We conclude from Lemma 3.6.2 that
For an ideal I of
![]() $Z(H)$
, recall that
$Z(H)$
, recall that
![]() $V(I)$
denotes the subset of
$V(I)$
denotes the subset of
![]() ${\mathrm {Spec}}(Z(H))$
consisting of all prime ideals containing I.
${\mathrm {Spec}}(Z(H))$
consisting of all prime ideals containing I.
Proposition 3.6.4. Let W be a generalization-closed subset of
![]() ${\mathrm {Spec}}(Z(H))$
. The following are equivalent for an H-module M:
${\mathrm {Spec}}(Z(H))$
. The following are equivalent for an H-module M:
-
a) M lies in
 $\mathcal {L}_{\varphi ^{-1}(W)}$
;
$\mathcal {L}_{\varphi ^{-1}(W)}$
; -
b)
 $V({\mathrm {Ann}}_{Z(H)}(v)) \cap W = \emptyset $
for all nonzero
$V({\mathrm {Ann}}_{Z(H)}(v)) \cap W = \emptyset $
for all nonzero
 $v \in M$
;
$v \in M$
; -
c)
 $V({\mathrm {Ann}}_{Z(H)}(N)) \cap W = \emptyset $
for all noetherian submodules
$V({\mathrm {Ann}}_{Z(H)}(N)) \cap W = \emptyset $
for all noetherian submodules
 $N \subseteq M$
.
$N \subseteq M$
.
Proof. Since
![]() $\mathcal {L}_{\varphi ^{-1}(W)}$
is localising we may assume that M is finitely generated. If
$\mathcal {L}_{\varphi ^{-1}(W)}$
is localising we may assume that M is finitely generated. If
![]() $v_1, \ldots , v_r$
are generators of the H-module M, then
$v_1, \ldots , v_r$
are generators of the H-module M, then
 $$ \begin{align*} V({\mathrm{Ann}}_{Z(H)}(M)) = V\left(\bigcap_{i=1}^r {\mathrm{Ann}}_{Z(H)}(v_i)\right) = \bigcup_{i=1}^r V({\mathrm{Ann}}_{Z(H)}(v_i)) . \end{align*} $$
$$ \begin{align*} V({\mathrm{Ann}}_{Z(H)}(M)) = V\left(\bigcap_{i=1}^r {\mathrm{Ann}}_{Z(H)}(v_i)\right) = \bigcup_{i=1}^r V({\mathrm{Ann}}_{Z(H)}(v_i)) . \end{align*} $$
This shows the equivalence of b) and c).
For the equivalence of a) and b), we first note that, because H is noetherian, M contains an essential submodule N of the form
![]() $N = N_1 \oplus \cdots \oplus N_r$
, where each
$N = N_1 \oplus \cdots \oplus N_r$
, where each
![]() $N_i$
is a uniform H-module ([Reference Goodearl and WarfieldGW] Corollary 5.18 and Proposition 5.15). Hence,
$N_i$
is a uniform H-module ([Reference Goodearl and WarfieldGW] Corollary 5.18 and Proposition 5.15). Hence,
![]() $E(M) = E(N) \cong \bigoplus _{i=1}^n E(N_i)$
. By [Reference Goodearl and WarfieldGW] Lemma 5.26, for each
$E(M) = E(N) \cong \bigoplus _{i=1}^n E(N_i)$
. By [Reference Goodearl and WarfieldGW] Lemma 5.26, for each
![]() $i = 1,\cdots , r$
there is a unique prime ideal
$i = 1,\cdots , r$
there is a unique prime ideal
![]() $\mathfrak {p}_i$
of H which is equal to the annihilator of some nonzero H-submodule
$\mathfrak {p}_i$
of H which is equal to the annihilator of some nonzero H-submodule
![]() $N_i'$
of
$N_i'$
of
![]() $N_i$
, and which contains the annihilators of all nonzero H-submodules of
$N_i$
, and which contains the annihilators of all nonzero H-submodules of
![]() $N_i$
. This
$N_i$
. This
![]() $\mathfrak {p}_i$
is the assassinator of
$\mathfrak {p}_i$
is the assassinator of
![]() $N_i$
in the sense of [Reference Goodearl and WarfieldGW] Definition on p. 102.
$N_i$
in the sense of [Reference Goodearl and WarfieldGW] Definition on p. 102.
Since H is assumed to be a finitely generated module over its centre, it is an FBN-ring by [Reference Goodearl and WarfieldGW] Proposition 9.1(a). Then we can apply [Reference Goodearl and WarfieldGW] Proposition 9.14 to see that the uniform injective H-module
![]() $E(N_i)$
is isomorphic to the H-injective hull
$E(N_i)$
is isomorphic to the H-injective hull
![]() $E(L_i)$
of any uniform left ideal
$E(L_i)$
of any uniform left ideal
![]() $L_i$
of
$L_i$
of
![]() $H/\mathfrak {p}_i$
. In other words, ([Reference Goodearl and WarfieldGW] Lemma 5.14),
$H/\mathfrak {p}_i$
. In other words, ([Reference Goodearl and WarfieldGW] Lemma 5.14),
![]() $E(N_i) \cong E_{\mathfrak {p}_i}$
and
$E(N_i) \cong E_{\mathfrak {p}_i}$
and
 $$ \begin{align*} E(M) \cong E(N) \cong \bigoplus_{i=1}^r E(N_i) \cong \bigoplus_{i=1}^r E_{\mathfrak{p}_i} . \end{align*} $$
$$ \begin{align*} E(M) \cong E(N) \cong \bigoplus_{i=1}^r E(N_i) \cong \bigoplus_{i=1}^r E_{\mathfrak{p}_i} . \end{align*} $$
We identify M with its image inside
![]() $E(M)$
. Note that M is not contained in the direct sum
$E(M)$
. Note that M is not contained in the direct sum
![]() $\bigoplus _{i \neq j} E_{\mathfrak {p}_i}$
for any j because otherwise we would have
$\bigoplus _{i \neq j} E_{\mathfrak {p}_i}$
for any j because otherwise we would have
![]() $M \cap E_{\mathfrak {p}_j} = 0$
, which contradicts the fact that M is essential in
$M \cap E_{\mathfrak {p}_j} = 0$
, which contradicts the fact that M is essential in
![]() $E(M)$
. So,
$E(M)$
. So,
![]() ${\mathrm {Hom}}_H(M, E_{\mathfrak {p}_j})$
is nonzero for any j.
${\mathrm {Hom}}_H(M, E_{\mathfrak {p}_j})$
is nonzero for any j.
a)
![]() $\Rightarrow $
b). Suppose that M lies in
$\Rightarrow $
b). Suppose that M lies in
![]() $\mathcal {L}_{\varphi ^{-1}(W)}$
. From
$\mathcal {L}_{\varphi ^{-1}(W)}$
. From
![]() ${\mathrm {Hom}}_H(M,E_{\mathfrak {p}_j}) \neq 0$
for any j, we deduce that
${\mathrm {Hom}}_H(M,E_{\mathfrak {p}_j}) \neq 0$
for any j, we deduce that
![]() $\mathfrak {p}_j \notin \varphi ^{-1}(W)$
for all j. Now, consider any nonzero
$\mathfrak {p}_j \notin \varphi ^{-1}(W)$
for all j. Now, consider any nonzero
![]() $v \in M$
and any
$v \in M$
and any
![]() $\mathfrak {p} \in \varphi ^{-1}(V({\mathrm {Ann}}_{Z(H)}(v)))$
. Because
$\mathfrak {p} \in \varphi ^{-1}(V({\mathrm {Ann}}_{Z(H)}(v)))$
. Because
![]() $\mathfrak {p}_i \cap Z(H)$
acts locally nilpotently on
$\mathfrak {p}_i \cap Z(H)$
acts locally nilpotently on
![]() $E_{\mathfrak {p}_i}$
by Lemma 3.6.3.a, we see that
$E_{\mathfrak {p}_i}$
by Lemma 3.6.3.a, we see that
for some
![]() $k> 0$
. This implies that
$k> 0$
. This implies that
![]() $\mathfrak {p}_j \cap Z(H) \subseteq \mathfrak {p} \cap Z(H)$
for some j. Since W is generalization-closed and
$\mathfrak {p}_j \cap Z(H) \subseteq \mathfrak {p} \cap Z(H)$
for some j. Since W is generalization-closed and
![]() $\mathfrak {p}_j \cap Z(H) \notin W$
, we see that
$\mathfrak {p}_j \cap Z(H) \notin W$
, we see that
![]() $\mathfrak {p} \cap Z(H) \notin W$
. Hence,
$\mathfrak {p} \cap Z(H) \notin W$
. Hence,
![]() $V({\mathrm {Ann}}_{Z(H)}(v)) \cap W = \emptyset $
.
$V({\mathrm {Ann}}_{Z(H)}(v)) \cap W = \emptyset $
.
b)
![]() $\Rightarrow $
a). Suppose that
$\Rightarrow $
a). Suppose that
![]() ${\mathrm {Hom}}_H(M, E_{\mathfrak {q}}) \neq 0$
for some
${\mathrm {Hom}}_H(M, E_{\mathfrak {q}}) \neq 0$
for some
![]() $\mathfrak {q} \in \varphi ^{-1}(W)$
. Then
$\mathfrak {q} \in \varphi ^{-1}(W)$
. Then
![]() ${\mathrm {Hom}}_H(E_{\mathfrak {p}_i}, E_{\mathfrak {q}}) \neq 0$
for some
${\mathrm {Hom}}_H(E_{\mathfrak {p}_i}, E_{\mathfrak {q}}) \neq 0$
for some
![]() $1 \leq i \leq r$
and so
$1 \leq i \leq r$
and so
![]() $\mathfrak {p}_i \cap Z(H) \subseteq \mathfrak {q} \cap Z(H)$
by Lemma 3.6.3.b. Hence,
$\mathfrak {p}_i \cap Z(H) \subseteq \mathfrak {q} \cap Z(H)$
by Lemma 3.6.3.b. Hence,
![]() $\mathfrak {p}_i \cap Z(H) \in W$
since W is generalization-closed.
$\mathfrak {p}_i \cap Z(H) \in W$
since W is generalization-closed.
Choose a nonzero element
![]() $v \in N_i'$
; since
$v \in N_i'$
; since
![]() $\mathfrak {p}_i$
kills
$\mathfrak {p}_i$
kills
![]() $N_i' \supseteq Hv$
, we have
$N_i' \supseteq Hv$
, we have
![]() $\mathfrak {p}_i \subseteq {\mathrm {Ann}}_H(Hv)$
; on the other hand,
$\mathfrak {p}_i \subseteq {\mathrm {Ann}}_H(Hv)$
; on the other hand,
![]() $\mathfrak {p}_i$
contains
$\mathfrak {p}_i$
contains
![]() ${\mathrm {Ann}}_H(Hv)$
as we saw above and hence
${\mathrm {Ann}}_H(Hv)$
as we saw above and hence
![]() $\mathfrak {p}_i = {\mathrm {Ann}}_H(Hv)$
. Since
$\mathfrak {p}_i = {\mathrm {Ann}}_H(Hv)$
. Since
![]() $Z(H)$
is central in H, we have
$Z(H)$
is central in H, we have
![]() ${\mathrm {Ann}}_{Z(H)}(v) = {\mathrm {Ann}}_{Z(H)}(Hv)$
. This ideal of
${\mathrm {Ann}}_{Z(H)}(v) = {\mathrm {Ann}}_{Z(H)}(Hv)$
. This ideal of
![]() $Z(H)$
is equal to
$Z(H)$
is equal to
![]() ${\mathrm {Ann}}_H(Hv) \cap Z(H) = \mathfrak {p}_i \cap Z(H)$
. Thus,
${\mathrm {Ann}}_H(Hv) \cap Z(H) = \mathfrak {p}_i \cap Z(H)$
. Thus,
![]() ${\mathrm {Ann}}_{Z(H)}(v) = \mathfrak {p}_i \cap Z(H)$
lies in W and therefore
${\mathrm {Ann}}_{Z(H)}(v) = \mathfrak {p}_i \cap Z(H)$
lies in W and therefore
![]() $V({\mathrm {Ann}}_{Z(H)}(v)) \cap W \neq \emptyset $
.
$V({\mathrm {Ann}}_{Z(H)}(v)) \cap W \neq \emptyset $
.
Obviously, we have a corresponding result for modules over
![]() $Z(H)$
.
$Z(H)$
.
Remark 3.6.5. Let W be a generalization-closed subset of
![]() ${\mathrm {Spec}}(Z(H))$
. The following are equivalent for a
${\mathrm {Spec}}(Z(H))$
. The following are equivalent for a
![]() $Z(H)$
-module M:
$Z(H)$
-module M:
-
a) M lies in
 $\mathcal {L}_W^Z$
;
$\mathcal {L}_W^Z$
; -
b)
 $V({\mathrm {Ann}}_{Z(H)}(v)) \cap W = \emptyset $
for all nonzero
$V({\mathrm {Ann}}_{Z(H)}(v)) \cap W = \emptyset $
for all nonzero
 $v \in M$
;
$v \in M$
; -
c)
 $V({\mathrm {Ann}}_{Z(H)}(N)) \cap W = \emptyset $
for all noetherian submodules
$V({\mathrm {Ann}}_{Z(H)}(N)) \cap W = \emptyset $
for all noetherian submodules
 $N \subseteq M$
.
$N \subseteq M$
.
3.7 A stability criterion for thickenings
Throughout this section, let
![]() $\mathcal {C}$
be a locally noetherian Grothendieck category which is a thickening of its full abelian subcategory
$\mathcal {C}$
be a locally noetherian Grothendieck category which is a thickening of its full abelian subcategory
![]() $\mathcal {A}$
. Recall from
$\mathcal {A}$
. Recall from
![]() $\S $
3 that we then have the increasing filtration
$\S $
3 that we then have the increasing filtration
![]() $\mathcal {A} = \mathcal {A}_0 \hookrightarrow \mathcal {A}_1 \hookrightarrow \ldots \hookrightarrow \mathcal {A}_j \hookrightarrow \ldots $
of
$\mathcal {A} = \mathcal {A}_0 \hookrightarrow \mathcal {A}_1 \hookrightarrow \ldots \hookrightarrow \mathcal {A}_j \hookrightarrow \ldots $
of
![]() $\mathcal {C}$
by full abelian subcategories, which all are locally noetherian Grothendieck categories. By Equation (2), the corresponding injective spectra all are in bijection
$\mathcal {C}$
by full abelian subcategories, which all are locally noetherian Grothendieck categories. By Equation (2), the corresponding injective spectra all are in bijection
 $$ \begin{align*} \mathbf{Sp}(\mathcal{C}) & \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}_j) \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}) \\ [E] & \longmapsto r_j([E]) \longmapsto r([E]) . \nonumber \end{align*} $$
$$ \begin{align*} \mathbf{Sp}(\mathcal{C}) & \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}_j) \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}) \\ [E] & \longmapsto r_j([E]) \longmapsto r([E]) . \nonumber \end{align*} $$
By Corollary 3.4.6 and Corollary 3.5.4, the inverses of these bijections are continuous for the stable as well as the stable Zariski topologies. Actually, it is straightforward to deduce that, for
![]() $i \leq j$
, the map
$i \leq j$
, the map
 $$ \begin{align*} \mathbf{Sp}(\mathcal{A}_j) & \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}_i) \\ x = [E_x] & \longmapsto r_{j,i}(x) := r_i(x) = [r_i(E_x)] \end{align*} $$
$$ \begin{align*} \mathbf{Sp}(\mathcal{A}_j) & \xrightarrow{\;\simeq\;} \mathbf{Sp}(\mathcal{A}_i) \\ x = [E_x] & \longmapsto r_{j,i}(x) := r_i(x) = [r_i(E_x)] \end{align*} $$
is a bijection with inverse
![]() $[U] \mapsto [E_{\mathcal {A}_j}(U)]$
, and this inverse is continuous for the stable as well as the stable Zariski topologies.
$[U] \mapsto [E_{\mathcal {A}_j}(U)]$
, and this inverse is continuous for the stable as well as the stable Zariski topologies.
In this section, we will present a technique to actually find stable subsets in
![]() $\mathbf {Sp}(\mathcal {C})$
. For this, we assume again from now on that
$\mathbf {Sp}(\mathcal {C})$
. For this, we assume again from now on that
![]() $\mathcal {A}$
has a noetherian projective generator P. Recall that
$\mathcal {A}$
has a noetherian projective generator P. Recall that
![]() $H = {\mathrm {End}}_{\mathcal {A}}(P)^{{\mathrm {op}}} = {\mathrm {End}}_{\mathcal {C}}(P)^{{\mathrm {op}}}$
, and let
$H = {\mathrm {End}}_{\mathcal {A}}(P)^{{\mathrm {op}}} = {\mathrm {End}}_{\mathcal {C}}(P)^{{\mathrm {op}}}$
, and let
![]() $Z = Z(H)$
denote its centre. By the equivalence of categories (4), this centre Z acts naturally on any object in
$Z = Z(H)$
denote its centre. By the equivalence of categories (4), this centre Z acts naturally on any object in
![]() $\mathcal {A}$
, that is,
$\mathcal {A}$
, that is,
![]() $Z = Z(\mathcal {A})$
is the centre of the category
$Z = Z(\mathcal {A})$
is the centre of the category
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
But we need further assumptions. The first one is:
-
(A1) H is finitely generated as a module over its centre Z.
The central tool for our investigation will be the (graded)
![]() $(H,H)$
-bimodule
$(H,H)$
-bimodule
 $$ \begin{align*} {\mathrm{Ext}}_{\mathcal{C}}^*(P,P) := \bigoplus_{i=0}^\infty {\mathrm{Ext}}_{\mathcal{C}}^i(P,P) . \end{align*} $$
$$ \begin{align*} {\mathrm{Ext}}_{\mathcal{C}}^*(P,P) := \bigoplus_{i=0}^\infty {\mathrm{Ext}}_{\mathcal{C}}^i(P,P) . \end{align*} $$
This, in particular, is a module for
![]() $Z \otimes Z := Z \otimes _{\mathbb {Z}} Z$
. We let
$Z \otimes Z := Z \otimes _{\mathbb {Z}} Z$
. We let
![]() $\mathcal {J} := {\mathrm {Ann}}_{Z \otimes Z}({\mathrm {Ext}}_{\mathcal {C}}^*(P,P))$
be its annihilator ideal and
$\mathcal {J} := {\mathrm {Ann}}_{Z \otimes Z}({\mathrm {Ext}}_{\mathcal {C}}^*(P,P))$
be its annihilator ideal and
![]() $\mathcal {R} := V(\mathcal {J}) \subseteq {\mathrm {Spec}}(Z \otimes Z)$
be the corresponding Zariski closed subset. Further, let
$\mathcal {R} := V(\mathcal {J}) \subseteq {\mathrm {Spec}}(Z \otimes Z)$
be the corresponding Zariski closed subset. Further, let
![]() $\pi _i : \mathcal {R} \rightarrow \Xi := {\mathrm {Spec}}(Z)$
, for
$\pi _i : \mathcal {R} \rightarrow \Xi := {\mathrm {Spec}}(Z)$
, for
![]() $i = 1, 2$
, denote the restrictions of the two projection maps
$i = 1, 2$
, denote the restrictions of the two projection maps
![]() ${\mathrm {Spec}}(Z \otimes Z) \rightrightarrows \Xi $
. We then have a coequaliser diagram
${\mathrm {Spec}}(Z \otimes Z) \rightrightarrows \Xi $
. We then have a coequaliser diagram
in the category of locally ringed spaces (cf. [Reference Demazure and GabrielDG] Proposition I.1.1.6). We briefly recall that
![]() $\mathbf {q}$
is a topological quotient map which identifies the points
$\mathbf {q}$
is a topological quotient map which identifies the points
![]() $\pi _1(x)$
and
$\pi _1(x)$
and
![]() $\pi _2(x)$
for all
$\pi _2(x)$
for all
![]() $x \in \mathcal {R}$
and that the sheaf
$x \in \mathcal {R}$
and that the sheaf
![]() $\mathcal {O}_{\mathfrak {Z}}$
is given, for any open subset
$\mathcal {O}_{\mathfrak {Z}}$
is given, for any open subset
![]() $U \subseteq \Xi $
, by the equalizer diagram
$U \subseteq \Xi $
, by the equalizer diagram

In section 3.6, we considered, for any generalization-closed subset
![]() $W \subseteq \Xi $
, the localising subcategories
$W \subseteq \Xi $
, the localising subcategories
![]() $\mathcal {L}_W^Z$
of
$\mathcal {L}_W^Z$
of
![]() ${\mathrm {Mod}}(Z)$
and
${\mathrm {Mod}}(Z)$
and
![]() $\mathcal {L}_W^H := \mathcal {L}_{\varphi ^{-1}(W)}$
of
$\mathcal {L}_W^H := \mathcal {L}_{\varphi ^{-1}(W)}$
of
![]() ${\mathrm {Mod}}(H)$
. These satisfy
${\mathrm {Mod}}(H)$
. These satisfy
![]() $\varrho ^{-1}(\mathcal {L}_W^Z) = \mathcal {L}_W^H$
by Equation (7). Under the category equivalence (4), the subcategory
$\varrho ^{-1}(\mathcal {L}_W^Z) = \mathcal {L}_W^H$
by Equation (7). Under the category equivalence (4), the subcategory
![]() $\mathcal {L}_W^H$
corresponds to the localising subcategory
$\mathcal {L}_W^H$
corresponds to the localising subcategory
of
![]() $\mathcal {A}$
. Finally, by Proposition 3.4.3, we have the localising subcategory
$\mathcal {A}$
. Finally, by Proposition 3.4.3, we have the localising subcategory
![]() $\mathcal {L}_W^{\mathcal {C}} := \langle \mathcal {L}_W^{\mathcal {A}} \rangle $
of
$\mathcal {L}_W^{\mathcal {C}} := \langle \mathcal {L}_W^{\mathcal {A}} \rangle $
of
![]() $\mathcal {C}$
, which is the unique localising subcategory of
$\mathcal {C}$
, which is the unique localising subcategory of
![]() $\mathcal {C}$
such that
$\mathcal {C}$
such that
![]() $\mathcal {A} \cap \mathcal {L}_W^{\mathcal {C}} = \mathcal {L}_W^{\mathcal {A}}$
.
$\mathcal {A} \cap \mathcal {L}_W^{\mathcal {C}} = \mathcal {L}_W^{\mathcal {A}}$
.
Theorem 3.7.1. In addition to (A1), we assume:
-
(A2) There is an integer d such that
 ${\mathrm {Ext}}_{\mathcal {C}}^j(P,-)|_{\mathcal {A}} = 0$
for any
${\mathrm {Ext}}_{\mathcal {C}}^j(P,-)|_{\mathcal {A}} = 0$
for any
 $j> d$
.
$j> d$
. -
(A3)
 $Z \otimes Z/\mathcal {J}^{d+1}$
is noetherian.
$Z \otimes Z/\mathcal {J}^{d+1}$
is noetherian.
Then, for any generalization-closed subset
![]() $W \subseteq \Xi $
with the property that
$W \subseteq \Xi $
with the property that
![]() $\pi _2(\pi _1^{-1}(W)) \subseteq W$
, the localising subcategory
$\pi _2(\pi _1^{-1}(W)) \subseteq W$
, the localising subcategory
![]() $\mathcal {L}_W^{\mathcal {C}}$
is stable.
$\mathcal {L}_W^{\mathcal {C}}$
is stable.
We begin the proof by recalling the following useful fact.
Lemma 3.7.2. Let M be a noetherian object in
![]() $\mathcal {C}$
. Then
$\mathcal {C}$
. Then
![]() ${\mathrm {Ext}}^j_{\mathcal {C}}(M,-)$
commutes with filtered colimits for all
${\mathrm {Ext}}^j_{\mathcal {C}}(M,-)$
commutes with filtered colimits for all
![]() $j \geq 0$
.
$j \geq 0$
.
Proof. In the Grothendieck category
![]() $\mathcal {C}$
filtered colimits are exact. Moreover, because
$\mathcal {C}$
filtered colimits are exact. Moreover, because
![]() $\mathcal {C}$
is locally noetherian and M is a noetherian object in
$\mathcal {C}$
is locally noetherian and M is a noetherian object in
![]() $\mathcal {C}$
, [Reference GabrielGab] Corollary 1 on p. 358 tells us that:
$\mathcal {C}$
, [Reference GabrielGab] Corollary 1 on p. 358 tells us that:
-
– the full subcategory of injective objects in
 $\mathcal {C}$
is closed under filtered colimits;
$\mathcal {C}$
is closed under filtered colimits; -
– the functor
 $F := {\mathrm {Hom}}_{\mathcal {C}}(M,-)$
from
$F := {\mathrm {Hom}}_{\mathcal {C}}(M,-)$
from
 $\mathcal {C}$
to the category of abelian groups commutes with filtered colimits.
$\mathcal {C}$
to the category of abelian groups commutes with filtered colimits.
In this situation, [Reference Kashiwara and SchapiraKS] Proposition 15.3.3 implies that the derived functors
![]() $R^jF = {\mathrm {Ext}}^j_{\mathcal {C}}(M,-)$
of F commute with filtered colimits.
$R^jF = {\mathrm {Ext}}^j_{\mathcal {C}}(M,-)$
of F commute with filtered colimits.
Next, we first need an auxiliary result. Since
![]() $Z = Z(\mathcal {A})$
the ring
$Z = Z(\mathcal {A})$
the ring
![]() $Z \otimes Z$
acts, for any two objects
$Z \otimes Z$
acts, for any two objects
![]() $A_1$
and
$A_1$
and
![]() $A_2$
in
$A_2$
in
![]() $\mathcal {A}$
, naturally on the groups
$\mathcal {A}$
, naturally on the groups
![]() ${\mathrm {Ext}}^j_{\mathcal {C}}(A_1,A_2)$
with the first and second factor in
${\mathrm {Ext}}^j_{\mathcal {C}}(A_1,A_2)$
with the first and second factor in
![]() $Z \otimes Z$
acting through endomorphisms in the category
$Z \otimes Z$
acting through endomorphisms in the category
![]() $\mathcal {C}$
on
$\mathcal {C}$
on
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, respectively.
$A_2$
, respectively.
Lemma 3.7.3. Suppose that (A2) holds true, and let A be an arbitrary object in
![]() $\mathcal {A}$
; then, for any
$\mathcal {A}$
; then, for any
![]() $j \geq 0$
, the
$j \geq 0$
, the
![]() $Z \otimes Z$
-module
$Z \otimes Z$
-module
![]() ${\mathrm {Ext}}^j_{\mathcal {C}}(P,A)$
is annihilated by
${\mathrm {Ext}}^j_{\mathcal {C}}(P,A)$
is annihilated by
![]() $\mathcal {J}^{d+1-j}$
.
$\mathcal {J}^{d+1-j}$
.
Proof. By Lemma 3.7.2, the functors
![]() ${\mathrm {Ext}}^j_{\mathcal {C}}(P,-)$
, for any
${\mathrm {Ext}}^j_{\mathcal {C}}(P,-)$
, for any
![]() $j \geq 0$
, commute with arbitrary direct sums. It follows that
$j \geq 0$
, commute with arbitrary direct sums. It follows that
![]() $\mathcal {J}$
annihilates
$\mathcal {J}$
annihilates
![]() ${\mathrm {Ext}}_{\mathcal {C}}^*(P,F)$
for any F which is a possibly infinite direct sums of copies of P. Since P is a generatorFootnote
2
of
${\mathrm {Ext}}_{\mathcal {C}}^*(P,F)$
for any F which is a possibly infinite direct sums of copies of P. Since P is a generatorFootnote
2
of
![]() $\mathcal {A}$
, using [Reference StenströmSte] p. 93 Proposition 6.2 repeatedly we find an exact sequence in
$\mathcal {A}$
, using [Reference StenströmSte] p. 93 Proposition 6.2 repeatedly we find an exact sequence in
![]() $\mathcal {A}$
of the form
$\mathcal {A}$
of the form
where each
![]() $F_n$
is a direct sum of copies of P. We break it up into short exact sequences
$F_n$
is a direct sum of copies of P. We break it up into short exact sequences
 $$ \begin{align*} & 0 \rightarrow Y_0 \rightarrow F_0 \rightarrow A \rightarrow 0 \\ & 0 \rightarrow Y_1 \rightarrow F_1 \rightarrow Y_0 \rightarrow 0 \\ & \cdots \\ & 0 \rightarrow Y_n \rightarrow F_n \rightarrow Y_{n-1} \rightarrow 0 \\ & \cdots \end{align*} $$
$$ \begin{align*} & 0 \rightarrow Y_0 \rightarrow F_0 \rightarrow A \rightarrow 0 \\ & 0 \rightarrow Y_1 \rightarrow F_1 \rightarrow Y_0 \rightarrow 0 \\ & \cdots \\ & 0 \rightarrow Y_n \rightarrow F_n \rightarrow Y_{n-1} \rightarrow 0 \\ & \cdots \end{align*} $$
Applying
![]() ${\mathrm {Ext}}^*_{\mathcal {C}}(P,-)$
we obtain exact sequences
${\mathrm {Ext}}^*_{\mathcal {C}}(P,-)$
we obtain exact sequences
 $$ \begin{align*} & {\mathrm{Ext}}^i_{\mathcal{C}}(P,F_0) \rightarrow {\mathrm{Ext}}^i_{\mathcal{C}}(P,A) \xrightarrow{\delta} {\mathrm{Ext}}^{i+1}_{\mathcal{C}}(P,Y_0) \\ & {\mathrm{Ext}}^{i+1}_{\mathcal{C}}(P,F_1) \rightarrow {\mathrm{Ext}}^{i+1}_{\mathcal{C}}(P,Y_0) \xrightarrow{\delta} {\mathrm{Ext}}^{i+2}_{\mathcal{C}}(P,Y_1) \\ & \cdots \\ & {\mathrm{Ext}}^{i+n}_{\mathcal{C}}(P,F_n) \rightarrow {\mathrm{Ext}}^{i+n}_{\mathcal{C}}(P,Y_{n-1}) \xrightarrow{\delta} {\mathrm{Ext}}^{i+n+1}_{\mathcal{C}}(P,Y_n) \ , \\ & \cdots \end{align*} $$
$$ \begin{align*} & {\mathrm{Ext}}^i_{\mathcal{C}}(P,F_0) \rightarrow {\mathrm{Ext}}^i_{\mathcal{C}}(P,A) \xrightarrow{\delta} {\mathrm{Ext}}^{i+1}_{\mathcal{C}}(P,Y_0) \\ & {\mathrm{Ext}}^{i+1}_{\mathcal{C}}(P,F_1) \rightarrow {\mathrm{Ext}}^{i+1}_{\mathcal{C}}(P,Y_0) \xrightarrow{\delta} {\mathrm{Ext}}^{i+2}_{\mathcal{C}}(P,Y_1) \\ & \cdots \\ & {\mathrm{Ext}}^{i+n}_{\mathcal{C}}(P,F_n) \rightarrow {\mathrm{Ext}}^{i+n}_{\mathcal{C}}(P,Y_{n-1}) \xrightarrow{\delta} {\mathrm{Ext}}^{i+n+1}_{\mathcal{C}}(P,Y_n) \ , \\ & \cdots \end{align*} $$
where
![]() $\delta $
denotes the connecting homomorphisms. These are sequences of
$\delta $
denotes the connecting homomorphisms. These are sequences of
![]() $Z\otimes Z$
-bimodules. The first term in each sequence is annihilated by
$Z\otimes Z$
-bimodules. The first term in each sequence is annihilated by
![]() $\mathcal {J}$
. Now, choose
$\mathcal {J}$
. Now, choose
![]() $n := d - i$
. Then
$n := d - i$
. Then
![]() ${\mathrm {Ext}}^{i+n+1}_{\mathcal {C}}(P,Y_n) = 0$
. The assertion now follows by downward induction along the above sequences.
${\mathrm {Ext}}^{i+n+1}_{\mathcal {C}}(P,Y_n) = 0$
. The assertion now follows by downward induction along the above sequences.
Proof of Theorem 3.7.1.
Since
![]() $\mathcal {L}_W^H = \varrho ^{-1}(\mathcal {L}_W^Z)$
, it follows from Lemma 3.6.1 that
$\mathcal {L}_W^H = \varrho ^{-1}(\mathcal {L}_W^Z)$
, it follows from Lemma 3.6.1 that
![]() $\mathcal {L}_W^H$
is stable in
$\mathcal {L}_W^H$
is stable in
![]() ${\mathrm {Mod}}(H)$
. Hence,
${\mathrm {Mod}}(H)$
. Hence,
![]() $\mathcal {L}_W^{\mathcal {A}} = \mathcal {L}_W^{\mathcal {C}} \cap \mathcal {A}$
is stable in
$\mathcal {L}_W^{\mathcal {A}} = \mathcal {L}_W^{\mathcal {C}} \cap \mathcal {A}$
is stable in
![]() $\mathcal {A}$
. Therefore, by Theorem 3.5.8, it is enough to show that the functor
$\mathcal {A}$
. Therefore, by Theorem 3.5.8, it is enough to show that the functor
![]() ${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
maps
${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
maps
![]() $\mathcal {L}_W^{\mathcal {A}}$
to
$\mathcal {L}_W^{\mathcal {A}}$
to
![]() $\mathcal {L}_W^H$
. By Lemma 3.7.2, the functor
$\mathcal {L}_W^H$
. By Lemma 3.7.2, the functor
![]() ${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
commutes with filtered colimits. Hence, it suffices to show that for any noetherian object A in
${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
commutes with filtered colimits. Hence, it suffices to show that for any noetherian object A in
![]() $\mathcal {L}_W^{\mathcal {C}} \cap \mathcal {A}$
, the H-module
$\mathcal {L}_W^{\mathcal {C}} \cap \mathcal {A}$
, the H-module
![]() $M := {\mathrm {Ext}}^1_{\mathcal {C}}(P,A)$
lies in
$M := {\mathrm {Ext}}^1_{\mathcal {C}}(P,A)$
lies in
![]() $\mathcal {L}_W^H$
. Since the functor
$\mathcal {L}_W^H$
. Since the functor
![]() ${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
is also half-exact, we may assume further, using a prime series for
${\mathrm {Ext}}^1_{\mathcal {C}}(P,-)$
is also half-exact, we may assume further, using a prime series for
![]() ${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
as in [Reference Goodearl and WarfieldGW] Proposition 3.13, that the annihilator of any nonzero H-submodule of
${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
as in [Reference Goodearl and WarfieldGW] Proposition 3.13, that the annihilator of any nonzero H-submodule of
![]() ${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
is a prime ideal
${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
is a prime ideal
![]() $\mathfrak {p}$
of H. Then necessarily
$\mathfrak {p}$
of H. Then necessarily
![]() $\mathfrak {p} = {\mathrm {Ann}}_H({\mathrm {Hom}}_{\mathcal {A}}(P,A))$
, and we write
$\mathfrak {p} = {\mathrm {Ann}}_H({\mathrm {Hom}}_{\mathcal {A}}(P,A))$
, and we write
![]() $\mathfrak {p}_Z := \mathfrak {p} \cap Z \in \Xi $
.
$\mathfrak {p}_Z := \mathfrak {p} \cap Z \in \Xi $
.
By Lemma 3.7.3, the
![]() $Z \otimes Z$
-module
$Z \otimes Z$
-module
![]() $M = {\mathrm {Ext}}^1_{\mathcal {C}}(P,A)$
is killed by
$M = {\mathrm {Ext}}^1_{\mathcal {C}}(P,A)$
is killed by
![]() $\mathcal {J}^{d+1}$
. Letting
$\mathcal {J}^{d+1}$
. Letting
![]() $\mathcal {R}_d := {\mathrm {Spec}}((Z \otimes Z) / \mathcal {J}^{d+1})$
, we can then regard M as an
$\mathcal {R}_d := {\mathrm {Spec}}((Z \otimes Z) / \mathcal {J}^{d+1})$
, we can then regard M as an
![]() $\mathcal {O}(\mathcal {R}_d) = (Z \otimes Z) / \mathcal {J}^{d+1}$
-module in a natural way. Next, consider the commutative diagram
$\mathcal {O}(\mathcal {R}_d) = (Z \otimes Z) / \mathcal {J}^{d+1}$
-module in a natural way. Next, consider the commutative diagram

where i is the closed embedding, and the
![]() $f_j$
are, similarly as before, the restrictions of the two projection maps.
$f_j$
are, similarly as before, the restrictions of the two projection maps.
Let
![]() $S := \Xi \setminus W$
; then our assumption
$S := \Xi \setminus W$
; then our assumption
![]() $\pi _2(\pi _1^{-1}(W)) \subseteq W$
is equivalent to
$\pi _2(\pi _1^{-1}(W)) \subseteq W$
is equivalent to
![]() $\pi _1^{-1}(W) \subseteq \pi _2^{-1}(W)$
, which is the same as
$\pi _1^{-1}(W) \subseteq \pi _2^{-1}(W)$
, which is the same as
![]() $\pi _2^{-1}(S) \subseteq \pi _1^{-1}(S)$
. Since
$\pi _2^{-1}(S) \subseteq \pi _1^{-1}(S)$
. Since
![]() $\pi _j = f_j \circ i$
, this is equivalent to
$\pi _j = f_j \circ i$
, this is equivalent to
![]() $i^{-1} f_2^{-1}(S) \subseteq i^{-1} f_1^{-1}(S)$
. However, i is a bijection because
$i^{-1} f_2^{-1}(S) \subseteq i^{-1} f_1^{-1}(S)$
. However, i is a bijection because
![]() $\mathcal {J}$
is nilpotent modulo
$\mathcal {J}$
is nilpotent modulo
![]() $\mathcal {J}^{d+1}$
, so this is in turn equivalent to
$\mathcal {J}^{d+1}$
, so this is in turn equivalent to
![]() $f_2^{-1}(S) \subseteq f_1^{-1}(S)$
.
$f_2^{-1}(S) \subseteq f_1^{-1}(S)$
.
Now,
![]() $\mathfrak {p}$
is the annihilator of any nonzero H-submodule of
$\mathfrak {p}$
is the annihilator of any nonzero H-submodule of
![]() ${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
, so
${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
, so
![]() $\mathfrak {p}_Z = \mathfrak {p} \cap Z = {\mathrm {Ann}}_Z(v)$
for all nonzero
$\mathfrak {p}_Z = \mathfrak {p} \cap Z = {\mathrm {Ann}}_Z(v)$
for all nonzero
![]() $v \in {\mathrm {Hom}}_{\mathcal {A}}(P,A)$
. Since
$v \in {\mathrm {Hom}}_{\mathcal {A}}(P,A)$
. Since
![]() ${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
lies in
${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
lies in
![]() $\mathcal {L}_W^H$
, this means that
$\mathcal {L}_W^H$
, this means that
![]() $V(\mathfrak {p}_Z) \cap W = \emptyset $
by Proposition 3.6.4, and hence
$V(\mathfrak {p}_Z) \cap W = \emptyset $
by Proposition 3.6.4, and hence
![]() $V(\mathfrak {p}_Z) \subseteq S = \Xi \setminus W$
.
$V(\mathfrak {p}_Z) \subseteq S = \Xi \setminus W$
.
By assumption,
![]() $\mathcal {O}(\mathcal {R}_d) = (Z \otimes Z) / \mathcal {J}^{d+1}$
is noetherian. Let
$\mathcal {O}(\mathcal {R}_d) = (Z \otimes Z) / \mathcal {J}^{d+1}$
is noetherian. Let
![]() $\overline {i}_2 : Z \to (Z \otimes Z) / \mathcal {J}^{d+1}$
, sending z to
$\overline {i}_2 : Z \to (Z \otimes Z) / \mathcal {J}^{d+1}$
, sending z to
![]() $1 \otimes z + \mathcal {J}^{d+1}$
, be the ring homomorphism which induces
$1 \otimes z + \mathcal {J}^{d+1}$
, be the ring homomorphism which induces
![]() $f_2$
. Let
$f_2$
. Let
![]() $Q_1,\cdots , Q_k \subseteq \mathcal {O}(\mathcal {R}_d)$
be the minimal prime ideals lying above
$Q_1,\cdots , Q_k \subseteq \mathcal {O}(\mathcal {R}_d)$
be the minimal prime ideals lying above
![]() $\overline {i}_2(\mathfrak {p}_Z) \mathcal {O}(\mathcal {R}_d)$
; then
$\overline {i}_2(\mathfrak {p}_Z) \mathcal {O}(\mathcal {R}_d)$
; then
![]() $Q_1^{a_1}\cdots Q_k^{a_k} \subseteq \overline {i}_2(\mathfrak {p}_Z) \mathcal {O}(\mathcal {R}_d)$
for some positive integers
$Q_1^{a_1}\cdots Q_k^{a_k} \subseteq \overline {i}_2(\mathfrak {p}_Z) \mathcal {O}(\mathcal {R}_d)$
for some positive integers
![]() $a_1,\cdots , a_k$
. We have
$a_1,\cdots , a_k$
. We have
![]() $f_2(Q_j) = (\overline {i}_2)^{-1}(Q_j) \in V(\mathfrak {p}_Z)$
because
$f_2(Q_j) = (\overline {i}_2)^{-1}(Q_j) \in V(\mathfrak {p}_Z)$
because
![]() $Q_j$
contains
$Q_j$
contains
![]() $\overline {i}_2(\mathfrak {p}_Z)$
. Therefore,
$\overline {i}_2(\mathfrak {p}_Z)$
. Therefore,
![]() $Q_j \in f_2^{-1}(V(\mathfrak {p}_Z)) \subseteq f_2^{-1}(S) \subseteq f_1^{-1}(S)$
. Thus, we see that
$Q_j \in f_2^{-1}(V(\mathfrak {p}_Z)) \subseteq f_2^{-1}(S) \subseteq f_1^{-1}(S)$
. Thus, we see that
![]() $\mathfrak {q}_j := f_1(Q_j)$
lies in S for all
$\mathfrak {q}_j := f_1(Q_j)$
lies in S for all
![]() $j = 1,\cdots , k$
. Hence,
$j = 1,\cdots , k$
. Hence,
![]() $V(\mathfrak {q}_j) \subseteq S$
for all j because S is specialization-closed.
$V(\mathfrak {q}_j) \subseteq S$
for all j because S is specialization-closed.
With
![]() ${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
also A is killed by
${\mathrm {Hom}}_{\mathcal {A}}(P,A)$
also A is killed by
![]() $\mathfrak {p}_Z$
. Hence,
$\mathfrak {p}_Z$
. Hence,
![]() $M = {\mathrm {Ext}}^1_{\mathcal {C}}(P, A)$
is killed by
$M = {\mathrm {Ext}}^1_{\mathcal {C}}(P, A)$
is killed by
![]() $Z \otimes \mathfrak {p}_Z$
as well as
$Z \otimes \mathfrak {p}_Z$
as well as
![]() $\mathcal {J}^{d+1}$
. We see that M is killed by
$\mathcal {J}^{d+1}$
. We see that M is killed by
![]() $\overline {i}_2(\mathfrak {p}_Z) \mathcal {O}(\mathcal {R}_d) \supseteq Q_1^{a_1}\cdots Q_k^{a_k}$
. Hence,
$\overline {i}_2(\mathfrak {p}_Z) \mathcal {O}(\mathcal {R}_d) \supseteq Q_1^{a_1}\cdots Q_k^{a_k}$
. Hence,
![]() $\mathfrak {q}_1^{a_1} \cdots \mathfrak {q}_k^{a_k} \cdot v = 0$
for any
$\mathfrak {q}_1^{a_1} \cdots \mathfrak {q}_k^{a_k} \cdot v = 0$
for any
![]() $v \in M$
, so
$v \in M$
, so
![]() $V({\mathrm {Ann}}_Z(v)) \subseteq V(\mathfrak {q}_1) \cup \cdots \cup V(\mathfrak {q}_k) \subseteq S$
. Therefore, the H-module M (where H acts on M through its action on P) lies in
$V({\mathrm {Ann}}_Z(v)) \subseteq V(\mathfrak {q}_1) \cup \cdots \cup V(\mathfrak {q}_k) \subseteq S$
. Therefore, the H-module M (where H acts on M through its action on P) lies in
![]() $\mathcal {L}^H_W$
by Proposition 3.6.4 as required.
$\mathcal {L}^H_W$
by Proposition 3.6.4 as required.
Now, we form the following diagram, which defines the map
![]() $\tau $
:
$\tau $
:

Proposition 3.7.4. Assume (A1), (A2), (A3). If
![]() $U \subseteq \mathfrak {Z}$
is an intersection of open subsets, then
$U \subseteq \mathfrak {Z}$
is an intersection of open subsets, then
![]() $\tau ^{-1}(U)$
is stable.
$\tau ^{-1}(U)$
is stable.
Proof. Put
![]() $W = \mathbf {q}^{-1}(U)$
. Then
$W = \mathbf {q}^{-1}(U)$
. Then
Now, apply Theorem 3.7.1.
Remark 3.7.5. Suppose that our category
![]() $\mathcal {C}$
is k-linear. Then the
$\mathcal {C}$
is k-linear. Then the
![]() $Z \otimes _{\mathbb {Z}} Z$
-action on the
$Z \otimes _{\mathbb {Z}} Z$
-action on the
![]() ${\mathrm {Ext}}$
-groups
${\mathrm {Ext}}$
-groups
![]() ${\mathrm {Ext}}^j_{\mathcal {C}}(M,N)$
for
${\mathrm {Ext}}^j_{\mathcal {C}}(M,N)$
for
![]() $M,N$
in
$M,N$
in
![]() $\mathcal {A}$
, factors through
$\mathcal {A}$
, factors through
![]() $Z \otimes _k Z$
. Therefore, the proof of Theorem 3.7.1 goes through if we replace
$Z \otimes _k Z$
. Therefore, the proof of Theorem 3.7.1 goes through if we replace
![]() $\mathbf {(A3)}$
by the weaker assumption that
$\mathbf {(A3)}$
by the weaker assumption that
![]() $(Z \otimes _k Z) / \overline {\mathcal {J}}^{d+1}$
is noetherian, where
$(Z \otimes _k Z) / \overline {\mathcal {J}}^{d+1}$
is noetherian, where
![]() $\overline {\mathcal {J}}$
is the image of
$\overline {\mathcal {J}}$
is the image of
![]() $\mathcal {J}$
under the surjection
$\mathcal {J}$
under the surjection
![]() $Z \otimes _{\mathbb {Z}} Z \twoheadrightarrow Z \otimes _k Z$
.
$Z \otimes _{\mathbb {Z}} Z \twoheadrightarrow Z \otimes _k Z$
.
We also apply Theorem 3.7.1 to give a sufficient criterion for the stability of the Krull-dimension filtration of the locally noetherian category
![]() $\mathcal {C}$
. For every ordinal
$\mathcal {C}$
. For every ordinal
![]() $\alpha $
, the set
$\alpha $
, the set
is a generalization-stable subset of
![]() $\Xi $
. We identify the corresponding localising subcategory
$\Xi $
. We identify the corresponding localising subcategory
![]() $\mathcal {L}^{\mathcal {C}}_{W_\alpha }$
of
$\mathcal {L}^{\mathcal {C}}_{W_\alpha }$
of
![]() $\mathcal {C}$
in Lemma 3.7.7 below, but first we recall a standard fact about Krull dimension.
$\mathcal {C}$
in Lemma 3.7.7 below, but first we recall a standard fact about Krull dimension.
Lemma 3.7.6. Let M be a finitely generated module over a commutative noetherian ring A. Then
Proof. An induction on the number of generators of M together with [Reference McConnell and RobsonMCR] Lemma 6.2.4 shows the first equality, namely
![]() $\kappa (M) = \sup _{v \in M} \kappa (Av)$
.
$\kappa (M) = \sup _{v \in M} \kappa (Av)$
.
Let I be an ideal of A. Since A is noetherian, [Reference McConnell and RobsonMCR] Lemma 6.2.4 implies that
![]() $\kappa (A/I) = \kappa (A / I^m)$
for all
$\kappa (A/I) = \kappa (A / I^m)$
for all
![]() $m \geq 0$
. Since
$m \geq 0$
. Since
![]() $(\sqrt {I})^m \subseteq I$
for sufficiently large m, we have
$(\sqrt {I})^m \subseteq I$
for sufficiently large m, we have
![]() $\kappa (A/I) \geq \kappa (A/\sqrt {I}) = \kappa (A/(\sqrt {I})^m) \geq \kappa (A/I)$
, so in fact we have the equality
$\kappa (A/I) \geq \kappa (A/\sqrt {I}) = \kappa (A/(\sqrt {I})^m) \geq \kappa (A/I)$
, so in fact we have the equality
![]() $\kappa (A/I) = \kappa (A/\sqrt {I})$
. Since
$\kappa (A/I) = \kappa (A/\sqrt {I})$
. Since
![]() $\sqrt {I}$
is equal to the intersection of the finitely many minimal primes
$\sqrt {I}$
is equal to the intersection of the finitely many minimal primes
![]() $\mathfrak {p}_1, \cdots , \mathfrak {p}_n$
containing it, there is a natural A-linear embedding
$\mathfrak {p}_1, \cdots , \mathfrak {p}_n$
containing it, there is a natural A-linear embedding
![]() $A / \sqrt {I} \hookrightarrow \oplus _{i=1}^n A / \mathfrak {p}_i$
. So
$A / \sqrt {I} \hookrightarrow \oplus _{i=1}^n A / \mathfrak {p}_i$
. So
Therefore, for any
![]() $v \in M$
,
$v \in M$
,
![]() $\kappa (Av) = \kappa (A/{\mathrm {Ann}}_A(v)) = \sup \limits _{\mathfrak {p} \in V({\mathrm {ann}}(v))} \kappa (A/\mathfrak {p})$
.
$\kappa (Av) = \kappa (A/{\mathrm {Ann}}_A(v)) = \sup \limits _{\mathfrak {p} \in V({\mathrm {ann}}(v))} \kappa (A/\mathfrak {p})$
.
Recall (
![]() $\S$
2.2) that
$\S$
2.2) that
![]() $\mathcal {C}_\alpha $
is the full subcategory of
$\mathcal {C}_\alpha $
is the full subcategory of
![]() $\mathcal {C}$
consisting of objects V such that
$\mathcal {C}$
consisting of objects V such that
![]() $\kappa (V) \leq \alpha $
.
$\kappa (V) \leq \alpha $
.
Lemma 3.7.7. For any ordinal
![]() $\alpha $
, we have
$\alpha $
, we have
![]() $\mathcal {L}^{\mathcal {C}}_{W_\alpha } = \mathcal {C}_\alpha $
.
$\mathcal {L}^{\mathcal {C}}_{W_\alpha } = \mathcal {C}_\alpha $
.
Proof. By Gabriel’s definition of Krull dimension found at [Reference GabrielGab] p. 382, we see that
![]() $\kappa (V) = \sup _i \kappa (V_i)$
if we write
$\kappa (V) = \sup _i \kappa (V_i)$
if we write
![]() $V = \varinjlim V_i$
as a filtered colimit of its noetherian subobjects
$V = \varinjlim V_i$
as a filtered colimit of its noetherian subobjects
![]() $V_i$
. Therefore, it is enough to show that for noetherian
$V_i$
. Therefore, it is enough to show that for noetherian
![]() $V \in \mathcal {C}$
, we have
$V \in \mathcal {C}$
, we have
![]() $V \in \mathcal {L}^{\mathcal {C}}_{W_\alpha }$
if and only if
$V \in \mathcal {L}^{\mathcal {C}}_{W_\alpha }$
if and only if
![]() $\kappa (V) \leq \alpha $
. Since
$\kappa (V) \leq \alpha $
. Since
![]() $\mathcal {C}$
is a thickening of
$\mathcal {C}$
is a thickening of
![]() $\mathcal {A}$
, we may further assume that
$\mathcal {A}$
, we may further assume that
![]() $V \in \mathcal {A}$
. Hence, we are reduced to showing that for finitely generated H-modules M, we have
$V \in \mathcal {A}$
. Hence, we are reduced to showing that for finitely generated H-modules M, we have
However, since H is a finitely generated Z-module,
![]() $\kappa (M) = \kappa (\rho (M))$
by [Reference McConnell and RobsonMCR] Corollary 10.1.10, whereas
$\kappa (M) = \kappa (\rho (M))$
by [Reference McConnell and RobsonMCR] Corollary 10.1.10, whereas
![]() $M \in \mathcal {L}^H_{W_\alpha }$
if and only if
$M \in \mathcal {L}^H_{W_\alpha }$
if and only if
![]() $\rho (M) \in \mathcal {L}^Z_{W_\alpha }$
by equation (7). Next,
$\rho (M) \in \mathcal {L}^Z_{W_\alpha }$
by equation (7). Next,
![]() $\rho (M) \in \mathcal {L}^Z_{W_\alpha }$
if and only if for all
$\rho (M) \in \mathcal {L}^Z_{W_\alpha }$
if and only if for all
![]() $v \in M$
and all
$v \in M$
and all
![]() $\mathfrak {p} \in {\mathrm {Spec}}(Z)$
containing
$\mathfrak {p} \in {\mathrm {Spec}}(Z)$
containing
![]() ${\mathrm {Ann}}_Z(v)$
, we have
${\mathrm {Ann}}_Z(v)$
, we have
![]() $\kappa (Z/\mathfrak {p}) \leq \alpha $
. As
$\kappa (Z/\mathfrak {p}) \leq \alpha $
. As
![]() $\rho (M)$
is a finitely generated Z-module, this is equivalent to
$\rho (M)$
is a finitely generated Z-module, this is equivalent to
![]() $\kappa (\rho (M)) \leq \alpha $
by Lemma 3.7.6.
$\kappa (\rho (M)) \leq \alpha $
by Lemma 3.7.6.
We can now establish the stability of the Krull-dimension filtration on
![]() $\mathcal {C}$
under certain fairly restrictive hypotheses on
$\mathcal {C}$
under certain fairly restrictive hypotheses on
![]() $\Xi $
and
$\Xi $
and
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Proposition 3.7.8. Suppose that
![]() $\mathcal {C}$
is k-linear, that Z is a finitely generated k-algebra and that there is an integer d such that
$\mathcal {C}$
is k-linear, that Z is a finitely generated k-algebra and that there is an integer d such that
![]() ${\mathrm {Ext}}^j_{\mathcal {C}}(P,.)|_{\mathcal {A}} = 0$
for any
${\mathrm {Ext}}^j_{\mathcal {C}}(P,.)|_{\mathcal {A}} = 0$
for any
![]() $j> d$
. Suppose further that
$j> d$
. Suppose further that
![]() ${\mathrm {pr}}_2 : \mathcal {R} \to \Xi $
is quasi-finite. Then
${\mathrm {pr}}_2 : \mathcal {R} \to \Xi $
is quasi-finite. Then
![]() $\mathcal {L}_{W_\alpha }^{\mathcal {C}}$
is a stable localising subcategory of
$\mathcal {L}_{W_\alpha }^{\mathcal {C}}$
is a stable localising subcategory of
![]() $\mathcal {C}$
for all
$\mathcal {C}$
for all
![]() $\alpha $
.
$\alpha $
.
Proof. By assumption, the k-algebra
![]() $Z \otimes _k Z$
is also finitely generated, so it is noetherian by Hilbert’s basis theorem. By Theorem 3.7.1 and Remark 3.7.5, it is enough to show that
$Z \otimes _k Z$
is also finitely generated, so it is noetherian by Hilbert’s basis theorem. By Theorem 3.7.1 and Remark 3.7.5, it is enough to show that
Let
![]() $\mathcal {S}_\alpha := \Xi \backslash W_\alpha $
be the complement of
$\mathcal {S}_\alpha := \Xi \backslash W_\alpha $
be the complement of
![]() $W_\alpha $
in
$W_\alpha $
in
![]() $\Xi $
; then it is enough to show that
$\Xi $
; then it is enough to show that
Let
![]() $P \in {\mathrm {pr}}_2^{-1}(\mathcal {S}_\alpha )$
, and set
$P \in {\mathrm {pr}}_2^{-1}(\mathcal {S}_\alpha )$
, and set
![]() $\mathfrak {p}_i := {\mathrm {pr}}_i(P)$
for
$\mathfrak {p}_i := {\mathrm {pr}}_i(P)$
for
![]() $i=1,2$
. Then
$i=1,2$
. Then
![]() $\mathfrak {p}_2 \in \mathcal {S}_\alpha $
, so
$\mathfrak {p}_2 \in \mathcal {S}_\alpha $
, so
![]() $\kappa (Z/\mathfrak {p}_2) \leq \alpha $
. The morphisms
$\kappa (Z/\mathfrak {p}_2) \leq \alpha $
. The morphisms
![]() ${\mathrm {pr}}_1$
and
${\mathrm {pr}}_1$
and
![]() ${\mathrm {pr}}_2$
induce the following diagram of residue fields:
${\mathrm {pr}}_2$
induce the following diagram of residue fields:
Since
![]() ${\mathrm {pr}}_2 : \mathcal {R} \to \Xi $
is quasi-finite,
${\mathrm {pr}}_2 : \mathcal {R} \to \Xi $
is quasi-finite,
![]() $k(P)$
is a finite-dimensional
$k(P)$
is a finite-dimensional
![]() $k(\mathfrak {p}_2)$
-vector space. Hence,
$k(\mathfrak {p}_2)$
-vector space. Hence,
Since Z is a finitely generated k-algebra, we can apply a version of the Noether normalisation theorem – see [Reference MatsumuraMat] Theorem 5.6 – to deduce that
Hence,
![]() $\kappa (Z/\mathfrak {p}_1) \leq \kappa (Z/\mathfrak {p}_2) \leq \alpha $
, which means that
$\kappa (Z/\mathfrak {p}_1) \leq \kappa (Z/\mathfrak {p}_2) \leq \alpha $
, which means that
![]() $\mathfrak {p}_1 = {\mathrm {pr}}_1(P) \in \mathcal {S}_\alpha $
.
$\mathfrak {p}_1 = {\mathrm {pr}}_1(P) \in \mathcal {S}_\alpha $
.
4 The quotient space for
 ${\mathrm {Mod}}_k(SL_2(\mathbb {Q}_p))$
${\mathrm {Mod}}_k(SL_2(\mathbb {Q}_p))$
4.1 The pro-p Iwahori–Hecke algebra and its centre
4.1.1 The setup
Let
![]() $\mathfrak {F}$
be a finite extension of
$\mathfrak {F}$
be a finite extension of
![]() $\mathbb {Q}_p$
with ring of integers
$\mathbb {Q}_p$
with ring of integers
![]() $\mathfrak {O}$
, maximal ideal
$\mathfrak {O}$
, maximal ideal
![]() $\mathfrak {M}$
and residue field
$\mathfrak {M}$
and residue field
![]() $\mathfrak {f}$
. We fix a choice of generator
$\mathfrak {f}$
. We fix a choice of generator
![]() $\pi $
of
$\pi $
of
![]() $\mathfrak {M}$
. Necessarily,
$\mathfrak {M}$
. Necessarily,
![]() $\mathfrak {f} \cong \mathbb {F}_q$
for some power q of p. We assume that our ground field k contains
$\mathfrak {f} \cong \mathbb {F}_q$
for some power q of p. We assume that our ground field k contains
![]() $\mathfrak {f}$
.
$\mathfrak {f}$
.
4.1.2 Groups
Let
![]() $G = {\mathrm {SL}}_2(\mathfrak {F})$
and
$G = {\mathrm {SL}}_2(\mathfrak {F})$
and
![]() $K = {\mathrm {SL}}_2(\mathfrak {O})$
, and define the pro- p Iwahori subgroup
$K = {\mathrm {SL}}_2(\mathfrak {O})$
, and define the pro- p Iwahori subgroup
 $$\begin{align*}I := \begin{pmatrix} 1 + \mathfrak{M} & \mathfrak{O} \\ \mathfrak{M} & 1 + \mathfrak{M} \end{pmatrix} \cap G.\end{align*}$$
$$\begin{align*}I := \begin{pmatrix} 1 + \mathfrak{M} & \mathfrak{O} \\ \mathfrak{M} & 1 + \mathfrak{M} \end{pmatrix} \cap G.\end{align*}$$
Let
 $T = \begin {pmatrix} {\mathfrak {F}}^\times & 0 \\ 0 & {\mathfrak {F}}^\times \end {pmatrix} \cap G$
be the subgroup of diagonal matrices in G, and let
$T = \begin {pmatrix} {\mathfrak {F}}^\times & 0 \\ 0 & {\mathfrak {F}}^\times \end {pmatrix} \cap G$
be the subgroup of diagonal matrices in G, and let
![]() $T^0 := T \cap K$
. The projection onto the
$T^0 := T \cap K$
. The projection onto the
![]() $(1,1)$
-entry gives group isomorphisms
$(1,1)$
-entry gives group isomorphisms
![]() $T \stackrel {\cong }{\longrightarrow } {\mathfrak {F}}^\times $
and
$T \stackrel {\cong }{\longrightarrow } {\mathfrak {F}}^\times $
and
![]() $T^0 \stackrel {\cong }{\longrightarrow } {\mathfrak {O}}^\times $
. Hence,
$T^0 \stackrel {\cong }{\longrightarrow } {\mathfrak {O}}^\times $
. Hence,
![]() $T / T^0$
is an infinite cyclic group. The normaliser
$T / T^0$
is an infinite cyclic group. The normaliser
![]() $N_G(T)$
of T in G is generated by T and
$N_G(T)$
of T in G is generated by T and
 $s_0 := \begin {pmatrix} 0 & 1 \\ -1 & 0 \end {pmatrix}$
, and
$s_0 := \begin {pmatrix} 0 & 1 \\ -1 & 0 \end {pmatrix}$
, and
![]() $N_G(T)$
is isomorphic to the semidirect product
$N_G(T)$
is isomorphic to the semidirect product
![]() $T \rtimes \langle s_0 \rangle $
, where
$T \rtimes \langle s_0 \rangle $
, where
![]() $s_0$
acts on T by inversion. This action preserves the subgroup
$s_0$
acts on T by inversion. This action preserves the subgroup
![]() $T^0$
, so that
$T^0$
, so that
![]() $T^0$
is normal in
$T^0$
is normal in
![]() $N_G(T)$
. Then we can form the affine Weyl group
$N_G(T)$
. Then we can form the affine Weyl group
![]() $W := N_G(T) / T^0$
which is isomorphic to the infinite dihedral group, generated by the
$W := N_G(T) / T^0$
which is isomorphic to the infinite dihedral group, generated by the
![]() $T^0$
-cosets of
$T^0$
-cosets of
![]() $s_0$
and
$s_0$
and
 $s_1 := \begin {pmatrix} 0 & - \pi ^{-1} \\ \pi & 0 \end {pmatrix}$
. The subgroup
$s_1 := \begin {pmatrix} 0 & - \pi ^{-1} \\ \pi & 0 \end {pmatrix}$
. The subgroup
![]() $T^1 := T \cap I$
is also normal in
$T^1 := T \cap I$
is also normal in
![]() $N_G(T)$
, and this gives the extended Weyl group
$N_G(T)$
, and this gives the extended Weyl group
![]() $\widetilde {W} := N_G(T) / T^1$
. Let
$\widetilde {W} := N_G(T) / T^1$
. Let
![]() $\Omega := T^0 / T^1$
; then
$\Omega := T^0 / T^1$
; then
![]() $\Omega \cong {\mathfrak {f}}^\times $
and we have the short exact sequence
$\Omega \cong {\mathfrak {f}}^\times $
and we have the short exact sequence
Note that
![]() $\Omega $
is isomorphic to
$\Omega $
is isomorphic to
![]() $\mathbb {F}_q^\times $
and is therefore a finite cyclic group of order
$\mathbb {F}_q^\times $
and is therefore a finite cyclic group of order
![]() $q-1$
.
$q-1$
.
4.1.3 The pro-p Iwahori–Hecke algebra
Let
![]() $\widehat {\Omega } := {\mathrm {Hom}}(\Omega , k^\times )$
be the group of k-linear characters of
$\widehat {\Omega } := {\mathrm {Hom}}(\Omega , k^\times )$
be the group of k-linear characters of
![]() $\Omega $
. Since k contains the residue field
$\Omega $
. Since k contains the residue field
![]() $\mathfrak {f}$
of
$\mathfrak {f}$
of
![]() $\mathfrak {F}$
by assumption,
$\mathfrak {F}$
by assumption,
![]() $\widehat {\Omega }$
is a cyclic group of order
$\widehat {\Omega }$
is a cyclic group of order
![]() $q-1$
, generated by the identity character
$q-1$
, generated by the identity character
 $$\begin{align*}{\mathrm{id}} : \Omega \to k^\times, \quad \begin{pmatrix} a & 0 \\ 0 & a^{-1} \end{pmatrix} T^1 \mapsto a^{-1} + \mathfrak{M} \in {\mathfrak{f}}^\times \hookrightarrow k^\times.\end{align*}$$
$$\begin{align*}{\mathrm{id}} : \Omega \to k^\times, \quad \begin{pmatrix} a & 0 \\ 0 & a^{-1} \end{pmatrix} T^1 \mapsto a^{-1} + \mathfrak{M} \in {\mathfrak{f}}^\times \hookrightarrow k^\times.\end{align*}$$
In other words, we have
![]() $\widehat {\Omega } = \{{\mathrm {id}}^j : 0 \leq j \leq q-2\}$
where
$\widehat {\Omega } = \{{\mathrm {id}}^j : 0 \leq j \leq q-2\}$
where ![]() is the trivial character. The group algebra
is the trivial character. The group algebra
![]() $k[\Omega ]$
contains
$k[\Omega ]$
contains
![]() $q-1$
primitive idempotents
$q-1$
primitive idempotents
that form a basis for
![]() $k[\Omega ]$
as a k-vector space. These idempotents are pairwise orthogonal:
$k[\Omega ]$
as a k-vector space. These idempotents are pairwise orthogonal:
We have the compactly induced G-representation
from the trivial representation k of I. It is a smooth k-linear representation of G, so
![]() $k[G/I]$
is an object in
$k[G/I]$
is an object in
![]() ${\mathrm {Mod}}_k(G)$
. The pro- p Iwahori–Hecke algebra is the opposite ring of the endomorphism ring of this representation:
${\mathrm {Mod}}_k(G)$
. The pro- p Iwahori–Hecke algebra is the opposite ring of the endomorphism ring of this representation:
The following facts are known about H.
Lemma 4.1.1.
-
a) The double cosets
 $\{\tau _w := IwI : w \in \widetilde {W}\}$
form a k-basis for H.
$\{\tau _w := IwI : w \in \widetilde {W}\}$
form a k-basis for H. -
b) The map
 $k[\Omega ] \to H$
given by
$k[\Omega ] \to H$
given by
 $\Omega \ni \omega \mapsto \tau _\omega $
is an injection of k-algebras.
$\Omega \ni \omega \mapsto \tau _\omega $
is an injection of k-algebras. -
c) The elements
 $\tau _0 := \tau _{s_0}$
and
$\tau _0 := \tau _{s_0}$
and
 $\tau _1 := \tau _{s_1}$
generate H as a k-algebra together with
$\tau _1 := \tau _{s_1}$
generate H as a k-algebra together with
 $k[\Omega ]$
.
$k[\Omega ]$
. -
d) We have
 $\tau _i e_\lambda = e_{\lambda ^{-1}} \tau _i$
for
$\tau _i e_\lambda = e_{\lambda ^{-1}} \tau _i$
for
 $i=0,1$
and any
$i=0,1$
and any
 $\lambda \in \widehat {\Omega }$
.
$\lambda \in \widehat {\Omega }$
. -
e) We have the quadratic relations
 for
for
 $i=0,1$
.
$i=0,1$
.
We will never use the notation
![]() $\tau _w$
when w is the identity element of
$\tau _w$
when w is the identity element of
![]() $\widetilde {W}$
because this is equal to the identity element in H. Therefore, writing
$\widetilde {W}$
because this is equal to the identity element in H. Therefore, writing
![]() $\tau _1 = \tau _{s_1}$
should not lead to any confusion.
$\tau _1 = \tau _{s_1}$
should not lead to any confusion.
4.1.4 The centre of H
The centre
![]() $Z = Z(H)$
of this k-algebra can be described explicitly. The following statement is well known, but see also [Reference Ollivier and SchneiderOS18]
$Z = Z(H)$
of this k-algebra can be described explicitly. The following statement is well known, but see also [Reference Ollivier and SchneiderOS18]
![]() $\S $
3.2.2.
$\S $
3.2.2.
Lemma 4.1.2. The element
generates a polynomial ring
![]() $k[\zeta ]$
inside
$k[\zeta ]$
inside
![]() $Z(H)$
.
$Z(H)$
.
Later on, the localisations
![]() $Z_\zeta $
of Z and
$Z_\zeta $
of Z and
![]() $H_\zeta $
of H at
$H_\zeta $
of H at
![]() $\zeta $
will play an important technical role.
$\zeta $
will play an important technical role.
Definition 4.1.3. For each
![]() $\lambda \in \widehat {\Omega }$
, we define the following elements of H:
$\lambda \in \widehat {\Omega }$
, we define the following elements of H:

Again, we omit the proof of the following well-known result.
Lemma 4.1.4. Let
![]() $\lambda \in \widehat {\Omega }$
.
$\lambda \in \widehat {\Omega }$
.
-
a)
 $X_\lambda $
is central in H.
$X_\lambda $
is central in H. -
b) If
 $\lambda \neq \lambda ^{-1}$
, then
$\lambda \neq \lambda ^{-1}$
, then
 $(e_\lambda + e_{\lambda ^{-1}}) \zeta = X_\lambda + X_{\lambda ^{-1}}$
.
$(e_\lambda + e_{\lambda ^{-1}}) \zeta = X_\lambda + X_{\lambda ^{-1}}$
. -
c) If
 $\lambda = \lambda ^{-1}$
, then
$\lambda = \lambda ^{-1}$
, then
 $e_\lambda \zeta = X_\lambda $
.
$e_\lambda \zeta = X_\lambda $
. -
d) We have
 $\sum \limits _{\alpha \in \widehat {\Omega }} X_\alpha = \zeta $
.
$\sum \limits _{\alpha \in \widehat {\Omega }} X_\alpha = \zeta $
.
We will now describe Z completely as a k-algebra with relations and generators. Suppose that
![]() $\lambda \in \widehat {\Omega }$
satisfies
$\lambda \in \widehat {\Omega }$
satisfies
![]() $\lambda \neq \lambda ^{-1}$
; then using Lemma 4.1.1, we see that the idempotent
$\lambda \neq \lambda ^{-1}$
; then using Lemma 4.1.1, we see that the idempotent
![]() $e_\lambda + e_{\lambda ^{-1}}$
is central in H. It is known, furthermore, that in this case
$e_\lambda + e_{\lambda ^{-1}}$
is central in H. It is known, furthermore, that in this case
For simplicity, we assume from now on that
![]() $p \neq 2$
. Then precisely two characters
$p \neq 2$
. Then precisely two characters
![]() $\lambda \in \widehat {\Omega }$
satisfy
$\lambda \in \widehat {\Omega }$
satisfy
![]() $\lambda = \lambda ^{-1}$
, namely the trivial character
$\lambda = \lambda ^{-1}$
, namely the trivial character ![]() and ‘the quadratic character’
and ‘the quadratic character’
![]() ${\mathrm {id}}^{\frac {q-1}{2}}$
. All other elements of
${\mathrm {id}}^{\frac {q-1}{2}}$
. All other elements of
![]() $\widehat {\Omega }$
are not equal to their inverse. This gives us the decomposition of Z as a direct product of nonunital subrings:
$\widehat {\Omega }$
are not equal to their inverse. This gives us the decomposition of Z as a direct product of nonunital subrings:

From
![]() $\S 3.2$
of [Reference Ollivier and SchneiderOS18], we deduce the following
$\S 3.2$
of [Reference Ollivier and SchneiderOS18], we deduce the following
Proposition 4.1.5. Let
![]() $\lambda \in \widehat {\Omega }$
, and let
$\lambda \in \widehat {\Omega }$
, and let
![]() $x,y$
be indeterminates.
$x,y$
be indeterminates.
-
a) Suppose that
 $\lambda = \lambda ^{-1}$
. Then the k-algebra homomorphism is an isomorphism.
$\lambda = \lambda ^{-1}$
. Then the k-algebra homomorphism is an isomorphism. $$\begin{align*}k[x] \to e_\lambda Z, \quad 1 \mapsto e_\lambda, \quad x \mapsto X_\lambda\end{align*}$$
$$\begin{align*}k[x] \to e_\lambda Z, \quad 1 \mapsto e_\lambda, \quad x \mapsto X_\lambda\end{align*}$$
-
b) Suppose that
 $\lambda \neq \lambda ^{-1}$
. Then the k-algebra homomorphism is an isomorphism.
$\lambda \neq \lambda ^{-1}$
. Then the k-algebra homomorphism is an isomorphism. $$\begin{align*}b_\lambda : \frac{ k[x, y] } {\langle xy\rangle} \to (e_\lambda + e_{\lambda^{-1}}) Z, \quad 1 \mapsto e_{\lambda} + e_{\lambda^{-1}}, \quad x \mapsto X_\lambda, \quad y \mapsto X_{\lambda^{-1}} \end{align*}$$
$$\begin{align*}b_\lambda : \frac{ k[x, y] } {\langle xy\rangle} \to (e_\lambda + e_{\lambda^{-1}}) Z, \quad 1 \mapsto e_{\lambda} + e_{\lambda^{-1}}, \quad x \mapsto X_\lambda, \quad y \mapsto X_{\lambda^{-1}} \end{align*}$$
4.2 The normalisation of
 ${\mathrm {Spec}}(Z)$
${\mathrm {Spec}}(Z)$
4.2.1 Categorical quotients of schemes
Let ![]() be two morphisms of schemes. Recall that a morphism of schemes
be two morphisms of schemes. Recall that a morphism of schemes
![]() $\psi : X \to Y$
is said to be a categorical quotient of X by
$\psi : X \to Y$
is said to be a categorical quotient of X by
![]() $\mathcal {R}$
if it is a coequaliser of this diagram in the category of schemes.
$\mathcal {R}$
if it is a coequaliser of this diagram in the category of schemes.
Given a morphism of locally ringed spaces
![]() $f : X \to Y$
, we write
$f : X \to Y$
, we write
![]() $|f| : |X| \to |Y|$
for the underlying continuous map of topological spaces.
$|f| : |X| \to |Y|$
for the underlying continuous map of topological spaces.
Let ![]() be a diagram of schemes such that
be a diagram of schemes such that
![]() $\psi f = \psi g$
, and let
$\psi f = \psi g$
, and let
![]() $\{Y_i : i \in I\}$
be an open covering of Y. For each
$\{Y_i : i \in I\}$
be an open covering of Y. For each
![]() $i \in I$
, form the fibre products
$i \in I$
, form the fibre products
![]() $X_i := X \times _Y Y_i$
and
$X_i := X \times _Y Y_i$
and
![]() $\mathcal {R}_i := \mathcal {R} \times _Y Y_i$
, and consider the diagram
$\mathcal {R}_i := \mathcal {R} \times _Y Y_i$
, and consider the diagram ![]() , where
, where
![]() $f_i,g_i$
and
$f_i,g_i$
and
![]() $\psi _i$
are the pullbacks of
$\psi _i$
are the pullbacks of
![]() $f,g$
and
$f,g$
and
![]() $\psi $
, respectively.
$\psi $
, respectively.
We denote the category of schemes by
![]() ${\mathrm {Sch}}$
, and the category of locally commutatively ringed topological spaces by
${\mathrm {Sch}}$
, and the category of locally commutatively ringed topological spaces by
![]() ${\mathrm {LRS}}$
.
${\mathrm {LRS}}$
.
Lemma 4.2.1. Let ![]() be a diagram of schemes such that
be a diagram of schemes such that
![]() $\psi f = \psi g$
, and let
$\psi f = \psi g$
, and let
![]() $\{Y_i : i \in I\}$
be an open covering of Y. Suppose that
$\{Y_i : i \in I\}$
be an open covering of Y. Suppose that
-
a)
 is a coequaliser diagram of topological spaces,
is a coequaliser diagram of topological spaces, -
b)
 $Y_i$
,
$Y_i$
,
 $X_i$
and
$X_i$
and
 $\mathcal {R}_i$
is affine for all
$\mathcal {R}_i$
is affine for all
 $i \in I$
, and
$i \in I$
, and -
c)
 is an equaliser diagram of commutative rings for all
is an equaliser diagram of commutative rings for all
 $i \in I$
.
$i \in I$
.
Then ![]() is a coequaliser in
is a coequaliser in
![]() ${\mathrm {LRS}}$
.Footnote
3
, and
${\mathrm {LRS}}$
.Footnote
3
, and
![]() $\psi $
is a categorical quotient of
$\psi $
is a categorical quotient of ![]() .
.
Proof. By the construction of colimits in
![]() ${\mathrm {LRS}}$
([Reference Demazure and GabrielDG] Proposition I.1.1.6), the first statement is equivalent to the following conditions:
${\mathrm {LRS}}$
([Reference Demazure and GabrielDG] Proposition I.1.1.6), the first statement is equivalent to the following conditions:
-
–
 is a coequaliser diagram of topological spaces;
is a coequaliser diagram of topological spaces; -
–
 is an equaliser diagram of sheaves of commutative rings on Y.
is an equaliser diagram of sheaves of commutative rings on Y.
The second condition can be checked after restriction to the open subschemes
![]() $Y_i$
. By the second assumption, these and their preimages in X and
$Y_i$
. By the second assumption, these and their preimages in X and
![]() $\mathcal {R}$
all are affine. Hence, these restricted sheaves are determined by their global sections in these affine schemes. Therefore, this reduces to the third assumption.
$\mathcal {R}$
all are affine. Hence, these restricted sheaves are determined by their global sections in these affine schemes. Therefore, this reduces to the third assumption.
Since
![]() ${\mathrm {Sch}}$
is a full subcategory of
${\mathrm {Sch}}$
is a full subcategory of
![]() ${\mathrm {LRS}}$
, the second statement follows from the first.
${\mathrm {LRS}}$
, the second statement follows from the first.
We will now give an example of Lemma 4.2.1 in action, which will come in useful later. Consider the union of two crossing affine lines:
We will ‘separate’ the two crossing affine lines to form a disjoint union of two affine lines
and then reglue them together to form
![]() $\mathcal {X}$
as a quotient of
$\mathcal {X}$
as a quotient of
![]() $\mathcal {X}'$
by a certain relation.
$\mathcal {X}'$
by a certain relation.
To be more precise, note that
![]() $\mathcal {X}'$
is the disjoint union of
$\mathcal {X}'$
is the disjoint union of
![]() ${\mathrm {Spec}} k[x]$
and
${\mathrm {Spec}} k[x]$
and
![]() ${\mathrm {Spec}} k[y]$
. Let
${\mathrm {Spec}} k[y]$
. Let
![]() $\mathcal {S} := {\mathrm {Spec}} k = \{s\}$
be a point, let
$\mathcal {S} := {\mathrm {Spec}} k = \{s\}$
be a point, let
![]() $a : \mathcal {S} \to \mathcal {X}'$
be the inclusion of the origin into the first affine line and let
$a : \mathcal {S} \to \mathcal {X}'$
be the inclusion of the origin into the first affine line and let
![]() $b : \mathcal {S} \to \mathcal {X}'$
be the inclusion of the origin into the second affine line.
$b : \mathcal {S} \to \mathcal {X}'$
be the inclusion of the origin into the second affine line.
Consider the k-algebra homomorphism
and let
![]() $\theta := {\mathrm {Spec}}(\varphi ) : \mathcal {X}' \to \mathcal {X}$
be the corresponding morphism of affine schemes.
$\theta := {\mathrm {Spec}}(\varphi ) : \mathcal {X}' \to \mathcal {X}$
be the corresponding morphism of affine schemes.
Proposition 4.2.2.
![]() $\theta : \mathcal {X}' \to \mathcal {X}$
is a categorical quotient of
$\theta : \mathcal {X}' \to \mathcal {X}$
is a categorical quotient of ![]() .
.
Proof. We will apply Lemma 4.2.1. The comorphism
![]() $a^\sharp : \mathcal {O}(\mathcal {X}') \to \mathcal {O}(\mathcal {S})$
(respectively,
$a^\sharp : \mathcal {O}(\mathcal {X}') \to \mathcal {O}(\mathcal {S})$
(respectively,
![]() $b^\sharp :\mathcal {O}(\mathcal {X}') \to \mathcal {O}(\mathcal {S})$
) is equal to the composition of the first projection from
$b^\sharp :\mathcal {O}(\mathcal {X}') \to \mathcal {O}(\mathcal {S})$
) is equal to the composition of the first projection from
![]() $k[x] \times k[y]$
onto
$k[x] \times k[y]$
onto
![]() $k[x]$
(respectively, the second projection
$k[x]$
(respectively, the second projection
![]() $k[x] \times k[y]$
onto
$k[x] \times k[y]$
onto
![]() $k[y]$
) with the evaluation-at-zero map
$k[y]$
) with the evaluation-at-zero map
![]() $k[x] \to k$
,
$k[x] \to k$
,
![]() $f(x) \mapsto f(0)$
(respectively,
$f(x) \mapsto f(0)$
(respectively,
![]() $k[y] \to k$
,
$k[y] \to k$
,
![]() $f(y) \mapsto f(0)$
). The k-algebra homomorphisms
$f(y) \mapsto f(0)$
). The k-algebra homomorphisms
![]() $a^\sharp \varphi $
and
$a^\sharp \varphi $
and
![]() $b^\sharp \varphi $
both kill
$b^\sharp \varphi $
both kill
![]() $\overline {x}$
and
$\overline {x}$
and
![]() $\overline {y}$
; since these two elements generate
$\overline {y}$
; since these two elements generate
![]() $\mathcal {O}(\mathcal {X})$
as a k-algebra, we see that
$\mathcal {O}(\mathcal {X})$
as a k-algebra, we see that
![]() $a^\sharp \varphi = b^\sharp \varphi $
. This gives us a complex of
$a^\sharp \varphi = b^\sharp \varphi $
. This gives us a complex of
![]() $\mathcal {O}(\mathcal {X})$
-modules
$\mathcal {O}(\mathcal {X})$
-modules
Since
![]() $\langle x \rangle \cap \langle y \rangle = \langle xy \rangle $
in
$\langle x \rangle \cap \langle y \rangle = \langle xy \rangle $
in
![]() $k[x,y]$
, the k-algebra homomorphism
$k[x,y]$
, the k-algebra homomorphism
![]() $\varphi $
is injective. If
$\varphi $
is injective. If
![]() $u = (f(x), g(y)) \in k[x] \times k[y]$
is such that
$u = (f(x), g(y)) \in k[x] \times k[y]$
is such that
![]() $a^\sharp (u) = b^\sharp (u)$
, then
$a^\sharp (u) = b^\sharp (u)$
, then
![]() $f(0) = g(0)$
and then
$f(0) = g(0)$
and then
shows that
![]() $\ker (a^\sharp - b^\sharp ) = \mathrm {Im}(\varphi )$
. So the complex (12) is in fact exact, and this verifies condition c) of Lemma 4.2.1.
$\ker (a^\sharp - b^\sharp ) = \mathrm {Im}(\varphi )$
. So the complex (12) is in fact exact, and this verifies condition c) of Lemma 4.2.1.
We have already observed that
![]() $\overline {x},\overline {y} \in \mathcal {O}(\mathcal {X})$
both kill
$\overline {x},\overline {y} \in \mathcal {O}(\mathcal {X})$
both kill
![]() $\mathcal {O}(\mathcal {S}) = k$
when we consider
$\mathcal {O}(\mathcal {S}) = k$
when we consider
![]() $\mathcal {O}(\mathcal {S})$
as an
$\mathcal {O}(\mathcal {S})$
as an
![]() $\mathcal {O}(\mathcal {X})$
-module via
$\mathcal {O}(\mathcal {X})$
-module via
![]() $a^\sharp \varphi = b^\sharp \varphi $
. So it is also killed by
$a^\sharp \varphi = b^\sharp \varphi $
. So it is also killed by
![]() $\overline {x} + \overline {y}$
. Therefore, if we localise the exact sequence (12) at the element
$\overline {x} + \overline {y}$
. Therefore, if we localise the exact sequence (12) at the element
![]() $\overline {x} + \overline {y}\in \mathcal {O}(\mathcal {X})$
, then we obtain the isomorphism
$\overline {x} + \overline {y}\in \mathcal {O}(\mathcal {X})$
, then we obtain the isomorphism
 $$\begin{align*}\left(\frac{k[x,y]}{\langle xy \rangle}\right)\left[ \frac{1}{\overline{x} + \overline{y}} \right] \quad \stackrel{\cong}{\longrightarrow} \quad k[x, x^{-1}] \times k[y, y^{-1}].\end{align*}$$
$$\begin{align*}\left(\frac{k[x,y]}{\langle xy \rangle}\right)\left[ \frac{1}{\overline{x} + \overline{y}} \right] \quad \stackrel{\cong}{\longrightarrow} \quad k[x, x^{-1}] \times k[y, y^{-1}].\end{align*}$$
Let
![]() $O := \langle \overline {x}, \overline {y} \rangle \in \mathcal {X}$
be the intersection point of the two crossing affine lines. Then the restriction of
$O := \langle \overline {x}, \overline {y} \rangle \in \mathcal {X}$
be the intersection point of the two crossing affine lines. Then the restriction of
![]() $\theta = {\mathrm {Spec}}(\varphi )$
to
$\theta = {\mathrm {Spec}}(\varphi )$
to
![]() $\mathcal {X}' - \{a(s),b(s)\} = {\mathrm {Spec}} \left (k[x, x^{-1}] \times k[y, y^{-1}]\right )$
is an isomorphism onto
$\mathcal {X}' - \{a(s),b(s)\} = {\mathrm {Spec}} \left (k[x, x^{-1}] \times k[y, y^{-1}]\right )$
is an isomorphism onto
![]() $\mathcal {X} \backslash \{O\}$
. Since
$\mathcal {X} \backslash \{O\}$
. Since
![]() $\theta $
maps both origins in
$\theta $
maps both origins in
![]() $\mathcal {X}'$
to
$\mathcal {X}'$
to
![]() $O \in \mathcal {X}$
, we see that
$O \in \mathcal {X}$
, we see that
![]() $|\theta |$
is surjective and that if
$|\theta |$
is surjective and that if
![]() $p,q \in |\mathcal {X}'|$
satisfy
$p,q \in |\mathcal {X}'|$
satisfy
![]() $|\theta |(p) = |\theta |(q)$
but
$|\theta |(p) = |\theta |(q)$
but
![]() $p\neq q$
, then necessarily
$p\neq q$
, then necessarily
![]() $p,q \in \{a(s), b(s)\}$
. Thus,
$p,q \in \{a(s), b(s)\}$
. Thus,
![]() $|\mathcal {X}|$
is obtained as a set by identifying
$|\mathcal {X}|$
is obtained as a set by identifying
![]() $a(s)$
with
$a(s)$
with
![]() $b(s)$
in
$b(s)$
in
![]() $|\mathcal {X}'|$
.
$|\mathcal {X}'|$
.
Finally, both
![]() $|\mathcal {X}'|$
and
$|\mathcal {X}'|$
and
![]() $|\mathcal {X}|$
carry the cofinite Zariski topologies, and the quotient topology on
$|\mathcal {X}|$
carry the cofinite Zariski topologies, and the quotient topology on
![]() $|\mathcal {X}'| / (a(s) \sim b(s))$
is still the cofinite topology. Hence,
$|\mathcal {X}'| / (a(s) \sim b(s))$
is still the cofinite topology. Hence,  is a coequaliser diagram of topological spaces, as required for condition a) of Lemma 4.2.1.
is a coequaliser diagram of topological spaces, as required for condition a) of Lemma 4.2.1.
4.2.2 The normalisation of
 ${\mathrm {Spec}}(Z)$
${\mathrm {Spec}}(Z)$
We return to the notation of
![]() $\S$
4.1.4.
$\S$
4.1.4.
Definition 4.2.3.
-
a) Let
 $\Xi = {\mathrm {Spec}} (Z)$
.
$\Xi = {\mathrm {Spec}} (Z)$
. -
b) Let
 $Z' := k[\Omega ][t]$
, where t is a formal variable, and let
$Z' := k[\Omega ][t]$
, where t is a formal variable, and let
 $\Xi ' := {\mathrm {Spec}} Z'$
.
$\Xi ' := {\mathrm {Spec}} Z'$
. -
c) Let
 $\varphi : Z \to Z'$
be the k-algebra homomorphism defined by
$\varphi : Z \to Z'$
be the k-algebra homomorphism defined by  $$\begin{align*}\varphi(X_\lambda) = e_\lambda t \quad\text{for all}\quad \lambda \in \widehat{\Omega}.\end{align*}$$
$$\begin{align*}\varphi(X_\lambda) = e_\lambda t \quad\text{for all}\quad \lambda \in \widehat{\Omega}.\end{align*}$$
-
d) Let
 $\theta : \Xi ' \to \Xi $
be defined by
$\theta : \Xi ' \to \Xi $
be defined by
 $\theta = {\mathrm {Spec}}(\varphi )$
.
$\theta = {\mathrm {Spec}}(\varphi )$
.
Note that
![]() $\Xi '$
is the disjoint union of
$\Xi '$
is the disjoint union of
![]() $|\widehat {\Omega }| = q-1$
affine lines
$|\widehat {\Omega }| = q-1$
affine lines
![]() $\Xi ^{\prime }_\lambda := {\mathrm {Spec}} k[t_\lambda ]$
, where
$\Xi ^{\prime }_\lambda := {\mathrm {Spec}} k[t_\lambda ]$
, where
![]() $t_\lambda := e_\lambda t \in Z'$
. We call
$t_\lambda := e_\lambda t \in Z'$
. We call
![]() $\Xi ^{\prime }_\lambda $
the
$\Xi ^{\prime }_\lambda $
the
![]() $\lambda $
-component of
$\lambda $
-component of
![]() $\Xi '$
. We denote the image of the origin
$\Xi '$
. We denote the image of the origin
![]() $\langle t_\lambda \rangle \in \Xi ^{\prime }_\lambda $
inside
$\langle t_\lambda \rangle \in \Xi ^{\prime }_\lambda $
inside
![]() $\Xi '$
by
$\Xi '$
by
![]() $O_\lambda $
. Equivalently,
$O_\lambda $
. Equivalently,
![]() $O_\lambda $
is the maximal ideal
$O_\lambda $
is the maximal ideal
![]() $\langle 1 - e_{\lambda }, t \rangle $
of
$\langle 1 - e_{\lambda }, t \rangle $
of
![]() $Z'$
.
$Z'$
.
Definition 4.2.4.
-
a) Let
 $\Xi _{{\mathrm {sing}}} := \{s_1,s_2,\cdots , s_{\frac {q-3}{2}}\}$
be the disjoint union of
$\Xi _{{\mathrm {sing}}} := \{s_1,s_2,\cdots , s_{\frac {q-3}{2}}\}$
be the disjoint union of
 $\frac {q-3}{2}$
copies of
$\frac {q-3}{2}$
copies of
 ${\mathrm {Spec}} k$
.
${\mathrm {Spec}} k$
. -
b) Define
 $a : \Xi _{{\mathrm {sing}}} \to \Xi '$
and
$a : \Xi _{{\mathrm {sing}}} \to \Xi '$
and
 $b : \Xi _{{\mathrm {sing}}} \to \Xi '$
to be the closed embeddings, given by
$b : \Xi _{{\mathrm {sing}}} \to \Xi '$
to be the closed embeddings, given by  $$\begin{align*}a(s_j) = O_{{\mathrm{id}}^j} \quad\text{and}\quad b(s_j) = O_{{\mathrm{id}}^{-j}} \quad\text{for all}\quad j = 1,\cdots, \frac{q-3}{2}.\end{align*}$$
$$\begin{align*}a(s_j) = O_{{\mathrm{id}}^j} \quad\text{and}\quad b(s_j) = O_{{\mathrm{id}}^{-j}} \quad\text{for all}\quad j = 1,\cdots, \frac{q-3}{2}.\end{align*}$$
The notation is intended to indicate that
![]() $\Xi _{{\mathrm {sing}}}$
is a copy of the singular locus of the scheme
$\Xi _{{\mathrm {sing}}}$
is a copy of the singular locus of the scheme
![]() $\Xi $
: indeed, in view of the decomposition (11) and Proposition 4.1.5.b,
$\Xi $
: indeed, in view of the decomposition (11) and Proposition 4.1.5.b,
![]() $\Xi $
contains
$\Xi $
contains
![]() $\frac {q-3}{2}$
copies of the pair of crossing lines
$\frac {q-3}{2}$
copies of the pair of crossing lines
![]() ${\mathrm {Spec}} \frac {k[x,y]}{\langle xy \rangle }$
, so the singular locus of
${\mathrm {Spec}} \frac {k[x,y]}{\langle xy \rangle }$
, so the singular locus of
![]() $\Xi $
consists of
$\Xi $
consists of
![]() $\frac {q-3}{2}$
closed points.
$\frac {q-3}{2}$
closed points.
Proposition 4.2.5.
![]() $\theta : \Xi ' \to \Xi $
is a categorical quotient of
$\theta : \Xi ' \to \Xi $
is a categorical quotient of ![]() .
.
Proof. The decomposition of
![]() $Z = \mathcal {O}(\Xi )$
as a direct product of nonunital subrings given in Equation (11) means that
$Z = \mathcal {O}(\Xi )$
as a direct product of nonunital subrings given in Equation (11) means that
![]() $\Xi $
decomposes into the disjoint union of connected components
$\Xi $
decomposes into the disjoint union of connected components
 $$ \begin{align} \Xi = \Xi_0 \quad \cup \quad \Xi_{\frac{q-1}{2}} \quad \cup \quad \coprod\limits_{j=1}^{\frac{q-3}{2}} \Xi_{j,-j},\end{align} $$
$$ \begin{align} \Xi = \Xi_0 \quad \cup \quad \Xi_{\frac{q-1}{2}} \quad \cup \quad \coprod\limits_{j=1}^{\frac{q-3}{2}} \Xi_{j,-j},\end{align} $$
where these connected components are defined by
for all
![]() $j = 1,\cdots , \frac {q-3}{2}$
. On the other hand, we can write
$j = 1,\cdots , \frac {q-3}{2}$
. On the other hand, we can write

Fix
![]() $j = 1,\cdots , \frac {q-3}{2}$
. The morphism
$j = 1,\cdots , \frac {q-3}{2}$
. The morphism
![]() $\theta $
maps
$\theta $
maps
![]() $(\Xi ^{\prime }_{{\mathrm {id}}^j} \cup \Xi ^{\prime }_{{\mathrm {id}}^{-j}})$
onto
$(\Xi ^{\prime }_{{\mathrm {id}}^j} \cup \Xi ^{\prime }_{{\mathrm {id}}^{-j}})$
onto
![]() $\Xi _{j,-j}$
; let
$\Xi _{j,-j}$
; let
![]() $\theta _j$
denote the restriction of
$\theta _j$
denote the restriction of
![]() $\theta $
to
$\theta $
to
![]() $(\Xi ^{\prime }_{{\mathrm {id}}^j} \cup \Xi ^{\prime }_{{\mathrm {id}}^{-j}})$
. Then we have the commutative diagram of affine schemes
$(\Xi ^{\prime }_{{\mathrm {id}}^j} \cup \Xi ^{\prime }_{{\mathrm {id}}^{-j}})$
. Then we have the commutative diagram of affine schemes

where
![]() $\theta _0 : \mathcal {X}' \to \mathcal {X}$
is the morphism that was denoted
$\theta _0 : \mathcal {X}' \to \mathcal {X}$
is the morphism that was denoted
![]() $\theta $
in Proposition 4.2.2,
$\theta $
in Proposition 4.2.2,
![]() $\beta _j := {\mathrm {Spec}}(b_{{\mathrm {id}}^j})$
is the isomorphism of affine schemes defined by the isomorphism
$\beta _j := {\mathrm {Spec}}(b_{{\mathrm {id}}^j})$
is the isomorphism of affine schemes defined by the isomorphism
![]() $b_{{\mathrm {id}}^j}$
from Proposition 4.1.5.b, and
$b_{{\mathrm {id}}^j}$
from Proposition 4.1.5.b, and
![]() $\alpha _j$
is the isomorphism of affine schemes defined by the k-algebra isomorphism
$\alpha _j$
is the isomorphism of affine schemes defined by the k-algebra isomorphism
given by
![]() $\alpha _j^\sharp (x)= t_{{\mathrm {id}}^j}$
and
$\alpha _j^\sharp (x)= t_{{\mathrm {id}}^j}$
and
![]() $\alpha _j^\sharp (y)= t_{{\mathrm {id}}^{-j}}$
. This gives us the commutative diagram of schemes
$\alpha _j^\sharp (y)= t_{{\mathrm {id}}^{-j}}$
. This gives us the commutative diagram of schemes

where
![]() $a_0$
and
$a_0$
and
![]() $b_0$
are the morphisms that were denoted a and b in the statement of Proposition 4.2.2. Now, we can apply Proposition 4.2.2 to see that
$b_0$
are the morphisms that were denoted a and b in the statement of Proposition 4.2.2. Now, we can apply Proposition 4.2.2 to see that
![]() $\theta _j$
is a coequaliser of
$\theta _j$
is a coequaliser of
![]() $a_j, b_j$
.
$a_j, b_j$
.
Note that the morphism
![]() $\theta $
sends
$\theta $
sends ![]() (respectively,
(respectively,
![]() $\Xi ^{\prime }_{{\mathrm {id}}^{\frac {q-1}{2}}}$
) isomorphically onto
$\Xi ^{\prime }_{{\mathrm {id}}^{\frac {q-1}{2}}}$
) isomorphically onto
![]() $\Xi _0$
(respectively,
$\Xi _0$
(respectively,
![]() $\Xi ^{\prime }_{\frac {q-1}{2}}$
). Taking coproducts of the diagrams (16) over
$\Xi ^{\prime }_{\frac {q-1}{2}}$
). Taking coproducts of the diagrams (16) over
![]() $j = 1,\cdots , \frac {q-3}{2}$
and bearing in mind the decompositions (13) and (14) now gives the result in view of Lemma A.3.
$j = 1,\cdots , \frac {q-3}{2}$
and bearing in mind the decompositions (13) and (14) now gives the result in view of Lemma A.3.
4.2.3 The nonsingular locus of
 $\Xi $
$\Xi $
Let
![]() $V(t)$
denote the set of
$V(t)$
denote the set of
![]() $q-1$
closed points in
$q-1$
closed points in
![]() $\Xi '$
consisting of the disjoint union of the origins in the
$\Xi '$
consisting of the disjoint union of the origins in the
![]() $q-1$
affine lines
$q-1$
affine lines
![]() $\Xi ^{\prime }_\lambda = {\mathrm {Spec}} k[t_\lambda ]$
.
$\Xi ^{\prime }_\lambda = {\mathrm {Spec}} k[t_\lambda ]$
.
Lemma 4.2.6. The morphism
![]() $\theta $
restricts to an isomorphism
$\theta $
restricts to an isomorphism
Proof. Let
![]() $\lambda \in \widehat {\Omega }$
, and write
$\lambda \in \widehat {\Omega }$
, and write
![]() $\lambda = {\mathrm {id}}^j$
for some
$\lambda = {\mathrm {id}}^j$
for some
![]() $j = 0,\cdots , q-2$
. Suppose first that
$j = 0,\cdots , q-2$
. Suppose first that
![]() $j \neq 0$
and
$j \neq 0$
and
![]() $j \neq \frac {q-1}{2}$
. Then the image of
$j \neq \frac {q-1}{2}$
. Then the image of
![]() $\zeta $
in
$\zeta $
in
![]() $\mathcal {O}(\Xi _{\lambda ,\lambda ^{-1}})$
under the restriction map
$\mathcal {O}(\Xi _{\lambda ,\lambda ^{-1}})$
under the restriction map
![]() $Z = \mathcal {O}(\Xi ) \to \mathcal {O}(\Xi _{j,-j})$
is
$Z = \mathcal {O}(\Xi ) \to \mathcal {O}(\Xi _{j,-j})$
is
![]() $(e_\lambda + e_{\lambda ^{-1}}) \zeta $
, which is equal to
$(e_\lambda + e_{\lambda ^{-1}}) \zeta $
, which is equal to
![]() $X_\lambda + X_{\lambda ^{-1}}$
by Lemma 4.1.4.b. We see that
$X_\lambda + X_{\lambda ^{-1}}$
by Lemma 4.1.4.b. We see that
![]() $\beta _j(V(\zeta ) \cap \Xi _{j,-j})$
is the origin O in the pair of crossing lines
$\beta _j(V(\zeta ) \cap \Xi _{j,-j})$
is the origin O in the pair of crossing lines
![]() $\mathcal {X}$
. Likewise, if
$\mathcal {X}$
. Likewise, if
![]() $j = 0$
or
$j = 0$
or
![]() $j = \frac {q-1}{2}$
, Lemma 4.1.4.c implies that
$j = \frac {q-1}{2}$
, Lemma 4.1.4.c implies that
![]() $V(\zeta ) \cap \Xi _{\frac {q-1}{2}} = V( e_\lambda \zeta ) $
is the origin in the affine line
$V(\zeta ) \cap \Xi _{\frac {q-1}{2}} = V( e_\lambda \zeta ) $
is the origin in the affine line
![]() $\Xi _j$
. So
$\Xi _j$
. So
![]() $V(\zeta ) \subset \Xi $
consists of precisely
$V(\zeta ) \subset \Xi $
consists of precisely
![]() $\frac {q-3}{2} + 2 = \frac {q+1}{2}$
closed points and contains the singular locus of
$\frac {q-3}{2} + 2 = \frac {q+1}{2}$
closed points and contains the singular locus of
![]() $\Xi $
, whereas
$\Xi $
, whereas
![]() $V(t)$
consists of
$V(t)$
consists of
![]() $|{\mathrm {Spec}} k[\Omega ]| = |\widehat {\Omega }| = q-1$
closed points in
$|{\mathrm {Spec}} k[\Omega ]| = |\widehat {\Omega }| = q-1$
closed points in
![]() $\Xi '$
.
$\Xi '$
.
The result now follows from the commutative diagram (15), together with the observation we made in the proof of Proposition 4.2.2 that
![]() $\theta _0$
restricts to an isomorphism between
$\theta _0$
restricts to an isomorphism between
![]() $\mathcal {X}' \backslash \{a_0(s),b_0(s)\}$
and
$\mathcal {X}' \backslash \{a_0(s),b_0(s)\}$
and
![]() $\mathcal {X} \backslash \{O\}$
.
$\mathcal {X} \backslash \{O\}$
.
Corollary 4.2.7. The map
![]() $\mathring {\theta }^\sharp : Z_\zeta = \mathcal {O}(\Xi - V(\zeta )) \quad \stackrel {\cong }{\longrightarrow } \quad \mathcal {O}(\Xi ' - V(t)) = k[\Omega ][t,t^{-1}]$
is a k-algebra isomorphism which sends
$\mathring {\theta }^\sharp : Z_\zeta = \mathcal {O}(\Xi - V(\zeta )) \quad \stackrel {\cong }{\longrightarrow } \quad \mathcal {O}(\Xi ' - V(t)) = k[\Omega ][t,t^{-1}]$
is a k-algebra isomorphism which sends
![]() $\zeta $
to t.
$\zeta $
to t.
Of course,
![]() $\mathring {\theta }^\sharp $
restricts to the basic map
$\mathring {\theta }^\sharp $
restricts to the basic map
![]() $\varphi : Z \to Z'$
on Z from Definition 4.2.3.c.
$\varphi : Z \to Z'$
on Z from Definition 4.2.3.c.
Definition 4.2.8. For each
![]() $\lambda \in \widehat {\Omega }$
, we define
$\lambda \in \widehat {\Omega }$
, we define
![]() $\epsilon _\lambda := (\mathring {\theta }^\sharp )^{-1}(e_\lambda )$
.
$\epsilon _\lambda := (\mathring {\theta }^\sharp )^{-1}(e_\lambda )$
.
The family
![]() $\{\epsilon _\lambda : \lambda \in \widehat {\Omega }\}$
form a complete set of primitive idempotents in
$\{\epsilon _\lambda : \lambda \in \widehat {\Omega }\}$
form a complete set of primitive idempotents in
![]() $Z_\zeta $
.
$Z_\zeta $
.
Lemma 4.2.9. We have
![]() $\epsilon _\lambda = \frac {X_\lambda }{\zeta }$
for all
$\epsilon _\lambda = \frac {X_\lambda }{\zeta }$
for all
![]() $\lambda \in \widehat {\Omega }$
.
$\lambda \in \widehat {\Omega }$
.
Proof. Since
![]() $\zeta $
is a unit in
$\zeta $
is a unit in
![]() $Z_\zeta $
, it’s enough to show
$Z_\zeta $
, it’s enough to show
![]() $\epsilon _\lambda \zeta ^2 = X_\lambda \zeta $
. Since
$\epsilon _\lambda \zeta ^2 = X_\lambda \zeta $
. Since
![]() $\mathring {\theta }^\sharp $
is a ring isomorphism that restricts to
$\mathring {\theta }^\sharp $
is a ring isomorphism that restricts to
![]() $\varphi $
on Z, it is enough to show that the equation
$\varphi $
on Z, it is enough to show that the equation
![]() $e_\lambda \varphi (\zeta )^2 = \varphi (X_\lambda \zeta )$
holds in
$e_\lambda \varphi (\zeta )^2 = \varphi (X_\lambda \zeta )$
holds in
![]() $k[\Omega ][t,t^{-1}]$
. However, using Lemma 4.1.4.d together with Definition 4.2.3.c, we have
$k[\Omega ][t,t^{-1}]$
. However, using Lemma 4.1.4.d together with Definition 4.2.3.c, we have
 $$ \begin{align} \varphi(\zeta) = \varphi\left(\sum\limits_{\alpha \in \widehat{\Omega}} X_\alpha \right) = \left( \sum\limits_{\alpha \in \widehat{\Omega}} e_\alpha t\right) = t\end{align} $$
$$ \begin{align} \varphi(\zeta) = \varphi\left(\sum\limits_{\alpha \in \widehat{\Omega}} X_\alpha \right) = \left( \sum\limits_{\alpha \in \widehat{\Omega}} e_\alpha t\right) = t\end{align} $$
and therefore
![]() $e_\lambda \varphi (\zeta )^2 = e_\lambda t^2 = (e_\lambda t) t = \varphi (X_\lambda ) \varphi (\zeta ) = \varphi (X_\lambda \zeta )$
as required.
$e_\lambda \varphi (\zeta )^2 = e_\lambda t^2 = (e_\lambda t) t = \varphi (X_\lambda ) \varphi (\zeta ) = \varphi (X_\lambda \zeta )$
as required.
Corollary 4.2.10. As a
![]() $k[\zeta ,\zeta ^{-1}]$
-module,
$k[\zeta ,\zeta ^{-1}]$
-module,
![]() $Z_\zeta $
decomposes as follows:
$Z_\zeta $
decomposes as follows:
 $$\begin{align*}Z_\zeta = \bigoplus\limits_{\lambda \in \widehat{\Omega}} \epsilon_\lambda k[\zeta, \zeta^{-1}].\end{align*}$$
$$\begin{align*}Z_\zeta = \bigoplus\limits_{\lambda \in \widehat{\Omega}} \epsilon_\lambda k[\zeta, \zeta^{-1}].\end{align*}$$
Proof. The isomorphism
![]() $\mathring {\theta }^\sharp : Z_\zeta \stackrel {\cong }{\longrightarrow } k[\Omega ][t, t^{-1}]$
given by Lemma 4.2.6 sends
$\mathring {\theta }^\sharp : Z_\zeta \stackrel {\cong }{\longrightarrow } k[\Omega ][t, t^{-1}]$
given by Lemma 4.2.6 sends
![]() $\zeta $
to t by Equation (17), and it sends
$\zeta $
to t by Equation (17), and it sends
![]() $\epsilon _\lambda \in Z_\zeta $
to
$\epsilon _\lambda \in Z_\zeta $
to
![]() $e_\lambda \in k[\Omega ][t,t^{-1}]$
for each
$e_\lambda \in k[\Omega ][t,t^{-1}]$
for each
![]() $\lambda \in \widehat {\Omega }$
. Since
$\lambda \in \widehat {\Omega }$
. Since
![]() $\{e_\lambda : \lambda \in \widehat {\Omega }\}$
forms a
$\{e_\lambda : \lambda \in \widehat {\Omega }\}$
forms a
![]() $k[t,t^{-1}]$
-module basis for
$k[t,t^{-1}]$
-module basis for
![]() $k[\Omega ][t,t^{-1}]$
, it follows that
$k[\Omega ][t,t^{-1}]$
, it follows that
![]() $\{\epsilon _\lambda : \lambda \in \widehat {\Omega }\}$
forms a
$\{\epsilon _\lambda : \lambda \in \widehat {\Omega }\}$
forms a
![]() $k[\zeta ,\zeta ^{-1}]$
-module basis for
$k[\zeta ,\zeta ^{-1}]$
-module basis for
![]() $Z_\zeta $
.
$Z_\zeta $
.
4.3 Bimodule annihilators
4.3.1 Some generalities about annihilators and bimodules
Definition 4.3.1. Let A be a k-algebra, and let
![]() $\phi : A \to A$
be a k-algebra automorphism. Let M be an A-bimodule. We write
$\phi : A \to A$
be a k-algebra automorphism. Let M be an A-bimodule. We write
![]() $M_\phi $
to denote the
$M_\phi $
to denote the
![]() $(A,A)$
-bimodule M, with action given by
$(A,A)$
-bimodule M, with action given by
and we call
![]() $M_\phi $
the right
$M_\phi $
the right
![]() $\phi $
-twist of M.
$\phi $
-twist of M.
Thus, the left A-action on
![]() $M_\phi $
is the usual one, whereas the right A-action is twisted by
$M_\phi $
is the usual one, whereas the right A-action is twisted by
![]() $\phi $
.
$\phi $
.
Lemma 4.3.2. Let A be a k-algebra, let M be an
![]() $(A,A)$
-bimodule and let
$(A,A)$
-bimodule and let
![]() $\phi : A \to A$
be a k-algebra automorphism. Then
$\phi : A \to A$
be a k-algebra automorphism. Then
Proof. Let
![]() $x = \sum _{i=1}^n a_i \otimes b_i \in A \otimes _k A$
. Then
$x = \sum _{i=1}^n a_i \otimes b_i \in A \otimes _k A$
. Then
![]() $x \cdot M_\phi = 0$
if and only if
$x \cdot M_\phi = 0$
if and only if
![]() $\sum _{i=1}^n a_i m \phi (b_i) = 0$
for all
$\sum _{i=1}^n a_i m \phi (b_i) = 0$
for all
![]() $m \in M$
. This is equivalent to
$m \in M$
. This is equivalent to
![]() $(1 \otimes \phi )(x) \cdot M = 0$
, and the result follows.
$(1 \otimes \phi )(x) \cdot M = 0$
, and the result follows.
Lemma 4.3.3. Let A be a k-algebra with centre Z, and let
![]() ${\mathrm {mult}}_Z : Z \otimes _k Z \to Z$
be the multiplication map. Then
${\mathrm {mult}}_Z : Z \otimes _k Z \to Z$
be the multiplication map. Then
Proof. For an element
![]() $x = \sum _{i=1}^n a_i\otimes b_i \in Z \otimes _k Z$
, we have
$x = \sum _{i=1}^n a_i\otimes b_i \in Z \otimes _k Z$
, we have
![]() $x \cdot 1 = \sum \limits _{i=1}^n a_ib_i = {\mathrm {mult}}_Z(x)$
. This shows the last equality. Since
$x \cdot 1 = \sum \limits _{i=1}^n a_ib_i = {\mathrm {mult}}_Z(x)$
. This shows the last equality. Since
![]() $A \supseteq Z \ni 1$
, we have
$A \supseteq Z \ni 1$
, we have
![]() ${\mathrm {Ann}}_{Z \otimes _k Z}(A) \subseteq {\mathrm {Ann}}_{Z \otimes _k Z}(Z) \subseteq {\mathrm {Ann}}_{Z \otimes _k Z}(1) = \ker {\mathrm {mult}}_Z$
by the above. Let
${\mathrm {Ann}}_{Z \otimes _k Z}(A) \subseteq {\mathrm {Ann}}_{Z \otimes _k Z}(Z) \subseteq {\mathrm {Ann}}_{Z \otimes _k Z}(1) = \ker {\mathrm {mult}}_Z$
by the above. Let
![]() $x = \sum _{i=1}^n a_i \otimes b_i \in \ker {\mathrm {mult}}_Z$
, and let
$x = \sum _{i=1}^n a_i \otimes b_i \in \ker {\mathrm {mult}}_Z$
, and let
![]() $c \in A$
. Then because
$c \in A$
. Then because
![]() $a_i, b_i$
are central in A, we have
$a_i, b_i$
are central in A, we have
![]() $x \cdot c = \sum _{i=1}^n a_i c b_i = \left (\sum _{i=1}^n a_i b_i\right ) c = {\mathrm {mult}}_Z(x)c = 0$
. Hence,
$x \cdot c = \sum _{i=1}^n a_i c b_i = \left (\sum _{i=1}^n a_i b_i\right ) c = {\mathrm {mult}}_Z(x)c = 0$
. Hence,
![]() $\ker {\mathrm {mult}}_Z \subseteq {\mathrm {Ann}}_{Z \otimes _kZ}(A)$
.
$\ker {\mathrm {mult}}_Z \subseteq {\mathrm {Ann}}_{Z \otimes _kZ}(A)$
.
Lemma 4.3.4. Let A be a commutative k-algebra, and let
![]() ${\mathrm {mult}}_A : A \otimes _k A \to A$
be the multiplication map.
${\mathrm {mult}}_A : A \otimes _k A \to A$
be the multiplication map.
-
a)
 $\ker {\mathrm {mult}}_A$
is generated as an ideal in
$\ker {\mathrm {mult}}_A$
is generated as an ideal in
 $A \otimes _k A$
by
$A \otimes _k A$
by
 $\{ a \otimes 1 - 1 \otimes a : a \in A\}$
.
$\{ a \otimes 1 - 1 \otimes a : a \in A\}$
. -
b) Suppose that
 $a_1,\cdots , a_m$
generate A as a k-algebra. Then
$a_1,\cdots , a_m$
generate A as a k-algebra. Then
 $\{a_i \otimes 1 - 1 \otimes a_i : i=1,\cdots , m\}$
generates
$\{a_i \otimes 1 - 1 \otimes a_i : i=1,\cdots , m\}$
generates
 $\ker {\mathrm {mult}}_A$
as an ideal in
$\ker {\mathrm {mult}}_A$
as an ideal in
 $A \otimes _kA$
.
$A \otimes _kA$
.
Proof. a) Certainly,
![]() ${\mathrm {mult}}_A$
kills
${\mathrm {mult}}_A$
kills
![]() $a \otimes 1 - 1 \otimes a$
for all
$a \otimes 1 - 1 \otimes a$
for all
![]() $a \in A$
. Conversely, if
$a \in A$
. Conversely, if
![]() $x = \sum _{i=1}^n a_i \otimes b_i \in A \otimes A$
is such that
$x = \sum _{i=1}^n a_i \otimes b_i \in A \otimes A$
is such that
![]() ${\mathrm {mult}}_A(x) = \sum _{i=1}^n a_i b_i = 0$
, then
${\mathrm {mult}}_A(x) = \sum _{i=1}^n a_i b_i = 0$
, then
 $$\begin{align*}x = \sum_{i=1}^n (a_i \otimes b_i - 1 \otimes a_i b_i) = \sum_{i=1}^n (a_i \otimes 1 - 1 \otimes a_i) (1 \otimes b_i)\end{align*}$$
$$\begin{align*}x = \sum_{i=1}^n (a_i \otimes b_i - 1 \otimes a_i b_i) = \sum_{i=1}^n (a_i \otimes 1 - 1 \otimes a_i) (1 \otimes b_i)\end{align*}$$
lies in the ideal in
![]() $A \otimes A$
generated by
$A \otimes A$
generated by
![]() $\{ a \otimes 1 - 1 \otimes a : a \in A\}$
.
$\{ a \otimes 1 - 1 \otimes a : a \in A\}$
.
b) Write
![]() $\partial (a) = a \otimes 1 - 1 \otimes a$
for
$\partial (a) = a \otimes 1 - 1 \otimes a$
for
![]() $a \in A$
. Then for all
$a \in A$
. Then for all
![]() $a,b \in A$
we have
$a,b \in A$
we have
 $$\begin{align*}\partial(ab) &= ab \otimes 1 - 1 \otimes ab = (a \otimes 1 - 1 \otimes a)(b \otimes 1) + (1 \otimes a)(b \otimes 1 - 1 \otimes b) \\ & = \partial(a) (b \otimes 1) + (1 \otimes a) \partial(b).\end{align*}$$
$$\begin{align*}\partial(ab) &= ab \otimes 1 - 1 \otimes ab = (a \otimes 1 - 1 \otimes a)(b \otimes 1) + (1 \otimes a)(b \otimes 1 - 1 \otimes b) \\ & = \partial(a) (b \otimes 1) + (1 \otimes a) \partial(b).\end{align*}$$
Hence, the ideal generated by
![]() $\{\partial (a_i) : i=1,\cdots , m\}$
contains
$\{\partial (a_i) : i=1,\cdots , m\}$
contains
![]() $\partial (a_1^{k_1}\cdots a_m^{k_m})$
for all nonnegative integers
$\partial (a_1^{k_1}\cdots a_m^{k_m})$
for all nonnegative integers
![]() $k_1,\cdots , k_m$
. Since
$k_1,\cdots , k_m$
. Since
![]() $a \mapsto \partial (a)$
is k-linear, and since
$a \mapsto \partial (a)$
is k-linear, and since
![]() $A = k[a_1,\cdots ,a_m]$
by assumption, this ideal contains
$A = k[a_1,\cdots ,a_m]$
by assumption, this ideal contains
![]() $\partial (a)$
for all
$\partial (a)$
for all
![]() $a \in A$
. Hence, it contains
$a \in A$
. Hence, it contains
![]() $\ker {\mathrm {mult}}_A$
by part a). The reverse inclusion is clear because
$\ker {\mathrm {mult}}_A$
by part a). The reverse inclusion is clear because
![]() ${\mathrm {mult}}_A(\partial (a_i)) = 0$
for all i.
${\mathrm {mult}}_A(\partial (a_i)) = 0$
for all i.
4.3.2 The bimodule
 $\frac {(H_\zeta \oplus H_\zeta )[\kappa , z, \mu ]}{H_\zeta \tau _0 \oplus H_\zeta \tau _1}$
$\frac {(H_\zeta \oplus H_\zeta )[\kappa , z, \mu ]}{H_\zeta \tau _0 \oplus H_\zeta \tau _1}$
Recall the canonical involution
![]() $\unicode{x3b9} : H \to H$
from [Reference Ollivier and SchneiderOS22], §2.4.3: it is a self-inverse k-algebra automorphism of H that fixes the subalgebra
$\unicode{x3b9} : H \to H$
from [Reference Ollivier and SchneiderOS22], §2.4.3: it is a self-inverse k-algebra automorphism of H that fixes the subalgebra
![]() $k[\Omega ]$
pointwise and satisfies
$k[\Omega ]$
pointwise and satisfies
Lemma 4.3.5.
![]() $\unicode{x3b9} $
fixes the centre Z of H pointwise.
$\unicode{x3b9} $
fixes the centre Z of H pointwise.
Proof. The decomposition (11) together with Proposition 4.1.5 implies that the central elements
![]() $\{X_\lambda : \lambda \in \widehat {\Omega }\}$
generate Z as a k-algebra. Since
$\{X_\lambda : \lambda \in \widehat {\Omega }\}$
generate Z as a k-algebra. Since
![]() $\unicode{x3b9} $
is a
$\unicode{x3b9} $
is a
![]() $k[\Omega ]$
-linear involution, it therefore suffices to check that
$k[\Omega ]$
-linear involution, it therefore suffices to check that
![]() $\unicode{x3b9} $
fixes each
$\unicode{x3b9} $
fixes each
![]() $X_\lambda $
. Now, if
$X_\lambda $
. Now, if ![]() , then since
, then since ![]() by Equation (10), we compute
by Equation (10), we compute
On the other hand, since ![]() and since
and since
![]() $\unicode{x3b9} $
fixes
$\unicode{x3b9} $
fixes ![]() , we have
, we have
where we used the second formula for
![]() $\zeta $
from Lemma 4.1.2.
$\zeta $
from Lemma 4.1.2.
Let
![]() $\kappa : H \to R$
be a homomorphism of k-algebras, let
$\kappa : H \to R$
be a homomorphism of k-algebras, let
![]() $z \in Z(R)$
and let
$z \in Z(R)$
and let
![]() $\mu \in \widehat {\Omega }$
. Then in [Reference Ollivier and SchneiderOS22], §2.4.7, Ollivier and Schneider explain how to use these parameters to endow the left R-module
$\mu \in \widehat {\Omega }$
. Then in [Reference Ollivier and SchneiderOS22], §2.4.7, Ollivier and Schneider explain how to use these parameters to endow the left R-module
![]() $R \oplus R$
with the structure of a right H-module, in fact forming an
$R \oplus R$
with the structure of a right H-module, in fact forming an
![]() $(R,H)$
-bimodule, that they denote
$(R,H)$
-bimodule, that they denote
![]() $(R \oplus R)[\kappa , z, \mu ]$
. The left R-action on
$(R \oplus R)[\kappa , z, \mu ]$
. The left R-action on
![]() $(R \oplus R)[\kappa , z, \mu ]$
is the obvious one, but H acts from the right as follows:
$(R \oplus R)[\kappa , z, \mu ]$
is the obvious one, but H acts from the right as follows:
Here,
![]() $\kappa _2 : H \to M_2(R)$
is the explicit k-algebra homomorphism into the ring of
$\kappa _2 : H \to M_2(R)$
is the explicit k-algebra homomorphism into the ring of
![]() $2 \times 2$
-matrices with entries in R from [Reference Ollivier and SchneiderOS22] §2.4.7. In this generality, we will explicitly compute the right action of Z on this bimodule.
$2 \times 2$
-matrices with entries in R from [Reference Ollivier and SchneiderOS22] §2.4.7. In this generality, we will explicitly compute the right action of Z on this bimodule.
Lemma 4.3.6. We have
 $\kappa _2(X_\alpha ) = z^2 \begin {pmatrix} \kappa ( e_{\alpha ^{-1}\mu } \tau _0\tau _1 ) & 0 \\ 0 & \kappa ( e_{\alpha \mu ^{-1}} \tau _1\tau _0 ) \end {pmatrix}$
for all
$\kappa _2(X_\alpha ) = z^2 \begin {pmatrix} \kappa ( e_{\alpha ^{-1}\mu } \tau _0\tau _1 ) & 0 \\ 0 & \kappa ( e_{\alpha \mu ^{-1}} \tau _1\tau _0 ) \end {pmatrix}$
for all
![]() $\alpha \in \widehat {\Omega }$
.
$\alpha \in \widehat {\Omega }$
.
Proof. Recall from [Reference Ollivier and SchneiderOS22]§2.4.7 that
 $\kappa _2(\tau _\omega ) = M_\omega = \begin {pmatrix} \mu ^{-1}(\omega ) \kappa (\tau _\omega ) & 0 \\ 0 & \mu (\omega )\kappa (\tau _\omega )\end {pmatrix}$
. Then
$\kappa _2(\tau _\omega ) = M_\omega = \begin {pmatrix} \mu ^{-1}(\omega ) \kappa (\tau _\omega ) & 0 \\ 0 & \mu (\omega )\kappa (\tau _\omega )\end {pmatrix}$
. Then
 $$ \begin{align}\begin{array}{lll} \kappa_2(e_\alpha) &=& - \sum\limits_{\omega \in \Omega} \alpha^{-1}(\omega) \kappa_2(\tau_\omega) = - \sum\limits_{\omega \in \Omega} \alpha^{-1}(\omega) M_\omega \\ &=&\begin{pmatrix} - \sum\limits_{\omega \in \Omega} \alpha^{-1}(\omega)\mu^{-1}(\omega) \kappa(\tau_\omega) & 0 \\ 0 & - \sum\limits_{\omega \in \Omega} \alpha^{-1}(\omega) \mu(\omega) \kappa(\tau_\omega) \end{pmatrix} \\ &=& \begin{pmatrix} \kappa(e_{\alpha \mu}) & 0 \\ 0 & \kappa(e_{\alpha\mu^{-1}}) \end{pmatrix} \end{array}\end{align} $$
$$ \begin{align}\begin{array}{lll} \kappa_2(e_\alpha) &=& - \sum\limits_{\omega \in \Omega} \alpha^{-1}(\omega) \kappa_2(\tau_\omega) = - \sum\limits_{\omega \in \Omega} \alpha^{-1}(\omega) M_\omega \\ &=&\begin{pmatrix} - \sum\limits_{\omega \in \Omega} \alpha^{-1}(\omega)\mu^{-1}(\omega) \kappa(\tau_\omega) & 0 \\ 0 & - \sum\limits_{\omega \in \Omega} \alpha^{-1}(\omega) \mu(\omega) \kappa(\tau_\omega) \end{pmatrix} \\ &=& \begin{pmatrix} \kappa(e_{\alpha \mu}) & 0 \\ 0 & \kappa(e_{\alpha\mu^{-1}}) \end{pmatrix} \end{array}\end{align} $$
using Equation (9). On the other hand, we have
 $$\begin{align*}\kappa_2(\tau_0) = M_0 = \begin{pmatrix} -\kappa(e_\mu) & 0 \\ z \kappa(\tau_1) & 0 \end{pmatrix} \quad\text{and}\quad \kappa_2(\tau_1) = M_1 = \begin{pmatrix} 0 & z \kappa(\tau_0) \\0 & - \kappa(e_{\mu^{-1}}) \end{pmatrix}.\end{align*}$$
$$\begin{align*}\kappa_2(\tau_0) = M_0 = \begin{pmatrix} -\kappa(e_\mu) & 0 \\ z \kappa(\tau_1) & 0 \end{pmatrix} \quad\text{and}\quad \kappa_2(\tau_1) = M_1 = \begin{pmatrix} 0 & z \kappa(\tau_0) \\0 & - \kappa(e_{\mu^{-1}}) \end{pmatrix}.\end{align*}$$
Then using Equation (18) together with Equation (10), we compute

Similarly,

Suppose first that ![]() so that
so that
![]() $X_\alpha = e_\alpha \tau _0\tau _1 + e_{\alpha ^{-1}} \tau _1\tau _0$
. Then
$X_\alpha = e_\alpha \tau _0\tau _1 + e_{\alpha ^{-1}} \tau _1\tau _0$
. Then ![]() , and adding the last two displayed equations together gives the result in this case.
, and adding the last two displayed equations together gives the result in this case.
Suppose now that ![]() so that
so that ![]() . Adding the above two equations in this case gives
. Adding the above two equations in this case gives

Since  and
and
 $\kappa _2(\tau _0+\tau _1+1) = \begin {pmatrix} \kappa (1-e_\mu ) & z \kappa (\tau _0) \\ z \kappa (\tau _1) & \kappa (1-e_{\mu ^{-1}}) \end {pmatrix}$
, we have
$\kappa _2(\tau _0+\tau _1+1) = \begin {pmatrix} \kappa (1-e_\mu ) & z \kappa (\tau _0) \\ z \kappa (\tau _1) & \kappa (1-e_{\mu ^{-1}}) \end {pmatrix}$
, we have

Adding together Equations (19) and (20) finishes the calculation.
Corollary 4.3.7.
 $\kappa _2(\zeta ) = z^2 \begin {pmatrix} \kappa (\tau _0\tau _1) & 0 \\ 0 & \kappa (\tau _1\tau _0) \end {pmatrix}$
.
$\kappa _2(\zeta ) = z^2 \begin {pmatrix} \kappa (\tau _0\tau _1) & 0 \\ 0 & \kappa (\tau _1\tau _0) \end {pmatrix}$
.
Proof. Note that
![]() $\sum \limits _{\alpha \in \widehat {\Omega }} e_{\alpha ^{-1}\mu } = \sum \limits _{\lambda \in \widehat {\Omega }} e_\lambda = 1$
. Now, apply Lemma 4.3.6 and Lemma 4.1.4.d.
$\sum \limits _{\alpha \in \widehat {\Omega }} e_{\alpha ^{-1}\mu } = \sum \limits _{\lambda \in \widehat {\Omega }} e_\lambda = 1$
. Now, apply Lemma 4.3.6 and Lemma 4.1.4.d.
Now, we specialise slightly and take R to be the central localization
![]() $H_\zeta $
of H at
$H_\zeta $
of H at
![]() $\zeta $
. Let
$\zeta $
. Let
![]() $\kappa $
be the composition of
$\kappa $
be the composition of
![]() $\unicode{x3b9} : H \to H$
with the natural map
$\unicode{x3b9} : H \to H$
with the natural map
![]() $H \hookrightarrow H_\zeta $
, noting that the latter map is an injection as a consequence of [Reference Ollivier and SchneiderOS18] Corollary 3.4, and set
$H \hookrightarrow H_\zeta $
, noting that the latter map is an injection as a consequence of [Reference Ollivier and SchneiderOS18] Corollary 3.4, and set
 $$\begin{align*}z := -\tau_{\omega_{-1}} \zeta^{-1} \in H_\zeta \quad\text{where}\quad \omega_{-1} = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} T^1 \in \Omega.\end{align*}$$
$$\begin{align*}z := -\tau_{\omega_{-1}} \zeta^{-1} \in H_\zeta \quad\text{where}\quad \omega_{-1} = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} T^1 \in \Omega.\end{align*}$$
Then we have at our disposal the
![]() $(H_\zeta ,H)$
-bimodule
$(H_\zeta ,H)$
-bimodule
![]() $(H_\zeta \oplus H_\zeta )[\kappa , z, \mu ]$
.
$(H_\zeta \oplus H_\zeta )[\kappa , z, \mu ]$
.
Lemma 4.3.8.
![]() $H_\zeta \tau _0 \oplus H_\zeta \tau _1$
is an
$H_\zeta \tau _0 \oplus H_\zeta \tau _1$
is an
![]() $(H_\zeta ,H)$
-submodule of
$(H_\zeta ,H)$
-submodule of
![]() $(H_\zeta \oplus H_\zeta )[\kappa , z, \mu ]$
.
$(H_\zeta \oplus H_\zeta )[\kappa , z, \mu ]$
.
Proof. When
![]() $\mu = {\mathrm {id}}^2$
and
$\mu = {\mathrm {id}}^2$
and
![]() $k = \mathbb {F}_p$
, this is proved in [Reference Ollivier and SchneiderOS22]
$k = \mathbb {F}_p$
, this is proved in [Reference Ollivier and SchneiderOS22]
![]() $\S $
3.7.3.2. The computation for general
$\S $
3.7.3.2. The computation for general
![]() $\mu $
is entirely analogous and does not use the restriction on k.
$\mu $
is entirely analogous and does not use the restriction on k.
Definition 4.3.9. Let
![]() $B_\mu := \frac {(H_\zeta \oplus H_\zeta )[\kappa , z, \mu ]}{H_\zeta \tau _0 \oplus H_\zeta \tau _1}$
, an
$B_\mu := \frac {(H_\zeta \oplus H_\zeta )[\kappa , z, \mu ]}{H_\zeta \tau _0 \oplus H_\zeta \tau _1}$
, an
![]() $(H_\zeta ,H)$
-bimodule.
$(H_\zeta ,H)$
-bimodule.
We will now calculate the right action of Z on this bimodule.
Proposition 4.3.10.
-
a) We have
 $v \zeta = \zeta ^{-1} v$
for all
$v \zeta = \zeta ^{-1} v$
for all
 $v \in B_\mu $
.
$v \in B_\mu $
. -
b) Let
 $\mathbf {1} := (\overline {1},\overline {1})\in B_\mu $
. Then
$\mathbf {1} := (\overline {1},\overline {1})\in B_\mu $
. Then
 $\mathbf {1} \epsilon _\alpha = \epsilon _{\alpha ^{-1} \mu } \mathbf {1}$
for all
$\mathbf {1} \epsilon _\alpha = \epsilon _{\alpha ^{-1} \mu } \mathbf {1}$
for all
 $\alpha \in \widehat {\Omega }$
.
$\alpha \in \widehat {\Omega }$
.
Proof. a) We have
![]() $z = -\tau _{\omega _{-1}}\zeta ^{-1}$
so
$z = -\tau _{\omega _{-1}}\zeta ^{-1}$
so
![]() $z^2 = \zeta ^{-2}$
because
$z^2 = \zeta ^{-2}$
because
![]() $\zeta $
is central and
$\zeta $
is central and
![]() $(\omega _{-1})^2 = \omega _1 = 1$
. Note that
$(\omega _{-1})^2 = \omega _1 = 1$
. Note that ![]() , and similarly
, and similarly
![]() $\kappa (\tau _1\tau _0) = \zeta - \tau _0\tau _1 \equiv \zeta \mod H\tau _1$
, by Lemma 4.1.2. Writing
$\kappa (\tau _1\tau _0) = \zeta - \tau _0\tau _1 \equiv \zeta \mod H\tau _1$
, by Lemma 4.1.2. Writing
![]() $v = (\overline {v_1},\overline {v_2})$
, we apply Corollary 4.3.7:
$v = (\overline {v_1},\overline {v_2})$
, we apply Corollary 4.3.7:
 $$\begin{align*}(\overline{v_1},\overline{v_2})\zeta = (\overline{v_1},\overline{v_2})\kappa_2(\zeta) = (\overline{v_1},\overline{v_2}) \zeta^{-2} \begin{pmatrix} \zeta - \tau_1\tau_0 & 0 \\ 0 & \zeta - \tau_0\tau_1 \end{pmatrix} = (\overline{v_1\zeta^{-1}}, \overline{v_2\zeta^{-1}}) = \zeta^{-1}(\overline{v_1},\overline{v_2}).\end{align*}$$
$$\begin{align*}(\overline{v_1},\overline{v_2})\zeta = (\overline{v_1},\overline{v_2})\kappa_2(\zeta) = (\overline{v_1},\overline{v_2}) \zeta^{-2} \begin{pmatrix} \zeta - \tau_1\tau_0 & 0 \\ 0 & \zeta - \tau_0\tau_1 \end{pmatrix} = (\overline{v_1\zeta^{-1}}, \overline{v_2\zeta^{-1}}) = \zeta^{-1}(\overline{v_1},\overline{v_2}).\end{align*}$$
b) Recall that
![]() $\epsilon _\alpha = X_\alpha /\zeta $
by Lemma 4.2.9. We will show that
$\epsilon _\alpha = X_\alpha /\zeta $
by Lemma 4.2.9. We will show that
Applying Lemma 4.3.6, we calculate
 $$ \begin{align} (\overline{1},\overline{1})\kappa_2(X_\alpha)= (\overline{1},\overline{1})z^2 \begin{pmatrix} \kappa( e_{\alpha^{-1}\mu} \tau_0\tau_1 ) & 0 \\ 0 & \kappa( e_{\alpha\mu^{-1}} \tau_1 \tau_0 ) \end{pmatrix}=\zeta^{-2} \left(\overline{e_{\alpha^{-1}\mu} \unicode{x3b9}(\tau_0\tau_1)}, \overline{e_{\alpha\mu^{-1}} \unicode{x3b9}(\tau_1\tau_0)}\right).\end{align} $$
$$ \begin{align} (\overline{1},\overline{1})\kappa_2(X_\alpha)= (\overline{1},\overline{1})z^2 \begin{pmatrix} \kappa( e_{\alpha^{-1}\mu} \tau_0\tau_1 ) & 0 \\ 0 & \kappa( e_{\alpha\mu^{-1}} \tau_1 \tau_0 ) \end{pmatrix}=\zeta^{-2} \left(\overline{e_{\alpha^{-1}\mu} \unicode{x3b9}(\tau_0\tau_1)}, \overline{e_{\alpha\mu^{-1}} \unicode{x3b9}(\tau_1\tau_0)}\right).\end{align} $$
Next,
Suppose first that
![]() $\alpha \neq \mu $
. Then since
$\alpha \neq \mu $
. Then since ![]() by Equation (10),
by Equation (10),
On the other hand, using Definition 4.1.3, we have the congruences
 $$\begin{align*}X_{\alpha^{-1} \mu} = e_{\alpha^{-1}\mu} \tau_0\tau_1 + e_{\alpha\mu^{-1}} \tau_1\tau_0 \equiv \left\{\begin{array}{ll} e_{\alpha^{-1}\mu} \tau_0\tau_1 & \mod H\tau_0\\ e_{\alpha\mu^{-1}} \tau_1\tau_0 & \mod H\tau_1. \end{array} \right.\end{align*}$$
$$\begin{align*}X_{\alpha^{-1} \mu} = e_{\alpha^{-1}\mu} \tau_0\tau_1 + e_{\alpha\mu^{-1}} \tau_1\tau_0 \equiv \left\{\begin{array}{ll} e_{\alpha^{-1}\mu} \tau_0\tau_1 & \mod H\tau_0\\ e_{\alpha\mu^{-1}} \tau_1\tau_0 & \mod H\tau_1. \end{array} \right.\end{align*}$$
Putting these together shows that
as required. Suppose now that
![]() $\alpha = \mu $
. Then applying Equations (22) and (23) again, we have
$\alpha = \mu $
. Then applying Equations (22) and (23) again, we have
whereas since ![]() in this case, we see that
in this case, we see that
Having shown that Equation (21) holds, we use part a) to obtain
4.3.3 The annihilator of
 $B_\mu $
in
$B_\mu $
in
 $Z_\zeta \otimes Z_\zeta $
$Z_\zeta \otimes Z_\zeta $
Recall from Corollary 4.2.7 that
![]() $Z_\zeta $
is isomorphic to
$Z_\zeta $
is isomorphic to
![]() $k[\Omega ][t,t^{-1}]$
. Noting that
$k[\Omega ][t,t^{-1}]$
. Noting that
![]() $k[\Omega ]$
is isomorphic to the direct product of
$k[\Omega ]$
is isomorphic to the direct product of
![]() $|\widehat {\Omega }| = q-1$
copies of the ground field k, the following statement is clear:
$|\widehat {\Omega }| = q-1$
copies of the ground field k, the following statement is clear:
Lemma 4.3.11. There is a unique k-algebra automorphism
![]() $\phi _\mu : Z_\zeta \to Z_\zeta $
such that
$\phi _\mu : Z_\zeta \to Z_\zeta $
such that
Note that this
![]() $\phi _\mu $
is in fact an involution.
$\phi _\mu $
is in fact an involution.
Proposition 4.3.12. The map
![]() $\psi : (H_\zeta )_{\phi _\mu } \to B_\mu $
given by
$\psi : (H_\zeta )_{\phi _\mu } \to B_\mu $
given by
![]() $\psi (h) = h \mathbf {1}$
for all
$\psi (h) = h \mathbf {1}$
for all
![]() $h \in H_\zeta $
is an injective homomorphism of
$h \in H_\zeta $
is an injective homomorphism of
![]() $(H_\zeta ,Z_\zeta )$
-bimodules.
$(H_\zeta ,Z_\zeta )$
-bimodules.
Proof. The map
![]() $\psi $
is clearly left
$\psi $
is clearly left
![]() $H_\zeta $
-linear. Using Proposition 4.3.10, we have
$H_\zeta $
-linear. Using Proposition 4.3.10, we have
for any
![]() $\alpha \in \widehat {\Omega }$
. After Corollary 4.2.7, we know that
$\alpha \in \widehat {\Omega }$
. After Corollary 4.2.7, we know that
![]() $Z_\zeta $
is generated as a k-algebra by the
$Z_\zeta $
is generated as a k-algebra by the
![]() $\epsilon _\alpha $
’s,
$\epsilon _\alpha $
’s,
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta ^{-1}$
. It follows that
$\zeta ^{-1}$
. It follows that
![]() $\psi $
is right
$\psi $
is right
![]() $Z_\zeta $
-linear.
$Z_\zeta $
-linear.
We have
![]() $\ker \psi = H_\zeta \tau _0 \cap H_\zeta \tau _1$
by definition of
$\ker \psi = H_\zeta \tau _0 \cap H_\zeta \tau _1$
by definition of
![]() $B_\mu $
. This is equal to
$B_\mu $
. This is equal to
![]() $(H \tau _0 \cap H \tau _1)_\zeta $
. But
$(H \tau _0 \cap H \tau _1)_\zeta $
. But
![]() $H \tau _0 \cap H \tau _1 = 0$
by Lemma 4.3.13 below.
$H \tau _0 \cap H \tau _1 = 0$
by Lemma 4.3.13 below.
Lemma 4.3.13. The sum of left ideals
![]() $H\tau _0 + H\tau _1$
is direct.
$H\tau _0 + H\tau _1$
is direct.
Proof. Recall that
![]() $\{\tau _w : w \in \widetilde {W}\}$
forms a basis for H as a k-vector space. Now,
$\{\tau _w : w \in \widetilde {W}\}$
forms a basis for H as a k-vector space. Now,
![]() $\widetilde {W}$
contains
$\widetilde {W}$
contains
![]() $\Omega $
as a normal subgroup and the images of
$\Omega $
as a normal subgroup and the images of
![]() $s_0$
and
$s_0$
and
![]() $s_1$
in
$s_1$
in
![]() $\widetilde {W} / \Omega $
generate a copy of the infinite dihedral group. It follows that every element of
$\widetilde {W} / \Omega $
generate a copy of the infinite dihedral group. It follows that every element of
![]() $\widetilde {W}$
has a unique representation in the form
$\widetilde {W}$
has a unique representation in the form
![]() $\omega w$
, where
$\omega w$
, where
![]() $\omega \in \Omega $
and w is a reduced word in
$\omega \in \Omega $
and w is a reduced word in
![]() $s_0$
and
$s_0$
and
![]() $s_1$
. Therefore, the reduced words in
$s_1$
. Therefore, the reduced words in
![]() $\tau _0$
and
$\tau _0$
and
![]() $\tau _1$
form a basis for H as a
$\tau _1$
form a basis for H as a
![]() $k[\Omega ]$
-module. Every nonempty such word ends in exactly one of either
$k[\Omega ]$
-module. Every nonempty such word ends in exactly one of either
![]() $\tau _0$
or
$\tau _0$
or
![]() $\tau _1$
, which gives the result.
$\tau _1$
, which gives the result.
Now, we study
![]() ${\mathrm {coker}}\ \psi $
.
${\mathrm {coker}}\ \psi $
.
Lemma 4.3.14. The left H-module
![]() $H / (H\tau _0 + H\tau _1)$
is killed by
$H / (H\tau _0 + H\tau _1)$
is killed by
![]() $\zeta (\zeta - 1)$
.
$\zeta (\zeta - 1)$
.
Proof. The fact that
![]() $\{\tau _w : w \in \widetilde {W}\}$
spans H implies that
$\{\tau _w : w \in \widetilde {W}\}$
spans H implies that
![]() $H = k[\Omega ] \oplus (H\tau _0 + H\tau _1)$
as a k-vector space. Therefore, it is enough to show that
$H = k[\Omega ] \oplus (H\tau _0 + H\tau _1)$
as a k-vector space. Therefore, it is enough to show that
![]() $\zeta (\zeta -1)e_\lambda \in H\tau _0 + H\tau _1$
for all
$\zeta (\zeta -1)e_\lambda \in H\tau _0 + H\tau _1$
for all
![]() $\lambda \in \widehat {\Omega }$
. However,
$\lambda \in \widehat {\Omega }$
. However, ![]() , so already
, so already
![]() $\zeta e_\lambda \equiv 0 \mod H\tau _0 + H \tau _1$
if
$\zeta e_\lambda \equiv 0 \mod H\tau _0 + H \tau _1$
if ![]() , whereas if
, whereas if ![]() , then
, then ![]() .
.
Corollary 4.3.15. There exist elements
![]() $u,v \in H$
such that
$u,v \in H$
such that
![]() $\zeta (\zeta - 1) = u\tau _0 + v\tau _1$
.
$\zeta (\zeta - 1) = u\tau _0 + v\tau _1$
.
Proposition 4.3.16. We have
![]() $(\zeta - 1) \cdot {\mathrm {coker}}\ \psi = 0$
.
$(\zeta - 1) \cdot {\mathrm {coker}}\ \psi = 0$
.
Proof. Let
![]() $(\overline {a}, \overline {b}) \in B_\mu $
for some
$(\overline {a}, \overline {b}) \in B_\mu $
for some
![]() $a,b \in H_\zeta $
. Define
$a,b \in H_\zeta $
. Define
![]() $c:= av\tau _1 + bu\tau _0$
, where
$c:= av\tau _1 + bu\tau _0$
, where
![]() $u,v \in H$
given by Corollary 4.3.15. Then
$u,v \in H$
given by Corollary 4.3.15. Then
and similarly
![]() $c \equiv b \zeta (\zeta -1) \mod H_\zeta \tau _1$
. Hence,
$c \equiv b \zeta (\zeta -1) \mod H_\zeta \tau _1$
. Hence,
![]() $\zeta (\zeta - 1)(\overline {a}, \overline {b}) = (\overline {c}, \overline {c}) = c\mathbf {1} = \psi (c)$
, so
$\zeta (\zeta - 1)(\overline {a}, \overline {b}) = (\overline {c}, \overline {c}) = c\mathbf {1} = \psi (c)$
, so
![]() ${\mathrm {coker}}\ \psi $
is killed by
${\mathrm {coker}}\ \psi $
is killed by
![]() $\zeta (\zeta -1)$
. Since
$\zeta (\zeta -1)$
. Since
![]() $\zeta $
is invertible in
$\zeta $
is invertible in
![]() $H_\zeta $
,
$H_\zeta $
,
![]() ${\mathrm {coker}}\ \psi $
is already killed by
${\mathrm {coker}}\ \psi $
is already killed by
![]() $\zeta - 1$
.
$\zeta - 1$
.
Lemma 4.3.17.
![]() $H/H \tau _0$
and
$H/H \tau _0$
and
![]() $H/H\tau _1$
are
$H/H\tau _1$
are
![]() $k[\zeta ]$
-torsion-free.
$k[\zeta ]$
-torsion-free.
Proof. Let
![]() $H_0$
be the k-subalgebra of H generated by
$H_0$
be the k-subalgebra of H generated by
![]() $k[\Omega ]$
and
$k[\Omega ]$
and
![]() $\tau _0$
. We have
$\tau _0$
. We have
Next, by [Reference Ollivier and SchneiderOS18] Corollary 3.4, H is free of rank
![]() $2$
as a
$2$
as a
![]() $H_0 \otimes _k k[\zeta ]$
-module, with basis
$H_0 \otimes _k k[\zeta ]$
-module, with basis
![]() $\{1, \tau _1\}$
. If
$\{1, \tau _1\}$
. If
![]() $H_0[\zeta ]$
denotes the subalgebra of H generated by
$H_0[\zeta ]$
denotes the subalgebra of H generated by
![]() $H_0$
and
$H_0$
and
![]() $\zeta $
, then this means that the multiplication map
$\zeta $
, then this means that the multiplication map
![]() $H_0 \otimes _k k[\zeta ] \to H_0[\zeta ]$
is a k-algebra isomorphism and also that H is free of rank
$H_0 \otimes _k k[\zeta ] \to H_0[\zeta ]$
is a k-algebra isomorphism and also that H is free of rank
![]() $2$
as a left
$2$
as a left
![]() $H_0[\zeta ]$
-module, with basis
$H_0[\zeta ]$
-module, with basis
![]() $\{1, \tau _1\}$
:
$\{1, \tau _1\}$
:
Let
![]() $A := k[\Omega ][\zeta ] \subset H_0[\zeta ]$
; clearly, A is isomorphic as a k-algebra to the polynomial ring in one variable over
$A := k[\Omega ][\zeta ] \subset H_0[\zeta ]$
; clearly, A is isomorphic as a k-algebra to the polynomial ring in one variable over
![]() $k[\Omega ]$
. Combining the two displayed equations above, we obtain the decomposition
$k[\Omega ]$
. Combining the two displayed equations above, we obtain the decomposition
of H as a left A-module. Now, ![]() by Lemma 4.1.1, and
by Lemma 4.1.1, and ![]() is central in H. This implies that right-multiplication by
is central in H. This implies that right-multiplication by
![]() $\tau _1$
sends H into
$\tau _1$
sends H into
![]() $A \tau _1 \oplus A \tau _0 \tau _1$
. Since this A-module is clearly contained in
$A \tau _1 \oplus A \tau _0 \tau _1$
. Since this A-module is clearly contained in
![]() $H \tau _1$
, we conclude that
$H \tau _1$
, we conclude that
![]() $H \tau _1 = A \tau _1 \oplus A \tau _0 \tau _1$
, and therefore
$H \tau _1 = A \tau _1 \oplus A \tau _0 \tau _1$
, and therefore
as a left A-module. Since A is itself free as a
![]() $k[\zeta ]$
-module, we see that
$k[\zeta ]$
-module, we see that
![]() $H / H \tau _1$
is free of rank
$H / H \tau _1$
is free of rank
![]() $2(q-1)$
as a
$2(q-1)$
as a
![]() $k[\zeta ]$
-module. It is in particular
$k[\zeta ]$
-module. It is in particular
![]() $k[\zeta ]$
-torsion-free.
$k[\zeta ]$
-torsion-free.
The argument for
![]() $H / H \tau _0$
is the same, after switching
$H / H \tau _0$
is the same, after switching
![]() $\tau _0$
with
$\tau _0$
with
![]() $\tau _1$
.
$\tau _1$
.
Corollary 4.3.18. The left H-module
![]() $B_\mu $
is
$B_\mu $
is
![]() $k[\zeta ]$
-torsion-free.
$k[\zeta ]$
-torsion-free.
Proof. As a left
![]() $k[\zeta ]$
-module,
$k[\zeta ]$
-module,
![]() $B_\mu $
is isomorphic to
$B_\mu $
is isomorphic to
![]() $k[\zeta , \zeta ^{-1}] \otimes _{k[\zeta ]} \left (\frac {H}{H \tau _0}\oplus \frac {H}{ H \tau _1}\right )$
. The expression in the brackets is
$k[\zeta , \zeta ^{-1}] \otimes _{k[\zeta ]} \left (\frac {H}{H \tau _0}\oplus \frac {H}{ H \tau _1}\right )$
. The expression in the brackets is
![]() $k[\zeta ]$
-torsion-free by Lemma 4.3.17, and the result follows easily.
$k[\zeta ]$
-torsion-free by Lemma 4.3.17, and the result follows easily.
Theorem 4.3.19. . We have
![]() ${\mathrm {Ann}}_{Z_\zeta \otimes Z_\zeta }(B_\mu ) = (1 \otimes \phi _\mu )(\ker {\mathrm {mult}}_{Z_\zeta })$
.
${\mathrm {Ann}}_{Z_\zeta \otimes Z_\zeta }(B_\mu ) = (1 \otimes \phi _\mu )(\ker {\mathrm {mult}}_{Z_\zeta })$
.
Proof. Write
![]() $R = Z_\zeta \otimes Z_\zeta $
. Using Proposition 4.3.12, we see that
$R = Z_\zeta \otimes Z_\zeta $
. Using Proposition 4.3.12, we see that
Suppose that
![]() $r \in R$
kills
$r \in R$
kills
![]() $(H_\zeta )_{\phi _\mu }$
; then r kills
$(H_\zeta )_{\phi _\mu }$
; then r kills
![]() $\operatorname {im}(\psi )$
. By Proposition 4.3.16,
$\operatorname {im}(\psi )$
. By Proposition 4.3.16,
![]() $(\zeta - 1)B_\mu \subseteq \operatorname {im}(\psi )$
. Hence,
$(\zeta - 1)B_\mu \subseteq \operatorname {im}(\psi )$
. Hence,
![]() $r \cdot \left ( (\zeta - 1) \otimes 1 \right )$
kills
$r \cdot \left ( (\zeta - 1) \otimes 1 \right )$
kills
![]() $B_\mu $
, so
$B_\mu $
, so
![]() $\zeta - 1$
kills
$\zeta - 1$
kills
![]() $r \cdot B_\mu $
. But
$r \cdot B_\mu $
. But
![]() $B_\mu $
is
$B_\mu $
is
![]() $k[\zeta ]$
-torsion-free by Corollary 4.3.18, so
$k[\zeta ]$
-torsion-free by Corollary 4.3.18, so
![]() $r \cdot B_\mu = 0$
. This shows that
$r \cdot B_\mu = 0$
. This shows that
Now, we apply Lemma 4.3.2 to the
![]() $(Z_\zeta ,Z_\zeta )$
-bimodule
$(Z_\zeta ,Z_\zeta )$
-bimodule
![]() $H_\zeta $
to see that
$H_\zeta $
to see that
Now,
![]() $Z_\zeta $
is the centre of
$Z_\zeta $
is the centre of
![]() $H_\zeta $
, so
$H_\zeta $
, so
![]() ${\mathrm {Ann}}_R(H_\zeta ) = {\mathrm {Ann}}_R(Z_\zeta )$
by Lemma 4.3.3. Since
${\mathrm {Ann}}_R(H_\zeta ) = {\mathrm {Ann}}_R(Z_\zeta )$
by Lemma 4.3.3. Since
![]() $\phi _\mu = \phi _\mu ^{-1}$
,
$\phi _\mu = \phi _\mu ^{-1}$
,
The result now follows from Lemma 4.3.3 applied with
![]() $A = Z_\zeta $
.
$A = Z_\zeta $
.
Write
![]() $\delta _\mu (a) := a\otimes 1 - 1 \otimes {\phi _\mu }(a)$
for all
$\delta _\mu (a) := a\otimes 1 - 1 \otimes {\phi _\mu }(a)$
for all
![]() $a \in Z_\zeta $
. The following finite set of ideal generators for
$a \in Z_\zeta $
. The following finite set of ideal generators for
![]() ${\mathrm {Ann}}_{Z_\zeta \otimes Z_\zeta }(B_\mu )$
will be useful to us later.
${\mathrm {Ann}}_{Z_\zeta \otimes Z_\zeta }(B_\mu )$
will be useful to us later.
Corollary 4.3.20. We have
![]() ${\mathrm {Ann}}_{Z_\zeta \otimes Z_\zeta }(B_\mu ) = (Z_\zeta \otimes Z_\zeta ) \delta _\mu (\zeta ) + \sum \limits _{\alpha \in \widehat {\Omega }} (Z_\zeta \otimes Z_\zeta ) \delta _\mu (\epsilon _\alpha )$
.
${\mathrm {Ann}}_{Z_\zeta \otimes Z_\zeta }(B_\mu ) = (Z_\zeta \otimes Z_\zeta ) \delta _\mu (\zeta ) + \sum \limits _{\alpha \in \widehat {\Omega }} (Z_\zeta \otimes Z_\zeta ) \delta _\mu (\epsilon _\alpha )$
.
Proof. By Corollary 4.2.7, there is a k-algebra isomorphism
![]() $Z_\zeta \stackrel {\cong }{\longrightarrow } k[\Omega ][t, t^{-1}]$
that sends
$Z_\zeta \stackrel {\cong }{\longrightarrow } k[\Omega ][t, t^{-1}]$
that sends
![]() $\epsilon _\alpha $
to
$\epsilon _\alpha $
to
![]() $e_\alpha $
and
$e_\alpha $
and
![]() $\zeta $
to t. Therefore,
$\zeta $
to t. Therefore,
![]() $\{\zeta , \zeta ^{-1}\} \cup \{\epsilon _\alpha : \alpha \in \widehat {\Omega }\} $
forms a set of k-algebra generators for
$\{\zeta , \zeta ^{-1}\} \cup \{\epsilon _\alpha : \alpha \in \widehat {\Omega }\} $
forms a set of k-algebra generators for
![]() $Z_\zeta $
. Write
$Z_\zeta $
. Write
![]() $\partial (a) = a \otimes 1 - 1 \otimes a$
for all
$\partial (a) = a \otimes 1 - 1 \otimes a$
for all
![]() $a \in Z_\zeta $
, and
$a \in Z_\zeta $
, and
![]() $R = Z_\zeta \otimes Z_\zeta $
; then by Lemma 4.3.4.b, we have
$R = Z_\zeta \otimes Z_\zeta $
; then by Lemma 4.3.4.b, we have
 $$ \begin{align} \ker {\mathrm{mult}}_{Z_\zeta} = R \partial(\zeta) + R \partial(\zeta^{-1}) + \sum\limits_{\alpha \in \widehat{\Omega}} R \partial(\epsilon_\alpha).\end{align} $$
$$ \begin{align} \ker {\mathrm{mult}}_{Z_\zeta} = R \partial(\zeta) + R \partial(\zeta^{-1}) + \sum\limits_{\alpha \in \widehat{\Omega}} R \partial(\epsilon_\alpha).\end{align} $$
Note that
![]() $\partial (\zeta ^{-1}) = \zeta ^{-1} \otimes 1 + 1 \otimes \zeta ^{-1} = (\zeta ^{-1} \otimes \zeta ^{-1})\partial (\zeta )$
, so
$\partial (\zeta ^{-1}) = \zeta ^{-1} \otimes 1 + 1 \otimes \zeta ^{-1} = (\zeta ^{-1} \otimes \zeta ^{-1})\partial (\zeta )$
, so
![]() $R \partial (\zeta ^{-1}) = R \partial (\zeta )$
. Also, note that
$R \partial (\zeta ^{-1}) = R \partial (\zeta )$
. Also, note that
![]() $(1 \otimes {\phi _\mu }) \partial = \delta _\mu $
. Therefore, applying
$(1 \otimes {\phi _\mu }) \partial = \delta _\mu $
. Therefore, applying
![]() $1 \otimes {\phi _\mu }$
to Equation (24) gives
$1 \otimes {\phi _\mu }$
to Equation (24) gives
 $$\begin{align*}(1 \otimes {\phi_\mu})\left(\ker {\mathrm{mult}}_{Z_\zeta}\right) = R \delta_\mu(\zeta) + \sum\limits_{\alpha \in \widehat{\Omega}} R \delta_\mu(\epsilon_\alpha).\end{align*}$$
$$\begin{align*}(1 \otimes {\phi_\mu})\left(\ker {\mathrm{mult}}_{Z_\zeta}\right) = R \delta_\mu(\zeta) + \sum\limits_{\alpha \in \widehat{\Omega}} R \delta_\mu(\epsilon_\alpha).\end{align*}$$
The result now follows from Theorem 4.3.19.
4.4 The bimodule annihilator of
 ${\mathrm {Ext}}^{\ast} _G(X,X)$
${\mathrm {Ext}}^{\ast} _G(X,X)$
Our goal will be to compute the ideal
Recall that
![]() $X = {\mathrm {ind}}_I^G(k)$
. For brevity, we will write for each
$X = {\mathrm {ind}}_I^G(k)$
. For brevity, we will write for each
![]() $n \geq 0$
$n \geq 0$
First, we will use the Poincaré duality isomorphisms from [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19] to relate
![]() $J_n$
with
$J_n$
with
![]() $J_{d-n}$
, where d is the dimension of G as a p-adic Lie group. For this, we need to look at the anti-involution
$J_{d-n}$
, where d is the dimension of G as a p-adic Lie group. For this, we need to look at the anti-involution ![]() that was introduced in [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19],
that was introduced in [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19],
![]() $\S 6$
: it is an antiautomorphism of the graded algebra
$\S 6$
: it is an antiautomorphism of the graded algebra
![]() $E^{\ast} $
by [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19], Proposition 6.1, and therefore in particular restricts to a k-algebra antiautomorphism of
$E^{\ast} $
by [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19], Proposition 6.1, and therefore in particular restricts to a k-algebra antiautomorphism of
![]() $H = E^0$
.
$H = E^0$
.
Lemma 4.4.1.
![]() fixes Z pointwise.
fixes Z pointwise.
Proof. By [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19] Proposition 6.1, we know that ![]() for all
for all
![]() $g \in G$
, where
$g \in G$
, where
![]() $\tau _g$
denotes the characteristic function of the double coset
$\tau _g$
denotes the characteristic function of the double coset
![]() $IgI$
– see [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19],
$IgI$
– see [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19],
![]() $\S $
2.2. It follows therefore that
$\S $
2.2. It follows therefore that ![]() restricts to the standard anti-involution on the group algebra
restricts to the standard anti-involution on the group algebra
![]() $k[\Omega ] \subset H$
that sends the group elements
$k[\Omega ] \subset H$
that sends the group elements
![]() $\tau _\omega $
to
$\tau _\omega $
to
![]() $\tau _{\omega ^{-1}}$
, for each
$\tau _{\omega ^{-1}}$
, for each
![]() $\omega \in \Omega $
. Equation (9) now implies that
$\omega \in \Omega $
. Equation (9) now implies that
Next, we have
![]() $s_i^{-1} = -s_i$
for
$s_i^{-1} = -s_i$
for
![]() $i=0,1$
inside G. Writing
$i=0,1$
inside G. Writing
![]() $\epsilon = \tau _{\omega _{-1}}$
, it follows that
$\epsilon = \tau _{\omega _{-1}}$
, it follows that
With these two pieces of information in hand, we can now compute the effect of ![]() on the algebra generators
on the algebra generators
![]() $X_\lambda $
of Z from Definition 4.1.3, for each
$X_\lambda $
of Z from Definition 4.1.3, for each
![]() $\lambda \in \widehat {\Omega }$
. When
$\lambda \in \widehat {\Omega }$
. When ![]() , we have
, we have

We have used here the fact that
![]() $\epsilon $
is a central involution in H, as well as the relations
$\epsilon $
is a central involution in H, as well as the relations
from Lemma 4.1.1. Next, recall from Lemma 4.1.2 that ![]() . When
. When ![]() , the calculation goes as follows:
, the calculation goes as follows:

We have used here the fact that ![]() . We have shown that
. We have shown that ![]() fixes each
fixes each
![]() $X_\lambda $
. Since these generate Z as a k-algebra in view of Proposition 4.1.5,
$X_\lambda $
. Since these generate Z as a k-algebra in view of Proposition 4.1.5, ![]() is the identity map.
is the identity map.
For our next result, we need to introduce the k-algebra involution
![]() $\sigma : Z \otimes _k Z \to Z \otimes _k Z$
, given by
$\sigma : Z \otimes _k Z \to Z \otimes _k Z$
, given by
![]() $\sigma (z_1 \otimes z_2) = z_2 \otimes z_1$
for
$\sigma (z_1 \otimes z_2) = z_2 \otimes z_1$
for
![]() $z_1,z_2 \in Z$
.
$z_1,z_2 \in Z$
.
Lemma 4.4.2. For each
![]() $n = 0,\cdots , d$
, we have
$n = 0,\cdots , d$
, we have
![]() $J_{d-n} = \sigma (J_n)$
.
$J_{d-n} = \sigma (J_n)$
.
Proof. For a k-vector space V, let
![]() $V^\vee $
denote the full k-linear dual
$V^\vee $
denote the full k-linear dual
![]() $V^\vee = {\mathrm {Hom}}_k(V,k)$
. When V happens to be an
$V^\vee = {\mathrm {Hom}}_k(V,k)$
. When V happens to be an
![]() $(H,H)$
-bimodule, then
$(H,H)$
-bimodule, then
![]() $V^\vee $
is also an
$V^\vee $
is also an
![]() $(H,H)$
-bimodule. Following [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19],
$(H,H)$
-bimodule. Following [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19],
![]() $\S $
7.1, this bimodule structure is given by the following rule:
$\S $
7.1, this bimodule structure is given by the following rule:
We are only interested in
![]() $(Z,Z)$
-bimodules here. Regarding every
$(Z,Z)$
-bimodules here. Regarding every
![]() $(Z,Z)$
-bimodule V as a left
$(Z,Z)$
-bimodule V as a left
![]() $A := Z \otimes _kZ$
-module in the standard way, we can write this action of A on
$A := Z \otimes _kZ$
-module in the standard way, we can write this action of A on
![]() $V^\vee $
as follows:
$V^\vee $
as follows:
It follows immediately that for every
![]() $(Z,Z)$
-bimodule V we have
$(Z,Z)$
-bimodule V we have
Now, [Reference Ollivier, Schneider, Aizenbud, Gourevitch, Kazhdan and LapidOS19] Proposition 7.18 gives us an injective homomorphism of
![]() $(H,H)$
-bimodules
$(H,H)$
-bimodules
Since ![]() fixes Z pointwise by Lemma 4.4.1, we may write this as
fixes Z pointwise by Lemma 4.4.1, we may write this as
an injective homomorphism of
![]() $(Z,Z)$
-bimodules. Using Equation (25), we obtain
$(Z,Z)$
-bimodules. Using Equation (25), we obtain
Replacing n with
![]() $d-n$
gives
$d-n$
gives
![]() $J_n \subseteq \sigma (J_{d-n})$
, so
$J_n \subseteq \sigma (J_{d-n})$
, so
![]() $J_{d-n} \subseteq \sigma (J_n) \subseteq \sigma ^2(J_{d-n}) = J_{d-n}$
.
$J_{d-n} \subseteq \sigma (J_n) \subseteq \sigma ^2(J_{d-n}) = J_{d-n}$
.
Recall the multiplication map
![]() ${\mathrm {mult}}_Z : Z \otimes _k Z \to Z$
from
${\mathrm {mult}}_Z : Z \otimes _k Z \to Z$
from
![]() $\S$
4.3.1.
$\S$
4.3.1.
Lemma 4.4.3.
-
a) We have
 $J_0 = \ker {\mathrm {mult}}_Z$
.
$J_0 = \ker {\mathrm {mult}}_Z$
. -
b)
 $J_0 = \sigma (J_0)$
.
$J_0 = \sigma (J_0)$
.
Proof. Since
![]() ${\mathrm {Ext}}^0_G(X,X) = {\mathrm {Hom}}_G(X,X) = H$
and since
${\mathrm {Ext}}^0_G(X,X) = {\mathrm {Hom}}_G(X,X) = H$
and since
![]() $Z = Z(H)$
, Lemma 4.3.3 implies that
$Z = Z(H)$
, Lemma 4.3.3 implies that
![]() $J_0 = \ker {\mathrm {mult}}_Z$
. The second statement follows from Lemma 4.3.4.a.
$J_0 = \ker {\mathrm {mult}}_Z$
. The second statement follows from Lemma 4.3.4.a.
We assume from now on that
![]() $\mathfrak {F} = \mathbb {Q}_p$
,
$\mathfrak {F} = \mathbb {Q}_p$
,
![]() $p \neq 2,3$
and
$p \neq 2,3$
and
![]() $\pi = p$
. This assumption allows us to apply the results of [Reference Ollivier and SchneiderOS22] to study
$\pi = p$
. This assumption allows us to apply the results of [Reference Ollivier and SchneiderOS22] to study
![]() $J_1$
. Recall first that by [Reference Ollivier and SchneiderOS22] Proposition 6.10(1), there is a certain short exact sequence of
$J_1$
. Recall first that by [Reference Ollivier and SchneiderOS22] Proposition 6.10(1), there is a certain short exact sequence of
![]() $(H,H)$
-bimodules
$(H,H)$
-bimodules
Here, C is a certain
![]() $(H,H)$
-bimodule with
$(H,H)$
-bimodule with
![]() $\dim _k C = 4$
.
$\dim _k C = 4$
.
Lemma 4.4.4. We have
![]() ${\mathrm {Ann}}_{Z \otimes _k Z}(\ker g_1)) = J_0$
.
${\mathrm {Ann}}_{Z \otimes _k Z}(\ker g_1)) = J_0$
.
Proof. By [Reference Ollivier and SchneiderOS22] Proposition 6.3,
![]() $\ker (g_1) \cong F^1H$
as an
$\ker (g_1) \cong F^1H$
as an
![]() $(H,H)$
-bimodule, where
$(H,H)$
-bimodule, where
![]() $(F^nH)_{n \geq 0}$
is the descending filtration on H defined at [Reference Ollivier and SchneiderOS22], §2.2.4. Writing
$(F^nH)_{n \geq 0}$
is the descending filtration on H defined at [Reference Ollivier and SchneiderOS22], §2.2.4. Writing
![]() $A = Z\otimes _kZ$
, we then have
$A = Z\otimes _kZ$
, we then have
For the reverse inclusion, note that
![]() $F^1H = H \tau _0 + H \tau _1$
, so
$F^1H = H \tau _0 + H \tau _1$
, so
![]() $\zeta (\zeta - 1)$
kills
$\zeta (\zeta - 1)$
kills
![]() $H/F^1H$
from the left by Lemma 4.3.14. Since H is
$H/F^1H$
from the left by Lemma 4.3.14. Since H is
![]() $k[\zeta ]$
-torsion-free and since
$k[\zeta ]$
-torsion-free and since
![]() $\zeta $
is central in H, left-multiplication by
$\zeta $
is central in H, left-multiplication by
![]() $\zeta (\zeta -1)$
gives an injective homomorphism of
$\zeta (\zeta -1)$
gives an injective homomorphism of
![]() $(H,H)$
-bimodules
$(H,H)$
-bimodules
![]() $H \hookrightarrow F^1H$
. Hence,
$H \hookrightarrow F^1H$
. Hence,
On p. 38 of [Reference Ollivier and SchneiderOS22], Ollivier and Schneider consider a certain twist of
![]() $(H_\zeta \oplus H_\zeta )[\kappa , z, {\mathrm {id}}^2]$
that they denote
$(H_\zeta \oplus H_\zeta )[\kappa , z, {\mathrm {id}}^2]$
that they denote
![]() $(H_\zeta \oplus H_\zeta )^\pm $
. The left action of H on
$(H_\zeta \oplus H_\zeta )^\pm $
. The left action of H on
![]() $(H_\zeta \oplus H_\zeta )$
is unchanged, but the right H-action is twisted by precomposing the previous right H-action by
$(H_\zeta \oplus H_\zeta )$
is unchanged, but the right H-action is twisted by precomposing the previous right H-action by
![]() $\unicode{x3b9} $
. They show that the left
$\unicode{x3b9} $
. They show that the left
![]() $H_\zeta $
-submodule
$H_\zeta $
-submodule
![]() $H_\zeta \tau _0 \oplus H_\zeta \tau _1$
of this direct sum is stable under this new right H-action, which allows them to pass to the quotient to form the
$H_\zeta \tau _0 \oplus H_\zeta \tau _1$
of this direct sum is stable under this new right H-action, which allows them to pass to the quotient to form the
![]() $(H_\zeta ,H)$
-bimodule
$(H_\zeta ,H)$
-bimodule
 $$\begin{align*}\left(\frac{H_\zeta}{H_\zeta \tau_0} \oplus \frac{H_\zeta}{H_\zeta \tau_1}\right)^\pm = \frac{(H_\zeta \oplus H_\zeta )^\pm}{(H_\zeta \tau_0 \oplus H_\zeta \tau_1)^{\pm}}.\end{align*}$$
$$\begin{align*}\left(\frac{H_\zeta}{H_\zeta \tau_0} \oplus \frac{H_\zeta}{H_\zeta \tau_1}\right)^\pm = \frac{(H_\zeta \oplus H_\zeta )^\pm}{(H_\zeta \tau_0 \oplus H_\zeta \tau_1)^{\pm}}.\end{align*}$$
Then they prove the following theorem – see [Reference Ollivier and SchneiderOS22] Proposition 3.28 and Theorem 6.8:
Theorem 4.4.5. There is an
![]() $(H_\zeta ,H)$
-bimodule isomorphism
$(H_\zeta ,H)$
-bimodule isomorphism
 $$\begin{align*}\left(\frac{H_\zeta}{H_\zeta \tau_0} \oplus \frac{H_\zeta}{H_\zeta \tau_1}\right)^\pm \stackrel{\cong}{\longrightarrow} \ker(f_1).\end{align*}$$
$$\begin{align*}\left(\frac{H_\zeta}{H_\zeta \tau_0} \oplus \frac{H_\zeta}{H_\zeta \tau_1}\right)^\pm \stackrel{\cong}{\longrightarrow} \ker(f_1).\end{align*}$$
We are only interested in the
![]() $(Z_\zeta ,Z_\zeta )$
-bimodule structure on
$(Z_\zeta ,Z_\zeta )$
-bimodule structure on
![]() $\ker (f_1)$
. Recall the
$\ker (f_1)$
. Recall the
![]() $(H_\zeta ,H)$
-bimodule
$(H_\zeta ,H)$
-bimodule
![]() $B_{{\mathrm {id}}^2}$
from Definition 4.3.9.
$B_{{\mathrm {id}}^2}$
from Definition 4.3.9.
Corollary 4.4.6. There is an
![]() $(H_\zeta ,Z_\zeta )$
-bimodule isomorphism
$(H_\zeta ,Z_\zeta )$
-bimodule isomorphism
![]() $B_{{\mathrm {id}}^2} \stackrel {\cong }{\longrightarrow } \ker (f_1)$
.
$B_{{\mathrm {id}}^2} \stackrel {\cong }{\longrightarrow } \ker (f_1)$
.
Proof. Note that
![]() $\zeta $
acts invertibly on
$\zeta $
acts invertibly on
![]() $\ker (f_1)$
from both sides by its definition: Indeed, the left
$\ker (f_1)$
from both sides by its definition: Indeed, the left
![]() $\zeta $
-actions and the right
$\zeta $
-actions and the right
![]() $\zeta $
-actions are mutually inverse. Therefore,
$\zeta $
-actions are mutually inverse. Therefore,
![]() $\ker (f_1)$
is in fact a
$\ker (f_1)$
is in fact a
![]() $(H_\zeta ,H_\zeta )$
-bimodule. Since
$(H_\zeta ,H_\zeta )$
-bimodule. Since
![]() $\unicode{x3b9} $
fixes Z by Lemma 4.3.5, precomposing with
$\unicode{x3b9} $
fixes Z by Lemma 4.3.5, precomposing with
![]() $\unicode{x3b9} $
makes no difference to the right action of Z. Now, we can apply Theorem 4.4.5.
$\unicode{x3b9} $
makes no difference to the right action of Z. Now, we can apply Theorem 4.4.5.
Theorem 4.4.7. Suppose that
![]() $\mathfrak {F} = \mathbb {Q}_p$
,
$\mathfrak {F} = \mathbb {Q}_p$
,
![]() $p \neq 2,3$
and
$p \neq 2,3$
and
![]() $\pi = p$
.
$\pi = p$
.
-
a) We have
 $J_1 = J_0 \cap {\mathrm {Ann}}_{Z \otimes _k Z}(B_{{\mathrm {id}}^2})$
.
$J_1 = J_0 \cap {\mathrm {Ann}}_{Z \otimes _k Z}(B_{{\mathrm {id}}^2})$
. -
b)
 $J_1 = \sigma (J_1)$
.
$J_1 = \sigma (J_1)$
.
Proof. a) Again, write
![]() $A = Z \otimes _k Z$
. Using Equation (26), we see that
$A = Z \otimes _k Z$
. Using Equation (26), we see that
For the reverse inclusion, suppose that
![]() $x \in {\mathrm {Ann}}_A(\ker (f_1) \oplus \ker (g_1))$
. Since the
$x \in {\mathrm {Ann}}_A(\ker (f_1) \oplus \ker (g_1))$
. Since the
![]() $(H,H)$
-bimodule C appearing in Equation (26) satisfies
$(H,H)$
-bimodule C appearing in Equation (26) satisfies
![]() $\dim _k C < \infty $
, there is a nonzero
$\dim _k C < \infty $
, there is a nonzero
![]() $g(\zeta ) \in k[\zeta ]$
such that
$g(\zeta ) \in k[\zeta ]$
such that
![]() $g(\zeta )E^1 \subseteq \ker (f_1) \oplus \ker (g_1)$
. Hence,
$g(\zeta )E^1 \subseteq \ker (f_1) \oplus \ker (g_1)$
. Hence,
![]() $x \cdot (g(\zeta )E^1) = 0$
, so
$x \cdot (g(\zeta )E^1) = 0$
, so
![]() $g(\zeta )(x \cdot E^1) = 0$
. Since
$g(\zeta )(x \cdot E^1) = 0$
. Since
![]() $E^1$
is
$E^1$
is
![]() $k[\zeta ]$
-torsion-free by [Reference Ollivier and SchneiderOS22] Lemma 5.1, this forces
$k[\zeta ]$
-torsion-free by [Reference Ollivier and SchneiderOS22] Lemma 5.1, this forces
![]() $x \cdot E^1 = 0$
. Hence,
$x \cdot E^1 = 0$
. Hence,
![]() $x \in {\mathrm {Ann}}_A(E^1)$
and
$x \in {\mathrm {Ann}}_A(E^1)$
and
Using Corollary 4.4.6 and Lemma 4.4.4, we see that
b) We know that
![]() $B_{{\mathrm {id}}^2}$
is in fact a
$B_{{\mathrm {id}}^2}$
is in fact a
![]() $(Z_\zeta ,Z_\zeta )$
-bimodule so that
$(Z_\zeta ,Z_\zeta )$
-bimodule so that
In view of formula (27) and Lemma 4.4.3.b, it is enough to show that the obvious extension of
![]() $\sigma $
to
$\sigma $
to
![]() $Z_\zeta \otimes Z_\zeta $
preserves
$Z_\zeta \otimes Z_\zeta $
preserves
![]() ${\mathrm {Ann}}_{Z_\zeta \otimes _k Z_\zeta }(B_{{\mathrm {id}}^2})$
.
${\mathrm {Ann}}_{Z_\zeta \otimes _k Z_\zeta }(B_{{\mathrm {id}}^2})$
.
Recall from Theorem 4.3.19 that this ideal is generated by
![]() $\{\delta _{{\mathrm {id}}^2}(a) : a \in Z_\zeta \}$
, where we define
$\{\delta _{{\mathrm {id}}^2}(a) : a \in Z_\zeta \}$
, where we define
![]() $\delta _{{\mathrm {id}}^2}(a) := a \otimes 1 - 1 \otimes {\phi _{{\mathrm {id}}^2}}(a)$
for each
$\delta _{{\mathrm {id}}^2}(a) := a \otimes 1 - 1 \otimes {\phi _{{\mathrm {id}}^2}}(a)$
for each
![]() $a \in A$
. Since
$a \in A$
. Since
![]() $(\phi _{{\mathrm {id}}^2})^2(a) = a$
for all
$(\phi _{{\mathrm {id}}^2})^2(a) = a$
for all
![]() $a \in Z_\zeta $
, we calculate
$a \in Z_\zeta $
, we calculate
Therefore,
![]() $\sigma $
preserves
$\sigma $
preserves
![]() ${\mathrm {Ann}}_{Z_\zeta \otimes _k Z_\zeta }(B_{{\mathrm {id}}^2})$
as required.
${\mathrm {Ann}}_{Z_\zeta \otimes _k Z_\zeta }(B_{{\mathrm {id}}^2})$
as required.
Putting everything together, we obtain
Corollary 4.4.8. Suppose that
![]() $\mathfrak {F} = \mathbb {Q}_p$
,
$\mathfrak {F} = \mathbb {Q}_p$
,
![]() $p \neq 2,3$
and
$p \neq 2,3$
and
![]() $\pi = p$
. Then
$\pi = p$
. Then
Proof. Here,
![]() $d = 3$
, so
$d = 3$
, so
![]() ${\mathrm {Ann}}_{Z \otimes _kZ}(E^{\ast} ) = J_0 \cap J_1 \cap J_2 \cap J_3$
. However,
${\mathrm {Ann}}_{Z \otimes _kZ}(E^{\ast} ) = J_0 \cap J_1 \cap J_2 \cap J_3$
. However,
![]() $J_2 = \sigma (J_1)$
and
$J_2 = \sigma (J_1)$
and
![]() $J_3 = \sigma (J_0)$
by Lemma 4.4.2. Using Lemma 4.4.3.b and Theorem 4.4.7.b, we obtain
$J_3 = \sigma (J_0)$
by Lemma 4.4.2. Using Lemma 4.4.3.b and Theorem 4.4.7.b, we obtain
4.5 The computation of the quotient space
Our goal is to compute the quotient locally ringed space
![]() $\Xi / \mathcal {R}$
, where
$\Xi / \mathcal {R}$
, where
4.5.1 Passing to the normalisation
Corollary 4.4.8 tells us that
Recall from Definition 4.2.3 that
![]() $\theta : \Xi ' \to \Xi $
is the normalisation of
$\theta : \Xi ' \to \Xi $
is the normalisation of
![]() $\Xi $
, where
$\Xi $
, where
![]() $\theta = {\mathrm {Spec}}(\varphi )$
and
$\theta = {\mathrm {Spec}}(\varphi )$
and
![]() $\varphi : Z \to Z'$
is the map sending
$\varphi : Z \to Z'$
is the map sending
![]() $X_\alpha \in Z$
to
$X_\alpha \in Z$
to
![]() $e_\alpha t \in Z' = k[\Omega ][t]$
. Because the localisation map
$e_\alpha t \in Z' = k[\Omega ][t]$
. Because the localisation map
![]() $Z \to Z_\zeta $
factors through
$Z \to Z_\zeta $
factors through
![]() $Z'$
, we see that the
$Z'$
, we see that the
![]() $(Z_\zeta ,Z_\zeta )$
-bimodule
$(Z_\zeta ,Z_\zeta )$
-bimodule
![]() $B_{\mu }$
from Definition 4.3.9 can be viewed as a
$B_{\mu }$
from Definition 4.3.9 can be viewed as a
![]() $(Z',Z')$
-bimodule via restriction along
$(Z',Z')$
-bimodule via restriction along
![]() $Z' \hookrightarrow Z_\zeta $
.
$Z' \hookrightarrow Z_\zeta $
.
Definition 4.5.1. We define
![]() $\mathcal {R}^{\prime }_\mu := V\left (\ker {\mathrm {mult}}_{Z'} \hspace {0.1cm} \cap \hspace {0.1cm} {\mathrm {Ann}}_{Z' \otimes _k Z'}(B_\mu )\right ) \subset \Xi ' \times \Xi '.$
$\mathcal {R}^{\prime }_\mu := V\left (\ker {\mathrm {mult}}_{Z'} \hspace {0.1cm} \cap \hspace {0.1cm} {\mathrm {Ann}}_{Z' \otimes _k Z'}(B_\mu )\right ) \subset \Xi ' \times \Xi '.$
Lemma 4.5.2. Write
![]() $A' = Z' \otimes _k Z'$
. Then we have
$A' = Z' \otimes _k Z'$
. Then we have
 $$\begin{align*}\ker {\mathrm{mult}}_{Z'} = A'(t \otimes 1 - 1 \otimes t) + \sum\limits_{\alpha \in \widehat{\Omega}} A'(e_\alpha \otimes 1 - 1 \otimes e_\alpha).\end{align*}$$
$$\begin{align*}\ker {\mathrm{mult}}_{Z'} = A'(t \otimes 1 - 1 \otimes t) + \sum\limits_{\alpha \in \widehat{\Omega}} A'(e_\alpha \otimes 1 - 1 \otimes e_\alpha).\end{align*}$$
Proof. The k-algebra
![]() $Z' = k[\Omega ][t]$
is generated by
$Z' = k[\Omega ][t]$
is generated by
![]() $\{t\} \cup \{e_\alpha : \alpha \in \widehat {\Omega }\}$
. Use Lemma 4.3.4.b.
$\{t\} \cup \{e_\alpha : \alpha \in \widehat {\Omega }\}$
. Use Lemma 4.3.4.b.
It turns out that
![]() ${\mathrm {Ann}}_{Z' \otimes _k Z'}(B_\mu )$
is slightly easier to compute than
${\mathrm {Ann}}_{Z' \otimes _k Z'}(B_\mu )$
is slightly easier to compute than
![]() ${\mathrm {Ann}}_{Z \otimes _k Z}(B_\mu )$
.
${\mathrm {Ann}}_{Z \otimes _k Z}(B_\mu )$
.
Proposition 4.5.3. Write
![]() $A' = Z' \otimes _k Z'$
. Then for any
$A' = Z' \otimes _k Z'$
. Then for any
![]() $\mu \in \widehat {\Omega }$
, we have
$\mu \in \widehat {\Omega }$
, we have
 $$\begin{align*}{\mathrm{Ann}}_{A'}(B_{\mu}) = A'(t \otimes t - 1 \otimes 1) + \sum\limits_{\alpha \in \widehat{\Omega}} A'(e_\alpha \otimes 1 - 1 \otimes e_{\mu/\alpha}).\end{align*}$$
$$\begin{align*}{\mathrm{Ann}}_{A'}(B_{\mu}) = A'(t \otimes t - 1 \otimes 1) + \sum\limits_{\alpha \in \widehat{\Omega}} A'(e_\alpha \otimes 1 - 1 \otimes e_{\mu/\alpha}).\end{align*}$$
Proof. By Corollary 4.2.7, there is a k-algebra isomorphism
![]() $Z^{\prime }_t \cong Z_\zeta $
. Under this isomorphism,
$Z^{\prime }_t \cong Z_\zeta $
. Under this isomorphism,
![]() $t \in Z'$
maps to
$t \in Z'$
maps to
![]() $\zeta \in Z_\zeta $
and
$\zeta \in Z_\zeta $
and
![]() $e_\alpha \in Z'$
maps to
$e_\alpha \in Z'$
maps to
![]() $\epsilon _\alpha = X_\alpha /\zeta \in Z_\zeta $
, for each
$\epsilon _\alpha = X_\alpha /\zeta \in Z_\zeta $
, for each
![]() $\alpha \in \widehat {\Omega }$
. This isomorphism also induces k-algebra isomorphisms
$\alpha \in \widehat {\Omega }$
. This isomorphism also induces k-algebra isomorphisms
![]() $A^{\prime }_{t \otimes t} \cong (Z^{\prime }_t) \otimes _k (Z^{\prime }_t) \cong (Z_\zeta ) \otimes _k (Z_\zeta ) \cong R$
. Regarding
$A^{\prime }_{t \otimes t} \cong (Z^{\prime }_t) \otimes _k (Z^{\prime }_t) \cong (Z_\zeta ) \otimes _k (Z_\zeta ) \cong R$
. Regarding
![]() $B_{\mu }$
as an
$B_{\mu }$
as an
![]() $A^{\prime }_{t \otimes t}$
-module via this isomorphism, we can apply Corollary 4.3.20 to obtain
$A^{\prime }_{t \otimes t}$
-module via this isomorphism, we can apply Corollary 4.3.20 to obtain
 $$\begin{align*}{\mathrm{Ann}}_{A^{\prime}_{t \otimes t}}(B_{\mu}) = A^{\prime}_{t \otimes t} (t \otimes 1 - 1 \otimes t^{-1}) + \sum\limits_{\alpha \in \widehat{\Omega}} A^{\prime}_{t \otimes t}(e_\alpha \otimes 1 - 1 \otimes e_{\mu/\alpha}).\end{align*}$$
$$\begin{align*}{\mathrm{Ann}}_{A^{\prime}_{t \otimes t}}(B_{\mu}) = A^{\prime}_{t \otimes t} (t \otimes 1 - 1 \otimes t^{-1}) + \sum\limits_{\alpha \in \widehat{\Omega}} A^{\prime}_{t \otimes t}(e_\alpha \otimes 1 - 1 \otimes e_{\mu/\alpha}).\end{align*}$$
Let I denote the ideal of
![]() $A'$
appearing on the right-hand side of the statement. Then
$A'$
appearing on the right-hand side of the statement. Then
![]() $A'/I$
is isomorphic to
$A'/I$
is isomorphic to
![]() $S[t, t^{-1}]$
as a k-algebra, where
$S[t, t^{-1}]$
as a k-algebra, where
![]() $S := k[\Omega ]^{\otimes 2} / \left \langle e_\alpha \otimes 1 - 1 \otimes e_{\mu /\alpha } : \alpha \in \widehat {\Omega }\right \rangle $
. This ring is t-torsion-free. Therefore,
$S := k[\Omega ]^{\otimes 2} / \left \langle e_\alpha \otimes 1 - 1 \otimes e_{\mu /\alpha } : \alpha \in \widehat {\Omega }\right \rangle $
. This ring is t-torsion-free. Therefore,
![]() $A'/I$
is
$A'/I$
is
![]() $t \otimes t$
-torsion-free, so
$t \otimes t$
-torsion-free, so
![]() $A' \cap (I \cdot A^{\prime }_{t \otimes t}) = I$
. Hence,
$A' \cap (I \cdot A^{\prime }_{t \otimes t}) = I$
. Hence,
![]() ${\mathrm {Ann}}_{A'}(B_{\mu }) = A' \cap {\mathrm {Ann}}_{A^{\prime }_{t \otimes t}}(B_{\mu }) = A' \cap (I \cdot A^{\prime }_{t \otimes t}) = I.$
${\mathrm {Ann}}_{A'}(B_{\mu }) = A' \cap {\mathrm {Ann}}_{A^{\prime }_{t \otimes t}}(B_{\mu }) = A' \cap (I \cdot A^{\prime }_{t \otimes t}) = I.$
Recall the coequaliser diagram ![]() from Proposition 4.2.5.
from Proposition 4.2.5.
Proposition 4.5.4. Let
![]() $q' : \Xi ' \to \Xi '/\mathcal {R}^{\prime }_\mu $
be a coequaliser in
$q' : \Xi ' \to \Xi '/\mathcal {R}^{\prime }_\mu $
be a coequaliser in
![]() ${\mathrm {LRS}}$
of
${\mathrm {LRS}}$
of  , and let
, and let
![]() $s : \Xi '/\mathcal {R}^{\prime }_\mu \to (\Xi '/\mathcal {R}^{\prime }_\mu )/\Xi _{{\mathrm {sing}}}$
be a coequaliser in
$s : \Xi '/\mathcal {R}^{\prime }_\mu \to (\Xi '/\mathcal {R}^{\prime }_\mu )/\Xi _{{\mathrm {sing}}}$
be a coequaliser in
![]() ${\mathrm {LRS}}$
of
${\mathrm {LRS}}$
of  . Then
. Then
Proof. The situation is summarised in the following diagram:

The result now follows from Lemma A.2, provided we can find an epimorphism
![]() $\theta ' : \mathcal {R}^{\prime }_\mu \to \mathcal {R}_\mu $
in
$\theta ' : \mathcal {R}^{\prime }_\mu \to \mathcal {R}_\mu $
in
![]() ${\mathrm {LRS}}$
making the diagram commute, in the sense that
${\mathrm {LRS}}$
making the diagram commute, in the sense that
![]() ${\mathrm {pr}}_i \theta ' = \theta {\mathrm {pr}}^{\prime }_i$
holds for
${\mathrm {pr}}_i \theta ' = \theta {\mathrm {pr}}^{\prime }_i$
holds for
![]() $i=1,2$
.
$i=1,2$
.
Write
![]() $A = Z \otimes _k Z$
and
$A = Z \otimes _k Z$
and
![]() $A' = Z' \otimes _k Z'$
; then by definition, we have
$A' = Z' \otimes _k Z'$
; then by definition, we have
 $$\begin{align*}\mathcal{O}(\mathcal{R}_\mu) = \frac{A}{\ker {\mathrm{mult}}_Z \hspace{0.1cm} \cap \hspace{0.1cm} {\mathrm{Ann}}_A(B_\mu)} \quad\text{and}\quad \mathcal{O}(\mathcal{R}^{\prime}_\mu) = \frac{A'}{\ker {\mathrm{mult}}_{Z'} \hspace{0.1cm} \cap \hspace{0.1cm} {\mathrm{Ann}}_{A'}(B_\mu)}.\end{align*}$$
$$\begin{align*}\mathcal{O}(\mathcal{R}_\mu) = \frac{A}{\ker {\mathrm{mult}}_Z \hspace{0.1cm} \cap \hspace{0.1cm} {\mathrm{Ann}}_A(B_\mu)} \quad\text{and}\quad \mathcal{O}(\mathcal{R}^{\prime}_\mu) = \frac{A'}{\ker {\mathrm{mult}}_{Z'} \hspace{0.1cm} \cap \hspace{0.1cm} {\mathrm{Ann}}_{A'}(B_\mu)}.\end{align*}$$
The map
![]() $\varphi \otimes \varphi : A \to A'$
is an injective k-algebra homomorphism; furthermore we have
$\varphi \otimes \varphi : A \to A'$
is an injective k-algebra homomorphism; furthermore we have
Therefore,
![]() $\varphi \otimes \varphi $
descends to a natural injective k-algebra homomorphism
$\varphi \otimes \varphi $
descends to a natural injective k-algebra homomorphism
We define
![]() $\theta ' := {\mathrm {Spec}}(\overline {\varphi \otimes \varphi }) : \mathcal {R}^{\prime }_\mu \to \mathcal {R}_\mu $
to be the corresponding morphism of affine schemes. The following diagram of commutative rings
$\theta ' := {\mathrm {Spec}}(\overline {\varphi \otimes \varphi }) : \mathcal {R}^{\prime }_\mu \to \mathcal {R}_\mu $
to be the corresponding morphism of affine schemes. The following diagram of commutative rings

is readily checked to be commutative: For example, we have
Because the schemes
![]() $\Xi ,\Xi ',\mathcal {R}_\mu ,\mathcal {R}^{\prime }_\mu $
are all affine, it follows that
$\Xi ,\Xi ',\mathcal {R}_\mu ,\mathcal {R}^{\prime }_\mu $
are all affine, it follows that
![]() ${\mathrm {pr}}_i \theta ' = \theta {\mathrm {pr}}^{\prime }_i$
holds for
${\mathrm {pr}}_i \theta ' = \theta {\mathrm {pr}}^{\prime }_i$
holds for
![]() $i=1,2$
. It remains to show that
$i=1,2$
. It remains to show that
![]() $\theta '$
is an epimorphism in
$\theta '$
is an epimorphism in
![]() ${\mathrm {LRS}}$
, and this follows from Lemma 4.5.5 below, once we check its two conditions.
${\mathrm {LRS}}$
, and this follows from Lemma 4.5.5 below, once we check its two conditions.
a) We note that
![]() $Z' = k[\Omega ][t]$
is a finitely generated Z-module via
$Z' = k[\Omega ][t]$
is a finitely generated Z-module via
![]() $\varphi : Z \to Z'$
: indeed,
$\varphi : Z \to Z'$
: indeed,
![]() $\Omega \subset Z'$
is a finite generating set as a
$\Omega \subset Z'$
is a finite generating set as a
![]() $k[t]$
-module, and
$k[t]$
-module, and
![]() $k[t] = k[\varphi (\zeta )] \subseteq \varphi (Z)$
. Hence,
$k[t] = k[\varphi (\zeta )] \subseteq \varphi (Z)$
. Hence,
![]() $A'$
is a finitely generated A-module, so
$A'$
is a finitely generated A-module, so
![]() $\mathcal {O}(\mathcal {R}^{\prime }_\mu )$
is a finitely generated
$\mathcal {O}(\mathcal {R}^{\prime }_\mu )$
is a finitely generated
![]() $\mathcal {O}(\mathcal {R}_\mu )$
-module. Hence,
$\mathcal {O}(\mathcal {R}_\mu )$
-module. Hence,
![]() $|\theta '|$
is surjective by [Reference Atiyah and MacDonaldAM] Proposition 5.1 and Theorem 5.10.
$|\theta '|$
is surjective by [Reference Atiyah and MacDonaldAM] Proposition 5.1 and Theorem 5.10.
b) The map
![]() $(\theta ')^\sharp (\mathcal {R}_\mu ) = \overline {\varphi \otimes \varphi }$
is injective, as we saw above in Equation (29).
$(\theta ')^\sharp (\mathcal {R}_\mu ) = \overline {\varphi \otimes \varphi }$
is injective, as we saw above in Equation (29).
Lemma 4.5.5.
Footnote
4
Let
![]() $f : Y \to X$
be a morphism of affine schemes. Suppose that
$f : Y \to X$
be a morphism of affine schemes. Suppose that
-
a)
 $|f| : |Y| \to |X|$
is surjective,
$|f| : |Y| \to |X|$
is surjective, -
b)
 $f^\sharp (X) : \mathcal {O}(X) \to \mathcal {O}(Y)$
is injective.
$f^\sharp (X) : \mathcal {O}(X) \to \mathcal {O}(Y)$
is injective.
Then
![]() $f : Y \to X$
is an epimorphism in
$f : Y \to X$
is an epimorphism in
![]() ${\mathrm {LRS}}$
.
${\mathrm {LRS}}$
.
Proof. Suppose that
![]() $uf = vf$
for some morphisms
$uf = vf$
for some morphisms
![]() $u,v : X \to Z$
in
$u,v : X \to Z$
in
![]() ${\mathrm {LRS}}$
. Then
${\mathrm {LRS}}$
. Then
![]() $|u| |f| = |v| |f|$
implies that
$|u| |f| = |v| |f|$
implies that
![]() $|u| = |v|$
because
$|u| = |v|$
because
![]() $|f|$
is surjective. Hence, it remains to show that
$|f|$
is surjective. Hence, it remains to show that
![]() $u^\sharp = v^\sharp $
. Now,
$u^\sharp = v^\sharp $
. Now,
![]() $|u|_\ast (f^\sharp ) \circ u^\sharp = (uf)^\sharp = (vf)^\sharp = |v|_\ast (f^\sharp ) \circ v^\sharp $
, so it is enough to show that
$|u|_\ast (f^\sharp ) \circ u^\sharp = (uf)^\sharp = (vf)^\sharp = |v|_\ast (f^\sharp ) \circ v^\sharp $
, so it is enough to show that
![]() $f^\sharp : \mathcal {O}_X \to f_\ast \mathcal {O}_Y$
is injective. This can be checked on basic open subsets
$f^\sharp : \mathcal {O}_X \to f_\ast \mathcal {O}_Y$
is injective. This can be checked on basic open subsets
![]() $D(g)$
of X,
$D(g)$
of X,
![]() $g \in \mathcal {O}(X)$
. But since
$g \in \mathcal {O}(X)$
. But since
![]() $X, Y$
are affine, the map
$X, Y$
are affine, the map
![]() $f^\sharp (D(g)) : \mathcal {O}(D(g)) \to \mathcal {O}(f^{-1}D(g))$
is the localisation of the injective map
$f^\sharp (D(g)) : \mathcal {O}(D(g)) \to \mathcal {O}(f^{-1}D(g))$
is the localisation of the injective map
![]() $f^\sharp (X) : \mathcal {O}(X) \to \mathcal {O}(Y)$
at g and is therefore also injective.
$f^\sharp (X) : \mathcal {O}(X) \to \mathcal {O}(Y)$
at g and is therefore also injective.
4.5.2 Calculating
 $\Xi '/\mathcal {R}^{\prime }_\mu $
$\Xi '/\mathcal {R}^{\prime }_\mu $
For each
![]() $\alpha \in \widehat {\Omega }$
, we let
$\alpha \in \widehat {\Omega }$
, we let
![]() $\Xi _\alpha := V(1 - e_\alpha ) \subset \Xi '$
be the closed subscheme cut out by the idempotent
$\Xi _\alpha := V(1 - e_\alpha ) \subset \Xi '$
be the closed subscheme cut out by the idempotent
![]() $1 - e_\alpha \in \mathcal {O}(\Xi ') = k[\Omega ][t]$
. Let
$1 - e_\alpha \in \mathcal {O}(\Xi ') = k[\Omega ][t]$
. Let
![]() $t_\alpha $
be the image of
$t_\alpha $
be the image of
![]() $t \in \mathcal {O}(\Xi ')$
in
$t \in \mathcal {O}(\Xi ')$
in
![]() $\mathcal {O}(\Xi ^{\prime }_\alpha )$
; then
$\mathcal {O}(\Xi ^{\prime }_\alpha )$
; then
![]() $\mathcal {O}(\Xi ^{\prime }_\alpha ) = k[t_\alpha ]$
and
$\mathcal {O}(\Xi ^{\prime }_\alpha ) = k[t_\alpha ]$
and
![]() $\Xi ' = \coprod _{\alpha \in \widehat {\Omega }} \Xi ^{\prime }_\alpha $
. It follows that
$\Xi ' = \coprod _{\alpha \in \widehat {\Omega }} \Xi ^{\prime }_\alpha $
. It follows that
 $$\begin{align*}\Xi' \times \Xi' = \coprod_{\alpha,\beta \in \widehat{\Omega}} \Xi^{\prime}_\alpha \times \Xi^{\prime}_\beta.\end{align*}$$
$$\begin{align*}\Xi' \times \Xi' = \coprod_{\alpha,\beta \in \widehat{\Omega}} \Xi^{\prime}_\alpha \times \Xi^{\prime}_\beta.\end{align*}$$
We write
![]() $\mathcal {R}^{\prime }_{\mu ,\alpha ,\beta } := \mathcal {R}^{\prime }_\mu \cap (\Xi ^{\prime }_\alpha \times \Xi ^{\prime }_\beta )$
for all
$\mathcal {R}^{\prime }_{\mu ,\alpha ,\beta } := \mathcal {R}^{\prime }_\mu \cap (\Xi ^{\prime }_\alpha \times \Xi ^{\prime }_\beta )$
for all
![]() $\alpha , \beta \in \widehat {\Omega }$
so that
$\alpha , \beta \in \widehat {\Omega }$
so that
 $$\begin{align*}\mathcal{R}^{\prime}_\mu = \coprod_{\alpha,\beta \in \widehat{\Omega}} \mathcal{R}^{\prime}_{\mu,\alpha,\beta}.\end{align*}$$
$$\begin{align*}\mathcal{R}^{\prime}_\mu = \coprod_{\alpha,\beta \in \widehat{\Omega}} \mathcal{R}^{\prime}_{\mu,\alpha,\beta}.\end{align*}$$
For each
![]() $\alpha , \beta \in \widehat {\Omega }$
, will identify
$\alpha , \beta \in \widehat {\Omega }$
, will identify
![]() $\mathcal {O}(\Xi ^{\prime }_\alpha \times \Xi ^{\prime }_\beta ) = k[t_\alpha ] \otimes _k k[t_\beta ]$
with the polynomial algebra
$\mathcal {O}(\Xi ^{\prime }_\alpha \times \Xi ^{\prime }_\beta ) = k[t_\alpha ] \otimes _k k[t_\beta ]$
with the polynomial algebra
![]() $k[x,y]$
, via
$k[x,y]$
, via
![]() $x \mapsto t_\alpha \otimes 1$
and
$x \mapsto t_\alpha \otimes 1$
and
![]() $y \mapsto 1 \otimes t_\beta $
. With this notation in hand, we can now calculate the defining equations for each
$y \mapsto 1 \otimes t_\beta $
. With this notation in hand, we can now calculate the defining equations for each
![]() $\mathcal {R}^{\prime }_{\mu ,\alpha ,\beta }$
.
$\mathcal {R}^{\prime }_{\mu ,\alpha ,\beta }$
.
Proposition 4.5.6. For every
![]() $\mu ,\alpha , \beta \in \widehat {\Omega }$
, we have
$\mu ,\alpha , \beta \in \widehat {\Omega }$
, we have
Proof. Consider the canonical projection
![]() $\pi _{\alpha ,\beta } : A' = \mathcal {O}(\Xi ' \times \Xi ') \twoheadrightarrow \mathcal {O}(\Xi ^{\prime }_\alpha \times \Xi ^{\prime }_\beta ) = k[x,y]$
with kernel
$\pi _{\alpha ,\beta } : A' = \mathcal {O}(\Xi ' \times \Xi ') \twoheadrightarrow \mathcal {O}(\Xi ^{\prime }_\alpha \times \Xi ^{\prime }_\beta ) = k[x,y]$
with kernel
![]() $\ker \pi _{\alpha ,\beta } = \langle (1 - e_\alpha ) \otimes 1, 1 \otimes (1 - e_\beta ) \rangle $
. Then for all
$\ker \pi _{\alpha ,\beta } = \langle (1 - e_\alpha ) \otimes 1, 1 \otimes (1 - e_\beta ) \rangle $
. Then for all
![]() $\gamma ,\delta \in \widehat {\Omega }$
, we have
$\gamma ,\delta \in \widehat {\Omega }$
, we have
 $$ \begin{align} \begin{array}{lll}\pi_{\alpha,\beta}( e_{\gamma} \otimes e_{\delta} ) &= \delta_{\alpha,\gamma} \delta_{\beta,\delta}, \\ \pi_{\alpha,\beta}(e_\gamma \otimes 1) &= \delta_{\alpha,\gamma}, \\ \pi_{\alpha,\beta}(1 \otimes e_\delta) &= \delta_{\beta,\delta}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{lll}\pi_{\alpha,\beta}( e_{\gamma} \otimes e_{\delta} ) &= \delta_{\alpha,\gamma} \delta_{\beta,\delta}, \\ \pi_{\alpha,\beta}(e_\gamma \otimes 1) &= \delta_{\alpha,\gamma}, \\ \pi_{\alpha,\beta}(1 \otimes e_\delta) &= \delta_{\beta,\delta}. \end{array} \end{align} $$
Using Lemma 4.5.2 together with Equations (30), we have
 $$ \begin{align*} \pi_{\alpha,\beta}(\ker {\mathrm{mult}}_{Z'}) &= \langle x - y \rangle + \sum\limits_{\nu \in \widehat{\Omega}} \langle \pi_{\alpha,\beta}(e_\nu \otimes 1) - \pi_{\alpha,\beta}(1 \otimes e_\nu) \rangle \\ &= \langle x - y \rangle + \sum\limits_{\nu \in \widehat{\Omega}} \langle \delta_{\alpha,\nu} - \delta_{\beta,\nu} \rangle \\ &= \langle (x - y)^{\delta_{\alpha,\beta}} \rangle.\end{align*} $$
$$ \begin{align*} \pi_{\alpha,\beta}(\ker {\mathrm{mult}}_{Z'}) &= \langle x - y \rangle + \sum\limits_{\nu \in \widehat{\Omega}} \langle \pi_{\alpha,\beta}(e_\nu \otimes 1) - \pi_{\alpha,\beta}(1 \otimes e_\nu) \rangle \\ &= \langle x - y \rangle + \sum\limits_{\nu \in \widehat{\Omega}} \langle \delta_{\alpha,\nu} - \delta_{\beta,\nu} \rangle \\ &= \langle (x - y)^{\delta_{\alpha,\beta}} \rangle.\end{align*} $$
Similarly, using Proposition 4.5.3 together with Equations (30), we have
 $$ \begin{align*} \pi_{\alpha,\beta}({\mathrm{Ann}}_{A'}(B_\mu)) &= \langle xy-1 \rangle + \sum\limits_{\nu \in \widehat{\Omega}} \langle \pi_{\alpha,\beta}(e_\nu \otimes 1) - \pi_{\alpha,\beta}(1 \otimes e_{\mu/\nu}) \rangle \\ &= \langle xy - 1 \rangle + \sum\limits_{\nu \in \widehat{\Omega}} \langle \delta_{\alpha,\nu} - \delta_{\beta,\mu/\nu} \rangle \\ &= \langle (xy - 1)^{\delta_{\alpha,\mu/\beta}} \rangle.\end{align*} $$
$$ \begin{align*} \pi_{\alpha,\beta}({\mathrm{Ann}}_{A'}(B_\mu)) &= \langle xy-1 \rangle + \sum\limits_{\nu \in \widehat{\Omega}} \langle \pi_{\alpha,\beta}(e_\nu \otimes 1) - \pi_{\alpha,\beta}(1 \otimes e_{\mu/\nu}) \rangle \\ &= \langle xy - 1 \rangle + \sum\limits_{\nu \in \widehat{\Omega}} \langle \delta_{\alpha,\nu} - \delta_{\beta,\mu/\nu} \rangle \\ &= \langle (xy - 1)^{\delta_{\alpha,\mu/\beta}} \rangle.\end{align*} $$
By the elementary Lemma 4.5.7 below, we then have
 $$ \begin{align*} \pi_{\alpha,\beta}(\ker {\mathrm{mult}}_{Z'} \hspace{0.1cm} \cap \hspace{0.1cm} {\mathrm{Ann}}_{A'}(B_\mu)) &= \pi_{\alpha,\beta}(\ker {\mathrm{mult}}_{Z'}) \hspace{0.1cm} \cap \hspace{0.1cm} \pi_{\alpha,\beta}({\mathrm{Ann}}_{A'}(B_\mu)) \\ &= \langle (x-y)^{\delta_{\alpha,\beta}} \rangle \hspace{0.1cm} \cap \hspace{0.1cm} \langle (xy-1)^{\delta_{\alpha, \mu/\beta}}\rangle \\ &= \langle (x-y)^{\delta_{\alpha,\beta}} (xy-1)^{\delta_{\alpha, \mu/\beta}}\rangle. \end{align*} $$
$$ \begin{align*} \pi_{\alpha,\beta}(\ker {\mathrm{mult}}_{Z'} \hspace{0.1cm} \cap \hspace{0.1cm} {\mathrm{Ann}}_{A'}(B_\mu)) &= \pi_{\alpha,\beta}(\ker {\mathrm{mult}}_{Z'}) \hspace{0.1cm} \cap \hspace{0.1cm} \pi_{\alpha,\beta}({\mathrm{Ann}}_{A'}(B_\mu)) \\ &= \langle (x-y)^{\delta_{\alpha,\beta}} \rangle \hspace{0.1cm} \cap \hspace{0.1cm} \langle (xy-1)^{\delta_{\alpha, \mu/\beta}}\rangle \\ &= \langle (x-y)^{\delta_{\alpha,\beta}} (xy-1)^{\delta_{\alpha, \mu/\beta}}\rangle. \end{align*} $$
Recalling that
![]() $\mathcal {R}^{\prime }_{\mu ,\alpha ,\beta } = \mathcal {R}^{\prime }_\mu \cap (\Xi ^{\prime }_\alpha \times \Xi ^{\prime }_\beta )$
and using Definition 4.5.1, we have
$\mathcal {R}^{\prime }_{\mu ,\alpha ,\beta } = \mathcal {R}^{\prime }_\mu \cap (\Xi ^{\prime }_\alpha \times \Xi ^{\prime }_\beta )$
and using Definition 4.5.1, we have
The result follows.
Lemma 4.5.7. Let A be a ring, let
![]() $e,f \in A$
be two central idempotents and consider the canonical projection
$e,f \in A$
be two central idempotents and consider the canonical projection
![]() $\pi : A \twoheadrightarrow A / \langle 1-e,1-f\rangle $
. Then for every pair of ideals
$\pi : A \twoheadrightarrow A / \langle 1-e,1-f\rangle $
. Then for every pair of ideals
![]() $I,J$
of A we have
$I,J$
of A we have
![]() $\pi (I \cap J) = \pi (I) \cap \pi (J)$
.
$\pi (I \cap J) = \pi (I) \cap \pi (J)$
.
Proof. Let
![]() $a \in \pi (I) \cap \pi (J)$
. Then we can find
$a \in \pi (I) \cap \pi (J)$
. Then we can find
![]() $x \in I$
and
$x \in I$
and
![]() $y \in J$
such that
$y \in J$
such that
![]() $a = \pi (x) = \pi (y)$
. Now,
$a = \pi (x) = \pi (y)$
. Now,
![]() $x = (1-e+e)(1-f+f)x$
implies that
$x = (1-e+e)(1-f+f)x$
implies that
![]() $\pi (x) = \pi (efx)$
and similarly
$\pi (x) = \pi (efx)$
and similarly
![]() $\pi (y) = \pi (efy)$
. Hence,
$\pi (y) = \pi (efy)$
. Hence,
![]() $\pi (efx) = \pi (x) = \pi (y) = \pi (efy)$
, so
$\pi (efx) = \pi (x) = \pi (y) = \pi (efy)$
, so
![]() $efx - efy \in \ker \pi $
. But
$efx - efy \in \ker \pi $
. But
![]() $ef(1-e) = ef(1-f) = 0$
, so
$ef(1-e) = ef(1-f) = 0$
, so
![]() $ef \ker \pi = 0$
. Hence,
$ef \ker \pi = 0$
. Hence,
![]() $ef(efx - efy) = 0$
, so
$ef(efx - efy) = 0$
, so
![]() $efx = e^2f^2x = e^2f^2y = efy$
. Since
$efx = e^2f^2x = e^2f^2y = efy$
. Since
![]() $efx \in I$
and
$efx \in I$
and
![]() $efy \in J$
, we see that
$efy \in J$
, we see that
![]() $efx = efy \in I \cap J$
. Hence,
$efx = efy \in I \cap J$
. Hence,
![]() $a = \pi (x) = \pi (efx) \in \pi (I \cap J)$
, so
$a = \pi (x) = \pi (efx) \in \pi (I \cap J)$
, so
![]() $\pi (I) \cap \pi (J) \subseteq \pi (I \cap J)$
. The reverse inclusion is clear.
$\pi (I) \cap \pi (J) \subseteq \pi (I \cap J)$
. The reverse inclusion is clear.
We introduce an equivalence relation
![]() $\underset {\mu }{\sim }{}$
on
$\underset {\mu }{\sim }{}$
on
![]() $\widehat {\Omega }$
by setting
$\widehat {\Omega }$
by setting
![]() $\alpha \underset {\mu }{\sim }{} \beta $
if and only if
$\alpha \underset {\mu }{\sim }{} \beta $
if and only if
![]() $\beta \in \{\alpha , \mu /\alpha \}$
. For an equivalence class
$\beta \in \{\alpha , \mu /\alpha \}$
. For an equivalence class
![]() $\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}$
, we write
$\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}$
, we write
 $$ \begin{align} \Xi^{\prime}_\gamma := \coprod_{\alpha \in \gamma} \Xi^{\prime}_\alpha \quad\text{and}\quad \mathcal{R}^{\prime}_{\mu,\gamma} := \coprod_{\alpha,\beta \in \gamma} \mathcal{R}^{\prime}_{\mu,\alpha,\beta}.\end{align} $$
$$ \begin{align} \Xi^{\prime}_\gamma := \coprod_{\alpha \in \gamma} \Xi^{\prime}_\alpha \quad\text{and}\quad \mathcal{R}^{\prime}_{\mu,\gamma} := \coprod_{\alpha,\beta \in \gamma} \mathcal{R}^{\prime}_{\mu,\alpha,\beta}.\end{align} $$
We use the projection maps
![]() ${\mathrm {pr}}_1^{\Xi ^{\prime }_\gamma }, {\mathrm {pr}}_2^{\Xi ^{\prime }_\gamma } : \Xi ^{\prime }_\gamma \times \Xi ^{\prime }_\gamma \to \Xi ^{\prime }_\gamma $
to define the map
${\mathrm {pr}}_1^{\Xi ^{\prime }_\gamma }, {\mathrm {pr}}_2^{\Xi ^{\prime }_\gamma } : \Xi ^{\prime }_\gamma \times \Xi ^{\prime }_\gamma \to \Xi ^{\prime }_\gamma $
to define the map
Then for each
![]() $\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}$
, we may form the coequaliser diagram in
$\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}$
, we may form the coequaliser diagram in
![]() ${\mathrm {LRS}}$
${\mathrm {LRS}}$

Lemma 4.5.8. We have
![]() $\Xi ' = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} \Xi ^{\prime }_\gamma $
and
$\Xi ' = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} \Xi ^{\prime }_\gamma $
and
![]() $\mathcal {R}^{\prime }_\mu = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}}\mathcal {R}^{\prime }_{\mu ,\gamma }$
.
$\mathcal {R}^{\prime }_\mu = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}}\mathcal {R}^{\prime }_{\mu ,\gamma }$
.
Proof. Only the second statement needs proof. For this, we have
 $$\begin{align*}\mathcal{R}^{\prime}_\mu = \coprod\limits_{\alpha,\beta \in \widehat{\Omega}} \mathcal{R}^{\prime}_{\mu,\alpha,\beta} = \coprod\limits_{\gamma \in \widehat{\Omega}/\underset{\mu}{\sim}{}}\coprod\limits_{\alpha \in \gamma} \coprod\limits_{\beta \in \widehat{\Omega}} \mathcal{R}^{\prime}_{\mu,\alpha,\beta}.\end{align*}$$
$$\begin{align*}\mathcal{R}^{\prime}_\mu = \coprod\limits_{\alpha,\beta \in \widehat{\Omega}} \mathcal{R}^{\prime}_{\mu,\alpha,\beta} = \coprod\limits_{\gamma \in \widehat{\Omega}/\underset{\mu}{\sim}{}}\coprod\limits_{\alpha \in \gamma} \coprod\limits_{\beta \in \widehat{\Omega}} \mathcal{R}^{\prime}_{\mu,\alpha,\beta}.\end{align*}$$
But by Proposition 4.5.6, we have
![]() $\mathcal {R}^{\prime }_{\mu ,\alpha ,\beta } = \emptyset $
if
$\mathcal {R}^{\prime }_{\mu ,\alpha ,\beta } = \emptyset $
if
![]() $\beta \notin \{\alpha , \mu /\alpha \}$
. Hence,
$\beta \notin \{\alpha , \mu /\alpha \}$
. Hence,
![]() $\mathcal {R}^{\prime }_\mu = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} \mathcal {R}^{\prime }_{\mu ,\gamma }$
.
$\mathcal {R}^{\prime }_\mu = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} \mathcal {R}^{\prime }_{\mu ,\gamma }$
.
Corollary 4.5.9. We have
![]() $\Xi '/\mathcal {R}^{\prime }_\mu \cong \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} \Xi ^{\prime }_\gamma / \mathcal {R}^{\prime }_{\mu ,\gamma }$
in
$\Xi '/\mathcal {R}^{\prime }_\mu \cong \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} \Xi ^{\prime }_\gamma / \mathcal {R}^{\prime }_{\mu ,\gamma }$
in
![]() ${\mathrm {LRS}}$
.
${\mathrm {LRS}}$
.
Proof. We have
![]() $\Xi ' = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} \Xi ^{\prime }_\gamma $
and
$\Xi ' = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} \Xi ^{\prime }_\gamma $
and
![]() $\mathcal {R}^{\prime }_\mu = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}}\mathcal {R}^{\prime }_{\mu ,\gamma }$
by Lemma 4.5.8. Note also that
$\mathcal {R}^{\prime }_\mu = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}}\mathcal {R}^{\prime }_{\mu ,\gamma }$
by Lemma 4.5.8. Note also that
 ${\mathrm {pr}}_i^{\Xi '} = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} f_i^\gamma $
for
${\mathrm {pr}}_i^{\Xi '} = \coprod \limits _{\gamma \in \widehat {\Omega }/\underset {\mu }{\sim }{}} f_i^\gamma $
for
![]() $i = 1,2$
. Now, the result follows from Lemma A.3.
$i = 1,2$
. Now, the result follows from Lemma A.3.
Recall [Reference de JongSta] Section 01JA that a gluing datum in
![]() ${\mathrm {LRS}}$
consists of the following data:
${\mathrm {LRS}}$
consists of the following data:
-
• an index set I,
-
• a locally ringed space
 $X_i$
for each
$X_i$
for each
 $i \in I$
,
$i \in I$
, -
• an open subspace
 $\iota _{i,j} : U_{i,j} \hookrightarrow X_i$
for each
$\iota _{i,j} : U_{i,j} \hookrightarrow X_i$
for each
 $i,j \in I$
,
$i,j \in I$
, -
• an isomorphism
 $\varphi _{i,j} : U_{i,j} \stackrel {\cong }{\longrightarrow } U_{j,i}$
in
$\varphi _{i,j} : U_{i,j} \stackrel {\cong }{\longrightarrow } U_{j,i}$
in
 ${\mathrm {LRS}}$
for all
${\mathrm {LRS}}$
for all
 $i,j \in I$
$i,j \in I$
such that
-
1.
 $U_{i,i} = X_i$
for all
$U_{i,i} = X_i$
for all
 $i \in I$
, and
$i \in I$
, and -
2.
 $\varphi _{j,k} \circ \varphi _{i,j}|_{U_{i,j} \cap U_{i,k}} = \varphi _{i,k}|_{U_{i,j} \cap U_{i,k}}$
holds for all
$\varphi _{j,k} \circ \varphi _{i,j}|_{U_{i,j} \cap U_{i,k}} = \varphi _{i,k}|_{U_{i,j} \cap U_{i,k}}$
holds for all
 $i,j,k \in I$
.
$i,j,k \in I$
.
Recall from [Reference Demazure and GabrielDG] Proposition I.1.1.6 that
![]() ${\mathrm {LRS}}$
admits all colimits.
${\mathrm {LRS}}$
admits all colimits.
Definition 4.5.10. Let
![]() $\left (I, \{X_i\}_{i \in I}, \{\iota _{i,j}\}_{i,j \in I}, \{\varphi _{i,j}\}_{i,j\in I}\right )$
be a gluing datum in
$\left (I, \{X_i\}_{i \in I}, \{\iota _{i,j}\}_{i,j \in I}, \{\varphi _{i,j}\}_{i,j\in I}\right )$
be a gluing datum in
![]() ${\mathrm {LRS}}$
. Form the coproduct
${\mathrm {LRS}}$
. Form the coproduct
![]() $U := \coprod \limits _{i \in I} X_i$
and let
$U := \coprod \limits _{i \in I} X_i$
and let
![]() $\ell _i : X_i \hookrightarrow U$
be the canonical inclusions for each
$\ell _i : X_i \hookrightarrow U$
be the canonical inclusions for each
![]() $i \in I$
. Define
$i \in I$
. Define
by setting
![]() $u = (u_{i,j})_{i,j \in I}$
and
$u = (u_{i,j})_{i,j \in I}$
and
![]() $v = (v_{i,j})_{i,j \in I}$
, where
$v = (v_{i,j})_{i,j \in I}$
, where
If
![]() $q : U \to X$
is a coequaliser of diagram (33) in
$q : U \to X$
is a coequaliser of diagram (33) in
![]() ${\mathrm {LRS}}$
, then we call X the gluing of the
${\mathrm {LRS}}$
, then we call X the gluing of the
![]() $X_i$
’s with respect to the gluing datum.
$X_i$
’s with respect to the gluing datum.
Remark 4.5.11. It is shown in [Reference de JongSta], Lemma 01JA that the glued locally ringed space X admits an open covering
![]() $\{U_i : i \in I\}$
such that
$\{U_i : i \in I\}$
such that
![]() $U_i \cong X_i$
for all
$U_i \cong X_i$
for all
![]() $i \in I$
. It follows immediately that X is a scheme whenever each
$i \in I$
. It follows immediately that X is a scheme whenever each
![]() $U_i$
is a scheme.
$U_i$
is a scheme.
Theorem 4.5.12. Suppose that
![]() $\gamma = \{\alpha ,\beta \}$
, where
$\gamma = \{\alpha ,\beta \}$
, where
![]() $\beta = \mu /\alpha $
and
$\beta = \mu /\alpha $
and
![]() $\alpha \neq \beta $
. Then
$\alpha \neq \beta $
. Then
![]() $\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{\mu ,\gamma }$
is isomorphic to the projective line
$\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{\mu ,\gamma }$
is isomorphic to the projective line
![]() $\mathbb {P}^1$
.
$\mathbb {P}^1$
.
Proof. We will first recall the well-known gluing datum that is used in the construction of the projective line
![]() $\mathbb {P}^1$
: See, for example, [Reference de JongSta], Example 01JE. The indexing set is
$\mathbb {P}^1$
: See, for example, [Reference de JongSta], Example 01JE. The indexing set is
![]() $I := \{\alpha ,\beta \}$
. The spaces to be glued are
$I := \{\alpha ,\beta \}$
. The spaces to be glued are
![]() $X_\alpha := \Xi ^{\prime }_\alpha = {\mathrm {Spec}} k[t_\alpha ]$
and
$X_\alpha := \Xi ^{\prime }_\alpha = {\mathrm {Spec}} k[t_\alpha ]$
and
![]() $X_ \beta := \Xi ^{\prime }_\beta = {\mathrm {Spec}} k[t_\beta ]$
. The
$X_ \beta := \Xi ^{\prime }_\beta = {\mathrm {Spec}} k[t_\beta ]$
. The
![]() $U_{i,j}$
’s are as follows:
$U_{i,j}$
’s are as follows:
The inclusions
![]() $\iota _{\alpha ,\beta }$
are made clear by the notation, and the gluing isomorphisms
$\iota _{\alpha ,\beta }$
are made clear by the notation, and the gluing isomorphisms
![]() $\varphi _{i,j}$
are as follows:
$\varphi _{i,j}$
are as follows:
![]() $\varphi _{\alpha ,\alpha } = {\mathrm {id}}_{U_\alpha }$
,
$\varphi _{\alpha ,\alpha } = {\mathrm {id}}_{U_\alpha }$
,
![]() $\varphi _{\beta ,\beta } = {\mathrm {id}}_{U_\beta }$
,
$\varphi _{\beta ,\beta } = {\mathrm {id}}_{U_\beta }$
,
![]() $\varphi _{\beta ,\alpha } = \varphi _{\alpha ,\beta }^{-1}$
, and
$\varphi _{\beta ,\alpha } = \varphi _{\alpha ,\beta }^{-1}$
, and
![]() $\varphi _{\alpha ,\beta } : U_{\alpha ,\beta } \stackrel {\cong }{\longrightarrow } U_{\beta ,\alpha }$
is determined by the corresponding map
$\varphi _{\alpha ,\beta } : U_{\alpha ,\beta } \stackrel {\cong }{\longrightarrow } U_{\beta ,\alpha }$
is determined by the corresponding map
![]() $\varphi _{\alpha ,\beta }^\sharp $
on coordinate rings, which is given by
$\varphi _{\alpha ,\beta }^\sharp $
on coordinate rings, which is given by
![]() $\varphi _{\alpha ,\beta }^\sharp (t_\beta ) = t_{\alpha }^{-1}$
. Hence, we have the coequaliser diagram
$\varphi _{\alpha ,\beta }^\sharp (t_\beta ) = t_{\alpha }^{-1}$
. Hence, we have the coequaliser diagram
Recall that
![]() $\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{\mu ,\gamma }$
is defined by the coequaliser diagram (32). We see that to show that
$\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{\mu ,\gamma }$
is defined by the coequaliser diagram (32). We see that to show that
![]() $\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{\mu ,\gamma } \cong \mathbb {P}^1$
as locally ringed spaces it will be enough find an isomorphism of schemes
$\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{\mu ,\gamma } \cong \mathbb {P}^1$
as locally ringed spaces it will be enough find an isomorphism of schemes
such that the following two diagrams of affine schemes are commutative:

Here, both of the top horizontal arrows are the closed embedding of
![]() $\mathcal {R}^{\prime }_{\mu ,\gamma }$
into
$\mathcal {R}^{\prime }_{\mu ,\gamma }$
into
![]() $\Xi ^{\prime }_\gamma \times \Xi ^{\prime }_\gamma $
. Now, the relation
$\Xi ^{\prime }_\gamma \times \Xi ^{\prime }_\gamma $
. Now, the relation
![]() $\mathcal {R}^{\prime }_{\mu ,\gamma }$
also decomposes as a disjoint union
$\mathcal {R}^{\prime }_{\mu ,\gamma }$
also decomposes as a disjoint union
 $$\begin{align*}\mathcal{R}^{\prime}_{\mu,\gamma} =\coprod\limits_{i,j \in \{\alpha,\beta\}} \mathcal{R}^{\prime}_{\mu,i,j} \quad \subset \quad \Xi^{\prime}_\gamma \times\Xi^{\prime}_\gamma = \coprod\limits_{i,j \in \{\alpha,\beta\}} \Xi^{\prime}_i \times \Xi^{\prime}_j,\end{align*}$$
$$\begin{align*}\mathcal{R}^{\prime}_{\mu,\gamma} =\coprod\limits_{i,j \in \{\alpha,\beta\}} \mathcal{R}^{\prime}_{\mu,i,j} \quad \subset \quad \Xi^{\prime}_\gamma \times\Xi^{\prime}_\gamma = \coprod\limits_{i,j \in \{\alpha,\beta\}} \Xi^{\prime}_i \times \Xi^{\prime}_j,\end{align*}$$
so it will be enough to work componentwise, and for each
![]() $i,j \in \gamma $
to find an isomorphism
$i,j \in \gamma $
to find an isomorphism
such that the following two diagrams of affine schemes are commutative:

Because
![]() $\alpha \neq \beta $
, the connected components
$\alpha \neq \beta $
, the connected components
![]() $\mathcal {R}^{\prime }_{\mu ,i,j}$
of
$\mathcal {R}^{\prime }_{\mu ,i,j}$
of
![]() $\mathcal {R}^{\prime }_{\mu ,\gamma }$
are given by Proposition 4.5.6 as follows:
$\mathcal {R}^{\prime }_{\mu ,\gamma }$
are given by Proposition 4.5.6 as follows:
 $$ \begin{align} \begin{array}{lll}\mathcal{R}^{\prime}_{\mu,\alpha,\alpha} &= V(\langle t_\alpha \otimes 1 - 1 \otimes t_\alpha \rangle), \\ \mathcal{R}^{\prime}_{\mu,\beta,\beta} &= V(\langle t_\beta \otimes 1 - 1 \otimes t_\beta \rangle), \\ \mathcal{R}^{\prime}_{\mu,\alpha,\beta} &= V(\langle t_\alpha \otimes t_\beta - 1 \otimes 1\rangle), \quad\text{and}\quad \\ \mathcal{R}^{\prime}_{\mu,\beta,\alpha} &= V(\langle t_\beta \otimes t_\alpha - 1 \otimes 1\rangle).\end{array} \end{align} $$
$$ \begin{align} \begin{array}{lll}\mathcal{R}^{\prime}_{\mu,\alpha,\alpha} &= V(\langle t_\alpha \otimes 1 - 1 \otimes t_\alpha \rangle), \\ \mathcal{R}^{\prime}_{\mu,\beta,\beta} &= V(\langle t_\beta \otimes 1 - 1 \otimes t_\beta \rangle), \\ \mathcal{R}^{\prime}_{\mu,\alpha,\beta} &= V(\langle t_\alpha \otimes t_\beta - 1 \otimes 1\rangle), \quad\text{and}\quad \\ \mathcal{R}^{\prime}_{\mu,\beta,\alpha} &= V(\langle t_\beta \otimes t_\alpha - 1 \otimes 1\rangle).\end{array} \end{align} $$
Suppose first that
![]() $j = i$
. In this case
$j = i$
. In this case
![]() $u_{i,i} = {\mathrm {id}}_{\Xi ^{\prime }_i}$
, so we define
$u_{i,i} = {\mathrm {id}}_{\Xi ^{\prime }_i}$
, so we define
![]() $\tau _{i,i} := {\mathrm {pr}}_1|_{\mathcal {R}^{\prime }_{\mu ,i,j}}$
; then the first diagram in Equation (35) commutes by definition. For the second diagram, note that
$\tau _{i,i} := {\mathrm {pr}}_1|_{\mathcal {R}^{\prime }_{\mu ,i,j}}$
; then the first diagram in Equation (35) commutes by definition. For the second diagram, note that
![]() $v_{i,i} = u_{i,i} \circ \varphi _{i,i}$
is also equal to
$v_{i,i} = u_{i,i} \circ \varphi _{i,i}$
is also equal to
![]() ${\mathrm {id}}_{\Xi ^{\prime }_i}$
, so
${\mathrm {id}}_{\Xi ^{\prime }_i}$
, so
![]() $v_{i,i} \circ \tau _{i,i} = {\mathrm {pr}}_1|_{\mathcal {R}^{\prime }_{\mu ,i,i}} = {\mathrm {pr}}_2|_{\mathcal {R}^{\prime }_{\mu ,i,i}}$
in view of the first two equations in Equation (36). Hence, the second diagram in Equation (35) commutes as well.
$v_{i,i} \circ \tau _{i,i} = {\mathrm {pr}}_1|_{\mathcal {R}^{\prime }_{\mu ,i,i}} = {\mathrm {pr}}_2|_{\mathcal {R}^{\prime }_{\mu ,i,i}}$
in view of the first two equations in Equation (36). Hence, the second diagram in Equation (35) commutes as well.
Suppose now that
![]() $j \neq i$
. Looking at the last two equations in Equation (36), we see that the element
$j \neq i$
. Looking at the last two equations in Equation (36), we see that the element
![]() ${\mathrm {pr}}_1^\sharp (t_i)|_{\mathcal {R}^{\prime }_{\mu ,i,j}} = \overline {t_i \otimes 1}$
is a unit in
${\mathrm {pr}}_1^\sharp (t_i)|_{\mathcal {R}^{\prime }_{\mu ,i,j}} = \overline {t_i \otimes 1}$
is a unit in
![]() $\mathcal {O}(\mathcal {R}^{\prime }_{\mu ,i,j})$
. Therefore, the k-algebra homomorphism
$\mathcal {O}(\mathcal {R}^{\prime }_{\mu ,i,j})$
. Therefore, the k-algebra homomorphism
![]() $({\mathrm {pr}}_1|_{\mathcal {R}^{\prime }_{i,j}})^\sharp : \mathcal {O}(\Xi ^{\prime }_i) \to \mathcal {O}(\mathcal {R}^{\prime }_{\mu ,i,j})$
extends to the localisation
$({\mathrm {pr}}_1|_{\mathcal {R}^{\prime }_{i,j}})^\sharp : \mathcal {O}(\Xi ^{\prime }_i) \to \mathcal {O}(\mathcal {R}^{\prime }_{\mu ,i,j})$
extends to the localisation
![]() $\mathcal {O}(U_{i,j})$
of
$\mathcal {O}(U_{i,j})$
of
![]() $\mathcal {O}(\Xi ^{\prime }_i)$
, which means that
$\mathcal {O}(\Xi ^{\prime }_i)$
, which means that
![]() ${\mathrm {pr}}_1|_{\mathcal {R}^{\prime }_{\mu ,i,j}}$
factors through the Zariski open subset
${\mathrm {pr}}_1|_{\mathcal {R}^{\prime }_{\mu ,i,j}}$
factors through the Zariski open subset
![]() $U_{i,j}$
of
$U_{i,j}$
of
![]() $\Xi ^{\prime }_i$
. In other words, there exists a morphism
$\Xi ^{\prime }_i$
. In other words, there exists a morphism
![]() $\tau _{i,j} : \mathcal {R}^{\prime }_{\mu ,i,j} \to U_{i,j}$
, making the first diagram in Equation (35) commutative. Looking at the last two equations in Equation (36) again, we see that the corresponding map on coordinate rings
$\tau _{i,j} : \mathcal {R}^{\prime }_{\mu ,i,j} \to U_{i,j}$
, making the first diagram in Equation (35) commutative. Looking at the last two equations in Equation (36) again, we see that the corresponding map on coordinate rings
 $$\begin{align*}\tau_{i,j}^\sharp : k[t_i, t_i^{-1}] \to \frac{k[t_i] \otimes k[t_j]}{\langle t_i \otimes t_j - 1 \otimes 1 \rangle}\end{align*}$$
$$\begin{align*}\tau_{i,j}^\sharp : k[t_i, t_i^{-1}] \to \frac{k[t_i] \otimes k[t_j]}{\langle t_i \otimes t_j - 1 \otimes 1 \rangle}\end{align*}$$
sends
![]() $t_i$
to
$t_i$
to
![]() $\overline {t_i \otimes 1}$
and
$\overline {t_i \otimes 1}$
and
![]() $t_i^{-1}$
to
$t_i^{-1}$
to
![]() $\overline {t_i \otimes 1}^{-1} = \overline {1 \otimes t_j}$
and that it is an isomorphism. Therefore,
$\overline {t_i \otimes 1}^{-1} = \overline {1 \otimes t_j}$
and that it is an isomorphism. Therefore,
![]() $\tau _{i,j}$
is also an isomorphism. It remains to check that the second diagram in Equation (35) is commutative. Since all schemes involved are affine, it will be enough to check this on coordinate rings.
$\tau _{i,j}$
is also an isomorphism. It remains to check that the second diagram in Equation (35) is commutative. Since all schemes involved are affine, it will be enough to check this on coordinate rings.
Suppose that
![]() $(i,j) = (\alpha ,\beta )$
. Since
$(i,j) = (\alpha ,\beta )$
. Since
![]() $v_{\alpha ,\beta } = u_{\beta ,\alpha } \circ \varphi _{\alpha ,\beta }$
by Equation (34), this diagram is
$v_{\alpha ,\beta } = u_{\beta ,\alpha } \circ \varphi _{\alpha ,\beta }$
by Equation (34), this diagram is

and it is commutative because
![]() $\tau _{\alpha ,\beta }^\sharp (\varphi _{\alpha ,\beta }^\sharp (t_\beta )) = \tau _{\alpha ,\beta }^\sharp (t_\alpha ^{-1}) = \overline {1 \otimes t_\beta } = \overline {{\mathrm {pr}}_2^\sharp (t_\beta )}$
.
$\tau _{\alpha ,\beta }^\sharp (\varphi _{\alpha ,\beta }^\sharp (t_\beta )) = \tau _{\alpha ,\beta }^\sharp (t_\alpha ^{-1}) = \overline {1 \otimes t_\beta } = \overline {{\mathrm {pr}}_2^\sharp (t_\beta )}$
.
Similarly, when
![]() $(i,j) = (\beta ,\alpha )$
because
$(i,j) = (\beta ,\alpha )$
because
![]() $v_{\beta ,\alpha } = u_{\alpha ,\beta } \circ \varphi _{\beta ,\alpha }$
by Equation (34), this diagram is
$v_{\beta ,\alpha } = u_{\alpha ,\beta } \circ \varphi _{\beta ,\alpha }$
by Equation (34), this diagram is

and it is commutative because
![]() $\tau _{\beta ,\alpha }^\sharp (\varphi _{\beta ,\alpha }^\sharp (t_\alpha )) = \tau _{\beta ,\alpha }^\sharp (t_\beta ^{-1}) = \overline {1 \otimes t_\alpha } = \overline {{\mathrm {pr}}_2^\sharp (t_\alpha )}$
.
$\tau _{\beta ,\alpha }^\sharp (\varphi _{\beta ,\alpha }^\sharp (t_\alpha )) = \tau _{\beta ,\alpha }^\sharp (t_\beta ^{-1}) = \overline {1 \otimes t_\alpha } = \overline {{\mathrm {pr}}_2^\sharp (t_\alpha )}$
.
Next, we will study the following diagram of k-schemes:
where
![]() $\mathbb {A}^1 = {\mathrm {Spec}} k[x]$
is an affine line,
$\mathbb {A}^1 = {\mathrm {Spec}} k[x]$
is an affine line,
![]() $\mathbb {R} = \Delta \cup \mathbb {H} = V((x-y)(xy-1)) \subseteq \mathbb {A}^2 = {\mathrm {Spec}} k[x,y]$
is the union of the hyperbola
$\mathbb {R} = \Delta \cup \mathbb {H} = V((x-y)(xy-1)) \subseteq \mathbb {A}^2 = {\mathrm {Spec}} k[x,y]$
is the union of the hyperbola
![]() $\mathbb {H} = V(xy-1)$
and the diagonal
$\mathbb {H} = V(xy-1)$
and the diagonal
![]() $\Delta = V(x-y)$
,
$\Delta = V(x-y)$
,
![]() ${\mathrm {pr}}_1, {\mathrm {pr}}_2$
are the projection morphisms whose respective comorphisms are determined by
${\mathrm {pr}}_1, {\mathrm {pr}}_2$
are the projection morphisms whose respective comorphisms are determined by
![]() ${\mathrm {pr}}_1^\sharp (x) = x$
and
${\mathrm {pr}}_1^\sharp (x) = x$
and
![]() ${\mathrm {pr}}_2^\sharp (x) = y$
, and the morphism
${\mathrm {pr}}_2^\sharp (x) = y$
, and the morphism
![]() $\psi : \mathbb {A}^1 \to \mathbb {P}^1$
, viewed as a natural transformation between the corresponding functors of points, is given by the rule
$\psi : \mathbb {A}^1 \to \mathbb {P}^1$
, viewed as a natural transformation between the corresponding functors of points, is given by the rule
Lemma 4.5.13. We have
![]() $\psi \circ {\mathrm {pr}}_1 = \psi \circ {\mathrm {pr}}_2$
.
$\psi \circ {\mathrm {pr}}_1 = \psi \circ {\mathrm {pr}}_2$
.
Proof. Let
![]() $(a,b) \in \mathbb {R}$
. Then
$(a,b) \in \mathbb {R}$
. Then
![]() $\psi ({\mathrm {pr}}_1(a,b)) = \psi (a) = (a^2+1:a)$
and
$\psi ({\mathrm {pr}}_1(a,b)) = \psi (a) = (a^2+1:a)$
and
![]() $\psi ({\mathrm {pr}}_2(a,b)) = \psi (b) = (b^2 + 1 : b)$
. However,
$\psi ({\mathrm {pr}}_2(a,b)) = \psi (b) = (b^2 + 1 : b)$
. However,
![]() $(a,b) \in \mathbb {R}$
implies that
$(a,b) \in \mathbb {R}$
implies that
![]() $a = b$
or
$a = b$
or
![]() $ab = 1$
, and in either case we have
$ab = 1$
, and in either case we have
![]() $(a^2+1)b = a(b^2+1)$
. Hence,
$(a^2+1)b = a(b^2+1)$
. Hence,
![]() $\psi ({\mathrm {pr}}_1(a,b)) = \psi ({\mathrm {pr}}_2(a,b))$
.
$\psi ({\mathrm {pr}}_1(a,b)) = \psi ({\mathrm {pr}}_2(a,b))$
.
We let y be a local coordinate on
![]() $\mathbb {P}^1$
, determined by
$\mathbb {P}^1$
, determined by
![]() $y( (a:1)) = a$
so that
$y( (a:1)) = a$
so that
![]() $Y_0 := {\mathrm {Spec}} k[y]$
and
$Y_0 := {\mathrm {Spec}} k[y]$
and
![]() $Y_\infty := {\mathrm {Spec}} k[1/y]$
form a standard open covering of
$Y_\infty := {\mathrm {Spec}} k[1/y]$
form a standard open covering of
![]() $\mathbb {P}^1$
by two affine lines.
$\mathbb {P}^1$
by two affine lines.
Lemma 4.5.14. Let
![]() $X_i = \psi ^{-1}(Y_i)$
and
$X_i = \psi ^{-1}(Y_i)$
and
![]() $\mathbb {R}_i = {\mathrm {pr}}_1^{-1}(X_i)$
for
$\mathbb {R}_i = {\mathrm {pr}}_1^{-1}(X_i)$
for
![]() $i = 0, \infty $
. Then
$i = 0, \infty $
. Then
![]() $X_i$
is a basic affine open in
$X_i$
is a basic affine open in
![]() $\mathbb {A}^1$
, and
$\mathbb {A}^1$
, and
![]() $\mathbb {R}_i$
is a basic affine open in
$\mathbb {R}_i$
is a basic affine open in
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Proof. We have
![]() $X_0 = \{a \in \mathbb {A}^1 : (a^2 + 1 : a) \in Y_0\} = \{a \in \mathbb {A}^1 : a \neq 0\}$
, which is the basic affine open
$X_0 = \{a \in \mathbb {A}^1 : (a^2 + 1 : a) \in Y_0\} = \{a \in \mathbb {A}^1 : a \neq 0\}$
, which is the basic affine open
![]() $D(x) \subset \mathbb {A}^1$
. Similarly,
$D(x) \subset \mathbb {A}^1$
. Similarly,
![]() $X_\infty = \{a \in \mathbb {A}^1 : (a^2+1:a) \in Y_\infty \} = \{a \in \mathbb {A}^1 : a^2+1\neq 0\}$
, which is the basic affine open
$X_\infty = \{a \in \mathbb {A}^1 : (a^2+1:a) \in Y_\infty \} = \{a \in \mathbb {A}^1 : a^2+1\neq 0\}$
, which is the basic affine open
![]() $D(x^2+1) \subset \mathbb {A}^1$
. The preimage of any basic affine open
$D(x^2+1) \subset \mathbb {A}^1$
. The preimage of any basic affine open
![]() $D(f) \subset {\mathrm {Spec}} k[x]$
under the morphism of affine schemes
$D(f) \subset {\mathrm {Spec}} k[x]$
under the morphism of affine schemes
![]() ${\mathrm {pr}}_1: \mathbb {R} \to \mathbb {A}^1$
is
${\mathrm {pr}}_1: \mathbb {R} \to \mathbb {A}^1$
is
![]() $D({\mathrm {pr}}_1^\sharp (f))$
, which is a basic affine open in
$D({\mathrm {pr}}_1^\sharp (f))$
, which is a basic affine open in
![]() $\mathbb {R}$
. Therefore,
$\mathbb {R}$
. Therefore,
![]() $\mathbb {R}_0$
and
$\mathbb {R}_0$
and
![]() $\mathbb {R}_\infty $
are basic affine opens in
$\mathbb {R}_\infty $
are basic affine opens in
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Proposition 4.5.15.
 is an equaliser diagram of commutative rings if
is an equaliser diagram of commutative rings if
![]() $i = 0$
or
$i = 0$
or
![]() $i = \infty $
.
$i = \infty $
.
Proof. Let
![]() $\mathbb {H}_i = \mathbb {R}_i \cap \mathbb {H}$
for
$\mathbb {H}_i = \mathbb {R}_i \cap \mathbb {H}$
for
![]() $i=0,\infty $
. By postcomposing
$i=0,\infty $
. By postcomposing
![]() ${\mathrm {pr}}_1^\sharp , {\mathrm {pr}}_2^\sharp $
with the restriction maps
${\mathrm {pr}}_1^\sharp , {\mathrm {pr}}_2^\sharp $
with the restriction maps
![]() $\mathcal {O}(\mathbb {R}_i) \twoheadrightarrow \mathcal {O}(\mathbb {H}_i)$
, we can replace
$\mathcal {O}(\mathbb {R}_i) \twoheadrightarrow \mathcal {O}(\mathbb {H}_i)$
, we can replace
![]() $\mathbb {R}_i$
by
$\mathbb {R}_i$
by
![]() $\mathbb {H}_i$
in this proof.
$\mathbb {H}_i$
in this proof.
First, we consider the case
![]() $i = 0$
, where the diagram becomes
$i = 0$
, where the diagram becomes

and the maps are given by
![]() $\psi ^\sharp (y) = x + x^{-1}$
,
$\psi ^\sharp (y) = x + x^{-1}$
,
![]() ${\mathrm {pr}}_1^\sharp (x) = x$
,
${\mathrm {pr}}_1^\sharp (x) = x$
,
![]() ${\mathrm {pr}}_2^\sharp (x) = x^{-1}$
. Clearly,
${\mathrm {pr}}_2^\sharp (x) = x^{-1}$
. Clearly,
![]() $\psi ^\sharp $
is injective, and
$\psi ^\sharp $
is injective, and
![]() ${\mathrm {pr}}_1^\sharp \psi ^\sharp = {\mathrm {pr}}_2^\sharp \psi ^\sharp $
by Lemma 4.5.13.
${\mathrm {pr}}_1^\sharp \psi ^\sharp = {\mathrm {pr}}_2^\sharp \psi ^\sharp $
by Lemma 4.5.13.
Suppose that
![]() $a = \sum \limits _{i=-n}^n a_ix^i \in \ker ({\mathrm {pr}}_1^\sharp - {\mathrm {pr}}_2^\sharp )$
for some
$a = \sum \limits _{i=-n}^n a_ix^i \in \ker ({\mathrm {pr}}_1^\sharp - {\mathrm {pr}}_2^\sharp )$
for some
![]() $a_i \in k$
. Then
$a_i \in k$
. Then
![]() $a_i = a_{-i}$
for all i, so a lies in the k-linear span of
$a_i = a_{-i}$
for all i, so a lies in the k-linear span of
![]() $\{x^n + x^{-n} : n \geq 0\}$
. Hence,
$\{x^n + x^{-n} : n \geq 0\}$
. Hence,
![]() $a \in F_m := \sum \limits _{n=0}^m k(x^n + x^{-n})$
for some
$a \in F_m := \sum \limits _{n=0}^m k(x^n + x^{-n})$
for some
![]() $m \geq 0$
. We will show by induction that
$m \geq 0$
. We will show by induction that
![]() $F_r \subseteq k[x + x^{-1}]$
for all
$F_r \subseteq k[x + x^{-1}]$
for all
![]() $r \geq 0$
. The base case
$r \geq 0$
. The base case
![]() $r = 0$
is clear. Assuming inductively that
$r = 0$
is clear. Assuming inductively that
![]() $F_{r-1} \subseteq k[x+x^{-1}]$
for some
$F_{r-1} \subseteq k[x+x^{-1}]$
for some
![]() $r \geq 1$
, we see that
$r \geq 1$
, we see that
![]() $x^r + x^{-r} \equiv (x+x^{-1})^r \mod F_{r-1}$
, so
$x^r + x^{-r} \equiv (x+x^{-1})^r \mod F_{r-1}$
, so
![]() $x^r + x^{-r} \in k[x+x^{-1}]$
as well. Hence,
$x^r + x^{-r} \in k[x+x^{-1}]$
as well. Hence,
and the sequence is exact in the middle as required.
Next, we consider the case where
![]() $i = \infty $
. The diagram becomes
$i = \infty $
. The diagram becomes

where the maps are now given by
![]() $\psi ^\sharp (y^{-1}) = \frac {1}{x + x^{-1}} = \frac {x}{x^2+1}$
,
$\psi ^\sharp (y^{-1}) = \frac {1}{x + x^{-1}} = \frac {x}{x^2+1}$
,
![]() ${\mathrm {pr}}_1^\sharp (x) = x$
and
${\mathrm {pr}}_1^\sharp (x) = x$
and
![]() ${\mathrm {pr}}_2^\sharp (x) = x^{-1}$
. It is again clear that
${\mathrm {pr}}_2^\sharp (x) = x^{-1}$
. It is again clear that
![]() $\psi ^\sharp $
is injective and that
$\psi ^\sharp $
is injective and that
![]() ${\mathrm {pr}}_1^\sharp \psi ^\sharp = {\mathrm {pr}}_2^\sharp \psi ^\sharp $
by Lemma 4.5.13.
${\mathrm {pr}}_1^\sharp \psi ^\sharp = {\mathrm {pr}}_2^\sharp \psi ^\sharp $
by Lemma 4.5.13.
Suppose that
![]() $\frac {a(x)}{(x^2+1)^n} \in \ker ({\mathrm {pr}}_1^\sharp - {\mathrm {pr}}_2^\sharp )$
for some
$\frac {a(x)}{(x^2+1)^n} \in \ker ({\mathrm {pr}}_1^\sharp - {\mathrm {pr}}_2^\sharp )$
for some
![]() $a(x) \in k[x]$
and some
$a(x) \in k[x]$
and some
![]() $n \geq 0$
. Then
$n \geq 0$
. Then
 $$\begin{align*}\frac{a(x)}{(x^2+1)^n} = \frac{a(x^{-1})}{(x^{-2} + 1)^n}.\end{align*}$$
$$\begin{align*}\frac{a(x)}{(x^2+1)^n} = \frac{a(x^{-1})}{(x^{-2} + 1)^n}.\end{align*}$$
Multiplying through by
![]() $(x^2+1)^n$
shows that
$(x^2+1)^n$
shows that
![]() $a(x) = a(x^{-1})x^{2n}$
. Hence,
$a(x) = a(x^{-1})x^{2n}$
. Hence,
![]() $\deg (a) \leq 2n$
, and dividing through by
$\deg (a) \leq 2n$
, and dividing through by
![]() $x^n$
shows that
$x^n$
shows that
![]() $a(x)x^{-n} \in k[x,x^{-1}]$
is invariant under the substitution
$a(x)x^{-n} \in k[x,x^{-1}]$
is invariant under the substitution
![]() $x \mapsto x^{-1}$
. Using Equation (38), we see that
$x \mapsto x^{-1}$
. Using Equation (38), we see that
![]() $a(x)x^{-n} = b(x + x^{-1})$
for some
$a(x)x^{-n} = b(x + x^{-1})$
for some
![]() $b(x) \in k[x]$
with
$b(x) \in k[x]$
with
![]() $\deg b \leq n$
. Write
$\deg b \leq n$
. Write
![]() $b(x) = b_0 + b_1 x + \cdots + b_nx^n$
for some
$b(x) = b_0 + b_1 x + \cdots + b_nx^n$
for some
![]() $b_0,\cdots ,b_n \in k$
; then
$b_0,\cdots ,b_n \in k$
; then
 $$\begin{align*}\frac{a(x)}{(x^2+1)^n} = \frac{x^n}{(x^2+1)^n}\sum\limits_{i=0}^n b_i \left(\frac{x^2+1}{x}\right)^i = \sum_{i=0}^n b_i \left(\frac{x}{x^2+1}\right)^{n-i} \in k\left[\frac{x}{x^2+1}\right].\end{align*}$$
$$\begin{align*}\frac{a(x)}{(x^2+1)^n} = \frac{x^n}{(x^2+1)^n}\sum\limits_{i=0}^n b_i \left(\frac{x^2+1}{x}\right)^i = \sum_{i=0}^n b_i \left(\frac{x}{x^2+1}\right)^{n-i} \in k\left[\frac{x}{x^2+1}\right].\end{align*}$$
Hence,
![]() $\frac {a(x)}{(x^2+1)^n} \in k\left [\frac {x}{x^2+1}\right ]$
and the sequence is exact in the middle as required.
$\frac {a(x)}{(x^2+1)^n} \in k\left [\frac {x}{x^2+1}\right ]$
and the sequence is exact in the middle as required.
Proposition 4.5.16.
![]() is a coequaliser diagram in
is a coequaliser diagram in
![]() ${\mathrm {LRS}}$
.
${\mathrm {LRS}}$
.
Proof. Noting that
![]() $\psi \circ {\mathrm {pr}}_1 = \psi \circ {\mathrm {pr}}_2$
by Lemma 4.5.13, this follows from Lemma 4.2.1, applied with the standard covering
$\psi \circ {\mathrm {pr}}_1 = \psi \circ {\mathrm {pr}}_2$
by Lemma 4.5.13, this follows from Lemma 4.2.1, applied with the standard covering
![]() $\{Y_0 = {\mathrm {Spec}} k[y], Y_\infty = {\mathrm {Spec}} k[y^{-1}]\}$
of
$\{Y_0 = {\mathrm {Spec}} k[y], Y_\infty = {\mathrm {Spec}} k[y^{-1}]\}$
of
![]() $Y = \mathbb {P}^1$
, once we have checked its three conditions. Condition b) follows from Lemma 4.5.14 and condition c) follows from Proposition 4.5.15, so it remains to check condition a). This amounts to checking the following:
$Y = \mathbb {P}^1$
, once we have checked its three conditions. Condition b) follows from Lemma 4.5.14 and condition c) follows from Proposition 4.5.15, so it remains to check condition a). This amounts to checking the following:
-
(i)
 $|\psi | : |\mathbb {A}^1| \to |\mathbb {P}^1|$
is surjective,
$|\psi | : |\mathbb {A}^1| \to |\mathbb {P}^1|$
is surjective, -
(ii) the equivalence classes of the equivalence relation
 $\underset {\mu }{\sim }{}$
on
$\underset {\mu }{\sim }{}$
on
 $|\mathbb {A}^1|$
defined by
$|\mathbb {A}^1|$
defined by  are equal to the fibres of
are equal to the fibres of
 $|\psi |$
,
$|\psi |$
, -
(iii) the induced map
 $|\mathbb {A}^1|/\underset {\mu }{\sim }{} \quad \longrightarrow \quad |\mathbb {P}^1|$
is a homeomorphism.
$|\mathbb {A}^1|/\underset {\mu }{\sim }{} \quad \longrightarrow \quad |\mathbb {P}^1|$
is a homeomorphism.
For (i) and (ii), for any k-variety of finite type X, we use [Reference Mumford and OdaMO], Chapter IV, Theorem 2.3 to identify
![]() $|X|$
with the set of
$|X|$
with the set of
![]() $\mathcal {G}$
-orbits in
$\mathcal {G}$
-orbits in
![]() $|X_{\overline {k}}|$
, where
$|X_{\overline {k}}|$
, where
![]() $\mathcal {G} = {\mathrm {Aut}}(\overline {k}/k)$
and
$\mathcal {G} = {\mathrm {Aut}}(\overline {k}/k)$
and
![]() $X_{\overline {k}} = X \times _k \overline {k}$
is the base-change of X to
$X_{\overline {k}} = X \times _k \overline {k}$
is the base-change of X to
![]() $\overline {k}$
. Then we have the following commutative diagram
$\overline {k}$
. Then we have the following commutative diagram

where the vertical arrows are surjective. Chasing this diagram reduces us to the case
![]() $k = \overline {k}$
.
$k = \overline {k}$
.
(i) The map
![]() $|\psi |$
sends the generic point in
$|\psi |$
sends the generic point in
![]() $|\mathbb {A}^1|$
to the generic point in
$|\mathbb {A}^1|$
to the generic point in
![]() $|\mathbb {P}^1|$
, and
$|\mathbb {P}^1|$
, and
![]() $0 \in \mathbb {A}^1$
to the point at infinity
$0 \in \mathbb {A}^1$
to the point at infinity
![]() $(1:0) \in \mathbb {P}^1$
. Any other point in
$(1:0) \in \mathbb {P}^1$
. Any other point in
![]() $|\mathbb {P}^1|$
is of the form
$|\mathbb {P}^1|$
is of the form
![]() $(c : 1)$
for some
$(c : 1)$
for some
![]() $c \in k$
; since k is algebraically closed, the equation
$c \in k$
; since k is algebraically closed, the equation
![]() $a + a^{-1} = c$
has a solution, so
$a + a^{-1} = c$
has a solution, so
![]() $(c:1) \in \operatorname {im}(|\psi |)$
.
$(c:1) \in \operatorname {im}(|\psi |)$
.
(ii) Let
![]() $a, b \in |\mathbb {A}^1|$
be such that
$a, b \in |\mathbb {A}^1|$
be such that
![]() $\psi (a) = \psi (b)$
. If
$\psi (a) = \psi (b)$
. If
![]() $\psi (a)$
is the generic point of
$\psi (a)$
is the generic point of
![]() $\mathbb {P}^1$
, then a and b must both be equal to the generic point of
$\mathbb {P}^1$
, then a and b must both be equal to the generic point of
![]() $\mathbb {A}^1$
, so assume otherwise. Then necessarily
$\mathbb {A}^1$
, so assume otherwise. Then necessarily
![]() $a,b$
are closed points in
$a,b$
are closed points in
![]() $\mathbb {A}^1$
. Since
$\mathbb {A}^1$
. Since
![]() $k = \overline {k}$
, we may assume that
$k = \overline {k}$
, we may assume that
![]() $a,b \in \mathbb {A}^1(k) = k$
. Now,
$a,b \in \mathbb {A}^1(k) = k$
. Now,
![]() $\psi (a) = \psi (b)$
implies that
$\psi (a) = \psi (b)$
implies that
![]() $(a^2+1:a) = (b^2+1:b)$
, hence
$(a^2+1:a) = (b^2+1:b)$
, hence
![]() $(a^2+1)b = a(b^2+1)$
, so
$(a^2+1)b = a(b^2+1)$
, so
![]() $(a-b)(ab-1) = 0$
and
$(a-b)(ab-1) = 0$
and
![]() $(a,b) \in \mathbb {R}(k)$
. Setting
$(a,b) \in \mathbb {R}(k)$
. Setting
![]() $u = (a,b) \in |\mathbb {R}|$
, we see that
$u = (a,b) \in |\mathbb {R}|$
, we see that
![]() $a = {\mathrm {pr}}_1(u)$
and
$a = {\mathrm {pr}}_1(u)$
and
![]() $b = {\mathrm {pr}}_2(u)$
as required.
$b = {\mathrm {pr}}_2(u)$
as required.
(iii) The map
![]() $|\psi | : |\mathbb {A}^1| \to |\mathbb {P}^1|$
is surjective and has finite fibres. Hence, the quotient topology on
$|\psi | : |\mathbb {A}^1| \to |\mathbb {P}^1|$
is surjective and has finite fibres. Hence, the quotient topology on
![]() $|\mathbb {P}^1|$
induced by this map from the Zariski topology on
$|\mathbb {P}^1|$
induced by this map from the Zariski topology on
![]() $|\mathbb {A}^1|$
is the cofinite topology and therefore coincides with the Zariski topology on
$|\mathbb {A}^1|$
is the cofinite topology and therefore coincides with the Zariski topology on
![]() $|\mathbb {P}^1|$
.
$|\mathbb {P}^1|$
.
Theorem 4.5.17. Suppose that
![]() $\gamma = \{\alpha \}$
, where
$\gamma = \{\alpha \}$
, where
![]() $\alpha = \mu /\alpha $
. Then
$\alpha = \mu /\alpha $
. Then
![]() $\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{\mu ,\gamma }$
is also isomorphic to the projective line
$\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{\mu ,\gamma }$
is also isomorphic to the projective line
![]() $\mathbb {P}^1$
.
$\mathbb {P}^1$
.
Proof. Since
![]() $\gamma = \{\alpha \}$
, we have
$\gamma = \{\alpha \}$
, we have
![]() $\Xi ^{\prime }_\gamma = \Xi ^{\prime }_\alpha = {\mathrm {Spec}} k[t_\alpha ]$
and
$\Xi ^{\prime }_\gamma = \Xi ^{\prime }_\alpha = {\mathrm {Spec}} k[t_\alpha ]$
and
![]() $\mathcal {R}^{\prime }_{\mu ,\gamma } = \mathcal {R}^{\prime }_{\mu ,\alpha ,\alpha }$
in view of Equation (31). Since
$\mathcal {R}^{\prime }_{\mu ,\gamma } = \mathcal {R}^{\prime }_{\mu ,\alpha ,\alpha }$
in view of Equation (31). Since
![]() $\alpha = \mu /\alpha $
, Proposition 4.5.6 tells us that
$\alpha = \mu /\alpha $
, Proposition 4.5.6 tells us that
![]() $\mathcal {R}^{\prime }_{\mu ,\alpha ,\alpha } = V((x-y)(xy-1))$
, where
$\mathcal {R}^{\prime }_{\mu ,\alpha ,\alpha } = V((x-y)(xy-1))$
, where
![]() $x = t_\alpha \otimes 1$
and
$x = t_\alpha \otimes 1$
and
![]() $y = 1 \otimes t_\alpha $
. Hence, we have a commutative diagram of schemes
$y = 1 \otimes t_\alpha $
. Hence, we have a commutative diagram of schemes

where the top line is the diagram (32), and the vertical arrows are the isomorphisms of schemes whose corresponding comorphisms are
given by
![]() $x \mapsto t_\alpha \otimes 1, y \mapsto 1 \otimes t_\beta $
and
$x \mapsto t_\alpha \otimes 1, y \mapsto 1 \otimes t_\beta $
and
![]() $x \mapsto t_\alpha $
, respectively. Since
$x \mapsto t_\alpha $
, respectively. Since
![]() $\psi $
is a coequaliser of
$\psi $
is a coequaliser of
![]() ${\mathrm {pr}}_1,{\mathrm {pr}}_2$
in
${\mathrm {pr}}_1,{\mathrm {pr}}_2$
in
![]() ${\mathrm {LRS}}$
by Proposition 4.5.16, this gives the required isomorphism of schemes
${\mathrm {LRS}}$
by Proposition 4.5.16, this gives the required isomorphism of schemes
![]() $\Xi ^{\prime }_\gamma / \mathcal {R}^{\prime }_{\mu ,\gamma } \stackrel {\cong }{\longrightarrow } \mathbb {P}^1$
.
$\Xi ^{\prime }_\gamma / \mathcal {R}^{\prime }_{\mu ,\gamma } \stackrel {\cong }{\longrightarrow } \mathbb {P}^1$
.
We specialize from now on to the case where
![]() $\mu = {\mathrm {id}}^2$
.
$\mu = {\mathrm {id}}^2$
.
Corollary 4.5.18.
![]() $\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
is isomorphic to the disjoint union of
$\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
is isomorphic to the disjoint union of
![]() $\frac {p+1}{2}$
projective lines.
$\frac {p+1}{2}$
projective lines.
Proof. After Corollary 4.5.9, Theorem 4.5.12 and Theorem 4.5.17,
![]() $\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
is isomorphic to the disjoint union of
$\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
is isomorphic to the disjoint union of
![]() $|\widehat {\Omega }/\!\!\!\underset {{\mathrm {id}}^2}{\sim }{}\!\!\!|$
projective lines. There are exactly two elements
$|\widehat {\Omega }/\!\!\!\underset {{\mathrm {id}}^2}{\sim }{}\!\!\!|$
projective lines. There are exactly two elements
![]() $\alpha \in \widehat {\Omega }$
that satisfy
$\alpha \in \widehat {\Omega }$
that satisfy
![]() $\alpha = {\mathrm {id}}^2/\alpha $
: If
$\alpha = {\mathrm {id}}^2/\alpha $
: If
![]() $\alpha = {\mathrm {id}}^j$
for some
$\alpha = {\mathrm {id}}^j$
for some
![]() $j = 0,\cdots , p-2$
, then
$j = 0,\cdots , p-2$
, then
![]() $\alpha = {\mathrm {id}}^2/\alpha $
if and only if
$\alpha = {\mathrm {id}}^2/\alpha $
if and only if
![]() $2j \equiv 2 \mod p-1$
which is equivalent to
$2j \equiv 2 \mod p-1$
which is equivalent to
![]() $j = 1$
or
$j = 1$
or
![]() $j = \frac {p+1}{2}$
. These correspond to the singleton equivalence classes, and all other classes have size two. Therefore,
$j = \frac {p+1}{2}$
. These correspond to the singleton equivalence classes, and all other classes have size two. Therefore,
![]() $|\widehat {\Omega }/\!\!\underset {{\mathrm {id}}^2}{\sim }{}\!\!| = 2 + \frac {p-3}{2} = \frac {p+1}{2}$
.
$|\widehat {\Omega }/\!\!\underset {{\mathrm {id}}^2}{\sim }{}\!\!| = 2 + \frac {p-3}{2} = \frac {p+1}{2}$
.
4.5.3 Regluing the projective lines to form
 $\Xi /\mathcal {R}$
$\Xi /\mathcal {R}$
At this point, we have to introduce more notation.
Definition 4.5.19. For each
![]() $1 \leq r \leq \frac {p+1}{2}$
, let
$1 \leq r \leq \frac {p+1}{2}$
, let
![]() $\gamma _r := \{ {\mathrm {id}}^r, {\mathrm {id}}^{2-r} \}$
and define
$\gamma _r := \{ {\mathrm {id}}^r, {\mathrm {id}}^{2-r} \}$
and define
Note that
![]() $\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2} \cong Z_1 \coprod Z_2 \coprod \cdots \coprod Z_{\frac {p+1}{2}}$
by Corollary 4.5.9 and Corollary 4.5.18. After Theorem 4.5.12 and Theorem 4.5.17, we know that each
$\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2} \cong Z_1 \coprod Z_2 \coprod \cdots \coprod Z_{\frac {p+1}{2}}$
by Corollary 4.5.9 and Corollary 4.5.18. After Theorem 4.5.12 and Theorem 4.5.17, we know that each
![]() $Z_r$
is isomorphic to the projective line
$Z_r$
is isomorphic to the projective line
![]() $\mathbb {P}^1$
. Note also that if
$\mathbb {P}^1$
. Note also that if
![]() $\alpha = {\mathrm {id}}^r$
, then
$\alpha = {\mathrm {id}}^r$
, then
![]() $\alpha = \mu /\alpha $
if and only if
$\alpha = \mu /\alpha $
if and only if
![]() $r = 1$
or
$r = 1$
or
![]() $r = \frac {p+1}{2}$
.
$r = \frac {p+1}{2}$
.
Definition 4.5.20. Let
![]() $1 \leq r \leq \frac {p+1}{2}$
, and write
$1 \leq r \leq \frac {p+1}{2}$
, and write
![]() $\alpha = {\mathrm {id}}^r$
.
$\alpha = {\mathrm {id}}^r$
.
-
• If
 $r = 1$
, let
$r = 1$
, let
 $z_r$
be the local coordinate on
$z_r$
be the local coordinate on
 $Z_r$
that pulls back to
$Z_r$
that pulls back to
 $\frac {t_{\alpha }}{t_{\alpha }^2+1}$
under the morphism
$\frac {t_{\alpha }}{t_{\alpha }^2+1}$
under the morphism
 $\Xi ^{\prime }_{\alpha } \twoheadrightarrow \mathbb {P}^1$
from the proof of Theorem 4.5.17.
$\Xi ^{\prime }_{\alpha } \twoheadrightarrow \mathbb {P}^1$
from the proof of Theorem 4.5.17. -
• If
 $r \neq 1$
and
$r \neq 1$
and
 $r \neq \frac {p+1}{2}$
, let
$r \neq \frac {p+1}{2}$
, let
 $z_r$
be the local coordinate on
$z_r$
be the local coordinate on
 $Z_r$
that pulls back to
$Z_r$
that pulls back to
 $t_{\alpha }$
under the morphism
$t_{\alpha }$
under the morphism
 $\Xi ^{\prime }_\alpha \coprod \Xi ^{\prime }_{{\mathrm {id}}^2/\alpha } \twoheadrightarrow \mathbb {P}^1$
from the proof of Theorem 4.5.12.
$\Xi ^{\prime }_\alpha \coprod \Xi ^{\prime }_{{\mathrm {id}}^2/\alpha } \twoheadrightarrow \mathbb {P}^1$
from the proof of Theorem 4.5.12. -
• If
 $r = \frac {p+1}{2}$
, let
$r = \frac {p+1}{2}$
, let
 $z_r$
be the local coordinate on
$z_r$
be the local coordinate on
 $Z_r$
that pulls back to
$Z_r$
that pulls back to
 $t_{\alpha } + t_{\alpha }^{-1}$
under the morphism
$t_{\alpha } + t_{\alpha }^{-1}$
under the morphism
 $\Xi ^{\prime }_\alpha \twoheadrightarrow \mathbb {P}^1$
from the proof of Theorem 4.5.17.
$\Xi ^{\prime }_\alpha \twoheadrightarrow \mathbb {P}^1$
from the proof of Theorem 4.5.17. -
• Let
 $O_r, \infty _r \in Z_r$
be the closed points defined by
$O_r, \infty _r \in Z_r$
be the closed points defined by
 $O_r := \{z_r = 0\}$
and
$O_r := \{z_r = 0\}$
and
 $\infty _r := \{z_r = \infty \}$
.
$\infty _r := \{z_r = \infty \}$
.
Recall that for any
![]() $\alpha \in \widehat {\Omega }$
, the origin on the affine line
$\alpha \in \widehat {\Omega }$
, the origin on the affine line
![]() $\Xi ^{\prime }_{\alpha }$
is denoted by
$\Xi ^{\prime }_{\alpha }$
is denoted by
![]() $O_\alpha $
and that
$O_\alpha $
and that
![]() $q' : \Xi ' \twoheadrightarrow \Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
denotes the quotient map. After revisiting the proofs of Theorem 4.5.12 and Theorem 4.5.17, we have the following
$q' : \Xi ' \twoheadrightarrow \Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
denotes the quotient map. After revisiting the proofs of Theorem 4.5.12 and Theorem 4.5.17, we have the following
Lemma 4.5.21. Let
![]() $1 \leq r \leq \frac {p+1}{2}$
.
$1 \leq r \leq \frac {p+1}{2}$
.
-
• If
 $r = 1$
, then
$r = 1$
, then
 $q'(O_{{\mathrm {id}}^1}) = O_1$
.
$q'(O_{{\mathrm {id}}^1}) = O_1$
. -
• If
 $r \neq 1$
and
$r \neq 1$
and
 $r \neq \frac {p+1}{2}$
, then
$r \neq \frac {p+1}{2}$
, then
 $q'(O_{{\mathrm {id}}^r}) = O_r$
and
$q'(O_{{\mathrm {id}}^r}) = O_r$
and
 $q'(O_{{\mathrm {id}}^{2-r}}) = \infty _r$
.
$q'(O_{{\mathrm {id}}^{2-r}}) = \infty _r$
. -
• If
 $r = \frac {p+1}{2}$
, then
$r = \frac {p+1}{2}$
, then
 $q'(O_{{\mathrm {id}}^{\frac {p+1}{2}}}) = \infty _{\frac {p+1}{2}}$
.
$q'(O_{{\mathrm {id}}^{\frac {p+1}{2}}}) = \infty _{\frac {p+1}{2}}$
.
Recall the coequaliser diagram ![]() from Proposition 4.2.5. After Proposition 4.5.4, we wish to better understand the coequaliser diagram
from Proposition 4.2.5. After Proposition 4.5.4, we wish to better understand the coequaliser diagram

Lemma 4.5.22. The pairs
![]() $\{\left (q'a(s_r), q'b(s_r)\right ) : r = 1, \cdots , \frac {p-3}{2}\}$
are explicitly given as follows:
$\{\left (q'a(s_r), q'b(s_r)\right ) : r = 1, \cdots , \frac {p-3}{2}\}$
are explicitly given as follows:
Proof. Suppose first that
![]() $r \neq \frac {p-3}{2}$
. Then using Definition 4.2.4.b and Lemma 4.5.21, we have
$r \neq \frac {p-3}{2}$
. Then using Definition 4.2.4.b and Lemma 4.5.21, we have
where the last equality holds because
![]() $1 \leq r < \frac {p-3}{2}$
implies that
$1 \leq r < \frac {p-3}{2}$
implies that
![]() $1 < r + 2 < \frac {p+1}{2}$
.
$1 < r + 2 < \frac {p+1}{2}$
.
Suppose now that
![]() $r = \frac {p-3}{2}$
. Then we still have
$r = \frac {p-3}{2}$
. Then we still have
![]() $q'(a(s_r)) = q'(O_{{\mathrm {id}}^r}) = O_r$
, but now the last case in Lemma 4.5.21 gives
$q'(a(s_r)) = q'(O_{{\mathrm {id}}^r}) = O_r$
, but now the last case in Lemma 4.5.21 gives
Theorem 4.5.23. The locally ringed space
![]() $\Xi /\mathcal {R}$
is a scheme.
$\Xi /\mathcal {R}$
is a scheme.
Proof. We know that
![]() $\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{{\mathrm {id}}^2,\gamma }$
is a scheme for each
$\Xi ^{\prime }_\gamma /\mathcal {R}^{\prime }_{{\mathrm {id}}^2,\gamma }$
is a scheme for each
![]() $\gamma \in \widehat {\Omega } /\!\!\underset {{\mathrm {id}}^2}{\sim }{}\!$
by Theorem 4.5.12 and Theorem 4.5.17. Hence,
$\gamma \in \widehat {\Omega } /\!\!\underset {{\mathrm {id}}^2}{\sim }{}\!$
by Theorem 4.5.12 and Theorem 4.5.17. Hence,
![]() $\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
is a scheme by Corollary 4.5.9. By Proposition 4.5.4, it remains to show that the locally ringed space
$\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
is a scheme by Corollary 4.5.9. By Proposition 4.5.4, it remains to show that the locally ringed space
![]() $(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}) / \Xi _{{\mathrm {sing}}}$
is a scheme. Now,
$(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}) / \Xi _{{\mathrm {sing}}}$
is a scheme. Now,
 $\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2} \cong \coprod \limits _{r=1}^{\frac {p+1}{2}} Z_r$
and we define
$\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2} \cong \coprod \limits _{r=1}^{\frac {p+1}{2}} Z_r$
and we define
so that
![]() $X_1 \coprod X_2 = \Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
. We also define maps
$X_1 \coprod X_2 = \Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
. We also define maps
![]() $\theta _1,\theta _2 : \Xi _{{\mathrm {sing}}} \to \Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
as follows:
$\theta _1,\theta _2 : \Xi _{{\mathrm {sing}}} \to \Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
as follows:
 $$\begin{align*}\theta_1(s_r) = \left\{ \begin{array}{lll} O_r & \text{ if } &r \equiv 1\ \text{or}\ 2\ \mod 4 \\ \infty_{r+2} & \text{ if } & r \equiv 3\ \text{or}\ 0\ \mod 4\end{array} \right. \quad \text{and}\quad \theta_2(s_r) = \left\{ \begin{array}{lll} \infty_{r+2} & \text{ if } &r \equiv 1 \ \text{or}\ 2\ \mod 4 \\ O_r & \text{ if } & r \equiv 3\ \text{or}\ 0\ \mod 4\end{array} \right.\end{align*}$$
$$\begin{align*}\theta_1(s_r) = \left\{ \begin{array}{lll} O_r & \text{ if } &r \equiv 1\ \text{or}\ 2\ \mod 4 \\ \infty_{r+2} & \text{ if } & r \equiv 3\ \text{or}\ 0\ \mod 4\end{array} \right. \quad \text{and}\quad \theta_2(s_r) = \left\{ \begin{array}{lll} \infty_{r+2} & \text{ if } &r \equiv 1 \ \text{or}\ 2\ \mod 4 \\ O_r & \text{ if } & r \equiv 3\ \text{or}\ 0\ \mod 4\end{array} \right.\end{align*}$$
so that
![]() $\theta _1(\Xi _{{\mathrm {sing}}}) \subseteq X_1$
and
$\theta _1(\Xi _{{\mathrm {sing}}}) \subseteq X_1$
and
![]() $\theta _2(\Xi _{{\mathrm {sing}}}) \subseteq X_2$
. Using Lemma 4.5.22, for all
$\theta _2(\Xi _{{\mathrm {sing}}}) \subseteq X_2$
. Using Lemma 4.5.22, for all
![]() $s_r \in \Xi _{{\mathrm {sing}}}$
we have
$s_r \in \Xi _{{\mathrm {sing}}}$
we have
Let
![]() $s : \Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2} \to (\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}) / \Xi _{{\mathrm {sing}}}$
be a coequaliser of
$s : \Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2} \to (\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}) / \Xi _{{\mathrm {sing}}}$
be a coequaliser of  ; it follows that
; it follows that
is a coequaliser diagram in
![]() ${\mathrm {LRS}}$
. Hence,
${\mathrm {LRS}}$
. Hence,
![]() $(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}) / \Xi _{{\mathrm {sing}}}$
is isomorphic to the gluing of
$(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}) / \Xi _{{\mathrm {sing}}}$
is isomorphic to the gluing of
![]() $X_1$
and
$X_1$
and
![]() $X_2$
along
$X_2$
along
![]() $\theta _1 : \Xi _{{\mathrm {sing}}} \to X_1$
and
$\theta _1 : \Xi _{{\mathrm {sing}}} \to X_1$
and
![]() $\theta _2 : \Xi _{{\mathrm {sing}}} \to X_2$
. Since
$\theta _2 : \Xi _{{\mathrm {sing}}} \to X_2$
. Since
![]() $\theta _1$
and
$\theta _1$
and
![]() $\theta _2$
are both closed embeddings, this gluing is a scheme by Proposition 1.1.1 [Reference AnantharamanAna].
$\theta _2$
are both closed embeddings, this gluing is a scheme by Proposition 1.1.1 [Reference AnantharamanAna].
Using Lemma 4.5.22, we can also deduce the following
Corollary 4.5.24. Write
![]() $P_r := s(Z_r) \subset (\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
for
$P_r := s(Z_r) \subset (\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
for
![]() $r = 1,\cdots , \frac {p+1}{2}$
.
$r = 1,\cdots , \frac {p+1}{2}$
.
-
a) Suppose that
 $p \equiv 1 \mod 4$
so that
$p \equiv 1 \mod 4$
so that
 $\frac {p+1}{2}$
is odd and
$\frac {p+1}{2}$
is odd and
 $\frac {p-1}{2}$
is even. Then the connected component of
$\frac {p-1}{2}$
is even. Then the connected component of
 $P_1$
in
$P_1$
in
 $(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
is given by and the connected component of
$(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
is given by and the connected component of $$\begin{align*}P_1 \cup P_3 \cup P_5 \cup \cdots \cup P_{\frac{p+1}{2}}\end{align*}$$
$$\begin{align*}P_1 \cup P_3 \cup P_5 \cup \cdots \cup P_{\frac{p+1}{2}}\end{align*}$$
 $P_2$
in
$P_2$
in
 $(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
is given by
$(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
is given by  $$\begin{align*}P_2 \cup P_4 \cup P_6 \cup \cdots \cup P_{\frac{p-1}{2}}.\end{align*}$$
$$\begin{align*}P_2 \cup P_4 \cup P_6 \cup \cdots \cup P_{\frac{p-1}{2}}.\end{align*}$$
-
b) Suppose that
 $p \equiv 3 \mod 4$
so that
$p \equiv 3 \mod 4$
so that
 $\frac {p-1}{2}$
is odd and
$\frac {p-1}{2}$
is odd and
 $\frac {p+1}{2}$
is even. Then the connected component of
$\frac {p+1}{2}$
is even. Then the connected component of
 $P_1$
in
$P_1$
in
 $(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
is given by and the connected component of
$(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
is given by and the connected component of $$\begin{align*}P_1 \cup P_3 \cup P_5 \cup \cdots \cup P_{\frac{p-1}{2}}\end{align*}$$
$$\begin{align*}P_1 \cup P_3 \cup P_5 \cup \cdots \cup P_{\frac{p-1}{2}}\end{align*}$$
 $P_2$
in
$P_2$
in
 $(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
is given by
$(\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2})/\Xi _{{\mathrm {sing}}}$
is given by  $$\begin{align*}P_2 \cup P_4 \cup P_6 \cup \cdots \cup P_{\frac{p+1}{2}}.\end{align*}$$
$$\begin{align*}P_2 \cup P_4 \cup P_6 \cup \cdots \cup P_{\frac{p+1}{2}}.\end{align*}$$
Example 4.5.25. When
![]() $p=13$
, the schemes
$p=13$
, the schemes
![]() $\Xi $
,
$\Xi $
,
![]() $\Xi '$
,
$\Xi '$
,
![]() $\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
and
$\Xi '/\mathcal {R}^{\prime }_{{\mathrm {id}}^2}$
and
![]() $\Xi /\mathcal {R}$
look as follows:
$\Xi /\mathcal {R}$
look as follows:

The blue colour indicates those connected components of
![]() $\Xi '$
that are glued only to themselves in
$\Xi '$
that are glued only to themselves in
![]() $\Xi '/\mathcal {R}'$
.
$\Xi '/\mathcal {R}'$
.
A Appendices
A.1 Some categorical results about colimits and coequalisers
We omit the proof of the following standard result.
Lemma A.1. Suppose that
![]() $q : \mathcal {Y} \to \mathcal {Z}$
is a coequaliser of the arrows
$q : \mathcal {Y} \to \mathcal {Z}$
is a coequaliser of the arrows
![]() $f,g : \mathcal {X} \to \mathcal {Y}$
in a category
$f,g : \mathcal {X} \to \mathcal {Y}$
in a category
![]() $\mathcal {C}$
. Then q is an epimorphism.
$\mathcal {C}$
. Then q is an epimorphism.
Lemma A.2. Let
![]() $\mathcal {C}$
be a category, containing the following diagram:
$\mathcal {C}$
be a category, containing the following diagram:

Suppose that in this diagram, we have
-
a) q is a coequaliser of
 ,
, -
b)
 $q'$
is a coequaliser of
$q'$
is a coequaliser of  ,
, -
c)
 $\theta $
is a coequaliser of
$\theta $
is a coequaliser of  , and
, and -
d) s is a coequaliser of
 .
.
Suppose further that there exists a morphism
![]() $\theta ' : \mathcal {R}' \to \mathcal {R}$
such that:
$\theta ' : \mathcal {R}' \to \mathcal {R}$
such that:
-
e)
 $\theta '$
is an epimorphism, and
$\theta '$
is an epimorphism, and -
f)
 $\theta f' = f \theta '$
and
$\theta f' = f \theta '$
and
 $\theta g' = g \theta '$
.
$\theta g' = g \theta '$
.
Then there exists an isomorphism
![]() $\varphi : \mathcal {Y} \stackrel {\cong }{\longrightarrow } \mathcal {Z}$
such that
$\varphi : \mathcal {Y} \stackrel {\cong }{\longrightarrow } \mathcal {Z}$
such that
![]() $sq' = \varphi q \theta $
.
$sq' = \varphi q \theta $
.
Proof. By d), we have
![]() $sq'a = sq'b$
. Hence, by c), there is a unique morphism
$sq'a = sq'b$
. Hence, by c), there is a unique morphism
![]() $\alpha : \mathcal {X} \to \mathcal {Z}$
such that
$\alpha : \mathcal {X} \to \mathcal {Z}$
such that
![]() $\boxed {sq' = \alpha \theta }$
. Using this, we have
$\boxed {sq' = \alpha \theta }$
. Using this, we have
![]() $\alpha f \theta ' \stackrel {f)}{=} \alpha \theta f' = sq' f' \stackrel {b)}{=} sq'g' = \alpha \theta g' \stackrel {f)}{=} \alpha g \theta '.$
Then
$\alpha f \theta ' \stackrel {f)}{=} \alpha \theta f' = sq' f' \stackrel {b)}{=} sq'g' = \alpha \theta g' \stackrel {f)}{=} \alpha g \theta '.$
Then
![]() $\alpha f = \alpha g$
by e), so by a), there is a unique morphism
$\alpha f = \alpha g$
by e), so by a), there is a unique morphism
![]() $\varphi : \mathcal {Y} \to \mathcal {Z}$
such that
$\varphi : \mathcal {Y} \to \mathcal {Z}$
such that
![]() $\boxed {\alpha = \varphi q}$
.
$\boxed {\alpha = \varphi q}$
.
Next, we have
![]() $q \theta f' \stackrel {f)}{=} q f \theta ' \stackrel {a)}{=} q g \theta ' \stackrel {f)}{=} q \theta g'$
, so by b), there is a unique morphism
$q \theta f' \stackrel {f)}{=} q f \theta ' \stackrel {a)}{=} q g \theta ' \stackrel {f)}{=} q \theta g'$
, so by b), there is a unique morphism
![]() $\tau : \mathcal {Y}' \to \mathcal {Y}$
such that
$\tau : \mathcal {Y}' \to \mathcal {Y}$
such that
![]() $\boxed {q \theta = \tau q'}$
. Then
$\boxed {q \theta = \tau q'}$
. Then
![]() $\tau q' a = q \theta a \stackrel {c)}{=} q \theta b = \tau q' b$
, so by d), there is a unique morphism
$\tau q' a = q \theta a \stackrel {c)}{=} q \theta b = \tau q' b$
, so by d), there is a unique morphism
![]() $\psi : \mathcal {Z} \to \mathcal {Y}$
such that
$\psi : \mathcal {Z} \to \mathcal {Y}$
such that
![]() $\boxed {\psi s = \tau }$
. We will show that
$\boxed {\psi s = \tau }$
. We will show that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are mutually inverse.
$\psi $
are mutually inverse.
Firstly,
![]() $\varphi \psi s q' = \varphi \tau q' = \varphi q \theta = \alpha \theta = s q'$
. But
$\varphi \psi s q' = \varphi \tau q' = \varphi q \theta = \alpha \theta = s q'$
. But
![]() $q'$
and s are coequalisers by b) and d), hence they are epimorphisms by Lemma A.1. Therefore,
$q'$
and s are coequalisers by b) and d), hence they are epimorphisms by Lemma A.1. Therefore,
![]() $\varphi \psi = 1_{\mathcal {Z}}$
. Secondly,
$\varphi \psi = 1_{\mathcal {Z}}$
. Secondly,
![]() $\psi \varphi q \theta = \psi \alpha \theta = \psi sq' = \tau q' = q\theta $
. Since
$\psi \varphi q \theta = \psi \alpha \theta = \psi sq' = \tau q' = q\theta $
. Since
![]() $\theta $
and q are coequalisers by c) and a), they are epimorphisms by Lemma A.1. Hence,
$\theta $
and q are coequalisers by c) and a), they are epimorphisms by Lemma A.1. Hence,
![]() $\psi \varphi = 1_{\mathcal {Y}}$
. Finally,
$\psi \varphi = 1_{\mathcal {Y}}$
. Finally,
![]() $\varphi q \theta = \alpha \theta = sq'$
.
$\varphi q \theta = \alpha \theta = sq'$
.
We omit the proof of the following standard result.
Lemma A.3. Let
![]() $\mathcal {I}$
be a set, and let
$\mathcal {I}$
be a set, and let
![]() $\mathcal {C}$
be a category with coproducts. Suppose that
$\mathcal {C}$
be a category with coproducts. Suppose that

is a family of coequaliser diagrams in
![]() $\mathcal {C}$
. Then
$\mathcal {C}$
. Then

is also a coequaliser diagram in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
A.2 An alternative stability proof
By Proposition 2.2.3,
![]() ${\mathrm {Mod}}_k(G)$
has Krull dimension
${\mathrm {Mod}}_k(G)$
has Krull dimension
![]() $1$
, so the only nontrivial term in the Krull-dimension filtration of
$1$
, so the only nontrivial term in the Krull-dimension filtration of
![]() ${\mathrm {Mod}}_k(G)$
is
${\mathrm {Mod}}_k(G)$
is
![]() ${\mathrm {Mod}}_k(G)_0$
. Its stability then follows from our general result, Proposition 3.7.8. Here, we give an alternative, more direct, argument for the stability of
${\mathrm {Mod}}_k(G)_0$
. Its stability then follows from our general result, Proposition 3.7.8. Here, we give an alternative, more direct, argument for the stability of
![]() ${\mathrm {Mod}}_k(G)_0$
. Our argument is inspired by Paškūnas’ proof of the corresponding result for the group
${\mathrm {Mod}}_k(G)_0$
. Our argument is inspired by Paškūnas’ proof of the corresponding result for the group
![]() $GL_2(\mathbb {Q}_p)$
and representations with a fixed central character ([Reference PaškūnasPas] Proposition 5.16).
$GL_2(\mathbb {Q}_p)$
and representations with a fixed central character ([Reference PaškūnasPas] Proposition 5.16).
An H-module is called locally finite if each of its elements is contained in a submodule of finite length. By Remark 2.2.2, the locally finite H-modules form the localising subcategory
![]() ${\mathrm {Mod}}(\mathcal {H})_0$
of objects of Krull dimension
${\mathrm {Mod}}(\mathcal {H})_0$
of objects of Krull dimension
![]() $0$
.
$0$
.
Lemma A.2.1.
![]() ${\mathrm {Mod}}(H)_0$
is stable.
${\mathrm {Mod}}(H)_0$
is stable.
Proof. By [Reference McConnell and RobsonMCR] Corollary 13.1.13(iii) and Theorem 13.10.3(i), any simple module over the affine PI k-algebra H is finite dimensional over k. Hence, a locally finite module is the same as a module in which every element is contained in a finite-dimensional submodule. It easily follows that
![]() ${\mathrm {Mod}}(H)_0$
satisfies the criterion [Reference GabrielGab] Proposition V.6.12.
${\mathrm {Mod}}(H)_0$
satisfies the criterion [Reference GabrielGab] Proposition V.6.12.
Correspondingly, a G-representation in
![]() ${\mathrm {Mod}}_k(G)$
is locally finite if each of its elements is contained in a subrepresentation of finite length.
${\mathrm {Mod}}_k(G)$
is locally finite if each of its elements is contained in a subrepresentation of finite length.
Lemma A.2.2. If the representation V in
![]() ${\mathrm {Mod}}_k(SL_2(\mathbb {Z}_p))$
is admissible, then also its injective hull in
${\mathrm {Mod}}_k(SL_2(\mathbb {Z}_p))$
is admissible, then also its injective hull in
![]() ${\mathrm {Mod}}_k(SL_2(\mathbb {Z}_p))$
is admissible.
${\mathrm {Mod}}_k(SL_2(\mathbb {Z}_p))$
is admissible.
Proof. Put
![]() $K := SL_2(\mathbb {Z}_p)$
. It is well known that a representation V in
$K := SL_2(\mathbb {Z}_p)$
. It is well known that a representation V in
![]() ${\mathrm {Mod}}_k(K)$
is admissible if and only if its Pontrjagin dual
${\mathrm {Mod}}_k(K)$
is admissible if and only if its Pontrjagin dual
![]() $V^\vee $
is finitely generated as a module over the completed group ring
$V^\vee $
is finitely generated as a module over the completed group ring
![]() $k[[K]]$
. The inclusion
$k[[K]]$
. The inclusion
![]() $V \hookrightarrow E(V)$
into an injective hull dualizes to a projective cover
$V \hookrightarrow E(V)$
into an injective hull dualizes to a projective cover
![]() $E(V)^\vee \twoheadrightarrow V^\vee $
. Since the ring
$E(V)^\vee \twoheadrightarrow V^\vee $
. Since the ring
![]() $k[[H]]$
is noetherian (cf. the explanations in the proof of [Reference SchneiderSch] Proposition 5) this cover
$k[[H]]$
is noetherian (cf. the explanations in the proof of [Reference SchneiderSch] Proposition 5) this cover
![]() $E(V)^\vee $
must be finitely generated as a
$E(V)^\vee $
must be finitely generated as a
![]() $k[[H]]$
-module. It follows that
$k[[H]]$
-module. It follows that
![]() $E(V)$
is admissible.
$E(V)$
is admissible.
Lemma A.2.3. For a representation V in
![]() ${\mathrm {Mod}}_k(G)$
, we have:
${\mathrm {Mod}}_k(G)$
, we have:
-
a) V is of finite length if and only if V is finitely generated and admissible.
-
b) V is locally finite if and only if it is locally admissible (in the sense of [Reference Emerton and PaskunasEP]).
Proof. a) Suppose that V is of finite length. Then it obviously is finitely generated. In order to see that V is admissible, we may assume that it is irreducible. But then, by Theorem 2.1.1 the H-module
![]() $V^I$
is finite dimensional, which means that V is admissible. Now, assume, vice versa, that V is finitely generated and admissible. Using a filtration of V as in Lemma 2.1.3 and the fact that admissibility is preserved by passing to subquotients ([Reference EmertonEme] Proposition 2.2.13), we may assume that V lies in
$V^I$
is finite dimensional, which means that V is admissible. Now, assume, vice versa, that V is finitely generated and admissible. Using a filtration of V as in Lemma 2.1.3 and the fact that admissibility is preserved by passing to subquotients ([Reference EmertonEme] Proposition 2.2.13), we may assume that V lies in
![]() ${\mathrm {Mod}}^I(G)$
. Since
${\mathrm {Mod}}^I(G)$
. Since
![]() $V^I$
is finite dimensional, the equivalence in Theorem 2.1.1 tells us that V is of finite length.
$V^I$
is finite dimensional, the equivalence in Theorem 2.1.1 tells us that V is of finite length.
b) If V is locally finite then, by a), it is locally admissible. Suppose therefore that V is locally admissible. But then it is the union of admissible and finitely generated subrepresentations. Again, by a) it follows that V is the union of subrepresentations of finite length.
Lemma A.2.4. If V is an injective object in
![]() ${\mathrm {Mod}}_k(G)_0$
, then V is also an injective object in
${\mathrm {Mod}}_k(G)_0$
, then V is also an injective object in
![]() ${\mathrm {Mod}}_k(SL_2(\mathbb {Z}_p))$
.
${\mathrm {Mod}}_k(SL_2(\mathbb {Z}_p))$
.
Proof. The proof is almost literally the same as for [Reference Emerton and PaskunasEP] Corollary 3.8. For the convenience of the reader, we note:
-
– Use Lemma A.3.b to replace the assumption that V is locally finite by the assumption that V is locally admissible, which loc. cit. uses.
-
– The group
 $SL_2(\mathbb {Q}_p)$
is the amalgam of
$SL_2(\mathbb {Q}_p)$
is the amalgam of
 $SL_2(\mathbb {Z}_p)$
and
$SL_2(\mathbb {Z}_p)$
and
 $(\begin {smallmatrix} 0 & 1 \\ p & 0 \end {smallmatrix}) SL_2(\mathbb {Z}_p) (\begin {smallmatrix} 0 & p^{-1} \\ 1 & 0 \end {smallmatrix})$
along the Iwahori subgroup (cf. [Reference SerreSer] II.4.1 Corollary 1).
$(\begin {smallmatrix} 0 & 1 \\ p & 0 \end {smallmatrix}) SL_2(\mathbb {Z}_p) (\begin {smallmatrix} 0 & p^{-1} \\ 1 & 0 \end {smallmatrix})$
along the Iwahori subgroup (cf. [Reference SerreSer] II.4.1 Corollary 1).
We also point out that in loc. cit. a version of Lemma A.2 is used without mentioning it.
Proposition A.2.5.
![]() ${\mathrm {Mod}}_k(G)_0$
is stable.
${\mathrm {Mod}}_k(G)_0$
is stable.
Proof. By Gabriel’s criterion (cf. [Reference StenströmSte] Proposition VI.7.1), we have to check the following: Let
![]() $V_0 \subseteq V$
be any essential extension in
$V_0 \subseteq V$
be any essential extension in
![]() ${\mathrm {Mod}}_k(G)$
(in particular
${\mathrm {Mod}}_k(G)$
(in particular
![]() $V_0 \neq \{0\}$
) such that
$V_0 \neq \{0\}$
) such that
![]() $V_0$
is locally finite. We then have to show that V is locally finite as well. First of all, by replacing V by an injective hull, we may assume that V is an injective object. Secondly, since
$V_0$
is locally finite. We then have to show that V is locally finite as well. First of all, by replacing V by an injective hull, we may assume that V is an injective object. Secondly, since
![]() ${\mathrm {Mod}}_k(G)_0$
is localising, by possibly enlarging
${\mathrm {Mod}}_k(G)_0$
is localising, by possibly enlarging
![]() $V_0$
, we may assume that
$V_0$
, we may assume that
![]() $V_0$
is the maximal locally finite subrepresentation of V. It is then straightforward to see that
$V_0$
is the maximal locally finite subrepresentation of V. It is then straightforward to see that
![]() $V_0$
is an injective object in
$V_0$
is an injective object in
![]() ${\mathrm {Mod}}_k(G)_0$
. Hence, using Frobenius reciprocity we deduce from Lemma A.4 that
${\mathrm {Mod}}_k(G)_0$
. Hence, using Frobenius reciprocity we deduce from Lemma A.4 that
for any smooth representation
![]() $\sigma $
of the subgroup
$\sigma $
of the subgroup
![]() $K := SL_2(\mathbb {Z}_p)$
.
$K := SL_2(\mathbb {Z}_p)$
.
Reasoning by contradiction we assume that
![]() $V_0 \neq V$
. It suffices to construct a nonzero locally finite subrepresentation of
$V_0 \neq V$
. It suffices to construct a nonzero locally finite subrepresentation of
![]() $V/V_0$
. For this, we pick an irreducible K-subrepresentation
$V/V_0$
. For this, we pick an irreducible K-subrepresentation
![]() $\sigma $
in the K-socle of
$\sigma $
in the K-socle of
![]() $V/V_0$
. We also pick a vector
$V/V_0$
. We also pick a vector
![]() $v \in (V/V_0)^I$
which generates
$v \in (V/V_0)^I$
which generates
![]() $\sigma $
as a K-representation. We let
$\sigma $
as a K-representation. We let
![]() $\bar {X} \subseteq V/V_0$
denote the G-subrepresentation generated by v and by X its preimage in V. We obtain:
$\bar {X} \subseteq V/V_0$
denote the G-subrepresentation generated by v and by X its preimage in V. We obtain:
-
a) The short exact sequence
 $0 \rightarrow V_0 \rightarrow X \rightarrow \bar {X} \rightarrow 0$
in
$0 \rightarrow V_0 \rightarrow X \rightarrow \bar {X} \rightarrow 0$
in
 ${\mathrm {Mod}}_k(G)$
does not split since
${\mathrm {Mod}}_k(G)$
does not split since
 $V_0 \hookrightarrow X$
is an essential extension.
$V_0 \hookrightarrow X$
is an essential extension. -
b) By the Frobenius reciprocity equality
 ${\mathrm {Hom}}_{k[K]}(\sigma ,\bar {X}) = {\mathrm {Hom}}_{k[G]}({\mathrm {ind}}_K^G(\sigma ),\bar {X})$
the inclusion
${\mathrm {Hom}}_{k[K]}(\sigma ,\bar {X}) = {\mathrm {Hom}}_{k[G]}({\mathrm {ind}}_K^G(\sigma ),\bar {X})$
the inclusion
 $\sigma \subseteq \bar {X}$
corresponds to a G-homomorphism
$\sigma \subseteq \bar {X}$
corresponds to a G-homomorphism
 $\bar {\psi } : {\mathrm {ind}}_K^G(\sigma ) \twoheadrightarrow \bar {X}$
, which is surjective since v lies in its image.
$\bar {\psi } : {\mathrm {ind}}_K^G(\sigma ) \twoheadrightarrow \bar {X}$
, which is surjective since v lies in its image.
Applying Equation (A.2) to a) shows that the map
![]() ${\mathrm {Hom}}_{k[G]}({\mathrm {ind}}_K^G(\sigma ),X) \twoheadrightarrow {\mathrm {Hom}}_{k[G]}({\mathrm {ind}}_K^G(\sigma ),\bar {X})$
is surjective so that
${\mathrm {Hom}}_{k[G]}({\mathrm {ind}}_K^G(\sigma ),X) \twoheadrightarrow {\mathrm {Hom}}_{k[G]}({\mathrm {ind}}_K^G(\sigma ),\bar {X})$
is surjective so that
![]() $\bar {\psi }$
has a preimage
$\bar {\psi }$
has a preimage
![]() $\psi : {\mathrm {ind}}_K^G(\sigma ) \rightarrow X$
. If
$\psi : {\mathrm {ind}}_K^G(\sigma ) \rightarrow X$
. If
![]() $\bar {\psi }$
would also be injective, then
$\bar {\psi }$
would also be injective, then
![]() $\psi \circ \bar {\psi }^{-1} : \bar {X} \rightarrow X$
would split the sequence in a). It follows that
$\psi \circ \bar {\psi }^{-1} : \bar {X} \rightarrow X$
would split the sequence in a). It follows that
![]() $\bar {\psi }$
is a proper quotient map. Since
$\bar {\psi }$
is a proper quotient map. Since
![]() $\bar {\psi }$
is a map in
$\bar {\psi }$
is a map in
![]() ${\mathrm {Mod}}_k^I(G)$
the equivalence of categories in Theorem 2.1.1 implies that the sequence
${\mathrm {Mod}}_k^I(G)$
the equivalence of categories in Theorem 2.1.1 implies that the sequence
![]() $\bar {\psi }^I : {\mathrm {ind}}_K^G(\sigma )^I \twoheadrightarrow \bar {X}^I$
is a proper quotient map of H-modules. We claim that any proper H-quotient of
$\bar {\psi }^I : {\mathrm {ind}}_K^G(\sigma )^I \twoheadrightarrow \bar {X}^I$
is a proper quotient map of H-modules. We claim that any proper H-quotient of
![]() ${\mathrm {ind}}_K^G(\sigma )^I$
has finite k-dimension. Again, Theorem 2.1.1 then implies that
${\mathrm {ind}}_K^G(\sigma )^I$
has finite k-dimension. Again, Theorem 2.1.1 then implies that
![]() $\bar {X}$
has finite length, which would contradict the maximality of
$\bar {X}$
has finite length, which would contradict the maximality of
![]() $V_0$
.
$V_0$
.
In order to determine the H-module structure of
![]() ${\mathrm {ind}}_K^G(\sigma )^I$
, we introduce the finite-dimensional subalgebra
${\mathrm {ind}}_K^G(\sigma )^I$
, we introduce the finite-dimensional subalgebra
![]() $H_0 := {\mathrm {End}}_{k[K]}(k[K/I])^{\mathrm {op}}$
of H. It is well known that the
$H_0 := {\mathrm {End}}_{k[K]}(k[K/I])^{\mathrm {op}}$
of H. It is well known that the
![]() $H_0$
-module of invariants
$H_0$
-module of invariants
![]() $\sigma ^I$
is one-dimensional and therefore provides a character
$\sigma ^I$
is one-dimensional and therefore provides a character
![]() $\chi : H_0 \rightarrow k$
. By [Reference OllivierOll] Lemma 3.6, there is an isomorphism of H-modules
$\chi : H_0 \rightarrow k$
. By [Reference OllivierOll] Lemma 3.6, there is an isomorphism of H-modules
![]() ${\mathrm {ind}}_K^G(\sigma )^I \cong H \otimes _{H_0} \chi $
.Footnote
5
${\mathrm {ind}}_K^G(\sigma )^I \cong H \otimes _{H_0} \chi $
.Footnote
5
On the other hand recall the notations introduced in
![]() $\S$
4.1. Note
$\S$
4.1. Note
![]() $\tau _0$
and
$\tau _0$
and
![]() $e_1$
lie in
$e_1$
lie in
![]() $H_0$
and that
$H_0$
and that
![]() $Z(H)$
contains the polynomial ring
$Z(H)$
contains the polynomial ring
![]() $k[\zeta ]$
by Lemma 4.1.2. As a consequence of [Reference Ollivier and SchneiderOS18] Corollary 3.4, we have the isomorphism of
$k[\zeta ]$
by Lemma 4.1.2. As a consequence of [Reference Ollivier and SchneiderOS18] Corollary 3.4, we have the isomorphism of
![]() $k[\zeta ]$
-modules
$k[\zeta ]$
-modules
which sends
![]() $(1,0)$
to
$(1,0)$
to
![]() $1 \otimes 1$
and
$1 \otimes 1$
and
![]() $(0,1)$
to
$(0,1)$
to
![]() $\tau _1 \otimes 1$
.
$\tau _1 \otimes 1$
.
Let
![]() $Q := k(\zeta )$
be the field of fractions of
$Q := k(\zeta )$
be the field of fractions of
![]() $k[\zeta ]$
, and let
$k[\zeta ]$
, and let
![]() $V := Q \otimes _{k[\zeta ]} (H \otimes _{H_0} \chi )$
. Then V is a two-dimensional vector space over Q with basis
$V := Q \otimes _{k[\zeta ]} (H \otimes _{H_0} \chi )$
. Then V is a two-dimensional vector space over Q with basis
![]() ${v,w}$
, where
${v,w}$
, where
![]() $v := 1 \otimes 1 \otimes 1$
and
$v := 1 \otimes 1 \otimes 1$
and
![]() $w := 1 \otimes \tau _1 \otimes 1$
. Suppose now that we have a nonzero H-submodule of infinite codimension in
$w := 1 \otimes \tau _1 \otimes 1$
. Suppose now that we have a nonzero H-submodule of infinite codimension in
![]() $H \otimes _{H_0} \chi $
. It gives rise to a line in the vector space V which is respected by the Q-linear action of
$H \otimes _{H_0} \chi $
. It gives rise to a line in the vector space V which is respected by the Q-linear action of
![]() $\tau _0$
and
$\tau _0$
and
![]() $\tau _1$
. Let
$\tau _1$
. Let
![]() $a := \chi (e_1)$
and
$a := \chi (e_1)$
and
![]() $b := \chi (\tau _0)$
. So, a is
$b := \chi (\tau _0)$
. So, a is
![]() $0$
or
$0$
or
![]() $1$
and b is some element of k. We calculate that the matrix A of the action of
$1$
and b is some element of k. We calculate that the matrix A of the action of
![]() $\tau _0$
with respect to the basis
$\tau _0$
with respect to the basis
![]() ${v,w}$
is
${v,w}$
is
![]() $(\begin {smallmatrix} b & \zeta - a(b+1) \\ 0 & -(a+b) \end {smallmatrix})$
and the matrix B of the action of
$(\begin {smallmatrix} b & \zeta - a(b+1) \\ 0 & -(a+b) \end {smallmatrix})$
and the matrix B of the action of
![]() $\tau _1$
with respect to the same basis is
$\tau _1$
with respect to the same basis is
![]() $(\begin {smallmatrix} 0 & 0 \\ 1 & -a \end {smallmatrix})$
. The minimum polynomial of B is visibly
$(\begin {smallmatrix} 0 & 0 \\ 1 & -a \end {smallmatrix})$
. The minimum polynomial of B is visibly
![]() $X^2 + a X$
. If
$X^2 + a X$
. If
![]() $a = 0$
, then B is nilpotent and the only
$a = 0$
, then B is nilpotent and the only
![]() $\tau _1$
-stable line in V is spanned by w. If
$\tau _1$
-stable line in V is spanned by w. If
![]() $a = 1$
, then B is diagonalizable, and there is an additional
$a = 1$
, then B is diagonalizable, and there is an additional
![]() $\tau _1$
-stable line spanned by
$\tau _1$
-stable line spanned by
![]() $v + w$
. So we just need to check that these two lines are not
$v + w$
. So we just need to check that these two lines are not
![]() $\tau _0$
-stable. Passing to the matrices we need to check that the column vectors
$\tau _0$
-stable. Passing to the matrices we need to check that the column vectors
![]() $(\begin {smallmatrix}0\\1\end {smallmatrix})$
and
$(\begin {smallmatrix}0\\1\end {smallmatrix})$
and
![]() $(\begin {smallmatrix}a\\1\end {smallmatrix})$
are not A-eigenvectors:
$(\begin {smallmatrix}a\\1\end {smallmatrix})$
are not A-eigenvectors:
-
–
 $A(\begin {smallmatrix}0\\1\end {smallmatrix}) = (\begin {smallmatrix}\zeta - a(b+1)\\ -(a+b)\end {smallmatrix})$
is not in
$A(\begin {smallmatrix}0\\1\end {smallmatrix}) = (\begin {smallmatrix}\zeta - a(b+1)\\ -(a+b)\end {smallmatrix})$
is not in
 $Q(\begin {smallmatrix}0 \\ 1 \end {smallmatrix})$
since
$Q(\begin {smallmatrix}0 \\ 1 \end {smallmatrix})$
since
 $\zeta - a(b+1)$
is not zero in Q;
$\zeta - a(b+1)$
is not zero in Q; -
–
 $A(\begin {smallmatrix}a\\1\end {smallmatrix}) = (\begin {smallmatrix}\zeta -a\\-(a+b)\end {smallmatrix}) = c (\begin {smallmatrix}a\\1\end {smallmatrix})$
for some
$A(\begin {smallmatrix}a\\1\end {smallmatrix}) = (\begin {smallmatrix}\zeta -a\\-(a+b)\end {smallmatrix}) = c (\begin {smallmatrix}a\\1\end {smallmatrix})$
for some
 $c \in Q$
implies
$c \in Q$
implies
 $c = -(a+b) \in k$
, but also
$c = -(a+b) \in k$
, but also
 $\zeta - a = ca \in k$
, which is impossible.
$\zeta - a = ca \in k$
, which is impossible.
Competing interest
The authors have no competing interest to declare.
Financial support
The authors acknowledge support from Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under SFB 1442, Geometry: Deformations and Rigidity, project-ID 427320536 and Germany’s Excellence Strategy EXC 2044 390685587, Mathematics Münster: Dynamics–Geometry–Structure. The second author also acknowledges support from the Mathematical Institute and Brasenose College, Oxford.




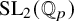
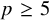
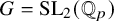
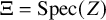

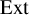
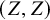
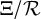
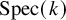
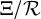
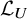


 is a coequaliser diagram of topological spaces,
is a coequaliser diagram of topological spaces, is a coequaliser diagram of topological spaces;
is a coequaliser diagram of topological spaces; is an equaliser diagram of sheaves of commutative rings on Y.
is an equaliser diagram of sheaves of commutative rings on Y. are equal to the fibres of
are equal to the fibres of  ,
, .
.