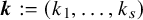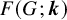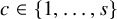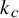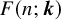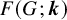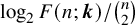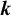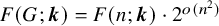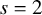1 Introduction
Let a nonincreasing sequence
![]() $\boldsymbol {k} = (k_1,\ldots ,k_s) \in \mathbb {N}^s$
of natural numbers be given. By an s-edge-colouring (or colouring for brevity) of a graph
$\boldsymbol {k} = (k_1,\ldots ,k_s) \in \mathbb {N}^s$
of natural numbers be given. By an s-edge-colouring (or colouring for brevity) of a graph
![]() $G=(V,E)$
, we mean a function
$G=(V,E)$
, we mean a function
![]() $\chi :E\to [s]$
, where we denote
$\chi :E\to [s]$
, where we denote
![]() $[s]:=\{1,\dots ,s\}$
. Note that colourings do not have to be proper, that is, adjacent edges can have the same colour. A colouring
$[s]:=\{1,\dots ,s\}$
. Note that colourings do not have to be proper, that is, adjacent edges can have the same colour. A colouring
![]() $\chi $
of G is called
$\chi $
of G is called
![]() $\boldsymbol {k}$
-valid if, for every
$\boldsymbol {k}$
-valid if, for every
![]() $c\in [s]$
, the colour-c subgraph
$c\in [s]$
, the colour-c subgraph
![]() $\chi ^{-1}(c)$
contains no copy of
$\chi ^{-1}(c)$
contains no copy of
![]() $K_{k_c}$
, the complete graph of order
$K_{k_c}$
, the complete graph of order
![]() $k_c$
. Write
$k_c$
. Write
![]() $F(G; \boldsymbol {k})$
for the number of
$F(G; \boldsymbol {k})$
for the number of
![]() $\boldsymbol {k}$
-valid colourings of G.
$\boldsymbol {k}$
-valid colourings of G.
In a previous paper with Yilma [Reference Pikhurko, Staden and Yilma24], we investigated the Erdős-Rothschild problem of determining
![]() $F(n;\boldsymbol {k})$
, the maximum of
$F(n;\boldsymbol {k})$
, the maximum of
![]() $F(G;\boldsymbol {k})$
over all graphs G on n vertices, and the
$F(G;\boldsymbol {k})$
over all graphs G on n vertices, and the
![]() $\boldsymbol {k}$
-extremal graphs, that is order-n graphs which attain this maximum. We assume throughout the paper, as we did there, that
$\boldsymbol {k}$
-extremal graphs, that is order-n graphs which attain this maximum. We assume throughout the paper, as we did there, that
![]() $s\ge 2$
and that
$s\ge 2$
and that
![]() $k_c \geq 3$
for all
$k_c \geq 3$
for all
![]() $c \in [s]$
(since
$c \in [s]$
(since
![]() $k_c=2$
just forbids colour c and the problem reduces to one with
$k_c=2$
just forbids colour c and the problem reduces to one with
![]() $s-1$
colours).
$s-1$
colours).
The case when
![]() $k_1 = \ldots = k_s =: k$
, which we denote by
$k_1 = \ldots = k_s =: k$
, which we denote by
![]() $\boldsymbol {k}=(k_1,\ldots ,k_s)=(k;s)$
, was first considered by Erdős and Rothschild in 1974 (see [Reference Erdős7, Reference Erdős8]). A trivial lower bound on
$\boldsymbol {k}=(k_1,\ldots ,k_s)=(k;s)$
, was first considered by Erdős and Rothschild in 1974 (see [Reference Erdős7, Reference Erdős8]). A trivial lower bound on
![]() $F(n;(k;s))$
is obtained by taking the largest
$F(n;(k;s))$
is obtained by taking the largest
![]() $K_k$
-free graph on n vertices, namely, the Turán graph
$K_k$
-free graph on n vertices, namely, the Turán graph
![]() $T_{k-1}(n)$
which is the complete
$T_{k-1}(n)$
which is the complete
![]() $(k-1)$
-partite graph with parts as equal as possible. Any s-edge-colouring of this graph is
$(k-1)$
-partite graph with parts as equal as possible. Any s-edge-colouring of this graph is
![]() $\boldsymbol {k}$
-valid, so we have
$\boldsymbol {k}$
-valid, so we have
where
![]() $t_{k-1}(n)$
is the number of edges in
$t_{k-1}(n)$
is the number of edges in
![]() $T_{k-1}(n)$
. In particular, Erdős and Rothschild conjectured that, when
$T_{k-1}(n)$
. In particular, Erdős and Rothschild conjectured that, when
![]() $\boldsymbol {k}=(3,3)$
and n is sufficiently large, the trivial lower bound (1.1) is in fact tight and, furthermore,
$\boldsymbol {k}=(3,3)$
and n is sufficiently large, the trivial lower bound (1.1) is in fact tight and, furthermore,
![]() $T_{2}(n)$
is the unique
$T_{2}(n)$
is the unique
![]() $\boldsymbol {k}$
-extremal graph on n vertices. The conjecture was verified for all
$\boldsymbol {k}$
-extremal graph on n vertices. The conjecture was verified for all
![]() $n \geq 6$
by Yuster [Reference Yuster29] (who also computed
$n \geq 6$
by Yuster [Reference Yuster29] (who also computed
![]() $F(n;(3,3))$
for smaller n). Proving Yuster’s extension of the conjecture, Alon et al. [Reference Alon, Balogh, Keevash and Sudakov1] showed that an analogous result holds for two and three colours: for large n, the Turán graph
$F(n;(3,3))$
for smaller n). Proving Yuster’s extension of the conjecture, Alon et al. [Reference Alon, Balogh, Keevash and Sudakov1] showed that an analogous result holds for two and three colours: for large n, the Turán graph
![]() $T_{k-1}(n)$
is the unique
$T_{k-1}(n)$
is the unique
![]() $\boldsymbol {k}$
-extremal graph for
$\boldsymbol {k}$
-extremal graph for
![]() $\boldsymbol {k}=(k,k)$
and
$\boldsymbol {k}=(k,k)$
and
![]() $\boldsymbol {k}=(k,k,k)$
. The proof of this result uses Szemerédi’s regularity lemma, so the graphs to which it applies are very large indeed. However, the assertions are not true for all numbers n of vertices. As was remarked in [Reference Alon, Balogh, Keevash and Sudakov1], the assertions do not hold when
$\boldsymbol {k}=(k,k,k)$
. The proof of this result uses Szemerédi’s regularity lemma, so the graphs to which it applies are very large indeed. However, the assertions are not true for all numbers n of vertices. As was remarked in [Reference Alon, Balogh, Keevash and Sudakov1], the assertions do not hold when
![]() $k \leq n < s^{(k-2)/2}$
, as in this case, a random colouring of the edges of
$k \leq n < s^{(k-2)/2}$
, as in this case, a random colouring of the edges of
![]() $K_n$
with s colours contains no monochromatic
$K_n$
with s colours contains no monochromatic
![]() $K_k$
with probability more than
$K_k$
with probability more than
![]() $\frac {1}{2}$
. Thus, for this range of n, we have
$\frac {1}{2}$
. Thus, for this range of n, we have
![]() $F(n;(k;s))> s^{\binom {n}{2}}/2 \geq s^{t_{k-1}(n)}$
. Hàn and Jiménez [Reference Hàn and Jiménez9] used graph containers to obtain an essentially optimal lower bound for the order n of graphs for which the trivial lower bound (1.1) for
$F(n;(k;s))> s^{\binom {n}{2}}/2 \geq s^{t_{k-1}(n)}$
. Hàn and Jiménez [Reference Hàn and Jiménez9] used graph containers to obtain an essentially optimal lower bound for the order n of graphs for which the trivial lower bound (1.1) for
![]() $s=2,3$
is tight.
$s=2,3$
is tight.
In this paper, we are only interested in large n. It was proved in [Reference Alon, Balogh, Keevash and Sudakov1, Proposition 5.1] that the limit
exists (and is positive) when
![]() $\boldsymbol {k}=(k;s)$
. It can be easily seen that the proof from [Reference Alon, Balogh, Keevash and Sudakov1] extends to an arbitrary fixed sequence
$\boldsymbol {k}=(k;s)$
. It can be easily seen that the proof from [Reference Alon, Balogh, Keevash and Sudakov1] extends to an arbitrary fixed sequence
![]() $\boldsymbol {k}$
. The authors of [Reference Alon, Balogh, Keevash and Sudakov1] noted that when more than three colours are used, the behaviour of
$\boldsymbol {k}$
. The authors of [Reference Alon, Balogh, Keevash and Sudakov1] noted that when more than three colours are used, the behaviour of
![]() $F(n;(k;s))$
changes, making its determination both harder and more interesting. Namely, it was shown in [Reference Alon, Balogh, Keevash and Sudakov1, page 287] that if
$F(n;(k;s))$
changes, making its determination both harder and more interesting. Namely, it was shown in [Reference Alon, Balogh, Keevash and Sudakov1, page 287] that if
![]() $s \geq 4$
(and
$s \geq 4$
(and
![]() $k \geq 3$
), then
$k \geq 3$
), then
![]() $F(n;(k;s))$
is exponentially in
$F(n;(k;s))$
is exponentially in
![]() $n^2$
larger than
$n^2$
larger than
![]() $s^{t_{k-1}(n)}$
.
$s^{t_{k-1}(n)}$
.
Table 1 Known results.

(*) These graphs are known to be asymptotically extremal only: they achieve the right exponent in
![]() $F(n;\boldsymbol {k})$
.
$F(n;\boldsymbol {k})$
.
In particular, any extremal graph has to contain many copies of
![]() $K_k$
. The authors of [Reference Alon, Balogh, Keevash and Sudakov1] determined
$K_k$
. The authors of [Reference Alon, Balogh, Keevash and Sudakov1] determined
![]() $F(\boldsymbol {k})$
for
$F(\boldsymbol {k})$
for
![]() $\boldsymbol {k}=(3,3,3,3)$
and
$\boldsymbol {k}=(3,3,3,3)$
and
![]() $\boldsymbol {k}=(4,4,4,4)$
, where
$\boldsymbol {k}=(4,4,4,4)$
, where
![]() $T_4(n)$
and
$T_4(n)$
and
![]() $T_9(n)$
, respectively, achieve the right exponent. Pikhurko and Yilma [Reference Pikhurko and Yilma25] were able to obtain an exact result for these cases: that these Turán graphs are the unique respective extremal graphs. Recently, Botler et al. [Reference Botler, Corsten, Dankovics, Frankl, Hàn, Jiménez and Skokan4] announced the determination of
$T_9(n)$
, respectively, achieve the right exponent. Pikhurko and Yilma [Reference Pikhurko and Yilma25] were able to obtain an exact result for these cases: that these Turán graphs are the unique respective extremal graphs. Recently, Botler et al. [Reference Botler, Corsten, Dankovics, Frankl, Hàn, Jiménez and Skokan4] announced the determination of
![]() $F(\boldsymbol {k})$
for
$F(\boldsymbol {k})$
for
![]() $\boldsymbol {k}=(3;5),(3;6)$
. For
$\boldsymbol {k}=(3;5),(3;6)$
. For
![]() $s=6$
, they proved that
$s=6$
, they proved that
![]() $T_8(n)$
is the unique extremal graph, and also proved a stability result. For
$T_8(n)$
is the unique extremal graph, and also proved a stability result. For
![]() $s=5$
, they uncovered new behaviour: for large n, there is an infinite family
$s=5$
, they uncovered new behaviour: for large n, there is an infinite family
![]() $\{S_{\alpha ,\beta }(n): 0 \leq \alpha +\beta \leq \frac {1}{4}\} \cup \{T_{\alpha ,\beta }(n): 0 \leq \alpha , \beta \leq \frac {1}{4}\}$
of asymptotically optimal graphs with either
$\{S_{\alpha ,\beta }(n): 0 \leq \alpha +\beta \leq \frac {1}{4}\} \cup \{T_{\alpha ,\beta }(n): 0 \leq \alpha , \beta \leq \frac {1}{4}\}$
of asymptotically optimal graphs with either
![]() $4$
,
$4$
,
![]() $6$
or
$6$
or
![]() $8$
parts, where
$8$
parts, where
![]() $S_{\alpha ,\beta }(n)$
denotes the complete partite graph with parts of size
$S_{\alpha ,\beta }(n)$
denotes the complete partite graph with parts of size
![]() $\frac {n}{4},\frac {n}{4},\alpha n,\alpha n,\beta n,\beta n,(\frac {1}{4}-\alpha -\beta ) n,(\frac {1}{4}-\alpha -\beta ) n$
and
$\frac {n}{4},\frac {n}{4},\alpha n,\alpha n,\beta n,\beta n,(\frac {1}{4}-\alpha -\beta ) n,(\frac {1}{4}-\alpha -\beta ) n$
and
![]() $T_{\alpha ,\beta }(n)$
denotes the complete partite graph with parts of size
$T_{\alpha ,\beta }(n)$
denotes the complete partite graph with parts of size
![]() $\alpha n, \alpha n, (\frac {1}{4}-\alpha )n, (\frac {1}{4}-\alpha )n, \beta n, \beta n, (\frac {1}{4}-\beta )n, (\frac {1}{4}-\beta )n$
. These are the only known results, asymptotic or exact.
$\alpha n, \alpha n, (\frac {1}{4}-\alpha )n, (\frac {1}{4}-\alpha )n, \beta n, \beta n, (\frac {1}{4}-\beta )n, (\frac {1}{4}-\beta )n$
. These are the only known results, asymptotic or exact.
Many other versions of the Erdős-Rothschild problem have been studied, where the goal is to maximise the number of colourings of some discrete object when one forbids certain coloured substructures. Erdős and Rothschild themselves considered the generalisation where one forbids a monochromatic graph H. In [Reference Alon, Balogh, Keevash and Sudakov1], the authors showed that the trivial lower bound (1.1) is tight for large n when H is colour-critical, that is, the removal of any edge from H reduces its chromatic number (note that every clique is colour-critical). In a further generalisation, Balogh [Reference Balogh3] considered edge-colourings in which a specific colouring of a fixed graph H is forbidden. Other authors have addressed this question in the cases of forbidden monochromatic matchings, stars, paths, trees and some other graphs in [Reference Hoppen, Kohayakawa and Lefmann12, Reference Hoppen, Kohayakawa and Lefmann13], matchings with a prescribed colour pattern in [Reference Hoppen and Lefmann14], rainbow stars in [Reference Hoppen, Lefmann, Odermann and Sanches17] and multicoloured cliques in [Reference Hoppen, Lefmann and Nolibos15]. A so-called ‘q-analogue’ was addressed in [Reference Hoppen, Lefmann and Odermann16], which considers a related problem in the context of vector spaces over a finite field
![]() $GF(q)$
. Alon and Yuster [Reference Alon and Yuster2] studied a directed version of the problem, to determine the maximum number of T-free orientations of an n-vertex graph, where T is a given k-vertex tournament. The problem of counting monochromatic H-free edge-colourings in hypergraphs was studied in [Reference Hoppen, Kohayakawa and Lefmann11, Reference Lefmann, Person, Rödl and Schacht20, Reference Lefmann, Person and Schacht21]. Additive versions have also been studied, where an underlying group [Reference Hàn and Jiménez10] or set [Reference Liu, Sharifzadeh and Staden22] with addition is coloured, and monochromatic triples
$GF(q)$
. Alon and Yuster [Reference Alon and Yuster2] studied a directed version of the problem, to determine the maximum number of T-free orientations of an n-vertex graph, where T is a given k-vertex tournament. The problem of counting monochromatic H-free edge-colourings in hypergraphs was studied in [Reference Hoppen, Kohayakawa and Lefmann11, Reference Lefmann, Person, Rödl and Schacht20, Reference Lefmann, Person and Schacht21]. Additive versions have also been studied, where an underlying group [Reference Hàn and Jiménez10] or set [Reference Liu, Sharifzadeh and Staden22] with addition is coloured, and monochromatic triples
![]() $(x,y,z)$
with
$(x,y,z)$
with
![]() $x+y=z$
are forbidden.
$x+y=z$
are forbidden.
1.1 An optimisation problem
This paper concerns the relation between the structure of almost extremal graphs for
![]() $F(n,\boldsymbol {k})$
and optimal solutions of a certain optimisation problem, Problem
$F(n,\boldsymbol {k})$
and optimal solutions of a certain optimisation problem, Problem
![]() $Q_t$
, which we now define.
$Q_t$
, which we now define.
Problem
![]() $Q_t$
: Given a sequence
$Q_t$
: Given a sequence
![]() $\boldsymbol {k} := (k_1,\ldots ,k_s) \in \mathbb {N}^s$
of natural numbers and
$\boldsymbol {k} := (k_1,\ldots ,k_s) \in \mathbb {N}^s$
of natural numbers and
![]() $t\in \{0,1,2\}$
, determine
$t\in \{0,1,2\}$
, determine
the maximum value of
 $$ \begin{align} q(\phi,\boldsymbol{\alpha}) := 2\sum_{\stackrel{1 \leq i < j \leq r}{\phi(ij) \neq \emptyset}} \alpha_i \alpha_j \log_2 |\phi(ij)| \end{align} $$
$$ \begin{align} q(\phi,\boldsymbol{\alpha}) := 2\sum_{\stackrel{1 \leq i < j \leq r}{\phi(ij) \neq \emptyset}} \alpha_i \alpha_j \log_2 |\phi(ij)| \end{align} $$
over the set
![]() of feasible solutions, that is, triples
of feasible solutions, that is, triples
![]() $(r,\phi ,\boldsymbol {\alpha })$
, such that
$(r,\phi ,\boldsymbol {\alpha })$
, such that
-
•
 $r \in \mathbb {N}$
and
$r \in \mathbb {N}$
and
 $\phi \in \Phi _t(r;\boldsymbol {k})$
, where
$\phi \in \Phi _t(r;\boldsymbol {k})$
, where
 $\Phi _t(r;\boldsymbol {k})$
is the set of all functions
$\Phi _t(r;\boldsymbol {k})$
is the set of all functions
 $\phi : \binom {[r]}{2} \rightarrow 2^{[s]}$
, such that is
$\phi : \binom {[r]}{2} \rightarrow 2^{[s]}$
, such that is $$\begin{align*}\phi^{-1}(c) := \left\{ ij \in \binom{[r]}{2} : c \in \phi(ij) \right\} \end{align*}$$
$$\begin{align*}\phi^{-1}(c) := \left\{ ij \in \binom{[r]}{2} : c \in \phi(ij) \right\} \end{align*}$$
 $K_{k_c}$
-free for every colour
$K_{k_c}$
-free for every colour
 $c \in [s]$
and
$c \in [s]$
and
 $|\phi (ij)|\ge t$
for all
$|\phi (ij)|\ge t$
for all
 $ij\in \binom {[r]}{2}$
;
$ij\in \binom {[r]}{2}$
;
-
•
 $\boldsymbol {\alpha } = (\alpha _1,\ldots ,\alpha _r) \in \Delta ^r$
, where
$\boldsymbol {\alpha } = (\alpha _1,\ldots ,\alpha _r) \in \Delta ^r$
, where
 $\Delta ^r$
is the set of all
$\Delta ^r$
is the set of all
 $\boldsymbol {\alpha } \in \mathbb {R}^r$
with
$\boldsymbol {\alpha } \in \mathbb {R}^r$
with
 $\alpha _i \geq 0$
for all
$\alpha _i \geq 0$
for all
 $i \in [r]$
, and
$i \in [r]$
, and
 $\alpha _1 + \ldots + \alpha _r = 1$
.
$\alpha _1 + \ldots + \alpha _r = 1$
.
Note that for
![]() $t=1,2$
, a triple
$t=1,2$
, a triple
![]() necessarily has
necessarily has
![]() $r<R(\boldsymbol {k})$
where
$r<R(\boldsymbol {k})$
where
![]() $R(\boldsymbol {k})$
is the Ramsey number of
$R(\boldsymbol {k})$
is the Ramsey number of
![]() $\boldsymbol {k}$
(i.e. the minimum R, such that
$\boldsymbol {k}$
(i.e. the minimum R, such that
![]() $K_R$
admits no
$K_R$
admits no
![]() $\boldsymbol {k}$
-valid s-edge-colouring). Thus, the maximum in (1.3) is attained for
$\boldsymbol {k}$
-valid s-edge-colouring). Thus, the maximum in (1.3) is attained for
![]() $t=1,2$
since
$t=1,2$
since
![]() $q(r,\phi ,\cdot )$
is continuous for each of the finitely many pairs
$q(r,\phi ,\cdot )$
is continuous for each of the finitely many pairs
![]() $(r,\phi )$
, and
$(r,\phi )$
, and
![]() is a (nonempty) compact space. It is also attained for
is a (nonempty) compact space. It is also attained for
![]() $t=0$
by (1.5) below. We call
$t=0$
by (1.5) below. We call
![]() $\phi \in \Phi _0(r;\boldsymbol {k})$
a colour pattern and
$\phi \in \Phi _0(r;\boldsymbol {k})$
a colour pattern and
![]() $\boldsymbol {\alpha } \in \Delta ^r$
a vertex weighting. A triple
$\boldsymbol {\alpha } \in \Delta ^r$
a vertex weighting. A triple
![]() $(r,\phi ,\boldsymbol {\alpha })$
is called
$(r,\phi ,\boldsymbol {\alpha })$
is called
![]() $Q_t$
-optimal if it attains the maximum, that is,
$Q_t$
-optimal if it attains the maximum, that is,
![]() and
and
![]() $q(r,\phi ,\boldsymbol {\alpha })=Q_t(\boldsymbol {k})$
. One can easily show [Reference Pikhurko, Staden and Yilma24, Lemma 6] that
$q(r,\phi ,\boldsymbol {\alpha })=Q_t(\boldsymbol {k})$
. One can easily show [Reference Pikhurko, Staden and Yilma24, Lemma 6] that
Note that a
![]() $Q_0$
-optimal triple can have r arbitrarily large, by, for example, adding vertices of weight 0 or splitting an existing vertex into two clones. Let
$Q_0$
-optimal triple can have r arbitrarily large, by, for example, adding vertices of weight 0 or splitting an existing vertex into two clones. Let
![]() be the set of
be the set of
![]() $Q_t$
-optimal triples
$Q_t$
-optimal triples
![]() $(r,\phi ,\boldsymbol {\alpha })$
. Let
$(r,\phi ,\boldsymbol {\alpha })$
. Let
![]() be the set of
be the set of
![]() with
with
![]() $\alpha _i>0$
for every
$\alpha _i>0$
for every
![]() $i \in [r]$
. Let
$i \in [r]$
. Let
![]() be the set of basic optimal solutions, which are
be the set of basic optimal solutions, which are
![]() $Q_2$
-optimal triples
$Q_2$
-optimal triples
![]() $(r,\phi ,\boldsymbol {\alpha })$
with
$(r,\phi ,\boldsymbol {\alpha })$
with
![]() $\alpha _i>0$
for every
$\alpha _i>0$
for every
![]() $i \in [r]$
.
$i \in [r]$
.
Given vectors
![]() $\boldsymbol {a}=(a_1,\ldots ,a_s)$
and
$\boldsymbol {a}=(a_1,\ldots ,a_s)$
and
![]() $\boldsymbol {b}=(b_1,\ldots ,b_t)$
, write
$\boldsymbol {b}=(b_1,\ldots ,b_t)$
, write
![]() $\boldsymbol {a}\leq \boldsymbol {b}$
if
$\boldsymbol {a}\leq \boldsymbol {b}$
if
![]() $a_i \leq b_i$
for all
$a_i \leq b_i$
for all
![]() $i \leq \max \{s,t\}$
where
$i \leq \max \{s,t\}$
where
![]() $a_i:=0$
for all
$a_i:=0$
for all
![]() $i>s$
and
$i>s$
and
![]() $b_i:=0$
for all
$b_i:=0$
for all
![]() $i>t$
. We write
$i>t$
. We write
![]() $\| \boldsymbol {a}-\boldsymbol {b}\|_1 := \sum _{i \leq \max \{s,t\}}|a_i-b_i|$
for the
$\| \boldsymbol {a}-\boldsymbol {b}\|_1 := \sum _{i \leq \max \{s,t\}}|a_i-b_i|$
for the
![]() $\ell ^1$
-distance between
$\ell ^1$
-distance between
![]() $\boldsymbol {a}$
and
$\boldsymbol {a}$
and
![]() $\boldsymbol {b}$
. In this paper, we always take
$\boldsymbol {b}$
. In this paper, we always take
![]() $\log $
to the base
$\log $
to the base
![]() $2$
; from now on, we omit any subscript.
$2$
; from now on, we omit any subscript.
One should think of feasible triples
![]() $(r,\phi ,\boldsymbol {\alpha })$
as vertex-weighted edge-coloured multigraphs. It is not hard to show that
$(r,\phi ,\boldsymbol {\alpha })$
as vertex-weighted edge-coloured multigraphs. It is not hard to show that
![]() $F(\boldsymbol {k})\geq Q(\boldsymbol {k})$
. Indeed, given
$F(\boldsymbol {k})\geq Q(\boldsymbol {k})$
. Indeed, given
![]() $\boldsymbol {k}$
, a
$\boldsymbol {k}$
, a
![]() $Q_1$
-optimal triple
$Q_1$
-optimal triple
![]() $(r,\phi ,\boldsymbol {\alpha })$
and
$(r,\phi ,\boldsymbol {\alpha })$
and
![]() $n \in \mathbb {N}$
, take the complete r-partite n-vertex graph
$n \in \mathbb {N}$
, take the complete r-partite n-vertex graph
![]() $K_{\boldsymbol {\alpha }}(n)$
whose parts
$K_{\boldsymbol {\alpha }}(n)$
whose parts
![]() $X_1,\ldots ,X_r$
satisfy
$X_1,\ldots ,X_r$
satisfy
![]() $|\,|X_i|-\alpha _i n\,| \leq 1$
for all
$|\,|X_i|-\alpha _i n\,| \leq 1$
for all
![]() $i \in [r]$
. Consider those s-edge-colourings of
$i \in [r]$
. Consider those s-edge-colourings of
![]() $K_{\boldsymbol {\alpha }}(n)$
in which, for
$K_{\boldsymbol {\alpha }}(n)$
in which, for
![]() $x \in X_i$
and
$x \in X_i$
and
![]() $y \in X_j$
, we only allow colours in
$y \in X_j$
, we only allow colours in
![]() $\phi (ij)$
to be used on
$\phi (ij)$
to be used on
![]() $xy$
. Every such colouring is
$xy$
. Every such colouring is
![]() $\boldsymbol {k}$
-valid, since every
$\boldsymbol {k}$
-valid, since every
![]() $\phi ^{-1}(c)$
is
$\phi ^{-1}(c)$
is
![]() $K_{k_c}$
-free. Clearly,
$K_{k_c}$
-free. Clearly,
![]() $F(n;\boldsymbol {k})$
is bounded below by the number of such colourings of
$F(n;\boldsymbol {k})$
is bounded below by the number of such colourings of
![]() $K_{\boldsymbol {\alpha }}(n)$
, which is
$K_{\boldsymbol {\alpha }}(n)$
, which is
 $$ \begin{align*}\prod_{ij\in\binom{[r]}{2}}|\phi(ij)|^{|X_i||X_j|} = 2^{q(\phi,\boldsymbol{\alpha})n^2/2+O(n)} = 2^{Q(\boldsymbol{k})n^2/2+O(n)}. \end{align*} $$
$$ \begin{align*}\prod_{ij\in\binom{[r]}{2}}|\phi(ij)|^{|X_i||X_j|} = 2^{q(\phi,\boldsymbol{\alpha})n^2/2+O(n)} = 2^{Q(\boldsymbol{k})n^2/2+O(n)}. \end{align*} $$
Taking the limit as
![]() $n\to \infty $
, we have
$n\to \infty $
, we have
![]() $F(\boldsymbol {k})\geq Q(\boldsymbol {k})$
. With Yilma, we proved the following results relating the determination of
$F(\boldsymbol {k})\geq Q(\boldsymbol {k})$
. With Yilma, we proved the following results relating the determination of
![]() $F(n;\boldsymbol {k})$
to Problem
$F(n;\boldsymbol {k})$
to Problem
![]() $Q_1$
, including a matching upper bound.
$Q_1$
, including a matching upper bound.
Theorem 1.1 [Reference Pikhurko, Staden and Yilma24].
The following hold for every
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
.
$\boldsymbol {k} \in \mathbb {N}^s$
.
-
(i) For every
 $n \in \mathbb {N}$
, at least one of the
$n \in \mathbb {N}$
, at least one of the
 $\boldsymbol {k}$
-extremal graphs of order n is complete multipartite.
$\boldsymbol {k}$
-extremal graphs of order n is complete multipartite. -
(ii)
 $F(n;\boldsymbol {k})=2^{Q(\boldsymbol {k}){n\choose 2}+o(n^2)}$
, that is,
$F(n;\boldsymbol {k})=2^{Q(\boldsymbol {k}){n\choose 2}+o(n^2)}$
, that is,
 $F(\boldsymbol {k})=Q(\boldsymbol {k})$
.
$F(\boldsymbol {k})=Q(\boldsymbol {k})$
. -
(iii) For every
 $\delta>0$
, there are
$\delta>0$
, there are
 $\eta>0$
and
$\eta>0$
and
 $n_0$
, such that if
$n_0$
, such that if
 $G=(V,E)$
is a complete multipartite graph of order
$G=(V,E)$
is a complete multipartite graph of order
 $n\ge n_0$
with (nonempty) parts
$n\ge n_0$
with (nonempty) parts
 $V_1,\dots ,V_r$
and
$V_1,\dots ,V_r$
and
 $F(G;\boldsymbol {k})\ge 2^{(Q(\boldsymbol {k})-\eta )n^2/2}$
, then there is a
$F(G;\boldsymbol {k})\ge 2^{(Q(\boldsymbol {k})-\eta )n^2/2}$
, then there is a
 $Q_1$
-optimal triple
$Q_1$
-optimal triple
 $(r,\phi ,\boldsymbol {\alpha '})$
, such that
$(r,\phi ,\boldsymbol {\alpha '})$
, such that
 $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }'\|_1 \leq \delta $
, where
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }'\|_1 \leq \delta $
, where
 $\boldsymbol {\alpha }:=(\frac {|V_1|}{n},\dots ,\frac {|V_r|}{n})$
.
$\boldsymbol {\alpha }:=(\frac {|V_1|}{n},\dots ,\frac {|V_r|}{n})$
.
Thus, by (1.5), to determine
![]() $F(\boldsymbol {k})$
, it suffices to find the optimal solutions to Problem
$F(\boldsymbol {k})$
, it suffices to find the optimal solutions to Problem
![]() $Q_2$
, which has the smallest feasible set among the problems
$Q_2$
, which has the smallest feasible set among the problems
![]() $Q_t$
. Unfortunately, this is difficult even when
$Q_t$
. Unfortunately, this is difficult even when
![]() $\boldsymbol {k}$
is small. Given a pair
$\boldsymbol {k}$
is small. Given a pair
![]() $(r,\phi )$
, one can use the method of Lagrange multipliers to find a best possible
$(r,\phi )$
, one can use the method of Lagrange multipliers to find a best possible
![]() $\boldsymbol {\alpha }$
for this pair; though the number of pairs
$\boldsymbol {\alpha }$
for this pair; though the number of pairs
![]() $(r,\phi )$
is finite, there are generally too many for a computer search. Indeed, the upper bound of
$(r,\phi )$
is finite, there are generally too many for a computer search. Indeed, the upper bound of
![]() $R(\boldsymbol {k})$
for r grows large very quickly, though we expect the optimal r to be much smaller than
$R(\boldsymbol {k})$
for r grows large very quickly, though we expect the optimal r to be much smaller than
![]() $R(\boldsymbol {k})$
.
$R(\boldsymbol {k})$
.
1.2 New results
The main contribution of this paper is a general stability theorem that determines the structure of any n-vertex graph G which is almost
![]() $\boldsymbol {k}$
-extremal, that is with
$\boldsymbol {k}$
-extremal, that is with
![]() $F(G,\boldsymbol {k})=F(n;\boldsymbol {k})\cdot 2^{o(n^2)}$
. This will show that the structure of any such graph is similar to an optimal solution to Problem
$F(G,\boldsymbol {k})=F(n;\boldsymbol {k})\cdot 2^{o(n^2)}$
. This will show that the structure of any such graph is similar to an optimal solution to Problem
![]() $Q_0$
, and almost all valid colourings almost follow an optimal colour pattern. This stability result holds for all
$Q_0$
, and almost all valid colourings almost follow an optimal colour pattern. This stability result holds for all
![]() $\boldsymbol {k}$
satisfying a rather general condition, which we call the extension property. Given
$\boldsymbol {k}$
satisfying a rather general condition, which we call the extension property. Given
![]() , one can easily check whether this condition holds. Indeed, we show that in almost all instances for which
, one can easily check whether this condition holds. Indeed, we show that in almost all instances for which
![]() $F(\boldsymbol {k})$
is known,
$F(\boldsymbol {k})$
is known,
![]() $\boldsymbol {k}$
satisfies a strong version of this property.
$\boldsymbol {k}$
satisfies a strong version of this property.
Definition 1.2 (Clones and extension property).
Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Given
$\boldsymbol {k} \in \mathbb {N}^s$
. Given
![]() $r \in \mathbb {N}$
and
$r \in \mathbb {N}$
and
![]() $\phi \in \Phi _0(r;\boldsymbol {k})$
, we say that
$\phi \in \Phi _0(r;\boldsymbol {k})$
, we say that
![]() $i \in [r]$
is
$i \in [r]$
is
-
• a clone of
 $j \in [r]\setminus \{ i \}$
(under
$j \in [r]\setminus \{ i \}$
(under
 $\phi $
) if
$\phi $
) if
 $\phi (ik) = \phi (jk)$
for all
$\phi (ik) = \phi (jk)$
for all
 $k \in [r] \setminus \{ i,j\}$
and
$k \in [r] \setminus \{ i,j\}$
and
 $|\phi (ij)| \leq 1$
;
$|\phi (ij)| \leq 1$
; -
• a strong clone of j (under
 $\phi $
) if additionally
$\phi $
) if additionally
 $\phi (ij) = \emptyset $
.
$\phi (ij) = \emptyset $
.
We say that
![]() $\boldsymbol {k}$
has
$\boldsymbol {k}$
has
-
• the extension property if, for every
 and
and
 $\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
, such that
$\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
, such that
 $\phi |_{\binom {[r^*]}{2}} = \phi ^*$
and
$\phi |_{\binom {[r^*]}{2}} = \phi ^*$
and
 $\sum _{i \in [r^*]: \phi (\{i,r^*+1\})\neq \emptyset }\alpha _i\log |\phi (\{ i,r^*+1 \})| = Q(\boldsymbol {k})$
, there exists
$\sum _{i \in [r^*]: \phi (\{i,r^*+1\})\neq \emptyset }\alpha _i\log |\phi (\{ i,r^*+1 \})| = Q(\boldsymbol {k})$
, there exists
 $j \in [r^*]$
, such that
$j \in [r^*]$
, such that
 $r^*+1$
is a clone of j under
$r^*+1$
is a clone of j under
 $\phi $
;
$\phi $
; -
• the strong extension property if in fact
 $r^*+1$
is a strong clone of j.
$r^*+1$
is a strong clone of j.
We explain the intuition and motivation behind this property in Section 2.1. For now, we remark that it is generally easy to check whether
![]() $\boldsymbol {k}$
has the extension property, when
$\boldsymbol {k}$
has the extension property, when
![]() is known. We check it for some cases in Section 5. For
is known. We check it for some cases in Section 5. For
![]() $\boldsymbol {k}$
with the extension property, one can describe all solutions to
$\boldsymbol {k}$
with the extension property, one can describe all solutions to
![]() in terms of basic optimal solutions. Every solution can be obtained by ‘blowing up’ a basic optimal solution
in terms of basic optimal solutions. Every solution can be obtained by ‘blowing up’ a basic optimal solution
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
; that is, taking arbitrarily many clones of the vertices and modifying part sizes so that the sum of vertex weights of clones of j equals
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
; that is, taking arbitrarily many clones of the vertices and modifying part sizes so that the sum of vertex weights of clones of j equals
![]() $\alpha _j^*$
for every j; and then possibly adding colour c edges between clones of each j, without creating a c-coloured copy of
$\alpha _j^*$
for every j; and then possibly adding colour c edges between clones of each j, without creating a c-coloured copy of
![]() $K_{k_c}$
, where c is the colour with the largest forbidden clique. Without loss of generality, we assume
$K_{k_c}$
, where c is the colour with the largest forbidden clique. Without loss of generality, we assume
![]() $k_1 \geq \ldots \geq k_s$
, so that
$k_1 \geq \ldots \geq k_s$
, so that
![]() $c=1$
. If
$c=1$
. If
![]() $k_1=k_2$
, then one cannot add any colour
$k_1=k_2$
, then one cannot add any colour
![]() $1$
edges between clones without creating a forbidden clique.
$1$
edges between clones without creating a forbidden clique.
Lemma 1.3. Let
![]() $s \in \mathbb {N}$
and suppose that
$s \in \mathbb {N}$
and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
with
$\boldsymbol {k} \in \mathbb {N}^s$
with
![]() $k_1 \geq \ldots \geq k_s$
has the extension property. Let
$k_1 \geq \ldots \geq k_s$
has the extension property. Let
![]() . Then
. Then
![]() if and only if there exist
if and only if there exist
![]() and a partition
and a partition
![]() $V_1 \cup \ldots \cup V_{r^*}$
of
$V_1 \cup \ldots \cup V_{r^*}$
of
![]() $\{i: \alpha _i>0\}$
, such that the following hold.
$\{i: \alpha _i>0\}$
, such that the following hold.
-
(i) For all
 $j \in [r^*]$
,
$j \in [r^*]$
,
 $\alpha ^*_j = \sum _{i \in V_j}\alpha _i$
.
$\alpha ^*_j = \sum _{i \in V_j}\alpha _i$
. -
(ii) For all
 $ij \in \binom {[r^*]}{2}$
,
$ij \in \binom {[r^*]}{2}$
,
 $i' \in V_i$
and
$i' \in V_i$
and
 $j' \in V_j$
, we have that
$j' \in V_j$
, we have that
 $\phi (i'j') = \phi ^*(ij)$
.
$\phi (i'j') = \phi ^*(ij)$
. -
(iii) For all
 $i \in [r^*]$
and distinct
$i \in [r^*]$
and distinct
 $i',j' \in V_i$
, we have that
$i',j' \in V_i$
, we have that
 $\phi (i'j') \subseteq \{ 1 \}$
. Moreover, if at least one
$\phi (i'j') \subseteq \{ 1 \}$
. Moreover, if at least one
 $\phi (i'i")$
for distinct
$\phi (i'i")$
for distinct
 $i',i"\in V_i$
and
$i',i"\in V_i$
and
 $i \in [r^*]$
is nonempty, then
$i \in [r^*]$
is nonempty, then
 $k_1>k_2$
and there is an integer vector
$k_1>k_2$
and there is an integer vector
 $\boldsymbol {\ell } \in \mathbb {N}^{r^*}$
, such that
$\boldsymbol {\ell } \in \mathbb {N}^{r^*}$
, such that
 $\|\boldsymbol {\ell }\|_1 \leq k_1-1$
and
$\|\boldsymbol {\ell }\|_1 \leq k_1-1$
and
 $\phi ^{-1}(1)[V_i]$
is
$\phi ^{-1}(1)[V_i]$
is
 $K_{\ell _i+1}$
-free for all
$K_{\ell _i+1}$
-free for all
 $i \in [r^*]$
.
$i \in [r^*]$
.
Our main result is the following stability theorem. The edit distance
![]() $d_{\mathrm {edit}}(G,G')$
of two graphs
$d_{\mathrm {edit}}(G,G')$
of two graphs
![]() $G,G'$
of the same order is the minimum number of edges that need to be added/removed to make
$G,G'$
of the same order is the minimum number of edges that need to be added/removed to make
![]() $G'$
isomorphic to G. Given graphs G and H and
$G'$
isomorphic to G. Given graphs G and H and
![]() $\delta>0$
, we say that G is
$\delta>0$
, we say that G is
![]() $\delta $
-far from being H-free if it has edit distance at least
$\delta $
-far from being H-free if it has edit distance at least
![]() $\delta |V(G)|^2$
to every H-free graph with the same number of vertices (note that we only need to delete edges here). Given disjoint
$\delta |V(G)|^2$
to every H-free graph with the same number of vertices (note that we only need to delete edges here). Given disjoint
![]() $A,B \subseteq V(G)$
and
$A,B \subseteq V(G)$
and
![]() $0 \leq d \leq 1$
, we say that
$0 \leq d \leq 1$
, we say that
![]() $G[A,B]$
is
$G[A,B]$
is
![]() $(\delta ,d)$
-regular if
$(\delta ,d)$
-regular if
![]() $d_G(A,B) := e_G(A,B)|A|^{-1}|B|^{-1} \in (d-\delta ,d+\delta )$
, and
$d_G(A,B) := e_G(A,B)|A|^{-1}|B|^{-1} \in (d-\delta ,d+\delta )$
, and
![]() $|d_G(X,Y)-d_G(A,B)|<\delta $
for all
$|d_G(X,Y)-d_G(A,B)|<\delta $
for all
![]() $X\subseteq A$
,
$X\subseteq A$
,
![]() $Y \subseteq B$
with
$Y \subseteq B$
with
![]() $|X|/|A|, |Y|/|B| \geq \delta $
. We are now ready to state the stability theorem. It says that, for any large n-vertex graph G which has close to the maximum number of valid colourings; that is,
$|X|/|A|, |Y|/|B| \geq \delta $
. We are now ready to state the stability theorem. It says that, for any large n-vertex graph G which has close to the maximum number of valid colourings; that is,
![]() $F(G;\boldsymbol {k})=F(n,\boldsymbol {k}) \cdot 2^{o(n^2)}$
, for almost all of its valid colourings
$F(G;\boldsymbol {k})=F(n,\boldsymbol {k}) \cdot 2^{o(n^2)}$
, for almost all of its valid colourings
![]() $\chi $
, there is a solution to
$\chi $
, there is a solution to
![]() which describes the structure of
which describes the structure of
![]() $\chi $
: it looks like a ‘blow-up’ of the solution. Lemma 1.3 describes the structure of solutions in terms of basic optimal solutions, and, therefore, there is a basic optimal solution
$\chi $
: it looks like a ‘blow-up’ of the solution. Lemma 1.3 describes the structure of solutions in terms of basic optimal solutions, and, therefore, there is a basic optimal solution
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
which describes the structure of
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
which describes the structure of
![]() $\chi $
. Part (ii) implies that, not only is there a partition of
$\chi $
. Part (ii) implies that, not only is there a partition of
![]() $V(G)$
, such that
$V(G)$
, such that
![]() $\chi $
has many edges of every colour
$\chi $
has many edges of every colour
![]() $c \in \phi ^*(ij)$
between the i-th and j-th parts (and few edges of any other colour), these edges are in fact well-distributed and of roughly equal densities between these parts.
$c \in \phi ^*(ij)$
between the i-th and j-th parts (and few edges of any other colour), these edges are in fact well-distributed and of roughly equal densities between these parts.
Theorem 1.4 (Stability).
Let
![]() $s \in \mathbb {N}$
, and suppose that
$s \in \mathbb {N}$
, and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
with
$\boldsymbol {k} \in \mathbb {N}^s$
with
![]() $k_1\geq \ldots \geq k_s$
has the extension property. Then for all
$k_1\geq \ldots \geq k_s$
has the extension property. Then for all
![]() $\delta> 0$
, there exist
$\delta> 0$
, there exist
![]() $n_0 \in \mathbb {N}$
and
$n_0 \in \mathbb {N}$
and
![]() $\varepsilon> 0$
, such that the following holds. If G is a graph on
$\varepsilon> 0$
, such that the following holds. If G is a graph on
![]() $n \geq n_0$
vertices, such that
$n \geq n_0$
vertices, such that
 $$ \begin{align*}\frac{\log F(G;\textbf{k})}{\binom{n}{2}} \geq Q(\textbf{k}) - \varepsilon, \end{align*} $$
$$ \begin{align*}\frac{\log F(G;\textbf{k})}{\binom{n}{2}} \geq Q(\textbf{k}) - \varepsilon, \end{align*} $$
then, for at least
![]() $(1-2^{-\varepsilon n^2})F(G;\boldsymbol {k})$
colourings
$(1-2^{-\varepsilon n^2})F(G;\boldsymbol {k})$
colourings
![]() $\chi : E(G) \rightarrow [s]$
which are
$\chi : E(G) \rightarrow [s]$
which are
![]() $\boldsymbol {k}$
-valid, there are
$\boldsymbol {k}$
-valid, there are
![]() and a partition
and a partition
![]() $Y_1 \cup \ldots \cup Y_{r^*}$
of
$Y_1 \cup \ldots \cup Y_{r^*}$
of
![]() $V(G)$
, such that the following hold.
$V(G)$
, such that the following hold.
-
(i) For all
 $i \in [r^*]$
, we have that
$i \in [r^*]$
, we have that
 $|\,|Y_i| - \alpha ^*_in\,| < 1$
.
$|\,|Y_i| - \alpha ^*_in\,| < 1$
. -
(ii) For all
 $c \in \phi ^*(ij)$
and
$c \in \phi ^*(ij)$
and
 $ij \in \binom {[r^*]}{2}$
, we have that
$ij \in \binom {[r^*]}{2}$
, we have that
 $\chi ^{-1}(c)[Y_i,Y_j]$
is
$\chi ^{-1}(c)[Y_i,Y_j]$
is
 $(\delta ,|\phi ^*(ij)|^{-1})$
-regular. In particular,
$(\delta ,|\phi ^*(ij)|^{-1})$
-regular. In particular,
 $e_G(Y_i,Y_j) \geq (1-s\delta )|Y_i||Y_j|$
.
$e_G(Y_i,Y_j) \geq (1-s\delta )|Y_i||Y_j|$
. -
(iii) Suppose
 $\sum _{i \in [r^*]}e(G[Y_i])> \delta n^2$
. Then
$\sum _{i \in [r^*]}e(G[Y_i])> \delta n^2$
. Then
 $\boldsymbol {k}$
does not have the strong extension property, and all but at most
$\boldsymbol {k}$
does not have the strong extension property, and all but at most
 $\delta n^2$
edges in
$\delta n^2$
edges in
 $\bigcup _{i \in [r^*]}G[Y_i]$
are coloured with
$\bigcup _{i \in [r^*]}G[Y_i]$
are coloured with
 $1$
under
$1$
under
 $\chi $
. Moreover, if
$\chi $
. Moreover, if
 $\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$
is such that
$\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$
is such that
 $G[Y_i]$
is
$G[Y_i]$
is
 $\delta $
-far from being
$\delta $
-far from being
 $K_{\ell _i}$
-free, then
$K_{\ell _i}$
-free, then
 $\|\boldsymbol {\ell }\|_1 \leq k_{1}-1$
.
$\|\boldsymbol {\ell }\|_1 \leq k_{1}-1$
.
Somewhat conversely, if (i), (iii) and
![]() $e_G(Y_i,Y_j)\geq (1-s\delta )|Y_i||Y_j|$
hold for some triple
$e_G(Y_i,Y_j)\geq (1-s\delta )|Y_i||Y_j|$
hold for some triple
![]() , a partition
, a partition
![]() $Y_1,\ldots ,Y_{r^*}$
of an n-vertex graph G, and
$Y_1,\ldots ,Y_{r^*}$
of an n-vertex graph G, and
![]() $\delta =o(1)$
, and each
$\delta =o(1)$
, and each
![]() $G[Y_i]$
is
$G[Y_i]$
is
![]() $K_{\ell_i+1}$
-free for some vector
$K_{\ell_i+1}$
-free for some vector
![]() $\boldsymbol {\ell }$
of
$\boldsymbol {\ell }$
of
![]() $1$
-norm at most
$1$
-norm at most
![]() $k_1-1$
, then
$k_1-1$
, then
![]() $F(G;\boldsymbol {k})\geq 2^{(Q(\boldsymbol {k})-o(1))n^2/2}$
.
$F(G;\boldsymbol {k})\geq 2^{(Q(\boldsymbol {k})-o(1))n^2/2}$
.
One should note the similarities between the statements of Theorem 1.4 and Lemma 1.3. Indeed, this parallel shows that the gist of Theorem 1.4 is ‘near-extremal graphs look like blow-ups of solutions to
![]() ’. This is not quite true within parts, as here, G could be very far from a complete partite graph. Note also that the partition
’. This is not quite true within parts, as here, G could be very far from a complete partite graph. Note also that the partition
![]() $Y_1 \cup \ldots \cup Y_{r^*}$
may be different for different colourings
$Y_1 \cup \ldots \cup Y_{r^*}$
may be different for different colourings
![]() $\chi $
.
$\chi $
.
We illustrate these statements with the example
![]() $\boldsymbol {k} = (5,3)$
. As it is not hard to show (or see Lemma 1.8),
$\boldsymbol {k} = (5,3)$
. As it is not hard to show (or see Lemma 1.8),
![]() consists of just one element, namely,
consists of just one element, namely,
![]() $(2,\phi ^*,(\frac {1}{2},\frac {1}{2}))$
, where
$(2,\phi ^*,(\frac {1}{2},\frac {1}{2}))$
, where
![]() $\phi ^*(12):=\{1,2\}$
. Thus, by Theorem 1.4 and the remark after it, the set of almost extremal graphs can be described as consisting of graphs that are
$\phi ^*(12):=\{1,2\}$
. Thus, by Theorem 1.4 and the remark after it, the set of almost extremal graphs can be described as consisting of graphs that are
![]() $o(n^2)$
-close to
$o(n^2)$
-close to
![]() $T_2(n)$
with triangle-free graphs added into each part, or a
$T_2(n)$
with triangle-free graphs added into each part, or a
![]() $K_4$
-free graph added into one part. Note that the partition
$K_4$
-free graph added into one part. Note that the partition
![]() $Y_1\cup Y_2$
of Theorem 1.4 may depend on the colouring. For example, if G is
$Y_1\cup Y_2$
of Theorem 1.4 may depend on the colouring. For example, if G is
![]() $T_4(n)$
with parts
$T_4(n)$
with parts
![]() $V_1,\ldots ,V_4$
, then Theorem 1.4 gives that for a typical colouring, there are disjoint pairs
$V_1,\ldots ,V_4$
, then Theorem 1.4 gives that for a typical colouring, there are disjoint pairs
![]() $ij,\ell m$
, such that almost all edges between
$ij,\ell m$
, such that almost all edges between
![]() $V_i$
and
$V_i$
and
![]() $V_j$
and between
$V_j$
and between
![]() $V_{\ell }$
and
$V_{\ell }$
and
![]() $V_m$
are coloured with colour
$V_m$
are coloured with colour
![]() $1$
; then
$1$
; then
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
in Theorem 1.4 have to be
$Y_2$
in Theorem 1.4 have to be
![]() $V_i\cup V_j$
and
$V_i\cup V_j$
and
![]() $V_{\ell } \cup V_m$
, up to changing
$V_{\ell } \cup V_m$
, up to changing
![]() $o(n)$
vertices.
$o(n)$
vertices.
If
![]() $\boldsymbol {k}$
has the strong extension property, then G is close to a complete multipartite graph by Theorem 1.4. So the pairs
$\boldsymbol {k}$
has the strong extension property, then G is close to a complete multipartite graph by Theorem 1.4. So the pairs
![]() $(r^*,\boldsymbol {\alpha }^*)$
associated with the colourings specified by the theorem are close to each other up to a relabelling of colours. We have the following corollary of Theorem 1.4 for
$(r^*,\boldsymbol {\alpha }^*)$
associated with the colourings specified by the theorem are close to each other up to a relabelling of colours. We have the following corollary of Theorem 1.4 for
![]() $\boldsymbol {k}$
with the strong extension property.
$\boldsymbol {k}$
with the strong extension property.
Corollary 1.5. Let
![]() $s \in \mathbb {N}$
, and suppose that
$s \in \mathbb {N}$
, and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
with
$\boldsymbol {k} \in \mathbb {N}^s$
with
![]() $k_1\geq \ldots \geq k_s$
has the strong extension property. Then for all
$k_1\geq \ldots \geq k_s$
has the strong extension property. Then for all
![]() $\delta> 0$
, there exists
$\delta> 0$
, there exists
![]() $n_0 \in \mathbb {N}$
and
$n_0 \in \mathbb {N}$
and
![]() $\varepsilon> 0$
, such that the following holds. Let G be a graph on
$\varepsilon> 0$
, such that the following holds. Let G be a graph on
![]() $n \geq n_0$
vertices, such that
$n \geq n_0$
vertices, such that
 $$ \begin{align*} \frac{\log F(G;\boldsymbol{k})}{\binom{n}{2}} \geq Q(\boldsymbol{k}) - \varepsilon. \end{align*} $$
$$ \begin{align*} \frac{\log F(G;\boldsymbol{k})}{\binom{n}{2}} \geq Q(\boldsymbol{k}) - \varepsilon. \end{align*} $$
Then there are
![]() $r^*,\boldsymbol {\alpha }^*$
and a partition V(G) =
$r^*,\boldsymbol {\alpha }^*$
and a partition V(G) =
![]() $V_1 \cup \ldots \cup V_{r^*}$
with
$V_1 \cup \ldots \cup V_{r^*}$
with
![]() $\left |\,|V_i|-\alpha ^*_i n \,\right | < 1$
for all
$\left |\,|V_i|-\alpha ^*_i n \,\right | < 1$
for all
![]() $i \in [r^*]$
, such that the edit distance between G and
$i \in [r^*]$
, such that the edit distance between G and
![]() $K[V_1,\ldots ,V_{r^*}]$
is at most
$K[V_1,\ldots ,V_{r^*}]$
is at most
![]() $\delta n^2$
. Moreover, for at least
$\delta n^2$
. Moreover, for at least
![]() $(1-2^{-\varepsilon n^2}) \cdot F(G;\boldsymbol {k}) \ \boldsymbol {k}$
-valid s-edge-colourings
$(1-2^{-\varepsilon n^2}) \cdot F(G;\boldsymbol {k}) \ \boldsymbol {k}$
-valid s-edge-colourings
![]() $\chi $
of G, there exists
$\chi $
of G, there exists
![]() where
where
![]() $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta $
, such that
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \leq \delta $
, such that
![]() $\chi ^{-1}(c)[V_i,V_j]$
is
$\chi ^{-1}(c)[V_i,V_j]$
is
![]() $(\delta ,|\phi ^*(ij)|^{-1})$
-regular for all
$(\delta ,|\phi ^*(ij)|^{-1})$
-regular for all
![]() $ij \in \binom {[r^*]}{2}$
and
$ij \in \binom {[r^*]}{2}$
and
![]() $c \in \phi ^*(ij)$
.
$c \in \phi ^*(ij)$
.
Recall from Theorem 1.1 (i) that at least one extremal graph is complete multipartite. The following conjecture was made in [Reference Pikhurko, Staden and Yilma24]:
Conjecture 1.6. For every
![]() $\boldsymbol {k}$
, every
$\boldsymbol {k}$
, every
![]() $\boldsymbol {k}$
-extremal graph is complete multipartite.
$\boldsymbol {k}$
-extremal graph is complete multipartite.
In [Reference Pikhurko and Staden23], we will use Corollary 1.5 to prove an exact result for all
![]() $\boldsymbol {k}$
with the strong extension property: that for such
$\boldsymbol {k}$
with the strong extension property: that for such
![]() $\boldsymbol {k}$
, every large extremal graph is a complete multipartite graph with part ratios roughly
$\boldsymbol {k}$
, every large extremal graph is a complete multipartite graph with part ratios roughly
![]() $\alpha _1^*,\ldots ,\alpha _{r^*}^*$
for some
$\alpha _1^*,\ldots ,\alpha _{r^*}^*$
for some
![]() $\boldsymbol {\alpha }^*$
coming from a basic optimal triple
$\boldsymbol {\alpha }^*$
coming from a basic optimal triple
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
. However, it seems much harder to prove an exact result for
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
. However, it seems much harder to prove an exact result for
![]() $\boldsymbol {k}$
without the strong extension property, as Theorem 1.4 as well as the example
$\boldsymbol {k}$
without the strong extension property, as Theorem 1.4 as well as the example
![]() $\boldsymbol {k}=(5,3)$
above show that, in general, there are many asymptotically extremal graphs which are far from complete multipartite.
$\boldsymbol {k}=(5,3)$
above show that, in general, there are many asymptotically extremal graphs which are far from complete multipartite.
1.3 Applications
Armed with Theorem 1.4, to determine asymptotically
![]() $\boldsymbol {k}$
-extremal graphs, one need only solve Problem
$\boldsymbol {k}$
-extremal graphs, one need only solve Problem
![]() $Q_2$
for
$Q_2$
for
![]() $\boldsymbol {k}$
, and then check for the extension property using the optimal solutions.
$\boldsymbol {k}$
, and then check for the extension property using the optimal solutions.
We apply our stability theorem to reprove stability for most of the cases in which
![]() $F(n;\boldsymbol {k})$
has already been determined, in a systematic fashion. For this, it suffices to solve Problem
$F(n;\boldsymbol {k})$
has already been determined, in a systematic fashion. For this, it suffices to solve Problem
![]() $Q_2$
(which follows from these earlier works), and to prove the extension property. Proving the extension property is straightforward: there are
$Q_2$
(which follows from these earlier works), and to prove the extension property. Proving the extension property is straightforward: there are
![]() $O(s^r)$
possible attachments of a new vertex to some
$O(s^r)$
possible attachments of a new vertex to some
![]() $(r,\phi ,\boldsymbol {\alpha })$
so a computer could check these for reasonable
$(r,\phi ,\boldsymbol {\alpha })$
so a computer could check these for reasonable
![]() $s,r$
. Actually, when optimal solutions have a particular nice form, which they do in almost all known cases, one can reduce the problem to determining solutions to some simple exponential equation over the integers (see Lemma 5.3). We cannot prove stability for
$s,r$
. Actually, when optimal solutions have a particular nice form, which they do in almost all known cases, one can reduce the problem to determining solutions to some simple exponential equation over the integers (see Lemma 5.3). We cannot prove stability for
![]() $\boldsymbol {k}=(3,3,3,3,3)$
, which does not have the extension property, strong or otherwise.
$\boldsymbol {k}=(3,3,3,3,3)$
, which does not have the extension property, strong or otherwise.
Theorem 1.7. Each
![]() $\boldsymbol {k}$
among
$\boldsymbol {k}$
among
![]() $(k,k)$
,
$(k,k)$
,
![]() $(k,k,k)$
,
$(k,k,k)$
,
![]() $(3,3,3,3)$
,
$(3,3,3,3)$
,
![]() $(4,4,4,4)$
has the strong extension property, for all integers
$(4,4,4,4)$
has the strong extension property, for all integers
![]() $k \geq 3$
. Thus, Theorem 1.4 applies to every such
$k \geq 3$
. Thus, Theorem 1.4 applies to every such
![]() $\boldsymbol {k}$
.
$\boldsymbol {k}$
.
As an example, we solve the optimisation problem for
![]() $s=2$
and state a version of Theorem 1.4 to illustrate it. Note that it would not be too difficult to prove stability for
$s=2$
and state a version of Theorem 1.4 to illustrate it. Note that it would not be too difficult to prove stability for
![]() $s=2$
directly.
$s=2$
directly.
Lemma 1.8. Let
![]() $k \geq \ell \geq 3$
be positive integers,
$k \geq \ell \geq 3$
be positive integers,
![]() $\boldsymbol {k} := (k,\ell )$
and
$\boldsymbol {k} := (k,\ell )$
and
![]() $\phi $
be the function on
$\phi $
be the function on
![]() $\binom {[\ell -1]}{2}$
that assumes value
$\binom {[\ell -1]}{2}$
that assumes value
![]() $\{1,2\}$
for every pair. Then
$\{1,2\}$
for every pair. Then
![]() $Q(\boldsymbol {k}) = 1 - \frac {1}{\ell -1}$
and
$Q(\boldsymbol {k}) = 1 - \frac {1}{\ell -1}$
and
![]() where
where
![]() $\boldsymbol {u}$
is uniform, and
$\boldsymbol {u}$
is uniform, and
![]() $\boldsymbol {k}$
has the extension property. Moreover,
$\boldsymbol {k}$
has the extension property. Moreover,
![]() $\boldsymbol {k}$
has the strong extension property if and only if
$\boldsymbol {k}$
has the strong extension property if and only if
![]() $k=\ell $
.
$k=\ell $
.
We write
![]() $\omega (G)$
for the clique number of a graph G; that is, the size of its largest clique.
$\omega (G)$
for the clique number of a graph G; that is, the size of its largest clique.
Theorem 1.9. Let
![]() $k \geq \ell \geq 3$
be integers. For all
$k \geq \ell \geq 3$
be integers. For all
![]() $\delta>0$
, there exist
$\delta>0$
, there exist
![]() $n_0\in \mathbb {N}$
and
$n_0\in \mathbb {N}$
and
![]() $\varepsilon>0$
, such that the following holds. Let G be a graph on
$\varepsilon>0$
, such that the following holds. Let G be a graph on
![]() $n\geq n_0$
vertices, such that
$n\geq n_0$
vertices, such that
![]() $\log F(G;(k,\ell )) \geq (Q(k,\ell )-\varepsilon )\binom {n}{2}$
. Then there is a graph
$\log F(G;(k,\ell )) \geq (Q(k,\ell )-\varepsilon )\binom {n}{2}$
. Then there is a graph
![]() $G'$
which can be obtained from G by modifying at most
$G'$
which can be obtained from G by modifying at most
![]() $\delta n^2$
adjacencies, and an equipartition
$\delta n^2$
adjacencies, and an equipartition
![]() $V(G')=A_1 \cup \ldots \cup A_{\ell-1}$
, such that
$V(G')=A_1 \cup \ldots \cup A_{\ell-1}$
, such that
![]() $G'[A_i,A_j]$
is complete for all distinct
$G'[A_i,A_j]$
is complete for all distinct
![]() $i,j \in [\ell-1]$
, and
$i,j \in [\ell-1]$
, and
![]() $\sum_{i \in [\ell-1]}\omega(G'[A_i]) \leq k-1$
.
$\sum_{i \in [\ell-1]}\omega(G'[A_i]) \leq k-1$
.
Moreover, for at least
![]() $(1-2^{-\varepsilon n^2})F(G;\boldsymbol {k})$
valid colourings
$(1-2^{-\varepsilon n^2})F(G;\boldsymbol {k})$
valid colourings
![]() $\chi $
of G,
$\chi $
of G,
![]() $\chi ^{-1}(c)[A_i,A_j]$
is
$\chi ^{-1}(c)[A_i,A_j]$
is
![]() $(\delta ,\frac {1}{2})$
-regular for
$(\delta ,\frac {1}{2})$
-regular for
![]() $c=1,2$
and distinct
$c=1,2$
and distinct
![]() $i,j \in [\ell-1]$
, and all but at most
$i,j \in [\ell-1]$
, and all but at most
![]() $\delta n^2$
edges in
$\delta n^2$
edges in
![]() $\bigcup_{i \in [\ell-1]}G[A_i]$
are coloured with colour
$\bigcup_{i \in [\ell-1]}G[A_i]$
are coloured with colour
![]() $1$
.
$1$
.
1.4 A sketch of the proof of Theorem 1.4
Since the proof of Theorem 1.4 is quite involved, we give a fairly detailed sketch first. Let G be a graph on n vertices, such that
![]() $\log F(G;\boldsymbol {k}) \geq (Q(\boldsymbol {k})-\varepsilon ) \binom {n}{2}$
. There are several ingredients to the proof.
$\log F(G;\boldsymbol {k}) \geq (Q(\boldsymbol {k})-\varepsilon ) \binom {n}{2}$
. There are several ingredients to the proof.
Regularity lemma: G is close to some nearly optimal
![]() $(r,\phi ,\boldsymbol {\alpha })$
in
$(r,\phi ,\boldsymbol {\alpha })$
in
![]() . The multicolour version of Szemerédi’s regularity lemma was already used to prove the existing results on
. The multicolour version of Szemerédi’s regularity lemma was already used to prove the existing results on
![]() $F(n;\boldsymbol {k})$
in [Reference Alon, Balogh, Keevash and Sudakov1, Reference Pikhurko and Yilma25] (for definitions and statements related to the regularity lemma, see Section 4.1). Given a
$F(n;\boldsymbol {k})$
in [Reference Alon, Balogh, Keevash and Sudakov1, Reference Pikhurko and Yilma25] (for definitions and statements related to the regularity lemma, see Section 4.1). Given a
![]() $\boldsymbol {k}$
-valid colouring
$\boldsymbol {k}$
-valid colouring
![]() $\chi $
of G, we obtain an equitable partition
$\chi $
of G, we obtain an equitable partition
![]() $U_1 \cup \ldots \cup U_r$
in which almost all pairs are regular in all colours in
$U_1 \cup \ldots \cup U_r$
in which almost all pairs are regular in all colours in
![]() $[s]$
. Define a colour pattern
$[s]$
. Define a colour pattern
![]() $\phi : \binom {[r]}{2} \rightarrow 2^{[s]}$
by adding the colour c to
$\phi : \binom {[r]}{2} \rightarrow 2^{[s]}$
by adding the colour c to
![]() $\phi (ij)$
if
$\phi (ij)$
if
![]() $\chi ^{-1}(c)[V_i,V_j]$
is regular, and has density that is not too small. The embedding lemma (Lemma 4.6) implies that
$\chi ^{-1}(c)[V_i,V_j]$
is regular, and has density that is not too small. The embedding lemma (Lemma 4.6) implies that
![]() $\phi ^{-1}(c)$
is
$\phi ^{-1}(c)$
is
![]() $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
![]() $c \in [s]$
. In this way, much of the information carried by
$c \in [s]$
. In this way, much of the information carried by
![]() $\chi $
is transferred to the tuple
$\chi $
is transferred to the tuple
![]() $\mathop {\mathrm {RL}}(\chi ) := (r,\phi ,\mathcal {U})$
, where
$\mathop {\mathrm {RL}}(\chi ) := (r,\phi ,\mathcal {U})$
, where
![]() $\mathcal {U} := \{ U_1,\ldots ,U_r \}$
.
$\mathcal {U} := \{ U_1,\ldots ,U_r \}$
.
Of course, one still needs to prove that this process is in some sense reversible: that the structure of G itself, as well as the structure of its colourings, can be recovered from
![]() $(r,\phi ,\mathcal {U})$
. This may not always be the case: we could have chosen some pathological
$(r,\phi ,\mathcal {U})$
. This may not always be the case: we could have chosen some pathological
![]() $\chi $
to generate
$\chi $
to generate
![]() $(r,\phi ,\mathcal {U})$
. For example, in the case
$(r,\phi ,\mathcal {U})$
. For example, in the case
![]() $\boldsymbol {k} = (3,3)$
, the unique extremal graph is
$\boldsymbol {k} = (3,3)$
, the unique extremal graph is
![]() $T_2(n) = K_{\lfloor n/2 \rfloor , \lceil n/2 \rceil }$
, but we could have chosen
$T_2(n) = K_{\lfloor n/2 \rfloor , \lceil n/2 \rceil }$
, but we could have chosen
![]() $\chi $
which colours every edge with colour
$\chi $
which colours every edge with colour
![]() $1$
. Then we cannot recover many further colourings from
$1$
. Then we cannot recover many further colourings from
![]() $(r,\phi ,\mathcal {U})$
.
$(r,\phi ,\mathcal {U})$
.
For this reason, we only wish to consider tuples
![]() $(r,\phi ,\mathcal {U})$
which are the image of many colourings; that is, some nontrivial proportion of all colourings. Such a tuple is called popular; and we think of colourings
$(r,\phi ,\mathcal {U})$
which are the image of many colourings; that is, some nontrivial proportion of all colourings. Such a tuple is called popular; and we think of colourings
![]() $\chi $
which map to this tuple as being good representatives of the set of all colourings of G. Since, as we show in Proposition 4.10, almost every colouring maps to a popular tuple, it suffices to fix a popular tuple
$\chi $
which map to this tuple as being good representatives of the set of all colourings of G. Since, as we show in Proposition 4.10, almost every colouring maps to a popular tuple, it suffices to fix a popular tuple
![]() $(r,\phi ,\mathcal {U})$
and only consider colourings which map to this tuple. Intuitively, all such colourings should be similar.
$(r,\phi ,\mathcal {U})$
and only consider colourings which map to this tuple. Intuitively, all such colourings should be similar.
Let
![]() $\alpha _i := 1/r$
for all
$\alpha _i := 1/r$
for all
![]() $i \in [r]$
. Then
$i \in [r]$
. Then
![]() . So the regularity lemma allows us to pass from G to a feasible solution to Problem
. So the regularity lemma allows us to pass from G to a feasible solution to Problem
![]() $Q_0$
. It turns out that since
$Q_0$
. It turns out that since
![]() $(r,\phi ,\mathcal {U})$
is popular, we have that
$(r,\phi ,\mathcal {U})$
is popular, we have that
and, moreover, that
![]() $G[U_i,U_j]$
is almost complete for all
$G[U_i,U_j]$
is almost complete for all
![]() $ij \in \binom {[r]}{2}$
(see Claim 4.1). Since we can choose r large (but still bounded), the number of edges of G within any
$ij \in \binom {[r]}{2}$
(see Claim 4.1). Since we can choose r large (but still bounded), the number of edges of G within any
![]() $U_i$
can be made very small. Therefore, the structure of G can be recovered from
$U_i$
can be made very small. Therefore, the structure of G can be recovered from
![]() $(r,\phi ,\mathcal {U})$
.
$(r,\phi ,\mathcal {U})$
.
Symmetrisation: from
![]() to some
to some
![]() . This is the main part of the proof (Lemma 3.1), and in it, we forget about G entirely, and instead concentrate on
. This is the main part of the proof (Lemma 3.1), and in it, we forget about G entirely, and instead concentrate on
![]() $(r,\phi ,\boldsymbol {\alpha })$
. We think of this object as a vertex-weighted coloured multigraph: the weights are given by
$(r,\phi ,\boldsymbol {\alpha })$
. We think of this object as a vertex-weighted coloured multigraph: the weights are given by
![]() $\boldsymbol {\alpha }$
, and the coloured edges by
$\boldsymbol {\alpha }$
, and the coloured edges by
![]() $\phi $
. We will apply a version of symmetrisation to
$\phi $
. We will apply a version of symmetrisation to
![]() $(r,\phi ,\boldsymbol {\alpha })$
. Symmetrisation was originally used in (ordinary) graphs by Zykov [Reference Zykov30] to give a new proof of Turán’s theorem. In its most basic form, it is the process of considering two nonadjacent vertices x and y in a graph G, and replacing x by a clone of y, that is a vertex
$(r,\phi ,\boldsymbol {\alpha })$
. Symmetrisation was originally used in (ordinary) graphs by Zykov [Reference Zykov30] to give a new proof of Turán’s theorem. In its most basic form, it is the process of considering two nonadjacent vertices x and y in a graph G, and replacing x by a clone of y, that is a vertex
![]() $y'$
whose neighbourhood is the same as that of y. With Yilma [Reference Pikhurko, Staden and Yilma24], we used symmetrisation to modify any
$y'$
whose neighbourhood is the same as that of y. With Yilma [Reference Pikhurko, Staden and Yilma24], we used symmetrisation to modify any
![]() $\boldsymbol {k}$
-extremal graph into one which is both extremal and complete multipartite (Theorem 1.1
(i)). Here, we use a version of symmetrisation as follows. Suppose that there is some
$\boldsymbol {k}$
-extremal graph into one which is both extremal and complete multipartite (Theorem 1.1
(i)). Here, we use a version of symmetrisation as follows. Suppose that there is some
![]() $ij \in \binom {[r]}{2}$
, such that
$ij \in \binom {[r]}{2}$
, such that
![]() $|\phi (ij)| \leq 1$
. Then we create a new feasible solution on r parts by making vertex j a clone of vertex i, or vice versa. One of these choices will be such that the new solution
$|\phi (ij)| \leq 1$
. Then we create a new feasible solution on r parts by making vertex j a clone of vertex i, or vice versa. One of these choices will be such that the new solution
![]() $(r,\phi ',\boldsymbol {\alpha })$
satisfies
$(r,\phi ',\boldsymbol {\alpha })$
satisfies
![]() $q(\phi ',\boldsymbol {\alpha }) \geq q(\phi ,\boldsymbol {\alpha })$
. At the end of this process, we will obtain
$q(\phi ',\boldsymbol {\alpha }) \geq q(\phi ,\boldsymbol {\alpha })$
. At the end of this process, we will obtain
![]() (where f is for final), such that
(where f is for final), such that
![]() $|\phi _f(ij)| \geq 2$
whenever
$|\phi _f(ij)| \geq 2$
whenever
![]() $i,j$
are not clones and
$i,j$
are not clones and
(in fact, we split each step into small steps to get slowly evolving colour patterns
![]() $\phi =\phi _0,\ldots ,\phi _f$
). The solution
$\phi =\phi _0,\ldots ,\phi _f$
). The solution
![]() $(r,\phi _f,\boldsymbol {\alpha })$
corresponds to a smaller solution
$(r,\phi _f,\boldsymbol {\alpha })$
corresponds to a smaller solution
![]() $(r_f,\psi _f,\boldsymbol {\alpha }_f)$
in which all clones are merged, so
$(r_f,\psi _f,\boldsymbol {\alpha }_f)$
in which all clones are merged, so
![]() (and
(and
![]() $q(\psi _f,\boldsymbol {\alpha }_f)=q(\phi _f,\boldsymbol {\alpha })$
is near-optimal). A compactness argument (Lemma 2.3) shows that there is some basic optimal solution
$q(\psi _f,\boldsymbol {\alpha }_f)=q(\phi _f,\boldsymbol {\alpha })$
is near-optimal). A compactness argument (Lemma 2.3) shows that there is some basic optimal solution
![]() $(r^*,\phi ^*,\boldsymbol {\alpha } ^*)$
which is very close to the near-optimal
$(r^*,\phi ^*,\boldsymbol {\alpha } ^*)$
which is very close to the near-optimal
![]() $(r_f,\phi _f,\boldsymbol {\alpha }_f)$
in a very strong sense:
$(r_f,\phi _f,\boldsymbol {\alpha }_f)$
in a very strong sense:
![]() $\boldsymbol {\alpha }^*$
and
$\boldsymbol {\alpha }^*$
and
![]() $\boldsymbol {\alpha }_f$
are close in
$\boldsymbol {\alpha }_f$
are close in
![]() $\ell ^1$
-distance, and
$\ell ^1$
-distance, and
![]() $\phi _f$
equals
$\phi _f$
equals
![]() $\phi ^*$
between pairs with nonnegligible weights.
$\phi ^*$
between pairs with nonnegligible weights.
The extension property:
![]() $(r,\phi,\boldsymbol{\alpha})$
and
$(r,\phi,\boldsymbol{\alpha})$
and
![]() $(r^*,\phi^*,\boldsymbol{\alpha}^*)$
are close. Here, we mean ‘close’ in the sense of Lemma 1.3. So we would like to show that when we merge pairs
$(r^*,\phi^*,\boldsymbol{\alpha}^*)$
are close. Here, we mean ‘close’ in the sense of Lemma 1.3. So we would like to show that when we merge pairs
![]() $ij$
with
$ij$
with
![]() $|\phi(ij)| \leq 1$
in
$|\phi(ij)| \leq 1$
in
![]() $(r,\phi,\boldsymbol{\alpha})$
we obtain a weight vector
$(r,\phi,\boldsymbol{\alpha})$
we obtain a weight vector
![]() $\boldsymbol {u}$
which is close to
$\boldsymbol {u}$
which is close to
![]() $\boldsymbol{\alpha}^*$
in
$\boldsymbol{\alpha}^*$
in
![]() $\ell^1$
-distance, and
$\ell^1$
-distance, and
![]() $\phi \subseteq \phi^*$
on pairs of non-negligible size. (This turns out to be a simplification; see below.) It is of course far from clear that we have not changed
$\phi \subseteq \phi^*$
on pairs of non-negligible size. (This turns out to be a simplification; see below.) It is of course far from clear that we have not changed
![]() $(r,\phi,\boldsymbol{\alpha})$
drastically to obtain
$(r,\phi,\boldsymbol{\alpha})$
drastically to obtain
![]() $(r^*,\phi^*,\boldsymbol{\alpha}^*)$
. That this is not so is effectively a consequence of the extension property.
$(r^*,\phi^*,\boldsymbol{\alpha}^*)$
. That this is not so is effectively a consequence of the extension property.
Having obtained
![]() $(r^*,\phi^*,\boldsymbol{\alpha}^*)$
from symmetrisation, we can now, with the benefit of hindsight, follow the procedure backwards. At each stage, we check whether the attachments of each vertex are large; if not we sequentially put bad vertices into an exceptional set, called
$(r^*,\phi^*,\boldsymbol{\alpha}^*)$
from symmetrisation, we can now, with the benefit of hindsight, follow the procedure backwards. At each stage, we check whether the attachments of each vertex are large; if not we sequentially put bad vertices into an exceptional set, called
![]() $U_{i}^0$
at the i-th step. At each stage, the extension property implies that every vertex x is either in
$U_{i}^0$
at the i-th step. At each stage, the extension property implies that every vertex x is either in
![]() $U_{i}^0$
or it corresponds to some vertex k in the optimal solution
$U_{i}^0$
or it corresponds to some vertex k in the optimal solution
![]() $(r^*,\phi^*,\boldsymbol{\alpha}^*)$
; that is,
$(r^*,\phi^*,\boldsymbol{\alpha}^*)$
; that is,
![]() $\phi_i(xy) \subseteq \phi^*(kj)$
for all
$\phi_i(xy) \subseteq \phi^*(kj)$
for all
![]() $j \in [r^*] \setminus \{ k \}$
and all vertices y corresponding to j. Let
$j \in [r^*] \setminus \{ k \}$
and all vertices y corresponding to j. Let
![]() $U_{i}^k$
be the set of vertices corresponding to k at Step i. Note that
$U_{i}^k$
be the set of vertices corresponding to k at Step i. Note that
![]() $|\phi_i(xy)| \leq 1$ if $x,y \in U_{i}^k$
.
$|\phi_i(xy)| \leq 1$ if $x,y \in U_{i}^k$
.
So, going back through the procedure, at each step there are a small fraction of vertices x which were exceptional but are no longer exceptional, and these are moved to the
![]() $U_{i}^k$
for which x corresponds to k; and there are a small fraction of vertices moved into
$U_{i}^k$
for which x corresponds to k; and there are a small fraction of vertices moved into
![]() $U_{i}^0$
. When we return to Step 0, we want to show that
$U_{i}^0$
. When we return to Step 0, we want to show that
![]() $\phi \subseteq \phi^*$
between any two classes
$\phi \subseteq \phi^*$
between any two classes
![]() $U_0^j$
and
$U_0^j$
and
![]() $U_0^k$
, even though the attachment between
$U_0^k$
, even though the attachment between
![]() $U_{0}^0$
and the rest of the vertices, as well as the colour pattern within a class
$U_{0}^0$
and the rest of the vertices, as well as the colour pattern within a class
![]() $U_{i}^k$
may have changed. Therefore, if we can show that
$U_{i}^k$
may have changed. Therefore, if we can show that
![]() $U_{0}^0$
is small (Claim 3.1.2) and every
$U_{0}^0$
is small (Claim 3.1.2) and every
![]() $U_{0}^k$
,
$U_{0}^k$
,
![]() $k>0$
, is about the same size throughout, then the procedure did not really change
$k>0$
, is about the same size throughout, then the procedure did not really change
![]() $(r,\phi,\boldsymbol{\alpha})$
much at all. Furthermore, we have a partition
$(r,\phi,\boldsymbol{\alpha})$
much at all. Furthermore, we have a partition
![]() $U_{0}^0,U_{0}^1,\ldots,U_{0}^{r^*}$
of
$U_{0}^0,U_{0}^1,\ldots,U_{0}^{r^*}$
of
![]() $[r]$
such that
$[r]$
such that
![]() $\phi \subseteq \phi^*$
between
$\phi \subseteq \phi^*$
between
![]() $U_{0}^i,U_{0}^j$
,
$U_{0}^i,U_{0}^j$
,
![]() $i,j \neq 0$
; and
$i,j \neq 0$
; and
![]() $|\phi(ij)| \leq 1$
within a class. In fact, the above sketch is a simplification, and though the exceptional set is always small, the other parts could change significantly in size. Nevertheless, we show that for each i there are
$|\phi(ij)| \leq 1$
within a class. In fact, the above sketch is a simplification, and though the exceptional set is always small, the other parts could change significantly in size. Nevertheless, we show that for each i there are
![]() $\tilde{r}_i$
nonzero nonexceptional parts with part ratios given by some
$\tilde{r}_i$
nonzero nonexceptional parts with part ratios given by some
![]() $\tilde{\boldsymbol{\alpha}}_i$
, and
$\tilde{\boldsymbol{\alpha}}_i$
, and
![]() , where
, where
![]() $\phi_i\subseteq\tilde{\phi}_i$
between pairs and
$\phi_i\subseteq\tilde{\phi}_i$
between pairs and
![]() $|\phi_i(jk)| \leq 1$
within a class.
$|\phi_i(jk)| \leq 1$
within a class.
Recovering G from
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
. We now transfer the information we have gleaned about
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
. We now transfer the information we have gleaned about
![]() $(r,\phi ,\boldsymbol {\alpha })$
back to G itself. The partition of
$(r,\phi ,\boldsymbol {\alpha })$
back to G itself. The partition of
![]() $[r]$
induces a partition
$[r]$
induces a partition
![]() $X_0,X_1,\ldots ,X_{r^*}$
on
$X_0,X_1,\ldots ,X_{r^*}$
on
![]() $V(G)$
. For every
$V(G)$
. For every
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
, we almost always have
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
, we almost always have
![]() $\chi (xy) \in \phi ^*(ij)$
when
$\chi (xy) \in \phi ^*(ij)$
when
![]() $ij \in \binom {[r^*]}{2}$
and
$ij \in \binom {[r^*]}{2}$
and
![]() $x \in X_i, y \in X_j$
. In Claims 4.2 and 4.3, we show, for almost all these
$x \in X_i, y \in X_j$
. In Claims 4.2 and 4.3, we show, for almost all these
![]() $\chi $
, that
$\chi $
, that
![]() $\chi ^{-1}(c)[X_i,X_j]$
is regular. Indeed, if
$\chi ^{-1}(c)[X_i,X_j]$
is regular. Indeed, if
![]() $\chi ^{-1}(c)[X_i,X_j]$
is not regular, then Lemma 4.4 implies that there is
$\chi ^{-1}(c)[X_i,X_j]$
is not regular, then Lemma 4.4 implies that there is
![]() $c^* \in [s]$
and large sets
$c^* \in [s]$
and large sets
![]() $X \subseteq X_i$
and
$X \subseteq X_i$
and
![]() $Y \subseteq X_j$
between which the density of colour
$Y \subseteq X_j$
between which the density of colour
![]() $c^*$
edges is significantly less than it is between
$c^*$
edges is significantly less than it is between
![]() $X_i$
and
$X_i$
and
![]() $X_j$
. But Corollary 4.8 implies that very few s-edge colourings of
$X_j$
. But Corollary 4.8 implies that very few s-edge colourings of
![]() $G[X_i,X_j]$
are such that some colour class (
$G[X_i,X_j]$
are such that some colour class (
![]() $c \in \phi ^*(ij)$
) has size much less than the average
$c \in \phi ^*(ij)$
) has size much less than the average
![]() $|\phi ^*(ij)|^{-1}$
.
$|\phi ^*(ij)|^{-1}$
.
The final step is to look inside the classes. We discretise by applying the regularity lemma again within each class (which is large by Lemma 2.8). This allows us to apply Lemma 2.5 to prove (iii).
1.5 Organisation
Most of the paper concerns optimal triples for Problem
![]() $Q_t$
rather than graphs. In Section 2, we collect some tools concerning these optimal triples, and some consequences of the extension property. The main result in Section 3 is the stability of optimal solutions given the extension property, which is the key component of the proof of our graph stability result, Theorem 1.4. In Section 4, we transfer statements on optimal triples to graphs, and prove Theorem 1.4, after stating and proving some tools concerning the regularity lemma. Then we prove Corollary 1.5. Section 5 concerns applications of Theorem 1.4, in particular, it contains the derivations of Theorems 1.7 and 1.9. We finish with some concluding remarks in Section 6.
$Q_t$
rather than graphs. In Section 2, we collect some tools concerning these optimal triples, and some consequences of the extension property. The main result in Section 3 is the stability of optimal solutions given the extension property, which is the key component of the proof of our graph stability result, Theorem 1.4. In Section 4, we transfer statements on optimal triples to graphs, and prove Theorem 1.4, after stating and proving some tools concerning the regularity lemma. Then we prove Corollary 1.5. Section 5 concerns applications of Theorem 1.4, in particular, it contains the derivations of Theorems 1.7 and 1.9. We finish with some concluding remarks in Section 6.
2 Optimal solutions of Problem
 $Q_t$
$Q_t$
We will now explore some properties of optimal solutions, which will be useful in later sections. The following proposition states that, in an optimal solution
![]() , every vertex i of positive weight attaches optimally, in that the normalised contribution
, every vertex i of positive weight attaches optimally, in that the normalised contribution
![]() $q_i(\phi ,\boldsymbol {\alpha })$
to the sum
$q_i(\phi ,\boldsymbol {\alpha })$
to the sum
 $$ \begin{align*}q(\phi,\boldsymbol{\alpha}) = \sum_{i \in [r]}\alpha_i q_i(\phi,\boldsymbol{\alpha})\quad\text{where}\quad q_i(\phi,\boldsymbol{\alpha}) := \sum_{\substack{j \in [r] \setminus \{ i \}\\ \phi(ij)\neq\emptyset}}\alpha_j\log|\phi(ij)| \end{align*} $$
$$ \begin{align*}q(\phi,\boldsymbol{\alpha}) = \sum_{i \in [r]}\alpha_i q_i(\phi,\boldsymbol{\alpha})\quad\text{where}\quad q_i(\phi,\boldsymbol{\alpha}) := \sum_{\substack{j \in [r] \setminus \{ i \}\\ \phi(ij)\neq\emptyset}}\alpha_j\log|\phi(ij)| \end{align*} $$
is equal to
![]() $Q(\boldsymbol {k})$
.
$Q(\boldsymbol {k})$
.
Proposition 2.1. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
, and suppose that
$\boldsymbol {k} \in \mathbb {N}^s$
, and suppose that
![]() . For every
. For every
![]() $i \in [r]$
with
$i \in [r]$
with
![]() $\alpha _i> 0$
, we have that
$\alpha _i> 0$
, we have that
![]() $ q_i(\phi ,\boldsymbol {\alpha }) = Q(\boldsymbol {k}) $
.
$ q_i(\phi ,\boldsymbol {\alpha }) = Q(\boldsymbol {k}) $
.
Proof. Without affecting the statement, we can remove all indices i with
![]() $\alpha _i=0$
. So assume that
$\alpha _i=0$
. So assume that
![]() $\alpha _i>0$
for all
$\alpha _i>0$
for all
![]() $i \in [r]$
. We use the method of Lagrange multipliers. Recall that the constraint is that
$i \in [r]$
. We use the method of Lagrange multipliers. Recall that the constraint is that
![]() $g(\boldsymbol {\alpha }) = 0$
, where
$g(\boldsymbol {\alpha }) = 0$
, where
![]() $g(\boldsymbol {\alpha }) := \|\boldsymbol {\alpha }\|_1 - 1$
. Fix
$g(\boldsymbol {\alpha }) := \|\boldsymbol {\alpha }\|_1 - 1$
. Fix
![]() $\phi \in \Phi _0(r;\boldsymbol {k})$
, and let
$\phi \in \Phi _0(r;\boldsymbol {k})$
, and let
Since the optimal vertex weighting
![]() $\boldsymbol {\alpha }$
is in the interior of
$\boldsymbol {\alpha }$
is in the interior of
![]() $\Delta ^r$
(and
$\Delta ^r$
(and
![]() $\mathcal {L}$
is continuously differentiable there), there is
$\mathcal {L}$
is continuously differentiable there), there is
![]() $\lambda $
, such that
$\lambda $
, such that
![]() $(\boldsymbol {\alpha },\lambda )$
is a critical point of
$(\boldsymbol {\alpha },\lambda )$
is a critical point of
![]() $\mathcal {L}$
. Thus,
$\mathcal {L}$
. Thus,
We see that
![]() $q_i(\phi ,\boldsymbol {\alpha })$
,
$q_i(\phi ,\boldsymbol {\alpha })$
,
![]() $i \in [r]$
, are equal to each other and the common value is
$i \in [r]$
, are equal to each other and the common value is
![]() $\lambda /2=\|\boldsymbol {\alpha }\|_1\lambda /2 = \sum _{i \in [r]}\alpha _iq_i(\phi ,\boldsymbol {\alpha })=q(\phi ,\boldsymbol {\alpha })=Q(\boldsymbol {k})$
. Therefore, every
$\lambda /2=\|\boldsymbol {\alpha }\|_1\lambda /2 = \sum _{i \in [r]}\alpha _iq_i(\phi ,\boldsymbol {\alpha })=q(\phi ,\boldsymbol {\alpha })=Q(\boldsymbol {k})$
. Therefore, every
![]() satisfies the equation in the statement of the proposition.
satisfies the equation in the statement of the proposition.
The next proposition shows that the objective function
![]() $q(\phi ,\cdot )$
is Lipschitz continuous.
$q(\phi ,\cdot )$
is Lipschitz continuous.
Proposition 2.2 [Reference Pikhurko, Staden and Yilma24, Proposition 11].
Let
![]() $s,r \in \mathbb {N}$
and
$s,r \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Let
$\boldsymbol {k} \in \mathbb {N}^s$
. Let
![]() $\phi \in \Phi _0(r;\boldsymbol {k})$
and
$\phi \in \Phi _0(r;\boldsymbol {k})$
and
![]() $\boldsymbol {\alpha },\boldsymbol {\beta } \in \Delta ^r$
. Then
$\boldsymbol {\alpha },\boldsymbol {\beta } \in \Delta ^r$
. Then
The next lemma states that whenever we have a feasible solution
![]() which is almost optimal, there is some vertex weighting
which is almost optimal, there is some vertex weighting
![]() $\boldsymbol {\alpha }^*$
which is close to
$\boldsymbol {\alpha }^*$
which is close to
![]() $\boldsymbol {\alpha }$
, such that
$\boldsymbol {\alpha }$
, such that
![]() $(r,\phi ,\boldsymbol {\alpha }^*)$
is an optimal solution.
$(r,\phi ,\boldsymbol {\alpha }^*)$
is an optimal solution.
Lemma 2.3 [Reference Pikhurko, Staden and Yilma24, Claim 15].
Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. For all
$\boldsymbol {k} \in \mathbb {N}^s$
. For all
![]() $\delta> 0$
, there exists
$\delta> 0$
, there exists
![]() $\varepsilon> 0$
, such that the following holds. Let
$\varepsilon> 0$
, such that the following holds. Let
![]() be such that
be such that
![]() $q(\phi ,\boldsymbol {\alpha }) \geq Q(\textbf {k}) - \varepsilon $
. Then there exists
$q(\phi ,\boldsymbol {\alpha }) \geq Q(\textbf {k}) - \varepsilon $
. Then there exists
![]() $\boldsymbol {\alpha }^* \in \Delta ^{r}$
, such that
$\boldsymbol {\alpha }^* \in \Delta ^{r}$
, such that
![]() $\| \boldsymbol {\alpha }-\boldsymbol {\alpha }^* \|_1 < \delta $
and
$\| \boldsymbol {\alpha }-\boldsymbol {\alpha }^* \|_1 < \delta $
and
![]() .
.
Consider the following definition.
Definition 2.4 (Capacity).
Given
![]() $r \in \mathbb {N}$
, a graph G with vertex set
$r \in \mathbb {N}$
, a graph G with vertex set
![]() $[r]$
and positive integers
$[r]$
and positive integers
![]() $\ell _1,\ldots ,\ell _r$
, we write
$\ell _1,\ldots ,\ell _r$
, we write
![]() $(\ell _1,\ldots ,\ell _r)G$
to denote the graph obtained from G by, for each
$(\ell _1,\ldots ,\ell _r)G$
to denote the graph obtained from G by, for each
![]() $i \in [r]$
, replacing vertex i with a clique
$i \in [r]$
, replacing vertex i with a clique
![]() $K_{\ell _i}$
, and joining every vertex in
$K_{\ell _i}$
, and joining every vertex in
![]() $K_{\ell _i}$
to all vertices in the cliques
$K_{\ell _i}$
to all vertices in the cliques
![]() $K_{\ell _j}$
, such that j is a neighbour of i in G.
$K_{\ell _j}$
, such that j is a neighbour of i in G.
Let
![]() $\mathop {\mathrm {Cap}}(G,k)$
be the set of those
$\mathop {\mathrm {Cap}}(G,k)$
be the set of those
![]() $(\ell _1,\ldots ,\ell _r) \in \mathbb {N}^r$
for which
$(\ell _1,\ldots ,\ell _r) \in \mathbb {N}^r$
for which
![]() $(\ell _1,\ldots ,\ell _r)G$
is
$(\ell _1,\ldots ,\ell _r)G$
is
![]() $K_k$
-free.
$K_k$
-free.
Since
![]() $(1,\ldots ,1)G = G$
, certainly
$(1,\ldots ,1)G = G$
, certainly
![]() $\mathop {\mathrm {Cap}}(G,k) \neq \emptyset $
whenever G is
$\mathop {\mathrm {Cap}}(G,k) \neq \emptyset $
whenever G is
![]() $K_k$
-free. It is easy to see that, if
$K_k$
-free. It is easy to see that, if
![]() $\boldsymbol {b} \in \mathbb {N}^r$
satisfies
$\boldsymbol {b} \in \mathbb {N}^r$
satisfies
![]() $\boldsymbol {b} \in \mathop {\mathrm {Cap}}(G,k)$
, then
$\boldsymbol {b} \in \mathop {\mathrm {Cap}}(G,k)$
, then
![]() $\boldsymbol {a} \in \mathop {\mathrm {Cap}}(G,k)$
for all
$\boldsymbol {a} \in \mathop {\mathrm {Cap}}(G,k)$
for all
![]() $\boldsymbol {a} \in \mathbb {N}^r$
with
$\boldsymbol {a} \in \mathbb {N}^r$
with
![]() $\boldsymbol {a} \leq \boldsymbol {b}$
. We think of
$\boldsymbol {a} \leq \boldsymbol {b}$
. We think of
![]() $\mathop {\mathrm {Cap}}(G,k)$
as being a measure of how far a
$\mathop {\mathrm {Cap}}(G,k)$
as being a measure of how far a
![]() $K_k$
-free graph G is from containing a copy of
$K_k$
-free graph G is from containing a copy of
![]() $K_k$
. For example,
$K_k$
. For example,
![]() $(1,2,2) \in \mathop {\mathrm {Cap}}(K_3,6)$
, but
$(1,2,2) \in \mathop {\mathrm {Cap}}(K_3,6)$
, but
![]() $\mathop {\mathrm {Cap}}(K_3,4) = \{ (1,1,1) \}$
.
$\mathop {\mathrm {Cap}}(K_3,4) = \{ (1,1,1) \}$
.
We now prove some facts about the capacity of
![]() $(\phi ^*)^{-1}(c)$
in a basic optimal solution
$(\phi ^*)^{-1}(c)$
in a basic optimal solution
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
, that is
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
, that is
![]() $q(\phi ^*,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
,
$q(\phi ^*,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
,
![]() $|\phi ^*(ij)| \geq 2$
for all
$|\phi ^*(ij)| \geq 2$
for all
![]() $ij \in \binom {[r^*]}{2}$
, and
$ij \in \binom {[r^*]}{2}$
, and
![]() $\alpha _i^*>0$
for all
$\alpha _i^*>0$
for all
![]() $i \in [r^*]$
. The most important part is (ii), which is essentially a consequence of the fact that maximally
$i \in [r^*]$
. The most important part is (ii), which is essentially a consequence of the fact that maximally
![]() $K_k$
-free graphs on r vertices have nontrivial capacity if and only if
$K_k$
-free graphs on r vertices have nontrivial capacity if and only if
![]() $r<k-1$
. This lemma will be important in proving Theorem 1.4
(iii).
$r<k-1$
. This lemma will be important in proving Theorem 1.4
(iii).
Lemma 2.5. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
with
$\boldsymbol {k} \in \mathbb {N}^s$
with
![]() $k_1\geq \ldots \geq k_s$
. Let
$k_1\geq \ldots \geq k_s$
. Let
![]() , and define
, and define
![]() $J_c := ([r^*],(\phi ^*)^{-1}(c))$
. Then the following statements hold.
$J_c := ([r^*],(\phi ^*)^{-1}(c))$
. Then the following statements hold.
-
(i)
 $J_c$
is maximally
$J_c$
is maximally
 $K_{k_c}$
-free.
$K_{k_c}$
-free. -
(ii) With
 $\boldsymbol {1} \in \mathbb {N}^{r^*}$
denoting the all-
$\boldsymbol {1} \in \mathbb {N}^{r^*}$
denoting the all-
 $1$
vector, we have furthermore, if
$1$
vector, we have furthermore, if $$ \begin{align*}\mathop{\mathrm{Cap}}(J_c,k_c) = \begin{cases} \{ \boldsymbol{1} \} \cup \{ \boldsymbol{\ell} \in \mathbb{N}^{r^*} : \|\boldsymbol{\ell}\|_1 \leq k_c-1 \} &\mbox{if } c = 1 \text{ and } k_1> k_2 \\ \{ \boldsymbol{1} \} &\mbox{otherwise;} \end{cases} \end{align*} $$
$$ \begin{align*}\mathop{\mathrm{Cap}}(J_c,k_c) = \begin{cases} \{ \boldsymbol{1} \} \cup \{ \boldsymbol{\ell} \in \mathbb{N}^{r^*} : \|\boldsymbol{\ell}\|_1 \leq k_c-1 \} &\mbox{if } c = 1 \text{ and } k_1> k_2 \\ \{ \boldsymbol{1} \} &\mbox{otherwise;} \end{cases} \end{align*} $$
 $\mathop {\mathrm {Cap}}(J_1,k_1) \neq \{ \boldsymbol {1} \}$
, then
$\mathop {\mathrm {Cap}}(J_1,k_1) \neq \{ \boldsymbol {1} \}$
, then
 $J_1 \cong K_{r^*}$
.
$J_1 \cong K_{r^*}$
.
-
(iii)
 $r^* \geq k_{2}-1$
.
$r^* \geq k_{2}-1$
.
Proof. Suppose that (i) does not hold for some
![]() $c \in [s]$
. Then there exist distinct
$c \in [s]$
. Then there exist distinct
![]() $i',j' \in [r^*]$
, such that
$i',j' \in [r^*]$
, such that
![]() $i'j' \notin E(J_c)$
, and
$i'j' \notin E(J_c)$
, and
![]() $J_c \cup \{ i'j' \}$
is
$J_c \cup \{ i'j' \}$
is
![]() $K_{k_c}$
-free. Let
$K_{k_c}$
-free. Let
![]() $\phi ' : \binom {[r^*]}{2} \rightarrow 2^{[s]}$
be defined by setting
$\phi ' : \binom {[r^*]}{2} \rightarrow 2^{[s]}$
be defined by setting
![]() $\phi '(ij) := \phi ^*(ij)$
whenever
$\phi '(ij) := \phi ^*(ij)$
whenever
![]() $ij \neq i'j'$
; and setting
$ij \neq i'j'$
; and setting
![]() $\phi '(i'j') := \phi ^*(ij) \cup \{ c \}$
. By construction,
$\phi '(i'j') := \phi ^*(ij) \cup \{ c \}$
. By construction,
![]() $\phi ' \in \Phi _2(r^*;\boldsymbol {k})$
. So
$\phi ' \in \Phi _2(r^*;\boldsymbol {k})$
. So
![]() . But
. But
 $$ \begin{align*}q(\phi',\boldsymbol{\alpha}^*) - q(\phi^*,\boldsymbol{\alpha}^*) = 2\alpha^*_{i'}\alpha^*_{j'}\log\left(1+\frac{1}{|\phi^*(i'j')|}\right) \geq 2\alpha^*_{i'}\alpha^*_{j'}\log \left( 1 + \frac{1}{s} \right)> 0, \end{align*} $$
$$ \begin{align*}q(\phi',\boldsymbol{\alpha}^*) - q(\phi^*,\boldsymbol{\alpha}^*) = 2\alpha^*_{i'}\alpha^*_{j'}\log\left(1+\frac{1}{|\phi^*(i'j')|}\right) \geq 2\alpha^*_{i'}\alpha^*_{j'}\log \left( 1 + \frac{1}{s} \right)> 0, \end{align*} $$
a contradiction. This proves (i).
We now prove (ii). To do this, we need the following simple claim.
Claim 2.5.1. Let
![]() $k \in \mathbb {N}$
, and let H be maximally
$k \in \mathbb {N}$
, and let H be maximally
![]() $K_k$
-free. Then every
$K_k$
-free. Then every
![]() $x \in V(H)$
lies in a copy of
$x \in V(H)$
lies in a copy of
![]() $K_{k-1}$
if and only if
$K_{k-1}$
if and only if
![]() $|V(H)| \geq k-1$
.
$|V(H)| \geq k-1$
.
Proof of Claim.
To prove the claim, note that the ‘only if’ direction is trivial. Suppose now that the other direction does not hold; that is,
![]() $r := |V(H)| \geq k-1$
and there exists
$r := |V(H)| \geq k-1$
and there exists
![]() $x \in V(H)$
which does not lie in a copy of
$x \in V(H)$
which does not lie in a copy of
![]() $K_{k-1}$
. First consider the case when
$K_{k-1}$
. First consider the case when
![]() $N_H(x) = V(H) \setminus \{ x \}$
. Then
$N_H(x) = V(H) \setminus \{ x \}$
. Then
![]() $H-x$
is a
$H-x$
is a
![]() $K_{k-2}$
-free graph on at least
$K_{k-2}$
-free graph on at least
![]() $k-2$
vertices. Thus, there is a nonedge e in
$k-2$
vertices. Thus, there is a nonedge e in
![]() $H-x$
. Let
$H-x$
. Let
![]() $H' := H \cup \{ e \}$
. Then
$H' := H \cup \{ e \}$
. Then
![]() $H'-x$
is
$H'-x$
is
![]() $K_{k-1}$
-free, and since x not does lie in a
$K_{k-1}$
-free, and since x not does lie in a
![]() $K_{k-1}$
in H, x does not lie in a copy of
$K_{k-1}$
in H, x does not lie in a copy of
![]() $K_k$
in
$K_k$
in
![]() $H'$
. Therefore,
$H'$
. Therefore,
![]() $H'$
is
$H'$
is
![]() $K_k$
-free, a contradiction.
$K_k$
-free, a contradiction.
Consider now the case when there is some
![]() $y \in V(H-x)$
, such that
$y \in V(H-x)$
, such that
![]() $xy \notin E(H)$
. Then
$xy \notin E(H)$
. Then
![]() $H" := H \cup \{ xy \}$
is
$H" := H \cup \{ xy \}$
is
![]() $K_k$
-free, since any clique which lies in
$K_k$
-free, since any clique which lies in
![]() $H"$
but not H must contain x. Again, this is a contradiction, proving the claim.
$H"$
but not H must contain x. Again, this is a contradiction, proving the claim.
Suppose that
![]() $\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c) \neq \{ \boldsymbol {1} \}$
. Then there exists
$\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c) \neq \{ \boldsymbol {1} \}$
. Then there exists
![]() $j \in [r^*]$
, such that
$j \in [r^*]$
, such that
![]() $\boldsymbol {1}+\boldsymbol {e}_j \in \mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c))$
. Observe that the graph
$\boldsymbol {1}+\boldsymbol {e}_j \in \mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c))$
. Observe that the graph
![]() $(\boldsymbol {1}+\boldsymbol {e}_j)J_c$
is obtained from
$(\boldsymbol {1}+\boldsymbol {e}_j)J_c$
is obtained from
![]() $J_c$
by inserting a twin
$J_c$
by inserting a twin
![]() $j'$
of j and adding the edge
$j'$
of j and adding the edge
![]() $jj'$
. If
$jj'$
. If
![]() $r^* \geq k_c-1$
, then j lies in a copy of
$r^* \geq k_c-1$
, then j lies in a copy of
![]() $K_{k_c-1}$
in
$K_{k_c-1}$
in
![]() $J_c$
by Part (i) and the claim. So
$J_c$
by Part (i) and the claim. So
![]() $j'$
together with the vertices in this copy form a copy of
$j'$
together with the vertices in this copy form a copy of
![]() $K_{k_c}$
in
$K_{k_c}$
in
![]() $(\boldsymbol {1}+\boldsymbol {e}_j)J_c$
, a contradiction. So
$(\boldsymbol {1}+\boldsymbol {e}_j)J_c$
, a contradiction. So
![]() $r^* \leq k_c-2$
.
$r^* \leq k_c-2$
.
Suppose instead that
![]() $\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c) = \{ \boldsymbol {1} \}$
. Then
$\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c) = \{ \boldsymbol {1} \}$
. Then
![]() $(\boldsymbol {1}+\boldsymbol {e}_j)J_c$
contains a copy of
$(\boldsymbol {1}+\boldsymbol {e}_j)J_c$
contains a copy of
![]() $K_{k_c}$
for every
$K_{k_c}$
for every
![]() $j \in [r^*]$
, and this copy necessarily contains j (since
$j \in [r^*]$
, and this copy necessarily contains j (since
![]() $J_c$
itself is
$J_c$
itself is
![]() $K_{k_c}$
-free). Trivially,
$K_{k_c}$
-free). Trivially,
![]() $r^* = |V(J_c)| \geq k_c-1$
. We have proved that
$r^* = |V(J_c)| \geq k_c-1$
. We have proved that
Let
![]() $C := \{ c \in [s] : r^* \leq k_c-2 \}$
. If
$C := \{ c \in [s] : r^* \leq k_c-2 \}$
. If
![]() $C = \emptyset $
, then
$C = \emptyset $
, then
![]() $\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c) = \{ \boldsymbol {1} \}$
for all
$\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c) = \{ \boldsymbol {1} \}$
for all
![]() $ c \in [s]$
. Note also that
$ c \in [s]$
. Note also that
![]() $\{ \boldsymbol {\ell } \in \mathbb {N}^{r^*} : \|\boldsymbol {\ell }\|_1 \leq k_c - 1 \} \subseteq \{ \boldsymbol {1} \}$
. So we are done in this case and may assume that
$\{ \boldsymbol {\ell } \in \mathbb {N}^{r^*} : \|\boldsymbol {\ell }\|_1 \leq k_c - 1 \} \subseteq \{ \boldsymbol {1} \}$
. So we are done in this case and may assume that
![]() $C \neq \emptyset $
.
$C \neq \emptyset $
.
By Part (i), for all
![]() $c \in C$
, we have
$c \in C$
, we have
![]() $(\phi ^*)^{-1}(c) \cong K_{r^*}$
since this is the unique maximally
$(\phi ^*)^{-1}(c) \cong K_{r^*}$
since this is the unique maximally
![]() $K_{k_c}$
-free graph on
$K_{k_c}$
-free graph on
![]() $r^*$
vertices. Define a new solution on
$r^*$
vertices. Define a new solution on
![]() $r^*+1$
vertices as follows. Suppose, without loss of generality, that
$r^*+1$
vertices as follows. Suppose, without loss of generality, that
![]() $\alpha _{r^*} \geq \alpha _i$
for all
$\alpha _{r^*} \geq \alpha _i$
for all
![]() $i \in [r^*]$
. Let
$i \in [r^*]$
. Let
 $$ \begin{align*} \phi(ij) &:= \begin{cases} \phi^*(ij) &\mbox{if } ij \in \binom{[r^*]}{2} \\ \phi^*(ir^*) &\mbox{if } i \in [r^*-1], j = r^*+1\\ C &\mbox{if } \{ i,j \} = \{ r^*,r^*+1 \} \end{cases}\\[-15pt] \end{align*} $$
$$ \begin{align*} \phi(ij) &:= \begin{cases} \phi^*(ij) &\mbox{if } ij \in \binom{[r^*]}{2} \\ \phi^*(ir^*) &\mbox{if } i \in [r^*-1], j = r^*+1\\ C &\mbox{if } \{ i,j \} = \{ r^*,r^*+1 \} \end{cases}\\[-15pt] \end{align*} $$
and
 $$ \begin{align*} \alpha_i &:= \begin{cases} \alpha^*_i &\mbox{if } i \in [r^*-1] \\ \alpha^*_{r^*}/2 &\mbox{if } i \in \{ r^*,r^*+1 \}. \end{cases}\\[-15pt] \end{align*} $$
$$ \begin{align*} \alpha_i &:= \begin{cases} \alpha^*_i &\mbox{if } i \in [r^*-1] \\ \alpha^*_{r^*}/2 &\mbox{if } i \in \{ r^*,r^*+1 \}. \end{cases}\\[-15pt] \end{align*} $$
Then
![]() $\phi ^{-1}(c)$
is
$\phi ^{-1}(c)$
is
![]() $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
![]() $c \in [s]$
, so
$c \in [s]$
, so
![]() . Furthermore,
. Furthermore,
 $$ \begin{align*} 0 \geq q(\phi,\boldsymbol{\alpha})-q(\phi^*,\boldsymbol{\alpha}^*) = 2\left(\frac{\alpha_{r^*}^*}{2}\right)^2 \log |C|,\\[-15pt] \end{align*} $$
$$ \begin{align*} 0 \geq q(\phi,\boldsymbol{\alpha})-q(\phi^*,\boldsymbol{\alpha}^*) = 2\left(\frac{\alpha_{r^*}^*}{2}\right)^2 \log |C|,\\[-15pt] \end{align*} $$
and so
![]() $|C|=1$
. Let
$|C|=1$
. Let
![]() $C = \{ c^* \}$
. Then
$C = \{ c^* \}$
. Then
![]() $k_{c^*}-2 \geq r^* \geq k_c -1$
for all
$k_{c^*}-2 \geq r^* \geq k_c -1$
for all
![]() $c \in [s] \setminus \{ c^* \}$
. That is,
$c \in [s] \setminus \{ c^* \}$
. That is,
![]() $c^*=1$
and
$c^*=1$
and
![]() $k_1> k_2$
. Suppose that
$k_1> k_2$
. Suppose that
![]() $(\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$
. Since
$(\ell _1,\ldots ,\ell _{r^*}) \in \mathbb {N}^{r^*}$
. Since
![]() $(\phi ^*)^{-1}(1) \cong K_{r^*}$
, the graph
$(\phi ^*)^{-1}(1) \cong K_{r^*}$
, the graph
![]() $(\ell _1,\ldots ,\ell _{r^*})(\phi ^*)^{-1}(1)$
is a clique of order
$(\ell _1,\ldots ,\ell _{r^*})(\phi ^*)^{-1}(1)$
is a clique of order
![]() $r^* + \sum _{i \in [r^*]}(\ell _i-1) = \sum _{i \in [r^*]}\ell _i$
. Therefore,
$r^* + \sum _{i \in [r^*]}(\ell _i-1) = \sum _{i \in [r^*]}\ell _i$
. Therefore,
![]() $\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(1),k_1) = \{ \boldsymbol {\ell } \in \mathbb {N}^{r^*} : \|\boldsymbol {\ell }\|_1 \leq k_1-1 \}$
(note that this set contains
$\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(1),k_1) = \{ \boldsymbol {\ell } \in \mathbb {N}^{r^*} : \|\boldsymbol {\ell }\|_1 \leq k_1-1 \}$
(note that this set contains
![]() $\boldsymbol {1}$
). This completes the proof of (ii).
$\boldsymbol {1}$
). This completes the proof of (ii).
Finally, Part (iii) is an immediate consequence of Part (ii) and (2.1).
2.1 The extension property
In this section, we explore the consequences of the extension property. Recall the equality from Proposition 2.1 which is necessary for all vertices of positive weight in an optimal solution. Suppose we wish to extend an optimal solution by adding a new vertex of zero weight. The following proposition shows that the normalised contribution of this new vertex cannot be more than
![]() $Q(\boldsymbol {k})$
. Given
$Q(\boldsymbol {k})$
. Given
![]() $\phi \in \Phi _0(r+1,\boldsymbol {k})$
and
$\phi \in \Phi _0(r+1,\boldsymbol {k})$
and
![]() $\boldsymbol {\alpha } \in \Delta ^r$
, let
$\boldsymbol {\alpha } \in \Delta ^r$
, let
 $$ \begin{align*} \mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}) := q_{r+1}(\phi,(\alpha_1,\ldots,\alpha_r,0)) = \sum_{\substack{i \in [r]\\ \phi(\{i,r+1\}) \neq \emptyset}}\alpha_i\log|\phi(\{ i,r+1 \})|, \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}) := q_{r+1}(\phi,(\alpha_1,\ldots,\alpha_r,0)) = \sum_{\substack{i \in [r]\\ \phi(\{i,r+1\}) \neq \emptyset}}\alpha_i\log|\phi(\{ i,r+1 \})|, \end{align*} $$
which is the ‘normalised contribution’ of the zero-weighted vertex
![]() $r+1$
to
$r+1$
to
![]() $q(\phi ,(\alpha _1,\ldots ,\alpha _r,0))$
.
$q(\phi ,(\alpha _1,\ldots ,\alpha _r,0))$
.
Proposition 2.6. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Suppose that
$\boldsymbol {k} \in \mathbb {N}^s$
. Suppose that
![]() . Let
. Let
![]() $\phi \in \Phi (r+1,\boldsymbol {k})$
be such that
$\phi \in \Phi (r+1,\boldsymbol {k})$
be such that
![]() $\phi |_{\binom {[r]}{2}} = \phi '$
. Then
$\phi |_{\binom {[r]}{2}} = \phi '$
. Then
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) \leq Q(\boldsymbol {k})$
.
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) \leq Q(\boldsymbol {k})$
.
Proof. Suppose not. We will show that we can transfer a small amount of weight from
![]() $[r]$
to
$[r]$
to
![]() $r+1$
, and in so doing, increase
$r+1$
, and in so doing, increase
![]() $q(\phi ,\cdot )$
. Let
$q(\phi ,\cdot )$
. Let
![]() $\gamma>0$
satisfy
$\gamma>0$
satisfy
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) = (1+\gamma )Q(\boldsymbol {k})$
. Let
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) = (1+\gamma )Q(\boldsymbol {k})$
. Let
![]() $\varepsilon \in (0,2\gamma /(2\gamma +1))$
. Define
$\varepsilon \in (0,2\gamma /(2\gamma +1))$
. Define
![]() $\boldsymbol {\beta } \in \mathbb {R}^{r+1}$
by setting
$\boldsymbol {\beta } \in \mathbb {R}^{r+1}$
by setting
 $$ \begin{align*}\beta_i := \begin{cases} (1-\varepsilon)\alpha_i &\mbox{if } i \in [r] \\ \varepsilon &\mbox{if } i = r+1. \end{cases} \end{align*} $$
$$ \begin{align*}\beta_i := \begin{cases} (1-\varepsilon)\alpha_i &\mbox{if } i \in [r] \\ \varepsilon &\mbox{if } i = r+1. \end{cases} \end{align*} $$
Then
![]() $\boldsymbol {\alpha } \in \Delta ^r$
implies that
$\boldsymbol {\alpha } \in \Delta ^r$
implies that
![]() $\boldsymbol {\beta } \in \Delta ^{r+1}$
. Now,
$\boldsymbol {\beta } \in \Delta ^{r+1}$
. Now,
a contradiction.
This motivates the extension property, which we repeat for the reader’s convenience:
Definition 2.7 (Clones and extension property).
Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Given
$\boldsymbol {k} \in \mathbb {N}^s$
. Given
![]() $r \in \mathbb {N}$
and
$r \in \mathbb {N}$
and
![]() $\phi \in \Phi _0(r;\boldsymbol {k})$
, we say that
$\phi \in \Phi _0(r;\boldsymbol {k})$
, we say that
![]() $i \in [r]$
is
$i \in [r]$
is
-
• a clone of
 $j \in [r]\setminus \{ i \}$
(under
$j \in [r]\setminus \{ i \}$
(under
 $\phi $
) if
$\phi $
) if
 $\phi (ik) = \phi (jk)$
for all
$\phi (ik) = \phi (jk)$
for all
 $k \in [r] \setminus \{ i,j\}$
and
$k \in [r] \setminus \{ i,j\}$
and
 $|\phi (ij)| \leq 1$
;
$|\phi (ij)| \leq 1$
; -
• a strong clone of j (under
 $\phi $
) if, additionally,
$\phi $
) if, additionally,
 $\phi (ij) = \emptyset $
.
$\phi (ij) = \emptyset $
.
We say that
![]() $\boldsymbol {k}$
has
$\boldsymbol {k}$
has
-
• the extension property if, for every
 and
and
 $\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
, such that
$\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
, such that
 $\phi |_{\binom {[r^*]}{2}} = \phi ^*$
and
$\phi |_{\binom {[r^*]}{2}} = \phi ^*$
and
 $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) = Q(\boldsymbol {k})$
; there exists
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) = Q(\boldsymbol {k})$
; there exists
 $j \in [r^*]$
, such that
$j \in [r^*]$
, such that
 $r^*+1$
is a clone of j under
$r^*+1$
is a clone of j under
 $\phi $
;
$\phi $
; -
• the strong extension property if in fact
 $r^*+1$
is a strong clone of j.
$r^*+1$
is a strong clone of j.
The extension property says that if we extend any basic optimal solution by adding an infinitesimal part with optimal contribution
![]() $Q(\boldsymbol {k})$
, then the new vertex clones an existing one (with perhaps one colour on the pair spanned by the two clones). Assuming that
$Q(\boldsymbol {k})$
, then the new vertex clones an existing one (with perhaps one colour on the pair spanned by the two clones). Assuming that
![]() $\boldsymbol {k}$
has the extension property, we can prove some properties of elements in
$\boldsymbol {k}$
has the extension property, we can prove some properties of elements in
![]() , including a uniform lower bound for vertex weightings in
, including a uniform lower bound for vertex weightings in
![]() $Q^*$
-optimal solutions.
$Q^*$
-optimal solutions.
Lemma 2.8. Let
![]() $s \in \mathbb {N}$
, and suppose that
$s \in \mathbb {N}$
, and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
has the extension property. Then there exists
$\boldsymbol {k} \in \mathbb {N}^s$
has the extension property. Then there exists
![]() $\mu> 0$
, such that
$\mu> 0$
, such that
![]() $\alpha _i^*> \mu $
for all
$\alpha _i^*> \mu $
for all
![]() and
and
![]() $i \in [r^*]$
.
$i \in [r^*]$
.
Proof. Suppose not; then, for all
![]() $n \in \mathbb {N}$
, there exists
$n \in \mathbb {N}$
, there exists
![]() and
and
![]() $i_n \in [r^*_n]$
, such that
$i_n \in [r^*_n]$
, such that
![]() $\alpha ^*_{i_n} < 1/n$
. By passing to a subsequence, since
$\alpha ^*_{i_n} < 1/n$
. By passing to a subsequence, since
![]() $r^*_n < R(\boldsymbol {k})$
, we may assume that
$r^*_n < R(\boldsymbol {k})$
, we may assume that
![]() $r^*_n \equiv r$
and
$r^*_n \equiv r$
and
![]() $\phi ^*_n \equiv \phi $
and, without loss of generality, that
$\phi ^*_n \equiv \phi $
and, without loss of generality, that
![]() $i_n \equiv r$
. Since
$i_n \equiv r$
. Since
![]() $\boldsymbol {\alpha }^*_n \in \Delta ^{r}$
and the simplex is closed and bounded, the Heine-Borel theorem implies that
$\boldsymbol {\alpha }^*_n \in \Delta ^{r}$
and the simplex is closed and bounded, the Heine-Borel theorem implies that
![]() $\boldsymbol {\alpha }^*_1,\boldsymbol {\alpha }^*_2,\ldots $
has a convergent subsequence
$\boldsymbol {\alpha }^*_1,\boldsymbol {\alpha }^*_2,\ldots $
has a convergent subsequence
![]() $\boldsymbol {\alpha }^*_{i_1},\boldsymbol {\alpha }^*_{i_2},\ldots $
, with limit
$\boldsymbol {\alpha }^*_{i_1},\boldsymbol {\alpha }^*_{i_2},\ldots $
, with limit
![]() $\boldsymbol {\beta } \in \Delta ^{r}$
. Observe that
$\boldsymbol {\beta } \in \Delta ^{r}$
. Observe that
![]() $\beta _{r} = 0$
. Without loss of generality, assume that
$\beta _{r} = 0$
. Without loss of generality, assume that
![]() $\boldsymbol {\beta } = (\beta _1,\ldots ,\beta _t,0,\ldots ,0)$
, where
$\boldsymbol {\beta } = (\beta _1,\ldots ,\beta _t,0,\ldots ,0)$
, where
![]() $t \in [r-1]$
and
$t \in [r-1]$
and
![]() $\beta _j> 0$
for all
$\beta _j> 0$
for all
![]() $j \in [t]$
. By continuity (Proposition 2.2),
$j \in [t]$
. By continuity (Proposition 2.2),
![]() $q(\phi ,(\beta _1,\ldots ,\beta _t))=q(\phi ,\boldsymbol {\beta })=Q(\boldsymbol {k})$
, so
$q(\phi ,(\beta _1,\ldots ,\beta _t))=q(\phi ,\boldsymbol {\beta })=Q(\boldsymbol {k})$
, so
![]() . Recall that
. Recall that
![]() $\alpha ^*_{i_m,r}> 0$
for all
$\alpha ^*_{i_m,r}> 0$
for all
![]() $m \in \mathbb {N}$
. By continuity and Proposition 2.1,
$m \in \mathbb {N}$
. By continuity and Proposition 2.1,
 $$ \begin{align*}\sum_{j \in [t]}\beta_j\log|\phi(rj)| = \mathop{\mathrm{ext}}(\phi,(\beta_1,\ldots,\beta_{r-1})) = \lim_{m\to\infty}q_r(\phi,(\alpha^*_{i_m,1},\ldots,\alpha^*_{i_m,r})) = Q(\boldsymbol{k}). \end{align*} $$
$$ \begin{align*}\sum_{j \in [t]}\beta_j\log|\phi(rj)| = \mathop{\mathrm{ext}}(\phi,(\beta_1,\ldots,\beta_{r-1})) = \lim_{m\to\infty}q_r(\phi,(\alpha^*_{i_m,1},\ldots,\alpha^*_{i_m,r})) = Q(\boldsymbol{k}). \end{align*} $$
The extension property implies that there exists
![]() $i \in [t]$
, such that
$i \in [t]$
, such that
![]() $\phi (rj)=\phi (ij)$
for all
$\phi (rj)=\phi (ij)$
for all
![]() $j \in [t] \setminus \{ i \}$
and
$j \in [t] \setminus \{ i \}$
and
![]() $|\phi (ir)| \leq 1$
, a contradiction to
$|\phi (ir)| \leq 1$
, a contradiction to
![]() $\phi \in \Phi _2(r;\boldsymbol {k})$
. This completes the proof of the lemma.
$\phi \in \Phi _2(r;\boldsymbol {k})$
. This completes the proof of the lemma.
Next, we prove that the strong extension property implies that optimal colour patterns have trivial capacity.
Lemma 2.9. Let
![]() $s \in \mathbb {N}$
, and suppose that
$s \in \mathbb {N}$
, and suppose that
![]() $\boldsymbol {k} \in \mathbb {N}^s$
with
$\boldsymbol {k} \in \mathbb {N}^s$
with
![]() $k_1 \geq \ldots \geq k_s$
has the extension property.
$k_1 \geq \ldots \geq k_s$
has the extension property.
-
(i) If
 $\boldsymbol {k}$
has the strong extension property, then for every
$\boldsymbol {k}$
has the strong extension property, then for every
 and
and
 $c \in [s]$
, we have that
$c \in [s]$
, we have that
 $\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c) = \{ \boldsymbol {1} \}$
.
$\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c) = \{ \boldsymbol {1} \}$
. -
(ii) If
 $k_1=k_2$
, then
$k_1=k_2$
, then
 $\boldsymbol {k}$
has the strong extension property.
$\boldsymbol {k}$
has the strong extension property. -
(iii) If
 and
and
 $\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
is such that
$\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
is such that
 $\phi |_{\binom {[r^*]}{2}}=\phi ^*$
and
$\phi |_{\binom {[r^*]}{2}}=\phi ^*$
and
 $r^*+1$
is a clone of
$r^*+1$
is a clone of
 $i \in [r^*]$
under
$i \in [r^*]$
under
 $\phi $
, then
$\phi $
, then
 $\phi (\{ i,r^*+1 \}) \subseteq \{ 1 \}$
.
$\phi (\{ i,r^*+1 \}) \subseteq \{ 1 \}$
.
Proof. For
![]() $c \in [s]$
, write
$c \in [s]$
, write
![]() $C(c):=\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c)$
as shorthand. We use the following claim to prove all three parts.
$C(c):=\mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c)$
as shorthand. We use the following claim to prove all three parts.
Claim 2.9.1. Let
![]() ,
,
![]() $c \in [s]$
and
$c \in [s]$
and
![]() $j \in [r^*]$
. Define
$j \in [r^*]$
. Define
![]() $\boldsymbol {\alpha } \in \Delta ^{r^*+1}$
by setting
$\boldsymbol {\alpha } \in \Delta ^{r^*+1}$
by setting
![]() $\alpha _i := \alpha ^*_i$
for all
$\alpha _i := \alpha ^*_i$
for all
![]() $i \in [r^*]$
and
$i \in [r^*]$
and
![]() $\alpha _{r^*+1} := 0$
. Define
$\alpha _{r^*+1} := 0$
. Define
![]() $\phi \in \Phi _1(r^*+1;\boldsymbol {k})$
by setting
$\phi \in \Phi _1(r^*+1;\boldsymbol {k})$
by setting
![]() $\phi |_{\binom {[r^*]}{2}} := \phi ^*$
and
$\phi |_{\binom {[r^*]}{2}} := \phi ^*$
and
![]() $\phi (\{ i,r^*+1 \}) := \phi ^*(ij)$
for all
$\phi (\{ i,r^*+1 \}) := \phi ^*(ij)$
for all
![]() $i \in [r^*]\setminus \{ j \}$
and
$i \in [r^*]\setminus \{ j \}$
and
![]() $\phi (\{ j,r^*+1 \}) := \{ c \}$
. Then,
$\phi (\{ j,r^*+1 \}) := \{ c \}$
. Then,
![]() $\boldsymbol {1} + \boldsymbol {e}_j \in C(c)$
if and only if
$\boldsymbol {1} + \boldsymbol {e}_j \in C(c)$
if and only if
![]() .
.
Proof of Claim.
We need to show that
![]() $\boldsymbol {1}+\boldsymbol {e}_j \in C(c)$
if and only if both
$\boldsymbol {1}+\boldsymbol {e}_j \in C(c)$
if and only if both
![]() and
and
![]() $q(\phi ,\boldsymbol {\alpha })=Q(\boldsymbol {k})$
. Firstly, we have
$q(\phi ,\boldsymbol {\alpha })=Q(\boldsymbol {k})$
. Firstly, we have
![]() if and only if
if and only if
![]() $\phi ^{-1}(c)$
is
$\phi ^{-1}(c)$
is
![]() $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
![]() $c \in [s]$
. For
$c \in [s]$
. For
![]() $c'\in [s]\setminus \{c\}$
,
$c'\in [s]\setminus \{c\}$
,
![]() $\phi ^{-1}(c')$
is obtained from
$\phi ^{-1}(c')$
is obtained from
![]() $(\phi ^*)^{-1}(c')$
by cloning vertex
$(\phi ^*)^{-1}(c')$
by cloning vertex
![]() $r^*$
, so is
$r^*$
, so is
![]() $K_{k_{c'}}$
-free. By definition,
$K_{k_{c'}}$
-free. By definition,
![]() $\phi ^{-1}(c)$
is
$\phi ^{-1}(c)$
is
![]() $K_{k_c}$
-free if and only if
$K_{k_c}$
-free if and only if
![]() $\boldsymbol {1} + \boldsymbol {e}_j \in C(c)$
. Secondly,
$\boldsymbol {1} + \boldsymbol {e}_j \in C(c)$
. Secondly,
![]() $q(\phi ,\boldsymbol {\alpha })=q(\phi ^*,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
. This proves the claim.
$q(\phi ,\boldsymbol {\alpha })=q(\phi ^*,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
. This proves the claim.
For (i), suppose that
![]() $\boldsymbol {k}$
has the strong extension property but there is
$\boldsymbol {k}$
has the strong extension property but there is
![]() and
and
![]() $c \in [s]$
for which
$c \in [s]$
for which
![]() $C(c) \neq \{\boldsymbol {1}\}$
. Then there is
$C(c) \neq \{\boldsymbol {1}\}$
. Then there is
![]() $j \in [r^*]$
, such that
$j \in [r^*]$
, such that
![]() $\boldsymbol {1}+\boldsymbol {e}_j \in C(c)$
. Let
$\boldsymbol {1}+\boldsymbol {e}_j \in C(c)$
. Let
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\phi $
be defined as in Claim 2.9.1. By the claim,
$\phi $
be defined as in Claim 2.9.1. By the claim,
![]() . So
. So
 $$ \begin{align*}\sum_{i \in [r^*]}\alpha_i \log|\phi(\{ i,r^*+1\})| = \sum_{i \in [r^*]\setminus \{ j \}}\alpha^*_i\log|\phi^*(ij)| = Q(\boldsymbol{k}) \end{align*} $$
$$ \begin{align*}\sum_{i \in [r^*]}\alpha_i \log|\phi(\{ i,r^*+1\})| = \sum_{i \in [r^*]\setminus \{ j \}}\alpha^*_i\log|\phi^*(ij)| = Q(\boldsymbol{k}) \end{align*} $$
by Proposition 2.1 applied to
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
. But
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
. But
![]() $r^*+1$
is not a strong clone of any
$r^*+1$
is not a strong clone of any
![]() $j' \in [r^*]$
under
$j' \in [r^*]$
under
![]() $\phi $
since
$\phi $
since
![]() $|\phi (\{r^*+1,j\})|=1$
(and
$|\phi (\{r^*+1,j\})|=1$
(and
![]() $|\phi (\{r^*+1,i\})| = |\phi (ji)| \geq 2$
for all
$|\phi (\{r^*+1,i\})| = |\phi (ji)| \geq 2$
for all
![]() $i \in [r^*]\setminus \{j\}$
). So
$i \in [r^*]\setminus \{j\}$
). So
![]() $\boldsymbol {k}$
does not have the strong extension property, a contradiction.
$\boldsymbol {k}$
does not have the strong extension property, a contradiction.
Next, we prove (ii). So suppose that
![]() $\boldsymbol {k}$
does not have the strong extension property. Then there is some
$\boldsymbol {k}$
does not have the strong extension property. Then there is some
![]() and an extension
and an extension
![]() $\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
, such that
$\phi \in \Phi _0(r^*+1;\boldsymbol {k})$
, such that
![]() $\phi |_{\binom {[r^*]}{2}}=\phi ^*$
,
$\phi |_{\binom {[r^*]}{2}}=\phi ^*$
,
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
and
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
and
![]() $r^*+1$
is a clone of some
$r^*+1$
is a clone of some
![]() $j \in [r^*]$
under
$j \in [r^*]$
under
![]() $\phi $
, but not a strong clone. So
$\phi $
, but not a strong clone. So
![]() $\phi (\{i,r^*+1\})=\phi ^*(ij)$
for all
$\phi (\{i,r^*+1\})=\phi ^*(ij)$
for all
![]() $i \in [r^*]\setminus \{j\}$
, and
$i \in [r^*]\setminus \{j\}$
, and
![]() $\phi (\{j,r^*+1\})=\{c\}$
for some
$\phi (\{j,r^*+1\})=\{c\}$
for some
![]() $c \in [s]$
. Note that
$c \in [s]$
. Note that
![]() , where
, where
![]() $\boldsymbol {\alpha }$
is defined as in the claim. Thus, by the claim,
$\boldsymbol {\alpha }$
is defined as in the claim. Thus, by the claim,
![]() $\boldsymbol {1}+\boldsymbol {e}_j \in C(c)$
. By Lemma 2.5
(ii), this implies
$\boldsymbol {1}+\boldsymbol {e}_j \in C(c)$
. By Lemma 2.5
(ii), this implies
![]() $c=1$
and
$c=1$
and
![]() $k_1>k_2$
. This also gives Part (iii).
$k_1>k_2$
. This also gives Part (iii).
2.2 The proof of Lemma 1.3
Recall that Lemma 1.3, informally speaking, enables us to characterise all solutions to Problem
![]() $Q_0$
in terms of the basic optimal solutions
$Q_0$
in terms of the basic optimal solutions
![]() .
.
Proof of Lemma 1.3.
Note that the ‘if’ direction is trivial, so it remains to prove the ‘only if’ direction. Let
![]() . We can assume that
. We can assume that
![]() $\alpha _i>0$
for all
$\alpha _i>0$
for all
![]() $i \in [r]$
.
$i \in [r]$
.
It is convenient to consider triples
![]() $(A,\phi ,\boldsymbol {\alpha })$
which are as feasible solutions
$(A,\phi ,\boldsymbol {\alpha })$
which are as feasible solutions
![]() $(r,\phi ,\boldsymbol {\alpha })$
except A is a set of r vertices (as opposed to
$(r,\phi ,\boldsymbol {\alpha })$
except A is a set of r vertices (as opposed to
![]() $[r]$
),
$[r]$
),
![]() $\phi : \binom {A}{2}\to 2^{[s]}$
and
$\phi : \binom {A}{2}\to 2^{[s]}$
and
![]() $\boldsymbol {\alpha } \in \Delta ^A := \{(\alpha _i: i \in A): \alpha _i>0 \text { for all } i \in A \text { and }\sum _{i \in A}\alpha _i=1\}$
. Given
$\boldsymbol {\alpha } \in \Delta ^A := \{(\alpha _i: i \in A): \alpha _i>0 \text { for all } i \in A \text { and }\sum _{i \in A}\alpha _i=1\}$
. Given
![]() $x,y \in A$
, define a new vertex weighting
$x,y \in A$
, define a new vertex weighting
![]() $\overline {\boldsymbol {\alpha }} \in \Delta ^{A\setminus \{y\}}$
, the
$\overline {\boldsymbol {\alpha }} \in \Delta ^{A\setminus \{y\}}$
, the
![]() $(x,y)$
-merging of
$(x,y)$
-merging of
![]() $\boldsymbol {\alpha }$
, by setting
$\boldsymbol {\alpha }$
, by setting
![]() $\overline {\alpha }_x := \alpha _x+\alpha _y$
and
$\overline {\alpha }_x := \alpha _x+\alpha _y$
and
![]() $\overline {\alpha }_z := \alpha _z$
for all
$\overline {\alpha }_z := \alpha _z$
for all
![]() $z \in [r] \setminus \{ x,y \}$
. Suppose
$z \in [r] \setminus \{ x,y \}$
. Suppose
![]() $|\phi (xy)| \leq 1$
. Then
$|\phi (xy)| \leq 1$
. Then
![]() where
where
![]() $\phi ':=\phi |_{\binom {A\setminus \{y\}}{2}}$
, and
$\phi ':=\phi |_{\binom {A\setminus \{y\}}{2}}$
, and
 $$ \begin{align} q_y(\phi,\overline{\boldsymbol{\alpha}}) &= \sum_{z \in [r]\setminus \{ x,y \}}\alpha_z\log|\phi(zy)| + (\alpha_x+\alpha_y)\log|\phi(xy)| = q_y(\phi,\boldsymbol{\alpha})= Q(\boldsymbol{k}),\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} q_y(\phi,\overline{\boldsymbol{\alpha}}) &= \sum_{z \in [r]\setminus \{ x,y \}}\alpha_z\log|\phi(zy)| + (\alpha_x+\alpha_y)\log|\phi(xy)| = q_y(\phi,\boldsymbol{\alpha})= Q(\boldsymbol{k}),\\[-16pt]\nonumber \end{align} $$
where the last equality follows from Proposition 2.1.
Consider the following claim.
Claim 2.1.
![]() $\{ ij \in \binom {[r]}{2} : |\phi (ij)| \leq 1\}$
is a disjoint union of cliques.
$\{ ij \in \binom {[r]}{2} : |\phi (ij)| \leq 1\}$
is a disjoint union of cliques.
Proof of Claim.
Suppose for a contradiction to the claim that, without loss of generality, there is some
![]() $ij \in \binom {[r-1]}{2}$
, such that
$ij \in \binom {[r-1]}{2}$
, such that
![]() $|\phi (ir)|,|\phi (jr)|\leq 1$
but
$|\phi (ir)|,|\phi (jr)|\leq 1$
but
![]() $|\phi (ij)| \geq 2$
. Suppose first that there exists
$|\phi (ij)| \geq 2$
. Suppose first that there exists
![]() $i'j' \in \binom {[r]}{2}\setminus \{ir,jr\}$
, such that
$i'j' \in \binom {[r]}{2}\setminus \{ir,jr\}$
, such that
![]() $|\phi (i'j')| \leq 1$
. At least one of
$|\phi (i'j')| \leq 1$
. At least one of
![]() $i',j'$
is not in
$i',j'$
is not in
![]() $\{i,j,r\}$
, say
$\{i,j,r\}$
, say
![]() $j'$
. Take the
$j'$
. Take the
![]() $(i',j')$
-merging
$(i',j')$
-merging
![]() $\overline {\boldsymbol {\alpha }}$
of
$\overline {\boldsymbol {\alpha }}$
of
![]() $\boldsymbol {\alpha }$
. By the above observations,
$\boldsymbol {\alpha }$
. By the above observations,
![]() , where
, where
![]() $\phi ':=\phi |_{\binom {[r]\setminus \{j'\}}{2}}$
. Note that
$\phi ':=\phi |_{\binom {[r]\setminus \{j'\}}{2}}$
. Note that
![]() $ir,jr,ij\in \binom {[r]\setminus \{j'\}}{2}$
, and
$ir,jr,ij\in \binom {[r]\setminus \{j'\}}{2}$
, and
![]() $\phi '(xy)=\phi (xy)$
for all
$\phi '(xy)=\phi (xy)$
for all
![]() $xy\in \binom {[r]\setminus \{j'\}}{2}$
.
$xy\in \binom {[r]\setminus \{j'\}}{2}$
.
Do this repeatedly until the only pairs
![]() $i'j'$
with
$i'j'$
with
![]() $|\phi (i'j')| \leq 1$
among the set A of remaining vertices are
$|\phi (i'j')| \leq 1$
among the set A of remaining vertices are
![]() $ir$
and
$ir$
and
![]() $jr$
. Let
$jr$
. Let
![]() $\boldsymbol {\beta }$
be the weight function and
$\boldsymbol {\beta }$
be the weight function and
![]() $\psi := \phi |_A$
the colour pattern. We have
$\psi := \phi |_A$
the colour pattern. We have
![]() . Now obtain the
. Now obtain the
![]() $(i,r)$
-merging
$(i,r)$
-merging
![]() $\overline {\boldsymbol {\beta }}$
of
$\overline {\boldsymbol {\beta }}$
of
![]() $\boldsymbol {\beta }$
and let
$\boldsymbol {\beta }$
and let
![]() $A':=A\setminus \{r\}$
. By the above,
$A':=A\setminus \{r\}$
. By the above,
![]() and
and
![]() $\psi ,\overline {\boldsymbol {\beta }},r$
satisfy (2.2). Further,
$\psi ,\overline {\boldsymbol {\beta }},r$
satisfy (2.2). Further,
![]() $|\psi '(xy)| = |\phi (xy)| \geq 2$
for every
$|\psi '(xy)| = |\phi (xy)| \geq 2$
for every
![]() $xy \in \binom {A'}{2}$
and
$xy \in \binom {A'}{2}$
and
![]() $\overline {\beta }_x>0$
for every
$\overline {\beta }_x>0$
for every
![]() $x \in A'$
, so in fact
$x \in A'$
, so in fact
![]() . Since
. Since
![]() $\boldsymbol {k}$
has the extension property, there exists
$\boldsymbol {k}$
has the extension property, there exists
![]() $y \in A'$
, such that
$y \in A'$
, such that
![]() $\psi '(r\ell ) = \psi '(y\ell )$
for all
$\psi '(r\ell ) = \psi '(y\ell )$
for all
![]() $\ell \in A'$
, and
$\ell \in A'$
, and
![]() $|\psi '(yr)|\leq 1$
. In particular,
$|\psi '(yr)|\leq 1$
. In particular,
![]() $|\psi '(rj)| = |\psi '(yj)| \geq 2$
, a contradiction to our assumption.
$|\psi '(rj)| = |\psi '(yj)| \geq 2$
, a contradiction to our assumption.
Proposition 2.1 implies that, for every
![]() $i \in [r]$
, we have that
$i \in [r]$
, we have that
![]() $q_i(\phi ,\boldsymbol {\alpha }) = Q(\boldsymbol {k})$
. By the claim, there is a (unique up to relabelling) partition
$q_i(\phi ,\boldsymbol {\alpha }) = Q(\boldsymbol {k})$
. By the claim, there is a (unique up to relabelling) partition
![]() $[r] = V_1 \cup \ldots \cup V_{r^*}$
, such that
$[r] = V_1 \cup \ldots \cup V_{r^*}$
, such that
 $$ \begin{align} \left\{ ij \in \binom{[r]}{2} : |\phi(ij)| \leq 1 \right\} = \bigcup_{j \in [r^*]}\binom{V_j}{2}\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} \left\{ ij \in \binom{[r]}{2} : |\phi(ij)| \leq 1 \right\} = \bigcup_{j \in [r^*]}\binom{V_j}{2}\\[-16pt]\nonumber \end{align} $$
(where a vertex
![]() $i'$
is the only member of some
$i'$
is the only member of some
![]() $V_{i}$
if and only if
$V_{i}$
if and only if
![]() $|\phi (i'j)| \geq 2$
for all
$|\phi (i'j)| \geq 2$
for all
![]() $j \in [r]\setminus \{ i' \}$
). Assume, without loss of generality, that
$j \in [r]\setminus \{ i' \}$
). Assume, without loss of generality, that
![]() $i \in V_i$
for all
$i \in V_i$
for all
![]() $i \in [r^*]$
. Let
$i \in [r^*]$
. Let
![]() $\boldsymbol {\alpha }^* \in \Delta ^{r^*}$
, such that
$\boldsymbol {\alpha }^* \in \Delta ^{r^*}$
, such that
![]() $\alpha ^*_i = \sum _{i' \in V_i}\alpha _{i'}$
, and set
$\alpha ^*_i = \sum _{i' \in V_i}\alpha _{i'}$
, and set
![]() $\phi ^* := \phi |_{\binom {[r^*]}{2}}$
.
$\phi ^* := \phi |_{\binom {[r^*]}{2}}$
.
Claim 2.2. We have the following:
-
(a)
 .
. -
(b) For all
 $i \in [r^*]$
and
$i \in [r^*]$
and
 $i' \in V_i$
, we have that
$i' \in V_i$
, we have that
 $\phi (i'j) = \phi (ij)$
for all
$\phi (i'j) = \phi (ij)$
for all
 $j \in [r^*]\setminus \{ i \}$
.
$j \in [r^*]\setminus \{ i \}$
.
Proof of Claim.
Let
 $$ \begin{align*}K := \bigcup_{j \in [r^*]}\{ (j,j') : j' \in V_j\setminus\{j\} \}\\[-15pt] \end{align*} $$
$$ \begin{align*}K := \bigcup_{j \in [r^*]}\{ (j,j') : j' \in V_j\setminus\{j\} \}\\[-15pt] \end{align*} $$
and
![]() $t := |K|$
. So K is a union of spanning stars in the
$t := |K|$
. So K is a union of spanning stars in the
![]() $V_j$
’s. We will form a new solution by transferring the total weight from
$V_j$
’s. We will form a new solution by transferring the total weight from
![]() $V_j$
to j.
$V_j$
to j.
Let
![]() $\boldsymbol {\alpha }_0 := \boldsymbol {\alpha }$
,
$\boldsymbol {\alpha }_0 := \boldsymbol {\alpha }$
,
![]() $\phi _0 := \phi $
and
$\phi _0 := \phi $
and
![]() $A_0 := [r]$
. Order the elements
$A_0 := [r]$
. Order the elements
![]() $(j_1,x_1), \ldots , (j_t,x_{t})$
of K, and, for each
$(j_1,x_1), \ldots , (j_t,x_{t})$
of K, and, for each
![]() $\ell \geq 1$
, let
$\ell \geq 1$
, let
![]() $\boldsymbol {\alpha }_{\ell }$
be the
$\boldsymbol {\alpha }_{\ell }$
be the
![]() $(j_{\ell },x_{\ell })$
-merging of
$(j_{\ell },x_{\ell })$
-merging of
![]() $\boldsymbol {\alpha }_{\ell -1}$
and
$\boldsymbol {\alpha }_{\ell -1}$
and
![]() $A_{\ell } := A_{\ell -1}\setminus \{x_{\ell }\}$
and
$A_{\ell } := A_{\ell -1}\setminus \{x_{\ell }\}$
and
![]() $\phi _{\ell } := \phi |_{\binom {A_{\ell }}{2}}$
. Precisely as in (2.2), we have that
$\phi _{\ell } := \phi |_{\binom {A_{\ell }}{2}}$
. Precisely as in (2.2), we have that
![]() , and
, and
 $$ \begin{align} \sum_{k \in \binom{A_{\ell}}{2}}\alpha_{\ell,k}\log|\phi(x_{\ell} k)| = Q(\boldsymbol{k}).\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \sum_{k \in \binom{A_{\ell}}{2}}\alpha_{\ell,k}\log|\phi(x_{\ell} k)| = Q(\boldsymbol{k}).\\[-15pt]\nonumber \end{align} $$
By construction,
![]() $A_t=[r^*]$
and
$A_t=[r^*]$
and
![]() $\alpha _{t,i}> 0$
for all
$\alpha _{t,i}> 0$
for all
![]() $i \in [r^*]$
. Let
$i \in [r^*]$
. Let
![]() $\boldsymbol {\alpha }^* := (\alpha _{t,1},\ldots ,\alpha _{t,r^*})$
and
$\boldsymbol {\alpha }^* := (\alpha _{t,1},\ldots ,\alpha _{t,r^*})$
and
![]() $\phi ' := \phi _t|_{\binom {[r^*]}{2}} = \phi |_{\binom {[r^*]}{2}}$
. Then
$\phi ' := \phi _t|_{\binom {[r^*]}{2}} = \phi |_{\binom {[r^*]}{2}}$
. Then
![]() . Moreover, by (2.4), we have that
. Moreover, by (2.4), we have that
![]() $ \sum _{i \in [r^*]}\alpha ^*_i\log |\phi (\{ i,r^*+j \})|= Q(\boldsymbol {k}) $
for all
$ \sum _{i \in [r^*]}\alpha ^*_i\log |\phi (\{ i,r^*+j \})|= Q(\boldsymbol {k}) $
for all
![]() $j \in [r-r^*]$
, and
$j \in [r-r^*]$
, and
![]() $ \alpha ^*_i = \sum _{i' \in V_i}\alpha _{i'} $
. So
$ \alpha ^*_i = \sum _{i' \in V_i}\alpha _{i'} $
. So
![]() $\boldsymbol {\alpha }^*$
and
$\boldsymbol {\alpha }^*$
and
![]() $\phi ^*$
satisfy (a).
$\phi ^*$
satisfy (a).
It remains to prove (b). For each
![]() $i' \in \{ r^*+1,\ldots ,r \}$
, let
$i' \in \{ r^*+1,\ldots ,r \}$
, let
![]() $i \in [r^*]$
be such that
$i \in [r^*]$
be such that
![]() $i' \in V_i$
. Apply the extension property to
$i' \in V_i$
. Apply the extension property to
![]() $(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
with
$(r^*,\phi ^*,\boldsymbol {\alpha }^*)$
with
![]() $i'$
playing the role of the additional vertex, whose colour pattern is given by
$i'$
playing the role of the additional vertex, whose colour pattern is given by
![]() $\phi $
. So there is some
$\phi $
. So there is some
![]() $x_{i'} \in [r^*]$
which is a clone of
$x_{i'} \in [r^*]$
which is a clone of
![]() $i'$
under
$i'$
under
![]() $\phi $
in
$\phi $
in
![]() $[r^*]$
. But, by the definition of
$[r^*]$
. But, by the definition of
![]() $V_i$
,
$V_i$
,
![]() $|\phi (\{ k,i' \})| \leq 1$
if and only if
$|\phi (\{ k,i' \})| \leq 1$
if and only if
![]() $k \in V_i$
. But there is a unique member of
$k \in V_i$
. But there is a unique member of
![]() $V_{i}$
which lies in
$V_{i}$
which lies in
![]() $[r^*]$
, namely, i. Certainly i is a clone of itself. So for all
$[r^*]$
, namely, i. Certainly i is a clone of itself. So for all
![]() $i \in [r^*]$
and
$i \in [r^*]$
and
![]() $i' \in [r]\cap V_i$
, we have that
$i' \in [r]\cap V_i$
, we have that
![]() $i'$
is a clone of vertex i under
$i'$
is a clone of vertex i under
![]() $\phi $
in
$\phi $
in
![]() $[r^*]$
. So (b) holds, completing the proof of the claim.
$[r^*]$
. So (b) holds, completing the proof of the claim.
So Part (i) of Lemma 1.3 holds by (2.3) and Claim 2.2
(a). For (ii), we need to prove that
![]() $\phi (i'j') = \phi (ij)$
for all
$\phi (i'j') = \phi (ij)$
for all
![]() $i' \in V_i$
and
$i' \in V_i$
and
![]() $j' \in V_j$
, whenever
$j' \in V_j$
, whenever
![]() $i \neq j$
. Suppose that there is some
$i \neq j$
. Suppose that there is some
![]() $c \in \phi (i'j') \setminus \phi (ij)$
. Thus,
$c \in \phi (i'j') \setminus \phi (ij)$
. Thus,
![]() $c \notin \phi (ij)=\phi ^*(ij)$
, and by Lemma 2.5
(i),
$c \notin \phi (ij)=\phi ^*(ij)$
, and by Lemma 2.5
(i),
![]() $(\phi ^*)^{-1}(c)$
is maximally
$(\phi ^*)^{-1}(c)$
is maximally
![]() $K_{k_c}$
-free, so there are vertices
$K_{k_c}$
-free, so there are vertices
![]() $\{ x_1,\ldots ,x_{k_c-2} \} \in [r^*]\setminus \{ i,j \}$
which, together with
$\{ x_1,\ldots ,x_{k_c-2} \} \in [r^*]\setminus \{ i,j \}$
which, together with
![]() $i,j$
, span a copy of
$i,j$
, span a copy of
![]() $K_{k_c}$
in
$K_{k_c}$
in
![]() $(\phi ^*)^{-1}(c)$
. But Claim 2.2
(b) implies that, for all
$(\phi ^*)^{-1}(c)$
. But Claim 2.2
(b) implies that, for all
![]() $\ell \in [k_c-2]$
, we have
$\ell \in [k_c-2]$
, we have
![]() $c \in \phi ^*(ix_{\ell }) = \phi (i'x_{\ell })$
and
$c \in \phi ^*(ix_{\ell }) = \phi (i'x_{\ell })$
and
![]() $c \in \phi ^*(jx_{\ell }) = \phi (j'x_{\ell })$
. Therefore,
$c \in \phi ^*(jx_{\ell }) = \phi (j'x_{\ell })$
. Therefore,
![]() $x_1,\ldots ,x_{k_c-2},i',j'$
span a copy of
$x_1,\ldots ,x_{k_c-2},i',j'$
span a copy of
![]() $K_{k_c}$
in
$K_{k_c}$
in
![]() $\phi ^{-1}(c)$
, a contradiction. So
$\phi ^{-1}(c)$
, a contradiction. So
![]() $\phi (i'j') \subseteq \phi (ij)$
. Using Proposition 2.1 and the fact that
$\phi (i'j') \subseteq \phi (ij)$
. Using Proposition 2.1 and the fact that
![]() $|\phi (i'i")| \leq 1$
for all
$|\phi (i'i")| \leq 1$
for all
![]() $i" \in V_i$
, we have that
$i" \in V_i$
, we have that
 $$ \begin{align*} Q(\boldsymbol{k}) &= q_{i'}(\phi,\boldsymbol{\alpha}) = \sum_{j \in [r^*]\setminus \{ i \}}\sum_{j' \in V_j}\alpha_{j'}\log|\phi(i'j')| \leq \sum_{j \in [r^*]\setminus \{ i \}}\sum_{j' \in V_j}\alpha_{j'}\log|\phi(ij)|\\ &= q_i(\phi^*,\boldsymbol{\alpha}^*) = Q(\boldsymbol{k}).\\[-15pt] \end{align*} $$
$$ \begin{align*} Q(\boldsymbol{k}) &= q_{i'}(\phi,\boldsymbol{\alpha}) = \sum_{j \in [r^*]\setminus \{ i \}}\sum_{j' \in V_j}\alpha_{j'}\log|\phi(i'j')| \leq \sum_{j \in [r^*]\setminus \{ i \}}\sum_{j' \in V_j}\alpha_{j'}\log|\phi(ij)|\\ &= q_i(\phi^*,\boldsymbol{\alpha}^*) = Q(\boldsymbol{k}).\\[-15pt] \end{align*} $$
Therefore, we have equality everywhere, and so
![]() $\phi (i'j') = \phi (ij) = \phi ^*(ij)$
for all
$\phi (i'j') = \phi (ij) = \phi ^*(ij)$
for all
![]() $ij \in \binom {[r^*]}{2}$
and
$ij \in \binom {[r^*]}{2}$
and
![]() $i' \in V_i$
,
$i' \in V_i$
,
![]() $j' \in V_j$
. This completes the proof of (ii).
$j' \in V_j$
. This completes the proof of (ii).
For (iii), let
![]() $c \in [s]$
,
$c \in [s]$
,
![]() $i \in [r^*]$
and
$i \in [r^*]$
and
![]() $i'i" \in \binom {V_i}{2}$
with
$i'i" \in \binom {V_i}{2}$
with
![]() $c \in \phi (i'i")$
. Then
$c \in \phi (i'i")$
. Then
![]() $\boldsymbol {1} + \boldsymbol {e}_i \in \mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c)$
. Lemma 2.5
(ii) implies that
$\boldsymbol {1} + \boldsymbol {e}_i \in \mathop {\mathrm {Cap}}((\phi ^*)^{-1}(c),k_c)$
. Lemma 2.5
(ii) implies that
![]() $c = 1$
and
$c = 1$
and
![]() $k_1>k_2$
. Now, for each
$k_1>k_2$
. Now, for each
![]() $i \in [r^*]$
, let
$i \in [r^*]$
, let
![]() $\ell _i$
be the size of the largest clique in
$\ell _i$
be the size of the largest clique in
![]() $\phi ^{-1}(1)[V_i]$
. By definition,
$\phi ^{-1}(1)[V_i]$
. By definition,
![]() $\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathop {\mathrm {Cap}}((\phi ^*)^{-1}(1),k_1)$
, and so
$\boldsymbol {\ell } := (\ell _1,\ldots ,\ell _{r^*}) \in \mathop {\mathrm {Cap}}((\phi ^*)^{-1}(1),k_1)$
, and so
![]() $\|\boldsymbol {\ell }\|_1 \leq k_1-1$
by Lemma 2.5
(ii). This complete the proof of (iii) and hence of the lemma.
$\|\boldsymbol {\ell }\|_1 \leq k_1-1$
by Lemma 2.5
(ii). This complete the proof of (iii) and hence of the lemma.
2.3 Nonoptimal attachments
We derive a further quantifiable consequence of the extension property in the following lemma, which shows that if a basic optimal solution is extended by an infinitesimal part, if it is not a clone of an existing vertex, then the deficit of its contribution is bounded away from zero.
Lemma 2.10. Let
![]() $s \in \mathbb {N}$
, and let
$s \in \mathbb {N}$
, and let
![]() $\boldsymbol {k} \in \mathbb {N}^s$
have the extension property. Then there exists
$\boldsymbol {k} \in \mathbb {N}^s$
have the extension property. Then there exists
![]() $\eta> 0$
, such that the following holds. Let
$\eta> 0$
, such that the following holds. Let
![]() and
and
![]() $\phi \in \Phi _0(r^*+1,\boldsymbol {k})$
, such that
$\phi \in \Phi _0(r^*+1,\boldsymbol {k})$
, such that
![]() $\phi |_{\binom {[r^*]}{2}}=\phi ^*$
and
$\phi |_{\binom {[r^*]}{2}}=\phi ^*$
and
![]() $r^*+1$
is not a clone of any
$r^*+1$
is not a clone of any
![]() $i \in [r^*]$
under
$i \in [r^*]$
under
![]() $\phi $
. Then
$\phi $
. Then
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) \leq Q(\boldsymbol {k}) - \eta $
.
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) \leq Q(\boldsymbol {k}) - \eta $
.
Proof. Suppose that the statement of the lemma does not hold. Then for all
![]() $n \in \mathbb {N}$
, there exist
$n \in \mathbb {N}$
, there exist
![]() and
and
![]() $\phi _n \in \Phi _0(r^*_n+1,\boldsymbol {k})$
, such that
$\phi _n \in \Phi _0(r^*_n+1,\boldsymbol {k})$
, such that
![]() $\phi _n|_{\binom {[r^*_n]}{2}} = \phi ^*_n$
and
$\phi _n|_{\binom {[r^*_n]}{2}} = \phi ^*_n$
and
![]() $r^*_n+1$
is not a clone of any
$r^*_n+1$
is not a clone of any
![]() $i \in [r^*_n]$
under
$i \in [r^*_n]$
under
![]() $\phi _n$
, but
$\phi _n$
, but
![]() $ \mathop {\mathrm {ext}}(\phi _n,\boldsymbol {\alpha }_n^*)> Q(\boldsymbol {k}) - \frac {1}{n} $
. By passing to a subsequence (since
$ \mathop {\mathrm {ext}}(\phi _n,\boldsymbol {\alpha }_n^*)> Q(\boldsymbol {k}) - \frac {1}{n} $
. By passing to a subsequence (since
![]() $r_n^*<R(\boldsymbol {k})$
), we may assume that
$r_n^*<R(\boldsymbol {k})$
), we may assume that
![]() $r^*_n \equiv r$
;
$r^*_n \equiv r$
;
![]() $\phi ^*_n \equiv \phi ^*$
and
$\phi ^*_n \equiv \phi ^*$
and
![]() $\phi _n \equiv \phi $
, so
$\phi _n \equiv \phi $
, so
and
![]() $r+1$
is not a clone of any
$r+1$
is not a clone of any
![]() $i \in [r]$
under
$i \in [r]$
under
![]() $\phi $
. Since
$\phi $
. Since
![]() $\Delta ^{r}$
is compact, we may choose a convergent subsequence
$\Delta ^{r}$
is compact, we may choose a convergent subsequence
![]() $\boldsymbol {\alpha }^*_{i_1},\boldsymbol {\alpha }^*_{i_2},\ldots $
of
$\boldsymbol {\alpha }^*_{i_1},\boldsymbol {\alpha }^*_{i_2},\ldots $
of
![]() $\boldsymbol {\alpha }^*_1,\boldsymbol {\alpha }^*_2,\ldots $
, with limit
$\boldsymbol {\alpha }^*_1,\boldsymbol {\alpha }^*_2,\ldots $
, with limit
![]() $\boldsymbol {\beta }$
. Now, since
$\boldsymbol {\beta }$
. Now, since
![]() $q(\phi ^*,\cdot )$
is continuous (by Proposition 2.2),
$q(\phi ^*,\cdot )$
is continuous (by Proposition 2.2),
and Lemma 2.8 implies that
![]() $\beta _j =\lim _{n \rightarrow \infty }\alpha _{i_n,j}^*>0$
for every
$\beta _j =\lim _{n \rightarrow \infty }\alpha _{i_n,j}^*>0$
for every
![]() $j \in [r]$
. So
$j \in [r]$
. So
![]() . But taking the limit in (2.5) implies that
. But taking the limit in (2.5) implies that
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\beta }) = Q(\boldsymbol {k})$
. Now the extension property implies that there is some
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\beta }) = Q(\boldsymbol {k})$
. Now the extension property implies that there is some
![]() $i \in [r]$
, such that
$i \in [r]$
, such that
![]() $r+1$
is a clone of i under
$r+1$
is a clone of i under
![]() $\phi $
, a contradiction.
$\phi $
, a contradiction.
Given colour patterns
![]() $\psi \in \Phi _0(r;\boldsymbol {k})$
and
$\psi \in \Phi _0(r;\boldsymbol {k})$
and
![]() $\psi ' \in \Phi _0(r';\boldsymbol {k})$
and a partition
$\psi ' \in \Phi _0(r';\boldsymbol {k})$
and a partition
![]() $\mathcal {V}=\{V_1,\ldots ,V_r\}$
of
$\mathcal {V}=\{V_1,\ldots ,V_r\}$
of
![]() $[r']$
, we will say
$[r']$
, we will say
![]() $\psi ' =_{\mathcal {V}} \psi $
if
$\psi ' =_{\mathcal {V}} \psi $
if
![]() $\psi '(i'j')=\psi (ij)$
for all
$\psi '(i'j')=\psi (ij)$
for all
![]() $ij \in \binom {[r]}{2}$
,
$ij \in \binom {[r]}{2}$
,
![]() $i' \in V_i$
and
$i' \in V_i$
and
![]() $j' \in V_j$
, and
$j' \in V_j$
, and
![]() $\psi (i'i")=\emptyset $
for all
$\psi (i'i")=\emptyset $
for all
![]() $i \in [r]$
and
$i \in [r]$
and
![]() $i'i" \in \binom {V_i}{2}$
. Similarly, given
$i'i" \in \binom {V_i}{2}$
. Similarly, given
![]() $\boldsymbol {\alpha } \in \Delta ^r$
and
$\boldsymbol {\alpha } \in \Delta ^r$
and
![]() $\boldsymbol {\alpha }' \in \Delta ^{r'}$
and a partition
$\boldsymbol {\alpha }' \in \Delta ^{r'}$
and a partition
![]() $\mathcal {V}=\{V_1,\ldots ,V_r\}$
of
$\mathcal {V}=\{V_1,\ldots ,V_r\}$
of
![]() $[r']$
, we will say
$[r']$
, we will say
![]() $\boldsymbol {\alpha }' =_{\mathcal {V}} \boldsymbol {\alpha }$
if
$\boldsymbol {\alpha }' =_{\mathcal {V}} \boldsymbol {\alpha }$
if
![]() $\sum _{j \in V_i}\alpha _j' = \alpha _i$
for all
$\sum _{j \in V_i}\alpha _j' = \alpha _i$
for all
![]() $i \in [r]$
.
$i \in [r]$
.
Let
![]() , let
, let
![]() $r \in \mathbb {N}$
and let
$r \in \mathbb {N}$
and let
![]() $[r]$
have partition
$[r]$
have partition
![]() $\mathcal {V}=\{V_1,\ldots ,V_{r^*}\}$
. Let
$\mathcal {V}=\{V_1,\ldots ,V_{r^*}\}$
. Let
![]() $\phi \in \Phi _0(r+1;\boldsymbol {k})$
be such that
$\phi \in \Phi _0(r+1;\boldsymbol {k})$
be such that
![]() $\phi |_{\binom {[r]}{2}}=_{\mathcal {V}} \phi ^*$
and
$\phi |_{\binom {[r]}{2}}=_{\mathcal {V}} \phi ^*$
and
![]() $\boldsymbol {\alpha } =_{\mathcal {V}} \boldsymbol {\alpha }^*$
. For
$\boldsymbol {\alpha } =_{\mathcal {V}} \boldsymbol {\alpha }^*$
. For
![]() $i \in [r^*]$
, let
$i \in [r^*]$
, let
be the minimum weight of edits of pairs at
![]() $r+1$
needed to make
$r+1$
needed to make
![]() $r+1$
a clone of i. If
$r+1$
a clone of i. If
![]() $d_i \leq \delta $
, we say that
$d_i \leq \delta $
, we say that
![]() $r+1$
is
$r+1$
is
![]() $\delta $
-close to being a
$\delta $
-close to being a
![]() $\phi ^*$
-clone of i, otherwise,
$\phi ^*$
-clone of i, otherwise,
![]() $r+1$
is
$r+1$
is
![]() $\delta $
-far from being a
$\delta $
-far from being a
![]() $\phi ^*$
-clone of i.
$\phi ^*$
-clone of i.
The next lemma extends the previous one by allowing an arbitrary feasible attachment to a (blow-up of a) basic optimal solution and supposing the new part is far from being a clone.
Lemma 2.11. Let
![]() $s \in \mathbb {N}$
, and let
$s \in \mathbb {N}$
, and let
![]() $\boldsymbol {k}$
have the extension property. Then there exists
$\boldsymbol {k}$
have the extension property. Then there exists
![]() $\eta>0$
, such that the following holds. Let
$\eta>0$
, such that the following holds. Let
![]() $\delta>0$
and
$\delta>0$
and
![]() , let
, let
![]() $r \in \mathbb {N}$
and let
$r \in \mathbb {N}$
and let
![]() $[r]$
have partition
$[r]$
have partition
![]() $\mathcal {V}=\{V_1,\ldots ,V_{r^*}\}$
. Let
$\mathcal {V}=\{V_1,\ldots ,V_{r^*}\}$
. Let
![]() $\phi \in \Phi _0(r+1;\boldsymbol {k})$
and
$\phi \in \Phi _0(r+1;\boldsymbol {k})$
and
![]() $\boldsymbol {\alpha } \in \Delta ^r$
be such that
$\boldsymbol {\alpha } \in \Delta ^r$
be such that
![]() $\phi |_{\binom {[r]}{2}}=_{\mathcal {V}} \phi ^*$
and
$\phi |_{\binom {[r]}{2}}=_{\mathcal {V}} \phi ^*$
and
![]() $\boldsymbol {\alpha } =_{\mathcal {V}} \boldsymbol {\beta }$
for some
$\boldsymbol {\alpha } =_{\mathcal {V}} \boldsymbol {\beta }$
for some
![]() $\boldsymbol {\beta } \in \Delta ^{r^*}$
with
$\boldsymbol {\beta } \in \Delta ^{r^*}$
with
![]() $\|\boldsymbol {\beta } - \boldsymbol {\alpha }^*\|_1 \leq \eta \delta $
. Suppose that
$\|\boldsymbol {\beta } - \boldsymbol {\alpha }^*\|_1 \leq \eta \delta $
. Suppose that
![]() $r+1$
is
$r+1$
is
![]() $\delta $
-far from being a
$\delta $
-far from being a
![]() $\phi ^*$
-clone of any
$\phi ^*$
-clone of any
![]() $i \in [r^*]$
. Then
$i \in [r^*]$
. Then
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) \leq Q(\boldsymbol {k})-\eta \delta $
.
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) \leq Q(\boldsymbol {k})-\eta \delta $
.
Proof. We will derive the lemma from the following claim.
Claim 2.11.1. There exists
![]() $\eta>0$
, such that when additionally
$\eta>0$
, such that when additionally
![]() $\boldsymbol {\beta }=\boldsymbol {\alpha }^*$
, we have
$\boldsymbol {\beta }=\boldsymbol {\alpha }^*$
, we have
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) \leq Q(\boldsymbol {k})-2\eta \delta \log s$
.
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) \leq Q(\boldsymbol {k})-2\eta \delta \log s$
.
Suppose that the claim holds and we wish to prove the lemma. Let
![]() $\boldsymbol {\alpha }' \in \Delta ^{r^*}$
be such that
$\boldsymbol {\alpha }' \in \Delta ^{r^*}$
be such that
![]() $\boldsymbol {\alpha }' =_{\mathcal {V}} \boldsymbol {\alpha }^*$
and
$\boldsymbol {\alpha }' =_{\mathcal {V}} \boldsymbol {\alpha }^*$
and
![]() $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }'\|_1 \leq \eta \delta $
. Such an
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }'\|_1 \leq \eta \delta $
. Such an
![]() $\boldsymbol {\alpha }'$
exists: for example, for all
$\boldsymbol {\alpha }'$
exists: for example, for all
![]() $j \in [r^*]$
and all
$j \in [r^*]$
and all
![]() $i \in V_j$
, take
$i \in V_j$
, take
![]() $\alpha ^{\prime }_i := \alpha_i\alpha_j^*/\beta_j$
. Since
$\alpha ^{\prime }_i := \alpha_i\alpha_j^*/\beta_j$
. Since
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }') \leq Q(\boldsymbol {k})-2\eta \delta \log s$
, we have
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }') \leq Q(\boldsymbol {k})-2\eta \delta \log s$
, we have
as required. So it remains to prove the claim.
Proof of Claim.
Let
![]() $\eta '>0$
be the constant obtained from Lemma 2.10. We will show that we can take
$\eta '>0$
be the constant obtained from Lemma 2.10. We will show that we can take
![]() $\eta := \eta '/(2\log s)$
.
$\eta := \eta '/(2\log s)$
.
It will be convenient to write
![]() $0$
instead of
$0$
instead of
![]() $r+1$
for the attachment. So we require an upper bound for
$r+1$
for the attachment. So we require an upper bound for
![]() $q_0(\phi ,\boldsymbol {\alpha })$
. Let
$q_0(\phi ,\boldsymbol {\alpha })$
. Let
![]() $1/n \ll 1/r,\delta ,\eta '$
, and for each
$1/n \ll 1/r,\delta ,\eta '$
, and for each
![]() $j \in [r^*]$
, subdivide the parts in each
$j \in [r^*]$
, subdivide the parts in each
![]() $V_j$
to get a total of n subparts, so that as many of these subparts as possible have the same size. We may assume that in fact every subpart of parts in
$V_j$
to get a total of n subparts, so that as many of these subparts as possible have the same size. We may assume that in fact every subpart of parts in
![]() $V_j$
have the same size
$V_j$
have the same size
![]() $\alpha ^*_j/n$
, since the total size of smaller parts is at most
$\alpha ^*_j/n$
, since the total size of smaller parts is at most
![]() $r/n$
which is negligible compared to
$r/n$
which is negligible compared to
![]() $\eta '$
and
$\eta '$
and
![]() $\delta $
. So, relabelling, we have a partition
$\delta $
. So, relabelling, we have a partition
![]() $\mathcal {U} := \{U_1,\ldots ,U_r\}$
of
$\mathcal {U} := \{U_1,\ldots ,U_r\}$
of
![]() $[r^*n]$
and
$[r^*n]$
and
![]() $\boldsymbol {\alpha }_n \in \Delta ^{r^*n}$
, such that
$\boldsymbol {\alpha }_n \in \Delta ^{r^*n}$
, such that
![]() $\boldsymbol {\alpha }_{n,k} = \alpha _j^*/n$
for every
$\boldsymbol {\alpha }_{n,k} = \alpha _j^*/n$
for every
![]() $k \in \mathcal {U}_j := \{U_{j'} : j' \in V_j\}$
, and
$k \in \mathcal {U}_j := \{U_{j'} : j' \in V_j\}$
, and
![]() $|\mathcal {U}_j|=n$
. Write
$|\mathcal {U}_j|=n$
. Write
![]() $\mathcal {U}_j := \{x_{j,1},\ldots ,x_{j,n}\}$
.
$\mathcal {U}_j := \{x_{j,1},\ldots ,x_{j,n}\}$
.
For all
![]() $\ell \in [n]$
, let
$\ell \in [n]$
, let
![]() $T_{\ell } := \{x_{1,\ell },\ldots ,x_{r^*,\ell }\}$
be the
$T_{\ell } := \{x_{1,\ell },\ldots ,x_{r^*,\ell }\}$
be the
![]() $\ell $
-th transversal, and let
$\ell $
-th transversal, and let
![]() $\phi _{\ell } := \phi |_{\{0\} \cup T_{\ell }}$
. Recall that
$\phi _{\ell } := \phi |_{\{0\} \cup T_{\ell }}$
. Recall that
![]() $\phi |_{T_{\ell }} = \phi ^*$
. For each
$\phi |_{T_{\ell }} = \phi ^*$
. For each
![]() $j \in [r^*]$
, let
$j \in [r^*]$
, let
![]() $C_j$
be the set of all
$C_j$
be the set of all
![]() $\ell \in [n]$
, such that
$\ell \in [n]$
, such that
![]() $0$
is a clone of j under
$0$
is a clone of j under
![]() $\phi _{\ell }$
. So
$\phi _{\ell }$
. So
![]() $C := C_1\cup \ldots \cup C_{r^*}$
is a disjoint union. By rearranging the transversals, we are going to make all sets
$C := C_1\cup \ldots \cup C_{r^*}$
is a disjoint union. By rearranging the transversals, we are going to make all sets
![]() $C_j$
empty except at most one. For this, partition C into pairs
$C_j$
empty except at most one. For this, partition C into pairs
![]() $\{\ell _1,\ell _2\}$
and a set
$\{\ell _1,\ell _2\}$
and a set
![]() $C_{0}$
, such that in every pair
$C_{0}$
, such that in every pair
![]() $\{\ell _1,\ell _2\}$
, we have
$\{\ell _1,\ell _2\}$
, we have
![]() $\ell _1 \in C_{j_1}$
and
$\ell _1 \in C_{j_1}$
and
![]() $\ell _2 \in C_{j_2}$
for distinct
$\ell _2 \in C_{j_2}$
for distinct
![]() $j_1,j_2 \in [r^*]$
, and there is at most one
$j_1,j_2 \in [r^*]$
, and there is at most one
![]() $j \in [r^*]$
, such that
$j \in [r^*]$
, such that
![]() $C_0 \cap C_j \neq \emptyset $
. For all pairs
$C_0 \cap C_j \neq \emptyset $
. For all pairs
![]() $\{\ell _1,\ell _2\}$
, swap the labels of
$\{\ell _1,\ell _2\}$
, swap the labels of
![]() $x_{j_1,\ell _1}$
and
$x_{j_1,\ell _1}$
and
![]() $x_{j_1,\ell _2}$
. Update C. Notice that now, C is our previous
$x_{j_1,\ell _2}$
. Update C. Notice that now, C is our previous
![]() $C_0$
, as neither
$C_0$
, as neither
![]() $\ell _1$
nor
$\ell _1$
nor
![]() $\ell _2$
gives a transversal where
$\ell _2$
gives a transversal where
![]() $0$
is a clone (since
$0$
is a clone (since
![]() $\phi _{\ell _1}$
has size two on every pair in
$\phi _{\ell _1}$
has size two on every pair in
![]() $\{0\} \cup T_{\ell _1}$
, and
$\{0\} \cup T_{\ell _1}$
, and
![]() $\phi _{\ell _2}$
has size at most
$\phi _{\ell _2}$
has size at most
![]() $1$
on exactly two pairs in
$1$
on exactly two pairs in
![]() $\{0\} \cup T_{\ell _2}$
).
$\{0\} \cup T_{\ell _2}$
).
Let
![]() $\Phi $
be the set of all
$\Phi $
be the set of all
![]() $\phi _{\ell }$
. Let
$\phi _{\ell }$
. Let
![]() $\Phi _{\mathrm {clone}} \subseteq \Phi $
be such that
$\Phi _{\mathrm {clone}} \subseteq \Phi $
be such that
![]() $\phi _{\ell } \in \Phi _{\mathrm {clone}}$
if and only if
$\phi _{\ell } \in \Phi _{\mathrm {clone}}$
if and only if
![]() $0$
is a clone under
$0$
is a clone under
![]() $\phi_\ell$
of some
$\phi_\ell$
of some
![]() $j \in [r^*]$
. By construction, every such
$j \in [r^*]$
. By construction, every such
![]() $\ell $
lies in C and there is a unique such
$\ell $
lies in C and there is a unique such
![]() $j=j^* \in [r^*]$
.
$j=j^* \in [r^*]$
.
We can make edits of weight at most
![]() $1-|C|/n$
to make
$1-|C|/n$
to make
![]() $0$
a clone of
$0$
a clone of
![]() $j^*$
under
$j^*$
under
![]() $\phi $
. Indeed, we can edit each
$\phi $
. Indeed, we can edit each
![]() $\phi _{\ell }$
with
$\phi _{\ell }$
with
![]() $\ell \in [n]\setminus C$
, requiring edits to parts of size
$\ell \in [n]\setminus C$
, requiring edits to parts of size
![]() $\alpha^*_1/n,\ldots,\alpha^*_{r^*}/n$
of total size
$\alpha^*_1/n,\ldots,\alpha^*_{r^*}/n$
of total size
![]() $1/n$
. Thus, our hypothesis implies that
$1/n$
. Thus, our hypothesis implies that
Lemma 2.10 implies that
![]() $q_0(\psi ,\boldsymbol {\alpha }^*) \leq Q(\boldsymbol {k}) - \eta '$
whenever
$q_0(\psi ,\boldsymbol {\alpha }^*) \leq Q(\boldsymbol {k}) - \eta '$
whenever
![]() $\psi \in \Phi \setminus \Phi _{\mathrm {clone}}$
. Therefore, using Proposition 2.6,
$\psi \in \Phi \setminus \Phi _{\mathrm {clone}}$
. Therefore, using Proposition 2.6,
 $$ \begin{align*} q_0(\phi,\boldsymbol{\alpha}) &= \sum_{\ell \in [n]}q_0(\phi_{\ell},\boldsymbol{\alpha}_n) = \sum_{\ell \in C}q_0(\phi_{\ell},\boldsymbol{\alpha}^*)/n + \sum_{\ell \in [n]\setminus C}q_0(\phi_{\ell},\boldsymbol{\alpha}^*)/n\\ &\leq |C|Q(\boldsymbol{k})/n + (n-|C|)((Q(\boldsymbol{k})-\eta')/n = Q(\boldsymbol{k})-(1-|C|/n)\eta' \leq Q(\boldsymbol{k})-\eta'\delta, \end{align*} $$
$$ \begin{align*} q_0(\phi,\boldsymbol{\alpha}) &= \sum_{\ell \in [n]}q_0(\phi_{\ell},\boldsymbol{\alpha}_n) = \sum_{\ell \in C}q_0(\phi_{\ell},\boldsymbol{\alpha}^*)/n + \sum_{\ell \in [n]\setminus C}q_0(\phi_{\ell},\boldsymbol{\alpha}^*)/n\\ &\leq |C|Q(\boldsymbol{k})/n + (n-|C|)((Q(\boldsymbol{k})-\eta')/n = Q(\boldsymbol{k})-(1-|C|/n)\eta' \leq Q(\boldsymbol{k})-\eta'\delta, \end{align*} $$
as required.
This completes the proof of the lemma.
The final lemma in this subsection considers an arbitrary not necessarily feasible attachment. Now, either the new part is far from being a clone, or it lies in many forbidden monochromatic cliques. This is the key tool in the proof of Lemma 3.1.
Lemma 2.12. Let
![]() $s \in \mathbb {N}$
, and let
$s \in \mathbb {N}$
, and let
![]() $\boldsymbol {k}=(k_1,\ldots ,k_s)$
have the extension property, where
$\boldsymbol {k}=(k_1,\ldots ,k_s)$
have the extension property, where
![]() $k_1 \geq \ldots \geq k_s$
. There exists
$k_1 \geq \ldots \geq k_s$
. There exists
![]() $\eta>0$
, such that the following hold. Let
$\eta>0$
, such that the following hold. Let
![]() $\delta>0$
, and let
$\delta>0$
, and let
![]() , let
, let
![]() $r \in \mathbb {N}$
, and let
$r \in \mathbb {N}$
, and let
![]() $[r]$
have partition
$[r]$
have partition
![]() $\mathcal {V}=\{V_1,\ldots, V_{r^*}\}$
. Let
$\mathcal {V}=\{V_1,\ldots, V_{r^*}\}$
. Let
![]() $\phi : \binom {[r+1]}{2} \to 2^{[s]}$
and
$\phi : \binom {[r+1]}{2} \to 2^{[s]}$
and
![]() $\boldsymbol {\alpha } \in \Delta ^r$
be such that
$\boldsymbol {\alpha } \in \Delta ^r$
be such that
![]() $\phi |_{\binom {[r]}{2}}=_{\mathcal {V}} \phi ^*$
and
$\phi |_{\binom {[r]}{2}}=_{\mathcal {V}} \phi ^*$
and
![]() $\boldsymbol {\alpha } =_{\mathcal {V}} \boldsymbol {\beta }$
for some
$\boldsymbol {\alpha } =_{\mathcal {V}} \boldsymbol {\beta }$
for some
![]() $\boldsymbol {\beta } \in \Delta ^{r^*}$
with
$\boldsymbol {\beta } \in \Delta ^{r^*}$
with
![]() $\|\boldsymbol {\beta }- \boldsymbol {\alpha }^*\|_1 \leq \eta \delta $
, and
$\|\boldsymbol {\beta }- \boldsymbol {\alpha }^*\|_1 \leq \eta \delta $
, and
![]() $\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) \geq Q(\boldsymbol {k})-\eta \delta $
. Then one of the following hold.
$\mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }) \geq Q(\boldsymbol {k})-\eta \delta $
. Then one of the following hold.
-
• There exists
 $\ell \in [r]$
, such that
$\ell \in [r]$
, such that
 $r+1$
is
$r+1$
is
 $\delta $
-close to a
$\delta $
-close to a
 $\phi ^*$
-clone of
$\phi ^*$
-clone of
 $\ell $
.
$\ell $
. -
• Let L be the set of sets
 $\{x_1,\ldots ,x_{k_1-1}\} \in \binom {[r]}{k_1-1}$
, such that
$\{x_1,\ldots ,x_{k_1-1}\} \in \binom {[r]}{k_1-1}$
, such that
 $\phi ^{-1}(c)[\{r+1,x_1,\ldots ,x_{k_1-1}\}] \supseteq K_{k_c}$
for some
$\phi ^{-1}(c)[\{r+1,x_1,\ldots ,x_{k_1-1}\}] \supseteq K_{k_c}$
for some
 $c \in [s]$
. Then
$c \in [s]$
. Then
 $\sum _{(x_1,\ldots ,x_{k_1-1}) \in L}\alpha _{x_1}\ldots \alpha _{x_{k_1-1}} \geq \eta $
.
$\sum _{(x_1,\ldots ,x_{k_1-1}) \in L}\alpha _{x_1}\ldots \alpha _{x_{k_1-1}} \geq \eta $
.
Proof. Let
![]() $\eta '>0$
be the constant obtained from Lemma 2.11. Suppose for a contradiction that for all
$\eta '>0$
be the constant obtained from Lemma 2.11. Suppose for a contradiction that for all
![]() $n \in \mathbb {N}$
, there exist
$n \in \mathbb {N}$
, there exist
![]() ,
,
![]() $r_n$
,
$r_n$
,
![]() $\mathcal {V}_n$
,
$\mathcal {V}_n$
,
![]() $\phi _n : \binom {[r_n+1]}{2} \to 2^{[s]}$
,
$\phi _n : \binom {[r_n+1]}{2} \to 2^{[s]}$
,
![]() $\boldsymbol {\beta }_n$
, such that
$\boldsymbol {\beta }_n$
, such that
![]() $\boldsymbol {\alpha }_n =_{\mathcal {V}_n} \boldsymbol {\beta }_n$
and
$\boldsymbol {\alpha }_n =_{\mathcal {V}_n} \boldsymbol {\beta }_n$
and
![]() $\|\boldsymbol {\beta }_n-\boldsymbol {\alpha }^*_n\|_1 \leq \eta '\delta /2$
,
$\|\boldsymbol {\beta }_n-\boldsymbol {\alpha }^*_n\|_1 \leq \eta '\delta /2$
,
![]() $\phi _n |_{\binom {[r_n]}{2}} =_{\mathcal {V}_n} \phi ^*_n$
,
$\phi _n |_{\binom {[r_n]}{2}} =_{\mathcal {V}_n} \phi ^*_n$
,
![]() $\mathop {\mathrm {ext}}(\phi _n,\boldsymbol {\alpha }_n) \geq Q(\boldsymbol {k})-\eta '\delta /2$
,
$\mathop {\mathrm {ext}}(\phi _n,\boldsymbol {\alpha }_n) \geq Q(\boldsymbol {k})-\eta '\delta /2$
,
![]() $r_n+1$
is
$r_n+1$
is
![]() $\delta $
-far from being a clone of any
$\delta $
-far from being a clone of any
![]() $\ell \in [r_n]$
under
$\ell \in [r_n]$
under
![]() $\phi _n$
, and defining the set of tuples
$\phi _n$
, and defining the set of tuples
![]() $L_n$
as in the statement of the lemma, we have
$L_n$
as in the statement of the lemma, we have
![]() $\sum _{(x_1,\ldots ,x_{k_1-1}) \in L_n}\alpha _{n,x_1}\ldots \alpha _{n,x_{k_1-1}} < \frac {1}{n}$
. Note that we may assume that
$\sum _{(x_1,\ldots ,x_{k_1-1}) \in L_n}\alpha _{n,x_1}\ldots \alpha _{n,x_{k_1-1}} < \frac {1}{n}$
. Note that we may assume that
![]() $r_n \leq 2^{s r_n^*}$
as
$r_n \leq 2^{s r_n^*}$
as
![]() $r_n+1$
has at most
$r_n+1$
has at most
![]() $2^s$
different attachments to parts in each
$2^s$
different attachments to parts in each
![]() $V_{n,i}$
in
$V_{n,i}$
in
![]() $\mathcal {V}_n$
, so if
$\mathcal {V}_n$
, so if
![]() $|V_{n,i}|> 2^{s r_n^*}$
, at least two of its parts are clones under
$|V_{n,i}|> 2^{s r_n^*}$
, at least two of its parts are clones under
![]() $\phi ^*_n$
, and we can merge them. As usual, we may assume that
$\phi ^*_n$
, and we can merge them. As usual, we may assume that
![]() $r_n^*=r^*$
and
$r_n^*=r^*$
and
![]() $\phi ^*_n=\phi ^*$
, and thus also
$\phi ^*_n=\phi ^*$
, and thus also
![]() $r_n=p$
,
$r_n=p$
,
![]() $\phi _n=\psi $
and
$\phi _n=\psi $
and
![]() $\mathcal {V}_n = \mathcal {V}$
. Choose a convergent subsequence
$\mathcal {V}_n = \mathcal {V}$
. Choose a convergent subsequence
![]() $\boldsymbol {\alpha }^*_{i_1},\boldsymbol {\alpha }^*_{i_2},\ldots $
of
$\boldsymbol {\alpha }^*_{i_1},\boldsymbol {\alpha }^*_{i_2},\ldots $
of
![]() $\boldsymbol {\alpha }^*_1,\boldsymbol {\alpha }^*_2,\ldots $
with limit
$\boldsymbol {\alpha }^*_1,\boldsymbol {\alpha }^*_2,\ldots $
with limit
![]() $\boldsymbol {\beta }^*$
, and a convergent subsequence
$\boldsymbol {\beta }^*$
, and a convergent subsequence
![]() $\boldsymbol {\alpha }_{i_{j_1}},\boldsymbol {\alpha }_{i_{j_2}},\ldots $
of
$\boldsymbol {\alpha }_{i_{j_1}},\boldsymbol {\alpha }_{i_{j_2}},\ldots $
of
![]() $\boldsymbol {\alpha }_{i_1},\boldsymbol {\alpha }_{i_2},\ldots $
with limit
$\boldsymbol {\alpha }_{i_1},\boldsymbol {\alpha }_{i_2},\ldots $
with limit
![]() $\boldsymbol {\beta }$
. The function
$\boldsymbol {\beta }$
. The function
![]() $\mathop {\mathrm {ext}}(\psi ,\cdot )$
is continuous, so
$\mathop {\mathrm {ext}}(\psi ,\cdot )$
is continuous, so
![]() $\mathop {\mathrm {ext}}(\psi ,\boldsymbol {\beta }) \geq Q(\boldsymbol {k})-\eta '\delta /2$
. Also, writing
$\mathop {\mathrm {ext}}(\psi ,\boldsymbol {\beta }) \geq Q(\boldsymbol {k})-\eta '\delta /2$
. Also, writing
![]() $\boldsymbol {\beta }_{\mathcal {V}}$
to be such that
$\boldsymbol {\beta }_{\mathcal {V}}$
to be such that
![]() $\boldsymbol {\beta } =_{\mathcal {V}} \boldsymbol {\beta }_{\mathcal {V}}$
, we have
$\boldsymbol {\beta } =_{\mathcal {V}} \boldsymbol {\beta }_{\mathcal {V}}$
, we have
![]() $\|\boldsymbol {\beta }_{\mathcal {V}}-\boldsymbol {\beta }^*\|_1 \leq \eta '\delta /2$
. Let
$\|\boldsymbol {\beta }_{\mathcal {V}}-\boldsymbol {\beta }^*\|_1 \leq \eta '\delta /2$
. Let
![]() $L_c$
be the set of sets
$L_c$
be the set of sets
![]() $(x_1,\ldots ,x_{k_1-1}) \in \binom {[p]}{k_1-1}$
, such that
$(x_1,\ldots ,x_{k_1-1}) \in \binom {[p]}{k_1-1}$
, such that
![]() $\psi ^{-1}(c)[\{p+1,x_1,\ldots ,x_{k_1-1}\}] \supseteq K_{k_c}$
. Note that by our assumption above,
$\psi ^{-1}(c)[\{p+1,x_1,\ldots ,x_{k_1-1}\}] \supseteq K_{k_c}$
. Note that by our assumption above,
![]() $L_c$
does not change with n. We have
$L_c$
does not change with n. We have
![]() $\sum _{(x_1,\ldots ,x_{k_1-1}) \in L_c}\beta _{x_1}\ldots \beta _{x_{k_1-1}} = 0$
. Thus, the density of
$\sum _{(x_1,\ldots ,x_{k_1-1}) \in L_c}\beta _{x_1}\ldots \beta _{x_{k_1-1}} = 0$
. Thus, the density of
![]() $K_{k_c}$
containing
$K_{k_c}$
containing
![]() $p+1$
is
$p+1$
is
![]() $0$
, and we can remove parts of size
$0$
, and we can remove parts of size
![]() $0$
from
$0$
from
![]() $[p]$
to obtain a set (without loss of generality
$[p]$
to obtain a set (without loss of generality
![]() $[p']$
), such that
$[p']$
), such that
![]() $\psi ^{-1}(c)[\{p+1\} \cup [p']]$
is
$\psi ^{-1}(c)[\{p+1\} \cup [p']]$
is
![]() $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
![]() $c \in [s]$
. Thus
$c \in [s]$
. Thus
![]() $\psi \in \Phi _0(\{p+1\} \cup [p'];\boldsymbol {k})$
, that is the attachment of
$\psi \in \Phi _0(\{p+1\} \cup [p'];\boldsymbol {k})$
, that is the attachment of
![]() $p+1$
under
$p+1$
under
![]() $\psi $
is feasible. Lemma 2.11 implies that
$\psi $
is feasible. Lemma 2.11 implies that
![]() $\mathop {\mathrm {ext}}(\psi ,\boldsymbol {\beta }) \leq Q(\boldsymbol {k})-\eta '\delta $
, a contradiction.
$\mathop {\mathrm {ext}}(\psi ,\boldsymbol {\beta }) \leq Q(\boldsymbol {k})-\eta '\delta $
, a contradiction.
Thus, there exists
![]() $N \in \mathbb {N}$
, such that the required sum of tuples is always at least
$N \in \mathbb {N}$
, such that the required sum of tuples is always at least
![]() $1/N$
. We can now take
$1/N$
. We can now take
![]() $\eta $
to be the minimum of
$\eta $
to be the minimum of
![]() $\eta '/2$
and
$\eta '/2$
and
![]() $1/N$
.
$1/N$
.
3 Stability of optimal solutions
The aim of this section is to prove the following lemma, which forms the core of our proof of Theorem 1.4. Roughly speaking, it says that Problem
![]() $Q_0$
is stable, in the sense that both the vertex-weighting and the colour pattern of an almost
$Q_0$
is stable, in the sense that both the vertex-weighting and the colour pattern of an almost
![]() $Q_0$
-optimal solution are close to that of a
$Q_0$
-optimal solution are close to that of a
![]() $Q_0$
-optimal solution (which can in turn be described in terms of a
$Q_0$
-optimal solution (which can in turn be described in terms of a
![]() $Q_2$
-optimal solution by Lemma 1.3). To prove Theorem 1.4, we will later ‘transfer’ this result to an almost optimal graph G.
$Q_2$
-optimal solution by Lemma 1.3). To prove Theorem 1.4, we will later ‘transfer’ this result to an almost optimal graph G.
Lemma 3.1 (Stability of optimal solutions).
Let
![]() $s \in \mathbb {N}$
, and let
$s \in \mathbb {N}$
, and let
![]() $\boldsymbol {k}=(k_1,\ldots ,k_s) \in \mathbb {N}^s$
have the extension property, where
$\boldsymbol {k}=(k_1,\ldots ,k_s) \in \mathbb {N}^s$
have the extension property, where
![]() $k_1 \geq \ldots \geq k_s$
. Let
$k_1 \geq \ldots \geq k_s$
. Let
![]() $\nu>0$
. Then there exists
$\nu>0$
. Then there exists
![]() $\varepsilon>0$
, such that for every
$\varepsilon>0$
, such that for every
![]() with
with
there is
![]() and a partition
and a partition
![]() $[r]=Y_0 \cup \ldots \cup Y_{r^*}$
, such that, defining
$[r]=Y_0 \cup \ldots \cup Y_{r^*}$
, such that, defining
![]() $\beta _i := \sum _{i' \in Y_i}\alpha _{i'}$
for all
$\beta _i := \sum _{i' \in Y_i}\alpha _{i'}$
for all
![]() $i \in [r^*]$
, the following holds.
$i \in [r^*]$
, the following holds.
-
(i)
 $\|\boldsymbol {\beta }-\boldsymbol {\alpha }^*\|_1 < \nu $
(and, in particular,
$\|\boldsymbol {\beta }-\boldsymbol {\alpha }^*\|_1 < \nu $
(and, in particular,
 $\sum _{i' \in Y_0}\alpha _{i'} < \nu $
).
$\sum _{i' \in Y_0}\alpha _{i'} < \nu $
). -
(ii) For all
 $ij \in \binom {[r^*]}{2}$
,
$ij \in \binom {[r^*]}{2}$
,
 $j' \in Y_j$
and
$j' \in Y_j$
and
 $i' \in Y_i$
, we have
$i' \in Y_i$
, we have
 $\phi (i'j') \subseteq \phi ^*(ij)$
.
$\phi (i'j') \subseteq \phi ^*(ij)$
. -
(iii) For all
 $i \in [r^*]$
and every
$i \in [r^*]$
and every
 $i'j' \in \binom {Y_{i}}{2}$
, we have
$i'j' \in \binom {Y_{i}}{2}$
, we have
 $\phi (i'j') \subseteq \{ 1 \}$
.
$\phi (i'j') \subseteq \{ 1 \}$
.
Note that the density of pairs (that is, the sum of the
![]() $\alpha _i\alpha _j$
) where the inclusion
$\alpha _i\alpha _j$
) where the inclusion
![]() $\phi (i'j') \subseteq \phi ^*(ij)$
in (ii) is strict is
$\phi (i'j') \subseteq \phi ^*(ij)$
in (ii) is strict is
![]() $O(\nu )$
.
$O(\nu )$
.
Proof. We will apply a version of symmetrisation to the graph
![]() $([r],E)$
, where E is the set of pairs
$([r],E)$
, where E is the set of pairs
![]() $ij$
on which
$ij$
on which
![]() $\phi $
has size at least two. That is, at each step, we will consider two vertices
$\phi $
has size at least two. That is, at each step, we will consider two vertices
![]() $j,j'$
with
$j,j'$
with
![]() $|\phi (jj')| \leq 1$
and replace one of them with a clone of the other, where the cloned vertex is the one which contributes the most to q. In the first part of the proof, we will perform this ‘forwards symmetrisation’.
$|\phi (jj')| \leq 1$
and replace one of them with a clone of the other, where the cloned vertex is the one which contributes the most to q. In the first part of the proof, we will perform this ‘forwards symmetrisation’.
Let
![]() $\mu $
be the output of Lemma 2.8 applied to
$\mu $
be the output of Lemma 2.8 applied to
![]() $\boldsymbol {k}$
, so
$\boldsymbol {k}$
, so
![]() $\alpha _j^*> \mu $
for all
$\alpha _j^*> \mu $
for all
![]() and
and
![]() $j \in [r^*]$
. Choose additional constants
$j \in [r^*]$
. Choose additional constants
![]() $\varepsilon ,\gamma ,\eta ,\delta $
, such that
$\varepsilon ,\gamma ,\eta ,\delta $
, such that
![]() $ \varepsilon \ll \gamma \ll \eta \ll \delta \ll \mu ,\nu $
where
$ \varepsilon \ll \gamma \ll \eta \ll \delta \ll \mu ,\nu $
where
![]() $\sqrt{\delta} $
is at most the output of Lemma 2.9,
$\sqrt{\delta} $
is at most the output of Lemma 2.9,
![]() $\eta $
is at most the output of Lemma 2.12, and
$\eta $
is at most the output of Lemma 2.12, and
![]() $\varepsilon^{1/4}$
is at most the output of Lemma 2.3 with
$\varepsilon^{1/4}$
is at most the output of Lemma 2.3 with
![]() $\gamma$
playing the role of
$\gamma$
playing the role of
![]() $\delta$
.
$\delta$
.
Now let
![]() satisfy
satisfy
![]() $q(\phi ,\boldsymbol {\alpha })>Q(\boldsymbol {k})-2\varepsilon $
. Add all i with
$q(\phi ,\boldsymbol {\alpha })>Q(\boldsymbol {k})-2\varepsilon $
. Add all i with
![]() $\alpha _i=0$
to
$\alpha _i=0$
to
![]() $Y_0$
. We can take
$Y_0$
. We can take
![]() $\tau \ll \varepsilon , \min _{i \in [r]}\alpha _i \leq 1/r$
so that, subdividing each part, we can remove subparts of total size at most
$\tau \ll \varepsilon , \min _{i \in [r]}\alpha _i \leq 1/r$
so that, subdividing each part, we can remove subparts of total size at most
![]() $r\tau $
so that every other subpart has size exactly
$r\tau $
so that every other subpart has size exactly
![]() $\tau $
. Since we can put the removed parts into
$\tau $
. Since we can put the removed parts into
![]() $Y_0$
, we may assume, without loss of generality, that all
$Y_0$
, we may assume, without loss of generality, that all
![]() $\alpha _i$
are equal to each other (and
$\alpha _i$
are equal to each other (and
![]() $\phi $
takes the value
$\phi $
takes the value
![]() $\emptyset $
between parts obtained from subdividing a single original part). So we may assume that
$\emptyset $
between parts obtained from subdividing a single original part). So we may assume that
![]() $\alpha _i = 1/r \ll \varepsilon $
for all
$\alpha _i = 1/r \ll \varepsilon $
for all
![]() $i \in [r]$
. Altogether, we have
$i \in [r]$
. Altogether, we have
3.1 The forwards symmetrisation procedure
Let
![]() $\mathcal {X}_0 := \{\{1\},\ldots ,\{r\}\}$
and
$\mathcal {X}_0 := \{\{1\},\ldots ,\{r\}\}$
and
![]() $\phi _0 := \phi $
.
$\phi _0 := \phi $
.
Claim 3.1.1. There is
![]() $f \in \mathbb {N}$
, such that, after relabelling
$f \in \mathbb {N}$
, such that, after relabelling
![]() $[r]$
, for all
$[r]$
, for all
![]() $i=0,\ldots ,f$
, there is a partition
$i=0,\ldots ,f$
, there is a partition
![]() $\mathcal {X}_i$
of
$\mathcal {X}_i$
of
![]() $[r]$
and colour pattern
$[r]$
and colour pattern
![]() $\phi _i \in \Phi _0(r;\boldsymbol {k})$
, such that the following hold.
$\phi _i \in \Phi _0(r;\boldsymbol {k})$
, such that the following hold.
-
(i) There is a single
 $x_{i} \in [r]$
, such that
$x_{i} \in [r]$
, such that
 $\mathcal {X}_{i}$
consists of the same elements as
$\mathcal {X}_{i}$
consists of the same elements as
 $\mathcal {X}_{i-1}$
, except that
$\mathcal {X}_{i-1}$
, except that
 $x_i$
has moved from one part to another.
$x_i$
has moved from one part to another. -
(ii)
 $\phi _i =_{\mathcal {X}_{i}} \psi _i$
where
$\phi _i =_{\mathcal {X}_{i}} \psi _i$
where
 $\psi _i = \phi |_{\binom {[r_i]}{2}}$
, and
$\psi _i = \phi |_{\binom {[r_i]}{2}}$
, and
 $\psi _f \in \Phi _2(r_f;\boldsymbol {k})$
for some
$\psi _f \in \Phi _2(r_f;\boldsymbol {k})$
for some
 $2 \leq r_f \leq \ldots \leq r_0 = r$
.
$2 \leq r_f \leq \ldots \leq r_0 = r$
. -
(iii)
 $q(\phi _{i},\boldsymbol {\alpha }) - q(\phi _{i-1},\boldsymbol {\alpha }) \geq 0$
(where
$q(\phi _{i},\boldsymbol {\alpha }) - q(\phi _{i-1},\boldsymbol {\alpha }) \geq 0$
(where
 $\phi_{-1} := \phi_0$
).
$\phi_{-1} := \phi_0$
).
Proof of Claim.
Let
![]() $W_0 := [r]$
,
$W_0 := [r]$
,
![]() $\phi _0 = \psi _0 := \phi $
, and let
$\phi _0 = \psi _0 := \phi $
, and let
![]() $V_{0,x} := X_{0,x} := \{ x \}$
for all
$V_{0,x} := X_{0,x} := \{ x \}$
for all
![]() $x \in [r]$
. Let
$x \in [r]$
. Let
![]() $\mathcal {V}_0 := \{\{x\}: x \in [r]\}$
and
$\mathcal {V}_0 := \{\{x\}: x \in [r]\}$
and
![]() $\boldsymbol {\beta }_0 := \boldsymbol {\alpha }$
. Initialise
$\boldsymbol {\beta }_0 := \boldsymbol {\alpha }$
. Initialise
![]() $i_1:=0$
.
$i_1:=0$
.
Inductively for
![]() $j \geq 0$
, perform forwards superstep
$j \geq 0$
, perform forwards superstep
![]() $j+1$
by defining
$j+1$
by defining
![]() $W_{j+1}$
,
$W_{j+1}$
,
![]() $\psi _{j+1}$
,
$\psi _{j+1}$
,
![]() $\mathcal {V}_{j+1} := \{V_{j+1,x} : x \in W_{j+1}\}$
,
$\mathcal {V}_{j+1} := \{V_{j+1,x} : x \in W_{j+1}\}$
,
![]() $\boldsymbol {\beta }_{j+1}$
as follows. Choose a pair
$\boldsymbol {\beta }_{j+1}$
as follows. Choose a pair
![]() $p_jt_j \in \binom {W_j}{2}$
with
$p_jt_j \in \binom {W_j}{2}$
with
![]() $|\psi _j(p_jt_j)| \leq 1$
, labelled so that
$|\psi _j(p_jt_j)| \leq 1$
, labelled so that
![]() $t_j$
has larger attachment under
$t_j$
has larger attachment under
![]() $\phi _j$
; that is
$\phi _j$
; that is
 $$ \begin{align} \sum_{\substack{yt_j \in \binom{W_j}{2}:\\ \psi_j(yt_j) \neq \emptyset}}\beta_{j,y}\log|\psi_j(yt_j)| \geq \sum_{\substack{yp_j \in \binom{W_j}{2}:\\ \psi_j(yp_j) \neq \emptyset}}\beta_{j,y}\log|\psi_j(yp_j)|.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \sum_{\substack{yt_j \in \binom{W_j}{2}:\\ \psi_j(yt_j) \neq \emptyset}}\beta_{j,y}\log|\psi_j(yt_j)| \geq \sum_{\substack{yp_j \in \binom{W_j}{2}:\\ \psi_j(yp_j) \neq \emptyset}}\beta_{j,y}\log|\psi_j(yp_j)|.\\[-15pt]\nonumber \end{align} $$
If there is no such pair, terminate the iteration. Otherwise, let
![]() $W_{j+1} := W_j \setminus \{ p_j \}$
. Obtain
$W_{j+1} := W_j \setminus \{ p_j \}$
. Obtain
![]() $\mathcal {V}_{j+1}$
from
$\mathcal {V}_{j+1}$
from
![]() $\mathcal {V}_j$
by replacing
$\mathcal {V}_j$
by replacing
![]() $V_{j,p_j},V_{j,t_j}$
with their union, so
$V_{j,p_j},V_{j,t_j}$
with their union, so
![]() $V_{j+1,t_j} := V_{j,t_j} \cup V_{j,p_j}$
and
$V_{j+1,t_j} := V_{j,t_j} \cup V_{j,p_j}$
and
![]() $V_{j+1,x} := V_{j,x}$
for all
$V_{j+1,x} := V_{j,x}$
for all
![]() $x \in W_{j+1}\setminus \{t_j\}$
. For all
$x \in W_{j+1}\setminus \{t_j\}$
. For all
![]() $x \in W_{j+1}$
, let
$x \in W_{j+1}$
, let
![]() $\beta _{j+1,x} := |V_{j+1,x}|/r$
. Let
$\beta _{j+1,x} := |V_{j+1,x}|/r$
. Let
![]() $\psi _{j+1} := \psi _j|_{\binom {W_{j+1}}{2}}$
. Note that
$\psi _{j+1} := \psi _j|_{\binom {W_{j+1}}{2}}$
. Note that
 $$ \begin{align} \nonumber &\phantom{=} \sum_{\substack{xy \in \binom{W_{j+1}}{2}:\\ \psi_{j+1}(xy) \neq \emptyset}}\beta_{j+1,x}\beta_{j+1,y}\log|\psi_{j+1}(xy)| - \sum_{\substack{xy \in \binom{W_j}{2}:\\ \psi_j(xy) \neq \emptyset}}\beta_{j,x}\beta_{j,y}\log|\psi_{j}(xy)|\\ &= \beta_{j,p_j} \left( \sum_{\substack{yt_j \in \binom{W_j}{2}:\\ \psi_j(yt_j) \neq \emptyset}}\beta_{j,y}\log|\psi_j(yt_j)| - \sum_{\substack{yp_j \in \binom{W_j}{2}:\\ \psi_j(yp_j) \neq \emptyset}}\beta_{j,y}\log|\psi_j(yp_j)| \right) \stackrel{(3.1)}{\geq} 0.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \nonumber &\phantom{=} \sum_{\substack{xy \in \binom{W_{j+1}}{2}:\\ \psi_{j+1}(xy) \neq \emptyset}}\beta_{j+1,x}\beta_{j+1,y}\log|\psi_{j+1}(xy)| - \sum_{\substack{xy \in \binom{W_j}{2}:\\ \psi_j(xy) \neq \emptyset}}\beta_{j,x}\beta_{j,y}\log|\psi_{j}(xy)|\\ &= \beta_{j,p_j} \left( \sum_{\substack{yt_j \in \binom{W_j}{2}:\\ \psi_j(yt_j) \neq \emptyset}}\beta_{j,y}\log|\psi_j(yt_j)| - \sum_{\substack{yp_j \in \binom{W_j}{2}:\\ \psi_j(yp_j) \neq \emptyset}}\beta_{j,y}\log|\psi_j(yp_j)| \right) \stackrel{(3.1)}{\geq} 0.\\[-15pt]\nonumber \end{align} $$
Now we will symmetrise each part in
![]() $V_{j,p_j}$
one by one, defining
$V_{j,p_j}$
one by one, defining
![]() $\phi _{i+1} : \binom {[r]}{2} \to 2^{[s]}$
for
$\phi _{i+1} : \binom {[r]}{2} \to 2^{[s]}$
for
![]() $i_j \leq i < i_{j+1}$
where
$i_j \leq i < i_{j+1}$
where
![]() $i_{j+1} := i_j+|V_{j,p_j}|$
. Let
$i_{j+1} := i_j+|V_{j,p_j}|$
. Let
![]() $y^* \in V_{j,t_j}$
be arbitrary. Let
$y^* \in V_{j,t_j}$
be arbitrary. Let
![]() $s_{j+1} := |V_{j,p_j}|$
, and write
$s_{j+1} := |V_{j,p_j}|$
, and write
![]() $V_{j,p_j} := \{v_1,\ldots ,v_{s_{j+1}}\}$
. We will perform
$V_{j,p_j} := \{v_1,\ldots ,v_{s_{j+1}}\}$
. We will perform
![]() $s_{j+1}$
forwards steps, as follows. Inductively for
$s_{j+1}$
forwards steps, as follows. Inductively for
![]() $i \geq i_j$
, obtain
$i \geq i_j$
, obtain
![]() $\mathcal {X}_{i+1}$
from
$\mathcal {X}_{i+1}$
from
![]() $\mathcal {X}_{i}$
by moving
$\mathcal {X}_{i}$
by moving
![]() $v_i$
from
$v_i$
from
![]() $X_{i,p_j}$
to
$X_{i,p_j}$
to
![]() $X_{i,t_j}$
. That is, for
$X_{i,t_j}$
. That is, for
![]() $i_j \leq i < i_{j+1}-1$
, let
$i_j \leq i < i_{j+1}-1$
, let
![]() $X_{i+1,t_j} := X_{i,t_j} \cup \{v_i\}$
,
$X_{i+1,t_j} := X_{i,t_j} \cup \{v_i\}$
,
![]() $X_{i+1,p_j} := X_{i,p_j}\setminus \{v_i\}$
and
$X_{i+1,p_j} := X_{i,p_j}\setminus \{v_i\}$
and
![]() $X_{i+1,x} := X_{i,x}$
for all
$X_{i+1,x} := X_{i,x}$
for all
![]() $x \in W_{j+1}\setminus \{t_j\}$
; if
$x \in W_{j+1}\setminus \{t_j\}$
; if
![]() $i=i_{j+1}-1$
, we do the same but instead discard the (empty)
$i=i_{j+1}-1$
, we do the same but instead discard the (empty)
![]() $p_j$
-th part, so
$p_j$
-th part, so
![]() $|\mathcal {X}_{i+1}|=|W_j|$
for
$|\mathcal {X}_{i+1}|=|W_j|$
for
![]() $i_j \leq i < i_{j+1}$
, while
$i_j \leq i < i_{j+1}$
, while
![]() $|\mathcal {X}_{i_{j+1}}|=|W_{j+1}|$
. Let
$|\mathcal {X}_{i_{j+1}}|=|W_{j+1}|$
. Let
![]() $v_i$
become a strong clone of
$v_i$
become a strong clone of
![]() $y^*$
in
$y^*$
in
![]() $\phi _{i+1}$
; that is, for distinct
$\phi _{i+1}$
; that is, for distinct
![]() $x,y \in [r]$
, define
$x,y \in [r]$
, define
 $$ \begin{align*}\phi_{i+1}(xy) := \begin{cases} \phi_{i}(xy) &\mbox{if } x,y \neq v_i \\\phi_i(y^*z) &\mbox{if } \{x,y\}=\{v_i,z\} \text{ and } z \neq y^*\\\emptyset &\mbox{if } \{x,y\}=\{v_i,y^*\}. \end{cases}\\[-15pt] \end{align*} $$
$$ \begin{align*}\phi_{i+1}(xy) := \begin{cases} \phi_{i}(xy) &\mbox{if } x,y \neq v_i \\\phi_i(y^*z) &\mbox{if } \{x,y\}=\{v_i,z\} \text{ and } z \neq y^*\\\emptyset &\mbox{if } \{x,y\}=\{v_i,y^*\}. \end{cases}\\[-15pt] \end{align*} $$
After defining
![]() $\phi _{i+1}$
and
$\phi _{i+1}$
and
![]() $\mathcal {X}_{i+1}$
for all
$\mathcal {X}_{i+1}$
for all
![]() $i_j \leq i < i_{j+1}$
, we proceed with superstep
$i_j \leq i < i_{j+1}$
, we proceed with superstep
![]() $j+2$
.
$j+2$
.
The iteration will run until some forwards step
![]() $i=f$
(for final) when
$i=f$
(for final) when
![]() $|\phi _f(xy)| \geq 2$
for all
$|\phi _f(xy)| \geq 2$
for all
![]() $x,y$
in different parts of
$x,y$
in different parts of
![]() $\mathcal {X}_f$
. The process terminates in a finite number of steps since
$\mathcal {X}_f$
. The process terminates in a finite number of steps since
![]() $|W_j|$
is strictly decreasing (so there are finitely many supersteps j), and there are finitely many steps
$|W_j|$
is strictly decreasing (so there are finitely many supersteps j), and there are finitely many steps
![]() $s_j$
at each superstep j.
$s_j$
at each superstep j.
Let
![]() $r_i := |\mathcal {X}_i|$
. By relabelling the elements of
$r_i := |\mathcal {X}_i|$
. By relabelling the elements of
![]() $[r]$
, for all supersteps j, we can assume that
$[r]$
, for all supersteps j, we can assume that
![]() $W_j$
is always an initial segment of
$W_j$
is always an initial segment of
![]() $[r]$
so we have
$[r]$
so we have
![]() $\psi _j = \phi |_{\binom {[|W_j|]}{2}}$
. Let
$\psi _j = \phi |_{\binom {[|W_j|]}{2}}$
. Let
![]() $\boldsymbol {\alpha }_i := (\alpha _{i,1},\ldots ,\alpha _{i,r_i}) := (|X_{i,1}|/r,\ldots ,|X_{i,r_i}|/r) \in \Delta ^{r_i}$
. We have shown that for each
$\boldsymbol {\alpha }_i := (\alpha _{i,1},\ldots ,\alpha _{i,r_i}) := (|X_{i,1}|/r,\ldots ,|X_{i,r_i}|/r) \in \Delta ^{r_i}$
. We have shown that for each
![]() $i \in [f]$
, we can obtain a function
$i \in [f]$
, we can obtain a function
![]() $\phi _i$
, and sets
$\phi _i$
, and sets
![]() $\mathcal {X}_i$
, such that Claim 3.1.1
(i) and Claim 3.1.1
(ii) hold.
$\mathcal {X}_i$
, such that Claim 3.1.1
(i) and Claim 3.1.1
(ii) hold.
We still need to prove Claim 3.1.1
(iii). It is true by definition for
![]() $i=0$
. Equation (3.1) implies that
$i=0$
. Equation (3.1) implies that
![]() $q_{t_j}(\psi _{j},\boldsymbol {\beta }_{j}) - q_{p_j}(\psi _j,\boldsymbol {\beta }_j) \geq 0$
. At step
$q_{t_j}(\psi _{j},\boldsymbol {\beta }_{j}) - q_{p_j}(\psi _j,\boldsymbol {\beta }_j) \geq 0$
. At step
![]() $i+1$
during the
$i+1$
during the
![]() $j+1$
superstep, we change the attachment of a single vertex
$j+1$
superstep, we change the attachment of a single vertex
![]() $v_i$
, and we have
$v_i$
, and we have
![]() $|\phi _i(v_iy)| \leq 1$
for all
$|\phi _i(v_iy)| \leq 1$
for all
![]() $y \in V_{j,p_j} \cup V_{j,t_j}$
. Thus, the only change to
$y \in V_{j,p_j} \cup V_{j,t_j}$
. Thus, the only change to
![]() $q_{v_i}$
is for pairs
$q_{v_i}$
is for pairs
![]() $v_ix$
with
$v_ix$
with
![]() $x \in V_{j,j'}$
for
$x \in V_{j,j'}$
for
![]() $j' \in W_{j+1}\setminus \{t_j\}$
. Thus,
$j' \in W_{j+1}\setminus \{t_j\}$
. Thus,
![]() $q_{v_i}(\phi _{i+1},\boldsymbol {\alpha }) - q_{v_i}(\phi _i,\boldsymbol {\alpha })$
is the difference of the left- and right-hand sides of (3.1). The required statement follows since
$q_{v_i}(\phi _{i+1},\boldsymbol {\alpha }) - q_{v_i}(\phi _i,\boldsymbol {\alpha })$
is the difference of the left- and right-hand sides of (3.1). The required statement follows since
![]() $q(\phi _{i+1},\boldsymbol {\alpha })-q(\phi _i,\boldsymbol {\alpha }) = \alpha _{v_i}(q_{v_i}(\phi _{i+1},\boldsymbol {\alpha }) - q_{v_i}(\phi _i,\boldsymbol {\alpha }))$
.
$q(\phi _{i+1},\boldsymbol {\alpha })-q(\phi _i,\boldsymbol {\alpha }) = \alpha _{v_i}(q_{v_i}(\phi _{i+1},\boldsymbol {\alpha }) - q_{v_i}(\phi _i,\boldsymbol {\alpha }))$
.
Since
![]() $\phi _f =_{\mathcal {X}_f} \psi _f \in \Phi _2(r_f;\boldsymbol {k})$
by definition, we also have that
$\phi _f =_{\mathcal {X}_f} \psi _f \in \Phi _2(r_f;\boldsymbol {k})$
by definition, we also have that
Moreover, Claim 3.1.1 (iii) implies that
Note that Lemma 2.3 implies that there is some vertex weighting
![]() $\boldsymbol {\beta}$
close to
$\boldsymbol {\beta}$
close to
![]() $\boldsymbol {\alpha}_f$
such that
$\boldsymbol {\alpha}_f$
such that
![]() $(r_f,\psi_f,\boldsymbol {\beta})$
is optimal (but it could have zero parts). So ‘forwards symmetrisation’ has allowed us to pass from our original feasible solution
$(r_f,\psi_f,\boldsymbol {\beta})$
is optimal (but it could have zero parts). So ‘forwards symmetrisation’ has allowed us to pass from our original feasible solution
![]() $(r,\phi ,\boldsymbol {\alpha })$
to a new feasible solution
$(r,\phi ,\boldsymbol {\alpha })$
to a new feasible solution
![]() $(r_f,\psi _f,\boldsymbol {\alpha }_f)$
, which is very close to a
$(r_f,\psi _f,\boldsymbol {\alpha }_f)$
, which is very close to a
![]() $Q_2$
-optimal solution (both in terms of vertex weighting and colour pattern). But our eventual aim is to show that
$Q_2$
-optimal solution (both in terms of vertex weighting and colour pattern). But our eventual aim is to show that
![]() $(r,\phi ,\boldsymbol {\alpha })$
itself is close to this optimal solution. So we need to show that few ‘significant’ changes were made during the forwards symmetrisation procedure. To this end, our next step will be to follow the procedure backwards, using the partitions
$(r,\phi ,\boldsymbol {\alpha })$
itself is close to this optimal solution. So we need to show that few ‘significant’ changes were made during the forwards symmetrisation procedure. To this end, our next step will be to follow the procedure backwards, using the partitions
![]() $\mathcal {X}_i$
of
$\mathcal {X}_i$
of
![]() $[r]$
at each step, to form a new partition
$[r]$
at each step, to form a new partition
![]() $\mathcal {U}_i$
of
$\mathcal {U}_i$
of
![]() $[r]$
, which records how the solution at each step differs from
$[r]$
, which records how the solution at each step differs from
![]() $(r_f,\phi _f,\boldsymbol {\alpha }_f)$
.
$(r_f,\phi _f,\boldsymbol {\alpha }_f)$
.
It will be convenient to define some normalised versions
![]() $\hat {q},\hat {q}_x$
of
$\hat {q},\hat {q}_x$
of
![]() $q,q_x$
(for
$q,q_x$
(for
![]() $x \in [r]$
). Here we recall that
$x \in [r]$
). Here we recall that
![]() $\alpha _1=\ldots =\alpha _r=1/r$
which makes the normalisation simpler. Given
$\alpha _1=\ldots =\alpha _r=1/r$
which makes the normalisation simpler. Given
![]() $(r,\phi ,\boldsymbol {\boldsymbol {\alpha }}) \in \Phi _0(r;\boldsymbol {k})$
and
$(r,\phi ,\boldsymbol {\boldsymbol {\alpha }}) \in \Phi _0(r;\boldsymbol {k})$
and
![]() $P \subseteq [r]$
, write
$P \subseteq [r]$
, write
 $$ \begin{align*} &q(P,\phi) := 2\sum_{\substack{xy \in \binom{P}{2}:\\ \phi(xy) \neq \emptyset}}\alpha_x\alpha_y|\log\phi(xy)| \quad\text{and}\quad q_x(P,\phi) := \sum_{\substack{y \in P\setminus\{x\}:\\ \phi(xy) \neq \emptyset}}\alpha_y|\log\phi(xy)|,\quad\text{and}\\ &\hat{q}(P,\phi) := \left(\frac{r}{|P|}\right)^2 \cdot q(P,\phi) \quad\text{and}\quad \hat{q}_x(P,\phi) := \frac{r}{|P|} \cdot q_x(P,\phi), \end{align*} $$
$$ \begin{align*} &q(P,\phi) := 2\sum_{\substack{xy \in \binom{P}{2}:\\ \phi(xy) \neq \emptyset}}\alpha_x\alpha_y|\log\phi(xy)| \quad\text{and}\quad q_x(P,\phi) := \sum_{\substack{y \in P\setminus\{x\}:\\ \phi(xy) \neq \emptyset}}\alpha_y|\log\phi(xy)|,\quad\text{and}\\ &\hat{q}(P,\phi) := \left(\frac{r}{|P|}\right)^2 \cdot q(P,\phi) \quad\text{and}\quad \hat{q}_x(P,\phi) := \frac{r}{|P|} \cdot q_x(P,\phi), \end{align*} $$
so that
(if this inequality were not true, then setting
![]() $\beta _x:=1/|P|$
for
$\beta _x:=1/|P|$
for
![]() $x \in P$
and
$x \in P$
and
![]() $\beta _x:=0$
otherwise gives
$\beta _x:=0$
otherwise gives
![]() $q(\phi ,\boldsymbol {\beta })>Q(\boldsymbol {k})$
).
$q(\phi ,\boldsymbol {\beta })>Q(\boldsymbol {k})$
).
3.2 The backwards symmetrisation procedure
The forwards symmetrisation procedure ended with
![]() which is very close to optimal. We now want to go backwards through each forwards step i in turn, each time defining a partition of
which is very close to optimal. We now want to go backwards through each forwards step i in turn, each time defining a partition of
![]() $[r]$
into
$[r]$
into
![]() $r_f$
sets
$r_f$
sets
![]() $U^1,\ldots , U^{r_f}$
corresponding to the vertices of
$U^1,\ldots , U^{r_f}$
corresponding to the vertices of
![]() $\psi _f$
as well as a small exceptional set
$\psi _f$
as well as a small exceptional set
![]() $U^0$
. The desired conclusion is that, at the end of this process, the final sets
$U^0$
. The desired conclusion is that, at the end of this process, the final sets
![]() $U^1,\ldots ,U^{r_f}$
, that is, those corresponding to the original
$U^1,\ldots ,U^{r_f}$
, that is, those corresponding to the original
![]() $\phi $
we started with, have sizes roughly
$\phi $
we started with, have sizes roughly
![]() $\alpha _1'r,\ldots , \alpha ^{\prime }_{r_f} r$
for some vertex weighting
$\alpha _1'r,\ldots , \alpha ^{\prime }_{r_f} r$
for some vertex weighting
![]() ${\boldsymbol {\alpha }}'$
where
${\boldsymbol {\alpha }}'$
where
![]() (so
(so
![]() ${\boldsymbol {\alpha }}'$
could differ significantly from
${\boldsymbol {\alpha }}'$
could differ significantly from
![]() ${\boldsymbol {\alpha }}_f$
and could have zero parts, but is nevertheless optimal). Thus the exceptional set together with the ‘extra’ parts outside of the support of
${\boldsymbol {\alpha }}_f$
and could have zero parts, but is nevertheless optimal). Thus the exceptional set together with the ‘extra’ parts outside of the support of
![]() ${\boldsymbol {\alpha }}'$
are small. This will mean that between parts,
${\boldsymbol {\alpha }}'$
are small. This will mean that between parts,
![]() $\phi _i$
resembles
$\phi _i$
resembles
![]() $\psi _f$
throughout the process, but the sizes of the parts
$\psi _f$
throughout the process, but the sizes of the parts
![]() $U^1,\ldots ,U^{r_f}$
could change during the process. Thus
$U^1,\ldots ,U^{r_f}$
could change during the process. Thus
![]() $\phi $
resembles
$\phi $
resembles
![]() $\psi _f$
on the support of
$\psi _f$
on the support of
![]() ${\boldsymbol {\alpha }}'$
in the required sense.
${\boldsymbol {\alpha }}'$
in the required sense.
At each forwards step i, we modified the solution
![]() $\phi _{i-1}$
to obtain a new solution
$\phi _{i-1}$
to obtain a new solution
![]() $\phi _i$
by changing the attachment at a single vertex
$\phi _i$
by changing the attachment at a single vertex
![]() $x_i$
, so that q did not decrease. Now, in the corresponding backwards step, initially no vertex is exceptional. Then, we reconsider the attachment at
$x_i$
, so that q did not decrease. Now, in the corresponding backwards step, initially no vertex is exceptional. Then, we reconsider the attachment at
![]() $x_i$
: if it was small in
$x_i$
: if it was small in
![]() $\phi _i$
we remove it into the exceptional set
$\phi _i$
we remove it into the exceptional set
![]() $U^0$
. If any other vertex y also has small attachment in
$U^0$
. If any other vertex y also has small attachment in
![]() $\phi _i$
we also remove it to
$\phi _i$
we also remove it to
![]() $U^0$
. If
$U^0$
. If
![]() $x_i$
was not removed, we assign it to the part
$x_i$
was not removed, we assign it to the part
![]() $U^j$
where
$U^j$
where
![]() $x_i$
looks most like a
$x_i$
looks most like a
![]() $\psi _f$
-clone of j in
$\psi _f$
-clone of j in
![]() $\phi _i$
, and similarly assign vertices which are no longer exceptional.
$\phi _i$
, and similarly assign vertices which are no longer exceptional.
The extension property guarantees that any vertex which was not moved into the exceptional set, and therefore has large attachment, looks similar to a
![]() $\psi_f$
-clone. There cannot be too many exceptional vertices since they all have small attachment, whereas q is large.
$\psi_f$
-clone. There cannot be too many exceptional vertices since they all have small attachment, whereas q is large.
We now formally describe the i-th backwards step. Define
![]() $\mathcal {U}_{f} := \{ U^0_{f},\ldots ,U^{r_f}_{f} \}$
by setting
$\mathcal {U}_{f} := \{ U^0_{f},\ldots ,U^{r_f}_{f} \}$
by setting
![]() $U^j_{f} := X_{f,j}$
for all
$U^j_{f} := X_{f,j}$
for all
![]() $j \in [r_f]$
and
$j \in [r_f]$
and
![]() $U^0_{f} := \emptyset $
. For each
$U^0_{f} := \emptyset $
. For each
![]() $i=f-1,\ldots ,0$
, define
$i=f-1,\ldots ,0$
, define
![]() $U_i$
and
$U_i$
and
![]() $\mathcal {U}_{i} := \{ U^0_{i},\ldots ,U^{r_f}_{i} \}$
inductively as follows. Initially,
$\mathcal {U}_{i} := \{ U^0_{i},\ldots ,U^{r_f}_{i} \}$
inductively as follows. Initially,
![]() $U_i=[r]$
and
$U_i=[r]$
and
![]() $U^0_i=\emptyset $
. If
$U^0_i=\emptyset $
. If
![]() $\hat {q}_{x_i}(U_{i},\phi _{i}) < Q(\boldsymbol {k})-\sqrt {\varepsilon }$
, move
$\hat {q}_{x_i}(U_{i},\phi _{i}) < Q(\boldsymbol {k})-\sqrt {\varepsilon }$
, move
![]() $x_i$
from
$x_i$
from
![]() $U_i$
into
$U_i$
into
![]() $U^0_{i}$
. Next, if there is
$U^0_{i}$
. Next, if there is
![]() $y \in U_{i}$
such that
$y \in U_{i}$
such that
![]() $\hat {q}_y(U_{i},\phi _{i})<Q(\boldsymbol {k})-\sqrt {\varepsilon }$
, move y into
$\hat {q}_y(U_{i},\phi _{i})<Q(\boldsymbol {k})-\sqrt {\varepsilon }$
, move y into
![]() $U^0_{i}$
(we also include the special vertex
$U^0_{i}$
(we also include the special vertex
![]() $x_i$
here, if at some point its attachment becomes too small). Update
$x_i$
here, if at some point its attachment becomes too small). Update
![]() $U_{i}$
and repeat until there are no such vertices left in
$U_{i}$
and repeat until there are no such vertices left in
![]() $U_{i}$
.
$U_{i}$
.
Next, for each
![]() $j \in [r_f]$
, let
$j \in [r_f]$
, let
![]() $U_i^j$
be the restriction of
$U_i^j$
be the restriction of
![]() $U_{i+1}^j$
to
$U_{i+1}^j$
to
![]() $U_i\setminus \{x_i\}$
. For each
$U_i\setminus \{x_i\}$
. For each
![]() $z \in B_i := (U_{i+1}^0 \cup \{x_i\}) \cap U_i$
, add z to the part
$z \in B_i := (U_{i+1}^0 \cup \{x_i\}) \cap U_i$
, add z to the part
![]() $U_i^j$
such that z looks most like a
$U_i^j$
such that z looks most like a
![]() $\psi _f$
-clone of j under
$\psi _f$
-clone of j under
![]() $\phi _i|_{U_i}$
; that is, choose the index
$\phi _i|_{U_i}$
; that is, choose the index
![]() $j\in [r_f]$
such that
$j\in [r_f]$
such that
 $$\begin{align*}\left(\kern1.5pt\sum_{j' \in [r_f]\setminus \{j\}}|\{y \in U_i^{j'}: \phi_i(yz) \neq \psi_f(j'j)\}|\right)+|\{y \in U_i^j: |\phi_i(yz)| \geq 2\}| \end{align*}$$
$$\begin{align*}\left(\kern1.5pt\sum_{j' \in [r_f]\setminus \{j\}}|\{y \in U_i^{j'}: \phi_i(yz) \neq \psi_f(j'j)\}|\right)+|\{y \in U_i^j: |\phi_i(yz)| \geq 2\}| \end{align*}$$
is minimal (breaking ties arbitrarily). This completes backwards step i; now move on to backwards step
![]() $i-1$
.
$i-1$
.
We show that the exceptional set
![]() $U_i^0$
is always small.
$U_i^0$
is always small.
Claim 3.1.2. For all
![]() $i=f,\ldots ,0$
, we have
$i=f,\ldots ,0$
, we have
![]() $|U^0_{i}| \leq 2\sqrt {\varepsilon }r$
.
$|U^0_{i}| \leq 2\sqrt {\varepsilon }r$
.
Proof of Claim.
Let
![]() $y_1,\ldots ,y_\ell $
be the vertices which are moved into
$y_1,\ldots ,y_\ell $
be the vertices which are moved into
![]() $U_{i}^0$
at step i, in this order. So
$U_{i}^0$
at step i, in this order. So
![]() $|U_{i}^0| = \ell $
.
$|U_{i}^0| = \ell $
.
Given distinct
![]() $x,y \in [r]$
, write
$x,y \in [r]$
, write
![]() $d_i(xy) := \log |\phi _i(xy)|$
if
$d_i(xy) := \log |\phi _i(xy)|$
if
![]() $\phi _i(xy)\neq \emptyset $
and
$\phi _i(xy)\neq \emptyset $
and
![]() $d_i(xy):=0$
otherwise. For
$d_i(xy):=0$
otherwise. For
![]() $1 \leq k \leq \ell $
, the vertex
$1 \leq k \leq \ell $
, the vertex
![]() $y_k$
is moved to
$y_k$
is moved to
![]() $U^0_{i}$
due to
$U^0_{i}$
due to
![]() $\hat {q}_{y_k}(U_{i,k},\phi _{i}) < Q(\boldsymbol {k})-\sqrt {\varepsilon }$
, where
$\hat {q}_{y_k}(U_{i,k},\phi _{i}) < Q(\boldsymbol {k})-\sqrt {\varepsilon }$
, where
![]() $U_{i,k} := [r]\setminus \{y_1,\ldots ,y_{k-1}\}$
. Note that
$U_{i,k} := [r]\setminus \{y_1,\ldots ,y_{k-1}\}$
. Note that
![]() $\hat {q}_{y_k}(U_{i,k},\phi _i)|U_{i,k}|=\sum _{x \in U_{i,k+1}}d_i(xy_k)$
. We have
$\hat {q}_{y_k}(U_{i,k},\phi _i)|U_{i,k}|=\sum _{x \in U_{i,k+1}}d_i(xy_k)$
. We have
 $$ \begin{align*} Q(\boldsymbol{k})\frac{(r-\ell)^2}{2} &\stackrel{({\scriptstyle 3.5})}{\geq} \hat{q}(U_i,\phi_i)\frac{|U_i|^2}{2} = \sum_{xy \in \binom{U_i}{2}}d_i(xy) = \sum_{xy \in \binom{[r]}{2}}d_i(xy) - \sum_{k \in [\ell]}\hat{q}_{y_k}(U_{i,k},\phi_i)|U_{i,k}|\\ &\ \ \geq \sum_{xy \in \binom{[r]}{2}}d_i(xy) - \sum_{k \in [\ell]}(Q(\boldsymbol{k})-\sqrt{\varepsilon})(r-k+1)\\ &\ \ = q(\phi_i,{\boldsymbol{\alpha}})\frac{r^2}{2} - (Q(\boldsymbol{k})-\sqrt{\varepsilon})\left(r\ell - \binom{\ell}{2}\right)\\ &\stackrel{({\scriptstyle 3.4})}{\geq} (Q(\boldsymbol{k})-2{\varepsilon})\frac{r^2}{2}- (Q(\boldsymbol{k})-\sqrt{\varepsilon})\left((r-\ell)\ell + \binom{\ell+1}{2}\right). \end{align*} $$
$$ \begin{align*} Q(\boldsymbol{k})\frac{(r-\ell)^2}{2} &\stackrel{({\scriptstyle 3.5})}{\geq} \hat{q}(U_i,\phi_i)\frac{|U_i|^2}{2} = \sum_{xy \in \binom{U_i}{2}}d_i(xy) = \sum_{xy \in \binom{[r]}{2}}d_i(xy) - \sum_{k \in [\ell]}\hat{q}_{y_k}(U_{i,k},\phi_i)|U_{i,k}|\\ &\ \ \geq \sum_{xy \in \binom{[r]}{2}}d_i(xy) - \sum_{k \in [\ell]}(Q(\boldsymbol{k})-\sqrt{\varepsilon})(r-k+1)\\ &\ \ = q(\phi_i,{\boldsymbol{\alpha}})\frac{r^2}{2} - (Q(\boldsymbol{k})-\sqrt{\varepsilon})\left(r\ell - \binom{\ell}{2}\right)\\ &\stackrel{({\scriptstyle 3.4})}{\geq} (Q(\boldsymbol{k})-2{\varepsilon})\frac{r^2}{2}- (Q(\boldsymbol{k})-\sqrt{\varepsilon})\left((r-\ell)\ell + \binom{\ell+1}{2}\right). \end{align*} $$
Rearranging, we have
![]() $\sqrt {\varepsilon }((r-\ell )\ell +\binom {\ell +1}{2}) \leq {\varepsilon } r^2 +Q(\boldsymbol {k})\ell /2 < 3\varepsilon r^2/2$
. But if
$\sqrt {\varepsilon }((r-\ell )\ell +\binom {\ell +1}{2}) \leq {\varepsilon } r^2 +Q(\boldsymbol {k})\ell /2 < 3\varepsilon r^2/2$
. But if
![]() $2\sqrt {\varepsilon }r \leq \ell \leq r/2$
, we have
$2\sqrt {\varepsilon }r \leq \ell \leq r/2$
, we have
![]() $\sqrt {\varepsilon }(r-\ell )\ell \geq \sqrt {\varepsilon }(1-2\sqrt {\varepsilon })\cdot 2\sqrt {\varepsilon }r^2> 3{\varepsilon } r^2/2$
. Thus, at the moment when
$\sqrt {\varepsilon }(r-\ell )\ell \geq \sqrt {\varepsilon }(1-2\sqrt {\varepsilon })\cdot 2\sqrt {\varepsilon }r^2> 3{\varepsilon } r^2/2$
. Thus, at the moment when
![]() $2\sqrt {\varepsilon }r$
vertices are added to
$2\sqrt {\varepsilon }r$
vertices are added to
![]() $U^0_i$
, we obtain a contradiction.
$U^0_i$
, we obtain a contradiction.
Every
![]() $x \in U_i$
satisfies
$x \in U_i$
satisfies
![]() $\hat {q}_x(U_i,\phi _i) \geq Q(\boldsymbol {k})-\sqrt {\varepsilon }$
. Let
$\hat {q}_x(U_i,\phi _i) \geq Q(\boldsymbol {k})-\sqrt {\varepsilon }$
. Let
![]() $n := |U_i|$
and let
$n := |U_i|$
and let
![]() $G_i$
be the complete graph with vertex set
$G_i$
be the complete graph with vertex set
![]() $U_i$
whose edges are coloured red (for missing), blue (for extra) or green (for perfect) as follows. For each
$U_i$
whose edges are coloured red (for missing), blue (for extra) or green (for perfect) as follows. For each
![]() $x \in U_i$
, let
$x \in U_i$
, let
![]() $j_x \in [r_f]$
be such that
$j_x \in [r_f]$
be such that
![]() $x \in U^{j_x}_i$
. For each
$x \in U^{j_x}_i$
. For each
![]() $xy \in E(G_i)$
,
$xy \in E(G_i)$
,
-
•
 $xy$
is red if
$xy$
is red if
 $j_x \neq j_y$
and
$j_x \neq j_y$
and
 $\phi _i(xy) \subsetneq \psi _f(j_xj_y)$
, so there are missing colours.
$\phi _i(xy) \subsetneq \psi _f(j_xj_y)$
, so there are missing colours. -
•
 $xy$
is blue if either
$xy$
is blue if either
 $j_x \neq j_y$
and
$j_x \neq j_y$
and
 $\phi _i(xy) \setminus \psi _f(j_xj_y) \neq \emptyset $
, or
$\phi _i(xy) \setminus \psi _f(j_xj_y) \neq \emptyset $
, or
 $j_x=j_y$
and
$j_x=j_y$
and
 $\phi _i(xy) \not \subseteq \{1\}$
, so there are extra colours.
$\phi _i(xy) \not \subseteq \{1\}$
, so there are extra colours. -
•
 $xy$
is green otherwise.
$xy$
is green otherwise.
Recall that we defined
by Claim 3.1.2. The colouring of
![]() $G_i-B_i$
depends only on the previous partition
$G_i-B_i$
depends only on the previous partition
![]() $\mathcal {U}_{i+1}$
and the colour pattern
$\mathcal {U}_{i+1}$
and the colour pattern
![]() $\phi _{i+1}$
since every vertex in
$\phi _{i+1}$
since every vertex in
![]() $U_i \setminus B_i$
lies in
$U_i \setminus B_i$
lies in
![]() $U^j_{i+1} \cap U^j_i$
for some
$U^j_{i+1} \cap U^j_i$
for some
![]() $j \in [r_f]$
, and the colour patterns
$j \in [r_f]$
, and the colour patterns
![]() $\phi _i$
and
$\phi _i$
and
![]() $\phi _{i+1}$
only differ at
$\phi _{i+1}$
only differ at
![]() $x_i$
. Also,
$x_i$
. Also,
Write
![]() ${\boldsymbol {\beta }}_i := (|U_i^1|,\ldots ,|U_i^{r_f}|)/|U_i| \in \Delta ^{r_f}$
.
${\boldsymbol {\beta }}_i := (|U_i^1|,\ldots ,|U_i^{r_f}|)/|U_i| \in \Delta ^{r_f}$
.
Claim 3.1.3. For all
![]() $i=f,\ldots ,0$
,
$i=f,\ldots ,0$
,
![]() $G_i$
has no blue edges.
$G_i$
has no blue edges.
Proof of Claim.
We prove this by backwards induction for
![]() $i=f,\ldots ,0$
. The claim is true for
$i=f,\ldots ,0$
. The claim is true for
![]() $i=f$
, as every edge in
$i=f$
, as every edge in
![]() $G_f$
is green. Suppose it is true for all backwards steps
$G_f$
is green. Suppose it is true for all backwards steps
![]() $f,\ldots ,i+1$
. The induction hypothesis and the fact that
$f,\ldots ,i+1$
. The induction hypothesis and the fact that
![]() $\phi _i$
differs from
$\phi _i$
differs from
![]() $\phi _{i+1}$
only at
$\phi _{i+1}$
only at
![]() $x_i$
implies that only vertices in
$x_i$
implies that only vertices in
![]() $B_i$
can be incident with blue edges in
$B_i$
can be incident with blue edges in
![]() $G_i$
.
$G_i$
.
First we show that
![]() $G_i$
contains few red edges and
$G_i$
contains few red edges and
![]() ${\boldsymbol {\beta }}_i$
is close to an optimal vertex weighting. Indeed,
${\boldsymbol {\beta }}_i$
is close to an optimal vertex weighting. Indeed,
 $$ \begin{align*} Q(\boldsymbol{k})-\sqrt{\varepsilon} &\leq \sum_{x \in U_i}\hat{q}_x(U_i,\phi_i)/|U_i| = \hat{q}(U_i,\phi_i)\\&\leq\left(\frac{r}{|U_i|}\right)^2\left(\frac{2}{r^2}\sum_{\substack{xy \in E(G_i) \\ \psi_f(j_xj_y) \neq \emptyset}}\log|\psi_f(j_xj_y)| - \frac{2}{r^2}\sum_{xy \text{ red}}\log\left(\frac{|\psi_f(j_xj_y)|}{|\psi_f(j_xj_y)|-1}\right)+\frac{2\log s}{r}|B_i|\right)\\&\leq q(\psi_f,{\boldsymbol{\beta}}_i)-2\log\left(\frac{s}{s-1}\right)\frac{e_{\mathrm{red}}(G_i)}{n^2} + \frac{2r\log s|B_i|}{n^2}\\&\leq Q(\boldsymbol{k})-2\log\left(\frac{s}{s-1}\right)\frac{e_{\mathrm{red}}(G_i)}{n^2} + 7\sqrt{\varepsilon}\log s. \end{align*} $$
$$ \begin{align*} Q(\boldsymbol{k})-\sqrt{\varepsilon} &\leq \sum_{x \in U_i}\hat{q}_x(U_i,\phi_i)/|U_i| = \hat{q}(U_i,\phi_i)\\&\leq\left(\frac{r}{|U_i|}\right)^2\left(\frac{2}{r^2}\sum_{\substack{xy \in E(G_i) \\ \psi_f(j_xj_y) \neq \emptyset}}\log|\psi_f(j_xj_y)| - \frac{2}{r^2}\sum_{xy \text{ red}}\log\left(\frac{|\psi_f(j_xj_y)|}{|\psi_f(j_xj_y)|-1}\right)+\frac{2\log s}{r}|B_i|\right)\\&\leq q(\psi_f,{\boldsymbol{\beta}}_i)-2\log\left(\frac{s}{s-1}\right)\frac{e_{\mathrm{red}}(G_i)}{n^2} + \frac{2r\log s|B_i|}{n^2}\\&\leq Q(\boldsymbol{k})-2\log\left(\frac{s}{s-1}\right)\frac{e_{\mathrm{red}}(G_i)}{n^2} + 7\sqrt{\varepsilon}\log s. \end{align*} $$
Thus
and additionally, from the penultimate inequality,
![]() $q(\psi _f,{\boldsymbol {\beta }}_i) \geq Q(\boldsymbol {k}) - {\varepsilon }^{1/4}$
. Lemma 2.3 applied with parameters
$q(\psi _f,{\boldsymbol {\beta }}_i) \geq Q(\boldsymbol {k}) - {\varepsilon }^{1/4}$
. Lemma 2.3 applied with parameters
![]() $s,\boldsymbol {k},\gamma $
implies that there exists
$s,\boldsymbol {k},\gamma $
implies that there exists
![]() ${\boldsymbol {\alpha }}^{\prime }_i \in \Delta ^{r_f}$
such that
${\boldsymbol {\alpha }}^{\prime }_i \in \Delta ^{r_f}$
such that
![]() and
and
Without loss of generality, suppose the nonzero entries of
![]() ${\boldsymbol {\alpha }}^{\prime }_i$
form an initial segment of length
${\boldsymbol {\alpha }}^{\prime }_i$
form an initial segment of length
![]() $\tilde {r}_i$
, and let
$\tilde {r}_i$
, and let
![]() $\tilde {{\boldsymbol {\alpha }}}_i$
be this initial segment. Let
$\tilde {{\boldsymbol {\alpha }}}_i$
be this initial segment. Let
![]() $\tilde {\phi }_i := \psi _f|_{\binom {[\tilde {r}_i]}{2}}$
. Then
$\tilde {\phi }_i := \psi _f|_{\binom {[\tilde {r}_i]}{2}}$
. Then
![]() . We claim that
. We claim that
Indeed, if
![]() $j \in [\tilde {r}_i]$
, then Proposition 2.1 implies that
$j \in [\tilde {r}_i]$
, then Proposition 2.1 implies that
![]() $q_{j}(\psi _f,{\boldsymbol {\alpha }}_i')=q_j(\tilde {\phi }_i,\tilde {{\boldsymbol {\alpha }}}_i) = Q(\boldsymbol {k})$
. If
$q_{j}(\psi _f,{\boldsymbol {\alpha }}_i')=q_j(\tilde {\phi }_i,\tilde {{\boldsymbol {\alpha }}}_i) = Q(\boldsymbol {k})$
. If
![]() $\tilde {r}_i < j \leq r_f$
, then Proposition 2.6 implies the bound
$\tilde {r}_i < j \leq r_f$
, then Proposition 2.6 implies the bound
![]() $q_{j}(\psi _f,{\boldsymbol {\alpha }}^{\prime }_i)={\mathop {\mathrm {ext}}}(\psi _f|_{\binom {[\tilde {r}_i] \cup \{j\}}{2}},\tilde {{\boldsymbol {\alpha }}}_i) \leq Q(\boldsymbol {k})$
.
$q_{j}(\psi _f,{\boldsymbol {\alpha }}^{\prime }_i)={\mathop {\mathrm {ext}}}(\psi _f|_{\binom {[\tilde {r}_i] \cup \{j\}}{2}},\tilde {{\boldsymbol {\alpha }}}_i) \leq Q(\boldsymbol {k})$
.
Next we claim that every
![]() $z \in B_i$
is
$z \in B_i$
is
![]() $\delta $
-close under
$\delta $
-close under
![]() $\phi _i|_{\binom {U_i}{2}}$
to being a
$\phi _i|_{\binom {U_i}{2}}$
to being a
![]() $\psi _f$
-clone of some
$\psi _f$
-clone of some
![]() $j \in [\tilde {r}_i] \subseteq [r_f]$
, which will follow from an application of Lemma 2.12. Suppose not. To apply the lemma, let
$j \in [\tilde {r}_i] \subseteq [r_f]$
, which will follow from an application of Lemma 2.12. Suppose not. To apply the lemma, let
![]() $U'_i := \bigcup_{j \in [\tilde{r}_i]}U^j_i$
and
$U'_i := \bigcup_{j \in [\tilde{r}_i]}U^j_i$
and
![]() $U^z_i := \{z\} \cup (U_i' \setminus B_i)$
and
$U^z_i := \{z\} \cup (U_i' \setminus B_i)$
and
![]() $t:=|U_i' \setminus B_i|$
. Let
$t:=|U_i' \setminus B_i|$
. Let
![]() $\tilde {{\boldsymbol {\beta }}}_i := (|U_i^1\setminus B_i|,\ldots ,|U_i^{\tilde {r}_i}\setminus B_i|)/|U_i' \setminus B_i|$
, so
$\tilde {{\boldsymbol {\beta }}}_i := (|U_i^1\setminus B_i|,\ldots ,|U_i^{\tilde {r}_i}\setminus B_i|)/|U_i' \setminus B_i|$
, so
![]() $\|\tilde {{\boldsymbol {\beta }}}_i-\tilde {{\boldsymbol {\alpha }}}_i\|_1 \leq 2\gamma $
by (3.8). Let
$\|\tilde {{\boldsymbol {\beta }}}_i-\tilde {{\boldsymbol {\alpha }}}_i\|_1 \leq 2\gamma $
by (3.8). Let
![]() $\phi ': \binom {U^z_i}{2} \to 2^{[s]}$
be obtained from
$\phi ': \binom {U^z_i}{2} \to 2^{[s]}$
be obtained from
![]() $\phi _i$
as follows. Let
$\phi _i$
as follows. Let
![]() $\phi '(zy):=\phi _i(zy)$
for all
$\phi '(zy):=\phi _i(zy)$
for all
![]() $y \in U_i^z\setminus \{z\}$
, and let
$y \in U_i^z\setminus \{z\}$
, and let
![]() $\phi '$
agree with
$\phi '$
agree with
![]() $\phi _f$
elsewhere, that is,
$\phi _f$
elsewhere, that is,
![]() $\phi '(xy):=\psi _f(j_xj_y)$
whenever
$\phi '(xy):=\psi _f(j_xj_y)$
whenever
![]() $j_x \neq j_y$
, and
$j_x \neq j_y$
, and
![]() $\phi '(xy):=\emptyset $
if
$\phi '(xy):=\emptyset $
if
![]() $j_x=j_y$
. Let
$j_x=j_y$
. Let
![]() ${\boldsymbol {\alpha }}_t$
be the length-t vector which is identically
${\boldsymbol {\alpha }}_t$
be the length-t vector which is identically
![]() $1/t$
. We have
$1/t$
. We have
We can apply Lemma 2.12 with
![]() $(\tilde {r}_i,\tilde {\phi }_i,\tilde {{\boldsymbol {\alpha }}}_i),(U^j_i \setminus B_i: j \in [\tilde{r}_i])$
,
$(\tilde {r}_i,\tilde {\phi }_i,\tilde {{\boldsymbol {\alpha }}}_i),(U^j_i \setminus B_i: j \in [\tilde{r}_i])$
,
![]() ${\boldsymbol {\alpha }}_t,\tilde {{\boldsymbol {\beta }}_i},z$
playing the roles of
${\boldsymbol {\alpha }}_t,\tilde {{\boldsymbol {\beta }}_i},z$
playing the roles of
![]() $(r^*,\phi ^*,{\boldsymbol {\alpha }}^*),\mathcal {V},{\boldsymbol {\alpha }},{\boldsymbol {\beta }},r+1$
to see that, writing L for the set of sets
$(r^*,\phi ^*,{\boldsymbol {\alpha }}^*),\mathcal {V},{\boldsymbol {\alpha }},{\boldsymbol {\beta }},r+1$
to see that, writing L for the set of sets
![]() $\{y_1,\ldots ,y_{k_1-1}\} \in \binom {U_i'\setminus B_i}{k_1-1}$
(i.e.
$\{y_1,\ldots ,y_{k_1-1}\} \in \binom {U_i'\setminus B_i}{k_1-1}$
(i.e.
![]() $(k_1-1)$
-subsets of vertices of
$(k_1-1)$
-subsets of vertices of
![]() $G_i[U_i']-B_i$
) such that
$G_i[U_i']-B_i$
) such that
![]() $(\phi ')^{-1}(c)[\{z,y_1,\ldots ,y_{k_1-1}\}] \supseteq K_{k_c}$
for some
$(\phi ')^{-1}(c)[\{z,y_1,\ldots ,y_{k_1-1}\}] \supseteq K_{k_c}$
for some
![]() $c \in [s]$
, we have
$c \in [s]$
, we have
![]() $|L| \geq \eta n^{k_1-1}$
.
$|L| \geq \eta n^{k_1-1}$
.
For every
![]() $\{y_1,\ldots ,y_{k_1-1}\} \in L$
, there are
$\{y_1,\ldots ,y_{k_1-1}\} \in L$
, there are
![]() $\ell ,\ell ' \in [k_1-1]$
such that
$\ell ,\ell ' \in [k_1-1]$
such that
![]() $y_\ell y_{\ell '}$
is red (recalling that these edges are either red or green), otherwise
$y_\ell y_{\ell '}$
is red (recalling that these edges are either red or green), otherwise
![]() $\phi _i$
is identical to
$\phi _i$
is identical to
![]() $\phi '$
on all pairs of these vertices, and thus
$\phi '$
on all pairs of these vertices, and thus
![]() $\phi_i^{-1}(c)$
contains a copy of
$\phi_i^{-1}(c)$
contains a copy of
![]() $K_{k_c}$
for some c. Each pair appears in at most
$K_{k_c}$
for some c. Each pair appears in at most
![]() $n^{k_1-3}$
sets in L, so the number of red edges in
$n^{k_1-3}$
sets in L, so the number of red edges in
![]() $G_i$
is at least
$G_i$
is at least
![]() $ \eta n^{k_1-1}/n^{k_1-3} = \eta n^2> 2{\varepsilon }^{1/3} n^2 $
, a contradiction to (3.7). Thus z is
$ \eta n^{k_1-1}/n^{k_1-3} = \eta n^2> 2{\varepsilon }^{1/3} n^2 $
, a contradiction to (3.7). Thus z is
![]() $\delta $
-close to being a
$\delta $
-close to being a
![]() $\psi _f$
-clone of some
$\psi _f$
-clone of some
![]() $j \in [\tilde {r}_i]$
under
$j \in [\tilde {r}_i]$
under
![]() $\phi _i|_{\binom {U_i^z}{2}}$
.
$\phi _i|_{\binom {U_i^z}{2}}$
.
During backwards symmetrisation we added z to the part
![]() $U_i^{j_{z}}$
such that z was closest to a
$U_i^{j_{z}}$
such that z was closest to a
![]() $\psi _f$
-clone of
$\psi _f$
-clone of
![]() $j_{z}$
under
$j_{z}$
under
![]() $\phi _i$
, so
$\phi _i$
, so
 $$ \begin{align*} d_{\mathrm{red}}(z)+d_{\mathrm{blue}}(z) &\leq \sum_{j' \in [r_f]\setminus\{j_z\}}|\{y \in U^{j'}_i: \phi_i(zy) \neq \psi_f(j_zj_y)\}|+|\{y \in U^{j_z}_i: |\phi_i(zy)| \geq 2\}|\\ &\leq \sum_{j' \in [r_f]\setminus\{j\}}|\{y \in U^{j'}_i: \phi_i(zy) \neq \psi_f(jj_y)\}|+|\{y \in U^{j}_i: |\phi_i(zy)| \geq 2\}|\\ &\leq \delta t + |B_i| \leq 2\delta n. \end{align*} $$
$$ \begin{align*} d_{\mathrm{red}}(z)+d_{\mathrm{blue}}(z) &\leq \sum_{j' \in [r_f]\setminus\{j_z\}}|\{y \in U^{j'}_i: \phi_i(zy) \neq \psi_f(j_zj_y)\}|+|\{y \in U^{j_z}_i: |\phi_i(zy)| \geq 2\}|\\ &\leq \sum_{j' \in [r_f]\setminus\{j\}}|\{y \in U^{j'}_i: \phi_i(zy) \neq \psi_f(jj_y)\}|+|\{y \in U^{j}_i: |\phi_i(zy)| \geq 2\}|\\ &\leq \delta t + |B_i| \leq 2\delta n. \end{align*} $$
Therefore the green degree of z in
![]() $G_i$
is
$G_i$
is
Thus
 $$\begin{align*} \nonumber Q(\boldsymbol{k})-\sqrt{\varepsilon} &\leq \hat{q}_z(U_i,\phi_i)\leq \frac{r}{|U_i|}\left( \frac{1}{r}\sum_{\substack{y \in U_i \\ \psi_f(j_zj_y) \neq \emptyset}}\log|\psi_f(j_zj_y)| + \frac{\log s}{r}(n-1-d_\mathrm{green}(z))\right)\\\nonumber &\leq q_{j_z}(\psi_f,{\boldsymbol{\beta}}_i) + 3\delta\log s \leq q_{j_z}(\psi_f,{\boldsymbol{\alpha}}^{\prime}_i) + 2(\log s)\|{\boldsymbol{\alpha}}^{\prime}_i-{\boldsymbol{\beta}}_i\|_1 + 3\delta\log s\\\nonumber &\kern-5pt\stackrel{({\scriptstyle 3.8})}{\leq} q_{j_z}(\psi_f,{\boldsymbol{\alpha}}^{\prime}_i) + 4\delta\log s \end{align*}$$
$$\begin{align*} \nonumber Q(\boldsymbol{k})-\sqrt{\varepsilon} &\leq \hat{q}_z(U_i,\phi_i)\leq \frac{r}{|U_i|}\left( \frac{1}{r}\sum_{\substack{y \in U_i \\ \psi_f(j_zj_y) \neq \emptyset}}\log|\psi_f(j_zj_y)| + \frac{\log s}{r}(n-1-d_\mathrm{green}(z))\right)\\\nonumber &\leq q_{j_z}(\psi_f,{\boldsymbol{\beta}}_i) + 3\delta\log s \leq q_{j_z}(\psi_f,{\boldsymbol{\alpha}}^{\prime}_i) + 2(\log s)\|{\boldsymbol{\alpha}}^{\prime}_i-{\boldsymbol{\beta}}_i\|_1 + 3\delta\log s\\\nonumber &\kern-5pt\stackrel{({\scriptstyle 3.8})}{\leq} q_{j_z}(\psi_f,{\boldsymbol{\alpha}}^{\prime}_i) + 4\delta\log s \end{align*}$$
and therefore
(By the optimality of
![]() $(r_f,\psi _f,{\boldsymbol {\alpha }}_i')$
this is automatically true for nonzero parts.) Next, we show the number of red edges incident to a vertex x in
$(r_f,\psi _f,{\boldsymbol {\alpha }}_i')$
this is automatically true for nonzero parts.) Next, we show the number of red edges incident to a vertex x in
![]() $U_i\setminus B_i$
is
$U_i\setminus B_i$
is
Indeed, the second part follows from the first since every edge incident to x in
![]() $G_i-B_i$
is either green or red. To prove the first part, let
$G_i-B_i$
is either green or red. To prove the first part, let
![]() $x \in U_i\setminus B_i$
. Since x can have blue neighbours only in
$x \in U_i\setminus B_i$
. Since x can have blue neighbours only in
![]() $B_i$
, we have
$B_i$
, we have
 $$ \begin{align} \nonumber Q(\boldsymbol{k})-\sqrt{\varepsilon} &\leq \hat{q}_x(U_i,\phi_i)\\\nonumber &\leq \frac{r}{|U_i|}\left( \frac{1}{r}\sum_{\substack{y \in U_i \setminus B_i \\ \psi_f(j_xj_y) \neq \emptyset}}\log|\psi_f(j_xj_y)| - \frac{1}{r}\sum_{y \in N_\mathrm{ red}(x)}\log\left(\frac{|\psi_f(j_xj_y)|}{|\psi_f(j_xj_y)|-1}\right) + \frac{\log s}{r}|B_i|\right)\\\nonumber &\leq q_{j_x}(\psi_f,{\boldsymbol{\beta}}_i) - \log\left(\frac{s}{s-1}\right)\frac{d_{\mathrm{red}}(x)}{n} + 4\log s\sqrt{\varepsilon}\\\nonumber &\leq q_{j_x}(\psi_f,{\boldsymbol{\alpha}}^{\prime}_i) - \frac{d_{\mathrm{red}}(x)}{sn}+3\gamma\log s\\ &\leq Q(\boldsymbol{k}) - \frac{d_{\mathrm{red}}(x)}{sn}+3\gamma\log s, \end{align} $$
$$ \begin{align} \nonumber Q(\boldsymbol{k})-\sqrt{\varepsilon} &\leq \hat{q}_x(U_i,\phi_i)\\\nonumber &\leq \frac{r}{|U_i|}\left( \frac{1}{r}\sum_{\substack{y \in U_i \setminus B_i \\ \psi_f(j_xj_y) \neq \emptyset}}\log|\psi_f(j_xj_y)| - \frac{1}{r}\sum_{y \in N_\mathrm{ red}(x)}\log\left(\frac{|\psi_f(j_xj_y)|}{|\psi_f(j_xj_y)|-1}\right) + \frac{\log s}{r}|B_i|\right)\\\nonumber &\leq q_{j_x}(\psi_f,{\boldsymbol{\beta}}_i) - \log\left(\frac{s}{s-1}\right)\frac{d_{\mathrm{red}}(x)}{n} + 4\log s\sqrt{\varepsilon}\\\nonumber &\leq q_{j_x}(\psi_f,{\boldsymbol{\alpha}}^{\prime}_i) - \frac{d_{\mathrm{red}}(x)}{sn}+3\gamma\log s\\ &\leq Q(\boldsymbol{k}) - \frac{d_{\mathrm{red}}(x)}{sn}+3\gamma\log s, \end{align} $$
where the final inequality follows from (3.9). Therefore,
![]() $d_{{\mathrm {red}}}(x) \leq \sqrt {\gamma }n$
, as required, and the penultimate inequality implies that
$d_{{\mathrm {red}}}(x) \leq \sqrt {\gamma }n$
, as required, and the penultimate inequality implies that
![]() $q_{j_x}(\psi _f,{\boldsymbol {\alpha }}^{\prime }_i) \geq Q(\boldsymbol {k})-\gamma ^{1/3}$
.
$q_{j_x}(\psi _f,{\boldsymbol {\alpha }}^{\prime }_i) \geq Q(\boldsymbol {k})-\gamma ^{1/3}$
.
Combined with (3.11), we have shown that
![]() $q_{j_y}(\psi _f,{\boldsymbol {\alpha }}^{\prime }_i) \geq Q(\boldsymbol {k})-\sqrt {\delta }$
for all
$q_{j_y}(\psi _f,{\boldsymbol {\alpha }}^{\prime }_i) \geq Q(\boldsymbol {k})-\sqrt {\delta }$
for all
![]() $y \in U_i$
. We will now show that this means that
$y \in U_i$
. We will now show that this means that
![]() ${\boldsymbol {\beta }}_i$
has the same support as
${\boldsymbol {\beta }}_i$
has the same support as
![]() ${\boldsymbol {\alpha }}^{\prime }_i$
; that is, either
${\boldsymbol {\alpha }}^{\prime }_i$
; that is, either
![]() $\tilde {r}_i=r_f$
, or for all
$\tilde {r}_i=r_f$
, or for all
![]() $\tilde {r}_i<j \leq r_f$
, we have
$\tilde {r}_i<j \leq r_f$
, we have
![]() $\beta _{i,j}=0$
. Suppose not; then without loss of generality there is some
$\beta _{i,j}=0$
. Suppose not; then without loss of generality there is some
![]() $x \in U^{\tilde {r}_i+1}_i$
(so
$x \in U^{\tilde {r}_i+1}_i$
(so
![]() $j_x=\tilde {r}_i+1$
). We have
$j_x=\tilde {r}_i+1$
). We have
![]() ${\mathop {\mathrm {ext}}}(\psi _f|_{\binom {[\tilde {r}_i+1]}{2}},\tilde {{\boldsymbol {\alpha }}}_i) = q_{\tilde {r}_i+1}(\psi _f,(\alpha ^{\prime }_{i,1},\ldots ,\alpha ^{\prime }_{i,\tilde {r}_i},0)) \geq Q(\boldsymbol {k})-\sqrt {\delta }$
. Thus Lemma 2.10 implies that
${\mathop {\mathrm {ext}}}(\psi _f|_{\binom {[\tilde {r}_i+1]}{2}},\tilde {{\boldsymbol {\alpha }}}_i) = q_{\tilde {r}_i+1}(\psi _f,(\alpha ^{\prime }_{i,1},\ldots ,\alpha ^{\prime }_{i,\tilde {r}_i},0)) \geq Q(\boldsymbol {k})-\sqrt {\delta }$
. Thus Lemma 2.10 implies that
![]() $\tilde {r}_i+1$
is a
$\tilde {r}_i+1$
is a
![]() $\psi _f$
-clone of some
$\psi _f$
-clone of some
![]() $j^* \in [\tilde {r}_i]$
under
$j^* \in [\tilde {r}_i]$
under
![]() $\psi _f$
, which is a contradiction since
$\psi _f$
, which is a contradiction since
![]() $|\psi _f(\{\tilde {r}_i+1,j^*\})| \geq 2$
for all
$|\psi _f(\{\tilde {r}_i+1,j^*\})| \geq 2$
for all
![]() $j^* \in [\tilde {r}_i]$
. Thus
$j^* \in [\tilde {r}_i]$
. Thus
![]() $U^j_i=\emptyset $
for all
$U^j_i=\emptyset $
for all
![]() $\tilde {r}_i < j \leq r_f$
, so (3.8) implies that
$\tilde {r}_i < j \leq r_f$
, so (3.8) implies that
 $$ \begin{align} \beta_{i,j} \geq \tilde{\alpha}_{i,j}-\gamma \geq \mu-\gamma \geq \mu/2\quad\text{for all }j \in [\tilde{r}_i], \quad\text{and}\quad U_i = \bigcup_{j \in [\tilde{r}_i]}U^j_i. \end{align} $$
$$ \begin{align} \beta_{i,j} \geq \tilde{\alpha}_{i,j}-\gamma \geq \mu-\gamma \geq \mu/2\quad\text{for all }j \in [\tilde{r}_i], \quad\text{and}\quad U_i = \bigcup_{j \in [\tilde{r}_i]}U^j_i. \end{align} $$
We can now complete the claim, comparing
![]() $\phi _i$
and the partition
$\phi _i$
and the partition
![]() $\bigcup _{j \in [\tilde {r}_i]}U^j_i$
of
$\bigcup _{j \in [\tilde {r}_i]}U^j_i$
of
![]() $U_i$
to
$U_i$
to
![]() . Suppose for a contradiction that there is a blue edge
. Suppose for a contradiction that there is a blue edge
![]() $zy$
, so
$zy$
, so
![]() $z \in B_i$
and
$z \in B_i$
and
![]() $y \in U_i$
(where y could also be in
$y \in U_i$
(where y could also be in
![]() $B_i$
). Let
$B_i$
). Let
![]() $j_1 := j_{z}$
and
$j_1 := j_{z}$
and
![]() $j_2 := j_y$
, so
$j_2 := j_y$
, so
![]() $\{j_1,j_2\} \subseteq [\tilde {r}_i]$
by (3.14). By definition, either
$\{j_1,j_2\} \subseteq [\tilde {r}_i]$
by (3.14). By definition, either
-
(i)
 $j_1 \neq j_2$
and there is
$j_1 \neq j_2$
and there is
 $c \in \phi _i(zy)\setminus \tilde {\phi }_i(j_1j_2)$
, or
$c \in \phi _i(zy)\setminus \tilde {\phi }_i(j_1j_2)$
, or -
(ii)
 $j_1=j_2$
and there is some
$j_1=j_2$
and there is some
 $1 \neq c \in \phi _i(zy)$
.
$1 \neq c \in \phi _i(zy)$
.
We claim that, in both cases, there exist
![]() $j_3,\ldots ,j_{k_c} \in [\tilde {r}_i]\setminus \{j_1,j_2\}$
such that
$j_3,\ldots ,j_{k_c} \in [\tilde {r}_i]\setminus \{j_1,j_2\}$
such that
![]() $c \in \tilde {\phi }_i(j_\ell j_{\ell '})$
for all pairs among
$c \in \tilde {\phi }_i(j_\ell j_{\ell '})$
for all pairs among
![]() $\{j_1,\ldots ,j_{k_c}\}$
except
$\{j_1,\ldots ,j_{k_c}\}$
except
![]() $j_1j_2$
if they are distinct. Indeed, suppose (i) holds. By Lemma 2.5(i), the graph
$j_1j_2$
if they are distinct. Indeed, suppose (i) holds. By Lemma 2.5(i), the graph
![]() $([\tilde {r}_i],(\tilde {\phi }_i)^{-1}(c))$
is maximally
$([\tilde {r}_i],(\tilde {\phi }_i)^{-1}(c))$
is maximally
![]() $K_{k_c}$
-free. Since it is not complete, we are done. Suppose (ii) holds. By Lemma 2.5(ii),
$K_{k_c}$
-free. Since it is not complete, we are done. Suppose (ii) holds. By Lemma 2.5(ii),
![]() $(\boldsymbol {1}+\boldsymbol {e}_{j_1})(\tilde {\phi }_i)^{-1}(c)$
contains a copy of
$(\boldsymbol {1}+\boldsymbol {e}_{j_1})(\tilde {\phi }_i)^{-1}(c)$
contains a copy of
![]() $K_{k_c}$
as
$K_{k_c}$
as
![]() $c \neq 1$
.
$c \neq 1$
.
We say that a subset
![]() $\{y_3,\ldots ,y_{k_c}\}$
with
$\{y_3,\ldots ,y_{k_c}\}$
with
![]() $y_\ell \in U_i^{j_\ell }$
for
$y_\ell \in U_i^{j_\ell }$
for
![]() $3 \leq \ell \leq k_c$
is bad if
$3 \leq \ell \leq k_c$
is bad if
![]() $zy_\ell $
,
$zy_\ell $
,
![]() $yy_\ell $
and
$yy_\ell $
and
![]() $y_{\ell }y_{\ell '}$
for every
$y_{\ell }y_{\ell '}$
for every
![]() $\ell \ell '\in \binom {[k_c]}{2}$
are green. Since
$\ell \ell '\in \binom {[k_c]}{2}$
are green. Since
![]() $c \in \phi _i(zy)$
, there can be no bad subsets in
$c \in \phi _i(zy)$
, there can be no bad subsets in
![]() $G_i$
since then
$G_i$
since then
![]() $c \in \phi _i(xy)$
for every pair
$c \in \phi _i(xy)$
for every pair
![]() $xy$
among vertices in the subset, contradicting
$xy$
among vertices in the subset, contradicting
![]() $K_{k_c} \notin \tilde {\phi }_i^{-1}(c)([\tilde {r}_i])$
. On the other hand, at least, say,
$K_{k_c} \notin \tilde {\phi }_i^{-1}(c)([\tilde {r}_i])$
. On the other hand, at least, say,
![]() $\prod _{3 \leq \ell \leq k_c}(|U_i^{j_\ell }|/2)$
subsets are bad. Indeed, (3.14) implies that
$\prod _{3 \leq \ell \leq k_c}(|U_i^{j_\ell }|/2)$
subsets are bad. Indeed, (3.14) implies that
![]() $|U_i^j| =\beta _{i,j}n \geq \mu n/2$
for all
$|U_i^j| =\beta _{i,j}n \geq \mu n/2$
for all
![]() $j \in [\tilde {r}_i]$
. Also, (3.12) and (3.10) imply that every vertex has at most
$j \in [\tilde {r}_i]$
. Also, (3.12) and (3.10) imply that every vertex has at most
![]() $2\delta n$
nongreen neighbours. Thus, choosing
$2\delta n$
nongreen neighbours. Thus, choosing
![]() $y_3,\ldots ,y_{k_c}$
sequentially, among the vertices in
$y_3,\ldots ,y_{k_c}$
sequentially, among the vertices in
![]() $U_i^{j_\ell }$
, there are at most
$U_i^{j_\ell }$
, there are at most
![]() $2(\ell -1)\delta n < \mu n/4 < |U_i^{j_\ell }|/2$
vertices forbidden for
$2(\ell -1)\delta n < \mu n/4 < |U_i^{j_\ell }|/2$
vertices forbidden for
![]() $y_\ell $
due to not being a green neighbour of every
$y_\ell $
due to not being a green neighbour of every
![]() $y_1,\ldots ,y_{\ell -1}$
, as required. This contradiction implies that z is not incident to any blue edges, and thus
$y_1,\ldots ,y_{\ell -1}$
, as required. This contradiction implies that z is not incident to any blue edges, and thus
![]() $G_i$
contains no blue edges. This finishes the proof of Claim 3.1.3.
$G_i$
contains no blue edges. This finishes the proof of Claim 3.1.3.
As before, let us assume that nonzero entries of
![]() ${\boldsymbol {\alpha }}^{\prime }_0$
are indexed by
${\boldsymbol {\alpha }}^{\prime }_0$
are indexed by
![]() $[\tilde {r}_0]$
. So Lemma 3.1 holds when we set
$[\tilde {r}_0]$
. So Lemma 3.1 holds when we set
![]() $Y_0 := U_0^0 \cup \bigcup _{\tilde {r}_0+1 \leq j \leq r_f}U_0^j$
and
$Y_0 := U_0^0 \cup \bigcup _{\tilde {r}_0+1 \leq j \leq r_f}U_0^j$
and
![]() $Y_j := U_0^j$
for all
$Y_j := U_0^j$
for all
![]() $j \in [\tilde {r}_0]$
and
$j \in [\tilde {r}_0]$
and
![]() $(\tilde {r}_0,\tilde {\phi }_0,\tilde {{\boldsymbol {\alpha }}}_0)$
plays the role of
$(\tilde {r}_0,\tilde {\phi }_0,\tilde {{\boldsymbol {\alpha }}}_0)$
plays the role of
![]() $(r^*,\phi ^*,{\boldsymbol {\alpha }}^*)$
. This completes the proof of Lemma 3.1.
$(r^*,\phi ^*,{\boldsymbol {\alpha }}^*)$
. This completes the proof of Lemma 3.1.
4 Stability of asymptotically extremal graphs
4.1 Tools for large graphs
One of our main tools is Szemerédi’s regularity lemma, which allows us to discretise a large edge-coloured graph and thus approximate it by a feasible solution to Problem
![]() $Q_0$
. We will need the following definitions relating to regularity.
$Q_0$
. We will need the following definitions relating to regularity.
Definition 4.1 (Edge density, regularity of pairs and partitions).
Given a graph G and disjoint nonempty sets
![]() $A,B \subseteq V(G)$
, we define the edge density between A and B to be
$A,B \subseteq V(G)$
, we define the edge density between A and B to be
Given
![]() $\varepsilon ,d> 0$
, the pair
$\varepsilon ,d> 0$
, the pair
![]() $(A,B)$
is called
$(A,B)$
is called
-
•
 $\varepsilon $
-regular, if for every
$\varepsilon $
-regular, if for every
 $X \subseteq A$
and
$X \subseteq A$
and
 $Y \subseteq B$
with
$Y \subseteq B$
with
 $|X| \geq \varepsilon |A|$
and
$|X| \geq \varepsilon |A|$
and
 $|Y| \geq \varepsilon |B|$
, we have that
$|Y| \geq \varepsilon |B|$
, we have that
 $|d(X,Y) - d(A,B)| \leq \varepsilon $
.
$|d(X,Y) - d(A,B)| \leq \varepsilon $
. -
•
 $(\varepsilon , d)$
-regular, if
$(\varepsilon , d)$
-regular, if
 $(A,B)$
is
$(A,B)$
is
 $\varepsilon $
-regular and
$\varepsilon $
-regular and
 $d_G(A,B) = d \pm \varepsilon $
.
$d_G(A,B) = d \pm \varepsilon $
. -
•
 $(\varepsilon ,\geq \! d)$
-regular, if it is
$(\varepsilon ,\geq \! d)$
-regular, if it is
 $\varepsilon $
-regular and has density at least
$\varepsilon $
-regular and has density at least
 $d-\varepsilon $
.
$d-\varepsilon $
.
An equitable partition of a set V is a partition of V into parts
![]() $V_1,\ldots ,V_m$
, such that
$V_1,\ldots ,V_m$
, such that
![]() $|\,|V_i| - |V_j|\,| \leq 1$
for all
$|\,|V_i| - |V_j|\,| \leq 1$
for all
![]() $i,j \in [m]$
. An equitable partition of
$i,j \in [m]$
. An equitable partition of
![]() $V(G)$
into parts
$V(G)$
into parts
![]() $V_1,\ldots ,V_m$
is called
$V_1,\ldots ,V_m$
is called
![]() $\varepsilon $
-regular if
$\varepsilon $
-regular if
![]() $|V_i| \leq \varepsilon |V(G)|$
for every
$|V_i| \leq \varepsilon |V(G)|$
for every
![]() $i \in [m]$
, and all but at most
$i \in [m]$
, and all but at most
![]() $\varepsilon \binom {m}{2}$
of the pairs
$\varepsilon \binom {m}{2}$
of the pairs
![]() $(V_i,V_j)$
are
$(V_i,V_j)$
are
![]() $\varepsilon $
-regular.
$\varepsilon $
-regular.
We use the following multicolour version of Szemerédi’s regularity lemma [Reference Szemerédi27]. This version can be deduced from the original (see, for example, Theorems 1.8 and 1.18 in Komlós and Simonovits [Reference Komlós, Simonovits, Miklós, Sós and Szőni19]).
Theorem 4.2 (Multicolour regularity lemma).
For every
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $s \in \mathbb {N}$
, there exists
$s \in \mathbb {N}$
, there exists
![]() $M \in \mathbb {N}$
, such that for any graph G on
$M \in \mathbb {N}$
, such that for any graph G on
![]() $n \geq M$
vertices and any edge s-colouring
$n \geq M$
vertices and any edge s-colouring
![]() $\chi : E(G) \rightarrow [s]$
, there is an equitable partition
$\chi : E(G) \rightarrow [s]$
, there is an equitable partition
![]() $V(G) = V_1 \cup \ldots \cup V_m$
with
$V(G) = V_1 \cup \ldots \cup V_m$
with
![]() $1/\varepsilon \leq m \leq M$
, which is
$1/\varepsilon \leq m \leq M$
, which is
![]() $\varepsilon $
-regular simultaneously with respect to all graphs
$\varepsilon $
-regular simultaneously with respect to all graphs
![]() $(V(G),\chi ^{-1}(i))$
, with
$(V(G),\chi ^{-1}(i))$
, with
![]() $i \in [s]$
.
$i \in [s]$
.
![]() $\Box $
$\Box $
Our first tool states that a subgraph of a regular pair is still regular, provided both parts are not too small.
Proposition 4.3 [Reference Pikhurko, Staden and Yilma24, Proposition 9].
Let
![]() $\varepsilon ,\delta $
be such that
$\varepsilon ,\delta $
be such that
![]() $0 < 2\delta \leq \varepsilon < 1$
. Suppose that
$0 < 2\delta \leq \varepsilon < 1$
. Suppose that
![]() $(X,Y)$
is a
$(X,Y)$
is a
![]() $\delta $
-regular pair, and let
$\delta $
-regular pair, and let
![]() $X' \subseteq X$
and
$X' \subseteq X$
and
![]() $Y' \subseteq Y$
. If
$Y' \subseteq Y$
. If
 $$ \begin{align*}\min \left\{ \frac{|X'|}{|X|} , \frac{|Y'|}{|Y|} \right\} \geq \frac{\delta}{\varepsilon}, \end{align*} $$
$$ \begin{align*}\min \left\{ \frac{|X'|}{|X|} , \frac{|Y'|}{|Y|} \right\} \geq \frac{\delta}{\varepsilon}, \end{align*} $$
then
![]() $(X',Y')$
is
$(X',Y')$
is
![]() $\varepsilon $
-regular.
$\varepsilon $
-regular.
![]() $\Box $
$\Box $
The next proposition states that, given a set of edge-disjoint subgraphs
![]() $G_1,\ldots ,G_s$
of a bipartite graph, if at least one of the graphs
$G_1,\ldots ,G_s$
of a bipartite graph, if at least one of the graphs
![]() $G_i$
is not regular of density
$G_i$
is not regular of density
![]() $s^{-1}$
, then there is a
$s^{-1}$
, then there is a
![]() $G_j$
whose density on a pair of large sets is reduced.
$G_j$
whose density on a pair of large sets is reduced.
Proposition 4.4. Let
![]() $A,B$
be disjoint sets of vertices,
$A,B$
be disjoint sets of vertices,
![]() $s \in \mathbb {N}$
, and let
$s \in \mathbb {N}$
, and let
![]() $\varepsilon> 0$
be a constant with
$\varepsilon> 0$
be a constant with
![]() $1/|A|,1/|B| \ll \varepsilon \ll 1/s$
. Let
$1/|A|,1/|B| \ll \varepsilon \ll 1/s$
. Let
![]() $G_1,\ldots ,G_s$
be pairwise edge-disjoint subgraphs of
$G_1,\ldots ,G_s$
be pairwise edge-disjoint subgraphs of
![]() $K[A,B]$
. Suppose that not all of
$K[A,B]$
. Suppose that not all of
![]() $G_1,\ldots ,G_s$
are
$G_1,\ldots ,G_s$
are
![]() $(\varepsilon ,s^{-1})$
-regular graphs. Then there exists
$(\varepsilon ,s^{-1})$
-regular graphs. Then there exists
![]() $c \in [s]$
and
$c \in [s]$
and
![]() $X \subseteq A$
,
$X \subseteq A$
,
![]() $Y \subseteq B$
with
$Y \subseteq B$
with
![]() $|X| = \lceil \varepsilon |A|\rceil $
and
$|X| = \lceil \varepsilon |A|\rceil $
and
![]() $|Y| = \lceil \varepsilon |B| \rceil $
, such that
$|Y| = \lceil \varepsilon |B| \rceil $
, such that
Proof. Given
![]() $c \in [s]$
,
$c \in [s]$
,
![]() $X \subseteq A, Y \subseteq B$
, let
$X \subseteq A, Y \subseteq B$
, let
If
![]() $G_c$
is not
$G_c$
is not
![]() $(\varepsilon ,s^{-1})$
-regular, then either
$(\varepsilon ,s^{-1})$
-regular, then either
-
(i)
 $|\text {diff}_c(A,B)|> \frac {\varepsilon }{2}|A||B|$
; or
$|\text {diff}_c(A,B)|> \frac {\varepsilon }{2}|A||B|$
; or -
(ii) there is some
 $X \subseteq A$
and
$X \subseteq A$
and
 $Y \subseteq B$
with
$Y \subseteq B$
with
 $|X| \geq \varepsilon |A|$
and
$|X| \geq \varepsilon |A|$
and
 $|Y| \geq \varepsilon |B|$
, such that
$|Y| \geq \varepsilon |B|$
, such that  $$ \begin{align*} \bigg|\frac{e_{G_c}(X,Y)}{|X||Y|}-\frac{e_{G_c}(A,B)}{|A||B|}\bigg|> \varepsilon; \end{align*} $$
$$ \begin{align*} \bigg|\frac{e_{G_c}(X,Y)}{|X||Y|}-\frac{e_{G_c}(A,B)}{|A||B|}\bigg|> \varepsilon; \end{align*} $$
or both (the immediate implication from the definition of
![]() $(\varepsilon ,s^{-1})$
-regular would have (i) replaced by
$(\varepsilon ,s^{-1})$
-regular would have (i) replaced by
![]() $|\text {diff}_c(A,B)|> \varepsilon |A||B|$
, which is stronger than the statement of (i)). To prove the proposition, it is enough to exhibit
$|\text {diff}_c(A,B)|> \varepsilon |A||B|$
, which is stronger than the statement of (i)). To prove the proposition, it is enough to exhibit
![]() $c^* \in [s]$
,
$c^* \in [s]$
,
![]() $X' \subseteq A$
and
$X' \subseteq A$
and
![]() $Y' \subseteq B$
with
$Y' \subseteq B$
with
![]() $|X'| \geq \varepsilon |A|$
and
$|X'| \geq \varepsilon |A|$
and
![]() $|Y'| \geq \varepsilon |B|$
so that
$|Y'| \geq \varepsilon |B|$
so that
Indeed, if we can find such
![]() $c^*,X',Y'$
, then, setting
$c^*,X',Y'$
, then, setting
![]() $k_1 := \lceil \varepsilon |A|\rceil $
and
$k_1 := \lceil \varepsilon |A|\rceil $
and
![]() $k_2 := \lceil \varepsilon |B|\rceil $
, we have that
$k_2 := \lceil \varepsilon |B|\rceil $
, we have that
 $$ \begin{align*} \sum_{\stackrel{X \subseteq X'}{|X|=k_1}}\sum_{\stackrel{Y \subseteq Y'}{|Y|=k_2}} \text{diff}_{c^*}(X,Y) &= \binom{|X'|}{k_1}\binom{|Y'|}{k_2}s^{-1}k_1k_2 - \binom{|X'|-1}{k_1-1}\binom{|Y'|-1}{k_2-1}e_{G_{c^*}}(X',Y')\\ &= \binom{|X'|-1}{k_1-1}\binom{|Y'|-1}{k_2-1} \text{diff}_{c^*}(X',Y'); \end{align*} $$
$$ \begin{align*} \sum_{\stackrel{X \subseteq X'}{|X|=k_1}}\sum_{\stackrel{Y \subseteq Y'}{|Y|=k_2}} \text{diff}_{c^*}(X,Y) &= \binom{|X'|}{k_1}\binom{|Y'|}{k_2}s^{-1}k_1k_2 - \binom{|X'|-1}{k_1-1}\binom{|Y'|-1}{k_2-1}e_{G_{c^*}}(X',Y')\\ &= \binom{|X'|-1}{k_1-1}\binom{|Y'|-1}{k_2-1} \text{diff}_{c^*}(X',Y'); \end{align*} $$
so, by averaging, there is some
![]() $X \subseteq X'$
and
$X \subseteq X'$
and
![]() $Y \subseteq Y'$
with
$Y \subseteq Y'$
with
![]() $|X|=k_1$
,
$|X|=k_1$
,
![]() $|Y|=k_2$
, such that
$|Y|=k_2$
, such that
as required. So we will now concentrate on finding
![]() $c^*,X',Y'$
so that (4.1) holds. Suppose first that (i) holds for some
$c^*,X',Y'$
so that (4.1) holds. Suppose first that (i) holds for some
![]() $c \in [s]$
. If
$c \in [s]$
. If
![]() $\text {diff}_c(A,B)> 0$
, then we are done by setting
$\text {diff}_c(A,B)> 0$
, then we are done by setting
![]() $c^* := c$
,
$c^* := c$
,
![]() $X' := A$
and
$X' := A$
and
![]() $Y' := B$
. So we may assume that
$Y' := B$
. So we may assume that
![]() $\text {diff}_c(A,B) < 0$
. Observe that
$\text {diff}_c(A,B) < 0$
. Observe that
So
![]() $\sum _{i \in [s]\setminus \{ c \}}\text {diff}_i(A,B) \geq \varepsilon |A||B|/2$
. By averaging, there is some
$\sum _{i \in [s]\setminus \{ c \}}\text {diff}_i(A,B) \geq \varepsilon |A||B|/2$
. By averaging, there is some
![]() $c' \in [s]$
, such that
$c' \in [s]$
, such that
So we are done by setting
![]() $c^* := c'$
,
$c^* := c'$
,
![]() $X' := A$
and
$X' := A$
and
![]() $Y' := B$
.
$Y' := B$
.
Suppose instead that (ii) holds for some
![]() $c \in [s]$
. So there are
$c \in [s]$
. So there are
![]() $X \subseteq A$
,
$X \subseteq A$
,
![]() $Y \subseteq B$
with
$Y \subseteq B$
with
![]() $|X| \geq \varepsilon |A|$
,
$|X| \geq \varepsilon |A|$
,
![]() $|Y| \geq \varepsilon |B|$
, such that
$|Y| \geq \varepsilon |B|$
, such that
 $$ \begin{align*}\varepsilon < \bigg| \frac{\text{diff}_c(X,Y)}{|X||Y|} - \frac{\text{diff}(A,B)}{|A||B|} \bigg| < \frac{| \text{diff}_c(X,Y)|}{|X||Y|} + \frac{\varepsilon}{2}. \end{align*} $$
$$ \begin{align*}\varepsilon < \bigg| \frac{\text{diff}_c(X,Y)}{|X||Y|} - \frac{\text{diff}(A,B)}{|A||B|} \bigg| < \frac{| \text{diff}_c(X,Y)|}{|X||Y|} + \frac{\varepsilon}{2}. \end{align*} $$
Therefore,
![]() $|\text {diff}_c(X,Y)|> \varepsilon |X||Y|/2$
. Again, we may assume that
$|\text {diff}_c(X,Y)|> \varepsilon |X||Y|/2$
. Again, we may assume that
![]() $\text {diff}_c(X,Y) < 0$
, or we are done. Then an almost identical argument to the one above yields
$\text {diff}_c(X,Y) < 0$
, or we are done. Then an almost identical argument to the one above yields
![]() $c' \in [s]$
, such that
$c' \in [s]$
, such that
![]() $\text {diff}_{c'}(X,Y) \geq \varepsilon |A||B|/2s$
. This completes the proof.
$\text {diff}_{c'}(X,Y) \geq \varepsilon |A||B|/2s$
. This completes the proof.
The next proposition states that regular pairs are robust under small perturbations; the version stated here is a slight variation of Proposition 8 in [Reference Böttcher, Schacht and Taraz5].
Proposition 4.5. Let
![]() $(A,B)$
be an
$(A,B)$
be an
![]() $(\varepsilon , d)$
-regular pair, and let
$(\varepsilon , d)$
-regular pair, and let
![]() $(A',B')$
be a pair, such that
$(A',B')$
be a pair, such that
![]() $|A' \bigtriangleup A| \leq \alpha |A'|$
and
$|A' \bigtriangleup A| \leq \alpha |A'|$
and
![]() $|B' \bigtriangleup B| \leq \alpha |B'|$
for some
$|B' \bigtriangleup B| \leq \alpha |B'|$
for some
![]() $0 \leq \alpha \leq 1$
. Then
$0 \leq \alpha \leq 1$
. Then
![]() $(A',B')$
is an
$(A',B')$
is an
![]() $(\varepsilon +7\sqrt {\alpha }, d)$
-regular pair.
$(\varepsilon +7\sqrt {\alpha }, d)$
-regular pair.
We will also frequently use the following standard embedding lemma (see, for example, Theorem 2.1 in [Reference Komlós, Simonovits, Miklós, Sós and Szőni19]).
Lemma 4.6 (Embedding lemma).
For every
![]() $\eta>0$
and integer
$\eta>0$
and integer
![]() $k \geq 2$
, there exist
$k \geq 2$
, there exist
![]() $\varepsilon>0\ \text{and}\ m_0 \in \mathbb {N}$
, such that the following holds. Suppose that G is a graph with a partition
$\varepsilon>0\ \text{and}\ m_0 \in \mathbb {N}$
, such that the following holds. Suppose that G is a graph with a partition
![]() $V(G) = V_1 \cup \ldots \cup V_k$
, such that
$V(G) = V_1 \cup \ldots \cup V_k$
, such that
![]() $|V_i| \geq m_0$
for all
$|V_i| \geq m_0$
for all
![]() $i \in [k]$
, and every pair
$i \in [k]$
, and every pair
![]() $(V_i,V_j)$
for
$(V_i,V_j)$
for
![]() $1 \leq i < j \leq k$
is
$1 \leq i < j \leq k$
is
![]() $(\varepsilon ,\geq \! \eta )$
-regular. Then G contains
$(\varepsilon ,\geq \! \eta )$
-regular. Then G contains
![]() $K_k$
.
$K_k$
.
4.1.1 Binomial tails
In order to prove Part (ii) of Theorem 1.4, we will need Corollary 4.8 below, which is a simple consequence of the Chernoff inequality. The combinatorial interpretation of this fact is that almost every partition of
![]() $[n]$
into k parts is such that every part has size roughly
$[n]$
into k parts is such that every part has size roughly
![]() $n/k$
. Write
$n/k$
. Write
![]() $X \sim \text {Bin}(n,p)$
if a random variable X is binomially distributed with parameters
$X \sim \text {Bin}(n,p)$
if a random variable X is binomially distributed with parameters
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $p \in (0,1)$
.
$p \in (0,1)$
.
Proposition 4.7 [Reference Janson, Łuczak and Ruciński18, Theorem 2.1].
Suppose
![]() $X \sim \text {Bin}(n,p)$
where
$X \sim \text {Bin}(n,p)$
where
![]() $0<p<1$
. Let
$0<p<1$
. Let
![]() $k \leq np$
. Then
$k \leq np$
. Then
 $$ \begin{align*}\mathbb{P}(X \leq k) \leq \exp \left( \frac{-(np-k)^2}{2np}\right). \end{align*} $$
$$ \begin{align*}\mathbb{P}(X \leq k) \leq \exp \left( \frac{-(np-k)^2}{2np}\right). \end{align*} $$
Corollary 4.8. Let
![]() $n,k \in \mathbb {N}$
and
$n,k \in \mathbb {N}$
and
![]() $\delta \in \mathbb {R}$
, where
$\delta \in \mathbb {R}$
, where
![]() $0 < 1/n \ll \delta \ll 1/k$
. Then
$0 < 1/n \ll \delta \ll 1/k$
. Then
 $$ \begin{align*}\sum_{i=0}^{\lfloor (k^{-1}-\delta) n \rfloor}\binom{n}{i} (k-1)^{n-i} \leq e^{-\delta^2 kn/3} \cdot k^n. \end{align*} $$
$$ \begin{align*}\sum_{i=0}^{\lfloor (k^{-1}-\delta) n \rfloor}\binom{n}{i} (k-1)^{n-i} \leq e^{-\delta^2 kn/3} \cdot k^n. \end{align*} $$
Proof. Let
![]() $X \sim \text {Bin}(n,k^{-1})$
be a binomial random variable. Then Proposition 4.7 implies that
$X \sim \text {Bin}(n,k^{-1})$
be a binomial random variable. Then Proposition 4.7 implies that
 $$ \begin{align*}\mathbb{P}(X \leq \lfloor(k^{-1}-\delta)n\rfloor) \leq \exp \left( \frac{-(n/k-\lfloor (k^{-1}-\delta)n \rfloor)^2}{2n/k} \right) \leq e^{-\delta^2kn/3}. \end{align*} $$
$$ \begin{align*}\mathbb{P}(X \leq \lfloor(k^{-1}-\delta)n\rfloor) \leq \exp \left( \frac{-(n/k-\lfloor (k^{-1}-\delta)n \rfloor)^2}{2n/k} \right) \leq e^{-\delta^2kn/3}. \end{align*} $$
But
 $$ \begin{align*}\mathbb{P}(X \leq \lfloor (k^{-1}-\delta)n\rfloor) = \sum_{i=0}^{\lfloor(k^{-1}-\delta)n\rfloor}\binom{n}{i}\left(\frac{1}{k}\right)^i \left(1-\frac{1}{k}\right)^{n-i} = k^{-n} \cdot \sum_{i=0}^{(k^{-1}-\delta)n\rfloor}\binom{n}{i}(k-1)^{n-i}, \end{align*} $$
$$ \begin{align*}\mathbb{P}(X \leq \lfloor (k^{-1}-\delta)n\rfloor) = \sum_{i=0}^{\lfloor(k^{-1}-\delta)n\rfloor}\binom{n}{i}\left(\frac{1}{k}\right)^i \left(1-\frac{1}{k}\right)^{n-i} = k^{-n} \cdot \sum_{i=0}^{(k^{-1}-\delta)n\rfloor}\binom{n}{i}(k-1)^{n-i}, \end{align*} $$
as required.
We will also need the following simple bound, which we state without proof. Let
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $\varepsilon ,\delta> 0$
, such that
$\varepsilon ,\delta> 0$
, such that
![]() $0 < 1/n \ll \varepsilon \ll \delta < 1$
. Then
$0 < 1/n \ll \varepsilon \ll \delta < 1$
. Then
 $$ \begin{align} \binom{n}{\leq \varepsilon n} \leq 2^{\delta n}, \end{align} $$
$$ \begin{align} \binom{n}{\leq \varepsilon n} \leq 2^{\delta n}, \end{align} $$
where for integers
![]() $m \geq t$
, we write
$m \geq t$
, we write
![]() $\binom {m}{\leq t}:=\sum _{0 \leq i \leq t}\binom {m}{i}$
.
$\binom {m}{\leq t}:=\sum _{0 \leq i \leq t}\binom {m}{i}$
.
4.2 Preparation for the proof of Theorem 1.4
We define a hierarchy of constants and assume that these relations hold throughout the remainder of this section. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
, and let
$\boldsymbol {k} \in \mathbb {N}^s$
, and let
![]() $\delta> 0$
. In what follows, whenever we assume that a constant is sufficiently small, it is because a larger constant gives a weaker conclusion. Let
$\delta> 0$
. In what follows, whenever we assume that a constant is sufficiently small, it is because a larger constant gives a weaker conclusion. Let
![]() $\mu> 0$
be such that
$\mu> 0$
be such that
![]() $\alpha ^*_i \geq \mu $
for all
$\alpha ^*_i \geq \mu $
for all
![]() and
and
![]() $i \in [r^*]$
(which exists by Lemma 2.8). We may assume that
$i \in [r^*]$
(which exists by Lemma 2.8). We may assume that
![]() $\delta \ll \mu , 1/s, 1/R(\boldsymbol {k})$
. Choose
$\delta \ll \mu , 1/s, 1/R(\boldsymbol {k})$
. Choose
![]() $\gamma _3, \ldots , \gamma _6 \in \mathbb {R}$
, such that
$\gamma _3, \ldots , \gamma _6 \in \mathbb {R}$
, such that
![]() $0 < \gamma _3 \ll \ldots \ll \gamma _6 \ll \delta $
. In particular, we may assume that
$0 < \gamma _3 \ll \ldots \ll \gamma _6 \ll \delta $
. In particular, we may assume that
![]() $\gamma _4 \leq \gamma _5/2M_{\gamma _5}$
, where
$\gamma _4 \leq \gamma _5/2M_{\gamma _5}$
, where
![]() $M_{\gamma _5}$
is the integer output of Theorem 4.2 applied with parameter
$M_{\gamma _5}$
is the integer output of Theorem 4.2 applied with parameter
![]() $\gamma _5$
; and
$\gamma _5$
; and
![]() $\gamma _5$
is at most the output of Lemma 4.6 applied with parameter
$\gamma _5$
is at most the output of Lemma 4.6 applied with parameter
![]() $\gamma _6$
. Let
$\gamma _6$
. Let
![]() $0 < \nu \ll \gamma _3$
. Let
$0 < \nu \ll \gamma _3$
. Let
![]() $\varepsilon> 0$
be such that
$\varepsilon> 0$
be such that
![]() $8\varepsilon $
is the output of Lemma 2.3 applied with
$8\varepsilon $
is the output of Lemma 2.3 applied with
![]() $2\nu $
; we may assume that
$2\nu $
; we may assume that
![]() $\varepsilon \ll \nu $
. Choose
$\varepsilon \ll \nu $
. Choose
![]() $\gamma _2 \in \mathbb {R}$
, such that
$\gamma _2 \in \mathbb {R}$
, such that
![]() $0 < \gamma _2 \ll \varepsilon $
. Let
$0 < \gamma _2 \ll \varepsilon $
. Let
![]() $\gamma _1> 0$
be the minimum constant obtained when Lemma 4.6 is applied with
$\gamma _1> 0$
be the minimum constant obtained when Lemma 4.6 is applied with
![]() $\gamma _2$
playing the role of
$\gamma _2$
playing the role of
![]() $\eta $
, and with
$\eta $
, and with
![]() $k_1,\ldots ,k_c$
playing the role of k. We may assume that
$k_1,\ldots ,k_c$
playing the role of k. We may assume that
![]() $0 < \gamma _1 \ll \gamma _2$
. Apply Theorem 4.2 with parameter
$0 < \gamma _1 \ll \gamma _2$
. Apply Theorem 4.2 with parameter
![]() $\gamma _1$
to obtain
$\gamma _1$
to obtain
![]() $M \in \mathbb {N}$
, such that the conclusions of the theorem hold. We may assume that
$M \in \mathbb {N}$
, such that the conclusions of the theorem hold. We may assume that
![]() $1/M \ll \gamma _1$
. Now let
$1/M \ll \gamma _1$
. Now let
![]() $n_0 \in \mathbb {N}$
be such that
$n_0 \in \mathbb {N}$
be such that
![]() $1/n_0 \ll 1/M$
. We have the hierarchy
$1/n_0 \ll 1/M$
. We have the hierarchy
We need the following somewhat technical definition of ‘popular vectors’ from [Reference Pikhurko and Yilma25], which allows us to choose colourings
![]() $\chi $
of G whose coloured regularity partition is a witness of many other valid colourings of G.
$\chi $
of G whose coloured regularity partition is a witness of many other valid colourings of G.
Definition 4.9 (Popular vectors).
Let G be a graph on
![]() $n \geq n_0$
vertices and
$n \geq n_0$
vertices and
![]() $\chi : E(G) \rightarrow [s]$
be an s-edge colouring of G which is
$\chi : E(G) \rightarrow [s]$
be an s-edge colouring of G which is
![]() $\boldsymbol {k}$
-valid. Apply Theorem 4.2 to the pair
$\boldsymbol {k}$
-valid. Apply Theorem 4.2 to the pair
![]() $(G,\chi )$
with parameter
$(G,\chi )$
with parameter
![]() $\gamma _1$
to obtain an equitable partition
$\gamma _1$
to obtain an equitable partition
![]() $V(G) = U_1 \cup \ldots \cup U_r$
with
$V(G) = U_1 \cup \ldots \cup U_r$
with
![]() $1/\gamma _1 \leq r \leq M$
, which is
$1/\gamma _1 \leq r \leq M$
, which is
![]() $\gamma _1$
-regular simultaneously with respect to all graphs
$\gamma _1$
-regular simultaneously with respect to all graphs
![]() $(V(G),\chi ^{-1}(c))$
, with
$(V(G),\chi ^{-1}(c))$
, with
![]() $c \in [s]$
. Let
$c \in [s]$
. Let
Let
![]() $\mathcal {U} := \{ U_i : i \in [r] \}$
. We define the function
$\mathcal {U} := \{ U_i : i \in [r] \}$
. We define the function
![]() $\mathop {\mathrm {RL}}$
by setting
$\mathop {\mathrm {RL}}$
by setting
(where we arbitrarily fix a single output if there is more than one choice of
![]() $(r,\phi ,\mathcal {U})$
). We say that
$(r,\phi ,\mathcal {U})$
). We say that
![]() $(r,\phi ,\mathcal {U})$
is popular if
$(r,\phi ,\mathcal {U})$
is popular if
and unpopular otherwise. Let
![]() $\mathrm {Pop}(G)$
be the set of popular
$\mathrm {Pop}(G)$
be the set of popular
![]() $(r,\phi ,\mathcal {U})$
, and let
$(r,\phi ,\mathcal {U})$
, and let
![]() $\mathrm {Col}(G)$
be the set of
$\mathrm {Col}(G)$
be the set of
![]() $\boldsymbol {k}$
-valid colourings
$\boldsymbol {k}$
-valid colourings
![]() $\chi $
of G, such that
$\chi $
of G, such that
![]() $\mathop {\mathrm {RL}}(\chi ) \in \mathrm {Pop}(G)$
.
$\mathop {\mathrm {RL}}(\chi ) \in \mathrm {Pop}(G)$
.
As the following proposition shows, almost every colouring
![]() $\chi $
maps to a popular vector.
$\chi $
maps to a popular vector.
Proposition 4.10. For all graphs G on
![]() $n \geq n_0$
vertices,
$n \geq n_0$
vertices,
Proof. Let M be the integer output of Theorem 4.2 applied with parameter
![]() $\gamma _1$
. Let
$\gamma _1$
. Let
![]() $n \geq M$
, and let G be a graph on n vertices. The function
$n \geq M$
, and let G be a graph on n vertices. The function
![]() $\mathop {\mathrm {RL}}$
is well-defined. Then the number of outputs
$\mathop {\mathrm {RL}}$
is well-defined. Then the number of outputs
![]() $(r,\phi ,\mathcal {U})$
is at most
$(r,\phi ,\mathcal {U})$
is at most
Now,
 $$ \begin{align*} \sum_{(r,\phi,\mathcal{U}) \in \mathrm{Pop}(G)}|\textstyle{\mathop{\mathrm{RL}}^{-1}}((r,\phi,\mathcal{U}))| &= F(G;\boldsymbol{k}) - \sum_{(r,\phi,\mathcal{U}) \notin \mathrm{Pop}(G)}|\textstyle{\mathop{\mathrm{RL}}^{-1}}((r,\phi,\mathcal{U}))|\\ &\geq \left(1 - 2^{O(\log n)} \cdot 2^{-3\varepsilon n^2} \right) F(G;\boldsymbol{k}) \geq (1-2^{-2\varepsilon n^2})F(G;\boldsymbol{k}),\\[-16pt] \end{align*} $$
$$ \begin{align*} \sum_{(r,\phi,\mathcal{U}) \in \mathrm{Pop}(G)}|\textstyle{\mathop{\mathrm{RL}}^{-1}}((r,\phi,\mathcal{U}))| &= F(G;\boldsymbol{k}) - \sum_{(r,\phi,\mathcal{U}) \notin \mathrm{Pop}(G)}|\textstyle{\mathop{\mathrm{RL}}^{-1}}((r,\phi,\mathcal{U}))|\\ &\geq \left(1 - 2^{O(\log n)} \cdot 2^{-3\varepsilon n^2} \right) F(G;\boldsymbol{k}) \geq (1-2^{-2\varepsilon n^2})F(G;\boldsymbol{k}),\\[-16pt] \end{align*} $$
as required.
4.3 The proof of Theorem 1.4
Using Lemma 3.1, we can now prove Theorem 1.4. Although this lemma is really the heart of the proof, there are still many steps required to ‘transfer’ its conclusion to the graph setting. For this reason, we split the proof into a series of claims, and continue to use the constants defined in (4.3).
Proof of Theorem 1.4. Suppose that G is a graph on
![]() $n \geq n_0$
vertices, and
$n \geq n_0$
vertices, and
 $$ \begin{align} \frac{\log F(G;\boldsymbol{k})}{\binom{n}{2}} \geq Q(\boldsymbol{k})-\varepsilon.\\[-16pt]\nonumber \end{align} $$
$$ \begin{align} \frac{\log F(G;\boldsymbol{k})}{\binom{n}{2}} \geq Q(\boldsymbol{k})-\varepsilon.\\[-16pt]\nonumber \end{align} $$
We will show that the conclusion of Theorem 1.4 holds with parameter
![]() $\delta $
. If we decrease
$\delta $
. If we decrease
![]() $\delta $
, then the conclusion of Theorem 1.4 becomes only stronger, so we can assume that
$\delta $
, then the conclusion of Theorem 1.4 becomes only stronger, so we can assume that
![]() $\delta $
satisfies (4.3). Let
$\delta $
satisfies (4.3). Let
![]() $(r,\phi ,\mathcal {U}) \in \mathrm {Pop}(G)$
. That is,
$(r,\phi ,\mathcal {U}) \in \mathrm {Pop}(G)$
. That is,
We will (for now) suppress the dependence of what follows on
![]() $(r,\phi ,\mathcal {U})$
. Thus, there is an equitable partition
$(r,\phi ,\mathcal {U})$
. Thus, there is an equitable partition
![]() $V(G) = U_1 \cup \ldots \cup U_r$
, where
$V(G) = U_1 \cup \ldots \cup U_r$
, where
![]() $1/\gamma _1 \leq r \leq M$
, which is, for all
$1/\gamma _1 \leq r \leq M$
, which is, for all
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
,
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
,
![]() $\gamma _1$
-regular simultaneously with respect to all graphs
$\gamma _1$
-regular simultaneously with respect to all graphs
![]() $(V(G),\chi ^{-1}(c))$
, with
$(V(G),\chi ^{-1}(c))$
, with
![]() $c \in [s]$
. Furthermore, for each
$c \in [s]$
. Furthermore, for each
![]() $ij \in \binom {[r]}{2}$
and
$ij \in \binom {[r]}{2}$
and
![]() $c \in [s]$
, we have that
$c \in [s]$
, we have that
![]() $c \in \phi (ij)$
if and only if
$c \in \phi (ij)$
if and only if
![]() $\chi ^{-1}(c)[U_i,U_j]$
is
$\chi ^{-1}(c)[U_i,U_j]$
is
![]() $(\gamma _1,\geq \! \gamma _2)$
-regular. Lemma 4.6 and our choice of parameters in (4.3) imply that
$(\gamma _1,\geq \! \gamma _2)$
-regular. Lemma 4.6 and our choice of parameters in (4.3) imply that
![]() $\phi ^{-1}(c)$
is
$\phi ^{-1}(c)$
is
![]() $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
![]() $c \in [s]$
.
$c \in [s]$
.
The next claim shows that G gives rise to a feasible solution
![]() $(r,\phi ,\boldsymbol {\alpha })$
of Problem
$(r,\phi ,\boldsymbol {\alpha })$
of Problem
![]() $Q_0$
which is almost optimal. Moreover,
$Q_0$
which is almost optimal. Moreover,
![]() $\boldsymbol {\alpha }$
is a good approximation of the structure of G, and because
$\boldsymbol {\alpha }$
is a good approximation of the structure of G, and because
![]() $(r,\phi ,\mathcal {U})$
is popular,
$(r,\phi ,\mathcal {U})$
is popular,
![]() $\phi $
is a good approximation of many valid colourings of G.
$\phi $
is a good approximation of many valid colourings of G.
Claim 4.1. Let
![]() $\boldsymbol {\alpha }:= ( |U_1|/n, \ldots , |U_r|/n )$
. Then
$\boldsymbol {\alpha }:= ( |U_1|/n, \ldots , |U_r|/n )$
. Then
![]() and
and
 $$ \begin{align*}q(\phi,\boldsymbol{\alpha}) \geq Q(\boldsymbol{k})-8\varepsilon + 2\sum_{\stackrel{ij \in \binom{[r]}{2}}{|\phi(ij)| \geq 2}} \left( \frac{e(\overline{G}[U_i,U_j])}{n^2} \right). \end{align*} $$
$$ \begin{align*}q(\phi,\boldsymbol{\alpha}) \geq Q(\boldsymbol{k})-8\varepsilon + 2\sum_{\stackrel{ij \in \binom{[r]}{2}}{|\phi(ij)| \geq 2}} \left( \frac{e(\overline{G}[U_i,U_j])}{n^2} \right). \end{align*} $$
Moreover, for every
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
, we have
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
, we have
 $$ \begin{align} \sum_{\stackrel{ij \in \binom{[r]}{2}}{|\phi(ij)|\geq2}}\frac{e(\overline{G}[U_i,U_j])}{n^2} \leq 4\varepsilon ,\end{align} $$
$$ \begin{align} \sum_{\stackrel{ij \in \binom{[r]}{2}}{|\phi(ij)|\geq2}}\frac{e(\overline{G}[U_i,U_j])}{n^2} \leq 4\varepsilon ,\end{align} $$
and there are at most
![]() $s\gamma _2 n^2$
edges
$s\gamma _2 n^2$
edges
![]() $xy \in E(G)$
where
$xy \in E(G)$
where
![]() $x \in U_i$
and
$x \in U_i$
and
![]() $y \in U_j$
, such that either
$y \in U_j$
, such that either
![]() $i=j$
, or
$i=j$
, or
![]() $i \neq j$
and
$i \neq j$
and
![]() $\chi (xy) \notin \phi (ij)$
.
$\chi (xy) \notin \phi (ij)$
.
Proof of Claim. Consider the following procedure for producing colourings of G whose image under
![]() $\mathop {\mathrm {RL}}$
is
$\mathop {\mathrm {RL}}$
is
![]() $(r,\phi ,\mathcal {U})$
.
$(r,\phi ,\mathcal {U})$
.
4.4 Standard colouring procedure
-
1. Colour ‘atypical’ edges as follows:
-
(i) Assign arbitrary colours to all edges of G that lie inside some part
 $U_i$
.
$U_i$
. -
(ii) Select at most
 $s\gamma _1\binom {r}{2}$
elements of
$s\gamma _1\binom {r}{2}$
elements of
 $\binom {[r]}{2}$
and, for each selected pair
$\binom {[r]}{2}$
and, for each selected pair
 $ij$
, assign colours to
$ij$
, assign colours to
 $G[U_i,U_j]$
arbitrarily.
$G[U_i,U_j]$
arbitrarily. -
(iii) For every colour
 $c \in [s]$
and every
$c \in [s]$
and every
 $ij \in \binom {[r]}{2}$
, colour an arbitrary subset of edges of
$ij \in \binom {[r]}{2}$
, colour an arbitrary subset of edges of
 $G[U_i,U_j]$
of size at most
$G[U_i,U_j]$
of size at most
 $\gamma _2|U_i||U_j|$
by colour c.
$\gamma _2|U_i||U_j|$
by colour c.
-
-
2. Colour most edges according to
 $\phi $
: for every edge
$\phi $
: for every edge
 $ij \in \binom {[s]}{2}$
and
$ij \in \binom {[s]}{2}$
and
 $x \in U_i$
,
$x \in U_i$
,
 $y \in U_j$
where
$y \in U_j$
where
 $xy \in E(G)$
and
$xy \in E(G)$
and
 $xy$
is not yet coloured, pick an arbitrary colour from the set
$xy$
is not yet coloured, pick an arbitrary colour from the set
 $\phi (ij)$
. If
$\phi (ij)$
. If
 $\phi (ij) = \emptyset $
, colour
$\phi (ij) = \emptyset $
, colour
 $xy$
with colour
$xy$
with colour
 $1$
.
$1$
.
This procedure will generate every
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
(as well as some further colourings, which may not even be
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
(as well as some further colourings, which may not even be
![]() $\boldsymbol {k}$
-valid). Indeed, this follows from Theorem 4.2, and the statement that
$\boldsymbol {k}$
-valid). Indeed, this follows from Theorem 4.2, and the statement that
![]() $\phi ^{-1}(c)$
is
$\phi ^{-1}(c)$
is
![]() $K_{k_c}$
-free for all
$K_{k_c}$
-free for all
![]() $c \in [s]$
.
$c \in [s]$
.
Let
![]() $S_1$
be the number of choices in step 1. We will call those edges which are not coloured according to
$S_1$
be the number of choices in step 1. We will call those edges which are not coloured according to
![]() $\phi $
(i.e. not coloured in step 2) the atypical edges. The number of these is at most
$\phi $
(i.e. not coloured in step 2) the atypical edges. The number of these is at most
 $$ \begin{align*} r\left\lceil \frac{n}{r}\right\rceil^2 + s\gamma_1\binom{r}{2}\left\lceil \frac{n}{r} \right\rceil^2 + s\cdot \binom{r}{2} \cdot \gamma_2\left\lceil \frac{n}{r}\right\rceil^2 < s\gamma_2 n^2, \end{align*} $$
$$ \begin{align*} r\left\lceil \frac{n}{r}\right\rceil^2 + s\gamma_1\binom{r}{2}\left\lceil \frac{n}{r} \right\rceil^2 + s\cdot \binom{r}{2} \cdot \gamma_2\left\lceil \frac{n}{r}\right\rceil^2 < s\gamma_2 n^2, \end{align*} $$
proving the second part of the claim. This also implies that
 $$ \begin{align*}S_1 \leq \binom{\binom{n}{2}}{\leq s\gamma_2 n^2}s^{s\gamma_2 n^2} \stackrel{(4.2)}{<} 2^{\varepsilon n^2/3}. \end{align*} $$
$$ \begin{align*}S_1 \leq \binom{\binom{n}{2}}{\leq s\gamma_2 n^2}s^{s\gamma_2 n^2} \stackrel{(4.2)}{<} 2^{\varepsilon n^2/3}. \end{align*} $$
Let
![]() $S_2$
be the number of choices in step 2 given a fixed choice at step 1. Since
$S_2$
be the number of choices in step 2 given a fixed choice at step 1. Since
![]() $(r,\phi ,\mathcal {U})$
is popular, we have that
$(r,\phi ,\mathcal {U})$
is popular, we have that
 $$ \begin{align} \log S_2 \stackrel{(4.5)}{\geq} \log \left( 2^{-3\varepsilon n^2} \cdot F(G;\boldsymbol{k}) \right) - \log S_1 \stackrel{(4.4)}{\geq} \binom{n}{2}\left( Q(\boldsymbol{k})-\varepsilon \right) - \frac{\varepsilon n^2}{3} - 3\varepsilon n^2. \end{align} $$
$$ \begin{align} \log S_2 \stackrel{(4.5)}{\geq} \log \left( 2^{-3\varepsilon n^2} \cdot F(G;\boldsymbol{k}) \right) - \log S_1 \stackrel{(4.4)}{\geq} \binom{n}{2}\left( Q(\boldsymbol{k})-\varepsilon \right) - \frac{\varepsilon n^2}{3} - 3\varepsilon n^2. \end{align} $$
We would now like to bound
![]() $S_2$
from above. For each
$S_2$
from above. For each
![]() $ij \in \binom {[r]}{2}$
, define
$ij \in \binom {[r]}{2}$
, define
![]() $\delta _{ij}$
by setting
$\delta _{ij}$
by setting
Now,
 $$ \begin{align} S_2 \leq \prod_{ij \in \binom{[r]}{2}} \left( \max \{ 1, |\phi(ij)| \} \right)^{|U_i||U_j|-\delta_{ij}n^2}. \end{align} $$
$$ \begin{align} S_2 \leq \prod_{ij \in \binom{[r]}{2}} \left( \max \{ 1, |\phi(ij)| \} \right)^{|U_i||U_j|-\delta_{ij}n^2}. \end{align} $$
So
 $$ \begin{align} \nonumber \log S_2 &\leq \sum_{\stackrel{ij \in \binom{[r]}{2}}{\phi(ij) \neq \emptyset}}\left(|U_i||U_j|-\delta_{ij}n^2 \right)\log|\phi(ij)| = n^2 \sum_{\stackrel{ij \in \binom{[r]}{2}}{\phi(ij) \neq \emptyset}}\left(\alpha_i\alpha_j-\delta_{ij} \right)\log|\phi(ij)|\\ &= \frac{n^2}{2} q(\phi,\boldsymbol{\alpha}) - n^2\sum_{\stackrel{ij \in \binom{[r]}{2}}{|\phi(ij)| \geq 2}}\delta_{ij}\log|\phi(ij)|. \end{align} $$
$$ \begin{align} \nonumber \log S_2 &\leq \sum_{\stackrel{ij \in \binom{[r]}{2}}{\phi(ij) \neq \emptyset}}\left(|U_i||U_j|-\delta_{ij}n^2 \right)\log|\phi(ij)| = n^2 \sum_{\stackrel{ij \in \binom{[r]}{2}}{\phi(ij) \neq \emptyset}}\left(\alpha_i\alpha_j-\delta_{ij} \right)\log|\phi(ij)|\\ &= \frac{n^2}{2} q(\phi,\boldsymbol{\alpha}) - n^2\sum_{\stackrel{ij \in \binom{[r]}{2}}{|\phi(ij)| \geq 2}}\delta_{ij}\log|\phi(ij)|. \end{align} $$
Combining this with (4.7), we have that
 $$ \begin{align*}q(\phi,\boldsymbol{\alpha}) \geq Q(\boldsymbol{k}) - 8\varepsilon + 2\sum_{\stackrel{ij \in \binom{[r]}{2}}{|\phi(ij)|\geq 2}} \delta_{ij}, \end{align*} $$
$$ \begin{align*}q(\phi,\boldsymbol{\alpha}) \geq Q(\boldsymbol{k}) - 8\varepsilon + 2\sum_{\stackrel{ij \in \binom{[r]}{2}}{|\phi(ij)|\geq 2}} \delta_{ij}, \end{align*} $$
proving the first part of the claim. Every edge that the second part of the claim counts is atypical, and by construction, there are at most
![]() $s\gamma _2 n^2$
of these. The final part of the claim follows from (4.7), (4.8) and (4.9).
$s\gamma _2 n^2$
of these. The final part of the claim follows from (4.7), (4.8) and (4.9).
![]() $\Box $
$\Box $
Apply Lemma 3.1 with parameter
![]() $2\nu $
to
$2\nu $
to
![]() $(r,\phi ,\boldsymbol {\alpha })$
to obtain
$(r,\phi ,\boldsymbol {\alpha })$
to obtain
![]() , such that the following hold: there is a partition
, such that the following hold: there is a partition
![]() $ [r] = V_0 \cup \ldots \cup V_{r^*} $
where for all
$ [r] = V_0 \cup \ldots \cup V_{r^*} $
where for all
![]() $i \in [r^*]$
, we have
$i \in [r^*]$
, we have
 $$ \begin{align} \|\boldsymbol{x}-\boldsymbol{\alpha}^*\|_1 < 2\nu \text{ where }x_i := \sum_{j \in V_i}\alpha_j; \end{align} $$
$$ \begin{align} \|\boldsymbol{x}-\boldsymbol{\alpha}^*\|_1 < 2\nu \text{ where }x_i := \sum_{j \in V_i}\alpha_j; \end{align} $$
for all
![]() $ij \in \binom {[r^*]}{2}$
,
$ij \in \binom {[r^*]}{2}$
,
![]() $i' \in V_i$
and
$i' \in V_i$
and
![]() $j' \in V_j$
, we have that
$j' \in V_j$
, we have that
![]() $\phi (i'j')\subseteq \phi ^*(ij)$
; and for all
$\phi (i'j')\subseteq \phi ^*(ij)$
; and for all
![]() $i \in [r^*]$
and every
$i \in [r^*]$
and every
![]() $i'j' \in \binom {V_i}{2}$
, we have
$i'j' \in \binom {V_i}{2}$
, we have
![]() $\phi (i'j') \subseteq \{ 1 \}$
.
$\phi (i'j') \subseteq \{ 1 \}$
.
We would like to transfer this partition to G itself. So for all
![]() $0 \leq i \leq r^*$
, let
$0 \leq i \leq r^*$
, let
 $$ \begin{align} X_i := \bigcup_{j \in V_i}U_j,\ \text{ so } \ V(G) = X_0 \cup \ldots \cup X_{r^*}. \end{align} $$
$$ \begin{align} X_i := \bigcup_{j \in V_i}U_j,\ \text{ so } \ V(G) = X_0 \cup \ldots \cup X_{r^*}. \end{align} $$
Then it is easy to see that
 $$ \begin{align} \boldsymbol{x} = \left( \frac{|X_1|}{n},\ldots,\frac{|X_{r^*}|}{n} \right). \end{align} $$
$$ \begin{align} \boldsymbol{x} = \left( \frac{|X_1|}{n},\ldots,\frac{|X_{r^*}|}{n} \right). \end{align} $$
Now (4.3) and (4.10) imply that, for all
![]() $i \in [r^*]$
,
$i \in [r^*]$
,
 $$ \begin{align} 2\nu> \|\boldsymbol{\alpha}^*-\boldsymbol{x}\|_1 \geq \bigg| \|\boldsymbol{\alpha}^*\|_1 - \|\boldsymbol{x}\|_1 \bigg| = \left| 1 - \left(1-\frac{|X_0|}{n}\right) \right| = \frac{|X_0|}{n}. \end{align} $$
$$ \begin{align} 2\nu> \|\boldsymbol{\alpha}^*-\boldsymbol{x}\|_1 \geq \bigg| \|\boldsymbol{\alpha}^*\|_1 - \|\boldsymbol{x}\|_1 \bigg| = \left| 1 - \left(1-\frac{|X_0|}{n}\right) \right| = \frac{|X_0|}{n}. \end{align} $$
Note that
![]() $\boldsymbol {x}$
,
$\boldsymbol {x}$
,
![]() $(r^*,\phi ^*)$
,
$(r^*,\phi ^*)$
,
![]() $[r]=V_0 \cup \ldots \cup V_{r^*}$
,
$[r]=V_0 \cup \ldots \cup V_{r^*}$
,
![]() $X_0, \ldots , X_{r^*}$
are fixed for every
$X_0, \ldots , X_{r^*}$
are fixed for every
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
. Claim 4.1 implies that
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
. Claim 4.1 implies that
Say that
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
is good if
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
is good if
-
•
 $\chi ^{-1}(c)[X_i,X_j]$
is
$\chi ^{-1}(c)[X_i,X_j]$
is
 $(\gamma _3,|\phi ^*(ij)|^{-1})$
-regular for all
$(\gamma _3,|\phi ^*(ij)|^{-1})$
-regular for all
 $ij \in \binom {[r^*]}{2}$
and
$ij \in \binom {[r^*]}{2}$
and
 $c \in \phi ^*(ij)$
.
$c \in \phi ^*(ij)$
.
Say that
![]() $\chi $
is bad otherwise. Let
$\chi $
is bad otherwise. Let
![]() $\mathcal {G}=\mathcal {G}(r,\phi ,\mathcal {U})$
be the set of good colourings
$\mathcal {G}=\mathcal {G}(r,\phi ,\mathcal {U})$
be the set of good colourings
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
. We will show that almost every
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
. We will show that almost every
![]() $\chi $
is good. The idea here is that, in every bad colouring
$\chi $
is good. The idea here is that, in every bad colouring
![]() $\chi $
, there is a pair
$\chi $
, there is a pair
![]() $(X_{i^*},X_{j^*})$
in which some colour graph of
$(X_{i^*},X_{j^*})$
in which some colour graph of
![]() $\chi $
is not regular of the correct density. Lemma 4.4 implies that there must be some colour c and large sets
$\chi $
is not regular of the correct density. Lemma 4.4 implies that there must be some colour c and large sets
![]() $X \subseteq X_{i^*}$
and
$X \subseteq X_{i^*}$
and
![]() $Y \subseteq X_{j^*}$
between which
$Y \subseteq X_{j^*}$
between which
![]() $\chi ^{-1}(c)$
has density which is significantly smaller than expected. So there are significantly fewer choices for colouring the edges between this pair, a loss which is quantified by Corollary 4.8.
$\chi ^{-1}(c)$
has density which is significantly smaller than expected. So there are significantly fewer choices for colouring the edges between this pair, a loss which is quantified by Corollary 4.8.
Consider the following procedure for generating a set of colourings of G which (as we will show) includes every bad colouring.
4.5 Bad colouring procedure
-
1. Choose at most
 $3\nu n^2$
edges of G and colour them arbitrarily. For each
$3\nu n^2$
edges of G and colour them arbitrarily. For each
 $i \in [r^*]$
, colour every remaining edge in
$i \in [r^*]$
, colour every remaining edge in
 $G[X_i]$
with colour
$G[X_i]$
with colour
 $1$
.
$1$
. -
2. Pick
 $i^*j^* \in \binom {[r^*]}{2}$
;
$i^*j^* \in \binom {[r^*]}{2}$
;
 $c^* \in \phi ^*(i^*j^*)$
and subsets
$c^* \in \phi ^*(i^*j^*)$
and subsets
 $X \subseteq X_{i^*}$
and
$X \subseteq X_{i^*}$
and
 $Y \subseteq X_{j^*}$
of size
$Y \subseteq X_{j^*}$
of size
 $\lceil \gamma _3|X_{i^*}| \rceil , \lceil \gamma _3|X_{j^*}|\rceil $
, respectively.
$\lceil \gamma _3|X_{i^*}| \rceil , \lceil \gamma _3|X_{j^*}|\rceil $
, respectively. -
3. Choose at most
 $(|\phi ^*(i^*j^*)|^{-1}-\gamma _3/2s)|X||Y|$
edges in
$(|\phi ^*(i^*j^*)|^{-1}-\gamma _3/2s)|X||Y|$
edges in
 $G[X,Y]$
and colour them with colour
$G[X,Y]$
and colour them with colour
 $c^*$
. Arbitrarily colour the remaining edges in
$c^*$
. Arbitrarily colour the remaining edges in
 $G[X,Y]$
with colours from
$G[X,Y]$
with colours from
 $\phi ^*(i^*j^*) \setminus \{ c^* \}$
.
$\phi ^*(i^*j^*) \setminus \{ c^* \}$
. -
4. Arbitrarily colour the remaining edges in
 $G[X_{i^*},X_{j^*}]$
with colours from
$G[X_{i^*},X_{j^*}]$
with colours from
 $\phi ^*(i^*j^*)$
.
$\phi ^*(i^*j^*)$
. -
5. For all
 $ij \in \binom {[r^*]}{2} \setminus \{ i^*j^* \}$
, arbitrarily colour all remaining edges in
$ij \in \binom {[r^*]}{2} \setminus \{ i^*j^* \}$
, arbitrarily colour all remaining edges in
 $G[X_i,X_j]$
using colours from
$G[X_i,X_j]$
using colours from
 $\phi ^*(ij)$
.
$\phi ^*(ij)$
.
Let
![]() $S_{p_1\ldots p_2}$
be the number of choices in steps
$S_{p_1\ldots p_2}$
be the number of choices in steps
![]() $p_1$
–
$p_1$
–
![]() $p_2$
, having fixed choices in previous steps, where
$p_2$
, having fixed choices in previous steps, where
![]() $[p_1,p_2] \subseteq [5]$
.
$[p_1,p_2] \subseteq [5]$
.
Claim 4.2. The number of bad
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
is at most
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
is at most
![]() $S_{1\ldots 5}$
.
$S_{1\ldots 5}$
.
Proof of Claim.
It suffices to show that for any bad
![]() $\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
, there is a set of choices in the bad colouring procedure which generates it. So fix such a
$\chi \in \mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))$
, there is a set of choices in the bad colouring procedure which generates it. So fix such a
![]() $\chi $
. Say that an edge
$\chi $
. Say that an edge
![]() $xy$
is contrary if one of the following holds:
$xy$
is contrary if one of the following holds:
-
(a) at least one of
 $x,y$
is in
$x,y$
is in
 $X_0$
;
$X_0$
; -
(b)
 $\chi (xy) \notin \phi ^*(ij)$
, where
$\chi (xy) \notin \phi ^*(ij)$
, where
 $i \neq j$
and
$i \neq j$
and
 $x \in X_i$
and
$x \in X_i$
and
 $y \in X_j$
;
$y \in X_j$
; -
(c)
 $x,y \in X_i$
and
$x,y \in X_i$
and
 $xy$
is not coloured with colour
$xy$
is not coloured with colour
 $1$
.
$1$
.
By (4.14), the number of edges of type (a) is at most
![]() $|X_0|n \leq 2\nu n^2$
. By Claim 4.1, there at most
$|X_0|n \leq 2\nu n^2$
. By Claim 4.1, there at most
![]() $s\gamma _2 n^2$
edges
$s\gamma _2 n^2$
edges
![]() $xy$
with
$xy$
with
![]() $x \in U_i$
,
$x \in U_i$
,
![]() $y \in U_j$
, such that either
$y \in U_j$
, such that either
![]() $i=j$
, or
$i=j$
, or
![]() $i \neq j$
and
$i \neq j$
and
![]() $\chi (xy) \notin \phi (ij)$
. Combining this with Lemma 3.1
(iii), we see that the number of edges of types (b) and (c) is at most
$\chi (xy) \notin \phi (ij)$
. Combining this with Lemma 3.1
(iii), we see that the number of edges of types (b) and (c) is at most
![]() $s\gamma _2 n^2$
. Therefore, there are at most
$s\gamma _2 n^2$
. Therefore, there are at most
![]() $3\nu n^2$
contrary edges in G. We colour these edges in step 1.
$3\nu n^2$
contrary edges in G. We colour these edges in step 1.
Since
![]() $\chi $
is bad, there is some
$\chi $
is bad, there is some
![]() $i^*j^* \in \binom {[r^*]}{2}$
and
$i^*j^* \in \binom {[r^*]}{2}$
and
![]() $c \in [s]$
, such that
$c \in [s]$
, such that
![]() $\chi ^{-1}(c)[X_{i^*},X_{j^*}]$
is not
$\chi ^{-1}(c)[X_{i^*},X_{j^*}]$
is not
![]() $(\gamma _3,|\phi ^*(i^*j^*)|^{-1})$
-regular. Proposition 4.4 applied with
$(\gamma _3,|\phi ^*(i^*j^*)|^{-1})$
-regular. Proposition 4.4 applied with
![]() $|\phi ^*(i^*j^*)|,X_{i^*},X_{j^*}, \chi ^{-1}(c)[X_{i^*},X_{j^*}],\gamma _3$
playing the roles of
$|\phi ^*(i^*j^*)|,X_{i^*},X_{j^*}, \chi ^{-1}(c)[X_{i^*},X_{j^*}],\gamma _3$
playing the roles of
![]() $r,A,B,G_c,\varepsilon $
implies that there exists
$r,A,B,G_c,\varepsilon $
implies that there exists
![]() $c^* \in [s]$
, such that there are
$c^* \in [s]$
, such that there are
![]() $X \subseteq X_{i^*}$
,
$X \subseteq X_{i^*}$
,
![]() $Y \subseteq X_{j^*}$
with
$Y \subseteq X_{j^*}$
with
![]() $|X| = \lceil \gamma _3 |X_{i^*}| \rceil $
,
$|X| = \lceil \gamma _3 |X_{i^*}| \rceil $
,
![]() $|Y| = \lceil \gamma _3|X_{j^*}|\rceil $
where
$|Y| = \lceil \gamma _3|X_{j^*}|\rceil $
where
So in step 2, we can take
![]() $i^*j^* \in \binom {[r^*]}{2}$
,
$i^*j^* \in \binom {[r^*]}{2}$
,
![]() $c^* \in [s]$
and
$c^* \in [s]$
and
![]() $X \subseteq X_{i^*}$
,
$X \subseteq X_{i^*}$
,
![]() $Y \subseteq X_{j^*}$
and choose a suitable colouring in steps 3 and 4, which will generate
$Y \subseteq X_{j^*}$
and choose a suitable colouring in steps 3 and 4, which will generate
![]() $\chi [X_{i^*},X_{j^*}]$
. The only uncoloured edges are noncontrary edges in
$\chi [X_{i^*},X_{j^*}]$
. The only uncoloured edges are noncontrary edges in
![]() $(X_i,X_j)$
for
$(X_i,X_j)$
for
![]() $ij \in \binom {[r^*]}{2} \setminus \{ i^*j^* \}$
, which can only use colours allowed by
$ij \in \binom {[r^*]}{2} \setminus \{ i^*j^* \}$
, which can only use colours allowed by
![]() $\phi $
, which form a subset of the colours allowed by
$\phi $
, which form a subset of the colours allowed by
![]() $\phi ^*$
, by Lemma 3.1. So we can colour them as in
$\phi ^*$
, by Lemma 3.1. So we can colour them as in
![]() $\chi $
in step 5. This proves that the bad colouring procedure will generate
$\chi $
in step 5. This proves that the bad colouring procedure will generate
![]() $\chi $
. Since
$\chi $
. Since
![]() $\chi $
was an arbitrary bad colouring, the claim is proved.
$\chi $
was an arbitrary bad colouring, the claim is proved.
![]() $\Box $
$\Box $
Therefore, we can give an upper bound for the number of bad colourings by counting the number of steps in the bad colouring procedure.
Claim 4.3.
![]() $ |\mathcal {G}| \geq (1-2^{-\gamma _3^5 n^2})|\mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))|. $
$ |\mathcal {G}| \geq (1-2^{-\gamma _3^5 n^2})|\mathop {\mathrm {RL}}^{-1}((r,\phi ,\mathcal {U}))|. $
Proof of Claim.
By the previous claim, it suffices to bound
![]() $S_{1\ldots 5}$
from above. Then
$S_{1\ldots 5}$
from above. Then
 $$ \begin{align*}S_{12} \leq \binom{n^2}{\leq 3\nu n^2} \cdot s^{3\nu n^2} \cdot \binom{r^*}{2} \cdot s \cdot \binom{|X_{i^*}|}{\leq\lceil \gamma_3|X_{i^*}|\rceil}\binom{|X_{j^*}|}{\leq\lceil \gamma_3|X_{j^*}|\rceil} \stackrel{(4.2)}{\leq} 2^{\gamma_3^6 n^2}.\\[-9pt] \end{align*} $$
$$ \begin{align*}S_{12} \leq \binom{n^2}{\leq 3\nu n^2} \cdot s^{3\nu n^2} \cdot \binom{r^*}{2} \cdot s \cdot \binom{|X_{i^*}|}{\leq\lceil \gamma_3|X_{i^*}|\rceil}\binom{|X_{j^*}|}{\leq\lceil \gamma_3|X_{j^*}|\rceil} \stackrel{(4.2)}{\leq} 2^{\gamma_3^6 n^2}.\\[-9pt] \end{align*} $$
Let
![]() $X \subseteq X_{i^*}$
and
$X \subseteq X_{i^*}$
and
![]() $Y \subseteq X_{j^*}$
be chosen at step 2. Now, (4.13) implies that
$Y \subseteq X_{j^*}$
be chosen at step 2. Now, (4.13) implies that
![]() $|X|,|Y| \geq \gamma _3 \mu n/2$
. Using
$|X|,|Y| \geq \gamma _3 \mu n/2$
. Using
![]() $e(G[X,Y]) \leq |X||Y|$
, we have
$e(G[X,Y]) \leq |X||Y|$
, we have
 $$ \begin{align*} S_{3} &\leq \sum_{i=0}^{\lfloor(|\phi^*(i^*j^*)|^{-1}-\gamma_3/2s)|X||Y|\rfloor}\binom{|X||Y|}{i} \left( |\phi^*(i^*j^*)|-1\right)^{|X||Y|-i}\\ &\leq e^{-\gamma_3^2|X||Y|/12s^2} \cdot |\phi^*(i^*j^*)|^{|X||Y|} \leq e^{-\gamma_3^4\mu^2n^2/48s^2} \cdot |\phi^*(i^*j^*)|^{|X||Y|}.\\[-9pt] \end{align*} $$
$$ \begin{align*} S_{3} &\leq \sum_{i=0}^{\lfloor(|\phi^*(i^*j^*)|^{-1}-\gamma_3/2s)|X||Y|\rfloor}\binom{|X||Y|}{i} \left( |\phi^*(i^*j^*)|-1\right)^{|X||Y|-i}\\ &\leq e^{-\gamma_3^2|X||Y|/12s^2} \cdot |\phi^*(i^*j^*)|^{|X||Y|} \leq e^{-\gamma_3^4\mu^2n^2/48s^2} \cdot |\phi^*(i^*j^*)|^{|X||Y|}.\\[-9pt] \end{align*} $$
where, in the second inequality, we used Corollary 4.8 with
![]() $|X||Y|,|\phi ^*(i^*j^*)|,\gamma _3/2s$
playing the roles of
$|X||Y|,|\phi ^*(i^*j^*)|,\gamma _3/2s$
playing the roles of
![]() $n,k,\delta $
. Therefore
$n,k,\delta $
. Therefore
Let B be the number of bad
![]() $\chi $
. Then, by Claim 4.2,
$\chi $
. Then, by Claim 4.2,
 $$ \begin{align*} \log B &\leq \log S_{1\ldots 5} \leq \log \left( 2^{\gamma_3^6n^2} \cdot e^{-\gamma_3^4\mu^2n^2/48s^2} \cdot s^{4\varepsilon n^2} \prod_{ij \in \binom{[r^*]}{2}} |\phi^*(ij)|^{|X_i||X_j|} \right)\\ &\leq \gamma_3^6 n^2 - \frac{\log e \cdot \gamma_3^4 \mu^2 n^2}{48s^2} + \log s \cdot 4\varepsilon n^2 + \sum_{ij \in \binom{[r^*]}{2}} |X_i||X_j|\log|\phi^*(ij)|\\ &\stackrel{(4.12)}{\leq} -4\gamma_3^5 n^2 + \frac{q(\phi^*,\boldsymbol{x})n^2}{2} \leq -4\gamma_3^5 n^2 + \left(q(\phi^*,\boldsymbol{\alpha}^*) + 2\log s\|\boldsymbol{x}-\boldsymbol{\alpha}^*\|_1 \right) \frac{n^2}{2}\\ &\stackrel{(4.10)}{\leq} Q(\boldsymbol{k})\binom{n}{2} - 3\gamma_3^5 n^2, \end{align*} $$
$$ \begin{align*} \log B &\leq \log S_{1\ldots 5} \leq \log \left( 2^{\gamma_3^6n^2} \cdot e^{-\gamma_3^4\mu^2n^2/48s^2} \cdot s^{4\varepsilon n^2} \prod_{ij \in \binom{[r^*]}{2}} |\phi^*(ij)|^{|X_i||X_j|} \right)\\ &\leq \gamma_3^6 n^2 - \frac{\log e \cdot \gamma_3^4 \mu^2 n^2}{48s^2} + \log s \cdot 4\varepsilon n^2 + \sum_{ij \in \binom{[r^*]}{2}} |X_i||X_j|\log|\phi^*(ij)|\\ &\stackrel{(4.12)}{\leq} -4\gamma_3^5 n^2 + \frac{q(\phi^*,\boldsymbol{x})n^2}{2} \leq -4\gamma_3^5 n^2 + \left(q(\phi^*,\boldsymbol{\alpha}^*) + 2\log s\|\boldsymbol{x}-\boldsymbol{\alpha}^*\|_1 \right) \frac{n^2}{2}\\ &\stackrel{(4.10)}{\leq} Q(\boldsymbol{k})\binom{n}{2} - 3\gamma_3^5 n^2, \end{align*} $$
where the penultimate inequality follows from Proposition 2.2 (here, we also define
![]() $q(\phi ^*,\boldsymbol {x})$
as in (1.4) even though
$q(\phi ^*,\boldsymbol {x})$
as in (1.4) even though
![]() $x_1+\ldots +x_{r^*} \leq 1$
, as opposed to equal to
$x_1+\ldots +x_{r^*} \leq 1$
, as opposed to equal to
![]() $1$
). Therefore
$1$
). Therefore
 $$ \begin{align*} \log B &\leq Q(\boldsymbol{k})\binom{n}{2}-3\gamma_3^5 n^2 \stackrel{(4.4)}{\leq} \left( \log F(G;\boldsymbol{k}) + \varepsilon\binom{n}{2} \right) - 3\gamma_3^5 n^2\\ &\leq \log F(G;\boldsymbol{k}) - 2\gamma_3^5 n^2 \stackrel{(4.5)}{\leq} \log |\textstyle{\mathop{\mathrm{RL}}^{-1}}((r,\phi,\mathcal{U}))| - \gamma_3^5 n^2. \end{align*} $$
$$ \begin{align*} \log B &\leq Q(\boldsymbol{k})\binom{n}{2}-3\gamma_3^5 n^2 \stackrel{(4.4)}{\leq} \left( \log F(G;\boldsymbol{k}) + \varepsilon\binom{n}{2} \right) - 3\gamma_3^5 n^2\\ &\leq \log F(G;\boldsymbol{k}) - 2\gamma_3^5 n^2 \stackrel{(4.5)}{\leq} \log |\textstyle{\mathop{\mathrm{RL}}^{-1}}((r,\phi,\mathcal{U}))| - \gamma_3^5 n^2. \end{align*} $$
The claim now follows.
We would now like to adjust our partition
![]() $V(G) = X_0 \cup \ldots \cup X_{r^*}$
so that
$V(G) = X_0 \cup \ldots \cup X_{r^*}$
so that
![]() $X_0 = \emptyset $
and
$X_0 = \emptyset $
and
![]() $|\,|X_i|-\alpha ^*_i n\,| \leq 1$
for all
$|\,|X_i|-\alpha ^*_i n\,| \leq 1$
for all
![]() $i \in [r^*]$
, and the other properties we have proved are maintained (with slightly weaker parameters). Clearly
$i \in [r^*]$
, and the other properties we have proved are maintained (with slightly weaker parameters). Clearly
 $$ \begin{align} \|\boldsymbol{\alpha^*}-\boldsymbol{x}\|_1 = \sum_{x_i < \alpha^*_i}(\alpha^*_i-x_i) + \sum_{x_i \geq \alpha^*_i}(x_i-\alpha^*_i). \end{align} $$
$$ \begin{align} \|\boldsymbol{\alpha^*}-\boldsymbol{x}\|_1 = \sum_{x_i < \alpha^*_i}(\alpha^*_i-x_i) + \sum_{x_i \geq \alpha^*_i}(x_i-\alpha^*_i). \end{align} $$
For each
![]() $i \in [r^*]$
, let
$i \in [r^*]$
, let
![]() $w_i := \min \{ \alpha ^*_i,x_i \}$
(recall from (4.12) that
$w_i := \min \{ \alpha ^*_i,x_i \}$
(recall from (4.12) that
![]() $x_i = |X_i|/n$
). Choose
$x_i = |X_i|/n$
). Choose
![]() $|X_i| - \lfloor w_i n \rfloor $
vertices from each
$|X_i| - \lfloor w_i n \rfloor $
vertices from each
![]() $X_i$
with
$X_i$
with
![]() $i \in [r^*]$
, and choose every vertex in
$i \in [r^*]$
, and choose every vertex in
![]() $X_0$
. Distribute them among the remainders of the
$X_0$
. Distribute them among the remainders of the
![]() $X_j$
,
$X_j$
,
![]() $j \in [r^*]$
, to create a new partition
$j \in [r^*]$
, to create a new partition
![]() $V(G) = Y_1 \cup \ldots \cup Y_{r^*}$
, such that
$V(G) = Y_1 \cup \ldots \cup Y_{r^*}$
, such that
![]() $|\,|Y_i|-\alpha ^*_i n\,| \leq 1$
for all
$|\,|Y_i|-\alpha ^*_i n\,| \leq 1$
for all
![]() $i \in [r^*]$
. This partition satisfies Theorem 1.4
(i).
$i \in [r^*]$
. This partition satisfies Theorem 1.4
(i).
Recall Definition 4.9. For every
![]() $(r',\phi ',\mathcal {U}') \in \mathrm {Pop}(G)$
, define
$(r',\phi ',\mathcal {U}') \in \mathrm {Pop}(G)$
, define
![]() $\mathcal {G}(r',\phi ',\mathcal {U}')$
in analogy with
$\mathcal {G}(r',\phi ',\mathcal {U}')$
in analogy with
![]() $\mathcal {G}$
(defined with respect to
$\mathcal {G}$
(defined with respect to
![]() $(r,\phi ,\mathcal {U})$
). Since
$(r,\phi ,\mathcal {U})$
). Since
![]() $(r,\phi ,\mathcal {U}) \in \mathrm {Pop}(G)$
chosen at the beginning of the proof was arbitrary,
$(r,\phi ,\mathcal {U}) \in \mathrm {Pop}(G)$
chosen at the beginning of the proof was arbitrary,
 $$ \begin{align*} \sum_{(r',\phi',\mathcal{U}') \in \mathrm{Pop}(G)} |\mathcal{G}(r',\phi',\mathcal{U}')| &\geq \left(1 - 2^{-\gamma_3^5 n^2} \right) \sum_{(r',\phi',\mathcal{U}') \in \mathrm{Pop}(G)} |\textstyle{\mathop{\mathrm{RL}}^{-1}}((r',\phi',\mathcal{U}'))|\\ &= \left(1 - 2^{-\gamma_3^5 n^2} \right) |\mathrm{Col}(G)| \geq \left(1 - 2^{-\gamma_3^5 n^2} \right)(1-2^{-2\varepsilon n^2}) \cdot F(G;\boldsymbol{k})\\ &\geq \left(1 - 2^{-\varepsilon n^2} \right) \cdot F(G;\boldsymbol{k}), \end{align*} $$
$$ \begin{align*} \sum_{(r',\phi',\mathcal{U}') \in \mathrm{Pop}(G)} |\mathcal{G}(r',\phi',\mathcal{U}')| &\geq \left(1 - 2^{-\gamma_3^5 n^2} \right) \sum_{(r',\phi',\mathcal{U}') \in \mathrm{Pop}(G)} |\textstyle{\mathop{\mathrm{RL}}^{-1}}((r',\phi',\mathcal{U}'))|\\ &= \left(1 - 2^{-\gamma_3^5 n^2} \right) |\mathrm{Col}(G)| \geq \left(1 - 2^{-\gamma_3^5 n^2} \right)(1-2^{-2\varepsilon n^2}) \cdot F(G;\boldsymbol{k})\\ &\geq \left(1 - 2^{-\varepsilon n^2} \right) \cdot F(G;\boldsymbol{k}), \end{align*} $$
where we used Claim 4.3 and Proposition 4.10 in the first and third inequalities, respectively. Therefore, to prove the remainder of Theorem 1.4, it suffices to show that every
![]() $\chi \in \mathcal {G}$
satisfies (ii) and (iii).
$\chi \in \mathcal {G}$
satisfies (ii) and (iii).
So we will now fix
![]() $\chi \in \mathcal {G}$
. Then the number of vertices which do not lie in
$\chi \in \mathcal {G}$
. Then the number of vertices which do not lie in
![]() $X_i \cap Y_i$
for any
$X_i \cap Y_i$
for any
![]() $i \in [r^*]$
is
$i \in [r^*]$
is
 $$ \begin{align*} n - \sum_{i \in [r^*]}|X_i \cap Y_i| &\leq n - \sum_{x_i < \alpha^*_i}|X_i| - \sum_{x_i \geq \alpha^*_i}\lfloor \alpha^*_i n \rfloor\\ &\leq n + \sum_{x_i < \alpha^*_i} (\alpha^*_i n - |X_i|) + \sum_{x_i \geq \alpha^*_i}(|X_i|-\alpha^*_i n) - \sum_{x_i < \alpha^*_i}\alpha^*_in - \sum_{x_i \geq \alpha^*_i}|X_i| + R(\boldsymbol{k})\\ &\stackrel{(4.16)}{\leq} n + \|\boldsymbol{\alpha}^*-\boldsymbol{x}\|_1 n - \sum_{i \in [r^*]}\alpha^*_i n + R(\boldsymbol{k}) \stackrel{(4.10)}{\leq} 2\nu n + R(\boldsymbol{k}) \leq 3\nu n. \end{align*} $$
$$ \begin{align*} n - \sum_{i \in [r^*]}|X_i \cap Y_i| &\leq n - \sum_{x_i < \alpha^*_i}|X_i| - \sum_{x_i \geq \alpha^*_i}\lfloor \alpha^*_i n \rfloor\\ &\leq n + \sum_{x_i < \alpha^*_i} (\alpha^*_i n - |X_i|) + \sum_{x_i \geq \alpha^*_i}(|X_i|-\alpha^*_i n) - \sum_{x_i < \alpha^*_i}\alpha^*_in - \sum_{x_i \geq \alpha^*_i}|X_i| + R(\boldsymbol{k})\\ &\stackrel{(4.16)}{\leq} n + \|\boldsymbol{\alpha}^*-\boldsymbol{x}\|_1 n - \sum_{i \in [r^*]}\alpha^*_i n + R(\boldsymbol{k}) \stackrel{(4.10)}{\leq} 2\nu n + R(\boldsymbol{k}) \leq 3\nu n. \end{align*} $$
Therefore
So, for all
![]() $i \in [r^*]$
, our choice of
$i \in [r^*]$
, our choice of
![]() $\mu $
in (4.3) implies that
$\mu $
in (4.3) implies that
![]() $|X_i \bigtriangleup Y_i| \leq 6\nu n \leq 7\nu |Y_i|/\mu $
. Now Proposition 4.5 implies that
$|X_i \bigtriangleup Y_i| \leq 6\nu n \leq 7\nu |Y_i|/\mu $
. Now Proposition 4.5 implies that
![]() $\chi ^{-1}(c)[Y_i,Y_j]$
is
$\chi ^{-1}(c)[Y_i,Y_j]$
is
![]() $(\gamma _4,|\phi ^*(ij)|^{-1})$
-regular. So
$(\gamma _4,|\phi ^*(ij)|^{-1})$
-regular. So
![]() $\chi $
satisfies Theorem 1.4
(ii).
$\chi $
satisfies Theorem 1.4
(ii).
We will now show that
![]() $\chi $
satisfies Theorem 1.4
(iii). Assume that
$\chi $
satisfies Theorem 1.4
(iii). Assume that
We have that
 $$\begin{align*} &\phantom{+} \hspace{-4cm} + \sum_{i \in [r^*]}(e_G(X_i)-|\chi^{-1}(1)[X_i]|) + \sum_{i \in [r^*]}(|\chi^{-1}(1)[X_i]| -|\chi^{-1}(1)[Y_i]|) \nonumber \\ &\stackrel{(4.15),(4.17)}{\leq} 2 \cdot 6\nu n\cdot n + 3\nu n^2 = 15\nu n^2. \nonumber \end{align*}$$
$$\begin{align*} &\phantom{+} \hspace{-4cm} + \sum_{i \in [r^*]}(e_G(X_i)-|\chi^{-1}(1)[X_i]|) + \sum_{i \in [r^*]}(|\chi^{-1}(1)[X_i]| -|\chi^{-1}(1)[Y_i]|) \nonumber \\ &\stackrel{(4.15),(4.17)}{\leq} 2 \cdot 6\nu n\cdot n + 3\nu n^2 = 15\nu n^2. \nonumber \end{align*}$$
For each
![]() $i \in [r^*]$
, do the following (independently). Let
$i \in [r^*]$
, do the following (independently). Let
![]() $M_{\gamma _5}$
be the integer output of Theorem 4.2 applied with
$M_{\gamma _5}$
be the integer output of Theorem 4.2 applied with
![]() $\gamma _5,1,1$
playing the roles of
$\gamma _5,1,1$
playing the roles of
![]() $\varepsilon ,s,M'$
. Recall that
$\varepsilon ,s,M'$
. Recall that
![]() $|Y_i| \geq \mu n/2> M_{\gamma _5}$
. Apply Theorem 4.2 to the monochromatic graph
$|Y_i| \geq \mu n/2> M_{\gamma _5}$
. Apply Theorem 4.2 to the monochromatic graph
![]() $\chi ^{-1}(1)[Y_i]$
, with parameter
$\chi ^{-1}(1)[Y_i]$
, with parameter
![]() $\gamma _5$
. Thus, obtain an equitable partition
$\gamma _5$
. Thus, obtain an equitable partition
![]() $Y_i = Z_{i,1}\cup \ldots \cup Z_{i,n_i}$
with
$Y_i = Z_{i,1}\cup \ldots \cup Z_{i,n_i}$
with
![]() $1/\gamma _5 \leq n_i \leq M_{\gamma _5}$
which is
$1/\gamma _5 \leq n_i \leq M_{\gamma _5}$
which is
![]() $\gamma _5$
-regular with respect to
$\gamma _5$
-regular with respect to
![]() $\chi ^{-1}(1)[Y_i]$
. For each
$\chi ^{-1}(1)[Y_i]$
. For each
![]() $i \in [r^*]$
and
$i \in [r^*]$
and
![]() $j \in [n_i]$
, we have that
$j \in [n_i]$
, we have that
![]() $|Z_{i,j}|/|Y_i| \geq M_{\gamma _5}^{-1}/2 \geq \gamma _4/\gamma _5$
. Proposition 4.3 now implies that, whenever
$|Z_{i,j}|/|Y_i| \geq M_{\gamma _5}^{-1}/2 \geq \gamma _4/\gamma _5$
. Proposition 4.3 now implies that, whenever
![]() $1 \in \phi ^*(ii')$
, we have that
$1 \in \phi ^*(ii')$
, we have that
![]() $\chi ^{-1}(1)[Z_{i,j},Z_{i',j'}]$
is
$\chi ^{-1}(1)[Z_{i,j},Z_{i',j'}]$
is
![]() $(\gamma _5,|\phi ^*(ii')|^{-1})$
-regular. Now, for each
$(\gamma _5,|\phi ^*(ii')|^{-1})$
-regular. Now, for each
![]() $i \in [r^*]$
, we will remove any edge
$i \in [r^*]$
, we will remove any edge
![]() $xy$
from
$xy$
from
![]() $\chi ^{-1}(1)[Y_i]$
with
$\chi ^{-1}(1)[Y_i]$
with
![]() $x \in Z_{i,j}$
and
$x \in Z_{i,j}$
and
![]() $y \in Z_{i,j'}$
, such that either
$y \in Z_{i,j'}$
, such that either
![]() $\chi ^{-1}(1)[Z_{i,j},Z_{i,j'}]$
is not
$\chi ^{-1}(1)[Z_{i,j},Z_{i,j'}]$
is not
![]() $(\gamma _5,\geq \! \gamma _6)$
-regular; or
$(\gamma _5,\geq \! \gamma _6)$
-regular; or
![]() $j=j'$
. Let
$j=j'$
. Let
![]() $G'[Y_i]$
be the graph obtained after these removals. Now,
$G'[Y_i]$
be the graph obtained after these removals. Now,
 $$ \begin{align} \nonumber \sum_{i \in [r^*]} (e_G(Y_i) - e_{G'}(Y_i)) &\stackrel{(4.19)}{\leq} 15 \nu n^2 + \sum_{i \in [r^*]} \gamma_5\binom{n_i}{2}\left\lceil \frac{|Y_i|}{n_i} \right\rceil^2 + \sum_{i \in [r^*]}\gamma_6 \binom{n_i}{2} \left\lceil \frac{|Y_i|}{n_i} \right\rceil^2\\ \nonumber &\phantom{+} \hspace{2cm} + \sum_{i \in [r^*]}\left\lceil \frac{|Y_i|}{n_i} \right\rceil^2\\ &\leq 15\nu n^2 + \gamma_5 n^2/2 + \gamma_6 n^2/2 + \gamma_5 n^2 \leq \gamma_6 n^2. \end{align} $$
$$ \begin{align} \nonumber \sum_{i \in [r^*]} (e_G(Y_i) - e_{G'}(Y_i)) &\stackrel{(4.19)}{\leq} 15 \nu n^2 + \sum_{i \in [r^*]} \gamma_5\binom{n_i}{2}\left\lceil \frac{|Y_i|}{n_i} \right\rceil^2 + \sum_{i \in [r^*]}\gamma_6 \binom{n_i}{2} \left\lceil \frac{|Y_i|}{n_i} \right\rceil^2\\ \nonumber &\phantom{+} \hspace{2cm} + \sum_{i \in [r^*]}\left\lceil \frac{|Y_i|}{n_i} \right\rceil^2\\ &\leq 15\nu n^2 + \gamma_5 n^2/2 + \gamma_6 n^2/2 + \gamma_5 n^2 \leq \gamma_6 n^2. \end{align} $$
Observe that for every
![]() $i \in [r^*]$
, every edge in
$i \in [r^*]$
, every edge in
![]() $G'[Y_i]$
is coloured with colour
$G'[Y_i]$
is coloured with colour
![]() $1$
by
$1$
by
![]() $\chi $
, and lies in a
$\chi $
, and lies in a
![]() $(\gamma _5, \geq \! \gamma _6)$
-regular pair. Let
$(\gamma _5, \geq \! \gamma _6)$
-regular pair. Let
![]() $J_i$
be the graph on vertex set
$J_i$
be the graph on vertex set
![]() $[n_i]$
in which
$[n_i]$
in which
![]() $jj'$
is an edge if and only if
$jj'$
is an edge if and only if
![]() $\chi ^{-1}(1)[Z_{i,j},Z_{i,j'}]$
is a
$\chi ^{-1}(1)[Z_{i,j},Z_{i,j'}]$
is a
![]() $(\gamma _5,\geq \!\gamma _6)$
-regular pair. Let
$(\gamma _5,\geq \!\gamma _6)$
-regular pair. Let
![]() $\omega _i := \omega (J_i)$
be the size of a maximal clique in
$\omega _i := \omega (J_i)$
be the size of a maximal clique in
![]() $J_i$
, and let
$J_i$
, and let
![]() $\boldsymbol {\omega } := (\omega _1,\ldots ,\omega _{r^*})$
.
$\boldsymbol {\omega } := (\omega _1,\ldots ,\omega _{r^*})$
.
Claim 4.4.
![]() $ \boldsymbol {\omega } \in \{ \boldsymbol {1} \} \cup \{ \boldsymbol {\ell } \in \mathbb {N}^{r^*} : \|\boldsymbol {\ell }\|_1 \leq k_1-1 \}. $
$ \boldsymbol {\omega } \in \{ \boldsymbol {1} \} \cup \{ \boldsymbol {\ell } \in \mathbb {N}^{r^*} : \|\boldsymbol {\ell }\|_1 \leq k_1-1 \}. $
Proof of Claim.
Without loss of generality, we may suppose that, for each
![]() $i \in [r^*]$
,
$i \in [r^*]$
,
![]() $Z_{i,1},\ldots ,Z_{i,\omega _{i}}$
span a clique in
$Z_{i,1},\ldots ,Z_{i,\omega _{i}}$
span a clique in
![]() $J_i$
. Let H be the graph with vertex set
$J_i$
. Let H be the graph with vertex set
![]() $\{ (i,j) : i \in [r^*], j \in [\omega _{i}] \}$
in which
$\{ (i,j) : i \in [r^*], j \in [\omega _{i}] \}$
in which
![]() $\{(i,j),(i',j')\}$
is an edge if
$\{(i,j),(i',j')\}$
is an edge if
![]() $i=i'$
; or
$i=i'$
; or
![]() $i \neq i'$
and
$i \neq i'$
and
![]() $1 \in \phi^* (ii')$
. Then (recalling Definition 2.4)
$1 \in \phi^* (ii')$
. Then (recalling Definition 2.4)
Suppose that H contains a copy of
![]() $K_{k_1}$
. Observe that, for every
$K_{k_1}$
. Observe that, for every
![]() $\{(i,j),(i',j')\} \in E(H)$
, we have that
$\{(i,j),(i',j')\} \in E(H)$
, we have that
![]() $\chi ^{-1}(1)[Z_{i,j},Z_{i',j'}]$
is
$\chi ^{-1}(1)[Z_{i,j},Z_{i',j'}]$
is
![]() $(\gamma _5,\geq \! \gamma _6)$
-regular. Lemma 4.6 and our choice of parameters implies that
$(\gamma _5,\geq \! \gamma _6)$
-regular. Lemma 4.6 and our choice of parameters implies that
![]() $G'$
contains a
$G'$
contains a
![]() $K_{k_1}$
of colour
$K_{k_1}$
of colour
![]() $1$
, a contradiction. Therefore,
$1$
, a contradiction. Therefore,
![]() $(\omega _1,\ldots ,\omega _{r^*}) \in \mathop {\mathrm {Cap}}((\phi ^*)^{-1}(1),k_1)$
, and Lemma 2.5 proves the claim.
$(\omega _1,\ldots ,\omega _{r^*}) \in \mathop {\mathrm {Cap}}((\phi ^*)^{-1}(1),k_1)$
, and Lemma 2.5 proves the claim.
For each
![]() $i \in [r^*]$
, let
$i \in [r^*]$
, let
![]() $\ell _i$
be such that
$\ell _i$
be such that
![]() $G[Y_i]$
is
$G[Y_i]$
is
![]() $\delta $
-far from being
$\delta $
-far from being
![]() $K_{\ell _i}$
-free. Then, by (4.20),
$K_{\ell _i}$
-free. Then, by (4.20),
![]() $G'[Y_i]$
is
$G'[Y_i]$
is
![]() $(\delta /2)$
-far from being
$(\delta /2)$
-far from being
![]() $K_{\ell _i}$
-free. So we can remove
$K_{\ell _i}$
-free. So we can remove
![]() $\delta |Y_i|^2/3$
edges from
$\delta |Y_i|^2/3$
edges from
![]() $G'[Y_i]$
, and there will still be a copy T of
$G'[Y_i]$
, and there will still be a copy T of
![]() $K_{\ell _i}$
. But, by the definition of
$K_{\ell _i}$
. But, by the definition of
![]() $G'[Y_i]$
, every edge in T lies in a pair
$G'[Y_i]$
, every edge in T lies in a pair
![]() $(Z_{i,j},Z_{i,j'})$
which is
$(Z_{i,j},Z_{i,j'})$
which is
![]() $(\gamma _5,\geq \! \gamma _6)$
-regular. Thus,
$(\gamma _5,\geq \! \gamma _6)$
-regular. Thus,
![]() $J_i$
contains a copy of
$J_i$
contains a copy of
![]() $K_{\ell _i}$
, and so
$K_{\ell _i}$
, and so
![]() $\ell _i \leq \omega _i$
. Therefore
$\ell _i \leq \omega _i$
. Therefore
![]() $\boldsymbol {\ell } = \boldsymbol {1}$
, or
$\boldsymbol {\ell } = \boldsymbol {1}$
, or
![]() $\|\boldsymbol {\ell }\|_1 \leq k_1-1$
.
$\|\boldsymbol {\ell }\|_1 \leq k_1-1$
.
We claim that our assumption (4.18) means that the first alternative cannot hold. Indeed, (4.18) and (4.20) imply that
![]() $\sum _{i \in [r^*]}e_{G'}(Y_i) \geq (\sqrt {\gamma _6}-\gamma _6) n^2$
. So there is some
$\sum _{i \in [r^*]}e_{G'}(Y_i) \geq (\sqrt {\gamma _6}-\gamma _6) n^2$
. So there is some
![]() $i \in [r^*]$
with
$i \in [r^*]$
with
![]() $e_{G'}(Y_i) \geq (\sqrt {\gamma _6}-\gamma _6)n^2/R(\boldsymbol {k})> 0$
. Thus,
$e_{G'}(Y_i) \geq (\sqrt {\gamma _6}-\gamma _6)n^2/R(\boldsymbol {k})> 0$
. Thus,
![]() $J_i$
contains at least one edge, and so
$J_i$
contains at least one edge, and so
![]() $\omega _i \geq 2$
. We have proved that
$\omega _i \geq 2$
. We have proved that
![]() $\|\boldsymbol {\ell }\|_1 \leq k_1-1$
as required. This together with Lemma 2.9 further implies that
$\|\boldsymbol {\ell }\|_1 \leq k_1-1$
as required. This together with Lemma 2.9 further implies that
![]() $\boldsymbol {k}$
does not have the strong extension property. This completes the proof that
$\boldsymbol {k}$
does not have the strong extension property. This completes the proof that
![]() $\chi $
satisfies Theorem 1.4
(iii).
$\chi $
satisfies Theorem 1.4
(iii).
We end this section with a proof of Corollary 1.5, a stability theorem for
![]() $\boldsymbol {k}$
with the strong extension property.
$\boldsymbol {k}$
with the strong extension property.
Proof of Corollary 1.5.
Let
![]() $\delta> 0$
. Let
$\delta> 0$
. Let
![]() $\varepsilon $
be the output of Theorem 1.4 applied with parameter
$\varepsilon $
be the output of Theorem 1.4 applied with parameter
![]() $\delta ' \leq \delta /(5s),\mu /10$
, where
$\delta ' \leq \delta /(5s),\mu /10$
, where
![]() $\mu $
is the output of Lemma 2.8. Now let G be a graph on
$\mu $
is the output of Lemma 2.8. Now let G be a graph on
![]() $n \geq n_0$
vertices, such that
$n \geq n_0$
vertices, such that
![]() $\log F(G;\boldsymbol {k})/\binom {n}{2} \geq Q(\boldsymbol {k})-\varepsilon $
.
$\log F(G;\boldsymbol {k})/\binom {n}{2} \geq Q(\boldsymbol {k})-\varepsilon $
.
Let
![]() be such that at least one of the specified
be such that at least one of the specified
![]() $(1-2^{-\varepsilon n^2}) \cdot F(n;\boldsymbol {k})$
colourings is associated with this triple by Theorem 1.4. Let
$(1-2^{-\varepsilon n^2}) \cdot F(n;\boldsymbol {k})$
colourings is associated with this triple by Theorem 1.4. Let
![]() $Y_1, \ldots , Y_{r^*}$
be the partition of
$Y_1, \ldots , Y_{r^*}$
be the partition of
![]() $V(G)$
given by (i). Writing
$V(G)$
given by (i). Writing
![]() $K_{\boldsymbol {\alpha }^*}(n)$
for the n-vertex complete partite graph whose ith part has size
$K_{\boldsymbol {\alpha }^*}(n)$
for the n-vertex complete partite graph whose ith part has size
![]() $\alpha _i^* n \pm 1$
, we have
$\alpha _i^* n \pm 1$
, we have
 $$ \begin{align} d_{\text{edit}}(G,K_{\boldsymbol{\alpha}^*}(n)) \leq \sum_{ij \in \binom{[r^*]}{2}}e(\overline{G}[V_i,V_j]) + \sum_{i \in [r^*]}e(G[V_i]). \end{align} $$
$$ \begin{align} d_{\text{edit}}(G,K_{\boldsymbol{\alpha}^*}(n)) \leq \sum_{ij \in \binom{[r^*]}{2}}e(\overline{G}[V_i,V_j]) + \sum_{i \in [r^*]}e(G[V_i]). \end{align} $$
Now, Part (ii) of Theorem 1.4 implies that, for all
![]() $ij \in \binom {[r^*]}{2}$
, we have that
$ij \in \binom {[r^*]}{2}$
, we have that
 $$ \begin{align*}e(G[V_i,V_j]) \geq \sum_{c \in \phi^*(ij)}|\chi^{-1}(c)[V_i,V_j]| \geq \sum_{c \in \phi^*(ij)}\left(\phi^*(ij)^{-1}-\delta'\right)|V_i||V_j| \geq \left(1-s\delta'\right)|V_i||V_j|. \end{align*} $$
$$ \begin{align*}e(G[V_i,V_j]) \geq \sum_{c \in \phi^*(ij)}|\chi^{-1}(c)[V_i,V_j]| \geq \sum_{c \in \phi^*(ij)}\left(\phi^*(ij)^{-1}-\delta'\right)|V_i||V_j| \geq \left(1-s\delta'\right)|V_i||V_j|. \end{align*} $$
So
 $$ \begin{align*}\sum_{ij \in \binom{[r^*]}{2}}e(\overline{G}[V_i,V_j]) \leq \frac{\delta}{5}\cdot\sum_{ij \in \binom{[r^*]}{2}}|V_i||V_j| \leq \frac{\delta n^2}{10}. \end{align*} $$
$$ \begin{align*}\sum_{ij \in \binom{[r^*]}{2}}e(\overline{G}[V_i,V_j]) \leq \frac{\delta}{5}\cdot\sum_{ij \in \binom{[r^*]}{2}}|V_i||V_j| \leq \frac{\delta n^2}{10}. \end{align*} $$
Finally, by Part (iii) of Theorem 1.4,
![]() $ \sum _{i \in [r^*]}e(G[V_i]) \leq \delta n^2/(5s) $
. Together with (4.21), we have
$ \sum _{i \in [r^*]}e(G[V_i]) \leq \delta n^2/(5s) $
. Together with (4.21), we have
![]() $d_{\text {edit}}(G,K_{\boldsymbol {\alpha }^*}(n)) \leq \delta n^2/5$
. Suppose
$d_{\text {edit}}(G,K_{\boldsymbol {\alpha }^*}(n)) \leq \delta n^2/5$
. Suppose
![]() $(r,\phi ,\boldsymbol {\alpha })$
is another triple associated with one of the specified colourings. Then
$(r,\phi ,\boldsymbol {\alpha })$
is another triple associated with one of the specified colourings. Then
![]() $\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \cdot n^2/2 + o(n^2) \leq d_{\text {edit}}(K_{\boldsymbol {\alpha }}(n),K_{\boldsymbol {\alpha }^*}(n)) \leq 2\delta n^2/5$
. Moreover, each entry of
$\|\boldsymbol {\alpha }-\boldsymbol {\alpha }^*\|_1 \cdot n^2/2 + o(n^2) \leq d_{\text {edit}}(K_{\boldsymbol {\alpha }}(n),K_{\boldsymbol {\alpha }^*}(n)) \leq 2\delta n^2/5$
. Moreover, each entry of
![]() $\boldsymbol {\alpha }$
and
$\boldsymbol {\alpha }$
and
![]() $\boldsymbol {\alpha }^*$
is at least
$\boldsymbol {\alpha }^*$
is at least
![]() $\mu $
by Lemma 2.8, and the above inequality can only be satisfied if
$\mu $
by Lemma 2.8, and the above inequality can only be satisfied if
![]() $r=r^*$
. This completes the proof.
$r=r^*$
. This completes the proof.
5 Applications
5.1 Recovering some previous results
Previous works [Reference Alon, Balogh, Keevash and Sudakov1, Reference Pikhurko and Yilma25] have (implicitly) solved the optimisation problem by solving a linear program with real variables
![]() $\boldsymbol {x}=(x_1,\ldots ,x_t)$
, such that any
$\boldsymbol {x}=(x_1,\ldots ,x_t)$
, such that any
![]() corresponds to some feasible
corresponds to some feasible
![]() $\boldsymbol {x}$
(but not necessarily vice versa). If, for every optimal
$\boldsymbol {x}$
(but not necessarily vice versa). If, for every optimal
![]() $\boldsymbol {x}$
, there is some
$\boldsymbol {x}$
, there is some
![]() which corresponds to it, then this triple is a basic optimal solution. Unfortunately, for all but a few small cases, the optimal solutions of the linear program do not correspond to a feasible triple.
which corresponds to it, then this triple is a basic optimal solution. Unfortunately, for all but a few small cases, the optimal solutions of the linear program do not correspond to a feasible triple.
We define a ‘basic’ linear program, to which we will then add extra constraints.
Problem L: Given a sequence
![]() $\boldsymbol {k}:=(k_1,\ldots ,k_s)\in \mathbb {N}^s$
of natural numbers, determine
$\boldsymbol {k}:=(k_1,\ldots ,k_s)\in \mathbb {N}^s$
of natural numbers, determine
![]() $\ell ^{\mathrm {max}}(\boldsymbol {k}) := \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d})$
, the maximum value of
$\ell ^{\mathrm {max}}(\boldsymbol {k}) := \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d})$
, the maximum value of
over the set
![]() $D(\boldsymbol {k})$
of tuples
$D(\boldsymbol {k})$
of tuples
![]() $\boldsymbol {d}=(d_2,\ldots ,d_s)$
, such that
$\boldsymbol {d}=(d_2,\ldots ,d_s)$
, such that
![]() $0 \leq d_t \leq 1$
for all
$0 \leq d_t \leq 1$
for all
![]() $2 \leq t \leq s$
, and
$2 \leq t \leq s$
, and
![]() $\sum _{2 \leq t \leq s}td_t \leq \sum _{c \in [s]}\left (1-(k_c-1)^{-1}\right )$
.
$\sum _{2 \leq t \leq s}td_t \leq \sum _{c \in [s]}\left (1-(k_c-1)^{-1}\right )$
.
Say that
![]() $\boldsymbol {d}$
which is feasible for Problem L is realisable if there is some
$\boldsymbol {d}$
which is feasible for Problem L is realisable if there is some
![]() with
with
 $$ \begin{align} d_t=2\sum_{ij \in \binom{[r]}{2}:|\phi(ij)|=t}\alpha_i \alpha_j\quad \text{for all }2 \leq t \leq s \end{align} $$
$$ \begin{align} d_t=2\sum_{ij \in \binom{[r]}{2}:|\phi(ij)|=t}\alpha_i \alpha_j\quad \text{for all }2 \leq t \leq s \end{align} $$
and call such a feasible triple a realisation (of
![]() $\boldsymbol {d}$
).
$\boldsymbol {d}$
).
Lemma 5.1. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}$
. Then
$\boldsymbol {k} \in \mathbb {N}$
. Then
![]() $Q(\boldsymbol {k}) \leq \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d})$
. Moreover, the following is true. Suppose that at least one optimal solution
$Q(\boldsymbol {k}) \leq \max _{\boldsymbol {d} \in D(\boldsymbol {k})}\ell (\boldsymbol {d})$
. Moreover, the following is true. Suppose that at least one optimal solution
![]() $\boldsymbol {d}$
to Problem L is realisable. Then
$\boldsymbol {d}$
to Problem L is realisable. Then
![]() $\max _{\boldsymbol {d}\in D(\boldsymbol {k})}\ell (\boldsymbol {d})=Q(\boldsymbol {k})$
and
$\max _{\boldsymbol {d}\in D(\boldsymbol {k})}\ell (\boldsymbol {d})=Q(\boldsymbol {k})$
and
![]() is the set of all
is the set of all
![]() which are realisations of some optimal (realisable)
which are realisations of some optimal (realisable)
![]() $\boldsymbol {d}$
.
$\boldsymbol {d}$
.
Proof. Let
![]() . For all
. For all
![]() $L \subseteq [s]$
, let
$L \subseteq [s]$
, let
![]() $f_L := 2\sum _{ij \in \binom {[r]}{2} :\phi (ij) = L} \alpha _i\alpha _j$
, and for all
$f_L := 2\sum _{ij \in \binom {[r]}{2} :\phi (ij) = L} \alpha _i\alpha _j$
, and for all
![]() $2 \leq t \leq s$
, let
$2 \leq t \leq s$
, let
![]() $d_t:=\sum _{|L|=t}f_L$
. Then
$d_t:=\sum _{|L|=t}f_L$
. Then
![]() $q(\phi ,\boldsymbol {\alpha }) = \ell (\boldsymbol {d})$
. We have
$q(\phi ,\boldsymbol {\alpha }) = \ell (\boldsymbol {d})$
. We have
so it suffices to show that
![]() $\sum _{L \subseteq [s]\setminus \{c\}}f_{L\cup \{c\}} \leq 1-(k_c-1)^{-1}$
for all
$\sum _{L \subseteq [s]\setminus \{c\}}f_{L\cup \{c\}} \leq 1-(k_c-1)^{-1}$
for all
![]() $c \in [s]$
. For this, let
$c \in [s]$
. For this, let
![]() $n \in \mathbb {N}$
and let
$n \in \mathbb {N}$
and let
![]() $H_c:=H^n_c(\phi ,\boldsymbol {\alpha })$
be the graph on n vertices with vertex classes
$H_c:=H^n_c(\phi ,\boldsymbol {\alpha })$
be the graph on n vertices with vertex classes
![]() $X_1,\ldots ,X_r$
where
$X_1,\ldots ,X_r$
where
![]() $|\,|X_i|-\alpha _i n\,| \leq 1$
for all
$|\,|X_i|-\alpha _i n\,| \leq 1$
for all
![]() $i \in [r]$
and
$i \in [r]$
and
![]() $xy \in E(H_c)$
for
$xy \in E(H_c)$
for
![]() $x \in X_i$
,
$x \in X_i$
,
![]() $y \in X_j$
if and only if
$y \in X_j$
if and only if
![]() $c \in \phi (ij)$
. Then
$c \in \phi (ij)$
. Then
![]() $H_c$
is
$H_c$
is
![]() $K_{k_c}$
-free since
$K_{k_c}$
-free since
![]() $\phi ^{-1}(c)$
is. Therefore, Turán’s Theorem [Reference Turán28] implies that
$\phi ^{-1}(c)$
is. Therefore, Turán’s Theorem [Reference Turán28] implies that
![]() $ e(H_c) \leq (1 - (k_c-1)^{-1}) n^2/2 $
. Let
$ e(H_c) \leq (1 - (k_c-1)^{-1}) n^2/2 $
. Let
![]() $c \in [s]$
. So
$c \in [s]$
. So
 $$ \begin{align*} \frac{n^2}{2}\sum_{L \subseteq [s]\setminus \{ c \}} f_{L\cup \{ c \}} &= \sum_{L \subseteq [s]\setminus\{c\}} \sum_{\stackrel{ij \in \binom{[r]}{2}}{\phi(ij)=L\cup \{ c \}}}\alpha_i n \cdot \alpha_j n \leq \sum_{L \subseteq [s]\setminus \{ c \}}\sum_{\stackrel{ij \in \binom{[r]}{2}}{\phi(ij)=L\cup \{ c \}}}|X_i||X_j| + 2s^2 n\\ &= \sum_{\stackrel{ij \in \binom{[r]}{2} }{c \in \phi(ij)}} |X_i||X_j| + 2s^2n= e(H_c) + 2s^2 n \leq \left(1-\frac{1}{k_c-1}\right)\frac{n^2}{2} + 2s^2n. \end{align*} $$
$$ \begin{align*} \frac{n^2}{2}\sum_{L \subseteq [s]\setminus \{ c \}} f_{L\cup \{ c \}} &= \sum_{L \subseteq [s]\setminus\{c\}} \sum_{\stackrel{ij \in \binom{[r]}{2}}{\phi(ij)=L\cup \{ c \}}}\alpha_i n \cdot \alpha_j n \leq \sum_{L \subseteq [s]\setminus \{ c \}}\sum_{\stackrel{ij \in \binom{[r]}{2}}{\phi(ij)=L\cup \{ c \}}}|X_i||X_j| + 2s^2 n\\ &= \sum_{\stackrel{ij \in \binom{[r]}{2} }{c \in \phi(ij)}} |X_i||X_j| + 2s^2n= e(H_c) + 2s^2 n \leq \left(1-\frac{1}{k_c-1}\right)\frac{n^2}{2} + 2s^2n. \end{align*} $$
Dividing through by
![]() $n^2/2$
and taking the limit as
$n^2/2$
and taking the limit as
![]() $n \rightarrow \infty $
gives the required inequality.
$n \rightarrow \infty $
gives the required inequality.
We wish to add more constraints to Problem L. Indeed, without additional constraints, Problem L only yields realisable solutions in some very special cases, for example,
![]() $\boldsymbol {k}=(k,k)$
or
$\boldsymbol {k}=(k,k)$
or
![]() $\boldsymbol {k}=(k,k,k)$
. A constraint is valid if every
$\boldsymbol {k}=(k,k,k)$
. A constraint is valid if every
![]() $\boldsymbol {d}$
which has a realisation
$\boldsymbol {d}$
which has a realisation
![]() must satisfy the constraint. We use I for a set of constraints, each of the type
must satisfy the constraint. We use I for a set of constraints, each of the type
![]() $\sum _{t \in T}d_t \leq 1-\frac {1}{k-1}$
for some
$\sum _{t \in T}d_t \leq 1-\frac {1}{k-1}$
for some
![]() $T \subseteq \{2,\ldots ,s\}$
and integer
$T \subseteq \{2,\ldots ,s\}$
and integer
![]() $k \geq 3$
. We call this constraint a
$k \geq 3$
. We call this constraint a
![]() $(T,k)$
-constraint. Let Problem
$(T,k)$
-constraint. Let Problem
![]() $(L,I)$
be Problem L with the constraints in I added to it, and let
$(L,I)$
be Problem L with the constraints in I added to it, and let
![]() $\ell ^{\mathrm {max}}_I(\boldsymbol {k})$
be the optimal solution of Problem
$\ell ^{\mathrm {max}}_I(\boldsymbol {k})$
be the optimal solution of Problem
![]() $(L,I)$
. We will still discuss realisable solutions
$(L,I)$
. We will still discuss realisable solutions
![]() $\boldsymbol {d}$
and realisations of
$\boldsymbol {d}$
and realisations of
![]() $\boldsymbol {d}$
for Problem
$\boldsymbol {d}$
for Problem
![]() $(L,I)$
without referring to I when it is clear from the context.
$(L,I)$
without referring to I when it is clear from the context.
For our purposes, it suffices to consider constraints as follows. Let
![]() $T \subseteq \{2,\ldots ,s\}$
. Next, given
$T \subseteq \{2,\ldots ,s\}$
. Next, given
![]() , let
, let
 $$ \begin{align} H_{\phi}(T):=\left\{ij\in\binom{[r]}{2}: |\phi(ij)|\in T\right\}. \end{align} $$
$$ \begin{align} H_{\phi}(T):=\left\{ij\in\binom{[r]}{2}: |\phi(ij)|\in T\right\}. \end{align} $$
Suppose that
![]() $H_{\phi }(T)$
is
$H_{\phi }(T)$
is
![]() $K_k$
-free for all
$K_k$
-free for all
![]() . Then
. Then
 $$ \begin{align*}\sum_{t \in T}d_t \leq 1-\frac{1}{k-1} \end{align*} $$
$$ \begin{align*}\sum_{t \in T}d_t \leq 1-\frac{1}{k-1} \end{align*} $$
is a valid constraint. This follows as in the proof of Lemma 5.1 from defining
![]() $H^n_T(\phi ,\boldsymbol {\alpha })$
to be the n-vertex
$H^n_T(\phi ,\boldsymbol {\alpha })$
to be the n-vertex
![]() $\boldsymbol {\alpha }$
-blow-up of
$\boldsymbol {\alpha }$
-blow-up of
![]() $H_{\phi }(T)$
(in analogy with
$H_{\phi }(T)$
(in analogy with
![]() $H^n_c(\phi ,\boldsymbol {\alpha })$
) and using the observation that
$H^n_c(\phi ,\boldsymbol {\alpha })$
) and using the observation that
 $$ \begin{align*}e(H^{n}_T(\phi,\boldsymbol{\alpha})) = \left(\sum_{t \in T}d_t\right)\frac{n^2}{2}+O(n). \end{align*} $$
$$ \begin{align*}e(H^{n}_T(\phi,\boldsymbol{\alpha})) = \left(\sum_{t \in T}d_t\right)\frac{n^2}{2}+O(n). \end{align*} $$
Lemma 5.2. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}$
. Let I be a set of valid
$\boldsymbol {k} \in \mathbb {N}$
. Let I be a set of valid
![]() $(T,k)$
-constraints, where each
$(T,k)$
-constraints, where each
![]() $T \subseteq \{2,\ldots ,s\}$
and
$T \subseteq \{2,\ldots ,s\}$
and
![]() $k \geq 3$
is an integer. Then
$k \geq 3$
is an integer. Then
![]() $Q(\boldsymbol {k}) \leq \ell ^{\mathrm {max}}_I(\boldsymbol {k})$
. Moreover, the following is true. Suppose that at least one optimal solution
$Q(\boldsymbol {k}) \leq \ell ^{\mathrm {max}}_I(\boldsymbol {k})$
. Moreover, the following is true. Suppose that at least one optimal solution
![]() $\boldsymbol {d}$
to Problem
$\boldsymbol {d}$
to Problem
![]() $(L,I)$
is realisable. Then
$(L,I)$
is realisable. Then
![]() $\ell ^{\mathrm {max}}_I(\boldsymbol {k})=Q(\boldsymbol {k})$
and
$\ell ^{\mathrm {max}}_I(\boldsymbol {k})=Q(\boldsymbol {k})$
and
![]() is the set of all
is the set of all
![]() which are realisations of some optimal (realisable)
which are realisations of some optimal (realisable)
![]() $\boldsymbol {d}$
.
$\boldsymbol {d}$
.
![]() $\Box $
$\Box $
The following lemma will enable us to prove that many of the sequences
![]() $\boldsymbol {k}$
for which Problem
$\boldsymbol {k}$
for which Problem
![]() $Q_2$
has been solved do indeed have the strong extension property.
$Q_2$
has been solved do indeed have the strong extension property.
Lemma 5.3. Let
![]() $s \in \mathbb {N}$
and
$s \in \mathbb {N}$
and
![]() $\boldsymbol {k} \in \mathbb {N}^s$
. Suppose that, for all
$\boldsymbol {k} \in \mathbb {N}^s$
. Suppose that, for all
![]() , we have that
, we have that
-
(i)
 $(\phi ^*)^{-1}(c) \cong T_{k_c-1}(r^*)$
and
$(\phi ^*)^{-1}(c) \cong T_{k_c-1}(r^*)$
and
 $(k_c-1)|r^*$
for all
$(k_c-1)|r^*$
for all
 $c \in [s]$
;
$c \in [s]$
; -
(ii)
 $|\,|\phi ^*(ij)|-|\phi ^*(i'j')|\,| \leq 1$
for all
$|\,|\phi ^*(ij)|-|\phi ^*(i'j')|\,| \leq 1$
for all
 $ij,i'j' \in \binom {[r^*]}{2}$
and
$ij,i'j' \in \binom {[r^*]}{2}$
and
 $\boldsymbol {\alpha }^*$
is uniform;
$\boldsymbol {\alpha }^*$
is uniform; -
(iii) every solution
 $\boldsymbol {t} := (t_1,\ldots ,t_{r^*}) \in [s]^{r^*}$
of (5.3)is such that
$\boldsymbol {t} := (t_1,\ldots ,t_{r^*}) \in [s]^{r^*}$
of (5.3)is such that $$ \begin{align} \prod_{i \in [r^*]} t_i^{\alpha_i^*} = 2^{Q(\boldsymbol{k})} \end{align} $$
$$ \begin{align} \prod_{i \in [r^*]} t_i^{\alpha_i^*} = 2^{Q(\boldsymbol{k})} \end{align} $$
 $t_i = 1$
for exactly one value
$t_i = 1$
for exactly one value
 $i \in [r^*]$
.
$i \in [r^*]$
.
Then
![]() $\boldsymbol {k}$
has the strong extension property.
$\boldsymbol {k}$
has the strong extension property.
Proof. Let
![]() $r^*+1$
be a new vertex, and let
$r^*+1$
be a new vertex, and let
![]() $\phi : \binom {[r^*+1]}{2} \rightarrow 2^{[s]}$
be such that
$\phi : \binom {[r^*+1]}{2} \rightarrow 2^{[s]}$
be such that
![]() $\phi |_{\binom {[r^*]}{2}} = \phi ^*$
and
$\phi |_{\binom {[r^*]}{2}} = \phi ^*$
and
Since
![]() $(\phi ^*)^{-1}(c) \cong T_{k_c-1}(r^*)$
for each
$(\phi ^*)^{-1}(c) \cong T_{k_c-1}(r^*)$
for each
![]() $c \in [s]$
, we have equally sized sets
$c \in [s]$
, we have equally sized sets
![]() $P^c_1,\ldots ,P^c_{k_c-1}$
which partition
$P^c_1,\ldots ,P^c_{k_c-1}$
which partition
![]() $[r^*]$
and which are the vertex classes of
$[r^*]$
and which are the vertex classes of
![]() $(\phi ^*)^{-1}(c)$
. Let
$(\phi ^*)^{-1}(c)$
. Let
![]() $\phi '$
be obtained from
$\phi '$
be obtained from
![]() $\phi $
by maximally enlarging the values on the pairs that contain
$\phi $
by maximally enlarging the values on the pairs that contain
![]() $r^*+1$
so that
$r^*+1$
so that
![]() $(\phi ')^{-1}(c)$
still does not contain a clique on
$(\phi ')^{-1}(c)$
still does not contain a clique on
![]() $k_c$
vertices. Clearly, for each colour c, this can be done independently of the other colours, and every maximal
$k_c$
vertices. Clearly, for each colour c, this can be done independently of the other colours, and every maximal
![]() $K_{k_c}$
-free attachment of a new vertex to
$K_{k_c}$
-free attachment of a new vertex to
![]() $(\phi ^*)^{-1}(c)\cong T_{k_c-1}(r^*)$
is to connect the vertex to all but one part of the Turán graph. Thus, for each
$(\phi ^*)^{-1}(c)\cong T_{k_c-1}(r^*)$
is to connect the vertex to all but one part of the Turán graph. Thus, for each
![]() $c\in [s]$
, there is
$c\in [s]$
, there is
![]() $j_c \in [k_c-1]$
, such that
$j_c \in [k_c-1]$
, such that
![]() $c \notin \phi '(\{ x,r^*+1\})$
if and only if
$c \notin \phi '(\{ x,r^*+1\})$
if and only if
![]() $x \in P^c_{j_c}$
. For each
$x \in P^c_{j_c}$
. For each
![]() $x \in [r^*]$
, let
$x \in [r^*]$
, let
![]() $i_c(x)$
be the unique member of
$i_c(x)$
be the unique member of
![]() $[k_c-1]$
, such that
$[k_c-1]$
, such that
![]() $x \in P^c_{i_c(x)}$
. So
$x \in P^c_{i_c(x)}$
. So
![]() $c \notin \phi '(\{ y,r^*+1 \})$
if and only if
$c \notin \phi '(\{ y,r^*+1 \})$
if and only if
![]() $i_c(y) = j_c$
. Then
$i_c(y) = j_c$
. Then
![]() $\mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) \geq \mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
, so by Proposition 2.6,
$\mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) \geq \mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*)=Q(\boldsymbol {k})$
, so by Proposition 2.6,
![]() $\mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) = \mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) = Q(\boldsymbol {k})$
, so
$\mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) = \mathop {\mathrm {ext}}(\phi ,\boldsymbol {\alpha }^*) = Q(\boldsymbol {k})$
, so
![]() $\phi (xy) \neq \phi '(xy)$
only if
$\phi (xy) \neq \phi '(xy)$
only if
![]() $|\phi '(xy)| = 1$
. Observe that
$|\phi '(xy)| = 1$
. Observe that
![]() $\phi '$
is determined completely by
$\phi '$
is determined completely by
![]() $\phi ^*$
and
$\phi ^*$
and
![]() $\{ j_1,\ldots , j_s \}$
.
$\{ j_1,\ldots , j_s \}$
.
Define
![]() $\boldsymbol {t} \in \mathbb {N}^{r^*}$
by setting
$\boldsymbol {t} \in \mathbb {N}^{r^*}$
by setting
![]() $t_i := \max \{ |\phi '(\{ i,r^*+1 \})|,1\}$
. Exponentiating (5.4) implies that
$t_i := \max \{ |\phi '(\{ i,r^*+1 \})|,1\}$
. Exponentiating (5.4) implies that
![]() $\prod _{i \in [r^*]}t_i^{\alpha ^*_i} = 2^{Q(\boldsymbol {k})}$
. So, by our hypothesis (iii), there exists
$\prod _{i \in [r^*]}t_i^{\alpha ^*_i} = 2^{Q(\boldsymbol {k})}$
. So, by our hypothesis (iii), there exists
![]() $x^* \in [r^*]$
, such that
$x^* \in [r^*]$
, such that
![]() $|\phi '(\{ x^*,r^*+1 \})| \leq 1$
and
$|\phi '(\{ x^*,r^*+1 \})| \leq 1$
and
![]() $|\phi '(\{ i,r^*+1 \})| \geq 2$
for all
$|\phi '(\{ i,r^*+1 \})| \geq 2$
for all
![]() $i \in [r^*] \setminus \{ x^* \}$
. Suppose first that
$i \in [r^*] \setminus \{ x^* \}$
. Suppose first that
![]() $\phi '(\{ x^*,r^*+1\}) = \emptyset $
. Then
$\phi '(\{ x^*,r^*+1\}) = \emptyset $
. Then
![]() $j_c = i_c(x^*)$
for all
$j_c = i_c(x^*)$
for all
![]() $c \in [s]$
, and so
$c \in [s]$
, and so
![]() $r^*+1$
is a twin of
$r^*+1$
is a twin of
![]() $x^*$
, as required.
$x^*$
, as required.
Therefore, we may assume that
![]() $\phi '(\{ x^*,r^*+1\}) = \{ c^* \}$
for some
$\phi '(\{ x^*,r^*+1\}) = \{ c^* \}$
for some
![]() $c^* \in [s]$
. Note that
$c^* \in [s]$
. Note that
![]() $j_c = i_c(x^*)$
for all
$j_c = i_c(x^*)$
for all
![]() $c \in [s]\setminus \{ c^* \}$
. So the attachment of
$c \in [s]\setminus \{ c^* \}$
. So the attachment of
![]() $r^*+1$
is almost the same as that of
$r^*+1$
is almost the same as that of
![]() $x^*$
, and we will compare them to obtain a contradiction. Without loss of generality, assume that
$x^*$
, and we will compare them to obtain a contradiction. Without loss of generality, assume that
![]() $i_{c^*}(x^*) = 1$
and
$i_{c^*}(x^*) = 1$
and
![]() $j_{c^*} = 2$
. Now, for
$j_{c^*} = 2$
. Now, for
![]() $i \in [k_{c^*}-1]$
and
$i \in [k_{c^*}-1]$
and
![]() $y \in P^{c^*}_i\setminus \{x^*\}$
, we have that
$y \in P^{c^*}_i\setminus \{x^*\}$
, we have that
 $$ \begin{align*}\phi'(\{ y,r^*+1 \}) = \begin{cases} \phi^*(x^*y) \cup \{ c^*\} &\mbox{if } i=1. \\ \phi^*(x^*y) \setminus \{ c^*\} &\mbox{if } i=2. \\ \phi^*(x^*y) &\mbox{if } 3 \leq i \leq k_{c^*}-1. \end{cases} \end{align*} $$
$$ \begin{align*}\phi'(\{ y,r^*+1 \}) = \begin{cases} \phi^*(x^*y) \cup \{ c^*\} &\mbox{if } i=1. \\ \phi^*(x^*y) \setminus \{ c^*\} &\mbox{if } i=2. \\ \phi^*(x^*y) &\mbox{if } 3 \leq i \leq k_{c^*}-1. \end{cases} \end{align*} $$
Since
![]() $\mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) = Q(\boldsymbol {k}) = q_{x^*}(\phi ^*,\boldsymbol {\alpha }^*) = \sum _{x \in [r^*]}\alpha ^*_x \log |\phi ^*(x^*x)|$
by Lemma 2.1, we have that
$\mathop {\mathrm {ext}}(\phi ',\boldsymbol {\alpha }^*) = Q(\boldsymbol {k}) = q_{x^*}(\phi ^*,\boldsymbol {\alpha }^*) = \sum _{x \in [r^*]}\alpha ^*_x \log |\phi ^*(x^*x)|$
by Lemma 2.1, we have that
 $$ \begin{align} \sum_{y \in P^{c^*}_1 \cup P^{c^*}_2 \setminus \{ x^*\}} \alpha^*_i\log|\phi^*(x^*y)| = \sum_{y \in P^{c^*}_1}\alpha^*_i\log \left(|\phi^*(x^*y)|-1 \right) + \sum_{y \in P^{c^*}_2 \setminus \{ x^*\}} \alpha^*_i\log \left(|\phi^*(x^*y)|+1\right). \end{align} $$
$$ \begin{align} \sum_{y \in P^{c^*}_1 \cup P^{c^*}_2 \setminus \{ x^*\}} \alpha^*_i\log|\phi^*(x^*y)| = \sum_{y \in P^{c^*}_1}\alpha^*_i\log \left(|\phi^*(x^*y)|-1 \right) + \sum_{y \in P^{c^*}_2 \setminus \{ x^*\}} \alpha^*_i\log \left(|\phi^*(x^*y)|+1\right). \end{align} $$
Let
![]() $p \in \mathbb {N}$
be such that
$p \in \mathbb {N}$
be such that
![]() $|\phi ^*(xy)| \in \{ p,p+1 \}$
for all
$|\phi ^*(xy)| \in \{ p,p+1 \}$
for all
![]() $xy \in \binom {[r^*]}{2}$
(which exists by (ii)). Note that
$xy \in \binom {[r^*]}{2}$
(which exists by (ii)). Note that
![]() $p \geq 2$
. Since
$p \geq 2$
. Since
![]() $(k_{c^*}-1)|r^*$
, we may write
$(k_{c^*}-1)|r^*$
, we may write
![]() $|P^{c^*}_1| =|P^{c^*}_2| = r^*/(k_c-1) =:r$
. Suppose
$|P^{c^*}_1| =|P^{c^*}_2| = r^*/(k_c-1) =:r$
. Suppose
![]() $\ell \leq r-1$
and
$\ell \leq r-1$
and
![]() $k \leq r$
are such that
$k \leq r$
are such that
![]() $|\phi ^*(x^*y)| = p$
for
$|\phi ^*(x^*y)| = p$
for
![]() $\ell $
elements y in
$\ell $
elements y in
![]() $P^{c^*}_1$
and
$P^{c^*}_1$
and
![]() $|\phi ^*(x^*y)| = p$
for k elements y in
$|\phi ^*(x^*y)| = p$
for k elements y in
![]() $P^{c^*}_2$
. Then, since
$P^{c^*}_2$
. Then, since
![]() $\boldsymbol {\alpha }^*$
is uniform, exponentiating (5.5) gives
$\boldsymbol {\alpha }^*$
is uniform, exponentiating (5.5) gives
that is
![]() $p^{\ell +2k-r}(p+1)^{2r-1-k-\ell } = (p+2)^{r-1-\ell }(p-1)^k$
. But
$p^{\ell +2k-r}(p+1)^{2r-1-k-\ell } = (p+2)^{r-1-\ell }(p-1)^k$
. But
![]() $p,p-1$
are coprime, and so are
$p,p-1$
are coprime, and so are
![]() $p+1,p+2$
. So
$p+1,p+2$
. So
![]() $p|(p+2)$
and
$p|(p+2)$
and
![]() $(p-1)|(p+1)$
. Therefore,
$(p-1)|(p+1)$
. Therefore,
![]() $p = 2$
, giving
$p = 2$
, giving
So
![]() $\ell +2k-r=2r-2-2\ell $
and
$\ell +2k-r=2r-2-2\ell $
and
![]() $2r-1-k-2\ell =0$
, and, hence,
$2r-1-k-2\ell =0$
, and, hence,
![]() $3(k+1) = 6(r-\ell ) = 4(k+1)$
, which implies
$3(k+1) = 6(r-\ell ) = 4(k+1)$
, which implies
![]() $k=-1$
, a contradiction.
$k=-1$
, a contradiction.
Therefore,
![]() $\phi '(\{ x^*,r^*+1 \}) = \emptyset $
, and
$\phi '(\{ x^*,r^*+1 \}) = \emptyset $
, and
![]() $\phi '(\{ x,r^*+1 \}) = \phi ^*(x^*x)$
for all
$\phi '(\{ x,r^*+1 \}) = \phi ^*(x^*x)$
for all
![]() $x \in [r^*]\setminus \{ x^*\}$
. By our earlier observation,
$x \in [r^*]\setminus \{ x^*\}$
. By our earlier observation,
![]() $\phi \equiv \phi '$
. Therefore,
$\phi \equiv \phi '$
. Therefore,
![]() $r^*+1$
is a twin of
$r^*+1$
is a twin of
![]() $x^*$
, as required.
$x^*$
, as required.
Proof of Theorem 1.7.
First we must solve Problem
![]() $Q_2$
for all specified
$Q_2$
for all specified
![]() $\boldsymbol {k}$
. This was implicitly done in [Reference Alon, Balogh, Keevash and Sudakov1, Reference Pikhurko and Yilma25], but we repeat the arguments here for completeness, and to demonstrate that the arguments are much cleaner and shorter when one is working with optimal solutions rather than regularity partitions of large graphs. We will solve Problem
$\boldsymbol {k}$
. This was implicitly done in [Reference Alon, Balogh, Keevash and Sudakov1, Reference Pikhurko and Yilma25], but we repeat the arguments here for completeness, and to demonstrate that the arguments are much cleaner and shorter when one is working with optimal solutions rather than regularity partitions of large graphs. We will solve Problem
![]() $Q_2$
by solving Problem L, sometimes with some additional valid constraints I, and then applying Lemma 5.2. First, we make some general observations. Suppose
$Q_2$
by solving Problem L, sometimes with some additional valid constraints I, and then applying Lemma 5.2. First, we make some general observations. Suppose
![]() $\boldsymbol {d}$
is a feasible solution of Problem L with additional constraints I, each constraint corresponding to some
$\boldsymbol {d}$
is a feasible solution of Problem L with additional constraints I, each constraint corresponding to some
![]() $(T,k)$
, and
$(T,k)$
, and
![]() $\boldsymbol {d}$
has realisation
$\boldsymbol {d}$
has realisation
![]() $(r,\phi ,\boldsymbol {\alpha })$
.
$(r,\phi ,\boldsymbol {\alpha })$
.
-
• Let
 $T \subseteq \{2,\ldots ,s\}$
and
$T \subseteq \{2,\ldots ,s\}$
and
 $k \geq 3$
be such that the
$k \geq 3$
be such that the
 $(T,k)$
-constraint is valid and in I. Suppose further that
$(T,k)$
-constraint is valid and in I. Suppose further that
 $\sum _{t \in T}d_{t}=1-\frac {1}{k-1}$
(that is, there is equality in the
$\sum _{t \in T}d_{t}=1-\frac {1}{k-1}$
(that is, there is equality in the
 $(T,k)$
-constraint). Then there is a partition of
$(T,k)$
-constraint). Then there is a partition of
 $[r]$
into parts
$[r]$
into parts
 $A_1,\ldots ,A_{k-1}$
, such that
$A_1,\ldots ,A_{k-1}$
, such that
 $\sum _{i \in A_{i'}}\alpha _{i}=\frac {1}{k-1}$
for all
$\sum _{i \in A_{i'}}\alpha _{i}=\frac {1}{k-1}$
for all
 $i' \in [k-1]$
, and
$i' \in [k-1]$
, and
 $ij \in H_{\phi }(T)$
if and only if
$ij \in H_{\phi }(T)$
if and only if
 $i,j$
lie in different parts
$i,j$
lie in different parts
 $A_{i'},A_{j'}$
(recall that
$A_{i'},A_{j'}$
(recall that
 $H_{\phi }(T)$
was defined in (5.2)).
$H_{\phi }(T)$
was defined in (5.2)). -
• If
 $S \subseteq [r]$
has
$S \subseteq [r]$
has
 $|S| \leq k$
, then
$|S| \leq k$
, then
 $2\sum _{ij \in \binom {S}{2}}\alpha _i\alpha _j \leq \sum _{i \in S}\alpha _i\left (1-\frac {1}{k-1}\right )$
.
$2\sum _{ij \in \binom {S}{2}}\alpha _i\alpha _j \leq \sum _{i \in S}\alpha _i\left (1-\frac {1}{k-1}\right )$
.
These follow as in the proof of Lemma 5.1 by taking
![]() $\boldsymbol {\alpha }$
-weighted blow-ups of
$\boldsymbol {\alpha }$
-weighted blow-ups of
![]() $H_{\phi }(T)$
and
$H_{\phi }(T)$
and
![]() $\phi |_{\binom {S}{2}}$
, respectively. For the first assertion, apply the stability theorem of Erdős [Reference Erdős6] and Simonovits [Reference Simonovits26] for the Turán problem, which states that any large n-vertex
$\phi |_{\binom {S}{2}}$
, respectively. For the first assertion, apply the stability theorem of Erdős [Reference Erdős6] and Simonovits [Reference Simonovits26] for the Turán problem, which states that any large n-vertex
![]() $K_k$
-free graph with density close to
$K_k$
-free graph with density close to
![]() $1-\frac {1}{k-1}$
must be close in edit distance to
$1-\frac {1}{k-1}$
must be close in edit distance to
![]() $T_{k-1}(n)$
. For the second, apply Turán’s theorem.
$T_{k-1}(n)$
. For the second, apply Turán’s theorem.
For ease of notation, we will write
![]() $H_{\phi }(t_1,\ldots ,t_{\ell })$
for
$H_{\phi }(t_1,\ldots ,t_{\ell })$
for
![]() $H_{\phi }(\{t_1,\ldots ,t_{\ell }\})$
below.
$H_{\phi }(\{t_1,\ldots ,t_{\ell }\})$
below.
The cases
![]() $\boldsymbol {k}\boldsymbol {=(k,k)}$
and
$\boldsymbol {k}\boldsymbol {=(k,k)}$
and
![]() $\boldsymbol {k}\boldsymbol {=(k,k,k)}$
$\boldsymbol {k}\boldsymbol {=(k,k,k)}$
We omit
![]() $\boldsymbol {k}=(k,k)$
since it is similar to
$\boldsymbol {k}=(k,k)$
since it is similar to
![]() $\boldsymbol {k}=(k,k,k)$
. Problem L for
$\boldsymbol {k}=(k,k,k)$
. Problem L for
![]() $\boldsymbol {k}=(k,k,k)$
is to maximise
$\boldsymbol {k}=(k,k,k)$
is to maximise
![]() $d_2+\log 3\cdot d_3$
subject to
$d_2+\log 3\cdot d_3$
subject to
![]() $\boldsymbol {d}\geq \boldsymbol {0}$
and
$\boldsymbol {d}\geq \boldsymbol {0}$
and
![]() $2d_2+3d_3 \leq 3(1-\frac {1}{k-1})$
. It is easy to see that the maximum is
$2d_2+3d_3 \leq 3(1-\frac {1}{k-1})$
. It is easy to see that the maximum is
![]() $\frac {k-2}{k-1}\log 3$
with unique optimal solution
$\frac {k-2}{k-1}\log 3$
with unique optimal solution
![]() $(d_2,d_3)=(0,1-\frac {1}{k-1})$
. Now, if
$(d_2,d_3)=(0,1-\frac {1}{k-1})$
. Now, if
![]() is a realisation of
is a realisation of
![]() $\boldsymbol {d}$
, then
$\boldsymbol {d}$
, then
![]() $H_{\phi }(3) \cong \phi ^{-1}(c)$
for all colours c, so
$H_{\phi }(3) \cong \phi ^{-1}(c)$
for all colours c, so
![]() $H_{\phi }(3)$
is
$H_{\phi }(3)$
is
![]() $K_k$
-free. Thus,
$K_k$
-free. Thus,
![]() $H_{\phi }(3)$
is a complete
$H_{\phi }(3)$
is a complete
![]() $(k-1)$
-partite graph and the sum of
$(k-1)$
-partite graph and the sum of
![]() $\alpha _{i'}$
over
$\alpha _{i'}$
over
![]() $i'$
in a single part is
$i'$
in a single part is
![]() $\frac {1}{k-1}$
, and in fact each part is a singleton. So
$\frac {1}{k-1}$
, and in fact each part is a singleton. So
![]() $r=k-1$
and
$r=k-1$
and
![]() $\alpha _i=\frac {1}{k-1}$
for all
$\alpha _i=\frac {1}{k-1}$
for all
![]() $i \in [r]$
, and
$i \in [r]$
, and
![]() $\phi ^{-1}(c) = H_{\phi }(3) \cong K_{k-1}$
for all colours c.
$\phi ^{-1}(c) = H_{\phi }(3) \cong K_{k-1}$
for all colours c.
The case
![]() $\boldsymbol {k}\boldsymbol {=(3,3,3,3)}$
$\boldsymbol {k}\boldsymbol {=(3,3,3,3)}$
We use the argument from [Reference Pikhurko and Yilma25], which requires an additional constraint. Let
![]() $T := \{3,4\}$
. We claim that
$T := \{3,4\}$
. We claim that
![]() $H_{\phi }(T)$
is
$H_{\phi }(T)$
is
![]() $K_3$
-free for all
$K_3$
-free for all
![]() . Indeed, if it contained a triangle
. Indeed, if it contained a triangle
![]() $i_1i_2i_3$
, then there is at most one colour in
$i_1i_2i_3$
, then there is at most one colour in
![]() $[4]$
missing from each
$[4]$
missing from each
![]() $\phi (i_si_t)$
, and, thus, there is one colour in
$\phi (i_si_t)$
, and, thus, there is one colour in
![]() $[4]$
which appears on every edge, a contradiction. Thus, the
$[4]$
which appears on every edge, a contradiction. Thus, the
![]() $(\{3,4\},3)$
-constraint is valid. So adding this constraint to Problem L, we seek to maximise
$(\{3,4\},3)$
-constraint is valid. So adding this constraint to Problem L, we seek to maximise
![]() $d_2 + \log 3\cdot d_3 + 2d_4$
subject to
$d_2 + \log 3\cdot d_3 + 2d_4$
subject to
![]() $\boldsymbol {d}\geq \boldsymbol {0}$
,
$\boldsymbol {d}\geq \boldsymbol {0}$
,
![]() $2d_2+3d_3+4d_4 \leq 2$
and
$2d_2+3d_3+4d_4 \leq 2$
and
![]() $d_3+d_4 \leq \frac {1}{2}$
. This has maximum
$d_3+d_4 \leq \frac {1}{2}$
. This has maximum
![]() $\frac {1}{4}+\frac {1}{2}\log 3$
with unique optimal solution
$\frac {1}{4}+\frac {1}{2}\log 3$
with unique optimal solution
![]() $(d_2,d_3,d_4)=(\frac {1}{4},\frac {1}{2},0)$
. Thus, if
$(d_2,d_3,d_4)=(\frac {1}{4},\frac {1}{2},0)$
. Thus, if
![]() $(r,\phi ,\boldsymbol {\alpha })$
is a realisation of
$(r,\phi ,\boldsymbol {\alpha })$
is a realisation of
![]() $\boldsymbol {d}$
, there is a partition of
$\boldsymbol {d}$
, there is a partition of
![]() $[r]$
into
$[r]$
into
![]() $A,B$
, such that
$A,B$
, such that
![]() $H_{\phi }(3,4)=H_{\phi }(3)$
is a complete bipartite graph with parts
$H_{\phi }(3,4)=H_{\phi }(3)$
is a complete bipartite graph with parts
![]() $A,B$
, and
$A,B$
, and
![]() $\sum _{i \in A}\alpha _{i}=\sum _{i\in B}\alpha _i=\frac {1}{2}$
. Since
$\sum _{i \in A}\alpha _{i}=\sum _{i\in B}\alpha _i=\frac {1}{2}$
. Since
![]() $d_4=0$
, for distinct
$d_4=0$
, for distinct
![]() $i,j \in A$
or
$i,j \in A$
or
![]() $i,j \in B$
, we have
$i,j \in B$
, we have
![]() $|\phi (ij)|=2$
, and, because
$|\phi (ij)|=2$
, and, because
![]() $H_{\phi }(2)$
is disjoint from
$H_{\phi }(2)$
is disjoint from
![]() $H_{\phi }(3)$
,
$H_{\phi }(3)$
,
 $$ \begin{align} \frac{1}{4}=d_2\stackrel{(5.1)}{=}2\sum_{ij\in\binom{A}{2}}\alpha_{i}\alpha_{j}+2\sum_{ij\in\binom{B}{2}}\alpha_i\alpha_j. \end{align} $$
$$ \begin{align} \frac{1}{4}=d_2\stackrel{(5.1)}{=}2\sum_{ij\in\binom{A}{2}}\alpha_{i}\alpha_{j}+2\sum_{ij\in\binom{B}{2}}\alpha_i\alpha_j. \end{align} $$
Without loss of generality, suppose that
![]() $|A| \leq |B|$
. Next we show that
$|A| \leq |B|$
. Next we show that
![]() $|A|=|B|=2$
via a series of claims. Note that
$|A|=|B|=2$
via a series of claims. Note that
![]() $|A|+|B| \geq 4$
, otherwise,
$|A|+|B| \geq 4$
, otherwise,
![]() $|A|=1$
and
$|A|=1$
and
![]() $|B|\leq 2$
and the second bullet point above implies that
$|B|\leq 2$
and the second bullet point above implies that
![]() $2d_2 \leq \frac {1}{2}\cdot \frac {1}{2}$
, a contradiction. The first claim is that
$2d_2 \leq \frac {1}{2}\cdot \frac {1}{2}$
, a contradiction. The first claim is that
![]() $|A| \leq |B| \leq 4$
. If not, then there are
$|A| \leq |B| \leq 4$
. If not, then there are
![]() $a \in A$
and
$a \in A$
and
![]() $b_1,\ldots ,b_5 \in B$
. Since
$b_1,\ldots ,b_5 \in B$
. Since
![]() $|\phi (ab_j)|=3$
for all
$|\phi (ab_j)|=3$
for all
![]() $j\in [5]$
, we may assume that
$j\in [5]$
, we may assume that
![]() $\phi (ab_1)=\phi (ab_2)$
. But then
$\phi (ab_1)=\phi (ab_2)$
. But then
![]() $\phi (b_1b_2)$
, of size
$\phi (b_1b_2)$
, of size
![]() $2$
, has nonempty intersection with this set, so
$2$
, has nonempty intersection with this set, so
![]() $\{a,b_1,b_2\}$
span a monochromatic triangle, a contradiction which proves the claim. The second claim is that if
$\{a,b_1,b_2\}$
span a monochromatic triangle, a contradiction which proves the claim. The second claim is that if
![]() $|A| \geq 2$
, then
$|A| \geq 2$
, then
![]() $|A|=|B|=2$
. If not, then there are
$|A|=|B|=2$
. If not, then there are
![]() $a_1,a_2 \in A$
and
$a_1,a_2 \in A$
and
![]() $b_1,b_2,b_3 \in B$
. Let S be the multiset obtained by collecting all
$b_1,b_2,b_3 \in B$
. Let S be the multiset obtained by collecting all
![]() $\phi (a_1a_2),\phi (a_ib_j), \phi (b_jb_{j'})$
for
$\phi (a_1a_2),\phi (a_ib_j), \phi (b_jb_{j'})$
for
![]() $i \in [2]$
,
$i \in [2]$
,
![]() $j,j'\in [3]$
. Then
$j,j'\in [3]$
. Then
![]() $|S|= 6\cdot 3 + 4\cdot 2 = 26$
. So there is
$|S|= 6\cdot 3 + 4\cdot 2 = 26$
. So there is
![]() $c \in [4]$
which appears in
$c \in [4]$
which appears in
![]() $\phi $
on
$\phi $
on
![]() $\lceil \frac {26}{4}\rceil =7$
pairs among five vertices, so
$\lceil \frac {26}{4}\rceil =7$
pairs among five vertices, so
![]() $\phi ^{-1}(c)$
contains a triangle by Turán’s theorem. It remains to rule out the case
$\phi ^{-1}(c)$
contains a triangle by Turán’s theorem. It remains to rule out the case
![]() $|A|=1$
and
$|A|=1$
and
![]() $|B| \geq 3$
. Since
$|B| \geq 3$
. Since
![]() $|B| \leq 4$
, we have
$|B| \leq 4$
, we have
![]() $2\sum _{ij \in \binom {B}{2}}\alpha _i\alpha _j \leq \frac {1}{2}\cdot \frac {3}{4}$
, so
$2\sum _{ij \in \binom {B}{2}}\alpha _i\alpha _j \leq \frac {1}{2}\cdot \frac {3}{4}$
, so
![]() $d_2 \leq \frac {3}{16}$
, a contradiction. This completes the proof that
$d_2 \leq \frac {3}{16}$
, a contradiction. This completes the proof that
![]() $|A|=|B|=2$
. So
$|A|=|B|=2$
. So
![]() $r=4$
, and (5.6) holds if and only if
$r=4$
, and (5.6) holds if and only if
![]() $\alpha _i=\frac {1}{4}$
for all
$\alpha _i=\frac {1}{4}$
for all
![]() $i\in [4]$
. We have
$i\in [4]$
. We have
![]() $\sum _{c \in [4]}|\phi ^{-1}(c)| = \sum _{ij\in \binom {[r]}{2}}|\phi (ij)|=2\cdot 2+ 4\cdot 3=16$
and every
$\sum _{c \in [4]}|\phi ^{-1}(c)| = \sum _{ij\in \binom {[r]}{2}}|\phi (ij)|=2\cdot 2+ 4\cdot 3=16$
and every
![]() $|\phi ^{-1}(c)| \leq 4$
, otherwise, there would be a triangle in colour c. Thus, every
$|\phi ^{-1}(c)| \leq 4$
, otherwise, there would be a triangle in colour c. Thus, every
![]() $|\phi ^{-1}(c)|=4$
and, moreover,
$|\phi ^{-1}(c)|=4$
and, moreover,
![]() $\phi ^{-1}(c) \cong K_{2,2}=T_2(4)$
. One can check that, up to relabelling, there is a unique way to choose the
$\phi ^{-1}(c) \cong K_{2,2}=T_2(4)$
. One can check that, up to relabelling, there is a unique way to choose the
![]() $\phi ^{-1}(c)$
to attain the given multiplicities (as in Table 2).
$\phi ^{-1}(c)$
to attain the given multiplicities (as in Table 2).
Table 2 Basic optimal solutions. In all these results, every basic optimal
![]() $(r,\phi ,\boldsymbol {\alpha })$
has
$(r,\phi ,\boldsymbol {\alpha })$
has
![]() $\phi ^{-1}(c) \cong T_{k-1}(r)$
for all
$\phi ^{-1}(c) \cong T_{k-1}(r)$
for all
![]() $c \in [s]$
and
$c \in [s]$
and
![]() $\boldsymbol {\alpha }$
is the uniform vector of length r. The figure for
$\boldsymbol {\alpha }$
is the uniform vector of length r. The figure for
![]() $k=4$
,
$k=4$
,
![]() $s=4$
is the complement of the optimal solution.
$s=4$
is the complement of the optimal solution.

The case
![]() $\boldsymbol {k}\boldsymbol {=(4,4,4,4)}$
$\boldsymbol {k}\boldsymbol {=(4,4,4,4)}$
No additional constraints are necessary in this case. Problem L is to maximise
![]() $d_2+\log 3\cdot d_3 + 2\cdot d_4$
subject to
$d_2+\log 3\cdot d_3 + 2\cdot d_4$
subject to
![]() $\boldsymbol {d}\geq \boldsymbol {0}$
and
$\boldsymbol {d}\geq \boldsymbol {0}$
and
![]() $2d_2+3d_3+4d_4 \leq \frac {8}{3}$
. This has maximum
$2d_2+3d_3+4d_4 \leq \frac {8}{3}$
. This has maximum
![]() $\frac {8}{9}\cdot \log 3$
, attained uniquely by
$\frac {8}{9}\cdot \log 3$
, attained uniquely by
![]() $(d_2,d_3,d_4)=(0,\frac {8}{9},0)$
. Suppose
$(d_2,d_3,d_4)=(0,\frac {8}{9},0)$
. Suppose
![]() is a realisation of
is a realisation of
![]() $\boldsymbol {d}$
. Since
$\boldsymbol {d}$
. Since
![]() $d_3$
is the only nonzero entry in
$d_3$
is the only nonzero entry in
![]() $\boldsymbol {d}$
, we have
$\boldsymbol {d}$
, we have
![]() $H_{\phi }(3) \cong K_r$
. We claim
$H_{\phi }(3) \cong K_r$
. We claim
![]() $r \leq 9$
. If not, then
$r \leq 9$
. If not, then
 $$ \begin{align*}\sum_{c\in[4]}|\phi^{-1}(c)[[10]]|=\sum_{ij\in\binom{[10]}{2}}|\phi(ij)|= 3\cdot\binom{10}{2}=135, \end{align*} $$
$$ \begin{align*}\sum_{c\in[4]}|\phi^{-1}(c)[[10]]|=\sum_{ij\in\binom{[10]}{2}}|\phi(ij)|= 3\cdot\binom{10}{2}=135, \end{align*} $$
so there is some
![]() $c \in [4]$
, such that
$c \in [4]$
, such that
![]() $\phi ^{-1}(c)$
has at least
$\phi ^{-1}(c)$
has at least
![]() $\lceil \frac {135}{4}\rceil = 34$
edges among
$\lceil \frac {135}{4}\rceil = 34$
edges among
![]() $10$
vertices. But by Turán’s theorem,
$10$
vertices. But by Turán’s theorem,
![]() $\phi ^{-1}(c)$
contains a
$\phi ^{-1}(c)$
contains a
![]() $K_4$
, a contradiction. So
$K_4$
, a contradiction. So
![]() $H_{\phi }(3)$
is
$H_{\phi }(3)$
is
![]() $K_{10}$
-free and
$K_{10}$
-free and
![]() $d_3=\frac {8}{9}$
, so the first bullet point implies that
$d_3=\frac {8}{9}$
, so the first bullet point implies that
![]() $H_{\phi }(3)$
is a complete
$H_{\phi }(3)$
is a complete
![]() $9$
-partite graph and the sum of
$9$
-partite graph and the sum of
![]() $\alpha _i$
over all i in a single part is
$\alpha _i$
over all i in a single part is
![]() $\frac {1}{9}$
. But
$\frac {1}{9}$
. But
![]() $ij \in H_{\phi }(3)$
if and only if
$ij \in H_{\phi }(3)$
if and only if
![]() $\phi (ij)\neq 0$
, so
$\phi (ij)\neq 0$
, so
![]() $r=9$
and
$r=9$
and
![]() $\alpha _i=\frac {1}{9}$
for all
$\alpha _i=\frac {1}{9}$
for all
![]() $i \in [9]$
. Again, we must have
$i \in [9]$
. Again, we must have
![]() $\phi ^{-1}(c) \cong T_3(9)$
for all
$\phi ^{-1}(c) \cong T_3(9)$
for all
![]() $c \in [4]$
, and one can check that there is a unique way, up to relabelling, so choose the
$c \in [4]$
, and one can check that there is a unique way, up to relabelling, so choose the
![]() $\phi ^{-1}(c)$
to attain the given multiplicities (see Table 2, where the complement of
$\phi ^{-1}(c)$
to attain the given multiplicities (see Table 2, where the complement of
![]() $(r,\phi ,\boldsymbol {\alpha })$
is drawn, that is there is an edge of colour c drawn between i and j if and only if
$(r,\phi ,\boldsymbol {\alpha })$
is drawn, that is there is an edge of colour c drawn between i and j if and only if
![]() $c \notin \phi (ij)$
).
$c \notin \phi (ij)$
).
The strong extension property
Given
![]() $\boldsymbol {k} \in \mathbb {N}^s$
, and
$\boldsymbol {k} \in \mathbb {N}^s$
, and
![]() , and let
, and let
![]() $\boldsymbol {t} \in [s]^{r}$
be such that
$\boldsymbol {t} \in [s]^{r}$
be such that
Using what we have just proved about basic optimal solutions, summarised in Table 2, we have the following.

We can easily solve all of these using Lemma 5.3. Indeed, in every case,
![]() $2^{Q(\boldsymbol {k})}$
is a product
$2^{Q(\boldsymbol {k})}$
is a product
![]() $p_1\ldots p_{r-1}$
of
$p_1\ldots p_{r-1}$
of
![]() $r-1$
primes, each larger than
$r-1$
primes, each larger than
![]() $\sqrt {s}$
. If
$\sqrt {s}$
. If
![]() $t_1\ldots t_{r}=2^{Q(\boldsymbol {k})}$
for positive integers
$t_1\ldots t_{r}=2^{Q(\boldsymbol {k})}$
for positive integers
![]() $t_1,\ldots ,t_{r}$
, since the
$t_1,\ldots ,t_{r}$
, since the
![]() $p_i$
are prime, each
$p_i$
are prime, each
![]() $t_i$
is a product of
$t_i$
is a product of
![]() $k_i$
elements of
$k_i$
elements of
![]() $p_1,\ldots ,p_{r-1}$
for some
$p_1,\ldots ,p_{r-1}$
for some
![]() $k_i$
. But
$k_i$
. But
![]() $p_jp_k> s$
for any
$p_jp_k> s$
for any
![]() $jk \in \binom {[r-1]}{2}$
, so
$jk \in \binom {[r-1]}{2}$
, so
![]() $k_i \in \{ 0,1\}$
. By the pigeonhole principle, there is exactly one
$k_i \in \{ 0,1\}$
. By the pigeonhole principle, there is exactly one
![]() $i \in [r]$
with
$i \in [r]$
with
![]() $t_i = 1$
. Now, every
$t_i = 1$
. Now, every
![]() $\boldsymbol {k}$
in the table satisfies the hypotheses of Lemma 5.3. So each of these
$\boldsymbol {k}$
in the table satisfies the hypotheses of Lemma 5.3. So each of these
![]() $\boldsymbol {k}$
have the strong extension property.
$\boldsymbol {k}$
have the strong extension property.
5.2 The two colour case
We will now compute
![]() $Q(\boldsymbol {k})$
in the case when
$Q(\boldsymbol {k})$
in the case when
![]() $s =2$
. When
$s =2$
. When
![]() $k \geq \ell $
and
$k \geq \ell $
and
![]() $\boldsymbol {k} = (k,\ell )$
, we will show that
$\boldsymbol {k} = (k,\ell )$
, we will show that
![]() depends only on
depends only on
![]() $\ell $
but
$\ell $
but
![]() depends on both
depends on both
![]() $k,\ell $
.
$k,\ell $
.
Proof of Lemma 1.8.
Let
![]() . Since
. Since
![]() $2 = s \geq |\phi ^*(ij)| \geq 2$
for all
$2 = s \geq |\phi ^*(ij)| \geq 2$
for all
![]() $ij \in \binom {[r^*]}{2}$
, we must have that
$ij \in \binom {[r^*]}{2}$
, we must have that
![]() $(\phi ^*)^{-1}(c) \cong K_{r^*}$
for
$(\phi ^*)^{-1}(c) \cong K_{r^*}$
for
![]() $c=1,2$
. Lemma 2.5
(iii) implies that
$c=1,2$
. Lemma 2.5
(iii) implies that
![]() $r^* \geq \ell -1$
. Therefore,
$r^* \geq \ell -1$
. Therefore,
![]() $r^* = \ell -1$
. So we have that
$r^* = \ell -1$
. So we have that
 $$ \begin{align*}q(\phi^*,\boldsymbol{\alpha}^*) = 2\sum_{ij \in \binom{[\ell-1]}{2}}\alpha^*_i\alpha^*_j = 1 - \sum_{i \in [\ell-1]}(\alpha^*_i)^2 \leq 1 - \frac{1}{\ell-1}, \end{align*} $$
$$ \begin{align*}q(\phi^*,\boldsymbol{\alpha}^*) = 2\sum_{ij \in \binom{[\ell-1]}{2}}\alpha^*_i\alpha^*_j = 1 - \sum_{i \in [\ell-1]}(\alpha^*_i)^2 \leq 1 - \frac{1}{\ell-1}, \end{align*} $$
with equality if and only if
![]() $\alpha ^*_i = 1/(\ell -1)$
for all
$\alpha ^*_i = 1/(\ell -1)$
for all
![]() $i \in [\ell -1]$
.
$i \in [\ell -1]$
.
Next we show that
![]() $\boldsymbol {k}$
has the extension property. So suppose we can attach a vertex
$\boldsymbol {k}$
has the extension property. So suppose we can attach a vertex
![]() $\ell $
and extend
$\ell $
and extend
![]() $\phi ^*$
to
$\phi ^*$
to
![]() $\phi $
as in Definition 1.2. Then
$\phi $
as in Definition 1.2. Then
 $$ \begin{align*}1 - \frac{1}{\ell-1} = \mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}^*) = \sum_{i \in [\ell-1] : \phi(i\ell) \neq \emptyset}\frac{\log|\phi(i\ell)|}{\ell-1} \end{align*} $$
$$ \begin{align*}1 - \frac{1}{\ell-1} = \mathop{\mathrm{ext}}(\phi,\boldsymbol{\alpha}^*) = \sum_{i \in [\ell-1] : \phi(i\ell) \neq \emptyset}\frac{\log|\phi(i\ell)|}{\ell-1} \end{align*} $$
so
 $$ \begin{align*}\prod_{i \in [\ell-1] : \phi(i\ell) \neq \emptyset}|\phi(i\ell)| = 2^{\ell-2}. \end{align*} $$
$$ \begin{align*}\prod_{i \in [\ell-1] : \phi(i\ell) \neq \emptyset}|\phi(i\ell)| = 2^{\ell-2}. \end{align*} $$
The left-hand side is a product of at most
![]() $\ell -1 \ 1$
-s and
$\ell -1 \ 1$
-s and
![]() $2$
-s. So there is some
$2$
-s. So there is some
![]() $j \in [\ell -1]$
, such that
$j \in [\ell -1]$
, such that
![]() $|\phi (i\ell )| = 2$
for all
$|\phi (i\ell )| = 2$
for all
![]() $i \in [\ell -1] \setminus \{ j \}$
and
$i \in [\ell -1] \setminus \{ j \}$
and
![]() $|\phi (\ell j)| \leq 1$
. This proves that
$|\phi (\ell j)| \leq 1$
. This proves that
![]() $\boldsymbol {k}$
has the extension property. If
$\boldsymbol {k}$
has the extension property. If
![]() $k=\ell $
, then we must have
$k=\ell $
, then we must have
![]() $\phi (\ell j) = \emptyset $
. But if
$\phi (\ell j) = \emptyset $
. But if
![]() $k> \ell $
, we can set
$k> \ell $
, we can set
![]() $\phi (\ell j) = \{ 1 \}$
; then
$\phi (\ell j) = \{ 1 \}$
; then
![]() $\phi ^{-1}(1) \cong K_{\ell }$
and so
$\phi ^{-1}(1) \cong K_{\ell }$
and so
![]() $\phi \in \Phi _1(\ell ;\boldsymbol {k})$
. So
$\phi \in \Phi _1(\ell ;\boldsymbol {k})$
. So
![]() $\boldsymbol {k}$
has the strong extension property if and only if
$\boldsymbol {k}$
has the strong extension property if and only if
![]() $k=\ell $
.
$k=\ell $
.
Theorem 1.9 follows from combining Lemma 1.8 with Theorem 1.4.
6 Concluding remarks
In this paper, we have proved a stability theorem which roughly says that all almost optimal graphs for the Erdős-Rothschild problem are similar in structure to the blow-up of a basic optimal solution with graphs of controlled clique number added inside parts. From this, one can systematically recover almost all known stability results. Unfortunately, Problem
![]() $Q_2$
is difficult to solve in general. It would be very interesting to see it solved in further cases. Currently, all known solutions have been obtained by relaxing it to a linear program (which is easy to solve), whose variables are graph densities and whose constraints essentially replace combinatorial constraints such as some graph being
$Q_2$
is difficult to solve in general. It would be very interesting to see it solved in further cases. Currently, all known solutions have been obtained by relaxing it to a linear program (which is easy to solve), whose variables are graph densities and whose constraints essentially replace combinatorial constraints such as some graph being
![]() $K_k$
-free, with the linear constraint that its density must be at most
$K_k$
-free, with the linear constraint that its density must be at most
![]() $1-\frac {1}{k-1}$
, by Turán’s theorem. For some few cases, solutions of this linear program correspond to feasible solutions of Problem
$1-\frac {1}{k-1}$
, by Turán’s theorem. For some few cases, solutions of this linear program correspond to feasible solutions of Problem
![]() $Q_2$
, but, in general, they do not. So one possible avenue to solve it in more cases is to add more sophisticated constraints to decrease the feasible set of the linear program, which is typically much larger than that of Problem
$Q_2$
, but, in general, they do not. So one possible avenue to solve it in more cases is to add more sophisticated constraints to decrease the feasible set of the linear program, which is typically much larger than that of Problem
![]() $Q_2$
.
$Q_2$
.
In [Reference Pikhurko and Staden23], we apply our stability theorem to prove an exact result for every
![]() $\boldsymbol {k}$
with the strong extension property, proving a part of Conjecture 1.6. Given Theorem 1.7, this will systematically recover most existing exact results (see Table 1). For the weak extension property, it is harder to obtain an exact result as there is typically a large family of asymptotically extremal graphs, with similar structures, and these graphs could have small parts.
$\boldsymbol {k}$
with the strong extension property, proving a part of Conjecture 1.6. Given Theorem 1.7, this will systematically recover most existing exact results (see Table 1). For the weak extension property, it is harder to obtain an exact result as there is typically a large family of asymptotically extremal graphs, with similar structures, and these graphs could have small parts.
Acknowledgments
We are grateful to Zelealem Yilma, our collaborator on an earlier paper on this topic, for helpful discussions at the beginning of this project; and to Emil Powierski who found and helped us correct an error in the proof of Lemma 3.1. We also thank an anonymous referee for their careful reading of our paper. Oleg Pikhurko was supported by European Research Council Advanced Grant 101020255 and Leverhulme Research Project Grant RPG-2018-424. Katherine Staden was supported by Engineering and Physical Sciences Research Council Fellowship EP/V025953/1.
Competing interest
The authors have no competing interest to declare.