Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T08:55:56.440Z Has data issue: false hasContentIssue false
  • English
  • Français

SPLITTING LOOPS AND NECKLACES: VARIANTS OF THE SQUARE PEG PROBLEM

Part of: Real and complex geometry Classical differential geometry

Published online by Cambridge University Press:  20 January 2020

JAI ASLAM ,
SHUJIAN CHEN ,
FLORIAN FRICK ,
SAM SALOFF-COSTE ,
LINUS SETIABRATA  and
HUGH THOMAS
JAI ASLAM
Affiliation:
Department of Mathematics, North Carolina State University, Raleigh, NC27695, USA; [email protected]
SHUJIAN CHEN
Affiliation:
Department of Mathematics, Brandeis University, Waltham, MA02453, USA; [email protected]
FLORIAN FRICK
Affiliation:
Department of Mathematics Sciences, Carnegie Mellon University, Pittsburgh, PA15213, USA; [email protected]
SAM SALOFF-COSTE
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY14853, USA; [email protected], [email protected]
LINUS SETIABRATA
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY14853, USA; [email protected], [email protected]
HUGH THOMAS
Affiliation:
Math. Dept., Université du Québec á Montréal, QuebecH2X 3Y7, Canada; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Toeplitz conjectured that any simple planar loop inscribes a square. Here we prove variants of Toeplitz’s square peg problem. We prove Hadwiger’s 1971 conjecture that any simple loop in 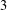$3$-space inscribes a parallelogram. We show that any simple planar loop inscribes sufficiently many rectangles that their vertices are dense in the loop. If the loop is rectifiable, there is a rectangle that cuts the loop into four pieces which can be rearranged to form two loops of equal length. (The previous two results are independently due to Schwartz.) A rectifiable loop in 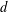$d$-space can be cut into 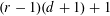$(r-1)(d+1)+1$ pieces that can be rearranged by translations to form $r$ loops of equal length. We relate our results to fair divisions of necklaces in the sense of Alon and to Tverberg-type results. This provides a new approach and a common framework to obtain inscribability results for the class of all continuous curves.

MSC classification

Primary: 53A04: Curves in Euclidean space
Secondary: 51M04: Elementary problems in Euclidean geometries
Type
Analysis
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e5
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Akopyan, A. and Avvakumov, S., ‘Any cyclic quadrilateral can be inscribed in any closed convex smooth curve’, Forum Math. Sigma 6 (2018), E7.CrossRefGoogle Scholar
Alishahi, M. and Meunier, F., ‘Fair splitting of colored paths’, Electron. J. Combin. 24(3) (2017), #P3.41.Google Scholar
Alon, N., ‘Splitting necklaces’, Adv. Math. 63(3) (1987), 247–253.CrossRefGoogle Scholar
Asada, M., Frick, F., Pisharody, V., Polevy, M., Stoner, D., Tsang, L. H. and Wellner, Z., ‘Fair division and generalizations of Sperner- and KKM-type results’, SIAM J. Discrete Math. 32(1) (2018), 591–610.CrossRefGoogle Scholar
Blagojević, P. V. M., Frick, F. and Ziegler, G. M., ‘Barycenters of polytope skeleta and counterexamples to the topological Tverberg conjecture, via constraints’, J. Eur. Math. Soc. 21(7) (2019), 2107–2116.CrossRefGoogle Scholar
Blagojević, P. V. M., Matschke, B. and Ziegler, G. M., ‘Optimal bounds for the colored Tverberg problem’, J. Eur. Math. Soc. 17(4) (2015), 739–754.CrossRefGoogle Scholar
Blagojević, P. V. M. and Soberón, P., ‘Thieves can make sandwiches’, Bull. Lond. Math. Soc. 50(1) (2018), 108–123.CrossRefGoogle Scholar
Blagojević, P. V. M. and Ziegler, G. M., ‘Beyond the Borsuk–Ulam theorem: the topological Tverberg story’, inA Journey through Discrete Mathematics (Springer, Cham, 2017), 273–341.CrossRefGoogle Scholar
de Longueville, M. and Živaljević, R., ‘Splitting multidimensional necklaces’, Adv. Math. 218(3) (2008), 926–939.CrossRefGoogle Scholar
Dold, A., ‘Simple proofs of some Borsuk–Ulam results’, Contemp. Math. 19 (1983), 65–69.CrossRefGoogle Scholar
Emch, A., ‘On some properties of the medians of closed continuous curves formed by analytic arcs’, Amer. J. Math. 38(1) (1916), 6–18.CrossRefGoogle Scholar
Frick, F., ‘Counterexamples to the topological Tverberg conjecture’, Oberwolfach Rep. 12(1) (2015), 318–321.Google Scholar
Guggenheimer, H., ‘Finite sets on curves and surfaces’, Israel J. Math. 3(2) (1965), 104–112.CrossRefGoogle Scholar
Guggenheimer, H., ‘Proof of a conjecture of H. Hadwiger’, Elem. Math. 29 (1974), 35–36.Google Scholar
Hadwiger, H., ‘Ungelöste Probleme Nr. 53’, Elem. Math. 26 (1971), 58.Google Scholar
Hobby, C. R. and Rice, J. R., ‘A moment problem in L 1 approximation’, Proc. Amer. Math. Soc. 16(4) (1965), 665–670.Google Scholar
Hugelmeyer, C., ‘Every smooth Jordan curve has an inscribed rectangle with aspect ratio equal to $\sqrt{3}$’, Preprint, 2018, arXiv:1803.07417.Google Scholar
Karasev, R., Roldán-Pensado, E. and Soberón, P., ‘Measure partitions using hyperplanes with fixed directions’, Israel J. Math. 212(2) (2016), 705–728.CrossRefGoogle Scholar
Mabillard, I. and Wagner, U., ‘Eliminating higher-multiplicity intersections, I. A whitney trick for tverberg-type problems’, Preprint, 2015, arXiv:1508.02349.Google Scholar
Makeev, V., ‘Quadrangles inscribed in a closed curve and the vertices of a curve’, J. Math. Sci. 131(1) (2005), 5395–5400.CrossRefGoogle Scholar
Matoušek, J., ‘Using the Borsuk–Ulam Theorem’, inLectures on Topological Methods in Combinatorics and Geometry, 2nd edn, Universitext (Springer, Heidelberg, 2008).Google Scholar
Matschke, B., ‘Equivariant topology methods in discrete geometry’, PhD Thesis, Freie Universität Berlin, 2011.Google Scholar
Matschke, B., ‘A survey on the square peg problem’, Not. Amer. Math. Soc. 61(4) (2014), 346–352.CrossRefGoogle Scholar
Matschke, B., ‘Quadrilaterals inscribed in convex curves’, Preprint, 2018, arXiv:1801.01945.Google Scholar
Meyerson, M. D., ‘Balancing acts’, Topol. Proc. 6 (1981), 59–75.Google Scholar
Nielsen, M. J., ‘Rhombi inscribed in simple closed curves’, Geom. Ded. 54(3) (1995), 245–254.CrossRefGoogle Scholar
Pak, I., Lectures on Discrete and Polyhedral Geometry, http://math.ucla.edu/∼pak/book.htm, 2010.Google Scholar
Schnirelman, L. G., ‘On some geometric properties of closed curves’, Uspekhi Mat. Nauk 10 (1944), 34–44 (in Russian).Google Scholar
Schwartz, R. E., ‘A trichotomy for rectangles inscribed in Jordan loops’, Preprint, 2018,arXiv:1804.00740.Google Scholar
Stromquist, W., ‘Inscribed squares and square-like quadrilaterals in closed curves’, Mathematika 36(2) (1989), 187–197.CrossRefGoogle Scholar
Tao, T., ‘An integration approach to the Toeplitz square peg problem’, Forum Math. Sigma 5 (2017), E30.CrossRefGoogle Scholar
Toeplitz, O., ‘Ueber einige Aufgaben der Analysis situs’, Verhandlungen der Schweizerischen Naturforschenden Gesellschaft in Solothurn 4(197) (1911), 29–30.Google Scholar
Vrećica, S. T. and Živaljević, R. T., ‘Fulton-MacPherson compactification, cyclohedra, and the polygonal pegs problem’, Israel J. Math. 184(1) (2011), 184–221.CrossRefGoogle Scholar