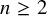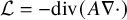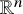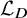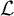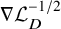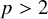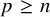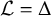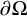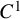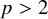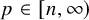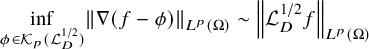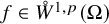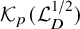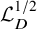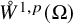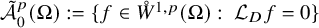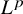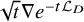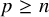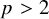1 Introduction and main results
In this paper, motivated by the recent works [Reference Hassell and Sikora10, Reference Jiang and Lin16, Reference Killip, Visan and Zhang20] on the Riesz transform on exterior Lipschitz domains, we continue to study the boundedness of the Riesz transform, associated with second-order divergence form elliptic operators on the exterior Lipschitz domain
![]() $\Omega $
having the Dirichlet boundary condition, on
$\Omega $
having the Dirichlet boundary condition, on
![]() $L^p(\Omega )$
with
$L^p(\Omega )$
with
![]() $p\in (2,\infty )$
.
$p\in (2,\infty )$
.
Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain; that is,
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain; that is,
![]() ${{{\mathbb R}}^n}\setminus \overline {\Omega }$
is a bounded Lipschitz domain of
${{{\mathbb R}}^n}\setminus \overline {\Omega }$
is a bounded Lipschitz domain of
![]() ${{{\mathbb R}}^n}$
, where
${{{\mathbb R}}^n}$
, where
![]() $\overline {\Omega }$
denotes the closure of
$\overline {\Omega }$
denotes the closure of
![]() $\Omega $
in
$\Omega $
in
![]() ${{{\mathbb R}}^n}$
. Recall that a bounded domain O is Lipschitz provided for each point x in the boundary
${{{\mathbb R}}^n}$
. Recall that a bounded domain O is Lipschitz provided for each point x in the boundary
![]() $\partial O$
, there is
$\partial O$
, there is
![]() $r>0$
, such that
$r>0$
, such that
![]() $B(x,r)\cap \partial O$
is a rotated graph of Lipschitz function. Furthermore, assume that
$B(x,r)\cap \partial O$
is a rotated graph of Lipschitz function. Furthermore, assume that
![]() $A\in L^\infty ({{{\mathbb R}}^n})$
is a real-valued and symmetric matrix that satisfies the uniformly elliptic condition; that is, there exists a constant
$A\in L^\infty ({{{\mathbb R}}^n})$
is a real-valued and symmetric matrix that satisfies the uniformly elliptic condition; that is, there exists a constant
![]() $\mu _0\in (0,1]$
such that, for any
$\mu _0\in (0,1]$
such that, for any
![]() $\xi \in {{{\mathbb R}}^n}$
and
$\xi \in {{{\mathbb R}}^n}$
and
![]() $x\in {{{\mathbb R}}^n}$
,
$x\in {{{\mathbb R}}^n}$
,
where
![]() $(\cdot ,\cdot )$
denotes the inner product in
$(\cdot ,\cdot )$
denotes the inner product in
![]() ${{{\mathbb R}}^n}$
.
${{{\mathbb R}}^n}$
.
Denote by
![]() $\mathcal {L}$
the operator
$\mathcal {L}$
the operator
![]() $-\mathrm {div}(A\nabla \cdot )$
on
$-\mathrm {div}(A\nabla \cdot )$
on
![]() ${{{\mathbb R}}^n}$
, and by
${{{\mathbb R}}^n}$
, and by
![]() $\mathcal {L}_D$
the operator
$\mathcal {L}_D$
the operator
![]() $-\mathrm {div}(A\nabla \cdot )$
on
$-\mathrm {div}(A\nabla \cdot )$
on
![]() $\Omega $
subject to the Dirichlet boundary condition (see, for instance, [Reference Ouhabaz24, Section 4.1] for the detailed definitions of
$\Omega $
subject to the Dirichlet boundary condition (see, for instance, [Reference Ouhabaz24, Section 4.1] for the detailed definitions of
![]() $\mathcal {L}$
,
$\mathcal {L}$
,
![]() $\mathcal {L}_D$
). When
$\mathcal {L}_D$
). When
![]() $A:=I_{n\times n}$
(the unit matrix), we simply denote these operators respectively by
$A:=I_{n\times n}$
(the unit matrix), we simply denote these operators respectively by
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta _D$
. Moreover, let
$\Delta _D$
. Moreover, let
![]() $O\subset {{{\mathbb R}}^n}$
be a bounded Lipschitz domain. Denote by
$O\subset {{{\mathbb R}}^n}$
be a bounded Lipschitz domain. Denote by
![]() $\mathcal {L}_{D,O}$
the operator
$\mathcal {L}_{D,O}$
the operator
![]() $-\mathrm {div}(A\nabla \cdot )$
on O subject to the Dirichlet boundary condition.
$-\mathrm {div}(A\nabla \cdot )$
on O subject to the Dirichlet boundary condition.
Let U be a domain in
![]() ${{{\mathbb R}}^n}$
or
${{{\mathbb R}}^n}$
or
![]() $U={{{\mathbb R}}^n}$
. Denote by
$U={{{\mathbb R}}^n}$
. Denote by
![]() $\mathcal {D}(U)$
the space of all infinitely differentiable functions with compact support in U endowed with the inductive topology, and by
$\mathcal {D}(U)$
the space of all infinitely differentiable functions with compact support in U endowed with the inductive topology, and by
![]() $\mathcal {D}'(U)$
the topological dual of
$\mathcal {D}'(U)$
the topological dual of
![]() $\mathcal {D}(U)$
with the weak-
$\mathcal {D}(U)$
with the weak-
![]() $\ast $
topology which is called the space of distributions on U. Let
$\ast $
topology which is called the space of distributions on U. Let
![]() $p\in (1,\infty )$
. For any
$p\in (1,\infty )$
. For any
![]() $x\in {{{\mathbb R}}^n}$
, let
$x\in {{{\mathbb R}}^n}$
, let
![]() $\rho (|x|):=(1+|x|^2)^{1/2}$
and
$\rho (|x|):=(1+|x|^2)^{1/2}$
and
![]() $\lg (|x|):=\ln (2+|x|^2)$
.
$\lg (|x|):=\ln (2+|x|^2)$
.
We define the weighted Sobolev space
![]() $W^{1,p}({{{\mathbb R}}^n})$
by
$W^{1,p}({{{\mathbb R}}^n})$
by
 $$ \begin{align*}W^{1,p}({{{\mathbb R}}^n}):=\left\{u\in\mathcal{D}'({{{\mathbb R}}^n}):\ \|u\|_{W^{1,p}({{{\mathbb R}}^n})}:=\left\|\frac{u}{\rho(|x|)}\right\|_{L^p({{{\mathbb R}}^n})} +\|\,|\nabla u|\,\|_{L^p({{{\mathbb R}}^n})}<\infty\right\} \end{align*} $$
$$ \begin{align*}W^{1,p}({{{\mathbb R}}^n}):=\left\{u\in\mathcal{D}'({{{\mathbb R}}^n}):\ \|u\|_{W^{1,p}({{{\mathbb R}}^n})}:=\left\|\frac{u}{\rho(|x|)}\right\|_{L^p({{{\mathbb R}}^n})} +\|\,|\nabla u|\,\|_{L^p({{{\mathbb R}}^n})}<\infty\right\} \end{align*} $$
when
![]() $p\neq n$
, and
$p\neq n$
, and
 $$ \begin{align*}W^{1,n}({{{\mathbb R}}^n}):=\left\{u\in\mathcal{D}'({{{\mathbb R}}^n}):\ \|u\|_{W^{1,n}({{{\mathbb R}}^n})}:=\left\|\frac{u}{\rho(|x|)\lg(|x|)}\right\|_{L^p({{{\mathbb R}}^n})} +\|\,|\nabla u|\,\|_{L^p({{{\mathbb R}}^n})}<\infty\right\}, \end{align*} $$
$$ \begin{align*}W^{1,n}({{{\mathbb R}}^n}):=\left\{u\in\mathcal{D}'({{{\mathbb R}}^n}):\ \|u\|_{W^{1,n}({{{\mathbb R}}^n})}:=\left\|\frac{u}{\rho(|x|)\lg(|x|)}\right\|_{L^p({{{\mathbb R}}^n})} +\|\,|\nabla u|\,\|_{L^p({{{\mathbb R}}^n})}<\infty\right\}, \end{align*} $$
where
![]() $\nabla u$
denotes the distributional gradient of u; see [Reference Amrouche, Girault and Giroire1, Reference Amrouche, Girault and Giroire2], for instance. Moreover, for the exterior domain
$\nabla u$
denotes the distributional gradient of u; see [Reference Amrouche, Girault and Giroire1, Reference Amrouche, Girault and Giroire2], for instance. Moreover, for the exterior domain
![]() $\Omega $
, the weighted Sobolev space
$\Omega $
, the weighted Sobolev space
![]() $W^{1,p}(\Omega )$
is defined via replacing
$W^{1,p}(\Omega )$
is defined via replacing
![]() $\mathcal {D}'({{{\mathbb R}}^n})$
and
$\mathcal {D}'({{{\mathbb R}}^n})$
and
![]() $L^p({{{\mathbb R}}^n})$
in the definition of
$L^p({{{\mathbb R}}^n})$
in the definition of
![]() $W^{1,p}({{{\mathbb R}}^n})$
, respectively, by
$W^{1,p}({{{\mathbb R}}^n})$
, respectively, by
![]() $\mathcal {D}'(\Omega )$
and
$\mathcal {D}'(\Omega )$
and
![]() $L^p(\Omega )$
, and the weighted Sobolev space
$L^p(\Omega )$
, and the weighted Sobolev space
![]() $\mathring {W}^{1,p}(\Omega )$
is defined as the completion of
$\mathring {W}^{1,p}(\Omega )$
is defined as the completion of
![]() $\mathcal {D}(\Omega )$
under the norm
$\mathcal {D}(\Omega )$
under the norm
![]() $\|\cdot \|_{W^{1,p}(\Omega )}$
. Moreover, for any
$\|\cdot \|_{W^{1,p}(\Omega )}$
. Moreover, for any
![]() $q\in (1,\infty )$
, denote by
$q\in (1,\infty )$
, denote by
![]() $W^{-1,q}({{{\mathbb R}}^n})$
,
$W^{-1,q}({{{\mathbb R}}^n})$
,
![]() $W^{-1,q}(\Omega )$
, and
$W^{-1,q}(\Omega )$
, and
![]() $\mathring {W}^{-1,q}(\Omega )$
, respectively, the dual spaces of
$\mathring {W}^{-1,q}(\Omega )$
, respectively, the dual spaces of
![]() $W^{1,q'}({{{\mathbb R}}^n})$
,
$W^{1,q'}({{{\mathbb R}}^n})$
,
![]() $W^{1,q'}(\Omega )$
, and
$W^{1,q'}(\Omega )$
, and
![]() $\mathring {W}^{1,q'}(\Omega )$
, where
$\mathring {W}^{1,q'}(\Omega )$
, where
![]() $q':=q/(q-1)$
.
$q':=q/(q-1)$
.
We also recall some useful properties for the Sobolev spaces
![]() $W^{1,p}({{{\mathbb R}}^n})$
,
$W^{1,p}({{{\mathbb R}}^n})$
,
![]() $W^{1,p}(\Omega )$
, and
$W^{1,p}(\Omega )$
, and
![]() $\mathring {W}^{1,p}(\Omega )$
established in [Reference Amrouche, Girault and Giroire1, Reference Amrouche, Girault and Giroire2] as following.
$\mathring {W}^{1,p}(\Omega )$
established in [Reference Amrouche, Girault and Giroire1, Reference Amrouche, Girault and Giroire2] as following.
Remark 1.1. Let
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain, and
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain, and
![]() $p\in (1,\infty )$
.
$p\in (1,\infty )$
.
-
(i)
 $\mathcal {D}({{{\mathbb R}}^n})$
is dense in
$\mathcal {D}({{{\mathbb R}}^n})$
is dense in
 $W^{1,p}({{{\mathbb R}}^n})$
and
$W^{1,p}({{{\mathbb R}}^n})$
and
 $\mathcal {D}(\overline {\Omega })$
is dense in
$\mathcal {D}(\overline {\Omega })$
is dense in
 $W^{1,p}(\Omega )$
. Here,
$W^{1,p}(\Omega )$
. Here,
 $\mathcal {D}(\overline {\Omega })$
denotes the space of all infinitely differentiable functions with compact support in
$\mathcal {D}(\overline {\Omega })$
denotes the space of all infinitely differentiable functions with compact support in
 $\overline {\Omega }$
. Furthermore, constants belong to
$\overline {\Omega }$
. Furthermore, constants belong to
 $W^{1,p}({{{\mathbb R}}^n})$
or
$W^{1,p}({{{\mathbb R}}^n})$
or
 $W^{1,p}(\Omega )$
when
$W^{1,p}(\Omega )$
when
 $p\in [n,\infty )$
, but constants do not belong to
$p\in [n,\infty )$
, but constants do not belong to
 $W^{1,p}({{{\mathbb R}}^n})$
and
$W^{1,p}({{{\mathbb R}}^n})$
and
 $W^{1,p}(\Omega )$
when
$W^{1,p}(\Omega )$
when
 $p\in (1,n)$
.
$p\in (1,n)$
. -
(ii) Let
 $U={{{\mathbb R}}^n}$
or
$U={{{\mathbb R}}^n}$
or
 $U=\Omega $
. For any
$U=\Omega $
. For any
 $u\in W^{1,p}(U)$
, define the semi-norm
$u\in W^{1,p}(U)$
, define the semi-norm
 $[u]_{W^{1,p}(U)}:=\|\,|\nabla u|\,\|_{L^p(U)}$
. When
$[u]_{W^{1,p}(U)}:=\|\,|\nabla u|\,\|_{L^p(U)}$
. When
 $p\in (1,n)$
, the semi-norm
$p\in (1,n)$
, the semi-norm
 $[\cdot ]_{W^{1,p}(U)}$
is a norm on
$[\cdot ]_{W^{1,p}(U)}$
is a norm on
 $W^{1,p}(U)$
equivalent to the full norm
$W^{1,p}(U)$
equivalent to the full norm
 $\|\cdot \|_{W^{1,p}(U)}$
; when
$\|\cdot \|_{W^{1,p}(U)}$
; when
 $p\in [n,\infty )$
, the semi-norm
$p\in [n,\infty )$
, the semi-norm
 $[\cdot ]_{W^{1,p}(U)}$
defines on the quotient space
$[\cdot ]_{W^{1,p}(U)}$
defines on the quotient space
 $W^{1,p}(U)/C$
a norm which is equivalent to the quotient norm (see [Reference Amrouche, Girault and Giroire2, Proposition 9.3] and [Reference Amrouche, Girault and Giroire1, Theorem 1.1]). Moreover, the semi-norm
$W^{1,p}(U)/C$
a norm which is equivalent to the quotient norm (see [Reference Amrouche, Girault and Giroire2, Proposition 9.3] and [Reference Amrouche, Girault and Giroire1, Theorem 1.1]). Moreover, the semi-norm
 $[\cdot ]_{W^{1,p}(\Omega )}$
is a norm on
$[\cdot ]_{W^{1,p}(\Omega )}$
is a norm on
 $\mathring {W}^{1,p}(\Omega )$
that is equivalent to the full norm
$\mathring {W}^{1,p}(\Omega )$
that is equivalent to the full norm
 $\|\cdot \|_{W^{1,p}(\Omega )}$
for all
$\|\cdot \|_{W^{1,p}(\Omega )}$
for all
 $1<p<\infty $
(see [Reference Amrouche, Girault and Giroire1, Theorem 1.2]).
$1<p<\infty $
(see [Reference Amrouche, Girault and Giroire1, Theorem 1.2]).
For a bounded Lipschitz domain
![]() $O\subset {{{\mathbb R}}^n}$
and
$O\subset {{{\mathbb R}}^n}$
and
![]() $1<p<\infty $
, the Sobolev space
$1<p<\infty $
, the Sobolev space
![]() $W^{1,p}(O)$
is defined as usual – that is,
$W^{1,p}(O)$
is defined as usual – that is,
![]() $f\in \mathcal {D}'(O)$
with
$f\in \mathcal {D}'(O)$
with
Furthermore,
![]() $\mathring {W}^{1,p}(O)$
is defined to be the closure of
$\mathring {W}^{1,p}(O)$
is defined to be the closure of
![]() $\mathcal {D}(O)$
in
$\mathcal {D}(O)$
in
![]() $W^{1,p}(O)$
, and
$W^{1,p}(O)$
, and
![]() $W^{-1,p}(O)$
and
$W^{-1,p}(O)$
and
![]() $\mathring {W}^{-1,p}(O)$
are defined as the dual spaces of
$\mathring {W}^{-1,p}(O)$
are defined as the dual spaces of
![]() $W^{1,p'}(O)$
and
$W^{1,p'}(O)$
and
![]() $\mathring {W}^{1,p'}(O)$
, respectively.
$\mathring {W}^{1,p'}(O)$
, respectively.
It is well known that the boundedness of the Riesz transform associated with some differential operators on various function spaces has important applications in harmonic analysis and partial differential equations and has aroused great interests in recent years (see, for instance, [Reference Auscher, Coulhon, Duong and Hofmann3, Reference Auscher and Tchamitchian4, Reference Coulhon and Duong7, Reference Coulhon, Jiang, Koskela and Sikora8, Reference Hassell and Sikora10, Reference Jiang15, Reference Jiang and Lin17, Reference Killip, Visan and Zhang20, Reference Shen25, Reference Song and Yan28]). In particular, let O be a bounded Lipschitz domain of
![]() ${{{\mathbb R}}^n}$
. The sharp boundedness of the Riesz transform
${{{\mathbb R}}^n}$
. The sharp boundedness of the Riesz transform
![]() $\nabla \mathcal {L}_{D,O}^{-1/2}$
associated with the operator
$\nabla \mathcal {L}_{D,O}^{-1/2}$
associated with the operator
![]() $\mathcal {L}_{D,O}$
having the Dirichlet boundary condition on the Lebesgue space
$\mathcal {L}_{D,O}$
having the Dirichlet boundary condition on the Lebesgue space
![]() $L^p(O)$
was established by Shen [Reference Shen25].
$L^p(O)$
was established by Shen [Reference Shen25].
Compared with the boundedness of the Riesz transform associated with differential operators on bounded Lipschitz domains, there are relatively few literatures for the Riesz transform associated with differential operators on exterior Lipschitz domains. Since the heat kernel generated by
![]() $\mathcal {L}_D$
satisfies the Gaussian upper bound estimate, it follows from the results of Sikora [Reference Sikora27] (see also [Reference Coulhon and Duong7]) that the Riesz transform
$\mathcal {L}_D$
satisfies the Gaussian upper bound estimate, it follows from the results of Sikora [Reference Sikora27] (see also [Reference Coulhon and Duong7]) that the Riesz transform
![]() $\nabla \mathcal {L}^{-1/2}_D$
is always bounded on
$\nabla \mathcal {L}^{-1/2}_D$
is always bounded on
![]() $L^p(\Omega )$
for
$L^p(\Omega )$
for
![]() $p\in (1,2]$
. By studying weighted operators in the one dimension, Hassell and Sikora [Reference Hassell and Sikora10] discovered that the Riesz transform
$p\in (1,2]$
. By studying weighted operators in the one dimension, Hassell and Sikora [Reference Hassell and Sikora10] discovered that the Riesz transform
![]() $\nabla \Delta _D^{-1/2}$
on the exterior of the unit ball is not bounded on
$\nabla \Delta _D^{-1/2}$
on the exterior of the unit ball is not bounded on
![]() $L^p$
for
$L^p$
for
![]() $p\in (2,\infty )$
if
$p\in (2,\infty )$
if
![]() $n=2$
, and
$n=2$
, and
![]() $p\in [n,\infty )$
if
$p\in [n,\infty )$
if
![]() $n\ge 3$
; see also [Reference Li, Smith and Zhang22] for the case
$n\ge 3$
; see also [Reference Li, Smith and Zhang22] for the case
![]() $n=3$
. Moreover, Killip, Visan and Zhang [Reference Killip, Visan and Zhang20] proved that the Riesz transform
$n=3$
. Moreover, Killip, Visan and Zhang [Reference Killip, Visan and Zhang20] proved that the Riesz transform
![]() $\nabla \Delta _D^{-1/2}$
on the exterior of a smooth convex obstacle in
$\nabla \Delta _D^{-1/2}$
on the exterior of a smooth convex obstacle in
![]() ${{{\mathbb R}}^n}$
(
${{{\mathbb R}}^n}$
(
![]() $n\ge 3$
) is bounded for
$n\ge 3$
) is bounded for
![]() $p\in (1,n)$
. Very recently, characterizations for the boundedness of the Riesz transform
$p\in (1,n)$
. Very recently, characterizations for the boundedness of the Riesz transform
![]() $\nabla \mathcal {L}_{D}^{-1/2}$
on
$\nabla \mathcal {L}_{D}^{-1/2}$
on
![]() $L^p(\Omega )$
with
$L^p(\Omega )$
with
![]() $p\in (2,n)$
was obtained in [Reference Jiang and Lin16].
$p\in (2,n)$
was obtained in [Reference Jiang and Lin16].
Let
Furthermore, denote by
![]() $L^{1}_{\mathrm {loc}}(\mathbb {R}^n)$
the set of all locally integrable functions on
$L^{1}_{\mathrm {loc}}(\mathbb {R}^n)$
the set of all locally integrable functions on
![]() ${\mathbb R}^n$
. Recall that the space
${\mathbb R}^n$
. Recall that the space
![]() $\mathrm {BMO}({{{\mathbb R}}^n})$
is defined as the set of all
$\mathrm {BMO}({{{\mathbb R}}^n})$
is defined as the set of all
![]() $f\in L^1_{\mathrm {loc}}({{{\mathbb R}}^n})$
satisfying
$f\in L^1_{\mathrm {loc}}({{{\mathbb R}}^n})$
satisfying
 $$ \begin{align*}\|f\|_{\mathrm{BMO}({{{\mathbb R}}^n})}:=\sup_{B\subset{{{\mathbb R}}^n}}\frac{1}{|B|}\int_{B}\left|f(x)-\frac{1}{|B|}\int_B f(y)\,dy\right|\,dx<\infty, \end{align*} $$
$$ \begin{align*}\|f\|_{\mathrm{BMO}({{{\mathbb R}}^n})}:=\sup_{B\subset{{{\mathbb R}}^n}}\frac{1}{|B|}\int_{B}\left|f(x)-\frac{1}{|B|}\int_B f(y)\,dy\right|\,dx<\infty, \end{align*} $$
where the supremum is taken over all balls B of
![]() ${{{\mathbb R}}^n}$
(see, for instance, [Reference John and Nirenberg19, Reference Stein29]). Moreover, the space
${{{\mathbb R}}^n}$
(see, for instance, [Reference John and Nirenberg19, Reference Stein29]). Moreover, the space
![]() $\mathrm {CMO}({{{\mathbb R}}^n})$
is defined as the completion of
$\mathrm {CMO}({{{\mathbb R}}^n})$
is defined as the completion of
![]() $\mathcal {D}({{{\mathbb R}}^n})$
in the space
$\mathcal {D}({{{\mathbb R}}^n})$
in the space
![]() $\mathrm {BMO}({{{\mathbb R}}^n})$
(see, for instance, [Reference Coifman and Weiss6]). The space
$\mathrm {BMO}({{{\mathbb R}}^n})$
(see, for instance, [Reference Coifman and Weiss6]). The space
![]() $\mathrm {VMO}({{{\mathbb R}}^n})$
is defined as the set of
$\mathrm {VMO}({{{\mathbb R}}^n})$
is defined as the set of
![]() $f\in \mathrm {BMO}({{{\mathbb R}}^n})$
satisfying
$f\in \mathrm {BMO}({{{\mathbb R}}^n})$
satisfying
 $$ \begin{align*}{\lim_{r\to 0}\sup_{x\in {{{\mathbb R}}^n}}\frac{1}{|B(x,r)|}\int_{B(x,r)}\left|f(y)-\frac{1}{|B(x,r)|}\int_{B(x,r)} f(z)\,dz\right|\,dy=0.}\end{align*} $$
$$ \begin{align*}{\lim_{r\to 0}\sup_{x\in {{{\mathbb R}}^n}}\frac{1}{|B(x,r)|}\int_{B(x,r)}\left|f(y)-\frac{1}{|B(x,r)|}\int_{B(x,r)} f(z)\,dz\right|\,dy=0.}\end{align*} $$
Note that
![]() $\mathrm {CMO}({{{\mathbb R}}^n})\varsubsetneq \mathrm {VMO}({{{\mathbb R}}^n}) \varsubsetneq \mathrm {BMO}({{{\mathbb R}}^n}).$
Let us recall some results proved in [Reference Jiang and Lin16, Theorems 1.3 and 1.4].
$\mathrm {CMO}({{{\mathbb R}}^n})\varsubsetneq \mathrm {VMO}({{{\mathbb R}}^n}) \varsubsetneq \mathrm {BMO}({{{\mathbb R}}^n}).$
Let us recall some results proved in [Reference Jiang and Lin16, Theorems 1.3 and 1.4].
Theorem 1.2 [Reference Jiang and Lin16].
Let
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain,
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain,
![]() $n\ge 2$
.
$n\ge 2$
.
(i) For all
![]() $p\in (1,\infty )$
, it holds for all
$p\in (1,\infty )$
, it holds for all
![]() $f\in \mathring {W}^{1,p}(\Omega )$
that
$f\in \mathring {W}^{1,p}(\Omega )$
that
(ii) Suppose that
![]() $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
and
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
and
![]() $n\ge 3$
. There exist
$n\ge 3$
. There exist
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $C>1$
such that, for all
$C>1$
such that, for all
![]() $f\in \mathring {W}^{1,p}(\Omega )$
, it holds that
$f\in \mathring {W}^{1,p}(\Omega )$
, it holds that
where
![]() $1<p<\min \{n,p({\mathcal {L}}),3+\epsilon \}$
. If
$1<p<\min \{n,p({\mathcal {L}}),3+\epsilon \}$
. If
![]() $\Omega $
is
$\Omega $
is
![]() $C^1$
, then (1.2) holds for all
$C^1$
, then (1.2) holds for all
![]() $1<p<\min \{n,p({\mathcal {L}})\}$
.
$1<p<\min \{n,p({\mathcal {L}})\}$
.
Remark 1.3. The version of (1.1) for Neumann boundary operators
![]() $\mathcal {L}_N$
has been recently proved in [Reference Devyver and Russ9] on complete manifolds with ends. Although the results in [Reference Devyver and Russ9] were presented in smooth manifolds setting, their proofs extend to exterior Lipschitz domains almost identically and show that, for all
$\mathcal {L}_N$
has been recently proved in [Reference Devyver and Russ9] on complete manifolds with ends. Although the results in [Reference Devyver and Russ9] were presented in smooth manifolds setting, their proofs extend to exterior Lipschitz domains almost identically and show that, for all
![]() $p\in (1,\infty )$
,
$p\in (1,\infty )$
,
Note that the heat kernel satisfies two side Gaussian bounds; see [Reference Jiang and Lin16, Proof of Theorem 1.2].
For the case
![]() $\mathcal {L}=\Delta $
being the Laplacian operator and
$\mathcal {L}=\Delta $
being the Laplacian operator and
![]() $\Omega $
being
$\Omega $
being
![]() $C^1$
,
$C^1$
,
![]() $p(\mathcal {L})=\infty $
and
$p(\mathcal {L})=\infty $
and
![]() $\epsilon =\infty $
. In this case, it follows from the above results that
$\epsilon =\infty $
. In this case, it follows from the above results that
![]() $\nabla \Delta _D^{-1/2}$
is bounded on
$\nabla \Delta _D^{-1/2}$
is bounded on
![]() $L^p(\Omega )$
for
$L^p(\Omega )$
for
![]() $1<p<n$
. By the unboundedness results on the Riesz transform
$1<p<n$
. By the unboundedness results on the Riesz transform
![]() $\nabla \Delta _D^{-1/2}$
established in [Reference Hassell and Sikora10], the range
$\nabla \Delta _D^{-1/2}$
established in [Reference Hassell and Sikora10], the range
![]() $(1,\min \{n,3+\varepsilon \})$
of p for (1.2) is sharp; see also [Reference Jiang and Lin16, Reference Killip, Visan and Zhang20].
$(1,\min \{n,3+\varepsilon \})$
of p for (1.2) is sharp; see also [Reference Jiang and Lin16, Reference Killip, Visan and Zhang20].
The main purpose of this paper is to further investigate the case
![]() $p\ge n$
. Note that from Theorem 1.2, the boundedness of the Riesz transform
$p\ge n$
. Note that from Theorem 1.2, the boundedness of the Riesz transform
![]() $\nabla \mathcal {L}_D^{-1/2}$
depends on
$\nabla \mathcal {L}_D^{-1/2}$
depends on
![]() $n,p(\mathcal {L})$
, and the geometry of the boundary
$n,p(\mathcal {L})$
, and the geometry of the boundary
![]() $\partial \Omega $
. All the dependences are essential; see the characterizations obtained by [Reference Jiang and Lin16, Theorem 1.1], the regularity dependence of the boundary by [Reference Jerison and Kenig18], and the counterexamples provided in [Reference Hassell and Sikora10, Reference Killip, Visan and Zhang20, Reference Jiang and Lin16]. However, for operator with nice coefficients and domain with nice boundary (
$\partial \Omega $
. All the dependences are essential; see the characterizations obtained by [Reference Jiang and Lin16, Theorem 1.1], the regularity dependence of the boundary by [Reference Jerison and Kenig18], and the counterexamples provided in [Reference Hassell and Sikora10, Reference Killip, Visan and Zhang20, Reference Jiang and Lin16]. However, for operator with nice coefficients and domain with nice boundary (
![]() $C^1$
or small Lipschitz constant) such that
$C^1$
or small Lipschitz constant) such that
![]() $p(\mathcal {L}),3+\epsilon \ge n$
, we can find a suitable substitution of
$p(\mathcal {L}),3+\epsilon \ge n$
, we can find a suitable substitution of
![]() $\mathring {W}^{1,p}(\Omega )$
space for the inequality (1.2) as following.
$\mathring {W}^{1,p}(\Omega )$
space for the inequality (1.2) as following.
Let us assume that the matrix A in the operator
![]() $\mathcal {L}$
is in the space
$\mathcal {L}$
is in the space
![]() $\mathrm {VMO}({{{\mathbb R}}^n})$
and satisfies the perturbation
$\mathrm {VMO}({{{\mathbb R}}^n})$
and satisfies the perturbation

for some
![]() $\delta>0$
, all
$\delta>0$
, all
![]() $r>1$
, and all
$r>1$
, and all
![]() $x_0\in {{{\mathbb R}}^n}$
. Or we assume that
$x_0\in {{{\mathbb R}}^n}$
. Or we assume that
![]() $A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. In both cases, from [Reference Jiang and Lin17] and [Reference Iwaniec and Sbordone14, Theorem 1], respectively, it is known that
$A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. In both cases, from [Reference Jiang and Lin17] and [Reference Iwaniec and Sbordone14, Theorem 1], respectively, it is known that
We have the following replacement for the Riesz inequality for
![]() $p\ge n$
and
$p\ge n$
and
![]() $p>2$
.
$p>2$
.
Theorem 1.4. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior
![]() $C^1$
domain. Assume that
$C^1$
domain. Assume that
![]() $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
![]() $(GD)$
or
$(GD)$
or
![]() $A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. Let
$A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. Let
![]() $p>2$
and
$p>2$
and
![]() $p\in [n,\infty )$
.
$p\in [n,\infty )$
.
(i) The kernel space
![]() $\mathcal {K}_{p}(\mathcal {L}_D^{1/2})$
of
$\mathcal {K}_{p}(\mathcal {L}_D^{1/2})$
of
![]() $\mathcal {L}_D^{1/2}$
in
$\mathcal {L}_D^{1/2}$
in
![]() $\mathring {W}^{1,p}(\Omega )$
coincides with
$\mathring {W}^{1,p}(\Omega )$
coincides with
![]() $\tilde {\mathcal {A}}^p_0(\Omega ):=\{\phi \in \mathring {W}^{1,p}(\Omega ): \mathcal {L}_D f=0\}.$
Moreover, when
$\tilde {\mathcal {A}}^p_0(\Omega ):=\{\phi \in \mathring {W}^{1,p}(\Omega ): \mathcal {L}_D f=0\}.$
Moreover, when
![]() $n\ge 3$
,
$n\ge 3$
,
![]() $\tilde {\mathcal {A}}^p_0(\Omega )=\mathcal {A}^p_0(\Omega ):=\{c(u_0-1): \ c\in {\mathbb R}\},$
where
$\tilde {\mathcal {A}}^p_0(\Omega )=\mathcal {A}^p_0(\Omega ):=\{c(u_0-1): \ c\in {\mathbb R}\},$
where
![]() $u_0$
is the unique solution in
$u_0$
is the unique solution in
![]() $W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem
$W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem
 $$ \begin{align*} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_0)=0\ \ &\text{in}\ \Omega,\\ u_0=1\ &\text{on}\ \partial\Omega; \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_0)=0\ \ &\text{in}\ \Omega,\\ u_0=1\ &\text{on}\ \partial\Omega; \end{array}\right. \end{align*} $$
when
![]() $n=2$
,
$n=2$
,
![]() $\tilde {\mathcal {A}}^p_0(\Omega )=\mathcal {A}^p_0(\Omega ):=\{c(u_0-u_1): \ c\in {\mathbb R}\},$
where
$\tilde {\mathcal {A}}^p_0(\Omega )=\mathcal {A}^p_0(\Omega ):=\{c(u_0-u_1): \ c\in {\mathbb R}\},$
where
![]() $u_0$
is the unique solution in
$u_0$
is the unique solution in
![]() $W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem
$W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem
 $$ \begin{align*} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_0)=0\ \ &\text{in}\ \Omega,\\ u_0=u_1\ &\text{on}\ \partial\Omega, \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_0)=0\ \ &\text{in}\ \Omega,\\ u_0=u_1\ &\text{on}\ \partial\Omega, \end{array}\right. \end{align*} $$
and
![]() $u_1\in W^{1,p}({\mathbb R}^2)$
is a solution of the problem
$u_1\in W^{1,p}({\mathbb R}^2)$
is a solution of the problem
![]() $\mathcal {L}u=\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }$
in
$\mathcal {L}u=\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }$
in
![]() ${\mathbb R}^2$
. Here and thereafter,
${\mathbb R}^2$
. Here and thereafter,
![]() $\sigma (\partial \Omega )$
denotes the surface measure of
$\sigma (\partial \Omega )$
denotes the surface measure of
![]() $\partial \Omega $
, and
$\partial \Omega $
, and
![]() $\delta _{\partial \Omega }$
is the distribution on
$\delta _{\partial \Omega }$
is the distribution on
![]() $\mathcal {D}({\mathbb R}^2)$
as
$\mathcal {D}({\mathbb R}^2)$
as
(ii) It holds for all
![]() $f\in \mathring {W}^{1,p}(\Omega )$
that
$f\in \mathring {W}^{1,p}(\Omega )$
that
and consequently, it holds that
The symbol
![]() $f\sim g$
means
$f\sim g$
means
![]() $f\lesssim g$
and
$f\lesssim g$
and
![]() $g\lesssim f$
, which stands for
$g\lesssim f$
, which stands for
![]() $f\le Cg$
and
$f\le Cg$
and
![]() $g\le Ch$
. The main new ingredient that appeared in Theorem 1.4 is identifying the kernel
$g\le Ch$
. The main new ingredient that appeared in Theorem 1.4 is identifying the kernel
![]() $\mathcal {K}_{p}(\mathcal {L}_D^{1/2})$
of
$\mathcal {K}_{p}(\mathcal {L}_D^{1/2})$
of
![]() $\mathcal {L}_D^{1/2}$
in
$\mathcal {L}_D^{1/2}$
in
![]() $\mathring {W}^{1,p}(\Omega )$
as the space
$\mathring {W}^{1,p}(\Omega )$
as the space
![]() $\mathcal {A}^p_0(\Omega )$
, which is motivated by the work of Amrouche, Girault and Giroire [Reference Amrouche, Girault and Giroire1]. We can actually establish a more general version of Theorem 1.4, provided that
$\mathcal {A}^p_0(\Omega )$
, which is motivated by the work of Amrouche, Girault and Giroire [Reference Amrouche, Girault and Giroire1]. We can actually establish a more general version of Theorem 1.4, provided that
![]() $p(\mathcal {L})\ge n$
and the boundary
$p(\mathcal {L})\ge n$
and the boundary
![]() $\partial \Omega $
is
$\partial \Omega $
is
![]() $C^1$
or with small Lipschitz constant; see Theorem 2.4 below.
$C^1$
or with small Lipschitz constant; see Theorem 2.4 below.
Let us remark that we can have an explicit description in the exterior setting due to the boundedness of the Riesz transform in
![]() ${{{\mathbb R}}^n}$
for
${{{\mathbb R}}^n}$
for
![]() $1<p<\infty $
and the special geometry of exterior domains. From previous results of Riesz transforms from [Reference Auscher, Coulhon, Duong and Hofmann3, Reference Coulhon, Jiang, Koskela and Sikora8, Reference Jiang and Lin17], we know in case of
$1<p<\infty $
and the special geometry of exterior domains. From previous results of Riesz transforms from [Reference Auscher, Coulhon, Duong and Hofmann3, Reference Coulhon, Jiang, Koskela and Sikora8, Reference Jiang and Lin17], we know in case of
![]() $p\in (2,\infty )$
, both local and global geometry can destroy the boundedness of the Riesz transform. In particular, a local perturbation of A may result in huge difference of behavior of the Riesz transform for
$p\in (2,\infty )$
, both local and global geometry can destroy the boundedness of the Riesz transform. In particular, a local perturbation of A may result in huge difference of behavior of the Riesz transform for
![]() $p>2$
; see [Reference Jiang and Lin17], for instance. So generally speaking, it is hard (at least to us) to have an explicit description of the kernel space. For the case of exterior domains, under the assumption of
$p>2$
; see [Reference Jiang and Lin17], for instance. So generally speaking, it is hard (at least to us) to have an explicit description of the kernel space. For the case of exterior domains, under the assumption of
![]() $p(\mathcal {L})=\infty $
, we see that the kernel space that breaks down the boundedness of the Riesz transform for
$p(\mathcal {L})=\infty $
, we see that the kernel space that breaks down the boundedness of the Riesz transform for
![]() $p\ge n$
and
$p\ge n$
and
![]() $p>2$
is actually only one-dimensional subspace of
$p>2$
is actually only one-dimensional subspace of
![]() $\mathring {W}^{1,p}(\Omega )$
.
$\mathring {W}^{1,p}(\Omega )$
.
Finally, let us apply Theorem 1.4 to the mapping property of the gradient of heat semigroup, which plays important roles in the study of of Schrödinger equations; see [Reference Ivanovici11, Reference Ivanovici and Planchon12, Reference Ivanovici and Planchon13, Reference Killip, Visan and Zhang21, Reference Li, Smith and Zhang22], for instance. For the operator
![]() $\sqrt t\nabla e^{-t\mathcal {L}_D}$
, it was known that there are no uniform
$\sqrt t\nabla e^{-t\mathcal {L}_D}$
, it was known that there are no uniform
![]() $L^p$
-bounds in t for
$L^p$
-bounds in t for
![]() $p>n$
; see [Reference Killip, Visan and Zhang20, Proposition 8.1]. As an application of (1.3) of Theorem 1.4, we have the following substitution.
$p>n$
; see [Reference Killip, Visan and Zhang20, Proposition 8.1]. As an application of (1.3) of Theorem 1.4, we have the following substitution.
Theorem 1.5. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior
![]() $C^1$
domain. Assume that
$C^1$
domain. Assume that
![]() $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
![]() $(GD)$
or
$(GD)$
or
![]() $A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. Let
$A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. Let
![]() $p>2$
and
$p>2$
and
![]() $p\in [n,\infty )$
. Then it holds that
$p\in [n,\infty )$
. Then it holds that
The proof is straightforward by using (1.3) and the analyticity of the heat semigroup, as
Moreover, noting that, for all
![]() $\phi \in \mathcal {K}_p(\mathcal {L}_D^{1/2})$
,
$\phi \in \mathcal {K}_p(\mathcal {L}_D^{1/2})$
,
we find that
![]() $e^{-t\mathcal {L}_D}\phi =\phi $
for all
$e^{-t\mathcal {L}_D}\phi =\phi $
for all
![]() $t>0$
.
$t>0$
.
In the particular case
![]() $\mathcal {L}:=\Delta $
and
$\mathcal {L}:=\Delta $
and
![]() $\Omega :={{{\mathbb R}}^n}\setminus \overline {B(0,1)}$
, it is clear that the kernel space is exactly as
$\Omega :={{{\mathbb R}}^n}\setminus \overline {B(0,1)}$
, it is clear that the kernel space is exactly as
 $$ \begin{align} \mathcal{K}_{p}(\Delta_D^{1/2})=\tilde{\mathcal{A}}^p_0(\Omega)= \begin{cases} \{c(1-|x|^{2-n}):\ |x|>1,\,c\in{\mathbb R}\}, & n\ge 3,\\ \{c\log|x|:\ |x|>1,\, c\in{\mathbb R}\}, & n=2, \end{cases} \end{align} $$
$$ \begin{align} \mathcal{K}_{p}(\Delta_D^{1/2})=\tilde{\mathcal{A}}^p_0(\Omega)= \begin{cases} \{c(1-|x|^{2-n}):\ |x|>1,\,c\in{\mathbb R}\}, & n\ge 3,\\ \{c\log|x|:\ |x|>1,\, c\in{\mathbb R}\}, & n=2, \end{cases} \end{align} $$
where
![]() $p\ge n$
and
$p\ge n$
and
![]() $p>2$
. We therefore have the following corollary.
$p>2$
. We therefore have the following corollary.
Corollary 1.6. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $\Omega :={{{\mathbb R}}^n}\setminus \overline {B(0,1)}$
. Let
$\Omega :={{{\mathbb R}}^n}\setminus \overline {B(0,1)}$
. Let
![]() $p>2$
and
$p>2$
and
![]() $p\in [n,\infty )$
. Then it holds that
$p\in [n,\infty )$
. Then it holds that
 $$ \begin{align*} \inf_{c\in{\mathbb R}} \left\|\sqrt t \nabla e^{-t\Delta_D}f-\frac{cx}{|x|^n}\right\|_{L^p(\Omega)}\le C\|f\|_{L^p(\Omega)},\,\forall\,t>0. \end{align*} $$
$$ \begin{align*} \inf_{c\in{\mathbb R}} \left\|\sqrt t \nabla e^{-t\Delta_D}f-\frac{cx}{|x|^n}\right\|_{L^p(\Omega)}\le C\|f\|_{L^p(\Omega)},\,\forall\,t>0. \end{align*} $$
It is clear from [Reference Killip, Visan and Zhang20, Proposition 8.1] that in the LHS of the last inequality, the infimum for large time t is not attained at
![]() $c=0$
. Moreover, since for
$c=0$
. Moreover, since for
![]() $f\in L^p(\Omega )$
,
$f\in L^p(\Omega )$
,
![]() $\sqrt t \nabla e^{-t\mathcal {L}_D}f$
does belong to
$\sqrt t \nabla e^{-t\mathcal {L}_D}f$
does belong to
![]() $L^p(\Omega )$
(without uniform bound in t), the infimum shall be attained at the finite c which depends on f and t.
$L^p(\Omega )$
(without uniform bound in t), the infimum shall be attained at the finite c which depends on f and t.
We shall first prove an intermediate version of Theorem 1.4 in Section 2. We shall then show the equivalence of the spaces
![]() $\mathcal {A}^p_0(\Omega )$
,
$\mathcal {A}^p_0(\Omega )$
,
![]() $\tilde {\mathcal {A}}^p_0(\Omega )$
and
$\tilde {\mathcal {A}}^p_0(\Omega )$
and
![]() $K_p(\mathcal {L}_D^{1/2})$
and complete the proof of Theorem 1.4 in Section 3.
$K_p(\mathcal {L}_D^{1/2})$
and complete the proof of Theorem 1.4 in Section 3.
Throughout the whole paper, we always denote by C or c a positive constant which is independent of the main parameters, but it may vary from line to line. Furthermore, for any
![]() $q\in [1,\infty ]$
, we denote by
$q\in [1,\infty ]$
, we denote by
![]() $q'$
its conjugate exponent – namely,
$q'$
its conjugate exponent – namely,
![]() $1/q+1/q'= 1$
. Finally, for any measurable set
$1/q+1/q'= 1$
. Finally, for any measurable set
![]() $E\subset {{{\mathbb R}}^n}$
and (vector-valued or matrix-valued) function
$E\subset {{{\mathbb R}}^n}$
and (vector-valued or matrix-valued) function
![]() $f\in L^1(E)$
, we denote the integral
$f\in L^1(E)$
, we denote the integral
![]() $\int _{E}|f(x)|\,dx$
simply by
$\int _{E}|f(x)|\,dx$
simply by
![]() $\int _{E}|f|\,dx$
and, when
$\int _{E}|f|\,dx$
and, when
![]() $|E|<\infty $
, we use the notation
$|E|<\infty $
, we use the notation
2 On boundedness of the Riesz transform
In this section, we prove the following more general version Theorem 2.4 of Theorem 1.4(ii) with
![]() $\mathcal {K}_p(\mathcal {L}_D^{1/2})$
replaced by
$\mathcal {K}_p(\mathcal {L}_D^{1/2})$
replaced by
![]() $\tilde {\mathcal {A}}^p_0(\Omega )$
, which is defined as
$\tilde {\mathcal {A}}^p_0(\Omega )$
, which is defined as
Let us begin with some necessary notations.
Definition 2.1. Let
![]() $\mathcal {L}:=-\mathrm {div}(A\nabla \cdot )$
be a second-order divergence form elliptic operator on
$\mathcal {L}:=-\mathrm {div}(A\nabla \cdot )$
be a second-order divergence form elliptic operator on
![]() ${{{\mathbb R}}^n}$
. Denote by
${{{\mathbb R}}^n}$
. Denote by
![]() $(q(\mathcal {L})', q(\mathcal {L}))$
the interior of the maximal interval of exponents
$(q(\mathcal {L})', q(\mathcal {L}))$
the interior of the maximal interval of exponents
![]() $q\in [1,\infty ]$
such that the operator
$q\in [1,\infty ]$
such that the operator
![]() $\nabla \mathcal {L}^{-1}\mathrm {div}$
is bounded on
$\nabla \mathcal {L}^{-1}\mathrm {div}$
is bounded on
![]() $L^q({{{\mathbb R}}^n})$
.
$L^q({{{\mathbb R}}^n})$
.
Furthermore, let O be a bounded Lipschitz domain of
![]() ${{{\mathbb R}}^n}$
and let
${{{\mathbb R}}^n}$
and let
![]() $\mathcal {L}_{D,O}:=-\mathrm {div}(A\nabla \cdot )$
be a second-order divergence form elliptic operator on O subject to the Dirichlet boundary condition. Similarly, denote by
$\mathcal {L}_{D,O}:=-\mathrm {div}(A\nabla \cdot )$
be a second-order divergence form elliptic operator on O subject to the Dirichlet boundary condition. Similarly, denote by
![]() $(q(\mathcal {L}_{D,O})', q(\mathcal {L}_{D,O}))$
the interior of the maximal interval of exponents
$(q(\mathcal {L}_{D,O})', q(\mathcal {L}_{D,O}))$
the interior of the maximal interval of exponents
![]() $q\in [1,\infty ]$
such that
$q\in [1,\infty ]$
such that
![]() $\nabla \mathcal {L}_{D,O}^{-1}\mathrm {div}$
is bounded on
$\nabla \mathcal {L}_{D,O}^{-1}\mathrm {div}$
is bounded on
![]() $L^q(O)$
.
$L^q(O)$
.
Remark 2.2. It is well known that there exists a constant
![]() $\varepsilon _0\in (0,\infty )$
depending on the matrix A and n such that
$\varepsilon _0\in (0,\infty )$
depending on the matrix A and n such that
![]() $(2-\varepsilon _0,2+\varepsilon _0)\subset (q(\mathcal {L})', q(\mathcal {L}))$
(see, for instance, [Reference Iwaniec and Sbordone14]). Similarly, there exists a constant
$(2-\varepsilon _0,2+\varepsilon _0)\subset (q(\mathcal {L})', q(\mathcal {L}))$
(see, for instance, [Reference Iwaniec and Sbordone14]). Similarly, there exists a constant
![]() $\varepsilon _1\in (0,\infty )$
depending on A, n, and the Lipschitz constant of O such that
$\varepsilon _1\in (0,\infty )$
depending on A, n, and the Lipschitz constant of O such that
![]() $(2-\varepsilon _1,2+\varepsilon _1)\subset (q(\mathcal {L}_{D,O})', q(\mathcal {L}_{D,O}))$
.
$(2-\varepsilon _1,2+\varepsilon _1)\subset (q(\mathcal {L}_{D,O})', q(\mathcal {L}_{D,O}))$
.
Remark 2.3. Note that
![]() $q(\mathcal {L})=p(\mathcal {L})$
. In fact, since for
$q(\mathcal {L})=p(\mathcal {L})$
. In fact, since for
![]() $1<p<\infty $
it holds that
$1<p<\infty $
it holds that
(see [Reference Auscher and Tchamitchian4]), one further has
which by duality implies that the
![]() $L^p$
-boundedness of
$L^p$
-boundedness of
![]() $\nabla \mathcal {L}^{-1}\mathrm {div}$
implies
$\nabla \mathcal {L}^{-1}\mathrm {div}$
implies
![]() $L^{p'}$
-boundedness of
$L^{p'}$
-boundedness of
![]() $\nabla \mathcal {L}^{-1/2}.$
However, note that for
$\nabla \mathcal {L}^{-1/2}.$
However, note that for
![]() $p\in (1,p(\mathcal {L}))$
,
$p\in (1,p(\mathcal {L}))$
,
![]() $\nabla \mathcal {L}^{-1/2}$
is bounded on
$\nabla \mathcal {L}^{-1/2}$
is bounded on
![]() $L^p({{{\mathbb R}}^n})$
. Therefore, for
$L^p({{{\mathbb R}}^n})$
. Therefore, for
![]() $p\in (p(\mathcal {L})',p(\mathcal {L}))$
, we have that
$p\in (p(\mathcal {L})',p(\mathcal {L}))$
, we have that
Thus, we have
![]() $q(\mathcal {L})=p(\mathcal {L})$
.
$q(\mathcal {L})=p(\mathcal {L})$
.
In what follows, for any
![]() $x\in {{{\mathbb R}}^n}$
and
$x\in {{{\mathbb R}}^n}$
and
![]() $r\in (0,\infty )$
, we always let
$r\in (0,\infty )$
, we always let
![]() $B(x,r):=\{y\in {{{\mathbb R}}^n}:\ |y-x|<r\}$
. Note that on
$B(x,r):=\{y\in {{{\mathbb R}}^n}:\ |y-x|<r\}$
. Note that on
![]() ${{{\mathbb R}}^n}$
, the maximal interval for the
${{{\mathbb R}}^n}$
, the maximal interval for the
![]() $L^p$
-boundedness of the Riesz transform is open (see, for instance, [Reference Coulhon, Jiang, Koskela and Sikora8]), so we may assume that
$L^p$
-boundedness of the Riesz transform is open (see, for instance, [Reference Coulhon, Jiang, Koskela and Sikora8]), so we may assume that
![]() $p(\mathcal {L})=q(\mathcal {L})>n$
.
$p(\mathcal {L})=q(\mathcal {L})>n$
.
Theorem 2.4. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain. Take a large
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain. Take a large
![]() $R\in (0,\infty )$
such that
$R\in (0,\infty )$
such that
![]() $\Omega ^c\subset B(0,R)$
. Let
$\Omega ^c\subset B(0,R)$
. Let
![]() $\Omega _R:=\Omega \cap B(0,R)$
. Assume that
$\Omega _R:=\Omega \cap B(0,R)$
. Assume that
![]() $\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}>n$
and
$\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}>n$
and
![]() $2<p\in [n, \min \{q(\mathcal {L}), q(\mathcal {L}_{D,\Omega _R})\})$
. Then there exists a positive constant C such that, for any
$2<p\in [n, \min \{q(\mathcal {L}), q(\mathcal {L}_{D,\Omega _R})\})$
. Then there exists a positive constant C such that, for any
![]() $f\in \mathring {W}^{1,p}(\Omega )$
,
$f\in \mathring {W}^{1,p}(\Omega )$
,
where
![]() $\tilde {\mathcal {A}}^p_0(\Omega )=\{\phi \in \mathring {W}^{1,p}(\Omega ):\ \mathcal {L}_D f=0\}$
.
$\tilde {\mathcal {A}}^p_0(\Omega )=\{\phi \in \mathring {W}^{1,p}(\Omega ):\ \mathcal {L}_D f=0\}$
.
To prove Theorem 2.4, let us first begin with the following several lemmas.
Let X be a Banach space and Y a closed subspace of X. Denote by
![]() $X^\ast $
the dual space of X. Let
$X^\ast $
the dual space of X. Let
where
![]() $\langle \cdot ,\cdot \rangle $
denotes the duality pairing between
$\langle \cdot ,\cdot \rangle $
denotes the duality pairing between
![]() $X^\ast $
and X. That is,
$X^\ast $
and X. That is,
![]() $X^\ast \bot Y$
denotes the subspace of
$X^\ast \bot Y$
denotes the subspace of
![]() $X^\ast $
orthogonal to Y.
$X^\ast $
orthogonal to Y.
Meanwhile, for any given
![]() $m\in {\mathbb N}\cup \{0\}$
, we denote by
$m\in {\mathbb N}\cup \{0\}$
, we denote by
![]() $\mathcal {P}_m$
the space of polynomials on
$\mathcal {P}_m$
the space of polynomials on
![]() ${{{\mathbb R}}^n}$
of degree less than or equal to m; if m is a strictly negative integer, we set by convention
${{{\mathbb R}}^n}$
of degree less than or equal to m; if m is a strictly negative integer, we set by convention
![]() $\mathcal {P}_m=\{0\}$
. Moreover, for any
$\mathcal {P}_m=\{0\}$
. Moreover, for any
![]() $s\in {\mathbb R}$
, denote by
$s\in {\mathbb R}$
, denote by
![]() $\lfloor s\rfloor $
the maximal integer not more than s.
$\lfloor s\rfloor $
the maximal integer not more than s.
Then we have the following conclusion on the isomorphism property of the divergence operator
![]() $\mathrm {div}$
which was obtained in [Reference Amrouche, Girault and Giroire2, Propositions 4.1 and 9.2].
$\mathrm {div}$
which was obtained in [Reference Amrouche, Girault and Giroire2, Propositions 4.1 and 9.2].
Lemma 2.5. Let
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $p\in (1,\infty )$
and
$p\in (1,\infty )$
and
![]() $p'\in (1,\infty )$
be given by
$p'\in (1,\infty )$
be given by
![]() $1/p+1/p'=1$
. Then the divergence operator
$1/p+1/p'=1$
. Then the divergence operator
![]() $\mathrm {div}$
is an isomorphism from
$\mathrm {div}$
is an isomorphism from
![]() $L^{p}({{{\mathbb R}}^n})/H_{p}$
to
$L^{p}({{{\mathbb R}}^n})/H_{p}$
to
![]() $W^{-1,p}({{{\mathbb R}}^n})\bot \mathcal {P}_{\lfloor 1-n/p'\rfloor }$
, where
$W^{-1,p}({{{\mathbb R}}^n})\bot \mathcal {P}_{\lfloor 1-n/p'\rfloor }$
, where
![]() $H_{p}:=\{v\in L^{p}({{{\mathbb R}}^n}):\ \mathrm {div}(v)=0\ \text {in the sense of distributions}\}$
.
$H_{p}:=\{v\in L^{p}({{{\mathbb R}}^n}):\ \mathrm {div}(v)=0\ \text {in the sense of distributions}\}$
.
Lemma 2.6. Let
![]() $p\in (2,\infty )$
and
$p\in (2,\infty )$
and
![]() $f\in W^{-1,p}({{{\mathbb R}}^n})$
with compact support. Then
$f\in W^{-1,p}({{{\mathbb R}}^n})$
with compact support. Then
![]() $f\in W^{-1,2}({{{\mathbb R}}^n})$
, and there exists a positive constant C, depending only on p and the support of f, such that
$f\in W^{-1,2}({{{\mathbb R}}^n})$
, and there exists a positive constant C, depending only on p and the support of f, such that
Lemma 2.6 is just [Reference Amrouche, Girault and Giroire1, Lemma 2.1].
Lemma 2.7. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $p\in (2,q(\mathcal {L}))$
. Assume that
$p\in (2,q(\mathcal {L}))$
. Assume that
![]() $f\in W^{-1,p}({{{\mathbb R}}^n})$
has compact support. When
$f\in W^{-1,p}({{{\mathbb R}}^n})$
has compact support. When
![]() $n\ge 3$
, the problem
$n\ge 3$
, the problem
has a unique solution u in
![]() $W^{1,2}({{{\mathbb R}}^n})\cap W^{1,p}({{{\mathbb R}}^n})$
.
$W^{1,2}({{{\mathbb R}}^n})\cap W^{1,p}({{{\mathbb R}}^n})$
.
When
![]() $n=2$
, if f further satisfies the compatibility condition
$n=2$
, if f further satisfies the compatibility condition
![]() $\langle f,1\rangle =0$
, then the problem (2.1) has a unique solution u in
$\langle f,1\rangle =0$
, then the problem (2.1) has a unique solution u in
![]() $W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)$
up to constants.
$W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)$
up to constants.
Proof. When
![]() $n\ge 3$
, by the assumption that
$n\ge 3$
, by the assumption that
![]() $f\in W^{-1,p}({{{\mathbb R}}^n})$
has compact support and Lemma 2.6, we conclude that
$f\in W^{-1,p}({{{\mathbb R}}^n})$
has compact support and Lemma 2.6, we conclude that
![]() $f\in W^{-1,2}({{{\mathbb R}}^n})$
. From Lemma 2.5, there exists
$f\in W^{-1,2}({{{\mathbb R}}^n})$
. From Lemma 2.5, there exists
![]() $F\in L^p({{{\mathbb R}}^n})\cap L^2({{{\mathbb R}}^n})$
such that
$F\in L^p({{{\mathbb R}}^n})\cap L^2({{{\mathbb R}}^n})$
such that
![]() $f=\mathrm {div}\,F.$
From this, the definition of the interval
$f=\mathrm {div}\,F.$
From this, the definition of the interval
![]() $(q(\mathcal {L})',q(\mathcal {L}))$
, and the assumption
$(q(\mathcal {L})',q(\mathcal {L}))$
, and the assumption
![]() $p\in (2,q(\mathcal {L}))$
, it follows that the equation (2.1) has a unique solution
$p\in (2,q(\mathcal {L}))$
, it follows that the equation (2.1) has a unique solution
![]() $u\in W^{1,2}({{{\mathbb R}}^n})\cap W^{1,p}({{{\mathbb R}}^n})$
.
$u\in W^{1,2}({{{\mathbb R}}^n})\cap W^{1,p}({{{\mathbb R}}^n})$
.
When
![]() $n=2$
, by the assumption that
$n=2$
, by the assumption that
![]() $f\in W^{-1,p}({{{\mathbb R}}^n})$
has compact support and Lemma 2.6, we conclude that
$f\in W^{-1,p}({{{\mathbb R}}^n})$
has compact support and Lemma 2.6, we conclude that
![]() $f\in W^{-1,2}({{{\mathbb R}}^n})$
. From this together with the compatibility condition
$f\in W^{-1,2}({{{\mathbb R}}^n})$
. From this together with the compatibility condition
![]() $\langle f,1\rangle =0$
, we deduce from Lemma 2.5 that there exists
$\langle f,1\rangle =0$
, we deduce from Lemma 2.5 that there exists
![]() $F\in L^p({{{\mathbb R}}^n})\cap L^2({{{\mathbb R}}^n})$
such that
$F\in L^p({{{\mathbb R}}^n})\cap L^2({{{\mathbb R}}^n})$
such that
![]() $f=\mathrm {div}\,F.$
Using this and the assumption
$f=\mathrm {div}\,F.$
Using this and the assumption
![]() $p\in (2,q(\mathcal {L}))$
again, we conclude that the problem (2.1) has a unique solution
$p\in (2,q(\mathcal {L}))$
again, we conclude that the problem (2.1) has a unique solution
![]() $u\in W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)$
up to constants. This finishes the proof of Lemma 2.7.
$u\in W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)$
up to constants. This finishes the proof of Lemma 2.7.
Lemma 2.8. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain. Take a large
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain. Take a large
![]() $R\in (0,\infty )$
such that
$R\in (0,\infty )$
such that
![]() $\Omega ^c\subset B(0,R)$
and let
$\Omega ^c\subset B(0,R)$
and let
![]() $\Omega _R:=\Omega \cap B(0,R)$
. Let
$\Omega _R:=\Omega \cap B(0,R)$
. Let
![]() $p\in (2, \min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
. Assume that
$p\in (2, \min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
. Assume that
![]() $f\in \mathring {W}^{-1,p}(\Omega )$
has compact support and its support is contained in
$f\in \mathring {W}^{-1,p}(\Omega )$
has compact support and its support is contained in
![]() $B(0,R)$
. Then the Dirichlet problem
$B(0,R)$
. Then the Dirichlet problem
 $$ \begin{align} \left\{\begin{array}{ll} -{{\mathrm {div}}}(A\nabla u)=f\ \ &\text{in}\ \Omega,\\ u=0\ &\text{on}\ \partial\Omega \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -{{\mathrm {div}}}(A\nabla u)=f\ \ &\text{in}\ \Omega,\\ u=0\ &\text{on}\ \partial\Omega \end{array}\right. \end{align} $$
has a unique solution u in
![]() $\mathring {W}^{1,2}(\Omega )\cap \mathring {W}^{1,p}(\Omega )$
.
$\mathring {W}^{1,2}(\Omega )\cap \mathring {W}^{1,p}(\Omega )$
.
Let
![]() $s\in (0,1)$
and
$s\in (0,1)$
and
![]() $p\in (1,\infty )$
. For the exterior Lipschitz domain (or the bounded Lipschitz domain)
$p\in (1,\infty )$
. For the exterior Lipschitz domain (or the bounded Lipschitz domain)
![]() $\Omega $
of
$\Omega $
of
![]() ${{{\mathbb R}}^n}$
, denote by
${{{\mathbb R}}^n}$
, denote by
![]() $W^{s,p}(\partial \Omega )$
the fractional Sobolev space on
$W^{s,p}(\partial \Omega )$
the fractional Sobolev space on
![]() $\partial \Omega $
(see, for instance, [Reference Nečas23, Section 2.4.3] for its definition). To show Lemma 2.8, we need the following conclusion.
$\partial \Omega $
(see, for instance, [Reference Nečas23, Section 2.4.3] for its definition). To show Lemma 2.8, we need the following conclusion.
Lemma 2.9. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $O\subset {{{\mathbb R}}^n}$
be a bounded Lipschitz domain. Let
$O\subset {{{\mathbb R}}^n}$
be a bounded Lipschitz domain. Let
![]() $p\in (2, q(\mathcal {L}_{D,O}))$
. Assume that
$p\in (2, q(\mathcal {L}_{D,O}))$
. Assume that
![]() $f\in \mathring {W}^{-1,p}(O)$
and
$f\in \mathring {W}^{-1,p}(O)$
and
![]() $g\in W^{1/p',p}(\partial O)$
. Then the Dirichlet problem
$g\in W^{1/p',p}(\partial O)$
. Then the Dirichlet problem
 $$ \begin{align} \left\{\begin{array}{ll} -{{\mathrm {div}}}(A\nabla v)=f\ \ &\text{in}\ O,\\ v=g\ &\text{on}\ \partial O \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -{{\mathrm {div}}}(A\nabla v)=f\ \ &\text{in}\ O,\\ v=g\ &\text{on}\ \partial O \end{array}\right. \end{align} $$
has a unique solution v in
![]() $W^{1,p}(O)$
.
$W^{1,p}(O)$
.
Proof. We first prove that there exists a solution
![]() $v\in W^{1,p}(O)$
for the problem (2.3). Indeed, by
$v\in W^{1,p}(O)$
for the problem (2.3). Indeed, by
![]() $g\in W^{1/p',p}(\partial O)$
and the converse trace theorem for Sobolev spaces (see, for instance, [Reference Nečas23, Section 2.5.7, Theorem 5.7]), we find that there exists a function
$g\in W^{1/p',p}(\partial O)$
and the converse trace theorem for Sobolev spaces (see, for instance, [Reference Nečas23, Section 2.5.7, Theorem 5.7]), we find that there exists a function
![]() $w_1\in W^{1,p}(O)$
such that
$w_1\in W^{1,p}(O)$
such that
![]() $w_1=g$
on
$w_1=g$
on
![]() $\partial O$
. Moreover, it is easy to find that
$\partial O$
. Moreover, it is easy to find that
![]() $-\mathrm {div}(A\nabla w_1)\in \mathring {W}^{-1,p}(O)$
. Furthermore, from the assumption that
$-\mathrm {div}(A\nabla w_1)\in \mathring {W}^{-1,p}(O)$
. Furthermore, from the assumption that
![]() $p\in (2, q(\mathcal {L}_{D,O}))$
, it follows that there exists a unique
$p\in (2, q(\mathcal {L}_{D,O}))$
, it follows that there exists a unique
![]() $w_2\in \mathring {W}^{1,p}(O)$
satisfying
$w_2\in \mathring {W}^{1,p}(O)$
satisfying
 $$ \begin{align*} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla w_2)=f+\mathrm{div}(A\nabla w_1)\ \ &\text{in}\ O,\\ w_2=0\ &\text{on}\ \partial O. \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla w_2)=f+\mathrm{div}(A\nabla w_1)\ \ &\text{in}\ O,\\ w_2=0\ &\text{on}\ \partial O. \end{array}\right. \end{align*} $$
Thus,
![]() $v:=w_1+w_2\in W^{1,p}(O)$
is a solution of the problem (2.3).
$v:=w_1+w_2\in W^{1,p}(O)$
is a solution of the problem (2.3).
Now, we show that the solution of (2.3) is unique. Assume that
![]() $v_1,v_2\in W^{1,p}(O)$
are solutions of (2.3). Then
$v_1,v_2\in W^{1,p}(O)$
are solutions of (2.3). Then
![]() $\mathrm {div}(A\nabla (v_1-v_2))=0$
in O and
$\mathrm {div}(A\nabla (v_1-v_2))=0$
in O and
![]() $v_1-v_2=0$
on
$v_1-v_2=0$
on
![]() $\partial O$
. Thus,
$\partial O$
. Thus,
![]() $v_1=v_2$
almost everywhere in O. This finishes the proof of Lemma 2.9.
$v_1=v_2$
almost everywhere in O. This finishes the proof of Lemma 2.9.
Now, we prove Lemma 2.8 by using Lemmas 2.7 and 2.9.
Proof of Lemma 2.8.
Suppose that
![]() ${\mathrm {\,supp\,}} f\subset B(0,R)$
and take a bump function
${\mathrm {\,supp\,}} f\subset B(0,R)$
and take a bump function
![]() $\psi _R$
such that
$\psi _R$
such that
![]() $\psi _R=1$
on
$\psi _R=1$
on
![]() $B(0,R)$
,
$B(0,R)$
,
![]() ${\mathrm {\,supp\,}}\psi _R\subset B(0,R+1)$
and
${\mathrm {\,supp\,}}\psi _R\subset B(0,R+1)$
and
![]() $|\nabla \psi _R|\le 1$
.
$|\nabla \psi _R|\le 1$
.
For any
![]() $g\in \mathcal {D}(\Omega )$
, by the fact
$g\in \mathcal {D}(\Omega )$
, by the fact
![]() $\|g\|_{\mathring {W}^{1,p'}(\Omega )}$
is equivalent to
$\|g\|_{\mathring {W}^{1,p'}(\Omega )}$
is equivalent to
![]() $\|\nabla g\|_{L^{p'}(\Omega )}$
(see Remark 1.1), we have
$\|\nabla g\|_{L^{p'}(\Omega )}$
(see Remark 1.1), we have
 $$ \begin{align} |\langle f,g\rangle|&=|\langle f,g\psi_R\rangle| \le \|f\|_{\mathring{W}^{-1,p}(\Omega)} \|\nabla (g\psi_R)\|_{L^{p'}(\Omega)}\\ \nonumber &\le \|f\|_{\mathring{W}^{-1,p}(\Omega)}\left[\|\nabla g\|_{L^{p'}(B(0,R+1)\cap\Omega)}+ C(R)\|g\|_{L^{p'}(B(0,R+1)\cap\Omega)}\right]\\ \nonumber &\le C(R)\|f\|_{\mathring{W}^{-1,p}(\Omega)} \left[\|\nabla g\|_{L^{2}(\Omega)}+ \left(\int_{\Omega}\frac{|g(x)|^2}{1+|x|^2} \,dx\right)^{1/2}\right]\\ \nonumber &\le C(R)\|f\|_{\mathring{W}^{-1,p}(\Omega)}\|g\|_{\mathring{W}^{1,2}(\Omega)}, \end{align} $$
$$ \begin{align} |\langle f,g\rangle|&=|\langle f,g\psi_R\rangle| \le \|f\|_{\mathring{W}^{-1,p}(\Omega)} \|\nabla (g\psi_R)\|_{L^{p'}(\Omega)}\\ \nonumber &\le \|f\|_{\mathring{W}^{-1,p}(\Omega)}\left[\|\nabla g\|_{L^{p'}(B(0,R+1)\cap\Omega)}+ C(R)\|g\|_{L^{p'}(B(0,R+1)\cap\Omega)}\right]\\ \nonumber &\le C(R)\|f\|_{\mathring{W}^{-1,p}(\Omega)} \left[\|\nabla g\|_{L^{2}(\Omega)}+ \left(\int_{\Omega}\frac{|g(x)|^2}{1+|x|^2} \,dx\right)^{1/2}\right]\\ \nonumber &\le C(R)\|f\|_{\mathring{W}^{-1,p}(\Omega)}\|g\|_{\mathring{W}^{1,2}(\Omega)}, \end{align} $$
for
![]() $n\ge 3$
, which implies that
$n\ge 3$
, which implies that
![]() $f\in \mathring {W}^{-1,2}(\Omega )$
. For
$f\in \mathring {W}^{-1,2}(\Omega )$
. For
![]() $n=2$
, simply replacing
$n=2$
, simply replacing
![]() $\int _{\Omega }\frac {|g(x)|^2}{1+|x|^2} \,dx$
by
$\int _{\Omega }\frac {|g(x)|^2}{1+|x|^2} \,dx$
by
![]() $\int _{\Omega }\frac {|g(x)|^2}{(1+|x|^2) \ln ^2(2+|x|^2) } \,dx$
gives the same conclusion.
$\int _{\Omega }\frac {|g(x)|^2}{(1+|x|^2) \ln ^2(2+|x|^2) } \,dx$
gives the same conclusion.
Thus,
![]() $f\in \mathring {W}^{-1,2}(\Omega )$
, which, together with the Lax–Milgram theorem, further implies that the Dirichlet problem (2.2) has a unique solution
$f\in \mathring {W}^{-1,2}(\Omega )$
, which, together with the Lax–Milgram theorem, further implies that the Dirichlet problem (2.2) has a unique solution
![]() $u\in \mathring {W}^{1,2}(\Omega )$
.
$u\in \mathring {W}^{1,2}(\Omega )$
.
Next, we show
![]() $u\in \mathring {W}^{1,p}(\Omega )$
. We first assume that
$u\in \mathring {W}^{1,p}(\Omega )$
. We first assume that
 $$ \begin{align*}p\in\left(2,\min\left\{q(\mathcal{L}),q(\mathcal{L}_{D,\Omega_R}),\frac{2n}{n-2}\right\}\right)\end{align*} $$
$$ \begin{align*}p\in\left(2,\min\left\{q(\mathcal{L}),q(\mathcal{L}_{D,\Omega_R}),\frac{2n}{n-2}\right\}\right)\end{align*} $$
when
![]() $n\ge 3$
or
$n\ge 3$
or
![]() $p\in (2,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
when
$p\in (2,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
when
![]() $n=2$
.
$n=2$
.
Let
![]() $\varphi _1,\varphi _2\in C^\infty ({{{\mathbb R}}^n})$
satisfy
$\varphi _1,\varphi _2\in C^\infty ({{{\mathbb R}}^n})$
satisfy
![]() $0\le \varphi _1,\varphi _2\le 1$
,
$0\le \varphi _1,\varphi _2\le 1$
,
![]() ${\mathrm {\,supp\,}}(\varphi _1)\subset B(0,R+1)$
,
${\mathrm {\,supp\,}}(\varphi _1)\subset B(0,R+1)$
,
![]() $\varphi _1\equiv 1$
on
$\varphi _1\equiv 1$
on
![]() $B(0,R)$
, and
$B(0,R)$
, and
![]() $\varphi _1+\varphi _2\equiv 1$
in
$\varphi _1+\varphi _2\equiv 1$
in
![]() ${{{\mathbb R}}^n}$
. Extend u by zero in
${{{\mathbb R}}^n}$
. Extend u by zero in
![]() $\Omega ^c$
and let
$\Omega ^c$
and let
![]() $u=u_1+u_2$
, where
$u=u_1+u_2$
, where
![]() $u_1:=u\varphi _1$
and
$u_1:=u\varphi _1$
and
![]() $u_2:=u\varphi _2$
. Then
$u_2:=u\varphi _2$
. Then
From
![]() $u\in \mathring {W}^{1,2}(\Omega )$
and the assumptions that
$u\in \mathring {W}^{1,2}(\Omega )$
and the assumptions that
![]() $\varphi _2\in C^\infty ({{{\mathbb R}}^n})$
and
$\varphi _2\in C^\infty ({{{\mathbb R}}^n})$
and
![]() $\varphi _2\equiv 1$
on
$\varphi _2\equiv 1$
on
![]() ${{{\mathbb R}}^n}\backslash B(0,R+1)$
, we infer that
${{{\mathbb R}}^n}\backslash B(0,R+1)$
, we infer that
![]() $u\varphi _2\in W^{1,2}(\Omega \cap B(0,R+1))$
and hence
$u\varphi _2\in W^{1,2}(\Omega \cap B(0,R+1))$
and hence
![]() $\nabla (u\varphi _2)\in L^2({{{\mathbb R}}^n})$
, which, together with the assumption
$\nabla (u\varphi _2)\in L^2({{{\mathbb R}}^n})$
, which, together with the assumption
![]() $A\in L^\infty ({{{\mathbb R}}^n};{\mathbb R}^{n\times n})$
, further implies that
$A\in L^\infty ({{{\mathbb R}}^n};{\mathbb R}^{n\times n})$
, further implies that
![]() $A\nabla (u\varphi _2)\in L^2({{{\mathbb R}}^n})$
.
$A\nabla (u\varphi _2)\in L^2({{{\mathbb R}}^n})$
.
Furthermore, it is straight to see that
in the weak sense. By the assumption
![]() $f\in \mathring {W}^{-1,p}(\Omega )$
, we conclude that
$f\in \mathring {W}^{-1,p}(\Omega )$
, we conclude that
![]() $f\varphi _2\in \mathring {W}^{-1,p}(\Omega )$
. Meanwhile, from
$f\varphi _2\in \mathring {W}^{-1,p}(\Omega )$
. Meanwhile, from
![]() $u\in \mathring {W}^{1,2}(\Omega )$
and the assumptions that
$u\in \mathring {W}^{1,2}(\Omega )$
and the assumptions that
![]() $\varphi _2\in C^\infty ({{{\mathbb R}}^n})$
,
$\varphi _2\in C^\infty ({{{\mathbb R}}^n})$
,
![]() $0\le \varphi _2\le 1$
, and
$0\le \varphi _2\le 1$
, and
![]() $\varphi _2\equiv 1$
on
$\varphi _2\equiv 1$
on
![]() ${{{\mathbb R}}^n}\backslash B(0,R+1)$
, we deduce that
${{{\mathbb R}}^n}\backslash B(0,R+1)$
, we deduce that
![]() $A\nabla u\cdot \nabla \varphi _2\in L^2(\Omega \cap B(0,R+1))$
, which, combined with the Sobolev inequality, further implies that
$A\nabla u\cdot \nabla \varphi _2\in L^2(\Omega \cap B(0,R+1))$
, which, combined with the Sobolev inequality, further implies that
![]() $A\nabla u\cdot \nabla \varphi _2\in W^{-1,p}(B(0,R+1))$
. Moreover, by
$A\nabla u\cdot \nabla \varphi _2\in W^{-1,p}(B(0,R+1))$
. Moreover, by
![]() $u\in W^{1,2}(\Omega )$
, we find that
$u\in W^{1,2}(\Omega )$
, we find that
![]() $u\in L^{p}_{\mathrm {loc}}(\Omega )$
, which, together with the assumptions that
$u\in L^{p}_{\mathrm {loc}}(\Omega )$
, which, together with the assumptions that
![]() $\varphi _2\in C^\infty ({{{\mathbb R}}^n})$
and
$\varphi _2\in C^\infty ({{{\mathbb R}}^n})$
and
![]() ${\mathrm {\,supp\,}}(\nabla \varphi _2)\subset B(0,R+1)$
, further implies that
${\mathrm {\,supp\,}}(\nabla \varphi _2)\subset B(0,R+1)$
, further implies that
![]() $Au\nabla \varphi _2\in L^{p}(\Omega \cap B(0,R+1))$
and hence
$Au\nabla \varphi _2\in L^{p}(\Omega \cap B(0,R+1))$
and hence
![]() $\mathrm {div}(Au\nabla \varphi _2)\in \mathring {W}^{-1,p}(\Omega \cap B(0,R+1))$
. Thus, we have
$\mathrm {div}(Au\nabla \varphi _2)\in \mathring {W}^{-1,p}(\Omega \cap B(0,R+1))$
. Thus, we have
![]() $g\in \mathring {W}^{-1,p}(\Omega \cap B(0,R+1))$
. Extend g by zero in
$g\in \mathring {W}^{-1,p}(\Omega \cap B(0,R+1))$
. Extend g by zero in
![]() $\Omega ^c$
. Then
$\Omega ^c$
. Then
![]() $g\in W^{-1,p}({{{\mathbb R}}^n})$
. Therefore,
$g\in W^{-1,p}({{{\mathbb R}}^n})$
. Therefore,
which, combined with Lemma 2.5 and
![]() $p\in (2,q(\mathcal {L}))$
, further implies that
$p\in (2,q(\mathcal {L}))$
, further implies that
![]() $u_2\in W^{1,p}({{{\mathbb R}}^n})$
.
$u_2\in W^{1,p}({{{\mathbb R}}^n})$
.
Furthermore, from
![]() $u=u_2$
on
$u=u_2$
on
![]() $\partial B(0,R+1)$
and the trace theorem for Sobolev spaces (see, for instance, [Reference Nečas23, Section 2.5.4, Theorem 5.5]), it follows that
$\partial B(0,R+1)$
and the trace theorem for Sobolev spaces (see, for instance, [Reference Nečas23, Section 2.5.4, Theorem 5.5]), it follows that
![]() $u\in W^{1/p',p}(\partial B(0,R+1))$
. Meanwhile, we have
$u\in W^{1/p',p}(\partial B(0,R+1))$
. Meanwhile, we have
 $$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u)=f\ \ &\text{in}\ \Omega_{R+1},\\ u=0\ &\text{on}\ \partial\Omega,\\ u=u_2\ &\text{on}\ \partial B(0,R+1),\\ \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u)=f\ \ &\text{in}\ \Omega_{R+1},\\ u=0\ &\text{on}\ \partial\Omega,\\ u=u_2\ &\text{on}\ \partial B(0,R+1),\\ \end{array}\right. \end{align} $$
where
![]() $\Omega _{R+1}:=\Omega \cap B(0,R+1)$
. By the assumption
$\Omega _{R+1}:=\Omega \cap B(0,R+1)$
. By the assumption
![]() $p<q(\mathcal {L}_{D,\Omega _{R+1}})$
and Lemma 2.9, we conclude that the problem (2.5) has a unique solution in
$p<q(\mathcal {L}_{D,\Omega _{R+1}})$
and Lemma 2.9, we conclude that the problem (2.5) has a unique solution in
![]() $W^{1,p}(\Omega _{R+1})$
, which further implies that
$W^{1,p}(\Omega _{R+1})$
, which further implies that
![]() $u\in W^{1,p}(\Omega _{R+1})$
. From this,
$u\in W^{1,p}(\Omega _{R+1})$
. From this,
![]() $u\in \mathring {W}^{1,2}(\Omega )$
,
$u\in \mathring {W}^{1,2}(\Omega )$
,
![]() $u_2\in W^{1,p}({{{\mathbb R}}^n})$
, and the fact that
$u_2\in W^{1,p}({{{\mathbb R}}^n})$
, and the fact that
![]() $u=u_2$
on
$u=u_2$
on
![]() ${{{\mathbb R}}^n}\backslash B(0,R+1)$
, we deduce that
${{{\mathbb R}}^n}\backslash B(0,R+1)$
, we deduce that
![]() $u\in W^{1,p}(\Omega )$
with any given
$u\in W^{1,p}(\Omega )$
with any given
 $$ \begin{align*}p\in\left(2,\min\left\{q(\mathcal{L}),q(\mathcal{L}_{D,\Omega_{R+1}}),\frac{2n}{n-2}\right\}\right)\end{align*} $$
$$ \begin{align*}p\in\left(2,\min\left\{q(\mathcal{L}),q(\mathcal{L}_{D,\Omega_{R+1}}),\frac{2n}{n-2}\right\}\right)\end{align*} $$
when
![]() $n\ge 3$
or any given
$n\ge 3$
or any given
![]() $p\in (2,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _{R+1}})\})$
when
$p\in (2,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _{R+1}})\})$
when
![]() $n=2$
. Then, using a bootstrap argument (see, for instance, [Reference Amrouche, Girault and Giroire1, p. 63]), we find that
$n=2$
. Then, using a bootstrap argument (see, for instance, [Reference Amrouche, Girault and Giroire1, p. 63]), we find that
![]() $u\in \mathring {W}^{1,p}(\Omega )$
with any given
$u\in \mathring {W}^{1,p}(\Omega )$
with any given
![]() $p\in (2,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _{R+1}})\})$
. This finishes the proof of Lemma 2.8.
$p\in (2,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _{R+1}})\})$
. This finishes the proof of Lemma 2.8.
Lemma 2.10. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain. Take a large
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain. Take a large
![]() $R\in (0,\infty )$
such that
$R\in (0,\infty )$
such that
![]() $\Omega ^c\subset B(0,R)$
and let
$\Omega ^c\subset B(0,R)$
and let
![]() $\Omega _R:=\Omega \cap B(0,R)$
. Assume that
$\Omega _R:=\Omega \cap B(0,R)$
. Assume that
![]() $\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}>n$
. Let
$\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}>n$
. Let
![]() $p>2$
and
$p>2$
and
![]() $p\in [n,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
. Assume further that
$p\in [n,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
. Assume further that
![]() $f\in \mathring {W}^{-1,p}(\Omega )$
and
$f\in \mathring {W}^{-1,p}(\Omega )$
and
Then the problem
 $$ \begin{align} \left\{\begin{array}{ll} -{{\mathrm {div}}}(A\nabla u)=f\ \ &\text{in}\ \Omega,\\ u=0\ &\text{on}\ \partial\Omega \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -{{\mathrm {div}}}(A\nabla u)=f\ \ &\text{in}\ \Omega,\\ u=0\ &\text{on}\ \partial\Omega \end{array}\right. \end{align} $$
has a unique solution u in
![]() $\mathring {W}^{1,p}(\Omega )/\tilde {\mathcal {A}}^p_0(\Omega )$
, and there exists a positive constant C independent of f such that
$\mathring {W}^{1,p}(\Omega )/\tilde {\mathcal {A}}^p_0(\Omega )$
, and there exists a positive constant C independent of f such that
Remark 2.11. Note that the above lemma is nontrivial only if
![]() $\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}\ge n$
and
$\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}\ge n$
and
![]() $\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}>2$
. This is not surprise, since by [Reference Jiang and Lin16, Theorem 1.1] and a similar proof of [Reference Jiang and Lin16, Theorem 1.4] via using the role of
$\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}>2$
. This is not surprise, since by [Reference Jiang and Lin16, Theorem 1.1] and a similar proof of [Reference Jiang and Lin16, Theorem 1.4] via using the role of
![]() $q(\mathcal {L}_{D,\Omega _R})$
instead of using [Reference Shen25, Theorem B & Theorem C] there, the Riesz operator
$q(\mathcal {L}_{D,\Omega _R})$
instead of using [Reference Shen25, Theorem B & Theorem C] there, the Riesz operator
![]() $\nabla \mathcal {L}^{-1/2}$
is bounded for
$\nabla \mathcal {L}^{-1/2}$
is bounded for
![]() $p\in (1,n)\cup (1,2]$
. In this case, the kernel
$p\in (1,n)\cup (1,2]$
. In this case, the kernel
![]() $\mathcal {A}^p_0(\Omega )$
must be trivial (i.e., equal zero).
$\mathcal {A}^p_0(\Omega )$
must be trivial (i.e., equal zero).
Proof of Lemma 2.10.
By the Closed Range Theorem of Banach (see, for instance, [Reference Ciarlet5, Theorem 5.11-5]), we find that there exists a vector-valued function
![]() $F\in L^p(\Omega )$
such that
$F\in L^p(\Omega )$
such that
![]() $f=\mathrm {div}F$
in
$f=\mathrm {div}F$
in
![]() $\Omega $
. Extend F by zero in
$\Omega $
. Extend F by zero in
![]() $\Omega ^c$
and still denote this extension by F. Let
$\Omega ^c$
and still denote this extension by F. Let
![]() $\widetilde {f}:=\mathrm {div}F$
. Then
$\widetilde {f}:=\mathrm {div}F$
. Then
![]() $\widetilde {f}\in W^{-1,p}({{{\mathbb R}}^n})$
. From Lemma 2.5, the assumption that
$\widetilde {f}\in W^{-1,p}({{{\mathbb R}}^n})$
. From Lemma 2.5, the assumption that
![]() $p\in (2,q(\mathcal {L}))$
, and the definition of the interval
$p\in (2,q(\mathcal {L}))$
, and the definition of the interval
![]() $(q(\mathcal {L})',q(\mathcal {L}))$
, it follows that there exists a unique
$(q(\mathcal {L})',q(\mathcal {L}))$
, it follows that there exists a unique
![]() $w\in W^{1,p}({{{\mathbb R}}^n})$
up to constants such that
$w\in W^{1,p}({{{\mathbb R}}^n})$
up to constants such that
Moreover, consider the Dirichlet problem
 $$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla z)=0\ \ &\text{in}\ \Omega,\\ z=-w\ &\text{on}\ \partial\Omega. \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla z)=0\ \ &\text{in}\ \Omega,\\ z=-w\ &\text{on}\ \partial\Omega. \end{array}\right. \end{align} $$
Then the problem (2.7) has a unique solution
![]() $z\in W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
. Indeed, take a large
$z\in W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
. Indeed, take a large
![]() $R\in (0,\infty )$
such that
$R\in (0,\infty )$
such that
![]() $\Omega ^c\subset B(0,R)$
and let
$\Omega ^c\subset B(0,R)$
and let
![]() $\Omega _R:=\Omega \cap B(0,R)$
. By
$\Omega _R:=\Omega \cap B(0,R)$
. By
![]() $w\in W^{1,p}({{{\mathbb R}}^n})$
, we conclude that
$w\in W^{1,p}({{{\mathbb R}}^n})$
, we conclude that
![]() $w\in W^{1/p',p}(\partial \Omega )$
. Let
$w\in W^{1/p',p}(\partial \Omega )$
. Let
![]() $u_z$
satisfy
$u_z$
satisfy
 $$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_z)=0\ \ &\text{in}\ \Omega_R,\\ u_z=-w\ &\text{on}\ \partial\Omega,\\ u_z=0\ &\text{on}\ \partial B(0,R).\\ \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_z)=0\ \ &\text{in}\ \Omega_R,\\ u_z=-w\ &\text{on}\ \partial\Omega,\\ u_z=0\ &\text{on}\ \partial B(0,R).\\ \end{array}\right. \end{align} $$
Then, from Lemma 2.9, we infer that the problem (2.8) has a unique solution
![]() $u_z\in W^{1,p}(\Omega _R)$
. Extend
$u_z\in W^{1,p}(\Omega _R)$
. Extend
![]() $u_z$
by zero on
$u_z$
by zero on
![]() ${{{\mathbb R}}^n}\backslash B(0,R)$
. Then
${{{\mathbb R}}^n}\backslash B(0,R)$
. Then
![]() $u_z\in W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
. Let v satisfy
$u_z\in W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
. Let v satisfy
 $$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla v)=\mathrm{div}(A\nabla u_z)\ \ &\text{in}\ \Omega,\\ v=0\ &\text{on}\ \partial\Omega. \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla v)=\mathrm{div}(A\nabla u_z)\ \ &\text{in}\ \Omega,\\ v=0\ &\text{on}\ \partial\Omega. \end{array}\right. \end{align} $$
By
![]() $u_z\in W^{1,p}(\Omega )$
and
$u_z\in W^{1,p}(\Omega )$
and
![]() $u_z\equiv 0$
on
$u_z\equiv 0$
on
![]() ${{{\mathbb R}}^n}\backslash B(0,R)$
, we conclude that
${{{\mathbb R}}^n}\backslash B(0,R)$
, we conclude that
![]() $\mathrm {div}(A\nabla u_z)\in \mathring {W}^{-1,p}(\Omega )$
has compact support. From this and Lemma 2.8, it follows that the problem (2.9) has a unique solution
$\mathrm {div}(A\nabla u_z)\in \mathring {W}^{-1,p}(\Omega )$
has compact support. From this and Lemma 2.8, it follows that the problem (2.9) has a unique solution
![]() $v\in \mathring {W}^{1,2}(\Omega )\cap \mathring {W}^{1,p}(\Omega )$
. Thus, the problem (2.7) has a unique solution
$v\in \mathring {W}^{1,2}(\Omega )\cap \mathring {W}^{1,p}(\Omega )$
. Thus, the problem (2.7) has a unique solution
![]() $z=u_z+v\in W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
. Then
$z=u_z+v\in W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
. Then
![]() $u=w+z\in \mathring {W}^{1,p}(\Omega )$
is a solution of the problem (2.6).
$u=w+z\in \mathring {W}^{1,p}(\Omega )$
is a solution of the problem (2.6).
Meanwhile, by the definition of the space
![]() $\tilde {\mathcal {A}}^p_0(\Omega )$
, we find that the problem (2.6) has a unique solution in
$\tilde {\mathcal {A}}^p_0(\Omega )$
, we find that the problem (2.6) has a unique solution in
![]() $\mathring {W}^{1,p}(\Omega )/\tilde {\mathcal {A}}^p_0(\Omega )$
. Furthermore, a duality argument shows that
$\mathring {W}^{1,p}(\Omega )/\tilde {\mathcal {A}}^p_0(\Omega )$
. Furthermore, a duality argument shows that
which, together with the Open Mapping Theorem of Banach (see, for instance, [Reference Ciarlet5, Theorem 5.6-2]), further implies that
namely,
This finishes the proof of Lemma 2.10.
Now, we prove Theorem 2.4 by using Lemma 2.10 and Theorem 1.2(i).
Proof of Theorem 2.4.
Let
![]() $2<p\in [n, \min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
. By Theorem 1.2(i) together with a duality argument, we see that, for any given
$2<p\in [n, \min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
. By Theorem 1.2(i) together with a duality argument, we see that, for any given
![]() $q\in (1,\infty )$
and any
$q\in (1,\infty )$
and any
![]() $g\in L^q(\Omega )$
,
$g\in L^q(\Omega )$
,
From this and Lemma 2.10, we infer that
This finishes the proof of Theorem 2.4.
3 On the kernel space and completion of the proof
In this section, we first identify
![]() $\mathcal {A}^p_0(\Omega )$
with
$\mathcal {A}^p_0(\Omega )$
with
![]() $\tilde {\mathcal {A}}^p_0(\Omega )$
, and then with
$\tilde {\mathcal {A}}^p_0(\Omega )$
, and then with
![]() $\mathcal {K}_p(\mathcal {L}_D^{1/2})$
, and finally complete the proof of Theorem 1.4.
$\mathcal {K}_p(\mathcal {L}_D^{1/2})$
, and finally complete the proof of Theorem 1.4.
Lemma 3.1. Let
![]() $n=2$
,
$n=2$
,
![]() $\Omega \subset {\mathbb R}^2$
be an exterior Lipschitz domain, and
$\Omega \subset {\mathbb R}^2$
be an exterior Lipschitz domain, and
![]() $p\in (2,q(\mathcal {L}))$
. Then the problem
$p\in (2,q(\mathcal {L}))$
. Then the problem
has a unique solution
![]() $u\in W^{1,p}({\mathbb R}^2)$
up to constants.
$u\in W^{1,p}({\mathbb R}^2)$
up to constants.
Proof. Let
![]() $q\in (2,\infty )$
and
$q\in (2,\infty )$
and
![]() $t\in (1,\infty )$
be given by
$t\in (1,\infty )$
be given by
![]() $\frac {1}{t}=\frac {2}{q'}-1$
. Then, by the Sobolev trace embedding theorem (see, for instance, [Reference Nečas23, Section 2.4.2, Theorem 4.2]), we find that, for any
$\frac {1}{t}=\frac {2}{q'}-1$
. Then, by the Sobolev trace embedding theorem (see, for instance, [Reference Nečas23, Section 2.4.2, Theorem 4.2]), we find that, for any
![]() $\varphi \in \mathcal {D}({\mathbb R}^2)$
,
$\varphi \in \mathcal {D}({\mathbb R}^2)$
,
 $$ \begin{align*} \left|\left\langle \frac{1}{\sigma(\partial\Omega)}\delta_{\partial\Omega},\varphi\right\rangle\right| &=\left|\frac{1}{\sigma(\partial\Omega)}\int_{\partial\Omega}\varphi(x)\,d\sigma(x)\right| \le\frac{1}{[\sigma(\partial\Omega)]^{1/t}}\|\varphi\|_{L^t(\partial\Omega)}\\ &\lesssim\frac{1}{[\sigma(\partial\Omega)]^{1/t}}\|\varphi\|_{W^{1,q'}(\Omega^c)} \lesssim\frac{1}{[\sigma(\partial\Omega)]^{1/t}}\|\varphi\|_{W^{1,q'}({\mathbb R}^2)}, \end{align*} $$
$$ \begin{align*} \left|\left\langle \frac{1}{\sigma(\partial\Omega)}\delta_{\partial\Omega},\varphi\right\rangle\right| &=\left|\frac{1}{\sigma(\partial\Omega)}\int_{\partial\Omega}\varphi(x)\,d\sigma(x)\right| \le\frac{1}{[\sigma(\partial\Omega)]^{1/t}}\|\varphi\|_{L^t(\partial\Omega)}\\ &\lesssim\frac{1}{[\sigma(\partial\Omega)]^{1/t}}\|\varphi\|_{W^{1,q'}(\Omega^c)} \lesssim\frac{1}{[\sigma(\partial\Omega)]^{1/t}}\|\varphi\|_{W^{1,q'}({\mathbb R}^2)}, \end{align*} $$
which, together with the fact that
![]() $\mathcal {D}({\mathbb R}^2)$
is dense in
$\mathcal {D}({\mathbb R}^2)$
is dense in
![]() $W^{1,q'}({\mathbb R}^2)$
, implies that
$W^{1,q'}({\mathbb R}^2)$
, implies that
![]() $\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }\in W^{-1,q}({\mathbb R}^2)$
with any given
$\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }\in W^{-1,q}({\mathbb R}^2)$
with any given
![]() $q\in (2,\infty )$
.
$q\in (2,\infty )$
.
Let
![]() $p\in (2,q(\mathcal {L}))$
. From Lemma 2.5 with
$p\in (2,q(\mathcal {L}))$
. From Lemma 2.5 with
![]() $n=2$
, we deduce that there exists
$n=2$
, we deduce that there exists
![]() $f\in L^p({\mathbb R}^2)$
such that
$f\in L^p({\mathbb R}^2)$
such that
![]() $\mathrm {div}f=\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }$
. By this and the assumption
$\mathrm {div}f=\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }$
. By this and the assumption
![]() $p\in (2,q(\mathcal {L}))$
, we further conclude that there exists
$p\in (2,q(\mathcal {L}))$
, we further conclude that there exists
![]() $u\in W^{1,p}({\mathbb R}^2)$
such that
$u\in W^{1,p}({\mathbb R}^2)$
such that
![]() $\mathcal {L}u=\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }$
.
$\mathcal {L}u=\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }$
.
Moreover, if there exist
![]() $u_1,u_2\in W^{1,p}({\mathbb R}^2)$
satisfying
$u_1,u_2\in W^{1,p}({\mathbb R}^2)$
satisfying
![]() $\mathcal {L}u_1=\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }=\mathcal {L}u_2$
, then
$\mathcal {L}u_1=\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }=\mathcal {L}u_2$
, then
![]() $u_1-u_2\in W^{1,p}({\mathbb R}^2)$
and
$u_1-u_2\in W^{1,p}({\mathbb R}^2)$
and
![]() $\mathcal {L}(u_1-u_2)=0$
, which, together with
$\mathcal {L}(u_1-u_2)=0$
, which, together with
![]() $p\in (q(\mathcal {L})',q(\mathcal {L}))$
, further implies that
$p\in (q(\mathcal {L})',q(\mathcal {L}))$
, further implies that
![]() $u_1-u_2=c$
. Thus, the problem (3.1) has a unique solution
$u_1-u_2=c$
. Thus, the problem (3.1) has a unique solution
![]() $u\in W^{1,p}({\mathbb R}^2)$
up to constants. This finishes the proof of Lemma 3.1.
$u\in W^{1,p}({\mathbb R}^2)$
up to constants. This finishes the proof of Lemma 3.1.
The following was essentially obtained in [Reference Shen25].
Lemma 3.2. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $O\subset {{{\mathbb R}}^n}$
be a bounded Lipschitz domain. If
$O\subset {{{\mathbb R}}^n}$
be a bounded Lipschitz domain. If
![]() $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
, then there exists a positive constant
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
, then there exists a positive constant
![]() $\varepsilon _0$
, depending only on n and the Lipschitz constant of O, such that, for any given
$\varepsilon _0$
, depending only on n and the Lipschitz constant of O, such that, for any given
![]() $p\in (\frac {4+\varepsilon _0}{3+\varepsilon _0},4+\varepsilon _0)$
when
$p\in (\frac {4+\varepsilon _0}{3+\varepsilon _0},4+\varepsilon _0)$
when
![]() $n=2$
or
$n=2$
or
![]() $p\in (\frac {3+\varepsilon _0}{2+\varepsilon _0},3+\varepsilon _0)$
when
$p\in (\frac {3+\varepsilon _0}{2+\varepsilon _0},3+\varepsilon _0)$
when
![]() $n\ge 3$
,
$n\ge 3$
,
![]() $\nabla \mathcal {L}_{D,O}^{-1}\mathrm {div}$
is bounded on
$\nabla \mathcal {L}_{D,O}^{-1}\mathrm {div}$
is bounded on
![]() $L^p(O)$
. In particular, if
$L^p(O)$
. In particular, if
![]() $\partial O\in C^1$
, it holds that
$\partial O\in C^1$
, it holds that
![]() $\varepsilon _0=\infty $
; that is,
$\varepsilon _0=\infty $
; that is,
![]() $\nabla \mathcal {L}_{D,O}^{-1}\mathrm {div}$
is bounded on
$\nabla \mathcal {L}_{D,O}^{-1}\mathrm {div}$
is bounded on
![]() $L^p(O)$
for any
$L^p(O)$
for any
![]() $p\in (1,\infty )$
.
$p\in (1,\infty )$
.
We now identify
![]() $\mathcal {A}^p_0(\Omega )$
with
$\mathcal {A}^p_0(\Omega )$
with
![]() $\tilde {\mathcal {A}}^p_0(\Omega )$
.
$\tilde {\mathcal {A}}^p_0(\Omega )$
.
Proposition 3.3. Let
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain, and
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain, and
![]() $p\in (1,\infty )$
. Take a large
$p\in (1,\infty )$
. Take a large
![]() $R\in (0,\infty )$
such that
$R\in (0,\infty )$
such that
![]() $\Omega ^c\subset B(0,R)$
and let
$\Omega ^c\subset B(0,R)$
and let
![]() $\Omega _R:=\Omega \cap B(0,R)$
. Assume that
$\Omega _R:=\Omega \cap B(0,R)$
. Assume that
![]() $\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}>n$
and
$\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\}>n$
and
![]() $2<p\in [n,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
. When
$2<p\in [n,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
. When
![]() $n\ge 3$
,
$n\ge 3$
,
where
![]() $u_0$
is the unique solution in
$u_0$
is the unique solution in
![]() $W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem
$W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem
 $$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_0)=0\ \ &\text{in}\ \Omega,\\ u_0=1\ &\text{on}\ \partial\Omega. \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_0)=0\ \ &\text{in}\ \Omega,\\ u_0=1\ &\text{on}\ \partial\Omega. \end{array}\right. \end{align} $$
When
![]() $n=2$
,
$n=2$
,
where
![]() $u_1$
is a solution of the problem (3.1) and
$u_1$
is a solution of the problem (3.1) and
![]() $u_0$
is the unique solution in
$u_0$
is the unique solution in
![]() $W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem
$W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem
 $$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_0)=0\ \ &\text{in}\ \Omega,\\ u_0=u_1\ &\text{on}\ \partial\Omega. \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} -\mathrm{div}(A\nabla u_0)=0\ \ &\text{in}\ \Omega,\\ u_0=u_1\ &\text{on}\ \partial\Omega. \end{array}\right. \end{align} $$
Proof. For
![]() $2<p\in [n,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
and
$2<p\in [n,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
and
![]() $\phi \in \tilde {\mathcal {A}}^p_0(\Omega )$
, extend
$\phi \in \tilde {\mathcal {A}}^p_0(\Omega )$
, extend
![]() $\phi $
by zero in
$\phi $
by zero in
![]() $\Omega ^c$
. Then the extension of
$\Omega ^c$
. Then the extension of
![]() $\phi $
, still denoted by
$\phi $
, still denoted by
![]() $\phi $
, belongs to
$\phi $
, belongs to
![]() $W^{1,p}({{{\mathbb R}}^n})$
and satisfies that
$W^{1,p}({{{\mathbb R}}^n})$
and satisfies that
Since
![]() $\phi \in W^{1,p}({{{\mathbb R}}^n})$
, it follows that
$\phi \in W^{1,p}({{{\mathbb R}}^n})$
, it follows that
![]() $\frac {\partial \phi }{\partial \boldsymbol {\nu }}\in W^{-1/p,p}(\partial \Omega )$
, where
$\frac {\partial \phi }{\partial \boldsymbol {\nu }}\in W^{-1/p,p}(\partial \Omega )$
, where
![]() $\frac {\partial \phi }{\partial \boldsymbol {\nu }}:=(A\nabla \phi )\cdot \boldsymbol {\nu }$
denotes the conormal derivative of
$\frac {\partial \phi }{\partial \boldsymbol {\nu }}:=(A\nabla \phi )\cdot \boldsymbol {\nu }$
denotes the conormal derivative of
![]() $\phi $
on
$\phi $
on
![]() $\partial \Omega $
, and
$\partial \Omega $
, and
![]() $W^{-1/p,p}(\partial \Omega )$
denotes the dual space of
$W^{-1/p,p}(\partial \Omega )$
denotes the dual space of
![]() $W^{1/p,p'}(\partial \Omega )$
. Moreover, it is easy to show that
$W^{1/p,p'}(\partial \Omega )$
. Moreover, it is easy to show that
![]() $\mathrm {div}(A\nabla \phi )$
, as a distribution in
$\mathrm {div}(A\nabla \phi )$
, as a distribution in
![]() ${{{\mathbb R}}^n}$
, satisfies that, for any
${{{\mathbb R}}^n}$
, satisfies that, for any
![]() $\varphi \in \mathcal {D}({{{\mathbb R}}^n})$
,
$\varphi \in \mathcal {D}({{{\mathbb R}}^n})$
,
 $$ \begin{align} \langle\mathrm{div}(A\nabla\phi),\varphi\rangle=-\left\langle\frac{\partial\phi}{\partial\boldsymbol{\nu}},\varphi\right\rangle_{\partial\Omega}, \end{align} $$
$$ \begin{align} \langle\mathrm{div}(A\nabla\phi),\varphi\rangle=-\left\langle\frac{\partial\phi}{\partial\boldsymbol{\nu}},\varphi\right\rangle_{\partial\Omega}, \end{align} $$
where
![]() $\langle \cdot ,\cdot \rangle _{\partial \Omega }$
denotes the duality pairing between
$\langle \cdot ,\cdot \rangle _{\partial \Omega }$
denotes the duality pairing between
![]() $W^{-1/p,p}(\partial \Omega )$
and
$W^{-1/p,p}(\partial \Omega )$
and
![]() $W^{1/p,p'}(\partial \Omega )$
. Furthermore, let h denote the distribution defined by
$W^{1/p,p'}(\partial \Omega )$
. Furthermore, let h denote the distribution defined by
![]() $\mathrm {div}(A\nabla \phi )$
; that is, for any
$\mathrm {div}(A\nabla \phi )$
; that is, for any
![]() $\varphi \in \mathcal {D}({{{\mathbb R}}^n})$
,
$\varphi \in \mathcal {D}({{{\mathbb R}}^n})$
,
 $$ \begin{align*}\langle h,\varphi\rangle=\langle\mathrm{div}(A\nabla\phi),\varphi\rangle=-\left\langle\frac{\partial\phi}{\partial\boldsymbol{\nu}}, \varphi\right\rangle_{\partial\Omega}, \end{align*} $$
$$ \begin{align*}\langle h,\varphi\rangle=\langle\mathrm{div}(A\nabla\phi),\varphi\rangle=-\left\langle\frac{\partial\phi}{\partial\boldsymbol{\nu}}, \varphi\right\rangle_{\partial\Omega}, \end{align*} $$
which, combined with the Sobolev trace embedding theorem (see, for instance, [Reference Nečas23, Section 2.5.4, Theorem 5.5]), further implies that, for any
![]() $\varphi \in \mathcal {D}({{{\mathbb R}}^n})$
,
$\varphi \in \mathcal {D}({{{\mathbb R}}^n})$
,
 $$ \begin{align*} |\langle h,\varphi\rangle|&\le\left\|\frac{\partial\phi}{\partial\boldsymbol{\nu}}\right\|_{W^{-1/p,p}(\partial\Omega)} \|\varphi\|_{W^{1/p,p'}(\partial\Omega)}\lesssim\left\|\frac{\partial\phi}{\partial\boldsymbol{\nu}}\right\|_{W^{-1/p,p}(\partial\Omega)} \|\varphi\|_{W^{1,p'}(\Omega^c)}\\ &\lesssim\left\|\frac{\partial\phi}{\partial\boldsymbol{\nu}}\right\|_{W^{-1/p,p}(\partial\Omega)} \|\varphi\|_{W^{1,p'}({{{\mathbb R}}^n})}. \end{align*} $$
$$ \begin{align*} |\langle h,\varphi\rangle|&\le\left\|\frac{\partial\phi}{\partial\boldsymbol{\nu}}\right\|_{W^{-1/p,p}(\partial\Omega)} \|\varphi\|_{W^{1/p,p'}(\partial\Omega)}\lesssim\left\|\frac{\partial\phi}{\partial\boldsymbol{\nu}}\right\|_{W^{-1/p,p}(\partial\Omega)} \|\varphi\|_{W^{1,p'}(\Omega^c)}\\ &\lesssim\left\|\frac{\partial\phi}{\partial\boldsymbol{\nu}}\right\|_{W^{-1/p,p}(\partial\Omega)} \|\varphi\|_{W^{1,p'}({{{\mathbb R}}^n})}. \end{align*} $$
By this and the fact that
![]() $\mathcal {D}({{{\mathbb R}}^n})$
is dense in
$\mathcal {D}({{{\mathbb R}}^n})$
is dense in
![]() $W^{1,p'}({{{\mathbb R}}^n})$
, we conclude that
$W^{1,p'}({{{\mathbb R}}^n})$
, we conclude that
![]() $h\in W^{-1,p}({{{\mathbb R}}^n})$
and h has a compact support.
$h\in W^{-1,p}({{{\mathbb R}}^n})$
and h has a compact support.
When
![]() $n\ge 3$
, from Lemma 2.7, it follows that the problem, that
$n\ge 3$
, from Lemma 2.7, it follows that the problem, that
![]() $\mathrm {div}(A\nabla w)=h$
in
$\mathrm {div}(A\nabla w)=h$
in
![]() ${{{\mathbb R}}^n}$
, has a unique solution in
${{{\mathbb R}}^n}$
, has a unique solution in
![]() $W^{1,2}({{{\mathbb R}}^n})\cap W^{1,p}({{{\mathbb R}}^n})$
. Therefore,
$W^{1,2}({{{\mathbb R}}^n})\cap W^{1,p}({{{\mathbb R}}^n})$
. Therefore,
![]() $w-\phi \in W^{1,p}({{{\mathbb R}}^n})$
and
$w-\phi \in W^{1,p}({{{\mathbb R}}^n})$
and
![]() $\mathrm {div}(A\nabla (w-\phi ))=0$
in
$\mathrm {div}(A\nabla (w-\phi ))=0$
in
![]() ${{{\mathbb R}}^n}$
. By this and the assumption
${{{\mathbb R}}^n}$
. By this and the assumption
![]() $2<p\in [n,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
, we find that
$2<p\in [n,\min \{q(\mathcal {L}),q(\mathcal {L}_{D,\Omega _R})\})$
, we find that
![]() $w-\phi =c$
with
$w-\phi =c$
with
![]() $c\in {\mathbb R}$
, which, together with the fact that
$c\in {\mathbb R}$
, which, together with the fact that
![]() $\mathrm {div}(A\nabla \phi )=0$
in
$\mathrm {div}(A\nabla \phi )=0$
in
![]() $\Omega $
, implies that the restriction of w to
$\Omega $
, implies that the restriction of w to
![]() $\Omega $
is the unique solution in
$\Omega $
is the unique solution in
![]() $W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem that
$W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem that
![]() $\mathrm {div}(A\nabla w)=0$
in
$\mathrm {div}(A\nabla w)=0$
in
![]() $\Omega $
and
$\Omega $
and
![]() $w=c$
on
$w=c$
on
![]() $\partial \Omega $
. Thus,
$\partial \Omega $
. Thus,
![]() $w=cu_0$
with
$w=cu_0$
with
![]() $u_0$
being the same as in (3.2) and
$u_0$
being the same as in (3.2) and
![]() $\phi =c(u_0-1)$
. This shows
$\phi =c(u_0-1)$
. This shows
![]() $\tilde {\mathcal {A}}^p_0(\Omega )\subset {\mathcal {A}}^p_0(\Omega ).$
$\tilde {\mathcal {A}}^p_0(\Omega )\subset {\mathcal {A}}^p_0(\Omega ).$
When
![]() $n=2$
, without the loss of generality, we can assume that
$n=2$
, without the loss of generality, we can assume that
![]() $\langle h,1\rangle \neq 0$
. Otherwise,
$\langle h,1\rangle \neq 0$
. Otherwise,
![]() $\langle h,1\rangle =0$
, and we see that
$\langle h,1\rangle =0$
, and we see that
![]() $h\in W^{-1,2}({\mathbb R}^2)\cap W^{-1,p}({\mathbb R}^2)$
. Then the same proof as in the case of
$h\in W^{-1,2}({\mathbb R}^2)\cap W^{-1,p}({\mathbb R}^2)$
. Then the same proof as in the case of
![]() $n\ge 3$
yields that
$n\ge 3$
yields that
![]() $\phi =c(u_0-1)$
with
$\phi =c(u_0-1)$
with
![]() $u_0$
obtained by (3.2). However, since
$u_0$
obtained by (3.2). However, since
![]() $1\in W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)$
, the uniqueness then implies
$1\in W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)$
, the uniqueness then implies
![]() $u_0=1$
and
$u_0=1$
and
![]() $\phi =0$
.
$\phi =0$
.
Suppose now
![]() $\langle h,1\rangle \neq 0$
. Let
$\langle h,1\rangle \neq 0$
. Let
![]() $u_1\in W^{1,p}({\mathbb R}^2)$
be a solution of the problem (3.1). Then
$u_1\in W^{1,p}({\mathbb R}^2)$
be a solution of the problem (3.1). Then
![]() $u_1$
satisfies
$u_1$
satisfies
Let
![]() $w\in W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)$
satisfy
$w\in W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)$
satisfy
Indeed, by
![]() $h\in W^{-1,p}({\mathbb R}^2)$
and
$h\in W^{-1,p}({\mathbb R}^2)$
and
we conclude that the right-hand side of (3.5) belongs to
![]() $W^{-1,p}({\mathbb R}^2)$
. This, together with the fact that both h and
$W^{-1,p}({\mathbb R}^2)$
. This, together with the fact that both h and
![]() $\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }$
have compact supports and Lemma 2.6, further implies that
$\frac {1}{\sigma (\partial \Omega )}\delta _{\partial \Omega }$
have compact supports and Lemma 2.6, further implies that
Moreover, it is easy to find that
Therefore, from this and Lemma 2.7, we deduce that the problem (3.5) has a unique solution
![]() ${w\in W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)}$
up to constants. Then, by the fact that w satisfies (3.5), we conclude that
${w\in W^{1,2}({\mathbb R}^2)\cap W^{1,p}({\mathbb R}^2)}$
up to constants. Then, by the fact that w satisfies (3.5), we conclude that
![]() ${w-\langle h,1\rangle u_1-\phi \in W^{1,p}({\mathbb R}^2)}$
and
${w-\langle h,1\rangle u_1-\phi \in W^{1,p}({\mathbb R}^2)}$
and
where
![]() $\phi $
is as in (3.4), which, combined with
$\phi $
is as in (3.4), which, combined with
![]() $p\in (2,q(\mathcal {L}))$
, implies that
$p\in (2,q(\mathcal {L}))$
, implies that
where c is a constant.
From the boundary condition that
![]() $\phi =0$
on
$\phi =0$
on
![]() $\partial \Omega $
and (3.6), we deduce that
$\partial \Omega $
and (3.6), we deduce that
![]() $w=c+\langle h,1\rangle u_1$
on
$w=c+\langle h,1\rangle u_1$
on
![]() $\partial \Omega $
. Then the restriction of w to
$\partial \Omega $
. Then the restriction of w to
![]() $\Omega $
is the unique solution in
$\Omega $
is the unique solution in
![]() $W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem that
$W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
of the problem that
![]() $\mathrm {div}(A\nabla w)=0$
in
$\mathrm {div}(A\nabla w)=0$
in
![]() $\Omega $
and
$\Omega $
and
![]() $w=c+\langle h,1\rangle u_1$
on
$w=c+\langle h,1\rangle u_1$
on
![]() $\partial \Omega $
. Moreover, let
$\partial \Omega $
. Moreover, let
![]() $w_1\in W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
be the unique solution of the problem
$w_1\in W^{1,2}(\Omega )\cap W^{1,p}(\Omega )$
be the unique solution of the problem
 $$ \begin{align*} \left\{\begin{array}{ll} \mathrm{div}(A\nabla w_1)=0\ \ &\text{in}\ \Omega,\\ w_1=\langle h,1\rangle u_1\ &\text{on}\ \partial\Omega, \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{ll} \mathrm{div}(A\nabla w_1)=0\ \ &\text{in}\ \Omega,\\ w_1=\langle h,1\rangle u_1\ &\text{on}\ \partial\Omega, \end{array}\right. \end{align*} $$
that is,
![]() $w_1=\langle h,1\rangle u_0$
. Then, we find that
$w_1=\langle h,1\rangle u_0$
. Then, we find that
![]() $w=w_1+c=\langle h,1\rangle u_0+c.$
This, combined with (3.6), further concludes that
$w=w_1+c=\langle h,1\rangle u_0+c.$
This, combined with (3.6), further concludes that
This shows
![]() $\tilde {\mathcal {A}}^p_0(\Omega )\subset {\mathcal {A}}^p_0(\Omega )$
for
$\tilde {\mathcal {A}}^p_0(\Omega )\subset {\mathcal {A}}^p_0(\Omega )$
for
![]() $n=2$
.
$n=2$
.
The converse inclusion
![]() ${\mathcal {A}}^p_0(\Omega )\subset \tilde {\mathcal {A}}^p_0(\Omega )$
is obvious, since constants belongs to
${\mathcal {A}}^p_0(\Omega )\subset \tilde {\mathcal {A}}^p_0(\Omega )$
is obvious, since constants belongs to
![]() $W^{1,p}({{{\mathbb R}}^n})$
for
$W^{1,p}({{{\mathbb R}}^n})$
for
![]() $p\ge n$
and
$p\ge n$
and
![]() $u_1\in W^{1,p}(\Omega )$
for
$u_1\in W^{1,p}(\Omega )$
for
![]() $n=2$
.
$n=2$
.
Lemma 3.4. Let
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $p\in (1,\infty )$
. Suppose that
$p\in (1,\infty )$
. Suppose that
![]() $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
![]() $(GD)$
, or
$(GD)$
, or
![]() $A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. Then the operator
$A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. Then the operator
![]() $\nabla \mathcal {L}^{-1}\mathrm {div}$
is bounded on
$\nabla \mathcal {L}^{-1}\mathrm {div}$
is bounded on
![]() $L^p({{{\mathbb R}}^n})$
.
$L^p({{{\mathbb R}}^n})$
.
Proof. The case
![]() $A\in \mathrm {CMO}({{{\mathbb R}}^n})$
follows from [Reference Iwaniec and Sbordone14, Theorem 1]. For the case
$A\in \mathrm {CMO}({{{\mathbb R}}^n})$
follows from [Reference Iwaniec and Sbordone14, Theorem 1]. For the case
![]() $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfying
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfying
![]() $(GD)$
, it follows from [Reference Jiang and Lin17] (see also [Reference Jiang and Lin16, Theorem 5.1 and Proposition 5.2]) that
$(GD)$
, it follows from [Reference Jiang and Lin17] (see also [Reference Jiang and Lin16, Theorem 5.1 and Proposition 5.2]) that
![]() $\nabla \mathcal {L}^{-1/2}$
is bounded on
$\nabla \mathcal {L}^{-1/2}$
is bounded on
![]() $L^p({{{\mathbb R}}^n})$
for
$L^p({{{\mathbb R}}^n})$
for
![]() $1<p<\infty $
. Thus, we have
$1<p<\infty $
. Thus, we have
which gives the desired conclusion.
We also point out that when both the matrix A and
![]() $\Omega $
have nice smoothness, the function u as in (3.1) can be represented by using the fundamental solution associated with
$\Omega $
have nice smoothness, the function u as in (3.1) can be represented by using the fundamental solution associated with
![]() $\mathcal {L}$
(see, for instance, [Reference Amrouche, Girault and Giroire1, Theorem 2.7]).
$\mathcal {L}$
(see, for instance, [Reference Amrouche, Girault and Giroire1, Theorem 2.7]).
Proposition 3.5. Let
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain, and
$\Omega \subset {{{\mathbb R}}^n}$
be an exterior Lipschitz domain, and
![]() $p\in (1,\infty )$
.
$p\in (1,\infty )$
.
-
(i) If
 $\Omega $
is
$\Omega $
is
 $C^1$
, and
$C^1$
, and
 $A\in \mathrm {CMO}({{{\mathbb R}}^n})$
, or
$A\in \mathrm {CMO}({{{\mathbb R}}^n})$
, or
 $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
 $(GD)$
, then, when
$(GD)$
, then, when
 $n\ge 3$
, for any
$n\ge 3$
, for any
 $p\in [n, \infty )$
,
$p\in [n, \infty )$
,
 $\tilde {\mathcal {A}}^p_0(\Omega )=\{c(u_0-1): \ c\in {\mathbb R}\}$
with
$\tilde {\mathcal {A}}^p_0(\Omega )=\{c(u_0-1): \ c\in {\mathbb R}\}$
with
 $u_0$
being the same as in (3.2); when
$u_0$
being the same as in (3.2); when
 $n=2$
, for any
$n=2$
, for any
 $p\in (2, \infty )$
,
$p\in (2, \infty )$
,
 $\tilde {\mathcal {A}}^p_0(\Omega )=\{c(u_0-u_1): \ c\in {\mathbb R}\}$
with
$\tilde {\mathcal {A}}^p_0(\Omega )=\{c(u_0-u_1): \ c\in {\mathbb R}\}$
with
 $u_0$
being the same as in (3.2) and
$u_0$
being the same as in (3.2) and
 $u_1$
being a solution of the problem (3.1).
$u_1$
being a solution of the problem (3.1). -
(ii) Assume
 $\mathcal {L}_D:=\Delta _D$
and
$\mathcal {L}_D:=\Delta _D$
and
 $\Omega $
is
$\Omega $
is
 $C^{1}$
. If
$C^{1}$
. If
 $n\ge 3$
and
$n\ge 3$
and
 $p\in [n,\infty )$
, then
$p\in [n,\infty )$
, then
 $\tilde {\mathcal {A}}^p_0(\Omega ) =\{c\phi _\ast :\ c\in {\mathbb R}\}$
, where
$\tilde {\mathcal {A}}^p_0(\Omega ) =\{c\phi _\ast :\ c\in {\mathbb R}\}$
, where
 $\phi _\ast $
is the unique solution of the Dirichlet problem
$\phi _\ast $
is the unique solution of the Dirichlet problem  $$ \begin{align*} \left\{\begin{array}{ll} \Delta \phi_\ast=0\ \ &\text{in}\ \Omega,\\ \phi_\ast=0\ &\text{on}\ \partial\Omega,\\ \phi_\ast(x)\to1\ &\text{as}\ |x|\to\infty.\\ \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{ll} \Delta \phi_\ast=0\ \ &\text{in}\ \Omega,\\ \phi_\ast=0\ &\text{on}\ \partial\Omega,\\ \phi_\ast(x)\to1\ &\text{as}\ |x|\to\infty.\\ \end{array}\right. \end{align*} $$
If
 $n=2$
and
$n=2$
and
 $p\in (2,\infty )$
, then
$p\in (2,\infty )$
, then
 $\tilde {\mathcal {A}}^p_0(\Omega )=\{c\phi _\ast :\ c\in {\mathbb R}\}$
, where
$\tilde {\mathcal {A}}^p_0(\Omega )=\{c\phi _\ast :\ c\in {\mathbb R}\}$
, where
 $\phi _\ast $
is a harmonic function in
$\phi _\ast $
is a harmonic function in
 $\Omega $
satisfying that
$\Omega $
satisfying that
 $\phi _\ast =0$
on
$\phi _\ast =0$
on
 $\partial \Omega $
and as
$\partial \Omega $
and as $$ \begin{align*} \left\{\begin{array}{ll} \phi_\ast(x)=-c_0\ln|x|+O(|x|^{-1}),\\ \nabla\phi_\ast(x)=-c_0\nabla\ln|x|+O(|x|^{-2}),\\ \nabla^2\phi_\ast(x)=O(|x|^{-2}),\\ \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{\begin{array}{ll} \phi_\ast(x)=-c_0\ln|x|+O(|x|^{-1}),\\ \nabla\phi_\ast(x)=-c_0\nabla\ln|x|+O(|x|^{-2}),\\ \nabla^2\phi_\ast(x)=O(|x|^{-2}),\\ \end{array}\right. \end{align*} $$
 $|x|\to \infty $
. Here,
$|x|\to \infty $
. Here,
 $c_0$
is a constant, and the notation
$c_0$
is a constant, and the notation
 $O(|x|^{-2})$
means that
$O(|x|^{-2})$
means that
 $\lim _{|x|\to \infty }\frac {|x|^{-2}}{O(|x|^{-2})}$
exists and is finite.
$\lim _{|x|\to \infty }\frac {|x|^{-2}}{O(|x|^{-2})}$
exists and is finite.
Proof. If
![]() $A\in \mathrm {CMO}({{{\mathbb R}}^n})$
, or
$A\in \mathrm {CMO}({{{\mathbb R}}^n})$
, or
![]() $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
![]() $(GD)$
, from Lemma 3.4, we infer that
$(GD)$
, from Lemma 3.4, we infer that
![]() $q(\mathcal {L})=\infty $
. Moreover, by Lemma 3.2, it holds that
$q(\mathcal {L})=\infty $
. Moreover, by Lemma 3.2, it holds that
![]() $ q(\mathcal {L}_{D,\Omega _R})=\infty .$
Therefore, by Proposition 3.3, we find that (i) holds.
$ q(\mathcal {L}_{D,\Omega _R})=\infty .$
Therefore, by Proposition 3.3, we find that (i) holds.
The conclusion of (ii) was obtained in [Reference Amrouche, Girault and Giroire1, Theorem 2.7 and Remark 2.8] (see also [Reference Shen and Wallace26, Remarks 5.3, 5.4, and 5.5]), and we omit the details here. This finishes the proof of Proposition 3.5.
We prove Theorem 1.4 by using Theorem 2.4 and Proposition 3.5.
Proof of Theorem 1.4.
(i) Assume that
![]() $A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
$A\in \mathrm {VMO}({{{\mathbb R}}^n})$
satisfies
![]() $(GD)$
, or
$(GD)$
, or
![]() $A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. Let
$A\in \mathrm {CMO}({{{\mathbb R}}^n})$
. Let
![]() $2<p\in [n,\infty )$
. Let us show that
$2<p\in [n,\infty )$
. Let us show that
![]() $\mathcal {K}_p(\mathcal {L}_D^{1/2})$
coincides with
$\mathcal {K}_p(\mathcal {L}_D^{1/2})$
coincides with
![]() $\tilde {\mathcal {A}}^p_0(\Omega )$
.
$\tilde {\mathcal {A}}^p_0(\Omega )$
.
Take a large constant
![]() $R\in (0,\infty )$
such that
$R\in (0,\infty )$
such that
![]() $\Omega ^c\subset B(0,R-1)$
and let
$\Omega ^c\subset B(0,R-1)$
and let
![]() $\Omega _R:=\Omega \cap B(0,R)$
. Then
$\Omega _R:=\Omega \cap B(0,R)$
. Then
![]() $\Omega _R$
is a bounded
$\Omega _R$
is a bounded
![]() $C^1$
domain of
$C^1$
domain of
![]() ${{{\mathbb R}}^n}$
. By Lemma 3.4, we find that
${{{\mathbb R}}^n}$
. By Lemma 3.4, we find that
![]() $q(\mathcal {L})=\infty $
. Moreover, from Lemma 3.2, we infer that
$q(\mathcal {L})=\infty $
. Moreover, from Lemma 3.2, we infer that
![]() $q(\mathcal {L}_{D,\Omega _R})=\infty $
. Therefore, by Theorem 2.4 and Proposition 3.5, it holds for any
$q(\mathcal {L}_{D,\Omega _R})=\infty $
. Therefore, by Theorem 2.4 and Proposition 3.5, it holds for any
![]() $f\in \mathring {W}^{1,p}(\Omega )$
that
$f\in \mathring {W}^{1,p}(\Omega )$
that
This implies that
![]() $\mathcal {K}_p(\mathcal {L}_D^{1/2})\subset \tilde {\mathcal {A}}^p_0(\Omega )$
.
$\mathcal {K}_p(\mathcal {L}_D^{1/2})\subset \tilde {\mathcal {A}}^p_0(\Omega )$
.
Let us show the converse inclusion. Let
![]() $u\in \mathcal {A}^p_0(\Omega )$
. By Theorem 1.2(i), we see that
$u\in \mathcal {A}^p_0(\Omega )$
. By Theorem 1.2(i), we see that
![]() $\mathcal {L}_D^{1/2}u\in L^p(\Omega )$
. Denote by
$\mathcal {L}_D^{1/2}u\in L^p(\Omega )$
. Denote by
![]() $\{p^D_t\}_{t>0}$
the heat kernels of the heat semigroup
$\{p^D_t\}_{t>0}$
the heat kernels of the heat semigroup
![]() $\{e^{-t\mathcal {L}_D}\}_{t>0}$
. By [Reference Coulhon and Duong7, Lemma 2.3], we further find that there exists
$\{e^{-t\mathcal {L}_D}\}_{t>0}$
. By [Reference Coulhon and Duong7, Lemma 2.3], we further find that there exists
![]() $\gamma>0$
such that, for all
$\gamma>0$
such that, for all
![]() $t>0$
,
$t>0$
,
which implies for
![]() $1<q<2$
that
$1<q<2$
that
Thus,
![]() $p_t^D(x,\cdot )\in \mathring {W}^{1,q}(\Omega )$
for
$p_t^D(x,\cdot )\in \mathring {W}^{1,q}(\Omega )$
for
![]() $1< q< 2$
and all
$1< q< 2$
and all
![]() $t>0$
. Therefore, for each
$t>0$
. Therefore, for each
![]() $t>0$
,
$t>0$
,
![]() $\mathcal {L}_De^{-t\mathcal {L}_D}u$
satisfies that, for all
$\mathcal {L}_De^{-t\mathcal {L}_D}u$
satisfies that, for all
![]() $x\in \Omega $
,
$x\in \Omega $
,
 $$ \begin{align*} \mathcal{L}_De^{-t\mathcal{L}_D}u(x)&=\int_\Omega(\mathcal{L}_D)_xp_t^D(x,y)u(y)\,dy=\int_\Omega (\mathcal{L}_D)_yp_t^D(x,y)u(y)\,dy\\ &=-\int_\Omega A(y)\nabla_yp_t^D(x,y)\cdot\nabla u(y)\,dy=\int_\Omega p_t^D(x,y)\mathcal{L}_D u(y)\,dy=0, \end{align*} $$
$$ \begin{align*} \mathcal{L}_De^{-t\mathcal{L}_D}u(x)&=\int_\Omega(\mathcal{L}_D)_xp_t^D(x,y)u(y)\,dy=\int_\Omega (\mathcal{L}_D)_yp_t^D(x,y)u(y)\,dy\\ &=-\int_\Omega A(y)\nabla_yp_t^D(x,y)\cdot\nabla u(y)\,dy=\int_\Omega p_t^D(x,y)\mathcal{L}_D u(y)\,dy=0, \end{align*} $$
where the second equality by symmetry of the heat kernel, the third equality by
![]() $u\in \mathring {W}^{1,p}(\Omega )$
and
$u\in \mathring {W}^{1,p}(\Omega )$
and
![]() $p_t^D(x,\cdot )\in \mathring {W}^{1,p'}(\Omega )$
,
$p_t^D(x,\cdot )\in \mathring {W}^{1,p'}(\Omega )$
,
![]() $1/p+1/p'=1$
,
$1/p+1/p'=1$
,
![]() $p>n$
when
$p>n$
when
![]() $n=2$
and
$n=2$
and
![]() $p\ge n$
when
$p\ge n$
when
![]() $n\ge 3$
. We thus see that
$n\ge 3$
. We thus see that
 $$ \begin{align*}\mathcal{L}_D^{1/2}u=\frac{1}{\sqrt{\pi}} \int_{0}^{\infty}\mathcal{L}_D e^{-s \mathcal{L}_D} u\frac{\,ds}{\sqrt{s}} =\frac{1}{\sqrt{\pi}} \int_{0}^{\infty} e^{-s \mathcal{L}_D} \mathcal{L}_D u\frac{\,ds}{\sqrt{s}}=0, \end{align*} $$
$$ \begin{align*}\mathcal{L}_D^{1/2}u=\frac{1}{\sqrt{\pi}} \int_{0}^{\infty}\mathcal{L}_D e^{-s \mathcal{L}_D} u\frac{\,ds}{\sqrt{s}} =\frac{1}{\sqrt{\pi}} \int_{0}^{\infty} e^{-s \mathcal{L}_D} \mathcal{L}_D u\frac{\,ds}{\sqrt{s}}=0, \end{align*} $$
which implies that
![]() $\tilde {\mathcal {A}}^p_0(\Omega )\subset \mathcal {K}_p(\mathcal {L}_D^{1/2})$
.
$\tilde {\mathcal {A}}^p_0(\Omega )\subset \mathcal {K}_p(\mathcal {L}_D^{1/2})$
.
(ii) By (i) and Theorem 2.4, we conclude that, for all
![]() $f\in \mathring {W}^{1,p}(\Omega )$
,
$f\in \mathring {W}^{1,p}(\Omega )$
,
This further implies that, for all
![]() $f\in \mathring {W}^{1,p}(\Omega )$
,
$f\in \mathring {W}^{1,p}(\Omega )$
,
Moreover, by Theorem 1.2(i), it holds for all
![]() $f\in \mathring {W}^{1,p}(\Omega )$
and
$f\in \mathring {W}^{1,p}(\Omega )$
and
![]() $\phi \in \mathcal {K}_p(\mathcal {L}_D^{1/2})$
that
$\phi \in \mathcal {K}_p(\mathcal {L}_D^{1/2})$
that
The last two inequalities give the desired conclusion and complete the proof.
Acknowledgements
The authors would like to sincerely thank the editor and the referee for their careful reading and several motivating remarks which lead the authors to improve this paper. The second author would like to thank Professor Zhongwei Shen for some helpful discussions on the topic of this paper.
Competing interest
The authors have no competing interests to declare.
Funding statement
R. Jiang is partially supported by NNSF of China (Grant Nos. 12471094 & 11922114). S. Yang is partially supported by NNSF of China (Grant No. 12431006), the Key Project of Gansu Provincial National Science Foundation (Grant No. 23JRRA1022) and the Innovative Groups of Basic Research in Gansu Province (Grant No. 22JR5RA391).
Data availability statement
No data is needed.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Author contributions
Both authors contributed equally.