Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
TAO, TERENCE
2016.
THE LOGARITHMICALLY AVERAGED CHOWLA AND ELLIOTT CONJECTURES FOR TWO-POINT CORRELATIONS.
Forum of Mathematics, Pi,
Vol. 4,
Issue. ,
Houcein El Abdalaoui, El
Kułaga-Przymus, Joanna
Lemańczyk, Mariusz
and
de la Rue, Thierry
2017.
The Chowla and the Sarnak conjectures from ergodic theory point of view.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 6,
p.
2899.
Tao, Terence
2017.
Number Theory – Diophantine Problems, Uniform Distribution and Applications.
p.
391.
TERÄVÄINEN, JONI
2018.
ON BINARY CORRELATIONS OF MULTIPLICATIVE FUNCTIONS.
Forum of Mathematics, Sigma,
Vol. 6,
Issue. ,
Ramaré, Olivier
2018.
Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics.
Vol. 2213,
Issue. ,
p.
317.
Frantzikinakis, Nikos
and
Host, Bernard
2018.
The logarithmic Sarnak conjecture for ergodic weights.
Annals of Mathematics,
Vol. 187,
Issue. 3,
Ferenczi, Sébastien
Kułaga-Przymus, Joanna
and
Lemańczyk, Mariusz
2018.
Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics.
Vol. 2213,
Issue. ,
p.
163.
Maynard, James
2019.
The twin prime conjecture.
Japanese Journal of Mathematics,
Vol. 14,
Issue. 2,
p.
175.
Tao, Terence
and
Teräväinen, Joni
2019.
The structure of correlations of multiplicative functions at almost all scales, with applications to the Chowla and Elliott conjectures.
Algebra & Number Theory,
Vol. 13,
Issue. 9,
p.
2103.
Semenov, Evgenii Mikhailovich
Sukochev, Fedor Anatol'evich
and
Usachev, Alexandr
2019.
Основные классы инвариантных банаховых пределов.
Известия Российской академии наук. Серия математическая,
Vol. 83,
Issue. 1,
p.
140.
Cellarosi, F.
2019.
The Abel Prize 2013-2017.
p.
207.
Tao, Terence
and
Teräväinen, Joni
2019.
The structure of logarithmically averaged correlations of multiplicative functions, with applications to the Chowla and Elliott conjectures.
Duke Mathematical Journal,
Vol. 168,
Issue. 11,
TAO, TERENCE
and
TERÄVÄINEN, JONI
2019.
VALUE PATTERNS OF MULTIPLICATIVE FUNCTIONS AND RELATED SEQUENCES.
Forum of Mathematics, Sigma,
Vol. 7,
Issue. ,
Semenov, E. M.
Sukochev, F. A.
and
Usachev, A. S.
2019.
The main classes of invariant Banach limits.
Izvestiya: Mathematics,
Vol. 83,
Issue. 1,
p.
124.
Sawin, Will
2020.
Dynamical models for Liouville and obstructions to further progress on sign patterns.
Journal of Number Theory,
Vol. 213,
Issue. ,
p.
1.
Trojovský, Pavel
2020.
On some properties of a meta-Fibonacci sequence connected to Hofstadter sequence and Möbius function.
Chaos, Solitons & Fractals,
Vol. 134,
Issue. ,
p.
109708.
Semenov, Evgenii Mikhailovich
Sukochev, Fedor Anatol'evich
and
Usachev, Aleksandr Sergeevich
2020.
Геометрия банаховых пределов и их приложения.
Успехи математических наук,
Vol. 75,
Issue. 4(454),
p.
153.
Semenov, E. M.
Sukochev, F. A.
and
Usachev, A. S.
2020.
Geometry of Banach limits and their applications.
Russian Mathematical Surveys,
Vol. 75,
Issue. 4,
p.
725.
Grechuk, Bogdan
2021.
Landscape of 21st Century Mathematics.
p.
1.
MCNAMARA, REDMOND
2021.
Sarnak’s conjecture for sequences of almost quadratic word growth.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 10,
p.
3060.
 ${\it\lambda}$ and
${\it\lambda}$ and 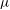 ${\it\mu}$ denote the Liouville and Möbius functions, respectively. Hildebrand showed that all eight possible sign patterns for
${\it\mu}$ denote the Liouville and Möbius functions, respectively. Hildebrand showed that all eight possible sign patterns for 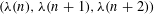 $({\it\lambda}(n),{\it\lambda}(n+1),{\it\lambda}(n+2))$ occur infinitely often. By using the recent result of the first two authors on mean values of multiplicative functions in short intervals, we strengthen Hildebrand’s result by proving that each of these eight sign patterns occur with positive lower natural density. We also obtain an analogous result for the nine possible sign patterns for
$({\it\lambda}(n),{\it\lambda}(n+1),{\it\lambda}(n+2))$ occur infinitely often. By using the recent result of the first two authors on mean values of multiplicative functions in short intervals, we strengthen Hildebrand’s result by proving that each of these eight sign patterns occur with positive lower natural density. We also obtain an analogous result for the nine possible sign patterns for 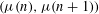 $({\it\mu}(n),{\it\mu}(n+1))$ . A new feature in the latter argument is the need to demonstrate that a certain random graph is almost surely connected.
$({\it\mu}(n),{\it\mu}(n+1))$ . A new feature in the latter argument is the need to demonstrate that a certain random graph is almost surely connected.