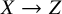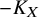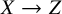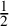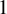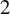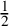1 Introduction
We work over the field of complex numbers
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
A
![]() $\mathbb {Q}$
-conic bundle is a proper morphism
$\mathbb {Q}$
-conic bundle is a proper morphism
![]() $X\to Z$
from a
$X\to Z$
from a
![]() $3$
-fold with only terminal singularities to a normal surface such that all fibres are connected and 1-dimensional, and
$3$
-fold with only terminal singularities to a normal surface such that all fibres are connected and 1-dimensional, and
![]() $-K_X$
is relatively ample over Z. A conjecture of Iskovskikh predicts that the base surface Z has only canonical singularities, or equivalently Z is
$-K_X$
is relatively ample over Z. A conjecture of Iskovskikh predicts that the base surface Z has only canonical singularities, or equivalently Z is
![]() $1$
-lc. This conjecture has important applications to the rationality problem of conic bundles [Reference Iskovskikh21]. Mori and Prokhorov proved Iskovskikh’s conjecture by showing that Z has only Du Val singularities of type A and giving a complete local classification of
$1$
-lc. This conjecture has important applications to the rationality problem of conic bundles [Reference Iskovskikh21]. Mori and Prokhorov proved Iskovskikh’s conjecture by showing that Z has only Du Val singularities of type A and giving a complete local classification of
![]() $\mathbb {Q}$
-conic bundles over a singular base in [Reference Mori and Prokhorov30, Reference Mori and Prokhorov31].
$\mathbb {Q}$
-conic bundles over a singular base in [Reference Mori and Prokhorov30, Reference Mori and Prokhorov31].
Motivated by Iskovskikh’s conjecture, it is natural to study the singularities of the base surface Z when X has worse singularities: for example, canonical singularities. Such a contraction also appears naturally in the birational classification of
![]() $3$
-dimensional algebraic varieties. Indeed when
$3$
-dimensional algebraic varieties. Indeed when
![]() $\rho (X/Z)=1$
, it is one of the three possible outcomes of the minimal model program for canonical
$\rho (X/Z)=1$
, it is one of the three possible outcomes of the minimal model program for canonical
![]() $3$
-folds of negative Kodaira dimension. However, Z may no longer be
$3$
-folds of negative Kodaira dimension. However, Z may no longer be
![]() $1$
-lc for such contractions. Shokurov conjectured that Z is always
$1$
-lc for such contractions. Shokurov conjectured that Z is always
![]() $\frac {1}{2}$
-lc, and the value
$\frac {1}{2}$
-lc, and the value
![]() $\frac {1}{2}$
is optimal (see Remark 1.2). More generally, Shokurov’s conjecture is expected to hold for conic bundles with canonical singularities in all dimensions.
$\frac {1}{2}$
is optimal (see Remark 1.2). More generally, Shokurov’s conjecture is expected to hold for conic bundles with canonical singularities in all dimensions.
Conjecture 1.1 Shokurov, compare [Reference Shokurov38, Reference Prokhorov34]
Let
![]() $\pi :X\to Z$
be a contraction between normal varieties such that
$\pi :X\to Z$
be a contraction between normal varieties such that
-
1.
 $\dim X-\dim Z=1$
,
$\dim X-\dim Z=1$
, -
2. X is canonical,
-
3.
 $K_Z$
is
$K_Z$
is
 $\mathbb {Q}$
-Cartier, and
$\mathbb {Q}$
-Cartier, and -
4.
 $-K_X$
is ample over Z.
$-K_X$
is ample over Z.
Then Z is
![]() $\frac {1}{2}$
-lc.
$\frac {1}{2}$
-lc.
Remark 1.2.
-
1. In Conjecture 1.1, the assumption in (4) can be replaced by ‘
 $-K_X$
is nef and big over Z’, which can be reduced to Conjecture 1.1 by taking the anti-canonical model over Z.
$-K_X$
is nef and big over Z’, which can be reduced to Conjecture 1.1 by taking the anti-canonical model over Z. -
2. In a private communication, Prokhorov shared his expectation that Z should be
 $\frac {1}{2}$
-klt in Conjecture 1.1 motivated by [Reference Prokhorov34, Example 10.6.1]. However, this is not always the case if
$\frac {1}{2}$
-klt in Conjecture 1.1 motivated by [Reference Prokhorov34, Example 10.6.1]. However, this is not always the case if
 $\dim X\geq 3$
; see Example 1.3.
$\dim X\geq 3$
; see Example 1.3.
Example 1.3 (compare [Reference Prokhorov34, Example 10.6.1])
Consider the following action of
![]() ${\boldsymbol{\mu} }_{4m}$
on
${\boldsymbol{\mu} }_{4m}$
on
![]() $\mathbb {P}_x^1\times \mathbb {C}^2_{u, v}$
:
$\mathbb {P}_x^1\times \mathbb {C}^2_{u, v}$
:
where m is a positive integer and
![]() $\xi $
is a primitive
$\xi $
is a primitive
![]() $4m$
th root of unity. Let
$4m$
th root of unity. Let
![]() $X=(\mathbb {P}^1\times \mathbb {C}^2)/{\boldsymbol{\mu} }_{4m}$
,
$X=(\mathbb {P}^1\times \mathbb {C}^2)/{\boldsymbol{\mu} }_{4m}$
,
![]() $Z= \mathbb {C}^2/{\boldsymbol{\mu} }_{4m}$
and
$Z= \mathbb {C}^2/{\boldsymbol{\mu} }_{4m}$
and
![]() $\pi : X\to Z$
the natural projection. Since
$\pi : X\to Z$
the natural projection. Since
![]() ${\boldsymbol{\mu} }_{4m}$
acts freely in codimension
${\boldsymbol{\mu} }_{4m}$
acts freely in codimension
![]() $1$
,
$1$
,
![]() $-K_X$
is
$-K_X$
is
![]() $\pi $
-ample. Note that Z has an isolated cyclic quotient singularity of type
$\pi $
-ample. Note that Z has an isolated cyclic quotient singularity of type
![]() $\frac {1}{4m}(1, 2m-1)$
at the origin
$\frac {1}{4m}(1, 2m-1)$
at the origin
![]() $o\in Z$
, and
$o\in Z$
, and
![]() $\mathrm {{mld}}(Z\ni o)=\frac {1}{2}$
(see [Reference Ambro4] for the computation of minimal log discrepancies of toric varieties). On the other hand, X is covered by
$\mathrm {{mld}}(Z\ni o)=\frac {1}{2}$
(see [Reference Ambro4] for the computation of minimal log discrepancies of toric varieties). On the other hand, X is covered by
![]() $2$
open affine charts
$2$
open affine charts
![]() $(x\neq 0)$
and
$(x\neq 0)$
and
![]() $(x\neq \infty )$
, and each chart is isomorphic to the affine toric variety
$(x\neq \infty )$
, and each chart is isomorphic to the affine toric variety
![]() $\mathbb {C}^3/\frac {1}{4m}(2m, 1, 2m-1)$
, which is canonical (see [Reference Reid36, Theorem (4.11)]) and Gorenstein. Note that in this case,
$\mathbb {C}^3/\frac {1}{4m}(2m, 1, 2m-1)$
, which is canonical (see [Reference Reid36, Theorem (4.11)]) and Gorenstein. Note that in this case,
![]() $\rho (X/Z)=1$
and the singular locus of X is the whole fibre
$\rho (X/Z)=1$
and the singular locus of X is the whole fibre
![]() $\pi ^{-1}(o)$
, which is
$\pi ^{-1}(o)$
, which is
![]() $1$
-dimensional. It is not clear yet whether there are such examples where X has isolated canonical singularities.
$1$
-dimensional. It is not clear yet whether there are such examples where X has isolated canonical singularities.
The main purpose of this paper is to give an affirmative answer to Shokurov’s conjecture.
Theorem 1.4. Conjecture 1.1 holds.
Theorem 1.4 follows from a more general result; see Theorem 1.7. In order to state the result, we recall some background. Let
![]() $\pi :(X,B)\to Z$
be an lc-trivial fibration (see Definition 2.12: for example,
$\pi :(X,B)\to Z$
be an lc-trivial fibration (see Definition 2.12: for example,
![]() $\pi : X\to Z$
is a contraction between normal varieties, and
$\pi : X\to Z$
is a contraction between normal varieties, and
![]() $(X, B)$
is an lc pair with
$(X, B)$
is an lc pair with
![]() $K_X+B\sim _{\mathbb {R},Z}0$
). By the work of Kawamata [Reference Kawamata24, Reference Kawamata25] and Ambro [Reference Ambro3], we have the so-called canonical bundle formula
$K_X+B\sim _{\mathbb {R},Z}0$
). By the work of Kawamata [Reference Kawamata24, Reference Kawamata25] and Ambro [Reference Ambro3], we have the so-called canonical bundle formula
where
![]() $B_Z$
is the discriminant part and
$B_Z$
is the discriminant part and
![]() $M_Z$
is the moduli part; see Section 2.4 for more details. For inductive purposes, it is useful and important to study the relation between singularities of
$M_Z$
is the moduli part; see Section 2.4 for more details. For inductive purposes, it is useful and important to study the relation between singularities of
![]() $(X,B)$
and those of
$(X,B)$
and those of
![]() $(Z,B_Z+M_Z)$
. In this context, Shokurov proposed the following conjecture. Recall that
$(Z,B_Z+M_Z)$
. In this context, Shokurov proposed the following conjecture. Recall that
![]() $\mathrm {{mld}}(X/Z\ni z,B)$
is the infimum of all the log discrepancies of prime divisors over X whose image on Z is
$\mathrm {{mld}}(X/Z\ni z,B)$
is the infimum of all the log discrepancies of prime divisors over X whose image on Z is
![]() $\overline {z}$
(see Definition 2.5).
$\overline {z}$
(see Definition 2.5).
Conjecture 1.5 Shokurov, compare [Reference Alexeev and Borisov2, Conjecture 1.2]
Let d be a positive integer and
![]() $\epsilon $
a positive real number. Then there is a positive real number
$\epsilon $
a positive real number. Then there is a positive real number
![]() $\delta =\delta (d,\epsilon )$
depending only on
$\delta =\delta (d,\epsilon )$
depending only on
![]() $d,\epsilon $
satisfying the following. Let
$d,\epsilon $
satisfying the following. Let
![]() $\pi : (X,B)\to Z$
be an lc-trivial fibration and
$\pi : (X,B)\to Z$
be an lc-trivial fibration and
![]() $z\in Z$
a point of codimension
$z\in Z$
a point of codimension
![]() $\ge 1$
such that
$\ge 1$
such that
-
1.
 $\dim X-\dim Z=d$
,
$\dim X-\dim Z=d$
, -
2.
 $\mathrm {{mld}}(X/Z\ni z,B)\ge \epsilon $
, and
$\mathrm {{mld}}(X/Z\ni z,B)\ge \epsilon $
, and -
3. the generic fibre of
 $\pi $
is of Fano type.
$\pi $
is of Fano type.
Then we can choose
![]() $M_Z\geq 0$
representing the moduli part such that
$M_Z\geq 0$
representing the moduli part such that
![]() $(Z\ni z,B_Z+M_Z)$
is
$(Z\ni z,B_Z+M_Z)$
is
![]() $\delta $
-lc.
$\delta $
-lc.
Remark 1.6.
-
1. The formulation of Conjecture 1.5 here is stronger than that in the previous literature [Reference Alexeev and Borisov2, Reference Birkar5], where a stronger assumption (2’) that ‘
 $(X, B)$
is an
$(X, B)$
is an
 $\epsilon $
-lc pair’ is required instead of the assumption in (2), and
$\epsilon $
-lc pair’ is required instead of the assumption in (2), and
 $\delta $
depends on
$\delta $
depends on
 $\dim X$
and
$\dim X$
and
 $\epsilon $
instead of just
$\epsilon $
instead of just
 $\dim X-\dim Z$
and
$\dim X-\dim Z$
and
 $\epsilon $
. In our formulation, B can be non-effective and
$\epsilon $
. In our formulation, B can be non-effective and
 $(X, B)$
can have non-klt centers over
$(X, B)$
can have non-klt centers over
 $Z\setminus \{z\}$
.
$Z\setminus \{z\}$
. -
2. Birkar [Reference Birkar5] proved Conjecture 1.5 under assumption (2’) for the following cases: (a)
 $(F,B|_F)$
belongs to a bounded family, where F is a general fibre of
$(F,B|_F)$
belongs to a bounded family, where F is a general fibre of
 $\pi $
, or (b)
$\pi $
, or (b)
 $\dim X=\dim Z+1$
. Hence, under assumption (2’), Conjecture 1.5 holds when the coefficients of
$\dim X=\dim Z+1$
. Hence, under assumption (2’), Conjecture 1.5 holds when the coefficients of
 $B|_F$
are bounded from below away from zero as a consequence of the Borisov–Alexeev–Borisov conjecture proved by Birkar [Reference Birkar7, Reference Birkar8]. Very recently, Birkar and Y. Chen [Reference Birkar and Chen10] proved Conjecture 1.5 under assumption (2’) for toric morphisms between toric varieties. We refer the reader to [Reference Birkar6, Theorems 1.9 and 2.5] for more related results.
$B|_F$
are bounded from below away from zero as a consequence of the Borisov–Alexeev–Borisov conjecture proved by Birkar [Reference Birkar7, Reference Birkar8]. Very recently, Birkar and Y. Chen [Reference Birkar and Chen10] proved Conjecture 1.5 under assumption (2’) for toric morphisms between toric varieties. We refer the reader to [Reference Birkar6, Theorems 1.9 and 2.5] for more related results. -
3. Following ideas in [Reference Birkar5], it is indicated by [Reference Chen and Han11, Proposition 7.6] (see [Reference Filipazzi and Moraga13, Theorem 1.10] for an embryonic form) that Conjecture 1.5 might be a consequence of Shokurov’s
 $\epsilon $
-lc complements conjecture. Moreover, following the proof of [Reference Birkar5, Corollary 1.7], [Reference Chen and Han11, Theorem 1.3] implies that Conjecture 1.5 holds for
$\epsilon $
-lc complements conjecture. Moreover, following the proof of [Reference Birkar5, Corollary 1.7], [Reference Chen and Han11, Theorem 1.3] implies that Conjecture 1.5 holds for
 $\dim X=\dim Z+1$
.
$\dim X=\dim Z+1$
. -
4. It is worthwhile to mention that Conjecture 1.5 implies McKernan’s conjecture on Mori fibre spaces [Reference Alexeev and Borisov2, Conjecture 1.1], which is closely related to Iskovskikh’s conjecture. Alexeev and Borisov [Reference Alexeev and Borisov2] proved McKernan’s conjecture for toric morphisms between toric varieties.
Our second main result gives the optimal value of
![]() $\delta (1,\epsilon )=\epsilon -\frac {1}{2}$
for any
$\delta (1,\epsilon )=\epsilon -\frac {1}{2}$
for any
![]() $\epsilon \ge 1$
.
$\epsilon \ge 1$
.
Theorem 1.7. Let
![]() $\pi : (X,B)\to Z$
be an lc-trivial fibration and
$\pi : (X,B)\to Z$
be an lc-trivial fibration and
![]() $z\in Z$
a codimension
$z\in Z$
a codimension
![]() $\ge 1$
point such that
$\ge 1$
point such that
-
1.
 $\dim X-\dim Z=1$
, the geometric generic fibre of
$\dim X-\dim Z=1$
, the geometric generic fibre of
 $\pi $
is a rational curve, and
$\pi $
is a rational curve, and -
2.
 $\mathrm {{mld}}(X/Z\ni z,B)\ge 1$
.
$\mathrm {{mld}}(X/Z\ni z,B)\ge 1$
.
Then we can choose
![]() $M_Z\geq 0$
representing the moduli part such that
$M_Z\geq 0$
representing the moduli part such that
The lower bound in Theorem 1.7 is optimal by Example 4.1.
As a corollary, we have the following global version of Theorem 1.7 with less technical notation involved.
Corollary 1.8. Let
![]() $(X,B)$
be a pair and
$(X,B)$
be a pair and
![]() $\pi : X\to Z$
a contraction between normal varieties such that
$\pi : X\to Z$
a contraction between normal varieties such that
-
1.
 $\dim X-\dim Z=1$
,
$\dim X-\dim Z=1$
, -
2.
 $(X,B)$
is canonical and B has no vertical irreducible component over Z,
$(X,B)$
is canonical and B has no vertical irreducible component over Z, -
3.
 $K_X+B\sim _{\mathbb {R},Z} 0$
, and
$K_X+B\sim _{\mathbb {R},Z} 0$
, and -
4. X is of Fano type over Z.
Then we can choose
![]() $M_Z\geq 0$
representing the moduli part such that
$M_Z\geq 0$
representing the moduli part such that
![]() $(Z,B_Z+M_Z)$
is
$(Z,B_Z+M_Z)$
is
![]() $\frac {1}{2}$
-lc.
$\frac {1}{2}$
-lc.
Remark 1.9.
-
1. We remark that if
 $\dim X-\dim Z=1$
, then exceptional divisors over X cannot dominate Z, so the assumption in (2) in Corollary 1.8 is equivalent to the assumption that
$\dim X-\dim Z=1$
, then exceptional divisors over X cannot dominate Z, so the assumption in (2) in Corollary 1.8 is equivalent to the assumption that
 $\mathrm {{mld}}(X/Z\ni z, B)\geq 1$
for any codimension
$\mathrm {{mld}}(X/Z\ni z, B)\geq 1$
for any codimension
 $\geq 1$
point
$\geq 1$
point
 $z\in Z$
.
$z\in Z$
. -
2. Note that
 $\frac {1}{2}$
is the maximal accumulation point of the set of minimal log discrepancies in dimension
$\frac {1}{2}$
is the maximal accumulation point of the set of minimal log discrepancies in dimension
 $2$
(see [Reference Alexeev1, Corollary 3.4], [Reference Shokurov37]). Thus it would be interesting if one could give a new proof of Iskovskikh’s conjecture by applying Theorems 1.4 and 1.7 without using the classification of terminal singularities in dimension
$2$
(see [Reference Alexeev1, Corollary 3.4], [Reference Shokurov37]). Thus it would be interesting if one could give a new proof of Iskovskikh’s conjecture by applying Theorems 1.4 and 1.7 without using the classification of terminal singularities in dimension
 $3$
. In fact, we can apply Corollary 1.8 to show that in the setting of Iskovskikh’s conjecture, Z is
$3$
. In fact, we can apply Corollary 1.8 to show that in the setting of Iskovskikh’s conjecture, Z is
 $\frac {1}{2}$
-klt; see Corollary 4.5. Recall that in order to prove Iskovskikh’s conjecture, it suffices to show that Z is
$\frac {1}{2}$
-klt; see Corollary 4.5. Recall that in order to prove Iskovskikh’s conjecture, it suffices to show that Z is
 $\frac {2}{3}$
-klt (see [Reference Jiang22, Lemma 5.1]), but our method could not achieve this. The reason is that in Corollary 4.5, there is no assumption on
$\frac {2}{3}$
-klt (see [Reference Jiang22, Lemma 5.1]), but our method could not achieve this. The reason is that in Corollary 4.5, there is no assumption on
 $\dim X$
, but Prokhorov provides us with Example 4.7 showing that Corollary 4.5 cannot be improved if
$\dim X$
, but Prokhorov provides us with Example 4.7 showing that Corollary 4.5 cannot be improved if
 $\dim X\geq 4.$
$\dim X\geq 4.$
Theorem 1.7 is a consequence of the following result, which gives a lower bound of certain log canonical thresholds for lc-trivial fibrations. We refer the reader to [Reference Chen and Han11, Problem 7.18] for more discussions.
Theorem 1.10 (compare [Reference Shokurov38, Conjecture])
Let
![]() $\pi : (X,B)\to Z$
be an lc-trivial fibration and
$\pi : (X,B)\to Z$
be an lc-trivial fibration and
![]() $z\in Z$
a codimension
$z\in Z$
a codimension
![]() $1$
point such that
$1$
point such that
-
1.
 $\dim X-\dim Z=1$
, the geometric generic fibre of
$\dim X-\dim Z=1$
, the geometric generic fibre of
 $\pi $
is a rational curve, and
$\pi $
is a rational curve, and -
2.
 $\mathrm {{mld}}(X/Z\ni z,B)\geq 1$
.
$\mathrm {{mld}}(X/Z\ni z,B)\geq 1$
.
Then
In particular, if B is effective, then the multiplicity of each irreducible component of
![]() $\pi ^{-1}(z)$
is bounded from above by
$\pi ^{-1}(z)$
is bounded from above by
![]() $2$
.
$2$
.
The bounds in Theorem 1.10 are optimal by Example 4.1.
Y. Chen informed us that together with Birkar, they also got the lower bound
![]() $\frac {1}{2}$
in Theorem 1.10 for toric morphisms between toric varieties in an earlier version of [Reference Birkar and Chen10]. As a related result, when
$\frac {1}{2}$
in Theorem 1.10 for toric morphisms between toric varieties in an earlier version of [Reference Birkar and Chen10]. As a related result, when
![]() $\dim X-\dim Z=2$
, Mori and Prokhorov [Reference Mori and Prokhorov32] showed that any 3-dimensional terminal del Pezzo fibration has no fibres of multiplicity
$\dim X-\dim Z=2$
, Mori and Prokhorov [Reference Mori and Prokhorov32] showed that any 3-dimensional terminal del Pezzo fibration has no fibres of multiplicity
![]() $>6$
.
$>6$
.
It turns out that Theorem 1.10 can be reduced to a local problem on estimating the lower bound of the log canonical threshold of a smooth curve with respect to a canonical pair on a smooth surface germ; see Corollary 3.12. Here, we prove a general result as it might have broader applications in other topics in birational geometry (compare [Reference Kollár, Smith and Corti28, Corollary 6.46]).
Theorem 1.11. Let
![]() $(X\ni P, B)$
be a germ of surface pair such that X is smooth and
$(X\ni P, B)$
be a germ of surface pair such that X is smooth and
![]() $\operatorname {mult}_P B\leq 1$
. Let C be a smooth curve at P such that
$\operatorname {mult}_P B\leq 1$
. Let C be a smooth curve at P such that
![]() $C\nsubseteq \operatorname {Supp}(B)$
. Set
$C\nsubseteq \operatorname {Supp}(B)$
. Set
![]() $\operatorname {mult}_P B=m$
,
$\operatorname {mult}_P B=m$
,
![]() $(B\cdot C)_P=I$
. Then
$(B\cdot C)_P=I$
. Then
![]() $\operatorname {lct}(X\ni P,B;C)\geq \min \{1, 1+\frac {m}{I}-m\}$
.
$\operatorname {lct}(X\ni P,B;C)\geq \min \{1, 1+\frac {m}{I}-m\}$
.
Example 3.10 shows that the lower bound in Theorem 1.11 is optimal (even in the case when
![]() $\operatorname {Supp} B$
is irreducible). It would be interesting to get an optimal lower bound of
$\operatorname {Supp} B$
is irreducible). It would be interesting to get an optimal lower bound of
![]() $\operatorname {lct}(X\ni P,B;C)$
if we do not assume that C is smooth in Theorem 1.11, as it might be related to alpha invariants; see [Reference Jiang and Zou23, Lemmas 3.1, 3.2] for an attempt in this direction.
$\operatorname {lct}(X\ni P,B;C)$
if we do not assume that C is smooth in Theorem 1.11, as it might be related to alpha invariants; see [Reference Jiang and Zou23, Lemmas 3.1, 3.2] for an attempt in this direction.
It would also be interesting to ask the following question.
Question 1.12. When
![]() $\dim X=3$
, can one give a complete local classification of the extremal case in Conjecture 1.1 when Z is strictly
$\dim X=3$
, can one give a complete local classification of the extremal case in Conjecture 1.1 when Z is strictly
![]() $\frac {1}{2}$
-lc? Or, more generally, can one give a complete local classification in Conjecture 1.1 when Z is singular?
$\frac {1}{2}$
-lc? Or, more generally, can one give a complete local classification in Conjecture 1.1 when Z is singular?
Sketch of proofs
By applying [Reference Prokhorov and Shokurov35, Theorem 8.1], we may reduce Theorem 1.7 to Theorem 1.10. Here, the sub-pair setting plays a key role, since it makes this reduction step simpler than that of the pair setting (compare [Reference Birkar5, Lemma 3.4, Proposition 3.5]), and it enables us to treat the case
![]() $\mathrm {{mld}}(X/Z\ni z,B)>1$
. On the other hand, the sub-pair setting causes new technical difficulties in the proof of Theorem 1.10. By taking hyperplane sections of the base Z, we may reduce Theorem 1.10 to the case
$\mathrm {{mld}}(X/Z\ni z,B)>1$
. On the other hand, the sub-pair setting causes new technical difficulties in the proof of Theorem 1.10. By taking hyperplane sections of the base Z, we may reduce Theorem 1.10 to the case
![]() $\dim X=2$
. By an MMP argument, we may reduce Theorem 1.10 to the case when
$\dim X=2$
. By an MMP argument, we may reduce Theorem 1.10 to the case when
![]() $X\to Z$
is a
$X\to Z$
is a
![]() $\mathbb {P}^1$
-bundle and
$\mathbb {P}^1$
-bundle and
![]() $B\ge 0$
, so the problem is reduced to a special case of Theorem 1.11 when
$B\ge 0$
, so the problem is reduced to a special case of Theorem 1.11 when
![]() $\operatorname {mult}_P B\leq 1$
and
$\operatorname {mult}_P B\leq 1$
and
![]() $(B\cdot C)_P\leq 2$
. Since the conditions
$(B\cdot C)_P\leq 2$
. Since the conditions
![]() $\operatorname {mult}_P B\leq 1$
and
$\operatorname {mult}_P B\leq 1$
and
![]() $(B\cdot C)_P\leq 2$
do not behave well under blow-ups, one may encounter difficulties in applying the ideas in [Reference Alexeev1, Reference Chen and Han11, Reference Han and Luo18], which deal with the minimal log discrepancies for surfaces. The key idea is to consider
$(B\cdot C)_P\leq 2$
do not behave well under blow-ups, one may encounter difficulties in applying the ideas in [Reference Alexeev1, Reference Chen and Han11, Reference Han and Luo18], which deal with the minimal log discrepancies for surfaces. The key idea is to consider
![]() $\widehat {X}$
, the completion of X along P, and decompose B into irreducible components on
$\widehat {X}$
, the completion of X along P, and decompose B into irreducible components on
![]() $\widehat {X}$
. By using the log canonical threshold polytope and applying the convexity of log canonical thresholds carefully, we may reduce Theorem 1.11 to the case when
$\widehat {X}$
. By using the log canonical threshold polytope and applying the convexity of log canonical thresholds carefully, we may reduce Theorem 1.11 to the case when
![]() $\operatorname {Supp} (B)$
is irreducible on
$\operatorname {Supp} (B)$
is irreducible on
![]() $\widehat {X}$
. Here, recall that
$\widehat {X}$
. Here, recall that
![]() $\operatorname {lct}(X\ni P, B;C)=\operatorname {lct}(\widehat {X}\ni P, B;C)$
. Finally, for this last case, following the ideas in [Reference Kuwata29], we may give a lower bound of
$\operatorname {lct}(X\ni P, B;C)=\operatorname {lct}(\widehat {X}\ni P, B;C)$
. Finally, for this last case, following the ideas in [Reference Kuwata29], we may give a lower bound of
![]() $\operatorname {lct}(\widehat {X}\ni P,B;C)$
by using the first pair of Puiseux exponents of B. The proof of Theorem 1.11 is provided in Section 3, and the proofs of other main results in this paper are provided in Section 4.
$\operatorname {lct}(\widehat {X}\ni P,B;C)$
by using the first pair of Puiseux exponents of B. The proof of Theorem 1.11 is provided in Section 3, and the proofs of other main results in this paper are provided in Section 4.
2 Preliminaries
In this section, we collect basic definitions and results. We adopt the standard notation and definitions in [Reference Kollár and Mori27] and [Reference Birkar, Cascini and Hacon9]. Recall that we work over the complex number field.
2.1 Divisors
Let
![]() $\mathbb {K}$
be either the rational number field
$\mathbb {K}$
be either the rational number field
![]() $\mathbb {Q}$
or the real number field
$\mathbb {Q}$
or the real number field
![]() $\mathbb {R}$
. Let X be a normal variety. A
$\mathbb {R}$
. Let X be a normal variety. A
![]() $\mathbb {K}$
-divisor is a finite
$\mathbb {K}$
-divisor is a finite
![]() $\mathbb {K}$
-linear combination
$\mathbb {K}$
-linear combination
![]() $D=\sum d_{i} D_{i}$
of prime Weil divisors
$D=\sum d_{i} D_{i}$
of prime Weil divisors
![]() $D_{i}$
, and
$D_{i}$
, and
![]() $d_{i}$
denotes the coefficient of
$d_{i}$
denotes the coefficient of
![]() $D_i$
in D. A
$D_i$
in D. A
![]() $\mathbb {K}$
-Cartier divisor is a
$\mathbb {K}$
-Cartier divisor is a
![]() $\mathbb {K}$
-linear combination of Cartier divisors.
$\mathbb {K}$
-linear combination of Cartier divisors.
We use
![]() $\sim _{\mathbb {K}}$
to denote the
$\sim _{\mathbb {K}}$
to denote the
![]() $\mathbb {K}$
-linear equivalence between
$\mathbb {K}$
-linear equivalence between
![]() $\mathbb {K}$
-divisors. For a projective morphism
$\mathbb {K}$
-divisors. For a projective morphism
![]() $X\to Z$
, we use
$X\to Z$
, we use
![]() $\sim _{\mathbb {K},Z}$
to denote the relative
$\sim _{\mathbb {K},Z}$
to denote the relative
![]() $\mathbb {K}$
-linear equivalence and
$\mathbb {K}$
-linear equivalence and
![]() $\equiv _{Z}$
to denote the relative numerical equivalence.
$\equiv _{Z}$
to denote the relative numerical equivalence.
Definition 2.1 (compare [Reference Prokhorov and Shokurov35])
Let X be a normal variety. Consider an infinite linear combination
![]() $\mathbf {D}:=\sum _D d_D D$
, where
$\mathbf {D}:=\sum _D d_D D$
, where
![]() $d_D\in \mathbb {K}$
and the infinite sum runs over all divisorial valuations of the function field of X. For any birational model Y of X, the trace of
$d_D\in \mathbb {K}$
and the infinite sum runs over all divisorial valuations of the function field of X. For any birational model Y of X, the trace of
![]() $\mathbf {D}$
on Y is defined by
$\mathbf {D}$
on Y is defined by
![]() $\mathbf {D}_Y:=\sum _{\mathrm {codim}_Y D=1} d_D D $
. Such a
$\mathbf {D}_Y:=\sum _{\mathrm {codim}_Y D=1} d_D D $
. Such a
![]() $\mathbf {D}$
is called a b-
$\mathbf {D}$
is called a b-
![]() $\mathbb {K}$
-divisor (or b-divisor for short when the base field is clear) if on each birational model Y of X, the trace
$\mathbb {K}$
-divisor (or b-divisor for short when the base field is clear) if on each birational model Y of X, the trace
![]() $\mathbf {D}_Y$
is a
$\mathbf {D}_Y$
is a
![]() $\mathbb {K}$
-divisor, or equivalently,
$\mathbb {K}$
-divisor, or equivalently,
![]() $\mathbf {D}_Y$
is a finite sum. If
$\mathbf {D}_Y$
is a finite sum. If
![]() $d_D\neq 0$
in
$d_D\neq 0$
in
![]() $\mathbf {D}$
for some D, D is called a birational component of
$\mathbf {D}$
for some D, D is called a birational component of
![]() $\mathbf {D}$
.
$\mathbf {D}$
.
Let D be a
![]() $\mathbb {K}$
-Cartier divisor on X. The Cartier closure of D is the b-
$\mathbb {K}$
-Cartier divisor on X. The Cartier closure of D is the b-
![]() $\mathbb {K}$
-divisor
$\mathbb {K}$
-divisor
![]() $\overline {D}$
whose trace on every birational model
$\overline {D}$
whose trace on every birational model
![]() $f:Y\to X$
is
$f:Y\to X$
is
![]() $f^*D$
.
$f^*D$
.
A b-
![]() $\mathbb {K}$
-divisor
$\mathbb {K}$
-divisor
![]() $\mathbf {D}$
is said to be b-semi-ample if there is a birational model
$\mathbf {D}$
is said to be b-semi-ample if there is a birational model
![]() $X'$
over X such that
$X'$
over X such that
![]() $\mathbf {D}_{X'}$
is
$\mathbf {D}_{X'}$
is
![]() $\mathbb {K}$
-Cartier and semi-ample, and
$\mathbb {K}$
-Cartier and semi-ample, and
![]() $\mathbf {D}=\overline {\mathbf {D}_{X'}}$
.
$\mathbf {D}=\overline {\mathbf {D}_{X'}}$
.
2.2 Pairs and singularities
Definition 2.2. Let
![]() $\pi : X\to Z$
be a morphism between varieties. We say that
$\pi : X\to Z$
be a morphism between varieties. We say that
![]() $\pi : X \to Z$
is a contraction if
$\pi : X \to Z$
is a contraction if
![]() $\pi $
is projective and
$\pi $
is projective and
![]() $\pi _*\mathcal {O}_X = \mathcal {O}_Z$
. In particular,
$\pi _*\mathcal {O}_X = \mathcal {O}_Z$
. In particular,
![]() $\pi $
is surjective and has connected fibres.
$\pi $
is surjective and has connected fibres.
Definition 2.3. Let
![]() $\pi : X\to Z$
be a contraction between normal varieties. For a prime divisor E on X, E is said to be horizontal over Z if E dominates Z, and E is said to be vertical over Z if E does not dominate Z. An
$\pi : X\to Z$
be a contraction between normal varieties. For a prime divisor E on X, E is said to be horizontal over Z if E dominates Z, and E is said to be vertical over Z if E does not dominate Z. An
![]() $\mathbb {R}$
-divisor on X is said to be vertical over Z if all its irreducible components are vertical over Z.
$\mathbb {R}$
-divisor on X is said to be vertical over Z if all its irreducible components are vertical over Z.
Definition 2.4 (compare [Reference Chen and Han11, Definition 3.2])
A sub-pair
![]() $(X, B)$
consists of a normal variety X and an
$(X, B)$
consists of a normal variety X and an
![]() $\mathbb {R}$
-divisor B on X such that
$\mathbb {R}$
-divisor B on X such that
![]() $K_X + B$
is
$K_X + B$
is
![]() $\mathbb {R}$
-Cartier. We say that
$\mathbb {R}$
-Cartier. We say that
![]() $(X, B)$
is a pair if
$(X, B)$
is a pair if
![]() $(X, B)$
is a sub-pair and B is effective.
$(X, B)$
is a sub-pair and B is effective.
A (relative) sub-pair
![]() $(X/Z\ni z, B)$
consists of normal varieties
$(X/Z\ni z, B)$
consists of normal varieties
![]() $X,Z$
, a contraction
$X,Z$
, a contraction
![]() $\pi : X\to Z$
, a scheme-theoretic point
$\pi : X\to Z$
, a scheme-theoretic point
![]() $z\in Z$
and an
$z\in Z$
and an
![]() $\mathbb {R}$
-divisor B on X such that
$\mathbb {R}$
-divisor B on X such that
![]() $K_X + B$
is
$K_X + B$
is
![]() $\mathbb {R}$
-Cartier over an open neighbourhood of z and
$\mathbb {R}$
-Cartier over an open neighbourhood of z and
![]() $\dim z < \dim X$
. We say that
$\dim z < \dim X$
. We say that
![]() $(X/Z\ni z, B)$
is a (relative) pair if
$(X/Z\ni z, B)$
is a (relative) pair if
![]() $(X/Z\ni z, B)$
is a sub-pair and B is effective. We say that a pair
$(X/Z\ni z, B)$
is a sub-pair and B is effective. We say that a pair
![]() $(X/Z\ni z, B)$
is a germ near z if z is a closed point. When
$(X/Z\ni z, B)$
is a germ near z if z is a closed point. When
![]() $Z=X$
,
$Z=X$
,
![]() $z=x$
and
$z=x$
and
![]() $\pi $
is the identity map, we will use
$\pi $
is the identity map, we will use
![]() $(X\ni x, B)$
instead of
$(X\ni x, B)$
instead of
![]() $(X/Z\ni z, B)$
for simplicity. When
$(X/Z\ni z, B)$
for simplicity. When
![]() $B=0$
, we will use X or
$B=0$
, we will use X or
![]() $X/Z\ni z$
instead of
$X/Z\ni z$
instead of
![]() $(X, 0)$
or
$(X, 0)$
or
![]() $(X/Z\ni z, 0)$
for simplicity.
$(X/Z\ni z, 0)$
for simplicity.
Definition 2.5. Let
![]() $(X/Z\ni z,B)$
be a sub-pair with contraction
$(X/Z\ni z,B)$
be a sub-pair with contraction
![]() $\pi : X\to Z$
and E a prime divisor over X. Let
$\pi : X\to Z$
and E a prime divisor over X. Let
![]() $\phi :Y\to X$
be a proper birational morphism such that E is a divisor on Y and write
$\phi :Y\to X$
be a proper birational morphism such that E is a divisor on Y and write
![]() $K_Y+B_Y=\phi ^{*}(K_X +B)$
. The log discrepancy of E with respect to
$K_Y+B_Y=\phi ^{*}(K_X +B)$
. The log discrepancy of E with respect to
![]() $(X, B)$
is defined to be
$(X, B)$
is defined to be
![]() $a(E, X, B):= 1-\operatorname {mult}_EB_Y$
, which is independent of the choice of Y.
$a(E, X, B):= 1-\operatorname {mult}_EB_Y$
, which is independent of the choice of Y.
Set
The minimal log discrepancy of
![]() $(X/Z\ni z,B)$
is defined to be
$(X/Z\ni z,B)$
is defined to be
By [Reference Chen and Han11, Lemma 3.5], the infimum is a minimum if
![]() $(X/Z\ni z,B)$
is an lc sub-pair, and it can be computed on a log resolution
$(X/Z\ni z,B)$
is an lc sub-pair, and it can be computed on a log resolution
![]() $\phi : Y\to (X, B)$
, where
$\phi : Y\to (X, B)$
, where
![]() $\operatorname {Supp} (\phi ^{-1}(\pi ^{-1}(\overline {z})))+\phi _*^{-1}\operatorname {Supp} (B)+\operatorname {Exc}(\phi )$
is a simple normal crossing divisor.
$\operatorname {Supp} (\phi ^{-1}(\pi ^{-1}(\overline {z})))+\phi _*^{-1}\operatorname {Supp} (B)+\operatorname {Exc}(\phi )$
is a simple normal crossing divisor.
When
![]() $X=Z$
,
$X=Z$
,
![]() $z=x$
, and
$z=x$
, and
![]() $\pi $
is the identity map, we use
$\pi $
is the identity map, we use
![]() $\mathrm {{mld}}(X\ni x,B)$
instead of
$\mathrm {{mld}}(X\ni x,B)$
instead of
![]() $\mathrm {{mld}}(X/Z\ni z,B)$
for simplicity.
$\mathrm {{mld}}(X/Z\ni z,B)$
for simplicity.
Example 2.6. We emphasise that our definition of
![]() $\mathrm {{mld}}(X/Z\ni z,B)$
requires that
$\mathrm {{mld}}(X/Z\ni z,B)$
requires that
![]() $\pi (\operatorname {center}_{X}(E))=\overline {z}$
, so it only reflects the singularities in a neighbourhood of z. For example, if
$\pi (\operatorname {center}_{X}(E))=\overline {z}$
, so it only reflects the singularities in a neighbourhood of z. For example, if
![]() $X=Z=\mathbb {P}^2$
,
$X=Z=\mathbb {P}^2$
,
![]() $B=L_1+L_2$
,
$B=L_1+L_2$
,
![]() $B'=\frac {1}{2}L_1+2L_2$
, where
$B'=\frac {1}{2}L_1+2L_2$
, where
![]() $L_1, L_2$
are
$L_1, L_2$
are
![]() $2$
distinct lines. Then
$2$
distinct lines. Then
 $$ \begin{align*}\mathrm{{mld}}(X/Z\ni z,B)=\begin{cases}2&\text{if } z\not \in L_1\cup L_2;\\1&\text{if } z \in L_1\cup L_2\setminus L_1\cap L_2; \\0 & \text{if } z \in L_1\cap L_2,\end{cases}\\[-16pt]\end{align*} $$
$$ \begin{align*}\mathrm{{mld}}(X/Z\ni z,B)=\begin{cases}2&\text{if } z\not \in L_1\cup L_2;\\1&\text{if } z \in L_1\cup L_2\setminus L_1\cap L_2; \\0 & \text{if } z \in L_1\cap L_2,\end{cases}\\[-16pt]\end{align*} $$
and
 $$ \begin{align*}\mathrm{{mld}}(X/Z\ni z,B')=\begin{cases}2&\text{if } z\not \in L_1\cup L_2;\\\frac{3}{2}&\text{if } z \in L_1\setminus L_1\cap L_2; \\-\infty & \text{if } z \in L_2.\end{cases}\\[-16pt]\end{align*} $$
$$ \begin{align*}\mathrm{{mld}}(X/Z\ni z,B')=\begin{cases}2&\text{if } z\not \in L_1\cup L_2;\\\frac{3}{2}&\text{if } z \in L_1\setminus L_1\cap L_2; \\-\infty & \text{if } z \in L_2.\end{cases}\\[-16pt]\end{align*} $$
Definition 2.7. Fix a non-negative real number
![]() $\epsilon $
. We say that the sub-pair
$\epsilon $
. We say that the sub-pair
![]() $(X/Z\ni z, B)$
is
$(X/Z\ni z, B)$
is
![]() $\epsilon $
-lc (respectively,
$\epsilon $
-lc (respectively,
![]() $\epsilon $
-klt, klt, lc) if
$\epsilon $
-klt, klt, lc) if
![]() $\mathrm {{mld}}(X/Z\ni z,B)\ge \epsilon $
(respectively,
$\mathrm {{mld}}(X/Z\ni z,B)\ge \epsilon $
(respectively,
![]() $> \epsilon $
,
$> \epsilon $
,
![]() $>0$
,
$>0$
,
![]() $\ge 0$
).
$\ge 0$
).
We say that
![]() $(X, B)$
is
$(X, B)$
is
![]() $\epsilon $
-lc (respectively,
$\epsilon $
-lc (respectively,
![]() $\epsilon $
-klt, klt, lc) if
$\epsilon $
-klt, klt, lc) if
![]() $(X\ni x, B)$
is so for any codimension
$(X\ni x, B)$
is so for any codimension
![]() $\geq 1$
point
$\geq 1$
point
![]() $x\in X$
; we say that
$x\in X$
; we say that
![]() $(X, B)$
is canonical (respectively, terminal) if
$(X, B)$
is canonical (respectively, terminal) if
![]() $a(E,X,B)\ge 1$
(respectively,
$a(E,X,B)\ge 1$
(respectively,
![]() $a(E,X,B)> 1$
) for any exceptional prime divisor E over X. These coincide with the usual definitions (compare [Reference Kollár and Mori27, Definition 2.34]).
$a(E,X,B)> 1$
) for any exceptional prime divisor E over X. These coincide with the usual definitions (compare [Reference Kollár and Mori27, Definition 2.34]).
The following lemma is well-known to experts, saying that being lc over
![]() $z\in Z$
is an open condition.
$z\in Z$
is an open condition.
Lemma 2.8. Let
![]() $(X/Z\ni z, B)$
be a sub-pair with contraction
$(X/Z\ni z, B)$
be a sub-pair with contraction
![]() $\pi : X\to Z$
, and fix a log resolution
$\pi : X\to Z$
, and fix a log resolution
![]() $f:Y\to (X, B)$
such that
$f:Y\to (X, B)$
such that
![]() $f^{-1}_*\operatorname {Supp} B+f^{-1}\pi ^{-1}(\overline {z})$
is a simple normal crossing divisor, and write
$f^{-1}_*\operatorname {Supp} B+f^{-1}\pi ^{-1}(\overline {z})$
is a simple normal crossing divisor, and write
![]() $K_Y+B_Y=f^*(K_X+B)$
. The following are equivalent:
$K_Y+B_Y=f^*(K_X+B)$
. The following are equivalent:
-
1.
 $(X/Z\ni z, B)$
is lc.
$(X/Z\ni z, B)$
is lc. -
2. For any prime divisor E on Y with
 $\pi (f(E))\ni z$
,
$\pi (f(E))\ni z$
,
 $\operatorname {mult}_{E} B_Y\leq 1$
.
$\operatorname {mult}_{E} B_Y\leq 1$
. -
3. There exists an open neighbourhood U of
 $z\in Z$
such that
$z\in Z$
such that
 $(\pi ^{-1}(U), B|_{\pi ^{-1}(U)})$
is lc.
$(\pi ^{-1}(U), B|_{\pi ^{-1}(U)})$
is lc.
Proof. By definition, (3) implies (2). By direct computations ([Reference Kollár and Mori27, Corollary 2.31]), if (2) holds for the given log resolution Y, it holds for any log resolution. Thus (2) implies (3). It is obvious that (3) implies (1). It suffices to show that (1) implies (2).
Suppose that sub-pair
![]() $(X/Z\ni z, B)$
is lc. Assume to the contrary that there exists a prime divisor E such that
$(X/Z\ni z, B)$
is lc. Assume to the contrary that there exists a prime divisor E such that
![]() $\operatorname {mult}_EB_Y>1$
and
$\operatorname {mult}_EB_Y>1$
and
![]() $E\cap f^{-1}\pi ^{-1}(z)\neq \emptyset .$
Then by successively blowing up some components of the closure of
$E\cap f^{-1}\pi ^{-1}(z)\neq \emptyset .$
Then by successively blowing up some components of the closure of
![]() $E\cap f^{-1}\pi ^{-1}(z)$
several times, we can replace Y by a higher model such that there exists a prime divisor
$E\cap f^{-1}\pi ^{-1}(z)$
several times, we can replace Y by a higher model such that there exists a prime divisor
![]() $E'$
on Y with
$E'$
on Y with
![]() $\pi (f(E'))=\overline {z}$
and
$\pi (f(E'))=\overline {z}$
and
![]() $\operatorname {mult}_{E'} B_Y>1$
(compare [Reference Kollár and Mori27, Corollary 2.31]), a contradiction. To be more precise, suppose that there exists a prime divisor D in
$\operatorname {mult}_{E'} B_Y>1$
(compare [Reference Kollár and Mori27, Corollary 2.31]), a contradiction. To be more precise, suppose that there exists a prime divisor D in
![]() $f^{-1}\pi ^{-1}(\bar z)$
, which maps to
$f^{-1}\pi ^{-1}(\bar z)$
, which maps to
![]() $\bar z$
such that
$\bar z$
such that
![]() $D\cap E\neq \emptyset $
, and suppose
$D\cap E\neq \emptyset $
, and suppose
![]() $\operatorname {mult}_D B_Y=d$
and
$\operatorname {mult}_D B_Y=d$
and
![]() $\operatorname {mult}_E B_Y=e>1$
; then we can blow up
$\operatorname {mult}_E B_Y=e>1$
; then we can blow up
![]() $D\cap E$
to get a new log resolution
$D\cap E$
to get a new log resolution
![]() $f': Y'\to X$
with
$f': Y'\to X$
with
![]() $K_{Y'}+B_{Y'}=f^{\prime *}(K_X+B)$
such that there exists a prime divisor in
$K_{Y'}+B_{Y'}=f^{\prime *}(K_X+B)$
such that there exists a prime divisor in
![]() $D'\cap f^{\prime -1}\pi ^{-1}(\bar z)$
, which maps to
$D'\cap f^{\prime -1}\pi ^{-1}(\bar z)$
, which maps to
![]() $\bar z$
with
$\bar z$
with
![]() $\operatorname {mult}_{D'} B_{Y'}=d+e-1$
. So, inductively, we can replace Y by a higher model to find the required
$\operatorname {mult}_{D'} B_{Y'}=d+e-1$
. So, inductively, we can replace Y by a higher model to find the required
![]() $E'$
.
$E'$
.
Definition 2.9. A non-klt place of a sub-pair
![]() $(X, B)$
(respectively,
$(X, B)$
(respectively,
![]() $(X/Z\ni z, B)$
) is a prime divisor E over X (respectively,
$(X/Z\ni z, B)$
) is a prime divisor E over X (respectively,
![]() $E\in \mathfrak {D}(X/Z\ni z)$
) such that
$E\in \mathfrak {D}(X/Z\ni z)$
) such that
![]() $a(E,X,B)\leq 0$
, and a non-klt center is the center of a non-klt place on X.
$a(E,X,B)\leq 0$
, and a non-klt center is the center of a non-klt place on X.
2.3 Log canonical thresholds
Definition 2.10. Let
![]() $(X/Z\ni z, B)$
be an lc sub-pair with contraction
$(X/Z\ni z, B)$
be an lc sub-pair with contraction
![]() $\pi : X\to Z$
, and let
$\pi : X\to Z$
, and let
![]() $D\neq 0$
be an effective
$D\neq 0$
be an effective
![]() $\mathbb {R}$
-Cartier
$\mathbb {R}$
-Cartier
![]() $\mathbb {R}$
-divisor on X such that
$\mathbb {R}$
-divisor on X such that
![]() $z\in \pi (\operatorname {Supp}(D))$
. The log canonical threshold of D with respect to
$z\in \pi (\operatorname {Supp}(D))$
. The log canonical threshold of D with respect to
![]() $(X/Z\ni z,B)$
is
$(X/Z\ni z,B)$
is
When
![]() $z\in Z$
is a codimension
$z\in Z$
is a codimension
![]() $1$
point, we may assume that
$1$
point, we may assume that
![]() $\overline {z}$
is a Cartier divisor on a neighbourhood U of
$\overline {z}$
is a Cartier divisor on a neighbourhood U of
![]() $z\in Z$
. Then we define
$z\in Z$
. Then we define
and this definition does not depend on the choice of the neighbourhood U of
![]() $z\in Z$
.
$z\in Z$
.
We may write
![]() $\operatorname {lct}(X/Z\ni z; D):=\operatorname {lct}(X/Z\ni z, 0; D)$
when
$\operatorname {lct}(X/Z\ni z; D):=\operatorname {lct}(X/Z\ni z, 0; D)$
when
![]() $B=0$
. When
$B=0$
. When
![]() $X=Z$
,
$X=Z$
,
![]() $z=x$
and
$z=x$
and
![]() $\pi $
is the identity map, we may write
$\pi $
is the identity map, we may write
![]() $\operatorname {lct}(X\ni x,B;D):=\operatorname {lct}(X/Z\ni z,B;D)$
.
$\operatorname {lct}(X\ni x,B;D):=\operatorname {lct}(X/Z\ni z,B;D)$
.
Remark 2.11 ([Reference Kollár26])
Keep the same setting as in Definition 2.10. Log canonical thresholds can be computed by a log resolution. In fact, take
![]() $g: X'\to X$
to be a log resolution of
$g: X'\to X$
to be a log resolution of
![]() $(X, B+D)$
, and write
$(X, B+D)$
, and write
![]() $K_{X'}+B'=g^*(K_X+B)$
. Then
$K_{X'}+B'=g^*(K_X+B)$
. Then
where the minimum runs over all prime divisors
![]() $E\subseteq \operatorname {Supp} (g^*D)$
such that
$E\subseteq \operatorname {Supp} (g^*D)$
such that
![]() $\pi (g(E))\ni z$
(compare Lemma 2.8(3)).
$\pi (g(E))\ni z$
(compare Lemma 2.8(3)).
2.4 Canonical bundle formula
The discrepancy b-divisor
![]() $\mathbf {A}=\mathbf {A}(X,B)$
of a sub-pair
$\mathbf {A}=\mathbf {A}(X,B)$
of a sub-pair
![]() $(X,B)$
is the b-divisor of X with the trace
$(X,B)$
is the b-divisor of X with the trace
![]() $\mathbf {A}_Y$
defined by the formula
$\mathbf {A}_Y$
defined by the formula
for any proper birational morphism
![]() $f: Y\to X$
between normal varieties. Similarly, we define
$f: Y\to X$
between normal varieties. Similarly, we define
![]() $\mathbf {A}^*=\mathbf {A}^*(X,B)$
by
$\mathbf {A}^*=\mathbf {A}^*(X,B)$
by
![]() $ \mathbf {A}^*_Y=\sum _{a_i>-1}a_iE_i $
for any proper birational morphism
$ \mathbf {A}^*_Y=\sum _{a_i>-1}a_iE_i $
for any proper birational morphism
![]() $f: Y\to X$
between normal varieties, where
$f: Y\to X$
between normal varieties, where
![]() $\mathbf {A}_Y=\sum a_iE_i$
. Note that
$\mathbf {A}_Y=\sum a_iE_i$
. Note that
![]() $\mathbf {A}^*(X,B)=\mathbf {A}(X,B)$
if and only if
$\mathbf {A}^*(X,B)=\mathbf {A}(X,B)$
if and only if
![]() $(X, B)$
is klt. See [Reference Fujino and Gongyo14, 2.3] for more details.
$(X, B)$
is klt. See [Reference Fujino and Gongyo14, 2.3] for more details.
Definition 2.12 (compare [Reference Fujino and Gongyo14, Definition 3.2], [Reference Hu20, Definition 3.1])
An lc-trivial fibration
![]() $\pi : (X, B)\to Z$
consists of a contraction
$\pi : (X, B)\to Z$
consists of a contraction
![]() $\pi : X\to Z$
between normal varieties and a sub-pair
$\pi : X\to Z$
between normal varieties and a sub-pair
![]() $(X, B)$
satisfying the following properties:
$(X, B)$
satisfying the following properties:
-
1.
 $(X, B)$
is lc over the generic point of Z,
$(X, B)$
is lc over the generic point of Z, -
2.
 $\operatorname {rank} \pi _*\mathcal {O}_X(\lceil \mathbf {A}^*(X, B)\rceil )=1$
, and
$\operatorname {rank} \pi _*\mathcal {O}_X(\lceil \mathbf {A}^*(X, B)\rceil )=1$
, and -
3. there exists an
 $\mathbb {R}$
-Cartier
$\mathbb {R}$
-Cartier
 $\mathbb {R}$
-divisor L on Z such that
$\mathbb {R}$
-divisor L on Z such that
 $K_X+B\sim _{\mathbb {R}}\pi ^*L.$
$K_X+B\sim _{\mathbb {R}}\pi ^*L.$
Remark 2.13. Here, we discuss more details about the condition in (2). If B is effective on the generic fibre of
![]() $\pi $
, then
$\pi $
, then
![]() $\mathcal {O}_X(\lceil \mathbf {A}^*(X, B)\rceil )=\mathcal {O}_X$
over the generic point of Z, so in this case the condition in (2) holds. Conversely, if the geometric generic fibre of
$\mathcal {O}_X(\lceil \mathbf {A}^*(X, B)\rceil )=\mathcal {O}_X$
over the generic point of Z, so in this case the condition in (2) holds. Conversely, if the geometric generic fibre of
![]() $\pi $
is a rational curve, then
$\pi $
is a rational curve, then
![]() $\operatorname {rank} \pi _*\mathcal {O}_X(\lceil \mathbf {A}^*(X, B)\rceil )=1$
implies that B is effective on the generic fibre of
$\operatorname {rank} \pi _*\mathcal {O}_X(\lceil \mathbf {A}^*(X, B)\rceil )=1$
implies that B is effective on the generic fibre of
![]() $\pi $
.
$\pi $
.
Let
![]() $\pi : (X, B)\to Z$
be an lc-trivial fibration. Then we may write
$\pi : (X, B)\to Z$
be an lc-trivial fibration. Then we may write
![]() $K_X+B\sim _{\mathbb {R}} \pi ^*L$
for some
$K_X+B\sim _{\mathbb {R}} \pi ^*L$
for some
![]() $\mathbb {R}$
-Cartier
$\mathbb {R}$
-Cartier
![]() $\mathbb {R}$
-divisor L. By the work of Kawamata [Reference Kawamata24, Reference Kawamata25] and Ambro [Reference Ambro3] (see [Reference Hu20, Section 3] for
$\mathbb {R}$
-divisor L. By the work of Kawamata [Reference Kawamata24, Reference Kawamata25] and Ambro [Reference Ambro3] (see [Reference Hu20, Section 3] for
![]() $\mathbb {R}$
-divisors), we have the so-called canonical bundle formula
$\mathbb {R}$
-divisors), we have the so-called canonical bundle formula
where
![]() $B_Z$
is defined by
$B_Z$
is defined by
and
Here, the sum runs over all prime divisors P on Z,
![]() $\eta _P$
is the generic point of P and it is known that it is a finite sum. So
$\eta _P$
is the generic point of P and it is known that it is a finite sum. So
![]() $B_Z$
is uniquely determined by
$B_Z$
is uniquely determined by
![]() $(X, B)$
, and
$(X, B)$
, and
![]() $M_Z$
is determined up to
$M_Z$
is determined up to
![]() $\mathbb {R}$
-linear equivalence. Here,
$\mathbb {R}$
-linear equivalence. Here,
![]() $B_Z$
is called the discriminant part and
$B_Z$
is called the discriminant part and
![]() $M_Z$
is called the moduli part of the canonical bundle formula. Recall that if B is effective, then
$M_Z$
is called the moduli part of the canonical bundle formula. Recall that if B is effective, then
![]() $B_Z$
is also effective.
$B_Z$
is also effective.
In the following, we suppose that B is a
![]() $\mathbb {Q}$
-divisor for simplicity. In fact, the canonical bundle formula satisfies certain functorial properties as follows. By [Reference Prokhorov and Shokurov35, Remark 7.7] or [Reference Fujino and Gongyo14, 3.4], there are b-divisors
$\mathbb {Q}$
-divisor for simplicity. In fact, the canonical bundle formula satisfies certain functorial properties as follows. By [Reference Prokhorov and Shokurov35, Remark 7.7] or [Reference Fujino and Gongyo14, 3.4], there are b-divisors
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {M}$
of Z such that
$\mathbf {M}$
of Z such that
-
○
 $\mathbf {B}_Z=B_Z$
,
$\mathbf {B}_Z=B_Z$
,
 $\mathbf {M}_Z=M_Z$
, and
$\mathbf {M}_Z=M_Z$
, and -
○ for any birational contraction
 $g: Z'\to Z$
, let
$g: Z'\to Z$
, let
 $X'$
be a resolution of the main component of
$X'$
be a resolution of the main component of
 $X\times _{Z} Z'$
with induced morphisms
$X\times _{Z} Z'$
with induced morphisms
 $g': X' \to X$
and
$g': X' \to X$
and
 $\pi ': X'\to Z'$
. Let
$\pi ': X'\to Z'$
. Let
 $K_{X'}+B'$
be the crepant pull back of
$K_{X'}+B'$
be the crepant pull back of
 $K_X+B$
—that is,
$K_X+B$
—that is,
 $K_{X'}+B'=g^{\prime *}(K_X+B)$
—then
$K_{X'}+B'=g^{\prime *}(K_X+B)$
—then
 $\mathbf {B}_{Z'}$
(respectively,
$\mathbf {B}_{Z'}$
(respectively,
 $\mathbf {M}_{Z'}$
) is the discriminant part (respectively, the moduli part) of the canonical bundle formula of
$\mathbf {M}_{Z'}$
) is the discriminant part (respectively, the moduli part) of the canonical bundle formula of
 $K_{X'}+B'$
on
$K_{X'}+B'$
on
 $Z'$
defined by equations (2.1) and (2.2):
$Z'$
defined by equations (2.1) and (2.2): 
The effective adjunction conjecture ([Reference Prokhorov and Shokurov35, Conjecture 7.13]) predicts that
![]() $\mathbf {M}$
is b-semi-ample. It was confirmed in the case of relative dimension
$\mathbf {M}$
is b-semi-ample. It was confirmed in the case of relative dimension
![]() $1$
.
$1$
.
Theorem 2.14 ([Reference Prokhorov and Shokurov35, Theorem 8.1])
Keep the notation in this subsection. Assume that B is a
![]() $\mathbb {Q}$
-divisor. If
$\mathbb {Q}$
-divisor. If
![]() $\dim X-\dim Z=1$
and the geometric generic fibre of
$\dim X-\dim Z=1$
and the geometric generic fibre of
![]() $\pi $
is a rational curve, then
$\pi $
is a rational curve, then
![]() $\mathbf {M}$
is b-semi-ample.
$\mathbf {M}$
is b-semi-ample.
Remark 2.15. Note that [Reference Prokhorov and Shokurov35, Theorem 8.1] holds for an lc-trivial fibration
![]() $\pi : (X, B)\to Z$
under two additional assumptions:
$\pi : (X, B)\to Z$
under two additional assumptions:
-
1. B is effective over the generic point of Z [Reference Prokhorov and Shokurov35, Assumption 7.1], and
-
2. there exists a
 $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
 $\Theta $
on X such that
$\Theta $
on X such that
 $K_X+\Theta \sim _{\mathbb {Q}, Z}0$
and
$K_X+\Theta \sim _{\mathbb {Q}, Z}0$
and
 $(X, \Theta )$
is klt over the generic point of Z [Reference Prokhorov and Shokurov35, Assumption 7.11].
$(X, \Theta )$
is klt over the generic point of Z [Reference Prokhorov and Shokurov35, Assumption 7.11].
Here, (i) is automatically satisfied by Remark 2.13. Also, (ii) is automatically satisfied by the following. Since the generic fibre
![]() $X_\eta $
of
$X_\eta $
of
![]() $\pi $
is a rational curve, we can find an effective
$\pi $
is a rational curve, we can find an effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $D_\eta $
on
$D_\eta $
on
![]() $X_\eta $
such that
$X_\eta $
such that
![]() $K_{X_\eta }+D_\eta \sim _{\mathbb {Q}}0$
and
$K_{X_\eta }+D_\eta \sim _{\mathbb {Q}}0$
and
![]() $(X_\eta , D_\eta )$
is klt. Denote D to be the closure of
$(X_\eta , D_\eta )$
is klt. Denote D to be the closure of
![]() $D_\eta $
on X; then
$D_\eta $
on X; then
![]() $K_{X}+D\sim _{\mathbb {Q}} E$
, where E is vertical over Z. Then we just take
$K_{X}+D\sim _{\mathbb {Q}} E$
, where E is vertical over Z. Then we just take
![]() $\Theta =D-E$
.
$\Theta =D-E$
.
2.5 Contractions of Fano type
Definition 2.16 ([Reference Prokhorov and Shokurov35])
Let
![]() $\pi : X\to Z$
be a contraction between normal varieties. We say that X is of Fano type over Z if one of the following equivalent conditions holds:
$\pi : X\to Z$
be a contraction between normal varieties. We say that X is of Fano type over Z if one of the following equivalent conditions holds:
-
1. there exists a klt pair
 $(X,B)$
such that
$(X,B)$
such that
 $-(K_X+B)$
is ample over Z;
$-(K_X+B)$
is ample over Z; -
2. there exists a klt pair
 $(X,B')$
such that
$(X,B')$
such that
 $-(K_X+B')$
is nef and big over Z;
$-(K_X+B')$
is nef and big over Z; -
3. there exists a klt pair
 $(X,B'')$
such that
$(X,B'')$
such that
 $K_X+B''\equiv _Z 0$
and
$K_X+B''\equiv _Z 0$
and
 $B''$
is big over Z.
$B''$
is big over Z.
When Z is a point, we just say that X is of Fano type.
2.6 Formal surface germs
Let P be a smooth closed point on a surface X. By the Cohen structure theorem,
![]() $\widehat {\mathcal {O}}_{X,P}\cong \widehat {\mathcal {O}}_{\mathbb {C}^2,o}=\mathbb {C}[[x,y]]$
. Denote by
$\widehat {\mathcal {O}}_{X,P}\cong \widehat {\mathcal {O}}_{\mathbb {C}^2,o}=\mathbb {C}[[x,y]]$
. Denote by
![]() $\widehat {X}_P$
the completion of X along P. We will use
$\widehat {X}_P$
the completion of X along P. We will use
![]() $\widehat {X}$
instead of
$\widehat {X}$
instead of
![]() $\widehat {X}_P$
if P is clear from the context.
$\widehat {X}_P$
if P is clear from the context.
We call
![]() ${C}$
a Cartier divisor on
${C}$
a Cartier divisor on
![]() $\widehat {X}$
if
$\widehat {X}$
if
![]() ${C}$
is defined by
${C}$
is defined by
![]() $(g=0)$
for some
$(g=0)$
for some
![]() $g\in \widehat {\mathcal {O}}_{X,P}$
. We call
$g\in \widehat {\mathcal {O}}_{X,P}$
. We call
![]() ${B}$
an
${B}$
an
![]() $\mathbb {R}$
-divisor (respectively, a
$\mathbb {R}$
-divisor (respectively, a
![]() $\mathbb {Q}$
-divisor) on
$\mathbb {Q}$
-divisor) on
![]() $\widehat {X}$
if
$\widehat {X}$
if
![]() ${B}=\sum _i b_i{B_i}$
for some Cartier divisors
${B}=\sum _i b_i{B_i}$
for some Cartier divisors
![]() ${B_i}$
on
${B_i}$
on
![]() $\widehat {X}$
and
$\widehat {X}$
and
![]() $b_i\in \mathbb {R}$
(respectively
$b_i\in \mathbb {R}$
(respectively
![]() $b_i\in \mathbb {Q}$
).
$b_i\in \mathbb {Q}$
).
Since the resolution of singularities is known for complete local rings ([Reference Temkin39]), the definition of singularities of pairs and log canonical thresholds can be extended to the formal case (see [Reference Kollár26] and [Reference de Fernex, Ein and Mustaţă12]).
Definition 2.17. Let
![]() $(\widehat {X}\ni P, {B}=\sum _i b_i{B_i})$
be an lc pair where
$(\widehat {X}\ni P, {B}=\sum _i b_i{B_i})$
be an lc pair where
![]() $P\in X$
is a smooth formal surface germ and
$P\in X$
is a smooth formal surface germ and
![]() ${B_i}$
is defined by
${B_i}$
is defined by
![]() $(f_i=0)$
for some
$(f_i=0)$
for some
![]() $f_i\in \widehat {\mathcal {O}}_{X,x}$
. Let
$f_i\in \widehat {\mathcal {O}}_{X,x}$
. Let
![]() ${C}=\sum _i c_i{C_i}\neq 0$
be an effective
${C}=\sum _i c_i{C_i}\neq 0$
be an effective
![]() $\mathbb {R}$
-divisor, where
$\mathbb {R}$
-divisor, where
![]() ${C_i}$
is defined by
${C_i}$
is defined by
![]() $(g_i=0)$
for some
$(g_i=0)$
for some
![]() $g_i\in \widehat {\mathcal {O}}_{X,x}$
. Let
$g_i\in \widehat {\mathcal {O}}_{X,x}$
. Let
![]() ${\phi }: \widehat {Y}\to (\widehat {X}, {B}+{C})$
be a log resolution ([Reference Temkin39]); then
${\phi }: \widehat {Y}\to (\widehat {X}, {B}+{C})$
be a log resolution ([Reference Temkin39]); then
 $$ \begin{align} \operatorname{lct}(\widehat{X}\ni P, {B};{C}):=\min_{E}\frac{1+\operatorname{mult}_E K_{\widehat{Y}/\widehat{X}}-\sum_i b_i\operatorname{mult}_E (f_i)}{\sum_i c_i\operatorname{mult}_E (g_i)}, \end{align} $$
$$ \begin{align} \operatorname{lct}(\widehat{X}\ni P, {B};{C}):=\min_{E}\frac{1+\operatorname{mult}_E K_{\widehat{Y}/\widehat{X}}-\sum_i b_i\operatorname{mult}_E (f_i)}{\sum_i c_i\operatorname{mult}_E (g_i)}, \end{align} $$
where the minimum runs over all prime divisors E in
![]() $\operatorname {Supp} ({\phi }^{*}C)$
such that
$\operatorname {Supp} ({\phi }^{*}C)$
such that
![]() $P\in \phi (E)$
. The definition does not depend on the choice of log resolutions. Here,
$P\in \phi (E)$
. The definition does not depend on the choice of log resolutions. Here,
![]() $\operatorname {mult}_E$
means the vanishing order of a function along E or the coefficient of E in a divisor.
$\operatorname {mult}_E$
means the vanishing order of a function along E or the coefficient of E in a divisor.
Remark 2.18. Let
![]() $(X\ni P, B)$
be a germ of an lc surface pair such that
$(X\ni P, B)$
be a germ of an lc surface pair such that
![]() $P\in X$
is smooth, and let C be an effective
$P\in X$
is smooth, and let C be an effective
![]() $\mathbb {R}$
-divisor near P. Consider
$\mathbb {R}$
-divisor near P. Consider
![]() $\widehat {X}$
(respectively
$\widehat {X}$
(respectively
![]() $B',C'$
), the completion of X (respectively
$B',C'$
), the completion of X (respectively
![]() $B,C$
) along P. Since a log resolution of
$B,C$
) along P. Since a log resolution of
![]() $(X\ni P, B+C)$
also gives a log resolution of
$(X\ni P, B+C)$
also gives a log resolution of
![]() $(\widehat {X},B'+C')$
,
$(\widehat {X},B'+C')$
,
![]() $\operatorname {lct}(\widehat {X}\ni P, B';C')=\operatorname {lct}(X\ni P, B;C)$
. In other words, in order to study the log canonical threshold of a smooth surface germ
$\operatorname {lct}(\widehat {X}\ni P, B';C')=\operatorname {lct}(X\ni P, B;C)$
. In other words, in order to study the log canonical threshold of a smooth surface germ
![]() $(X\ni P,B)$
, it is equivalent to study that of the corresponding smooth formal surface germ
$(X\ni P,B)$
, it is equivalent to study that of the corresponding smooth formal surface germ
![]() $(\widehat {X}\ni P, B')$
.
$(\widehat {X}\ni P, B')$
.
Recall that log canonical thresholds satisfy convexity with respect to the coefficients.
Lemma 2.19 (compare [Reference Han, Li and Qi16, Lemma 3.8])
Let
![]() $P\in X$
be a smooth surface germ or a smooth formal surface germ. Let
$P\in X$
be a smooth surface germ or a smooth formal surface germ. Let
![]() $({X}\ni P,{B_i})$
be an lc pair for
$({X}\ni P,{B_i})$
be an lc pair for
![]() $1\leq i\leq m$
,
$1\leq i\leq m$
,
![]() ${C}\neq 0$
an effective
${C}\neq 0$
an effective
![]() $\mathbb {R}$
-divisor on
$\mathbb {R}$
-divisor on
![]() ${X}$
and
${X}$
and
![]() $\lambda _i$
non-negative real numbers such that
$\lambda _i$
non-negative real numbers such that
![]() $\sum _{i=1}^m\lambda _i= 1$
. Then
$\sum _{i=1}^m\lambda _i= 1$
. Then
 $$ \begin{align*}\operatorname{lct}({X}\ni P,\sum_{i=1}^m \lambda_i {B_i};{C})\geq \sum_{i=1}^m \lambda_i \operatorname{lct}({X}\ni P,{B_i};{C}).\end{align*} $$
$$ \begin{align*}\operatorname{lct}({X}\ni P,\sum_{i=1}^m \lambda_i {B_i};{C})\geq \sum_{i=1}^m \lambda_i \operatorname{lct}({X}\ni P,{B_i};{C}).\end{align*} $$
3 Log canonical thresholds on a smooth surface germ
In this section, we study the lower bounds of log canonical thresholds on a smooth surface germ. The main goal of this section is to prove Theorem 1.11.
Recall the following result on computing log canonical thresholds of hypersurfaces.
Proposition 3.1 ([Reference Kuwata29, Proposition 2.1])
Let
![]() ${B}$
be a Cartier divisor in a neighbourhood of
${B}$
be a Cartier divisor in a neighbourhood of
![]() $o\in \widehat {\mathbb {C}^n}$
defined by
$o\in \widehat {\mathbb {C}^n}$
defined by
![]() $(f=0)$
, where
$(f=0)$
, where
![]() $f\in \mathbb {C}[[x_1, \dots , x_n]]$
. Assign rational weights
$f\in \mathbb {C}[[x_1, \dots , x_n]]$
. Assign rational weights
![]() $w(x_i)$
to the variables, and let
$w(x_i)$
to the variables, and let
![]() $w(f)$
be the weighted multiplicity of f. Let
$w(f)$
be the weighted multiplicity of f. Let
denote the weighted homogeneous leading term of f. Take
![]() $b=\frac {\sum _{i=1}^n w(x_i)}{w(f)}$
. If
$b=\frac {\sum _{i=1}^n w(x_i)}{w(f)}$
. If
![]() $(\widehat {\mathbb {C}^n}, b\cdot (f_w=0))$
is lc outside o, then
$(\widehat {\mathbb {C}^n}, b\cdot (f_w=0))$
is lc outside o, then
![]() $\operatorname {lct}(\widehat {\mathbb {C}^n}\ni o; B)=b$
.
$\operatorname {lct}(\widehat {\mathbb {C}^n}\ni o; B)=b$
.
To warm up, the following proposition is an application of Proposition 3.1.
Proposition 3.2. Let
![]() ${B}$
be a Cartier divisor in a neighbourhood of
${B}$
be a Cartier divisor in a neighbourhood of
![]() $o\in \widehat {\mathbb {C}^2}$
defined by
$o\in \widehat {\mathbb {C}^2}$
defined by
![]() $(f=0)$
, where
$(f=0)$
, where
![]() $f=x^{n } (x^{m_1}+y^{m_2})^k$
for some positive integers k, n,
$f=x^{n } (x^{m_1}+y^{m_2})^k$
for some positive integers k, n,
![]() $m_1$
,
$m_1$
,
![]() $m_2$
. Then
$m_2$
. Then
 $$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o; B)=\min\left\{ \frac{m_1+m_2}{km_1m_2+ {n }{m_2}}, \frac{1}{n }, \frac{1}{k} \right\}.\end{align*} $$
$$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o; B)=\min\left\{ \frac{m_1+m_2}{km_1m_2+ {n }{m_2}}, \frac{1}{n }, \frac{1}{k} \right\}.\end{align*} $$
Proof. Consider
![]() $C_1$
defined by
$C_1$
defined by
![]() $(x=0)$
and
$(x=0)$
and
![]() $C_2$
defined by
$C_2$
defined by
![]() $(x^{m_1}+y^{m_2}=0)$
; then
$(x^{m_1}+y^{m_2}=0)$
; then
![]() $(C_1\cdot C_2)_{o}=m_2.$
Consider the weight
$(C_1\cdot C_2)_{o}=m_2.$
Consider the weight
![]() $w=(m_2, m_1)$
; then
$w=(m_2, m_1)$
; then
![]() $f_w=f$
and
$f_w=f$
and
![]() $b=\frac {m_1+m_2}{km_1m_2+ {n }{m_2}}$
as in Proposition 3.1.
$b=\frac {m_1+m_2}{km_1m_2+ {n }{m_2}}$
as in Proposition 3.1.
If
![]() $b\leq \min \{ \frac {1}{n}, \frac {1}{k}\}$
, then
$b\leq \min \{ \frac {1}{n}, \frac {1}{k}\}$
, then
![]() $(\widehat {\mathbb {C}^2}, b\cdot (f_w=0))$
is lc outside o, and hence
$(\widehat {\mathbb {C}^2}, b\cdot (f_w=0))$
is lc outside o, and hence
![]() $\operatorname {lct}(\widehat {\mathbb {C}^2}\ni o; B)=b$
by Proposition 3.1. If
$\operatorname {lct}(\widehat {\mathbb {C}^2}\ni o; B)=b$
by Proposition 3.1. If
![]() $b> \frac {1}{n}$
, then
$b> \frac {1}{n}$
, then
![]() $n>km_2$
. Then [Reference Kollár and Mori27, Corollary 5.57] implies that
$n>km_2$
. Then [Reference Kollár and Mori27, Corollary 5.57] implies that
![]() $(\widehat {\mathbb {C}^2}\ni o, C_1+\frac {k}{n}C_2)$
is lc. If
$(\widehat {\mathbb {C}^2}\ni o, C_1+\frac {k}{n}C_2)$
is lc. If
![]() $b> \frac {1}{k}$
, then either
$b> \frac {1}{k}$
, then either
![]() $m_1=1$
or
$m_1=1$
or
![]() $m_2=1$
. In either case,
$m_2=1$
. In either case,
![]() $C_2$
is smooth and
$C_2$
is smooth and
![]() $k>nm_2$
. Then [Reference Kollár and Mori27, Corollary 5.57] implies that
$k>nm_2$
. Then [Reference Kollár and Mori27, Corollary 5.57] implies that
![]() $(\widehat {\mathbb {C}^2}\ni o, \frac {n}{k}C_1+C_2)$
is lc.
$(\widehat {\mathbb {C}^2}\ni o, \frac {n}{k}C_1+C_2)$
is lc.
Definition 3.3 (compare [Reference Kuwata29, Definition 2.10])
Let
![]() $B=(f=0)$
be an irreducible curve in a neighbourhood of
$B=(f=0)$
be an irreducible curve in a neighbourhood of
![]() $o\in \widehat {\mathbb {C}^2}$
. If B is smooth, then we set
$o\in \widehat {\mathbb {C}^2}$
. If B is smooth, then we set
![]() $m=1$
and
$m=1$
and
![]() $n=\infty $
. Otherwise, the Puiseux expansion of B (under suitable local parameters
$n=\infty $
. Otherwise, the Puiseux expansion of B (under suitable local parameters
![]() $x, y$
) is expressed as
$x, y$
) is expressed as
![]() $x=t^m, y=\sum _{i=n}^\infty \alpha _i t^i$
for some local parameter t, where
$x=t^m, y=\sum _{i=n}^\infty \alpha _i t^i$
for some local parameter t, where
![]() $m,n\in \mathbb {Z}_{\ge 2}$
,
$m,n\in \mathbb {Z}_{\ge 2}$
,
![]() $m<n$
, and m does not divide n. Here,
$m<n$
, and m does not divide n. Here,
![]() $(m, n)$
is called the first pair of Puiseux exponents of f. Note that
$(m, n)$
is called the first pair of Puiseux exponents of f. Note that
![]() $m=\operatorname {mult}_o f$
is the multiplicity of f at
$m=\operatorname {mult}_o f$
is the multiplicity of f at
![]() $o\in \widehat {\mathbb {C}^2}$
.
$o\in \widehat {\mathbb {C}^2}$
.
Example 3.4. If
![]() $n>m>1$
and
$n>m>1$
and
![]() $m,n$
are coprime, then the first pair of Puiseux exponents of
$m,n$
are coprime, then the first pair of Puiseux exponents of
![]() $f=x^m+y^n$
is just
$f=x^m+y^n$
is just
![]() $(m,n)$
.
$(m,n)$
.
The close relation between the first pair of Puiseux exponents and log canonical thresholds can be illustrated by the following result.
Theorem 3.5 ([Reference Kuwata29, Theorem 1.3])
Let
![]() ${B}$
be a Cartier divisor in a neighbourhood of
${B}$
be a Cartier divisor in a neighbourhood of
![]() $o\in \widehat {\mathbb {C}^2}$
defined by
$o\in \widehat {\mathbb {C}^2}$
defined by
![]() $(f=0)$
, where
$(f=0)$
, where
![]() $f\in \mathbb {C}[[x, y]]$
. Write
$f\in \mathbb {C}[[x, y]]$
. Write
![]() $f=\prod _{j=1}^r f_j^{\alpha _j}$
, where each
$f=\prod _{j=1}^r f_j^{\alpha _j}$
, where each
![]() $f_j$
is irreducible. Write
$f_j$
is irreducible. Write
![]() $B=\sum _j \alpha _j B_j$
, where
$B=\sum _j \alpha _j B_j$
, where
![]() $B_j$
is defined by
$B_j$
is defined by
![]() $(f_j=0)$
. Then
$(f_j=0)$
. Then
![]() $\operatorname {lct}(\widehat {\mathbb {C}^2}\ni o; B)$
depends only on the first pairs of Puiseux exponents of
$\operatorname {lct}(\widehat {\mathbb {C}^2}\ni o; B)$
depends only on the first pairs of Puiseux exponents of
![]() $f_j$
,
$f_j$
,
![]() $(B_i\cdot B_j)_o$
, and
$(B_i\cdot B_j)_o$
, and
![]() $\alpha _j$
.
$\alpha _j$
.
Following the ideas in [Reference Kuwata29, Theorem 1.2], we have the following.
Proposition 3.6. Let
![]() ${B}$
be a Cartier divisor in a neighbourhood of
${B}$
be a Cartier divisor in a neighbourhood of
![]() $o\in \widehat {\mathbb {C}^2}$
defined by
$o\in \widehat {\mathbb {C}^2}$
defined by
![]() $(f=0)$
, where
$(f=0)$
, where
![]() $f\in \mathbb {C}[[x, y]]$
. Suppose that f is irreducible. Let
$f\in \mathbb {C}[[x, y]]$
. Suppose that f is irreducible. Let
![]() $\operatorname {mult}_o f=m$
, and let
$\operatorname {mult}_o f=m$
, and let
![]() $(m, n)$
be the first pair of Puiseux exponents of f. Let
$(m, n)$
be the first pair of Puiseux exponents of f. Let
![]() $C\neq B$
be a smooth curve passing through o and
$C\neq B$
be a smooth curve passing through o and
![]() $(B\cdot C)_o=I.$
Then for every positive real numbers
$(B\cdot C)_o=I.$
Then for every positive real numbers
![]() $s,t$
,
$s,t$
,
 $$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o; sB+tC)=\min\left\{\frac{m+n}{smn+tI}, \frac{m+I}{(sm+t)I}, \frac{1}{s}, \frac{1}{t}\right\}.\end{align*} $$
$$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o; sB+tC)=\min\left\{\frac{m+n}{smn+tI}, \frac{m+I}{(sm+t)I}, \frac{1}{s}, \frac{1}{t}\right\}.\end{align*} $$
Remark 3.7.
-
1. By convention, if
 $(m,n)=(1,\infty )$
, we set
$(m,n)=(1,\infty )$
, we set
 $\frac {1+\infty }{s\cdot \infty +tI}:=\frac {1}{s}$
.
$\frac {1+\infty }{s\cdot \infty +tI}:=\frac {1}{s}$
. -
2. In the case that
 $s=t=1$
, Proposition 3.6 is a special case of [Reference Kuwata29, Theorem 1.2]. We also remark that Proposition 3.6 might be indicated by more general results in [Reference Galindo, Hernando and Monserrat15], but the formulation there is complicated, and we give a simple proof in this special case for the reader’s convenience.
$s=t=1$
, Proposition 3.6 is a special case of [Reference Kuwata29, Theorem 1.2]. We also remark that Proposition 3.6 might be indicated by more general results in [Reference Galindo, Hernando and Monserrat15], but the formulation there is complicated, and we give a simple proof in this special case for the reader’s convenience. -
3. Recall that under the setting of Proposition 3.6, by [Reference Kuwata29, Proof of Theorem 1.2, Case 2, Page 711–712],
 $$ \begin{align*}I\in \left\{m, 2m, \dots, \left\lfloor{\frac{n}{m}}\right\rfloor m, n\right\}.\end{align*} $$
$$ \begin{align*}I\in \left\{m, 2m, \dots, \left\lfloor{\frac{n}{m}}\right\rfloor m, n\right\}.\end{align*} $$
Proof. Set
 $$ \begin{align*}c:=\min\left\{\frac{m+n}{smn+tI}, \frac{m+I}{(sm+t)I}, \frac{1}{s}, \frac{1}{t}\right\}. \end{align*} $$
$$ \begin{align*}c:=\min\left\{\frac{m+n}{smn+tI}, \frac{m+I}{(sm+t)I}, \frac{1}{s}, \frac{1}{t}\right\}. \end{align*} $$
As being lc is a closed condition on coefficients, we may assume that
![]() $s, t\in \mathbb {Q}$
. Possibly replacing
$s, t\in \mathbb {Q}$
. Possibly replacing
![]() $s, t$
by a multiple, we may assume that
$s, t$
by a multiple, we may assume that
![]() $s, t$
are integers.
$s, t$
are integers.
If
![]() $m=1$
, then by Theorem 3.5, we may assume that
$m=1$
, then by Theorem 3.5, we may assume that
![]() $sB+tC$
is defined by
$sB+tC$
is defined by
![]() $(x^s (x +y^I)^t=0)$
. Then the proposition follows from Proposition 3.2. In the following, we may assume that
$(x^s (x +y^I)^t=0)$
. Then the proposition follows from Proposition 3.2. In the following, we may assume that
![]() $m>1$
, and in particular, B is singular at o.
$m>1$
, and in particular, B is singular at o.
Suppose that
![]() $\frac {1}{s}\leq \frac {m+n}{smn+tI}$
; then we have
$\frac {1}{s}\leq \frac {m+n}{smn+tI}$
; then we have
![]() $m=1$
(recall that
$m=1$
(recall that
![]() $n>1$
), which is absurd.
$n>1$
), which is absurd.
Suppose that
![]() $\frac {1}{t}\leq \frac {m+I}{(sm+t)I}$
; then
$\frac {1}{t}\leq \frac {m+I}{(sm+t)I}$
; then
![]() $sI\leq t$
. Then [Reference Kollár and Mori27, Corollary 5.57] implies that
$sI\leq t$
. Then [Reference Kollár and Mori27, Corollary 5.57] implies that
![]() $(\widehat {\mathbb {C}^2}\ni o, \frac {s}{t}B+C)$
is lc. Since
$(\widehat {\mathbb {C}^2}\ni o, \frac {s}{t}B+C)$
is lc. Since
![]() $n\ge I\ge m$
, we have
$n\ge I\ge m$
, we have
![]() $\frac {m+n}{smn+tI}\ge \frac {1}{t}$
, and hence
$\frac {m+n}{smn+tI}\ge \frac {1}{t}$
, and hence
![]() $\frac {1}{t}=c$
.
$\frac {1}{t}=c$
.
So from now on, we may assume that
in particular,
 $$ \begin{align*}c= \min\left\{\frac{m+n}{smn+tI}, \frac{m+I}{(sm+t)I}\right\}. \end{align*} $$
$$ \begin{align*}c= \min\left\{\frac{m+n}{smn+tI}, \frac{m+I}{(sm+t)I}\right\}. \end{align*} $$
If
![]() $I=n$
, then by Theorem 3.5, we may assume that
$I=n$
, then by Theorem 3.5, we may assume that
![]() $sB+tC$
is defined by
$sB+tC$
is defined by
![]() $((x^{m}+y^n)^s x^t=0)$
. Then by Proposition 3.2,
$((x^{m}+y^n)^s x^t=0)$
. Then by Proposition 3.2,
 $$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o; sB+tC)=\min\left\{\frac{m+n}{smn+tn}, \frac{1}{s}, \frac{1}{t}\right\}=c.\end{align*} $$
$$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o; sB+tC)=\min\left\{\frac{m+n}{smn+tn}, \frac{1}{s}, \frac{1}{t}\right\}=c.\end{align*} $$
If
![]() $I=pm$
for some
$I=pm$
for some
![]() $1\leq p\leq \lfloor {\frac {n}{m}}\rfloor $
, then by Theorem 3.5, we may assume that
$1\leq p\leq \lfloor {\frac {n}{m}}\rfloor $
, then by Theorem 3.5, we may assume that
![]() $sB+tC$
is defined by
$sB+tC$
is defined by
![]() $(h=0)$
, where
$(h=0)$
, where
![]() $h=(x^{m}+y^n)^s (x+y^p)^t$
.
$h=(x^{m}+y^n)^s (x+y^p)^t$
.
If
![]() $tp\leq sm$
, consider the weight
$tp\leq sm$
, consider the weight
![]() $w=(n, m)$
; then
$w=(n, m)$
; then
![]() $h_w=y^{pt}(x^m+y^n)^s$
and
$h_w=y^{pt}(x^m+y^n)^s$
and
![]() $b=\frac {m+n}{smn+tI}$
, as defined in Proposition 3.1. Moreover,
$b=\frac {m+n}{smn+tI}$
, as defined in Proposition 3.1. Moreover,
![]() $(\widehat {\mathbb {C}^2},bh_w)$
is lc outside o as
$(\widehat {\mathbb {C}^2},bh_w)$
is lc outside o as
![]() $b\leq \frac {1}{pt}$
by
$b\leq \frac {1}{pt}$
by
![]() $tp\leq sm$
and
$tp\leq sm$
and
![]() $b< \frac {1}{s}$
by equation (3.1). Hence, by Proposition 3.1,
$b< \frac {1}{s}$
by equation (3.1). Hence, by Proposition 3.1,
If
![]() $tp> sm$
, consider the weight
$tp> sm$
, consider the weight
![]() $w'=(p, 1)$
; then
$w'=(p, 1)$
; then
![]() $h_{w'}=x^{ms}(x+y^{p})^t$
and
$h_{w'}=x^{ms}(x+y^{p})^t$
and
![]() $b'=\frac {1+p}{(sm+t)p}=\frac {m+I}{(sm+t)I}$
, as defined in Proposition 3.1. Moreover,
$b'=\frac {1+p}{(sm+t)p}=\frac {m+I}{(sm+t)I}$
, as defined in Proposition 3.1. Moreover,
![]() $(\widehat {\mathbb {C}^2},b'h_{w'})$
is lc outside o as
$(\widehat {\mathbb {C}^2},b'h_{w'})$
is lc outside o as
![]() $b'< \frac {1}{ms}$
by
$b'< \frac {1}{ms}$
by
![]() $tp> sm$
and
$tp> sm$
and
![]() $b'<\frac {1}{t}$
by equation (3.1). Hence, by Proposition 3.1,
$b'<\frac {1}{t}$
by equation (3.1). Hence, by Proposition 3.1,
Corollary 3.8. Let
![]() ${B}$
be a Cartier divisor in a neighbourhood of
${B}$
be a Cartier divisor in a neighbourhood of
![]() $o\in \widehat {\mathbb {C}^2}$
defined by
$o\in \widehat {\mathbb {C}^2}$
defined by
![]() $(f=0)$
, where
$(f=0)$
, where
![]() $f\in \mathbb {C}[[x, y]]$
. Suppose that f is irreducible,
$f\in \mathbb {C}[[x, y]]$
. Suppose that f is irreducible,
![]() $\operatorname {mult}_o f=m$
, and let
$\operatorname {mult}_o f=m$
, and let
![]() $(m, n)$
be the first pair of Puiseux exponents of f. Let
$(m, n)$
be the first pair of Puiseux exponents of f. Let
![]() $C\neq B$
be a smooth curve passing through o, and
$C\neq B$
be a smooth curve passing through o, and
![]() $(B\cdot C)_o=I.$
Let
$(B\cdot C)_o=I.$
Let
![]() $\lambda $
be a positive real number. Suppose that one of the following conditions holds:
$\lambda $
be a positive real number. Suppose that one of the following conditions holds:
-
1.
 $\lambda m \leq 1$
;
$\lambda m \leq 1$
; -
2.
 $n=I$
and
$n=I$
and
 $\lambda \leq \min \{1, \frac {1}{m}+\frac {1}{I}\}$
; or
$\lambda \leq \min \{1, \frac {1}{m}+\frac {1}{I}\}$
; or -
3.
 $I\neq m$
and
$I\neq m$
and
 $\lambda I\leq 2$
.
$\lambda I\leq 2$
.
Then
![]() $(\widehat {\mathbb {C}^2}\ni o, \lambda B)$
is lc and
$(\widehat {\mathbb {C}^2}\ni o, \lambda B)$
is lc and
Proof. First we remark that if (c) holds, then (a) holds. In fact, suppose that
![]() $\lambda I\leq 2$
and
$\lambda I\leq 2$
and
![]() $\lambda m> 1$
; then
$\lambda m> 1$
; then
![]() $I<2m$
. Then by Remark 3.7(3),
$I<2m$
. Then by Remark 3.7(3),
![]() $I=m$
, so we get a contradiction by assumption (c). So in the following, we only assume that (a) or (b) holds.
$I=m$
, so we get a contradiction by assumption (c). So in the following, we only assume that (a) or (b) holds.
Here, note that under condition (a),
![]() $\lambda \leq \min \{1, \frac {1}{m}+\frac {1}{I}\}$
automatically holds. So we always have
$\lambda \leq \min \{1, \frac {1}{m}+\frac {1}{I}\}$
automatically holds. So we always have
![]() $\lambda \leq \min \{1,\frac {1}{I}+\frac {1}{m}\}$
.
$\lambda \leq \min \{1,\frac {1}{I}+\frac {1}{m}\}$
.
Set
![]() $t:=\min \{1, 1+\frac {m}{I}-\lambda m\}\geq 0.$
The statement is equivalent to
$t:=\min \{1, 1+\frac {m}{I}-\lambda m\}\geq 0.$
The statement is equivalent to
![]() $\operatorname {lct}(\widehat {\mathbb {C}^2}\ni o; \lambda B+tC)\geq 1$
. By Proposition 3.6, this is equivalent to showing that
$\operatorname {lct}(\widehat {\mathbb {C}^2}\ni o; \lambda B+tC)\geq 1$
. By Proposition 3.6, this is equivalent to showing that
-
1.
 $\frac {m+n}{\lambda mn+tI}\geq 1$
,
$\frac {m+n}{\lambda mn+tI}\geq 1$
, -
2.
 ${m+I}\geq {(\lambda m+t)I}$
,
${m+I}\geq {(\lambda m+t)I}$
, -
3.
 $1\geq \lambda $
, and
$1\geq \lambda $
, and -
4.
 $1\geq t$
.
$1\geq t$
.
Here, (2) and (4) follow from the definition of t, and (3) follows from
![]() $\lambda \leq \min \{1,\frac {1}{I}+\frac {1}{m}\}$
. It is enough to show (1).
$\lambda \leq \min \{1,\frac {1}{I}+\frac {1}{m}\}$
. It is enough to show (1).
If
![]() $m=1$
, then
$m=1$
, then
![]() $n=\infty $
, so (1) is equivalent to
$n=\infty $
, so (1) is equivalent to
![]() $\lambda =\lambda m \leq 1$
under the convention in Lemma 3.7(1), which is already proved in (3).
$\lambda =\lambda m \leq 1$
under the convention in Lemma 3.7(1), which is already proved in (3).
In the following, we assume that
![]() $m\ge 2$
. It suffices to prove that
$m\ge 2$
. It suffices to prove that
which is equivalent to
![]() $(n-I)(1-\lambda m)\geq 0$
. Recall that
$(n-I)(1-\lambda m)\geq 0$
. Recall that
![]() $n\geq I$
, so (1) holds if either
$n\geq I$
, so (1) holds if either
![]() $n=I$
or
$n=I$
or
![]() $\lambda m\leq 1$
holds. This proves the conclusion for (a) and (b).
$\lambda m\leq 1$
holds. This proves the conclusion for (a) and (b).
Remark 3.9. In applications, we only use Corollary 3.8 when condition (a) holds. The advantage of this corollary is that we can get rid of n in the first pair of Puiseux exponents of f, and the log canonical threshold can be estimated by only m and I. In practice, n is usually hard to control, while m and I can be controlled easily by geometric conditions.
The following example shows that both Theorem 1.11 and Corollary 3.8 are optimal.
Example 3.10. Consider two coprime positive integers m and I such that
![]() $m < I$
. Take a positive real number
$m < I$
. Take a positive real number
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda m\leq 1 \leq \lambda I$
. Consider
$\lambda m\leq 1 \leq \lambda I$
. Consider
![]() $(\mathbb {C}^2, \lambda B)$
, where
$(\mathbb {C}^2, \lambda B)$
, where
![]() $B=(x^{m}+y^{I}=0)$
and
$B=(x^{m}+y^{I}=0)$
and
![]() $C=(x=0)$
. Then
$C=(x=0)$
. Then
![]() $\operatorname {mult}_o \lambda B=\lambda m$
,
$\operatorname {mult}_o \lambda B=\lambda m$
,
![]() $(\lambda B\cdot C)_o= \lambda I$
. A direct computation by Proposition 3.6 shows that
$(\lambda B\cdot C)_o= \lambda I$
. A direct computation by Proposition 3.6 shows that
![]() $(\mathbb {C}^2\ni o, \lambda B+(1+\frac {m}{I}-\lambda m)C)$
is lc but
$(\mathbb {C}^2\ni o, \lambda B+(1+\frac {m}{I}-\lambda m)C)$
is lc but
![]() $(\mathbb {C}^2\ni o, \lambda B+(1+\frac {m}{I}-\lambda m+\epsilon )C)$
is not lc for any
$(\mathbb {C}^2\ni o, \lambda B+(1+\frac {m}{I}-\lambda m+\epsilon )C)$
is not lc for any
![]() $\epsilon>0$
. So in this case,
$\epsilon>0$
. So in this case,
Now we may show Theorem 1.11, which could be regarded as an
![]() $\mathbb {R}$
-divisor version of Corollary 3.8.
$\mathbb {R}$
-divisor version of Corollary 3.8.
Proof of Theorem 1.11
Possibly approximating
![]() $\mathbb {R}$
-coefficients with
$\mathbb {R}$
-coefficients with
![]() $\mathbb {Q}$
-coefficients, we may assume that B is a
$\mathbb {Q}$
-coefficients, we may assume that B is a
![]() $\mathbb {Q}$
-divisor. Recall that
$\mathbb {Q}$
-divisor. Recall that
![]() $(B\cdot C)_P=I$
and
$(B\cdot C)_P=I$
and
![]() $\operatorname {mult}_P B=m$
.
$\operatorname {mult}_P B=m$
.
If
![]() $I\leq 1$
, then
$I\leq 1$
, then
![]() $(X\ni P,B+C)$
is lc by [Reference Kollár and Mori27, Corollary 5.57]. Hence we may assume that
$(X\ni P,B+C)$
is lc by [Reference Kollár and Mori27, Corollary 5.57]. Hence we may assume that
![]() $I>1$
.
$I>1$
.
We may replace
![]() $P\in X$
by the formal neighbourhood
$P\in X$
by the formal neighbourhood
![]() $\widehat {X}$
of
$\widehat {X}$
of
![]() $P\in X$
, which is isomorphic to the formal neighbourhood
$P\in X$
, which is isomorphic to the formal neighbourhood
![]() $o\in \widehat {\mathbb {C}^2}$
. So from now on we may assume that
$o\in \widehat {\mathbb {C}^2}$
. So from now on we may assume that
![]() $P\in X$
is just
$P\in X$
is just
![]() $o\in \widehat {\mathbb {C}^2}$
. Write
$o\in \widehat {\mathbb {C}^2}$
. Write
![]() ${B}=\sum _{i=1}^{n} b_i {B_i}$
, where
${B}=\sum _{i=1}^{n} b_i {B_i}$
, where
![]() $b_i\in (0,1]$
, and
$b_i\in (0,1]$
, and
![]() $\{B_i\}_{1\leq i\leq n}$
are distinct irreducible curves on
$\{B_i\}_{1\leq i\leq n}$
are distinct irreducible curves on
![]() $\widehat {\mathbb {C}^2}$
passing through o.
$\widehat {\mathbb {C}^2}$
passing through o.
If
![]() $n=1$
, then we are done by Corollary 3.8. So we may assume that
$n=1$
, then we are done by Corollary 3.8. So we may assume that
![]() $n\geq 2$
.
$n\geq 2$
.
Set
![]() $s:=1+\frac {m}{I}-m$
. The goal is to show that
$s:=1+\frac {m}{I}-m$
. The goal is to show that
![]() $(\widehat {\mathbb {C}^2} \ni o,B+s{C})$
is lc. Consider the log canonical threshold polytope of the pair
$(\widehat {\mathbb {C}^2} \ni o,B+s{C})$
is lc. Consider the log canonical threshold polytope of the pair
![]() $(\widehat {\mathbb {C}^2} \ni o,s{C})$
with respect to the divisors
$(\widehat {\mathbb {C}^2} \ni o,s{C})$
with respect to the divisors
![]() ${B_1},\ldots ,{B_n}$
,
${B_1},\ldots ,{B_n}$
,
 $$ \begin{align*}P(\widehat{\mathbb{C}^2}\ni o,s{C};{B_1},\ldots,{B_n}):=\left\{(t_1,\ldots,t_n)\in \mathbb{R}^n_{\geq 0}\,\bigg\vert \left(\widehat{\mathbb{C}^2}\ni o ,s{C}+\sum_{i=1}^n t_i{B_i}\right)\text{ is lc}\right\}.\end{align*} $$
$$ \begin{align*}P(\widehat{\mathbb{C}^2}\ni o,s{C};{B_1},\ldots,{B_n}):=\left\{(t_1,\ldots,t_n)\in \mathbb{R}^n_{\geq 0}\,\bigg\vert \left(\widehat{\mathbb{C}^2}\ni o ,s{C}+\sum_{i=1}^n t_i{B_i}\right)\text{ is lc}\right\}.\end{align*} $$
By Lemma 2.19,
![]() $P(\widehat {\mathbb {C}^2}\ni o,s{C};{B_1},\ldots ,{B_n})$
is a compact convex polytope in
$P(\widehat {\mathbb {C}^2}\ni o,s{C};{B_1},\ldots ,{B_n})$
is a compact convex polytope in
![]() $\mathbb {R}^n$
. It suffices to show that the convex polytope
$\mathbb {R}^n$
. It suffices to show that the convex polytope
 $$ \begin{align*}\mathcal{P}:=\left\{(t_1,\ldots,t_n)\in\mathbb{R}^n_{\geq 0}\,\bigg\vert \operatorname{mult}_o\sum_{i=1}^n t_i{B_i}=m,\ \sum_{i=1}^n t_i({B_i}\cdot{C})_o=I\right\}\end{align*} $$
$$ \begin{align*}\mathcal{P}:=\left\{(t_1,\ldots,t_n)\in\mathbb{R}^n_{\geq 0}\,\bigg\vert \operatorname{mult}_o\sum_{i=1}^n t_i{B_i}=m,\ \sum_{i=1}^n t_i({B_i}\cdot{C})_o=I\right\}\end{align*} $$
is contained in
![]() $P(\widehat {\mathbb {C}^2}\ni o ,s{C};{B_1},\ldots ,{B_n})$
, here we remark that
$P(\widehat {\mathbb {C}^2}\ni o ,s{C};{B_1},\ldots ,{B_n})$
, here we remark that
![]() $\mathcal {P}\neq \emptyset $
. By Lemma 3.11, all the vertices of
$\mathcal {P}\neq \emptyset $
. By Lemma 3.11, all the vertices of
![]() $\mathcal {P}$
are contained in
$\mathcal {P}$
are contained in
![]() $\bigcup _{i\neq j} E_{i,j}$
, where
$\bigcup _{i\neq j} E_{i,j}$
, where
![]() $E_{i,j}:=\{(t_1,\cdots ,t_n)\mid t_k=0 \text { for } k\neq i,j\}$
. Hence it suffices to show that
$E_{i,j}:=\{(t_1,\cdots ,t_n)\mid t_k=0 \text { for } k\neq i,j\}$
. Hence it suffices to show that
for all
![]() $1\leq i< j\leq n$
.
$1\leq i< j\leq n$
.
Without loss of generality, we may just consider the case
![]() $(i, j)=(1,2)$
. It suffices to show that any vertex point of
$(i, j)=(1,2)$
. It suffices to show that any vertex point of
![]() $E_{1,2}\cap \mathcal {P}$
is contained in
$E_{1,2}\cap \mathcal {P}$
is contained in
![]() $P(\widehat {\mathbb {C}^2} \ni o,s{C};{B_1},{B_2})$
, where
$P(\widehat {\mathbb {C}^2} \ni o,s{C};{B_1},{B_2})$
, where
![]() $E_{1,2}$
is identified with
$E_{1,2}$
is identified with
![]() $\mathbb {R}^2$
. Set
$\mathbb {R}^2$
. Set
![]() $\operatorname {mult}_o B_i=m_i, (B_i\cdot C)_o=I_i\ge 1$
for
$\operatorname {mult}_o B_i=m_i, (B_i\cdot C)_o=I_i\ge 1$
for
![]() $i=1,2$
. Take
$i=1,2$
. Take
![]() $(c_1, c_2)$
to be a vertex point of
$(c_1, c_2)$
to be a vertex point of
![]() $E_{1,2}\cap \mathcal {P}$
; then
$E_{1,2}\cap \mathcal {P}$
; then
![]() $(c_1, c_2)$
satisfies the following equations:
$(c_1, c_2)$
satisfies the following equations:
Here, we recall that
![]() $m_1, m_2, I_1, I_2$
are positive integers,
$m_1, m_2, I_1, I_2$
are positive integers,
![]() $m_1\leq I_1$
,
$m_1\leq I_1$
,
![]() $m_2\leq I_2$
and
$m_2\leq I_2$
and
![]() $m\leq 1<I$
.
$m\leq 1<I$
.
Suppose that either
![]() $c_1=0$
or
$c_1=0$
or
![]() $c_2=0$
; then
$c_2=0$
; then
![]() $(c_1, c_2)\in P(\widehat {\mathbb {C}^2}\ni o,s{C};{B_1},{B_2})$
follows directly from Corollary 3.8.
$(c_1, c_2)\in P(\widehat {\mathbb {C}^2}\ni o,s{C};{B_1},{B_2})$
follows directly from Corollary 3.8.
Suppose that
![]() $c_1>0$
and
$c_1>0$
and
![]() $c_2>0$
. Since
$c_2>0$
. Since
![]() $(c_1, c_2)$
is a vertex of
$(c_1, c_2)$
is a vertex of
![]() $E_{1,2}\cap \mathcal {P}$
, it is the unique solution of equation (3.2). Thus
$E_{1,2}\cap \mathcal {P}$
, it is the unique solution of equation (3.2). Thus
![]() $\frac {m_1}{I_1}\neq \frac {m_2}{I_2}$
, and
$\frac {m_1}{I_1}\neq \frac {m_2}{I_2}$
, and
Without loss of generality, we may assume that
![]() $\frac {m_1}{I_1}<\frac {m}{I}<\frac {m_2}{I_2}$
. See Figure 1.
$\frac {m_1}{I_1}<\frac {m}{I}<\frac {m_2}{I_2}$
. See Figure 1.

Figure 1 Two cases.
If
![]() $m\geq \frac {m_2}{I_2}>\frac {m_1}{I_1}$
, then we may write
$m\geq \frac {m_2}{I_2}>\frac {m_1}{I_1}$
, then we may write
![]() $c_1B_1+c_2B_2=\mu _1 \frac {m}{m_1}B_1+\mu _2 \frac {m}{m_2}B_2$
for
$c_1B_1+c_2B_2=\mu _1 \frac {m}{m_1}B_1+\mu _2 \frac {m}{m_2}B_2$
for
![]() $\mu _1=\frac {m_1c_1}{m}$
and
$\mu _1=\frac {m_1c_1}{m}$
and
![]() $ \mu _2=\frac {m_2c_2}{m}$
. Note that
$ \mu _2=\frac {m_2c_2}{m}$
. Note that
![]() $\mu _1+\mu _2=1$
. By Corollary 3.8 and
$\mu _1+\mu _2=1$
. By Corollary 3.8 and
![]() $m\leq 1$
,
$m\leq 1$
,
 $$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{m}{m_i}B_i;C)\geq \min\left\{1, 1+\frac{m_i}{I_i}-m\right\}=1+\frac{m_i}{I_i}-m\end{align*} $$
$$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{m}{m_i}B_i;C)\geq \min\left\{1, 1+\frac{m_i}{I_i}-m\right\}=1+\frac{m_i}{I_i}-m\end{align*} $$
for
![]() $i=1,2$
. By Lemma 2.19 and the Cauchy–Schwarz inequality, we have
$i=1,2$
. By Lemma 2.19 and the Cauchy–Schwarz inequality, we have
 $$ \begin{align*} \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,c_1B_1+c_2B_2;C)&\geq \mu_1 \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{m}{m_1}B_1;C)+\mu_2 \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{m}{m_2}B_2;C)\\ &\geq 1-m+\mu_1\frac{m_1}{I_1}+\mu_2\frac{m_2}{I_2}=1-m+\frac{m_1^2c_1}{I_1m}+\frac{m_2^2c_2}{I_2m}\\ &\geq 1-m+ \frac{(m_1c_1+m_2c_2)^2}{(I_1c_1+I_2c_2)m}=1-m+\frac{m}{I}=s. \end{align*} $$
$$ \begin{align*} \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,c_1B_1+c_2B_2;C)&\geq \mu_1 \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{m}{m_1}B_1;C)+\mu_2 \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{m}{m_2}B_2;C)\\ &\geq 1-m+\mu_1\frac{m_1}{I_1}+\mu_2\frac{m_2}{I_2}=1-m+\frac{m_1^2c_1}{I_1m}+\frac{m_2^2c_2}{I_2m}\\ &\geq 1-m+ \frac{(m_1c_1+m_2c_2)^2}{(I_1c_1+I_2c_2)m}=1-m+\frac{m}{I}=s. \end{align*} $$
Otherwise,
![]() $\frac {m_2}{I_2}>m$
. We may write
$\frac {m_2}{I_2}>m$
. We may write
![]() $c_1B_1+c_2B_2=\mu ^{\prime }_1 \lambda _1B_1+\mu ^{\prime }_2 \frac {1}{I_2}B_2$
, where
$c_1B_1+c_2B_2=\mu ^{\prime }_1 \lambda _1B_1+\mu ^{\prime }_2 \frac {1}{I_2}B_2$
, where
![]() $\mu ^{\prime }_2=I_2c_2$
,
$\mu ^{\prime }_2=I_2c_2$
,
![]() $\mu ^{\prime }_1=1-I_2c_2$
,
$\mu ^{\prime }_1=1-I_2c_2$
,
![]() $\lambda _1=\frac {c_1}{1-I_2c_2}$
. Note that
$\lambda _1=\frac {c_1}{1-I_2c_2}$
. Note that
![]() $\mu ^{\prime }_1> 1-\frac {m_2c_2}{m}> 0$
,
$\mu ^{\prime }_1> 1-\frac {m_2c_2}{m}> 0$
,
![]() $\mu ^{\prime }_1+\mu ^{\prime }_2=1$
and
$\mu ^{\prime }_1+\mu ^{\prime }_2=1$
and
![]() $\lambda _1\leq \frac {c_1}{1-\frac {m_2c_2}{m}}=\frac {m}{m_1}\leq \frac {1}{m_1}$
. By Corollary 3.8, we have
$\lambda _1\leq \frac {c_1}{1-\frac {m_2c_2}{m}}=\frac {m}{m_1}\leq \frac {1}{m_1}$
. By Corollary 3.8, we have
 $$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\lambda_1B_1;C)\geq \min\left\{1, 1+\frac{m_1}{I_1}-\lambda_1 m_1\right\}\ \ \ \text{and}\ \ \ \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{1}{I_2}B_2;C)\geq 1.\end{align*} $$
$$ \begin{align*}\operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\lambda_1B_1;C)\geq \min\left\{1, 1+\frac{m_1}{I_1}-\lambda_1 m_1\right\}\ \ \ \text{and}\ \ \ \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{1}{I_2}B_2;C)\geq 1.\end{align*} $$
By Lemma 2.19, we have
 $$ \begin{align*} \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,c_1B_1+c_2B_2;C) &\geq \mu^{\prime}_1 \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o, \lambda_1 B_1;C)+\mu^{\prime}_2 \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{1}{I_2}B_2;C)\\ &\geq \min\left\{1, 1+\mu^{\prime}_1m_1(\frac{1}{I_1}-\lambda_1)\right\}= \min\left\{1, 1+\frac{m_1}{I_1}(1-I)\right\}\\ &\geq\min\left\{1, 1+\frac{m}{I}(1-I)\right\}=s. \end{align*} $$
$$ \begin{align*} \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,c_1B_1+c_2B_2;C) &\geq \mu^{\prime}_1 \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o, \lambda_1 B_1;C)+\mu^{\prime}_2 \operatorname{lct}(\widehat{\mathbb{C}^2}\ni o,\frac{1}{I_2}B_2;C)\\ &\geq \min\left\{1, 1+\mu^{\prime}_1m_1(\frac{1}{I_1}-\lambda_1)\right\}= \min\left\{1, 1+\frac{m_1}{I_1}(1-I)\right\}\\ &\geq\min\left\{1, 1+\frac{m}{I}(1-I)\right\}=s. \end{align*} $$
Here, for the equality, we use the fact that
In summary, we have showed that
![]() $(c_1, c_2)\in P(\widehat {\mathbb {C}^2}\ni o,s{C};{B_1},{B_2})$
, and the proof is completed.
$(c_1, c_2)\in P(\widehat {\mathbb {C}^2}\ni o,s{C};{B_1},{B_2})$
, and the proof is completed.
Lemma 3.11. Let
![]() $b_j\geq 0$
and
$b_j\geq 0$
and
![]() $\mathbf {n}_j\in \mathbb {R}^n_{>0}$
for
$\mathbf {n}_j\in \mathbb {R}^n_{>0}$
for
![]() $j=1,2$
. Assume that
$j=1,2$
. Assume that
![]() $n\geq 2$
; then
$n\geq 2$
; then
is a convex polytope, and all the vertices of
![]() $\mathcal {P}$
belong to
$\mathcal {P}$
belong to
![]() $\bigcup _{1\leq i\neq j\leq n} E_{i,j}$
, where
$\bigcup _{1\leq i\neq j\leq n} E_{i,j}$
, where
Proof. It is easy to check that
![]() $\mathcal {P}$
, if non-empty, is a convex polytope of dimension at least
$\mathcal {P}$
, if non-empty, is a convex polytope of dimension at least
![]() $n-2$
. Note that each vertex of
$n-2$
. Note that each vertex of
![]() $\mathcal {P}$
belongs to at least
$\mathcal {P}$
belongs to at least
![]() $n-2$
faces of
$n-2$
faces of
![]() $\mathcal {P}$
. Since
$\mathcal {P}$
. Since
![]() $\mathcal {P}$
has at most n faces
$\mathcal {P}$
has at most n faces
![]() $\{(t_1,\cdots ,t_n)\in \mathbb {R}^n\mid t_i=0\}\cap \mathcal {P}$
for
$\{(t_1,\cdots ,t_n)\in \mathbb {R}^n\mid t_i=0\}\cap \mathcal {P}$
for
![]() $i=1,2,\ldots ,n$
, we conclude that each vertex of
$i=1,2,\ldots ,n$
, we conclude that each vertex of
![]() $\mathcal {P}$
belongs to
$\mathcal {P}$
belongs to
![]() $\bigcup _{1\leq i< j\leq n} E_{i,j}$
.
$\bigcup _{1\leq i< j\leq n} E_{i,j}$
.
Corollary 3.12. Let
![]() $(X\ni P, B)$
be a germ of surface pair such that X is smooth and
$(X\ni P, B)$
be a germ of surface pair such that X is smooth and
![]() $\mathrm {{mld}}(X\ni P, B)\geq 1$
. Let C be a smooth curve at P such that
$\mathrm {{mld}}(X\ni P, B)\geq 1$
. Let C be a smooth curve at P such that
![]() $C\nsubseteq \operatorname {Supp} (B)$
and
$C\nsubseteq \operatorname {Supp} (B)$
and
![]() $(B\cdot C)_P\le 2$
. Then
$(B\cdot C)_P\le 2$
. Then
![]() $\operatorname {lct}(X\ni P,B;C)\geq \frac {1}{2}$
.
$\operatorname {lct}(X\ni P,B;C)\geq \frac {1}{2}$
.
Proof. Note that
![]() $\mathrm {{mld}}(X\ni P, B)\geq 1$
implies that
$\mathrm {{mld}}(X\ni P, B)\geq 1$
implies that
![]() $m:=\operatorname {mult}_{P} B\le 1$
(compare [Reference Han and Luo18, Lemma 3.15]). By Theorem 1.11 and the fact that
$m:=\operatorname {mult}_{P} B\le 1$
(compare [Reference Han and Luo18, Lemma 3.15]). By Theorem 1.11 and the fact that
![]() $I\leq 2$
,
$I\leq 2$
,
4 Proofs of the main theorems
4.1 Proof of Theorem 1.10
In this subsection, we give the proof of Theorem 1.10. We first treat the case when
![]() $\dim X=2$
.
$\dim X=2$
.
Proof of Theorem 1.10 when
 $\dim X=2$
$\dim X=2$
Observe that when
![]() $\dim X=2$
, Z is a curve and z is a closed point. We split the proof into two steps.
$\dim X=2$
, Z is a curve and z is a closed point. We split the proof into two steps.
Step 1. First we treat the case when X is smooth,
![]() $B\geq 0$
.
$B\geq 0$
.
In this case, we have
![]() $\mathrm {{mld}}(X/Z\ni z, B)= 1$
. As the geometric generic fibre of
$\mathrm {{mld}}(X/Z\ni z, B)= 1$
. As the geometric generic fibre of
![]() $\pi $
is a rational curve, we may run a
$\pi $
is a rational curve, we may run a
![]() $K_X$
-MMP over Z and reach a minimal ruled surface
$K_X$
-MMP over Z and reach a minimal ruled surface
![]() $\pi ':X'\to Z$
. Denote by
$\pi ':X'\to Z$
. Denote by
![]() $\phi : X\to X'$
the induced morphism and
$\phi : X\to X'$
the induced morphism and
![]() $B'=\phi _*B$
. Since
$B'=\phi _*B$
. Since
![]() $K_{X}+B\sim _{\mathbb {R},Z} 0$
, by the negativity lemma [Reference Birkar, Cascini and Hacon9, Lemma 3.6.2],
$K_{X}+B\sim _{\mathbb {R},Z} 0$
, by the negativity lemma [Reference Birkar, Cascini and Hacon9, Lemma 3.6.2],
![]() $\phi ^*(K_{X'}+B')=K_X+B$
. Thus,
$\phi ^*(K_{X'}+B')=K_X+B$
. Thus,
![]() $K_{X'}+B'\sim _{\mathbb {R},Z} 0$
,
$K_{X'}+B'\sim _{\mathbb {R},Z} 0$
,
![]() $\mathrm {{mld}}(X'/Z\ni z, B')=\mathrm {{mld}}(X/Z\ni z, B)$
and
$\mathrm {{mld}}(X'/Z\ni z, B')=\mathrm {{mld}}(X/Z\ni z, B)$
and
![]() $\operatorname {lct}(X'/Z\ni z, B';\pi ^{\prime *}z)=\operatorname {lct}(X/Z\ni z, B;\pi ^*z)$
. Now
$\operatorname {lct}(X'/Z\ni z, B';\pi ^{\prime *}z)=\operatorname {lct}(X/Z\ni z, B;\pi ^*z)$
. Now
![]() $F:=\pi ^{\prime *}(z)\cong \mathbb {P}^1$
and
$F:=\pi ^{\prime *}(z)\cong \mathbb {P}^1$
and
![]() $(K_{X'}+B')\cdot F=0$
. By the adjunction formula,
$(K_{X'}+B')\cdot F=0$
. By the adjunction formula,
![]() $K_{X'}\cdot F=-2$
. Hence
$K_{X'}\cdot F=-2$
. Hence
![]() $(B'\cdot F)_P\leq 2$
for any closed point
$(B'\cdot F)_P\leq 2$
for any closed point
![]() $P\in F$
. Recall that
$P\in F$
. Recall that
![]() $\mathrm {{mld}}(X'/Z\ni z, B')= 1$
implies that
$\mathrm {{mld}}(X'/Z\ni z, B')= 1$
implies that
![]() $F\nsubseteq \operatorname {Supp} (B')$
. By Corollary 3.12,
$F\nsubseteq \operatorname {Supp} (B')$
. By Corollary 3.12,
![]() $\operatorname {lct}(X'\ni P, B';F)\geq \frac {1}{2}$
for any closed point
$\operatorname {lct}(X'\ni P, B';F)\geq \frac {1}{2}$
for any closed point
![]() $P\in F$
, which implies that
$P\in F$
, which implies that
![]() $\operatorname {lct}(X'/Z\ni z, B'; \pi ^{\prime *}z)\geq \frac {1}{2}$
. Hence
$\operatorname {lct}(X'/Z\ni z, B'; \pi ^{\prime *}z)\geq \frac {1}{2}$
. Hence
![]() $\operatorname {lct}(X/Z\ni z, B; \pi ^{*}z)\geq \frac {1}{2}$
.
$\operatorname {lct}(X/Z\ni z, B; \pi ^{*}z)\geq \frac {1}{2}$
.
Step 2. We treat the general case.
Write
![]() $\mathrm {{mld}}(X/Z\ni z, B)= 1+\epsilon $
for some
$\mathrm {{mld}}(X/Z\ni z, B)= 1+\epsilon $
for some
![]() $\epsilon \geq 0$
. Let
$\epsilon \geq 0$
. Let
![]() $f:W\to X$
be a log resolution of
$f:W\to X$
be a log resolution of
![]() $(X,\operatorname {Supp}(B)+\pi ^*z)$
. We may write
$(X,\operatorname {Supp}(B)+\pi ^*z)$
. We may write
![]() $K_W+B_W=f^{*}(K_X+B).$
Since
$K_W+B_W=f^{*}(K_X+B).$
Since
![]() $\mathrm {{mld}}(X/Z\ni z, B)= 1+\epsilon $
, for any curve
$\mathrm {{mld}}(X/Z\ni z, B)= 1+\epsilon $
, for any curve
![]() $C\subset \operatorname {Supp} (f^*\pi ^*z)$
,
$C\subset \operatorname {Supp} (f^*\pi ^*z)$
,
![]() $\operatorname {mult}_C B_W\leq -\epsilon $
. We can take
$\operatorname {mult}_C B_W\leq -\epsilon $
. We can take
![]() $s\geq 0$
such that for any curve
$s\geq 0$
such that for any curve
![]() $C\subset \operatorname {Supp}( f^*\pi ^*z)$
,
$C\subset \operatorname {Supp}( f^*\pi ^*z)$
,
![]() $\operatorname {mult}_C (B_W+sf^*\pi ^*z)\leq 0$
, and there exists a curve
$\operatorname {mult}_C (B_W+sf^*\pi ^*z)\leq 0$
, and there exists a curve
![]() $C_0\subset \operatorname {Supp} ( f^*\pi ^*z)$
with
$C_0\subset \operatorname {Supp} ( f^*\pi ^*z)$
with
![]() $\operatorname {mult}_{C_0} (B_W+sf^*\pi ^*z)= 0$
. By Lemma 2.8, possibly shrinking Z near z, we may assume that
$\operatorname {mult}_{C_0} (B_W+sf^*\pi ^*z)= 0$
. By Lemma 2.8, possibly shrinking Z near z, we may assume that
![]() $(X, B)$
is lc, so the coefficients of
$(X, B)$
is lc, so the coefficients of
![]() $B_W$
are at most
$B_W$
are at most
![]() $1$
. Since
$1$
. Since
![]() $B_W+sf^*\pi ^*z$
is a simple normal crossing divisor, by [Reference Chen and Han11, Lemma 3.3],
$B_W+sf^*\pi ^*z$
is a simple normal crossing divisor, by [Reference Chen and Han11, Lemma 3.3],
![]() $\mathrm {{mld}}(W/Z\ni z, B_W+sf^*\pi ^*z)= 1$
. Note that
$\mathrm {{mld}}(W/Z\ni z, B_W+sf^*\pi ^*z)= 1$
. Note that
![]() $B_W+sf^*\pi ^*z$
is not necessarily effective, so we cannot apply Step 1 directly.
$B_W+sf^*\pi ^*z$
is not necessarily effective, so we cannot apply Step 1 directly.
We may write
![]() $B_W+sf^*\pi ^*z=D-G$
, where D and G are effective
$B_W+sf^*\pi ^*z=D-G$
, where D and G are effective
![]() $\mathbb {R}$
-divisors with no common components. Then
$\mathbb {R}$
-divisors with no common components. Then
By Remark 2.13, B is effective on the generic fibre of
![]() $\pi $
, so
$\pi $
, so
![]() $\operatorname {Supp} (G)$
does not dominate Z. Possibly shrinking Z near z, we may assume that
$\operatorname {Supp} (G)$
does not dominate Z. Possibly shrinking Z near z, we may assume that
![]() $\operatorname {Supp} (G)\subset \operatorname {Supp} (f^{*}\pi ^*z)$
. By the construction,
$\operatorname {Supp} (G)\subset \operatorname {Supp} (f^{*}\pi ^*z)$
. By the construction,
![]() $C_0\subset \operatorname {Supp} (f^{*}\pi ^*z)$
but
$C_0\subset \operatorname {Supp} (f^{*}\pi ^*z)$
but
![]() $C_0\not \subset \operatorname {Supp} (G)$
. Note that
$C_0\not \subset \operatorname {Supp} (G)$
. Note that
![]() $(W, D)$
is lc as the coefficients of D are at most
$(W, D)$
is lc as the coefficients of D are at most
![]() $1$
.
$1$
.
If E is a curve on W that is contracted over Z with
![]() $(K_W+D)\cdot E<0$
, then
$(K_W+D)\cdot E<0$
, then
![]() $G\cdot E<0$
, and hence
$G\cdot E<0$
, and hence
![]() $E\subset \operatorname {Supp} (G)$
. Then
$E\subset \operatorname {Supp} (G)$
. Then
![]() $E\not \subset \operatorname {Supp} (D)$
and
$E\not \subset \operatorname {Supp} (D)$
and
![]() $K_W\cdot E<0$
. This implies that any
$K_W\cdot E<0$
. This implies that any
![]() $(K_W+D)$
-MMP over Z is also a
$(K_W+D)$
-MMP over Z is also a
![]() $K_W$
-MMP over Z, and it only contracts curves in
$K_W$
-MMP over Z, and it only contracts curves in
![]() $\operatorname {Supp} (G)$
.
$\operatorname {Supp} (G)$
.
We may run a
![]() $(K_W+D)$
-MMP over Z and reach a minimal model Y with induced maps
$(K_W+D)$
-MMP over Z and reach a minimal model Y with induced maps
![]() $g:W\to Y$
and
$g:W\to Y$
and
![]() $h:Y \to Z$
such that
$h:Y \to Z$
such that
![]() $K_Y+D_Y\sim _{\mathbb {R},Z}G_Y$
is nef over Z, where
$K_Y+D_Y\sim _{\mathbb {R},Z}G_Y$
is nef over Z, where
![]() $D_Y$
and
$D_Y$
and
![]() $G_Y$
are the strict transforms of D and G on Y, respectively.
$G_Y$
are the strict transforms of D and G on Y, respectively.
As this MMP is also a
![]() $K_W$
-MMP, Y is a smooth surface. Recall that
$K_W$
-MMP, Y is a smooth surface. Recall that
![]() $C_0\not \subseteq \operatorname {Supp} (G)$
, so
$C_0\not \subseteq \operatorname {Supp} (G)$
, so
![]() $C_0$
is not contracted by this MMP and
$C_0$
is not contracted by this MMP and
![]() $\operatorname {Supp} (G_Y)\subsetneq \operatorname {Supp} (h^{*}z)$
. Hence
$\operatorname {Supp} (G_Y)\subsetneq \operatorname {Supp} (h^{*}z)$
. Hence
![]() $G_Y=0$
as
$G_Y=0$
as
![]() $G_Y$
is nef over Z. Since
$G_Y$
is nef over Z. Since
![]() $K_Y+D_Y=g_{*}(K_W+D-G)\sim _{\mathbb {R},Z}0$
, by the negativity lemma [Reference Birkar, Cascini and Hacon9, Lemma 3.6.2],
$K_Y+D_Y=g_{*}(K_W+D-G)\sim _{\mathbb {R},Z}0$
, by the negativity lemma [Reference Birkar, Cascini and Hacon9, Lemma 3.6.2],
Thus,
![]() $\mathrm {{mld}}(Y/Z\ni z, D_Y)=\mathrm {{mld}}(W/Z\ni z, B_W+sf^*\pi ^*z)=1$
, and
$\mathrm {{mld}}(Y/Z\ni z, D_Y)=\mathrm {{mld}}(W/Z\ni z, B_W+sf^*\pi ^*z)=1$
, and
Since X and Y are isomorphic over the generic point of Z, the geometric generic fibre of h is again a rational curve. So
![]() $(Y,D_Y)$
satisfies the setting in Step 1. By Step 1, we get
$(Y,D_Y)$
satisfies the setting in Step 1. By Step 1, we get
![]() $\operatorname {lct}(Y/Z\ni z, D_Y; h^{*}z)\geq \frac {1}{2}$
.
$\operatorname {lct}(Y/Z\ni z, D_Y; h^{*}z)\geq \frac {1}{2}$
.
To conclude the proof, we need to give a lower bound for s. As Y is smooth, Y dominates a
![]() $\mathbb {P}^1$
-bundle over Z. So there exists a curve
$\mathbb {P}^1$
-bundle over Z. So there exists a curve
![]() $C_1$
on Y such that
$C_1$
on Y such that
![]() $C_1\subset \operatorname {Supp} (h^{*}z)$
and
$C_1\subset \operatorname {Supp} (h^{*}z)$
and
![]() $\operatorname {mult}_{C_1} h^{*}z=1$
. Denote
$\operatorname {mult}_{C_1} h^{*}z=1$
. Denote
![]() $C_1'$
to be the strict transform of
$C_1'$
to be the strict transform of
![]() $C_1$
on W; then
$C_1$
on W; then
![]() $C^{\prime }_1\subset \operatorname {Supp} (f^*\pi ^*z)$
and
$C^{\prime }_1\subset \operatorname {Supp} (f^*\pi ^*z)$
and
![]() $\operatorname {mult}_{C^{\prime }_1} f^*\pi ^*z=1$
. Note that
$\operatorname {mult}_{C^{\prime }_1} f^*\pi ^*z=1$
. Note that
![]() $\operatorname {mult}_{C^{\prime }_1} (B_W+sf^*\pi ^*z)=\operatorname {mult}_{C_1} (D_Y)\geq 0$
. On the other hand,
$\operatorname {mult}_{C^{\prime }_1} (B_W+sf^*\pi ^*z)=\operatorname {mult}_{C_1} (D_Y)\geq 0$
. On the other hand,
![]() $\operatorname {mult}_{C^{\prime }_1} (B_W+sf^*\pi ^*z)\leq 0$
by the definition of s. So
$\operatorname {mult}_{C^{\prime }_1} (B_W+sf^*\pi ^*z)\leq 0$
by the definition of s. So
![]() $\operatorname {mult}_{C^{\prime }_1} (B_W+sf^*\pi ^*z)= 0$
. As
$\operatorname {mult}_{C^{\prime }_1} (B_W+sf^*\pi ^*z)= 0$
. As
![]() $\operatorname {mult}_{C^{\prime }_1} B_W\leq -\epsilon $
, we have
$\operatorname {mult}_{C^{\prime }_1} B_W\leq -\epsilon $
, we have
![]() $s\geq \epsilon $
. Hence
$s\geq \epsilon $
. Hence
This concludes the proof.
Next we give the proof of Theorem 1.10 by induction on dimensions.
Proof of Theorem 1.10
We prove the theorem by induction on the dimension of X. We have proved the case when
![]() $\dim X=2$
. Suppose that Theorem 1.10 holds when
$\dim X=2$
. Suppose that Theorem 1.10 holds when
![]() $\dim X=n$
for some integer
$\dim X=n$
for some integer
![]() $n\ge 2$
; we will show that the theorem holds when
$n\ge 2$
; we will show that the theorem holds when
![]() $\dim X=n+1$
.
$\dim X=n+1$
.
As the statement is local around
![]() $z\in Z$
, we are free to shrink Z. Possibly shrinking Z near z, we may assume that
$z\in Z$
, we are free to shrink Z. Possibly shrinking Z near z, we may assume that
![]() $\overline {z}$
is a Cartier divisor on Z. Set
$\overline {z}$
is a Cartier divisor on Z. Set
![]() $t:=\operatorname {lct}(X/Z\ni z, B; \pi ^*{\overline {z}})$
. Possibly shrinking Z near z, we may assume that
$t:=\operatorname {lct}(X/Z\ni z, B; \pi ^*{\overline {z}})$
. Possibly shrinking Z near z, we may assume that
![]() $(X, B+ t\pi ^*\overline {z})$
is lc.
$(X, B+ t\pi ^*\overline {z})$
is lc.
Pick a general hyperplane section
![]() $H\subset Z$
intersecting
$H\subset Z$
intersecting
![]() $\overline {z}$
. Possibly shrinking Z near z, we may assume that
$\overline {z}$
. Possibly shrinking Z near z, we may assume that
![]() $H\cap \overline {z}$
is irreducible. Let
$H\cap \overline {z}$
is irreducible. Let
![]() $z_H$
be the generic point of
$z_H$
be the generic point of
![]() $H\cap \overline {z}$
and
$H\cap \overline {z}$
and
![]() $G:=\pi ^* H$
; then by Bertini’s theorem, the restriction
$G:=\pi ^* H$
; then by Bertini’s theorem, the restriction
![]() $\pi _G=\pi |_G: G\to H$
is a contraction between normal varieties such that
$\pi _G=\pi |_G: G\to H$
is a contraction between normal varieties such that
![]() $K_G+B|_G\sim _{\mathbb {R},H} 0$
. Since H is general, by [Reference Kollár and Mori27, Lemma 5.17(2)], we may assume that
$K_G+B|_G\sim _{\mathbb {R},H} 0$
. Since H is general, by [Reference Kollár and Mori27, Lemma 5.17(2)], we may assume that
-
○ the geometric generic fibre of
 $\pi _G$
is a rational curve, and
$\pi _G$
is a rational curve, and -
○
 $(X, B+G+t\pi ^*\overline {z})$
is lc.
$(X, B+G+t\pi ^*\overline {z})$
is lc.
Let
![]() $\phi : Y\to X$
be a log resolution of
$\phi : Y\to X$
be a log resolution of
![]() $(X,\operatorname {Supp} B+\pi ^*\overline {z})$
, we may write
$(X,\operatorname {Supp} B+\pi ^*\overline {z})$
, we may write
where
![]() $E_i$
are
$E_i$
are
![]() $\phi $
-exceptional prime divisors. Possibly shrinking Z near z, we may further assume that
$\phi $
-exceptional prime divisors. Possibly shrinking Z near z, we may further assume that
![]() $z\in \pi \circ \phi (E_i)$
for each i. By taking H general enough, we may assume that
$z\in \pi \circ \phi (E_i)$
for each i. By taking H general enough, we may assume that
-
○
 $\phi ^*G=\phi _{*}^{-1}G$
, and
$\phi ^*G=\phi _{*}^{-1}G$
, and -
○
 $\phi $
is a log resolution of
$\phi $
is a log resolution of
 $(X,\operatorname {Supp} B+\pi ^*\overline {z}+G)$
.
$(X,\operatorname {Supp} B+\pi ^*\overline {z}+G)$
.
Since
![]() $\phi _{*}^{-1}G=\phi ^*G=\phi ^{*}\pi ^*H$
, we have
$\phi _{*}^{-1}G=\phi ^*G=\phi ^{*}\pi ^*H$
, we have
![]() $\pi \circ \phi (E_i\cap \phi _{*}^{-1}G)=(\pi \circ \phi (E_i))\cap H$
for each i.
$\pi \circ \phi (E_i\cap \phi _{*}^{-1}G)=(\pi \circ \phi (E_i))\cap H$
for each i.
Since
by the adjunction formula [Reference Kollár and Mori27, Proposition 5.73],
which implies that the induced morphism
![]() $\phi _{*}^{-1} (G)\to G$
is a log resolution of
$\phi _{*}^{-1} (G)\to G$
is a log resolution of
![]() $(G, B|_G+ \pi _G^*\overline {z_H})$
. Since z and
$(G, B|_G+ \pi _G^*\overline {z_H})$
. Since z and
![]() $z_H$
are codimension
$z_H$
are codimension
![]() $1$
points of Z and H, respectively, we have
$1$
points of Z and H, respectively, we have
 $$ \begin{align*} \mathrm{{mld}}(G/H\ni z_H, B|_G){}&=\min\{a_i\mid \pi\circ\phi(E_i\cap \phi_{*}^{-1}G)=\overline{z_H} \}\\{}&= \min\{a_i\mid \pi\circ\phi(E_i)=\overline{z} \}=\mathrm{{mld}}(X/Z\ni z,B). \end{align*} $$
$$ \begin{align*} \mathrm{{mld}}(G/H\ni z_H, B|_G){}&=\min\{a_i\mid \pi\circ\phi(E_i\cap \phi_{*}^{-1}G)=\overline{z_H} \}\\{}&= \min\{a_i\mid \pi\circ\phi(E_i)=\overline{z} \}=\mathrm{{mld}}(X/Z\ni z,B). \end{align*} $$
Here, the formula computing minimal log discrepancies is by [Reference Chen and Han11, Lemma 3.5], which says that one can compute the minimal log discrepancy of an lc sub-pair on a log resolution. Similarly, we have
As
![]() $(X, B+G+t\pi ^*\overline {z})$
is lc, so is
$(X, B+G+t\pi ^*\overline {z})$
is lc, so is
![]() $(G, B|_G+t \pi _G^*\overline {z_H})$
. On the other hand, by the definition of t, there exists an index i such that
$(G, B|_G+t \pi _G^*\overline {z_H})$
. On the other hand, by the definition of t, there exists an index i such that
![]() $a_i'=0$
and
$a_i'=0$
and
![]() $E_i \subseteq \operatorname {Supp}(\phi ^*\pi ^*\overline {z})$
. In particular,
$E_i \subseteq \operatorname {Supp}(\phi ^*\pi ^*\overline {z})$
. In particular,
![]() $ \pi \circ \phi (E_i)=\overline {z}$
. Then by the construction,
$ \pi \circ \phi (E_i)=\overline {z}$
. Then by the construction,
![]() $E_{i}\cap \phi ^{-1}_{*}G\neq \emptyset $
, which gives a non-klt place of
$E_{i}\cap \phi ^{-1}_{*}G\neq \emptyset $
, which gives a non-klt place of
![]() $(G, B|_G+t \pi _G^*\overline {z_H})$
whose image on H is
$(G, B|_G+t \pi _G^*\overline {z_H})$
whose image on H is
![]() $\overline {z_H}$
. Thus
$\overline {z_H}$
. Thus
![]() $t=\operatorname {lct}(G/H\ni z_{H},B|_G; \pi _G^{*}\overline {z_H})$
. As
$t=\operatorname {lct}(G/H\ni z_{H},B|_G; \pi _G^{*}\overline {z_H})$
. As
![]() $(G/H\ni z_{H},B|_G)$
satisfies the conditions of Theorem 1.10,
$(G/H\ni z_{H},B|_G)$
satisfies the conditions of Theorem 1.10,
 $$ \begin{align*} &\operatorname{lct}(X/Z\ni z, B; \pi^*{\overline{z}})={}\operatorname{lct}(G/H\ni z_{H},B|_G; \pi_G^{*}\overline{z_H})\\ \geq{}& \mathrm{{mld}}(G/H\ni z_H, B|_G)-\frac{1}{2} ={}\mathrm{{mld}}(X/Z\ni z,B)-\frac{1}{2} \end{align*} $$
$$ \begin{align*} &\operatorname{lct}(X/Z\ni z, B; \pi^*{\overline{z}})={}\operatorname{lct}(G/H\ni z_{H},B|_G; \pi_G^{*}\overline{z_H})\\ \geq{}& \mathrm{{mld}}(G/H\ni z_H, B|_G)-\frac{1}{2} ={}\mathrm{{mld}}(X/Z\ni z,B)-\frac{1}{2} \end{align*} $$
by the induction hypothesis.
For the last statement, note that
![]() $\operatorname {lct}(X/Z\ni z, B; \pi ^*\overline {z})\geq \frac {1}{2}$
implies that the coefficients of
$\operatorname {lct}(X/Z\ni z, B; \pi ^*\overline {z})\geq \frac {1}{2}$
implies that the coefficients of
![]() $B+\frac {1}{2}\pi ^*\overline {z}$
are at most
$B+\frac {1}{2}\pi ^*\overline {z}$
are at most
![]() $1$
over a neighbourhood of
$1$
over a neighbourhood of
![]() $z\in Z$
. So if B is effective, then the multiplicity of each irreducible component of
$z\in Z$
. So if B is effective, then the multiplicity of each irreducible component of
![]() $\pi ^*{z}$
is bounded from above by
$\pi ^*{z}$
is bounded from above by
![]() $2$
.
$2$
.
The following example shows that the bounds in Theorems 1.7 and 1.10 are optimal.
Example 4.1. Consider
![]() $C\simeq \mathbb {P}^1$
. Consider
$C\simeq \mathbb {P}^1$
. Consider
![]() $Y=C\times \mathbb {P}^1$
and the natural projection
$Y=C\times \mathbb {P}^1$
and the natural projection
![]() $\pi : Y\to C$
. Let D be a smooth curve on Y of type
$\pi : Y\to C$
. Let D be a smooth curve on Y of type
![]() $(1,2)$
. Note that there exists a closed point
$(1,2)$
. Note that there exists a closed point
![]() $p\in C$
such that D intersects
$p\in C$
such that D intersects
![]() $\pi ^{-1} (p)$
at a single closed point with intersection multiplicity
$\pi ^{-1} (p)$
at a single closed point with intersection multiplicity
![]() $2$
. Set
$2$
. Set
![]() $F=\pi ^{-1} (p)$
. Then for any real number
$F=\pi ^{-1} (p)$
. Then for any real number
![]() $s\geq 0$
, we consider the sub-pair
$s\geq 0$
, we consider the sub-pair
![]() $(Y, D-sF)$
. We can get a log resolution of
$(Y, D-sF)$
. We can get a log resolution of
![]() $(Y, D-sF)$
by blowing up twice as follows. Let
$(Y, D-sF)$
by blowing up twice as follows. Let
![]() $Y_1\to Y$
be the blow-up at
$Y_1\to Y$
be the blow-up at
![]() $F\cap D$
. Denote by
$F\cap D$
. Denote by
![]() $F_1, D_1$
the strict transforms of
$F_1, D_1$
the strict transforms of
![]() $F, D$
on
$F, D$
on
![]() $Y_1$
, respectively, and
$Y_1$
, respectively, and
![]() $E_1$
the exceptional divisor. Then
$E_1$
the exceptional divisor. Then
![]() $F_1, D_1, E_1$
intersect at one point. Let
$F_1, D_1, E_1$
intersect at one point. Let
![]() $Y_2\to Y_1$
be the blow-up at
$Y_2\to Y_1$
be the blow-up at
![]() $F_1\cap D_1\cap E_1$
, denote by
$F_1\cap D_1\cap E_1$
, denote by
![]() $F_2,D_2, E_2$
the strict transforms of
$F_2,D_2, E_2$
the strict transforms of
![]() $F_1,D_1, E_1$
on
$F_1,D_1, E_1$
on
![]() $Y_2$
, respectively, and
$Y_2$
, respectively, and
![]() $G_2$
the exceptional divisor on
$G_2$
the exceptional divisor on
![]() $Y_2$
. Then
$Y_2$
. Then
![]() $Y_2$
is a log resolution of
$Y_2$
is a log resolution of
![]() $(Y, D-sF)$
. Let
$(Y, D-sF)$
. Let
![]() $\pi : Y_2\to C$
and
$\pi : Y_2\to C$
and
![]() $f: Y_2\to Y$
be the induced maps. Then we have
$f: Y_2\to Y$
be the induced maps. Then we have
and
Set
![]() $B_2=D_2-sF_2-sE_2-2sG_2$
. Then
$B_2=D_2-sF_2-sE_2-2sG_2$
. Then
![]() $(Y_2/C\ni p, B_2)$
satisfies the conditions of Theorem 1.10. It is easy to compute that
$(Y_2/C\ni p, B_2)$
satisfies the conditions of Theorem 1.10. It is easy to compute that
![]() $\mathrm {{mld}}(Y_2/C\ni p, B_2)=1+s$
and
$\mathrm {{mld}}(Y_2/C\ni p, B_2)=1+s$
and
![]() $\operatorname {lct}(Y_2/C\ni p, B_2;\pi ^{*}p)=\frac {1}{2}+s$
. We also have
$\operatorname {lct}(Y_2/C\ni p, B_2;\pi ^{*}p)=\frac {1}{2}+s$
. We also have
![]() $\operatorname {mult}_{G_2}\pi ^*p=2.$
This shows that Theorem 1.10 is optimal.
$\operatorname {mult}_{G_2}\pi ^*p=2.$
This shows that Theorem 1.10 is optimal.
In this case, if we consider the canonical bundle formula for
![]() $(Y_2, B_2)$
over C, then the discriminant part is
$(Y_2, B_2)$
over C, then the discriminant part is
![]() $B_C=(\frac {1}{2}-s)p$
, and hence for any
$B_C=(\frac {1}{2}-s)p$
, and hence for any
![]() $M_C\geq 0$
on C,
$M_C\geq 0$
on C,
This shows that Theorem 1.7 is optimal.
The next example shows that Theorem 1.10 does not hold when B is not effective on the generic fibre.
Example 4.2. Consider
![]() $C\simeq \mathbb {P}^1$
. Consider the pair
$C\simeq \mathbb {P}^1$
. Consider the pair
![]() $(C\times \mathbb {P}^1, B:=B_1-B_2)$
and the natural projection
$(C\times \mathbb {P}^1, B:=B_1-B_2)$
and the natural projection
![]() $\pi : C\times \mathbb {P}^1\to C$
, where
$\pi : C\times \mathbb {P}^1\to C$
, where
![]() $B_1$
is a curve on
$B_1$
is a curve on
![]() $C\times \mathbb {P}^1$
of type
$C\times \mathbb {P}^1$
of type
![]() $(2,3)$
with a cusp
$(2,3)$
with a cusp
![]() $q\in B_1$
, and
$q\in B_1$
, and
![]() $B_2$
is the section of
$B_2$
is the section of
![]() $\pi $
containing q. Set
$\pi $
containing q. Set
![]() $p=\pi (q)$
and
$p=\pi (q)$
and
![]() $D=\pi ^{-1}(p)=\pi ^{*}p$
. We can take
$D=\pi ^{-1}(p)=\pi ^{*}p$
. We can take
![]() $B_1,B_2$
such that
$B_1,B_2$
such that
![]() $B_1$
,
$B_1$
,
![]() $B_2$
and D are locally defined by
$B_2$
and D are locally defined by
![]() $(x^2+y^3=0)$
,
$(x^2+y^3=0)$
,
![]() $(y=0)$
and
$(y=0)$
and
![]() $(x=0)$
, respectively, for some local coordinates
$(x=0)$
, respectively, for some local coordinates
![]() $x,y$
near
$x,y$
near
![]() $q\in C\times \mathbb {P}^1$
. Then
$q\in C\times \mathbb {P}^1$
. Then
![]() $\operatorname {lct}(C\times \mathbb {P}^1/C\ni p,B;D)=\frac {1}{3}<\frac {1}{2}$
. More generally, if B is not effective on the generic fibre, then there is no uniform lower bound for
$\operatorname {lct}(C\times \mathbb {P}^1/C\ni p,B;D)=\frac {1}{3}<\frac {1}{2}$
. More generally, if B is not effective on the generic fibre, then there is no uniform lower bound for
![]() $\operatorname {lct}(C\times \mathbb {P}^1/C\ni p,B;D)$
as in Theorem 1.10.
$\operatorname {lct}(C\times \mathbb {P}^1/C\ni p,B;D)$
as in Theorem 1.10.
4.2 Proofs of Theorems 1.4 and 1.7
We first reduce Theorem 1.7 to the case when B is a
![]() $\mathbb {Q}$
-divisor.
$\mathbb {Q}$
-divisor.
Lemma 4.3. Assume that Theorem 1.7 holds when B is a
![]() $\mathbb {Q}$
-divisor; then Theorem 1.7 holds.
$\mathbb {Q}$
-divisor; then Theorem 1.7 holds.
Proof. Fix the choice of the Weil divisor
![]() $K_X$
. We may write
$K_X$
. We may write
 $$ \begin{align*}K_X+B=\sum_{i=1}^m d_iD_i,\end{align*} $$
$$ \begin{align*}K_X+B=\sum_{i=1}^m d_iD_i,\end{align*} $$
where
![]() $D_i$
are Cartier divisors on X and
$D_i$
are Cartier divisors on X and
![]() $ d_1,\ldots ,d_m$
are
$ d_1,\ldots ,d_m$
are
![]() $\mathbb {Q}$
-linearly independent real numbers. By [Reference Han, Liu and Shokurov17, Lemma 5.3],
$\mathbb {Q}$
-linearly independent real numbers. By [Reference Han, Liu and Shokurov17, Lemma 5.3],
![]() $D_i$
is
$D_i$
is
![]() $\mathbb {R}$
-Cartier and
$\mathbb {R}$
-Cartier and
![]() $D_i\sim _{\mathbb {R},Z}0$
for any
$D_i\sim _{\mathbb {R},Z}0$
for any
![]() $1\leq i\leq m$
.
$1\leq i\leq m$
.
For a point
![]() $\mathbf {t}=(t_1, \dots , t_m)\in \mathbb {R}^m$
, we set
$\mathbf {t}=(t_1, \dots , t_m)\in \mathbb {R}^m$
, we set
 $$ \begin{align*}B(\mathbf{t})=\sum_{i=1}^m t_iD_i-K_X.\end{align*} $$
$$ \begin{align*}B(\mathbf{t})=\sum_{i=1}^m t_iD_i-K_X.\end{align*} $$
Then for any
![]() $\mathbf {t}\in \mathbb {R}^m$
,
$\mathbf {t}\in \mathbb {R}^m$
,
![]() $K_X+B(\mathbf {t})\sim _{\mathbb {R},Z}0$
. Set
$K_X+B(\mathbf {t})\sim _{\mathbb {R},Z}0$
. Set
![]() $\mathbf {d}=(d_1, \dots , d_m)$
.
$\mathbf {d}=(d_1, \dots , d_m)$
.
Let
![]() $f:Y\to X$
be a log resolution of
$f:Y\to X$
be a log resolution of
![]() $(X,B+\sum _{i=1}^m D_i)$
such that
$(X,B+\sum _{i=1}^m D_i)$
such that
![]() $\operatorname {Supp} (f^{-1}\pi ^{-1}(\overline {z}))$
is a simple normal crossing divisor. Write
$\operatorname {Supp} (f^{-1}\pi ^{-1}(\overline {z}))$
is a simple normal crossing divisor. Write
![]() $K_Y+B_Y(\mathbf {t})=f^{*}(K_X+B(\mathbf {t}))$
.
$K_Y+B_Y(\mathbf {t})=f^{*}(K_X+B(\mathbf {t}))$
.
Possibly shrinking Z near z, we may assume that
![]() $(X, B)$
is lc. Note that
$(X, B)$
is lc. Note that
![]() $(X, B(\mathbf {t}))$
is lc if and only if the coefficients of
$(X, B(\mathbf {t}))$
is lc if and only if the coefficients of
![]() $B_Y(\mathbf {t})$
are at most
$B_Y(\mathbf {t})$
are at most
![]() $1$
. Note that
$1$
. Note that
![]() $\mathrm {{mld}}(X/Z\ni z, B(\mathbf {t}))\geq 1$
if and only if for any prime divisor E on Y with
$\mathrm {{mld}}(X/Z\ni z, B(\mathbf {t}))\geq 1$
if and only if for any prime divisor E on Y with
![]() $f(E)=\overline {z}$
,
$f(E)=\overline {z}$
,
![]() $\operatorname {mult}_E B_Y(\mathbf {t})\leq 0$
(compare [Reference Chen and Han11, Lemma 3.3]). So the subset
$\operatorname {mult}_E B_Y(\mathbf {t})\leq 0$
(compare [Reference Chen and Han11, Lemma 3.3]). So the subset
is determined by finitely many linear functions in
![]() $\mathbf {t}$
with coefficients in
$\mathbf {t}$
with coefficients in
![]() $\mathbb {Q}$
. In other words,
$\mathbb {Q}$
. In other words,
![]() $\mathcal {P}_1$
is a non-compact rational polytope containing
$\mathcal {P}_1$
is a non-compact rational polytope containing
![]() $\mathbf {d}$
. Note that
$\mathbf {d}$
. Note that
![]() $\mathrm {{mld}}(X/Z\ni z, B(\mathbf {t}))$
can be computed on Y as the minimum of finitely many linear functions in
$\mathrm {{mld}}(X/Z\ni z, B(\mathbf {t}))$
can be computed on Y as the minimum of finitely many linear functions in
![]() $\mathbf {t}$
with coefficients in
$\mathbf {t}$
with coefficients in
![]() $\mathbb {Q}$
. Possibly replacing
$\mathbb {Q}$
. Possibly replacing
![]() $\mathcal {P}_1$
with a smaller rational polytope containing
$\mathcal {P}_1$
with a smaller rational polytope containing
![]() $\mathbf {d}$
, we may assume that
$\mathbf {d}$
, we may assume that
![]() $\mathrm {{mld}}(X/Z\ni z, B(\mathbf {t}))$
is linear on
$\mathrm {{mld}}(X/Z\ni z, B(\mathbf {t}))$
is linear on
![]() $\mathcal {P}_1$
and
$\mathcal {P}_1$
and
![]() $\mathcal {P}_1$
is bounded.
$\mathcal {P}_1$
is bounded.
By Remark 2.13, B is effective on the generic fibre of
![]() $\pi $
. It is easy to see that
$\pi $
. It is easy to see that
is a rational polytope.
By the construction,
![]() $\mathcal {P}:=\mathcal {P}_1\cap \mathcal {P}_2$
is a bounded rational polytope containing
$\mathcal {P}:=\mathcal {P}_1\cap \mathcal {P}_2$
is a bounded rational polytope containing
![]() $\mathbf {d}$
. If
$\mathbf {d}$
. If
![]() $\mathbf {t}\in \mathcal {P}$
, then
$\mathbf {t}\in \mathcal {P}$
, then
![]() $\pi : (X, B(\mathbf {t}))\to Z$
is an lc-trivial fibration satisfying the assumptions of Theorem 1.7. So we can consider the canonical bundle formula
$\pi : (X, B(\mathbf {t}))\to Z$
is an lc-trivial fibration satisfying the assumptions of Theorem 1.7. So we can consider the canonical bundle formula
By the convexity of log canonical thresholds, the irreducible components of
![]() $\operatorname {Supp} (B(\mathbf {t})_Z)$
belong to a finite set
$\operatorname {Supp} (B(\mathbf {t})_Z)$
belong to a finite set
![]() $\{P_1, P_2, \dots , P_k\}$
for any
$\{P_1, P_2, \dots , P_k\}$
for any
![]() $\mathbf {t}\in \mathcal {P}$
, here
$\mathbf {t}\in \mathcal {P}$
, here
![]() $\{P_1, P_2, \dots , P_k\}$
is the set of prime divisors on Z in
$\{P_1, P_2, \dots , P_k\}$
is the set of prime divisors on Z in
![]() $\bigcup _{\mathbf {t}'}\operatorname {Supp} (B(\mathbf {t}')_Z)$
, where the union runs over all vertex points
$\bigcup _{\mathbf {t}'}\operatorname {Supp} (B(\mathbf {t}')_Z)$
, where the union runs over all vertex points
![]() $\mathbf {t}'\in \mathcal {P}$
. Denote the generic point of
$\mathbf {t}'\in \mathcal {P}$
. Denote the generic point of
![]() $P_j$
by
$P_j$
by
![]() $z_j$
for
$z_j$
for
![]() $1\leq j\leq k$
. Note that for any
$1\leq j\leq k$
. Note that for any
![]() $1\leq j\leq k$
,
$1\leq j\leq k$
,
![]() $\operatorname {lct}(X/Z\ni z_j, B(\mathbf {t}); \pi ^*P_j)$
is computed on a log resolution as the minimum of finitely many linear functions in
$\operatorname {lct}(X/Z\ni z_j, B(\mathbf {t}); \pi ^*P_j)$
is computed on a log resolution as the minimum of finitely many linear functions in
![]() $\mathbf {t}$
with coefficients in
$\mathbf {t}$
with coefficients in
![]() $\mathbb {Q}$
. So possibly replacing
$\mathbb {Q}$
. So possibly replacing
![]() $\mathcal {P}$
with a smaller rational polytope containing
$\mathcal {P}$
with a smaller rational polytope containing
![]() $\mathbf {d}$
, we may assume that
$\mathbf {d}$
, we may assume that
![]() $\operatorname {lct}(X/Z\ni z_j, B(\mathbf {t}); \pi ^*P_j)$
is linear in
$\operatorname {lct}(X/Z\ni z_j, B(\mathbf {t}); \pi ^*P_j)$
is linear in
![]() $\mathbf {t}$
for any
$\mathbf {t}$
for any
![]() $1\leq j\leq k$
.
$1\leq j\leq k$
.
Now we can take
![]() $\mathbf {t}_1, \dots , \mathbf {t}_l\in \mathcal {P} \cap \mathbb {Q}^m$
and positive real numbers
$\mathbf {t}_1, \dots , \mathbf {t}_l\in \mathcal {P} \cap \mathbb {Q}^m$
and positive real numbers
![]() $s_1,\dots , s_l$
such that
$s_1,\dots , s_l$
such that
![]() $\sum _{i=1}^ls_i=1$
and
$\sum _{i=1}^ls_i=1$
and
![]() $\sum _{i=1}^ls_i\mathbf {t}_i=\mathbf {d}$
. By the construction,
$\sum _{i=1}^ls_i\mathbf {t}_i=\mathbf {d}$
. By the construction,
 $$ \begin{align*} B_Z={}&\sum_{j=1}^k (1-\operatorname{lct}(X/Z\ni z_j, B; \pi^*P_j))P_j\\ ={}&\sum_{j=1}^k \sum_{i=1}^ls_i (1-\operatorname{lct}(X/Z\ni z_j, B(\mathbf{t}_i); \pi^*P_j))P_j=\sum_{i=1}^ls_i B(\mathbf{t}_i)_Z. \end{align*} $$
$$ \begin{align*} B_Z={}&\sum_{j=1}^k (1-\operatorname{lct}(X/Z\ni z_j, B; \pi^*P_j))P_j\\ ={}&\sum_{j=1}^k \sum_{i=1}^ls_i (1-\operatorname{lct}(X/Z\ni z_j, B(\mathbf{t}_i); \pi^*P_j))P_j=\sum_{i=1}^ls_i B(\mathbf{t}_i)_Z. \end{align*} $$
By assumption, Theorem 1.7 holds for
![]() $(X/Z\ni z, B(\mathbf {t}_i))$
for each i: that is, we can choose
$(X/Z\ni z, B(\mathbf {t}_i))$
for each i: that is, we can choose
![]() $M(\mathbf {t}_i)_Z\geq 0$
such that
$M(\mathbf {t}_i)_Z\geq 0$
such that
Then setting
![]() $M_Z:=\sum _{i=1}^l s_i M(\mathbf {t}_i)_Z\geq 0$
, we have
$M_Z:=\sum _{i=1}^l s_i M(\mathbf {t}_i)_Z\geq 0$
, we have
 $$ \begin{align*} &\mathrm{{mld}}(Z\ni z,B_Z+M_Z)\geq {} \sum_{i=1}^l s_i \mathrm{{mld}}(Z\ni z,B(\mathbf{t}_i)_Z+M(\mathbf{t}_i)_Z)\\ \geq {}& \sum_{i=1}^l s_i\mathrm{{mld}}(X/Z\ni z, B(\mathbf{t}_i))-\frac{1}{2} ={}\mathrm{{mld}}(X/Z\ni z, B)-\frac{1}{2}. \end{align*} $$
$$ \begin{align*} &\mathrm{{mld}}(Z\ni z,B_Z+M_Z)\geq {} \sum_{i=1}^l s_i \mathrm{{mld}}(Z\ni z,B(\mathbf{t}_i)_Z+M(\mathbf{t}_i)_Z)\\ \geq {}& \sum_{i=1}^l s_i\mathrm{{mld}}(X/Z\ni z, B(\mathbf{t}_i))-\frac{1}{2} ={}\mathrm{{mld}}(X/Z\ni z, B)-\frac{1}{2}. \end{align*} $$
Here, for the first inequality, we use the convexity of minimal log discrepancies, and for the last equality, we use the linearity of
![]() $\mathrm {{mld}}(X/Z\ni z, B(\mathbf {t}))$
on
$\mathrm {{mld}}(X/Z\ni z, B(\mathbf {t}))$
on
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Proof of Theorem 1.7
By Lemma 4.3, we may assume that B is a
![]() $\mathbb {Q}$
-divisor. As we described in Section 2.4, there are b-divisors
$\mathbb {Q}$
-divisor. As we described in Section 2.4, there are b-divisors
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {M}$
such that
$\mathbf {M}$
such that
-
○
 $\mathbf {B}_Z=B_Z$
,
$\mathbf {B}_Z=B_Z$
,
 $\mathbf {M}_Z=M_Z$
, and
$\mathbf {M}_Z=M_Z$
, and -
○ for any birational contraction
 $g: Z'\to Z$
, let
$g: Z'\to Z$
, let
 $X'$
be a resolution of the main component of
$X'$
be a resolution of the main component of
 $X\times _{Z} Z'$
with induced morphisms
$X\times _{Z} Z'$
with induced morphisms
 $g': X' \to X$
and
$g': X' \to X$
and
 $\pi ': X'\to Z'$
. Write
$\pi ': X'\to Z'$
. Write
 $K_{X'}+B'=g^{\prime *}(K_X+B)$
; then
$K_{X'}+B'=g^{\prime *}(K_X+B)$
; then
 $\mathbf {B}_{Z'}$
(respectively,
$\mathbf {B}_{Z'}$
(respectively,
 $\mathbf {M}_{Z'}$
) is the discriminant part (respectively, the moduli part) of the canonical bundle formula of
$\mathbf {M}_{Z'}$
) is the discriminant part (respectively, the moduli part) of the canonical bundle formula of
 $K_{X'}+B'$
on
$K_{X'}+B'$
on
 $Z'$
.
$Z'$
.
We may write
![]() $\mathbf {B}=\sum d_P P$
, where P is the birational component of
$\mathbf {B}=\sum d_P P$
, where P is the birational component of
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $d_P$
the corresponding coefficient.
$d_P$
the corresponding coefficient.
Claim 4.4. For any birational component P of
![]() $\mathbf {B}$
whose center on Z is
$\mathbf {B}$
whose center on Z is
![]() $\overline {z}$
,
$\overline {z}$
,
![]() $d_P\leq \frac {3}{2}-\mathrm {{mld}}(X/Z\ni z, B)$
.
$d_P\leq \frac {3}{2}-\mathrm {{mld}}(X/Z\ni z, B)$
.
We will proceed with the proof assuming Claim 4.4. The proof of Claim 4.4 will be given after the proof.
By [Reference Prokhorov and Shokurov35, Theorem 8.1] (see Remark 2.15),
![]() $\mathbf {M}$
is b-semi-ample. Then there exists a resolution
$\mathbf {M}$
is b-semi-ample. Then there exists a resolution
![]() $g:Z'\to Z$
such that
$g:Z'\to Z$
such that
![]() $\mathbf {M}_{Z'}$
is semi-ample, and
$\mathbf {M}_{Z'}$
is semi-ample, and
![]() $\mathbf {B}_{Z'}+\operatorname {Supp}(g^{-1}(\overline {z}))$
is a simple normal crossing divisor. Thus we may take a general
$\mathbf {B}_{Z'}+\operatorname {Supp}(g^{-1}(\overline {z}))$
is a simple normal crossing divisor. Thus we may take a general
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $L_{Z'}\geq 0$
on
$L_{Z'}\geq 0$
on
![]() $Z'$
such that
$Z'$
such that
![]() $\mathbf {M}_{Z'}\sim _{\mathbb {Q}} L_{Z'}$
,
$\mathbf {M}_{Z'}\sim _{\mathbb {Q}} L_{Z'}$
,
![]() $\mathbf {B}_{Z'}+L_{Z'}$
is simple normal crossing, and for each prime divisor P on
$\mathbf {B}_{Z'}+L_{Z'}$
is simple normal crossing, and for each prime divisor P on
![]() $Z'$
whose center on Z is
$Z'$
whose center on Z is
![]() $\overline {z}$
, the coefficient of P in
$\overline {z}$
, the coefficient of P in
![]() $\mathbf {B}_{Z'}+L_{Z'}$
is at most
$\mathbf {B}_{Z'}+L_{Z'}$
is at most
![]() $\frac {3}{2}-\mathrm {{mld}}(X/Z\ni z, B)$
. In this case,
$\frac {3}{2}-\mathrm {{mld}}(X/Z\ni z, B)$
. In this case,
![]() $ \mathrm {{mld}}(Z'/Z\ni z, \mathbf {B}_{Z'}+L_{Z'})\geq \mathrm {{mld}}(X/Z\ni z, B)-\frac {1}{2}. $
Note that
$ \mathrm {{mld}}(Z'/Z\ni z, \mathbf {B}_{Z'}+L_{Z'})\geq \mathrm {{mld}}(X/Z\ni z, B)-\frac {1}{2}. $
Note that
hence by the negativity lemma [Reference Birkar, Cascini and Hacon9, Lemma 3.6.2],
Thus
![]() $ M_Z\sim _{\mathbb {Q}} g_*L_{Z'}\geq 0$
and
$ M_Z\sim _{\mathbb {Q}} g_*L_{Z'}\geq 0$
and
![]() $ \mathrm {{mld}}(Z\ni z, B_{Z}+g_*L_{Z'})\geq \mathrm {{mld}}(X/Z\ni z, B)-\frac {1}{2}.$
$ \mathrm {{mld}}(Z\ni z, B_{Z}+g_*L_{Z'})\geq \mathrm {{mld}}(X/Z\ni z, B)-\frac {1}{2}.$
Proof of Claim 4.4
Fix a birational component
![]() $P_0$
of
$P_0$
of
![]() $\mathbf {B}$
whose center on Z is
$\mathbf {B}$
whose center on Z is
![]() $\overline {z}$
:
$\overline {z}$
:

Take a resolution
![]() $g: Z'\to Z$
such that
$g: Z'\to Z$
such that
![]() $P_0$
is a prime divisor on
$P_0$
is a prime divisor on
![]() $Z'$
. Denote the generic point of
$Z'$
. Denote the generic point of
![]() $P_0$
on
$P_0$
on
![]() $Z'$
by
$Z'$
by
![]() $z'$
and hence
$z'$
and hence
![]() $P_0=\overline {z'}$
. Let
$P_0=\overline {z'}$
. Let
![]() $X'$
be a resolution of the main component of
$X'$
be a resolution of the main component of
![]() $X\times _Z Z'$
with induced maps
$X\times _Z Z'$
with induced maps
![]() $g': {X'}\to X$
and
$g': {X'}\to X$
and
![]() $\pi ': {X'}\to Z'$
. We may write
$\pi ': {X'}\to Z'$
. We may write
![]() $K_{X'}+B'=g^{\prime *}{(K_X+B)}$
. Then
$K_{X'}+B'=g^{\prime *}{(K_X+B)}$
. Then
In particular, this implies that
By the construction, the geometric generic fibre of
![]() $\pi '$
is a rational curve. So
$\pi '$
is a rational curve. So
![]() $({X'}/Z'\ni z', B')$
satisfies the assumptions of Theorem 1.10. By Theorem 1.10,
$({X'}/Z'\ni z', B')$
satisfies the assumptions of Theorem 1.10. By Theorem 1.10,
Hence by the definition of
![]() $\mathbf {B}$
,
$\mathbf {B}$
,
 $$ \begin{align*} d_{P_0}={}&1-\operatorname{lct}({X'}/Z'\ni z',B';\pi^{\prime*}\overline{z'})\\\leq{}& \frac{3}{2}-\mathrm{{mld}}({X'}/Z'\ni z', B')\leq \frac{3}{2}-\mathrm{{mld}}(X/Z\ni z, B).\\[-40pt] \end{align*} $$
$$ \begin{align*} d_{P_0}={}&1-\operatorname{lct}({X'}/Z'\ni z',B';\pi^{\prime*}\overline{z'})\\\leq{}& \frac{3}{2}-\mathrm{{mld}}({X'}/Z'\ni z', B')\leq \frac{3}{2}-\mathrm{{mld}}(X/Z\ni z, B).\\[-40pt] \end{align*} $$
Proof of Corollary 1.8
Note that we cannot get Corollary 1.8 by directly applying Theorem 1.7 to all codimension
![]() $\geq 1$
points on Z, as the choice of
$\geq 1$
points on Z, as the choice of
![]() $M_Z$
depends on
$M_Z$
depends on
![]() $z\in Z$
in Theorem 1.7. But we can follow the same line as in Theorem 1.7 to prove Corollary 1.8.
$z\in Z$
in Theorem 1.7. But we can follow the same line as in Theorem 1.7 to prove Corollary 1.8.
By the same reduction in Lemma 4.3, we may assume that B is a
![]() $\mathbb {Q}$
-divisor. As we described in Section 2.4, there are b-divisors
$\mathbb {Q}$
-divisor. As we described in Section 2.4, there are b-divisors
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {M}$
such that
$\mathbf {M}$
such that
-
○
 $\mathbf {B}_Z=B_Z$
,
$\mathbf {B}_Z=B_Z$
,
 $\mathbf {M}_Z=M_Z$
, and
$\mathbf {M}_Z=M_Z$
, and -
○ for any birational contraction
 $g: Z'\to Z$
, let
$g: Z'\to Z$
, let
 $X'$
be a resolution of the main component of
$X'$
be a resolution of the main component of
 $X\times _{Z} Z'$
with induced morphisms
$X\times _{Z} Z'$
with induced morphisms
 $g': X' \to X$
and
$g': X' \to X$
and
 $\pi ': X'\to Z'$
. Write
$\pi ': X'\to Z'$
. Write
 $K_{X'}+B'=g^{\prime *}(K_X+B)$
; then
$K_{X'}+B'=g^{\prime *}(K_X+B)$
; then
 $\mathbf {B}_{Z'}$
(respectively,
$\mathbf {B}_{Z'}$
(respectively,
 $\mathbf {M}_{Z'}$
) is the discriminant part (respectively, the moduli part) of the canonical bundle formula of
$\mathbf {M}_{Z'}$
) is the discriminant part (respectively, the moduli part) of the canonical bundle formula of
 $K_{X'}+B'$
on
$K_{X'}+B'$
on
 $Z'$
.
$Z'$
.
By [Reference Prokhorov and Shokurov35, Theorem 8.1] (see Remark 2.15),
![]() $\mathbf {M}$
is b-semi-ample. Then there exists a resolution
$\mathbf {M}$
is b-semi-ample. Then there exists a resolution
![]() $g:Z'\to Z$
such that
$g:Z'\to Z$
such that
![]() $\mathbf {M}_{Z'}$
is semi-ample, and
$\mathbf {M}_{Z'}$
is semi-ample, and
![]() $\mathbf {B}_{Z'}+\operatorname {Supp}(g^{-1}(\overline {z}))$
is a simple normal crossing divisor. By applying Claim 4.4 to all codimension
$\mathbf {B}_{Z'}+\operatorname {Supp}(g^{-1}(\overline {z}))$
is a simple normal crossing divisor. By applying Claim 4.4 to all codimension
![]() $\geq 1$
points on Z, we get that the coefficients of
$\geq 1$
points on Z, we get that the coefficients of
![]() $\mathbf {B}_{Z'}$
are at most
$\mathbf {B}_{Z'}$
are at most
![]() $\frac {1}{2}$
. Thus we may take a general
$\frac {1}{2}$
. Thus we may take a general
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $L_{Z'}\geq 0$
on
$L_{Z'}\geq 0$
on
![]() $Z'$
such that
$Z'$
such that
![]() $\mathbf {M}_{Z'}\sim _{\mathbb {Q}} L_{Z'}$
,
$\mathbf {M}_{Z'}\sim _{\mathbb {Q}} L_{Z'}$
,
![]() $\mathbf {B}_{Z'}+L_{Z'}$
is simple normal crossing, and the coefficients of
$\mathbf {B}_{Z'}+L_{Z'}$
is simple normal crossing, and the coefficients of
![]() $\mathbf {B}_{Z'}+L_{Z'}$
are at most
$\mathbf {B}_{Z'}+L_{Z'}$
are at most
![]() $\frac {1}{2}$
. In this case,
$\frac {1}{2}$
. In this case,
![]() $ (Z', \mathbf {B}_{Z'}+L_{Z'}) $
is
$ (Z', \mathbf {B}_{Z'}+L_{Z'}) $
is
![]() $\frac {1}{2}$
-lc. Note that
$\frac {1}{2}$
-lc. Note that
hence by the negativity lemma [Reference Birkar, Cascini and Hacon9, Lemma 3.6.2],
Thus
![]() $ M_Z\sim _{\mathbb {Q}} g_*L_{Z'}\geq 0$
and
$ M_Z\sim _{\mathbb {Q}} g_*L_{Z'}\geq 0$
and
![]() $ (Z, B_{Z}+g_*L_{Z'})$
is
$ (Z, B_{Z}+g_*L_{Z'})$
is
![]() $\frac {1}{2}$
-lc.
$\frac {1}{2}$
-lc.
Proof of Theorem 1.4
As the statement is local, we may assume that Z is affine. Since
![]() $-K_X$
is ample over Z, there exists a positive integer N such that
$-K_X$
is ample over Z, there exists a positive integer N such that
![]() $-NK_X$
is very ample over Z. Let H be a general very ample divisor on X such that
$-NK_X$
is very ample over Z. Let H be a general very ample divisor on X such that
![]() $H\sim _{Z} -NK_X$
, and take
$H\sim _{Z} -NK_X$
, and take
![]() $B=\frac {1}{N}H$
. Then
$B=\frac {1}{N}H$
. Then
![]() $K_X+B\sim _{\mathbb {Q},Z}0$
, B has no vertical irreducible component over Z, and
$K_X+B\sim _{\mathbb {Q},Z}0$
, B has no vertical irreducible component over Z, and
![]() $(X,B)$
is canonical. By Corollary 1.8, we can choose
$(X,B)$
is canonical. By Corollary 1.8, we can choose
![]() $M_Z\geq 0$
representing the moduli part and
$M_Z\geq 0$
representing the moduli part and
![]() $B_Z$
the discriminant part of the canonical bundle formula of
$B_Z$
the discriminant part of the canonical bundle formula of
![]() $K_X+B$
on Z such that
$K_X+B$
on Z such that
![]() $(Z,B_Z+M_Z)$
is
$(Z,B_Z+M_Z)$
is
![]() $\frac {1}{2}$
-lc. Note that
$\frac {1}{2}$
-lc. Note that
![]() $B\geq 0$
implies that
$B\geq 0$
implies that
![]() $B_Z\geq 0$
. Thus Z is
$B_Z\geq 0$
. Thus Z is
![]() $\frac {1}{2}$
-lc.
$\frac {1}{2}$
-lc.
Finally, as an application of Corollary 1.8, we show the following weaker version of Iskovskikh’s conjecture under a more general setting without using the classification of terminal singularities in dimension
![]() $3$
as in [Reference Mori and Prokhorov30].
$3$
as in [Reference Mori and Prokhorov30].
Corollary 4.5. Let
![]() $\pi :X\to Z$
be a contraction between normal varieties such that
$\pi :X\to Z$
be a contraction between normal varieties such that
-
1.
 $\dim X-\dim Z=1$
,
$\dim X-\dim Z=1$
, -
2. there is no prime divisor D on X such that
 $\mathrm {codim}(\pi (D), Z)\geq 2$
,
$\mathrm {codim}(\pi (D), Z)\geq 2$
, -
3. X is terminal,
-
4.
 $K_Z$
is
$K_Z$
is
 $\mathbb {Q}$
-Cartier, and
$\mathbb {Q}$
-Cartier, and -
5.
 $-K_X$
is ample over Z.
$-K_X$
is ample over Z.
Then Z is
![]() $\frac {1}{2}$
-klt.
$\frac {1}{2}$
-klt.
Here, the assumption in (2) is a natural geometric condition: for example, it holds if all fibres of
![]() $\pi $
are 1-dimensional or if
$\pi $
are 1-dimensional or if
![]() $\rho (X/Z)=1$
.
$\rho (X/Z)=1$
.
Proof. As the statement is local, we may assume that Z is affine. By Theorem 1.4, Z is
![]() $\frac {1}{2}$
-lc. Assume to the contrary that Z is not
$\frac {1}{2}$
-lc. Assume to the contrary that Z is not
![]() $\frac {1}{2}$
-klt; then there exists an exceptional prime divisor E over Z such that
$\frac {1}{2}$
-klt; then there exists an exceptional prime divisor E over Z such that
![]() $a(E, Z )=\frac {1}{2}$
. Denote by
$a(E, Z )=\frac {1}{2}$
. Denote by
![]() $c_Z(E)$
the center of E on Z.
$c_Z(E)$
the center of E on Z.
By [Reference Birkar, Cascini and Hacon9, Corollary 1.4.3], we can find a proper birational morphism
![]() $g: Z'\to Z$
such that E is the only g-exceptional divisor. Let
$g: Z'\to Z$
such that E is the only g-exceptional divisor. Let
![]() $X'$
be a resolution of the main component of
$X'$
be a resolution of the main component of
![]() $X\times _{Z} Z'$
with induced morphisms
$X\times _{Z} Z'$
with induced morphisms
![]() $g': X' \to X$
and
$g': X' \to X$
and
![]() $\pi ': X'\to Z'$
:
$\pi ': X'\to Z'$
:

We can write
![]() $K_{X'}+G=g^{\prime *}K_X$
,
$K_{X'}+G=g^{\prime *}K_X$
,
![]() $K_{Z'}+\frac {1}{2}E=g^*K_Z.$
$K_{Z'}+\frac {1}{2}E=g^*K_Z.$
As
![]() $-K_X$
is ample over Z, for any
$-K_X$
is ample over Z, for any
![]() $t\in (0, 1)\cap \mathbb {Q}$
, we can take an effective
$t\in (0, 1)\cap \mathbb {Q}$
, we can take an effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $B^t$
on X such that
$B^t$
on X such that
-
○
 $(X,B^t)$
is canonical,
$(X,B^t)$
is canonical, -
○
 $B^t$
has no vertical irreducible component over Z,
$B^t$
has no vertical irreducible component over Z, -
○
 $K_X+B^t\sim _{\mathbb {Q},Z} 0$
, and
$K_X+B^t\sim _{\mathbb {Q},Z} 0$
, and -
○
 $\operatorname {Supp} (B^t)\supset \operatorname {Supp}(\pi ^{-1}(c_Z(E)))$
, and the multiplicity of each irreducible component of
$\operatorname {Supp} (B^t)\supset \operatorname {Supp}(\pi ^{-1}(c_Z(E)))$
, and the multiplicity of each irreducible component of
 $\operatorname {Supp}(\pi ^{-1}(c_Z(E)))$
in
$\operatorname {Supp}(\pi ^{-1}(c_Z(E)))$
in
 $B^t$
is a non-constant linear function in t.
$B^t$
is a non-constant linear function in t.
The construction is as follows. Take a sufficiently large N such that
![]() $-NK_X\sim _{Z} H$
is a very ample divisor on X, and
$-NK_X\sim _{Z} H$
is a very ample divisor on X, and
![]() $\mathcal {O}_X(H)$
and
$\mathcal {O}_X(H)$
and
![]() $\mathcal {O}_X(H)\otimes I_{\operatorname {Supp}(\pi ^{-1}(c_Z(E)))}$
are generated by global sections. Now take
$\mathcal {O}_X(H)\otimes I_{\operatorname {Supp}(\pi ^{-1}(c_Z(E)))}$
are generated by global sections. Now take
![]() $B_1$
to be a general global section of
$B_1$
to be a general global section of
![]() $\mathcal {O}_X(H)$
and
$\mathcal {O}_X(H)$
and
![]() $B_2$
a general global section of
$B_2$
a general global section of
![]() $\mathcal {O}_X(H)\otimes I_{\operatorname {Supp}(\pi ^{-1}(c_Z(E)))}$
. Then
$\mathcal {O}_X(H)\otimes I_{\operatorname {Supp}(\pi ^{-1}(c_Z(E)))}$
. Then
![]() $B^t=\frac {(1-st)}{N}B_1+\frac {st}{N} B_2$
satisfies the requirements for sufficiently small positive rational number s. Here, the assumption in (3) guarantees that
$B^t=\frac {(1-st)}{N}B_1+\frac {st}{N} B_2$
satisfies the requirements for sufficiently small positive rational number s. Here, the assumption in (3) guarantees that
![]() $(X, B^t)$
is canonical, and the assumption in (2) guarantees that
$(X, B^t)$
is canonical, and the assumption in (2) guarantees that
![]() $B^t$
has no vertical irreducible component over Z as
$B^t$
has no vertical irreducible component over Z as
![]() $\operatorname {Supp}(\pi ^{-1}(c_Z(E)))$
has codimension at least
$\operatorname {Supp}(\pi ^{-1}(c_Z(E)))$
has codimension at least
![]() $2$
in X.
$2$
in X.
Then by Corollary 1.8, for any
![]() $t\in (0, 1)\cap \mathbb {Q}$
, we can choose
$t\in (0, 1)\cap \mathbb {Q}$
, we can choose
![]() $M^t_Z\geq 0$
representing the moduli part of the canonical bundle formula of
$M^t_Z\geq 0$
representing the moduli part of the canonical bundle formula of
![]() $K_X+B^t$
on Z such that
$K_X+B^t$
on Z such that
![]() $(Z,B^t_Z+M^t_Z)$
is
$(Z,B^t_Z+M^t_Z)$
is
![]() $\frac {1}{2}$
-lc, where
$\frac {1}{2}$
-lc, where
![]() $B^t_Z\geq 0$
is the discriminant part. In particular,
$B^t_Z\geq 0$
is the discriminant part. In particular,
![]() $c_Z(E)$
is not contained in
$c_Z(E)$
is not contained in
![]() $\operatorname {Supp}(B^t_Z+M^t_Z)$
, otherwise
$\operatorname {Supp}(B^t_Z+M^t_Z)$
, otherwise
![]() $a(E, Z, B^t_Z+M^t_Z)<a(E, Z)=\frac {1}{2}$
, which is absurd. As we described in Section 2.4, there are b-divisors
$a(E, Z, B^t_Z+M^t_Z)<a(E, Z)=\frac {1}{2}$
, which is absurd. As we described in Section 2.4, there are b-divisors
![]() $\mathbf {B}^t$
and
$\mathbf {B}^t$
and
![]() $\mathbf {M}^t$
such that
$\mathbf {M}^t$
such that
-
○
 $\mathbf {B}^t_Z=B^t_Z$
,
$\mathbf {B}^t_Z=B^t_Z$
,
 $\mathbf {M}^t_Z=M^t_Z$
,
$\mathbf {M}^t_Z=M^t_Z$
, -
○
 $K_{X'}+G+g^{\prime *}B^t=\pi ^{\prime *}(K_{Z'}+\mathbf {B}^t_{Z'}+\mathbf {M}^t_{Z'})$
,
$K_{X'}+G+g^{\prime *}B^t=\pi ^{\prime *}(K_{Z'}+\mathbf {B}^t_{Z'}+\mathbf {M}^t_{Z'})$
, -
○
 $K_{Z'}+\mathbf {B}^t_{Z'}+\mathbf {M}^t_{Z'}=g^*(K_Z+B^t_Z+M^t_Z)=K_{Z'}+\frac {1}{2}E+g^*(B^t_Z+M^t_Z).$
$K_{Z'}+\mathbf {B}^t_{Z'}+\mathbf {M}^t_{Z'}=g^*(K_Z+B^t_Z+M^t_Z)=K_{Z'}+\frac {1}{2}E+g^*(B^t_Z+M^t_Z).$
Recall that
![]() $\mathbf {M}^t$
is b-semi-ample by [Reference Prokhorov and Shokurov35, Theorem 8.1] (see Remark 2.15), so
$\mathbf {M}^t$
is b-semi-ample by [Reference Prokhorov and Shokurov35, Theorem 8.1] (see Remark 2.15), so
![]() $\mathbf {M}^t_{Z'}\leq g^*M^t_Z$
by the negativity lemma [Reference Birkar, Cascini and Hacon9, Lemma 3.6.2]. As
$\mathbf {M}^t_{Z'}\leq g^*M^t_Z$
by the negativity lemma [Reference Birkar, Cascini and Hacon9, Lemma 3.6.2]. As
![]() $c_Z(E)$
is not contained in
$c_Z(E)$
is not contained in
![]() $\operatorname {Supp}(B^t_Z+M^t_Z)$
, we get
$\operatorname {Supp}(B^t_Z+M^t_Z)$
, we get
![]() $\operatorname {mult}_E \mathbf {M}^t_{Z'}=0$
and then
$\operatorname {mult}_E \mathbf {M}^t_{Z'}=0$
and then
![]() $\operatorname {mult}_E\mathbf {B}^t_{Z'}=\frac {1}{2}$
. The latter one implies that
$\operatorname {mult}_E\mathbf {B}^t_{Z'}=\frac {1}{2}$
. The latter one implies that
![]() $\operatorname {lct}(X'/Z'\ni \eta _E, G+g^{\prime *}B^t; \pi ^{\prime *}E)=\frac {1}{2}$
by definition, where
$\operatorname {lct}(X'/Z'\ni \eta _E, G+g^{\prime *}B^t; \pi ^{\prime *}E)=\frac {1}{2}$
by definition, where
![]() $\eta _E$
is the generic point of E. This is absurd, as by the construction of
$\eta _E$
is the generic point of E. This is absurd, as by the construction of
![]() $B^t$
,
$B^t$
,
![]() $\operatorname {lct}(X'/Z'\ni \eta _E, G+g^{\prime *}B^t; \pi ^{\prime *}E)$
is a non-constant function in t.
$\operatorname {lct}(X'/Z'\ni \eta _E, G+g^{\prime *}B^t; \pi ^{\prime *}E)$
is a non-constant function in t.
Remark 4.6.
Prokhorov provided us with the following example, which shows that Corollary 4.5 cannot be improved if
![]() $\dim X\geq 4.$
$\dim X\geq 4.$
Example 4.7. Consider the following action of
![]() ${\boldsymbol{\mu} }_{2m+1}$
on
${\boldsymbol{\mu} }_{2m+1}$
on
![]() $\mathbb {P}_x^1\times \mathbb {C}^3_{u, v, w}$
:
$\mathbb {P}_x^1\times \mathbb {C}^3_{u, v, w}$
:
where m is a positive integer and
![]() $\xi $
is a primitive
$\xi $
is a primitive
![]() $(2m+1)$
th root of unity. Let
$(2m+1)$
th root of unity. Let
![]() $X=(\mathbb {P}^1\times \mathbb {C}^3)/{\boldsymbol{\mu} }_{2m+1}$
,
$X=(\mathbb {P}^1\times \mathbb {C}^3)/{\boldsymbol{\mu} }_{2m+1}$
,
![]() $Z= \mathbb {C}^3/{\boldsymbol{\mu} }_{2m+1}$
and
$Z= \mathbb {C}^3/{\boldsymbol{\mu} }_{2m+1}$
and
![]() $\pi : X\to Z$
the natural projection. Since
$\pi : X\to Z$
the natural projection. Since
![]() ${\boldsymbol{\mu} }_{2m+1}$
acts freely in codimension
${\boldsymbol{\mu} }_{2m+1}$
acts freely in codimension
![]() $1$
,
$1$
,
![]() $-K_X$
is
$-K_X$
is
![]() $\pi $
-ample and
$\pi $
-ample and
![]() $\rho (X/Z)=1$
. Note that Z has an isolated cyclic quotient singularity of type
$\rho (X/Z)=1$
. Note that Z has an isolated cyclic quotient singularity of type
![]() $\frac {1}{2m+1}(1, 1, m)$
at the origin
$\frac {1}{2m+1}(1, 1, m)$
at the origin
![]() $o\in Z$
, and
$o\in Z$
, and
![]() $\mathrm {{mld}}(Z\ni o)=\frac {m+2}{2m+1}$
(see [Reference Ambro4] for the computation of minimal log discrepancies of toric varieties). On the other hand, X has two isolated cyclic quotient singularities of types
$\mathrm {{mld}}(Z\ni o)=\frac {m+2}{2m+1}$
(see [Reference Ambro4] for the computation of minimal log discrepancies of toric varieties). On the other hand, X has two isolated cyclic quotient singularities of types
![]() $\frac {1}{2m+1}(m, 1, 1, m)$
and
$\frac {1}{2m+1}(m, 1, 1, m)$
and
![]() $\frac {1}{2m+1}(m+1, 1, 1, m)$
that are terminal (see [Reference Reid36, (4.11) Theorem]).
$\frac {1}{2m+1}(m+1, 1, 1, m)$
that are terminal (see [Reference Reid36, (4.11) Theorem]).
Acknowledgments
We are grateful to V. V. Shokurov for sharing with us his conjecture (Conjecture 1.1) and for many useful discussions and insightful suggestions. In particular, Shokurov suggested that we consider sub-pairs in the formulation of the main results, which greatly simplified our previous proof. The third named author would like to thank his advisor Chenyang Xu for his support. Part of this work was done while the third named author visited Zhiyu Tian at BICMR, Peking University, during the 2020 Fall Semester, and he would like to thank them for their hospitality. We would like to thank Caucher Birkar, Yifei Chen, Jihao Liu, Shigefumi Mori and Yuri Prokhorov for helpful comments. We thank the referees for useful suggestions and comments.
Financial Support
The first named author was supported by a grant from the Simons Foundation (Grant Number 814268, MSRI) and Start-up Grant No. JIH1414011Y of Fudan University. The second named author was supported by NSFC for Innovative Research Groups (Grant No. 12121001) and the National Key Research and Development Program of China (Grant No. 2020YFA0713200).
Conflicts of interest
None.