Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T03:22:10.426Z Has data issue: false hasContentIssue false
  • English
  • Français

SERRE WEIGHTS AND WILD RAMIFICATION IN TWO-DIMENSIONAL GALOIS REPRESENTATIONS

Part of: Algebraic number theory: local and $p$-adic fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  23 December 2016

LASSINA DEMBÉLÉ ,
FRED DIAMOND  and
DAVID P. ROBERTS
LASSINA DEMBÉLÉ
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK; [email protected]
FRED DIAMOND
Affiliation:
Department of Mathematics, King’s College London, London WC2R 2LS, UK; [email protected]
DAVID P. ROBERTS
Affiliation:
Division of Science and Mathematics, University of Minnesota Morris, Morris, MN 56267, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A generalization of Serre’s Conjecture asserts that if 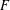$F$ is a totally real field, then certain characteristic 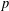$p$ representations of Galois groups over $F$ arise from Hilbert modular forms. Moreover, it predicts the set of weights of such forms in terms of the local behaviour of the Galois representation at primes over 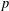 $p$ . This characterization of the weights, which is formulated using 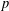$p$ -adic Hodge theory, is known under mild technical hypotheses if 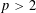$p>2$ . In this paper we give, under the assumption that 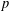$p$ is unramified in 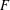$F$ , a conjectural alternative description for the set of weights. Our approach is to use the Artin–Hasse exponential and local class field theory to construct bases for local Galois cohomology spaces in terms of which we identify subspaces that should correspond to ones defined using 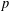$p$ -adic Hodge theory. The resulting conjecture amounts to an explicit description of wild ramification in reductions of certain crystalline Galois representations. It enables the direct computation of the set of Serre weights of a Galois representation, which we illustrate with numerical examples. A proof of this conjecture has been announced by Calegari, Emerton, Gee and Mavrides.

MSC classification

Primary: 11F80: Galois representations
Secondary: 11S15: Ramification and extension theory 11S25: Galois cohomology
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e33
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Abrashkin, V., ‘Modular representations of the Galois group of a local field and a generalization of a conjecture of Shafarevich’, Izv. Akad. Nauk SSSR Ser. Mat. 53(6) (1989), 1135–1182. 1337; MR 1039960.Google Scholar
Ash, A. and Sinnott, W., ‘An analogue of Serre’s conjecture for Galois representations and Hecke eigenclasses in the mod p cohomology of GL(n, Z)’, Duke Math. J. 105(1) (2000), 1–24; MR 1788040.Google Scholar
Breuil, C., ‘Sur un problème de compatibilité local-global modulo p pour GL2 ’, J. Reine Angew. Math. 692 (2014), 1–76; MR 3274546.Google Scholar
Buzzard, K., Diamond, F. and Jarvis, F., ‘On Serre’s conjecture for mod ℓ Galois representations over totally real fields’, Duke Math. J. 155(1) (2010), 105–161; MR 2730374.Google Scholar
Calegari, F., Emerton, M., Gee, T. and Mavrides, L., ‘Explicit Serre weights for two-dimensional Galois representations’, Preprint, 2016, arXiv:1608.06059.Google Scholar
Chang, S. and Diamond, F., ‘Extensions of rank one (𝜙, 𝛤)-modules and crystalline representations’, Compositio Math. 147(2) (2011), 375–427; MR 2776609.Google Scholar
Dembélé , L., ‘Explicit computations of Hilbert modular forms on ℚ(√5)’, Exp. Math. 14(4) (2005), 457–466; MR 2193808.Google Scholar
Dembélé, L., ‘Quaternionic Manin symbols, Brandt matrices, and Hilbert modular forms’, Math. Comp. 76(258) (2007), 1039–1057; MR 2291849.Google Scholar
Dembélé, L., Diamond, F. and Roberts, D. P., ‘On the computation and combinatorics of Serre weights for two-dimensional Galois representations’, in preparation.Google Scholar
Dokchitser, T. and Dokchitser, V., ‘Identifying Frobenius elements in Galois groups’, Algebra Number Theory 7(6) (2013), 1325–1352; MR 3107565.Google Scholar
Fontaine, J.-M., ‘Il n’y a pas de variété abélienne sur Z ’, Invent. Math. 81(3) (1985), 515–538; MR 807070.Google Scholar
Gee, T., ‘Automorphic lifts of prescribed types’, Math. Ann. 350(1) (2011), 107–144; MR 2785764.Google Scholar
Gee, T., Herzig, F. and Savitt, D., ‘General Serre weight conjectures’, Preprint, 2015,arXiv:1509.02527.Google Scholar
Gee, T. and Kisin, M., ‘The Breuil–Mézard conjecture for potentially Barsotti–Tate representations’, Forum Math. Pi 2 (2014), e1 56; MR 3292675.Google Scholar
Gee, T., Liu, T. and Savitt, D., ‘The Buzzard–Diamond–Jarvis conjecture for unitary groups’, J. Amer. Math. Soc. 27(2) (2014), 389–435; MR 3164985.Google Scholar
Jones, J. W. and Roberts, D. P., ‘A database of number fields’, LMS J. Comput. Math. 17(1) (2014), 595–618; MR 3356048.Google Scholar
Khare, C. and Wintenberger, J.-P., ‘Serre’s modularity conjecture. I’, Invent. Math. 178(3) (2009), 485–504; MR 2551763.Google Scholar
Khare, C. and Wintenberger, J.-P., ‘Serre’s modularity conjecture. II’, Invent. Math. 178(3) (2009), 505–586; MR 2551764.Google Scholar
Mavrides, L., ‘On wild ramification in reductions of two-dimensional crystalline Galois representations’. PhD Thesis, King’s College London, 2016.Google Scholar
Newton, J., ‘Serre weights and Shimura curves’, Proc. Lond. Math. Soc. (3) 108(6) (2014), 1471–1500; MR 3218316.CrossRefGoogle Scholar
Robert, A. M., A Course in p-Adic Analysis, Graduate Texts in Mathematics, 198 (Springer, New York, 2000), MR 1760253.Google Scholar
Schein, M. M., ‘Weights in Serre’s conjecture for Hilbert modular forms: the ramified case’, Israel J. Math. 166 (2008), 369–391; MR 2430440.Google Scholar
Serre, J.-P., Local Fields, Graduate Texts in Mathematics, 67 (Springer, New York–Berlin, 1979), translated from the French by Marvin Jay Greenberg; MR 554237.Google Scholar
Serre, J.-P., ‘Sur les représentations modulaires de degré 2 de Gal( Q /Q )’, Duke Math. J. 54(1) (1987), 179–230; MR 885783.Google Scholar
Taylor, R., ‘On Galois representations associated to Hilbert modular forms’, Invent. Math. 98(2) (1989), 265–280; MR 1016264.Google Scholar