Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-05T12:34:41.691Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigid automorphisms of linking systems

Part of: Representation theory of groups

Published online by Cambridge University Press:  15 March 2021

George Glauberman  and
Justin Lynd Open the ORCID record for Justin Lynd [Opens in a new window]
George Glauberman
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Ave, Chicago, IL60637; E-mail: [email protected]
Justin Lynd
Affiliation:
Department of Mathematics, University of Louisiana at Lafayette, Lafayette, LA70504; E-mail: [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A rigid automorphism of a linking system is an automorphism that restricts to the identity on the Sylow subgroup. A rigid inner automorphism is conjugation by an element in the center of the Sylow subgroup. At odd primes, it is known that each rigid automorphism of a centric linking system is inner. We prove that the group of rigid outer automorphisms of a linking system at the prime 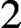$2$ is elementary abelian and that it splits over the subgroup of rigid inner automorphisms. In a second result, we show that if an automorphism of a finite group G restricts to the identity on the centric linking system for G, then it is of 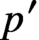$p'$-order modulo the group of inner automorphisms, provided G has no nontrivial normal 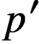$p'$-subgroups. We present two applications of this last result, one to tame fusion systems.

MSC classification

Primary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Secondary: 20D45: Automorphisms
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e23
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Andersen, K. K. S., Oliver, B. and Ventura, J., ‘Reduced, tame and exotic fusion systems’, Proc. Lond. Math. Soc. (3) 105(1) (2012), 87–152.CrossRefGoogle Scholar
Aschbacher, M., Kessar, R. and Oliver, B., Fusion Systems in Algebra and Topology, London Mathematical Society Lecture Note Series, Vol. 391 (Cambridge University Press, Cambridge, UK, 2011).CrossRefGoogle Scholar
Broto, C., Levi, R. and Oliver, B., ‘The homotopy theory of fusion systems’, J. Amer. Math. Soc. 16(4) (2003), 779–856.CrossRefGoogle Scholar
Broto, C., Møller, J. and Oliver, B., ‘Automorphisms of fusion systems of finite simple groups of Lie type’, Mem. Amer. Math. Soc. 262(1267) (2019), 1–120.Google Scholar
Chermak, A., ‘Fusion systems and localities’, Acta Math. 211(1) (2013), 47–139.CrossRefGoogle Scholar
Chermak, A., ‘Finite localities II’, Preprint, 2015, arXiv:1505.08110.Google Scholar
Chermak, A., ‘Finite localities III’, Preprint, 2016 arXiv:1610.06161.Google Scholar
Craven, D. A., ‘Normal subsystems of fusion systems’, J. Lond. Math. Soc. (2) 84(1) (2011), 137–158.CrossRefGoogle Scholar
Glauberman, G., ‘Central elements in core-free groups’, J. Algebra 4 (1966), 403–420.CrossRefGoogle Scholar
Glauberman, G., ‘On the automorphism groups of a finite group having no non-identity normal subgroups of odd order’, Math. Z. 93 (1966), 154–160.CrossRefGoogle Scholar
Glauberman, G., ‘Weakly closed elements of Sylow subgroups’, Math. Z. 107 (1968), 1–20.CrossRefGoogle Scholar
Glauberman, G., Guralnick, R., Lynd, J. and Navarro, G., ‘Centers of Sylow subgroups and automorphisms’, Israel J. Math. 240 (2020), 253–266.CrossRefGoogle Scholar
Glauberman, G. and Lynd, J., ‘Control of fixed points and existence and uniqueness of centric linking systems’, Invent. Math. 206(2) (2016), 441–484.CrossRefGoogle Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups. Number 3. Part I. Chapter A, Mathematical Surveys and Monographs, Vol. 40 (American Mathematical Society, Providence, RI, 1998).Google Scholar
Gross, F., ‘Automorphisms which centralize a Sylow $\mathrm{p}$-subgroup’, J. Algebra 77(1) (1982), 202–233.CrossRefGoogle Scholar
Henke, E., ‘Subcentric linking systems’, Trans. Amer. Math. Soc. 371(5) (2019), 3325–3373.CrossRefGoogle Scholar
Levi, R. and Oliver, B., ‘Construction of 2-local finite groups of a type studied by Solomon and Benson’, Geom. Topol. 6 (2002), 917–990.CrossRefGoogle Scholar
Oliver, B., ‘Equivalences of classifying spaces completed at odd primes’, Math. Proc. Cambridge Philos. Soc. 137(2) (2004), 321–347.CrossRefGoogle Scholar
Oliver, B., ‘Equivalences of classifying spaces completed at the prime two’, Mem. Amer. Math. Soc. 180(848) (2006), vi+102 pp.Google Scholar
Oliver, B., ‘Existence and uniqueness of linking systems: Chermak’s proof via obstruction theory’, Acta Math. 211 (2013), no. 1, 141–175. MR 3118306CrossRefGoogle Scholar
Oliver, B. and Ventura, J., ‘Extensions of linking systems with $\mathrm{p}$-group kernel’, Math. Ann. 338(4) (2007), 983–1043.CrossRefGoogle Scholar
Puig, L., ‘Frobenius categories’, J. Algebra 303(1) (2006), 309–357.CrossRefGoogle Scholar