Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T10:02:48.515Z Has data issue: false hasContentIssue false
  • English
  • Français

REGULARIZATION OF NON-NORMAL MATRICES BY GAUSSIAN NOISE—THE BANDED TOEPLITZ AND TWISTED TOEPLITZ CASES

Part of: Probability theory on algebraic and topological structures Special matrices

Published online by Cambridge University Press:  13 February 2019

ANIRBAN BASAK Open the ORCID record for ANIRBAN BASAK [Opens in a new window] ,
ELLIOT PAQUETTE Open the ORCID record for ELLIOT PAQUETTE [Opens in a new window]  and
OFER ZEITOUNI Open the ORCID record for OFER ZEITOUNI [Opens in a new window]
ANIRBAN BASAK
Affiliation:
International Centre for Theoretical Sciences, Tata Institute of Fundamental Research, Bangalore 560089, India; [email protected] Department of Mathematics, Weizmann Institute of Science, POB 26, Rehovot 76100, Israel
ELLIOT PAQUETTE
Affiliation:
Department of Mathematics, The Ohio State University, Tower 100, 231 W 18th Ave, Columbus, Ohio 43210, USA; [email protected]
OFER ZEITOUNI
Affiliation:
Department of Mathematics, Weizmann Institute of Science, POB 26, Rehovot 76100, Israel Courant Institute, New York University, 251 Mercer St, New York, NY 10012, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the spectrum of additive, polynomially vanishing random perturbations of deterministic matrices, as follows. Let 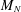$M_{N}$ be a deterministic 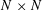$N\times N$ matrix, and let 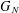$G_{N}$ be a complex Ginibre matrix. We consider the matrix 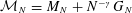${\mathcal{M}}_{N}=M_{N}+N^{-\unicode[STIX]{x1D6FE}}G_{N}$, where 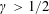$\unicode[STIX]{x1D6FE}>1/2$. With 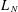$L_{N}$ the empirical measure of eigenvalues of 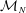${\mathcal{M}}_{N}$, we provide a general deterministic equivalence theorem that ties 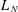$L_{N}$ to the singular values of 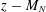$z-M_{N}$, with 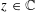$z\in \mathbb{C}$. We then compute the limit of 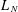$L_{N}$ when 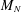$M_{N}$ is an upper-triangular Toeplitz matrix of finite symbol: if 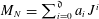$M_{N}=\sum _{i=0}^{\mathfrak{d}}a_{i}J^{i}$ where 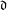$\mathfrak{d}$ is fixed, 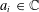$a_{i}\in \mathbb{C}$ are deterministic scalars and 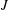$J$ is the nilpotent matrix 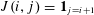$J(i,j)=\mathbf{1}_{j=i+1}$, then 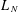$L_{N}$ converges, as 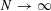$N\rightarrow \infty$, to the law of 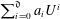$\sum _{i=0}^{\mathfrak{d}}a_{i}U^{i}$ where 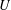$U$ is a uniform random variable on the unit circle in the complex plane. We also consider the case of slowly varying diagonals (twisted Toeplitz matrices), and, when 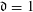$\mathfrak{d}=1$, also of independent and identically distributed entries on the diagonals in 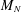$M_{N}$.

MSC classification

Primary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Secondary: 15B05: Toeplitz, Cauchy, and related matrices 15B52: Random matrices
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e3
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Basak, A., Cook, N. A. and Zeitouni, O., ‘Circular law for the sum of random permutation matrices’, Electron. J. Probab. 23 (2018), paper no. 33, 51 pp.Google Scholar
Basak, A., Paquette, E. and Zeitouni, O., ‘Spectrum of random perturbations of Toeplitz matrices with finite symbols’, Preprint, 2018, arXiv:1812.06207.Google Scholar
Bhatia, R., Matrix Analysis (Springer, Berlin, 1997).Google Scholar
Craig, W. and Simon, B., ‘Log Hölder continuity of the integrated density of states for stochastic Jacobi matrices’, Comm. Math. Phys. 90(2) (1983), 207–218.Google Scholar
Davies, R. B. and Hager, M., ‘Perturbations of Jordan matrices’, J. Approx. Theory 156 (2009), 82–94.Google Scholar
Feldheim, O. N., Paquette, E. and Zeitouni, O., ‘Regularization of non-normal matrices by Gaussian noise’, Int. Math. Res. Not. IMRN 18 (2015), 8724–8751.Google Scholar
Goodman, N. R., ‘Distribution of the determinant of a complex wishart distributed matrix’, Ann. of Math. Stat. 34(1) (1963), 178–180.Google Scholar
Gordon, Y., ‘On Milman’s inequality and random subspaces which escape through a mesh in ℝ n ’, Geom. Aspects Funct. Anal. (2002), 84–106. (Springer, 1988).Google Scholar
Guionnet, A., Krishnapur, M. and Zeitouni, O., ‘The single ring theorem’, Ann. of Math. 174(2) (2011), 1189–1217.Google Scholar
Guionnet, A., Wood, P. M. and Zeitouni, O., ‘Convergence of the spectral measure of non-normal matrices’, Proc. Amer. Math. Soc. 142 (2014), 667–679.Google Scholar
Hachem, W., Loubaton, P. and Najim, J., ‘Deterministic equivalents for certain random functionals of large random matrices’, Ann. Appl. Probab. 3 (2007), 875–930.Google Scholar
Horn, R. A. and Johnson, C. R., Topics in Matrix Analysis (Cambridge University Press, 1991).Google Scholar
Horn, R. A. and Johnson, C. R., Matrix Analysis, (Cambridge University Press, 2012).Google Scholar
Marcus, M., ‘Determinant of sums’, College Math. J. 21 (1990), 130–135.Google Scholar
Reichel, L. and Trefethen, L. N., ‘Eigenvalues and pseudo–eigenvalues of Toeplitz matrices’, Linear Algebra Appl. 162 (1992), 153–185.Google Scholar
Simon, B., A Comprehensive Course in Analysis, Part 3. Harmonic Analysis (American Mathematical Society, Providence, RI, 2015).Google Scholar
Sjöstrand, J. and Vogel, M., ‘Large bi-diagonal matrices and random perturbations’, J. Spectr. Theor. 6 (2016), 977–1020.Google Scholar
Sjöstrand, J. and Vogel, M., ‘Interior eigenvalue density of large bi-diagonal matrices subject to random perturbations’, inMicrolocal Analysis and Singular Perturbation Theory, RIMS Kôkyûroku Bessatsu, B61 (Res. Inst. Math. Sci. (RIMS), Kyoto, 2017), 201–227.Google Scholar
Śniady, P., ‘Random regularization of Brown spectral measure’, J. Funct. Anal. 193 (2002), 291–313.Google Scholar
Tao, T., Topics in Random Matrix Theory, Graduate Studies in Mathematics, 132 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Tao, T., Vu, V. and Manjunath, K., ‘Random matrices: universality of ESDs and the circular law’, Ann. Probab. 38(5) (2010), 2023–2065.Google Scholar
Trefethen, L. N., ‘Pseudospectra of Matrices’, inNumerical Analysis 1991, Vol. 260 (eds. Griffiths, D. F. and Watson, G. A.) (Longman Sci. Tech., Harlow, UK, 1992), 234–266.Google Scholar
Trefethen, L. N., ‘Wave packet pseudomodes of variable coefficient differential operators’, Proc. R. Soc. Lond. Ser. A 461 (2005), 3099–3122.Google Scholar
Trefethen, L. N. and Chapman, S. J., ‘Wave packet pseudomodes of twisted Toeplitz matrices’, Comm. Pure Appl. Math. 57(9) (2004), 1233–1264.Google Scholar
Trefethen, L. N., Contedini, M. and Embree, M., ‘Spectra, pseudospectra, and localization for random bidiagonal matrices’, Commun. Pure Appl. Math. 54(5) (2001), 595–623.Google Scholar
Trefethen, L. N. and Embree, M., Spectra and Pseudospectra: the Behavior of Nonnormal Matrices and Operators (Princeton University Press, Princeton, 2005).Google Scholar
Wood, P. M., ‘Universality of the ESD for a fixed matrix plus small random noise: A stability approach’, Ann. Inst. H. Poincaré Probab. Stat. 52(4) (2016), 1877–1896.Google Scholar