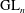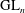Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sorensen, Claus M.
2016.
The local Langlands correspondence in families and Ihara's lemma for U(n).
Journal of Number Theory,
Vol. 164,
Issue. ,
p.
127.
Thorne, Jack A.
2016.
Automorphy of some residually dihedral Galois representations.
Mathematische Annalen,
Vol. 364,
Issue. 1-2,
p.
589.
Caraiani, Ana
and
Scholze, Peter
2017.
On the generic part of the cohomology of compact unitary Shimura varieties.
Annals of Mathematics,
Vol. 186,
Issue. 3,
Clozel, Laurent
and
Thorne, Jack A.
2017.
Level-raising and symmetric power functoriality, III.
Duke Mathematical Journal,
Vol. 166,
Issue. 2,
Wong, Peng-Jie
2019.
On the Chebotarev–Sato–Tate phenomenon.
Journal of Number Theory,
Vol. 196,
Issue. ,
p.
272.
Newton, James
and
Thorne, Jack A.
2021.
Symmetric power functoriality for holomorphic modular forms.
Publications mathématiques de l'IHÉS,
Vol. 134,
Issue. 1,
p.
1.
van Hoften, Pol
2021.
A geometric Jacquet–Langlands correspondence for paramodular Siegel threefolds.
Mathematische Zeitschrift,
Vol. 299,
Issue. 3-4,
p.
2029.
Karnataki, Aditya
2021.
Level-raising for automorphic forms on 𝐺𝐿_{𝑛}.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 12,
p.
8547.
Moss, Gilbert
2021.
The universal unramified module for GL(n) and
the Ihara conjecture.
Algebra & Number Theory,
Vol. 15,
Issue. 5,
p.
1181.
Anastassiades, Christos
and
Thorne, Jack A.
2022.
RAISING THE LEVEL OF AUTOMORPHIC REPRESENTATIONS OF OF UNITARY TYPE.
Journal of the Institute of Mathematics of Jussieu,
Vol. 21,
Issue. 4,
p.
1421.