Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-20T12:23:55.798Z Has data issue: false hasContentIssue false
  • English
  • Français

PERIOD IDENTITIES OF CM FORMS ON QUATERNION ALGEBRAS

Part of: Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  20 May 2020

CHARLOTTE CHAN
CHARLOTTE CHAN*
Affiliation:
Department of Mathematics, University of Michigan, 530 Church St., Ann Arbor 48109, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Waldspurger’s formula gives an identity between the norm of a torus period and an 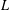$L$-function of the twist of an automorphic representation on GL(2). For any two Hecke characters of a fixed quadratic extension, one can consider the two torus periods coming from integrating one character against the automorphic induction of the other. Because the corresponding 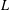$L$-functions agree, (the norms of) these periods—which occur on different quaternion algebras—are closely related. In this paper, we give a direct proof of an explicit identity between the torus periods themselves.

MSC classification

Primary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols 11F27: Theta series; Weil representation; theta correspondences 11R52: Quaternion and other division algebras
Type
Number Theory
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e25
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2020

References

Bertolini, M., Darmon, H. and Prasanna, K., ‘Generalized Heegner cycles and p-adic Rankin L-series. With an appendix by Brian Conrad’, Duke Math. J. 162(6) (2013), 1033–1148.CrossRefGoogle Scholar
Casselman, W., ‘On some results of Atkin and Lehner’, Math. Ann. 201 (1973), 301–314.CrossRefGoogle Scholar
Chan, C., ‘Period identities of CM forms on quaternion algebras’, PhD Thesis, University of Michigan, 2018.Google Scholar
Collins, D., ‘Numerical computation of Petersson inner products and $q$-expansions’, Preprint, 2018, arXiv:1802.09740.Google Scholar
Gan, W. T. and Ichino, A., ‘Formal degrees and local theta correspondence’, Invent. Math. 195(3) (2014), 509–672.CrossRefGoogle Scholar
Gan, W. T., Qiu, Y. and Takeda, S., ‘The regularized Siegel–Weil formula (the second term identity) and the Rallis inner product formula’, Invent. Math. 198(3) (2014), 739–831.CrossRefGoogle Scholar
Gross, B., ‘Local orders, root numbers, and modular curves’, Amer. J. Math. 110 (1988), 1153–1182.CrossRefGoogle Scholar
Gross, B. and Prasad, D., ‘Test vectors for linear forms’, Math. Ann. 291(2) (1991), 343–355.CrossRefGoogle Scholar
Harris, M., Kudla, S. and Sweet, W., ‘Theta dichotomy for unitary groups’, J. Amer. Math. Soc. 9(4) (1996), 941–1004.CrossRefGoogle Scholar
Hida, H., ‘Congruence of cusp forms and special values of their zeta functions’, Invent. Math. 63(2) (1981), 225–261.CrossRefGoogle Scholar
Ichino, A. and Prasanna, K., ‘Periods of quaternionic Shimura varieties’, Mem. Amer. Math. Soc, to appear.Google Scholar
Ichino, A. and Prasanna, K., ‘Periods of quaternionic Shimura varieties, II’, Preprint, 2020.Google Scholar
Jacquet, H. and Langlands, R., Automorphic Forms for GL2, Lecture Notes in Mathematics, 114 (Springer, Berlin, New York, 1970), vii + 548.CrossRefGoogle Scholar
Kudla, S., ‘Splitting metaplectic covers of dual reductive pairs’, Israel J. Math. 87(1–3) (1994), 361–401.CrossRefGoogle Scholar
Kudla, S. and Sweet, W., ‘Degenerate principal series representations for U (n, n)’, Israel J. Math. 98 (1997), 253–306.CrossRefGoogle Scholar
Lapid, E. M. and Rallis, S., ‘On the local factors of representations of classical groups’, inAutomorphic Representations, L-Functions and Applications: Progress and Prospects, Ohio State University Mathematics Research Institute, 11 (de Gruyter, Berlin, 2005), 309–359.Google Scholar
Moeglin, C., Vignéras, M.-F. and Waldspurger, J.-L., Correspondances de Howe sur Uncorps p-Adique, Lecture Notes in Mathematics, 1291 (Springer, Berlin, 1987), viii + 163.CrossRefGoogle Scholar
Piatetski-Shapiro, I. and Rallis, S., ‘L-functions for the classical groups’, inModular Forms (Durham, 1983), Ellis Horwood Ser. Mat. Appl: Statist. Oper. Res. (Horwood, Chichester, 1984), 251–261.Google Scholar
Popa, A., ‘Central values of Rankin L-series over real quadratic fields’, Compos. Math. 142 (2006), 811–866.CrossRefGoogle Scholar
Prasad, D., ‘Weil representation, Howe duality, and the theta correspondence’, inTheta Functions: from the Classical to the Modern, CRM Proc. Lecture Notes (American Mathematical Society, Providence, RI, 1993), 105–127.CrossRefGoogle Scholar
Rallis, S., ‘On the Howe duality conjecture’, Compos. Math. 51 (1984), 333–399.Google Scholar
Ranga Rao, R., ‘On some explicit formulas in the theory of Weil representations’, Pacific J. Math. 157(2) (1993), 335–371.CrossRefGoogle Scholar
Rohrlich, D., ‘On the L-function of canonical Hecke characters of imaginary quadratic fields’, Duke Math. J. 47(3) (1980), 547–557.CrossRefGoogle Scholar
Saito, H., ‘On Tunnell’s formula for characters of GL(2)’, Compos. Math. 85(1) (1993), 99–108.Google Scholar
Shimura, G., ‘The special values of the zeta functions associated with cusp forms’, Comm. Pure Appl. Math. 29(6) (1976), 783–804.CrossRefGoogle Scholar
Sun, B. and Zhu, C.-B., ‘Conservation relations for local theta correspondence’, J. Amer. Math. Soc. 28(4) (2015), 939–983.CrossRefGoogle Scholar
Tunnell, J., ‘Local 𝜖-factors and characters of GL(2)’, Amer. J. Math. 105(6) (1983), 1277–1307.CrossRefGoogle Scholar
Vilenkin, N. J. and Klimyk, V. U., Representations of Lie Groups and Special Functions, Vol. 1, Mathematics and its Applications (Soviet Ser.), 72 (Kluwer Academic, Dordrecht, 1991).CrossRefGoogle Scholar
Waldspurger, J.-L., ‘Sur les valeurs de certaines fonctions L automorphes en leur centre de symétrie’, Compos. Math. 54(2) (1985), 173–242.Google Scholar
Xue, H., ‘Central values of L-functions over CM fields’, J. Number Theory 122 (2007), 342–378.CrossRefGoogle Scholar
Yang, T., ‘Theta liftings and the $L$-function of elliptic curves’, PhD Thesis, University of Maryland, College Park, 1995, 126 pages, ProQuest LLC.Google Scholar