Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T08:21:07.518Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE STRUCTURE OF GRAPHS WHICH ARE LOCALLY INDISTINGUISHABLE FROM A LATTICE

Part of: Graph theory

Published online by Cambridge University Press:  05 December 2016

ITAI BENJAMINI  and
DAVID ELLIS
ITAI BENJAMINI
Affiliation:
Department of Mathematics, Weizmann Institute of Science, Rehovot 76100, Israel; [email protected]
DAVID ELLIS
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London E1 4NS, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each integer 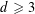$d\geqslant 3$ , we obtain a characterization of all graphs in which the ball of radius 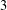$3$ around each vertex is isomorphic to the ball of radius 3 in 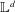$\mathbb{L}^{d}$ , the graph of the 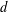$d$ -dimensional integer lattice. The finite, connected graphs with this property have a highly rigid, ‘global’ algebraic structure; they can be viewed as quotient lattices of 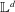$\mathbb{L}^{d}$ in various compact 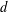$d$ -dimensional orbifolds which arise from crystallographic groups. We give examples showing that ‘radius 3’ cannot be replaced by ‘radius 2’, and that ‘orbifold’ cannot be replaced by ‘manifold’. In the 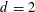$d=2$ case, our methods yield new proofs of structure theorems of Thomassen [‘Tilings of the Torus and Klein bottle and vertex-transitive graphs on a fixed surface’, Trans. Amer. Math. Soc.323 (1991), 605–635] and of Márquez et al. [‘Locally grid graphs: classification and Tutte uniqueness’, Discrete Math.266 (2003), 327–352], and also yield short, ‘algebraic’ restatements of these theorems. Our proofs use a mixture of techniques and results from combinatorics, geometry and group theory.

MSC classification

Primary: 05C75: Structural characterization of families of graphs
Secondary: 05C10: Planar graphs; geometric and topological aspects of graph theory
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e31
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Ballman, W. and Brin, M., ‘Polygonal complexes and combinatorial group theory’, Geom. Dedicata 50 (1994), 165–191.Google Scholar
Benjamini, I., ‘Coarse geometry and randomness’, inLecture notes from the 41st Probability Summer School held in Saint-Flour, 2011, Lecture Notes in Mathematics (Springer, New York, 2013), 2100.Google Scholar
Bieberbach, L., ‘Über die Bewegungsgruppen der Euklidischen Räume I’, Math. Ann. 70 (1911), 297–336.Google Scholar
Bieberbach, L., ‘Über die Bewegungsgruppen der Euklidischen Räume II’, Math. Ann. 72 (1912), 400–412.Google Scholar
Bollobás, B., ‘A probabilistic proof of an asymptotic formula for the number of labelled regular graphs’, Preprint Series, Matematisk Institut, Aarhus Universitet, 1979.Google Scholar
Bollobás, B., ‘A probabilistic proof of an asymptotic formula for the number of labelled regular graphs’, Eur. J. Combin. 1 (1980), 311–316.Google Scholar
Bollobás, B., ‘The asymptotic number of unlabelled d-regular graphs’, J. Lond. Math. Soc. (2) 26 (1982), 201–206.Google Scholar
Brown, M. and Connelly, R., ‘On graphs with a constant link, II’, Discrete Math. 11 (1975), 199–232.Google Scholar
Bugata, P., Horňák, M. and Jendrol, S., ‘On graphs with given neighbourhoods’, Casopis pro pestovani matermatiky 2 (1989), 146–154.Google Scholar
Charlap, L. S., Bieberbach Groups and Flat Manifolds (Springer, New York, 1986).Google Scholar
Csaba, B., Kühn, D., Lo, A., Osthus, D. and Treglown, A., ‘Proof of the 1-factorization and Hamilton decomposition conjectures’, Mem. Amer. Math. Soc. 244(1154) (2016).Google Scholar
Davis, M. W., ‘Lectures on Orbifolds and reflection groups’, inAdvanced Lectures in Mathematics, Volume XVI: Transformation Groups and Moduli Spaces of Curves (eds. Ji, L. and Yau, S.-T.) (International Press, Somerville, MA, USA /Higher Education Press, Beijing, China, 2011), Available at http://math.osu.edu/files/08-05-MRI-preprint.pdf.Google Scholar
de la Salle, M. and Tessera, R., ‘Characterizing a vertex-transitive graph by a large ball’, Preprint, 2015, arXiv:1508.02247.Google Scholar
Doyen, J., Hubaud, X. and Reynnert, U., ‘Finite graphs with isomorphic neighbourhoods,’, inProblèmes Combinatoires et Théorie des Graphes (Colloque C.N.R.S., Orsay, 1976).Google Scholar
Gross, J. L. and Tucker, T. W., Topological Graph Theory (Wiley, New York, 1987).Google Scholar
Hall, J. and Shult, E. E., ‘Locally cotriangular graphs’, Geom. Dedicata 18 (1985), 113–159.Google Scholar
Hatcher, A., Algebraic Topology (Cambridge University Press, Cambridge, UK, 2002).Google Scholar
Hell, P., ‘Graphs with given neighbourhoods’, inProblèmes Combinatoires et Théorie des Graphes (Proc. Coll. Int. C.N.R.S., Orsay, 1976), 219–223.Google Scholar
Hoory, S., ‘On graphs of high girth’, PhD thesis, Hebrew University of Jerusalem, 2002.Google Scholar
Kim, J. H., Sudakov, B. and Vu, V. H., ‘On the asymmetry of random regular graphs and random graphs’, Random Structures Algorithms 21 (2002), 216–224.Google Scholar
Lazebnik, F., Ustimenko, V. A. and Woldar, A. J., ‘A new series of dense graphs of high girth’, Bull. Amer. Math. Soc. (N.S.) 32 (1995), 73–79.Google Scholar
Lubotzsky, A., Phillips, R. and Sarnak, P., ‘Ramanujan graphs’, Combinatorica 8 (1988), 261–277.Google Scholar
Kwak, J. H. and Nedela, R., Graphs and their Coverings, Lecture Notes Series, 17 (Combinatorial and Computational Mathematics Center, POSTECH, Pohang, 2005), Available at http://www.savbb.sk/∼nedela/graphcov.pdf.Google Scholar
Márquez, A., de Mier, A., Noy, M. and Revuelta, M. P., ‘Locally grid graphs: classification and Tutte uniqueness’, Discrete Math. 266 (2003), 327–352.Google Scholar
McKay, B. D. and Wormald, N., ‘Automorphisms of random graphs with specified vertices’, Combinatorica 4 (1984), 325–338.Google Scholar
Nedela, R., ‘Covering projections of graphs preserving links of vertices and edges’, Discrete Math. 134 (1994), 111–124.Google Scholar
Nedela, R., ‘Covering spaces of locally homogeneous graphs’, Discrete Math. 121 (1993), 177–188.Google Scholar
Sedlaček, J., ‘Local properties of graphs’, Casopis pro pestovani matermatiky 106 (1981), 290–298.Google Scholar
Światkowski, J., ‘Trivalent polygonal complexes of nonpositive curvature and platonic symmetry’, Geom. Dedicata 70 (1998), 87–110.Google Scholar
Thom, R., ‘Espaces fibrés en sphères et carrés de Steenrod’, Ann. Sci. Éc. Norm. Supér. (4) 69 (1952), 109–182.Google Scholar
Thomassen, C., ‘Tilings of the Torus and Klein bottle and vertex-transitive graphs on a fixed surface’, Trans. Amer. Math. Soc. 323 (1991), 605–635.Google Scholar
Thurston, W., ‘Lectures on orbifolds’, inThe Geometry and Topology of 3-Manifolds Ch. 13, unpublished manuscript, available at http://library.msri.org/books/gt3m/PDF/13.pdf.Google Scholar
Tits, J., ‘A local approach to buildings’, inThe Geometric Vein: The Coxeter Festschrift (Springer, New York, 1981), 519–547.Google Scholar
Tits, J., Buildings of Spherical type and Finite BN-pairs, Lecture Notes in Mathematics, 386 (Springer, New York, 1974).Google Scholar
Weetman, G., ‘A construction of locally homogeneous graphs’, J. Lond. Math. Soc. (2) 50 (1994), 68–86.Google Scholar
Wise, D. T., ‘Non-positively curved square complexes, aperiodic tilings, and non-residually finite groups’, PhD Thesis, Princeton University, 1996.Google Scholar
Wormald, N., ‘Some problems in the enumeration of labelled graphs’, PhD thesis, University of Newcastle, 1978.Google Scholar