Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T01:16:43.420Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE IRREDUCIBLE COMPONENTS OF SOME CRYSTALLINE DEFORMATION RINGS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  24 April 2020

ROBIN BARTLETT
ROBIN BARTLETT*
Affiliation:
Max Planck Institute for Mathematics, Germany; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We adapt a technique of Kisin to construct and study crystalline deformation rings of 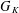$G_{K}$ for a finite extension 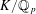$K/\mathbb{Q}_{p}$. This is done by considering a moduli space of Breuil–Kisin modules, satisfying an additional Galois condition, over the unrestricted deformation ring. For 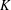$K$ unramified over 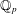$\mathbb{Q}_{p}$ and Hodge–Tate weights in 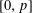$[0,p]$, we study the geometry of this space. As a consequence, we prove that, under a mild cyclotomic-freeness assumption, all crystalline representations of an unramified extension of 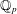$\mathbb{Q}_{p}$, with Hodge–Tate weights in 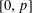$[0,p]$, are potentially diagonalizable.

MSC classification

Primary: 11F80: Galois representations
Secondary: 11F33: Congruences for modular and $p$-adic modular forms
Type
Number Theory
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e22
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2020

References

Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., ‘Potential automorphy and change of weight’, Ann. of Math. (2) 179(2) (2014), 501–609.CrossRefGoogle Scholar
Bartlett, R., ‘Inertial and Hodge–Tate weights of crystalline representations’, Math. Ann. 376 (2020), 645–681.CrossRefGoogle Scholar
Bartlett, R., ‘Potentially diagonalisable lifts with controlled Hodge–Tate weights’ Preprint, 2018, arXiv:1812.02042.Google Scholar
Bartlett, R., ‘Potential diagonalisability of pseudo-Barsotti–Tate representations’, Preprint, 2020, arXiv:2001.08660.Google Scholar
Bhatt, B., Morrow, M. and Scholze, P., ‘Integral p-adic Hodge theory’, Publ. Math. Inst. Hautes Études Sci. 128 (2018), 219–397.CrossRefGoogle Scholar
Bourbaki, N., Éléments de mathématique. Fascicule XXVIII. Algèbre commutative. Chapitre 3: Graduations, filtrations et topologies. Chapitre 4: Idéaux premiers associés et décomposition primaire. Actualités Scientifiques et Industrielles, No. 1293. Hermann, Paris, 1961.Google Scholar
Breuil, C. and Mézard, A., ‘Multiplicités modulaires et représentations de GL2(Zp) et de Gal(Qp/Qp) en l = p’, Duke Math. J. 115(2) (2002), 205–310. With an appendix by Guy Henniart.Google Scholar
Colmez, P., ‘Théorie d’Iwasawa des représentations de de Rham d’un corps local’, Ann. of Math. (2) 148(2) (1998), 485–571.CrossRefGoogle Scholar
Fontaine, J.-M., ‘Représentations p-adiques des corps locaux. I’, inThe Grothendieck Festschrift, Vol. II, Progress in Mathematics, 87 (Birkhäuser Boston, Boston, MA, 1990), 249–309.Google Scholar
Fontaine, J.-M., ‘Le corps des périodes p-adiques’, Astérisque 223 (1994), 59–111. With an appendix by Pierre Colmez, Périodes $p$-adiques (Bures-sur-Yvette, 1988).Google Scholar
Gao, H., ‘Crystalline liftings and weight part of Serre’s conjecture’, Israel J. Math 221(1) (2017), 117–164.CrossRefGoogle Scholar
Gao, H., ‘Breuil–Kisin modules and integral $p$-adic Hodge theory’, Preprint, 2019, arXiv:1905.08555.Google Scholar
Gao, H. and Liu, T., ‘A note on potential diagonalizability of crystalline representations’, Math. Ann. 360(1–2) (2014), 481–487.CrossRefGoogle Scholar
Gee, T., ‘A modularity lifting theorem for weight two Hilbert modular forms’, Math. Res. Lett. 13(5–6) (2006), 805–811.CrossRefGoogle Scholar
Gee, T. and Kisin, M., ‘The Breuil–Mézard conjecture for potentially Barsotti–Tate representations’, Forum Math. Pi 2, e1 (2014), 56.CrossRefGoogle Scholar
Gee, T., Liu, T. and Savitt, D., ‘The Buzzard–Diamond–Jarvis conjecture for unitary groups’, J. Amer. Math. Soc. 27(2) (2014), 389–435.CrossRefGoogle Scholar
Gee, T., Liu, T. and Savitt, D., ‘The weight part of Serre’s conjecture for GL(2)’, Forum Math. Pi 3 e2 (2015).CrossRefGoogle Scholar
Grothendieck, A., ‘Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I’, Inst. Hautes Études Sci. Publ. Math. 11 (1961), 167.Google Scholar
Grothendieck, A., ‘Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV’, Inst. Hautes Études Sci. Publ. Math. 32 (1967), 361.Google Scholar
Kisin, M., ‘Crystalline representations and F-crystals’, inAlgebraic Geometry and Number Theory, Progress in Mathematics, 253 (Birkhäuser Boston, Boston, MA, 2006), 459–496.CrossRefGoogle Scholar
Kisin, M., ‘Potentially semi-stable deformation rings’, J. Amer. Math. Soc. 21(2) (2008), 513–546.CrossRefGoogle Scholar
Kisin, M., ‘Moduli of finite flat group schemes, and modularity’, Ann. of Math. (2) 170(3) (2009), 1085–1180.CrossRefGoogle Scholar
Kisin, M., ‘The Fontaine–Mazur conjecture for GL2’, J. Amer. Math. Soc. 22(3) (2009), 641–690.CrossRefGoogle Scholar
Kisin, M., ‘Integral models for Shimura varieties of abelian type’, J. Amer. Math. Soc. 23(4) (2010), 967–1012.CrossRefGoogle Scholar
Liu, T., ‘The correspondence between Barsotti–Tate groups and Kisin modules when p = 2’, J. Théor. Nombres Bordeaux 25(3) (2013), 661–676.CrossRefGoogle Scholar
Ozeki, Y., ‘Full faithfulness theorem for torsion crystalline representations’, New York J. Math. 20 (2014), 1043–1061.Google Scholar
Sander, F., ‘Hilbert–Samuel multiplicities of certain deformation rings’, Math. Res. Lett. 21(3) (2014), 605–615.CrossRefGoogle Scholar
The Stacks Project Authors. Stacks Project. http://stacks.math.columbia.edu, 2017.Google Scholar
Wang, X., ‘Weight elimination in two dimensions when $p=2$’, Preprint, 2017, arXiv:1711.09035.Google Scholar