Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T06:07:16.202Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE HARD SPHERE MODEL AND SPHERE PACKINGS IN HIGH DIMENSIONS

Part of: Discrete geometry Equilibrium statistical mechanics

Published online by Cambridge University Press:  14 January 2019

MATTHEW JENSSEN ,
FELIX JOOS  and
WILL PERKINS
MATTHEW JENSSEN
Affiliation:
Mathematics Institute, University of Oxford, UK; [email protected]
FELIX JOOS
Affiliation:
School of Mathematics, University of Birmingham, UK; [email protected]
WILL PERKINS
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a lower bound on the entropy of sphere packings of 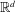$\mathbb{R}^{d}$ of density 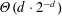$\unicode[STIX]{x1D6E9}(d\cdot 2^{-d})$. The entropy measures how plentiful such packings are, and our result is significantly stronger than the trivial lower bound that can be obtained from the mere existence of a dense packing. Our method also provides a new, statistical-physics-based proof of the 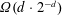$\unicode[STIX]{x1D6FA}(d\cdot 2^{-d})$ lower bound on the maximum sphere packing density by showing that the expected packing density of a random configuration from the hard sphere model is at least 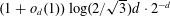$(1+o_{d}(1))\log (2/\sqrt{3})d\cdot 2^{-d}$ when the ratio of the fugacity parameter to the volume covered by a single sphere is at least 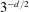$3^{-d/2}$. Such a bound on the sphere packing density was first achieved by Rogers, with subsequent improvements to the leading constant by Davenport and Rogers, Ball, Vance, and Venkatesh.

MSC classification

Primary: 52C17: Packing and covering in $n$ dimensions
Secondary: 82B21: Continuum models (systems of particles, etc.)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e1
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Ajtai, M., Komlós, J. and Szemerédi, E., ‘A note on Ramsey numbers’, J. Combin. Theory Ser. A 29 (1980), 354–360.Google Scholar
Ball, K., ‘A lower bound for the optimal density of lattice packings’, Int. Math. Res. Not. IMRN 10 (1992), 217–221.Google Scholar
Charbonneau, P., Kurchan, J., Parisi, G., Urbani, P. and Zamponi, F., ‘Glass and jamming transitions: from exact results to finite-dimensional descriptions’, Annu. Rev. Condens. Matter Phys. 8 (2017), 265–288.Google Scholar
Cohn, H., ‘Packing, coding, and ground states’. Park City Mathematics Institute Lecture Notes, available at arXiv:1603.05202, 2016.Google Scholar
Cohn, H., ‘A conceptual breakthrough in sphere packing’, Notices Amer. Math. Soc. 64 (2017), 102–115.Google Scholar
Cohn, H., Kumar, A., Miller, S. D., Radchenko, D. and Viazovska, M., ‘The sphere packing problem in dimension 24’, Ann. of Math. (2) 185 (2017), 1017–1033.Google Scholar
Cohn, H. and Zhao, Y., ‘Sphere packing bounds via spherical codes’, Duke Math. J. 163 (2014), 1965–2002.Google Scholar
Conway, J. H. and Sloane, N. J. A., Sphere Packings, Lattices and Groups, Vol. 290, 3rd edn, (Springer, New York, 1999).Google Scholar
Davenport, H. and Rogers, C. A., ‘Hlawka’s theorem in the geometry of numbers’, Duke Math. J. 14 (1947), 367–375.Google Scholar
Davies, E., Jenssen, M., Perkins, W. and Roberts, B., ‘Independent sets, matchings, and occupancy fractions’, J. Lond. Math. Soc. (2) 96.1 (2017), 47–66.Google Scholar
Davies, E., Jenssen, M., Perkins, W. and Roberts, B., ‘On the average size of independent sets in triangle-free graphs’, Proc. Amer. Math. Soc. 146 (2018), 111–124.Google Scholar
Diaconis, P., Lebeau, G. and Michel, L., ‘Geometric analysis for the Metropolis algorithm on Lipschitz domains’, Invent. Math. 185 (2011), 239–281.Google Scholar
Fernández, R., Procacci, A. and Scoppola, B., ‘The analyticity region of the hard sphere gas. Improved bounds’, J. Stat. Phys. 5 (2007), 1139–1143.Google Scholar
Frisch, H. L. and Percus, J. K., ‘High dimensionality as an organizing device for classical fluids’, Phys. Rev. E 60(3) (1999), 2942–2948.Google Scholar
Hales, T. C., ‘A proof of the Kepler conjecture’, Ann. of Math. (2) 162(3) (2005), 1065–1185.Google Scholar
Hayes, T. P. and Moore, C., ‘Lower bounds on the critical density in the hard disk model via optimized metrics’. Preprint, 2014, arXiv:1407.1930.Google Scholar
Hofer-Temmel, C., ‘Disagreement percolation for the hard-sphere model’. Preprint, 2015,arXiv:1507.02521.Google Scholar
Jenssen, M., Joos, F. and Perkins, W., ‘On kissing numbers and spherical codes in high dimensions’, Adv. Math. 335 (2018), 307–321.Google Scholar
Jiang, T. and Vardy, A., ‘Asymptotic improvement of the Gilbert–Varshamov bound on the size of binary codes’, IEEE Trans. Inform. Theory 50 (2004), 1655–1664.Google Scholar
Kabatjanskiĭ, G. A. and Levenšteĭn, V. I., ‘Bounds for packings on the sphere and in space’, Problemy Peredači Informacii 14 (1978), 3–25.Google Scholar
Kannan, R., Mahoney, M. W. and Montenegro, R., ‘Rapid mixing of several Markov chains for a hard-core model’, inAlgorithms and Computation, Lecture Notes in Comput. Sci., 2906 (Springer, Berlin, 2003), 663–675.Google Scholar
Krivelevich, M., Litsyn, S. and Vardy, A., ‘A lower bound on the density of sphere packings via graph theory’, Int. Math. Res. Not. IMRN 2004(43) (2004), 2271–2279.Google Scholar
Löwen, H., ‘Fun with hard spheres’, inStatistical Physics and Spatial Statistics (Springer, Berlin, 2000), 295–331.Google Scholar
Mase, S., Møller, J., Stoyan, D., Waagepetersen, R. P. and Döge, G., ‘Packing densities and simulated tempering for hard core Gibbs point processes’, Ann. Inst. Statist. Math. 53(4) (2001), 661–680.Google Scholar
Parisi, G. and Zamponi, F., ‘Mean-field theory of hard sphere glasses and jamming’, Rev. Mod. Phys. 82(1) (2010), 789–845.Google Scholar
Pulvirenti, E. and Tsagkarogiannis, D., ‘Cluster expansion in the canonical ensemble’, Comm. Math. Phys. 316(2) (2012), 289–306.Google Scholar
Radin, C. and Sadun, L., ‘Structure of the hard sphere solid’, Phys. Rev. Lett. 94(1)015502 (2005).Google Scholar
Richthammer, T., ‘Translation-invariance of two-dimensional Gibbsian point processes’, Comm. Math. Phys. 274(1) (2007), 81–122.Google Scholar
Rogers, C. A., ‘Existence theorems in the geometry of numbers’, Ann. of Math. (2) 48 (1947), 994–1002.Google Scholar
Rogers, C. A., Packing and Covering, (Cambridge University Press, Cambridge, 1964).Google Scholar
Ruelle, D., Statistical Mechanics: Rigorous Results, (Imperial College Press and World Scientific, London, 1999).Google Scholar
Shearer, J. B., ‘A note on the independence number of triangle-free graphs’, Discrete Math. 46 (1983), 83–87.Google Scholar
Siegel, C. L., ‘A mean value theorem in geometry of numbers’, Ann. of Math. (2) 46 (1945), 340–347.Google Scholar
Torquato, S. and Stillinger, F. H., ‘New conjectural lower bounds on the optimal density of sphere packings’, Exp. Math. 15(3) (2006), 307–331.Google Scholar
Vance, S., ‘Improved sphere packing lower bounds from Hurwitz lattices’, Adv. Math. 227 (2011), 2144–2156.Google Scholar
Venkatesh, A., ‘A note on sphere packings in high dimension’, Int. Math. Res. Not. IMRN 2013(7) (2013), 1628–1642.Google Scholar
Viazovska, M. S., ‘The sphere packing problem in dimension 8’, Ann. of Math. (2) 185 (2017), 991–1015.Google Scholar