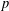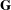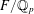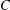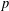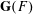Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Anastassiades, Christos
and
Thorne, Jack A.
2022.
RAISING THE LEVEL OF AUTOMORPHIC REPRESENTATIONS OF OF UNITARY TYPE.
Journal of the Institute of Mathematics of Jussieu,
Vol. 21,
Issue. 4,
p.
1421.