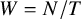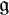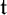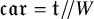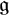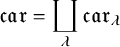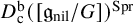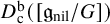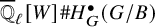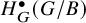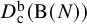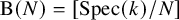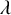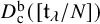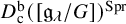1 Introduction
Let G be a connected reductive algebraic group over an algebraic closure k of a finite field. Let T be a maximal torus of G, and let B be the Borel subgroup of G containing T. We denote by N the normalizer of T in G, and we let
![]() $W=N/T$
be the Weyl group of G. We denote by
$W=N/T$
be the Weyl group of G. We denote by
![]() ${\mathfrak {g}}$
,
${\mathfrak {g}}$
,
![]() ${\mathfrak {t}}$
, and
${\mathfrak {t}}$
, and
![]() ${\mathfrak {b}}$
the Lie algebras of G, T and B, respectively, and we denote by
${\mathfrak {b}}$
the Lie algebras of G, T and B, respectively, and we denote by
![]() ${\mathfrak {g}}_{\mathrm {nil}}$
the nilpotent cone of
${\mathfrak {g}}_{\mathrm {nil}}$
the nilpotent cone of
![]() ${\mathfrak {g}}$
.
${\mathfrak {g}}$
.
In [Reference Rider17], Rider considered the triangulated subcategory
![]() $D_{\mathrm {c}}^{\mathrm {b}}([{\mathfrak {g}}_{\mathrm {nil}}/G])^{\mathrm {Spr}}$
of
$D_{\mathrm {c}}^{\mathrm {b}}([{\mathfrak {g}}_{\mathrm {nil}}/G])^{\mathrm {Spr}}$
of
![]() $D_{\mathrm {c}}^{\mathrm {b}}([{\mathfrak {g}}_{\mathrm {nil}}/G])$
generated by the direct summand of the Springer sheaf. She proved that it is equivalent to the derived category of finitely generated dg modules over the smash product algebra
$D_{\mathrm {c}}^{\mathrm {b}}([{\mathfrak {g}}_{\mathrm {nil}}/G])$
generated by the direct summand of the Springer sheaf. She proved that it is equivalent to the derived category of finitely generated dg modules over the smash product algebra
![]() ${\overline {\mathbb {Q}}_{\ell }}[W]\# H^{\bullet }_G(G/B)$
, where
${\overline {\mathbb {Q}}_{\ell }}[W]\# H^{\bullet }_G(G/B)$
, where
![]() $H^{\bullet }_G(G/B)$
is the G-equivariant cohomology of the flag variety (see also [Reference Li12] for a similar result).
$H^{\bullet }_G(G/B)$
is the G-equivariant cohomology of the flag variety (see also [Reference Li12] for a similar result).
We denote by
![]() $\mathrm {B}(N)=[\mathrm {Spec}(k)/N]$
the classifying stack of N-torsors. Rider’s result can be then reformulated as an equivalence of categories between
$\mathrm {B}(N)=[\mathrm {Spec}(k)/N]$
the classifying stack of N-torsors. Rider’s result can be then reformulated as an equivalence of categories between
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathrm {B}(N))$
and
$D_{\mathrm {c}}^{\mathrm {b}}(\mathrm {B}(N))$
and
![]() $D_{\mathrm {c}}^{\mathrm {b}}([{\mathfrak {g}}_{\mathrm {nil}}/G])^{\mathrm {Spr}}$
. The aim of this paper is to construct this equivalence via a cohomological correspondence between
$D_{\mathrm {c}}^{\mathrm {b}}([{\mathfrak {g}}_{\mathrm {nil}}/G])^{\mathrm {Spr}}$
. The aim of this paper is to construct this equivalence via a cohomological correspondence between
![]() $\mathrm {B}(N)$
and
$\mathrm {B}(N)$
and
![]() $[{\mathfrak {g}}_{\mathrm {nil}}/G]$
in the spirit of Lusztig induction. Namely, we construct a complex
$[{\mathfrak {g}}_{\mathrm {nil}}/G]$
in the spirit of Lusztig induction. Namely, we construct a complex
![]() ${\overline {{\mathcal {N}}}}_{\mathrm {nil}}$
on
${\overline {{\mathcal {N}}}}_{\mathrm {nil}}$
on
![]() $\mathrm {B}(N)\times [{\mathfrak {g}}_{\mathrm {nil}}/G]$
, such that the functor
$\mathrm {B}(N)\times [{\mathfrak {g}}_{\mathrm {nil}}/G]$
, such that the functor
is an equivalence of categories, where
![]() $\mathrm {pr}_1$
and
$\mathrm {pr}_1$
and
![]() $\mathrm {pr}_2$
are the two obvious projections.
$\mathrm {pr}_2$
are the two obvious projections.
Let us remark that
![]() $\mathrm {B}(N)$
and
$\mathrm {B}(N)$
and
![]() $[{\mathfrak {g}}_{\mathrm {nil}}/G]$
are the zero fibres of the canonical maps
$[{\mathfrak {g}}_{\mathrm {nil}}/G]$
are the zero fibres of the canonical maps
where
In this paper we consider more generally the analogous equivalences above the strata of the natural stratification
where
![]() $\mathfrak {L}$
is the set of G-conjugacy classes of Levi subgroups (of parabolic subgroups) of G.
$\mathfrak {L}$
is the set of G-conjugacy classes of Levi subgroups (of parabolic subgroups) of G.
We consider the quotient stacks
with respect to the adjoint actions
![]() $\mathrm {Ad}$
(which is trivial for T), and we denote by
$\mathrm {Ad}$
(which is trivial for T), and we denote by
![]() $\pi :\mathcal {T}\rightarrow {\overline {\mathcal {T}}}$
the induced map. Notice that our stacks are algebraic stacks over
$\pi :\mathcal {T}\rightarrow {\overline {\mathcal {T}}}$
the induced map. Notice that our stacks are algebraic stacks over
![]() $\mathfrak {car}$
.
$\mathfrak {car}$
.
We consider the following commutative diagram:

where q is induced by the projection
![]() ${\mathfrak {b}}\rightarrow {\mathfrak {t}}$
, and p is induced by the inclusion
${\mathfrak {b}}\rightarrow {\mathfrak {t}}$
, and p is induced by the inclusion
![]() ${\mathfrak {b}}\subset {\mathfrak {g}}$
.
${\mathfrak {b}}\subset {\mathfrak {g}}$
.
We put
The Lusztig induction and restriction functors are defined by
 $$ \begin{align*} &\mathrm{Ind}:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{T})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}),\,\,\,\,\,K\mapsto p_*q^!K=\mathrm{pr}_{\mathcal{G}\, *}\underline{\mathrm{ Hom}}\left({\mathcal{N}},\mathrm{pr}_{\mathcal{T}}^!(K)\right)\\ &\mathrm{Res}:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{T}),\,\,\,\,\, K\mapsto q_!p^*K=\mathrm{pr}_{\mathcal{T}\, !}\left({\mathcal{N}}\otimes\mathrm{pr}_{\mathcal{G}}^*(K)\right) \end{align*} $$
$$ \begin{align*} &\mathrm{Ind}:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{T})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}),\,\,\,\,\,K\mapsto p_*q^!K=\mathrm{pr}_{\mathcal{G}\, *}\underline{\mathrm{ Hom}}\left({\mathcal{N}},\mathrm{pr}_{\mathcal{T}}^!(K)\right)\\ &\mathrm{Res}:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{T}),\,\,\,\,\, K\mapsto q_!p^*K=\mathrm{pr}_{\mathcal{T}\, !}\left({\mathcal{N}}\otimes\mathrm{pr}_{\mathcal{G}}^*(K)\right) \end{align*} $$
For a stack
![]() $\mathcal {X}$
over
$\mathcal {X}$
over
![]() $\mathfrak {car}$
, we put
$\mathfrak {car}$
, we put
We prove the following result (see Theorem 5.1).
Theorem 1.1 (Descent).
For
![]() $\lambda \in \mathfrak {L}$
, the restriction
$\lambda \in \mathfrak {L}$
, the restriction
![]() ${\mathcal {N}}_{\lambda }$
of
${\mathcal {N}}_{\lambda }$
of
![]() ${\mathcal {N}}$
to
${\mathcal {N}}$
to
![]() $(\mathcal {T}\times _{\mathfrak {car}}\mathcal {G})_{\lambda }$
descends to
$(\mathcal {T}\times _{\mathfrak {car}}\mathcal {G})_{\lambda }$
descends to
![]() ${\overline {{\mathcal {N}}}}_{\lambda }$
on
${\overline {{\mathcal {N}}}}_{\lambda }$
on
![]() $({\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G})_{\lambda }$
.
$({\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G})_{\lambda }$
.
To prove the existence of
![]() ${\overline {{\mathcal {N}}}}_{\lambda }$
, we regard the complex
${\overline {{\mathcal {N}}}}_{\lambda }$
, we regard the complex
![]() $(q_{\lambda },p_{\lambda })_!{\overline {\mathbb {Q}}_{\ell }}$
, (where
$(q_{\lambda },p_{\lambda })_!{\overline {\mathbb {Q}}_{\ell }}$
, (where
![]() $(q_{\lambda },p_{\lambda })$
is obtained from
$(q_{\lambda },p_{\lambda })$
is obtained from
![]() $(q,p)$
by base change) as the outcome of a Postnikov diagram, which descends in a natural way to a Postnikov diagram on
$(q,p)$
by base change) as the outcome of a Postnikov diagram, which descends in a natural way to a Postnikov diagram on
![]() $({\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G})_{\lambda }$
using weight arguments. The complex
$({\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G})_{\lambda }$
using weight arguments. The complex
![]() ${\overline {{\mathcal {N}}}}_{\lambda }$
is then defined as the outcome of the descended Postnikov diagram.
${\overline {{\mathcal {N}}}}_{\lambda }$
is then defined as the outcome of the descended Postnikov diagram.
Remark 1.2.
-
(1) As a particular case, the restriction of
 ${\mathcal {N}}$
to
${\mathcal {N}}$
to
 $\mathrm {B}(T)\times [{\mathfrak {g}}_{\mathrm {nil}}/G]$
descends to a complex
$\mathrm {B}(T)\times [{\mathfrak {g}}_{\mathrm {nil}}/G]$
descends to a complex
 ${\overline {{\mathcal {N}}}}_{\mathrm { nil}}$
on
${\overline {{\mathcal {N}}}}_{\mathrm { nil}}$
on
 $\mathrm {B}(N)\times [{\mathfrak {g}}_{\mathrm {nil}}/G]$
.
$\mathrm {B}(N)\times [{\mathfrak {g}}_{\mathrm {nil}}/G]$
. -
(2) As noticed by S. Gunningham [Reference Gunningham6], the functor
 $\mathrm {Res}$
depends on the choice of the Borel subgroup containing T, and so the restriction of a complex
$\mathrm {Res}$
depends on the choice of the Borel subgroup containing T, and so the restriction of a complex
 $K\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G})$
cannot be W-equivariant. Therefore, we cannot expect that
$K\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G})$
cannot be W-equivariant. Therefore, we cannot expect that
 ${\mathcal {N}}$
descends to
${\mathcal {N}}$
descends to
 ${\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G}$
. In 5.4, we use an old computation of Verdier that explains more directly why
${\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G}$
. In 5.4, we use an old computation of Verdier that explains more directly why
 ${\mathcal {N}}$
cannot descend. Therefore, the above descent result seems to be optimal.
${\mathcal {N}}$
cannot descend. Therefore, the above descent result seems to be optimal. -
(3) We also prove that
 ${\mathcal {N}}$
descends over regular elements, which stratum intersects with all strata above
${\mathcal {N}}$
descends over regular elements, which stratum intersects with all strata above
 $\mathfrak {car}$
(see §5.3).
$\mathfrak {car}$
(see §5.3).
For each
![]() $\lambda \in \mathfrak {L}$
we define the pair of adjoint functors
$\lambda \in \mathfrak {L}$
we define the pair of adjoint functors
![]() $(\mathrm {R}_{\lambda },\mathrm {I}_{\lambda })$
by
$(\mathrm {R}_{\lambda },\mathrm {I}_{\lambda })$
by
 $$ \begin{align*} &\mathrm{R}_{\lambda}:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}_{\lambda})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}({\overline{\mathcal{T}}}_{\lambda}),\hspace{.5cm}K\mapsto\mathrm{pr}_{1!}\left({\overline{{\mathcal{N}}}}_{\lambda}\otimes \mathrm{pr}_2^*(K)\right),\\ &\mathrm{I}_{\lambda}:D_{\mathrm{c}}^{\mathrm{b}}({\overline{\mathcal{T}}}_{\lambda})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}_{\lambda}),\hspace{.5cm}K\mapsto \mathrm{pr}_{2*}\,\underline{\mathrm{ Hom}}\left({\overline{{\mathcal{N}}}}_{\lambda},\mathrm{pr}_1^!(K)\right) \end{align*} $$
$$ \begin{align*} &\mathrm{R}_{\lambda}:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}_{\lambda})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}({\overline{\mathcal{T}}}_{\lambda}),\hspace{.5cm}K\mapsto\mathrm{pr}_{1!}\left({\overline{{\mathcal{N}}}}_{\lambda}\otimes \mathrm{pr}_2^*(K)\right),\\ &\mathrm{I}_{\lambda}:D_{\mathrm{c}}^{\mathrm{b}}({\overline{\mathcal{T}}}_{\lambda})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}_{\lambda}),\hspace{.5cm}K\mapsto \mathrm{pr}_{2*}\,\underline{\mathrm{ Hom}}\left({\overline{{\mathcal{N}}}}_{\lambda},\mathrm{pr}_1^!(K)\right) \end{align*} $$
If
![]() $\mathrm {Ind}_{\lambda }$
and
$\mathrm {Ind}_{\lambda }$
and
![]() $\mathrm {Res}_{\lambda }$
denote the induction and restriction above
$\mathrm {Res}_{\lambda }$
denote the induction and restriction above
![]() $\mathfrak {car}_{\lambda }$
and
$\mathfrak {car}_{\lambda }$
and
![]() $\pi _{\lambda }:\mathcal {T}_{\lambda }\rightarrow {\overline {\mathcal {T}}}_{\lambda }$
the morphism obtained by base change from
$\pi _{\lambda }:\mathcal {T}_{\lambda }\rightarrow {\overline {\mathcal {T}}}_{\lambda }$
the morphism obtained by base change from
![]() $\pi $
, then
$\pi $
, then
For each geometric point c of
![]() $\mathfrak {car}_{\lambda }$
, we have the functor
$\mathfrak {car}_{\lambda }$
, we have the functor
which is compatible by base change with the functors
![]() $\mathrm {Ind}_{\lambda }$
.
$\mathrm {Ind}_{\lambda }$
.
For each geometric point c of
![]() $\mathfrak {car}$
, we define
$\mathfrak {car}$
, we define
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {{Spr}}}$
as the triangulated subcategory of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {{Spr}}}$
as the triangulated subcategory of
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)$
generated by the direct factors of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)$
generated by the direct factors of
![]() $\mathrm {Ind}_c({\overline {\mathbb {Q}}_{\ell }})$
. We then define
$\mathrm {Ind}_c({\overline {\mathbb {Q}}_{\ell }})$
. We then define
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
as the full subcategory of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
as the full subcategory of
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
of complexes K such that
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
of complexes K such that
![]() $K_c\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
for all geometric points c of
$K_c\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
for all geometric points c of
![]() $\mathfrak {car}_{\lambda }$
.
$\mathfrak {car}_{\lambda }$
.
We prove the following theorem (see Theorem 7.7 and Remark 7.6):
Theorem 1.3. The functor
![]() $\mathrm {I}_{\lambda }$
induces an equivalence of categories
$\mathrm {I}_{\lambda }$
induces an equivalence of categories
![]() $D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\lambda })\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
with inverse given by
$D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\lambda })\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
with inverse given by
![]() $\mathrm {R}_{\lambda }$
.
$\mathrm {R}_{\lambda }$
.
If G is of type A with connected center, then
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}=D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
, and so
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}=D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
, and so
![]() $\mathrm {I}_{\lambda }:D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\lambda })\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
is an equivalence of categories with inverse functor
$\mathrm {I}_{\lambda }:D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\lambda })\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
is an equivalence of categories with inverse functor
![]() $\mathrm {R}_{\lambda }$
.
$\mathrm {R}_{\lambda }$
.
Remark 1.4.
-
(1) Notice that the stack
 $\overline {\mathcal {T}_c}$
with
$\overline {\mathcal {T}_c}$
with
 $c=0$
is
$c=0$
is
 $\mathrm {B}(N)=[\mathrm {Spec}(k)/N]$
. It follows from Theorem 1.3 that the category
$\mathrm {B}(N)=[\mathrm {Spec}(k)/N]$
. It follows from Theorem 1.3 that the category
 $D_{\mathrm {c}}^{\mathrm {b}}(\mathrm {B}(N))$
is equivalent to
$D_{\mathrm {c}}^{\mathrm {b}}(\mathrm {B}(N))$
is equivalent to
 $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_0)^{\mathrm {Spr}}$
.
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_0)^{\mathrm {Spr}}$
. -
(2) When
 $\lambda $
is the stratum of semisimple regular elements, the two stacks
$\lambda $
is the stratum of semisimple regular elements, the two stacks
 ${\overline {\mathcal {T}}}_{\lambda }$
and
${\overline {\mathcal {T}}}_{\lambda }$
and
 $\mathcal {G}_{\lambda }$
are isomorphic, and the functors
$\mathcal {G}_{\lambda }$
are isomorphic, and the functors
 $\mathrm {I}_{\lambda }$
,
$\mathrm {I}_{\lambda }$
,
 $\mathrm {R}_{\lambda }$
are the identity functors (see §6.2).
$\mathrm {R}_{\lambda }$
are the identity functors (see §6.2). -
(3) The interested reader may follow the methods of [Reference Beilinson, Bernstein and Deligne2 Reference Beilinson, Bernstein and Deligne, §6] to get similar results over the complex numbers.
Consider the projection
The functor
![]() $s^$
is an equivalence
$s^$
is an equivalence
![]() $\mathcal {M}({\mathfrak {t}})\rightarrow \mathcal {M}(\mathcal {T})$
between the categories of perverse sheaves. Therefore, when working with perverse sheaves, we may work with the diagram
$\mathcal {M}({\mathfrak {t}})\rightarrow \mathcal {M}(\mathcal {T})$
between the categories of perverse sheaves. Therefore, when working with perverse sheaves, we may work with the diagram

which is more convenient, as the kernel
![]() $(q',p)_!{\overline {\mathbb {Q}}_{\ell }}$
is the intersection cohomology complex of
$(q',p)_!{\overline {\mathbb {Q}}_{\ell }}$
is the intersection cohomology complex of
![]() ${\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}$
, and so it descends naturally to
${\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}$
, and so it descends naturally to
![]() $[{\mathfrak {t}}/W]\times _{\mathfrak {car}}\mathcal {G}$
. Moreover, by Bezrukavnikov and Yom Din [Reference Bezrukavnikov and Yom Din3], the functor
$[{\mathfrak {t}}/W]\times _{\mathfrak {car}}\mathcal {G}$
. Moreover, by Bezrukavnikov and Yom Din [Reference Bezrukavnikov and Yom Din3], the functor
![]() $\mathrm {Ind}$
and
$\mathrm {Ind}$
and
![]() $\mathrm {Res}$
maps perverse sheaves to perverse sheaves.
$\mathrm {Res}$
maps perverse sheaves to perverse sheaves.
The above factorization of p via
![]() $(q',p)$
and its generalisation in the framework of the generalised Springer correspondence is due to Lusztig (see [Reference Letellier11, Proof of Proposition 5.5.3] for more details and [Reference Lusztig15] for the case where G is not necessarily connected).
$(q',p)$
and its generalisation in the framework of the generalised Springer correspondence is due to Lusztig (see [Reference Letellier11, Proof of Proposition 5.5.3] for more details and [Reference Lusztig15] for the case where G is not necessarily connected).
In §2.9, we define a pair of adjoint functors
![]() ${^p}\mathrm {I}:\mathcal {M}([{\mathfrak {t}}/W])\rightarrow \mathcal {M}(\mathcal {G})$
, and
${^p}\mathrm {I}:\mathcal {M}([{\mathfrak {t}}/W])\rightarrow \mathcal {M}(\mathcal {G})$
, and
![]() ${^p}\mathrm {R}:\mathcal {M}(\mathcal {G})\rightarrow \mathcal {M}([{\mathfrak {t}}/W])$
and we prove the following theorem (see Theorem 7.10).
${^p}\mathrm {R}:\mathcal {M}(\mathcal {G})\rightarrow \mathcal {M}([{\mathfrak {t}}/W])$
and we prove the following theorem (see Theorem 7.10).
Theorem 1.5. The functor
![]() ${^p}\mathrm {I}$
induces an equivalence of categories
${^p}\mathrm {I}$
induces an equivalence of categories
![]() $\mathcal {M}([{\mathfrak {t}}/W])\rightarrow \mathcal {M}(\mathcal {G})^{\mathrm {Spr}}$
with inverse functor
$\mathcal {M}([{\mathfrak {t}}/W])\rightarrow \mathcal {M}(\mathcal {G})^{\mathrm {Spr}}$
with inverse functor
![]() ${^p}\mathrm {R}$
. In particular, if G is of type A with connected center, then
${^p}\mathrm {R}$
. In particular, if G is of type A with connected center, then
![]() $\mathcal {M}(\mathcal {G})^{\mathrm {Spr}}=\mathcal {M}(\mathcal {G})$
, and so the categories
$\mathcal {M}(\mathcal {G})^{\mathrm {Spr}}=\mathcal {M}(\mathcal {G})$
, and so the categories
![]() $\mathcal {M}([{\mathfrak {t}}/W])$
and
$\mathcal {M}([{\mathfrak {t}}/W])$
and
![]() $\mathcal {M}(\mathcal {G})$
are equivalent.
$\mathcal {M}(\mathcal {G})$
are equivalent.
This result is an analogue in the
![]() $\ell $
-adic setting of (a special case of) the main result of S. Gunningham [Reference Gunningham7] in the D-module setting. We were informed by the anonymous referee that, using the result of Bezrukavnikov and Yom Din, the proof of Gunningham works also in the
$\ell $
-adic setting of (a special case of) the main result of S. Gunningham [Reference Gunningham7] in the D-module setting. We were informed by the anonymous referee that, using the result of Bezrukavnikov and Yom Din, the proof of Gunningham works also in the
![]() $\ell $
-adic setting (although this is not published).
$\ell $
-adic setting (although this is not published).
2 Preliminaries
2.1 Postnikov diagrams in triangulated categories
Let
![]() ${\mathcal {D}}$
be a triangulated category. We will need the following lemma:
${\mathcal {D}}$
be a triangulated category. We will need the following lemma:
Lemma 2.1. Consider a diagram in
![]() ${\mathcal {D}}$
${\mathcal {D}}$

where
![]() $(u,v,w)$
and
$(u,v,w)$
and
![]() $(u',v',w')$
are distinguished triangles. Suppose that
$(u',v',w')$
are distinguished triangles. Suppose that
Then there exists a unique morphism
![]() $C\rightarrow C'$
which extends the above diagram into a morphism of distinguished triangles.
$C\rightarrow C'$
which extends the above diagram into a morphism of distinguished triangles.
Proof. Only the unicity needs to be proved (the existence follows from the axioms of a triangulated category). We are thus reduced to prove that if we have a morphism of triangles,

then
![]() $\beta =0$
.
$\beta =0$
.
As
![]() $\beta \circ u=0$
, there exists
$\beta \circ u=0$
, there exists
![]() $\gamma :A\rightarrow C'$
such that
$\gamma :A\rightarrow C'$
such that
![]() $\gamma \circ v=\beta $
. Since
$\gamma \circ v=\beta $
. Since
there exists
![]() $\varepsilon :B\rightarrow A'$
such that
$\varepsilon :B\rightarrow A'$
such that
![]() $v'\circ \gamma =\varepsilon \circ w$
. By assumption,
$v'\circ \gamma =\varepsilon \circ w$
. By assumption,
![]() $\varepsilon =0$
and so
$\varepsilon =0$
and so
![]() $v'\circ \gamma =0$
.
$v'\circ \gamma =0$
.
There exists thus
![]() $\overline {\gamma }:A\rightarrow B'[-1]$
such that
$\overline {\gamma }:A\rightarrow B'[-1]$
such that
![]() $u'\circ \overline {\gamma }=\gamma $
. By assumption, we must have
$u'\circ \overline {\gamma }=\gamma $
. By assumption, we must have
![]() $\overline {\gamma }=0$
, and so
$\overline {\gamma }=0$
, and so
![]() $\gamma =0$
from which we get that
$\gamma =0$
from which we get that
![]() $\beta =0$
.
$\beta =0$
.
A Postnikov diagram
![]() $\Lambda $
[Reference Orlov16] consists of a complex
$\Lambda $
[Reference Orlov16] consists of a complex
in
![]() ${\mathcal {D}}$
, called the base and denoted by
${\mathcal {D}}$
, called the base and denoted by
![]() $\Lambda _b$
, together with a finite sequence of distinguished triangles
$\Lambda _b$
, together with a finite sequence of distinguished triangles
with
![]() $i=1,\dots ,m$
, such that
$i=1,\dots ,m$
, such that
![]() $\partial _i=\alpha _{i-1}\circ d_i$
for all i. We visualize
$\partial _i=\alpha _{i-1}\circ d_i$
for all i. We visualize
![]() $\Lambda $
as
$\Lambda $
as

The length of
![]() $\Lambda $
is the integer m.
$\Lambda $
is the integer m.
The object
![]() $C_m$
will be called the outcome of the Postnikov diagram
$C_m$
will be called the outcome of the Postnikov diagram
![]() $\Lambda $
.
$\Lambda $
.
Notice that if
![]() ${\mathcal {D}}$
is equipped with a nondegenerate t-structure, then we can define the Postnikov diagram
${\mathcal {D}}$
is equipped with a nondegenerate t-structure, then we can define the Postnikov diagram
![]() $\Lambda (K)$
with outcome K for any complex
$\Lambda (K)$
with outcome K for any complex
![]() $K\in {\mathcal {D}}^{[n,n+m]}$
as
$K\in {\mathcal {D}}^{[n,n+m]}$
as


using the distinguished triangles
The construction of
![]() $\Lambda (K)$
is functorial in K.
$\Lambda (K)$
is functorial in K.
Remark 2.2. Given
![]() $K\in {\mathcal {D}}^{[n,n+m]}$
, then
$K\in {\mathcal {D}}^{[n,n+m]}$
, then
![]() $\Lambda (K)$
is the unique (up to a unique isomorphism) Postnikov diagram of the form (2.1) with outcome K such that
$\Lambda (K)$
is the unique (up to a unique isomorphism) Postnikov diagram of the form (2.1) with outcome K such that
for all
![]() $i=1,\dots ,m$
. This follows from [Reference Beilinson, Bernstein and Deligne2, Proposition 1.3.3(ii)].
$i=1,\dots ,m$
. This follows from [Reference Beilinson, Bernstein and Deligne2, Proposition 1.3.3(ii)].
Lemma 2.3. Given
![]() $K\in {\mathcal {D}}^{[n,n+m]}$
, the Postnikov diagram
$K\in {\mathcal {D}}^{[n,n+m]}$
, the Postnikov diagram
![]() $\Lambda (K)$
is the unique one (up a unique isomorphism) that completes the subdiagram
$\Lambda (K)$
is the unique one (up a unique isomorphism) that completes the subdiagram

Proof. By Remark 2.2, it is enough to prove that if we are given a Postnikov diagram of the form (2.1) where
![]() $A_i=P_i[m-n-2i]$
with
$A_i=P_i[m-n-2i]$
with
![]() $P_i$
a perverse sheaf, then
$P_i$
a perverse sheaf, then
![]() $C_i\in {\mathcal {D}}^{[i-(m-n),2i-(m-n)]}$
for all
$C_i\in {\mathcal {D}}^{[i-(m-n),2i-(m-n)]}$
for all
![]() $i=1,\dots ,m$
. The proof goes by recurrence on
$i=1,\dots ,m$
. The proof goes by recurrence on
![]() $m\geq 1$
using the long exact sequence of perverse cohomology.
$m\geq 1$
using the long exact sequence of perverse cohomology.
Lemma 2.4. Assume that we have a Postnikov diagram with the notation as in diagram (2.1) and that for each
![]() $i=0,\dots ,m-2$
, any
$i=0,\dots ,m-2$
, any
![]() $j\geq i+2$
and any
$j\geq i+2$
and any
![]() $k\geq 1$
we have
$k\geq 1$
we have
Then if
![]() $(d^{\prime }_m,d^{\prime }_{m-1},\dots ,d^{\prime }_1)$
is a sequence of arrows
$(d^{\prime }_m,d^{\prime }_{m-1},\dots ,d^{\prime }_1)$
is a sequence of arrows
![]() $d^{\prime }_i:A_i\rightarrow C_{i-1}$
such that
$d^{\prime }_i:A_i\rightarrow C_{i-1}$
such that
![]() $\partial _i=\alpha _{i-1}\circ d^{\prime }_i$
for all i, then
$\partial _i=\alpha _{i-1}\circ d^{\prime }_i$
for all i, then
Proof. We need to prove that
for all
![]() $i=0,\dots ,m-2$
.
$i=0,\dots ,m-2$
.
Since we have a distinguished triangle
we have an exact sequence
By assumption, the right-hand side is
![]() $0$
, and so we are reduced to prove that
$0$
, and so we are reduced to prove that
Repeating the argument as many times as needed, we end up proving that
![]() $\mathrm {Hom}(A_{i+2},C_0[-1-i])=0$
, which follows also from the assumption as
$\mathrm {Hom}(A_{i+2},C_0[-1-i])=0$
, which follows also from the assumption as
![]() $C_0=A_0$
.
$C_0=A_0$
.
Proposition 2.5. Assume given a complex
![]() $\Lambda _b$
in
$\Lambda _b$
in
![]() ${\mathcal {D}}$
${\mathcal {D}}$
and suppose that it satisfies
and
Then the complex (2.4) can be completed in a unique way (up to a unique isomorphism) into a Postnikov diagram
![]() $\Lambda $
in
$\Lambda $
in
![]() ${\mathcal {D}}$
.
${\mathcal {D}}$
.
Proof. The proof goes by induction on
![]() $0\leq r <m$
. If
$0\leq r <m$
. If
![]() $r=0$
, then this is obvious. Suppose that we have proved the proposition up to the rank r. Therefore, we have the complex
$r=0$
, then this is obvious. Suppose that we have proved the proposition up to the rank r. Therefore, we have the complex
![]() $C_r$
. By Lemma 2.4, there exists a unique map
$C_r$
. By Lemma 2.4, there exists a unique map
![]() $d_{r+1}$
such that the following diagram commutes:
$d_{r+1}$
such that the following diagram commutes:

We complete
![]() $d_{r+1}$
into a distinguished triangle
$d_{r+1}$
into a distinguished triangle
Now we notice that
Indeed, the complexes
![]() $C_r$
being successive extensions of the complexes
$C_r$
being successive extensions of the complexes
![]() $A_i$
, with
$A_i$
, with
![]() $i=0,\dots ,r$
, this follows from the assumptions (2.5) and (2.6) .
$i=0,\dots ,r$
, this follows from the assumptions (2.5) and (2.6) .
By Lemma 2.1, such a
![]() $C_{r+1}$
is thus unique (up to a unique isomorphism).
$C_{r+1}$
is thus unique (up to a unique isomorphism).
2.2 Stacks and sheaves: notation and convention
Let k be an algebraic closure of a finite field. In these notes, unless specified, our stacks are k-algebraic stacks of finite type, and quotient stacks are denoted by
![]() $[X/G]$
if G is an algebraic group over k acting a k-scheme X. If
$[X/G]$
if G is an algebraic group over k acting a k-scheme X. If
![]() $X=\mathrm {Spec}(k)$
, we put
$X=\mathrm {Spec}(k)$
, we put
![]() $\mathrm {B}(G)=[X/G]$
.
$\mathrm {B}(G)=[X/G]$
.
For a morphism
![]() $f:\mathcal {X}\rightarrow {\mathcal {Y}}$
of stacks, we have the usual functors
$f:\mathcal {X}\rightarrow {\mathcal {Y}}$
of stacks, we have the usual functors
between derived categories of constructible
![]() ${\overline {\mathbb {Q}}_{\ell }}$
-sheaves (see [Reference Laszlo and Olsson9]).
${\overline {\mathbb {Q}}_{\ell }}$
-sheaves (see [Reference Laszlo and Olsson9]).
Remark 2.6. The fact that
![]() $f^!$
preserves
$f^!$
preserves
![]() $-,+,b$
follows from from our assumption that our stacks are of finite type over a field. Indeed, the statement reduces to the case where
$-,+,b$
follows from from our assumption that our stacks are of finite type over a field. Indeed, the statement reduces to the case where
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() ${\mathcal {Y}}$
are schemes of finite type over a field which is known [Reference Deligne5, Corollary 2.9].
${\mathcal {Y}}$
are schemes of finite type over a field which is known [Reference Deligne5, Corollary 2.9].
We will use freely the properties of these functors (adjunction, projection formula, base change,…). When there is no ambiguity, we will sometimes write
![]() $K|_{\mathcal {X}}$
instead of
$K|_{\mathcal {X}}$
instead of
![]() $f^*(K)$
.
$f^*(K)$
.
Remark 2.7.
-
(i) Notice that if
 $d\in \mathbb {Z}$
is the dimension of a fibre of f whose absolute value is maximal, then
$d\in \mathbb {Z}$
is the dimension of a fibre of f whose absolute value is maximal, then  $$ \begin{align*}f_!:D_{\mathrm{c}}^{]-\infty,n]}(\mathcal{X})\rightarrow D_{\mathrm{c}}^{]-\infty,n+2d]}({\mathcal{Y}}). \end{align*} $$
$$ \begin{align*}f_!:D_{\mathrm{c}}^{]-\infty,n]}(\mathcal{X})\rightarrow D_{\mathrm{c}}^{]-\infty,n+2d]}({\mathcal{Y}}). \end{align*} $$
For instance
 $$ \begin{align*}H_c^i([X/G],{\overline{\mathbb{Q}}_{\ell}})=0\hspace{.5cm} \text{ if }\hspace{.5cm}i> 2(\mathrm{dim}\, X-\mathrm{dim}\, G). \end{align*} $$
$$ \begin{align*}H_c^i([X/G],{\overline{\mathbb{Q}}_{\ell}})=0\hspace{.5cm} \text{ if }\hspace{.5cm}i> 2(\mathrm{dim}\, X-\mathrm{dim}\, G). \end{align*} $$
-
(ii) If f is representable, then
 $f_!$
induces
$f_!$
induces  $$ \begin{align*}f_!:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{X})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}({\mathcal{Y}}). \end{align*} $$
$$ \begin{align*}f_!:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{X})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}({\mathcal{Y}}). \end{align*} $$
-
(iii) If f is smooth with fibres of pure relative dimension d, then [Reference Laszlo and Olsson9, 9.1.2]
 $$ \begin{align*}f^!=f^*[2d](d). \end{align*} $$
$$ \begin{align*}f^!=f^*[2d](d). \end{align*} $$
Except in some rare occasions, we will only need the category
![]() $D_{\mathrm {c}}^{\mathrm {b}}$
.
$D_{\mathrm {c}}^{\mathrm {b}}$
.
We will denote by
![]() $\overline {\mathbb {Q}}_{\ell ,\, \mathcal {X}}$
the constant sheaf on
$\overline {\mathbb {Q}}_{\ell ,\, \mathcal {X}}$
the constant sheaf on
![]() $\mathcal {X}$
. If there are no ambiguities, we will sometimes denote it simply by
$\mathcal {X}$
. If there are no ambiguities, we will sometimes denote it simply by
![]() ${\overline {\mathbb {Q}}_{\ell }}$
to alleviate the notation.
${\overline {\mathbb {Q}}_{\ell }}$
to alleviate the notation.
For two
![]() ${\mathcal {Y}}$
-stacks
${\mathcal {Y}}$
-stacks
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {X}'$
, we define the external tensor product of
$\mathcal {X}'$
, we define the external tensor product of
![]() $K\in D_{\mathrm {c}}^-(\mathcal {X})$
and
$K\in D_{\mathrm {c}}^-(\mathcal {X})$
and
![]() $K'\in D_{\mathrm {c}}^-(\mathcal {X}')$
above
$K'\in D_{\mathrm {c}}^-(\mathcal {X}')$
above
![]() ${\mathcal {Y}}$
as
${\mathcal {Y}}$
as
where
![]() $\mathrm {pr}_1$
and
$\mathrm {pr}_1$
and
![]() $\mathrm {pr}_2$
are the two projections.
$\mathrm {pr}_2$
are the two projections.
We consider the auto-dual perversity p and we denote by
![]() $\mathcal {M}(\mathcal {X})$
the full subcategory of
$\mathcal {M}(\mathcal {X})$
the full subcategory of
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
of perverse sheaves on
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
of perverse sheaves on
![]() $\mathcal {X}$
. Then, if
$\mathcal {X}$
. Then, if
![]() $\mathcal {X}$
is an equidimensional stack with smooth dense open substack
$\mathcal {X}$
is an equidimensional stack with smooth dense open substack
![]() ${\mathcal {U}}$
, the intersection cohomology complex on
${\mathcal {U}}$
, the intersection cohomology complex on
![]() $\mathcal {X}$
with coefficient in a local system
$\mathcal {X}$
with coefficient in a local system
![]() $\mathcal {E}$
on U is denoted by
$\mathcal {E}$
on U is denoted by
![]() ${\mathrm {IC}}_{\mathcal {X}}(\mathcal {E})$
;its restriction to
${\mathrm {IC}}_{\mathcal {X}}(\mathcal {E})$
;its restriction to
![]() ${\mathcal {U}}$
is
${\mathcal {U}}$
is
![]() $\mathcal {E}$
. If
$\mathcal {E}$
. If
![]() $\mathcal {E}={\overline {\mathbb {Q}}_{\ell }}$
, we will simply write
$\mathcal {E}={\overline {\mathbb {Q}}_{\ell }}$
, we will simply write
![]() ${\mathrm {IC}}_{\mathcal {X}}$
instead of
${\mathrm {IC}}_{\mathcal {X}}$
instead of
![]() ${\mathrm {IC}}_{\mathcal {X}}({\overline {\mathbb {Q}}_{\ell }})$
. Recall that
${\mathrm {IC}}_{\mathcal {X}}({\overline {\mathbb {Q}}_{\ell }})$
. Recall that
![]() ${\mathrm {IC}}_{\mathcal {X}}(\mathcal {E})[\mathrm {dim}\,\mathcal {X}]\in \mathcal {M}(\mathcal {X})$
is the image of
${\mathrm {IC}}_{\mathcal {X}}(\mathcal {E})[\mathrm {dim}\,\mathcal {X}]\in \mathcal {M}(\mathcal {X})$
is the image of
where
![]() $j:{\mathcal {U}}\rightarrow \mathcal {X}$
is the inclusion. Recall also that if
$j:{\mathcal {U}}\rightarrow \mathcal {X}$
is the inclusion. Recall also that if
![]() $\mathcal {X}'\rightarrow \mathcal {X}$
is a small resolution of singularities (representable, proper, birational,
$\mathcal {X}'\rightarrow \mathcal {X}$
is a small resolution of singularities (representable, proper, birational,
![]() $\mathcal {X}'$
smooth), then
$\mathcal {X}'$
smooth), then
![]() $f_*{\overline {\mathbb {Q}}_{\ell }}={\mathrm {IC}}_{\mathcal {X}}$
.
$f_*{\overline {\mathbb {Q}}_{\ell }}={\mathrm {IC}}_{\mathcal {X}}$
.
If
![]() $D_{\mathcal {X}}$
denotes the Verdier dual, then
$D_{\mathcal {X}}$
denotes the Verdier dual, then
![]() $D_{\mathcal {X}}({\mathrm {IC}}_{\mathcal {X}}(\mathcal {E}))={\mathrm {IC}}_{\mathcal {X}}(\mathcal {E}^{\vee })[2\mathrm {dim}(\mathcal {X})](\mathrm {dim}(\mathcal {X}))$
, where
$D_{\mathcal {X}}({\mathrm {IC}}_{\mathcal {X}}(\mathcal {E}))={\mathrm {IC}}_{\mathcal {X}}(\mathcal {E}^{\vee })[2\mathrm {dim}(\mathcal {X})](\mathrm {dim}(\mathcal {X}))$
, where
![]() $\mathcal {E}^{\vee }$
denotes the dual local system.
$\mathcal {E}^{\vee }$
denotes the dual local system.
Proposition 2.8. Let
![]() $\mathcal {X}$
be an equidimensional algebraic stack, and let
$\mathcal {X}$
be an equidimensional algebraic stack, and let
![]() ${\mathcal {U}}$
be a dense open smooth substack of
${\mathcal {U}}$
be a dense open smooth substack of
![]() $\mathcal {X}$
. Suppose that we have a short exact sequence
$\mathcal {X}$
. Suppose that we have a short exact sequence
in the category of perverse sheaves on
![]() $\mathcal {X}$
. If both
$\mathcal {X}$
. If both
![]() $A'$
and
$A'$
and
![]() $A"$
are the intermediate extension of their restriction to
$A"$
are the intermediate extension of their restriction to
![]() ${\mathcal {U}}$
, then A is also the intermediate extension of its restriction to
${\mathcal {U}}$
, then A is also the intermediate extension of its restriction to
![]() ${\mathcal {U}}$
.
${\mathcal {U}}$
.
Proof. Let j be the inclusion of
![]() ${\mathcal {U}}$
in
${\mathcal {U}}$
in
![]() $\mathcal {X}$
. From
$\mathcal {X}$
. From
![]() $j_!j^*\rightarrow 1\rightarrow j_*j^*$
and the fact that A is a perverse sheaf, we have a commutative diagram:
$j_!j^*\rightarrow 1\rightarrow j_*j^*$
and the fact that A is a perverse sheaf, we have a commutative diagram:

from which we can identify
![]() $j_{!*}j^*A$
as a subquotient of A. In particular,
$j_{!*}j^*A$
as a subquotient of A. In particular,
It is thus enough to prove that
We have the commutative diagram of perverse sheaves

where the top and bottom horizontal sequences are exact. We thus deduce that the middle sequence is exact at
![]() $A'$
and
$A'$
and
![]() $A"$
and the composition
$A"$
and the composition
![]() $A'\rightarrow A"$
is zero, from which we deduce the inequality (2.7) as
$A'\rightarrow A"$
is zero, from which we deduce the inequality (2.7) as
As we assume that k is the algebraic closure of a finite field and that all our stacks are of finite type, any stack we consider in this paper will be defined over some finite subfield of k.
If
![]() $\mathcal {X}$
is defined over finite subfield
$\mathcal {X}$
is defined over finite subfield
![]() $k_o\subset k$
, we denote by
$k_o\subset k$
, we denote by
![]() $\mathcal {X}_o$
the corresponding
$\mathcal {X}_o$
the corresponding
![]() $k_o$
-structure on
$k_o$
-structure on
![]() $\mathcal {X}$
(if no confusion arises) and we denote by
$\mathcal {X}$
(if no confusion arises) and we denote by
![]() $\mathrm {Frob}_o:\mathcal {X}\rightarrow \mathcal {X}$
the induced geometric Frobenius on
$\mathrm {Frob}_o:\mathcal {X}\rightarrow \mathcal {X}$
the induced geometric Frobenius on
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
Let
![]() $K,K'\in D_{\mathrm {c}}^b(\mathcal {X})$
. We recall that
$K,K'\in D_{\mathrm {c}}^b(\mathcal {X})$
. We recall that
![]() $H_c^i(\mathcal {X},K)$
(resp.
$H_c^i(\mathcal {X},K)$
(resp.
![]() $\mathrm {Ext}^i(K,K')=\mathrm {Hom}(K,K'[i])$
) is said to be pure of weight r if there exists a finite subfield
$\mathrm {Ext}^i(K,K')=\mathrm {Hom}(K,K'[i])$
) is said to be pure of weight r if there exists a finite subfield
![]() $k_o$
of k such that
$k_o$
of k such that
![]() $\mathcal {X}$
and K (resp. K and
$\mathcal {X}$
and K (resp. K and
![]() $K'$
) are defined over
$K'$
) are defined over
![]() $k_o$
, and the eigenvalues of the induced automorphism
$k_o$
, and the eigenvalues of the induced automorphism
![]() $\mathrm {Frob}_o^*$
on
$\mathrm {Frob}_o^*$
on
![]() $H_c^i(\mathcal {X},K)$
(resp.
$H_c^i(\mathcal {X},K)$
(resp.
![]() $\mathrm {Ext}^i(K,K')$
) are algebraic numbers whose complex conjugates are all of absolute value
$\mathrm {Ext}^i(K,K')$
) are algebraic numbers whose complex conjugates are all of absolute value
![]() $|k_o|^{r/2}$
. It is well known that this notion of weight does not depend on the choice of
$|k_o|^{r/2}$
. It is well known that this notion of weight does not depend on the choice of
![]() $k_o$
. In particular, the Tate twist
$k_o$
. In particular, the Tate twist
![]() ${\overline {\mathbb {Q}}_{\ell }}(i)$
makes sense over k.
${\overline {\mathbb {Q}}_{\ell }}(i)$
makes sense over k.
Let
![]() $\mathcal {X}_o$
be a
$\mathcal {X}_o$
be a
![]() $k_o$
-structure on
$k_o$
-structure on
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $K_o, K^{\prime }_o\in D_{\mathrm {c}}^b(\mathcal {X}_o)$
, and let us denote by K and
$K_o, K^{\prime }_o\in D_{\mathrm {c}}^b(\mathcal {X}_o)$
, and let us denote by K and
![]() $K'$
the induced complexes in
$K'$
the induced complexes in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
. Then the following sequence [Reference Beilinson, Bernstein and Deligne2, (5.1.2.5)]
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
. Then the following sequence [Reference Beilinson, Bernstein and Deligne2, (5.1.2.5)]
is exact for all i.
Notice that if
![]() $\mathrm {Ext}^j(K,K')=0$
for odd values of j, then it follows from the above exact sequence that for all i,
$\mathrm {Ext}^j(K,K')=0$
for odd values of j, then it follows from the above exact sequence that for all i,
is an isomorphism.
2.3 Cohomology of
 $\mathrm {B}(T)$
$\mathrm {B}(T)$
Let T be a rank d torus over k. Recall that for any k-scheme S, the category
![]() $\mathrm {B}(T)(S)$
is the category of T-torsors over S, and the algebraic stack
$\mathrm {B}(T)(S)$
is the category of T-torsors over S, and the algebraic stack
![]() $\mathrm {B}(T)$
is of dimension
$\mathrm {B}(T)$
is of dimension
![]() $-d$
.
$-d$
.
The cohomology
![]() $H^{\bullet }(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
is concentrated in nonnegative even degrees, and the morphism
$H^{\bullet }(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
is concentrated in nonnegative even degrees, and the morphism
given by Chern classes induces an isomorphism
As
![]() ${\overline {\mathbb {Q}}_{\ell }}$
-algebras,
${\overline {\mathbb {Q}}_{\ell }}$
-algebras,
![]() $H^{2\bullet }(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
is isomorphic to
$H^{2\bullet }(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
is isomorphic to
![]() $\mathrm {Sym}^{\bullet }\big (X^*(T)\otimes {\overline {\mathbb {Q}}_{\ell }}(-1)\big )$
.
$\mathrm {Sym}^{\bullet }\big (X^*(T)\otimes {\overline {\mathbb {Q}}_{\ell }}(-1)\big )$
.
By duality,
![]() $H_c^{\bullet }(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
is thus concentrated in even degrees
$H_c^{\bullet }(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
is thus concentrated in even degrees
![]() $\leq -2\,\mathrm {dim}(T)$
, and
$\leq -2\,\mathrm {dim}(T)$
, and
![]() $H_c^{2i}(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
is pure of weight
$H_c^{2i}(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
is pure of weight
![]() $2i$
.
$2i$
.
2.4 W-equivariant complexes
Let W be a finite group and a stack
![]() $\mathcal {X}$
. An action of W on a complex
$\mathcal {X}$
. An action of W on a complex
![]() $K\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
is a group homomorphism
$K\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
is a group homomorphism
In this case we define the W-invariant part
![]() $K^W\rightarrow K$
in
$K^W\rightarrow K$
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
of
![]() $(K,\theta )$
as follows.
$(K,\theta )$
as follows.
Notice first that in any additive category, if for some morphism
![]() $e:A\rightarrow A$
, there exist two morphisms
$e:A\rightarrow A$
, there exist two morphisms
![]() $u:A\rightarrow A'$
and
$u:A\rightarrow A'$
and
![]() $v:A'\rightarrow A$
such that
$v:A'\rightarrow A$
such that
![]() $v\circ u=e$
and
$v\circ u=e$
and
![]() $u\circ v=1_{K'}$
(in which case e is an idempotent which is said to be split), then
$u\circ v=1_{K'}$
(in which case e is an idempotent which is said to be split), then
![]() $1-e$
admits a kernel which is v and a cokernel which is u. In particular,
$1-e$
admits a kernel which is v and a cokernel which is u. In particular,
![]() $(A',u,v)$
is unique up to a unique isomorphism and we call it the splitting of e.
$(A',u,v)$
is unique up to a unique isomorphism and we call it the splitting of e.
Since
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
is a triangulated category with bounded t-structure, by the main theorem of [Reference Le and Chen10], every idempotent element e of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
is a triangulated category with bounded t-structure, by the main theorem of [Reference Le and Chen10], every idempotent element e of
![]() $\mathrm {End}(K)$
splits. Considering the indempotent
$\mathrm {End}(K)$
splits. Considering the indempotent
 $$ \begin{align} e=e_K:=\frac{1}{|W|}\sum_{w\in W}\theta(w)\in\mathrm{End}(K),\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} e=e_K:=\frac{1}{|W|}\sum_{w\in W}\theta(w)\in\mathrm{End}(K),\\[-15pt]\nonumber \end{align} $$
we define
![]() $K^W\rightarrow K$
as the kernel of
$K^W\rightarrow K$
as the kernel of
![]() $1-e$
.
$1-e$
.
A W-torsor is a morphism of stacks
![]() $\pi :\mathcal {X}\rightarrow \overline {\mathcal {X}}$
that fits to a cartesian diagram
$\pi :\mathcal {X}\rightarrow \overline {\mathcal {X}}$
that fits to a cartesian diagram

Remark 2.9. (1) A W-torsor
![]() $\pi :\mathcal {X}\rightarrow \overline {\mathcal {X}}$
is thus finite étale representable and for any scheme S and morphism
$\pi :\mathcal {X}\rightarrow \overline {\mathcal {X}}$
is thus finite étale representable and for any scheme S and morphism
![]() $S\rightarrow {\mathcal {Y}}$
, the projection
$S\rightarrow {\mathcal {Y}}$
, the projection
has a natural structure of W-torsor (between schemes).
(2) If
![]() $\pi :\mathcal {X}\rightarrow \overline {\mathcal {X}}$
is a W-torsor, then
$\pi :\mathcal {X}\rightarrow \overline {\mathcal {X}}$
is a W-torsor, then
![]() $\mathcal {X}$
is equipped with a right action of W in the sense of [Reference Romagny18] and conversely, from right action of W on
$\mathcal {X}$
is equipped with a right action of W in the sense of [Reference Romagny18] and conversely, from right action of W on
![]() $\mathcal {X}$
we get a W-torsor by taking the quotient morphism of
$\mathcal {X}$
we get a W-torsor by taking the quotient morphism of
![]() $\mathcal {X}$
by W. However, although this is implicit, we will not use the definition of group actions on stacks or the notion of quotient of stacks by group action.
$\mathcal {X}$
by W. However, although this is implicit, we will not use the definition of group actions on stacks or the notion of quotient of stacks by group action.
An
![]() $\ell $
-adic sheaf on
$\ell $
-adic sheaf on
![]() $\mathrm {B}(W)$
is a vector space equipped with a right action of W and
$\mathrm {B}(W)$
is a vector space equipped with a right action of W and
for right multiplication of W on itself. The left multiplication corresponds to the Galois action. We thus have a decomposition
where the sum is over the irreducible
![]() ${\overline {\mathbb {Q}}_{\ell }}$
-characters of W,
${\overline {\mathbb {Q}}_{\ell }}$
-characters of W,
![]() $V_{\chi }$
is a W-module affording the character
$V_{\chi }$
is a W-module affording the character
![]() $\chi $
and
$\chi $
and
![]() $\mathcal {L}_{o,\chi }$
is the irreducible smooth
$\mathcal {L}_{o,\chi }$
is the irreducible smooth
![]() $\ell $
-adic sheaf on
$\ell $
-adic sheaf on
![]() $\mathrm {B}(W)$
corresponding to
$\mathrm {B}(W)$
corresponding to
![]() $V_{\chi }^*$
.
$V_{\chi }^*$
.
By base change from Diagram (2.10) we get the analogous decomposition
Notice that
![]() $\mathcal {L}_{\chi }$
may not be irreducible and that
$\mathcal {L}_{\chi }$
may not be irreducible and that
![]() $(\pi _*{\overline {\mathbb {Q}}_{\ell }})^W={\overline {\mathbb {Q}}_{\ell }}$
.
$(\pi _*{\overline {\mathbb {Q}}_{\ell }})^W={\overline {\mathbb {Q}}_{\ell }}$
.
Given a W-torsor
![]() $\pi :\mathcal {X}\rightarrow \overline {\mathcal {X}}$
, we denote by
$\pi :\mathcal {X}\rightarrow \overline {\mathcal {X}}$
, we denote by
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)$
the subcategory of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)$
the subcategory of
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
whose objects are isomorphic to objects of the form
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
whose objects are isomorphic to objects of the form
![]() $\pi ^*(\overline {K})$
with
$\pi ^*(\overline {K})$
with
![]() $\overline {K}\in D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
and morphisms are given by
$\overline {K}\in D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
and morphisms are given by
We call
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)$
the category of W-equivariant complexes on
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)$
the category of W-equivariant complexes on
![]() $\mathcal {X}$
(with respect to
$\mathcal {X}$
(with respect to
![]() $\pi $
).
$\pi $
).
Remark 2.10. The inverse functor of
![]() $\pi ^*:D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)$
is given by
$\pi ^*:D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)$
is given by
Indeed this follows from the above discussion and
which is a consequence of the projection formula.
Given two W-equivariant complexes
![]() $A=\pi ^*\overline {A}$
and
$A=\pi ^*\overline {A}$
and
![]() $B=\pi ^*\overline {B}$
in
$B=\pi ^*\overline {B}$
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
, we define an action of W on
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
, we define an action of W on
![]() $\mathrm { Hom}_{D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})}(A,B)$
as follows.
$\mathrm { Hom}_{D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})}(A,B)$
as follows.
We have
 $$ \begin{align*} \mathrm{Hom}_{D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{X})}(A,B)&=\mathrm{ Hom}_{D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{X})}(\pi^*\overline{A},\pi^*\overline{B})\\ &=\mathrm{Hom}_{D_{\mathrm{c}}^{\mathrm{b}}(\overline{\mathcal{X}})}(\overline{A},\pi_*\pi^*\overline{B})\\ &= \bigoplus_{\chi} V_{\chi}\otimes\mathrm{Hom}_{D_{\mathrm{c}}^{\mathrm{b}}(\overline{\mathcal{X}})}\left(\overline{A}, \mathcal{L}_{\chi}\otimes\overline{B}\right). \end{align*} $$
$$ \begin{align*} \mathrm{Hom}_{D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{X})}(A,B)&=\mathrm{ Hom}_{D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{X})}(\pi^*\overline{A},\pi^*\overline{B})\\ &=\mathrm{Hom}_{D_{\mathrm{c}}^{\mathrm{b}}(\overline{\mathcal{X}})}(\overline{A},\pi_*\pi^*\overline{B})\\ &= \bigoplus_{\chi} V_{\chi}\otimes\mathrm{Hom}_{D_{\mathrm{c}}^{\mathrm{b}}(\overline{\mathcal{X}})}\left(\overline{A}, \mathcal{L}_{\chi}\otimes\overline{B}\right). \end{align*} $$
The action of W on the
![]() $V_{\chi }$
defines thus an action of W on
$V_{\chi }$
defines thus an action of W on
![]() $\mathrm { Hom}_{D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})}(A,B)$
, and we have
$\mathrm { Hom}_{D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})}(A,B)$
, and we have
Remark 2.11. Our definition of W-equivariant complexes is consistent with the usual one. If W acts (on the right) on a scheme X, then following [Reference Kiehl and Weissauer8, III, 15], a W-equivariant complex on X is a pair
![]() $(K,\theta )$
with
$(K,\theta )$
with
![]() $K\in D_{\mathrm {c}}^{\mathrm {b}}(X)$
and
$K\in D_{\mathrm {c}}^{\mathrm {b}}(X)$
and
![]() $\theta =(\theta _w)_{w\in W}$
a collection of isomorphisms
$\theta =(\theta _w)_{w\in W}$
a collection of isomorphisms
such that
-
(i)
 $\theta _{ww'}=\theta _w\circ w^*(\theta _{w'})$
for all
$\theta _{ww'}=\theta _w\circ w^*(\theta _{w'})$
for all
 $w,w'\in W$
, and
$w,w'\in W$
, and -
(ii)
 $\theta _1=1_K$
,
$\theta _1=1_K$
,
where
![]() $1_K:K\rightarrow K$
denotes the identity morphism.
$1_K:K\rightarrow K$
denotes the identity morphism.
Moreover, if
![]() $(K,\theta ),(K',\theta ')\in D_{\mathrm {c}}^{\mathrm {b}}(X,W)$
, then the group W acts (on the left) on
$(K,\theta ),(K',\theta ')\in D_{\mathrm {c}}^{\mathrm {b}}(X,W)$
, then the group W acts (on the left) on
![]() $\mathrm {Hom}_{D_{\mathrm {c}}^{\mathrm {b}}(X)}(K,K')$
as
$\mathrm {Hom}_{D_{\mathrm {c}}^{\mathrm {b}}(X)}(K,K')$
as
for all
![]() $w\in W$
and
$w\in W$
and
![]() $f\in \mathrm {Hom}(K,K')$
, and
$f\in \mathrm {Hom}(K,K')$
, and
A commutative diagram

where
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are W-torsors, induces a functor
$\pi '$
are W-torsors, induces a functor
![]() $f^*:D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X}',W)\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)$
, and, moreover, if the above diagram is cartesian and f is representable, then we also get a functor
$f^*:D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X}',W)\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)$
, and, moreover, if the above diagram is cartesian and f is representable, then we also get a functor
![]() $f_!:D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X}',W)$
. Both are compatible with the usual functors
$f_!:D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X},W)\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X}',W)$
. Both are compatible with the usual functors
![]() $f^*$
and
$f^*$
and
![]() $f_!$
where we forget the actions of W.
$f_!$
where we forget the actions of W.
Remark 2.12. Notice that if K is W-equivariant, then its Postnikov diagram
![]() $\Lambda (K)$
is W-equivariant (i.e., the vertices and the arrows of the diagram are W-equivariant).
$\Lambda (K)$
is W-equivariant (i.e., the vertices and the arrows of the diagram are W-equivariant).
In the next two following lemmas we assume given a W-torsor
Lemma 2.13. Assume that we have a distinguished triangle
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
and that d is W-equivariant. Then there exists a distinguished triangle
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
and that d is W-equivariant. Then there exists a distinguished triangle
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
and an isomorphism of triangles
$D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
and an isomorphism of triangles

If, moreover, we assume that
then the triangle (2.12) is unique (up to a unique isomorphism), and the morphism s is unique.
Proof. As
![]() $d:\pi ^*\overline {A}\rightarrow \pi ^*\overline {C}$
is W-equivariant, by definition it descends to a unique morphism
$d:\pi ^*\overline {A}\rightarrow \pi ^*\overline {C}$
is W-equivariant, by definition it descends to a unique morphism
![]() $\overline {d}:\overline {A}\rightarrow \overline {C}$
in
$\overline {d}:\overline {A}\rightarrow \overline {C}$
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
. We complete this morphism into a distinguished triangle
$D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
. We complete this morphism into a distinguished triangle
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
.
$D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
.
There exists an isomorphism
![]() $s:C'\rightarrow \pi ^*(\overline {C}')$
, such that the following diagram commutes:
$s:C'\rightarrow \pi ^*(\overline {C}')$
, such that the following diagram commutes:

The second statement follows from Lemma 2.1.
Proposition 2.14. Assume that we have a Postnikov diagram
![]() $\Lambda $
of the form (2.1) in
$\Lambda $
of the form (2.1) in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
, such that the complex
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
, such that the complex
![]() $\Lambda _b$
is the image by
$\Lambda _b$
is the image by
![]() $\pi ^*$
of a complex
$\pi ^*$
of a complex
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
. Suppose also that
$D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
. Suppose also that
and
Then the complex (2.13) can be completed in a unique way (up to a unique isomorphism) into a Postnikov diagram
![]() $\overline {\Lambda }$
in
$\overline {\Lambda }$
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
, such that
$D_{\mathrm {c}}^{\mathrm {b}}(\overline {\mathcal {X}})$
, such that
Proof. The conditions (2.14) and (2.15) imply the analogous conditions with
![]() $A_i$
replaced by
$A_i$
replaced by
![]() $\overline {A}_i$
. Therefore, by Lemma 2.5 we can extend in a unique way the complex (2.13) into a Postnikov diagram
$\overline {A}_i$
. Therefore, by Lemma 2.5 we can extend in a unique way the complex (2.13) into a Postnikov diagram
![]() $\overline {\Lambda }$
. We prove by induction on
$\overline {\Lambda }$
. We prove by induction on
![]() $0\leq r <m$
that
$0\leq r <m$
that
![]() $\pi ^*(\overline {\Lambda })=\Lambda $
using Lemma 2.13 and the unicity of
$\pi ^*(\overline {\Lambda })=\Lambda $
using Lemma 2.13 and the unicity of
![]() $d_{r+1}$
(Lemma 2.4).
$d_{r+1}$
(Lemma 2.4).
2.5 Cohomological correspondences
By a cohomological correspondence
![]() $\Gamma =({\mathcal {C}},N,p,q)$
we shall mean a correspondence of S-algebraic stacks
$\Gamma =({\mathcal {C}},N,p,q)$
we shall mean a correspondence of S-algebraic stacks

together with a kernel
![]() $N\in D_{\mathrm {c}}^-({\mathcal {C}})$
.
$N\in D_{\mathrm {c}}^-({\mathcal {C}})$
.
The correspondence
![]() $\Gamma $
comes with a functor
$\Gamma $
comes with a functor
which we call the restriction functor associated to
![]() $\Gamma $
, whose right adjoint is the induction functor
$\Gamma $
, whose right adjoint is the induction functor
Lemma 2.15. If we have a morphism of correspondences
![]() $f:({\mathcal {C}},p,q)\rightarrow ({\mathcal {C}}',p',q')$
(i.e., a commutative diagram)
$f:({\mathcal {C}},p,q)\rightarrow ({\mathcal {C}}',p',q')$
(i.e., a commutative diagram)

then we have natural isomorphisms
Proof. This is an obvious consequence of the projection formulas (see [Reference Laszlo and Olsson9, 9.1.1 and 9.1.i]).
Lemma 2.16 (Composition).
Assume that we have two cohomological correspondences
![]() $\Gamma =({\mathcal {C}},N,p,q)$
and
$\Gamma =({\mathcal {C}},N,p,q)$
and
![]() $\Gamma '=({\mathcal {C}}',N',p',q')$
. Consider the following diagram:
$\Gamma '=({\mathcal {C}}',N',p',q')$
. Consider the following diagram:

Then
where
We keep the correspondence (2.16), and we assume that it can be completed into a diagram

where
![]() $\pi $
and
$\pi $
and
![]() $\rho $
are W-torsors and where the square is cartesian.
$\rho $
are W-torsors and where the square is cartesian.
If N is W-equivariant (i.e., descends to a complex
![]() $\overline {N}$
on
$\overline {N}$
on
![]() $\overline {{\mathcal {C}}}$
), then we have the following factorization
$\overline {{\mathcal {C}}}$
), then we have the following factorization
where
![]() $\mathrm {I}:D_{\mathrm {c}}^+(\overline {{\mathcal {Y}}})\rightarrow D_{\mathrm {c}}^+(\mathcal {X})$
and
$\mathrm {I}:D_{\mathrm {c}}^+(\overline {{\mathcal {Y}}})\rightarrow D_{\mathrm {c}}^+(\mathcal {X})$
and
![]() $\mathrm {R}:D_{\mathrm {c}}^-(\mathcal {X})\rightarrow D_{\mathrm {c}}^-(\overline {{\mathcal {Y}}})$
are respectively the induction and restriction functors defined from the correspondence
$\mathrm {R}:D_{\mathrm {c}}^-(\mathcal {X})\rightarrow D_{\mathrm {c}}^-(\overline {{\mathcal {Y}}})$
are respectively the induction and restriction functors defined from the correspondence
![]() $(\overline {{\mathcal {C}}},\overline {N},\overline {p},\overline {q})$
.
$(\overline {{\mathcal {C}}},\overline {N},\overline {p},\overline {q})$
.
Remark 2.17. Notice that
![]() $\mathrm {I}$
can be computed as
$\mathrm {I}$
can be computed as
since
 $$ \begin{align*} \mathrm{Ind}(\pi^*\overline{K})&=\mathrm{I}\circ\pi_*\circ\pi^*(\overline{K})\\ &=\bigoplus_{\chi} V_{\chi}\otimes \mathrm{I}(\mathcal{L}_{\chi}\otimes \overline{K}), \end{align*} $$
$$ \begin{align*} \mathrm{Ind}(\pi^*\overline{K})&=\mathrm{I}\circ\pi_*\circ\pi^*(\overline{K})\\ &=\bigoplus_{\chi} V_{\chi}\otimes \mathrm{I}(\mathcal{L}_{\chi}\otimes \overline{K}), \end{align*} $$
where
![]() $\pi _*{\overline {\mathbb {Q}}_{\ell }}=\bigoplus _{\chi } V_{\chi }\otimes \mathcal {L}_{\chi }$
is the decomposition indexed by the irreducible characters of W (see Remark 2.10).
$\pi _*{\overline {\mathbb {Q}}_{\ell }}=\bigoplus _{\chi } V_{\chi }\otimes \mathcal {L}_{\chi }$
is the decomposition indexed by the irreducible characters of W (see Remark 2.10).
2.6 Reductive groups
For an affine connected algebraic group H over k, we denote by
![]() $\mathfrak {h}$
the Lie algebra of H. We denote by
$\mathfrak {h}$
the Lie algebra of H. We denote by
![]() $Z(H)$
the center of H and by
$Z(H)$
the center of H and by
![]() $z(\mathfrak {h})$
the center of
$z(\mathfrak {h})$
the center of
![]() $\mathfrak {h}$
. We will also denote by
$\mathfrak {h}$
. We will also denote by
![]() ${\mathcal {H}}:=[\mathfrak {h}/H]$
the quotient stack of
${\mathcal {H}}:=[\mathfrak {h}/H]$
the quotient stack of
![]() $\mathfrak {h}$
by H for the adjoint action
$\mathfrak {h}$
by H for the adjoint action
![]() $\mathrm {Ad}:H\rightarrow \mathrm {GL}(\mathfrak {h})$
.
$\mathrm {Ad}:H\rightarrow \mathrm {GL}(\mathfrak {h})$
.
If, moreover, H is reductive, we denote by
the variety of characteristic polynomials of the elements of
![]() $\mathfrak {h}$
, and we have a canonical map
$\mathfrak {h}$
, and we have a canonical map
![]() $\chi _{\mathfrak {h}}:\mathcal {H}\rightarrow \mathfrak {car}_{\mathfrak {h}}$
.
$\chi _{\mathfrak {h}}:\mathcal {H}\rightarrow \mathfrak {car}_{\mathfrak {h}}$
.
If H is commutative, then
![]() ${\mathcal {H}}\simeq \mathfrak {h}\times \mathrm {B}(H)$
,
${\mathcal {H}}\simeq \mathfrak {h}\times \mathrm {B}(H)$
,
![]() $\mathfrak {car}_{\mathfrak {h}}\simeq \mathfrak {h}$
and
$\mathfrak {car}_{\mathfrak {h}}\simeq \mathfrak {h}$
and
![]() $\chi _{\mathfrak {h}}$
is the first projection.
$\chi _{\mathfrak {h}}$
is the first projection.
From now, G is a connected reductive group over k, T is a maximal torus of G, B a Borel subgroup of G containing T, U the unipotent radical of B, N the normalizer
![]() $\mathrm {N}_G(T)$
of T in G and W the Weyl group
$\mathrm {N}_G(T)$
of T in G and W the Weyl group
![]() $N/T$
. Through this paper we put
$N/T$
. Through this paper we put
We will simply use the notation
![]() $\mathfrak {car}$
instead of
$\mathfrak {car}$
instead of
![]() $\mathfrak {car}_{\mathfrak {g}}$
, and we recall that
$\mathfrak {car}_{\mathfrak {g}}$
, and we recall that
We let
be the canonical map.
The character group is denoted by
![]() $X^*(T)$
and the cocharacter group by
$X^*(T)$
and the cocharacter group by
![]() $X_*(T)$
.
$X_*(T)$
.
When it makes sense, we use freely the subscripts
![]() ${\mathrm {reg}}$
and
${\mathrm {reg}}$
and
![]() ${\mathrm {rss}}$
for restriction to G-regular or G-regular semisimple elements. Similarly we will use the subscript
${\mathrm {rss}}$
for restriction to G-regular or G-regular semisimple elements. Similarly we will use the subscript
![]() $\mathrm {nil}$
for restriction to nilpotent elements.
$\mathrm {nil}$
for restriction to nilpotent elements.
We assume throughout this paper that the characteristic of k is not too small so that
![]() ${\mathfrak {t}}_{{\mathrm {reg}}}\neq \emptyset $
and centralizers of semisimple elements of
${\mathfrak {t}}_{{\mathrm {reg}}}\neq \emptyset $
and centralizers of semisimple elements of
![]() ${\mathfrak {g}}$
are Levi subgroups (of parabolic subgroups) of G (see [Reference Letellier11, §2.6] for an explicit bound on p).
${\mathfrak {g}}$
are Levi subgroups (of parabolic subgroups) of G (see [Reference Letellier11, §2.6] for an explicit bound on p).
2.7 Lusztig correspondence
Consider the correspondence (which we call Lusztig correspondence)
where the arrows are induced by the inclusion
![]() ${\mathfrak {b}}\subset {\mathfrak {g}}$
and by the projection
${\mathfrak {b}}\subset {\mathfrak {g}}$
and by the projection
![]() ${\mathfrak {b}}\rightarrow {\mathfrak {t}}$
.
${\mathfrak {b}}\rightarrow {\mathfrak {t}}$
.
Consider
The group G acts on X by
![]() $g\cdot (x,hB)=( \mathrm {Ad}(g)(x),ghB)$
, and the map
$g\cdot (x,hB)=( \mathrm {Ad}(g)(x),ghB)$
, and the map
induces an isomorphism
![]() $\mathcal {B}\rightarrow \mathcal {X}:=[X/G]$
.
$\mathcal {B}\rightarrow \mathcal {X}:=[X/G]$
.
Under the identification
![]() $\mathcal {B}\simeq \mathcal {X}$
, the morphism p is the quotient by G of the Grothendieck-Springer resolution
$\mathcal {B}\simeq \mathcal {X}$
, the morphism p is the quotient by G of the Grothendieck-Springer resolution
from which we deduce the first assertion of the theorem below.
Theorem 2.18.
-
(i) The morphism
 $p:\mathcal {B}\rightarrow \mathcal {G}$
is representable, proper and semi-small.
$p:\mathcal {B}\rightarrow \mathcal {G}$
is representable, proper and semi-small. -
(ii) We have a factorization of p (Stein factorization)

where
 $q'=\chi _{\mathfrak {t}}\circ q:\mathcal {B}\rightarrow \mathcal {T}\rightarrow {\mathfrak {t}}$
, and
$q'=\chi _{\mathfrak {t}}\circ q:\mathcal {B}\rightarrow \mathcal {T}\rightarrow {\mathfrak {t}}$
, and
 $(q',p)$
is a small resolution of singularities.
$(q',p)$
is a small resolution of singularities.
Proof. Above,
![]() ${\mathcal {S}}_{{\mathrm {rss}}}:={\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}_{{\mathrm {rss}}}$
,
${\mathcal {S}}_{{\mathrm {rss}}}:={\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}_{{\mathrm {rss}}}$
,
![]() $(q',p)$
is an isomorphism, and so
$(q',p)$
is an isomorphism, and so
![]() $\mathcal {G}_{{\mathrm {rss}}}$
is smooth. The complementary of
$\mathcal {G}_{{\mathrm {rss}}}$
is smooth. The complementary of
![]() $\mathcal {G}_{{\mathrm {rss}}}$
in
$\mathcal {G}_{{\mathrm {rss}}}$
in
![]() ${\mathcal {S}}$
is of codimension at least
${\mathcal {S}}$
is of codimension at least
![]() $2$
. Therefore,
$2$
. Therefore,
![]() ${\mathcal {S}}$
satisfies the condition
${\mathcal {S}}$
satisfies the condition
![]() $(R_1)$
of Serres’s criterion for normality. Moreover,
$(R_1)$
of Serres’s criterion for normality. Moreover,
![]() ${\mathfrak {t}}$
is a complete intersection over
${\mathfrak {t}}$
is a complete intersection over
![]() $\mathfrak {car}$
, and so by base change, the same is true for
$\mathfrak {car}$
, and so by base change, the same is true for
![]() ${\mathcal {S}}$
over
${\mathcal {S}}$
over
![]() $\mathcal {G}$
. As
$\mathcal {G}$
. As
![]() $\mathcal {G}$
is smooth, the stack
$\mathcal {G}$
is smooth, the stack
![]() ${\mathcal {S}}$
satisfies the condition
${\mathcal {S}}$
satisfies the condition
![]() $(S_2)$
of Serres’s criterion. Therefore
$(S_2)$
of Serres’s criterion. Therefore
![]() ${\mathcal {S}}$
is normal from which we deduce the proposition.
${\mathcal {S}}$
is normal from which we deduce the proposition.
2.8 Lusztig induction and restriction
The morphism p is representable, proper and q is smooth of pure dimension
![]() $0$
. We thus have
$0$
. We thus have
![]() $p_*=p_!$
and
$p_*=p_!$
and
![]() $q^*=q^!$
. The Lusztig induction and restriction functors [Reference Lusztig14, (7.1.7)] are the induction and restriction defined from the correspondence (2.19) with the constant sheaf as a kernel:
$q^*=q^!$
. The Lusztig induction and restriction functors [Reference Lusztig14, (7.1.7)] are the induction and restriction defined from the correspondence (2.19) with the constant sheaf as a kernel:
Remark 2.19. Notice that
![]() $\mathrm {Res}$
is well-defined as
$\mathrm {Res}$
is well-defined as
![]() $q_!$
maps bounded complexes to bounded complexes. To see that, we consider the commutative triangle
$q_!$
maps bounded complexes to bounded complexes. To see that, we consider the commutative triangle

Since h is an affine fibration, the adjunction morphism
is an isomorphism, and so we conclude by noticing that a is representable.
By the main result of [Reference Bezrukavnikov and Yom Din3], the functors
![]() $\mathrm {Ind}$
and
$\mathrm {Ind}$
and
![]() $\mathrm {Res}$
map perverse sheaves to perverse sheaves.
$\mathrm {Res}$
map perverse sheaves to perverse sheaves.
Consider the factorization

where the map
![]() $\mathcal {T}\rightarrow \mathfrak {car}$
is either the composition
$\mathcal {T}\rightarrow \mathfrak {car}$
is either the composition
![]() $\mathcal {T}\rightarrow \mathcal {G}\rightarrow \mathfrak {car}$
or the composition
$\mathcal {T}\rightarrow \mathcal {G}\rightarrow \mathfrak {car}$
or the composition
![]() $\mathcal {T}\rightarrow {\mathfrak {t}}\rightarrow \mathfrak {car}$
.
$\mathcal {T}\rightarrow {\mathfrak {t}}\rightarrow \mathfrak {car}$
.
By §2.5, we have
 $$ \begin{align*} \mathrm{Res}(K)&={\mathrm{pr}_{\mathcal{T}}}_!\left(\mathrm{pr}^*_{\mathcal{G}}(K)\otimes (q,p)_!{\overline{\mathbb{Q}}_{\ell}}\right),\\ \mathrm{Ind}(K)&={\mathrm{pr}_{\mathcal{G}}}_*\,\underline{\mathrm{ Hom}}\left((q,p)_!{\overline{\mathbb{Q}}_{\ell}},\mathrm{pr}_{\mathcal{T}}^!(K)\right)\\ &={\mathrm{pr}_{\mathcal{G}}}_!\left(\mathrm{pr}^*_{\mathcal{T}}(K)\otimes (q,p)_!{\overline{\mathbb{Q}}_{\ell}}\right). \end{align*} $$
$$ \begin{align*} \mathrm{Res}(K)&={\mathrm{pr}_{\mathcal{T}}}_!\left(\mathrm{pr}^*_{\mathcal{G}}(K)\otimes (q,p)_!{\overline{\mathbb{Q}}_{\ell}}\right),\\ \mathrm{Ind}(K)&={\mathrm{pr}_{\mathcal{G}}}_*\,\underline{\mathrm{ Hom}}\left((q,p)_!{\overline{\mathbb{Q}}_{\ell}},\mathrm{pr}_{\mathcal{T}}^!(K)\right)\\ &={\mathrm{pr}_{\mathcal{G}}}_!\left(\mathrm{pr}^*_{\mathcal{T}}(K)\otimes (q,p)_!{\overline{\mathbb{Q}}_{\ell}}\right). \end{align*} $$
The last identity follows from the fact that
![]() $q^!=q^*$
and
$q^!=q^*$
and
![]() $p_!=p_*$
since we can then regard
$p_!=p_*$
since we can then regard
![]() $\mathrm {Ind}$
as the restriction functor associated to the correspondence
$\mathrm {Ind}$
as the restriction functor associated to the correspondence
![]() $(\mathcal {B},q,p)$
.
$(\mathcal {B},q,p)$
.
Notice also that
![]() $(q,p)_!{\overline {\mathbb {Q}}_{\ell }}\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {T}\times _{\mathfrak {car}}\mathcal {G})$
.
$(q,p)_!{\overline {\mathbb {Q}}_{\ell }}\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {T}\times _{\mathfrak {car}}\mathcal {G})$
.
2.9 Induction and restriction for perverse sheaves
As we say in the previous section, the two functors
![]() $\mathrm {Ind}$
and
$\mathrm {Ind}$
and
![]() $\mathrm {Res}$
are t-exact but, as we will see later, the kernel
$\mathrm {Res}$
are t-exact but, as we will see later, the kernel
![]() $(q,p)_!{\overline {\mathbb {Q}}_{\ell }}$
is not W-equivariant. In this section we introduce slightly modified functors
$(q,p)_!{\overline {\mathbb {Q}}_{\ell }}$
is not W-equivariant. In this section we introduce slightly modified functors
![]() ${^p}\underline {\mathrm {Ind}}$
and
${^p}\underline {\mathrm {Ind}}$
and
![]() ${^p}\underline {\mathrm {Res}}$
defined from a kernel which is naturally W-equivariant.
${^p}\underline {\mathrm {Res}}$
defined from a kernel which is naturally W-equivariant.
We consider the following commutative diagram

where
![]() $s:\mathcal {T}\simeq {\mathfrak {t}}\times \mathrm {B}(T)\rightarrow {\mathfrak {t}}$
is the projection on
$s:\mathcal {T}\simeq {\mathfrak {t}}\times \mathrm {B}(T)\rightarrow {\mathfrak {t}}$
is the projection on
![]() ${\mathfrak {t}}$
. Notice that s is not representable.
${\mathfrak {t}}$
. Notice that s is not representable.
Consider the induction functor
Since the functor
![]() $s^:\mathcal {M}({\mathfrak {t}})\rightarrow \mathcal {M}(\mathcal {T})$
is an equivalence of categories with inverse functor
$s^:\mathcal {M}({\mathfrak {t}})\rightarrow \mathcal {M}(\mathcal {T})$
is an equivalence of categories with inverse functor
![]() ${^p}{\mathcal {H}}^0\circ \left (s_\right )$
and since
${^p}{\mathcal {H}}^0\circ \left (s_\right )$
and since
![]() $\mathrm {Ind}$
maps perverse sheaves to perverse sheaves (see §2.8), the functor
$\mathrm {Ind}$
maps perverse sheaves to perverse sheaves (see §2.8), the functor
![]() $\underline {\mathrm {Ind}}$
preserves perversity and we denote by
$\underline {\mathrm {Ind}}$
preserves perversity and we denote by
![]() ${^p}\underline {\mathrm {Ind}}$
the induced functor on perverse sheaves:
${^p}\underline {\mathrm {Ind}}$
the induced functor on perverse sheaves:
The functor
![]() $\underline {\mathrm {Ind}}$
admits a left adjoint
$\underline {\mathrm {Ind}}$
admits a left adjoint
which is right t-exact but not left t-exact (unlike
![]() $\underline {\mathrm {Ind}}$
).
$\underline {\mathrm {Ind}}$
).
Since
![]() $\mathrm {Res}$
preserves perversity, for
$\mathrm {Res}$
preserves perversity, for
![]() $K\in \mathcal {M}(\mathcal {G})$
, we have
$K\in \mathcal {M}(\mathcal {G})$
, we have
where
![]() $K'\in \mathcal {M}({\mathfrak {t}})$
is defined as
$K'\in \mathcal {M}({\mathfrak {t}})$
is defined as
![]() $s^!(K')[n](n)=\mathrm {Res}(K)$
.
$s^!(K')[n](n)=\mathrm {Res}(K)$
.
Define the restriction
Lemma 2.20.
![]() ${^p}\underline {\mathrm {Res}}$
is left adjoint to
${^p}\underline {\mathrm {Res}}$
is left adjoint to
![]() ${^p}\underline {\mathrm {Ind}}$
.
${^p}\underline {\mathrm {Ind}}$
.
Proof. We have
 $$ \begin{align*} \mathrm{Hom}_{\mathcal{M}({\mathfrak{t}})}\left({^p}\underline{\mathrm{Res}}(A),B\right)&=\mathrm{ Hom}_{\mathcal{M}(\mathcal{T})}\left(s^!({^p}\underline{\mathrm{Res}}(A))[n](n),s^!B[n](n)\right)\\ &=\mathrm{Hom}_{\mathcal{M}(\mathcal{T})}\left(\mathrm{Res}(A),s^!B[n](n)\right)\\ &=\mathrm{Hom}_{\mathcal{M}(\mathcal{G})}\left(A,\mathrm{Ind}(s^!B[n](n))\right)\\ &=\mathrm{Hom}_{\mathcal{M}(\mathcal{G})}\left(A,{^p}\underline{\mathrm{Ind}}(B)\right). \\[-36pt] \end{align*} $$
$$ \begin{align*} \mathrm{Hom}_{\mathcal{M}({\mathfrak{t}})}\left({^p}\underline{\mathrm{Res}}(A),B\right)&=\mathrm{ Hom}_{\mathcal{M}(\mathcal{T})}\left(s^!({^p}\underline{\mathrm{Res}}(A))[n](n),s^!B[n](n)\right)\\ &=\mathrm{Hom}_{\mathcal{M}(\mathcal{T})}\left(\mathrm{Res}(A),s^!B[n](n)\right)\\ &=\mathrm{Hom}_{\mathcal{M}(\mathcal{G})}\left(A,\mathrm{Ind}(s^!B[n](n))\right)\\ &=\mathrm{Hom}_{\mathcal{M}(\mathcal{G})}\left(A,{^p}\underline{\mathrm{Ind}}(B)\right). \\[-36pt] \end{align*} $$
Put
and let
![]() $\pi _{\mathfrak {t}}:{\mathfrak {t}}\rightarrow \overline {{\mathfrak {t}}}$
be the quotient map.
$\pi _{\mathfrak {t}}:{\mathfrak {t}}\rightarrow \overline {{\mathfrak {t}}}$
be the quotient map.
Proposition 2.21. The functors
![]() ${{}^p}\underline {\mathrm {Ind}}$
and
${{}^p}\underline {\mathrm {Ind}}$
and
![]() ${{}^p}\underline {\mathrm {Res}}$
factorize as
${{}^p}\underline {\mathrm {Res}}$
factorize as
where
![]() ${{}^p}\mathrm {I}:\mathcal {M}(\overline {{\mathfrak {t}}})\rightarrow \mathcal {M}(\mathcal {G})$
and
${{}^p}\mathrm {I}:\mathcal {M}(\overline {{\mathfrak {t}}})\rightarrow \mathcal {M}(\mathcal {G})$
and
![]() ${{}^p}\mathrm {R}:\mathcal {M}(\mathcal {G})\rightarrow \mathcal {M}(\overline {{\mathfrak {t}}})$
are defined as
${{}^p}\mathrm {R}:\mathcal {M}(\mathcal {G})\rightarrow \mathcal {M}(\overline {{\mathfrak {t}}})$
are defined as
 $$ \begin{align*} &{{}^p}\mathrm{I}(K):=\mathrm{pr}_{2\, *}\,\underline{\mathrm{ Hom}}\left({\mathrm{IC}}_{\overline{{\mathfrak{t}}}\times_{\mathfrak{car}}\mathcal{G}},\mathrm{pr}_1^!K\right)[n](n),\\ &{{}^p}\mathrm{R}(K):={{}^p}{\mathcal{H}}^0\left(\mathrm{pr}_{1\, !}\left({\mathrm{IC}}_{\overline{{\mathfrak{t}}}\times_{\mathfrak{car}}\mathcal{G}}\otimes\mathrm{pr}_2^*(K)\right)[-n](-n)\right). \end{align*} $$
$$ \begin{align*} &{{}^p}\mathrm{I}(K):=\mathrm{pr}_{2\, *}\,\underline{\mathrm{ Hom}}\left({\mathrm{IC}}_{\overline{{\mathfrak{t}}}\times_{\mathfrak{car}}\mathcal{G}},\mathrm{pr}_1^!K\right)[n](n),\\ &{{}^p}\mathrm{R}(K):={{}^p}{\mathcal{H}}^0\left(\mathrm{pr}_{1\, !}\left({\mathrm{IC}}_{\overline{{\mathfrak{t}}}\times_{\mathfrak{car}}\mathcal{G}}\otimes\mathrm{pr}_2^*(K)\right)[-n](-n)\right). \end{align*} $$
Proof. Follows from the diagram (2.21) using that
![]() $(q',p)_!{\overline {\mathbb {Q}}_{\ell }}={\mathrm {IC}}_{{\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}}$
, which follows from the fact that
$(q',p)_!{\overline {\mathbb {Q}}_{\ell }}={\mathrm {IC}}_{{\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}}$
, which follows from the fact that
![]() $(q',p)$
is a small resolution of singularities by Theorem 2.18 (ii).
$(q',p)$
is a small resolution of singularities by Theorem 2.18 (ii).
We have the following proposition.
Proposition 2.22.
-
(1) Let
 $K\in \mathcal {M}({\mathfrak {t}})$
be W-equivariant, and let
$K\in \mathcal {M}({\mathfrak {t}})$
be W-equivariant, and let
 $L\in \mathcal {M}(\mathcal {G})$
. The adjunction isomorphism
$L\in \mathcal {M}(\mathcal {G})$
. The adjunction isomorphism  $$ \begin{align*}\mathrm{Hom}_{\mathcal{M}({\mathfrak{t}})}\big({{}^p}\underline{\mathrm{Res}}(L),K\big)\simeq \mathrm{Hom}_{\mathcal{M}(\mathcal{G})}\big(L,{{}^p}\underline{\mathrm{Ind}}(K)\big) \end{align*} $$
$$ \begin{align*}\mathrm{Hom}_{\mathcal{M}({\mathfrak{t}})}\big({{}^p}\underline{\mathrm{Res}}(L),K\big)\simeq \mathrm{Hom}_{\mathcal{M}(\mathcal{G})}\big(L,{{}^p}\underline{\mathrm{Ind}}(K)\big) \end{align*} $$
is W-equivariant.
-
(2) The functor
 ${{}^p}\mathrm {R}$
is left adjoint to
${{}^p}\mathrm {R}$
is left adjoint to
 ${{}^p}\mathrm {I}$
.
${{}^p}\mathrm {I}$
.
Proof. From Proposition 2.21 we find that
for any
![]() $f\in \mathrm {Hom}({{}^p}\underline {\mathrm {Res}}(L),K)$
and
$f\in \mathrm {Hom}({{}^p}\underline {\mathrm {Res}}(L),K)$
and
![]() $w\in W$
, from which we deduce the assertion (1). The second assertion is a consequence of (1) together with following identities:
$w\in W$
, from which we deduce the assertion (1). The second assertion is a consequence of (1) together with following identities:
 $$ \begin{align*} &\mathrm{Hom}_{\mathcal{M}(\overline{{\mathfrak{t}}})}\left({{}^p}\mathrm{R}(L),\overline{K}\right)=\mathrm{ Hom}_{\mathcal{M}({\mathfrak{t}})}\left({{}^p}\underline{\mathrm{Res}}(L),K\right)^W,\\ &\mathrm{Hom}_{\mathcal{M}(\mathcal{G})}\left(L,{{}^p}\mathrm{I}(\overline{K})\right)=\mathrm{ Hom}_{\mathcal{M}(\mathcal{G})}\left(L,{{}^p}\underline{\mathrm{Ind}}(K)\right)^W \end{align*} $$
$$ \begin{align*} &\mathrm{Hom}_{\mathcal{M}(\overline{{\mathfrak{t}}})}\left({{}^p}\mathrm{R}(L),\overline{K}\right)=\mathrm{ Hom}_{\mathcal{M}({\mathfrak{t}})}\left({{}^p}\underline{\mathrm{Res}}(L),K\right)^W,\\ &\mathrm{Hom}_{\mathcal{M}(\mathcal{G})}\left(L,{{}^p}\mathrm{I}(\overline{K})\right)=\mathrm{ Hom}_{\mathcal{M}(\mathcal{G})}\left(L,{{}^p}\underline{\mathrm{Ind}}(K)\right)^W \end{align*} $$
where
![]() $K=\pi _{\mathfrak {t}}^*(\overline {K})$
.
$K=\pi _{\mathfrak {t}}^*(\overline {K})$
.
2.10 Springer action
From Borho-MacPherson construction of the Springer action [Reference Borho and MacPherson4], the complex
![]() $p_!{\overline {\mathbb {Q}}_{\ell }}$
is endowed with an action of the Weyl group W (i.e., a group homomorphism
$p_!{\overline {\mathbb {Q}}_{\ell }}$
is endowed with an action of the Weyl group W (i.e., a group homomorphism
![]() $W\rightarrow \mathrm {Aut}(p_!({\overline {\mathbb {Q}}_{\ell }}))$
). Their strategy was to prove that
$W\rightarrow \mathrm {Aut}(p_!({\overline {\mathbb {Q}}_{\ell }}))$
). Their strategy was to prove that
![]() $p_*{\overline {\mathbb {Q}}_{\ell }}$
is the intermediate extension of some smooth
$p_*{\overline {\mathbb {Q}}_{\ell }}$
is the intermediate extension of some smooth
![]() $\ell $
-adic sheaf on
$\ell $
-adic sheaf on
![]() $\mathcal {G}_{\mathrm {rss}}$
on which W acts. From the diagram (2.21), we see that
$\mathcal {G}_{\mathrm {rss}}$
on which W acts. From the diagram (2.21), we see that
![]() $p_!{\overline {\mathbb {Q}}_{\ell }}=\mathrm {pr}_{2\, !}{\mathrm {IC}}_{{\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}}$
, and so the action of W follows from the fact that
$p_!{\overline {\mathbb {Q}}_{\ell }}=\mathrm {pr}_{2\, !}{\mathrm {IC}}_{{\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}}$
, and so the action of W follows from the fact that
![]() ${\mathrm {IC}}_{{\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}}$
is naturally W-equivariant.
${\mathrm {IC}}_{{\mathfrak {t}}\times _{\mathfrak {car}}\mathcal {G}}$
is naturally W-equivariant.
This defines an action of W on
![]() $H^i(\mathcal {B},{\overline {\mathbb {Q}}_{\ell }})$
as well as an action on the cohomology of the fibres. These actions are compatible with the restriction maps from the cohomology of
$H^i(\mathcal {B},{\overline {\mathbb {Q}}_{\ell }})$
as well as an action on the cohomology of the fibres. These actions are compatible with the restriction maps from the cohomology of
![]() $\mathcal {B}$
to the cohomology of the fibres.
$\mathcal {B}$
to the cohomology of the fibres.
On the other hand, the natural map
![]() $\mathrm {B}(T)\rightarrow \mathrm {B}(B)$
is a U-fibration, and so
$\mathrm {B}(T)\rightarrow \mathrm {B}(B)$
is a U-fibration, and so
![]() $H^i(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})=H^i(\mathrm {B}(B),{\overline {\mathbb {Q}}_{\ell }})$
. The action of W on
$H^i(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})=H^i(\mathrm {B}(B),{\overline {\mathbb {Q}}_{\ell }})$
. The action of W on
![]() $\mathrm {B}(T)$
induces thus an action of W on
$\mathrm {B}(T)$
induces thus an action of W on
![]() $H^i(\mathrm {B}(B),{\overline {\mathbb {Q}}_{\ell }})$
. This action coincides with the Springer action (regarding
$H^i(\mathrm {B}(B),{\overline {\mathbb {Q}}_{\ell }})$
. This action coincides with the Springer action (regarding
![]() $\mathrm {B}(B)$
as the zero fibre of p).
$\mathrm {B}(B)$
as the zero fibre of p).
Lemma 2.23. The restriction map
![]() $H^i(\mathrm {B}(B),{\overline {\mathbb {Q}}_{\ell }})\rightarrow H^i(\mathcal {B},{\overline {\mathbb {Q}}_{\ell }})$
induced by the map
$H^i(\mathrm {B}(B),{\overline {\mathbb {Q}}_{\ell }})\rightarrow H^i(\mathcal {B},{\overline {\mathbb {Q}}_{\ell }})$
induced by the map
![]() $\mathcal {B}\rightarrow \mathrm {B}(B)$
(given by the B-torsor
$\mathcal {B}\rightarrow \mathrm {B}(B)$
(given by the B-torsor
![]() ${\mathfrak {b}}\rightarrow \mathcal {B}$
) is W-equivariant for the Springer actions.
${\mathfrak {b}}\rightarrow \mathcal {B}$
) is W-equivariant for the Springer actions.
Proof. We know that the restriction map
of the inclusion
![]() $i:\mathrm {B}(B)\hookrightarrow \mathcal {B}$
is W-equivariant for the Springer actions.
$i:\mathrm {B}(B)\hookrightarrow \mathcal {B}$
is W-equivariant for the Springer actions.
The morphism
![]() $b:\mathcal {B}\rightarrow \mathrm {B}(B)$
is a vector bundle with fibre
$b:\mathcal {B}\rightarrow \mathrm {B}(B)$
is a vector bundle with fibre
![]() ${\mathfrak {b}}$
. Hence
${\mathfrak {b}}$
. Hence
![]() $b^*$
is an isomorphism with inverse
$b^*$
is an isomorphism with inverse
![]() $i^*$
and so is W-equivariant.
$i^*$
and so is W-equivariant.
3 Steinberg stacks
3.1 Geometry of Steinberg stacks
We consider the following stacks
We have the following cartesian diagrams

where the top horizontal arrow is the natural map, and the last two arrows are the diagonal morphisms. Since the diagonal morphism
![]() ${\mathfrak {t}}\rightarrow {\mathfrak {t}}\times _{\mathfrak {car}}{\mathfrak {t}}$
is closed, the stack
${\mathfrak {t}}\rightarrow {\mathfrak {t}}\times _{\mathfrak {car}}{\mathfrak {t}}$
is closed, the stack
![]() ${\mathcal {Y}}$
is a closed substack of
${\mathcal {Y}}$
is a closed substack of
![]() $\mathcal {Z}$
.
$\mathcal {Z}$
.
Remark 3.1. Consider
so that
![]() $\mathcal {Z}=[Z/G]$
where G acts on Z by
$\mathcal {Z}=[Z/G]$
where G acts on Z by
The canonical morphisms
![]() $\mathcal {B}\rightarrow \mathrm {B}(B)$
and
$\mathcal {B}\rightarrow \mathrm {B}(B)$
and
![]() $\mathcal {G}\rightarrow \mathrm {B}(G)$
induce a morphism
$\mathcal {G}\rightarrow \mathrm {B}(G)$
induce a morphism
and the canonical map
![]() $[B\backslash G/B]\rightarrow \mathrm {B}(B)\times _{\mathrm {B}(G)}\mathrm {B}(B)$
is an isomorphism.
$[B\backslash G/B]\rightarrow \mathrm {B}(B)\times _{\mathrm {B}(G)}\mathrm {B}(B)$
is an isomorphism.
Consider the stratification
where
![]() $\mathcal {O}_w=[B\backslash BwB/B]$
. Notice that the natural map
$\mathcal {O}_w=[B\backslash BwB/B]$
. Notice that the natural map
![]() $\mathrm {B}(B_w)\rightarrow \mathcal {O}_w$
is an isomorphism.
$\mathrm {B}(B_w)\rightarrow \mathcal {O}_w$
is an isomorphism.
This induces partitions into locally closed substacks
For
![]() $w\in W$
, put
$w\in W$
, put
Then
where
![]() $B_w$
acts by the adjoint action and
$B_w$
acts by the adjoint action and
![]() ${\mathfrak {t}}^w$
are the points of
${\mathfrak {t}}^w$
are the points of
![]() ${\mathfrak {t}}$
fixed by w.
${\mathfrak {t}}$
fixed by w.
Since
![]() $B_w=TU_w$
, we proved the following proposition.
$B_w=TU_w$
, we proved the following proposition.
Proposition 3.2.
-
(1) For all
 $w\in W$
, the projection
$w\in W$
, the projection  $$ \begin{align*}\mathcal{Z}_w\rightarrow\mathcal{T} \end{align*} $$
$$ \begin{align*}\mathcal{Z}_w\rightarrow\mathcal{T} \end{align*} $$
induced by the canonical projection
 ${\mathfrak {b}}\rightarrow {\mathfrak {t}}$
is a fibration with fibre isomorphic to
${\mathfrak {b}}\rightarrow {\mathfrak {t}}$
is a fibration with fibre isomorphic to
 $ [{\mathfrak {u}}_w/U_w]$
, where
$ [{\mathfrak {u}}_w/U_w]$
, where
 $U_w$
acts by the adjoint action.
$U_w$
acts by the adjoint action. -
(2) The fibres of the projection
 $\mathcal {Z}_w\rightarrow \mathcal {O}_w$
(resp.
$\mathcal {Z}_w\rightarrow \mathcal {O}_w$
(resp.
 ${\mathcal {Y}}_w\rightarrow \mathcal {O}_w$
) are affine spaces all of same dimension
${\mathcal {Y}}_w\rightarrow \mathcal {O}_w$
) are affine spaces all of same dimension
 ${\mathfrak {b}}_w$
(resp.
${\mathfrak {b}}_w$
(resp.
 $\mathrm {dim}\,{\mathfrak {t}}^w+\mathrm {dim}\,{\mathfrak {u}}_w$
).
$\mathrm {dim}\,{\mathfrak {t}}^w+\mathrm {dim}\,{\mathfrak {u}}_w$
).
3.2 Purity of cohomology
Proposition 3.3. The compactly supported cohomology of
![]() $\mathcal {Z}$
and
$\mathcal {Z}$
and
![]() ${\mathcal {Y}}$
is pure and vanishes in odd degree.
${\mathcal {Y}}$
is pure and vanishes in odd degree.
Proof. We prove it for
![]() ${\mathcal {Y}}$
, but the proof is completely similar for
${\mathcal {Y}}$
, but the proof is completely similar for
![]() $\mathcal {Z}$
. Let us choose
$\mathcal {Z}$
. Let us choose
![]() $k_o$
, a finite subfield of k such that G, B and T are defined over
$k_o$
, a finite subfield of k such that G, B and T are defined over
![]() $k_o$
and T is split. Then
$k_o$
and T is split. Then
![]() $\mathrm {Gal}(k/k_o)$
acts trivially on W.
$\mathrm {Gal}(k/k_o)$
acts trivially on W.
Recall (see §3) that we have a partition into locally closed substacks
By our choice of
![]() $k_o$
, each stratum is defined over
$k_o$
, each stratum is defined over
![]() $k_o$
.
$k_o$
.
We choose a total order
![]() $\{w_0,w_1,\dots \}$
on W so that we have a decreasing filtration of closed substacks
$\{w_0,w_1,\dots \}$
on W so that we have a decreasing filtration of closed substacks
satisfying
![]() ${\mathcal {Y}}_i\backslash {\mathcal {Y}}_{i+1}={\mathcal {Y}}_{w_i}$
for all i. This defines a spectral sequence [Reference Deligne5, Chapter 6, Formula (2.5.2)] from which we can reduce the proof of the purity of the cohomology of
${\mathcal {Y}}_i\backslash {\mathcal {Y}}_{i+1}={\mathcal {Y}}_{w_i}$
for all i. This defines a spectral sequence [Reference Deligne5, Chapter 6, Formula (2.5.2)] from which we can reduce the proof of the purity of the cohomology of
![]() ${\mathcal {Y}}$
and the vanishing in odd degrees to the analogous statement for
${\mathcal {Y}}$
and the vanishing in odd degrees to the analogous statement for
![]() ${\mathcal {Y}}_w$
.
${\mathcal {Y}}_w$
.
The fibres of the projection
![]() ${\mathcal {Y}}_w\rightarrow \mathcal {O}_w$
are affine spaces all of same dimension
${\mathcal {Y}}_w\rightarrow \mathcal {O}_w$
are affine spaces all of same dimension
![]() $n(w)=\mathrm {dim}\,{\mathfrak {t}}^w+\mathrm {dim}\,{\mathfrak {u}}_w$
by Proposition 3, and so
$n(w)=\mathrm {dim}\,{\mathfrak {t}}^w+\mathrm {dim}\,{\mathfrak {u}}_w$
by Proposition 3, and so
Recall also that the map
![]() $\mathrm {B}(B_w)\rightarrow \mathcal {O}_w$
is an isomorphism and that
$\mathrm {B}(B_w)\rightarrow \mathcal {O}_w$
is an isomorphism and that
Therefore,
Since the cohomology of
![]() $\mathrm {B}(T)$
is pure and vanishes in odd degree, the same is true for
$\mathrm {B}(T)$
is pure and vanishes in odd degree, the same is true for
![]() $H_c^i({\mathcal {Y}}_w,{\overline {\mathbb {Q}}_{\ell }})$
.
$H_c^i({\mathcal {Y}}_w,{\overline {\mathbb {Q}}_{\ell }})$
.
3.3 Restriction to the diagonal
Notice that
and so
![]() $H_c^i(\mathcal {Z},{\overline {\mathbb {Q}}_{\ell }})$
is naturally equipped with an action of
$H_c^i(\mathcal {Z},{\overline {\mathbb {Q}}_{\ell }})$
is naturally equipped with an action of
![]() $W\times W$
.
$W\times W$
.
The aim of this section is to prove the following theorem.
Theorem 3.4. The cohomological restriction
of the diagonal morphism
![]() $\mathcal {B}\rightarrow \mathcal {Z}$
is W-equivariant for the Springer actions (where we consider the diagonal action of W on the source).
$\mathcal {B}\rightarrow \mathcal {Z}$
is W-equivariant for the Springer actions (where we consider the diagonal action of W on the source).
Let
![]() $q':\mathcal {B}\rightarrow {\mathfrak {t}}$
be induced by the canonical projection
$q':\mathcal {B}\rightarrow {\mathfrak {t}}$
be induced by the canonical projection
![]() ${\mathfrak {b}}\rightarrow {\mathfrak {t}}$
. Then
${\mathfrak {b}}\rightarrow {\mathfrak {t}}$
. Then
Choose a total ordering
![]() $\{w_0,w_1,\dots \}$
on W so that we have a decreasing filtration of closed substacks
$\{w_0,w_1,\dots \}$
on W so that we have a decreasing filtration of closed substacks
satisfying
![]() $\mathcal {Z}_i\backslash \mathcal {Z}_{i+1}=\mathcal {Z}_{w_i}$
for all i.
$\mathcal {Z}_i\backslash \mathcal {Z}_{i+1}=\mathcal {Z}_{w_i}$
for all i.
By [Reference Deligne5, Chapter 6, Formula (2.5.2)], we have a spectral sequence
For
![]() $w\in W$
, consider the morphism
$w\in W$
, consider the morphism
and the following commutative diagram:

Then
As
![]() $H^{\mathrm {odd}}_c(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
vanishes, the spectral sequence degenerates at
$H^{\mathrm {odd}}_c(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
vanishes, the spectral sequence degenerates at
![]() $E_1$
.
$E_1$
.
Proof of Theorem 3.4.
Since the above spectral sequence degenerates at
![]() $E_1$
, we have
$E_1$
, we have
![]() ${\mathcal {H}}_c^{\mathrm {odd}}(q',q')_!{\overline {\mathbb {Q}}_{\ell }}=0$
, and
${\mathcal {H}}_c^{\mathrm {odd}}(q',q')_!{\overline {\mathbb {Q}}_{\ell }}=0$
, and
![]() ${\mathcal {H}}^{\mathrm {even}}(q',q')_!{\overline {\mathbb {Q}}_{\ell }}$
is a successive extension of the
${\mathcal {H}}^{\mathrm {even}}(q',q')_!{\overline {\mathbb {Q}}_{\ell }}$
is a successive extension of the
![]() $\Delta _{{\mathfrak {t}},w\,*}{\overline {\mathbb {Q}}_{\ell }}\otimes H^{\mathrm { even}}_c(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
. By Proposition 2.8,
$\Delta _{{\mathfrak {t}},w\,*}{\overline {\mathbb {Q}}_{\ell }}\otimes H^{\mathrm { even}}_c(\mathrm {B}(T),{\overline {\mathbb {Q}}_{\ell }})$
. By Proposition 2.8,
![]() ${\mathcal {H}}^{2i}(q',q')_!{\overline {\mathbb {Q}}_{\ell }}$
is thus a perverse sheaf (up to a shift) that is the intermediate extension of its restriction to
${\mathcal {H}}^{2i}(q',q')_!{\overline {\mathbb {Q}}_{\ell }}$
is thus a perverse sheaf (up to a shift) that is the intermediate extension of its restriction to
![]() ${\mathfrak {t}}_{\mathrm {reg}}\times _{\mathfrak {car}}{\mathfrak {t}}_{\mathrm {reg}}$
.
${\mathfrak {t}}_{\mathrm {reg}}\times _{\mathfrak {car}}{\mathfrak {t}}_{\mathrm {reg}}$
.
We thus have
where
![]() $\Delta :W\times {\mathfrak {t}}\rightarrow {\mathfrak {t}}\times _{\mathfrak {car}}{\mathfrak {t}}$
,
$\Delta :W\times {\mathfrak {t}}\rightarrow {\mathfrak {t}}\times _{\mathfrak {car}}{\mathfrak {t}}$
,
![]() $(w,t)\mapsto (w(t),t)$
is the normalization morphism.
$(w,t)\mapsto (w(t),t)$
is the normalization morphism.
Using the spectral sequence
together with the fact that
![]() $H_c^i({\mathfrak {t}}\times _{\mathfrak {car}}{\mathfrak {t}},\Delta _*{\overline {\mathbb {Q}}_{\ell }})=0$
unless
$H_c^i({\mathfrak {t}}\times _{\mathfrak {car}}{\mathfrak {t}},\Delta _*{\overline {\mathbb {Q}}_{\ell }})=0$
unless
![]() $i=2n$
, we deduce that
$i=2n$
, we deduce that
The restriction morphism
![]() $H_c^i(\mathcal {Z},{\overline {\mathbb {Q}}_{\ell }})\rightarrow H_c^i(\mathcal {B},{\overline {\mathbb {Q}}_{\ell }})$
is induced by the restriction morphism
$H_c^i(\mathcal {Z},{\overline {\mathbb {Q}}_{\ell }})\rightarrow H_c^i(\mathcal {B},{\overline {\mathbb {Q}}_{\ell }})$
is induced by the restriction morphism
which is W-equivariant, hence the theorem.
4 Postnikov diagrams of kernels
The aim of this section is to compute the kernel
as well as its restriction to nilpotent elements.
To alleviate the notation, we will denote by f the representable morphism
considered in Theorem 2.18.
The map
![]() $(q,p)$
decomposes as
$(q,p)$
decomposes as
or equivalently as
under the identification
![]() $\mathcal {T}={\mathfrak {t}}\times \mathrm {B}(T)$
. Notice that
$\mathcal {T}={\mathfrak {t}}\times \mathrm {B}(T)$
. Notice that
![]() $\tau $
corresponds to the T-torsor
$\tau $
corresponds to the T-torsor
![]() $\dot {\mathcal {B}}=[{\mathfrak {b}}/U]\rightarrow [{\mathfrak {b}}/B]=\mathcal {B}$
.
$\dot {\mathcal {B}}=[{\mathfrak {b}}/U]\rightarrow [{\mathfrak {b}}/B]=\mathcal {B}$
.
The first map is a T-torsor which fits into the cartesian diagram

where the map
![]() $\mathrm {B}(T)\rightarrow \mathrm {B}(T)\times \mathrm {B}(T)$
is the diagonal embbeding, and
$\mathrm {B}(T)\rightarrow \mathrm {B}(T)\times \mathrm {B}(T)$
is the diagonal embbeding, and
![]() $\mathrm {B}(T)\times \mathrm {B}(T)\rightarrow \mathrm {B}(T)$
is induced by
$\mathrm {B}(T)\times \mathrm {B}(T)\rightarrow \mathrm {B}(T)$
is induced by
![]() $T\times T\rightarrow T, (t,h)\mapsto th^{-1}$
.
$T\times T\rightarrow T, (t,h)\mapsto th^{-1}$
.
4.1 Postnikov diagrams associated to T-torsors
Let
![]() ${\mathcal {V}}$
be an algebraic stack and
${\mathcal {V}}$
be an algebraic stack and
![]() $\dot {{\mathcal {V}}}$
a T-torsor
$\dot {{\mathcal {V}}}$
a T-torsor
![]() $\rho :\dot {{\mathcal {V}}}\rightarrow {\mathcal {V}}$
. We want to compute
$\rho :\dot {{\mathcal {V}}}\rightarrow {\mathcal {V}}$
. We want to compute
![]() $\rho _!{\overline {\mathbb {Q}}_{\ell }}$
.
$\rho _!{\overline {\mathbb {Q}}_{\ell }}$
.
This torsor corresponds to a morphism
We have a Chern class morphism
associated to the canonical T-torsor
![]() $\mathrm {Spec}(k)\rightarrow \mathrm {B}(T)$
, which induces an isomorphism
$\mathrm {Spec}(k)\rightarrow \mathrm {B}(T)$
, which induces an isomorphism
Composed with
![]() $\sigma ^*$
, it induces a Chern class morphism
$\sigma ^*$
, it induces a Chern class morphism
Concretely, if
![]() $\chi \in X^*(T)$
, then
$\chi \in X^*(T)$
, then
![]() $c_{\rho }(\chi )$
is the Chern class of the line bundle
$c_{\rho }(\chi )$
is the Chern class of the line bundle
where T acts on
![]() $\mathbb {A}^1$
as
$\mathbb {A}^1$
as
![]() $x\cdot t=\chi (t^{-1})x$
, for
$x\cdot t=\chi (t^{-1})x$
, for
![]() $(x,t)\in \mathbb {A}^1\times T$
.
$(x,t)\in \mathbb {A}^1\times T$
.
Since
![]() $H^2({\mathcal {V}},{\overline {\mathbb {Q}}_{\ell }})={\mathrm {Ext}}^2_{\mathcal {V}}({\overline {\mathbb {Q}}_{\ell }},{\overline {\mathbb {Q}}_{\ell }})=\mathrm {Hom}_{\mathcal {V}}({\overline {\mathbb {Q}}_{\ell }},{\overline {\mathbb {Q}}_{\ell }}[2])$
, we can regard c as a map
$H^2({\mathcal {V}},{\overline {\mathbb {Q}}_{\ell }})={\mathrm {Ext}}^2_{\mathcal {V}}({\overline {\mathbb {Q}}_{\ell }},{\overline {\mathbb {Q}}_{\ell }})=\mathrm {Hom}_{\mathcal {V}}({\overline {\mathbb {Q}}_{\ell }},{\overline {\mathbb {Q}}_{\ell }}[2])$
, we can regard c as a map
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}({\mathcal {V}})$
.
$D_{\mathrm {c}}^{\mathrm {b}}({\mathcal {V}})$
.
This defines a complex of objects of
![]() $D_{\mathrm {c}}^{\mathrm {b}}({\mathcal {V}})$
$D_{\mathrm {c}}^{\mathrm {b}}({\mathcal {V}})$
where
![]() $\partial _{n-i+1}[2n-2i+2](n-i+1)$
is induced by the morphism
$\partial _{n-i+1}[2n-2i+2](n-i+1)$
is induced by the morphism
that maps v to
![]() $v\wedge c_{\rho }(1)$
.
$v\wedge c_{\rho }(1)$
.
Proposition 4.1.
-
(1) We have
 $$ \begin{align*}{{}^p}{\mathcal{H}}^i(\rho_!{\overline{\mathbb{Q}}_{\ell}})={\mathcal{H}}^i(\rho_!{\overline{\mathbb{Q}}_{\ell}})\simeq\bigwedge^{2n-i}X_*(T)\otimes{\overline{\mathbb{Q}}_{\ell}}(n-i). \end{align*} $$
$$ \begin{align*}{{}^p}{\mathcal{H}}^i(\rho_!{\overline{\mathbb{Q}}_{\ell}})={\mathcal{H}}^i(\rho_!{\overline{\mathbb{Q}}_{\ell}})\simeq\bigwedge^{2n-i}X_*(T)\otimes{\overline{\mathbb{Q}}_{\ell}}(n-i). \end{align*} $$
-
(2) The complex (4.2) is the base
 $\Lambda _b(\rho _!{\overline {\mathbb {Q}}_{\ell }})$
of the Postnikov diagram
$\Lambda _b(\rho _!{\overline {\mathbb {Q}}_{\ell }})$
of the Postnikov diagram
 $\Lambda (\rho _!{\overline {\mathbb {Q}}_{\ell }})$
.
$\Lambda (\rho _!{\overline {\mathbb {Q}}_{\ell }})$
.
Proof. The proposition reduces to the case
![]() $n=1$
using an isomorphism
$n=1$
using an isomorphism
![]() $T\simeq (\mathbb {G}_m)^n$
. Indeed, the complex (4.2) can be realized as the tensor product of analogous complexes associated to rank
$T\simeq (\mathbb {G}_m)^n$
. Indeed, the complex (4.2) can be realized as the tensor product of analogous complexes associated to rank
![]() $1$
tori.
$1$
tori.
4.2 Postnikov diagram of
 ${\mathcal {N}}$
${\mathcal {N}}$
Since the map
![]() $\hat {f}:\hat {\mathcal {B}}\rightarrow \hat {{\mathcal {S}}}$
is a small resolution of singularities, we have
$\hat {f}:\hat {\mathcal {B}}\rightarrow \hat {{\mathcal {S}}}$
is a small resolution of singularities, we have
Following §4.1 we now regard the Chern class morphism
associated to the T-torsor
![]() $\delta :\mathcal {B}\rightarrow \hat {\mathcal {B}}$
as a morphism
$\delta :\mathcal {B}\rightarrow \hat {\mathcal {B}}$
as a morphism
Applying
![]() $\hat {f}_!$
we get
$\hat {f}_!$
we get
Applying the functor
![]() $\hat {f}_!$
to the complex
$\hat {f}_!$
to the complex
![]() $\Lambda _b(\delta _!{\overline {\mathbb {Q}}_{\ell }})$
we obtain a complex
$\Lambda _b(\delta _!{\overline {\mathbb {Q}}_{\ell }})$
we obtain a complex
 $$\begin{align*} &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \cdots \overset{\partial_1}{\longrightarrow}\left(\bigwedge^{n}X_*(T)\right)\otimes{\mathrm{IC}}_{\hat{{\mathcal{S}}}}, \notag \end{align*}$$
$$\begin{align*} &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \cdots \overset{\partial_1}{\longrightarrow}\left(\bigwedge^{n}X_*(T)\right)\otimes{\mathrm{IC}}_{\hat{{\mathcal{S}}}}, \notag \end{align*}$$
where
![]() $\partial _{n-i+1}[2n-2i+2](n-i+1)$
is induced by the morphism
$\partial _{n-i+1}[2n-2i+2](n-i+1)$
is induced by the morphism
 $$ \begin{align*}\left(\bigwedge^{i-1}X_*(T)\right)\otimes{\mathrm{IC}}_{\hat{{\mathcal{S}}}}\longrightarrow\left(\bigwedge^iX_*(T)\right)\otimes{\mathrm{IC}}_{\hat{{\mathcal{S}}}}[2](1) \end{align*} $$
$$ \begin{align*}\left(\bigwedge^{i-1}X_*(T)\right)\otimes{\mathrm{IC}}_{\hat{{\mathcal{S}}}}\longrightarrow\left(\bigwedge^iX_*(T)\right)\otimes{\mathrm{IC}}_{\hat{{\mathcal{S}}}}[2](1) \end{align*} $$
given by
![]() $v\otimes s\mapsto v\wedge f_!(c_{\delta })(s)$
.
$v\otimes s\mapsto v\wedge f_!(c_{\delta })(s)$
.
Proposition 4.2.
-
(1) The perverse cohomology sheaves of
 ${\mathcal {N}}$
are
${\mathcal {N}}$
are  $$ \begin{align*}{^{\mathrm{p}}}{\mathcal{H}}^i\left({\mathcal{N}}\right) =\left(\bigwedge^{2n-i}X_*(T)\right)\otimes{\mathrm{IC}}_{\hat{{\mathcal{S}}}}(n-i). \end{align*} $$
$$ \begin{align*}{^{\mathrm{p}}}{\mathcal{H}}^i\left({\mathcal{N}}\right) =\left(\bigwedge^{2n-i}X_*(T)\right)\otimes{\mathrm{IC}}_{\hat{{\mathcal{S}}}}(n-i). \end{align*} $$
-
(2) We have
 $\Lambda ({\mathcal {N}})=\hat {f}_!\left (\Lambda (\delta _!{\overline {\mathbb {Q}}_{\ell }})\right )$
.
$\Lambda ({\mathcal {N}})=\hat {f}_!\left (\Lambda (\delta _!{\overline {\mathbb {Q}}_{\ell }})\right )$
. -
(3) Assume that G, B and T are defined over a finite subfield
 $k_o$
of k. The diagram
$k_o$
of k. The diagram
 $\Lambda ({\mathcal {N}})$
is the unique Postnikov diagram defined over
$\Lambda ({\mathcal {N}})$
is the unique Postnikov diagram defined over
 $k_o$
whose base is the complex (4.3).
$k_o$
whose base is the complex (4.3).
Proof. The assertion (1) follows from the fact that the morphism
![]() $\hat {f}$
is small and that the cohomology groups of
$\hat {f}$
is small and that the cohomology groups of
![]() $\Lambda (\delta _!{\overline {\mathbb {Q}}_{\ell }})$
are constant (see Proposition 4.1(1)). The assertion (2) follows from Lemma 2.3.
$\Lambda (\delta _!{\overline {\mathbb {Q}}_{\ell }})$
are constant (see Proposition 4.1(1)). The assertion (2) follows from Lemma 2.3.
To prove assertion (3), we choose a finite subfield
![]() $k_o$
of k on which G, T and B are defined, and we let
$k_o$
of k on which G, T and B are defined, and we let
![]() $T_o$
and
$T_o$
and
![]() $\hat {{\mathcal {S}}}_o$
be the induced
$\hat {{\mathcal {S}}}_o$
be the induced
![]() $k_o$
-structure on T and
$k_o$
-structure on T and
![]() $\hat {{\mathcal {S}}}$
. We want to prove that
$\hat {{\mathcal {S}}}$
. We want to prove that
![]() $\hat {f}_{o!}\left (\Lambda (\delta _{o!}{\overline {\mathbb {Q}}_{\ell }})\right )$
is the unique Postnikov diagram that completes the complex (4.3) with T and
$\hat {f}_{o!}\left (\Lambda (\delta _{o!}{\overline {\mathbb {Q}}_{\ell }})\right )$
is the unique Postnikov diagram that completes the complex (4.3) with T and
![]() $\hat {{\mathcal {S}}}$
replaced by
$\hat {{\mathcal {S}}}$
replaced by
![]() $T_o$
and
$T_o$
and
![]() $\hat {{\mathcal {S}}}_o$
.
$\hat {{\mathcal {S}}}_o$
.
We need to prove that the hypothesis of Lemma 2.5 is satisfied. The condition (2.5) is verified as
for all
![]() $j<i$
.
$j<i$
.
The proof of the condition (2.6) reduces to prove that
for all
![]() $j>i$
and
$j>i$
and
![]() $k\geq 1$
. But this is clear from the next proposition using the exact sequence (2.8).
$k\geq 1$
. But this is clear from the next proposition using the exact sequence (2.8).
Proposition 4.3.
![]() $\mathrm {Ext}^j_{\hat {{\mathcal {S}}}}({\mathrm {IC}}_{\hat {{\mathcal {S}}}},{\mathrm {IC}}_{\hat {{\mathcal {S}}}})=0$
if j is odd and
$\mathrm {Ext}^j_{\hat {{\mathcal {S}}}}({\mathrm {IC}}_{\hat {{\mathcal {S}}}},{\mathrm {IC}}_{\hat {{\mathcal {S}}}})=0$
if j is odd and
![]() $\mathrm {Ext}^{2i}_{\hat {{\mathcal {S}}}}({\mathrm {IC}}_{\hat {{\mathcal {S}}}},{\mathrm {IC}}_{\hat {{\mathcal {S}}}})$
is pure of weight
$\mathrm {Ext}^{2i}_{\hat {{\mathcal {S}}}}({\mathrm {IC}}_{\hat {{\mathcal {S}}}},{\mathrm {IC}}_{\hat {{\mathcal {S}}}})$
is pure of weight
![]() $2i$
.
$2i$
.
Proof. We need to compute
Since
![]() $\hat {{\mathcal {S}}}=\mathrm {B}(T)\times {\mathcal {S}}$
and since the statement of the proposition is true if we replace
$\hat {{\mathcal {S}}}=\mathrm {B}(T)\times {\mathcal {S}}$
and since the statement of the proposition is true if we replace
![]() $\hat {S}$
by
$\hat {S}$
by
![]() $\mathrm {B}(T)$
(noticing that
$\mathrm {B}(T)$
(noticing that
![]() ${\mathrm {IC}}_{\mathrm {B}(T)}={\overline {\mathbb {Q}}_{\ell }}$
), by Künneth formula we are reduced to prove the proposition with
${\mathrm {IC}}_{\mathrm {B}(T)}={\overline {\mathbb {Q}}_{\ell }}$
), by Künneth formula we are reduced to prove the proposition with
![]() ${\mathcal {S}}$
instead of
${\mathcal {S}}$
instead of
![]() $\hat {{\mathcal {S}}}$
.
$\hat {{\mathcal {S}}}$
.
Consider the cartesian diagram

Since f is representable, the morphism
![]() $\mathrm {pr}_1$
is also representable. We have
$\mathrm {pr}_1$
is also representable. We have
 $$ \begin{align*} \mathrm{Hom}({\mathrm{IC}}_{\mathcal{S}},{\mathrm{IC}}_{\mathcal{S}}[i])&=\mathrm{Hom}(f_!{\overline{\mathbb{Q}}_{\ell}},f_!{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=\mathrm{Hom}(f^*f_!{\overline{\mathbb{Q}}_{\ell}},{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=\mathrm{Hom}(\mathrm{pr}_{1!}{\overline{\mathbb{Q}}_{\ell}},{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=\mathrm{Hom}({\overline{\mathbb{Q}}_{\ell}},\mathrm{pr}_1^!{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=H^i({\mathcal{Y}},\mathrm{pr}_1^!{\overline{\mathbb{Q}}_{\ell}})\\ &=H_c^{-i}({\mathcal{Y}},{\overline{\mathbb{Q}}_{\ell}}), \end{align*} $$
$$ \begin{align*} \mathrm{Hom}({\mathrm{IC}}_{\mathcal{S}},{\mathrm{IC}}_{\mathcal{S}}[i])&=\mathrm{Hom}(f_!{\overline{\mathbb{Q}}_{\ell}},f_!{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=\mathrm{Hom}(f^*f_!{\overline{\mathbb{Q}}_{\ell}},{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=\mathrm{Hom}(\mathrm{pr}_{1!}{\overline{\mathbb{Q}}_{\ell}},{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=\mathrm{Hom}({\overline{\mathbb{Q}}_{\ell}},\mathrm{pr}_1^!{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=H^i({\mathcal{Y}},\mathrm{pr}_1^!{\overline{\mathbb{Q}}_{\ell}})\\ &=H_c^{-i}({\mathcal{Y}},{\overline{\mathbb{Q}}_{\ell}}), \end{align*} $$
where the last identity is by Poincaré duality (notice that
![]() $\mathrm {dim}\,{\mathcal {Y}}=0$
). We thus conclude from Proposition 3.3.
$\mathrm {dim}\,{\mathcal {Y}}=0$
). We thus conclude from Proposition 3.3.
4.3 Restriction to nilpotent elements
We let
![]() $\mathfrak {z}$
be a locally closed subset of
$\mathfrak {z}$
be a locally closed subset of
![]() $z(\mathfrak {g})$
. We consider the Lusztig correspondence
$z(\mathfrak {g})$
. We consider the Lusztig correspondence

over
![]() $\mathfrak {z}=\mathfrak {z}/\!/W\subset \mathfrak {car}$
.
$\mathfrak {z}=\mathfrak {z}/\!/W\subset \mathfrak {car}$
.
The T-torsor
![]() $\delta _{\mathfrak {z}}:\mathcal {B}_{\mathfrak {z}}\rightarrow \hat {\mathcal {B}}_{\mathfrak {z}}=\mathrm {B}(T)\times \mathcal {B}_{\mathfrak {z}}$
induced from
$\delta _{\mathfrak {z}}:\mathcal {B}_{\mathfrak {z}}\rightarrow \hat {\mathcal {B}}_{\mathfrak {z}}=\mathrm {B}(T)\times \mathcal {B}_{\mathfrak {z}}$
induced from
![]() $\delta $
gives rise to a Chern class morphism
$\delta $
gives rise to a Chern class morphism
and so following the same lines as in §4.2, we end up with a complex
 $$\begin{align*} &\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdots\longrightarrow\left(\bigwedge^nX_*(T)\right)\otimes \left(\overline{\mathbb{Q}}_{\ell,\,\mathrm{B}(T)}\boxtimes p_{\mathfrak{z}\,!}{\overline{\mathbb{Q}}_{\ell}}\right).\notag \end{align*}$$
$$\begin{align*} &\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdots\longrightarrow\left(\bigwedge^nX_*(T)\right)\otimes \left(\overline{\mathbb{Q}}_{\ell,\,\mathrm{B}(T)}\boxtimes p_{\mathfrak{z}\,!}{\overline{\mathbb{Q}}_{\ell}}\right).\notag \end{align*}$$
which is the restriction of the complex (4.3) to
![]() $\hat {{\mathcal {S}}}_{\mathfrak {z}}$
.
$\hat {{\mathcal {S}}}_{\mathfrak {z}}$
.
If
![]() $\mathfrak {z}=0$
, we will replace the subscript
$\mathfrak {z}=0$
, we will replace the subscript
![]() $\mathfrak {z}$
by nil.
$\mathfrak {z}$
by nil.
Let
![]() $\mathrm {pr}_{\mathrm {nil}}:\hat {{\mathcal {S}}}_{\mathfrak {z}}\rightarrow \hat {{\mathcal {S}}}_{\mathrm { nil}}=\mathrm {B}(T)\times \mathcal {G}_{\mathrm {nil}}$
be the morphism induced by the projection
$\mathrm {pr}_{\mathrm {nil}}:\hat {{\mathcal {S}}}_{\mathfrak {z}}\rightarrow \hat {{\mathcal {S}}}_{\mathrm { nil}}=\mathrm {B}(T)\times \mathcal {G}_{\mathrm {nil}}$
be the morphism induced by the projection
![]() $\mathfrak {z}+{\mathfrak {g}}_{\mathrm {nil}}\rightarrow {\mathfrak {g}}_{\mathrm {nil}}$
.
$\mathfrak {z}+{\mathfrak {g}}_{\mathrm {nil}}\rightarrow {\mathfrak {g}}_{\mathrm {nil}}$
.
Proposition 4.4.
-
(1) We have
 $$ \begin{align*}(q_{\mathfrak{z}},p_{\mathfrak{z}})_!{\overline{\mathbb{Q}}_{\ell}}=\mathrm{pr}_{\mathrm{nil}}^*\left((q_{\mathrm{nil}},p_{\mathrm{nil}})_!{\overline{\mathbb{Q}}_{\ell}}\right). \end{align*} $$
$$ \begin{align*}(q_{\mathfrak{z}},p_{\mathfrak{z}})_!{\overline{\mathbb{Q}}_{\ell}}=\mathrm{pr}_{\mathrm{nil}}^*\left((q_{\mathrm{nil}},p_{\mathrm{nil}})_!{\overline{\mathbb{Q}}_{\ell}}\right). \end{align*} $$
-
(2) Assume also that
 $G, B$
and T are defined over a finite subfield
$G, B$
and T are defined over a finite subfield
 $k_o$
of k. The Postnikov diagram
$k_o$
of k. The Postnikov diagram
 $\Lambda ((q_{\mathrm {nil}},p_{\mathrm {nil}})_!{\overline {\mathbb {Q}}_{\ell }})=\hat {f}_{\mathrm {nil}\, !}\big (\Lambda (\delta _{\mathrm {nil}\, !}{\overline {\mathbb {Q}}_{\ell }})\big )$
is the unique Postnikov diagram defined over
$\Lambda ((q_{\mathrm {nil}},p_{\mathrm {nil}})_!{\overline {\mathbb {Q}}_{\ell }})=\hat {f}_{\mathrm {nil}\, !}\big (\Lambda (\delta _{\mathrm {nil}\, !}{\overline {\mathbb {Q}}_{\ell }})\big )$
is the unique Postnikov diagram defined over
 $k_o$
whose base is the complex (4.4) with
$k_o$
whose base is the complex (4.4) with
 $\mathfrak {z}=0$
.
$\mathfrak {z}=0$
.
Proof. The assertion (1) is clear. The proof of assertion (2) goes exactly along the same lines as the proof of Proposition 4.2.
5 Descent
As explained in §5.4, the kernel
![]() ${\mathcal {N}}$
does not descend to
${\mathcal {N}}$
does not descend to
![]() ${\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G}$
. However, we will prove in this section that we have a descent result if we restrict ourselves to strata of
${\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G}$
. However, we will prove in this section that we have a descent result if we restrict ourselves to strata of
![]() $\mathfrak {car}$
that we are now defining.
$\mathfrak {car}$
that we are now defining.
5.1 The main theorem
We have a natural stratification of
![]() $\mathfrak {car}$
into smooth locally closed subsets indexed by the set
$\mathfrak {car}$
into smooth locally closed subsets indexed by the set
![]() $\mathfrak {L}$
of G-conjugacy classes of Levi subgroups (of parabolic subgroups) of G
$\mathfrak {L}$
of G-conjugacy classes of Levi subgroups (of parabolic subgroups) of G
Concretely, let L be a representative of
![]() $\lambda \in \mathfrak {L}$
containing T. Then
$\lambda \in \mathfrak {L}$
containing T. Then
![]() $\mathfrak {car}_{\lambda }$
is the image of
$\mathfrak {car}_{\lambda }$
is the image of
by the quotient map
![]() ${\mathfrak {t}}\rightarrow \mathfrak {car}$
.
${\mathfrak {t}}\rightarrow \mathfrak {car}$
.
If
![]() $\mathcal {X}$
is either
$\mathcal {X}$
is either
![]() $\mathcal {T},\mathcal {B},\hat {\mathcal {B}}, {\mathcal {S}}, \hat {{\mathcal {S}}}, {\overline {\mathcal {T}}} $
or
$\mathcal {T},\mathcal {B},\hat {\mathcal {B}}, {\mathcal {S}}, \hat {{\mathcal {S}}}, {\overline {\mathcal {T}}} $
or
![]() $\mathcal {G}$
we put
$\mathcal {G}$
we put
for any
![]() $\lambda \in \mathfrak {L}$
.
$\lambda \in \mathfrak {L}$
.
We consider the Lusztig correspondence over
![]() $\lambda \in \mathfrak {L}$
$\lambda \in \mathfrak {L}$
Notice that
![]() $\mathcal {T}_{\lambda }=[{\mathfrak {t}}_{\lambda }/T]\simeq {\mathfrak {t}}_{\lambda }\times \mathrm {B}(T)$
with
$\mathcal {T}_{\lambda }=[{\mathfrak {t}}_{\lambda }/T]\simeq {\mathfrak {t}}_{\lambda }\times \mathrm {B}(T)$
with
 $$ \begin{align*}{\mathfrak{t}}_{\lambda}=\coprod_{g\in N_G(T)/N_G(L,T)}g\,z(\mathfrak{l})^og^{-1}. \end{align*} $$
$$ \begin{align*}{\mathfrak{t}}_{\lambda}=\coprod_{g\in N_G(T)/N_G(L,T)}g\,z(\mathfrak{l})^og^{-1}. \end{align*} $$
Notice that if for some
![]() $g\in G$
and
$g\in G$
and
![]() $s\in z(\mathfrak {l})^o$
we have
$s\in z(\mathfrak {l})^o$
we have
![]() $\mathrm {Ad}(g)(s)\in z(\mathfrak {l})^o$
, then
$\mathrm {Ad}(g)(s)\in z(\mathfrak {l})^o$
, then
![]() $g\in N_G(L)$
[Reference Letellier11, Lemma 2.6.16].
$g\in N_G(L)$
[Reference Letellier11, Lemma 2.6.16].
We thus have isomorphisms of stacks
Put
![]() $B^L:=B\cap L$
, and let
$B^L:=B\cap L$
, and let
![]() ${\mathfrak {u}}^L$
be the Lie algebra of the unipotent radical of
${\mathfrak {u}}^L$
be the Lie algebra of the unipotent radical of
![]() $B^L$
. We consider the following commutative diagram (as in §4.3 with
$B^L$
. We consider the following commutative diagram (as in §4.3 with
![]() $G=L$
and
$G=L$
and
![]() $\mathfrak {z}=z(\mathfrak {l})^o$
):
$\mathfrak {z}=z(\mathfrak {l})^o$
):

Put
We have an exact sequence
and the group
![]() $\widehat {W}^L$
acts on
$\widehat {W}^L$
acts on
in the natural way on the first factor and via
![]() $W_L$
on the second factor.
$W_L$
on the second factor.
The first two vertical arrows of the diagram (5.1) are
![]() $\widehat {W}^L$
-torsors while the right vertical arrow is
$\widehat {W}^L$
-torsors while the right vertical arrow is
![]() $W_L$
-torsor.
$W_L$
-torsor.
Theorem 5.1. The complex
![]() ${\mathcal {N}}^L:=(q^L,p^L)_!{\overline {\mathbb {Q}}_{\ell }}$
is
${\mathcal {N}}^L:=(q^L,p^L)_!{\overline {\mathbb {Q}}_{\ell }}$
is
![]() $\widehat {W}^L$
-equivariant (i.e., it descends to a complex
$\widehat {W}^L$
-equivariant (i.e., it descends to a complex
![]() ${\overline {{\mathcal {N}}}}_{\lambda }$
on
${\overline {{\mathcal {N}}}}_{\lambda }$
on
![]() $\overline {\mathcal {T}}_{\lambda }\times _{\mathfrak {car}_{\lambda }}\mathcal {G}_{\lambda }$
).
$\overline {\mathcal {T}}_{\lambda }\times _{\mathfrak {car}_{\lambda }}\mathcal {G}_{\lambda }$
).
Remark 5.2. We have the following commutative diagram

where the top square is cartesian. From this diagram we see that
where
![]() ${\mathcal {N}}$
is as in §4. In other words, the complex
${\mathcal {N}}$
is as in §4. In other words, the complex
![]() ${\mathcal {N}}_{\lambda }:={\mathcal {N}}|_{\mathcal {T}_{\lambda }\times _{\mathfrak {car}}\mathcal {G}_{\lambda }}$
is W-equivariant.
${\mathcal {N}}_{\lambda }:={\mathcal {N}}|_{\mathcal {T}_{\lambda }\times _{\mathfrak {car}}\mathcal {G}_{\lambda }}$
is W-equivariant.
5.2 Proof of Theorem 5.1
The essential case is when
![]() $L=G$
which case reduces to the nilpotent elements (see §4.3). We thus consider the following diagram:
$L=G$
which case reduces to the nilpotent elements (see §4.3). We thus consider the following diagram:

and we want to prove that the complex
![]() $(q_{\mathrm {nil}},p_{\mathrm {nil}})_!{\overline {\mathbb {Q}}_{\ell }}$
is W-equivariant and so descends to
$(q_{\mathrm {nil}},p_{\mathrm {nil}})_!{\overline {\mathbb {Q}}_{\ell }}$
is W-equivariant and so descends to
![]() $\mathrm {B}(N)\times \mathcal {G}_{\mathrm {nil}}$
.
$\mathrm {B}(N)\times \mathcal {G}_{\mathrm {nil}}$
.
Consider now the diagram

Notice that the complex
![]() $(q_{\mathrm {nil}},p_{\mathrm {nil}})_!{\overline {\mathbb {Q}}_{\ell }}$
is the restriction of
$(q_{\mathrm {nil}},p_{\mathrm {nil}})_!{\overline {\mathbb {Q}}_{\ell }}$
is the restriction of
![]() $(\tau ,p)_!{\overline {\mathbb {Q}}_{\ell }}$
to
$(\tau ,p)_!{\overline {\mathbb {Q}}_{\ell }}$
to
![]() $\mathrm {B}(T)\times \mathcal {G}_{\mathrm {nil}}$
.
$\mathrm {B}(T)\times \mathcal {G}_{\mathrm {nil}}$
.
It is thus enough to prove that
![]() $(\tau ,p)_!{\overline {\mathbb {Q}}_{\ell }}$
is W-equivariant.
$(\tau ,p)_!{\overline {\mathbb {Q}}_{\ell }}$
is W-equivariant.
The map
![]() $(\tau ,p)$
decomposes as
$(\tau ,p)$
decomposes as
Following the strategy of §4.1, we see that the complex
![]() $(\tau ,p)_!{\overline {\mathbb {Q}}_{\ell }}$
is the outcome of the Postnikov diagram
$(\tau ,p)_!{\overline {\mathbb {Q}}_{\ell }}$
is the outcome of the Postnikov diagram
![]() $\hat {p}_!\Lambda (\delta _!{\overline {\mathbb {Q}}_{\ell }})$
. The base of this Postnikov diagram is the complex
$\hat {p}_!\Lambda (\delta _!{\overline {\mathbb {Q}}_{\ell }})$
. The base of this Postnikov diagram is the complex
 $$\begin{align*} &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \cdots\overset{\partial_1}{\longrightarrow} \left(\bigwedge^nX_*(T)\right)\otimes{\mathrm{IC}}_{\hat{\mathcal{G}}}(\hat{\mathcal{L}}), \notag \end{align*}$$
$$\begin{align*} &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \cdots\overset{\partial_1}{\longrightarrow} \left(\bigwedge^nX_*(T)\right)\otimes{\mathrm{IC}}_{\hat{\mathcal{G}}}(\hat{\mathcal{L}}), \notag \end{align*}$$
where
![]() $\hat {\mathcal {L}}$
is the semisimple local system
$\hat {\mathcal {L}}$
is the semisimple local system
![]() ${\overline {\mathbb {Q}}_{\ell }}\boxtimes \mathcal {L}$
with
${\overline {\mathbb {Q}}_{\ell }}\boxtimes \mathcal {L}$
with
![]() $\mathcal {L}=p_{{\mathrm {rss}}\, !}{\overline {\mathbb {Q}}_{\ell }}$
where
$\mathcal {L}=p_{{\mathrm {rss}}\, !}{\overline {\mathbb {Q}}_{\ell }}$
where
![]() $p_{\mathrm {rss}}:\mathcal {B}_{\mathrm {rss}}\rightarrow \mathcal {G}_{\mathrm {rss}}$
is the restriction of p to semisimple regular elements.
$p_{\mathrm {rss}}:\mathcal {B}_{\mathrm {rss}}\rightarrow \mathcal {G}_{\mathrm {rss}}$
is the restriction of p to semisimple regular elements.
We consider on vertices of (5.2) the W-action given by the Springer action on
![]() ${\mathrm {IC}}_{\mathcal {G}}(\mathcal {L})=p_!{\overline {\mathbb {Q}}_{\ell }}$
and the obvious one on
${\mathrm {IC}}_{\mathcal {G}}(\mathcal {L})=p_!{\overline {\mathbb {Q}}_{\ell }}$
and the obvious one on
![]() $X_*(T)$
.
$X_*(T)$
.
Theorem 5.3. The arrows of the complex (5.2) are W-equivariant.
Theorem 5.3 will be a consequence of Theorem 5.6 below.
Corollary 5.4. The complex (5.2) descends to a unique complex
![]() $\overline {\Lambda }_b$
in
$\overline {\Lambda }_b$
in
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\hat {\mathcal {G}})$
whose vertices are
$D_{\mathrm {c}}^{\mathrm {b}}(\hat {\mathcal {G}})$
whose vertices are
 $$ \begin{align*}\left(\bigwedge^{2n-i}X_*(T)\right)\otimes\left(\overline{\mathbb{Q}}_{\ell,\, \mathrm{B}(N)}\boxtimes {\mathrm{IC}}_{\mathcal{G}}(\mathcal{L})\right)[2n-2i](n-i). \end{align*} $$
$$ \begin{align*}\left(\bigwedge^{2n-i}X_*(T)\right)\otimes\left(\overline{\mathbb{Q}}_{\ell,\, \mathrm{B}(N)}\boxtimes {\mathrm{IC}}_{\mathcal{G}}(\mathcal{L})\right)[2n-2i](n-i). \end{align*} $$
If
![]() $k_o$
is a finite subfield of k on which
$k_o$
is a finite subfield of k on which
![]() $G, T$
and B are defined, then
$G, T$
and B are defined, then
![]() $\overline {\Lambda }_b$
is naturally defined over
$\overline {\Lambda }_b$
is naturally defined over
![]() $k_o$
.
$k_o$
.
Theorem 5.5. The complex
![]() $\overline {\Lambda }_b$
of Corollary 5.4 can be completed into a unique Postnikov diagram
$\overline {\Lambda }_b$
of Corollary 5.4 can be completed into a unique Postnikov diagram
![]() $\overline {\Lambda }$
(up to a unique isomorphism) such that for any finite subfield
$\overline {\Lambda }$
(up to a unique isomorphism) such that for any finite subfield
![]() $k_o$
of k on which
$k_o$
of k on which
![]() $G,T$
and B are defined, the diagram
$G,T$
and B are defined, the diagram
![]() $\overline {\Lambda }$
is also defined over
$\overline {\Lambda }$
is also defined over
![]() $k_o$
with
$k_o$
with
![]() $\overline {\Lambda }_b$
equipped with its natural
$\overline {\Lambda }_b$
equipped with its natural
![]() $k_o$
-structure.
$k_o$
-structure.
We have
In particular, the outcome
![]() $(\tau ,p)_!{\overline {\mathbb {Q}}_{\ell }}$
of
$(\tau ,p)_!{\overline {\mathbb {Q}}_{\ell }}$
of
![]() $\hat {p}_!\Lambda (\delta _!{\overline {\mathbb {Q}}_{\ell }})$
descends naturally to
$\hat {p}_!\Lambda (\delta _!{\overline {\mathbb {Q}}_{\ell }})$
descends naturally to
![]() $\mathrm {B}(N)\times \mathcal {G}$
.
$\mathrm {B}(N)\times \mathcal {G}$
.
Proof. We choose a finite subfield
![]() $k_o$
on which G, T and B are defined. By the proof of Proposition 4.2, the conditions of Proposition 2.14 are satisfied over
$k_o$
on which G, T and B are defined. By the proof of Proposition 4.2, the conditions of Proposition 2.14 are satisfied over
![]() $k_o$
. Therefore, by Proposition 2.14, there is a unique Postnikov diagram
$k_o$
. Therefore, by Proposition 2.14, there is a unique Postnikov diagram
![]() $\overline {\Lambda }_o$
that completes the natural descent of
$\overline {\Lambda }_o$
that completes the natural descent of
![]() $\overline {\Lambda }_b$
to
$\overline {\Lambda }_b$
to
![]() $k_o$
. The wanted Postnikov diagram
$k_o$
. The wanted Postnikov diagram
![]() $\overline {\Lambda }$
is the one induced by
$\overline {\Lambda }$
is the one induced by
![]() $\overline {\Lambda }_o$
from
$\overline {\Lambda }_o$
from
![]() $k_o$
to k.
$k_o$
to k.
As explained in §2.4, the group W acts on
Theorem 5.6. The map
where the first arrow is the Chern class morphism of
![]() $\delta $
and the second arrow is given by
$\delta $
and the second arrow is given by
![]() $\hat {p}_!$
, is W-equivariant.
$\hat {p}_!$
, is W-equivariant.
This is apriori not obvious as the natural action of W on
![]() $\hat {\mathcal {G}}$
does not lift to
$\hat {\mathcal {G}}$
does not lift to
![]() $\hat {\mathcal {B}}$
.
$\hat {\mathcal {B}}$
.
We have the following proposition.
Proposition 5.7. The Chern class morphism
of the T-torsor
![]() $\delta $
is W-equivariant.
$\delta $
is W-equivariant.
Proof. As
![]() $\hat {\mathcal {B}}=\mathrm {B}(T)\times \mathcal {B}$
, by Künneth formula we have
$\hat {\mathcal {B}}=\mathrm {B}(T)\times \mathcal {B}$
, by Künneth formula we have
Then
where
![]() $\pi $
is the T-torsor
$\pi $
is the T-torsor
![]() $\dot {\mathcal {B}}\rightarrow \mathcal {B}$
. The Chern class morphism
$\dot {\mathcal {B}}\rightarrow \mathcal {B}$
. The Chern class morphism
![]() $c_{\mathrm {can}}$
of the trivial T-torsor
$c_{\mathrm {can}}$
of the trivial T-torsor
![]() $\mathrm {Spec}(k)\rightarrow \mathrm {B}(T)$
is W-equivariant.
$\mathrm {Spec}(k)\rightarrow \mathrm {B}(T)$
is W-equivariant.
We thus need to prove that
![]() $c_{\pi }$
is W-equivariant.
$c_{\pi }$
is W-equivariant.
The Chern class morphism
![]() $c_{\pi }$
decomposes as
$c_{\pi }$
decomposes as
where the first map is
![]() $c_{\mathrm {can}}$
and the second map is the cohomological restriction of the canonical map
$c_{\mathrm {can}}$
and the second map is the cohomological restriction of the canonical map
![]() $\mathcal {B}\rightarrow \mathrm {B}(B)$
. It is W-equivariant by Lemma 2.23.
$\mathcal {B}\rightarrow \mathrm {B}(B)$
. It is W-equivariant by Lemma 2.23.
Theorem 5.6 is a consequence of Proposition 5.7 together with the following one.
Proposition 5.8. The map
induced by
![]() $\hat {p}_!$
is W-equivariant.
$\hat {p}_!$
is W-equivariant.
Proof. By Künneth formula, we are reduced to prove that the same statement is true with
![]() $\hat {\mathcal {B}}$
and
$\hat {\mathcal {B}}$
and
![]() $\hat {\mathcal {G}}$
replaced by
$\hat {\mathcal {G}}$
replaced by
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {G}$
. That is, we need to see that the map
$\mathcal {G}$
. That is, we need to see that the map
given by the functor
![]() $p_!$
is W-equivariant.
$p_!$
is W-equivariant.
Consider the cartesian diagram

We have
 $$ \begin{align*} {\mathrm{Ext}}^i_{\mathcal{G}}({\mathrm{IC}}_{\mathcal{G}}(\mathcal{L}),{\mathrm{IC}}_{\mathcal{G}}(\mathcal{L}))&=\mathrm{ Hom}(p_!{\overline{\mathbb{Q}}_{\ell}},p_!{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=\mathrm{Hom}(p^*p_!{\overline{\mathbb{Q}}_{\ell}},{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=H^i(\mathcal{Z},\mathrm{pr}_1^!{\overline{\mathbb{Q}}_{\ell}})\\ &=H^{-i}_c(\mathcal{Z},{\overline{\mathbb{Q}}_{\ell}}). \end{align*} $$
$$ \begin{align*} {\mathrm{Ext}}^i_{\mathcal{G}}({\mathrm{IC}}_{\mathcal{G}}(\mathcal{L}),{\mathrm{IC}}_{\mathcal{G}}(\mathcal{L}))&=\mathrm{ Hom}(p_!{\overline{\mathbb{Q}}_{\ell}},p_!{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=\mathrm{Hom}(p^*p_!{\overline{\mathbb{Q}}_{\ell}},{\overline{\mathbb{Q}}_{\ell}}[i])\\ &=H^i(\mathcal{Z},\mathrm{pr}_1^!{\overline{\mathbb{Q}}_{\ell}})\\ &=H^{-i}_c(\mathcal{Z},{\overline{\mathbb{Q}}_{\ell}}). \end{align*} $$
The dual of the map (5.4) is the cohomological restriction
of the diagonal morphism
![]() $\mathcal {B}\rightarrow \mathcal {Z}$
. The proposition is thus a consequence of Theorem 3.4.
$\mathcal {B}\rightarrow \mathcal {Z}$
. The proposition is thus a consequence of Theorem 3.4.
5.3 Descent over regular elements
We consider the diagram (4.1) over regular elements

and put
Theorem 5.9. The kernel
![]() ${\mathcal {N}}_{\mathrm {reg}}$
is W-equivariant (i.e., it descends to
${\mathcal {N}}_{\mathrm {reg}}$
is W-equivariant (i.e., it descends to
![]() ${\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G}_{\mathrm {reg}}$
).
${\overline {\mathcal {T}}}\times _{\mathfrak {car}}\mathcal {G}_{\mathrm {reg}}$
).
Proof. Following the strategy of §5.2, we need to prove that the base
![]() $\Lambda _b({\mathcal {N}}_{\mathrm {reg}})$
of the Postnikov diagram
$\Lambda _b({\mathcal {N}}_{\mathrm {reg}})$
of the Postnikov diagram
![]() $\Lambda ({\mathcal {N}}_{\mathrm {reg}})$
is W-equivariant. With the map
$\Lambda ({\mathcal {N}}_{\mathrm {reg}})$
is W-equivariant. With the map
![]() $\hat {f}_{\mathrm {reg}}$
being an isomorphism, the vertices of
$\hat {f}_{\mathrm {reg}}$
being an isomorphism, the vertices of
![]() $\Lambda _b({\mathcal {N}}_{\mathrm {reg}})$
are constant sheaves (up to a shift) and so are clearly W-equivariant. To prove that the arrows are W-equivariant, we need to prove (analogously to Theorem 5.6) that the map
$\Lambda _b({\mathcal {N}}_{\mathrm {reg}})$
are constant sheaves (up to a shift) and so are clearly W-equivariant. To prove that the arrows are W-equivariant, we need to prove (analogously to Theorem 5.6) that the map
is W-equivariant. The first map being W-equivariant (see Proposition 5.7), we need to see that the second map too. However, notice that
![]() $\hat {f}_{\mathrm {reg}}$
is an isomorphism, and so the second map is an isomorphism
$\hat {f}_{\mathrm {reg}}$
is an isomorphism, and so the second map is an isomorphism
which is dual to the restriction morphism
By Künneth formula, we are reduced to prove that the restriction map (which is an isomorphism)
is W-equivariant. Notice that
![]() $H_c^{-2}({\mathcal {S}}_{\mathrm {reg}},{\overline {\mathbb {Q}}_{\ell }})$
and
$H_c^{-2}({\mathcal {S}}_{\mathrm {reg}},{\overline {\mathbb {Q}}_{\ell }})$
and
![]() $H^{-2}_c(\mathcal {B}_{\mathrm {reg}},{\overline {\mathbb {Q}}_{\ell }})$
are both the hypercohomology of the proper pushforwards of
$H^{-2}_c(\mathcal {B}_{\mathrm {reg}},{\overline {\mathbb {Q}}_{\ell }})$
are both the hypercohomology of the proper pushforwards of
![]() ${\overline {\mathbb {Q}}_{\ell }}$
along the maps
${\overline {\mathbb {Q}}_{\ell }}$
along the maps
![]() $\mathrm {pr}_2:{\mathcal {S}}_{\mathrm {reg}}\rightarrow \mathcal {G}_{\mathrm {reg}}$
and
$\mathrm {pr}_2:{\mathcal {S}}_{\mathrm {reg}}\rightarrow \mathcal {G}_{\mathrm {reg}}$
and
![]() $p_{\mathrm {reg}}:\mathcal {B}_{\mathrm {reg}}\rightarrow \mathcal {G}_{\mathrm {reg}}$
, respectively, and these pushforwards are the intermediate extensions of the pushforwards over semisimple regular elements. The result follows from the fact that W acts on
$p_{\mathrm {reg}}:\mathcal {B}_{\mathrm {reg}}\rightarrow \mathcal {G}_{\mathrm {reg}}$
, respectively, and these pushforwards are the intermediate extensions of the pushforwards over semisimple regular elements. The result follows from the fact that W acts on
![]() $\mathcal {B}_{\mathrm {rss}}$
and that the isomorphism
$\mathcal {B}_{\mathrm {rss}}$
and that the isomorphism
![]() $\mathcal {B}_{\mathrm {rss}}\simeq {\mathcal {S}}_{\mathrm {rss}}$
is W-equivariant.
$\mathcal {B}_{\mathrm {rss}}\simeq {\mathcal {S}}_{\mathrm {rss}}$
is W-equivariant.
5.4 “Un calcul triste”
In this section we give an example where the kernel
![]() ${\mathcal {N}}$
is not W-equivariant.
${\mathcal {N}}$
is not W-equivariant.
5.10. Notice that if
![]() ${\mathcal {N}}$
were W-equivariant, then by Remark 2.12, the diagram
${\mathcal {N}}$
were W-equivariant, then by Remark 2.12, the diagram
![]() $\Lambda ({\mathcal {N}})$
would be also W-equivariant and by Proposition 4.2(2), so would be the arrows of the complex
$\Lambda ({\mathcal {N}})$
would be also W-equivariant and by Proposition 4.2(2), so would be the arrows of the complex
![]() $\Lambda _b({\mathcal {N}})$
.
$\Lambda _b({\mathcal {N}})$
.
For
![]() $w\in W$
, put
$w\in W$
, put
![]() $\mathcal {B}_w:=[\mathrm {Ad}(w){\mathfrak {b}}/wBw^{-1}]$
. We then have a cartesian diagram
$\mathcal {B}_w:=[\mathrm {Ad}(w){\mathfrak {b}}/wBw^{-1}]$
. We then have a cartesian diagram

from which we get a commutative diagram (base change)

where the horizontal arrows are given by the functors
![]() $(q^{\prime }_w,p_w)_!$
and
$(q^{\prime }_w,p_w)_!$
and
![]() $(q,p)_!$
, respectively. Identifying
$(q,p)_!$
, respectively. Identifying
![]() $H^2(\mathcal {B},{\overline {\mathbb {Q}}_{\ell }})$
and
$H^2(\mathcal {B},{\overline {\mathbb {Q}}_{\ell }})$
and
![]() $H^2(\mathcal {B}_w,{\overline {\mathbb {Q}}_{\ell }})$
with
$H^2(\mathcal {B}_w,{\overline {\mathbb {Q}}_{\ell }})$
with
![]() $IH^2({\mathcal {S}},{\overline {\mathbb {Q}}_{\ell }})$
on one hand, and
$IH^2({\mathcal {S}},{\overline {\mathbb {Q}}_{\ell }})$
on one hand, and
![]() $(q',p)_!{\overline {\mathbb {Q}}_{\ell }}$
and
$(q',p)_!{\overline {\mathbb {Q}}_{\ell }}$
and
![]() $(q^{\prime }_w,p_w)_!{\overline {\mathbb {Q}}_{\ell }}$
with
$(q^{\prime }_w,p_w)_!{\overline {\mathbb {Q}}_{\ell }}$
with
![]() ${\mathrm {IC}}_{\mathcal {S}}$
on the other hand, we end up with a commutative diagram
${\mathrm {IC}}_{\mathcal {S}}$
on the other hand, we end up with a commutative diagram

Similarly to §5.2, we see that that the arrows of the diagram
![]() $\Lambda _b({\mathcal {N}})$
are W-equivariant if and only if
$\Lambda _b({\mathcal {N}})$
are W-equivariant if and only if
![]() $a=a_w$
for all
$a=a_w$
for all
![]() $w\in W$
.
$w\in W$
.
5.11. Assume that
![]() $G=\mathrm {SL}_2$
and put
$G=\mathrm {SL}_2$
and put
![]() $a_-:=a_w$
for
$a_-:=a_w$
for
![]() $w\neq 1$
and
$w\neq 1$
and
![]() $a_+:=a$
. We prove below that
$a_+:=a$
. We prove below that
![]() $a_+\neq a_-$
, proving thus the nonequivariance of
$a_+\neq a_-$
, proving thus the nonequivariance of
![]() ${\mathcal {N}}$
.
${\mathcal {N}}$
.
Note that
 $$ \begin{align*} &S:={\mathfrak{t}}\times_{\mathfrak{car}}{\mathfrak{g}}=\{(x,t)\in {\mathfrak{sl}}_2\times\mathbb{A}^1\,|\, \det(x)=-t^2\}\\ &X_+=\{(x,t,D)\in{\mathfrak{sl}}_2\times\mathbb{A}^1\times\mathbb{P}^1\,|\, (x,t)\in S, D\subset\mathrm{ Ker}(x-t\mathrm{Id})\}\\[-15pt] \end{align*} $$
$$ \begin{align*} &S:={\mathfrak{t}}\times_{\mathfrak{car}}{\mathfrak{g}}=\{(x,t)\in {\mathfrak{sl}}_2\times\mathbb{A}^1\,|\, \det(x)=-t^2\}\\ &X_+=\{(x,t,D)\in{\mathfrak{sl}}_2\times\mathbb{A}^1\times\mathbb{P}^1\,|\, (x,t)\in S, D\subset\mathrm{ Ker}(x-t\mathrm{Id})\}\\[-15pt] \end{align*} $$
and denote by
![]() $\rho _+:X_+\rightarrow S$
the map
$\rho _+:X_+\rightarrow S$
the map
![]() $(x,t,D)\mapsto (x,t)$
. We consider also the analogous map
$(x,t,D)\mapsto (x,t)$
. We consider also the analogous map
![]() $\rho _-:X_-\rightarrow S$
, where we replace
$\rho _-:X_-\rightarrow S$
, where we replace
![]() $\mathrm {Ker}(x-t\mathrm {Id})$
in the definition of
$\mathrm {Ker}(x-t\mathrm {Id})$
in the definition of
![]() $X_+$
by
$X_+$
by
![]() $\mathrm { Ker}(x+t\mathrm {Id})$
.
$\mathrm { Ker}(x+t\mathrm {Id})$
.
Note that if B denotes the Borel subgroup of upper triangular matrices, then
and
![]() $X_-$
corresponds to choosing the opposite Borel subgroup of lower triangular matrices.
$X_-$
corresponds to choosing the opposite Borel subgroup of lower triangular matrices.
We have compactifications
 $$ \begin{align*} &\overline{S}:=\{(X;T;Z)\in\mathbb{P}^4\,|\, \det(X)=-T^2\}\\ &\overline{X}_+:=\{((X;T;Z),D)\in\overline{S}\times\mathbb{P}^1\,|\, D\subset\mathrm{Ker}(X-T\mathrm{Id})\}\\ &\overline{X}_-:=\{((X;T;Z),D)\in\overline{S}\times\mathbb{P}^1\,|\, D\subset\mathrm{Ker}(X+T\mathrm{Id})\}\ \end{align*} $$
$$ \begin{align*} &\overline{S}:=\{(X;T;Z)\in\mathbb{P}^4\,|\, \det(X)=-T^2\}\\ &\overline{X}_+:=\{((X;T;Z),D)\in\overline{S}\times\mathbb{P}^1\,|\, D\subset\mathrm{Ker}(X-T\mathrm{Id})\}\\ &\overline{X}_-:=\{((X;T;Z),D)\in\overline{S}\times\mathbb{P}^1\,|\, D\subset\mathrm{Ker}(X+T\mathrm{Id})\}\ \end{align*} $$
where we identify
![]() ${\mathfrak {sl}}_2$
with
${\mathfrak {sl}}_2$
with
![]() $\mathbb {A}^3$
in the obvious way, and the small resolutions
$\mathbb {A}^3$
in the obvious way, and the small resolutions
![]() $\overline {\rho }_+:\overline {X}_+\rightarrow \overline {S}$
and
$\overline {\rho }_+:\overline {X}_+\rightarrow \overline {S}$
and
![]() $\overline {\rho }_-:\overline {X}_-\rightarrow \overline {S}$
.
$\overline {\rho }_-:\overline {X}_-\rightarrow \overline {S}$
.
Identifying
![]() $IH^2(\overline {S},{\overline {\mathbb {Q}}_{\ell }})$
with
$IH^2(\overline {S},{\overline {\mathbb {Q}}_{\ell }})$
with
![]() $H^2(\overline {X}_+,{\overline {\mathbb {Q}}_{\ell }})$
(resp. with
$H^2(\overline {X}_+,{\overline {\mathbb {Q}}_{\ell }})$
(resp. with
![]() $H^2(\overline {X}_-,{\overline {\mathbb {Q}}_{\ell }})$
) and
$H^2(\overline {X}_-,{\overline {\mathbb {Q}}_{\ell }})$
) and
![]() ${\mathrm {IC}}_{\overline {S}}$
with
${\mathrm {IC}}_{\overline {S}}$
with
![]() $\overline {\rho }_{+*}{\overline {\mathbb {Q}}_{\ell }}$
(resp.
$\overline {\rho }_{+*}{\overline {\mathbb {Q}}_{\ell }}$
(resp.
![]() $\overline {\rho }_{-\, *}{\overline {\mathbb {Q}}_{\ell }}$
) we get a map
$\overline {\rho }_{-\, *}{\overline {\mathbb {Q}}_{\ell }}$
) we get a map
(resp. we get a map
![]() $\overline {a}_-:IH^2(\overline {S},{\overline {\mathbb {Q}}_{\ell }})\rightarrow {\mathrm {Ext}}^2\left ({\mathrm {IC}}_{\overline {S}},{\mathrm {IC}}_{\overline {S}}\right )$
).
$\overline {a}_-:IH^2(\overline {S},{\overline {\mathbb {Q}}_{\ell }})\rightarrow {\mathrm {Ext}}^2\left ({\mathrm {IC}}_{\overline {S}},{\mathrm {IC}}_{\overline {S}}\right )$
).
If we compose
![]() $\overline {a}_+$
(resp.
$\overline {a}_+$
(resp.
![]() $\overline {a}_-$
) with the natural map
$\overline {a}_-$
) with the natural map
we get the cup-product
induced by the one on
![]() $H^*(\overline {X}_+,{\overline {\mathbb {Q}}_{\ell }})$
(resp. we get the cup-product
$H^*(\overline {X}_+,{\overline {\mathbb {Q}}_{\ell }})$
(resp. we get the cup-product
![]() $\smile _-$
induced by the one on
$\smile _-$
induced by the one on
![]() $H^*(\overline {X}_-,{\overline {\mathbb {Q}}_{\ell }})$
).
$H^*(\overline {X}_-,{\overline {\mathbb {Q}}_{\ell }})$
).
We have the following result [Reference Verdier20].
Proposition 5.12 (Verdier).
The two cup-products
are not the same.
Proof. For the convenience of the reader, we outline the proof.
Consider the following commutative diagram

Consider the divisors
 $$ \begin{align*} &D_{1,+}:=\mathrm{pr}_+\left(f^{-1}(\{\infty\}\times\mathbb{P}^1)\right)=f_+^{-1}(\infty),\hspace{.5cm}D_{2,+}:=\mathrm{pr}_+\left(f^{-1}(\mathbb{P}^1\times\{\infty\})\right)\\ &D_{1,-}:=\mathrm{pr}_-\left(f^{-1}(\mathbb{P}^1\times\{\infty\})\right)=f_-^{-1}(\infty),\hspace{.5cm}D_{2,-}:=\mathrm{pr}_-\left(f^{-1}(\{\infty\}\times\mathbb{P}^1)\right)\\[-15pt] \end{align*} $$
$$ \begin{align*} &D_{1,+}:=\mathrm{pr}_+\left(f^{-1}(\{\infty\}\times\mathbb{P}^1)\right)=f_+^{-1}(\infty),\hspace{.5cm}D_{2,+}:=\mathrm{pr}_+\left(f^{-1}(\mathbb{P}^1\times\{\infty\})\right)\\ &D_{1,-}:=\mathrm{pr}_-\left(f^{-1}(\mathbb{P}^1\times\{\infty\})\right)=f_-^{-1}(\infty),\hspace{.5cm}D_{2,-}:=\mathrm{pr}_-\left(f^{-1}(\{\infty\}\times\mathbb{P}^1)\right)\\[-15pt] \end{align*} $$
Under the natural identifications
the class
![]() $\mathrm {cl}(D_{1,+/-})\in H^2(\overline {X}_{+/-},{\overline {\mathbb {Q}}_{\ell }})$
corresponds to
$\mathrm {cl}(D_{1,+/-})\in H^2(\overline {X}_{+/-},{\overline {\mathbb {Q}}_{\ell }})$
corresponds to
![]() $\mathrm { cl}(D_{2,-/+})\in H^2(\overline {X}_{-/+},{\overline {\mathbb {Q}}_{\ell }})$
, and so the proposition follows from the calculations
$\mathrm { cl}(D_{2,-/+})\in H^2(\overline {X}_{-/+},{\overline {\mathbb {Q}}_{\ell }})$
, and so the proposition follows from the calculations
As a consequence of the proposition, we get that the two maps
![]() $\overline {a}_+$
and
$\overline {a}_+$
and
![]() $\overline {a}_-$
are different.
$\overline {a}_-$
are different.
Let us now deduce from this that
![]() $a_+$
and
$a_+$
and
![]() $a_-$
are also different.
$a_-$
are also different.
Put
Notice that
Put
 $$ \begin{align*} &\overline{\sigma}:=\overline{a}_+-\overline{a}_-:IH^2(\overline{S},{\overline{\mathbb{Q}}_{\ell}})\rightarrow {\mathrm{Ext}}^2({\mathrm{IC}}_{\overline{S}},{\mathrm{IC}}_{\overline{S}})=H^2(\overline{S},K)\\ &\sigma:=a_+-a_-:IH^2(S,{\overline{\mathbb{Q}}_{\ell}})\rightarrow {\mathrm{Ext}}^2({\mathrm{IC}}_S,{\mathrm{IC}}_S)=H^2(S,K|_S).\\[-15pt] \end{align*} $$
$$ \begin{align*} &\overline{\sigma}:=\overline{a}_+-\overline{a}_-:IH^2(\overline{S},{\overline{\mathbb{Q}}_{\ell}})\rightarrow {\mathrm{Ext}}^2({\mathrm{IC}}_{\overline{S}},{\mathrm{IC}}_{\overline{S}})=H^2(\overline{S},K)\\ &\sigma:=a_+-a_-:IH^2(S,{\overline{\mathbb{Q}}_{\ell}})\rightarrow {\mathrm{Ext}}^2({\mathrm{IC}}_S,{\mathrm{IC}}_S)=H^2(S,K|_S).\\[-15pt] \end{align*} $$
We have the following commutative diagram:

where the vertical arrows are the restriction maps.
Let
![]() $\overline {\alpha }\in IH^2(\overline {S},{\overline {\mathbb {Q}}_{\ell }})$
be such that
$\overline {\alpha }\in IH^2(\overline {S},{\overline {\mathbb {Q}}_{\ell }})$
be such that
![]() $\overline {\sigma }(\overline {\alpha })\neq 0$
, and denote by
$\overline {\sigma }(\overline {\alpha })\neq 0$
, and denote by
![]() $\alpha \in IH^2(S,{\overline {\mathbb {Q}}_{\ell }})$
the image of
$\alpha \in IH^2(S,{\overline {\mathbb {Q}}_{\ell }})$
the image of
![]() $\overline {\alpha }$
.
$\overline {\alpha }$
.
Proposition 5.13. We have
and so
![]() $a_+\neq a_-$
.
$a_+\neq a_-$
.
Proof. We need to prove that
We have the open covering
where
![]() $\overline {S}_{\mathrm {reg}}$
is the smooth open subset of elements
$\overline {S}_{\mathrm {reg}}$
is the smooth open subset of elements
![]() $(X;T;Z)$
in
$(X;T;Z)$
in
![]() $\overline {S}$
such that
$\overline {S}$
such that
![]() $X\neq 0$
.
$X\neq 0$
.
Notice that
![]() $S_{\mathrm {reg}}=\overline {S}_{\mathrm {reg}}\cap S$
, and so we have the exact sequence (Mayer-Vietoris)
$S_{\mathrm {reg}}=\overline {S}_{\mathrm {reg}}\cap S$
, and so we have the exact sequence (Mayer-Vietoris)
Since
![]() $S_{\mathrm {reg}}$
and
$S_{\mathrm {reg}}$
and
![]() $\overline {S}_{\mathrm {reg}}$
are smooth open subsets of S and
$\overline {S}_{\mathrm {reg}}$
are smooth open subsets of S and
![]() $\overline {S}$
, respectively, we have
$\overline {S}$
, respectively, we have
Notice also that
as
![]() $\rho |_{X_{\mathrm {reg}}}:X_{\mathrm {reg}}\simeq S_{\mathrm {reg}}$
and
$\rho |_{X_{\mathrm {reg}}}:X_{\mathrm {reg}}\simeq S_{\mathrm {reg}}$
and
![]() $H^1(X_{\mathrm {reg}},{\overline {\mathbb {Q}}_{\ell }})\simeq H^1(X,{\overline {\mathbb {Q}}_{\ell }})=0$
.
$H^1(X_{\mathrm {reg}},{\overline {\mathbb {Q}}_{\ell }})\simeq H^1(X,{\overline {\mathbb {Q}}_{\ell }})=0$
.
The map
![]() $\varphi $
is thus injective, and so to prove (5.5), we are reduced to prove that
$\varphi $
is thus injective, and so to prove (5.5), we are reduced to prove that
where
![]() $\varphi _{\overline {S}_{\mathrm {reg}}}:H^2(\overline {S},K)\rightarrow H^2(\overline {S}_{\mathrm {reg}},{\overline {\mathbb {Q}}_{\ell }})$
is the restriction map.
$\varphi _{\overline {S}_{\mathrm {reg}}}:H^2(\overline {S},K)\rightarrow H^2(\overline {S}_{\mathrm {reg}},{\overline {\mathbb {Q}}_{\ell }})$
is the restriction map.
As the restrictions of
![]() $\overline {\rho }_+$
and
$\overline {\rho }_+$
and
![]() $\overline {\rho }_-$
over regular elements induce isomorphisms
$\overline {\rho }_-$
over regular elements induce isomorphisms
![]() $\overline {X}_{+,{\mathrm {reg}}}\simeq \overline {S}_{\mathrm {reg}}$
and
$\overline {X}_{+,{\mathrm {reg}}}\simeq \overline {S}_{\mathrm {reg}}$
and
![]() $\overline {X}_{-,{\mathrm {reg}}}\simeq \overline {S}_{\mathrm {reg}}$
we have the following commutative diagram:
$\overline {X}_{-,{\mathrm {reg}}}\simeq \overline {S}_{\mathrm {reg}}$
we have the following commutative diagram:

and the analogous diagram with
![]() $\overline {X}_-$
instead of
$\overline {X}_-$
instead of
![]() $\overline {X}_+$
. From these two commutative diagrams we deduce that
$\overline {X}_+$
. From these two commutative diagrams we deduce that
6 The functors
 $\mathrm {I}_{\lambda }$
and
$\mathrm {I}_{\lambda }$
and
 $\mathrm {R}_{\lambda }$
$\mathrm {R}_{\lambda }$
6.1 Definition
We consider the cohomological correspondence where
![]() $\mathrm {pr}_i$
is the i-th projection
$\mathrm {pr}_i$
is the i-th projection
with kernel
![]() ${\overline {{\mathcal {N}}}}_{\lambda }$
.
${\overline {{\mathcal {N}}}}_{\lambda }$
.
We define the associated restriction and induction functors
 $$ \begin{align*} &\mathrm{R}_{\lambda}:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}_{\lambda})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}({\overline{\mathcal{T}}}_{\lambda}),\hspace{.5cm}K\mapsto\mathrm{pr}_{1!}\left(\mathrm{pr}_2^*(K)\otimes{\overline{{\mathcal{N}}}}_{\lambda}\right),\\ &\mathrm{I}_{\lambda}:D_{\mathrm{c}}^{\mathrm{b}}({\overline{\mathcal{T}}}_{\lambda})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}_{\lambda}),\hspace{.5cm}K\mapsto \mathrm{pr}_{2*}\,\underline{\mathrm{ Hom}}\left({\overline{{\mathcal{N}}}}_{\lambda},\mathrm{pr}_1^!(K)\right) \end{align*} $$
$$ \begin{align*} &\mathrm{R}_{\lambda}:D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}_{\lambda})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}({\overline{\mathcal{T}}}_{\lambda}),\hspace{.5cm}K\mapsto\mathrm{pr}_{1!}\left(\mathrm{pr}_2^*(K)\otimes{\overline{{\mathcal{N}}}}_{\lambda}\right),\\ &\mathrm{I}_{\lambda}:D_{\mathrm{c}}^{\mathrm{b}}({\overline{\mathcal{T}}}_{\lambda})\rightarrow D_{\mathrm{c}}^{\mathrm{b}}(\mathcal{G}_{\lambda}),\hspace{.5cm}K\mapsto \mathrm{pr}_{2*}\,\underline{\mathrm{ Hom}}\left({\overline{{\mathcal{N}}}}_{\lambda},\mathrm{pr}_1^!(K)\right) \end{align*} $$
as in §2.5.
If we denote
![]() $\mathrm {Ind}_{\lambda }$
and
$\mathrm {Ind}_{\lambda }$
and
![]() $\mathrm {Res}_{\lambda }$
the induction and restriction functors associated to the correspondence
$\mathrm {Res}_{\lambda }$
the induction and restriction functors associated to the correspondence
with kernel
![]() ${\mathcal {N}}_{\lambda }={\mathcal {N}}|_{\mathcal {T}_{\lambda }\times _{\mathfrak {car}}\mathcal {G}_{\lambda }}$
, then by Remark 5.2,
${\mathcal {N}}_{\lambda }={\mathcal {N}}|_{\mathcal {T}_{\lambda }\times _{\mathfrak {car}}\mathcal {G}_{\lambda }}$
, then by Remark 5.2,
Since
![]() $q_{\lambda }^!=q_{\lambda }^*$
and
$q_{\lambda }^!=q_{\lambda }^*$
and
![]() $p_{\lambda \,!}=p_{\lambda \, *}$
, we see that
$p_{\lambda \,!}=p_{\lambda \, *}$
, we see that
![]() $\mathrm {Ind}_{\lambda }$
decomposes also as the composition of
$\mathrm {Ind}_{\lambda }$
decomposes also as the composition of
![]() $\pi _{\lambda \, !}$
followed by the functor
$\pi _{\lambda \, !}$
followed by the functor
and so by Remark 2.17, we have
As in §2.9, we define a pair of adjoint functors
![]() $({^p}\mathrm {R}_{\lambda },{^p}\mathrm {I}_{\lambda })$
$({^p}\mathrm {R}_{\lambda },{^p}\mathrm {I}_{\lambda })$

where
![]() $\overline {{\mathfrak {t}}}_{\lambda }:=[{\mathfrak {t}}_{\lambda }/W]$
. We let
$\overline {{\mathfrak {t}}}_{\lambda }:=[{\mathfrak {t}}_{\lambda }/W]$
. We let
![]() $\overline {s}_{\lambda }:{\overline {\mathcal {T}}}_{\lambda }\rightarrow \overline {{\mathfrak {t}}}_{\lambda }$
be the quotient map of the identity map
$\overline {s}_{\lambda }:{\overline {\mathcal {T}}}_{\lambda }\rightarrow \overline {{\mathfrak {t}}}_{\lambda }$
be the quotient map of the identity map
![]() ${\mathfrak {t}}_{\lambda }\rightarrow {\mathfrak {t}}_{\lambda }$
by
${\mathfrak {t}}_{\lambda }\rightarrow {\mathfrak {t}}_{\lambda }$
by
![]() $N\rightarrow W$
.
$N\rightarrow W$
.
Lemma 6.1. We have
Proof. Since the functors
![]() $\overline {s}_{\lambda }^$
and
$\overline {s}_{\lambda }^$
and
![]() ${^p}{\mathcal {H}}^0\circ \overline {s}_{\lambda \, !}[-n](-n)$
between
${^p}{\mathcal {H}}^0\circ \overline {s}_{\lambda \, !}[-n](-n)$
between
![]() $\mathcal {M}(\overline {{\mathfrak {t}}}_{\lambda })$
and
$\mathcal {M}(\overline {{\mathfrak {t}}}_{\lambda })$
and
![]() $\mathcal {M}({\overline {\mathcal {T}}}_{\lambda })$
are inverse to each other, by adjunction we deduce the second equality from the first one.
$\mathcal {M}({\overline {\mathcal {T}}}_{\lambda })$
are inverse to each other, by adjunction we deduce the second equality from the first one.
Analogously to the definition
![]() ${^p}\underline {\mathrm {Ind}}$
(see §2.9) we define
${^p}\underline {\mathrm {Ind}}$
(see §2.9) we define
![]() ${^p}\underline {\mathrm {Ind}}_{\lambda }$
by
${^p}\underline {\mathrm {Ind}}_{\lambda }$
by
where

By Remark 2.17, to prove the first equality, we need to see that
Using that
![]() $\mathrm {Ind}_{\lambda }=\mathrm {I}_{\lambda }\circ \pi _{\lambda \, !}$
, we are reduced to prove that
$\mathrm {Ind}_{\lambda }=\mathrm {I}_{\lambda }\circ \pi _{\lambda \, !}$
, we are reduced to prove that
But this follows from the base change theorem as
![]() $\overline {s}_{\lambda }$
and
$\overline {s}_{\lambda }$
and
![]() $s_{\lambda }$
are smooth and of the same relative dimension.
$s_{\lambda }$
are smooth and of the same relative dimension.
6.2 Semisimple regular elements
Let us see that
![]() $\mathrm {I}_{\lambda }$
and
$\mathrm {I}_{\lambda }$
and
![]() $\mathrm {R}_{\lambda }$
are the identity functors when
$\mathrm {R}_{\lambda }$
are the identity functors when
![]() $\lambda $
represents semisimple regular elements (i.e., when
$\lambda $
represents semisimple regular elements (i.e., when
![]() $\lambda $
is the conjugacy class of maximal tori), in which case we use the subscript
$\lambda $
is the conjugacy class of maximal tori), in which case we use the subscript
![]() ${\mathrm {rss}}$
instead of
${\mathrm {rss}}$
instead of
![]() $\lambda $
in the notation.
$\lambda $
in the notation.
Recall that
is an isomorphism and so, taking the quotient by B on both sides, we end up with an isomorphism
Moreover, the natural injection
![]() ${\mathfrak {t}}_{{\mathrm {reg}}}\rightarrow {\mathfrak {g}}_{{\mathrm {rss}}}$
induces an isomorphism
${\mathfrak {t}}_{{\mathrm {reg}}}\rightarrow {\mathfrak {g}}_{{\mathrm {rss}}}$
induces an isomorphism
Therefore, the morphism
![]() $(q_{\mathrm {rss}},p_{\mathrm {rss}})$
is the diagonal morphism
$(q_{\mathrm {rss}},p_{\mathrm {rss}})$
is the diagonal morphism
We thus have the following cartesian diagram:

where the horizontal arrows are the quotient maps by W, and the vertical arrows are the diagonal morphisms (which are T-torsors). Therefore,
(i.e.,
![]() ${\overline {{\mathcal {N}}}}_{{\mathrm {rss}}}=\Delta _{{\overline {\mathcal {T}}}_{\!{\mathrm {reg}}}!}{\overline {\mathbb {Q}}_{\ell }}$
). The functors
${\overline {{\mathcal {N}}}}_{{\mathrm {rss}}}=\Delta _{{\overline {\mathcal {T}}}_{\!{\mathrm {reg}}}!}{\overline {\mathbb {Q}}_{\ell }}$
). The functors
![]() $\mathrm {I}_{{\mathrm {rss}}}:D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\!{\mathrm {reg}}})\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{{\mathrm {rss}}})\simeq D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\!{\mathrm {reg}}})$
and
$\mathrm {I}_{{\mathrm {rss}}}:D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\!{\mathrm {reg}}})\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{{\mathrm {rss}}})\simeq D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\!{\mathrm {reg}}})$
and
![]() $\mathrm {R}_{{\mathrm {rss}}}:D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\!{\mathrm {reg}}})\simeq D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{{\mathrm {rss}}})\rightarrow D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\!{\mathrm {reg}}})$
are thus the identity functors.
$\mathrm {R}_{{\mathrm {rss}}}:D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\!{\mathrm {reg}}})\simeq D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{{\mathrm {rss}}})\rightarrow D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\!{\mathrm {reg}}})$
are thus the identity functors.
6.3 The isomorphism
 $\mathrm {R}_{\lambda }\circ \mathrm {I}_{\lambda }\simeq 1$
$\mathrm {R}_{\lambda }\circ \mathrm {I}_{\lambda }\simeq 1$
By (6.1) we can regard
![]() $\mathrm {I}_{\lambda }$
as a restriction functor. We thus consider the composition of correspondences
$\mathrm {I}_{\lambda }$
as a restriction functor. We thus consider the composition of correspondences

where the arrows are the obvious projections.
We put
Then it follows from §2.5 that the functor
![]() $\mathrm {R}_{\lambda }\circ \mathrm {I}_{\lambda }$
is the restriction functor of the cohomological correspondence
$\mathrm {R}_{\lambda }\circ \mathrm {I}_{\lambda }$
is the restriction functor of the cohomological correspondence
Theorem 6.2. There is a natural isomorphism
where
is the diagonal morphism. In particular we have
![]() $\mathrm {R}_{\lambda }\circ \mathrm {I}_{\lambda }\simeq 1$
.
$\mathrm {R}_{\lambda }\circ \mathrm {I}_{\lambda }\simeq 1$
.
As we did in §5.2, we explain the proof in the nilpotent case, which is the essential case. We thus consider the first diagram of §5.2, and we put
We have
where
is the obvious projection.
Consider the decomposition of
![]() $(q_{\mathrm {nil}},q_{\mathrm {nil}})$
as
$(q_{\mathrm {nil}},q_{\mathrm {nil}})$
as
By Künneth formula, we have
We consider the following commutative diagram

with diagonal morphisms
![]() $\Delta _{\mathcal {B}_{\mathrm {nil}}}$
and
$\Delta _{\mathcal {B}_{\mathrm {nil}}}$
and
![]() $\Delta _{\mathrm {B}(T)}$
.
$\Delta _{\mathrm {B}(T)}$
.
The morphism
![]() $\Delta _{\mathcal {B}_{\mathrm {nil}}}:\mathcal {B}_{\mathrm {nil}}\rightarrow \mathcal {Z}_{\mathrm {nil}}$
is schematic closed, and so by adjunction we have a morphism
$\Delta _{\mathcal {B}_{\mathrm {nil}}}:\mathcal {B}_{\mathrm {nil}}\rightarrow \mathcal {Z}_{\mathrm {nil}}$
is schematic closed, and so by adjunction we have a morphism
and by applying the functor
![]() $(q_{\mathrm {nil}},q_{\mathrm {nil}})_!$
, we get a morphism
$(q_{\mathrm {nil}},q_{\mathrm {nil}})_!$
, we get a morphism
On the other hand, the morphism
![]() $q_{\mathrm {nil}}$
being smooth with fibres isomorphic to
$q_{\mathrm {nil}}$
being smooth with fibres isomorphic to
![]() $[{\mathfrak {u}}/U]$
, we have by adjunction a morphism
$[{\mathfrak {u}}/U]$
, we have by adjunction a morphism
which is an isomorphism, and so we obtain an isomorphism
Composing (6.4) with (6.6), we end up with a morphism
From (6.2) together with (6.7) we get a morphism
where
![]() $\pi _{\mathrm {nil}}$
is the canonical map
$\pi _{\mathrm {nil}}$
is the canonical map
![]() $\mathrm {B}(T)\rightarrow \mathrm {B}(N)$
.
$\mathrm {B}(T)\rightarrow \mathrm {B}(N)$
.
Composing with the adjunction morphism
we find
Consider the cartesian diagram

where the top arrow is given by
![]() $(w,t)\mapsto (w(t),t)$
and the bottom arrow is the diagonal morphism.
$(w,t)\mapsto (w(t),t)$
and the bottom arrow is the diagonal morphism.
If we denote by
![]() $\Delta _{\mathrm {B}(T),w}:\mathrm {B}(T)\rightarrow \mathrm {B}(T)\times \mathrm {B}(T)$
the w-twisted diagonal morphism induced by
$\Delta _{\mathrm {B}(T),w}:\mathrm {B}(T)\rightarrow \mathrm {B}(T)\times \mathrm {B}(T)$
the w-twisted diagonal morphism induced by
![]() $t\mapsto (w(t),t)$
, then
$t\mapsto (w(t),t)$
, then
and so the pullback of (6.8) along the map
![]() $\pi _{\mathrm {nil}}\times \pi _{\mathrm {nil}}$
provides a morphism
$\pi _{\mathrm {nil}}\times \pi _{\mathrm {nil}}$
provides a morphism
of
![]() $W\times W$
-equivariant complexes.
$W\times W$
-equivariant complexes.
Theorem 6.2 is thus a consequence of the following result.
It is enough to show that the morphism
 $$ \begin{align*}{\mathcal{H}}^i(q_{\mathrm{nil}},q_{\mathrm{nil}})_!{\overline{\mathbb{Q}}_{\ell}}\rightarrow {\mathcal{H}}^i\left(\bigoplus_{w\in W}\Delta_{\mathrm{B}(T),w\,!}{\overline{\mathbb{Q}}_{\ell}}\right) \end{align*} $$
$$ \begin{align*}{\mathcal{H}}^i(q_{\mathrm{nil}},q_{\mathrm{nil}})_!{\overline{\mathbb{Q}}_{\ell}}\rightarrow {\mathcal{H}}^i\left(\bigoplus_{w\in W}\Delta_{\mathrm{B}(T),w\,!}{\overline{\mathbb{Q}}_{\ell}}\right) \end{align*} $$
induced by the morphism (6.9) is an isomorphism for all i.
To prove this, we prove that we have an isomorphism
 $$ \begin{align*}{\mathcal{H}}^i(q,q)_!{\overline{\mathbb{Q}}_{\ell}}\rightarrow {\mathcal{H}}^i\left(\bigoplus_{w\in W}\Delta_{\mathcal{T},w\,!}{\overline{\mathbb{Q}}_{\ell}}\right) \end{align*} $$
$$ \begin{align*}{\mathcal{H}}^i(q,q)_!{\overline{\mathbb{Q}}_{\ell}}\rightarrow {\mathcal{H}}^i\left(\bigoplus_{w\in W}\Delta_{\mathcal{T},w\,!}{\overline{\mathbb{Q}}_{\ell}}\right) \end{align*} $$
where
![]() $\Delta _{\mathcal {T},w}:\mathcal {T}\rightarrow \mathcal {T}\times _{\mathfrak {car}}\mathcal {T}$
is induced by
$\Delta _{\mathcal {T},w}:\mathcal {T}\rightarrow \mathcal {T}\times _{\mathfrak {car}}\mathcal {T}$
is induced by
![]() $t\mapsto (w(t),t)$
.
$t\mapsto (w(t),t)$
.
Proposition 6.4. The sheaf
![]() ${\mathcal {H}}^i(q,q)_!{\overline {\mathbb {Q}}_{\ell }}$
is (up to a shift by
${\mathcal {H}}^i(q,q)_!{\overline {\mathbb {Q}}_{\ell }}$
is (up to a shift by
![]() $-n$
) perverse and is the intermediate extension of its restriction to the open substack of regular elements of
$-n$
) perverse and is the intermediate extension of its restriction to the open substack of regular elements of
![]() $\mathcal {T}\times _{\mathfrak {car}}\mathcal {T}$
. In particular, it is
$\mathcal {T}\times _{\mathfrak {car}}\mathcal {T}$
. In particular, it is
![]() $W\times W$
-equivariant.
$W\times W$
-equivariant.
To prove the proposition, we will use a weight argument. Therefore, we choose a finite subfield
![]() $k_o$
of k such that
$k_o$
of k such that
![]() $G, T,$
and B are defined over
$G, T,$
and B are defined over
![]() $k_o$
, and T is split over
$k_o$
, and T is split over
![]() $k_o$
.
$k_o$
.
Recall that we have a stratification (see §3)
The restriction of
![]() $(q,q)$
to
$(q,q)$
to
![]() $\mathcal {Z}_w$
is the composition of the projection
$\mathcal {Z}_w$
is the composition of the projection
![]() $q_w:\mathcal {Z}_w\rightarrow \mathcal {T}$
followed by the morphism
$q_w:\mathcal {Z}_w\rightarrow \mathcal {T}$
followed by the morphism
![]() $ \Delta _{\mathcal {T},w}:\mathcal {T}\rightarrow \mathcal {T}\times _{\mathfrak {car}}\mathcal {T}$
.
$ \Delta _{\mathcal {T},w}:\mathcal {T}\rightarrow \mathcal {T}\times _{\mathfrak {car}}\mathcal {T}$
.
As the cohomology of
![]() $[{\mathfrak {u}}_w/U_w]$
is trivial, we deduce that
$[{\mathfrak {u}}_w/U_w]$
is trivial, we deduce that
We choose a total order
![]() $\{w_0,w_1,\dots \}$
on W so that we have a decreasing filtration of closed substacks
$\{w_0,w_1,\dots \}$
on W so that we have a decreasing filtration of closed substacks
satisfying
![]() $\mathcal {Z}_i\backslash \mathcal {Z}_{i+1}=\mathcal {Z}_{w_i}$
for all i.
$\mathcal {Z}_i\backslash \mathcal {Z}_{i+1}=\mathcal {Z}_{w_i}$
for all i.
By [Reference Deligne5, Chapitre 6, 2.5], we have a spectral sequence
Lemma 6.5. This spectral sequence degenerates at
![]() $E_1$
.
$E_1$
.
Proof. As
![]() $\mathcal {Z}_i\backslash \mathcal {Z}_{i+1}=\mathcal {Z}_{w_i}$
and
$\mathcal {Z}_i\backslash \mathcal {Z}_{i+1}=\mathcal {Z}_{w_i}$
and
![]() $\mathcal {T}=T\times \mathrm {B}(T)$
, by (6.10) we have
$\mathcal {T}=T\times \mathrm {B}(T)$
, by (6.10) we have
 $$ \begin{align} E_1^{ij}={\mathcal{H}}^{i+j}\Delta_{\mathcal{T},w_i\,!}{\overline{\mathbb{Q}}_{\ell}}=\bigwedge^{2n-i-j}X_*(T)\otimes\left(\Delta_{{\mathfrak{t}},w_i\, !}{\overline{\mathbb{Q}}_{\ell}}\boxtimes {{\overline{\mathbb{Q}}_{\ell}}}_{,\mathrm{B}(T)\times\mathrm{B}(T)}\right)(n-i-j) \end{align} $$
$$ \begin{align} E_1^{ij}={\mathcal{H}}^{i+j}\Delta_{\mathcal{T},w_i\,!}{\overline{\mathbb{Q}}_{\ell}}=\bigwedge^{2n-i-j}X_*(T)\otimes\left(\Delta_{{\mathfrak{t}},w_i\, !}{\overline{\mathbb{Q}}_{\ell}}\boxtimes {{\overline{\mathbb{Q}}_{\ell}}}_{,\mathrm{B}(T)\times\mathrm{B}(T)}\right)(n-i-j) \end{align} $$
where
![]() $\Delta _{{\mathfrak {t}},w}:{\mathfrak {t}}\rightarrow {\mathfrak {t}}\times _{\mathfrak {car}} {\mathfrak {t}}$
is given by
$\Delta _{{\mathfrak {t}},w}:{\mathfrak {t}}\rightarrow {\mathfrak {t}}\times _{\mathfrak {car}} {\mathfrak {t}}$
is given by
![]() $t\mapsto (w(t),t)$
. Notice that
$t\mapsto (w(t),t)$
. Notice that
is (up to a shift) perverse and pure of weight
![]() $0$
. Hence
$0$
. Hence
![]() $E_1^{ij}$
is (up to a shift) pure of weight
$E_1^{ij}$
is (up to a shift) pure of weight
![]() $2(i+j)$
.
$2(i+j)$
.
Therefore, the sources and the targets of the differentials
![]() $d_1$
are (up to a shift) perverse of different weight, and so
$d_1$
are (up to a shift) perverse of different weight, and so
![]() $d_1$
vanishes. We keep applying the same argument for the other differentials and we deduce that the spectral sequence degenerates at
$d_1$
vanishes. We keep applying the same argument for the other differentials and we deduce that the spectral sequence degenerates at
![]() $E_1$
, i.e.
$E_1$
, i.e.
![]() $E_1=E_{\infty }$
.
$E_1=E_{\infty }$
.
Proof of Proposition 6.4.
It follows from Lemma 6.5 that
![]() ${\mathcal {H}}^k(q,q)_!{\overline {\mathbb {Q}}_{\ell }}$
is a successive extension of
${\mathcal {H}}^k(q,q)_!{\overline {\mathbb {Q}}_{\ell }}$
is a successive extension of
![]() $E_1^{ij}$
’s which are intermediate extensions of their restriction to the open substack of regular elements by (6.11). It is thus perverse (up to a shift by
$E_1^{ij}$
’s which are intermediate extensions of their restriction to the open substack of regular elements by (6.11). It is thus perverse (up to a shift by
![]() $-n$
), and so the proposition is a consequence of Proposition 2.8.
$-n$
), and so the proposition is a consequence of Proposition 2.8.
Following the proof of (6.4), we have also a morphism
where
![]() $\Delta _{\mathcal {T}}:\mathcal {T}\rightarrow \mathcal {T}\times _{\mathfrak {car}}\mathcal {T}$
is the diagonal morphism. We thus get a morphism
$\Delta _{\mathcal {T}}:\mathcal {T}\rightarrow \mathcal {T}\times _{\mathfrak {car}}\mathcal {T}$
is the diagonal morphism. We thus get a morphism
and since, by Proposition 6.4, the sheaf
![]() ${\mathcal {H}}^i(q,q)_!{\overline {\mathbb {Q}}_{\ell }}$
is
${\mathcal {H}}^i(q,q)_!{\overline {\mathbb {Q}}_{\ell }}$
is
![]() $W\times W$
-equivariant, we get a morphism
$W\times W$
-equivariant, we get a morphism
The source and the target of this morphism are intermediate extensions of their restriction to regular elements (see Proposition 6.4). It is thus an isomorphism, as its restriction to regular element is an isomorphism.
7 Main results
7.1 Derived categories
Fix
![]() $\lambda \in \mathfrak {L}$
. In this section we choose a geometric point
$\lambda \in \mathfrak {L}$
. In this section we choose a geometric point
![]() $c:\mathrm {Spec}(k)\rightarrow \mathfrak {car}_{\lambda }$
. For any stack
$c:\mathrm {Spec}(k)\rightarrow \mathfrak {car}_{\lambda }$
. For any stack
![]() $\mathcal {X}$
above
$\mathcal {X}$
above
![]() $\mathfrak {car}_{\lambda }$
we put
$\mathfrak {car}_{\lambda }$
we put
and for any complex
![]() $K\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
we denote by
$K\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X})$
we denote by
![]() $K_c\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X}_c)$
the pullback of K along the base change morphism
$K_c\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {X}_c)$
the pullback of K along the base change morphism
![]() $\mathcal {X}_c\rightarrow \mathcal {X}$
.
$\mathcal {X}_c\rightarrow \mathcal {X}$
.
We have a commutative diagram with Cartesian squares

We then define the pair
![]() $(\mathrm {R}_c,\mathrm {I}_c)$
of adjoint functors
$(\mathrm {R}_c,\mathrm {I}_c)$
of adjoint functors

by
The following lemma follows from the base change theorem and the projection formula.
Lemma 7.1. We have the commutation formulas.
-
(a)
 $$ \begin{align*}\iota_!\circ\mathrm{I}_c=\mathrm{I}_{\lambda}\circ\iota_!,\hspace{1cm}\mathrm{I}_c\circ\iota^*=\iota^*\circ\mathrm{I}_{\lambda}. \end{align*} $$
$$ \begin{align*}\iota_!\circ\mathrm{I}_c=\mathrm{I}_{\lambda}\circ\iota_!,\hspace{1cm}\mathrm{I}_c\circ\iota^*=\iota^*\circ\mathrm{I}_{\lambda}. \end{align*} $$
-
(b)
 $$ \begin{align*}\iota_!\circ\mathrm{R}_c=\mathrm{R}_{\lambda}\circ\iota_!,\hspace{1cm}\mathrm{R}_c\circ\iota^*=\iota^*\circ\mathrm{R}_{\lambda}. \end{align*} $$
$$ \begin{align*}\iota_!\circ\mathrm{R}_c=\mathrm{R}_{\lambda}\circ\iota_!,\hspace{1cm}\mathrm{R}_c\circ\iota^*=\iota^*\circ\mathrm{R}_{\lambda}. \end{align*} $$
Theorem 7.2. We have
Proof. The isomorphism of functors
![]() $\mathrm {R}_c\circ \mathrm {I}_c\simeq 1$
is obtained by taking the pullback along
$\mathrm {R}_c\circ \mathrm {I}_c\simeq 1$
is obtained by taking the pullback along
![]() $\overline {\mathcal {T}_c}\times \overline {\mathcal {T}_c}\rightarrow {\overline {\mathcal {T}}}_{\lambda }\times _{\mathfrak {car}_{\lambda }}{\overline {\mathcal {T}}}_{\lambda }$
of the isomorphism of complexes
$\overline {\mathcal {T}_c}\times \overline {\mathcal {T}_c}\rightarrow {\overline {\mathcal {T}}}_{\lambda }\times _{\mathfrak {car}_{\lambda }}{\overline {\mathcal {T}}}_{\lambda }$
of the isomorphism of complexes
of Theorem 6.2.
We have also the functor
defined by base change from the diagram (2.20). It satisfies
where
![]() $\pi _c$
is the W-torsor
$\pi _c$
is the W-torsor
![]() $\mathcal {T}_c\rightarrow {\overline {\mathcal {T}}}_c$
. When
$\mathcal {T}_c\rightarrow {\overline {\mathcal {T}}}_c$
. When
![]() $c=0$
, we will use the notation
$c=0$
, we will use the notation
![]() $\pi _{\mathrm {nil}}$
instead of
$\pi _{\mathrm {nil}}$
instead of
![]() $\pi _c$
.
$\pi _c$
.
We define
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
as the triangulated subcategory of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
as the triangulated subcategory of
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)$
generated by the simple direct factors of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)$
generated by the simple direct factors of
![]() $\mathrm {Ind}_c({\overline {\mathbb {Q}}_{\ell }})$
which, by Springer theory, are indexed by the irreducible characters of the Weyl group
$\mathrm {Ind}_c({\overline {\mathbb {Q}}_{\ell }})$
which, by Springer theory, are indexed by the irreducible characters of the Weyl group
![]() $W_c$
of the centralizer of c.
$W_c$
of the centralizer of c.
Proposition 7.3. The functor
![]() $\mathrm {I}_c:D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_c)\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
induces a bijection between simple perverse sheaves compatible with parametrization by irreducible representations of
$\mathrm {I}_c:D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_c)\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
induces a bijection between simple perverse sheaves compatible with parametrization by irreducible representations of
![]() $W_c$
.
$W_c$
.
Proof. The essential case is
![]() $c=0$
in which case we have
$c=0$
in which case we have
![]() $\mathcal {T}_c=\mathrm {B}(T)$
,
$\mathcal {T}_c=\mathrm {B}(T)$
,
![]() ${\overline {\mathcal {T}}}_c=\mathrm {B}(N)$
and
${\overline {\mathcal {T}}}_c=\mathrm {B}(N)$
and
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm { Spr}}=D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\mathrm {nil}})^{\mathrm {Spr}}$
. The simple objects of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm { Spr}}=D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\mathrm {nil}})^{\mathrm {Spr}}$
. The simple objects of
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathrm {B}(N))$
and
$D_{\mathrm {c}}^{\mathrm {b}}(\mathrm {B}(N))$
and
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\mathrm {nil}})^{\mathrm {Spr}}$
are both parametrized by the irreducible characters of W. This is Springer theory in the second case and, in the first case, the simple objects are the simple direct summands of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\mathrm {nil}})^{\mathrm {Spr}}$
are both parametrized by the irreducible characters of W. This is Springer theory in the second case and, in the first case, the simple objects are the simple direct summands of
![]() $\pi _{\mathrm { nil}\,*}{\overline {\mathbb {Q}}_{\ell }}$
. The pullback functor
$\pi _{\mathrm { nil}\,*}{\overline {\mathbb {Q}}_{\ell }}$
. The pullback functor
![]() $\overline {s}_{\mathrm {nil}}^$
along the obvious morphism
$\overline {s}_{\mathrm {nil}}^$
along the obvious morphism
![]() $\overline {s}_{\mathrm {nil}}:\mathrm {B}(N)\rightarrow \mathrm {B}(W)$
induces an equivalence between the categories of perverse sheaves that is compatible with the indexation of the simple perverse sheaves by the irreducible characters of W. By Lemma 6.1 applied to nilpotents, we have
$\overline {s}_{\mathrm {nil}}:\mathrm {B}(N)\rightarrow \mathrm {B}(W)$
induces an equivalence between the categories of perverse sheaves that is compatible with the indexation of the simple perverse sheaves by the irreducible characters of W. By Lemma 6.1 applied to nilpotents, we have
We are thus reduced to prove the statement of the proposition for
![]() ${^p}\mathrm {I}_{\mathrm { nil}}:\mathcal {M}(\mathrm {B}(W))\rightarrow \mathcal {M}(\mathcal {G}_{\mathrm {nil}})^{\mathrm {Spr}}$
. Unlike
${^p}\mathrm {I}_{\mathrm { nil}}:\mathcal {M}(\mathrm {B}(W))\rightarrow \mathcal {M}(\mathcal {G}_{\mathrm {nil}})^{\mathrm {Spr}}$
. Unlike
![]() $\mathrm {I}_{\mathrm {nil}}$
, the construction of
$\mathrm {I}_{\mathrm {nil}}$
, the construction of
![]() ${^p}\mathrm {I}_{\mathrm {nil}}$
extends to a global functor
${^p}\mathrm {I}_{\mathrm {nil}}$
extends to a global functor
![]() ${^p}\mathrm {I}$
. A standard argument using the functor
${^p}\mathrm {I}$
. A standard argument using the functor
![]() ${^p}\mathrm {I}$
and its restriction to semisimple regular elements proves the proposition for
${^p}\mathrm {I}$
and its restriction to semisimple regular elements proves the proposition for
![]() ${^p}\mathrm {I}_{\mathrm {nil}}$
.
${^p}\mathrm {I}_{\mathrm {nil}}$
.
Proposition 7.4. The functor
![]() $\mathrm {I}_c$
induces an equivalence of categories
$\mathrm {I}_c$
induces an equivalence of categories
![]() $D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_c)\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
with inverse functor
$D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_c)\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
with inverse functor
![]() $\mathrm {R}_c$
.
$\mathrm {R}_c$
.
Proof. Since
![]() $\mathrm {R}_c\circ \mathrm {I}_c\simeq 1$
, the functor
$\mathrm {R}_c\circ \mathrm {I}_c\simeq 1$
, the functor
![]() $\mathrm {I}_c$
induces an injection between the
$\mathrm {I}_c$
induces an injection between the
![]() $\mathrm {Ext}^i$
of simple perverse sheaves. On the other hand, by the proposition below together with [Reference Achar1, Theorem 4.6] and Proposition 7.3, we know that the
$\mathrm {Ext}^i$
of simple perverse sheaves. On the other hand, by the proposition below together with [Reference Achar1, Theorem 4.6] and Proposition 7.3, we know that the
![]() $\mathrm { Ext}^i$
of the simple objects that corresponds under
$\mathrm { Ext}^i$
of the simple objects that corresponds under
![]() $\mathrm {I}_c$
have the same dimension and so
$\mathrm {I}_c$
have the same dimension and so
![]() $\mathrm {I}_c$
induces an isomorphism between the
$\mathrm {I}_c$
induces an isomorphism between the
![]() $\mathrm {Ext}^i$
. By a lemma of Beilinson [Reference Schnürer19, Lemma 6], the functor
$\mathrm {Ext}^i$
. By a lemma of Beilinson [Reference Schnürer19, Lemma 6], the functor
![]() $\mathrm {I}_c$
induces thus an equivalence of categories
$\mathrm {I}_c$
induces thus an equivalence of categories
![]() $D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_c)\simeq D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
.
$D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_c)\simeq D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
.
Consider the decomposition
where the sum runs over the irreducible
![]() ${\overline {\mathbb {Q}}_{\ell }}$
-characters of W,
${\overline {\mathbb {Q}}_{\ell }}$
-characters of W,
![]() $V_{\varphi }$
is an irreducible representation affording the character
$V_{\varphi }$
is an irreducible representation affording the character
![]() $\varphi $
and the
$\varphi $
and the
![]() $\mathcal {L}_{\varphi }$
are the irreducible smooth
$\mathcal {L}_{\varphi }$
are the irreducible smooth
![]() $\ell $
-adic sheaves on
$\ell $
-adic sheaves on
![]() $\mathrm {B}(N)$
.
$\mathrm {B}(N)$
.
Proposition 7.5. For any irreducible characters
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
of W, we have
$\varphi '$
of W, we have
Proof. The proof is similar to that of [Reference Achar1, Theorem 4.6]. We give it for the convenience of the reader. We have
 $$ \begin{align*} \mathrm{Ext}^i(\mathcal{L}_{\varphi},\mathcal{L}_{\varphi'})&=\mathrm{Hom}_W\left(V_{\varphi}^*,\mathrm{ Ext}^i(\pi_{\mathrm{nil}\,!}{\overline{\mathbb{Q}}_{\ell}},\mathcal{L}_{\varphi'})\right)\\ &=\mathrm{Hom}_W\left(V_{\varphi}^*,\mathrm{Ext}^i({\overline{\mathbb{Q}}_{\ell}},\pi_{\mathrm{nil}}^*(\mathcal{L}_{\varphi'}))\right)\\ &=\mathrm{Hom}_W\left(V_{\varphi}^*,\mathrm{ Ext}^i_{\mathrm{B}(T)}({\overline{\mathbb{Q}}_{\ell}},{\overline{\mathbb{Q}}_{\ell}})\otimes\mathrm{ Hom}({\overline{\mathbb{Q}}_{\ell}},\pi_{\mathrm{nil}}^*(\mathcal{L}_{\varphi'}))\right)\\ &=\mathrm{Hom}_W\left(V_{\varphi}^*,H^i(\mathrm{B}(T),{\overline{\mathbb{Q}}_{\ell}})\otimes\mathrm{Hom}(\pi_{\mathrm{ nil}\,!}{\overline{\mathbb{Q}}_{\ell}},\mathcal{L}_{\varphi'})\right)\\ &=\left(V_{\varphi}\otimes H^i(\mathrm{B}(T),{\overline{\mathbb{Q}}_{\ell}})\otimes V_{\varphi'}^*\right)^W. \end{align*} $$
$$ \begin{align*} \mathrm{Ext}^i(\mathcal{L}_{\varphi},\mathcal{L}_{\varphi'})&=\mathrm{Hom}_W\left(V_{\varphi}^*,\mathrm{ Ext}^i(\pi_{\mathrm{nil}\,!}{\overline{\mathbb{Q}}_{\ell}},\mathcal{L}_{\varphi'})\right)\\ &=\mathrm{Hom}_W\left(V_{\varphi}^*,\mathrm{Ext}^i({\overline{\mathbb{Q}}_{\ell}},\pi_{\mathrm{nil}}^*(\mathcal{L}_{\varphi'}))\right)\\ &=\mathrm{Hom}_W\left(V_{\varphi}^*,\mathrm{ Ext}^i_{\mathrm{B}(T)}({\overline{\mathbb{Q}}_{\ell}},{\overline{\mathbb{Q}}_{\ell}})\otimes\mathrm{ Hom}({\overline{\mathbb{Q}}_{\ell}},\pi_{\mathrm{nil}}^*(\mathcal{L}_{\varphi'}))\right)\\ &=\mathrm{Hom}_W\left(V_{\varphi}^*,H^i(\mathrm{B}(T),{\overline{\mathbb{Q}}_{\ell}})\otimes\mathrm{Hom}(\pi_{\mathrm{ nil}\,!}{\overline{\mathbb{Q}}_{\ell}},\mathcal{L}_{\varphi'})\right)\\ &=\left(V_{\varphi}\otimes H^i(\mathrm{B}(T),{\overline{\mathbb{Q}}_{\ell}})\otimes V_{\varphi'}^*\right)^W. \end{align*} $$
The third equality follows from the canonical isomorphism
as the category
![]() $\mathcal {M}(\mathrm {B}(T))$
is semisimple linear with unique simple object
$\mathcal {M}(\mathrm {B}(T))$
is semisimple linear with unique simple object
![]() ${\overline {\mathbb {Q}}_{\ell }}[-n]$
.
${\overline {\mathbb {Q}}_{\ell }}[-n]$
.
Define
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
as the full subcategory of
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
as the full subcategory of
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
of complexes K such that
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
of complexes K such that
![]() $K_c\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
for all geometric point c of
$K_c\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
for all geometric point c of
![]() $\mathfrak {car}_{\lambda }$
.
$\mathfrak {car}_{\lambda }$
.
Remark 7.6. If G is of type A with connected center then we have
![]() $D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}=D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
for all
$D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}=D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })$
for all
![]() $\lambda $
.
$\lambda $
.
Theorem 7.7. The functor
![]() $\mathrm {I}_{\lambda }$
induces an equivalence of categories
$\mathrm {I}_{\lambda }$
induces an equivalence of categories
![]() $D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\lambda })\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
with inverse functor
$D_{\mathrm {c}}^{\mathrm {b}}({\overline {\mathcal {T}}}_{\lambda })\rightarrow D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
with inverse functor
![]() $\mathrm {R}_{\lambda }$
.
$\mathrm {R}_{\lambda }$
.
Proof. Since
![]() $\mathrm {R}_{\lambda }\circ \mathrm {I}_{\lambda }\simeq 1$
, it suffices to see that the morphism
$\mathrm {R}_{\lambda }\circ \mathrm {I}_{\lambda }\simeq 1$
, it suffices to see that the morphism
is an isomorphism for all
![]() $K\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
. But it follows from the fact that it is true over
$K\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_{\lambda })^{\mathrm {Spr}}$
. But it follows from the fact that it is true over
![]() $\mathcal {G}_c$
for any geometrical point c of
$\mathcal {G}_c$
for any geometrical point c of
![]() $\mathfrak {car}_{\lambda }$
by the above proposition.
$\mathfrak {car}_{\lambda }$
by the above proposition.
7.2 Perverse sheaves
Let
![]() $({^p}\mathrm {R},{^p}\mathrm {I})$
be the pair of adjoint functors defined in §2.9.
$({^p}\mathrm {R},{^p}\mathrm {I})$
be the pair of adjoint functors defined in §2.9.
Theorem 7.8. The adjunction map
is an isomorphism.
It is enough to prove that for any
![]() $\lambda \in \mathfrak {L}$
and any
$\lambda \in \mathfrak {L}$
and any
![]() $K\in \mathcal {M}(\overline {{\mathfrak {t}}})$
, the restriction
$K\in \mathcal {M}(\overline {{\mathfrak {t}}})$
, the restriction
of the adjunction morphism
![]() ${^p}\mathrm {R}\circ {{}^p}\mathrm {I}(K)\rightarrow K$
along the map
${^p}\mathrm {R}\circ {{}^p}\mathrm {I}(K)\rightarrow K$
along the map
![]() ${\overline {\mathcal {T}}}_{\lambda }\rightarrow \overline {{\mathfrak {t}}}$
is an isomorphism.
${\overline {\mathcal {T}}}_{\lambda }\rightarrow \overline {{\mathfrak {t}}}$
is an isomorphism.
Therefore, the theorem is a consequence of Theorem 6.2 together with the following result, which is straightforward.
Proposition 7.9. For any
![]() $K\in \mathcal {M}(\overline {{\mathfrak {t}}})$
and
$K\in \mathcal {M}(\overline {{\mathfrak {t}}})$
and
![]() $L\in \mathcal {M}(\mathcal {G})$
, we have
$L\in \mathcal {M}(\mathcal {G})$
, we have
Denote by
![]() $\mathcal {M}(\mathcal {G})^{\mathrm {Spr}}$
the full subcategory if
$\mathcal {M}(\mathcal {G})^{\mathrm {Spr}}$
the full subcategory if
![]() $\mathcal {M}(\mathcal {G})$
of perverse sheaves K such that
$\mathcal {M}(\mathcal {G})$
of perverse sheaves K such that
![]() $K_c\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
for all geometric point c of
$K_c\in D_{\mathrm {c}}^{\mathrm {b}}(\mathcal {G}_c)^{\mathrm {Spr}}$
for all geometric point c of
![]() $\mathfrak {car}$
.
$\mathfrak {car}$
.
Theorem 7.10. The functor
![]() ${^p}\mathrm {I}$
induces an equivalence of catgeories
${^p}\mathrm {I}$
induces an equivalence of catgeories
![]() $\mathcal {M}(\overline {{\mathfrak {t}}})\rightarrow \mathcal {M}(\mathcal {G})^{\mathrm {Spr}}$
with inverse functor
$\mathcal {M}(\overline {{\mathfrak {t}}})\rightarrow \mathcal {M}(\mathcal {G})^{\mathrm {Spr}}$
with inverse functor
![]() ${^p}\mathrm {R}$
.
${^p}\mathrm {R}$
.
In particular, if G is of type A with connected center, then
![]() $\mathcal {M}(\mathcal {G})^{\mathrm {Spr}}=\mathcal {M}(\mathcal {G})$
, and so the categories
$\mathcal {M}(\mathcal {G})^{\mathrm {Spr}}=\mathcal {M}(\mathcal {G})$
, and so the categories
![]() $\mathcal {M}(\overline {{\mathfrak {t}}})$
and
$\mathcal {M}(\overline {{\mathfrak {t}}})$
and
![]() $\mathcal {M}(\mathcal {G})$
are equivalent.
$\mathcal {M}(\mathcal {G})$
are equivalent.
Proof. Thanks to Theorem 7.8, it remains to prove that
is an isomorphism for all
![]() $K\in \mathcal {M}(\mathcal {G})^{\mathrm {Spr}}$
. We are thus reduced to prove that this is an isomorphism after restriction to
$K\in \mathcal {M}(\mathcal {G})^{\mathrm {Spr}}$
. We are thus reduced to prove that this is an isomorphism after restriction to
![]() $\mathcal {G}_{\lambda }$
for all
$\mathcal {G}_{\lambda }$
for all
![]() $\lambda \in \mathfrak {L}$
. But this is a consequence of Proposition 7.9 and Theorem 7.7.
$\lambda \in \mathfrak {L}$
. But this is a consequence of Proposition 7.9 and Theorem 7.7.
Acknowledgements
It is a pleasure to thank P. Achar, O. Dudas, S. Gunningham, B. Hennion, L. Illusie, B. Keller and O. Schiffmann for useful discussions, O. Gabber for telling us about Verdier’s paper “Un calcul triste” and M. Romagny for his help with group action on stacks.
Conflict of Interest
The authors have no conflict of interest to declare.