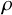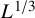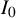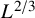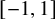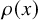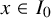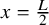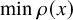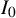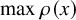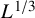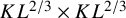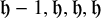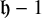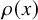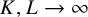1 Introduction
We consider the solid-on-solid (SOS) model on ![]() , an
, an
![]() $L\times L$
square in
$L\times L$
square in
![]() $\mathbb {Z}^2$
, at large inverse-temperature
$\mathbb {Z}^2$
, at large inverse-temperature
![]() $\beta>0$
, with zero boundary conditions and a floor at height
$\beta>0$
, with zero boundary conditions and a floor at height
![]() $0$
: Denoting by
$0$
: Denoting by
![]() $\mathsf {x}\sim \mathsf {y}$
a pair of adjacent sites
$\mathsf {x}\sim \mathsf {y}$
a pair of adjacent sites
![]() $\mathsf {x},\mathsf {y}\in \mathbb {Z}^2$
, and setting
$\mathsf {x},\mathsf {y}\in \mathbb {Z}^2$
, and setting
![]() $\varphi _{\mathsf {x}} = 0$
for all
$\varphi _{\mathsf {x}} = 0$
for all
![]() $\mathsf {x}\notin \Lambda _L$
, the model assigns a height function
$\mathsf {x}\notin \Lambda _L$
, the model assigns a height function
![]() $\varphi :\Lambda _L \to \mathbb {Z}_{\geq 0}$
(taking nonnegative integer heights) the probability
$\varphi :\Lambda _L \to \mathbb {Z}_{\geq 0}$
(taking nonnegative integer heights) the probability
 $$ \begin{align}\pi^0_{\Lambda_L}(\varphi) \propto \exp\Big(-\beta\sum_{\mathsf{x}\sim \mathsf{y}} |\varphi_{\mathsf{x}}-\varphi_{\mathsf{y}}|\Big). \end{align} $$
$$ \begin{align}\pi^0_{\Lambda_L}(\varphi) \propto \exp\Big(-\beta\sum_{\mathsf{x}\sim \mathsf{y}} |\varphi_{\mathsf{x}}-\varphi_{\mathsf{y}}|\Big). \end{align} $$
The model was introduced in the early 1950s (see [Reference Burton, Cabrera and Frank5, Reference Temperley39]) to approximate the formation of crystals and the interface separating the plus and minus phases in the low-temperature three-dimensional (3D) Ising model.
While of interest in any dimension d, the study of the model on
![]() $\mathbb {Z}^2$
has special importance, as it is the only dimension associated with the roughening phase transition. For the low-temperature 3D Ising model, which the
$\mathbb {Z}^2$
has special importance, as it is the only dimension associated with the roughening phase transition. For the low-temperature 3D Ising model, which the
![]() $(2+1)$
D SOS model approximates for large
$(2+1)$
D SOS model approximates for large
![]() $\beta $
, rigorously establishing the roughening phase transition is a tantalizing open problem which has seen very little progress since being observed some 50 years ago (numerical experiments suggest it takes place at
$\beta $
, rigorously establishing the roughening phase transition is a tantalizing open problem which has seen very little progress since being observed some 50 years ago (numerical experiments suggest it takes place at ![]() , compared to the critical 3D Ising temperature
, compared to the critical 3D Ising temperature
![]() $\beta _c \approx 0.221$
). The corresponding phase transition for the
$\beta _c \approx 0.221$
). The corresponding phase transition for the
![]() $(2+1)$
D SOS with no floor
$(2+1)$
D SOS with no floor
![]() $\widehat \pi $
(where
$\widehat \pi $
(where
![]() $\varphi $
can be negative) was rigorously confirmed as follows: (i) (Localization) for
$\varphi $
can be negative) was rigorously confirmed as follows: (i) (Localization) for
![]() $\beta $
large enough, the surface is rigid, in that
$\beta $
large enough, the surface is rigid, in that
![]() $\operatorname {Var}(\varphi _{\mathsf {x}})=O(1)$
at
$\operatorname {Var}(\varphi _{\mathsf {x}})=O(1)$
at
![]() $\mathsf {x}$
in the bulk, and furthermore
$\mathsf {x}$
in the bulk, and furthermore
![]() $|\varphi _{\mathsf {x}}|$
has an exponential tail [Reference Brandenberger and Wayne3]; (ii) (Delocalization) for
$|\varphi _{\mathsf {x}}|$
has an exponential tail [Reference Brandenberger and Wayne3]; (ii) (Delocalization) for
![]() $\beta $
small enough, Fröhlich and Spencer [Reference Fröhlich and Spencer26, Reference Fröhlich and Spencer27] famously showed that
$\beta $
small enough, Fröhlich and Spencer [Reference Fröhlich and Spencer26, Reference Fröhlich and Spencer27] famously showed that
![]() $\operatorname {Var}(\varphi _{\mathsf {x}}) \asymp \log L$
, just as in the case where
$\operatorname {Var}(\varphi _{\mathsf {x}}) \asymp \log L$
, just as in the case where
![]() $\varphi $
takes values in
$\varphi $
takes values in
![]() $\mathbb {R}$
. (iii) Very recently, Lammers [Reference Lammers37] showed the phase transition in
$\mathbb {R}$
. (iii) Very recently, Lammers [Reference Lammers37] showed the phase transition in
![]() $\operatorname {Var}(\varphi _{\mathsf {x}})$
is sharp: There exists
$\operatorname {Var}(\varphi _{\mathsf {x}})$
is sharp: There exists ![]() such that
such that
![]() $\operatorname {Var}(\varphi _{\mathsf {x}})\to \infty $
for all
$\operatorname {Var}(\varphi _{\mathsf {x}})\to \infty $
for all ![]() whereas it is
whereas it is
![]() $O(1)$
for all
$O(1)$
for all ![]() ; numerical experiments suggest that
; numerical experiments suggest that ![]() . (See [Reference Lammers37] for additional details on the recent developments in the SOS model with no floor and related models of integer-valued height functions.)
. (See [Reference Lammers37] for additional details on the recent developments in the SOS model with no floor and related models of integer-valued height functions.)
Our setting is the low-temperature regime (
![]() $\beta $
large), yet with the restriction that the surface must lie above above a hard wall (the assumption
$\beta $
large), yet with the restriction that the surface must lie above above a hard wall (the assumption
![]() $\varphi \geq 0$
). Bricmont, El-Mellouki and Fröhlich [Reference Bricmont, El Mellouki and Fröhlich4] showed that this induces entropic repulsion, regarded as a key feature of the physics of random surfaces: The restriction
$\varphi \geq 0$
). Bricmont, El-Mellouki and Fröhlich [Reference Bricmont, El Mellouki and Fröhlich4] showed that this induces entropic repulsion, regarded as a key feature of the physics of random surfaces: The restriction
![]() $\varphi \geq 0$
propels the surface (despite the energy cost) so as to gain entropy. Namely, it was shown in [Reference Bricmont, El Mellouki and Fröhlich4] that
$\varphi \geq 0$
propels the surface (despite the energy cost) so as to gain entropy. Namely, it was shown in [Reference Bricmont, El Mellouki and Fröhlich4] that
![]() $ \frac {c}\beta \log L \leq \mathbb {E}[\varphi _{\mathsf {x}} \mid \varphi \geq 0] \leq \frac {C}\beta \log L$
for absolute constants
$ \frac {c}\beta \log L \leq \mathbb {E}[\varphi _{\mathsf {x}} \mid \varphi \geq 0] \leq \frac {C}\beta \log L$
for absolute constants
![]() $c,C>0$
.
$c,C>0$
.
The gap between these bounds was closed in [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli13], where it was established that
![]() $\mathbb {E}[\varphi _{\mathsf {x}} \mid \varphi \geq 0]$
is
$\mathbb {E}[\varphi _{\mathsf {x}} \mid \varphi \geq 0]$
is
![]() $\frac 1{4\beta }\log L + O(1)$
, and moreover,
$\frac 1{4\beta }\log L + O(1)$
, and moreover,
![]() $(1-\epsilon _\beta )L^2$
sites are at such a height with high probability (w.h.p.). The following intuition explains the height asymptotics: If the surface lies rigid about height h, then the cost of raising every site by
$(1-\epsilon _\beta )L^2$
sites are at such a height with high probability (w.h.p.). The following intuition explains the height asymptotics: If the surface lies rigid about height h, then the cost of raising every site by
![]() $1$
is
$1$
is
![]() $4\beta L$
(incurred at the sites along the boundary); the benefit in doing so would be to gain the ability to feature spikes of depth
$4\beta L$
(incurred at the sites along the boundary); the benefit in doing so would be to gain the ability to feature spikes of depth
![]() $h+1$
(forbidden at level h due to the restriction
$h+1$
(forbidden at level h due to the restriction
![]() $\varphi \geq 0$
), and as such a spike has an energetic cost of about
$\varphi \geq 0$
), and as such a spike has an energetic cost of about
![]() $e^{-4\beta h}$
, the entropy gain is about
$e^{-4\beta h}$
, the entropy gain is about
![]() $\mathsf H(e^{-4\beta h})L^2$
, where
$\mathsf H(e^{-4\beta h})L^2$
, where
![]() $\mathsf H(\cdot )$
is the Shannon entropy; the two terms are equated at
$\mathsf H(\cdot )$
is the Shannon entropy; the two terms are equated at
![]() $h\sim \frac 1{4\beta }\log L$
.
$h\sim \frac 1{4\beta }\log L$
.
Significant progress in the understanding of the shape of the SOS surface above a hard wall was obtained in the sequel by the same authors [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14]. The height-h level lines of the surface are the loops formed by placing dual bonds between every pair
![]() $\mathsf {x}\sim \mathsf {y}$
such that
$\mathsf {x}\sim \mathsf {y}$
such that
![]() $\varphi _{\mathsf {x}}<h$
and
$\varphi _{\mathsf {x}}<h$
and
![]() $\varphi _{\mathsf {y}}\geq h$
. To account for local thermal fluctuations, call a loop macroscopic if its length is at least
$\varphi _{\mathsf {y}}\geq h$
. To account for local thermal fluctuations, call a loop macroscopic if its length is at least
![]() $(\log L)^2$
. With this notation, (a more detailed version of) the following theorem was given in [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14] (see also [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli12]):
$(\log L)^2$
. With this notation, (a more detailed version of) the following theorem was given in [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14] (see also [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli12]):
Theorem [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Thms. 1,2,3 and Rem. 1.3].
For
![]() $\beta $
large enough, the
$\beta $
large enough, the
![]() $(2+1)$
D SOS model with zero boundary conditions on a square
$(2+1)$
D SOS model with zero boundary conditions on a square ![]() above the wall
above the wall
![]() $\varphi \geq 0$
, satisfies the following w.h.p.:
$\varphi \geq 0$
, satisfies the following w.h.p.:
-
(i) Shape: At least
 $(1-\epsilon _\beta )L^2$
of the sites
$(1-\epsilon _\beta )L^2$
of the sites
 $\mathsf {x}\in \Lambda _L$
have height
$\mathsf {x}\in \Lambda _L$
have height
 $\varphi _{\mathsf {x}} = \mathfrak h^\star $
, where the random
$\varphi _{\mathsf {x}} = \mathfrak h^\star $
, where the random
 $\mathfrak h^\star $
is either
$\mathfrak h^\star $
is either
 $ \lfloor \frac 1{4\beta }\log L\rfloor $
or
$ \lfloor \frac 1{4\beta }\log L\rfloor $
or
 $\lfloor \frac 1{4\beta }\log L\rfloor -1$
. Moreover, there is a unique macroscopic loop at each height
$\lfloor \frac 1{4\beta }\log L\rfloor -1$
. Moreover, there is a unique macroscopic loop at each height
 $0,1,\ldots ,\mathfrak h^\star $
and none above height
$0,1,\ldots ,\mathfrak h^\star $
and none above height
 $\mathfrak h^\star $
. Further, for a diverging sequenceFootnote
1
of L’s, the sequence of nested loops
$\mathfrak h^\star $
. Further, for a diverging sequenceFootnote
1
of L’s, the sequence of nested loops
 $\mathcal L_0 \subset \mathcal L_1 \subset \ldots $
, when rescaled to
$\mathcal L_0 \subset \mathcal L_1 \subset \ldots $
, when rescaled to
 $[0,1]^2$
, converges in probability in Hausdorff distance to a deterministic limit defined by a Wulff shape
$[0,1]^2$
, converges in probability in Hausdorff distance to a deterministic limit defined by a Wulff shape
 $\mathcal W$
, which is the convex body of area
$\mathcal W$
, which is the convex body of area
 $1$
minimizing the line integral of a surface tension
$1$
minimizing the line integral of a surface tension
 $\tau _\beta (\cdot )$
along its perimeter
$\tau _\beta (\cdot )$
along its perimeter
 $\partial \mathcal W$
; the scaling limit of
$\partial \mathcal W$
; the scaling limit of
 $\mathcal L_k$
(where
$\mathcal L_k$
(where
 $\mathcal L_0$
is the top level line at height
$\mathcal L_0$
is the top level line at height
 $\mathfrak h^\star $
) is given by the union of all possible translates of
$\mathfrak h^\star $
) is given by the union of all possible translates of
 $\mathcal W$
, rescaled by an explicit radius
$\mathcal W$
, rescaled by an explicit radius
 $r_k$
that is decreasing in k.
$r_k$
that is decreasing in k. -
(ii) Fluctuations: For a diverging sequenceFootnote 2 of L’s, the maximum displacement of the top level line
 $\mathcal L_0$
from the boundary segment
$\mathcal L_0$
from the boundary segment
 $I\times \{0\}$
for
$I\times \{0\}$
for  is
is
 $L^{1/3+o(1)}$
. That is, if is the maximum y-coordinate of a point
$L^{1/3+o(1)}$
. That is, if is the maximum y-coordinate of a point $$\begin{align*}\overline\rho(x)=\max\{ y \leq L/2\,:\; (x,y)\in\mathcal L_0\} \end{align*}$$
$$\begin{align*}\overline\rho(x)=\max\{ y \leq L/2\,:\; (x,y)\in\mathcal L_0\} \end{align*}$$
 $(x,y)$
visited by
$(x,y)$
visited by
 $\mathcal L_0$
in the bottom-half of
$\mathcal L_0$
in the bottom-half of
 $\Lambda _L$
, then (1.2)for any fixed
$\Lambda _L$
, then (1.2)for any fixed $$ \begin{align} \max_{x\in I} \overline\rho(x) \leq L^{1/3+\epsilon} , \end{align} $$
$$ \begin{align} \max_{x\in I} \overline\rho(x) \leq L^{1/3+\epsilon} , \end{align} $$
 $\epsilon>0$
, whereas for every interval
$\epsilon>0$
, whereas for every interval
 $I'\subset I$
of length
$I'\subset I$
of length
 $L^{2/3-\epsilon }$
, (1.3)
$L^{2/3-\epsilon }$
, (1.3) $$ \begin{align} \max_{x\in I'} \overline\rho(x) \geq L^{1/3-\epsilon} . \end{align} $$
$$ \begin{align} \max_{x\in I'} \overline\rho(x) \geq L^{1/3-\epsilon} . \end{align} $$
Consider the distance of the top level line loop
![]() $\mathcal L_0$
from a point
$\mathcal L_0$
from a point
![]() $(x_0,0)$
on the bottom boundary of the box, where the scaling limit is flat – for example, the center side
$(x_0,0)$
on the bottom boundary of the box, where the scaling limit is flat – for example, the center side
![]() $x_0=L/2$
(see Figure 1 for a depiction). The above theorem shows that
$x_0=L/2$
(see Figure 1 for a depiction). The above theorem shows that
![]() $\overline \rho (x_0) \leq L^{1/3+\epsilon } $
w.h.p., yet it gives no nontrivial lower bound on it. It is believed that
$\overline \rho (x_0) \leq L^{1/3+\epsilon } $
w.h.p., yet it gives no nontrivial lower bound on it. It is believed that
![]() $\overline \rho (x_0)$
should have order
$\overline \rho (x_0)$
should have order
![]() $L^{1/3}$
(with no poly-log corrections); more precisely, one expects
$L^{1/3}$
(with no poly-log corrections); more precisely, one expects
![]() $\overline \rho (x_0)\asymp _{\texttt P} L^{1/3}$
, where we write
$\overline \rho (x_0)\asymp _{\texttt P} L^{1/3}$
, where we write
![]() $f\lesssim _{\texttt P} g$
if
$f\lesssim _{\texttt P} g$
if
![]() $f/g$
is uniformly tight, and
$f/g$
is uniformly tight, and
![]() $f\asymp _{\texttt P} g$
if
$f\asymp _{\texttt P} g$
if
![]() $f\lesssim _{\texttt P} g \lesssim _{\texttt P} f$
.
$f\lesssim _{\texttt P} g \lesssim _{\texttt P} f$
.

Figure 1 Fluctuations of the SOS level lines about the flat portions of their scaling limits. Maximal fluctuation is known to be at most
![]() $L^{1/3+\epsilon }$
w.h.p., and it is believed that the distance of the top level line from a given boundary point (e.g., the center side) is of order
$L^{1/3+\epsilon }$
w.h.p., and it is believed that the distance of the top level line from a given boundary point (e.g., the center side) is of order
![]() $ L^{1/3}$
.
$ L^{1/3}$
.
Moreover, one expects that if one were to rescale
![]() $\overline \rho (x)$
by
$\overline \rho (x)$
by
![]() $L^{1/3}$
along an interval of order
$L^{1/3}$
along an interval of order
![]() $L^{2/3}$
positioned on bottom boundary (within the flat portion of the scaling limit) – take, for example,
$L^{2/3}$
positioned on bottom boundary (within the flat portion of the scaling limit) – take, for example,
for concreteness – then, after rescaling said interval by
![]() $L^{2/3}$
(in the concrete example, to
$L^{2/3}$
(in the concrete example, to
![]() $[-1,1]$
), one would arrive at a limit law of a nontrivial diffusion, a variant of a Ferrari–Spohn diffusion [Reference Ferrari and Spohn25]. (This prediction was stated here in terms of
$[-1,1]$
), one would arrive at a limit law of a nontrivial diffusion, a variant of a Ferrari–Spohn diffusion [Reference Ferrari and Spohn25]. (This prediction was stated here in terms of
![]() $\overline \rho (x)$
, the maximal vertical displacement of
$\overline \rho (x)$
, the maximal vertical displacement of
![]() $\mathcal L_0$
, so as to be well-defined, as
$\mathcal L_0$
, so as to be well-defined, as
![]() $\mathcal L_0$
can have many points with a given x-coordinate; the same statement is expected to hold for
$\mathcal L_0$
can have many points with a given x-coordinate; the same statement is expected to hold for
![]() $\underline \rho (x)$
measuring the minimal displacement of
$\underline \rho (x)$
measuring the minimal displacement of
![]() $\mathcal L_0$
, as defined in Theorem 1.1.)
$\mathcal L_0$
, as defined in Theorem 1.1.)
To explain this prediction, note first that it is well known that the law of a Brownian excursion on
![]() $[-N,N]$
tilted (penalized) by
$[-N,N]$
tilted (penalized) by
![]() $\exp (-\lambda A)$
, where A is the area under it, tends as
$\exp (-\lambda A)$
, where A is the area under it, tends as
![]() $N\to \infty $
to that of a Ferrari–Spohn diffusion. The entropic repulsion that propels the SOS level line loop
$N\to \infty $
to that of a Ferrari–Spohn diffusion. The entropic repulsion that propels the SOS level line loop
![]() $\mathcal L$
to height h acts much like an area tilt: If a loop has internal area
$\mathcal L$
to height h acts much like an area tilt: If a loop has internal area
![]() $\mathsf S$
, then its probability (roughly) gains a tilt of
$\mathsf S$
, then its probability (roughly) gains a tilt of
![]() $\exp (\lambda \mathsf S)$
for
$\exp (\lambda \mathsf S)$
for
![]() $\lambda = \mathsf {H}(e^{-4\beta h})$
as described earlier, or equivalently, a tilt of
$\lambda = \mathsf {H}(e^{-4\beta h})$
as described earlier, or equivalently, a tilt of
![]() $\exp (-\lambda A)$
, where
$\exp (-\lambda A)$
, where
![]() $A = L^2-\mathsf S $
is the area exterior to it. Consider
$A = L^2-\mathsf S $
is the area exterior to it. Consider
![]() $\mathcal L_k$
, which is at height
$\mathcal L_k$
, which is at height
![]() $\mathfrak h^\star -k$
: There
$\mathfrak h^\star -k$
: There
![]() $\lambda \approx e^{-4\beta (\mathfrak h^\star - k)} \approx L^{-1} e^{4\beta k}$
(recall
$\lambda \approx e^{-4\beta (\mathfrak h^\star - k)} \approx L^{-1} e^{4\beta k}$
(recall
![]() $\mathfrak h^\star \approx \tfrac 1{4\beta }\log L$
), and we see that the rescaling of
$\mathfrak h^\star \approx \tfrac 1{4\beta }\log L$
), and we see that the rescaling of
![]() $\rho (x)$
by
$\rho (x)$
by
![]() $L^{1/3}$
and
$L^{1/3}$
and
![]() $I_0$
by
$I_0$
by
![]() $L^{2/3}$
cancels the
$L^{2/3}$
cancels the
![]() $L^{-1}$
factor in
$L^{-1}$
factor in
![]() $\lambda $
and translates into a tilt of
$\lambda $
and translates into a tilt of
![]() $\exp (-e^{4\beta k} \hat {A})$
, where
$\exp (-e^{4\beta k} \hat {A})$
, where
![]() $\hat {A}$
is the rescaled area, as in the above continuous approximation (see also [Reference Ioffe, Shlosman and Velenik33, Reference Ioffe and Velenik35]). Related to this, the famous problem of establishing a Ferrari–Spohn law for the two-dimensional (2D) Ising interface under critical prewetting (which may be seen as a version of the SOS problem only with a single contour as opposed to
$\hat {A}$
is the rescaled area, as in the above continuous approximation (see also [Reference Ioffe, Shlosman and Velenik33, Reference Ioffe and Velenik35]). Related to this, the famous problem of establishing a Ferrari–Spohn law for the two-dimensional (2D) Ising interface under critical prewetting (which may be seen as a version of the SOS problem only with a single contour as opposed to
![]() $c\log L$
many) was finally settled in a recent seminal work by Ioffe, Ott, Shlosman and Velenik [Reference Ioffe, Ott, Shlosman and Velenik30] (prior to that, the
$c\log L$
many) was finally settled in a recent seminal work by Ioffe, Ott, Shlosman and Velenik [Reference Ioffe, Ott, Shlosman and Velenik30] (prior to that, the
![]() $L^{1/3+o(1)}$
fluctuations were established by Velenik [Reference Velenik40] and the tightness of the rescaled area was proved by Ganguly and Gheissari [Reference Ganguly and Gheissari28]). The challenges in handling a diverging number of interacting (noncrossing) contours with distinct area tilts (the k-th one is tilted by
$L^{1/3+o(1)}$
fluctuations were established by Velenik [Reference Velenik40] and the tightness of the rescaled area was proved by Ganguly and Gheissari [Reference Ganguly and Gheissari28]). The challenges in handling a diverging number of interacting (noncrossing) contours with distinct area tilts (the k-th one is tilted by
![]() $\approx \exp (-e^{4\beta k}\hat {A})$
) are such that the simplified problem that has Brownian excursions with area tilts is already nontrivial; see [Reference Caputo and Ganguly9, Reference Caputo, Ioffe and Wachtel10, Reference Caputo, Ioffe and Wachtel11, Reference Dembo, Lubetzky and Zeitouni16] for recent progress on it.
$\approx \exp (-e^{4\beta k}\hat {A})$
) are such that the simplified problem that has Brownian excursions with area tilts is already nontrivial; see [Reference Caputo and Ganguly9, Reference Caputo, Ioffe and Wachtel10, Reference Caputo, Ioffe and Wachtel11, Reference Dembo, Lubetzky and Zeitouni16] for recent progress on it.
In accordance with this prediction for the scaling limit of
![]() $L^{-1/3}\rho (x)$
along
$L^{-1/3}\rho (x)$
along
![]() $I_0$
, one expects that both
$I_0$
, one expects that both
![]() $\max _{x\in I_0} \rho (x)$
and
$\max _{x\in I_0} \rho (x)$
and
![]() $\min _{x\in I_0} \rho (x)$
would be of the same order as our rescaling factor
$\min _{x\in I_0} \rho (x)$
would be of the same order as our rescaling factor
![]() $L^{1/3}$
; that is, to be precise, that
$L^{1/3}$
; that is, to be precise, that
![]() $\max \overline \rho (x) \lesssim _{\texttt P} L^{1/3}$
and that
$\max \overline \rho (x) \lesssim _{\texttt P} L^{1/3}$
and that
![]() $\min \underline \rho (x) \gtrsim _{\texttt P} L^{1/3}$
. Our main result is the latter part (readily implying
$\min \underline \rho (x) \gtrsim _{\texttt P} L^{1/3}$
. Our main result is the latter part (readily implying
![]() $\rho (x_0)\gtrsim _{\texttt P} L^{1/3}$
at any given
$\rho (x_0)\gtrsim _{\texttt P} L^{1/3}$
at any given
![]() $\epsilon _\beta L \leq x_0 \leq (1-\epsilon _\beta )L$
, for example, the center side
$\epsilon _\beta L \leq x_0 \leq (1-\epsilon _\beta )L$
, for example, the center side
![]() $x_0=L/2$
).
$x_0=L/2$
).
Theorem 1.1. Fix
![]() $\beta $
large, and consider the
$\beta $
large, and consider the
![]() $(2+1)$
D SOS model with zero boundary conditions on
$(2+1)$
D SOS model with zero boundary conditions on ![]() as per Equation (1.1) above a wall
as per Equation (1.1) above a wall
![]() $\varphi \geq 0$
. Let
$\varphi \geq 0$
. Let
![]() $\mathcal L_0$
be the (w.h.p. unique) top macroscopic level line, consider the interval
$\mathcal L_0$
be the (w.h.p. unique) top macroscopic level line, consider the interval ![]() centered on the bottom boundary and let
centered on the bottom boundary and let
denote the minimum vertical displacement of
![]() $\mathcal L_0$
from the bottom boundary at the coordinate x. Then for every
$\mathcal L_0$
from the bottom boundary at the coordinate x. Then for every
![]() $\epsilon>0$
there exists
$\epsilon>0$
there exists
![]() $\delta>0$
such that for large enough L, with probability at least
$\delta>0$
such that for large enough L, with probability at least
![]() $1-\epsilon $
,
$1-\epsilon $
,
As we later explain, we obtain Equation (1.4) by moving from
![]() $\rho (x)$
, at a constant probability cost, to a curve whose limit (after the same rescaling) is a Brownian excursion, yielding the
$\rho (x)$
, at a constant probability cost, to a curve whose limit (after the same rescaling) is a Brownian excursion, yielding the
![]() $L^{1/3}$
bound. This refines the lower bound in Equation (1.3) into the estimate
$L^{1/3}$
bound. This refines the lower bound in Equation (1.3) into the estimate
![]() $\max _{x\in I_0}\overline \rho (x) \geq \min _{x\in I_0}\underline \rho (x) \gtrsim _{\texttt P} L^{1/3} $
. Note though that one cannot replace the
$\max _{x\in I_0}\overline \rho (x) \geq \min _{x\in I_0}\underline \rho (x) \gtrsim _{\texttt P} L^{1/3} $
. Note though that one cannot replace the
![]() $L^{1/3+o(1)}$
in the upper bound of Equation (1.2) by
$L^{1/3+o(1)}$
in the upper bound of Equation (1.2) by
![]() $O(L^{1/3})$
, as it addresses
$O(L^{1/3})$
, as it addresses
![]() $\max \overline \rho (x)$
over all
$\max \overline \rho (x)$
over all ![]() . Our comparison to a Brownian excursion implies that
. Our comparison to a Brownian excursion implies that
![]() $\max _{x\in I}\underline \rho (x) \geq c L^{1/3}\sqrt {\log L}$
w.h.p.; as we later explain, Theorem 1.3 will imply that
$\max _{x\in I}\underline \rho (x) \geq c L^{1/3}\sqrt {\log L}$
w.h.p.; as we later explain, Theorem 1.3 will imply that
![]() $\max _{x\in I}\underline \rho (x) \gtrsim _{\texttt P} L^{1/3} (\log L)^{2/3}$
, its predicted order (see Remark 1.6 as well as Question 1.7).
$\max _{x\in I}\underline \rho (x) \gtrsim _{\texttt P} L^{1/3} (\log L)^{2/3}$
, its predicted order (see Remark 1.6 as well as Question 1.7).
To derive the Brownian excursion law, we rely on the powerful Ornstein–Zernike framework as developed by Campanino, Ioffe and Velenik [Reference Ioffe29, Reference Campanino and Ioffe6, Reference Campanino, Ioffe and Velenik7, Reference Campanino, Ioffe and Velenik8], that allows one to couple the interface in hand to a directed random walk. This machinery was the key to several recent advances in the understanding 2D Ising interfaces (e.g., [Reference Ioffe, Ott, Shlosman and Velenik30] mentioned earlier) and Potts interfaces (e.g., [Reference Ott and Velenik38, Reference Ioffe, Ott, Velenik and Wachtel31]). In fact, the work [Reference Ioffe, Ott, Velenik and Wachtel31], due to Ioffe, Ott, Velenik and Wachtel, is of particular interest in our setting: There it was shown that the interface of the 2D Potts model in a box with Dobrushin’s boundary conditions has the scaling limit of a Brownian excursion for all
![]() $\beta>\beta _c$
. As in our case, one of the main obstacles is the interaction of the interface with the boundary and, in particular, ruling out the scenario whereby the interface is pinned to the wall. This was achieved for the Potts interface in [Reference Ioffe, Ott, Velenik and Wachtel31] (and later used as an ingredient in [Reference Ioffe, Ott, Shlosman and Velenik30]) via a direct analysis of its random cluster counterpart and then combined with a version of Ornstein–Zernike theory tailored to that model.
$\beta>\beta _c$
. As in our case, one of the main obstacles is the interaction of the interface with the boundary and, in particular, ruling out the scenario whereby the interface is pinned to the wall. This was achieved for the Potts interface in [Reference Ioffe, Ott, Velenik and Wachtel31] (and later used as an ingredient in [Reference Ioffe, Ott, Shlosman and Velenik30]) via a direct analysis of its random cluster counterpart and then combined with a version of Ornstein–Zernike theory tailored to that model.
Here, we instead appeal to the framework of Ioffe, Shlosman and Toninelli [Reference Ioffe, Shlosman and Toninelli32] to rule out pinning. That approach, while valid only for large enough
![]() $\beta $
(whereas the analysis in [Reference Ioffe, Ott, Shlosman and Velenik30] holds for all
$\beta $
(whereas the analysis in [Reference Ioffe, Ott, Shlosman and Velenik30] holds for all
![]() $\beta>\beta _c$
), is fairly generic and applicable to SOS contours as part of the following family of Ising polymers (to aid the exposition, we describe it briefly here, deferring its full definition to Sections 2.2 and 2.3). Call a path
$\beta>\beta _c$
), is fairly generic and applicable to SOS contours as part of the following family of Ising polymers (to aid the exposition, we describe it briefly here, deferring its full definition to Sections 2.2 and 2.3). Call a path
![]() $\gamma $
of distinct adjacent edges in
$\gamma $
of distinct adjacent edges in
![]() $(\mathbb {Z}^2)^* = \mathbb {Z}^2+(\frac 12,\frac 12)$
(vertices may repeat according to a splitting rule) a polymer, or contour, if it connects the origin
$(\mathbb {Z}^2)^* = \mathbb {Z}^2+(\frac 12,\frac 12)$
(vertices may repeat according to a splitting rule) a polymer, or contour, if it connects the origin
![]() $\mathsf {o}^*=(\frac 12,\frac 12)$
to a marked
$\mathsf {o}^*=(\frac 12,\frac 12)$
to a marked
![]() $\mathsf {x}_N$
at distance N from
$\mathsf {x}_N$
at distance N from
![]() $\mathsf {o}^*$
while staying in a half-plane
$\mathsf {o}^*$
while staying in a half-plane
![]() ${\mathbb H}_{\vec {n}}$
. The model gives
${\mathbb H}_{\vec {n}}$
. The model gives
![]() $\gamma $
a probability proportional to
$\gamma $
a probability proportional to
 $$\begin{align*}q(\gamma) := \exp\bigg(-\beta|\gamma| + \sum_{\mathcal{C}} \Phi(\mathcal{C};\gamma)\bigg),\end{align*}$$
$$\begin{align*}q(\gamma) := \exp\bigg(-\beta|\gamma| + \sum_{\mathcal{C}} \Phi(\mathcal{C};\gamma)\bigg),\end{align*}$$
where the sum goes over every finite connected subset
![]() $\mathcal {C}$
in
$\mathcal {C}$
in
![]() $\mathbb {Z}^2$
that intersects
$\mathbb {Z}^2$
that intersects
![]() $\Delta _\gamma $
, the vertex boundary of
$\Delta _\gamma $
, the vertex boundary of
![]() $\gamma $
, and the potential function
$\gamma $
, and the potential function
![]() $\Phi $
satisfies the following properties: ( P1)
$\Phi $
satisfies the following properties: ( P1)
![]() $\Phi (\mathcal {C};\cdot )$
is local, in the sense that it only depends on
$\Phi (\mathcal {C};\cdot )$
is local, in the sense that it only depends on
![]() $\gamma $
through
$\gamma $
through
![]() $\mathcal {C}\cap \Delta _\gamma $
; ( P2)
$\mathcal {C}\cap \Delta _\gamma $
; ( P2)
![]() $\sup _\gamma |\Phi (\mathcal {C},\gamma )|$
decays exponentially in the size of
$\sup _\gamma |\Phi (\mathcal {C},\gamma )|$
decays exponentially in the size of
![]() $\mathcal {C}$
(more precisely, in the minimum size of a graph connecting its boundary edges), and ( P3)
$\mathcal {C}$
(more precisely, in the minimum size of a graph connecting its boundary edges), and ( P3)
![]() $\Phi $
is invariant under translations of the form
$\Phi $
is invariant under translations of the form
![]() $(\mathcal {C},\gamma )\mapsto (\mathcal {C}+{\mathsf {v}},\gamma +{\mathsf {v}})$
. The final requirement in [Reference Ioffe, Shlosman and Toninelli32] is to have that ( P4) the surface tension is symmetric: If one defines the surface tension as
$(\mathcal {C},\gamma )\mapsto (\mathcal {C}+{\mathsf {v}},\gamma +{\mathsf {v}})$
. The final requirement in [Reference Ioffe, Shlosman and Toninelli32] is to have that ( P4) the surface tension is symmetric: If one defines the surface tension as
 $$\begin{align*}\tau_\beta(\vec{n}):=-\lim_{N \to\infty}\frac1{ N}\log\Big(\sum_\gamma q(\gamma)\Big),\end{align*}$$
$$\begin{align*}\tau_\beta(\vec{n}):=-\lim_{N \to\infty}\frac1{ N}\log\Big(\sum_\gamma q(\gamma)\Big),\end{align*}$$
then the function
![]() $\vec {n}\mapsto \tau _{\beta }(\vec {n})$
should have all discrete symmetries of
$\vec {n}\mapsto \tau _{\beta }(\vec {n})$
should have all discrete symmetries of
![]() $\mathbb {Z}^2$
. Under these conditions, the main result of [Reference Ioffe, Shlosman and Toninelli32] was that modifying the potential function
$\mathbb {Z}^2$
. Under these conditions, the main result of [Reference Ioffe, Shlosman and Toninelli32] was that modifying the potential function
![]() $\Phi $
into
$\Phi $
into
![]() $\Phi '$
along
$\Phi '$
along
![]() $\partial {\mathbb H}_{\vec {n}}$
does not affect the surface tension. That is, if we let
$\partial {\mathbb H}_{\vec {n}}$
does not affect the surface tension. That is, if we let
![]() $\Phi '(\mathcal {C},\gamma )=\Phi (\mathcal {C},\gamma )$
whenever
$\Phi '(\mathcal {C},\gamma )=\Phi (\mathcal {C},\gamma )$
whenever
![]() $\mathcal {C}$
is fully contained in
$\mathcal {C}$
is fully contained in
![]() ${\mathbb H}_{\vec {n}}$
and the modified
${\mathbb H}_{\vec {n}}$
and the modified
![]() $\Phi '$
still obeys the decay condition in Property (P2), then the modified
$\Phi '$
still obeys the decay condition in Property (P2), then the modified
![]() $\tau ^{\prime }_\beta $
agrees with the original
$\tau ^{\prime }_\beta $
agrees with the original
![]() $\tau _\beta $
. Moreover, the corresponding partition functions are comparable (see Theorem 5.1).
$\tau _\beta $
. Moreover, the corresponding partition functions are comparable (see Theorem 5.1).
The main ingredient in our proof of Theorem 1.1 is the following result, which establishes a Brownian excursion limit law for (a) Ising polymers as defined by [Reference Ioffe, Shlosman and Toninelli32] in the positive half-plane
![]() ${\mathbb H}$
and (b) Ising polymers in a box of side length N. Our proof of Part (a) hinges on the ‘no pinning’ main result of [Reference Ioffe, Shlosman and Toninelli32] (mentioned above) en route to refining its conclusion and deriving the limit law. Part (b), proved similarly, may be viewed as an analogue of [Reference Ioffe, Ott, Velenik and Wachtel31] for any Ising polymer at large
${\mathbb H}$
and (b) Ising polymers in a box of side length N. Our proof of Part (a) hinges on the ‘no pinning’ main result of [Reference Ioffe, Shlosman and Toninelli32] (mentioned above) en route to refining its conclusion and deriving the limit law. Part (b), proved similarly, may be viewed as an analogue of [Reference Ioffe, Ott, Velenik and Wachtel31] for any Ising polymer at large
![]() $\beta $
.
$\beta $
.
Theorem 1.2. Fix
![]() $\beta $
large, and consider the family of Ising polymers
$\beta $
large, and consider the family of Ising polymers
![]() $\gamma $
(see Definitions 2.3 and 2.6) in a domain D, where the potential function
$\gamma $
(see Definitions 2.3 and 2.6) in a domain D, where the potential function
![]() $\Phi '$
is modified along its boundary
$\Phi '$
is modified along its boundary
![]() $\partial D$
, and D is either
$\partial D$
, and D is either
-
(a) the positive half-plane
 ${\mathbb H}$
with the marked end points
${\mathbb H}$
with the marked end points
 $\mathsf {o}^*=(\frac 12,\frac 12)$
and
$\mathsf {o}^*=(\frac 12,\frac 12)$
and
 $\mathsf {x}_N = (\frac 12,N-\frac 12)$
; or
$\mathsf {x}_N = (\frac 12,N-\frac 12)$
; or -
(b) a box of side length N whose bottom corners are the same marked end points
 $\mathsf {o}^*$
and
$\mathsf {o}^*$
and
 $\mathsf {x}_N$
.
$\mathsf {x}_N$
.
There exists
![]() $\sigma>0$
such that, if
$\sigma>0$
such that, if
![]() $\overline \gamma (x)=\max \{y : (x,y)\in \gamma \}$
, then
$\overline \gamma (x)=\max \{y : (x,y)\in \gamma \}$
, then
![]() $\overline \gamma (\lfloor x N\rfloor )/(\sigma \sqrt {N})$
converges weakly to a standard Brownian excursion on
$\overline \gamma (\lfloor x N\rfloor )/(\sigma \sqrt {N})$
converges weakly to a standard Brownian excursion on
![]() $[0,1]$
, and the same holds for
$[0,1]$
, and the same holds for
![]() $\underline \gamma (x)=\min \{y : (x,y)\in \gamma \}$
.
$\underline \gamma (x)=\min \{y : (x,y)\in \gamma \}$
.
In particular, Part (b) applies to the SOS model
![]() $\widehat \pi _{\Lambda }^{0,1,1,1}$
with no floor on a box
$\widehat \pi _{\Lambda }^{0,1,1,1}$
with no floor on a box
![]() $\Lambda $
of side length N, for
$\Lambda $
of side length N, for
![]() $\beta>\beta _0$
and boundary conditions
$\beta>\beta _0$
and boundary conditions
![]() $0$
on the bottom side and
$0$
on the bottom side and
![]() $1$
elsewhere: Namely, the height-
$1$
elsewhere: Namely, the height-
![]() $1$
level line that connects the bottom corners of the box
$1$
level line that connects the bottom corners of the box
![]() $\Lambda $
has a scaling limit of a Brownian excursion.
$\Lambda $
has a scaling limit of a Brownian excursion.
While Theorem 1.2 addressed level lines in the SOS model (and more generally, Ising polymers) with no floor – whereby the scaling limit is a Brownian excursion – its application for Theorem 1.1 (addressing SOS above a floor) used the fact that in that setting the effect of the floor is uniformly bounded. Indeed, in an
![]() $L^{2/3}\times L^{2/3}$
box centered on the bottom boundary, the tilting effect of the floor on the top level line (as a Radon–Nikodym derivative) amounts to a factor of
$L^{2/3}\times L^{2/3}$
box centered on the bottom boundary, the tilting effect of the floor on the top level line (as a Radon–Nikodym derivative) amounts to a factor of
![]() $\exp [ c A / L ]$
, where A is the area under the nontilted curve (note
$\exp [ c A / L ]$
, where A is the area under the nontilted curve (note
![]() $A \lesssim _{\texttt P} L$
for a Brownian excursion on an interval of length
$A \lesssim _{\texttt P} L$
for a Brownian excursion on an interval of length
![]() $L^{2/3}$
). Since, as mentioned above, a Brownian excursion tilted by an area term is known to converge to a Ferrari–Spohn diffusion, one expects that the top level line of SOS in that box will actually dominate a Ferrari–Spohn diffusion. This is the content of Theorem 1.3 below.
$L^{2/3}$
). Since, as mentioned above, a Brownian excursion tilted by an area term is known to converge to a Ferrari–Spohn diffusion, one expects that the top level line of SOS in that box will actually dominate a Ferrari–Spohn diffusion. This is the content of Theorem 1.3 below.
We first define the limiting object formally. Let
![]() $\mathsf {Ai}(x)$
denote the Airy function (of the first kind), that is, the solution to
$\mathsf {Ai}(x)$
denote the Airy function (of the first kind), that is, the solution to
![]() $y"(x) = x y$
with the initial condition
$y"(x) = x y$
with the initial condition
![]() $y=0$
at
$y=0$
at
![]() $x=\infty $
. For
$x=\infty $
. For
![]() $\lambda ,\sigma>0$
, define
$\lambda ,\sigma>0$
, define
![]() $f_{\lambda ,\sigma }(x) := \mathsf {Ai}((2\lambda \sigma )^{1/3}x +\omega _1)$
, where
$f_{\lambda ,\sigma }(x) := \mathsf {Ai}((2\lambda \sigma )^{1/3}x +\omega _1)$
, where
![]() $\omega _1$
is the ‘first’ zero of
$\omega _1$
is the ‘first’ zero of
![]() $\mathsf {Ai}$
(
$\mathsf {Ai}$
(
![]() $\omega _1<0$
and closest to
$\omega _1<0$
and closest to
![]() $0$
).Footnote
3
The stationary Ferrari–Spohn diffusion we consider is the diffusion on
$0$
).Footnote
3
The stationary Ferrari–Spohn diffusion we consider is the diffusion on
![]() $(0,\infty )$
with generator
$(0,\infty )$
with generator
 $$ \begin{align} \mathsf{L}\psi = \frac{1}2 \psi" + \frac{f_{\lambda,\sigma}'}{f_{\lambda,\sigma}}\psi' \end{align} $$
$$ \begin{align} \mathsf{L}\psi = \frac{1}2 \psi" + \frac{f_{\lambda,\sigma}'}{f_{\lambda,\sigma}}\psi' \end{align} $$
and Dirichlet boundary condition at
![]() $0$
.
$0$
.
The following result establishes that if we consider the SOS model on a
![]() $KL^{2/3}\times KL^{2/3}$
box with boundary conditions
$KL^{2/3}\times KL^{2/3}$
box with boundary conditions
![]() $H-1,H,H,H$
, where H is the typical height of the top level line (up to
$H-1,H,H,H$
, where H is the typical height of the top level line (up to
![]() $1$
integer), then the H-level line will converge weakly to a Ferrari–Spohn diffusion in
$1$
integer), then the H-level line will converge weakly to a Ferrari–Spohn diffusion in
![]() $(C[-T,T], \|\cdot \|_{\infty })$
for any
$(C[-T,T], \|\cdot \|_{\infty })$
for any
![]() $T>0$
. A direct consequence (via the monotonicity argument in Section 3) is a refinement of Theorem 1.1, showing that
$T>0$
. A direct consequence (via the monotonicity argument in Section 3) is a refinement of Theorem 1.1, showing that
![]() $\rho (x)$
from that theorem essentially dominates a Ferrari–Spohn diffusion (thus
$\rho (x)$
from that theorem essentially dominates a Ferrari–Spohn diffusion (thus
![]() $\rho (x) \gtrsim _{\texttt P} L^{1/3}$
; see Remark 1.5).
$\rho (x) \gtrsim _{\texttt P} L^{1/3}$
; see Remark 1.5).
Theorem 1.3. Fix
![]() $\beta $
large, and consider the SOS model on a
$\beta $
large, and consider the SOS model on a
![]() $K L^{2/3}\times K L^{2/3}$
box with a floor at
$K L^{2/3}\times K L^{2/3}$
box with a floor at
![]() $0$
and boundary conditions
$0$
and boundary conditions
![]() $H = \lfloor \frac 1{4\beta }\log L\rfloor $
everywhere except the bottom side, where they are
$H = \lfloor \frac 1{4\beta }\log L\rfloor $
everywhere except the bottom side, where they are
![]() $H-1$
. Suppose that
$H-1$
. Suppose that
![]() $a_L$
, the fractional part of
$a_L$
, the fractional part of
![]() $\frac 1{4\beta }\log L$
, converges to a limit, and let
$\frac 1{4\beta }\log L$
, converges to a limit, and let
![]() $\overline \rho (x)$
denote the maximum vertical distance of the H-level line (connecting the bottom corners of the box) from the bottom side at horizontal location
$\overline \rho (x)$
denote the maximum vertical distance of the H-level line (connecting the bottom corners of the box) from the bottom side at horizontal location
![]() $x\in \mathbb {R}$
. Let
$x\in \mathbb {R}$
. Let
![]() $\sigma>0$
be the constant from Theorem 1.2, Part (b). Then there exists
$\sigma>0$
be the constant from Theorem 1.2, Part (b). Then there exists
![]() $\lambda>0$
such that
$\lambda>0$
such that
![]() $ \overline \rho (\lfloor x L^{2/3} \rfloor ) / (\sigma L^{1/3})$
converges weakly as
$ \overline \rho (\lfloor x L^{2/3} \rfloor ) / (\sigma L^{1/3})$
converges weakly as
![]() $L\to \infty $
followed by
$L\to \infty $
followed by
![]() $K\to \infty $
to the stationary Ferrari–Spohn diffusion on
$K\to \infty $
to the stationary Ferrari–Spohn diffusion on
![]() $(0,\infty )$
with generator
$(0,\infty )$
with generator
![]() $\mathsf {L}$
and Dirichlet boundary condition at 0. The same holds for
$\mathsf {L}$
and Dirichlet boundary condition at 0. The same holds for
![]() $\underline {\rho }(x)$
, the minimum height fluctuation of the level line at
$\underline {\rho }(x)$
, the minimum height fluctuation of the level line at
![]() $x\in \mathbb {R}$
.
$x\in \mathbb {R}$
.
Remark 1.4. Using the same methods, a Ferrari–Spohn diffusion limit may also be derived for Ising polymers with the appropriate area tilt. Furthermore, it is possible to take any diverging sequence of
![]() $K:= K(L) \in (0,L^{1/20})$
. See Theorem 7.1 for a more detailed version of Theorem 1.3.
$K:= K(L) \in (0,L^{1/20})$
. See Theorem 7.1 for a more detailed version of Theorem 1.3.
Remark 1.5. As mentioned above, Theorem 1.2 is proved via coupling the Ising polymer to a 2D directed random walk excursion. The proof of Theorem 1.3, taking into account the floor in the SOS model, proceeds by using the same machinery to couple the polymer to a random walk excursionbn yet this time with an area tilt. We then appeal to the approach of [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6] for handling the convergence of such 2D random walks to the Ferrari–Spohn diffusion. As a byproduct of this argument, one can read off quantitative results on the model before taking
![]() $K,L\to \infty $
; namely, the top level line of the SOS model with zero boundary conditions on
$K,L\to \infty $
; namely, the top level line of the SOS model with zero boundary conditions on
![]() $\Lambda _L$
above a wall dominates a random walk excursion with end points
$\Lambda _L$
above a wall dominates a random walk excursion with end points
![]() $0$
and an area tilt on any interval of length
$0$
and an area tilt on any interval of length
![]() $L^{2/3}$
at distance at least
$L^{2/3}$
at distance at least
![]() $\epsilon _\beta L$
from the box corners (a stronger result than Theorem 1.1).
$\epsilon _\beta L$
from the box corners (a stronger result than Theorem 1.1).
Remark 1.6. Consider the aforementioned stronger version of Theorem 1.1, whereby the vertical displacement
![]() $\underline \rho (x)$
of the top level line
$\underline \rho (x)$
of the top level line
![]() $\mathcal L_0$
of the SOS model, along any interval of length
$\mathcal L_0$
of the SOS model, along any interval of length
![]() $L^{2/3}$
bounded away from the corners, stochastically dominates a random walk with area tilt
$L^{2/3}$
bounded away from the corners, stochastically dominates a random walk with area tilt
![]() $e^{-cA / L}$
. Standard tools will then imply that
$e^{-cA / L}$
. Standard tools will then imply that
![]() $\max _{x\in I}\underline \rho (x)$
is
$\max _{x\in I}\underline \rho (x)$
is
![]() $\Omega ( L^{1/3}(\log L)^{2/3})$
for
$\Omega ( L^{1/3}(\log L)^{2/3})$
for ![]() . Namely, one could show, for some absolute constant
. Namely, one could show, for some absolute constant
![]() $c>0$
, a lower bound on the upper tail of
$c>0$
, a lower bound on the upper tail of
![]() $\underline \rho (x_0)$
, valid for all
$\underline \rho (x_0)$
, valid for all
![]() $x_0\in I$
, à la Tracy–Widom distribution:
$x_0\in I$
, à la Tracy–Widom distribution:
Considering about
![]() $L^{1/3}$
such
$L^{1/3}$
such
![]() $x_0$
taken in disjoint boxes of length
$x_0$
taken in disjoint boxes of length
![]() $L^{2/3}$
each, along with monotonicity arguments similar to those employed in Section 3 will then imply
$L^{2/3}$
each, along with monotonicity arguments similar to those employed in Section 3 will then imply
![]() $\max _{x\in I} \underline \rho (x) \gtrsim _{\texttt P} L^{1/3}(\log L)^{2/3}$
.
$\max _{x\in I} \underline \rho (x) \gtrsim _{\texttt P} L^{1/3}(\log L)^{2/3}$
.
It is plausible that this gives the correct order of the upper tail large deviation rate function, and that consequently,
![]() $\max _x\underline \rho (x) \asymp _{\texttt P} L^{1/3}(\log L)^{2/3}$
(see, e.g., [Reference Ganguly and Gheissari28], where an estimate of this type was obtained for the 2D Ising interface in critical prewetting, as well the work of Alexander [Reference Alexander1] on local roughness of droplet boundaries in the random cluster model).
$\max _x\underline \rho (x) \asymp _{\texttt P} L^{1/3}(\log L)^{2/3}$
(see, e.g., [Reference Ganguly and Gheissari28], where an estimate of this type was obtained for the 2D Ising interface in critical prewetting, as well the work of Alexander [Reference Alexander1] on local roughness of droplet boundaries in the random cluster model).
Question 1.7. Let ![]() . What is the rate function
. What is the rate function
![]() $a\mapsto -\log \pi _{\Lambda _L}^0(\underline \rho (x_0)>a L^{1/3})$
?
$a\mapsto -\log \pi _{\Lambda _L}^0(\underline \rho (x_0)>a L^{1/3})$
?
As for lower tails, to our knowledge these are still open for the 2D Ising under critical prewetting, where one expects the Ising interface to reach the bottom in
![]() $O_{\texttt P}(1)$
locations along
$O_{\texttt P}(1)$
locations along ![]() . One should stress though that it is unclear that the SOS large deviations would take after the behavior of the 2D Ising interface under prewetting – particularly for the lower tails, where in SOS there are
. One should stress though that it is unclear that the SOS large deviations would take after the behavior of the 2D Ising interface under prewetting – particularly for the lower tails, where in SOS there are
![]() $\Theta (\log L)$
level lines below
$\Theta (\log L)$
level lines below
![]() $\mathcal L_0$
, all of which must cooperate with a downward deviation.
$\mathcal L_0$
, all of which must cooperate with a downward deviation.
Question 1.8. Let ![]() . What is the order of
. What is the order of
![]() $\pi _{\Lambda _L}^0(\underline \rho (x_0)=0)$
?
$\pi _{\Lambda _L}^0(\underline \rho (x_0)=0)$
?
The paper is organized as follows. In Section 2, we formalize the setting of Ising polymers, as well as the inputs we need from Ornstein–Zernike theory. We also establish that the SOS model satisfies the required hypotheses of Ising polymers, and thus Theorem 1.2 is applicable to it. Section 3 proves Theorem 1.1, addressing the SOS measure
![]() $\pi $
, using a monotonicity argument and the conclusion of Theorem 1.2 on
$\pi $
, using a monotonicity argument and the conclusion of Theorem 1.2 on
![]() $\widehat \pi $
, the SOS measure without a floor. In Section 4, we introduce a random walk in
$\widehat \pi $
, the SOS measure without a floor. In Section 4, we introduce a random walk in
![]() ${\mathbb H}$
that is closely related to Ising polymers and state the key limit theorems for this random walk. In turn, Section 5 provides the proof of Theorem 1.2 modulo these random walks results that are deferred to Section 6. In Section 7, we prove Theorem 1.3.
${\mathbb H}$
that is closely related to Ising polymers and state the key limit theorems for this random walk. In turn, Section 5 provides the proof of Theorem 1.2 modulo these random walks results that are deferred to Section 6. In Section 7, we prove Theorem 1.3.
2 Cluster expansion, Ising polymers and Ornstein–Zernike theory
In this section, we review the tools needed for our proofs – notably, cluster expansion, prior work on Ising polymers and the Ornstein–Zernike theory. In several cases, we will need variants of existing results, which are not covered by the results proved in the literature. In those cases, we provide proofs of these analogues (either in the main text or in the appendix).
Throughout the paper, we say that an event holds with high probability (w.h.p.) if its probability tends to
![]() $1$
as the system size (typically, L or N) tends to
$1$
as the system size (typically, L or N) tends to
![]() $\infty $
. For two functions
$\infty $
. For two functions
![]() $f: \mathbb {N} \to (0,\infty )$
and
$f: \mathbb {N} \to (0,\infty )$
and
![]() $g: \mathbb {N} \to (0,\infty )$
, write
$g: \mathbb {N} \to (0,\infty )$
, write
![]() $ f \sim g $
to denote that
$ f \sim g $
to denote that
![]() $\lim _{N\to \infty } f(N)/g(N) = 1$
; write
$\lim _{N\to \infty } f(N)/g(N) = 1$
; write
![]() $ f \lesssim g$
when there exists a constant
$ f \lesssim g$
when there exists a constant
![]() $K>0$
such that
$K>0$
such that
![]() $f(N) \leq K g(N)$
for all
$f(N) \leq K g(N)$
for all
![]() $N \in \mathbb {N}$
; and write
$N \in \mathbb {N}$
; and write
![]() $f \asymp g $
when
$f \asymp g $
when
![]() $f\lesssim g$
and
$f\lesssim g$
and
![]() $g\lesssim f$
.
$g\lesssim f$
.
2.1 Contours and cluster expansion
A contour
![]() $\gamma $
is a collection of bonds
$\gamma $
is a collection of bonds
![]() $(e_i)_{i=1}^m$
in the dual lattice
$(e_i)_{i=1}^m$
in the dual lattice
![]() $(\mathbb {Z}^2)^*$
, where all bonds are distinct except possibly
$(\mathbb {Z}^2)^*$
, where all bonds are distinct except possibly
![]() $e_1$
and
$e_1$
and
![]() $e_m$
may coincide, every two consecutive edges share a vertex, and the path formed is simple except in accordance with a splitting rule: If the pair
$e_m$
may coincide, every two consecutive edges share a vertex, and the path formed is simple except in accordance with a splitting rule: If the pair
![]() $e_{i}, e_{i+1}$
and
$e_{i}, e_{i+1}$
and
![]() $e_j, e_{j+1}$
all intersect at a vertex
$e_j, e_{j+1}$
all intersect at a vertex
![]() $\mathsf {x}$
, then the two other end points of
$\mathsf {x}$
, then the two other end points of
![]() $e_i,e_{i+1}$
are on the same side of the line through
$e_i,e_{i+1}$
are on the same side of the line through
![]() $\mathsf {x}$
with slope
$\mathsf {x}$
with slope
![]() $1$
(from southwest to northeast) and similarly for
$1$
(from southwest to northeast) and similarly for
![]() $e_j,e_{j+1}$
(this is the northeast splitting rule). We call
$e_j,e_{j+1}$
(this is the northeast splitting rule). We call
![]() $\gamma $
an open contour if
$\gamma $
an open contour if
![]() $e_1\neq e_m$
.
$e_1\neq e_m$
.
In the context of the SOS model in a finite, connected
![]() $\Lambda \Subset \mathbb {Z}^2$
under
$\Lambda \Subset \mathbb {Z}^2$
under
![]() $0$
boundary conditions, for any h, the h-level lines (recall that for any configuration
$0$
boundary conditions, for any h, the h-level lines (recall that for any configuration
![]() $\varphi $
and integer h, these are the bonds dual to
$\varphi $
and integer h, these are the bonds dual to
![]() $\mathsf {x}\sim \mathsf {y}$
with
$\mathsf {x}\sim \mathsf {y}$
with
![]() $\varphi _{\mathsf {x}}<h$
and
$\varphi _{\mathsf {x}}<h$
and
![]() $\varphi _{\mathsf {y}}\geq h$
) give rise to a collection of disjoint loops after applying the global splitting rule. In the presence of a boundary condition
$\varphi _{\mathsf {y}}\geq h$
) give rise to a collection of disjoint loops after applying the global splitting rule. In the presence of a boundary condition
![]() $\xi \in \{0,1\}^{\partial \Lambda }$
consisting of a connected stretch of
$\xi \in \{0,1\}^{\partial \Lambda }$
consisting of a connected stretch of
![]() $0$
’s (and
$0$
’s (and
![]() $1$
’s elsewhere), this gives rise to a unique open contour among the height-
$1$
’s elsewhere), this gives rise to a unique open contour among the height-
![]() $1$
level lines (accompanied by a collection of closed contours). We refer to this path as the open
$1$
level lines (accompanied by a collection of closed contours). We refer to this path as the open
![]() $1$
-contour. Let
$1$
-contour. Let
![]() $\Delta _{\gamma }^+$
and
$\Delta _{\gamma }^+$
and
![]() $\Delta _{\gamma }^-$
denote the set of sites (of
$\Delta _{\gamma }^-$
denote the set of sites (of
![]() $\mathbb {Z}^2$
) immediately above and below
$\mathbb {Z}^2$
) immediately above and below
![]() $\gamma $
, respectively, and define
$\gamma $
, respectively, and define
Note that the sites in
![]() $\Delta _{\gamma }^+$
have height
$\Delta _{\gamma }^+$
have height
![]() $\geq 1$
, while the sites in
$\geq 1$
, while the sites in
![]() $\Delta _{\gamma }^-$
have height
$\Delta _{\gamma }^-$
have height
![]() $\leq 0$
. Each
$\leq 0$
. Each
![]() $\gamma $
divides
$\gamma $
divides
![]() $\Lambda $
into two regions,
$\Lambda $
into two regions,
![]() $\Lambda _{\gamma }^+$
and
$\Lambda _{\gamma }^+$
and
![]() $\Lambda _{\gamma }^-$
, where we write
$\Lambda _{\gamma }^-$
, where we write
![]() $\Lambda _{\gamma }^+$
to denote the region that contains
$\Lambda _{\gamma }^+$
to denote the region that contains
![]() $\Delta _{\gamma }^+$
as part of its inner boundary. The next proposition addresses the law of this unique SOS open contour
$\Delta _{\gamma }^+$
as part of its inner boundary. The next proposition addresses the law of this unique SOS open contour
![]() $\gamma $
.
$\gamma $
.
Proposition 2.1 [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli13, Lem. A.2].
Consider the SOS model
![]() $\widehat \pi _\Lambda ^\xi $
on any finite, connected
$\widehat \pi _\Lambda ^\xi $
on any finite, connected
![]() $\Lambda \subset \mathbb {Z}^2$
and under any boundary condition
$\Lambda \subset \mathbb {Z}^2$
and under any boundary condition
![]() $\xi \in \{0, 1\}^{\partial \Lambda }$
that induces a unique open
$\xi \in \{0, 1\}^{\partial \Lambda }$
that induces a unique open
![]() $1$
-contour
$1$
-contour
![]() $\gamma $
. Then there exists a constant
$\gamma $
. Then there exists a constant
![]() $\beta _0>0$
such that for all
$\beta _0>0$
such that for all
![]() $\beta \geq \beta _0$
,
$\beta \geq \beta _0$
,

for some ‘decoration functions’
![]() $\{\phi (\mathcal {C}, \gamma )\}_{\mathcal {C} \subset \mathbb {Z}^2}$
satisfying the following properties:
$\{\phi (\mathcal {C}, \gamma )\}_{\mathcal {C} \subset \mathbb {Z}^2}$
satisfying the following properties:
-
(i) If
 $\mathcal {C}$
is not connected, then
$\mathcal {C}$
is not connected, then
 $\phi (\mathcal {C}; \gamma ) = 0$
.
$\phi (\mathcal {C}; \gamma ) = 0$
. -
(ii) The decoration function
 $\phi (\mathcal {C};\cdot )$
depends on
$\phi (\mathcal {C};\cdot )$
depends on
 $\gamma $
only through
$\gamma $
only through
 $\mathcal {C} \cap \Delta _{\gamma }$
.
$\mathcal {C} \cap \Delta _{\gamma }$
. -
(iii) For all
 ${\mathsf {v}} \in \mathbb {Z}^2$
,
${\mathsf {v}} \in \mathbb {Z}^2$
,
 $\phi (\mathcal {C}; \gamma ) = \phi (\mathcal {C}+{\mathsf {v}}; \gamma +{\mathsf {v}})$
.
$\phi (\mathcal {C}; \gamma ) = \phi (\mathcal {C}+{\mathsf {v}}; \gamma +{\mathsf {v}})$
. -
(iv) Letting
 $d(\mathcal {C})$
denote the cardinality of the smallest connected set of bonds of
$d(\mathcal {C})$
denote the cardinality of the smallest connected set of bonds of
 $\mathbb {Z}^2$
containing all boundary bonds of
$\mathbb {Z}^2$
containing all boundary bonds of
 $\mathcal {C}$
(i.e., bonds connecting
$\mathcal {C}$
(i.e., bonds connecting
 $\mathcal {C}$
to
$\mathcal {C}$
to
 $\mathcal {C}^c$
), we have the decay bound (2.2)
$\mathcal {C}^c$
), we have the decay bound (2.2) $$ \begin{align} \sup_{\gamma} |\phi(\mathcal{C}; \gamma)| \leq \exp\Big(- (\beta-\beta_0) d(\mathcal{C})\Big). \end{align} $$
$$ \begin{align} \sup_{\gamma} |\phi(\mathcal{C}; \gamma)| \leq \exp\Big(- (\beta-\beta_0) d(\mathcal{C})\Big). \end{align} $$
Furthermore, if
![]() $\widehat Z_{\Lambda }^\xi $
is the partition function of the SOS model
$\widehat Z_{\Lambda }^\xi $
is the partition function of the SOS model
![]() $\widehat \pi _{\Lambda }^\xi $
and
$\widehat \pi _{\Lambda }^\xi $
and
is the interface partition function corresponding to the distribution Equation (2.1), then
The decoration functions come from cluster expansion applied to the partition functions in
![]() $\Lambda _{\gamma }^+$
and
$\Lambda _{\gamma }^+$
and
![]() $\Lambda _{\gamma }^-$
. In Appendix A, we recall cluster expansion for the SOS model and provide the proof of Proposition 2.1, as the expression for the decoration function
$\Lambda _{\gamma }^-$
. In Appendix A, we recall cluster expansion for the SOS model and provide the proof of Proposition 2.1, as the expression for the decoration function
![]() $\phi $
is needed to verify that it meets the criteria of modified Ising polymers (Definition 2.6). In light of Property (i), from now on we will write
$\phi $
is needed to verify that it meets the criteria of modified Ising polymers (Definition 2.6). In light of Property (i), from now on we will write
![]() $\mathcal {C}$
to denote a connected subset (or cluster) of
$\mathcal {C}$
to denote a connected subset (or cluster) of
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Next, we recall the notion of surface tension for the SOS model.
Definition 2.2 (Dobrushin boundary conditions, surface tension).
Fix
![]() $\vec {u} \in \mathbb {S}^{1}$
in the first quadrant, that is, with
$\vec {u} \in \mathbb {S}^{1}$
in the first quadrant, that is, with
![]() $\theta _{\vec {u}} \in [0,\pi /2)$
, where
$\theta _{\vec {u}} \in [0,\pi /2)$
, where
![]() $\theta _{\vec {u}}$
is the angle
$\theta _{\vec {u}}$
is the angle
![]() $\vec {u}$
makes with the positive horizontal axis. Set
$\vec {u}$
makes with the positive horizontal axis. Set ![]() , and let
, and let
![]() $\xi (\vec {u})$
denote the boundary condition defined by
$\xi (\vec {u})$
denote the boundary condition defined by
![]() $\xi (\vec {u})_v = 0$
for all
$\xi (\vec {u})_v = 0$
for all
![]() $v\in \partial \Lambda $
lying on or below
$v\in \partial \Lambda $
lying on or below
![]() $\mathrm {span}(\vec {u})$
, and
$\mathrm {span}(\vec {u})$
, and
![]() $\xi (\vec {u})_v= 1$
otherwise. Our main focus is on the boundary condition
$\xi (\vec {u})_v= 1$
otherwise. Our main focus is on the boundary condition
![]() $\xi (\mathsf {e}_1)$
, which we denote by
$\xi (\mathsf {e}_1)$
, which we denote by
![]() $0,1,1,1$
(after the values induced by
$0,1,1,1$
(after the values induced by
![]() $\xi (\mathsf {e}_1)$
on the four sides of the box
$\xi (\mathsf {e}_1)$
on the four sides of the box ![]() ). Define
). Define
![]() $d_{N,\vec {u}} := N/\cos (\theta _{\vec {u}})$
. The surface tension
$d_{N,\vec {u}} := N/\cos (\theta _{\vec {u}})$
. The surface tension ![]() is defined by
is defined by
The value of ![]() for the other quadrants is defined symmetrically so that
for the other quadrants is defined symmetrically so that ![]() when
when
![]() $\theta _{\vec u} = -\theta _{\vec v}$
or
$\theta _{\vec u} = -\theta _{\vec v}$
or
![]() $\theta _{\vec u} = \pi -\theta _{\vec v}$
.
$\theta _{\vec u} = \pi -\theta _{\vec v}$
.
Finally, ![]() extends to an even function on all of
extends to an even function on all of
![]() $\mathbb {R}^2$
via homogeneity:
$\mathbb {R}^2$
via homogeneity:
The proof of the existence of ![]() as well as many of its properties can be found in [Reference Dobrushin, Kotecký and Shlosman20, §1–2].
as well as many of its properties can be found in [Reference Dobrushin, Kotecký and Shlosman20, §1–2].
2.2 The free Ising polymer model
In this section, we define the class of Ising polymer models, as given by [Reference Ioffe, Shlosman and Toninelli32].Footnote 4 The reader is also referred to [Reference Dobrushin, Kotecký and Shlosman20] for many useful results on such polymer models. It will be shown that the SOS open contour from Equation (2.1) falls in this class.
Recall that we write
![]() $\mathcal {C}$
to denote a finite, connected subset of
$\mathcal {C}$
to denote a finite, connected subset of
![]() $\mathbb {Z}^2$
. For every contour
$\mathbb {Z}^2$
. For every contour
![]() $\gamma $
, consider any decoration function
$\gamma $
, consider any decoration function
![]() $\Phi (\mathcal {C}; \gamma )$
satisfying the following four properties:
$\Phi (\mathcal {C}; \gamma )$
satisfying the following four properties:
-
(P1) Locality:
 $\Phi (\mathcal {C}; \cdot )$
depends on
$\Phi (\mathcal {C}; \cdot )$
depends on
 $\gamma $
only through
$\gamma $
only through
 $\mathcal {C}\cap \Delta _{\gamma }$
.
$\mathcal {C}\cap \Delta _{\gamma }$
. -
(P2) Decay: There exists some
 $\chi>1/2$
such that, for all
$\chi>1/2$
such that, for all
 $\beta>0$
sufficiently large, (2.5)where
$\beta>0$
sufficiently large, (2.5)where $$ \begin{align} \sup_{\gamma} |\Phi(\mathcal{C},\gamma)| \leq \exp(-\chi \beta (d(\mathcal{C})+1)), \end{align} $$
$$ \begin{align} \sup_{\gamma} |\Phi(\mathcal{C},\gamma)| \leq \exp(-\chi \beta (d(\mathcal{C})+1)), \end{align} $$
 $d(\mathcal {C})$
is defined as in Property (iv) of Proposition 2.1.
$d(\mathcal {C})$
is defined as in Property (iv) of Proposition 2.1.
-
(P3) Translational symmetry: For all
 ${\mathsf {v}}\in \mathbb {Z}^2$
,
${\mathsf {v}}\in \mathbb {Z}^2$
,
 $\Phi (\mathcal {C}; \gamma ) = \Phi (\mathcal {C}+{\mathsf {v}};\gamma +{\mathsf {v}})$
.
$\Phi (\mathcal {C}; \gamma ) = \Phi (\mathcal {C}+{\mathsf {v}};\gamma +{\mathsf {v}})$
. -
(P4) Symmetry of the surface tension: The surface tension
 $\tau _{\beta }(\mathsf {x})$
defined below in Equation (2.8) possesses all discrete symmetries of
$\tau _{\beta }(\mathsf {x})$
defined below in Equation (2.8) possesses all discrete symmetries of
 $\mathbb {Z}^2$
(rotations by
$\mathbb {Z}^2$
(rotations by
 $\pi /4$
and reflections w.r.t. axes and the diagonals
$\pi /4$
and reflections w.r.t. axes and the diagonals
 $y=\pm x$
).
$y=\pm x$
).
Towards specifying the probability that the model assigns to each polymer – as well as the surface tension
![]() $\tau _\beta $
mentioned in Property (P4) – define the free (polymer) weight via
$\tau _\beta $
mentioned in Property (P4) – define the free (polymer) weight via
 $$ \begin{align} q(\gamma) = \exp\Big(-\beta|\gamma| + \sum_{\mathcal{C} \cap \Delta_{\gamma} \neq \emptyset} \Phi(\mathcal{C};\gamma)\Big), \end{align} $$
$$ \begin{align} q(\gamma) = \exp\Big(-\beta|\gamma| + \sum_{\mathcal{C} \cap \Delta_{\gamma} \neq \emptyset} \Phi(\mathcal{C};\gamma)\Big), \end{align} $$
where, here and throughout the article, sums over
![]() $\mathcal {C}$
are assumed to only go over connected subsets
$\mathcal {C}$
are assumed to only go over connected subsets
![]() $\mathcal {C} \subset \mathbb {Z}^2$
. Next, for any
$\mathcal {C} \subset \mathbb {Z}^2$
. Next, for any
![]() $\mathsf {x} \in (\mathbb {Z}^2)^*$
, consider the partition function going over all contours
$\mathsf {x} \in (\mathbb {Z}^2)^*$
, consider the partition function going over all contours
![]() $\gamma $
with the start point given by the dual origin
$\gamma $
with the start point given by the dual origin
![]() $\mathsf {o}^* := (1/2,1/2)$
and end point
$\mathsf {o}^* := (1/2,1/2)$
and end point
![]() $\mathsf {x}$
:
$\mathsf {x}$
:
For any set of contours E, consider also the partition function going over all contours in E with end points
![]() $0$
and
$0$
and
![]() $\mathsf {x}$
:
$\mathsf {x}$
:
Lastly, define the Ising polymer surface tension
![]() $\tau _{\beta }(\cdot )$
viaFootnote
5
$\tau _{\beta }(\cdot )$
viaFootnote
5
where the limit is taken over N such that
![]() $N \vec {n}$
is in
$N \vec {n}$
is in
![]() $(\mathbb {Z}^2)^*$
. By homogeneity,
$(\mathbb {Z}^2)^*$
. By homogeneity,
![]() $\tau _{\beta }$
extends to all of
$\tau _{\beta }$
extends to all of
![]() $\mathbb {R}^2$
.
$\mathbb {R}^2$
.
Definition 2.3 (Free Ising polymer).
The free Ising polymer model in a subset
![]() $D\subset \mathbb {R}^2$
is given by the probability measure over contours
$D\subset \mathbb {R}^2$
is given by the probability measure over contours
![]() $\gamma :\mathsf {o}^* \to \mathsf {x}$
contained in D:
$\gamma :\mathsf {o}^* \to \mathsf {x}$
contained in D:
 $$ \begin{align} \mathbf{P}^{\mathsf{x}}( \cdot \;\big|\; \gamma \subset D) := \frac{\mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset D, \gamma \in \cdot )}{\mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset D)}, \end{align} $$
$$ \begin{align} \mathbf{P}^{\mathsf{x}}( \cdot \;\big|\; \gamma \subset D) := \frac{\mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset D, \gamma \in \cdot )}{\mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset D)}, \end{align} $$
for a partition function
![]() $\mathcal {G}$
as above with a decoration function
$\mathcal {G}$
as above with a decoration function
![]() $\Phi $
satisfying Properties (P1) to (P4).
$\Phi $
satisfying Properties (P1) to (P4).
Below, we list some needed properties of
![]() $\tau _{\beta }$
, proven in [Reference Dobrushin, Kotecký and Shlosman20].
$\tau _{\beta }$
, proven in [Reference Dobrushin, Kotecký and Shlosman20].
Proposition 2.4 (Surface tension properties, [Reference Dobrushin, Kotecký and Shlosman20]).
There exists
![]() $\beta _0>0$
such that for all
$\beta _0>0$
such that for all
![]() $\beta \geq \beta _0$
:
$\beta \geq \beta _0$
:
-
(i) The formula in Equation (2.8) converges uniformly.
-
(ii) The surface tension
 $\tau _{\beta }: \mathbb {R}^2 \to \mathbb {R}^2$
is analytic.
$\tau _{\beta }: \mathbb {R}^2 \to \mathbb {R}^2$
is analytic. -
(iii) (Strong triangle inequality) For any two noncollinear vectors
 ${\mathsf {u}}$
and
${\mathsf {u}}$
and
 ${\mathsf {v}}$
in
${\mathsf {v}}$
in
 $\mathbb {Z}^2$
, we have
$\mathbb {Z}^2$
, we have  $$\begin{align*}\tau_{\beta}({\mathsf{u}}) + \tau_{\beta}({\mathsf{v}})> \tau_{\beta}({\mathsf{u}}+{\mathsf{v}}). \end{align*}$$
$$\begin{align*}\tau_{\beta}({\mathsf{u}}) + \tau_{\beta}({\mathsf{v}})> \tau_{\beta}({\mathsf{u}}+{\mathsf{v}}). \end{align*}$$
Proof. Properties (i) and (ii) follow from the combination of Theorem 4.8 and Proposition 4.12 of [Reference Dobrushin, Kotecký and Shlosman20].Footnote 6 Lastly, Property (iii) appeared in [Reference Dobrushin, Kotecký and Shlosman20, Proposition 1, Section 4.21].
For our main application of Theorem 1.2, the SOS model, the following result relates the surface tension ![]() defined in Equation (2.4) to the Ising polymer surface tension
defined in Equation (2.4) to the Ising polymer surface tension
![]() $\tau _\beta $
defined above. We suspect it is known, though could not find an exact reference for it, and as it follows from our other arguments in Section 5, we include its proof in Section 5.3 for completeness.
$\tau _\beta $
defined above. We suspect it is known, though could not find an exact reference for it, and as it follows from our other arguments in Section 5, we include its proof in Section 5.3 for completeness.
Proposition 2.5. Fix
![]() $\beta \geq \beta _0$
. Let
$\beta \geq \beta _0$
. Let
![]() $q(\gamma )$
denote the free polymer weight as per Equation (2.6) with
$q(\gamma )$
denote the free polymer weight as per Equation (2.6) with
![]() $\Phi (\mathcal {C};\gamma )$
taken to be
$\Phi (\mathcal {C};\gamma )$
taken to be
![]() $\phi (\mathcal {C};\gamma )$
from Proposition 2.1. Consider the Ising polymer surface tension
$\phi (\mathcal {C};\gamma )$
from Proposition 2.1. Consider the Ising polymer surface tension
![]() $\tau _{\beta }$
corresponding to the free polymer weights
$\tau _{\beta }$
corresponding to the free polymer weights
![]() $q(\gamma )$
as per Equation (2.8). For all
$q(\gamma )$
as per Equation (2.8). For all
![]() $\mathsf {u} \in \mathbb {R}^2$
,
$\mathsf {u} \in \mathbb {R}^2$
,
Observe that the decoration function
![]() $\phi (\mathcal {C};\gamma )$
appearing in the law of the unique open
$\phi (\mathcal {C};\gamma )$
appearing in the law of the unique open
![]() $1$
-contour under
$1$
-contour under
![]() $\widehat {\pi }_{\Lambda }^{\xi }$
satisfies Properties (P1) to (P4). Indeed, Proposition 2.1 states that the decoration function
$\widehat {\pi }_{\Lambda }^{\xi }$
satisfies Properties (P1) to (P4). Indeed, Proposition 2.1 states that the decoration function
![]() $\phi (\mathcal {C};\gamma )$
satisfies Properties (P1) to (P3). Property (P4) holds for
$\phi (\mathcal {C};\gamma )$
satisfies Properties (P1) to (P3). Property (P4) holds for ![]() because of the symmetry of the SOS model and thus for
because of the symmetry of the SOS model and thus for
![]() $\tau _{\beta }$
thanks to Proposition 2.5.
$\tau _{\beta }$
thanks to Proposition 2.5.
However, the open
![]() $1$
-contour in the SOS model is not a free Ising polymer due to the
$1$
-contour in the SOS model is not a free Ising polymer due to the ![]() term appearing in Equation (2.1), which introduces an interaction of
term appearing in Equation (2.1), which introduces an interaction of
![]() $\gamma $
with the boundary via the decoration function
$\gamma $
with the boundary via the decoration function
![]() $\phi $
. This served as one of the motivations of [Reference Ioffe, Shlosman and Toninelli32] to study modified Ising polymers – the generalization of the free Ising polymers described above to allow domain-induced modifications on the ‘free’ weights (the SOS open contour does belong to that family of models: See Observation 2.7).
$\phi $
. This served as one of the motivations of [Reference Ioffe, Shlosman and Toninelli32] to study modified Ising polymers – the generalization of the free Ising polymers described above to allow domain-induced modifications on the ‘free’ weights (the SOS open contour does belong to that family of models: See Observation 2.7).
2.3 The modified Ising polymer model
For any
![]() $D \subset \mathbb {R}^2$
and for any decoration function
$D \subset \mathbb {R}^2$
and for any decoration function
![]() $\Phi (\mathcal {C};\gamma )$
satisfying Properties (P1) to (P4), consider any function
$\Phi (\mathcal {C};\gamma )$
satisfying Properties (P1) to (P4), consider any function
![]() $\Phi _D(\mathcal {C};\gamma )$
satisfying
$\Phi _D(\mathcal {C};\gamma )$
satisfying
-
(M1)
 $\Phi _D(\mathcal {C}; \gamma ) = \Phi (\mathcal {C}; \gamma )$
for any
$\Phi _D(\mathcal {C}; \gamma ) = \Phi (\mathcal {C}; \gamma )$
for any
 $\mathcal {C} \subset D$
, and
$\mathcal {C} \subset D$
, and -
(M2)
 $\Phi _D(\mathcal {C};\gamma )$
satisfies the same decay bound in Equation (2.5) for all
$\Phi _D(\mathcal {C};\gamma )$
satisfies the same decay bound in Equation (2.5) for all
 $\mathcal {C}$
.
$\mathcal {C}$
.
Call
![]() $\Phi _D(\mathcal {C};\gamma )$
a modified decoration function (with modifications outside of D), and define the modified polymer weight
$\Phi _D(\mathcal {C};\gamma )$
a modified decoration function (with modifications outside of D), and define the modified polymer weight
 $$\begin{align*}q_{D}(\gamma) = \exp\Big(-\beta|\gamma| + \sum_{\mathcal{C} \cap \Delta_{\gamma} \neq \emptyset} \Phi_D(\mathcal{C};\gamma)\Big) \end{align*}$$
$$\begin{align*}q_{D}(\gamma) = \exp\Big(-\beta|\gamma| + \sum_{\mathcal{C} \cap \Delta_{\gamma} \neq \emptyset} \Phi_D(\mathcal{C};\gamma)\Big) \end{align*}$$
as well as the partition function

Definition 2.6 (Modified Ising polymer).
The modified Ising polymer in a subset
![]() $D \subset \mathbb {R}^2$
is given by the probability measure on contours
$D \subset \mathbb {R}^2$
is given by the probability measure on contours
![]() $\gamma :\mathsf {o}^*\to \mathsf {x}$
contained in D:
$\gamma :\mathsf {o}^*\to \mathsf {x}$
contained in D:
 $$ \begin{align} \mathbf{P}_{D}^{\mathsf{x}}(\cdot) := \frac{\mathcal{G}_D(\mathsf{x} \;\big|\; \gamma \in \cdot)}{\mathcal{G}_D(\mathsf{x})} , \end{align} $$
$$ \begin{align} \mathbf{P}_{D}^{\mathsf{x}}(\cdot) := \frac{\mathcal{G}_D(\mathsf{x} \;\big|\; \gamma \in \cdot)}{\mathcal{G}_D(\mathsf{x})} , \end{align} $$
where the partition function
![]() $\mathcal {G}_D$
is defined for a decoration function
$\mathcal {G}_D$
is defined for a decoration function
![]() $\Phi $
satisfying Properties (P1) to (P4) and a modified decoration function
$\Phi $
satisfying Properties (P1) to (P4) and a modified decoration function
![]() $\Phi _D$
satisfying Properties (M1) and (M2).
$\Phi _D$
satisfying Properties (M1) and (M2).
Note that the SOS open contour with law
![]() $\widehat {\pi }_{\Lambda }^{\xi }$
given by Equation (2.1) is of the form above, with
$\widehat {\pi }_{\Lambda }^{\xi }$
given by Equation (2.1) is of the form above, with
![]() $\Phi (\mathcal {C};\gamma )=\phi (\mathcal {C};\gamma )$
,
$\Phi (\mathcal {C};\gamma )=\phi (\mathcal {C};\gamma )$
,
![]() $D=\Lambda $
, and
$D=\Lambda $
, and ![]() for
for
![]() $\phi (\mathcal {C};\gamma )$
from Proposition 2.1 (in which this choice of
$\phi (\mathcal {C};\gamma )$
from Proposition 2.1 (in which this choice of
![]() $\Phi _D(\mathcal {C};\gamma )$
clearly satisfies Properties (M1) and (M2)). Namely, the following holds:
$\Phi _D(\mathcal {C};\gamma )$
clearly satisfies Properties (M1) and (M2)). Namely, the following holds:
Observation 2.7 (SOS is a modified Ising polymer).
Fix
![]() $\beta \geq \beta _0$
, and consider the SOS model
$\beta \geq \beta _0$
, and consider the SOS model
![]() $\widehat \pi _{\Lambda }^{\xi }$
in a finite, connected subset
$\widehat \pi _{\Lambda }^{\xi }$
in a finite, connected subset
![]() $\Lambda \subset \mathbb {Z}^2$
and boundary condition
$\Lambda \subset \mathbb {Z}^2$
and boundary condition
![]() $\xi \in \{0,1\}^{\partial \Lambda }$
that induces a unique open
$\xi \in \{0,1\}^{\partial \Lambda }$
that induces a unique open
![]() $1$
-contour
$1$
-contour
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $\bar {\Lambda }$
denote the region in
$\bar {\Lambda }$
denote the region in
![]() $\mathbb {R}^2$
enclosed by
$\mathbb {R}^2$
enclosed by
![]() $\partial \Lambda $
(i.e., the region enclosed by the
$\partial \Lambda $
(i.e., the region enclosed by the
![]() $\mathbb {Z}^2$
-edges connecting the boundary vertices of
$\mathbb {Z}^2$
-edges connecting the boundary vertices of
![]() $\Lambda $
). Assume for convenience that the start point of
$\Lambda $
). Assume for convenience that the start point of
![]() $\gamma $
is
$\gamma $
is
![]() $\mathsf {o}^*$
, and denote its end point by
$\mathsf {o}^*$
, and denote its end point by
![]() $\mathsf {x}$
. Then
$\mathsf {x}$
. Then
![]() $\gamma $
has the Ising polymer law
$\gamma $
has the Ising polymer law
![]() $\mathbf {P}^{\mathsf {x}}_{\bar \Lambda }$
defined with decoration weights
$\mathbf {P}^{\mathsf {x}}_{\bar \Lambda }$
defined with decoration weights
![]() $\Phi (\mathcal {C};\gamma ) := \phi (\mathcal {C};\gamma )$
and
$\Phi (\mathcal {C};\gamma ) := \phi (\mathcal {C};\gamma )$
and ![]() .
.
It will be very convenient to view Ising polymers as connected paths in the lattice
![]() $\mathbb {Z}^2$
rather than the dual lattice
$\mathbb {Z}^2$
rather than the dual lattice
![]() $(\mathbb {Z}^2)^*$
via the translation map
$(\mathbb {Z}^2)^*$
via the translation map
![]() $\iota : \mathsf {o}^* \mapsto 0$
, and this is the convention we will follow for the remainder of the article (for clarity, note also that, through this mapping, clusters
$\iota : \mathsf {o}^* \mapsto 0$
, and this is the convention we will follow for the remainder of the article (for clarity, note also that, through this mapping, clusters
![]() $\mathcal {C}$
will henceforth denote finite, connected subsets of
$\mathcal {C}$
will henceforth denote finite, connected subsets of
![]() $(\mathbb {Z}^2)^*$
instead of
$(\mathbb {Z}^2)^*$
instead of
![]() $\mathbb {Z}^2$
), excluding Section 3.
$\mathbb {Z}^2$
), excluding Section 3.
Let us now restate Theorem 1.2 in the above language, which is the form in which we will prove it (Section 5.7). For
![]() $N \in \mathbb {N}$
, define
$N \in \mathbb {N}$
, define
![]() $Q:= [0,N]^2$
.
$Q:= [0,N]^2$
.
Theorem 2.8. Fix
![]() $\beta>0$
large, take D to be either
$\beta>0$
large, take D to be either
![]() ${\mathbb H}$
or Q and set
${\mathbb H}$
or Q and set
![]() $\mathsf {x} := (N,0)$
. Consider an Ising polymer
$\mathsf {x} := (N,0)$
. Consider an Ising polymer
![]() $\gamma \sim \mathbf {P}_D^{\mathsf {x}}(\cdot )$
. There exists
$\gamma \sim \mathbf {P}_D^{\mathsf {x}}(\cdot )$
. There exists
![]() $\sigma>0$
such that, if
$\sigma>0$
such that, if
![]() $\overline \gamma (x)=\max \{y : (x,y)\in \gamma \}$
, then
$\overline \gamma (x)=\max \{y : (x,y)\in \gamma \}$
, then
![]() $\overline \gamma (\lfloor xN \rfloor )/(\sigma \sqrt {N})$
converges weakly to a standard Brownian excursion in the Skorokhod space
$\overline \gamma (\lfloor xN \rfloor )/(\sigma \sqrt {N})$
converges weakly to a standard Brownian excursion in the Skorokhod space
![]() $(D[0,1], \|\cdot \|_{\infty })$
and the same holds for
$(D[0,1], \|\cdot \|_{\infty })$
and the same holds for
![]() $\underline \gamma (x)=\min \{y : (x,y)\in \gamma \}$
.
$\underline \gamma (x)=\min \{y : (x,y)\in \gamma \}$
.
Remark 2.9. The variance
![]() $\sigma ^2$
with
$\sigma ^2$
with
![]() $\sigma $
as in Theorem 2.8 (and by extension, the one in Theorem 1.2) is given above Theorem 4.3. It is related to the curvature of the Wulff shape (defined in Section 2.6) associated to the Ising polymer. See [Reference Dobrushin, Kotecký and Shlosman20, Appendix B] for details.
$\sigma $
as in Theorem 2.8 (and by extension, the one in Theorem 1.2) is given above Theorem 4.3. It is related to the curvature of the Wulff shape (defined in Section 2.6) associated to the Ising polymer. See [Reference Dobrushin, Kotecký and Shlosman20, Appendix B] for details.
2.4 Nonnegative decoration functions and a product structure
Following [Reference Ioffe, Shlosman and Toninelli32, Section 3.1], we employ a construction going back to [Reference Dobrushin and Shlosman21] that allows us to consider decoration functions which are nonnegative. In this discussion, we allow for the case
![]() $D =\mathbb {R}^2$
, in which case
$D =\mathbb {R}^2$
, in which case
![]() $\Phi _D(\mathcal {C};\gamma ) = \Phi (\mathcal {C};\gamma )$
and
$\Phi _D(\mathcal {C};\gamma ) = \Phi (\mathcal {C};\gamma )$
and
![]() $q_D(\gamma ) =q(\gamma )$
.
$q_D(\gamma ) =q(\gamma )$
.
For a contour
![]() $\gamma $
, we consider the set of (not necessarily distinct) bonds in
$\gamma $
, we consider the set of (not necessarily distinct) bonds in
![]() $\mathbb {Z}^2$
(recall we have applied the translation map
$\mathbb {Z}^2$
(recall we have applied the translation map
![]() $\iota : \mathsf {o}^* \mapsto 0$
):
$\iota : \mathsf {o}^* \mapsto 0$
):
 $$\begin{align*}\nabla_{\gamma} := \bigcup_{b = (\mathsf{y}, \mathsf{y}+\mathsf{e}_i) \in \gamma} \{ b, b+\mathsf{e}_i,b-\mathsf{e}_i\} . \end{align*}$$
$$\begin{align*}\nabla_{\gamma} := \bigcup_{b = (\mathsf{y}, \mathsf{y}+\mathsf{e}_i) \in \gamma} \{ b, b+\mathsf{e}_i,b-\mathsf{e}_i\} . \end{align*}$$
To be clear, b is a bond in
![]() $\gamma $
,
$\gamma $
,
![]() $\mathsf {e}_i$
denotes a standard basis vector, and
$\mathsf {e}_i$
denotes a standard basis vector, and
![]() $b\pm \mathsf {e}_i$
denotes the bond obtained by translating b by
$b\pm \mathsf {e}_i$
denotes the bond obtained by translating b by
![]() $\pm \mathsf {e}_i$
. Thus,
$\pm \mathsf {e}_i$
. Thus,
![]() $\nabla _{\gamma }$
contains three bonds for each bond of
$\nabla _{\gamma }$
contains three bonds for each bond of
![]() $\gamma $
. Define
$\gamma $
. Define
where
![]() $|\mathcal {C} \cap \nabla _{\gamma }|$
is equal to the number of bonds, counted with multiplicity, in
$|\mathcal {C} \cap \nabla _{\gamma }|$
is equal to the number of bonds, counted with multiplicity, in
![]() $\nabla _{\gamma }$
that
$\nabla _{\gamma }$
that
![]() $\mathcal {C}$
intersects:
$\mathcal {C}$
intersects:

Observe that
![]() $\Phi ^{\prime }_D \geq 0$
by Equation (2.5) and Property (M2). For any fixed bond
$\Phi ^{\prime }_D \geq 0$
by Equation (2.5) and Property (M2). For any fixed bond
![]() $b \in \mathbb {Z}^2$
, let
$b \in \mathbb {Z}^2$
, let
![]() $c(\beta )$
denote the value of
$c(\beta )$
denote the value of
 $$\begin{align*}c(\beta) := \sum_{\mathcal{C} \subset (\mathbb{Z}^2)^* ,\, \mathcal{C} \cap b \neq \emptyset} e^{-\chi\beta( d(\mathcal{C})+1)}. \end{align*}$$
$$\begin{align*}c(\beta) := \sum_{\mathcal{C} \subset (\mathbb{Z}^2)^* ,\, \mathcal{C} \cap b \neq \emptyset} e^{-\chi\beta( d(\mathcal{C})+1)}. \end{align*}$$
Note that
where we used that
![]() $\left |\{\mathcal {C} \subset (\mathbb {Z}^2)^*: \mathcal {C} \cap b \neq \emptyset ,d(\mathcal {C}) = m \}\right | \leq e^{c m}$
for some
$\left |\{\mathcal {C} \subset (\mathbb {Z}^2)^*: \mathcal {C} \cap b \neq \emptyset ,d(\mathcal {C}) = m \}\right | \leq e^{c m}$
for some
![]() $c>0$
. (To see this, replace the marked
$c>0$
. (To see this, replace the marked
![]() $e\in \mathcal {C}$
intersecting b by a marked boundary edge
$e\in \mathcal {C}$
intersecting b by a marked boundary edge
![]() $e_0\in \partial \mathcal {C}$
with the same y-coordinate (say) at the cost of a factor of m; then, when enumerating the smallest connected set of edges of
$e_0\in \partial \mathcal {C}$
with the same y-coordinate (say) at the cost of a factor of m; then, when enumerating the smallest connected set of edges of
![]() $\mathbb {Z}^2$
containing the marked
$\mathbb {Z}^2$
containing the marked
![]() $e_0$
and specified edges
$e_0$
and specified edges
![]() $\partial \mathcal {C}$
, regard
$\partial \mathcal {C}$
, regard
![]() $\partial \mathcal {C}$
as the vertices of a 6-regular graph (whose vertices are the
$\partial \mathcal {C}$
as the vertices of a 6-regular graph (whose vertices are the
![]() $\mathbb {Z}^2$
bonds and two are adjacent if they share an end point; that is, the line graph of
$\mathbb {Z}^2$
bonds and two are adjacent if they share an end point; that is, the line graph of
![]() $\mathbb {Z}^2$
), and recall that in a graph whose maximum degree is
$\mathbb {Z}^2$
), and recall that in a graph whose maximum degree is
![]() $\Delta $
, the number of m-vertex connected subgraphs rooted at a given vertex is at most
$\Delta $
, the number of m-vertex connected subgraphs rooted at a given vertex is at most
![]() $(e \Delta )^m$
.) Using the fact that
$(e \Delta )^m$
.) Using the fact that
![]() $\mathcal {C}\cap \Delta _{\gamma } \neq \emptyset $
implies
$\mathcal {C}\cap \Delta _{\gamma } \neq \emptyset $
implies
![]() $\mathcal {C}\cap \nabla _{\gamma } \neq \emptyset $
, we have
$\mathcal {C}\cap \nabla _{\gamma } \neq \emptyset $
, we have
 $$ \begin{align*} \sum_{\mathcal{C} \cap \Delta_{\gamma} \neq \emptyset} \Phi_D(\mathcal{C};\gamma) = -3c(\beta)|\gamma| + \sum_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Phi_{D}'(\mathcal{C};\gamma). \end{align*} $$
$$ \begin{align*} \sum_{\mathcal{C} \cap \Delta_{\gamma} \neq \emptyset} \Phi_D(\mathcal{C};\gamma) = -3c(\beta)|\gamma| + \sum_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Phi_{D}'(\mathcal{C};\gamma). \end{align*} $$
Thus, we have
 $$ \begin{align*} q_{D}(\gamma) = \exp \Big( -(\beta+3c(\beta))|\gamma| + \sum_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Phi_{D}'(\mathcal{C};\gamma)\Big). \end{align*} $$
$$ \begin{align*} q_{D}(\gamma) = \exp \Big( -(\beta+3c(\beta))|\gamma| + \sum_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Phi_{D}'(\mathcal{C};\gamma)\Big). \end{align*} $$
Since
![]() $f(\beta ):= \beta +3c(\beta )$
is strictly increasing for all
$f(\beta ):= \beta +3c(\beta )$
is strictly increasing for all
![]() $\beta $
large enough, we will henceforth redefine
$\beta $
large enough, we will henceforth redefine
![]() $\beta = f(\beta )$
so that we may drop the laborious
$\beta = f(\beta )$
so that we may drop the laborious
![]() $3c(\beta )$
from our weights:
$3c(\beta )$
from our weights:
 $$ \begin{align} q_{D}(\gamma) = \exp \Big( -\beta|\gamma| + \sum_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Phi_{D}'(\mathcal{C};\gamma)\Big) . \end{align} $$
$$ \begin{align} q_{D}(\gamma) = \exp \Big( -\beta|\gamma| + \sum_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Phi_{D}'(\mathcal{C};\gamma)\Big) . \end{align} $$
A useful comparison to record at this stage is that, for any
![]() $D \subset \mathbb {R}^2$
,
$D \subset \mathbb {R}^2$
,
 $$ \begin{align} \left| \log \frac{q_D(\gamma)}{q(\gamma)}\right| \leq 6 e^{-\chi \beta}|\gamma|. \end{align} $$
$$ \begin{align} \left| \log \frac{q_D(\gamma)}{q(\gamma)}\right| \leq 6 e^{-\chi \beta}|\gamma|. \end{align} $$
Remark 2.10. For any domain
![]() $D \subset \mathbb {R}^2$
, the nonnegative decoration functions
$D \subset \mathbb {R}^2$
, the nonnegative decoration functions
![]() $\Phi '(\mathcal {C};\gamma )$
still satisfy Properties (P1) to (P4) above, and the modified nonnegative decoration functions
$\Phi '(\mathcal {C};\gamma )$
still satisfy Properties (P1) to (P4) above, and the modified nonnegative decoration functions
![]() $\Phi _D'(\mathcal {C};\gamma )$
still satisfy Properties (M1) and (M2).
$\Phi _D'(\mathcal {C};\gamma )$
still satisfy Properties (M1) and (M2).
We next uncover the product structure of
![]() $q_D$
. Defining
$q_D$
. Defining ![]() , we may write
, we may write
 $$\begin{align*}\exp\Big(\sum_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Phi_{D}'(\mathcal{C};\gamma)\Big) = \prod_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Big(\big(e^{ \Phi_{D}'(\mathcal{C};\gamma)} -1\big) +1\Big) = \sum_{\underline{\mathcal{C}} = \{\mathcal{C}_i\}} \prod_i \Psi_{D}(\mathcal{C}_i;\gamma), \end{align*}$$
$$\begin{align*}\exp\Big(\sum_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Phi_{D}'(\mathcal{C};\gamma)\Big) = \prod_{\mathcal{C} \cap \nabla_{\gamma} \neq \emptyset} \Big(\big(e^{ \Phi_{D}'(\mathcal{C};\gamma)} -1\big) +1\Big) = \sum_{\underline{\mathcal{C}} = \{\mathcal{C}_i\}} \prod_i \Psi_{D}(\mathcal{C}_i;\gamma), \end{align*}$$
where the sum goes over all possible finite collections
![]() $\underline {\mathcal {C}}$
of clusters. Given this, for any contour
$\underline {\mathcal {C}}$
of clusters. Given this, for any contour
![]() $\gamma $
and any collection
$\gamma $
and any collection
![]() $\underline {\mathcal {C}}$
of clusters, we define the animal weight
$\underline {\mathcal {C}}$
of clusters, we define the animal weight
![]() $q_{D}(\Gamma )$
of the animal
$q_{D}(\Gamma )$
of the animal
![]() $\Gamma = [\gamma , \underline {\mathcal {C}}]$
by
$\Gamma = [\gamma , \underline {\mathcal {C}}]$
by
 $$ \begin{align} q_{D}(\Gamma) = q_{D}([\gamma,\underline{\mathcal{C}}]) := e^{-\beta|\gamma|}\prod_{\mathcal{C} \in \underline{\mathcal{C}}} \Psi_{D}(\mathcal{C}; \gamma) , \end{align} $$
$$ \begin{align} q_{D}(\Gamma) = q_{D}([\gamma,\underline{\mathcal{C}}]) := e^{-\beta|\gamma|}\prod_{\mathcal{C} \in \underline{\mathcal{C}}} \Psi_{D}(\mathcal{C}; \gamma) , \end{align} $$
and observe
 $$\begin{align*}q_{D}(\gamma) = \sum_{\Gamma = [\gamma,\underline{\mathcal{C}}]}q_{D}(\Gamma). \end{align*}$$
$$\begin{align*}q_{D}(\gamma) = \sum_{\Gamma = [\gamma,\underline{\mathcal{C}}]}q_{D}(\Gamma). \end{align*}$$
The above allows us to consider the free and modified Ising polymer measures as probability measures on animals:
 $$ \begin{align} \mathbf{P}^{\mathsf{x}}(\cdot \;\big|\; \gamma \subset D) = \frac{\mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset D, \Gamma \in \cdot)}{\mathcal{G}(\mathsf{x}\;\big|\; \gamma \subset D)} \qquad \text{and}\qquad \mathbf{P}_{D}^{\mathsf{x}}(\cdot) := \frac{\mathcal{G}_D(\mathsf{x} \;\big|\; \Gamma \in \cdot)}{\mathcal{G}_D(\mathsf{x})} . \end{align} $$
$$ \begin{align} \mathbf{P}^{\mathsf{x}}(\cdot \;\big|\; \gamma \subset D) = \frac{\mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset D, \Gamma \in \cdot)}{\mathcal{G}(\mathsf{x}\;\big|\; \gamma \subset D)} \qquad \text{and}\qquad \mathbf{P}_{D}^{\mathsf{x}}(\cdot) := \frac{\mathcal{G}_D(\mathsf{x} \;\big|\; \Gamma \in \cdot)}{\mathcal{G}_D(\mathsf{x})} . \end{align} $$
Due to the product structure of
![]() $q_{D}(\Gamma )$
, it is often convenient to consider animals rather than contours; indeed, we will see in Section 4.1 that the product structure begets a connection with a random walk, which is crucial to our analysis.
$q_{D}(\Gamma )$
, it is often convenient to consider animals rather than contours; indeed, we will see in Section 4.1 that the product structure begets a connection with a random walk, which is crucial to our analysis.
When D is taken to be
![]() $\mathbb {R}^2$
, we will omit D from the notation laid out above.
$\mathbb {R}^2$
, we will omit D from the notation laid out above.
2.5 Notation for Ising polymers and animals
Below, we set notation that will be used throughout the article in the context of Ising polymers and animals. Recall that we regard Ising polymers as connected paths in the lattice
![]() $\mathbb {Z}^2$
rather than the dual lattice
$\mathbb {Z}^2$
rather than the dual lattice
![]() $(\mathbb {Z}^2)^*$
via the translation map
$(\mathbb {Z}^2)^*$
via the translation map
![]() $\iota : \mathsf {o}^* \mapsto 0$
(the convention hereafter, excluding Section 3).
$\iota : \mathsf {o}^* \mapsto 0$
(the convention hereafter, excluding Section 3).
-
• We write
 $Q:= [0,N]^2$
.
$Q:= [0,N]^2$
. -
• For a point
 $\mathsf {u} \in \mathbb {Z}^2$
, we will write
$\mathsf {u} \in \mathbb {Z}^2$
, we will write
 $\mathsf {u}_{1}$
and
$\mathsf {u}_{1}$
and
 $\mathsf {u}_{2}$
to denote the x-coordinate and y-coordinate of
$\mathsf {u}_{2}$
to denote the x-coordinate and y-coordinate of
 $\mathsf {u}$
, respectively.
$\mathsf {u}$
, respectively. -
• For a subset
 $E \subset \mathbb {Z}^2$
, we’ll write
$E \subset \mathbb {Z}^2$
, we’ll write
 $\mathsf {u}+ E$
to denote the translation of E by the vector defined by
$\mathsf {u}+ E$
to denote the translation of E by the vector defined by
 $\mathsf {u}$
.
$\mathsf {u}$
. -
• For a contour
 $\gamma $
, we write
$\gamma $
, we write
 $|\gamma |$
to denote the number of bonds in
$|\gamma |$
to denote the number of bonds in
 $\gamma $
. We write
$\gamma $
. We write
 $(\gamma (0), \dots , \gamma (|\gamma |))$
to denote the ordered vertices of
$(\gamma (0), \dots , \gamma (|\gamma |))$
to denote the ordered vertices of
 $\gamma $
.
$\gamma $
. -
• For an animal
 $\Gamma := [\gamma , \underline {\mathcal {C}}]$
, we write
$\Gamma := [\gamma , \underline {\mathcal {C}}]$
, we write
 $|\Gamma | := |\gamma |$
, and
$|\Gamma | := |\gamma |$
, and
 $\mathsf {X}(\Gamma ) := \mathsf {X}(\gamma )$
to denote the displacement of
$\mathsf {X}(\Gamma ) := \mathsf {X}(\gamma )$
to denote the displacement of
 $\gamma $
; that is, the vector in
$\gamma $
; that is, the vector in
 $\mathbb {Z}^2$
given by the end point of
$\mathbb {Z}^2$
given by the end point of
 $\gamma $
minus the start point of
$\gamma $
minus the start point of
 $\gamma $
.
$\gamma $
. -
• For a pair of contours
 $\gamma := (\gamma (0), \dots , \gamma (|\gamma |))$
and
$\gamma := (\gamma (0), \dots , \gamma (|\gamma |))$
and
 $\gamma ':= (\gamma '(0), \dots , \gamma '(|\gamma '|))$
, let
$\gamma ':= (\gamma '(0), \dots , \gamma '(|\gamma '|))$
, let
 $\Delta := \gamma (|\gamma |) - \gamma '(0)$
. We define their concatenation to be Similarly, for a pair of animals
$\Delta := \gamma (|\gamma |) - \gamma '(0)$
. We define their concatenation to be Similarly, for a pair of animals $$\begin{align*}\gamma \circ \gamma' := \big( \gamma(0), \dots, \gamma(|\gamma|),\Delta+ \gamma'(1), \dots, \Delta+ \gamma'(|\gamma'|) \big ) . \end{align*}$$
$$\begin{align*}\gamma \circ \gamma' := \big( \gamma(0), \dots, \gamma(|\gamma|),\Delta+ \gamma'(1), \dots, \Delta+ \gamma'(|\gamma'|) \big ) . \end{align*}$$
 $\Gamma := [\gamma , \underline {\mathcal {C}}]$
and
$\Gamma := [\gamma , \underline {\mathcal {C}}]$
and
 $\Gamma ':= [\gamma ', \underline {\mathcal {C}}']$
, we define their concatenation to be
$\Gamma ':= [\gamma ', \underline {\mathcal {C}}']$
, we define their concatenation to be  $$\begin{align*}\Gamma \circ \Gamma' := [ \gamma \circ \gamma', ~\underline{\mathcal{C}} \cup \underline{\mathcal{C}}']. \end{align*}$$
$$\begin{align*}\Gamma \circ \Gamma' := [ \gamma \circ \gamma', ~\underline{\mathcal{C}} \cup \underline{\mathcal{C}}']. \end{align*}$$
-
• For
 ${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
, we write
${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
, we write
 $\gamma : {\mathsf {u}} \to {\mathsf {v}}$
to indicate that
$\gamma : {\mathsf {u}} \to {\mathsf {v}}$
to indicate that
 $\gamma (0) = {\mathsf {u}}$
and
$\gamma (0) = {\mathsf {u}}$
and
 $\gamma (|\gamma |) = {\mathsf {v}}$
. We write
$\gamma (|\gamma |) = {\mathsf {v}}$
. We write
 $\Gamma : {\mathsf {u}} \to {\mathsf {v}}$
to indicate that
$\Gamma : {\mathsf {u}} \to {\mathsf {v}}$
to indicate that
 $\Gamma = [\gamma , \underline {\mathcal {C}}]$
for some contour
$\Gamma = [\gamma , \underline {\mathcal {C}}]$
for some contour
 $\gamma : {\mathsf {u}} \to {\mathsf {v}}$
.
$\gamma : {\mathsf {u}} \to {\mathsf {v}}$
. -
• For a set
 $D\subset \mathbb {R}^2$
, we say
$D\subset \mathbb {R}^2$
, we say
 $\Gamma = [\gamma , \underline {\mathcal {C}}] \subset D$
if
$\Gamma = [\gamma , \underline {\mathcal {C}}] \subset D$
if
 $\gamma $
as well as all clusters
$\gamma $
as well as all clusters
 $\mathcal {C} \in \underline {\mathcal {C}}$
are contained in D.
$\mathcal {C} \in \underline {\mathcal {C}}$
are contained in D. -
• For any
 $D \subset \mathbb {R}^2$
, we define the set of contours When
$D \subset \mathbb {R}^2$
, we define the set of contours When $$\begin{align*}\mathcal P_D({\mathsf{u}},{\mathsf{v}}):= \{\gamma: \gamma \subset D ,\, \gamma : {\mathsf{u}} \to {\mathsf{v}} \}. \end{align*}$$
$$\begin{align*}\mathcal P_D({\mathsf{u}},{\mathsf{v}}):= \{\gamma: \gamma \subset D ,\, \gamma : {\mathsf{u}} \to {\mathsf{v}} \}. \end{align*}$$
 ${\mathsf {u}} = 0$
, we will simply write
${\mathsf {u}} = 0$
, we will simply write
 $\mathcal P_D({\mathsf {v}})$
. We’ll write
$\mathcal P_D({\mathsf {v}})$
. We’ll write
 $\Gamma \in \mathcal P_D({\mathsf {u}},{\mathsf {v}})$
for animals
$\Gamma \in \mathcal P_D({\mathsf {u}},{\mathsf {v}})$
for animals
 $\Gamma $
to mean
$\Gamma $
to mean
 $\Gamma = [\gamma , \underline {\mathcal {C}}]$
for some contour
$\Gamma = [\gamma , \underline {\mathcal {C}}]$
for some contour
 $\gamma \in \mathcal P_D({\mathsf {u}},{\mathsf {v}})$
.
$\gamma \in \mathcal P_D({\mathsf {u}},{\mathsf {v}})$
.
2.6 The Wulff shape
Now, define the Wulff shape
 $$\begin{align*}\mathcal W := \bigcap_{\mathsf{y} \in \mathbb{R}^2} \{\mathsf{h} \in \mathbb{R}^2: \mathsf{h} \cdot \mathsf{y} \leq \tau_\beta(\mathsf{y}) \}, \end{align*}$$
$$\begin{align*}\mathcal W := \bigcap_{\mathsf{y} \in \mathbb{R}^2} \{\mathsf{h} \in \mathbb{R}^2: \mathsf{h} \cdot \mathsf{y} \leq \tau_\beta(\mathsf{y}) \}, \end{align*}$$
which is clearly closed and convex (as it is the intersection of half-spaces). Observe that
 $$\begin{align*}\mathcal W = \overline{\left\{\mathsf{h} \in \mathbb{R}^2: \sum_{\mathsf{y} \in \mathbb{Z}^2} e^{\mathsf{h}\cdot \mathsf{y}} \mathcal{G}(\mathsf{y}) < \infty\right\}}. \end{align*}$$
$$\begin{align*}\mathcal W = \overline{\left\{\mathsf{h} \in \mathbb{R}^2: \sum_{\mathsf{y} \in \mathbb{Z}^2} e^{\mathsf{h}\cdot \mathsf{y}} \mathcal{G}(\mathsf{y}) < \infty\right\}}. \end{align*}$$
Indeed, from Equation (2.8), we have
It follows that the sum in the second expression for
![]() $\mathcal W$
converges if and only if
$\mathcal W$
converges if and only if
![]() $\mathsf {h} \cdot \mathsf {y} < \tau _\beta (\mathsf {y})$
for all
$\mathsf {h} \cdot \mathsf {y} < \tau _\beta (\mathsf {y})$
for all
![]() $\mathsf {y}\in \mathbb {Z}^2$
large, which by homogeneity and continuity of
$\mathsf {y}\in \mathbb {Z}^2$
large, which by homogeneity and continuity of
![]() $\tau _{\beta }$
is equivalent to the same holding for all
$\tau _{\beta }$
is equivalent to the same holding for all
![]() $\mathsf {y} \in \mathbb {R}^2$
. Including the equality case
$\mathsf {y} \in \mathbb {R}^2$
. Including the equality case
![]() $\mathsf {h}\cdot \mathsf {y} = \tau _{\beta }(\mathsf {y})$
in the first expression for
$\mathsf {h}\cdot \mathsf {y} = \tau _{\beta }(\mathsf {y})$
in the first expression for
![]() $\mathcal W$
is equivalent to taking the closure of the set in the second expression.
$\mathcal W$
is equivalent to taking the closure of the set in the second expression.
2.7 Cone points, the irreducible decomposition of animals and weight factorization
Let us define the forward cone
![]() $\mathcal {Y}^\blacktriangleleft := \{(x,y) \in \mathbb {Z}^2 : |y|\leq x \}$
and the backward cone
$\mathcal {Y}^\blacktriangleleft := \{(x,y) \in \mathbb {Z}^2 : |y|\leq x \}$
and the backward cone
![]() $\mathcal {Y}^\blacktriangleright := -\mathcal {Y}^\blacktriangleleft $
. We will also need
$\mathcal {Y}^\blacktriangleright := -\mathcal {Y}^\blacktriangleleft $
. We will also need
![]() $\mathcal {Y}^\blacktriangleleft _{\delta }:= \{ (x,y) \in \mathbb {Z}^2 : |y|\leq \delta x\}$
for
$\mathcal {Y}^\blacktriangleleft _{\delta }:= \{ (x,y) \in \mathbb {Z}^2 : |y|\leq \delta x\}$
for
![]() $\delta>0$
. Given a contour
$\delta>0$
. Given a contour
![]() $\gamma $
and an animal
$\gamma $
and an animal
![]() $\Gamma =[\gamma ,\underline {\mathcal {C}}]$
, we say that
$\Gamma =[\gamma ,\underline {\mathcal {C}}]$
, we say that
![]() ${\mathsf {u}}\in \gamma $
is a cone point for
${\mathsf {u}}\in \gamma $
is a cone point for
![]() $\gamma $
if
$\gamma $
if
and we say
![]() ${\mathsf {u}}\in \gamma $
is a cone point for
${\mathsf {u}}\in \gamma $
is a cone point for
![]() $\Gamma $
if
$\Gamma $
if
Recall from Section 2.5 that the previous display means that the forward and backward cones emanating from
![]() ${\mathsf {u}}$
fully contain
${\mathsf {u}}$
fully contain
![]() $\gamma $
as well as all clusters
$\gamma $
as well as all clusters
![]() $\mathcal {C}$
in
$\mathcal {C}$
in
![]() $\underline {\mathcal {C}}$
. Of course if
$\underline {\mathcal {C}}$
. Of course if
![]() ${\mathsf {u}} \in \gamma $
is a cone point for
${\mathsf {u}} \in \gamma $
is a cone point for
![]() $\Gamma $
, then
$\Gamma $
, then
![]() ${\mathsf {u}}$
is a cone point for
${\mathsf {u}}$
is a cone point for
![]() $\gamma $
as well. Note that for any
$\gamma $
as well. Note that for any
![]() ${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
,
${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
,
![]() ${\mathsf {u}} \in {\mathsf {v}} + \mathcal {Y}^\blacktriangleleft $
if and only if
${\mathsf {u}} \in {\mathsf {v}} + \mathcal {Y}^\blacktriangleleft $
if and only if
![]() ${\mathsf {v}} \in {\mathsf {u}} +\mathcal {Y}^\blacktriangleright $
.
${\mathsf {v}} \in {\mathsf {u}} +\mathcal {Y}^\blacktriangleright $
.
If
![]() $\Gamma $
has two cone points
$\Gamma $
has two cone points
![]() ${\mathsf {u}}$
and
${\mathsf {u}}$
and
![]() ${\mathsf {v}}$
, the contour part of
${\mathsf {v}}$
, the contour part of
![]() $\Gamma $
between
$\Gamma $
between
![]() ${\mathsf {u}}$
and
${\mathsf {u}}$
and
![]() ${\mathsf {v}}$
as well as all associated clusters are entirely contained within the ‘diamond’
${\mathsf {v}}$
as well as all associated clusters are entirely contained within the ‘diamond’
![]() ${\mathsf {u}}+\mathcal {Y}^\blacktriangleleft \cap {\mathsf {v}}+\mathcal {Y}^\blacktriangleright $
. An animal is called left-irreducible if it contains no cone points and if it is entirely contained in the backwards cone emanating from its end point. Similarly, an animal is called right-irreducible if it contains no cone points and it is contained in the forward cone emanating from its start point. An animal is called irreducible if it is both left- and right-irreducible. We let
${\mathsf {u}}+\mathcal {Y}^\blacktriangleleft \cap {\mathsf {v}}+\mathcal {Y}^\blacktriangleright $
. An animal is called left-irreducible if it contains no cone points and if it is entirely contained in the backwards cone emanating from its end point. Similarly, an animal is called right-irreducible if it contains no cone points and it is contained in the forward cone emanating from its start point. An animal is called irreducible if it is both left- and right-irreducible. We let
![]() $\mathsf {A_L}, \mathsf {A_R}$
and
$\mathsf {A_L}, \mathsf {A_R}$
and
![]() $\mathsf {A}$
be the sets of left-irreducible, right-irreducible and irreducible animals, respectively, with start point at the origin.
$\mathsf {A}$
be the sets of left-irreducible, right-irreducible and irreducible animals, respectively, with start point at the origin.
Consider now an animal
![]() $\Gamma $
with at least two cone points, and decompose it into (left-/right-) irreducible animals as follows:
$\Gamma $
with at least two cone points, and decompose it into (left-/right-) irreducible animals as follows:
for some
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $\Gamma ^{(L)} \in \mathsf {A_L}$
,
$\Gamma ^{(L)} \in \mathsf {A_L}$
,
![]() $\Gamma ^{(R)} \in \mathsf {A_R}$
, and
$\Gamma ^{(R)} \in \mathsf {A_R}$
, and
![]() $\Gamma ^{(i)} \in \mathsf {A}$
for
$\Gamma ^{(i)} \in \mathsf {A}$
for
![]() $i =1,\dots ,n$
. For
$i =1,\dots ,n$
. For
![]() $i\in \{L, 1,\dots ,n, R\}$
, we will write
$i\in \{L, 1,\dots ,n, R\}$
, we will write
From the definition of a cone point, any cluster
![]() $\mathcal {C} \in \underline {\mathcal {C}}_i$
will be such that
$\mathcal {C} \in \underline {\mathcal {C}}_i$
will be such that
![]() $\mathcal {C} \cap \nabla _{\gamma ^{(j)}} = \emptyset $
for
$\mathcal {C} \cap \nabla _{\gamma ^{(j)}} = \emptyset $
for
![]() $j \neq i$
. Informally, this means that any cluster of
$j \neq i$
. Informally, this means that any cluster of
![]() $\Gamma ^{(i)}$
will not be a cluster of
$\Gamma ^{(i)}$
will not be a cluster of
![]() $\Gamma ^{(j)}$
. Thus, the weights
$\Gamma ^{(j)}$
. Thus, the weights
![]() $q_D(\Gamma )$
‘factorize’ into a product of the weights of the irreducible pieces:
$q_D(\Gamma )$
‘factorize’ into a product of the weights of the irreducible pieces:
 $$ \begin{align} q_D(\Gamma) = \prod_{i \in \{L, 1,\dots, n,R\}} e^{- \beta |\gamma^{(i)}|} \prod_{\mathcal{C} \in \underline{\mathcal{C}}_i} \Psi_D(\mathcal{C};\gamma) = q_D(\Gamma^{(L)}) q_D(\Gamma^{(R)})\prod_{i=1}^n q_D(\Gamma^{(i)}). \end{align} $$
$$ \begin{align} q_D(\Gamma) = \prod_{i \in \{L, 1,\dots, n,R\}} e^{- \beta |\gamma^{(i)}|} \prod_{\mathcal{C} \in \underline{\mathcal{C}}_i} \Psi_D(\mathcal{C};\gamma) = q_D(\Gamma^{(L)}) q_D(\Gamma^{(R)})\prod_{i=1}^n q_D(\Gamma^{(i)}). \end{align} $$
When
![]() $\gamma \subset Q$
, note that the shape of the forward and backward cones necessitates
$\gamma \subset Q$
, note that the shape of the forward and backward cones necessitates
so that Equation (2.18) becomes
 $$ \begin{align} q_Q(\Gamma) = q_Q(\Gamma^{(L)}) q_Q(\Gamma^{(R)}) \prod_{i=1}^n q_{{\mathbb H}}(\Gamma^{(i)}). \end{align} $$
$$ \begin{align} q_Q(\Gamma) = q_Q(\Gamma^{(L)}) q_Q(\Gamma^{(R)}) \prod_{i=1}^n q_{{\mathbb H}}(\Gamma^{(i)}). \end{align} $$
We write
![]() $\mathsf {Cpts}(\gamma )$
and
$\mathsf {Cpts}(\gamma )$
and
![]() $\mathsf {Cpts}(\Gamma )$
to denote the set of cone points of
$\mathsf {Cpts}(\Gamma )$
to denote the set of cone points of
![]() $\gamma $
and the set of cone points of
$\gamma $
and the set of cone points of
![]() $\Gamma $
, respectively. Let
$\Gamma $
, respectively. Let
![]() $n:= n(\Gamma ) = |\mathsf {Cpts}(\Gamma )|-1$
as above so that n is equal to the number of irreducible pieces of
$n:= n(\Gamma ) = |\mathsf {Cpts}(\Gamma )|-1$
as above so that n is equal to the number of irreducible pieces of
![]() $\Gamma $
. We label the cone points of
$\Gamma $
. We label the cone points of
![]() $\Gamma $
by
$\Gamma $
by
![]() $\zeta ^{(1)}, \dots , \zeta ^{(n+1)}$
, where the ordering is strictly increasing in the x-coordinates, that is,
$\zeta ^{(1)}, \dots , \zeta ^{(n+1)}$
, where the ordering is strictly increasing in the x-coordinates, that is,
The set
![]() $\mathsf {Cpts}(\Gamma )$
therefore takes on a natural meaning as an ordered
$\mathsf {Cpts}(\Gamma )$
therefore takes on a natural meaning as an ordered
![]() $n(\Gamma )-$
tuple, and so we will abuse notation and write
$n(\Gamma )-$
tuple, and so we will abuse notation and write
The following result of [Reference Ioffe, Shlosman and Toninelli32] states that the free weight of contours in
![]() $\mathbb {Z}^2$
that have large length and contain a sublinear number of cone points compared to the distance of the end point is exponentially small compared to
$\mathbb {Z}^2$
that have large length and contain a sublinear number of cone points compared to the distance of the end point is exponentially small compared to
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Lemma 2.11 ([Reference Ioffe, Shlosman and Toninelli32, Eq. (4.5)]Footnote 7 ).
Fix any
![]() $\epsilon ,\delta \in (0,1)$
. There exist
$\epsilon ,\delta \in (0,1)$
. There exist
![]() $\beta _0 \in (0, \infty )$
,
$\beta _0 \in (0, \infty )$
,
![]() $\nu _0>0$
,
$\nu _0>0$
,
![]() $\delta _0>0$
and
$\delta _0>0$
and
![]() $c>0$
such that the following bounds hold uniformly over
$c>0$
such that the following bounds hold uniformly over
![]() $\beta \geq \beta _0$
,
$\beta \geq \beta _0$
,
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
and
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
and
![]() $r \geq 1+\epsilon $
:
$r \geq 1+\epsilon $
:
In [Reference Ioffe, Shlosman and Toninelli32],Footnote 8 it is claimed without proof that the an analogue of Lemma 2.11 also holds for animals. For completeness, we supply the result as well as a proof below.
Proposition 2.12. For any
![]() $\delta \in (0,1)$
, there exist
$\delta \in (0,1)$
, there exist
![]() $\nu>0$
and
$\nu>0$
and
![]() $c>0$
such that the following bounds hold uniformly over
$c>0$
such that the following bounds hold uniformly over
![]() $\beta \geq \beta _0$
, and
$\beta \geq \beta _0$
, and
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
:
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
:
where
![]() $\delta _0$
is as in Lemma 2.11.
$\delta _0$
is as in Lemma 2.11.
Proof. The idea is to show that, for a typical
![]() $\Gamma = [\gamma ,\underline {\mathcal {C}}]$
, many of the cone points for
$\Gamma = [\gamma ,\underline {\mathcal {C}}]$
, many of the cone points for
![]() $\gamma $
are also cone points for
$\gamma $
are also cone points for
![]() $\Gamma $
. We do this by showing that typically,
$\Gamma $
. We do this by showing that typically,
![]() $\mathcal {C}$
does not contain many clusters (more precisely, the total
$\mathcal {C}$
does not contain many clusters (more precisely, the total
![]() $d(\cdot )$
-size is not too big). The result then follows from Equation (2.22).
$d(\cdot )$
-size is not too big). The result then follows from Equation (2.22).
Our starting point is the following, which comes from Property (P2) and Remark 2.10 and states that for some constant
![]() $c_1>0$
, for all
$c_1>0$
, for all
![]() $\beta>0$
sufficiently large, and for any animal
$\beta>0$
sufficiently large, and for any animal
![]() $[\gamma , \underline {\mathcal {C}}]$
,
$[\gamma , \underline {\mathcal {C}}]$
,
 $$ \begin{align} q([\gamma, \underline{\mathcal{C}}]) \leq e^{-\beta|\gamma|}\exp\bigg({-c_1\beta\sum_{\mathcal{C} \in \underline{\mathcal{C}}} d(\mathcal{C})}\bigg). \end{align} $$
$$ \begin{align} q([\gamma, \underline{\mathcal{C}}]) \leq e^{-\beta|\gamma|}\exp\bigg({-c_1\beta\sum_{\mathcal{C} \in \underline{\mathcal{C}}} d(\mathcal{C})}\bigg). \end{align} $$
Now, define the events
 $$ \begin{align*} A &= \{\Gamma = [\gamma,\underline{\mathcal{C}}] \;\big|\; |\mathsf{Cpts}(\Gamma)| < \delta_0\|\mathsf{y}\|_1\} \\ B &= \{\Gamma = [\gamma,\underline{\mathcal{C}}] \;\big|\; |\mathsf{Cpts}(\gamma)| \geq 2\delta_0\|\mathsf{y}\|_1, \,|\gamma| \leq 1.1 \|\mathsf{y}\|_1 \}. \end{align*} $$
$$ \begin{align*} A &= \{\Gamma = [\gamma,\underline{\mathcal{C}}] \;\big|\; |\mathsf{Cpts}(\Gamma)| < \delta_0\|\mathsf{y}\|_1\} \\ B &= \{\Gamma = [\gamma,\underline{\mathcal{C}}] \;\big|\; |\mathsf{Cpts}(\gamma)| \geq 2\delta_0\|\mathsf{y}\|_1, \,|\gamma| \leq 1.1 \|\mathsf{y}\|_1 \}. \end{align*} $$
Then, from Equations (2.21) and (2.22), we have
 $$\begin{align*}\frac{\mathcal{G}(\mathsf{y} \;\big|\; A)}{\mathcal{G}(\mathsf{y})} = \frac{\mathcal{G}(\mathsf{y} \;\big|\; A, B)}{\mathcal{G}(\mathsf{y})} + O\big( e^{-\nu_0 \beta \left\Vert \mathsf{y} \right\Vert{}_1}\big). \end{align*}$$
$$\begin{align*}\frac{\mathcal{G}(\mathsf{y} \;\big|\; A)}{\mathcal{G}(\mathsf{y})} = \frac{\mathcal{G}(\mathsf{y} \;\big|\; A, B)}{\mathcal{G}(\mathsf{y})} + O\big( e^{-\nu_0 \beta \left\Vert \mathsf{y} \right\Vert{}_1}\big). \end{align*}$$
Now, consider a contour
![]() $\gamma $
with at least
$\gamma $
with at least
![]() $2\delta _0\|\mathsf {y}\|_1$
cone points and an animal
$2\delta _0\|\mathsf {y}\|_1$
cone points and an animal
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\Gamma = [\gamma , \underline {\mathcal {C}}]$
for some set of clusters
$\Gamma = [\gamma , \underline {\mathcal {C}}]$
for some set of clusters
![]() $\underline {\mathcal {C}}$
. Note that if
$\underline {\mathcal {C}}$
. Note that if
![]() $\Gamma $
has less than
$\Gamma $
has less than
![]() $\delta _0\|\mathsf {y}\|_1$
cone points, then the clusters of
$\delta _0\|\mathsf {y}\|_1$
cone points, then the clusters of
![]() $\underline {\mathcal {C}}$
must intersect
$\underline {\mathcal {C}}$
must intersect
![]() $\gamma $
in such a way that at least
$\gamma $
in such a way that at least
![]() $\delta _0\|\mathsf {y}\|_1$
cone points of
$\delta _0\|\mathsf {y}\|_1$
cone points of
![]() $\gamma $
are not cone points of
$\gamma $
are not cone points of
![]() $\Gamma $
. This necessitates that the sum of
$\Gamma $
. This necessitates that the sum of
![]() $d(\mathcal {C})$
over
$d(\mathcal {C})$
over
![]() $\mathcal {C} \in \underline {\mathcal {C}}$
exceeds
$\mathcal {C} \in \underline {\mathcal {C}}$
exceeds
![]() $\delta _0 \|\mathsf {y}\|_1$
. Hence, we can write
$\delta _0 \|\mathsf {y}\|_1$
. Hence, we can write
 $$ \begin{align*} &\mathcal{G}(\mathsf{y} \;\big|\; A, B) \\ \leq &\sum_{\substack{\gamma:0\to \mathsf{y} \\ |\gamma|\leq 1.1 \|\mathsf{y}\|_1}}\sum_{m \geq \delta_0 \left\Vert \mathsf{y} \right\Vert{}_1} \sum_{n=1}^{m}\sum_{k=1}^{n}\binom{3|\gamma|}{k} \sum_{\substack{\underline{n} = (n_1,\dots,n_k) \\ n_1+\dots+n_k=n}} \sum_{\substack{\underline{m} = (m_1,\dots,m_n) \\ m_1+\dots+m_n=m}} \bigg(\prod_{i=1}^k|G_{i, \underline{n}, \underline{m}}|\bigg) e^{-\beta|\gamma|-c_1\beta m}, \end{align*} $$
$$ \begin{align*} &\mathcal{G}(\mathsf{y} \;\big|\; A, B) \\ \leq &\sum_{\substack{\gamma:0\to \mathsf{y} \\ |\gamma|\leq 1.1 \|\mathsf{y}\|_1}}\sum_{m \geq \delta_0 \left\Vert \mathsf{y} \right\Vert{}_1} \sum_{n=1}^{m}\sum_{k=1}^{n}\binom{3|\gamma|}{k} \sum_{\substack{\underline{n} = (n_1,\dots,n_k) \\ n_1+\dots+n_k=n}} \sum_{\substack{\underline{m} = (m_1,\dots,m_n) \\ m_1+\dots+m_n=m}} \bigg(\prod_{i=1}^k|G_{i, \underline{n}, \underline{m}}|\bigg) e^{-\beta|\gamma|-c_1\beta m}, \end{align*} $$
where: the second sum accounts for the possible values of
![]() $m =\sum _{\mathcal {C}\in \underline {\mathcal {C}}} d(\mathcal {C})$
; the third sum accounts for the possible values of
$m =\sum _{\mathcal {C}\in \underline {\mathcal {C}}} d(\mathcal {C})$
; the third sum accounts for the possible values of
![]() $n=|\underline {\mathcal {C}}|$
given m; the fourth sum and the binominal coefficient account for the number of possible bonds of
$n=|\underline {\mathcal {C}}|$
given m; the fourth sum and the binominal coefficient account for the number of possible bonds of
![]() $\nabla _{\gamma }$
that the clusters of
$\nabla _{\gamma }$
that the clusters of
![]() $\underline {\mathcal {C}}$
intersect; the fifth sum accounts for the number of clusters that intersect a particular bond of
$\underline {\mathcal {C}}$
intersect; the fifth sum accounts for the number of clusters that intersect a particular bond of
![]() $\nabla _{\gamma }$
(given k and an arbitrary labeling of the bonds
$\nabla _{\gamma }$
(given k and an arbitrary labeling of the bonds
![]() $b_1, \dots , b_k$
); the sixth sum accounts for the possible
$b_1, \dots , b_k$
); the sixth sum accounts for the possible
![]() $d(\cdot )$
-value of each of the n clusters given that their total
$d(\cdot )$
-value of each of the n clusters given that their total
![]() $d(\cdot )$
-sum is m, and where
$d(\cdot )$
-sum is m, and where
![]() $\underline {m}=(m_1,\dots ,m_n)$
is ordered such that
$\underline {m}=(m_1,\dots ,m_n)$
is ordered such that
![]() $m_1,\dots ,m_{n_1}$
represent the
$m_1,\dots ,m_{n_1}$
represent the
![]() $d(\cdot )$
-values of the
$d(\cdot )$
-values of the
![]() $n_1$
clusters intersecting
$n_1$
clusters intersecting
![]() $b_1$
,
$b_1$
,
![]() $m_{n_1+1},\dots ,m_{n_1+n_2}$
represent the
$m_{n_1+1},\dots ,m_{n_1+n_2}$
represent the
![]() $d(\cdot )$
-values of the
$d(\cdot )$
-values of the
![]() $n_2$
clusters intersecting
$n_2$
clusters intersecting
![]() $b_2$
and so on; each
$b_2$
and so on; each
![]() $G_{i, \underline {n}, \underline {m}}$
denotes the set of all possible collections of the
$G_{i, \underline {n}, \underline {m}}$
denotes the set of all possible collections of the
![]() $n_i$
clusters intersecting
$n_i$
clusters intersecting
![]() $b_i$
given the aforementioned
$b_i$
given the aforementioned
![]() $\underline {n}$
and
$\underline {n}$
and
![]() $\underline {m}$
; and lastly, the exponential is the cumulative upper bound on
$\underline {m}$
; and lastly, the exponential is the cumulative upper bound on
![]() $q([\gamma ,\underline {\mathcal {C}}])$
given by Equation (2.23) (given that the cumulative
$q([\gamma ,\underline {\mathcal {C}}])$
given by Equation (2.23) (given that the cumulative
![]() $d(\cdot )$
is m).
$d(\cdot )$
is m).
Now, similar to Equation (2.11), the number of clusters
![]() $\mathcal {C}$
with
$\mathcal {C}$
with
![]() $d(\mathcal {C})= r$
and intersecting some fixed bond b is bounded from above by
$d(\mathcal {C})= r$
and intersecting some fixed bond b is bounded from above by
![]() $e^{c_2 r}$
, and therefore,
$e^{c_2 r}$
, and therefore,
 $$\begin{align*}\prod_{i=1}^k|G_{i, \underline{n}, \underline{m}}| \leq e^{c_2 (m_1+\dots+m_n)} = e^{c_2 m}. \end{align*}$$
$$\begin{align*}\prod_{i=1}^k|G_{i, \underline{n}, \underline{m}}| \leq e^{c_2 (m_1+\dots+m_n)} = e^{c_2 m}. \end{align*}$$
Hence,
![]() $\mathcal {G}(\mathsf {y} \;\big |\; A, B)$
is upper bounded by
$\mathcal {G}(\mathsf {y} \;\big |\; A, B)$
is upper bounded by
 $$ \begin{align*} &\sum_{\substack{\gamma:0\to \mathsf{y} \\ |\gamma|\leq 1.1 \|\mathsf{y}\|_1}}e^{-\beta|\gamma|}\sum_{m \geq \delta_0 \left\Vert \mathsf{y} \right\Vert{}_1} \sum_{n=1}^{m}\sum_{k=1}^{n}\binom{3|\gamma|}{k} \sum_{\substack{\underline{n} = (n_1,\dots,n_k) \\ n_1+\dots+n_k=n}} \sum_{\substack{\underline{m} = (m_1,\dots,m_n) \\ m_1+\dots+m_n=m}} e^{-c_1\beta m}e^{c_2 m} \\& \quad \leq\sum_{\substack{\gamma:0\to \mathsf{y} \\ |\gamma|\leq 1.1 \|\mathsf{y}\|_1}}e^{-\beta|\gamma|}\sum_{m \geq \delta_0 \left\Vert \mathsf{y} \right\Vert{}_1}e^{-c_3\beta m} \sum_{n=1}^{m}\sum_{k=1}^{n}\binom{3|\gamma|}{k} \binom{n-1} {k-1} \binom{m-1}{n-1} \\& \quad \leq\sum_{\substack{\gamma:0 \to \mathsf{y} \\ |\gamma|\leq 1.1 \|\mathsf{y}\|_1}}e^{-\beta|\gamma|} \sum_{m \geq \delta_0 \left\Vert \mathsf{y} \right\Vert{}_1}e^{-c_3\beta m} 2^m (2^m-1) 2^{3|\gamma|} \leq \ e^{-c_4\beta \left\Vert \mathsf{y} \right\Vert{}_1}\sum_{\gamma:0\to\mathsf{y}}e^{-\beta|\gamma|}. \end{align*} $$
$$ \begin{align*} &\sum_{\substack{\gamma:0\to \mathsf{y} \\ |\gamma|\leq 1.1 \|\mathsf{y}\|_1}}e^{-\beta|\gamma|}\sum_{m \geq \delta_0 \left\Vert \mathsf{y} \right\Vert{}_1} \sum_{n=1}^{m}\sum_{k=1}^{n}\binom{3|\gamma|}{k} \sum_{\substack{\underline{n} = (n_1,\dots,n_k) \\ n_1+\dots+n_k=n}} \sum_{\substack{\underline{m} = (m_1,\dots,m_n) \\ m_1+\dots+m_n=m}} e^{-c_1\beta m}e^{c_2 m} \\& \quad \leq\sum_{\substack{\gamma:0\to \mathsf{y} \\ |\gamma|\leq 1.1 \|\mathsf{y}\|_1}}e^{-\beta|\gamma|}\sum_{m \geq \delta_0 \left\Vert \mathsf{y} \right\Vert{}_1}e^{-c_3\beta m} \sum_{n=1}^{m}\sum_{k=1}^{n}\binom{3|\gamma|}{k} \binom{n-1} {k-1} \binom{m-1}{n-1} \\& \quad \leq\sum_{\substack{\gamma:0 \to \mathsf{y} \\ |\gamma|\leq 1.1 \|\mathsf{y}\|_1}}e^{-\beta|\gamma|} \sum_{m \geq \delta_0 \left\Vert \mathsf{y} \right\Vert{}_1}e^{-c_3\beta m} 2^m (2^m-1) 2^{3|\gamma|} \leq \ e^{-c_4\beta \left\Vert \mathsf{y} \right\Vert{}_1}\sum_{\gamma:0\to\mathsf{y}}e^{-\beta|\gamma|}. \end{align*} $$
Finally, the nonnegativity of the decorations
![]() $\Phi '$
implies
$\Phi '$
implies
 $$\begin{align*}\mathcal{G}(\mathsf{y}) = \sum_{\substack{\Gamma = [\gamma, \underline{\mathcal{C}}] \\ \gamma:0 \to\mathsf{y}}}q([\gamma, \underline{\mathcal{C}}]) = \sum_{\gamma:0 \to\mathsf{y}}\exp\bigg({-\beta|\gamma|+\sum_{\substack{\mathcal{C} \subset \Lambda \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} \Phi'(\mathcal{C};\gamma)}\bigg) \geq \sum_{\gamma:0 \to\mathsf{y}}e^{-\beta|\gamma|}, \end{align*}$$
$$\begin{align*}\mathcal{G}(\mathsf{y}) = \sum_{\substack{\Gamma = [\gamma, \underline{\mathcal{C}}] \\ \gamma:0 \to\mathsf{y}}}q([\gamma, \underline{\mathcal{C}}]) = \sum_{\gamma:0 \to\mathsf{y}}\exp\bigg({-\beta|\gamma|+\sum_{\substack{\mathcal{C} \subset \Lambda \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} \Phi'(\mathcal{C};\gamma)}\bigg) \geq \sum_{\gamma:0 \to\mathsf{y}}e^{-\beta|\gamma|}, \end{align*}$$
and thus
 $$\begin{align*}\frac{\mathcal{G}(\mathsf{y} \;\big|\; A, B)}{\mathcal{G}(\mathsf{y})} \leq e^{-c_5\beta \left\Vert \mathsf{y} \right\Vert{}_1}, \end{align*}$$
$$\begin{align*}\frac{\mathcal{G}(\mathsf{y} \;\big|\; A, B)}{\mathcal{G}(\mathsf{y})} \leq e^{-c_5\beta \left\Vert \mathsf{y} \right\Vert{}_1}, \end{align*}$$
concluding the proof.
Remark 2.13. Note that the proof of Proposition 2.12 is such that, for any Ising polymer model
![]() $\mathcal {G}_D$
or
$\mathcal {G}_D$
or
![]() $\mathcal {G}(\cdot \;\big |\; \gamma \subset D)$
satisfying the analogous bounds in Lemma 2.11, Proposition 2.12 follows with
$\mathcal {G}(\cdot \;\big |\; \gamma \subset D)$
satisfying the analogous bounds in Lemma 2.11, Proposition 2.12 follows with
![]() $\mathcal {G}$
replaced by
$\mathcal {G}$
replaced by
![]() $\mathcal {G}_D$
or
$\mathcal {G}_D$
or
![]() $\mathcal {G}(\cdot \;\big |\; \gamma \subset D)$
. This is used when we prove the existence of cone points for
$\mathcal {G}(\cdot \;\big |\; \gamma \subset D)$
. This is used when we prove the existence of cone points for
![]() $\Gamma $
in these models in Lemma 5.7.
$\Gamma $
in these models in Lemma 5.7.
2.8 Ornstein–Zernike theory and its applications
For
![]() $\mathsf {h} \in \mathbb {R}^2$
, we define
$\mathsf {h} \in \mathbb {R}^2$
, we define
![]() $W^{\mathsf {h}}(\cdot )$
by
$W^{\mathsf {h}}(\cdot )$
by
for any animal
![]() $\Gamma $
(not necessarily irreducible). For
$\Gamma $
(not necessarily irreducible). For
![]() $\mathsf {y}\neq 0$
, define the dual parameter
$\mathsf {y}\neq 0$
, define the dual parameter
![]() $\mathsf {h}_{\mathsf {y}}$
by
$\mathsf {h}_{\mathsf {y}}$
by
The homogeneity of
![]() $\tau _\beta (\mathsf {y})$
as per Equation (2.8) implies that
$\tau _\beta (\mathsf {y})$
as per Equation (2.8) implies that
![]() $\mathsf {h}_{\mathsf {y}} \in \partial \mathcal W$
(since
$\mathsf {h}_{\mathsf {y}} \in \partial \mathcal W$
(since
![]() $\mathsf {h}_{\mathsf {y}} \cdot \mathsf {y} = \nabla \tau _\beta (\mathsf {y})\cdot \mathsf {y} = \tau _\beta (\mathsf {y})$
and recalling the first definition of
$\mathsf {h}_{\mathsf {y}} \cdot \mathsf {y} = \nabla \tau _\beta (\mathsf {y})\cdot \mathsf {y} = \tau _\beta (\mathsf {y})$
and recalling the first definition of
![]() $\mathcal W$
).
$\mathcal W$
).
Proposition 2.14 below, which forms the main result of the Ornstein–Zernike theory for the Ising polymer models, was stated in [Reference Ioffe, Shlosman and Toninelli32, Thm. 5] in a slightly different setting (namely, the cones are defined differently here), pointing to [Reference Ioffe and Velenik34] as its relevant input. Indeed, one may infer this result via an Ornstein–Zernike analysis as in [Reference Ioffe and Velenik34, Sec 3.3 and 3.4], but since (a) the models considered in that work do not include Ising polymers, and (b) our setting differs somewhat from that of [Reference Ioffe, Shlosman and Toninelli32], we include a full proof of this proposition in Appendix B.
Proposition 2.14. For any
![]() $\delta \in (0,1)$
, there exists
$\delta \in (0,1)$
, there exists
![]() $\beta _0>0$
such that for all
$\beta _0>0$
such that for all
![]() $\beta>\beta _0$
and for any
$\beta>\beta _0$
and for any
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
, the collection of weights
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
, the collection of weights
![]() $W^{\mathsf {h}_{\mathsf {y}}}$
defines a probability distribution on the set
$W^{\mathsf {h}_{\mathsf {y}}}$
defines a probability distribution on the set
![]() $\mathsf {A}$
of irreducible animals. To emphasize that
$\mathsf {A}$
of irreducible animals. To emphasize that
![]() $W^{\mathsf {h}_{\mathsf {y}}}$
defines a probability distribution (on irreducible animals), and for consistency with [Reference Ioffe, Shlosman and Toninelli32], we use the notation
$W^{\mathsf {h}_{\mathsf {y}}}$
defines a probability distribution (on irreducible animals), and for consistency with [Reference Ioffe, Shlosman and Toninelli32], we use the notation
Let
![]() $\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}$
denote expectation under
$\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}$
denote expectation under
![]() $\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
. Then
$\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
. Then
for some constant
![]() $\alpha := \alpha (\beta , \mathsf {y})>0$
– in particular, the expectation of
$\alpha := \alpha (\beta , \mathsf {y})>0$
– in particular, the expectation of
![]() $\mathsf {X}(\Gamma )$
under
$\mathsf {X}(\Gamma )$
under
![]() $\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
is collinear to
$\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
is collinear to
![]() $\mathsf {y}$
. Finally, there exists a ‘mass-gap’ constant
$\mathsf {y}$
. Finally, there exists a ‘mass-gap’ constant
![]() $\nu _g>0$
such that for all
$\nu _g>0$
such that for all
![]() $\beta>0$
large,
$\beta>0$
large,
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta } \setminus \{0\}$
, and
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta } \setminus \{0\}$
, and
![]() $k \geq 1$
,
$k \geq 1$
,
where
![]() $C:= C(\beta )>0$
is a positive constant.
$C:= C(\beta )>0$
is a positive constant.
Note that, since
![]() $\mathsf {h}_{\mathsf {y}} \cdot \mathsf {y} = \tau _{\beta }(\mathsf {y})$
(by the homogeneity of
$\mathsf {h}_{\mathsf {y}} \cdot \mathsf {y} = \tau _{\beta }(\mathsf {y})$
(by the homogeneity of
![]() $\tau _\beta $
as mentioned above), we have the following from Equation (2.18)
$\tau _\beta $
as mentioned above), we have the following from Equation (2.18)
 $$ \begin{align} q(\Gamma) = e^{-\tau_{\beta}(\mathsf{y})} \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(L)}) \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(R)}) \prod_{i=1}^n \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(i)}) , \end{align} $$
$$ \begin{align} q(\Gamma) = e^{-\tau_{\beta}(\mathsf{y})} \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(L)}) \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(R)}) \prod_{i=1}^n \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(i)}) , \end{align} $$
for any
![]() $\Gamma $
with at least two cone points. For
$\Gamma $
with at least two cone points. For
![]() ${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
and a set of animals E, introduce
${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
and a set of animals E, introduce

When E is taken to be the set of all possible animals, we’ll simply write
![]() $\mathcal {A}({\mathsf {u}},{\mathsf {v}}; E) = \mathcal {A}({\mathsf {u}},{\mathsf {v}})$
. Then, for
$\mathcal {A}({\mathsf {u}},{\mathsf {v}}; E) = \mathcal {A}({\mathsf {u}},{\mathsf {v}})$
. Then, for
![]() $D = Q$
or
$D = Q$
or
![]() ${\mathbb H}$
, Equation (2.27) allows us to write
${\mathbb H}$
, Equation (2.27) allows us to write
 $$ \begin{align} &\mathcal{G}(\mathsf{y} \;\big|\; \gamma \subset D, |\mathsf{Cpts}(\Gamma)|\geq 2) \nonumber\\ &\quad= \ e^{-\tau_{\beta}(\mathsf{y})} \sum_{\substack{\Gamma^{(L)} \in \mathsf{A_L} \\ \gamma^{(L)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(L)}) \ \sum_{\substack{\Gamma^{(R)} \in \mathsf{A_R} \\ \gamma^{(R)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(R)}) \ \mathcal{A}( \mathsf{X}(\Gamma^{(L)}), \mathsf{y}- \mathsf{X}(\Gamma^{(R)}) ). \end{align} $$
$$ \begin{align} &\mathcal{G}(\mathsf{y} \;\big|\; \gamma \subset D, |\mathsf{Cpts}(\Gamma)|\geq 2) \nonumber\\ &\quad= \ e^{-\tau_{\beta}(\mathsf{y})} \sum_{\substack{\Gamma^{(L)} \in \mathsf{A_L} \\ \gamma^{(L)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(L)}) \ \sum_{\substack{\Gamma^{(R)} \in \mathsf{A_R} \\ \gamma^{(R)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{y}}}(\Gamma^{(R)}) \ \mathcal{A}( \mathsf{X}(\Gamma^{(L)}), \mathsf{y}- \mathsf{X}(\Gamma^{(R)}) ). \end{align} $$
Note that the sum over n in Equation (2.28) above closely resembles the probability of a random walk event. This product structure of probability weights
![]() $\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
naturally leads to considering the random walk model related to the law of
$\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
naturally leads to considering the random walk model related to the law of
![]() $\mathsf {Cpts}(\Gamma )$
described in Section 4.1.
$\mathsf {Cpts}(\Gamma )$
described in Section 4.1.
3 Proof of Theorem 1.1 modulo Theorem 1.2
In this section, we infer Theorem 1.1 from Theorem 1.2(a). Throughout the section, let
![]() $H_L=\lfloor \frac 1{4\beta }\log L\rfloor $
. Recall that, as per Equation (1.4), we wish to give a lower bound on the event
$H_L=\lfloor \frac 1{4\beta }\log L\rfloor $
. Recall that, as per Equation (1.4), we wish to give a lower bound on the event
The fact that the definition of
![]() $\underline \rho (x)$
pertains to the height-
$\underline \rho (x)$
pertains to the height-
![]() $\mathfrak h^*$
(top) level line, where
$\mathfrak h^*$
(top) level line, where
![]() $\mathfrak h^*$
is random in
$\mathfrak h^*$
is random in
![]() $\{H_{L-1}, H_L\}$
(as mentioned in the Introduction, the results of [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14] determine it w.h.p. for side lengths L outside of a critical subsequence) make this event delicate to work with. We will derive the required lower bound on E via more tractable events, tailored to the analysis of a local rectangle of side length
$\{H_{L-1}, H_L\}$
(as mentioned in the Introduction, the results of [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14] determine it w.h.p. for side lengths L outside of a critical subsequence) make this event delicate to work with. We will derive the required lower bound on E via more tractable events, tailored to the analysis of a local rectangle of side length
![]() $\asymp L^{2/3}$
located at the center of the bottom side of
$\asymp L^{2/3}$
located at the center of the bottom side of
![]() $\Lambda _L$
.
$\Lambda _L$
.
Let
and let
![]() $R_1\subset \Lambda _L$
be the set of
$R_1\subset \Lambda _L$
be the set of
![]() $\mathsf {x}\in \Lambda _L$
at distance at most
$\mathsf {x}\in \Lambda _L$
at distance at most
![]() $(\log L)^2+1$
from
$(\log L)^2+1$
from
![]() $R_0$
. For fixed
$R_0$
. For fixed
![]() $\delta>0$
, define the marked region
$\delta>0$
, define the marked region ![]() . Theorem 1.1 will follow from the next proposition, where here and in what follows, x and y are
. Theorem 1.1 will follow from the next proposition, where here and in what follows, x and y are
![]() $*$
-connected if their Euclidean distance is at most
$*$
-connected if their Euclidean distance is at most
![]() $\sqrt 2$
.
$\sqrt 2$
.
Proposition 3.1. Fix
![]() $\beta \geq \beta _0$
. Let
$\beta \geq \beta _0$
. Let
![]() $B_n$
be the event that there is a
$B_n$
be the event that there is a
![]() $*$
-connected path in
$*$
-connected path in
![]() $R_0$
, intersecting
$R_0$
, intersecting
![]() $\mathfrak {M}$
, whose length is
$\mathfrak {M}$
, whose length is
![]() $\geq (\log L)^2$
and whose sites have height
$\geq (\log L)^2$
and whose sites have height
![]() $\geq H_L-n$
. Let
$\geq H_L-n$
. Let
![]() $C_n$
be the event that there is no simple path in
$C_n$
be the event that there is no simple path in
![]() $R_1$
of length
$R_1$
of length
![]() $\geq (\log L)^2$
whose sites have height
$\geq (\log L)^2$
whose sites have height
![]() $\geq H_L-n+1$
. Then, for every fixed
$\geq H_L-n+1$
. Then, for every fixed
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\epsilon>0$
there exists
$\epsilon>0$
there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\pi _{\Lambda _L}^0(B_n\cap C_n) < \epsilon $
for all L large.
$\pi _{\Lambda _L}^0(B_n\cap C_n) < \epsilon $
for all L large.
Proof of Theorem 1.1.
Observe that
Indeed, [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Theorem 2a] implies that there are w.h.p. no level lines of length at least
![]() $\log ^2 L$
nested in the height-
$\log ^2 L$
nested in the height-
![]() $\mathfrak h^{*}$
level line loop
$\mathfrak h^{*}$
level line loop
![]() $\mathcal L^{*}$
(implying
$\mathcal L^{*}$
(implying
![]() $C_0$
), whereas
$C_0$
), whereas
![]() $E^c $
implies that
$E^c $
implies that
![]() $\mathcal L^*$
intersects
$\mathcal L^*$
intersects
![]() $\mathfrak M$
; thus, following its interior boundary for length at least
$\mathfrak M$
; thus, following its interior boundary for length at least
![]() $(\log L)^2$
will produce the path as per
$(\log L)^2$
will produce the path as per
![]() $B_0$
.
$B_0$
.
Similarly,
again using that the height-
![]() $\mathfrak h^{*}$
level line loop
$\mathfrak h^{*}$
level line loop
![]() $\mathcal L^{*}$
must encompass a
$\mathcal L^{*}$
must encompass a
![]() $*$
-chain of sites crossing the marked region
$*$
-chain of sites crossing the marked region
![]() $\mathfrak {M}$
as in
$\mathfrak {M}$
as in
![]() $B_1$
and that
$B_1$
and that
![]() $C_1$
holds w.h.p. when
$C_1$
holds w.h.p. when
![]() $\mathfrak h^{*} = H_L-1$
by [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Theorem 2a]. The conclusion now follows from Proposition 3.1.
$\mathfrak h^{*} = H_L-1$
by [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Theorem 2a]. The conclusion now follows from Proposition 3.1.
Proof of Proposition 3.1.
Fix
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\epsilon>0$
. The following procedure will reveal the ‘outermost’ chain
$\epsilon>0$
. The following procedure will reveal the ‘outermost’ chain
![]() $\mathfrak C$
of
$\mathfrak C$
of
![]() $\mathbb {Z}^2$
-connected sites of height at most
$\mathbb {Z}^2$
-connected sites of height at most
![]() $H_L-n$
that encloses, together with the southern boundary of
$H_L-n$
that encloses, together with the southern boundary of
![]() $\Lambda _L$
, the box
$\Lambda _L$
, the box
![]() $R_0$
. For each site
$R_0$
. For each site
![]() $\mathsf {x}$
in the north, east and west boundaries of
$\mathsf {x}$
in the north, east and west boundaries of
![]() $R_1$
, reveal its
$R_1$
, reveal its
![]() $\mathbb {Z}^2$
-connected component of sites
$\mathbb {Z}^2$
-connected component of sites
![]() $\mathsf {y} \in R_1$
for which
$\mathsf {y} \in R_1$
for which
![]() $\varphi _{\mathsf {y}}> H_L-n$
. Let U denote the collection of all revealed vertices, and let
$\varphi _{\mathsf {y}}> H_L-n$
. Let U denote the collection of all revealed vertices, and let
![]() $\mathfrak {C}$
be the exterior boundary of U contained in
$\mathfrak {C}$
be the exterior boundary of U contained in
![]() $R_1$
. By definition,
$R_1$
. By definition,
![]() $\varphi _{\mathsf {y}} \leq H_L-n$
for all
$\varphi _{\mathsf {y}} \leq H_L-n$
for all
![]() $\mathsf {y} \in \mathfrak {C}$
. Now, let W denote the collection of sites whose exterior boundary is formed by
$\mathsf {y} \in \mathfrak {C}$
. Now, let W denote the collection of sites whose exterior boundary is formed by
![]() $\mathfrak {C}$
and the southern boundary of
$\mathfrak {C}$
and the southern boundary of
![]() $\Lambda _L$
. On the event
$\Lambda _L$
. On the event
![]() $C_{n}$
, each connected component comprising U has diameter strictly less than
$C_{n}$
, each connected component comprising U has diameter strictly less than
![]() $(\log L)^2$
; in particular,
$(\log L)^2$
; in particular,
![]() $R_0 \subset W$
.
$R_0 \subset W$
.
Now, condition on
![]() $\mathfrak {C}$
, and let
$\mathfrak {C}$
, and let
![]() $\xi (\mathfrak {C})$
denote the boundary condition of W given by the heights on
$\xi (\mathfrak {C})$
denote the boundary condition of W given by the heights on
![]() $\mathfrak {C}$
and the sites of height
$\mathfrak {C}$
and the sites of height
![]() $0$
on
$0$
on
![]() $\partial \Lambda $
. From the domain Markov property, we may deduce our desired bound
$\partial \Lambda $
. From the domain Markov property, we may deduce our desired bound
![]() $\pi _{\Lambda _L}^0(B_n \cap C_n) <\epsilon $
if we can show
$\pi _{\Lambda _L}^0(B_n \cap C_n) <\epsilon $
if we can show
uniformly over
![]() $\mathfrak {C}$
. Define
$\mathfrak {C}$
. Define
![]() $\mathsf {x}_{\ell } := \lfloor \tfrac {L}2 -2L^{2/3} \rfloor $
and
$\mathsf {x}_{\ell } := \lfloor \tfrac {L}2 -2L^{2/3} \rfloor $
and
![]() $\mathsf {x}_r:=\mathsf {x}_{\ell } + \lfloor 4L^{2/3} \rfloor $
. Using that all heights on
$\mathsf {x}_r:=\mathsf {x}_{\ell } + \lfloor 4L^{2/3} \rfloor $
. Using that all heights on
![]() $\mathfrak {C}$
are bounded by
$\mathfrak {C}$
are bounded by
![]() $H_L-n$
, that all heights on
$H_L-n$
, that all heights on
![]() $\partial \Lambda _L$
are
$\partial \Lambda _L$
are
![]() $0$
(in particular, bounded by
$0$
(in particular, bounded by
![]() $H_L-n-1$
), and that
$H_L-n-1$
), and that
![]() $B_n$
is an increasing event, we have
$B_n$
is an increasing event, we have
where the boundary conditions
![]() $\texttt {{legs}}$
are
$\texttt {{legs}}$
are
![]() $H_L-n-1$
on the horizontal line of sites
$H_L-n-1$
on the horizontal line of sites ![]() and
and
![]() $H_L-n$
elsewhere (see Figure 2, noting the ‘legs’ of sites of height
$H_L-n$
elsewhere (see Figure 2, noting the ‘legs’ of sites of height
![]() $H_L-n$
protruding inwards from the bottom boundary of W). Thus, it suffices to show the right hand is bounded by
$H_L-n$
protruding inwards from the bottom boundary of W). Thus, it suffices to show the right hand is bounded by
![]() $\epsilon $
.
$\epsilon $
.

Figure 2 The rectangles
![]() $R_0$
(purple) and
$R_0$
(purple) and
![]() $R_1$
(gray), and in between the region W (blue) whose boundary conditions are raised via monotonicity to
$R_1$
(gray), and in between the region W (blue) whose boundary conditions are raised via monotonicity to
![]() $H_L-n$
except on the segment between
$H_L-n$
except on the segment between
![]() $\mathsf {x}_{\ell }$
and
$\mathsf {x}_{\ell }$
and
![]() $\mathsf {x}_r$
, where they are set to
$\mathsf {x}_r$
, where they are set to
![]() $H_L-n-1$
.
$H_L-n-1$
.
Moving to
![]() $\pi _{W}^{\texttt {{legs}}}$
has two main advantages. The first is that there exists a unique open
$\pi _{W}^{\texttt {{legs}}}$
has two main advantages. The first is that there exists a unique open
![]() $H_L-n$
-contour
$H_L-n$
-contour
![]() $\gamma $
under this measure, and in particular, the sites of height
$\gamma $
under this measure, and in particular, the sites of height
![]() $\geq H_L-n$
along
$\geq H_L-n$
along
![]() $\gamma $
form a
$\gamma $
form a
![]() $*$
-chain of sites of length larger than
$*$
-chain of sites of length larger than
![]() $(\log L)^2$
(typically of order
$(\log L)^2$
(typically of order
![]() $L^{2/3}$
). Further, a standard Peierls argument shows that, w.h.p. under
$L^{2/3}$
). Further, a standard Peierls argument shows that, w.h.p. under
![]() $\pi _{W}^{\texttt {{legs}}}$
, there are no such
$\pi _{W}^{\texttt {{legs}}}$
, there are no such
![]() $*$
-chains of length larger than
$*$
-chains of length larger than
![]() $\log L$
. In particular, defining
$\log L$
. In particular, defining
we have
The second advantage of moving to
![]() $\pi _{W}^{\texttt {{legs}}}$
is that we may couple
$\pi _{W}^{\texttt {{legs}}}$
is that we may couple
![]() $\gamma $
under the no-floor measure
$\gamma $
under the no-floor measure
![]() $\widehat \pi _{W}^{\texttt {{legs}}}$
with a modified Ising polymer law in the half-space
$\widehat \pi _{W}^{\texttt {{legs}}}$
with a modified Ising polymer law in the half-space
![]() $\mathbf {P}_{{\mathbb H}}^{\mathsf {x}}$
(see Definition 2.6), for which we have Theorem 1.2. After exhibiting this in Claim 3.2, we compare
$\mathbf {P}_{{\mathbb H}}^{\mathsf {x}}$
(see Definition 2.6), for which we have Theorem 1.2. After exhibiting this in Claim 3.2, we compare
![]() $\widehat \pi _{W}^{\texttt {{legs}}}$
and
$\widehat \pi _{W}^{\texttt {{legs}}}$
and
![]() $\pi _{W}^{\texttt {{legs}}}$
via Equation (A.8).
$\pi _{W}^{\texttt {{legs}}}$
via Equation (A.8).
We begin with the argument relating
![]() $\hat \pi _W^{\texttt {{legs}}}$
to
$\hat \pi _W^{\texttt {{legs}}}$
to
![]() $\mathbf {P}_{{\mathbb H}}^{\mathsf {x}}$
. From now on, we shift W to the left so that
$\mathbf {P}_{{\mathbb H}}^{\mathsf {x}}$
. From now on, we shift W to the left so that
![]() $\mathsf {x}_{\ell } = 0$
and
$\mathsf {x}_{\ell } = 0$
and
![]() $\mathsf {x}_r = \lfloor 4L^{2/3} \rfloor $
. Note that
$\mathsf {x}_r = \lfloor 4L^{2/3} \rfloor $
. Note that
![]() $\gamma $
is a contour in W with start point
$\gamma $
is a contour in W with start point
![]() $\mathsf {o}^* \in (\mathbb {Z}^2)^*$
and end point
$\mathsf {o}^* \in (\mathbb {Z}^2)^*$
and end point
![]() $\mathsf {x}:= \mathsf {x}_r - (1/2,1/2)$
. We will couple
$\mathsf {x}:= \mathsf {x}_r - (1/2,1/2)$
. We will couple
![]() $\widehat \pi _{W}^{\texttt {{legs}}}$
with the Ising polymer law
$\widehat \pi _{W}^{\texttt {{legs}}}$
with the Ising polymer law
![]() $\mathbf {P}_{{\mathbb H}}^{\mathsf {x}}$
, defined using the SOS decoration weights
$\mathbf {P}_{{\mathbb H}}^{\mathsf {x}}$
, defined using the SOS decoration weights
![]() $\Phi (\mathcal {C}; \gamma ) := \phi (\mathcal {C};\gamma )$
and
$\Phi (\mathcal {C}; \gamma ) := \phi (\mathcal {C};\gamma )$
and ![]() from Proposition 2.1. This coupling is natural in light of the very far distance of
from Proposition 2.1. This coupling is natural in light of the very far distance of
![]() $\mathfrak {C}$
from both
$\mathfrak {C}$
from both
![]() $\mathsf {o}^*$
and
$\mathsf {o}^*$
and
![]() $\mathsf {x}$
. Define
$\mathsf {x}$
. Define
![]() $N:= \lfloor 4L^{2/3} \rfloor $
. Recall the set
$N:= \lfloor 4L^{2/3} \rfloor $
. Recall the set
![]() $\mathcal P_{D}({\mathsf {u}},{\mathsf {v}})$
from Section 2.5. Let
$\mathcal P_{D}({\mathsf {u}},{\mathsf {v}})$
from Section 2.5. Let
![]() $\bar {W}$
denote the region in
$\bar {W}$
denote the region in
![]() $\mathbb {R}^2$
enclosed by W, that is, the region enclosed by the
$\mathbb {R}^2$
enclosed by W, that is, the region enclosed by the
![]() $\mathbb {Z}^2$
-edges connecting the boundary vertices of W. Then
$\mathbb {Z}^2$
-edges connecting the boundary vertices of W. Then
![]() $\gamma \in \mathcal P_{\bar {W}}(\mathsf {o}^*, \mathsf {x})$
. Lower the boundary conditions of
$\gamma \in \mathcal P_{\bar {W}}(\mathsf {o}^*, \mathsf {x})$
. Lower the boundary conditions of
![]() $\widehat \pi _{W}^{\texttt {{legs}}}$
to
$\widehat \pi _{W}^{\texttt {{legs}}}$
to
![]() $0,1,1,1$
using the shift invariance of the no-floor model. Then Observation 2.7 states that
$0,1,1,1$
using the shift invariance of the no-floor model. Then Observation 2.7 states that
![]() $\gamma \sim \widehat \pi _{W}^{\texttt {{legs}}}$
has the Ising polymer law
$\gamma \sim \widehat \pi _{W}^{\texttt {{legs}}}$
has the Ising polymer law
![]() $\mathbf {P}_{\bar {W}}^{\mathsf {x}}$
, and the decoration weights are defined via
$\mathbf {P}_{\bar {W}}^{\mathsf {x}}$
, and the decoration weights are defined via
![]() $ \Phi (\mathcal {C}; \gamma ) := \phi (\mathcal {C};\gamma )$
and
$ \Phi (\mathcal {C}; \gamma ) := \phi (\mathcal {C};\gamma )$
and ![]() .
.
Claim 3.2. Extend
![]() $\widehat \pi _{W}^{\texttt {{legs}}}$
to a probability measure on all contours in
$\widehat \pi _{W}^{\texttt {{legs}}}$
to a probability measure on all contours in
![]() $\mathcal P_{{\mathbb H}}(\mathsf {o}^*, \mathsf {x})$
via
$\mathcal P_{{\mathbb H}}(\mathsf {o}^*, \mathsf {x})$
via
![]() $\widehat \pi _{W}^{\texttt {{legs}}}(\gamma ) = 0$
for all
$\widehat \pi _{W}^{\texttt {{legs}}}(\gamma ) = 0$
for all
![]() $\gamma \not \in \mathcal P_{\bar {W}}(\mathsf {o}^*, \mathsf {x})$
. For some constant
$\gamma \not \in \mathcal P_{\bar {W}}(\mathsf {o}^*, \mathsf {x})$
. For some constant
![]() $C>0$
and for all
$C>0$
and for all
![]() $\beta>0$
large enough, we have
$\beta>0$
large enough, we have
Proof of Claim 3.2.
We use the identification of the law of the contour induced by
![]() $\widehat \pi _{W}^{\texttt {{legs}}}$
with
$\widehat \pi _{W}^{\texttt {{legs}}}$
with
![]() $\mathbf {P}_{\bar {W}}^{\mathsf {x}}$
throughout this proof.
$\mathbf {P}_{\bar {W}}^{\mathsf {x}}$
throughout this proof.
The main input for the proof is the following: for any
![]() $\delta \in (0,1)$
and for all
$\delta \in (0,1)$
and for all
![]() $\beta ,N>0$
large,
$\beta ,N>0$
large,
We prove Equation (3.3) now. Using the decay of
![]() $\phi (\mathcal {C};\gamma )$
(Proposition 2.1(iv)) as in Equation (2.11), we have the following for any
$\phi (\mathcal {C};\gamma )$
(Proposition 2.1(iv)) as in Equation (2.11), we have the following for any
![]() $\gamma : \mathsf {o}^* \to \mathsf {x}$
:
$\gamma : \mathsf {o}^* \to \mathsf {x}$
:
 $$ \begin{align} \sum_{\mathcal{C} \cap \Delta_{\gamma} \neq \emptyset } \left|\phi(\mathcal{C};\gamma)\right| \leq \sum_{\mathsf{y} \in \Delta_{\gamma}} \, \sum_{\mathcal{C} \ni \mathsf{y}} \sup_{\gamma} |\phi(\mathcal{C};\gamma)| \leq 3|\gamma| e^{-(\beta-\beta_0)}. \end{align} $$
$$ \begin{align} \sum_{\mathcal{C} \cap \Delta_{\gamma} \neq \emptyset } \left|\phi(\mathcal{C};\gamma)\right| \leq \sum_{\mathsf{y} \in \Delta_{\gamma}} \, \sum_{\mathcal{C} \ni \mathsf{y}} \sup_{\gamma} |\phi(\mathcal{C};\gamma)| \leq 3|\gamma| e^{-(\beta-\beta_0)}. \end{align} $$
Since
![]() $|\gamma |$
is always larger than N, we have
$|\gamma |$
is always larger than N, we have
On the other hand, Equation (3.4) implies
 $$ \begin{align*} &\max\Big(\mathcal{G}_{{\mathbb H}}\big(\mathsf{x} \;\big|\; |\gamma| \geq (1+\delta)N\big),\,\mathcal{G}_{\bar{W}}\big(\mathsf{x} \;\big|\; |\gamma| \geq (1+\delta)N\big) \Big) \\&\qquad\qquad\qquad\qquad\qquad\qquad\leq \sum_{\substack{\gamma \subset {\mathbb H} \\ |\gamma| \geq (1+\delta)N}} \exp\Big( -(\beta - 3e^{-(\beta -\beta_0)})|\gamma| \Big) \leq e^{-(\beta -c)(1+\delta)N}, \end{align*} $$
$$ \begin{align*} &\max\Big(\mathcal{G}_{{\mathbb H}}\big(\mathsf{x} \;\big|\; |\gamma| \geq (1+\delta)N\big),\,\mathcal{G}_{\bar{W}}\big(\mathsf{x} \;\big|\; |\gamma| \geq (1+\delta)N\big) \Big) \\&\qquad\qquad\qquad\qquad\qquad\qquad\leq \sum_{\substack{\gamma \subset {\mathbb H} \\ |\gamma| \geq (1+\delta)N}} \exp\Big( -(\beta - 3e^{-(\beta -\beta_0)})|\gamma| \Big) \leq e^{-(\beta -c)(1+\delta)N}, \end{align*} $$
where
![]() $c>0$
is a constant independent of
$c>0$
is a constant independent of
![]() $\beta $
and N. The above two bounds yield Equation (3.3). Note that a consequence of Equation (3.3) is
$\beta $
and N. The above two bounds yield Equation (3.3). Note that a consequence of Equation (3.3) is
Now, fix any
![]() $\delta \in (0,1/2)$
. Observe that
$\delta \in (0,1/2)$
. Observe that

For any contour
![]() $\gamma $
such that
$\gamma $
such that
![]() $d_{L^{\infty }}(\gamma ,\mathfrak {C})> (1-2\delta )N$
, we have the following for all
$d_{L^{\infty }}(\gamma ,\mathfrak {C})> (1-2\delta )N$
, we have the following for all
![]() $\beta>0$
large:
$\beta>0$
large:

where in the last inequality,
![]() $c>0$
is a constant independent of N and
$c>0$
is a constant independent of N and
![]() $\beta $
large, and the bound follows similarly to Equation (3.4). For any
$\beta $
large, and the bound follows similarly to Equation (3.4). For any
![]() $|\gamma |<(1+\delta )N$
, Equation (3.4) yields an upper bound on
$|\gamma |<(1+\delta )N$
, Equation (3.4) yields an upper bound on
![]() $\mathcal {G}_{\mathbb H}(\mathsf {x})$
of
$\mathcal {G}_{\mathbb H}(\mathsf {x})$
of
![]() $\exp (-(\beta - 3(1+\delta )e^{-(\beta -\beta _0)}) N)$
. This upper bound, the lower bound on
$\exp (-(\beta - 3(1+\delta )e^{-(\beta -\beta _0)}) N)$
. This upper bound, the lower bound on
![]() $\mathcal {G}_{\bar {W}}(\mathsf {x})$
in Equation (3.5), and the previous display imply the following for any
$\mathcal {G}_{\bar {W}}(\mathsf {x})$
in Equation (3.5), and the previous display imply the following for any
![]() $|\gamma |<(1+\delta )N$
:
$|\gamma |<(1+\delta )N$
:
where
![]() $c'>0$
is a constant independent of
$c'>0$
is a constant independent of
![]() $\beta $
and N. Since the number of connected paths in
$\beta $
and N. Since the number of connected paths in
![]() $(\mathbb {Z}^2)^*$
rooted at
$(\mathbb {Z}^2)^*$
rooted at
![]() $\mathsf {o}^*$
of length at most
$\mathsf {o}^*$
of length at most
![]() $(1+\delta )N$
is trivially bounded
$(1+\delta )N$
is trivially bounded
![]() $4^{(1+\delta )N}$
, the previous display along with Equation (3.3) imply that the total variation distance between
$4^{(1+\delta )N}$
, the previous display along with Equation (3.3) imply that the total variation distance between
![]() $\widehat {\pi }_{W}^{\texttt {{legs}}}$
viewed as a probability measure on
$\widehat {\pi }_{W}^{\texttt {{legs}}}$
viewed as a probability measure on
![]() $\mathcal P_{{\mathbb H}}(\mathsf {o}^*, \mathsf {x})$
and
$\mathcal P_{{\mathbb H}}(\mathsf {o}^*, \mathsf {x})$
and
![]() $\mathbf {P}_{{\mathbb H}}^{\mathsf {x}}$
is bounded by
$\mathbf {P}_{{\mathbb H}}^{\mathsf {x}}$
is bounded by
![]() $e^{-c"\beta N}$
.
$e^{-c"\beta N}$
.
Now, from Equation (A.8), we have
 $$ \begin{align} \pi_{\tilde R_0}^{\texttt{{legs}}}(\gamma) \propto \widehat\pi_{\tilde R_0}^{\texttt{{legs}}}(\gamma) \exp\left(- \frac{\lambda^{(n)}}{L}A(\gamma)+o(1)\right) , \end{align} $$
$$ \begin{align} \pi_{\tilde R_0}^{\texttt{{legs}}}(\gamma) \propto \widehat\pi_{\tilde R_0}^{\texttt{{legs}}}(\gamma) \exp\left(- \frac{\lambda^{(n)}}{L}A(\gamma)+o(1)\right) , \end{align} $$
where
![]() $A(\gamma )$
denotes the area under
$A(\gamma )$
denotes the area under
![]() $\gamma $
in W. From Equation (3.1) and Equation (3.2), the claim will be proven if we can show that for any
$\gamma $
in W. From Equation (3.1) and Equation (3.2), the claim will be proven if we can show that for any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\delta>0$
such that
$\delta>0$
such that
for L sufficiently large. Theorem 1.2 and Claim 3.2 imply that, under horizontal rescaling by
![]() $|\mathsf {x}|_1 = \lfloor 4L^{2/3} \rfloor $
and vertical rescaling by
$|\mathsf {x}|_1 = \lfloor 4L^{2/3} \rfloor $
and vertical rescaling by
![]() $\lfloor 4L^{2/3} \rfloor ^{1/2}$
,
$\lfloor 4L^{2/3} \rfloor ^{1/2}$
,
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat \pi _{W}^{\texttt {{legs}}}$
converges weakly to a Brownian excursion as
$\widehat \pi _{W}^{\texttt {{legs}}}$
converges weakly to a Brownian excursion as
![]() $L\to \infty $
. In particular,
$L\to \infty $
. In particular,
![]() $\widehat \pi _{W}^{\texttt {{legs}}}(\min _{x \in I_0} \underline {\rho }^{\gamma }(x) < \delta L^{1/3})$
can be made arbitrarily close to
$\widehat \pi _{W}^{\texttt {{legs}}}(\min _{x \in I_0} \underline {\rho }^{\gamma }(x) < \delta L^{1/3})$
can be made arbitrarily close to
![]() $0$
by taking
$0$
by taking
![]() $\delta $
small enough. Letting
$\delta $
small enough. Letting
![]() $\tilde {\mathbb {E}}$
denote expectation with respect to
$\tilde {\mathbb {E}}$
denote expectation with respect to
![]() $\widehat \pi _{W}^{\texttt {{legs}}}$
, we have
$\widehat \pi _{W}^{\texttt {{legs}}}$
, we have

The denominator is bounded away from
![]() $0$
because
$0$
because
![]() $\lambda ^{(n)}$
is bounded for fixed
$\lambda ^{(n)}$
is bounded for fixed
![]() $\beta $
, and the Brownian excursion limit of
$\beta $
, and the Brownian excursion limit of
![]() $\gamma $
implies that, for any
$\gamma $
implies that, for any
![]() $c>0$
,
$c>0$
,
![]() $\tilde {\mathbb {E}}[e^{-\frac {c}{L}A(\gamma )}]$
converges to
$\tilde {\mathbb {E}}[e^{-\frac {c}{L}A(\gamma )}]$
converges to
![]() $\mathbb {E}[e^{-cA(\xi )}]$
, where
$\mathbb {E}[e^{-cA(\xi )}]$
, where
![]() $\xi $
has the law of a Brownian excursion on
$\xi $
has the law of a Brownian excursion on
![]() $[0,4]$
(see also Claim 7.4 below, where this is explained in more detail in the more delicate setting of Theorem 7.1).
$[0,4]$
(see also Claim 7.4 below, where this is explained in more detail in the more delicate setting of Theorem 7.1).
![]() $A(\gamma )$
is unlikely to be much bigger than
$A(\gamma )$
is unlikely to be much bigger than
![]() $L^{2/3}\cdot L^{1/3} = L$
(making the expectation strictly positive). Hence, since the exponential in the numerator is bounded above by
$L^{2/3}\cdot L^{1/3} = L$
(making the expectation strictly positive). Hence, since the exponential in the numerator is bounded above by
![]() $1+o(1)$
, we get
$1+o(1)$
, we get
for some C depending only on
![]() $\beta $
and L large enough. Since the right-hand side can be made arbitrarily small by taking
$\beta $
and L large enough. Since the right-hand side can be made arbitrarily small by taking
![]() $\delta $
small enough, as discussed above, this implies Equation (3.8), thereby concluding the proof.
$\delta $
small enough, as discussed above, this implies Equation (3.8), thereby concluding the proof.
4 The effective random walk model, free Ising polymers and limit theorems
The factorization of
![]() $q(\Gamma )$
from Equation (2.27) and the input from Ornstein–Zernike theory (Proposition 2.14) naturally leads one to consider the 2D effective random walk defined in Section 4.1. In that subsection, we further expose the connection between this effective random walk and the cone points of the free Ising polymer model in
$q(\Gamma )$
from Equation (2.27) and the input from Ornstein–Zernike theory (Proposition 2.14) naturally leads one to consider the 2D effective random walk defined in Section 4.1. In that subsection, we further expose the connection between this effective random walk and the cone points of the free Ising polymer model in
![]() ${\mathbb H}$
. A key result there is Proposition 4.1, which enables a quantitative comparison between the partition function
${\mathbb H}$
. A key result there is Proposition 4.1, which enables a quantitative comparison between the partition function
![]() $\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset {\mathbb H})$
and the probability that the random walk stays in
$\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset {\mathbb H})$
and the probability that the random walk stays in
![]() ${\mathbb H}$
. In particular, we will be able to rule out bad events for the cone points of the free Ising polymer in
${\mathbb H}$
. In particular, we will be able to rule out bad events for the cone points of the free Ising polymer in
![]() ${\mathbb H}$
using random walk estimates. In the next section, we develop comparison results between free and modified Ising polymers such that bad events for the cone points of modified Ising polymers can also be ruled out using random walk estimates. Eventually, this will lead to a coupling between the cone points of the modified Ising polymer and our random walk.
${\mathbb H}$
using random walk estimates. In the next section, we develop comparison results between free and modified Ising polymers such that bad events for the cone points of modified Ising polymers can also be ruled out using random walk estimates. Eventually, this will lead to a coupling between the cone points of the modified Ising polymer and our random walk.
In the rest of this section, we develop various limit theorems for our random walk that will be used in the analysis of (modified) Ising polymers in Section 5, culminating in the proof of Theorem 2.8 (and thus Theorem 1.2).
4.1 The random walk model and free Ising polymers
Consider the random walk
![]() $(\mathsf {S}(i))_{i \in \mathbb {Z}_{\geq 0}}$
, whose law will be denoted by
$(\mathsf {S}(i))_{i \in \mathbb {Z}_{\geq 0}}$
, whose law will be denoted by
![]() $\mathbb {P}$
, with i.i.d. increments
$\mathbb {P}$
, with i.i.d. increments
![]() $\{X(i) = (X_1(i), X_2(i))\}_{i \geq 1}$
of step distribution X, where for any
$\{X(i) = (X_1(i), X_2(i))\}_{i \geq 1}$
of step distribution X, where for any
![]() $\vec {v} \in \mathbb {Z}^2$
,
$\vec {v} \in \mathbb {Z}^2$
,
We will denote by
![]() $(\mathsf {S}_1(\cdot ),\mathsf {S}_2(\cdot ))$
the two coordinates of
$(\mathsf {S}_1(\cdot ),\mathsf {S}_2(\cdot ))$
the two coordinates of
![]() $\mathsf {S}(\cdot )$
. For
$\mathsf {S}(\cdot )$
. For
![]() ${\mathsf {u}} \in \mathbb {Z}^2$
, we will write
${\mathsf {u}} \in \mathbb {Z}^2$
, we will write
![]() $\mathbb {P}_{{\mathsf {u}}}$
to denote the law of
$\mathbb {P}_{{\mathsf {u}}}$
to denote the law of
![]() $\mathsf {S}(\cdot )$
started from
$\mathsf {S}(\cdot )$
started from
![]() $\mathsf {S}(0) = {\mathsf {u}}$
. From Equation (2.25), we have
$\mathsf {S}(0) = {\mathsf {u}}$
. From Equation (2.25), we have
![]() $\mathbb {E}[X] = \alpha \mathsf {x}$
, and from Equation (2.26), we inherit exponential tail decay: For all
$\mathbb {E}[X] = \alpha \mathsf {x}$
, and from Equation (2.26), we inherit exponential tail decay: For all
![]() $\beta $
sufficiently large, there exists a constant
$\beta $
sufficiently large, there exists a constant
![]() $C':= C'(\beta )>0$
such that for all
$C':= C'(\beta )>0$
such that for all
![]() $k \geq 1$
, we have
$k \geq 1$
, we have
 $$ \begin{align} \sum_{\vec{v} \in \mathbb{Z}^2: \left\Vert \vec{v} \right\Vert{}_1 \geq k} \mathbb{P}(X = \vec{v}) \leq C' e^{-\nu_g \beta k}. \end{align} $$
$$ \begin{align} \sum_{\vec{v} \in \mathbb{Z}^2: \left\Vert \vec{v} \right\Vert{}_1 \geq k} \mathbb{P}(X = \vec{v}) \leq C' e^{-\nu_g \beta k}. \end{align} $$
We remark that the step distribution of X need not be symmetric in the y-coordinate
![]() $X_2$
due to the northeast splitting rule (this is the key difference between our random walk and the random walk considered in [Reference Ioffe, Ott, Velenik and Wachtel31] and why we cannot use their random walk results here). Also note that
$X_2$
due to the northeast splitting rule (this is the key difference between our random walk and the random walk considered in [Reference Ioffe, Ott, Velenik and Wachtel31] and why we cannot use their random walk results here). Also note that
![]() $\mathbb {P}(X \in \mathcal {Y}^\blacktriangleleft ) = 1$
, and thus the x-coordinate
$\mathbb {P}(X \in \mathcal {Y}^\blacktriangleleft ) = 1$
, and thus the x-coordinate
![]() $X_1>0$
a.s.
$X_1>0$
a.s.
We will write
![]() $H_{E}^A$
to denote the first hitting time of a set
$H_{E}^A$
to denote the first hitting time of a set
![]() $E \subset \mathbb {R}^2$
by a stochastic process
$E \subset \mathbb {R}^2$
by a stochastic process
![]() $A_.$
, omitting the A from the notation when the stochastic process is clear. For singleton sets, we will simply write
$A_.$
, omitting the A from the notation when the stochastic process is clear. For singleton sets, we will simply write
![]() $H_{{\mathsf {u}}}^A$
rather than
$H_{{\mathsf {u}}}^A$
rather than
![]() $H_{\{{\mathsf {u}}\}}^A$
. Let
$H_{\{{\mathsf {u}}\}}^A$
. Let
![]() ${\mathbb H}_{-} := \mathbb {R} \times \mathbb {R}_{<0}$
. In light of the factorization (2.27), for fixed
${\mathbb H}_{-} := \mathbb {R} \times \mathbb {R}_{<0}$
. In light of the factorization (2.27), for fixed
![]() $\Gamma ^{(L)}$
and
$\Gamma ^{(L)}$
and
![]() $\Gamma ^{(R)}$
, we will be interested in our random walk
$\Gamma ^{(R)}$
, we will be interested in our random walk
![]() $\mathsf {S}(\cdot )$
started from
$\mathsf {S}(\cdot )$
started from
![]() $\Gamma ^{(L)}$
and conditioned on the event
$\Gamma ^{(L)}$
and conditioned on the event
It will therefore be helpful to obtain an expression for
![]() $\mathbb {P}_{{\mathsf {u}}}(H_{{\mathsf {v}}} < H_{{\mathbb H}_-})$
in terms of animal weights, for any
$\mathbb {P}_{{\mathsf {u}}}(H_{{\mathsf {v}}} < H_{{\mathbb H}_-})$
in terms of animal weights, for any
![]() ${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
. Towards this end, define the sets
${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
. Towards this end, define the sets
 $$ \begin{align} \mathsf{V}^+_{{\mathsf{u}}, {\mathsf{v}}} &:= \{ (\vec{v}_1, \dots, \vec{v}_n) \in (\mathbb{Z}^2)^n : n \geq 1, {\mathsf{u}}+\vec{v}_1+ \dots+ \vec{v}_m = {\mathsf{v}}, {\mathsf{u}}+\vec{v}_1+\dots+\vec{v}_i \in {\mathbb H} \ ~\forall 1 \leq i \leq n \} \nonumber \\ \mathsf{A}^+_{{\mathsf{u}},{\mathsf{v}}} &:= \{ (\Gamma^{(1)}, \dots, \Gamma^{(n)}) \in \mathsf{A}^n : n \geq 1 , \big(\mathsf{X}(\Gamma^{(1)}), \dots, \mathsf{X}(\Gamma^{(n)})\big) \in \mathsf{V}^+_{{\mathsf{u}}, {\mathsf{v}}} \}, \end{align} $$
$$ \begin{align} \mathsf{V}^+_{{\mathsf{u}}, {\mathsf{v}}} &:= \{ (\vec{v}_1, \dots, \vec{v}_n) \in (\mathbb{Z}^2)^n : n \geq 1, {\mathsf{u}}+\vec{v}_1+ \dots+ \vec{v}_m = {\mathsf{v}}, {\mathsf{u}}+\vec{v}_1+\dots+\vec{v}_i \in {\mathbb H} \ ~\forall 1 \leq i \leq n \} \nonumber \\ \mathsf{A}^+_{{\mathsf{u}},{\mathsf{v}}} &:= \{ (\Gamma^{(1)}, \dots, \Gamma^{(n)}) \in \mathsf{A}^n : n \geq 1 , \big(\mathsf{X}(\Gamma^{(1)}), \dots, \mathsf{X}(\Gamma^{(n)})\big) \in \mathsf{V}^+_{{\mathsf{u}}, {\mathsf{v}}} \}, \end{align} $$
and, for a set of animals E, introduce

When E is taken to be the set of all possible animals, we’ll simply write
![]() $\mathcal {A}^+({\mathsf {u}},{\mathsf {v}}; E) = \mathcal {A}^+({\mathsf {u}},{\mathsf {v}})$
. Observe that
$\mathcal {A}^+({\mathsf {u}},{\mathsf {v}}; E) = \mathcal {A}^+({\mathsf {u}},{\mathsf {v}})$
. Observe that
 $$ \begin{align} \mathbb{P}_{{\mathsf{u}}}\big(H_{{\mathsf{v}}} < H_{{\mathbb H}_{-}} \big) = \sum_{n \geq 1} \sum_{(\vec{v}_1, \dots, \vec{v}_n) \in \mathsf{V}^+_{{\mathsf{u}}, {\mathsf{v}}}} \prod_{i=1}^n \mathbb{P}(X=\vec{v}_i) = \mathcal{A}^+({\mathsf{u}}, {\mathsf{v}}). \end{align} $$
$$ \begin{align} \mathbb{P}_{{\mathsf{u}}}\big(H_{{\mathsf{v}}} < H_{{\mathbb H}_{-}} \big) = \sum_{n \geq 1} \sum_{(\vec{v}_1, \dots, \vec{v}_n) \in \mathsf{V}^+_{{\mathsf{u}}, {\mathsf{v}}}} \prod_{i=1}^n \mathbb{P}(X=\vec{v}_i) = \mathcal{A}^+({\mathsf{u}}, {\mathsf{v}}). \end{align} $$
In words, the above equation states that the probability of the random walk hitting
![]() ${\mathsf {v}}$
before leaving
${\mathsf {v}}$
before leaving
![]() ${\mathbb H}_{-}$
is equal to a sum over all possible products of weights of irreducible animals whose concatenation has all cone points in
${\mathbb H}_{-}$
is equal to a sum over all possible products of weights of irreducible animals whose concatenation has all cone points in
![]() ${\mathbb H}$
.
${\mathbb H}$
.
Recall
![]() $\mathcal {A}(\cdot ,\cdot ;\cdot )$
from Equation (2.28), and note that for any
$\mathcal {A}(\cdot ,\cdot ;\cdot )$
from Equation (2.28), and note that for any
![]() ${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
and any set of animals E,
${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
and any set of animals E,
since the (only) difference between
![]() $\mathcal {A}^+({\mathsf {u}}, {\mathsf {v}};E)$
and
$\mathcal {A}^+({\mathsf {u}}, {\mathsf {v}};E)$
and
![]() $\mathcal {A}({\mathsf {u}}, {\mathsf {v}};E)$
is that the sum defining
$\mathcal {A}({\mathsf {u}}, {\mathsf {v}};E)$
is that the sum defining
![]() $\mathcal {A}({\mathsf {u}}, {\mathsf {v}};E)$
restricts to tuples of irreducible animals such that the entire concatenation
$\mathcal {A}({\mathsf {u}}, {\mathsf {v}};E)$
restricts to tuples of irreducible animals such that the entire concatenation
![]() ${\mathsf {u}}+ \Gamma ^{(1)} \circ \cdots \circ \Gamma ^{(n)}$
is contained in
${\mathsf {u}}+ \Gamma ^{(1)} \circ \cdots \circ \Gamma ^{(n)}$
is contained in
![]() ${\mathbb H}$
, while the sum defining
${\mathbb H}$
, while the sum defining
![]() $\mathcal {A}^+({\mathsf {u}}, {\mathsf {v}};E)$
requires only the cone points to stay in
$\mathcal {A}^+({\mathsf {u}}, {\mathsf {v}};E)$
requires only the cone points to stay in
![]() ${\mathbb H}$
. In particular,
${\mathbb H}$
. In particular,
![]() $\mathsf {Cpts}(\Gamma )$
(viewed as an ordered tuple, see Equation (2.20)) under the conditioned law
$\mathsf {Cpts}(\Gamma )$
(viewed as an ordered tuple, see Equation (2.20)) under the conditioned law
![]() $\mathbf {P}^{\mathsf {x}}(\cdot \;\big |\; \Gamma ^{(L)}, \Gamma ^{(R)}, \gamma \subset {\mathbb H})$
and the trajectory of the random walk
$\mathbf {P}^{\mathsf {x}}(\cdot \;\big |\; \Gamma ^{(L)}, \Gamma ^{(R)}, \gamma \subset {\mathbb H})$
and the trajectory of the random walk
![]() $\mathbb {P}_{\mathsf {X}(\Gamma ^{(L)})}(\cdot \;\big |\; H_{\mathsf {x}- \mathsf {X}(\Gamma ^{(R)})} < H_{{\mathbb H}_-})$
only differ due to these requirements.
$\mathbb {P}_{\mathsf {X}(\Gamma ^{(L)})}(\cdot \;\big |\; H_{\mathsf {x}- \mathsf {X}(\Gamma ^{(R)})} < H_{{\mathbb H}_-})$
only differ due to these requirements.
Ultimately, we will achieve a coupling between
![]() $\mathsf {Cpts}(\Gamma )$
with the trajectory of the random walk because of an entropic repulsion result (Proposition 5.11): The cone points of
$\mathsf {Cpts}(\Gamma )$
with the trajectory of the random walk because of an entropic repulsion result (Proposition 5.11): The cone points of
![]() $\Gamma $
in the ‘bulk’ of the strip
$\Gamma $
in the ‘bulk’ of the strip
![]() $[0,N] \times [0,\infty )$
stay far away from the boundary of
$[0,N] \times [0,\infty )$
stay far away from the boundary of
![]() ${\mathbb H}$
with high probability so that the aforementioned difference between
${\mathbb H}$
with high probability so that the aforementioned difference between
![]() $\mathcal {A}^+$
and
$\mathcal {A}^+$
and
![]() $\mathcal {A}$
becomes negligible. A major step towards showing entropic repulsion is is the following crucial result from [Reference Ioffe, Shlosman and Toninelli32].Footnote
9
$\mathcal {A}$
becomes negligible. A major step towards showing entropic repulsion is is the following crucial result from [Reference Ioffe, Shlosman and Toninelli32].Footnote
9
Proposition 4.1 [Reference Ioffe, Shlosman and Toninelli32, Theorem 7].
Recall
![]() $\nu _g$
from Proposition 2.14. There exists
$\nu _g$
from Proposition 2.14. There exists
![]() $\overline {\delta } \in (0,\nu _g/4)$
and
$\overline {\delta } \in (0,\nu _g/4)$
and
![]() $\beta _0>0$
such that for all
$\beta _0>0$
such that for all
![]() $\beta> \beta _0$
, there exists a constant
$\beta> \beta _0$
, there exists a constant
![]() $C:=C(\beta )> 0$
such that
$C:=C(\beta )> 0$
such that
 $$\begin{align*}\sup_{\substack{{\mathsf{u}}, \mathsf{x} - {\mathsf{v}} \in \mathcal{Y} \\ {\mathsf{u}}, {\mathsf{v}} \in {\mathbb H}}} e^{-\overline{\delta} \beta ( \left\Vert {\mathsf{u}} \right\Vert{}_1 + \left\Vert \mathsf{x}-{\mathsf{v}} \right\Vert{}_1 )} \mathbb{P}_{{\mathsf{u}}}(H_{{\mathsf{v}}} < H_{{\mathbb H}_{-}}) \leq C e^{\tau_{\beta}(\mathsf{x})} \mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H}). \end{align*}$$
$$\begin{align*}\sup_{\substack{{\mathsf{u}}, \mathsf{x} - {\mathsf{v}} \in \mathcal{Y} \\ {\mathsf{u}}, {\mathsf{v}} \in {\mathbb H}}} e^{-\overline{\delta} \beta ( \left\Vert {\mathsf{u}} \right\Vert{}_1 + \left\Vert \mathsf{x}-{\mathsf{v}} \right\Vert{}_1 )} \mathbb{P}_{{\mathsf{u}}}(H_{{\mathsf{v}}} < H_{{\mathbb H}_{-}}) \leq C e^{\tau_{\beta}(\mathsf{x})} \mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H}). \end{align*}$$
Proposition 4.1 combined with the exponential tail decay of
![]() $\Gamma ^{(L)}$
and
$\Gamma ^{(L)}$
and
![]() $\Gamma ^{(R)}$
(2.26) (note the significance of
$\Gamma ^{(R)}$
(2.26) (note the significance of
![]() $\bar {\delta } < \nu _g/4$
) will allow us to eliminate bad events for
$\bar {\delta } < \nu _g/4$
) will allow us to eliminate bad events for
![]() $\mathsf {Cpts}(\Gamma )$
under the free Ising polymer law via estimates for random walks in a half-space, which are significantly easier to obtain compared to directly analyzing the polymer law.
$\mathsf {Cpts}(\Gamma )$
under the free Ising polymer law via estimates for random walks in a half-space, which are significantly easier to obtain compared to directly analyzing the polymer law.
4.2 Limit theorems for our random walk, confined to the half-space
We now state two important limit theorems, Theorems 4.2 and 4.3, for our random walk
![]() $\mathsf {S}(\cdot )$
confined to positive half-space, though our results apply to a more general class of 2D random walks. Our random walk
$\mathsf {S}(\cdot )$
confined to positive half-space, though our results apply to a more general class of 2D random walks. Our random walk
![]() $\mathsf {S}(\cdot )$
is on
$\mathsf {S}(\cdot )$
is on
![]() $\mathbb {Z}^2$
and has i.i.d. increments X with mean
$\mathbb {Z}^2$
and has i.i.d. increments X with mean
![]() $(\mu ,0)$
for some
$(\mu ,0)$
for some
![]() $\mu>0$
, exponential tails and satisfies
$\mu>0$
, exponential tails and satisfies
![]() $X_1>0$
a.s. Let us also write
$X_1>0$
a.s. Let us also write
![]() $\operatorname {Var}(X) = (\sigma _1^2, \sigma _2^2)$
.
$\operatorname {Var}(X) = (\sigma _1^2, \sigma _2^2)$
.
Let
![]() $V_1$
denote the unique positive harmonic function for the one-dimensional random walk
$V_1$
denote the unique positive harmonic function for the one-dimensional random walk
![]() $\mathsf {S}_2$
killed upon leaving
$\mathsf {S}_2$
killed upon leaving
![]() $(0,\infty )$
satisfying
$(0,\infty )$
satisfying
The uniqueness of
![]() $V_1$
was established by Doney in [Reference Doney22]. Similarly, let
$V_1$
was established by Doney in [Reference Doney22]. Similarly, let
![]() $V_1'$
denote the analogous harmonic function for the random walk
$V_1'$
denote the analogous harmonic function for the random walk
![]() $-\mathsf {S}_2$
.
$-\mathsf {S}_2$
.
Theorem 4.2. Fix any
![]() $A>0$
and any
$A>0$
and any
![]() $\delta \in (0,1/2)$
. Uniformly over
$\delta \in (0,1/2)$
. Uniformly over
![]() $k \in [N/\mu - A\sqrt {N}, N/\mu + A \sqrt {N}]$
and
$k \in [N/\mu - A\sqrt {N}, N/\mu + A \sqrt {N}]$
and
![]() $u, v \in (0, N^{1/2-\delta }] \cap \mathbb {N}$
, we have the following results.
$u, v \in (0, N^{1/2-\delta }] \cap \mathbb {N}$
, we have the following results.
-
1. There exist constants
 $\mathbf {C}>0$
and
$\mathbf {C}>0$
and
 $\kappa := \kappa (X)>0$
such that (4.6)Furthermore, if
$\kappa := \kappa (X)>0$
such that (4.6)Furthermore, if $$ \begin{align} \mathbb{P}_{(0,u)}\Big(\mathsf{S}(k) = (N,v) ,\, H_{{\mathbb H}_{-}}> k \Big) \sim \mathbf{C} \kappa \frac{V_1(u) V_1'(v)}{k^2} \exp\Big(-\frac{(N-k\mu)^2}{2k \sigma_1^2 }\Big). \end{align} $$
then
$$ \begin{align} \mathbb{P}_{(0,u)}\Big(\mathsf{S}(k) = (N,v) ,\, H_{{\mathbb H}_{-}}> k \Big) \sim \mathbf{C} \kappa \frac{V_1(u) V_1'(v)}{k^2} \exp\Big(-\frac{(N-k\mu)^2}{2k \sigma_1^2 }\Big). \end{align} $$
then $$\begin{align*}p_{N,A} := \mathbb{P}_{(0,u)}\Big( H_{(N,v)} \in [\tfrac{N}{\mu} - A\sqrt{N}, \tfrac{N}{\mu}+ A\sqrt{N}] \;\big|\; H_{(N,v)} < H_{{\mathbb H}_{-}} \Big),\end{align*}$$
(4.7)
$$\begin{align*}p_{N,A} := \mathbb{P}_{(0,u)}\Big( H_{(N,v)} \in [\tfrac{N}{\mu} - A\sqrt{N}, \tfrac{N}{\mu}+ A\sqrt{N}] \;\big|\; H_{(N,v)} < H_{{\mathbb H}_{-}} \Big),\end{align*}$$
(4.7) $$ \begin{align} \lim_{A \to \infty} \liminf_{N\to\infty} p_{N,A}= 1. \end{align} $$
$$ \begin{align} \lim_{A \to \infty} \liminf_{N\to\infty} p_{N,A}= 1. \end{align} $$
-
2. Let
 $\widehat {\mathsf {S}}_2(\cdot )$
denote the denote the linear interpolation of the points
$\widehat {\mathsf {S}}_2(\cdot )$
denote the denote the linear interpolation of the points
 $(n, \mathsf {S}_2(n))_{n\in \mathbb {N}}$
, viewed as an element of
$(n, \mathsf {S}_2(n))_{n\in \mathbb {N}}$
, viewed as an element of
 $C[0,\infty )$
. The family of conditional laws converges as
$C[0,\infty )$
. The family of conditional laws converges as $$\begin{align*}\mathbb{Q}_{u,v}^k(\cdot) := \mathbb{P}_{(0,u)}\bigg( \Big(\frac{\widehat{\mathsf{S}}_2(tk)}{\sigma_2\sqrt{k}}\Big)_{t\in [0,1]} \in \cdot \;\big|\; \mathsf{S}(k) = (N,v) ,\, H_{{\mathbb H}_{-}}>k \bigg) \end{align*}$$
$$\begin{align*}\mathbb{Q}_{u,v}^k(\cdot) := \mathbb{P}_{(0,u)}\bigg( \Big(\frac{\widehat{\mathsf{S}}_2(tk)}{\sigma_2\sqrt{k}}\Big)_{t\in [0,1]} \in \cdot \;\big|\; \mathsf{S}(k) = (N,v) ,\, H_{{\mathbb H}_{-}}>k \bigg) \end{align*}$$
 $k \to \infty $
to the law of the standard Brownian excursion in
$k \to \infty $
to the law of the standard Brownian excursion in
 $C[0,1]$
.
$C[0,1]$
.
Next, we describe the diffusive limit of our random walk. For
![]() $\ell , n\in \mathbb {N}$
and any ordered
$\ell , n\in \mathbb {N}$
and any ordered
![]() $\ell $
-tuple of points
$\ell $
-tuple of points
![]() $\mathcal S$
in
$\mathcal S$
in
![]() $\mathbb {R}^2$
, enumerated as
$\mathbb {R}^2$
, enumerated as
and satisfying
![]() $s_1(i) < s_1(i+1)$
for each
$s_1(i) < s_1(i+1)$
for each
![]() $i \in [1,\ell -1]$
, we define
$i \in [1,\ell -1]$
, we define
![]() $\mathfrak {J}_n(\mathcal S)$
to be the linear interpolation through the diffusively rescaled points
$\mathfrak {J}_n(\mathcal S)$
to be the linear interpolation through the diffusively rescaled points
 $$ \begin{align} \mathfrak{J}_n(\mathcal S) := \Big(\frac{1}{n}s_1(i), \frac{1}{\sigma\sqrt{n}}s_2(i) \Big)_{i=1}^k \end{align} $$
$$ \begin{align} \mathfrak{J}_n(\mathcal S) := \Big(\frac{1}{n}s_1(i), \frac{1}{\sigma\sqrt{n}}s_2(i) \Big)_{i=1}^k \end{align} $$
where
![]() $\sigma ^2 := \sigma _2^2/\mu $
(c.f. Remark 2.9). Consider now the linear interpolation corresponding to our random walk
$\sigma ^2 := \sigma _2^2/\mu $
(c.f. Remark 2.9). Consider now the linear interpolation corresponding to our random walk
![]() $\mathsf {S}(\cdot )$
up to time
$\mathsf {S}(\cdot )$
up to time
![]() $H_{(N,v)}$
:
$H_{(N,v)}$
:
Viewing
![]() $\mathfrak {e}_N^{\mathsf {S},v}$
as a random element of
$\mathfrak {e}_N^{\mathsf {S},v}$
as a random element of
![]() $C[0,1]$
, Theorem 4.3 below gives a convergence result to the Brownian excursion on
$C[0,1]$
, Theorem 4.3 below gives a convergence result to the Brownian excursion on
![]() $[0,1]$
.
$[0,1]$
.
Theorem 4.3. Fix any
![]() $\delta \in (0,1/2)$
. Uniformly over
$\delta \in (0,1/2)$
. Uniformly over
![]() $u, v \in (0,N^{1/2-\delta }] \cap \mathbb {N}$
, we have the following. The family of conditional laws
$u, v \in (0,N^{1/2-\delta }] \cap \mathbb {N}$
, we have the following. The family of conditional laws
converges weakly as
![]() $N \to \infty $
to the law of the standard Brownian excursion in
$N \to \infty $
to the law of the standard Brownian excursion in
![]() $(C[0,1], \|\cdot \|_{\infty })$
.
$(C[0,1], \|\cdot \|_{\infty })$
.
Theorems 4.2 and 4.3 are proved in Section 6.3. These results are modifications of a ballot-type theorem from [Reference Denisov and Wachtel17] and an invariance principle from [Reference Duraj and Wachtel23], respectively. Those important results were proved for a much broader class of random walks in very general cones; however, they were only proved for fixed start points and end points. The two results above have been modified to hold uniformly in appropriate ranges of start points and end points, which is crucial for our application. We remark that [Reference Ioffe, Ott, Velenik and Wachtel31, Section 5] states and proves results that similarly modify the results of [Reference Denisov and Wachtel17] and [Reference Duraj and Wachtel23]. However, first, the random walk they consider is symmetric in the y-coordinate, which simplifies their analysis, and second, their proofs do not always make explicit the aforementioned uniformity, in particular for the x-coordinate of the end point of their random walk. In Section 6, where our random walk estimates are proved, we take care to describe explicitly how we modify the proofs in [Reference Denisov and Wachtel17] and [Reference Duraj and Wachtel23] to handle uniformity in a broad range of start and end points.
5 Proof of Theorem 1.2 via random walk coupling
Throughout this Section, set
![]() $\mathsf {x} := \mathsf {x}(N) = (N,0) \in \mathbb {Z}^2$
. Recall the notation set forth in Section 2.5.
$\mathsf {x} := \mathsf {x}(N) = (N,0) \in \mathbb {Z}^2$
. Recall the notation set forth in Section 2.5.
In this section, we prove Theorem 2.8, thereby proving Theorem 1.2, via a certain coupling between
![]() $\mathsf {Cpts}(\Gamma )$
under the modified Ising polymer law
$\mathsf {Cpts}(\Gamma )$
under the modified Ising polymer law
![]() $\mathbf {P}_D^{\mathsf {x}}$
and the effective random walk, where
$\mathbf {P}_D^{\mathsf {x}}$
and the effective random walk, where
![]() $D = Q$
or
$D = Q$
or
![]() ${\mathbb H}$
. This is accomplished as follows.
${\mathbb H}$
. This is accomplished as follows.
In Section 4.1, we described the particular role played by the free Ising polymer model in the half-space due to its direct connection with an effective random walk. It is then crucial for our analysis to be able to compare the modified Ising polymers we are interested in with free Ising polymers. In Section 5.1, we state our needed comparison results, Theorem 5.1 (the main theorem of [Reference Ioffe, Shlosman and Toninelli32]) and Proposition 5.2, the latter being an extension of the former that allows us to handle the
![]() $D = Q$
case. The key consequence of these comparisons is that contour events of small probability in one model are still small in the other model (Corollary 5.3).
$D = Q$
case. The key consequence of these comparisons is that contour events of small probability in one model are still small in the other model (Corollary 5.3).
In Section 5.2, we prove Proposition 5.2, showing along the way that
![]() $\Gamma $
under the modified Ising polymer law in D typically has many cone points (Lemma 5.7). In Section 5.3, we prove Proposition 2.5 in a similar way to Proposition 5.2.
$\Gamma $
under the modified Ising polymer law in D typically has many cone points (Lemma 5.7). In Section 5.3, we prove Proposition 2.5 in a similar way to Proposition 5.2.
In Section 5.4, we show that each (left/right-)irreducible piece
![]() $\Gamma ^{(i)}$
has size bounded by
$\Gamma ^{(i)}$
has size bounded by
![]() $(\log N)^2$
,
$(\log N)^2$
,
![]() $i \in \{L, 1, \dots , n, R\}$
, w.h.p. under
$i \in \{L, 1, \dots , n, R\}$
, w.h.p. under
![]() $\mathbf {P}_D^{\mathsf {x}}$
.
$\mathbf {P}_D^{\mathsf {x}}$
.
In Section 5.5, we show the key result enabling a coupling between
![]() $\mathsf {Cpts}(\Gamma )$
and the effective random walk, Proposition 5.11. This result, which is an expression of entropic repulsion, states that, with high
$\mathsf {Cpts}(\Gamma )$
and the effective random walk, Proposition 5.11. This result, which is an expression of entropic repulsion, states that, with high
![]() $\mathbf {P}_D^{\mathsf {x}}$
-probability, each cone point of
$\mathbf {P}_D^{\mathsf {x}}$
-probability, each cone point of
![]() $\Gamma $
stays above height
$\Gamma $
stays above height
![]() $N^{\delta }$
in the large interval
$N^{\delta }$
in the large interval
![]() $[N^{4\delta }, N-N^{4\delta }]$
, for any
$[N^{4\delta }, N-N^{4\delta }]$
, for any
![]() $\delta \in (0,1/4)$
. This is achieved via Corollary 5.3, which reduces the result to the result in the free polymer model, and Proposition 4.1, which will allow us to reduce the result to an entropic repulsion result for the random walk conditioned to stay in
$\delta \in (0,1/4)$
. This is achieved via Corollary 5.3, which reduces the result to the result in the free polymer model, and Proposition 4.1, which will allow us to reduce the result to an entropic repulsion result for the random walk conditioned to stay in
![]() ${\mathbb H}$
.
${\mathbb H}$
.
The entropic repulsion, the shape of the cones
![]() $\mathcal {Y}^\blacktriangleleft $
and
$\mathcal {Y}^\blacktriangleleft $
and
![]() $\mathcal {Y}^\blacktriangleright $
, and the bound
$\mathcal {Y}^\blacktriangleright $
, and the bound
![]() $|\Gamma ^{(i)}| \leq (\log N)^2$
implies that the entire animal stays bounded away from
$|\Gamma ^{(i)}| \leq (\log N)^2$
implies that the entire animal stays bounded away from
![]() $\partial {\mathbb H}$
, the boundary of the half-plane, in the strip
$\partial {\mathbb H}$
, the boundary of the half-plane, in the strip
![]() $[N^{4\delta }, N-N^{4\delta }] \times [0,\infty )$
. The first consequence of this is that the weight modifications play no role in this strip; that is, for each cluster
$[N^{4\delta }, N-N^{4\delta }] \times [0,\infty )$
. The first consequence of this is that the weight modifications play no role in this strip; that is, for each cluster
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\Gamma $
in this strip, we have
$\Gamma $
in this strip, we have
![]() $\Phi _D(\mathcal {C};\gamma ) = \Phi (\mathcal {C};\gamma )$
. Thus, the portion of
$\Phi _D(\mathcal {C};\gamma ) = \Phi (\mathcal {C};\gamma )$
. Thus, the portion of
![]() $\Gamma $
contained in this strip behaves like a free Ising polymer, which can be related to the random walk. The second consequence is that the requirement that
$\Gamma $
contained in this strip behaves like a free Ising polymer, which can be related to the random walk. The second consequence is that the requirement that
![]() $\gamma $
stays in D in this strip becomes trivial. In particular, following the discussion after Equation (4.5), we will be able to couple the cone points of
$\gamma $
stays in D in this strip becomes trivial. In particular, following the discussion after Equation (4.5), we will be able to couple the cone points of
![]() $\Gamma $
in this strip with an effective random walk. This is achieved in Section 5.6.
$\Gamma $
in this strip with an effective random walk. This is achieved in Section 5.6.
Theorem 2.8 is finally proved in Section 5.7.
5.1 Comparing Ising polymers with modified and unmodified weights
We begin with the main theorem of [Reference Ioffe, Shlosman and Toninelli32], which states that the partition functions of the Ising polymers in
![]() ${\mathbb H}$
, with and without modifications, are equivalent up to a
${\mathbb H}$
, with and without modifications, are equivalent up to a
![]() $\beta $
-dependent constant.
$\beta $
-dependent constant.
Theorem 5.1 [Reference Ioffe, Shlosman and Toninelli32, Theorem 1].
For all
![]() $\beta>0$
large enough, we have
$\beta>0$
large enough, we have
In fact, there exist constants
![]() $C_1:=C_1(\beta ), C_2:=C_2(\beta )>0$
such that for all
$C_1:=C_1(\beta ), C_2:=C_2(\beta )>0$
such that for all
![]() $\beta $
large enough,
$\beta $
large enough,
Though we only consider
![]() ${\mathbb H}$
in this article, [Reference Ioffe, Shlosman and Toninelli32, Theorem 1] is stated more generally for half-spaces whose interior normal has argument lying in
${\mathbb H}$
in this article, [Reference Ioffe, Shlosman and Toninelli32, Theorem 1] is stated more generally for half-spaces whose interior normal has argument lying in
![]() $[-\pi /4, 3\pi /4]$
.
$[-\pi /4, 3\pi /4]$
.
The next proposition can be seen as an extension of Theorem 5.1 to address polymers in Q.
Proposition 5.2. For all
![]() $\beta>0$
sufficiently large, there exists a constant
$\beta>0$
sufficiently large, there exists a constant
![]() $C:= C(\beta )>0$
such that for any
$C:= C(\beta )>0$
such that for any
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
and
The proof of Proposition 5.2 is given in Section 5.2.
One can readily imply from Equations (5.2) and (5.4) the following, relating
![]() $\mathbf {P}^{\mathsf {x}}(\cdot \mid \gamma \subset D)$
and
$\mathbf {P}^{\mathsf {x}}(\cdot \mid \gamma \subset D)$
and
![]() $\mathbf {P}_D^{\mathsf {x}}$
, exactly as [Reference Ioffe, Shlosman and Toninelli32] derived its analogue from Equation (5.2) (see the discussion below Equation (2.7) in that paper):
$\mathbf {P}_D^{\mathsf {x}}$
, exactly as [Reference Ioffe, Shlosman and Toninelli32] derived its analogue from Equation (5.2) (see the discussion below Equation (2.7) in that paper):
Corollary 5.3. Let
![]() $D = {\mathbb H}$
or Q. There exists a constant
$D = {\mathbb H}$
or Q. There exists a constant
![]() $C:= C(\beta )>0$
such that for any set of contours A contained in D,
$C:= C(\beta )>0$
such that for any set of contours A contained in D,
For instance, if
![]() $Y_\gamma := \sum _{\mathcal {C} \cap \nabla _{\gamma } \neq \emptyset } \Phi _D'(\mathcal {C};\gamma ) - \Phi '(\mathcal {C};\gamma )$
and
$Y_\gamma := \sum _{\mathcal {C} \cap \nabla _{\gamma } \neq \emptyset } \Phi _D'(\mathcal {C};\gamma ) - \Phi '(\mathcal {C};\gamma )$
and
![]() $\mathbf {E}[\cdot ]$
denotes expectation under
$\mathbf {E}[\cdot ]$
denotes expectation under
![]() $\mathbf {P}^{\mathsf {x}}(\cdot \mid \gamma \subset D)$
, then
$\mathbf {P}^{\mathsf {x}}(\cdot \mid \gamma \subset D)$
, then
![]() $\mathbf {E}[e^{Y_{\gamma }}]$
is just
$\mathbf {E}[e^{Y_{\gamma }}]$
is just
![]() $\mathcal {G}_D(\mathsf {x})/\mathcal {G}(\mathsf {x} \mid \gamma \subset D)$
, and therefore
$\mathcal {G}_D(\mathsf {x})/\mathcal {G}(\mathsf {x} \mid \gamma \subset D)$
, and therefore ![]() . Notice
. Notice
![]() $C^{-1} \leq \mathbf {E}[e^{Y_{\gamma }}] \leq C$
by Equation (5.2) (for
$C^{-1} \leq \mathbf {E}[e^{Y_{\gamma }}] \leq C$
by Equation (5.2) (for
![]() $D={\mathbb H}$
) and Equation (5.4) (for
$D={\mathbb H}$
) and Equation (5.4) (for
![]() $D=Q$
). By Cauchy–Schwarz,
$D=Q$
). By Cauchy–Schwarz,
![]() $\mathbf {P}_D^{\mathsf {x}}(A) \leq C \sqrt {\mathbf {P}^{\mathsf {x}}(A\mid \gamma \subset D )}\sqrt {\mathbf {E}[e^{2Y_\gamma }]}$
, and the last expectation is uniformly bounded (as
$\mathbf {P}_D^{\mathsf {x}}(A) \leq C \sqrt {\mathbf {P}^{\mathsf {x}}(A\mid \gamma \subset D )}\sqrt {\mathbf {E}[e^{2Y_\gamma }]}$
, and the last expectation is uniformly bounded (as
![]() $\mathbf {E}[e^{2Y_{\gamma }}] =\tilde {\mathcal {G}}_D(\mathsf {x})/\mathcal {G}(\mathsf {x} \mid \gamma \subset D)$
, where
$\mathbf {E}[e^{2Y_{\gamma }}] =\tilde {\mathcal {G}}_D(\mathsf {x})/\mathcal {G}(\mathsf {x} \mid \gamma \subset D)$
, where
![]() $\tilde {\mathcal {G}}_D(\mathsf {x})$
is defined w.r.t.
$\tilde {\mathcal {G}}_D(\mathsf {x})$
is defined w.r.t.
![]() $\tilde {\Phi }^{\prime }_D(\mathcal {C};\gamma ) := 2\Phi _D'(\mathcal {C};\gamma )-\Phi '(\mathcal {C};\gamma )$
).
$\tilde {\Phi }^{\prime }_D(\mathcal {C};\gamma ) := 2\Phi _D'(\mathcal {C};\gamma )-\Phi '(\mathcal {C};\gamma )$
).
A particular consequence of Corollary 5.3 is that contour events that hold with probability tending to
![]() $1$
in the unmodified models (which are much easier to study) still hold with probability tending to
$1$
in the unmodified models (which are much easier to study) still hold with probability tending to
![]() $1$
in the modified models. The most significant application of this fact is in the proof of entropic repulsion under
$1$
in the modified models. The most significant application of this fact is in the proof of entropic repulsion under
![]() $\mathbf {P}_Q^{\mathsf {x}}(\cdot )$
(Proposition 5.11), which, as explained at the start of this Section, is a crucial step towards the random walk coupling achieved in Section 5.6.
$\mathbf {P}_Q^{\mathsf {x}}(\cdot )$
(Proposition 5.11), which, as explained at the start of this Section, is a crucial step towards the random walk coupling achieved in Section 5.6.
Remark 5.4. In Corollary 5.3, we specified that the event A should be a set of contours. The reason this was emphasized is that in Equation (2.15) we extended the measure
![]() $\mathbf {P}_D^{\mathsf {x}}$
from contours to animals, but Corollary 5.3 does not hold for general animal events A. Indeed, it is not true that small animal events in one model stay small in another model, as the ratio
$\mathbf {P}_D^{\mathsf {x}}$
from contours to animals, but Corollary 5.3 does not hold for general animal events A. Indeed, it is not true that small animal events in one model stay small in another model, as the ratio
![]() $|q(\Gamma )/q_D(\Gamma )|$
is not bounded away from
$|q(\Gamma )/q_D(\Gamma )|$
is not bounded away from
![]() $0$
nor
$0$
nor
![]() $\infty $
(as there are no such bounds on
$\infty $
(as there are no such bounds on
![]() $|\Phi ^{\prime }_Q(\mathcal {C};\gamma )|/|\Phi '(\mathcal {C};\gamma )|$
in the generality of weight modifications that we must consider).
$|\Phi ^{\prime }_Q(\mathcal {C};\gamma )|/|\Phi '(\mathcal {C};\gamma )|$
in the generality of weight modifications that we must consider).
5.2 Proof of Proposition 5.2
We will need two auxiliary lemmas. The first, Lemma 5.5, states that in any model where at least two cone points exist, the partition function is dominated by animals whose first (left) and last (right) irreducible pieces have size of order
![]() $1$
.
$1$
.
Lemma 5.5. Let D be either Q or
![]() ${\mathbb H}$
. For any
${\mathbb H}$
. For any
![]() $\epsilon \in (0,1)$
, there exists
$\epsilon \in (0,1)$
, there exists
![]() $K_{\epsilon } := K_{\epsilon ,\beta }>0$
such that
$K_{\epsilon } := K_{\epsilon ,\beta }>0$
such that
and
Remark 5.6. Observe that once Proposition 5.2 is proved, the domain
![]() ${\mathbb H}$
in the right-hand side of Equations (5.5) and (5.6) may be replaced by D, for D either Q or
${\mathbb H}$
in the right-hand side of Equations (5.5) and (5.6) may be replaced by D, for D either Q or
![]() ${\mathbb H}$
.
${\mathbb H}$
.
The second auxiliary result, Lemma 5.7, extends Lemma 2.11, and thus Proposition 2.12 thanks to Remark 2.13, to the modified models on Q and
![]() ${\mathbb H}$
.
${\mathbb H}$
.
Lemma 5.7. Let D be either Q or
![]() ${\mathbb H}$
. Fix any
${\mathbb H}$
. Fix any
![]() $\epsilon ,\delta \in (0,1)$
. There exist positive constants
$\epsilon ,\delta \in (0,1)$
. There exist positive constants
![]() $\beta _0, \delta _0$
and
$\beta _0, \delta _0$
and
![]() $\nu _0>0$
such that for all
$\nu _0>0$
such that for all
![]() $\beta \geq \beta _0$
, there exists
$\beta \geq \beta _0$
, there exists
![]() $C:= C(\beta )>0$
such that the following hold uniformly over all
$C:= C(\beta )>0$
such that the following hold uniformly over all
![]() $N \in \mathbb {N}$
and
$N \in \mathbb {N}$
and
![]() $r \geq 1+\epsilon $
:
$r \geq 1+\epsilon $
:
In particular, there exists
![]() $\nu>0$
such that for all
$\nu>0$
such that for all
![]() $\beta \geq \beta _0$
, there exists
$\beta \geq \beta _0$
, there exists
![]() $C:= C(\beta )>0$
such that the following holds uniformly over all
$C:= C(\beta )>0$
such that the following holds uniformly over all
![]() $N\in \mathbb {N}$
:
$N\in \mathbb {N}$
:
We postpone the proof of Lemma 5.5 to the end of the subsection. We prove Proposition 5.2 and Lemma 5.7 in tandem, proceeding as follows:
-
(a) We begin by proving Lemma 5.7 for
 $D={\mathbb H}$
.
$D={\mathbb H}$
. -
(b) We then prove the first part of Proposition 5.2 (Equation (5.3)), as well as its analog for
 $\mathcal {G}_{{\mathbb H}}$
, that is, (5.10)
$\mathcal {G}_{{\mathbb H}}$
, that is, (5.10) $$ \begin{align} C^{-1}\mathcal{G}_{{\mathbb H}}(\mathsf{x})\leq \mathcal{G}_{{\mathbb H}}(\mathsf{x} \;\big|\; \gamma \subset Q) \leq C\mathcal{G}_{{\mathbb H}}(\mathsf{x}). \end{align} $$
$$ \begin{align} C^{-1}\mathcal{G}_{{\mathbb H}}(\mathsf{x})\leq \mathcal{G}_{{\mathbb H}}(\mathsf{x} \;\big|\; \gamma \subset Q) \leq C\mathcal{G}_{{\mathbb H}}(\mathsf{x}). \end{align} $$
-
(c) These results are then used to prove Lemma 5.7 for
 $D=Q$
.
$D=Q$
. -
(d) Finally, we prove Equation (5.4), thereby completing the proof of Proposition 5.2.
Proof of Part (a). For each bound, we will first apply Lemma 2.11, then Theorem 5.1. Recall that Lemma 2.11 states that the analogous bounds to Equation (5.7) and Equation (5.8) hold for
![]() $\mathcal {G}(\mathsf {x})$
. Equation (5.1) implies that
$\mathcal {G}(\mathsf {x})$
. Equation (5.1) implies that
![]() $\log \mathcal {G}(\mathsf {x})$
and
$\log \mathcal {G}(\mathsf {x})$
and
![]() $\log \mathcal {G}(\mathsf {x}\;\big |\; \gamma \subset {\mathbb H})$
have the same leading order; thus, for some
$\log \mathcal {G}(\mathsf {x}\;\big |\; \gamma \subset {\mathbb H})$
have the same leading order; thus, for some
![]() $\nu _0' \in (0, \nu _0]$
, we have
$\nu _0' \in (0, \nu _0]$
, we have
 $$ \begin{align*} \mathcal{G}\big(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H} ,\, |\gamma| \geq r \left\Vert \mathsf{x} \right\Vert{}_1\big) &\leq \mathcal{G}\big(\mathsf{x} \;\big|\; |\gamma| \geq r \left\Vert \mathsf{x} \right\Vert{}_1\big) \leq Ce^{-\nu_0' \beta r \left\Vert \mathsf{x} \right\Vert{}_1} \mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H}), \text{ and} \\ \mathcal{G}\big(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H} ,\, \mathsf{Cpts}(\gamma) < 2\delta_0 \left\Vert \mathsf{x} \right\Vert{}_1 \big) &\leq \mathcal{G}\big(\mathsf{x} \;\big|\; |\mathsf{Cpts}(\gamma)| < 2\delta_0 \left\Vert \mathsf{x} \right\Vert{}_1 \big) \leq C e^{-\nu_0' \beta \left\Vert \mathsf{x} \right\Vert{}_1} \mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H}). \end{align*} $$
$$ \begin{align*} \mathcal{G}\big(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H} ,\, |\gamma| \geq r \left\Vert \mathsf{x} \right\Vert{}_1\big) &\leq \mathcal{G}\big(\mathsf{x} \;\big|\; |\gamma| \geq r \left\Vert \mathsf{x} \right\Vert{}_1\big) \leq Ce^{-\nu_0' \beta r \left\Vert \mathsf{x} \right\Vert{}_1} \mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H}), \text{ and} \\ \mathcal{G}\big(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H} ,\, \mathsf{Cpts}(\gamma) < 2\delta_0 \left\Vert \mathsf{x} \right\Vert{}_1 \big) &\leq \mathcal{G}\big(\mathsf{x} \;\big|\; |\mathsf{Cpts}(\gamma)| < 2\delta_0 \left\Vert \mathsf{x} \right\Vert{}_1 \big) \leq C e^{-\nu_0' \beta \left\Vert \mathsf{x} \right\Vert{}_1} \mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset {\mathbb H}). \end{align*} $$
Equation (5.7) and Equation (5.8) for
![]() $D ={\mathbb H}$
now follow from Corollary 5.3, and Equation (5.9) from Remark 2.13.
$D ={\mathbb H}$
now follow from Corollary 5.3, and Equation (5.9) from Remark 2.13.
Proof of Part (b). The upper bounds in both Equations (5.3) and (5.10) hold with
![]() $C = 1$
, since
$C = 1$
, since
![]() $Q \subset {\mathbb H}$
.
$Q \subset {\mathbb H}$
.
We now show the lower bound for Equation (5.10). The lower bound in Equation (5.3) is obtained simply by replacing
![]() $q_{{\mathbb H}}$
with q in what follows. By Lemmas 5.5 and 5.7 (for
$q_{{\mathbb H}}$
with q in what follows. By Lemmas 5.5 and 5.7 (for
![]() $D={\mathbb H}$
), we have the following: for any
$D={\mathbb H}$
), we have the following: for any
![]() $\epsilon \in (0,1)$
, there exists
$\epsilon \in (0,1)$
, there exists
![]() $K:=K(\beta ,\epsilon )>0$
such that for
$K:=K(\beta ,\epsilon )>0$
such that for
![]() $\|\mathsf {x}\|_1$
large,
$\|\mathsf {x}\|_1$
large,
Now, using the weight factorization of
![]() $q_{{\mathbb H}}(\Gamma )$
in Equation (2.18), we may express the right-hand side of the above (for
$q_{{\mathbb H}}(\Gamma )$
in Equation (2.18), we may express the right-hand side of the above (for
![]() $N=\left \Vert \mathsf {x} \right \Vert {}_1 \geq 2/\delta _0$
) as
$N=\left \Vert \mathsf {x} \right \Vert {}_1 \geq 2/\delta _0$
) as

For any
![]() ${\mathsf {u}} \in \mathcal {Y}^\blacktriangleleft $
, let
${\mathsf {u}} \in \mathcal {Y}^\blacktriangleleft $
, let
![]() $\gamma ^{(L)}({\mathsf {u}})$
denote an arbitrary up-right path from
$\gamma ^{(L)}({\mathsf {u}})$
denote an arbitrary up-right path from
![]() $0$
to
$0$
to
![]() ${\mathsf {u}}$
, and let
${\mathsf {u}}$
, and let
![]() $\gamma ^{(R)}({\mathsf {u}})$
denote an arbitrary down-right path from
$\gamma ^{(R)}({\mathsf {u}})$
denote an arbitrary down-right path from
![]() $\mathsf {x}-{\mathsf {u}}$
to
$\mathsf {x}-{\mathsf {u}}$
to
![]() $\mathsf {x}$
(if one exists). Since the backwards cone of
$\mathsf {x}$
(if one exists). Since the backwards cone of
![]() $\Gamma ^{(L)}$
must contain the origin and the forwards cone of
$\Gamma ^{(L)}$
must contain the origin and the forwards cone of
![]() $\mathsf {x}-\Gamma ^{(R)}$
must contain
$\mathsf {x}-\Gamma ^{(R)}$
must contain
![]() $\mathsf {x}$
, it follows that
$\mathsf {x}$
, it follows that
for any collection
![]() $\{\Gamma ^{(L)}, \Gamma ^{(1)} ,\dots , \Gamma ^{(m)}, \Gamma ^{(R)}\}$
contributing to a nonzero term in the second-to-last display. In particular, for any
$\{\Gamma ^{(L)}, \Gamma ^{(1)} ,\dots , \Gamma ^{(m)}, \Gamma ^{(R)}\}$
contributing to a nonzero term in the second-to-last display. In particular, for any
![]() $\Gamma ^{(L)} \in \mathsf {A_L}$
and
$\Gamma ^{(L)} \in \mathsf {A_L}$
and
![]() $\Gamma ^{(R)} \in \mathsf {A_R}$
such that
$\Gamma ^{(R)} \in \mathsf {A_R}$
such that
![]() $\{|\Gamma ^{(L)}|, |\Gamma ^{(R)}|\leq K\}$
, we have
$\{|\Gamma ^{(L)}|, |\Gamma ^{(R)}|\leq K\}$
, we have

Since
![]() $ q_{{\mathbb H}}(\Gamma ^{(L)}) \leq q_{{\mathbb H}}(\gamma ^{(L)}(\mathsf {X}(\Gamma ^{(L)}))) $
and
$ q_{{\mathbb H}}(\Gamma ^{(L)}) \leq q_{{\mathbb H}}(\gamma ^{(L)}(\mathsf {X}(\Gamma ^{(L)}))) $
and
![]() $q_{{\mathbb H}}(\Gamma ^{(R)}) \leq q_{{\mathbb H}}(\gamma ^{(R)}(\mathsf {X}(\Gamma ^{(R)}))) $
, it follows from the last three displays that the right-hand side of Equation (5.11) is bounded above by
$q_{{\mathbb H}}(\Gamma ^{(R)}) \leq q_{{\mathbb H}}(\gamma ^{(R)}(\mathsf {X}(\Gamma ^{(R)}))) $
, it follows from the last three displays that the right-hand side of Equation (5.11) is bounded above by

The prefactor in the last display is a constant depending only
![]() $K:=K(\beta ,\epsilon )$
, finishing the proof.
$K:=K(\beta ,\epsilon )$
, finishing the proof.
Proof of Part (c). In Part (a), we proved Equations (5.7) and (5.8) for
![]() $D={\mathbb H}$
. Bounding below the left-hand sides of these equations by adding the restriction
$D={\mathbb H}$
. Bounding below the left-hand sides of these equations by adding the restriction
![]() $\gamma \subset Q$
, and giving an upper bound on the right-hand sides by using Equation (5.10) to replace
$\gamma \subset Q$
, and giving an upper bound on the right-hand sides by using Equation (5.10) to replace
![]() $\mathcal {G}_{{\mathbb H}}(\mathsf {x})$
by
$\mathcal {G}_{{\mathbb H}}(\mathsf {x})$
by
![]() $C\mathcal {G}_{{\mathbb H}}(\mathsf {x} \;\big |\; \gamma \subset Q)$
yields the same results for
$C\mathcal {G}_{{\mathbb H}}(\mathsf {x} \;\big |\; \gamma \subset Q)$
yields the same results for
![]() $\mathcal {G}_{{\mathbb H}}(\mathsf {x} \;\big |\; \gamma \subset Q, \cdot )$
:
$\mathcal {G}_{{\mathbb H}}(\mathsf {x} \;\big |\; \gamma \subset Q, \cdot )$
:
uniformly in
![]() $\beta $
large enough and
$\beta $
large enough and
![]() $\mathsf {x}$
. Similar to Equation (2.13), we have
$\mathsf {x}$
. Similar to Equation (2.13), we have
 $$ \begin{align} \left| \log \frac{q_{{\mathbb H}}(\gamma)}{q_{Q}(\gamma)}\right| \leq 6e^{-\chi\beta} |\gamma|. \end{align} $$
$$ \begin{align} \left| \log \frac{q_{{\mathbb H}}(\gamma)}{q_{Q}(\gamma)}\right| \leq 6e^{-\chi\beta} |\gamma|. \end{align} $$
Equation (5.7) and Equation (5.8) for
![]() $D=Q$
are then simple consequences of Equations (5.13) to (5.15). Once again, Equation (5.9) for
$D=Q$
are then simple consequences of Equations (5.13) to (5.15). Once again, Equation (5.9) for
![]() $D=Q$
follows by Remark 2.13.
$D=Q$
follows by Remark 2.13.
Proof of Part (d). Let us start by proving the upper bound in Equation (5.4). As in Equation (5.11), Lemmas 5.5 and 5.7 (now for
![]() $D=Q$
) yield the following for any
$D=Q$
) yield the following for any
![]() $\epsilon \in (0,1)$
, some
$\epsilon \in (0,1)$
, some
![]() $K:= K(\beta ,\epsilon )>0$
, and all
$K:= K(\beta ,\epsilon )>0$
, and all
![]() $\|\mathsf {x}\|_1$
large enough:
$\|\mathsf {x}\|_1$
large enough:
The first term on the right-hand side,
![]() $\epsilon \mathcal {G}_{{\mathbb H}}(\mathsf {x})$
, may be bounded by
$\epsilon \mathcal {G}_{{\mathbb H}}(\mathsf {x})$
, may be bounded by
![]() $C_0(\beta )\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset Q)$
via Equations (5.2) and (5.3). We now follow the proof of Part (b) to bound the second term: Using the factorization Equation (2.19) of
$C_0(\beta )\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset Q)$
via Equations (5.2) and (5.3). We now follow the proof of Part (b) to bound the second term: Using the factorization Equation (2.19) of
![]() $q_Q(\Gamma )$
, expanding the right-hand side as in Part (b) and replacing
$q_Q(\Gamma )$
, expanding the right-hand side as in Part (b) and replacing
![]() $\Gamma ^{(L)}$
and
$\Gamma ^{(L)}$
and
![]() $\Gamma ^{(R)}$
by clusterless up-right paths
$\Gamma ^{(R)}$
by clusterless up-right paths
![]() $\gamma ^{(L)}(\mathsf {X}(\Gamma ^{(L)}))$
and
$\gamma ^{(L)}(\mathsf {X}(\Gamma ^{(L)}))$
and
![]() $\gamma ^{(R)}(\mathsf {X}(\Gamma ^{(R)}))$
, we obtain an upper bound by
$\gamma ^{(R)}(\mathsf {X}(\Gamma ^{(R)}))$
, we obtain an upper bound by
![]() $C_1\mathcal {G}_{{\mathbb H}}(\mathsf {x} \;\big |\; \gamma \subset Q)$
, which by Equations (5.2) and (5.3) is bounded above by
$C_1\mathcal {G}_{{\mathbb H}}(\mathsf {x} \;\big |\; \gamma \subset Q)$
, which by Equations (5.2) and (5.3) is bounded above by
![]() $C_1'\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset Q)$
.
$C_1'\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset Q)$
.
For the lower bound in Equation (5.4), start instead from
![]() $\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset Q)$
. Bound it from above by
$\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset Q)$
. Bound it from above by
![]() $C_2\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset {\mathbb H})$
using Equation (5.3), and bound the latter by
$C_2\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset {\mathbb H})$
using Equation (5.3), and bound the latter by
![]() $C_2'\mathcal {G}_{{\mathbb H}}(\mathsf {x})$
using Equation (5.2). Now, use the inequality in Equation (5.11), expand the right-hand side exactly as in the proceeding display and again replace
$C_2'\mathcal {G}_{{\mathbb H}}(\mathsf {x})$
using Equation (5.2). Now, use the inequality in Equation (5.11), expand the right-hand side exactly as in the proceeding display and again replace
![]() $\Gamma ^{(L)}$
and
$\Gamma ^{(L)}$
and
![]() $\Gamma ^{(R)}$
by clusterless, up-right paths. Observe that the bound in Equation (5.12) holds with the right-hand side replaced with
$\Gamma ^{(R)}$
by clusterless, up-right paths. Observe that the bound in Equation (5.12) holds with the right-hand side replaced with
![]() $\mathcal {G}_Q(\mathsf {x})$
, since all animals on the left-hand side are contained in Q (and therefore the
$\mathcal {G}_Q(\mathsf {x})$
, since all animals on the left-hand side are contained in Q (and therefore the
![]() $q_{{\mathbb H}}$
-weights of these animals are equal to the
$q_{{\mathbb H}}$
-weights of these animals are equal to the
![]() $q_Q$
-weights). Following the remainder of the proof of Part (b), we obtain the lower bound in Equation (5.4).
$q_Q$
-weights). Following the remainder of the proof of Part (b), we obtain the lower bound in Equation (5.4).
Proof of Lemma 5.5.
For any
![]() ${\mathsf {u}},{\mathsf {v}} \in \mathbb {Z}^2$
and for any set of animals E, define the partition functions
${\mathsf {u}},{\mathsf {v}} \in \mathbb {Z}^2$
and for any set of animals E, define the partition functions
 $$ \begin{align} \mathcal{G}_D({\mathsf{u}} \to {\mathsf{v}}) := \sum_{ \substack{\gamma : {\mathsf{u}} \to {\mathsf{v}}\\ \gamma \subset D}} q_D(\gamma)\quad \text{and} \quad \mathcal{G}_D({\mathsf{u}} \to {\mathsf{v}} \;\big|\; E) := \sum_{ \Gamma \in \mathcal P_D( {\mathsf{u}} , {\mathsf{v}}) \cap E} q_D(\Gamma) . \end{align} $$
$$ \begin{align} \mathcal{G}_D({\mathsf{u}} \to {\mathsf{v}}) := \sum_{ \substack{\gamma : {\mathsf{u}} \to {\mathsf{v}}\\ \gamma \subset D}} q_D(\gamma)\quad \text{and} \quad \mathcal{G}_D({\mathsf{u}} \to {\mathsf{v}} \;\big|\; E) := \sum_{ \Gamma \in \mathcal P_D( {\mathsf{u}} , {\mathsf{v}}) \cap E} q_D(\Gamma) . \end{align} $$
We begin with three estimates pertaining to
![]() $\mathcal {G}_D({\mathsf {u}} \to {\mathsf {v}})$
.
$\mathcal {G}_D({\mathsf {u}} \to {\mathsf {v}})$
.
First, we have the analogue of Equation (2.26) for the modified animal weights: For all
![]() $\beta>0$
sufficiently large, there exists a constant
$\beta>0$
sufficiently large, there exists a constant
![]() $c':=c'(\beta )>0$
such that for all
$c':=c'(\beta )>0$
such that for all
![]() $k, N\geq 1$
,
$k, N\geq 1$
,
This is proved at the end of Appendix B.
Next, below Theorem 3 of [Reference Ioffe, Shlosman and Toninelli32], it is noted that Equation (5.2) in the current article actually holds if the end points of the contour are not on the line
![]() $\partial {\mathbb H}$
; that is, for any
$\partial {\mathbb H}$
; that is, for any
![]() ${\mathsf {u}},{\mathsf {v}} \in {\mathbb H}$
, we have
${\mathsf {u}},{\mathsf {v}} \in {\mathbb H}$
, we have
Similarly, in Sections 4.1 and 4.2 of [Reference Ioffe, Shlosman and Toninelli32], it is shown that contours with linear size and many cone points dominate
![]() $\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset {\mathbb H})$
, and the arguments there yield that the same is true when the end points of the contour are not on
$\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset {\mathbb H})$
, and the arguments there yield that the same is true when the end points of the contour are not on
![]() $\partial {\mathbb H}$
; that is, for any fixed
$\partial {\mathbb H}$
; that is, for any fixed
![]() $\epsilon \in (0,1)$
, there exist constants
$\epsilon \in (0,1)$
, there exist constants
![]() $\delta _0, \nu , c>0$
such that the following bounds hold uniformly over
$\delta _0, \nu , c>0$
such that the following bounds hold uniformly over
![]() $\beta>0$
sufficiently large, over
$\beta>0$
sufficiently large, over
![]() ${\mathsf {u}},{\mathsf {v}} \in {\mathbb H}$
satisfying
${\mathsf {u}},{\mathsf {v}} \in {\mathbb H}$
satisfying
![]() ${\mathsf {v}}\in {\mathsf {u}} +\mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
, and over
${\mathsf {v}}\in {\mathsf {u}} +\mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
, and over
![]() $r \geq 1+\epsilon $
:
$r \geq 1+\epsilon $
:
and
As a consequence of Remark 2.13, we have many cone points for animals
![]() $\Gamma $
as well:
$\Gamma $
as well:
Now, towards Equation (5.5), we only show
![]() $\mathcal {G}_{D}(\mathsf {x} \;\big |\; |\mathsf {Cpts}(\Gamma )|\geq 2 ,\, |\Gamma ^{(L)}|> K_{\epsilon }) \leq \epsilon \mathcal {G}_{D}(\mathsf {x})$
, as the analogous bound with
$\mathcal {G}_{D}(\mathsf {x} \;\big |\; |\mathsf {Cpts}(\Gamma )|\geq 2 ,\, |\Gamma ^{(L)}|> K_{\epsilon }) \leq \epsilon \mathcal {G}_{D}(\mathsf {x})$
, as the analogous bound with
![]() $\Gamma ^{(R)}$
instead of
$\Gamma ^{(R)}$
instead of
![]() $\Gamma ^{(L)}$
follows via the same argument. We begin by using Equations (2.18) and (2.19) to obtain the expansion
$\Gamma ^{(L)}$
follows via the same argument. We begin by using Equations (2.18) and (2.19) to obtain the expansion

The above double sum over n and irreducible animals is bounded by
![]() $\mathcal {G}_{{\mathbb H}}({\mathsf {u}} \to {\mathsf {v}})$
, which by Equation (5.19) is bounded by
$\mathcal {G}_{{\mathbb H}}({\mathsf {u}} \to {\mathsf {v}})$
, which by Equation (5.19) is bounded by
![]() $C_2(\beta )\mathcal {G}({\mathsf {u}} \to {\mathsf {v}} \;\big |\; \gamma \subset {\mathbb H})$
. It then suffices to show
$C_2(\beta )\mathcal {G}({\mathsf {u}} \to {\mathsf {v}} \;\big |\; \gamma \subset {\mathbb H})$
. It then suffices to show
where
![]() $C:= C(\beta )>0$
is a constant and
$C:= C(\beta )>0$
is a constant and
![]() $\bar {\delta }$
is as in Proposition 4.1. Indeed, substituting the bound in Equation (5.22) into Equation (5.21), using the exponential tail from Equation (5.18), and recalling
$\bar {\delta }$
is as in Proposition 4.1. Indeed, substituting the bound in Equation (5.22) into Equation (5.21), using the exponential tail from Equation (5.18), and recalling
![]() $\bar {\delta }< \nu _g/4$
yields
$\bar {\delta }< \nu _g/4$
yields
By Theorem 5.1, the right-hand side above is bounded by
![]() $\epsilon \mathcal {G}_{{\mathbb H}}(\mathsf {x})$
for
$\epsilon \mathcal {G}_{{\mathbb H}}(\mathsf {x})$
for
![]() $K_{\epsilon }:= K_{\epsilon , \beta }>0$
large enough.
$K_{\epsilon }:= K_{\epsilon , \beta }>0$
large enough.
To show Equation (5.22), we use the existence of cone points Equation (5.20) (for which we write a
![]() $1+o(1)$
, where the
$1+o(1)$
, where the
![]() $o(1)$
term vanishes as
$o(1)$
term vanishes as
![]() $\|{\mathsf {v}}-{\mathsf {u}}\|_1$
tends to infinity) and the weight factorization in Equation (2.27):
$\|{\mathsf {v}}-{\mathsf {u}}\|_1$
tends to infinity) and the weight factorization in Equation (2.27):

In the second-to-last line we used Equations (4.4) and (4.5) and then Proposition 4.1 to bound the
![]() $\mathcal {A}({\mathsf {u}}',{\mathsf {v}}')$
term, as well as
$\mathcal {A}({\mathsf {u}}',{\mathsf {v}}')$
term, as well as
![]() $\mathsf {h}_{\mathsf {x}} \cdot \mathsf {x} = \tau _{\beta }(\mathsf {x})$
. In the third line, we used the triangle inequality. Equation (5.22) then follows from the exponential tails of
$\mathsf {h}_{\mathsf {x}} \cdot \mathsf {x} = \tau _{\beta }(\mathsf {x})$
. In the third line, we used the triangle inequality. Equation (5.22) then follows from the exponential tails of
![]() $\Gamma ^{(L)}$
and
$\Gamma ^{(L)}$
and
![]() $\Gamma ^{(R)}$
in Equation (2.26), again recalling
$\Gamma ^{(R)}$
in Equation (2.26), again recalling
![]() $\bar {\delta }<\nu _g/4$
. This yields Equation (5.5). The proof of Equation (5.6) is identical, just replace the left-hand side of Equation (5.21) by
$\bar {\delta }<\nu _g/4$
. This yields Equation (5.5). The proof of Equation (5.6) is identical, just replace the left-hand side of Equation (5.21) by
![]() $\mathcal {G}(\mathsf {x} \;\big |\; |\mathsf {Cpts}(\Gamma )|\geq 2 , |\Gamma ^{(L)}|>K_{\epsilon }, \gamma \subset D)$
and then replace all modified weights
$\mathcal {G}(\mathsf {x} \;\big |\; |\mathsf {Cpts}(\Gamma )|\geq 2 , |\Gamma ^{(L)}|>K_{\epsilon }, \gamma \subset D)$
and then replace all modified weights
![]() $q_D$
by q.
$q_D$
by q.
5.3 Proof of Proposition 2.5
Fix a direction
![]() $\vec {u} \in \mathbb {S}^{d-1}$
, and let
$\vec {u} \in \mathbb {S}^{d-1}$
, and let
![]() $t_N^-(\vec {u}):= (N, y_N) \in \mathbb {Z}^2$
denote the lattice point whose x-coordinate is equal to N and is on or below the line
$t_N^-(\vec {u}):= (N, y_N) \in \mathbb {Z}^2$
denote the lattice point whose x-coordinate is equal to N and is on or below the line
![]() $\mathrm {span}(\vec {u})$
. Let
$\mathrm {span}(\vec {u})$
. Let
![]() $\mathsf {o}^*:= (1/2, 1/2)$
be the origin of the dual lattice
$\mathsf {o}^*:= (1/2, 1/2)$
be the origin of the dual lattice
![]() $(\mathbb {Z}^2)^*$
, and define
$(\mathbb {Z}^2)^*$
, and define
![]() $\mathsf {x}_N(\vec {u}):= t_N^-(\vec {u})+(-1/2,1/2) \in (\mathbb {Z}^2)^*$
. Then we have the formula
$\mathsf {x}_N(\vec {u}):= t_N^-(\vec {u})+(-1/2,1/2) \in (\mathbb {Z}^2)^*$
. Then we have the formula
where
![]() $\mathcal {I}_{N,M}$
denotes the strip
$\mathcal {I}_{N,M}$
denotes the strip
![]() $[0,N] \times [-M,M]$
. [Reference Dobrushin, Kotecký and Shlosman20, Theorem 4.16] implies that the surface tension
$[0,N] \times [-M,M]$
. [Reference Dobrushin, Kotecký and Shlosman20, Theorem 4.16] implies that the surface tension
![]() $\tau _{\beta }$
is equal to the surface tension of the model in
$\tau _{\beta }$
is equal to the surface tension of the model in
![]() $\mathcal {I}_{N,M}$
with the same (free) weights
$\mathcal {I}_{N,M}$
with the same (free) weights
![]() $q(\gamma )$
, that is:Footnote
10
$q(\gamma )$
, that is:Footnote
10
Thus, the proof will be finished if we can compare to exponential order the partition function with modified weights
![]() $\mathcal {G}_{\mathcal {I}_{N,M}}(\mathsf {x}_N(\vec {u}))$
and the partition function with free weights
$\mathcal {G}_{\mathcal {I}_{N,M}}(\mathsf {x}_N(\vec {u}))$
and the partition function with free weights
![]() $\mathcal {G}(\mathsf {x}_N(\vec {u})\;\big |\; \gamma \subset \mathcal {I}_{N,M})$
. The proof of this comparison is extremely similar to the proof of Equation (5.4) above, though much simpler, and so it is omitted for brevity’s sake.Footnote
11
$\mathcal {G}(\mathsf {x}_N(\vec {u})\;\big |\; \gamma \subset \mathcal {I}_{N,M})$
. The proof of this comparison is extremely similar to the proof of Equation (5.4) above, though much simpler, and so it is omitted for brevity’s sake.Footnote
11
5.4 Boundedness of the irreducible pieces
The main result of this subsection is Proposition 5.8, which states that each irreducible piece of
![]() $\Gamma $
has size bounded by
$\Gamma $
has size bounded by
![]() $(\log N)^2$
with high
$(\log N)^2$
with high
![]() $\mathbf {P}_D^{\mathsf {x}}(\cdot )-$
probability.
$\mathbf {P}_D^{\mathsf {x}}(\cdot )-$
probability.
When
![]() $\Gamma $
has at least two cone points, recall from Equation (2.17) that we write
$\Gamma $
has at least two cone points, recall from Equation (2.17) that we write
![]() $\Gamma ^{(1)}, \dots , \Gamma ^{(n)}$
to denote the irreducible components of
$\Gamma ^{(1)}, \dots , \Gamma ^{(n)}$
to denote the irreducible components of
![]() $\Gamma $
, where
$\Gamma $
, where
![]() $n := |\mathsf {Cpts}(\Gamma )|-1$
.
$n := |\mathsf {Cpts}(\Gamma )|-1$
.
Proposition 5.8. For
![]() $D=Q$
or
$D=Q$
or
![]() $D={\mathbb H}$
,
$D={\mathbb H}$
,
We will need the following two results on the asymptotic size of the partition functions of interest. Recall the notation for asymptotic relations set out at the start of Section 2.
Lemma 5.9. There exists some
![]() $C:= C(\beta )>0$
$C:= C(\beta )>0$
Proof. Similar to Equation (2.29), we have from Equation (4.4)
 $$ \begin{align*} e^{\tau_{\beta}(\mathsf{x})} \mathcal{G}(x \;\big|\; |\mathsf{Cpts}(\Gamma)| \geq 2) &= \sum_{\Gamma^{(L)} \in \mathsf{A_L}} \sum_{\Gamma^{(R)} \in \mathsf{A_R}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) \mathbb{P}_{\mathsf{X}(\Gamma^{(L)})}(H_{\mathsf{x}- \mathsf{X}(\Gamma^{(R)})} < \infty) \\ &\leq \Big(\sum_{\Gamma^{(L)} \in \mathsf{A_L}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) \Big) \Big( \sum_{\Gamma^{(R)} \in \mathsf{A_R}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) \Big) . \end{align*} $$
$$ \begin{align*} e^{\tau_{\beta}(\mathsf{x})} \mathcal{G}(x \;\big|\; |\mathsf{Cpts}(\Gamma)| \geq 2) &= \sum_{\Gamma^{(L)} \in \mathsf{A_L}} \sum_{\Gamma^{(R)} \in \mathsf{A_R}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) \mathbb{P}_{\mathsf{X}(\Gamma^{(L)})}(H_{\mathsf{x}- \mathsf{X}(\Gamma^{(R)})} < \infty) \\ &\leq \Big(\sum_{\Gamma^{(L)} \in \mathsf{A_L}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) \Big) \Big( \sum_{\Gamma^{(R)} \in \mathsf{A_R}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) \Big) . \end{align*} $$
The above summations are finite by Claim B.1. The lemma then follows from Equation (2.22).
We remark that a precise first-order asymptotic for
![]() $\mathcal {G}(\mathsf {x})$
is given in [Reference Dobrushin, Kotecký and Shlosman20, Eq. (4.12.3)]. The asymptotic can be proved by showing
$\mathcal {G}(\mathsf {x})$
is given in [Reference Dobrushin, Kotecký and Shlosman20, Eq. (4.12.3)]. The asymptotic can be proved by showing
![]() $\mathbb {P}_{\mathsf {X}(\Gamma ^{(L)})}(H_{\mathsf {x}- \mathsf {X}(\Gamma ^{(R)})} < \infty )$
is of order
$\mathbb {P}_{\mathsf {X}(\Gamma ^{(L)})}(H_{\mathsf {x}- \mathsf {X}(\Gamma ^{(R)})} < \infty )$
is of order
![]() $|\mathsf {x}|^{-1/2}$
via random walk estimates, similar to the proof of Theorem 4.2.
$|\mathsf {x}|^{-1/2}$
via random walk estimates, similar to the proof of Theorem 4.2.
Lemma 5.10. We have
where the implied constant depends on
![]() $\beta $
.
$\beta $
.
Proof. Item (1) of Theorem 4.2 shows that for any positive, fixed u and v in
![]() $\mathbb {N}$
(independent of N), we have
$\mathbb {N}$
(independent of N), we have
The lower-bound of Equation (5.24) then follows immediately from Proposition 4.1 and Equation (5.25).
It is not too hard to show a matching upper bound so that
![]() $\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset {\mathbb H}) \asymp e^{-\tau _{\beta }(\mathsf {x})} N^{-3/2}$
. Again, we do not pursue this here as the lower bound suffices.
$\mathcal {G}(\mathsf {x} \;\big |\; \gamma \subset {\mathbb H}) \asymp e^{-\tau _{\beta }(\mathsf {x})} N^{-3/2}$
. Again, we do not pursue this here as the lower bound suffices.
Proof of Proposition 5.8.
Define the set of animals
In Lemmas 5.5 and 5.7 and Remark 5.6, it was shown that this set of animals dominates
![]() $\mathbf {P}_D^{\mathsf {x}}$
, that is,
$\mathbf {P}_D^{\mathsf {x}}$
, that is,
Therefore, in light of Lemma 5.10, the proof of Proposition 5.8 will be complete upon showing
for any fixed K.
Define the sets of animals
Using the factorization of weights (Equation (2.18) and Equation (2.19) for
![]() $D=Q$
), we have
$D=Q$
), we have

For any
![]() $\mathsf {a}, \mathsf {b} \in {\mathbb H}$
, Equations (5.19) and (5.23) along with the trivial bound
$\mathsf {a}, \mathsf {b} \in {\mathbb H}$
, Equations (5.19) and (5.23) along with the trivial bound
![]() $ \mathcal {G}(\mathsf {a} \to \mathsf {b} \;\big |\; \gamma \subset {\mathbb H}) \leq \mathcal {G}(\mathsf {b}-\mathsf {a})\, $
implies
$ \mathcal {G}(\mathsf {a} \to \mathsf {b} \;\big |\; \gamma \subset {\mathbb H}) \leq \mathcal {G}(\mathsf {b}-\mathsf {a})\, $
implies
![]() $ \mathcal {G}_{{\mathbb H}}(\mathsf {a} \to \mathsf {b}) \leq C e^{\tau _{\beta }(\mathsf {b}-\mathsf {a})} $
for some constant
$ \mathcal {G}_{{\mathbb H}}(\mathsf {a} \to \mathsf {b}) \leq C e^{\tau _{\beta }(\mathsf {b}-\mathsf {a})} $
for some constant
![]() $C:=C(\beta )>0$
. Define the weights
$C:=C(\beta )>0$
. Define the weights
![]() $W_{{\mathbb H}}^{\mathsf {h}}(\Gamma ) := e^{\mathsf {h}\cdot \mathsf {X}(\Gamma )}q_{{\mathbb H}}(\Gamma )$
, under which
$W_{{\mathbb H}}^{\mathsf {h}}(\Gamma ) := e^{\mathsf {h}\cdot \mathsf {X}(\Gamma )}q_{{\mathbb H}}(\Gamma )$
, under which
![]() $\Gamma $
has exponential tails by Equation (5.18). Then
$\Gamma $
has exponential tails by Equation (5.18). Then

The exponential tails in Equation (5.18) implies both
 $$\begin{align*}\sum_{\substack{\Gamma^{(L)} \in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset D}} q_D(\Gamma^{(L)})e^{\tau_{\beta}(\mathsf{X}(\Gamma^{(L)}))} \quad \text{and} \quad \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset D}} q_D(\Gamma^{(R)})e^{\tau_{\beta}(\mathsf{X}(\Gamma^{(R)}))} \end{align*}$$
$$\begin{align*}\sum_{\substack{\Gamma^{(L)} \in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset D}} q_D(\Gamma^{(L)})e^{\tau_{\beta}(\mathsf{X}(\Gamma^{(L)}))} \quad \text{and} \quad \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset D}} q_D(\Gamma^{(R)})e^{\tau_{\beta}(\mathsf{X}(\Gamma^{(R)}))} \end{align*}$$
are bounded by a constant
![]() $C_K>0$
, while
$C_K>0$
, while
These bounds, the strong triangle inequality (Proposition 2.4) and the fact that there are at most
![]() $|0+\mathcal {Y}^\blacktriangleleft \cap \mathsf {x} +\mathcal {Y}^\blacktriangleright \cap \mathbb {Z}^2| \leq (N+1)^2$
possible values for
$|0+\mathcal {Y}^\blacktriangleleft \cap \mathsf {x} +\mathcal {Y}^\blacktriangleright \cap \mathbb {Z}^2| \leq (N+1)^2$
possible values for
![]() ${\mathsf {u}}$
and for
${\mathsf {u}}$
and for
![]() ${\mathsf {v}}$
yield
${\mathsf {v}}$
yield
for some constant
![]() $C^{\prime }_K>0$
. Thus, we have Equation (5.27), finishing the proof.
$C^{\prime }_K>0$
. Thus, we have Equation (5.27), finishing the proof.
5.5 Entropic repulsion of the animal
Fix any
![]() $\delta \in (0,1/4)$
, and define the rectangles
$\delta \in (0,1/4)$
, and define the rectangles
![]() $\mathfrak {R}_0(\delta ) := [N^{4\delta }, N- N^{4\delta }] \times [0, 2N^{\delta }]$
and
$\mathfrak {R}_0(\delta ) := [N^{4\delta }, N- N^{4\delta }] \times [0, 2N^{\delta }]$
and
![]() $\mathfrak {R}(\delta ) := [N^{4\delta }, N- N^{4\delta }] \times [0, N^{\delta }]$
. The main result in this subsection is the entropic repulsion result Proposition 5.11, which states that, under
$\mathfrak {R}(\delta ) := [N^{4\delta }, N- N^{4\delta }] \times [0, N^{\delta }]$
. The main result in this subsection is the entropic repulsion result Proposition 5.11, which states that, under
![]() $\mathbf {P}_D^{\mathsf {x}}(\cdot )$
, the cone points of
$\mathbf {P}_D^{\mathsf {x}}(\cdot )$
, the cone points of
![]() $\Gamma $
do not intersect
$\Gamma $
do not intersect
![]() $\mathfrak {R}(\delta )$
with probability tending to
$\mathfrak {R}(\delta )$
with probability tending to
![]() $1$
as
$1$
as
![]() $N \to \infty $
.
$N \to \infty $
.
Proposition 5.11. Let
![]() $D=Q$
or
$D=Q$
or
![]() $D={\mathbb H}$
. For any
$D={\mathbb H}$
. For any
![]() $\delta \in (0,1/4)$
,
$\delta \in (0,1/4)$
,
From the shape of
![]() $\mathcal {Y}^\blacktriangleleft $
and the
$\mathcal {Y}^\blacktriangleleft $
and the
![]() $(\log N)^2$
bound on each
$(\log N)^2$
bound on each
![]() $|\Gamma ^{(i)}|$
(Proposition 5.8), Proposition 5.11 is enough to deduce that, with high
$|\Gamma ^{(i)}|$
(Proposition 5.8), Proposition 5.11 is enough to deduce that, with high
![]() $\mathbf {P}_D^{\mathsf {x}}$
-probability, the entire animal (contour and clusters) stays away from
$\mathbf {P}_D^{\mathsf {x}}$
-probability, the entire animal (contour and clusters) stays away from
![]() $\partial {\mathbb H}$
in a slightly shorter rectangle (5.31). We will use this fact in the following subsection to couple
$\partial {\mathbb H}$
in a slightly shorter rectangle (5.31). We will use this fact in the following subsection to couple
![]() $\mathsf {Cpts}(\Gamma )$
with the random walk. We begin with an analogous result in the free Ising polymer case, where we can exploit the connection with the random walk and associated estimates, à la Proposition 4.1.
$\mathsf {Cpts}(\Gamma )$
with the random walk. We begin with an analogous result in the free Ising polymer case, where we can exploit the connection with the random walk and associated estimates, à la Proposition 4.1.
Lemma 5.12. Let
![]() $D=Q$
or
$D=Q$
or
![]() $D={\mathbb H}$
. For any
$D={\mathbb H}$
. For any
![]() $\delta \in (0,1/8)$
,
$\delta \in (0,1/8)$
,
Proof. In light of Proposition 5.8 and the shape of
![]() $\mathcal {Y}^\blacktriangleleft $
, it suffices to show that the cone points of
$\mathcal {Y}^\blacktriangleleft $
, it suffices to show that the cone points of
![]() $\Gamma $
avoid the larger rectangle
$\Gamma $
avoid the larger rectangle
![]() $\mathfrak {R}_0(\delta )$
with high probability, that is,
$\mathfrak {R}_0(\delta )$
with high probability, that is,
Recall
![]() $\mathcal P_D^{\mathrm {cp},\mathrm {len}}(\mathsf {x},K)$
from Equation (5.26), and observe that Lemmas 5.5 and 5.7 and Remark 5.6 imply
$\mathcal P_D^{\mathrm {cp},\mathrm {len}}(\mathsf {x},K)$
from Equation (5.26), and observe that Lemmas 5.5 and 5.7 and Remark 5.6 imply
From the previous two displays, the proof of the Lemma will be complete upon showing
Now, fix
![]() $K \geq 1$
and N large compared to K. Recall the sets
$K \geq 1$
and N large compared to K. Recall the sets
![]() $\mathsf {A}_{\mathsf {L},K}$
and
$\mathsf {A}_{\mathsf {L},K}$
and
![]() $\mathsf {A}_{\mathsf {R},K}$
from Equation (5.28). Using Equation (2.29), we have
$\mathsf {A}_{\mathsf {R},K}$
from Equation (5.28). Using Equation (2.29), we have
 $$ \begin{align*} &\mathbf{P}^{\mathsf{x}}\big(\mathcal P_D^{\mathrm{cp},\mathrm{len}}(\mathsf{x}, K) , E_{\delta} \;\big|\; \gamma \subset D \big) \\ &\quad\leq \frac{1}{\mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset D) } e^{-\tau_{\beta}(\mathsf{x})} \sum_{\substack{\Gamma^{(L)}\in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) \ \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) \ \mathcal{A}\big( \mathsf{X}(\Gamma^{(L)}), \mathsf{x}- \mathsf{X}(\Gamma^{(R)}); E_{\delta} \big). \end{align*} $$
$$ \begin{align*} &\mathbf{P}^{\mathsf{x}}\big(\mathcal P_D^{\mathrm{cp},\mathrm{len}}(\mathsf{x}, K) , E_{\delta} \;\big|\; \gamma \subset D \big) \\ &\quad\leq \frac{1}{\mathcal{G}(\mathsf{x} \;\big|\; \gamma \subset D) } e^{-\tau_{\beta}(\mathsf{x})} \sum_{\substack{\Gamma^{(L)}\in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) \ \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) \ \mathcal{A}\big( \mathsf{X}(\Gamma^{(L)}), \mathsf{x}- \mathsf{X}(\Gamma^{(R)}); E_{\delta} \big). \end{align*} $$
Using Equation (5.3), Equation (4.5) and Proposition 4.1, we may bound from above the right-hand side of the previous display
 $$ \begin{align} &C^{-1} \sum_{\substack{\Gamma^{(L)} \in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) e^{\overline{\delta} \beta \|\mathsf{X}(\Gamma^{(L)})\|_1} \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) e^{\overline{\delta} \beta \|\mathsf{X}(\Gamma^{(R)})\|_1} \ \frac{\mathcal{A}^+\big( \mathsf{X}(\Gamma^{(L)}), \mathsf{x}- \mathsf{X}(\Gamma^{(R)}); E_{\delta} \big)}{\mathbb{P}_{X(\Gamma^{(L)})}(H_{\mathsf{x}-\mathsf{X}(\Gamma^{(R)})}> H_{{\mathbb H}_{-}})} \nonumber \\& \quad = C^{-1} \sum_{\substack{\Gamma^{(L)} \in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) e^{\overline{\delta} \beta \|\mathsf{X}(\Gamma^{(L)})\|_1} \ \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) e^{\overline{\delta} \beta \|\mathsf{X}(\Gamma^{(R)})\|_1} \nonumber \\& \qquad \times \mathbb{P}_{\mathsf{X}(\Gamma^{(L)})}\big( \exists i < H_{\mathsf{x} -\mathsf{X}(\Gamma^{(R)})} : \mathsf{S}_1(i) \in [N^{4\delta}, N-N^{4\delta}] ,\, \mathsf{S}_2(i) \in [0, 2N^{\delta}] \;\big|\; H_{\mathsf{x}-\mathsf{X}(\Gamma^{(R)})} < H_{{\mathbb H}_{-}}\big). \end{align} $$
$$ \begin{align} &C^{-1} \sum_{\substack{\Gamma^{(L)} \in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) e^{\overline{\delta} \beta \|\mathsf{X}(\Gamma^{(L)})\|_1} \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) e^{\overline{\delta} \beta \|\mathsf{X}(\Gamma^{(R)})\|_1} \ \frac{\mathcal{A}^+\big( \mathsf{X}(\Gamma^{(L)}), \mathsf{x}- \mathsf{X}(\Gamma^{(R)}); E_{\delta} \big)}{\mathbb{P}_{X(\Gamma^{(L)})}(H_{\mathsf{x}-\mathsf{X}(\Gamma^{(R)})}> H_{{\mathbb H}_{-}})} \nonumber \\& \quad = C^{-1} \sum_{\substack{\Gamma^{(L)} \in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) e^{\overline{\delta} \beta \|\mathsf{X}(\Gamma^{(L)})\|_1} \ \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset D}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) e^{\overline{\delta} \beta \|\mathsf{X}(\Gamma^{(R)})\|_1} \nonumber \\& \qquad \times \mathbb{P}_{\mathsf{X}(\Gamma^{(L)})}\big( \exists i < H_{\mathsf{x} -\mathsf{X}(\Gamma^{(R)})} : \mathsf{S}_1(i) \in [N^{4\delta}, N-N^{4\delta}] ,\, \mathsf{S}_2(i) \in [0, 2N^{\delta}] \;\big|\; H_{\mathsf{x}-\mathsf{X}(\Gamma^{(R)})} < H_{{\mathbb H}_{-}}\big). \end{align} $$
The ballot-type result Theorem 4.2(1) and standard random walk estimates yield
uniformly over
![]() $\Gamma ^{(L)}\in \mathsf {A}_{\mathsf L, K}$
and
$\Gamma ^{(L)}\in \mathsf {A}_{\mathsf L, K}$
and
![]() $\Gamma ^{(R)} \in \mathsf {A}_{\mathsf R, K}$
. On the other hand, the exponential tails in Equation (2.26) and the relation
$\Gamma ^{(R)} \in \mathsf {A}_{\mathsf R, K}$
. On the other hand, the exponential tails in Equation (2.26) and the relation
![]() $4\overline {\delta } < \nu _g$
yield
$4\overline {\delta } < \nu _g$
yield
 $$\begin{align*}C^{-1} \Big(\sum_{\substack{\Gamma^{(L)} \in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset Q}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) e^{\overline{\delta} \beta \left\Vert \mathsf{X}(\Gamma^{(L)}) \right\Vert{}_1} \Big) \Big( \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset Q}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) e^{\overline{\delta} \beta \left\Vert \mathsf{X}(\Gamma^{(R)}) \right\Vert{}_1} \Big) \leq C_K, \end{align*}$$
$$\begin{align*}C^{-1} \Big(\sum_{\substack{\Gamma^{(L)} \in \mathsf{A}_{\mathsf{L},K} \\ \gamma^{(L)} \subset Q}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(L)}) e^{\overline{\delta} \beta \left\Vert \mathsf{X}(\Gamma^{(L)}) \right\Vert{}_1} \Big) \Big( \sum_{\substack{\Gamma^{(R)} \in \mathsf{A}_{\mathsf{R},K} \\ \gamma^{(R)} \subset Q}} \mathbb{P}^{\mathsf{h}_{\mathsf{x}}}(\Gamma^{(R)}) e^{\overline{\delta} \beta \left\Vert \mathsf{X}(\Gamma^{(R)}) \right\Vert{}_1} \Big) \leq C_K, \end{align*}$$
for some constant
![]() $C_K:= C_{K,\beta }> 0$
. Taking the limit as N, then
$C_K:= C_{K,\beta }> 0$
. Taking the limit as N, then
![]() $K\to \infty $
in Equation (5.30) yields Equation (5.29).
$K\to \infty $
in Equation (5.30) yields Equation (5.29).
5.6 Coupling with the effective random walk
Let
![]() $D=Q$
or
$D=Q$
or
![]() $D={\mathbb H}$
, and fix
$D={\mathbb H}$
, and fix
![]() $\delta \in (0,1/8)$
. The entropic repulsion result, Proposition 5.11, sets the stage for a coupling between the cone points of
$\delta \in (0,1/8)$
. The entropic repulsion result, Proposition 5.11, sets the stage for a coupling between the cone points of
![]() $\Gamma $
lying in the strip
$\Gamma $
lying in the strip
![]() $\mathcal {S}_{N^{4\delta }, N-N^{4\delta }}:= [N^{4\delta }, N-N^{4\delta }]\times [0,\infty )$
and the random walk
$\mathcal {S}_{N^{4\delta }, N-N^{4\delta }}:= [N^{4\delta }, N-N^{4\delta }]\times [0,\infty )$
and the random walk
![]() $\mathsf {S}(\cdot )$
defined in Section 4.1. Before defining this coupling explicitly, we set up some notation.
$\mathsf {S}(\cdot )$
defined in Section 4.1. Before defining this coupling explicitly, we set up some notation.
For
![]() ${\mathsf {u}},{\mathsf {v}} \in \mathbb {Z}^2$
, define
${\mathsf {u}},{\mathsf {v}} \in \mathbb {Z}^2$
, define
 $$ \begin{align*} &\mathcal P_{D,*}^{\delta}({\mathsf{u}}, {\mathsf{v}}) \\ &:= \Big\{ \Gamma \in \mathcal P_D({\mathsf{u}},{\mathsf{v}}) : |\mathsf{Cpts}(\Gamma)| \geq 2 ,\, \max_{i\in \{L,1,\dots, |\mathsf{Cpts}(\Gamma)|-1,R\}} |\Gamma^{(i)}| < (\log N)^2 ,\, \mathsf{Cpts}(\Gamma) \cap \mathfrak{R}(\delta) = \emptyset \Big\}, \end{align*} $$
$$ \begin{align*} &\mathcal P_{D,*}^{\delta}({\mathsf{u}}, {\mathsf{v}}) \\ &:= \Big\{ \Gamma \in \mathcal P_D({\mathsf{u}},{\mathsf{v}}) : |\mathsf{Cpts}(\Gamma)| \geq 2 ,\, \max_{i\in \{L,1,\dots, |\mathsf{Cpts}(\Gamma)|-1,R\}} |\Gamma^{(i)}| < (\log N)^2 ,\, \mathsf{Cpts}(\Gamma) \cap \mathfrak{R}(\delta) = \emptyset \Big\}, \end{align*} $$
where, as usual, we write
![]() $\mathcal P_{D,*}^{\delta }(\mathsf {x}) := \mathcal P_{D,*}^{\delta }(0,\mathsf {x})$
. Observe that the last two conditions in the definition, along with the shape of
$\mathcal P_{D,*}^{\delta }(\mathsf {x}) := \mathcal P_{D,*}^{\delta }(0,\mathsf {x})$
. Observe that the last two conditions in the definition, along with the shape of
![]() $\mathcal {Y}^\blacktriangleleft $
, ensure that
$\mathcal {Y}^\blacktriangleleft $
, ensure that
where the intersection pertains to both contour and clusters of
![]() $\Gamma $
. From Lemma 5.7 and Propositions 5.8 and 5.11, we know that
$\Gamma $
. From Lemma 5.7 and Propositions 5.8 and 5.11, we know that
Define the measure
For
![]() $\Gamma \in \mathcal P_{D,*}^{\delta }$
, let
$\Gamma \in \mathcal P_{D,*}^{\delta }$
, let
![]() $\zeta ^{(\mathsf {L}*)}$
and
$\zeta ^{(\mathsf {L}*)}$
and
![]() $\zeta ^{(\mathsf {R}*)}$
denote the leftmost and rightmost cone points of
$\zeta ^{(\mathsf {R}*)}$
denote the leftmost and rightmost cone points of
![]() $\Gamma $
in
$\Gamma $
in
![]() $\mathcal {S}_{N^{4\delta }, N-N^{4\delta }}$
, respectively. Note that, since
$\mathcal {S}_{N^{4\delta }, N-N^{4\delta }}$
, respectively. Note that, since
![]() $\Gamma \in \mathcal P_{D,*}^{\delta }$
, we have
$\Gamma \in \mathcal P_{D,*}^{\delta }$
, we have
and
Let
![]() $\Gamma ^{(\mathsf {L}*)} \in \mathcal P_{D,*}^{\delta }(0,\zeta ^{(\mathsf {L}*)})$
denote the portion of
$\Gamma ^{(\mathsf {L}*)} \in \mathcal P_{D,*}^{\delta }(0,\zeta ^{(\mathsf {L}*)})$
denote the portion of
![]() $\Gamma $
connecting
$\Gamma $
connecting
![]() $0$
to
$0$
to
![]() $\zeta ^{(\mathsf {L}*)}$
(including all clusters connected to
$\zeta ^{(\mathsf {L}*)}$
(including all clusters connected to
![]() $\gamma ^{(\mathsf {L}*)}$
). Similarly, define
$\gamma ^{(\mathsf {L}*)}$
). Similarly, define
![]() $\Gamma ^{(\mathsf {R}*)}\in \mathcal P_{D,*}^{\delta }(\zeta ^{(\mathsf {R}*)},\mathsf {x})$
as the portion of
$\Gamma ^{(\mathsf {R}*)}\in \mathcal P_{D,*}^{\delta }(\zeta ^{(\mathsf {R}*)},\mathsf {x})$
as the portion of
![]() $\Gamma $
connecting
$\Gamma $
connecting
![]() $\zeta _{\mathsf {R}*}$
to
$\zeta _{\mathsf {R}*}$
to
![]() $\mathsf {x}$
, and define
$\mathsf {x}$
, and define
![]() $\Gamma ^* \in \mathcal P_{D,*}^{\delta }(\zeta ^{(\mathsf {L}*)},\zeta ^{(\mathsf {R}*)})$
as the portion of
$\Gamma ^* \in \mathcal P_{D,*}^{\delta }(\zeta ^{(\mathsf {L}*)},\zeta ^{(\mathsf {R}*)})$
as the portion of
![]() $\Gamma $
connecting
$\Gamma $
connecting
![]() $\zeta _{\mathsf {L}*}$
to
$\zeta _{\mathsf {L}*}$
to
![]() $\zeta _{\mathsf {R}*}$
so that
$\zeta _{\mathsf {R}*}$
so that
Note that
![]() $\Gamma ^*$
is a concatenation of irreducible animals, each of which are completely contained in Q by Equation (5.31). Therefore, from Equation (2.18), we have
$\Gamma ^*$
is a concatenation of irreducible animals, each of which are completely contained in Q by Equation (5.31). Therefore, from Equation (2.18), we have
Crucially, the
![]() $q_D$
-weight of
$q_D$
-weight of
![]() $\Gamma ^*$
is equal to its (free) q-weight.
$\Gamma ^*$
is equal to its (free) q-weight.
For any fixed
![]() $\overline {\zeta }^{(\mathsf {L}*)}$
and
$\overline {\zeta }^{(\mathsf {L}*)}$
and
![]() $\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34), respectively, and for any fixed animals
$\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34), respectively, and for any fixed animals
![]() $\overline {\Gamma }^{(\mathsf {L}*)} \in \mathcal P_D(0, \overline {\zeta }^{(\mathsf {L}*)})$
and
$\overline {\Gamma }^{(\mathsf {L}*)} \in \mathcal P_D(0, \overline {\zeta }^{(\mathsf {L}*)})$
and
![]() $\overline {\Gamma }^{(\mathsf {R}*)} \in \mathcal P_D(\overline {\zeta }^{(\mathsf {R}*)}, \mathsf {x})$
, consider the measure
$\overline {\Gamma }^{(\mathsf {R}*)} \in \mathcal P_D(\overline {\zeta }^{(\mathsf {R}*)}, \mathsf {x})$
, consider the measure
which describes the conditional law of
![]() $\Gamma ^*$
and defines a probability measure on the following set of animals:
$\Gamma ^*$
and defines a probability measure on the following set of animals:
Note that, for fixed
![]() $\overline {\zeta }^{(\mathsf {L}*)}$
and
$\overline {\zeta }^{(\mathsf {L}*)}$
and
![]() $\overline {\zeta }^{(\mathsf {R}*)}$
, the choice of
$\overline {\zeta }^{(\mathsf {R}*)}$
, the choice of
![]() $\bar {\Gamma }^{(\mathsf {L}*)}$
and
$\bar {\Gamma }^{(\mathsf {L}*)}$
and
![]() $\bar {\Gamma }^{(\mathsf {R}*)}$
does not change
$\bar {\Gamma }^{(\mathsf {R}*)}$
does not change
![]() $\mathbf {P}_{D,*}^{\overline {\zeta }^{(\mathsf {L}*)},\overline {\zeta }^{(\mathsf {R}*)}}(\cdot )$
. In particular, we have the formula
$\mathbf {P}_{D,*}^{\overline {\zeta }^{(\mathsf {L}*)},\overline {\zeta }^{(\mathsf {R}*)}}(\cdot )$
. In particular, we have the formula
 $$ \begin{align} \mathbf{P}_{D,*}^{\overline{\zeta}^{(\mathsf{L}*)},\overline{\zeta}^{(\mathsf{R}*)}}(E) = \sum_{\Gamma \in E \cap \mathcal P_{D,\delta}^{*,A}(\overline{\zeta}^{(\mathsf{L}*)},\overline{\zeta}^{(\mathsf{R}*)}) } q(\Gamma) \ \ / \ \sum_{\Gamma \in \mathcal P_{D,\delta}^{*,A}(\overline{\zeta}^{(\mathsf{L}*)},\overline{\zeta}^{(\mathsf{R}*)})} q(\Gamma) . \end{align} $$
$$ \begin{align} \mathbf{P}_{D,*}^{\overline{\zeta}^{(\mathsf{L}*)},\overline{\zeta}^{(\mathsf{R}*)}}(E) = \sum_{\Gamma \in E \cap \mathcal P_{D,\delta}^{*,A}(\overline{\zeta}^{(\mathsf{L}*)},\overline{\zeta}^{(\mathsf{R}*)}) } q(\Gamma) \ \ / \ \sum_{\Gamma \in \mathcal P_{D,\delta}^{*,A}(\overline{\zeta}^{(\mathsf{L}*)},\overline{\zeta}^{(\mathsf{R}*)})} q(\Gamma) . \end{align} $$
Again, note that only the free weight appears in the above formula.
Lastly, for any
![]() $c>0$
, define the half-space
$c>0$
, define the half-space
![]() ${\mathbb H}_c := \{(x,y) \in \mathbb {R}^2 : y \geq c\}$
.
${\mathbb H}_c := \{(x,y) \in \mathbb {R}^2 : y \geq c\}$
.
Proposition 5.13. Let
![]() $D=Q$
or
$D=Q$
or
![]() $D={\mathbb H}$
. There exists
$D={\mathbb H}$
. There exists
![]() $\nu _2>0$
such that for all
$\nu _2>0$
such that for all
![]() $N\in \mathbb {N}$
, for all
$N\in \mathbb {N}$
, for all
![]() $\beta>0$
sufficiently large, and for all
$\beta>0$
sufficiently large, and for all
![]() $\overline {\zeta }^{(\mathsf {L}*)}$
and
$\overline {\zeta }^{(\mathsf {L}*)}$
and
![]() $\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34), respectively, if we let
$\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34), respectively, if we let
![]() $T= H_{\overline {\zeta }^{(\mathsf {R}*)}}$
and view
$T= H_{\overline {\zeta }^{(\mathsf {R}*)}}$
and view
![]() $\mathsf {Cpts}(\Gamma ^*)$
as an ordered tuple (see Equation (2.20)),
$\mathsf {Cpts}(\Gamma ^*)$
as an ordered tuple (see Equation (2.20)),
for some constant
![]() $C:=C(\beta )>0$
.
$C:=C(\beta )>0$
.
Proof. Fix
![]() $\overline {\zeta }^{(\mathsf {L}*)}$
and
$\overline {\zeta }^{(\mathsf {L}*)}$
and
![]() $\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34), respectively. Recall
$\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34), respectively. Recall
![]() $\mathsf {V}_{{\mathsf {u}},{\mathsf {v}}}^+$
from Equation (4.3), and define
$\mathsf {V}_{{\mathsf {u}},{\mathsf {v}}}^+$
from Equation (4.3), and define
 $$ \begin{align*} \mathsf{V}_{\overline\zeta^{(\mathsf{L}*)}, \overline\zeta^{(\mathsf{R}*)}}^{\delta} :=& \Big \{ (\vec v_1, \dots, \vec v_n) \in \mathsf{V}_{\overline\zeta^{(\mathsf{L}*)}, \overline\zeta^{(\mathsf{R}*)}}^+ : n \geq 1, \ \left\Vert \vec v_k \right\Vert{}_1 \leq (\log N)^2 \\&\quad \text{ and } \overline{\zeta}^{(\mathsf{L}*)} + \sum_{i=1}^k \vec v_i \geq N^{\delta} ~\forall k \in [1, n] \Big \}, \\\mathsf{A}_{\overline\zeta^{(\mathsf{L}*)}, \overline\zeta^{(\mathsf{R}*)}}^{\delta} :=& \Big \{ (\overline \Gamma^{(1)}, \dots, \overline \Gamma^{(n)}) \in \mathsf{A}^n : \ n \geq 1, \ \big( X(\overline \Gamma^{(1)}), \dots, X(\overline \Gamma^{(n)}) \big) \in \mathsf{V}_{\overline\zeta^{(\mathsf{L}*)}, \overline\zeta^{(\mathsf{R}*)}}^{\delta} \Big \}. \end{align*} $$
$$ \begin{align*} \mathsf{V}_{\overline\zeta^{(\mathsf{L}*)}, \overline\zeta^{(\mathsf{R}*)}}^{\delta} :=& \Big \{ (\vec v_1, \dots, \vec v_n) \in \mathsf{V}_{\overline\zeta^{(\mathsf{L}*)}, \overline\zeta^{(\mathsf{R}*)}}^+ : n \geq 1, \ \left\Vert \vec v_k \right\Vert{}_1 \leq (\log N)^2 \\&\quad \text{ and } \overline{\zeta}^{(\mathsf{L}*)} + \sum_{i=1}^k \vec v_i \geq N^{\delta} ~\forall k \in [1, n] \Big \}, \\\mathsf{A}_{\overline\zeta^{(\mathsf{L}*)}, \overline\zeta^{(\mathsf{R}*)}}^{\delta} :=& \Big \{ (\overline \Gamma^{(1)}, \dots, \overline \Gamma^{(n)}) \in \mathsf{A}^n : \ n \geq 1, \ \big( X(\overline \Gamma^{(1)}), \dots, X(\overline \Gamma^{(n)}) \big) \in \mathsf{V}_{\overline\zeta^{(\mathsf{L}*)}, \overline\zeta^{(\mathsf{R}*)}}^{\delta} \Big \}. \end{align*} $$
Note that the sets
![]() $\mathsf {A}_{\overline \zeta ^{(\mathsf {L}*)}, \overline \zeta ^{(\mathsf {R}*)}}^{\delta }$
and
$\mathsf {A}_{\overline \zeta ^{(\mathsf {L}*)}, \overline \zeta ^{(\mathsf {R}*)}}^{\delta }$
and
![]() $\mathcal P_{D,\delta }^{*,\mathsf {A}}(\overline \zeta ^{(\mathsf {L}*)}, \overline \zeta ^{(\mathsf {R}*)})$
are in bijection with one another, since for any
$\mathcal P_{D,\delta }^{*,\mathsf {A}}(\overline \zeta ^{(\mathsf {L}*)}, \overline \zeta ^{(\mathsf {R}*)})$
are in bijection with one another, since for any
![]() $(\overline \Gamma ^{(1)}, \dots , \overline \Gamma ^{(n)}) \in \mathsf {A}_{\overline \zeta ^{(\mathsf {L}*)}, \overline \zeta ^{(\mathsf {R}*)}}^{\delta }$
, the animal
$(\overline \Gamma ^{(1)}, \dots , \overline \Gamma ^{(n)}) \in \mathsf {A}_{\overline \zeta ^{(\mathsf {L}*)}, \overline \zeta ^{(\mathsf {R}*)}}^{\delta }$
, the animal
![]() $\overline \Gamma ^{(1)} \circ \cdots \circ \overline \Gamma ^{(n)}$
is in
$\overline \Gamma ^{(1)} \circ \cdots \circ \overline \Gamma ^{(n)}$
is in
![]() $\mathcal P_{D,\delta }^{*,\mathsf {A}}(\overline \zeta ^{(\mathsf {L}*)}, \overline \zeta ^{(\mathsf {R}*)})$
. The above observations, along with Equation (2.27) (where we substitute
$\mathcal P_{D,\delta }^{*,\mathsf {A}}(\overline \zeta ^{(\mathsf {L}*)}, \overline \zeta ^{(\mathsf {R}*)})$
. The above observations, along with Equation (2.27) (where we substitute
![]() $\mathsf {y} := \mathsf {x}$
and use that
$\mathsf {y} := \mathsf {x}$
and use that
![]() $\mathbb {P}^{\mathsf {h}_{\mathsf {x}}}(\Gamma ^{(i)})=e^{\mathsf {h}_{\mathsf {x}} \cdot \mathsf {X}(\Gamma ^{(i)})}q(\Gamma ^{(i)})$
) yields the following:
$\mathbb {P}^{\mathsf {h}_{\mathsf {x}}}(\Gamma ^{(i)})=e^{\mathsf {h}_{\mathsf {x}} \cdot \mathsf {X}(\Gamma ^{(i)})}q(\Gamma ^{(i)})$
) yields the following:

where we define the random walk event
A nearly identical calculation but for the numerator of the right-hand side of Equation (5.36) yields the following: For any
![]() $n\geq 1$
and for any
$n\geq 1$
and for any
![]() $(\vec {v}_1, \dots , \vec {v}_n) \in (\mathbb {Z}^2)^n$
,
$(\vec {v}_1, \dots , \vec {v}_n) \in (\mathbb {Z}^2)^n$
,

Thus, the law of
![]() $\mathsf {Cpts}(\overline \Gamma )$
under
$\mathsf {Cpts}(\overline \Gamma )$
under
![]() $\mathbf {P}_{D,*}^{\overline {\zeta }^{(\mathsf {L}*)},\overline {\zeta }^{(\mathsf {R}*)}}$
is equal to the law of
$\mathbf {P}_{D,*}^{\overline {\zeta }^{(\mathsf {L}*)},\overline {\zeta }^{(\mathsf {R}*)}}$
is equal to the law of
![]() $(\mathsf {S}(i))_{i=0}^{H_{\overline {\zeta }^{(\mathsf {R}*)}}}$
under
$(\mathsf {S}(i))_{i=0}^{H_{\overline {\zeta }^{(\mathsf {R}*)}}}$
under
![]() $\mathbb {P}_{\overline {\zeta }^{(\mathsf {L}*)}}(\cdot \;\big |\; E_{\delta }^{*})$
. Now, observe that Theorem 4.2 along with shift invariance of the random walk (to shift the walk downwards by
$\mathbb {P}_{\overline {\zeta }^{(\mathsf {L}*)}}(\cdot \;\big |\; E_{\delta }^{*})$
. Now, observe that Theorem 4.2 along with shift invariance of the random walk (to shift the walk downwards by
![]() $N^{\delta }$
) give the following estimate, which holds uniformly over our ranges of
$N^{\delta }$
) give the following estimate, which holds uniformly over our ranges of
![]() $\overline {\zeta }^{(\mathsf {L}*)}$
and
$\overline {\zeta }^{(\mathsf {L}*)}$
and
![]() $\overline {\zeta }^{(\mathsf {R}*)}$
:
$\overline {\zeta }^{(\mathsf {R}*)}$
:
Exponential tails of the random walk increments (4.2) and the above estimate then imply that
for some constant
![]() $\nu>0$
independent of
$\nu>0$
independent of
![]() $\beta $
and a constant
$\beta $
and a constant
![]() $C:=C(\beta )>0$
, finishing the proof.
$C:=C(\beta )>0$
, finishing the proof.
5.7 Proof of Theorem 2.8
We see from the shape of the cone
![]() $\mathcal {Y}^\blacktriangleleft $
and the restriction on
$\mathcal {Y}^\blacktriangleleft $
and the restriction on
![]() $|\Gamma ^{(i)}|$
that for all
$|\Gamma ^{(i)}|$
that for all
![]() $\Gamma \in \mathcal P_{D,\delta }^*(\mathsf {x})$
,
$\Gamma \in \mathcal P_{D,\delta }^*(\mathsf {x})$
,
 $$\begin{align*}\frac{1}{ \sqrt N}\max_{x\in [0,N]} |\overline\gamma(x) - \underline\gamma(x)| \leq \frac{2(\log N)^2}{ \sqrt N}. \end{align*}$$
$$\begin{align*}\frac{1}{ \sqrt N}\max_{x\in [0,N]} |\overline\gamma(x) - \underline\gamma(x)| \leq \frac{2(\log N)^2}{ \sqrt N}. \end{align*}$$
In addition to Equation (5.32), this tells us that it suffices to show
![]() $\mathfrak {J}_N(\mathsf {Cpts}(\Gamma ))$
under
$\mathfrak {J}_N(\mathsf {Cpts}(\Gamma ))$
under
![]() $\mathbf {P}_{D,*}^{\mathsf {x}}(\cdot )$
converges weakly to a Brownian excursion. Now, we have the following on
$\mathbf {P}_{D,*}^{\mathsf {x}}(\cdot )$
converges weakly to a Brownian excursion. Now, we have the following on
![]() $\mathcal P_{D,\delta }^*$
:
$\mathcal P_{D,\delta }^*$
:
as well as the bounds in Equations (5.33) and (5.34). These bounds imply that
![]() $\Gamma ^{(\mathsf {L}*)}$
and
$\Gamma ^{(\mathsf {L}*)}$
and
![]() $\Gamma ^{(\mathsf {R}*)}$
do not impact the diffusive scaling limit of
$\Gamma ^{(\mathsf {R}*)}$
do not impact the diffusive scaling limit of
![]() $\mathsf {Cpts}(\Gamma )$
. Thus, recalling the linear interpolation
$\mathsf {Cpts}(\Gamma )$
. Thus, recalling the linear interpolation
![]() $\mathfrak {J}_N$
from Equation (4.8), it suffices to show
$\mathfrak {J}_N$
from Equation (4.8), it suffices to show
![]() $ \mathfrak {J}_N(\mathsf {Cpts}(\Gamma ^*)) $
under law
$ \mathfrak {J}_N(\mathsf {Cpts}(\Gamma ^*)) $
under law
![]() $\mathbf {P}_{D,*}^{\overline {\zeta }^{(\mathsf {L}*)},\overline {\zeta }^{(\mathsf {R}*)}}(\cdot )$
converges weakly to a Brownian excursion, uniformly in
$\mathbf {P}_{D,*}^{\overline {\zeta }^{(\mathsf {L}*)},\overline {\zeta }^{(\mathsf {R}*)}}(\cdot )$
converges weakly to a Brownian excursion, uniformly in
![]() $\overline {\zeta }^{(\mathsf {L}*)}$
and
$\overline {\zeta }^{(\mathsf {L}*)}$
and
![]() $\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34). But this is an immediate consequence of Proposition 5.13, the shift invariance of the random walk and Theorem 4.3.
$\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34). But this is an immediate consequence of Proposition 5.13, the shift invariance of the random walk and Theorem 4.3.
This concludes the proof of Theorem 2.8 and hence also Theorem 1.2.
6 Random walks in a half-space
This section is devoted to the proofs of Theorems 4.2 and 4.3 via the analysis of random walks in a half-space.
As mentioned after Theorem 4.3, we seek to extend many of the results from [Reference Denisov and Wachtel17] and [Reference Duraj and Wachtel23]. These papers are written for random walks whose coordinates are uncorrelated. Though
![]() $\mathsf {S}(\cdot )$
may not have this property, we can obtain such a random walk by rotating – this is done in Section 6.3.
$\mathsf {S}(\cdot )$
may not have this property, we can obtain such a random walk by rotating – this is done in Section 6.3.
As such, we must consider random walks in general half-spaces. Throughout the rest of this section, fix a unit vector
![]() $\vec {n} \in \mathbb {S}^1$
, and consider the half-space through the origin with inward normal
$\vec {n} \in \mathbb {S}^1$
, and consider the half-space through the origin with inward normal
![]() $\vec {n}$
, and call this space
$\vec {n}$
, and call this space
![]() ${\mathbb H}_{\vec {n}} \subset \mathbb {R}^2$
. Let
${\mathbb H}_{\vec {n}} \subset \mathbb {R}^2$
. Let
![]() $\vec {n}^{\perp } \in \mathbb {S}^1$
be a unit vector orthogonal to
$\vec {n}^{\perp } \in \mathbb {S}^1$
be a unit vector orthogonal to
![]() $\vec {n}$
(the choice between
$\vec {n}$
(the choice between
![]() $\vec {n}$
and
$\vec {n}$
and
![]() $-\vec {n}$
does not matter). We will think of our random walk in terms of coordinates with respect to
$-\vec {n}$
does not matter). We will think of our random walk in terms of coordinates with respect to
![]() $\vec {n}$
and
$\vec {n}$
and
![]() $\vec {n}^{\perp }$
instead of
$\vec {n}^{\perp }$
instead of
![]() $\mathsf {e}_1$
and
$\mathsf {e}_1$
and
![]() $\mathsf {e}_2$
. Let
$\mathsf {e}_2$
. Let
![]() $S(\cdot )$
denote a general
$S(\cdot )$
denote a general
![]() $2$
D random walk with step distribution
$2$
D random walk with step distribution
![]() $X = (X_1, X_2)$
such that
$X = (X_1, X_2)$
such that
![]() $\mathbb {E} X =\vec {0}$
,
$\mathbb {E} X =\vec {0}$
,
![]() $\operatorname {Cov} X = \mathrm {Id}$
, and
$\operatorname {Cov} X = \mathrm {Id}$
, and
![]() $\mathbb {P}(|X|>m) \leq c_1e^{-c_2m}$
for some constants
$\mathbb {P}(|X|>m) \leq c_1e^{-c_2m}$
for some constants
![]() $c_1, c_2>0$
and for all
$c_1, c_2>0$
and for all
![]() $m \geq 1$
. Additionally, we impose a lattice assumption: Assume that X takes values on a lattice
$m \geq 1$
. Additionally, we impose a lattice assumption: Assume that X takes values on a lattice
![]() $\mathcal {L}$
that is a nondegenerate linear transformation of
$\mathcal {L}$
that is a nondegenerate linear transformation of
![]() $\mathbb {Z}^2$
and that the distribution of X is strongly aperiodic; that is, for each
$\mathbb {Z}^2$
and that the distribution of X is strongly aperiodic; that is, for each
![]() ${\mathsf {u}} \in \mathcal {L}$
,
${\mathsf {u}} \in \mathcal {L}$
,
![]() $\mathcal {L}$
is the smallest subgroup of
$\mathcal {L}$
is the smallest subgroup of
![]() $\mathbb {Z}^2$
containing
$\mathbb {Z}^2$
containing
The theory of random walks confined to a half-space is intimately related to the theory of harmonic functions for processes killed upon exiting a half-space, and so we recall the relevant facts from this theory before proceeding.
6.1 Harmonic functions for processes in a half-space
Our domain of interest is a relatively simple one, the half-space
![]() ${\mathbb H}_{\vec {n}}$
, and we are concerned with the harmonic functions of the Brownian motion and of the random walk
${\mathbb H}_{\vec {n}}$
, and we are concerned with the harmonic functions of the Brownian motion and of the random walk
![]() $S(\cdot )$
killed upon exit from
$S(\cdot )$
killed upon exit from
![]() ${\mathbb H}_{\vec {n}}$
.
${\mathbb H}_{\vec {n}}$
.
The harmonic function of the Brownian motion killed at
![]() $\partial {\mathbb H}_{\vec {n}}$
is given by the minimal (up to a constant), strictly positive harmonic function on
$\partial {\mathbb H}_{\vec {n}}$
is given by the minimal (up to a constant), strictly positive harmonic function on
![]() ${\mathbb H}_{\vec {n}}$
with zero boundary conditions. For us, such functions take a very explicit form. Consider the rotation that sends
${\mathbb H}_{\vec {n}}$
with zero boundary conditions. For us, such functions take a very explicit form. Consider the rotation that sends
![]() $\vec {n} \mapsto \mathsf {e}_2$
, and thus
$\vec {n} \mapsto \mathsf {e}_2$
, and thus
![]() ${\mathbb H}_{\vec {n}}$
to
${\mathbb H}_{\vec {n}}$
to
![]() ${\mathbb H}$
. This is a conformal mapping that induces a bijection between positive harmonic functions in
${\mathbb H}$
. This is a conformal mapping that induces a bijection between positive harmonic functions in
![]() ${\mathbb H}$
that vanish on
${\mathbb H}$
that vanish on
![]() $\partial {\mathbb H}$
to positive harmonic functions in
$\partial {\mathbb H}$
to positive harmonic functions in
![]() ${\mathbb H}_{\vec {n}}$
that vanish on
${\mathbb H}_{\vec {n}}$
that vanish on
![]() $\partial {\mathbb H}_{\vec {n}}$
. SinceFootnote
12
every such harmonic function in
$\partial {\mathbb H}_{\vec {n}}$
. SinceFootnote
12
every such harmonic function in
![]() ${\mathbb H}$
takes the form
${\mathbb H}$
takes the form
![]() $h({\mathsf {v}}) = c {\mathsf {v}}\cdot \mathsf {e}_2$
, for some constant
$h({\mathsf {v}}) = c {\mathsf {v}}\cdot \mathsf {e}_2$
, for some constant
![]() $c>0$
, it follows that every harmonic h function in
$c>0$
, it follows that every harmonic h function in
![]() ${\mathbb H}_{\vec {n}}$
takes the form
${\mathbb H}_{\vec {n}}$
takes the form
![]() $h({\mathsf {v}}) = c {\mathsf {v}}\cdot \vec {n}$
. In particular, the harmonic function only depends on the projection of
$h({\mathsf {v}}) = c {\mathsf {v}}\cdot \vec {n}$
. In particular, the harmonic function only depends on the projection of
![]() ${\mathsf {v}}$
onto
${\mathsf {v}}$
onto
![]() $\vec {n}$
. In what follows, we take
$\vec {n}$
. In what follows, we take
![]() $c=1$
and define
$c=1$
and define
We refer to [Reference DeBlassie15] for a general discussion of the harmonic function of the Brownian motion in cones.
One of the many achievements of [Reference Denisov and Wachtel17] is the construction of a positive harmonic function V for a wide class of random walks
![]() $S(\cdot )$
killed upon exit from K, that is, V solves the equationFootnote
13
$S(\cdot )$
killed upon exit from K, that is, V solves the equationFootnote
13
where K is an element of a wide class of cones.Footnote 14 Many of their limit theorems that we wish to extend were stated in terms of V. The function V was constructed as
where h is a choice of the harmonic function for Brownian motion killed at
![]() $\partial K$
. For
$\partial K$
. For
![]() $K := H_{{\mathbb H}_{\vec {n}}}$
,
$K := H_{{\mathbb H}_{\vec {n}}}$
,
![]() $h := u$
, and so we see
$h := u$
, and so we see
where
![]() $V_1 := V_1^{\vec {n}}$
is the unique positive harmonic function for the one-dimensional random walk
$V_1 := V_1^{\vec {n}}$
is the unique positive harmonic function for the one-dimensional random walk
![]() $\vec {n} \cdot S(\cdot )$
killed at leaving
$\vec {n} \cdot S(\cdot )$
killed at leaving
![]() $(0,\infty )$
satisfying
$(0,\infty )$
satisfying
The uniqueness of
![]() $V_1$
, as well as an exact formula for
$V_1$
, as well as an exact formula for
![]() $V_1$
, was established by Doney in [Reference Doney22].
$V_1$
, was established by Doney in [Reference Doney22].
6.2 Limit theorems for general random walks in a half-space
The following two results, Propositions 6.1 and 6.2, are modifications of a ballot-type theorem from [Reference Denisov and Wachtel17] and an invariance principle from [Reference Duraj and Wachtel23], respectively. We’ll write
![]() $\mathfrak {e}(\cdot )$
to denote the standard Brownian excursion on
$\mathfrak {e}(\cdot )$
to denote the standard Brownian excursion on
![]() $[0,1]$
.
$[0,1]$
.
Proposition 6.1 (Modification of [Reference Denisov and Wachtel17, Theorem 6]).
Fix any
![]() $A> 0$
and
$A> 0$
and
![]() $\delta \in (0,1/2)$
. Then there exists a constant
$\delta \in (0,1/2)$
. Then there exists a constant
![]() $C_1>0$
such that, uniformly over sequences
$C_1>0$
such that, uniformly over sequences
![]() $a_k, b_k$
and
$a_k, b_k$
and
![]() $u_k$
satisfying
$u_k$
satisfying
we have
where
![]() $V_1'$
is the positive harmonic function for
$V_1'$
is the positive harmonic function for
![]() $-\vec {n}\cdot S_2(\cdot )$
killed upon leaving
$-\vec {n}\cdot S_2(\cdot )$
killed upon leaving
![]() $(0,\infty )$
.
$(0,\infty )$
.
Proposition 6.2 (Modification of [Reference Duraj and Wachtel23, Theorem 6]).
Fix any
![]() $\delta \in (0,1/2)$
. Uniformly over sequences
$\delta \in (0,1/2)$
. Uniformly over sequences
the family of conditional laws
 $$ \begin{align*} \mathbf{Q}_{u_k, a_k, b_k}^k (\cdot) := \mathbb{P}_{u_k \vec{n}}\bigg( \Big(\frac{\vec{n} \cdot S(\left\lfloor tk\right\rfloor)}{\sqrt{k}}\Big)_{t\in [0,1]} \in \cdot \;\big|\; S(k) = a_k \vec{n}^{\perp} + b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^{S}> k \bigg) \end{align*} $$
$$ \begin{align*} \mathbf{Q}_{u_k, a_k, b_k}^k (\cdot) := \mathbb{P}_{u_k \vec{n}}\bigg( \Big(\frac{\vec{n} \cdot S(\left\lfloor tk\right\rfloor)}{\sqrt{k}}\Big)_{t\in [0,1]} \in \cdot \;\big|\; S(k) = a_k \vec{n}^{\perp} + b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^{S}> k \bigg) \end{align*} $$
converge as
![]() $k \to \infty $
to the law of
$k \to \infty $
to the law of
![]() $\mathfrak {e}(\cdot )$
in the Skorokhod space
$\mathfrak {e}(\cdot )$
in the Skorokhod space
![]() $(D[0,1], \|\cdot \|_{\infty })$
.
$(D[0,1], \|\cdot \|_{\infty })$
.
For the next result, let
![]() $\mathbf {S}(\cdot )$
denote a 2D random walk with step distribution
$\mathbf {S}(\cdot )$
denote a 2D random walk with step distribution
![]() $\mathbf {X} = (\mathbf {X}_1, \mathbf {X}_2)$
satisfying the same lattice, covariance and tail decay assumptions as X but with mean
$\mathbf {X} = (\mathbf {X}_1, \mathbf {X}_2)$
satisfying the same lattice, covariance and tail decay assumptions as X but with mean
![]() $\mathbb {E} \mathbf {X} =\mu \vec {n}^{\perp }$
for some
$\mathbb {E} \mathbf {X} =\mu \vec {n}^{\perp }$
for some
![]() $\mu>0$
.
$\mu>0$
.
Proposition 6.3. Fix any
![]() $\delta \in (0,1/2)$
. There exists a constant
$\delta \in (0,1/2)$
. There exists a constant
![]() $\mathbf {C'}:= \mathbf {C'}(\mathbf {X})>0$
such that, uniformly over
$\mathbf {C'}:= \mathbf {C'}(\mathbf {X})>0$
such that, uniformly over
![]() $u, v \in (0,N^{1/2-\delta }]$
and
$u, v \in (0,N^{1/2-\delta }]$
and
![]() $\{u\vec {n},\,N\vec {n}^{\perp }+v \vec {n}\} \subset \mathcal {L}$
, we have
$\{u\vec {n},\,N\vec {n}^{\perp }+v \vec {n}\} \subset \mathcal {L}$
, we have
where
![]() $V_1'$
denotes the harmonic function for
$V_1'$
denotes the harmonic function for
![]() $-\vec {n}\cdot \mathbf {S}_2(\cdot )$
killed upon leaving
$-\vec {n}\cdot \mathbf {S}_2(\cdot )$
killed upon leaving
![]() $(0,\infty )$
.
$(0,\infty )$
.
Furthermore, if
then
Propositions 6.1 to 6.3 will be proved in Section 6.5. Note that when
![]() $\vec {n} = \mathsf {e}_2$
(so
$\vec {n} = \mathsf {e}_2$
(so
![]() ${\mathbb H}_{\vec {n}} = {\mathbb H}$
), Proposition 6.3 reduces to [Reference Ioffe, Ott, Velenik and Wachtel31, Theorem 5.1].
${\mathbb H}_{\vec {n}} = {\mathbb H}$
), Proposition 6.3 reduces to [Reference Ioffe, Ott, Velenik and Wachtel31, Theorem 5.1].
6.3 Proof of Theorems 4.2 and 4.3
Recall that the random walk
![]() $\mathsf {S}(\cdot )$
is a 2D random walk whose step distribution
$\mathsf {S}(\cdot )$
is a 2D random walk whose step distribution
![]() $X= ( X_1, X_2)$
satisfies
$X= ( X_1, X_2)$
satisfies
![]() $\mathbb {E}[ X] = (\mu ,0)$
, for some
$\mathbb {E}[ X] = (\mu ,0)$
, for some
![]() $\mu>0$
, and exponential tail decay for
$\mu>0$
, and exponential tail decay for
![]() $| X|$
. Recall
$| X|$
. Recall
![]() $\sigma _1^2 := \operatorname {Var}(X_1)$
and
$\sigma _1^2 := \operatorname {Var}(X_1)$
and
![]() $\sigma _2^2 := \operatorname {Var}(X_2)$
.
$\sigma _2^2 := \operatorname {Var}(X_2)$
.
Proof of Theorem 4.2.
Theorem 4.2 follows from Propositions 6.1 to 6.3 by linearly transforming the random walk
![]() $\mathsf {S}(\cdot )$
to satisfy the hypotheses of these results. We demonstrate this explicitly for item (2) of Theorem 4.2; the proof of item (1) follows readily.
$\mathsf {S}(\cdot )$
to satisfy the hypotheses of these results. We demonstrate this explicitly for item (2) of Theorem 4.2; the proof of item (1) follows readily.
Following from [Reference Denisov and Wachtel17, Example 2], we derive the aforementioned linear transformation, Consider the recentered, normalized random walk
 $$\begin{align*}\overline{\mathsf{S}}(n) := \begin{pmatrix} \sigma_1^{-1} & 0 \\ 0 & \sigma_2^{-1} \end{pmatrix} \bigg( \mathsf{S}(n) - n\begin{pmatrix} \mu \\ 0 \end{pmatrix} \bigg). \end{align*}$$
$$\begin{align*}\overline{\mathsf{S}}(n) := \begin{pmatrix} \sigma_1^{-1} & 0 \\ 0 & \sigma_2^{-1} \end{pmatrix} \bigg( \mathsf{S}(n) - n\begin{pmatrix} \mu \\ 0 \end{pmatrix} \bigg). \end{align*}$$
This is a random walk with increments
![]() $\bar {X}:= (\bar {X}_1, \bar {X}_2)$
of mean
$\bar {X}:= (\bar {X}_1, \bar {X}_2)$
of mean
![]() $0$
such that, for some
$0$
such that, for some
![]() $\rho \in (0,1)$
, we have
$\rho \in (0,1)$
, we have
 $C:= \operatorname {Cov} \bar {X} = \mathbb {E} \bar {X}\bar {X}^t = \begin {pmatrix} 1&\rho \\ \rho &1 \end {pmatrix}$
. Let
$C:= \operatorname {Cov} \bar {X} = \mathbb {E} \bar {X}\bar {X}^t = \begin {pmatrix} 1&\rho \\ \rho &1 \end {pmatrix}$
. Let
![]() $C = ODO^t$
. Since C is a covariance matrix, it is positive semidefinite; however, if C had
$C = ODO^t$
. Since C is a covariance matrix, it is positive semidefinite; however, if C had
![]() $0$
as an eigenvalue, then that would imply the random walk lives on a line, which we know is not true as X can be
$0$
as an eigenvalue, then that would imply the random walk lives on a line, which we know is not true as X can be
![]() $\mathsf {e}_1$
or
$\mathsf {e}_1$
or
![]() $\mathsf {e}_1+\mathsf {e}_2$
with positive probability. So, C is positive-definite. Consider the transformation matrix
$\mathsf {e}_1+\mathsf {e}_2$
with positive probability. So, C is positive-definite. Consider the transformation matrix
![]() $M := O^t\sqrt {D^{-1}} O$
. Then
$M := O^t\sqrt {D^{-1}} O$
. Then
To be explicit, straightforward calculations reveal that if
![]() $\theta \in [-\pi ,\pi ]$
solves
$\theta \in [-\pi ,\pi ]$
solves
![]() $\sin 2\theta = \rho $
, then we may take
$\sin 2\theta = \rho $
, then we may take
 $$\begin{align*}M = \frac{1}{\sqrt{1- \rho^2}} \begin{pmatrix} \cos \theta & - \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix}, \end{align*}$$
$$\begin{align*}M = \frac{1}{\sqrt{1- \rho^2}} \begin{pmatrix} \cos \theta & - \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix}, \end{align*}$$
though we will not need this explicit form.
Now, observe that
![]() $\vec {n} := M^{-1}\mathsf {e}_2$
has norm
$\vec {n} := M^{-1}\mathsf {e}_2$
has norm
![]() $1$
(explicitly,
$1$
(explicitly,
![]() $\vec {n} = (\sin \theta , \cos \theta )$
). Using the fact that
$\vec {n} = (\sin \theta , \cos \theta )$
). Using the fact that
![]() $M^{-1}$
is symmetric and
$M^{-1}$
is symmetric and
![]() $\vec {n}$
is outward normal to
$\vec {n}$
is outward normal to
![]() $M{\mathbb H}_{-} = {\mathbb H}_{-\vec {n}}$
,
$M{\mathbb H}_{-} = {\mathbb H}_{-\vec {n}}$
,
 $$ \begin{align*} &\big\{ H_{{\mathbb H}_-}^{\mathsf{S}}> k \big\} = \big\{\mathsf{e}_2^{t} \mathsf{S}(i) >0 ,\, \forall i \in [0,k] \big\} = \big\{\mathsf{e}_2^{t} \overline{\mathsf{S}}(i) >0 ,\, \forall i \in [0,k] \big\} \\ &\quad= \big\{ M \overline{\mathsf{S}}(i) \cdot M^{-1}\mathsf{e}_2 >0 ,\, \forall i \in [0,k]\big\} = \big\{ H_{{\mathbb H}_{-\vec{n}}}^{M\overline{\mathsf{S}}} >k \big\}. \end{align*} $$
$$ \begin{align*} &\big\{ H_{{\mathbb H}_-}^{\mathsf{S}}> k \big\} = \big\{\mathsf{e}_2^{t} \mathsf{S}(i) >0 ,\, \forall i \in [0,k] \big\} = \big\{\mathsf{e}_2^{t} \overline{\mathsf{S}}(i) >0 ,\, \forall i \in [0,k] \big\} \\ &\quad= \big\{ M \overline{\mathsf{S}}(i) \cdot M^{-1}\mathsf{e}_2 >0 ,\, \forall i \in [0,k]\big\} = \big\{ H_{{\mathbb H}_{-\vec{n}}}^{M\overline{\mathsf{S}}} >k \big\}. \end{align*} $$
In what follows, we write
![]() $M(a,b)$
to denote the matrix applied to the vector
$M(a,b)$
to denote the matrix applied to the vector
![]() $a \mathsf {e}_1 + b\mathsf {e}_2$
. Then for any measurable set
$a \mathsf {e}_1 + b\mathsf {e}_2$
. Then for any measurable set
![]() $\mathrm {B}$
,
$\mathrm {B}$
,
 $$ \begin{align} &\mathbb{P}_{(0,u)}\Big(\mathsf{S}(\cdot) \in \mathrm{B} \;\big|\; S(k) = (N,v) ,\, H_{{\mathbb H}_-}^{\mathsf{S}(\cdot)}> k \Big) \nonumber\\ &\quad= \mathbb{P}_{(0,\sigma_2^{-1} u)}\Big(\overline{\mathsf{S}}(\cdot) \in \mathrm{B}-k(\mu,0) \;\big|\; \overline{\mathsf{S}}(k) = (\tfrac{N-k\mu}{\sigma_1},\tfrac{v}{\sigma_2}) ,\, H_{{\mathbb H}_-}^{\overline{\mathsf{S}}} > k \Big) \nonumber\\ &\quad= \mathbb{P}_{M(0,u)}\Big(M\overline{\mathsf{S}}(\cdot) \in M(\mathrm{B}-k(\mu,0)) \;\big|\; M\overline{\mathsf{S}}(k) = M(\tfrac{N-k\mu}{\sigma_1},\tfrac{v}{\sigma_2}) ,\, H_{{\mathbb H}_{-\vec{n}}}^{M\overline{\mathsf{S}}} >k \Big). \end{align} $$
$$ \begin{align} &\mathbb{P}_{(0,u)}\Big(\mathsf{S}(\cdot) \in \mathrm{B} \;\big|\; S(k) = (N,v) ,\, H_{{\mathbb H}_-}^{\mathsf{S}(\cdot)}> k \Big) \nonumber\\ &\quad= \mathbb{P}_{(0,\sigma_2^{-1} u)}\Big(\overline{\mathsf{S}}(\cdot) \in \mathrm{B}-k(\mu,0) \;\big|\; \overline{\mathsf{S}}(k) = (\tfrac{N-k\mu}{\sigma_1},\tfrac{v}{\sigma_2}) ,\, H_{{\mathbb H}_-}^{\overline{\mathsf{S}}} > k \Big) \nonumber\\ &\quad= \mathbb{P}_{M(0,u)}\Big(M\overline{\mathsf{S}}(\cdot) \in M(\mathrm{B}-k(\mu,0)) \;\big|\; M\overline{\mathsf{S}}(k) = M(\tfrac{N-k\mu}{\sigma_1},\tfrac{v}{\sigma_2}) ,\, H_{{\mathbb H}_{-\vec{n}}}^{M\overline{\mathsf{S}}} >k \Big). \end{align} $$
Let us now check the hypotheses of Proposition 6.2. Take
![]() $\vec {n}^{\perp } := M\mathsf {e}_1/\left \Vert M\mathsf {e}_1 \right \Vert $
. Note that
$\vec {n}^{\perp } := M\mathsf {e}_1/\left \Vert M\mathsf {e}_1 \right \Vert $
. Note that
![]() $\vec {n}^{\perp }$
spans
$\vec {n}^{\perp }$
spans
![]() $\partial {\mathbb H}_{-\vec {n}}$
and
$\partial {\mathbb H}_{-\vec {n}}$
and
![]() $\vec {n}$
is the inward normal of
$\vec {n}$
is the inward normal of
![]() $M{\mathbb H}={\mathbb H}_{\vec {n}}$
.
$M{\mathbb H}={\mathbb H}_{\vec {n}}$
.
![]() $M\mathsf {S}(\cdot )$
is a random walk on the lattice
$M\mathsf {S}(\cdot )$
is a random walk on the lattice
![]() $\mathcal {L}$
generated by
$\mathcal {L}$
generated by
![]() $\left \Vert M\mathsf {e}_1 \right \Vert \vec {n}^{\perp }$
and
$\left \Vert M\mathsf {e}_1 \right \Vert \vec {n}^{\perp }$
and
![]() $M\mathsf {e}_2$
, the latter of which can be expressed as
$M\mathsf {e}_2$
, the latter of which can be expressed as
 $$ \begin{align*} M\mathsf{e}_2 = (M\mathsf{e}_2\cdot \vec{n}^{\perp}) \vec{n}^{\perp} + \vec{n} = \frac{ \mathsf{e}_1^t M^tM\mathsf{e}_2}{\left\Vert M\mathsf{e}_1 \right\Vert} \vec{n}^{\perp} + \vec{n} = \frac{\mathsf{e}_1^tC^{-1}\mathsf{e}_2}{\left\Vert M\mathsf{e}_1 \right\Vert} \vec{n}^{\perp} + \vec{n}. \end{align*} $$
$$ \begin{align*} M\mathsf{e}_2 = (M\mathsf{e}_2\cdot \vec{n}^{\perp}) \vec{n}^{\perp} + \vec{n} = \frac{ \mathsf{e}_1^t M^tM\mathsf{e}_2}{\left\Vert M\mathsf{e}_1 \right\Vert} \vec{n}^{\perp} + \vec{n} = \frac{\mathsf{e}_1^tC^{-1}\mathsf{e}_2}{\left\Vert M\mathsf{e}_1 \right\Vert} \vec{n}^{\perp} + \vec{n}. \end{align*} $$
Thus, for any
![]() $x, y \in \mathbb {R}$
,
$x, y \in \mathbb {R}$
,
 $$\begin{align*}M(x,y) = \frac{x + y\mathsf{e}_2^t C^{-1} \mathsf{e}_1}{\left\Vert M\mathsf{e}_1 \right\Vert} \vec{n}^{\perp} + y\vec{n} . \end{align*}$$
$$\begin{align*}M(x,y) = \frac{x + y\mathsf{e}_2^t C^{-1} \mathsf{e}_1}{\left\Vert M\mathsf{e}_1 \right\Vert} \vec{n}^{\perp} + y\vec{n} . \end{align*}$$
For any
![]() $k \in [N/\mu -A\sqrt {N}, N/\mu +A\sqrt {N}]$
, for A arbitrarily large (but fixed with respect to N), and for any
$k \in [N/\mu -A\sqrt {N}, N/\mu +A\sqrt {N}]$
, for A arbitrarily large (but fixed with respect to N), and for any
![]() $u,v \in [1, N^{1/2-\delta }]$
, we see that
$u,v \in [1, N^{1/2-\delta }]$
, we see that
satisfies Equation (6.2). With the hypotheses of Proposition 6.2 satisfied, it follows from Equation (6.7) and
that item (2) of Theorem 4.2 is an immediate consequence of Proposition 6.2.
We now use Theorem 4.2 to prove the Brownian excursion limit.
Proof of Theorem 4.3.
Due to Equation (4.7), it suffices to show that, for each fixed k, uniformly in the number of steps
![]() $k \in [N/\mu - A\sqrt {N}, N\mu + A\sqrt {N}]$
, the family of conditional laws
$k \in [N/\mu - A\sqrt {N}, N\mu + A\sqrt {N}]$
, the family of conditional laws
converges as
![]() $k \to \infty $
to the law of the standard Brownian excursion on
$k \to \infty $
to the law of the standard Brownian excursion on
![]() $[0,1]$
. We begin with Claim 6.4, which localizes the x-coordinate
$[0,1]$
. We begin with Claim 6.4, which localizes the x-coordinate
![]() $\mathsf {S}_1(j)$
to an interval of size
$\mathsf {S}_1(j)$
to an interval of size
![]() $o(N)$
, for
$o(N)$
, for
![]() $j\in [0,k]$
and allows us to compare the linear interpolation
$j\in [0,k]$
and allows us to compare the linear interpolation
![]() $\mathfrak {e}^{\mathsf {S},v}$
with the linear interpolation in item (2) of Theorem 4.2.
$\mathfrak {e}^{\mathsf {S},v}$
with the linear interpolation in item (2) of Theorem 4.2.
Claim 6.4. For any
![]() $\eta>0$
, uniformly over u and v as in the theorem statement, we have
$\eta>0$
, uniformly over u and v as in the theorem statement, we have
Proof. In light of the bound on
![]() $\mathbb {P}_{(0,u)}(\mathsf {S}(k) = (N,v) ,\, k < H_{{\mathbb H}_{-}}^{\mathsf {S}})$
provided by Equation (4.6), it suffices to show
$\mathbb {P}_{(0,u)}(\mathsf {S}(k) = (N,v) ,\, k < H_{{\mathbb H}_{-}}^{\mathsf {S}})$
provided by Equation (4.6), it suffices to show
This follows from a union bound over j, the exponential tail bound on the steps of
![]() $\mathsf {S}_1(\cdot )$
from Equation (4.2), and Hoeffding’s inequality:
$\mathsf {S}_1(\cdot )$
from Equation (4.2), and Hoeffding’s inequality:
 $$ \begin{align*} &\mathbb{P}_{0} \Big( \max_{j \in [0,N]} \big|\mathsf{S}_1(j) - \mu j\big|> N^{1/2+\eta} \Big) \leq N \max_{j \in [0,N]} \mathbb{P}_0\Big(\big|\mathsf{S}_1(j)- \mu j\big| > N^{1/2+\eta} \Big) \\ &\leq N \max_{j \in [0,N]} \mathbb{P}_0\Big(\big|\mathsf{S}_1(j)- \mu j\big| > N^{1/2+\eta} ,\, \max_{i \in [0,j-1]} \big|\mathsf{S}(i) - \mathsf{S}(i+1) \big| \leq (\log N)^2 \Big) \\ &\qquad+ c' N^2 e^{-\nu_g \beta (\log N)^2} \\ &\leq 2N e^{-\frac{2N^{2\eta}}{(\log N)^4}}+ c' N^2 e^{-\nu_g \beta (\log N)^2} = o(N^{-3/2}).\\[-37pt] \end{align*} $$
$$ \begin{align*} &\mathbb{P}_{0} \Big( \max_{j \in [0,N]} \big|\mathsf{S}_1(j) - \mu j\big|> N^{1/2+\eta} \Big) \leq N \max_{j \in [0,N]} \mathbb{P}_0\Big(\big|\mathsf{S}_1(j)- \mu j\big| > N^{1/2+\eta} \Big) \\ &\leq N \max_{j \in [0,N]} \mathbb{P}_0\Big(\big|\mathsf{S}_1(j)- \mu j\big| > N^{1/2+\eta} ,\, \max_{i \in [0,j-1]} \big|\mathsf{S}(i) - \mathsf{S}(i+1) \big| \leq (\log N)^2 \Big) \\ &\qquad+ c' N^2 e^{-\nu_g \beta (\log N)^2} \\ &\leq 2N e^{-\frac{2N^{2\eta}}{(\log N)^4}}+ c' N^2 e^{-\nu_g \beta (\log N)^2} = o(N^{-3/2}).\\[-37pt] \end{align*} $$
Note that Theorem 4.2(2) and Claim 6.4 are the equivalents of [Reference Ioffe, Ott, Velenik and Wachtel31, Eqs. (76) and (77)] for our random walk. We therefore finish the proof of our Theorem 4.3 exactly as in the proof of [Reference Ioffe, Ott, Velenik and Wachtel31, Theorem 5.3].
6.4 Uniform estimates for the random walk in a half-space
Before proving Propositions 6.1 to 6.3, we need to modify several key estimates of [Reference Denisov and Wachtel17] to address the range of parameters in Equations (6.2) and (6.4). In what follows, we will repeatedly refer back to [Reference Denisov and Wachtel17], explaining how their arguments can be adapted to give the desired uniformity. When stating or citing the results of [Reference Denisov and Wachtel17] and [Reference Duraj and Wachtel23], we will for the most part use their notation, pointing out any discrepancies explicitly.
6.4.1 Needed inputs
The results of [Reference Denisov and Wachtel17] are often stated in terms of the dimension d and a positive constant p, where p is related to the asymptotic behavior of the relevant harmonic function in the cone. For us,
![]() $d=2$
and
$d=2$
and
![]() $p=1$
.
$p=1$
.
Our first input is an extension of two estimates of [Reference Denisov and Wachtel17] uniformly over our range of initial positions.
Proposition 6.5 (Modification of [Reference Denisov and Wachtel17, Eq. (7)]).
Fix any
![]() $\delta \in (0,1/2)$
. The following estimate holds uniformly over all
$\delta \in (0,1/2)$
. The following estimate holds uniformly over all
![]() $a_k \in \mathbb {R}$
and
$a_k \in \mathbb {R}$
and
![]() $b_k \in (0 , k^{1/2-\delta }]$
such that
$b_k \in (0 , k^{1/2-\delta }]$
such that
![]() $a_k \vec {n}^{\perp } +b_k\vec {n} \in \mathcal {L}$
:
$a_k \vec {n}^{\perp } +b_k\vec {n} \in \mathcal {L}$
:
Proof. Equation (6.10), for
![]() $a_k := \mathfrak {a}$
and
$a_k := \mathfrak {a}$
and
![]() $b_k := \mathfrak {b}$
fixed, is proved in [Reference Denisov and Wachtel17] as an immediate consequence of the lemmas of [Reference Denisov and Wachtel17, Sections 3 and 4]. Of these, only [Reference Denisov and Wachtel17, Lemma 21] is insufficient for the uniformity that we require.Footnote
15
That is, we must show that for all
$b_k := \mathfrak {b}$
fixed, is proved in [Reference Denisov and Wachtel17] as an immediate consequence of the lemmas of [Reference Denisov and Wachtel17, Sections 3 and 4]. Of these, only [Reference Denisov and Wachtel17, Lemma 21] is insufficient for the uniformity that we require.Footnote
15
That is, we must show that for all
![]() $\epsilon>0$
sufficiently small,
$\epsilon>0$
sufficiently small,
where
![]() $\nu _k$
is defined as the first hitting time of
$\nu _k$
is defined as the first hitting time of
![]() $k^{1/2-\epsilon } \vec {n} + {\mathbb H}_{\vec {n}}$
and
$k^{1/2-\epsilon } \vec {n} + {\mathbb H}_{\vec {n}}$
and
![]() $o(1) \to 0$
as
$o(1) \to 0$
as
![]() $k \to \infty $
uniformly over the ranges of interest for
$k \to \infty $
uniformly over the ranges of interest for
![]() $a_k$
and
$a_k$
and
![]() $b_k$
. Uniformity in
$b_k$
. Uniformity in
![]() $a_k$
is trivial. Uniformity of
$a_k$
is trivial. Uniformity of
![]() $b_k$
was proven in [Reference Ioffe, Ott, Velenik and Wachtel31, Sec. 5.6] (see their Equation
$b_k$
was proven in [Reference Ioffe, Ott, Velenik and Wachtel31, Sec. 5.6] (see their Equation
![]() $(60)$
, and recall that
$(60)$
, and recall that
![]() $u(S(\nu _k)) = S(\nu _k) \cdot \vec {n}$
and
$u(S(\nu _k)) = S(\nu _k) \cdot \vec {n}$
and
![]() $V(a_k \vec {n}^{\perp } + b_k\vec {n}) = V_1(b_k)$
). Thus, the proof of [Reference Denisov and Wachtel17, Eq. (7)] given at the end of [Reference Denisov and Wachtel17, Sec. 4] extends to prove our proposition.
$V(a_k \vec {n}^{\perp } + b_k\vec {n}) = V_1(b_k)$
). Thus, the proof of [Reference Denisov and Wachtel17, Eq. (7)] given at the end of [Reference Denisov and Wachtel17, Sec. 4] extends to prove our proposition.
Proposition 6.6 (Modification of [Reference Denisov and Wachtel17, Theorem 3]).
Uniformly over sequences
![]() $a_k$
and
$a_k$
and
![]() $b_k$
satisfying Equation (6.2), the family of measures
$b_k$
satisfying Equation (6.2), the family of measures
 $$\begin{align*}\mathbb{P}_{a_k \vec{n}^{\perp}+ b_k \vec{n}} \Big( \frac{S(k)}{\sqrt k} \in \cdot \;\big|\; H_{{\mathbb H}_{-\vec{n}}}^S>k \Big) \end{align*}$$
$$\begin{align*}\mathbb{P}_{a_k \vec{n}^{\perp}+ b_k \vec{n}} \Big( \frac{S(k)}{\sqrt k} \in \cdot \;\big|\; H_{{\mathbb H}_{-\vec{n}}}^S>k \Big) \end{align*}$$
converges weakly, as k tends to
![]() $\infty $
, to the probability measure on
$\infty $
, to the probability measure on
![]() ${\mathbb H}_{\vec {n}}$
with density given by
${\mathbb H}_{\vec {n}}$
with density given by
![]() $H_0 (\mathsf {y}\cdot \vec {n}) e^{-\|a\vec {n}^{\perp }-\mathsf {y}\|^2/2} {\mathrm {d}} \mathsf {y}$
, where
$H_0 (\mathsf {y}\cdot \vec {n}) e^{-\|a\vec {n}^{\perp }-\mathsf {y}\|^2/2} {\mathrm {d}} \mathsf {y}$
, where
![]() $H_0> 0$
is the normalizing constant.
$H_0> 0$
is the normalizing constant.
Proof. Let B denote a measurable subset of K. Theorem 3 of [Reference Denisov and Wachtel17] gives us
 $$\begin{align*}\lim_{k\to\infty} \mathbb{P}\Big( \frac{S(k)}{\sqrt k} \in B- a \vec{n}^{\perp} \;\big|\; H_{{\mathbb H}_{-\vec{n}}}^S>k \Big) = H_0 \int_{B- a\vec{n}^{\perp}} (\mathsf{y}\cdot \vec{n}) e^{-|\mathsf{y}|^2/2} {\mathrm{d}} \mathsf{y} = H_0 \int_{B} (\mathsf{y}\cdot \vec{n}) e^{-|a\vec{n}^{\perp} -\mathsf{y}|^2/2} {\mathrm{d}} \mathsf{y}. \end{align*}$$
$$\begin{align*}\lim_{k\to\infty} \mathbb{P}\Big( \frac{S(k)}{\sqrt k} \in B- a \vec{n}^{\perp} \;\big|\; H_{{\mathbb H}_{-\vec{n}}}^S>k \Big) = H_0 \int_{B- a\vec{n}^{\perp}} (\mathsf{y}\cdot \vec{n}) e^{-|\mathsf{y}|^2/2} {\mathrm{d}} \mathsf{y} = H_0 \int_{B} (\mathsf{y}\cdot \vec{n}) e^{-|a\vec{n}^{\perp} -\mathsf{y}|^2/2} {\mathrm{d}} \mathsf{y}. \end{align*}$$
A simple continuity argument then yields
 $$\begin{align*}\lim_{k \to \infty} \mathbb{P}\Big( \frac{S(k)+a_k \vec{n}^{\perp} + b_k \vec{n}}{\sqrt k} \in B \;\big|\; H_{{\mathbb H}_{-\vec{n}}}^S>k \Big)= H_0 \int_{B} (\mathsf{y}\cdot \vec{n}) e^{-|a\vec{n}^{\perp} -\mathsf{y}|^2/2} {\mathrm{d}} \mathsf{y} \end{align*}$$
$$\begin{align*}\lim_{k \to \infty} \mathbb{P}\Big( \frac{S(k)+a_k \vec{n}^{\perp} + b_k \vec{n}}{\sqrt k} \in B \;\big|\; H_{{\mathbb H}_{-\vec{n}}}^S>k \Big)= H_0 \int_{B} (\mathsf{y}\cdot \vec{n}) e^{-|a\vec{n}^{\perp} -\mathsf{y}|^2/2} {\mathrm{d}} \mathsf{y} \end{align*}$$
as well. This concludes the proof.
Proposition 6.7 (Modification of [Reference Denisov and Wachtel17, Theorem 5]).
Recall
![]() $H_0$
from Proposition 6.6. Then uniformly over sequences
$H_0$
from Proposition 6.6. Then uniformly over sequences
![]() $a_k$
and
$a_k$
and
![]() $b_k$
satisfying Equation (6.2),
$b_k$
satisfying Equation (6.2),
 $$ \begin{align} \limsup_{k \to \infty} \sup_{\mathsf{y} \in {\mathbb H}_{\vec{n}}} \left|\frac{k^{3/2}}{V_1(b_k)} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k) = \mathsf{y} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k \big) - \kappa H_0 \frac{\mathsf{y}\cdot \vec{n}}{\sqrt{k}} e^{- \|a\sqrt{k}\vec{n}^{\perp} - \mathsf{y}\|^2/2k}\right| = 0. \end{align} $$
$$ \begin{align} \limsup_{k \to \infty} \sup_{\mathsf{y} \in {\mathbb H}_{\vec{n}}} \left|\frac{k^{3/2}}{V_1(b_k)} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k) = \mathsf{y} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k \big) - \kappa H_0 \frac{\mathsf{y}\cdot \vec{n}}{\sqrt{k}} e^{- \|a\sqrt{k}\vec{n}^{\perp} - \mathsf{y}\|^2/2k}\right| = 0. \end{align} $$
Proof of Proposition 6.7.
Below, we adapt the proof of Theorem 5 given in [Reference Denisov and Wachtel17, Section 6.2], beginning as in [Reference Denisov and Wachtel17] by splitting
![]() $K := {\mathbb H}_{\vec {n}}$
into three parts:
$K := {\mathbb H}_{\vec {n}}$
into three parts:
 $$ \begin{align*} K^{(1)} &:= \{ \mathsf{y} \in {\mathbb H}_{\vec{n}} : \left\Vert \mathsf{y} \right\Vert> R \sqrt k \} \, \\ K^{(2)} &:= \{ \mathsf{y} \in {\mathbb H}_{\vec{n}} : \left\Vert \mathsf{y} \right\Vert \leq R \sqrt{n},\, \mathsf{y} \cdot \vec{n} \leq 2 \epsilon \sqrt{n} \} \, \\ K^{(3)} &:= \{\mathsf{y} \in {\mathbb H}_{\vec{n}} : \left\Vert \mathsf{y} \right\Vert \leq R \sqrt k ,\, \mathsf{y} \cdot \vec{n} > 2\epsilon\sqrt k \} , \end{align*} $$
$$ \begin{align*} K^{(1)} &:= \{ \mathsf{y} \in {\mathbb H}_{\vec{n}} : \left\Vert \mathsf{y} \right\Vert> R \sqrt k \} \, \\ K^{(2)} &:= \{ \mathsf{y} \in {\mathbb H}_{\vec{n}} : \left\Vert \mathsf{y} \right\Vert \leq R \sqrt{n},\, \mathsf{y} \cdot \vec{n} \leq 2 \epsilon \sqrt{n} \} \, \\ K^{(3)} &:= \{\mathsf{y} \in {\mathbb H}_{\vec{n}} : \left\Vert \mathsf{y} \right\Vert \leq R \sqrt k ,\, \mathsf{y} \cdot \vec{n} > 2\epsilon\sqrt k \} , \end{align*} $$
for some
![]() $R>0$
and
$R>0$
and
![]() $\epsilon>0$
. Below, we let
$\epsilon>0$
. Below, we let
![]() $C>0$
denote a constant independent of k,
$C>0$
denote a constant independent of k,
![]() $\mathsf {y}$
, R and
$\mathsf {y}$
, R and
![]() $\epsilon $
that may change from line to line. Since
$\epsilon $
that may change from line to line. Since
 $$ \begin{align*} \lim_{R \to \infty} \lim_{\epsilon \to 0} \sup_{\mathsf{y} \in K^{(1)} \cup K^{(2)}} \frac{\mathsf{y} \cdot \vec{n}}{\sqrt{k}} e^{- \|a\sqrt{k}\vec{n}^{\perp} - \mathsf{y}\|^2/2k} = 0 . \end{align*} $$
$$ \begin{align*} \lim_{R \to \infty} \lim_{\epsilon \to 0} \sup_{\mathsf{y} \in K^{(1)} \cup K^{(2)}} \frac{\mathsf{y} \cdot \vec{n}}{\sqrt{k}} e^{- \|a\sqrt{k}\vec{n}^{\perp} - \mathsf{y}\|^2/2k} = 0 . \end{align*} $$
Proposition 6.7 will be proved if we can show
 $$ \begin{align} \lim_{R \to \infty} \lim_{\epsilon \to 0} \limsup_{k \to\infty} \frac{k^{3/2}}{V_1(b_k)}\sup_{\mathsf{y} \in K^{(1)} \cup K^{(2)}} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k) = \mathsf{y} ,\,H_{{\mathbb H}_{-\vec{n}}}^S>k\big) = 0 \end{align} $$
$$ \begin{align} \lim_{R \to \infty} \lim_{\epsilon \to 0} \limsup_{k \to\infty} \frac{k^{3/2}}{V_1(b_k)}\sup_{\mathsf{y} \in K^{(1)} \cup K^{(2)}} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k) = \mathsf{y} ,\,H_{{\mathbb H}_{-\vec{n}}}^S>k\big) = 0 \end{align} $$
and
 $$ \begin{align} \lim_{\epsilon \to 0} \limsup_{k\to\infty} \sup_{\mathsf{y} \in K^{(3)}} \left|\frac{k^{3/2}}{V_1(b_k)} \mathbb{P}_{a_k\vec{n}^{\perp}+b_k\vec{n}}\big(S(k) = \mathsf{y},\, H_{{\mathbb H}_{-\vec{n}}}>k\big) - \kappa H_0 \frac{\mathsf{y}\cdot\vec{n}}{\sqrt{k}} e^{-\frac{\|a\vec{n}^{\perp} - \mathsf{y}\|^2}{2k}}\right| = 0. \end{align} $$
$$ \begin{align} \lim_{\epsilon \to 0} \limsup_{k\to\infty} \sup_{\mathsf{y} \in K^{(3)}} \left|\frac{k^{3/2}}{V_1(b_k)} \mathbb{P}_{a_k\vec{n}^{\perp}+b_k\vec{n}}\big(S(k) = \mathsf{y},\, H_{{\mathbb H}_{-\vec{n}}}>k\big) - \kappa H_0 \frac{\mathsf{y}\cdot\vec{n}}{\sqrt{k}} e^{-\frac{\|a\vec{n}^{\perp} - \mathsf{y}\|^2}{2k}}\right| = 0. \end{align} $$
We begin with the more complicated Equation (6.13).
Set
![]() $m: = \lfloor \epsilon ^3k \rfloor $
. Our starting point is [Reference Denisov and Wachtel17, Eq. (82)], reproduced below:
$m: = \lfloor \epsilon ^3k \rfloor $
. Our starting point is [Reference Denisov and Wachtel17, Eq. (82)], reproduced below:
 $$ \begin{align} &\mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k) = \mathsf{y} ,\,H_{{\mathbb H}_{-\vec{n}}}^S> k \big) \nonumber\\ &\quad= \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(n-m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k-m \big) \mathbb{P}_z\big(S(m) = \mathsf{y} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > m\big). \end{align} $$
$$ \begin{align} &\mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k) = \mathsf{y} ,\,H_{{\mathbb H}_{-\vec{n}}}^S> k \big) \nonumber\\ &\quad= \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(n-m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k-m \big) \mathbb{P}_z\big(S(m) = \mathsf{y} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > m\big). \end{align} $$
Let
![]() ${\mathbb H}_{\vec {n}}^{(1)}(\mathsf {y}) := \{ \mathsf {z} \in {\mathbb H}_{\vec {n}} : \left \Vert \mathsf {z}-\mathsf {y} \right \Vert < \epsilon \sqrt {k} \}$
. Then we may follow the computations in [Reference Denisov and Wachtel17, Eqs. (83),(84)] exactly, yielding a constant
${\mathbb H}_{\vec {n}}^{(1)}(\mathsf {y}) := \{ \mathsf {z} \in {\mathbb H}_{\vec {n}} : \left \Vert \mathsf {z}-\mathsf {y} \right \Vert < \epsilon \sqrt {k} \}$
. Then we may follow the computations in [Reference Denisov and Wachtel17, Eqs. (83),(84)] exactly, yielding a constant
![]() $a> 0$
such that the following inequalities hold uniformly interm
$a> 0$
such that the following inequalities hold uniformly interm
![]() $a_k, b_k$
and
$a_k, b_k$
and
![]() $\mathsf {y}$
such that
$\mathsf {y}$
such that
![]() $\mathsf {y}\cdot \vec {n}> 2\epsilon \sqrt {k}$
:
$\mathsf {y}\cdot \vec {n}> 2\epsilon \sqrt {k}$
:
 $$ \begin{align} &\frac{k^{3/2}}{V_1(b_k)}\sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}\setminus {\mathbb H}_{\vec{n}}^{(1)}(\mathsf{y})} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k-m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k-m \big) \mathbb{P}_z\big(S(m) = \mathsf{y} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > m \big) \leq C \epsilon^{-3} e^{-\frac{a}{\epsilon}} \end{align} $$
$$ \begin{align} &\frac{k^{3/2}}{V_1(b_k)}\sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}\setminus {\mathbb H}_{\vec{n}}^{(1)}(\mathsf{y})} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k-m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k-m \big) \mathbb{P}_z\big(S(m) = \mathsf{y} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > m \big) \leq C \epsilon^{-3} e^{-\frac{a}{\epsilon}} \end{align} $$
and
 $$ \begin{align} &\frac{k^{3/2}}{V_1(b_k)}\sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}^{(1)}(\mathsf{y})} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k-m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k-m \big) \mathbb{P}_z\big(S(m) = \mathsf{y} ,\, H_{{\mathbb H}_{-\vec{n}}}^S < k \big) \leq C \epsilon^{-3}e^{-\frac{a}{\epsilon}} . \end{align} $$
$$ \begin{align} &\frac{k^{3/2}}{V_1(b_k)}\sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}^{(1)}(\mathsf{y})} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k-m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k-m \big) \mathbb{P}_z\big(S(m) = \mathsf{y} ,\, H_{{\mathbb H}_{-\vec{n}}}^S < k \big) \leq C \epsilon^{-3}e^{-\frac{a}{\epsilon}} . \end{align} $$
Both right-hand sides go to
![]() $0$
as
$0$
as
![]() $\epsilon \to 0$
, and so we turn our attention to the following expression:
$\epsilon \to 0$
, and so we turn our attention to the following expression:
 $$ \begin{align*} \Sigma(\mathsf{y}) = \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}^{(1)}(\mathsf{y})} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S (k-m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k-m \big) \mathbb{P}_z\big(S(m) = \mathsf{y}\big). \end{align*} $$
$$ \begin{align*} \Sigma(\mathsf{y}) = \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}^{(1)}(\mathsf{y})} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S (k-m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k-m \big) \mathbb{P}_z\big(S(m) = \mathsf{y}\big). \end{align*} $$
The bound in [Reference Denisov and Wachtel17, Eq. (85)] also holds uniformly over
![]() $a_k, b_k$
, and
$a_k, b_k$
, and
![]() $\mathsf {y}\cdot \vec {n}> 2 \epsilon \sqrt {k}$
, except that there should be a
$\mathsf {y}\cdot \vec {n}> 2 \epsilon \sqrt {k}$
, except that there should be a
![]() $V(\mathsf {x})$
factor in the
$V(\mathsf {x})$
factor in the
![]() $O(\cdot )$
-expression of Equation (85) there, where for us
$O(\cdot )$
-expression of Equation (85) there, where for us
![]() $\mathsf {x} := a_k \vec {n}^{\perp } +b_k \vec {n}$
and so
$\mathsf {x} := a_k \vec {n}^{\perp } +b_k \vec {n}$
and so
![]() $V(\mathsf {x}) = V_1(b_k)$
.Footnote
16
Altogether, we find
$V(\mathsf {x}) = V_1(b_k)$
.Footnote
16
Altogether, we find
where
 $$\begin{align*}\Sigma_1(\mathsf{y}):= \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}^{(1)}(\mathsf{y})} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k-m) = \mathsf{z} \;\big|\; H_{{\mathbb H}_{-\vec{n}}}^S> k-m \big) e^{-\frac{\left\Vert \mathsf{y}-\mathsf{z} \right\Vert{}^2}{2\epsilon^3k}}. \end{align*}$$
$$\begin{align*}\Sigma_1(\mathsf{y}):= \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}^{(1)}(\mathsf{y})} \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\big(S(k-m) = \mathsf{z} \;\big|\; H_{{\mathbb H}_{-\vec{n}}}^S> k-m \big) e^{-\frac{\left\Vert \mathsf{y}-\mathsf{z} \right\Vert{}^2}{2\epsilon^3k}}. \end{align*}$$
From Proposition 6.6 and a compactness argument, we have
 $$ \begin{align*} \limsup_{k\to\infty} \sup_{\mathsf{y}\in K^{(3)}} \left| \Sigma_1(\mathsf{y}) - H_0 \int_{\|(1-\epsilon^3)^{1/2}r - \mathsf{y}/\sqrt{k}\|<\epsilon} (\mathsf{r} \cdot \vec{n}) e^{-\|a \vec{n}^{\perp} - \mathsf{r}\|^2/2} e^{-\| (1-\epsilon^3)^{1/2}\mathsf{r} - \mathsf{y}/\sqrt{k} \|/2\epsilon^3} {\mathrm{d}} \mathsf{r} \right| = 0. \end{align*} $$
$$ \begin{align*} \limsup_{k\to\infty} \sup_{\mathsf{y}\in K^{(3)}} \left| \Sigma_1(\mathsf{y}) - H_0 \int_{\|(1-\epsilon^3)^{1/2}r - \mathsf{y}/\sqrt{k}\|<\epsilon} (\mathsf{r} \cdot \vec{n}) e^{-\|a \vec{n}^{\perp} - \mathsf{r}\|^2/2} e^{-\| (1-\epsilon^3)^{1/2}\mathsf{r} - \mathsf{y}/\sqrt{k} \|/2\epsilon^3} {\mathrm{d}} \mathsf{r} \right| = 0. \end{align*} $$
We can follow the steps up to the display before [Reference Denisov and Wachtel17, Eq. (86)], appealing this time to the uniform continuity of
![]() $(\mathsf {r}\cdot \vec {n}^{\perp }) e^{-\|a\vec {n}^{\perp }-\mathsf {r}\|^2/2}$
(instead of the function
$(\mathsf {r}\cdot \vec {n}^{\perp }) e^{-\|a\vec {n}^{\perp }-\mathsf {r}\|^2/2}$
(instead of the function
![]() $u(\mathsf {r})e^{-\|r\|^2/2}$
as in [Reference Denisov and Wachtel17]), to obtain
$u(\mathsf {r})e^{-\|r\|^2/2}$
as in [Reference Denisov and Wachtel17]), to obtain
 $$ \begin{align*} \limsup_{k \to \infty} \sup_{\mathsf{y}\in K^{(3)}} \left|\Sigma_1(\mathsf{y}) - H_0 \frac{\mathsf{y}\cdot \vec{n}}{\sqrt{k}} e^{-\frac{\|a\vec{n}^{\perp} - \mathsf{y}\|^2}{2k}}\right| = o(\epsilon^{3}). \end{align*} $$
$$ \begin{align*} \limsup_{k \to \infty} \sup_{\mathsf{y}\in K^{(3)}} \left|\Sigma_1(\mathsf{y}) - H_0 \frac{\mathsf{y}\cdot \vec{n}}{\sqrt{k}} e^{-\frac{\|a\vec{n}^{\perp} - \mathsf{y}\|^2}{2k}}\right| = o(\epsilon^{3}). \end{align*} $$
Combining the above with Equation (6.17) and applying Proposition 6.5, we find
 $$ \begin{align*} \lim_{\epsilon \to 0} \limsup_{k\to\infty} \sup_{\mathsf{y} \in K^{(3)}} \left|\frac{k^{3/2}}{V_1(b_k)} \Sigma(\mathsf{y}) - \kappa H_0 \frac{\mathsf{y}\cdot\vec{n}}{\sqrt{k}} e^{-\frac{\|a\vec{n}^{\perp} - \mathsf{y}\|^2}{2k}}\right| = 0. \end{align*} $$
$$ \begin{align*} \lim_{\epsilon \to 0} \limsup_{k\to\infty} \sup_{\mathsf{y} \in K^{(3)}} \left|\frac{k^{3/2}}{V_1(b_k)} \Sigma(\mathsf{y}) - \kappa H_0 \frac{\mathsf{y}\cdot\vec{n}}{\sqrt{k}} e^{-\frac{\|a\vec{n}^{\perp} - \mathsf{y}\|^2}{2k}}\right| = 0. \end{align*} $$
Combining this with Equations (6.15) and (6.16) yields Equation (6.13).
The modifications of [Reference Denisov and Wachtel17, Section 6.2] required to obtain Equation (6.12) are much simpler than those needed to obtain Equation (6.13). Equation (6.12) follows very similarly to the proofs of [Reference Denisov and Wachtel17, Eqs. (77) and (81)], and so we just highlight the main differences. The main technical modification comes from the following, which adapts their Lemmas 27 and 28:
for all
![]() $u, a, b \geq 0$
. Indeed, note that Proposition 6.5 gives the bound
$u, a, b \geq 0$
. Indeed, note that Proposition 6.5 gives the bound
Then the proofs of Lemmas 27 and 28 of [Reference Denisov and Wachtel17] can be repeated to yield Equation (6.18) (in particular, the
![]() $C(\mathsf {x})$
in Lemma 27 can be expressed as
$C(\mathsf {x})$
in Lemma 27 can be expressed as
![]() $C V_1(\mathsf {x}\cdot \vec {n})$
, and the
$C V_1(\mathsf {x}\cdot \vec {n})$
, and the
![]() $C(\mathsf {x},\mathsf {y})$
in Lemma 28 can be expressed as
$C(\mathsf {x},\mathsf {y})$
in Lemma 28 can be expressed as
![]() $C V_1(\mathsf {x}\cdot \vec {n})V_1(\mathsf {y}\cdot \vec {n})$
). So all
$C V_1(\mathsf {x}\cdot \vec {n})V_1(\mathsf {y}\cdot \vec {n})$
). So all
![]() $C(\mathsf {x})$
terms from the proofs of [Reference Denisov and Wachtel17, Eqs. (77),(81)] should be replaced by
$C(\mathsf {x})$
terms from the proofs of [Reference Denisov and Wachtel17, Eqs. (77),(81)] should be replaced by
![]() $V_1(b_k)$
, after which one finds that their work up to [Reference Denisov and Wachtel17, Eq. (81)] yields Equation (6.12).
$V_1(b_k)$
, after which one finds that their work up to [Reference Denisov and Wachtel17, Eq. (81)] yields Equation (6.12).
6.5 Proofs of Propositions 6.1 to 6.3
Proof of Proposition 6.1.
In what follows, all estimates will be uniform over
![]() $a_k, b_k$
and
$a_k, b_k$
and
![]() $u_k$
satisfying Equation (6.2).
$u_k$
satisfying Equation (6.2).
We begin by following the proof given in [Reference Denisov and Wachtel17, Section 6.3]. In particular, we also set
![]() $m = \lfloor (1-t)k \rfloor $
for some
$m = \lfloor (1-t)k \rfloor $
for some
![]() $t \in (0,1)$
and write the decomposition
$t \in (0,1)$
and write the decomposition
 $$ \begin{align} &\mathbb{P}_{u_k \vec{n}}\Big(S(k) = a_k \vec{n}^{\perp} + b_k \vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k \Big) \nonumber \\ & \quad = \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}} \mathbb{P}_{u_k \vec{n}}\Big(S(k-m)= \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k-m \Big)\mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\Big(S'(m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^{S'} > m \Big), \end{align} $$
$$ \begin{align} &\mathbb{P}_{u_k \vec{n}}\Big(S(k) = a_k \vec{n}^{\perp} + b_k \vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k \Big) \nonumber \\ & \quad = \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}} \mathbb{P}_{u_k \vec{n}}\Big(S(k-m)= \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k-m \Big)\mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\Big(S'(m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^{S'} > m \Big), \end{align} $$
where
![]() $S'$
is distributed as
$S'$
is distributed as
![]() $-S$
. Letting
$-S$
. Letting
![]() $\mathsf {x}:= u_k \vec {n}$
and
$\mathsf {x}:= u_k \vec {n}$
and
![]() $\mathsf {y}:= a_k \vec {n}^{\perp }+ b_k \vec {n}$
, and recalling Equation (6.18) as the needed modification of Lemmas 27 and 28 of [Reference Denisov and Wachtel17], we can follow the proof given in [Reference Denisov and Wachtel17, Sec. 6.3] up to their Equation (89) to find
$\mathsf {y}:= a_k \vec {n}^{\perp }+ b_k \vec {n}$
, and recalling Equation (6.18) as the needed modification of Lemmas 27 and 28 of [Reference Denisov and Wachtel17], we can follow the proof given in [Reference Denisov and Wachtel17, Sec. 6.3] up to their Equation (89) to find
where
 $$\begin{align*}\Sigma_1(R,k) := \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}} : |\mathsf{z}|> R \sqrt{k}} \mathbb{P}_{u_k \vec{n}}\Big(S(k-m)= \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k-m \Big)\mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\Big(S'(m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^{S'} > m \Big) . \end{align*}$$
$$\begin{align*}\Sigma_1(R,k) := \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}} : |\mathsf{z}|> R \sqrt{k}} \mathbb{P}_{u_k \vec{n}}\Big(S(k-m)= \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k-m \Big)\mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\Big(S'(m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^{S'} > m \Big) . \end{align*}$$
We are now in a position to apply Proposition 6.7 to the remainder term
 $$ \begin{align*} \Sigma_2 (R,k) &:= \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}: \|\mathsf{z}\| \leq R\sqrt k} \mathbb{P}_{u_k \vec{n}}\Big(S(k-m)= \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k-m \Big) \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\Big(S'(m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^{S'} > m \Big) \\&= \frac{H_0^2\kappa^2 V_1(u_k)V_1(b_k)}{\big(t(1-t)\big)^{3/2}k^3} \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}: \|\mathsf{z}\| \leq R\sqrt k} \Big(\frac{\mathsf{z}\cdot\vec{n}}{\sqrt{tk}}\Big) \Big(\frac{\mathsf{z}\cdot\vec{n}}{\sqrt{(1-t)k}}\Big) e^{-\frac{|\mathsf{z}|^2}{2tk} - \frac{|a\sqrt{k}\vec{n}^{\perp}-\mathsf{z}|^2}{2(1-t)k}} \nonumber \\&\quad +o\big(V_1(u_k)V'(b_k)k^{-2}\big) \\&= \frac{H_0^2\kappa^2 V_1(u_k)V_1(b_k)}{\big(t(1-t)\big)^{3/2}k^3}e^{-\frac{a^2}{2}} \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}: \|\mathsf{z}\| \leq R\sqrt k} \Big(\frac{\mathsf{z}\cdot\vec{n}}{\sqrt{tk}}\Big) \Big(\frac{\mathsf{z}\cdot\vec{n}}{\sqrt{(1-t)k}}\Big) e^{-\frac{(\mathsf{z}\cdot\vec{n})^2}{2t(1-t)k} - \frac{(\mathsf{z}\cdot\vec{n}^{\perp}-ta\sqrt{k})^2}{2t(1-t)k}} \nonumber \\&\quad + o\big(V_1(u_k)V'(b_k)k^{-2}\big). \end{align*} $$
$$ \begin{align*} \Sigma_2 (R,k) &:= \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}: \|\mathsf{z}\| \leq R\sqrt k} \mathbb{P}_{u_k \vec{n}}\Big(S(k-m)= \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^S> k-m \Big) \mathbb{P}_{a_k \vec{n}^{\perp} + b_k \vec{n}}\Big(S'(m) = \mathsf{z} ,\, H_{{\mathbb H}_{-\vec{n}}}^{S'} > m \Big) \\&= \frac{H_0^2\kappa^2 V_1(u_k)V_1(b_k)}{\big(t(1-t)\big)^{3/2}k^3} \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}: \|\mathsf{z}\| \leq R\sqrt k} \Big(\frac{\mathsf{z}\cdot\vec{n}}{\sqrt{tk}}\Big) \Big(\frac{\mathsf{z}\cdot\vec{n}}{\sqrt{(1-t)k}}\Big) e^{-\frac{|\mathsf{z}|^2}{2tk} - \frac{|a\sqrt{k}\vec{n}^{\perp}-\mathsf{z}|^2}{2(1-t)k}} \nonumber \\&\quad +o\big(V_1(u_k)V'(b_k)k^{-2}\big) \\&= \frac{H_0^2\kappa^2 V_1(u_k)V_1(b_k)}{\big(t(1-t)\big)^{3/2}k^3}e^{-\frac{a^2}{2}} \sum_{\mathsf{z} \in {\mathbb H}_{\vec{n}}: \|\mathsf{z}\| \leq R\sqrt k} \Big(\frac{\mathsf{z}\cdot\vec{n}}{\sqrt{tk}}\Big) \Big(\frac{\mathsf{z}\cdot\vec{n}}{\sqrt{(1-t)k}}\Big) e^{-\frac{(\mathsf{z}\cdot\vec{n})^2}{2t(1-t)k} - \frac{(\mathsf{z}\cdot\vec{n}^{\perp}-ta\sqrt{k})^2}{2t(1-t)k}} \nonumber \\&\quad + o\big(V_1(u_k)V'(b_k)k^{-2}\big). \end{align*} $$
Note that, compared to the first display after [Reference Denisov and Wachtel17, Eq. (89)], the only different terms are those involving a and the little-oh terms: This is a consequence of the modifications in our Proposition 6.7 compared to their Theorem 5. From here, we can follow their proof step-by-step until the end, yielding Equation (6.3).
Proof of Proposition 6.2.
We begin by showing convergence of the finite-dimensional distributions. For this, it is enough to consider sequences
![]() $a_k\in [-A\sqrt {k}, A\sqrt {k}]$
such that
$a_k\in [-A\sqrt {k}, A\sqrt {k}]$
such that
![]() $a_k/\sqrt {k} \to a$
and show that, for any
$a_k/\sqrt {k} \to a$
and show that, for any
![]() $a \in [-A,A]$
, the finite-dimensional distributions converge to the same limit (as then every subsequence has a further subsequence converging to the same distribution).
$a \in [-A,A]$
, the finite-dimensional distributions converge to the same limit (as then every subsequence has a further subsequence converging to the same distribution).
We proceed by following the arguments as in [Reference Duraj and Wachtel23, Sec. 4], making adaptions as necessary. We begin with [Reference Duraj and Wachtel23, Eq. (40)], which states that for any
![]() $t \in [0,1)$
and
$t \in [0,1)$
and
![]() $B \in \sigma (\{S_2(i) , i \leq kt\})$
, we have
$B \in \sigma (\{S_2(i) , i \leq kt\})$
, we have
where
![]() $X_{k,t} := S(\left \lfloor tk\right \rfloor )/\sqrt {k}$
and
$X_{k,t} := S(\left \lfloor tk\right \rfloor )/\sqrt {k}$
and
 $$ \begin{align*} h_{u_k,a_k,b_k}^{(k)}(t,\mathsf{w}) = \frac{\mathbb{P}_{u_k\vec{n}}\big(H_{{\mathbb H}_{-\vec{n}}}> kt \big) \mathbb{P}_{\mathsf{w}\sqrt{n}}\Big(S((1-t)k) = a_k \vec{n}^{\perp}+b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S >(1-t)k \Big)}{\mathbb{P}_{u_k \vec{n}}\Big(S(k) = a_k\vec{n}^{\perp}+b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k\Big)}. \end{align*} $$
$$ \begin{align*} h_{u_k,a_k,b_k}^{(k)}(t,\mathsf{w}) = \frac{\mathbb{P}_{u_k\vec{n}}\big(H_{{\mathbb H}_{-\vec{n}}}> kt \big) \mathbb{P}_{\mathsf{w}\sqrt{n}}\Big(S((1-t)k) = a_k \vec{n}^{\perp}+b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S >(1-t)k \Big)}{\mathbb{P}_{u_k \vec{n}}\Big(S(k) = a_k\vec{n}^{\perp}+b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k\Big)}. \end{align*} $$
From Propositions 6.1 and 6.5, we have
 $$\begin{align*}\frac{\mathbb{P}_{u_k\vec{n}}\big(H_{{\mathbb H}_{-\vec{n}}}> kt \big) }{\mathbb{P}_{u_k \vec{n}}\Big(S(k) = a_k\vec{n}^{\perp}+b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k\Big)} \sim \frac{ t^{-1/2} e^{a^2/2}}{C_1 \kappa V_1'(b_k)}k^{3/2} . \end{align*}$$
$$\begin{align*}\frac{\mathbb{P}_{u_k\vec{n}}\big(H_{{\mathbb H}_{-\vec{n}}}> kt \big) }{\mathbb{P}_{u_k \vec{n}}\Big(S(k) = a_k\vec{n}^{\perp}+b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S > k\Big)} \sim \frac{ t^{-1/2} e^{a^2/2}}{C_1 \kappa V_1'(b_k)}k^{3/2} . \end{align*}$$
Now, let
![]() $S'(\cdot )$
denote the random walk whose increments are independent copies of
$S'(\cdot )$
denote the random walk whose increments are independent copies of
![]() $-X$
. Considering the walk
$-X$
. Considering the walk
![]() $S(\cdot )$
in reversed time, we have
$S(\cdot )$
in reversed time, we have
Applying Proposition 6.7 yields
 $$ \begin{align*} &\limsup_{k\to\infty} \sup_{\mathsf{w}\in {\mathbb H}_{\vec{n}}} \bigg| \frac{(1-t)^{3/2}k^{3/2}}{V_1'(b_k)} \mathbb{P}_{\mathsf{w}\sqrt{k}}\Big(S((1-t)k) = a_k \vec{n}^{\perp}+b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S>(1-t)k \Big ) \\&\qquad\qquad\qquad - \kappa H_0 \frac{\mathsf{w}\cdot \vec{n}}{(1-t)^{1/2}} e^{-\frac{|a\vec{n}^{\perp} - \mathsf{w}|^2}{2(1-t)}} \bigg| = 0 \end{align*} $$
$$ \begin{align*} &\limsup_{k\to\infty} \sup_{\mathsf{w}\in {\mathbb H}_{\vec{n}}} \bigg| \frac{(1-t)^{3/2}k^{3/2}}{V_1'(b_k)} \mathbb{P}_{\mathsf{w}\sqrt{k}}\Big(S((1-t)k) = a_k \vec{n}^{\perp}+b_k\vec{n} ,\, H_{{\mathbb H}_{-\vec{n}}}^S>(1-t)k \Big ) \\&\qquad\qquad\qquad - \kappa H_0 \frac{\mathsf{w}\cdot \vec{n}}{(1-t)^{1/2}} e^{-\frac{|a\vec{n}^{\perp} - \mathsf{w}|^2}{2(1-t)}} \bigg| = 0 \end{align*} $$
uniformly over
![]() $a_k$
and
$a_k$
and
![]() $b_k$
. Altogether, we find
$b_k$
. Altogether, we find
uniformly over
![]() $\mathsf {w} \in {\mathbb H}_{\vec {n}}$
, where
$\mathsf {w} \in {\mathbb H}_{\vec {n}}$
, where
 $$\begin{align*}h(a,t,\mathsf{w}) := \frac{H_0}{C_1} t^{-\frac{1}2} (1-t)^2 (\mathsf{w}\cdot \vec{n}) e^{- \frac{|\mathsf{w}\cdot \vec{n}|^2}{2(1-t)} } \exp \Big(- \frac{|\mathsf{w}\cdot \vec{n}^{\perp}|^2}{2(1-t)} + \frac{a \mathsf{w}\cdot\vec{n}^{\perp}}{1-t} - \frac{ta^2}{2(1-t)} \Big) . \end{align*}$$
$$\begin{align*}h(a,t,\mathsf{w}) := \frac{H_0}{C_1} t^{-\frac{1}2} (1-t)^2 (\mathsf{w}\cdot \vec{n}) e^{- \frac{|\mathsf{w}\cdot \vec{n}|^2}{2(1-t)} } \exp \Big(- \frac{|\mathsf{w}\cdot \vec{n}^{\perp}|^2}{2(1-t)} + \frac{a \mathsf{w}\cdot\vec{n}^{\perp}}{1-t} - \frac{ta^2}{2(1-t)} \Big) . \end{align*}$$
Recall
![]() $D[0,t]$
the space of cadlag functions from
$D[0,t]$
the space of cadlag functions from
![]() $[0,t]$
to
$[0,t]$
to
![]() $\mathbb {R}$
. For any bounded and continuous functional
$\mathbb {R}$
. For any bounded and continuous functional
![]() $g_t : D[0,t] \to \mathbb {R}$
, Equation (6.20) gives us
$g_t : D[0,t] \to \mathbb {R}$
, Equation (6.20) gives us
where we have used that for fixed a and t,
![]() $h(a,t,\mathsf {w})$
is uniformly bounded in
$h(a,t,\mathsf {w})$
is uniformly bounded in
![]() $\mathsf {w}$
. Applying the convergence result [Reference Duraj and Wachtel23, Theorem 2] (see also Remark 1 in [Reference Duraj and Wachtel23]), we find
$\mathsf {w}$
. Applying the convergence result [Reference Duraj and Wachtel23, Theorem 2] (see also Remark 1 in [Reference Duraj and Wachtel23]), we find
where
![]() $(\mathfrak {M}_{{\mathbb H}_{\vec {n}}}(s))_{s\in [0,1]}$
denotes the Brownian meander in
$(\mathfrak {M}_{{\mathbb H}_{\vec {n}}}(s))_{s\in [0,1]}$
denotes the Brownian meander in
![]() ${\mathbb H}_{\vec {n}}$
started from the origin. Recall that
${\mathbb H}_{\vec {n}}$
started from the origin. Recall that
![]() $\mathfrak {M}_{{\mathbb H}_{\vec {n}}}(s) = W_s \vec {n}^{\perp } + M_s \vec {n}$
, where
$\mathfrak {M}_{{\mathbb H}_{\vec {n}}}(s) = W_s \vec {n}^{\perp } + M_s \vec {n}$
, where
![]() $(W_s)_{s\in [0,1]}$
is a standard one-dimensional Brownian motion,
$(W_s)_{s\in [0,1]}$
is a standard one-dimensional Brownian motion,
![]() $(M_s)_{s\in [0,1]}$
is a standard one-dimensional Brownian meander, and
$(M_s)_{s\in [0,1]}$
is a standard one-dimensional Brownian meander, and
![]() $W_.$
and
$W_.$
and
![]() $M_.$
are independent processes. Then the expectation over
$M_.$
are independent processes. Then the expectation over
![]() $W_.$
factors out of the right-hand side of Equation (6.22) as follows:
$W_.$
factors out of the right-hand side of Equation (6.22) as follows:
 $$\begin{align*}\mathbb{E}\Big[\frac{H_0}{C_1}(1-t)^{-\frac{3}2} M_1 e^{-\frac{t|M_1|^2}{2(1-t)} }g_t(t^{1/2}M_.) \Big] \mathbb{E} \Big[ \exp \Big(- \frac{t\mathcal{N}^2}{2(1-t)}+ \frac{a\sqrt{t}}{1-t}\mathcal{N}-\frac{ta^2}{2(1-t)}\Big) \Big], \end{align*}$$
$$\begin{align*}\mathbb{E}\Big[\frac{H_0}{C_1}(1-t)^{-\frac{3}2} M_1 e^{-\frac{t|M_1|^2}{2(1-t)} }g_t(t^{1/2}M_.) \Big] \mathbb{E} \Big[ \exp \Big(- \frac{t\mathcal{N}^2}{2(1-t)}+ \frac{a\sqrt{t}}{1-t}\mathcal{N}-\frac{ta^2}{2(1-t)}\Big) \Big], \end{align*}$$
where
![]() $\mathcal {N} \sim N(0,1)$
. That second expectation evaluates to
$\mathcal {N} \sim N(0,1)$
. That second expectation evaluates to
![]() $\sqrt {1-t}$
(in particular, there is no dependence on a in the above expression). So, letting
$\sqrt {1-t}$
(in particular, there is no dependence on a in the above expression). So, letting
![]() $C_2:=H_0/C_1$
, we’ve found
$C_2:=H_0/C_1$
, we’ve found
Thus, for every fixed
![]() $t <1$
, we have shown convergence in distribution on
$t <1$
, we have shown convergence in distribution on
![]() $D[0,t]$
to the same limit for every a. This in particular implies convergence of all finite -dimensional distributions to the same limit for every a, as well as tightness on
$D[0,t]$
to the same limit for every a. This in particular implies convergence of all finite -dimensional distributions to the same limit for every a, as well as tightness on
![]() $[0,1-\delta ]$
, for any
$[0,1-\delta ]$
, for any
![]() $\delta \in (0,1)$
. Tightness on
$\delta \in (0,1)$
. Tightness on
![]() $[1-\delta ,1]$
follows by applying the exact same arguments for the random walk reversed in time, just as in the end of [Reference Duraj and Wachtel23, Section 4].
$[1-\delta ,1]$
follows by applying the exact same arguments for the random walk reversed in time, just as in the end of [Reference Duraj and Wachtel23, Section 4].
Thus, we have the convergence of the family of laws
![]() $\mathbf {Q}^k_{u_k,a_k,b_k}$
. The limit may be identified as that of the standard Brownian excursion by taking
$\mathbf {Q}^k_{u_k,a_k,b_k}$
. The limit may be identified as that of the standard Brownian excursion by taking
![]() $S(i) := \hat {S}_1(i) \vec {n}^{\perp } + \hat {S}_2(i) \vec {n}$
, where
$S(i) := \hat {S}_1(i) \vec {n}^{\perp } + \hat {S}_2(i) \vec {n}$
, where
![]() $\hat {S}_1(\cdot )$
and
$\hat {S}_1(\cdot )$
and
![]() $\hat {S}_2(\cdot )$
are independent simple symmetric random walks on
$\hat {S}_2(\cdot )$
are independent simple symmetric random walks on
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Proof of Proposition 6.3.
Following the proof of [Reference Ioffe, Ott, Velenik and Wachtel31, Thm 5.1] until their Equation (59) yields Equation (6.6). Equation (6.5) is then an immediate consequence of Proposition 6.1.
7 Proof of Theorem 1.3
This section is dedicated to the proof of Theorem 1.3. We prove a slightly more detailed result below. Recall the generator
![]() $\mathsf {L}$
of the relevant Ferrari–Spohn diffusion defined in Equation (1.5).
$\mathsf {L}$
of the relevant Ferrari–Spohn diffusion defined in Equation (1.5).
Theorem 7.1. Fix an integer
![]() $n \geq 0$
. Suppose that
$n \geq 0$
. Suppose that
![]() $a_L$
, the fractional part of
$a_L$
, the fractional part of
![]() $\tfrac {1}{4\beta }\log L$
, converges to some limit a, and let
$\tfrac {1}{4\beta }\log L$
, converges to some limit a, and let
![]() $\lambda>0$
denote the
$\lambda>0$
denote the
![]() $L\to \infty $
limit of
$L\to \infty $
limit of
![]() $\lambda ^{(n)}(L):= c_{\infty }e^{4\beta a_L}(1-e^{-4\beta })e^{4\beta n}$
. Define
$\lambda ^{(n)}(L):= c_{\infty }e^{4\beta a_L}(1-e^{-4\beta })e^{4\beta n}$
. Define
![]() $\mathsf {y}:= (\lfloor KL^{2/3} \rfloor ,0) $
, for some
$\mathsf {y}:= (\lfloor KL^{2/3} \rfloor ,0) $
, for some
![]() $K>0$
, and the box
$K>0$
, and the box ![]() . Consider the modified Ising polymer
. Consider the modified Ising polymer
![]() $\gamma $
in
$\gamma $
in
![]() $D =Q$
or
$D =Q$
or
![]() ${\mathbb H}$
with start point
${\mathbb H}$
with start point
![]() $-\mathsf {y}$
and end point
$-\mathsf {y}$
and end point
![]() $\mathsf {y}$
with area tilt
$\mathsf {y}$
with area tilt
![]() $\exp (-\frac {\lambda ^{(n)}(L)A(\gamma )}{L})$
. Let
$\exp (-\frac {\lambda ^{(n)}(L)A(\gamma )}{L})$
. Let
![]() $\overline {\gamma }(x)$
denote the maximum vertical distance of
$\overline {\gamma }(x)$
denote the maximum vertical distance of
![]() $\gamma $
at
$\gamma $
at
![]() $x \in \mathbb {R}$
. Let
$x \in \mathbb {R}$
. Let
![]() $\sigma>0$
be the constant from Theorem 1.2, Part (b). For any fixed
$\sigma>0$
be the constant from Theorem 1.2, Part (b). For any fixed
![]() $T>0$
, the diffusively rescaled interface
$T>0$
, the diffusively rescaled interface
![]() $\sigma ^{-\frac {1}2}L^{-\frac {1}3}\overline {\gamma }(L^{\frac {2}3} x)$
converges weakly in
$\sigma ^{-\frac {1}2}L^{-\frac {1}3}\overline {\gamma }(L^{\frac {2}3} x)$
converges weakly in
![]() $(D[-T,T], \|\cdot \|_{\infty })$
as first
$(D[-T,T], \|\cdot \|_{\infty })$
as first
![]() $L\to \infty $
then
$L\to \infty $
then
![]() $K\to \infty $
to the stationary Ferrari–Spohn diffusion on
$K\to \infty $
to the stationary Ferrari–Spohn diffusion on
![]() $(0,\infty )$
with generator
$(0,\infty )$
with generator
![]() $\mathsf {L}$
and Dirichlet boundary condition at
$\mathsf {L}$
and Dirichlet boundary condition at
![]() $0$
. The same holds for
$0$
. The same holds for
![]() $\underline {\gamma }(x)$
, the minimum vertical distance at x.
$\underline {\gamma }(x)$
, the minimum vertical distance at x.
Remark 7.2. Fix
![]() $\beta $
sufficiently large, and consider the SOS model with a floor on the box Q with boundary conditions
$\beta $
sufficiently large, and consider the SOS model with a floor on the box Q with boundary conditions
![]() $H-n$
everywhere, except on the bottom where they are
$H-n$
everywhere, except on the bottom where they are
![]() $H-n-1$
. Equation (A.8) and Observation 2.7 imply that the law of the
$H-n-1$
. Equation (A.8) and Observation 2.7 imply that the law of the
![]() $H-n$
-level line (connecting the bottom corners of Q) is given by a modified Ising polymer with area tilt as in Theorem 7.1. Thus, Theorem 7.1 implies Theorem 1.3.
$H-n$
-level line (connecting the bottom corners of Q) is given by a modified Ising polymer with area tilt as in Theorem 7.1. Thus, Theorem 7.1 implies Theorem 1.3.
Remark 7.3. The argument used to prove the above theorem holds mutatis mutandis for
![]() $K\in (0,L^\epsilon )$
for, say,
$K\in (0,L^\epsilon )$
for, say,
![]() $0<\epsilon <\frac 1{20}$
, where the restriction on
$0<\epsilon <\frac 1{20}$
, where the restriction on
![]() $\epsilon $
is due to the fact that we are able to control the effect of the area tilt term
$\epsilon $
is due to the fact that we are able to control the effect of the area tilt term
![]() $\exp [-\frac \lambda L A(\gamma )]$
on boxes of side-length
$\exp [-\frac \lambda L A(\gamma )]$
on boxes of side-length
![]() $L^{2/3+\epsilon }$
(via [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Prop. A.1]).
$L^{2/3+\epsilon }$
(via [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Prop. A.1]).
7.1 Proof of Theorem 7.1
Let
![]() $\mathbf {P}_D^{{\mathsf {u}},{\mathsf {v}}}$
be the modified Ising polymer in
$\mathbf {P}_D^{{\mathsf {u}},{\mathsf {v}}}$
be the modified Ising polymer in
![]() $D = Q$
or
$D = Q$
or
![]() ${\mathbb H}$
with start point
${\mathbb H}$
with start point
![]() ${\mathsf {u}}\in \mathbb {Z}^2$
and end point
${\mathsf {u}}\in \mathbb {Z}^2$
and end point
![]() ${\mathsf {v}}\in \mathbb {Z}^2$
, that is,
${\mathsf {v}}\in \mathbb {Z}^2$
, that is,
 $$\begin{align*}\mathbf{P}_D^{{\mathsf{u}},{\mathsf{v}}}(\cdot) := \frac{\mathcal{G}_D({\mathsf{u}} \to {\mathsf{v}} \;\big|\; \gamma \in \cdot)}{\mathcal{G}_D({\mathsf{u}} \to {\mathsf{v}})}, \end{align*}$$
$$\begin{align*}\mathbf{P}_D^{{\mathsf{u}},{\mathsf{v}}}(\cdot) := \frac{\mathcal{G}_D({\mathsf{u}} \to {\mathsf{v}} \;\big|\; \gamma \in \cdot)}{\mathcal{G}_D({\mathsf{u}} \to {\mathsf{v}})}, \end{align*}$$
where we recall the partition functions
![]() $\mathcal {G}_D({\mathsf {u}} \to {\mathsf {v}})$
from Equation (5.17).Footnote
17
Let
$\mathcal {G}_D({\mathsf {u}} \to {\mathsf {v}})$
from Equation (5.17).Footnote
17
Let
![]() $\mathbf {E}_{D}^{{\mathsf {u}},{\mathsf {v}}}$
denote expectation with respect to
$\mathbf {E}_{D}^{{\mathsf {u}},{\mathsf {v}}}$
denote expectation with respect to
![]() $\mathbf {P}_D^{{\mathsf {u}},{\mathsf {v}}}$
. Next, define the modified Ising polymer with area tilt
$\mathbf {P}_D^{{\mathsf {u}},{\mathsf {v}}}$
. Next, define the modified Ising polymer with area tilt

As explained above Equation (2.15), we will also view
![]() $\mathbf {P}_{D,\lambda }^{-\mathsf {y},\mathsf {y}}$
as a measure on animals
$\mathbf {P}_{D,\lambda }^{-\mathsf {y},\mathsf {y}}$
as a measure on animals
![]() $\Gamma $
(in which
$\Gamma $
(in which
![]() $A(\Gamma ) := A(\gamma )$
). Note that we have replaced
$A(\Gamma ) := A(\gamma )$
). Note that we have replaced
![]() $\lambda ^{(n)}(L)$
with its
$\lambda ^{(n)}(L)$
with its
![]() $L\to \infty $
limit
$L\to \infty $
limit
![]() $\lambda $
, and as the next claim (controlling the influence of the area tilt) will show, the difference between these will play no role in our estimates.
$\lambda $
, and as the next claim (controlling the influence of the area tilt) will show, the difference between these will play no role in our estimates.
Claim 7.4. For each fixed
![]() $K>0$
, with
$K>0$
, with
![]() $\mathsf {y}=(\lfloor K L^{2/3}\rfloor ,0)$
as in Theorem 7.1, there exists
$\mathsf {y}=(\lfloor K L^{2/3}\rfloor ,0)$
as in Theorem 7.1, there exists
![]() $a_K>0$
such that
$a_K>0$
such that
![]() $\mathbf {E}_D^{-\mathsf {y},\mathsf {y}}\big [e^{-\frac {\lambda }{L} A(\gamma )}\big ] \to a_K$
as
$\mathbf {E}_D^{-\mathsf {y},\mathsf {y}}\big [e^{-\frac {\lambda }{L} A(\gamma )}\big ] \to a_K$
as
![]() $L\to \infty $
.
$L\to \infty $
.
Proof. From Theorem 1.2, we know that both
![]() $L^{-1/3}\underline {\gamma }(\lfloor L^{2/3}x\rfloor )$
and
$L^{-1/3}\underline {\gamma }(\lfloor L^{2/3}x\rfloor )$
and
![]() $L^{-1/3}\overline {\gamma }(\lfloor L^{2/3}x\rfloor )$
converge weakly in
$L^{-1/3}\overline {\gamma }(\lfloor L^{2/3}x\rfloor )$
converge weakly in
![]() $D([-K,K], \|\cdot \|_{\infty })$
to the Brownian excursion from
$D([-K,K], \|\cdot \|_{\infty })$
to the Brownian excursion from
![]() $0$
to
$0$
to
![]() $0$
. Since the function
$0$
. Since the function
 $$ \begin{align*} f: (D[-K,K],\|\cdot\|_{\infty}) &\to \mathbb{R} \\ g &\mapsto \exp\Big(-\int_{-K}^K |g(x)| {\mathrm{d}} x\Big) \end{align*} $$
$$ \begin{align*} f: (D[-K,K],\|\cdot\|_{\infty}) &\to \mathbb{R} \\ g &\mapsto \exp\Big(-\int_{-K}^K |g(x)| {\mathrm{d}} x\Big) \end{align*} $$
is a bounded, continuous function, it follows after a change of variables
![]() $x \mapsto L^{2/3}x$
that
$x \mapsto L^{2/3}x$
that
where
![]() $\xi $
denotes a Brownian excursion from
$\xi $
denotes a Brownian excursion from
![]() $0$
to
$0$
to
![]() $0$
on
$0$
on
![]() $[-K,K]$
. This concludes the proof.
$[-K,K]$
. This concludes the proof.
The above claim (applied to the denominator of Equation (7.1) to show the effect of the area tilt there is uniformly bounded, whereas its effect on the numerator can be isolated via Cauchy–Schwarz) now implies that the total-variation distance between
![]() $\tilde {\mathbf {P}}^{-\mathsf {y},\mathsf {y}}_{D,\lambda }$
and
$\tilde {\mathbf {P}}^{-\mathsf {y},\mathsf {y}}_{D,\lambda }$
and
![]() $\tilde {\mathbf {P}}^{-\mathsf {y},\mathsf {y}}_{D,\lambda ^{(n)}}$
vanishes as
$\tilde {\mathbf {P}}^{-\mathsf {y},\mathsf {y}}_{D,\lambda ^{(n)}}$
vanishes as
![]() $L\to \infty $
.
$L\to \infty $
.
We prove Theorem 7.1 by first coupling the cone points of
![]() $\Gamma \sim \mathbf {P}_{D,\lambda }^{-\mathsf {y},\mathsf {y}}$
that lie inside some strip (those cone points for which we will have entropic repulsion) with the trajectory of a random walk with area tilt. We then fit this random walk into the framework of [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6], where a Ferrari–Spohn limit was proved for a broad class of directed, 2D random walks with area tilt.
$\Gamma \sim \mathbf {P}_{D,\lambda }^{-\mathsf {y},\mathsf {y}}$
that lie inside some strip (those cone points for which we will have entropic repulsion) with the trajectory of a random walk with area tilt. We then fit this random walk into the framework of [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6], where a Ferrari–Spohn limit was proved for a broad class of directed, 2D random walks with area tilt.
7.1.1 Coupling with an area-tilted random walk
This subsection will closely follow the notation and work in Section 5.6, where the existence of a coupling between the cone points of a modified Ising polymer (without area tilt) and the corresponding random walk was proved. The inputs to construct such a coupling were:
-
(a) existence of many cone points and boundedness of the polymer length (Lemma 5.7);
-
(b) boundedness of the irreducible pieces (Proposition 5.8); and
-
(c) entropic repulsion (Proposition 5.11).
These results all held with probability tending to
![]() $1$
as N (the side length of the box) tends to infinity. In the current situation, we take
$1$
as N (the side length of the box) tends to infinity. In the current situation, we take
![]() $N= 2\|\mathsf {y}\|_1 = 2\lfloor KL^{2/3} \rfloor $
and we shift
$N= 2\|\mathsf {y}\|_1 = 2\lfloor KL^{2/3} \rfloor $
and we shift
![]() $\mathsf {x}$
(as in the statement of the above results) to
$\mathsf {x}$
(as in the statement of the above results) to
![]() $\mathsf {y}$
so that these results hold under
$\mathsf {y}$
so that these results hold under
![]() $\mathbf {P}_D^{-\mathsf {y},\mathsf {y}}$
with probability tending to
$\mathbf {P}_D^{-\mathsf {y},\mathsf {y}}$
with probability tending to
![]() $1$
as L tends to
$1$
as L tends to
![]() $\infty $
. Claim 7.4 states that
$\infty $
. Claim 7.4 states that
![]() $\mathbf {P}_D^{-\mathsf {y},\mathsf {y}}[e^{-\frac {\lambda }{L}A(\gamma )}]$
is bounded away from
$\mathbf {P}_D^{-\mathsf {y},\mathsf {y}}[e^{-\frac {\lambda }{L}A(\gamma )}]$
is bounded away from
![]() $0$
uniformly in L so that Items (a) and (c) above hold with probability tending to
$0$
uniformly in L so that Items (a) and (c) above hold with probability tending to
![]() $1$
as L tends to
$1$
as L tends to
![]() $\infty $
under
$\infty $
under
![]() $\mathbf {P}_{D,\lambda }^{-\mathsf {y},\mathsf {y}}$
as well. Thus, we are in good position to establish a coupling between the area-tilted Ising polymer and an area-tilted random walk that we define below.
$\mathbf {P}_{D,\lambda }^{-\mathsf {y},\mathsf {y}}$
as well. Thus, we are in good position to establish a coupling between the area-tilted Ising polymer and an area-tilted random walk that we define below.
Fix
![]() $\delta \in (0,1/8)$
. Analogous to Equation (5.35), define the measure
$\delta \in (0,1/8)$
. Analogous to Equation (5.35), define the measure
where
![]() $\overline {\zeta }^{(\mathsf {L}*)}$
and
$\overline {\zeta }^{(\mathsf {L}*)}$
and
![]() $\overline {\zeta }^{(\mathsf {R}*)}$
are points in
$\overline {\zeta }^{(\mathsf {R}*)}$
are points in
![]() $\mathbb {Z}^2$
satisfying
$\mathbb {Z}^2$
satisfying
(these are the analogues of Equations (5.33) and (5.34), respectively). Recall that, thanks to Item (b) and Item (c), the first and last cone points of
![]() $\Gamma $
in the strip
$\Gamma $
in the strip
![]() $\mathcal {S}_{-\frac {N}2+N^{4\delta }, \frac {N}2- N^{4\delta }}$
satisfy Equations (7.2) and (7.3) with
$\mathcal {S}_{-\frac {N}2+N^{4\delta }, \frac {N}2- N^{4\delta }}$
satisfy Equations (7.2) and (7.3) with
![]() $\mathbf {P}_{D,\lambda }^{-\mathsf {y},\mathsf {y}}$
-probability tending to
$\mathbf {P}_{D,\lambda }^{-\mathsf {y},\mathsf {y}}$
-probability tending to
![]() $1$
as L tends to
$1$
as L tends to
![]() $\infty $
. It is between these cone points that we couple with an area-tilted random walk.
$\infty $
. It is between these cone points that we couple with an area-tilted random walk.
Recall the random walk
![]() $\mathsf {S}$
and its law
$\mathsf {S}$
and its law
![]() $\mathbb {P}$
defined in Section 4.1. Write
$\mathbb {P}$
defined in Section 4.1. Write
![]() $\mathbb {E}$
and
$\mathbb {E}$
and
![]() $\mathbb {E}_{{\mathsf {u}}}$
for expectation under
$\mathbb {E}_{{\mathsf {u}}}$
for expectation under
![]() $\mathbb {P}$
and
$\mathbb {P}$
and
![]() $\mathbb {P}_{{\mathsf {u}}}$
, respectively. Define the area under
$\mathbb {P}_{{\mathsf {u}}}$
, respectively. Define the area under
![]() $\mathsf {S}$
as follows: For an l-steps walk
$\mathsf {S}$
as follows: For an l-steps walk
![]() $\mathsf {S}=\{(\mathsf {S}_1(0),\mathsf {S}_2(0)),\dots ,(\mathsf {S}_1(l),\mathsf {S}_2(l))\}$
, we write
$\mathsf {S}=\{(\mathsf {S}_1(0),\mathsf {S}_2(0)),\dots ,(\mathsf {S}_1(l),\mathsf {S}_2(l))\}$
, we write
 $$ \begin{align} A(\mathsf{S}) := \sum_{i=1}^l(\mathsf{S}_1(i)-\mathsf{S}_1(i-1))\mathsf{S}_2(i). \end{align} $$
$$ \begin{align} A(\mathsf{S}) := \sum_{i=1}^l(\mathsf{S}_1(i)-\mathsf{S}_1(i-1))\mathsf{S}_2(i). \end{align} $$
To indicate the law of the random walk
![]() $\mathsf {S}$
with area tilt, started from
$\mathsf {S}$
with area tilt, started from
![]() $\mathsf {S}(0) = {\mathsf {u}}$
, we write
$\mathsf {S}(0) = {\mathsf {u}}$
, we write

Proposition 7.5. There exists
![]() $\nu>0$
such that for all
$\nu>0$
such that for all
![]() $K>0$
and L large enough with respect to K, for all
$K>0$
and L large enough with respect to K, for all
![]() $\beta>0$
sufficiently large, and for all
$\beta>0$
sufficiently large, and for all
![]() $\overline {\zeta }^{(\mathsf {L}*)}$
and
$\overline {\zeta }^{(\mathsf {L}*)}$
and
![]() $\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34) respectively, if we let
$\overline {\zeta }^{(\mathsf {R}*)}$
satisfying Equations (5.33) and (5.34) respectively, if we let
![]() $T= H_{\overline {\zeta }^{(\mathsf {R}*)}}$
and view
$T= H_{\overline {\zeta }^{(\mathsf {R}*)}}$
and view
![]() $\mathsf {Cpts}(\Gamma ^*)$
as an ordered tuple (see Equation (2.20)), then
$\mathsf {Cpts}(\Gamma ^*)$
as an ordered tuple (see Equation (2.20)), then
for some constant
![]() $C:=C(\beta )>0$
.
$C:=C(\beta )>0$
.
Proof. This follows from the coupling of the untilted measures given by Proposition 5.13. One just needs to check that the difference in the definitions of area for
![]() $\Gamma ^*$
and
$\Gamma ^*$
and
![]() $\mathsf {S}$
results in a negligible difference in the tilts. This is easy to see: By Item (b), the distance between two consecutive cone points is at most
$\mathsf {S}$
results in a negligible difference in the tilts. This is easy to see: By Item (b), the distance between two consecutive cone points is at most
![]() $(\log L)^2$
, and hence one can enclose the diamond between them in a square of area
$(\log L)^2$
, and hence one can enclose the diamond between them in a square of area
![]() $(\log L)^4$
. Since the total area of such squares is an upper bound on
$(\log L)^4$
. Since the total area of such squares is an upper bound on
![]() $|A(\Gamma ^*)-A(S)|$
, we find
$|A(\Gamma ^*)-A(S)|$
, we find
 $$\begin{align*}\left|\frac{A(\Gamma^*)}{L} - \frac{A(\mathsf{S})}{L}\right| \leq 2K\frac{(\log L)^4}{L^{1/3}} = o(1). \end{align*}$$
$$\begin{align*}\left|\frac{A(\Gamma^*)}{L} - \frac{A(\mathsf{S})}{L}\right| \leq 2K\frac{(\log L)^4}{L^{1/3}} = o(1). \end{align*}$$
This shows that the tilts are equivalent up to a
![]() $o(1)$
factor. Since Claim 7.4 implies that the expectations of
$o(1)$
factor. Since Claim 7.4 implies that the expectations of
![]() $e^{-\frac {\lambda }LA(\Gamma ^*)}$
and
$e^{-\frac {\lambda }LA(\Gamma ^*)}$
and
![]() $e^{-\frac {\lambda }{L}A(\mathsf {S})}$
are bounded away from
$e^{-\frac {\lambda }{L}A(\mathsf {S})}$
are bounded away from
![]() $0$
, the result follows.
$0$
, the result follows.
7.1.2 Convergence to Ferrari–Spohn
We have reduced to a 2D random walk bridge with area tilt conditioned to stay in
![]() ${\mathbb H}_{N^{\delta }}$
, with start point
${\mathbb H}_{N^{\delta }}$
, with start point
![]() $\bar {\mathsf {u}}:= \overline \zeta ^{(\mathsf {L}*)}$
and end point
$\bar {\mathsf {u}}:= \overline \zeta ^{(\mathsf {L}*)}$
and end point
![]() $\bar {\mathsf {v}}:= \overline \zeta ^{(\mathsf {R}*)}$
satisfying Equations (7.2) and (7.3), respectively. In [Reference Ioffe, Ott, Shlosman and Velenik30, Sections 6.6 and 6.7], the Ferrari–Spohn diffusion limit is proved for a wide class of such random walks, with the stronger condition ([Reference Ioffe, Ott, Shlosman and Velenik30, Eq. (6.10)]) on the start point
$\bar {\mathsf {v}}:= \overline \zeta ^{(\mathsf {R}*)}$
satisfying Equations (7.2) and (7.3), respectively. In [Reference Ioffe, Ott, Shlosman and Velenik30, Sections 6.6 and 6.7], the Ferrari–Spohn diffusion limit is proved for a wide class of such random walks, with the stronger condition ([Reference Ioffe, Ott, Shlosman and Velenik30, Eq. (6.10)]) on the start point
![]() ${\mathsf {u}}$
and end point
${\mathsf {u}}$
and end point
![]() ${\mathsf {v}}$
of the random walk:
${\mathsf {v}}$
of the random walk:
where
![]() $\epsilon>0$
is any small constant,
$\epsilon>0$
is any small constant,
![]() $C>c>0$
are fixed constants and
$C>c>0$
are fixed constants and
![]() $\bar {K}\leq K$
is a parameter tending to
$\bar {K}\leq K$
is a parameter tending to
![]() $\infty $
after L (these conditions are stronger than Equations (7.2) and (7.3) in the y-coordinates only). Lemma 7.6 shows that our random walk indeed passes through points satisfying Equations (7.6) and (7.7) with high probability, thereby putting us in the same setting as [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6.6]. We prove it using the Brownian excursion limit Theorem 4.3.
$\infty $
after L (these conditions are stronger than Equations (7.2) and (7.3) in the y-coordinates only). Lemma 7.6 shows that our random walk indeed passes through points satisfying Equations (7.6) and (7.7) with high probability, thereby putting us in the same setting as [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6.6]. We prove it using the Brownian excursion limit Theorem 4.3.
For brevity, we will write the law of the area-tilted random walk bridge as
Similarly, we write the law of the untilted random walk bridge via
We will denote expectation under these measures by replacing
![]() $\mathbb {P}$
with
$\mathbb {P}$
with
![]() $\mathbb {E}$
.
$\mathbb {E}$
.
Lemma 7.6. Let
![]() $E_{c,C}$
denote the event that the random walk
$E_{c,C}$
denote the event that the random walk
![]() $\mathsf {S}$
passes through
$\mathsf {S}$
passes through
![]() ${\mathsf {u}}$
and
${\mathsf {u}}$
and
![]() ${\mathsf {v}}$
satisfying Equations (7.6) and (7.7), for some
${\mathsf {v}}$
satisfying Equations (7.6) and (7.7), for some
![]() $C>c>0$
. Then for some constant
$C>c>0$
. Then for some constant
![]() $K_0>0$
, the following limit holds uniformly in
$K_0>0$
, the following limit holds uniformly in
![]() $\bar {\mathsf {u}}$
satisfying Equation (7.2) and
$\bar {\mathsf {u}}$
satisfying Equation (7.2) and
![]() $\bar {\mathsf {v}}$
satisfying Equation (7.3):
$\bar {\mathsf {v}}$
satisfying Equation (7.3):
Proof. We will show that
![]() $\mathsf {S}$
passes through a point
$\mathsf {S}$
passes through a point
![]() ${\mathsf {u}}$
satisfying Equation (7.2) with high probability; the same argument will show the same is true for
${\mathsf {u}}$
satisfying Equation (7.2) with high probability; the same argument will show the same is true for
![]() ${\mathsf {v}}$
. Further, one only needs to check that
${\mathsf {v}}$
. Further, one only needs to check that
![]() ${\mathsf {u}}_2 \geq cL^{1/3}$
(the upper bound by
${\mathsf {u}}_2 \geq cL^{1/3}$
(the upper bound by
![]() $CL^{1/3}$
is not needed), since
$CL^{1/3}$
is not needed), since
![]() $\mathsf {S}_2(0) = \bar {\mathsf {u}}_2< cL^{1/3}$
, and so the first time
$\mathsf {S}_2(0) = \bar {\mathsf {u}}_2< cL^{1/3}$
, and so the first time
![]() $\mathsf {S}_2$
rises above
$\mathsf {S}_2$
rises above
![]() $cL^{1/3}$
, it will also be below
$cL^{1/3}$
, it will also be below
![]() $CL^{1/3}$
for L large enough (recall from Equation (5.38) that under the nonarea-tilted measure,
$CL^{1/3}$
for L large enough (recall from Equation (5.38) that under the nonarea-tilted measure,
![]() $\mathsf {S}$
has increments bounded by
$\mathsf {S}$
has increments bounded by
![]() $(\log L)^2$
with probability tending to
$(\log L)^2$
with probability tending to
![]() $1$
as
$1$
as
![]() $L\to \infty $
, and so by Claim 7.4, the same is true under the area-tilted measure).
$L\to \infty $
, and so by Claim 7.4, the same is true under the area-tilted measure).
Now, using the localization of
![]() $\mathsf {S}_1$
(Claim 6.4) and the triviality-in-L of the area tilt (Claim 7.4), we have that for all
$\mathsf {S}_1$
(Claim 6.4) and the triviality-in-L of the area tilt (Claim 7.4), we have that for all
![]() $\epsilon>0$
small, the following hold with
$\epsilon>0$
small, the following hold with
![]() $\mathbb {P}_{\lambda ,+}^{\bar {\mathsf {u}},\bar {\mathsf {v}}}$
-probability tending to
$\mathbb {P}_{\lambda ,+}^{\bar {\mathsf {u}},\bar {\mathsf {v}}}$
-probability tending to
![]() $1$
as
$1$
as
![]() $L\to \infty $
:
$L\to \infty $
:
 $$ \begin{align} \mathcal{E}_1(L^{2/3}) &:= \big\{\mathsf{S}_1(L^{2/3}) \in [-(K-\mu) L^{2/3} - L^{1/3+\epsilon}, -(K-\mu)L^{2/3} +L^{1/3+\epsilon}] \big\}, \text{ and} \nonumber\\ \mathcal{E}_1(2L^{2/3}) &:= \big\{\mathsf{S}_1(2L^{2/3}) \in [-(K-2\mu) L^{2/3} - L^{1/3+\epsilon}, -(K-2\mu)L^{2/3} +L^{1/3+\epsilon}] \big\} . \end{align} $$
$$ \begin{align} \mathcal{E}_1(L^{2/3}) &:= \big\{\mathsf{S}_1(L^{2/3}) \in [-(K-\mu) L^{2/3} - L^{1/3+\epsilon}, -(K-\mu)L^{2/3} +L^{1/3+\epsilon}] \big\}, \text{ and} \nonumber\\ \mathcal{E}_1(2L^{2/3}) &:= \big\{\mathsf{S}_1(2L^{2/3}) \in [-(K-2\mu) L^{2/3} - L^{1/3+\epsilon}, -(K-2\mu)L^{2/3} +L^{1/3+\epsilon}] \big\} . \end{align} $$
Thus, the lemma will be proved upon showing
Write the above probability as

where
Due to the restriction on
![]() $\mathsf {S}(2L^{2/3})$
imposed by the indicator defining F, Equation (7.9) will be shown if we can prove
$\mathsf {S}(2L^{2/3})$
imposed by the indicator defining F, Equation (7.9) will be shown if we can prove

uniformly over
Note that the
![]() $\sup $
over K is trivial: Indeed, K plays no role in the limit in Equation (7.11), since by horizontal shift invariance, we may shift to the right by
$\sup $
over K is trivial: Indeed, K plays no role in the limit in Equation (7.11), since by horizontal shift invariance, we may shift to the right by
![]() $KL^{2/3}$
. The denominator may be bounded from below as a constant, by shifting both
$KL^{2/3}$
. The denominator may be bounded from below as a constant, by shifting both
![]() $\bar {\mathsf {u}}_2$
and
$\bar {\mathsf {u}}_2$
and
![]() $\bar {\mathsf {w}}_2$
up to
$\bar {\mathsf {w}}_2$
up to
![]() $cL^{1/3}$
, and then applying the Brownian excursion limit as in the proof of Claim 7.4. The area tilt in the numerator may be bounded from above by
$cL^{1/3}$
, and then applying the Brownian excursion limit as in the proof of Claim 7.4. The area tilt in the numerator may be bounded from above by
![]() $1$
. Thus, we have reduced to showing the following:
$1$
. Thus, we have reduced to showing the following:
uniformly over
![]() $\bar u$
and
$\bar u$
and
![]() $\bar w$
. By monotonicity, we may assume
$\bar w$
. By monotonicity, we may assume
![]() $\bar {w}_2 = 0$
. The result now follows from the Brownian excursion limit of
$\bar {w}_2 = 0$
. The result now follows from the Brownian excursion limit of
![]() $\mathsf {S}_2$
under
$\mathsf {S}_2$
under
![]() $\mathbb {P}_{+}^{\bar {\mathsf {u}}, \bar {\mathsf {w}}}$
(Theorem 4.3).
$\mathbb {P}_{+}^{\bar {\mathsf {u}}, \bar {\mathsf {w}}}$
(Theorem 4.3).
Following [Reference Ioffe, Ott, Shlosman and Velenik30], we are now ready to prove Theorem 7.1.
Proof of Theorem 7.1.
We have reduced to an area-tilted, directed 2D random walk bridge between
![]() ${\mathsf {u}}$
and
${\mathsf {u}}$
and
![]() ${\mathsf {v}}$
satisfying Equations (7.2) and (7.3), respectively, conditioned to stay positive. That is, we have a random walk
${\mathsf {v}}$
satisfying Equations (7.2) and (7.3), respectively, conditioned to stay positive. That is, we have a random walk
![]() $\mathsf {S}$
under law
$\mathsf {S}$
under law
This puts us in the framework of the proof of the Ferrari–Spohn limit for such random walks given in [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6.6 and 6.7]. Tightness follows exactly as in [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6.6]. The proof of finite-dimensional distributions in [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6.7] had just two additional inputs: their Proposition 6.2 and Lemma 6.3, and so we will be done as soon as we establish our analogues of these results.
Their Proposition 6.2 holds exactly the same for us. Their Lemma 6.3 does as well, with the exception that the constant in front of our area tilt is slightly different, and thus the resulting generator is slightly different as well. We restate and prove that result in our setting.
For any
![]() $n\in \mathbb {N}$
, we will write
$n\in \mathbb {N}$
, we will write
![]() $\mathsf {S}[0,n]:= (\mathsf {S}(i))_{i\in [0,n]}$
. Following [Reference Ioffe, Ott, Shlosman and Velenik30, Eq.(6.6)], for any function
$\mathsf {S}[0,n]:= (\mathsf {S}(i))_{i\in [0,n]}$
. Following [Reference Ioffe, Ott, Shlosman and Velenik30, Eq.(6.6)], for any function
![]() $f: \mathbb {N} \to \mathbb {R}$
and
$f: \mathbb {N} \to \mathbb {R}$
and
![]() $u \in {\mathbb H}$
, define the n-step partition function
$u \in {\mathbb H}$
, define the n-step partition function
Recall from Section 4.1 that
![]() $\mathsf {S}$
under law
$\mathsf {S}$
under law
![]() $\mathbb {P}$
has step-distribution
$\mathbb {P}$
has step-distribution
![]() $X = (X_1, X_2)$
. Recall also
$X = (X_1, X_2)$
. Recall also
![]() $\sigma ^2 := \operatorname {Var}(X_2)/\mu $
from the discussion above Theorem 4.3. Following [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6.5], define the following operator on smooth test functions f with compact support in
$\sigma ^2 := \operatorname {Var}(X_2)/\mu $
from the discussion above Theorem 4.3. Following [Reference Ioffe, Ott, Shlosman and Velenik30, Section 6.5], define the following operator on smooth test functions f with compact support in
![]() $(0,\infty )$
:
$(0,\infty )$
:
Note that the indicator may be dropped, as f is supported above
![]() $0$
. By Taylor expanding f to second order and
$0$
. By Taylor expanding f to second order and
![]() $e^x-1$
to first order (the errors are
$e^x-1$
to first order (the errors are
![]() $o(L^{-2/3})$
), we have
$o(L^{-2/3})$
), we have
 $$ \begin{align*} &\lim_{L\to\infty} \frac{\mathbf{T}_L-\mathrm{Id}}{L^{-2/3}}f(r) \\ &\quad= \lim_{L\to\infty} L^{2/3} \mathbb{E}\Big[\big(e^{-\frac{\lambda}{L}X_1 r L^{1/3} \sigma} -1\big)f(r) + e^{-\frac{\lambda}{L}X_1 r L^{1/3} \sigma} \Big(f'(r)\frac{X_2}{L^{1/3}\sigma} + \tfrac{1}2 f"(r)\frac{X_2^2}{L^{2/3}\sigma^2}\Big) \Big] \\ &\quad=\lim_{L\to\infty} L^{2/3} \mathbb{E}\Big[-\frac{\lambda}{L^{2/3}}X_1 r \sigma f(r) + e^{-\frac{\lambda}{L}X_1 r L^{1/3} \sigma} \Big(f'(r)\frac{X_2}{L^{1/3}\sigma} + \tfrac{1}2 f"(r)\frac{X_2^2}{L^{2/3}\sigma^2} \Big) \Big]. \end{align*} $$
$$ \begin{align*} &\lim_{L\to\infty} \frac{\mathbf{T}_L-\mathrm{Id}}{L^{-2/3}}f(r) \\ &\quad= \lim_{L\to\infty} L^{2/3} \mathbb{E}\Big[\big(e^{-\frac{\lambda}{L}X_1 r L^{1/3} \sigma} -1\big)f(r) + e^{-\frac{\lambda}{L}X_1 r L^{1/3} \sigma} \Big(f'(r)\frac{X_2}{L^{1/3}\sigma} + \tfrac{1}2 f"(r)\frac{X_2^2}{L^{2/3}\sigma^2}\Big) \Big] \\ &\quad=\lim_{L\to\infty} L^{2/3} \mathbb{E}\Big[-\frac{\lambda}{L^{2/3}}X_1 r \sigma f(r) + e^{-\frac{\lambda}{L}X_1 r L^{1/3} \sigma} \Big(f'(r)\frac{X_2}{L^{1/3}\sigma} + \tfrac{1}2 f"(r)\frac{X_2^2}{L^{2/3}\sigma^2} \Big) \Big]. \end{align*} $$
Now, use
![]() $\mu := \mathbb {E}[X_1]$
,
$\mu := \mathbb {E}[X_1]$
,
![]() $\mathbb {E}[X_2] = 0$
and
$\mathbb {E}[X_2] = 0$
and
![]() $\operatorname {Var}(X_2) = \mathbb {E}[X_2^2]$
so that the
$\operatorname {Var}(X_2) = \mathbb {E}[X_2^2]$
so that the
![]() $f'(r)$
term vanishes and we find
$f'(r)$
term vanishes and we find
Kurtz’s semigroup convergence theorem ([Reference Ethier and Kurtz24, Theorem 1.6.5], see also [Reference Ioffe, Shlosman and Velenik33, Eq.(2.34)]) then gives
uniformly over t in bounded intervals of
![]() $\mathbb {R}_+$
. Define the rescaling operator
$\mathbb {R}_+$
. Define the rescaling operator
Observing that
![]() $\mathcal {G}_{\lambda ,L,+}^{k}[ \mathrm {Sc}_L f] =\mathbf {T}_L^k f$
, the second-to-last-display immediately yields
$\mathcal {G}_{\lambda ,L,+}^{k}[ \mathrm {Sc}_L f] =\mathbf {T}_L^k f$
, the second-to-last-display immediately yields
which is our version of [Reference Ioffe, Ott, Shlosman and Velenik30, Lemma 6.3].
A Cluster expansion and open contours in the SOS model
A.1 Cluster expansion
Consider the SOS model in a region
![]() $\Lambda \Subset \mathbb {Z}^2$
without floor, with boundary condition
$\Lambda \Subset \mathbb {Z}^2$
without floor, with boundary condition
![]() $j\in \mathbb {Z}$
. Fix any subset U of the inner boundary of
$j\in \mathbb {Z}$
. Fix any subset U of the inner boundary of
![]() $\Lambda $
, and condition on
$\Lambda $
, and condition on
![]() $\{\varphi |_U\geq j\}$
. Let
$\{\varphi |_U\geq j\}$
. Let
![]() $\widehat Z_{\Lambda , U} := \widehat {Z}_{\Lambda ,U}^{j,+}$
denote the partition function of this model. Note that the partition function has no dependence on j and is also unchanged by a replacement of the conditioning with
$\widehat Z_{\Lambda , U} := \widehat {Z}_{\Lambda ,U}^{j,+}$
denote the partition function of this model. Note that the partition function has no dependence on j and is also unchanged by a replacement of the conditioning with
![]() $\{\varphi |_U \leq j\}$
. [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli13] proves that there exists a constant
$\{\varphi |_U \leq j\}$
. [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli13] proves that there exists a constant
![]() $\beta _0>0$
such that for all
$\beta _0>0$
such that for all
![]() $\beta>\beta _0$
, one has
$\beta>\beta _0$
, one has
for some function
![]() $f_U$
. Equation (A.1) was proven using the main theorem from [Reference Kotecký and Preiss36], which can actually be used to show (with the same proof as in [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli13]) that the formula holds simultaneously for all subsets
$f_U$
. Equation (A.1) was proven using the main theorem from [Reference Kotecký and Preiss36], which can actually be used to show (with the same proof as in [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli13]) that the formula holds simultaneously for all subsets
![]() $\Lambda '\subset \Lambda $
(with the same
$\Lambda '\subset \Lambda $
(with the same
![]() $f_U$
):
$f_U$
):
(here,
![]() $Z_{\Lambda ',U}$
is defined as before, with the understanding that the condition on U only needs to be satisfied on
$Z_{\Lambda ',U}$
is defined as before, with the understanding that the condition on U only needs to be satisfied on
![]() $\Lambda '\cap U$
, or in other words
$\Lambda '\cap U$
, or in other words
![]() $Z_{\Lambda ',U}:=Z_{\Lambda ',U \cap \Lambda '}$
). The latter observation leads, using Möbius inversion, to the following formula for
$Z_{\Lambda ',U}:=Z_{\Lambda ',U \cap \Lambda '}$
). The latter observation leads, using Möbius inversion, to the following formula for
![]() $f_U$
:
$f_U$
:
From Equation (A.3), we can read off some properties of the function
![]() $f_U$
:
$f_U$
:
-
1.
 $f_U(V)$
only depends on U only through
$f_U(V)$
only depends on U only through
 $U\cap V$
, and in particular, if
$U\cap V$
, and in particular, if
 $U\cap V = \emptyset $
,
$U\cap V = \emptyset $
,
 $f_U(V) = f_0(V)$
for some universal function
$f_U(V) = f_0(V)$
for some universal function
 $f_0$
. Moreover,
$f_0$
. Moreover,
 $f_0(V)$
only depends on the ‘shape’ and size of the volume V, that is,
$f_0(V)$
only depends on the ‘shape’ and size of the volume V, that is,
 $f_0(\cdot )$
is invariant with respect to lattice symmetries.
$f_0(\cdot )$
is invariant with respect to lattice symmetries. -
2. If V is not connected,
 $f_U(V)=0$
. Indeed, if
$f_U(V)=0$
. Indeed, if
 $V=V_1 \sqcup V_2$
, each log-partition function on the right-hand side of Equation (A.3) splits into the sum of two terms, both of which appear in the global sum with the same frequency of plus and minus signs.
$V=V_1 \sqcup V_2$
, each log-partition function on the right-hand side of Equation (A.3) splits into the sum of two terms, both of which appear in the global sum with the same frequency of plus and minus signs. -
3. There exists a constant
 $\beta _0>0$
such that (A.4)where
$\beta _0>0$
such that (A.4)where $$ \begin{align} \sup_U |f_U(\mathcal{C})| \leq \exp\big((\beta-\beta_0)d(\mathcal{C})\big), \end{align} $$
$$ \begin{align} \sup_U |f_U(\mathcal{C})| \leq \exp\big((\beta-\beta_0)d(\mathcal{C})\big), \end{align} $$
 $d(\mathcal {C})$
denotes the cardinality of the smallest connected set of bonds of
$d(\mathcal {C})$
denotes the cardinality of the smallest connected set of bonds of
 $\mathbb {Z}^2$
containing all boundary bonds of
$\mathbb {Z}^2$
containing all boundary bonds of
 $\mathcal {C}$
(i.e., bonds connecting
$\mathcal {C}$
(i.e., bonds connecting
 $\mathcal {C}$
to
$\mathcal {C}$
to
 $\mathcal {C}^c$
), see [Reference Dobrushin, Kotecký and Shlosman20, Proposition 3.9] for details.
$\mathcal {C}^c$
), see [Reference Dobrushin, Kotecký and Shlosman20, Proposition 3.9] for details.
A.2 Proof of Proposition 2.1
Recall
![]() $\widehat {Z}_{\Lambda ,U}^{j,+}$
from above Equation (A.1), and define
$\widehat {Z}_{\Lambda ,U}^{j,+}$
from above Equation (A.1), and define
![]() $\widehat {Z}_{\Lambda ,U}^{j,-}$
similarly but with the conditioning
$\widehat {Z}_{\Lambda ,U}^{j,-}$
similarly but with the conditioning
![]() $\{\varphi |_U \leq j\}$
(as noted above Equation (A.1),
$\{\varphi |_U \leq j\}$
(as noted above Equation (A.1),
![]() $\widehat {Z}_{\Lambda ,U}^{j,+} = \widehat {Z}_{\Lambda ,U}^{j,-}$
. The different notation is mostly for clarity in the calculations that follow). Recall also
$\widehat {Z}_{\Lambda ,U}^{j,+} = \widehat {Z}_{\Lambda ,U}^{j,-}$
. The different notation is mostly for clarity in the calculations that follow). Recall also
![]() $\Lambda _{\gamma }^+, \Lambda _{\gamma }^-, \Delta _{\gamma }^+,$
and
$\Lambda _{\gamma }^+, \Lambda _{\gamma }^-, \Delta _{\gamma }^+,$
and
![]() $\Delta _{\gamma }^{-}$
from above Proposition 2.1.
$\Delta _{\gamma }^{-}$
from above Proposition 2.1.
Observe that
This is a simple consequence of the following identity: For any
![]() ${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
such that
${\mathsf {u}}, {\mathsf {v}} \in \mathbb {Z}^2$
such that
![]() $\varphi _{\mathsf {u}} \geq 1$
and
$\varphi _{\mathsf {u}} \geq 1$
and
![]() $\varphi _{{\mathsf {v}}} \leq 0$
, we have
$\varphi _{{\mathsf {v}}} \leq 0$
, we have
Now, cluster-expanding each of the partition functions on the right-hand side of Equation (A.5) yields
 $$ \begin{align} \widehat Z_{\Lambda_{\gamma}^+, \Delta_{\gamma}^+}^{1} \widehat Z_{\Lambda_{\gamma}^-,\Delta_{\gamma}^-}^{0} &= \exp \Big(\sum_{\substack{\mathcal{C} \subset \Lambda \\ \mathcal{C} \cap \Delta_{\gamma} = \emptyset}} f_0(\mathcal{C}) + \sum_{\substack{\mathcal{C} \subset \Lambda_{\gamma}^+ \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_{\Delta_{\gamma}^+}(\mathcal{C}) + \sum_{\substack{\mathcal{C} \subset \Lambda_{\gamma}^- \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_{\Delta_{\gamma}^-} (\mathcal{C}) \Big) \nonumber \\ &= e^{\sum_{\mathcal{C}\subset \Lambda} f_0(\mathcal{C})} \exp\Big( \Psi_{\Lambda}(\gamma)\Big) =\widehat Z_{\Lambda}^{0} \exp\Big( \Psi_{\Lambda}(\gamma)\Big) , \end{align} $$
$$ \begin{align} \widehat Z_{\Lambda_{\gamma}^+, \Delta_{\gamma}^+}^{1} \widehat Z_{\Lambda_{\gamma}^-,\Delta_{\gamma}^-}^{0} &= \exp \Big(\sum_{\substack{\mathcal{C} \subset \Lambda \\ \mathcal{C} \cap \Delta_{\gamma} = \emptyset}} f_0(\mathcal{C}) + \sum_{\substack{\mathcal{C} \subset \Lambda_{\gamma}^+ \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_{\Delta_{\gamma}^+}(\mathcal{C}) + \sum_{\substack{\mathcal{C} \subset \Lambda_{\gamma}^- \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_{\Delta_{\gamma}^-} (\mathcal{C}) \Big) \nonumber \\ &= e^{\sum_{\mathcal{C}\subset \Lambda} f_0(\mathcal{C})} \exp\Big( \Psi_{\Lambda}(\gamma)\Big) =\widehat Z_{\Lambda}^{0} \exp\Big( \Psi_{\Lambda}(\gamma)\Big) , \end{align} $$
where
 $$\begin{align*}\Psi_{\Lambda}(\gamma) := - \sum_{\substack{\mathcal{C} \subset \Lambda \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_0(\mathcal{C}) + \sum_{\substack{\mathcal{C} \subset \Lambda_{\gamma}^+ \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_{\Delta_{\gamma}^+}(\mathcal{C}) + \sum_{\substack{\mathcal{C} \subset \Lambda_{\gamma}^- \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_{\Delta_{\gamma}^-}(\mathcal{C}). \end{align*}$$
$$\begin{align*}\Psi_{\Lambda}(\gamma) := - \sum_{\substack{\mathcal{C} \subset \Lambda \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_0(\mathcal{C}) + \sum_{\substack{\mathcal{C} \subset \Lambda_{\gamma}^+ \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_{\Delta_{\gamma}^+}(\mathcal{C}) + \sum_{\substack{\mathcal{C} \subset \Lambda_{\gamma}^- \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} f_{\Delta_{\gamma}^-}(\mathcal{C}). \end{align*}$$
Defining
it follows from Equations (A.5) and (A.6) that
 $$\begin{align*}\widehat{Z}_{\Lambda}^{\xi} =\widehat{Z}_{\Lambda}^0\sum_{\gamma} \exp\Big(-\beta|\gamma| + \sum_{\substack{\mathcal{C} \subset \Lambda \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} \phi(\mathcal{C};\gamma)\Big). \end{align*}$$
$$\begin{align*}\widehat{Z}_{\Lambda}^{\xi} =\widehat{Z}_{\Lambda}^0\sum_{\gamma} \exp\Big(-\beta|\gamma| + \sum_{\substack{\mathcal{C} \subset \Lambda \\ \mathcal{C} \cap \Delta_{\gamma} \neq \emptyset}} \phi(\mathcal{C};\gamma)\Big). \end{align*}$$
Equations (2.1) and (2.3) follow immediately. From the definition of
![]() $\phi $
in Equation (A.7) and the properties of
$\phi $
in Equation (A.7) and the properties of
![]() $f_U$
from Appendix A.1, we obtain Properties (i) to (iv) of the proposition.
$f_U$
from Appendix A.1, we obtain Properties (i) to (iv) of the proposition.
A.3 Law of an open contour in the SOS model with floor
Consider the SOS model
![]() $\pi _{R}^{\xi }$
in a domain R with floor at
$\pi _{R}^{\xi }$
in a domain R with floor at
![]() $0$
and boundary condition
$0$
and boundary condition
![]() $\xi \in \{h-1, h\}^{\partial \Lambda }$
inducing a unique open h-contour
$\xi \in \{h-1, h\}^{\partial \Lambda }$
inducing a unique open h-contour
![]() $\gamma $
. Consider
$\gamma $
. Consider
![]() $h=\lfloor \frac {1}{4\beta }\log L \rfloor - n$
, for
$h=\lfloor \frac {1}{4\beta }\log L \rfloor - n$
, for
![]() $n \in \mathbb {N}$
fixed relative to L, and assume that the domain R satisfies
$n \in \mathbb {N}$
fixed relative to L, and assume that the domain R satisfies
![]() $|R| \leq L^{\frac {4}{3}+2\epsilon }$
and
$|R| \leq L^{\frac {4}{3}+2\epsilon }$
and
![]() $|\partial R| \leq L^{\frac {2}{3}+2\epsilon }$
, for some
$|\partial R| \leq L^{\frac {2}{3}+2\epsilon }$
, for some
![]() $\epsilon \in (0,1/20)$
. In this subsection, we derive an asymptotic expression for the law of the random contour
$\epsilon \in (0,1/20)$
. In this subsection, we derive an asymptotic expression for the law of the random contour
![]() $\gamma $
in terms of the no-floor law
$\gamma $
in terms of the no-floor law
![]() $\widehat {\pi }_R^{\xi }$
.
$\widehat {\pi }_R^{\xi }$
.
For a subset U of the inner boundary of R, recall
![]() $\widehat {Z}_{R,U}^{j, \pm }$
as in Appendix A.2, and define
$\widehat {Z}_{R,U}^{j, \pm }$
as in Appendix A.2, and define
![]() $Z_{R,U}^{j,\pm }$
similarly but with a floor at
$Z_{R,U}^{j,\pm }$
similarly but with a floor at
![]() $0$
. As in Equation (A.5), we can write the law of
$0$
. As in Equation (A.5), we can write the law of
![]() $\gamma $
in terms of the partition functions above and below it:
$\gamma $
in terms of the partition functions above and below it:
The partition functions
![]() $Z_{R, U}^{j,\pm }$
can be related to the corresponding partition function
$Z_{R, U}^{j,\pm }$
can be related to the corresponding partition function
![]() $\widehat Z_{R, U}^{j,\pm }$
of the model without floor via the following (taken from [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Prop. A.1]):
$\widehat Z_{R, U}^{j,\pm }$
of the model without floor via the following (taken from [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Prop. A.1]):
where
![]() $\widehat \pi $
is the infinite volume measure obtained as the thermodynamic limit of
$\widehat \pi $
is the infinite volume measure obtained as the thermodynamic limit of
![]() $\widehat {\pi }_{\Lambda }^0$
, see [Reference Brandenberger and Wayne3]. It follows that
$\widehat {\pi }_{\Lambda }^0$
, see [Reference Brandenberger and Wayne3]. It follows that
where we used
![]() $|R_{\gamma }^{+}| = |R| - |R_{\gamma }^{-}|$
and dropped the term
$|R_{\gamma }^{+}| = |R| - |R_{\gamma }^{-}|$
and dropped the term
![]() $|R|\widehat \pi (\varphi _o> h)$
, which is independent of
$|R|\widehat \pi (\varphi _o> h)$
, which is independent of
![]() $\gamma $
. It was proved in [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Lemma 2.4] that there exists a constant
$\gamma $
. It was proved in [Reference Caputo, Lubetzky, Martinelli, Sly and Toninelli14, Lemma 2.4] that there exists a constant
![]() $c_{\infty }:= c_\infty (\beta )$
such that, for
$c_{\infty }:= c_\infty (\beta )$
such that, for
![]() $j \geq 1$
,
$j \geq 1$
,
Define
![]() $a_L := \frac 1{4\beta }\log L - \lfloor \frac 1{4\beta }\log L\rfloor $
,
$a_L := \frac 1{4\beta }\log L - \lfloor \frac 1{4\beta }\log L\rfloor $
,
![]() $\lambda := \lambda (L) = c_{\infty }e^{4\beta a_L}(1-e^{-4\beta })$
and
$\lambda := \lambda (L) = c_{\infty }e^{4\beta a_L}(1-e^{-4\beta })$
and
![]() $\lambda ^{(n)} := \lambda e^{4\beta n}$
. We have
$\lambda ^{(n)} := \lambda e^{4\beta n}$
. We have
 $$ \begin{align*} &\widehat\pi(\varphi_o> h-1) - \widehat\pi(\varphi_o > h) = c_{\infty} e^{-4\beta h}(1-e^{-4\beta})+O(e^{-6\beta h}) \\&\qquad\qquad\qquad\quad\qquad= c_{\infty}e^{4\beta a_L- \log L + 4\beta n}(1-e^{-4\beta})+O(e^{-6\beta h}) = \lambda^{(n)}/L + O(e^{-6\beta h}). \end{align*} $$
$$ \begin{align*} &\widehat\pi(\varphi_o> h-1) - \widehat\pi(\varphi_o > h) = c_{\infty} e^{-4\beta h}(1-e^{-4\beta})+O(e^{-6\beta h}) \\&\qquad\qquad\qquad\quad\qquad= c_{\infty}e^{4\beta a_L- \log L + 4\beta n}(1-e^{-4\beta})+O(e^{-6\beta h}) = \lambda^{(n)}/L + O(e^{-6\beta h}). \end{align*} $$
Putting everything together, we find
where
![]() $A(\gamma )=|R_{\gamma }^{-}|$
is the area under
$A(\gamma )=|R_{\gamma }^{-}|$
is the area under
![]() $\gamma $
in R.
$\gamma $
in R.
B Proof of Proposition 2.14 and Equation (5.18)
Proof of Proposition 2.14.
Fix
![]() $\delta \in (0,1)$
. We begin by showing that for any
$\delta \in (0,1)$
. We begin by showing that for any
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
, we have
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
, we have
![]() $f(\mathsf {h}_{\mathsf {y}}) = 1$
, where
$f(\mathsf {h}_{\mathsf {y}}) = 1$
, where
Let
and
where
![]() $\nu $
is the same as in Proposition 2.12. In words,
$\nu $
is the same as in Proposition 2.12. In words,
![]() $\mathcal W_{\textrm {in}}^\blacktriangleleft $
is the sector of the Wulff shape
$\mathcal W_{\textrm {in}}^\blacktriangleleft $
is the sector of the Wulff shape
![]() $\mathcal W$
where the sector boundary (part of
$\mathcal W$
where the sector boundary (part of
![]() $\partial \mathcal W$
) is
$\partial \mathcal W$
) is
![]() $\{\mathsf {h}_{\mathsf {y}} : \mathsf {y}\in \mathcal {Y}^\blacktriangleleft _{\delta }\}$
, while
$\{\mathsf {h}_{\mathsf {y}} : \mathsf {y}\in \mathcal {Y}^\blacktriangleleft _{\delta }\}$
, while
![]() $\mathcal W_{\textrm {out}}^{\blacktriangleleft }$
lies right outside of
$\mathcal W_{\textrm {out}}^{\blacktriangleleft }$
lies right outside of
![]() $\mathcal W$
along the continuation of such sector (note that
$\mathcal W$
along the continuation of such sector (note that
![]() $\mathcal W_{\textrm {in}}^\blacktriangleleft \subset \mathcal W$
comes from
$\mathcal W_{\textrm {in}}^\blacktriangleleft \subset \mathcal W$
comes from
![]() $0 \in \mathcal W$
and the convexity of
$0 \in \mathcal W$
and the convexity of
![]() $\mathcal W$
).
$\mathcal W$
).
In what follows, we let
![]() $C:= C(\beta )>0$
denote a constant that may depend on
$C:= C(\beta )>0$
denote a constant that may depend on
![]() $\beta $
and may change from line-to-line. We begin with two claims.
$\beta $
and may change from line-to-line. We begin with two claims.
Claim B.1. For all
![]() $\mathsf {h} \in \mathcal W_{\textrm {in}}^\blacktriangleleft \cup \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
, we have
$\mathsf {h} \in \mathcal W_{\textrm {in}}^\blacktriangleleft \cup \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
, we have
and the series converges uniformly over
![]() $\mathsf {h}$
. In particular,
$\mathsf {h}$
. In particular,
![]() $f(\mathsf {h})$
is continuous on
$f(\mathsf {h})$
is continuous on
![]() $\mathcal W_{\textrm {in}}^\blacktriangleleft \cup \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
.
$\mathcal W_{\textrm {in}}^\blacktriangleleft \cup \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
.
Proof of Claim B.1.
We will use the following bound many times: From Equation (2.16), we have that for any
![]() $\epsilon \in (0,1)$
and for all
$\epsilon \in (0,1)$
and for all
![]() $\beta>0$
sufficiently large, there exists a constant
$\beta>0$
sufficiently large, there exists a constant
![]() $C:= C(\epsilon , \beta )>0$
such that for all
$C:= C(\epsilon , \beta )>0$
such that for all
![]() $\mathsf {y} \in \mathbb {Z}^2$
$\mathsf {y} \in \mathbb {Z}^2$
For
![]() $\mathsf {h}\in \mathcal W_{\textrm {in}}^\blacktriangleleft \cup \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
, we have
$\mathsf {h}\in \mathcal W_{\textrm {in}}^\blacktriangleleft \cup \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
, we have
![]() $\mathsf {h}\cdot \mathsf {y} - \tau _{\beta }(\mathsf {y}) \leq \frac {\beta \nu }{2}\|\mathsf {y}\|_2 \leq \frac {\beta \nu }{2}\|\mathsf {y}\|_1$
for all
$\mathsf {h}\cdot \mathsf {y} - \tau _{\beta }(\mathsf {y}) \leq \frac {\beta \nu }{2}\|\mathsf {y}\|_2 \leq \frac {\beta \nu }{2}\|\mathsf {y}\|_1$
for all
![]() $\mathsf {y} \in \mathbb {Z}^2 \setminus \{0\}$
. Then Proposition 2.12 and Equation (B.1) yield
$\mathsf {y} \in \mathbb {Z}^2 \setminus \{0\}$
. Then Proposition 2.12 and Equation (B.1) yield
 $$ \begin{align} \sum_{\substack{\Gamma \in \mathsf{A_L} \cup \mathsf{A_R} \\ \Gamma: 0 \to\mathsf{y}}} W^{\mathsf{h}}(\Gamma) \leq e^{\mathsf{h}\cdot\mathsf{y}} \mathcal{G}(\mathsf{y} \;\big|\; |\mathsf{Cpts}(\Gamma)| = 0) \leq C\exp\Big(-(\tfrac{\nu \beta}2 - \epsilon)\left\Vert \mathsf{y} \right\Vert{}_1\Big) . \end{align} $$
$$ \begin{align} \sum_{\substack{\Gamma \in \mathsf{A_L} \cup \mathsf{A_R} \\ \Gamma: 0 \to\mathsf{y}}} W^{\mathsf{h}}(\Gamma) \leq e^{\mathsf{h}\cdot\mathsf{y}} \mathcal{G}(\mathsf{y} \;\big|\; |\mathsf{Cpts}(\Gamma)| = 0) \leq C\exp\Big(-(\tfrac{\nu \beta}2 - \epsilon)\left\Vert \mathsf{y} \right\Vert{}_1\Big) . \end{align} $$
Take
![]() $\epsilon < \nu \beta /2$
. Then since
$\epsilon < \nu \beta /2$
. Then since
![]() $\mathsf {A} \subset \mathsf {A_L}$
, the sequence of continuous functions
$\mathsf {A} \subset \mathsf {A_L}$
, the sequence of continuous functions
 $$\begin{align*}f_N(\mathsf{h}) := \sum_{\substack{\mathsf{y} \in \mathbb{Z}^2 \setminus \{0\} \\ \left\Vert \mathsf{y} \right\Vert{}_1 \leq N}} \sum_{\substack{\Gamma \in \mathsf{A} \\ \Gamma: 0 \to\mathsf{y}}} W^{\mathsf{h}}(\Gamma) \end{align*}$$
$$\begin{align*}f_N(\mathsf{h}) := \sum_{\substack{\mathsf{y} \in \mathbb{Z}^2 \setminus \{0\} \\ \left\Vert \mathsf{y} \right\Vert{}_1 \leq N}} \sum_{\substack{\Gamma \in \mathsf{A} \\ \Gamma: 0 \to\mathsf{y}}} W^{\mathsf{h}}(\Gamma) \end{align*}$$
converges uniformly to
![]() $f(\mathsf {h})$
, and so the claim follows.
$f(\mathsf {h})$
, and so the claim follows.
Claim B.2. For
![]() $\mathsf {h} \in \mathcal W_{\textrm {in}}^\blacktriangleleft $
,
$\mathsf {h} \in \mathcal W_{\textrm {in}}^\blacktriangleleft $
,
![]() $f(\mathsf {h})\leq 1$
. For
$f(\mathsf {h})\leq 1$
. For
![]() $\mathsf {h} \in \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
,
$\mathsf {h} \in \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
,
![]() $f(\mathsf {h})\geq 1$
.
$f(\mathsf {h})\geq 1$
.
Proof of Claim B.2.
Similar to Equation (B.2), we have the following for any
![]() $\mathsf {h} \in \mathcal W_{\textrm {in}}^\blacktriangleleft \cup \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
:
$\mathsf {h} \in \mathcal W_{\textrm {in}}^\blacktriangleleft \cup \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
:

Using the factorization of
![]() $q(\Gamma )$
(2.18) and (B.3), we have
$q(\Gamma )$
(2.18) and (B.3), we have

where in the inequality we replaced
![]() $\mathcal {Y}^\blacktriangleleft _{\delta }$
by the full cone
$\mathcal {Y}^\blacktriangleleft _{\delta }$
by the full cone
![]() $\mathcal {Y}^\blacktriangleleft $
and in the next line we exchanged the sums and used the fact that an animal with at least one cone point must necessarily satisfy
$\mathcal {Y}^\blacktriangleleft $
and in the next line we exchanged the sums and used the fact that an animal with at least one cone point must necessarily satisfy
![]() $\mathsf {X}(\Gamma ) \in \mathcal {Y}^\blacktriangleleft $
. Hence, we have the chain of inequalities
$\mathsf {X}(\Gamma ) \in \mathcal {Y}^\blacktriangleleft $
. Hence, we have the chain of inequalities
 $$ \begin{align} \sum_{\mathsf{y}\in \mathcal{Y}^\blacktriangleleft_{\delta}}e^{\mathsf{h}\cdot\mathsf{y}} \mathcal{G}(\mathsf{y}) \leq C + B_L(\mathsf{h})B_R(\mathsf{h})\sum_{m\geq1} f(\mathsf{h})^m \leq C + \sum_{\mathsf{y}\in \mathbb{Z}^2}e^{\mathsf{h}\cdot\mathsf{y}} \mathcal{G}(\mathsf{y}). \end{align} $$
$$ \begin{align} \sum_{\mathsf{y}\in \mathcal{Y}^\blacktriangleleft_{\delta}}e^{\mathsf{h}\cdot\mathsf{y}} \mathcal{G}(\mathsf{y}) \leq C + B_L(\mathsf{h})B_R(\mathsf{h})\sum_{m\geq1} f(\mathsf{h})^m \leq C + \sum_{\mathsf{y}\in \mathbb{Z}^2}e^{\mathsf{h}\cdot\mathsf{y}} \mathcal{G}(\mathsf{y}). \end{align} $$
Since
![]() $B_L(\mathsf {h}),B_R(\mathsf {h})<\infty $
by Claim B.1, finiteness of the middle term in Equation (B.4) depends only on the convergence of
$B_L(\mathsf {h}),B_R(\mathsf {h})<\infty $
by Claim B.1, finiteness of the middle term in Equation (B.4) depends only on the convergence of
![]() $\sum _{m\geq 1}f(\mathsf {h})^m$
.
$\sum _{m\geq 1}f(\mathsf {h})^m$
.
Now, if
![]() $\mathsf {h}$
is in the interior of
$\mathsf {h}$
is in the interior of
![]() $\mathcal W_{\textrm {in}}^\blacktriangleleft $
(and thus in the interior of
$\mathcal W_{\textrm {in}}^\blacktriangleleft $
(and thus in the interior of
![]() $\mathcal W$
), the rightmost term in Equation (B.4) converges due to the second definition of
$\mathcal W$
), the rightmost term in Equation (B.4) converges due to the second definition of
![]() $\mathcal W$
, and thus
$\mathcal W$
, and thus
![]() $\sum _{m\geq 1}f(\mathsf {h})^m<\infty $
, and thus
$\sum _{m\geq 1}f(\mathsf {h})^m<\infty $
, and thus
![]() $f(\mathsf {h})<1$
. By continuity of f, we get
$f(\mathsf {h})<1$
. By continuity of f, we get
![]() $f(\mathsf {h})\leq 1$
on
$f(\mathsf {h})\leq 1$
on
![]() $\mathcal W_{\textrm {in}}^\blacktriangleleft $
. On the other hand, if
$\mathcal W_{\textrm {in}}^\blacktriangleleft $
. On the other hand, if
![]() $\mathsf {h}$
is in the interior of
$\mathsf {h}$
is in the interior of
![]() $\mathcal W_{\textrm {out}}^{\blacktriangleleft }$
, the leftmost term in Equation (B.4) diverges (by the same argument that showed the equivalence of the two definitions of
$\mathcal W_{\textrm {out}}^{\blacktriangleleft }$
, the leftmost term in Equation (B.4) diverges (by the same argument that showed the equivalence of the two definitions of
![]() $\mathcal W$
in subsection 2.6), and thus
$\mathcal W$
in subsection 2.6), and thus
![]() $\sum _{m\geq 1}f(\mathsf {h})^m=\infty $
, and thus
$\sum _{m\geq 1}f(\mathsf {h})^m=\infty $
, and thus
![]() $f(\mathsf {h})\geq 1$
.
$f(\mathsf {h})\geq 1$
.
By continuity of f, it follows that
![]() $f(\mathsf {h})=1$
on
$f(\mathsf {h})=1$
on
![]() $\mathcal W_{\textrm {in}}^\blacktriangleleft \cap \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
, that is,
$\mathcal W_{\textrm {in}}^\blacktriangleleft \cap \mathcal W_{\textrm {out}}^{\blacktriangleleft }$
, that is,
![]() $f(\mathsf {h}_{\mathsf {y}})=1$
for
$f(\mathsf {h}_{\mathsf {y}})=1$
for
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }$
. This proves that
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }$
. This proves that
![]() $\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
defines a probability distribution on
$\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
defines a probability distribution on
![]() $\mathsf {A}$
for
$\mathsf {A}$
for
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }$
.
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }$
.
Next, we show Equation (2.25). For any
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
, define
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
, define
From above, we know that
![]() $F(\mathsf {y}) \equiv 1$
. Since
$F(\mathsf {y}) \equiv 1$
. Since
![]() $\tau _\beta $
is analytic outside of the origin (Proposition 2.4), it is in particular twice differentiable and thus so is
$\tau _\beta $
is analytic outside of the origin (Proposition 2.4), it is in particular twice differentiable and thus so is
![]() $\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}(\Gamma )$
with
$\mathbb {P}^{\mathsf {h}_{\mathsf {y}}}(\Gamma )$
with
![]() $\nabla \mathbb {P}^{\mathsf {h}_{\mathsf {y}}}(\Gamma ) = J_{\mathsf {h}_{\mathsf {y}}} \mathsf {X}(\Gamma ) \mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
, where
$\nabla \mathbb {P}^{\mathsf {h}_{\mathsf {y}}}(\Gamma ) = J_{\mathsf {h}_{\mathsf {y}}} \mathsf {X}(\Gamma ) \mathbb {P}^{\mathsf {h}_{\mathsf {y}}}$
, where
![]() $J_{\mathsf {h}_{\mathsf {y}}}$
is the Jacobian matrix of
$J_{\mathsf {h}_{\mathsf {y}}}$
is the Jacobian matrix of
![]() $\mathsf {y} \mapsto \mathsf {h}_{\mathsf {y}}$
. Using the same argument as in Claim B.1 and boundedness of
$\mathsf {y} \mapsto \mathsf {h}_{\mathsf {y}}$
. Using the same argument as in Claim B.1 and boundedness of
![]() $J_{\mathsf {h}_{\mathsf {y}}}$
, we find that
$J_{\mathsf {h}_{\mathsf {y}}}$
, we find that
![]() $\sum _{\Gamma \in \mathsf {A}}J_{\mathsf {h}_{\mathsf {y}}} \mathsf {X}(\Gamma )\mathbb {P}^{\mathsf {h}_{\mathsf {x}}}(\Gamma )$
converges uniformly for
$\sum _{\Gamma \in \mathsf {A}}J_{\mathsf {h}_{\mathsf {y}}} \mathsf {X}(\Gamma )\mathbb {P}^{\mathsf {h}_{\mathsf {x}}}(\Gamma )$
converges uniformly for
![]() $\mathsf {y}\in \mathbb {Z}^2\setminus \{0\}$
, and thus we can differentiate
$\mathsf {y}\in \mathbb {Z}^2\setminus \{0\}$
, and thus we can differentiate
![]() $F(\mathsf {y})$
under the sum to get
$F(\mathsf {y})$
under the sum to get
that is,
![]() $\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}[\mathsf {X}(\Gamma )] \in \text {Ker}(J_{\mathsf {h}_{\mathsf {y}}})$
. Differentiating the relation
$\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}[\mathsf {X}(\Gamma )] \in \text {Ker}(J_{\mathsf {h}_{\mathsf {y}}})$
. Differentiating the relation
![]() $\mathsf {h}_{\mathsf {y}} \cdot \mathsf {y} = \tau _\beta (y)$
, we see that
$\mathsf {h}_{\mathsf {y}} \cdot \mathsf {y} = \tau _\beta (y)$
, we see that
![]() $\mathsf {y} \in \text {Ker}(J_{\mathsf {h}_{\mathsf {y}}})$
, and so if
$\mathsf {y} \in \text {Ker}(J_{\mathsf {h}_{\mathsf {y}}})$
, and so if
![]() $J_{\mathsf {h}_{\mathsf {y}}}$
is nondegenerate we get that
$J_{\mathsf {h}_{\mathsf {y}}}$
is nondegenerate we get that
![]() $\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}[\mathsf {X}(\Gamma )]$
is collinear to
$\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}[\mathsf {X}(\Gamma )]$
is collinear to
![]() $\mathsf {y}$
, that is,
$\mathsf {y}$
, that is,
![]() $\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}[\mathsf {X}(\Gamma )] = \alpha \mathsf {y}$
for some scalar
$\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}[\mathsf {X}(\Gamma )] = \alpha \mathsf {y}$
for some scalar
![]() $\alpha =\alpha (\mathsf {y})$
. Finally, the nondegeneracy condition can be removed: Since
$\alpha =\alpha (\mathsf {y})$
. Finally, the nondegeneracy condition can be removed: Since
![]() $\tau _\beta $
is analytic (outside of the origin), the points at which
$\tau _\beta $
is analytic (outside of the origin), the points at which
![]() $J_{\mathsf {h}_{\mathsf {y}}}$
is fully degenerate form a discrete set, and since collinearity must hold outside of such set and
$J_{\mathsf {h}_{\mathsf {y}}}$
is fully degenerate form a discrete set, and since collinearity must hold outside of such set and
![]() $\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}[\mathsf {X}(\Gamma )]$
is continuous, we get the result for any
$\mathbb {E}^{\mathsf {h}_{\mathsf {y}}}[\mathsf {X}(\Gamma )]$
is continuous, we get the result for any
![]() $\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
.
$\mathsf {y} \in \mathcal {Y}^\blacktriangleleft _{\delta }\setminus \{0\}$
.
It remains to show the exponential tail decay (2.26), which actually holds for the weights
![]() $W^{\mathsf {h}}$
for any
$W^{\mathsf {h}}$
for any
![]() $\mathsf {h} \in \mathcal W$
. Below,
$\mathsf {h} \in \mathcal W$
. Below,
![]() $\nu _1>0$
and
$\nu _1>0$
and
![]() $\nu _2>0$
denote constants independent of
$\nu _2>0$
denote constants independent of
![]() $\mathsf {h}$
and
$\mathsf {h}$
and
![]() $\beta $
, while
$\beta $
, while
![]() $C_1>0$
and
$C_1>0$
and
![]() $C_2>0$
may depend on
$C_2>0$
may depend on
![]() $\beta $
but not
$\beta $
but not
![]() $\mathsf {h}$
. We express the left-hand side of Equations (2.26) as follows:
$\mathsf {h}$
. We express the left-hand side of Equations (2.26) as follows:
 $$ \begin{align} \sum_{\substack{\Gamma \in \mathsf{A_L} \cup \mathsf{A_R} \\|\Gamma| \geq k}} W^{\mathsf{h}}(\Gamma) \leq \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 \geq k/2} \sum_{\substack{ \Gamma \in \mathsf{A_L} \cup \mathsf{A_R} \\|\Gamma| \geq k\\ \Gamma: 0 \to \mathsf{y}}} W^{\mathsf{h}}(\Gamma) + \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 < k/2} \sum_{\substack{|\Gamma| \geq k \\ \Gamma: 0 \to \mathsf{y}}} W^{\mathsf{h}}(\Gamma). \end{align} $$
$$ \begin{align} \sum_{\substack{\Gamma \in \mathsf{A_L} \cup \mathsf{A_R} \\|\Gamma| \geq k}} W^{\mathsf{h}}(\Gamma) \leq \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 \geq k/2} \sum_{\substack{ \Gamma \in \mathsf{A_L} \cup \mathsf{A_R} \\|\Gamma| \geq k\\ \Gamma: 0 \to \mathsf{y}}} W^{\mathsf{h}}(\Gamma) + \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 < k/2} \sum_{\substack{|\Gamma| \geq k \\ \Gamma: 0 \to \mathsf{y}}} W^{\mathsf{h}}(\Gamma). \end{align} $$
The first term in the above sum can be bounded using Equation (B.1), Proposition 2.12, and the bound
![]() $\mathsf {h} \cdot \mathsf {y} \leq \tau _{\beta }(\mathsf {y})$
for any
$\mathsf {h} \cdot \mathsf {y} \leq \tau _{\beta }(\mathsf {y})$
for any
![]() $\mathsf {h} \in \mathcal W$
:
$\mathsf {h} \in \mathcal W$
:
 $$\begin{align*}\sum_{\left\Vert \mathsf{y} \right\Vert{}_1 \geq k/2} \sum_{\substack{ \Gamma \in \mathsf{A_L} \cup \mathsf{A_R} \\|\Gamma| \geq k\\ \Gamma: 0 \to \mathsf{y}}} W^{\mathsf{h}}(\Gamma) \leq \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 \geq k/2} e^{\mathsf{h} \cdot \mathsf{y}} \mathcal{G}(\mathsf{y} \;\big|\; |\mathsf{Cpts}(\Gamma)| = 0) \leq \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 \geq k/2} e^{-(\nu \beta -\epsilon)\left\Vert \mathsf{y} \right\Vert{}_1} \leq C_1 e^{-\nu_1 \beta k}. \end{align*}$$
$$\begin{align*}\sum_{\left\Vert \mathsf{y} \right\Vert{}_1 \geq k/2} \sum_{\substack{ \Gamma \in \mathsf{A_L} \cup \mathsf{A_R} \\|\Gamma| \geq k\\ \Gamma: 0 \to \mathsf{y}}} W^{\mathsf{h}}(\Gamma) \leq \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 \geq k/2} e^{\mathsf{h} \cdot \mathsf{y}} \mathcal{G}(\mathsf{y} \;\big|\; |\mathsf{Cpts}(\Gamma)| = 0) \leq \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 \geq k/2} e^{-(\nu \beta -\epsilon)\left\Vert \mathsf{y} \right\Vert{}_1} \leq C_1 e^{-\nu_1 \beta k}. \end{align*}$$
The second term in Equation (B.5) is bounded by
 $$ \begin{align*} &\sum_{\left\Vert \mathsf{y} \right\Vert{}_1 <k/2}e^{\mathsf{h}\cdot \mathsf{y}} \mathcal{G}(\mathsf{y} \;\big|\; |\gamma| \geq k) \leq \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 < k/2} e^{\tau_{\beta}(\mathsf{y})} \Big(c e^{-\nu_0 \beta (k/\left\Vert \mathsf{y} \right\Vert{}_1) \left\Vert \mathsf{y} \right\Vert{}_1} \Big) \mathcal{G}(\mathsf{y})\\ &\quad \leq C_2 e^{-\nu_0 \beta k}\sum_{\left\Vert \mathsf{y} \right\Vert{}_1 < k/2} e^{\epsilon \|\mathsf{y}\|_1} \leq C_2 e^{-\nu_2 \beta k}, \end{align*} $$
$$ \begin{align*} &\sum_{\left\Vert \mathsf{y} \right\Vert{}_1 <k/2}e^{\mathsf{h}\cdot \mathsf{y}} \mathcal{G}(\mathsf{y} \;\big|\; |\gamma| \geq k) \leq \sum_{\left\Vert \mathsf{y} \right\Vert{}_1 < k/2} e^{\tau_{\beta}(\mathsf{y})} \Big(c e^{-\nu_0 \beta (k/\left\Vert \mathsf{y} \right\Vert{}_1) \left\Vert \mathsf{y} \right\Vert{}_1} \Big) \mathcal{G}(\mathsf{y})\\ &\quad \leq C_2 e^{-\nu_0 \beta k}\sum_{\left\Vert \mathsf{y} \right\Vert{}_1 < k/2} e^{\epsilon \|\mathsf{y}\|_1} \leq C_2 e^{-\nu_2 \beta k}, \end{align*} $$
where the first inequality uses Equation (2.21) and
![]() $\mathsf {h} \cdot \mathsf {y} \leq \tau _{\beta }(\mathsf {y})$
, and the second inequality uses Equation (B.1).
$\mathsf {h} \cdot \mathsf {y} \leq \tau _{\beta }(\mathsf {y})$
, and the second inequality uses Equation (B.1).
Proof of Equation (5.18).
Define the partition function over contours
![]() $\gamma \subset \mathbb {Z}^2$
such that
$\gamma \subset \mathbb {Z}^2$
such that
![]() $\gamma :0 \to \mathsf {y}$
:
$\gamma :0 \to \mathsf {y}$
:
 $$\begin{align*}\mathcal{G}_D^{\texttt{{full}}}(\mathsf{y}) := \sum_{ \gamma : 0 \to \mathsf{y} } q_D(\gamma). \end{align*}$$
$$\begin{align*}\mathcal{G}_D^{\texttt{{full}}}(\mathsf{y}) := \sum_{ \gamma : 0 \to \mathsf{y} } q_D(\gamma). \end{align*}$$
Equation (2.13) gives us
![]() $q_D(\gamma ) \leq \exp (6 e^{-\chi \beta }|\gamma |)q(\gamma )$
, from which we find
$q_D(\gamma ) \leq \exp (6 e^{-\chi \beta }|\gamma |)q(\gamma )$
, from which we find
 $$ \begin{align*} \mathcal{G}_D^{\texttt{{full}}}(\mathsf{y}) \leq \sum_{\gamma:0\to\mathsf{y}} e^{6 e^{-\chi \beta}|\gamma|}q(\gamma) \leq e^{6.6e^{-\chi\beta}\|\mathsf{y}\|_1}\mathcal{G}(\mathsf{y}) + \sum_{\substack{\gamma: 0 \to \mathsf{y} \\ |\gamma| \geq 1.1 \|\mathsf{y}\|_1}} e^{6 e^{-\chi \beta}|\gamma|}q(\gamma) \leq e^{7e^{-\chi\beta}\|\mathsf{y}\|_1} \mathcal{G}(\mathsf{y}), \end{align*} $$
$$ \begin{align*} \mathcal{G}_D^{\texttt{{full}}}(\mathsf{y}) \leq \sum_{\gamma:0\to\mathsf{y}} e^{6 e^{-\chi \beta}|\gamma|}q(\gamma) \leq e^{6.6e^{-\chi\beta}\|\mathsf{y}\|_1}\mathcal{G}(\mathsf{y}) + \sum_{\substack{\gamma: 0 \to \mathsf{y} \\ |\gamma| \geq 1.1 \|\mathsf{y}\|_1}} e^{6 e^{-\chi \beta}|\gamma|}q(\gamma) \leq e^{7e^{-\chi\beta}\|\mathsf{y}\|_1} \mathcal{G}(\mathsf{y}), \end{align*} $$
where in the final inequality we used Equation (2.21). We then obtain the analogue of Equation (B.1) by applying Equation (B.1) to the above: For any
![]() $\epsilon \in (0,1)$
, there exists
$\epsilon \in (0,1)$
, there exists
![]() $\beta _0:= \beta _0(\epsilon )>0$
such that for all
$\beta _0:= \beta _0(\epsilon )>0$
such that for all
![]() $\beta \geq \beta _0$
and for all
$\beta \geq \beta _0$
and for all
![]() $\mathsf {y} \in \mathbb {Z}^2$
,
$\mathsf {y} \in \mathbb {Z}^2$
,
for some
![]() $C:= C(\epsilon ,\beta )>0$
. Similarly, we obtain the length and contour cone points bound Lemma 2.11 and the animal cone points bound Proposition 2.12 with
$C:= C(\epsilon ,\beta )>0$
. Similarly, we obtain the length and contour cone points bound Lemma 2.11 and the animal cone points bound Proposition 2.12 with
![]() $\mathcal {G}_D^{\texttt {{full}}}(\mathsf {y})$
replacing
$\mathcal {G}_D^{\texttt {{full}}}(\mathsf {y})$
replacing
![]() $\mathcal {G}(\mathsf {y})$
there. With these bounds, we may rerun the proof of Equation (2.26), replacing
$\mathcal {G}(\mathsf {y})$
there. With these bounds, we may rerun the proof of Equation (2.26), replacing
![]() $W^{\mathsf {h}}(\Gamma )$
with
$W^{\mathsf {h}}(\Gamma )$
with
![]() $e^{\mathsf {h}\cdot \mathsf {X}(\Gamma )} q_D(\Gamma )$
.
$e^{\mathsf {h}\cdot \mathsf {X}(\Gamma )} q_D(\Gamma )$
.
Acknowledgements
We thank Milind Hegde for a useful discussion.
Competing interests
The authors have no competing interest to declare.
Funding statement
Y.H.K. acknowledges the support of the NSF Graduate Research Fellowship 1839302. E.L. acknowledges the support of NSF DMS-2054833.


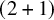
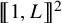 with zero boundary conditions and nonnegative heights (a floor at height
with zero boundary conditions and nonnegative heights (a floor at height 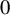
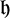
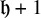
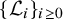
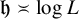
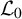
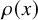
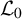
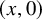
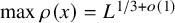
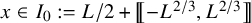 . It is believed that rescaling
. It is believed that rescaling