Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T09:41:57.006Z Has data issue: false hasContentIssue false
  • English
  • Français

OBSTRUCTIONS TO ALGEBRAIZING TOPOLOGICAL VECTOR BUNDLES

Part of: (Co)homology theory Holomorphic fiber spaces Theory of modules and ideals Fiber spaces and bundles

Published online by Cambridge University Press:  21 March 2019

A. ASOK ,
J. FASEL  and
M. J. HOPKINS
A. ASOK
Affiliation:
Department of Mathematics, University of Southern California, 3620 S. Vermont Ave., Los Angeles, CA 90089-2532, USA; [email protected]
J. FASEL
Affiliation:
Institut Fourier - UMR 5582, Université Grenoble Alpes CS 40700, 38058 Grenoble Cedex 09, France; [email protected]
M. J. HOPKINS
Affiliation:
Department of Mathematics, Harvard University, One Oxford Street, Cambridge, MA 02138, USA; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose $X$ is a smooth complex algebraic variety. A necessary condition for a complex topological vector bundle on 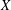$X$ (viewed as a complex manifold) to be algebraic is that all Chern classes must be algebraic cohomology classes, that is, lie in the image of the cycle class map. We analyze the question of whether algebraicity of Chern classes is sufficient to guarantee algebraizability of complex topological vector bundles. For affine varieties of dimension ${\leqslant}3$, it is known that algebraicity of Chern classes of a vector bundle guarantees algebraizability of the vector bundle. In contrast, we show in dimension 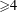${\geqslant}4$ that algebraicity of Chern classes is insufficient to guarantee algebraizability of vector bundles. To do this, we construct a new obstruction to algebraizability using Steenrod operations on Chow groups. By means of an explicit example, we observe that our obstruction is nontrivial in general.

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory
Secondary: 32L05: Holomorphic bundles and generalizations 55R25: Sphere bundles and vector bundles 13C10: Projective and free modules and ideals
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e6
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Asok, A. and Fasel, J., ‘Algebraic vector bundles on spheres’, J. Topol. 7(3) (2014), 894–926.Google Scholar
Asok, A. and Fasel, J., ‘A cohomological classification of vector bundles on smooth affine threefolds’, Duke Math. J. 163(14) (2014), 2561–2601.Google Scholar
Asok, A. and Fasel, J., ‘Secondary characteristic classes and the Euler class’, Doc. Math. (2015), 7–29. (Extra vol.: Alexander S. Merkurjev’s Sixtieth Birthday).Google Scholar
Asok, A. and Fasel, J., ‘Splitting vector bundles outside the stable range and homotopy theory of punctured affine spaces’, J. Amer. Math. Soc. 28(4) (2015), 1031–1062.Google Scholar
Asok, A. and Fasel, J., ‘An explicit KO-degree map and applications’, J. Topol. 10(1) (2017), 268–300.Google Scholar
Asok, A., Hoyois, M. and Wendt, M., ‘Affine representability results in A1 -homotopy theory I: vector bundles’, Duke Math. J. 166(10) (2017), 1923–1953.Google Scholar
Atiyah, M. F. and Rees, E., ‘Vector bundles on projective 3-space’, Invent. Math. 35 (1976), 131–153.Google Scholar
Bănică, C. and Putinar, M., ‘On complex vector bundles on projective threefolds’, Invent. Math. 88(2) (1987), 427–438.Google Scholar
Brosnan, P., ‘Steenrod operations in Chow theory’, Trans. Amer. Math. Soc. 355(5) (2003), 1869–1903 (electronic).Google Scholar
Deligne, P., ‘Voevodsky’s lectures on motivic cohomology 2000/2001’, inAlgebraic Topology, Abel Symp., 4 (Springer, Berlin, 2009), 355–409.Google Scholar
Dugger, D. and Isaksen, D. C., ‘Motivic cell structures’, Algebr. Geom. Topol. 5 (2005), 615–652.Google Scholar
Edidin, D. and Graham, W., ‘Equivariant intersection theory’, Invent. Math. 131(3) (1998), 595–634.Google Scholar
Fasel, J., ‘The projective bundle theorem for j -cohomology’, J. K-Theory I(2) (2013), 413–464.Google Scholar
Forstnerič, F., Stein Manifolds and Holomorphic Mappings, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, 56 (Springer, Heidelberg, 2011).Google Scholar
Fulton, W., Intersection Theory, 2nd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, 2 (Springer, Berlin, 1998).Google Scholar
Gillet, H., ‘Riemann-Roch theorems for higher algebraic K-theory’, Adv. Math. 40(3) (1981), 203–289.Google Scholar
Grauert, H., ‘Analytische Faserungen über holomorph-vollständigen Räumen’, Math. Ann. 135 (1958), 263–273.Google Scholar
Griffiths, P. A., ‘Function theory of finite order on algebraic varieties. i(a)’, J. Differential Geometry 6 (1971/72), 285–306.Google Scholar
Hartshorne, R., Ample Subvarieties of Algebraic Varieties, Lecture Notes in Mathematics, 156 (Springer, Berlin-New York, 1970), Notes written in collaboration with C. Musili.Google Scholar
Kumar, N. M. and Murthy, M. P., ‘Algebraic cycles and vector bundles over affine three-folds’, Ann. of Math. (2) 116(3) (1982), 579–591.Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture Notes on Motivic Cohomology, Clay Mathematics Monographs, 2 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Morel, F., ‘Sur les puissances de l’idéal fondamental de l’anneau de Witt’, Comment. Math. Helv. 79(4) (2004), 689–703.Google Scholar
Morel, F., A1 -Algebraic Topology Over a Field, Lecture Notes in Mathematics, 2052 (Springer, Heidelberg, 2012).Google Scholar
Morel, F. and Voevodsky, V., ‘A1 -homotopy theory of schemes’, Publ. Math. Inst. Hautes Études Sci. 90(2001) (1999), 45–143.Google Scholar
Murthy, M. P. and Swan, R. G., ‘Vector bundles over affine surfaces’, Invent. Math. 36 (1976), 125–165.Google Scholar
Orlov, D., Vishik, A. and Voevodsky, V., ‘An exact sequence for K ∗ M /2 with applications to quadratic forms’, Ann. of Math. (2) 165(1) (2007), 1–13.Google Scholar
Pushin, O., ‘Higher Chern classes and Steenrod operations in motivic cohomology’, J. K-Theory 31(4) (2004), 307–321.Google Scholar
Schwarzenberger, R. L. E., ‘Vector bundles on algebraic surfaces’, Proc. Lond. Math. Soc. (3) 11 (1961), 601–622.Google Scholar
Serre, J.-P., ‘Modules projectifs et espaces fibrés à fibre vectorielle’, inSéminaire P. Dubreil, M.-L. Dubreil-Jacotin et C. Pisot, 1957/58, Fasc. 2, Exposé 23 (Secrétariat mathématique, Paris, 1958), 18.Google Scholar
Serre, J.-P., ‘On the fundamental group of a unirational variety’, J. Lond. Math. Soc. 34 (1959), 481–484.Google Scholar
Suslin, A. A., ‘Torsion in K 2 of fields’, K-Theory 1(1) (1987), 5–29.Google Scholar
Soulé, C. and Voisin, C., ‘Torsion cohomology classes and algebraic cycles on complex projective manifolds’, Adv. Math. 198(1) (2005), 107–127.Google Scholar
Totaro, B., ‘Non-injectivity of the map from the Witt group of a variety to the Witt group of its function field’, J. Inst. Math. Jussieu 2(3) (2003), 483–493.Google Scholar
Totaro, B., ‘On the integral Hodge and Tate conjectures over a number field’, Forum Math. Sigma 1 (2013), e4, 13pp.Google Scholar
Trento examples, Classification of Irregular Varieties (Trento 1990), Lecture Notes in Mathematics, 1515(Springer, Berlin, 1992), 134–139.Google Scholar
Voevodsky, V., ‘Reduced power operations in motivic cohomology’, Publ. Math. Inst. Hautes Études Sci. 98 (2003), 1–57.Google Scholar
Voevodsky, V., ‘On the zero slice of the sphere spectrum’, Tr. Mat. Inst. Steklova 246(Algebr. Geom. Metody, Svyazi i Prilozh) (2004), 106–115.Google Scholar
Voisin, C., Hodge Theory and Complex Algebraic Geometry. II, English edn, Cambridge Studies in Advanced Mathematics, 77 (Cambridge University Press, Cambridge, 2007), Translated from the French by Leila Schneps.Google Scholar