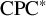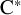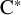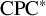Introduction
Nuclear
$\mathrm {C}^*$
-algebras are those for which the identity map can be approximated in point norm topology by completely positive contractions through finite-dimensional
$\mathrm {C}^*$
-algebras. More formally, a
$\mathrm {C}^*$
-algebra A has the completely positive approximation property if there are a net
$(F_\lambda )_{\lambda \in \Lambda }$
of finite-dimensional
$\mathrm {C}^*$
-algebras and completely positive contractive (c.p.c.) maps
such that
$\varphi _\lambda \circ \psi _\lambda $
converges pointwise in norm to the identity map
$\mathrm {id}_A$
. For separable
$\mathrm {C}^*$
-algebras (the case we are mostly interested in in this paper), one can always restrict to systems of approximations with countable index sets. Upon composing such approximations one obtains a system of the form
with commuting lower triangles, 
, and approximately commuting upper triangles (i.e.,
$\varphi _n \circ \psi _n \longrightarrow \mathrm {id}_A$
in point-norm topology). The sequence of upper triangles
$(A, \varphi _n \circ \psi _n)_n$
may be regarded as an inductive system in the category of operator spaces with c.p.c. maps as morphisms, and with the inductive limit again being an operator space, more precisely a self-adjoint subspace of the sequence algebra
$A_\infty = \prod _n A / \bigoplus _n A$
, the quotient of bounded sequences modulo null sequences in A. At least after passing to a subsystem (so that the approximation errors become summable on larger and larger subsets), this inductive limit will agree with the embedding of A into
$A_\infty $
as constant sequences, and in particular, it will indeed be a
$\mathrm {C}^*$
-algebra. In this situation, it is then reasonable to expect that the lower row
also encodes all pertinent information about A. This is a tempting point of view, since it would allow one to write any separable nuclear
$\mathrm {C}^*$
-algebra as an inductive limit of finite-dimensional ones in a suitable category: Such a limit, say X, will be contained in the sequence algebra
$F_\infty = \prod _n F_n / \bigoplus _n F_n$
. It can be described as (the norm closure of) the union
$\bigcup _n \rho _n(F_n)$
, where
$\rho _n\colon F_n \longrightarrow F_\infty $
denotes the limit map for each n, and there will be an induced c.p.c. isometry
$\Psi \colon A \longrightarrow X$
. The space X will certainly reflect the linear structure of A and also the order (even after passing to matrix amplifications), since the maps involved are completely positive. It will, however, in general not be a sub-
$\mathrm {C}^*$
-algebra of
$F_\infty $
, and the map
$\Psi $
will not be multiplicative.
Studying operator algebras as inductive limits has a long history, spanning from Murray and von Neumann’s work on hyperfiniteness in [Reference Murray and von Neumann18] to semidiscreteness and Connes’ celebrated classification of injective
$\mathrm {II}_1$
factors ([Reference Connes7]) on the von Neumann algebra side, and featuring the classification of UHF, AF, AT and AH algebras on the
$\mathrm {C}^*$
-algebra side (see [Reference Elliott8, Reference Elliott9, Reference Glimm10]). Inductive limits have been used to construct fundamental
$\mathrm {C}^*$
-algebras with prescribed structural,
$\mathrm {K}$
-theoretic and tracial data, such as the Jiang–Su Algebra
$\mathcal {Z}$
[Reference Jiang and Su13, Reference Rørdam and Winter21] and the Razak–Jacelon Algebra
$\mathcal {W}$
[Reference Jacelon12]. More recently, inductive limits of Cartan pairs as described in [Reference Barlak and Li2] were used in [Reference Li17] to show that all classifiable stably-finite
$\mathrm {C}^*$
-algebras admit groupoid models. The inductive systems appearing in these results all have
$^*$
-homomorphisms as connecting maps. This entails that, at least on the
$\mathrm {C}^*$
-algebra side, one has to admit more complicated building block algebras than just finite-dimensional ones in order to reach a reasonable bandwidth of examples. (Often one uses algebras built from bundles of finite-dimensional
$\mathrm {C}^*$
-algebras over locally compact spaces, which poses limitations on the existence of sufficiently many connecting maps.)
In this paper, we explore how to relax conditions on the connecting maps while keeping the building blocks finite-dimensional, and hence as easy as possible. Our Ansatz is it to write an arbitrary separable nuclear
$\mathrm {C}^*$
-algebra as an inductive limit of finite-dimensional
$\mathrm {C}^*$
-algebras in the category of operator spaces. In order to be conceptually satisfactory and to give access to applications, such an approach would have to meet some minimal requirements: One needs to be able to recover the
$\mathrm {C}^*$
-algebra structure from the operator system X (or from the inductive system, for that matter) in a practical way, and one needs to be able to concisely describe the limit operator spaces arising in this manner. There are, however, two obstacles to overcome.
First, the connecting maps
$\rho _{n,n-1}$
can in general not be arranged to be multiplicative, not even approximately: requiring multiplicativity would only grant access to AF algebras, a small albeit interesting subclass of nuclear C*-algebras. In [Reference Blackadar and Kirchberg4], Blackadar and Kirchberg suggested the notion of NF systems, which incorporates a certain type of asymptotic multiplicativity and which covers the substantially larger class of NF algebras. While much broader than AF algebras, this class is still far from covering all nuclear
$\mathrm {C}^*$
-algebras. Therefore, we are looking for a notion of inductive systems of finite-dimensional
$\mathrm {C}^*$
-algebras which is sufficiently flexible in the sense that every separable nuclear
$\mathrm {C}^*$
-algebra can be written as the inductive limit of such a system, while at the same, time it is rigid enough to encode not only the linear and matrix order structure, but also the multiplicative structure of an initially given
$\mathrm {C}^*$
-algebra. It will be important that the algebraic structure is not only encoded in the system, but that it can actually be accessed and extracted in a meaningful and sufficiently concrete way.
Second, assuming one has a notion of inductive systems as above, we need to distinguish them from arbitrary inductive systems of finite-dimensional
$\mathrm {C}^*$
-algebras in the category of operator spaces. Ideally, we will want to derive an intrinsic characterization of the respective limits. (Theoretically, one could compare the limit to every
$\mathrm {C}^*$
-algebra and check for the existence of an isomorphism in a suitable sense, but such an extrinsic characterization would be unsatisfactory both conceptually and practically, since it would largely obscure any information related to the finite-dimensional approximations.)
The aforementioned notion of NF algebras as introduced by Blackadar and Kirchberg addresses the first obstacle and reveals a subtle facet of the second.
Definition [Reference Blackadar and Kirchberg4].
A system
$(F_n,\rho _{n+1,n})_n$
consisting of a sequence
$(F_n)_n$
of finite-dimensional
$\mathrm {C}^*$
-algebras together with c.p.c. connecting maps
$\rho _{n+1,n}\colon F_n\longrightarrow F_{n+1}$
is called an NF system if it is asymptotically multiplicative in the sense that for any
$\varepsilon>0$
,
$k\geq 0$
and
$x,y\in F_k$
, there exists an
$M>k$
so that for all
$m>n>M$
, we have
$$ \begin{align} \|\rho_{m,n}\big(\rho_{n,k}(x)\rho_{n,k}(y)\big)-\rho_{m,n}\big(\rho_{n,k}(x)\big)\rho_{m,n}\big(\rho_{n,k}(y)\big)\|<\varepsilon. \end{align} $$
The limit of such a system is indeed a sub-
$\mathrm {C}^*$
-algebra of
$F_\infty $
, with product given by
for any
$k\geq 0$
and
$x,y\in F_k$
. Therefore, asymptotic multiplicativity of the involved connecting maps does encode the multiplicative structure of the limit, thus addressing the first obstacle above.
Blackadar and Kirchberg then characterize limits of NF systems, so-called NF algebras, as nuclear and quasidiagonal
$\mathrm {C}^*$
-algebras. While this is a large and highly relevant class of
$\mathrm {C}^*$
-algebras, it is not closed under taking quotients or extensions, which restricts the range of applications of NF systems considerably. This is subtly related to the fact that quasidiagonality is an external approximation property, characterized extrinsically, in terms of comparison maps into other
$\mathrm {C}^*$
-algebras.
We propose here a generalization of NF systems which permits to encode the multiplicative structure of the limit in terms of the connecting maps between its finite dimensional approximands, yet renders access to all separable nuclear
$\mathrm {C}^*$
-algebras, and therefore allows for an intrinsic characterization. As the key feature of our main definition, we ask the connecting maps to become more and more order zero, thus replacing the asymptotic multiplicativity of NF systems. We recall from [Reference Winter and Zacharias24] that, for a c.p.c. map, ‘order zero’ just means ‘orthogonality preserving’, and that order zero c.p.c. maps remember a lot of the multiplicative structure through formulae of the type
$\theta (x) \theta (yz) = \theta (xy)\theta (z)$
. In case the domain is unital, one can characterize order zero maps via
$$ \begin{align} \theta(1) \theta(yz) = \theta(y)\theta(z). \end{align} $$
Definition A (Definition 2.2).
A system
$(F_n,\rho _{n+1,n})_n$
consisting of a sequence
$(F_n)_n$
of finite-dimensional
$\mathrm {C}^*$
-algebras along with c.p.c. connecting maps
$\rho _{n+1,n}\colon F_n\longrightarrow F_{n+1}$
is called a
${\mathrm {CPC}^*}$
-system if it is asymptotically order zero in the sense that for any
$\varepsilon>0$
,
$k\geq 0$
and
$x,y\in F_k$
, there exists an
$M>k$
so that for all
$m>n,l>M$
, we have
$$ \begin{align} \|\rho_{m,l}(1_{F_l})\rho_{m,n}\big(\rho_{n,k}(x)\rho_{n,k}(y)\big)-\rho_{m,n}\big(\rho_{n,k}(x)\big)\rho_{m,n}\big(\rho_{n,k}(y)\big)\|<\varepsilon. \end{align} $$
Note that in view of (c), the approximate identity (d) may indeed be viewed as an order zero version of (a). For inductive limits of such systems, one may still describe a product as in (b).
Proposition B (Proposition 2.6).
Let
$X\subset F_\infty $
be the limit of a
${\mathrm {CPC}^*}$
-system
$(F_n,\rho _{n+1,n})_n$
. Then there exists an associative bilinear map 
satisfying
for all
$k\geq 0$
and
$x,y\in F_k$
, so that 
is a
$\mathrm {C}^*$
-algebra with the involution and norm inherited as a subspace of
$F_\infty $
.
We denote the
$\mathrm {C}^*$
-algebra above by 
and call it the
${\mathrm {CPC}^*}$
-limit of the system
$(F_n,\rho _{n+1,n})_n$
.
With a
$\mathrm {C}^*$
-algebra structure established, the next question is: When is the limit nuclear? Thanks to Ozawa and Sato’s ‘one-way-CPAP’ from [Reference Sato22, Theorem 5.1] (an approximation property which only involves the upwards maps
$\varphi _n$
), the answer is ‘always’. Remarkably, while
${\mathrm {CPC}^*}$
-limits readily satisfy the one-way-CPAP, in order to arrive at nuclearity, the proof of [Reference Sato22, Theorem 5.1] first confirms that 
is injective, which by Connes’ theorem implies that 
is nuclear. Hence, this result is non-constructive, meaning one does not build a completely positive approximation directly from the system
$(F_n,\rho _{n+1,n})_n$
. This is in line with Blackadar and Kirchberg’s characterization of NF algebras as the nuclear and quasidiagonal
$\mathrm {C}^*$
-algebras, which involves the fact that nuclearity passes to quotients, and hence also relies on Connes’ theorem and is non-constructive in a similar way.
As a converse, we show that any system of c.p.c. approximations of a separable nuclear
$\mathrm {C}^*$
-algebra A with approximately order zero downwards maps has a subsystem which gives rise to a
${\mathrm {CPC}^*}$
-system with
${\mathrm {CPC}^*}$
-limit isomorphic to A. It follows implicitly from [Reference Blackadar and Kirchberg4, Reference Winter and Zacharias24] and explicitly from [Reference Brown, Carrión and White5] that every nuclear
$\mathrm {C}^*$
-algebra does admit such a system of approximations.
Combining these results, we can now describe all separable nuclear
$\mathrm {C}^*$
-algebras as inductive limits of finite-dimensional
$\mathrm {C}^*$
-algebras:
Theorem C. For a separable
$\mathrm {C}^*$
-algebra A, the following are equivalent:
-
(i) A is nuclear.
-
(ii) A is
$^*$
-isomorphic to a
${\mathrm {CPC}^*}$
-limit.
Proposition B shows how to extract the multiplicative structure from a
${\mathrm {CPC}^*}$
-limit, thus addressing the first of the two issues raised above. As for the second, our description of
${\mathrm {CPC}^*}$
-systems and the characterization of their limits is indeed an intrinsic one, not requiring any comparison with
$\mathrm {C}^*$
-algebras outside. In upcoming work, we will explore how to apply this notion practically, in particular how to describe permanence properties of nuclearity and how to access K-theory in terms of
${\mathrm {CPC}^*}$
-systems.
The article is arranged as follows. Section 1 establishes results on c.p.c. and order zero maps that will be used throughout. Some results in this section are well-known and some are new. In Section 2, we define
${\mathrm {CPC}^*}$
-systems and prove (ii)
$\Longrightarrow $
(i) of Theorem C. Section 3 is dedicated to proving the reverse implication, and Section 4 relates
${\mathrm {CPC}^*}$
-systems to NF systems.
1 Order zero maps and order embeddings
In this section, we highlight some properties of completely positive maps, with a particular focus on order zero maps and on complete order embeddings.
We write
$A_+$
for the cone of positive elements of a
$\mathrm {C}^*$
-algebra A,
$A^1$
and
$A^1_+$
for the respective closed unit balls,
$X' \cap A\subset M$
for the relative commutant in A of a set X (with A and X both contained in a larger
$\mathrm {C}^*$
-algebra M),
$CA = C_0((0,1],A)$
for the cone,
$\mathrm {M}_r(A)$
for
$r \times r$
matrices over A, and
$\mathcal {M}(A)$
for the multiplier algebra of A (regarded as a subalgebra of the double dual
$A^{**}$
).
Definition 1.1. Let A and B be
$\mathrm {C}^*$
-algebras with self-adjoint subspaces
$X\subset A$
,
$Y\subset B$
and
$\theta \colon X\longrightarrow Y$
a linear map. We say
$\theta $
is positive if
$\theta (x)\in Y\cap B_+$
for all
$x\in X\cap A_+$
. We say it is completely positive (c.p.) if this holds for all matrix amplifications
$\theta ^{(r)}\colon \mathrm {M}_r(X)\longrightarrow \mathrm {M}_r(Y)$
. We say
$\theta $
is completely contractive if
$\sup _{r\geq 1} \|\theta ^{(r)}\|\leq 1$
. A map which is completely positive and completely contractive is referred to as completely positive contractive (c.p.c.).
Remark 1.2. When
$1_A\in X$
is a unital self-adjoint subspace of a unital
$\mathrm {C}^*$
-algebra A (what is usually called an operator (sub)system), then for any c.p. map
$\theta \colon X\longrightarrow Y$
, we have
$$ \begin{align*} \|\theta\|\leq \sup_{r\geq 1}\|\theta^{(r)}\|\leq \|\theta(1_A)\|. \end{align*} $$
It follows that any completely positive and contractive map from a unital self-adjoint subspace of a
$\mathrm {C}^*$
-algebra is automatically completely contractive. The respective statement holds when A is a (not necessarily unital)
$\mathrm {C}^*$
-algebra.
A particularly special class of completely positive maps consists of orthogonality preserving or order zero maps. At the end of this section, we will highlight several properties that order zero maps share with
$^*$
-homomorphisms and that may fail for general c.p.c. maps.
Definition 1.3. A c.p. map
$\theta \colon A\longrightarrow B$
between
$\mathrm {C}^*$
-algebras is order zero if it maps orthogonal elements to orthogonal elements, or equivalently if for any
$a,b\in A_+$
,
$$\begin{align*}ab=0\ \Longrightarrow\ \theta(a)\theta(b)=0.\end{align*}$$
Examples of c.p. order zero maps include
$^*$
-homomorphisms, but there exist c.p. order zero maps which are not multiplicative, such as the canonical embedding
$\iota \colon A\longrightarrow CA$
of a
$\mathrm {C}^*$
-algebra into its cone. Nonetheless, order zero maps are remarkably close to
$^*$
-homomorphisms, as is made evident by the structure theorem for c.p. order zero maps [Reference Winter and Zacharias24, Theorem 3.3]. The following rendition combines elements of [Reference Winter and Zacharias24, Theorem 3.3] and [Reference Winter and Zacharias24, Proposition 3.2].
Theorem 1.4 (Structure theorem for order zero maps [Reference Winter and Zacharias24]).
Let A and B be
$\mathrm {C}^*$
-algebras,
$\theta \colon A\longrightarrow B$
a c.p. order zero map,
$C=\mathrm {C}^*(\theta (A))$
,
$\{u_\lambda \}_\lambda $
an increasing approximate identity for A, and 
. Then
$0\leq h\in \mathcal {M}(C)\cap C'\subset C^{**}$
with
$\|h\|=\|\theta \|$
, and there exists a
$^*$
-homomorphism
$\pi _\theta \colon A\longrightarrow \mathcal {M}(C)$
so that for all
$a\in A$
,
$$\begin{align*}\theta(a)=h\pi_\theta(a)=h^{1/2}\pi_\theta(a)h^{1/2}.\end{align*}$$
Remarks 1.5. (i) ([Reference Winter and Zacharias24, Proposition 3.2]) When A is unital, we have
$h=\theta (1_A)$
, and in general, the map
$\theta ^{\sim }\colon A^{\sim }\longrightarrow \mathcal {M}(C)$
given by
$\theta ^{\sim }(a+\lambda 1_{A^\sim })=\theta (a)+\lambda h$
is the unique c.p. order zero extension of
$\theta $
. (By
$A^{\sim }$
we denote the minimal unitization of A, so that
$A^{\sim }=A$
when A is unital.) In any case,
$h\geq \theta (a)$
for all
$a\in A_+^1$
. Note that for
$\theta ^{\sim }$
to be order zero, one can replace h with
$1_{\mathcal {M}(C)}$
only if
$\theta $
is in fact multiplicative, since u.c.p. order zero maps are automatically
$^*$
-homomorphisms.
(ii) The structure theorem for order zero maps gives a useful characterization of when a c.p. map with unital domain is order zero: Assume A and B are
$\mathrm {C}^*$
-algebras with A unital. Then a c.p. map
$\theta \colon A\longrightarrow B$
is order zero if and only if
$\theta (a)\theta (b)=\theta (1_A)\theta (ab)$
for all
$a,b\in A$
.
Definition 1.6. Let A and B be
$\mathrm {C}^*$
-algebras and
$X\subset A$
,
$Y\subset B$
two self-adjoint subspaces. We say a linear map
$\theta \colon X\longrightarrow Y$
is a complete order embedding if
$\theta $
is c.p. and completely isometric with c.p. inverse
$\theta ^{-1}\colon \theta (X)\longrightarrow A$
(i.e., for all
$r\geq 1$
,
$\theta ^{(r)}\colon \mathrm {M}_r(X)\longrightarrow \mathrm {M}_r(Y)$
is isometric and
$x\in \mathrm {M}_r(X)\cap \mathrm {M}_r(A)_+ \Longleftrightarrow \theta ^{(r)}(x)\in \mathrm {M}_r(Y)\cap \mathrm {M}_r(B)_+$
for all
$x\in \mathrm {M}_r(X)$
). A surjective complete order embedding is called a complete order isomorphism.
Remarks 1.7. (i) A complete order isomorphism between
$\mathrm {C}^*$
-algebras is automatically a
$^*$
-isomorphism (cf. [Reference Blackadar3, Theorem II.6.9.17]).
(ii) If
$X=A$
and
$\theta \colon A\longrightarrow Y\subset B$
is c.p. and completely isometric, then it is automatically a complete order embedding: If
$\theta (a)\geq 0$
for some
$0\neq a\in A^1$
, then
$a=a^*$
since
$\theta $
is injective and
$^*$
-linear. If
$a_-\neq 0$
, then for 
, we have
$$ \begin{align*} \|a\|+\|a_-\|&=\|b-a\|\\ &=\|\theta(b)-\theta(a)\|\\ &\leq \| \|\theta(b)\|1_{B^\sim}-\theta(a)\|\\ &=\|\|\theta(a)\|1_{B^\sim}-\theta(a)\|\\ &\leq \|\theta(a)\|\\ &=\|a\|, \end{align*} $$
a contradiction, so a was positive. The respective argument applies when a lives in some matrix algebra over A, whence indeed the inverse of
$\theta $
is completely positive.
(iii) An isometric c.p. map
$\theta \colon A\longrightarrow B$
between
$\mathrm {C}^*$
-algebras which is not surjective and not unital may fail to be a complete order embedding – even if it has a c.p. inverse
$\theta ^{-1}\colon \theta (A)\longrightarrow A$
. We will work out such an example in forthcoming work. The proposition below shows that for all order zero maps, this issue does not occur. We will use this in Proposition 2.7.
Proposition 1.8. Suppose
$\theta \colon A\longrightarrow B$
is a c.p. order zero map between
$\mathrm {C}^*$
-algebras A and B. Then
$\theta $
is isometric if and only if it is a complete order embedding.
Proof. A complete order embedding is by definition isometric, so we only need to show that an isometric c.p. order zero map
$\theta \colon A\to B$
is a complete order embedding; by Remark 1.7(ii), this reduces to showing that
$\theta $
is completely isometric. Without loss of generality, we assume
$B=\mathrm {C}^*(\theta (A))$
. Let
$\iota \colon A\longrightarrow CA$
denote the canonical embedding
$a\mapsto \mathrm {id}_{(0,1])}\otimes a$
of A into its cone. Then by [Reference Winter and Zacharias24, Corollary 4.1],
$\theta $
induces a surjective
$^*$
-homomorphism
$\hat {\theta }:CA\longrightarrow B$
so that
$\hat {\theta } \circ \iota =\theta $
.
Set
$\pi \colon B\longrightarrow B/\hat {\theta }(SA)$
and 
, where 
denotes the suspension of A. Then there exists a surjective
$^*$
-homomorphism
$\varphi \colon A\longrightarrow B/\hat {\theta }(SA)$
so that
$\hat {\pi }=\varphi \circ \text {ev}_1$
. Altogether, we have the commutative diagram
We claim that
$\varphi $
is injective. If so, then we have
$\varphi ^{-1}\circ \pi \circ \theta =\mathrm {id}_A$
, and hence,
$(\varphi ^{-1})^{(r)}\circ \pi ^{(r)} \circ \theta ^{(r)} =\mathrm {id}_A^{(r)}$
for each
$r\geq 1$
. Since
$\varphi ^{-1}$
and
$\pi $
are in this case completely contractive, it will then follow that
$\theta $
must be completely isometric.
It suffices to check injectivity on
$A_+$
, and so we fix
$a\in A_+$
with
$\|a\|=1$
. Let
$\rho \in S(B)$
be a pure state on B with
$\|\theta (a)\|=\rho (\theta (a))$
. Then
$\rho \circ \hat {\theta }$
is a pure state on
$CA$
, and hence, its restriction to the algebraic tensor product
$C_0((0,1])\odot A$
is of the form
$\text {ev}_t\otimes \rho $
for some
$t\in (0,1]$
and some (pure) state
$\rho _A$
on A. Since
$$\begin{align*}1=\|a\|=\|\theta(a)\|=\rho\circ\hat{\theta}(\mathrm{id}_{(0,1]}\otimes a)=t\rho_A(a)\leq \rho_A(a)\leq \|a\|,\end{align*}$$
we must have
$t=1$
. In particular,
$SA\subset \text {ker}(\rho \circ \hat {\theta })$
, and hence,
$\hat {\theta }(SA)\subset \text {ker}(\rho )$
. Since
$\rho (\theta (a))=1$
, we conclude that
$\theta (a)\notin \hat {\theta }(SA)$
, and so
$\varphi (a)\neq 0$
.
2
$\mathrm{CPC}^*$
-systems and their limits
Recall from Remark 1.5(ii) that for
$\mathrm {C}^*$
-algebras A and B with A unital a c.p.c. map
$\theta \colon A\longrightarrow B$
is order zero precisely when
$\theta (a)\theta (b)=\theta (1_A)\theta (ab)$
for all
$a,b\in A$
. The following definition gives an asymptotic version of this characterization.
Definition 2.1. Given a sequence of
$\mathrm {C}^*$
-algebras
$(F_n)_n$
, we let
be the quotient
$\mathrm {C}^*$
-algebra of norm bounded sequences modulo null sequences, denoting elements of the quotient in the form
$[(x_n)_n]$
.
If in addition we have c.p.c. connecting maps
$\rho _{n+1,n}\colon F_n\longrightarrow F_{n+1}$
for all
$n\geq 0$
, we set 
and
$\rho _{n,n}=\mathrm {id}_{F_n}$
for all
$m>n\geq 0$
, and define induced maps
$\rho _n\colon F_n\longrightarrow F_\infty $
by
$$ \begin{align*} \rho_n(x)=[(\rho_{m,n}(x))_{m>n}] \end{align*} $$
for all
$x\in F_n$
and define the inductive limit of the system
$(F_n, \rho _{n+1,n})_n$
to be the closed self-adjoint subspace
In general, such an inductive limit exists in the category of operator spaces; in order to equip it with the structure of a
$\mathrm {C}^*$
-algebra, one needs additional hypotheses.
Definition 2.2. Let
$(F_n)_n$
be a sequence of finite-dimensional
$\mathrm {C}^*$
-algebras together with c.p.c. maps
$\rho _{n+1,n}\colon F_n\longrightarrow F_{n+1}$
for all
$n\geq 0$
. We call
$(F_n,\rho _{n+1,n})_n$
a
${\mathrm {CPC}^*}$
-system if for any
$k\geq 0$
,
$x,y\in F_k$
, and
$\varepsilon>0$
, there exists
$M>k$
so that for all
$m>n,l>M$
,
$$ \begin{align} \|\rho_{m,l}(1_{F_l})\rho_{m,n}(\rho_{n,k}(x)\rho_{n,k}(y))-\rho_{m,k}(x)\rho_{m,k}(y)\|<\varepsilon. \end{align} $$
In this situation, we call the limit 
a
${\mathrm {CPC}^*}$
-limit.
The aim of this section is to prove that a
${\mathrm {CPC}^*}$
-limit can be turned, in a very robust sense, into a
$\mathrm {C}^*$
-algebra (Proposition 2.6), denoted by 
, which is nuclear (Theorem 2.13), and such that the map 
is an order zero complete order embedding (Proposition 2.7). We begin by accumulating some tools and observations.
Systems as in Definition 2.1 involve c.p.c. maps; hence, they are clearly compatible with taking matrix amplifications. It is slightly less obvious that the process of lifting individual elements of the inductive limit is also compatible with the system in the following sense.
Lemma 2.3. Let
$(F_n,\rho _{n+1,n})_n$
be a system as in Definition 2.1. For any
$r\geq 1$
and 
, if
$(x_n)_n\in \prod \mathrm {M}_r(F_n)$
is some lift of
$\bar {x}$
, then 
.
Proof. Consider
$r=1$
and fix 
, a lift
$(x_n)_n\in \prod F_n$
of
$\bar {x}$
, and
$\varepsilon>0$
. Let
$y_{k_j}\in F_{k_j}$
so that 
. Since the maps are coherent, we can assume for simplicity that the
$k_j$
are increasing and set 
for
$k_j<n<k_{j+1}$
. Then we have 
. Now fix
$k>0$
so that
$\|\rho _k(y_k)-\bar {x}\|<\varepsilon /4$
. Then we may choose
$M>k$
so that
$\|\rho _{n,k}(y_k)-x_n\|<\varepsilon /2$
for all
$n>M$
. Then for all
$m>n>M$
,
$$ \begin{align*} \|\rho_{m,n}(x_n)-x_m\|&\leq \|\rho_{m,n}(x_n-\rho_{n,k}(y_k))\| + \|\rho_{m,k}(y_k)-x_m\|\\&\leq \|x_n-\rho_{n,k}(y_k)\| + \|\rho_{m,k}(y_k)-x_m\|\\ &<\varepsilon. \end{align*} $$
It follows that 
.
Note that the argument for
$r=1$
uses only that the maps
$\rho _{m,n}$
are coherent and c.p.c., which is also true for their matrix amplifications, and so the exact same proof goes through for
$r\geq 1$
.
A key tool for us will be a distinguished matrix order unitFootnote 1 for the limit of a
${\mathrm {CPC}^*}$
-system
$(F_n,\rho _{n+1,n})_n$
, which we define to be
Note that we do not in general assume that e is an element of 
. That latter situation would correspond to 
being unital (with 
), in which case, (2.1) can be slightly simplified by eliminating the variable l.
We also set
Remark 2.4. Note that (2.1) implies that for any
$k\geq 0$
and
$x,y\in F_k$
, we have
The following lemma will allow us to interpret e as a commuting nondegenerate order unit for 
.
Lemma 2.5. Let
$(F_n,\rho _{n+1,n})_n$
be a
${\mathrm {CPC}^*}$
-system, and let e be as defined in (2.2).
-
(1) For each
$k\geq 0$
,
$x\in F_k$
and
$\varepsilon>0$
, there exists
$M>k$
so that for all
$m>n>M$
,
$$\begin{align*}\|\rho_{m,n}(1_{F_n})\rho_{m,k}(x)-\rho_{m,k}(x)\rho_{m,n}(1_{F_n})\|<\varepsilon.\end{align*}$$
In particular,
. -
(2) For any
$r\geq 1$
and any self-adjoint , we have
$\|\bar {x}\|e^{(r)}\geq \bar {x}$
in
$\mathrm {M}_r(F_\infty )$
. -
(3) For any
and any
$j\geq 1$
, we have
$\|e^j\bar {x}\|=\|\bar {x}\|$
. In particular, for any and
$j\geq 1$
, if
$e^j\bar {x}=e^j\bar {y}$
, then
$\bar {x}=\bar {y}$
.
.
, we have 
and any 
and 
Proof. For (i), we fix
$k\geq 0$
,
$x\in F_k$
and
$\varepsilon>0$
; without loss of generality, it suffices to assume
$x\in (F_k)_+^1$
. It follows from a standard functional calculus argument using polynomial approximations of
$t\mapsto t^{1/2}$
on
$[0,1]$
that we are finished when we find for any
$\eta>0$
an
$M>k$
so that for all
$m>n>M$
,
$$ \begin{align} \|\rho_{m,n}(1_{F_n})\rho_{m,k}(x)^2-\rho_{m,k}(x)^2\rho_{m,n}(1_{F_n})\|<\eta. \end{align} $$
To that end, we utilize (2.1) to choose
$M>k$
so that for all
$m>n>M$
,
$$ \begin{align} \|\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2)-\rho_{m,k}(x)^2\|<\eta/6.\end{align} $$
Then we have
$$ \begin{align*} &\|\rho_{m,n}(1_{F_n})\rho_{m,k}(x)^2-\rho_{m,k}(x)^2\rho_{m,n}(1_{F_n})\|\\&\overset{\phantom{(2.4)}}{\leq} \|\rho_{m,n}(1_{F_n})\rho_{m,k}(x)^2-\rho_{m,n}(1_{F_n})^2\rho_{m,n}(\rho_{n,k}(x)^2)\| \\& \phantom{\overset{(2.4)}{<}} + \|\rho_{m,n}(1_{F_n})^2\rho_{m,n}(\rho_{n,k}(x)^2)-\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})\|\\& \phantom{\overset{(2.4)}{<}} + \|\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})-\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})^2\|\\&\phantom{\overset{(2.4)}{<}} +\|\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})^2-\rho_{m,k}(x)^2\rho_{m,n}(1_{F_n})\|\\&\overset{\phantom{(2.4)}}{\leq} \|\rho_{m,n}(1_{F_n})\|\|\rho_{m,k}(x)^2-\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2)\| \\& \phantom{\overset{(2.4)}{<}} + \|\rho_{m,n}(1_{F_n})\|\|\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2)-\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})\|\\& \phantom{\overset{(2.4)}{<}} + \|\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2)-\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})\|\|\rho_{m,n}(1_{F_n})\|\\&\phantom{\overset{(2.4)}{<}} +\|\big(\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})-\rho_{m,k}(x)^2\big)^*\|\|\rho_{m,n}(1_{F_n})\|\\&\leq 2\|\rho_{m,k}(x)^2-\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2)\|\\&\phantom{\overset{(2.4)}{<}} + 2\|\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2)-\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})\| \\&\overset{({2.4})}{<} \eta/3+ 2\|\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2) - \rho_{m,k}(x)^2\|\\&\phantom{\overset{(2.4)}{<}} + 2\|\rho_{m,k}(x)^2-\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})\|\\&\overset{\phantom{(2.4)}}{=} \eta/3 + 2\|\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2) - \rho_{m,k}(x)^2\|\\&\phantom{\overset{(2.4)}{<}} + 2\|\big(\rho_{m,k}(x)^2-\rho_{m,n}(\rho_{n,k}(x)^2)\rho_{m,n}(1_{F_n})\big)^*\|\\&\overset{\phantom{(2.4)}}{=} \eta/3+4\|\rho_{m,n}(1_{F_n})\rho_{m,n}(\rho_{n,k}(x)^2) - \rho_{m,k}(x)^2\|\\&\overset{({2.4})}{<}\eta, \end{align*} $$
which establishes (2.3) and hence (i).
For the order unit condition (ii), we first consider
$r=1$
. For any self-adjoint 
and any self-adjoint lift
$(x_n)_n\in \prod F_n$
of
$\bar {x}$
, Lemma 2.3 tells us 
. Hence, it suffices to prove the claim for
$\rho _k(x)$
for any fixed
$k\geq 0$
and any self-adjoint
$x\in F_k$
. For each
$n>k$
, we have
$\|\rho _{n,k}(x)\|1_{F_n}\geq \rho _{n,k}(x)$
, and so
$\|\rho _{n,k}(x)\|\rho _n(1_{F_n})\geq \rho _n(\rho _{n,k}(x))=\rho _k(x)$
. Since all the maps are c.p.c., it follows that
$e\geq \rho _n(1_{F_n})$
for all
$n\geq 0$
, and hence,
$\|\rho _{n,k}(x)\| e \geq \rho _k(x)$
for all
$n>k$
. Moreover,
$(\|\rho _{n,k}(x)\|)_{n>k}$
is bounded and non-increasing, which means 
, and so
Since the argument for
$r=1$
uses only Lemma 2.3 and that the maps are c.p.c., we may repeat the same argument for
$r\geq 1$
.
For the nondegeneracy condition (iii), we assume 
(otherwise, the claim is trivial). We first consider the case where 
is self-adjoint, and we assume moreover that
$\|\bar {x}\|=1$
. By possibly replacing
$\bar {x}$
with
$-\bar {x}$
, we may assume
$1\in \sigma (\bar {x})$
, the spectrum of
$\bar {x}$
. From (i), we know e and
$\bar {x}$
commute, and so we may identify
$\mathrm {C}^*(e,\bar {x})\subset F_\infty $
with
$C_0(\Omega )$
for some locally compact Hausdorff space
$\Omega \subset \sigma (e)\times \sigma (\bar {x})\subset [0,1]\times [-1,1]$
. Then (ii) implies
$s\geq t$
for all
$(s,t)\in \Omega $
. Since we assumed
$1\in \sigma (\bar {x})$
, it follows that
$(1,1)\in \Omega $
, and so for any
$m\geq 1$
,
$$\begin{align*}1=\|\bar{x}\|\geq \|e^m\bar{x}\|=\sup_{(s,t)\in \Omega} |s^m t|\geq 1.\end{align*}$$
Now, we handle the general case of any 
. Because
$\bigcup _n \rho _n(F_n)$
is dense in 
, it suffices to check that (iii) holds for any fixed
$\bar {x}=\rho _k(x)$
with
$k\geq 0$
and
$x\in F_k$
. From Remark 2.4, we know that
Since 
is self-adjoint for all
$m>n>k$
, we already know that
$$ \begin{align*} &\|e \rho_m\big(\rho_{m,k}(x)^*\rho_{m,k}(x)\big) - e \rho_n\big(\rho_{n,k}(x)^*\rho_{n,k}(x)\big)\|\\ &= \|\rho_m\big(\rho_{m,k}(x)^*\rho_{m,k}(x)\big) - \rho_n\big(\rho_{n,k}(x)^*\rho_{n,k}(x)\big)\|, \end{align*} $$
which together with (2.5) implies that
$\big (\rho _n\big (\rho _{n,k}(x)^*\rho _{n,k}(x)\big )\big )_n$
is Cauchy and hence converges to some self-adjoint 
with
$e \bar {z}=\rho _k(x)^*\rho _k(x)$
. From this and the self-adjoint case, we have
$$ \begin{align*} \|\rho_k(x)\|^2=\|\rho_k(x)^*\rho_k(x)\|=\|e\bar{z}\|=\|\bar{z}\|. \end{align*} $$
Since
$\bar {z}$
is self-adjoint, (ii) tells us
$ \|\rho _k(x)\|^2 e =\|\bar {z}\|e\geq \bar {z}$
. By (i), e commutes with
$\bar {z}$
and moreover with
$|\rho _k(x)|$
. It follows that
$$\begin{align*}\|\rho_k(x)\|^2 e^2 \geq e\bar{z} = \rho_k(x)^*\rho_k(x),\end{align*}$$
which implies
$$\begin{align*}\|\rho_k(x)\| e \geq |\rho_k(x)|.\end{align*}$$
With this, the proof of the self-adjoint case also shows that
$\|e^m |\rho _k(x)|\|\\ =\| |\rho _k(x)| \|$
for any
$m\geq 1$
, and so it follows that for any
$m\geq 1$
, we have
$$ \begin{align*}\|e^m\rho_k(x)\|^2&= \|e^{2m}|\rho_k(x)|^2\|\\ &=\|(e^m|\rho_k(x)|)^2\|\\ &=\|e^m|\rho_k(x)|\|^2\\ &=\||\rho_k(x)|\|^2\\ &=\|\rho_k(x)\|^2.\\[-37pt]\end{align*} $$
With these preliminary observations covered, we are now ready to prove our first structural result about
${\mathrm {CPC}^*}$
-limits.
Proposition 2.6. Let 
be the limit of a
${\mathrm {CPC}^*}$
-system
$(F_n,\rho _{n+1,n})_n$
. Then there exists an associative bilinear map 
satisfying
for all
$k\geq 0$
and
$x,y\in F_k$
and
for all 
, so that with respect to the multiplication 
, 
is a
$\mathrm {C}^*$
-algebra with norm
$\|\cdot \|_{F_\infty }$
, denoted 
.Footnote 2
Proof. We begin by defining 
. For elements
$\bar {x},\bar {y}$
in the nested union
$\bigcup _n \rho _n(F_n)$
, we may choose
$k\geq 0$
and
$x,y\in F_k$
so that
$\bar {x}=\rho _k(x)$
and
$\bar {y}=\rho _k(y)$
and define 
by
That the given limit exists follows immediately from Remark 2.4 and Lemma 2.5(iii). Moreover, this definition is independent of the particular choice of k and
$x,y\in F_k$
. Indeed, for any
$(x_n)_n, (y_n)_n\in \prod F_n$
with
$[(x_n)_n]=\rho _k(x)=\bar {x}$
and
$[(y_n)_n]=\rho _k(y)=\bar {y}$
, we have
$[(\rho _{n,k}(x)\rho _{n,k}(y))_n]=[(x_ny_n)_n]$
. Then for any
$\varepsilon>0$
and
$M>k$
with
$\sup _{n>M}\|\rho _{n,k}(x)\rho _{n,k}(y)-x_ny_n\|<\varepsilon $
, we have
$\|\rho _n(\rho _{n,k}(x)\rho _{n,k}(y))-\rho _n(x_ny_n)\|<\varepsilon $
for all
$n>M$
, and so the sequence 
also converges to 
.
Bilinearity of this map follows from that of the usual product in the
$F_n$
’s. For each
$k\geq 0$
and
$x,y\in F_k$
, we have from Remark 2.4 that
which by the nondegeneracy condition in Lemma 2.5(iii) implies
For 
and
$(x_n)_n, (y_n)_n\in \prod F_n$
with
$\bar {x}=[(x_n)_n]$
and
$\bar {y}=[(y_n)_n]$
, it follows from (2.9) and Lemma 2.3 that
Moreover, by Lemma 2.5(iii), we have for all
$m>n\geq 0$
,
Hence, 
exists, and we may extend the map to 
by defining
for each 
, where
$(x_n)_n, (y_n)_n\in \prod F_n$
are any lifts of
$\bar {x}$
and
$\bar {y}$
. Note that we still have
and so it follows again from nondegeneracy (Lemma 2.5(iii)) that 
is the unique element 
so that
$e \bar {z} = \bar {x}\bar {y}$
. In summary, our map 
is well-defined, bilinear and satisfies (2.7) and (2.6). To see that it is associative, fix 
. Then we have
It follows from nondegeneracy that
So, 
is an algebra. To see that it is a
$^*$
-algebra with respect to the involution it inherits from
$F_\infty $
, we set 
, and observe that
Again, it follows from nondegeneracy that 
, so indeed, 
is a
$^*$
-algebra.
Since 
is already a Banach space with respect to the given norm on
$F_\infty $
, it remains to confirm that it is in fact a Banach
$^*$
-algebra and that the norm still satisfies the
$\mathrm {C}^*$
-identity. Both of these follow immediately from the fact that
for any 
.
Proposition 2.7. Let
$(F_n,\rho _{n+1,n})_n$
be a
${\mathrm {CPC}^*}$
-system. Then
is an order zero complete order embedding.
Proof. Clearly, the map is isometric,
$^*$
-preserving and linear since the given
$^*$
-linear structures and norms on 
and 
are the same. Moreover, from (2.11), we can conclude that
$\Theta $
is order zero. By Proposition 1.8, it remains only to show that it is completely positive (i.e., for any
$r\geq 1$
and 
, the element 
is in
$\mathrm {M}_r(F_\infty )_+$
). (We still use 
to denote the multiplication in 
.)
Fix
$r\geq 1$
, and note that by applying (2.7) coordinate-wise, we have for any 
that
So it suffices to show that
$e^{(r)}\bar {y}\geq 0$
implies
$\bar {y}\geq 0$
for any 
.
To that end, fix 
and assume
$e^{(r)}\bar {y}\geq 0$
. If
$y=0$
, there is nothing to show, so we assume
$\|\bar {y}\|=1$
. Using Lemma 2.5(iii), we also get a nondegeneracy condition for
$e^{(r)}$
, which says that
$e^{(r)}\bar {z}=0$
implies
$\bar {z}=0$
for any 
. Then since
$$\begin{align*}e^{(r)}\bar{y}= (e^{(r)}\bar{y})^*= e^{(r)}\bar{y}^*,\end{align*}$$
we conclude that
$\bar {y}= \bar {y}^*$
.
From Lemma 2.5(ii), we know
$e^{(r)}- \bar {y}$
and
$e^{(r)}+ \bar {y}\in \mathrm {M}_r(F_\infty )_+$
. Since
$e^{(r)}$
and
$\bar {y}$
commute (by Lemma 2.5(i)), this implies that
$e^{(r)} \geq |\bar {y}|$
and that we can identify
$\mathrm {C}^*(e^{(r)},\bar {y})\subset \mathrm {M}_r(F_\infty )$
with
$C_0(\Omega )$
for some locally compact
$\Omega \subset \sigma (e^{(r)})\times \sigma (\bar {y})$
, where
$e^{(r)}$
corresponds to the map
$(s,t)\mapsto s$
and
$\bar {y}$
corresponds to the map
$(s,t)\mapsto t$
. Since
$e^{(r)} \geq |\bar {y}|$
, we have
$s \geq |t|$
for all
$(s,t)\in \Omega $
. Now, suppose there exists
$t_0\in \sigma (\bar {y})\cap (-\infty ,0)$
, and let
$s_0\in \sigma (e^{(r)})$
so that
$(s_0,t_0)\in \Omega $
. Then
$s_0 \geq |t_0|>0$
implies
$s_0>0$
, whence
$s_0t_0<0$
, contradicting
$e^{(r)}\bar {y}\geq 0$
. Hence,
$\bar {y}\geq 0$
, and our proof is complete.
Corollary 2.8. Let
$(F_n,\rho _{n+1,n})_n$
be a
${\mathrm {CPC}^*}$
-system, and let
$\Theta $
be as in Proposition 2.7. Then for any
$\mathrm {C}^*$
-algebra A and complete order embedding
$\psi \colon A\longrightarrow F_\infty $
with 
, the map 
is a
$^*$
-isomorphim.
Proof. With Proposition 2.7, we see that 
is a surjective complete order isomorphism. The claim then follows from Remark 1.7(i).
Remark 2.9. By definition, 
and 
are identical as involutive Banach spaces. With the previous results at hand, we may describe the
$\mathrm {C}^*$
-algebra structure in two alternative ways: Let C denote the
$\mathrm {C}^*$
-algebra generated by 
in
$F_\infty $
and 
the
$^*$
-homomorphism guaranteed by Theorem 1.4. From Theorem 1.4, we see that
$\ker (\pi _\Theta )=\ker (\Theta )=\{0\}$
, which means
$\pi _\Theta $
is injective, and 
, so we may regard 
as a
$\mathrm {C}^*$
-algebra of multipliers of C. Moreover, if 
, then
$\Theta (x)=x=e\pi _\Theta (x)$
for all 
.
On the other hand, if 
, then one can also show that 
forms an abstract operator system (cf. [Reference Choi and Effros6] or [Reference Paulsen20, Chapter 13]). As an operator system, this is equal to the operator system 
, which happens to also be a
$\mathrm {C}^*$
-algebra, and so for each
$r\geq 1$
, the norm on 
agrees with the matrix norm on 
induced by the matrix order. Hence, by [Reference Hamana11, Corollary 4.2], we may identify 
with the enveloping
$\mathrm {C}^*$
-algebra of this operator system.
Remark 2.10. Though the subspace 
might not be a sub-
$\mathrm {C}^*$
-algebra in general, the correspondence between 
and 
is so robust that we take the liberty to call both 
and 
the limit of a
${\mathrm {CPC}^*}$
-system, and we refer to 
as a
${\mathrm {CPC}^*}$
-limit.
As we mentioned before, e need not be in 
. Nonetheless, the sequence
$(\rho _n(1_{F_n}))_n$
will still provide an approximate identity for the limit of the system.
Corollary 2.11. Let
$(F_n,\rho _{n+1,n})_n$
be a
${\mathrm {CPC}^*}$
-system. Then
$(\rho _n(1_{F_n}))_n$
forms an increasing approximate identity for 
.
Proof. The sequence
$(\rho _n(1_{F_n}))_n$
is increasing in
$F_\infty $
since the maps
$\rho _{m,n}$
are all c.p.c., and so by Proposition 2.7, it is also increasing in 
.
To see that this forms an approximate identity, it suffices to consider elements of the form 
for some
$k\geq 0$
and
$x,y\in F_k$
. Indeed, since 
is a
$\mathrm {C}^*$
-algebra, it follows that for any 
, there exists 
so that 
. Then for any lift
$(x_n)_n, (y_n)_n$
of
$\bar {x}$
and
$\bar {y}$
, respectively, Lemma 2.3 tells us
$\rho _n(x_n)\longrightarrow \bar {x}$
and
$\rho _n(y_n)\longrightarrow \bar {y}$
, and so 
.
Now fix
$k\geq 0, x,y \in F_k$
, and
$\varepsilon>0$
, and choose
$M>k$
so that
for all
$m>n>M$
. Then using Lemma 2.5(iii) and (2.7), we have for all
$n>M$
,
It remains to show that all
${\mathrm {CPC}^*}$
-limits are nuclear. For this, we will use Ozawa and Sato’s one-way-CPAP, which appeared implicitly in [Reference Ozawa19] (via [Reference Kishimoto, Ozawa and Sakai16]); see [Reference Sato22, Theorem 5.1] for the explicit statement and its proof.
Theorem 2.12 [Reference Ozawa19, Reference Sato22].
A
$\mathrm {C}^*$
-algebra A is nuclear if and only if there exists a net
$\{\varphi _\lambda \colon F_\lambda \longrightarrow A\}_{\lambda \in \Lambda }$
of c.p.c. maps from finite-dimensional
$\mathrm {C}^*$
-algebras
$\{F_\lambda \}_{\lambda \in \Lambda }$
such that the induced c.p.c. map
$$ \begin{align*} \Phi=(\varphi_\lambda)_\lambda\colon \textstyle{\prod} F_\lambda/\textstyle{\bigoplus} F_\lambda &\longrightarrow \ell^\infty (\Lambda,A)/c_0(\Lambda, A), \end{align*} $$
given by
$\Phi ([(x_\lambda )_{\lambda \in \Lambda }])=[(\varphi _\lambda (x_\lambda ))_{\lambda \in \Lambda }], $
satisfies
$$\begin{align*}\iota(A^1)\subset \Phi\big((\textstyle{\prod} F_\lambda/ \textstyle{\bigoplus} F_\lambda)^1\big),\end{align*}$$
where
$\iota \colon A \longrightarrow \ell ^\infty (\Lambda ,A)/c_0(\Lambda , A)$
denotes the identification of A with the sub-
$\mathrm {C}^*$
-algebra of
$\ell ^\infty (\Lambda ,A)/c_0(\Lambda , A)$
consisting of equivalence classes of constant nets.
Theorem 2.13.
${\mathrm {CPC}^*}$
-limits are nuclear.
Proof. Let
$(F_n,\rho _{n+1,n})_n$
be a
${\mathrm {CPC}^*}$
-system with complete order embedding 
from Proposition 2.7. For each
$m\geq 0$
, we define 
. It follows from Proposition 2.7 that each
$\varphi _m$
is a c.p.c. map. We denote the sequence algebra 
by 
, and we write 
for the embedding as equivalence classes of constant sequences. Let 
be the c.p.c. map induced by the
$\varphi _m$
as in Theorem 2.12 with
$\Phi ([(x_m)_m])=[(\varphi _m(x_m))_m]$
. Note that for
$k\geq 0$
and
$x\in F_k$
, we have
$$ \begin{align*} \Phi(\rho_k(x))&=\Phi([(\rho_{m,k}(x))_{m>k}])\\&=[(\varphi_m(\rho_{m,k}(x)))_{m>k}]\\ &=[((\Theta^{-1}\circ\rho_m)(\rho_{m,k}(x))_{m>k}]\\ &=[(\Theta^{-1}\circ\rho_k(x))_{m>k}]\\ &=\iota\circ\Theta^{-1}\circ\rho_k(x)\\ &=\iota\circ\varphi_k(x). \end{align*} $$
Since these elements are dense in 
, it follows that
$\Phi (\bar {x})=\iota \circ \Theta ^{-1}(\bar {x})$
for each 
. Since
$\Theta ^{-1}$
is isometric, that gives us
Now with [Reference Sato22, Theorem 5.1] (as stated above in Theorem 2.12), we conclude that 
is nuclear.
3
${\mathrm {CPC}^*}$
-systems from systems of c.p.c. approximations
The goal of this section is a converse to Theorem 2.12: Any separable nuclear
$\mathrm {C}^*$
-algebra is
$^*$
-isomorphic to a
${\mathrm {CPC}^*}$
-limit. Moreover, the
${\mathrm {CPC}^*}$
-system will arise from a system of c.p.c. approximations. We first recall some facts regarding systems of c.p.c. approximations of separable nuclear
$\mathrm {C}^*$
-algebras.
Definition 3.1. Let A be a separable nuclear
$\mathrm {C}^*$
-algebra.
(i) A system of c.p.c. approximations for A is a sequence 
, where the
$F_n$
are finite-dimensional
$\mathrm {C}^*$
-algebras and 
are c.p.c. maps so that for all
$a\in A$
,
(ii) We call a system of c.p.c. approximations as above summable if there exists a decreasing sequence
$(\varepsilon _n)_n\in \ell ^1(\mathbb {N})_+^1$
such that for all
$n>k\geq 0$
,
$$ \begin{align*} \|\varphi_k-\varphi_n \circ \psi_n\circ\varphi_k\|<\varepsilon_n. \end{align*} $$
(iii) We say a system of c.p.c. approximations as in (i) has approximately multiplicative downwards maps if for any
$a,b\in A$
, we have 
.
(iv) We say a system of c.p.c. approximations as in (i) has approximately order zero downwards maps if for any
$a,b\in A_+$
with
$ab=0$
, we have 
.
(v) Given a system of c.p.c. approximations as in (i), we define for all
$m>n\geq 0$
,
thus obtaining an associated system
$(F_n,\rho _{n+1,n})_n$
.
Remarks 3.2. (i) We will usually consider summable systems of c.p.c. approximations, in which case
$\rho _{m,n}$
and
$\psi _m\circ \varphi _n$
become arbitrarily close for
$m>n$
sufficiently large. Moreover, for any
$k\geq 0$
and
$x\in F_k$
, the sequence
$(\varphi _n(\rho _{n,k}(x)))_n$
converges in A.
(ii) Asking for summability will not result in any loss of generality, since after passing to a subsystem, we can always arrange this for any choice of
$(\varepsilon _n)_n \in \ell ^1(\mathbb {N})^1_+$
. Indeed, given a system 
of c.p.c. approximations of a nuclear
$\mathrm {C}^*$
-algebra A and a decreasing sequence
$(\varepsilon _j)\in \ell ^1(\mathbb {N})^1_+$
, we can use compactness of the unit balls of the
$F_n$
to find an increasing sequence
$(n_j)_j \subset \mathbb {N}$
so that for all
$n_k\geq 0$
and
$j>k$
,
$$\begin{align*}\|\varphi_{n_k}-\varphi_{n_j} \circ \psi_{n_j} \circ \varphi_{n_k}\|<\varepsilon_{n_j}.\end{align*}$$
(iii) For a system of c.p.c. approximations of a
$\mathrm {C}^*$
-algebra A as in 3.1 and any
$a\in A$
, we have
To see this, it suffices to consider
$a\in A_+^1$
. Let
$\varepsilon>0$
, and choose
$\eta>0$
so that
$2\eta +\sqrt {3\eta }<\varepsilon $
and
$N>0$
so that
$\|a-\varphi _n(\psi _n(a))\|<\eta $
and
$\|a^2-\varphi _n(\psi _n(a^2))\|<\eta $
for all
$n>N$
. Then a consequence of Stinespring’s Theorem ([Reference Kirchberg and Winter15, Lemma 3.5]), guarantees that
$\|\varphi _n(\psi _n(a)b)-\varphi _n(\psi _n(a))\varphi _n(b)\|<\sqrt {3\eta }$
for any
$b\in (F_n)^1$
. Applying this to
$b=1_{F_n}$
yields
$$ \begin{align*} \|a-a\varphi_n(1_{F_n})\|&\leq 2\eta + \|\varphi_n(\psi_n(a))-\varphi_n(\psi_n(a))\varphi_n(1_{F_n})\|\\ &= 2\eta + \|\varphi_n(\psi_n(a)1_{F_n})-\varphi_n(\psi_n(a))\varphi_n(1_{F_n})\|\\ &<2\eta + \sqrt{3\eta}\\ &<\varepsilon. \end{align*} $$
One can always ask for approximately order zero downwards maps, as follows from [Reference Blackadar and Kirchberg4] in connection with [Reference Voiculescu23, Theorem 5]); see [Reference Brown, Carrión and White5, Theorem 3.1] for an explicit statement:
Theorem 3.3. For a separable
$\mathrm {C}^*$
-algebra A, the following are equivalent.
-
(i) A is nuclear.
-
(ii) A admits a system of c.p.c. approximations with approximately order zero downwards maps.
Lemma 3.4. Let 
be a system of c.p.c. approximations of a separable nuclear
$\mathrm {C}^*$
-algebra A. Then the induced map
$\Psi \colon A\longrightarrow F_\infty $
given for all
$a\in A$
by
is a complete order embedding.
If the system of approximations is summable, then we have 
, (i.e., the image of
$\Psi $
agrees with the limit of the associated system in the sense of Definitions 3.1
(v) and 2.1).
Proof. Since each
$\psi _n$
is c.p.c., it follows that
$\Psi $
is a c.p.c. map. Moreover, since the maps
$\psi _n,\varphi _n$
are all c.p.c., it follows that
for all
$r\geq 1$
and
$a\in \mathrm {M}_r(A)$
. Hence,
$\|\Psi ^{(r)}(a)\|\geq \|a\|$
for all
$r\geq 0$
and
$a\in \mathrm {M}_r(A)$
, and so
$\Psi $
is completely isometric and hence a complete order embedding.
Now we assume moreover that the system is summable with respect to some decreasing sequence
$(\varepsilon _n)_n\in \ell ^1(\mathbb {N})^1_+$
. Let
$k\geq 0$
and
$x\in F_k$
, and set 
. (Recall that the limit exists by Remark 3.2(i).) Then we have
$$ \begin{align} \rho_k(x)&=[(\rho_{m,k}(x))_{m>k}]\\ &=[(\psi_m(\varphi_{m-1}(\rho_{m-1,k}(x))))_{m>k}] \nonumber\\ &=[(\psi_m(a))_m] \nonumber\\ &=\Psi(a), \nonumber \end{align} $$
and so
On the other hand, it follows from summability that
$$ \begin{align*} \|\varphi_m\circ \rho_{m,n} \circ \psi_n-\varphi_n\circ\psi_n\|< \textstyle{\sum}_{j=n+1}^m\varepsilon_j \end{align*} $$
for all
$m>n\geq 0$
. Hence, for any given
$a\in A$
and
$\varepsilon>0$
, we can find
$M>0$
such that for all
$m>n>M$
,
$$ \begin{align} &\|\varphi_m \circ \rho_{m,n} \circ \psi_n(a)-a\|\\& \quad \leq \|\varphi_m \circ \rho_{m,n} \circ \psi_n(a)-\varphi_n\circ\psi_n(a)\|+\|\varphi_n\circ\psi_n(a)-a\|\nonumber \\& \quad <\varepsilon. \nonumber \end{align} $$
From this, we conclude that the set 
is dense in A, and so by (3.2),
$\textstyle {\bigcup _n} \rho _n(F_n)$
is dense in
$\Psi (A)$
. Since
$\Psi $
is isometric, that means 
.
In the situation of Lemma 3.4, if the system of c.p.c. approximations has approximately order zero downwards maps, then the map
$\Psi $
clearly is order zero. In this case, since the codomain is
$F_\infty $
, we obtain refined information about the positive contraction appearing in the structure theorem for order zero maps (Theorem 1.4).
Proposition 3.5. Let 
be a system of c.p.c. approximations of a separable nuclear
$\mathrm {C}^*$
-algebra A with approximately order zero downwards maps, and let
$\Psi \colon A\longrightarrow F_\infty $
be the order zero complete order embedding from Lemma 3.4. We write C for the
$\mathrm {C}^*$
-algebra generated by
$\Psi (A)$
in
$F_\infty $
and
$J_C=\{b\in F_\infty \mid b C\cup C b\subset C\}$
for the idealizer of C in
$F_\infty $
, and we denote by h the element in
$\mathcal {M}(C)$
provided by the structure theorem for order zero maps; cf. Theorem 1.4.
Then there exists
$\bar {h}\in (J_C)_+^1 \subset F_\infty $
so that
$\bar {h}c=hc$
for all
$c\in C$
. In particular, for all
$a,b\in A$
,
$$ \begin{align} \bar{h}\Psi(a)&=\Psi(a)\bar{h}, \end{align} $$
$$ \begin{align} \|\bar{h}\Psi(a)\|&=\|\Psi(a)\|=\|a\|,\ \text{ and } \end{align} $$
$$ \begin{align} \bar{h}\Psi(ab)&=\Psi(a)\Psi(b). \end{align} $$
Moreover, (3.4), (3.5) and (3.6) still holds when replacing
$\bar {h}$
by any
$\bar {e}\in (F_\infty )_+^1$
such that
$\bar {e} \Psi (a)=\bar {h}\Psi (a)$
for all
$a\in A$
.
Proof. Since C is an ideal in
$J_C$
, there is a unique
$^*$
-homorphism
$\theta \colon J_C\longrightarrow \mathcal {M}(C)$
extending the canonical embedding
$C \longrightarrow \mathcal {M}(C)$
so that
$\theta (b)c=bc$
and
$c\theta (b)=cb$
for all
$b\in J_C$
and
$c\in C$
. We claim that
$\theta $
is surjective. Indeed, let
$\pi \colon \prod F_n\longrightarrow F_\infty $
denote the quotient map. Since C is separable, we can find a separable sub-
$\mathrm {C}^*$
-algebra
$D\subset \prod F_n$
with
$\pi (D)=C$
. Though D may be degenerate in
$\prod F_n$
(in the sense that its support projection is not
$1_{\prod F_n}$
), it is nondegenerate in its ultra-weak closure
$\overline {D}^{\sigma \text {-wk}}\subset \prod F_n$
(in the same sense), and so [Reference Akemann, Pedersen and Tomiyama1, Proposition 2.4] tells us we can identify
$\mathcal {M}(D)$
with
$\{b\in \overline {D}^{\sigma \text {-wk}} \mid b D\cup D b\subset D\}\subset \prod F_n$
, and with this identification, we have
$\pi (\mathcal {M}(D))\subset J_C$
. Since D is separable and
$\pi |_D\colon D\longrightarrow C$
is a surjection, [Reference Akemann, Pedersen and Tomiyama1, Theorem 4.2] guarantees a surjective
$^*$
-homomorphism
$\hat {\pi }\colon \mathcal {M}(D)\longrightarrow \mathcal {M}(C)$
so that for all
$d\in D$
and
$x\in \mathcal {M}(D)$
, we have
$\hat {\pi }(x)\pi (d)=\pi (xd)$
and
$\pi (d)\hat {\pi }(x)=\pi (dx)$
. All this together gives us the following diagram, which we claim commutes:
To see that
$\hat {\pi }=\theta \circ \pi |_{\mathcal {M}(D)}$
, let
$x\in \mathcal {M}(D)$
and
$c\in C$
, and choose
$d\in D$
such that
$\pi (d)=c$
. Then
$$ \begin{align*} \theta(\pi(x))c=\pi(x)c=\pi(x)\pi(d)=\pi(xd)=\hat{\pi}(x)\pi(d)=\hat{\pi}(x)c, \end{align*} $$
and likewise,
$c\theta (\pi (c))=c\hat {\pi }(x)$
. Hence,
$\hat {\pi }=\theta \circ \pi |_{\mathcal {M}(D)}$
, and
$\theta $
is surjective, as desired.
Now let
$\bar {h}\in (J_C)_+^1$
be a lift of h. Then we have for each
$c\in C$
$$ \begin{align*} \bar{h}c=\theta(\bar{h})c=hc\hspace{.5 cm} \text{ and } \hspace{.5 cm} c\bar{h}=c\theta(\bar{h})=ch. \end{align*} $$
It then follows from our choice of h that for all
$a,b\in A$
,
$$ \begin{align*} \bar{h}\Psi(ab)&=h\Psi(ab)=\Psi(a)\Psi(b),\ \text{ and }\\ \bar{h}\Psi(a)&=h\Psi(a)=\Psi(a)h=\Psi(a)\bar{h}. \end{align*} $$
Since
$\Psi $
is isometric,
$\|a\|^2h=\|\Psi (aa^*)\|h\geq \Psi (aa^*)$
for all
$a\in A$
(see Remark 1.5(i)), and so
$$ \begin{align*} \|a\|^4&=\|\Psi(a)\|^4\\ &=\|\Psi(a)^*\Psi(a)\Psi(a)^*\Psi(a)\|\\ &\leq \|\Psi(a)^*\Psi(aa^*)\Psi(a)\|\\ &\leq \|\Psi(a)^*\|a\|^2h\Psi(a)\|\\ &\leq \|a\|^3\|h\Psi(a)\|. \end{align*} $$
In particular, for all
$a\in A$
,
$$ \begin{align*} \|\bar{h}\Psi(a)\|= \|h\Psi(a)\|=\|\Psi(a)\|=\|a\|. \end{align*} $$
Finally, suppose
$\bar {e}\in (F_\infty )_+^1$
and
$\bar {e} \Psi (a)=\bar {h}\Psi (a)=h\Psi (a)$
for all
$a\in A$
. Then for each
$a\in A$
,
$$\begin{align*}\|\bar{e} \Psi(a)-\Psi(a) \bar{e}\|=\|h\Psi(a)-\Psi(a) \bar{e}\|=\|h\Psi(a)^*-\bar{e} \Psi(a)^*\|=0,\end{align*}$$
and it follows that
$\Psi (a)\bar {e} = \Psi (a)\bar {h} = \Psi (a)h$
for all
$a\in A$
as well. Since this extends to all
$c\in C$
, it follows that
$\bar {e}\in (J_C)_+^1$
and
$\theta (\bar {e})=h$
. Since
$\bar {e}$
is also a lift of h, the preceding arguments establish (3.4), (3.5) and (3.6) for
$\bar {e}$
.
Now we are ready to prove the main result of this section.
Theorem 3.6. Let 
be a system of c.p.c. approximations of a separable nuclear
$\mathrm {C}^*$
-algebra A with approximately order zero downwards maps. After possibly passing to a subsystem of approximations, the associated system
$(F_n,\rho _{n+1,n})_n$
is a
${\mathrm {CPC}^*}$
-system in the sense of Definition 2.2, and the map
$\Psi \colon A\longrightarrow F_\infty $
from Lemma 3.4 is an order zero complete order embedding with 
.
Upon composing
$\Psi $
with the inverse of
$\Theta $
from Proposition 2.7, we obtain an isomorphism 
. In particular, any separable nuclear
$\mathrm {C}^*$
-algebra is
$^*$
-isomorphic to a
${\mathrm {CPC}^*}$
-limit.
Proof. As we saw in Remark 3.2(ii), after possibly passing to a subsystem, we may assume that the system of approximations (and any further subsystem) is summable.
Let
$\Psi \colon A\longrightarrow F_\infty $
be the induced order zero complete order embedding from Lemma 3.4, h be the element in
$\mathcal {M}(\mathrm {C}^*(\Psi (A)))$
from the structure theorem for order zero maps (Theorem 1.4), and
$\bar {h}\in (F_\infty )_+^1$
be an element guaranteed by Proposition 3.5 so that
$\bar {h}\Psi (a)=h\Psi (a)$
for all
$a\in A$
. We fix a lift
$(h_n)_n\in (\prod F_n)_+^1$
of
$\bar {h}$
and note that since
$$ \begin{align*}\|\Psi(b)\Psi(a)-\bar{h}\Psi(a)\|&\overset{({3.6})}{=}\|\bar{h}\Psi(ba)-\bar{h}\Psi(a)\|\\ &\overset{\phantom{(3.5)}}{=}\|\bar{h}\Psi(ba-a)\|\\ &\overset{({3.5})}{=} \|ba-a\|\end{align*} $$
for all
$a,b\in A$
, we have that for any
$a,b\in A$
and
$\varepsilon>0$
, there exists
$M>0$
so that for all
$m\geq M$
,
$$ \begin{align} \|\psi_m(b)\psi_m(a)-h_m\psi_m(a)\|< \|ba-a\|+ \varepsilon. \end{align} $$
Now we are ready to determine an appropriate subsystem of approximations. Fix a countable dense subset
$\{a_k\}_k\subset A^1$
and a strictly decreasing sequence
$(\varepsilon _n)_n\in \ell ^1(\mathbb {N})_+^1$
. By Remark 3.2(iii), we may choose
$j_0>0$
so that
$$ \begin{align*} \|\varphi_{j_0}(1_{F_{j_0}})a_0-a_0\|<\varepsilon_0/2.\end{align*} $$
Then we can choose
$j_1>j_0$
so that for all
$m\geq j_1$
and
$i\in \{1,2\}$
,
$$ \begin{align*} \|\psi_m(\varphi_{j_0}(1_{F_{j_0}}))\psi_m(a_0)-h_m\psi_m(a_0)\|&\overset{({3.7})}{<}\|\varphi_{j_0}(1_{F_{j_0}})a_0-a_0\|+ \varepsilon_0/2 \\ &\overset{\phantom{(3.7)}}{<}\varepsilon_0,\\ \max_{0\leq k\leq 1}\|\varphi_{j_1}(1_{F_{j_1}})a_k-a_k\|&\overset{\phantom{(3.7)}}{<}\varepsilon_1/2, \text{ and}\\ \|\varphi_{j_1}(\psi_{j_1}(\varphi_{j_0}(1_{F_{j_0}})^i))-\varphi_{j_0}(1_{F_{j_0}})^i\|&\overset{\phantom{(3.7)}}{<}\varepsilon_1^2/3. \end{align*} $$
For all
$n>0$
, we may inductively choose
$j_n>j_{n-1}$
so that for all
$m\geq j_n$
and
$i\in \{1,2\}$
,
$$ \begin{align} \max_{0\leq k <n} \|\psi_m(\varphi_{j_{n-1}}(1_{F_{j_{n-1}}}))\psi_m(a_k)-h_m\psi_m(a_k)\|&<\varepsilon_{n-1}, \end{align} $$
$$ \begin{align} \max_{0\leq k\leq n} \|\varphi_{j_n}(1_{F_{j_n}})a_k-a_k\|&<\varepsilon_n/2, \text{ and} \end{align} $$
$$ \begin{align} \|\varphi_{j_n}(\psi_{j_n}(\varphi_{j_{n-1}}(1_{F_{j_{n-1}}})^i))-\varphi_{j_{n-1}}(1_{F_{j_{n-1}}})^i\|&<\varepsilon_n^2/3. \end{align} $$
Let
$\hat {\Psi }\colon A\longrightarrow \prod F_{j_n}/\textstyle {\bigoplus } F_{j_n}$
denote the map induced by the subsystem 
. Then
$\hat {\Psi }$
is still an order zero complete order embedding, and for
$\hat {\bar {h}}=[(h_{j_n})_n]\in \prod F_{j_n}/\textstyle {\bigoplus } F_{j_n}$
, we still have
$\hat {\bar {h}}\hat {\Psi }(a)=\hat {h}\hat {\Psi }(a)$
for all
$a\in A$
, where
$\hat {h}\in \mathcal {M}(\mathrm {C}^*(\hat {\Psi (A)}))$
is the element guaranteed by Theorem 1.4. Thus, we may pass to the (summable) subsystem 
, drop the subscripts and write
$\Psi $
, h and
$\bar {h}$
for
$\hat {\Psi }$
,
$\hat {h}$
and
$\hat {\bar {h}}$
, respectively. Now (3.8)–(3.10) say that for any
$n>0$
, we have for for
$m> n$
and
$i\in \{1,2\}$
$$ \begin{align} \max_{0\leq k \leq n} \|\psi_m(\varphi_{n}(1_{F_{n}}))\psi_m(a_k)-h_m\psi_m(a_k)\|&<\varepsilon_{n}, \end{align} $$
$$ \begin{align} \max_{0\leq k\leq n}\|\varphi_{n}(1_{F_{n}})a_k-a_k\|&<\varepsilon_n/2, \text{ and} \end{align} $$
$$ \begin{align} \|\varphi_n(\psi_n(\varphi_{n-1}(1_{F_{n-1}})^i))-\varphi_{n-1}(1_{F_{n-1}})^i\|&<\varepsilon_n^2/3. \end{align} $$
We aim to show that the associated system
$(F_n,\rho _{n+1,n})_n$
as in Definition 3.1(v) is
${\mathrm {CPC}^*}$
.
Claim 1. For all
$a\in A$
, we have
$[(\rho _{n+1,n}(1_{F_n}))_n] \Psi (a)=\bar {h}\Psi (a)$
, and (3.4), (3.5) and (3.6) also hold for
$[(\rho _{n+1,n}(1_{F_n}))_n]$
in place of
$\bar {h}$
.
We check the claim on an element
$a_k$
from our fixed dense subset of
$A^1$
. Since
$$ \begin{align} &\|\rho_{n,n-1}(1_{F_{n-1}}) \psi_n(a_k)-h_n\psi_n(a_k)\| \\ &\overset{\phantom{(3.11)}}{=}\|\psi_n(\varphi_{n-1}(1_{F_{n-1}})) \psi_n(a_k)-h_n\psi_n(a_k)\| \nonumber\\ &\overset{({3.11})}{<}\varepsilon_{n-1}\nonumber \end{align} $$
for all
$n>k$
, it follows that
$[(\rho _{n+1,n}(1_{F_n}))_n]\Psi (a)=\bar {h}\Psi (a)$
for all
$a\in A$
, which establishes the claim by Proposition 3.5 with
$\bar {e}=[(\rho _{n+1,n}(1_{F_n}))_n]$
.
Claim 2. For any
$a\in A$
and
$\varepsilon>0$
, there exists an
$M>0$
so that for
$m>n>M$
,
$$ \begin{align*} \|\rho_{m,n}(1_{F_n})\psi_m(a)-\rho_{m,m-1}(1_{F_{m-1}})\psi_m(a)\|<\varepsilon.\end{align*} $$
Again, we check the claim on some
$a_k$
from our fixed dense subset of
$A^1$
. Fix
$\varepsilon>0$
. It follows from summability (see Remark 3.2(i)) that we may choose
$M>k$
with
$\varepsilon _M<\varepsilon /3$
so that
$\|\rho _{m,n}-\psi _m\circ \varphi _n\|<\varepsilon /3$
for all
$m>n>M$
. Then it follows from (3.11) and (3.14) that for all
$m>n>M$
,
$$ \begin{align*} &\|\rho_{m,n}(1_{F_n})\psi_m(a_k)-\rho_{m,m-1}(1_{F_{m-1}})\psi_m(a_k)\|\\& \quad < \|\psi_m(\varphi_{n}(1_{F_{n}}))\psi_m(a_k)-\rho_{m,m-1}(1_{F_{m-1}})\psi_m(a_k)\| + \varepsilon/3\\& \quad \leq \|\psi_m(\varphi_{n}(1_{F_{n}}))\psi_m(a_k)-h_m\psi_m(a_k)\| \\& \qquad + \|h_m\psi_m(a_k)-\rho_{m,m-1}(1_{F_{m-1}})\psi_m(a_k)\| +\varepsilon/3 \\& \quad < \varepsilon_{n}+\varepsilon_{m-1}+\varepsilon/3\\& \quad <\varepsilon. \end{align*} $$
Claim 3. For any
$a,b\in A$
and
$\varepsilon>0$
, there exists an
$M>0$
so that
$m> n>M$
$$ \begin{align*} \|\psi_m(a)\psi_m(b)-\rho_{m,n}(1_{F_n})\psi_m(ab)\|&<\varepsilon. \end{align*} $$
Let
$a,b\in A^1$
and
$\varepsilon>0$
. Claim 1 tells us that
$[(\rho _{n+1,n}(1_{F_n}))_n] \Psi (ab)=\Psi (a)\Psi (b)$
, and so there is an
$M_0>0$
so that for all
$m>M_0$
,
$$ \begin{align*} \|\psi_m(a)\psi_m(b)-\rho_{m,m-1}(1_{F_{m-1}})\psi_m(ab)\| <\varepsilon/2. \end{align*} $$
Then this with Claim 2 (for
$ab$
in place of
$a\in A$
and
$\varepsilon /2$
in place of
$\varepsilon $
) tells us that there exists
$M>M_0$
so that for all
$m> n>M$
,
$$ \begin{align*} &\|\psi_m(a)\psi_m(b)-\rho_{m,n}(1_{F_n})\psi_m(ab)\| \\ & \quad <\|\rho_{m,m-1}(1_{F_{m-1}})\psi_m(ab)-\rho_{m,n}(1_{F_n})\psi_m(ab)\| + \varepsilon/2\\ & \quad <\varepsilon. \end{align*} $$
Claim 4. For any
$a\in A$
and
$\varepsilon>0$
, there exists an
$M>0$
so that for all
$m>n>M$
,
$$ \begin{align*} \|\rho_{m,n}\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(a)\big)-\psi_m(a)\|&<\varepsilon. \end{align*} $$
Again, we check the claim on some
$a_k$
from our fixed dense subset of
$A^1$
. Fix
$1>\varepsilon >0$
. By (3.13) and [Reference Kirchberg and Rørdam14, Lemma 7.11], for each
$n>0$
,
$$ \begin{align*} &\|\varphi_n\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(a_k)\big)-\varphi_n(\rho_{n,n-1}(1_{F_{n-1}}))\ \varphi_n(\psi_n(a_k))\|\\& \quad <\big(3\varepsilon_n^2/3\big)^{1/2}\\& \quad =\varepsilon_n. \end{align*} $$
We now can choose
$M>k$
with
$\varepsilon _M<\varepsilon /6$
so that for all
$m>n>M$
,
$$ \begin{align} &\|\varphi_n\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(a_k)\big)-\varphi_n(\rho_{n,n-1}(1_{F_{n-1}}))\ \varphi_n(\psi_n(a_k))\|\\& \quad <\varepsilon_n \nonumber\\& \quad <\varepsilon/6,\nonumber \end{align} $$
$$ \begin{align} \|\varphi_n(\psi_n(a_k))-a_k\|&<\varepsilon/6, \end{align} $$
and
$$ \begin{align} \|\rho_{m,n}(\psi_n(a_k))-\psi_m(a_k)\|&\leq \|\varphi_{m-1}\circ\rho_{m-1,n}(\psi_n(a_k))-a_k\| \\ &<\varepsilon/2. \nonumber \end{align} $$
Then we have for all
$m>n>M$
,
$$ \begin{align*} & \|\rho_{m,n}\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(a_k)\big)-\psi_m(a_k)\|\\&\overset{\phantom{(3.13)}}{\leq} \|\rho_{m,n}\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(a_k)\big)-\rho_{m,n+1}(\psi_{n+1}(a_k))\|\\&\phantom{{}\overset{(3.13)}{\leq}{}}+\|\rho_{m,n+1}(\psi_{n+1}(a_k))-\psi_m(a_k)\| \\&\overset{({3.17})}{<} \varepsilon/2 + \|\rho_{m,n}\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(a_k)\big)-\rho_{m,n+1}(\psi_{n+1}(a_k))\|\\&\overset{\phantom{(3.13)}}{=} \varepsilon/2 + \|\rho_{m,n+1}\circ\psi_{n+1}\big(\varphi_n\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(a_k)\big)-a_k\big)\|\\&\overset{\phantom{(3.13)}}{\leq} \varepsilon/2 + \|\varphi_n\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(a_k)\big)-a_k\|\\&\overset{({3.15})}{<} \varepsilon/2 +\varepsilon/6 + \|\varphi_n(\rho_{n,n-1}(1_{F_{n-1}}))\ \varphi_n(\psi_n(a_k))-a_k\|\\&\overset{({3.16})}{<} 2\varepsilon/3 + \varepsilon/6 + \|\varphi_n(\rho_{n,n-1}(1_{F_{n-1}}))a_k-a_k\|\\&\overset{\phantom{(3.13)}}{\leq} 5\varepsilon/6+ \|\varphi_n(\rho_{n,n-1}(1_{F_{n-1}}))a_k-\varphi_{n-1}(1_{F_{n-1}})a_k\|\\&\phantom{{}\overset{(3.13)}{\leq}{}}+ \|\varphi_{n-1}(1_{F_{n-1}})a_k-a_k\|\\&\overset{({3.13})}{<} 5\varepsilon/6+ \varepsilon_n^2/3+\|\varphi_{n-1}(1_{F_{n-1}})a_k-a_k\|\\&\overset{({3.12})}{<} 5\varepsilon/6+ \varepsilon_n^2/3+\varepsilon_{n-1}/2\\[-3pt]&\overset{\phantom{(3.13)}}{<}\varepsilon. \end{align*} $$
This finishes the proof of the claim.
Now we are ready to verify that
$(F_n,\rho _{n+1,n})_n$
is a
${\mathrm {CPC}^*}$
-system. Let
$k\geq 0$
,
$x,y\in F^1_k$
, and
$\varepsilon>0$
. Define 
and 
. (Recall that these limits exist by Remark 3.2(i).) We then in particular have
Combining this with Claims 3 and 4, we can choose
$M>0$
so that for all
$m>n\geq M$
,
$$ \begin{align*} \|\rho_{m,k}(x)\rho_{m,k}(y)-\rho_{m,n}(1_{F_n})\psi_m(ab)\|&<\varepsilon/4\ \text{ and} \\ \|\rho_{m,n}\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(ab)\big)-\psi_m(ab)\|&<\varepsilon/2. \end{align*} $$
Using these two approximations, we compute for
$m>n,l>M$
,
$$ \begin{align*} &\|\rho_{m,l}(1_{F_l})\rho_{m,n}\big(\rho_{n,k}(x)\rho_{n,k}(y)\big)-\rho_{m,k}(x)\rho_{m,k}(y)\|\\& \quad \leq \|\rho_{m,l}(1_{F_l})\ \rho_{m,n}\big(\rho_{n,k}(x)\rho_{n,k}(y)-\rho_{n,n-1}(1_{F_{n-1}})\psi_n(ab)\big)\| \\& \qquad + \|\rho_{m,l}(1_{F_l})\ \rho_{m,n}\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(ab)\big)-\rho_{m,l}(1_{F_l})\ \psi_m(ab)\| \\& \qquad +\|\rho_{m,l}(1_{F_l})\psi_m(ab)-\rho_{m,k}(x)\rho_{m,k}(y)\| \\& \quad \leq \|\rho_{n,k}(x)\rho_{n,k}(y)-\rho_{n,n-1}(1_{F_{n-1}})\psi_n(ab)\| \\& \qquad + \|\rho_{m,n}\big(\rho_{n,n-1}(1_{F_{n-1}})\psi_n(ab)\big)-\psi_m(ab)\| \\& \qquad +\|\rho_{m,l}(1_{F_l})\psi_m(ab)-\rho_{m,k}(x)\rho_{m,k}(y)\| \\& \quad < \varepsilon. \end{align*} $$
Finally, since our subsystem is still summable, 
by Lemma 3.4, so by Corollary 2.8, A is
$^*$
-isomorphic to a
${\mathrm {CPC}^*}$
-limit.
Remark 3.7. If A is a separable unital nuclear
$\mathrm {C}^*$
-algebra with a summable system 
of c.p.c. approximations with approximately order zero downwards maps, then
$(\varphi _n(1_{F_n}))_n$
converges to
$1_A$
, and hence, 
. In this case, the associated system
$(F_n,\rho _{n+1,n})_n$
will automatically be a
${\mathrm {CPC}^*}$
-system even without passing to a subsystem.
We close this section with a description of the product of a nuclear
$\mathrm {C}^*$
-algebra in terms of an associated
${\mathrm {CPC}^*}$
-system, interpreting Corollary 2.8 along the lines of Proposition 2.6.
Corollary 3.8. Let 
be a summable system of c.p.c. approximations of a separable nuclear
$\mathrm {C}^*$
-algebra A with approximately order zero downwards maps so that the associated system
$(F_n,\rho _{n+1,n})_n$
is a
${\mathrm {CPC}^*}$
-system. Let
$\Psi \colon A\longrightarrow F_\infty $
be the induced order zero complete order embedding. Then for any
$k\geq 0$
,
$x,y\in F_k$
, and 
, 
, we have 
.
4 NF systems and
${\mathrm {CPC}^*}$
-systems
We conclude by comparing our
${\mathrm {CPC}^*}$
-systems with Blackadar and Kirchberg’s NF systems from [Reference Blackadar and Kirchberg4] and establish that the latter may indeed be regarded as a special case of the former.
Definition 4.1 [Reference Blackadar and Kirchberg4, Definitions 2.1.1 and 5.2.1].
A system
$(F_n,\rho _{n+1,n})_n$
consisting of finite dimensional
$\mathrm {C}^*$
-algebras and c.p.c. maps as in Definition 2.1 is called an NF system if the maps
$\rho _{m,n}$
are asymptotically multiplicative, in the sense that for all
$k\geq 0$
,
$x,y\in F_k$
, and
$\varepsilon>0$
, there exists
$M>k$
so that for all
$m>n>M$
,
$$\begin{align*}\|\rho_{m,n}(\rho_{n,k}(x)\rho_{n,k}(y))-\rho_{m,k}(x)\rho_{m,k}(y)\|<\varepsilon.\end{align*}$$
The limit of this system (in the sense of Definition 2.1) is a
$\mathrm {C}^*$
-algebra with multiplication given for all
$k\geq 0$
and
$x,y\in F_k$
by
A
$\mathrm {C}^*$
-algebra that is
$^*$
-isomorphic to the inductive limit of an NF system is called an NF algebra.
Remark 4.2. A unital
${\mathrm {CPC}^*}$
-system is NF, and if
$(F_n,\rho _{n+1,n})_n$
is an NF system such that for any
$\varepsilon>0$
there exists
$M>0$
so that for all
$m>n>M$
,
$$ \begin{align*} \|\rho_{m,n}(1_{F_n})-1_{F_m}\|<\varepsilon, \end{align*} $$
then it is also a
${\mathrm {CPC}^*}$
-system. With Theorem 4.4 below, one can drop this condition upon passing to a subsystem.
The following excerpt from [Reference Blackadar and Kirchberg4, Theorem 5.2.2] characterizes nuclear and quasidiagonal
$\mathrm {C}^*$
-algebras in terms of NF systems. In comparison with Theorem 3.6, here one asks for approximately multiplicative downwards maps as opposed to just approximately order zero ones; this corresponds to adding quasidiagonality to the nuclearity hypothesis.
Theorem 4.3. For a separable
$\mathrm {C}^*$
-algebra A, the following are equivalent:
-
(i) A is an NF algebra.
-
(ii) A is nuclear and quasidiagonal.
-
(iii) There exists a system
of c.p.c. approximations with approximately multiplicative downwards maps.
of c.p.c. approximations with approximately multiplicative downwards maps.Theorem 4.4. Any NF system admits a
${\mathrm {CPC}^*}$
-subsystem.
Proof. Let
$(F_n,\rho _{n+1,n})_n$
be an NF system. From this, we form another NF system
$(B_n,\varphi _{n+1,n})$
(with a different limit) just as in [Reference Blackadar and Kirchberg4, Proposition 5.1.3] by taking
$B_n=\bigoplus _{j=0}^n F_j$
and 
:
Then for each
$k\geq 0$
,
$\hat {x}=(x_0,...,x_k)\in B_k$
, and
$n>k$
, we have
$$\begin{align*}\varphi_{n,k}(\hat{x})= \hat{x} \oplus \oplus_{j=k+1}^n \rho_{j,k}(x_k).\end{align*}$$
We claim we can find a subsystem
$(B_{n_j},\varphi _{n_j+1,n_j})_j$
which is
${\mathrm {CPC}^*}$
. Set 
. Then each
$\varphi _{n+1,n}$
is a complete order embedding, and hence, so are the induced c.p.c. maps
$\varphi _n\colon B_n\longrightarrow B\subset B_\infty $
. Using Arveson’s Extension Theorem (cf. [Reference Blackadar and Kirchberg4, Lemma 5.1.2]), we extend each c.p.c. contraction
$\varphi _n^{-1}\colon \varphi _n(B_n)\longrightarrow B_n$
to a c.p.c. map
$\psi _n\colon B\longrightarrow B_n$
with
$\psi _n\circ \varphi _n=\mathrm {id}_{B_n}$
. Since the union
$\bigcup _n \varphi _n(B_n)$
is nested,
$(\varphi _m\circ \psi _m)|_{\varphi _n(B_n)}=\mathrm {id}_{\varphi _n(B_n)}$
for all
$m>n\geq 0$
, and so 
is a system of c.p.c. approximations of B. Note that the associated system
$(B_n,\psi _{n+1}\circ \varphi _n)_n$
is exactly
$(B_n,\varphi _{n+1,n})_n$
: Indeed, for any
$n\geq 0$
and
$x\in B_n$
, we have for all
$m>n$
,
Moreover, the downwards maps of our system 
of c.p.c. approximations are approximately multiplicative. To see this, it suffices to consider
$\varphi _k(x),\varphi _k(y)$
for some
$k\geq 0$
and
$x,y\in B_k$
. Fix
$\varepsilon>0$
. Since
$\bigcup _n \varphi _n(B_n)$
is dense in B, we may choose
$N>k$
and
$z\in B_N$
so that
$\|\varphi _N(z)-\varphi _k(x)\varphi _k(y)\|<\varepsilon /3$
. Since the system is NF, we have
and so we may choose
$M>N$
so that
$$\begin{align*}\|\varphi_k(x)\varphi_k(y)-\varphi_m\big(\psi_m(\varphi_k(x))\psi_m(\varphi_k(y))\big)\|<\varepsilon/3\end{align*}$$
for all
$m>M$
. Since each
$\varphi _n$
is isometric, we have for all
$m>M>N$
,
$$ \begin{align*} &\|\psi_m(\varphi_k(x)\varphi_k(y))-\psi_m(\varphi_k(x))\psi_m(\varphi_k(y))\|\\& \quad < \|\psi_m(\varphi_N(z))-\psi_m(\varphi_k(x))\psi_m(\varphi_k(y))\| + \varepsilon/3 \\& \quad =\|\varphi_m\big(\psi_m(\varphi_N(z))\big)-\varphi_m\big(\psi_m(\varphi_k(x))\psi_m(\varphi_k(y)))\big)\| + \varepsilon/3 \\& \quad =\|\varphi_N(z)-\varphi_m\big(\psi_m(\varphi_k(x))\psi_m(\varphi_k(y))\big)\| + \varepsilon/3 \\& \quad <\varepsilon. \end{align*} $$
Since the downwards maps are approximately multiplicative, they are also approximately order zero, and so Theorem 3.6 guarantees that the associated system
$(B_n,\psi _{n+1}\circ \varphi _n)_n=(B_n,\varphi _{n+1,n})_n$
, has a
${\mathrm {CPC}^*}$
-subsystem
$(B_{n_j},\varphi _{n_{j+1},n_j})_j$
.
We claim that the system
$(F_{n_j},\rho _{n_{j+1},n_j})_j$
is also
${\mathrm {CPC}^*}$
. Since this will hold without passing to a further subsystem, at this point, we may drop the subscripts for ease of notation. Fix
$k\geq 0$
,
$x,y\in F_k$
, and
$\varepsilon>0$
. Let
$\hat {x}=(0,...,0,x), \hat {y}=(0,...,0,y)\in B_k$
, and choose
$M>k$
so that for all
$m>n,l>M$
, we have
$$ \begin{align} \|\varphi_{m,l}(1_{B_l})\varphi_{m,n}\big(\varphi_{n,k}(\hat{x})\varphi_{n,k}(\hat{y})\big)-\varphi_{m,k}(\hat{x})\varphi_{m,k}(\hat{y})\|&<\varepsilon. \end{align} $$
Expanding these terms, we get
$$ \begin{align*} \varphi_{m,k}(\hat{x})\varphi_{m,k}(\hat{y})&=\big(\hat{x} \oplus \big(\oplus_{j=k+1}^m \rho_{j,k}(x)\big)\big)\big(\hat{y} \oplus \big(\oplus_{j=k+1}^m \rho_{j,k}(y)\big)\big)\\ &=\hat{x}\hat{y} \oplus \big(\oplus_{j=k+1}^m \rho_{j,k}(x)\rho_{j,k}(y)\big),\\ \varphi_{m,l}(1_{B_l})&=1_{B_l}\oplus \big(\oplus_{j=l+1}^m \rho_{j,l}(1_{F_l})\big), \end{align*} $$
and
$$ \begin{align*} &\varphi_{m,n}(\varphi_{n,k}(\hat{x})\varphi_{n,k}(\hat{y}))\\& \quad = \varphi_{m,n}\big(\hat{x}\hat{y} \oplus \big(\oplus_{j=k+1}^n \rho_{j,k}(x)\rho_{j,k}(y)\big)\big)\\& \quad =\hat{x}\hat{y} \oplus \big(\oplus_{j=k+1}^n \rho_{j,k}(x)\rho_{j,k}(y)\big) \oplus \big(\oplus_{j=n+1}^m \rho_{j,k}\big(\rho_{n,k}(x)\rho_{n,k}(y)\big)\big). \end{align*} $$
By considering only the
$m^{\text {th}}$
entries of these, it follows from (4.2) that
$$ \begin{align*} \|\rho_{m,n}(1_{F_n})\rho_{m,n}\big(\rho_{n,k}(x)\rho_{n,k}(y)\big)-\rho_{m,k}(x)\rho_{m,k}(y)\|<\varepsilon, \end{align*} $$
which shows that
$(F_n,\rho _{n+1,n})_n$
is a
${\mathrm {CPC}^*}$
-system.
Acknowledgements
We are grateful to Jamie Gabe for helpful comments on a draft of this paper and to the referee for their careful reading and helpful comments.
Competing interest
The authors have no competing interest to declare.
Funding statement
This research was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2044 – 390685587, Mathematics Münster – Dynamics – Geometry – Structure, the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 427320536 – SFB 1442, and ERC Advanced Grant 834267 – AMAREC
as a subspace of 
. For the sake of clarity, multiplication in 
will always be denoted with the 
(e.g., 
). So, for 
, we are taking the 
.
Open access
