Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T11:05:38.807Z Has data issue: false hasContentIssue false
  • English
  • Français

NONCROSSING SETS AND A GRASSMANN ASSOCIAHEDRON

Part of: Polytopes and polyhedra Ordered sets

Published online by Cambridge University Press:  20 February 2017

FRANCISCO SANTOS ,
CHRISTIAN STUMP  and
VOLKMAR WELKER
FRANCISCO SANTOS
Affiliation:
Departamento de Matemáticas, Estadística y Computación Universidad de Cantabria, Santander, Spain; [email protected]
CHRISTIAN STUMP
Affiliation:
Institut für Mathematik, Freie Universität Berlin, Germany; [email protected]
VOLKMAR WELKER
Affiliation:
Fachbereich Mathematik und Informatik, Philipps-Universität Marburg, Germany; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a natural generalization of the noncrossing relation between pairs of elements in 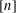$[n]$ to 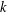$k$-tuples in 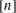$[n]$ that was first considered by Petersen et al. [J. Algebra324(5) (2010), 951–969]. We give an alternative approach to their result that the flag simplicial complex on 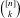$\binom{[n]}{k}$ induced by this relation is a regular, unimodular and flag triangulation of the order polytope of the poset given by the product 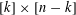$[k]\times [n-k]$ of two chains (also called Gelfand–Tsetlin polytope), and that it is the join of a simplex and a sphere (that is, it is a Gorenstein triangulation). We then observe that this already implies the existence of a flag simplicial polytope generalizing the dual associahedron, whose Stanley–Reisner ideal is an initial ideal of the Grassmann–Plücker ideal, while previous constructions of such a polytope did not guarantee flagness nor reduced to the dual associahedron for 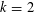$k=2$. On our way we provide general results about order polytopes and their triangulations. We call the simplicial complex the noncrossing complex, and the polytope derived from it the dual Grassmann associahedron. We extend results of Petersen et al. [J. Algebra324(5) (2010), 951–969] showing that the noncrossing complex and the Grassmann associahedron naturally reflect the relations between Grassmannians with different parameters, in particular the isomorphism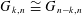$G_{k,n}\cong G_{n-k,n}$. Moreover, our approach allows us to show that the adjacency graph of the noncrossing complex admits a natural acyclic orientation that allows us to define a Grassmann–Tamari order on maximal noncrossing families. Finally, we look at the precise relation of the noncrossing complex and the weak separability complex of Leclerc and Zelevinsky [Amer. Math. Soc. Transl.181(2) (1998), 85–108]; see also Scott [J. Algebra290(1) (2005), 204–220] among others. We show that the weak separability complex is not only a subcomplex of the noncrossing complex as noted by Petersen et al. [J. Algebra324(5) (2010), 951–969] but actually its cyclically invariant part.

MSC classification

Primary: 52B20: Lattice polytopes (including relations with commutative algebra and algebraic geometry)
Secondary: 06A11: Algebraic aspects of posets
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e5
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Athanasiadis, C. A., ‘On noncrossing and nonnesting partitions for classical reflection groups’, Electron. J. Combin. 5 (1998), R42, 1–16.Google Scholar
Athanasiadis, C. A., ‘Ehrhart polynomials, simplicial polytopes, magic square and a conjecture of Stanley’, J. Reine Angew. Math. 583 (2005), 163–174.Google Scholar
Birkhoff, G., ‘Rings of sets’, Duke Math. J. 3(3) (1937), 443–454.Google Scholar
Brändén, P., ‘Sign-graded posets, unimodality of w-polynomials and the charney-davis conjecture’, Electron. J. Combin. 11(2) (2004), Research paper 9, 15 p.Google Scholar
Bruns, W. and Römer, T., ‘ h-vectors of Gorenstein polytopes’, J. Combin. Theory Ser. A 114 (2007), 65–76.Google Scholar
Conca, A., Hosten, S. and Thomas, R. R., ‘Nice initial complexes of some classical ideals’, inAlgebraic and Geometric Combinatorics, Contemporary Mathematics, 423 (American Mathematical Society, Providence, RI, 2006), 11–42.Google Scholar
De Loera, J., Rambau, J. and Santos, F., Triangulations, Algorithms and Computation in Mathematics, 25 (Springer, Berlin, 2010).CrossRefGoogle Scholar
Danilov, V. I., Karzanov, A. V. and Koshevoy, G. A., ‘Separated set-systems and their geometric models’, Russian Math. Surveys 65(4) (2010), 659–740.CrossRefGoogle Scholar
Gonciulea, N. and Lakshmibai, V., ‘Degenerations of flag and schubert varieties to toric varieties’, Transform. Groups 1 (1996), 215–248.Google Scholar
Górska, K. and Penson, K. A., ‘Multidimensional Catalan and related numbers as Hausdorff moments’, Probab. Math. Stat. 33(2) (2013), 265–274.Google Scholar
Hess, D. and Hirsch, B., ‘On the topology of weakly and strongly separated set complexes’, preliminary version available at http://www.math.umn.edu/∼reiner/REU/HessHirsch2011.pdf, (2011).Google Scholar
Hess, D. and Hirsch, B., ‘On the topology of weakly and strongly separated set complexes’, Topology Appl. 160(2) (2013), 328–336.CrossRefGoogle Scholar
Hibi, T., ‘Distributive lattices, affine semigroup rings and algebras with straightening laws’, inCommutative Algebra and Combinatorics (Kyoto, 1985), Advanced Studies in Pure Mathematics, 11 (North-Holland, Amsterdam, 1987), 93–109.CrossRefGoogle Scholar
Lakshmibai, V. and Raghavan, K. N., Standard Monomial Theory, Encyclopedia of Mathematical Science, 137 (Springer, Berlin, 2008).Google Scholar
Lam, T. and Postnikov, A., ‘Alcoved polytopes I’, Discrete Comput. Geom. 38 (2007), 453–478.CrossRefGoogle Scholar
Leclerc, B. and Zelevinsky, A., ‘Quasi-commuting families of quantum Plücker coordinates’, Amer. Math. Soc. Transl. 181(2) (1998), 85–108.Google Scholar
McConville, T., ‘Lattice structure of Grid-Tamari orders’, J. Combin. Theory Ser. A 148 (2017), 27–56.Google Scholar
Oh, S., Postnikov, A. and Speyer, D. E., ‘Weak separation and plabic graphs’, Proc. Lond. Math. Soc. (3) 110 (2015), 721–754.Google Scholar
Petersen, T. K., Pylyavskyy, P. and Speyer, D. E., ‘A non-crossing standard monomial theory’, J. Algebra 324(5) (2010), 951–969.Google Scholar
Pournin, L., ‘The diameter of associahedra’, Adv. Math. 259 (2014), 13–42.Google Scholar
Pylyavskyy, P., ‘Non-crossing tableaux’, Ann. Comb. 13(3) (2009), 323–339.CrossRefGoogle Scholar
Reading, N., ‘From the Tamari lattice to Cambrian lattices and beyond’, inAssociahedra, Tamari Lattices, and Related Structures, Tamari Memorial Festschrift, Progress in Mathematics, 299 (Birkhäuser, Basel, 2012), 293–322.CrossRefGoogle Scholar
Reiner, V. and Welker, V., ‘On the Charney–Davis and Neggers–Stanley conjectures’, J. Combin. Theory Ser. A 109(2) (2005), 247–280.Google Scholar
Rubey, M. and Stump, C., ‘Crossings and nestings in set partitions of classical types’, Electron. J. Combin. 17 (2010), R120, 1–19.CrossRefGoogle Scholar
Scott, J. S., ‘Quasi-commuting families of quantum minors’, J. Algebra 290(1) (2005), 204–220.Google Scholar
Scott, J. S., ‘Grassmannians and cluster algebras’, Proc. Lond. Math. Soc. 92(2) (2006), 345–380.Google Scholar
Sleator, D. D., Tarjan, R. E. and Thurston, W. P., ‘Rotation distance, triangulations and hyperbolic geometry’, J. Amer. Math. Soc. 1 (1988), 647–681.Google Scholar
Sloane, N. J. A., OEIS Foundation Inc., ‘The on-line encyclopedia of integer sequences’, (2017), http://oeis.org.Google Scholar
Stanley, R. P., ‘Eulerian partitions of a unit hypercube’, inHigher Combinatorics (ed. Aigner, M.) Proceedings of the NATO Advanced Study Institute (Reidel, Dordrecht/Boston, 1977), 51–62.Google Scholar
Stanley, R. P., ‘Two poset polytopes’, Discrete Comput. Geom. 1 (1986), 9–23.Google Scholar
Sturmfels, B., Gröbner Bases and Convex Polytopes, University Lecture Series, 8 (American Mathematical Society, Providence, RI, 1996).Google Scholar
Sulanke, R. A., ‘Generalizing Narayana and Schröder numbers to higher dimensions’, Electron. J. Combin. 11 (2004), R54.Google Scholar
Ziegler, G. M., Lectures on Polytopes (Springer, New York, 1994).Google Scholar