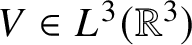1 Introduction and main result
We consider N bosons in a finite box
 $\Lambda _L=[-\tfrac L 2, \tfrac L 2]^3 \subset \mathbb {R}^3$
, interacting via a two-body nonnegative, radial, compactly supported potential V with scattering length
$\Lambda _L=[-\tfrac L 2, \tfrac L 2]^3 \subset \mathbb {R}^3$
, interacting via a two-body nonnegative, radial, compactly supported potential V with scattering length
![]() $\mathfrak {a}$
. The Hamilton operator has the form
$\mathfrak {a}$
. The Hamilton operator has the form
 $$ \begin{align} H_L = -\sum_{i=1}^N \Delta_i+\sum_{1 \leq i<j \leq N}V(x_i-x_j) \end{align} $$
$$ \begin{align} H_L = -\sum_{i=1}^N \Delta_i+\sum_{1 \leq i<j \leq N}V(x_i-x_j) \end{align} $$
and acts on the Hilbert space
 $L^2_s(\Lambda _L^N)$
, the subspace of
$L^2_s(\Lambda _L^N)$
, the subspace of
 $L^2(\Lambda _L^N)$
consisting of functions that are symmetric with respect to permutations of the N particles (we use here units with particle mass
$L^2(\Lambda _L^N)$
consisting of functions that are symmetric with respect to permutations of the N particles (we use here units with particle mass
![]() $m=1/2$
and
$m=1/2$
and
![]() $\hbar =1$
). We assume Dirichlet boundary conditions and denote by
$\hbar =1$
). We assume Dirichlet boundary conditions and denote by
![]() $E(N,L)$
the corresponding ground state energy. We are interested in the energy per unit volume in the thermodynamic limit, defined by
$E(N,L)$
the corresponding ground state energy. We are interested in the energy per unit volume in the thermodynamic limit, defined by
 $$ \begin{align} e(\rho)=\lim_{\substack{N,L\to+\infty\\ \rho=N/L^3}} \frac{E(N,L)}{L^3}. \end{align} $$
$$ \begin{align} e(\rho)=\lim_{\substack{N,L\to+\infty\\ \rho=N/L^3}} \frac{E(N,L)}{L^3}. \end{align} $$
Bogoliubov [Reference Bogoliubov4] and, later, in more explicit terms, Lee–Huang–Yang [Reference Lee, Huang and Yang14] predicted that, in the dilute limit
![]() $\rho \mathfrak {a}^3 \ll 1$
, the specific ground state energy (1.2) is so that
$\rho \mathfrak {a}^3 \ll 1$
, the specific ground state energy (1.2) is so that
 $$ \begin{align} e(\rho)= 4 \pi \mathfrak{a} \rho^2 \left[ 1+ \frac{128}{15\sqrt \pi} (\rho \mathfrak{a}^3)^{1/2}+ o( (\rho \mathfrak{a}^3)^{1/2}) \right]. \end{align} $$
$$ \begin{align} e(\rho)= 4 \pi \mathfrak{a} \rho^2 \left[ 1+ \frac{128}{15\sqrt \pi} (\rho \mathfrak{a}^3)^{1/2}+ o( (\rho \mathfrak{a}^3)^{1/2}) \right]. \end{align} $$
In particular, up to lower order corrections, it only depends on the interaction potential through the scattering length
![]() $\mathfrak {a}$
. An alternative heuristic derivation of (1.3) was proposed in [Reference Lieb15] (this approach was based on a partial differential equation with a convolution nonlinearity, whose mathematical properties were recently studied in [Reference Carlen, Jauslin and Lieb7]).
$\mathfrak {a}$
. An alternative heuristic derivation of (1.3) was proposed in [Reference Lieb15] (this approach was based on a partial differential equation with a convolution nonlinearity, whose mathematical properties were recently studied in [Reference Carlen, Jauslin and Lieb7]).
On the rigorous level, the validity of the leading term on the right-hand side of (1.3) was established by Dyson, who obtained an upper bound in [Reference Dyson8], and by Lieb–Yngvason, who proved the matching lower bound in [Reference Lieb and Yngvason16]. An upper bound with the correct second-order contribution was first derived in [Reference Yau and Yin20] by Yau–Yin for regular potentials, improving a previous estimate from [Reference Erdős, Schlein and Yau9], which only recovered the correct formula (as an upper bound) in the limit of weak coupling. The approach of [Reference Yau and Yin20] has been reviewed and adapted to a grand canonical setting in [Reference Aaen1]. As for the lower bound, preliminary results have been obtained in [Reference Giuliani and Seiringer13] and [Reference Brietzke and Solovey6], where (1.3) was shown in particular regimes, where the potential scales with the density
![]() $\rho $
. Finally, a rigorous lower bound matching (1.3) has been obtained by Fournais–Solovej, in [Reference Fournais and Solovej10] for
$\rho $
. Finally, a rigorous lower bound matching (1.3) has been obtained by Fournais–Solovej, in [Reference Fournais and Solovej10] for
![]() $L^1$
potentials and, very recently, in [Reference Fournais and Solovej11] for a hard sphere interaction (a nonoptimal bound for hard spheres had been previously obtained in [Reference Brietzke, Fournais and Solovej5]).
$L^1$
potentials and, very recently, in [Reference Fournais and Solovej11] for a hard sphere interaction (a nonoptimal bound for hard spheres had been previously obtained in [Reference Brietzke, Fournais and Solovej5]).
Our goal in this article is to show a new upper bound for (1.3). With respect to the upper bound established in [Reference Yau and Yin20], our result holds for a larger class of potentials (in [Reference Yau and Yin20], the upper bound is proven for smooth potentials), it gives a better rate (although still far from optimal) and, most important in our opinion, it relies on a simpler proof.
Theorem 1.1. Let
![]() $V \in L^{3}(\mathbb {R}^3)$
be nonnegative, radially symmetric, with
$V \in L^{3}(\mathbb {R}^3)$
be nonnegative, radially symmetric, with
![]() $\mathrm {supp}(V)\subset B_R(0)$
and scattering length
$\mathrm {supp}(V)\subset B_R(0)$
and scattering length
![]() $\mathfrak {a}$
. Then, the specific ground state energy
$\mathfrak {a}$
. Then, the specific ground state energy
![]() $e(\rho )$
of the Hamilton operator
$e(\rho )$
of the Hamilton operator
![]() $H_L$
defined in (1.1) satisfies
$H_L$
defined in (1.1) satisfies
 $$ \begin{align} e(\rho)\leq 4\pi \rho^2 \mathfrak{a} \Big[ 1 + \frac{128}{15 \sqrt \pi} (\rho \mathfrak{a}^3)^{1/2} \Big] + C \rho^{5/2+ 1/10} \end{align} $$
$$ \begin{align} e(\rho)\leq 4\pi \rho^2 \mathfrak{a} \Big[ 1 + \frac{128}{15 \sqrt \pi} (\rho \mathfrak{a}^3)^{1/2} \Big] + C \rho^{5/2+ 1/10} \end{align} $$
for some
![]() $C>0$
(depending on
$C>0$
(depending on
![]() $\| V \|_3$
and on R) and for
$\| V \|_3$
and on R) and for
![]() $\rho $
small enough.
$\rho $
small enough.
Remark. Since Dirichlet boundary conditions lead to the largest energy, the upper bound (1.4) holds in fact for arbitrary boundary conditions.
Remark. At the cost of a longer proof, we could improve the bound on the error, up to the order
![]() $\rho ^{5/2+2/9}$
(this is the rate determined by Lemma 5.1).
$\rho ^{5/2+2/9}$
(this is the rate determined by Lemma 5.1).
The proof of 1.4 is based on the construction of an appropriate trial state. However, we do not directly construct a trial state in
 $L^2_s (\Lambda _L^N)$
for the Hamiltonian (1.1). Instead, to simplify the analysis, it is very convenient to (1) consider smaller boxes (rather than letting
$L^2_s (\Lambda _L^N)$
for the Hamiltonian (1.1). Instead, to simplify the analysis, it is very convenient to (1) consider smaller boxes (rather than letting
![]() $N, L \to \infty $
first and considering small
$N, L \to \infty $
first and considering small
![]() $\rho $
at the end, we will consider a diagonal limit, with
$\rho $
at the end, we will consider a diagonal limit, with
![]() $L = \rho ^{-\gamma }$
, for some
$L = \rho ^{-\gamma }$
, for some
![]() $\gamma> 1$
), (2) work with periodic rather than Dirichlet boundary conditions and (3) work in the grand-canonical setting, considering states with variable number of particles, rather than the canonical setting. In other words, our trial state will be defined on the bosonic Fock space
$\gamma> 1$
), (2) work with periodic rather than Dirichlet boundary conditions and (3) work in the grand-canonical setting, considering states with variable number of particles, rather than the canonical setting. In other words, our trial state will be defined on the bosonic Fock space
 $$ \begin{align*} \mathcal{F}(\Lambda_{ L})= \bigoplus_{n \geq 0} L^2_s (\Lambda_L^{n}) = \bigoplus_{n \geq 0} L^2 (\Lambda_L)^{\otimes_s n} \end{align*} $$
$$ \begin{align*} \mathcal{F}(\Lambda_{ L})= \bigoplus_{n \geq 0} L^2_s (\Lambda_L^{n}) = \bigoplus_{n \geq 0} L^2 (\Lambda_L)^{\otimes_s n} \end{align*} $$
where
 $L^2_s (\Lambda _L^{n})$
is the subspace of
$L^2_s (\Lambda _L^{n})$
is the subspace of
 $L^2 (\Lambda _L^n)$
consisting of wave functions that are symmetric with respect to permutations. On
$L^2 (\Lambda _L^n)$
consisting of wave functions that are symmetric with respect to permutations. On
![]() $\mathcal {F}(\Lambda _{ L})$
, we consider the number of particles operator
$\mathcal {F}(\Lambda _{ L})$
, we consider the number of particles operator
![]() $\mathcal {N}$
defined through
$\mathcal {N}$
defined through
![]() $(\mathcal {N} \psi )^{(n)}= n \psi ^{(n)}$
. Moreover, we introduce the Hamiltonian operator
$(\mathcal {N} \psi )^{(n)}= n \psi ^{(n)}$
. Moreover, we introduce the Hamiltonian operator
![]() $\mathcal {H}$
, setting
$\mathcal {H}$
, setting
with
 $$ \begin{align*} \mathcal{H}^{(n)} = \sum_{j=1}^n -\Delta_{x_j} + \sum_{1 \leq i<j \leq n} V(x_i - x_j), \end{align*} $$
$$ \begin{align*} \mathcal{H}^{(n)} = \sum_{j=1}^n -\Delta_{x_j} + \sum_{1 \leq i<j \leq n} V(x_i - x_j), \end{align*} $$
imposing now (in contrast to what we did in (1.1)) periodic boundary conditions (with a slight abuse of notation, V denotes here the periodic extension of the potential introduced in (1.1)). The upper bound for the energy of (1.5) will then imply Theorem 1.1 thanks to the following localisation result.
Proposition 1.2. Let
![]() $e(\rho )$
be defined as in (1.2), with Dirichlet boundary conditions. Let
$e(\rho )$
be defined as in (1.2), with Dirichlet boundary conditions. Let
![]() $R < b < L$
, with R the radius of the support of the potential V, as defined in Theorem 1.1. Then, for any normalised
$R < b < L$
, with R the radius of the support of the potential V, as defined in Theorem 1.1. Then, for any normalised
![]() $\Psi _{L} \in \mathcal {F} (\Lambda _{L})$
satisfying periodic boundary conditions and such that
$\Psi _{L} \in \mathcal {F} (\Lambda _{L})$
satisfying periodic boundary conditions and such that
for some
![]() $c' , C'> 0$
, we have
$c' , C'> 0$
, we have
 $$ \begin{align} e(\rho) \leq \frac{\langle \Psi_{L}, \mathcal{H} \Psi_{L} \rangle }{L^3} + \frac{C}{L^{4} b} \langle \Psi_{L}, \mathcal{N} \Psi_{L} \rangle \end{align} $$
$$ \begin{align} e(\rho) \leq \frac{\langle \Psi_{L}, \mathcal{H} \Psi_{L} \rangle }{L^3} + \frac{C}{L^{4} b} \langle \Psi_{L}, \mathcal{N} \Psi_{L} \rangle \end{align} $$
for a universal constant
![]() $C> 0$
.
$C> 0$
.
The proof of Proposition 1.2 is standard; see [Reference Robinson18, Reference Yau and Yin20, Reference Aaen1]. Roughly speaking, the idea consists in using
![]() $\Psi _L$
(satisfying periodic boundary conditions on the box
$\Psi _L$
(satisfying periodic boundary conditions on the box
![]() $\Lambda _L$
) to construct a trial state satisfying Dirichlet boundary conditions on a slightly larger box of side length
$\Lambda _L$
) to construct a trial state satisfying Dirichlet boundary conditions on a slightly larger box of side length
![]() $L + 2b$
and then in approaching the thermodynamic limit by replicating the Dirichlet state on several boxes of side length
$L + 2b$
and then in approaching the thermodynamic limit by replicating the Dirichlet state on several boxes of side length
![]() $L+2b$
, separated by corridors of size R (to avoid interactions among different boxes). For completeness, we provide a detailed proof of Proposition 1.2 in Appendix A.
$L+2b$
, separated by corridors of size R (to avoid interactions among different boxes). For completeness, we provide a detailed proof of Proposition 1.2 in Appendix A.
The bulk of the article contains the proof of the following proposition, establishing the existence of a trial state with the correct energy per unit volume and the correct expected number of particles on boxes of size
![]() $L = {\tilde {\rho }}^{-\gamma }$
. We use here the notation
$L = {\tilde {\rho }}^{-\gamma }$
. We use here the notation
![]() ${\tilde {\rho }}$
for the density to stress the fact that the upper bound (1.9) will be inserted in (1.7) to prove an upper bound for the specific ground state energy
${\tilde {\rho }}$
for the density to stress the fact that the upper bound (1.9) will be inserted in (1.7) to prove an upper bound for the specific ground state energy
![]() $e (\rho )$
, for a slightly different density
$e (\rho )$
, for a slightly different density
![]() $\rho < {\tilde {\rho }}$
(to make up for the corrections on the right-hand side of (1.6)).
$\rho < {\tilde {\rho }}$
(to make up for the corrections on the right-hand side of (1.6)).
Proposition 1.3. As in Theorem 1.1, assume that
![]() $V \in L^3 (\mathbb {R}^3)$
is nonnegative, radially symmetric with
$V \in L^3 (\mathbb {R}^3)$
is nonnegative, radially symmetric with
![]() $\text {supp } V \subset B_R (0)$
and scattering length
$\text {supp } V \subset B_R (0)$
and scattering length
![]() $\frak {a}$
. For
$\frak {a}$
. For
![]() $\gamma> 1$
and
$\gamma> 1$
and
![]() ${\tilde {\rho }}> 0$
let
${\tilde {\rho }}> 0$
let
![]() $L = {\tilde {\rho }}^{-\gamma }$
. Then, for every
$L = {\tilde {\rho }}^{-\gamma }$
. Then, for every
![]() $0< \varepsilon < 1/4$
, there exists
$0< \varepsilon < 1/4$
, there exists
![]() $\Phi _{{\tilde {\rho }}} \in \mathcal {F} (\Lambda _L)$
satisfying periodic boundary conditions such that
$\Phi _{{\tilde {\rho }}} \in \mathcal {F} (\Lambda _L)$
satisfying periodic boundary conditions such that
 $$ \begin{align} \langle \Phi_{{\tilde{\rho}}} , \mathcal{N} \Phi_{{\tilde{\rho}}} \rangle \geq {\tilde{\rho}} L^3 , \qquad \langle \Phi_{{\tilde{\rho}}} , \mathcal{N}^2 \Phi_{{\tilde{\rho}}} \rangle \leq C {\tilde{\rho}}^{2} L^6 \end{align} $$
$$ \begin{align} \langle \Phi_{{\tilde{\rho}}} , \mathcal{N} \Phi_{{\tilde{\rho}}} \rangle \geq {\tilde{\rho}} L^3 , \qquad \langle \Phi_{{\tilde{\rho}}} , \mathcal{N}^2 \Phi_{{\tilde{\rho}}} \rangle \leq C {\tilde{\rho}}^{2} L^6 \end{align} $$
and
 $$ \begin{align} \frac{{\bigl\langle\Phi_{{\tilde{\rho}}},\mathcal{H} \Phi_{{\tilde{\rho}}}\bigr\rangle}}{ L^3} \leq 4\pi\mathfrak{a} {\tilde{\rho}}^{\,2}\bigg(1+\frac{128}{15\sqrt{\pi}}(\mathfrak{a}^3 {\tilde{\rho}})^{1/2}\bigg)+ \mathcal{E} , \end{align} $$
$$ \begin{align} \frac{{\bigl\langle\Phi_{{\tilde{\rho}}},\mathcal{H} \Phi_{{\tilde{\rho}}}\bigr\rangle}}{ L^3} \leq 4\pi\mathfrak{a} {\tilde{\rho}}^{\,2}\bigg(1+\frac{128}{15\sqrt{\pi}}(\mathfrak{a}^3 {\tilde{\rho}})^{1/2}\bigg)+ \mathcal{E} , \end{align} $$
with
Remark. the condition
![]() $\gamma> 1$
is needed to make sure that the localisation error in (1.7) is negligible. While we will choose
$\gamma> 1$
is needed to make sure that the localisation error in (1.7) is negligible. While we will choose
![]() $\gamma = 11/10$
to optimise the rate, our analysis allows us to take any
$\gamma = 11/10$
to optimise the rate, our analysis allows us to take any
![]() $1 < \gamma < 4/3$
. With a longer proof, our techniques could be extended to all
$1 < \gamma < 4/3$
. With a longer proof, our techniques could be extended to all
![]() $1 < \gamma < 5/3$
. This suggests that our trial state captures the correct correlations of the ground state, up to length scales of the order
$1 < \gamma < 5/3$
. This suggests that our trial state captures the correct correlations of the ground state, up to length scales of the order
![]() $\rho ^{-5/3}$
.
$\rho ^{-5/3}$
.
With Proposition 1.2 and Proposition 1.3 we can prove Theorem 1.1.
Proof Proof of Theorem 1.1.
For given
![]() $\rho> 0$
, we would like to choose
$\rho> 0$
, we would like to choose
![]() ${\tilde {\rho }}$
or, equivalently,
${\tilde {\rho }}$
or, equivalently,
![]() $L = {\tilde {\rho }}^{-\gamma }$
, so that (1.8) implies (1.6). Fixing
$L = {\tilde {\rho }}^{-\gamma }$
, so that (1.8) implies (1.6). Fixing
![]() $c'> 0$
and
$c'> 0$
and
![]() $b = L^\alpha $
, for some
$b = L^\alpha $
, for some
![]() $\alpha \in (0;1)$
, this leads to the implicit equation
$\alpha \in (0;1)$
, this leads to the implicit equation
 $$ \begin{align} L = {\tilde{\rho}}^{-\gamma} = \left[ \rho (1+ c' \rho) (1 + 2 L^{\alpha-1} + R L^{-1})^3 \right]^{-\gamma}. \end{align} $$
$$ \begin{align} L = {\tilde{\rho}}^{-\gamma} = \left[ \rho (1+ c' \rho) (1 + 2 L^{\alpha-1} + R L^{-1})^3 \right]^{-\gamma}. \end{align} $$
Setting
![]() $L = \big (\rho (1+c' \rho ) \big )^{-\gamma } x$
, we rewrite (1.10) as
$L = \big (\rho (1+c' \rho ) \big )^{-\gamma } x$
, we rewrite (1.10) as
 $$ \begin{align*} x = \big(1 + 2 \, \big(\rho(1+c' \rho) \big)^{\gamma (1-\alpha)} / x^{1-\alpha} + R \, \big(\rho(1+c' \rho) \big)^\gamma /x \big)^{-3\gamma} \end{align*} $$
$$ \begin{align*} x = \big(1 + 2 \, \big(\rho(1+c' \rho) \big)^{\gamma (1-\alpha)} / x^{1-\alpha} + R \, \big(\rho(1+c' \rho) \big)^\gamma /x \big)^{-3\gamma} \end{align*} $$
and we conclude that the existence of a solution
![]() $L = L(\rho )$
of (1.10) follows from the implicit function theorem, if
$L = L(\rho )$
of (1.10) follows from the implicit function theorem, if
![]() $\rho> 0$
is small enough (the solution stems from
$\rho> 0$
is small enough (the solution stems from
![]() $x=1$
for
$x=1$
for
![]() $\rho = 0$
). By construction,
$\rho = 0$
). By construction,
![]() $L = {\tilde {\rho }}^{-\gamma }$
, with
$L = {\tilde {\rho }}^{-\gamma }$
, with
and thus
From Proposition 1.3, we find
![]() $\Phi _{{\tilde {\rho }}} \in \mathcal {F} (\Lambda _L)$
such that (1.8) and (1.9) hold true. In particular, (1.8) implies (1.6) (with
$\Phi _{{\tilde {\rho }}} \in \mathcal {F} (\Lambda _L)$
such that (1.8) and (1.9) hold true. In particular, (1.8) implies (1.6) (with
![]() $b = L^\alpha $
,
$b = L^\alpha $
,
![]() $C'=C$
). Thus, from Proposition 1.2 we conclude
$C'=C$
). Thus, from Proposition 1.2 we conclude
 $$ \begin{align*} e(\rho) \leq \frac{\langle \Phi_{{\tilde{\rho}}}, \mathcal{H} \Phi_{{\tilde{\rho}}} \rangle}{L^3} + \frac{C}{L^4 b} \langle \Phi_{{\tilde{\rho}}} , \mathcal{N} \Phi_{{\tilde{\rho}}} \rangle. \end{align*} $$
$$ \begin{align*} e(\rho) \leq \frac{\langle \Phi_{{\tilde{\rho}}}, \mathcal{H} \Phi_{{\tilde{\rho}}} \rangle}{L^3} + \frac{C}{L^4 b} \langle \Phi_{{\tilde{\rho}}} , \mathcal{N} \Phi_{{\tilde{\rho}}} \rangle. \end{align*} $$
Inserting (1.9) and (1.8), we obtain (since (1.8) also implies that
![]() $\langle \Phi _{{\tilde {\rho }}} , \mathcal {N} \Phi _{{\tilde {\rho }}} \rangle \leq C \widetilde {\rho } L^3$
)
$\langle \Phi _{{\tilde {\rho }}} , \mathcal {N} \Phi _{{\tilde {\rho }}} \rangle \leq C \widetilde {\rho } L^3$
)
 $$ \begin{align*} e (\rho) \leq 4 \pi \frak{a} {\tilde{\rho}}^2 \left[ 1 + \frac{128}{15\sqrt{\pi}} (\frak{a}^3 {\tilde{\rho}})^{1/2} \right] + C {\tilde{\rho}}^{1+\gamma (1+\alpha)} + C {\tilde{\rho}}^{\,5/2} \cdot \max \{{\tilde{\rho}}^\varepsilon , \, {\tilde{\rho}}^{4-3\gamma -6\varepsilon} , \, {\tilde{\rho}}^{9/4-3\gamma/2-3\varepsilon} \}. \end{align*} $$
$$ \begin{align*} e (\rho) \leq 4 \pi \frak{a} {\tilde{\rho}}^2 \left[ 1 + \frac{128}{15\sqrt{\pi}} (\frak{a}^3 {\tilde{\rho}})^{1/2} \right] + C {\tilde{\rho}}^{1+\gamma (1+\alpha)} + C {\tilde{\rho}}^{\,5/2} \cdot \max \{{\tilde{\rho}}^\varepsilon , \, {\tilde{\rho}}^{4-3\gamma -6\varepsilon} , \, {\tilde{\rho}}^{9/4-3\gamma/2-3\varepsilon} \}. \end{align*} $$
With (1.11), we conclude that
 $$ \begin{align*} e (\rho) \leq \; &4 \pi \frak{a} \rho^2 \left[ 1 + \frac{128}{15\sqrt{\pi}} (\frak{a}^3 \rho )^{1/2} \right] \\ &+ C \rho^{5/2} \cdot \max \{ \rho^{\gamma (1-\alpha)-1/2} , \, \rho^{\gamma (1+\alpha) -3/2} , \, \rho^\varepsilon , \, \rho^{4-3\gamma -6\varepsilon} , \, \rho^{9/4-3\gamma/2-3\varepsilon} \} ,\end{align*} $$
$$ \begin{align*} e (\rho) \leq \; &4 \pi \frak{a} \rho^2 \left[ 1 + \frac{128}{15\sqrt{\pi}} (\frak{a}^3 \rho )^{1/2} \right] \\ &+ C \rho^{5/2} \cdot \max \{ \rho^{\gamma (1-\alpha)-1/2} , \, \rho^{\gamma (1+\alpha) -3/2} , \, \rho^\varepsilon , \, \rho^{4-3\gamma -6\varepsilon} , \, \rho^{9/4-3\gamma/2-3\varepsilon} \} ,\end{align*} $$
where we neglected errors of order
![]() $C \rho ^3$
, which are subleading compared with
$C \rho ^3$
, which are subleading compared with
![]() $C\rho^{5/2+\varepsilon}$
, since
$C\rho^{5/2+\varepsilon}$
, since
![]() $\varepsilon \in (0;1/4)$
.
$\varepsilon \in (0;1/4)$
.
Comparing the first two errors, we choose
![]() $\alpha = 1/(2\gamma )$
. Comparing instead third and fourth errors, we set
$\alpha = 1/(2\gamma )$
. Comparing instead third and fourth errors, we set
![]() $\varepsilon = (4-3\gamma )/7$
(both choices are consistent with the conditions
$\varepsilon = (4-3\gamma )/7$
(both choices are consistent with the conditions
![]() $\alpha \in (0;1)$
and
$\alpha \in (0;1)$
and
![]() $\varepsilon \in (0;1/4)$
, because
$\varepsilon \in (0;1/4)$
, because
![]() $\gamma> 1$
). Since, with these choices, the last error is of smaller order, we obtain
$\gamma> 1$
). Since, with these choices, the last error is of smaller order, we obtain
 $$ \begin{align*} e (\rho) \leq \; 4 \pi \frak{a} \rho^2 \left[ 1 + \frac{128}{15\sqrt{\pi}} (\frak{a}^3 \rho )^{1/2} \right] + C \rho^{5/2} \cdot \max \{ \rho^{\gamma-1}, \rho^{(4-3\gamma)/7} \}. \end{align*} $$
$$ \begin{align*} e (\rho) \leq \; 4 \pi \frak{a} \rho^2 \left[ 1 + \frac{128}{15\sqrt{\pi}} (\frak{a}^3 \rho )^{1/2} \right] + C \rho^{5/2} \cdot \max \{ \rho^{\gamma-1}, \rho^{(4-3\gamma)/7} \}. \end{align*} $$
Choosing
![]() $\gamma = 11/10$
, we find (1.4).
$\gamma = 11/10$
, we find (1.4).
The proof of Proposition 1.3 occupies the rest of the article (excluding Appendix A, where we show Proposition 1.2). In Section 2 we define our trial state. To this end, we will start with a coherent state describing the Bose–Einstein condensate. Similar to [Reference Girardeau and Arnowitt12, Reference Erdős, Schlein and Yau9], we will then act on the coherent state with a Bogoliubov transformation to add the expected correlation structure. Finally, we will apply the exponential of a cubic expression in creation operators. While the Bogoliubov transformation creates pairs of excitations with opposite momenta
![]() $p, -p$
, the cubic operator creates three excitations at a time, two with large momenta
$p, -p$
, the cubic operator creates three excitations at a time, two with large momenta
![]() $r+v, -r$
and one with low momentum v. This last step is essential, since, as follows from [Reference Erdős, Schlein and Yau9, Reference Napiórkowski, Reuvers and Solovej17], quasi-free states cannot approximate the ground state energy to the precision of (1.3). We remark that the idea of creating triples of excitations originally appeared in the work of Yau–Yin [Reference Yau and Yin20] (a brief comparison with the trial state of [Reference Yau and Yin20] can be found after the precise definition of our trial state in (2.25)). Recently, it has been also applied to establish the validity of Bogoliubov theory in the Gross–Pitaevskii regime in [Reference Boccato, Brennecke, Cenatiempo and Schlein3, Reference Boccato, Brennecke, Cenatiempo and Schlein2]; while our approach is inspired by these papers, we need new tools to deal with the large boxes considered in Proposition 1.3 (a simple computation shows that the Gross–Pitaevskii regime corresponds to the exponent
$r+v, -r$
and one with low momentum v. This last step is essential, since, as follows from [Reference Erdős, Schlein and Yau9, Reference Napiórkowski, Reuvers and Solovej17], quasi-free states cannot approximate the ground state energy to the precision of (1.3). We remark that the idea of creating triples of excitations originally appeared in the work of Yau–Yin [Reference Yau and Yin20] (a brief comparison with the trial state of [Reference Yau and Yin20] can be found after the precise definition of our trial state in (2.25)). Recently, it has been also applied to establish the validity of Bogoliubov theory in the Gross–Pitaevskii regime in [Reference Boccato, Brennecke, Cenatiempo and Schlein3, Reference Boccato, Brennecke, Cenatiempo and Schlein2]; while our approach is inspired by these papers, we need new tools to deal with the large boxes considered in Proposition 1.3 (a simple computation shows that the Gross–Pitaevskii regime corresponds to the exponent
![]() $\gamma = 1/2$
; to control localisation errors, we need instead to choose
$\gamma = 1/2$
; to control localisation errors, we need instead to choose
![]() $\gamma> 1$
). In Section 3, we combine the contributions to the energy of the trial state arising from the conjugation with the Bogoliubov transformation and from the action of the cubic phase, proving the desired upper bound. In Section 4 and Section 5, we prove technical bounds which allow us to identify the leading contributions collected in Section 3.
$\gamma> 1$
). In Section 3, we combine the contributions to the energy of the trial state arising from the conjugation with the Bogoliubov transformation and from the action of the cubic phase, proving the desired upper bound. In Section 4 and Section 5, we prove technical bounds which allow us to identify the leading contributions collected in Section 3.
2 Setting and trial state
To show Proposition 1.3, we find it convenient to work with rescaled variables. We consider the transformation
![]() $x_j \to x_j / L$
and, motivated by the choice
$x_j \to x_j / L$
and, motivated by the choice
![]() $L = {\tilde {\rho }}^{-\gamma }$
in Proposition 1.3, we set
$L = {\tilde {\rho }}^{-\gamma }$
in Proposition 1.3, we set
![]() $N = {\tilde {\rho }}^{1-3\gamma }$
(we will look for trial states with expected number of particles close to N to make sure that (1.8) holds true). It follows that the Hamiltonian (1.5) is unitarily equivalent to the operator
$N = {\tilde {\rho }}^{1-3\gamma }$
(we will look for trial states with expected number of particles close to N to make sure that (1.8) holds true). It follows that the Hamiltonian (1.5) is unitarily equivalent to the operator
![]() $L^{-2} \mathcal {H}_N = {\tilde {\rho }}^{2\gamma } \mathcal {H}_N$
, with
$L^{-2} \mathcal {H}_N = {\tilde {\rho }}^{2\gamma } \mathcal {H}_N$
, with
![]() $\mathcal {H}_N$
acting on the Fock space
$\mathcal {H}_N$
acting on the Fock space
![]() $\mathcal {F} (\Lambda )$
defined over the unit box
$\mathcal {F} (\Lambda )$
defined over the unit box
![]() $\Lambda = \Lambda _1 = [-1/2; 1/2 ]^3$
(with periodic boundary conditions) so that
$\Lambda = \Lambda _1 = [-1/2; 1/2 ]^3$
(with periodic boundary conditions) so that
 $(\mathcal {H}_N \Psi )^{(n)} = \mathcal {H}_N^{(n)} \Psi ^{(n)}$
, with
$(\mathcal {H}_N \Psi )^{(n)} = \mathcal {H}_N^{(n)} \Psi ^{(n)}$
, with
 $$ \begin{align*} \mathcal{H}_N^{(n)} = \sum_{j=1}^n -\Delta_{x_j} + \sum_{1 \leq i,j \leq n} N^{2-2\kappa} V (N^{1-\kappa} (x_i - x_j)) \end{align*} $$
$$ \begin{align*} \mathcal{H}_N^{(n)} = \sum_{j=1}^n -\Delta_{x_j} + \sum_{1 \leq i,j \leq n} N^{2-2\kappa} V (N^{1-\kappa} (x_i - x_j)) \end{align*} $$
and
![]() $\kappa = (2\gamma - 1)/ (3\gamma -1)$
. The assumption
$\kappa = (2\gamma - 1)/ (3\gamma -1)$
. The assumption
![]() $\gamma> 1$
in Proposition 1.3 allows us to restrict our attention to
$\gamma> 1$
in Proposition 1.3 allows us to restrict our attention to
![]() $\kappa \in (1/2; 2/3)$
.
$\kappa \in (1/2; 2/3)$
.
For any momentum
![]() $p \in \Lambda ^* = 2\pi \mathbb {Z}^3$
, we introduce on the Fock space
$p \in \Lambda ^* = 2\pi \mathbb {Z}^3$
, we introduce on the Fock space
 $\mathcal {F} (\Lambda ) = \bigoplus _{n \geq 0} L^2_s (\Lambda ^{n})$
the operators
$\mathcal {F} (\Lambda ) = \bigoplus _{n \geq 0} L^2_s (\Lambda ^{n})$
the operators
![]() $a_p^*, a_p$
, creating and, respectively, annihilating a particle with momentum p. Creation and annihilation operators satisfy the canonical commutation relations
$a_p^*, a_p$
, creating and, respectively, annihilating a particle with momentum p. Creation and annihilation operators satisfy the canonical commutation relations
 $$ \begin{align} \left[ a_p , a_q^* \right] = \delta_{pq} , \qquad \left[ a_p , a_q \right] = \left[ a^*_p, a_q^* \right] = 0. \end{align} $$
$$ \begin{align} \left[ a_p , a_q^* \right] = \delta_{pq} , \qquad \left[ a_p , a_q \right] = \left[ a^*_p, a_q^* \right] = 0. \end{align} $$
On
![]() $\mathcal {F}(\Lambda )$
, we define the number of particles operator
$\mathcal {F}(\Lambda )$
, we define the number of particles operator
![]() $\mathcal {N} = \sum _{p \in \Lambda ^*} a_p^* a_p$
. Expressed in terms of creation and annihilation operators, the Hamiltonian
$\mathcal {N} = \sum _{p \in \Lambda ^*} a_p^* a_p$
. Expressed in terms of creation and annihilation operators, the Hamiltonian
![]() $\mathcal {H}_N$
takes the form
$\mathcal {H}_N$
takes the form
 $$ \begin{align} \mathcal{H}_N=\sum_{p\in\Lambda^*}p^2a_p^*a_p+\frac{1}{2N^{1-\kappa}} \sum_{p,q,r\in \Lambda^*} \widehat{V} (r/N^{1-\kappa}) \, a_{p+r}^*a_q^*a_{q+r}a_{p}. \end{align} $$
$$ \begin{align} \mathcal{H}_N=\sum_{p\in\Lambda^*}p^2a_p^*a_p+\frac{1}{2N^{1-\kappa}} \sum_{p,q,r\in \Lambda^*} \widehat{V} (r/N^{1-\kappa}) \, a_{p+r}^*a_q^*a_{q+r}a_{p}. \end{align} $$
We now construct our trial state. To generate a condensate, we use a Weyl operator
 $$ \begin{align} W_{N_0}=\exp \big[ \sqrt{N_0} a_0^* - \sqrt{N_0}a_0 \big] \end{align} $$
$$ \begin{align} W_{N_0}=\exp \big[ \sqrt{N_0} a_0^* - \sqrt{N_0}a_0 \big] \end{align} $$
with a parameter
![]() $N_0$
to be specified later on. While
$N_0$
to be specified later on. While
![]() $W_{N_0}$
leaves
$W_{N_0}$
leaves
![]() $a_p, a_p^*$
invariant, for all
$a_p, a_p^*$
invariant, for all
![]() $p \in \Lambda ^* \backslash \{ 0 \}$
, it produces shifts of
$p \in \Lambda ^* \backslash \{ 0 \}$
, it produces shifts of
![]() $a_0, a_0^*$
; in other words,
$a_0, a_0^*$
; in other words,
 $$ \begin{align} W_{N_0}^* a_0 \, W_{N_0} = a_0 + \sqrt{N_0} , \qquad W_{N_0}^* a_0^* \, W_{N_0} = a_0^* + \sqrt{N_0}. \end{align} $$
$$ \begin{align} W_{N_0}^* a_0 \, W_{N_0} = a_0 + \sqrt{N_0} , \qquad W_{N_0}^* a_0^* \, W_{N_0} = a_0^* + \sqrt{N_0}. \end{align} $$
When acting on the vacuum vector
![]() $\Omega = \{ 1, 0, \dots \}$
, (2.3) generates a coherent state in the zero-momentum mode
$\Omega = \{ 1, 0, \dots \}$
, (2.3) generates a coherent state in the zero-momentum mode
![]() $\varphi _0 (x) \equiv 1$
, with expected number of particles
$\varphi _0 (x) \equiv 1$
, with expected number of particles
![]() $N_0$
.
$N_0$
.
It turns out, however, that the coherent state does not approximate the ground state energy, not even to leading order. To get closer to the ground state energy, it is crucial to add correlations among particles. To this end, we fix
![]() $0 < \ell < 1/2$
and we consider the lowest energy solution
$0 < \ell < 1/2$
and we consider the lowest energy solution
![]() $f_{\ell }$
of the Neumann problem
$f_{\ell }$
of the Neumann problem
 $$ \begin{align} \left[ -\Delta + \frac{1}{2} V \right] f_{\ell} = \lambda_{\ell} f_{\ell} \end{align} $$
$$ \begin{align} \left[ -\Delta + \frac{1}{2} V \right] f_{\ell} = \lambda_{\ell} f_{\ell} \end{align} $$
on the ball
![]() $|x| \leq N^{1-\kappa }\ell $
, with the normalisation
$|x| \leq N^{1-\kappa }\ell $
, with the normalisation
![]() $f_\ell (x) = 1$
if
$f_\ell (x) = 1$
if
![]() $|x| =N^{1-\kappa } \ell $
. Furthermore, by rescaling, we define
$|x| =N^{1-\kappa } \ell $
. Furthermore, by rescaling, we define
![]() $f_{N,\ell } (x) := f_\ell \big ( N^{1-\kappa }x\big )$
for
$f_{N,\ell } (x) := f_\ell \big ( N^{1-\kappa }x\big )$
for
![]() $|x| \leq \ell $
. We extend
$|x| \leq \ell $
. We extend
![]() $f_{N,\ell }$
to a function on
$f_{N,\ell }$
to a function on
![]() $\Lambda $
, by fixing
$\Lambda $
, by fixing
![]() $f_{N,\ell } (x) = 1$
, for all
$f_{N,\ell } (x) = 1$
, for all
![]() $x \in \Lambda $
, with
$x \in \Lambda $
, with
![]() $|x|> \ell $
. Then
$|x|> \ell $
. Then
 $$ \begin{align} \left[ -\Delta + \frac12 N^{2-2\kappa} V ( N^{1-\kappa}x ) \right] f_{N,\ell} (x) = N^{2-2\kappa} \lambda_\ell f_{N,\ell} (x) \chi_\ell(x) \end{align} $$
$$ \begin{align} \left[ -\Delta + \frac12 N^{2-2\kappa} V ( N^{1-\kappa}x ) \right] f_{N,\ell} (x) = N^{2-2\kappa} \lambda_\ell f_{N,\ell} (x) \chi_\ell(x) \end{align} $$
for all
![]() $x \in \Lambda $
, where
$x \in \Lambda $
, where
![]() $\chi _\ell $
denotes the characteristic function of the ball of radius
$\chi _\ell $
denotes the characteristic function of the ball of radius
![]() $\ell $
. We denote by
$\ell $
. We denote by
 $ \widehat {f}_{N,\ell } (p)$
the Fourier coefficients of the function
$ \widehat {f}_{N,\ell } (p)$
the Fourier coefficients of the function
![]() $f_{N,\ell }$
, for
$f_{N,\ell }$
, for
![]() $p \in \Lambda ^*$
. We also define
$p \in \Lambda ^*$
. We also define
![]() $w_\ell (x) = 1 - f_\ell (x)$
(with
$w_\ell (x) = 1 - f_\ell (x)$
(with
![]() $w_\ell (x) = 0$
for
$w_\ell (x) = 0$
for
![]() $|x|> N^{1-\kappa } \ell $
) and its rescaled version
$|x|> N^{1-\kappa } \ell $
) and its rescaled version
![]() $w_{N,\ell } : \Lambda \to \mathbb {R}$
through
$w_{N,\ell } : \Lambda \to \mathbb {R}$
through
![]() $w_{N,\ell } (x) = w_\ell (N^{1-\kappa } x) = 1 - f_{N,\ell } (x)$
. The Fourier coefficients of
$w_{N,\ell } (x) = w_\ell (N^{1-\kappa } x) = 1 - f_{N,\ell } (x)$
. The Fourier coefficients of
![]() $w_{N,\ell }$
are given by
$w_{N,\ell }$
are given by
 $$ \begin{align*} \widehat{w}_{N,\ell} (p) = \int_{\Lambda} w_\ell ( N^{1-\kappa} x) e^{-i p \cdot x} dx =\frac1{N^{3-3\kappa}}\, \widehat{w}_\ell \big(p/N^{1-\kappa}\big) \end{align*} $$
$$ \begin{align*} \widehat{w}_{N,\ell} (p) = \int_{\Lambda} w_\ell ( N^{1-\kappa} x) e^{-i p \cdot x} dx =\frac1{N^{3-3\kappa}}\, \widehat{w}_\ell \big(p/N^{1-\kappa}\big) \end{align*} $$
where
![]() $\widehat {w}_\ell (k)$
denotes the Fourier transform of the (compactly supported) function
$\widehat {w}_\ell (k)$
denotes the Fourier transform of the (compactly supported) function
![]() $w_\ell $
. Some important properties of the solution of the eigenvalue problem (2.5) are summarised in the following lemma, whose proof can be found in [Reference Boccato, Brennecke, Cenatiempo and Schlein3, Appendix A] (replacing
$w_\ell $
. Some important properties of the solution of the eigenvalue problem (2.5) are summarised in the following lemma, whose proof can be found in [Reference Boccato, Brennecke, Cenatiempo and Schlein3, Appendix A] (replacing
![]() $N\in \mathbb {N}$
by
$N\in \mathbb {N}$
by
![]() $N^{1-\kappa }$
).
$N^{1-\kappa }$
).
Lemma 2.1. Let
![]() $V \in L^3 (\mathbb {R}^3)$
be nonnegative, compactly supported and spherically symmetric. Fix
$V \in L^3 (\mathbb {R}^3)$
be nonnegative, compactly supported and spherically symmetric. Fix
![]() $\ell> 0$
and let
$\ell> 0$
and let
![]() $f_\ell $
denote the solution of (2.5). For
$f_\ell $
denote the solution of (2.5). For
![]() $N\in \mathbb {N}$
large enough, the following properties hold true:
$N\in \mathbb {N}$
large enough, the following properties hold true:
-
i) We have
 $$ \begin{align*} \bigg| \lambda_\ell - \frac{3\mathfrak{a} }{N^{3-3\kappa}\ell^3} \bigg| \leq \frac{1}{N^{3-3\kappa}\ell^3} \frac{C \mathfrak{a}^2}{\ell N^{1-\kappa}}. \end{align*} $$
$$ \begin{align*} \bigg| \lambda_\ell - \frac{3\mathfrak{a} }{N^{3-3\kappa}\ell^3} \bigg| \leq \frac{1}{N^{3-3\kappa}\ell^3} \frac{C \mathfrak{a}^2}{\ell N^{1-\kappa}}. \end{align*} $$
-
ii) We have
 $0\leq f_\ell , w_\ell \leq 1$
. Moreover, there exists a constant
$0\leq f_\ell , w_\ell \leq 1$
. Moreover, there exists a constant
 $C> 0$
such that
$C> 0$
such that  $$ \begin{align*} \left| \int V(x) f_\ell (x) dx - 8\pi \mathfrak{a} \right| \leq \frac{C \mathfrak{a}^2 }{\ell N^{1-\kappa}}. \end{align*} $$
$$ \begin{align*} \left| \int V(x) f_\ell (x) dx - 8\pi \mathfrak{a} \right| \leq \frac{C \mathfrak{a}^2 }{\ell N^{1-\kappa}}. \end{align*} $$
-
iii) There exists a constant
 $C>0 $
such that, for all
$C>0 $
such that, for all
 $x \in \mathbb {R}^3$
,
$x \in \mathbb {R}^3$
,  $$ \begin{align*} w_\ell(x)\leq \frac{C}{|x|+1} \quad\text{ and }\quad |\nabla w_\ell(x)|\leq \frac{C }{x^2+1}. \end{align*} $$
$$ \begin{align*} w_\ell(x)\leq \frac{C}{|x|+1} \quad\text{ and }\quad |\nabla w_\ell(x)|\leq \frac{C }{x^2+1}. \end{align*} $$
-
iv) There exists a constant
 $C> 0$
such that, for all
$C> 0$
such that, for all
 $p \in \mathbb {R}^3$
,
$p \in \mathbb {R}^3$
,  $$ \begin{align*} |\widehat{w}_{N,\ell} (p)| \leq \frac{C}{ N^{1-\kappa}p^2} . \end{align*} $$
$$ \begin{align*} |\widehat{w}_{N,\ell} (p)| \leq \frac{C}{ N^{1-\kappa}p^2} . \end{align*} $$
We consider the coefficients
![]() $\eta : \Lambda ^* \to \mathbb {R}$
defined through
$\eta : \Lambda ^* \to \mathbb {R}$
defined through
 $$ \begin{align} \eta_p = -N \widehat{w}_{N,\ell} (p) = - \frac{N^\kappa}{N^{2-2\kappa}} \,\widehat{w}_\ell(p/N^{1-\kappa}). \end{align} $$
$$ \begin{align} \eta_p = -N \widehat{w}_{N,\ell} (p) = - \frac{N^\kappa}{N^{2-2\kappa}} \,\widehat{w}_\ell(p/N^{1-\kappa}). \end{align} $$
Lemma 2.1 implies that
 $$ \begin{align} |\eta_p| \leq \frac{C N^\kappa}{p^2} \end{align} $$
$$ \begin{align} |\eta_p| \leq \frac{C N^\kappa}{p^2} \end{align} $$
for all
![]() $p \in \Lambda _+^*=2\pi \mathbb {Z}^3 \backslash \{0\}$
and for some constant
$p \in \Lambda _+^*=2\pi \mathbb {Z}^3 \backslash \{0\}$
and for some constant
![]() $C>0$
independent of
$C>0$
independent of
![]() $N\in \mathbb {N}$
(for
$N\in \mathbb {N}$
(for
![]() $N\in \mathbb {N}$
large enough). From (2.6), we find the relation
$N\in \mathbb {N}$
large enough). From (2.6), we find the relation
 $$ \begin{align} p^2 \eta_p + \frac{N^\kappa}{2}\widehat{V} (p/N^{1-\kappa}) + \frac{1}{2N} \sum_{q \in \Lambda^*} N^\kappa\widehat{V} ((p-q) /N^{1-\kappa})\eta_q = N^{3-2\kappa} \lambda_{\ell} (\widehat{\chi}_\ell * \widehat{f}_{N,\ell}) (p). \end{align} $$
$$ \begin{align} p^2 \eta_p + \frac{N^\kappa}{2}\widehat{V} (p/N^{1-\kappa}) + \frac{1}{2N} \sum_{q \in \Lambda^*} N^\kappa\widehat{V} ((p-q) /N^{1-\kappa})\eta_q = N^{3-2\kappa} \lambda_{\ell} (\widehat{\chi}_\ell * \widehat{f}_{N,\ell}) (p). \end{align} $$
From Lemma 2.1, part iii), we also obtain
 $$ \begin{align} |\eta_0| \leq N^{3-2\kappa} \int_{\mathbb{R}^3} w_\ell (x) dx \leq C N^\kappa . \end{align} $$
$$ \begin{align} |\eta_0| \leq N^{3-2\kappa} \int_{\mathbb{R}^3} w_\ell (x) dx \leq C N^\kappa . \end{align} $$
The coefficients
![]() $\eta _p$
will be used to model, through a Bogoliubov transformation, short-distance correlations among particles. To reach this goal, it is enough to act on momenta
$\eta _p$
will be used to model, through a Bogoliubov transformation, short-distance correlations among particles. To reach this goal, it is enough to act on momenta
![]() $|p| \gg N^{\kappa /2}$
. On low momenta, the Bogoliubov transformation is needed to diagonalise the (renormalised) quadratic part of the Hamiltonian. For
$|p| \gg N^{\kappa /2}$
. On low momenta, the Bogoliubov transformation is needed to diagonalise the (renormalised) quadratic part of the Hamiltonian. For
![]() $\varepsilon> 0$
small enough, we therefore define the set
$\varepsilon> 0$
small enough, we therefore define the set
 $$ \begin{align} P_L \; = \Big\{ p \in \Lambda^*_+ : |p| \leq N^{\kappa/2+\varepsilon} \Big\}\, \end{align} $$
$$ \begin{align} P_L \; = \Big\{ p \in \Lambda^*_+ : |p| \leq N^{\kappa/2+\varepsilon} \Big\}\, \end{align} $$
of low momenta. We will denote its complement by
![]() $P_L^c = \Lambda _+^* \backslash P_L$
. For
$P_L^c = \Lambda _+^* \backslash P_L$
. For
![]() $p \in \Lambda ^*_+$
we set
$p \in \Lambda ^*_+$
we set
with
![]() $\eta _p$
defined in (2.7),
$\eta _p$
defined in (2.7),
![]() $\tau _p \in \mathbb {R}$
defined by
$\tau _p \in \mathbb {R}$
defined by
 $$ \begin{align} \tanh(2\tau_p) = - \frac{8 \pi \mathfrak{a} N^\kappa}{p^2 +8 \pi \mathfrak{a} N^\kappa}\, \end{align} $$
$$ \begin{align} \tanh(2\tau_p) = - \frac{8 \pi \mathfrak{a} N^\kappa}{p^2 +8 \pi \mathfrak{a} N^\kappa}\, \end{align} $$
and
![]() $\chi (p \in S)$
denoting the indicator function of the set S. With these coefficients, we define the Bogoliubov transformation
$\chi (p \in S)$
denoting the indicator function of the set S. With these coefficients, we define the Bogoliubov transformation
 $$ \begin{align} T_\nu \; = \exp \bigg(\;\frac 12 \sum_{p \in \Lambda^*_+} \nu_p \big(a^*_p a^*_{-p} - \mbox{h.c.} \big) \;\bigg). \end{align} $$
$$ \begin{align} T_\nu \; = \exp \bigg(\;\frac 12 \sum_{p \in \Lambda^*_+} \nu_p \big(a^*_p a^*_{-p} - \mbox{h.c.} \big) \;\bigg). \end{align} $$
For any
![]() $p \neq 0$
we have
$p \neq 0$
we have
with the notation
![]() $\gamma _p = \cosh (\nu _p)$
and
$\gamma _p = \cosh (\nu _p)$
and
![]() $\sigma _p = \sinh (\nu _p)$
.
$\sigma _p = \sinh (\nu _p)$
.
With the Weyl operator (2.3) and the Bogoliubov transformation (2.13), we obtain the ‘squeezed’ coherent state
 $\widetilde {\Psi }_N = W_{N_0} T_\nu \Omega $
. Choosing
$\widetilde {\Psi }_N = W_{N_0} T_\nu \Omega $
. Choosing
![]() $N_0$
so that
$N_0$
so that
![]() $N = N_0 + \| \sigma \|^2$
, one can show that this trial state has approximately N particles and, to leading order, the correct ground state energy. However, as observed in [Reference Erdős, Schlein and Yau9] (for a similar trial state) and later in [Reference Napiórkowski, Reuvers and Solovej17], the energy of the quasi-free state
$N = N_0 + \| \sigma \|^2$
, one can show that this trial state has approximately N particles and, to leading order, the correct ground state energy. However, as observed in [Reference Erdős, Schlein and Yau9] (for a similar trial state) and later in [Reference Napiórkowski, Reuvers and Solovej17], the energy of the quasi-free state
![]() $\widetilde {\Psi }_N$
does not match the second-order correction in (1.3). To prove Proposition 1.3, we therefore need to modify the trial state. We do so by replacing the vacuum
$\widetilde {\Psi }_N$
does not match the second-order correction in (1.3). To prove Proposition 1.3, we therefore need to modify the trial state. We do so by replacing the vacuum
![]() $\Omega $
in the definition of
$\Omega $
in the definition of
![]() $\widetilde {\Psi }_N$
by the normalised Fock space vector
$\widetilde {\Psi }_N$
by the normalised Fock space vector
![]() $\xi _\nu / \| \xi _\nu \|$
, with
$\xi _\nu / \| \xi _\nu \|$
, with
![]() $\xi _\nu = e^{A_\nu } \Omega $
and the cubic phase
$\xi _\nu = e^{A_\nu } \Omega $
and the cubic phase
 $$ \begin{align} \begin{aligned} A_\nu =\frac 1 {\sqrt {N}} \sum_{\substack{r\in P_H,v \in P_S:\\r+v\in P_H}} \nu_r \sinh (\nu_v) \,a^*_{r+v} a^*_{-r} a^*_{-v} \Theta_{r,v} = \frac 1 {\sqrt {N}} \sum_{\substack{r\in P_H,v \in P_S:\\r+v\in P_H}} \eta_r \sigma_v \,a^*_{r+v} a^*_{-r} a^*_{-v} \Theta_{r,v}. \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} A_\nu =\frac 1 {\sqrt {N}} \sum_{\substack{r\in P_H,v \in P_S:\\r+v\in P_H}} \nu_r \sinh (\nu_v) \,a^*_{r+v} a^*_{-r} a^*_{-v} \Theta_{r,v} = \frac 1 {\sqrt {N}} \sum_{\substack{r\in P_H,v \in P_S:\\r+v\in P_H}} \eta_r \sigma_v \,a^*_{r+v} a^*_{-r} a^*_{-v} \Theta_{r,v}. \end{aligned}\end{align} $$
Here, we introduced the momentum sets
 $$ \begin{align} P_H &= \{ p \in \Lambda_+^* : |p|> N^{1-\kappa-\varepsilon} \}, \nonumber\\ P_S &=\Big\{p\in \Lambda^*_+: N^{\kappa/2-\varepsilon} \leq |p|\leq N^{\kappa/2 + \varepsilon}\Big\}. \end{align} $$
$$ \begin{align} P_H &= \{ p \in \Lambda_+^* : |p|> N^{1-\kappa-\varepsilon} \}, \nonumber\\ P_S &=\Big\{p\in \Lambda^*_+: N^{\kappa/2-\varepsilon} \leq |p|\leq N^{\kappa/2 + \varepsilon}\Big\}. \end{align} $$
Notice that
![]() $P_S \subset P_L$
. On the other hand, to make sure that
$P_S \subset P_L$
. On the other hand, to make sure that
![]() $P_H \cap P_L = \emptyset $
, from now on we will require that
$P_H \cap P_L = \emptyset $
, from now on we will require that
![]() $\varepsilon> 0$
is so small that
$\varepsilon> 0$
is so small that
![]() $3\kappa - 2 + 4 \varepsilon < 0$
. Moreover, in (2.15) we included, for every
$3\kappa - 2 + 4 \varepsilon < 0$
. Moreover, in (2.15) we included, for every
![]() $r \in P_H$
and every
$r \in P_H$
and every
![]() $v \in P_S$
, the cutoff
$v \in P_S$
, the cutoff
 $$ \begin{align*} \Theta_{r,v}&= \prod_{s \in P_H}\!\Big[ 1-\chi(\mathcal{N}_s>0)\chi(\mathcal{N}_{-s+v}>0)\Big] \nonumber\\ & \quad\times \prod_{w \in P_S}\! \Big[ 1-\chi(\mathcal{N}_w>0)\chi(\mathcal{N}_{r-w}+\mathcal{N}_{-r-v-w}>0) \Big] \end{align*} $$
$$ \begin{align*} \Theta_{r,v}&= \prod_{s \in P_H}\!\Big[ 1-\chi(\mathcal{N}_s>0)\chi(\mathcal{N}_{-s+v}>0)\Big] \nonumber\\ & \quad\times \prod_{w \in P_S}\! \Big[ 1-\chi(\mathcal{N}_w>0)\chi(\mathcal{N}_{r-w}+\mathcal{N}_{-r-v-w}>0) \Big] \end{align*} $$
where
![]() $\mathcal {N}_p = a^*_p a_p$
and
$\mathcal {N}_p = a^*_p a_p$
and
![]() $\chi (t>0)$
is the indicator function of the set
$\chi (t>0)$
is the indicator function of the set
![]() $\{ t>0 \}$
.
$\{ t>0 \}$
.
Remark. It is easy to check that the computation of the energy and the number of particles of the trial state we are constructing would not change substantially (and would still lead to a proof of Proposition 1.3), if in the definition (2.15) of
![]() $A_\nu $
we restricted the sum over r to the finite set
$A_\nu $
we restricted the sum over r to the finite set
![]() $P_H \cap \{ p \in \Lambda ^*_+ : |p| < N^{1-\kappa + \varepsilon } \} = \{ p \in \Lambda ^*_+ : N^{1-\kappa -\varepsilon } < |p| < N^{1-\kappa +\varepsilon } \}$
. With this choice, the infinite product over
$P_H \cap \{ p \in \Lambda ^*_+ : |p| < N^{1-\kappa + \varepsilon } \} = \{ p \in \Lambda ^*_+ : N^{1-\kappa -\varepsilon } < |p| < N^{1-\kappa +\varepsilon } \}$
. With this choice, the infinite product over
![]() $s \in P_H$
appearing in the definition of the cutoff
$s \in P_H$
appearing in the definition of the cutoff
![]() $\Theta _{r,v}$
would be replaced by a finite multiplication.
$\Theta _{r,v}$
would be replaced by a finite multiplication.
Let us briefly discuss the action of the cutoff
![]() $\Theta _{r,v}$
. To understand its role in the computation of
$\Theta _{r,v}$
. To understand its role in the computation of
![]() $e^{A_\nu } \Omega $
, we observe that, for every integer
$e^{A_\nu } \Omega $
, we observe that, for every integer
![]() $m \geq 2$
,
$m \geq 2$
,
![]() $r_1, \dots , r_m \in P_H$
,
$r_1, \dots , r_m \in P_H$
,
![]() $v_1, \dots , v_m \in P_S$
, with
$v_1, \dots , v_m \in P_S$
, with
![]() $r_1 + v_1, \dots , r_m +v_m \in P_H$
, we find
$r_1 + v_1, \dots , r_m +v_m \in P_H$
, we find
 $$ \begin{align*} \Theta_{r_m,v_m} &a^*_{r_{m-1}+v_{m-1}} a^*_{-r_{m-1}}a^*_{-v_{m-1}}\dots a^*_{r_1+v_1}a^*_{-r_1}a^*_{-v_1}\Omega=\\ &= \prod_{i,j=1}^{m-1}\prod_{\substack{p_\ell\in\{-r_\ell,r_\ell+v_\ell\},\\\ell=i,j,m}}\delta_{p_i\neq -p_j+v_m}\delta_{-p_m+v_i\neq p_j} \\ &\hspace{4cm} \times a^*_{r_{m-1}+v_{m-1}}a^*_{-r_{m-1}}a^*_{-v_{m-1}}\dots a^*_{r_1+v_1}a^*_{-r_1}a^*_{-v_1}\Omega. \end{align*} $$
$$ \begin{align*} \Theta_{r_m,v_m} &a^*_{r_{m-1}+v_{m-1}} a^*_{-r_{m-1}}a^*_{-v_{m-1}}\dots a^*_{r_1+v_1}a^*_{-r_1}a^*_{-v_1}\Omega=\\ &= \prod_{i,j=1}^{m-1}\prod_{\substack{p_\ell\in\{-r_\ell,r_\ell+v_\ell\},\\\ell=i,j,m}}\delta_{p_i\neq -p_j+v_m}\delta_{-p_m+v_i\neq p_j} \\ &\hspace{4cm} \times a^*_{r_{m-1}+v_{m-1}}a^*_{-r_{m-1}}a^*_{-v_{m-1}}\dots a^*_{r_1+v_1}a^*_{-r_1}a^*_{-v_1}\Omega. \end{align*} $$
The choice
![]() $i=j$
in the product on the second line introduces restrictions of the form
$i=j$
in the product on the second line introduces restrictions of the form
![]() $v_m \neq v_i$
and
$v_m \neq v_i$
and
![]() $p_m \neq p_i$
where
$p_m \neq p_i$
where
![]() $p_\ell \in \{-r_\ell ,r_\ell +v_\ell \}$
for
$p_\ell \in \{-r_\ell ,r_\ell +v_\ell \}$
for
![]() $\ell = m,i$
, for all
$\ell = m,i$
, for all
![]() $i \in \{1, \dots , m-1 \}$
(the condition
$i \in \{1, \dots , m-1 \}$
(the condition
![]() $p_i \neq -p_i + v_m$
, on the other hand, is trivially satisfied due to the assumption
$p_i \neq -p_i + v_m$
, on the other hand, is trivially satisfied due to the assumption
![]() $p_i\in P_H,v_m\in P_S$
). For
$p_i\in P_H,v_m\in P_S$
). For
![]() $m\geq 3$
, the cutoff
$m\geq 3$
, the cutoff
![]() $\Theta _{r_m,v_m}$
implements additional restrictions involving three indices of the form
$\Theta _{r_m,v_m}$
implements additional restrictions involving three indices of the form
![]() $-p_i+v_j \neq p_k$
with
$-p_i+v_j \neq p_k$
with
![]() $p_\ell \in \{-r_\ell ,r_\ell +v_\ell \}, \ell =i,j,k$
where
$p_\ell \in \{-r_\ell ,r_\ell +v_\ell \}, \ell =i,j,k$
where
![]() $i,j,k = 1,\dots ,m, i\neq j\neq k$
, so that exactly one of the three indices is m. We conclude that, for any
$i,j,k = 1,\dots ,m, i\neq j\neq k$
, so that exactly one of the three indices is m. We conclude that, for any
![]() $m\geq 2$
,
$m\geq 2$
,
 $$ \begin{align} A_\nu^m\Omega = &\frac1{N^{m/2}}\sum_{\substack{r_1\in P_H,v_1\in P_S:\\r_1+v_1\in P_H}}\dots\sum_{\substack{r_m\in P_H,v_m\in P_S:\nonumber\\r_m+v_m\in P_H}}\prod_{i=1}^m \eta_{r_i}\sigma_{v_i}\nonumber\\ &\hspace{2cm} \times \theta(\{r_j,v_j\}_{j=1}^m)a^*_{r_m+v_m}a^*_{-r_m}a^*_{-v_m}\dots a^*_{r_1+v_1}a^*_{-r_1}a^*_{v_1}\Omega \end{align} $$
$$ \begin{align} A_\nu^m\Omega = &\frac1{N^{m/2}}\sum_{\substack{r_1\in P_H,v_1\in P_S:\\r_1+v_1\in P_H}}\dots\sum_{\substack{r_m\in P_H,v_m\in P_S:\nonumber\\r_m+v_m\in P_H}}\prod_{i=1}^m \eta_{r_i}\sigma_{v_i}\nonumber\\ &\hspace{2cm} \times \theta(\{r_j,v_j\}_{j=1}^m)a^*_{r_m+v_m}a^*_{-r_m}a^*_{-v_m}\dots a^*_{r_1+v_1}a^*_{-r_1}a^*_{v_1}\Omega \end{align} $$
where
 $$ \begin{align} \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) = \prod_{\substack{i,j,k=1\\j\neq k}}^m\prod_{\substack{p_i\in\{-r_i,r_i+v_i\}\\ p_k\in\{-r_k,r_k+v_k\}}}\delta_{-p_i+v_j\neq p_k}. \end{align} $$
$$ \begin{align} \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) = \prod_{\substack{i,j,k=1\\j\neq k}}^m\prod_{\substack{p_i\in\{-r_i,r_i+v_i\}\\ p_k\in\{-r_k,r_k+v_k\}}}\delta_{-p_i+v_j\neq p_k}. \end{align} $$
To illustrate the reason for the introduction of the cutoff, let us compute the norm
![]() $\| \xi _\nu \|$
of the vector
$\| \xi _\nu \|$
of the vector
![]() $\xi _\nu = e^{A_\nu } \Omega $
. With (2.17), we find
$\xi _\nu = e^{A_\nu } \Omega $
. With (2.17), we find
 $$ \begin{align} \| \xi_\nu\|^2 &= \sum_{m\geq 0}\frac{1}{(m!)^2} \| (A_\nu)^m \Omega \|^2 \nonumber\\ &= \sum_{m\geq 0}\frac1{(m!)^2}\frac1{N^m} \sum_{\substack{v_1, {\tilde{v}}_1 \in P_S \\ r_1, {\tilde{r}}_1 \in P_H: \\ r_1 + v_1 ,\, {\tilde{r}}_1 + {\tilde{v}}_1 \in P_H}} \cdots \sum_{\substack{v_m, {\tilde{v}}_m \in P_S \\ r_m, {\tilde{r}}_m \in P_H: \\ r_m + v_m ,\, {\tilde{r}}_m + {\tilde{v}}_m \in P_H}} \theta\big(\{{\tilde{r}}_j,{\tilde{v}}_j\}_{j=1}^m\big) \theta\big(\{r_j,v_j\}_{j=1}^m\big) \nonumber\\ & \hspace{1cm}\times\prod_{i=1}^m \eta_{r_i}\eta_{{\tilde{r}}_i} \sigma_{v_i} \sigma_{{\tilde{v}}_i} {\bigl\langle a^*_{r_m+v_m}a^*_{-r_m}a^*_{-v_m}\dots a^*_{-v_1}\Omega, a^*_{\tilde{r}_m+\tilde{v}_m}a^*_{-\tilde{r}_m}a^*_{-\tilde{v}_m} \dots a^*_{-\tilde{v}_1}\Omega\bigr\rangle}. \end{align} $$
$$ \begin{align} \| \xi_\nu\|^2 &= \sum_{m\geq 0}\frac{1}{(m!)^2} \| (A_\nu)^m \Omega \|^2 \nonumber\\ &= \sum_{m\geq 0}\frac1{(m!)^2}\frac1{N^m} \sum_{\substack{v_1, {\tilde{v}}_1 \in P_S \\ r_1, {\tilde{r}}_1 \in P_H: \\ r_1 + v_1 ,\, {\tilde{r}}_1 + {\tilde{v}}_1 \in P_H}} \cdots \sum_{\substack{v_m, {\tilde{v}}_m \in P_S \\ r_m, {\tilde{r}}_m \in P_H: \\ r_m + v_m ,\, {\tilde{r}}_m + {\tilde{v}}_m \in P_H}} \theta\big(\{{\tilde{r}}_j,{\tilde{v}}_j\}_{j=1}^m\big) \theta\big(\{r_j,v_j\}_{j=1}^m\big) \nonumber\\ & \hspace{1cm}\times\prod_{i=1}^m \eta_{r_i}\eta_{{\tilde{r}}_i} \sigma_{v_i} \sigma_{{\tilde{v}}_i} {\bigl\langle a^*_{r_m+v_m}a^*_{-r_m}a^*_{-v_m}\dots a^*_{-v_1}\Omega, a^*_{\tilde{r}_m+\tilde{v}_m}a^*_{-\tilde{r}_m}a^*_{-\tilde{v}_m} \dots a^*_{-\tilde{v}_1}\Omega\bigr\rangle}. \end{align} $$
Clearly, for the expectation on the last line not to vanish, all creation and annihilation operators with momenta in
![]() $P_S$
must be contracted among themselves. Since, on the support of
$P_S$
must be contracted among themselves. Since, on the support of
 $\theta (\{ r_j, v_j \}_{j=1}^m)$
,
$\theta (\{ r_j, v_j \}_{j=1}^m)$
,
![]() $v_i \neq v_j$
for all
$v_i \neq v_j$
for all
![]() $i\neq j$
(and, similarly,
$i\neq j$
(and, similarly,
![]() ${\tilde {v}}_i \neq {\tilde {v}}_j$
for all
${\tilde {v}}_i \neq {\tilde {v}}_j$
for all
![]() $i\neq j$
on the support of
$i\neq j$
on the support of
 $\theta (\{ \widetilde {r}_j, \widetilde {v}_j \}_{j=1}^m)$
), we have
$\theta (\{ \widetilde {r}_j, \widetilde {v}_j \}_{j=1}^m)$
), we have
![]() $(m!)$
identical contributions arising from this pairing. We end up with
$(m!)$
identical contributions arising from this pairing. We end up with
 $$ \begin{align} & \| \xi_\nu\|^2 =\sum_{m\geq 0}\frac1{m!}\frac1{N^m} \sum_{\substack{v_1 \in P_S, r_1, {\tilde{r}}_1 \in P_H: \\ r_1 + v_1 ,\, {\tilde{r}}_1 + v_1 \in P_H}} \cdots \sum_{\substack{v_m \in P_S, r_m, {\tilde{r}}_m \in P_H: \\ r_m + v_m ,\, {\tilde{r}}_m + v_m \in P_H}} \hskip -0.5cm \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{ {\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \nonumber\\ & \hspace{4.5cm}\times \prod_{i=1}^m \eta_{r_i}\eta_{{\tilde{r}}_i} \sigma^2_{v_i} {\bigl\langle\Omega,A_{r_1,v_1}\dots A_{r_m,v_m} A^*_{\tilde{r}_m,v_m} \dots A^*_{\tilde{r}_1,v_1} \Omega\bigr\rangle} \end{align} $$
$$ \begin{align} & \| \xi_\nu\|^2 =\sum_{m\geq 0}\frac1{m!}\frac1{N^m} \sum_{\substack{v_1 \in P_S, r_1, {\tilde{r}}_1 \in P_H: \\ r_1 + v_1 ,\, {\tilde{r}}_1 + v_1 \in P_H}} \cdots \sum_{\substack{v_m \in P_S, r_m, {\tilde{r}}_m \in P_H: \\ r_m + v_m ,\, {\tilde{r}}_m + v_m \in P_H}} \hskip -0.5cm \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{ {\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \nonumber\\ & \hspace{4.5cm}\times \prod_{i=1}^m \eta_{r_i}\eta_{{\tilde{r}}_i} \sigma^2_{v_i} {\bigl\langle\Omega,A_{r_1,v_1}\dots A_{r_m,v_m} A^*_{\tilde{r}_m,v_m} \dots A^*_{\tilde{r}_1,v_1} \Omega\bigr\rangle} \end{align} $$
where we have introduced the notation
![]() $A_{r_i,v_i} = a_{r_i+v_i} a_{-r_i}$
.
$A_{r_i,v_i} = a_{r_i+v_i} a_{-r_i}$
.
It is now important to observe that, because of the presence of the cutoffs, the annihilation operators in
![]() $A_{r_j, v_j}$
must be contracted with the creation operators in
$A_{r_j, v_j}$
must be contracted with the creation operators in
![]() $A_{\widetilde {r}_j, v_j}$
. In fact, if this was not the case, we would have
$A_{\widetilde {r}_j, v_j}$
. In fact, if this was not the case, we would have
![]() $-r_j = -\widetilde {r}_\ell $
or
$-r_j = -\widetilde {r}_\ell $
or
![]() $-r_j = \widetilde {r}_\ell + v_\ell $
and
$-r_j = \widetilde {r}_\ell + v_\ell $
and
![]() $r_j + v_j = -\widetilde {r}_k$
or
$r_j + v_j = -\widetilde {r}_k$
or
![]() $r_j + v_j = \widetilde {r}_k + v_k$
, with at least one of the two indices
$r_j + v_j = \widetilde {r}_k + v_k$
, with at least one of the two indices
![]() $\ell , k$
different from j. This would imply one of the four relations
$\ell , k$
different from j. This would imply one of the four relations
![]() $\widetilde {r}_\ell + v_j = -\widetilde {r}_k$
,
$\widetilde {r}_\ell + v_j = -\widetilde {r}_k$
,
![]() $\widetilde {r}_\ell + v_j = \widetilde {r}_k + v_k$
,
$\widetilde {r}_\ell + v_j = \widetilde {r}_k + v_k$
,
![]() $ \widetilde {r}_\ell + v_\ell = \widetilde {r}_k + v_j$
,
$ \widetilde {r}_\ell + v_\ell = \widetilde {r}_k + v_j$
,
![]() $-\widetilde {r}_\ell - v_\ell + v_j = \widetilde {r}_k + v_k$
, all of which are forbidden by the cutoff
$-\widetilde {r}_\ell - v_\ell + v_j = \widetilde {r}_k + v_k$
, all of which are forbidden by the cutoff
 $\theta \big ( \{ \widetilde {r}_j, \widetilde {v}_j \}_{j=1}^{m} \big )$
. We conclude that
$\theta \big ( \{ \widetilde {r}_j, \widetilde {v}_j \}_{j=1}^{m} \big )$
. We conclude that
 $$ \begin{align} {\bigl\langle\Omega,A_{r_1,v_1}\dots A_{r_m,v_m} A^*_{\tilde{r}_m,v_m} \dots A^*_{\tilde{r}_1,v_1} \Omega\bigr\rangle} &\theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{ {\tilde{r}}_j, {\tilde{v}}_j \}_{j=1}^{m} \big) \nonumber\\ &\quad = \prod_{i=1}^m \Big(\delta_{{\tilde{r}}_i, r_i} + \delta_{-{\tilde{r}}_i, r_i+v_i}\Big) \theta\big( \{r_j, v_j \}_{j=1}^{m} \big)\, \end{align} $$
$$ \begin{align} {\bigl\langle\Omega,A_{r_1,v_1}\dots A_{r_m,v_m} A^*_{\tilde{r}_m,v_m} \dots A^*_{\tilde{r}_1,v_1} \Omega\bigr\rangle} &\theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{ {\tilde{r}}_j, {\tilde{v}}_j \}_{j=1}^{m} \big) \nonumber\\ &\quad = \prod_{i=1}^m \Big(\delta_{{\tilde{r}}_i, r_i} + \delta_{-{\tilde{r}}_i, r_i+v_i}\Big) \theta\big( \{r_j, v_j \}_{j=1}^{m} \big)\, \end{align} $$
(after identification of the momenta, the second cutoff becomes superfluous). From (2.20), we obtain
 $$ \begin{align} \|\xi_\nu \|^2 &= \sum_{m\geq 0}\frac1{m!}\frac1{N^{m}} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta\big(\{r_j, v_j\}_{j=1}^{m}\big) \, \prod_{i=1}^{m}\eta_{r_i} \big( \eta_{r_i} +\eta_{r_i+v_i} \big) \sigma_{v_i}^2\nonumber\\ &= \sum_{m\geq 0}\frac1{2^m m!}\frac1{N^{m}} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta\big(\{r_j, v_j\}_{j=1}^{m}\big) \, \prod_{i=1}^{m} \big( \eta_{r_i} +\eta_{r_i+v_i} \big)^2 \sigma_{v_i}^2 \end{align} $$
$$ \begin{align} \|\xi_\nu \|^2 &= \sum_{m\geq 0}\frac1{m!}\frac1{N^{m}} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta\big(\{r_j, v_j\}_{j=1}^{m}\big) \, \prod_{i=1}^{m}\eta_{r_i} \big( \eta_{r_i} +\eta_{r_i+v_i} \big) \sigma_{v_i}^2\nonumber\\ &= \sum_{m\geq 0}\frac1{2^m m!}\frac1{N^{m}} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta\big(\{r_j, v_j\}_{j=1}^{m}\big) \, \prod_{i=1}^{m} \big( \eta_{r_i} +\eta_{r_i+v_i} \big)^2 \sigma_{v_i}^2 \end{align} $$
where we used the invariance of
![]() $\theta $
, with respect to
$\theta $
, with respect to
![]() $-r_i \to r_i + v_i$
. The cutoffs have been used first to exclude coinciding momenta in
$-r_i \to r_i + v_i$
. The cutoffs have been used first to exclude coinciding momenta in
![]() $v_1, \dots , v_m$
and in
$v_1, \dots , v_m$
and in
![]() $\widetilde {v}_1, \dots , \widetilde {v}_m$
(which implies that, up to permutations, the pairing of the momenta in
$\widetilde {v}_1, \dots , \widetilde {v}_m$
(which implies that, up to permutations, the pairing of the momenta in
![]() $P_S$
is unique) and then in (2.21) to make sure that annihilation operators in
$P_S$
is unique) and then in (2.21) to make sure that annihilation operators in
![]() $A_{r_j, v_j}$
can only be contracted with the creation operators in
$A_{r_j, v_j}$
can only be contracted with the creation operators in
 $A^*_{\widetilde {r}_j, v_j}$
. This substantially simplifies computations. Similar simplifications will arise in the computation of the energy of our trial state.
$A^*_{\widetilde {r}_j, v_j}$
. This substantially simplifies computations. Similar simplifications will arise in the computation of the energy of our trial state.
Apart from the formula (2.22) for the norm
![]() $\| \xi _\nu \|^2$
, we will also need bounds on the expectation, in the state
$\| \xi _\nu \|^2$
, we will also need bounds on the expectation, in the state
![]() $\xi _\nu / \| \xi _\nu \|$
, of the number of particles operator
$\xi _\nu / \| \xi _\nu \|$
, of the number of particles operator
![]() $\mathcal {N}$
, of
$\mathcal {N}$
, of
![]() $\mathcal {N}^2$
, of the kinetic energy operator
$\mathcal {N}^2$
, of the kinetic energy operator
![]() $\mathcal {K}$
and of the product
$\mathcal {K}$
and of the product
![]() $\mathcal {K} \mathcal {N}$
. These bounds are collected in the next proposition, whose proof will be discussed in Section 5.
$\mathcal {K} \mathcal {N}$
. These bounds are collected in the next proposition, whose proof will be discussed in Section 5.
Proposition 2.2. Let
![]() $\xi _\nu =e^{A_\nu }\Omega $
with
$\xi _\nu =e^{A_\nu }\Omega $
with
![]() $e^{A_\nu }$
defined in (2.15) with
$e^{A_\nu }$
defined in (2.15) with
![]() $\kappa \in (1/2 ;2/3)$
and
$\kappa \in (1/2 ;2/3)$
and
![]() $\varepsilon> 0$
such that
$\varepsilon> 0$
such that
![]() $3\kappa -2 + 4\varepsilon < 0$
. Then, under the assumptions of Theorem 1.1, we have
$3\kappa -2 + 4\varepsilon < 0$
. Then, under the assumptions of Theorem 1.1, we have
 $$ \begin{align} \frac{\langle \xi_\nu, \mathcal{N}^{\,j} \xi_\nu \rangle}{\| \xi_\nu \|^2} & \leq C N^{(9\kappa/2-2+\varepsilon)j} \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu, \mathcal{N}^{\,j} \xi_\nu \rangle}{\| \xi_\nu \|^2} & \leq C N^{(9\kappa/2-2+\varepsilon)j} \end{align} $$
and
 $$ \begin{align} \frac{ {\bigl\langle\xi_\nu,\mathcal{K} \mathcal{N}^{j-1} \xi_\nu\bigr\rangle}}{\|\xi_\nu\|^2} \leq C N^{5\kappa/2}N^{(9\kappa/2-2+\varepsilon)(j-1)} \end{align} $$
$$ \begin{align} \frac{ {\bigl\langle\xi_\nu,\mathcal{K} \mathcal{N}^{j-1} \xi_\nu\bigr\rangle}}{\|\xi_\nu\|^2} \leq C N^{5\kappa/2}N^{(9\kappa/2-2+\varepsilon)(j-1)} \end{align} $$
for
![]() $j=1,2$
.
$j=1,2$
.
Using the Weyl operator
![]() $W_{N_0}$
from (2.3), the Bogoliubov transformation
$W_{N_0}$
from (2.3), the Bogoliubov transformation
![]() $T_\nu $
defined in (2.13) and the cubic phase
$T_\nu $
defined in (2.13) and the cubic phase
![]() $A_\nu $
introduced in (2.15) (or, equivalently, the vector
$A_\nu $
introduced in (2.15) (or, equivalently, the vector
![]() $\xi _\nu = e^{A_\nu } \Omega $
), we can now define our trial state
$\xi _\nu = e^{A_\nu } \Omega $
), we can now define our trial state
 $$ \begin{align} \Psi_N = \frac{W_{N_0} T_\nu e^{A_\nu} \Omega}{\| W_{N_0} T_\nu e^{A_\nu} \Omega \|} = W_{N_0} T_\nu \frac{\xi_\nu}{\| \xi_\nu \|} . \end{align} $$
$$ \begin{align} \Psi_N = \frac{W_{N_0} T_\nu e^{A_\nu} \Omega}{\| W_{N_0} T_\nu e^{A_\nu} \Omega \|} = W_{N_0} T_\nu \frac{\xi_\nu}{\| \xi_\nu \|} . \end{align} $$
Here, we choose
![]() $N_0> 0$
such that
$N_0> 0$
such that
where
![]() $\sigma _L$
denotes the restriction to the set
$\sigma _L$
denotes the restriction to the set
![]() $P_L$
of the coefficients
$P_L$
of the coefficients
![]() $\sigma _p = \sinh (\nu _p)$
, with
$\sigma _p = \sinh (\nu _p)$
, with
![]() $\nu _p$
defining the Bogoliubov transformation
$\nu _p$
defining the Bogoliubov transformation
![]() $T_\nu $
; see (2.13).
$T_\nu $
; see (2.13).
Let us briefly compare our trial state with the one of [Reference Yau and Yin20]. In both approaches, the condensate is perturbed with operators creating double and triple excitations, the latter having two particles with high momenta and one particle with low momentum. Moreover, similarly as in [Reference Yau and Yin20], we impose cutoffs making sure that each low momentum appears only once. In contrast to [Reference Yau and Yin20], we also impose cutoffs on high momenta. Moreover, we have a clearer separation between creation of pairs (obtained through the Bogoliubov transformation
![]() $T_\nu $
) and creation of triples. Finally, in our approach, we create triple excitations through the action of
$T_\nu $
) and creation of triples. Finally, in our approach, we create triple excitations through the action of
![]() $e^{A_\nu }$
on the vacuum; the algebraic structure of the exponential makes the analysis and the combinatorics much simpler.
$e^{A_\nu }$
on the vacuum; the algebraic structure of the exponential makes the analysis and the combinatorics much simpler.
As shown in the next proposition, the choice (2.26) of
![]() $N_0$
guarantees that
$N_0$
guarantees that
![]() $\Psi _N$
has the expected number of particles.
$\Psi _N$
has the expected number of particles.
Proposition 2.3. Let
![]() $\Psi _N$
be defined in (2.25) with the parameter
$\Psi _N$
be defined in (2.25) with the parameter
![]() $N_0$
appearing in (2.3) defined by (2.26). Let
$N_0$
appearing in (2.3) defined by (2.26). Let
![]() $\kappa \in (1/2; 2/3)$
and
$\kappa \in (1/2; 2/3)$
and
![]() $\varepsilon> 0$
so that
$\varepsilon> 0$
so that
![]() $3\kappa -2 + 4\varepsilon < 0$
. Then
$3\kappa -2 + 4\varepsilon < 0$
. Then
for all N large enough.
To prove Proposition 2.3 (and later to show other properties of the trial state
![]() $\Psi _N$
) in the next lemma we collect some bounds for norms of the coefficients appearing in the definition of
$\Psi _N$
) in the next lemma we collect some bounds for norms of the coefficients appearing in the definition of
![]() $A_\nu $
in (2.15). We denote here by
$A_\nu $
in (2.15). We denote here by
![]() $\eta _L, \eta _{L^c}, \eta _S, \eta _H$
the restriction of
$\eta _L, \eta _{L^c}, \eta _S, \eta _H$
the restriction of
![]() $\eta : \Lambda ^* \to \mathbb {R}$
to the set
$\eta : \Lambda ^* \to \mathbb {R}$
to the set
![]() $P_L, P_L^c, P_S$
and, respectively,
$P_L, P_L^c, P_S$
and, respectively,
![]() $P_H$
. Similarly, we define
$P_H$
. Similarly, we define
![]() $\gamma _L, \gamma _{L^c}, \gamma _H, \gamma _S$
and
$\gamma _L, \gamma _{L^c}, \gamma _H, \gamma _S$
and
![]() $\sigma _L, \sigma _{L^c}, \sigma _H, \sigma _S$
.
$\sigma _L, \sigma _{L^c}, \sigma _H, \sigma _S$
.
Lemma 2.4. We have
 $$ \begin{align*} &\| \eta_{L^c} \|^2 \leq C N^{3 \kappa/2 -\varepsilon} , \quad && \| \eta_{L^c} \|^2_{H^1} \leq C N^{1+\kappa}, \quad && \|\eta_{L^c} \|_\infty \leq C N^{-2\varepsilon} \\[0.2cm] &\| \eta_H \|^2 \leq C N^{3\kappa-1 +\varepsilon} , \quad && \| \eta_H \|^2_{H^1} \leq C N^{1+\kappa} , \quad && \|\eta_H \|_\infty \leq C N^{3\kappa-2 +2\varepsilon} . \end{align*} $$
$$ \begin{align*} &\| \eta_{L^c} \|^2 \leq C N^{3 \kappa/2 -\varepsilon} , \quad && \| \eta_{L^c} \|^2_{H^1} \leq C N^{1+\kappa}, \quad && \|\eta_{L^c} \|_\infty \leq C N^{-2\varepsilon} \\[0.2cm] &\| \eta_H \|^2 \leq C N^{3\kappa-1 +\varepsilon} , \quad && \| \eta_H \|^2_{H^1} \leq C N^{1+\kappa} , \quad && \|\eta_H \|_\infty \leq C N^{3\kappa-2 +2\varepsilon} . \end{align*} $$
In particular, this implies that
![]() $\|\gamma _H\|_\infty , \|\sigma _H\|_\infty \leq C$
. Moreover, we have
$\|\gamma _H\|_\infty , \|\sigma _H\|_\infty \leq C$
. Moreover, we have
and
 $$ \begin{align*} \| \gamma_L \|^2 \leq C N^{3\kappa/2 + 3\varepsilon}, \qquad \| \sigma_L \|^2 \leq C N^{3\kappa/2} \, , \qquad \quad \| \sigma_L \|^2_{H^1} \leq C N^{5\kappa/2 +\varepsilon}. \end{align*} $$
$$ \begin{align*} \| \gamma_L \|^2 \leq C N^{3\kappa/2 + 3\varepsilon}, \qquad \| \sigma_L \|^2 \leq C N^{3\kappa/2} \, , \qquad \quad \| \sigma_L \|^2_{H^1} \leq C N^{5\kappa/2 +\varepsilon}. \end{align*} $$
Finally, we observe that
 $$ \begin{align*} \| \sigma_S\|^2 \leq C N^{3\kappa/2}, \qquad \| \sigma_S\|^2_{H^1} \leq C N^{5\kappa/2+\varepsilon}, \qquad \| \gamma_S \|_\infty^2, \| \sigma_S \|^2_\infty \leq C N^\varepsilon . \end{align*} $$
$$ \begin{align*} \| \sigma_S\|^2 \leq C N^{3\kappa/2}, \qquad \| \sigma_S\|^2_{H^1} \leq C N^{5\kappa/2+\varepsilon}, \qquad \| \gamma_S \|_\infty^2, \| \sigma_S \|^2_\infty \leq C N^\varepsilon . \end{align*} $$
Proof. The bounds for
![]() $\|\eta _{L^c}\|$
,
$\|\eta _{L^c}\|$
,
![]() $\| \eta _H\|$
,
$\| \eta _H\|$
,
![]() $\|\eta _{L^c}\|_\infty $
and
$\|\eta _{L^c}\|_\infty $
and
![]() $\| \eta _H\|_\infty $
follow from (2.8). On the other hand, with the notation
$\| \eta _H\|_\infty $
follow from (2.8). On the other hand, with the notation
![]() $\check {\eta } (x) = - N w_\ell ( N^{1-\kappa } x)$
for the function on
$\check {\eta } (x) = - N w_\ell ( N^{1-\kappa } x)$
for the function on
![]() $\Lambda $
with Fourier coefficients
$\Lambda $
with Fourier coefficients
![]() $\eta _p$
, we find from Lemma 2.1, part iii),
$\eta _p$
, we find from Lemma 2.1, part iii),
 $$ \begin{align*} \| \eta_{L^c} \|_{H^1}^2 \leq C \sum_{p \in \Lambda^*} p^2 |\eta_p|^2 \leq C \int |\nabla \check{\eta} (x)|^2 dx \leq C N^{1+ \kappa} \int_{\mathbb{R}^3} \frac{1}{(|x|^2+1)^2}\, dx \leq C N^{1+\kappa} . \end{align*} $$
$$ \begin{align*} \| \eta_{L^c} \|_{H^1}^2 \leq C \sum_{p \in \Lambda^*} p^2 |\eta_p|^2 \leq C \int |\nabla \check{\eta} (x)|^2 dx \leq C N^{1+ \kappa} \int_{\mathbb{R}^3} \frac{1}{(|x|^2+1)^2}\, dx \leq C N^{1+\kappa} . \end{align*} $$
To show bounds for
![]() $\sigma _L, \gamma _L$
we observe that, with (2.12) and
$\sigma _L, \gamma _L$
we observe that, with (2.12) and
 $\gamma _p^2 = 1 + \sigma _p^2$
, we obtain
$\gamma _p^2 = 1 + \sigma _p^2$
, we obtain
 $$ \begin{align} \sigma^2_p = \frac{p^2 + 8\pi \frak{a} N^\kappa - \sqrt{|p|^4 + 16 \pi \frak{a} N^\kappa p^2}}{2 \sqrt{|p|^4 + 16 \pi \frak{a} N^\kappa p^2}} , \qquad \sigma_p \gamma_p = \frac{-8\pi \frak{a} N^\kappa}{2 \sqrt{|p|^4 + 16 \pi \frak{a} N^\kappa p^2}}. \end{align} $$
$$ \begin{align} \sigma^2_p = \frac{p^2 + 8\pi \frak{a} N^\kappa - \sqrt{|p|^4 + 16 \pi \frak{a} N^\kappa p^2}}{2 \sqrt{|p|^4 + 16 \pi \frak{a} N^\kappa p^2}} , \qquad \sigma_p \gamma_p = \frac{-8\pi \frak{a} N^\kappa}{2 \sqrt{|p|^4 + 16 \pi \frak{a} N^\kappa p^2}}. \end{align} $$
Recalling that
![]() $P_L = \{ p \in \Lambda ^*_+ : |p| \leq N^{\kappa /2+\varepsilon } \}$
, we find
$P_L = \{ p \in \Lambda ^*_+ : |p| \leq N^{\kappa /2+\varepsilon } \}$
, we find
 $$ \begin{align} \| \sigma_L\|^2_\infty \leq \mathop{\mathrm{sup}}\limits_{p \in P_L : |p| \leq N^{\kappa/2}} C \frac{N^{\kappa/2}}{|p|} + \mathop{\mathrm{sup}}\limits_{p \in P_L : |p|\geq N^{\kappa/2}} C \frac{N^{2\kappa}}{|p|^4} \leq C N^{\kappa /2}. \end{align} $$
$$ \begin{align} \| \sigma_L\|^2_\infty \leq \mathop{\mathrm{sup}}\limits_{p \in P_L : |p| \leq N^{\kappa/2}} C \frac{N^{\kappa/2}}{|p|} + \mathop{\mathrm{sup}}\limits_{p \in P_L : |p|\geq N^{\kappa/2}} C \frac{N^{2\kappa}}{|p|^4} \leq C N^{\kappa /2}. \end{align} $$
Moreover, by definition of
![]() $P_S$
we get
$P_S$
we get
 $$ \begin{align*} \|\sigma_S\|_\infty^2\leq \mathop{\mathrm{sup}}\limits_{N^{\kappa/2-\varepsilon}\leq|p|\leq N^{\kappa/2}} C \frac{N^{\kappa/2}}{|p|} + \mathop{\mathrm{sup}}\limits_{p \in P_L: |p|\geq N^{\kappa/2}} C \frac{N^{2\kappa}}{|p|^4} \leq C N^\varepsilon. \end{align*} $$
$$ \begin{align*} \|\sigma_S\|_\infty^2\leq \mathop{\mathrm{sup}}\limits_{N^{\kappa/2-\varepsilon}\leq|p|\leq N^{\kappa/2}} C \frac{N^{\kappa/2}}{|p|} + \mathop{\mathrm{sup}}\limits_{p \in P_L: |p|\geq N^{\kappa/2}} C \frac{N^{2\kappa}}{|p|^4} \leq C N^\varepsilon. \end{align*} $$
Using again
 $\gamma ^2_p= 1+ \sigma ^2_p$
, we find
$\gamma ^2_p= 1+ \sigma ^2_p$
, we find
![]() $\| \gamma _L\|_\infty \leq C N^{\kappa /2}$
and
$\| \gamma _L\|_\infty \leq C N^{\kappa /2}$
and
![]() $\|\gamma _S\|_\infty \leq C N^\varepsilon $
. Similarly, we obtain
$\|\gamma _S\|_\infty \leq C N^\varepsilon $
. Similarly, we obtain
 $$ \begin{align} \| \sigma_L\|^2 \leq C \sum_{p \in P_L : |p| \leq N^{\kappa/2}} \frac{N^{\kappa/2}}{|p|} + C \sum_{p \in P_L : |p|> N^{\kappa/2}} \frac{N^{2\kappa}}{|p|^4} \leq C N^{3\kappa/2} \end{align} $$
$$ \begin{align} \| \sigma_L\|^2 \leq C \sum_{p \in P_L : |p| \leq N^{\kappa/2}} \frac{N^{\kappa/2}}{|p|} + C \sum_{p \in P_L : |p|> N^{\kappa/2}} \frac{N^{2\kappa}}{|p|^4} \leq C N^{3\kappa/2} \end{align} $$
and thus
![]() $\|\gamma _L\|^2 \leq C N^{3\kappa /2 + 3 \varepsilon }$
. Moreover, we have
$\|\gamma _L\|^2 \leq C N^{3\kappa /2 + 3 \varepsilon }$
. Moreover, we have
 $$ \begin{align} \| \sigma_L\|^2_{H_1} \leq C \sum_{p \in P_L : |p| \leq N^{\kappa/2}} |p| N^{\kappa/2} + C \sum_{p \in P_L : |p| \geq N^{\kappa/2}} \frac{N^{2\kappa} }{p^2} \leq C N^{5\kappa/2 + \varepsilon}. \end{align} $$
$$ \begin{align} \| \sigma_L\|^2_{H_1} \leq C \sum_{p \in P_L : |p| \leq N^{\kappa/2}} |p| N^{\kappa/2} + C \sum_{p \in P_L : |p| \geq N^{\kappa/2}} \frac{N^{2\kappa} }{p^2} \leq C N^{5\kappa/2 + \varepsilon}. \end{align} $$
The bound for
![]() $\| \sigma _L \gamma _L\|_1$
is proved similarly, using the expression for
$\| \sigma _L \gamma _L\|_1$
is proved similarly, using the expression for
![]() $\gamma _p \sigma _p$
in (2.28). Finally, we note that the estimates (2.30) and (2.31) do not improve when we consider the restriction of
$\gamma _p \sigma _p$
in (2.28). Finally, we note that the estimates (2.30) and (2.31) do not improve when we consider the restriction of
![]() $\sigma _p$
to
$\sigma _p$
to
![]() $P_S\subset P_L$
; hence,
$P_S\subset P_L$
; hence,
![]() $\| \sigma _S\|^2 \leq C N^{3\kappa /2}$
and
$\| \sigma _S\|^2 \leq C N^{3\kappa /2}$
and
 $\| \sigma _S\|^2_{H^1} \leq C N^{5\kappa /2+\varepsilon }$
.
$\| \sigma _S\|^2_{H^1} \leq C N^{5\kappa /2+\varepsilon }$
.
We can now return to the proof of Proposition 2.3.
Proof Proof of Proposition 2.3.
 $$ \begin{align} T_\nu^* W_{N_0}^* \mathcal{N} W_{N_0} T_\nu =\; &N_0+\sum_{p\in \Lambda_+^*}\sigma_p^2+\sqrt{N_0}(a_0+a^*_0)+ a^*_0 a_0 \nonumber\\ & + \sum_{p\in \Lambda^*_+}\big[ (\sigma_p^2+\gamma_p^2)a_p^*a_p + \gamma_p \sigma_p (a_p a_{-p} + \mbox{h.c.}) \big] . \end{align} $$
$$ \begin{align} T_\nu^* W_{N_0}^* \mathcal{N} W_{N_0} T_\nu =\; &N_0+\sum_{p\in \Lambda_+^*}\sigma_p^2+\sqrt{N_0}(a_0+a^*_0)+ a^*_0 a_0 \nonumber\\ & + \sum_{p\in \Lambda^*_+}\big[ (\sigma_p^2+\gamma_p^2)a_p^*a_p + \gamma_p \sigma_p (a_p a_{-p} + \mbox{h.c.}) \big] . \end{align} $$
By definition of
![]() $\xi _\nu $
,
$\xi _\nu $
,
![]() $a_0 \xi _\nu = 0$
and
$a_0 \xi _\nu = 0$
and
![]() $\langle \xi _\nu , a_p a_{-p} \xi _\nu \rangle = 0$
for every
$\langle \xi _\nu , a_p a_{-p} \xi _\nu \rangle = 0$
for every
![]() $p \in \Lambda ^*$
, as well as the definition
$p \in \Lambda ^*$
, as well as the definition
![]() $N = N_0 + \| \sigma _L \|^2$
, we obtain that
$N = N_0 + \| \sigma _L \|^2$
, we obtain that
 $$ \begin{align} \langle \Psi_N, \mathcal{N} \Psi_N \rangle = \frac{\langle \xi_\nu , T_\nu^* W_{N_0}^* \mathcal{N} W_{N_0} T_\nu \xi_\nu \rangle}{\| \xi_\nu \|^2} = N +\sum_{p\in P_L^c}\sigma_p^2 + \sum_{p\in P_S\cup P_H} (\sigma_p^2+\gamma_p^2)\frac{\langle \xi_\nu,a_p^*a_p \xi_\nu\rangle}{\|\xi_\nu\|^2} . \end{align} $$
$$ \begin{align} \langle \Psi_N, \mathcal{N} \Psi_N \rangle = \frac{\langle \xi_\nu , T_\nu^* W_{N_0}^* \mathcal{N} W_{N_0} T_\nu \xi_\nu \rangle}{\| \xi_\nu \|^2} = N +\sum_{p\in P_L^c}\sigma_p^2 + \sum_{p\in P_S\cup P_H} (\sigma_p^2+\gamma_p^2)\frac{\langle \xi_\nu,a_p^*a_p \xi_\nu\rangle}{\|\xi_\nu\|^2} . \end{align} $$
This immediately implies that
![]() $\langle \Psi _N, \mathcal {N} \Psi _N \rangle \geq N$
.
$\langle \Psi _N, \mathcal {N} \Psi _N \rangle \geq N$
.
With
![]() $a_0 \xi _\nu = 0$
and the assumption
$a_0 \xi _\nu = 0$
and the assumption
![]() $3\kappa - 2 + 4 \varepsilon < 0$
, (2.32) also implies that
$3\kappa - 2 + 4 \varepsilon < 0$
, (2.32) also implies that
 $$ \begin{align*} \langle \xi_\nu , T_\nu^* W_{N_0}^* \mathcal{N}^2 W_{N_0} T_\nu \xi_\nu \rangle \leq \; &C N^2 + C \sum_{p,q \in \Lambda^*_+} (\sigma_p^2 + \gamma_p^2) (\sigma_q^2 + \gamma_q^2) \langle \xi_\nu, a_p^* a_p a_q^* a_q \xi_\nu \rangle \\ &+ C \sum_{p,q \in \Lambda^*_+} \gamma_p \sigma_p \gamma_q \sigma_q \langle \xi_\nu, (a_p a_{-p} + a^*_p a_{-p}^*) (a_q a_{-q} + a_q^* a_{-q}^*) \xi_\nu \rangle. \end{align*} $$
$$ \begin{align*} \langle \xi_\nu , T_\nu^* W_{N_0}^* \mathcal{N}^2 W_{N_0} T_\nu \xi_\nu \rangle \leq \; &C N^2 + C \sum_{p,q \in \Lambda^*_+} (\sigma_p^2 + \gamma_p^2) (\sigma_q^2 + \gamma_q^2) \langle \xi_\nu, a_p^* a_p a_q^* a_q \xi_\nu \rangle \\ &+ C \sum_{p,q \in \Lambda^*_+} \gamma_p \sigma_p \gamma_q \sigma_q \langle \xi_\nu, (a_p a_{-p} + a^*_p a_{-p}^*) (a_q a_{-q} + a_q^* a_{-q}^*) \xi_\nu \rangle. \end{align*} $$
Since
![]() $\xi _\nu $
is a superposition of states with
$\xi _\nu $
is a superposition of states with
![]() $3m$
particles with momenta in
$3m$
particles with momenta in
![]() $P_H \cup P_S$
, we obtain, writing
$P_H \cup P_S$
, we obtain, writing
![]() $a_p a_{-p} a_q^* a_{-q}^* = a_q^* a_p a_{-q}^* a_{-p} +(\delta _{p,q}+ \delta _{-p, q})( a_{p}^* a_{p} +1) + \delta _{p,q} a^*_{-p} a_{-p}$
and similarly for
$a_p a_{-p} a_q^* a_{-q}^* = a_q^* a_p a_{-q}^* a_{-p} +(\delta _{p,q}+ \delta _{-p, q})( a_{p}^* a_{p} +1) + \delta _{p,q} a^*_{-p} a_{-p}$
and similarly for
![]() $a_p^* a_{-p}^* a_q a_{-q}$
,
$a_p^* a_{-p}^* a_q a_{-q}$
,
 $$ \begin{align*} \langle \xi_\nu , T_\nu^* W_{N_0}^* \mathcal{N}^2 W_{N_0} T_\nu \xi_\nu \rangle \leq \; &CN^2 + C N^{2\varepsilon} \langle \xi_\nu , (\mathcal{N}+1)^2 \xi_\nu \rangle + C \sum_{p \in P_H \cup P_S} \gamma_p^2 \sigma_p^2 \langle \xi_\nu, a_p^* a_p \xi_\nu \rangle \\ & + C \sum_{p \in \Lambda^*_+} \gamma_p^2 \sigma_p^2 \| \xi_\nu \|^2 + C \hspace{-.3cm} \sum_{p,q \in P_H\cup P_S} \hspace{-.3cm} \gamma_p \sigma_p \gamma_q \sigma_q \langle \xi_\nu, a^*_p a_q a^*_{-p} a_{-q} \xi_\nu \rangle . \end{align*} $$
$$ \begin{align*} \langle \xi_\nu , T_\nu^* W_{N_0}^* \mathcal{N}^2 W_{N_0} T_\nu \xi_\nu \rangle \leq \; &CN^2 + C N^{2\varepsilon} \langle \xi_\nu , (\mathcal{N}+1)^2 \xi_\nu \rangle + C \sum_{p \in P_H \cup P_S} \gamma_p^2 \sigma_p^2 \langle \xi_\nu, a_p^* a_p \xi_\nu \rangle \\ & + C \sum_{p \in \Lambda^*_+} \gamma_p^2 \sigma_p^2 \| \xi_\nu \|^2 + C \hspace{-.3cm} \sum_{p,q \in P_H\cup P_S} \hspace{-.3cm} \gamma_p \sigma_p \gamma_q \sigma_q \langle \xi_\nu, a^*_p a_q a^*_{-p} a_{-q} \xi_\nu \rangle . \end{align*} $$
Estimating the last term through
 $$ \begin{align*} \Big| \sum_{p,q \in P_H \cup P_S} \gamma_p &\sigma_p \gamma_q \sigma_q \langle \xi_\nu, a^*_p a_q a^*_{-p} a_{-q} \xi_\nu \rangle \Big| \\ \leq \; & \sum_{p,q \in P_H \cup P_S} |\gamma_p | | \sigma_p | |\gamma_q | | \sigma_q | \, \| a^* _q a_p \xi_\nu \| \| a^*_{-p} a_{-q} \xi_\nu \| \\ \leq \; & \sum_{p,q \in P_H \cup P_S} | \gamma_p | |\sigma_p | |\gamma_q | |\sigma_q | \, \big[ \| a_q a_p \xi_\nu \| + \| a_p \xi_\nu \| \big] \big[ \| a_{-p} a_{-q} \xi_\nu \| + \| a_{-q} \xi_\nu \| \big] \\ \leq \; & C \| \gamma_{S \cup H} \|_\infty^2 \| \sigma_{S \cup H} \|_\infty^2 \| (\mathcal{N}+1) \xi_\nu \|^2 + C \| \gamma_{S \cup H} \|_\infty^2 \| \sigma_{S \cup H} \|^2 \| \mathcal{N}^{1/2} \xi_\nu \|^2\\ &+ C \| \gamma_{S \cup H} \|_\infty^2 \| \sigma_{S \cup H} \|_\infty \| \sigma_{S \cup H} \| \| (\mathcal{N}+1) \xi_\nu \| \| \mathcal{N}^{1/2} \xi_\nu \|, \end{align*} $$
$$ \begin{align*} \Big| \sum_{p,q \in P_H \cup P_S} \gamma_p &\sigma_p \gamma_q \sigma_q \langle \xi_\nu, a^*_p a_q a^*_{-p} a_{-q} \xi_\nu \rangle \Big| \\ \leq \; & \sum_{p,q \in P_H \cup P_S} |\gamma_p | | \sigma_p | |\gamma_q | | \sigma_q | \, \| a^* _q a_p \xi_\nu \| \| a^*_{-p} a_{-q} \xi_\nu \| \\ \leq \; & \sum_{p,q \in P_H \cup P_S} | \gamma_p | |\sigma_p | |\gamma_q | |\sigma_q | \, \big[ \| a_q a_p \xi_\nu \| + \| a_p \xi_\nu \| \big] \big[ \| a_{-p} a_{-q} \xi_\nu \| + \| a_{-q} \xi_\nu \| \big] \\ \leq \; & C \| \gamma_{S \cup H} \|_\infty^2 \| \sigma_{S \cup H} \|_\infty^2 \| (\mathcal{N}+1) \xi_\nu \|^2 + C \| \gamma_{S \cup H} \|_\infty^2 \| \sigma_{S \cup H} \|^2 \| \mathcal{N}^{1/2} \xi_\nu \|^2\\ &+ C \| \gamma_{S \cup H} \|_\infty^2 \| \sigma_{S \cup H} \|_\infty \| \sigma_{S \cup H} \| \| (\mathcal{N}+1) \xi_\nu \| \| \mathcal{N}^{1/2} \xi_\nu \|, \end{align*} $$
we conclude with the bounds in Lemma 2.4 and in Proposition 2.2 that, for
![]() $3\kappa -2 + 4\varepsilon < 0,$
$3\kappa -2 + 4\varepsilon < 0,$
 $$ \begin{align*} \langle \xi_\nu , T_\nu^* W_{N_0}^* \mathcal{N}^2 W_{N_0} T_\nu \xi_\nu \rangle \leq \;& C N^2 + C N^{2\varepsilon} \langle \xi_\nu, \mathcal{N}^2 \xi_\nu \rangle + C N^\varepsilon \| \sigma \|^2 \langle \xi_\nu, \mathcal{N} \xi_\nu \rangle + C \| \gamma \|_\infty^2 \| \sigma \|^2 \\ \leq \; & C N^2 + C N^{9\kappa -4 + 4\varepsilon} + C N^{6\kappa -2 +2\varepsilon} + C N^{2\kappa} \leq C N^2. \\[-36pt] \end{align*} $$
$$ \begin{align*} \langle \xi_\nu , T_\nu^* W_{N_0}^* \mathcal{N}^2 W_{N_0} T_\nu \xi_\nu \rangle \leq \;& C N^2 + C N^{2\varepsilon} \langle \xi_\nu, \mathcal{N}^2 \xi_\nu \rangle + C N^\varepsilon \| \sigma \|^2 \langle \xi_\nu, \mathcal{N} \xi_\nu \rangle + C \| \gamma \|_\infty^2 \| \sigma \|^2 \\ \leq \; & C N^2 + C N^{9\kappa -4 + 4\varepsilon} + C N^{6\kappa -2 +2\varepsilon} + C N^{2\kappa} \leq C N^2. \\[-36pt] \end{align*} $$
The next theorem, whose proof occupies the rest of the article, determines the energy of
![]() $\Psi _N$
and, combined with Proposition 2.3, allows us to conclude the proof of Proposition 1.3.
$\Psi _N$
and, combined with Proposition 2.3, allows us to conclude the proof of Proposition 1.3.
Theorem 2.5. Let
![]() $\mathcal {H}_N$
and
$\mathcal {H}_N$
and
![]() $\Psi _N \in \mathcal {F}$
be defined as in (2.2) and (2.25), respectively, and let
$\Psi _N \in \mathcal {F}$
be defined as in (2.2) and (2.25), respectively, and let
 $E_N^\Psi = \langle \Psi _N, \mathcal {H}_N \Psi _N \rangle $
. Let
$E_N^\Psi = \langle \Psi _N, \mathcal {H}_N \Psi _N \rangle $
. Let
![]() $\kappa \in (1/2; 2/3)$
,
$\kappa \in (1/2; 2/3)$
,
![]() $\varepsilon> 0$
so small that
$\varepsilon> 0$
so small that
![]() $3\kappa -2 + 4\varepsilon < 0$
. Then, under the assumption of Theorem 1.1, we have
$3\kappa -2 + 4\varepsilon < 0$
. Then, under the assumption of Theorem 1.1, we have
 $$ \begin{align} E_N^\Psi \leq 4 \pi \mathfrak{a} N^{1+\kappa} \bigg(1+\frac{128}{15\sqrt{\pi}}(\mathfrak{a}^3N^{3\kappa-2})^{1/2}\bigg)+ C N^{5\kappa/2} \max \{ N^{-\varepsilon} \hspace{-.1cm} , N^{9\kappa-5 +6\varepsilon} \hspace{-.1cm} ,N^{21\kappa/4-3+3\varepsilon}\} \end{align} $$
$$ \begin{align} E_N^\Psi \leq 4 \pi \mathfrak{a} N^{1+\kappa} \bigg(1+\frac{128}{15\sqrt{\pi}}(\mathfrak{a}^3N^{3\kappa-2})^{1/2}\bigg)+ C N^{5\kappa/2} \max \{ N^{-\varepsilon} \hspace{-.1cm} , N^{9\kappa-5 +6\varepsilon} \hspace{-.1cm} ,N^{21\kappa/4-3+3\varepsilon}\} \end{align} $$
for all N large enough.
Remark. Equation (2.34) gives the correct second-order term for all
![]() $\kappa < 5/9$
(choosing
$\kappa < 5/9$
(choosing
![]() $\varepsilon> 0$
small enough); this corresponds to exponents
$\varepsilon> 0$
small enough); this corresponds to exponents
![]() $\gamma < 4/3$
in Proposition 1.3. With a more complicated proof, we could have considered all
$\gamma < 4/3$
in Proposition 1.3. With a more complicated proof, we could have considered all
![]() $\kappa < 7/12$
(corresponding to
$\kappa < 7/12$
(corresponding to
![]() $\gamma < 5/3$
).
$\gamma < 5/3$
).
Proof Proof of Proposition 1.3.
Proposition 1.3 follows from Proposition 2.3 and Theorem 2.5, recalling that (1.5) is unitarily equivalent to
![]() $L^{-2} \mathcal {H}_N$
, with
$L^{-2} \mathcal {H}_N$
, with
![]() $\mathcal {H}_N$
as defined in (2.2),
$\mathcal {H}_N$
as defined in (2.2),
![]() $L = {\tilde {\rho }}^{-\gamma }$
,
$L = {\tilde {\rho }}^{-\gamma }$
,
![]() $N = {\tilde {\rho }} L^3 = {\tilde {\rho }}^{1-3\gamma }$
and
$N = {\tilde {\rho }} L^3 = {\tilde {\rho }}^{1-3\gamma }$
and
![]() $\kappa = (2\gamma - 1)/ (3\gamma -1)$
. At the end, to obtain (1.8) and (1.9), we have to rename
$\kappa = (2\gamma - 1)/ (3\gamma -1)$
. At the end, to obtain (1.8) and (1.9), we have to rename
![]() $\varepsilon (3\gamma - 1) \to \varepsilon $
.
$\varepsilon (3\gamma - 1) \to \varepsilon $
.
3 Energy of the trial state
In this section we prove Theorem 2.5. With (2.25) and introducing the notations
we write
 $$ \begin{align*} E^{\Psi}_N = \langle \Psi_N, \mathcal{H}_N \Psi_N \rangle = \frac{\langle \xi_\nu , \mathcal{G}_N \xi_\nu \rangle}{\| \xi_\nu \|^2 } \end{align*} $$
$$ \begin{align*} E^{\Psi}_N = \langle \Psi_N, \mathcal{H}_N \Psi_N \rangle = \frac{\langle \xi_\nu , \mathcal{G}_N \xi_\nu \rangle}{\| \xi_\nu \|^2 } \end{align*} $$
with
![]() $\xi _\nu = e^{A_\nu } \Omega $
, as defined before (2.15). With (2.2) and recalling from (2.4) that
$\xi _\nu = e^{A_\nu } \Omega $
, as defined before (2.15). With (2.2) and recalling from (2.4) that
 $$ \begin{align} W^*_{N_0} a_p W_{N_0}=a_p+\sqrt{N_0}\,\delta_{p,0} \end{align} $$
$$ \begin{align} W^*_{N_0} a_p W_{N_0}=a_p+\sqrt{N_0}\,\delta_{p,0} \end{align} $$
we obtain
 $\mathcal {L}_N= \mathcal {L}^{(0)}_N +\mathcal {L}^{(1)}_N+ \mathcal {L}^{(2)}_N + \mathcal {L}^{(3)}_N + \mathcal {L}^{(4)}_N $
, with
$\mathcal {L}_N= \mathcal {L}^{(0)}_N +\mathcal {L}^{(1)}_N+ \mathcal {L}^{(2)}_N + \mathcal {L}^{(3)}_N + \mathcal {L}^{(4)}_N $
, with
 $$ \begin{align} \mathcal{L}^{(0)}_N=\;&\frac {N_0^2} {2} \,N^{\kappa-1} \widehat{V}(0)\nonumber\\ \mathcal{L}^{(1)}_N=\; & N_0^{3/2}\, N^{\kappa-1}\widehat{V}(0)(a_0+\mbox{h.c.})\nonumber\\ \mathcal{L}^{(2)}_N=\;&\sum_{p\in \Lambda^*}p^2a^*_pa_p + \frac{N_0}{N} \sum_{p\in \Lambda^*} N^\kappa \big( \widehat{V}(p/N^{1-\kappa}) + \widehat V(0) \big) a_p^*a_p \nonumber\\ & \hskip 3cm + \frac{N_0}{2 N}\sum_{p\in \Lambda^*}N^\kappa \widehat{V}(p/N^{1-\kappa})(a_p^*a_{-p}^*+ a_p a_{-p})\nonumber\\ \mathcal{L}^{(3)}_N=\; & \frac{\sqrt{N_0}}N \sum_{p,r\in \Lambda^*} N^{\kappa} \widehat{V}(r/N^{1-\kappa})(a^*_pa^*_ra_{p+r}+ a^*_{p+r} a_r a_p )\nonumber \\ \mathcal{L}^{(4)}_N=\; &\frac1{2N}\sum_{p,q,r \in \Lambda^*} N^{\kappa} \widehat{V}(r/N^{1-\kappa})a^*_{p+r} a^*_q a_{p}a_{q+r}. \end{align} $$
$$ \begin{align} \mathcal{L}^{(0)}_N=\;&\frac {N_0^2} {2} \,N^{\kappa-1} \widehat{V}(0)\nonumber\\ \mathcal{L}^{(1)}_N=\; & N_0^{3/2}\, N^{\kappa-1}\widehat{V}(0)(a_0+\mbox{h.c.})\nonumber\\ \mathcal{L}^{(2)}_N=\;&\sum_{p\in \Lambda^*}p^2a^*_pa_p + \frac{N_0}{N} \sum_{p\in \Lambda^*} N^\kappa \big( \widehat{V}(p/N^{1-\kappa}) + \widehat V(0) \big) a_p^*a_p \nonumber\\ & \hskip 3cm + \frac{N_0}{2 N}\sum_{p\in \Lambda^*}N^\kappa \widehat{V}(p/N^{1-\kappa})(a_p^*a_{-p}^*+ a_p a_{-p})\nonumber\\ \mathcal{L}^{(3)}_N=\; & \frac{\sqrt{N_0}}N \sum_{p,r\in \Lambda^*} N^{\kappa} \widehat{V}(r/N^{1-\kappa})(a^*_pa^*_ra_{p+r}+ a^*_{p+r} a_r a_p )\nonumber \\ \mathcal{L}^{(4)}_N=\; &\frac1{2N}\sum_{p,q,r \in \Lambda^*} N^{\kappa} \widehat{V}(r/N^{1-\kappa})a^*_{p+r} a^*_q a_{p}a_{q+r}. \end{align} $$
To compute
![]() $\mathcal {G}_N$
, we have to conjugate the operators in (3.3) with the Bogoliubov transformation
$\mathcal {G}_N$
, we have to conjugate the operators in (3.3) with the Bogoliubov transformation
![]() $T_\nu $
. The result is described in the following proposition, whose proof will be discussed in Section 4.
$T_\nu $
. The result is described in the following proposition, whose proof will be discussed in Section 4.
Proposition 3.1. Let
 $$ \begin{align} \mathcal{K} = \sum_{p \in \Lambda^*_+} p^2 a^*_p a_p, \qquad \mathcal{V}_N^{(H)}= \frac{1}{2 N}\sum_{\substack{r\in \Lambda^*,\, p,q \in P_H:\\ p+r,q+r\in P_H}}N^\kappa \widehat{V}(r/N^{1-\kappa}) a_{p+r}^*a_q^*a_{p}a_{q+r} \, \end{align} $$
$$ \begin{align} \mathcal{K} = \sum_{p \in \Lambda^*_+} p^2 a^*_p a_p, \qquad \mathcal{V}_N^{(H)}= \frac{1}{2 N}\sum_{\substack{r\in \Lambda^*,\, p,q \in P_H:\\ p+r,q+r\in P_H}}N^\kappa \widehat{V}(r/N^{1-\kappa}) a_{p+r}^*a_q^*a_{p}a_{q+r} \, \end{align} $$
and (recalling from (2.26) that
![]() $N_0 = N - \| \sigma _L \|^2$
)
$N_0 = N - \| \sigma _L \|^2$
)
 $$ \begin{align} \mathcal{C}_N =\; \frac{\sqrt{N_0}}{ N} \sum_{\substack{p,r \in P_H\\ p+r \in P_S}} N^\kappa \widehat V(r/N^{1-\kappa})\, \sigma_{p+r} \gamma_p\gamma_r \,(a^*_{p+r} a^*_{-p} a^*_{-r} + \mbox{h.c.} ). \end{align} $$
$$ \begin{align} \mathcal{C}_N =\; \frac{\sqrt{N_0}}{ N} \sum_{\substack{p,r \in P_H\\ p+r \in P_S}} N^\kappa \widehat V(r/N^{1-\kappa})\, \sigma_{p+r} \gamma_p\gamma_r \,(a^*_{p+r} a^*_{-p} a^*_{-r} + \mbox{h.c.} ). \end{align} $$
Moreover, let
 $$ \begin{align} C_{\mathcal{G}_N} =\; & \frac{N^{1+\kappa}}{2} \widehat{V}(0) +\sum_{p\in {\Lambda}^*_+}p^2\sigma_p^2 + \sum_{p\in \Lambda^*_+} N^\kappa \widehat{V}(p/N^{1-\kappa})\sigma_p\gamma_p\nonumber\\ &+ \sum_{p\in P_L}N^\kappa \widehat{V}(p/N^{1-\kappa}) \sigma_p^2 +\frac{1}{2N}\sum_{\substack{p,r\in \Lambda^*_+\\r\neq p}} N^\kappa \widehat{V}(r/N^{1-\kappa})\sigma_p\sigma_{p-r}\gamma_p\gamma_{p-r} \nonumber\\ & - \frac 1 N \sum_{v \in P_L} \sigma^2_v \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p . \end{align} $$
$$ \begin{align} C_{\mathcal{G}_N} =\; & \frac{N^{1+\kappa}}{2} \widehat{V}(0) +\sum_{p\in {\Lambda}^*_+}p^2\sigma_p^2 + \sum_{p\in \Lambda^*_+} N^\kappa \widehat{V}(p/N^{1-\kappa})\sigma_p\gamma_p\nonumber\\ &+ \sum_{p\in P_L}N^\kappa \widehat{V}(p/N^{1-\kappa}) \sigma_p^2 +\frac{1}{2N}\sum_{\substack{p,r\in \Lambda^*_+\\r\neq p}} N^\kappa \widehat{V}(r/N^{1-\kappa})\sigma_p\sigma_{p-r}\gamma_p\gamma_{p-r} \nonumber\\ & - \frac 1 N \sum_{v \in P_L} \sigma^2_v \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p . \end{align} $$
Then, under the assumptions of Theorem 1.1, for all
![]() $\kappa \in (1/2; 2/3)$
and
$\kappa \in (1/2; 2/3)$
and
![]() $\varepsilon> 0$
with
$\varepsilon> 0$
with
![]() $3\kappa -2 + 4\varepsilon < 0$
and N sufficiently large, we have
$3\kappa -2 + 4\varepsilon < 0$
and N sufficiently large, we have
 $$ \begin{align} \frac{\langle \xi_\nu, \mathcal{G}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \; &C_{\mathcal{G}_N} + \frac{\langle \xi_\nu, (\mathcal{K}+\mathcal{V}_N^{(H)} +\mathcal{C}_N) \xi_\nu\rangle}{\| \xi_\nu \|^2}\nonumber \\ &+ C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon}, N^{9\kappa - 5 + 6\varepsilon} , N^{21 \kappa /4 - 3 + 3 \varepsilon } \}. \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu, \mathcal{G}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \; &C_{\mathcal{G}_N} + \frac{\langle \xi_\nu, (\mathcal{K}+\mathcal{V}_N^{(H)} +\mathcal{C}_N) \xi_\nu\rangle}{\| \xi_\nu \|^2}\nonumber \\ &+ C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon}, N^{9\kappa - 5 + 6\varepsilon} , N^{21 \kappa /4 - 3 + 3 \varepsilon } \}. \end{align} $$
Remark. In fact, (3.7) does not only hold true for
![]() $\xi _\nu $
but for any state satisfying the bounds in Proposition 2.2.
$\xi _\nu $
but for any state satisfying the bounds in Proposition 2.2.
The expectation of the operators
 $\mathcal {K}, \mathcal {V}_N^{(H)}, \mathcal {C}_N$
in the state
$\mathcal {K}, \mathcal {V}_N^{(H)}, \mathcal {C}_N$
in the state
![]() $\xi _\nu / \| \xi _\nu \|$
, appearing on the right-hand side of (3.7) is determined by the next proposition, which will be shown in Section 5.
$\xi _\nu / \| \xi _\nu \|$
, appearing on the right-hand side of (3.7) is determined by the next proposition, which will be shown in Section 5.
Proposition 3.2. Under the assumptions of Theorem 1.1, we have
 $$ \begin{align*} \frac{\langle \xi_\nu, (\mathcal{K}+\mathcal{V}^{(H)}_N +\mathcal{C}_{N}) \xi_\nu \rangle }{\|\xi_\nu\|^2} \leq \; & \frac1N\sum_{v\in P_L}\sigma_v^2\sum_{r\in P_H} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v}) \\ &+ C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon} ,\, N^{12\kappa-7 +5\varepsilon}\} \end{align*} $$
$$ \begin{align*} \frac{\langle \xi_\nu, (\mathcal{K}+\mathcal{V}^{(H)}_N +\mathcal{C}_{N}) \xi_\nu \rangle }{\|\xi_\nu\|^2} \leq \; & \frac1N\sum_{v\in P_L}\sigma_v^2\sum_{r\in P_H} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v}) \\ &+ C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon} ,\, N^{12\kappa-7 +5\varepsilon}\} \end{align*} $$
for all
![]() $\kappa \in (1/2; 2/3)$
and all
$\kappa \in (1/2; 2/3)$
and all
![]() $\varepsilon> 0$
so small that
$\varepsilon> 0$
so small that
![]() $3\kappa -2 + 4\varepsilon < 0$
.
$3\kappa -2 + 4\varepsilon < 0$
.
Let us now use the statements of Proposition 3.1 and Proposition 3.2 to obtain an upper bound for the energy of the trial state
![]() $\Psi _N$
and prove Theorem 2.5. From Proposition 3.1 and Proposition 3.2 we find
$\Psi _N$
and prove Theorem 2.5. From Proposition 3.1 and Proposition 3.2 we find
 $$ \begin{align} E_N^\Psi \leq \; & \frac{N^{1+\kappa}}{2}\,\widehat{V}(0)+ \sum_{p \in \Lambda^*_+} p^2 \sigma_p^2 + \sum_{p \in \Lambda^*_+} N^\kappa \widehat V(p/N^{1-\kappa}) \gamma_p \sigma_p \nonumber \\ & + \sum_{v \in P_L} N^\kappa \widehat V(v/N^{1-\kappa}) \sigma^2_v + \frac 1 {2N} \sum_{\substack{p,q \in \Lambda^*_+\nonumber\\ p \neq q}} N^\kappa \widehat V( (p-q)/N^{1-\kappa}) \gamma_p \gamma_{q} \sigma_p \sigma_{q}\nonumber\\ & - \frac 1 N \sum_{v \in P_L} \sigma^2_v \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p \nonumber\\ & + \frac1N\sum_{v\in P_L}\sigma_v^2\sum_{r\in P_H} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v})\, + \mathcal{E} \end{align} $$
$$ \begin{align} E_N^\Psi \leq \; & \frac{N^{1+\kappa}}{2}\,\widehat{V}(0)+ \sum_{p \in \Lambda^*_+} p^2 \sigma_p^2 + \sum_{p \in \Lambda^*_+} N^\kappa \widehat V(p/N^{1-\kappa}) \gamma_p \sigma_p \nonumber \\ & + \sum_{v \in P_L} N^\kappa \widehat V(v/N^{1-\kappa}) \sigma^2_v + \frac 1 {2N} \sum_{\substack{p,q \in \Lambda^*_+\nonumber\\ p \neq q}} N^\kappa \widehat V( (p-q)/N^{1-\kappa}) \gamma_p \gamma_{q} \sigma_p \sigma_{q}\nonumber\\ & - \frac 1 N \sum_{v \in P_L} \sigma^2_v \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p \nonumber\\ & + \frac1N\sum_{v\in P_L}\sigma_v^2\sum_{r\in P_H} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v})\, + \mathcal{E} \end{align} $$
with
for all
![]() $\kappa \in (1/2; 2/3)$
and all
$\kappa \in (1/2; 2/3)$
and all
![]() $\varepsilon> 0$
with
$\varepsilon> 0$
with
![]() $3\kappa -2 + 4\varepsilon < 0$
(in this range,
$3\kappa -2 + 4\varepsilon < 0$
(in this range,
![]() $12\kappa -7+5\varepsilon < 9\kappa -5+3\varepsilon $
). Since
$12\kappa -7+5\varepsilon < 9\kappa -5+3\varepsilon $
). Since
![]() $|\sigma _p - \eta _p| \leq C |\eta _p|^3$
for all
$|\sigma _p - \eta _p| \leq C |\eta _p|^3$
for all
![]() $p \in P_L^c$
, with (2.8) we find
$p \in P_L^c$
, with (2.8) we find
 $$ \begin{align} \sum_{p \in \Lambda^*_+} p^2 \sigma_p^2 \leq \sum_{v \in P_L} v^2 \sigma_v^2 + \sum_{p \in P_L^c} p^2 \eta_p^2 + C N^{5\kappa/2 - 3\varepsilon} . \end{align} $$
$$ \begin{align} \sum_{p \in \Lambda^*_+} p^2 \sigma_p^2 \leq \sum_{v \in P_L} v^2 \sigma_v^2 + \sum_{p \in P_L^c} p^2 \eta_p^2 + C N^{5\kappa/2 - 3\varepsilon} . \end{align} $$
Similarly, with
 $|\gamma _p \sigma _p - \eta _p| \leq C \eta _p^3$
for all
$|\gamma _p \sigma _p - \eta _p| \leq C \eta _p^3$
for all
![]() $p \in P_L^c $
, the last term on the first line of (3.8) can be written as
$p \in P_L^c $
, the last term on the first line of (3.8) can be written as
 $$ \begin{align} \sum_{p \in \Lambda^*_+} N^\kappa &\widehat V(p/N^{1-\kappa})\gamma_p \sigma_p \nonumber \\ & \leq \sum_{v \in P_L} N^\kappa \widehat V(v/N^{1-\kappa}) \gamma_v \sigma_v + \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p + C N^{5\kappa/2-3\varepsilon} . \end{align} $$
$$ \begin{align} \sum_{p \in \Lambda^*_+} N^\kappa &\widehat V(p/N^{1-\kappa})\gamma_p \sigma_p \nonumber \\ & \leq \sum_{v \in P_L} N^\kappa \widehat V(v/N^{1-\kappa}) \gamma_v \sigma_v + \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p + C N^{5\kappa/2-3\varepsilon} . \end{align} $$
Next, we focus on the last term on the second line of (3.8). We define
![]() $\mathcal {E}_1$
through the identity
$\mathcal {E}_1$
through the identity
 $$ \begin{align} &\frac 1 {2N} \sum_{\substack{p,q \in \Lambda^*_+\\ p \neq q}} N^\kappa \widehat V((p-q)/N^{1-\kappa}) \gamma_p \gamma_{q} \sigma_p \sigma_{q}\nonumber \\ &= \frac 1 {N} \!\!\sum_{\substack{p \in P_L^c, \\ q \in P_L}} N^\kappa \widehat V((p-q)/N^{1-\kappa}) \eta_p \gamma_{q} \sigma_{q} + \frac 1 {2N}\!\! \sum_{\substack{p,q \in P_L^c\\ p \neq q}} \!N^\kappa \widehat V((p-q)/N^{1-\kappa}) \eta_p \eta_q \!+ \mathcal{E}_1. \end{align} $$
$$ \begin{align} &\frac 1 {2N} \sum_{\substack{p,q \in \Lambda^*_+\\ p \neq q}} N^\kappa \widehat V((p-q)/N^{1-\kappa}) \gamma_p \gamma_{q} \sigma_p \sigma_{q}\nonumber \\ &= \frac 1 {N} \!\!\sum_{\substack{p \in P_L^c, \\ q \in P_L}} N^\kappa \widehat V((p-q)/N^{1-\kappa}) \eta_p \gamma_{q} \sigma_{q} + \frac 1 {2N}\!\! \sum_{\substack{p,q \in P_L^c\\ p \neq q}} \!N^\kappa \widehat V((p-q)/N^{1-\kappa}) \eta_p \eta_q \!+ \mathcal{E}_1. \end{align} $$
Using again
![]() $|\gamma _p \sigma _p - \eta _p | \leq C |\eta _p|^3$
for all
$|\gamma _p \sigma _p - \eta _p | \leq C |\eta _p|^3$
for all
![]() $p \in P_L^c$
, the estimate
$p \in P_L^c$
, the estimate
 $$ \begin{align} \mathop{\mathrm{sup}}\limits_{r\in \Lambda^*}\,\sum_{s \in \Lambda^*_+} N^\kappa |\widehat V((r-s)/N^{1-\kappa})| |\eta_s| \leq C N^{1+\kappa} \end{align} $$
$$ \begin{align} \mathop{\mathrm{sup}}\limits_{r\in \Lambda^*}\,\sum_{s \in \Lambda^*_+} N^\kappa |\widehat V((r-s)/N^{1-\kappa})| |\eta_s| \leq C N^{1+\kappa} \end{align} $$
and the bounds from Lemma 2.4, we conclude (using the condition
![]() $3\kappa -2 + 5\varepsilon < 0$
) that
$3\kappa -2 + 5\varepsilon < 0$
) that
 $$ \begin{align*} \mathcal{E}_1 &\leq C \left[ N^{\kappa} \| \eta_{L^c} \|_\infty \| \eta_{L^c} \|^2 + N^{\kappa-1} \| \eta_{L^c} \|_\infty \| \eta_{L^c} \|^2 \| \sigma_L \gamma_L \|_1 + N^{\kappa-1} \| \sigma_L \gamma_L \|_1^2 \right] \leq C N^{5\kappa/2-\varepsilon}. \end{align*} $$
$$ \begin{align*} \mathcal{E}_1 &\leq C \left[ N^{\kappa} \| \eta_{L^c} \|_\infty \| \eta_{L^c} \|^2 + N^{\kappa-1} \| \eta_{L^c} \|_\infty \| \eta_{L^c} \|^2 \| \sigma_L \gamma_L \|_1 + N^{\kappa-1} \| \sigma_L \gamma_L \|_1^2 \right] \leq C N^{5\kappa/2-\varepsilon}. \end{align*} $$
To prove (3.12) we use (2.8) and we remark that
 $$ \begin{align*} \sum_{s \in \Lambda^* : |s| \leq N^{1-\kappa}} N^\kappa |\widehat V((r-s)/N^{1-\kappa})| |\eta_s| \leq C N^{2\kappa} \sum_{s \in \Lambda^*_+: |s| \leq N^{1-\kappa}} |s|^{-2} \leq C N^{1+\kappa} \end{align*} $$
$$ \begin{align*} \sum_{s \in \Lambda^* : |s| \leq N^{1-\kappa}} N^\kappa |\widehat V((r-s)/N^{1-\kappa})| |\eta_s| \leq C N^{2\kappa} \sum_{s \in \Lambda^*_+: |s| \leq N^{1-\kappa}} |s|^{-2} \leq C N^{1+\kappa} \end{align*} $$
and that, rescaling variables (setting
![]() ${\tilde {r}} = r/ N^{1-\kappa }$
) and using an integral approximation,
${\tilde {r}} = r/ N^{1-\kappa }$
) and using an integral approximation,
 $$ \begin{align*} \sum_{s \in \Lambda^*_+ : |s|> N^{1-\kappa}} N^\kappa |\widehat V((r-s)/N^{1-\kappa})| |\eta_s| &\leq C N^{1+\kappa} \sum_{s \in \Lambda^* / N^{1-\kappa}: |s| > 1} N^{-3(1-\kappa)} \, |\widehat{V} ({\tilde{r}} - s)| |s|^{-2} \\ &\leq C N^{1+\kappa} \int_{|s| > 1} |\widehat{V} ({\tilde{r}} - s)| |s|^{-2} ds \leq C_q N^{1+\kappa} \| \widehat{V} \|_q \end{align*} $$
$$ \begin{align*} \sum_{s \in \Lambda^*_+ : |s|> N^{1-\kappa}} N^\kappa |\widehat V((r-s)/N^{1-\kappa})| |\eta_s| &\leq C N^{1+\kappa} \sum_{s \in \Lambda^* / N^{1-\kappa}: |s| > 1} N^{-3(1-\kappa)} \, |\widehat{V} ({\tilde{r}} - s)| |s|^{-2} \\ &\leq C N^{1+\kappa} \int_{|s| > 1} |\widehat{V} ({\tilde{r}} - s)| |s|^{-2} ds \leq C_q N^{1+\kappa} \| \widehat{V} \|_q \end{align*} $$
for any
![]() $q < 3$
. With the assumption
$q < 3$
. With the assumption
![]() $V \in L^{q'} (\mathbb {R}^3)$
, for some
$V \in L^{q'} (\mathbb {R}^3)$
, for some
![]() $q'> 3/2$
, (3.12) follows by the Hausdorff–Young inequality.
$q'> 3/2$
, (3.12) follows by the Hausdorff–Young inequality.
Finally, we remark that the terms in the last two lines of (3.8) can be combined, using (2.8) and the bound
![]() $\| \sigma _L \|^2 \leq C N^{3\kappa /2}$
from Lemma 2.4, into
$\| \sigma _L \|^2 \leq C N^{3\kappa /2}$
from Lemma 2.4, into
 $$ \begin{align} - \frac 1 N \sum_{v \in P_L} \sigma^2_v \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p& +\frac1N\sum_{v\in P_L}\sigma_v^2\sum_{r\in P_H} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v})\nonumber\\ &\leq \frac 1 N \sum_{v \in P_L} \sigma^2_v \sum_{r \in P_L^c} N^\kappa \widehat V(r/N^{1-\kappa}) \eta_{r+v} + C N^{5\kappa/2 - \varepsilon}. \end{align} $$
$$ \begin{align} - \frac 1 N \sum_{v \in P_L} \sigma^2_v \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p& +\frac1N\sum_{v\in P_L}\sigma_v^2\sum_{r\in P_H} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v})\nonumber\\ &\leq \frac 1 N \sum_{v \in P_L} \sigma^2_v \sum_{r \in P_L^c} N^\kappa \widehat V(r/N^{1-\kappa}) \eta_{r+v} + C N^{5\kappa/2 - \varepsilon}. \end{align} $$
Inserting (3.9), (3.10), (3.11) and (3.13) into (3.8), we obtain
 $$ \begin{align} E_N^\Psi \leq & \, \frac{N^{1+\kappa}}{2} \widehat{V} (0)+ \sum_{p \in P_L^c}\big[ p^2 \eta_p + N^\kappa \widehat V(p/N^{1-\kappa}) + \frac 1 {2N} \sum_{r \in P_L^c} N^\kappa \widehat V((r-p)/N^\kappa) \eta_r \big] \eta_p \nonumber\\ & + \sum_{v \in P_L} \Big[ v^2 \sigma_v^2 + \big(\sigma^2_v + \gamma_v \sigma_v \big)\Big( N^\kappa \widehat V(v/N^{1-\kappa}) +\frac 1 N \sum_{r \in P_L^c} N^\kappa \widehat V((r-v)/N^{1-\kappa})\eta_{r} \Big) \Big] \nonumber\\ & + C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\} . \end{align} $$
$$ \begin{align} E_N^\Psi \leq & \, \frac{N^{1+\kappa}}{2} \widehat{V} (0)+ \sum_{p \in P_L^c}\big[ p^2 \eta_p + N^\kappa \widehat V(p/N^{1-\kappa}) + \frac 1 {2N} \sum_{r \in P_L^c} N^\kappa \widehat V((r-p)/N^\kappa) \eta_r \big] \eta_p \nonumber\\ & + \sum_{v \in P_L} \Big[ v^2 \sigma_v^2 + \big(\sigma^2_v + \gamma_v \sigma_v \big)\Big( N^\kappa \widehat V(v/N^{1-\kappa}) +\frac 1 N \sum_{r \in P_L^c} N^\kappa \widehat V((r-v)/N^{1-\kappa})\eta_{r} \Big) \Big] \nonumber\\ & + C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\} . \end{align} $$
Let us now consider the first square bracket on the right-hand side of (3.14). Using the scattering equation (2.9) we obtain
 $$ \begin{align} &\sum_{p \in P_L^c} \Big[ p^2 \eta_p + N^\kappa \widehat V(p/N^{1-\kappa}) + \frac 1 {2N} \sum_{r \in P_L^c} N^\kappa \widehat V( (r-p)/N^{1-\kappa}) \eta_r \Big] \eta_p \nonumber\\ &\qquad\qquad= \frac 1 2 \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p - \frac 1 {2N} \sum_{\substack{p \in P_L^c\\ v \in P_L} } N^\kappa \widehat V((p-v)/N^{1-\kappa}) \eta_v \eta_p+ \mathcal{E}_2 \end{align} $$
$$ \begin{align} &\sum_{p \in P_L^c} \Big[ p^2 \eta_p + N^\kappa \widehat V(p/N^{1-\kappa}) + \frac 1 {2N} \sum_{r \in P_L^c} N^\kappa \widehat V( (r-p)/N^{1-\kappa}) \eta_r \Big] \eta_p \nonumber\\ &\qquad\qquad= \frac 1 2 \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa}) \eta_p - \frac 1 {2N} \sum_{\substack{p \in P_L^c\\ v \in P_L} } N^\kappa \widehat V((p-v)/N^{1-\kappa}) \eta_v \eta_p+ \mathcal{E}_2 \end{align} $$
with
 $$ \begin{align*} \mathcal{E}_2 =\; N^{3-2\kappa} \lambda_{\ell} \sum_{p \in P_L^c} \big( \widehat \chi_\ell \ast \widehat f_{N,\ell}\big)_p \eta_p - \frac 1 {2N} \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa})\eta_p \eta_0 . \end{align*} $$
$$ \begin{align*} \mathcal{E}_2 =\; N^{3-2\kappa} \lambda_{\ell} \sum_{p \in P_L^c} \big( \widehat \chi_\ell \ast \widehat f_{N,\ell}\big)_p \eta_p - \frac 1 {2N} \sum_{p \in P_L^c} N^\kappa \widehat V(p/N^{1-\kappa})\eta_p \eta_0 . \end{align*} $$
Using
![]() $N^{3-3\kappa } \lambda _{\ell } \leq C$
(Lemma 2.1),
$N^{3-3\kappa } \lambda _{\ell } \leq C$
(Lemma 2.1),
 $\| \widehat \chi _\ell \ast \widehat f_{N,\ell }\| = \| \chi _\ell f_{N,\ell } \| \leq C$
and
$\| \widehat \chi _\ell \ast \widehat f_{N,\ell }\| = \| \chi _\ell f_{N,\ell } \| \leq C$
and
![]() $\|\eta _{L^c}\|^2 \leq C N^{3\kappa /2 -\varepsilon }$
(Lemma 2.4) in the first term, (2.10) and (3.12) in the second term, we find
$\|\eta _{L^c}\|^2 \leq C N^{3\kappa /2 -\varepsilon }$
(Lemma 2.4) in the first term, (2.10) and (3.12) in the second term, we find
![]() $\mathcal {E}_2 \leq C N^{5\kappa /2-\varepsilon }$
(using that
$\mathcal {E}_2 \leq C N^{5\kappa /2-\varepsilon }$
(using that
![]() $3\kappa -2 + 4\varepsilon < 0$
and
$3\kappa -2 + 4\varepsilon < 0$
and
![]() $\kappa> 1/2$
).
$\kappa> 1/2$
).
As for the second square bracket on the right-hand side of (3.14), we write
 $$ \begin{align} \sum_{v \in P_L} \big(\sigma^2_v + \gamma_v \sigma_v \big) \Big( N^\kappa \widehat V(v/N^{1-\kappa}) & +\frac 1 N \sum_{r \in P_L^c} N^\kappa \widehat V((r-v)/N^{1-\kappa})\eta_{r} \Big) \nonumber\\ &= \sum_{v \in P_L} \big(\sigma^2_v + \gamma_v \sigma_v \big) N^\kappa \big( \widehat V(\cdot/N^{1-\kappa}) \ast \widehat f_{N,\ell} \big)_v + \mathcal{E}_3 \end{align} $$
$$ \begin{align} \sum_{v \in P_L} \big(\sigma^2_v + \gamma_v \sigma_v \big) \Big( N^\kappa \widehat V(v/N^{1-\kappa}) & +\frac 1 N \sum_{r \in P_L^c} N^\kappa \widehat V((r-v)/N^{1-\kappa})\eta_{r} \Big) \nonumber\\ &= \sum_{v \in P_L} \big(\sigma^2_v + \gamma_v \sigma_v \big) N^\kappa \big( \widehat V(\cdot/N^{1-\kappa}) \ast \widehat f_{N,\ell} \big)_v + \mathcal{E}_3 \end{align} $$
with
 $$ \begin{align*} \mathcal{E}_3 =\; -\frac 1 N \hskip -0.2cm \sum_{v,\,r\in P_L}\hskip -0.2cm N^\kappa \widehat V((r-v)/N^{1-\kappa}) \big(\sigma^2_v + \gamma_v \sigma_v \big)\eta_{r} - \frac {\eta_0} N \sum_{v \in P_L} N^\kappa \widehat V_{N}(v/N^{1-\kappa}) \big(\sigma^2_v + \gamma_v \sigma_v \big) . \end{align*} $$
$$ \begin{align*} \mathcal{E}_3 =\; -\frac 1 N \hskip -0.2cm \sum_{v,\,r\in P_L}\hskip -0.2cm N^\kappa \widehat V((r-v)/N^{1-\kappa}) \big(\sigma^2_v + \gamma_v \sigma_v \big)\eta_{r} - \frac {\eta_0} N \sum_{v \in P_L} N^\kappa \widehat V_{N}(v/N^{1-\kappa}) \big(\sigma^2_v + \gamma_v \sigma_v \big) . \end{align*} $$
With (2.8), Lemma 2.4,
![]() $|\eta _0| \leq C N^\kappa $
and the assumption
$|\eta _0| \leq C N^\kappa $
and the assumption
![]() $3\kappa -2 + 5\varepsilon < 0$
, we obtain
$3\kappa -2 + 5\varepsilon < 0$
, we obtain
![]() $\mathcal {E}_3 \leq N^{5\kappa /2-\varepsilon }$
.
$\mathcal {E}_3 \leq N^{5\kappa /2-\varepsilon }$
.
Inserting (3.15) and (3.16) in (3.14) and completing sums over p on the right-hand side of (3.15), we arrive at
 $$ \begin{align} E_N^\Psi \leq \; & \frac{N}{2} \big( N^\kappa \widehat V_{N}(\cdot/N^{1-\kappa}) \ast \widehat f_{N,\ell} \big)_0 \nonumber \\ &+ \sum_{v \in P_L} \Big[ v^2 \sigma_v^2 + \big(\sigma^2_v + \gamma_v \sigma_v \big) \big( N^\kappa \widehat V(\cdot/N^{1-\kappa}) \ast \widehat f_{N,\ell} \big)_v - \frac {1} 2 N^\kappa \big( \widehat V(\cdot/N^{1-\kappa}) \ast \widehat f_{N,\ell} \big)_v \eta_v \Big] \nonumber \\ &+ C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\}. \end{align} $$
$$ \begin{align} E_N^\Psi \leq \; & \frac{N}{2} \big( N^\kappa \widehat V_{N}(\cdot/N^{1-\kappa}) \ast \widehat f_{N,\ell} \big)_0 \nonumber \\ &+ \sum_{v \in P_L} \Big[ v^2 \sigma_v^2 + \big(\sigma^2_v + \gamma_v \sigma_v \big) \big( N^\kappa \widehat V(\cdot/N^{1-\kappa}) \ast \widehat f_{N,\ell} \big)_v - \frac {1} 2 N^\kappa \big( \widehat V(\cdot/N^{1-\kappa}) \ast \widehat f_{N,\ell} \big)_v \eta_v \Big] \nonumber \\ &+ C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\}. \end{align} $$
Let us now introduce the notation
 $\hat {g}_p = ( N^\kappa \widehat V(\cdot /N^{1-\kappa }) \ast \widehat f_{N,\ell })_p$
. Notice that
$\hat {g}_p = ( N^\kappa \widehat V(\cdot /N^{1-\kappa }) \ast \widehat f_{N,\ell })_p$
. Notice that
 $$ \begin{align} \big|\, \widehat g_0 - 8 \pi \mathfrak{a} N^\kappa \,\big| \leq C N^{2\kappa -1}, \qquad \big|\, \widehat g_p - \widehat g_0 \, \big| \leq C |p| N^{2\kappa -1} . \end{align} $$
$$ \begin{align} \big|\, \widehat g_0 - 8 \pi \mathfrak{a} N^\kappa \,\big| \leq C N^{2\kappa -1}, \qquad \big|\, \widehat g_p - \widehat g_0 \, \big| \leq C |p| N^{2\kappa -1} . \end{align} $$
With the expression (2.28), we obtain
 $$ \begin{align*} \sum_{v \in P_L} \Big[ v^2 \sigma_v^2 + \big(\sigma^2_v + \gamma_v \sigma_v \big) \widehat g_v \Big] & =\frac 12 \sum_{v \in P_L} \left[ -v^2 - \widehat g_v + \frac{v^4 + v^2 (8\pi \frak{a} N^\kappa + \widehat g_v)}{\sqrt{v^4 + 16 \pi \frak{a} N^\kappa v^2}} \right] \\ & = \frac 12 \sum_{v \in P_L} \left[ \sqrt{v^4 + 16 \pi \frak{a} N^\kappa v^2} - v^2 - 8 \pi \mathfrak{a} N^\kappa \right] + \mathcal{E}_{4} \end{align*} $$
$$ \begin{align*} \sum_{v \in P_L} \Big[ v^2 \sigma_v^2 + \big(\sigma^2_v + \gamma_v \sigma_v \big) \widehat g_v \Big] & =\frac 12 \sum_{v \in P_L} \left[ -v^2 - \widehat g_v + \frac{v^4 + v^2 (8\pi \frak{a} N^\kappa + \widehat g_v)}{\sqrt{v^4 + 16 \pi \frak{a} N^\kappa v^2}} \right] \\ & = \frac 12 \sum_{v \in P_L} \left[ \sqrt{v^4 + 16 \pi \frak{a} N^\kappa v^2} - v^2 - 8 \pi \mathfrak{a} N^\kappa \right] + \mathcal{E}_{4} \end{align*} $$
where, with (3.18) and
![]() $3\kappa -2 + 4\varepsilon < 0$
, we find
$3\kappa -2 + 4\varepsilon < 0$
, we find
 $$ \begin{align*} \mathcal{E}_{4} &= \frac 12 \sum_{v\in P_L} \left[ 8\pi \frak{a} N^\kappa - \widehat g_v + \frac{\widehat g_v - 8\pi \frak{a} N^\kappa}{\sqrt{1 + 16 \pi \frak{a} N^\kappa / v^2}} \right] \\ &\leq C \sum_{v\in P_L} | 8\pi \frak{a} N^\kappa - \widehat g_v | \;\frac{|\sqrt{1 + 16 \pi \frak{a} N^\kappa / v^2} - 1 |}{\sqrt{1 + 16 \pi \frak{a} N^\kappa /v^2}} \\ &\leq C N^{2\kappa-1} \Big[ \sum_{|v| < N^{\kappa/2}} (1+ |v|) + \sum_{v \in P_L : |v|> N^{\kappa/2}} \frac{N^{\kappa/2}}{|v|^2} \Big] \leq C N^{5\kappa/2-\varepsilon} . \end{align*} $$
$$ \begin{align*} \mathcal{E}_{4} &= \frac 12 \sum_{v\in P_L} \left[ 8\pi \frak{a} N^\kappa - \widehat g_v + \frac{\widehat g_v - 8\pi \frak{a} N^\kappa}{\sqrt{1 + 16 \pi \frak{a} N^\kappa / v^2}} \right] \\ &\leq C \sum_{v\in P_L} | 8\pi \frak{a} N^\kappa - \widehat g_v | \;\frac{|\sqrt{1 + 16 \pi \frak{a} N^\kappa / v^2} - 1 |}{\sqrt{1 + 16 \pi \frak{a} N^\kappa /v^2}} \\ &\leq C N^{2\kappa-1} \Big[ \sum_{|v| < N^{\kappa/2}} (1+ |v|) + \sum_{v \in P_L : |v|> N^{\kappa/2}} \frac{N^{\kappa/2}}{|v|^2} \Big] \leq C N^{5\kappa/2-\varepsilon} . \end{align*} $$
Moreover, from (3.17) and with the scattering equation (2.9), we obtain
 $$ \begin{align*} - \frac{N^\kappa}{2} \sum_{v \in P_L} \widehat{g}_v \eta_v \leq \sum_{v \in P_L} \frac{(8\pi \frak{a} N^\kappa )^2}{4v^2} + C N^{5\kappa/2-\varepsilon}. \end{align*} $$
$$ \begin{align*} - \frac{N^\kappa}{2} \sum_{v \in P_L} \widehat{g}_v \eta_v \leq \sum_{v \in P_L} \frac{(8\pi \frak{a} N^\kappa )^2}{4v^2} + C N^{5\kappa/2-\varepsilon}. \end{align*} $$
Thus,
 $$ \begin{align*} E^\Psi_N \leq \; & 4 \pi \mathfrak{a} N^{1+\kappa} + \frac 12 \sum_{v \in P_L} \Big[ \sqrt{v^4 + 16 \pi \mathfrak{a} N^\kappa v^2} - v^2 - 8 \pi \mathfrak{a} N^\kappa + \frac{(8 \pi \mathfrak{a} N^\kappa )^2}{2v^2} \Big] \\ &+ C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\} . \end{align*} $$
$$ \begin{align*} E^\Psi_N \leq \; & 4 \pi \mathfrak{a} N^{1+\kappa} + \frac 12 \sum_{v \in P_L} \Big[ \sqrt{v^4 + 16 \pi \mathfrak{a} N^\kappa v^2} - v^2 - 8 \pi \mathfrak{a} N^\kappa + \frac{(8 \pi \mathfrak{a} N^\kappa )^2}{2v^2} \Big] \\ &+ C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\} . \end{align*} $$
With
 $$ \begin{align*} \left| \sqrt{v^4 + 16 \pi \mathfrak{a} N^\kappa v^2} - v^2 - 8 \pi \mathfrak{a} N^\kappa + \frac{(8 \pi \mathfrak{a} N^\kappa )^2}{2v^2} \right| \leq C \frac{N^{2\kappa}}{|v|^4} \end{align*} $$
$$ \begin{align*} \left| \sqrt{v^4 + 16 \pi \mathfrak{a} N^\kappa v^2} - v^2 - 8 \pi \mathfrak{a} N^\kappa + \frac{(8 \pi \mathfrak{a} N^\kappa )^2}{2v^2} \right| \leq C \frac{N^{2\kappa}}{|v|^4} \end{align*} $$
we can replace, up to an error of order
![]() $N^{5\kappa /2-\varepsilon }$
, the sum over
$N^{5\kappa /2-\varepsilon }$
, the sum over
![]() $P_L$
with a sum over all
$P_L$
with a sum over all
![]() $\Lambda ^*_+$
. With the rescaling
$\Lambda ^*_+$
. With the rescaling
![]() $v \to N^{\kappa /2} v$
, we arrive at
$v \to N^{\kappa /2} v$
, we arrive at
 $$ \begin{align} E^\Psi_N \leq \; & 4 \pi \mathfrak{a} N^{1+\kappa} + \frac{N^\kappa}{2} \sum_{v \in 2\pi N^{-\kappa/2} \mathbb{Z}^3} \Big[ \sqrt{v^4 + 16 \pi \mathfrak{a} v^2} - v^2 - 8 \pi \mathfrak{a} + \frac{(8 \pi \mathfrak{a} )^2}{2v^2} \Big] \nonumber \\ &+ C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\}. \end{align} $$
$$ \begin{align} E^\Psi_N \leq \; & 4 \pi \mathfrak{a} N^{1+\kappa} + \frac{N^\kappa}{2} \sum_{v \in 2\pi N^{-\kappa/2} \mathbb{Z}^3} \Big[ \sqrt{v^4 + 16 \pi \mathfrak{a} v^2} - v^2 - 8 \pi \mathfrak{a} + \frac{(8 \pi \mathfrak{a} )^2}{2v^2} \Big] \nonumber \\ &+ C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\}. \end{align} $$
Recognising that (3.19) defines a Riemann sum and explicitly computing
 $$ \begin{align*} \frac{1}{2 (2\pi)^3} \int dv \, \Big[ \sqrt{v^4 + 16 \pi \mathfrak{a} v^2} - v^2 - 8 \pi \mathfrak{a} + \frac{(8 \pi \mathfrak{a} )^2}{2v^2} \Big] = 4 \pi \frak{a} \cdot \frac{128}{15 \sqrt{\pi}} \frak{a}^{3/2} \end{align*} $$
$$ \begin{align*} \frac{1}{2 (2\pi)^3} \int dv \, \Big[ \sqrt{v^4 + 16 \pi \mathfrak{a} v^2} - v^2 - 8 \pi \mathfrak{a} + \frac{(8 \pi \mathfrak{a} )^2}{2v^2} \Big] = 4 \pi \frak{a} \cdot \frac{128}{15 \sqrt{\pi}} \frak{a}^{3/2} \end{align*} $$
we conclude that
 $$ \begin{align*} E^\Psi_N \leq \; & 4 \pi \mathfrak{a} N^{1+\kappa} \cdot \left[ 1 + \frac{128}{15 \sqrt{\pi}} \, (\frak{a}^3 N^{3\kappa-2})^{1/2} \right] \\ &+ C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\} . \end{align*} $$
$$ \begin{align*} E^\Psi_N \leq \; & 4 \pi \mathfrak{a} N^{1+\kappa} \cdot \left[ 1 + \frac{128}{15 \sqrt{\pi}} \, (\frak{a}^3 N^{3\kappa-2})^{1/2} \right] \\ &+ C N^{5\kappa/2} \max \{ N^{-\varepsilon},\,N^{9\kappa-5 +6\varepsilon} ,\, N^{21\kappa/4-3+3\varepsilon}\} . \end{align*} $$
To compare the Riemann sum in (3.19) with the integral, we first removed contributions arising from
![]() $|v| \leq N^{-\varepsilon }$
using that
$|v| \leq N^{-\varepsilon }$
using that
![]() $|F(v)| \leq C / v^2$
, for small v, with the definition
$|F(v)| \leq C / v^2$
, for small v, with the definition
![]() $F(v) = \sqrt {v^4 + 16 \pi \mathfrak {a} v^2} - v^2 - 8 \pi \mathfrak {a} + (8 \pi \mathfrak {a} )^2 / 2v^2$
. For
$F(v) = \sqrt {v^4 + 16 \pi \mathfrak {a} v^2} - v^2 - 8 \pi \mathfrak {a} + (8 \pi \mathfrak {a} )^2 / 2v^2$
. For
![]() $|v|> N^{-\varepsilon }$
, we use that
$|v|> N^{-\varepsilon }$
, we use that
![]() $|\nabla F (v)| \leq C |v|^{-3} (1+v^2)^{-1}$
to compare the value of
$|\nabla F (v)| \leq C |v|^{-3} (1+v^2)^{-1}$
to compare the value of
![]() $F(q)$
with
$F(q)$
with
![]() $F(v)$
, for all q in the cube of size
$F(v)$
, for all q in the cube of size
![]() $2\pi N^{-\kappa /2}$
centred at v.
$2\pi N^{-\kappa /2}$
centred at v.
4 Bogoliubov transformation
In this section, we show Proposition 3.1. From the definition (3.1) and from (3.3), we obtain (since
![]() $T_\nu $
does not act on the zero momentum mode and since
$T_\nu $
does not act on the zero momentum mode and since
![]() $a_0 \xi _\nu = 0$
)
$a_0 \xi _\nu = 0$
)
 $$ \begin{align*} \frac{\langle \xi_\nu, \mathcal{G}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} = \frac{N_0^2}{2} N^{\kappa - 1} \widehat{V} (0) + \sum_{j=2}^4 \frac{\langle \xi_\nu, \mathcal{G}_N^{(j)} \xi_\nu \rangle}{\| \xi_\nu \|^2} \end{align*} $$
$$ \begin{align*} \frac{\langle \xi_\nu, \mathcal{G}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} = \frac{N_0^2}{2} N^{\kappa - 1} \widehat{V} (0) + \sum_{j=2}^4 \frac{\langle \xi_\nu, \mathcal{G}_N^{(j)} \xi_\nu \rangle}{\| \xi_\nu \|^2} \end{align*} $$
with
 $\mathcal {G}_N^{(j)} = T_\nu ^* \mathcal {L}_N^{(j)} T_\nu $
, for
$\mathcal {G}_N^{(j)} = T_\nu ^* \mathcal {L}_N^{(j)} T_\nu $
, for
![]() $j=2,3,4$
.
$j=2,3,4$
.
We start from the contribution of
 $\mathcal {G}_N^{(2)}$
. We write
$\mathcal {G}_N^{(2)}$
. We write
 $\mathcal {L}_N^{(2)}= \mathcal {K} + \mathcal {L}_N^{(2,V)}$
with
$\mathcal {L}_N^{(2)}= \mathcal {K} + \mathcal {L}_N^{(2,V)}$
with
 $$ \begin{align*} \mathcal{L}_N^{(2,V)} =\frac{N_0}{N}\sum_{p\in \Lambda^*} N^\kappa \big( \hat{V}(p/N^{1-\kappa}) + \hat V(0) \big) a_p^*a_p + \frac{N_0}{2N}\sum_{p\in \Lambda^*}N^\kappa \hat{V}(p/N^{1-\kappa})(a_p^*a_{-p}^*+\mbox{h.c.} ). \end{align*} $$
$$ \begin{align*} \mathcal{L}_N^{(2,V)} =\frac{N_0}{N}\sum_{p\in \Lambda^*} N^\kappa \big( \hat{V}(p/N^{1-\kappa}) + \hat V(0) \big) a_p^*a_p + \frac{N_0}{2N}\sum_{p\in \Lambda^*}N^\kappa \hat{V}(p/N^{1-\kappa})(a_p^*a_{-p}^*+\mbox{h.c.} ). \end{align*} $$
Using (2.14) we get
 $$ \begin{align*} T^*_{\nu} \mathcal{K} T_\nu - \left[ \mathcal{K} + \sum_{p \in \Lambda_+^*} p^2 \sigma_p^2 \right] = 2 \sum_{p\in \Lambda^*_+} p^2 \sigma_p^2 a^*_p a_p + \sum_{p \in \Lambda^*_+} p^2 \big[\gamma_p\sigma_p ( a^*_p a^*_{-p}+\mbox{h.c.}) \big] := E_1 + E_2. \end{align*} $$
$$ \begin{align*} T^*_{\nu} \mathcal{K} T_\nu - \left[ \mathcal{K} + \sum_{p \in \Lambda_+^*} p^2 \sigma_p^2 \right] = 2 \sum_{p\in \Lambda^*_+} p^2 \sigma_p^2 a^*_p a_p + \sum_{p \in \Lambda^*_+} p^2 \big[\gamma_p\sigma_p ( a^*_p a^*_{-p}+\mbox{h.c.}) \big] := E_1 + E_2. \end{align*} $$
From (2.15),
![]() $\langle \xi _\nu , \text {E}_2 \xi _\nu \rangle = 0$
(
$\langle \xi _\nu , \text {E}_2 \xi _\nu \rangle = 0$
(
![]() $\xi _\nu $
is a superposition of states with
$\xi _\nu $
is a superposition of states with
![]() $3m$
particles, for
$3m$
particles, for
![]() $m \in \mathbb {N}$
). To bound the expectation of
$m \in \mathbb {N}$
). To bound the expectation of
![]() $E_1$
on
$E_1$
on
![]() $\xi _\nu $
we notice that
$\xi _\nu $
we notice that
![]() $\langle \xi _\nu ,a^*_pa_p\xi _\nu \rangle =0$
if
$\langle \xi _\nu ,a^*_pa_p\xi _\nu \rangle =0$
if
![]() $p\in \Lambda ^*_+\backslash (P_S\cup P_H)$
. Moreover, proceeding as in (2.31), we have
$p\in \Lambda ^*_+\backslash (P_S\cup P_H)$
. Moreover, proceeding as in (2.31), we have
 $$ \begin{align*} \mathop{\mathrm{sup}}\limits_{p \in P_S} ( p^2 \sigma_p^2) \leq \mathop{\mathrm{sup}}\limits_{p \in P_S: |p|\leq N^{\kappa/2}} N^{\kappa/2} |p| + \mathop{\mathrm{sup}}\limits_{p \in P_S : |p|> N^{\kappa/2}} \frac{N^{2\kappa}}{p^2} \leq C N^{\kappa} \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{sup}}\limits_{p \in P_S} ( p^2 \sigma_p^2) \leq \mathop{\mathrm{sup}}\limits_{p \in P_S: |p|\leq N^{\kappa/2}} N^{\kappa/2} |p| + \mathop{\mathrm{sup}}\limits_{p \in P_S : |p|> N^{\kappa/2}} \frac{N^{2\kappa}}{p^2} \leq C N^{\kappa} \end{align*} $$
while
 $$ \begin{align*} \mathop{\mathrm{sup}}\limits_{p \in P_H} (p^2 \sigma_p^2) \leq \mathop{\mathrm{sup}}\limits_{|p| \geq N^{1-\kappa-\varepsilon}} \frac{N^{2\kappa}}{p^2} \leq C N^{-2+4\kappa+2\varepsilon} \leq C N^\kappa \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{sup}}\limits_{p \in P_H} (p^2 \sigma_p^2) \leq \mathop{\mathrm{sup}}\limits_{|p| \geq N^{1-\kappa-\varepsilon}} \frac{N^{2\kappa}}{p^2} \leq C N^{-2+4\kappa+2\varepsilon} \leq C N^\kappa \end{align*} $$
because, by assumption,
![]() $3\kappa -2+2\varepsilon < 0$
. Hence,
$3\kappa -2+2\varepsilon < 0$
. Hence,
 $$ \begin{align} |{\bigl\langle\xi_\nu, E_{1}\xi_\nu\bigr\rangle}|\leq C N^\kappa \, \| \mathcal{N}^{1/2}\xi_\nu \|^2 . \end{align} $$
$$ \begin{align} |{\bigl\langle\xi_\nu, E_{1}\xi_\nu\bigr\rangle}|\leq C N^\kappa \, \| \mathcal{N}^{1/2}\xi_\nu \|^2 . \end{align} $$
We now consider the contribution from
 $ \mathcal {L}_N^{(2,V)}$
. Using again
$ \mathcal {L}_N^{(2,V)}$
. Using again
![]() $\langle \xi _\nu , a_p^* a_{-p}^* \xi _\nu \rangle = 0$
for all
$\langle \xi _\nu , a_p^* a_{-p}^* \xi _\nu \rangle = 0$
for all
![]() $p \in \Lambda _+^*$
and
$p \in \Lambda _+^*$
and
![]() $\langle \xi _\nu , a_p^* a_{p} \xi _\nu \rangle = 0$
for all
$\langle \xi _\nu , a_p^* a_{p} \xi _\nu \rangle = 0$
for all
![]() $p \in \Lambda ^*_+\backslash (P_S \cup P_H)$
, a straightforward computation shows that
$p \in \Lambda ^*_+\backslash (P_S \cup P_H)$
, a straightforward computation shows that
 $$ \begin{align*} &\frac{\langle \xi_\nu, T^*_\nu \mathcal{L}_N^{(2,V)} T_\nu \xi_\nu \rangle}{\| \xi_\nu \|^2} \\ &\hspace{2cm} = \frac{N_0}{N} \sum_{p \in \Lambda^*_+} N^\kappa \widehat V(p/N^{1-\kappa}) \gamma_p \sigma_p + \frac{N_0}{N} \sum_{p \in \Lambda^*_+} N^\kappa \big(\widehat V(0) +\widehat V(p/N^{1-\kappa}) \big) \sigma^2_p \\ & \hspace{2.3cm} + \frac{N_0}{N} \sum_{p\in P_S \cup P_H} N^\kappa \big[\widehat V(p/N^{\kappa-1})(\gamma_p+\sigma_p)^2 +\widehat V(0) (\gamma^2_p + \sigma^2_p) \big] \frac{\langle \xi_\nu, a^*_p a_p \xi_\nu \rangle}{\| \xi_\nu \|^2} . \end{align*} $$
$$ \begin{align*} &\frac{\langle \xi_\nu, T^*_\nu \mathcal{L}_N^{(2,V)} T_\nu \xi_\nu \rangle}{\| \xi_\nu \|^2} \\ &\hspace{2cm} = \frac{N_0}{N} \sum_{p \in \Lambda^*_+} N^\kappa \widehat V(p/N^{1-\kappa}) \gamma_p \sigma_p + \frac{N_0}{N} \sum_{p \in \Lambda^*_+} N^\kappa \big(\widehat V(0) +\widehat V(p/N^{1-\kappa}) \big) \sigma^2_p \\ & \hspace{2.3cm} + \frac{N_0}{N} \sum_{p\in P_S \cup P_H} N^\kappa \big[\widehat V(p/N^{\kappa-1})(\gamma_p+\sigma_p)^2 +\widehat V(0) (\gamma^2_p + \sigma^2_p) \big] \frac{\langle \xi_\nu, a^*_p a_p \xi_\nu \rangle}{\| \xi_\nu \|^2} . \end{align*} $$
With the bounds
![]() $\|\gamma _S \|^2_\infty $
,
$\|\gamma _S \|^2_\infty $
,
![]() $\|\sigma _S\|^2_\infty $
,
$\|\sigma _S\|^2_\infty $
,
![]() $\|\sigma _H\|_\infty ^2$
,
$\|\sigma _H\|_\infty ^2$
,
![]() $\|\gamma _H\|_\infty ^2 \leq C N^{\varepsilon }$
from Lemma 2.4, with (4.1) and with the estimate
$\|\gamma _H\|_\infty ^2 \leq C N^{\varepsilon }$
from Lemma 2.4, with (4.1) and with the estimate
![]() $\langle \xi _\nu , \mathcal {N} \xi _\nu \rangle \leq C N^{9\kappa /2 -2+\varepsilon } \| \xi _\nu \|^2$
from Proposition 2.2, we conclude that
$\langle \xi _\nu , \mathcal {N} \xi _\nu \rangle \leq C N^{9\kappa /2 -2+\varepsilon } \| \xi _\nu \|^2$
from Proposition 2.2, we conclude that
 $$ \begin{align} \frac{\langle \xi_\nu, \mathcal{G}^{(2)}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \; &\frac{\langle \xi_\nu, \mathcal{K} \xi_\nu \rangle}{\| \xi_\nu \|^2} + \sum_{p \in \Lambda^*_+} p^2 \sigma_p^2 + \frac{N_0}{N} \sum_{p \in \Lambda^*_+} N^\kappa \widehat V(p/N^{1-\kappa}) \gamma_p \sigma_p \nonumber\\ &+ \frac{N_0}{N} \sum_{p \in \Lambda^*_+} N^\kappa \big(\widehat V(0) +\widehat V(p/N^{1-\kappa}) \big) \sigma^2_p + C N^{5\kappa/2-\varepsilon} \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu, \mathcal{G}^{(2)}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \; &\frac{\langle \xi_\nu, \mathcal{K} \xi_\nu \rangle}{\| \xi_\nu \|^2} + \sum_{p \in \Lambda^*_+} p^2 \sigma_p^2 + \frac{N_0}{N} \sum_{p \in \Lambda^*_+} N^\kappa \widehat V(p/N^{1-\kappa}) \gamma_p \sigma_p \nonumber\\ &+ \frac{N_0}{N} \sum_{p \in \Lambda^*_+} N^\kappa \big(\widehat V(0) +\widehat V(p/N^{1-\kappa}) \big) \sigma^2_p + C N^{5\kappa/2-\varepsilon} \end{align} $$
using again the condition
![]() $3\kappa - 2 +4\varepsilon < 0$
.
$3\kappa - 2 +4\varepsilon < 0$
.
Next, we study the contribution of
 $\mathcal {G}_N^{(3)} = T_\nu ^* \mathcal {L}^{(3)}_N T_\nu $
, with
$\mathcal {G}_N^{(3)} = T_\nu ^* \mathcal {L}^{(3)}_N T_\nu $
, with
 $\mathcal {L}^{(3)}_N$
as in (3.3). Recall the operator
$\mathcal {L}^{(3)}_N$
as in (3.3). Recall the operator
![]() $\mathcal {C}_N$
, defined in (3.5). Taking into account the fact that
$\mathcal {C}_N$
, defined in (3.5). Taking into account the fact that
![]() $\xi _\nu $
is a superposition of vectors with
$\xi _\nu $
is a superposition of vectors with
![]() $2m$
particles with momenta in
$2m$
particles with momenta in
![]() $P_H$
and m particles with momenta in
$P_H$
and m particles with momenta in
![]() $P_S$
, for
$P_S$
, for
![]() $m \in \mathbb {N}$
, we obtain that
$m \in \mathbb {N}$
, we obtain that
 $$ \begin{align*} \langle \xi_\nu, \mathcal{G}_N^{(3)} \xi_\nu \rangle = \langle \xi_\nu , \mathcal{C}_N \xi_\nu \rangle + \sum_{j=1}^3 \left[ \langle \xi_\nu, \text{F}_j \xi_\nu \rangle + \text{h.c.} \right] \end{align*} $$
$$ \begin{align*} \langle \xi_\nu, \mathcal{G}_N^{(3)} \xi_\nu \rangle = \langle \xi_\nu , \mathcal{C}_N \xi_\nu \rangle + \sum_{j=1}^3 \left[ \langle \xi_\nu, \text{F}_j \xi_\nu \rangle + \text{h.c.} \right] \end{align*} $$
with
 $$ \begin{align*} \text{F}_1 &= \frac{\sqrt{N_0}}{N} \sum_{p,r \in P_H : p+r \in P_S} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_{p+r} \sigma_p \sigma_r \, a^*_{p+r} a^*_{-p} a^*_{-r} \\ \text{F}_2 &= \frac{\sqrt{N_0}}{N} \sum_{p \in P_H , r \in P_S : p+r \in P_H} N^\kappa \left[ \widehat V(r/N^{1-\kappa}) + \widehat{V} (p / N^{1-\kappa}) \right] \gamma_{p+r} \sigma_p \sigma_r \, a^*_{p+r} a^*_{-p} a^*_{-r} \\ \text{F}_3 &= \frac{\sqrt{N_0}}{N} \sum_{p \in P_H, r \in P_S : p+r \in P_H} N^\kappa \left[ \widehat V(r/N^{1-\kappa}) + \widehat V(p /N^{1-\kappa}) \right] \sigma_{p+r} \gamma_p \gamma_r \, a_{-p-r} a_{p} a_{r} . \end{align*} $$
$$ \begin{align*} \text{F}_1 &= \frac{\sqrt{N_0}}{N} \sum_{p,r \in P_H : p+r \in P_S} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_{p+r} \sigma_p \sigma_r \, a^*_{p+r} a^*_{-p} a^*_{-r} \\ \text{F}_2 &= \frac{\sqrt{N_0}}{N} \sum_{p \in P_H , r \in P_S : p+r \in P_H} N^\kappa \left[ \widehat V(r/N^{1-\kappa}) + \widehat{V} (p / N^{1-\kappa}) \right] \gamma_{p+r} \sigma_p \sigma_r \, a^*_{p+r} a^*_{-p} a^*_{-r} \\ \text{F}_3 &= \frac{\sqrt{N_0}}{N} \sum_{p \in P_H, r \in P_S : p+r \in P_H} N^\kappa \left[ \widehat V(r/N^{1-\kappa}) + \widehat V(p /N^{1-\kappa}) \right] \sigma_{p+r} \gamma_p \gamma_r \, a_{-p-r} a_{p} a_{r} . \end{align*} $$
Using
![]() $\|a^*_{-r} (\mathcal {N}+1)^{1/2}\xi _\nu \|\leq \|a_{-r} (\mathcal {N}+1)^{1/2}\xi _\nu \| + \|(\mathcal {N}+1)^{1/2}\xi _\nu \|$
, we can bound
$\|a^*_{-r} (\mathcal {N}+1)^{1/2}\xi _\nu \|\leq \|a_{-r} (\mathcal {N}+1)^{1/2}\xi _\nu \| + \|(\mathcal {N}+1)^{1/2}\xi _\nu \|$
, we can bound
 $$ \begin{align*} \langle \xi_\nu , \text{F}_1 \xi_\nu \rangle \leq \; &C N^{\kappa -1/2} \| \gamma_S \|_\infty \sum_{p,r \in P_H} |\sigma_r| |\sigma_p | \, \| a_{p+r} a_{-p} (\mathcal{N} + 1)^{-1/2} \xi_\nu \| \\ &\hspace{4cm} \times \left[ \| a_{-r} (\mathcal{N} + 1)^{1/2} \xi_\nu \| + \| (\mathcal{N} + 1)^{1/2} \xi_{\nu} \| \right] \\ \leq \; &C N^{\kappa -1/2} \| \gamma_S \|_\infty \| \sigma_H \|_\infty \| \sigma_H \| \, \| (\mathcal{N} + 1)^{1/2} \xi_\nu \| \| (\mathcal{N}+ 1) \xi_\nu \| \\ &+ C N^{\kappa -1/2} \| \gamma_S \|_\infty \| \sigma_H \|^2 \, \| (\mathcal{N} + 1)^{1/2} \xi_\nu \|^2. \end{align*} $$
$$ \begin{align*} \langle \xi_\nu , \text{F}_1 \xi_\nu \rangle \leq \; &C N^{\kappa -1/2} \| \gamma_S \|_\infty \sum_{p,r \in P_H} |\sigma_r| |\sigma_p | \, \| a_{p+r} a_{-p} (\mathcal{N} + 1)^{-1/2} \xi_\nu \| \\ &\hspace{4cm} \times \left[ \| a_{-r} (\mathcal{N} + 1)^{1/2} \xi_\nu \| + \| (\mathcal{N} + 1)^{1/2} \xi_{\nu} \| \right] \\ \leq \; &C N^{\kappa -1/2} \| \gamma_S \|_\infty \| \sigma_H \|_\infty \| \sigma_H \| \, \| (\mathcal{N} + 1)^{1/2} \xi_\nu \| \| (\mathcal{N}+ 1) \xi_\nu \| \\ &+ C N^{\kappa -1/2} \| \gamma_S \|_\infty \| \sigma_H \|^2 \, \| (\mathcal{N} + 1)^{1/2} \xi_\nu \|^2. \end{align*} $$
With Lemma 2.4 and Proposition 2.2, we obtain
 $$ \begin{align*} \frac{\langle \xi_\nu , \text{F}_1 \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq CN^{37\kappa /4 - 4 +5\varepsilon/2} + C N^{17\kappa/2 - 7/2 + 5\varepsilon/2} \leq C N^{5\kappa/2} \cdot N^{21\kappa /4 - 7/2 + 3\varepsilon/2} \end{align*} $$
$$ \begin{align*} \frac{\langle \xi_\nu , \text{F}_1 \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq CN^{37\kappa /4 - 4 +5\varepsilon/2} + C N^{17\kappa/2 - 7/2 + 5\varepsilon/2} \leq C N^{5\kappa/2} \cdot N^{21\kappa /4 - 7/2 + 3\varepsilon/2} \end{align*} $$
from the assumption that
![]() $3\kappa -2 +4\varepsilon < 0$
. Similarly, we find
$3\kappa -2 +4\varepsilon < 0$
. Similarly, we find
 $$ \begin{align*} \langle \xi_\nu , \text{F}_2 \xi_\nu \rangle \leq \; & C N^{\kappa -1/2} \| \gamma_H \|_\infty \| \sigma_S \|_\infty \| \sigma_H \| \, \| (\mathcal{N}+ 1)^{1/2} \xi_\nu \| \| (\mathcal{N}+ 1) \xi_\nu \| \\ &+ C N^{\kappa -1/2} \| \gamma_H \|_\infty \| \sigma_S \| \| \sigma_H \| \, \| (\mathcal{N} + 1)^{1/2} \xi_\nu \|^2 \\ \leq \; &C \big[ N^{37\kappa/4-4+3\varepsilon} + N^{31\kappa/4-3+3\varepsilon/2} \big] \| \xi_\nu \|^2 \leq C N^{5\kappa/2} \cdot N^{21\kappa/4 - 3 + 3 \varepsilon /2} \| \xi_\nu \|^2 \end{align*} $$
$$ \begin{align*} \langle \xi_\nu , \text{F}_2 \xi_\nu \rangle \leq \; & C N^{\kappa -1/2} \| \gamma_H \|_\infty \| \sigma_S \|_\infty \| \sigma_H \| \, \| (\mathcal{N}+ 1)^{1/2} \xi_\nu \| \| (\mathcal{N}+ 1) \xi_\nu \| \\ &+ C N^{\kappa -1/2} \| \gamma_H \|_\infty \| \sigma_S \| \| \sigma_H \| \, \| (\mathcal{N} + 1)^{1/2} \xi_\nu \|^2 \\ \leq \; &C \big[ N^{37\kappa/4-4+3\varepsilon} + N^{31\kappa/4-3+3\varepsilon/2} \big] \| \xi_\nu \|^2 \leq C N^{5\kappa/2} \cdot N^{21\kappa/4 - 3 + 3 \varepsilon /2} \| \xi_\nu \|^2 \end{align*} $$
and also
 $$ \begin{align*} \langle \xi_\nu , \text{F}_3 \xi_\nu \rangle \leq \; & C N^{\kappa -1/2} \| \gamma_H \|_\infty \| \gamma_S \|_\infty \| \sigma_H \| \, \| (\mathcal{N}+ 1)^{1/2} \xi_\nu \| \| (\mathcal{N}+ 1) \xi_\nu \| \\ &+ C N^{\kappa -1/2} \| \gamma_H \|_\infty \| \gamma_S \| \| \sigma_H \| \, \| (\mathcal{N} + 1)^{1/2} \xi_\nu \|^2 \\ \leq \; &C N^{5\kappa/2} \cdot N^{21\kappa/4 - 3 + 3 \varepsilon} \| \xi_\nu \|^2 . \end{align*} $$
$$ \begin{align*} \langle \xi_\nu , \text{F}_3 \xi_\nu \rangle \leq \; & C N^{\kappa -1/2} \| \gamma_H \|_\infty \| \gamma_S \|_\infty \| \sigma_H \| \, \| (\mathcal{N}+ 1)^{1/2} \xi_\nu \| \| (\mathcal{N}+ 1) \xi_\nu \| \\ &+ C N^{\kappa -1/2} \| \gamma_H \|_\infty \| \gamma_S \| \| \sigma_H \| \, \| (\mathcal{N} + 1)^{1/2} \xi_\nu \|^2 \\ \leq \; &C N^{5\kappa/2} \cdot N^{21\kappa/4 - 3 + 3 \varepsilon} \| \xi_\nu \|^2 . \end{align*} $$
Summarising, we have
 $$ \begin{align} \frac{\langle \xi_\nu, \mathcal{G}_N^{(3)} \xi_\nu \rangle}{ \| \xi_\nu \|^2} \leq \frac{\langle \xi_\nu , \mathcal{C}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} + C N^{5\kappa/2} \cdot N^{21\kappa/4 - 3 + 3 \varepsilon} . \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu, \mathcal{G}_N^{(3)} \xi_\nu \rangle}{ \| \xi_\nu \|^2} \leq \frac{\langle \xi_\nu , \mathcal{C}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} + C N^{5\kappa/2} \cdot N^{21\kappa/4 - 3 + 3 \varepsilon} . \end{align} $$
Finally, let us consider
 $\mathcal {G}_N^{(4)} = T_\nu ^* \mathcal {L}_N^{(4)} T_\nu $
. We decompose
$\mathcal {G}_N^{(4)} = T_\nu ^* \mathcal {L}_N^{(4)} T_\nu $
. We decompose
 $\langle \xi _\nu , \mathcal {G}_N^{(4)} \xi _\nu \rangle = \sum _{j=1}^3 \langle \xi _\nu , \text {G}_j \xi _\nu \rangle $
with
$\langle \xi _\nu , \mathcal {G}_N^{(4)} \xi _\nu \rangle = \sum _{j=1}^3 \langle \xi _\nu , \text {G}_j \xi _\nu \rangle $
with
 $$ \begin{align*} \text{G}_1 &= \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ -r \neq q,p}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_q \gamma_{p+r} \gamma_{q+r} a^*_{p+r} a^*_q a_{p} a_{q+r} \\ \text{G}_2 & = \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ r \neq q,-p}} N^\kappa \widehat V(r/N^{1-\kappa}) \big( \gamma_{p+r} \sigma_q a^*_{p+r} a_{-q} + \sigma_{p+r} \gamma_q a_{-p-r} a^*_q \big) \\[-0.5cm] & \hskip5.5cm\times \big( \gamma_{p} \sigma_{q+r} a_{p}a^*_{-q-r} + \sigma_{p} \gamma_{q+r} a^*_{-p} a_{q+r}\big)\\[0.2cm] \text{G}_3 & = \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ r \neq q,-p}} N^\kappa \widehat V(r/N^{1-\kappa}) \sigma_p \sigma_q \sigma_{p+r} \sigma_{q+r} a_{p+r} a_{q} a^*_{p} a^*_{q+r}. \end{align*} $$
$$ \begin{align*} \text{G}_1 &= \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ -r \neq q,p}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_q \gamma_{p+r} \gamma_{q+r} a^*_{p+r} a^*_q a_{p} a_{q+r} \\ \text{G}_2 & = \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ r \neq q,-p}} N^\kappa \widehat V(r/N^{1-\kappa}) \big( \gamma_{p+r} \sigma_q a^*_{p+r} a_{-q} + \sigma_{p+r} \gamma_q a_{-p-r} a^*_q \big) \\[-0.5cm] & \hskip5.5cm\times \big( \gamma_{p} \sigma_{q+r} a_{p}a^*_{-q-r} + \sigma_{p} \gamma_{q+r} a^*_{-p} a_{q+r}\big)\\[0.2cm] \text{G}_3 & = \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ r \neq q,-p}} N^\kappa \widehat V(r/N^{1-\kappa}) \sigma_p \sigma_q \sigma_{p+r} \sigma_{q+r} a_{p+r} a_{q} a^*_{p} a^*_{q+r}. \end{align*} $$
To estimate contributions from
![]() $\text {G}_3$
, we arrange terms in normal order. We find
$\text {G}_3$
, we arrange terms in normal order. We find
 $$ \begin{align*} \text{G}_3 = \; & \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ -r \neq q,p}} N^\kappa \widehat V(r/N^{1-\kappa}) \sigma_p \sigma_q \sigma_{p+r} \sigma_{q+r} a^*_{p} a^*_{q+r} a_{p+r} a_{q} \\ &+ \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p \in \Lambda^*_+ \\ p \neq -r}} N^\kappa \widehat V(r/N^{1-\kappa}) \sigma_p^2 \sigma^2_{p+r} \big( a^*_p a_p + a^*_{p+r}a_{p+r}\big) \\ &+ \frac 1 {N} \sum_{\substack{p,q \in \Lambda^*_+ }} N^\kappa \widehat V(0) \sigma_p^2 \sigma^2_{q} a^*_p a_p \\ &+ \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p \in \Lambda^*_+ :\\ p\not = -r}} N^\kappa \widehat V(r/N^{1-\kappa}) \sigma^2_p \sigma^2_{p+r} + \frac 1 {2N} \sum_{\substack{p,q \in \Lambda^*_+}} N^\kappa \widehat V(0) \sigma^2_p \sigma^2_{q} . \end{align*} $$
$$ \begin{align*} \text{G}_3 = \; & \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ -r \neq q,p}} N^\kappa \widehat V(r/N^{1-\kappa}) \sigma_p \sigma_q \sigma_{p+r} \sigma_{q+r} a^*_{p} a^*_{q+r} a_{p+r} a_{q} \\ &+ \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p \in \Lambda^*_+ \\ p \neq -r}} N^\kappa \widehat V(r/N^{1-\kappa}) \sigma_p^2 \sigma^2_{p+r} \big( a^*_p a_p + a^*_{p+r}a_{p+r}\big) \\ &+ \frac 1 {N} \sum_{\substack{p,q \in \Lambda^*_+ }} N^\kappa \widehat V(0) \sigma_p^2 \sigma^2_{q} a^*_p a_p \\ &+ \frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p \in \Lambda^*_+ :\\ p\not = -r}} N^\kappa \widehat V(r/N^{1-\kappa}) \sigma^2_p \sigma^2_{p+r} + \frac 1 {2N} \sum_{\substack{p,q \in \Lambda^*_+}} N^\kappa \widehat V(0) \sigma^2_p \sigma^2_{q} . \end{align*} $$
Since
![]() $a_p\,\xi _\nu =0$
if
$a_p\,\xi _\nu =0$
if
![]() $p\in \Lambda ^*_+\backslash (P_S\cup P_H)$
and
$p\in \Lambda ^*_+\backslash (P_S\cup P_H)$
and
![]() $\|\sigma _H\|_\infty \leq \|\sigma _S\|_\infty $
, we find, by Cauchy–Schwarz,
$\|\sigma _H\|_\infty \leq \|\sigma _S\|_\infty $
, we find, by Cauchy–Schwarz,
 $$ \begin{align} \langle \xi_\nu, \text{G}_3 \xi_\nu \rangle &\leq C N^{\kappa -1} \left[ \| \sigma_S \|_\infty^2 \| \sigma \|^2 \| (\mathcal{N}+1) \xi_\nu \|^2 + \| \sigma \|^4 \| \xi_\nu \|^2 \right] \nonumber\\ &\leq C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon} , N^{9\kappa -5 + 3\varepsilon} \} \| \xi_\nu \|^2 \end{align} $$
$$ \begin{align} \langle \xi_\nu, \text{G}_3 \xi_\nu \rangle &\leq C N^{\kappa -1} \left[ \| \sigma_S \|_\infty^2 \| \sigma \|^2 \| (\mathcal{N}+1) \xi_\nu \|^2 + \| \sigma \|^4 \| \xi_\nu \|^2 \right] \nonumber\\ &\leq C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon} , N^{9\kappa -5 + 3\varepsilon} \} \| \xi_\nu \|^2 \end{align} $$
using Proposition 2.2 and
![]() $3\kappa -2 + 4\varepsilon < 0$
. We proceed similarly for
$3\kappa -2 + 4\varepsilon < 0$
. We proceed similarly for
![]() $\text {G}_2$
. Through normal ordering, we get
$\text {G}_2$
. Through normal ordering, we get
 $$ \begin{align*} \text{G}_2 = \; &\frac 1 {N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ -r \neq q,p}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_{p+r}\sigma_q \sigma_{q+r} a^*_{p+r} a^*_{-q-r} a_{p} a_{-q} \\ &+ \frac 1 {N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ -r \neq q,p}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_{p+r} \gamma_{q+r}\sigma_p \sigma_{q} a^*_{p+r} a^*_{-p} a_{-q} a_{q+r} \\ &+ \frac 1 {N} \sum_{\substack{p,q \in \Lambda^*_+ }} N^\kappa \widehat V(0) \gamma_p^2 \sigma^2_q a^*_p a_p + \frac 1 {N} \sum_{\substack{r \in \Lambda^*,\,p \in \Lambda^*_+ }} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p^2 \sigma^2_{p+r} a^*_p a_p \\ &+ \frac 2 {N} \sum_{\substack{r \in \Lambda^*,\,p \in \Lambda^*_+ }} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \sigma_p \gamma_{p+r} \sigma_{p+r} a^*_p a_p \\ &+ \frac 1 {2N} \sum_{\substack{p,r \in \Lambda^*_+}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_{p+r} \sigma_p \sigma_{p+r} . \end{align*} $$
$$ \begin{align*} \text{G}_2 = \; &\frac 1 {N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ -r \neq q,p}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_{p+r}\sigma_q \sigma_{q+r} a^*_{p+r} a^*_{-q-r} a_{p} a_{-q} \\ &+ \frac 1 {N} \sum_{\substack{r \in \Lambda^*,\, p,q \in \Lambda^*_+ \\ -r \neq q,p}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_{p+r} \gamma_{q+r}\sigma_p \sigma_{q} a^*_{p+r} a^*_{-p} a_{-q} a_{q+r} \\ &+ \frac 1 {N} \sum_{\substack{p,q \in \Lambda^*_+ }} N^\kappa \widehat V(0) \gamma_p^2 \sigma^2_q a^*_p a_p + \frac 1 {N} \sum_{\substack{r \in \Lambda^*,\,p \in \Lambda^*_+ }} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p^2 \sigma^2_{p+r} a^*_p a_p \\ &+ \frac 2 {N} \sum_{\substack{r \in \Lambda^*,\,p \in \Lambda^*_+ }} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \sigma_p \gamma_{p+r} \sigma_{p+r} a^*_p a_p \\ &+ \frac 1 {2N} \sum_{\substack{p,r \in \Lambda^*_+}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_{p+r} \sigma_p \sigma_{p+r} . \end{align*} $$
Keeping the last contribution intact and estimating the term on the fourth line distinguishing the two cases
![]() $(p+r) \in P_S$
and
$(p+r) \in P_S$
and
![]() $(p+r) \in P_H$
, we arrive at
$(p+r) \in P_H$
, we arrive at
 $$ \begin{align*} \langle \xi_\nu , \text{G}_2 \xi_\nu \rangle \leq \; &\frac 1 {2N} \sum_{\substack{p,r \in \Lambda^*_+}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_{p+r} \sigma_p \sigma_{p+r} \| \xi_\nu \|^2 \\ &+ C N^{\kappa -1} \| \gamma_S \|_\infty^2 \| \sigma \|^2 \| (\mathcal{N}+1) \xi_\nu \|^2 \\ &+ C N^{\kappa -1} \| \gamma_{S \cup H} \|_\infty \| \sigma_{S \cup H} \|_\infty \\ & \hspace{2cm} \times \left[ \| \gamma_S \sigma_S \|_1 + \| \gamma_H \|_\infty \mathop{\mathrm{sup}}\limits_p \sum_{r \in \Lambda^*} \widehat{V} (r/ N^{1-\kappa}) |\eta_{p+r}| \right] \| \mathcal{N}^{1/2} \xi_\nu \|^2 . \end{align*} $$
$$ \begin{align*} \langle \xi_\nu , \text{G}_2 \xi_\nu \rangle \leq \; &\frac 1 {2N} \sum_{\substack{p,r \in \Lambda^*_+}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_{p+r} \sigma_p \sigma_{p+r} \| \xi_\nu \|^2 \\ &+ C N^{\kappa -1} \| \gamma_S \|_\infty^2 \| \sigma \|^2 \| (\mathcal{N}+1) \xi_\nu \|^2 \\ &+ C N^{\kappa -1} \| \gamma_{S \cup H} \|_\infty \| \sigma_{S \cup H} \|_\infty \\ & \hspace{2cm} \times \left[ \| \gamma_S \sigma_S \|_1 + \| \gamma_H \|_\infty \mathop{\mathrm{sup}}\limits_p \sum_{r \in \Lambda^*} \widehat{V} (r/ N^{1-\kappa}) |\eta_{p+r}| \right] \| \mathcal{N}^{1/2} \xi_\nu \|^2 . \end{align*} $$
With the bounds in Lemma 2.4 and in Proposition 2.2 and with (3.12), we conclude that
 $$ \begin{align} \langle \xi_\nu , \text{G}_2 \xi_\nu \rangle \leq \frac 1 {2N} \sum_{\substack{p,r \in \Lambda^*_+}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_{p+r} \sigma_p \sigma_{p+r} \| \xi_\nu \|^2 + C N^{5\kappa /2} \cdot N^{9\kappa -5 + 3\varepsilon} \| \xi_\nu \|^2. \end{align} $$
$$ \begin{align} \langle \xi_\nu , \text{G}_2 \xi_\nu \rangle \leq \frac 1 {2N} \sum_{\substack{p,r \in \Lambda^*_+}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_{p+r} \sigma_p \sigma_{p+r} \| \xi_\nu \|^2 + C N^{5\kappa /2} \cdot N^{9\kappa -5 + 3\varepsilon} \| \xi_\nu \|^2. \end{align} $$
Finally, we consider
![]() $\text {G}_1$
. Recalling that
$\text {G}_1$
. Recalling that
![]() $a_p \xi _\nu = 0$
if
$a_p \xi _\nu = 0$
if
![]() $p \in \Lambda ^*_+ \backslash (P_S \cup P_H)$
and observing that
$p \in \Lambda ^*_+ \backslash (P_S \cup P_H)$
and observing that
![]() $\langle \xi _\nu , a^*_{p+r}a^*_qa_pa_{q+r}\xi _\nu \rangle \neq 0$
only if the operator
$\langle \xi _\nu , a^*_{p+r}a^*_qa_pa_{q+r}\xi _\nu \rangle \neq 0$
only if the operator
![]() $a^*_{p+r}a^*_q a_p a_{q+r}$
preserves the number of particles in
$a^*_{p+r}a^*_q a_p a_{q+r}$
preserves the number of particles in
![]() $P_S$
and in
$P_S$
and in
![]() $P_H$
, we arrive at
$P_H$
, we arrive at
 $$ \begin{align*} \langle \xi_\nu, \text{G}_1 \xi_\nu \rangle \leq \; &\frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in P_H: \\p+r,q+r\in P_H}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_q \gamma_{p+r} \gamma_{q-r} \langle \xi_\nu , a^*_{p+r} a^*_q a_{p} a_{q+r} \xi_\nu \rangle \\ &+ C N^{\kappa -1 } \| \gamma_{S \cup H} \|_\infty^2 \| \gamma_S \|^2 \| (\mathcal{N} + 1) \xi \|^2. \end{align*} $$
$$ \begin{align*} \langle \xi_\nu, \text{G}_1 \xi_\nu \rangle \leq \; &\frac 1 {2N} \sum_{\substack{r \in \Lambda^*,\, p,q \in P_H: \\p+r,q+r\in P_H}} N^\kappa \widehat V(r/N^{1-\kappa}) \gamma_p \gamma_q \gamma_{p+r} \gamma_{q-r} \langle \xi_\nu , a^*_{p+r} a^*_q a_{p} a_{q+r} \xi_\nu \rangle \\ &+ C N^{\kappa -1 } \| \gamma_{S \cup H} \|_\infty^2 \| \gamma_S \|^2 \| (\mathcal{N} + 1) \xi \|^2. \end{align*} $$
With
![]() $|\gamma _p \gamma _q \gamma _{p+r} \gamma _{q+r} - 1| \leq C \| \eta _H \|_\infty ^2$
for all
$|\gamma _p \gamma _q \gamma _{p+r} \gamma _{q+r} - 1| \leq C \| \eta _H \|_\infty ^2$
for all
![]() $p,q \in P_H$
, with
$p,q \in P_H$
, with
![]() $(p+r), (q+r) \in P_H$
and using the estimate (see the proof of (3.12))
$(p+r), (q+r) \in P_H$
and using the estimate (see the proof of (3.12))
 $$ \begin{align*} \mathop{\mathrm{sup}}\limits_{p\in \Lambda^*} \sum_{r \in \Lambda^*_+ : r \not = p} \frac{N^\kappa |\widehat{V} (r/N^{1-\kappa})|}{|p-r|^2} \leq C N \end{align*} $$
$$ \begin{align*} \mathop{\mathrm{sup}}\limits_{p\in \Lambda^*} \sum_{r \in \Lambda^*_+ : r \not = p} \frac{N^\kappa |\widehat{V} (r/N^{1-\kappa})|}{|p-r|^2} \leq C N \end{align*} $$
we conclude that
 $$ \begin{align*} \langle \xi_\nu, \text{G}_1 \xi_\nu \rangle \leq \langle \xi_\nu, \mathcal{V}_N^{(H)} \xi_\nu \rangle + C \| \eta_H \|_\infty^2 \| \mathcal{N}^{1/2} \mathcal{K}^{1/2} \xi_\nu \|^2 + C N^{\kappa -1 } \| \gamma_{S \cup H} \|_\infty^2 \| \gamma_S \|^2 \| \mathcal{N} \xi \|^2 \end{align*} $$
$$ \begin{align*} \langle \xi_\nu, \text{G}_1 \xi_\nu \rangle \leq \langle \xi_\nu, \mathcal{V}_N^{(H)} \xi_\nu \rangle + C \| \eta_H \|_\infty^2 \| \mathcal{N}^{1/2} \mathcal{K}^{1/2} \xi_\nu \|^2 + C N^{\kappa -1 } \| \gamma_{S \cup H} \|_\infty^2 \| \gamma_S \|^2 \| \mathcal{N} \xi \|^2 \end{align*} $$
with
 $\mathcal {V}_N^{(H)}$
defined as in (3.4). With Lemma 2.4 and Proposition 2.2, we find (using the assumption
$\mathcal {V}_N^{(H)}$
defined as in (3.4). With Lemma 2.4 and Proposition 2.2, we find (using the assumption
![]() $3\kappa - 2 + 4 \varepsilon < 0$
)
$3\kappa - 2 + 4 \varepsilon < 0$
)
 $$ \begin{align*} \langle \xi_\nu, \text{G}_1 \xi_\nu \rangle \leq \langle \xi_\nu, \mathcal{V}_N^{(H)} \xi_\nu \rangle + C N^{5\kappa/2} \cdot N^{9 \kappa - 5 + 6\varepsilon} \| \xi_\nu \|^2. \end{align*} $$
$$ \begin{align*} \langle \xi_\nu, \text{G}_1 \xi_\nu \rangle \leq \langle \xi_\nu, \mathcal{V}_N^{(H)} \xi_\nu \rangle + C N^{5\kappa/2} \cdot N^{9 \kappa - 5 + 6\varepsilon} \| \xi_\nu \|^2. \end{align*} $$
With (4.4) and (4.5), we have shown that
 $$ \begin{align*} \frac{\langle \xi_\nu, \mathcal{G}_N^{(4)} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \frac{\langle \xi_\nu, \mathcal{V}_N^{(H)} \xi_\nu \rangle}{\| \xi_\nu \|^2} + C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon}, N^{9\kappa - 5 + 6 \varepsilon} \}. \end{align*} $$
$$ \begin{align*} \frac{\langle \xi_\nu, \mathcal{G}_N^{(4)} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \frac{\langle \xi_\nu, \mathcal{V}_N^{(H)} \xi_\nu \rangle}{\| \xi_\nu \|^2} + C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon}, N^{9\kappa - 5 + 6 \varepsilon} \}. \end{align*} $$
Combining the last bound with (4.2) and (4.3), we obtain
 $$ \begin{align*} \frac{\langle \xi_\nu, \mathcal{G}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \; &\widetilde{C}_N + \frac{\langle \xi_\nu, (\mathcal{K} +\mathcal{V}_N^{(H)} + \mathcal{C}_N) \xi_\nu \rangle}{\| \xi_\nu \|^2} \\ &+ C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon}, N^{9\kappa - 5 + 6\varepsilon} , N^{21 \kappa /4 - 3 + 3 \varepsilon } \} \end{align*} $$
$$ \begin{align*} \frac{\langle \xi_\nu, \mathcal{G}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \; &\widetilde{C}_N + \frac{\langle \xi_\nu, (\mathcal{K} +\mathcal{V}_N^{(H)} + \mathcal{C}_N) \xi_\nu \rangle}{\| \xi_\nu \|^2} \\ &+ C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon}, N^{9\kappa - 5 + 6\varepsilon} , N^{21 \kappa /4 - 3 + 3 \varepsilon } \} \end{align*} $$
where we defined
 $$ \begin{align} \widetilde{C}_{N} =\; & \frac{N_0^2 }{2N} N^\kappa \widehat{V}(0) +\sum_{p\in {\Lambda}^*_+}p^2\sigma_p^2 + \frac{N_0}{N}\sum_{p\in \Lambda^*_+} N^\kappa \big( \widehat{V}(p/N^{1-\kappa}) + \widehat{V}(0) \big)\sigma_p^2\nonumber\\ & + \frac{N_0}{N}\sum_{p\in \Lambda^*_+}N^\kappa \widehat{V}(p/N^{1-\kappa})\sigma_p\gamma_p +\frac{1}{2N}\sum_{\substack{p,r\in \Lambda^*_+\\r\neq p}}N^\kappa \widehat{V}(r/N^{1-\kappa})\sigma_p\sigma_{p+r}\gamma_p\gamma_{p+r}. \end{align} $$
$$ \begin{align} \widetilde{C}_{N} =\; & \frac{N_0^2 }{2N} N^\kappa \widehat{V}(0) +\sum_{p\in {\Lambda}^*_+}p^2\sigma_p^2 + \frac{N_0}{N}\sum_{p\in \Lambda^*_+} N^\kappa \big( \widehat{V}(p/N^{1-\kappa}) + \widehat{V}(0) \big)\sigma_p^2\nonumber\\ & + \frac{N_0}{N}\sum_{p\in \Lambda^*_+}N^\kappa \widehat{V}(p/N^{1-\kappa})\sigma_p\gamma_p +\frac{1}{2N}\sum_{\substack{p,r\in \Lambda^*_+\\r\neq p}}N^\kappa \widehat{V}(r/N^{1-\kappa})\sigma_p\sigma_{p+r}\gamma_p\gamma_{p+r}. \end{align} $$
Inserting
![]() $N_0 = N - \| \sigma _L \|^2$
and recalling from Lemma 2.4 that
$N_0 = N - \| \sigma _L \|^2$
and recalling from Lemma 2.4 that
![]() $\| \sigma _L \|^2 \leq C N^{3\kappa /2}$
and
$\| \sigma _L \|^2 \leq C N^{3\kappa /2}$
and
![]() $\| \sigma _{L^c} \|^2 \leq C N^{3\kappa /2 - \varepsilon }$
, we obtain
$\| \sigma _{L^c} \|^2 \leq C N^{3\kappa /2 - \varepsilon }$
, we obtain
 $\widetilde {C}_N = C_{\mathcal {G}_N} + \mathcal {O} (N^{5\kappa /2 - \varepsilon })$
, with
$\widetilde {C}_N = C_{\mathcal {G}_N} + \mathcal {O} (N^{5\kappa /2 - \varepsilon })$
, with
![]() $C_{\mathcal {G}_N}$
as defined in (3.6) (with the assumption
$C_{\mathcal {G}_N}$
as defined in (3.6) (with the assumption
![]() $3\kappa - 2 + 4\varepsilon < 0$
). To handle the first term on the second line of (4.6), we used that
$3\kappa - 2 + 4\varepsilon < 0$
). To handle the first term on the second line of (4.6), we used that
 $|\sigma _p \gamma _p - \eta _p| \leq C \eta _p^3 \leq C N^{3\kappa }/|p|^6$
, for
$|\sigma _p \gamma _p - \eta _p| \leq C \eta _p^3 \leq C N^{3\kappa }/|p|^6$
, for
![]() $p \in P_L^c$
. This completes the proof of Proposition 3.1.
$p \in P_L^c$
. This completes the proof of Proposition 3.1.
5 Cubic conjugation
In this section we prove Proposition 2.2 and Proposition 3.2, as a consequence of the following lemma.
Lemma 5.1. Let
![]() $A_\nu $
be defined in (2.15) and
$A_\nu $
be defined in (2.15) and
![]() $\mathcal {K}$
,
$\mathcal {K}$
,
 $\mathcal {V}_N^{(H)}$
and
$\mathcal {V}_N^{(H)}$
and
![]() $\mathcal {C}_N$
be defined in (3.4) and (3.5), respectively. Then, for
$\mathcal {C}_N$
be defined in (3.4) and (3.5), respectively. Then, for
![]() $\xi _\nu =e^{A_\nu }\Omega $
,
$\xi _\nu =e^{A_\nu }\Omega $
,
 $$ \begin{align} \frac{\langle \xi_\nu, \mathcal{K} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq\; & \frac 2 {N} \sum_{\substack{v \in P_S, r \in P_H:\\r+v \in P_H}} r^2\eta_r (\eta_r+\eta_{r+v})\sigma_v^2 + \mathcal{E} , \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu, \mathcal{K} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq\; & \frac 2 {N} \sum_{\substack{v \in P_S, r \in P_H:\\r+v \in P_H}} r^2\eta_r (\eta_r+\eta_{r+v})\sigma_v^2 + \mathcal{E} , \end{align} $$
 $$ \begin{align} \frac{\langle \xi_\nu, \mathcal{C}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \; & \frac 2 {N} \sum_{\substack{v \in P_S, r \in P_H :\\ r+v \in P_H}} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r +\eta_{r+v}) \sigma_v^2 + \mathcal{E} , \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu, \mathcal{C}_N \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \; & \frac 2 {N} \sum_{\substack{v \in P_S, r \in P_H :\\ r+v \in P_H}} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r +\eta_{r+v}) \sigma_v^2 + \mathcal{E} , \end{align} $$
 $$ \begin{align} \frac{\langle \xi_\nu, \mathcal{V}_N^{(H)} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \;& \frac 1 {N^2} \sum_{\substack{v \in P_S, r \in P_H: \\ r+v \in P_H}} \, \big( N^\kappa \widehat V(\cdot/N^{1-\kappa}) \ast \eta \big)_r (\eta_r+\eta_{r+v}) \sigma_v^2 + \mathcal{E} , \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu, \mathcal{V}_N^{(H)} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \;& \frac 1 {N^2} \sum_{\substack{v \in P_S, r \in P_H: \\ r+v \in P_H}} \, \big( N^\kappa \widehat V(\cdot/N^{1-\kappa}) \ast \eta \big)_r (\eta_r+\eta_{r+v}) \sigma_v^2 + \mathcal{E} , \end{align} $$
with
for all
![]() $\kappa \in (1/2 ;2/3)$
,
$\kappa \in (1/2 ;2/3)$
,
![]() $\varepsilon>0$
so small that
$\varepsilon>0$
so small that
![]() $3\kappa - 2 + 4 \varepsilon < 0$
and N large enough.
$3\kappa - 2 + 4 \varepsilon < 0$
and N large enough.
With Lemma 5.1, we can immediately show Proposition 3.2.
Proof Proof of Proposition 3.2.
From Lemma 5.1 we have
 $$ \begin{align*} &\frac{\langle \xi_\nu, (\mathcal{K} + \mathcal{V}_N^{(H)} + \mathcal{C}_{N} ) \xi_\nu \rangle}{\| \xi_\nu \|^2} \\ & \leq \frac 2 N \sum_{v \in P_S} \sigma_v^2 \sum_{\substack{r \in P_H: \\ r+v \in P_H}}\Big[ r^2 \eta_r + N^\kappa \widehat V(r/N^{1-\kappa}) + \frac {N^\kappa} {2N} \big(\widehat V(\cdot/N^{1-\kappa}) \ast \eta \big)_r \Big] (\eta_r+\eta_{r+v}) + \mathcal{E} \end{align*} $$
$$ \begin{align*} &\frac{\langle \xi_\nu, (\mathcal{K} + \mathcal{V}_N^{(H)} + \mathcal{C}_{N} ) \xi_\nu \rangle}{\| \xi_\nu \|^2} \\ & \leq \frac 2 N \sum_{v \in P_S} \sigma_v^2 \sum_{\substack{r \in P_H: \\ r+v \in P_H}}\Big[ r^2 \eta_r + N^\kappa \widehat V(r/N^{1-\kappa}) + \frac {N^\kappa} {2N} \big(\widehat V(\cdot/N^{1-\kappa}) \ast \eta \big)_r \Big] (\eta_r+\eta_{r+v}) + \mathcal{E} \end{align*} $$
with
![]() $\mathcal {E} \leq CN^{5\kappa /2} \cdot \max \{ N^{-\varepsilon }, N^{12\kappa -7 + 5\varepsilon } \}$
. With the scattering equation (2.9), we obtain
$\mathcal {E} \leq CN^{5\kappa /2} \cdot \max \{ N^{-\varepsilon }, N^{12\kappa -7 + 5\varepsilon } \}$
. With the scattering equation (2.9), we obtain
 $$ \begin{align*} \frac{\langle \xi_\nu, (\mathcal{K} + \mathcal{V}_N^{(H)} + \mathcal{C}_{N} ) \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \frac1N\sum_{v\in P_S}\sigma_v^2\sum_{\substack{r \in P_H: \\r+v\in P_H}} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v})+ \mathcal{E}' \end{align*} $$
$$ \begin{align*} \frac{\langle \xi_\nu, (\mathcal{K} + \mathcal{V}_N^{(H)} + \mathcal{C}_{N} ) \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq \frac1N\sum_{v\in P_S}\sigma_v^2\sum_{\substack{r \in P_H: \\r+v\in P_H}} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v})+ \mathcal{E}' \end{align*} $$
with
 $$ \begin{align*} \mathcal{E}' \leq \; \frac 1 N \sum_{v \in P_S} \sigma_v^2 \sum_{\substack{r \in P_H:\, r+v \in P_H}} N^{3-2\kappa} \lambda_{\ell} (\widehat \chi_\ell \ast \widehat f_{N,\ell})_r \eta_r + \mathcal{E} . \end{align*} $$
$$ \begin{align*} \mathcal{E}' \leq \; \frac 1 N \sum_{v \in P_S} \sigma_v^2 \sum_{\substack{r \in P_H:\, r+v \in P_H}} N^{3-2\kappa} \lambda_{\ell} (\widehat \chi_\ell \ast \widehat f_{N,\ell})_r \eta_r + \mathcal{E} . \end{align*} $$
Using
![]() $|N^{3-3\kappa }\lambda _{\ell }|\leq C$
and
$|N^{3-3\kappa }\lambda _{\ell }|\leq C$
and
 $\|\widehat {\chi }_\ell \ast \widehat f_{N,\ell }\|\leq C$
, we conclude
$\|\widehat {\chi }_\ell \ast \widehat f_{N,\ell }\|\leq C$
, we conclude
 $$ \begin{align*} &\frac{\langle \xi_\nu, (\mathcal{K} + \mathcal{V}_N^{(H)} + \mathcal{C}_{N} ) \xi_\nu \rangle}{\| \xi_\nu \|^2} \\ &\hspace{.3cm} \leq \frac1N\sum_{v\in P_S}\sigma_v^2\sum_{\substack{r \in P_H: \\r+v\in P_H}} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v}) + C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon}, N^{12\kappa -7 + 5\varepsilon} \}. \end{align*} $$
$$ \begin{align*} &\frac{\langle \xi_\nu, (\mathcal{K} + \mathcal{V}_N^{(H)} + \mathcal{C}_{N} ) \xi_\nu \rangle}{\| \xi_\nu \|^2} \\ &\hspace{.3cm} \leq \frac1N\sum_{v\in P_S}\sigma_v^2\sum_{\substack{r \in P_H: \\r+v\in P_H}} N^\kappa \widehat V(r/N^{1-\kappa})(\eta_r+\eta_{r+v}) + C N^{5\kappa/2} \cdot \max \{ N^{-\varepsilon}, N^{12\kappa -7 + 5\varepsilon} \}. \end{align*} $$
Finally, with (3.12) and the expression (2.28) for
![]() $\sigma ^2_v$
, we can extend the sum over
$\sigma ^2_v$
, we can extend the sum over
![]() $v \in P_S$
to a sum over all
$v \in P_S$
to a sum over all
![]() $v \in P_L$
, without changing the size of the error. This completes the proof of Proposition 3.2.
$v \in P_L$
, without changing the size of the error. This completes the proof of Proposition 3.2.
We still have to show Proposition 2.2 and Lemma 5.1.
5.1 Expectation of the particle number and kinetic energy
In this section we prove (5.1) and Proposition 2.2. We start by computing the expectation
![]() $\langle \xi _\nu , \mathcal {K} \xi _\nu \rangle $
. We proceed as we did in (2.19)–(2.22) to compute
$\langle \xi _\nu , \mathcal {K} \xi _\nu \rangle $
. We proceed as we did in (2.19)–(2.22) to compute
![]() $\| \xi _\nu \|^2$
. With
$\| \xi _\nu \|^2$
. With
![]() $\mathcal {K} a_{r+v}^* a_{-r}^* a_{-v}^* = a_{r+v}^* a_{-r}^* a_{-v}^* (\mathcal {K} + (r+v)^2 + r^2 + v^2)$
we obtain
$\mathcal {K} a_{r+v}^* a_{-r}^* a_{-v}^* = a_{r+v}^* a_{-r}^* a_{-v}^* (\mathcal {K} + (r+v)^2 + r^2 + v^2)$
we obtain
 $$ \begin{align*} {\bigl\langle\xi_{\nu},\mathcal{K} \xi_{\nu}\bigr\rangle} = &\; \sum_{m\geq 1}\frac1{2^m (m-1)!}\frac1{N^m} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta \big( \{ r_j, v_j \}_{j=1}^{m} \big) \\&\hspace{3cm} \times [r_m^2+v_m^2+(r_m+v_m)^2]\, \prod_{i=1}^m (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 \, \end{align*} $$
$$ \begin{align*} {\bigl\langle\xi_{\nu},\mathcal{K} \xi_{\nu}\bigr\rangle} = &\; \sum_{m\geq 1}\frac1{2^m (m-1)!}\frac1{N^m} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta \big( \{ r_j, v_j \}_{j=1}^{m} \big) \\&\hspace{3cm} \times [r_m^2+v_m^2+(r_m+v_m)^2]\, \prod_{i=1}^m (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 \, \end{align*} $$
with the cutoff
![]() $\theta $
introduced in (2.18). Since all terms are positive, we can find an upper bound for
$\theta $
introduced in (2.18). Since all terms are positive, we can find an upper bound for
![]() $\langle \xi _\nu , \mathcal {K} \xi _\nu \rangle $
by replacing
$\langle \xi _\nu , \mathcal {K} \xi _\nu \rangle $
by replacing
 $\theta (\{r_j,v_j\}_{j=1}^m)$
with
$\theta (\{r_j,v_j\}_{j=1}^m)$
with
 $\theta (\{r_j,v_j\}_{j=1}^{m-1})$
, removing conditions involving momenta with index m. Recalling (2.22), we find
$\theta (\{r_j,v_j\}_{j=1}^{m-1})$
, removing conditions involving momenta with index m. Recalling (2.22), we find
 $$ \begin{align*} {\bigl\langle\xi_{\nu},\mathcal{K} \xi_{\nu}\bigr\rangle} &\leq \frac{1}{2N} \sum_{\substack{v\in P_S,r\in P_H:\\r+v\in P_H}}[r^2+v^2+(r+v)^2] (\eta_r + \eta_{r+v})^2 \sigma_v^2 \,\|\xi_\nu\|^2 \\ &\leq \frac{2}{N} \sum_{v \in P_S , r\in P_H} r^2 \eta_r(\eta_r + \eta_{r+v}) \sigma_v^2 \,\|\xi_\nu\|^2 + \mathcal{E} \end{align*} $$
$$ \begin{align*} {\bigl\langle\xi_{\nu},\mathcal{K} \xi_{\nu}\bigr\rangle} &\leq \frac{1}{2N} \sum_{\substack{v\in P_S,r\in P_H:\\r+v\in P_H}}[r^2+v^2+(r+v)^2] (\eta_r + \eta_{r+v})^2 \sigma_v^2 \,\|\xi_\nu\|^2 \\ &\leq \frac{2}{N} \sum_{v \in P_S , r\in P_H} r^2 \eta_r(\eta_r + \eta_{r+v}) \sigma_v^2 \,\|\xi_\nu\|^2 + \mathcal{E} \end{align*} $$
with (using Lemma 2.4 and the assumption
![]() $3\kappa -2 +4\varepsilon < 0$
)
$3\kappa -2 +4\varepsilon < 0$
)
 $$ \begin{align*} \frac{\mathcal{E}}{\|\xi_\nu\|^2} =& \frac2N \sum_{\substack{v\in P_S,r\in P_H : \\ r+v \in P_H}} \hspace{-.3cm} (v ^2+r\cdot v) \eta_r (\eta_r+\eta_{r+v})\sigma_v^2 \\&\leq \frac C N( \| \sigma_S \|_{H^1}^2 \| \eta_H \|^2 +\|\sigma_S\|\|\eta_H\|\|\sigma_S\|_{H^1}\|\eta_H\|_{H^1})\leq C N^{4\kappa -1+\varepsilon}\leq C N^{5\kappa/2-\varepsilon}. \end{align*} $$
$$ \begin{align*} \frac{\mathcal{E}}{\|\xi_\nu\|^2} =& \frac2N \sum_{\substack{v\in P_S,r\in P_H : \\ r+v \in P_H}} \hspace{-.3cm} (v ^2+r\cdot v) \eta_r (\eta_r+\eta_{r+v})\sigma_v^2 \\&\leq \frac C N( \| \sigma_S \|_{H^1}^2 \| \eta_H \|^2 +\|\sigma_S\|\|\eta_H\|\|\sigma_S\|_{H^1}\|\eta_H\|_{H^1})\leq C N^{4\kappa -1+\varepsilon}\leq C N^{5\kappa/2-\varepsilon}. \end{align*} $$
This proves (5.1). In particular, (5.1) implies, together with Lemma 2.4, that
 $$ \begin{align} \frac{\langle \xi_\nu , \mathcal{K} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq C N^{-1} \| \eta_H \|_{H^1}^2 \| \sigma_S \|^2 \leq C N^{5\kappa /2}, \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu , \mathcal{K} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq C N^{-1} \| \eta_H \|_{H^1}^2 \| \sigma_S \|^2 \leq C N^{5\kappa /2}, \end{align} $$
which shows (2.24) with
![]() $j=1$
in Proposition 2.2.
$j=1$
in Proposition 2.2.
Analogously, we find
 $$ \begin{align*} \langle \xi_\nu, \mathcal{K} \mathcal{N} \xi_\nu \rangle & \leq \sum_{m\geq 1}\frac{3m}{2^m (m-1)!}\frac1{N^m} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta \big( \{ r_j, v_j \}_{j=1}^{m} \big) \\&\hspace{3cm} \times [r_m^2+v_m^2+(r_m+v_m)^2]\, \prod_{i=1}^m (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 . \end{align*} $$
$$ \begin{align*} \langle \xi_\nu, \mathcal{K} \mathcal{N} \xi_\nu \rangle & \leq \sum_{m\geq 1}\frac{3m}{2^m (m-1)!}\frac1{N^m} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta \big( \{ r_j, v_j \}_{j=1}^{m} \big) \\&\hspace{3cm} \times [r_m^2+v_m^2+(r_m+v_m)^2]\, \prod_{i=1}^m (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 . \end{align*} $$
Writing
![]() $m = 1+ (m-1)$
and bounding
$m = 1+ (m-1)$
and bounding
 $\theta ( \{ r_j, v_j \}_{j=1}^{m} )$
by
$\theta ( \{ r_j, v_j \}_{j=1}^{m} )$
by
 $\theta ( \{ r_j, v_j \}_{j=1}^{m-2} )$
, we obtain
$\theta ( \{ r_j, v_j \}_{j=1}^{m-2} )$
, we obtain
 $$ \begin{align*} \langle \xi_\nu, \mathcal{K} \mathcal{N} \xi_\nu \rangle \leq \; & 3 \langle \xi_\nu , \mathcal{K} \xi_\nu \rangle + \frac{3}{4N^2} \sum_{r,r' \in P_H, v,v' \in P_S} [ r^2 + v^2 + (r+v)^2] \\ &\hspace{5cm} \times (\eta_r + \eta_{r+v})^2 (\eta_{r'} + \eta_{r' + v'})^2 \sigma_v^2 \sigma_{v'}^2 \| \xi_\nu \|^2. \end{align*} $$
$$ \begin{align*} \langle \xi_\nu, \mathcal{K} \mathcal{N} \xi_\nu \rangle \leq \; & 3 \langle \xi_\nu , \mathcal{K} \xi_\nu \rangle + \frac{3}{4N^2} \sum_{r,r' \in P_H, v,v' \in P_S} [ r^2 + v^2 + (r+v)^2] \\ &\hspace{5cm} \times (\eta_r + \eta_{r+v})^2 (\eta_{r'} + \eta_{r' + v'})^2 \sigma_v^2 \sigma_{v'}^2 \| \xi_\nu \|^2. \end{align*} $$
With (5.4) and with the bounds for
 $\| \eta _H \|_{H^1}^2, \| \eta _H \|^2, \| \sigma _S \|^2$
from Lemma 2.4, we find
$\| \eta _H \|_{H^1}^2, \| \eta _H \|^2, \| \sigma _S \|^2$
from Lemma 2.4, we find
 $$ \begin{align} \frac{\langle \xi_\nu, \mathcal{K} \mathcal{N} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq C N^{5\kappa /2} \cdot N^{9\kappa/2 - 2 + \varepsilon}, \end{align} $$
$$ \begin{align} \frac{\langle \xi_\nu, \mathcal{K} \mathcal{N} \xi_\nu \rangle}{\| \xi_\nu \|^2} \leq C N^{5\kappa /2} \cdot N^{9\kappa/2 - 2 + \varepsilon}, \end{align} $$
which shows (2.24) with
![]() $j=2$
.
$j=2$
.
To show (2.23) we observe that, by (2.15), the operator
![]() $A_\nu $
only creates particles with momenta in
$A_\nu $
only creates particles with momenta in
![]() $P_S \cup P_H$
and for each particle with momentum in
$P_S \cup P_H$
and for each particle with momentum in
![]() $P_S$
, it creates two particles with momenta in
$P_S$
, it creates two particles with momenta in
![]() $P_H$
. Since
$P_H$
. Since
![]() $|p|> N^{1-\kappa -\varepsilon }$
for all
$|p|> N^{1-\kappa -\varepsilon }$
for all
![]() $p \in P_H$
, we find, by (5.4),
$p \in P_H$
, we find, by (5.4),
 $$ \begin{align*} \langle \xi_\nu, \mathcal{N} \xi_\nu \rangle &= \sum_{p \in P_S \cup P_H} \langle \xi_\nu, a^*_p a_p \xi_\nu \rangle = \frac{3}{2} \sum_{p \in P_H} \langle \xi_\nu , a^*_p a_p \xi_\nu \rangle \\ &\leq C N^{-2+2\kappa+2\varepsilon} \langle \xi_\nu, \mathcal{K} \xi_\nu \rangle \leq N^{9\kappa/2 - 2 + 2\varepsilon} \| \xi_\nu \|^2, \end{align*} $$
$$ \begin{align*} \langle \xi_\nu, \mathcal{N} \xi_\nu \rangle &= \sum_{p \in P_S \cup P_H} \langle \xi_\nu, a^*_p a_p \xi_\nu \rangle = \frac{3}{2} \sum_{p \in P_H} \langle \xi_\nu , a^*_p a_p \xi_\nu \rangle \\ &\leq C N^{-2+2\kappa+2\varepsilon} \langle \xi_\nu, \mathcal{K} \xi_\nu \rangle \leq N^{9\kappa/2 - 2 + 2\varepsilon} \| \xi_\nu \|^2, \end{align*} $$
proving (2.23) for
![]() $j=1$
. Analogously, we find
$j=1$
. Analogously, we find
 $$ \begin{align*} \langle \xi_\nu, \mathcal{N}^2 \xi_\nu \rangle &= \; \sum_{p\in P_S\cup P_H} \langle \mathcal{N}^{1/2}\xi_\nu, a^*_p a_p \mathcal{N}^{1/2}\xi_\nu \rangle \\ &\leq \; \frac32 \sum_{p\in P_H} \langle \mathcal{N}^{1/2}\xi_\nu, a^*_p a_p \mathcal{N}^{1/2} \xi_\nu \rangle \leq C N^{-2+2\kappa+2\varepsilon} \langle \xi_\nu, \mathcal{K} \mathcal{N} \xi_\nu \rangle . \end{align*} $$
$$ \begin{align*} \langle \xi_\nu, \mathcal{N}^2 \xi_\nu \rangle &= \; \sum_{p\in P_S\cup P_H} \langle \mathcal{N}^{1/2}\xi_\nu, a^*_p a_p \mathcal{N}^{1/2}\xi_\nu \rangle \\ &\leq \; \frac32 \sum_{p\in P_H} \langle \mathcal{N}^{1/2}\xi_\nu, a^*_p a_p \mathcal{N}^{1/2} \xi_\nu \rangle \leq C N^{-2+2\kappa+2\varepsilon} \langle \xi_\nu, \mathcal{K} \mathcal{N} \xi_\nu \rangle . \end{align*} $$
By (5.5), we obtain (2.23) with
![]() $j=2$
. This completes the proof of Proposition 2.2.
$j=2$
. This completes the proof of Proposition 2.2.
5.2 Expectation of the cubic term
The goal of this section is to show (5.2). From (3.5), we have (using the reality of
![]() $\eta _p, \gamma _p, \sigma _p$
)
$\eta _p, \gamma _p, \sigma _p$
)
 $$ \begin{align*} &\langle\xi_\nu,\mathcal{C}_N\xi_\nu\rangle\\ &=2\frac{\sqrt{N_0}}{ N}\sum_{m\geq 1}\frac1{m!(m-1)!}\sum_{\substack{p,r \in P_H\\ p+r \in P_S}} N^\kappa \widehat V(r/N^{1-\kappa})\, \sigma_{p+r} \gamma_p\gamma_r \langle A_\nu^{m} \xi_\nu, \,a^*_{p+r} a^*_{-p} a^*_{-r} A_\nu^{m-1}\xi_\nu\rangle. \end{align*} $$
$$ \begin{align*} &\langle\xi_\nu,\mathcal{C}_N\xi_\nu\rangle\\ &=2\frac{\sqrt{N_0}}{ N}\sum_{m\geq 1}\frac1{m!(m-1)!}\sum_{\substack{p,r \in P_H\\ p+r \in P_S}} N^\kappa \widehat V(r/N^{1-\kappa})\, \sigma_{p+r} \gamma_p\gamma_r \langle A_\nu^{m} \xi_\nu, \,a^*_{p+r} a^*_{-p} a^*_{-r} A_\nu^{m-1}\xi_\nu\rangle. \end{align*} $$
Proceeding as in the previous section, we get
 $$ \begin{align*}\begin{aligned} & {\bigl\langle\xi_{\nu},\mathcal{C}_N\xi_{\nu}\bigr\rangle}\\ &= 2 \sqrt{\frac{N_0}{N}}\,\sum_{m\geq 1}\frac1{2^{m-1} (m-1)!}\frac1{N^m}\sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \hskip -0.5cm \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \\ & \hskip 0.5cm \times N^\kappa \widehat V(r_m/N^{1-\kappa})\,\big(\eta_{r_m} +\eta_{r_m+v_m}\big)\gamma_{r_m}\gamma_{r_m+v_m} \sigma^2_{v_m}\, \prod_{i=1}^{m-1} (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2. \end{aligned}\\[-17pt]\end{align*} $$
$$ \begin{align*}\begin{aligned} & {\bigl\langle\xi_{\nu},\mathcal{C}_N\xi_{\nu}\bigr\rangle}\\ &= 2 \sqrt{\frac{N_0}{N}}\,\sum_{m\geq 1}\frac1{2^{m-1} (m-1)!}\frac1{N^m}\sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \hskip -0.5cm \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \\ & \hskip 0.5cm \times N^\kappa \widehat V(r_m/N^{1-\kappa})\,\big(\eta_{r_m} +\eta_{r_m+v_m}\big)\gamma_{r_m}\gamma_{r_m+v_m} \sigma^2_{v_m}\, \prod_{i=1}^{m-1} (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2. \end{aligned}\\[-17pt]\end{align*} $$
To reconstruct the norm
![]() $\| \xi _\nu \|^2$
on the right-hand side, we need to free the momenta with index m. To this end, we recall the defintion (2.18) to write
$\| \xi _\nu \|^2$
on the right-hand side, we need to free the momenta with index m. To this end, we recall the defintion (2.18) to write
 $$ \begin{align} \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) = \theta\big( \{r_j, v_j \}_{j=1}^{m-1} \big)\, \theta_m\big( \{ r_j, v_j \}_{j=1}^{m} \big)\\[-17pt]\nonumber \end{align} $$
$$ \begin{align} \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) = \theta\big( \{r_j, v_j \}_{j=1}^{m-1} \big)\, \theta_m\big( \{ r_j, v_j \}_{j=1}^{m} \big)\\[-17pt]\nonumber \end{align} $$
with
 $$ \begin{align*} \theta_m\big( \{r_j, v_j \}_{j=1}^{m} \big)= \prod_{i,j=1}^{m-1}\prod_{\substack{p_i,p_j,p_m:\\p_\ell\in\{-r_\ell,r_\ell+v_\ell\}}}\delta_{p_i\neq -p_j+v_m}\delta_{-p_m+v_i\neq p_j} \\[-17pt]\end{align*} $$
$$ \begin{align*} \theta_m\big( \{r_j, v_j \}_{j=1}^{m} \big)= \prod_{i,j=1}^{m-1}\prod_{\substack{p_i,p_j,p_m:\\p_\ell\in\{-r_\ell,r_\ell+v_\ell\}}}\delta_{p_i\neq -p_j+v_m}\delta_{-p_m+v_i\neq p_j} \\[-17pt]\end{align*} $$
collecting all conditions involving
![]() $\{r_m, v_m\}$
. Writing
$\{r_m, v_m\}$
. Writing
![]() $\theta _m = 1 + [ \theta _m - 1]$
, we split
$\theta _m = 1 + [ \theta _m - 1]$
, we split
![]() $\langle \xi _\nu , \mathcal {C}_N \xi _\nu \rangle = I_{\mathcal {C}} + J_{\mathcal {C}}$
with (recall the expression (2.22) for
$\langle \xi _\nu , \mathcal {C}_N \xi _\nu \rangle = I_{\mathcal {C}} + J_{\mathcal {C}}$
with (recall the expression (2.22) for
![]() $\| \xi _\nu \|^2$
)
$\| \xi _\nu \|^2$
)
 $$ \begin{align*} I_{\mathcal{C}} = \; 2\,\sqrt{\frac{N_0}{N}}\,\sum_{\substack{ v \in P_S,\, r \in P_H: \\r+v \in P_H}} N^{\kappa-1}\widehat V(r/N^{1-\kappa})\,\big(\eta_{r}+\eta_{r+v}\big)\gamma_{r}\gamma_{r+v} \sigma^2_{v}\, \| \xi_\nu\|^2 \\[-17pt]\end{align*} $$
$$ \begin{align*} I_{\mathcal{C}} = \; 2\,\sqrt{\frac{N_0}{N}}\,\sum_{\substack{ v \in P_S,\, r \in P_H: \\r+v \in P_H}} N^{\kappa-1}\widehat V(r/N^{1-\kappa})\,\big(\eta_{r}+\eta_{r+v}\big)\gamma_{r}\gamma_{r+v} \sigma^2_{v}\, \| \xi_\nu\|^2 \\[-17pt]\end{align*} $$
and
 $$ \begin{align*}\begin{aligned} J_{\mathcal{C}} =\; & 2\sqrt{\frac{N_0}{N}}\sum_{m\geq 1}\frac1{2^{m-1} (m-1)!}\frac1{N^m} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta\big( \{r_j, v_j \}_{j=1}^{m-1} \big) \\ & \times \Big[ \theta_m\big( \{r_j, v_j \}_{j=1}^{m} \big) -1 \Big] N^\kappa\widehat V(r_m/N^{1-\kappa})\,\big(\eta_{r_m} +\eta_{r_m+v_m}\big)\gamma_{r_m}\gamma_{r_m+v_m} \sigma^2_{v_m} \\ &\hspace{8cm} \times \prod_{i=1}^{m-1} (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 . \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} J_{\mathcal{C}} =\; & 2\sqrt{\frac{N_0}{N}}\sum_{m\geq 1}\frac1{2^{m-1} (m-1)!}\frac1{N^m} \sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta\big( \{r_j, v_j \}_{j=1}^{m-1} \big) \\ & \times \Big[ \theta_m\big( \{r_j, v_j \}_{j=1}^{m} \big) -1 \Big] N^\kappa\widehat V(r_m/N^{1-\kappa})\,\big(\eta_{r_m} +\eta_{r_m+v_m}\big)\gamma_{r_m}\gamma_{r_m+v_m} \sigma^2_{v_m} \\ &\hspace{8cm} \times \prod_{i=1}^{m-1} (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 . \end{aligned}\end{align*} $$
With
 $|\sqrt {N_0/N} - 1| \leq C \| \sigma _L \|^2/N$
and
$|\sqrt {N_0/N} - 1| \leq C \| \sigma _L \|^2/N$
and
![]() $|\gamma _r \gamma _{r+v} - 1| \leq C N^{2\kappa } / |r|^4$
for all
$|\gamma _r \gamma _{r+v} - 1| \leq C N^{2\kappa } / |r|^4$
for all
![]() $r \in P_H, v\in P_S$
, we obtain (using (3.12) and the assumption
$r \in P_H, v\in P_S$
, we obtain (using (3.12) and the assumption
![]() $3\kappa - 2 + 4\varepsilon < 0$
) that
$3\kappa - 2 + 4\varepsilon < 0$
) that
 $$ \begin{align} \frac{I_{\mathcal{C}}}{\| \xi_\nu \|^2} \leq \frac{2}{N} \sum_{\substack{ v \in P_S,\, r \in P_H: \\r+v \in P_H}} N^{\kappa}\widehat V(r/N^{1-\kappa})\,\big(\eta_{r}+\eta_{r+v}\big) \sigma^2_{v} + C N^{5\kappa /2 - \varepsilon}.\\[-17pt]\nonumber \end{align} $$
$$ \begin{align} \frac{I_{\mathcal{C}}}{\| \xi_\nu \|^2} \leq \frac{2}{N} \sum_{\substack{ v \in P_S,\, r \in P_H: \\r+v \in P_H}} N^{\kappa}\widehat V(r/N^{1-\kappa})\,\big(\eta_{r}+\eta_{r+v}\big) \sigma^2_{v} + C N^{5\kappa /2 - \varepsilon}.\\[-17pt]\nonumber \end{align} $$
To complete the proof of (5.2), we focus now on the error term
![]() $J_{\mathcal {C}}$
. We observe that
$J_{\mathcal {C}}$
. We observe that
 $$ \begin{align} | \theta_m\big( \{r_j, v_j \}_{j=1}^{m} \big) -1 | \leq& \sum_{j=1}^{m-1} \Big[ \delta_{v_j , v_m} + \sum_{ \substack{ p_m \in \{ -r_m, r_m+v_m \} \\p_j \in \{ -r_j, r_j+v_j\} }}\delta_{p_m, p_j} \Big] \nonumber\\ & + \sum_{\substack{j,k=1\\j\neq k}}^{m-1} \Big[ \sum_{ \substack{ p_j \in \{ -r_j, r_j+v_j \} \\ p_k \in \{ -r_k, r_k+v_k\} }} \delta_{v_m, p_j+p_k} + \sum_{\substack{ p_m \in \{ -r_m, r_m+v_m \} \\ p_j \in \{ -r_j, r_j+v_j \} }}\delta_{p_m, -p_j+v_k} \Big] . \end{align} $$
$$ \begin{align} | \theta_m\big( \{r_j, v_j \}_{j=1}^{m} \big) -1 | \leq& \sum_{j=1}^{m-1} \Big[ \delta_{v_j , v_m} + \sum_{ \substack{ p_m \in \{ -r_m, r_m+v_m \} \\p_j \in \{ -r_j, r_j+v_j\} }}\delta_{p_m, p_j} \Big] \nonumber\\ & + \sum_{\substack{j,k=1\\j\neq k}}^{m-1} \Big[ \sum_{ \substack{ p_j \in \{ -r_j, r_j+v_j \} \\ p_k \in \{ -r_k, r_k+v_k\} }} \delta_{v_m, p_j+p_k} + \sum_{\substack{ p_m \in \{ -r_m, r_m+v_m \} \\ p_j \in \{ -r_j, r_j+v_j \} }}\delta_{p_m, -p_j+v_k} \Big] . \end{align} $$
We bound
![]() $|J_{\mathcal {C}}| \leq \text {X}_1+ \text {X}_2$
, with
$|J_{\mathcal {C}}| \leq \text {X}_1+ \text {X}_2$
, with
![]() $\text {X}_1$
denoting the contribution arising from the first term on the right-hand side of (5.8) (this term involves two indices, m and j) and
$\text {X}_1$
denoting the contribution arising from the first term on the right-hand side of (5.8) (this term involves two indices, m and j) and
![]() $\text {X}_2$
indicating the contribution from the second term on the right-hand side of (5.8) (this term involves three indices,
$\text {X}_2$
indicating the contribution from the second term on the right-hand side of (5.8) (this term involves three indices,
![]() $m,j,k$
). We can estimate
$m,j,k$
). We can estimate
 $$ \begin{align*} \text{X}_1 \leq \; &C \sum_{m\geq 2}\frac1{2^{m-2} (m-2)!}\frac1{N^m}\sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta\big( \{r_j, v_j \}_{j=1}^{m-1} \big) \\ &\times N^\kappa |\widehat V(r_m/N^{1-\kappa})| \,\big| \eta_{r_m} +\eta_{r_m+v_m}\big| |\gamma_{r_m}| |\gamma_{r_m+v_m}| \sigma^2_{v_m} \prod_{i=1}^{m-1} (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 \\ & \times \Big[ \delta_{v_m, v_{m-1}} +\sum_{\substack{p_{m-1},p_m:\\p_\ell\in \{-r_\ell,r_\ell+v_\ell\}}}\hspace{-0.3cm}\delta_{p_m, p_{m-1}}\Big] . \end{align*} $$
$$ \begin{align*} \text{X}_1 \leq \; &C \sum_{m\geq 2}\frac1{2^{m-2} (m-2)!}\frac1{N^m}\sum_{\substack{ v_1 \in P_S, r_1 \in P_H : \\ r_1 +v_1 \in P_H } } \cdots \sum_{\substack{ v_m \in P_S, r_m \in P_H : \\ r_m +v_m \in P_H } } \theta\big( \{r_j, v_j \}_{j=1}^{m-1} \big) \\ &\times N^\kappa |\widehat V(r_m/N^{1-\kappa})| \,\big| \eta_{r_m} +\eta_{r_m+v_m}\big| |\gamma_{r_m}| |\gamma_{r_m+v_m}| \sigma^2_{v_m} \prod_{i=1}^{m-1} (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 \\ & \times \Big[ \delta_{v_m, v_{m-1}} +\sum_{\substack{p_{m-1},p_m:\\p_\ell\in \{-r_\ell,r_\ell+v_\ell\}}}\hspace{-0.3cm}\delta_{p_m, p_{m-1}}\Big] . \end{align*} $$
With
 $\theta \big ( \{r_j, v_j \}_{j=1}^{m-1} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-2} \big )$
, we reconstruct
$\theta \big ( \{r_j, v_j \}_{j=1}^{m-1} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-2} \big )$
, we reconstruct
![]() $\| \xi _\nu \|^2$
. Since
$\| \xi _\nu \|^2$
. Since
![]() $\| \gamma _H \|_\infty \leq C$
, we end up with
$\| \gamma _H \|_\infty \leq C$
, we end up with
 $$ \begin{align*} \frac{\text{X}_1}{\| \xi_\nu \|^2} \leq\; & \frac{C}{N^2} \sum_{r , r' \in P_H, v,v' \in P_S} N^\kappa |\widehat{V} (r/N^{1-\kappa}) |\eta_r + \eta_{r+v}| |\eta_{r'} + \eta_{r'+v'}|^2 \sigma_v^2 \sigma_{v'}^2 \\ &\hspace{6cm} \times \Big[ \delta_{v,v'} + \sum_{\substack{p \in \{-r, r+v\} \\ p' \in \{ -r', r' +v' \}}} \delta_{p,p'} \Big] \\ \leq \; &C N^{2\kappa-2} \| \sigma_S \|_\infty^2 \| \sigma_S \|^2 \| \eta_H \|^2 \sum_{r \in P_H} \frac{|\widehat{V} (r/N^{1-\kappa})|}{r^2} + C N^{4\kappa -2} \| \sigma_S \|^4 \sum_{r \in P_H} |r|^{-6} \\ \leq \; &C N^{11\kappa/2-2+2\varepsilon} + C N^{10\kappa-5+3\varepsilon} \leq C N^{5\kappa/2-\varepsilon}, \end{align*} $$
$$ \begin{align*} \frac{\text{X}_1}{\| \xi_\nu \|^2} \leq\; & \frac{C}{N^2} \sum_{r , r' \in P_H, v,v' \in P_S} N^\kappa |\widehat{V} (r/N^{1-\kappa}) |\eta_r + \eta_{r+v}| |\eta_{r'} + \eta_{r'+v'}|^2 \sigma_v^2 \sigma_{v'}^2 \\ &\hspace{6cm} \times \Big[ \delta_{v,v'} + \sum_{\substack{p \in \{-r, r+v\} \\ p' \in \{ -r', r' +v' \}}} \delta_{p,p'} \Big] \\ \leq \; &C N^{2\kappa-2} \| \sigma_S \|_\infty^2 \| \sigma_S \|^2 \| \eta_H \|^2 \sum_{r \in P_H} \frac{|\widehat{V} (r/N^{1-\kappa})|}{r^2} + C N^{4\kappa -2} \| \sigma_S \|^4 \sum_{r \in P_H} |r|^{-6} \\ \leq \; &C N^{11\kappa/2-2+2\varepsilon} + C N^{10\kappa-5+3\varepsilon} \leq C N^{5\kappa/2-\varepsilon}, \end{align*} $$
where we used Lemma 2.4, (3.12), the assumption
![]() $3\kappa -2 + 4\varepsilon < 0$
and the remark that
$3\kappa -2 + 4\varepsilon < 0$
and the remark that
![]() $|\eta _{r+v}| \leq CN^\kappa |r|^{-2}$
, for all
$|\eta _{r+v}| \leq CN^\kappa |r|^{-2}$
, for all
![]() $r \in P_H$
and
$r \in P_H$
and
![]() $v \in P_S$
. We can proceed similarly to estimate
$v \in P_S$
. We can proceed similarly to estimate
![]() $X_2$
. In the second term on the right-hand side of (5.8), we have to sum over
$X_2$
. In the second term on the right-hand side of (5.8), we have to sum over
![]() $(m-1) (m-2)/2$
pairs of indices
$(m-1) (m-2)/2$
pairs of indices
![]() $j,k$
. With
$j,k$
. With
 $\theta \big ( \{r_j, v_j \}_{j=1}^{m-1} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-3} \big )$
and again with Lemma 2.4 and(3.12), we arrive at
$\theta \big ( \{r_j, v_j \}_{j=1}^{m-1} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-3} \big )$
and again with Lemma 2.4 and(3.12), we arrive at
 $$ \begin{align*} \frac{\text{X}_2}{\| \xi_\nu \|^2} \leq\; & \frac{C}{N^3} \sum_{\substack{r , r' , r'' \in P_H, \\ v,v', v'' \in P_S}} N^\kappa |\widehat{V} (r/N^{1-\kappa}) |\eta_r + \eta_{r+v}| |\eta_{r'} + \eta_{r'+v'}|^2 |\eta_{r''} + \eta_{r''+v''}|^2 \sigma_v^2 \sigma_{v'}^2 \sigma_{v''}^2 \\ &\hspace{4.5cm} \times \Big[ \sum_{ \substack{p \in \{ -r , r+v \}, \\ p' \in \{ -r', r' + v'\}}} \delta_{p,-p'+v''} + \sum_{\substack{p' \in \{-r', r'+v'\}, \\ p'' \in \{-r'', r'' + v''\}}} \delta_{v,p'+p''} \Big] \\ \leq \; &C N^{4\kappa - 3} \| \sigma_S \|^6 \| \eta_H \|^2 \sum_{r \in P_H} |r|^{-6} + C N^{6\kappa -3} \| \sigma_S \|^6 \sum_{r \in P_H} \frac{|\widehat{V} (r/N^{1-\kappa})|}{r^2} \sum_{r' \in P_H} |r'|^{-8} \\ \leq \; &C N^{29\kappa/2 -7 + 5\varepsilon} \leq C N^{5\kappa/2} \cdot N^{12 \kappa -7 + 5\varepsilon} . \end{align*} $$
$$ \begin{align*} \frac{\text{X}_2}{\| \xi_\nu \|^2} \leq\; & \frac{C}{N^3} \sum_{\substack{r , r' , r'' \in P_H, \\ v,v', v'' \in P_S}} N^\kappa |\widehat{V} (r/N^{1-\kappa}) |\eta_r + \eta_{r+v}| |\eta_{r'} + \eta_{r'+v'}|^2 |\eta_{r''} + \eta_{r''+v''}|^2 \sigma_v^2 \sigma_{v'}^2 \sigma_{v''}^2 \\ &\hspace{4.5cm} \times \Big[ \sum_{ \substack{p \in \{ -r , r+v \}, \\ p' \in \{ -r', r' + v'\}}} \delta_{p,-p'+v''} + \sum_{\substack{p' \in \{-r', r'+v'\}, \\ p'' \in \{-r'', r'' + v''\}}} \delta_{v,p'+p''} \Big] \\ \leq \; &C N^{4\kappa - 3} \| \sigma_S \|^6 \| \eta_H \|^2 \sum_{r \in P_H} |r|^{-6} + C N^{6\kappa -3} \| \sigma_S \|^6 \sum_{r \in P_H} \frac{|\widehat{V} (r/N^{1-\kappa})|}{r^2} \sum_{r' \in P_H} |r'|^{-8} \\ \leq \; &C N^{29\kappa/2 -7 + 5\varepsilon} \leq C N^{5\kappa/2} \cdot N^{12 \kappa -7 + 5\varepsilon} . \end{align*} $$
Thus,
![]() $|J_{\mathcal {C}}| / \| \xi _\nu \|^2 \leq N^{5\kappa /2} \cdot \max \{ N^{-\varepsilon } , N^{12\kappa -7 + 5\varepsilon } \}$
. With (5.7), this implies (5.2).
$|J_{\mathcal {C}}| / \| \xi _\nu \|^2 \leq N^{5\kappa /2} \cdot \max \{ N^{-\varepsilon } , N^{12\kappa -7 + 5\varepsilon } \}$
. With (5.7), this implies (5.2).
5.3 Expectation of the quartic term
In this section we show the bound (5.3) for the expectation of
 $\mathcal {V}_N^{(H)}$
. Pairing momenta in
$\mathcal {V}_N^{(H)}$
. Pairing momenta in
![]() $P_S$
, as we did in (2.20) and in the previous subsections, we obtain
$P_S$
, as we did in (2.20) and in the previous subsections, we obtain
 $$ \begin{align} \begin{aligned} {\bigl\langle\xi_\nu,\mathcal{V}_N^{(H)} \xi_\nu\bigr\rangle}=&\frac1{2N}\sum_{m\geq 1}\frac1{m!}\frac1{N^m} \sum_{\substack{v_1 \in P_S,\, r_1, {\tilde{r}}_1 \in P_H:\\ r_1+v_1,\, {\tilde{r}}_1 + v_1 \in P_H}} \cdots\sum_{\substack{v_m \in P_S,\, r_m, {\tilde{r}}_m \in P_H:\\ r_m+v_m,\, {\tilde{r}}_m + v_m \in P_H}} \\ &\times \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \prod_{i=1}^m\eta_{r_i}\eta_{\tilde{r}_i}\sigma_{v_i}^2\hspace{-0.3cm}\sum_{\substack{r\in \Lambda^*, p,q \in P_H: \\p+r,\,q+r\in P_H}}\hspace{-0.2cm} N^\kappa \widehat V(r/N^{1-\kappa})\\ &\times{\bigl\langle\Omega,A_{r_1,v_1}\dots A_{r_m,v_m}\,a^*_{p+r}a^*_{q} a_p a_{q+r} A^*_{\tilde{r}_1,v_1}\dots A^*_{\tilde{r}_m,v_m}\Omega\bigr\rangle} \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} {\bigl\langle\xi_\nu,\mathcal{V}_N^{(H)} \xi_\nu\bigr\rangle}=&\frac1{2N}\sum_{m\geq 1}\frac1{m!}\frac1{N^m} \sum_{\substack{v_1 \in P_S,\, r_1, {\tilde{r}}_1 \in P_H:\\ r_1+v_1,\, {\tilde{r}}_1 + v_1 \in P_H}} \cdots\sum_{\substack{v_m \in P_S,\, r_m, {\tilde{r}}_m \in P_H:\\ r_m+v_m,\, {\tilde{r}}_m + v_m \in P_H}} \\ &\times \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \prod_{i=1}^m\eta_{r_i}\eta_{\tilde{r}_i}\sigma_{v_i}^2\hspace{-0.3cm}\sum_{\substack{r\in \Lambda^*, p,q \in P_H: \\p+r,\,q+r\in P_H}}\hspace{-0.2cm} N^\kappa \widehat V(r/N^{1-\kappa})\\ &\times{\bigl\langle\Omega,A_{r_1,v_1}\dots A_{r_m,v_m}\,a^*_{p+r}a^*_{q} a_p a_{q+r} A^*_{\tilde{r}_1,v_1}\dots A^*_{\tilde{r}_m,v_m}\Omega\bigr\rangle} \end{aligned}\end{align} $$
where we use the notation
![]() $A_{r_i, v_i} = a_{r_i+v_i} a_{-r_i}$
that was already introduced in (2.20). Next we observe that because of the cutoffs
$A_{r_i, v_i} = a_{r_i+v_i} a_{-r_i}$
that was already introduced in (2.20). Next we observe that because of the cutoffs
 $\theta (\{r_j,v_j\}_{j=1}^m)$
and
$\theta (\{r_j,v_j\}_{j=1}^m)$
and
 $\theta (\{{\tilde {r}}_j,v_j\}_{j=1}^m)$
, at most two indices
$\theta (\{{\tilde {r}}_j,v_j\}_{j=1}^m)$
, at most two indices
![]() $i,j \in \{ 1, \dots , m \}$
can be involved in contractions with the observable
$i,j \in \{ 1, \dots , m \}$
can be involved in contractions with the observable
![]() $a_{p+r}^* a_q^* a_p a_{q+r}$
. We distinguish two possible cases:
$a_{p+r}^* a_q^* a_p a_{q+r}$
. We distinguish two possible cases:
-
1) There exists an index
 $i \in \{ 1,\dots ,m \}$
such that
$i \in \{ 1,\dots ,m \}$
such that
 $a_p$
,
$a_p$
,
 $a_{q+r}$
are contracted with
$a_{q+r}$
are contracted with
 $A^*_{{\tilde {r}}_i,v_i}$
and
$A^*_{{\tilde {r}}_i,v_i}$
and
 $a^*_{q}$
,
$a^*_{q}$
,
 $a^*_{p+r}$
are contracted with
$a^*_{p+r}$
are contracted with
 $A_{r_i,v_i}$
.
$A_{r_i,v_i}$
. -
2) There are two indices
 $i \neq j \in \{ 1, \dots , m \}$
such that the operators
$i \neq j \in \{ 1, \dots , m \}$
such that the operators
 $a_p$
and
$a_p$
and
 $a_{q+r}$
are contracted with
$a_{q+r}$
are contracted with
 $a^*_{{\tilde {p}}_i}$
and
$a^*_{{\tilde {p}}_i}$
and
 $a^*_{{\tilde {p}}_j}$
for some
$a^*_{{\tilde {p}}_j}$
for some
 ${\tilde {p}}_\ell \in \{-{\tilde {r}}_\ell , {\tilde {r}}_\ell + v_\ell \}, \ell =i,j$
and the operators
${\tilde {p}}_\ell \in \{-{\tilde {r}}_\ell , {\tilde {r}}_\ell + v_\ell \}, \ell =i,j$
and the operators
 $a^*_q, a^*_{p+r}$
are contracted with
$a^*_q, a^*_{p+r}$
are contracted with
 $a_{p_i}, a_{p_j}$
, with
$a_{p_i}, a_{p_j}$
, with
 $p_\ell \in \{-r_\ell ,r_\ell +v_\ell \}, \ell =i,j$
. Note that in this case the operators
$p_\ell \in \{-r_\ell ,r_\ell +v_\ell \}, \ell =i,j$
. Note that in this case the operators
 $a^*_{-{\tilde {p}}_i+v_i}, a^*_{-{\tilde {p}}_j+v_j}$
have to be contracted with
$a^*_{-{\tilde {p}}_i+v_i}, a^*_{-{\tilde {p}}_j+v_j}$
have to be contracted with
 $a_{-p_i+v_i}, a_{-p_j+v_j}.$
$a_{-p_i+v_i}, a_{-p_j+v_j}.$
We denote by
![]() $\text {V}_1$
and
$\text {V}_1$
and
![]() $\text {V}_2$
the contributions to
$\text {V}_2$
the contributions to
 ${\bigl \langle \xi _\nu ,\mathcal {V}_N^{(H)} \xi _\nu \bigr \rangle }$
arising from the two cases described above. Let us first consider
${\bigl \langle \xi _\nu ,\mathcal {V}_N^{(H)} \xi _\nu \bigr \rangle }$
arising from the two cases described above. Let us first consider
![]() $\text {V}_1$
. There are m choices (all leading to the same contribution) for the index
$\text {V}_1$
. There are m choices (all leading to the same contribution) for the index
![]() $i \in \{ 1, \dots , m \}$
labelling momenta to be contracted with the observable. Let us fix
$i \in \{ 1, \dots , m \}$
labelling momenta to be contracted with the observable. Let us fix
![]() $i = m$
. Then we have
$i = m$
. Then we have
![]() $p={\tilde {p}}_m, q+r=-{\tilde {p}}_m+v_m$
with
$p={\tilde {p}}_m, q+r=-{\tilde {p}}_m+v_m$
with
![]() ${\tilde {p}}_m \in \{-{\tilde {r}}_m,{\tilde {r}}_m +v_m \}$
and
${\tilde {p}}_m \in \{-{\tilde {r}}_m,{\tilde {r}}_m +v_m \}$
and
![]() $p+r=p_m, q=-p_m+v_m$
with
$p+r=p_m, q=-p_m+v_m$
with
![]() $p_m\in \{-r_m,r_m+v_m\}$
. Note that the choice of p and
$p_m\in \{-r_m,r_m+v_m\}$
. Note that the choice of p and
![]() $p+r$
also determines q and
$p+r$
also determines q and
![]() $q+r$
, since we always have
$q+r$
, since we always have
![]() $q = v_m - (p+r)$
. The presence of the cutoffs immediately implies that
$q = v_m - (p+r)$
. The presence of the cutoffs immediately implies that
![]() $A_{r_j,v_j}$
is fully contracted with
$A_{r_j,v_j}$
is fully contracted with
 $A^*_{{\tilde {r}}_j , v_j}$
, for all
$A^*_{{\tilde {r}}_j , v_j}$
, for all
![]() $j \not = m$
. We find
$j \not = m$
. We find
 $$ \begin{align} &\langle \xi_{\nu}, \text{V}_1 \xi_{\nu} \rangle \nonumber\\ &=\frac1{2N}\sum_{m\geq 1}\frac1{(m-1)!}\frac1{N^m} \;\sum_{\substack{v_1 \in P_S, r_1, {\tilde{r}}_1 \in P_H: \nonumber\\ r_1 + v_1 ,\, {\tilde{r}}_1 + v_1 \in P_H}} \cdots \sum_{\substack{v_{m} \in P_S, r_{m}, {\tilde{r}}_{m} \in P_H: \\ r_{m} + v_{m} ,\, {\tilde{r}}_{m} + v_{m} \in P_H}}\hskip -0.5cm\theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \nonumber\\[6pt] &\, \times \hskip -0.1cm \prod_{j=1}^{m-1}\hskip -0.1cm\eta_{r_j}\eta_{{\tilde{r}}_j}(\delta_{r_j,{\tilde{r}}_j}+\delta_{-r_j,{\tilde{r}}_j+v_j})\sigma_{v_j}^2\, \eta_{r_m} \eta_{{\tilde{r}}_m}\sigma_{v_m}^2\hspace{-.5cm} \sum_{\substack{r\in \Lambda^*,\,p\in P_H:\\p-v_m,p+r\in P_H}} \hskip -0.7cm N^\kappa\widehat{V}(r/N^{1-\kappa}) \hskip -0.5cm \sum_{\substack{p_m\in \{-r_m,r_m+v_m\}\\{\tilde{p}}_m\in \{-{\tilde{r}}_m,{\tilde{r}}_m+v_m\}}}\hspace{-0.8cm}\delta_{p,p_m}\delta_{p+r,{\tilde{p}}_m} . \end{align} $$
$$ \begin{align} &\langle \xi_{\nu}, \text{V}_1 \xi_{\nu} \rangle \nonumber\\ &=\frac1{2N}\sum_{m\geq 1}\frac1{(m-1)!}\frac1{N^m} \;\sum_{\substack{v_1 \in P_S, r_1, {\tilde{r}}_1 \in P_H: \nonumber\\ r_1 + v_1 ,\, {\tilde{r}}_1 + v_1 \in P_H}} \cdots \sum_{\substack{v_{m} \in P_S, r_{m}, {\tilde{r}}_{m} \in P_H: \\ r_{m} + v_{m} ,\, {\tilde{r}}_{m} + v_{m} \in P_H}}\hskip -0.5cm\theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \nonumber\\[6pt] &\, \times \hskip -0.1cm \prod_{j=1}^{m-1}\hskip -0.1cm\eta_{r_j}\eta_{{\tilde{r}}_j}(\delta_{r_j,{\tilde{r}}_j}+\delta_{-r_j,{\tilde{r}}_j+v_j})\sigma_{v_j}^2\, \eta_{r_m} \eta_{{\tilde{r}}_m}\sigma_{v_m}^2\hspace{-.5cm} \sum_{\substack{r\in \Lambda^*,\,p\in P_H:\\p-v_m,p+r\in P_H}} \hskip -0.7cm N^\kappa\widehat{V}(r/N^{1-\kappa}) \hskip -0.5cm \sum_{\substack{p_m\in \{-r_m,r_m+v_m\}\\{\tilde{p}}_m\in \{-{\tilde{r}}_m,{\tilde{r}}_m+v_m\}}}\hspace{-0.8cm}\delta_{p,p_m}\delta_{p+r,{\tilde{p}}_m} . \end{align} $$
Since here (in contrast to the previous subsections) the contraction does not fix
![]() ${\tilde {r}}_m$
to be either
${\tilde {r}}_m$
to be either
![]() $r_m$
or
$r_m$
or
![]() $-(r_m + v_m)$
, we cannot erase the cutoff
$-(r_m + v_m)$
, we cannot erase the cutoff
 $\theta (\{ {\tilde {r}}_j , v_j \}_{j=1}^m)$
. With the decomposition (5.6), we can replace, on the right-hand side of (5.10),
$\theta (\{ {\tilde {r}}_j , v_j \}_{j=1}^m)$
. With the decomposition (5.6), we can replace, on the right-hand side of (5.10),
 $$ \begin{align*} \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) = \theta \big( \{r_j, v_j \}_{j=1}^{m-1} \big) \theta_m \big( \{ r_j, v_j \}_{j=1}^{m} \big) \theta_m \big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big). \end{align*} $$
$$ \begin{align*} \theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) = \theta \big( \{r_j, v_j \}_{j=1}^{m-1} \big) \theta_m \big( \{ r_j, v_j \}_{j=1}^{m} \big) \theta_m \big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big). \end{align*} $$
Writing
 $$ \begin{align*} \theta_m \big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \theta_m \big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) = 1 + \Big[ \theta_m \big( \{ r_j, v_j \}_{j=1}^{m} \big) \theta_m \big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) - 1 \Big] \end{align*} $$
$$ \begin{align*} \theta_m \big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \theta_m \big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) = 1 + \Big[ \theta_m \big( \{ r_j, v_j \}_{j=1}^{m} \big) \theta_m \big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) - 1 \Big] \end{align*} $$
we split (as we did in the last subsection)
![]() $\langle \xi _\nu , \text {V}_1 \xi _\nu \rangle = I_{\mathcal {V}} + J_{\mathcal {V}}$
, with
$\langle \xi _\nu , \text {V}_1 \xi _\nu \rangle = I_{\mathcal {V}} + J_{\mathcal {V}}$
, with
 $$ \begin{align} I_{\mathcal{V}} = \frac 1 {N^2} \sum_{r \in \Lambda^*} \sum_{\substack{ v\in P_S, p \in P_H:\\ p+r,p-v,\, p+r-v \in P_H}} \hskip -0.5cm N^\kappa \widehat V(r/N^{1-\kappa}) \eta_{p} \big( \eta_{p+r} +\eta_{p+r-v} \big) \sigma_{v}^2 \, \| \xi_\nu \|^2 \end{align} $$
$$ \begin{align} I_{\mathcal{V}} = \frac 1 {N^2} \sum_{r \in \Lambda^*} \sum_{\substack{ v\in P_S, p \in P_H:\\ p+r,p-v,\, p+r-v \in P_H}} \hskip -0.5cm N^\kappa \widehat V(r/N^{1-\kappa}) \eta_{p} \big( \eta_{p+r} +\eta_{p+r-v} \big) \sigma_{v}^2 \, \| \xi_\nu \|^2 \end{align} $$
and
 $$ \begin{align} J_{\mathcal{V}} =&\frac1{2N}\sum_{m\geq 1}\frac1{2^{m-1} (m-1)!}\frac1{N^m}\sum_{\substack{v_1 \in P_S, r_1 \in P_H: \\ r_1 + v_1 \in P_H}} \cdots \sum_{\substack{v_{m-1} \in P_S, r_{m-1} \in P_H: \\ r_{m-1} + v_{m-1} \in P_H}} \sum_{\substack{v_{m} \in P_S , r_{m}, {\tilde{r}}_{m} \in P_H: \\ r_{m} + v_{m} ,\, {\tilde{r}}_{m} + v_{m} \in P_H}} \nonumber\\ & \times \theta\big( \{r_j, v_j \}_{j=1}^{m-1} \big) \big[ \theta_m(\{r_j, v_j\}_{j=1}^{m})\theta_m(\{ r^\sharp_j ,v_j\}_{j=1}^m)-1\big] \prod_{i=1}^{m-1} (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 \, \nonumber\\ &\times \eta_{r_m} \eta_{{\tilde{r}}_m} \sigma_{v_m}^2 \sum_{\substack{r\in \Lambda^*}} N^\kappa \widehat V(r/N^{1-\kappa})\hspace{-0.5cm} \sum_{\substack{ p \in P_H :\, p+r,\\ p-v_m,\, p+r-v_m\in P_H}} \sum_{\substack{p_m\in \{-r_m,r_m+v_m\}\\{\tilde{p}}_m\in \{-{\tilde{r}}_m,{\tilde{r}}_m+v_m\}}}\hspace{-0.3cm}\delta_{p,p_m}\delta_{p+r,{\tilde{p}}_m} \end{align} $$
$$ \begin{align} J_{\mathcal{V}} =&\frac1{2N}\sum_{m\geq 1}\frac1{2^{m-1} (m-1)!}\frac1{N^m}\sum_{\substack{v_1 \in P_S, r_1 \in P_H: \\ r_1 + v_1 \in P_H}} \cdots \sum_{\substack{v_{m-1} \in P_S, r_{m-1} \in P_H: \\ r_{m-1} + v_{m-1} \in P_H}} \sum_{\substack{v_{m} \in P_S , r_{m}, {\tilde{r}}_{m} \in P_H: \\ r_{m} + v_{m} ,\, {\tilde{r}}_{m} + v_{m} \in P_H}} \nonumber\\ & \times \theta\big( \{r_j, v_j \}_{j=1}^{m-1} \big) \big[ \theta_m(\{r_j, v_j\}_{j=1}^{m})\theta_m(\{ r^\sharp_j ,v_j\}_{j=1}^m)-1\big] \prod_{i=1}^{m-1} (\eta_{r_i} + \eta_{r_i + v_i})^2 \sigma_{v_i}^2 \, \nonumber\\ &\times \eta_{r_m} \eta_{{\tilde{r}}_m} \sigma_{v_m}^2 \sum_{\substack{r\in \Lambda^*}} N^\kappa \widehat V(r/N^{1-\kappa})\hspace{-0.5cm} \sum_{\substack{ p \in P_H :\, p+r,\\ p-v_m,\, p+r-v_m\in P_H}} \sum_{\substack{p_m\in \{-r_m,r_m+v_m\}\\{\tilde{p}}_m\in \{-{\tilde{r}}_m,{\tilde{r}}_m+v_m\}}}\hspace{-0.3cm}\delta_{p,p_m}\delta_{p+r,{\tilde{p}}_m} \end{align} $$
where
 $r^\sharp _j = r_j$
for
$r^\sharp _j = r_j$
for
![]() $j=1,\dots , m-1$
and
$j=1,\dots , m-1$
and
 $r^\sharp _m = {\tilde {r}}_m$
in the argument of
$r^\sharp _m = {\tilde {r}}_m$
in the argument of
![]() $\theta _m$
. Observing that, with Lemma 2.4 and (3.12),
$\theta _m$
. Observing that, with Lemma 2.4 and (3.12),
 $$ \begin{align*} \frac 1 {N^2} \sum_{r \in \Lambda^*} & \sum_{\substack{v \in P_S, p \in \Lambda^* : \\ p\in P_H^c \text{ or } p-v \in P_H^c}} N^\kappa |\widehat V(r/N^{1-\kappa})| |\eta_{p}| \big( |\eta_{p+r}| + |\eta_{p+r-v}| \big) \sigma_{v}^2 \\ &\leq C N^{-2+2\kappa} \| \sigma_S \|^2 \Big[ \sum_{|p| \leq N^{1-\kappa -\varepsilon}} |p|^{-2} \Big] \mathop{\mathrm{sup}}\limits_{p\in \Lambda^*} \sum_{r \in \Lambda^*} |\widehat V(r/N^{1-\kappa})| |\eta_{p+r}| \leq C N^{5\kappa/2 - \varepsilon}, \end{align*} $$
$$ \begin{align*} \frac 1 {N^2} \sum_{r \in \Lambda^*} & \sum_{\substack{v \in P_S, p \in \Lambda^* : \\ p\in P_H^c \text{ or } p-v \in P_H^c}} N^\kappa |\widehat V(r/N^{1-\kappa})| |\eta_{p}| \big( |\eta_{p+r}| + |\eta_{p+r-v}| \big) \sigma_{v}^2 \\ &\leq C N^{-2+2\kappa} \| \sigma_S \|^2 \Big[ \sum_{|p| \leq N^{1-\kappa -\varepsilon}} |p|^{-2} \Big] \mathop{\mathrm{sup}}\limits_{p\in \Lambda^*} \sum_{r \in \Lambda^*} |\widehat V(r/N^{1-\kappa})| |\eta_{p+r}| \leq C N^{5\kappa/2 - \varepsilon}, \end{align*} $$
we conclude from (5.11) (switching
![]() $p+r \to p$
and
$p+r \to p$
and
![]() $v \to -v$
) that
$v \to -v$
) that
 $$ \begin{align} \frac{I_{\mathcal{V}}}{\| \xi_\nu \|^2} \leq \frac 1 {N^2} \sum_{\substack{v \in P_S, p \in P_H: \\ p+v \in P_H}} \, \big( N^\kappa \widehat V(\cdot/N^{1-\kappa}) \ast \eta \big)_p (\eta_p +\eta_{p+v}) \sigma_v^2 + C N^{5\kappa/2-\varepsilon}. \end{align} $$
$$ \begin{align} \frac{I_{\mathcal{V}}}{\| \xi_\nu \|^2} \leq \frac 1 {N^2} \sum_{\substack{v \in P_S, p \in P_H: \\ p+v \in P_H}} \, \big( N^\kappa \widehat V(\cdot/N^{1-\kappa}) \ast \eta \big)_p (\eta_p +\eta_{p+v}) \sigma_v^2 + C N^{5\kappa/2-\varepsilon}. \end{align} $$
Let us now focus on the term
![]() $J_{\mathcal {V}}$
. With
$J_{\mathcal {V}}$
. With
 $$ \begin{align} \Big| \theta_m \big( &\{r_j, v_j \}_{j=1}^{m} \big) \theta_m\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) -1 \Big| \nonumber\\ \leq \; &\sum_{j=1}^{m-1} \delta_{v_m, v_j} + \sum_{j=1}^{m-1} \Big[ \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ p_m \in \{ - r_m , r_m + v_m \}}} \delta_{p_m, p_j} + \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ {\tilde{p}}_m \in \{ - {\tilde{r}}_m , {\tilde{r}}_m + v_m \}}} \delta_{{\tilde{p}}_m, p_j} \Big] \nonumber \\ &+ \sum_{\substack{j,k=1 \\ j \not = k}}^{m-1} \Big[ \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ p_m \in \{ - r_m , r_m + v_m \}}} \delta_{p_m, -p_j + v_k} + \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ {\tilde{p}}_m \in \{ - {\tilde{r}}_m , {\tilde{r}}_m + v_m \}}} \delta_{{\tilde{p}}_m, -p_j + v_k} \Big]\nonumber \\ &+ \sum_{\substack{j,k=1 \\ j \not = k}}^{m-1} \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ p_k \in \{ - r_k , r_k + v_k \}}} \delta_{v_m , p_j + p_k} \end{align} $$
$$ \begin{align} \Big| \theta_m \big( &\{r_j, v_j \}_{j=1}^{m} \big) \theta_m\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) -1 \Big| \nonumber\\ \leq \; &\sum_{j=1}^{m-1} \delta_{v_m, v_j} + \sum_{j=1}^{m-1} \Big[ \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ p_m \in \{ - r_m , r_m + v_m \}}} \delta_{p_m, p_j} + \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ {\tilde{p}}_m \in \{ - {\tilde{r}}_m , {\tilde{r}}_m + v_m \}}} \delta_{{\tilde{p}}_m, p_j} \Big] \nonumber \\ &+ \sum_{\substack{j,k=1 \\ j \not = k}}^{m-1} \Big[ \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ p_m \in \{ - r_m , r_m + v_m \}}} \delta_{p_m, -p_j + v_k} + \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ {\tilde{p}}_m \in \{ - {\tilde{r}}_m , {\tilde{r}}_m + v_m \}}} \delta_{{\tilde{p}}_m, -p_j + v_k} \Big]\nonumber \\ &+ \sum_{\substack{j,k=1 \\ j \not = k}}^{m-1} \sum_{\substack{p_j \in \{ - r_j, r_j + v_j \} \\ p_k \in \{ - r_k , r_k + v_k \}}} \delta_{v_m , p_j + p_k} \end{align} $$
we can bound
![]() $|J_{\mathcal {V}}| \leq \text {W}_1 + \text {W}_2 + \text {W}_3 + \text {W}_4$
, with
$|J_{\mathcal {V}}| \leq \text {W}_1 + \text {W}_2 + \text {W}_3 + \text {W}_4$
, with
![]() $W_\ell $
indicating the contribution to (5.12) arising from the
$W_\ell $
indicating the contribution to (5.12) arising from the
![]() $\ell $
th term on the right-hand side of (5.14).
$\ell $
th term on the right-hand side of (5.14).
The term
![]() $\text {W}_1$
contains the sum of
$\text {W}_1$
contains the sum of
![]() $(m-1)$
identical contributions, corresponding to
$(m-1)$
identical contributions, corresponding to
![]() $j \in \{ 1, \dots , m-1 \}$
in the first term on the right-hand side of (5.14). Let us fix
$j \in \{ 1, \dots , m-1 \}$
in the first term on the right-hand side of (5.14). Let us fix
![]() $j=m-1$
. Estimating
$j=m-1$
. Estimating
 $\theta \big ( \{r_j, v_j \}_{j=1}^{m-1} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-2} \big )$
and reconstructing the expression (2.22) for
$\theta \big ( \{r_j, v_j \}_{j=1}^{m-1} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-2} \big )$
and reconstructing the expression (2.22) for
![]() $\| \xi _\nu \|^2$
, we can bound (the momenta
$\| \xi _\nu \|^2$
, we can bound (the momenta
![]() $r',r'',\tilde {r}''$
correspond to
$r',r'',\tilde {r}''$
correspond to
![]() $r_{m-1}, r_m, \tilde {r}_m$
)
$r_{m-1}, r_m, \tilde {r}_m$
)
 $$ \begin{align*} \frac{\text{W}_1}{\| \xi_\nu \|^2} \leq C N^{-3} \sum_{r \in \Lambda^*} N^\kappa |\widehat{V} (r/N^{1-\kappa})| \hspace{-.3cm} \sum_{\substack{r', r'', {\tilde{r}}'' \in P_H \\ v' \in P_S}} \hspace{-.3cm} (\eta_{r'} + \eta_{r'+v'})^2 |\eta_{r''}| |\eta_{{\tilde{r}}''}| \sigma_{v'}^4 \hspace{-.4cm} \sum_{\substack{p'' \in \{ -r'', r''+v' \} \\ {\tilde{p}}'' \in \{ -{\tilde{r}}'', {\tilde{r}}'' +v' \}}} \hspace{-.5cm} \delta_{p''+r ,{\tilde{p}}''}. \end{align*} $$
$$ \begin{align*} \frac{\text{W}_1}{\| \xi_\nu \|^2} \leq C N^{-3} \sum_{r \in \Lambda^*} N^\kappa |\widehat{V} (r/N^{1-\kappa})| \hspace{-.3cm} \sum_{\substack{r', r'', {\tilde{r}}'' \in P_H \\ v' \in P_S}} \hspace{-.3cm} (\eta_{r'} + \eta_{r'+v'})^2 |\eta_{r''}| |\eta_{{\tilde{r}}''}| \sigma_{v'}^4 \hspace{-.4cm} \sum_{\substack{p'' \in \{ -r'', r''+v' \} \\ {\tilde{p}}'' \in \{ -{\tilde{r}}'', {\tilde{r}}'' +v' \}}} \hspace{-.5cm} \delta_{p''+r ,{\tilde{p}}''}. \end{align*} $$
With Lemma 2.4 and with the estimate
 $$ \begin{align} \mathop{\mathrm{sup}}\limits_{v \in P_S \cup \{ 0 \}} \frac{1}{N^2} \sum_{\substack{r \in \Lambda^*, q \in P_H : \\ q-r \in P_H}} N^\kappa |\widehat{V} (r/N^{1-\kappa})| |\eta_{q-v} | |\eta_{q-r}| \leq C N^{\kappa}, \end{align} $$
$$ \begin{align} \mathop{\mathrm{sup}}\limits_{v \in P_S \cup \{ 0 \}} \frac{1}{N^2} \sum_{\substack{r \in \Lambda^*, q \in P_H : \\ q-r \in P_H}} N^\kappa |\widehat{V} (r/N^{1-\kappa})| |\eta_{q-v} | |\eta_{q-r}| \leq C N^{\kappa}, \end{align} $$
which can be shown similarly to (3.12) (using
![]() $V \in L^q (\mathbb {R}^3)$
, for some
$V \in L^q (\mathbb {R}^3)$
, for some
![]() $q> 3/2$
), we find
$q> 3/2$
), we find
 $$ \begin{align} \frac{\text{W}_1}{\| \xi_\nu \|^2} \leq C N^{\kappa -1} \| \eta_H \|^2 \| \sigma_S \|_\infty^2 \| \sigma_S \|^2 \leq C N^{11\kappa/2 -2 + 2\varepsilon} \leq C N^{5\kappa/2-\varepsilon} \end{align} $$
$$ \begin{align} \frac{\text{W}_1}{\| \xi_\nu \|^2} \leq C N^{\kappa -1} \| \eta_H \|^2 \| \sigma_S \|_\infty^2 \| \sigma_S \|^2 \leq C N^{11\kappa/2 -2 + 2\varepsilon} \leq C N^{5\kappa/2-\varepsilon} \end{align} $$
since
![]() $3\kappa - 2 + 4\varepsilon < 0$
. Analogously, we bound, with (3.12) and Lemma 2.4,
$3\kappa - 2 + 4\varepsilon < 0$
. Analogously, we bound, with (3.12) and Lemma 2.4,
 $$ \begin{align} \frac{\text{W}_2}{\| \xi_\nu \|^2} \leq \; &C N^{-3} \sum_{r \in \Lambda^*} N^\kappa |\widehat{V} (r/N^{1-\kappa})| \hspace{-.3cm} \sum_{\substack{r', r'', {\tilde{r}}'' \in P_H \\ v', v'' \in P_S}} \hspace{-.3cm} (\eta_{r'} + \eta_{r'+v'})^2 |\eta_{r''}| |\eta_{{\tilde{r}}''}| \sigma_{v'}^2 \sigma_{v''}^2 \hspace{-.3cm}\nonumber\\ &\times \sum_{\substack{p'' \in \{ -r'', r''+v'' \} \\ {\tilde{p}}'' \in \{ -{\tilde{r}}'', {\tilde{r}}'' +v'' \}}} \hspace{-.3cm} \delta_{p'' + r , {\tilde{p}}''} \Big[ \sum_{\substack{p' \in \{ -r', r'+v' \} \\ p'' \in \{ -r'', r'' +v'' \}}} \delta_{p', p''} + \sum_{\substack{p' \in \{ -r', r'+v' \} \\ {\tilde{p}}'' \in \{ -{\tilde{r}}'', {\tilde{r}}'' +v'' \}}} \delta_{p', {\tilde{p}}''} \Big] \nonumber\\ \leq \; &C N^{-3+5\kappa} \| \sigma_S \|^4 \Big[\sum_{r' \in P_H} |r'|^{-6}\Big] \Big[ \mathop{\mathrm{sup}}\limits_{r' \in \Lambda^*} \sum_{r \in \Lambda^* , r \not = -r'} \frac{|\widehat{V} (r/N^{1-\kappa})|}{|r+r'|^{2}} \Big] \leq C N^{5\kappa/2-\varepsilon}. \end{align} $$
$$ \begin{align} \frac{\text{W}_2}{\| \xi_\nu \|^2} \leq \; &C N^{-3} \sum_{r \in \Lambda^*} N^\kappa |\widehat{V} (r/N^{1-\kappa})| \hspace{-.3cm} \sum_{\substack{r', r'', {\tilde{r}}'' \in P_H \\ v', v'' \in P_S}} \hspace{-.3cm} (\eta_{r'} + \eta_{r'+v'})^2 |\eta_{r''}| |\eta_{{\tilde{r}}''}| \sigma_{v'}^2 \sigma_{v''}^2 \hspace{-.3cm}\nonumber\\ &\times \sum_{\substack{p'' \in \{ -r'', r''+v'' \} \\ {\tilde{p}}'' \in \{ -{\tilde{r}}'', {\tilde{r}}'' +v'' \}}} \hspace{-.3cm} \delta_{p'' + r , {\tilde{p}}''} \Big[ \sum_{\substack{p' \in \{ -r', r'+v' \} \\ p'' \in \{ -r'', r'' +v'' \}}} \delta_{p', p''} + \sum_{\substack{p' \in \{ -r', r'+v' \} \\ {\tilde{p}}'' \in \{ -{\tilde{r}}'', {\tilde{r}}'' +v'' \}}} \delta_{p', {\tilde{p}}''} \Big] \nonumber\\ \leq \; &C N^{-3+5\kappa} \| \sigma_S \|^4 \Big[\sum_{r' \in P_H} |r'|^{-6}\Big] \Big[ \mathop{\mathrm{sup}}\limits_{r' \in \Lambda^*} \sum_{r \in \Lambda^* , r \not = -r'} \frac{|\widehat{V} (r/N^{1-\kappa})|}{|r+r'|^{2}} \Big] \leq C N^{5\kappa/2-\varepsilon}. \end{align} $$
As for
![]() $\text {W}_3$
, there are
$\text {W}_3$
, there are
![]() $(m-1)(m-2)$
possible choices of the indices
$(m-1)(m-2)$
possible choices of the indices
![]() $j,k$
in (5.14), all leading to the same contribution. We fix
$j,k$
in (5.14), all leading to the same contribution. We fix
![]() $j = m-1$
and
$j = m-1$
and
![]() $k =m-2$
. Estimating now
$k =m-2$
. Estimating now
 $\theta \big ( \{r_j, v_j \}_{j=1}^{m-1} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-3} \big )$
, we obtain, with (3.12),
$\theta \big ( \{r_j, v_j \}_{j=1}^{m-1} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-3} \big )$
, we obtain, with (3.12),
 $$ \begin{align} \frac{\text{W}_3}{\| \xi_\nu \|^2} \leq \; &C N^{-4} \sum_{r \in \Lambda^*} N^\kappa |\widehat{V} (r/N^{1-\kappa})| \nonumber\\ &\times \sum_{\substack{r', r'', r''', {\tilde{r}}''' \in P_H \nonumber\\ v', v'', v''' \in P_S}} \hspace{-.3cm} (\eta_{r'} + \eta_{r'+v'})^2 (\eta_{r''} + \eta_{r''+v''})^2 |\eta_{r'''}| |\eta_{{\tilde{r}}'''}| \sigma_{v'}^2 \sigma_{v''}^2 \sigma_{v'''}^2 \hspace{-.5cm}\nonumber\\ &\times \sum_{\substack{p''' \in \{ -r''', r'''+ v''' \} \nonumber\\ {\tilde{p}}''' \in \{ -{\tilde{r}}''' , {\tilde{r}}''' + v''' \}}} \hspace{-.5cm} \delta_{p'''+r , {\tilde{p}}'''} \Big[ \sum_{\substack{p' \in \{ -r', r'+v' \}\nonumber \\ p''' \in \{ -r''', r''' +v''' \}}} \hspace{-.5cm} \delta_{p''', -p'+v''} + \sum_{\substack{p' \in \{ -r', r'+v' \}\nonumber \\ {\tilde{p}}''' \in \{ -{\tilde{r}}''', {\tilde{r}}''' +v''' \}}} \hspace{-.3cm} \delta_{{\tilde{p}}''' , - p' + v''} \Big] \\ \leq \; &C N^{-3+ 4\kappa} \| \sigma_S \|^6 \| \eta_H \|^2 \sum_{r' \in P_H} |r'|^{-6} \leq C N^{5\kappa/2} \cdot N^{12\kappa - 7 +4\varepsilon}. \end{align} $$
$$ \begin{align} \frac{\text{W}_3}{\| \xi_\nu \|^2} \leq \; &C N^{-4} \sum_{r \in \Lambda^*} N^\kappa |\widehat{V} (r/N^{1-\kappa})| \nonumber\\ &\times \sum_{\substack{r', r'', r''', {\tilde{r}}''' \in P_H \nonumber\\ v', v'', v''' \in P_S}} \hspace{-.3cm} (\eta_{r'} + \eta_{r'+v'})^2 (\eta_{r''} + \eta_{r''+v''})^2 |\eta_{r'''}| |\eta_{{\tilde{r}}'''}| \sigma_{v'}^2 \sigma_{v''}^2 \sigma_{v'''}^2 \hspace{-.5cm}\nonumber\\ &\times \sum_{\substack{p''' \in \{ -r''', r'''+ v''' \} \nonumber\\ {\tilde{p}}''' \in \{ -{\tilde{r}}''' , {\tilde{r}}''' + v''' \}}} \hspace{-.5cm} \delta_{p'''+r , {\tilde{p}}'''} \Big[ \sum_{\substack{p' \in \{ -r', r'+v' \}\nonumber \\ p''' \in \{ -r''', r''' +v''' \}}} \hspace{-.5cm} \delta_{p''', -p'+v''} + \sum_{\substack{p' \in \{ -r', r'+v' \}\nonumber \\ {\tilde{p}}''' \in \{ -{\tilde{r}}''', {\tilde{r}}''' +v''' \}}} \hspace{-.3cm} \delta_{{\tilde{p}}''' , - p' + v''} \Big] \\ \leq \; &C N^{-3+ 4\kappa} \| \sigma_S \|^6 \| \eta_H \|^2 \sum_{r' \in P_H} |r'|^{-6} \leq C N^{5\kappa/2} \cdot N^{12\kappa - 7 +4\varepsilon}. \end{align} $$
Analogously, with Lemma 2.4 and (5.15), we find
 $$ \begin{align*} \frac{\text{W}_4}{\| \xi_\nu \|^2} \leq \; &C N^{-4} \sum_{r \in \Lambda^*} N^\kappa |\widehat{V} (r/N^{1-\kappa})| \\ &\times \sum_{\substack{r', r'', r''', {\tilde{r}}''' \in P_H \\ v', v'', v''' \in P_S}} \hspace{-.3cm} (\eta_{r'} + \eta_{r'+v'})^2 (\eta_{r''} + \eta_{r''+v''})^2 |\eta_{r'''}| |\eta_{{\tilde{r}}'''} | \sigma_{v'}^2 \sigma_{v''}^2 \sigma_{v'''}^2 \hspace{-.5cm}\\ &\times \sum_{\substack{p''' \in \{ -r''', r'''+ v''' \} \\ {\tilde{p}}''' \in \{ -{\tilde{r}}''' , {\tilde{r}}'''+ v''' \}}} \hspace{-.5cm} \delta_{p''' + r , {\tilde{p}}''' } \sum_{\substack{p' \in \{ -r', r'+v' \} \\ p'' \in \{ -r'', r'' +v'' \}}} \hspace{-.5cm} \delta_{v''', p' +p''} \\ \leq \; &C N^{-2+5\kappa}\| \sigma_S \|^6 \sum_{r' \in P_H} |r'|^{-8} \leq C N^{5\kappa/2} \cdot N^{12\kappa -7 + 5\varepsilon}. \end{align*} $$
$$ \begin{align*} \frac{\text{W}_4}{\| \xi_\nu \|^2} \leq \; &C N^{-4} \sum_{r \in \Lambda^*} N^\kappa |\widehat{V} (r/N^{1-\kappa})| \\ &\times \sum_{\substack{r', r'', r''', {\tilde{r}}''' \in P_H \\ v', v'', v''' \in P_S}} \hspace{-.3cm} (\eta_{r'} + \eta_{r'+v'})^2 (\eta_{r''} + \eta_{r''+v''})^2 |\eta_{r'''}| |\eta_{{\tilde{r}}'''} | \sigma_{v'}^2 \sigma_{v''}^2 \sigma_{v'''}^2 \hspace{-.5cm}\\ &\times \sum_{\substack{p''' \in \{ -r''', r'''+ v''' \} \\ {\tilde{p}}''' \in \{ -{\tilde{r}}''' , {\tilde{r}}'''+ v''' \}}} \hspace{-.5cm} \delta_{p''' + r , {\tilde{p}}''' } \sum_{\substack{p' \in \{ -r', r'+v' \} \\ p'' \in \{ -r'', r'' +v'' \}}} \hspace{-.5cm} \delta_{v''', p' +p''} \\ \leq \; &C N^{-2+5\kappa}\| \sigma_S \|^6 \sum_{r' \in P_H} |r'|^{-8} \leq C N^{5\kappa/2} \cdot N^{12\kappa -7 + 5\varepsilon}. \end{align*} $$
Together with (5.16), (5.17), (5.18), we conclude that
Finally, we consider the term
![]() $\text {V}_2$
, associated with the second case listed after (5.9). We fix
$\text {V}_2$
, associated with the second case listed after (5.9). We fix
![]() $i =m$
and
$i =m$
and
![]() $j=m-1$
and we consider all possible contractions of
$j=m-1$
and we consider all possible contractions of
![]() $a_p$
with
$a_p$
with
 $a^*_{{\tilde {p}}_m}$
, of
$a^*_{{\tilde {p}}_m}$
, of
![]() $a_{q+r}$
with
$a_{q+r}$
with
 $a^*_{{\tilde {p}}_{m-1}}$
and of
$a^*_{{\tilde {p}}_{m-1}}$
and of
![]() $a_q^*, a_{p+r}^*$
with
$a_q^*, a_{p+r}^*$
with
![]() $a_{p_m}, a_{p_{m-1}}$
, where
$a_{p_m}, a_{p_{m-1}}$
, where
![]() ${\tilde {p}}_\ell \in \{-{\tilde {r}}_\ell ,{\tilde {r}}_\ell +v_\ell \}$
and
${\tilde {p}}_\ell \in \{-{\tilde {r}}_\ell ,{\tilde {r}}_\ell +v_\ell \}$
and
![]() $p_\ell \in \{ -r_\ell , r_\ell + v_\ell \}$
, for
$p_\ell \in \{ -r_\ell , r_\ell + v_\ell \}$
, for
![]() $\ell =m,m-1$
. We obtain
$\ell =m,m-1$
. We obtain
 $$ \begin{align*}\begin{aligned} &{\bigl\langle\xi_\nu,\text{V}_2\, \xi_\nu\bigr\rangle} \\ & = \frac{1}{2N} \sum_{m\geq 2}\frac1{(m-2)!}\frac1{N^m} \sum_{\substack{v_1 \in P_S, r_1, {\tilde{r}}_1 \in P_H: \\ r_1 + v_1 ,\, {\tilde{r}}_1 + v_1 \in P_H}} \cdots \sum_{\substack{v_{m} \in P_S, r_{m}, {\tilde{r}}_{m} \in P_H: \\ r_{m} + v_{m} ,\, {\tilde{r}}_{m} + v_{m} \in P_H}}\hskip -0.5cm\theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \\ & \hskip 0.5cm \times \prod_{i=1}^{m-2}\eta_{r_i}\eta_{\tilde{r}_i} \big( \delta_{{\tilde{r}}_i,r_i}+\delta_{-{\tilde{r}}_i,r_i+v_i}\big)\sigma_{v_i}^2 \, \prod_{j=m,m-1} \eta_{r_j} \eta_{{\tilde{r}}_j} \sigma_{v_j}^2\\ &\hspace{0.5cm}\times \sum_{\substack{r \in \Lambda^*,\, p,q \in P_H: \\ p-r, q-r \in P_H }} N^\kappa \widehat V(r/N^{1-\kappa}) \sum_{\substack{{\tilde{p}}_\ell \in \{ -{\tilde{r}}_\ell, {\tilde{r}}_\ell+v_\ell\} \\ \ell=m-1,m } } \delta_{p, {\tilde{p}}_m} \delta_{q+r, {\tilde{p}}_{m-1}} \\ & \hspace{0.5cm} \times \hskip -0.5cm \sum_{\substack{ p_\ell \in \{ - r_\ell, r_\ell+v_\ell\} \\ \ell=m-1,m } } \big(\delta_{q, p_m} \delta_{p+r, p_{m-1}} + \delta_{q, p_{m-1}} \delta_{p+r, p_{m}} \big) \big( \delta_{{\tilde{p}}_m, p_m} + \delta_{-{\tilde{p}}_m+v_m, -p_{m-1}+v_{m-1}} \big). \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} &{\bigl\langle\xi_\nu,\text{V}_2\, \xi_\nu\bigr\rangle} \\ & = \frac{1}{2N} \sum_{m\geq 2}\frac1{(m-2)!}\frac1{N^m} \sum_{\substack{v_1 \in P_S, r_1, {\tilde{r}}_1 \in P_H: \\ r_1 + v_1 ,\, {\tilde{r}}_1 + v_1 \in P_H}} \cdots \sum_{\substack{v_{m} \in P_S, r_{m}, {\tilde{r}}_{m} \in P_H: \\ r_{m} + v_{m} ,\, {\tilde{r}}_{m} + v_{m} \in P_H}}\hskip -0.5cm\theta\big( \{r_j, v_j \}_{j=1}^{m} \big) \theta\big( \{{\tilde{r}}_j, v_j \}_{j=1}^{m} \big) \\ & \hskip 0.5cm \times \prod_{i=1}^{m-2}\eta_{r_i}\eta_{\tilde{r}_i} \big( \delta_{{\tilde{r}}_i,r_i}+\delta_{-{\tilde{r}}_i,r_i+v_i}\big)\sigma_{v_i}^2 \, \prod_{j=m,m-1} \eta_{r_j} \eta_{{\tilde{r}}_j} \sigma_{v_j}^2\\ &\hspace{0.5cm}\times \sum_{\substack{r \in \Lambda^*,\, p,q \in P_H: \\ p-r, q-r \in P_H }} N^\kappa \widehat V(r/N^{1-\kappa}) \sum_{\substack{{\tilde{p}}_\ell \in \{ -{\tilde{r}}_\ell, {\tilde{r}}_\ell+v_\ell\} \\ \ell=m-1,m } } \delta_{p, {\tilde{p}}_m} \delta_{q+r, {\tilde{p}}_{m-1}} \\ & \hspace{0.5cm} \times \hskip -0.5cm \sum_{\substack{ p_\ell \in \{ - r_\ell, r_\ell+v_\ell\} \\ \ell=m-1,m } } \big(\delta_{q, p_m} \delta_{p+r, p_{m-1}} + \delta_{q, p_{m-1}} \delta_{p+r, p_{m}} \big) \big( \delta_{{\tilde{p}}_m, p_m} + \delta_{-{\tilde{p}}_m+v_m, -p_{m-1}+v_{m-1}} \big). \end{aligned}\end{align*} $$
Estimating
 $\theta \big ( \{r_j, v_j \}_{j=1}^{m} \big ) \theta \big ( \{{\tilde {r}}_j, v_j \}_{j=1}^{m} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-2} \big )$
and using Lemma 2.4 and the condition
$\theta \big ( \{r_j, v_j \}_{j=1}^{m} \big ) \theta \big ( \{{\tilde {r}}_j, v_j \}_{j=1}^{m} \big ) \leq \theta \big ( \{r_j, v_j \}_{j=1}^{m-2} \big )$
and using Lemma 2.4 and the condition
![]() $3\kappa - 2 + 4\varepsilon < 0$
, we find
$3\kappa - 2 + 4\varepsilon < 0$
, we find
 $$ \begin{align*}\begin{aligned} \frac{|{\bigl\langle\xi_\nu,\text{V}_2\, \xi_\nu\bigr\rangle}|}{\| \xi_\nu \|^2} \\ \leq \; & C N^{-3} \sum_{r \in \Lambda^*} N^\kappa \widehat{V} (r/N^{1-\kappa}) \sum_{\substack{r',{\tilde{r}}',r'', {\tilde{r}}'' \in P_H \\ v',v'' \in P_S}} |\eta_{r'}| |\eta_{{\tilde{r}}'}| |\eta_{r''}| |\eta_{{\tilde{r}}''}| \sigma_{v'}^2 \sigma_{v''}^2 \\ &\times \sum_{\substack{p' \in \{ -r' , r' + v' \} \\ p'' \in \{ -r'' , r'' + v'' \}}} \sum_{\substack{{\tilde{p}}' \in \{ -{\tilde{r}}' , {\tilde{r}}' + v' \} \\ {\tilde{p}}'' \in \{ -{\tilde{r}}'' , {\tilde{r}}'' + v'' \} }} (\delta_{{\tilde{p}}', p''+r} \delta_{{\tilde{p}}'' + r, p'} + \delta_{{\tilde{p}}', p'+r} \delta_{{\tilde{p}}'' + r, p''}) \\ &\hspace{6cm} \times (\delta_{{\tilde{p}}'', p''} + \delta_{-{\tilde{p}}'' + v'', -p'+v'}) \\ \leq \; &C N^{-3+\kappa} \| \eta_H \|^4 \| \sigma_S \|^4 \leq C N^{10\kappa - 5 + 2\varepsilon} \leq C N^{5\kappa/2 -\varepsilon}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \frac{|{\bigl\langle\xi_\nu,\text{V}_2\, \xi_\nu\bigr\rangle}|}{\| \xi_\nu \|^2} \\ \leq \; & C N^{-3} \sum_{r \in \Lambda^*} N^\kappa \widehat{V} (r/N^{1-\kappa}) \sum_{\substack{r',{\tilde{r}}',r'', {\tilde{r}}'' \in P_H \\ v',v'' \in P_S}} |\eta_{r'}| |\eta_{{\tilde{r}}'}| |\eta_{r''}| |\eta_{{\tilde{r}}''}| \sigma_{v'}^2 \sigma_{v''}^2 \\ &\times \sum_{\substack{p' \in \{ -r' , r' + v' \} \\ p'' \in \{ -r'' , r'' + v'' \}}} \sum_{\substack{{\tilde{p}}' \in \{ -{\tilde{r}}' , {\tilde{r}}' + v' \} \\ {\tilde{p}}'' \in \{ -{\tilde{r}}'' , {\tilde{r}}'' + v'' \} }} (\delta_{{\tilde{p}}', p''+r} \delta_{{\tilde{p}}'' + r, p'} + \delta_{{\tilde{p}}', p'+r} \delta_{{\tilde{p}}'' + r, p''}) \\ &\hspace{6cm} \times (\delta_{{\tilde{p}}'', p''} + \delta_{-{\tilde{p}}'' + v'', -p'+v'}) \\ \leq \; &C N^{-3+\kappa} \| \eta_H \|^4 \| \sigma_S \|^4 \leq C N^{10\kappa - 5 + 2\varepsilon} \leq C N^{5\kappa/2 -\varepsilon}. \end{aligned} \end{align*} $$
A Proof of Proposition 1.2
The proof of Proposition 1.2 is based on standard results, which are collected in this section for the reader’s convenience. In particular, we follow [Reference Robinson18] (see Lemma 2.1.3) and [Reference Yau and Yin20, Sec. 12] for Lemmas A.1 and A.2 and the proof of Lemma 3.3.2 in [Reference Aaen1] for Lemma A.4 (control on the second moment of
![]() $\mathcal {N}$
allows us to avoid the condition imposed in [Reference Aaen1] that V is strictly positive around the origin).
$\mathcal {N}$
allows us to avoid the condition imposed in [Reference Aaen1] that V is strictly positive around the origin).
The proof of Proposition 1.2 is divided into three parts. First, we show how to switch from periodic boundary conditions to Dirichlet boundary conditions, increasing the size of the box a bit. In the second step, we replicate the Dirichlet trial state obtained in the first step to obtain an upper bound on the energy in a sequence of boxes whose size increases to infinity (but with fixed density). In the last step, we show how to pass from the grand canonical to the canonical setting.
Let
 $\Psi _L = \{ \Psi _L^{(n)} \}_{n \geq 0} \in \mathcal {F} (\Lambda _L)$
be a normalised trial state for the Fock-space Hamiltonian
$\Psi _L = \{ \Psi _L^{(n)} \}_{n \geq 0} \in \mathcal {F} (\Lambda _L)$
be a normalised trial state for the Fock-space Hamiltonian
![]() $\mathcal {H}$
defined on the box
$\mathcal {H}$
defined on the box
![]() $\Lambda _L$
with periodic boundary conditions (in fact, we denote by
$\Lambda _L$
with periodic boundary conditions (in fact, we denote by
 $\Psi _L^{(n)} (x_1, \dots , x_n)$
the L-periodic extension of
$\Psi _L^{(n)} (x_1, \dots , x_n)$
the L-periodic extension of
 $\Psi _L^{(n)}$
to the whole space
$\Psi _L^{(n)}$
to the whole space
![]() $\mathbb {R}^{3n}$
). For
$\mathbb {R}^{3n}$
). For
![]() $u \in \Lambda _L$
, we define
$u \in \Lambda _L$
, we define
 $\Psi _{L+2b,u}^D \in \mathcal {F} (\Lambda _{L+2b}^u)$
, where
$\Psi _{L+2b,u}^D \in \mathcal {F} (\Lambda _{L+2b}^u)$
, where
![]() $\Lambda _{L+2b}^u=u+\Lambda _{L+2b}$
is a box centred at u, with side length
$\Lambda _{L+2b}^u=u+\Lambda _{L+2b}$
is a box centred at u, with side length
![]() $L+2b$
, setting, for any
$L+2b$
, setting, for any
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $$ \begin{align} (\Psi_{L+2b,u}^{\mathrm{D}})^{(n)}(x_1, \dots , x_n) = \Psi_L^{(n)} (x_1, \dots , x_n) \prod_{i=1}^n Q_{L,b} (x_i - u) \end{align} $$
$$ \begin{align} (\Psi_{L+2b,u}^{\mathrm{D}})^{(n)}(x_1, \dots , x_n) = \Psi_L^{(n)} (x_1, \dots , x_n) \prod_{i=1}^n Q_{L,b} (x_i - u) \end{align} $$
where
 $Q_{L,b} (x_i) = \prod _{j=1}^3 q_{L,b} (x_i^{(j)})$
with
$Q_{L,b} (x_i) = \prod _{j=1}^3 q_{L,b} (x_i^{(j)})$
with
![]() $q_{L,b} : \mathbb {R} \to [0;1]$
defined by
$q_{L,b} : \mathbb {R} \to [0;1]$
defined by
 $$ \begin{align*} q_{L,b}(t)=\begin{cases} \cos\big(\frac{\pi(t+L/2-b)}{4b}\big) \qquad &\text{if}\ \big|t+\frac{L}{2}\big|\leq b\\ 1&\text{if}\ |t|<\frac{L}{2}-b\\ \cos\big(\frac{\pi(t-L/2+b)}{4b}\big) &\text{if}\ \big|t-\frac L2\big|\leq b\\ 0 &\text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} q_{L,b}(t)=\begin{cases} \cos\big(\frac{\pi(t+L/2-b)}{4b}\big) \qquad &\text{if}\ \big|t+\frac{L}{2}\big|\leq b\\ 1&\text{if}\ |t|<\frac{L}{2}-b\\ \cos\big(\frac{\pi(t-L/2+b)}{4b}\big) &\text{if}\ \big|t-\frac L2\big|\leq b\\ 0 &\text{otherwise.} \end{cases} \end{align*} $$
By definition
 $(\Psi _{L+2b,u}^{\mathrm {Dir}})^{(n)}$
satisfies Dirichlet boundary condition on the box
$(\Psi _{L+2b,u}^{\mathrm {Dir}})^{(n)}$
satisfies Dirichlet boundary condition on the box
![]() $\Lambda _{L+2b}^u$
. The following lemma allows us to compare energy and moments of the number of particles of
$\Lambda _{L+2b}^u$
. The following lemma allows us to compare energy and moments of the number of particles of
 $\Psi ^{\text {D}}_{L+2b , u}$
with those of
$\Psi ^{\text {D}}_{L+2b , u}$
with those of
![]() $\Psi _L$
.
$\Psi _L$
.
Lemma A.1. Under the assumptions of Proposition 1.2, let
 $\Psi _{L+2b, u}^{\text {D}}$
be defined as in (A.1) with
$\Psi _{L+2b, u}^{\text {D}}$
be defined as in (A.1) with
![]() $u\in \Lambda _L$
. Then we have
$u\in \Lambda _L$
. Then we have
 $\| \Psi _{L+2b,u}^{\mathrm {D}}\|=1$
. Moreover, for all
$\| \Psi _{L+2b,u}^{\mathrm {D}}\|=1$
. Moreover, for all
![]() $j \in \mathbb {N}$
,
$j \in \mathbb {N}$
,
 $$ \begin{align*} {\bigl\langle\Psi_{L+2b,u}^{\mathrm{D}},\mathcal{N}^j \Psi_{L+2b,u}^{\mathrm{D}}\bigr\rangle}={\bigl\langle\Psi_L, \mathcal{N}^j \Psi_L\bigr\rangle} , \end{align*} $$
$$ \begin{align*} {\bigl\langle\Psi_{L+2b,u}^{\mathrm{D}},\mathcal{N}^j \Psi_{L+2b,u}^{\mathrm{D}}\bigr\rangle}={\bigl\langle\Psi_L, \mathcal{N}^j \Psi_L\bigr\rangle} , \end{align*} $$
and there exists
![]() $\bar {u}\in \Lambda _{L}$
such that
$\bar {u}\in \Lambda _{L}$
such that
 $$ \begin{align} {\bigl\langle\Psi_{L+2b,\bar u}^{\mathrm{D}},\mathcal{H}\,\Psi_{L+2b,\bar u}^{\mathrm{D}}\bigr\rangle}\leq {\bigl\langle\Psi_L,\mathcal{H}\,\Psi_L\bigr\rangle}+\frac{C}{Lb}{\bigl\langle\Psi_L,\mathcal{N} \Psi_L\bigr\rangle} \end{align} $$
$$ \begin{align} {\bigl\langle\Psi_{L+2b,\bar u}^{\mathrm{D}},\mathcal{H}\,\Psi_{L+2b,\bar u}^{\mathrm{D}}\bigr\rangle}\leq {\bigl\langle\Psi_L,\mathcal{H}\,\Psi_L\bigr\rangle}+\frac{C}{Lb}{\bigl\langle\Psi_L,\mathcal{N} \Psi_L\bigr\rangle} \end{align} $$
for a universal constant
![]() $C> 0$
.
$C> 0$
.
Proof. For an arbitrary L-periodic function
 $\psi \in L^2_{\mathrm {loc}}(\mathbb {R})$
, we find
$\psi \in L^2_{\mathrm {loc}}(\mathbb {R})$
, we find
 $$ \begin{align} \int_{-\frac L2-b}^{\frac L2+b}dt |\psi(t)|^2 q(t)^2 = \int_{-\frac L2}^{\frac L2}dt |\psi(t)|^2. \end{align} $$
$$ \begin{align} \int_{-\frac L2-b}^{\frac L2+b}dt |\psi(t)|^2 q(t)^2 = \int_{-\frac L2}^{\frac L2}dt |\psi(t)|^2. \end{align} $$
To prove (A.3), we combine (using the periodicity of
![]() $\psi $
) the integral over
$\psi $
) the integral over
![]() $[-L/2-b; -L/2]$
with the integral over
$[-L/2-b; -L/2]$
with the integral over
![]() $[L/2 - b; L/2]$
and the integral over
$[L/2 - b; L/2]$
and the integral over
![]() $[-L/2; - L/2 + b ]$
with the integral over
$[-L/2; - L/2 + b ]$
with the integral over
![]() $[L/2; L/2 +b]$
(using that
$[L/2; L/2 +b]$
(using that
![]() $\cos ^2 x + \cos ^2 (x - \pi /2) = 1$
).
$\cos ^2 x + \cos ^2 (x - \pi /2) = 1$
).
Applying (A.3) (separately on each variable), we obtain that
 $\| (\Psi _{L+2b,u}^{\text {D}} )^{(n)} \| = \| \Psi _L^{(n)} \|$
, for all
$\| (\Psi _{L+2b,u}^{\text {D}} )^{(n)} \| = \| \Psi _L^{(n)} \|$
, for all
![]() $n \in \mathbb {N}$
. This implies that
$n \in \mathbb {N}$
. This implies that
 $\| \Psi _{L+2b,u}^{\text {D}} \| = \| \Psi _L \| = 1$
and that
$\| \Psi _{L+2b,u}^{\text {D}} \| = \| \Psi _L \| = 1$
and that
 $\langle \Psi _{L+2b,u}^{\text {D}} , \mathcal {N}^j \Psi _{L+2b , u}^{\text {D}} \rangle = \langle \Psi _L, \mathcal {N}^j \Psi _L \rangle $
for all
$\langle \Psi _{L+2b,u}^{\text {D}} , \mathcal {N}^j \Psi _{L+2b , u}^{\text {D}} \rangle = \langle \Psi _L, \mathcal {N}^j \Psi _L \rangle $
for all
![]() $j \in \mathbb {N}$
.
$j \in \mathbb {N}$
.
To compute the expectation of the kinetic energy in the state
 $\Psi _{L+2b,u}^{\mathrm {D}}$
, we observe that, for any L-periodic
$\Psi _{L+2b,u}^{\mathrm {D}}$
, we observe that, for any L-periodic
 $\psi \in L^2_{\mathrm {loc}}(\mathbb {R})$
with
$\psi \in L^2_{\mathrm {loc}}(\mathbb {R})$
with
 $\psi ' \in L^2_{\mathrm {loc}}(\mathbb {R})$
, we have (since
$\psi ' \in L^2_{\mathrm {loc}}(\mathbb {R})$
, we have (since
![]() $\psi '$
is also L-periodic)
$\psi '$
is also L-periodic)
 $$ \begin{align*} \int_{-\frac L2-b}^{\frac L2+b}dt \, |(q\psi)'(t)|^2=\int_{\frac L2}^{\frac L2}dt \, |\psi' (t)|^2 + \int_{-\frac L2-b}^{\frac L2+b}dt \, \big[ |\psi(t)|^2 q'(t)^2 + q(t) q'(t) \frac{d}{dt}|\psi(t)|^2\big] \end{align*} $$
$$ \begin{align*} \int_{-\frac L2-b}^{\frac L2+b}dt \, |(q\psi)'(t)|^2=\int_{\frac L2}^{\frac L2}dt \, |\psi' (t)|^2 + \int_{-\frac L2-b}^{\frac L2+b}dt \, \big[ |\psi(t)|^2 q'(t)^2 + q(t) q'(t) \frac{d}{dt}|\psi(t)|^2\big] \end{align*} $$
where we used periodicity of
![]() $\psi '$
and (A.3). Integrating by parts and using
$\psi '$
and (A.3). Integrating by parts and using
![]() $q(\pm (L/2+b)) = q' (\pm (L/2 - b)) = 0$
, we get
$q(\pm (L/2+b)) = q' (\pm (L/2 - b)) = 0$
, we get
 $$ \begin{align}\begin{aligned} \int_{-\frac L2-b}^{\frac L2+b}dt \, |(q\psi)'(t)|^2= &\int_{-\frac L2}^{\frac L2} dt \, |\psi'(t)|^2-\int_{-\frac L2-b}^{\frac L2+b}dt \, |\psi(t)|^2 \, q(t)q''(t) \\ \leq & \int_{-\frac L2}^{\frac L2}dt \, |\psi'(t)|^2 + \frac C {b^2} \int_{\mathbb{R}} dt \, |\psi(t)|^2 \chi_{L,b}(t) \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \int_{-\frac L2-b}^{\frac L2+b}dt \, |(q\psi)'(t)|^2= &\int_{-\frac L2}^{\frac L2} dt \, |\psi'(t)|^2-\int_{-\frac L2-b}^{\frac L2+b}dt \, |\psi(t)|^2 \, q(t)q''(t) \\ \leq & \int_{-\frac L2}^{\frac L2}dt \, |\psi'(t)|^2 + \frac C {b^2} \int_{\mathbb{R}} dt \, |\psi(t)|^2 \chi_{L,b}(t) \end{aligned}\end{align} $$
where
![]() $\chi _{L,b}(t)=\chi _b(t+L/2)+\chi _b(t-L/2)$
with
$\chi _{L,b}(t)=\chi _b(t+L/2)+\chi _b(t-L/2)$
with
![]() $\chi _r(t)$
the characteristic function of
$\chi _r(t)$
the characteristic function of
![]() $[-r,r]$
and we used
$[-r,r]$
and we used
![]() $|q'' (t)|\leq C b^{-2} \chi _{L,b}(t)$
. Applying (A.4) (separately in every direction), we obtain
$|q'' (t)|\leq C b^{-2} \chi _{L,b}(t)$
. Applying (A.4) (separately in every direction), we obtain
 $$ \begin{align} \| \nabla_{x_j} &(\Psi^{\text{D}}_{L+2b, u})^{(n)} \|^2 \nonumber\\ \leq \; & \| \nabla_{x_j} (\Psi^{\text{D}}_{L+2b,u})^{(n)} \|^2 \nonumber\\ &+ \frac{C}{b^2} \int_{\mathbb{R}^3} dx_j\, \widetilde{\chi}_{L,b} (x_j - u) \int_{\Lambda_L^{n-1}} dx_1 \dots dx_{j-1} dx_{j+1} \dots dx_n \; |\Psi_L^{(n)} (x_1, \dots , x_n) |^2 \end{align} $$
$$ \begin{align} \| \nabla_{x_j} &(\Psi^{\text{D}}_{L+2b, u})^{(n)} \|^2 \nonumber\\ \leq \; & \| \nabla_{x_j} (\Psi^{\text{D}}_{L+2b,u})^{(n)} \|^2 \nonumber\\ &+ \frac{C}{b^2} \int_{\mathbb{R}^3} dx_j\, \widetilde{\chi}_{L,b} (x_j - u) \int_{\Lambda_L^{n-1}} dx_1 \dots dx_{j-1} dx_{j+1} \dots dx_n \; |\Psi_L^{(n)} (x_1, \dots , x_n) |^2 \end{align} $$
where we defined
 $\widetilde {\chi }_{L,b} (x) =\sum _{k=1}^3 \chi _{L,b} (x^{(k)}) \prod _{\substack {j\neq k}}^3 \chi _{\frac L2}(x^{(j)})$
.
$\widetilde {\chi }_{L,b} (x) =\sum _{k=1}^3 \chi _{L,b} (x^{(k)}) \prod _{\substack {j\neq k}}^3 \chi _{\frac L2}(x^{(j)})$
.
To compute the potential energy of
![]() $\psi _L$
, we have to consider the L-periodic extension
$\psi _L$
, we have to consider the L-periodic extension
![]() $V_L (x) = \sum _{m\in \mathbb {Z}^3}V(x+mL)$
of V. Since we assumed V to be positive and supported in
$V_L (x) = \sum _{m\in \mathbb {Z}^3}V(x+mL)$
of V. Since we assumed V to be positive and supported in
![]() $B_R (0)$
and that
$B_R (0)$
and that
![]() $L>R$
, we get
$L>R$
, we get
![]() $V(x)\leq V_L(x)$
, which implies that, for any
$V(x)\leq V_L(x)$
, which implies that, for any
![]() $i \not = j$
,
$i \not = j$
,
 $$ \begin{align*} |(\Psi_{L+2b,u}^{\mathrm{D}})^{(n)}(x_1, &\dots , x_n)|^2 \, V(x_i-x_j) \\ &\leq \Big| \Psi_L^{(n)} (x_1, \dots , x_n) \, \sqrt{V_L (x_i-x_j)} \Big|^2 \, \prod_{k=1}^n Q_{L,b} (x_k-u)^2. \end{align*} $$
$$ \begin{align*} |(\Psi_{L+2b,u}^{\mathrm{D}})^{(n)}(x_1, &\dots , x_n)|^2 \, V(x_i-x_j) \\ &\leq \Big| \Psi_L^{(n)} (x_1, \dots , x_n) \, \sqrt{V_L (x_i-x_j)} \Big|^2 \, \prod_{k=1}^n Q_{L,b} (x_k-u)^2. \end{align*} $$
Applying (A.3), we obtain
 $$ \begin{align}\begin{aligned} \int_{(\Lambda_{L+2b}^u)^n} dx_1 \dots dx_n \, &|(\Psi_{L+2b,u}^{\mathrm{D}})^{(n)}(x_1, \dots , x_n)|^2 V (x_i-x_j) \\ &\leq \int_{\Lambda^n_L} dx_1 \dots dx_n \, |\Psi^{(n)}_L (x_1, \dots , x_n)|^2 \, V_L (x_i-x_j). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \int_{(\Lambda_{L+2b}^u)^n} dx_1 \dots dx_n \, &|(\Psi_{L+2b,u}^{\mathrm{D}})^{(n)}(x_1, \dots , x_n)|^2 V (x_i-x_j) \\ &\leq \int_{\Lambda^n_L} dx_1 \dots dx_n \, |\Psi^{(n)}_L (x_1, \dots , x_n)|^2 \, V_L (x_i-x_j). \end{aligned}\end{align} $$
From (A.5) and (A.6), we conclude (using the bosonic symmetry)
 $$ \begin{align*} &{\bigl\langle\Psi_{L+2b,u}^{\mathrm{D}},\mathcal{H} \Psi_{L+2b,u}^{\mathrm{D}}\bigr\rangle}\\ &\qquad\qquad \leq{\bigl\langle\Psi_L,\mathcal{H}\Psi_L\bigr\rangle}+\frac{C}{b^2}\sum_{n\geq0}n \int_{\mathbb{R}^3} dx_1 \, \widetilde{\chi}_{L,b}(x_1-u) \int_{\Lambda_L^{n-1}} dx_2\dots dx_n \, |\Psi_L^{(n)}(x_1,\dots,x_n)|^2. \end{align*} $$
$$ \begin{align*} &{\bigl\langle\Psi_{L+2b,u}^{\mathrm{D}},\mathcal{H} \Psi_{L+2b,u}^{\mathrm{D}}\bigr\rangle}\\ &\qquad\qquad \leq{\bigl\langle\Psi_L,\mathcal{H}\Psi_L\bigr\rangle}+\frac{C}{b^2}\sum_{n\geq0}n \int_{\mathbb{R}^3} dx_1 \, \widetilde{\chi}_{L,b}(x_1-u) \int_{\Lambda_L^{n-1}} dx_2\dots dx_n \, |\Psi_L^{(n)}(x_1,\dots,x_n)|^2. \end{align*} $$
Averaging over
![]() $u\in \Lambda _L$
we conclude (since
$u\in \Lambda _L$
we conclude (since
![]() $\| \widetilde {\chi }_{L,b} \|_1 \leq C L^2 b$
)
$\| \widetilde {\chi }_{L,b} \|_1 \leq C L^2 b$
)
 $$ \begin{align*}\int_{\Lambda_L}du\,{\bigl\langle\Psi_{L+2b,u}^{\mathrm{D}},\mathcal{H}\, \Psi_{L+2b,u}^{\mathrm{D}}\bigr\rangle}\leq L^3{\bigl\langle\Psi_L,\mathcal{H}\,\Psi_L\bigr\rangle}+\frac{C L^2}{b} \langle \Psi_L , \mathcal{N} \Psi_L \rangle. \end{align*} $$
$$ \begin{align*}\int_{\Lambda_L}du\,{\bigl\langle\Psi_{L+2b,u}^{\mathrm{D}},\mathcal{H}\, \Psi_{L+2b,u}^{\mathrm{D}}\bigr\rangle}\leq L^3{\bigl\langle\Psi_L,\mathcal{H}\,\Psi_L\bigr\rangle}+\frac{C L^2}{b} \langle \Psi_L , \mathcal{N} \Psi_L \rangle. \end{align*} $$
Hence, there exists
![]() $\bar {u}\in \Lambda _L$
so that (A.2) holds.
$\bar {u}\in \Lambda _L$
so that (A.2) holds.
From now on, let us define
 $\Psi _{L+2b}^{\text {D}} \in \mathcal {F} (\Lambda _{L+2b})$
, setting
$\Psi _{L+2b}^{\text {D}} \in \mathcal {F} (\Lambda _{L+2b})$
, setting
 $(\Psi _{L+2b}^{\text {D}})^{(n)} (x_1, \dots , x_n) = (\Psi _{L+2b , \bar {u}}^{\text {D}})^{(n)} (x_1 - \bar {u}, \dots , x_n - \bar {u})$
, with
$(\Psi _{L+2b}^{\text {D}})^{(n)} (x_1, \dots , x_n) = (\Psi _{L+2b , \bar {u}}^{\text {D}})^{(n)} (x_1 - \bar {u}, \dots , x_n - \bar {u})$
, with
 $\Psi _{L+2b,\bar {u}}^{\text {D}}$
from Lemma A.1. Since
$\Psi _{L+2b,\bar {u}}^{\text {D}}$
from Lemma A.1. Since
 $\Psi _{L+2b}^{\text {D}}$
satisfies Dirichlet boundary conditions, we can replicate it into several adjacent copies of
$\Psi _{L+2b}^{\text {D}}$
satisfies Dirichlet boundary conditions, we can replicate it into several adjacent copies of
![]() $\Lambda _{L+2b}$
, separated by corridors of size R (to avoid interactions between different boxes). This allows us to construct a sequence of trial states on boxes with increasing volume (but keeping the density fixed).
$\Lambda _{L+2b}$
, separated by corridors of size R (to avoid interactions between different boxes). This allows us to construct a sequence of trial states on boxes with increasing volume (but keeping the density fixed).
Let
![]() $t \in \mathbb {N}$
and
$t \in \mathbb {N}$
and
![]() ${\tilde {L}} = t (L+2b +R)$
. We think of the large box
${\tilde {L}} = t (L+2b +R)$
. We think of the large box
![]() $\Lambda _{{\tilde {L}}}$
as the (almost) disjoint union of
$\Lambda _{{\tilde {L}}}$
as the (almost) disjoint union of
![]() $t^3$
shifted copies of the small box
$t^3$
shifted copies of the small box
![]() $\Lambda _{L+2b+R}$
, centred at
$\Lambda _{L+2b+R}$
, centred at
with
![]() $i_1, i_2, i_3 \in \{ 1, \dots , t \}$
. Let
$i_1, i_2, i_3 \in \{ 1, \dots , t \}$
. Let
 $\{ c_i \}_{i=1}^{t^3}$
denote an enumeration of the centres (A.7). We define
$\{ c_i \}_{i=1}^{t^3}$
denote an enumeration of the centres (A.7). We define
 $\Psi ^{\text {D}}_{{\tilde {L}}} \in \mathcal {F} (\Lambda _{{\tilde {L}}})$
by setting
$\Psi ^{\text {D}}_{{\tilde {L}}} \in \mathcal {F} (\Lambda _{{\tilde {L}}})$
by setting
 $$ \begin{align} (\Psi_{{\tilde{L}}}^{\text{D}} )^{(m)} (x_1, \dots , x_{m}) = \frac{1}{\| (\Psi^{\text{D}}_{L+2b})^{(n)} \|^{t^3 -1}} \prod_{i=1}^{t^3} (\Psi_{L+2b}^{\text{D}})^{(n)} (x_{(i-1)n + 1} - c_i , \dots , x_{i n} - c_i) \end{align} $$
$$ \begin{align} (\Psi_{{\tilde{L}}}^{\text{D}} )^{(m)} (x_1, \dots , x_{m}) = \frac{1}{\| (\Psi^{\text{D}}_{L+2b})^{(n)} \|^{t^3 -1}} \prod_{i=1}^{t^3} (\Psi_{L+2b}^{\text{D}})^{(n)} (x_{(i-1)n + 1} - c_i , \dots , x_{i n} - c_i) \end{align} $$
if
![]() $m = n t^3$
for an
$m = n t^3$
for an
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
 $(\Psi _{{\tilde {L}}}^{\text {D}} )^{(m)} = 0$
otherwise (here we set
$(\Psi _{{\tilde {L}}}^{\text {D}} )^{(m)} = 0$
otherwise (here we set
 $(\Psi _{L+2b}^{\text {D}})^{(n)} = 0$
if one of its arguments lies outside
$(\Psi _{L+2b}^{\text {D}})^{(n)} = 0$
if one of its arguments lies outside
![]() $\Lambda _{L+2b}$
). More precisely,
$\Lambda _{L+2b}$
). More precisely,
 $(\Psi _{{\tilde {L}}}^{\text {D}} )^{(m)}$
should be defined as the symmetrisation of (A.8) (but we can use (A.8) to compute the expectation of permutation symmetric observables).
$(\Psi _{{\tilde {L}}}^{\text {D}} )^{(m)}$
should be defined as the symmetrisation of (A.8) (but we can use (A.8) to compute the expectation of permutation symmetric observables).
Lemma A.2. Under the assumptions of Proposition 1.2, let
 $\Psi _{{\tilde {L}}}^{\text {D}}$
be defined as above. Then
$\Psi _{{\tilde {L}}}^{\text {D}}$
be defined as above. Then
 $\| \Psi _{{\tilde {L}}}^{\text {D}} \| = 1$
,
$\| \Psi _{{\tilde {L}}}^{\text {D}} \| = 1$
,
 $$ \begin{align*} {\bigl\langle\Psi_{\tilde{L}}^{\mathrm{D}},\mathcal{N}^j\Psi_{\tilde{L}}^{\mathrm{D}}\bigr\rangle}=t^{3j}{\bigl\langle\Psi_{L+2b}^{\mathrm{D}},\mathcal{N}^j \Psi_{L+2b}^{\mathrm{D}}\bigr\rangle} \end{align*} $$
$$ \begin{align*} {\bigl\langle\Psi_{\tilde{L}}^{\mathrm{D}},\mathcal{N}^j\Psi_{\tilde{L}}^{\mathrm{D}}\bigr\rangle}=t^{3j}{\bigl\langle\Psi_{L+2b}^{\mathrm{D}},\mathcal{N}^j \Psi_{L+2b}^{\mathrm{D}}\bigr\rangle} \end{align*} $$
for all
![]() $j \in \mathbb {N}$
and
$j \in \mathbb {N}$
and
 $$ \begin{align} {\bigl\langle\Psi_{\tilde{L}}^{\mathrm{D}},\mathcal{H}\Psi_{\tilde{L}}^{\mathrm{D}}\bigr\rangle} = t^3 {\bigl\langle\Psi_{L+2b}^{\mathrm{D}}, \mathcal{H} \Psi_{L+2b}^{\mathrm{D}}\bigr\rangle}. \end{align} $$
$$ \begin{align} {\bigl\langle\Psi_{\tilde{L}}^{\mathrm{D}},\mathcal{H}\Psi_{\tilde{L}}^{\mathrm{D}}\bigr\rangle} = t^3 {\bigl\langle\Psi_{L+2b}^{\mathrm{D}}, \mathcal{H} \Psi_{L+2b}^{\mathrm{D}}\bigr\rangle}. \end{align} $$
Proof. From the definition (A.8), we have
 $\| (\Psi _{{\tilde {L}}}^{\text {D}})^{(nt^3)} \| = \| (\Psi ^{\text {D}}_{L+2b})^{(n)} \|$
for all
$\| (\Psi _{{\tilde {L}}}^{\text {D}})^{(nt^3)} \| = \| (\Psi ^{\text {D}}_{L+2b})^{(n)} \|$
for all
![]() $n \in \mathbb {N}$
. Since
$n \in \mathbb {N}$
. Since
 $(\Psi _{{\tilde {L}}}^{\text {D}})^{(m)} = 0$
, if
$(\Psi _{{\tilde {L}}}^{\text {D}})^{(m)} = 0$
, if
![]() $m \not = n t^3$
, we conclude that
$m \not = n t^3$
, we conclude that
 $\| \Psi _{{\tilde {L}}}^{\text {D}} \| = \| \Psi _{L+2b}^{\text {D}} \| = 1$
and also that, for
$\| \Psi _{{\tilde {L}}}^{\text {D}} \| = \| \Psi _{L+2b}^{\text {D}} \| = 1$
and also that, for
![]() $j \in \mathbb {N}$
,
$j \in \mathbb {N}$
,
 $$ \begin{align*} {\bigl\langle\Psi_{\tilde{L}}^{\mathrm{D}}, \mathcal{N}^j \Psi_{\tilde{L}}^{\mathrm{D}}\bigr\rangle} \hskip -0.05cm=\sum_{n\geq 0} (t^3 n)^j \|(\Psi_{\tilde{L}}^{\mathrm{D}})^{(t^3n)}\|^2 \hskip -0.05cm=t^{3j} \sum_{n\geq 0} n^j \|(\Psi_{L+2b}^{\mathrm{D}})^{(n)}\|^2 \hskip -0.05cm= t^{3j} {\bigl\langle\Psi_{L+2b}^{\mathrm{D}},\mathcal{N}^j \Psi_{L+2b}^{\mathrm{D}}\bigr\rangle}. \end{align*} $$
$$ \begin{align*} {\bigl\langle\Psi_{\tilde{L}}^{\mathrm{D}}, \mathcal{N}^j \Psi_{\tilde{L}}^{\mathrm{D}}\bigr\rangle} \hskip -0.05cm=\sum_{n\geq 0} (t^3 n)^j \|(\Psi_{\tilde{L}}^{\mathrm{D}})^{(t^3n)}\|^2 \hskip -0.05cm=t^{3j} \sum_{n\geq 0} n^j \|(\Psi_{L+2b}^{\mathrm{D}})^{(n)}\|^2 \hskip -0.05cm= t^{3j} {\bigl\langle\Psi_{L+2b}^{\mathrm{D}},\mathcal{N}^j \Psi_{L+2b}^{\mathrm{D}}\bigr\rangle}. \end{align*} $$
To prove (A.9), we observe, first of all, that for any
![]() $i=1, \dots , n t^3$
, when the operator
$i=1, \dots , n t^3$
, when the operator
![]() $\nabla _{x_i}$
acts on
$\nabla _{x_i}$
acts on
 $(\Psi ^{\text {D}}_{{\tilde {L}}})^{(n t^3)}$
, it only hits one of the factors
$(\Psi ^{\text {D}}_{{\tilde {L}}})^{(n t^3)}$
, it only hits one of the factors
 $(\Psi ^{\text {D}}_{L+2b})^{(n)}$
on the right-hand side of (A.8). Similarly, for any
$(\Psi ^{\text {D}}_{L+2b})^{(n)}$
on the right-hand side of (A.8). Similarly, for any
![]() $i,j \in \{ 1, \dots , m \}$
, the operator
$i,j \in \{ 1, \dots , m \}$
, the operator
![]() $V(x_i - x_j)$
has nonzero expectation in the state
$V(x_i - x_j)$
has nonzero expectation in the state
 $(\Psi ^{\text {D}}_{{\tilde {L}}})^{(n t^3)}$
only if
$(\Psi ^{\text {D}}_{{\tilde {L}}})^{(n t^3)}$
only if
![]() $x_i, x_j$
are arguments of the same factor
$x_i, x_j$
are arguments of the same factor
 $(\Psi ^{\text {D}}_{L+2b})^{(n)}$
on the right-hand side of (A.8) (this observation is exactly the reason for introducing corridors of size R between the small boxes, where the wave function vanishes). We conclude that
$(\Psi ^{\text {D}}_{L+2b})^{(n)}$
on the right-hand side of (A.8) (this observation is exactly the reason for introducing corridors of size R between the small boxes, where the wave function vanishes). We conclude that
 ${\bigl \langle \Psi _{\tilde {L}}^{\mathrm {D}},\mathcal {H} \Psi _{\tilde {L}}^{\mathrm {D}}\bigr \rangle } = t^3 {\bigl \langle \Psi _{L+2b}^{\mathrm {D}}, \mathcal {H} \Psi _{L+2b}^{\mathrm {D}}\bigr \rangle }$
, as claimed.
${\bigl \langle \Psi _{\tilde {L}}^{\mathrm {D}},\mathcal {H} \Psi _{\tilde {L}}^{\mathrm {D}}\bigr \rangle } = t^3 {\bigl \langle \Psi _{L+2b}^{\mathrm {D}}, \mathcal {H} \Psi _{L+2b}^{\mathrm {D}}\bigr \rangle }$
, as claimed.
Finally, in Lemma A.4 we show how to obtain an upper bound for the ground state energy per particle in the canonical ensemble, starting from a trial state in the grand-canonical setting. Recall the notation
![]() $E(N,L)$
for the ground state energy of the Hamiltonian (1.1), describing N particles in the box
$E(N,L)$
for the ground state energy of the Hamiltonian (1.1), describing N particles in the box
![]() $\Lambda _L$
, with Dirichlet boundary conditions. For
$\Lambda _L$
, with Dirichlet boundary conditions. For
![]() $\rho> 0$
with
$\rho> 0$
with
![]() $\rho L^3 \in \mathbb {N}$
, we introduce the notation
$\rho L^3 \in \mathbb {N}$
, we introduce the notation
 $$ \begin{align*} e_{L}(\rho)=\frac{E(\rho L^3, L)}{ L^3}. \end{align*} $$
$$ \begin{align*} e_{L}(\rho)=\frac{E(\rho L^3, L)}{ L^3}. \end{align*} $$
Comparing with the definition (1.2), we find
![]() $e (\rho ) = \lim _{L \to \infty } e_L (\rho )$
(where the limit has to be taken along sequences of L, with
$e (\rho ) = \lim _{L \to \infty } e_L (\rho )$
(where the limit has to be taken along sequences of L, with
![]() $\rho L^3 \in \mathbb {N}$
). In the proof of Lemma A.4 we use the existence of the thermodynamic limit of the specific energy and its convexity (see [Reference Ruelle19, Thm. 3.5.8 and 3.5.11]), together with the following result on the Legendre transform of convex functions.
$\rho L^3 \in \mathbb {N}$
). In the proof of Lemma A.4 we use the existence of the thermodynamic limit of the specific energy and its convexity (see [Reference Ruelle19, Thm. 3.5.8 and 3.5.11]), together with the following result on the Legendre transform of convex functions.
Lemma A.3. Let
![]() $D \subset \mathbb {R}$
be a closed interval and
$D \subset \mathbb {R}$
be a closed interval and
![]() $f : D \to \mathbb {R}$
be convex and continuous (also at the boundary of D). We define the Legendre transform
$f : D \to \mathbb {R}$
be convex and continuous (also at the boundary of D). We define the Legendre transform
![]() $f^* : \mathbb {R} \to \mathbb {R}$
of f by
$f^* : \mathbb {R} \to \mathbb {R}$
of f by
 $$ \begin{align} f^* (y) = \mathop{\mathrm{sup}}\limits_{x \in D} \left[ x y - f(x) \right]. \end{align} $$
$$ \begin{align} f^* (y) = \mathop{\mathrm{sup}}\limits_{x \in D} \left[ x y - f(x) \right]. \end{align} $$
Then
![]() $f^*$
is well-defined (because, by continuity,
$f^*$
is well-defined (because, by continuity,
![]() $x \to xy - f (x)$
is bounded on D, for all
$x \to xy - f (x)$
is bounded on D, for all
![]() $y \in \mathbb {R}$
) and, for all
$y \in \mathbb {R}$
) and, for all
![]() $x \in D$
,
$x \in D$
,
 $$ \begin{align} f (x) = \mathop{\mathrm{sup}}\limits_{y \in \mathbb{R}} \left[ xy - f^* (y) \right] . \end{align} $$
$$ \begin{align} f (x) = \mathop{\mathrm{sup}}\limits_{y \in \mathbb{R}} \left[ xy - f^* (y) \right] . \end{align} $$
Proof. By definition of
![]() $f^*$
, we have
$f^*$
, we have
![]() $f^* (y) \geq xy - f(x)$
for all
$f^* (y) \geq xy - f(x)$
for all
![]() $x \in D, y \in \mathbb {R}$
. This implies that
$x \in D, y \in \mathbb {R}$
. This implies that
![]() $f(x) \geq xy - f^* (y)$
for all
$f(x) \geq xy - f^* (y)$
for all
![]() $x \in D, y \in \mathbb {R}$
and therefore that
$x \in D, y \in \mathbb {R}$
and therefore that
 $$ \begin{align} f(x) \geq \mathop{\mathrm{sup}}\limits_{y \in \mathbb{R}} \left[ xy - f^* (y) \right] \end{align} $$
$$ \begin{align} f(x) \geq \mathop{\mathrm{sup}}\limits_{y \in \mathbb{R}} \left[ xy - f^* (y) \right] \end{align} $$
for all
![]() $x \in D$
. On the other hand, fix
$x \in D$
. On the other hand, fix
![]() $x_0 \in D$
and
$x_0 \in D$
and
![]() $t \leq f(x_0)$
. Then, by convexity of f (and by its continuity at the boundaries of D), we find a line through
$t \leq f(x_0)$
. Then, by convexity of f (and by its continuity at the boundaries of D), we find a line through
![]() $(x_0,t)$
lying below the graph of f. In other words, there exists
$(x_0,t)$
lying below the graph of f. In other words, there exists
![]() $y \in \mathbb {R}$
such that
$y \in \mathbb {R}$
such that
![]() $f(x) \geq t + y (x-x_0)$
for all
$f(x) \geq t + y (x-x_0)$
for all
![]() $x \in D$
. Thus,
$x \in D$
. Thus,
![]() $y x_0 - t \geq y x - f(x)$
for all
$y x_0 - t \geq y x - f(x)$
for all
![]() $x \in D$
, which implies that
$x \in D$
, which implies that
and therefore that
![]() $t \leq y x_0 - f^* (y)$
. In particular,
$t \leq y x_0 - f^* (y)$
. In particular,
 $t \leq \mathop {\mathrm {sup}}\limits _{y \in \mathbb {R}} [ y x_0 - f^* (y)]$
. Since
$t \leq \mathop {\mathrm {sup}}\limits _{y \in \mathbb {R}} [ y x_0 - f^* (y)]$
. Since
![]() $t \leq f(x_0)$
was arbitrary, we conclude that
$t \leq f(x_0)$
was arbitrary, we conclude that
 $f(x_0) \leq \mathop {\mathrm {sup}}\limits _{y \in \mathbb {R}} [ y x_0 - f^* (y)]$
. With (A.12), we obtain that
$f(x_0) \leq \mathop {\mathrm {sup}}\limits _{y \in \mathbb {R}} [ y x_0 - f^* (y)]$
. With (A.12), we obtain that
 $f(x) = \mathop {\mathrm {sup}}\limits _{y \in \mathbb {R}} \left [ xy - f^* (y) \right ]$
for all
$f(x) = \mathop {\mathrm {sup}}\limits _{y \in \mathbb {R}} \left [ xy - f^* (y) \right ]$
for all
![]() $x \in D$
.
$x \in D$
.
Lemma A.4. Under the assumptions of Proposition 1.2, fix
![]() $\rho> 0$
and suppose that there exists a sequence
$\rho> 0$
and suppose that there exists a sequence
 $\Psi _L^{\text {D}} \in \mathcal {F} (\Lambda _L)$
(parametrised by L with
$\Psi _L^{\text {D}} \in \mathcal {F} (\Lambda _L)$
(parametrised by L with
![]() $\rho L^3 \in \mathbb {N}$
), satisfying Dirichlet boundary conditions, such that
$\rho L^3 \in \mathbb {N}$
), satisfying Dirichlet boundary conditions, such that
 $$ \begin{align} \langle \Psi_L^{\text{D}} , \mathcal{N} \Psi^{\text{D}}_L \rangle \geq \rho ( 1 + c' \rho) L^3 , \qquad \langle \Psi_L^{\text{D}} , \mathcal{N}^{2} \Psi^{\text{D}}_L\rangle \leq C' (\rho L^3)^2 \,\end{align} $$
$$ \begin{align} \langle \Psi_L^{\text{D}} , \mathcal{N} \Psi^{\text{D}}_L \rangle \geq \rho ( 1 + c' \rho) L^3 , \qquad \langle \Psi_L^{\text{D}} , \mathcal{N}^{2} \Psi^{\text{D}}_L\rangle \leq C' (\rho L^3)^2 \,\end{align} $$
for some constants
![]() $c', C'> 0$
. Then we have
$c', C'> 0$
. Then we have
 $$ \begin{align*} e (\rho) \leq \lim_{L \to \infty} \frac{\langle \Psi_L^{\text{D}}, \mathcal{H} \Psi_L^{\text{D}} \rangle}{L^3} .\end{align*} $$
$$ \begin{align*} e (\rho) \leq \lim_{L \to \infty} \frac{\langle \Psi_L^{\text{D}}, \mathcal{H} \Psi_L^{\text{D}} \rangle}{L^3} .\end{align*} $$
Proof. Using positivity of
![]() $\mathcal {H}$
, we have, for any
$\mathcal {H}$
, we have, for any
![]() $\mu \geq 0$
and
$\mu \geq 0$
and
![]() $M>0$
,
$M>0$
,
 $$ \begin{align}\begin{aligned} &\frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3} \\ & \quad \geq \frac{\mu}{L^3}{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{N}\Psi_{L}^{\mathrm{D}}\bigr\rangle} +\frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},(\mathcal{H}-\mu\mathcal{N})\chi(\mathcal{N}\leq M L^3) \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{{L}^3} -\frac{\mu}{L^3}{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{N}\chi(\mathcal{N}>M L^3) \Psi_{L}^{\mathrm{D}}\bigr\rangle}\\ & \quad \geq \frac{\mu}{L^3}{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{N}\Psi_{L}^{\mathrm{D}}\bigr\rangle}+\sum_{m=0}^{M L^3}\bigg(e_{L}\bigg(\frac{m}{{L}^3}\bigg)-\mu \frac{m}{{L}^3}\bigg) \Big\|(\Psi_{{L}}^{\mathrm{D}})^{(m)}\Big\|^2 - \frac{\mu}{M L^6}{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{N}^2\Psi_{L}^{\mathrm{D}}\bigr\rangle} , \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} &\frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3} \\ & \quad \geq \frac{\mu}{L^3}{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{N}\Psi_{L}^{\mathrm{D}}\bigr\rangle} +\frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},(\mathcal{H}-\mu\mathcal{N})\chi(\mathcal{N}\leq M L^3) \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{{L}^3} -\frac{\mu}{L^3}{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{N}\chi(\mathcal{N}>M L^3) \Psi_{L}^{\mathrm{D}}\bigr\rangle}\\ & \quad \geq \frac{\mu}{L^3}{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{N}\Psi_{L}^{\mathrm{D}}\bigr\rangle}+\sum_{m=0}^{M L^3}\bigg(e_{L}\bigg(\frac{m}{{L}^3}\bigg)-\mu \frac{m}{{L}^3}\bigg) \Big\|(\Psi_{{L}}^{\mathrm{D}})^{(m)}\Big\|^2 - \frac{\mu}{M L^6}{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{N}^2\Psi_{L}^{\mathrm{D}}\bigr\rangle} , \end{aligned}\end{align} $$
where we used the inequality
![]() $\chi (\mathcal {N}> M L^3) \leq \mathcal {N}/ (M L^3)$
. Hence, with (A.13) and fixing M large enough (depending on
$\chi (\mathcal {N}> M L^3) \leq \mathcal {N}/ (M L^3)$
. Hence, with (A.13) and fixing M large enough (depending on
![]() $c', C'$
), we find
$c', C'$
), we find
 $$ \begin{align}\begin{aligned} \frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3} & \geq \mu \rho +\sum_{m=0}^{M L^3}\bigg(e_{L}\bigg(\frac{m}{{L}^3}\bigg)-\mu \frac{m}{{L}^3}\bigg) \Big\|(\Psi_{{L}}^{\mathrm{D}})^{(m)}\Big\|^2 . \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3} & \geq \mu \rho +\sum_{m=0}^{M L^3}\bigg(e_{L}\bigg(\frac{m}{{L}^3}\bigg)-\mu \frac{m}{{L}^3}\bigg) \Big\|(\Psi_{{L}}^{\mathrm{D}})^{(m)}\Big\|^2 . \end{aligned}\end{align} $$
Next, we claim that
 $$ \begin{align} e_{L}(\rho)\geq \Big(1+\frac R{L}\Big)^3e\bigg(\rho\Big(1+\frac{R}{L}\Big)^{-3}\bigg). \end{align} $$
$$ \begin{align} e_{L}(\rho)\geq \Big(1+\frac R{L}\Big)^3e\bigg(\rho\Big(1+\frac{R}{L}\Big)^{-3}\bigg). \end{align} $$
Indeed, starting from an arbitrary normalised trial state
![]() $\psi $
describing
$\psi $
describing
![]() $N = \rho L^3$
particles in a box of side length L, with Dirichlet boundary conditions, we can construct, for any
$N = \rho L^3$
particles in a box of side length L, with Dirichlet boundary conditions, we can construct, for any
![]() $r \in \mathbb {N}$
, a trial state describing
$r \in \mathbb {N}$
, a trial state describing
![]() $N'= N r^3 = \rho L^3 r^3$
particles in a box of side length
$N'= N r^3 = \rho L^3 r^3$
particles in a box of side length
![]() $L'= r (L+R)$
, again with Dirichlet boundary conditions, by placing
$L'= r (L+R)$
, again with Dirichlet boundary conditions, by placing
![]() $r^3$
copies of the state
$r^3$
copies of the state
![]() $\psi $
in adjacent boxes and using that (thanks to the corridors of size R between the boxes) particles in different boxes do not interact. This construction is very similar to the one presented around Lemma A.2 (the difference is that here we work in the canonical setting, which makes things slightly simpler). Since
$\psi $
in adjacent boxes and using that (thanks to the corridors of size R between the boxes) particles in different boxes do not interact. This construction is very similar to the one presented around Lemma A.2 (the difference is that here we work in the canonical setting, which makes things slightly simpler). Since
![]() $N' = [\rho / (1 +R/L)^3 ] L^{'3}$
, optimising the choice of
$N' = [\rho / (1 +R/L)^3 ] L^{'3}$
, optimising the choice of
![]() $\psi $
, we obtain that
$\psi $
, we obtain that
![]() $E ([\rho / (1 + R/L)^3] L^{'3} , L') \leq r^3 E (\rho L^3, L)$
and therefore that
$E ([\rho / (1 + R/L)^3] L^{'3} , L') \leq r^3 E (\rho L^3, L)$
and therefore that
Taking the limit
![]() $L' \to \infty $
(along the sequence
$L' \to \infty $
(along the sequence
![]() $L' = r (L+R)$
,
$L' = r (L+R)$
,
![]() $r \in \mathbb {N}$
), we obtain (A.16). Then (A.15) and (A.16) yield
$r \in \mathbb {N}$
), we obtain (A.16). Then (A.15) and (A.16) yield
 $$ \begin{align*} \frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3}\geq\;\mu\rho-\Big(1+\frac RL\Big)^3e^*(\mu), \end{align*} $$
$$ \begin{align*} \frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3}\geq\;\mu\rho-\Big(1+\frac RL\Big)^3e^*(\mu), \end{align*} $$
where
![]() $e^*$
denotes the Legendre transform of
$e^*$
denotes the Legendre transform of
![]() $e : D \to \mathbb {R}$
, defined on the domain
$e : D \to \mathbb {R}$
, defined on the domain
![]() $D=[0,M]$
, as in (A.10) (here we use the convexity of the specific energy e). It follows that
$D=[0,M]$
, as in (A.10) (here we use the convexity of the specific energy e). It follows that
 $$ \begin{align*} \lim_{L\to+\infty}\frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3}\geq\;\mu\rho-e^*(\mu) \end{align*} $$
$$ \begin{align*} \lim_{L\to+\infty}\frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3}\geq\;\mu\rho-e^*(\mu) \end{align*} $$
for all
![]() $\mu \geq 0$
. Thus,
$\mu \geq 0$
. Thus,
 $$ \begin{align*} \lim_{L\to+\infty}\frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3}\geq \; \mathop{\mathrm{sup}}\limits_{\mu \geq 0} \Big[ \mu\rho-e^*(\mu) \Big] = \mathop{\mathrm{sup}}\limits_{\mu \in \mathbb{R}} \Big[ \mu\rho-e^*(\mu) \Big] = e (\rho) \end{align*} $$
$$ \begin{align*} \lim_{L\to+\infty}\frac{{\bigl\langle\Psi_{L}^{\mathrm{D}},\mathcal{H} \Psi_{L}^{\mathrm{D}}\bigr\rangle}}{L^3}\geq \; \mathop{\mathrm{sup}}\limits_{\mu \geq 0} \Big[ \mu\rho-e^*(\mu) \Big] = \mathop{\mathrm{sup}}\limits_{\mu \in \mathbb{R}} \Big[ \mu\rho-e^*(\mu) \Big] = e (\rho) \end{align*} $$
where we used the fact that
![]() $e^* (0) = 0$
(because
$e^* (0) = 0$
(because
![]() $e (\rho ) \geq 0$
for all
$e (\rho ) \geq 0$
for all
![]() $\rho \geq 0$
and
$\rho \geq 0$
and
![]() $e (0) = 0$
) and
$e (0) = 0$
) and
![]() $e^* (\mu ) \geq -e (0) = 0$
for all
$e^* (\mu ) \geq -e (0) = 0$
for all
![]() $\mu \in \mathbb {R}$
in the second step and Lemma A.3 in the third step.
$\mu \in \mathbb {R}$
in the second step and Lemma A.3 in the third step.
With Lemmas A.1, A.2 and A.4 we are ready to show Proposition 1.2.
Proof Proof of Proposition 1.2.
Given a normalised
![]() $\Psi _L \in \mathcal {F} (\Lambda _L)$
satisfying periodic boundary conditions with
$\Psi _L \in \mathcal {F} (\Lambda _L)$
satisfying periodic boundary conditions with
we find with Lemma A.1 a normalised
 $\Psi _{L+2b}^{\text {D}} \in \mathcal {F} (\Lambda _{L+2b})$
satisfying Dirichlet conditions such that
$\Psi _{L+2b}^{\text {D}} \in \mathcal {F} (\Lambda _{L+2b})$
satisfying Dirichlet conditions such that
and
 $$ \begin{align*} \langle \Psi_{L+2b}^{\text{D}} , \mathcal{H} \Psi_{L+2b}^{\text{D}} \rangle \leq \langle \Psi_L , \mathcal{H} \Psi_L \rangle + \frac{C}{Lb} \langle \Psi_L , \mathcal{N} \Psi_L \rangle. \end{align*} $$
$$ \begin{align*} \langle \Psi_{L+2b}^{\text{D}} , \mathcal{H} \Psi_{L+2b}^{\text{D}} \rangle \leq \langle \Psi_L , \mathcal{H} \Psi_L \rangle + \frac{C}{Lb} \langle \Psi_L , \mathcal{N} \Psi_L \rangle. \end{align*} $$
With Lemma A.2, we obtain a sequence
 $\Psi ^{\text {D}}_{{\tilde {L}}} \in \mathcal {F} (\Lambda _{{\tilde {L}}})$
, with
$\Psi ^{\text {D}}_{{\tilde {L}}} \in \mathcal {F} (\Lambda _{{\tilde {L}}})$
, with
![]() ${\tilde {L}} =t (L+2b+R)$
for
${\tilde {L}} =t (L+2b+R)$
for
![]() $t \in \mathbb {N}$
, such that
$t \in \mathbb {N}$
, such that
 $$ \begin{align*} \langle \Psi_{{\tilde{L}}}^{\text{D}} , \mathcal{N} \Psi_{{\tilde{L}}}^{\text{D}} \rangle \geq \rho (1+ c' \rho) {\tilde{L}}^3 , \hskip 0.5cm \langle \Psi_{{\tilde{L}}}^{\text{D}} , \mathcal{N}^2 \Psi_{{\tilde{L}}}^{\text{D}} \rangle \leq C' \rho^2 {\tilde{L}}^6 \end{align*} $$
$$ \begin{align*} \langle \Psi_{{\tilde{L}}}^{\text{D}} , \mathcal{N} \Psi_{{\tilde{L}}}^{\text{D}} \rangle \geq \rho (1+ c' \rho) {\tilde{L}}^3 , \hskip 0.5cm \langle \Psi_{{\tilde{L}}}^{\text{D}} , \mathcal{N}^2 \Psi_{{\tilde{L}}}^{\text{D}} \rangle \leq C' \rho^2 {\tilde{L}}^6 \end{align*} $$
and
 $$ \begin{align*} \langle \Psi_{{\tilde{L}}}^{\text{D}} , \mathcal{H} \Psi_{{\tilde{L}}}^{\text{D}} \rangle \leq t^3 \langle \Psi_L , \mathcal{H} \Psi_L \rangle + \frac{C t^3}{Lb} \langle \Psi_L , \mathcal{N} \Psi_L \rangle . \end{align*} $$
$$ \begin{align*} \langle \Psi_{{\tilde{L}}}^{\text{D}} , \mathcal{H} \Psi_{{\tilde{L}}}^{\text{D}} \rangle \leq t^3 \langle \Psi_L , \mathcal{H} \Psi_L \rangle + \frac{C t^3}{Lb} \langle \Psi_L , \mathcal{N} \Psi_L \rangle . \end{align*} $$
With Lemma A.4, we conclude that
 $$ \begin{align*} e(\rho) &\leq \lim_{{\tilde{L}} \to \infty} \frac{\langle \Psi_{{\tilde{L}}}^{\text{D}} , \mathcal{H} \Psi_{{\tilde{L}}}^{\text{D}} \rangle}{{\tilde{L}}^3} \\ & \leq \frac{1}{(1+2b/L + R/L)^3} \left[ \frac{\langle \Psi_L, \mathcal{H} \Psi_L \rangle}{L^3} + \frac{C}{L^4 b} \langle \Psi_L, \mathcal{N} \Psi_L \rangle \right] \\ &\leq \frac{\langle \Psi_L, \mathcal{H} \Psi_L \rangle}{L^3} + \frac{C}{L^4 b} \langle \Psi_L, \mathcal{N} \Psi_L \rangle. \\[-39pt]\end{align*} $$
$$ \begin{align*} e(\rho) &\leq \lim_{{\tilde{L}} \to \infty} \frac{\langle \Psi_{{\tilde{L}}}^{\text{D}} , \mathcal{H} \Psi_{{\tilde{L}}}^{\text{D}} \rangle}{{\tilde{L}}^3} \\ & \leq \frac{1}{(1+2b/L + R/L)^3} \left[ \frac{\langle \Psi_L, \mathcal{H} \Psi_L \rangle}{L^3} + \frac{C}{L^4 b} \langle \Psi_L, \mathcal{N} \Psi_L \rangle \right] \\ &\leq \frac{\langle \Psi_L, \mathcal{H} \Psi_L \rangle}{L^3} + \frac{C}{L^4 b} \langle \Psi_L, \mathcal{N} \Psi_L \rangle. \\[-39pt]\end{align*} $$
Acknowledgement
We are grateful to C. Boccato and S. Fournais for valuable discussions. G.B. and S.C. gratefully acknowledge the support from the GNFM Gruppo Nazionale per la Fisica Matematica. B. S. gratefully acknowledges partial support from the NCCR SwissMAP, from the Swiss National Science Foundation through the Grant ‘Dynamical and Energetic Properties of Bose–Einstein Condensates’ and from the European Research Council through the ERC-AdG CLaQS.
Conflict of Interest
None.