Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T09:24:16.110Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLICATIVE PARAMETRIZED HOMOTOPY THEORY VIA SYMMETRIC SPECTRA IN RETRACTIVE SPACES

Part of: Homotopy theory

Published online by Cambridge University Press:  19 March 2020

FABIAN HEBESTREIT ,
STEFFEN SAGAVE  and
CHRISTIAN SCHLICHTKRULL
FABIAN HEBESTREIT
Affiliation:
Mathematical Institute, University of Bonn, Endenicher Allee 60, 53115Bonn, Germany; [email protected]
STEFFEN SAGAVE
Affiliation:
IMAPP, Radboud University Nijmegen, PO Box 9010, 6500GL Nijmegen, The Netherlands; [email protected]
CHRISTIAN SCHLICHTKRULL
Affiliation:
Department of Mathematics, University of Bergen, P.O. Box 7803, 5020Bergen, Norway; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In order to treat multiplicative phenomena in twisted (co)homology, we introduce a new point-set-level framework for parametrized homotopy theory. We provide a convolution smash product that descends to the corresponding 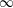$\infty$-categorical product and allows for convenient constructions of commutative parametrized ring spectra. As an immediate application, we compare various models for generalized Thom spectra. In a companion paper, this approach is used to compare homotopical and operator algebraic models for twisted 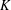$K$-theory.

MSC classification

Primary: 55P43: Spectra with additional structure ($E_infty$, $A_infty$, ring spectra, etc.)
Secondary: 55P42: Stable homotopy theory, spectra
Type
Topology
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e16
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits noncommercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© The Author(s) 2020

References

Ando, M., Blumberg, A. J. and Gepner, D., ‘Parametrized spectra, multiplicative Thom spectra, and the twisted Umkehr map’, Geom. Topol. 22 (2018), 3761–3825.CrossRefGoogle Scholar
Ando, M., Blumberg, A. J., Gepner, D., Hopkins, M. J. and Rezk, C., ‘An ∞-categorical approach to R-line bundles, R-module Thom spectra, and twisted R-homology’, J. Topol. 7(3) (2014), 869–893.CrossRefGoogle Scholar
Ando, M., Blumberg, A. J., Gepner, D., Hopkins, M. J. and Rezk, C., ‘Units of ring spectra, orientations and Thom spectra via rigid infinite loop space theory’, J. Topol. 7(4) (2014), 1077–1117.CrossRefGoogle Scholar
Antieau, B., Gepner, D. and Gómez, J. M., ‘Actions of K (𝜋, n) spaces on K-theory and uniqueness of twisted K-theory’, Trans. Amer. Math. Soc. 366(7) (2014), 3631–3648.CrossRefGoogle Scholar
Barwick, C., ‘On left and right model categories and left and right Bousfield localizations’, Homology Homotopy Appl. 12(2) (2010), 245–320.CrossRefGoogle Scholar
Basu, S., Sagave, S. and Schlichtkrull, C., ‘Generalized Thom spectra and their topological Hochschild homology’, J. Inst. Math. Jussieu 19(1) (2020), 21–64.CrossRefGoogle Scholar
Blumberg, A. J., Cohen, R. L. and Schlichtkrull, C., ‘Topological Hochschild homology of Thom spectra and the free loop space’, Geom. Topol. 14(2) (2010), 1165–1242.CrossRefGoogle Scholar
Borceux, F., Handbook of Categorical Algebra. 1, Encyclopedia of Mathematics and its Applications, 50 (Cambridge University Press, Cambridge, 1994).Google Scholar
Borceux, F., Handbook of Categorical Algebra. 2, Encyclopedia of Mathematics and its Applications, 51 (Cambridge University Press, Cambridge, 1994).Google Scholar
Bousfield, A. K., ‘On the telescopic homotopy theory of spaces’, Trans. Amer. Math. Soc. 353(6) (2001), 2391–2426.CrossRefGoogle Scholar
Braunack-Mayer, V. S., ‘Rational parametrised stable homotopy theory’, PhD Thesis, University of Zurich, 2018, available at https://doi.org/10.5167/uzh-153000.CrossRefGoogle Scholar
Cagne, P. and Melliès, P.-A., ‘On bifibrations of model categories’. Preprint, 2017,arXiv:1709.10484.Google Scholar
Clapp, M. and Puppe, D., ‘The homotopy category of parametrized spectra’, Manuscripta Math. 45(3) (1984), 219–247.CrossRefGoogle Scholar
Dugger, D., ‘Replacing model categories with simplicial ones’, Trans. Amer. Math. Soc. 353(12) (2001), 5003–5027.CrossRefGoogle Scholar
Gepner, D., Groth, M. and Nikolaus, T., ‘Universality of multiplicative infinite loop space machines’, Algebr. Geom. Topol. 15(6) (2015), 3107–3153.CrossRefGoogle Scholar
Glasman, S., ‘Day convolution for ∞-categories’, Math. Res. Lett. 23(5) (2016), 1369–1385.CrossRefGoogle Scholar
Goerss, P. G. and Jardine, J. F., Simplicial Homotopy Theory, Progress in Mathematics, 174 (Birkhäuser, Basel, 1999).CrossRefGoogle Scholar
Gorchinskiy, S. and Guletskiĭ, V., ‘Positive model structures for abstract symmetric spectra’, Appl. Categ. Structures 26(1) (2018), 29–46.CrossRefGoogle Scholar
Harpaz, Y., Nuiten, J. and Prasma, M., ‘The tangent bundle of a model category’, Theory Appl. Categ. 34 (2019), 1039–1072, Paper No. 33.Google Scholar
Harpaz, Y. and Prasma, M., ‘The Grothendieck construction for model categories’, Adv. Maths 281 (2015), 1306–1363.CrossRefGoogle Scholar
Hebestreit, F. and Sagave, S., ‘Homotopical and operator algebraic twisted $K$-theory’, Preprint, 2019, arXiv:1904.01872v1.Google Scholar
Hinich, V., ‘Dwyer–Kan localization revisited’, Homology Homotopy Appl. 18(1) (2016), 27–48.CrossRefGoogle Scholar
Hirschhorn, P. S., Model Categories and Their Localizations, Mathematical Surveys and Monographs, 99 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Hirschhorn, P. S., ‘Overcategories and undercategories of model categories’, Preprint, 2015,arXiv:1507.01624.Google Scholar
Hovey, M., Model Categories, Mathematical Surveys and Monographs, 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Hovey, M., ‘Spectra and symmetric spectra in general model categories’, J. Pure Appl. Algebra 165(1) (2001), 63–127.CrossRefGoogle Scholar
Hovey, M., Shipley, B. and Smith, J., ‘Symmetric spectra’, J. Amer. Math. Soc. 13(1) (2000), 149–208.CrossRefGoogle Scholar
Joachim, M., ‘Higher coherences for equivariant K-theory’, inStructured Ring Spectra, London Mathematical Society Lecture Note Series, 315 (Cambridge University Press, Cambridge, 2004), 87–114.CrossRefGoogle Scholar
Joyal, A., ‘The theory of quasi-categories and its applications’, 2008. Available athttp://mat.uab.cat/∼kock/crm/hocat/advanced-course/Quadern45-2.pdf.Google Scholar
Lewis, L. G. Jr., ‘The stable category and generalized Thom spectra’, PhD Thesis, University of Chicago, 1978.Google Scholar
Lewis, L. G. Jr., ‘When is the natural map X→𝛺𝛴X a cofibration?’, Trans. Amer. Math. Soc. 273(1) (1982), 147–155.Google Scholar
Lewis, L. G. Jr., ‘Open maps, colimits, and a convenient category of fibre spaces’, Topology Appl. 19(1) (1985), 75–89.CrossRefGoogle Scholar
Lewis, L. G. Jr., May, J. P., Steinberger, M. and McClure, J. E., Equivariant Stable Homotopy Theory, Lecture Notes in Mathematics, 1213 (Springer, Berlin, 1986), With contributions by J. E. McClure.CrossRefGoogle Scholar
Lurie, J., Higher Topos Theory, Annals of Mathematics Studies, 170 (Princeton University Press, Princeton, NJ, 2009).CrossRefGoogle Scholar
Lurie, J., ‘Higher algebra’, Preprint, 2016, available at http://www.math.harvard.edu/∼lurie/.Google Scholar
Mandell, M. A., May, J. P., Schwede, S. and Shipley, B., ‘Model categories of diagram spectra’, Proc. Lond. Math. Soc. (3) 82(2) (2001), 441–512.CrossRefGoogle Scholar
May, J. P. and Sigurdsson, J., Parametrized Homotopy Theory, Mathematical Surveys and Monographs, 132 (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
Nikolaus, T., ‘Stable $\infty$-operads and the multiplicative Yoneda lemma’, Preprint, 2016,arXiv:1608.02901.Google Scholar
Nikolaus, T. and Sagave, S., ‘Presentably symmetric monoidal ∞-categories are represented by symmetric monoidal model categories’, Algebr. Geom. Topol. 17(5) (2017), 3189–3212.CrossRefGoogle Scholar
Nikolaus, T. and Scholze, P., ‘On topological cyclic homology’, Acta Math. 221(2) (2018), 203–409.CrossRefGoogle Scholar
Pavlov, D. and Scholbach, J., ‘Symmetric operads in abstract symmetric spectra’, J. Inst. Math. Jussieu 18(4) (2019), 707–758.CrossRefGoogle Scholar
Sagave, S. and Schlichtkrull, C., ‘Diagram spaces and symmetric spectra’, Adv. Maths 231(3–4) (2012), 2116–2193.CrossRefGoogle Scholar
Sagave, S. and Schlichtkrull, C., ‘Group completion and units in 𝓘-spaces’, Algebr. Geom. Topol. 13(2) (2013), 625–686.CrossRefGoogle Scholar
Schlichtkrull, C., ‘Units of ring spectra and their traces in algebraic K-theory’, Geom. Topol. 8 (2004), 645–673 (electronic).CrossRefGoogle Scholar
Schlichtkrull, C., ‘Thom spectra that are symmetric spectra’, Doc. Math. 14 (2009), 699–748.Google Scholar
Schulz, J., ‘Logarithmic structures on commutative $Hk$-algebra spectra’, PhD Thesis, Universität Hamburg, 2018, available athttp://ediss.sub.uni-hamburg.de/volltexte/2018/9312/.Google Scholar
Schwede, S., ‘Symmetric spectra’, ‘Book project’, 2012, available athttp://www.math.uni-bonn.de/people/schwede/.Google Scholar
Schwede, S. and Shipley, B. E., ‘Algebras and modules in monoidal model categories’, Proc. Lond. Math. Soc. (3) 80(2) (2000), 491–511.CrossRefGoogle Scholar
Shipley, B., ‘A convenient model category for commutative ring spectra’, inHomotopy Theory: Relations with Algebraic Geometry, Group Cohomology, and Algebraic K-theory, Contemporary Mathematics, 346 (American Mathematical Society, Providence, RI, 2004), 473–483.Google Scholar
Thomason, R. W., ‘Homotopy colimits in the category of small categories’, Math. Proc. Cambridge Philos. Soc. 85(1) (1979), 91–109.CrossRefGoogle Scholar