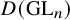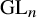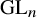1 Introduction
The present article is a continuation in a series of papers by Misha Gekhtman, Misha Shapiro and Alek Vainshtein that aim at proving the following conjecture:
Any simple complex Poisson–Lie group endowed with a Poisson bracket from the Belavin–Drinfeld classification possesses a compatible generalized cluster structure.
For conciseness, we refer to the above conjecture as the GSV conjecture and to Belavin–Drinfeld triples as BD triples. The conjecture was first formulated in [Reference Gekhtman, Shapiro and Vainshtein16] assuming ordinary cluster structures of geometric type, and later it was realized in [Reference Gekhtman, Shapiro and Vainshtein18] that a more general notion of cluster algebras is needed. Cluster algebras were invented by Fomin and Zelevinsky in [Reference Fomin and Zelevinsky14] as an algebraic framework for studying dual canonical bases and total positivity. The notion of generalized cluster algebra suitable for the GSV conjecture was first introduced in [Reference Gekhtman, Shapiro and Vainshtein18] as an adjustment of an earlier definition given in [Reference Chekhov and Shapiro6].
Progress on GSV conjecture
As the recent progress shows, the GSV conjecture might be extended beyond simple groups and brackets compatible with the group structure. At present, we know that
-
• Any simple complex Poisson–Lie group endowed with the standard Poisson bracket possesses a compatible cluster structure; see [Reference Gekhtman, Shapiro and Vainshtein16];
-
• For any Belavin–Drinfeld data, the existence of a compatible cluster structure for
 $\operatorname {\mathrm {SL}}_n$
for all
$\operatorname {\mathrm {SL}}_n$
for all
 $n < 5$
was shown in [Reference Gekhtman, Shapiro and Vainshtein16]; for
$n < 5$
was shown in [Reference Gekhtman, Shapiro and Vainshtein16]; for
 $\operatorname {\mathrm {SL}}_5$
, the conjecture was proved by Eisner in [Reference Eisner8];
$\operatorname {\mathrm {SL}}_5$
, the conjecture was proved by Eisner in [Reference Eisner8]; -
• For a large class of the so-called aperiodic oriented BD triples, the conjecture was proved for
 $\operatorname {\mathrm {SL}}_n$
in [Reference Gekhtman, Shapiro and Vainshtein20];
$\operatorname {\mathrm {SL}}_n$
in [Reference Gekhtman, Shapiro and Vainshtein20]; -
• For other Poisson–Lie groups, the conjecture was established for the Drinfeld double of
 $\operatorname {\mathrm {SL}}_n$
in [Reference Gekhtman, Shapiro and Vainshtein18] for the standard Poisson structure, as well as for
$\operatorname {\mathrm {SL}}_n$
in [Reference Gekhtman, Shapiro and Vainshtein18] for the standard Poisson structure, as well as for
 $\operatorname {\mathrm {SL}}_n^{\dagger }$
, which is an image of the dual group
$\operatorname {\mathrm {SL}}_n^{\dagger }$
, which is an image of the dual group
 $\operatorname {\mathrm {SL}}_n^*$
in
$\operatorname {\mathrm {SL}}_n^*$
in
 $\operatorname {\mathrm {SL}}_n$
. An alternative construction on the Drinfeld double of
$\operatorname {\mathrm {SL}}_n$
. An alternative construction on the Drinfeld double of
 $\operatorname {\mathrm {SL}}_n$
was also given in [Reference Gekhtman, Shapiro and Vainshtein19, Reference Gekhtman, Shapiro and Vainshtein21].
$\operatorname {\mathrm {SL}}_n$
was also given in [Reference Gekhtman, Shapiro and Vainshtein19, Reference Gekhtman, Shapiro and Vainshtein21].
The above results naturally extend to
![]() $\operatorname {\mathrm {GL}}_n$
. The present paper combines the cluster structures from [Reference Gekhtman, Shapiro and Vainshtein20] for aperiodic oriented BD triples with the generalized cluster structure from [Reference Gekhtman, Shapiro and Vainshtein18] for the Drinfeld double endowed with the standard bracket. As a result, we derive generalized cluster structures on the Drinfeld doubles of
$\operatorname {\mathrm {GL}}_n$
. The present paper combines the cluster structures from [Reference Gekhtman, Shapiro and Vainshtein20] for aperiodic oriented BD triples with the generalized cluster structure from [Reference Gekhtman, Shapiro and Vainshtein18] for the Drinfeld double endowed with the standard bracket. As a result, we derive generalized cluster structures on the Drinfeld doubles of
![]() $\operatorname {\mathrm {GL}}_n$
and
$\operatorname {\mathrm {GL}}_n$
and
![]() $\operatorname {\mathrm {SL}}_n$
compatible with Poisson brackets from the aperiodic oriented class of Belavin–Drinfeld triples.
$\operatorname {\mathrm {SL}}_n$
compatible with Poisson brackets from the aperiodic oriented class of Belavin–Drinfeld triples.
Belavin–Drinfeld triples
Let
![]() $\Pi :=[1,n-1]$
be a set of simple roots of type
$\Pi :=[1,n-1]$
be a set of simple roots of type
![]() $A_n$
identified with an interval
$A_n$
identified with an interval
![]() $[1,n-1]$
. Recall that a Belavin–Drinfeld triple is a triple
$[1,n-1]$
. Recall that a Belavin–Drinfeld triple is a triple
![]() $(\Gamma _1,\Gamma _2,\gamma )$
such that
$(\Gamma _1,\Gamma _2,\gamma )$
such that
![]() $\Gamma _1,\Gamma _2\subseteq \Pi $
and
$\Gamma _1,\Gamma _2\subseteq \Pi $
and
![]() $\gamma :\Gamma _1 \rightarrow \Gamma _2$
a nilpotent isometry; we say that the triple is trivial if
$\gamma :\Gamma _1 \rightarrow \Gamma _2$
a nilpotent isometry; we say that the triple is trivial if
![]() $\Gamma _1=\Gamma _2=\emptyset $
. As Belavin and Drinfeld showed in [Reference Belavin and Drinfeld1, Reference Belavin and Drinfeld2], such triples (together with some additional data) parametrize factorizable quasitriangular Poisson structures on connected simple complex Poisson–Lie groups (for details, see Section 2.2). As in [Reference Gekhtman, Shapiro and Vainshtein20], however, we consider even more general Poisson brackets that depend on a pair
$\Gamma _1=\Gamma _2=\emptyset $
. As Belavin and Drinfeld showed in [Reference Belavin and Drinfeld1, Reference Belavin and Drinfeld2], such triples (together with some additional data) parametrize factorizable quasitriangular Poisson structures on connected simple complex Poisson–Lie groups (for details, see Section 2.2). As in [Reference Gekhtman, Shapiro and Vainshtein20], however, we consider even more general Poisson brackets that depend on a pair
![]() $\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
of Belavin–Drinfeld triples
$\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
of Belavin–Drinfeld triples
![]() $\mathbf {\Gamma }^r:=(\Gamma _1^r,\Gamma _2^r,\gamma _r)$
and
$\mathbf {\Gamma }^r:=(\Gamma _1^r,\Gamma _2^r,\gamma _r)$
and
![]() $\mathbf {\Gamma }^c:=(\Gamma _1^c,\Gamma _2^c,\gamma _c)$
. A Belavin–Drinfeld triple
$\mathbf {\Gamma }^c:=(\Gamma _1^c,\Gamma _2^c,\gamma _c)$
. A Belavin–Drinfeld triple
![]() $(\Gamma _1,\Gamma _2,\gamma )$
is called oriented if for any
$(\Gamma _1,\Gamma _2,\gamma )$
is called oriented if for any
![]() $i,i+1 \in \Gamma _1$
,
$i,i+1 \in \Gamma _1$
,
![]() $\gamma (i+1) = \gamma (i)+1$
; a pair of Belavin–Drinfeld triples is called oriented if both
$\gamma (i+1) = \gamma (i)+1$
; a pair of Belavin–Drinfeld triples is called oriented if both
![]() $\mathbf {\Gamma }^r$
and
$\mathbf {\Gamma }^r$
and
![]() $\mathbf {\Gamma }^c$
are oriented. The pair is called aperiodic if the map
$\mathbf {\Gamma }^c$
are oriented. The pair is called aperiodic if the map
![]() $\gamma _c^{-1}w_0\gamma _rw_0$
is nilpotent, where
$\gamma _c^{-1}w_0\gamma _rw_0$
is nilpotent, where
![]() $w_0$
is the longest Weyl group element. Given a Cartan subalgebra
$w_0$
is the longest Weyl group element. Given a Cartan subalgebra
![]() $\mathfrak {h}$
of
$\mathfrak {h}$
of
![]() $\operatorname {\mathrm {sl}}_n(\mathbb {C})$
and a Belavin–Drinfeld triple
$\operatorname {\mathrm {sl}}_n(\mathbb {C})$
and a Belavin–Drinfeld triple
![]() $(\Gamma _1,\Gamma _2,\gamma )$
, set
$(\Gamma _1,\Gamma _2,\gamma )$
, set
and let
![]() $\mathcal {H}_{\mathbf {\Gamma }}$
be the connected subgroup of
$\mathcal {H}_{\mathbf {\Gamma }}$
be the connected subgroup of
![]() $\operatorname {\mathrm {SL}}_n(\mathbb {C})$
with Lie algebra
$\operatorname {\mathrm {SL}}_n(\mathbb {C})$
with Lie algebra
![]() $\mathfrak {h}_{\mathbf {\Gamma }}$
. The dimension of
$\mathfrak {h}_{\mathbf {\Gamma }}$
. The dimension of
![]() $\mathcal {H}_{\mathbf {\Gamma }}$
is given by
$\mathcal {H}_{\mathbf {\Gamma }}$
is given by
![]() $k_{\mathbf {\Gamma }}:=|\Pi \setminus \Gamma _1|$
.
$k_{\mathbf {\Gamma }}:=|\Pi \setminus \Gamma _1|$
.
Main results and the outline of the paper
In this paper, we consider generalized cluster structures in the rings of regular functions of
![]() $\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
and
$\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
and
![]() $\operatorname {\mathrm {SL}}_n \times \operatorname {\mathrm {SL}}_n$
(for the precise definition, see Section 2.1). Roughly, the difference between generalized cluster structures and ordinary cluster structures of geometric type (in the sense of Fomin and Zelevinsky) is that the former allows more than two monomials in exchange relations. In fact, there is only one generalized exchange relation in the initial seeds that we study in this paper (more generalized exchange relations appear in the case of nonaperiodic BD pairs; see [Reference Gekhtman, Shapiro and Vainshtein19]). Recall that an extended cluster
$\operatorname {\mathrm {SL}}_n \times \operatorname {\mathrm {SL}}_n$
(for the precise definition, see Section 2.1). Roughly, the difference between generalized cluster structures and ordinary cluster structures of geometric type (in the sense of Fomin and Zelevinsky) is that the former allows more than two monomials in exchange relations. In fact, there is only one generalized exchange relation in the initial seeds that we study in this paper (more generalized exchange relations appear in the case of nonaperiodic BD pairs; see [Reference Gekhtman, Shapiro and Vainshtein19]). Recall that an extended cluster
![]() $(x_1,\ldots ,x_{N+M})$
is called log-canonical (relative some Poisson bracket
$(x_1,\ldots ,x_{N+M})$
is called log-canonical (relative some Poisson bracket
![]() $\{\cdot ,\cdot \}$
) if
$\{\cdot ,\cdot \}$
) if
![]() $\{x_i,x_j\} = \omega _{ij} x_ix_j$
for some constants
$\{x_i,x_j\} = \omega _{ij} x_ix_j$
for some constants
![]() $\omega _{ij}$
and all
$\omega _{ij}$
and all
![]() $1 \leq i, j\leq N+M$
; a generalized cluster structure is called compatible with the Poisson bracket if all extended clusters are log-canonical. An extended cluster
$1 \leq i, j\leq N+M$
; a generalized cluster structure is called compatible with the Poisson bracket if all extended clusters are log-canonical. An extended cluster
![]() $(x_1,\ldots ,x_{N+M})$
is called regular if all
$(x_1,\ldots ,x_{N+M})$
is called regular if all
![]() $x_i$
’s are represented as regular functions on the given variety (
$x_i$
’s are represented as regular functions on the given variety (
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
or
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
or
![]() $\operatorname {\mathrm {SL}}_n \times \operatorname {\mathrm {SL}}_n$
in our case); the generalized cluster structure is called regular if all extended clusters are regular. The main part of the paper is devoted to proving the following theorem.
$\operatorname {\mathrm {SL}}_n \times \operatorname {\mathrm {SL}}_n$
in our case); the generalized cluster structure is called regular if all extended clusters are regular. The main part of the paper is devoted to proving the following theorem.
Theorem 1.1. Let
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be a pair of aperiodic oriented Belavin–Drinfeld triples. There exists a generalized cluster structure
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be a pair of aperiodic oriented Belavin–Drinfeld triples. There exists a generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma })$
on
$\mathcal {GC}(\mathbf {\Gamma })$
on
![]() $D(\operatorname {\mathrm {GL}}_n) = \operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
such that
$D(\operatorname {\mathrm {GL}}_n) = \operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
such that
-
(i) The number of stable variables is
 $k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c} + (n+1)$
, and the exchange matrix has full rank;
$k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c} + (n+1)$
, and the exchange matrix has full rank; -
(ii) The generalized cluster structure
 $\mathcal {GC}(\mathbf {\Gamma })$
is regular, and the ring of regular functions
$\mathcal {GC}(\mathbf {\Gamma })$
is regular, and the ring of regular functions
 $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
is naturally isomorphic to the upper cluster algebra
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
is naturally isomorphic to the upper cluster algebra
 $\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
;
$\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
; -
(iii) The global toric action of
 $(\mathbb {C}^*)^{k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c}+2}$
on
$(\mathbb {C}^*)^{k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c}+2}$
on
 $\mathcal {GC}(\mathbf {\Gamma })$
is induced by the left action of
$\mathcal {GC}(\mathbf {\Gamma })$
is induced by the left action of
 $\mathcal {H}_{\mathbf {\Gamma }^r}$
, the right action of
$\mathcal {H}_{\mathbf {\Gamma }^r}$
, the right action of
 $\mathcal {H}_{\mathbf {\Gamma }^c}$
and the action by scalar matrices on each component of
$\mathcal {H}_{\mathbf {\Gamma }^c}$
and the action by scalar matrices on each component of
 $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
;
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
; -
(iv) Any Poisson bracket defined by the pair
 $\mathbf {\Gamma }$
on
$\mathbf {\Gamma }$
on
 $D(\operatorname {\mathrm {GL}}_n)$
is compatible with
$D(\operatorname {\mathrm {GL}}_n)$
is compatible with
 $\mathcal {GC}(\mathbf {\Gamma })$
.
$\mathcal {GC}(\mathbf {\Gamma })$
.
For the trivial
![]() $\mathbf {\Gamma }^r$
and
$\mathbf {\Gamma }^r$
and
![]() $\mathbf {\Gamma }^c$
, the theorem was proved in [Reference Gekhtman, Shapiro and Vainshtein18] (we refer to the corresponding generalized cluster structure
$\mathbf {\Gamma }^c$
, the theorem was proved in [Reference Gekhtman, Shapiro and Vainshtein18] (we refer to the corresponding generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
as the standard one). When
$\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
as the standard one). When
![]() $\mathbf {\Gamma }^r = \mathbf {\Gamma }^c$
, the group
$\mathbf {\Gamma }^r = \mathbf {\Gamma }^c$
, the group
![]() $D(\operatorname {\mathrm {GL}}_n)$
together with its Poisson structure is the Drinfeld double of
$D(\operatorname {\mathrm {GL}}_n)$
together with its Poisson structure is the Drinfeld double of
![]() $\operatorname {\mathrm {GL}}_n$
. By default, we work over the field of complex numbers
$\operatorname {\mathrm {GL}}_n$
. By default, we work over the field of complex numbers
![]() $\mathbb {C}$
(however, the results hold over
$\mathbb {C}$
(however, the results hold over
![]() $\mathbb {R}$
for the same class of Poisson brackets). The initial seed is described in Section 3 (a rough description is available below). The proof of Theorem 1.1 is contained in Sections 4–8. In Section 4, we prove that all cluster variables in the seeds adjacent to the initial one are regular functions. In Section 5, we prove Part (ii) by induction on the size
$\mathbb {R}$
for the same class of Poisson brackets). The initial seed is described in Section 3 (a rough description is available below). The proof of Theorem 1.1 is contained in Sections 4–8. In Section 4, we prove that all cluster variables in the seeds adjacent to the initial one are regular functions. In Section 5, we prove Part (ii) by induction on the size
![]() $|\Gamma _1^r| + |\Gamma _1^c|$
. The step of the induction employs the construction of certain birational quasi-isomorphisms introduced in [Reference Gekhtman, Shapiro and Vainshtein20] (i.e., quasi-isomorphisms in the sense of [Reference Fraser12] that are also birational isomorphisms of the underlying varieties). Section 6 is devoted to Part (iii), and in Sections 7 and 8 we prove Part (iv) via a direct computation. A similar result holds in the case of
$|\Gamma _1^r| + |\Gamma _1^c|$
. The step of the induction employs the construction of certain birational quasi-isomorphisms introduced in [Reference Gekhtman, Shapiro and Vainshtein20] (i.e., quasi-isomorphisms in the sense of [Reference Fraser12] that are also birational isomorphisms of the underlying varieties). Section 6 is devoted to Part (iii), and in Sections 7 and 8 we prove Part (iv) via a direct computation. A similar result holds in the case of
![]() $D(\operatorname {\mathrm {SL}}_n)$
:
$D(\operatorname {\mathrm {SL}}_n)$
:
Theorem 1.2. Let
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be a pair of aperiodic oriented Belavin–Drinfeld triples. There exists a generalized cluster structure
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be a pair of aperiodic oriented Belavin–Drinfeld triples. There exists a generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma })$
on
$\mathcal {GC}(\mathbf {\Gamma })$
on
![]() $D(\operatorname {\mathrm {SL}}_n) = \operatorname {\mathrm {SL}}_n \times \operatorname {\mathrm {SL}}_n$
such that
$D(\operatorname {\mathrm {SL}}_n) = \operatorname {\mathrm {SL}}_n \times \operatorname {\mathrm {SL}}_n$
such that
-
(i) The number of stable variables is
 $k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c} + (n-1)$
, and the exchange matrix has full rank;
$k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c} + (n-1)$
, and the exchange matrix has full rank; -
(ii) The generalized cluster structure
 $\mathcal {GC}(\mathbf {\Gamma })$
is regular, and the ring of regular functions
$\mathcal {GC}(\mathbf {\Gamma })$
is regular, and the ring of regular functions
 $\mathcal {O}(D(\operatorname {\mathrm {SL}}_n))$
is naturally isomorphic to the upper cluster algebra
$\mathcal {O}(D(\operatorname {\mathrm {SL}}_n))$
is naturally isomorphic to the upper cluster algebra
 $\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
;
$\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
; -
(iii) The global toric action of
 $(\mathbb {C}^*)^{k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c}}$
on
$(\mathbb {C}^*)^{k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c}}$
on
 $\mathcal {GC}(\mathbf {\Gamma })$
is induced by the left action of
$\mathcal {GC}(\mathbf {\Gamma })$
is induced by the left action of
 $\mathcal {H}_{\mathbf {\Gamma }^r}$
and the right action of
$\mathcal {H}_{\mathbf {\Gamma }^r}$
and the right action of
 $\mathcal {H}_{\mathbf {\Gamma }^c}$
on
$\mathcal {H}_{\mathbf {\Gamma }^c}$
on
 $D(\operatorname {\mathrm {SL}}_n)$
;
$D(\operatorname {\mathrm {SL}}_n)$
; -
(iv) Any Poisson bracket defined by the pair
 $\mathbf {\Gamma }$
on
$\mathbf {\Gamma }$
on
 $D(\operatorname {\mathrm {SL}}_n)$
is compatible with
$D(\operatorname {\mathrm {SL}}_n)$
is compatible with
 $\mathcal {GC}(\mathbf {\Gamma })$
.
$\mathcal {GC}(\mathbf {\Gamma })$
.
In Section 9, we show how to derive Theorem 1.2 from Theorem 1.1, and in Section 10 we provide a few examples of the generalized cluster structures studied in this paper.
A rough description of the initial extended seed
The construction of the initial quiver consists of two parts: First, we construct the initial quiver for the case of the trivial
![]() $\mathbf {\Gamma }$
(this was described in [Reference Gekhtman, Shapiro and Vainshtein18]); second, for each root in
$\mathbf {\Gamma }$
(this was described in [Reference Gekhtman, Shapiro and Vainshtein18]); second, for each root in
![]() $\Gamma ^r_1$
and
$\Gamma ^r_1$
and
![]() $\Gamma ^c_2$
, we add three additional arrows (see Figure 12). The initial extended cluster consists of five types of regular functions: c-functions,
$\Gamma ^c_2$
, we add three additional arrows (see Figure 12). The initial extended cluster consists of five types of regular functions: c-functions,
![]() $\varphi $
-functions, f-functions, g-functions and h-functions. The c-,
$\varphi $
-functions, f-functions, g-functions and h-functions. The c-,
![]() $\varphi $
- and f-functions were constructed in [Reference Gekhtman, Shapiro and Vainshtein18] and are the same for any choice of
$\varphi $
- and f-functions were constructed in [Reference Gekhtman, Shapiro and Vainshtein18] and are the same for any choice of
![]() $\mathbf {\Gamma }$
. More specifically, the c-functions comprise
$\mathbf {\Gamma }$
. More specifically, the c-functions comprise
![]() $n-1$
CasimirsFootnote
1
of the given Poisson bracket which also serve as isolated frozen variables, and the
$n-1$
CasimirsFootnote
1
of the given Poisson bracket which also serve as isolated frozen variables, and the
![]() $\varphi $
- and f-functions are
$\varphi $
- and f-functions are
![]() $(n-1)n/2$
and
$(n-1)n/2$
and
![]() $(n-1)(n-2)/2$
cluster variables that satisfy the following invariance properties:
$(n-1)(n-2)/2$
cluster variables that satisfy the following invariance properties:
where
![]() $(X,Y)$
are the standard coordinates on
$(X,Y)$
are the standard coordinates on
![]() $D(\operatorname {\mathrm {GL}}_n)$
,
$D(\operatorname {\mathrm {GL}}_n)$
,
![]() $N_+$
is any unipotent upper triangular matrix,
$N_+$
is any unipotent upper triangular matrix,
![]() $N_-$
and
$N_-$
and
![]() $N_-^{\prime }$
are unipotent lower triangular matrices, A is any invertible matrix and
$N_-^{\prime }$
are unipotent lower triangular matrices, A is any invertible matrix and
![]() $\varphi (X,Y) = (\det X)^m\tilde {\varphi }(X,Y)$
for some number m that depends on
$\varphi (X,Y) = (\det X)^m\tilde {\varphi }(X,Y)$
for some number m that depends on
![]() $\varphi $
. Furthermore, for any BD data, the initial seed also contains the g-functions
$\varphi $
. Furthermore, for any BD data, the initial seed also contains the g-functions
![]() $\det X^{[i,n]}_{[i,n]}$
and the h-functions
$\det X^{[i,n]}_{[i,n]}$
and the h-functions
![]() $\det Y^{[i,n]}_{[i,n]}$
,
$\det Y^{[i,n]}_{[i,n]}$
,
![]() $1 \leq i \leq n$
(
$1 \leq i \leq n$
(
![]() $\det X$
and
$\det X$
and
![]() $\det Y$
are both frozen variables). All the other g- and h-functions are constructed via a combinatorial procedure based on the given root data
$\det Y$
are both frozen variables). All the other g- and h-functions are constructed via a combinatorial procedure based on the given root data
![]() $\mathbf {\Gamma }$
(there are
$\mathbf {\Gamma }$
(there are
![]() $n(n+1)/2 \ g$
-functions and
$n(n+1)/2 \ g$
-functions and
![]() $n(n+1)/2 \ h$
-functions). As in [Reference Gekhtman, Shapiro and Vainshtein20], we construct a list of so-called
$n(n+1)/2 \ h$
-functions). As in [Reference Gekhtman, Shapiro and Vainshtein20], we construct a list of so-called
![]() $\mathcal {L}$
-matrices, and then we set the g- and h-functions to be the trailing minors of the
$\mathcal {L}$
-matrices, and then we set the g- and h-functions to be the trailing minors of the
![]() $\mathcal {L}$
-matrices. The determinants of
$\mathcal {L}$
-matrices. The determinants of
![]() $\mathcal {L}$
-matrices are declared to be frozen variables. If we let
$\mathcal {L}$
-matrices are declared to be frozen variables. If we let
![]() $\psi $
to be any g- or h-variable, then it satisfies the following invariance properties:
$\psi $
to be any g- or h-variable, then it satisfies the following invariance properties:
where
![]() $\tilde {\gamma }_r$
and
$\tilde {\gamma }_r$
and
![]() $\tilde {\gamma }_c^*$
are group lifts of the Belavin–Drinfeld maps
$\tilde {\gamma }_c^*$
are group lifts of the Belavin–Drinfeld maps
![]() $\gamma _r$
and
$\gamma _r$
and
![]() $\gamma _c^*$
associated with
$\gamma _c^*$
associated with
![]() $\mathbf {\Gamma }^r$
and
$\mathbf {\Gamma }^r$
and
![]() $\mathbf {\Gamma }^c$
, respectively. The combinatorial construction relies on the nilpotency of the map
$\mathbf {\Gamma }^c$
, respectively. The combinatorial construction relies on the nilpotency of the map
![]() $\gamma _c^{-1}w_0\gamma _rw_0$
, where
$\gamma _c^{-1}w_0\gamma _rw_0$
, where
![]() $w_0$
is the longest Weyl group element. When
$w_0$
is the longest Weyl group element. When
![]() $\gamma _c^{-1} w_0 \gamma _r w_0$
is not nilpotent, the
$\gamma _c^{-1} w_0 \gamma _r w_0$
is not nilpotent, the
![]() $\mathcal {L}$
-matrices become infinite, so a different procedure has to be applied (one such example was studied in [Reference Gekhtman, Shapiro and Vainshtein19]). See Section 10 for some examples of
$\mathcal {L}$
-matrices become infinite, so a different procedure has to be applied (one such example was studied in [Reference Gekhtman, Shapiro and Vainshtein19]). See Section 10 for some examples of
![]() $\mathcal {L}$
-matrices and initial quivers.
$\mathcal {L}$
-matrices and initial quivers.
Future work
As explained in Remark 3.7 in [Reference Gekhtman, Shapiro and Vainshtein20], the authors of the conjecture have already identified generalized cluster structures in type A for any Belavin–Drinfeld data. However, there is a lack of tools for producing proofs. One new tool was introduced in [Reference Gekhtman, Shapiro and Vainshtein20], which consists in considering birational quasi-isomorphisms between different cluster structures and which significantly reduced labor in showing that the upper cluster algebra is naturally isomorphic to the algebra of regular functions. However, there’s yet no better tool for proving the compatibility with a Poisson bracket except a tedious and direct computation. We hope that the constructed birational quasi-isomorphisms might be used for proving log-canonicity as well, but this idea is still under development. Furthermore, Schrader and Shapiro recently in [Reference Schrader and Shapiro25] have embedded the quantum group
![]() $U_q(\operatorname {\mathrm {sl}}_n)$
into a quantum cluster
$U_q(\operatorname {\mathrm {sl}}_n)$
into a quantum cluster
![]() $\mathcal {X}$
-algebra introduced by Fock and Goncharov in [Reference Fock and Goncharov10]. As noted in [Reference Schrader and Shapiro25], one should be able to embed
$\mathcal {X}$
-algebra introduced by Fock and Goncharov in [Reference Fock and Goncharov10]. As noted in [Reference Schrader and Shapiro25], one should be able to embed
![]() $U_q(\operatorname {\mathrm {sl}}_n)$
into a quantum cluster
$U_q(\operatorname {\mathrm {sl}}_n)$
into a quantum cluster
![]() $\mathcal {A}$
-algebra in the sense of Berenstein and Zelevinsky [Reference Berenstein and Zelevinsky4], which is suggested by the existence of a generalized cluster structure on the dual group
$\mathcal {A}$
-algebra in the sense of Berenstein and Zelevinsky [Reference Berenstein and Zelevinsky4], which is suggested by the existence of a generalized cluster structure on the dual group
![]() $\operatorname {\mathrm {SL}}_n^*$
from [Reference Gekhtman, Shapiro and Vainshtein18]. We plan to address the question about
$\operatorname {\mathrm {SL}}_n^*$
from [Reference Gekhtman, Shapiro and Vainshtein18]. We plan to address the question about
![]() $\mathcal {A}$
-cluster realization of
$\mathcal {A}$
-cluster realization of
![]() $U_q(\operatorname {\mathrm {sl}}_n)$
, as well as the question of existence of other generalized cluster structures on
$U_q(\operatorname {\mathrm {sl}}_n)$
, as well as the question of existence of other generalized cluster structures on
![]() $\operatorname {\mathrm {SL}}_n^*$
in our future work.
$\operatorname {\mathrm {SL}}_n^*$
in our future work.
Software
During the course of working on this paper, we have developed a Matlab application that is able to produce the initial seed of any generalized cluster structure presented in the paper and which provides various tools for manipulating the quiver and the associated functions. It also presents some tools for working with Poisson brackets. The software is freely available under MIT license on the author’s GitHub repository: https://github.com/Grabovskii/GenClustGLn.
2 Background
2.1 Generalized cluster structures
In this section, we briefly recall the main definitions and propositions of the generalized cluster algebras theory from [Reference Gekhtman, Shapiro and Vainshtein18], which constitute a generalization of cluster algebras of geometric type invented by Fomin and Zelevinsky in [Reference Fomin and Zelevinsky14]. Throughout this section, let
![]() $\mathcal {F}$
be a field of rational functions in
$\mathcal {F}$
be a field of rational functions in
![]() $N+M$
independent variables with coefficients in
$N+M$
independent variables with coefficients in
![]() $\mathbb {Q}$
. Fix an algebraically independent set
$\mathbb {Q}$
. Fix an algebraically independent set
![]() $x_{N+1},\ldots , x_{N+M} \in \mathcal {F}$
over
$x_{N+1},\ldots , x_{N+M} \in \mathcal {F}$
over
![]() $\mathbb {Q}$
and call its elements stable (or frozen) variables.
$\mathbb {Q}$
and call its elements stable (or frozen) variables.
Seeds
To define a seed, we first define the following data:
-
• Let
 $\tilde {B} = (b_{ij})$
be an
$\tilde {B} = (b_{ij})$
be an
 $N\times (N+M)$
integer matrix whose principal part B is skew-symmetrizable (recall that the principal part of a matrix is its leading square submatrix). The matrices B and
$N\times (N+M)$
integer matrix whose principal part B is skew-symmetrizable (recall that the principal part of a matrix is its leading square submatrix). The matrices B and
 $\tilde {B}$
are called the exchange matrix and the extended exchange matrix, respectively;
$\tilde {B}$
are called the exchange matrix and the extended exchange matrix, respectively; -
• Let
 $x_1,\ldots , x_N$
be an algebraically independent subset of
$x_1,\ldots , x_N$
be an algebraically independent subset of
 $\mathcal {F}$
over
$\mathcal {F}$
over
 $\mathbb {Q}$
such that the elements
$\mathbb {Q}$
such that the elements
 $x_1,\ldots ,x_N,\ldots ,x_{N+M}$
generate the field
$x_1,\ldots ,x_N,\ldots ,x_{N+M}$
generate the field
 $\mathcal {F}$
. The elements
$\mathcal {F}$
. The elements
 $x_1,\ldots ,x_N$
are called cluster variables, and the tuples
$x_1,\ldots ,x_N$
are called cluster variables, and the tuples
 $\mathbf {x} := (x_1,\ldots ,x_N)$
and
$\mathbf {x} := (x_1,\ldots ,x_N)$
and
 $\tilde {\mathbf {x}} := (x_1,\ldots ,x_{N+M})$
are called a cluster and an extended cluster, respectively;
$\tilde {\mathbf {x}} := (x_1,\ldots ,x_{N+M})$
are called a cluster and an extended cluster, respectively; -
• For every
 $1 \leq i \leq N$
, let
$1 \leq i \leq N$
, let
 $d_i$
be a factor of
$d_i$
be a factor of
 $\gcd (b_{ij} \ | \ 1 \leq j \leq N)$
. The ith string
$\gcd (b_{ij} \ | \ 1 \leq j \leq N)$
. The ith string
 $p_i$
is a tuple
$p_i$
is a tuple
 $p_i := (p_{ir})_{0 \leq r \leq d_i}$
, where each
$p_i := (p_{ir})_{0 \leq r \leq d_i}$
, where each
 $p_{ir}$
is a monomial in the stable variables with an integer coefficient and such that
$p_{ir}$
is a monomial in the stable variables with an integer coefficient and such that
 $p_{i0} = p_{id_i} = 1$
. The ith string is called trivial if
$p_{i0} = p_{id_i} = 1$
. The ith string is called trivial if
 $d_i = 1$
. Set
$d_i = 1$
. Set
 $\mathcal {P} := \{ p_i \ | \ 1 \leq i \leq N\}$
.
$\mathcal {P} := \{ p_i \ | \ 1 \leq i \leq N\}$
.
Now, a seed is
![]() $\Sigma := (\mathbf {x}, \tilde {B}, \mathcal {P})$
and an extended seed is
$\Sigma := (\mathbf {x}, \tilde {B}, \mathcal {P})$
and an extended seed is
![]() $\tilde {\Sigma } := (\tilde {\mathbf {x}}, \tilde {B}, \mathcal {P})$
. In practice, one additionally names one of the seeds as the initial seed.
$\tilde {\Sigma } := (\tilde {\mathbf {x}}, \tilde {B}, \mathcal {P})$
. In practice, one additionally names one of the seeds as the initial seed.
Generalized cluster mutations
Let
![]() $\Sigma = (\mathbf {x}, \tilde {B},\mathcal {P})$
be a seed constructed via the recipe from the previous paragraph. A generalized cluster mutation in direction k produces a seed
$\Sigma = (\mathbf {x}, \tilde {B},\mathcal {P})$
be a seed constructed via the recipe from the previous paragraph. A generalized cluster mutation in direction k produces a seed
![]() $\Sigma ^{\prime } = (\mathbf {x}^{\prime }, \tilde {B}^{\prime }, \mathcal {P}^{\prime })$
that is constructed as follows.
$\Sigma ^{\prime } = (\mathbf {x}^{\prime }, \tilde {B}^{\prime }, \mathcal {P}^{\prime })$
that is constructed as follows.
-
• Define cluster
 $\tau $
-monomials
$\tau $
-monomials
 $u_{k;>}$
and
$u_{k;>}$
and
 $u_{k;<}$
,
$u_{k;<}$
,
 $1 \leq k \leq N$
, via and stable
$1 \leq k \leq N$
, via and stable $$\begin{align*}u_{k;>} := \prod_{\substack{1 \leq i \leq N, \\ b_{ki} > 0}} x_{i}^{b_{ki}/d_k}, \ \ u_{k;<} := \prod_{\substack{1 \leq i \leq N, \\ b_{ki} < 0}} x_{i}^{-b_{ki}/d_k}, \end{align*}$$
$$\begin{align*}u_{k;>} := \prod_{\substack{1 \leq i \leq N, \\ b_{ki} > 0}} x_{i}^{b_{ki}/d_k}, \ \ u_{k;<} := \prod_{\substack{1 \leq i \leq N, \\ b_{ki} < 0}} x_{i}^{-b_{ki}/d_k}, \end{align*}$$
 $\tau $
-monomials
$\tau $
-monomials
 $v_{k;>}^{[r]}$
and
$v_{k;>}^{[r]}$
and
 $v_{k;<}^{[r]}$
,
$v_{k;<}^{[r]}$
,
 $1 \leq k \leq N$
,
$1 \leq k \leq N$
,
 $0 \leq r \leq d_k$
, as where the product over an empty set by definition equals
$0 \leq r \leq d_k$
, as where the product over an empty set by definition equals $$\begin{align*}v_{k;>}^{[r]} := \prod_{\substack{N+1\leq i \leq N+M,\\ b_{ki} > 0}} x_i^{\lfloor rb_{ki}/d_k \rfloor}, \ \ v_{k;<}^{[r]} := \prod_{\substack{N+1 \leq i \leq N+M,\\ b_{ki} < 0}} x_i^{\lfloor-rb_{ki}/d_k\rfloor}, \end{align*}$$
$$\begin{align*}v_{k;>}^{[r]} := \prod_{\substack{N+1\leq i \leq N+M,\\ b_{ki} > 0}} x_i^{\lfloor rb_{ki}/d_k \rfloor}, \ \ v_{k;<}^{[r]} := \prod_{\substack{N+1 \leq i \leq N+M,\\ b_{ki} < 0}} x_i^{\lfloor-rb_{ki}/d_k\rfloor}, \end{align*}$$
 $1$
and
$1$
and
 $\lfloor m \rfloor $
denotes the floor of a number
$\lfloor m \rfloor $
denotes the floor of a number
 $m \in \mathbb {Z}$
. Define
$m \in \mathbb {Z}$
. Define
 $x_k^{\prime }$
via the generalized exchange relation (2.1)and set
$x_k^{\prime }$
via the generalized exchange relation (2.1)and set $$ \begin{align} x_k x_k^{\prime} := \sum_{r=0}^{d_k} p_{kr} u_{k;>}^{r} v_{k;>}^{[r]} u_{k;<}^{d_k-r} v_{k;<}^{[d_k-r]}, \end{align} $$
$$ \begin{align} x_k x_k^{\prime} := \sum_{r=0}^{d_k} p_{kr} u_{k;>}^{r} v_{k;>}^{[r]} u_{k;<}^{d_k-r} v_{k;<}^{[d_k-r]}, \end{align} $$
 $\mathbf {x}^{\prime } := (\mathbf {x} \setminus \{x_k\}) \cup \{x_k^{\prime }\}$
.
$\mathbf {x}^{\prime } := (\mathbf {x} \setminus \{x_k\}) \cup \{x_k^{\prime }\}$
.
-
• The matrix entries
 $b_{ij}^{\prime }$
of
$b_{ij}^{\prime }$
of
 $\tilde {B}^{\prime }$
are defined as
$\tilde {B}^{\prime }$
are defined as  $$\begin{align*}b_{ij}^{\prime} := \begin{cases} -b_{ij} \ \ &\text{if } i=k \text{ or }j=k;\\ b_{ij} + \dfrac{|b_{ik}|b_{kj} + b_{ik} |b_{kj}|}{2} \ \ &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}b_{ij}^{\prime} := \begin{cases} -b_{ij} \ \ &\text{if } i=k \text{ or }j=k;\\ b_{ij} + \dfrac{|b_{ik}|b_{kj} + b_{ik} |b_{kj}|}{2} \ \ &\text{otherwise.} \end{cases} \end{align*}$$
-
• The strings
 $p_i^{\prime } \in \mathcal {P}^{\prime }$
are given by the exchange coefficient mutation
$p_i^{\prime } \in \mathcal {P}^{\prime }$
are given by the exchange coefficient mutation  $$\begin{align*}p_{ir}^{\prime} := \begin{cases} p_{i,d_i-r} \ \ &\text{if }i = k; \\ p_{ir} \ \ &\text{otherwise.}\end{cases} \end{align*}$$
$$\begin{align*}p_{ir}^{\prime} := \begin{cases} p_{i,d_i-r} \ \ &\text{if }i = k; \\ p_{ir} \ \ &\text{otherwise.}\end{cases} \end{align*}$$
The seeds
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma ^{\prime }$
are also called adjacent. A few comments on the definition:
$\Sigma ^{\prime }$
are also called adjacent. A few comments on the definition:
-
1) Call a cluster variable
 $x_i$
isolated if
$x_i$
isolated if
 $b_{ij} = 0$
for all
$b_{ij} = 0$
for all
 $1 \leq j \leq N+M$
. The definition of
$1 \leq j \leq N+M$
. The definition of
 $b_{ij}^{\prime }$
implies that a mutation preserves the property of being isolated;
$b_{ij}^{\prime }$
implies that a mutation preserves the property of being isolated; -
2) Since
 $\gcd \{b_{ij} \ | \ 1 \leq j \leq N\} = \gcd \{b_{ij}^{\prime } \ | \ 1 \leq j \leq N\}$
, the numbers
$\gcd \{b_{ij} \ | \ 1 \leq j \leq N\} = \gcd \{b_{ij}^{\prime } \ | \ 1 \leq j \leq N\}$
, the numbers
 $d_1,\ldots , d_N$
retain their defining property after a mutation is performed;
$d_1,\ldots , d_N$
retain their defining property after a mutation is performed; -
3) If a string
 $p_k$
is trivial, then the generalized exchange relation in equation (2.1) becomes the exchange relation from the ordinary cluster theory of geometric type: (2.2)In fact, the generalized cluster structures studied in this paper have only one nontrivial string, hence all exchange relations except one are ordinary.
$p_k$
is trivial, then the generalized exchange relation in equation (2.1) becomes the exchange relation from the ordinary cluster theory of geometric type: (2.2)In fact, the generalized cluster structures studied in this paper have only one nontrivial string, hence all exchange relations except one are ordinary. $$ \begin{align} x_k x_k^{\prime} = \prod_{\substack{1 \leq i \leq N+M\\ b_{ki>0}}} x_i^{b_{ki}} + \prod_{\substack{1 \leq i \leq N+M\\ b_{ki<0}}} x_i^{-b_{ki}}. \end{align} $$
$$ \begin{align} x_k x_k^{\prime} = \prod_{\substack{1 \leq i \leq N+M\\ b_{ki>0}}} x_i^{b_{ki}} + \prod_{\substack{1 \leq i \leq N+M\\ b_{ki<0}}} x_i^{-b_{ki}}. \end{align} $$
-
4) The generalized exchange relation can also be written in the following form. For any i, denote
 $v_{i;>} := v_{i;>}^{[d_i]}$
,
$v_{i;>} := v_{i;>}^{[d_i]}$
,
 $v_{i;<} := v_{i;<}^{[d_i]}$
; set Note that the mutation rule for
$v_{i;<} := v_{i;<}^{[d_i]}$
; set Note that the mutation rule for $$\begin{align*}q_{ir} := \frac{v_{i;>}^r v_{i; < }^{d_i-r}}{(v_{i;>}^{[r]} v_{i;<}^{[d_i-r]})^{d_i}}, \ \ \hat{p}_{ir} := \frac{p_{ir}^{d_i}}{q_{ir}}, \ \ 1 \leq i \leq N,\ 0 \leq r \leq d_i. \end{align*}$$
$$\begin{align*}q_{ir} := \frac{v_{i;>}^r v_{i; < }^{d_i-r}}{(v_{i;>}^{[r]} v_{i;<}^{[d_i-r]})^{d_i}}, \ \ \hat{p}_{ir} := \frac{p_{ir}^{d_i}}{q_{ir}}, \ \ 1 \leq i \leq N,\ 0 \leq r \leq d_i. \end{align*}$$
 $\hat {p}_{ir}$
is the same as for
$\hat {p}_{ir}$
is the same as for
 $p_{ir}$
. Now, equation (2.1) becomes The expression
$p_{ir}$
. Now, equation (2.1) becomes The expression $$\begin{align*}x_k x_k^{\prime} = \sum_{r=0}^{d_k} (\hat{p}_{kr} v_{k;>}^r v_{k;<}^{d_k-r})^{1/d_k} u_{k;>}^r u_{k;<}^{d_k-r}. \end{align*}$$
$$\begin{align*}x_k x_k^{\prime} = \sum_{r=0}^{d_k} (\hat{p}_{kr} v_{k;>}^r v_{k;<}^{d_k-r})^{1/d_k} u_{k;>}^r u_{k;<}^{d_k-r}. \end{align*}$$
 $(\hat {p}_{kr} v_{k;>}^r v_{k;<}^{d_k-r})^{1/d_k}$
is a monomial in the stable variables.
$(\hat {p}_{kr} v_{k;>}^r v_{k;<}^{d_k-r})^{1/d_k}$
is a monomial in the stable variables.
Generalized cluster structure
Two seeds
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma ^{\prime }$
are called mutation equivalent if there’s a sequence
$\Sigma ^{\prime }$
are called mutation equivalent if there’s a sequence
![]() $\Sigma _1, \ldots , \Sigma _m$
such that
$\Sigma _1, \ldots , \Sigma _m$
such that
![]() $\Sigma _1 = \Sigma $
,
$\Sigma _1 = \Sigma $
,
![]() $\Sigma _m = \Sigma ^{\prime }$
and such that
$\Sigma _m = \Sigma ^{\prime }$
and such that
![]() $\Sigma _{i+1}$
and
$\Sigma _{i+1}$
and
![]() $\Sigma _i$
are adjacent for each i. For a fixed seed
$\Sigma _i$
are adjacent for each i. For a fixed seed
![]() $\Sigma $
, the set of all seeds that are mutation equivalent to
$\Sigma $
, the set of all seeds that are mutation equivalent to
![]() $\Sigma $
is called the generalized cluster structure and is denoted as
$\Sigma $
is called the generalized cluster structure and is denoted as
![]() $\mathcal {GC}(\Sigma )$
or simply
$\mathcal {GC}(\Sigma )$
or simply
![]() $\mathcal {GC}$
.
$\mathcal {GC}$
.
Generalized cluster algebra
Let
![]() $\mathcal {GC}$
be a generalized cluster structure constructed as above. Define
$\mathcal {GC}$
be a generalized cluster structure constructed as above. Define
![]() $\mathbb {A} := \mathbb {Z}[x_{N+1},\ldots ,x_{N+M}]$
and
$\mathbb {A} := \mathbb {Z}[x_{N+1},\ldots ,x_{N+M}]$
and
![]() $\bar {\mathbb {A}} := \mathbb {Z}[x_{N+1}^{\pm 1},\ldots , x_{N+M}^{\pm 1}]$
. Choose a ground ring
$\bar {\mathbb {A}} := \mathbb {Z}[x_{N+1}^{\pm 1},\ldots , x_{N+M}^{\pm 1}]$
. Choose a ground ring
![]() $\hat {\mathbb {A}}$
, which is a subring of
$\hat {\mathbb {A}}$
, which is a subring of
![]() $\bar {\mathbb {A}}$
that contains
$\bar {\mathbb {A}}$
that contains
![]() $\mathbb {A}$
. The
$\mathbb {A}$
. The
![]() $\hat {\mathbb {A}}$
-subalgebra of
$\hat {\mathbb {A}}$
-subalgebra of
![]() $\mathcal {F}$
given by
$\mathcal {F}$
given by
is called the generalized cluster algebra. For any seed
![]() $\Sigma := ((x_1,\ldots ,x_{N}),\tilde {B},\mathcal {P})$
, set
$\Sigma := ((x_1,\ldots ,x_{N}),\tilde {B},\mathcal {P})$
, set
to be the ring of Laurent polynomials associated with
![]() $\Sigma $
, and define
$\Sigma $
, and define
The algebra
![]() $\bar {\mathcal {A}}$
is called the generalized upper cluster algebra. The generalized Laurent phenomenon states that
$\bar {\mathcal {A}}$
is called the generalized upper cluster algebra. The generalized Laurent phenomenon states that
![]() $\mathcal {A} \subseteq \bar {\mathcal {A}}$
.
$\mathcal {A} \subseteq \bar {\mathcal {A}}$
.
Upper bounds
Let
![]() $\mathbb {T}_N$
be a labeled N-regular tree. Associate with each vertex a seed so that adjacent seeds are adjacent in the tree,Footnote
2
and if a seed
$\mathbb {T}_N$
be a labeled N-regular tree. Associate with each vertex a seed so that adjacent seeds are adjacent in the tree,Footnote
2
and if a seed
![]() $\Sigma ^{\prime }$
is adjacent to
$\Sigma ^{\prime }$
is adjacent to
![]() $\Sigma $
in direction k, label the corresponding edge in the tree with number k. A nerve
$\Sigma $
in direction k, label the corresponding edge in the tree with number k. A nerve
![]() $\mathcal {N}$
in
$\mathcal {N}$
in
![]() $\mathbb {T}_N$
is a subtree on
$\mathbb {T}_N$
is a subtree on
![]() $N+1$
vertices such that all its edges have different labels (for instance, a star is a nerve). An upper bound
$N+1$
vertices such that all its edges have different labels (for instance, a star is a nerve). An upper bound
![]() $\bar {\mathcal {A}}(\mathcal {N})$
is defined as the algebra
$\bar {\mathcal {A}}(\mathcal {N})$
is defined as the algebra
where
![]() $V(\mathcal {N})$
stands for the vertex set of
$V(\mathcal {N})$
stands for the vertex set of
![]() $\mathcal {N}$
. Upper bounds were first defined and studied in [Reference Berenstein, Fomin and Zelevinsky3]. Let L be the number of isolated variables in
$\mathcal {N}$
. Upper bounds were first defined and studied in [Reference Berenstein, Fomin and Zelevinsky3]. Let L be the number of isolated variables in
![]() $\mathcal {GC}$
. For the ith nontrivial string in
$\mathcal {GC}$
. For the ith nontrivial string in
![]() $\mathcal {P}$
, let
$\mathcal {P}$
, let
![]() $\tilde {B}(i)$
be a
$\tilde {B}(i)$
be a
![]() $(d_{i}-1) \times L$
matrix such that the rth row consists of the exponents of the isolated variables in
$(d_{i}-1) \times L$
matrix such that the rth row consists of the exponents of the isolated variables in
![]() $p_{ir}$
(recall that
$p_{ir}$
(recall that
![]() $p_{ir}$
is a monomial in the stable variables). The following result was proved in [Reference Gekhtman, Shapiro and Vainshtein18].
$p_{ir}$
is a monomial in the stable variables). The following result was proved in [Reference Gekhtman, Shapiro and Vainshtein18].
Proposition 2.1. Assume that the extended exchange matrix has full rank, and let
![]() $\operatorname {\mathrm {rank}} \tilde {B}(i) = d_i - 1$
for any nontrivial string in
$\operatorname {\mathrm {rank}} \tilde {B}(i) = d_i - 1$
for any nontrivial string in
![]() $\mathcal {P}$
. Then the upper bounds
$\mathcal {P}$
. Then the upper bounds
![]() $\bar {\mathcal {A}}(\mathcal {N})$
do not depend on the choice of
$\bar {\mathcal {A}}(\mathcal {N})$
do not depend on the choice of
![]() $\mathcal {N}$
and hence coincide with the generalized upper cluster algebra
$\mathcal {N}$
and hence coincide with the generalized upper cluster algebra
![]() $\bar {\mathcal {A}}$
.
$\bar {\mathcal {A}}$
.
Generalized cluster structures on varieties
Let V be a Zariski open subset of
![]() $\mathbb {C}^{N+M}$
,
$\mathbb {C}^{N+M}$
,
![]() $\mathcal {O}(V)$
be the ring of regular functions, and let
$\mathcal {O}(V)$
be the ring of regular functions, and let
![]() $\mathbb {C}(V)$
be the field of rational functions on V. As before, let
$\mathbb {C}(V)$
be the field of rational functions on V. As before, let
![]() $\mathcal {GC}$
be a generalized cluster structure, and assume that
$\mathcal {GC}$
be a generalized cluster structure, and assume that
![]() $f_1,\ldots , f_{N+M}$
is a transcendence basis of
$f_1,\ldots , f_{N+M}$
is a transcendence basis of
![]() $\mathbb {C}(V)$
over
$\mathbb {C}(V)$
over
![]() $\mathbb {C}$
. Pick an extended cluster
$\mathbb {C}$
. Pick an extended cluster
![]() $(x_1,\ldots ,x_{N+M})$
in
$(x_1,\ldots ,x_{N+M})$
in
![]() $\mathcal {GC}$
, and define a field isomorphism
$\mathcal {GC}$
, and define a field isomorphism
![]() $\theta : \mathcal {F}_{\mathbb {C}} \rightarrow \mathbb C(V)$
via
$\theta : \mathcal {F}_{\mathbb {C}} \rightarrow \mathbb C(V)$
via
![]() $\theta : x_i \mapsto f_i$
,
$\theta : x_i \mapsto f_i$
,
![]() $1 \leq i \leq N+M$
, where
$1 \leq i \leq N+M$
, where
![]() $\mathcal {F}_{\mathbb {C}} := \mathcal {F} \otimes \mathbb {C}$
is the extension by complex scalars of
$\mathcal {F}_{\mathbb {C}} := \mathcal {F} \otimes \mathbb {C}$
is the extension by complex scalars of
![]() $\mathcal {F}$
. The pair
$\mathcal {F}$
. The pair
![]() $(\mathcal {GC}, \theta )$
(or sometimes just
$(\mathcal {GC}, \theta )$
(or sometimes just
![]() $\mathcal {GC}$
) is called a generalized cluster structure on V. It’s called regular if
$\mathcal {GC}$
) is called a generalized cluster structure on V. It’s called regular if
![]() $\theta (x)$
is a regular function for every variable x. Choose a ground ring as
$\theta (x)$
is a regular function for every variable x. Choose a ground ring as
where
![]() $\theta (x_{N+i})$
does not vanish on V if and only if
$\theta (x_{N+i})$
does not vanish on V if and only if
![]() $1 \leq i \leq M^{\prime }$
. Set
$1 \leq i \leq M^{\prime }$
. Set
![]() $\mathcal {A}_{\mathbb C} := \mathcal {A} \otimes \mathbb {C}$
and
$\mathcal {A}_{\mathbb C} := \mathcal {A} \otimes \mathbb {C}$
and
![]() $\bar {\mathcal {A}}_{\mathbb C}:= \bar {\mathcal {A}}\otimes \mathbb C$
.
$\bar {\mathcal {A}}_{\mathbb C}:= \bar {\mathcal {A}}\otimes \mathbb C$
.
Proposition 2.2. Let V be a Zariski open subset of
![]() $\mathbb C^{N+M}$
and
$\mathbb C^{N+M}$
and
![]() $(\mathcal {GC},\theta )$
be a generalized cluster structure on V with N cluster and M stable variables. Suppose there exists an extended cluster
$(\mathcal {GC},\theta )$
be a generalized cluster structure on V with N cluster and M stable variables. Suppose there exists an extended cluster
![]() $\tilde {\mathbf {x}} = (x_1,\ldots ,x_{N+M})$
that satisfies the following properties:
$\tilde {\mathbf {x}} = (x_1,\ldots ,x_{N+M})$
that satisfies the following properties:
-
(i) For each
 $1 \leq i \leq N+M$
,
$1 \leq i \leq N+M$
,
 $\theta (x_i)$
is regular on V, and for each
$\theta (x_i)$
is regular on V, and for each
 $1 \leq i \neq j \leq N+M$
,
$1 \leq i \neq j \leq N+M$
,
 $\theta (x_i)$
is coprime with
$\theta (x_i)$
is coprime with
 $\theta (x_j)$
in
$\theta (x_j)$
in
 $\mathcal {O}(V)$
;
$\mathcal {O}(V)$
; -
(ii) For any cluster variable
 $x_k^{\prime }$
obtained via the generalized exchange relation (2.1) applied to
$x_k^{\prime }$
obtained via the generalized exchange relation (2.1) applied to
 $\tilde {\mathbf {x}}$
in direction k,
$\tilde {\mathbf {x}}$
in direction k,
 $\theta (x_k^{\prime })$
is regular on V and coprime with
$\theta (x_k^{\prime })$
is regular on V and coprime with
 $\theta (x_k)$
in
$\theta (x_k)$
in
 $\mathcal {O}(V)$
.
$\mathcal {O}(V)$
.
Then
![]() $(\mathcal {GC},\theta )$
is a regular generalized cluster structure on V. If additionally
$(\mathcal {GC},\theta )$
is a regular generalized cluster structure on V. If additionally
-
(iii) each regular function on V belongs to
 $\theta (\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}))$
,
$\theta (\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}))$
,
then
![]() $\theta $
is an isomorphism between
$\theta $
is an isomorphism between
![]() $\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC})$
and
$\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC})$
and
![]() $\mathcal {O}(V)$
.
$\mathcal {O}(V)$
.
In the case of ordinary cluster structures, the proof of Proposition 2.2 is available in [Reference Gekhtman, Shapiro and Vainshtein15] (Proposition 3.37) and in a more general setup in [Reference Fomin, Williams and Zelevinsky13] (Proposition 6.4.1). As explained in [Reference Gekhtman, Shapiro and Vainshtein18], Proposition 2.2 is a direct corollary of a natural extension of Proposition 3.6 in [Reference Fomin and Pylyavskyy11] to the case of generalized cluster structures. When
![]() $\theta $
is an isomorphism between
$\theta $
is an isomorphism between
![]() $\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC})$
and
$\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC})$
and
![]() $\mathcal {O}(V)$
, these algebras are also said to be naturally isomorphic. A practical way of verifying Condition 2.2 of Proposition 2.2 is based on Proposition 2.1.
$\mathcal {O}(V)$
, these algebras are also said to be naturally isomorphic. A practical way of verifying Condition 2.2 of Proposition 2.2 is based on Proposition 2.1.
Poisson structures in
 $\mathcal {GC}$
$\mathcal {GC}$
Let
![]() $\{\cdot , \cdot \}$
be a Poisson bracket on
$\{\cdot , \cdot \}$
be a Poisson bracket on
![]() $\mathcal {F}$
(or on
$\mathcal {F}$
(or on
![]() $\mathcal {F}_{\mathbb {C}}$
), and let
$\mathcal {F}_{\mathbb {C}}$
), and let
![]() $\tilde {\mathbf {x}}$
be any extended cluster in
$\tilde {\mathbf {x}}$
be any extended cluster in
![]() $\mathcal {GC}$
. We say that
$\mathcal {GC}$
. We say that
![]() $\tilde {\mathbf {x}}$
is log-canonical if
$\tilde {\mathbf {x}}$
is log-canonical if
![]() $\{x_i,x_j\} = \omega _{ij} x_i x_j$
for all
$\{x_i,x_j\} = \omega _{ij} x_i x_j$
for all
![]() $1 \leq i,j \leq N+M$
, where
$1 \leq i,j \leq N+M$
, where
![]() $\omega _{ij} \in \mathbb {Q}$
(or
$\omega _{ij} \in \mathbb {Q}$
(or
![]() $\omega _{ij} \in \mathbb {C}$
for
$\omega _{ij} \in \mathbb {C}$
for
![]() $\mathcal {F}_{\mathbb C}$
). We call the generalized cluster structure compatible with the bracket if any extended cluster in
$\mathcal {F}_{\mathbb C}$
). We call the generalized cluster structure compatible with the bracket if any extended cluster in
![]() $\mathcal {GC}$
is log-canonical. Let
$\mathcal {GC}$
is log-canonical. Let
![]() $\Omega :=(\omega _{ij})_{i,j=1}^{N+M}$
be the coefficient matrix of the bracket with respect to the extended cluster
$\Omega :=(\omega _{ij})_{i,j=1}^{N+M}$
be the coefficient matrix of the bracket with respect to the extended cluster
![]() $\tilde {\mathbf {x}}$
. The following proposition is a natural generalization of Theorem 4.5 from [Reference Gekhtman, Shapiro and Vainshtein15].
$\tilde {\mathbf {x}}$
. The following proposition is a natural generalization of Theorem 4.5 from [Reference Gekhtman, Shapiro and Vainshtein15].
Proposition 2.3. Let
![]() $\Sigma = (\tilde {\mathbf {x}}, \tilde {B}, \mathcal {P})$
be an extended seed in
$\Sigma = (\tilde {\mathbf {x}}, \tilde {B}, \mathcal {P})$
be an extended seed in
![]() $\mathcal {F}$
that satisfies the following properties:
$\mathcal {F}$
that satisfies the following properties:
-
(i) The extended cluster
 $\tilde {\mathbf {x}}$
is log-canonical with respect to the bracket;
$\tilde {\mathbf {x}}$
is log-canonical with respect to the bracket; -
(ii) For a diagonal matrix with positive entries D such that
 $DB$
is skew-symmetric, there exists a diagonal
$DB$
is skew-symmetric, there exists a diagonal
 $N \times N$
matrix
$N \times N$
matrix
 $\Delta $
such that
$\Delta $
such that
 $\tilde {B}\Omega = \begin {bmatrix}\Delta & 0\end {bmatrix}$
and such that
$\tilde {B}\Omega = \begin {bmatrix}\Delta & 0\end {bmatrix}$
and such that
 $D\Delta $
is a multiple of the identity matrix;
$D\Delta $
is a multiple of the identity matrix; -
(iii) The Laurent polynomials
 $\hat {p}_{ir}$
are Casimirs of the bracket.
$\hat {p}_{ir}$
are Casimirs of the bracket.
Then any other seed in
![]() $\mathcal {GC}$
satisfies properties i, ii (with the same
$\mathcal {GC}$
satisfies properties i, ii (with the same
![]() $\Delta $
) and iii. In particular,
$\Delta $
) and iii. In particular,
![]() $\mathcal {GC}$
is compatible with
$\mathcal {GC}$
is compatible with
![]() $\{\cdot , \cdot \}$
.
$\{\cdot , \cdot \}$
.
Condition ii has the following interpretation, which is used in practice. For each
![]() $1\leq i \leq N$
, define
$1\leq i \leq N$
, define
![]() $y_i := \prod _{j=1}^{N+M} x_j^{b_{ij}}$
. Then ii is equivalent to
$y_i := \prod _{j=1}^{N+M} x_j^{b_{ij}}$
. Then ii is equivalent to
![]() $\{\log y_i, \log x_j\} = \delta _{ij}\Delta _{ii}$
, where
$\{\log y_i, \log x_j\} = \delta _{ij}\Delta _{ii}$
, where
![]() $\delta _{ij}$
is the Kronecker symbol. The variable
$\delta _{ij}$
is the Kronecker symbol. The variable
![]() $y_i$
is called the y-coordinate of the cluster variable
$y_i$
is called the y-coordinate of the cluster variable
![]() $x_i$
. Note that Condition ii implies that
$x_i$
. Note that Condition ii implies that
![]() $\tilde {B}$
has full rank.
$\tilde {B}$
has full rank.
Toric actions
Given an extended cluster
![]() $(x_1,\ldots ,x_{N+M})$
in
$(x_1,\ldots ,x_{N+M})$
in
![]() $\mathcal {GC}$
, a local toric action (of rank s) is an action
$\mathcal {GC}$
, a local toric action (of rank s) is an action
![]() $\mathcal {F}_{\mathbb {C}} \curvearrowleft (\mathbb {C}^*)^s$
by field automorphisms given on the variables
$\mathcal {F}_{\mathbb {C}} \curvearrowleft (\mathbb {C}^*)^s$
by field automorphisms given on the variables
![]() $x_i$
’s as
$x_i$
’s as
 $$\begin{align*}x_i.(t_1,\ldots,t_s) \mapsto x_i \prod_{j=1}^{s} t_j^{\omega_{ij}}, \ \ \ t_j \in \mathbb{C}^*, \end{align*}$$
$$\begin{align*}x_i.(t_1,\ldots,t_s) \mapsto x_i \prod_{j=1}^{s} t_j^{\omega_{ij}}, \ \ \ t_j \in \mathbb{C}^*, \end{align*}$$
where
![]() $W:= (\omega _{ij})$
is an integer-valued
$W:= (\omega _{ij})$
is an integer-valued
![]() $(N+M) \times s$
matrix of rank s called the weight matrix of the action. We say that two local toric actions of rank s defined on some extended clusters
$(N+M) \times s$
matrix of rank s called the weight matrix of the action. We say that two local toric actions of rank s defined on some extended clusters
![]() $\tilde {\mathbf {x}}$
and
$\tilde {\mathbf {x}}$
and
![]() $\tilde {\mathbf {x}}^{\prime }$
are compatible if the composition of mutations that takes
$\tilde {\mathbf {x}}^{\prime }$
are compatible if the composition of mutations that takes
![]() $\tilde {\mathbf {x}}$
to
$\tilde {\mathbf {x}}$
to
![]() $\tilde {\mathbf {x}}^{\prime }$
intertwines the actions. A collection of pairwise compatible local toric actions of rank s defined for every extended cluster is called a global toric action. We also say that a local toric action is
$\tilde {\mathbf {x}}^{\prime }$
intertwines the actions. A collection of pairwise compatible local toric actions of rank s defined for every extended cluster is called a global toric action. We also say that a local toric action is
![]() $\mathcal {GC}$
-extendable if it belongs to some global toric action.
$\mathcal {GC}$
-extendable if it belongs to some global toric action.
Proposition 2.4. A local toric action with a weight matrix W is uniquely
![]() $\mathcal {GC}$
-extendable to a global toric action if
$\mathcal {GC}$
-extendable to a global toric action if
![]() $\tilde {B}W = 0$
and the Laurent polynomials
$\tilde {B}W = 0$
and the Laurent polynomials
![]() $\hat {p}_{ir}$
are invariant with respect to the action.
$\hat {p}_{ir}$
are invariant with respect to the action.
As noted in [Reference Gekhtman, Shapiro and Vainshtein18], this proposition is a natural extension of Lemma 5.3 in [Reference Gekhtman, Shapiro and Vainshtein15]. For the purposes of this paper, it suffices to assume that
![]() $\hat {p}_{ir}$
are invariant with respect to the action; however, in the case of ordinary cluster structures of geometric type, the statement of the proposition is if and only if.
$\hat {p}_{ir}$
are invariant with respect to the action; however, in the case of ordinary cluster structures of geometric type, the statement of the proposition is if and only if.
Quasi-isomorphisms that arise from global toric actions
Let
![]() $\mathcal {GC}_1(\Sigma _1)$
and
$\mathcal {GC}_1(\Sigma _1)$
and
![]() $\mathcal {GC}_2(\Sigma _2)$
be generalized cluster structures with initial extended seeds
$\mathcal {GC}_2(\Sigma _2)$
be generalized cluster structures with initial extended seeds
![]() $\Sigma _1:=(\tilde {\mathbf {x}}, \tilde {B}_1, \mathcal {P}_1)$
and
$\Sigma _1:=(\tilde {\mathbf {x}}, \tilde {B}_1, \mathcal {P}_1)$
and
![]() $\Sigma _2 := (\tilde {\mathbf {f}}, \tilde {B}_2, \mathcal {P}_2)$
, and let
$\Sigma _2 := (\tilde {\mathbf {f}}, \tilde {B}_2, \mathcal {P}_2)$
, and let
![]() $\mathcal {F}_1$
and
$\mathcal {F}_1$
and
![]() $\mathcal {F}_2$
be the corresponding ambient fields. Assume the following:
$\mathcal {F}_2$
be the corresponding ambient fields. Assume the following:
-
• There is the same number of cluster and stable variables in
 $\tilde {\mathbf {x}}$
and
$\tilde {\mathbf {x}}$
and
 $\tilde {\mathbf {f}}$
;
$\tilde {\mathbf {f}}$
; -
• The numbers
 $d_1,\ldots ,d_N$
from the definition of the generalized cluster structure are equal for both
$d_1,\ldots ,d_N$
from the definition of the generalized cluster structure are equal for both
 $\mathcal {GC}_1$
and
$\mathcal {GC}_1$
and
 $\mathcal {GC}_2$
;
$\mathcal {GC}_2$
; -
• The strings
 $\mathcal {P}_1$
and
$\mathcal {P}_1$
and
 $\mathcal {P}_2$
are the same in the following sense: If one picks
$\mathcal {P}_2$
are the same in the following sense: If one picks
 $p_{ir}$
and substitutes all
$p_{ir}$
and substitutes all
 $x_i$
’s with
$x_i$
’s with
 $f_i$
’s, one obtains the rth component of the ith string from
$f_i$
’s, one obtains the rth component of the ith string from
 $\mathcal {P}_2$
, and vice versa;
$\mathcal {P}_2$
, and vice versa; -
• The extended exchange matrices
 $\tilde {B}_1$
and
$\tilde {B}_1$
and
 $\tilde {B}_2$
are the same in all but the last column, which corresponds to a stable variable;
$\tilde {B}_2$
are the same in all but the last column, which corresponds to a stable variable; -
• There are integer-valued vectors
 $u = (u_1,\ldots ,u_{n+m})^t$
and
$u = (u_1,\ldots ,u_{n+m})^t$
and
 $v = (v_1,\ldots ,v_{n+m})^t$
that define local toric actions (of rank
$v = (v_1,\ldots ,v_{n+m})^t$
that define local toric actions (of rank
 $1$
) on
$1$
) on
 $\tilde {\mathbf {x}}$
and
$\tilde {\mathbf {x}}$
and
 $\tilde {\mathbf {f}}$
, respectively, and they are
$\tilde {\mathbf {f}}$
, respectively, and they are
 $\mathcal {GC}$
-extendable.
$\mathcal {GC}$
-extendable.
Proposition 2.5. Assume that
![]() $\frac {v_i-u_i}{u_{N+M}}$
is an integer for each
$\frac {v_i-u_i}{u_{N+M}}$
is an integer for each
![]() $1 \leq i \leq N+M$
. Define a field isomorphism
$1 \leq i \leq N+M$
. Define a field isomorphism
![]() $\theta :\mathcal {F}_2 \rightarrow \mathcal {F}_1$
on the generators as
$\theta :\mathcal {F}_2 \rightarrow \mathcal {F}_1$
on the generators as
![]() $\theta (f_i):=x_i x_{N+M}^{\left (\frac {v_i-u_i}{u_{N+M}}\right )}$
,
$\theta (f_i):=x_i x_{N+M}^{\left (\frac {v_i-u_i}{u_{N+M}}\right )}$
,
![]() $1 \leq i \leq N+M$
. If
$1 \leq i \leq N+M$
. If
![]() $\tilde {\mathbf {x}}^{\prime } := (x_1^{\prime },\ldots ,x_{N+M}^{\prime })$
and
$\tilde {\mathbf {x}}^{\prime } := (x_1^{\prime },\ldots ,x_{N+M}^{\prime })$
and
![]() $\tilde {\mathbf {f}}^{\prime } := (f_1^{\prime },\ldots ,f_{N+M}^{\prime })$
are two extended clusters obtained from
$\tilde {\mathbf {f}}^{\prime } := (f_1^{\prime },\ldots ,f_{N+M}^{\prime })$
are two extended clusters obtained from
![]() $\tilde {\mathbf {x}}$
and
$\tilde {\mathbf {x}}$
and
![]() $\tilde {\mathbf {f}}$
via the same sequence of mutations (i.e., the mutations followed the same indices), and
$\tilde {\mathbf {f}}$
via the same sequence of mutations (i.e., the mutations followed the same indices), and
![]() $(u_1^{\prime },\ldots , u^{\prime }_{N+M})^t$
and
$(u_1^{\prime },\ldots , u^{\prime }_{N+M})^t$
and
![]() $(v_1^{\prime },\ldots ,v^{\prime }_{N+M})^t$
are the weight vectors of the global toric actions in the extended clusters
$(v_1^{\prime },\ldots ,v^{\prime }_{N+M})^t$
are the weight vectors of the global toric actions in the extended clusters
![]() $\tilde {\mathbf {x}}^{\prime }$
and
$\tilde {\mathbf {x}}^{\prime }$
and
![]() $\tilde {\mathbf {f}}^{\prime }$
, then
$\tilde {\mathbf {f}}^{\prime }$
, then
 $$\begin{align*}\theta(f_i^{\prime}) = x_i^{\prime} x_{N+M}^{\left(\frac{v_i^{\prime} - u_i^{\prime}}{u_{N+M}}\right)}, \ \ 1 \leq i \leq N+M. \end{align*}$$
$$\begin{align*}\theta(f_i^{\prime}) = x_i^{\prime} x_{N+M}^{\left(\frac{v_i^{\prime} - u_i^{\prime}}{u_{N+M}}\right)}, \ \ 1 \leq i \leq N+M. \end{align*}$$
The above proposition is a generalization of Lemma 8.4 from [Reference Gekhtman, Shapiro and Vainshtein17] to the case of generalized cluster structures. The map
![]() $\theta $
is an instance of a quasi-isomorphism defined by Fraser in [Reference Fraser12].
$\theta $
is an instance of a quasi-isomorphism defined by Fraser in [Reference Fraser12].
Quiver
A quiver is a directed multigraph with no
![]() $1$
- and
$1$
- and
![]() $2$
-cycles. Pick an extended seed
$2$
-cycles. Pick an extended seed
![]() $(\tilde {\mathbf {x}},\tilde {B},\mathcal {P})$
, and let
$(\tilde {\mathbf {x}},\tilde {B},\mathcal {P})$
, and let
![]() $D:=\operatorname {\mathrm {diag}}(d_1^{-1},\ldots , d_N^{-1})$
be a diagonal matrix with
$D:=\operatorname {\mathrm {diag}}(d_1^{-1},\ldots , d_N^{-1})$
be a diagonal matrix with
![]() $d_i$
’s defined as above. Assume that
$d_i$
’s defined as above. Assume that
![]() $DB$
is skew-symmetric, where B is the principal part of
$DB$
is skew-symmetric, where B is the principal part of
![]() $\tilde {B}$
. Then the matrix
$\tilde {B}$
. Then the matrix
 $$\begin{align*}\hat{B}:= \begin{bmatrix} DB & \tilde{B}^{[N+1,N+M]} \\ -(\tilde{B}^{[N+1,N+M]})^T & 0 \end{bmatrix} \end{align*}$$
$$\begin{align*}\hat{B}:= \begin{bmatrix} DB & \tilde{B}^{[N+1,N+M]} \\ -(\tilde{B}^{[N+1,N+M]})^T & 0 \end{bmatrix} \end{align*}$$
is the adjacency matrix of a quiver Q, in which each vertex i corresponds to a variable
![]() $x_i \in \tilde {\mathbf {x}}$
. The vertices that correspond to cluster variables are called mutable, the vertices that correspond to stable variables are called frozen and the vertices that correspond to isolated variables are called isolated. For each i, the number
$x_i \in \tilde {\mathbf {x}}$
. The vertices that correspond to cluster variables are called mutable, the vertices that correspond to stable variables are called frozen and the vertices that correspond to isolated variables are called isolated. For each i, the number
![]() $d_i$
is called the multiplicity of the ith vertex. If one mutates the extended seed
$d_i$
is called the multiplicity of the ith vertex. If one mutates the extended seed
![]() $(\tilde {x},\tilde {B},\mathcal {P})$
, then the quiver of the new seed can be obtained from the initial quiver via the following steps:
$(\tilde {x},\tilde {B},\mathcal {P})$
, then the quiver of the new seed can be obtained from the initial quiver via the following steps:
-
1) For each path
 $i \rightarrow k \rightarrow j$
, add an arrow
$i \rightarrow k \rightarrow j$
, add an arrow
 $i \rightarrow j$
;
$i \rightarrow j$
; -
2) If there is a pair of arrows
 $i \rightarrow j$
and
$i \rightarrow j$
and
 $j \rightarrow i$
, remove both;
$j \rightarrow i$
, remove both; -
3) Flip the orientation of all arrows going in and out of the vertex k.
The above process is also called a quiver mutation in direction k (or at vertex k). Instead of describing the matrix
![]() $\tilde {B}$
, we describe the corresponding quiver and multiplicities
$\tilde {B}$
, we describe the corresponding quiver and multiplicities
![]() $d_i$
’s.
$d_i$
’s.
2.2 Poisson–Lie groups
In this section, we briefly recall relevant concepts from Poisson geometry. A more detailed account can be found in [Reference Chari and Pressley5], [Reference Etingof and Schiffmann9] and [Reference Reyman and Semenov-Tian-Shansky23].
Poisson–Lie groups
A Poisson bracket
![]() $\{\cdot , \cdot \}$
on a commutative algebra is a Lie bracket that satisfies the Leibniz rule in each slot. Given a manifold M, a Poisson bivector field on M is a section
$\{\cdot , \cdot \}$
on a commutative algebra is a Lie bracket that satisfies the Leibniz rule in each slot. Given a manifold M, a Poisson bivector field on M is a section
![]() $\pi \in \Gamma (M,\bigwedge ^2 TM)$
such that
$\pi \in \Gamma (M,\bigwedge ^2 TM)$
such that
![]() $\{f,g\}:=\pi (df\wedge dg)$
is a Poisson bracket on the space of smooth functions on M. A Lie group G endowed with a Poisson bivector field
$\{f,g\}:=\pi (df\wedge dg)$
is a Poisson bracket on the space of smooth functions on M. A Lie group G endowed with a Poisson bivector field
![]() $\pi $
is called a Poisson–Lie group if for any
$\pi $
is called a Poisson–Lie group if for any
![]() $g,h \in G$
,
$g,h \in G$
,
![]() $\pi _{gh} = (dL_g \otimes dL_g)\pi _h + (dR_h \otimes dR_h)\pi _g$
, where
$\pi _{gh} = (dL_g \otimes dL_g)\pi _h + (dR_h \otimes dR_h)\pi _g$
, where
![]() $L_g$
and
$L_g$
and
![]() $R_h$
are the left and right translations by g and h, respectively. Let
$R_h$
are the left and right translations by g and h, respectively. Let
![]() $\mathfrak {g}$
be the Lie algebra of G and
$\mathfrak {g}$
be the Lie algebra of G and
![]() $r \in \mathfrak g \otimes \mathfrak g$
. If G is a connected Lie group, then the bivector fieldFootnote
3
$r \in \mathfrak g \otimes \mathfrak g$
. If G is a connected Lie group, then the bivector fieldFootnote
3
![]() $\pi _g := (dL_g\otimes dL_g) r - (dR_g \otimes dR_g)r$
defines the structure of a Poisson-Lie group on G if and only if the following conditions are satisfied:
$\pi _g := (dL_g\otimes dL_g) r - (dR_g \otimes dR_g)r$
defines the structure of a Poisson-Lie group on G if and only if the following conditions are satisfied:
-
1) The symmetric part of r is
 $\operatorname {\mathrm {ad}}$
-invariant;
$\operatorname {\mathrm {ad}}$
-invariant; -
2) The
 $3$
-tensor
$3$
-tensor
 $[r,r]:=[r_{12},r_{13}] + [r_{12},r_{23}] + [r_{13},r_{23}]$
is
$[r,r]:=[r_{12},r_{13}] + [r_{12},r_{23}] + [r_{13},r_{23}]$
is
 $\operatorname {\mathrm {ad}}$
-invariant, where
$\operatorname {\mathrm {ad}}$
-invariant, where
 $(a\otimes b)_{12} = a \otimes b \otimes 1$
,
$(a\otimes b)_{12} = a \otimes b \otimes 1$
,
 $(a \otimes b)_{13} = a \otimes 1 \otimes b$
and
$(a \otimes b)_{13} = a \otimes 1 \otimes b$
and
 $(a\otimes b)_{23} = 1 \otimes a \otimes b$
,
$(a\otimes b)_{23} = 1 \otimes a \otimes b$
,
 $a,b \in \mathfrak {g}$
.
$a,b \in \mathfrak {g}$
.
The classical Yang–Baxter equation (CYBE) is the equation
![]() $[r,r] = 0$
. For simple complex Lie algebras
$[r,r] = 0$
. For simple complex Lie algebras
![]() $\mathfrak {g}$
, Belavin and Drinfeld in [Reference Belavin and Drinfeld1, Reference Belavin and Drinfeld2] classified solutions of the CYBE that have a nondegenerate symmetric part. The classification was partially extended by Hodges in [Reference Hodges22] to the case of reductive complex Lie algebras (however, Hodges required the symmetric part of r to be a multiple of the Casimir element). A full classification of solutions of the CYBE with an arbitrary nondegenerate
$\mathfrak {g}$
, Belavin and Drinfeld in [Reference Belavin and Drinfeld1, Reference Belavin and Drinfeld2] classified solutions of the CYBE that have a nondegenerate symmetric part. The classification was partially extended by Hodges in [Reference Hodges22] to the case of reductive complex Lie algebras (however, Hodges required the symmetric part of r to be a multiple of the Casimir element). A full classification of solutions of the CYBE with an arbitrary nondegenerate
![]() $\operatorname {\mathrm {ad}}$
-invariant symmetric part in the case of reductive complex Lie algebras was obtained by Delorme in [Reference Delorme7].
$\operatorname {\mathrm {ad}}$
-invariant symmetric part in the case of reductive complex Lie algebras was obtained by Delorme in [Reference Delorme7].
The Belavin–Drinfeld classification
Let
![]() $\mathfrak {g}$
be a reductive complex Lie algebra endowed with a nondegenerate symmetric invariant bilinear form
$\mathfrak {g}$
be a reductive complex Lie algebra endowed with a nondegenerate symmetric invariant bilinear form
![]() $\langle \,,\,\rangle $
, and let
$\langle \,,\,\rangle $
, and let
![]() $\Pi $
be a set of simple roots of
$\Pi $
be a set of simple roots of
![]() $\mathfrak {g}$
. A Belavin–Drinfeld triple (for conciseness, a BD triple) is a triple
$\mathfrak {g}$
. A Belavin–Drinfeld triple (for conciseness, a BD triple) is a triple
![]() $(\Gamma _1, \Gamma _2, \gamma )$
with
$(\Gamma _1, \Gamma _2, \gamma )$
with
![]() $\Gamma _1, \Gamma _2 \subset \Pi $
and
$\Gamma _1, \Gamma _2 \subset \Pi $
and
![]() $\gamma : \Gamma _1 \rightarrow \Gamma _2$
a nilpotent isometry. The nilpotency condition means that for any
$\gamma : \Gamma _1 \rightarrow \Gamma _2$
a nilpotent isometry. The nilpotency condition means that for any
![]() $\alpha \in \Gamma _1$
there exists a number j such that
$\alpha \in \Gamma _1$
there exists a number j such that
![]() $\gamma ^j(\alpha ) \notin \Gamma _1$
. Decompose
$\gamma ^j(\alpha ) \notin \Gamma _1$
. Decompose
![]() $\mathfrak {g}$
as
$\mathfrak {g}$
as
![]() $\mathfrak {g} = \mathfrak {n}_+ \oplus \mathfrak {h} \oplus \mathfrak {n}_-$
, where
$\mathfrak {g} = \mathfrak {n}_+ \oplus \mathfrak {h} \oplus \mathfrak {n}_-$
, where
![]() $\mathfrak {n}_+ = \bigoplus _{\alpha> 0} \mathfrak {g}_{\alpha }$
and
$\mathfrak {n}_+ = \bigoplus _{\alpha> 0} \mathfrak {g}_{\alpha }$
and
![]() $\mathfrak {n}_- = \bigoplus _{\alpha> 0} \mathfrak {g}_{-\alpha }$
are nilpotent subalgebras,
$\mathfrak {n}_- = \bigoplus _{\alpha> 0} \mathfrak {g}_{-\alpha }$
are nilpotent subalgebras,
![]() $\mathfrak {g}_{\alpha }$
are root subspaces and
$\mathfrak {g}_{\alpha }$
are root subspaces and
![]() $\mathfrak {h}$
is a Cartan subalgebra. For every positive root
$\mathfrak {h}$
is a Cartan subalgebra. For every positive root
![]() $\alpha $
, choose
$\alpha $
, choose
![]() $e_{\alpha } \in \mathfrak {g}_{\alpha }$
and
$e_{\alpha } \in \mathfrak {g}_{\alpha }$
and
![]() $e_{-\alpha } \in \mathfrak {g}_{-\alpha }$
such that
$e_{-\alpha } \in \mathfrak {g}_{-\alpha }$
such that
![]() $\langle e_{\alpha },e_{-\alpha }\rangle = 1$
, and set
$\langle e_{\alpha },e_{-\alpha }\rangle = 1$
, and set
![]() $h_{\alpha }:=[e_{\alpha },e_{-\alpha }]$
. Let
$h_{\alpha }:=[e_{\alpha },e_{-\alpha }]$
. Let
![]() $\mathfrak {g}_{\Gamma _1}$
and
$\mathfrak {g}_{\Gamma _1}$
and
![]() $\mathfrak {g}_{\Gamma _2}$
be the simple Lie subalgebras of
$\mathfrak {g}_{\Gamma _2}$
be the simple Lie subalgebras of
![]() $\mathfrak {g}$
generated by
$\mathfrak {g}$
generated by
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
. Extend
$\Gamma _2$
. Extend
![]() $\gamma $
to an isomorphism
$\gamma $
to an isomorphism
![]() $\mathbb {Z}\Gamma _1 \xrightarrow {\sim } \mathbb {Z}\Gamma _2$
, and then define
$\mathbb {Z}\Gamma _1 \xrightarrow {\sim } \mathbb {Z}\Gamma _2$
, and then define
![]() $\gamma : \mathfrak {g}_{\Gamma _1} \rightarrow \mathfrak {g}_{\Gamma _2}$
via
$\gamma : \mathfrak {g}_{\Gamma _1} \rightarrow \mathfrak {g}_{\Gamma _2}$
via
![]() $\gamma (e_{\alpha }) = e_{\gamma (\alpha )}$
and
$\gamma (e_{\alpha }) = e_{\gamma (\alpha )}$
and
![]() $\gamma (h_{\alpha }) = h_{\gamma (\alpha )}$
. Let
$\gamma (h_{\alpha }) = h_{\gamma (\alpha )}$
. Let
![]() $\gamma ^* : \mathfrak {g}_{\Gamma _2} \rightarrow \mathfrak {g}_{\Gamma _1}$
be the conjugate of
$\gamma ^* : \mathfrak {g}_{\Gamma _2} \rightarrow \mathfrak {g}_{\Gamma _1}$
be the conjugate of
![]() $\gamma $
with respect to the form on
$\gamma $
with respect to the form on
![]() $\mathfrak {g}$
. Extend both
$\mathfrak {g}$
. Extend both
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^*$
by zero to
$\gamma ^*$
by zero to
![]() $[\mathfrak {g},\mathfrak {g}]$
. For an element
$[\mathfrak {g},\mathfrak {g}]$
. For an element
![]() $r \in \mathfrak {g}\otimes \mathfrak {g}$
, set
$r \in \mathfrak {g}\otimes \mathfrak {g}$
, set
![]() $R_+, R_- :\mathfrak {g}\rightarrow \mathfrak {g}$
to be the linear transformations determined by
$R_+, R_- :\mathfrak {g}\rightarrow \mathfrak {g}$
to be the linear transformations determined by
![]() $\langle R_+(x), y\rangle = \langle r, x\otimes y\rangle $
and
$\langle R_+(x), y\rangle = \langle r, x\otimes y\rangle $
and
![]() $\langle R_-(y), x\rangle = -\langle r, x\otimes y\rangle $
,
$\langle R_-(y), x\rangle = -\langle r, x\otimes y\rangle $
,
![]() $x, y \in \mathfrak {g}$
. Let
$x, y \in \mathfrak {g}$
. Let
![]() $\pi _{>}$
,
$\pi _{>}$
,
![]() $\pi _{<}$
and
$\pi _{<}$
and
![]() $\pi _0$
be the projections onto
$\pi _0$
be the projections onto
![]() $\mathfrak {n}_+$
,
$\mathfrak {n}_+$
,
![]() $\mathfrak {n}_-$
and
$\mathfrak {n}_-$
and
![]() $\mathfrak {h}$
, respectively. In terms of
$\mathfrak {h}$
, respectively. In terms of
![]() $R_+$
and
$R_+$
and
![]() $R_-$
, the CYBE assumes the form
$R_-$
, the CYBE assumes the form
Let
![]() $R_0 : \mathfrak {h} \rightarrow \mathfrak {h}$
be a linear transformation that satisfies the following conditions:
$R_0 : \mathfrak {h} \rightarrow \mathfrak {h}$
be a linear transformation that satisfies the following conditions:
where
![]() $\operatorname {\mathrm {id}}_{\mathfrak {h}} : \mathfrak {h} \rightarrow \mathfrak {h}$
is the identity and
$\operatorname {\mathrm {id}}_{\mathfrak {h}} : \mathfrak {h} \rightarrow \mathfrak {h}$
is the identity and
![]() $R_0^*$
is the adjoint of
$R_0^*$
is the adjoint of
![]() $R_0$
. If
$R_0$
. If
![]() $\mathfrak {g}$
is simple, then the solutions
$\mathfrak {g}$
is simple, then the solutions
![]() $R_0$
of equations (2.8)–(2.9) form an affine subspace of
$R_0$
of equations (2.8)–(2.9) form an affine subspace of
![]() $\hom (\mathfrak {h},\mathfrak {h})$
(linear maps) of dimension
$\hom (\mathfrak {h},\mathfrak {h})$
(linear maps) of dimension
![]() $k_{\mathbf {\Gamma }}(k_{\mathbf {\Gamma }}-1)/2$
.
$k_{\mathbf {\Gamma }}(k_{\mathbf {\Gamma }}-1)/2$
.
Theorem 2.6. (Belavin, Drinfeld) Under the above setup, if
where
![]() $R_0$
is any solution of the system (2.8)–(2.9), then
$R_0$
is any solution of the system (2.8)–(2.9), then
![]() $R_+$
satisfies the CYBE (2.7). Moreover,
$R_+$
satisfies the CYBE (2.7). Moreover,
Conversely, if
![]() $R_+ : \mathfrak {g} \rightarrow \mathfrak {g}$
is any linear transformation that satisfies equation (2.11), then
$R_+ : \mathfrak {g} \rightarrow \mathfrak {g}$
is any linear transformation that satisfies equation (2.11), then
![]() $R_+$
assumes the form (2.10) for a suitable decomposition of
$R_+$
assumes the form (2.10) for a suitable decomposition of
![]() $\mathfrak {g}$
, for some Belavin–Drinfeld triple and some choice of root vectors
$\mathfrak {g}$
, for some Belavin–Drinfeld triple and some choice of root vectors
![]() $e_{\alpha }$
.
$e_{\alpha }$
.
The matrix
![]() $R_+$
from the theorem is called a classical R-matrix. In this form, the theorem follows from Theorem 6.3 in [Reference Hodges22]. It is important that the form on
$R_+$
from the theorem is called a classical R-matrix. In this form, the theorem follows from Theorem 6.3 in [Reference Hodges22]. It is important that the form on
![]() $\mathfrak {g}$
is fixed; however, if
$\mathfrak {g}$
is fixed; however, if
![]() $\mathfrak {g}$
is simple, then all nondegenerate symmetric invariant bilinear forms are multiples of one another, so the theorem yields a full classification of solutions
$\mathfrak {g}$
is simple, then all nondegenerate symmetric invariant bilinear forms are multiples of one another, so the theorem yields a full classification of solutions
![]() $r \in \mathfrak {g}\otimes \mathfrak {g}$
of the CYBE with nondegenerate
$r \in \mathfrak {g}\otimes \mathfrak {g}$
of the CYBE with nondegenerate
![]() $\operatorname {\mathrm {ad}}$
-invariant symmetric parts.
$\operatorname {\mathrm {ad}}$
-invariant symmetric parts.
The Drinfeld double
Let G be a reductive complex connected Poisson–Lie group endowed with a nondegenerate symmetric invariant bilinear form on
![]() $\mathfrak {g}$
and with a Poisson bivector field defined as
$\mathfrak {g}$
and with a Poisson bivector field defined as
for some
![]() $r \in \mathfrak {g}\otimes \mathfrak {g}$
that satisfies the conditions of Theorem 2.6. Let
$r \in \mathfrak {g}\otimes \mathfrak {g}$
that satisfies the conditions of Theorem 2.6. Let
![]() $R_+$
and
$R_+$
and
![]() $R_-$
be defined from r as in the previous paragraph, and set
$R_-$
be defined from r as in the previous paragraph, and set
![]() $\mathfrak {d} := \mathfrak g \oplus \mathfrak g$
to be the direct sum of Lie algebras. Define a nondegenerate symmetric invariant bilinear form on
$\mathfrak {d} := \mathfrak g \oplus \mathfrak g$
to be the direct sum of Lie algebras. Define a nondegenerate symmetric invariant bilinear form on
![]() $\mathfrak {d}$
as
$\mathfrak {d}$
as
As a vector space,
![]() $\mathfrak {d}$
splits into the direct sum of the following isotropic Lie subalgebras:
$\mathfrak {d}$
splits into the direct sum of the following isotropic Lie subalgebras:
Set
![]() $R^{\mathfrak {d}}_+ := P_{\mathfrak {g}^*}$
, where
$R^{\mathfrak {d}}_+ := P_{\mathfrak {g}^*}$
, where
![]() $P_{\mathfrak {g}^*}$
is the projection of
$P_{\mathfrak {g}^*}$
is the projection of
![]() $\mathfrak {d}$
onto
$\mathfrak {d}$
onto
![]() $\mathfrak {g}^*$
, and let
$\mathfrak {g}^*$
, and let
![]() $r^{\mathfrak {d}} \in \mathfrak {d}\otimes \mathfrak {d}$
be the
$r^{\mathfrak {d}} \in \mathfrak {d}\otimes \mathfrak {d}$
be the
![]() $2$
-tensor that corresponds to
$2$
-tensor that corresponds to
![]() $R^{\mathfrak {d}}_+$
. Then
$R^{\mathfrak {d}}_+$
. Then
![]() $R_+^{\mathfrak {d}}$
yields the structure of a Poisson–Lie group on the Lie group
$R_+^{\mathfrak {d}}$
yields the structure of a Poisson–Lie group on the Lie group
![]() $D(G):=G \times G$
via the Poisson bivector field
$D(G):=G \times G$
via the Poisson bivector field
![]() $\pi ^{\mathfrak {d}}_{(g,h)} := (dL_{(g,h)}\otimes dL_{(g,h)}) r^{\mathfrak {d}} - (dR_{(g,h)}\otimes dR_{(g,h)})r^{\mathfrak {d}}$
,
$\pi ^{\mathfrak {d}}_{(g,h)} := (dL_{(g,h)}\otimes dL_{(g,h)}) r^{\mathfrak {d}} - (dR_{(g,h)}\otimes dR_{(g,h)})r^{\mathfrak {d}}$
,
![]() ${(g,h)} \in D(G)$
. The Poisson–Lie group
${(g,h)} \in D(G)$
. The Poisson–Lie group
![]() $D(G)$
is called the Drinfeld double of G.
$D(G)$
is called the Drinfeld double of G.
The Poisson bracket on
![]() $D(G)$
can be written in the form
$D(G)$
can be written in the form
where
![]() $\nabla ^L f_i = (\nabla _X^L f_i, -\nabla _Y^L f_i)$
and
$\nabla ^L f_i = (\nabla _X^L f_i, -\nabla _Y^L f_i)$
and
![]() $\nabla ^R f_i = (\nabla _X^R f_i, -\nabla _Y^R f_i)$
are the left and the right gradients, respectively,
$\nabla ^R f_i = (\nabla _X^R f_i, -\nabla _Y^R f_i)$
are the left and the right gradients, respectively,
![]() $E_Lf_i = \nabla ^L_X f_i+ \nabla ^L_Yf_i$
and
$E_Lf_i = \nabla ^L_X f_i+ \nabla ^L_Yf_i$
and
![]() $E_Rf_i = \nabla ^R_Xf_i + \nabla ^R_Yf_i$
. We define the gradients on G asFootnote
4
$E_Rf_i = \nabla ^R_Xf_i + \nabla ^R_Yf_i$
. We define the gradients on G asFootnote
4
 $$\begin{align*}\langle \nabla^L f|_g, x\rangle = \left. \frac{d}{dt}\right|{}_{t=0} f(g\exp (tx)), \ \ \ \langle \nabla^R f|_g, x\rangle = \left. \frac{d}{dt}\right|{}_{t=0} f(\exp(tx)g), \ \ g \in G, \ x \in \mathfrak{g}. \end{align*}$$
$$\begin{align*}\langle \nabla^L f|_g, x\rangle = \left. \frac{d}{dt}\right|{}_{t=0} f(g\exp (tx)), \ \ \ \langle \nabla^R f|_g, x\rangle = \left. \frac{d}{dt}\right|{}_{t=0} f(\exp(tx)g), \ \ g \in G, \ x \in \mathfrak{g}. \end{align*}$$
The group G can be identified with the connected Poisson–Lie subgroup
![]() $G^{\delta }$
of
$G^{\delta }$
of
![]() $D(G)$
that corresponds to the Lie subalgebra
$D(G)$
that corresponds to the Lie subalgebra
![]() $\mathfrak {g}^{\delta }$
. The Poisson bracket
$\mathfrak {g}^{\delta }$
. The Poisson bracket
![]() $\{\cdot , \cdot \}_G$
on G can be expressed as
$\{\cdot , \cdot \}_G$
on G can be expressed as
Additionally, the connected Poisson–Lie subgroup
![]() $G^*$
of
$G^*$
of
![]() $D(G)$
that corresponds to
$D(G)$
that corresponds to
![]() $\mathfrak {g}^*$
is called the dual Poisson–Lie group of G. The Poisson structure on
$\mathfrak {g}^*$
is called the dual Poisson–Lie group of G. The Poisson structure on
![]() $G^*$
(which is induced from
$G^*$
(which is induced from
![]() $D(G)$
) can be modeled locally in the group G via the map
$D(G)$
) can be modeled locally in the group G via the map
The image of this map is an open dense subset of G denoted as
![]() $G^{\dagger }$
(however, the map is not injective in general).
$G^{\dagger }$
(however, the map is not injective in general).
Following [Reference Gekhtman, Shapiro and Vainshtein20], we consider a more general Poisson bracket on
![]() $G\times G$
that is defined by a pair of classical R-matrices
$G\times G$
that is defined by a pair of classical R-matrices
![]() $R_+^c$
and
$R_+^c$
and
![]() $R_+^r$
(the meaning of the upper indices is unveiled later in the text). For such a pair, the Poisson bracket is defined as
$R_+^r$
(the meaning of the upper indices is unveiled later in the text). For such a pair, the Poisson bracket is defined as
We will frequently abuse the terminology and call
![]() $G\times G$
endowed with bracket (2.12) the Drinfeld double of G. However, bracket (2.12) yields the structure of a Poisson–Lie group on
$G\times G$
endowed with bracket (2.12) the Drinfeld double of G. However, bracket (2.12) yields the structure of a Poisson–Lie group on
![]() $G\times G$
if and only if
$G\times G$
if and only if
![]() $R^c_+ = R^r_+$
.
$R^c_+ = R^r_+$
.
Symplectic foliation and Poisson submanifolds
Let
![]() $(M,\pi )$
be a Poisson manifold. An immersed submanfiold
$(M,\pi )$
be a Poisson manifold. An immersed submanfiold
![]() $S \subseteq M$
is called a Poisson submanifold if
$S \subseteq M$
is called a Poisson submanifold if
![]() $\pi |_S \in \Gamma (S,\bigwedge ^2TS)$
. Examples of Poisson submanifolds include nonsingular parts of the zero loci of frozen variables (see Section 3.8). Let
$\pi |_S \in \Gamma (S,\bigwedge ^2TS)$
. Examples of Poisson submanifolds include nonsingular parts of the zero loci of frozen variables (see Section 3.8). Let
![]() $\pi ^{\#} : TM^* \rightarrow TM$
be a morphism of vector bundles defined as
$\pi ^{\#} : TM^* \rightarrow TM$
be a morphism of vector bundles defined as
![]() $\langle \pi ^{\#}(\xi ),\eta \rangle := \langle \pi ,\xi \wedge \eta \rangle $
,
$\langle \pi ^{\#}(\xi ),\eta \rangle := \langle \pi ,\xi \wedge \eta \rangle $
,
![]() $\xi ,\eta \in T_p^*M$
,
$\xi ,\eta \in T_p^*M$
,
![]() $p \in M$
. The Poisson bivector
$p \in M$
. The Poisson bivector
![]() $\pi $
is called nondegenerate if
$\pi $
is called nondegenerate if
![]() $\pi ^{\#}$
is an isomorphism of vector bundles. A symplectic leaf is a maximal (by inclusion) connected Poisson submanifold S of M for which
$\pi ^{\#}$
is an isomorphism of vector bundles. A symplectic leaf is a maximal (by inclusion) connected Poisson submanifold S of M for which
![]() $\pi |_S$
is nondegenerate. It is a theorem that any Poisson manifold M is a union of its symplectic leaves.
$\pi |_S$
is nondegenerate. It is a theorem that any Poisson manifold M is a union of its symplectic leaves.
2.3 Desnanot–Jacobi identities
We will frequently use the following Desnanot–Jacobi identities, which can be easily derived from short Plücker relations:
Proposition 2.7. Let A be an
![]() $m \times (m+1)$
matrix with entries in an arbitrary field. Then for any
$m \times (m+1)$
matrix with entries in an arbitrary field. Then for any
![]() $1\leq i < j < k\leq (m+1)$
and
$1\leq i < j < k\leq (m+1)$
and
![]() $1\leq \alpha \leq m$
, the following identity holds:
$1\leq \alpha \leq m$
, the following identity holds:
where the hatted upper (lower) indices indicate that the corresponding column (row) is removed.
Proposition 2.8. Let A be an
![]() $m\times m$
matrix with entries in an arbitrary field. If
$m\times m$
matrix with entries in an arbitrary field. If
![]() $1 \leq i < j\leq m$
and
$1 \leq i < j\leq m$
and
![]() $1\leq k < l\leq m$
, then the following identity holds:
$1\leq k < l\leq m$
, then the following identity holds:
3 Description of
 $D(\operatorname {\mathrm {GL}}_n)$
and
$D(\operatorname {\mathrm {GL}}_n)$
and
 $\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
$\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
3.1 BD graphs in type A
In this section, we describe BD graphs that are attached to pairs of BD triples; the material is drawn from [Reference Gekhtman, Shapiro and Vainshtein20]. Let us identify the positive simple roots of
![]() $\operatorname {\mathrm {sl}}_n(\mathbb C)$
with an interval
$\operatorname {\mathrm {sl}}_n(\mathbb C)$
with an interval
![]() $[1, n-1]$
. We define
$[1, n-1]$
. We define
![]() $\mathbf {\Gamma }^r := (\Gamma _1^r, \Gamma _2^r, \gamma _r)$
and
$\mathbf {\Gamma }^r := (\Gamma _1^r, \Gamma _2^r, \gamma _r)$
and
![]() $\mathbf {\Gamma }^c := (\Gamma _1^c, \Gamma _2^c, \gamma _c)$
to be a pair of BD triples for
$\mathbf {\Gamma }^c := (\Gamma _1^c, \Gamma _2^c, \gamma _c)$
to be a pair of BD triples for
![]() $\operatorname {\mathrm {sl}}_n(\mathbb C)$
, and we name the first triple a row BD triple and the other one a column BD triple. Furthermore, if
$\operatorname {\mathrm {sl}}_n(\mathbb C)$
, and we name the first triple a row BD triple and the other one a column BD triple. Furthermore, if
![]() $\Gamma _1^r = \Gamma _1^c = \emptyset $
, we call
$\Gamma _1^r = \Gamma _1^c = \emptyset $
, we call
![]() $(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
the standard or trivial BD pair.
$(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
the standard or trivial BD pair.
BD graph for a pair of BD triples
The graph
![]() $G_{(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)}$
is defined in the following way. The vertex set of the graph consists of two copies of
$G_{(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)}$
is defined in the following way. The vertex set of the graph consists of two copies of
![]() $[1,n-1]$
, one of each is called the upper part and the other one is the lower part. We draw an edge between vertices i and
$[1,n-1]$
, one of each is called the upper part and the other one is the lower part. We draw an edge between vertices i and
![]() $n-i$
if they belong to the same part (if
$n-i$
if they belong to the same part (if
![]() $i = n-i$
, we draw a loop). If
$i = n-i$
, we draw a loop). If
![]() $\gamma _r(i) = j$
, draw a directed edge from i in the upper part to j in the lower part; if
$\gamma _r(i) = j$
, draw a directed edge from i in the upper part to j in the lower part; if
![]() $\gamma _c(i) = j$
, draw a directed edge from j in the lower part to i in the upper part. The edges between vertices of the same part are called horizontal, between different parts vertical. Figure 1 provides two examples of BD graphs.
$\gamma _c(i) = j$
, draw a directed edge from j in the lower part to i in the upper part. The edges between vertices of the same part are called horizontal, between different parts vertical. Figure 1 provides two examples of BD graphs.

Figure 1 Examples of BD graphs. The vertical directed edges coming from
![]() $\mathbf {\Gamma }^r$
and
$\mathbf {\Gamma }^r$
and
![]() $\mathbf {\Gamma }^c$
are painted in red and blue, respectively.
$\mathbf {\Gamma }^c$
are painted in red and blue, respectively.
Paths in
 $G_{(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)}$
and aperiodicity
$G_{(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)}$
and aperiodicity
There is no orientation assigned to horizontal edges, hence we allow them to be traversed in both directions. An alternating path in
![]() $G_{(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)}$
is a path in which horizontal and vertical edges alternate. A path is a cycle if it starts where it ends. Now, we call the pair
$G_{(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)}$
is a path in which horizontal and vertical edges alternate. A path is a cycle if it starts where it ends. Now, we call the pair
![]() $(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
aperiodic if
$(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
aperiodic if
![]() $G_{(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)}$
has no alternating cycles (equivalently, the map
$G_{(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)}$
has no alternating cycles (equivalently, the map
![]() $\gamma _c^{-1} w_0 \gamma _r w_0$
is nilpotent, where
$\gamma _c^{-1} w_0 \gamma _r w_0$
is nilpotent, where
![]() $w_0$
is the longest Weyl group element of
$w_0$
is the longest Weyl group element of
![]() $[1,n-1]$
). In examples in this paper, we denote alternating paths as
$[1,n-1]$
). In examples in this paper, we denote alternating paths as
![]() $\cdots \rightarrow i \xrightarrow {X} i^{\prime } \xrightarrow {\gamma _r} j \xrightarrow {Y} j^{\prime } \xrightarrow {\gamma _c^*} i^{\prime } \rightarrow \cdots $
, where X and Y indicate whether an edge is in the upper or the lower part of
$\cdots \rightarrow i \xrightarrow {X} i^{\prime } \xrightarrow {\gamma _r} j \xrightarrow {Y} j^{\prime } \xrightarrow {\gamma _c^*} i^{\prime } \rightarrow \cdots $
, where X and Y indicate whether an edge is in the upper or the lower part of
![]() $G_{(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)}$
, respectively, and
$G_{(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)}$
, respectively, and
![]() $\gamma _r$
and
$\gamma _r$
and
![]() $\gamma _c^*$
indicate a vertical edge directed downwards or upwards.
$\gamma _c^*$
indicate a vertical edge directed downwards or upwards.
Oriented BD triples
Let
![]() $\mathbf {\Gamma } = (\Gamma _1,\Gamma _2,\gamma )$
be a BD triple. Since
$\mathbf {\Gamma } = (\Gamma _1,\Gamma _2,\gamma )$
be a BD triple. Since
![]() $\gamma $
is an isometry, if
$\gamma $
is an isometry, if
![]() $\gamma (i) = j$
and
$\gamma (i) = j$
and
![]() $i+1 \in \Gamma _1$
, then
$i+1 \in \Gamma _1$
, then
![]() $\gamma (i+1) = j \pm 1$
. We call the BD triple
$\gamma (i+1) = j \pm 1$
. We call the BD triple
![]() $\mathbf {\Gamma }$
oriented if
$\mathbf {\Gamma }$
oriented if
![]() $\gamma (i+1) = j+1$
for every
$\gamma (i+1) = j+1$
for every
![]() $i \in \Gamma _1$
such that
$i \in \Gamma _1$
such that
![]() $i+1 \in \Gamma _1$
. A pair of BD triples
$i+1 \in \Gamma _1$
. A pair of BD triples
![]() $(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
is called oriented if both
$(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
is called oriented if both
![]() $\mathbf {\Gamma }^r$
and
$\mathbf {\Gamma }^r$
and
![]() $\mathbf {\Gamma }^c$
are oriented.
$\mathbf {\Gamma }^c$
are oriented.
Runs
Let
![]() $\mathbf {\Gamma } = (\Gamma _1,\Gamma _2,\gamma )$
be a BD triple. For an arbitrary
$\mathbf {\Gamma } = (\Gamma _1,\Gamma _2,\gamma )$
be a BD triple. For an arbitrary
![]() $i \in [1,n]$
, set
$i \in [1,n]$
, set
An X-run of i is the interval
![]() $\Delta (i) := [i_-+1, i_+]$
. Replacing
$\Delta (i) := [i_-+1, i_+]$
. Replacing
![]() $\Gamma _1$
with
$\Gamma _1$
with
![]() $\Gamma _2$
in the above formulas, we obtain the definition of a Y-run
$\Gamma _2$
in the above formulas, we obtain the definition of a Y-run
![]() $\bar {\Delta }(i)$
of i. The X-runs partition the set
$\bar {\Delta }(i)$
of i. The X-runs partition the set
![]() $[1,n]$
, and likewise the Y-runs. A run is called trivial if it consists of a single element. Evidently, the map
$[1,n]$
, and likewise the Y-runs. A run is called trivial if it consists of a single element. Evidently, the map
![]() $\gamma $
can be viewed as a bijection between the set of nontrivial X-runs and the set of nontrivial Y-runs. For a pair of BD triples
$\gamma $
can be viewed as a bijection between the set of nontrivial X-runs and the set of nontrivial Y-runs. For a pair of BD triples
![]() $(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, the runs that correspond to
$(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, the runs that correspond to
![]() $\mathbf {\Gamma }^r$
and
$\mathbf {\Gamma }^r$
and
![]() $\mathbf {\Gamma }^c$
are called row and column runs, respectively. We will indicate with an upper index r or c whether a run is from
$\mathbf {\Gamma }^c$
are called row and column runs, respectively. We will indicate with an upper index r or c whether a run is from
![]() $\mathbf {\Gamma }^r$
or
$\mathbf {\Gamma }^r$
or
![]() $\mathbf {\Gamma }^c$
.
$\mathbf {\Gamma }^c$
.
Example 3.1. Consider the BD graphs on Figure 1. Evidently, both are aperiodic and encode pairs of oriented BD triples. Here’s a list of all runs that correspond to the graph on the right:
-
• Row runs:
 $\Delta _1^r = [1, 4],\ \Delta _2^r = [5],\ \Delta _3^r = [6]; \ \ \bar {\Delta }_1^r = [1], \ \bar {\Delta }_2^r = [2, 5], \ \bar {\Delta }_3^r = [6]$
;
$\Delta _1^r = [1, 4],\ \Delta _2^r = [5],\ \Delta _3^r = [6]; \ \ \bar {\Delta }_1^r = [1], \ \bar {\Delta }_2^r = [2, 5], \ \bar {\Delta }_3^r = [6]$
; -
• Column runs:
 $\Delta _1^c = [1,2], \ \Delta _2^c = [3,4],\ \Delta _3^c = [5], \ \Delta _3^c = [6]; \ \ \bar {\Delta }_1^c = [1],\ \bar {\Delta }_2^c = [2]$
,
$\Delta _1^c = [1,2], \ \Delta _2^c = [3,4],\ \Delta _3^c = [5], \ \Delta _3^c = [6]; \ \ \bar {\Delta }_1^c = [1],\ \bar {\Delta }_2^c = [2]$
,
 $\bar {\Delta }_3^c = [3, 4]$
,
$\bar {\Delta }_3^c = [3, 4]$
,
 $\bar {\Delta }_4^c = [5,6].$
$\bar {\Delta }_4^c = [5,6].$
3.2 Construction of
 $\mathcal {L}$
-matrices
$\mathcal {L}$
-matrices
Let X and Y be two
![]() $n\times n$
matrices of indeterminates, which represent the standard coordinates on
$n\times n$
matrices of indeterminates, which represent the standard coordinates on
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
. For this section, fix an aperiodic oriented BD pair
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
. For this section, fix an aperiodic oriented BD pair
![]() $\mathbf {\Gamma }:=(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
, and let
$\mathbf {\Gamma }:=(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
, and let
![]() $G_{\mathbf {\Gamma }}$
be the BD graph associated with the pair, which is constructed in Section 3.1. The construction described in this section follows Section 3.2 from [Reference Gekhtman, Shapiro and Vainshtein20].
$G_{\mathbf {\Gamma }}$
be the BD graph associated with the pair, which is constructed in Section 3.1. The construction described in this section follows Section 3.2 from [Reference Gekhtman, Shapiro and Vainshtein20].
We associate a matrix
![]() $\mathcal {L} = \mathcal {L}(X,Y)$
to every maximal alternating path in
$\mathcal {L} = \mathcal {L}(X,Y)$
to every maximal alternating path in
![]() $G_{(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)}$
in the following way. If the path traverses a horizontal edge
$G_{(\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)}$
in the following way. If the path traverses a horizontal edge
![]() $i \rightarrow i^{\prime }$
in the upper part of the graph, we assign to the edge a submatrix of X viaFootnote
5
$i \rightarrow i^{\prime }$
in the upper part of the graph, we assign to the edge a submatrix of X viaFootnote
5
Similarly, we assign a submatrix of Y to every horizontal edge
![]() $j^{\prime } \rightarrow j$
in the lower part of the graph that appears in the path via
$j^{\prime } \rightarrow j$
in the lower part of the graph that appears in the path via
We call these submatrices X- and Y-blocks, respectively. Now, the first block in the path becomes the bottom right corner of the matrix
![]() $\mathcal {L}$
. As we move along the path, we collect the X- and Y-blocks and align them together according to the following patterns:
$\mathcal {L}$
. As we move along the path, we collect the X- and Y-blocks and align them together according to the following patterns:

The lower plus and minus in the first scheme correspond to
![]() $\mathbf {\Gamma }^r$
(aligning along rows), and in the second scheme they correspond to
$\mathbf {\Gamma }^r$
(aligning along rows), and in the second scheme they correspond to
![]() $\mathbf {\Gamma }^c$
(aligning along columns). In other words, once the first block is set in the bottom right part of
$\mathbf {\Gamma }^c$
(aligning along columns). In other words, once the first block is set in the bottom right part of
![]() $\mathcal {L}$
, the algorithm of adding the blocks as one moves along the path can be described as follows:
$\mathcal {L}$
, the algorithm of adding the blocks as one moves along the path can be described as follows:
-
1) If the X-block that corresponds to an edge
 $i^{\prime } \rightarrow i$
is placed in
$i^{\prime } \rightarrow i$
is placed in
 $\mathcal {L}$
and
$\mathcal {L}$
and
 $\gamma _r(i) = j$
, proceed to the edge
$\gamma _r(i) = j$
, proceed to the edge
 $j\rightarrow j^{\prime }$
in the lower part of the graph and put the corresponding Y-block to the left of the X-block so that
$j\rightarrow j^{\prime }$
in the lower part of the graph and put the corresponding Y-block to the left of the X-block so that
 $y_{jn}$
and
$y_{jn}$
and
 $x_{i1}$
are adjacent and belong to the same row;
$x_{i1}$
are adjacent and belong to the same row; -
2) If the Y-block that corresponds to an edge
 $j^{\prime } \rightarrow j$
is placed in
$j^{\prime } \rightarrow j$
is placed in
 $\mathcal {L}$
and
$\mathcal {L}$
and
 $\gamma _c^*(j) = i$
, proceed to the edge
$\gamma _c^*(j) = i$
, proceed to the edge
 $i \rightarrow i^{\prime }$
in the upper part of the graph and put the corresponding X-block on top of the Y-block so that
$i \rightarrow i^{\prime }$
in the upper part of the graph and put the corresponding X-block on top of the Y-block so that
 $x_{ni}$
and
$x_{ni}$
and
 $y_{1j}$
are adjacent and belong to the same column;
$y_{1j}$
are adjacent and belong to the same column; -
3) Repeat until the path reaches its end.
Example 3.2. Let
![]() $n=4$
and
$n=4$
and
![]() $\mathbf {\Gamma }^r$
and
$\mathbf {\Gamma }^r$
and
![]() $\mathbf {\Gamma }^c$
be Cremmer–Gervais triples. In other words,
$\mathbf {\Gamma }^c$
be Cremmer–Gervais triples. In other words,
![]() $\gamma _r(i) = \gamma _c(i) = i+1$
for
$\gamma _r(i) = \gamma _c(i) = i+1$
for
![]() $i \in \{1, 2\}$
(see the BD graph below).
$i \in \{1, 2\}$
(see the BD graph below).

Denote by
![]() $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
![]() $\mathcal {L}_2$
the matrices that correspond to these paths. For the first one, the blocks that correspond to the edges are
$\mathcal {L}_2$
the matrices that correspond to these paths. For the first one, the blocks that correspond to the edges are
![]() $X_{[1,4]}^{[1,3]}$
,
$X_{[1,4]}^{[1,3]}$
,
![]() $Y_{[1,4]}^{[2,4]}$
,
$Y_{[1,4]}^{[2,4]}$
,
![]() $X_{[1,1]}^{[1,3]}$
, in the order in the path. Aligning these blocks according to the algorithm, we obtain
$X_{[1,1]}^{[1,3]}$
, in the order in the path. Aligning these blocks according to the algorithm, we obtain
![]() $\mathcal {L}_1$
(see below). In a similar way one can obtain
$\mathcal {L}_1$
(see below). In a similar way one can obtain
![]() $\mathcal {L}_2$
.
$\mathcal {L}_2$
.
 $$\begin{align*}\mathcal{L}_1(X,Y) = \begin{bmatrix}x_{41} & x_{42} & x_{43} & 0 & 0 & 0\\ y_{12} & y_{13} & y_{14} & 0 & 0 & 0\\ y_{22} & y_{23} & y_{24} & x_{11} & x_{12} & x_{13} \\ y_{32} & y_{33} & y_{34} & x_{21} & x_{22} & x_{23}\\ y_{42} & y_{43} & y_{44} & x_{31} & x_{32} & x_{33}\\ 0 & 0 & 0 & x_{41} & x_{42} & x_{43} \end{bmatrix}, \ \ \ \mathcal{L}_2(X,Y) = \begin{bmatrix} y_{12} & y_{13} & y_{14} & 0 & 0 & 0\\ y_{22} & y_{23} & y_{24} & x_{11} & x_{12} & x_{13}\\ y_{32} & y_{33} & y_{34} & x_{21} & x_{22} & x_{23}\\ y_{42} & y_{43} & y_{44} & x_{31} & x_{32} & x_{33}\\ 0 & 0 & 0 & x_{41} & x_{42} & x_{43}\\ 0 & 0 & 0 & y_{12} & y_{13} & y_{14} \end{bmatrix}. \end{align*}$$
$$\begin{align*}\mathcal{L}_1(X,Y) = \begin{bmatrix}x_{41} & x_{42} & x_{43} & 0 & 0 & 0\\ y_{12} & y_{13} & y_{14} & 0 & 0 & 0\\ y_{22} & y_{23} & y_{24} & x_{11} & x_{12} & x_{13} \\ y_{32} & y_{33} & y_{34} & x_{21} & x_{22} & x_{23}\\ y_{42} & y_{43} & y_{44} & x_{31} & x_{32} & x_{33}\\ 0 & 0 & 0 & x_{41} & x_{42} & x_{43} \end{bmatrix}, \ \ \ \mathcal{L}_2(X,Y) = \begin{bmatrix} y_{12} & y_{13} & y_{14} & 0 & 0 & 0\\ y_{22} & y_{23} & y_{24} & x_{11} & x_{12} & x_{13}\\ y_{32} & y_{33} & y_{34} & x_{21} & x_{22} & x_{23}\\ y_{42} & y_{43} & y_{44} & x_{31} & x_{32} & x_{33}\\ 0 & 0 & 0 & x_{41} & x_{42} & x_{43}\\ 0 & 0 & 0 & y_{12} & y_{13} & y_{14} \end{bmatrix}. \end{align*}$$
Properties of
 $\mathcal {L}$
-matrices
$\mathcal {L}$
-matrices
Observe the following:
-
• The blocks are aligned in such a way that the indices in the blocks that correspond to the runs
 $\Delta ^r$
and
$\Delta ^r$
and
 $\bar {\Delta }^r$
(or
$\bar {\Delta }^r$
(or
 $\Delta ^c$
and
$\Delta ^c$
and
 $\bar {\Delta }^c$
) are in the same rows (columns);
$\bar {\Delta }^c$
) are in the same rows (columns); -
• For any variable
 $x_{ij}$
or
$x_{ij}$
or
 $y_{ji}$
with
$y_{ji}$
with
 $i> j$
, there is a unique
$i> j$
, there is a unique
 $\mathcal {L}(X,Y)$
that contains it on the diagonal;
$\mathcal {L}(X,Y)$
that contains it on the diagonal; -
• If
 $i_1 \rightarrow i_2 \rightarrow \cdots \rightarrow i_{2n}$
is the maximal alternating path that gives rise to
$i_1 \rightarrow i_2 \rightarrow \cdots \rightarrow i_{2n}$
is the maximal alternating path that gives rise to
 $\mathcal {L}$
, then the size
$\mathcal {L}$
, then the size
 $N(\mathcal {L}) \times N(\mathcal {L})$
of
$N(\mathcal {L}) \times N(\mathcal {L})$
of
 $\mathcal {L}$
can be determined as
$\mathcal {L}$
can be determined as  $$\begin{align*}N(\mathcal{L}) = \sum_{k=1}^{n} i_{2k-1}. \end{align*}$$
$$\begin{align*}N(\mathcal{L}) = \sum_{k=1}^{n} i_{2k-1}. \end{align*}$$
3.3 Initial cluster and
 $\mathcal {GC}(\mathbf {\Gamma })$
$\mathcal {GC}(\mathbf {\Gamma })$
In this section, we describe the initial extended cluster of the generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma })$
on
$\mathcal {GC}(\mathbf {\Gamma })$
on
![]() $\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
induced by an aperiodic oriented BD pair
$\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
induced by an aperiodic oriented BD pair
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, as well as the choice of the ground ring.
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, as well as the choice of the ground ring.
Description of
 $\varphi $
-, f- and c-functions
$\varphi $
-, f- and c-functions
Set
![]() $U:= X^{-1} Y$
and define
$U:= X^{-1} Y$
and define
set
![]() $\tilde {\varphi }_{kl}(X,Y) := \det \Phi _{kl}(X,Y)$
and
$\tilde {\varphi }_{kl}(X,Y) := \det \Phi _{kl}(X,Y)$
and
where
 $$\begin{align*}s_{kl} = \begin{cases} (-1)^{k(l+1)} &n \text{ is even,}\\ (-1)^{(n-1)/2 + k(k-1)/2 + l(l-1)/2} &n \text{ is odd.} \end{cases} \end{align*}$$
$$\begin{align*}s_{kl} = \begin{cases} (-1)^{k(l+1)} &n \text{ is even,}\\ (-1)^{(n-1)/2 + k(k-1)/2 + l(l-1)/2} &n \text{ is odd.} \end{cases} \end{align*}$$
All f- and
![]() $\varphi $
-functions are considered as cluster variables. The c-functions are defined via
$\varphi $
-functions are considered as cluster variables. The c-functions are defined via
 $$\begin{align*}\det (X+\lambda Y) = \sum_{i=0}^{n} \lambda^{i} s_i c_i(X,Y), \end{align*}$$
$$\begin{align*}\det (X+\lambda Y) = \sum_{i=0}^{n} \lambda^{i} s_i c_i(X,Y), \end{align*}$$
where
![]() $s_i = (-1)^{i(n-1)}$
. Note that
$s_i = (-1)^{i(n-1)}$
. Note that
![]() $c_{0} = \det X$
and
$c_{0} = \det X$
and
![]() $c_n = \det Y$
. The functions
$c_n = \det Y$
. The functions
![]() $c_1,\ldots ,c_{n-1}$
are considered as isolated stable variables, and the only nontrivial string, which is attached to
$c_1,\ldots ,c_{n-1}$
are considered as isolated stable variables, and the only nontrivial string, which is attached to
![]() $\varphi _{11}$
, is given by the tuple
$\varphi _{11}$
, is given by the tuple
![]() $(1,c_1,\ldots ,c_{n-1},1)$
.
$(1,c_1,\ldots ,c_{n-1},1)$
.
Description of g- and h-functions
For
![]() $i> j$
, let
$i> j$
, let
![]() $\mathcal {L}$
be an
$\mathcal {L}$
be an
![]() $\mathcal {L}$
-matrix such that
$\mathcal {L}$
-matrix such that
![]() $\mathcal {L}_{ss}(X,Y) = x_{ij}$
for some s, and let
$\mathcal {L}_{ss}(X,Y) = x_{ij}$
for some s, and let
![]() $N(\mathcal {L})$
be the size of
$N(\mathcal {L})$
be the size of
![]() $\mathcal {L}$
. Set
$\mathcal {L}$
. Set
![]() $g_{ij} := \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
. Similarly, if
$g_{ij} := \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
. Similarly, if
![]() $\mathcal {L}$
is such that
$\mathcal {L}$
is such that
![]() $\mathcal {L}_{ss}(X,Y) = y_{ji}$
, we set
$\mathcal {L}_{ss}(X,Y) = y_{ji}$
, we set
![]() $h_{ji} := \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
. In addition, we let
$h_{ji} := \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
. In addition, we let
![]() $g_{ii} := \det X^{[i,n]}_{[i,n]}$
and
$g_{ii} := \det X^{[i,n]}_{[i,n]}$
and
![]() $h_{ii} := \det Y^{[i,n]}_{[i,n]}$
,
$h_{ii} := \det Y^{[i,n]}_{[i,n]}$
,
![]() $1 \leq i \leq n$
. The functions
$1 \leq i \leq n$
. The functions
![]() $h_{11}$
and
$h_{11}$
and
![]() $g_{11}$
, as well as the determinants of the
$g_{11}$
, as well as the determinants of the
![]() $\mathcal {L}$
-matrices, are considered as stable variables.
$\mathcal {L}$
-matrices, are considered as stable variables.
Conventions
The following identifications are frequently used in the text:
 $$ \begin{align} \begin{aligned} f_{n-l,l} &:= \varphi_{n-l,l},& &1 \leq l \leq n-1;\\ f_{0,l} &:= h_{n-l+1,n-l+1},& &1 \leq l \leq n-1;\\ f_{k,0} & := g_{n-k+1,n-k+1},& &1 \leq k \leq n-1. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} f_{n-l,l} &:= \varphi_{n-l,l},& &1 \leq l \leq n-1;\\ f_{0,l} &:= h_{n-l+1,n-l+1},& &1 \leq l \leq n-1;\\ f_{k,0} & := g_{n-k+1,n-k+1},& &1 \leq k \leq n-1. \end{aligned} \end{align} $$
The above equalities are set in concordance with the defining formulas for the variables, for which one simply extends the range of the allowed indices. Furthermore, for g-functions we set
 $$ \begin{align} g_{n+1,i+1} := \begin{cases} h_{1,j+1} &\text{if} \ \gamma_c^*(j) = i,\\ 1 &\text{otherwise;} \end{cases} \ \ \ g_{i,0} := \begin{cases} h_{jn} & \text{if} \ \gamma_r(i)=j,\\ 1 & \text{otherwise;} \end{cases} \end{align} $$
$$ \begin{align} g_{n+1,i+1} := \begin{cases} h_{1,j+1} &\text{if} \ \gamma_c^*(j) = i,\\ 1 &\text{otherwise;} \end{cases} \ \ \ g_{i,0} := \begin{cases} h_{jn} & \text{if} \ \gamma_r(i)=j,\\ 1 & \text{otherwise;} \end{cases} \end{align} $$
and for h-functions we set
 $$ \begin{align} h_{j+1,n+1} := \begin{cases} g_{i+1,1} &\text{if} \ \gamma_r(i) = j,\\ 1 &\text{otherwise;} \end{cases} \ \ \ h_{0,j} := \begin{cases} g_{ni} &\text{if}\ \gamma_c^*(j) = i,\\ 1 &\text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} h_{j+1,n+1} := \begin{cases} g_{i+1,1} &\text{if} \ \gamma_r(i) = j,\\ 1 &\text{otherwise;} \end{cases} \ \ \ h_{0,j} := \begin{cases} g_{ni} &\text{if}\ \gamma_c^*(j) = i,\\ 1 &\text{otherwise.} \end{cases} \end{align} $$
The meaning of these identifications follows from the following observation: If
![]() $g_{ni} = \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
and
$g_{ni} = \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
and
![]() $\gamma _c^*(j) = i$
, then
$\gamma _c^*(j) = i$
, then
![]() $h_{1,j+1} = \det \mathcal {L}^{[s+1,N(\mathcal {L})]}_{[s+1,N(\mathcal {L})]}$
; similarly, if
$h_{1,j+1} = \det \mathcal {L}^{[s+1,N(\mathcal {L})]}_{[s+1,N(\mathcal {L})]}$
; similarly, if
![]() $h_{jn} = \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
and
$h_{jn} = \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
and
![]() $\gamma _r(i) = j$
, then
$\gamma _r(i) = j$
, then
![]() $g_{i+1,1} = \det \mathcal {L}^{[s+1,N(\mathcal {L})]}_{[s+1,N(\mathcal {L})]}$
.
$g_{i+1,1} = \det \mathcal {L}^{[s+1,N(\mathcal {L})]}_{[s+1,N(\mathcal {L})]}$
.
Description of
 $\mathcal {GC}(\mathbf {\Gamma })$
$\mathcal {GC}(\mathbf {\Gamma })$
The description of the initial quiver is given later in Section 3.6. The initial extended cluster is given by the union
 $$\begin{align*}\begin{aligned} \{g_{ij}, \ h_{ji} \ | \ 1 \leq j \leq i \leq n\} \cup \{f_{kl} \ | \ k, l \geq 1&, \ k+l \leq n-1 \}\cup \\ &\cup \{ \varphi_{kl} \ | \ k, l \geq 1, \ k+l \leq n \} \cup \{ c_{i} \ | \ 1 \leq i \leq n-1\}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{g_{ij}, \ h_{ji} \ | \ 1 \leq j \leq i \leq n\} \cup \{f_{kl} \ | \ k, l \geq 1&, \ k+l \leq n-1 \}\cup \\ &\cup \{ \varphi_{kl} \ | \ k, l \geq 1, \ k+l \leq n \} \cup \{ c_{i} \ | \ 1 \leq i \leq n-1\}. \end{aligned} \end{align*}$$
Let
![]() $\mathcal {L}_1(X,Y), \ldots , \mathcal {L}_m(X,Y)$
be the list of all
$\mathcal {L}_1(X,Y), \ldots , \mathcal {L}_m(X,Y)$
be the list of all
![]() $\mathcal {L}$
-matrices in
$\mathcal {L}$
-matrices in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
. The ground ring
$\mathcal {GC}(\mathbf {\Gamma })$
. The ground ring
![]() $\hat {\mathbb {A}} = \hat {\mathbb {A}}(\mathcal {GC}(\mathbf {\Gamma }))$
is set to be
$\hat {\mathbb {A}} = \hat {\mathbb {A}}(\mathcal {GC}(\mathbf {\Gamma }))$
is set to be
All mutation relations are ordinary except the mutation at
![]() $\varphi _{11}$
. It is given by
$\varphi _{11}$
. It is given by
 $$ \begin{align} \varphi_{11} \varphi_{11}^{\prime} = \sum_{r=0}^n c_r \varphi_{21}^r \varphi_{12}^{n-r}. \end{align} $$
$$ \begin{align} \varphi_{11} \varphi_{11}^{\prime} = \sum_{r=0}^n c_r \varphi_{21}^r \varphi_{12}^{n-r}. \end{align} $$
A variable
![]() $\psi $
is frozen if and only if either
$\psi $
is frozen if and only if either
![]() $\psi = c_i$
for
$\psi = c_i$
for
![]() $0 \leq i \leq n$
, or
$0 \leq i \leq n$
, or
![]() $\psi = g_{i+1,1}$
for
$\psi = g_{i+1,1}$
for
![]() $i \in \Pi \setminus \Gamma _1^r$
, or
$i \in \Pi \setminus \Gamma _1^r$
, or
![]() $\psi = h_{1,j+1}$
for
$\psi = h_{1,j+1}$
for
![]() $j \in \Pi \setminus \Gamma _2^c$
.
$j \in \Pi \setminus \Gamma _2^c$
.
3.4 Operators and the bracket
In this section, we describe various operators and their properties used throughout the text, especially in sections on compatibility.
The operators
 $\gamma , \gamma ^* : \operatorname {\mathrm {gl}}_n(\mathbb C) \rightarrow \operatorname {\mathrm {gl}}_n(\mathbb C)$
$\gamma , \gamma ^* : \operatorname {\mathrm {gl}}_n(\mathbb C) \rightarrow \operatorname {\mathrm {gl}}_n(\mathbb C)$
Let
![]() $\mathbf {\Gamma } := (\Gamma _1,\Gamma _2,\gamma )$
be an oriented BD triple. Let
$\mathbf {\Gamma } := (\Gamma _1,\Gamma _2,\gamma )$
be an oriented BD triple. Let
![]() $\Delta _1,\ldots ,\Delta _k$
be the list of all nontrivial X-runs, and set
$\Delta _1,\ldots ,\Delta _k$
be the list of all nontrivial X-runs, and set
![]() $\bar {\Delta }_1,\ldots ,\bar {\Delta }_k$
to be the list of the corresponding Y-runs, where
$\bar {\Delta }_1,\ldots ,\bar {\Delta }_k$
to be the list of the corresponding Y-runs, where
![]() $\gamma (\Delta _i) = \bar {\Delta }_i$
,
$\gamma (\Delta _i) = \bar {\Delta }_i$
,
![]() $1 \leq i \leq k$
. Set
$1 \leq i \leq k$
. Set
![]() $\operatorname {\mathrm {gl}}(\Delta _i)$
to be a subalgebra of
$\operatorname {\mathrm {gl}}(\Delta _i)$
to be a subalgebra of
![]() $\operatorname {\mathrm {gl}}_n(\mathbb {C})$
of the matrices that are zero outside of the block
$\operatorname {\mathrm {gl}}_n(\mathbb {C})$
of the matrices that are zero outside of the block
![]() $\Delta _i \times \Delta _i$
(and similarly for
$\Delta _i \times \Delta _i$
(and similarly for
![]() $\operatorname {\mathrm {gl}}(\Delta _i)$
). Define
$\operatorname {\mathrm {gl}}(\Delta _i)$
). Define
![]() $\gamma _i : \operatorname {\mathrm {gl}}_n(\Delta _i) \rightarrow \operatorname {\mathrm {gl}}_n(\bar {\Delta }_i)$
to be the map that shifts the
$\gamma _i : \operatorname {\mathrm {gl}}_n(\Delta _i) \rightarrow \operatorname {\mathrm {gl}}_n(\bar {\Delta }_i)$
to be the map that shifts the
![]() $\Delta _i\times \Delta _i$
block to
$\Delta _i\times \Delta _i$
block to
![]() $\bar {\Delta }_i \times \bar {\Delta }_i$
. Then the map
$\bar {\Delta }_i \times \bar {\Delta }_i$
. Then the map
![]() $\gamma : \operatorname {\mathrm {gl}}_n(\mathbb {C}) \rightarrow \operatorname {\mathrm {gl}}_n(\mathbb {C})$
is defined as the direct sum
$\gamma : \operatorname {\mathrm {gl}}_n(\mathbb {C}) \rightarrow \operatorname {\mathrm {gl}}_n(\mathbb {C})$
is defined as the direct sum
![]() $\gamma :=\bigoplus _{i=1}^k\gamma _i$
extended by zero to
$\gamma :=\bigoplus _{i=1}^k\gamma _i$
extended by zero to
![]() $\operatorname {\mathrm {gl}}_n(\mathbb {C})$
. Similarly, one sets
$\operatorname {\mathrm {gl}}_n(\mathbb {C})$
. Similarly, one sets
![]() $\gamma _i^* : \operatorname {\mathrm {gl}}_n(\bar {\Delta }_i)\rightarrow \operatorname {\mathrm {gl}}_n(\Delta _i)$
to be the map that shifts the
$\gamma _i^* : \operatorname {\mathrm {gl}}_n(\bar {\Delta }_i)\rightarrow \operatorname {\mathrm {gl}}_n(\Delta _i)$
to be the map that shifts the
![]() $\bar {\Delta }_i \times \bar {\Delta }_i$
block to
$\bar {\Delta }_i \times \bar {\Delta }_i$
block to
![]() $\Delta _i \times \Delta _i$
. The map
$\Delta _i \times \Delta _i$
. The map
![]() $\gamma ^* : \operatorname {\mathrm {gl}}_n(\mathbb {C}) \rightarrow \operatorname {\mathrm {gl}}_n(\mathbb {C})$
is obtained as the direct sum
$\gamma ^* : \operatorname {\mathrm {gl}}_n(\mathbb {C}) \rightarrow \operatorname {\mathrm {gl}}_n(\mathbb {C})$
is obtained as the direct sum
![]() $\gamma ^*:=\bigoplus _{i=1}^k\gamma _i^*$
extended by zero to
$\gamma ^*:=\bigoplus _{i=1}^k\gamma _i^*$
extended by zero to
![]() $\operatorname {\mathrm {gl}}_n(\mathbb {C})$
.
$\operatorname {\mathrm {gl}}_n(\mathbb {C})$
.
Remark 3.3. The resulting maps were denoted in [Reference Gekhtman, Shapiro and Vainshtein20] as
![]() $\mathring {\gamma }$
and
$\mathring {\gamma }$
and
![]() $\mathring {\gamma }^*$
, in order to distinguish them from their
$\mathring {\gamma }^*$
, in order to distinguish them from their
![]() $\operatorname {\mathrm {sl}}_{n}$
-counterparts that were constructed in Section 2.2 (note:
$\operatorname {\mathrm {sl}}_{n}$
-counterparts that were constructed in Section 2.2 (note:
![]() $\gamma |_{\operatorname {\mathrm {sl}}_n(\mathbb {C})}$
may be different from the map constructed in Section 2.2 on the Cartan subalgebra of
$\gamma |_{\operatorname {\mathrm {sl}}_n(\mathbb {C})}$
may be different from the map constructed in Section 2.2 on the Cartan subalgebra of
![]() $\operatorname {\mathrm {sl}}_n(\mathbb {C})$
).
$\operatorname {\mathrm {sl}}_n(\mathbb {C})$
).
Example 3.4. Let us consider a BD pair defined by its BD graph below (note:
![]() $\Gamma _1^c = \emptyset $
):
$\Gamma _1^c = \emptyset $
):

Similarly, the action of
![]() $\gamma ^*$
is given by
$\gamma ^*$
is given by
 $$\begin{align*}\gamma^* \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} & a_{15}\\a_{21} & a_{22} & a_{23} & a_{24} & a_{25}\\ a_{31} & a_{32} & a_{33} & a_{34} & a_{35}\\ a_{41} & a_{42} & a_{43} & a_{44} & a_{45}\\a_{51} & a_{52} & a_{53} & a_{54} & a_{55}\end{bmatrix} = \begin{bmatrix}a_{33} & a_{34} & a_{35} & 0 & 0\\ a_{43} & a_{44} & a_{45} & 0 & 0 \\ a_{53} & a_{54} & a_{55} & 0 & 0 \\ 0 & 0 & 0 & a_{11} & a_{12} \\ 0 & 0 & 0 & a_{21} & a_{22}\end{bmatrix}. \end{align*}$$
$$\begin{align*}\gamma^* \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} & a_{15}\\a_{21} & a_{22} & a_{23} & a_{24} & a_{25}\\ a_{31} & a_{32} & a_{33} & a_{34} & a_{35}\\ a_{41} & a_{42} & a_{43} & a_{44} & a_{45}\\a_{51} & a_{52} & a_{53} & a_{54} & a_{55}\end{bmatrix} = \begin{bmatrix}a_{33} & a_{34} & a_{35} & 0 & 0\\ a_{43} & a_{44} & a_{45} & 0 & 0 \\ a_{53} & a_{54} & a_{55} & 0 & 0 \\ 0 & 0 & 0 & a_{11} & a_{12} \\ 0 & 0 & 0 & a_{21} & a_{22}\end{bmatrix}. \end{align*}$$
The group homomorphisms
 $\tilde {\gamma }$
and
$\tilde {\gamma }$
and
 $\tilde {\gamma }^*$
$\tilde {\gamma }^*$
The maps
![]() $\gamma , \gamma ^* : \operatorname {\mathrm {gl}}_n(\mathbb C) \rightarrow \operatorname {\mathrm {gl}}_n(\mathbb C)$
are not Lie algebra homomorphisms; however, their restrictions to the Borel subalgebras
$\gamma , \gamma ^* : \operatorname {\mathrm {gl}}_n(\mathbb C) \rightarrow \operatorname {\mathrm {gl}}_n(\mathbb C)$
are not Lie algebra homomorphisms; however, their restrictions to the Borel subalgebras
![]() $\mathfrak {b}_+$
and
$\mathfrak {b}_+$
and
![]() $\mathfrak {b}_-$
are Lie algebra homomorphisms, hence we can define group homomorphisms
$\mathfrak {b}_-$
are Lie algebra homomorphisms, hence we can define group homomorphisms
![]() $\tilde {\gamma }, \tilde {\gamma }^* : \mathfrak {B}_{\pm } \rightarrow \mathfrak {B}_{\pm }$
, where
$\tilde {\gamma }, \tilde {\gamma }^* : \mathfrak {B}_{\pm } \rightarrow \mathfrak {B}_{\pm }$
, where
![]() $\mathfrak {B}_+$
and
$\mathfrak {B}_+$
and
![]() $\mathfrak {B}_-$
are the corresponding Borel subgroups. Notice that if the BD triple is oriented and
$\mathfrak {B}_-$
are the corresponding Borel subgroups. Notice that if the BD triple is oriented and
![]() $N_{\pm }$
is a unipotent (upper or lower) triangular matrix, then
$N_{\pm }$
is a unipotent (upper or lower) triangular matrix, then
![]() $\tilde {\gamma }(N_{\pm }) = \gamma (N_{\pm } - I) + I$
, where I is the identity matrix, and similarly for
$\tilde {\gamma }(N_{\pm }) = \gamma (N_{\pm } - I) + I$
, where I is the identity matrix, and similarly for
![]() $\tilde {\gamma }^*$
. Likewise, let
$\tilde {\gamma }^*$
. Likewise, let
![]() $\operatorname {\mathrm {GL}}(\Delta )\hookrightarrow \operatorname {\mathrm {GL}}_n$
be the group of invertible
$\operatorname {\mathrm {GL}}(\Delta )\hookrightarrow \operatorname {\mathrm {GL}}_n$
be the group of invertible
![]() $|\Delta |\times |\Delta |$
matrices viewed as a block in
$|\Delta |\times |\Delta |$
matrices viewed as a block in
![]() $\operatorname {\mathrm {GL}}_n$
that occupies
$\operatorname {\mathrm {GL}}_n$
that occupies
![]() $\Delta \times \Delta $
; since
$\Delta \times \Delta $
; since
![]() $\gamma : \operatorname {\mathrm {gl}}(\Delta ) \rightarrow \operatorname {\mathrm {gl}}(\bar {\Delta })$
is an isomorphism of Lie algebras, it can be integrated to an isomorphism of groups
$\gamma : \operatorname {\mathrm {gl}}(\Delta ) \rightarrow \operatorname {\mathrm {gl}}(\bar {\Delta })$
is an isomorphism of Lie algebras, it can be integrated to an isomorphism of groups
![]() $\gamma : \operatorname {\mathrm {GL}}(\Delta ) \rightarrow \operatorname {\mathrm {GL}}(\bar {\Delta })$
(and similarly for
$\gamma : \operatorname {\mathrm {GL}}(\Delta ) \rightarrow \operatorname {\mathrm {GL}}(\bar {\Delta })$
(and similarly for
![]() $\gamma ^*$
).
$\gamma ^*$
).
Remark 3.5. The maps
![]() $\tilde {\gamma }$
and
$\tilde {\gamma }$
and
![]() $\tilde {\gamma }^*$
were denoted in [Reference Gekhtman, Shapiro and Vainshtein20] as
$\tilde {\gamma }^*$
were denoted in [Reference Gekhtman, Shapiro and Vainshtein20] as
![]() $\exp (\gamma )$
and
$\exp (\gamma )$
and
![]() $\exp (\gamma ^*)$
. We have changed the notation to avoid a possible confusion with the matrix exponential.
$\exp (\gamma ^*)$
. We have changed the notation to avoid a possible confusion with the matrix exponential.
Differential operators
For a rational function
![]() $f \in \mathbb C(\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n)$
, set
$f \in \mathbb C(\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n)$
, set
 $$\begin{align*}\nabla_X f := \left( \frac{\partial f}{\partial x_{ji}} \right) _{i,j=1}^{n}, \ \ \nabla_Y f := \left( \frac{\partial f}{\partial y_{ji}} \right) _{i,j=1}^{n}. \end{align*}$$
$$\begin{align*}\nabla_X f := \left( \frac{\partial f}{\partial x_{ji}} \right) _{i,j=1}^{n}, \ \ \nabla_Y f := \left( \frac{\partial f}{\partial y_{ji}} \right) _{i,j=1}^{n}. \end{align*}$$
Define
 $$ \begin{align*} E_Lf &:= \nabla_X f \cdot X + \nabla_Y f \cdot Y, & E_R f &:= X \nabla_X f + Y \nabla_Y f, \\ \xi_L f &:= \gamma_c(\nabla_X f \cdot X) + \nabla_Y f \cdot Y, & \xi_R f &:= X\nabla_X f + \gamma_r^*(Y \nabla_Y f), \\ \eta_L f &:= \nabla_X f \cdot X + \gamma_c^*(\nabla_Y f \cdot Y), & \eta_R f&:= \gamma_r(X \nabla_X f) + Y \nabla_Y f. \end{align*} $$
$$ \begin{align*} E_Lf &:= \nabla_X f \cdot X + \nabla_Y f \cdot Y, & E_R f &:= X \nabla_X f + Y \nabla_Y f, \\ \xi_L f &:= \gamma_c(\nabla_X f \cdot X) + \nabla_Y f \cdot Y, & \xi_R f &:= X\nabla_X f + \gamma_r^*(Y \nabla_Y f), \\ \eta_L f &:= \nabla_X f \cdot X + \gamma_c^*(\nabla_Y f \cdot Y), & \eta_R f&:= \gamma_r(X \nabla_X f) + Y \nabla_Y f. \end{align*} $$
Let
![]() $\ell $
denote r or c. Define subalgebras
$\ell $
denote r or c. Define subalgebras
 $$\begin{align*}\mathfrak{g}_{\Gamma^{\ell}_1} := \bigoplus_{i=1}^{k} \operatorname{\mathrm{gl}}(\Delta_i^{\ell}), \ \ \ \ \mathfrak{g}_{\Gamma^{\ell}_2} := \bigoplus_{i=1}^{k} \operatorname{\mathrm{gl}}(\bar{\Delta}^{\ell}_i), \end{align*}$$
$$\begin{align*}\mathfrak{g}_{\Gamma^{\ell}_1} := \bigoplus_{i=1}^{k} \operatorname{\mathrm{gl}}(\Delta_i^{\ell}), \ \ \ \ \mathfrak{g}_{\Gamma^{\ell}_2} := \bigoplus_{i=1}^{k} \operatorname{\mathrm{gl}}(\bar{\Delta}^{\ell}_i), \end{align*}$$
where
![]() $\operatorname {\mathrm {gl}}(\Delta _i^{\ell })$
and
$\operatorname {\mathrm {gl}}(\Delta _i^{\ell })$
and
![]() $\operatorname {\mathrm {gl}}(\bar {\Delta }_i^{\ell })$
are constructed above. Let
$\operatorname {\mathrm {gl}}(\bar {\Delta }_i^{\ell })$
are constructed above. Let
![]() $\pi _{\Gamma _1^{\ell }}$
and
$\pi _{\Gamma _1^{\ell }}$
and
![]() $\pi _{\Gamma _2^{\ell }}$
be the projections onto
$\pi _{\Gamma _2^{\ell }}$
be the projections onto
![]() $\mathfrak {g}_{\Gamma ^{\ell }_1}$
and
$\mathfrak {g}_{\Gamma ^{\ell }_1}$
and
![]() $\mathfrak {g}_{\Gamma ^{\ell }_2}$
, respectively; also, let
$\mathfrak {g}_{\Gamma ^{\ell }_2}$
, respectively; also, let
![]() $\pi _{\hat {\Gamma }_1^{\ell }}$
and
$\pi _{\hat {\Gamma }_1^{\ell }}$
and
![]() $\pi _{\hat {\Gamma }_2^{\ell }}$
be the projections onto the orthogonal complements of
$\pi _{\hat {\Gamma }_2^{\ell }}$
be the projections onto the orthogonal complements of
![]() $\mathfrak {g}_{\Gamma ^{\ell }_1}$
and
$\mathfrak {g}_{\Gamma ^{\ell }_1}$
and
![]() $\mathfrak {g}_{\Gamma ^{\ell }_2}$
with respect to the trace form. There are numerous identities that relate the differential operators among each other and with the projections; they are easily derivable and extensively used in the paper. Let us mention some of them:
$\mathfrak {g}_{\Gamma ^{\ell }_2}$
with respect to the trace form. There are numerous identities that relate the differential operators among each other and with the projections; they are easily derivable and extensively used in the paper. Let us mention some of them:
 $$ \begin{align*} E_L &= \xi_L + (1-\gamma_c) (\nabla_X X), & E_R &= \xi_R + (1-\gamma_r^*)(Y\nabla_Y),\\ E_L &= \eta_L + (1-\gamma_c^*)(\nabla_Y Y), & E_R &= \eta_R + (1-\gamma_r)(X \nabla X),\\ \xi_L &= \gamma_c(\eta_L) + \pi_{\hat{\Gamma}_2^c}(\nabla_Y Y), & \xi_R &= \gamma_r^*(\eta_R) + \pi_{\hat{\Gamma}_1^r} (X \nabla_X),\\ \eta_L &= \gamma_c^*(\xi_L) + \pi_{\hat{\Gamma}_1^c} (\nabla_X X), & \eta_R &= \gamma_r(\xi_R) + \pi_{\hat{\Gamma}_2^r}(Y\nabla_Y). \end{align*} $$
$$ \begin{align*} E_L &= \xi_L + (1-\gamma_c) (\nabla_X X), & E_R &= \xi_R + (1-\gamma_r^*)(Y\nabla_Y),\\ E_L &= \eta_L + (1-\gamma_c^*)(\nabla_Y Y), & E_R &= \eta_R + (1-\gamma_r)(X \nabla X),\\ \xi_L &= \gamma_c(\eta_L) + \pi_{\hat{\Gamma}_2^c}(\nabla_Y Y), & \xi_R &= \gamma_r^*(\eta_R) + \pi_{\hat{\Gamma}_1^r} (X \nabla_X),\\ \eta_L &= \gamma_c^*(\xi_L) + \pi_{\hat{\Gamma}_1^c} (\nabla_X X), & \eta_R &= \gamma_r(\xi_R) + \pi_{\hat{\Gamma}_2^r}(Y\nabla_Y). \end{align*} $$
The bracket and
 $R_0$
$R_0$
For any choice of
![]() $(R_0^r,R_0^c)$
on
$(R_0^r,R_0^c)$
on
![]() $\operatorname {\mathrm {SL}}_n\times \operatorname {\mathrm {SL}}_n$
, the variables
$\operatorname {\mathrm {SL}}_n\times \operatorname {\mathrm {SL}}_n$
, the variables
![]() $c_0,c_1,\ldots ,c_{n-1},c_n$
are Casimirs of the Poisson bracket. However, there is only one choice of
$c_0,c_1,\ldots ,c_{n-1},c_n$
are Casimirs of the Poisson bracket. However, there is only one choice of
![]() $(R_0^r,R_0^c)$
for which these variables are Casimirs on
$(R_0^r,R_0^c)$
for which these variables are Casimirs on
![]() $\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
:
$\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
:
-
a) The functions
 $c_0, c_1,\ldots , c_{n-1},c_n$
are Casimirs if and only if the identity matrix is an eigenvector of both
$c_0, c_1,\ldots , c_{n-1},c_n$
are Casimirs if and only if the identity matrix is an eigenvector of both
 $R_0^r$
and
$R_0^r$
and
 $R_0^c$
(in this case,
$R_0^c$
(in this case,
 $R_0^r(I) = R_0^c(I) = (1/2)I$
from
$R_0^r(I) = R_0^c(I) = (1/2)I$
from
 $R_0 + R_0^* = \operatorname {\mathrm {id}}_{\mathfrak h}$
).
$R_0 + R_0^* = \operatorname {\mathrm {id}}_{\mathfrak h}$
).
However, there is an important alternative choice of
![]() $(R_0^r,R_0^c)$
:
$(R_0^r,R_0^c)$
:
-
b) For a BD triple
 $(\Gamma _1,\Gamma _2,\gamma )$
, a solution
$(\Gamma _1,\Gamma _2,\gamma )$
, a solution
 $R_0$
of equations (2.8) and (2.9) is such that (3.6)(the identities are viewed relative the Cartan subalgebra
$R_0$
of equations (2.8) and (2.9) is such that (3.6)(the identities are viewed relative the Cartan subalgebra $$ \begin{align}\begin{aligned} R_0 (1-\gamma) &= \pi_{\Gamma_1} + R_0 \pi_{\hat{\Gamma}_1} \qquad&\qquad R_0(1-\gamma^*) &= -\gamma^* +R_0 \pi_{\hat{\Gamma}_2}\\ R_0^*(1-\gamma) &= -\gamma + R_0^*\pi_{\hat{\Gamma_1}}\qquad&\qquad R_0^*(1-\gamma^*) &= \pi_{\Gamma_2} + R_0^*\pi_{\hat{\Gamma}_2} \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} R_0 (1-\gamma) &= \pi_{\Gamma_1} + R_0 \pi_{\hat{\Gamma}_1} \qquad&\qquad R_0(1-\gamma^*) &= -\gamma^* +R_0 \pi_{\hat{\Gamma}_2}\\ R_0^*(1-\gamma) &= -\gamma + R_0^*\pi_{\hat{\Gamma_1}}\qquad&\qquad R_0^*(1-\gamma^*) &= \pi_{\Gamma_2} + R_0^*\pi_{\hat{\Gamma}_2} \end{aligned} \end{align} $$
 $\mathfrak {h}$
of
$\mathfrak {h}$
of
 $\operatorname {\mathrm {gl}}_n$
).
$\operatorname {\mathrm {gl}}_n$
).
Note that these conditions do not follow from the system (2.8) and (2.9). For instance, if
![]() $I_{\Delta }:=\sum _{i\in \Delta }e_{ii}$
, the first condition specifies the value of
$I_{\Delta }:=\sum _{i\in \Delta }e_{ii}$
, the first condition specifies the value of
![]() $R_0$
on
$R_0$
on
![]() $I_{\Delta }-I_{\bar {\Delta }}$
as
$I_{\Delta }-I_{\bar {\Delta }}$
as
Choosing
![]() $R_0^r$
and
$R_0^r$
and
![]() $R_0^c$
that satisfy equation (3.6) eases some of the computations with Poisson brackets, so this choice is employed in the proofs; however, in Section 8.2 we show that the results of the paper hold regardless of the choice of
$R_0^c$
that satisfy equation (3.6) eases some of the computations with Poisson brackets, so this choice is employed in the proofs; however, in Section 8.2 we show that the results of the paper hold regardless of the choice of
![]() $(R_0^r,R_0^c)$
. Moreover, when
$(R_0^r,R_0^c)$
. Moreover, when
![]() $R_0:= R_0^r = R_0^c$
and
$R_0:= R_0^r = R_0^c$
and
![]() $R_0$
satisfies equation (3.6), the connected Poisson dual
$R_0$
satisfies equation (3.6), the connected Poisson dual
![]() $\operatorname {\mathrm {GL}}_n^*$
of
$\operatorname {\mathrm {GL}}_n^*$
of
![]() $\operatorname {\mathrm {GL}}_n$
can be viewed as a subgroup of the direct product of certain parabolic subgroups modulo a relation (see Section 3.8 for details). Lastly, the Poisson bracket (2.12) attains the following form on
$\operatorname {\mathrm {GL}}_n$
can be viewed as a subgroup of the direct product of certain parabolic subgroups modulo a relation (see Section 3.8 for details). Lastly, the Poisson bracket (2.12) attains the following form on
![]() $\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
:
$\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
:
3.5 Invariance properties
In this section, we describe the invariance properties of the functions from the initial extended cluster.
Invariance properties of f- and
 $\varphi $
-functions
$\varphi $
-functions
Let f be any f-function and
![]() $\tilde {\varphi }$
be any
$\tilde {\varphi }$
be any
![]() $\tilde {\varphi }$
-function (recall that
$\tilde {\varphi }$
-function (recall that
![]() $\tilde {\varphi }$
differs from
$\tilde {\varphi }$
differs from
![]() $\varphi $
by a factor of
$\varphi $
by a factor of
![]() $\det X$
; see equation (3.1)). Pick any unipotent upper triangular matrix
$\det X$
; see equation (3.1)). Pick any unipotent upper triangular matrix
![]() $N_+$
, a pair of any unipotent lower triangular matrices
$N_+$
, a pair of any unipotent lower triangular matrices
![]() $N_-$
and
$N_-$
and
![]() $N_-^{\prime }$
, and let A be any invertible matrix. Then
$N_-^{\prime }$
, and let A be any invertible matrix. Then
Let
![]() $\mathfrak {b}_+$
and
$\mathfrak {b}_+$
and
![]() $\mathfrak {b}_-$
be the subspaces of upper and lower triangular matrices. The infinitesimal version of equation (3.7) is
$\mathfrak {b}_-$
be the subspaces of upper and lower triangular matrices. The infinitesimal version of equation (3.7) is
 $$ \begin{align}\begin{aligned} \nabla_X f \cdot X, \ \nabla_Y f\cdot Y \in &\,\mathfrak{b}_-, \qquad&\qquad &E_Rf \in \mathfrak{b}_+;\\ E_L\tilde{\varphi} \in &\,\mathfrak{b}_-, \qquad&\qquad &E_R\tilde{\varphi} = 0. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \nabla_X f \cdot X, \ \nabla_Y f\cdot Y \in &\,\mathfrak{b}_-, \qquad&\qquad &E_Rf \in \mathfrak{b}_+;\\ E_L\tilde{\varphi} \in &\,\mathfrak{b}_-, \qquad&\qquad &E_R\tilde{\varphi} = 0. \end{aligned}\end{align} $$
Moreover,
 $$ \begin{align}\begin{aligned} \pi_0 E_L \log f &= \text{const}, \qquad&\qquad \pi_0 E_R \log f &= \text{const}, \\ \pi_0 E_L \log \varphi &= \text{const}, \qquad&\qquad \pi_0 E_R \log \varphi &= \text{const}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \pi_0 E_L \log f &= \text{const}, \qquad&\qquad \pi_0 E_R \log f &= \text{const}, \\ \pi_0 E_L \log \varphi &= \text{const}, \qquad&\qquad \pi_0 E_R \log \varphi &= \text{const}, \end{aligned}\end{align} $$
where
![]() $\pi _0$
is the projection onto the space of diagonal matrices; by const we mean that the left-hand sides (LHS) of the formulas do not depend on
$\pi _0$
is the projection onto the space of diagonal matrices; by const we mean that the left-hand sides (LHS) of the formulas do not depend on
![]() $(X,Y)$
. For the c-functions,
$(X,Y)$
. For the c-functions,
where I is the identity matrix.
Invariance properties of g- and h-functions
Let
![]() $\psi $
be any g- or h-function, and let
$\psi $
be any g- or h-function, and let
![]() $N_+$
and
$N_+$
and
![]() $N_-$
be any unipotent upper and lower triangular matrices. Then
$N_-$
be any unipotent upper and lower triangular matrices. Then
Let T be any diagonal matrix; then we also have
 $$ \begin{align} \begin{aligned} \psi(X\tilde{\gamma}_c^*(T),YT) &= \hat{\xi}_L(T)\psi(X,Y), & \psi(TX,\tilde{\gamma}_r(T)Y) &= \hat{\xi}_R(T) \psi(X,Y),\\ \psi(XT,Y\tilde{\gamma}_c(T)) &= \hat{\eta}_L(T) \psi(X,Y), & \psi(\tilde{\gamma}_r^*(T)X,TY) &= \hat{\eta}_R(T) \psi(X,Y), \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned} \psi(X\tilde{\gamma}_c^*(T),YT) &= \hat{\xi}_L(T)\psi(X,Y), & \psi(TX,\tilde{\gamma}_r(T)Y) &= \hat{\xi}_R(T) \psi(X,Y),\\ \psi(XT,Y\tilde{\gamma}_c(T)) &= \hat{\eta}_L(T) \psi(X,Y), & \psi(\tilde{\gamma}_r^*(T)X,TY) &= \hat{\eta}_R(T) \psi(X,Y), \end{aligned}\end{align} $$
where
![]() $\hat {\xi }_R$
,
$\hat {\xi }_R$
,
![]() $\hat {\xi }_L$
,
$\hat {\xi }_L$
,
![]() $\hat {\eta }_R$
and
$\hat {\eta }_R$
and
![]() $\hat {\eta }_L$
are constants that depend only on T and
$\hat {\eta }_L$
are constants that depend only on T and
![]() $\psi $
(they can be viewed as characters on the group of invertible diagonal matrices). The infinitesimal version of equation (3.10) is
$\psi $
(they can be viewed as characters on the group of invertible diagonal matrices). The infinitesimal version of equation (3.10) is
and the infinitesimal version of equation (3.11) is
 $$ \begin{align} \begin{aligned} \pi_0 \xi_L \log \psi &= \text{const}, \qquad&\qquad \pi_0 \xi_R \log \psi &= \text{const},\\ \pi_0 \eta_L \log \psi &= \text{const}, \qquad&\qquad \pi_0 \eta_R \log \psi &= \text{const}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \pi_0 \xi_L \log \psi &= \text{const}, \qquad&\qquad \pi_0 \xi_R \log \psi &= \text{const},\\ \pi_0 \eta_L \log \psi &= \text{const}, \qquad&\qquad \pi_0 \eta_R \log \psi &= \text{const}. \end{aligned} \end{align} $$
Finally, let us mention the results of Lemma 4.4 and Corollary 4.6 from [Reference Gekhtman, Shapiro and Vainshtein20]. If
![]() $\Delta ^r$
,
$\Delta ^r$
,
![]() $\Delta ^c$
,
$\Delta ^c$
,
![]() $\bar {\Delta }^r$
and
$\bar {\Delta }^r$
and
![]() $\bar {\Delta }^c$
are any X- and Y- row and column runs (trivial or not), then
$\bar {\Delta }^c$
are any X- and Y- row and column runs (trivial or not), then
 $$ \begin{align}\begin{aligned} \operatorname{\mathrm{tr}}( (\nabla_X\log \psi\cdot X)_{\Delta^c}^{\Delta^c}) &= \text{const}, \qquad&\qquad \operatorname{\mathrm{tr}}( (X \nabla_X\log \psi)_{\Delta^r}^{\Delta^r}) &= \text{const}, \\ \operatorname{\mathrm{tr}}( (\nabla_Y \log \psi\cdot Y)_{\bar{\Delta}^c}^{\bar{\Delta}^c}) & = \text{const}, \qquad&\qquad \operatorname{\mathrm{tr}}( (Y\nabla_Y \log \psi)_{\bar{\Delta}^r}^{\bar{\Delta}^r}) & = \text{const}; \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \operatorname{\mathrm{tr}}( (\nabla_X\log \psi\cdot X)_{\Delta^c}^{\Delta^c}) &= \text{const}, \qquad&\qquad \operatorname{\mathrm{tr}}( (X \nabla_X\log \psi)_{\Delta^r}^{\Delta^r}) &= \text{const}, \\ \operatorname{\mathrm{tr}}( (\nabla_Y \log \psi\cdot Y)_{\bar{\Delta}^c}^{\bar{\Delta}^c}) & = \text{const}, \qquad&\qquad \operatorname{\mathrm{tr}}( (Y\nabla_Y \log \psi)_{\bar{\Delta}^r}^{\bar{\Delta}^r}) & = \text{const}; \end{aligned}\end{align} $$
also,
 $$ \begin{align}\begin{aligned} \operatorname{\mathrm{tr}}( \nabla_X\log \psi\cdot X) &= \text{const}, \qquad&\qquad \operatorname{\mathrm{tr}}(X \nabla_X\log \psi) &= \text{const}, \\ \operatorname{\mathrm{tr}}( \nabla_Y \log \psi\cdot Y) & = \text{const}, \qquad&\qquad \operatorname{\mathrm{tr}}(Y\nabla_Y \log \psi) & = \text{const}. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \operatorname{\mathrm{tr}}( \nabla_X\log \psi\cdot X) &= \text{const}, \qquad&\qquad \operatorname{\mathrm{tr}}(X \nabla_X\log \psi) &= \text{const}, \\ \operatorname{\mathrm{tr}}( \nabla_Y \log \psi\cdot Y) & = \text{const}, \qquad&\qquad \operatorname{\mathrm{tr}}(Y\nabla_Y \log \psi) & = \text{const}. \end{aligned} \end{align} $$
3.6 Initial quiver
In this section, we describe the initial quiver for
![]() $\mathcal {GC}(\mathbf {\Gamma })$
defined by an aperiodic oriented BD pair
$\mathcal {GC}(\mathbf {\Gamma })$
defined by an aperiodic oriented BD pair
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
. We first describe the quiver for the trivial BD pair (based on [Reference Gekhtman, Shapiro and Vainshtein18]), and then we explain the necessary adjustments for a nontrivial BD pair. For particular examples of quivers, see Section 10. Throughout the section, we assume that
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
. We first describe the quiver for the trivial BD pair (based on [Reference Gekhtman, Shapiro and Vainshtein18]), and then we explain the necessary adjustments for a nontrivial BD pair. For particular examples of quivers, see Section 10. Throughout the section, we assume that
![]() $n \geq 3$
(the case
$n \geq 3$
(the case
![]() $n=2$
is described in [Reference Gekhtman, Shapiro and Vainshtein18]).
$n=2$
is described in [Reference Gekhtman, Shapiro and Vainshtein18]).
3.6.1 The quiver for the trivial BD pair
Below one can find pictures of the neighborhoods of all variables in the initial quiver in the case of the trivial BD pair. A few of remarks beforehand:
-
• The circled vertices are mutable (in the sense of ordinary exchange relations (2.2)), the square vertices are frozen, the rounded square vertices may or may not be mutable depending on the indices and the hexagon vertex is a mutable vertex with a generalized mutation relation (see equations (2.1) and (3.5));
-
• Since
 $c_1,\ldots ,c_{n-1}$
are isolated variables, they are not shown on the resulting quiver;
$c_1,\ldots ,c_{n-1}$
are isolated variables, they are not shown on the resulting quiver; -
• For
 $k=2$
and
$k=2$
and
 $n> 3$
, the vertices
$n> 3$
, the vertices
 $\varphi _{1k}$
and
$\varphi _{1k}$
and
 $\varphi _{k-1,2}$
coincide; hence, the pictures provided below suggest that there are two edges pointing from
$\varphi _{k-1,2}$
coincide; hence, the pictures provided below suggest that there are two edges pointing from
 $\varphi _{21}$
to
$\varphi _{21}$
to
 $\varphi _{12}$
(however, there is only one arrow in
$\varphi _{12}$
(however, there is only one arrow in
 $n = 3$
).
$n = 3$
).

Figure 2 The neighborhood of
![]() $\varphi _{kl}$
for
$\varphi _{kl}$
for
![]() $k,l \neq 1$
,
$k,l \neq 1$
,
![]() $k+l < n$
.
$k+l < n$
.

Figure 3 The neighborhood of
![]() $\varphi _{1l}$
for
$\varphi _{1l}$
for
![]() $2 \leq l \leq n-1$
.
$2 \leq l \leq n-1$
.

Figure 4 The neighborhood of
![]() $\varphi _{k1}$
for
$\varphi _{k1}$
for
![]() $2 \leq k \leq n-1$
.
$2 \leq k \leq n-1$
.

Figure 5 The neighborhood of
![]() $\varphi _{kl}$
for (a)
$\varphi _{kl}$
for (a)
![]() $k=l=1$
and (b)
$k=l=1$
and (b)
![]() $k+l=n$
.
$k+l=n$
.

Figure 6 The neighborhood of
![]() $f_{kl}$
for
$f_{kl}$
for
![]() $k+l <n$
(convention (3.2) is in place.).
$k+l <n$
(convention (3.2) is in place.).

Figure 7 The neighborhood of
![]() $g_{ij}$
for
$g_{ij}$
for
![]() $1 < j \leq i\leq n$
(convention (3.3) is in place).
$1 < j \leq i\leq n$
(convention (3.3) is in place).

Figure 8 The neighborhood of
![]() $g_{i1}$
for
$g_{i1}$
for
![]() $1 \leq i \leq n$
.
$1 \leq i \leq n$
.

Figure 9 The neighborhood of
![]() $h_{ij}$
for
$h_{ij}$
for
![]() $1 < i < j \leq n$
.
$1 < i < j \leq n$
.

Figure 10 The neighborhood of
![]() $h_{ij}$
for
$h_{ij}$
for
![]() $1 < i = j \leq n$
.
$1 < i = j \leq n$
.

Figure 11 The neighborhood of
![]() $h_{1j}$
.
$h_{1j}$
.
3.6.2 The quiver for a nontrivial BD pair (algorithm)
If
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
is nontrivial, one proceeds as follows. First, draw the quiver for the case of the trivial BD pair, employing the neighborhoods as described above. Second, add new arrows as prescribed by the following algorithm:
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
is nontrivial, one proceeds as follows. First, draw the quiver for the case of the trivial BD pair, employing the neighborhoods as described above. Second, add new arrows as prescribed by the following algorithm:
-
1) If
 $i \in \Gamma _1^r$
, unfreeze
$i \in \Gamma _1^r$
, unfreeze
 $g_{i+1,1}$
and add additional arrows, as indicated in Figure 12(a);
$g_{i+1,1}$
and add additional arrows, as indicated in Figure 12(a);
Figure 12 Additional arrows for
 $g_{i+1,1}$
and
$g_{i+1,1}$
and
 $h_{1,j+1}$
.
$h_{1,j+1}$
. -
2) If
 $j \in \Gamma _2^c$
, unfreeze
$j \in \Gamma _2^c$
, unfreeze
 $h_{1,j+1}$
and add additional arrows, as indicated in Figure 12(b);
$h_{1,j+1}$
and add additional arrows, as indicated in Figure 12(b); -
3) Repeat for all roots in
 $\Gamma _1^r$
and
$\Gamma _1^r$
and
 $\Gamma _2^c$
.
$\Gamma _2^c$
.
Note that the algorithm does not depend on the order of the roots of
![]() $\Gamma _1^r$
and
$\Gamma _1^r$
and
![]() $\Gamma _2^c$
. Indeed, adding new arrows corresponds to adding a certain matrix (determined by the figure) to the current adjacency matrix of the quiver; since addition of matrices is commutative, the order of the roots is irrelevant.
$\Gamma _2^c$
. Indeed, adding new arrows corresponds to adding a certain matrix (determined by the figure) to the current adjacency matrix of the quiver; since addition of matrices is commutative, the order of the roots is irrelevant.

Figure 13 The neighborhood of
![]() $g_{11}$
.
$g_{11}$
.

Figure 14 The neighborhood of
![]() $g_{i1}$
for
$g_{i1}$
for
![]() $1 < i < n$
.
$1 < i < n$
.

Figure 15 The neighborhood of
![]() $g_{n1}$
.
$g_{n1}$
.

Figure 16 The neighborhood of
![]() $g_{nj}$
for
$g_{nj}$
for
![]() $2 \leq j \leq n$
.
$2 \leq j \leq n$
.

Figure 17 The neighborhood of
![]() $h_{nn}$
.
$h_{nn}$
.

Figure 18 The neighborhood of
![]() $h_{in}$
for
$h_{in}$
for
![]() $2 \leq j \leq n-1$
.
$2 \leq j \leq n-1$
.

Figure 19 The neighborhood of
![]() $h_{1n}$
.
$h_{1n}$
.

Figure 20 The neighborhood of
![]() $h_{1j}$
for
$h_{1j}$
for
![]() $1<j<n$
.
$1<j<n$
.

Figure 21 The neighborhood of
![]() $h_{11}$
.
$h_{11}$
.
3.6.3 The quiver for a nontrivial BD pair (explicit)
As an alternative to the algorithm described in the previous paragraph, we provide explicit neighborhoods of the variables
![]() $g_{i1}$
,
$g_{i1}$
,
![]() $h_{1i}$
,
$h_{1i}$
,
![]() $g_{ni}$
,
$g_{ni}$
,
![]() $h_{in}$
,
$h_{in}$
,
![]() $1 \leq i \leq n$
in the case of a nontrivial BD pair. All the other neighborhoods are the same as in the case of the trivial BD pair.
$1 \leq i \leq n$
in the case of a nontrivial BD pair. All the other neighborhoods are the same as in the case of the trivial BD pair.
Remark 3.7. Once the initial quiver is constructed for a BD pair
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, one can obtain the initial quiver for the cluster structure
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, one can obtain the initial quiver for the cluster structure
![]() $\mathcal {C}(\mathbf {\Gamma })$
on
$\mathcal {C}(\mathbf {\Gamma })$
on
![]() $\operatorname {\mathrm {GL}}_n$
described in [Reference Gekhtman, Shapiro and Vainshtein20], in the following way: 1) remove all f- and
$\operatorname {\mathrm {GL}}_n$
described in [Reference Gekhtman, Shapiro and Vainshtein20], in the following way: 1) remove all f- and
![]() $\varphi $
-vertices; 2) for each
$\varphi $
-vertices; 2) for each
![]() $1 \leq i \leq n$
, merge the vertex
$1 \leq i \leq n$
, merge the vertex
![]() $h_{ii}$
with the vertex
$h_{ii}$
with the vertex
![]() $g_{ii}$
(but retain the edges); 3) in the resulting quiver, remove the loop at the vertex
$g_{ii}$
(but retain the edges); 3) in the resulting quiver, remove the loop at the vertex
![]() $g_{nn}$
.
$g_{nn}$
.
3.7 Toric action
Let
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be an aperiodic oriented BD pair that defines the generalized cluster structure
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be an aperiodic oriented BD pair that defines the generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma })$
, and let
$\mathcal {GC}(\mathbf {\Gamma })$
, and let
![]() $\mathfrak {h}^{\operatorname {\mathrm {sl}}_n}$
be the Cartan subalgebra of
$\mathfrak {h}^{\operatorname {\mathrm {sl}}_n}$
be the Cartan subalgebra of
![]() $\operatorname {\mathrm {sl}}_n$
. For each
$\operatorname {\mathrm {sl}}_n$
. For each
![]() $\ell \in \{r,c\}$
, define a subalgebra
$\ell \in \{r,c\}$
, define a subalgebra
Notice that its dimension is
where
![]() $\Pi $
is the set of simple roots. Let
$\Pi $
is the set of simple roots. Let
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
and
$\mathcal {H}_{\mathbf {\Gamma }^r}$
and
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
be the connected subgroups of
$\mathcal {H}_{\mathbf {\Gamma }^c}$
be the connected subgroups of
![]() $\operatorname {\mathrm {SL}}_n$
that correspond to
$\operatorname {\mathrm {SL}}_n$
that correspond to
![]() $\mathfrak {h}_{\mathbf {\Gamma }^r}$
and
$\mathfrak {h}_{\mathbf {\Gamma }^r}$
and
![]() $\mathfrak {h}_{\mathbf {\Gamma }^c}$
, respectively. We let
$\mathfrak {h}_{\mathbf {\Gamma }^c}$
, respectively. We let
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
act upon
$\mathcal {H}_{\mathbf {\Gamma }^r}$
act upon
![]() $D(\operatorname {\mathrm {GL}}_n)$
on the left and
$D(\operatorname {\mathrm {GL}}_n)$
on the left and
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
to act upon
$\mathcal {H}_{\mathbf {\Gamma }^c}$
to act upon
![]() $D(\operatorname {\mathrm {GL}}_n)$
on the right; that is,
$D(\operatorname {\mathrm {GL}}_n)$
on the right; that is,
 $$\begin{align*}\begin{aligned} H.(X,Y) = (HX,HY), \ \ &H \in \mathcal{H}_{\mathbf{\Gamma}^r};\\ (X,Y).H = (XH,YH), \ \ &H \in \mathcal{H}_{\mathbf{\Gamma}^c}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} H.(X,Y) = (HX,HY), \ \ &H \in \mathcal{H}_{\mathbf{\Gamma}^r};\\ (X,Y).H = (XH,YH), \ \ &H \in \mathcal{H}_{\mathbf{\Gamma}^c}. \end{aligned} \end{align*}$$
We also let scalar matrices act upon
![]() $D(\operatorname {\mathrm {GL}}_n)$
via
$D(\operatorname {\mathrm {GL}}_n)$
via
As we shall see in Section 6, the left-right action of
![]() $\mathcal {H}_{\mathbf {\Gamma }^r} \times \mathcal {H}_{\mathbf {\Gamma }^c}$
together with the action by scalar matrices induces a global toric action on
$\mathcal {H}_{\mathbf {\Gamma }^r} \times \mathcal {H}_{\mathbf {\Gamma }^c}$
together with the action by scalar matrices induces a global toric action on
![]() $\mathcal {GC}(\mathbf {\Gamma })$
of rank
$\mathcal {GC}(\mathbf {\Gamma })$
of rank
![]() $k_{\mathbf {\Gamma }^r} + k_{\mathbf {\Gamma }^c}+2$
.
$k_{\mathbf {\Gamma }^r} + k_{\mathbf {\Gamma }^c}+2$
.
3.8 Poisson-geometric properties of frozen variables
As we explained above, if
![]() $(R_0^r,R_0^c)$
is chosen in such a way that
$(R_0^r,R_0^c)$
is chosen in such a way that
![]() $R_0^r(I) = R_0^c(I) = 1/2$
, then the frozen variables
$R_0^r(I) = R_0^c(I) = 1/2$
, then the frozen variables
![]() $c_0,c_1,\ldots ,c_{n-1},c_n$
are Casimirs of the Poisson bracket (for the case of
$c_0,c_1,\ldots ,c_{n-1},c_n$
are Casimirs of the Poisson bracket (for the case of
![]() $D(\operatorname {\mathrm {SL}}_n)$
, the statement is true for any
$D(\operatorname {\mathrm {SL}}_n)$
, the statement is true for any
![]() $(R_0^r,R_0^c)$
). In particular, the symplectic leaves of the Poisson bracket are contained in the level sets of these Casimirs. The other frozen variables are given by the determinants of
$(R_0^r,R_0^c)$
). In particular, the symplectic leaves of the Poisson bracket are contained in the level sets of these Casimirs. The other frozen variables are given by the determinants of
![]() $\mathcal {L}$
-matrices. Given such a frozen variable
$\mathcal {L}$
-matrices. Given such a frozen variable
![]() $\psi (X,Y) := \det \mathcal {L}(X,Y)$
, the proposition below, which was proved in [Reference Gekhtman, Shapiro and Vainshtein20], implies that the nonsingular part of the zero locus of
$\psi (X,Y) := \det \mathcal {L}(X,Y)$
, the proposition below, which was proved in [Reference Gekhtman, Shapiro and Vainshtein20], implies that the nonsingular part of the zero locus of
![]() $\psi $
is a Poisson submanifold; hence, it foliates into a union of its own symplectic leaves. However, we do not know if those symplectic leaves are also symplectic leaves of
$\psi $
is a Poisson submanifold; hence, it foliates into a union of its own symplectic leaves. However, we do not know if those symplectic leaves are also symplectic leaves of
![]() $D(\operatorname {\mathrm {GL}}_n)$
.
$D(\operatorname {\mathrm {GL}}_n)$
.
For a Belavin–Drinfeld triple
![]() $\mathbf {\Gamma } = (\Gamma _1,\Gamma _2,\gamma )$
, let
$\mathbf {\Gamma } = (\Gamma _1,\Gamma _2,\gamma )$
, let
![]() $\mathcal {P}_+(\Gamma _1)$
and
$\mathcal {P}_+(\Gamma _1)$
and
![]() $\mathcal {P}_-(\Gamma _2)$
be the upper and lower parabolic subgroups of
$\mathcal {P}_-(\Gamma _2)$
be the upper and lower parabolic subgroups of
![]() $\operatorname {\mathrm {GL}}_n$
determined by the root data
$\operatorname {\mathrm {GL}}_n$
determined by the root data
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
, respectively. Define a subgroup
$\Gamma _2$
, respectively. Define a subgroup
![]() $\mathcal {D} \subseteq \mathcal {P}_+(\Gamma _1)\times \mathcal {P}_-(\Gamma _2)$
via
$\mathcal {D} \subseteq \mathcal {P}_+(\Gamma _1)\times \mathcal {P}_-(\Gamma _2)$
via
where
![]() $\Pi _{\Gamma _1} :\mathcal {P}_+(\Gamma _1) \rightarrow \Pi _{\Delta } \operatorname {\mathrm {GL}}_n(\Delta )$
and
$\Pi _{\Gamma _1} :\mathcal {P}_+(\Gamma _1) \rightarrow \Pi _{\Delta } \operatorname {\mathrm {GL}}_n(\Delta )$
and
![]() $\Pi _{\Gamma _2} : \mathcal {P}_-(\Gamma _2) \rightarrow \prod _{\bar {\Delta }} \operatorname {\mathrm {GL}}_n(\bar {\Delta })$
are group projections (
$\Pi _{\Gamma _2} : \mathcal {P}_-(\Gamma _2) \rightarrow \prod _{\bar {\Delta }} \operatorname {\mathrm {GL}}_n(\bar {\Delta })$
are group projections (
![]() $\Delta $
and
$\Delta $
and
![]() $\bar {\Delta }$
are nontrivial X- and Y-runs, respectively), and
$\bar {\Delta }$
are nontrivial X- and Y-runs, respectively), and
![]() $\operatorname {\mathrm {GL}}_n(\Delta )$
are invertible
$\operatorname {\mathrm {GL}}_n(\Delta )$
are invertible
![]() $|\Delta |\times |\Delta |$
matrices embedded into
$|\Delta |\times |\Delta |$
matrices embedded into
![]() $\operatorname {\mathrm {GL}}_n$
as a
$\operatorname {\mathrm {GL}}_n$
as a
![]() $\Delta \times \Delta $
block (and likewise
$\Delta \times \Delta $
block (and likewise
![]() $\operatorname {\mathrm {GL}}_n(\bar {\Delta })$
). Given a Belavin–Drinfeld pair
$\operatorname {\mathrm {GL}}_n(\bar {\Delta })$
). Given a Belavin–Drinfeld pair
![]() $(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, denote the respective groups
$(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, denote the respective groups
![]() $\mathcal {D}$
as
$\mathcal {D}$
as
![]() $\mathcal {D}^r$
and
$\mathcal {D}^r$
and
![]() $\mathcal {D}^c$
.
$\mathcal {D}^c$
.
Proposition 3.8. For any
![]() $\mathcal {L}$
-matrix in
$\mathcal {L}$
-matrix in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
, the following statements hold:
$\mathcal {GC}(\mathbf {\Gamma })$
, the following statements hold:
-
(i) For any
 $(g_1,g_2) \in \mathcal {D}^r$
,
$(g_1,g_2) \in \mathcal {D}^r$
,
 $\det \mathcal {L}(g_1X,g_2Y) = \chi ^r(g_1,g_2) \det \mathcal {L}(X,Y)$
, where
$\det \mathcal {L}(g_1X,g_2Y) = \chi ^r(g_1,g_2) \det \mathcal {L}(X,Y)$
, where
 $\chi ^r$
is a character on
$\chi ^r$
is a character on
 $\mathcal {D}^r$
;
$\mathcal {D}^r$
; -
(ii) For any
 $(g_1,g_2) \in \mathcal {D}^c$
,
$(g_1,g_2) \in \mathcal {D}^c$
,
 $\det \mathcal {L}(Xg_1,Yg_2) = \chi ^c(g_1,g_2) \det \mathcal {L}(X,Y)$
, where
$\det \mathcal {L}(Xg_1,Yg_2) = \chi ^c(g_1,g_2) \det \mathcal {L}(X,Y)$
, where
 $\chi ^c$
is a character on
$\chi ^c$
is a character on
 $\mathcal {D}^c$
;
$\mathcal {D}^c$
; -
(iii)
 $\det \mathcal {L}(X,Y)$
is log-canonical with any
$\det \mathcal {L}(X,Y)$
is log-canonical with any
 $x_{ij}$
or
$x_{ij}$
or
 $y_{ij}$
.
$y_{ij}$
.
Remark 3.9. Assume that
![]() $\mathbf {\Gamma }^r= \mathbf {\Gamma }^c$
and
$\mathbf {\Gamma }^r= \mathbf {\Gamma }^c$
and
![]() $R_0:=R_0^r=R_0^c$
is chosen so that equation (3.6) is satisfied. Then the connected dual Poisson group
$R_0:=R_0^r=R_0^c$
is chosen so that equation (3.6) is satisfied. Then the connected dual Poisson group
![]() $\operatorname {\mathrm {GL}}_n^*$
, viewed as a subgroup of
$\operatorname {\mathrm {GL}}_n^*$
, viewed as a subgroup of
![]() $D(\operatorname {\mathrm {GL}}_n)=\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
, is a subgroup of
$D(\operatorname {\mathrm {GL}}_n)=\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
, is a subgroup of
![]() $\mathcal {D}$
as well. In the case of
$\mathcal {D}$
as well. In the case of
![]() $D(\operatorname {\mathrm {SL}}_n)$
, such an issue with the choice of
$D(\operatorname {\mathrm {SL}}_n)$
, such an issue with the choice of
![]() $R_0$
does not arise, so
$R_0$
does not arise, so
![]() $\operatorname {\mathrm {SL}}_n^* \subseteq \mathcal {D}$
(hence, the determinants of the
$\operatorname {\mathrm {SL}}_n^* \subseteq \mathcal {D}$
(hence, the determinants of the
![]() $\mathcal {L}$
-matrices are semi-invariant with respect to the action of
$\mathcal {L}$
-matrices are semi-invariant with respect to the action of
![]() $\operatorname {\mathrm {SL}}_n^*$
on the right and on the left).
$\operatorname {\mathrm {SL}}_n^*$
on the right and on the left).
4 Regularity
Let
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be a BD pair that defines a generalized cluster structure
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be a BD pair that defines a generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma })$
on
$\mathcal {GC}(\mathbf {\Gamma })$
on
![]() $D(\operatorname {\mathrm {GL}}_n)$
with the initial seed described in Section 3. In this section, we show that the mutation of any cluster variable from the initial seed in
$D(\operatorname {\mathrm {GL}}_n)$
with the initial seed described in Section 3. In this section, we show that the mutation of any cluster variable from the initial seed in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
produces a regular function. We will prove in Section 5.5 that
$\mathcal {GC}(\mathbf {\Gamma })$
produces a regular function. We will prove in Section 5.5 that
![]() $\mathcal {GC}(\mathbf {\Gamma })$
satisfies coprimality conditions 2.2 and 2.2 of Proposition 2.2, which implies that
$\mathcal {GC}(\mathbf {\Gamma })$
satisfies coprimality conditions 2.2 and 2.2 of Proposition 2.2, which implies that
![]() $\mathcal {GC}(\mathbf {\Gamma })$
is a regular generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
is a regular generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
.
$D(\operatorname {\mathrm {GL}}_n)$
.
Proposition 4.1. The mutation of the initial cluster of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
in any direction yields a regular function.
$\mathcal {GC}(\mathbf {\Gamma })$
in any direction yields a regular function.
Proof. The regularity at
![]() $g_{ij}$
and
$g_{ij}$
and
![]() $h_{ji}$
for
$h_{ji}$
for
![]() $i> j$
follows from Theorem 6.1 in [Reference Gekhtman, Shapiro and Vainshtein20]; for
$i> j$
follows from Theorem 6.1 in [Reference Gekhtman, Shapiro and Vainshtein20]; for
![]() $\varphi $
- and f-functions, the regularity follows from Section 6.4 in [Reference Gekhtman, Shapiro and Vainshtein18]. Therefore, all we need to prove is that the mutation at any
$\varphi $
- and f-functions, the regularity follows from Section 6.4 in [Reference Gekhtman, Shapiro and Vainshtein18]. Therefore, all we need to prove is that the mutation at any
![]() $g_{ii}$
or
$g_{ii}$
or
![]() $h_{ii}$
in the case of an aperiodic oriented BD pair yields a regular function.
$h_{ii}$
in the case of an aperiodic oriented BD pair yields a regular function.
Mutation at
![]() $h_{ii}$
. First of all, note that if
$h_{ii}$
. First of all, note that if
![]() $n-1 \notin \Gamma ^r_2$
, then, according to the construction in Section 3.2, the functions
$n-1 \notin \Gamma ^r_2$
, then, according to the construction in Section 3.2, the functions
![]() $h_{i-1,i}$
for
$h_{i-1,i}$
for
![]() $2 \leq i \leq n$
coincide with the ones in the case of the standard BD pair. This situation was already studied in [Reference Gekhtman, Shapiro and Vainshtein18], so let us assume that
$2 \leq i \leq n$
coincide with the ones in the case of the standard BD pair. This situation was already studied in [Reference Gekhtman, Shapiro and Vainshtein18], so let us assume that
![]() $n-1 \in \Gamma ^r_2$
. For
$n-1 \in \Gamma ^r_2$
. For
![]() $i < n$
, the mutation at
$i < n$
, the mutation at
![]() $h_{ii}$
can be written as
$h_{ii}$
can be written as
Let
![]() $\mathcal {L}$
be the
$\mathcal {L}$
be the
![]() $\mathcal {L}$
-matrix that defines the functions
$\mathcal {L}$
-matrix that defines the functions
![]() $h_{i-1,i}$
,
$h_{i-1,i}$
,
![]() $2 \leq i \leq n$
, and let
$2 \leq i \leq n$
, and let
![]() $H_{i-1,i}$
be a submatrix of
$H_{i-1,i}$
be a submatrix of
![]() $\mathcal {L}$
such that
$\mathcal {L}$
such that
![]() $h_{i-1,i} = \det H_{i-1,i}$
. Then
$h_{i-1,i} = \det H_{i-1,i}$
. Then
![]() $H_{i-1,i}$
can be written as a block-diagonal matrix
$H_{i-1,i}$
can be written as a block-diagonal matrix
 $$\begin{align*}H_{i-1,i} = \begin{bmatrix} Y^{[i,n]}_{[i-1,n]} & * \\ 0 & C \end{bmatrix}, \end{align*}$$
$$\begin{align*}H_{i-1,i} = \begin{bmatrix} Y^{[i,n]}_{[i-1,n]} & * \\ 0 & C \end{bmatrix}, \end{align*}$$
where C is some
![]() $(m-1) \times m$
matrix and the asterisk denotes the part of
$(m-1) \times m$
matrix and the asterisk denotes the part of
![]() $H_{i-1,i}$
that’s not relevant to the proof. Recall that
$H_{i-1,i}$
that’s not relevant to the proof. Recall that
![]() $F_{1,n-i+1} = | X^{[n,n]}\, Y^{[i,n]} |_{[i-1,n]}$
. Define a block-diagonal matrix A as
$F_{1,n-i+1} = | X^{[n,n]}\, Y^{[i,n]} |_{[i-1,n]}$
. Define a block-diagonal matrix A as
 $$\begin{align*}A:= \begin{bmatrix} F_{1,n-i+1} & * \\ 0 & C\end{bmatrix}, \end{align*}$$
$$\begin{align*}A:= \begin{bmatrix} F_{1,n-i+1} & * \\ 0 & C\end{bmatrix}, \end{align*}$$
and let N be the index of the last column of A. According to the Desnanot–Jacobi identity from Proposition 2.7, we see that
Now, notice that
hence equation (4.2) becomes
Dividing both sides by
![]() $\det C^{\hat {m}}$
and comparing the resulting expression with equation (4.1), we see that
$\det C^{\hat {m}}$
and comparing the resulting expression with equation (4.1), we see that
![]() $h^{\prime }_{ii} = \det A^{\hat {2}}$
. Hence,
$h^{\prime }_{ii} = \det A^{\hat {2}}$
. Hence,
![]() $h^{\prime }_{ii}$
is a regular function.
$h^{\prime }_{ii}$
is a regular function.
Now, let’s study the mutation at
![]() $h_{nn}$
. Since we assume
$h_{nn}$
. Since we assume
![]() $n-1 \in \Gamma _2^r$
, let
$n-1 \in \Gamma _2^r$
, let
![]() $\gamma _r(i) = n-1$
. Then the mutation reads
$\gamma _r(i) = n-1$
. Then the mutation reads
Set
![]() $H:= H_{n-1,n}$
. Then
$H:= H_{n-1,n}$
. Then
![]() $h_{n-1,n} = y_{n-1,n} g_{i+1,1} - y_{nn} \det H^{\hat {1}}_{\hat {2}}$
and
$h_{n-1,n} = y_{n-1,n} g_{i+1,1} - y_{nn} \det H^{\hat {1}}_{\hat {2}}$
and
 $$\begin{align*}\begin{aligned} h_{nn} h^{\prime}_{nn} &= (y_{nn} x_{n,n-1} - y_{n-1,n} x_{nn}) g_{i+1,1} + x_{nn} (y_{n-1,n} g_{i+1,1} - y_{nn} \det H^{\hat{1}}_{\hat{2}}) = \\ &= h_{nn} (x_{n,n-1} g_{i+1,1} - x_{nn} \det H^{\hat{1}}_{\hat{2}}). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} h_{nn} h^{\prime}_{nn} &= (y_{nn} x_{n,n-1} - y_{n-1,n} x_{nn}) g_{i+1,1} + x_{nn} (y_{n-1,n} g_{i+1,1} - y_{nn} \det H^{\hat{1}}_{\hat{2}}) = \\ &= h_{nn} (x_{n,n-1} g_{i+1,1} - x_{nn} \det H^{\hat{1}}_{\hat{2}}). \end{aligned} \end{align*}$$
Therefore,
![]() $h^{\prime }_{nn} = x_{n,n-1} g_{i+1,1} - x_{nn} \det H^{\hat {1}}_{\hat {2}}$
is a regular function.
$h^{\prime }_{nn} = x_{n,n-1} g_{i+1,1} - x_{nn} \det H^{\hat {1}}_{\hat {2}}$
is a regular function.
Mutation at
![]() $g_{ii}$
. As in the previous case, if
$g_{ii}$
. As in the previous case, if
![]() $n-1 \notin \Gamma _1^c$
, then the functions
$n-1 \notin \Gamma _1^c$
, then the functions
![]() $g_{i+1,i}$
coincide with the ones in case of the standard BD pair, which was already treated in [Reference Gekhtman, Shapiro and Vainshtein18]. Therefore, assume
$g_{i+1,i}$
coincide with the ones in case of the standard BD pair, which was already treated in [Reference Gekhtman, Shapiro and Vainshtein18]. Therefore, assume
![]() $n-1 \in \Gamma _1^c$
, which implies there is a Y-block attached to the bottom of the leading X-block of the functions
$n-1 \in \Gamma _1^c$
, which implies there is a Y-block attached to the bottom of the leading X-block of the functions
![]() $g_{i+1,i}$
. For
$g_{i+1,i}$
. For
![]() $i < n$
, the mutation at
$i < n$
, the mutation at
![]() $g_{ii}$
is given by
$g_{ii}$
is given by
Define
![]() $\tilde {F}_{n-i,1} := [Y^{[n, n]} \, X^{[i, n]}]_{[i, n]}$
. Note that
$\tilde {F}_{n-i,1} := [Y^{[n, n]} \, X^{[i, n]}]_{[i, n]}$
. Note that
![]() $\det (\tilde {F}_{n-i,\ 1})^{\hat 2} = (-1)^{n-i}f_{n-i, 1}$
. Let
$\det (\tilde {F}_{n-i,\ 1})^{\hat 2} = (-1)^{n-i}f_{n-i, 1}$
. Let
![]() $G_{i,i-1}$
be a submatrix of the
$G_{i,i-1}$
be a submatrix of the
![]() $\mathcal {L}$
-matrix such that
$\mathcal {L}$
-matrix such that
![]() $\det G_{i,i-1} = g_{i,i-1}$
; it can be written as
$\det G_{i,i-1} = g_{i,i-1}$
; it can be written as
 $$\begin{align*}G_{i,i-1} = \begin{bmatrix} X^{[i-1,n]}_{[i, n]} & 0\\ \ast & C \end{bmatrix}, \end{align*}$$
$$\begin{align*}G_{i,i-1} = \begin{bmatrix} X^{[i-1,n]}_{[i, n]} & 0\\ \ast & C \end{bmatrix}, \end{align*}$$
where C is some
![]() $m \times (m-1)$
matrix. Define
$m \times (m-1)$
matrix. Define
 $$\begin{align*}A := A(i-1) := \begin{bmatrix} \tilde{F}_{n-i+1,1} & 0 \\ \ast & C \end{bmatrix} \end{align*}$$
$$\begin{align*}A := A(i-1) := \begin{bmatrix} \tilde{F}_{n-i+1,1} & 0 \\ \ast & C \end{bmatrix} \end{align*}$$
Let N be the index of the last row of A. The Desnanot–Jacobi identity from Proposition 2.8 tells us that
Deciphering the last identity yields
or
Let
![]() $B:= A(i) = A_{\hat 1}^{\hat 2}$
. The Desnanot–Jacobi identity from Proposition 2.8 for B yields
$B:= A(i) = A_{\hat 1}^{\hat 2}$
. The Desnanot–Jacobi identity from Proposition 2.8 for B yields
Now, multiply equations (4.3) by
![]() $g_{i+1,i+1}$
and (4.4) by
$g_{i+1,i+1}$
and (4.4) by
![]() $g_{i-1, i-1}$
, substitute
$g_{i-1, i-1}$
, substitute
![]() $\det A_{\hat {1}}^{\hat {2}} \cdot g_{i+1,i+1} \cdot g_{i-1, i-1}$
in equations (4.3) with the right-hand side (RHS) of equation (4.4) and combine the terms. These algebraic manipulations result in
$\det A_{\hat {1}}^{\hat {2}} \cdot g_{i+1,i+1} \cdot g_{i-1, i-1}$
in equations (4.3) with the right-hand side (RHS) of equation (4.4) and combine the terms. These algebraic manipulations result in
Thus, the mutation at
![]() $g_{ii}$
for
$g_{ii}$
for
![]() $1 < i < n$
yields a regular function.
$1 < i < n$
yields a regular function.
Now consider the mutation at
![]() $g_{nn}$
. Since we assume
$g_{nn}$
. Since we assume
![]() $n-1 \in \Gamma _1^c$
, let
$n-1 \in \Gamma _1^c$
, let
![]() $\gamma _c(n-1)=j$
. Then the mutation at
$\gamma _c(n-1)=j$
. Then the mutation at
![]() $g_{nn}$
reads
$g_{nn}$
reads
Since
![]() $g_{nn} = x_{nn}$
, all we need to check is that the RHS is divisible by
$g_{nn} = x_{nn}$
, all we need to check is that the RHS is divisible by
![]() $x_{nn}$
. Let
$x_{nn}$
. Let
![]() $G := G_{n, n-1}$
. Expanding
$G := G_{n, n-1}$
. Expanding
![]() $g_{n,n-1}$
along the first row, we obtain
$g_{n,n-1}$
along the first row, we obtain
![]() $g_{n, n-1} = x_{n, n-1} h_{1,j+1} - x_{nn} G^{\hat {2}}_{\hat {1}}$
. Writing out
$g_{n, n-1} = x_{n, n-1} h_{1,j+1} - x_{nn} G^{\hat {2}}_{\hat {1}}$
. Writing out
![]() $g_{n-1,n-1}$
and
$g_{n-1,n-1}$
and
![]() $f_{11}$
, we see that
$f_{11}$
, we see that
 $$\begin{align*}\begin{aligned} g_{nn} g^{\prime}_{nn} &= (x_{n-1,n-1}x_{nn} - x_{n-1,n}x_{n-1,n})y_{nn} h_{1,j+1} \\ &\quad + (x_{n-1,n}y_{nn} - y_{n-1,n}x_{nn})(x_{n, n-1} h_{1,j+1} - x_{nn} \det G^{\hat{2}}_{\hat{1}}). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} g_{nn} g^{\prime}_{nn} &= (x_{n-1,n-1}x_{nn} - x_{n-1,n}x_{n-1,n})y_{nn} h_{1,j+1} \\ &\quad + (x_{n-1,n}y_{nn} - y_{n-1,n}x_{nn})(x_{n, n-1} h_{1,j+1} - x_{nn} \det G^{\hat{2}}_{\hat{1}}). \end{aligned} \end{align*}$$
After expanding the brackets, it’s easy to see that there are two terms
![]() $x_{n-1,n}x_{n,n-1}y_{nn}h_{1,j+1}$
with opposite signs, hence they cancel each other out; all the other terms are divisible by
$x_{n-1,n}x_{n,n-1}y_{nn}h_{1,j+1}$
with opposite signs, hence they cancel each other out; all the other terms are divisible by
![]() $x_{nn}$
. Thus, the proposition is proved.
$x_{nn}$
. Thus, the proposition is proved.
5 Completeness
In this section, we prove part 2.2 of Proposition 2.2, which asserts that any regular function belongs to the upper cluster algebra. Together with the results on regularity from Section 4, we will conclude that the ring of regular functions on
![]() $D(\operatorname {\mathrm {GL}}_n)$
can be identified with the upper cluster algebra.
$D(\operatorname {\mathrm {GL}}_n)$
can be identified with the upper cluster algebra.
5.1 Birational quasi-isomorphisms
 $\mathcal {U}$
$\mathcal {U}$
For this section, let us fix an aperiodic oriented BD pair
![]() $\mathbf {\Gamma } := (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
, let
$\mathbf {\Gamma } := (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
, let
![]() $D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the corresponding Drinfeld double, and let
$D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the corresponding Drinfeld double, and let
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be the generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
be the generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
. We consider another BD pair
$D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
. We consider another BD pair
![]() $\tilde {\mathbf {\Gamma }}$
obtained from
$\tilde {\mathbf {\Gamma }}$
obtained from
![]() $\mathbf {\Gamma }$
by removing a root from
$\mathbf {\Gamma }$
by removing a root from
![]() $\Gamma _1^r$
(or from
$\Gamma _1^r$
(or from
![]() $\Gamma _1^c$
) and its image in
$\Gamma _1^c$
) and its image in
![]() $\Gamma _1^r$
(or in
$\Gamma _1^r$
(or in
![]() $\Gamma _2^c$
; see the cases below), and define another Drinfeld doubleFootnote
6
$\Gamma _2^c$
; see the cases below), and define another Drinfeld doubleFootnote
6
![]() $D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}}$
endowed with the generalized cluster structure
$D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}}$
endowed with the generalized cluster structure
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. The objective of this section is to construct a certain rational map
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. The objective of this section is to construct a certain rational map
which we later recognize as a quasi-isomorphism in the sense of Proposition 2.5 and as a birational automorphism of
![]() $\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
. In view of these two properties, we refer to the maps
$\operatorname {\mathrm {GL}}_n\times \operatorname {\mathrm {GL}}_n$
. In view of these two properties, we refer to the maps
![]() $\mathcal {U}$
as birational quasi-isomorphisms.Footnote
7
$\mathcal {U}$
as birational quasi-isomorphisms.Footnote
7
Notation
We denote by
![]() $(X,Y)$
the standard coordinates on
$(X,Y)$
the standard coordinates on
![]() $D(\operatorname {\mathrm {GL}}_n)$
(regardless of the associated BD pair). If
$D(\operatorname {\mathrm {GL}}_n)$
(regardless of the associated BD pair). If
![]() $\psi $
is a cluster or stable variable in
$\psi $
is a cluster or stable variable in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
, then by
$\mathcal {GC}(\mathbf {\Gamma })$
, then by
![]() $\tilde {\psi }$
we denote the corresponding variable in
$\tilde {\psi }$
we denote the corresponding variable in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
; that is,
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
; that is,
![]() $\psi $
and
$\psi $
and
![]() $\tilde {\psi }$
are either the variables attached to the same vertices in the initial quivers or in the quivers that are obtained via the same sequences of mutations. All g-, h-, f-,
$\tilde {\psi }$
are either the variables attached to the same vertices in the initial quivers or in the quivers that are obtained via the same sequences of mutations. All g-, h-, f-,
![]() $\varphi $
- and c- functions in the initial extended cluster of
$\varphi $
- and c- functions in the initial extended cluster of
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
are marked with a tilde as well.
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
are marked with a tilde as well.
Removing the rightmost root from a row run
Let
![]() $\Delta ^r = [p+1,p+k]$
be a nontrivial row X-run in
$\Delta ^r = [p+1,p+k]$
be a nontrivial row X-run in
![]() $\mathbf {\Gamma }$
, and let
$\mathbf {\Gamma }$
, and let
![]() $\bar {\Delta }^r = [q+1,q+k] := \gamma _r(\Delta ^r)$
be the corresponding row Y-run. Define
$\bar {\Delta }^r = [q+1,q+k] := \gamma _r(\Delta ^r)$
be the corresponding row Y-run. Define
![]() $\tilde {\mathbf {\Gamma }} = (\tilde {\mathbf {\Gamma }}^r, \mathbf {\Gamma }^c)$
with
$\tilde {\mathbf {\Gamma }} = (\tilde {\mathbf {\Gamma }}^r, \mathbf {\Gamma }^c)$
with
![]() $\tilde {\mathbf {\Gamma }}^r = (\tilde {\Gamma }_1^r, \tilde {\Gamma }_2^r, \gamma _r|_{\tilde {\Gamma }_1^r})$
given by
$\tilde {\mathbf {\Gamma }}^r = (\tilde {\Gamma }_1^r, \tilde {\Gamma }_2^r, \gamma _r|_{\tilde {\Gamma }_1^r})$
given by
![]() $\tilde {\Gamma }_1^r = \Gamma _1^r \setminus \{p+k-1\}$
and
$\tilde {\Gamma }_1^r = \Gamma _1^r \setminus \{p+k-1\}$
and
![]() $\tilde {\Gamma }_2^r = \Gamma _2^r \setminus \{q+k-1\}$
. Let us examine the difference between the
$\tilde {\Gamma }_2^r = \Gamma _2^r \setminus \{q+k-1\}$
. Let us examine the difference between the
![]() $\mathcal {L}$
-matrices in
$\mathcal {L}$
-matrices in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. For any
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. For any
![]() $\mathcal {L}$
-matrix
$\mathcal {L}$
-matrix
![]() $\mathcal {L}(X,Y)$
in
$\mathcal {L}(X,Y)$
in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
, let
$\mathcal {GC}(\mathbf {\Gamma })$
, let
![]() $\tilde {\mathcal {L}}(X,Y)$
be a matrix obtained from
$\tilde {\mathcal {L}}(X,Y)$
be a matrix obtained from
![]() $\mathcal {L}(X,Y)$
via removing the last row of each Y-block of the form
$\mathcal {L}(X,Y)$
via removing the last row of each Y-block of the form
![]() $Y^{J}_{[1,q+k]}$
. If
$Y^{J}_{[1,q+k]}$
. If
![]() $\mathcal {L}(X,Y)$
arises from a maximal alternating path in
$\mathcal {L}(X,Y)$
arises from a maximal alternating path in
![]() $G_{\mathbf {\Gamma }}$
that does not pass through the edge
$G_{\mathbf {\Gamma }}$
that does not pass through the edge
![]() $(p+k-1)\xrightarrow {\gamma _r}(q+k-1)$
, then
$(p+k-1)\xrightarrow {\gamma _r}(q+k-1)$
, then
![]() $\tilde {\mathcal {L}}(X,Y)$
is an
$\tilde {\mathcal {L}}(X,Y)$
is an
![]() $\mathcal {L}$
-matrix in
$\mathcal {L}$
-matrix in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
that arises from the same path in
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
that arises from the same path in
![]() $G_{\tilde {\mathbf {\Gamma }}}$
. However, if
$G_{\tilde {\mathbf {\Gamma }}}$
. However, if
![]() $\mathcal {L}^*(X,Y):=\mathcal {L}(X,Y)$
is constructed from a path that does pass through
$\mathcal {L}^*(X,Y):=\mathcal {L}(X,Y)$
is constructed from a path that does pass through
![]() $(p+k-1)\xrightarrow {\gamma _r}(q+k-1)$
, then
$(p+k-1)\xrightarrow {\gamma _r}(q+k-1)$
, then
![]() $\tilde {\mathcal {L}}^*(X,Y)$
is a reducible matrix with blocks that correspond to the remaining two
$\tilde {\mathcal {L}}^*(X,Y)$
is a reducible matrix with blocks that correspond to the remaining two
![]() $\mathcal {L}$
-matrices in
$\mathcal {L}$
-matrices in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. Let us set
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. Let us set
![]() $s_0$
to be the number such that
$s_0$
to be the number such that
![]() $\mathcal {L}^*_{s_0s_0}(X,Y) = x_{p+k,1}$
. Define a rational map
$\mathcal {L}^*_{s_0s_0}(X,Y) = x_{p+k,1}$
. Define a rational map
![]() $\mathcal {U} : D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
via the following data:
$\mathcal {U} : D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
via the following data:
 $$ \begin{align} U_0(X,Y) = I + \sum_{i = 1}^{k-1} \alpha_i(X,Y) e_{q+i,q+k}; \end{align} $$
$$ \begin{align} U_0(X,Y) = I + \sum_{i = 1}^{k-1} \alpha_i(X,Y) e_{q+i,q+k}; \end{align} $$
 $$ \begin{align} U_+(X,Y) := \left(\prod_{k\geq 1}^{\leftarrow} \tilde{\gamma}_r^k(U_0)\right)U_0; \end{align} $$
$$ \begin{align} U_+(X,Y) := \left(\prod_{k\geq 1}^{\leftarrow} \tilde{\gamma}_r^k(U_0)\right)U_0; \end{align} $$
Proposition 5.1. Let
![]() $\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the rational map given by equation (5.4). Then the map
$\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the rational map given by equation (5.4). Then the map
![]() $\mathcal {U}$
acts on the cluster and stable variables via the following formulas:
$\mathcal {U}$
acts on the cluster and stable variables via the following formulas:
 $$ \begin{align} \mathcal{U}^*(g_{ij}(X,Y)) = \begin{cases} \tilde{g}_{ij}(X,Y)\tilde{g}_{p+k,1}(X,Y) \ &\text{if}\ \mathcal{L}^*_{ss}(X,Y) = x_{ij} \ \text{for} \ s < s_0;\\ \tilde{g}_{ij}(X,Y) \ &\text{otherwise}; \end{cases} \end{align} $$
$$ \begin{align} \mathcal{U}^*(g_{ij}(X,Y)) = \begin{cases} \tilde{g}_{ij}(X,Y)\tilde{g}_{p+k,1}(X,Y) \ &\text{if}\ \mathcal{L}^*_{ss}(X,Y) = x_{ij} \ \text{for} \ s < s_0;\\ \tilde{g}_{ij}(X,Y) \ &\text{otherwise}; \end{cases} \end{align} $$
 $$ \begin{align} \mathcal{U}^*(h_{ij}(X,Y)) = \begin{cases} \tilde{h}_{ij}(X,Y)\tilde{g}_{p+k,1}(X,Y) \ &\text{if}\ \mathcal{L}^*_{ss}(X,Y) = y_{ij} \ \text{for} \ s < s_0;\\ \tilde{h}_{ij}(X,Y) \ &\text{otherwise}; \end{cases} \end{align} $$
$$ \begin{align} \mathcal{U}^*(h_{ij}(X,Y)) = \begin{cases} \tilde{h}_{ij}(X,Y)\tilde{g}_{p+k,1}(X,Y) \ &\text{if}\ \mathcal{L}^*_{ss}(X,Y) = y_{ij} \ \text{for} \ s < s_0;\\ \tilde{h}_{ij}(X,Y) \ &\text{otherwise}; \end{cases} \end{align} $$
if
![]() $\psi $
is any
$\psi $
is any
![]() $\varphi $
-, f- or c- function in the initial extended cluster, then
$\varphi $
-, f- or c- function in the initial extended cluster, then
Note that the first lines in equations (5.5) and (5.6) reflect the fact that
![]() $\tilde {\mathcal {L}}^*(X,Y)$
is a reducible matrix with blocks equal to a pair of
$\tilde {\mathcal {L}}^*(X,Y)$
is a reducible matrix with blocks equal to a pair of
![]() $\mathcal {L}$
-matrices from
$\mathcal {L}$
-matrices from
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. The proof of the above proposition is exactly the same as in [Reference Gekhtman, Shapiro and Vainshtein20].
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. The proof of the above proposition is exactly the same as in [Reference Gekhtman, Shapiro and Vainshtein20].
Motivation of formulas (5.1)–(5.4)
Though the formulas are complicated, they are designed in concordance with the invariance properties of the variables. The
![]() $\varphi $
-, f- and c-variables are the same in the initial extended clusters of
$\varphi $
-, f- and c-variables are the same in the initial extended clusters of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
, and they are all invariant with respect to the left action
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
, and they are all invariant with respect to the left action
![]() $N_+.(X,Y) = (N_+X,N_+Y)$
by unipotent upper triangular matrices. Since
$N_+.(X,Y) = (N_+X,N_+Y)$
by unipotent upper triangular matrices. Since
![]() $U_+$
is such, we see that formula (5.7) holds. Now, if
$U_+$
is such, we see that formula (5.7) holds. Now, if
![]() $\psi $
is a g- or h-function, recall that one of its invariance properties reads
$\psi $
is a g- or h-function, recall that one of its invariance properties reads
Notice that
![]() $\tilde {\gamma }_r(U_+)\cdot U_0 = U_+$
; therefore,
$\tilde {\gamma }_r(U_+)\cdot U_0 = U_+$
; therefore,
hence, the main part of the proof of Proposition 5.1 is to show that
for some
![]() $\varepsilon \geq 0$
. A similar reasoning explains formulas for
$\varepsilon \geq 0$
. A similar reasoning explains formulas for
![]() $\mathcal {U}$
for other choices of roots below.
$\mathcal {U}$
for other choices of roots below.
The inverse of
 $\mathcal {U}$
$\mathcal {U}$
Though we do not need formulas for the inverse of
![]() $\mathcal {U}$
in the proofs (except in some simple cases), let us state them for completeness. Let
$\mathcal {U}$
in the proofs (except in some simple cases), let us state them for completeness. Let
![]() $\theta _r:=\gamma _r|_{\tilde {\Gamma }_1^r}$
be the BD map for the triple
$\theta _r:=\gamma _r|_{\tilde {\Gamma }_1^r}$
be the BD map for the triple
![]() $\tilde {\mathbf {\Gamma }}^r$
. The verification of the formulas is similar to the proof of Proposition 5.1 and is based on an application of a series of long Plücker relations.
$\tilde {\mathbf {\Gamma }}^r$
. The verification of the formulas is similar to the proof of Proposition 5.1 and is based on an application of a series of long Plücker relations.
 $$ \begin{align} \tilde{U}_0(X,Y) = I + \sum_{i = 1}^{k-1} \beta_i(X,Y) e_{q+i,q+k}; \end{align} $$
$$ \begin{align} \tilde{U}_0(X,Y) = I + \sum_{i = 1}^{k-1} \beta_i(X,Y) e_{q+i,q+k}; \end{align} $$
 $$ \begin{align} \tilde{U}_+(X,Y) := \left(\prod_{k\geq 1}^{\leftarrow} \tilde{\theta}_r^k(\tilde{U}_0)\right)\tilde{U}_0; \end{align} $$
$$ \begin{align} \tilde{U}_+(X,Y) := \left(\prod_{k\geq 1}^{\leftarrow} \tilde{\theta}_r^k(\tilde{U}_0)\right)\tilde{U}_0; \end{align} $$
The formulas for the inverse of
![]() $\mathcal {U}$
in the other cases below are obtained via the same scheme: 1) add an extra negative sign in front of the coefficients; 2) substitute
$\mathcal {U}$
in the other cases below are obtained via the same scheme: 1) add an extra negative sign in front of the coefficients; 2) substitute
![]() $\tilde {\mathcal {L}}^*$
with
$\tilde {\mathcal {L}}^*$
with
![]() $\mathcal {L}^*$
and the frozen variable in the denominator with the corresponding cluster variable from
$\mathcal {L}^*$
and the frozen variable in the denominator with the corresponding cluster variable from
![]() $\mathcal {GC}(\mathbf {\Gamma })$
; 3) substitute
$\mathcal {GC}(\mathbf {\Gamma })$
; 3) substitute
![]() $\tilde {\gamma }$
with
$\tilde {\gamma }$
with
![]() $\tilde {\theta }$
.
$\tilde {\theta }$
.
Removing the leftmost root from a row run
As before, let
![]() $\Delta ^r = [p+1,p+k]$
be a nontrivial row X-run in
$\Delta ^r = [p+1,p+k]$
be a nontrivial row X-run in
![]() $\mathbf {\Gamma }$
and let
$\mathbf {\Gamma }$
and let
![]() $\bar {\Delta }^r = [q+1,q+k] := \gamma _r(\Delta ^r)$
be the corresponding row Y-run. Define
$\bar {\Delta }^r = [q+1,q+k] := \gamma _r(\Delta ^r)$
be the corresponding row Y-run. Define
![]() $\tilde {\mathbf {\Gamma }} = (\tilde {\mathbf {\Gamma }}^r, \mathbf {\Gamma }^c)$
with
$\tilde {\mathbf {\Gamma }} = (\tilde {\mathbf {\Gamma }}^r, \mathbf {\Gamma }^c)$
with
![]() $\tilde {\mathbf {\Gamma }}^r = (\tilde {\Gamma }_1^r, \tilde {\Gamma }_2^r, \gamma _r|_{\tilde {\Gamma }_1^r})$
given by
$\tilde {\mathbf {\Gamma }}^r = (\tilde {\Gamma }_1^r, \tilde {\Gamma }_2^r, \gamma _r|_{\tilde {\Gamma }_1^r})$
given by
![]() $\tilde {\Gamma }_1^r = \Gamma _1^r \setminus \{p+1\}$
and
$\tilde {\Gamma }_1^r = \Gamma _1^r \setminus \{p+1\}$
and
![]() $\tilde {\Gamma }_2^r = \Gamma _2^r \setminus \{q+1\}$
. For an
$\tilde {\Gamma }_2^r = \Gamma _2^r \setminus \{q+1\}$
. For an
![]() $\mathcal {L}$
-matrix
$\mathcal {L}$
-matrix
![]() $\mathcal {L}(X,Y)$
in
$\mathcal {L}(X,Y)$
in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
, let
$\mathcal {GC}(\mathbf {\Gamma })$
, let
![]() $\tilde {\mathcal {L}}(X,Y)$
be a matrix that is obtained from
$\tilde {\mathcal {L}}(X,Y)$
be a matrix that is obtained from
![]() $\mathcal {L}(X,Y)$
by removing the first row of each X-block of the form
$\mathcal {L}(X,Y)$
by removing the first row of each X-block of the form
![]() $X^{J}_{[p+1,n]}$
. If
$X^{J}_{[p+1,n]}$
. If
![]() $\mathcal {L}(X,Y)$
arises from a path that does not traverse the edge
$\mathcal {L}(X,Y)$
arises from a path that does not traverse the edge
![]() $(p+1) \xrightarrow {\gamma _r} (q+1)$
, then
$(p+1) \xrightarrow {\gamma _r} (q+1)$
, then
![]() $\tilde {\mathcal {L}}(X,Y)$
is an
$\tilde {\mathcal {L}}(X,Y)$
is an
![]() $\mathcal {L}$
-matrix in
$\mathcal {L}$
-matrix in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
; if it does traverse the latter edge,
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
; if it does traverse the latter edge,
![]() $\tilde {\mathcal {L}}(X,Y)$
is a reducible matrix with blocks that are
$\tilde {\mathcal {L}}(X,Y)$
is a reducible matrix with blocks that are
![]() $\mathcal {L}$
-matrices in
$\mathcal {L}$
-matrices in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. Let us denote the
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. Let us denote the
![]() $\mathcal {L}$
-matrix that corresponds to the latter path as
$\mathcal {L}$
-matrix that corresponds to the latter path as
![]() $\mathcal {L}^*(X,Y)$
, and let us denote by
$\mathcal {L}^*(X,Y)$
, and let us denote by
![]() $s_0$
the number for which
$s_0$
the number for which
![]() $\mathcal {L}^*_{s_0s_0}(X,Y) = x_{p+2,2}$
. We define the rational map
$\mathcal {L}^*_{s_0s_0}(X,Y) = x_{p+2,2}$
. We define the rational map
![]() $\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
via the following data:
$\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
via the following data:
 $$ \begin{align} U_0 := I + \sum_{i=1}^{k-1}\alpha_{i}(X,Y)e_{q+1,q+i+1}; \end{align} $$
$$ \begin{align} U_0 := I + \sum_{i=1}^{k-1}\alpha_{i}(X,Y)e_{q+1,q+i+1}; \end{align} $$
 $$ \begin{align} U_+:=\left(\prod_{k\geq 1}^{\leftarrow} \tilde{\gamma}_r^k(U_0)\right)U_0; \end{align} $$
$$ \begin{align} U_+:=\left(\prod_{k\geq 1}^{\leftarrow} \tilde{\gamma}_r^k(U_0)\right)U_0; \end{align} $$
The next proposition corresponds to Theorem 7.3 in [Reference Gekhtman, Shapiro and Vainshtein20] and can be proved in exactly the same way:
Proposition 5.2. Let
![]() $\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the rational map given by equation (5.15). Then the map
$\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the rational map given by equation (5.15). Then the map
![]() $\mathcal {U}$
acts on the cluster and stable variables via the following formulas:
$\mathcal {U}$
acts on the cluster and stable variables via the following formulas:
 $$ \begin{align} \mathcal{U}^*(g_{ij}(X,Y)) = \begin{cases} \tilde{g}_{ij}(X,Y)\tilde{g}_{p+2,1}(X,Y) \ &\text{if}\ \mathcal{L}^*_{ss}(X,Y) = x_{ij} \ \text{for} \ s < s_0;\\ \tilde{g}_{ij}(X,Y) \ &\text{otherwise}; \end{cases} \end{align} $$
$$ \begin{align} \mathcal{U}^*(g_{ij}(X,Y)) = \begin{cases} \tilde{g}_{ij}(X,Y)\tilde{g}_{p+2,1}(X,Y) \ &\text{if}\ \mathcal{L}^*_{ss}(X,Y) = x_{ij} \ \text{for} \ s < s_0;\\ \tilde{g}_{ij}(X,Y) \ &\text{otherwise}; \end{cases} \end{align} $$
 $$ \begin{align} \mathcal{U}^*(h_{ij}(X,Y)) = \begin{cases} \tilde{h}_{ij}(X,Y)\tilde{g}_{p+2,1}(X,Y) \ &\text{if}\ \mathcal{L}^*_{ss}(X,Y) = y_{ij} \ \text{for} \ s < s_0;\\ \tilde{h}_{ij}(X,Y) \ &\text{otherwise}; \end{cases} \end{align} $$
$$ \begin{align} \mathcal{U}^*(h_{ij}(X,Y)) = \begin{cases} \tilde{h}_{ij}(X,Y)\tilde{g}_{p+2,1}(X,Y) \ &\text{if}\ \mathcal{L}^*_{ss}(X,Y) = y_{ij} \ \text{for} \ s < s_0;\\ \tilde{h}_{ij}(X,Y) \ &\text{otherwise}; \end{cases} \end{align} $$
if
![]() $\psi $
is any
$\psi $
is any
![]() $\varphi $
-, f- or c- function in the initial extended cluster, then
$\varphi $
-, f- or c- function in the initial extended cluster, then
Removing roots from column runs
For a BD triple
![]() $\mathbf {\Gamma } = (\Gamma _1,\Gamma _2,\gamma )$
, let us define the opposite BD triple
$\mathbf {\Gamma } = (\Gamma _1,\Gamma _2,\gamma )$
, let us define the opposite BD triple
![]() $\mathbf {\Gamma }^{\text {op}}$
as
$\mathbf {\Gamma }^{\text {op}}$
as
![]() $\mathbf {\Gamma }^{\text {op}}:= (\Gamma _2,\Gamma _1,\gamma ^*)$
; likewise, if
$\mathbf {\Gamma }^{\text {op}}:= (\Gamma _2,\Gamma _1,\gamma ^*)$
; likewise, if
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is a BD pair, we call
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is a BD pair, we call
![]() $\mathbf {\Gamma }^{\text {op}} := ((\mathbf {\Gamma }^c)^{\text {op}}, (\mathbf {\Gamma }^r)^{\text {op}})$
the opposite BD pair. As explained in [Reference Gekhtman, Shapiro and Vainshtein20], the
$\mathbf {\Gamma }^{\text {op}} := ((\mathbf {\Gamma }^c)^{\text {op}}, (\mathbf {\Gamma }^r)^{\text {op}})$
the opposite BD pair. As explained in [Reference Gekhtman, Shapiro and Vainshtein20], the
![]() $\mathcal {L}$
-matrices in
$\mathcal {L}$
-matrices in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\mathbf {\Gamma }^{\text {op}})$
are related via the involution
$\mathcal {GC}(\mathbf {\Gamma }^{\text {op}})$
are related via the involution
In particular, the involution
![]() $(X,Y)\mapsto (Y^t, X^t)$
maps g- and h-functions from
$(X,Y)\mapsto (Y^t, X^t)$
maps g- and h-functions from
![]() $\mathcal {GC}(\mathbf {\Gamma })$
to h- and g-functions from
$\mathcal {GC}(\mathbf {\Gamma })$
to h- and g-functions from
![]() $\mathcal {GC}(\mathbf {\Gamma }^{\text {op}})$
. This allows one to translate the construction of the rational maps from the case of removing a pair of roots from row runs to the case of removing a pair of roots from column runs. In the latter case, for some unipotent lower triangular matrix
$\mathcal {GC}(\mathbf {\Gamma }^{\text {op}})$
. This allows one to translate the construction of the rational maps from the case of removing a pair of roots from row runs to the case of removing a pair of roots from column runs. In the latter case, for some unipotent lower triangular matrix
![]() $U_0:=U_0(X,Y)$
, we set
$U_0:=U_0(X,Y)$
, we set
 $$\begin{align*}U_- := U_0 \prod_{k \geq 1}^{\rightarrow} (\tilde{\gamma}_c^*)^k(U_0) \end{align*}$$
$$\begin{align*}U_- := U_0 \prod_{k \geq 1}^{\rightarrow} (\tilde{\gamma}_c^*)^k(U_0) \end{align*}$$
and define the rational map
![]() $\mathcal {U} : D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
via
$\mathcal {U} : D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
via
As one can observe in the previous cases, the entries of the matrix
![]() $U_0$
belong to the localization
$U_0$
belong to the localization
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))[\tilde {\psi }^{\pm }_{\square }]$
, where the variable
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))[\tilde {\psi }^{\pm }_{\square }]$
, where the variable
![]() $\tilde {\psi _{\square }}$
is a stable variable in
$\tilde {\psi _{\square }}$
is a stable variable in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
such that
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
such that
![]() $\psi _{\square }$
is a cluster variable in
$\psi _{\square }$
is a cluster variable in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
(see the paragraph on notation above). Let
$\mathcal {GC}(\mathbf {\Gamma })$
(see the paragraph on notation above). Let
![]() $\Delta ^c = [p+1,p+k]$
be a nontrivial column X-run and
$\Delta ^c = [p+1,p+k]$
be a nontrivial column X-run and
![]() $\gamma (\Delta ^c) = [q+1,q+k]$
be the corresponding column Y-run. Then, if
$\gamma (\Delta ^c) = [q+1,q+k]$
be the corresponding column Y-run. Then, if
![]() $p+1$
and
$p+1$
and
![]() $q+1$
are removed, the variable
$q+1$
are removed, the variable
![]() $\psi _{\square }$
is
$\psi _{\square }$
is
![]() $\psi _{\square }=h_{1,q+2}$
; if
$\psi _{\square }=h_{1,q+2}$
; if
![]() $p+k-1$
and
$p+k-1$
and
![]() $q+k-1$
are removed, then
$q+k-1$
are removed, then
![]() $\psi _{\square } = h_{1,q+k}$
.
$\psi _{\square } = h_{1,q+k}$
.
The action of
 $\mathcal {U}$
upon other clusters
$\mathcal {U}$
upon other clusters
Let
![]() $\tilde {\mathbf {\Gamma }}$
be obtained from
$\tilde {\mathbf {\Gamma }}$
be obtained from
![]() $\mathbf {\Gamma }$
in one of the four ways described above (i.e., by removing a pair of rightmost or leftmost roots from row or column runs), and let
$\mathbf {\Gamma }$
in one of the four ways described above (i.e., by removing a pair of rightmost or leftmost roots from row or column runs), and let
![]() $\psi _{\square }$
be the variable that is cluster in
$\psi _{\square }$
be the variable that is cluster in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and such that the corresponding variable
$\mathcal {GC}(\mathbf {\Gamma })$
and such that the corresponding variable
![]() $\tilde {\psi }_{\square }$
is stable in
$\tilde {\psi }_{\square }$
is stable in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. The following proposition corresponds to Proposition 7.4 in [Reference Gekhtman, Shapiro and Vainshtein20] and describes the action of the maps
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. The following proposition corresponds to Proposition 7.4 in [Reference Gekhtman, Shapiro and Vainshtein20] and describes the action of the maps
![]() $\mathcal {U}$
defined above upon an extended cluster other than the initial one.
$\mathcal {U}$
defined above upon an extended cluster other than the initial one.
Proposition 5.3. If
![]() $\psi $
and
$\psi $
and
![]() $\tilde {\psi }$
are cluster variables in
$\tilde {\psi }$
are cluster variables in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
that are obtained via the same sequences of mutations, then
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
that are obtained via the same sequences of mutations, then
 $$\begin{align*}\mathcal{U}^*(\psi(X,Y)) = \tilde{\psi}(X,Y) \tilde{\psi}_{\square}(X,Y)^{\lambda}, \ \ \ \lambda:={\frac{\deg(\psi)-\deg(\tilde{\psi})}{\deg{\tilde{\psi}_{\square}}}}, \end{align*}$$
$$\begin{align*}\mathcal{U}^*(\psi(X,Y)) = \tilde{\psi}(X,Y) \tilde{\psi}_{\square}(X,Y)^{\lambda}, \ \ \ \lambda:={\frac{\deg(\psi)-\deg(\tilde{\psi})}{\deg{\tilde{\psi}_{\square}}}}, \end{align*}$$
where
![]() $\deg $
denotes the polynomial degree.
$\deg $
denotes the polynomial degree.
Proof. The proposition is a straight consequence of Proposition 2.5. The required global toric actions in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
have their weight vectors formed by the degrees of the cluster and stable variables considered as polynomials, and the map
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
have their weight vectors formed by the degrees of the cluster and stable variables considered as polynomials, and the map
![]() $\theta $
coincides with the map
$\theta $
coincides with the map
![]() $\mathcal {U}$
. Indeed, if
$\mathcal {U}$
. Indeed, if
![]() $\psi $
is any variable from the initial extended cluster such that
$\psi $
is any variable from the initial extended cluster such that
![]() $\deg (\psi ) = \deg (\tilde {\psi })$
, then
$\deg (\psi ) = \deg (\tilde {\psi })$
, then
![]() $\theta (\psi ) = \tilde {\psi } = \mathcal {U}(\psi )$
. However, if
$\theta (\psi ) = \tilde {\psi } = \mathcal {U}(\psi )$
. However, if
![]() $\psi $
and
$\psi $
and
![]() $\tilde {\psi }$
have different degrees, then the formulas for
$\tilde {\psi }$
have different degrees, then the formulas for
![]() $\mathcal {U}$
(see Proposition 5.2 or Proposition 5.1) suggest that
$\mathcal {U}$
(see Proposition 5.2 or Proposition 5.1) suggest that
![]() $\deg \psi - \deg \tilde {\psi } = \deg \psi _{\square } = \deg \tilde {\psi }_{\square }$
. Therefore,
$\deg \psi - \deg \tilde {\psi } = \deg \psi _{\square } = \deg \tilde {\psi }_{\square }$
. Therefore,
Thus, the maps
![]() $\theta $
and
$\theta $
and
![]() $\mathcal {U}$
are the same (when viewed as maps between the rings generated by the initial extended clusters), and the conclusion of Proposition 2.5 for the map
$\mathcal {U}$
are the same (when viewed as maps between the rings generated by the initial extended clusters), and the conclusion of Proposition 2.5 for the map
![]() $\theta $
is exactly the statement of Proposition 5.3.
$\theta $
is exactly the statement of Proposition 5.3.
For the next corollaries, if
![]() $\Sigma $
is any seed in
$\Sigma $
is any seed in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
, we set
$\mathcal {GC}(\mathbf {\Gamma })$
, we set
![]() $\mathcal {L}_{\mathbb {C}}(\Sigma ):=\mathcal {L}(\Sigma )\otimes \mathbb {C}$
to be the complexification of the ring of Laurent polynomials associated with the seed
$\mathcal {L}_{\mathbb {C}}(\Sigma ):=\mathcal {L}(\Sigma )\otimes \mathbb {C}$
to be the complexification of the ring of Laurent polynomials associated with the seed
![]() $\Sigma $
(see equation (2.4) for the definition). Likewise,
$\Sigma $
(see equation (2.4) for the definition). Likewise,
![]() $\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })$
denotes the ring of Laurent polynomials associated to a seed
$\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })$
denotes the ring of Laurent polynomials associated to a seed
![]() $\tilde {\Sigma } \in \mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. The below corollaries appeared in [Reference Gekhtman, Shapiro and Vainshtein20] in a disguised form in the proof of Theorem 3.12.
$\tilde {\Sigma } \in \mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. The below corollaries appeared in [Reference Gekhtman, Shapiro and Vainshtein20] in a disguised form in the proof of Theorem 3.12.
Corollary 5.3.1. Let
![]() $\Sigma $
and
$\Sigma $
and
![]() $\tilde {\Sigma }$
be seeds in
$\tilde {\Sigma }$
be seeds in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
obtained via the same sequences of mutations from the initial seeds, and let
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
obtained via the same sequences of mutations from the initial seeds, and let
![]() $\mathcal {L}_{\mathbb {C}}(\Sigma )$
and
$\mathcal {L}_{\mathbb {C}}(\Sigma )$
and
![]() $\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })$
be the corresponding rings of Laurent polynomials. If
$\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })$
be the corresponding rings of Laurent polynomials. If
![]() $\mathcal {O}(\operatorname {\mathrm {GL}}_n) \subseteq \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })$
, then
$\mathcal {O}(\operatorname {\mathrm {GL}}_n) \subseteq \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })$
, then
![]() $\mathcal {O}(\operatorname {\mathrm {GL}}_n) \subseteq \mathcal {L}_{\mathbb {C}}(\Sigma )$
.
$\mathcal {O}(\operatorname {\mathrm {GL}}_n) \subseteq \mathcal {L}_{\mathbb {C}}(\Sigma )$
.
Proof. It’s a consequence of Proposition 5.3 that
![]() $\mathcal {U}^*$
can be viewed as an isomorphism
$\mathcal {U}^*$
can be viewed as an isomorphism
![]() $\mathcal {L}_{\mathbb {C}}(\Sigma ) \xrightarrow {\sim } \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })[\tilde {\psi }_{\square }^{\pm 1}]$
. Since
$\mathcal {L}_{\mathbb {C}}(\Sigma ) \xrightarrow {\sim } \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })[\tilde {\psi }_{\square }^{\pm 1}]$
. Since
![]() $\mathcal {U}^*(\mathcal {O}(\operatorname {\mathrm {GL}}_n)) \subseteq \mathcal {O}(\operatorname {\mathrm {GL}}_n)[\tilde {\psi }_{\square }^{\pm 1}] \subseteq \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })[\tilde {\psi }_{\square }^{\pm 1}]$
, we see that
$\mathcal {U}^*(\mathcal {O}(\operatorname {\mathrm {GL}}_n)) \subseteq \mathcal {O}(\operatorname {\mathrm {GL}}_n)[\tilde {\psi }_{\square }^{\pm 1}] \subseteq \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })[\tilde {\psi }_{\square }^{\pm 1}]$
, we see that
![]() $\mathcal {O}(\operatorname {\mathrm {GL}}_n) \subseteq \mathcal {L}_{\mathbb {C}}(\Sigma )$
.
$\mathcal {O}(\operatorname {\mathrm {GL}}_n) \subseteq \mathcal {L}_{\mathbb {C}}(\Sigma )$
.
![]() $\Box $
$\Box $
Corollary 5.3.2. Let
![]() $\tilde {\mathcal {N}}$
be a nerve in
$\tilde {\mathcal {N}}$
be a nerve in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
and
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
and
![]() $\mathcal {N}^{\prime }$
be the corresponding set of seeds in
$\mathcal {N}^{\prime }$
be the corresponding set of seeds in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
. Set
$\mathcal {GC}(\mathbf {\Gamma })$
. Set
![]() $\mathcal {N} := \mathcal {N}^{\prime } \cup \Sigma _{\psi _{\square }}$
to be a nerve in
$\mathcal {N} := \mathcal {N}^{\prime } \cup \Sigma _{\psi _{\square }}$
to be a nerve in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
, where
$\mathcal {GC}(\mathbf {\Gamma })$
, where
![]() $\Sigma _{\psi _{\square }}$
is a seed adjacent to any seed of
$\Sigma _{\psi _{\square }}$
is a seed adjacent to any seed of
![]() $\mathcal {N}^{\prime }$
in the direction of
$\mathcal {N}^{\prime }$
in the direction of
![]() $\psi _{\square }$
. If
$\psi _{\square }$
. If
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))\subseteq \bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\tilde {\mathbf {\Gamma }}))$
and
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))\subseteq \bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\tilde {\mathbf {\Gamma }}))$
and
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n)) \subseteq \mathcal {L}_{\mathbb {C}}(\Sigma _{\psi _{\square }})$
, then
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n)) \subseteq \mathcal {L}_{\mathbb {C}}(\Sigma _{\psi _{\square }})$
, then
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))\subseteq \bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
.
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))\subseteq \bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
.
Proof. Since
![]() $\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\tilde {\mathbf {\Gamma }}) = \bigcap _{\tilde {\Sigma } \in \tilde {\mathcal {N}}} \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })$
, it follows from Corollary 5.3.1 that
$\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\tilde {\mathbf {\Gamma }}) = \bigcap _{\tilde {\Sigma } \in \tilde {\mathcal {N}}} \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Sigma })$
, it follows from Corollary 5.3.1 that
since in addition
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n)) \subseteq \mathcal {L}_{\mathbb {C}}(\Sigma _{\psi _{\square }})$
, we conclude that
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n)) \subseteq \mathcal {L}_{\mathbb {C}}(\Sigma _{\psi _{\square }})$
, we conclude that
The conclusion of Corollary 5.3.2 corresponds to Condition 2.2 of Proposition 2.2. Hence, if the other two conditions of the proposition are satisfied, then
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
is naturally isomorphic to
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
is naturally isomorphic to
![]() $\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
.
$\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
.
5.2 Auxiliary mutation sequences
As in [Reference Gekhtman, Shapiro and Vainshtein20], we will use the same inductive argument on the size
![]() $|\Gamma _1^r|+|\Gamma _1^c|$
in order to prove that
$|\Gamma _1^r|+|\Gamma _1^c|$
in order to prove that
![]() $\bar {\mathcal {\mathcal {A}}}$
is naturally isomorphic to
$\bar {\mathcal {\mathcal {A}}}$
is naturally isomorphic to
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
. The step of the induction is simple and relies upon Corollary 5.3.2 and the existence of at least two different birational quasi-isomorphisms (i.e., arising from a removal of different roots). However, for the base of the induction, which is
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
. The step of the induction is simple and relies upon Corollary 5.3.2 and the existence of at least two different birational quasi-isomorphisms (i.e., arising from a removal of different roots). However, for the base of the induction, which is
![]() $|\Gamma _1^r|+|\Gamma _1^c| = 1$
, we will need to express manually the standard coordinates
$|\Gamma _1^r|+|\Gamma _1^c| = 1$
, we will need to express manually the standard coordinates
![]() $x_{ij}$
and
$x_{ij}$
and
![]() $y_{ij}$
as elements of
$y_{ij}$
as elements of
![]() $\mathcal {L}_{\mathbb {C}}(\Sigma _{\psi _{\square }})$
, where the seed
$\mathcal {L}_{\mathbb {C}}(\Sigma _{\psi _{\square }})$
, where the seed
![]() $\Sigma _{\psi _{\square }}$
is adjacent to the initial one in the direction of
$\Sigma _{\psi _{\square }}$
is adjacent to the initial one in the direction of
![]() $\psi _{\square }$
(see the previous section). This, in turn, will be substantially based on the Laurent phenomenon: If we know that a certain polynomial
$\psi _{\square }$
(see the previous section). This, in turn, will be substantially based on the Laurent phenomenon: If we know that a certain polynomial
![]() $p(X,Y)$
is a cluster variable, then
$p(X,Y)$
is a cluster variable, then
![]() $p(X,Y) \in \mathcal {L}_{\mathbb {C}}(\Sigma _{\psi _{\square }})$
, and therefore
$p(X,Y) \in \mathcal {L}_{\mathbb {C}}(\Sigma _{\psi _{\square }})$
, and therefore
![]() $p(X,Y)$
can be used in the production of Laurent expressionsFootnote
8
for
$p(X,Y)$
can be used in the production of Laurent expressionsFootnote
8
for
![]() $x_{ij}$
or
$x_{ij}$
or
![]() $y_{ij}$
even if we do not know a precise Laurent expansion of
$y_{ij}$
even if we do not know a precise Laurent expansion of
![]() $p(X,Y)$
in terms of the variables of
$p(X,Y)$
in terms of the variables of
![]() $\Sigma _{\psi _{\square }}$
. Thus, the objective of this section is to enrich our database of cluster variables, which will be used in manufacturing Laurent expressions of the standard coordinates
$\Sigma _{\psi _{\square }}$
. Thus, the objective of this section is to enrich our database of cluster variables, which will be used in manufacturing Laurent expressions of the standard coordinates
![]() $x_{ij}$
and
$x_{ij}$
and
![]() $y_{ij}$
.
$y_{ij}$
.
5.2.1 Sequence
 $B_s$
in the standard
$B_s$
in the standard
 $\mathcal {GC}$
$\mathcal {GC}$
For this section, let us consider only one generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
induced by the standard BD pair. For
$D(\operatorname {\mathrm {GL}}_n)$
induced by the standard BD pair. For
![]() $2 \leq s \leq n$
, define a sequence of mutations
$2 \leq s \leq n$
, define a sequence of mutations
![]() $B_s$
as
$B_s$
as
 $$\begin{align*}\begin{aligned} h_{sn} \rightarrow h_{s,n-1} \rightarrow \cdots \rightarrow h_{s,s+1} \rightarrow \\ \rightarrow h_{ss} \rightarrow f_{1,n-s} \rightarrow f_{2,n-s-1} \rightarrow \cdots \rightarrow f_{n-s,1} \rightarrow \\ \rightarrow g_{ss} \rightarrow g_{s,s-1} \rightarrow \cdots \rightarrow g_{s2}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} h_{sn} \rightarrow h_{s,n-1} \rightarrow \cdots \rightarrow h_{s,s+1} \rightarrow \\ \rightarrow h_{ss} \rightarrow f_{1,n-s} \rightarrow f_{2,n-s-1} \rightarrow \cdots \rightarrow f_{n-s,1} \rightarrow \\ \rightarrow g_{ss} \rightarrow g_{s,s-1} \rightarrow \cdots \rightarrow g_{s2}. \end{aligned} \end{align*}$$
The pathway of the sequence is illustrated in Figure 22.

Figure 22 The initial quiver of the standard
![]() $\mathcal {GC}$
in
$\mathcal {GC}$
in
![]() $n=5$
. The vertices of the sequence
$n=5$
. The vertices of the sequence
![]() $B_s$
for
$B_s$
for
![]() $s=3$
are highlighted.
$s=3$
are highlighted.
Lemma 5.4. Apply the mutation sequence
![]() $B_s$
to the initial seed. Then the resulting seed contains the following cluster variables:
$B_s$
to the initial seed. Then the resulting seed contains the following cluster variables:
Proof. The mutation at
![]() $h_{sn}$
reads
$h_{sn}$
reads
which is simply
 $$\begin{align*}y_{sn} h^{\prime}_{sn} = y_{s+1,n} \det \begin{bmatrix} y_{s-1,n-1} & y_{s-1,n}\\ y_{s,n-1} & y_{sn} \end{bmatrix} + y_{s-1,n} \det \begin{bmatrix} y_{s,n-1} & y_{sn} \\ y_{s+1,n-1} & y_{s+1,n} \end{bmatrix}; \end{align*}$$
$$\begin{align*}y_{sn} h^{\prime}_{sn} = y_{s+1,n} \det \begin{bmatrix} y_{s-1,n-1} & y_{s-1,n}\\ y_{s,n-1} & y_{sn} \end{bmatrix} + y_{s-1,n} \det \begin{bmatrix} y_{s,n-1} & y_{sn} \\ y_{s+1,n-1} & y_{s+1,n} \end{bmatrix}; \end{align*}$$
hence,
![]() $h^{\prime }_{sn} = \det Y^{[n,n-1]}_{\{s-1,s+1\}}$
. Once we’ve mutated along the sequence
$h^{\prime }_{sn} = \det Y^{[n,n-1]}_{\{s-1,s+1\}}$
. Once we’ve mutated along the sequence
![]() $h_{sn} \rightarrow \cdots \rightarrow h_{s,n-i+1}$
, the mutation at
$h_{sn} \rightarrow \cdots \rightarrow h_{s,n-i+1}$
, the mutation at
![]() $h_{s,n-i}$
reads
$h_{s,n-i}$
reads
This is a Desnanot–Jacobi identity from Proposition 2.7 applied to the matrix
 $$\begin{align*}\begin{matrix} & \downarrow & & & & \\ \rightarrow & y_{s-1,n-i-1} & y_{s-1,n-i} & y_{s-1,n-i+1} & \ldots & y_{s-1,n}\\ \rightarrow & y_{s,n-i-1} & y_{s,n-i} & y_{s,n-i+1} & \ldots & y_{s,n}\\ &\vdots & \vdots & \vdots & \ldots & \vdots\\ \rightarrow & y_{s+1+i,n-i-1} & y_{s+1+i,n-i} & y_{s+1+i,n-i+1} & \ldots & y_{s+1+i,n} \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & & \\ \rightarrow & y_{s-1,n-i-1} & y_{s-1,n-i} & y_{s-1,n-i+1} & \ldots & y_{s-1,n}\\ \rightarrow & y_{s,n-i-1} & y_{s,n-i} & y_{s,n-i+1} & \ldots & y_{s,n}\\ &\vdots & \vdots & \vdots & \ldots & \vdots\\ \rightarrow & y_{s+1+i,n-i-1} & y_{s+1+i,n-i} & y_{s+1+i,n-i+1} & \ldots & y_{s+1+i,n} \end{matrix} \end{align*}$$
with rows and columns chosen as indicated by arrows (the first two rows, the last row and the first column). We obtain
![]() $h^{\prime }_{s,n-i+1} = \det Y^{[n-i,n]}_{\{s-1\}\cup [s+1,s+i]}$
. Next, the mutation at
$h^{\prime }_{s,n-i+1} = \det Y^{[n-i,n]}_{\{s-1\}\cup [s+1,s+i]}$
. Next, the mutation at
![]() $h_{ss}$
is given by
$h_{ss}$
is given by
This is a Desnanot–Jacobi identity from Proposition 2.8 applied to the matrix
 $$\begin{align*}\begin{matrix} & \downarrow & \downarrow & & & \\ \rightarrow & x_{s-1,n} & y_{s-1,s} & y_{s-1,s+1} & \ldots & y_{s-1,n}\\ \rightarrow & x_{sn} & y_{ss} & y_{s,s+1} & \ldots & y_{sn}\\ & \vdots & \vdots &\vdots & \ldots & \vdots \\ & x_{nn} & y_{ns} & y_{n,s+1} & \ldots & y_{nn} \end{matrix}; \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & \downarrow & & & \\ \rightarrow & x_{s-1,n} & y_{s-1,s} & y_{s-1,s+1} & \ldots & y_{s-1,n}\\ \rightarrow & x_{sn} & y_{ss} & y_{s,s+1} & \ldots & y_{sn}\\ & \vdots & \vdots &\vdots & \ldots & \vdots \\ & x_{nn} & y_{ns} & y_{n,s+1} & \ldots & y_{nn} \end{matrix}; \end{align*}$$
hence,
![]() $h_{ss}^{\prime } = \det [X^{[n]} \ Y^{[s+1,n]}]_{\{s-1\}\cup [s+1,n]}$
. Next, assuming the conventions
$h_{ss}^{\prime } = \det [X^{[n]} \ Y^{[s+1,n]}]_{\{s-1\}\cup [s+1,n]}$
. Next, assuming the conventions
![]() $f_{0,n-j} = h_{j+1,j+1}$
and
$f_{0,n-j} = h_{j+1,j+1}$
and
![]() $f_{n-j,0} = g_{j+1,j+1}$
(see equation (3.2)), the subsequent mutations along the path
$f_{n-j,0} = g_{j+1,j+1}$
(see equation (3.2)), the subsequent mutations along the path
![]() $f_{1,n-s} \rightarrow \cdots \rightarrow f_{n-s,1}$
yield
$f_{1,n-s} \rightarrow \cdots \rightarrow f_{n-s,1}$
yield
Assuming by induction that
![]() $f_{i-1,n-s-i+2}^{\prime } = \det [X^{[n-i+1,n]} \ Y^{[s+i,n]}]_{\{s-1\}\cup [s+1,n]}$
, the latter relation becomes a Desnanot-Jacobi identity from Proposition 2.8 for the matrix
$f_{i-1,n-s-i+2}^{\prime } = \det [X^{[n-i+1,n]} \ Y^{[s+i,n]}]_{\{s-1\}\cup [s+1,n]}$
, the latter relation becomes a Desnanot-Jacobi identity from Proposition 2.8 for the matrix
![]() $[X^{[n-i,n]} \ Y^{[s+i-2,n]}]_{\{s-1\}\cup [s+1,n]}$
applied as indicated:
$[X^{[n-i,n]} \ Y^{[s+i-2,n]}]_{\{s-1\}\cup [s+1,n]}$
applied as indicated:
 $$\begin{align*}\begin{matrix} & \downarrow & & & \downarrow & & & &\\ \rightarrow & x_{s-1,n-i} & x_{s-1,n-i+1} & \ldots & x_{s-1,n} & y_{s-1,i+s} & y_{s-1,i+s+1} & \ldots & y_{s-1,n}\\ \rightarrow & x_{s,n-i} & x_{s,n-i+1} & \ldots & x_{s,n} & y_{s,i+s} & y_{s,i+s+1} & \ldots & y_{s,n}\\ &\vdots & \vdots & \ldots & \vdots & \vdots & \vdots & \ldots & \vdots\\ & x_{n,n-i} & x_{n,n-i+1} & \ldots & x_{nn} & y_{n,i+s} & y_{n,i+s+1} & \ldots & y_{n,n}. \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & \downarrow & & & &\\ \rightarrow & x_{s-1,n-i} & x_{s-1,n-i+1} & \ldots & x_{s-1,n} & y_{s-1,i+s} & y_{s-1,i+s+1} & \ldots & y_{s-1,n}\\ \rightarrow & x_{s,n-i} & x_{s,n-i+1} & \ldots & x_{s,n} & y_{s,i+s} & y_{s,i+s+1} & \ldots & y_{s,n}\\ &\vdots & \vdots & \ldots & \vdots & \vdots & \vdots & \ldots & \vdots\\ & x_{n,n-i} & x_{n,n-i+1} & \ldots & x_{nn} & y_{n,i+s} & y_{n,i+s+1} & \ldots & y_{n,n}. \end{matrix} \end{align*}$$
Therefore,
![]() $f_{i,n-s-i+1}^{\prime } = \det [X^{[n-i,n]} \ Y^{[s+i+1,n]}]_{\{s-1\}\cup [s+1,n]}$
(note that
$f_{i,n-s-i+1}^{\prime } = \det [X^{[n-i,n]} \ Y^{[s+i+1,n]}]_{\{s-1\}\cup [s+1,n]}$
(note that
![]() $f_{n-s,1}$
consists entirely of variables from X). Lastly, the mutations along the path
$f_{n-s,1}$
consists entirely of variables from X). Lastly, the mutations along the path
![]() $g_{ss} \rightarrow \cdots \rightarrow g_{s2}$
read
$g_{ss} \rightarrow \cdots \rightarrow g_{s2}$
read
Assuming by induction
![]() $g^{\prime }_{s,s-i+2} = \det X^{[s-i+1,n-i+1]}_{\{s-1\}\cup [s+1,n]}$
, apply the Desnanot–Jacobi identity to the matrix
$g^{\prime }_{s,s-i+2} = \det X^{[s-i+1,n-i+1]}_{\{s-1\}\cup [s+1,n]}$
, apply the Desnanot–Jacobi identity to the matrix
 $$\begin{align*}\begin{matrix} &\downarrow & & & \downarrow \\ \rightarrow & x_{s-1,s-i} & x_{s-1,s-i+1} & \ldots & x_{s-1,n-i+1} \\ \rightarrow & x_{s,s-i} & x_{s,s-i+1} & \ldots & x_{s,n-i+1}\\ &\vdots& \vdots & \ldots & \vdots \\ &x_{n,s-i} & x_{n,s-i+1} & \ldots & x_{n,n-i+1}.\\ \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} &\downarrow & & & \downarrow \\ \rightarrow & x_{s-1,s-i} & x_{s-1,s-i+1} & \ldots & x_{s-1,n-i+1} \\ \rightarrow & x_{s,s-i} & x_{s,s-i+1} & \ldots & x_{s,n-i+1}\\ &\vdots& \vdots & \ldots & \vdots \\ &x_{n,s-i} & x_{n,s-i+1} & \ldots & x_{n,n-i+1}.\\ \end{matrix} \end{align*}$$
At last, we obtain that
![]() $g_{s,s-i+1}^{\prime } = \det X^{[s-i,n-i]}_{\{s-1\} \cup [s+1,n]}$
.
$g_{s,s-i+1}^{\prime } = \det X^{[s-i,n-i]}_{\{s-1\} \cup [s+1,n]}$
.
5.2.2 Sequence
 $B_{s-k} \rightarrow \ldots \rightarrow B_{s}$
in the standard
$B_{s-k} \rightarrow \ldots \rightarrow B_{s}$
in the standard
 $\mathcal {GC}$
$\mathcal {GC}$
Lemma 5.5. Let us apply the mutation sequence
![]() $B_{s-k}\rightarrow \cdots \rightarrow B_s$
to the initial seed. Then the resulting seed contains the following cluster variables:
$B_{s-k}\rightarrow \cdots \rightarrow B_s$
to the initial seed. Then the resulting seed contains the following cluster variables:
Proof. We prove by induction on k. For
![]() $k=0$
, the formulas coincide with formulas (5.19)–(5.21). Let us apply the sequence
$k=0$
, the formulas coincide with formulas (5.19)–(5.21). Let us apply the sequence
![]() $B_{s-k} \rightarrow \cdots \rightarrow B_{s-1}$
to the initial seed and assume that the formulas hold. We will show that the same formulas hold after a further mutation along the sequence
$B_{s-k} \rightarrow \cdots \rightarrow B_{s-1}$
to the initial seed and assume that the formulas hold. We will show that the same formulas hold after a further mutation along the sequence
![]() $B_s$
. The mutation at
$B_s$
. The mutation at
![]() $h_{sn}$
reads
$h_{sn}$
reads
This is a Desnanot–Jacobi identity for the matrix
 $$\begin{align*}\begin{matrix} &\downarrow & \\ \rightarrow & y_{s-k-1,n-1} & y_{s-k-1,n}\\ \rightarrow & y_{s,n-1} & y_{sn}\\ \rightarrow & y_{s+1,n-1} & y_{s+1,n} \end{matrix}; \end{align*}$$
$$\begin{align*}\begin{matrix} &\downarrow & \\ \rightarrow & y_{s-k-1,n-1} & y_{s-k-1,n}\\ \rightarrow & y_{s,n-1} & y_{sn}\\ \rightarrow & y_{s+1,n-1} & y_{s+1,n} \end{matrix}; \end{align*}$$
hence,
![]() $h_{sn}^{\prime } = \det Y^{[n-1,n]}_{\{s-k-1,s+1\}}$
. The subsequent mutations are
$h_{sn}^{\prime } = \det Y^{[n-1,n]}_{\{s-k-1,s+1\}}$
. The subsequent mutations are
These are Desnanot–Jacobi identities applied to the matrix
 $$\begin{align*}\begin{matrix} & \downarrow & & & \\ \rightarrow & y_{s-k-1,n-i-1} & y_{s-k-1,n-i} &\ldots &y_{s-k-1,n}\\ \rightarrow & y_{s,n-i-1} & y_{s,n-i} & \ldots & y_{sn}\\ & y_{s+1,n-i-1} & y_{s,n-i} & \ldots & y_{s+1,n}\\ & \vdots & \vdots & \ldots & \vdots \\ \rightarrow & y_{s+i+1,n-i-1} & y_{s+i+1,n-i} & \ldots & y_{s+i+1,n}. \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & \\ \rightarrow & y_{s-k-1,n-i-1} & y_{s-k-1,n-i} &\ldots &y_{s-k-1,n}\\ \rightarrow & y_{s,n-i-1} & y_{s,n-i} & \ldots & y_{sn}\\ & y_{s+1,n-i-1} & y_{s,n-i} & \ldots & y_{s+1,n}\\ & \vdots & \vdots & \ldots & \vdots \\ \rightarrow & y_{s+i+1,n-i-1} & y_{s+i+1,n-i} & \ldots & y_{s+i+1,n}. \end{matrix} \end{align*}$$
Therefore,
![]() $h^{\prime }_{s,n-i} = \det Y^{[n-i-1,n]}_{\{s-k-1\}\cup [s+1,s+i+1]}$
. Next, the mutation at
$h^{\prime }_{s,n-i} = \det Y^{[n-i-1,n]}_{\{s-k-1\}\cup [s+1,s+i+1]}$
. Next, the mutation at
![]() $h_{ss}$
for
$h_{ss}$
for
![]() $s < n$
reads
$s < n$
reads
This is a Desnanot–Jacobi identity applied to the matrix
 $$\begin{align*}\begin{matrix} &\downarrow & \downarrow & & & \\ \rightarrow & x_{s-k-1,n} & y_{s-k-1,s} & y_{s-k-1,s+1} & \ldots & y_{s-k-1,n}\\ \rightarrow & x_{sn} & y_{ss} & y_{s,s+1} & \ldots & y_{sn}\\ & x_{s+1,n} & y_{s+1,s} & y_{s+1,s+1} & \ldots & y_{s+1,n}\\ & \vdots & \vdots & \vdots & \ldots & \vdots \\ & x_{nn} & y_{ns} & y_{n,s+1} & \ldots & y_{nn} \end{matrix}; \end{align*}$$
$$\begin{align*}\begin{matrix} &\downarrow & \downarrow & & & \\ \rightarrow & x_{s-k-1,n} & y_{s-k-1,s} & y_{s-k-1,s+1} & \ldots & y_{s-k-1,n}\\ \rightarrow & x_{sn} & y_{ss} & y_{s,s+1} & \ldots & y_{sn}\\ & x_{s+1,n} & y_{s+1,s} & y_{s+1,s+1} & \ldots & y_{s+1,n}\\ & \vdots & \vdots & \vdots & \ldots & \vdots \\ & x_{nn} & y_{ns} & y_{n,s+1} & \ldots & y_{nn} \end{matrix}; \end{align*}$$
hence,
![]() $h^{\prime }_{ss} = \det [X^{[n,n]} \ Y^{[s+1,n]}]_{\{s-k-1\}\cup [s+1,n]}$
. If
$h^{\prime }_{ss} = \det [X^{[n,n]} \ Y^{[s+1,n]}]_{\{s-k-1\}\cup [s+1,n]}$
. If
![]() $s = n$
, then the mutation is
$s = n$
, then the mutation is
which expands as
 $$\begin{align*}y_{nn} h_{nn}^{\prime} = \det \begin{bmatrix} x_{n-k-1,n} & y_{n-k-1,n}\\ x_{nn} & y_{nn} \end{bmatrix} + x_{nn} y_{n-k-1,n} = x_{n-k-1,n}y_{nn}, \end{align*}$$
$$\begin{align*}y_{nn} h_{nn}^{\prime} = \det \begin{bmatrix} x_{n-k-1,n} & y_{n-k-1,n}\\ x_{nn} & y_{nn} \end{bmatrix} + x_{nn} y_{n-k-1,n} = x_{n-k-1,n}y_{nn}, \end{align*}$$
hence
![]() $h_{nn}^{\prime } = x_{n-k-1,n}$
. The subsequent mutations along
$h_{nn}^{\prime } = x_{n-k-1,n}$
. The subsequent mutations along
![]() $f_{1,n-s} \rightarrow \cdots \rightarrow f_{n-s,1}$
read
$f_{1,n-s} \rightarrow \cdots \rightarrow f_{n-s,1}$
read
These are Desnanot–Jacobi identities applied to the matrices of the form
 $$\begin{align*}\begin{matrix} & \downarrow & & & & & \downarrow & & & \\ \rightarrow & x_{s-k-1,n-i} & x_{s-k-1,n-i+1} & \cdots &x_{s-k-1,n} & y_{s-k-1,i+s} & y_{s-k-1,i+s+1} & \cdots & y_{s-k-1,n}\\ \rightarrow & x_{s,n-i} & x_{s,n-i+1} & \cdots &x_{sn} & y_{s,i+s} & y_{s,i+s+1} & \cdots & y_{sn}\\ & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots &\cdots & \vdots \\ & x_{n,n-i} & x_{n,n-i+1} & \cdots & x_{nn} & y_{n,i+s} & y_{n,i+s+1} & \cdots & y_{nn}\\ \end{matrix}; \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & & & \downarrow & & & \\ \rightarrow & x_{s-k-1,n-i} & x_{s-k-1,n-i+1} & \cdots &x_{s-k-1,n} & y_{s-k-1,i+s} & y_{s-k-1,i+s+1} & \cdots & y_{s-k-1,n}\\ \rightarrow & x_{s,n-i} & x_{s,n-i+1} & \cdots &x_{sn} & y_{s,i+s} & y_{s,i+s+1} & \cdots & y_{sn}\\ & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots &\cdots & \vdots \\ & x_{n,n-i} & x_{n,n-i+1} & \cdots & x_{nn} & y_{n,i+s} & y_{n,i+s+1} & \cdots & y_{nn}\\ \end{matrix}; \end{align*}$$
hence,
![]() $f_{i,n-s-i+1}^{\prime } = \det [X^{[n-i,n]} \ Y^{[s+i+1,n]}]_{\{s-k-1\} \cup [s+1,n]}$
. Lastly, consider the consecutive mutations along the path
$f_{i,n-s-i+1}^{\prime } = \det [X^{[n-i,n]} \ Y^{[s+i+1,n]}]_{\{s-k-1\} \cup [s+1,n]}$
. Lastly, consider the consecutive mutations along the path
![]() $g_{ss} \rightarrow \cdots \rightarrow g_{s2}$
. The mutation at
$g_{ss} \rightarrow \cdots \rightarrow g_{s2}$
. The mutation at
![]() $g_{s,s-i+1}$
yields
$g_{s,s-i+1}$
yields
This is a Desnanot–Jacobi identity for the matrix
 $$\begin{align*}\begin{matrix} & \downarrow & & & & \downarrow\\ \rightarrow & x_{s-k-1,s-i} & x_{s-k-1,s-i+1} & \cdots & x_{s-k-1,n-i} & x_{s-k-1,n-i+1}\\ \rightarrow & x_{s,s-i} & x_{s,s-i+1} & \cdots & x_{s,n-i} & x_{s,n-i+1}\\ & x_{s+1,s-i} & x_{s+1,s-i+1} & \cdots & x_{s+1,n-i} & x_{s+1,n-i+1}\\ & \vdots & \vdots & \cdots & \vdots & \vdots\\ & x_{n,s-i} & x_{n,s-i+1} & \cdots & x_{n,n-i} & x_{n,n-i+1}. \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & & \downarrow\\ \rightarrow & x_{s-k-1,s-i} & x_{s-k-1,s-i+1} & \cdots & x_{s-k-1,n-i} & x_{s-k-1,n-i+1}\\ \rightarrow & x_{s,s-i} & x_{s,s-i+1} & \cdots & x_{s,n-i} & x_{s,n-i+1}\\ & x_{s+1,s-i} & x_{s+1,s-i+1} & \cdots & x_{s+1,n-i} & x_{s+1,n-i+1}\\ & \vdots & \vdots & \cdots & \vdots & \vdots\\ & x_{n,s-i} & x_{n,s-i+1} & \cdots & x_{n,n-i} & x_{n,n-i+1}. \end{matrix} \end{align*}$$
Thus, the lemma is proved.
Remark 5.6. Applying the sequence
![]() $B_{n-k} \rightarrow \cdots \rightarrow B_{n}$
to the initial seed, we obtain
$B_{n-k} \rightarrow \cdots \rightarrow B_{n}$
to the initial seed, we obtain
Therefore, this mutation sequence provides an alternative way of showing that
![]() $x_{ij}$
’s are cluster variables (another sequence is shown in [Reference Gekhtman, Shapiro and Vainshtein18], but it doesn’t translate well to a nontrivial BD pair). Figure 23 illustrates the quiver in
$x_{ij}$
’s are cluster variables (another sequence is shown in [Reference Gekhtman, Shapiro and Vainshtein18], but it doesn’t translate well to a nontrivial BD pair). Figure 23 illustrates the quiver in
![]() $n=5$
obtained after applying
$n=5$
obtained after applying
![]() $B_2\rightarrow B_3$
.
$B_2\rightarrow B_3$
.

Figure 23 The result of mutating the initial quiver along the sequence
![]() $B_2 \rightarrow B_3$
(
$B_2 \rightarrow B_3$
(
![]() $n=5$
, the standard
$n=5$
, the standard
![]() $\mathcal {GC}$
).
$\mathcal {GC}$
).
5.2.3 Sequence
 $B_{s-k} \rightarrow \ldots \rightarrow B_s$
in the case
$B_{s-k} \rightarrow \ldots \rightarrow B_s$
in the case
 $|\Gamma _1^r|+|\Gamma _1^c| = 1$
$|\Gamma _1^r|+|\Gamma _1^c| = 1$
Lemma 5.7. Let
![]() $\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be a BD pair such that
$\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be a BD pair such that
![]() $\Gamma _1^r = \{p\}$
,
$\Gamma _1^r = \{p\}$
,
![]() $\Gamma _2^r = \{q\}$
, and
$\Gamma _2^r = \{q\}$
, and
![]() $\Gamma _1^c = \emptyset $
, and let
$\Gamma _1^c = \emptyset $
, and let
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be the corresponding generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
be the corresponding generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
. Let s and k be nonnegative numbers that satisfy
$D(\operatorname {\mathrm {GL}}_n)$
. Let s and k be nonnegative numbers that satisfy
![]() $2 \leq s-k \leq n$
,
$2 \leq s-k \leq n$
,
![]() $2 \leq s \leq n$
,
$2 \leq s \leq n$
,
![]() $s-k \neq q+1$
. Apply the mutation sequence
$s-k \neq q+1$
. Apply the mutation sequence
![]() $B_{s-k} \rightarrow \cdots \rightarrow B_{s}$
to the initial seed of
$B_{s-k} \rightarrow \cdots \rightarrow B_{s}$
to the initial seed of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
. Then the resulting seed contains the following cluster variables:
$\mathcal {GC}(\mathbf {\Gamma })$
. Then the resulting seed contains the following cluster variables:
Proof. Let
![]() $\tilde {\mathbf {\Gamma }}$
be the standard BD pair. Let
$\tilde {\mathbf {\Gamma }}$
be the standard BD pair. Let
![]() $\mathcal {U} : D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the birational quasi-isomorphism from Section 5.1. In this case, it is given by
$\mathcal {U} : D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the birational quasi-isomorphism from Section 5.1. In this case, it is given by
 $$\begin{align*}\mathcal{U}(X,Y):= (U_0X,U_0Y), \ \ U_0(X,Y) := I + \alpha(X,Y) e_{q,q+1}, \ \ \alpha(X,Y):=\frac{\det X_{\{p\}\cup[p+2,n]}^{[1,n-p]}}{\det X_{[p+1,n]}^{[1,n-p]}}. \end{align*}$$
$$\begin{align*}\mathcal{U}(X,Y):= (U_0X,U_0Y), \ \ U_0(X,Y) := I + \alpha(X,Y) e_{q,q+1}, \ \ \alpha(X,Y):=\frac{\det X_{\{p\}\cup[p+2,n]}^{[1,n-p]}}{\det X_{[p+1,n]}^{[1,n-p]}}. \end{align*}$$
Now, notice that if
![]() $I \subseteq [1,n]$
and
$I \subseteq [1,n]$
and
![]() $J \subseteq [1,2n]$
are two sets of indices of the same size, and if either
$J \subseteq [1,2n]$
are two sets of indices of the same size, and if either
![]() $\{q,q+1\}\subseteq I$
or
$\{q,q+1\}\subseteq I$
or
![]() $I \cap \{q\} = \emptyset $
, then
$I \cap \{q\} = \emptyset $
, then
Therefore, if
![]() $p(X,Y)$
is any polynomial from equations (5.25)–(5.27),
$p(X,Y)$
is any polynomial from equations (5.25)–(5.27),
![]() $\mathcal {U}^*(p(X,Y)) = p(X,Y)$
; but since
$\mathcal {U}^*(p(X,Y)) = p(X,Y)$
; but since
![]() $\mathcal {U}$
is invertible and
$\mathcal {U}$
is invertible and
![]() $p(X,Y)$
is a cluster variable in
$p(X,Y)$
is a cluster variable in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
(see Lemma 5.5), it follows from Proposition 5.3 that
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
(see Lemma 5.5), it follows from Proposition 5.3 that
![]() $p(X,Y)$
is a cluster variable in
$p(X,Y)$
is a cluster variable in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
as well.
$\mathcal {GC}(\mathbf {\Gamma })$
as well.
Lemma 5.8. Let
![]() $\mathbf {\Gamma } :=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be a BD pair such that
$\mathbf {\Gamma } :=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be a BD pair such that
![]() $\Gamma _1^r = \emptyset $
,
$\Gamma _1^r = \emptyset $
,
![]() $\Gamma _1^c = \{p\}$
,
$\Gamma _1^c = \{p\}$
,
![]() $\Gamma _2^c = \{q\}$
. Let s and k be nonnegative numbers that satisfy
$\Gamma _2^c = \{q\}$
. Let s and k be nonnegative numbers that satisfy
![]() $2 \leq s-k \leq n$
,
$2 \leq s-k \leq n$
,
![]() $2 \leq s \leq n$
. Apply the mutation sequence
$2 \leq s \leq n$
. Apply the mutation sequence
![]() $B_{s-k} \rightarrow \cdots \rightarrow B_{s}$
to the initial seed of
$B_{s-k} \rightarrow \cdots \rightarrow B_{s}$
to the initial seed of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
. Then the resulting seed contains the following cluster variables:
$\mathcal {GC}(\mathbf {\Gamma })$
. Then the resulting seed contains the following cluster variables:
Proof. The proof proceeds along the same lines as the proof of Lemma 5.7. In this case, the birational quasi-isomorphism is given by
 $$\begin{align*}\mathcal{U}(X,Y):=(XU_0,YU_0), \ \ U_0(X,Y) := I + \alpha(X,Y) e_{p+1,p}, \ \ \alpha(X,Y) := \frac{\det Y^{\{q\}\cup[q+2,n]}_{[1,n-q]}}{\det Y^{[q+1,n]}_{[1,n-q]}}\\[-53pt] \end{align*}$$
$$\begin{align*}\mathcal{U}(X,Y):=(XU_0,YU_0), \ \ U_0(X,Y) := I + \alpha(X,Y) e_{p+1,p}, \ \ \alpha(X,Y) := \frac{\det Y^{\{q\}\cup[q+2,n]}_{[1,n-q]}}{\det Y^{[q+1,n]}_{[1,n-q]}}\\[-53pt] \end{align*}$$
5.2.4 Sequence W in the standard
 $\mathcal {GC}$
$\mathcal {GC}$
Let
![]() $\mathbf {\Gamma }$
be the trivial BD pair and
$\mathbf {\Gamma }$
be the trivial BD pair and
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be the corresponding generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
be the corresponding generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
. For
$D(\operatorname {\mathrm {GL}}_n)$
. For
![]() $2 \leq s \leq n-1$
and
$2 \leq s \leq n-1$
and
![]() $1 \leq t \leq n-s$
, define a sequence of mutations
$1 \leq t \leq n-s$
, define a sequence of mutations
![]() $V_{s,t}$
by
$V_{s,t}$
by
and define a sequence
![]() $W_{s,t}$
as
$W_{s,t}$
as
An illustration of the sequences is shown in Figure 24.

Figure 24 An illustration of the sequence
![]() $W_{21}$
and
$W_{21}$
and
![]() $W_{21}\rightarrow V_{22}$
in
$W_{21}\rightarrow V_{22}$
in
![]() $n=6$
. Vertices
$n=6$
. Vertices
![]() $h_{ii}$
are frozen for convenience, and the vertices that do not participate in mutations are removed.
$h_{ii}$
are frozen for convenience, and the vertices that do not participate in mutations are removed.
Lemma 5.9. Apply the mutation sequence
![]() $W_{s,1}\rightarrow W_{s,2} \rightarrow \cdots \rightarrow W_{s,t-1} \rightarrow V_{s,t}$
to the initial seed of
$W_{s,1}\rightarrow W_{s,2} \rightarrow \cdots \rightarrow W_{s,t-1} \rightarrow V_{s,t}$
to the initial seed of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
. Then the resulting seed contains the following cluster variables:
$\mathcal {GC}(\mathbf {\Gamma })$
. Then the resulting seed contains the following cluster variables:
where the upper index indicates the number of times the corresponding vertex of the quiver was mutated along the sequence.
Proof. Notice that
![]() $V_{s,1}$
is a part of
$V_{s,1}$
is a part of
![]() $B_{s}$
sequence. Moreover, the cluster variables obtained along the sequence
$B_{s}$
sequence. Moreover, the cluster variables obtained along the sequence
![]() $W_{s,1}$
can be as well collected from the sequence
$W_{s,1}$
can be as well collected from the sequence
![]() $B_{s} \rightarrow \cdots \rightarrow B_{n-1}$
. More generally, if we’ve already mutated along the sequence
$B_{s} \rightarrow \cdots \rightarrow B_{n-1}$
. More generally, if we’ve already mutated along the sequence
 $$\begin{align*}\begin{aligned} W_{s,1} \rightarrow W_{s,2} \rightarrow \cdots \rightarrow W_{s,t-2} \rightarrow V_{s,t-1} \rightarrow V_{s+1,t-1} &\rightarrow \cdots \rightarrow V_{s+k-1,t-1}\rightarrow \\ &\rightarrow h_{s+k,n}^{(t-2)} \rightarrow \cdots \rightarrow h_{s+k,n-i+1}^{(t-2)}, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} W_{s,1} \rightarrow W_{s,2} \rightarrow \cdots \rightarrow W_{s,t-2} \rightarrow V_{s,t-1} \rightarrow V_{s+1,t-1} &\rightarrow \cdots \rightarrow V_{s+k-1,t-1}\rightarrow \\ &\rightarrow h_{s+k,n}^{(t-2)} \rightarrow \cdots \rightarrow h_{s+k,n-i+1}^{(t-2)}, \end{aligned} \end{align*}$$
the mutation at
![]() $h_{s+k,n-i}^{(t-2)}$
yields a cluster variable
$h_{s+k,n-i}^{(t-2)}$
yields a cluster variable
Proceeding with the proof, the mutation of
![]() $h_{sn}^{(t-1)}$
can be written as
$h_{sn}^{(t-1)}$
can be written as
which is a Desnanot–Jacobi identity applied to the matrix
 $$\begin{align*}\begin{matrix} & \downarrow & & & \\ & y_{s-1,n-t} & y_{s-1,n-t+1} & \cdots & y_{s-1,n}\\ & y_{s,n-t} & y_{s,n-t+1} & \cdots & y_{sn} \\ & \vdots & \vdots & \cdots & \vdots \\ & y_{s+t-3,n-t} & y_{s+t-3,n-t+1} & \cdots & y_{s+t-3,n}\\ \rightarrow & y_{s+t-2,n-t} & y_{s+t-2,n-t+1} & \cdots & y_{s+t-2,n}\\ \rightarrow & y_{s+t-1,n-t} & y_{s+t-1,n-t+1} & \cdots & y_{s+t-1,n}\\ \rightarrow & y_{s+t,n-t} & y_{s+t-1,n-t+1} & \cdots & y_{s+t-1,n}. \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & \\ & y_{s-1,n-t} & y_{s-1,n-t+1} & \cdots & y_{s-1,n}\\ & y_{s,n-t} & y_{s,n-t+1} & \cdots & y_{sn} \\ & \vdots & \vdots & \cdots & \vdots \\ & y_{s+t-3,n-t} & y_{s+t-3,n-t+1} & \cdots & y_{s+t-3,n}\\ \rightarrow & y_{s+t-2,n-t} & y_{s+t-2,n-t+1} & \cdots & y_{s+t-2,n}\\ \rightarrow & y_{s+t-1,n-t} & y_{s+t-1,n-t+1} & \cdots & y_{s+t-1,n}\\ \rightarrow & y_{s+t,n-t} & y_{s+t-1,n-t+1} & \cdots & y_{s+t-1,n}. \end{matrix} \end{align*}$$
Proceeding along
![]() $h^{(t-1)}_{s,n} \rightarrow \cdots \rightarrow h^{(t-1)}_{s,n-i+1}$
, the subsequent mutation at
$h^{(t-1)}_{s,n} \rightarrow \cdots \rightarrow h^{(t-1)}_{s,n-i+1}$
, the subsequent mutation at
![]() $h^{(t-1)}_{s,n-i}$
reads
$h^{(t-1)}_{s,n-i}$
reads
This is again a Desnanot–Jacobi identity applied to the matrix
 $$\begin{align*}\begin{matrix} & \downarrow & & & \\ & y_{s-1,n-(t+i)} & y_{s-1,n-(t+i)+1} & \cdots & y_{s-1,n}\\ & \vdots & \vdots & \cdots & \vdots \\ \rightarrow & y_{s+t-2,n-(t+i)} & y_{s+t-2,n-(t+i)+1} & \cdots & y_{s+t-2,n}\\ \rightarrow & y_{s+t-1,n-(t+i)} & y_{s+t-1,n-(t+i)+1} & \cdots & y_{s+t-1,n}\\ & \vdots & \vdots & \cdots & \vdots \\ \rightarrow & y_{s+t+i,n-(t+i)} & y_{s+t+i,n-(t+i)+1} & \cdots & y_{s+t+i, n}. \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & \\ & y_{s-1,n-(t+i)} & y_{s-1,n-(t+i)+1} & \cdots & y_{s-1,n}\\ & \vdots & \vdots & \cdots & \vdots \\ \rightarrow & y_{s+t-2,n-(t+i)} & y_{s+t-2,n-(t+i)+1} & \cdots & y_{s+t-2,n}\\ \rightarrow & y_{s+t-1,n-(t+i)} & y_{s+t-1,n-(t+i)+1} & \cdots & y_{s+t-1,n}\\ & \vdots & \vdots & \cdots & \vdots \\ \rightarrow & y_{s+t+i,n-(t+i)} & y_{s+t+i,n-(t+i)+1} & \cdots & y_{s+t+i, n}. \end{matrix} \end{align*}$$
As for the variable
![]() $h_{s+k,n}^{(t-1)}$
in equation (5.31) for
$h_{s+k,n}^{(t-1)}$
in equation (5.31) for
![]() $k> 0$
, the mutation relation is
$k> 0$
, the mutation relation is
This is a Desnanot–Jacobi identity applied to the matrix
 $$\begin{align*}\begin{matrix} & \downarrow & & & \\ & y_{s-1,n-t} & y_{s-1,n-t+1} & \ldots & y_{s-1,n}\\ & y_{s,n-t} & y_{s,n-t+1} & \ldots & y_{sn}\\ & \vdots & \vdots & \ldots & \vdots\\ & y_{s+(t-1)-2,n-t} & y_{s+(t-1)-2,n-t+1} & \ldots & y_{s+(t-1)-2,n}\\ \rightarrow & y_{s+t-2,n-t} & y_{s+t-2,n-t+1} & \ldots & y_{s+t-2,n}\\ \rightarrow & y_{s+(t-1)+k,n-t} & y_{s+(t-1)+k,n-t+1} & \ldots & y_{s+(t-1)+k,n}\\ \rightarrow & y_{s+t+k,n-t} & y_{s+t+k,n-t+1} & \ldots & y_{s+t+k,n}. \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & \\ & y_{s-1,n-t} & y_{s-1,n-t+1} & \ldots & y_{s-1,n}\\ & y_{s,n-t} & y_{s,n-t+1} & \ldots & y_{sn}\\ & \vdots & \vdots & \ldots & \vdots\\ & y_{s+(t-1)-2,n-t} & y_{s+(t-1)-2,n-t+1} & \ldots & y_{s+(t-1)-2,n}\\ \rightarrow & y_{s+t-2,n-t} & y_{s+t-2,n-t+1} & \ldots & y_{s+t-2,n}\\ \rightarrow & y_{s+(t-1)+k,n-t} & y_{s+(t-1)+k,n-t+1} & \ldots & y_{s+(t-1)+k,n}\\ \rightarrow & y_{s+t+k,n-t} & y_{s+t+k,n-t+1} & \ldots & y_{s+t+k,n}. \end{matrix} \end{align*}$$
Lastly, for
![]() $i> 0$
and
$i> 0$
and
![]() $k> 0$
, the mutation at
$k> 0$
, the mutation at
![]() $h_{s+k,n-i}^{(t-1)}$
is
$h_{s+k,n-i}^{(t-1)}$
is
This is a Desnanot–Jacobi identity for
 $$\begin{align*}\begin{matrix} & \downarrow & & & \\ & y_{s-1,n-(t+i)} & y_{s-1,n-(t+i)+1} & \cdots & y_{s-1,n}\\ & \vdots & \vdots & \cdots & \vdots \\ \rightarrow & y_{s+t-2,n-(t+i)} & y_{s+t-2,n-(t+i)+1} & \cdots & y_{s+t-2,n}\\ \rightarrow & y_{s+(t-1)+k,n-(t+i)} & y_{s+(t-1)+k,n-(t+i)+1} & \cdots & y_{s+(t-1)+k,n}\\ & y_{s+t+k,n-(t+i)} & y_{s+t+k,n-(t+i)+1} & \cdots & y_{s+t+k,n}\\ & \vdots & \vdots & \cdots & \vdots \\ & y_{s+(t-1)+i+k,n-(t+i)} & y_{s+(t-1)+i+k,n-(t+i)+1} & \cdots & y_{s+(t-1)+i+k, n}\\ \rightarrow & y_{s+t+i+k,n-(t+i)} & y_{s+t+i+k,n-(t+i)+1} & \cdots & y_{s+t+i+k, n}.\\ \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} & \downarrow & & & \\ & y_{s-1,n-(t+i)} & y_{s-1,n-(t+i)+1} & \cdots & y_{s-1,n}\\ & \vdots & \vdots & \cdots & \vdots \\ \rightarrow & y_{s+t-2,n-(t+i)} & y_{s+t-2,n-(t+i)+1} & \cdots & y_{s+t-2,n}\\ \rightarrow & y_{s+(t-1)+k,n-(t+i)} & y_{s+(t-1)+k,n-(t+i)+1} & \cdots & y_{s+(t-1)+k,n}\\ & y_{s+t+k,n-(t+i)} & y_{s+t+k,n-(t+i)+1} & \cdots & y_{s+t+k,n}\\ & \vdots & \vdots & \cdots & \vdots \\ & y_{s+(t-1)+i+k,n-(t+i)} & y_{s+(t-1)+i+k,n-(t+i)+1} & \cdots & y_{s+(t-1)+i+k, n}\\ \rightarrow & y_{s+t+i+k,n-(t+i)} & y_{s+t+i+k,n-(t+i)+1} & \cdots & y_{s+t+i+k, n}.\\ \end{matrix} \end{align*}$$
Thus, the lemma is proved.
5.2.5 Sequence
 $\mathcal {S}$
in the standard
$\mathcal {S}$
in the standard
 $\mathcal {GC}$
$\mathcal {GC}$
Let us briefly recall a special sequence of mutations from [Reference Gekhtman, Shapiro and Vainshtein18] denoted as
![]() $\mathcal {S}$
. The sequence was used in order to show that the entries of the matrix
$\mathcal {S}$
. The sequence was used in order to show that the entries of the matrix
![]() $U = X^{-1}Y$
belong to the upper cluster algebra, as well as to produce a generalized cluster structure on the variety
$U = X^{-1}Y$
belong to the upper cluster algebra, as well as to produce a generalized cluster structure on the variety
![]() $\operatorname {\mathrm {GL}}_n^{\dagger }$
(see Section 2.2 for the definition).
$\operatorname {\mathrm {GL}}_n^{\dagger }$
(see Section 2.2 for the definition).
Quiver Q0
Let Q be the initial quiver of the standard generalized cluster algebra
![]() $\mathcal {GC}$
. Let us define a quiver
$\mathcal {GC}$
. Let us define a quiver
![]() $Q_0$
that consists of the vertices that contain all g- and f-functions, as well as all
$Q_0$
that consists of the vertices that contain all g- and f-functions, as well as all
![]() $h_{ii}$
for
$h_{ii}$
for
![]() $2 \leq i \leq n$
and all
$2 \leq i \leq n$
and all
![]() $\varphi _{i,n-i}$
for
$\varphi _{i,n-i}$
for
![]() $1 \leq i \leq n-1$
; for convenience, let us freeze the vertices
$1 \leq i \leq n-1$
; for convenience, let us freeze the vertices
![]() $\varphi _{i,n-i}$
and
$\varphi _{i,n-i}$
and
![]() $h_{ii}$
. Furthermore, we assign double indices
$h_{ii}$
. Furthermore, we assign double indices
![]() $(i,j)$
to the vertices of
$(i,j)$
to the vertices of
![]() $Q_0$
, with i enumerating the rows and running from top to bottom, and j being responsible for the columns, running from left to right. Figure 25 represents
$Q_0$
, with i enumerating the rows and running from top to bottom, and j being responsible for the columns, running from left to right. Figure 25 represents
![]() $Q_0$
for
$Q_0$
for
![]() $n=5$
. The quiver
$n=5$
. The quiver
![]() $Q_0$
together with the functions attached to the vertices defines an ordinary cluster algebra of geometric type.
$Q_0$
together with the functions attached to the vertices defines an ordinary cluster algebra of geometric type.

Figure 25 Quiver
![]() $Q_0$
for
$Q_0$
for
![]() $n=5$
.
$n=5$
.
Sequence
![]() $\mathbf{\mathcal {S}}$
1
$\mathbf{\mathcal {S}}$
1
Let us mutate the quiver
![]() $Q_0$
along the diagonals starting from the bottom left and proceeding to the top right corner. More precisely: first, mutate at
$Q_0$
along the diagonals starting from the bottom left and proceeding to the top right corner. More precisely: first, mutate at
![]() $(n,2)$
; second, mutate along
$(n,2)$
; second, mutate along
![]() $(n-1,2) \rightarrow (n,3)$
; third, mutate along
$(n-1,2) \rightarrow (n,3)$
; third, mutate along
![]() $(n-2,2) \rightarrow (n-1,3) \rightarrow (n,4)$
and so on. The last mutation in the sequence is at the vertex
$(n-2,2) \rightarrow (n-1,3) \rightarrow (n,4)$
and so on. The last mutation in the sequence is at the vertex
![]() $(2,n)$
. Let us denote the resulting quiver as
$(2,n)$
. Let us denote the resulting quiver as
![]() $Q_1$
and the resulting cluster variables as
$Q_1$
and the resulting cluster variables as
![]() $\chi _{ij}^1$
,
$\chi _{ij}^1$
,
![]() $2 \leq i,\ j \leq n$
. They are given by
$2 \leq i,\ j \leq n$
. They are given by
 $$ \begin{align} \chi_{ij}^1 = \begin{cases} \det X^{[1]\cup [j+1,n+j-i+1]}_{[i-1,n]} \ &\text{if} \ i> j\\ \det [X^{[1]\cup [j+1,n]} \ Y^{[n+i-j,n]}]_{[i-1,n]} \ & \text{if} \ i \leq j. \end{cases} \end{align} $$
$$ \begin{align} \chi_{ij}^1 = \begin{cases} \det X^{[1]\cup [j+1,n+j-i+1]}_{[i-1,n]} \ &\text{if} \ i> j\\ \det [X^{[1]\cup [j+1,n]} \ Y^{[n+i-j,n]}]_{[i-1,n]} \ & \text{if} \ i \leq j. \end{cases} \end{align} $$
Sequence
![]() $\mathbf{\mathcal{S}}$
k
$\mathbf{\mathcal{S}}$
k
Once we’ve mutated along the sequence
![]() $\mathcal {S}_{k-1}$
, the sequence
$\mathcal {S}_{k-1}$
, the sequence
![]() $\mathcal {S}_k$
is defined as follows. First, freeze all the vertices in the kth row and in the
$\mathcal {S}_k$
is defined as follows. First, freeze all the vertices in the kth row and in the
![]() $(n-k+2)$
th column of the quiver
$(n-k+2)$
th column of the quiver
![]() $Q_{k-1}$
. Then
$Q_{k-1}$
. Then
![]() $\mathcal {S}_k$
is defined as a sequence of mutations along the diagonals: First, mutate at
$\mathcal {S}_k$
is defined as a sequence of mutations along the diagonals: First, mutate at
![]() $(n,2)$
; then mutate along
$(n,2)$
; then mutate along
![]() $(n-1,2)\rightarrow (n,3)$
, and so on. The resulting cluster variables are denoted as
$(n-1,2)\rightarrow (n,3)$
, and so on. The resulting cluster variables are denoted as
![]() $\chi _{ij}^k$
and are given by
$\chi _{ij}^k$
and are given by
 $$\begin{align*}\chi_{ij}^k = \begin{cases} \det X^{[1,k]\cup [j+k,n+j-i+k]}_{[i-k,n]} \ &\text{if} \ i-k+1>j\\ \det [X^{[1,k]\cup [j+k,n]} \ Y^{[n+i-j+1-k,n]}]_{[i-k,n]} \ &\text{if} \ i-k+1 \leq j. \end{cases} \end{align*}$$
$$\begin{align*}\chi_{ij}^k = \begin{cases} \det X^{[1,k]\cup [j+k,n+j-i+k]}_{[i-k,n]} \ &\text{if} \ i-k+1>j\\ \det [X^{[1,k]\cup [j+k,n]} \ Y^{[n+i-j+1-k,n]}]_{[i-k,n]} \ &\text{if} \ i-k+1 \leq j. \end{cases} \end{align*}$$
Sequence
![]() $\mathbf{\mathcal{S}}$
$\mathbf{\mathcal{S}}$
The sequence
![]() $\mathcal {S}$
is defined as the composition
$\mathcal {S}$
is defined as the composition
![]() $\mathcal {S}_{n-1} \circ \mathcal {S}_{n-2} \circ \cdots \circ \mathcal {S}_1$
. The result of its application to the initial quiver is illustrated in Figure 26 for
$\mathcal {S}_{n-1} \circ \mathcal {S}_{n-2} \circ \cdots \circ \mathcal {S}_1$
. The result of its application to the initial quiver is illustrated in Figure 26 for
![]() $n=4$
. Notice that
$n=4$
. Notice that
It was shown in [Reference Gekhtman, Shapiro and Vainshtein18] that the entries of U in the standard
![]() $\mathcal {GC}$
can be written as Laurent polynomials in terms of the following variables: c-functions,
$\mathcal {GC}$
can be written as Laurent polynomials in terms of the following variables: c-functions,
![]() $\varphi $
-functions and the functions
$\varphi $
-functions and the functions
![]() $\chi _{k+1,j}^k$
obtained from the sequence
$\chi _{k+1,j}^k$
obtained from the sequence
![]() $\mathcal {S}$
.
$\mathcal {S}$
.

Figure 26 An application of the sequence
![]() $\mathcal {S}$
to the initial quiver of the standard
$\mathcal {S}$
to the initial quiver of the standard
![]() $\mathcal {GC}$
,
$\mathcal {GC}$
,
![]() $n=4$
.
$n=4$
.
5.2.6 Sequence
 $\mathcal {S}$
in the case
$\mathcal {S}$
in the case
 $|\Gamma _1^r|+|\Gamma _1^c| = 1$
$|\Gamma _1^r|+|\Gamma _1^c| = 1$
Lemma 5.10. Let
![]() $\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be a BD pair such that
$\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be a BD pair such that
![]() $\Gamma _1^r = \{p\}$
,
$\Gamma _1^r = \{p\}$
,
![]() $\Gamma _2^r = \{q\}$
and
$\Gamma _2^r = \{q\}$
and
![]() $\Gamma _1^c = \emptyset $
, and let
$\Gamma _1^c = \emptyset $
, and let
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be the corresponding generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
be the corresponding generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
. Apply the sequence
$D(\operatorname {\mathrm {GL}}_n)$
. Apply the sequence
![]() $\mathcal {S}$
to the initial seed of
$\mathcal {S}$
to the initial seed of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
. Then for
$\mathcal {GC}(\mathbf {\Gamma })$
. Then for
![]() $1 \leq k \leq n-1$
,
$1 \leq k \leq n-1$
,
![]() $2 \leq j \leq n-k+1$
, the resulting seed contains the cluster variables
$2 \leq j \leq n-k+1$
, the resulting seed contains the cluster variables
Remark 5.11. Though not needed in this paper, a similar lemma can be proved for the case
![]() $\Gamma _1^c = \emptyset $
and
$\Gamma _1^c = \emptyset $
and
![]() $\Gamma _1^r = \{p\}$
,
$\Gamma _1^r = \{p\}$
,
![]() $\Gamma _1^r = \{q\}$
. Then the resulting seed also contains the cluster variables (5.33) except for
$\Gamma _1^r = \{q\}$
. Then the resulting seed also contains the cluster variables (5.33) except for
![]() $k = p$
.
$k = p$
.
The case of a nontrivial
![]() $\mathbf {\Gamma }^c$
will require a different result.
$\mathbf {\Gamma }^c$
will require a different result.
Lemma 5.12. Let
![]() $\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be a BD pair such that
$\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be a BD pair such that
![]() $\Gamma _1^r = \emptyset $
,
$\Gamma _1^r = \emptyset $
,
![]() $\Gamma _1^c = \{p\}$
and
$\Gamma _1^c = \{p\}$
and
![]() $\Gamma _2^c = \{q\}$
, and let
$\Gamma _2^c = \{q\}$
, and let
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be the corresponding generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
be the corresponding generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
. There exist extended clusters
$D(\operatorname {\mathrm {GL}}_n)$
. There exist extended clusters
![]() $\Psi :=(\psi _1,\ldots ,\psi _{2n})$
and
$\Psi :=(\psi _1,\ldots ,\psi _{2n})$
and
![]() $\tilde {\Psi }:=(\tilde {\psi }_1,\ldots ,\tilde {\psi }_{2n})$
in
$\tilde {\Psi }:=(\tilde {\psi }_1,\ldots ,\tilde {\psi }_{2n})$
in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
, respectively, such that
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
, respectively, such that
![]() $\psi _i(X,Y) = \tilde {\psi }_i(X,Y)$
if and only if
$\psi _i(X,Y) = \tilde {\psi }_i(X,Y)$
if and only if
![]() $\psi _i \neq g_{n-p+1,1}$
.
$\psi _i \neq g_{n-p+1,1}$
.
Proof. Indeed, if
![]() $p = 1$
, then the initial extended clusters of
$p = 1$
, then the initial extended clusters of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
satisfy the requirement; if
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
satisfy the requirement; if
![]() $p> 1$
, then let
$p> 1$
, then let
![]() $\Psi _{\mathcal {S}_1}$
and
$\Psi _{\mathcal {S}_1}$
and
![]() $\tilde {\Psi }_{\mathcal {S}_1}$
be the extended clusters in
$\tilde {\Psi }_{\mathcal {S}_1}$
be the extended clusters in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
, respectively, that are obtained from the initial extended clusters via an application of
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
, respectively, that are obtained from the initial extended clusters via an application of
![]() $\mathcal {S}_1$
. Let
$\mathcal {S}_1$
. Let
![]() $\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the birational quasi-isomorphism described in Section 5.1. It is given by
$\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the birational quasi-isomorphism described in Section 5.1. It is given by
 $$\begin{align*}\mathcal{U}(X,Y):=(XU_0,YU_0), \ \ U_0(X,Y) := I + \alpha(X,Y) e_{p+1,p}, \ \ \alpha(X,Y) := \frac{\det Y^{\{q\}\cup[q+2,n]}_{[1,n-q]}}{\det Y^{[q+1,n]}_{[1,n-q]}}. \end{align*}$$
$$\begin{align*}\mathcal{U}(X,Y):=(XU_0,YU_0), \ \ U_0(X,Y) := I + \alpha(X,Y) e_{p+1,p}, \ \ \alpha(X,Y) := \frac{\det Y^{\{q\}\cup[q+2,n]}_{[1,n-q]}}{\det Y^{[q+1,n]}_{[1,n-q]}}. \end{align*}$$
It follows that
![]() $\mathcal {U}(\chi _{ij}^1(X,Y)) = \chi _{ij}^1(X,Y)$
, where
$\mathcal {U}(\chi _{ij}^1(X,Y)) = \chi _{ij}^1(X,Y)$
, where
![]() $\chi _{ij}^1$
are defined in equation (5.32); therefore, Proposition 5.3 implies that
$\chi _{ij}^1$
are defined in equation (5.32); therefore, Proposition 5.3 implies that
![]() $\chi _{ij}^1$
are cluster variables of
$\chi _{ij}^1$
are cluster variables of
![]() $\Psi _{\mathcal {S}_1}$
. Since all the other variables (except
$\Psi _{\mathcal {S}_1}$
. Since all the other variables (except
![]() $g_{n-p+1,1}(X,Y)$
and
$g_{n-p+1,1}(X,Y)$
and
![]() $\tilde {g}_{n-p+1,1}(X,Y)$
) are equal as elements of
$\tilde {g}_{n-p+1,1}(X,Y)$
) are equal as elements of
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
, we conclude that
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
, we conclude that
![]() $\Psi _{\mathcal {S}_1}$
and
$\Psi _{\mathcal {S}_1}$
and
![]() $\tilde {\Psi }_{\mathcal {S}_1}$
are the required extended clusters.
$\tilde {\Psi }_{\mathcal {S}_1}$
are the required extended clusters.
5.3 Completeness for
 $|\Gamma _1^r| = 1$
and
$|\Gamma _1^r| = 1$
and
 $|\Gamma _1^c| = 0$
$|\Gamma _1^c| = 0$
Let
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be a generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
be a generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
defined by a BD pair with
$D(\operatorname {\mathrm {GL}}_n)$
defined by a BD pair with
![]() $\Gamma _1^r = \{p\}$
,
$\Gamma _1^r = \{p\}$
,
![]() $\Gamma _2^r = \{q\}$
and
$\Gamma _2^r = \{q\}$
and
![]() $\Gamma _1^c = \emptyset $
, and let
$\Gamma _1^c = \emptyset $
, and let
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
be the standard generalized cluster structure.
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
be the standard generalized cluster structure.
Lemma 5.13. The entries of
![]() $U = X^{-1}Y$
in
$U = X^{-1}Y$
in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
belong to the upper cluster algebra.
$\mathcal {GC}(\mathbf {\Gamma })$
belong to the upper cluster algebra.
Proof. It was shown in [Reference Gekhtman, Shapiro and Vainshtein18] that the entries of U can be expressed as Laurent polynomials in terms of the
![]() $\varphi $
-variables, c-variables and the variables
$\varphi $
-variables, c-variables and the variables
![]() $\chi ^k_{k+1,j}$
(see Section 5.2.5), as well as in terms of any mutations of these variables. By Lemma 5.10, all of these variables are present in
$\chi ^k_{k+1,j}$
(see Section 5.2.5), as well as in terms of any mutations of these variables. By Lemma 5.10, all of these variables are present in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
; thus, the entries of U belong to
$\mathcal {GC}(\mathbf {\Gamma })$
; thus, the entries of U belong to
![]() $\bar {\mathcal {A}}(\mathcal {GC}(\mathbf {\Gamma }))$
.
$\bar {\mathcal {A}}(\mathcal {GC}(\mathbf {\Gamma }))$
.
Proposition 5.14. Under the setup of the current section, the entries of X and Y belong to the upper cluster algebra.
Proof. Due to Corollary 5.3.2, it suffices to show that the entries of X and Y can be expressed as Laurent polynomials in the cluster
![]() $\Psi $
adjacent to the initial one in the direction of
$\Psi $
adjacent to the initial one in the direction of
![]() $g_{p+1,1}$
. It follows from Lemma 5.7 and Remark 5.6 that all the entries of X except the qth row belong to the upper cluster algebra, for they are themselves cluster variables. Due to Lemma 5.13 and the relation
$g_{p+1,1}$
. It follows from Lemma 5.7 and Remark 5.6 that all the entries of X except the qth row belong to the upper cluster algebra, for they are themselves cluster variables. Due to Lemma 5.13 and the relation
![]() $XU = Y$
, all the entries of Y except the qth row also belong to the upper cluster algebra. Therefore, we only need to find Laurent expressions for the qth rows of X and Y.
$XU = Y$
, all the entries of Y except the qth row also belong to the upper cluster algebra. Therefore, we only need to find Laurent expressions for the qth rows of X and Y.
The mutation at
![]() $g_{p+1,1}$
yields
$g_{p+1,1}$
yields
 $$ \begin{align} g^{\prime}_{p+1,1}(X,Y) = \det \begin{bmatrix} y_{qn} & x_{p,2} & x_{p,3} & \ldots & x_{p,n-p+1}\\ y_{q+1,n} & x_{p+1,2} & x_{p+1,3} & \ldots & x_{p+1,n-p+1}\\ 0 & x_{p+2,2} & x_{p+2,3} & \ldots & x_{p+2,n-p+1}\\ \vdots & \vdots & \vdots & \ldots & \vdots \\ 0 & x_{n,2} & x_{n,3} & \ldots & x_{n,n-p+1} \end{bmatrix}, \end{align} $$
$$ \begin{align} g^{\prime}_{p+1,1}(X,Y) = \det \begin{bmatrix} y_{qn} & x_{p,2} & x_{p,3} & \ldots & x_{p,n-p+1}\\ y_{q+1,n} & x_{p+1,2} & x_{p+1,3} & \ldots & x_{p+1,n-p+1}\\ 0 & x_{p+2,2} & x_{p+2,3} & \ldots & x_{p+2,n-p+1}\\ \vdots & \vdots & \vdots & \ldots & \vdots \\ 0 & x_{n,2} & x_{n,3} & \ldots & x_{n,n-p+1} \end{bmatrix}, \end{align} $$
which can be seen via an appropriate application of a Plücker relation. Expanding
![]() $g^{\prime }_{p+1,1}(X,Y)$
along the first column yields
$g^{\prime }_{p+1,1}(X,Y)$
along the first column yields
Since
![]() $p \neq q$
, it follows from Lemma 5.7 that
$p \neq q$
, it follows from Lemma 5.7 that
![]() $\det X_{\{p\} \cup [p+2,n]}^{[2,n-p+1]}$
is a Laurent polynomial in terms of the variables of
$\det X_{\{p\} \cup [p+2,n]}^{[2,n-p+1]}$
is a Laurent polynomial in terms of the variables of
![]() $\Psi $
. Together with the above relation, we see that
$\Psi $
. Together with the above relation, we see that
![]() $y_{qn}$
is a Laurent polynomial in terms of the variables of
$y_{qn}$
is a Laurent polynomial in terms of the variables of
![]() $\Psi $
as well.
$\Psi $
as well.
Let us assume by induction that for
![]() $i> q$
the variables
$i> q$
the variables
![]() $y_{qj}$
are already recovered, where
$y_{qj}$
are already recovered, where
![]() $j \geq i$
. Expanding the function
$j \geq i$
. Expanding the function
![]() $h_{q,i-1}(Y) = \det Y^{[i-1,n]}_{[q,q+n-i+1]}$
along the first row, we see that
$h_{q,i-1}(Y) = \det Y^{[i-1,n]}_{[q,q+n-i+1]}$
along the first row, we see that
where
![]() $P_1(Y)$
is a polynomial in all entries of
$P_1(Y)$
is a polynomial in all entries of
![]() $Y^{[i-1,n]}_{[q,q+n-i+1]}$
except
$Y^{[i-1,n]}_{[q,q+n-i+1]}$
except
![]() $y_{q,i-1}$
, and hence,
$y_{q,i-1}$
, and hence,
![]() $P_1(Y)$
is a Laurent polynomial in the variables of
$P_1(Y)$
is a Laurent polynomial in the variables of
![]() $\Psi $
. Therefore, we’ve recovered all
$\Psi $
. Therefore, we’ve recovered all
![]() $y_{qi}$
for
$y_{qi}$
for
![]() $i \geq q$
. To proceed further, we make use of f-functions. The variable
$i \geq q$
. To proceed further, we make use of f-functions. The variable
![]() $x_{qn}$
can be recovered via expanding
$x_{qn}$
can be recovered via expanding
![]() $f_{1,n-q}(X,Y)$
along the first row:
$f_{1,n-q}(X,Y)$
along the first row:
where
![]() $P_2$
is now a polynomial in all entries of
$P_2$
is now a polynomial in all entries of
![]() $[X^{[n,n]}\, Y^{[q+1,n]}]_{[q,n]}$
except
$[X^{[n,n]}\, Y^{[q+1,n]}]_{[q,n]}$
except
![]() $x_{qn}$
, and therefore
$x_{qn}$
, and therefore
![]() $P_2(X,Y)$
is a Laurent polynomial in
$P_2(X,Y)$
is a Laurent polynomial in
![]() $\Psi $
. If for some
$\Psi $
. If for some
![]() $i> q+1$
the variables
$i> q+1$
the variables
![]() $x_{qj}$
are already recovered, where
$x_{qj}$
are already recovered, where
![]() $j \geq i$
, then
$j \geq i$
, then
![]() $x_{q,i-1}$
can be recovered via expanding
$x_{q,i-1}$
can be recovered via expanding
![]() $f_{n-i+1,i-q}(X,Y)$
along the first row:
$f_{n-i+1,i-q}(X,Y)$
along the first row:
where
![]() $P_3(X,Y)$
is again a polynomial in entries that are already known to be Laurent polynomials in terms of
$P_3(X,Y)$
is again a polynomial in entries that are already known to be Laurent polynomials in terms of
![]() $\Psi $
. We conclude at this moment that the variables
$\Psi $
. We conclude at this moment that the variables
![]() $x_{q,q+1},\ldots ,x_{qn}$
are Laurent polynomials in
$x_{q,q+1},\ldots ,x_{qn}$
are Laurent polynomials in
![]() $\Psi $
. Using the same idea, we recover the variables
$\Psi $
. Using the same idea, we recover the variables
![]() $x_{q1},\ldots ,x_{qq}$
consecutively starting from
$x_{q1},\ldots ,x_{qq}$
consecutively starting from
![]() $x_{qq}$
and using the g-functions: Each
$x_{qq}$
and using the g-functions: Each
![]() $x_{qi}$
is recovered via the expansion along the first row of the function
$x_{qi}$
is recovered via the expansion along the first row of the function
![]() $g_{qi}(X,Y)$
.
$g_{qi}(X,Y)$
.
Lastly, since
![]() $x_{q1}, \ldots , x_{qn}$
are recovered as Laurent polynomials in terms of
$x_{q1}, \ldots , x_{qn}$
are recovered as Laurent polynomials in terms of
![]() $\Psi $
, the remaining variables
$\Psi $
, the remaining variables
![]() $y_{q1},\ldots ,y_{q,q-1}$
are recovered via
$y_{q1},\ldots ,y_{q,q-1}$
are recovered via
![]() $XU = Y$
. Thus, all the entries of X and Y are Laurent polynomials in the variables of
$XU = Y$
. Thus, all the entries of X and Y are Laurent polynomials in the variables of
![]() $\Psi $
.
$\Psi $
.
5.4 Completeness for
 $|\Gamma _1^r| = 0$
and
$|\Gamma _1^r| = 0$
and
 $|\Gamma _1^c| = 1$
$|\Gamma _1^c| = 1$
Similarly to the previous section, let
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be a generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
be a generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
defined by a BD pair with
$D(\operatorname {\mathrm {GL}}_n)$
defined by a BD pair with
![]() $\Gamma _1^c = \{p\}$
,
$\Gamma _1^c = \{p\}$
,
![]() $\Gamma _2^c = \{q\}$
and
$\Gamma _2^c = \{q\}$
and
![]() $\Gamma _1^r = \emptyset $
, and let
$\Gamma _1^r = \emptyset $
, and let
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
be the standard generalized cluster structure. We need the following abstract result:
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
be the standard generalized cluster structure. We need the following abstract result:
Lemma 5.15. Let
![]() $\mathcal {F}$
be a field of characteristic zero, and let
$\mathcal {F}$
be a field of characteristic zero, and let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be distinct transcendental elements over
$\beta $
be distinct transcendental elements over
![]() $\mathcal {F}$
and such that
$\mathcal {F}$
and such that
![]() $\mathcal {F}(\alpha ) = \mathcal {F}(\beta )$
. If there is a relation
$\mathcal {F}(\alpha ) = \mathcal {F}(\beta )$
. If there is a relation
 $$ \begin{align} \sum_{k=1}^{m} (\alpha^k - \beta^k) p_k = 0 \end{align} $$
$$ \begin{align} \sum_{k=1}^{m} (\alpha^k - \beta^k) p_k = 0 \end{align} $$
for
![]() $p_k \in \mathcal {F}$
, then all
$p_k \in \mathcal {F}$
, then all
![]() $p_k = 0$
.
$p_k = 0$
.
Proof. Let us set
![]() $x:=\alpha $
for convenience. Since
$x:=\alpha $
for convenience. Since
![]() $\mathcal {F}(\alpha ) = \mathcal {F}(\beta )$
, we can express
$\mathcal {F}(\alpha ) = \mathcal {F}(\beta )$
, we can express
![]() $\beta $
as
$\beta $
as
![]() $\beta = \frac {a x + b}{cx + d}$
with
$\beta = \frac {a x + b}{cx + d}$
with
![]() $ad-bc \neq 0$
. Now, if
$ad-bc \neq 0$
. Now, if
![]() $c = 0$
, each
$c = 0$
, each
![]() $p_k$
in equation (5.35) must be zero due to the linear independence of the polynomials
$p_k$
in equation (5.35) must be zero due to the linear independence of the polynomials
![]() $x^k - ((a/d)x+(b/d))^k$
. Otherwise, if
$x^k - ((a/d)x+(b/d))^k$
. Otherwise, if
![]() $c \neq 0$
, we can look at the order of the pole
$c \neq 0$
, we can look at the order of the pole
![]() $x = -d/c$
and show that
$x = -d/c$
and show that
![]() $p_m = 0$
, and then, via a descending induction starting at m, that all
$p_m = 0$
, and then, via a descending induction starting at m, that all
![]() $p_k = 0$
. Thus, the statement holds.
$p_k = 0$
. Thus, the statement holds.
Contrary to Lemma 5.13, in the case of a nontrivial column BD triple we first treat the entries of
![]() $YX^{-1}$
:
$YX^{-1}$
:
Lemma 5.16. The entries of
![]() $YX^{-1}$
belong to the upper cluster algebra of
$YX^{-1}$
belong to the upper cluster algebra of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
.
$\mathcal {GC}(\mathbf {\Gamma })$
.
Proof. By Lemma 5.12, there exist extended clusters
![]() $\Psi :=(\psi _1,\ldots ,\psi _{2n})$
and
$\Psi :=(\psi _1,\ldots ,\psi _{2n})$
and
![]() $\tilde {\Psi }:=(\tilde {\psi }_1,\ldots ,\tilde {\psi }_{2n})$
in
$\tilde {\Psi }:=(\tilde {\psi }_1,\ldots ,\tilde {\psi }_{2n})$
in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
and
$\mathcal {GC}(\mathbf {\Gamma })$
and
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
, respectively, that differ only in the variable
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
, respectively, that differ only in the variable
![]() $g_{n-p+1,1}$
. Let
$g_{n-p+1,1}$
. Let
![]() $\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}}\dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the birational quasi-isomorphism defined in Section 5.1. Let
$\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}}\dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the birational quasi-isomorphism defined in Section 5.1. Let
![]() $\Psi ^{\prime }$
be the extended cluster adjacent to
$\Psi ^{\prime }$
be the extended cluster adjacent to
![]() $\Psi $
in the direction of
$\Psi $
in the direction of
![]() $h_{1,q+1}$
. By Corollary 5.3.2, it suffices to show that the entries of
$h_{1,q+1}$
. By Corollary 5.3.2, it suffices to show that the entries of
![]() $YX^{-1}$
belong to the ring of Laurent polynomials
$YX^{-1}$
belong to the ring of Laurent polynomials
![]() $\mathcal {L}_{\mathbb {C}}(\Psi ^{\prime })$
. Let us fix an entry
$\mathcal {L}_{\mathbb {C}}(\Psi ^{\prime })$
. Let us fix an entry
![]() $v:=(YX^{-1})_{ij}$
; since
$v:=(YX^{-1})_{ij}$
; since
![]() $v \in \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Psi })$
, we can write v as
$v \in \tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Psi })$
, we can write v as
where
![]() $p_{i}$
are elements of
$p_{i}$
are elements of
![]() $\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Psi })$
that do not contain
$\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Psi })$
that do not contain
![]() $\tilde {g}_{n-p+1,1}$
(in other words, we view
$\tilde {g}_{n-p+1,1}$
(in other words, we view
![]() $\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Psi })$
as a polynomial ring in one variable
$\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Psi })$
as a polynomial ring in one variable
![]() $\tilde {g}_{n-p+1,1}$
). Since
$\tilde {g}_{n-p+1,1}$
). Since
![]() $\mathcal {U}(YX^{-1}) = YX^{-1}$
and due to the choice of
$\mathcal {U}(YX^{-1}) = YX^{-1}$
and due to the choice of
![]() $\Psi $
and
$\Psi $
and
![]() $\tilde {\Psi }$
, we see that an application of
$\tilde {\Psi }$
, we see that an application of
![]() $(\mathcal {U}^*)^{-1}$
yields
$(\mathcal {U}^*)^{-1}$
yields
 $$ \begin{align} v = p_0 + \sum_{k \geq 1}\left( \frac{{g}_{n-p+1,1}}{{h}_{1,q+1}}\right)^k p_k, \end{align} $$
$$ \begin{align} v = p_0 + \sum_{k \geq 1}\left( \frac{{g}_{n-p+1,1}}{{h}_{1,q+1}}\right)^k p_k, \end{align} $$
hence subtracting equation (5.37) from equation (5.36), we arrive at
 $$\begin{align*}\sum_{k \geq 1}\left(\tilde{g}_{n-p+1,1}^k - \left( \frac{g_{n-p+1,1}}{h_{1,q+1}}\right)^k \right) p_k = 0. \end{align*}$$
$$\begin{align*}\sum_{k \geq 1}\left(\tilde{g}_{n-p+1,1}^k - \left( \frac{g_{n-p+1,1}}{h_{1,q+1}}\right)^k \right) p_k = 0. \end{align*}$$
By Lemma 5.15,
![]() $p_k = 0$
for all
$p_k = 0$
for all
![]() $k \geq 1$
. Therefore, there exists a Laurent expression for v in terms of
$k \geq 1$
. Therefore, there exists a Laurent expression for v in terms of
![]() $\mathcal {L}_{\mathbb {C}}(\Psi )$
that does not involve a division by
$\mathcal {L}_{\mathbb {C}}(\Psi )$
that does not involve a division by
![]() $h_{1,q+1}$
(for
$h_{1,q+1}$
(for
![]() $\tilde {h}_{1,q+1}$
is not invertible in
$\tilde {h}_{1,q+1}$
is not invertible in
![]() $\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Psi })$
); therefore, if
$\tilde {\mathcal {L}}_{\mathbb {C}}(\tilde {\Psi })$
); therefore, if
![]() $h_{1,q+1} h_{1,q+1}^{\prime } = M$
is an exchange relation for
$h_{1,q+1} h_{1,q+1}^{\prime } = M$
is an exchange relation for
![]() $h_{1,q+1}$
, substituting
$h_{1,q+1}$
, substituting
![]() $h_{1,q+1}$
with
$h_{1,q+1}$
with
![]() $M/h_{1,q+1}^{\prime }$
in the Laurent expression for v yields an expression in the ring
$M/h_{1,q+1}^{\prime }$
in the Laurent expression for v yields an expression in the ring
![]() $\mathcal {L}_{\mathbb {C}}(\Psi ^{\prime })$
. Thus, the lemma is proved.
$\mathcal {L}_{\mathbb {C}}(\Psi ^{\prime })$
. Thus, the lemma is proved.
Proposition 5.17. In the setup of the current section, all entries of X and Y belong to the upper cluster algebra of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
.
$\mathcal {GC}(\mathbf {\Gamma })$
.
Proof. It follows from Lemma 5.8 that all entries of X except the pth column are cluster variables in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
. Since the entries of
$\mathcal {GC}(\mathbf {\Gamma })$
. Since the entries of
![]() $YX^{-1}$
belong to the upper cluster algebra due to Lemma 5.16 and since
$YX^{-1}$
belong to the upper cluster algebra due to Lemma 5.16 and since
![]() $Y = (YX^{-1})X$
, we see that all entries of Y except the pth column also belong to the upper cluster algebra. The mutation at
$Y = (YX^{-1})X$
, we see that all entries of Y except the pth column also belong to the upper cluster algebra. The mutation at
![]() $h_{1,q+1}(X,Y)$
yields
$h_{1,q+1}(X,Y)$
yields
 $$ \begin{align} h^{\prime}_{1,q+1}(X,Y) = \begin{bmatrix} x_{np} & x_{n,p+1} & 0 & \cdots & 0\\ y_{2q} & y_{2,q+1} & y_{2,q+2} & \cdots & y_{2n}\\ \vdots & \vdots & \vdots & \cdots & \vdots\\ y_{n-q+1,q} & y_{n-q+1,q+1} & y_{n-q+1,q+2} &\cdots & y_{n-q+1,n} \end{bmatrix}, \end{align} $$
$$ \begin{align} h^{\prime}_{1,q+1}(X,Y) = \begin{bmatrix} x_{np} & x_{n,p+1} & 0 & \cdots & 0\\ y_{2q} & y_{2,q+1} & y_{2,q+2} & \cdots & y_{2n}\\ \vdots & \vdots & \vdots & \cdots & \vdots\\ y_{n-q+1,q} & y_{n-q+1,q+1} & y_{n-q+1,q+2} &\cdots & y_{n-q+1,n} \end{bmatrix}, \end{align} $$
and the expansion along the first row yields
A further expansion of the minor
![]() $\det Y^{\{q\}\cup [q+2,n]}_{[2,n-q+1]}$
along its first column yields
$\det Y^{\{q\}\cup [q+2,n]}_{[2,n-q+1]}$
along its first column yields
 $$\begin{align*}\det Y^{\{q\}\cup[q+2,n]}_{[2,n-q+1]} = \sum_{k=2}^{n-q+1} y_{kq} \det Y^{[q+2,n]}_{[2,k-1]\cup[k+1,n-q+1]}. \end{align*}$$
$$\begin{align*}\det Y^{\{q\}\cup[q+2,n]}_{[2,n-q+1]} = \sum_{k=2}^{n-q+1} y_{kq} \det Y^{[q+2,n]}_{[2,k-1]\cup[k+1,n-q+1]}. \end{align*}$$
In turn, the minors
![]() $\det Y^{[q+2,n]}_{[2,k-1]\cup [k+1,n-q+1]}$
are known to be cluster variables:
$\det Y^{[q+2,n]}_{[2,k-1]\cup [k+1,n-q+1]}$
are known to be cluster variables:
 $$\begin{align*}\det Y^{[q+2,n]}_{[2,k-1]\cup[k+1,n-q+1]} = \begin{cases} h_{3,q+2} \ &k=2,\\ h^{(k-2)}_{3,q+k} \ &2 < k < n-q+1,\\ h_{2,q+2} \ &k = n-q+1, \end{cases} \end{align*}$$
$$\begin{align*}\det Y^{[q+2,n]}_{[2,k-1]\cup[k+1,n-q+1]} = \begin{cases} h_{3,q+2} \ &k=2,\\ h^{(k-2)}_{3,q+k} \ &2 < k < n-q+1,\\ h_{2,q+2} \ &k = n-q+1, \end{cases} \end{align*}$$
where the variables
![]() $h^{(k-2)}_{3,q+k}$
come from the W-sequences studied in Lemma 5.9 (they are applicable in
$h^{(k-2)}_{3,q+k}$
come from the W-sequences studied in Lemma 5.9 (they are applicable in
![]() $|\Gamma _1^c| = 1$
as well, for the h-functions are the same as in the standard structure). It follows from equation (5.39) that
$|\Gamma _1^c| = 1$
as well, for the h-functions are the same as in the standard structure). It follows from equation (5.39) that
![]() $x_{np}$
belongs to the upper cluster structure. Now, the rest of the proof is similar to Proposition 5.14: To recover the variables
$x_{np}$
belongs to the upper cluster structure. Now, the rest of the proof is similar to Proposition 5.14: To recover the variables
![]() $x_{n-i,p}$
for
$x_{n-i,p}$
for
![]() $1 \leq i \leq p$
, one uses the functions
$1 \leq i \leq p$
, one uses the functions
![]() $g_{n-i,p}$
; due to the relation
$g_{n-i,p}$
; due to the relation
![]() $Y = (YX^{-1})X$
and Lemma 5.16, these variables together with
$Y = (YX^{-1})X$
and Lemma 5.16, these variables together with
![]() $x_{np}$
yield
$x_{np}$
yield
![]() $y_{np},\ldots , y_{pp}$
. To proceed further, one recovers consecutively
$y_{np},\ldots , y_{pp}$
. To proceed further, one recovers consecutively
![]() $y_{p,p+i}$
from
$y_{p,p+i}$
from
![]() $h_{p,p+i}$
, and then one can obtain
$h_{p,p+i}$
, and then one can obtain
![]() $x_{p,p+i}$
back from the relation
$x_{p,p+i}$
back from the relation
![]() $X = (YX^{-1})^{-1} Y$
. Thus the proposition is proved.
$X = (YX^{-1})^{-1} Y$
. Thus the proposition is proved.
5.5 Coprimality
Let
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be the generalized cluster structure on
$\mathcal {GC}(\mathbf {\Gamma })$
be the generalized cluster structure on
![]() $D(\operatorname {\mathrm {GL}}_n)$
induced by an aperiodic oriented BD pair
$D(\operatorname {\mathrm {GL}}_n)$
induced by an aperiodic oriented BD pair
![]() $\mathbf {\Gamma }$
. In this section, we prove that all cluster and frozen variables from the initial extended cluster are irreducible as elements of
$\mathbf {\Gamma }$
. In this section, we prove that all cluster and frozen variables from the initial extended cluster are irreducible as elements of
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
, as well as (for cluster variables) coprime with their mutations in
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
, as well as (for cluster variables) coprime with their mutations in
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
. Together with Proposition 4.1, we will conclude that
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
. Together with Proposition 4.1, we will conclude that
![]() $\mathcal {GC}(\mathbf {\Gamma })$
is a regular generalized cluster structure.
$\mathcal {GC}(\mathbf {\Gamma })$
is a regular generalized cluster structure.
Lemma 5.18. Assume that
![]() $\mathbf {\Gamma }$
is nontrivial and
$\mathbf {\Gamma }$
is nontrivial and
![]() $\tilde {\mathbf {\Gamma }}$
is obtained from
$\tilde {\mathbf {\Gamma }}$
is obtained from
![]() $\mathbf {\Gamma }$
by the removal of a pair of roots. Let
$\mathbf {\Gamma }$
by the removal of a pair of roots. Let
![]() $\psi _{\square }$
be the cluster variable from the initial cluster of
$\psi _{\square }$
be the cluster variable from the initial cluster of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
such that
$\mathcal {GC}(\mathbf {\Gamma })$
such that
![]() $\tilde {\psi }_{\square }$
is frozen in
$\tilde {\psi }_{\square }$
is frozen in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
(see Section 5.1). Let
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
(see Section 5.1). Let
![]() $\tilde {\psi }\neq \tilde {\psi }_{\square }$
be a cluster or frozen variable in
$\tilde {\psi }\neq \tilde {\psi }_{\square }$
be a cluster or frozen variable in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
and
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
and
![]() $\psi $
be the corresponding variable in
$\psi $
be the corresponding variable in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
. Suppose that
$\mathcal {GC}(\mathbf {\Gamma })$
. Suppose that
![]() $\tilde {\psi }$
and
$\tilde {\psi }$
and
![]() $\tilde {\psi }_{\square }$
are irreducible as elements of
$\tilde {\psi }_{\square }$
are irreducible as elements of
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
. Then there exist
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
. Then there exist
![]() $f \in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
and
$f \in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
and
![]() $\lambda \geq 0$
such that f is coprime with
$\lambda \geq 0$
such that f is coprime with
![]() $\psi _{\square }$
and
$\psi _{\square }$
and
![]() $\psi = f \psi _{\square }^{\lambda }$
; moreover,
$\psi = f \psi _{\square }^{\lambda }$
; moreover,
![]() $\psi $
is irreducible in
$\psi $
is irreducible in
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
if and only if
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
if and only if
![]() $\psi $
is not divisible by
$\psi $
is not divisible by
![]() $\psi _{\square }$
.
$\psi _{\square }$
.
Proof. Indeed, let
![]() $\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the birational quasi-isomorphism constructed in Section 5.1. By Proposition 5.3,
$\mathcal {U}:D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the birational quasi-isomorphism constructed in Section 5.1. By Proposition 5.3,
![]() $\mathcal {U}^*(\psi ) = \tilde {\psi } \tilde {\psi }_{\square }^{\varepsilon }$
for some
$\mathcal {U}^*(\psi ) = \tilde {\psi } \tilde {\psi }_{\square }^{\varepsilon }$
for some
![]() $\varepsilon \geq 0$
. Assume that
$\varepsilon \geq 0$
. Assume that
![]() $\psi = f_1\cdot f_2$
for some regular coprime functions
$\psi = f_1\cdot f_2$
for some regular coprime functions
![]() $f_1$
and
$f_1$
and
![]() $f_2$
. Set
$f_2$
. Set
where
![]() $\tilde {f}_i \in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
and
$\tilde {f}_i \in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
and
![]() $\tilde {\psi }_{\square }$
are coprime (by the assumption,
$\tilde {\psi }_{\square }$
are coprime (by the assumption,
![]() $\tilde {\psi }_{\square }$
is irreducible, so we can find such
$\tilde {\psi }_{\square }$
is irreducible, so we can find such
![]() $\tilde {f}_i$
). Applying
$\tilde {f}_i$
). Applying
![]() $\mathcal {U}^*$
to
$\mathcal {U}^*$
to
![]() $\psi $
, we arrive at
$\psi $
, we arrive at
Since
![]() $\tilde {\psi }_{\square }$
is coprime with
$\tilde {\psi }_{\square }$
is coprime with
![]() $\tilde {\psi }$
,
$\tilde {\psi }$
,
![]() $\tilde {f}_1$
and
$\tilde {f}_1$
and
![]() $\tilde {f}_2$
, we see that
$\tilde {f}_2$
, we see that
![]() $\varepsilon = \lambda _1 + \lambda _2$
; since
$\varepsilon = \lambda _1 + \lambda _2$
; since
![]() $\tilde {\psi }$
is irreducible by the assumption, without loss of generality
$\tilde {\psi }$
is irreducible by the assumption, without loss of generality
![]() $\tilde {f}_2$
is a unit in
$\tilde {f}_2$
is a unit in
![]() $\mathcal {O}(\operatorname {\mathrm {GL}}_n)$
; that is,
$\mathcal {O}(\operatorname {\mathrm {GL}}_n)$
; that is,
![]() $\tilde {f}_2 = a \det X^{k}\det Y^{l}$
for some
$\tilde {f}_2 = a \det X^{k}\det Y^{l}$
for some
![]() $k,l\in \mathbb {Z}$
and
$k,l\in \mathbb {Z}$
and
![]() $a \in \mathbb {C}$
. Since
$a \in \mathbb {C}$
. Since
![]() $(\mathcal {U}^*)^{-1}(\tilde {f}_2) = \tilde {f}_2$
, we see that
$(\mathcal {U}^*)^{-1}(\tilde {f}_2) = \tilde {f}_2$
, we see that
![]() $\psi = \tilde {f}_2 f_1\psi _{\square }^{\lambda _2}$
. Setting
$\psi = \tilde {f}_2 f_1\psi _{\square }^{\lambda _2}$
. Setting
![]() $f:=\tilde {f}_2f_1$
and
$f:=\tilde {f}_2f_1$
and
![]() $\lambda :=\lambda _2$
proves the first claim. Moreover, if
$\lambda :=\lambda _2$
proves the first claim. Moreover, if
![]() $\psi $
is not divisible by
$\psi $
is not divisible by
![]() $\psi _{\square }$
, then
$\psi _{\square }$
, then
![]() $\lambda _2 = 0$
, hence
$\lambda _2 = 0$
, hence
![]() $f_2$
is a unit and thus
$f_2$
is a unit and thus
![]() $\psi $
is irreducible.
$\psi $
is irreducible.
Proposition 5.19. All cluster and frozen variables in the initial extended cluster of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
are irreducible polynomials.
$\mathcal {GC}(\mathbf {\Gamma })$
are irreducible polynomials.
Proof. For the standard BD pair, it’s the statement of Theorem 3.10 in [Reference Gekhtman, Shapiro and Vainshtein18]. For other BD pairs, let us use an induction on the size
![]() $|\Gamma _1^r| + |\Gamma _1^c|$
. If
$|\Gamma _1^r| + |\Gamma _1^c|$
. If
![]() $|\Gamma _1^r| + |\Gamma _1^c| = 1$
, then the only variables from the initial extended cluster that differ from the case of the standard BD pair are g- and h-functions; these are irreducible by Frobenius theorem [Reference Schneider24, p. 15]. From now on, assume that
$|\Gamma _1^r| + |\Gamma _1^c| = 1$
, then the only variables from the initial extended cluster that differ from the case of the standard BD pair are g- and h-functions; these are irreducible by Frobenius theorem [Reference Schneider24, p. 15]. From now on, assume that
![]() $|\Gamma _1^r|+|\Gamma _1^c| \geq 2$
.
$|\Gamma _1^r|+|\Gamma _1^c| \geq 2$
.
Let
![]() $\tilde {\mathbf {\Gamma }}$
be obtained from
$\tilde {\mathbf {\Gamma }}$
be obtained from
![]() $\mathbf {\Gamma }$
by removing a pair of leftmost or rightmost roots, and let
$\mathbf {\Gamma }$
by removing a pair of leftmost or rightmost roots, and let
![]() $\psi _1$
be the variable that is cluster in
$\psi _1$
be the variable that is cluster in
![]() $\mathcal {GC}(\mathbf {\Gamma })$
but such that
$\mathcal {GC}(\mathbf {\Gamma })$
but such that
![]() $\tilde {\psi }_1$
is frozen in
$\tilde {\psi }_1$
is frozen in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. Let
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. Let
![]() $\mathcal {U}_1 : D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the associated birational quasi-isomorphism. Since
$\mathcal {U}_1 : D(\operatorname {\mathrm {GL}}_n)_{\tilde {\mathbf {\Gamma }}} \dashrightarrow D(\operatorname {\mathrm {GL}}_n)_{\mathbf {\Gamma }}$
be the associated birational quasi-isomorphism. Since
![]() $|\Gamma _1^r|+|\Gamma _1^c| \geq 2$
, we can find yet another pair of roots from
$|\Gamma _1^r|+|\Gamma _1^c| \geq 2$
, we can find yet another pair of roots from
![]() $\mathbf {\Gamma }$
to remove; let us denote by
$\mathbf {\Gamma }$
to remove; let us denote by
![]() $\psi _2$
the corresponding variable.
$\psi _2$
the corresponding variable.
The variables
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
are irreducible. Indeed, let us write
$\psi _2$
are irreducible. Indeed, let us write
![]() $\psi _1 = f\psi _2^{\lambda _2}$
and
$\psi _1 = f\psi _2^{\lambda _2}$
and
![]() $\psi _2 = g \psi _1^{\lambda _{1}}$
for some
$\psi _2 = g \psi _1^{\lambda _{1}}$
for some
![]() $\lambda _1,\lambda _2 \geq 0$
and
$\lambda _1,\lambda _2 \geq 0$
and
![]() $f,g\in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
coprime with
$f,g\in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
coprime with
![]() $\psi _2$
and
$\psi _2$
and
![]() $\psi _1$
, respectively. Applying
$\psi _1$
, respectively. Applying
![]() $\mathcal {U}_1$
to
$\mathcal {U}_1$
to
![]() $\psi _1 = f \psi ^{\lambda _2}_2$
, we see that there exists
$\psi _1 = f \psi ^{\lambda _2}_2$
, we see that there exists
![]() $\tilde {f}$
coprime with
$\tilde {f}$
coprime with
![]() $\tilde {\psi }_1$
and numbers
$\tilde {\psi }_1$
and numbers
![]() $\theta \in \mathbb {Z}$
,
$\theta \in \mathbb {Z}$
,
![]() $\eta \geq 0$
such that
$\eta \geq 0$
such that
It follows from the assumption of the induction that
![]() $1 = \theta + \eta \lambda _2$
and that
$1 = \theta + \eta \lambda _2$
and that
![]() $1 = \tilde {f}\tilde {\psi }_2^{\lambda _2}$
. Since
$1 = \tilde {f}\tilde {\psi }_2^{\lambda _2}$
. Since
![]() $\tilde {\psi }_2$
is not invertible in
$\tilde {\psi }_2$
is not invertible in
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
, we conclude that
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
, we conclude that
![]() $\lambda _2 = 0$
. A similar argument shows that
$\lambda _2 = 0$
. A similar argument shows that
![]() $\lambda _1 = 0$
(here, one applies the other birational quasi-isomorphism). By Lemma 5.18, both
$\lambda _1 = 0$
(here, one applies the other birational quasi-isomorphism). By Lemma 5.18, both
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
are irreducible.
$\psi _2$
are irreducible.
Any cluster or frozen variable from the initial extended cluster is irreducible. Indeed, let
![]() $\psi $
be such. If
$\psi $
be such. If
![]() $\psi $
is not divisible by
$\psi $
is not divisible by
![]() $\psi _1$
or
$\psi _1$
or
![]() $\psi _2$
, then it follows from Lemma 5.18 that
$\psi _2$
, then it follows from Lemma 5.18 that
![]() $\psi $
is irreducible; otherwise, since
$\psi $
is irreducible; otherwise, since
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
are irreducible, we can find
$\psi _2$
are irreducible, we can find
![]() $f \in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
coprime with both
$f \in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
coprime with both
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
, and numbers
$\psi _2$
, and numbers
![]() $\theta _1,\theta _2 \geq 1$
such that
$\theta _1,\theta _2 \geq 1$
such that
Applying
![]() $\mathcal {U}_1^*$
to the above identity, we arrive at
$\mathcal {U}_1^*$
to the above identity, we arrive at
where
![]() $\tilde {f}$
is coprime with
$\tilde {f}$
is coprime with
![]() $\tilde {\psi }_1$
,
$\tilde {\psi }_1$
,
![]() $\eta _1, \in \mathbb {Z}$
and
$\eta _1, \in \mathbb {Z}$
and
![]() $\zeta \geq 0$
. We see that
$\zeta \geq 0$
. We see that
![]() $\varepsilon _1 = \eta _1 + \theta _1 + \theta _2\zeta $
, hence
$\varepsilon _1 = \eta _1 + \theta _1 + \theta _2\zeta $
, hence
![]() $\tilde {\psi } = \tilde {f}\tilde {\psi }_2^{\theta _2}$
. But since both
$\tilde {\psi } = \tilde {f}\tilde {\psi }_2^{\theta _2}$
. But since both
![]() $\tilde {\psi }$
and
$\tilde {\psi }$
and
![]() $\tilde {\psi }_2$
are coprime irreducible elements of
$\tilde {\psi }_2$
are coprime irreducible elements of
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
, we conclude that
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
, we conclude that
![]() $\theta _2 = 0$
. By Lemma 5.18,
$\theta _2 = 0$
. By Lemma 5.18,
![]() $\psi $
is irreducible.
$\psi $
is irreducible.
Proposition 5.20. Any cluster variable
![]() $\psi $
from the initial cluster of
$\psi $
from the initial cluster of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
is coprime with
$\mathcal {GC}(\mathbf {\Gamma })$
is coprime with
![]() $\psi ^{\prime }$
.
$\psi ^{\prime }$
.
Proof. As in the previous proposition, let us run an induction on the size
![]() $|\Gamma _1^r| + |\Gamma _1^c|$
. For the standard BD pair, the statement was proved in [Reference Gekhtman, Shapiro and Vainshtein18]. For
$|\Gamma _1^r| + |\Gamma _1^c|$
. For the standard BD pair, the statement was proved in [Reference Gekhtman, Shapiro and Vainshtein18]. For
![]() $|\Gamma _1^r|+|\Gamma _1^c| \geq 1$
, let
$|\Gamma _1^r|+|\Gamma _1^c| \geq 1$
, let
![]() $\tilde {\mathbf {\Gamma }}$
be obtained from
$\tilde {\mathbf {\Gamma }}$
be obtained from
![]() $\mathbf {\Gamma }$
by the removal of a pair of leftmost or rightmost roots, and let
$\mathbf {\Gamma }$
by the removal of a pair of leftmost or rightmost roots, and let
![]() $\psi _{\square }$
be the cluster variable such that
$\psi _{\square }$
be the cluster variable such that
![]() $\tilde {\psi }_{\square }$
is frozen in
$\tilde {\psi }_{\square }$
is frozen in
![]() $\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. For any variable
$\mathcal {GC}(\tilde {\mathbf {\Gamma }})$
. For any variable
![]() $\psi \neq \psi _{\square }$
, since
$\psi \neq \psi _{\square }$
, since
![]() $\psi $
is irreducible (see Proposition 5.19), we can write
$\psi $
is irreducible (see Proposition 5.19), we can write
![]() $\psi ^{\prime } = p \cdot \psi ^{\lambda }$
for some
$\psi ^{\prime } = p \cdot \psi ^{\lambda }$
for some
![]() $\lambda \geq 0$
and some p coprime with
$\lambda \geq 0$
and some p coprime with
![]() $\psi $
. Applying the corresponding birational quasi-isomorphism, we find
$\psi $
. Applying the corresponding birational quasi-isomorphism, we find
![]() $\varepsilon , \eta \geq 0$
,
$\varepsilon , \eta \geq 0$
,
![]() $\theta \in \mathbb {Z}$
and an element
$\theta \in \mathbb {Z}$
and an element
![]() $\tilde {p}$
coprime with
$\tilde {p}$
coprime with
![]() $\tilde {\psi }_{\square }$
such that
$\tilde {\psi }_{\square }$
such that
Since
![]() $\tilde {\psi }^{\prime }$
and
$\tilde {\psi }^{\prime }$
and
![]() $\tilde {\psi }$
are coprime by the assumption of the induction, we see that
$\tilde {\psi }$
are coprime by the assumption of the induction, we see that
![]() $\lambda = 0$
. Therefore,
$\lambda = 0$
. Therefore,
![]() $\psi $
is coprime with
$\psi $
is coprime with
![]() $\psi ^{\prime }$
.
$\psi ^{\prime }$
.
Now, let us address the case of
![]() $\psi = \psi _{\square }$
. If
$\psi = \psi _{\square }$
. If
![]() $|\Gamma _1^r|+|\Gamma _1^c| \geq 2$
, the coprimality of
$|\Gamma _1^r|+|\Gamma _1^c| \geq 2$
, the coprimality of
![]() $\psi _{\square }$
with
$\psi _{\square }$
with
![]() $\psi _{\square }^{\prime }$
follows from the existence of another birational quasi-isomorphism, which is associated with a different pair of roots. If
$\psi _{\square }^{\prime }$
follows from the existence of another birational quasi-isomorphism, which is associated with a different pair of roots. If
![]() $|\Gamma _1^r|+|\Gamma _1^c| = 1$
, we observe from formula (5.34), formula (5.38) and Frobenius theorem [Reference Schneider24, p. 15] that
$|\Gamma _1^r|+|\Gamma _1^c| = 1$
, we observe from formula (5.34), formula (5.38) and Frobenius theorem [Reference Schneider24, p. 15] that
![]() $\psi _{\square }^{\prime }$
is irreducible and coprime with
$\psi _{\square }^{\prime }$
is irreducible and coprime with
![]() $\psi _{\square }$
. Thus, the proposition is proved.
$\psi _{\square }$
. Thus, the proposition is proved.
Combining Proposition 4.1, Proposition 5.19 and Proposition 5.20, we see that
![]() $\mathcal {GC}(\mathbf {\Gamma })$
satisfies the first two conditions of Proposition 2.2; thus,
$\mathcal {GC}(\mathbf {\Gamma })$
satisfies the first two conditions of Proposition 2.2; thus,
![]() $\mathcal {GC}(\mathbf {\Gamma })$
is a regular generalized cluster structure.
$\mathcal {GC}(\mathbf {\Gamma })$
is a regular generalized cluster structure.
5.6 The final proof
Proposition 5.21. Let
![]() $\mathcal {GC}(\mathbf {\Gamma })$
be a generalized cluster structure
$\mathcal {GC}(\mathbf {\Gamma })$
be a generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma })$
on
$\mathcal {GC}(\mathbf {\Gamma })$
on
![]() $D(\operatorname {\mathrm {GL}}_n)$
that arises from an aperiodic oriented BD pair
$D(\operatorname {\mathrm {GL}}_n)$
that arises from an aperiodic oriented BD pair
![]() $\mathbf {\Gamma }$
. Then the ring of regular functions on
$\mathbf {\Gamma }$
. Then the ring of regular functions on
![]() $D(\operatorname {\mathrm {GL}}_n)$
is naturally isomorphic to the the upper cluster algebra of
$D(\operatorname {\mathrm {GL}}_n)$
is naturally isomorphic to the the upper cluster algebra of
![]() $\mathcal {GC}(\mathbf {\Gamma })$
.
$\mathcal {GC}(\mathbf {\Gamma })$
.
Proof. The fact that
![]() $\mathcal {GC}(\mathbf {\Gamma })$
is a regular generalized cluster structure is the content of Section 4 and Section 5.5, hence we only need to verify the third condition of Proposition 2.2. The proof is based on an inductive argument on the size
$\mathcal {GC}(\mathbf {\Gamma })$
is a regular generalized cluster structure is the content of Section 4 and Section 5.5, hence we only need to verify the third condition of Proposition 2.2. The proof is based on an inductive argument on the size
![]() $|\Gamma _1^r| + |\Gamma _1^c|$
. The base of induction is
$|\Gamma _1^r| + |\Gamma _1^c|$
. The base of induction is
![]() ${|\Gamma _1^c| + |\Gamma _1^r| = 1}$
, which is the content of Proposition 5.14 and Proposition 5.17, and the inductive step is based on Corollary 5.3.2 and the existence of at least two distinct birational quasi-isomorphisms. The proof can be executed verbatim as in [Reference Gekhtman, Shapiro and Vainshtein20].
${|\Gamma _1^c| + |\Gamma _1^r| = 1}$
, which is the content of Proposition 5.14 and Proposition 5.17, and the inductive step is based on Corollary 5.3.2 and the existence of at least two distinct birational quasi-isomorphisms. The proof can be executed verbatim as in [Reference Gekhtman, Shapiro and Vainshtein20].
6 Toric action
Let
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be an aperiodic oriented BD pair that induces the generalized cluster structure
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be an aperiodic oriented BD pair that induces the generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma })$
on
$\mathcal {GC}(\mathbf {\Gamma })$
on
![]() $D(\operatorname {\mathrm {GL}}_n)$
. Let
$D(\operatorname {\mathrm {GL}}_n)$
. Let
![]() $\mathfrak {h}^{\operatorname {\mathrm {sl}}_n}$
be the Cartan subalgebra of
$\mathfrak {h}^{\operatorname {\mathrm {sl}}_n}$
be the Cartan subalgebra of
![]() $\operatorname {\mathrm {sl}}_n$
. In Section 3.7, we defined subalgebras
$\operatorname {\mathrm {sl}}_n$
. In Section 3.7, we defined subalgebras
and we let
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
and
$\mathcal {H}_{\mathbf {\Gamma }^r}$
and
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
be the connected subgroups of
$\mathcal {H}_{\mathbf {\Gamma }^c}$
be the connected subgroups of
![]() $\operatorname {\mathrm {SL}}_n$
that correspond to
$\operatorname {\mathrm {SL}}_n$
that correspond to
![]() $\mathfrak {h}_{\mathbf {\Gamma }^r}$
and
$\mathfrak {h}_{\mathbf {\Gamma }^r}$
and
![]() $\mathfrak {h}_{\mathbf {\Gamma }^c}$
, respectively. Then we let the groups
$\mathfrak {h}_{\mathbf {\Gamma }^c}$
, respectively. Then we let the groups
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
and
$\mathcal {H}_{\mathbf {\Gamma }^r}$
and
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
act upon
$\mathcal {H}_{\mathbf {\Gamma }^c}$
act upon
![]() $D(\operatorname {\mathrm {GL}}_n)$
on the left and on the right, respectively, and we also defined an action by scalar matrices on each component of
$D(\operatorname {\mathrm {GL}}_n)$
on the left and on the right, respectively, and we also defined an action by scalar matrices on each component of
![]() $D(\operatorname {\mathrm {GL}}_n) = \operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
. Note that
$D(\operatorname {\mathrm {GL}}_n) = \operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
. Note that
![]() $\dim \mathcal {H}_{\mathbf {\Gamma }^r} = k_{\mathbf {\Gamma }^r}:=|\Pi \setminus \Gamma _1^r|$
and
$\dim \mathcal {H}_{\mathbf {\Gamma }^r} = k_{\mathbf {\Gamma }^r}:=|\Pi \setminus \Gamma _1^r|$
and
![]() $\dim \mathcal {H}_{\mathbf {\Gamma }^c} = k_{\mathbf {\Gamma }^c}:=|\Pi \setminus \Gamma _1^c|$
, where
$\dim \mathcal {H}_{\mathbf {\Gamma }^c} = k_{\mathbf {\Gamma }^c}:=|\Pi \setminus \Gamma _1^c|$
, where
![]() $\Pi = [1,n-1]$
is the set of simple roots of type
$\Pi = [1,n-1]$
is the set of simple roots of type
![]() $A_n$
. In this section, we show that the cumulative action of the three groups induces a global toric action on
$A_n$
. In this section, we show that the cumulative action of the three groups induces a global toric action on
![]() $\mathcal {GC}(\mathbf {\Gamma })$
of rank
$\mathcal {GC}(\mathbf {\Gamma })$
of rank
![]() $k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c}+2$
.
$k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c}+2$
.
Lemma 6.1. All cluster and frozen variables from the initial extended cluster are semi-invariant with respect to the left action by
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
, the right action by
$\mathcal {H}_{\mathbf {\Gamma }^r}$
, the right action by
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
, and the action by scalar matrices.
$\mathcal {H}_{\mathbf {\Gamma }^c}$
, and the action by scalar matrices.
Proof. The
![]() $\varphi $
-, f- and c-functions are semi-invariant with respect to the left action
$\varphi $
-, f- and c-functions are semi-invariant with respect to the left action
![]() $T.(X,Y) = (TX,TY)$
and the right action
$T.(X,Y) = (TX,TY)$
and the right action
![]() $(X,Y).T = (XT,YT)$
, where T is any invertible diagonal matrix (see Theorem 6.1 in [Reference Gekhtman, Shapiro and Vainshtein18]). The g- and f-functions are semi-invariant with respect to the actions by
$(X,Y).T = (XT,YT)$
, where T is any invertible diagonal matrix (see Theorem 6.1 in [Reference Gekhtman, Shapiro and Vainshtein18]). The g- and f-functions are semi-invariant with respect to the actions by
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
and
$\mathcal {H}_{\mathbf {\Gamma }^r}$
and
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
by Lemma 6.2 from [Reference Gekhtman, Shapiro and Vainshtein20]. Their semi-invariance relative the action
$\mathcal {H}_{\mathbf {\Gamma }^c}$
by Lemma 6.2 from [Reference Gekhtman, Shapiro and Vainshtein20]. Their semi-invariance relative the action
![]() $(a,b).(X,Y) = (aX,bY)$
,
$(a,b).(X,Y) = (aX,bY)$
,
![]() $a,b \in \mathbb {C}^*$
, follows from its infinitesimal counterpart (3.15).
$a,b \in \mathbb {C}^*$
, follows from its infinitesimal counterpart (3.15).
How the toric action is induced
If
![]() $H \in \mathcal {H}_{\mathbf {\Gamma }^r}$
and
$H \in \mathcal {H}_{\mathbf {\Gamma }^r}$
and
![]() $\psi $
is any cluster or stable variable, then
$\psi $
is any cluster or stable variable, then
![]() $\psi (HX,HY) = \chi (H) \psi (X,Y)$
for some character
$\psi (HX,HY) = \chi (H) \psi (X,Y)$
for some character
![]() $\chi $
on
$\chi $
on
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
that depends on
$\mathcal {H}_{\mathbf {\Gamma }^r}$
that depends on
![]() $\psi $
. The character is a monomial in
$\psi $
. The character is a monomial in
![]() $k_{\mathbf {\Gamma }^r}$
independent parameters that describe the group
$k_{\mathbf {\Gamma }^r}$
independent parameters that describe the group
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
, and the exponents of the parameters become the weight vector assigned to
$\mathcal {H}_{\mathbf {\Gamma }^r}$
, and the exponents of the parameters become the weight vector assigned to
![]() $\psi $
. Thus, one induces a local toric action from the left-right action of
$\psi $
. Thus, one induces a local toric action from the left-right action of
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}\times \mathcal {H}_{\mathbf {\Gamma }^c}$
and the action by scalar matrices.
$\mathcal {H}_{\mathbf {\Gamma }^r}\times \mathcal {H}_{\mathbf {\Gamma }^c}$
and the action by scalar matrices.
Proposition 6.2. The toric action induced by the left action of
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
, the right action of
$\mathcal {H}_{\mathbf {\Gamma }^r}$
, the right action of
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
and the action by scalar matrices is
$\mathcal {H}_{\mathbf {\Gamma }^c}$
and the action by scalar matrices is
![]() $\mathcal {GC}$
-extendable.
$\mathcal {GC}$
-extendable.
Proof. Let
![]() $\tilde {B}$
be the initial extended exchange matrix and W be the weight matrix of the resulting toric action. The fact that W has the full rank can be proved in exactly the same way as in [Reference Gekhtman, Shapiro and Vainshtein20] using the fact that the upper cluster algebra can be identified with the ring of regular functions on
$\tilde {B}$
be the initial extended exchange matrix and W be the weight matrix of the resulting toric action. The fact that W has the full rank can be proved in exactly the same way as in [Reference Gekhtman, Shapiro and Vainshtein20] using the fact that the upper cluster algebra can be identified with the ring of regular functions on
![]() $D(\operatorname {\mathrm {GL}}_n)$
(which is proved in Section 5): If we assume that
$D(\operatorname {\mathrm {GL}}_n)$
(which is proved in Section 5): If we assume that
![]() $\operatorname {\mathrm {rank}} W < k_{\mathbf {\Gamma }^r} + k_{\mathbf {\Gamma }^c}+2$
, then one can construct a toric action of rank
$\operatorname {\mathrm {rank}} W < k_{\mathbf {\Gamma }^r} + k_{\mathbf {\Gamma }^c}+2$
, then one can construct a toric action of rank
![]() $1$
from the given action that leaves all cluster and stable variables invariant, but any
$1$
from the given action that leaves all cluster and stable variables invariant, but any
![]() $x_{ij}$
and
$x_{ij}$
and
![]() $y_{ij}$
is a Laurent polynomial in the initial cluster and stable variables, and the constructed action does not fix them, which leads to a contradiction. Thus,
$y_{ij}$
is a Laurent polynomial in the initial cluster and stable variables, and the constructed action does not fix them, which leads to a contradiction. Thus,
![]() $\operatorname {\mathrm {rank}} W = k_{\mathbf {\Gamma }^r} + k_{\mathbf {\Gamma }^c}+2$
.
$\operatorname {\mathrm {rank}} W = k_{\mathbf {\Gamma }^r} + k_{\mathbf {\Gamma }^c}+2$
.
Now, let us show that
![]() $\tilde {B}W = 0$
. This reduces to showing that if
$\tilde {B}W = 0$
. This reduces to showing that if
![]() $\psi (X,Y) \psi ^{\prime }(X,Y) = M(X,Y)$
is an exchange relation in the initial cluster, then
$\psi (X,Y) \psi ^{\prime }(X,Y) = M(X,Y)$
is an exchange relation in the initial cluster, then
![]() $M(X,Y)$
is a semi-invariant of the three actions. For the exchange relations for g- and h- functions (except
$M(X,Y)$
is a semi-invariant of the three actions. For the exchange relations for g- and h- functions (except
![]() $h_{ii}$
and
$h_{ii}$
and
![]() $g_{ii}$
,
$g_{ii}$
,
![]() $2 \leq i \leq n$
), the latter was already shown in [Reference Gekhtman, Shapiro and Vainshtein20]. For
$2 \leq i \leq n$
), the latter was already shown in [Reference Gekhtman, Shapiro and Vainshtein20]. For
![]() $\varphi $
- and f-functions, the statement was verified in [Reference Gekhtman, Shapiro and Vainshtein18]. Therefore, we need to check that
$\varphi $
- and f-functions, the statement was verified in [Reference Gekhtman, Shapiro and Vainshtein18]. Therefore, we need to check that
![]() $\tilde {B}W = 0$
holds for
$\tilde {B}W = 0$
holds for
![]() $h_{ii}$
and
$h_{ii}$
and
![]() $g_{ii}$
when
$g_{ii}$
when
![]() $2 \leq i \leq n$
(i.e., for the rows of
$2 \leq i \leq n$
(i.e., for the rows of
![]() $\tilde {B}$
that correspond to these functions).
$\tilde {B}$
that correspond to these functions).
The mutation at
![]() $h_{ii}$
reads
$h_{ii}$
reads
Set
![]() $H := \operatorname {\mathrm {diag}}(t_1,\ldots ,t_n) \in \mathcal {H}_{\mathbf {\Gamma }^r}$
and
$H := \operatorname {\mathrm {diag}}(t_1,\ldots ,t_n) \in \mathcal {H}_{\mathbf {\Gamma }^r}$
and
![]() $M(X,Y)$
the RHS of the above mutation relation, and let us act by H on
$M(X,Y)$
the RHS of the above mutation relation, and let us act by H on
![]() $M(X,Y)$
. If we set
$M(X,Y)$
. If we set
![]() $h_{i,i+1}(HX,HY) = \alpha h_{i,i+1}(X,Y)$
, where
$h_{i,i+1}(HX,HY) = \alpha h_{i,i+1}(X,Y)$
, where
![]() $\alpha = \alpha (t_1,\ldots ,t_n)$
, then
$\alpha = \alpha (t_1,\ldots ,t_n)$
, then
![]() $h_{i-1,i}(HX,HY) = t_{i-1}\alpha h_{i-1,i}(X,Y)$
; similarly, if we write
$h_{i-1,i}(HX,HY) = t_{i-1}\alpha h_{i-1,i}(X,Y)$
; similarly, if we write
![]() $f_{1,n-i}(HX,HY) = \beta f_{1,n-i}(X,Y)$
, then
$f_{1,n-i}(HX,HY) = \beta f_{1,n-i}(X,Y)$
, then
![]() $f_{1,n-i+1}(HX,HY) = t_{i-1} \beta f_{1,n-i+1}(X,Y)$
. Overall,
$f_{1,n-i+1}(HX,HY) = t_{i-1} \beta f_{1,n-i+1}(X,Y)$
. Overall,
that is, it’s a semi-invariant of
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
.
$\mathcal {H}_{\mathbf {\Gamma }^r}$
.
Next, the mutation at
![]() $g_{ii}$
is
$g_{ii}$
is
Let
![]() $M(X,Y)$
be the RHS of the latter mutation relation, and let us act by the same H on
$M(X,Y)$
be the RHS of the latter mutation relation, and let us act by the same H on
![]() $M(X,Y)$
. If we write
$M(X,Y)$
. If we write
![]() $g_{i+1,i+1}(HX,HY) = \alpha g_{i+1,i+1}(X,Y)$
, where now we have some different
$g_{i+1,i+1}(HX,HY) = \alpha g_{i+1,i+1}(X,Y)$
, where now we have some different
![]() $\alpha = \alpha (t_1,\ldots ,t_n)$
, then
$\alpha = \alpha (t_1,\ldots ,t_n)$
, then
![]() $g_{i-1,i-1}(HX,HY) = t_{i-1} t_i \alpha g_{i-1,i-1}(X,Y)$
; next, if we write
$g_{i-1,i-1}(HX,HY) = t_{i-1} t_i \alpha g_{i-1,i-1}(X,Y)$
; next, if we write
![]() $f_{n-i,1}(HX,HY) = \beta f_{n-i,1}(X,Y)$
, then
$f_{n-i,1}(HX,HY) = \beta f_{n-i,1}(X,Y)$
, then
![]() $f_{n-i+1,1}(HX,HY) = t_{i-1} \beta f_{n-i+1,1}(X,Y)$
; and lastly, if
$f_{n-i+1,1}(HX,HY) = t_{i-1} \beta f_{n-i+1,1}(X,Y)$
; and lastly, if
![]() $g_{i+1,i}(HX,HY) = \gamma g_{i+1,i}(X,Y)$
, then
$g_{i+1,i}(HX,HY) = \gamma g_{i+1,i}(X,Y)$
, then
![]() $g_{i,i-1}(HX,HY) = t_{i} \gamma g_{i,i-1}(X,Y)$
. Overall, the action by H on
$g_{i,i-1}(HX,HY) = t_{i} \gamma g_{i,i-1}(X,Y)$
. Overall, the action by H on
![]() $M(X,Y)$
yields
$M(X,Y)$
yields
Reasoning along the same lines, one can prove that the RHS of the above mutation relations are also semi-invariant with respect to the right action by
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
and the action by scalar matrices. Lastly, the Casimirs
$\mathcal {H}_{\mathbf {\Gamma }^c}$
and the action by scalar matrices. Lastly, the Casimirs
![]() $\hat {p}_{1r}$
from the statement of Proposition 2.4 are given by
$\hat {p}_{1r}$
from the statement of Proposition 2.4 are given by
![]() $\hat {p}_{1r} = c_{r}^n g_{11}^{r-n} h_{11}^{-r}$
,
$\hat {p}_{1r} = c_{r}^n g_{11}^{r-n} h_{11}^{-r}$
,
![]() $1\leq r \leq n-1$
. Their invariance was shown in [Reference Gekhtman, Shapiro and Vainshtein18]. Thus, the toric action is
$1\leq r \leq n-1$
. Their invariance was shown in [Reference Gekhtman, Shapiro and Vainshtein18]. Thus, the toric action is
![]() $\mathcal {GC}$
-extendable.
$\mathcal {GC}$
-extendable.
7 Log-canonicity in the initial cluster
The objective of this section is to prove that the brackets between all functions in the initial extended cluster are log-canonical. It was proved in [Reference Gekhtman, Shapiro and Vainshtein20] that the brackets between g- and h-functions are such, so the rest is to show that f- and
![]() $\varphi $
-functions are log-canonical between themselves and each other, as well as log-canonical with g- and h-functions. The former is straightforward.
$\varphi $
-functions are log-canonical between themselves and each other, as well as log-canonical with g- and h-functions. The former is straightforward.
Proposition 7.1. The f- and
![]() $\varphi $
-functions are log-canonical between themselves and each other.
$\varphi $
-functions are log-canonical between themselves and each other.
Proof. Notice that if a function
![]() $\phi $
satisfies
$\phi $
satisfies
![]() $\pi _0 E_R \phi \in \mathfrak {b}_+$
and
$\pi _0 E_R \phi \in \mathfrak {b}_+$
and
![]() $\pi _0 E_L \phi \in \mathfrak {b}_-$
, and if
$\pi _0 E_L \phi \in \mathfrak {b}_-$
, and if
![]() $\pi _0 E_R \log \phi = \text {const}$
and
$\pi _0 E_R \log \phi = \text {const}$
and
![]() $\pi _0 E_L \log \phi = \text {const}$
, then the first two terms of the bracket of two such functions are constant:
$\pi _0 E_L \log \phi = \text {const}$
, then the first two terms of the bracket of two such functions are constant:
 $$\begin{align*}\begin{aligned} &\langle R_+^c(E_L \log \phi_1), E_L \log \phi_2\rangle = \langle R_0^c\pi_0(E_L \log \phi_1), \pi_0 E_L\log \phi_2 \rangle = \text{const};\\ &-\langle R_+^r(E_R \log \phi_1), E_R \log \phi_2 \rangle = - \langle R_0^r\pi_0 (E_R \log \phi_1), E_R \log \phi_2 \rangle = \text{const}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\langle R_+^c(E_L \log \phi_1), E_L \log \phi_2\rangle = \langle R_0^c\pi_0(E_L \log \phi_1), \pi_0 E_L\log \phi_2 \rangle = \text{const};\\ &-\langle R_+^r(E_R \log \phi_1), E_R \log \phi_2 \rangle = - \langle R_0^r\pi_0 (E_R \log \phi_1), E_R \log \phi_2 \rangle = \text{const}. \end{aligned} \end{align*}$$
This means that the difference between
![]() $\{\log \phi _1, \log \phi _2 \}$
and
$\{\log \phi _1, \log \phi _2 \}$
and
![]() $\{\log \phi _1, \log \phi _2 \}_{\text {std}}$
(the standard bracket studied in [Reference Gekhtman, Shapiro and Vainshtein18]) is constant. Since f- and
$\{\log \phi _1, \log \phi _2 \}_{\text {std}}$
(the standard bracket studied in [Reference Gekhtman, Shapiro and Vainshtein18]) is constant. Since f- and
![]() $\varphi $
-functions enjoy such properties, they are log-canonical between themselves and each other.
$\varphi $
-functions enjoy such properties, they are log-canonical between themselves and each other.
Before we proceed to proving the log-canonicity for the remaining pairs, let us derive a preliminary formula, which is also needed in Section 8:
Lemma 7.2. Let
![]() $\phi $
be any f- or
$\phi $
be any f- or
![]() $\varphi $
-function, and let
$\varphi $
-function, and let
![]() $\psi $
be any g- or h-function. Then the following formula holds:
$\psi $
be any g- or h-function. Then the following formula holds:
Proof. If
![]() $\phi $
is either a
$\phi $
is either a
![]() $\varphi $
- or f-function, then
$\varphi $
- or f-function, then
![]() $\pi _0 E_R \phi \in \mathfrak {b}_+$
and
$\pi _0 E_R \phi \in \mathfrak {b}_+$
and
![]() $\pi _0 E_L \phi \in \mathfrak {b}_-$
. Let’s use the following form of the bracket:
$\pi _0 E_L \phi \in \mathfrak {b}_-$
. Let’s use the following form of the bracket:
Recall that
![]() $E_L \psi = \xi _L \psi + (1-\gamma _c) (\nabla _X \psi X)$
, where
$E_L \psi = \xi _L \psi + (1-\gamma _c) (\nabla _X \psi X)$
, where
![]() $\pi _0\xi _L \psi \in \mathfrak {b}_-$
; with that in mind, rewrite the first term as
$\pi _0\xi _L \psi \in \mathfrak {b}_-$
; with that in mind, rewrite the first term as
 $$\begin{align*}\begin{aligned} \langle R_+^c(E_L \phi), E_L \psi\rangle &= -\langle \frac{\gamma_c^*}{1-\gamma_c^*} \pi_{<} E_L\phi, E_L\psi\rangle + \langle R_0^c \pi_0 E_L\phi, E_L\psi \rangle \\ & = -\langle \pi_{<} E_L\phi, \gamma_c(\nabla_X\psi X) \rangle +\langle R_0^c \pi_0 E_L\phi, E_L\psi \rangle\\ &= \langle \pi_{<} E_L\phi, \nabla_Y \psi Y\rangle + \langle R_0^c \pi_0 E_L\phi, E_L\psi \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \langle R_+^c(E_L \phi), E_L \psi\rangle &= -\langle \frac{\gamma_c^*}{1-\gamma_c^*} \pi_{<} E_L\phi, E_L\psi\rangle + \langle R_0^c \pi_0 E_L\phi, E_L\psi \rangle \\ & = -\langle \pi_{<} E_L\phi, \gamma_c(\nabla_X\psi X) \rangle +\langle R_0^c \pi_0 E_L\phi, E_L\psi \rangle\\ &= \langle \pi_{<} E_L\phi, \nabla_Y \psi Y\rangle + \langle R_0^c \pi_0 E_L\phi, E_L\psi \rangle. \end{aligned} \end{align*}$$
Similarly, applying
![]() $E_R \psi = \xi _R \psi + (1-\gamma _r^*) (Y\nabla _Y \psi )$
, we can rewrite the second term of the bracket as
$E_R \psi = \xi _R \psi + (1-\gamma _r^*) (Y\nabla _Y \psi )$
, we can rewrite the second term of the bracket as
Combining all together, the result follows.
Proposition 7.3. All f- and
![]() $\varphi $
-functions are log-canonical with all g- and h-functions.
$\varphi $
-functions are log-canonical with all g- and h-functions.
Proof. Let
![]() $\phi $
be any f- or
$\phi $
be any f- or
![]() $\varphi $
-function, and let
$\varphi $
-function, and let
![]() $\psi $
be any g- or h-function. Only for this proof, call two rational functions log-equivalent (
$\psi $
be any g- or h-function. Only for this proof, call two rational functions log-equivalent (
![]() $\overset {\log }{\sim }$
) if their difference is a multiple of
$\overset {\log }{\sim }$
) if their difference is a multiple of
![]() $\phi \psi $
. Therefore, we aim at proving that
$\phi \psi $
. Therefore, we aim at proving that
![]() $\{\phi ,\psi \} \overset {\log }{\sim } 0$
. Let us pick a pair of solutions
$\{\phi ,\psi \} \overset {\log }{\sim } 0$
. Let us pick a pair of solutions
![]() $(R_0^r,R_0^c)$
of the system (2.8) and (2.9) with the properties (3.6) (as a reminder, in Section 8.2 we show that log-canonicity doesn’t depend on the choice of
$(R_0^r,R_0^c)$
of the system (2.8) and (2.9) with the properties (3.6) (as a reminder, in Section 8.2 we show that log-canonicity doesn’t depend on the choice of
![]() $R_0$
).
$R_0$
).
Recall from [Reference Gekhtman, Shapiro and Vainshtein20] or from Section 3.3 that all the following quantities
are multiples of
![]() $\psi $
. Also, recall from [Reference Gekhtman, Shapiro and Vainshtein18] or from Section 3.3 that
$\psi $
. Also, recall from [Reference Gekhtman, Shapiro and Vainshtein18] or from Section 3.3 that
![]() $\pi _0 E_R \phi $
and
$\pi _0 E_R \phi $
and
![]() $\pi _0 E_L \phi $
are multiples of
$\pi _0 E_L \phi $
are multiples of
![]() $\phi $
. Therefore, rewriting
$\phi $
. Therefore, rewriting
![]() $E_L \psi $
as
$E_L \psi $
as
![]() $E_L \psi = \eta _L \psi + (1-\gamma _c^*)(\nabla _Y \psi Y)$
and using
$E_L \psi = \eta _L \psi + (1-\gamma _c^*)(\nabla _Y \psi Y)$
and using
![]() $(R_0^c)^*(1-\gamma _c^*) = \pi _{\Gamma _2^c} + (R_0^c)^* \pi _{\hat {\Gamma }_2^c}$
, we see that
$(R_0^c)^*(1-\gamma _c^*) = \pi _{\Gamma _2^c} + (R_0^c)^* \pi _{\hat {\Gamma }_2^c}$
, we see that
 $$\begin{align*}\begin{aligned} \langle R_0^c \pi_0 E_L \phi, E_L\psi \rangle &= \overbrace{\langle R_0^c \pi_0 E_L \phi, \eta_L \psi \rangle}^{\overset{\log}{\sim} 0} + \langle \pi_0 E_L\phi, \pi_0(R_0^c)^*(1-\gamma_c^*)(\nabla_Y\psi Y)\rangle \overset{\log}{\sim}\\&\overset{\log}{\sim} \langle \pi_0 E_L\phi, \pi_{\Gamma_2^c} \nabla_Y\psi Y \rangle + \overbrace{\langle R_0^c \pi_0 E_L \phi, \pi_{\hat{\Gamma}_2^c} \nabla_Y \psi Y \rangle}^{\overset{\log}{\sim} 0} \overset{\log}{\sim} \langle \pi_0 E_L \phi, \pi_{\Gamma_2^c} \nabla_Y \psi Y \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \langle R_0^c \pi_0 E_L \phi, E_L\psi \rangle &= \overbrace{\langle R_0^c \pi_0 E_L \phi, \eta_L \psi \rangle}^{\overset{\log}{\sim} 0} + \langle \pi_0 E_L\phi, \pi_0(R_0^c)^*(1-\gamma_c^*)(\nabla_Y\psi Y)\rangle \overset{\log}{\sim}\\&\overset{\log}{\sim} \langle \pi_0 E_L\phi, \pi_{\Gamma_2^c} \nabla_Y\psi Y \rangle + \overbrace{\langle R_0^c \pi_0 E_L \phi, \pi_{\hat{\Gamma}_2^c} \nabla_Y \psi Y \rangle}^{\overset{\log}{\sim} 0} \overset{\log}{\sim} \langle \pi_0 E_L \phi, \pi_{\Gamma_2^c} \nabla_Y \psi Y \rangle. \end{aligned} \end{align*}$$
Similarly, rewriting
![]() $E_R\psi = \xi _R + (1-\gamma _r^*) Y\nabla _Y \psi $
and using
$E_R\psi = \xi _R + (1-\gamma _r^*) Y\nabla _Y \psi $
and using
![]() $(R_0^r)^*(1-\gamma _r^*) = \pi _{\Gamma _2^r} + (R_0^r)^* \pi _{\hat {\Gamma }_2^r}$
, we arrive at
$(R_0^r)^*(1-\gamma _r^*) = \pi _{\Gamma _2^r} + (R_0^r)^* \pi _{\hat {\Gamma }_2^r}$
, we arrive at
Now, combining these together with formula (7.1), we see that
 $$\begin{align*}\begin{aligned} \{\phi, \psi\} &\overset{\log}{\sim} -\langle \pi_0 E_L \phi, \nabla_Y \psi Y\rangle + \langle \pi_0 E_R \phi, Y\nabla_Y \psi \rangle + \langle \pi_0 E_L \phi, \pi_{\Gamma_2^c} \nabla_Y \psi Y \rangle - \langle \pi_0 E_R \phi, \pi_{\Gamma_2^r} Y\nabla_Y \psi \rangle \overset{\log}{\sim} \\ & \overset{\log}{\sim} -\langle \pi_0 E_L\phi, \pi_{\hat{\Gamma}_2^c} \nabla_Y \psi Y\rangle - \langle \pi_0 E_R\phi, \pi_{\hat{\Gamma}_2^r} Y\nabla_Y \psi \rangle \overset{\log}{\sim} 0. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{\phi, \psi\} &\overset{\log}{\sim} -\langle \pi_0 E_L \phi, \nabla_Y \psi Y\rangle + \langle \pi_0 E_R \phi, Y\nabla_Y \psi \rangle + \langle \pi_0 E_L \phi, \pi_{\Gamma_2^c} \nabla_Y \psi Y \rangle - \langle \pi_0 E_R \phi, \pi_{\Gamma_2^r} Y\nabla_Y \psi \rangle \overset{\log}{\sim} \\ & \overset{\log}{\sim} -\langle \pi_0 E_L\phi, \pi_{\hat{\Gamma}_2^c} \nabla_Y \psi Y\rangle - \langle \pi_0 E_R\phi, \pi_{\hat{\Gamma}_2^r} Y\nabla_Y \psi \rangle \overset{\log}{\sim} 0. \end{aligned} \end{align*}$$
Thus, the result follows.
8 Compatibility
The objective of this section is to prove Condition ii of Proposition 2.3. The matrix
![]() $\Delta $
from the proposition is the identity matrix; therefore, we show that
$\Delta $
from the proposition is the identity matrix; therefore, we show that
![]() $\{\log y_{i}, \log x_j\} = \delta _{ij}$
, where
$\{\log y_{i}, \log x_j\} = \delta _{ij}$
, where
![]() $y_i$
is the y-coordinate of a cluster variable
$y_i$
is the y-coordinate of a cluster variable
![]() $x_i$
. Together with the results from Section 7, we will conclude, in particular, that any extended cluster in
$x_i$
. Together with the results from Section 7, we will conclude, in particular, that any extended cluster in
![]() $\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is log-canonical with respect to the Poisson bracket. If
$\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is log-canonical with respect to the Poisson bracket. If
![]() $\psi _1$
is any cluster g- or h-function that is not equal to
$\psi _1$
is any cluster g- or h-function that is not equal to
![]() $g_{ii}$
or
$g_{ii}$
or
![]() $h_{ii}$
,
$h_{ii}$
,
![]() $1 \leq i \leq n$
, and
$1 \leq i \leq n$
, and
![]() $\psi _2$
is any g- or h-function, then it was shown in [Reference Gekhtman, Shapiro and Vainshtein20] that
$\psi _2$
is any g- or h-function, then it was shown in [Reference Gekhtman, Shapiro and Vainshtein20] that
 $$\begin{align*}\{\log y(\psi_1), \log \psi_2\} = \begin{cases} 1, \ &\psi_1 = \psi_2\\ 0, \ &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\{\log y(\psi_1), \log \psi_2\} = \begin{cases} 1, \ &\psi_1 = \psi_2\\ 0, \ &\text{otherwise.} \end{cases} \end{align*}$$
In this section, we treat all the other pairs of functions from the initial cluster.
8.1 Diagonal derivatives
In this subsection, we state technical formulas that compare the diagonal derivatives of the variables that are adjacent in the quiver. We remind the reader that when the indices are seemingly out of range, the conventions (3.2)–(3.4) are in place.
Case of f- and
 $\varphi $
-functions.
$\varphi $
-functions.
Set
![]() $\Delta (i,j) := \sum _{k=i}^{j} e_{kk}.$
The following formulas are drawn from the text of [Reference Gekhtman, Shapiro and Vainshtein18, p. 25]: for
$\Delta (i,j) := \sum _{k=i}^{j} e_{kk}.$
The following formulas are drawn from the text of [Reference Gekhtman, Shapiro and Vainshtein18, p. 25]: for
![]() $k,l\geq 0$
,
$k,l\geq 0$
,
![]() $1 \leq k+l\leq n$
,
$1 \leq k+l\leq n$
,
for
![]() $k,l \geq 1, \ k+l \leq n$
,
$k,l \geq 1, \ k+l \leq n$
,
 $$ \begin{align}\begin{aligned} \pi_0 E_L \log \varphi_{kl} &= (n-k-l)(I+\Delta(n,n))+ \Delta(n-k+1,n) + \Delta(n-l+1,n), \\ \pi_0 E_R \log\varphi_{kl} &= (n-k-l+1)I. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \pi_0 E_L \log \varphi_{kl} &= (n-k-l)(I+\Delta(n,n))+ \Delta(n-k+1,n) + \Delta(n-l+1,n), \\ \pi_0 E_R \log\varphi_{kl} &= (n-k-l+1)I. \end{aligned} \end{align} $$
Let
![]() $y(f_{kl})$
and
$y(f_{kl})$
and
![]() $y(\varphi _{kl})$
be y-coordinates. Examining the neighborhoods of
$y(\varphi _{kl})$
be y-coordinates. Examining the neighborhoods of
![]() $\varphi $
- and f-functions and applying the above formulas yield
$\varphi $
- and f-functions and applying the above formulas yield
 $$ \begin{align}\begin{aligned} &\pi_0 E_L y(f_{kl}) = \pi_0 E_R y(f_{kl}) = 0, \ \ k,l\geq 1, \ \ k+l \leq n-1;\\ &\pi_0 E_L y(\varphi_{kl}) = \pi_0 E_R y(\varphi_{kl}) = 0, \ \ k,l \geq 1, \ \ k+l \leq n. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} &\pi_0 E_L y(f_{kl}) = \pi_0 E_R y(f_{kl}) = 0, \ \ k,l\geq 1, \ \ k+l \leq n-1;\\ &\pi_0 E_L y(\varphi_{kl}) = \pi_0 E_R y(\varphi_{kl}) = 0, \ \ k,l \geq 1, \ \ k+l \leq n. \end{aligned} \end{align} $$
Case of g- and h-functions.
For
![]() $1 \leq i \leq j \leq n$
, let us denote
$1 \leq i \leq j \leq n$
, let us denote
 $$ \begin{align}\begin{aligned} g&:= \log g_{ij} - \log g_{i+1,j+1},\\ h&:= \log h_{ji} - \log h_{j+1,i+1}. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} g&:= \log g_{ij} - \log g_{i+1,j+1},\\ h&:= \log h_{ji} - \log h_{j+1,i+1}. \end{aligned} \end{align} $$
Then g satisfies the following list of formulas:
 $$ \begin{align} \begin{aligned} \pi_0 \xi_L g &= \gamma_c(e_{jj}), & \pi_0 \xi_R g &= e_{ii}, \\ \pi_0 \eta_L g &= e_{jj}, & \pi_0 \eta_R g &= \gamma_r(e_{ii}); \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \pi_0 \xi_L g &= \gamma_c(e_{jj}), & \pi_0 \xi_R g &= e_{ii}, \\ \pi_0 \eta_L g &= e_{jj}, & \pi_0 \eta_R g &= \gamma_r(e_{ii}); \end{aligned} \end{align} $$
 $$ \begin{align} \begin{aligned} \pi_0\pi_{\hat{\Gamma}_2^c} (\nabla_Y g \cdot Y) &= 0, & \pi_0 \pi_{\hat{\Gamma}_1^r} (X\nabla_X g) &= \pi_{\hat{\Gamma}_1^r} e_{ii},\\ \pi_0 \pi_{\hat{\Gamma}_1^c}(\nabla_X g \cdot X) &= \pi_{\hat{\Gamma}_1^c} (e_{jj}), & \pi_0 \pi_{\hat{\Gamma}_2^r}(Y\nabla_Y g) & = 0 \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \pi_0\pi_{\hat{\Gamma}_2^c} (\nabla_Y g \cdot Y) &= 0, & \pi_0 \pi_{\hat{\Gamma}_1^r} (X\nabla_X g) &= \pi_{\hat{\Gamma}_1^r} e_{ii},\\ \pi_0 \pi_{\hat{\Gamma}_1^c}(\nabla_X g \cdot X) &= \pi_{\hat{\Gamma}_1^c} (e_{jj}), & \pi_0 \pi_{\hat{\Gamma}_2^r}(Y\nabla_Y g) & = 0 \end{aligned} \end{align} $$
and for any runs
![]() $\Delta ^r$
,
$\Delta ^r$
,
![]() $\Delta ^c$
,
$\Delta ^c$
,
![]() $\bar {\Delta }^r$
and
$\bar {\Delta }^r$
and
![]() $\bar {\Delta }^c$
,
$\bar {\Delta }^c$
,
 $$ \begin{align} \begin{aligned} \operatorname{\mathrm{tr}}(\nabla_X g X)_{\Delta^c}^{\Delta^c} &= 1_{\Delta^c}(j), & \operatorname{\mathrm{tr}}(X\nabla_X g)_{\Delta^r}^{\Delta^r} &= 1_{\Delta^r}(i),\\ \operatorname{\mathrm{tr}} (\nabla_Y g Y)_{\bar{\Delta}^c}^{\bar{\Delta}^c} &= 0, & \operatorname{\mathrm{tr}} (Y\nabla_Y g)_{\bar{\Delta}^r}^{\bar{\Delta}^r} & = 0, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{\mathrm{tr}}(\nabla_X g X)_{\Delta^c}^{\Delta^c} &= 1_{\Delta^c}(j), & \operatorname{\mathrm{tr}}(X\nabla_X g)_{\Delta^r}^{\Delta^r} &= 1_{\Delta^r}(i),\\ \operatorname{\mathrm{tr}} (\nabla_Y g Y)_{\bar{\Delta}^c}^{\bar{\Delta}^c} &= 0, & \operatorname{\mathrm{tr}} (Y\nabla_Y g)_{\bar{\Delta}^r}^{\bar{\Delta}^r} & = 0, \end{aligned} \end{align} $$
where
![]() $1_{\Delta ^c}$
and
$1_{\Delta ^c}$
and
![]() $1_{\Delta ^r}$
are indicators. Similarly, h satisfies the following list:
$1_{\Delta ^r}$
are indicators. Similarly, h satisfies the following list:
 $$ \begin{align} \begin{aligned} \pi_0 \xi_L h &= e_{ii}, & \pi_0 \xi_R h &= \gamma_r^*(e_{jj}), \\ \pi_0 \eta_L h &= \gamma_c^*(e_{ii}), & \pi_0 \eta_R h &= e_{jj}; \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \pi_0 \xi_L h &= e_{ii}, & \pi_0 \xi_R h &= \gamma_r^*(e_{jj}), \\ \pi_0 \eta_L h &= \gamma_c^*(e_{ii}), & \pi_0 \eta_R h &= e_{jj}; \end{aligned} \end{align} $$
 $$ \begin{align} \begin{aligned} \pi_0\pi_{\hat{\Gamma}_2^c} (\nabla_Y h \cdot Y) &= \pi_{\hat{\Gamma}_2^c}e_{ii}, & \pi_0 \pi_{\hat{\Gamma}_1^r} (X\nabla_X h) &= 0,\\ \pi_0 \pi_{\hat{\Gamma}_1^c}(\nabla_X h \cdot X) &=0, & \pi_0 \pi_{\hat{\Gamma}_2^r}(Y\nabla_Y h) & = \pi_{\hat{\Gamma}_2^r} e_{jj}; \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \pi_0\pi_{\hat{\Gamma}_2^c} (\nabla_Y h \cdot Y) &= \pi_{\hat{\Gamma}_2^c}e_{ii}, & \pi_0 \pi_{\hat{\Gamma}_1^r} (X\nabla_X h) &= 0,\\ \pi_0 \pi_{\hat{\Gamma}_1^c}(\nabla_X h \cdot X) &=0, & \pi_0 \pi_{\hat{\Gamma}_2^r}(Y\nabla_Y h) & = \pi_{\hat{\Gamma}_2^r} e_{jj}; \end{aligned} \end{align} $$
 $$ \begin{align} \begin{aligned} \operatorname{\mathrm{tr}}(\nabla_X h X)_{\Delta^c}^{\Delta^c} &= 0, & \operatorname{\mathrm{tr}}(X\nabla_X h)_{\Delta^r}^{\Delta^r} &= 0,\\ \operatorname{\mathrm{tr}} (\nabla_Y h Y)_{\bar{\Delta}^c}^{\bar{\Delta}^c} &= 1_{\bar{\Delta}^c}(i), & \operatorname{\mathrm{tr}} (Y\nabla_Y h)_{\bar{\Delta}^r}^{\bar{\Delta}^r} & = 1_{\bar{\Delta}^r}(j). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{\mathrm{tr}}(\nabla_X h X)_{\Delta^c}^{\Delta^c} &= 0, & \operatorname{\mathrm{tr}}(X\nabla_X h)_{\Delta^r}^{\Delta^r} &= 0,\\ \operatorname{\mathrm{tr}} (\nabla_Y h Y)_{\bar{\Delta}^c}^{\bar{\Delta}^c} &= 1_{\bar{\Delta}^c}(i), & \operatorname{\mathrm{tr}} (Y\nabla_Y h)_{\bar{\Delta}^r}^{\bar{\Delta}^r} & = 1_{\bar{\Delta}^r}(j). \end{aligned} \end{align} $$
The above formulas easily follow from a close inspection of the invariance properties from equation (3.11); the formulas for traces follow from the proof of Lemma 4.4 in [Reference Gekhtman, Shapiro and Vainshtein20]. As a corollary, if
![]() $D \in \{\xi _L,\xi _R, \eta _L, \eta _R\}$
, then
$D \in \{\xi _L,\xi _R, \eta _L, \eta _R\}$
, then
For
![]() $i=j$
, formula (8.11) is true only for
$i=j$
, formula (8.11) is true only for
![]() $D = \eta _L$
and
$D = \eta _L$
and
![]() $D=\xi _L$
. It follows from equation (8.7) that for any
$D=\xi _L$
. It follows from equation (8.7) that for any
![]() $1 \leq j \leq i \leq n$
,
$1 \leq j \leq i \leq n$
,
and for any
![]() $1 \leq j < i \leq n$
, it’s a consequence of equation (8.10) that
$1 \leq j < i \leq n$
, it’s a consequence of equation (8.10) that
8.2 Dependence on the choice of
 $R_0$
$R_0$
In this subsection, we show that the compatibility of the Poisson bracket with the generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
does not depend on the choice of the solutions of the system (2.8) and (2.9). Specifically, let
$\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
does not depend on the choice of the solutions of the system (2.8) and (2.9). Specifically, let
![]() $(R_0^r,R_0^c)$
and
$(R_0^r,R_0^c)$
and
![]() $(\tilde {R}_0^r,\tilde {R}_0^c)$
be solutions that correspond to
$(\tilde {R}_0^r,\tilde {R}_0^c)$
be solutions that correspond to
![]() $(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, and let us consider two Poisson brackets on
$(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
, and let us consider two Poisson brackets on
![]() $D(\operatorname {\mathrm {GL}}_n)$
that depend on these choices:
$D(\operatorname {\mathrm {GL}}_n)$
that depend on these choices:
![]() $\{\cdot ,\cdot \}_{(R_0^r,R_0^c)}$
and
$\{\cdot ,\cdot \}_{(R_0^r,R_0^c)}$
and
![]() $\{\cdot ,\cdot \}_{(\tilde {R}_0^r,\tilde {R}_0^c)}$
.
$\{\cdot ,\cdot \}_{(\tilde {R}_0^r,\tilde {R}_0^c)}$
.
Proposition 8.1. If the initial extended cluster of
![]() $\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is log-canonical with respect to
$\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is log-canonical with respect to
![]() $\{\cdot , \cdot \}_{(R_0^r,R_0^c)}$
, then it’s also log-canonical with respect to
$\{\cdot , \cdot \}_{(R_0^r,R_0^c)}$
, then it’s also log-canonical with respect to
![]() $\{\cdot ,\cdot \}_{(\tilde {R}_0^r,\tilde {R}_0^c)}$
.
$\{\cdot ,\cdot \}_{(\tilde {R}_0^r,\tilde {R}_0^c)}$
.
Proof. Indeed, let
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
be any two variables from the initial extended cluster and let
$\psi _2$
be any two variables from the initial extended cluster and let
![]() $\mathfrak {h}$
be the Cartan subalgebra of
$\mathfrak {h}$
be the Cartan subalgebra of
![]() $\operatorname {\mathrm {gl}}_n(\mathbb {C})$
. Then the difference of the brackets can be written as
$\operatorname {\mathrm {gl}}_n(\mathbb {C})$
. Then the difference of the brackets can be written as
where
![]() $s_0^{\ell } : \mathfrak {h}\rightarrow \mathfrak {h}$
is a skew-symmetric linear transformation such that
$s_0^{\ell } : \mathfrak {h}\rightarrow \mathfrak {h}$
is a skew-symmetric linear transformation such that
![]() $s_0^{\ell }(\alpha - \gamma _{\ell }(\alpha )) = 0$
for
$s_0^{\ell }(\alpha - \gamma _{\ell }(\alpha )) = 0$
for
![]() $\alpha \in \Gamma _1^{\ell }$
,
$\alpha \in \Gamma _1^{\ell }$
,
![]() $\ell \in \{r,c\}$
. Now, it suffices to prove thatFootnote
9
$\ell \in \{r,c\}$
. Now, it suffices to prove thatFootnote
9
![]() $s_0^c\pi _0 E_L\log \psi = \text {const}$
and
$s_0^c\pi _0 E_L\log \psi = \text {const}$
and
![]() $s_0^r \pi _0E_R \log \psi = \text {const}$
, where
$s_0^r \pi _0E_R \log \psi = \text {const}$
, where
![]() $\psi $
is any function from the initial extended cluster. Let us only deal with the case of
$\psi $
is any function from the initial extended cluster. Let us only deal with the case of
![]() $s_0^c$
, the other case is similar. If
$s_0^c$
, the other case is similar. If
![]() $\psi $
is a
$\psi $
is a
![]() $\varphi $
- or f-function, then it follows from equation (3.9) that
$\varphi $
- or f-function, then it follows from equation (3.9) that
![]() $\pi _0 E_L \log \psi = \text {const}$
; if
$\pi _0 E_L \log \psi = \text {const}$
; if
![]() $\psi $
is a g- or h-function, then we write
$\psi $
is a g- or h-function, then we write
![]() $\pi _0 E_L \psi = \pi _0\xi _L \psi + \pi _0(1-\gamma ^c) X \nabla _X \psi $
. Recall from equation (3.13) that
$\pi _0 E_L \psi = \pi _0\xi _L \psi + \pi _0(1-\gamma ^c) X \nabla _X \psi $
. Recall from equation (3.13) that
![]() $\pi _0 \xi _L \log \psi = \text {const}$
, hence it’s left to study
$\pi _0 \xi _L \log \psi = \text {const}$
, hence it’s left to study
![]() $s_0^c\pi _0 (1-\gamma ^c)(X\nabla _X \psi )$
. Let us enumerate all nontrivial column X-runs as
$s_0^c\pi _0 (1-\gamma ^c)(X\nabla _X \psi )$
. Let us enumerate all nontrivial column X-runs as
![]() $\Delta ^c_1,\ldots ,\Delta ^c_k$
, and let us decompose the space of all diagonal matrices
$\Delta ^c_1,\ldots ,\Delta ^c_k$
, and let us decompose the space of all diagonal matrices
![]() $\mathfrak {h}$
as
$\mathfrak {h}$
as
 $$ \begin{align} \mathfrak{h} = \left(\bigoplus_{i=1}^k \mathfrak{h}_i\right) \oplus \left( \bigoplus_{i=1}^k \langle I_i \rangle \right) \oplus (\mathfrak h_{\Gamma_1^c})^{\perp}, \end{align} $$
$$ \begin{align} \mathfrak{h} = \left(\bigoplus_{i=1}^k \mathfrak{h}_i\right) \oplus \left( \bigoplus_{i=1}^k \langle I_i \rangle \right) \oplus (\mathfrak h_{\Gamma_1^c})^{\perp}, \end{align} $$
where
![]() $\mathfrak {h}_i$
is a subspace generated by the roots
$\mathfrak {h}_i$
is a subspace generated by the roots
![]() $\Delta _i^c \cap \Gamma _1^c$
,
$\Delta _i^c \cap \Gamma _1^c$
,
![]() $I_i := \sum _{j \in \Delta _i^c} e_{jj}$
,
$I_i := \sum _{j \in \Delta _i^c} e_{jj}$
,
![]() $\langle I_i \rangle $
is the span of
$\langle I_i \rangle $
is the span of
![]() $I_i$
and
$I_i$
and
![]() $\mathfrak {h}_{\Gamma _1^c}$
is the span of
$\mathfrak {h}_{\Gamma _1^c}$
is the span of
![]() $\{e_{jj} \ | \ \exists i \in [1,k], \ j \in \Delta _i^c\}$
. Now,
$\{e_{jj} \ | \ \exists i \in [1,k], \ j \in \Delta _i^c\}$
. Now,
![]() $\pi _{\hat {\Gamma }_1^c}\pi _0 X\nabla _X\log \psi $
is constant by (3.13), and the application of
$\pi _{\hat {\Gamma }_1^c}\pi _0 X\nabla _X\log \psi $
is constant by (3.13), and the application of
![]() $s_0^c(1-\gamma _c)$
to
$s_0^c(1-\gamma _c)$
to
![]() $X\nabla _X\log \psi $
is zero on the first component of equation (8.14). The projection of
$X\nabla _X\log \psi $
is zero on the first component of equation (8.14). The projection of
![]() $X\nabla _X\log \psi $
onto the second component is equal to
$X\nabla _X\log \psi $
onto the second component is equal to
 $$ \begin{align} \sum_{i=1}^k \frac{1}{|\Delta_i^c|} \operatorname{\mathrm{tr}}(X\nabla_X\log \psi)_{\Delta_i^c}^{\Delta_i^c}, \end{align} $$
$$ \begin{align} \sum_{i=1}^k \frac{1}{|\Delta_i^c|} \operatorname{\mathrm{tr}}(X\nabla_X\log \psi)_{\Delta_i^c}^{\Delta_i^c}, \end{align} $$
which is constant by equation (3.14) (or by Lemma 4.4 from [Reference Gekhtman, Shapiro and Vainshtein20]). Thus, the statement holds.
Proposition 8.2. If
![]() $\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is compatible with the Poisson bracket
$\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is compatible with the Poisson bracket
![]() $\{\cdot ,\cdot \}_{(R_0^r,R_0^c)}$
, then it’s also compatible with
$\{\cdot ,\cdot \}_{(R_0^r,R_0^c)}$
, then it’s also compatible with
![]() $\{\cdot ,\cdot \}_{(\tilde {R}_0^r,\tilde {R}_0^c)}$
.
$\{\cdot ,\cdot \}_{(\tilde {R}_0^r,\tilde {R}_0^c)}$
.
Proof. Let
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
by any two variables from the initial extended cluster with
$\psi _2$
by any two variables from the initial extended cluster with
![]() $\psi _1$
being non-frozen. As the proof of Proposition 8.1 shows, we need to prove that
$\psi _1$
being non-frozen. As the proof of Proposition 8.1 shows, we need to prove that
If
![]() $\psi _1$
is any
$\psi _1$
is any
![]() $\varphi $
- or f-function, then the above identities follow from formulas (8.3). Assume that
$\varphi $
- or f-function, then the above identities follow from formulas (8.3). Assume that
![]() $\psi _1 = g_{ij}$
for
$\psi _1 = g_{ij}$
for
![]() $1 \leq j \leq i \leq n$
or
$1 \leq j \leq i \leq n$
or
![]() $\psi _1 = h_{ji}$
for
$\psi _1 = h_{ji}$
for
![]() $1 \leq j < i \leq n$
(and
$1 \leq j < i \leq n$
(and
![]() $\psi _1$
is not frozen). Then we can write
$\psi _1$
is not frozen). Then we can write
![]() $E_L = \xi _L + (1-\gamma _c)(\nabla _X X)$
and recall that
$E_L = \xi _L + (1-\gamma _c)(\nabla _X X)$
and recall that
![]() $\pi _0\xi _L y(\psi _1) = 0$
by equation (8.11),
$\pi _0\xi _L y(\psi _1) = 0$
by equation (8.11),
![]() $\operatorname {\mathrm {tr}}(\nabla _X y(\psi _1))_{\Delta _i^c}^{\Delta _i^c} = 0$
by equations (8.12) and (8.13); and finally,
$\operatorname {\mathrm {tr}}(\nabla _X y(\psi _1))_{\Delta _i^c}^{\Delta _i^c} = 0$
by equations (8.12) and (8.13); and finally,
![]() $\pi _0 \pi _{\hat {\Gamma }_1^c}(\nabla _X y(\psi _1) X) = 0$
by equation (8.11); therefore,
$\pi _0 \pi _{\hat {\Gamma }_1^c}(\nabla _X y(\psi _1) X) = 0$
by equation (8.11); therefore,
![]() $\langle s_0^c E_L y(\psi _1), \psi _2\rangle = 0$
. In a similar way one can prove
$\langle s_0^c E_L y(\psi _1), \psi _2\rangle = 0$
. In a similar way one can prove
![]() $\langle s_0^r E_R y(\psi _1),\psi _2\rangle = 0$
. The only exception is
$\langle s_0^r E_R y(\psi _1),\psi _2\rangle = 0$
. The only exception is
![]() $\psi _1 = h_{ii}$
for
$\psi _1 = h_{ii}$
for
![]() $2 \leq i \leq n$
. In this case, we set
$2 \leq i \leq n$
. In this case, we set
![]() $h = \log h_{i-1,i} - \log h_{i,i+1}$
and
$h = \log h_{i-1,i} - \log h_{i,i+1}$
and
![]() $f = \log f_{1,n-i} - \log f_{1,n-i+1}$
so that
$f = \log f_{1,n-i} - \log f_{1,n-i+1}$
so that
![]() $\log y(h_{ii}) = h + f$
, and let
$\log y(h_{ii}) = h + f$
, and let
![]() $\Delta _1^r,\ldots ,\Delta _{m}^r$
be the list of all nontrivial row X-runs; then, by equations (8.1), (8.8) and (8.10),
$\Delta _1^r,\ldots ,\Delta _{m}^r$
be the list of all nontrivial row X-runs; then, by equations (8.1), (8.8) and (8.10),
 $$\begin{align*}\begin{aligned} \langle s_0^r E_R \log y(h_{ii}),\psi_2\rangle &= \langle s_0^r \eta_R(h), E_R \psi \rangle + \langle s_0^r(1-\gamma_r)X\nabla_X h, E_R \psi\rangle + \langle s_0^r E_R f, E_R \psi \rangle \\ &= \langle s_0^r e_{i-1,i-1}, E_R\psi\rangle + \sum_{k=1}^m \frac{1}{|\Delta_k^r|} \operatorname{\mathrm{tr}}(X \nabla_X h)_{\Delta^r}^{\Delta^r}\langle s_0^r I_k, E_R \psi\rangle + \langle s_0(-e_{i-1,i-1}),E_R\psi\rangle\\ & = 0.\end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \langle s_0^r E_R \log y(h_{ii}),\psi_2\rangle &= \langle s_0^r \eta_R(h), E_R \psi \rangle + \langle s_0^r(1-\gamma_r)X\nabla_X h, E_R \psi\rangle + \langle s_0^r E_R f, E_R \psi \rangle \\ &= \langle s_0^r e_{i-1,i-1}, E_R\psi\rangle + \sum_{k=1}^m \frac{1}{|\Delta_k^r|} \operatorname{\mathrm{tr}}(X \nabla_X h)_{\Delta^r}^{\Delta^r}\langle s_0^r I_k, E_R \psi\rangle + \langle s_0(-e_{i-1,i-1}),E_R\psi\rangle\\ & = 0.\end{aligned} \end{align*}$$
8.3 Computation of
 $\{y(\phi ),\psi \}$
and
$\{y(\phi ),\psi \}$
and
 $\{y(\psi ),\phi \}$
$\{y(\psi ),\phi \}$
Let
![]() $\phi $
be any f- or
$\phi $
be any f- or
![]() $\varphi $
-function, and let
$\varphi $
-function, and let
![]() $\psi $
be any g- or h-function. The objective of this subsection is to show that
$\psi $
be any g- or h-function. The objective of this subsection is to show that
![]() $\{y(\phi ),\psi \} = \{y(\psi ), \phi \} = 0$
(for
$\{y(\phi ),\psi \} = \{y(\psi ), \phi \} = 0$
(for
![]() $y(\psi )$
, we assume that
$y(\psi )$
, we assume that
![]() $\psi $
is a cluster variable).
$\psi $
is a cluster variable).
Proposition 8.3.
![]() $\{y(\phi ),\psi \} = 0$
.
$\{y(\phi ),\psi \} = 0$
.
Proof. Let us apply formula (7.1):
 $$\begin{align*}\{y(\phi), \psi\} & = -\langle \pi_0 E_L y(\phi), \nabla_Y \psi Y\rangle + \langle \pi_0 E_R y(\phi), Y\nabla_Y \psi \rangle + \langle R_0^c \pi_0 E_L y(\phi), E_L\psi\rangle\\ &\quad - \langle R_0^r \pi_0 E_Ry(\phi), E_R \psi\rangle, \end{align*}$$
$$\begin{align*}\{y(\phi), \psi\} & = -\langle \pi_0 E_L y(\phi), \nabla_Y \psi Y\rangle + \langle \pi_0 E_R y(\phi), Y\nabla_Y \psi \rangle + \langle R_0^c \pi_0 E_L y(\phi), E_L\psi\rangle\\ &\quad - \langle R_0^r \pi_0 E_Ry(\phi), E_R \psi\rangle, \end{align*}$$
and now recall from equation (8.3) that
![]() $\pi _0E_Ly(\phi ) = \pi _0E_Ry(\phi ) = 0$
. Thus,
$\pi _0E_Ly(\phi ) = \pi _0E_Ry(\phi ) = 0$
. Thus,
![]() $\{y(\phi ),\psi \} = 0$
.
$\{y(\phi ),\psi \} = 0$
.
Proposition 8.4.
![]() $\{y(\psi ),\phi \} = 0$
.
$\{y(\psi ),\phi \} = 0$
.
Proof. Let us pick a pair
![]() $(R_0^r,R_0^c)$
of solutions of equations (2.8) and (2.9) such that both
$(R_0^r,R_0^c)$
of solutions of equations (2.8) and (2.9) such that both
![]() $R_0^r$
and
$R_0^r$
and
![]() $R_0^c$
satisfy the identities (3.6).
$R_0^c$
satisfy the identities (3.6).
Case 1,
![]() $i\neq j$
. Assume first that
$i\neq j$
. Assume first that
![]() $\psi $
is any cluster
$\psi $
is any cluster
![]() $g_{ij}$
or
$g_{ij}$
or
![]() $h_{ji}$
for
$h_{ji}$
for
![]() $1 \leq j < i \leq n$
. Similarly to equation (7.1), we can write
$1 \leq j < i \leq n$
. Similarly to equation (7.1), we can write
 $$ \begin{align} \{y(\psi),\phi\} &= \langle \pi_0 X \nabla_X y(\psi), E_R\phi\rangle - \langle \pi_0 \nabla_X y(\psi)\cdot X, E_L\phi\rangle + \langle R_0^c \pi_0 E_L y(\psi), E_L\phi\rangle\nonumber\\ &\quad -\langle R_0^r \pi_0 E_R y(\psi), E_R\phi\rangle. \end{align} $$
$$ \begin{align} \{y(\psi),\phi\} &= \langle \pi_0 X \nabla_X y(\psi), E_R\phi\rangle - \langle \pi_0 \nabla_X y(\psi)\cdot X, E_L\phi\rangle + \langle R_0^c \pi_0 E_L y(\psi), E_L\phi\rangle\nonumber\\ &\quad -\langle R_0^r \pi_0 E_R y(\psi), E_R\phi\rangle. \end{align} $$
Using equation (8.11) and the formula
![]() $E_L = \xi _L + (1-\gamma _c)(\nabla _X X)$
, we can write
$E_L = \xi _L + (1-\gamma _c)(\nabla _X X)$
, we can write
![]() $E_L y(\psi ) = (1-\gamma _c) \nabla _X y(\psi ) X$
and
$E_L y(\psi ) = (1-\gamma _c) \nabla _X y(\psi ) X$
and
![]() $\pi _0 \pi _{\hat {\Gamma }_1^c} \nabla _X y(\psi ) X = 0$
; hence, the second and the third terms combine into
$\pi _0 \pi _{\hat {\Gamma }_1^c} \nabla _X y(\psi ) X = 0$
; hence, the second and the third terms combine into
 $$\begin{align*}\begin{aligned} - \langle \pi_0 \nabla_X y(\psi)\cdot X&, E_L\phi\rangle + \langle R_0^c \pi_0 E_L y(\psi), E_L\phi\rangle =\\&= - \langle \pi_0\pi_{\Gamma_1^c} \nabla_X y(\psi)\cdot X, E_L\phi\rangle + \langle R_0^c \pi_0 (1-\gamma_c)\pi_{\Gamma_1^c} (\nabla_X y(\psi)\cdot X), E_L\phi\rangle= 0. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} - \langle \pi_0 \nabla_X y(\psi)\cdot X&, E_L\phi\rangle + \langle R_0^c \pi_0 E_L y(\psi), E_L\phi\rangle =\\&= - \langle \pi_0\pi_{\Gamma_1^c} \nabla_X y(\psi)\cdot X, E_L\phi\rangle + \langle R_0^c \pi_0 (1-\gamma_c)\pi_{\Gamma_1^c} (\nabla_X y(\psi)\cdot X), E_L\phi\rangle= 0. \end{aligned} \end{align*}$$
Similarly, the first term cancels out with the fourth one if we write
![]() $E_R y(\psi ) = (1-\gamma _r)(X\nabla _X y(\psi ))$
and apply
$E_R y(\psi ) = (1-\gamma _r)(X\nabla _X y(\psi ))$
and apply
![]() $R_0^r(1-\gamma _r)\pi _0 = \pi _0 \pi _{\Gamma _1^r} + R_0^r\pi _0 \pi _{\hat {\Gamma }_1^r}$
.
$R_0^r(1-\gamma _r)\pi _0 = \pi _0 \pi _{\Gamma _1^r} + R_0^r\pi _0 \pi _{\hat {\Gamma }_1^r}$
.
Case 2.
![]() $\psi = h_{ii}$
,
$\psi = h_{ii}$
,
![]() $2 \leq i \leq n$
. Let us denote
$2 \leq i \leq n$
. Let us denote
![]() $\hat {h}:= \log h_{i-1,i} - \log h_{i,i+1}$
,
$\hat {h}:= \log h_{i-1,i} - \log h_{i,i+1}$
,
![]() $\hat {f} := \log f_{1,n-i} - \log f_{1,n-i+1}$
,
$\hat {f} := \log f_{1,n-i} - \log f_{1,n-i+1}$
,
![]() $\hat {\phi } = \log \phi $
. Then
$\hat {\phi } = \log \phi $
. Then
![]() $\log y(h_{ii}) = \hat {h} + \hat {f}$
. The bracket
$\log y(h_{ii}) = \hat {h} + \hat {f}$
. The bracket
![]() $\{\hat {h}, \hat {\phi }\}$
can be expressed as in equation (8.16):
$\{\hat {h}, \hat {\phi }\}$
can be expressed as in equation (8.16):
Using the diagonal derivatives formulas from Section 8.1 and
![]() $E_L = \xi _L + (1-\gamma _c)(\nabla _X X)$
, we can expand the second and the third terms as
$E_L = \xi _L + (1-\gamma _c)(\nabla _X X)$
, we can expand the second and the third terms as
 $$\begin{align*}\begin{aligned} - \langle \pi_0 \nabla_X \hat{h}\cdot X&, E_L\hat{\phi}\rangle + \langle R_0^c \pi_0 E_L \hat{h}, E_L\hat{\phi}\rangle = - \langle \pi_0 \pi_{\Gamma_1^c}\nabla_X \hat{h}\cdot X, E_L\hat{\phi}\rangle + \langle R_0^c e_{ii}, E_L\hat{\phi}\rangle + \\ &+ \langle R_0^c(1-\gamma_c)(\nabla_X \hat{h} \cdot X), E_L\hat{\phi}\rangle = \langle R_0^c e_{ii}, E_L\hat{\phi}\rangle; \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} - \langle \pi_0 \nabla_X \hat{h}\cdot X&, E_L\hat{\phi}\rangle + \langle R_0^c \pi_0 E_L \hat{h}, E_L\hat{\phi}\rangle = - \langle \pi_0 \pi_{\Gamma_1^c}\nabla_X \hat{h}\cdot X, E_L\hat{\phi}\rangle + \langle R_0^c e_{ii}, E_L\hat{\phi}\rangle + \\ &+ \langle R_0^c(1-\gamma_c)(\nabla_X \hat{h} \cdot X), E_L\hat{\phi}\rangle = \langle R_0^c e_{ii}, E_L\hat{\phi}\rangle; \end{aligned} \end{align*}$$
similarly, using
![]() $E_R = \eta _R + (1-\gamma _r)(X\nabla _X)$
, we write
$E_R = \eta _R + (1-\gamma _r)(X\nabla _X)$
, we write
hence
![]() $\{\hat {h}, \hat {\phi }\} = \langle R_0^c e_{ii}, E_L\hat {\phi }\rangle - \langle R_0^r e_{i-1,i-1}, E_R \hat {\phi } \rangle $
. Using the invariance properties of f-functions together with the diagonal derivatives formulas for
$\{\hat {h}, \hat {\phi }\} = \langle R_0^c e_{ii}, E_L\hat {\phi }\rangle - \langle R_0^r e_{i-1,i-1}, E_R \hat {\phi } \rangle $
. Using the invariance properties of f-functions together with the diagonal derivatives formulas for
![]() $\hat {f}$
, we can write
$\hat {f}$
, we can write
![]() $\{\hat {f},\hat {\phi }\}$
as
$\{\hat {f},\hat {\phi }\}$
as
Altogether, we see that
The latter expression depends only on f- and
![]() $\varphi $
-functions, which stay the same for all oriented aperiodic BD pairs. Since it was proved in [Reference Gekhtman, Shapiro and Vainshtein18] that for the standard pair we have
$\varphi $
-functions, which stay the same for all oriented aperiodic BD pairs. Since it was proved in [Reference Gekhtman, Shapiro and Vainshtein18] that for the standard pair we have
![]() $\{y(\psi ), \phi \} = 0$
, we see that the same is true for any other BD pair.
$\{y(\psi ), \phi \} = 0$
, we see that the same is true for any other BD pair.
Case 2.
![]() $\psi = g_{ii}$
,
$\psi = g_{ii}$
,
![]() $2 \leq i \leq n$
. Let us denote
$2 \leq i \leq n$
. Let us denote
![]() $\hat {g}:=\log g_{i,i-1} - \log g_{i+1,i}$
,
$\hat {g}:=\log g_{i,i-1} - \log g_{i+1,i}$
,
![]() $\hat {g}^{\prime } := \log g_{i+1,i+1} - \log g_{i-1,i-1}$
,
$\hat {g}^{\prime } := \log g_{i+1,i+1} - \log g_{i-1,i-1}$
,
![]() $\hat {f} := \log f_{n-i+1,1} - \log f_{n-i,1}$
. Then
$\hat {f} := \log f_{n-i+1,1} - \log f_{n-i,1}$
. Then
![]() $\log y(g_{ii}) = \hat {g} + \hat {g}^{\prime } + \hat {f}$
. The bracket between these three pieces and
$\log y(g_{ii}) = \hat {g} + \hat {g}^{\prime } + \hat {f}$
. The bracket between these three pieces and
![]() $\phi $
can be computed as in the previous case:
$\phi $
can be computed as in the previous case:
 $$\begin{align*}\begin{aligned} \{ \hat{g}^{\prime}, \hat{\phi} \} &= -\langle R_0^c(e_{i-1,i-1} + e_{ii}), E_L \hat{\phi}\rangle + \langle R_0^r(e_{i-1,i-1} + e_{ii}), E_R \hat{\phi}\rangle \\ &\quad -\langle e_{i-1,i-1} + e_{ii}, E_R \hat{\phi} \rangle + \langle e_{ii} + e_{i-1,i-1}, E_L\hat{\phi} \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{ \hat{g}^{\prime}, \hat{\phi} \} &= -\langle R_0^c(e_{i-1,i-1} + e_{ii}), E_L \hat{\phi}\rangle + \langle R_0^r(e_{i-1,i-1} + e_{ii}), E_R \hat{\phi}\rangle \\ &\quad -\langle e_{i-1,i-1} + e_{ii}, E_R \hat{\phi} \rangle + \langle e_{ii} + e_{i-1,i-1}, E_L\hat{\phi} \rangle. \end{aligned} \end{align*}$$
Now, summing up the above three equations, we see that all terms with
![]() $R_0^c$
or
$R_0^c$
or
![]() $R_0^r$
cancel out. The remaining terms do not depend on the choice of BD pair, hence they coincide with the expression in the standard case, which is zero.
$R_0^r$
cancel out. The remaining terms do not depend on the choice of BD pair, hence they coincide with the expression in the standard case, which is zero.
8.4 Bracket for g- and h-functions
The main objective of this subsection is to derive a formula for the Poisson bracket between g- and h-functions that’s subsequently used below.
Shorthand notation
Whenever we fix two functions
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
, let us denote the gradients of their logarithms (and operators associated with them) via augmenting the operators with upper indices
$\psi _2$
, let us denote the gradients of their logarithms (and operators associated with them) via augmenting the operators with upper indices
![]() $1$
or
$1$
or
![]() $2$
. For instance,
$2$
. For instance,
![]() $\nabla ^1_X \cdot X := \nabla _X \log \psi _1 \cdot X$
or
$\nabla ^1_X \cdot X := \nabla _X \log \psi _1 \cdot X$
or
![]() $\eta _R^2 := \eta _R \log \psi _2$
. For conciseness, any other data associated with either of the two functions (e.g., blocks or
$\eta _R^2 := \eta _R \log \psi _2$
. For conciseness, any other data associated with either of the two functions (e.g., blocks or
![]() $\mathcal {L}$
-matrices) is also augmented with upper indices
$\mathcal {L}$
-matrices) is also augmented with upper indices
![]() $1$
or
$1$
or
![]() $2$
.
$2$
.
Lemma 8.5. Let
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
be any g- or h-functions. Then the bracket between them can be expressed as
$\psi _2$
be any g- or h-functions. Then the bracket between them can be expressed as
 $$ \begin{align} \begin{aligned} \{\log \psi_1,\log \psi_2\} = &= -\langle \pi_{<} \eta_L^1, \pi_{>} \eta_L^2 \rangle - \langle \pi_{>} \eta_R^1, \pi_{<} \eta_R^2 \rangle + \\ &+ \langle \gamma_r \xi_R^1, \gamma_r X \nabla_X^2 \rangle + \langle \gamma_c^* \xi_L^1, \gamma_c^* \nabla_Y^2 Y \rangle + D,\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \{\log \psi_1,\log \psi_2\} = &= -\langle \pi_{<} \eta_L^1, \pi_{>} \eta_L^2 \rangle - \langle \pi_{>} \eta_R^1, \pi_{<} \eta_R^2 \rangle + \\ &+ \langle \gamma_r \xi_R^1, \gamma_r X \nabla_X^2 \rangle + \langle \gamma_c^* \xi_L^1, \gamma_c^* \nabla_Y^2 Y \rangle + D,\\ \end{aligned} \end{align} $$
where D is given by
 $$ \begin{align}\begin{aligned} D &= -\langle \pi_0 \gamma_c^* \xi_L^1, \gamma_c^*(\nabla^2_Y Y)\rangle - \langle \pi_0 \gamma_r \xi_R^1, \gamma_r(X\nabla^2_X)\rangle + \langle R_0^c \pi_0 E_L^1, E_L^2 \rangle - \langle R_0^r \pi_0 E_R^1, E_R^2 \rangle \\ &\quad -\langle \pi_0 \nabla^1_X X, E_L^2\rangle + \langle \pi_0 X\nabla^1_X, E_R^2 \rangle. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} D &= -\langle \pi_0 \gamma_c^* \xi_L^1, \gamma_c^*(\nabla^2_Y Y)\rangle - \langle \pi_0 \gamma_r \xi_R^1, \gamma_r(X\nabla^2_X)\rangle + \langle R_0^c \pi_0 E_L^1, E_L^2 \rangle - \langle R_0^r \pi_0 E_R^1, E_R^2 \rangle \\ &\quad -\langle \pi_0 \nabla^1_X X, E_L^2\rangle + \langle \pi_0 X\nabla^1_X, E_R^2 \rangle. \end{aligned} \end{align} $$
We refer to D as the diagonal part of the bracket.
Proof. Recall that the bracket is defined as
Recall that
![]() $E_L^i = \xi _L^i + (1-\gamma _c) (\nabla _X^i X)$
with
$E_L^i = \xi _L^i + (1-\gamma _c) (\nabla _X^i X)$
with
![]() $\xi _L^i \in \mathfrak {b}_-$
,
$\xi _L^i \in \mathfrak {b}_-$
,
![]() $i \in \{1,2\}$
; with that, the first term becomes
$i \in \{1,2\}$
; with that, the first term becomes
 $$ \begin{align} \begin{aligned} \langle R_+^c(E_L^1), E_L^2 \rangle &= \left\langle \frac{1}{1-\gamma_c} \pi_{>} E_L^1, E_L^2 \right\rangle - \left\langle \frac{\gamma_c^*}{1-\gamma_c^*} \pi_{<} E_L^1, E_L^2 \right\rangle + \langle R_0^c \pi_0 E_L^1, E_L^2 \rangle \\ &= \langle \pi_{>} \nabla_X^1 X, E_L^2 \rangle - \langle \pi_{<} E_L^1, \gamma_c(\nabla_X^2 X)\rangle + \langle R_0^c \pi_0 E_L^1, E_L^2 \rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle R_+^c(E_L^1), E_L^2 \rangle &= \left\langle \frac{1}{1-\gamma_c} \pi_{>} E_L^1, E_L^2 \right\rangle - \left\langle \frac{\gamma_c^*}{1-\gamma_c^*} \pi_{<} E_L^1, E_L^2 \right\rangle + \langle R_0^c \pi_0 E_L^1, E_L^2 \rangle \\ &= \langle \pi_{>} \nabla_X^1 X, E_L^2 \rangle - \langle \pi_{<} E_L^1, \gamma_c(\nabla_X^2 X)\rangle + \langle R_0^c \pi_0 E_L^1, E_L^2 \rangle. \end{aligned} \end{align} $$
Similarly, recall that
![]() $E_R^i = \xi _R^i + (1-\gamma _r^*) (Y \nabla _Y^i)$
and
$E_R^i = \xi _R^i + (1-\gamma _r^*) (Y \nabla _Y^i)$
and
![]() $\xi _R^i \in \mathfrak {b}_+$
; using these formulas, we rewrite the second term of the bracket as
$\xi _R^i \in \mathfrak {b}_+$
; using these formulas, we rewrite the second term of the bracket as
 $$ \begin{align} \begin{aligned} -\langle R_+^r (E_R^1), E_R^1\rangle &= -\left\langle \frac{1}{1-\gamma_r}\pi_{>}E_R^1, E_R^2 \right\rangle + \left\langle \frac{\gamma_r^*}{1-\gamma_r^*} \pi_{<}E_R^1, E_R^2 \right\rangle - \langle R_0^r \pi_0 E_R^1, E_R^2 \rangle \\ &= -\langle \pi_{>} E_R^1, Y\nabla^2_Y\rangle + \langle \pi_{<}\gamma_r^* (Y\nabla^2_Y), E_R^2 \rangle - \langle R_0^r \pi_0 E_R^1, E_R^2 \rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} -\langle R_+^r (E_R^1), E_R^1\rangle &= -\left\langle \frac{1}{1-\gamma_r}\pi_{>}E_R^1, E_R^2 \right\rangle + \left\langle \frac{\gamma_r^*}{1-\gamma_r^*} \pi_{<}E_R^1, E_R^2 \right\rangle - \langle R_0^r \pi_0 E_R^1, E_R^2 \rangle \\ &= -\langle \pi_{>} E_R^1, Y\nabla^2_Y\rangle + \langle \pi_{<}\gamma_r^* (Y\nabla^2_Y), E_R^2 \rangle - \langle R_0^r \pi_0 E_R^1, E_R^2 \rangle. \end{aligned} \end{align} $$
With equations (8.20) and (8.21), we can rewrite equation (8.19) as
 $$ \begin{align} \begin{aligned} \{\log \psi_1,\log \psi_2\} &= \langle \pi_{>} \nabla^1_X X, E_L^2\rangle - \langle \pi_{<} E_L^1, \gamma_c (\nabla^2_X X)\rangle - \langle \nabla^1_X X, \nabla^2_Y Y\rangle \\ &\quad -\langle \pi_{>} E_R^1, Y\nabla^2_Y \rangle + \langle \pi_{<} \gamma_r^*(Y\nabla^1_Y), E_R^2\rangle + \langle X\nabla^1_X, Y\nabla^2_Y \rangle \\ &\quad + \langle R_0^c \pi_0 E_L^1, E_L^2\rangle - \langle R_0^r \pi_0 E_R^1, E_R^2 \rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \{\log \psi_1,\log \psi_2\} &= \langle \pi_{>} \nabla^1_X X, E_L^2\rangle - \langle \pi_{<} E_L^1, \gamma_c (\nabla^2_X X)\rangle - \langle \nabla^1_X X, \nabla^2_Y Y\rangle \\ &\quad -\langle \pi_{>} E_R^1, Y\nabla^2_Y \rangle + \langle \pi_{<} \gamma_r^*(Y\nabla^1_Y), E_R^2\rangle + \langle X\nabla^1_X, Y\nabla^2_Y \rangle \\ &\quad + \langle R_0^c \pi_0 E_L^1, E_L^2\rangle - \langle R_0^r \pi_0 E_R^1, E_R^2 \rangle. \end{aligned} \end{align} $$
Let’s deal with the first three terms of equation (8.22). Rewrite
![]() $E_L^1 = \xi _L^1 + (1-\gamma _c)(\nabla _X^1 X)$
and
$E_L^1 = \xi _L^1 + (1-\gamma _c)(\nabla _X^1 X)$
and
![]() $\pi _{>}\gamma _c(\nabla ^2_X X)=-\pi _{>}\nabla ^2_Y Y$
, and combine the first and the third terms:
$\pi _{>}\gamma _c(\nabla ^2_X X)=-\pi _{>}\nabla ^2_Y Y$
, and combine the first and the third terms:
 $$ \begin{align} \begin{aligned} &\langle \pi_{>} \nabla^1_X X, E_L^2\rangle - \langle \pi_{<} E_L^1, \gamma_c (\nabla^2_X X)\rangle - \langle \nabla^1_X X, \nabla^2_Y Y\rangle \\ &\quad =-\langle \pi_{\leq} \nabla^1_X X, \nabla^2_Y Y\rangle + \langle \pi_{>} \nabla^1_X X, \nabla^2_X X\rangle + \langle \pi_{<} \xi_L^1, \nabla_Y^2 Y\rangle + \langle \pi_{<} (1-\gamma_c)(\nabla_X^1 X), \nabla_Y^2 Y\rangle; \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\langle \pi_{>} \nabla^1_X X, E_L^2\rangle - \langle \pi_{<} E_L^1, \gamma_c (\nabla^2_X X)\rangle - \langle \nabla^1_X X, \nabla^2_Y Y\rangle \\ &\quad =-\langle \pi_{\leq} \nabla^1_X X, \nabla^2_Y Y\rangle + \langle \pi_{>} \nabla^1_X X, \nabla^2_X X\rangle + \langle \pi_{<} \xi_L^1, \nabla_Y^2 Y\rangle + \langle \pi_{<} (1-\gamma_c)(\nabla_X^1 X), \nabla_Y^2 Y\rangle; \end{aligned} \end{align} $$
the first and the fourth terms in the latter expression combine into
 $$\begin{align*}\begin{aligned} -\langle \pi_{\leq} \nabla^1_X X&, \nabla^2_Y Y\rangle + \langle \pi_{<} (1-\gamma_c)(\nabla_X^1 X), \nabla_Y^2 Y\rangle = - \langle \pi_0 \nabla^1_X X, \nabla^2_Y Y\rangle - \langle \pi_{<} \gamma_c \nabla^1_X X, \nabla^2_Y Y\rangle \\ &= - \langle \pi_0 \nabla^1_X X, \nabla^2_Y Y\rangle - \langle \pi_{<} \nabla^1_X X, \eta_L^2 \rangle + \langle \pi_{<} \nabla^1_X X, \nabla^2_X X\rangle \\ &= - \langle \pi_0 \nabla^1_X X, \nabla^2_Y Y\rangle - \langle \pi_{<} \eta_L^1, \eta_L^2 \rangle + \langle \pi_{<} \gamma_c^*(\nabla^1_Y Y), \eta_L^2 \rangle + \langle \pi_{<} \nabla^1_X X, \nabla^2_X X\rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} -\langle \pi_{\leq} \nabla^1_X X&, \nabla^2_Y Y\rangle + \langle \pi_{<} (1-\gamma_c)(\nabla_X^1 X), \nabla_Y^2 Y\rangle = - \langle \pi_0 \nabla^1_X X, \nabla^2_Y Y\rangle - \langle \pi_{<} \gamma_c \nabla^1_X X, \nabla^2_Y Y\rangle \\ &= - \langle \pi_0 \nabla^1_X X, \nabla^2_Y Y\rangle - \langle \pi_{<} \nabla^1_X X, \eta_L^2 \rangle + \langle \pi_{<} \nabla^1_X X, \nabla^2_X X\rangle \\ &= - \langle \pi_0 \nabla^1_X X, \nabla^2_Y Y\rangle - \langle \pi_{<} \eta_L^1, \eta_L^2 \rangle + \langle \pi_{<} \gamma_c^*(\nabla^1_Y Y), \eta_L^2 \rangle + \langle \pi_{<} \nabla^1_X X, \nabla^2_X X\rangle. \end{aligned} \end{align*}$$
Since
![]() $\xi _L^2 = \gamma _c(\eta _L^2) + \pi _{\hat {\Gamma }_2^c} (\nabla _Y^2 Y) \in \mathfrak {b}_-$
, we see that
$\xi _L^2 = \gamma _c(\eta _L^2) + \pi _{\hat {\Gamma }_2^c} (\nabla _Y^2 Y) \in \mathfrak {b}_-$
, we see that
![]() $\pi _>(\gamma _c(\eta _L^2)) = -\pi _{>}\pi _{\hat {\Gamma }_2^c}(\nabla _Y^2 Y)$
, hence the term
$\pi _>(\gamma _c(\eta _L^2)) = -\pi _{>}\pi _{\hat {\Gamma }_2^c}(\nabla _Y^2 Y)$
, hence the term
![]() $\langle \pi _{<} \gamma _c^* (\nabla ^1_Y Y), \eta _L^2 \rangle $
can be combined with
$\langle \pi _{<} \gamma _c^* (\nabla ^1_Y Y), \eta _L^2 \rangle $
can be combined with
![]() $\langle \pi _{<} \xi _L^1, \nabla ^2_Y Y\rangle $
from equation (8.23) as
$\langle \pi _{<} \xi _L^1, \nabla ^2_Y Y\rangle $
from equation (8.23) as
 $$\begin{align*}\begin{aligned} \langle \pi_{<} \xi_L^1, \nabla^2_Y Y\rangle + \langle \pi_{<} \gamma_c^* (\nabla^1_Y Y), \eta_L^2 \rangle &= \langle \pi_{<} \xi_L^1, \nabla^2_Y Y\rangle - \langle \pi_{<} \pi_{\hat{\Gamma}_2^c}(\nabla^1_Y Y), \nabla^2_Y Y \rangle = \langle \pi_{<} \pi_{\Gamma_2^c} \xi_L^1, \nabla_Y^2 Y\rangle \\ &= \langle \pi_{<} \gamma_c^*(\xi_L^1), \gamma_c^*(\nabla_Y^2 Y)\rangle, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \langle \pi_{<} \xi_L^1, \nabla^2_Y Y\rangle + \langle \pi_{<} \gamma_c^* (\nabla^1_Y Y), \eta_L^2 \rangle &= \langle \pi_{<} \xi_L^1, \nabla^2_Y Y\rangle - \langle \pi_{<} \pi_{\hat{\Gamma}_2^c}(\nabla^1_Y Y), \nabla^2_Y Y \rangle = \langle \pi_{<} \pi_{\Gamma_2^c} \xi_L^1, \nabla_Y^2 Y\rangle \\ &= \langle \pi_{<} \gamma_c^*(\xi_L^1), \gamma_c^*(\nabla_Y^2 Y)\rangle, \end{aligned} \end{align*}$$
for
![]() $\pi _{\hat {\Gamma }_2^c}(\xi _L^1) = \pi _{\hat {\Gamma }_2^c}(\nabla _Y^1 Y)$
. Overall, equation (8.23) (which is the first three terms of equation (8.22)) updates to
$\pi _{\hat {\Gamma }_2^c}(\xi _L^1) = \pi _{\hat {\Gamma }_2^c}(\nabla _Y^1 Y)$
. Overall, equation (8.23) (which is the first three terms of equation (8.22)) updates to
Next, let’s study the contribution of the fourth, fifth and the sixth terms in equation (8.22) together with
![]() $\langle \nabla ^1_X X, \nabla ^2_X X\rangle = \langle X \nabla ^1_X, X \nabla ^2_X \rangle $
. First, rewrite
$\langle \nabla ^1_X X, \nabla ^2_X X\rangle = \langle X \nabla ^1_X, X \nabla ^2_X \rangle $
. First, rewrite
![]() $-\langle \pi _{>} E_R^1, Y\nabla ^2_Y\rangle $
as
$-\langle \pi _{>} E_R^1, Y\nabla ^2_Y\rangle $
as
 $$ \begin{align} \begin{aligned} &-\langle \pi_{>} E_R^1, Y\nabla^2_Y\rangle = -\langle \pi_{>} \eta_R^1, Y\nabla^2_Y \rangle - \langle \pi_{>} (1-\gamma_r) (X\nabla^1_X), Y\nabla^2_Y\rangle \\ &\quad = -\langle \pi_{>} \eta_R^1, \eta_R^2\rangle + \langle \pi_{>} \eta_R^1, \gamma_r (X\nabla^2_X) \rangle - \langle \pi_{>} X\nabla^1_X, Y \nabla^2_Y\rangle + \langle \pi_{>} \gamma_r (X \nabla^1_X), Y\nabla^2_Y\rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &-\langle \pi_{>} E_R^1, Y\nabla^2_Y\rangle = -\langle \pi_{>} \eta_R^1, Y\nabla^2_Y \rangle - \langle \pi_{>} (1-\gamma_r) (X\nabla^1_X), Y\nabla^2_Y\rangle \\ &\quad = -\langle \pi_{>} \eta_R^1, \eta_R^2\rangle + \langle \pi_{>} \eta_R^1, \gamma_r (X\nabla^2_X) \rangle - \langle \pi_{>} X\nabla^1_X, Y \nabla^2_Y\rangle + \langle \pi_{>} \gamma_r (X \nabla^1_X), Y\nabla^2_Y\rangle. \end{aligned} \end{align} $$
Since
![]() $\gamma _r^*(\eta _R^1) = \pi _{\Gamma _1^r} \xi _R^1$
, we see that
$\gamma _r^*(\eta _R^1) = \pi _{\Gamma _1^r} \xi _R^1$
, we see that
![]() $\langle \pi _{>} \eta _R^1, \gamma _r(X \nabla ^2_X)\rangle = \langle \pi _{>} \pi _{\Gamma _1^r} \xi _R^1, X\nabla ^2_X\rangle $
. The last two terms in equation (8.24) together with
$\langle \pi _{>} \eta _R^1, \gamma _r(X \nabla ^2_X)\rangle = \langle \pi _{>} \pi _{\Gamma _1^r} \xi _R^1, X\nabla ^2_X\rangle $
. The last two terms in equation (8.24) together with
![]() $\langle \nabla ^1_X X, \nabla ^2_X X\rangle $
and the fifth and the sixth terms in equation (8.22) contribute
$\langle \nabla ^1_X X, \nabla ^2_X X\rangle $
and the fifth and the sixth terms in equation (8.22) contribute
 $$\begin{align*}\begin{aligned} &- \langle \pi_{>} X\nabla^1_X, Y \nabla^2_Y\rangle + \langle \pi_{>} \gamma_r (X \nabla^1_X), Y\nabla^2_Y\rangle + \langle X \nabla^1_X, X \nabla^2_X \rangle + \langle \pi_{<} \gamma_r^*(Y\nabla^1_Y), E_R^2\rangle + \langle X\nabla^1_X, Y\nabla^2_Y \rangle \\ &\quad = \langle \pi_{\leq} X\nabla^1_X, Y\nabla^2_Y\rangle - \langle \pi_{>} X\nabla^1_X, X\nabla^2_X \rangle + \langle X\nabla^1_X,X\nabla^2_X \rangle - \langle \pi_{<}X\nabla^1_X, E_R^2\rangle \\ &\quad = \langle \pi_0 X\nabla^1_X,Y\nabla^2_Y\rangle +\langle \pi_0 X\nabla^1_X,X\nabla^2_X \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &- \langle \pi_{>} X\nabla^1_X, Y \nabla^2_Y\rangle + \langle \pi_{>} \gamma_r (X \nabla^1_X), Y\nabla^2_Y\rangle + \langle X \nabla^1_X, X \nabla^2_X \rangle + \langle \pi_{<} \gamma_r^*(Y\nabla^1_Y), E_R^2\rangle + \langle X\nabla^1_X, Y\nabla^2_Y \rangle \\ &\quad = \langle \pi_{\leq} X\nabla^1_X, Y\nabla^2_Y\rangle - \langle \pi_{>} X\nabla^1_X, X\nabla^2_X \rangle + \langle X\nabla^1_X,X\nabla^2_X \rangle - \langle \pi_{<}X\nabla^1_X, E_R^2\rangle \\ &\quad = \langle \pi_0 X\nabla^1_X,Y\nabla^2_Y\rangle +\langle \pi_0 X\nabla^1_X,X\nabla^2_X \rangle. \end{aligned} \end{align*}$$
Combining everything together, we obtain the formula.
Lemma 8.6. If
![]() $(R_0^r,R_0^c)$
are chosen so that the identities (3.6) hold, then the diagonal part D from equation (8.18) can be further expanded as
$(R_0^r,R_0^c)$
are chosen so that the identities (3.6) hold, then the diagonal part D from equation (8.18) can be further expanded as
 $$ \begin{align}\begin{aligned} D &= -\langle \pi_0 \gamma_c^* \xi_L^1, \gamma_c^*(\nabla^2_Y Y)\rangle - \langle \pi_0 \gamma_r \xi_R^1, \gamma_r(X\nabla^2_X)\rangle + \langle R_0^c \pi_0 \xi_L^1, E_L^2 \rangle - \langle \pi_{\hat{\Gamma}_1^c} \pi_0 \nabla^1_X X, E_L^2 \rangle \\ &\quad + \langle R_0^c \pi_0 \pi_{\hat{\Gamma}_1^c} \nabla^1_X X, E_L^2 \rangle - \langle R_0^r \pi_0 \eta_R^1, E_R^2 \rangle + \langle \pi_0 \pi_{\hat{\Gamma}_1^r} X \nabla^1_X, E_R^2 \rangle - \langle R_0^r \pi_0 \pi_{\hat{\Gamma}_1^r} X \nabla^1_X, E_R^2 \rangle. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} D &= -\langle \pi_0 \gamma_c^* \xi_L^1, \gamma_c^*(\nabla^2_Y Y)\rangle - \langle \pi_0 \gamma_r \xi_R^1, \gamma_r(X\nabla^2_X)\rangle + \langle R_0^c \pi_0 \xi_L^1, E_L^2 \rangle - \langle \pi_{\hat{\Gamma}_1^c} \pi_0 \nabla^1_X X, E_L^2 \rangle \\ &\quad + \langle R_0^c \pi_0 \pi_{\hat{\Gamma}_1^c} \nabla^1_X X, E_L^2 \rangle - \langle R_0^r \pi_0 \eta_R^1, E_R^2 \rangle + \langle \pi_0 \pi_{\hat{\Gamma}_1^r} X \nabla^1_X, E_R^2 \rangle - \langle R_0^r \pi_0 \pi_{\hat{\Gamma}_1^r} X \nabla^1_X, E_R^2 \rangle. \end{aligned} \end{align} $$
Proof. Observe that
Therefore, the corresponding terms together with
![]() $-\langle \pi _0 \nabla ^1_X X, E_L^2\rangle $
contribute
$-\langle \pi _0 \nabla ^1_X X, E_L^2\rangle $
contribute
Similarly,
hence
Now, the result is obtained via combining the two formulas.
8.5 Block formulas
In this subsection, we state a further expansion from [Reference Gekhtman, Shapiro and Vainshtein20] of the first four terms in formula (8.17).
Block intervals
Let
![]() $\mathcal {L}$
be an
$\mathcal {L}$
be an
![]() $\mathcal {L}$
-matrix. We enumerate the blocks of
$\mathcal {L}$
-matrix. We enumerate the blocks of
![]() $\mathcal {L}$
in such a way that blocks
$\mathcal {L}$
in such a way that blocks
![]() $X_t$
and
$X_t$
and
![]() $Y_t$
are aligned along their rows (i.e., using
$Y_t$
are aligned along their rows (i.e., using
![]() $\gamma _r$
) and
$\gamma _r$
) and
![]() $Y_t$
and
$Y_t$
and
![]() $X_{t+1}$
are aligned along their columns,
$X_{t+1}$
are aligned along their columns,
![]() $t \geq 1$
. Let us denote by
$t \geq 1$
. Let us denote by
![]() $K_t$
and
$K_t$
and
![]() $L_t$
, respectively, the row and column indices in
$L_t$
, respectively, the row and column indices in
![]() $\mathcal {L}$
that are occupied by
$\mathcal {L}$
that are occupied by
![]() $X_t$
; similarly,
$X_t$
; similarly,
![]() $\bar {K}_t$
and
$\bar {K}_t$
and
![]() $\bar {L}_t$
are row and column indices occupied by
$\bar {L}_t$
are row and column indices occupied by
![]() $Y_t$
in
$Y_t$
in
![]() $\mathcal {L}$
. Furthermore, we set
$\mathcal {L}$
. Furthermore, we set
![]() $\Phi _t := K_t \cap \bar {K}_t$
and
$\Phi _t := K_t \cap \bar {K}_t$
and
![]() $\Psi _t := L_t \cap \bar {L}_{t-1}$
. Figure 27 depicts an
$\Psi _t := L_t \cap \bar {L}_{t-1}$
. Figure 27 depicts an
![]() $\mathcal {L}$
-matrix with the intervals.
$\mathcal {L}$
-matrix with the intervals.

Figure 27 An illustration of the intervals
![]() $\bar {K}_t$
,
$\bar {K}_t$
,
![]() $\bar {L}_t$
,
$\bar {L}_t$
,
![]() $L_t$
,
$L_t$
,
![]() $K_t$
,
$K_t$
,
![]() $\Phi _t$
,
$\Phi _t$
,
![]() $\Psi _t$
.
$\Psi _t$
.
Remark 8.7. The authors of [Reference Gekhtman, Shapiro and Vainshtein20] additionally define empty blocks in the beginning and in the end of the sequence so that it always starts with an X-block and ends with a Y-block; furthermore, they attach row or column intervals to the empty blocks depending on a set of conditions. The convention with empty blocks is rather complicated and only helps to avoid one term in two formulas. Ergo, we write all formulas without assuming that there are extra empty blocks.
 $\mathcal {L}$
-gradients
$\mathcal {L}$
-gradients
Let
![]() $\psi $
be any g- or h-function, and let
$\psi $
be any g- or h-function, and let
![]() $\mathcal {L}$
be an
$\mathcal {L}$
be an
![]() $\mathcal {L}$
-matrix such that
$\mathcal {L}$
-matrix such that
![]() $\psi = \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
(in the case of
$\psi = \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
(in the case of
![]() $\psi = g_{ii}$
or
$\psi = g_{ii}$
or
![]() $\psi = h_{ii}$
, set
$\psi = h_{ii}$
, set
![]() $\mathcal {L}(X,Y):=X$
or
$\mathcal {L}(X,Y):=X$
or
![]() $\mathcal {L}(X,Y): = Y$
accordingly). Notice that
$\mathcal {L}(X,Y): = Y$
accordingly). Notice that
![]() $(j,i)$
entry of
$(j,i)$
entry of
![]() $\nabla _X\psi $
is the sum of the cofactors computed at all occurrences of
$\nabla _X\psi $
is the sum of the cofactors computed at all occurrences of
![]() $x_{ij}$
in the matrix
$x_{ij}$
in the matrix
![]() $\mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
(and similarly for
$\mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
(and similarly for
![]() $(j,i)$
entry of
$(j,i)$
entry of
![]() $\nabla _Y\psi $
and
$\nabla _Y\psi $
and
![]() $y_{ij}$
). We define an
$y_{ij}$
). We define an
![]() $N(\mathcal {L}) \times N(\mathcal {L})$
matrix
$N(\mathcal {L}) \times N(\mathcal {L})$
matrix
![]() $\nabla _{\mathcal {L}}\psi $
that has as its
$\nabla _{\mathcal {L}}\psi $
that has as its
![]() $(j,i)$
entry the
$(j,i)$
entry the
![]() $(i-s+1,j-s+1)$
-cofactor of
$(i-s+1,j-s+1)$
-cofactor of
![]() $\mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
, where
$\mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}$
, where
![]() $i, j \geq s$
, and zero everywhere else. Consequently, if m is the last index in the block sequence in
$i, j \geq s$
, and zero everywhere else. Consequently, if m is the last index in the block sequence in
![]() $\mathcal {L}$
, we have
$\mathcal {L}$
, we have
 $$\begin{align*}\nabla_{X} \psi = \sum_{t=1}^{m} (\nabla_{\mathcal{L}} \psi)_{L_t \rightarrow J_t}^{K_t \rightarrow I_t}, \ \ \ \nabla_Y \psi = \sum_{t=1}^{m} (\nabla_{\mathcal{L}} \psi)_{\bar{L}_t \rightarrow \bar{J}_t}^{\bar{K}_t \rightarrow \bar{I}_t}, \end{align*}$$
$$\begin{align*}\nabla_{X} \psi = \sum_{t=1}^{m} (\nabla_{\mathcal{L}} \psi)_{L_t \rightarrow J_t}^{K_t \rightarrow I_t}, \ \ \ \nabla_Y \psi = \sum_{t=1}^{m} (\nabla_{\mathcal{L}} \psi)_{\bar{L}_t \rightarrow \bar{J}_t}^{\bar{K}_t \rightarrow \bar{I}_t}, \end{align*}$$
where
![]() $Y_t = Y^{\bar {J}_t}_{\bar {I}_t}$
and
$Y_t = Y^{\bar {J}_t}_{\bar {I}_t}$
and
![]() $X_t = X^{J_t}_{I_t}$
. Evidently, by
$X_t = X^{J_t}_{I_t}$
. Evidently, by
![]() $\nabla _{\mathcal {L}}\log \psi $
we mean
$\nabla _{\mathcal {L}}\log \psi $
we mean
![]() $(1/\psi ) \nabla _{\mathcal {L}}\psi $
. Let us mention the following simple formulas:
$(1/\psi ) \nabla _{\mathcal {L}}\psi $
. Let us mention the following simple formulas:
 $$\begin{align*}\mathcal{L}\nabla_{\mathcal{L}}\log\psi = \begin{bmatrix} 0 & * \\ 0 & I \end{bmatrix}, \ \ \ \nabla_{\mathcal{L}}\log\psi \cdot \mathcal{L} = \begin{bmatrix} 0 & 0 \\ * & I \end{bmatrix}, \end{align*}$$
$$\begin{align*}\mathcal{L}\nabla_{\mathcal{L}}\log\psi = \begin{bmatrix} 0 & * \\ 0 & I \end{bmatrix}, \ \ \ \nabla_{\mathcal{L}}\log\psi \cdot \mathcal{L} = \begin{bmatrix} 0 & 0 \\ * & I \end{bmatrix}, \end{align*}$$
where I is the identity matrix that occupies
![]() $[s,N(\mathcal {L})]\times [s,N(\mathcal {L})]$
and
$[s,N(\mathcal {L})]\times [s,N(\mathcal {L})]$
and
![]() $*$
indicates terms whose particular expressions are of no importance in the proofs.
$*$
indicates terms whose particular expressions are of no importance in the proofs.
Numbers p and q
Let
![]() $\psi (X,Y):= \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}(X,Y)$
for some s and
$\psi (X,Y):= \det \mathcal {L}^{[s,N(\mathcal {L})]}_{[s,N(\mathcal {L})]}(X,Y)$
for some s and
![]() $\mathcal {L}$
. Let us call the leading block of
$\mathcal {L}$
. Let us call the leading block of
![]() $\psi $
the X- or Y-block of
$\psi $
the X- or Y-block of
![]() $\mathcal {L}(X,Y)$
that contains the entry
$\mathcal {L}(X,Y)$
that contains the entry
![]() $(s,s)$
. The number q is defined as the index of the leading block. Furthermore, if the block is of type X, we set
$(s,s)$
. The number q is defined as the index of the leading block. Furthermore, if the block is of type X, we set
![]() $p:=q$
; if it’s of type Y, we set
$p:=q$
; if it’s of type Y, we set
![]() $p:=q+1$
.
$p:=q+1$
.
Embeddings
 $\rho $
and
$\rho $
and
 $\sigma $
$\sigma $
Let us pick a pair of g- or h-functions
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
, and let us mark all the data associated with either of the functions with an upper index
$\psi _2$
, and let us mark all the data associated with either of the functions with an upper index
![]() $1$
or
$1$
or
![]() $2$
. Pick the number p associated with
$2$
. Pick the number p associated with
![]() $\psi _1$
as in the previous paragraph, and let
$\psi _1$
as in the previous paragraph, and let
![]() $X_t^2 = X_{I_t^2}^{J_t^2}$
be an X-block of
$X_t^2 = X_{I_t^2}^{J_t^2}$
be an X-block of
![]() $\mathcal {L}^2$
. If
$\mathcal {L}^2$
. If
![]() $I_t^2 \subseteq I_p^1$
, define
$I_t^2 \subseteq I_p^1$
, define
![]() $\rho (K_t^2)$
to be a subset of
$\rho (K_t^2)$
to be a subset of
![]() $K_p^1$
that corresponds to
$K_p^1$
that corresponds to
![]() $I_t^2$
viewed as a subset of
$I_t^2$
viewed as a subset of
![]() $I_p^1$
; similarly, if
$I_p^1$
; similarly, if
![]() $J_t^2 \subseteq J_p^1$
, we define
$J_t^2 \subseteq J_p^1$
, we define
![]() $\rho (L_t^2)$
to be a subset of
$\rho (L_t^2)$
to be a subset of
![]() $L_p^1$
that occupies the column indices
$L_p^1$
that occupies the column indices
![]() $I_t^2$
in
$I_t^2$
in
![]() $X_p^1$
. Likewise, fix
$X_p^1$
. Likewise, fix
![]() $Y_u^1 = Y_{\bar {I}_u^1}^{\bar {J}_u^1}$
in
$Y_u^1 = Y_{\bar {I}_u^1}^{\bar {J}_u^1}$
in
![]() $\mathcal {L}^1$
and define an embedding
$\mathcal {L}^1$
and define an embedding
![]() $\sigma _u$
for Y-blocks as follows. If
$\sigma _u$
for Y-blocks as follows. If
![]() $\bar {J}_t^2 \subseteq \bar {J}_u^1$
, then
$\bar {J}_t^2 \subseteq \bar {J}_u^1$
, then
![]() $\sigma _u(\bar {L}_t^2)$
is a subset of
$\sigma _u(\bar {L}_t^2)$
is a subset of
![]() $\bar {L}_u^1$
that corresponds to
$\bar {L}_u^1$
that corresponds to
![]() $\bar {J}_t^2$
; similarly, if
$\bar {J}_t^2$
; similarly, if
![]() $\bar {I}_t^2 \subseteq \bar {I}_u^1$
, then
$\bar {I}_t^2 \subseteq \bar {I}_u^1$
, then
![]() $\sigma _u(\bar {K}_t^2)$
is a subset of
$\sigma _u(\bar {K}_t^2)$
is a subset of
![]() $\bar {K}_u^1$
that occupies the indices
$\bar {K}_u^1$
that occupies the indices
![]() $\bar {I}_t^2$
in
$\bar {I}_t^2$
in
![]() $Y_u^1$
. Note: The map
$Y_u^1$
. Note: The map
![]() $\rho $
always embeds into rows or columns of
$\rho $
always embeds into rows or columns of
![]() $X_p^1$
that is viewed as a submatrix of
$X_p^1$
that is viewed as a submatrix of
![]() $\mathcal {L}^1$
, whereas the targeting block for
$\mathcal {L}^1$
, whereas the targeting block for
![]() $\sigma $
might vary depending on its subscript u.
$\sigma $
might vary depending on its subscript u.
More on subblocks
Recall that X- and Y-blocks have the form
![]() $X^{[1,\beta ]}_{[\alpha ,n]}$
and
$X^{[1,\beta ]}_{[\alpha ,n]}$
and
![]() $Y^{[\bar {\beta },n]}_{[1,\bar {\alpha }]}$
, where
$Y^{[\bar {\beta },n]}_{[1,\bar {\alpha }]}$
, where
![]() $\alpha ,\beta ,\bar {\alpha },\bar {\beta }$
are defined in Section 3.2. For two matrices
$\alpha ,\beta ,\bar {\alpha },\bar {\beta }$
are defined in Section 3.2. For two matrices
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, let us write
$A_2$
, let us write
![]() $A_1 \subseteq A_2$
if
$A_1 \subseteq A_2$
if
![]() $A_1$
is a submatrix of
$A_1$
is a submatrix of
![]() $A_2$
. Let us recall Proposition 4.3 from [Reference Gekhtman, Shapiro and Vainshtein20]:
$A_2$
. Let us recall Proposition 4.3 from [Reference Gekhtman, Shapiro and Vainshtein20]:
Proposition 8.8. Let
![]() $X_1$
,
$X_1$
,
![]() $X_2$
,
$X_2$
,
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
be arbitrary X- and Y-blocks, with
$Y_2$
be arbitrary X- and Y-blocks, with
![]() $\alpha $
’s and
$\alpha $
’s and
![]() $\beta $
’s indexed accordingly. Then the following holds:
$\beta $
’s indexed accordingly. Then the following holds:
-
(i) If
 $\beta _2 < \beta _1$
or
$\beta _2 < \beta _1$
or
 $\alpha _2> \alpha _1$
, then
$\alpha _2> \alpha _1$
, then
 $X_2 \subseteq X_1$
;
$X_2 \subseteq X_1$
; -
(ii) If
 $\bar {\beta }_2> \bar {\beta }_1$
or
$\bar {\beta }_2> \bar {\beta }_1$
or
 $\bar {\alpha }_2 < \bar {\alpha }_1$
, then
$\bar {\alpha }_2 < \bar {\alpha }_1$
, then
 $Y_2 \subseteq Y_1$
.
$Y_2 \subseteq Y_1$
.
Notice that the proposition in particular states that if
![]() $\beta _2 < \beta _1$
, then necessarily
$\beta _2 < \beta _1$
, then necessarily
![]() $\alpha _2 \geq \alpha _1$
, and likewise in all other instances. We implicitly refer to this fact in the proofs that follow.
$\alpha _2 \geq \alpha _1$
, and likewise in all other instances. We implicitly refer to this fact in the proofs that follow.
The formulas
Let us pick any g- or h-functions
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
, and let p and q be the numbers defined above for
$\psi _2$
, and let p and q be the numbers defined above for
![]() $\psi _1$
, and let
$\psi _1$
, and let
![]() $q^{\prime }$
be the index of the leading block of
$q^{\prime }$
be the index of the leading block of
![]() $\psi _2$
. Following [Reference Gekhtman, Shapiro and Vainshtein20], define B-terms:
$\psi _2$
. Following [Reference Gekhtman, Shapiro and Vainshtein20], define B-terms:
 $$ \begin{align*} B_t^{\mathrm{I}} &:= -\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2})_{\Phi_t^2}^{\bar{L}_t^2} (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2}^{\Phi_t^2}\rangle, & B_t^{\mathrm{II}} &:= \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\rho(\Psi_t^2)}^{\rho(\Psi_t^2)}(\nabla^{2}_{\mathcal{L}})_{\Psi_t^2}^{\bar{K}_{t-1}^2}(\mathcal{L}^{2})_{\bar{K}_{t-1}^2}^{\Psi_t^2}\rangle,\\ B_t^{\mathrm{III}} &:= \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\Psi_p^1}^{L_p^1\setminus \Psi_p^1} (\nabla^{2}_{\mathcal{L}})_{L_t^2\setminus \Psi_t^2}^{K_t^2} (\mathcal{L}^{2})_{K_t^2}^{\Psi_t^2}\rangle, & B_t^{\mathrm{IV}} &:= \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2}(\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2}\rangle\\ \bar{B}_t^{\mathrm{I}}(u) &:= -\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_u(\Psi_{t+1}^2)}^{\sigma_u(\Psi_{t+1})} (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{K_{t+1}^2} (\mathcal{L}^{2})_{K_{t+1}^2}^{\Psi_{t+1}^2}\rangle, & \bar{B}_t^{\mathrm{II}}(u) &:= \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\sigma_u(\Phi_t^2)}^{\sigma_u(\Phi_t^2)} (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2}\rangle\\ \bar{B}_t^{\mathrm{III}} &:= \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_q^1\setminus \Phi_q^1}^{\Phi_q^1} (\mathcal{L}^{2})_{\Phi_t^2}^{\bar{L}_t^2} (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2}^{\bar{K}_t^2\setminus \Phi_t^2}\rangle, & \bar{B}_t^{\mathrm{IV}}(u) &:= \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_u(\Psi_{t+1}^2)}^{\sigma_u(\Psi_{t+1}^2)} (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2} (\nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\Psi_{t+1}^2}\rangle. \end{align*} $$
$$ \begin{align*} B_t^{\mathrm{I}} &:= -\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2})_{\Phi_t^2}^{\bar{L}_t^2} (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2}^{\Phi_t^2}\rangle, & B_t^{\mathrm{II}} &:= \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\rho(\Psi_t^2)}^{\rho(\Psi_t^2)}(\nabla^{2}_{\mathcal{L}})_{\Psi_t^2}^{\bar{K}_{t-1}^2}(\mathcal{L}^{2})_{\bar{K}_{t-1}^2}^{\Psi_t^2}\rangle,\\ B_t^{\mathrm{III}} &:= \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\Psi_p^1}^{L_p^1\setminus \Psi_p^1} (\nabla^{2}_{\mathcal{L}})_{L_t^2\setminus \Psi_t^2}^{K_t^2} (\mathcal{L}^{2})_{K_t^2}^{\Psi_t^2}\rangle, & B_t^{\mathrm{IV}} &:= \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2}(\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2}\rangle\\ \bar{B}_t^{\mathrm{I}}(u) &:= -\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_u(\Psi_{t+1}^2)}^{\sigma_u(\Psi_{t+1})} (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{K_{t+1}^2} (\mathcal{L}^{2})_{K_{t+1}^2}^{\Psi_{t+1}^2}\rangle, & \bar{B}_t^{\mathrm{II}}(u) &:= \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\sigma_u(\Phi_t^2)}^{\sigma_u(\Phi_t^2)} (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2}\rangle\\ \bar{B}_t^{\mathrm{III}} &:= \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_q^1\setminus \Phi_q^1}^{\Phi_q^1} (\mathcal{L}^{2})_{\Phi_t^2}^{\bar{L}_t^2} (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2}^{\bar{K}_t^2\setminus \Phi_t^2}\rangle, & \bar{B}_t^{\mathrm{IV}}(u) &:= \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_u(\Psi_{t+1}^2)}^{\sigma_u(\Psi_{t+1}^2)} (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2} (\nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\Psi_{t+1}^2}\rangle. \end{align*} $$
Now, the formulas for the first four terms of equation (8.17) are:
 $$ \begin{align}\begin{aligned} \langle \pi_{<}\eta_L^1,\pi_{>}\eta_L^2\rangle &= \sum_{\beta_t^2 < \beta_p^1} (B_t^{\mathrm{I}}+B_t^{\mathrm{II}}) + \sum_{\beta_t^2=\beta_p^1}B_t^{\mathrm{III}} \\ &\quad +\sum_{\beta_t^2 < \beta_p^1} \left( \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2)}^{\rho(K_t^2)}(\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2}^{K_t^2}\right\rangle-\left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\rho(L_t^2)}^{\rho(L_t^2)}(\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2}\right\rangle\right); \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \langle \pi_{<}\eta_L^1,\pi_{>}\eta_L^2\rangle &= \sum_{\beta_t^2 < \beta_p^1} (B_t^{\mathrm{I}}+B_t^{\mathrm{II}}) + \sum_{\beta_t^2=\beta_p^1}B_t^{\mathrm{III}} \\ &\quad +\sum_{\beta_t^2 < \beta_p^1} \left( \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2)}^{\rho(K_t^2)}(\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2}^{K_t^2}\right\rangle-\left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\rho(L_t^2)}^{\rho(L_t^2)}(\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2}\right\rangle\right); \end{aligned} \end{align} $$
 $$ \begin{align}\begin{aligned} \langle \pi_{>}\eta_R^1 ,\pi_{<}\eta_R^2 \rangle & = \sum_{\bar{\alpha}_t^2 < \bar{\alpha}_q^1} (\bar{B}_t^{\mathrm{I}}(q) + \bar{B}_t^{\mathrm{II}}(q)) + \sum_{\bar{\alpha}_t^2 = \bar{\alpha}^1_q} \bar{B}_t^{\mathrm{III}} \\ &\quad + \sum_{\bar{\alpha}_t^2 < \bar{\alpha}^1_q} \left( \left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_q(\bar{L}_t^2}^{\sigma_q(\bar{L}_t^2)}(\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2}^{\bar{L}_t^2}\right\rangle - \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\sigma_q(\bar{K}_t^2)}^{\sigma_q(\bar{K}_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\bar{K}_t^2}\right\rangle \right); \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \langle \pi_{>}\eta_R^1 ,\pi_{<}\eta_R^2 \rangle & = \sum_{\bar{\alpha}_t^2 < \bar{\alpha}_q^1} (\bar{B}_t^{\mathrm{I}}(q) + \bar{B}_t^{\mathrm{II}}(q)) + \sum_{\bar{\alpha}_t^2 = \bar{\alpha}^1_q} \bar{B}_t^{\mathrm{III}} \\ &\quad + \sum_{\bar{\alpha}_t^2 < \bar{\alpha}^1_q} \left( \left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_q(\bar{L}_t^2}^{\sigma_q(\bar{L}_t^2)}(\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2}^{\bar{L}_t^2}\right\rangle - \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\sigma_q(\bar{K}_t^2)}^{\sigma_q(\bar{K}_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\bar{K}_t^2}\right\rangle \right); \end{aligned} \end{align} $$
 $$ \begin{align} \begin{aligned} \langle \gamma_c^* (\xi_L^1), \gamma_c^*(\nabla_Y^2Y)\rangle &= \sum_{\beta_t^2 \leq \beta_p^1} B_t^{\mathrm{II}} + \sum_{\bar{\beta}_t^2> \bar{\beta}_{p-1}^1} \bar{B}_t^{\mathrm{IV}}(p-1) + (\Psi_p^1 = \emptyset) \sum_{\bar{\beta}_{p-1} = \bar{\beta}_t} \bar{B}_t^{\mathrm{IV}}(p-1) \\ &\quad +\sum_{u=1}^{p} \sum_{t=1}^{q^{\prime}} \langle (\nabla^1_{\mathcal{L}} \mathcal{L}^1)^{L_u^1 \rightarrow J_u^1}_{L_u^1 \rightarrow J_u^1}, \gamma_c^* (\nabla^2_{\mathcal{L}}\mathcal{L}^2)^{\bar{L}^2_t\setminus \Psi_{t+1} \rightarrow \bar{J}^2_t \setminus \bar{\Delta}(\bar{\beta}_t)}_{\bar{L}^2_t\setminus \Psi_{t+1} \rightarrow \bar{J}^2_t \setminus \bar{\Delta}(\bar{\beta}_t)} \rangle \\ &\quad + \sum_{u=1}^{p-1} \sum_{t=1}^{q^{\prime}} \langle (\nabla^1_{\mathcal{L}} \mathcal{L}^1)^{\bar{L}^1_u\setminus \Psi_{u+1} \rightarrow \bar{J}^1_u \setminus \bar{\Delta}(\bar{\beta}_u)}_{\bar{L}^1_u\setminus \Psi_{u+1} \rightarrow \bar{J}^1_u \setminus \bar{\Delta}(\bar{\beta}_u)}, \pi_{\Gamma_2^c} (\nabla^2_{\mathcal{L}}\mathcal{L}^2)^{\bar{L}^2_t\setminus \Psi_{t+1} \rightarrow \bar{J}^2_t \setminus \bar{\Delta}(\bar{\beta}_t)}_{\bar{L}^2_t\setminus \Psi_{t+1} \rightarrow \bar{J}^2_t \setminus \bar{\Delta}(\bar{\beta}_t)}\rangle \\ &\quad + \sum_{t=1}^{q^{\prime}} (| \{ u < p \ | \ \beta_u^1 \geq \beta_{t+1}^2 \}| + |\{u < p-1 \ | \ \bar{\beta}_u < \bar{\beta}_{t} \}|) \langle (\nabla^2_{\mathcal{L}})^{\bar{K}_t^2}_{\Psi_{t+1}^2} (\mathcal{L}^2)_{\bar{K}_t^2}^{\Psi_{t+1}^2}\rangle; \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle \gamma_c^* (\xi_L^1), \gamma_c^*(\nabla_Y^2Y)\rangle &= \sum_{\beta_t^2 \leq \beta_p^1} B_t^{\mathrm{II}} + \sum_{\bar{\beta}_t^2> \bar{\beta}_{p-1}^1} \bar{B}_t^{\mathrm{IV}}(p-1) + (\Psi_p^1 = \emptyset) \sum_{\bar{\beta}_{p-1} = \bar{\beta}_t} \bar{B}_t^{\mathrm{IV}}(p-1) \\ &\quad +\sum_{u=1}^{p} \sum_{t=1}^{q^{\prime}} \langle (\nabla^1_{\mathcal{L}} \mathcal{L}^1)^{L_u^1 \rightarrow J_u^1}_{L_u^1 \rightarrow J_u^1}, \gamma_c^* (\nabla^2_{\mathcal{L}}\mathcal{L}^2)^{\bar{L}^2_t\setminus \Psi_{t+1} \rightarrow \bar{J}^2_t \setminus \bar{\Delta}(\bar{\beta}_t)}_{\bar{L}^2_t\setminus \Psi_{t+1} \rightarrow \bar{J}^2_t \setminus \bar{\Delta}(\bar{\beta}_t)} \rangle \\ &\quad + \sum_{u=1}^{p-1} \sum_{t=1}^{q^{\prime}} \langle (\nabla^1_{\mathcal{L}} \mathcal{L}^1)^{\bar{L}^1_u\setminus \Psi_{u+1} \rightarrow \bar{J}^1_u \setminus \bar{\Delta}(\bar{\beta}_u)}_{\bar{L}^1_u\setminus \Psi_{u+1} \rightarrow \bar{J}^1_u \setminus \bar{\Delta}(\bar{\beta}_u)}, \pi_{\Gamma_2^c} (\nabla^2_{\mathcal{L}}\mathcal{L}^2)^{\bar{L}^2_t\setminus \Psi_{t+1} \rightarrow \bar{J}^2_t \setminus \bar{\Delta}(\bar{\beta}_t)}_{\bar{L}^2_t\setminus \Psi_{t+1} \rightarrow \bar{J}^2_t \setminus \bar{\Delta}(\bar{\beta}_t)}\rangle \\ &\quad + \sum_{t=1}^{q^{\prime}} (| \{ u < p \ | \ \beta_u^1 \geq \beta_{t+1}^2 \}| + |\{u < p-1 \ | \ \bar{\beta}_u < \bar{\beta}_{t} \}|) \langle (\nabla^2_{\mathcal{L}})^{\bar{K}_t^2}_{\Psi_{t+1}^2} (\mathcal{L}^2)_{\bar{K}_t^2}^{\Psi_{t+1}^2}\rangle; \end{aligned} \end{align} $$
 $$ \begin{align} \begin{aligned} \langle \gamma_r (\xi_R^1), \gamma_r(X\nabla_X^2)\rangle &= \sum_{\bar{\alpha}_t^2 \leq \bar{\alpha}^1_{p-1}} \bar{B}_t^{\mathrm{II}}(p-1) + \sum_{\bar{\alpha}_t^2 \leq \bar{\alpha}_p^1} \bar{B}_t^{\mathrm{II}}(p) + \sum_{\alpha_t^2> \alpha_p^1} B_t^{\mathrm{IV}} \\ &\quad + (\Phi_p^1 = \emptyset) \sum_{\alpha_t^2 = \alpha_p^1} B_t^{\mathrm{IV}} + \sum_{u=1}^p \sum_{t=1}^{q^{\prime}} \langle (\mathcal L \nabla^1_{\mathcal{L}})^{\bar{K}_u^1 \rightarrow \bar{I}_u^1}_{\bar{K}_u^1 \rightarrow \bar{I}_u^1}, \gamma_r(\mathcal{L}^2 \nabla^2_{\mathcal{L}})^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle \\ &\quad + \sum_{u=1}^p \sum_{t=1}^{q^{\prime}} \langle (\mathcal{L}^1 \nabla^1_{\mathcal{L}})^{K_u^1 \setminus \Phi_u^1 \rightarrow I_u^1 \setminus \Delta(\alpha_u^1)}_{K_u^1 \setminus \Phi_u^1 \rightarrow I_u^1 \setminus \Delta(\alpha_u^1)}, \pi_{\Gamma_1^r} (\mathcal{L}^2 \nabla^2_{\mathcal{L}})_{K_t^2\setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2\setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle \\ &\quad + \sum_{t=1}^{q^{\prime}} (|\{u < p-1 \ | \ \bar{\alpha}_u^1 \geq \bar{\alpha}_t^2\}| + |\{u < p \ | \ \alpha_u^1 < \alpha_t^2\}|)\langle (\mathcal{L}^2)_{\Phi_t^2}^{L_t^2} (\nabla^2_{\mathcal{L}})_{L_t^2}^{\Phi_t^2}\rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle \gamma_r (\xi_R^1), \gamma_r(X\nabla_X^2)\rangle &= \sum_{\bar{\alpha}_t^2 \leq \bar{\alpha}^1_{p-1}} \bar{B}_t^{\mathrm{II}}(p-1) + \sum_{\bar{\alpha}_t^2 \leq \bar{\alpha}_p^1} \bar{B}_t^{\mathrm{II}}(p) + \sum_{\alpha_t^2> \alpha_p^1} B_t^{\mathrm{IV}} \\ &\quad + (\Phi_p^1 = \emptyset) \sum_{\alpha_t^2 = \alpha_p^1} B_t^{\mathrm{IV}} + \sum_{u=1}^p \sum_{t=1}^{q^{\prime}} \langle (\mathcal L \nabla^1_{\mathcal{L}})^{\bar{K}_u^1 \rightarrow \bar{I}_u^1}_{\bar{K}_u^1 \rightarrow \bar{I}_u^1}, \gamma_r(\mathcal{L}^2 \nabla^2_{\mathcal{L}})^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle \\ &\quad + \sum_{u=1}^p \sum_{t=1}^{q^{\prime}} \langle (\mathcal{L}^1 \nabla^1_{\mathcal{L}})^{K_u^1 \setminus \Phi_u^1 \rightarrow I_u^1 \setminus \Delta(\alpha_u^1)}_{K_u^1 \setminus \Phi_u^1 \rightarrow I_u^1 \setminus \Delta(\alpha_u^1)}, \pi_{\Gamma_1^r} (\mathcal{L}^2 \nabla^2_{\mathcal{L}})_{K_t^2\setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2\setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle \\ &\quad + \sum_{t=1}^{q^{\prime}} (|\{u < p-1 \ | \ \bar{\alpha}_u^1 \geq \bar{\alpha}_t^2\}| + |\{u < p \ | \ \alpha_u^1 < \alpha_t^2\}|)\langle (\mathcal{L}^2)_{\Phi_t^2}^{L_t^2} (\nabla^2_{\mathcal{L}})_{L_t^2}^{\Phi_t^2}\rangle. \end{aligned} \end{align} $$
By
![]() $(\Psi _p^1 = \emptyset )$
and
$(\Psi _p^1 = \emptyset )$
and
![]() $(\Phi _p^1 = \emptyset )$
we mean an indicator that’s equal to
$(\Phi _p^1 = \emptyset )$
we mean an indicator that’s equal to
![]() $1$
if the condition is satisfied and
$1$
if the condition is satisfied and
![]() $0$
otherwise. It follows from the construction that
$0$
otherwise. It follows from the construction that
![]() $(\Psi _p^1 = \emptyset ) = 1$
if and only if
$(\Psi _p^1 = \emptyset ) = 1$
if and only if
![]() $Y_p^1$
is the last block in the alternating path that defines
$Y_p^1$
is the last block in the alternating path that defines
![]() $\mathcal {L}^1$
; similarly,
$\mathcal {L}^1$
; similarly,
![]() $(\Phi _p^1 = \emptyset ) = 1$
if and only if
$(\Phi _p^1 = \emptyset ) = 1$
if and only if
![]() $X_p^1$
is the last block in the path (hence, it sits in the upper left corner of
$X_p^1$
is the last block in the path (hence, it sits in the upper left corner of
![]() $\mathcal {L}^1$
, for blocks along the path are glued in
$\mathcal {L}^1$
, for blocks along the path are glued in
![]() $\mathcal {L}$
from bottom up). The terms with indicators are not present in the empty block convention from [Reference Gekhtman, Shapiro and Vainshtein20], for their contribution is accounted for in other terms.
$\mathcal {L}$
from bottom up). The terms with indicators are not present in the empty block convention from [Reference Gekhtman, Shapiro and Vainshtein20], for their contribution is accounted for in other terms.
Lastly, let us mention the total contribution of B-terms to equation (8.17). If
![]() $\psi _1$
is an h-function, then the total contribution is
$\psi _1$
is an h-function, then the total contribution is
 $$ \begin{align}\begin{aligned} &\sum_{\substack{\bar{\alpha}^2_{t-1} < \bar{\alpha}_{p-1}^1 \\ \bar{\beta}_{t-1}^2> \bar{\beta}_{p-1}^1}}\left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\Psi_t^2)}^{\sigma_{p-1}(\Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\Psi_t^2}^{\Psi_t^2}\right\rangle + \sum_{\substack{\bar{\alpha}_{t-1}^2 \neq \bar{\alpha}_{p-1}^1\\\bar{\beta}_{t-1}^2 = \bar{\beta}_{p-1}^1}} \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\Psi_p^1}^{\Psi_p^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\Psi_t^2}^{\Psi_t^2}\right\rangle \\ &\qquad +\sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 < \bar{\beta}_{p-1}^1}} \left\langle (\mathcal{L}^{2})_{\bar{K}_{t-1}^2}^{L^2_{t-1}} (\nabla^{2}_{\mathcal{L}})_{L_{t-1}^2}^{\bar{K}_{t-1}^2}\right\rangle + \sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 \geq \bar{\beta}_{p-1}^1 }} \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_{p-1}^1}^{\bar{K}_{p-1}^1} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_{t-1}^2}^{\bar{K}_{t-1}^2}\right\rangle \\ &\qquad - \sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 \geq \bar{\beta}_{p-1}^1 }} \left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)}^{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1}^2 \setminus \Psi_t^2}^{\bar{L}_{t-1}^2 \setminus \Psi_t^2} \right\rangle + \sideset{}{^l}\sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\\bar{\beta}_{t-1}^2 = \bar{\beta}_{p-1}^1 }} \left\langle (\mathcal{L}^{2})_{\Phi^2_{t-1}}^{L_{t-1}^2}(\nabla^{2}_{\mathcal{L}})_{L_{t-1}^2}^{\Phi_{t-1}^2}\right\rangle \\ &\qquad + \sideset{}{^l}\sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 = \bar{\beta}_{p-1}^1 }}\left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_{p-1}^1}^{\bar{L}_{p-1}^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1}^2}^{\bar{L}_{t-1}^2} \right\rangle - \sideset{}{^l}\sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 = \bar{\beta}_{p-1}^1}} \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_{p-1}^1}^{\bar{K}_{p-1}^1} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_{t-1}^2}^{\bar{K}_{t-1}^2} \right\rangle, \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} &\sum_{\substack{\bar{\alpha}^2_{t-1} < \bar{\alpha}_{p-1}^1 \\ \bar{\beta}_{t-1}^2> \bar{\beta}_{p-1}^1}}\left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\Psi_t^2)}^{\sigma_{p-1}(\Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\Psi_t^2}^{\Psi_t^2}\right\rangle + \sum_{\substack{\bar{\alpha}_{t-1}^2 \neq \bar{\alpha}_{p-1}^1\\\bar{\beta}_{t-1}^2 = \bar{\beta}_{p-1}^1}} \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\Psi_p^1}^{\Psi_p^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\Psi_t^2}^{\Psi_t^2}\right\rangle \\ &\qquad +\sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 < \bar{\beta}_{p-1}^1}} \left\langle (\mathcal{L}^{2})_{\bar{K}_{t-1}^2}^{L^2_{t-1}} (\nabla^{2}_{\mathcal{L}})_{L_{t-1}^2}^{\bar{K}_{t-1}^2}\right\rangle + \sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 \geq \bar{\beta}_{p-1}^1 }} \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_{p-1}^1}^{\bar{K}_{p-1}^1} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_{t-1}^2}^{\bar{K}_{t-1}^2}\right\rangle \\ &\qquad - \sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 \geq \bar{\beta}_{p-1}^1 }} \left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)}^{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1}^2 \setminus \Psi_t^2}^{\bar{L}_{t-1}^2 \setminus \Psi_t^2} \right\rangle + \sideset{}{^l}\sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\\bar{\beta}_{t-1}^2 = \bar{\beta}_{p-1}^1 }} \left\langle (\mathcal{L}^{2})_{\Phi^2_{t-1}}^{L_{t-1}^2}(\nabla^{2}_{\mathcal{L}})_{L_{t-1}^2}^{\Phi_{t-1}^2}\right\rangle \\ &\qquad + \sideset{}{^l}\sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 = \bar{\beta}_{p-1}^1 }}\left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_{p-1}^1}^{\bar{L}_{p-1}^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1}^2}^{\bar{L}_{t-1}^2} \right\rangle - \sideset{}{^l}\sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1\\ \bar{\beta}_{t-1}^2 = \bar{\beta}_{p-1}^1}} \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_{p-1}^1}^{\bar{K}_{p-1}^1} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_{t-1}^2}^{\bar{K}_{t-1}^2} \right\rangle, \end{aligned} \end{align} $$
where
![]() $\sum ^l$
means a summation over blocks the
$\sum ^l$
means a summation over blocks the
![]() $Y_{t-1}^2$
that have their exit point strictly to the left of the exit point of
$Y_{t-1}^2$
that have their exit point strictly to the left of the exit point of
![]() $Y_{p-1^1}$
(for the definition of exit points, see Section 3.2). If
$Y_{p-1^1}$
(for the definition of exit points, see Section 3.2). If
![]() $\psi _1$
is a g-function, then the contribution is
$\psi _1$
is a g-function, then the contribution is
 $$ \begin{align} \begin{aligned} &\sum_{\substack{\beta_t^2<\beta_p^1\\\alpha_t^2>\alpha_p^1}}\left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\Phi_t^2}^{\Phi_t^2} \right\rangle + \sum_{\substack{\beta_t^2 \neq \beta_p^1\\ \alpha_t^2 = \alpha_p^1}}\left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\Phi_p^1}^{\Phi_p^1} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\Phi_t^2}^{\Phi_t^2}\right\rangle \\ &\quad +\sum_{\substack{\beta_t^2 = \beta_p^1\\ \alpha_t^2 < \alpha_p^1}} \left\langle (\mathcal{L}^{2})_{\bar{K}_{t-1}^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\bar{K}_{t-1}^2}\right\rangle + \sum_{\substack{\beta_t^2 = \beta_p^1 \\ \alpha_t^2 \geq \alpha_p^1}} \left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{L_p^1}^{L_p^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2} \right\rangle \\ &\quad -\sum_{\substack{\beta_t^2=\beta_p^1 \\ \alpha_t^2 \geq \alpha_p^1}}\left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2\setminus \Phi_t^2)}^{\rho(K_t^2\setminus \Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \right\rangle +\sideset{}{^a}\sum_{\substack{\beta_t^2 = \beta_p^1\\\alpha_t^2=\alpha_p^1}}\mathop{} \left\langle (\mathcal{L}^{2})_{\bar{K}_{t-1}^2}^{\Psi_t^2} (\nabla^{2}_{\mathcal{L}})_{\Psi_t^2}^{\bar{K}_{t-1}^2}\right\rangle \\ &\quad + \sideset{}{^a}\sum_{\substack{\beta_t^2 = \beta_p^1\\ \alpha_t^2 = \alpha_p^1}} \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{K_p^1}^{K_p^1} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2}^{K_t^2}\right\rangle - \sideset{}{^a} \sum_{\substack{\beta_t^2 = \beta_p^1\\ \alpha_t^2 = \alpha_p^1}}\left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{L_p^1}^{L_p^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2}\right\rangle \\ &\quad + \sum_{\bar{\beta}_t^2> \bar{\beta}_{p-1}^1} \left\langle (\mathcal{L}^{2})_{\bar{K}_t^2}^{\Psi_{t+1}^2} (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2}\right\rangle + \sum_{\bar{\alpha}_{t}^2 \leq \bar{\alpha}_{p-1}^1} \left\langle (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2}\right\rangle, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\sum_{\substack{\beta_t^2<\beta_p^1\\\alpha_t^2>\alpha_p^1}}\left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\Phi_t^2}^{\Phi_t^2} \right\rangle + \sum_{\substack{\beta_t^2 \neq \beta_p^1\\ \alpha_t^2 = \alpha_p^1}}\left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\Phi_p^1}^{\Phi_p^1} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\Phi_t^2}^{\Phi_t^2}\right\rangle \\ &\quad +\sum_{\substack{\beta_t^2 = \beta_p^1\\ \alpha_t^2 < \alpha_p^1}} \left\langle (\mathcal{L}^{2})_{\bar{K}_{t-1}^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\bar{K}_{t-1}^2}\right\rangle + \sum_{\substack{\beta_t^2 = \beta_p^1 \\ \alpha_t^2 \geq \alpha_p^1}} \left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{L_p^1}^{L_p^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2} \right\rangle \\ &\quad -\sum_{\substack{\beta_t^2=\beta_p^1 \\ \alpha_t^2 \geq \alpha_p^1}}\left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2\setminus \Phi_t^2)}^{\rho(K_t^2\setminus \Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \right\rangle +\sideset{}{^a}\sum_{\substack{\beta_t^2 = \beta_p^1\\\alpha_t^2=\alpha_p^1}}\mathop{} \left\langle (\mathcal{L}^{2})_{\bar{K}_{t-1}^2}^{\Psi_t^2} (\nabla^{2}_{\mathcal{L}})_{\Psi_t^2}^{\bar{K}_{t-1}^2}\right\rangle \\ &\quad + \sideset{}{^a}\sum_{\substack{\beta_t^2 = \beta_p^1\\ \alpha_t^2 = \alpha_p^1}} \left\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{K_p^1}^{K_p^1} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2}^{K_t^2}\right\rangle - \sideset{}{^a} \sum_{\substack{\beta_t^2 = \beta_p^1\\ \alpha_t^2 = \alpha_p^1}}\left\langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{L_p^1}^{L_p^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2}\right\rangle \\ &\quad + \sum_{\bar{\beta}_t^2> \bar{\beta}_{p-1}^1} \left\langle (\mathcal{L}^{2})_{\bar{K}_t^2}^{\Psi_{t+1}^2} (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2}\right\rangle + \sum_{\bar{\alpha}_{t}^2 \leq \bar{\alpha}_{p-1}^1} \left\langle (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2}\right\rangle, \end{aligned} \end{align} $$
where
![]() $\sum ^a$
means that the summation is taken over blocks the
$\sum ^a$
means that the summation is taken over blocks the
![]() $X_t^2$
that have their exit point strictly above the exit point of
$X_t^2$
that have their exit point strictly above the exit point of
![]() $X_p^1$
.
$X_p^1$
.
8.6 Computation of
 $\{y(h_{ii}), \psi \}$
$\{y(h_{ii}), \psi \}$
Let
![]() $\psi $
be an arbitrary g- or h-function, and let
$\psi $
be an arbitrary g- or h-function, and let
![]() $h_{ii}$
be fixed,
$h_{ii}$
be fixed,
![]() $2 \leq i \leq n$
. For the shorthand notation from Section 8.4, the first function in this section is
$2 \leq i \leq n$
. For the shorthand notation from Section 8.4, the first function in this section is
![]() $\log h_{i-1,i} - \log h_{i,i+1}$
and the second function is
$\log h_{i-1,i} - \log h_{i,i+1}$
and the second function is
![]() $\log \psi $
, meaning that if an operator has an upper index
$\log \psi $
, meaning that if an operator has an upper index
![]() $1$
or
$1$
or
![]() $2$
, it’s applied to the first or the second function, respectively. We also assume throughout the subsection that a pair
$2$
, it’s applied to the first or the second function, respectively. We also assume throughout the subsection that a pair
![]() $(R_0^r,R_0^c)$
is chosen so that equation (3.6) holds.
$(R_0^r,R_0^c)$
is chosen so that equation (3.6) holds.
Proposition 8.9. The bracket of
![]() $y(h_{ii})$
and
$y(h_{ii})$
and
![]() $\psi $
can be expressed as
$\psi $
can be expressed as
 $$ \begin{align}\begin{aligned} \{\log y(h_{ii}),\log \psi\} &= -\langle \pi_{<} \eta_L^1, \pi_{>} \eta_L^2 \rangle - \langle \pi_{>} \eta_R^1, \pi_{<} \eta_R^2 \rangle \\ &\quad + \langle \gamma_r \xi_R^1, \gamma_r X \nabla_X^2 \rangle + \langle \gamma_c^* \xi_L^1, \gamma_c^* \nabla_Y^2 Y \rangle \\ &\quad + \langle \pi_{\hat{\Gamma}_2^c} e_{ii}, \pi_{\hat{\Gamma}_2^c} \nabla_Y^2 Y\rangle - \langle e_{i-1,i-1}, \eta_R^2 \rangle. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \{\log y(h_{ii}),\log \psi\} &= -\langle \pi_{<} \eta_L^1, \pi_{>} \eta_L^2 \rangle - \langle \pi_{>} \eta_R^1, \pi_{<} \eta_R^2 \rangle \\ &\quad + \langle \gamma_r \xi_R^1, \gamma_r X \nabla_X^2 \rangle + \langle \gamma_c^* \xi_L^1, \gamma_c^* \nabla_Y^2 Y \rangle \\ &\quad + \langle \pi_{\hat{\Gamma}_2^c} e_{ii}, \pi_{\hat{\Gamma}_2^c} \nabla_Y^2 Y\rangle - \langle e_{i-1,i-1}, \eta_R^2 \rangle. \end{aligned} \end{align} $$
Proof. Recall that the y-coordinate of
![]() $h_{ii}$
is given by
$h_{ii}$
is given by
Set
![]() $f:= f_{1,n-i}/f_{1,n-i+1}$
. Using the diagonal derivatives formulas for f from Section 8.1 and formula (7.1), we can express the bracket
$f:= f_{1,n-i}/f_{1,n-i+1}$
. Using the diagonal derivatives formulas for f from Section 8.1 and formula (7.1), we can express the bracket
![]() $\{\log f, \log \psi \}$
as
$\{\log f, \log \psi \}$
as
Combining the latter formula with the expression for D from equation (8.18),
![]() $D+ \{\log f, \log \psi \}$
becomes
$D+ \{\log f, \log \psi \}$
becomes
 $$\begin{align*}\begin{aligned} &-\langle \pi_{\Gamma_2^c} e_{ii}, \nabla^2_Y Y\rangle - \langle e_{i-1,i-1}, \gamma_r(X\nabla^2_X) \rangle + \langle R_0^c e_{ii}, E_L^2 \rangle - \langle R_0^r e_{i-1,i-1}, E_R^2 \rangle\\ &\qquad +\langle e_{ii}, \nabla^2_Y Y\rangle - \langle e_{i-1,i-1}, Y\nabla^2_Y \rangle - \langle R_0^c e_{ii}, E_L^2\rangle + \langle R_0^r e_{i-1,i-1}, E_R^2 \rangle \\ &\quad = \langle \pi_{\hat{\Gamma}_2^c} e_{ii}, \nabla^2_Y Y\rangle - \langle e_{i-1,i-1}, \eta_R^2 \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &-\langle \pi_{\Gamma_2^c} e_{ii}, \nabla^2_Y Y\rangle - \langle e_{i-1,i-1}, \gamma_r(X\nabla^2_X) \rangle + \langle R_0^c e_{ii}, E_L^2 \rangle - \langle R_0^r e_{i-1,i-1}, E_R^2 \rangle\\ &\qquad +\langle e_{ii}, \nabla^2_Y Y\rangle - \langle e_{i-1,i-1}, Y\nabla^2_Y \rangle - \langle R_0^c e_{ii}, E_L^2\rangle + \langle R_0^r e_{i-1,i-1}, E_R^2 \rangle \\ &\quad = \langle \pi_{\hat{\Gamma}_2^c} e_{ii}, \nabla^2_Y Y\rangle - \langle e_{i-1,i-1}, \eta_R^2 \rangle. \end{aligned} \end{align*}$$
Now, applying equation (8.17) to
![]() $\{\log h_{i-1,i} - \log h_{i,i+1}, \log \psi \}$
the formula follows.
$\{\log h_{i-1,i} - \log h_{i,i+1}, \log \psi \}$
the formula follows.
Corollary 8.9.1. As a consequence,
![]() $\{\log y(h_{ii}), \log h_{jj}\} = \delta _{ij}$
for any j.
$\{\log y(h_{ii}), \log h_{jj}\} = \delta _{ij}$
for any j.
Proof. The first two terms of equation (8.32) vanish, for
![]() $Y\nabla _Y \log h_{jj} \in \mathfrak {b}_+$
and
$Y\nabla _Y \log h_{jj} \in \mathfrak {b}_+$
and
![]() $\nabla _Y \log h_{jj} \cdot Y \in \mathfrak {b}_-$
; since
$\nabla _Y \log h_{jj} \cdot Y \in \mathfrak {b}_-$
; since
![]() $h_{jj}$
doesn’t depend on X, the third term vanishes as well. Now, recall from Section 8.1 that
$h_{jj}$
doesn’t depend on X, the third term vanishes as well. Now, recall from Section 8.1 that
and
![]() $\xi _L (\log h_{i-1,i} -\log h_{i,i+1}) = e_{ii}$
, where
$\xi _L (\log h_{i-1,i} -\log h_{i,i+1}) = e_{ii}$
, where
![]() $\Delta (j,n) = \sum _{k=j}^{n} e_{kk}$
. Therefore,
$\Delta (j,n) = \sum _{k=j}^{n} e_{kk}$
. Therefore,
 $$\begin{align*}\begin{aligned} \{\log y(h_{ii}),\log \psi\} &= \langle \gamma_c^* e_{ii}, \gamma_c^*\Delta(j,n) \rangle + \langle \pi_{\hat{\Gamma}^c_2}e_{ii}, \pi_{\hat{\Gamma}^c_2} \Delta(j,n) \rangle - \langle e_{i-1,i-1}, \Delta(j,n) \rangle \\ &= \langle e_{ii} - e_{i-1,i-1}, \Delta(j,n) \rangle = \delta_{ij}.\end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{\log y(h_{ii}),\log \psi\} &= \langle \gamma_c^* e_{ii}, \gamma_c^*\Delta(j,n) \rangle + \langle \pi_{\hat{\Gamma}^c_2}e_{ii}, \pi_{\hat{\Gamma}^c_2} \Delta(j,n) \rangle - \langle e_{i-1,i-1}, \Delta(j,n) \rangle \\ &= \langle e_{ii} - e_{i-1,i-1}, \Delta(j,n) \rangle = \delta_{ij}.\end{aligned} \end{align*}$$
Lemma 8.10. The following formulas for the last two terms of equation (8.32) hold:
 $$\begin{align*}\langle \pi_{\hat{\Gamma}_2^c} e_{ii}, \pi_{\hat{\Gamma}_2^c} \nabla_Y^2 Y\rangle = \sum_{t=1}^{q^{\prime}} \langle \pi_{\hat{\Gamma}_2^c} e_{ii}, \begin{bmatrix} 0 & 0\\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2} \end{bmatrix} \rangle; \end{align*}$$
$$\begin{align*}\langle \pi_{\hat{\Gamma}_2^c} e_{ii}, \pi_{\hat{\Gamma}_2^c} \nabla_Y^2 Y\rangle = \sum_{t=1}^{q^{\prime}} \langle \pi_{\hat{\Gamma}_2^c} e_{ii}, \begin{bmatrix} 0 & 0\\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2} \end{bmatrix} \rangle; \end{align*}$$
 $$\begin{align*}-\langle e_{i-1,i-1}, \eta_R^2 \rangle = - \sum_{t=1}^{q^{\prime}} \langle e_{i-1,i-1}, \begin{bmatrix} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\bar{K}_t^2} & 0 \\ 0 & 0 \end{bmatrix} \rangle - \sum_{t=1}^{q^{\prime}} \langle e_{i-1,i-1}, \gamma_r \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle. \end{align*}$$
$$\begin{align*}-\langle e_{i-1,i-1}, \eta_R^2 \rangle = - \sum_{t=1}^{q^{\prime}} \langle e_{i-1,i-1}, \begin{bmatrix} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\bar{K}_t^2} & 0 \\ 0 & 0 \end{bmatrix} \rangle - \sum_{t=1}^{q^{\prime}} \langle e_{i-1,i-1}, \gamma_r \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle. \end{align*}$$
Proof. The gradient
![]() $\nabla ^2_Y Y$
can be expressed as
$\nabla ^2_Y Y$
can be expressed as
 $$\begin{align*}\begin{aligned} \nabla^2_Y Y &= \sum_{t=1}^{q^{\prime}} (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2 \rightarrow \bar{J}_t^2}^{\bar{K}_t^2 \rightarrow \bar{I}_t^2} \cdot Y = \sum_{t=1}^{q^{\prime}} \begin{bmatrix} 0 & 0 \\ (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2}^{\bar{K}_t^2} Y_{\hat{\bar{J}}_t^2}^{\bar{I}_t^2} & (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\bar{L}_t^2} \end{bmatrix} \\ &= \sum_{t=1}^{q^{\prime}} \begin{bmatrix} 0 & 0 & 0 \\ (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2} Y_{\hat{\bar{J}}_t^2}^{\bar{I}_t^2} & (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\Psi_{t+1}^2} & (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\bar{K}_t^2 \setminus \Psi_{t+1}^2} \\ (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{K}_t^2} Y_{\hat{\bar{J}}_t^2}^{\bar{I}_t^2} & (\nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2 \setminus \Psi_{t+1}^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\Psi_{t+1}^2} & (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2} \end{bmatrix}, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \nabla^2_Y Y &= \sum_{t=1}^{q^{\prime}} (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2 \rightarrow \bar{J}_t^2}^{\bar{K}_t^2 \rightarrow \bar{I}_t^2} \cdot Y = \sum_{t=1}^{q^{\prime}} \begin{bmatrix} 0 & 0 \\ (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2}^{\bar{K}_t^2} Y_{\hat{\bar{J}}_t^2}^{\bar{I}_t^2} & (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\bar{L}_t^2} \end{bmatrix} \\ &= \sum_{t=1}^{q^{\prime}} \begin{bmatrix} 0 & 0 & 0 \\ (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2} Y_{\hat{\bar{J}}_t^2}^{\bar{I}_t^2} & (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\Psi_{t+1}^2} & (\nabla^{2}_{\mathcal{L}})_{\Psi_{t+1}^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\bar{K}_t^2 \setminus \Psi_{t+1}^2} \\ (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{K}_t^2} Y_{\hat{\bar{J}}_t^2}^{\bar{I}_t^2} & (\nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2 \setminus \Psi_{t+1}^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\Psi_{t+1}^2} & (\nabla^{2}_{\mathcal{L}})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{K}_t^2} (\mathcal{L}^{2})_{\bar{K}_t^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2} \end{bmatrix}, \end{aligned} \end{align*}$$
where
![]() $\hat {\bar {J}}_t^2 = [1,n] \setminus \bar {J}_t^2$
. Now, if one projects
$\hat {\bar {J}}_t^2 = [1,n] \setminus \bar {J}_t^2$
. Now, if one projects
![]() $\nabla ^2_Y Y$
onto the diagonal, only the central blocks survive; a further application of
$\nabla ^2_Y Y$
onto the diagonal, only the central blocks survive; a further application of
![]() $\pi _{\hat {\Gamma }_2^c}$
nullifies the middle block, for it occupies the location
$\pi _{\hat {\Gamma }_2^c}$
nullifies the middle block, for it occupies the location
![]() $\bar {\Delta }(\bar {\alpha }_t) \times \bar {\Delta }(\bar {\alpha }_t)$
, and thus the first formula follows. A block formula for
$\bar {\Delta }(\bar {\alpha }_t) \times \bar {\Delta }(\bar {\alpha }_t)$
, and thus the first formula follows. A block formula for
![]() $\eta _R^2$
, though easily derivable in a similar fashion, was deduced in [Reference Gekhtman, Shapiro and Vainshtein20]; hence, the second formula follows.
$\eta _R^2$
, though easily derivable in a similar fashion, was deduced in [Reference Gekhtman, Shapiro and Vainshtein20]; hence, the second formula follows.
Proposition 8.11. The following formula holds:
 $$\begin{align*}\{\log y(h_{ii}), \log\psi \} = \begin{cases} 1,\ &\psi = h_{ii} \\ 0,\ &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\{\log y(h_{ii}), \log\psi \} = \begin{cases} 1,\ &\psi = h_{ii} \\ 0,\ &\text{otherwise.} \end{cases} \end{align*}$$
Proof. First of all, let us assume that
![]() $\psi $
is not equal to some
$\psi $
is not equal to some
![]() $h_{jj}$
, for this case is covered by Corollary 8.9.1. Recall that Y blocks have the form
$h_{jj}$
, for this case is covered by Corollary 8.9.1. Recall that Y blocks have the form
![]() $Y_t = Y_{[1, \bar {\alpha }_t]}^{[\bar {\beta }_t,n]}$
. The assumption
$Y_t = Y_{[1, \bar {\alpha }_t]}^{[\bar {\beta }_t,n]}$
. The assumption
![]() $\psi \neq h_{jj}$
for all j implies that
$\psi \neq h_{jj}$
for all j implies that
![]() $\bar {\beta }_{p-1}^1 \leq \bar {\beta }_{t-1}^2$
and
$\bar {\beta }_{p-1}^1 \leq \bar {\beta }_{t-1}^2$
and
![]() $\bar {\alpha }_{p-1}^1 \geq \bar {\alpha }_{t-1}^2$
for all t. Indeed, if on the contrary
$\bar {\alpha }_{p-1}^1 \geq \bar {\alpha }_{t-1}^2$
for all t. Indeed, if on the contrary
![]() $\bar {\beta }_{p-1}^1> \bar {\beta }_{t-1}^2$
, then
$\bar {\beta }_{p-1}^1> \bar {\beta }_{t-1}^2$
, then
![]() $\bar {\beta }_{p-1}^1 = 2$
and
$\bar {\beta }_{p-1}^1 = 2$
and
![]() $\bar {\beta }_{t-1}^2 = 1$
; this means that
$\bar {\beta }_{t-1}^2 = 1$
; this means that
![]() $Y_{t-1}^2 = Y$
, and hence
$Y_{t-1}^2 = Y$
, and hence
![]() $\psi $
must be some
$\psi $
must be some
![]() $h_{jj}$
. A similar reasoning applies to
$h_{jj}$
. A similar reasoning applies to
![]() $\bar {\alpha }$
, for
$\bar {\alpha }$
, for
![]() $\bar {\alpha }^1_{p-1} \in \{n,n-1\}$
.
$\bar {\alpha }^1_{p-1} \in \{n,n-1\}$
.
Next, we need to collect block formulas of all terms in equation (8.32), which are given in Section 8.5 and in Lemma 8.10. Under the stated assumption, some of the terms of the block formulas readily vanish. Indeed, observe the following:
-
• All terms that do not contain the first function vanish (for instance,
 $\sum \langle (\mathcal {L}^{2})_{\bar {K}_{t-1}^2}^{L_{t-1}^2} (\nabla ^{2}_{\mathcal {L}})_{L_{t-1}^2}^{\bar {K}_{t-1}^2}\rangle = 0$
);
$\sum \langle (\mathcal {L}^{2})_{\bar {K}_{t-1}^2}^{L_{t-1}^2} (\nabla ^{2}_{\mathcal {L}})_{L_{t-1}^2}^{\bar {K}_{t-1}^2}\rangle = 0$
); -
• The sums
 $\sum ^l$
vanish. Indeed, these are sums over blocks
$\sum ^l$
vanish. Indeed, these are sums over blocks
 $Y_{t}^2$
which have their exit point to the left of
$Y_{t}^2$
which have their exit point to the left of
 $Y_{p-1}^1$
, hence the exit point of
$Y_{p-1}^1$
, hence the exit point of
 $Y_{t}^2$
must be
$Y_{t}^2$
must be
 $(1,1)$
. That’s precisely the case
$(1,1)$
. That’s precisely the case
 $\psi = h_{jj}$
, which was considered in Corollary 8.9.1;
$\psi = h_{jj}$
, which was considered in Corollary 8.9.1; -
•
 $(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{K_p^1}^{K_p^1} = 0$
, for the leading block of the first function is
$(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{K_p^1}^{K_p^1} = 0$
, for the leading block of the first function is
 $Y_{p-1}^1$
and
$Y_{p-1}^1$
and
 $K_p^1$
spans the rows of
$K_p^1$
spans the rows of
 $X_p^1$
;
$X_p^1$
; -
•
 $(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})_{\rho (L_t^2)}^{\rho (L_t^2)} = 0$
under the assumption
$(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})_{\rho (L_t^2)}^{\rho (L_t^2)} = 0$
under the assumption
 $\beta _t^2 < \beta _p^1$
, for then
$\beta _t^2 < \beta _p^1$
, for then
 $\rho (L_t^2) \subseteq L_p^1 \setminus \Psi _p^1$
;
$\rho (L_t^2) \subseteq L_p^1 \setminus \Psi _p^1$
; -
•
 $(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})_{L_u^1}^{L_u^1} = 0$
for all
$(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})_{L_u^1}^{L_u^1} = 0$
for all
 $u < p$
;
$u < p$
; -
• For
 $u = p$
, even though
$u = p$
, even though
 $(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})_{L_p^1}^{L_p^1}$
might be nonzero, the only term it belongs to vanishes: because if
$(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})_{L_p^1}^{L_p^1}$
might be nonzero, the only term it belongs to vanishes: because if $$\begin{align*}\begin{aligned} & \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})^{L_p^1 \rightarrow J_p^1}_{L_p^1 \rightarrow J_p^1}, \gamma_c^* (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)} \rangle\\ &\quad = \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})^{\Psi_p^1 \rightarrow \bar{\Delta}(\bar{\beta}_{p-1}^1)}_{\Psi_p^1 \rightarrow \bar{\Delta}(\bar{\beta}_{p-1}^1)}, (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)} \rangle = 0, \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} & \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})^{L_p^1 \rightarrow J_p^1}_{L_p^1 \rightarrow J_p^1}, \gamma_c^* (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)} \rangle\\ &\quad = \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})^{\Psi_p^1 \rightarrow \bar{\Delta}(\bar{\beta}_{p-1}^1)}_{\Psi_p^1 \rightarrow \bar{\Delta}(\bar{\beta}_{p-1}^1)}, (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)} \rangle = 0, \end{aligned}\end{align*}$$
 $\bar {\Delta }(\bar {\beta }_{p-1}^1)$
is nontrivial, it’s
$\bar {\Delta }(\bar {\beta }_{p-1}^1)$
is nontrivial, it’s
 $[1,1_+]$
(which is the leftmost Y-run, hence if we cut out a Y-run in the second slot, the nonzero blocks in the second matrix never overlap with such in the first one).
$[1,1_+]$
(which is the leftmost Y-run, hence if we cut out a Y-run in the second slot, the nonzero blocks in the second matrix never overlap with such in the first one).
-
•
 $(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{K_{u}^1 \setminus \Phi _u^1}^{K_{u}^1 \setminus \Phi _u^1} = 0$
for all u;
$(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{K_{u}^1 \setminus \Phi _u^1}^{K_{u}^1 \setminus \Phi _u^1} = 0$
for all u; -
• All terms that involve the blocks of the first function with indices
 $u < p-1$
vanish.
$u < p-1$
vanish.
Additionally, one term requires a special care. Observe that
 $$\begin{align*}(\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_{p-1}^1 \setminus \Psi_p^1 \rightarrow \bar{J}_{p-1}^1 \setminus \bar{\Delta}(\bar{\beta}_{p}^1)}^{\bar{L}_{p-1}^1 \setminus \Psi_p^1 \rightarrow \bar{J}_{p-1}^1 \setminus \bar{\Delta}(\bar{\beta}_{p}^1)} = \begin{cases} e_{ii}, \ &i \notin \bar{\Delta}(\bar{\beta}_{p}^1) \\ 0, \ &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}(\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_{p-1}^1 \setminus \Psi_p^1 \rightarrow \bar{J}_{p-1}^1 \setminus \bar{\Delta}(\bar{\beta}_{p}^1)}^{\bar{L}_{p-1}^1 \setminus \Psi_p^1 \rightarrow \bar{J}_{p-1}^1 \setminus \bar{\Delta}(\bar{\beta}_{p}^1)} = \begin{cases} e_{ii}, \ &i \notin \bar{\Delta}(\bar{\beta}_{p}^1) \\ 0, \ &\text{otherwise.} \end{cases} \end{align*}$$
Since we can assume
![]() $\bar {\beta }_{p-1}^1 \leq \bar {\beta }_{t-1}^2$
for any t, we find that
$\bar {\beta }_{p-1}^1 \leq \bar {\beta }_{t-1}^2$
for any t, we find that
 $$\begin{align*} & \sum_{t=1}^{q^{\prime}} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_{p-1}^1 \setminus \Psi_p^1 \rightarrow \bar{J}_{p-1}^1 \setminus \bar{\Delta}(\bar{\beta}_{p}^1)}^{\bar{L}_{p-1}^1 \setminus \Psi_p^1 \rightarrow \bar{J}_{p-1}^1 \setminus \bar{\Delta}(\bar{\beta}_{p}^1)}, \pi_{\Gamma_2^c} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t}^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)}^{\bar{L}_{t}^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)} \rangle\\ &\quad = \sum_{t=1}^{q^{\prime}}\langle \pi_{\Gamma_2^c} e_{ii}, \begin{bmatrix}0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2}\end{bmatrix} \rangle. \end{align*}$$
$$\begin{align*} & \sum_{t=1}^{q^{\prime}} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_{p-1}^1 \setminus \Psi_p^1 \rightarrow \bar{J}_{p-1}^1 \setminus \bar{\Delta}(\bar{\beta}_{p}^1)}^{\bar{L}_{p-1}^1 \setminus \Psi_p^1 \rightarrow \bar{J}_{p-1}^1 \setminus \bar{\Delta}(\bar{\beta}_{p}^1)}, \pi_{\Gamma_2^c} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t}^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)}^{\bar{L}_{t}^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)} \rangle\\ &\quad = \sum_{t=1}^{q^{\prime}}\langle \pi_{\Gamma_2^c} e_{ii}, \begin{bmatrix}0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2}\end{bmatrix} \rangle. \end{align*}$$
Indeed, this formula follows right away if
![]() $i \notin \bar {\Delta }(\bar {\beta }_p^1)$
. But if
$i \notin \bar {\Delta }(\bar {\beta }_p^1)$
. But if
![]() $i \in \bar {\Delta }(\bar {\beta }_p^1)$
, the LHS is zero; so is the expression on the right, for
$i \in \bar {\Delta }(\bar {\beta }_p^1)$
, the LHS is zero; so is the expression on the right, for
![]() $\bar {\Delta }(\bar {\beta }_p^1)$
is the leftmost Y-run and we cut out a Y-run in the second slot.
$\bar {\Delta }(\bar {\beta }_p^1)$
is the leftmost Y-run and we cut out a Y-run in the second slot.
With all above in mind, formula (8.32) expands in terms of blocks as
 $$\begin{align*}\begin{aligned} \{\log y(h_{ii}), \log \psi\} &= -\sum_{\bar{\alpha}_t^2 < \bar{\alpha}_{p-1}^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_t^2)}^{\sigma_{p-1}(\bar{L}_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2}^{\bar{L}_t^2} \rangle +\sum_{\bar{\alpha}_t^2 < \bar{\alpha}_{p-1}^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\sigma_{p-1}(\bar{K}_t^2)}^{\sigma_{p-1}(\bar{K}_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\bar{K}_t^2} \rangle \\ &\quad + \sum_{t=1}^{q^{\prime}} \langle \pi_{\Gamma_2^c} e_{ii}, \begin{bmatrix}0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2}\end{bmatrix} \rangle + \sum_{\bar{\alpha}_{t-1}^2 < \bar{\alpha}_{p-1}^1 } \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\Psi_t^2)}^{\sigma_{p-1}(\Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\Psi_t^2}^{\Psi_t^2} \rangle\\ &\quad +\sum_{t=1}^{q^{\prime}} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_{p-1}^1 \rightarrow \bar{I}_{p-1}^1}^{\bar{K}_{p-1}^1 \rightarrow \bar{I}_{p-1}^1}, \gamma_r (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle \\ &\quad - \sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1 \\ \bar{\beta}_{t-1}^2 \geq \bar{\beta}_{p-1}^1}} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)}^{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1}^2 \setminus \Psi_t^2}^{\bar{L}_{t-1}^2 \setminus \Psi_t^2} \rangle \\ &\quad + \sum_{\substack{\bar{\alpha}_{t-1} = \bar{\alpha}_{p-1} \\ \bar{\beta}^2_{t-1} \geq \bar{\beta}_{p-1}^1}} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_{p-1}}^{\bar{K}_{p-1}} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_{t-1}^2}^{\bar{K}_{t-1}^2} \rangle + \sum_{t=1}^{q^{\prime}} \langle \pi_{\hat{\Gamma}_2^c}e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t \setminus \Psi_{t+1}}^{\bar{L}_t \setminus \Psi_{t+1}} \end{bmatrix} \rangle \\ &\quad - \sum_{t=1}^{q^{\prime}} \langle e_{i-1,i-1}, \begin{bmatrix} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\bar{K}_t^2} & 0 \\ 0 & 0 \end{bmatrix} \rangle - \sum_{t=1}^{q^{\prime}} \langle e_{i-1,i-1}, \gamma_r \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{\log y(h_{ii}), \log \psi\} &= -\sum_{\bar{\alpha}_t^2 < \bar{\alpha}_{p-1}^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_t^2)}^{\sigma_{p-1}(\bar{L}_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2}^{\bar{L}_t^2} \rangle +\sum_{\bar{\alpha}_t^2 < \bar{\alpha}_{p-1}^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\sigma_{p-1}(\bar{K}_t^2)}^{\sigma_{p-1}(\bar{K}_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\bar{K}_t^2} \rangle \\ &\quad + \sum_{t=1}^{q^{\prime}} \langle \pi_{\Gamma_2^c} e_{ii}, \begin{bmatrix}0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2}\end{bmatrix} \rangle + \sum_{\bar{\alpha}_{t-1}^2 < \bar{\alpha}_{p-1}^1 } \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\Psi_t^2)}^{\sigma_{p-1}(\Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\Psi_t^2}^{\Psi_t^2} \rangle\\ &\quad +\sum_{t=1}^{q^{\prime}} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_{p-1}^1 \rightarrow \bar{I}_{p-1}^1}^{\bar{K}_{p-1}^1 \rightarrow \bar{I}_{p-1}^1}, \gamma_r (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle \\ &\quad - \sum_{\substack{\bar{\alpha}_{t-1}^2 = \bar{\alpha}_{p-1}^1 \\ \bar{\beta}_{t-1}^2 \geq \bar{\beta}_{p-1}^1}} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)}^{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1}^2 \setminus \Psi_t^2}^{\bar{L}_{t-1}^2 \setminus \Psi_t^2} \rangle \\ &\quad + \sum_{\substack{\bar{\alpha}_{t-1} = \bar{\alpha}_{p-1} \\ \bar{\beta}^2_{t-1} \geq \bar{\beta}_{p-1}^1}} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_{p-1}}^{\bar{K}_{p-1}} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_{t-1}^2}^{\bar{K}_{t-1}^2} \rangle + \sum_{t=1}^{q^{\prime}} \langle \pi_{\hat{\Gamma}_2^c}e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t \setminus \Psi_{t+1}}^{\bar{L}_t \setminus \Psi_{t+1}} \end{bmatrix} \rangle \\ &\quad - \sum_{t=1}^{q^{\prime}} \langle e_{i-1,i-1}, \begin{bmatrix} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\bar{K}_t^2}^{\bar{K}_t^2} & 0 \\ 0 & 0 \end{bmatrix} \rangle - \sum_{t=1}^{q^{\prime}} \langle e_{i-1,i-1}, \gamma_r \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle. \end{aligned} \end{align*}$$
Now, we combine the remaining terms to obtain zero. The conditions under the second and the seventh sums combine into a condition satisfied for all blocks, and the resulting sum cancels out with the ninth one. The fifth sum cancels out with the last one. The third sum combines with the eighth one, and the resulting sum is
 $$ \begin{align} \begin{aligned} \sum_{t=1}^{q^{\prime}} \langle \pi_{\Gamma_2^c} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2\setminus \Psi_{t+1}^2}^{\bar{L}_t^2\setminus \Psi_{t+1}^2}\end{bmatrix} \rangle + \sum_{t=1}^{q^{\prime}} \langle \pi_{\hat{\Gamma}_2^c} e_{ii},& \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2\setminus \Psi_{t+1}^2}^{\bar{L}_t^2\setminus \Psi_{t+1}^2}\end{bmatrix} \rangle = \sum_{t=1}^{q^{\prime}} \langle e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2\setminus \Psi_{t+1}^2}^{\bar{L}_t^2\setminus \Psi_{t+1}^2}\end{bmatrix} \rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sum_{t=1}^{q^{\prime}} \langle \pi_{\Gamma_2^c} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2\setminus \Psi_{t+1}^2}^{\bar{L}_t^2\setminus \Psi_{t+1}^2}\end{bmatrix} \rangle + \sum_{t=1}^{q^{\prime}} \langle \pi_{\hat{\Gamma}_2^c} e_{ii},& \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2\setminus \Psi_{t+1}^2}^{\bar{L}_t^2\setminus \Psi_{t+1}^2}\end{bmatrix} \rangle = \sum_{t=1}^{q^{\prime}} \langle e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2\setminus \Psi_{t+1}^2}^{\bar{L}_t^2\setminus \Psi_{t+1}^2}\end{bmatrix} \rangle. \end{aligned} \end{align} $$
All the remaining terms (the first, the fourth and the sixth) combine into
 $$ \begin{align} \begin{aligned} -\sum_{\bar{\alpha}_t^2 < \bar{\alpha}_{p-1}^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_t^2)}^{\sigma_{p-1}(\bar{L}_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t}^{\bar{L}_t}\rangle &+ \sum_{\bar{\alpha}_{t-1}^2 < \bar{\alpha}_{p-1}^1 } \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\Psi_t^2)}^{\sigma_{p-1}(\Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\Psi_t^2}^{\Psi_t^2} \rangle \\& - \sum_{\substack{\bar{\alpha}^2_{t-1} = \bar{\alpha}^1_{p-1} \\ \bar{\beta}^2_{t-1} \geq \bar{\beta}^1_{p-1} }} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)}^{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1}^2 \setminus \Psi_t^2}^{\bar{L}_{t-1}^2 \setminus \Psi_t^2}\rangle \\ =&- \sum_{\bar{\alpha}_{t-1}^2 \leq \bar{\alpha}_{p-1}^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_{t}^2)}^{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_{t}^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1} \setminus \Psi_{t}^2}^{\bar{L}_{t-1} \setminus \Psi_{t}^2}\rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} -\sum_{\bar{\alpha}_t^2 < \bar{\alpha}_{p-1}^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_t^2)}^{\sigma_{p-1}(\bar{L}_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t}^{\bar{L}_t}\rangle &+ \sum_{\bar{\alpha}_{t-1}^2 < \bar{\alpha}_{p-1}^1 } \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\Psi_t^2)}^{\sigma_{p-1}(\Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\Psi_t^2}^{\Psi_t^2} \rangle \\& - \sum_{\substack{\bar{\alpha}^2_{t-1} = \bar{\alpha}^1_{p-1} \\ \bar{\beta}^2_{t-1} \geq \bar{\beta}^1_{p-1} }} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)}^{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1}^2 \setminus \Psi_t^2}^{\bar{L}_{t-1}^2 \setminus \Psi_t^2}\rangle \\ =&- \sum_{\bar{\alpha}_{t-1}^2 \leq \bar{\alpha}_{p-1}^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_{t}^2)}^{\sigma_{p-1}(\bar{L}_{t-1}^2 \setminus \Psi_{t}^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_{t-1} \setminus \Psi_{t}^2}^{\bar{L}_{t-1} \setminus \Psi_{t}^2}\rangle. \end{aligned} \end{align} $$
Now, the contributions of equations (8.33) and (8.34) cancel each other out (note that the condition
![]() $\bar {\alpha }_{t-1}^2 \leq \bar {\alpha }_{p-1}^1$
is satisfied for all blocks, for this is a consequence of the assumption
$\bar {\alpha }_{t-1}^2 \leq \bar {\alpha }_{p-1}^1$
is satisfied for all blocks, for this is a consequence of the assumption
![]() $\psi \neq h_{jj}$
). Thus, the result follows.
$\psi \neq h_{jj}$
). Thus, the result follows.
8.7 Computation of
 $\{y(g_{ii}), \psi \}$
$\{y(g_{ii}), \psi \}$
Let
![]() $\psi $
be an arbitrary g- or h-function and let
$\psi $
be an arbitrary g- or h-function and let
![]() $g_{ii}$
be fixed,
$g_{ii}$
be fixed,
![]() $2 \leq i \leq n$
. We employ the shorthand notation from the previous sections, choosing the first function to be
$2 \leq i \leq n$
. We employ the shorthand notation from the previous sections, choosing the first function to be
![]() $\log g_{i,i-1} - \log g_{i+1,i}$
and the second function to be
$\log g_{i,i-1} - \log g_{i+1,i}$
and the second function to be
![]() $\log \psi $
. Let us assume throughout the subsection that a pair
$\log \psi $
. Let us assume throughout the subsection that a pair
![]() $(R_0^r,R_0^c)$
is chosen so that equation (3.6) holds.
$(R_0^r,R_0^c)$
is chosen so that equation (3.6) holds.
Proposition 8.12. The bracket of
![]() $y(g_{ii})$
and
$y(g_{ii})$
and
![]() $\psi $
can be expressed as
$\psi $
can be expressed as
 $$ \begin{align}\begin{aligned} \{\log y(g_{ii}),\log \psi\} &= -\langle \pi_{<} \eta_L^1, \pi_{>} \eta_L^2 \rangle - \langle \pi_{>} \eta_R^1, \pi_{<} \eta_R^2 \rangle \\ &\quad + \langle \gamma_r \xi_R^1, \gamma_r X \nabla_X^2 \rangle + \langle \gamma_c^* \xi_L^1, \gamma_c^* \nabla_Y^2 Y \rangle \\ &\quad + \langle \pi_{\hat{\Gamma}_1^r} e_{ii}, \pi_{\hat{\Gamma}_1^r} X\nabla_X^2\rangle - \langle e_{i-1,i-1}, \eta_L^2 \rangle. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \{\log y(g_{ii}),\log \psi\} &= -\langle \pi_{<} \eta_L^1, \pi_{>} \eta_L^2 \rangle - \langle \pi_{>} \eta_R^1, \pi_{<} \eta_R^2 \rangle \\ &\quad + \langle \gamma_r \xi_R^1, \gamma_r X \nabla_X^2 \rangle + \langle \gamma_c^* \xi_L^1, \gamma_c^* \nabla_Y^2 Y \rangle \\ &\quad + \langle \pi_{\hat{\Gamma}_1^r} e_{ii}, \pi_{\hat{\Gamma}_1^r} X\nabla_X^2\rangle - \langle e_{i-1,i-1}, \eta_L^2 \rangle. \end{aligned} \end{align} $$
Proof. Recall that we employ the conventions from Section 3.3 when indices are out of range. The y-coordinate of
![]() $g_{ii}$
is given by
$g_{ii}$
is given by
With formula (7.1) and the diagonal derivatives formulas from Section 8.1, we can write the bracket
![]() $\{\log g, \log \psi \}$
as
$\{\log g, \log \psi \}$
as
 $$\begin{align*}\begin{aligned} \{\log g, \log \psi\} &= \langle e_{i-1,i-1} + e_{ii}, \nabla_Y^2 Y\rangle - \langle e_{i-1,i-1} + e_{ii}, Y \nabla_Y^2 \rangle \\ &\quad -\langle R_0^c (e_{i-1,i-1} + e_{ii}), E_L^2 \rangle + \langle R_0^r (e_{i-1,i-1} + e_{ii}), E_R^2 \rangle \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{\log g, \log \psi\} &= \langle e_{i-1,i-1} + e_{ii}, \nabla_Y^2 Y\rangle - \langle e_{i-1,i-1} + e_{ii}, Y \nabla_Y^2 \rangle \\ &\quad -\langle R_0^c (e_{i-1,i-1} + e_{ii}), E_L^2 \rangle + \langle R_0^r (e_{i-1,i-1} + e_{ii}), E_R^2 \rangle \end{aligned} \end{align*}$$
and the bracket
![]() $\{\log f, \log \psi \}$
as
$\{\log f, \log \psi \}$
as
Now, the sum
![]() $\{\log f, \log \psi \} + \{\log g,\log \psi \}$
becomes
$\{\log f, \log \psi \} + \{\log g,\log \psi \}$
becomes
To derive the formula for
![]() $\{\log y(g_{ii}), \log \psi \}$
, we use formula (8.17). Notice that the first four terms are already in the appropriate form, so we only need to deal with the diagonal part D. Consequently, we need to show that
$\{\log y(g_{ii}), \log \psi \}$
, we use formula (8.17). Notice that the first four terms are already in the appropriate form, so we only need to deal with the diagonal part D. Consequently, we need to show that
Notice that
![]() $R_0 \gamma = -\pi _{\Gamma _1} + R_0 \pi _{\Gamma _1}$
. With this, we rewrite
$R_0 \gamma = -\pi _{\Gamma _1} + R_0 \pi _{\Gamma _1}$
. With this, we rewrite
 $$\begin{align*}\begin{aligned} \langle R_0^c \pi_0 \xi_L^1, E_L^2 \rangle &= \langle R_0^c \gamma_c(e_{i-1,i-1}), E_L^2 \rangle = -\langle \pi_{\Gamma_1^c} e_{i-1,i-1}, E_L^2 \rangle + \langle R_0^c \pi_{\Gamma_1^c} e_{i-1,i-1}, E_L^2 \rangle;\\ -\langle R_0^r\pi_0 \eta_R^1, E_R^2 \rangle &= -\langle R_0^r \gamma_r(e_{ii}), E_R^2 \rangle = \langle \pi_{\Gamma_1^r} e_{ii}, E_R^2 \rangle - \langle R_0^r \pi_{\Gamma_1^r} e_{ii}, E_R^2 \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \langle R_0^c \pi_0 \xi_L^1, E_L^2 \rangle &= \langle R_0^c \gamma_c(e_{i-1,i-1}), E_L^2 \rangle = -\langle \pi_{\Gamma_1^c} e_{i-1,i-1}, E_L^2 \rangle + \langle R_0^c \pi_{\Gamma_1^c} e_{i-1,i-1}, E_L^2 \rangle;\\ -\langle R_0^r\pi_0 \eta_R^1, E_R^2 \rangle &= -\langle R_0^r \gamma_r(e_{ii}), E_R^2 \rangle = \langle \pi_{\Gamma_1^r} e_{ii}, E_R^2 \rangle - \langle R_0^r \pi_{\Gamma_1^r} e_{ii}, E_R^2 \rangle. \end{aligned} \end{align*}$$
Now, expressing D as in equation (8.25), the full expression for
![]() $D + \{\log (fg), \log \psi \}$
expands as
$D + \{\log (fg), \log \psi \}$
expands as
 $$\begin{align*}\begin{aligned} &-\langle \pi_{\Gamma_1^c} e_{i-1,i-1}, \gamma_c^*(\nabla^2_Y Y) \rangle - \langle \pi_{\Gamma_1^r}e_{ii}, X \nabla^2_X \rangle - \langle \pi_{\Gamma_1^c} e_{i-1,i-1}, E_L^2 \rangle + \langle R_0^c \pi_{\Gamma_1^c} e_{i-1,i-1}, E_L^2\rangle \\ &\quad - \langle \pi_{\hat{\Gamma}_1^c} e_{i-1,i-1}, E_L^2 \rangle + \langle R_0^c \pi_{\hat{\Gamma}_1^c}e_{i-1,i-1}, E_L^2\rangle + \langle \pi_{\Gamma_1^r} e_{ii}, E_R^2 \rangle - \langle R_0^r \pi_{\Gamma_1^r} e_{ii}, E_R^2 \rangle \\ &\quad + \langle \pi_{\hat{\Gamma}_1^r} e_{ii}, E_R^2\rangle - \langle R_0^r \pi_{\hat{\Gamma}_1^r} e_{ii}, E_R^2 \rangle +\langle e_{i-1,i-1}, \nabla^2_Y Y\rangle - \langle e_{ii}, Y\nabla^2_Y \rangle \\ &\quad - \langle R_0^c e_{i-1,i-1}, E_L^2 \rangle + \langle R_0^r e_{ii}, E_R^2 \rangle\rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &-\langle \pi_{\Gamma_1^c} e_{i-1,i-1}, \gamma_c^*(\nabla^2_Y Y) \rangle - \langle \pi_{\Gamma_1^r}e_{ii}, X \nabla^2_X \rangle - \langle \pi_{\Gamma_1^c} e_{i-1,i-1}, E_L^2 \rangle + \langle R_0^c \pi_{\Gamma_1^c} e_{i-1,i-1}, E_L^2\rangle \\ &\quad - \langle \pi_{\hat{\Gamma}_1^c} e_{i-1,i-1}, E_L^2 \rangle + \langle R_0^c \pi_{\hat{\Gamma}_1^c}e_{i-1,i-1}, E_L^2\rangle + \langle \pi_{\Gamma_1^r} e_{ii}, E_R^2 \rangle - \langle R_0^r \pi_{\Gamma_1^r} e_{ii}, E_R^2 \rangle \\ &\quad + \langle \pi_{\hat{\Gamma}_1^r} e_{ii}, E_R^2\rangle - \langle R_0^r \pi_{\hat{\Gamma}_1^r} e_{ii}, E_R^2 \rangle +\langle e_{i-1,i-1}, \nabla^2_Y Y\rangle - \langle e_{ii}, Y\nabla^2_Y \rangle \\ &\quad - \langle R_0^c e_{i-1,i-1}, E_L^2 \rangle + \langle R_0^r e_{ii}, E_R^2 \rangle\rangle. \end{aligned} \end{align*}$$
It’s easy to see that all terms containing
![]() $R_0^r$
, as well as all terms containing
$R_0^r$
, as well as all terms containing
![]() $R_0^c$
, result in zero. The rest can be combined as follows:
$R_0^c$
, result in zero. The rest can be combined as follows:
Thus, the formula holds.
Corollary 8.12.1. As a consequence,
![]() $\{\log y(g_{ii}), \log g_{jj} \} = \delta _{ij}$
for any j.
$\{\log y(g_{ii}), \log g_{jj} \} = \delta _{ij}$
for any j.
Proof. Recall that
![]() $X \nabla _X g_{jj} \in \mathfrak {b}_+$
and
$X \nabla _X g_{jj} \in \mathfrak {b}_+$
and
![]() $\nabla _X g_{jj} \cdot X \in \mathfrak {b}_-$
, so the first two terms together with the fourth one vanish; since
$\nabla _X g_{jj} \cdot X \in \mathfrak {b}_-$
, so the first two terms together with the fourth one vanish; since
![]() $\pi _0(\xi _R^1) = e_{ii}$
and
$\pi _0(\xi _R^1) = e_{ii}$
and
![]() $\pi _0 (X \nabla ^2_X) = \pi _0 (\nabla ^2_XX) = \Delta (j,n)$
, where
$\pi _0 (X \nabla ^2_X) = \pi _0 (\nabla ^2_XX) = \Delta (j,n)$
, where
![]() $\Delta (j,n) = \sum _{k=j}^n e_{kk}$
, we see that
$\Delta (j,n) = \sum _{k=j}^n e_{kk}$
, we see that
 $$\begin{align*}\begin{aligned} \{\log y(g_{ii}), \log g_{jj} \} &= \langle \pi_{\Gamma_1^r} e_{ii}, \pi_{\Gamma_1^r} \Delta(j,n) \rangle + \langle \pi_{\hat{\Gamma}_1^r} e_{ii}, \pi_{\hat{\Gamma}_1^r} \Delta(j,n)\rangle - \langle e_{i-1,i-1}, \Delta(j,n)\rangle \\ &= \langle e_{ii} - e_{i-1,i-1}, \Delta(j,n) \rangle = \delta_{ij}.\end{aligned}\\[-40pt] \end{align*}$$
$$\begin{align*}\begin{aligned} \{\log y(g_{ii}), \log g_{jj} \} &= \langle \pi_{\Gamma_1^r} e_{ii}, \pi_{\Gamma_1^r} \Delta(j,n) \rangle + \langle \pi_{\hat{\Gamma}_1^r} e_{ii}, \pi_{\hat{\Gamma}_1^r} \Delta(j,n)\rangle - \langle e_{i-1,i-1}, \Delta(j,n)\rangle \\ &= \langle e_{ii} - e_{i-1,i-1}, \Delta(j,n) \rangle = \delta_{ij}.\end{aligned}\\[-40pt] \end{align*}$$
Lemma 8.13. The following formulas hold for the last two terms in equation (8.35):
 $$\begin{align*}\langle \pi_{\hat{\Gamma}_1^r} e_{ii}, X \nabla^2_X \rangle = \langle \pi_{\hat{\Gamma}_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\end{bmatrix}\rangle; \end{align*}$$
$$\begin{align*}\langle \pi_{\hat{\Gamma}_1^r} e_{ii}, X \nabla^2_X \rangle = \langle \pi_{\hat{\Gamma}_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\end{bmatrix}\rangle; \end{align*}$$
 $$\begin{align*}-\langle e_{i-1,i-1}, \eta_L^2 \rangle = -\sum_{u=1}^{s^2} \langle e_{i-1,i-1}, \begin{bmatrix} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2} & 0 \\ 0 & 0\end{bmatrix} \rangle - \sum_{t=1}^{s^2} \langle e_{i-1,i-1}, \gamma_c^* \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2} \end{bmatrix}\rangle. \end{align*}$$
$$\begin{align*}-\langle e_{i-1,i-1}, \eta_L^2 \rangle = -\sum_{u=1}^{s^2} \langle e_{i-1,i-1}, \begin{bmatrix} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2} & 0 \\ 0 & 0\end{bmatrix} \rangle - \sum_{t=1}^{s^2} \langle e_{i-1,i-1}, \gamma_c^* \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2} \end{bmatrix}\rangle. \end{align*}$$
Proof. The gradient
![]() $X \nabla ^2_X$
can be expressed as
$X \nabla ^2_X$
can be expressed as
 $$\begin{align*}\begin{aligned} X\nabla^2_X &= \sum_{t=1}^{s^2} X (\nabla_{\mathcal{L}}^2)_{L_t^2 \rightarrow J_t^2}^{K_t^2 \rightarrow I_t^2} = \sum_{t=1}^{s^2} \begin{bmatrix} 0 & X_{\hat{I}_t^2}^{J_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2} \\ 0 & (\mathcal{L}^{2})_{K_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2} \end{bmatrix} \\ &= \sum_{t=1}^{s^2} \begin{bmatrix} 0 & X_{\hat{I}_t^2}^{J_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2} & X_{\hat{I}_t^2}^{J_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2 \setminus \Phi_t^2} \\ 0 & (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2} & (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2 \setminus \Phi_t^2} \\ 0 & (\mathcal{L}^{2})_{K_t^2 \setminus \Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2} & (\mathcal{L}^{2})_{K_t^2 \setminus \Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \end{aligned}, \end{align*}$$
$$\begin{align*}\begin{aligned} X\nabla^2_X &= \sum_{t=1}^{s^2} X (\nabla_{\mathcal{L}}^2)_{L_t^2 \rightarrow J_t^2}^{K_t^2 \rightarrow I_t^2} = \sum_{t=1}^{s^2} \begin{bmatrix} 0 & X_{\hat{I}_t^2}^{J_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2} \\ 0 & (\mathcal{L}^{2})_{K_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2} \end{bmatrix} \\ &= \sum_{t=1}^{s^2} \begin{bmatrix} 0 & X_{\hat{I}_t^2}^{J_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2} & X_{\hat{I}_t^2}^{J_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2 \setminus \Phi_t^2} \\ 0 & (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2} & (\mathcal{L}^{2})_{\Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2 \setminus \Phi_t^2} \\ 0 & (\mathcal{L}^{2})_{K_t^2 \setminus \Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{\Phi_t^2} & (\mathcal{L}^{2})_{K_t^2 \setminus \Phi_t^2}^{L_t^2} (\nabla^{2}_{\mathcal{L}})_{L_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \end{aligned}, \end{align*}$$
where
![]() $\hat {I}_t^2 = [1,n] \setminus I_t^2$
. Now, the projection onto diagonal matrices eliminates all off-diagonal blocks; a further projection onto
$\hat {I}_t^2 = [1,n] \setminus I_t^2$
. Now, the projection onto diagonal matrices eliminates all off-diagonal blocks; a further projection onto
![]() $\mathfrak {g}_{\hat {\Gamma }_1^r}$
nullifies the middle block, for it occupies the location
$\mathfrak {g}_{\hat {\Gamma }_1^r}$
nullifies the middle block, for it occupies the location
![]() $\Delta (\alpha _t^2) \times \Delta (\alpha _t^2)$
. Thus, the first formula hold. For the second formula, one can use a block formula for
$\Delta (\alpha _t^2) \times \Delta (\alpha _t^2)$
. Thus, the first formula hold. For the second formula, one can use a block formula for
![]() $\eta _L^2$
derived in [Reference Gekhtman, Shapiro and Vainshtein20] (which is also easily derivable in a similar manner).
$\eta _L^2$
derived in [Reference Gekhtman, Shapiro and Vainshtein20] (which is also easily derivable in a similar manner).
Proposition 8.14. The following formula holds:
 $$\begin{align*}\{\log y(g_{ii}), \log \psi \} = \begin{cases} 1, \ &\psi = g_{ii}\\ 0, \ &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\{\log y(g_{ii}), \log \psi \} = \begin{cases} 1, \ &\psi = g_{ii}\\ 0, \ &\text{otherwise.} \end{cases} \end{align*}$$
Proof. First of all, let us assume that
![]() $\psi \neq g_{jj}$
for all j, for this case was studied in Corollary 8.12.1. As a consequence, we can assume throughout the proof that for any
$\psi \neq g_{jj}$
for all j, for this case was studied in Corollary 8.12.1. As a consequence, we can assume throughout the proof that for any
![]() $X_t^2 = X_{[\alpha _t^2,n]}^{[1,\beta ^2_t]}$
, we have
$X_t^2 = X_{[\alpha _t^2,n]}^{[1,\beta ^2_t]}$
, we have
![]() $\alpha _p^1 \leq \alpha _t^2$
and
$\alpha _p^1 \leq \alpha _t^2$
and
![]() $\beta _p^1 \geq \beta _{t}^2$
. Indeed, ifFootnote
10
$\beta _p^1 \geq \beta _{t}^2$
. Indeed, ifFootnote
10
![]() $\alpha _p^1> \alpha _t^2$
, then
$\alpha _p^1> \alpha _t^2$
, then
![]() $\alpha _p^1 = 2$
and
$\alpha _p^1 = 2$
and
![]() $\alpha _t^2 = 1$
, which implies that
$\alpha _t^2 = 1$
, which implies that
![]() $\psi = g_{jj}$
for some j. A similar reasoning applies to
$\psi = g_{jj}$
for some j. A similar reasoning applies to
![]() $\beta _p^1$
, for
$\beta _p^1$
, for
![]() $\beta _p^1 \in \{n-1,n\}$
.
$\beta _p^1 \in \{n-1,n\}$
.
Now, we need to expand every term in equation (8.35) using block formulas from Section 8.5 and Lemma 8.13. We can say right away that some of the terms in the block formulas vanish via the following observations:
-
• All terms that do not contain the first function are zero. For instance,
 $\sum \langle (\mathcal {L}^{2})_{\bar {K}_{t-1}^2}^{L_t^2} (\nabla ^{2}_{\mathcal {L}})_{L_t^2}^{\bar {K}_{t-1}^2} \rangle = 0$
;
$\sum \langle (\mathcal {L}^{2})_{\bar {K}_{t-1}^2}^{L_t^2} (\nabla ^{2}_{\mathcal {L}})_{L_t^2}^{\bar {K}_{t-1}^2} \rangle = 0$
; -
• The sums
 $\sum ^{a}$
vanish, for they are taken over the blocks
$\sum ^{a}$
vanish, for they are taken over the blocks
 $X_t^2$
that have their exit point above the exit point of
$X_t^2$
that have their exit point above the exit point of
 $X_p^1$
. Since the exit point of the latter is
$X_p^1$
. Since the exit point of the latter is
 $(2,1)$
, the exit point of the former must be
$(2,1)$
, the exit point of the former must be
 $(1,1)$
, which is precisely the case
$(1,1)$
, which is precisely the case
 $\psi = g_{jj}$
, which in turn is excluded from the consideration;
$\psi = g_{jj}$
, which in turn is excluded from the consideration; -
•
 $(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})^{\bar {L}_p^1}_{\bar {L}_p^1} = 0$
, for the leading block of the first function is
$(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})^{\bar {L}_p^1}_{\bar {L}_p^1} = 0$
, for the leading block of the first function is
 $X_p^1$
and
$X_p^1$
and
 $\bar {L}_p^1$
spans the rows of
$\bar {L}_p^1$
spans the rows of
 $Y_p^1$
;
$Y_p^1$
; -
•
 $(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{\sigma _{p}(\bar {K}_t^2)}^{\sigma _{p}(\bar {K}_t^2)} = 0$
if
$(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{\sigma _{p}(\bar {K}_t^2)}^{\sigma _{p}(\bar {K}_t^2)} = 0$
if
 $\bar {\alpha }_t^2 < \bar {\alpha }_p^1$
. This relation holds due to
$\bar {\alpha }_t^2 < \bar {\alpha }_p^1$
. This relation holds due to
 $\sigma _p(\bar {K}_t^2) \subseteq \bar {K}_p^1 \setminus \Phi _p^1$
, and the gradient is zero along the latter rows;
$\sigma _p(\bar {K}_t^2) \subseteq \bar {K}_p^1 \setminus \Phi _p^1$
, and the gradient is zero along the latter rows; -
•
 $(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{\bar {K}_u^1}^{\bar {K}_u^1} = 0$
for
$(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{\bar {K}_u^1}^{\bar {K}_u^1} = 0$
for
 $u < p$
;
$u < p$
; -
• For
 $u = p$
, even though
$u = p$
, even though
 $(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{\bar {K}_p^1}^{\bar {K}_p^1}$
might be nonzero, the only term it belongs to vanishes: for if
$(\mathcal {L}^{1} \nabla ^{1}_{\mathcal {L}})_{\bar {K}_p^1}^{\bar {K}_p^1}$
might be nonzero, the only term it belongs to vanishes: for if $$\begin{align*}\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_p^1 \rightarrow \bar{I}_p^1}^{\bar{K}_p^1 \rightarrow \bar{I}_p^1}, \gamma_r (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle = \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\Phi_p \rightarrow \Delta(\alpha_p^1)}^{\Phi_p \rightarrow \Delta(\alpha_p^1)}, (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle = 0, \end{align*}$$
$$\begin{align*}\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\bar{K}_p^1 \rightarrow \bar{I}_p^1}^{\bar{K}_p^1 \rightarrow \bar{I}_p^1}, \gamma_r (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle = \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\Phi_p \rightarrow \Delta(\alpha_p^1)}^{\Phi_p \rightarrow \Delta(\alpha_p^1)}, (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle = 0, \end{align*}$$
 $\Delta (\alpha _p^1)$
is nontrivial, it is the leftmost X-run, and since we cut out an X-run in the second matrix, the result is zero.
$\Delta (\alpha _p^1)$
is nontrivial, it is the leftmost X-run, and since we cut out an X-run in the second matrix, the result is zero.
-
•
 $(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})_{\bar {L}_u^1 \setminus \Psi _{u+1}^1 \rightarrow \bar {J}_u^1 \setminus \bar {\Delta }(\bar {\beta }_u^1)}^{\bar {L}_u^1 \setminus \Psi _{u+1}^1 \rightarrow \bar {J}_u^1 \setminus \bar {\Delta }(\bar {\beta }_u^1)} = 0$
for all u;
$(\nabla ^{1}_{\mathcal {L}}\mathcal {L}^{1})_{\bar {L}_u^1 \setminus \Psi _{u+1}^1 \rightarrow \bar {J}_u^1 \setminus \bar {\Delta }(\bar {\beta }_u^1)}^{\bar {L}_u^1 \setminus \Psi _{u+1}^1 \rightarrow \bar {J}_u^1 \setminus \bar {\Delta }(\bar {\beta }_u^1)} = 0$
for all u; -
• All terms that involve the blocks of the first function with indices
 $u < p-1$
vanish;
$u < p-1$
vanish;
Additionally, one term requires a special care. Observe that
 $$\begin{align*}(\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{K_p^1 \setminus \Phi_p^1 \rightarrow I_p^1 \setminus \Delta(\alpha_p^1)}^{K_p^1 \setminus \Phi_p^1 \rightarrow I_p^1 \setminus \Delta(\alpha_p^1)} = \begin{cases} e_{ii}, \ \ i \notin \Delta(\alpha_p^1)\\ 0, \ \ \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}(\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{K_p^1 \setminus \Phi_p^1 \rightarrow I_p^1 \setminus \Delta(\alpha_p^1)}^{K_p^1 \setminus \Phi_p^1 \rightarrow I_p^1 \setminus \Delta(\alpha_p^1)} = \begin{cases} e_{ii}, \ \ i \notin \Delta(\alpha_p^1)\\ 0, \ \ \text{otherwise.} \end{cases} \end{align*}$$
We argue that
 $$\begin{align*}\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{K_p^1 \setminus \Phi_p^1 \rightarrow I_p^1 \setminus \Delta(\alpha_p^1)}^{K_p^1 \setminus \Phi_p^1 \rightarrow I_p^1 \setminus \Delta(\alpha_p^1)}, \pi_{\Gamma_1^r} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle = \langle \pi_{\Gamma_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\end{bmatrix} \rangle. \end{align*}$$
$$\begin{align*}\langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{K_p^1 \setminus \Phi_p^1 \rightarrow I_p^1 \setminus \Delta(\alpha_p^1)}^{K_p^1 \setminus \Phi_p^1 \rightarrow I_p^1 \setminus \Delta(\alpha_p^1)}, \pi_{\Gamma_1^r} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)}^{K_t^2 \setminus \Phi_t^2 \rightarrow I_t^2 \setminus \Delta(\alpha_t^2)} \rangle = \langle \pi_{\Gamma_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\end{bmatrix} \rangle. \end{align*}$$
Indeed, the formula follows right away if
![]() $i \notin \Delta (\alpha _p^1)$
. On the contrary, if
$i \notin \Delta (\alpha _p^1)$
. On the contrary, if
![]() $i \in \Delta (\alpha _p^1)$
, then the LHS is zero; such is the RHS as well, for we remove an X-run from the second matrix.
$i \in \Delta (\alpha _p^1)$
, then the LHS is zero; such is the RHS as well, for we remove an X-run from the second matrix.
With all the above observations, formula (8.35) expands as
 $$\begin{align*}\begin{aligned} \{\log y(g_{ii}), \log \psi \} &= - \sum_{\beta_t^2 < \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2)}^{\rho(K_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2}^{K_t^2} + \sum_{\beta_t^2 < \beta_p^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\rho(L_t^2)}^{\rho(L_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2} \rangle \\ &\quad + \sum_{t=1}^{s^2}\langle \pi_{\Gamma_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\end{bmatrix} \rangle + \sum_{\beta_t^2 < \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\Phi_t^2}^{\Phi_t^2} \rangle\\ &\quad +\sum_{t=1}^{s^2} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{L_p^1 \rightarrow J_p^1}^{L_p^1 \rightarrow J_p^1}, \gamma_c^* (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)} \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{\log y(g_{ii}), \log \psi \} &= - \sum_{\beta_t^2 < \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2)}^{\rho(K_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2}^{K_t^2} + \sum_{\beta_t^2 < \beta_p^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\rho(L_t^2)}^{\rho(L_t^2)} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2} \rangle \\ &\quad + \sum_{t=1}^{s^2}\langle \pi_{\Gamma_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\end{bmatrix} \rangle + \sum_{\beta_t^2 < \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\Phi_t^2}^{\Phi_t^2} \rangle\\ &\quad +\sum_{t=1}^{s^2} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{L_p^1 \rightarrow J_p^1}^{L_p^1 \rightarrow J_p^1}, \gamma_c^* (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2 \rightarrow \bar{J}_t^2 \setminus \bar{\Delta}(\bar{\beta}_t^2)} \end{aligned} \end{align*}$$
 $$\begin{align*}\begin{aligned} &\quad - \sum_{\beta_t^2 = \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2 \setminus \Phi_t^2)}^{\rho(K_t^2 \setminus \Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \rangle \\ &\quad + \sum_{\beta_t^2 = \beta_p^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{L_p^1}^{L_p^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2} \rangle + \sum_{t=1}^{s^2} \langle \pi_{\hat{\Gamma}_1^r}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle \\ &\quad - \sum_{t=1}^{s^2} \langle e_{i-1,i-1}, \begin{bmatrix} (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{L_t^2}^{L_t^2} & 0 \\ 0 & 0 \end{bmatrix} \rangle - \sum_{t=1}^{s^2} \langle e_{i-1,i-1}, \gamma_c^* \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2} \end{bmatrix} \rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\quad - \sum_{\beta_t^2 = \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2 \setminus \Phi_t^2)}^{\rho(K_t^2 \setminus \Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \rangle \\ &\quad + \sum_{\beta_t^2 = \beta_p^1} \langle (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{L_p^1}^{L_p^1} (\nabla^{2}_{\mathcal{L}}\mathcal{L}^{2})_{L_t^2}^{L_t^2} \rangle + \sum_{t=1}^{s^2} \langle \pi_{\hat{\Gamma}_1^r}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle \\ &\quad - \sum_{t=1}^{s^2} \langle e_{i-1,i-1}, \begin{bmatrix} (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{L_t^2}^{L_t^2} & 0 \\ 0 & 0 \end{bmatrix} \rangle - \sum_{t=1}^{s^2} \langle e_{i-1,i-1}, \gamma_c^* \begin{bmatrix} 0 & 0 \\ 0 & (\nabla^{1}_{\mathcal{L}}\mathcal{L}^{1})_{\bar{L}_t^2 \setminus \Psi_{t+1}^2}^{\bar{L}_t^2 \setminus \Psi_{t+1}^2} \end{bmatrix} \rangle. \end{aligned} \end{align*}$$
Now, let’s combine these terms together. The conditions under the second and the seventh sums combine into
![]() $\beta _t^2 \leq \beta _p^1$
, which is satisfied for all blocks due to our assumption; hence, these terms cancel out with the ninth sum. The fifth term cancels out with the last one. The third and the eighth term combine into
$\beta _t^2 \leq \beta _p^1$
, which is satisfied for all blocks due to our assumption; hence, these terms cancel out with the ninth sum. The fifth term cancels out with the last one. The third and the eighth term combine into
 $$ \begin{align}\begin{aligned} &\sum_{t=1}^{s^2} \langle \pi_{\Gamma_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle + \sum_{t=1}^{s^2} \langle \pi_{\Gamma_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle \\ &\quad = \sum_{t=1}^{s^2} \langle e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} &\sum_{t=1}^{s^2} \langle \pi_{\Gamma_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle + \sum_{t=1}^{s^2} \langle \pi_{\Gamma_1^r} e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle \\ &\quad = \sum_{t=1}^{s^2} \langle e_{ii}, \begin{bmatrix} 0 & 0 \\ 0 & (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2} \end{bmatrix} \rangle. \end{aligned} \end{align} $$
The remaining terms (the first, the fourth and the sixth) add up to
 $$ \begin{align}\begin{aligned} - \sum_{\beta_t^2 < \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2)}^{\rho(K_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2}^{K_t^2} \rangle &+ \sum_{\beta_t^2 < \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\Phi_t^2}^{\Phi_t^2} \rangle \\ &- \sum_{\beta_t^2 = \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2 \setminus \Phi_t^2)}^{\rho(K_t^2\setminus \Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\rangle \\ = &-\sum_{t=1}^{s^2} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2 \setminus \Phi_t^2)}^{\rho(K_t^2\setminus \Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\rangle, \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} - \sum_{\beta_t^2 < \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2)}^{\rho(K_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2}^{K_t^2} \rangle &+ \sum_{\beta_t^2 < \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(\Phi_t^2)}^{\rho(\Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{\Phi_t^2}^{\Phi_t^2} \rangle \\ &- \sum_{\beta_t^2 = \beta_p^1} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2 \setminus \Phi_t^2)}^{\rho(K_t^2\setminus \Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\rangle \\ = &-\sum_{t=1}^{s^2} \langle (\mathcal{L}^{1} \nabla^{1}_{\mathcal{L}})_{\rho(K_t^2 \setminus \Phi_t^2)}^{\rho(K_t^2\setminus \Phi_t^2)} (\mathcal{L}^{2} \nabla^{2}_{\mathcal{L}})_{K_t^2 \setminus \Phi_t^2}^{K_t^2 \setminus \Phi_t^2}\rangle, \end{aligned} \end{align} $$
where we used the fact that
![]() $\beta _t^2 \leq \beta _p^1$
is satisfied for all blocks under the stated assumption. Now, notice that the total contribution of equations (8.36) and (8.37) is zero. Thus, the result follows.
$\beta _t^2 \leq \beta _p^1$
is satisfied for all blocks under the stated assumption. Now, notice that the total contribution of equations (8.36) and (8.37) is zero. Thus, the result follows.
9 Case of
 $D(\operatorname {\mathrm {SL}}_n)$
$D(\operatorname {\mathrm {SL}}_n)$
In this section, we show how to derive Theorem 1.2 from Theorem 1.1. Let us restate Theorem 1.2 here for convenience.
Theorem. Let
![]() $\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be a pair of aperiodic oriented Belavin–Drinfeld triples. There exists a generalized cluster structure
$\mathbf {\Gamma } = (\mathbf {\Gamma }^r, \mathbf {\Gamma }^c)$
be a pair of aperiodic oriented Belavin–Drinfeld triples. There exists a generalized cluster structure
![]() $\mathcal {GC}(\mathbf {\Gamma })$
on
$\mathcal {GC}(\mathbf {\Gamma })$
on
![]() $D(\operatorname {\mathrm {SL}}_n) = \operatorname {\mathrm {SL}}_n \times \operatorname {\mathrm {SL}}_n$
such that
$D(\operatorname {\mathrm {SL}}_n) = \operatorname {\mathrm {SL}}_n \times \operatorname {\mathrm {SL}}_n$
such that
-
(i) The number of stable variables is
 $k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c} + (n-1)$
, and the exchange matrix has full rank;
$k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c} + (n-1)$
, and the exchange matrix has full rank; -
(ii) The generalized cluster structure
 $\mathcal {GC}(\mathbf {\Gamma })$
is regular, and the ring of regular functions
$\mathcal {GC}(\mathbf {\Gamma })$
is regular, and the ring of regular functions
 $\mathcal {O}(D(\operatorname {\mathrm {SL}}_n))$
is naturally isomorphic to the upper cluster algebra
$\mathcal {O}(D(\operatorname {\mathrm {SL}}_n))$
is naturally isomorphic to the upper cluster algebra
 $\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
;
$\bar {\mathcal {A}}_{\mathbb {C}}(\mathcal {GC}(\mathbf {\Gamma }))$
; -
(iii) The global toric action of
 $(\mathbb {C}^*)^{k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c}}$
on
$(\mathbb {C}^*)^{k_{\mathbf {\Gamma }^r}+k_{\mathbf {\Gamma }^c}}$
on
 $\mathcal {GC}(\mathbf {\Gamma })$
is induced by the left action of
$\mathcal {GC}(\mathbf {\Gamma })$
is induced by the left action of
 $\mathcal {H}_{\mathbf {\Gamma }^r}$
and the right action of
$\mathcal {H}_{\mathbf {\Gamma }^r}$
and the right action of
 $\mathcal {H}_{\mathbf {\Gamma }^c}$
on
$\mathcal {H}_{\mathbf {\Gamma }^c}$
on
 $D(\operatorname {\mathrm {SL}}_n)$
;
$D(\operatorname {\mathrm {SL}}_n)$
; -
(iv) Any Poisson bracket defined by the pair
 $\mathbf {\Gamma }$
on
$\mathbf {\Gamma }$
on
 $D(\operatorname {\mathrm {SL}}_n)$
is compatible with
$D(\operatorname {\mathrm {SL}}_n)$
is compatible with
 $\mathcal {GC}(\mathbf {\Gamma })$
.
$\mathcal {GC}(\mathbf {\Gamma })$
.
Let
![]() $\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be an oriented aperiodic Belavin–Drinfeld pair. Fix a choice of
$\mathbf {\Gamma }:=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
be an oriented aperiodic Belavin–Drinfeld pair. Fix a choice of
![]() $(R_0^r,R_0^c)$
for the Poisson bracket
$(R_0^r,R_0^c)$
for the Poisson bracket
![]() $\{\cdot ,\cdot \}_{D(\operatorname {\mathrm {SL}}_n)}$
on
$\{\cdot ,\cdot \}_{D(\operatorname {\mathrm {SL}}_n)}$
on
![]() $D(\operatorname {\mathrm {SL}}_n)$
and extend both
$D(\operatorname {\mathrm {SL}}_n)$
and extend both
![]() $R_0^r$
and
$R_0^r$
and
![]() $R_0^c$
to the Cartan subalgebra of
$R_0^c$
to the Cartan subalgebra of
![]() $\operatorname {\mathrm {gl}}_n$
via
$\operatorname {\mathrm {gl}}_n$
via
![]() $R_0^r(I) := R_0^c(I) := (1/2)I$
, where I is the identity matrix. Let
$R_0^r(I) := R_0^c(I) := (1/2)I$
, where I is the identity matrix. Let
![]() $\{\cdot ,\cdot \}_{D(\operatorname {\mathrm {GL}}_n)}$
be the resulting Poisson bracket on
$\{\cdot ,\cdot \}_{D(\operatorname {\mathrm {GL}}_n)}$
be the resulting Poisson bracket on
![]() $D(\operatorname {\mathrm {GL}}_n)$
.
$D(\operatorname {\mathrm {GL}}_n)$
.
Lemma 9.1. Under the above choice of
![]() $(R_0^r,R_0^c)$
, the restriction map
$(R_0^r,R_0^c)$
, the restriction map
![]() $\mathcal {O}(D(\operatorname {\mathrm {GL}}_n)) \rightarrow \mathcal {O}(D(\operatorname {\mathrm {SL}}_n))$
is Poisson; in other words, for any
$\mathcal {O}(D(\operatorname {\mathrm {GL}}_n)) \rightarrow \mathcal {O}(D(\operatorname {\mathrm {SL}}_n))$
is Poisson; in other words, for any
![]() $f_1,f_2 \in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
,
$f_1,f_2 \in \mathcal {O}(D(\operatorname {\mathrm {GL}}_n))$
,
Proof. Let
![]() $\pi _*$
the projection of
$\pi _*$
the projection of
![]() $\operatorname {\mathrm {gl}}_n$
onto
$\operatorname {\mathrm {gl}}_n$
onto
![]() $\operatorname {\mathrm {sl}}_n$
$\operatorname {\mathrm {sl}}_n$
and let
![]() $f_1$
and
$f_1$
and
![]() $f_2$
be regular functions on
$f_2$
be regular functions on
![]() $D(\operatorname {\mathrm {GL}}_n)$
. Recall that
$D(\operatorname {\mathrm {GL}}_n)$
. Recall that
 $$\begin{align*}\begin{aligned} \{f_1,f_2\}_{D(\operatorname{\mathrm{GL}}_n)}(X,Y) &= \langle R_+^c(E_Lf_1),E_Lf_2\rangle - \langle R_+^r (E_R f_1), E_R f_2\rangle \\ &\quad +\langle X\nabla_X f_1, Y\nabla_Y f_2\rangle - \langle \nabla_X f_1 X, \nabla_Y f_2 Y\rangle; \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{f_1,f_2\}_{D(\operatorname{\mathrm{GL}}_n)}(X,Y) &= \langle R_+^c(E_Lf_1),E_Lf_2\rangle - \langle R_+^r (E_R f_1), E_R f_2\rangle \\ &\quad +\langle X\nabla_X f_1, Y\nabla_Y f_2\rangle - \langle \nabla_X f_1 X, \nabla_Y f_2 Y\rangle; \end{aligned} \end{align*}$$
 $$\begin{align*}\begin{aligned} \{f_1|_{D(\operatorname{\mathrm{SL}}_n)},f_2|_{D(\operatorname{\mathrm{SL}}_n)}\}_{D(\operatorname{\mathrm{SL}}_n)}(X,Y) & = \langle R_+^c(\pi_*(E_Lf_1)),\pi_*(E_Lf_2)\rangle - \langle R_+^r (\pi_*(E_R f_1)), \pi_*(E_R f_2)\rangle \\ &\quad +\langle \pi_*(X\nabla_X f_1), \pi_*(Y\nabla_Y f_2)\rangle - \langle \pi_*(\nabla_X f_1 X), \pi_*(\nabla_Y f_2 Y)\rangle. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \{f_1|_{D(\operatorname{\mathrm{SL}}_n)},f_2|_{D(\operatorname{\mathrm{SL}}_n)}\}_{D(\operatorname{\mathrm{SL}}_n)}(X,Y) & = \langle R_+^c(\pi_*(E_Lf_1)),\pi_*(E_Lf_2)\rangle - \langle R_+^r (\pi_*(E_R f_1)), \pi_*(E_R f_2)\rangle \\ &\quad +\langle \pi_*(X\nabla_X f_1), \pi_*(Y\nabla_Y f_2)\rangle - \langle \pi_*(\nabla_X f_1 X), \pi_*(\nabla_Y f_2 Y)\rangle. \end{aligned} \end{align*}$$
A simple computation shows that
Now, since
![]() $\operatorname {\mathrm {tr}}(AB) = \operatorname {\mathrm {tr}}(BA)$
, we see that
$\operatorname {\mathrm {tr}}(AB) = \operatorname {\mathrm {tr}}(BA)$
, we see that
![]() $\operatorname {\mathrm {tr}}(E_Lf_1) = \operatorname {\mathrm {tr}}(E_R f_1)$
,
$\operatorname {\mathrm {tr}}(E_Lf_1) = \operatorname {\mathrm {tr}}(E_R f_1)$
,
![]() $\operatorname {\mathrm {tr}}(X\nabla _X f_1) = \operatorname {\mathrm {tr}}(\nabla _X f_1 X)$
, and so on. Combining the above identities yields equation (9.1).
$\operatorname {\mathrm {tr}}(X\nabla _X f_1) = \operatorname {\mathrm {tr}}(\nabla _X f_1 X)$
, and so on. Combining the above identities yields equation (9.1).
Now, let us turn to the proof of Theorem 1.2:
Proof. The initial extended seed on
![]() $D(\operatorname {\mathrm {SL}}_n)$
is obtained from the initial extended seed on
$D(\operatorname {\mathrm {SL}}_n)$
is obtained from the initial extended seed on
![]() $D(\operatorname {\mathrm {GL}}_n)$
via setting
$D(\operatorname {\mathrm {GL}}_n)$
via setting
![]() $\det X = \det Y = 1$
and removing the frozen variables
$\det X = \det Y = 1$
and removing the frozen variables
![]() $g_{11}$
and
$g_{11}$
and
![]() $h_{11}$
. Therefore, the total number of frozen variables on
$h_{11}$
. Therefore, the total number of frozen variables on
![]() $D(\operatorname {\mathrm {SL}}_n)$
is
$D(\operatorname {\mathrm {SL}}_n)$
is
![]() $k_{\mathbf {\Gamma }^r} + k_{\mathbf {\Gamma }^c}$
. Part (ii) is trivial: Given any regular function on
$k_{\mathbf {\Gamma }^r} + k_{\mathbf {\Gamma }^c}$
. Part (ii) is trivial: Given any regular function on
![]() $D(\operatorname {\mathrm {SL}}_n)$
, one can extend it to a regular function on
$D(\operatorname {\mathrm {SL}}_n)$
, one can extend it to a regular function on
![]() $D(\operatorname {\mathrm {GL}}_n)$
, then express the function as a Laurent polynomial in terms of any extended cluster, and finally restrict it back to
$D(\operatorname {\mathrm {GL}}_n)$
, then express the function as a Laurent polynomial in terms of any extended cluster, and finally restrict it back to
![]() $D(\operatorname {\mathrm {SL}}_n)$
.
$D(\operatorname {\mathrm {SL}}_n)$
.
Any extended cluster on
![]() $D(\operatorname {\mathrm {SL}}_n)$
is log-canonical due to Lemma 9.1 and the fact that the statement is true for
$D(\operatorname {\mathrm {SL}}_n)$
is log-canonical due to Lemma 9.1 and the fact that the statement is true for
![]() $D(\operatorname {\mathrm {GL}}_n)$
. Let
$D(\operatorname {\mathrm {GL}}_n)$
. Let
![]() $\tilde {B}_{D(\operatorname {\mathrm {GL}}_n}$
and
$\tilde {B}_{D(\operatorname {\mathrm {GL}}_n}$
and
![]() $\tilde {B}_{D(\operatorname {\mathrm {SL}}_n)}$
be the extended exchange matrices for the initial extended seeds, and let
$\tilde {B}_{D(\operatorname {\mathrm {SL}}_n)}$
be the extended exchange matrices for the initial extended seeds, and let
![]() $\Omega _{D(\operatorname {\mathrm {GL}}_n)}$
and
$\Omega _{D(\operatorname {\mathrm {GL}}_n)}$
and
![]() $\Omega _{D(\operatorname {\mathrm {SL}}_n)}$
be the coefficient matrices of the brackets. Due to the choice of
$\Omega _{D(\operatorname {\mathrm {SL}}_n)}$
be the coefficient matrices of the brackets. Due to the choice of
![]() $(R^r_0,R^c_0)$
,
$(R^r_0,R^c_0)$
,
![]() $\det X$
and
$\det X$
and
![]() $\det Y$
are Casimirs on
$\det Y$
are Casimirs on
![]() $D(\operatorname {\mathrm {GL}}_n)$
, and therefore the corresponding rows and columns of
$D(\operatorname {\mathrm {GL}}_n)$
, and therefore the corresponding rows and columns of
![]() $\Omega _{D(\operatorname {\mathrm {GL}}_n)}$
are zero; furthermore, the log-coefficient of any pair of variables on
$\Omega _{D(\operatorname {\mathrm {GL}}_n)}$
are zero; furthermore, the log-coefficient of any pair of variables on
![]() $D(\operatorname {\mathrm {SL}}_n)$
coincides with the log-coefficient on
$D(\operatorname {\mathrm {SL}}_n)$
coincides with the log-coefficient on
![]() $D(\operatorname {\mathrm {GL}}_n)$
due to Lemma 9.1. Since in addition
$D(\operatorname {\mathrm {GL}}_n)$
due to Lemma 9.1. Since in addition
![]() $\tilde {B}_{D(\operatorname {\mathrm {GL}}_n)} \Omega _{D(\operatorname {\mathrm {GL}}_n)} = \begin {bmatrix} I & 0 \end {bmatrix}$
(compatibility with the Poisson bracket), it follows that
$\tilde {B}_{D(\operatorname {\mathrm {GL}}_n)} \Omega _{D(\operatorname {\mathrm {GL}}_n)} = \begin {bmatrix} I & 0 \end {bmatrix}$
(compatibility with the Poisson bracket), it follows that
![]() $\tilde {B}_{D(\operatorname {\mathrm {SL}}_n)} \Omega _{D(\operatorname {\mathrm {SL}}_n)} = \begin {bmatrix} I & 0 \end {bmatrix}$
, and thus, by Proposition 2.3, the Poisson bracket
$\tilde {B}_{D(\operatorname {\mathrm {SL}}_n)} \Omega _{D(\operatorname {\mathrm {SL}}_n)} = \begin {bmatrix} I & 0 \end {bmatrix}$
, and thus, by Proposition 2.3, the Poisson bracket
![]() $\{\cdot ,\cdot \}_{D(\operatorname {\mathrm {SL}}_n)}$
is compatible with the generalized cluster structure on
$\{\cdot ,\cdot \}_{D(\operatorname {\mathrm {SL}}_n)}$
is compatible with the generalized cluster structure on
![]() $D(\operatorname {\mathrm {SL}}_n)$
. In particular,
$D(\operatorname {\mathrm {SL}}_n)$
. In particular,
![]() $\tilde {B}_{D(\operatorname {\mathrm {SL}}_n)}$
has full rank.
$\tilde {B}_{D(\operatorname {\mathrm {SL}}_n)}$
has full rank.
For part (iii), we use the groups
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}$
and
$\mathcal {H}_{\mathbf {\Gamma }^r}$
and
![]() $\mathcal {H}_{\mathbf {\Gamma }^c}$
that were defined in Section 3.7 (the difference is that we no longer have the two-dimensional action by scalar matrices). Note that
$\mathcal {H}_{\mathbf {\Gamma }^c}$
that were defined in Section 3.7 (the difference is that we no longer have the two-dimensional action by scalar matrices). Note that
![]() $\mathcal {H}_{\mathbf {\Gamma }^r},\mathcal {H}_{\mathbf {\Gamma }^c}\subseteq \operatorname {\mathrm {SL}}_n$
, hence these groups induce zero weights on the frozen variables
$\mathcal {H}_{\mathbf {\Gamma }^r},\mathcal {H}_{\mathbf {\Gamma }^c}\subseteq \operatorname {\mathrm {SL}}_n$
, hence these groups induce zero weights on the frozen variables
![]() $g_{11} = \det X$
and
$g_{11} = \det X$
and
![]() $h_{11} = \det Y$
. As a result, if
$h_{11} = \det Y$
. As a result, if
![]() $W_{D(\operatorname {\mathrm {SL}}_n)}$
and
$W_{D(\operatorname {\mathrm {SL}}_n)}$
and
![]() $W_{D(\operatorname {\mathrm {GL}}_n)}$
are the weight matrices for the actions of
$W_{D(\operatorname {\mathrm {GL}}_n)}$
are the weight matrices for the actions of
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}\times \mathcal {H}_{\mathbf {\Gamma }^c}$
upon
$\mathcal {H}_{\mathbf {\Gamma }^r}\times \mathcal {H}_{\mathbf {\Gamma }^c}$
upon
![]() $D(\operatorname {\mathrm {GL}}_n)$
and
$D(\operatorname {\mathrm {GL}}_n)$
and
![]() $D(\operatorname {\mathrm {SL}}_n)$
, the identity
$D(\operatorname {\mathrm {SL}}_n)$
, the identity
![]() $\tilde {B}_{D(\operatorname {\mathrm {SL}}_n)}W_{D(\operatorname {\mathrm {SL}}_n)} = 0$
follows from the identity
$\tilde {B}_{D(\operatorname {\mathrm {SL}}_n)}W_{D(\operatorname {\mathrm {SL}}_n)} = 0$
follows from the identity
![]() $\tilde {B}_{D(\operatorname {\mathrm {GL}}_n)}W_{D(\operatorname {\mathrm {GL}}_n)} = 0$
, for the weights of
$\tilde {B}_{D(\operatorname {\mathrm {GL}}_n)}W_{D(\operatorname {\mathrm {GL}}_n)} = 0$
, for the weights of
![]() $g_{11}$
and
$g_{11}$
and
![]() $h_{11}$
are zero. We conclude from Proposition 2.4 that the local toric action induced by
$h_{11}$
are zero. We conclude from Proposition 2.4 that the local toric action induced by
![]() $\mathcal {H}_{\mathbf {\Gamma }^r}\times \mathcal {H}_{\mathbf {\Gamma }^c}$
on
$\mathcal {H}_{\mathbf {\Gamma }^r}\times \mathcal {H}_{\mathbf {\Gamma }^c}$
on
![]() $D(\operatorname {\mathrm {SL}}_n)$
is
$D(\operatorname {\mathrm {SL}}_n)$
is
![]() $\mathcal {GC}$
-extendable.
$\mathcal {GC}$
-extendable.
10 Selected examples
In this section, we provide three examples of generalized cluster structures on
![]() $\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
for
$\operatorname {\mathrm {GL}}_n \times \operatorname {\mathrm {GL}}_n$
for
![]() $n\in \{3,4,5\}$
. Note that some of the arrows in the quivers are dashed only for convenience; their weight is equal to
$n\in \{3,4,5\}$
. Note that some of the arrows in the quivers are dashed only for convenience; their weight is equal to
![]() $1$
, as the weight of all the other arrows.
$1$
, as the weight of all the other arrows.
10.1 Cremmer–Gervais
 $i\mapsto i-1$
,
$i\mapsto i-1$
,
 $n = 3$
$n = 3$
The initial quiver is illustrated in Figure 28. There are two
![]() $\mathcal {L}$
-matrices:
$\mathcal {L}$
-matrices:
 $$\begin{align*}\mathcal{L}_1(X,Y) = \begin{bmatrix} x_{21} & x_{22} & x_{23} & \\ x_{31} & x_{32} & x_{33} & \\ & y_{11} & y_{12} & y_{13}\\ & y_{21} & y_{22} & y_{23} \end{bmatrix}, \ \ \mathcal{L}_2(X,Y) = \begin{bmatrix} y_{13} & x_{21}\\ y_{23} & x_{31}\end{bmatrix}. \end{align*}$$
$$\begin{align*}\mathcal{L}_1(X,Y) = \begin{bmatrix} x_{21} & x_{22} & x_{23} & \\ x_{31} & x_{32} & x_{33} & \\ & y_{11} & y_{12} & y_{13}\\ & y_{21} & y_{22} & y_{23} \end{bmatrix}, \ \ \mathcal{L}_2(X,Y) = \begin{bmatrix} y_{13} & x_{21}\\ y_{23} & x_{31}\end{bmatrix}. \end{align*}$$

Figure 28 The initial quiver for the Cremmer–Gervais structure in
![]() $n=3$
,
$n=3$
,
![]() $\Gamma _1^r=\Gamma _1^c = \{2\}$
,
$\Gamma _1^r=\Gamma _1^c = \{2\}$
,
![]() $\Gamma _2^r=\Gamma _2^c = \{1\}$
.
$\Gamma _2^r=\Gamma _2^c = \{1\}$
.
10.2 Cremmer-Gervais
 $i \mapsto i+1$
,
$i \mapsto i+1$
,
 $n=4$
$n=4$
The initial quiver is illustrated in Figure 29. As we showed in Example 3.2, there are two
![]() $\mathcal {L}$
-matrices:
$\mathcal {L}$
-matrices:
 $$\begin{align*}\mathcal{L}_1(X,Y) = \begin{bmatrix}x_{41} & x_{42} & x_{43} & 0 & 0 & 0\\ y_{12} & y_{13} & y_{14} & 0 & 0 & 0\\ y_{22} & y_{23} & y_{24} & x_{11} & x_{12} & x_{13} \\ y_{32} & y_{33} & y_{34} & x_{21} & x_{22} & x_{23}\\ y_{42} & y_{43} & y_{44} & x_{31} & x_{32} & x_{33}\\ 0 & 0 & 0 & x_{41} & x_{42} & x_{43} \end{bmatrix}, \ \ \ \mathcal{L}_2(X,Y) = \begin{bmatrix} y_{12} & y_{13} & y_{14} & 0 & 0 & 0\\ y_{22} & y_{23} & y_{24} & x_{11} & x_{12} & x_{13}\\ y_{32} & y_{33} & y_{34} & x_{21} & x_{22} & x_{23}\\ y_{42} & y_{43} & y_{44} & x_{31} & x_{32} & x_{33}\\ 0 & 0 & 0 & x_{41} & x_{42} & x_{43}\\ 0 & 0 & 0 & y_{12} & y_{13} & y_{14} \end{bmatrix}. \end{align*}$$
$$\begin{align*}\mathcal{L}_1(X,Y) = \begin{bmatrix}x_{41} & x_{42} & x_{43} & 0 & 0 & 0\\ y_{12} & y_{13} & y_{14} & 0 & 0 & 0\\ y_{22} & y_{23} & y_{24} & x_{11} & x_{12} & x_{13} \\ y_{32} & y_{33} & y_{34} & x_{21} & x_{22} & x_{23}\\ y_{42} & y_{43} & y_{44} & x_{31} & x_{32} & x_{33}\\ 0 & 0 & 0 & x_{41} & x_{42} & x_{43} \end{bmatrix}, \ \ \ \mathcal{L}_2(X,Y) = \begin{bmatrix} y_{12} & y_{13} & y_{14} & 0 & 0 & 0\\ y_{22} & y_{23} & y_{24} & x_{11} & x_{12} & x_{13}\\ y_{32} & y_{33} & y_{34} & x_{21} & x_{22} & x_{23}\\ y_{42} & y_{43} & y_{44} & x_{31} & x_{32} & x_{33}\\ 0 & 0 & 0 & x_{41} & x_{42} & x_{43}\\ 0 & 0 & 0 & y_{12} & y_{13} & y_{14} \end{bmatrix}. \end{align*}$$

Figure 29 The initial quiver for Cremmer–Gervais structure
![]() $i \mapsto i+1$
,
$i \mapsto i+1$
,
![]() $\mathbf {\Gamma }^r=\mathbf {\Gamma }^c$
,
$\mathbf {\Gamma }^r=\mathbf {\Gamma }^c$
,
![]() $n=4$
.
$n=4$
.

Figure 30 The initial quiver for the generalized cluster structure on
![]() $\operatorname {\mathrm {GL}}_5 \times \operatorname {\mathrm {GL}}_5$
induced by the BD pair
$\operatorname {\mathrm {GL}}_5 \times \operatorname {\mathrm {GL}}_5$
induced by the BD pair
![]() $\mathbf {\Gamma }=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
with
$\mathbf {\Gamma }=(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
with
![]() $\Gamma _1^r = \{2,4\}$
,
$\Gamma _1^r = \{2,4\}$
,
![]() $\Gamma _2^r = \{1,3\}$
,
$\Gamma _2^r = \{1,3\}$
,
![]() $\gamma _r(2) = 1$
,
$\gamma _r(2) = 1$
,
![]() $\gamma _r(4) = 3$
,
$\gamma _r(4) = 3$
,
![]() $\Gamma _1^c = \{1\}$
,
$\Gamma _1^c = \{1\}$
,
![]() $\Gamma _2^c = \{4\}$
,
$\Gamma _2^c = \{4\}$
,
![]() $\gamma _c(1) = 4$
.
$\gamma _c(1) = 4$
.
10.3 An example with different
 $\mathbf {\Gamma }^r$
and
$\mathbf {\Gamma }^r$
and
 $\mathbf {\Gamma }^c$
,
$\mathbf {\Gamma }^c$
,
 $n=5$
$n=5$
Set
![]() $n:=5$
,
$n:=5$
,
![]() $\Gamma _1^r := \{2,4\}$
,
$\Gamma _1^r := \{2,4\}$
,
![]() $\Gamma _2^r := \{1,3\}$
,
$\Gamma _2^r := \{1,3\}$
,
![]() $\gamma _r(2): = 1$
,
$\gamma _r(2): = 1$
,
![]() $\gamma _r(4): = 3$
;
$\gamma _r(4): = 3$
;
![]() $\Gamma _1^c := \{1\}$
,
$\Gamma _1^c := \{1\}$
,
![]() $\Gamma _2^c: = \{4\}$
,
$\Gamma _2^c: = \{4\}$
,
![]() $\gamma _c(1) := 4$
. The initial quiver of the resulting
$\gamma _c(1) := 4$
. The initial quiver of the resulting
![]() $\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is illustrated in Figure 30. There are six
$\mathcal {GC}(\mathbf {\Gamma }^r,\mathbf {\Gamma }^c)$
is illustrated in Figure 30. There are six
![]() $\mathcal {L}$
-matrices, five of which are trivial and one nontrivial:
$\mathcal {L}$
-matrices, five of which are trivial and one nontrivial:
 $$\begin{align*}\mathcal{L}_1(X,Y):= \begin{bmatrix} y_{13} & y_{14} & y_{15} & & & & & \\ y_{23} & y_{24} & y_{25} & & & & & \\ y_{33} & y_{34} & y_{35} & x_{41} & x_{42} & & & \\ y_{43} & y_{44} & y_{45} & x_{51} & x_{52} & & & \\ & & & y_{14} & y_{15} & x_{21} & x_{22} & x_{23} \\ & & & y_{24} & y_{25} & x_{31} & x_{32} & x_{33}\\ & & & & & x_{41} & x_{42} & x_{43}\\ & & & & & x_{51} & x_{52} & x_{53} \end{bmatrix}; \end{align*}$$
$$\begin{align*}\mathcal{L}_1(X,Y):= \begin{bmatrix} y_{13} & y_{14} & y_{15} & & & & & \\ y_{23} & y_{24} & y_{25} & & & & & \\ y_{33} & y_{34} & y_{35} & x_{41} & x_{42} & & & \\ y_{43} & y_{44} & y_{45} & x_{51} & x_{52} & & & \\ & & & y_{14} & y_{15} & x_{21} & x_{22} & x_{23} \\ & & & y_{24} & y_{25} & x_{31} & x_{32} & x_{33}\\ & & & & & x_{41} & x_{42} & x_{43}\\ & & & & & x_{51} & x_{52} & x_{53} \end{bmatrix}; \end{align*}$$
Acknowledgements
The author would like to thank his advisor, Misha Gekhtman, for giving this problem to him and for numerous discussions and valuable suggestions. The author would also like to thank the anonymous referee, whose valuable comments have improved the exposition.
Competing interest
The authors have no competing interest to declare.
Funding statement
The first version of the paper was written at University of Notre Dame and was partially supported by NSF grant 2100785. The final version was written at Institute for Basic Science and supported by the grant IBS-R003-D1.