Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Karpenko, Nikita A.
2020.
Extended Petrov–Semenov’s connections.
Archiv der Mathematik,
Vol. 115,
Issue. 1,
p.
27.
Devyatov, Rostislav A.
Karpenko, Nikita A.
and
Merkurjev, Alexander S.
2021.
Maximal indexes of flag varieties for spin groups.
Forum of Mathematics, Sigma,
Vol. 9,
Issue. ,
Petrov, Victor
and
Semenov, Nikita
2021.
Hopf-theoretic approach to motives of twisted flag varieties.
Compositio Mathematica,
Vol. 157,
Issue. 5,
p.
963.
Primozic, Eric
2022.
On universal stably free modules in positive characteristic.
Journal of Pure and Applied Algebra,
Vol. 226,
Issue. 5,
p.
106918.
Scully, Stephen
2022.
On an Extension of Hoffmann’s Separation Theorem for Quadratic Forms.
International Mathematics Research Notices,
Vol. 2022,
Issue. 14,
p.
11092.
Karpenko, Nikita A.
2022.
On Classifying Spaces of Spin Groups.
Results in Mathematics,
Vol. 77,
Issue. 4,
Primozic, Eric
2022.
Motivic cohomology and infinitesimal group schemes.
Annals of K-Theory,
Vol. 7,
Issue. 3,
p.
441.
Harvey, Curtis R.
and
Karpenko, Nikita A.
2024.
On generic quadratic forms in a power of the fundamental ideal.
European Journal of Mathematics,
Vol. 10,
Issue. 4,
Harvey, Curtis R.
and
Karpenko, Nikita A.
2024.
Quadratic forms in I n of dimension 2 n +2 n-1 .
Comptes Rendus. Mathématique,
Vol. 362,
Issue. G11,
p.
1539.
Karpenko, Nikita A.
2025.
On special Clifford groups and their characteristic classes.
Ricerche di Matematica,
Vol. 74,
Issue. 1,
p.
449.
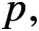 $p,$
we define Steenrod operations
$p,$
we define Steenrod operations
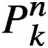 $P^{n}_{k}$
on motivic cohomology with
$P^{n}_{k}$
on motivic cohomology with
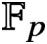 $\mathbb {F}_{p}$
-coefficients of smooth varieties defined over the base field
$\mathbb {F}_{p}$
-coefficients of smooth varieties defined over the base field
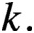 $k.$
We show that
$k.$
We show that
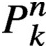 $P^{n}_{k}$
is the pth power on
$P^{n}_{k}$
is the pth power on
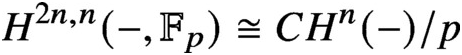 $H^{2n,n}(-,\mathbb {F}_{p}) \cong CH^{n}(-)/p$
and prove an instability result for the operations. Restricted to mod p Chow groups, we show that the operations satisfy the expected Adem relations and Cartan formula. Using these new operations, we remove previous restrictions on the characteristic of the base field for Rost’s degree formula. Over a base field of characteristic
$H^{2n,n}(-,\mathbb {F}_{p}) \cong CH^{n}(-)/p$
and prove an instability result for the operations. Restricted to mod p Chow groups, we show that the operations satisfy the expected Adem relations and Cartan formula. Using these new operations, we remove previous restrictions on the characteristic of the base field for Rost’s degree formula. Over a base field of characteristic
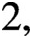 $2,$
we obtain new results on quadratic forms.
$2,$
we obtain new results on quadratic forms.