Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T13:52:06.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Modularity lifting results in parallel weight one and applications to the Artin conjecture: the tamely ramified case

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  10 July 2014

PAYMAN L. KASSAEI ,
SHU SASAKI  and
YICHAO TIAN
PAYMAN L. KASSAEI
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke St. W., Montreal H3A 0B9, QC, Canada; [email protected]
SHU SASAKI
Affiliation:
Fakultat fur Mathematik, Universitat Duisburg-Essen, Thea-Leymann-Strasse 9, 45127 Essen, Germany; [email protected]
YICHAO TIAN
Affiliation:
Morningside Center of Mathematics, Chinese Academy of Sciences, 55 Zhong Guan Cun East Road, Beijing, 100190, China; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend the modularity lifting result of P. Kassaei (‘Modularity lifting in parallel weight one’,J. Amer. Math. Soc.26 (1) (2013), 199–225) to allow Galois representations with some ramification at 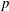$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$. We also prove modularity mod 5 of certain Galois representations. We use these results to prove new cases of the strong Artin conjecture over totally real fields in which 5 is unramified. As an ingredient of the proof, we provide a general result on the automatic analytic continuation of overconvergent 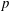$p$-adic Hilbert modular forms of finite slope which substantially generalizes a similar result in P. Kassaei (‘Modularity lifting in parallel weight one’, J. Amer. Math. Soc.26 (1) (2013), 199–225).

MSC classification

Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11F80: Galois representations
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e18
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author(s) 2014

References

Andreatta, F. and Goren, E., ‘Hilbert modular forms: mod p and p-adic aspects’, Mem. Amer. Math. Soc. 173 (2005).Google Scholar
Abbes, A. and Saito, T., ‘Ramification of local fields with imperfect residue fields’, Amer. J. Math. 124 (2002), 879–920.Google Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., ‘Congruences between Hilbert modular forms: constructing ordinary lifts, II’, Math. Res. Lett. 18 (2011).Google Scholar
Buzzard, K., ‘Analytic continuation of overconvergent eigenforms’, J. Amer. Math. Soc. 16 (2003), 29–55.Google Scholar
Buzzard, K., Dickinson, M., Shepherd-Barron, N. and Taylor, R., ‘On icosahedral Artin representations’, Duke Math. J. 109 (2001), 283–318.Google Scholar
Buzzard, K. and Taylor, R., ‘Companion forms and weight one forms’, Ann. of Math. 149 (1999), 905–919.CrossRefGoogle Scholar
Carayol, H., ‘Sur les représentations p-adiques associées aux formes modulaires de Hilbert’, Ann. Scient. de l’E.N.S. 19 (1986), 409–468.Google Scholar
Chevalley, C., ‘Deux theorems d’arithmetic’, J. Soc. Math. Japan 3 (1951), 36–44.Google Scholar
Cornell, G., Silverman, J. H. and Stevens, G. (Eds.), Modular Forms and Fermat’s Last Theorem (Springer-Verlag, 1998).Google Scholar
Deligne, P. and Ribet, K., ‘Values of abelian L-functions at negative integers over totally real fields’, Invent. Math. 59 (1980), 227–286.Google Scholar
Diamond, F., ‘On deformation rings and Hecke rings’, Ann. of Math. (2) 144 (1) (1996), 137–166.Google Scholar
Ekedahl, T., ‘An effective version of Hilbert’s irreducibility theorem’, inSéminaire de Théorie des Nombres, (Paris, 1988–1989), Progress in Mathematics, 91 (Birkhäuser).Google Scholar
Gee, T., ‘Companion forms over totally real fields, II’, Duke Math. J. 136 (2007), 275–284.Google Scholar
Goren, E. and Oort, F., ‘Stratifications of Hilbert modular varieties’, J. Algebraic Geom. 9 (1) (2000), 111–154.Google Scholar
Goren, E. and Kassaei, P., ‘Canonical subgroups over Hilbert modular varieties’, J. für die reine und angewandte Mathematik 670 (2012), 1–63.Google Scholar
Hida, H., ‘On p-adic Hecke algebras for G L 2over totally real fields’, Ann. of Math. 128 (1988), 295–384.Google Scholar
Jarvis, F., ‘Correspondences on Shimura curves and Mazur’s principle above p ’, Pac. J. Math. 213 (2004), 267–280.Google Scholar
Khare, C. and Wintenberger, J. P., ‘Serre’s modularity conjecture II’, Invent. Math. 178 (2009), 505–586.Google Scholar
Kassaei, P., ‘Modularity lifting in parallel weight one’, J. Amer. Math. Soc. 26 (1) (2013), 199–225.Google Scholar
Kassaei, P., ‘Overconvergence, analytic continuation, and classicality: the case of curves’, J. für die reine und angewandte Mathematik 631 (2009), 109–139.Google Scholar
Katz, N. and Mazur, B., Arithmetic Moduli of Elliptic Curves, Annals of Mathematical Studies, 108 (Princeton University Press, 1985).CrossRefGoogle Scholar
Kisin, M. and Lai, K. F., ‘Overconvergent Hilbert modular forms’, Amer. J. Math. 127 (2005), 735–783.CrossRefGoogle Scholar
Kisin, M., ‘Moduli of finite flat group schemes and modularity’, Ann. of Math. 170 (2009), 1085–1180.Google Scholar
Mokrane, A., ‘Quelques remarques sur l’ordinarité’, J. Number Theory 73 (1998), 162–181.CrossRefGoogle Scholar
Nyssen, L., ‘Pseudo-représentations’, Math. Ann. 306 (1996), 257–283.Google Scholar
Pappas, G., ‘Arithmetic models for Hilbert modular varieties’, Comput. Math. 98 (1995), 43–76.Google Scholar
Pilloni, V., ‘Formes modulaires $p$ -adiques de Hilbert de poids 1’, Preprint, 2012.Google Scholar
Pilloni, V., ‘Prolongement analytique sur les variétés de Siegel’, Duke Math. J. 157 (1) (2011), 167–222.CrossRefGoogle Scholar
Pilloni, V. and Stroh, B., ‘Surconvergence et Classicité: le cas Hilbert’, Preprint 2011.Google Scholar
Pilloni, V. and Stroh, B., ‘Surconvergence, ramification et modularité’, Preprint 2013.Google Scholar
Rappoport, M., ‘Compactification de l’espace de modules de Hilbert–Blumenthal’, Comput. Math. 36 (1978), 255–335.Google Scholar
Raynaud, M., ‘Schémas en groupes de type (p, …, p)’, Bull. de la S.M.F. 102 (1974), 241–280.Google Scholar
Rogawski, J. and Tunnell, J., ‘On Artin L-functions associated to Hilbert modular forms of weight one’, Invent. Math. 1983 1–42.Google Scholar
Rouquier, R., ‘Caractérisation des Caractères et pseudo-Caractères’, J. Algebra 180 (1996), 571–586.Google Scholar
Rubin, K., Modularity of mod 5 representations, in [9], p. 463–474.CrossRefGoogle Scholar
Sasaki, S., On Artin representations and nearly ordinary Hecke algebras over totally real fields, Preprint.Google Scholar
Serre, J. P., ‘Topics in Galois theory’, inResearch Notes in Mathematics Vol. 1 (Jones and Bartlett Publishers, 1992).Google Scholar
Shepherd-Barron, N. and Taylor, R, ‘Mod 2 and mod 5 icosahedral representations’, J. Amer. Math. Soc. 10 (1997), 283–298.Google Scholar
Shimura, G., ‘The special values of the zeta functions associated with Hilbert modular forms’, Duke Math. J. 45 (3) (1978), 637–679.Google Scholar
Stamm, H., ‘On the reduction of the Hilbert–Blumenthal-moduli scheme with Γ 0(p)-level structure’, Forum Math. 9 (4) (1990), 405–455.Google Scholar
Taylor, R., ‘On Galois representations associated to Hilbert modular forms’, Invent. Math. 98 (1989), 265–280.CrossRefGoogle Scholar
Taylor, R., ‘On icosahedral Artin representations II’, Amer. J. Math. 125 (2003), 549–566.Google Scholar
Tian, Y., Classicality of overconvergent Hilbert eigenforms: case of quadratic residue degree. arXiv:1104.4583.Google Scholar
Wiles, A., ‘On ordinary λ-adic representations associated to modular forms’, Invent. Math. 94 (1988), 529–573.Google Scholar