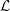Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2025-01-03T03:54:56.794Z Has data issue: false hasContentIssue false
  • English
  • Français

${\mathcal{L}}$ -INVARIANTS AND LOCAL–GLOBAL COMPATIBILITY FOR THE GROUP 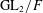$\text{GL}_{2}/F$

Part of: Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  10 June 2016

YIWEN DING
YIWEN DING*
Affiliation:
Department of Mathematics, Imperial College London, UK; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 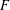$F$ be a totally real number field, 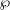${\wp}$ a place of 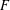$F$ above 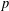$p$ . Let 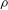${\it\rho}$ be a 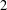$2$ -dimensional 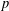$p$ -adic representation of 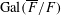$\text{Gal}(\overline{F}/F)$ which appears in the étale cohomology of quaternion Shimura curves (thus 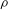${\it\rho}$ is associated to Hilbert eigenforms). When the restriction 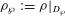${\it\rho}_{{\wp}}:={\it\rho}|_{D_{{\wp}}}$ at the decomposition group of 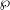${\wp}$ is semistable noncrystalline, one can associate to 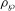${\it\rho}_{{\wp}}$ the so-called Fontaine–Mazur 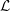${\mathcal{L}}$ -invariants, which are however invisible in the classical local Langlands correspondence. In this paper, we prove one can find these 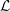${\mathcal{L}}$ -invariants in the completed cohomology group of quaternion Shimura curves, which generalizes some of Breuil’s results [Breuil, Astérisque, 331 (2010), 65–115] in the $\text{GL}_{2}/\mathbb{Q}$ -case.

MSC classification

Primary: 11S37: Langlands-Weil conjectures, nonabelian class field theory
Secondary: 11S80: Other analytic theory (analogues of beta and gamma functions, $p$-adic integration, etc.)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e13
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2016

References

Belaïche, J. and Chenevier, G., ‘Families of Galois representations and Selmer groups’, Astérisque 324 (2009).Google Scholar
Bergdall, J., ‘On the variation of $({\it\varphi},{\rm\Gamma})$ -modules over $p$ -adic famillies of automorphic forms’, Thesis, Brandeis University, 2013.Google Scholar
Berger, L., ‘Représentations p-adiques et équations différentielles’, Invent. Math. 148(2) (2002), 219–284.Google Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-archimedean Analysis, Grundlehren der math. Wiss. 261 (Springer, 1984).CrossRefGoogle Scholar
Breuil, C., ‘Invariant L et série spéciale p-adique’, Ann. Sci. Éc. Norm. Supér. (4) 37 (2004), 559–610.Google Scholar
Breuil, C., ‘Introduction générale aux volumes d’Astérisque sur le programme de Langlands p-adique pour GL2(ℚ p )’, Astérisque 319 (2008), 1–12.Google Scholar
Breuil, C., ‘Série spéciale p-adique et cohomologie étale complétée’, Astérisque 331 (2010), 65–115.Google Scholar
Breuil, C., ‘The emerging p-adic Langlands programme’, Proceedings of I.C.M.2010, Vol. II, 203–230.Google Scholar
Breuil, C., ‘Conjectures de classicité sur les formes de Hilbert surconvergentes de pente finie’, unpublished note, march 2010.Google Scholar
Breuil, C., ‘Remarks on some locally ℚ p analytic representations of GL2(F) in the crystalline case’, London Math. Soc. Lecture Note Ser. 393 (2012), 212–238.Google Scholar
Breuil, C., ‘Vers le socle localement analytique pour GL n II’, Math. Annalen 361 (2015), 741–785.CrossRefGoogle Scholar
Breuil, C. and Emerton, M., ‘Représentations p-adique ordinaires de GL2(ℚ p ) et compatibilité local-global’, Astérisque 331 (2010), 255–315.Google Scholar
Buzzard, K., ‘Eigenvarieties’, London Math. Soc. Lecture Note Ser. 320 (2007), 59–120.Google Scholar
Carayol, H., ‘Sur les représentations l-adiques associées aux formes modulaires de Hilbert’, Ann. Sci. Éc. Norm. Supér. 19 (1986), 409–468.CrossRefGoogle Scholar
Casselman, W. and Wigner, D., ‘Continuous cohomology and a conjecture of Serre’s’, Invent. Math. 25(3) (1974), 199–211.Google Scholar
Chenevier, G., ‘Familles p-adiques de formes automorphes pour GL n ’, J. Reine Angew. Math. 570 (2004), 143–217.Google Scholar
Chenevier, G., ‘On the infinite fern of Galois representations of unitary type’, Ann. Sci. Éc. Norm. Supér. (4) 44(6) (2011), 963–1019.Google Scholar
Colmez, P., ‘Représentations triangulines de dimension 2’, Astérisque 319 (2008), 213–258.Google Scholar
Colmez, P., ‘Invariants L et dérivées de valeurs propres de Frobenius’, Astérisque 331 (2010), 13–28.Google Scholar
Ding, Y., ‘Formes modulaires $p$ -adiques sur les courbes de Shimura unitares et compatibilité local-global’, Preprint.Google Scholar
Ding, Y., ‘ ${\mathcal{L}}$ -invariants, partially de Rham families and local-global compatibility’, Preprint, 2015, arXiv:1508.07420.Google Scholar
Emerton, M., ‘Locally analytic vectors in representations of locally p-adic analytic groups’, Mem. Amer. Math. Soc., (2004), to appear.Google Scholar
Emerton, M., ‘On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms’, Invent. Math. 164 (2006), 1–84.Google Scholar
Emerton, M., ‘Jacquet Modules of locally analytic representations of p-adic reductive groups I. constructions and first properties’, Ann. Sci. Éc. Norm. Supér. (4) 39(5) (2006), 775–839.Google Scholar
Emerton, M., ‘Jacquet modules of locally analytic representations of p-adic reductive groups II. The relation to parabolic induction’, J. Inst. Math. Jussieu (2007).Google Scholar
Emerton, M., ‘Local-global compatibiligty in the $p$ -adic Langlands programme for $\text{GL}_{2}/\mathbb{Q}$ ’, Preprint, 2010.Google Scholar
Fontaine, J.-M., ‘Le corps des périodes p-adiques’, Astérisque 223 (1994), 59–102.Google Scholar
Fontaine, J.-M. and Ouyang, Y., ‘Theory of $p$ -adic Galois representations’, Preprint, 2008.Google Scholar
Harris, M. and Taylor, R., On the Geometry and Cohomology of Some Simple Shimura Varieties, (Princeton University Press, 2001).Google Scholar
Kedlaya, K., Pottharst, J. and Xiao, L., ‘Cohomology of arithmetic families of (𝜙, Γ)-modules’, J. Amer. Math. Soc. 27 (2014), 1043–1115.Google Scholar
Kisin, M., ‘Overconvergent modular forms and the Fontaine–Mazur conjecture’, Invent. Math. 153(2) (2003), 373–454.Google Scholar
Liu, R., ‘Triangulation of refined families’, Comment. Math. Helv. 90(4) (2015), 831–904.CrossRefGoogle Scholar
Nakamura, K., ‘Classification of two-dimensional split trianguline representations of p-adic field’, Compositio Math. 145(4) (2009), 865–914.Google Scholar
Newton, J., ‘Completed cohomology of Shimura curves and a p-adic Jacquet–Langlands correspondence’, Math. Ann. 355(2) (2013), 729–763.CrossRefGoogle Scholar
Saito, T., ‘Hilbert modular forms and p-adic Hodge theory’, Compositio Math. 145 (2009), 1081–1113.CrossRefGoogle Scholar
Schneider, P. and Teitelbaum, J., ‘Locally analytic distributions and p-adic representation theory, with applications to GL2 ’, J. Amer. Math. Soc. 15.2 (2002), 443–468.Google Scholar
Schneider, P. and Teitelbaum, J., ‘Algebras of p-adic distributions and admissible representations’, Invent. Math. 153 (2003), 145–196.CrossRefGoogle Scholar
Schraen, B., ‘Représentations p-adiques de GL2(L) et catégories dérivées’, Israel J. Math. 176 (2012), 307–361.Google Scholar
Taylor, R., ‘Galois representations associated to Siegel modular forms of low weight’, Duke Math. J. 63(2) (1991), 281–332.Google Scholar
Tian, Y. and Xiao, L., ‘ p-adic cohomology and classicality of overconvergent Hilbert modular forms’, Astérisque, to appear.Google Scholar
Weibel, C. A., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics, 38 (Cambridge University Press, 1994).Google Scholar
Zhang, Y., ‘L-invariants and logarithm derivatives of eigenvalues of Frobenius’, Sci. China Math. 57(8) (2014), 1587–1604.Google Scholar