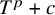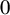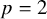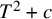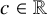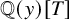1. Introduction
Let K be a field, and suppose
![]() $f\in K[T]$
has degree
$f\in K[T]$
has degree
![]() $\deg f\ge 2$
. For
$\deg f\ge 2$
. For
![]() $n\in \mathbb {N}=\{1,2,3,\ldots \}$
, we write
$n\in \mathbb {N}=\{1,2,3,\ldots \}$
, we write
![]() $f^{(n)}\in K[T]$
for the n-fold iterate of f and define
$f^{(n)}\in K[T]$
for the n-fold iterate of f and define
![]() $f^{(0)}=T$
. Let
$f^{(0)}=T$
. Let
![]() $x\in K$
. We call x an f-periodic point if there exists
$x\in K$
. We call x an f-periodic point if there exists
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $f^{(n)}(x)=x$
. We call x an f-preperiodic point if there exists an integer
$f^{(n)}(x)=x$
. We call x an f-preperiodic point if there exists an integer
![]() $m\ge 0$
such that
$m\ge 0$
such that
![]() $f^{(m)}(x)$
is f-periodic. Suppose x is f-preperiodic. The preperiod length of x is
$f^{(m)}(x)$
is f-periodic. Suppose x is f-preperiodic. The preperiod length of x is
and the minimum period of x is
An element of K is called an f-wandering point if it is not f-preperiodic. Equivalently,
![]() $x\in K$
is an f-wandering point if and only if
$x\in K$
is an f-wandering point if and only if
![]() $\{f^{(n)}(x) : n\in \mathbb {N}\}$
is infinite.
$\{f^{(n)}(x) : n\in \mathbb {N}\}$
is infinite.
Suppose for the moment that K is a subfield of
![]() $\mathbb {C}$
. We call f post-critically finite if its post-critical set
$\mathbb {C}$
. We call f post-critically finite if its post-critical set
is finite. For example,
![]() $T^2-1$
is post-critically finite as its post-critical set equals
$T^2-1$
is post-critically finite as its post-critical set equals
![]() $\{-1,0\}$
.
$\{-1,0\}$
.
Let
![]() $M_{\mathbb {Q}}$
denote the set consisting of the v-adic absolute value on
$M_{\mathbb {Q}}$
denote the set consisting of the v-adic absolute value on
![]() $\mathbb {Q}$
for all prime numbers v together with the Archimedean absolute value. For each prime number v, let
$\mathbb {Q}$
for all prime numbers v together with the Archimedean absolute value. For each prime number v, let
![]() $\mathbb {C}_v$
denote a completion of an algebraic closure of the valued field of v-adic numbers. We also set
$\mathbb {C}_v$
denote a completion of an algebraic closure of the valued field of v-adic numbers. We also set
![]() $\mathbb {C}_v=\mathbb {C}$
if v is Archimedean.
$\mathbb {C}_v=\mathbb {C}$
if v is Archimedean.
For a real number
![]() $t\ge 0$
, we set
$t\ge 0$
, we set
![]() $\log ^{+}t = \log \max \{1,t\}$
. Let
$\log ^{+}t = \log \max \{1,t\}$
. Let
![]() $v\in M_{\mathbb {Q}}$
, and suppose
$v\in M_{\mathbb {Q}}$
, and suppose
![]() $f\in \mathbb {C}_v[T]$
has degree
$f\in \mathbb {C}_v[T]$
has degree
![]() $d\ge 2$
. For all
$d\ge 2$
. For all
![]() $x\in \mathbb {C}_v$
, the limit
$x\in \mathbb {C}_v$
, the limit
exists and satisfies
![]() $\lambda _{f,v}(f(x)) = d\lambda _{f,v}(x)$
; see Chapter 3 and in particular Theorem 3.27 or Exercise 3.24 [Reference SilvermanSil07] for details. For example,
$\lambda _{f,v}(f(x)) = d\lambda _{f,v}(x)$
; see Chapter 3 and in particular Theorem 3.27 or Exercise 3.24 [Reference SilvermanSil07] for details. For example,
![]() $\lambda _{T^2,v}(x) = \log ^{+} |x|_v$
.
$\lambda _{T^2,v}(x) = \log ^{+} |x|_v$
.
If v is Archimedean, we often abbreviate
![]() $\lambda _{f,v} = \lambda _f$
. The local canonical height differs from
$\lambda _{f,v} = \lambda _f$
. The local canonical height differs from
![]() $z\mapsto \log ^{+}|z|$
by a bounded function on
$z\mapsto \log ^{+}|z|$
by a bounded function on
![]() $\mathbb {C}$
. We define
$\mathbb {C}$
. We define
 $$ \begin{align} \mathsf{C}(f) = \max\left\{1,\sup_{z\in\mathbb{C}} \frac{\max\{1,|z|\}}{e^{\lambda_f(z)}}\right\}<\infty. \end{align} $$
$$ \begin{align} \mathsf{C}(f) = \max\left\{1,\sup_{z\in\mathbb{C}} \frac{\max\{1,|z|\}}{e^{\lambda_f(z)}}\right\}<\infty. \end{align} $$
Thus, the filled Julia set attached to f is contained in the closed disk of radius
![]() $\mathsf {C}(f)$
centered at
$\mathsf {C}(f)$
centered at
![]() $0$
.
$0$
.
Next, we define the canonical height of an algebraic number with respect to f. Let K be a number field and
![]() $f\in K[T]$
be of degree
$f\in K[T]$
be of degree
![]() $\ge 2$
. Suppose x lies in a finite extension F of K. Let
$\ge 2$
. Suppose x lies in a finite extension F of K. Let
![]() $v\in M_{\mathbb {Q}}$
, and for a ring homomorphism
$v\in M_{\mathbb {Q}}$
, and for a ring homomorphism
![]() $\sigma \in \mathrm {Hom}(F,\mathbb {C}_v)$
we let
$\sigma \in \mathrm {Hom}(F,\mathbb {C}_v)$
we let
![]() $\sigma (f)$
be the polynomial obtained by applying
$\sigma (f)$
be the polynomial obtained by applying
![]() $\sigma $
to each coefficient of f. The canonical or Call–Silverman height of x (with respect to f) is
$\sigma $
to each coefficient of f. The canonical or Call–Silverman height of x (with respect to f) is
 $$ \begin{align} \hat h_f(x) = \frac{1}{[F:\mathbb{Q}]} \sum_{v\in M_{\mathbb{Q}}} \sum_{\sigma \in\mathrm{Hom}(F,\mathbb{C}_v)} \lambda_{\sigma(f),v}(\sigma(x)). \end{align} $$
$$ \begin{align} \hat h_f(x) = \frac{1}{[F:\mathbb{Q}]} \sum_{v\in M_{\mathbb{Q}}} \sum_{\sigma \in\mathrm{Hom}(F,\mathbb{C}_v)} \lambda_{\sigma(f),v}(\sigma(x)). \end{align} $$
This value does not depend on the number field
![]() $F\supseteq K$
containing x. Let
$F\supseteq K$
containing x. Let
![]() $\overline K$
denote an algebraic closure of K, we obtain a well-defined map
$\overline K$
denote an algebraic closure of K, we obtain a well-defined map
![]() $\hat h_f\colon \overline K\rightarrow [0,\infty )$
. For
$\hat h_f\colon \overline K\rightarrow [0,\infty )$
. For
![]() $x\in F$
, we define
$x\in F$
, we define
To formulate our results, we require Dimitrov’s notion of a hedgehog. A quill is a line segment
![]() $[0,1] z=\{tz : t\in [0,1]\}\subseteq \mathbb {C}$
, where
$[0,1] z=\{tz : t\in [0,1]\}\subseteq \mathbb {C}$
, where
![]() $z\in \mathbb {C}^\times = \mathbb {C}\smallsetminus \{0\}$
. A hedgehog with at most q quills is a finite union of quills
$z\in \mathbb {C}^\times = \mathbb {C}\smallsetminus \{0\}$
. A hedgehog with at most q quills is a finite union of quills
 $$ \begin{align*} \mathcal{H}(z_1,\ldots,z_q) = \bigcup_{i=1}^q [0,1] z_i, \end{align*} $$
$$ \begin{align*} \mathcal{H}(z_1,\ldots,z_q) = \bigcup_{i=1}^q [0,1] z_i, \end{align*} $$
where
![]() $z_1,\ldots ,z_q\in \mathbb {C}^\times $
; we also define
$z_1,\ldots ,z_q\in \mathbb {C}^\times $
; we also define
![]() $\mathcal {H}() = \{0\}$
to be the quill-less hedgehog. A hedgehog is a compact, path connected, topological tree.
$\mathcal {H}() = \{0\}$
to be the quill-less hedgehog. A hedgehog is a compact, path connected, topological tree.
We will also use Dubinin’s theorem [Reference DubininDub84] which states
if
![]() $q\ge 1$
, where
$q\ge 1$
, where
![]() $\mathrm {cap}(\mathcal {K})$
is the capacity, or equivalently the transfinite diameter, of a compact subset
$\mathrm {cap}(\mathcal {K})$
is the capacity, or equivalently the transfinite diameter, of a compact subset
![]() $\mathcal {K}\subseteq \mathbb {C}$
. We refer to Section 3 for basic properties of the capacity.
$\mathcal {K}\subseteq \mathbb {C}$
. We refer to Section 3 for basic properties of the capacity.
Quill Hypothesis. Let K be a number field, and let
![]() $f\in K[T]$
have degree
$f\in K[T]$
have degree
![]() $\ge 2$
. We say that f satisfies the quill hypothesis if there exist
$\ge 2$
. We say that f satisfies the quill hypothesis if there exist
![]() $\sigma _0\in \mathrm {Hom}(K,\mathbb {C})$
and an integer
$\sigma _0\in \mathrm {Hom}(K,\mathbb {C})$
and an integer
![]() $q\ge 0$
such that the post-critical set
$q\ge 0$
such that the post-critical set
![]() $\mathrm {PCO}^{+}(\sigma _0(f))$
is contained in a hedgehog with at most q quills and
$\mathrm {PCO}^{+}(\sigma _0(f))$
is contained in a hedgehog with at most q quills and
This hypothesis will be only be relevant for polynomials
![]() $f = T^p+c$
with p a prime number.
$f = T^p+c$
with p a prime number.
The condition and the constant
![]() $4$
are artefacts of Dubinin’s theorem. Our main results require f to satisfy the quill hypothesis, which should be unnecessary conjecturally.
$4$
are artefacts of Dubinin’s theorem. Our main results require f to satisfy the quill hypothesis, which should be unnecessary conjecturally.
Say
![]() $f=T^2-1$
. Then
$f=T^2-1$
. Then
![]() $\mathrm {PCO}^{+}(f)$
is contained in the single quill
$\mathrm {PCO}^{+}(f)$
is contained in the single quill
![]() $[-1,0]$
. We will see in Lemma 3.6 that
$[-1,0]$
. We will see in Lemma 3.6 that
![]() $\mathsf {C}(T^2-1) \le (\sqrt 5+1)/2<4$
. So
$\mathsf {C}(T^2-1) \le (\sqrt 5+1)/2<4$
. So
![]() $f=T^2-1$
satisfies the quill hypothesis.
$f=T^2-1$
satisfies the quill hypothesis.
We are now ready to state our results.
Theorem 1.1. Let p be a prime number, let K be a number field and let
![]() $f=T^p+c\in K[T]$
. Suppose that
$f=T^p+c\in K[T]$
. Suppose that
![]() $0$
is an f-periodic point and that f satisfies the quill hypothesis. Then there exists
$0$
is an f-periodic point and that f satisfies the quill hypothesis. Then there exists
![]() $\kappa =\kappa (f)>0$
with the following properties.
$\kappa =\kappa (f)>0$
with the following properties.
-
(i) If
 $x\in \overline K$
is an algebraic integer and also an f-wandering point, then
$x\in \overline K$
is an algebraic integer and also an f-wandering point, then
 $\lambda _f^{\mathrm {max}} (x) \ge \kappa /[K(x):K]$
.
$\lambda _f^{\mathrm {max}} (x) \ge \kappa /[K(x):K]$
. -
(ii) If
 $x\in \overline K$
is an f-wandering point, then
$x\in \overline K$
is an f-wandering point, then
 $\hat h_f (x) \ge \kappa /[K(x):K]^{2}$
.
$\hat h_f (x) \ge \kappa /[K(x):K]^{2}$
.
Let us explain why (i) can be seen as a dynamical Schinzel–Zassenhaus property for f. Indeed, let x be an algebraic integer with
![]() $\mathbb {Q}$
-minimal polynomial
$\mathbb {Q}$
-minimal polynomial
![]() $(X-x_1)\cdots (X-x_d)$
, where
$(X-x_1)\cdots (X-x_d)$
, where
![]() $x_1,\ldots ,x_d\in \mathbb {C}$
. The house
$x_1,\ldots ,x_d\in \mathbb {C}$
. The house ![]() of x is
of x is
![]() $\max _{1\le i\le d} |x_i|$
. We have
$\max _{1\le i\le d} |x_i|$
. We have ![]() if
if
![]() $x\not =0$
. Kronecker’s theorem states that
$x\not =0$
. Kronecker’s theorem states that ![]() vanishes if and only if x is
vanishes if and only if x is
![]() $0$
or a root of unity. Dimitrov [Reference DimitrovDim] proved
$0$
or a root of unity. Dimitrov [Reference DimitrovDim] proved ![]() for all remaining algebraic integers x. This is sometimes called the Schinzel–Zassenhaus conjecture [Reference Schinzel and ZassenhausSZ65]. Observe that if
for all remaining algebraic integers x. This is sometimes called the Schinzel–Zassenhaus conjecture [Reference Schinzel and ZassenhausSZ65]. Observe that if
![]() $x\not =0$
, then
$x\not =0$
, then ![]() . Moreover, x is
. Moreover, x is
![]() $T^2$
-preperiodic if and only if it is
$T^2$
-preperiodic if and only if it is
![]() $0$
or a root of unity.
$0$
or a root of unity.
Part (ii) of the theorem is conjectured to hold for all rational functions
![]() $f\in K(T)$
of degree
$f\in K(T)$
of degree
![]() $\ge 2$
with
$\ge 2$
with
![]() $[K(x):K]^2$
replaced by
$[K(x):K]^2$
replaced by
![]() $[K(x):K]$
. This is called the dynamical Lehmer conjecture; see Conjecture 3.25 [Reference SilvermanSil07] or Conjecture 16.2 [Reference Benedetto, Ingram, Jones, Manes, Silverman and TuckerBIJ+19] for a higher-dimensional version. The dynamical Lehmer conjecture is already open in the classical case
$[K(x):K]$
. This is called the dynamical Lehmer conjecture; see Conjecture 3.25 [Reference SilvermanSil07] or Conjecture 16.2 [Reference Benedetto, Ingram, Jones, Manes, Silverman and TuckerBIJ+19] for a higher-dimensional version. The dynamical Lehmer conjecture is already open in the classical case
![]() $f=T^2$
. In this case,
$f=T^2$
. In this case,
![]() $\hat h_{T^2}$
is the absolute logarithmic Weil height. Suppose x is a nonzero algebraic number that is not a root of unity. Dobrowolski’s theorem [Reference DobrowolskiDob79] implies
$\hat h_{T^2}$
is the absolute logarithmic Weil height. Suppose x is a nonzero algebraic number that is not a root of unity. Dobrowolski’s theorem [Reference DobrowolskiDob79] implies
![]() $\hat h_{T^2}(x)\ge \frac {c}{d} \left (\frac {\log \log d}{\log d}\right )^3$
with
$\hat h_{T^2}(x)\ge \frac {c}{d} \left (\frac {\log \log d}{\log d}\right )^3$
with
![]() $d=[\mathbb {Q}(x):\mathbb {Q}]$
and for an absolute constant
$d=[\mathbb {Q}(x):\mathbb {Q}]$
and for an absolute constant
![]() $c>0$
.
$c>0$
.
In the dynamical setting, little is known. However, we mention that M. Baker obtained a lower bound for the canonical height for general rational maps, up to an exceptional set. For a polynomial f as above, his Theorem 1.14 [Reference BakerBak06] states the following. There exist constants
![]() $c_1>0$
and
$c_1>0$
and
![]() $c_2>0$
that depend on K and f with the following property. Let
$c_2>0$
that depend on K and f with the following property. Let
![]() $F/K$
be a finite extension. Then
$F/K$
be a finite extension. Then
![]() $\hat h_f(x)> \frac {c_1}{[F:\mathbb {Q}]}$
for all
$\hat h_f(x)> \frac {c_1}{[F:\mathbb {Q}]}$
for all
![]() $x\in F$
with at most
$x\in F$
with at most
![]() $c_2 [F:\mathbb {Q}] \log (2[F:\mathbb {Q}])$
exceptions.
$c_2 [F:\mathbb {Q}] \log (2[F:\mathbb {Q}])$
exceptions.
Next, we exhibit some cases where the quill hypothesis is satisfied.
Lemma 1.2. Let p be a prime number, let K be a number field and let
![]() $f=T^p+c\in K[T]$
. Suppose that
$f=T^p+c\in K[T]$
. Suppose that
![]() $f\not = T^2-2$
. Then f satisfies the quill hypothesis in both of the following cases.
$f\not = T^2-2$
. Then f satisfies the quill hypothesis in both of the following cases.
-
(i) There exists a field embedding
 $\sigma _0\colon K\rightarrow \mathbb {R}$
with image in the real numbers such that
$\sigma _0\colon K\rightarrow \mathbb {R}$
with image in the real numbers such that
 $\mathrm {PCO}^{+}(\sigma _0(f))$
is bounded.
$\mathrm {PCO}^{+}(\sigma _0(f))$
is bounded. -
(ii) There exists a field embedding
 $\sigma _0\colon K\rightarrow \mathbb {C}$
such that
$\sigma _0\colon K\rightarrow \mathbb {C}$
such that
 $\#\mathrm {PCO}^{+}(\sigma _0(f)) \le 2p-2$
.
$\#\mathrm {PCO}^{+}(\sigma _0(f)) \le 2p-2$
.
Let
![]() $n\in \mathbb {N}$
, and let
$n\in \mathbb {N}$
, and let
![]() $G_n$
denote the monic polynomial whose roots are precisely those
$G_n$
denote the monic polynomial whose roots are precisely those
![]() $c\in \mathbb {C}$
for which
$c\in \mathbb {C}$
for which
![]() $0$
is
$0$
is
![]() $(T^2+c)$
-periodic with exact period n. Then
$(T^2+c)$
-periodic with exact period n. Then
![]() $G_n\in \mathbb {Z}[X]$
and work of Lutzky [Reference LutzkyLut93] implies that
$G_n\in \mathbb {Z}[X]$
and work of Lutzky [Reference LutzkyLut93] implies that
![]() $G_n$
has at least one real root. In particular, by Lemma 1.2(i) the quill hypothesis is met for infinitely many quadratic polynomials
$G_n$
has at least one real root. In particular, by Lemma 1.2(i) the quill hypothesis is met for infinitely many quadratic polynomials
![]() $T^2+c\in \overline {\mathbb {Q}}[T]$
with periodic critical point. It is a folklore conjecture that
$T^2+c\in \overline {\mathbb {Q}}[T]$
with periodic critical point. It is a folklore conjecture that
![]() $G_n$
is irreducible for all
$G_n$
is irreducible for all
![]() $n\in \mathbb {N}$
. Conditional on this conjecture, any
$n\in \mathbb {N}$
. Conditional on this conjecture, any
![]() $f=T^2+c$
with
$f=T^2+c$
with
![]() $c\not =-2$
for which
$c\not =-2$
for which
![]() $0$
is f-periodic satisfies the quill hypothesis.
$0$
is f-periodic satisfies the quill hypothesis.
Let us briefly address
![]() $f=T^2-2$
. Then
$f=T^2-2$
. Then
![]() $\lambda _{f}(w+w^{-1}) = \bigl |\log |w|\bigr |$
for all
$\lambda _{f}(w+w^{-1}) = \bigl |\log |w|\bigr |$
for all
![]() $w\in \mathbb {C}^\times $
. Moreover,
$w\in \mathbb {C}^\times $
. Moreover,
![]() $\hat h_f(w+w^{-1}) = 2h(w)$
for all nonzero algebraic w; here,
$\hat h_f(w+w^{-1}) = 2h(w)$
for all nonzero algebraic w; here,
![]() $h=h_{T^2}$
is the absolute logarithmic Weil height. For
$h=h_{T^2}$
is the absolute logarithmic Weil height. For
![]() $f=T^2-2$
, Theorem 1.1 follows from Dimitrov’s Theorem 1 [Reference DimitrovDim]. Moreover, part (ii) with a better exponent in
$f=T^2-2$
, Theorem 1.1 follows from Dimitrov’s Theorem 1 [Reference DimitrovDim]. Moreover, part (ii) with a better exponent in
![]() $[K(x):K]$
follows from Dobrowolski’s Theorem 1 [Reference DobrowolskiDob79].
$[K(x):K]$
follows from Dobrowolski’s Theorem 1 [Reference DobrowolskiDob79].
If
![]() $0$
is periodic of minimal period larger than 1, then
$0$
is periodic of minimal period larger than 1, then
![]() $f = T^p + c$
is not conjugate to a Chebyshev polynomial or
$f = T^p + c$
is not conjugate to a Chebyshev polynomial or
![]() $T^p$
. Using the lemma above, we find for each prime p an f not of this form that satisfies the quill hypothesis.
$T^p$
. Using the lemma above, we find for each prime p an f not of this form that satisfies the quill hypothesis.
The main technical results of this paper are in Section 4. For example, we also cover some cases where
![]() $0$
is an f-preperiodic point. In Theorem 4.4 below, we prove a more general version of Theorem 1.1.
$0$
is an f-preperiodic point. In Theorem 4.4 below, we prove a more general version of Theorem 1.1.
We now draw several corollaries.
Corollary 1.3. Let p be a prime number, let K be a number field and let
![]() $f=T^p+c\in K[T]$
. Suppose that
$f=T^p+c\in K[T]$
. Suppose that
![]() $0$
is an f-periodic point and that f satisfies the quill hypothesis. Suppose
$0$
is an f-periodic point and that f satisfies the quill hypothesis. Suppose
![]() $y\in K$
.
$y\in K$
.
-
(i) Suppose
 $K/\mathbb {Q}$
is unramified above p. Let y be an f-periodic point. Let
$K/\mathbb {Q}$
is unramified above p. Let y be an f-periodic point. Let
 $x\in \overline K$
satisfy
$x\in \overline K$
satisfy
 $f^{(n)}(x)=y$
with
$f^{(n)}(x)=y$
with
 $n\ge 0$
minimal. Then
$n\ge 0$
minimal. Then
 $[K(x):K]\ge p^{n-\mathrm {per}(y)}$
.
$[K(x):K]\ge p^{n-\mathrm {per}(y)}$
. -
(ii) Suppose
 $K/\mathbb {Q}$
is unramified above p. Let y be an f-preperiodic point and not f-periodic. Then
$K/\mathbb {Q}$
is unramified above p. Let y be an f-preperiodic point and not f-periodic. Then
 $f^{(n)}-y\in K[T]$
is irreducible for all
$f^{(n)}-y\in K[T]$
is irreducible for all
 $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
. -
(iii) Let y be an f-wandering point. Then there exists
 $\kappa =\kappa (f,y)>0$
such that, for all
$\kappa =\kappa (f,y)>0$
such that, for all
 $n\in \mathbb {N}$
, each irreducible factor of
$n\in \mathbb {N}$
, each irreducible factor of
 $f^{(n)} - y \in K[T]$
has degree at least
$f^{(n)} - y \in K[T]$
has degree at least
 $\kappa p^n$
.
$\kappa p^n$
.
By Lemma 4.1, the extension
![]() $\mathbb {Q}(c)/\mathbb {Q}$
is unramified above p if
$\mathbb {Q}(c)/\mathbb {Q}$
is unramified above p if
![]() $0$
is f-preperiodic.
$0$
is f-preperiodic.
For example, if
![]() $f=T^2-1$
, then
$f=T^2-1$
, then
![]() $f^{(n)}-1$
is irreducible in
$f^{(n)}-1$
is irreducible in
![]() $\mathbb {Q}[T]$
for all
$\mathbb {Q}[T]$
for all
![]() $n\in \mathbb {N}$
. Stoll [Reference StollSto92] showed that iterates of certain quadratic polynomials are irreducible over
$n\in \mathbb {N}$
. Stoll [Reference StollSto92] showed that iterates of certain quadratic polynomials are irreducible over
![]() $\mathbb {Q}$
. Part (iii) of Corollary 1.3 was proved in more general form by Jones and Levy [Reference Jones and LevyJL17] using different methods.
$\mathbb {Q}$
. Part (iii) of Corollary 1.3 was proved in more general form by Jones and Levy [Reference Jones and LevyJL17] using different methods.
The method presented here is effective in that it can produce explicit lower bounds for heights. In the next two corollaries, we take a closer look at the quadratic polynomial
![]() $f=T^2-1$
.
$f=T^2-1$
.
Corollary 1.4. Let
![]() $f = T^2-1$
.
$f = T^2-1$
.
-
(i) Let
 $x\in \overline {\mathbb {Q}}$
be an algebraic integer and an f-wandering point. Then
$x\in \overline {\mathbb {Q}}$
be an algebraic integer and an f-wandering point. Then  $$ \begin{align*} \lambda^{\mathrm{max}}_{f}(x)\ge \frac{\log(4^{11/10}/(\sqrt 5+1))}{48} \frac{1}{[\mathbb{Q}(x):\mathbb{Q}]}> \frac{0.007}{[\mathbb{Q}(x):\mathbb{Q}]}. \end{align*} $$
$$ \begin{align*} \lambda^{\mathrm{max}}_{f}(x)\ge \frac{\log(4^{11/10}/(\sqrt 5+1))}{48} \frac{1}{[\mathbb{Q}(x):\mathbb{Q}]}> \frac{0.007}{[\mathbb{Q}(x):\mathbb{Q}]}. \end{align*} $$
-
(ii) Let
 $x\in \overline {\mathbb {Q}}$
be an f-wandering point. Then
$x\in \overline {\mathbb {Q}}$
be an f-wandering point. Then  $$ \begin{align*} \hat h_f(x)\ge \frac{\log(4^{11/10}/(\sqrt 5+1))}{48} \frac{1}{[\mathbb{Q}(x):\mathbb{Q}]^2}> \frac{0.007}{[\mathbb{Q}(x):\mathbb{Q}]^2}. \end{align*} $$
$$ \begin{align*} \hat h_f(x)\ge \frac{\log(4^{11/10}/(\sqrt 5+1))}{48} \frac{1}{[\mathbb{Q}(x):\mathbb{Q}]^2}> \frac{0.007}{[\mathbb{Q}(x):\mathbb{Q}]^2}. \end{align*} $$
Corollary 1.5. Let
![]() $f=T^2-1\in \mathbb {Q}[T]$
, and let
$f=T^2-1\in \mathbb {Q}[T]$
, and let
![]() $x\in \overline {\mathbb {Q}}$
be an f-preperiodic point. Then
$x\in \overline {\mathbb {Q}}$
be an f-preperiodic point. Then
We now discuss the method of proof. It is an adaptation of Dimitrov’s proof of the Schinzel–Zassenhaus conjecture [Reference DimitrovDim].
Suppose we are given f as in Theorem 1.1 and an algebraic integer x such that
![]() $\lambda _f^{\mathrm {max}}(x)$
is sufficiently small. For simplicity, say
$\lambda _f^{\mathrm {max}}(x)$
is sufficiently small. For simplicity, say
![]() $f=T^p+c\in \mathbb {Q}[T]$
has rational coefficients.
$f=T^p+c\in \mathbb {Q}[T]$
has rational coefficients.
The
![]() $\mathbb {Q}$
-minimal polynomial
$\mathbb {Q}$
-minimal polynomial
![]() $A\in \mathbb {Q}[X]$
of x factors as
$A\in \mathbb {Q}[X]$
of x factors as
![]() $(X-x_1)\cdots (X-x_D)$
with
$(X-x_1)\cdots (X-x_D)$
with
![]() $x_1,\ldots ,x_D\in \mathbb {C}$
. For an integer
$x_1,\ldots ,x_D\in \mathbb {C}$
. For an integer
![]() $k\ge 1$
, we set
$k\ge 1$
, we set
![]() $A_k = (X-f^{(k)}(x_1))\cdots (X-f^{(k)}(x_D))$
. The basic idea is to consider a p-th root
$A_k = (X-f^{(k)}(x_1))\cdots (X-f^{(k)}(x_D))$
. The basic idea is to consider a p-th root
![]() $\phi $
of the rational function
$\phi $
of the rational function
![]() $(A_l/A_k)^{p-1}=1+O(1/X)$
for certain integers
$(A_l/A_k)^{p-1}=1+O(1/X)$
for certain integers
![]() $1\le k<l$
. A priori, we may consider
$1\le k<l$
. A priori, we may consider
![]() $\phi $
as a formal power series in
$\phi $
as a formal power series in
![]() $\mathbb {Q}[[1/X]]$
. However, an appropriate choice of k and l will imply
$\mathbb {Q}[[1/X]]$
. However, an appropriate choice of k and l will imply
![]() $\phi \in \mathbb {Z}[[1/X]]$
. This formal power series is constructed in Section 2 where we also analyze integrality properties via congruence conditions. This step requires that the degree of
$\phi \in \mathbb {Z}[[1/X]]$
. This formal power series is constructed in Section 2 where we also analyze integrality properties via congruence conditions. This step requires that the degree of
![]() $T^p+c$
is a prime number. The power series
$T^p+c$
is a prime number. The power series
![]() $\phi $
represents a holomorphic function on the complement of a large enough disk. This step is similar as in Dimitrov’s proof.
$\phi $
represents a holomorphic function on the complement of a large enough disk. This step is similar as in Dimitrov’s proof.
Our next step will be to construct a sufficiently nice connected domain
![]() $U\subseteq \mathbb {C}$
on which
$U\subseteq \mathbb {C}$
on which
![]() $\phi $
represents a holomorphic function. Our choice U will have bounded complement in
$\phi $
represents a holomorphic function. Our choice U will have bounded complement in
![]() $\mathbb {C}$
. This construction is done in Section 3, and it is the main new aspect of this paper. Let
$\mathbb {C}$
. This construction is done in Section 3, and it is the main new aspect of this paper. Let
![]() $\widehat {\mathbb {C}}={\mathbb {C}}\cup \{\infty \}$
denote the extended complex plane. The construction of U depends on a parameter
$\widehat {\mathbb {C}}={\mathbb {C}}\cup \{\infty \}$
denote the extended complex plane. The construction of U depends on a parameter
![]() $n\in \mathbb {N}$
. It takes as an input a hedgehog
$n\in \mathbb {N}$
. It takes as an input a hedgehog
![]() $I_0$
that contains the post-critical set of f (or at least part of it). The critical values of
$I_0$
that contains the post-critical set of f (or at least part of it). The critical values of
![]() $f^{(n)}$
are contained in the preimage
$f^{(n)}$
are contained in the preimage
![]() $(f^{(n)})^{-1}(I_0)$
, which one should think of as a finite topological tree. Thus,
$(f^{(n)})^{-1}(I_0)$
, which one should think of as a finite topological tree. Thus,
![]() $f^{(n)}$
has no critical points on
$f^{(n)}$
has no critical points on
![]() $\mathbb {C}\smallsetminus (f^{(n)})^{-1}(I_0)$
. Moreover, adding the point at infinity will make
$\mathbb {C}\smallsetminus (f^{(n)})^{-1}(I_0)$
. Moreover, adding the point at infinity will make
![]() $\mathbb {C}\smallsetminus (f^{(n)})^{-1}(I_0)$
simply connected.
$\mathbb {C}\smallsetminus (f^{(n)})^{-1}(I_0)$
simply connected.
However, this complement is not yet the desired U. We need to ensure that U does not contain the
![]() $f^{(k)}(x_i)$
and
$f^{(k)}(x_i)$
and
![]() $f^{(l)}(x_j)$
so that
$f^{(l)}(x_j)$
so that
![]() $A_l/A_k$
has neither poles nor zeros on U. This can be done by augmenting
$A_l/A_k$
has neither poles nor zeros on U. This can be done by augmenting
![]() $(f^{(n)})^{-1}(I_0)$
to a larger finite topological tree while retaining the property that
$(f^{(n)})^{-1}(I_0)$
to a larger finite topological tree while retaining the property that
![]() $U\cup \{\infty \}$
is simply connected. By monodromy, the p-th root
$U\cup \{\infty \}$
is simply connected. By monodromy, the p-th root
![]() $\phi $
extends to a holomorphic function on U.
$\phi $
extends to a holomorphic function on U.
Dubinin’s theorem is our tool to bound from above the capacity of a suitable hedgehog. We will be able to relate the capacity of
![]() $\mathbb {C}\smallsetminus U$
to the capacity of a hedgehog using transformation properties of the capacity under certain holomorphic mappings.
$\mathbb {C}\smallsetminus U$
to the capacity of a hedgehog using transformation properties of the capacity under certain holomorphic mappings.
Finally, in Section 4 we prove the results stated in the introduction. As did Dimitrov, we use the Pólya–Bertrandias theorem. It implies that
![]() $\phi $
is a rational function if
$\phi $
is a rational function if
![]() $\mathrm {cap}(\mathbb {C}\smallsetminus U)<1$
. The quill hypothesis, the post-critically finite hypothesis on f, and the fact that
$\mathrm {cap}(\mathbb {C}\smallsetminus U)<1$
. The quill hypothesis, the post-critically finite hypothesis on f, and the fact that
![]() $\lambda _f^{\mathrm {max}}(x)$
is small is used to ensure the capacity inequality. Here, we also choose the parameter n that controls the tree and ultimately U. If
$\lambda _f^{\mathrm {max}}(x)$
is small is used to ensure the capacity inequality. Here, we also choose the parameter n that controls the tree and ultimately U. If
![]() $\phi $
, whose p-th power is
$\phi $
, whose p-th power is
![]() $(A_l/A_k)^{p-1}$
, is a rational function, then we are in one of two cases. The first case is when
$(A_l/A_k)^{p-1}$
, is a rational function, then we are in one of two cases. The first case is when
![]() $A_k$
and
$A_k$
and
![]() $A_l$
have a common root that cancels out in
$A_l$
have a common root that cancels out in
![]() $A_l/A_k$
. Thus,
$A_l/A_k$
. Thus,
![]() $f^{(k)}(x_i) = f^{(l)}(x_j)$
for some
$f^{(k)}(x_i) = f^{(l)}(x_j)$
for some
![]() $i,j$
. A standard argument involving the canonical height and
$i,j$
. A standard argument involving the canonical height and
![]() $k<l$
shows that x is f-preperiodic. In the second case,
$k<l$
shows that x is f-preperiodic. In the second case,
![]() $A_k$
has a multiple root, say
$A_k$
has a multiple root, say
![]() $f^{(k)}(x_i) = f^{(k)}(x_j)$
for distinct
$f^{(k)}(x_i) = f^{(k)}(x_j)$
for distinct
![]() $i,j$
. This collision of Galois conjugates implies that
$i,j$
. This collision of Galois conjugates implies that
![]() $\mathbb {Q}(f^{(k)}(x))$
is a proper subfield of
$\mathbb {Q}(f^{(k)}(x))$
is a proper subfield of
![]() $\mathbb {Q}(x)$
. We can then proceed by an induction on the field degree. This case study is laid out in detail in Proposition 4.3 which then quickly leads to the results mentioned in the introduction.
$\mathbb {Q}(x)$
. We can then proceed by an induction on the field degree. This case study is laid out in detail in Proposition 4.3 which then quickly leads to the results mentioned in the introduction.
2. Constructing the power series
In this section, we construct an auxiliary power series. Our approach largely follows the approach laid out in Section 2 [Reference DimitrovDim] and in particular Proposition 2.2 and Lemma 2.5 loc.cit. We adapt it to the dynamical setting. Dimitrov’s crucial observation is that
![]() $\sqrt {1+4X}$
is a formal power series in X with integral coefficients.
$\sqrt {1+4X}$
is a formal power series in X with integral coefficients.
Throughout this section, let R denote an integrally closed domain of characteristic
![]() $0$
. Let p be a prime number.
$0$
. Let p be a prime number.
For
![]() $D\in \mathbb {N}$
and
$D\in \mathbb {N}$
and
![]() $j\in \{0,\ldots ,D\}$
, let
$j\in \{0,\ldots ,D\}$
, let
![]() $e_j \in \mathbb {Z}[X_1,\ldots ,X_D]$
denote the elementary symmetric polynomial of degree j. We set
$e_j \in \mathbb {Z}[X_1,\ldots ,X_D]$
denote the elementary symmetric polynomial of degree j. We set
So
![]() $\Psi _{p,j}\in \mathbb {Z}[X_1,\ldots ,X_D]$
by Fermat’s little theorem and
$\Psi _{p,j}\in \mathbb {Z}[X_1,\ldots ,X_D]$
by Fermat’s little theorem and
If R is subring of a ring S and
![]() $a,b\in S$
, we write
$a,b\in S$
, we write ![]() or
or ![]() to signify
to signify
![]() $a-b\in pS$
.
$a-b\in pS$
.
Lemma 2.1. For all
![]() $k\in \mathbb {N}$
and all
$k\in \mathbb {N}$
and all
![]() $j\in \{0,\ldots ,D\}$
, we have
$j\in \{0,\ldots ,D\}$
, we have
Proof. By Equation (2.1) our claim (2.2) holds for
![]() $k=1$
.
$k=1$
.
We assume that Equation (2.2) holds for
![]() $k\ge 1$
and will deduce it for
$k\ge 1$
and will deduce it for
![]() $k+1$
. So
$k+1$
. So

as ![]() .
.
We evaluate
![]() $\Psi _{p,j}$
at
$\Psi _{p,j}$
at
![]() $(X_1^{p^k},\ldots ,X_D^{p^k})$
and use Equation (2.1) to find
$(X_1^{p^k},\ldots ,X_D^{p^k})$
and use Equation (2.1) to find
Finally,
![]() $\Psi _{p,j}(X_1^{p^k},\ldots ,X_D^{p^k}) \in \Psi _{p,j}^{p^k} + p\mathbb {Z}[X_1,\ldots ,X_D]$
and hence
$\Psi _{p,j}(X_1^{p^k},\ldots ,X_D^{p^k}) \in \Psi _{p,j}^{p^k} + p\mathbb {Z}[X_1,\ldots ,X_D]$
and hence ![]() from Equation (2.4). Thus, Equation (2.2) for
from Equation (2.4). Thus, Equation (2.2) for
![]() $k+1$
follows from Equation (2.3).
$k+1$
follows from Equation (2.3).
Lemma 2.2. Let S be a ring of which R is a subring and suppose
![]() $x_1,\ldots ,x_D\in S$
such that
$x_1,\ldots ,x_D\in S$
such that
![]() $(X-x_1)\cdots (X-x_D)\in R[X]$
. Let p be a prime number.
$(X-x_1)\cdots (X-x_D)\in R[X]$
. Let p be a prime number.
-
(i) The value of a symmetric polynomial in
 $R[X_1,\ldots ,X_D]$
evaluated at
$R[X_1,\ldots ,X_D]$
evaluated at
 $(x_1,\ldots ,x_D)$
lies in R.
$(x_1,\ldots ,x_D)$
lies in R. -
(ii) Let
 $k,l\in \mathbb {N}$
with
$k,l\in \mathbb {N}$
with  for all
for all
 $a\in R$
. For all
$a\in R$
. For all
 $j\in \{0,\ldots ,D\}$
, we have
$j\in \{0,\ldots ,D\}$
, we have 
Proof. An elementary symmetric polynomial in
![]() $R[X_1,\ldots ,X_D]$
lies in
$R[X_1,\ldots ,X_D]$
lies in
![]() $R[e_1,\ldots ,e_D]$
. We conclude (i) as
$R[e_1,\ldots ,e_D]$
. We conclude (i) as
![]() $e_1(x_1,\ldots ,x_D),\ldots ,e_D(x_1,\ldots ,x_D)\in R$
by hypothesis.
$e_1(x_1,\ldots ,x_D),\ldots ,e_D(x_1,\ldots ,x_D)\in R$
by hypothesis.
For (ii), observe that
![]() $\Psi _{p,j}$
is symmetric so
$\Psi _{p,j}$
is symmetric so
![]() $\Psi _{p,j}(x_1,\ldots ,x_D)\in R$
by part (i). For the same reason,
$\Psi _{p,j}(x_1,\ldots ,x_D)\in R$
by part (i). For the same reason,
![]() $e_j(x_1^{p^k},\ldots ,x_D^{p^k})\in R$
and
$e_j(x_1^{p^k},\ldots ,x_D^{p^k})\in R$
and
![]() $e_j(x_1^{p^l},\ldots ,x_D^{p^l})\in R$
.
$e_j(x_1^{p^l},\ldots ,x_D^{p^l})\in R$
.
By the hypothesis in (ii), we conclude ![]() . Lemma 2.1 implies
. Lemma 2.1 implies
Raising ![]() to the p-th power gives
to the p-th power gives ![]() for all
for all
![]() $a\in R$
. In particular,
$a\in R$
. In particular,
![]() $e_j(x_1,\ldots ,x_D)^{p^k}$
and
$e_j(x_1,\ldots ,x_D)^{p^k}$
and
![]() $e_j(x_1,\ldots ,x_D)^{p^l}$
are equivalent modulo
$e_j(x_1,\ldots ,x_D)^{p^l}$
are equivalent modulo
![]() $p^2$
. Part (ii) now follows from Equation (2.5).
$p^2$
. Part (ii) now follows from Equation (2.5).
![]() $\Box $
$\Box $
Lemma 2.3. Let
![]() $f = T^p+c\in R[T]$
. We have
$f = T^p+c\in R[T]$
. We have
for all
![]() $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
.
Proof. As
![]() $f^{(0)}(0)=0$
, the claim holds for
$f^{(0)}(0)=0$
, the claim holds for
![]() $k=1$
. Say
$k=1$
. Say
![]() $k\ge 2$
. By induction on k, we have
$k\ge 2$
. By induction on k, we have ![]() for some
for some
![]() $g\in R[T]$
. So
$g\in R[T]$
. So

and the lemma follows from
![]() $f^{(k-1)}(0) = f^{(k-2)}(0)^p+c$
.
$f^{(k-1)}(0) = f^{(k-2)}(0)^p+c$
.
Let
![]() $f\in R[T]$
and
$f\in R[T]$
and
![]() $A=\prod _{j=1}^D (X-x_j)\in R[X]$
, where
$A=\prod _{j=1}^D (X-x_j)\in R[X]$
, where
![]() $x_1,\ldots ,x_D$
are in a splitting field of A. For all integers
$x_1,\ldots ,x_D$
are in a splitting field of A. For all integers
![]() $k\ge 0$
, we set
$k\ge 0$
, we set
 $$ \begin{align*}A_k = \prod_{j=1}^D (X-f^{(k)}(x_j)).\end{align*} $$
$$ \begin{align*}A_k = \prod_{j=1}^D (X-f^{(k)}(x_j)).\end{align*} $$
Then
![]() $A_k\in R[X]$
by Lemma 2.2(i).
$A_k\in R[X]$
by Lemma 2.2(i).
Lemma 2.4. Let
![]() $ f= T^p+c\in R[T]$
. Suppose that
$ f= T^p+c\in R[T]$
. Suppose that
![]() $k,l\in \mathbb {N}$
satisfy
$k,l\in \mathbb {N}$
satisfy
![]() $k\le l$
and
$k\le l$
and
![]() $f^{(k-1)}(0) = f^{(l-1)}(0)$
. Set
$f^{(k-1)}(0) = f^{(l-1)}(0)$
. Set
 $$ \begin{align} \delta = \left\{ \begin{array}{ll} 0 &: \text{if }k=1,\\ 1 &:\text{if }k\ge 2. \end{array} \right. \end{align} $$
$$ \begin{align} \delta = \left\{ \begin{array}{ll} 0 &: \text{if }k=1,\\ 1 &:\text{if }k\ge 2. \end{array} \right. \end{align} $$
We assume that
Then ![]() for all monic
for all monic
![]() $A\in R[X]$
.
$A\in R[X]$
.
Proof. If
![]() $k=1$
, then
$k=1$
, then
![]() $0=f^{(k-1)}(0)=f^{(l-1)}(0)$
. In this case, Lemma 2.3 implies
$0=f^{(k-1)}(0)=f^{(l-1)}(0)$
. In this case, Lemma 2.3 implies ![]() with
with
![]() $g = T+c$
. Observe that
$g = T+c$
. Observe that
![]() $f^{(k)} = f = g(T^p) = g(T^{p^k})$
.
$f^{(k)} = f = g(T^p) = g(T^{p^k})$
.
If
![]() $k\ge 2$
, Lemma 2.3 implies
$k\ge 2$
, Lemma 2.3 implies ![]() and
and ![]() , where
, where
![]() $g = (T+f^{(k-1)}(0))^p+c$
.
$g = (T+f^{(k-1)}(0))^p+c$
.
We can summarize both cases by ![]() and
and ![]() ; we sometimes drop the reference to base ring in
; we sometimes drop the reference to base ring in ![]() below.
below.
Let
![]() $j\in \{0,\ldots ,D\}$
; the polynomial
$j\in \{0,\ldots ,D\}$
; the polynomial
![]() $e_j(g(X_1),\ldots ,g(X_D))$
is symmetric. So
$e_j(g(X_1),\ldots ,g(X_D))$
is symmetric. So
for some
![]() ${P_{j}} \in R[X_1,\ldots ,X_D]$
. Next, we replace
${P_{j}} \in R[X_1,\ldots ,X_D]$
. Next, we replace
![]() $X_i$
by
$X_i$
by
![]() $X_i^{p^{k-\delta }}$
to get
$X_i^{p^{k-\delta }}$
to get
Hence,
The same argument for l yields
We factor
![]() $A = (X-x_1)\cdots (X-x_D)$
with
$A = (X-x_1)\cdots (X-x_D)$
with
![]() $x_1,\ldots ,x_D$
inside a fixed splitting field of A. We specialize
$x_1,\ldots ,x_D$
inside a fixed splitting field of A. We specialize
![]() $(x_1,\ldots ,x_D)$
in Equation (2.8) to get
$(x_1,\ldots ,x_D)$
in Equation (2.8) to get
both elements lie in R by Lemma 2.2(i). As any element in
![]() $R[x_1,\ldots ,x_D]$
is integral over R and since R is integrally closed, we conclude
$R[x_1,\ldots ,x_D]$
is integral over R and since R is integrally closed, we conclude
The same statement holds with k replaced by l by using Equation (2.9).
By hypothesis (2.7) and by Lemma 2.2(ii) applied to
![]() $k-\delta ,l-\delta $
, we have
$k-\delta ,l-\delta $
, we have
and hence
This holds for all j and so ![]() , as desired.
, as desired.
Let
 $$ \begin{align} \Phi_p = \sum_{k=0}^\infty {1/p \choose k} U^k \in \mathbb{Q}[[U]]; \end{align} $$
$$ \begin{align} \Phi_p = \sum_{k=0}^\infty {1/p \choose k} U^k \in \mathbb{Q}[[U]]; \end{align} $$
it satisfies
![]() $\Phi _p^p = 1+U$
. If
$\Phi _p^p = 1+U$
. If
![]() $k\ge 0$
is an integer, then
$k\ge 0$
is an integer, then
 $$ \begin{align*} {1/p\choose k} p^k = \frac{1}{k!} \frac 1p\left(\frac 1p -1\right)\cdots\left(\frac 1p -k+1\right) p^k \in \frac{1}{k!}\mathbb{Z}. \end{align*} $$
$$ \begin{align*} {1/p\choose k} p^k = \frac{1}{k!} \frac 1p\left(\frac 1p -1\right)\cdots\left(\frac 1p -k+1\right) p^k \in \frac{1}{k!}\mathbb{Z}. \end{align*} $$
The exponent of the prime p in
![]() $k!$
equals the finite sum
$k!$
equals the finite sum
![]() $\sum _{e=1}^{\infty }[k/p^e]$
which is at most
$\sum _{e=1}^{\infty }[k/p^e]$
which is at most
![]() $k\sum _{e=1}^\infty p^{-e}= k/(p-1)\le k$
. So p does not appear in the denominator of
$k\sum _{e=1}^\infty p^{-e}= k/(p-1)\le k$
. So p does not appear in the denominator of
![]() ${1/p\choose k} p^{2k}\in \mathbb {Q}$
for all
${1/p\choose k} p^{2k}\in \mathbb {Q}$
for all
![]() $k\ge 0$
. Moreover, if
$k\ge 0$
. Moreover, if
![]() $\ell $
is a prime distinct from p, then
$\ell $
is a prime distinct from p, then
![]() $\ell $
does not appear in the denominator of
$\ell $
does not appear in the denominator of
![]() ${1/p\choose k}$
. Therefore,
${1/p\choose k}$
. Therefore,
Let
![]() $R[[1/X]]$
be the ring of formal power series in X. We write
$R[[1/X]]$
be the ring of formal power series in X. We write
![]() $\mathrm {ord}_\infty $
for the natural valuation on
$\mathrm {ord}_\infty $
for the natural valuation on
![]() $R[[1/X]]$
, that is,
$R[[1/X]]$
, that is,
![]() $\mathrm {ord}_\infty (1/X) = 1$
. A nonconstant polynomial in
$\mathrm {ord}_\infty (1/X) = 1$
. A nonconstant polynomial in
![]() $R[X]$
does not lie in
$R[X]$
does not lie in
![]() $R[[1/X]]$
, rather it lies in the ring of formal Laurent series
$R[[1/X]]$
, rather it lies in the ring of formal Laurent series
![]() $R((1/X))$
to which we extend
$R((1/X))$
to which we extend
![]() $\mathrm {ord}_\infty $
in the unique fashion. So we will consider
$\mathrm {ord}_\infty $
in the unique fashion. So we will consider
![]() $R[X]\subseteq R((1/X))$
. For example, any monic polynomial in
$R[X]\subseteq R((1/X))$
. For example, any monic polynomial in
![]() $R[X]$
is a unit in
$R[X]$
is a unit in
![]() $R((1/X))$
.
$R((1/X))$
.
Proposition 2.5. Let p be a prime number, and let
![]() $f=T^p+c\in R[T]$
. Suppose that
$f=T^p+c\in R[T]$
. Suppose that
![]() $k,l\in \mathbb {N}$
satisfy
$k,l\in \mathbb {N}$
satisfy
![]() $k\le l$
and
$k\le l$
and
![]() $f^{(k-1)}(0) = f^{(l-1)}(0)$
. Let
$f^{(k-1)}(0) = f^{(l-1)}(0)$
. Let
![]() $\delta \in \{0,1\}$
be as in Lemma 2.4, and suppose
$\delta \in \{0,1\}$
be as in Lemma 2.4, and suppose ![]() for all
for all
![]() $a\in R$
. If
$a\in R$
. If
![]() $A\in R[T]$
is monic, there exists
$A\in R[T]$
is monic, there exists
![]() $B\in R[X]$
such that
$B\in R[X]$
such that
![]() $\deg B \le \deg A_k^p - 1$
,
$\deg B \le \deg A_k^p - 1$
,
![]() $\Phi _p(p^2 B/A_k^p) \in R[[1/X]]$
and
$\Phi _p(p^2 B/A_k^p) \in R[[1/X]]$
and
![]() $\Phi _p(p^2 B/A_k^p)^p =(A_l/A_k)^{p-1}$
.
$\Phi _p(p^2 B/A_k^p)^p =(A_l/A_k)^{p-1}$
.
Proof. Lemma 2.4 implies
![]() $A_k A_l^{p-1} = A_k^p + p^2 B$
for some
$A_k A_l^{p-1} = A_k^p + p^2 B$
for some
![]() $ B\in R[X]$
. As
$ B\in R[X]$
. As
![]() $A_k$
and
$A_k$
and
![]() $A_l$
are both monic of degree
$A_l$
are both monic of degree
![]() $D = \deg A$
, leading terms cancel and we find
$D = \deg A$
, leading terms cancel and we find
![]() $\deg B \le pD-1$
. Then,
$\deg B \le pD-1$
. Then,
with
![]() $C={B}/{A_k^p}$
. Since
$C={B}/{A_k^p}$
. Since
![]() $A_k$
is monic, we have
$A_k$
is monic, we have
![]() $C\in R((1/X))$
. So
$C\in R((1/X))$
. So
![]() $\mathrm {ord}_\infty (C) =-\deg B + p D \ge 1$
. Therefore, C is a formal power series in
$\mathrm {ord}_\infty (C) =-\deg B + p D \ge 1$
. Therefore, C is a formal power series in
![]() $1/X$
and even lies in the ideal
$1/X$
and even lies in the ideal
![]() $(1/X)R[[1/X]]$
.
$(1/X)R[[1/X]]$
.
Recall that
![]() $\Phi _p(p^2 U) \in \mathbb {Z}[[U]]$
by Equation (2.11). Therefore,
$\Phi _p(p^2 U) \in \mathbb {Z}[[U]]$
by Equation (2.11). Therefore,
![]() $\Phi _p(p^2C ) \in R[[1/X]]$
and
$\Phi _p(p^2C ) \in R[[1/X]]$
and
by the functional equation
![]() $\Phi _p^p=1+U$
; this is an identity in
$\Phi _p^p=1+U$
; this is an identity in
![]() $R((1/X))$
. We conclude the proof by dividing by
$R((1/X))$
. We conclude the proof by dividing by
![]() $A_k^p$
.
$A_k^p$
.
3. Constructing simply connected domains
Recall that
![]() $\widehat {\mathbb {C}}$
denotes the extended complex plane
$\widehat {\mathbb {C}}$
denotes the extended complex plane
![]() $\mathbb {C}\cup \{\infty \}$
, that is, the Riemann sphere. This section concerns the construction of a domain
$\mathbb {C}\cup \{\infty \}$
, that is, the Riemann sphere. This section concerns the construction of a domain
![]() $U\subseteq \widehat {\mathbb {C}}$
containing
$U\subseteq \widehat {\mathbb {C}}$
containing
![]() $\infty $
that is related to the discussion in the introduction. It depends on a polynomial
$\infty $
that is related to the discussion in the introduction. It depends on a polynomial
![]() $f=T^p+c$
and ultimately on an algebraic integer of small canonical height. The complement
$f=T^p+c$
and ultimately on an algebraic integer of small canonical height. The complement
![]() $\widehat {\mathbb {C}} \smallsetminus U$
will be a compact subset of
$\widehat {\mathbb {C}} \smallsetminus U$
will be a compact subset of
![]() $\mathbb {C}$
of capacity strictly less than
$\mathbb {C}$
of capacity strictly less than
![]() $1$
. The relevant properties are stated in Proposition 3.4. Later on, we will construct a holomorphic function on U using the power series introduced in Section 2.
$1$
. The relevant properties are stated in Proposition 3.4. Later on, we will construct a holomorphic function on U using the power series introduced in Section 2.
We begin with a topological lemma which is most likely well-known. We provide a proof as we could not find a proper reference.
Lemma 3.1. Let
![]() $f\in \mathbb {C}[T]\smallsetminus \mathbb {C}$
. Let
$f\in \mathbb {C}[T]\smallsetminus \mathbb {C}$
. Let
![]() $B\subseteq \mathbb {C}$
be compact such that
$B\subseteq \mathbb {C}$
be compact such that
![]() $\mathbb {C}\smallsetminus B$
is connected with cyclic fundamental group. Suppose B contains all critical values of f. Then
$\mathbb {C}\smallsetminus B$
is connected with cyclic fundamental group. Suppose B contains all critical values of f. Then
![]() $\mathbb {C}\smallsetminus f^{-1}(B)$
is connected and
$\mathbb {C}\smallsetminus f^{-1}(B)$
is connected and
![]() $\widehat {\mathbb {C}}\smallsetminus f^{-1}(B)$
is simply connected.
$\widehat {\mathbb {C}}\smallsetminus f^{-1}(B)$
is simply connected.
Proof. Let us denote the restriction
![]() $f|_{f^{-1}(\mathbb {C}\smallsetminus B)} \colon f^{-1}(\mathbb {C}\smallsetminus B)=\mathbb {C} \smallsetminus f^{-1}(B)\rightarrow \mathbb {C}\smallsetminus B$
by
$f|_{f^{-1}(\mathbb {C}\smallsetminus B)} \colon f^{-1}(\mathbb {C}\smallsetminus B)=\mathbb {C} \smallsetminus f^{-1}(B)\rightarrow \mathbb {C}\smallsetminus B$
by
![]() $\psi $
. Then
$\psi $
. Then
![]() $\psi $
is a surjective continuous map. As a nonconstant polynomial induces a proper map, we see that
$\psi $
is a surjective continuous map. As a nonconstant polynomial induces a proper map, we see that
![]() $\psi $
is proper and thus closed. By hypothesis,
$\psi $
is proper and thus closed. By hypothesis,
![]() $f^{-1}(\mathbb {C}\smallsetminus B)$
does not contain any critical point of f. So
$f^{-1}(\mathbb {C}\smallsetminus B)$
does not contain any critical point of f. So
![]() $\psi $
is a local homeomorphism and thus open. As
$\psi $
is a local homeomorphism and thus open. As
![]() $\psi $
is closed and open, the image of a connected component of
$\psi $
is closed and open, the image of a connected component of
![]() $\mathbb {C}\smallsetminus f^{-1}(B)$
under
$\mathbb {C}\smallsetminus f^{-1}(B)$
under
![]() $\psi $
is all of
$\psi $
is all of
![]() $\mathbb {C}\smallsetminus B$
. As
$\mathbb {C}\smallsetminus B$
. As
![]() $\psi $
is the restriction of a polynomial, we conclude that all connected components of
$\psi $
is the restriction of a polynomial, we conclude that all connected components of
![]() $\mathbb {C}\smallsetminus f^{-1}(B)$
are unbounded. The preimage
$\mathbb {C}\smallsetminus f^{-1}(B)$
are unbounded. The preimage
![]() $f^{-1}(B)$
is compact, and so
$f^{-1}(B)$
is compact, and so
![]() $\mathbb {C} \smallsetminus f^{-1}(B)$
has a only one unbounded connected component. Therefore,
$\mathbb {C} \smallsetminus f^{-1}(B)$
has a only one unbounded connected component. Therefore,
![]() $\mathbb {C}\smallsetminus f^{-1}(B)$
is connected and so is
$\mathbb {C}\smallsetminus f^{-1}(B)$
is connected and so is
![]() $\widehat {\mathbb {C}}\smallsetminus f^{-1}(B)$
.
$\widehat {\mathbb {C}}\smallsetminus f^{-1}(B)$
.
We fix a base point
![]() $z_0\in \mathbb {C}\smallsetminus f^{-1}(B)$
. The proper, surjective, local homeomorphism
$z_0\in \mathbb {C}\smallsetminus f^{-1}(B)$
. The proper, surjective, local homeomorphism
![]() $\psi $
is a topological covering by Lemma 2 [Reference HoHo75]. Then
$\psi $
is a topological covering by Lemma 2 [Reference HoHo75]. Then
![]() $\pi _1(\mathbb {C} \smallsetminus f^{-1}(B),z_0)$
is isomorphic to a subgroup of
$\pi _1(\mathbb {C} \smallsetminus f^{-1}(B),z_0)$
is isomorphic to a subgroup of
![]() $\pi _1(\mathbb {C} \smallsetminus B,p(z_0))$
of finite index and thus cyclic.
$\pi _1(\mathbb {C} \smallsetminus B,p(z_0))$
of finite index and thus cyclic.
Let
![]() $U_\infty $
be the complement in
$U_\infty $
be the complement in
![]() $\mathbb {C}$
of a closed disk centered at
$\mathbb {C}$
of a closed disk centered at
![]() $0$
containing the compact set
$0$
containing the compact set
![]() $f^{-1}(B)$
. We suppose
$f^{-1}(B)$
. We suppose
![]() $z_0\in U_\infty $
. Adding the point at infinity gives us a simply connected domain
$z_0\in U_\infty $
. Adding the point at infinity gives us a simply connected domain
![]() $U_\infty \cup \{\infty \}\subseteq \widehat {\mathbb {C}}$
and we have
$U_\infty \cup \{\infty \}\subseteq \widehat {\mathbb {C}}$
and we have
![]() $\widehat {\mathbb {C}} \smallsetminus f^{-1}(B) = (U_\infty \cup \{\infty \})\cup (\mathbb {C}\smallsetminus f^{-1}(B))$
. The theorem of Seifert and van Kampen tells us that the inclusion induces a short exact sequence
$\widehat {\mathbb {C}} \smallsetminus f^{-1}(B) = (U_\infty \cup \{\infty \})\cup (\mathbb {C}\smallsetminus f^{-1}(B))$
. The theorem of Seifert and van Kampen tells us that the inclusion induces a short exact sequence
We may assume
![]() $B\not =\emptyset $
. Consider the loop
$B\not =\emptyset $
. Consider the loop
![]() $t\mapsto z_0 e^{2\pi \sqrt {-1} t}$
, its image lies in
$t\mapsto z_0 e^{2\pi \sqrt {-1} t}$
, its image lies in
![]() $U_\infty $
. Fix any
$U_\infty $
. Fix any
![]() $w\in f^{-1}(B)$
. It is well-known that such loop represents a generator of
$w\in f^{-1}(B)$
. It is well-known that such loop represents a generator of
![]() $\pi _1(\mathbb {C} \smallsetminus \{w\},z_0)\cong \mathbb {Z}$
and that the natural homomorphism
$\pi _1(\mathbb {C} \smallsetminus \{w\},z_0)\cong \mathbb {Z}$
and that the natural homomorphism
![]() $\pi _1(U_\infty ,z_0)\rightarrow \pi _1(\mathbb {C}\smallsetminus f^{-1}(B),z_0) \rightarrow \pi _1(\mathbb {C}\smallsetminus \{w\},z_0)$
is an isomorphism. So also the middle group is isomorphic to
$\pi _1(U_\infty ,z_0)\rightarrow \pi _1(\mathbb {C}\smallsetminus f^{-1}(B),z_0) \rightarrow \pi _1(\mathbb {C}\smallsetminus \{w\},z_0)$
is an isomorphism. So also the middle group is isomorphic to
![]() $\mathbb {Z}$
and the first arrow is a group isomorphism. Therefore,
$\mathbb {Z}$
and the first arrow is a group isomorphism. Therefore,
![]() $\widehat {\mathbb {C}}\smallsetminus f^{-1}(B)$
is simply connected by Equation (3.1).
$\widehat {\mathbb {C}}\smallsetminus f^{-1}(B)$
is simply connected by Equation (3.1).
We recall the definition of the transfinite diameter of a nonempty compact subset
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $\mathbb {C}$
; see Chapter 5.5 [Reference RansfordRan95] for details. For an integer
$\mathbb {C}$
; see Chapter 5.5 [Reference RansfordRan95] for details. For an integer
![]() $n\ge 2$
, we define
$n\ge 2$
, we define
 $$ \begin{align*} d_n(\mathcal{K}) = \sup \left\{ \prod_{1\le i<j\le n} |z_i-z_j|^{2/(n(n-1))} : z_1,\ldots,z_n\in\mathcal{K}\right\}. \end{align*} $$
$$ \begin{align*} d_n(\mathcal{K}) = \sup \left\{ \prod_{1\le i<j\le n} |z_i-z_j|^{2/(n(n-1))} : z_1,\ldots,z_n\in\mathcal{K}\right\}. \end{align*} $$
The sequence
![]() $\bigl (d_n(\mathcal {K})\bigr )_{n\ge 2}$
is nonincreasing, and the transfinite diameter of
$\bigl (d_n(\mathcal {K})\bigr )_{n\ge 2}$
is nonincreasing, and the transfinite diameter of
![]() $\mathcal {K}$
is its limit. The transfinite diameter is known to equal the capacity
$\mathcal {K}$
is its limit. The transfinite diameter is known to equal the capacity
![]() $\mathrm {cap}(\mathcal {K})$
of
$\mathrm {cap}(\mathcal {K})$
of
![]() $\mathcal {K}$
by the Fekete–Szegö theorem; see Theorem 5.5.2 [Reference RansfordRan95]. It is convenient to define
$\mathcal {K}$
by the Fekete–Szegö theorem; see Theorem 5.5.2 [Reference RansfordRan95]. It is convenient to define
![]() $\mathrm {cap}(\emptyset )=0$
.
$\mathrm {cap}(\emptyset )=0$
.
For
![]() $f\in \mathbb {C}[T]$
and for
$f\in \mathbb {C}[T]$
and for
![]() $n\in \mathbb {N}$
, we introduce the truncated post-critical set
$n\in \mathbb {N}$
, we introduce the truncated post-critical set
In the next proposition we will use Dubinin’s theorem.
Proposition 3.2. Let
![]() $f\in \mathbb {C}[T]$
be monic of degree
$f\in \mathbb {C}[T]$
be monic of degree
![]() $d\ge 2$
such that
$d\ge 2$
such that
![]() $f'(0)=0$
. Let
$f'(0)=0$
. Let
![]() $n\in \mathbb {N}$
such that there exist
$n\in \mathbb {N}$
such that there exist
![]() $q\ge 0$
and
$q\ge 0$
and
![]() $\gamma _1,\ldots ,\gamma _q\in \mathbb {C}^\times $
with
$\gamma _1,\ldots ,\gamma _q\in \mathbb {C}^\times $
with
![]() $\mathrm {PCO}_{n}^{+}(f)\subseteq \mathcal {H}(\gamma _1,\ldots ,\gamma _q)$
. Let
$\mathrm {PCO}_{n}^{+}(f)\subseteq \mathcal {H}(\gamma _1,\ldots ,\gamma _q)$
. Let
![]() $m\ge 1$
, and let
$m\ge 1$
, and let
![]() $\alpha _1,\ldots ,\alpha _m \in \mathbb {C}$
be arbitrary. There is a simply connected domain
$\alpha _1,\ldots ,\alpha _m \in \mathbb {C}$
be arbitrary. There is a simply connected domain
![]() $U\subseteq \widehat {\mathbb {C}}$
containing
$U\subseteq \widehat {\mathbb {C}}$
containing
![]() $\infty $
with the following properties.
$\infty $
with the following properties.
-
(i) We have
 $0,\alpha _1,\ldots ,\alpha _m\not \in U$
and
$0,\alpha _1,\ldots ,\alpha _m\not \in U$
and
 $\widehat {\mathbb {C}}\smallsetminus U$
is a compact subset of
$\widehat {\mathbb {C}}\smallsetminus U$
is a compact subset of
 $\mathbb {C}$
.
$\mathbb {C}$
. -
(ii) We have
 $$ \begin{align*} \mathrm{cap}(\widehat{\mathbb{C}}\smallsetminus U)\le 4^{-1/(qd^n+m)} \max\{|\gamma_1|,\ldots,|\gamma_q|,|f^{(n)}(\alpha_1)|,\ldots,|f^{(n)}(\alpha_m)|\}^{1/d^n}. \end{align*} $$
$$ \begin{align*} \mathrm{cap}(\widehat{\mathbb{C}}\smallsetminus U)\le 4^{-1/(qd^n+m)} \max\{|\gamma_1|,\ldots,|\gamma_q|,|f^{(n)}(\alpha_1)|,\ldots,|f^{(n)}(\alpha_m)|\}^{1/d^n}. \end{align*} $$
To prepare for the proof of Proposition 3.2, let
![]() $f\in \mathbb {C}[T]$
denote a monic polynomial of degree
$f\in \mathbb {C}[T]$
denote a monic polynomial of degree
![]() $d\ge 2$
with
$d\ge 2$
with
![]() $f'(0)=0$
. Let
$f'(0)=0$
. Let
![]() $n\in \mathbb {N}$
, and suppose
$n\in \mathbb {N}$
, and suppose
![]() $\gamma _1,\ldots ,\gamma _q\in \mathbb {C}^\times $
are such that
$\gamma _1,\ldots ,\gamma _q\in \mathbb {C}^\times $
are such that
![]() $I_0=\mathcal {H}(\gamma _1,\ldots ,\gamma _q)$
contains
$I_0=\mathcal {H}(\gamma _1,\ldots ,\gamma _q)$
contains
![]() $\mathrm {PCO}_{n}^{+}(f)$
.
$\mathrm {PCO}_{n}^{+}(f)$
.
We apply Lemma 3.1 to
![]() $f^{(n)}$
and
$f^{(n)}$
and
![]() $B=I_0$
; the fundamental group of
$B=I_0$
; the fundamental group of
![]() $\mathbb {C}\smallsetminus I_0$
is cyclic and generated by a large enough loop. We set
$\mathbb {C}\smallsetminus I_0$
is cyclic and generated by a large enough loop. We set
By Lemma 3.1, the complement
![]() $\mathbb {C}\smallsetminus H_f^{(n)}$
is connected and
$\mathbb {C}\smallsetminus H_f^{(n)}$
is connected and
![]() $\widehat {\mathbb {C}} \smallsetminus H_f^{(n)}$
is simply connected. Observe that
$\widehat {\mathbb {C}} \smallsetminus H_f^{(n)}$
is simply connected. Observe that
![]() $0\in H_f^{(n)}$
because
$0\in H_f^{(n)}$
because
![]() $0$
is a critical point of f.
$0$
is a critical point of f.
We will show that a branch of
![]() $z\mapsto f^{(n)}(z)^{1/d^n}$
admits a holomorphic continuation on
$z\mapsto f^{(n)}(z)^{1/d^n}$
admits a holomorphic continuation on
![]() $\mathbb {C}\smallsetminus H_f^{(n)}$
. Moreover, this continuation will be a biholomorphic map between
$\mathbb {C}\smallsetminus H_f^{(n)}$
. Moreover, this continuation will be a biholomorphic map between
![]() $\mathbb {C}\smallsetminus H_f^{(n)}$
and the complement of a hedgehog.
$\mathbb {C}\smallsetminus H_f^{(n)}$
and the complement of a hedgehog.
Let
![]() $z\in \mathbb {C}$
satisfy
$z\in \mathbb {C}$
satisfy
![]() $f^{(n)}(z)=0$
. Then
$f^{(n)}(z)=0$
. Then
![]() $z\in H_f^{(n)}$
as
$z\in H_f^{(n)}$
as
![]() $0\in I_0$
. Therefore,
$0\in I_0$
. Therefore,
![]() $f^{(n)}$
has no roots in
$f^{(n)}$
has no roots in
![]() $\mathbb {C}\smallsetminus H_f^{(n)}$
. The association
$\mathbb {C}\smallsetminus H_f^{(n)}$
. The association
![]() $w\mapsto f^{(n)}(w^{-1})$
is meromorphic on
$w\mapsto f^{(n)}(w^{-1})$
is meromorphic on
![]() $\mathbb {C} \smallsetminus \tilde H$
with
$\mathbb {C} \smallsetminus \tilde H$
with
![]() $\tilde H = \{w \in \mathbb {C}^\times : w^{-1} \in H_f^{(n)}\}$
closed in
$\tilde H = \{w \in \mathbb {C}^\times : w^{-1} \in H_f^{(n)}\}$
closed in
![]() $\mathbb {C}$
. It never vanishes and has only one pole at
$\mathbb {C}$
. It never vanishes and has only one pole at
![]() $0\in \mathbb {C}\smallsetminus \tilde H$
the order of which is
$0\in \mathbb {C}\smallsetminus \tilde H$
the order of which is
![]() $d^n$
. It follows that
$d^n$
. It follows that
![]() $\tilde f \colon w\mapsto w^{d^n} f^{(n)}(w^{-1})$
is holomorphic on
$\tilde f \colon w\mapsto w^{d^n} f^{(n)}(w^{-1})$
is holomorphic on
![]() $\mathbb {C} \smallsetminus \tilde H$
without zeros. Moreover,
$\mathbb {C} \smallsetminus \tilde H$
without zeros. Moreover,
![]() $\tilde f(0)=1$
as f is monic.
$\tilde f(0)=1$
as f is monic.
The complements
![]() $\widehat {\mathbb {C}} \smallsetminus H_f^{(n)}$
and
$\widehat {\mathbb {C}} \smallsetminus H_f^{(n)}$
and
![]() $\mathbb {C} \smallsetminus \tilde H$
are homeomorphic via the Möbius transformation
$\mathbb {C} \smallsetminus \tilde H$
are homeomorphic via the Möbius transformation
![]() $z\mapsto z^{-1}$
. In particular, the latter is simply connected. So there exists a holomorphic function
$z\mapsto z^{-1}$
. In particular, the latter is simply connected. So there exists a holomorphic function
![]() $\tilde g_n \colon \mathbb {C}\smallsetminus \tilde H \rightarrow \mathbb {C}$
with
$\tilde g_n \colon \mathbb {C}\smallsetminus \tilde H \rightarrow \mathbb {C}$
with
![]() $\tilde g_n(w)^{d^n}=\tilde f(w)$
for all
$\tilde g_n(w)^{d^n}=\tilde f(w)$
for all
![]() $w\in \mathbb {C}\smallsetminus \tilde H$
and with
$w\in \mathbb {C}\smallsetminus \tilde H$
and with
![]() $\tilde g_n(0)=1$
. We resubstitute
$\tilde g_n(0)=1$
. We resubstitute
![]() $z=1/w$
and define
$z=1/w$
and define
![]() $g_n(z) = z\tilde g_n(z^{-1})$
to find
$g_n(z) = z\tilde g_n(z^{-1})$
to find
for all
![]() $z\in \mathbb {C} \smallsetminus H_f^{(n)}$
. Then
$z\in \mathbb {C} \smallsetminus H_f^{(n)}$
. Then
![]() $g_n$
is holomorphic and
$g_n$
is holomorphic and
![]() $g_n(z) = z + O(1)$
as
$g_n(z) = z + O(1)$
as
![]() $z\rightarrow \infty $
.
$z\rightarrow \infty $
.
Let
![]() $z\in \mathbb {C} \smallsetminus H_f^{(n)}$
. Then
$z\in \mathbb {C} \smallsetminus H_f^{(n)}$
. Then
![]() $g_n(z) \in \mathbb {C}\smallsetminus I_n$
with
$g_n(z) \in \mathbb {C}\smallsetminus I_n$
with
![]() $I_n = \{z\in \mathbb {C} : z^{d^n} \in I_0\}$
by Equation (3.2). Now,
$I_n = \{z\in \mathbb {C} : z^{d^n} \in I_0\}$
by Equation (3.2). Now,
is a hedgehog with at most
![]() $q d^n$
quills where the
$q d^n$
quills where the
![]() $w_i$
satisfy
$w_i$
satisfy
![]() $w_i^{d^n}=\gamma _i$
.
$w_i^{d^n}=\gamma _i$
.
Let us consider two examples.
First, suppose
![]() $f = T^2$
. In this case, the post-critical set equals
$f = T^2$
. In this case, the post-critical set equals
![]() $\{0\}$
. We may take
$\{0\}$
. We may take
![]() $q=0$
and
$q=0$
and
![]() $I_0 = \mathcal {H}()=\{0\}$
. For all
$I_0 = \mathcal {H}()=\{0\}$
. For all
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
![]() $H_f^{(n)} = I_n = \{0\}$
. Moreover,
$H_f^{(n)} = I_n = \{0\}$
. Moreover,
![]() $g_n(z) = z$
for all
$g_n(z) = z$
for all
![]() $z\in \mathbb {C}^\times $
.
$z\in \mathbb {C}^\times $
.
Second, say
![]() $f = T^2-2$
. Its post-critical set is
$f = T^2-2$
. Its post-critical set is
![]() $\{-2,2\}$
. This time the hedgehog
$\{-2,2\}$
. This time the hedgehog
![]() $I_0 = \mathcal {H}(-2,2) = [-2,0]\cup [0,2]$
has
$I_0 = \mathcal {H}(-2,2) = [-2,0]\cup [0,2]$
has
![]() $q=2$
quills. As
$q=2$
quills. As
![]() $f^{-1}([-2,2])=[-2,2]$
, we have
$f^{-1}([-2,2])=[-2,2]$
, we have
![]() $H^{(n)}_f = [-2,2]$
for all
$H^{(n)}_f = [-2,2]$
for all
![]() $n\in \mathbb {N}$
. In particular,
$n\in \mathbb {N}$
. In particular,
![]() $f^{(n)}(z)\not =0$
for all
$f^{(n)}(z)\not =0$
for all
![]() $z\in \mathbb {C} \smallsetminus [-2,2]$
. The polynomial mapping
$z\in \mathbb {C} \smallsetminus [-2,2]$
. The polynomial mapping
![]() $w\mapsto w^{2^n}f^{(n)}(w^{-1})$
does not vanish on the simply connected domain
$w\mapsto w^{2^n}f^{(n)}(w^{-1})$
does not vanish on the simply connected domain
![]() $\mathbb {C}\smallsetminus ((-\infty ,-1/2]\cup [1/2,\infty ))$
and attains
$\mathbb {C}\smallsetminus ((-\infty ,-1/2]\cup [1/2,\infty ))$
and attains
![]() $1$
at
$1$
at
![]() $z=0$
. So it has a holomorphic
$z=0$
. So it has a holomorphic
![]() $2^n$
-th root
$2^n$
-th root
![]() $\tilde g_n$
that maps
$\tilde g_n$
that maps
![]() $0$
to
$0$
to
![]() $1$
. As above, we set
$1$
. As above, we set
![]() $g_n(z) = z \tilde g_n(z^{-1})$
for all
$g_n(z) = z \tilde g_n(z^{-1})$
for all
![]() $z\in \mathbb {C} \smallsetminus [-2,2]$
. Then
$z\in \mathbb {C} \smallsetminus [-2,2]$
. Then
![]() $g_n$
takes values in
$g_n$
takes values in
![]() $\mathbb {C}\smallsetminus I_n$
. Here,
$\mathbb {C}\smallsetminus I_n$
. Here,
![]() $I_n$
is a hedgehog with
$I_n$
is a hedgehog with
![]() $2^{n+1}$
quills ending at
$2^{n+1}$
quills ending at
![]() $2^{1/2^n} e^{2\pi \sqrt {-1} (k+\delta )/2^n}$
for
$2^{1/2^n} e^{2\pi \sqrt {-1} (k+\delta )/2^n}$
for
![]() $k\in \mathbb {Z}$
and
$k\in \mathbb {Z}$
and
![]() $\delta \in \{0,1/2\}$
.
$\delta \in \{0,1/2\}$
.
We return to the general case. The map
![]() $g_n$
is a key tool in constructing U from Proposition 3.2. Let us first show that it is injective and determine its image.
$g_n$
is a key tool in constructing U from Proposition 3.2. Let us first show that it is injective and determine its image.
Lemma 3.3. The holomorphic function
![]() $g_n$
induces a bijection
$g_n$
induces a bijection
![]() $\mathbb {C}\smallsetminus H_f^{(n)}\rightarrow \mathbb {C}\smallsetminus I_n$
.
$\mathbb {C}\smallsetminus H_f^{(n)}\rightarrow \mathbb {C}\smallsetminus I_n$
.
Proof. Suppose
![]() $z\in \mathbb {C}\smallsetminus H_f^{(n)}$
is a critical point of
$z\in \mathbb {C}\smallsetminus H_f^{(n)}$
is a critical point of
![]() $g_n$
. Taking the derivative of Equation (3.2) gives
$g_n$
. Taking the derivative of Equation (3.2) gives
![]() $d^n g_n(z)^{d^n-1}g_n'(z) = ({f^{(n)}})'(z)$
and hence
$d^n g_n(z)^{d^n-1}g_n'(z) = ({f^{(n)}})'(z)$
and hence
![]() $(f^{(n)})'(z)=0$
. The chain rule yields
$(f^{(n)})'(z)=0$
. The chain rule yields
![]() $f'(f^{(n-1)}(z))\cdots f'(z)=0$
, so
$f'(f^{(n-1)}(z))\cdots f'(z)=0$
, so
![]() $f'$
vanishes at
$f'$
vanishes at
![]() $f^{(j)}(z)$
for some
$f^{(j)}(z)$
for some
![]() $j\in \{0,\ldots ,n-1\}$
. Hence,
$j\in \{0,\ldots ,n-1\}$
. Hence,
![]() $f^{(n)}(z) \in \mathrm {PCO}_{n}^{+}(f)$
. But
$f^{(n)}(z) \in \mathrm {PCO}_{n}^{+}(f)$
. But
![]() $\mathrm {PCO}_n^{+}(f) \subseteq I_0$
by our standing hypothesis and so
$\mathrm {PCO}_n^{+}(f) \subseteq I_0$
by our standing hypothesis and so
![]() $z\in H_f^{(n)}$
. This is a contradiction. We conclude that
$z\in H_f^{(n)}$
. This is a contradiction. We conclude that
![]() $g_n$
has no critical points on its domain
$g_n$
has no critical points on its domain
![]() $\mathbb {C}\smallsetminus H_f^{(n)}$
and that it is a local homeomorphism.
$\mathbb {C}\smallsetminus H_f^{(n)}$
and that it is a local homeomorphism.
Let us verify that the map
![]() $\mathbb {C}\smallsetminus H_f^{(n)}\rightarrow \mathbb {C}\smallsetminus I_n$
is proper. Indeed, let
$\mathbb {C}\smallsetminus H_f^{(n)}\rightarrow \mathbb {C}\smallsetminus I_n$
is proper. Indeed, let
![]() $\mathcal {K}$
be compact with
$\mathcal {K}$
be compact with
![]() $\mathcal {K}\subseteq \mathbb {C}\smallsetminus I_n$
. We need to verify that
$\mathcal {K}\subseteq \mathbb {C}\smallsetminus I_n$
. We need to verify that
![]() $g_n^{-1}(\mathcal {K})$
is compact. To this end, let
$g_n^{-1}(\mathcal {K})$
is compact. To this end, let
![]() $(x_k)_{k\in \mathbb {N}}$
be a sequence in
$(x_k)_{k\in \mathbb {N}}$
be a sequence in
![]() $g_n^{-1}(\mathcal {K})$
. If the sequence is unbounded, then so is
$g_n^{-1}(\mathcal {K})$
. If the sequence is unbounded, then so is
![]() $(f^{(n)}(x_k))_{k\in \mathbb {N}}$
. This is impossible as
$(f^{(n)}(x_k))_{k\in \mathbb {N}}$
. This is impossible as
![]() $f^{(n)}(x_k) = g_n(x_k)^{d^n}$
lies in the image of
$f^{(n)}(x_k) = g_n(x_k)^{d^n}$
lies in the image of
![]() $\mathcal {K}$
in
$\mathcal {K}$
in
![]() $\mathbb {C}$
under the
$\mathbb {C}$
under the
![]() $d^n$
-th power map, itself a bounded set. So we may replace
$d^n$
-th power map, itself a bounded set. So we may replace
![]() $(x_k)_{k\in \mathbb {N}}$
by a convergent subsequence with limit
$(x_k)_{k\in \mathbb {N}}$
by a convergent subsequence with limit
![]() $x\in \mathbb {C}$
. To verify our claim, it suffices to check
$x\in \mathbb {C}$
. To verify our claim, it suffices to check
![]() $x\in g_n^{-1}(\mathcal {K})$
. If
$x\in g_n^{-1}(\mathcal {K})$
. If
![]() $x\in \mathbb {C}\smallsetminus H_f^{(n)}$
, then
$x\in \mathbb {C}\smallsetminus H_f^{(n)}$
, then
![]() $g_n(x)=\lim _{k\rightarrow \infty } g_n(x_k) \in \mathcal {K}$
and we are done. Let us assume
$g_n(x)=\lim _{k\rightarrow \infty } g_n(x_k) \in \mathcal {K}$
and we are done. Let us assume
![]() $x\in H_f^{(n)}$
. As
$x\in H_f^{(n)}$
. As
![]() $\mathcal {K}$
is compact, we may pass to a subsequence for which
$\mathcal {K}$
is compact, we may pass to a subsequence for which
![]() $(g_n(x_k))_{k\in \mathbb {N}}$
converges to
$(g_n(x_k))_{k\in \mathbb {N}}$
converges to
![]() $y\in \mathcal {K}$
. Now,
$y\in \mathcal {K}$
. Now,
![]() $y^{d^n}=\lim _{k\rightarrow \infty } f^{(n)}(x_k) = f^{(n)}(x)\in I_0$
using that
$y^{d^n}=\lim _{k\rightarrow \infty } f^{(n)}(x_k) = f^{(n)}(x)\in I_0$
using that
![]() $f^{(n)}$
is a polynomial. Hence,
$f^{(n)}$
is a polynomial. Hence,
![]() $y\in I_n$
, but this contradicts
$y\in I_n$
, but this contradicts
![]() $\mathcal {K}\subseteq \mathbb {C}\smallsetminus I_n$
.
$\mathcal {K}\subseteq \mathbb {C}\smallsetminus I_n$
.
The continuous map
![]() $\mathbb {C}\smallsetminus H_f^{(n)}\rightarrow \mathbb {C}\smallsetminus I_n$
is a proper local homeomorphism. So it is open and closed, hence surjective as both
$\mathbb {C}\smallsetminus H_f^{(n)}\rightarrow \mathbb {C}\smallsetminus I_n$
is a proper local homeomorphism. So it is open and closed, hence surjective as both
![]() $\mathbb {C}\smallsetminus H_f^{(n)}$
and
$\mathbb {C}\smallsetminus H_f^{(n)}$
and
![]() $\mathbb {C}\smallsetminus I_n$
are connected. We find that
$\mathbb {C}\smallsetminus I_n$
are connected. We find that
![]() $\mathbb {C}\smallsetminus H_f^{(n)}\rightarrow \mathbb {C}\smallsetminus I_n$
is a topological covering using again Lemma 2 [Reference HoHo75].
$\mathbb {C}\smallsetminus H_f^{(n)}\rightarrow \mathbb {C}\smallsetminus I_n$
is a topological covering using again Lemma 2 [Reference HoHo75].
Recall that
![]() $I_0$
contains all critical values of
$I_0$
contains all critical values of
![]() $z\mapsto z^{d^n}$
and
$z\mapsto z^{d^n}$
and
![]() $z\mapsto f^{(n)}(z)$
. The fiber of either map above a point of
$z\mapsto f^{(n)}(z)$
. The fiber of either map above a point of
![]() $\mathbb {C}\smallsetminus I_0$
contains
$\mathbb {C}\smallsetminus I_0$
contains
![]() $d^n = \deg f^{(n)}$
elements. So Equation (3.2) implies that
$d^n = \deg f^{(n)}$
elements. So Equation (3.2) implies that
![]() $g_n$
is injective.
$g_n$
is injective.
The inverse of a holomorphic bijection is again holomorphic. So the inverse
of
![]() $g_n$
is also holomorphic; the function
$g_n$
is also holomorphic; the function
![]() $h_n$
is a branch of
$h_n$
is a branch of
![]() $z\mapsto (f^{(n)})^{-1}(z^{d^n})$
. We have
$z\mapsto (f^{(n)})^{-1}(z^{d^n})$
. We have
by the same property of
![]() $g_n$
. Thus,
$g_n$
. Thus,
![]() $h_n$
extends to a homeomorphism
$h_n$
extends to a homeomorphism
![]() $\widehat {\mathbb {C}}\smallsetminus I_n\rightarrow \widehat {\mathbb {C}}\smallsetminus H_f^{(n)}$
.
$\widehat {\mathbb {C}}\smallsetminus I_n\rightarrow \widehat {\mathbb {C}}\smallsetminus H_f^{(n)}$
.
Proof of Proposition 3.2.
If
![]() $\alpha _i\in \mathbb {C}\smallsetminus H_f^{(n)}$
, then the value
$\alpha _i\in \mathbb {C}\smallsetminus H_f^{(n)}$
, then the value
![]() $g_n(\alpha _i)$
is well-defined. We define a further hedgehog
$g_n(\alpha _i)$
is well-defined. We define a further hedgehog
with at most
![]() $qd^n+m$
quills; see Equation (3.3).
$qd^n+m$
quills; see Equation (3.3).
The hedgehog complement
![]() $\widehat {\mathbb {C}}\smallsetminus I^{\prime }_n$
is connected and simply connected, and therefore so is its homeomorphic image
$\widehat {\mathbb {C}}\smallsetminus I^{\prime }_n$
is connected and simply connected, and therefore so is its homeomorphic image
The image U lies open in
![]() $\widehat {\mathbb {C}}\smallsetminus H_f^{(n)}$
and thus in
$\widehat {\mathbb {C}}\smallsetminus H_f^{(n)}$
and thus in
![]() $\widehat {\mathbb {C}}$
. Because
$\widehat {\mathbb {C}}$
. Because
![]() $\infty \in U$
, we find that
$\infty \in U$
, we find that
![]() $\widehat {\mathbb {C}}\smallsetminus U=\mathbb {C}\smallsetminus U$
is compact; this yields part of the claim of (i).
$\widehat {\mathbb {C}}\smallsetminus U=\mathbb {C}\smallsetminus U$
is compact; this yields part of the claim of (i).
Recall
![]() $0 \in H_f^{(n)}$
, so
$0 \in H_f^{(n)}$
, so
![]() $0\not \in U$
. Suppose
$0\not \in U$
. Suppose
![]() $\alpha _i\in U$
for some i. So
$\alpha _i\in U$
for some i. So
![]() $\alpha _i\not \in H_f^{(n)}$
and thus
$\alpha _i\not \in H_f^{(n)}$
and thus
![]() $g_n(\alpha _i) \in I^{\prime }_n$
by construction. But
$g_n(\alpha _i) \in I^{\prime }_n$
by construction. But
![]() $\alpha _i$
also lies in the image of
$\alpha _i$
also lies in the image of
![]() $h_n$
, that is,
$h_n$
, that is,
![]() $\alpha _i=h_n(\beta )$
for some
$\alpha _i=h_n(\beta )$
for some
![]() $\beta \in \mathbb {C}\smallsetminus I^{\prime }_n$
. We deduce
$\beta \in \mathbb {C}\smallsetminus I^{\prime }_n$
. We deduce
![]() $g_n(\alpha _i) = g_n(h_n(\beta ))=\beta $
, which is a contradiction. So no
$g_n(\alpha _i) = g_n(h_n(\beta ))=\beta $
, which is a contradiction. So no
![]() $\alpha _i$
lies in U. This implies the rest of (i).
$\alpha _i$
lies in U. This implies the rest of (i).
We apply Theorem 5.2.3 [Reference RansfordRan95] with
![]() $K_1 =I^{\prime }_n,K_2=\widehat {\mathbb {C}}\smallsetminus U,D_1=\widehat {\mathbb {C}}\smallsetminus I^{\prime }_n,D_2= U,$
and f as
$K_1 =I^{\prime }_n,K_2=\widehat {\mathbb {C}}\smallsetminus U,D_1=\widehat {\mathbb {C}}\smallsetminus I^{\prime }_n,D_2= U,$
and f as
![]() ${h_n}|_{D_1}\colon {D_1}\rightarrow {D_2}$
extended as above to send
${h_n}|_{D_1}\colon {D_1}\rightarrow {D_2}$
extended as above to send
![]() $\infty \mapsto \infty $
. Hence,
$\infty \mapsto \infty $
. Hence,
Recall that
![]() $I^{\prime }_n$
is a hedgehog with at most
$I^{\prime }_n$
is a hedgehog with at most
![]() $qd^n+m$
quills and lengths given in Equations (3.3) and (3.4). Dubinin’s theorem [Reference DubininDub84] implies
$qd^n+m$
quills and lengths given in Equations (3.3) and (3.4). Dubinin’s theorem [Reference DubininDub84] implies
Combining these two estimates and using
![]() $|g_n(\alpha _i)| = |f^{(n)}(\alpha _i)|^{1/d^{n}}$
if
$|g_n(\alpha _i)| = |f^{(n)}(\alpha _i)|^{1/d^{n}}$
if
![]() $\alpha _i\in \mathbb {C}\smallsetminus H_f^{(n)}$
yields
$\alpha _i\in \mathbb {C}\smallsetminus H_f^{(n)}$
yields
This completes the proof of (ii).
We keep the notation of the previous proof and make a final expository remark. The complement of U as in Equation (3.5) is obtained by augmenting
![]() $H_f^{(n)}$
. More precisely, we claim that
$H_f^{(n)}$
. More precisely, we claim that
Indeed, note that
![]() $U = h_n(\widehat {\mathbb {C}}\smallsetminus I^{\prime }_n) \subseteq h_n(\widehat {\mathbb {C}}\smallsetminus I_n) = \widehat {\mathbb {C}}\smallsetminus H^{(n)}_f$
as
$U = h_n(\widehat {\mathbb {C}}\smallsetminus I^{\prime }_n) \subseteq h_n(\widehat {\mathbb {C}}\smallsetminus I_n) = \widehat {\mathbb {C}}\smallsetminus H^{(n)}_f$
as
![]() $I_n\subseteq I^{\prime }_n$
. Taking the complement in
$I_n\subseteq I^{\prime }_n$
. Taking the complement in
![]() $\mathbb {C}$
yields
$\mathbb {C}$
yields
![]() $H_f^{(n)}\subseteq \mathbb {C} \smallsetminus U$
. Suppose
$H_f^{(n)}\subseteq \mathbb {C} \smallsetminus U$
. Suppose
![]() $z=h_n(w)$
with
$z=h_n(w)$
with
![]() $w\in I^{\prime }_n\smallsetminus I_n$
. If
$w\in I^{\prime }_n\smallsetminus I_n$
. If
![]() $z\in U$
, then
$z\in U$
, then
![]() $z=h_n(w')$
for some
$z=h_n(w')$
for some
![]() $w\in \widehat {\mathbb {C}}\smallsetminus I^{\prime }_n$
. But then
$w\in \widehat {\mathbb {C}}\smallsetminus I^{\prime }_n$
. But then
![]() $w=w'$
because
$w=w'$
because
![]() $h_n$
is injective; this is a contradiction. So the right-hand side of Equation (3.6) is contained in its left-hand side. To see the converse inclusion, we suppose
$h_n$
is injective; this is a contradiction. So the right-hand side of Equation (3.6) is contained in its left-hand side. To see the converse inclusion, we suppose
![]() $z\in \mathbb {C}\smallsetminus U$
and
$z\in \mathbb {C}\smallsetminus U$
and
![]() $z\not \in H_f^{(n)}$
. As
$z\not \in H_f^{(n)}$
. As
![]() $h_n$
maps onto
$h_n$
maps onto
![]() $\widehat {\mathbb {C}}\smallsetminus H_f^{(n)}$
, there is
$\widehat {\mathbb {C}}\smallsetminus H_f^{(n)}$
, there is
![]() $w\in \widehat {\mathbb {C}}\smallsetminus I_n$
with
$w\in \widehat {\mathbb {C}}\smallsetminus I_n$
with
![]() $z=h_n(w)$
. Because
$z=h_n(w)$
. Because
![]() $z\not \in U$
, we must have
$z\not \in U$
, we must have
![]() $w\in I^{\prime }_n$
. Thus,
$w\in I^{\prime }_n$
. Thus,
![]() $z\in h_n(I^{\prime }_n\smallsetminus I_n)$
. This completes the proof of Equation (3.6).
$z\in h_n(I^{\prime }_n\smallsetminus I_n)$
. This completes the proof of Equation (3.6).
Next, we make the estimate in Proposition 3.2 more explicit for polynomials of the shape
![]() $T^d+c$
.
$T^d+c$
.
Proposition 3.4. Let
![]() $d\ge 2$
be an integer, and let
$d\ge 2$
be an integer, and let
![]() $f=T^d+c\in \mathbb {C}[T]$
. Let
$f=T^d+c\in \mathbb {C}[T]$
. Let
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $\mathrm {PCO}_{n}^{+}(f)$
is contained in a hedgehog with at most
$\mathrm {PCO}_{n}^{+}(f)$
is contained in a hedgehog with at most
![]() $q\ge 0$
quills. Let
$q\ge 0$
quills. Let
![]() $m\ge 1$
, and let
$m\ge 1$
, and let
![]() $\alpha _1,\ldots ,\alpha _m \in \mathbb {C}$
. There is a simply connected domain
$\alpha _1,\ldots ,\alpha _m \in \mathbb {C}$
. There is a simply connected domain
![]() $U\subseteq \widehat {\mathbb {C}}$
with the following properties.
$U\subseteq \widehat {\mathbb {C}}$
with the following properties.
-
(i) We have
 $0,\alpha _1,\ldots ,\alpha _m\not \in U$
and
$0,\alpha _1,\ldots ,\alpha _m\not \in U$
and
 $\widehat {\mathbb {C}}\smallsetminus U$
is a compact subset of
$\widehat {\mathbb {C}}\smallsetminus U$
is a compact subset of
 $\mathbb {C}$
.
$\mathbb {C}$
. -
(ii) We have
 $$ \begin{align*} \mathrm{cap}(\widehat{\mathbb{C}}\smallsetminus U)\le 4^{-1/(qd^n+m)} \mathsf{C}(f)^{1/d^n} e^{\max\{\lambda_f(0),\lambda_f(\alpha_1), \ldots, \lambda_f(\alpha_m)\}}. \end{align*} $$
$$ \begin{align*} \mathrm{cap}(\widehat{\mathbb{C}}\smallsetminus U)\le 4^{-1/(qd^n+m)} \mathsf{C}(f)^{1/d^n} e^{\max\{\lambda_f(0),\lambda_f(\alpha_1), \ldots, \lambda_f(\alpha_m)\}}. \end{align*} $$
Proof. By hypothesis, there are
![]() $\gamma _1,\ldots ,\gamma _q\in \mathbb {C}^\times $
with
$\gamma _1,\ldots ,\gamma _q\in \mathbb {C}^\times $
with
![]() $\mathrm {PCO}_{n}^{+}(f)\subseteq \mathcal {H}(\gamma _1,\ldots ,\gamma _q)$
. By shortening and omitting quills, we may assume that each
$\mathrm {PCO}_{n}^{+}(f)\subseteq \mathcal {H}(\gamma _1,\ldots ,\gamma _q)$
. By shortening and omitting quills, we may assume that each
![]() $\gamma _i$
lies in
$\gamma _i$
lies in
![]() $\mathrm {PCO}_{n}^{+}(f)$
. In other words, for each i there is
$\mathrm {PCO}_{n}^{+}(f)$
. In other words, for each i there is
![]() $n_i\in \{1,\ldots ,n\}$
with
$n_i\in \{1,\ldots ,n\}$
with
![]() $\gamma _i = f^{(n_i)}(0)$
. By the definition (1.2) of
$\gamma _i = f^{(n_i)}(0)$
. By the definition (1.2) of
![]() $\mathsf {C}(f)$
, we have
$\mathsf {C}(f)$
, we have
![]() $|\gamma _i|\le \mathsf {C}(f) e^{\lambda _f(f^{(n_i)}(0))} \le \mathsf {C}(f) e^{d^{n_i} \lambda _f(0)} \le \mathsf {C}(f) e^{d^n \lambda _f(0)}$
. The same definition also gives
$|\gamma _i|\le \mathsf {C}(f) e^{\lambda _f(f^{(n_i)}(0))} \le \mathsf {C}(f) e^{d^{n_i} \lambda _f(0)} \le \mathsf {C}(f) e^{d^n \lambda _f(0)}$
. The same definition also gives
![]() $|f^{(n)}(\alpha _i)|\le \mathsf {C}(f) e^{d^n\lambda _f(\alpha _i)}$
for all i. The proof follows from Proposition 3.2.
$|f^{(n)}(\alpha _i)|\le \mathsf {C}(f) e^{d^n\lambda _f(\alpha _i)}$
for all i. The proof follows from Proposition 3.2.
Our applications require
![]() $\lambda _f(0)=0$
in Equation (3.4).
$\lambda _f(0)=0$
in Equation (3.4).
We conclude this section by deducing upper bounds for
![]() $\mathsf {C}(f)$
when
$\mathsf {C}(f)$
when
![]() $f=T^d+c\in \mathbb {C}[T]$
. Ingram has related estimates; see Section 2 [Reference IngramIng09].
$f=T^d+c\in \mathbb {C}[T]$
. Ingram has related estimates; see Section 2 [Reference IngramIng09].
Lemma 3.5. Let
![]() $d\ge 2$
be an integer, and let
$d\ge 2$
be an integer, and let
![]() $c\in \mathbb {C}$
. The polynomial
$c\in \mathbb {C}$
. The polynomial
![]() $T^d -T- |c|$
has a unique root r in
$T^d -T- |c|$
has a unique root r in
![]() $(0,\infty )$
. Moreover,
$(0,\infty )$
. Moreover,
![]() $r\ge 1$
and
$r\ge 1$
and
![]() $\log ^{+}|z^d+c| \ge -(d-1)\log r + d\log ^{+} |z|$
for all
$\log ^{+}|z^d+c| \ge -(d-1)\log r + d\log ^{+} |z|$
for all
![]() $z\in \mathbb {C}$
with
$z\in \mathbb {C}$
with
![]() $|z|\ge r$
.
$|z|\ge r$
.
Proof. Both statements are invariant under rotating c. So we may assume
![]() $c\in [0,\infty )$
.
$c\in [0,\infty )$
.
The polynomial
![]() $T^d-T-c$
is a convex function on
$T^d-T-c$
is a convex function on
![]() $(0,\infty )$
, and it is negative for small positive arguments. So it has exact one root r in
$(0,\infty )$
, and it is negative for small positive arguments. So it has exact one root r in
![]() $(0,\infty )$
. We must have
$(0,\infty )$
. We must have
![]() $r\ge 1$
as
$r\ge 1$
as
![]() $1^d-1-c\le 0$
.
$1^d-1-c\le 0$
.
Let
![]() $z\in \mathbb {C}$
. We prove the lemma by showing
$z\in \mathbb {C}$
. We prove the lemma by showing
 $$ \begin{align} \frac{\max\{1,|z^d+c|\}}{\max\{1,|z|^d\}} \ge \frac{1}{r^{d-1}} \end{align} $$
$$ \begin{align} \frac{\max\{1,|z^d+c|\}}{\max\{1,|z|^d\}} \ge \frac{1}{r^{d-1}} \end{align} $$
for all
![]() $z\in \mathbb {C}$
with
$z\in \mathbb {C}$
with
![]() $|z|\ge r$
. Note that
$|z|\ge r$
. Note that
![]() $|z|\ge r\ge 1$
gives
$|z|\ge r\ge 1$
gives
![]() $|z|^d-c\ge |z|$
. The triangle inequality implies
$|z|^d-c\ge |z|$
. The triangle inequality implies
![]() $|z^d+c|\ge \bigl ||z^d|-c\bigr |\ge |z|\ge 1$
. So the left-hand side of Equation (3.7) equals
$|z^d+c|\ge \bigl ||z^d|-c\bigr |\ge |z|\ge 1$
. So the left-hand side of Equation (3.7) equals
![]() $|z^d+c|/|z^d|=|1+c/z^d|>0$
. By the minimum modulus principle, we have
$|z^d+c|/|z^d|=|1+c/z^d|>0$
. By the minimum modulus principle, we have
![]() $|1+c/z^d|\ge 1$
for all z with
$|1+c/z^d|\ge 1$
for all z with
![]() $|z|\ge r$
, or
$|z|\ge r$
, or
![]() $|1+c/z^d|$
attains a minimum
$|1+c/z^d|$
attains a minimum
![]() $<1$
on the boundary
$<1$
on the boundary
![]() $|z|=r$
. In the first case, Equation (3.7) holds true. Finally, if
$|z|=r$
. In the first case, Equation (3.7) holds true. Finally, if
![]() $|z|=r$
and
$|z|=r$
and
![]() $|1+c/z^d|$
is minimal, then necessarily
$|1+c/z^d|$
is minimal, then necessarily
![]() $z^d = -r^d$
by elementary geometry. In this case,
$z^d = -r^d$
by elementary geometry. In this case,
![]() $|1+c/z^d| = |1-c/r^d|=|(r^d-c)/r^d| = r^{1-d}$
and we recover Equation (3.7).
$|1+c/z^d| = |1-c/r^d|=|(r^d-c)/r^d| = r^{1-d}$
and we recover Equation (3.7).
Lemma 3.6. Let
![]() $d\ge 2$
be an integer, and let
$d\ge 2$
be an integer, and let
![]() $c\in \mathbb {C}$
. Let
$c\in \mathbb {C}$
. Let
![]() $r\ge 1$
be as in Lemma 3.5. Then
$r\ge 1$
be as in Lemma 3.5. Then
![]() $\mathsf {C}(T^d+c) \le r$
.
$\mathsf {C}(T^d+c) \le r$
.
Proof. Set
![]() $f=T^d+c$
. Observe that by Lemma 3.5 we have
$f=T^d+c$
. Observe that by Lemma 3.5 we have
![]() $|f(z)|\ge r$
if
$|f(z)|\ge r$
if
![]() $|z|\ge r$
. By a simple induction, we find
$|z|\ge r$
. By a simple induction, we find
![]() $\log ^{+} |f^{(n)}(z)| \ge -(d-1)\log r + d\log ^{+} |f^{(n-1)}(z)|$
for all
$\log ^{+} |f^{(n)}(z)| \ge -(d-1)\log r + d\log ^{+} |f^{(n-1)}(z)|$
for all
![]() $n\ge 1$
if
$n\ge 1$
if
![]() $|z|\ge r$
. Considering the telescoping sum, we get
$|z|\ge r$
. Considering the telescoping sum, we get
 $$ \begin{align*} \frac{\log^{+}|f^{(n)}(z)|}{d^n} - \log^{+}|z| &= \sum_{j=1}^n \frac{\log^{+}|f^{(j)}(z)|}{d^j} - \frac{d\log^{+} |f^{(j-1)}(z)|}{d^{j}} \\ & \ge \sum_{j=1}^n \frac{-(d-1)\log r}{d^j} \ge \sum_{j=1}^\infty \frac{-(d-1)\log r}{d^j} = -\log r. \end{align*} $$
$$ \begin{align*} \frac{\log^{+}|f^{(n)}(z)|}{d^n} - \log^{+}|z| &= \sum_{j=1}^n \frac{\log^{+}|f^{(j)}(z)|}{d^j} - \frac{d\log^{+} |f^{(j-1)}(z)|}{d^{j}} \\ & \ge \sum_{j=1}^n \frac{-(d-1)\log r}{d^j} \ge \sum_{j=1}^\infty \frac{-(d-1)\log r}{d^j} = -\log r. \end{align*} $$
On taking the limit
![]() $n\rightarrow \infty $
, the left-hand side becomes
$n\rightarrow \infty $
, the left-hand side becomes
![]() $\lambda _f(z)-\log ^{+}|z|$
by Equation (1.1). So we obtain
$\lambda _f(z)-\log ^{+}|z|$
by Equation (1.1). So we obtain
![]() $\log ^{+}|z| \le \log r + \lambda _f(z)$
if
$\log ^{+}|z| \le \log r + \lambda _f(z)$
if
![]() $|z|\ge r$
. Since
$|z|\ge r$
. Since
![]() $\lambda _f$
is nonnegative, this bound also holds if
$\lambda _f$
is nonnegative, this bound also holds if
![]() $|z|<r$
. We obtain
$|z|<r$
. We obtain
![]() $\log ^{+}|z|-\lambda _f(z)\le \log r$
for all
$\log ^{+}|z|-\lambda _f(z)\le \log r$
for all
![]() $z\in \mathbb {C}$
. The lemma follows from the definition (1.2).
$z\in \mathbb {C}$
. The lemma follows from the definition (1.2).
Lemma 3.7. Let
![]() $d\ge 2$
be an integer, let
$d\ge 2$
be an integer, let
![]() $c\in \mathbb {C}$
and let
$c\in \mathbb {C}$
and let
![]() $f=T^d+c$
. Suppose
$f=T^d+c$
. Suppose
![]() $\mathrm {PCO}^{+}(f)=\{f^{(n)}(0) : n\in \mathbb {N}\}$
is a bounded set.
$\mathrm {PCO}^{+}(f)=\{f^{(n)}(0) : n\in \mathbb {N}\}$
is a bounded set.
-
(i) We have
 $|c|\le 2^{1/(d-1)}$
and
$|c|\le 2^{1/(d-1)}$
and
 $\mathsf {C}(f) \le 2^{1/(d-1)}$
.
$\mathsf {C}(f) \le 2^{1/(d-1)}$
. -
(ii) Suppose
 $c^{d-1}\not =-2$
. Then
$c^{d-1}\not =-2$
. Then
 $\mathsf {C}(f) < 2^{1/(d-1)}$
.
$\mathsf {C}(f) < 2^{1/(d-1)}$
. -
(iii) Suppose d is odd. Then
 $\mathsf {C}(f) < 2^{1/(d-1)}$
.
$\mathsf {C}(f) < 2^{1/(d-1)}$
.
Proof. By hypothesis, we have
![]() $\lambda _f(c)=\lambda _f(f(0))=0$
. Thus,
$\lambda _f(c)=\lambda _f(f(0))=0$
. Thus,
![]() $|c| \le \mathsf {C}(f)\le r$
by Lemma 3.6, where r is the unique positive real number with
$|c| \le \mathsf {C}(f)\le r$
by Lemma 3.6, where r is the unique positive real number with
![]() $r^d=r+|c|$
. As
$r^d=r+|c|$
. As
![]() $T^d-T-|c|$
has no roots on
$T^d-T-|c|$
has no roots on
![]() $(0,r)$
by Lemma 3.5 we find that it takes negative values on
$(0,r)$
by Lemma 3.5 we find that it takes negative values on
![]() $(0,r)$
. So
$(0,r)$
. So
![]() $|c|^d \le |c|+|c|$
and therefore
$|c|^d \le |c|+|c|$
and therefore
![]() $|c|\le t$
, where
$|c|\le t$
, where
![]() $t=2^{1/(d-1)}$
. We note
$t=2^{1/(d-1)}$
. We note
![]() $t^d-t-|c|\ge t^d-t-t=0$
and hence
$t^d-t-|c|\ge t^d-t-t=0$
and hence
![]() $t\ge r$
. We conclude
$t\ge r$
. We conclude
![]() $\mathsf {C}(f)\le r\le t = 2^{1/(d-1)}$
. Part (i) follows.
$\mathsf {C}(f)\le r\le t = 2^{1/(d-1)}$
. Part (i) follows.
For the proof of (ii), let us assume
![]() $\mathsf {C}(f) = 2^{1/(d-1)}$
and retain the notation from the proof of part (i). Then
$\mathsf {C}(f) = 2^{1/(d-1)}$
and retain the notation from the proof of part (i). Then
![]() $r=t$
and hence
$r=t$
and hence
![]() $2^{1/(d-1)}$
is a root of
$2^{1/(d-1)}$
is a root of
![]() $T^d-T-|c|$
. This yields
$T^d-T-|c|$
. This yields
![]() $|c|=2^{1/(d-1)}$
after a short calculation.
$|c|=2^{1/(d-1)}$
after a short calculation.
Suppose
![]() $d=2$
. Then it is well-known that the Mandelbrot set meets the circle of radius
$d=2$
. Then it is well-known that the Mandelbrot set meets the circle of radius
![]() $2$
with center
$2$
with center
![]() $0$
in the single point
$0$
in the single point
![]() $-2$
. This implies (ii) for
$-2$
. This implies (ii) for
![]() $d=2$
. Here is a direct verification that extends to all
$d=2$
. Here is a direct verification that extends to all
![]() $d\ge 2$
. It involves
$d\ge 2$
. It involves
![]() $c^d+c$
, the second iterate of
$c^d+c$
, the second iterate of
![]() $0$
under f. Indeed, its orbit under f is also bounded and so
$0$
under f. Indeed, its orbit under f is also bounded and so
![]() $|c||c^{d-1}+1|=|c^d+c|\le \mathsf {C}(f)=2^{1/(d-1)}$
. But
$|c||c^{d-1}+1|=|c^d+c|\le \mathsf {C}(f)=2^{1/(d-1)}$
. But
![]() $|c|=2^{1/(d-1)}$
and thus
$|c|=2^{1/(d-1)}$
and thus
![]() $|c^{d-1}+1|\le 1$
. The circle around
$|c^{d-1}+1|\le 1$
. The circle around
![]() $0$
of radius
$0$
of radius
![]() $2$
meets the closed disk around
$2$
meets the closed disk around
![]() $-1$
of radius
$-1$
of radius
![]() $1$
in the single point
$1$
in the single point
![]() $-2$
. We conclude
$-2$
. We conclude
![]() $c^{d-1}=-2$
, and this implies (ii).
$c^{d-1}=-2$
, and this implies (ii).
In (iii), we have that d is odd. We will prove
![]() $c^{d-1}\not =-2$
by contradiction; (iii) then follows from (ii). Indeed, if
$c^{d-1}\not =-2$
by contradiction; (iii) then follows from (ii). Indeed, if
![]() $c^{d-1}=-2$
, then
$c^{d-1}=-2$
, then
![]() $f^{(2)}(0)=c^d+c=-c$
. So
$f^{(2)}(0)=c^d+c=-c$
. So
![]() $f^{(3)}(0) = -c^d+c$
has absolute value
$f^{(3)}(0) = -c^d+c$
has absolute value
![]() $|c||c^{d-1}-1| = 3|c|> 2^{1/(d-1)}\ge \mathsf {C}(f)$
. But then
$|c||c^{d-1}-1| = 3|c|> 2^{1/(d-1)}\ge \mathsf {C}(f)$
. But then
![]() $\lambda _f(f^{3}(0))>0$
and this contradicts the hypothesis that the f-orbit of
$\lambda _f(f^{3}(0))>0$
and this contradicts the hypothesis that the f-orbit of
![]() $0$
is bounded.
$0$
is bounded.
We are now ready to prove Lemma 1.2 from the introduction.
Proof of Lemma 1.2.
Let
![]() $\sigma _0$
be a complex embedding of K as in (i) or (ii). By hypothesis,
$\sigma _0$
be a complex embedding of K as in (i) or (ii). By hypothesis,
![]() $\sigma _0(f)\not =T^2-2$
and
$\sigma _0(f)\not =T^2-2$
and
![]() $d=p$
is a prime. Moreover,
$d=p$
is a prime. Moreover,
![]() $\mathrm {PCO}^{+}(\sigma _0(f))$
is bounded in both (i) and (ii). So Lemma 3.7 yields
$\mathrm {PCO}^{+}(\sigma _0(f))$
is bounded in both (i) and (ii). So Lemma 3.7 yields
![]() $\mathsf {C}(\sigma _0(f))<2^{1/(p-1)}\le 2$
; if
$\mathsf {C}(\sigma _0(f))<2^{1/(p-1)}\le 2$
; if
![]() $p=2$
we use part (ii), and if
$p=2$
we use part (ii), and if
![]() $p\ge 3$
we use (iii).
$p\ge 3$
we use (iii).
For case (i), the embedding
![]() $\sigma _0$
is real. The set
$\sigma _0$
is real. The set
![]() $\mathrm {PCO}^{+}(\sigma _0(f))=\{\sigma _0(f)(0),\sigma _0(f)^{(2)}(0),\ldots \}$
lies in
$\mathrm {PCO}^{+}(\sigma _0(f))=\{\sigma _0(f)(0),\sigma _0(f)^{(2)}(0),\ldots \}$
lies in
![]() $\mathbb {R}$
. So it is contained in the union
$\mathbb {R}$
. So it is contained in the union
![]() $[-\alpha ,0]\cup [0,\beta ]$
of
$[-\alpha ,0]\cup [0,\beta ]$
of
![]() $q=2$
quills. Thus,
$q=2$
quills. Thus,
![]() $q\log \mathsf {C}(\sigma _0(f))<\log 4$
and Equation (1.4) is satisfied.
$q\log \mathsf {C}(\sigma _0(f))<\log 4$
and Equation (1.4) is satisfied.
In case (ii), the set
![]() $\mathrm {PCO}^{+}(\sigma _0(f))$
is finite and can be covered by
$\mathrm {PCO}^{+}(\sigma _0(f))$
is finite and can be covered by
![]() $q\le 2p-2$
quills. Now, we find
$q\le 2p-2$
quills. Now, we find
![]() $q\log \mathsf {C}(\sigma _0(f)) < 2(p-1) \log 2^{1/(p-1)} = \log 4$
and Equation (1.4) is again satisfied.
$q\log \mathsf {C}(\sigma _0(f)) < 2(p-1) \log 2^{1/(p-1)} = \log 4$
and Equation (1.4) is again satisfied.
4. Proof of main results
The following lemma is well-known; the second claim goes back to Gleason. See Lemme 2, Exposé XIX [Reference Douady and HubbardDH84] for
![]() $p=2$
, and to Epstein and Poonen [Reference EpsteinEps12]. For the reader’s convenience, we give a proof.
$p=2$
, and to Epstein and Poonen [Reference EpsteinEps12]. For the reader’s convenience, we give a proof.
Lemma 4.1. Let p be a prime number and
![]() $f=T^p+c \in \mathbb {C}[T]$
.
$f=T^p+c \in \mathbb {C}[T]$
.
-
(i) Suppose
 $0$
is f-preperiodic. Then c is an algebraic integer.
$0$
is f-preperiodic. Then c is an algebraic integer. -
(ii) Suppose
 $0$
is f-periodic. Then
$0$
is f-periodic. Then
 $\mathbb {Q}(c)/\mathbb {Q}$
is unramified above p.
$\mathbb {Q}(c)/\mathbb {Q}$
is unramified above p.
Proof. We shall consider
![]() $P=T^p+X$
as polynomial in
$P=T^p+X$
as polynomial in
![]() $\mathbb {Z}[T,X]$
.
$\mathbb {Z}[T,X]$
.
We set
![]() $P^{(0)}=T,P^{(1)}=P=T^p+X, P^{(2)} = P(P(T,X),X)=(T^p+X)^p+X, P^{(3)}=P(P^{(2)}(T,X),X)=((T^p+X)^p+X)^p+X$
, etc. A simple induction shows that
$P^{(0)}=T,P^{(1)}=P=T^p+X, P^{(2)} = P(P(T,X),X)=(T^p+X)^p+X, P^{(3)}=P(P^{(2)}(T,X),X)=((T^p+X)^p+X)^p+X$
, etc. A simple induction shows that
![]() $P^{(k)}$
is monic of degree
$P^{(k)}$
is monic of degree
![]() $p^{k-1}$
in X for all
$p^{k-1}$
in X for all
![]() $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
.
Suppose
![]() $c\in \mathbb {C}$
such that
$c\in \mathbb {C}$
such that
![]() $0$
is f-preperiodic, where
$0$
is f-preperiodic, where
![]() $f=T^p+c$
. So there exist integers
$f=T^p+c$
. So there exist integers
![]() $k,l$
with
$k,l$
with
![]() $0\le k<l$
such that
$0\le k<l$
such that
![]() $P^{(k)}(0,c)=P^{(l)}(0,c)$
. This produces a monic polynomial in integral coefficients of degree
$P^{(k)}(0,c)=P^{(l)}(0,c)$
. This produces a monic polynomial in integral coefficients of degree
![]() $p^{l-1}$
that vanishes at c. Part (i) follows.
$p^{l-1}$
that vanishes at c. Part (i) follows.
For part (ii), we observe that
![]() $P^{(k)}=(P^{(k-1)})^p+X$
for
$P^{(k)}=(P^{(k-1)})^p+X$
for
![]() $k\in \mathbb {N}$
. The derivative by X satisfies
$k\in \mathbb {N}$
. The derivative by X satisfies
![]() $\frac {\partial }{\partial X} P^{(k)} = pP^{(k-1)} \frac {\partial }{\partial X}P^{(k-1)}+1 \in 1 + p\mathbb {Z}[T,X]$
. We specialize T to
$\frac {\partial }{\partial X} P^{(k)} = pP^{(k-1)} \frac {\partial }{\partial X}P^{(k-1)}+1 \in 1 + p\mathbb {Z}[T,X]$
. We specialize T to
![]() $0$
and get
$0$
and get
![]() $\frac {\partial }{\partial X} P^{(k)}(0,X) \in 1 + p\mathbb {Z}[X]$
.
$\frac {\partial }{\partial X} P^{(k)}(0,X) \in 1 + p\mathbb {Z}[X]$
.
The determinant of the Sylvester matrix of the pair
![]() $P^{(k)}(0,X),\frac {\partial }{\partial X} P^{(k)}(0,X)$
is up to sign the discriminant of
$P^{(k)}(0,X),\frac {\partial }{\partial X} P^{(k)}(0,X)$
is up to sign the discriminant of
![]() $P^{(k)}(0,X)$
. The reduction modulo p of this matrix has upper triangular form with diagonal entries
$P^{(k)}(0,X)$
. The reduction modulo p of this matrix has upper triangular form with diagonal entries ![]() . In particular, the discriminant is not divisible by p.
. In particular, the discriminant is not divisible by p.
If
![]() $0$
is f-periodic with
$0$
is f-periodic with
![]() $f=T^p+c$
, then
$f=T^p+c$
, then
![]() $f^{(k)}(0)=0$
for some
$f^{(k)}(0)=0$
for some
![]() $k\in \mathbb {N}$
. The
$k\in \mathbb {N}$
. The
![]() $\mathbb {Q}$
-minimal polynomial of c has integral coefficients by (i), and it divides
$\mathbb {Q}$
-minimal polynomial of c has integral coefficients by (i), and it divides
![]() $P^{(k)}(0,X)$
. So its discriminant is not divisible by p either. This implies (ii).
$P^{(k)}(0,X)$
. So its discriminant is not divisible by p either. This implies (ii).
The following result is a special case of the Pólya–Bertrandias theorem; it is crucial for our application and is also at the core of Dimitrov’s proof of the Schinzel–Zassenhaus conjecture.
Let K be a number field, and let
![]() $\mathcal {O}_K$
denote the ring of algebraic integers of K. For
$\mathcal {O}_K$
denote the ring of algebraic integers of K. For
![]() $\phi = \sum _{j\ge 0} \phi _j/X^{j}\in K[[1/X]]$
and
$\phi = \sum _{j\ge 0} \phi _j/X^{j}\in K[[1/X]]$
and
![]() $\sigma \in \mathrm {Hom}(K,\mathbb {C})$
, we define
$\sigma \in \mathrm {Hom}(K,\mathbb {C})$
, we define
![]() $\sigma (\phi ) = \sum _{j\ge 0} \sigma (\phi _j)/X^{j}\in \mathbb {C}[[1/X]]$
. Recall that
$\sigma (\phi ) = \sum _{j\ge 0} \sigma (\phi _j)/X^{j}\in \mathbb {C}[[1/X]]$
. Recall that
![]() $\mathrm {cap}(\mathcal {K})$
is the transfinite diameter of a nonempty compact subset
$\mathrm {cap}(\mathcal {K})$
is the transfinite diameter of a nonempty compact subset
![]() $\mathcal {K}\subseteq \mathbb {C}$
.
$\mathcal {K}\subseteq \mathbb {C}$
.
Theorem 4.2 (Pólya–Bertrandias).
Let K be a number field and
![]() $\phi \in \mathcal {O}_K[[1/X]]$
. Suppose that for each
$\phi \in \mathcal {O}_K[[1/X]]$
. Suppose that for each
![]() $\sigma \in \mathrm {Hom}(K,\mathbb {C})$
there exists a connected open subset
$\sigma \in \mathrm {Hom}(K,\mathbb {C})$
there exists a connected open subset
![]() $U_\sigma \subseteq \mathbb {C}$
with the following properties.
$U_\sigma \subseteq \mathbb {C}$
with the following properties.
-
(i) The complement
 $\mathbb {C}\smallsetminus U_\sigma $
is compact.
$\mathbb {C}\smallsetminus U_\sigma $
is compact. -
(ii) The formal power series
 $\sigma (\phi )$
converges at all
$\sigma (\phi )$
converges at all
 $z\in \mathbb {C}$
with
$z\in \mathbb {C}$
with
 $|z|$
sufficiently large.
$|z|$
sufficiently large. -
(iii) The holomorphic function induced by
 $\sigma (\phi )$
as in (ii) extends to a holomorphic function on
$\sigma (\phi )$
as in (ii) extends to a holomorphic function on
 $U_\sigma $
.
$U_\sigma $
.
If
![]() $\prod _{\sigma \in \mathrm {Hom}(K,\mathbb {C})} \mathrm {cap}(\mathbb {C}\smallsetminus U_\sigma )<1$
, then
$\prod _{\sigma \in \mathrm {Hom}(K,\mathbb {C})} \mathrm {cap}(\mathbb {C}\smallsetminus U_\sigma )<1$
, then
![]() $\phi $
is a rational function.
$\phi $
is a rational function.
Proof. This is a special case of Théorème 5.4.6 [Reference AmiceAmi75]. Note that our power series has integral coefficients, so we can take
![]() $P_1(K)=\emptyset $
in the reference. Let
$P_1(K)=\emptyset $
in the reference. Let
![]() $\overline \sigma $
denote
$\overline \sigma $
denote
![]() $\sigma $
composed with complex conjugation. Then we may take
$\sigma $
composed with complex conjugation. Then we may take
![]() $U_{\overline \sigma }$
to be the complex conjugate of
$U_{\overline \sigma }$
to be the complex conjugate of
![]() $U_{\sigma }$
.
$U_{\sigma }$
.
We come to the main technical result of our paper.
Proposition 4.3. Let p be a prime number, let K be a number field and let
![]() $f=T^p+c\in K[T]$
. Suppose further that there are
$f=T^p+c\in K[T]$
. Suppose further that there are
![]() $k,l\in \mathbb {N}$
with
$k,l\in \mathbb {N}$
with
![]() $k<l, f^{(k-1)}(0)=f^{(l-1)}(0)$
and the following properties.
$k<l, f^{(k-1)}(0)=f^{(l-1)}(0)$
and the following properties.
-
(i) Let
 $\delta $
be as in Equation (2.6), and assume
$\delta $
be as in Equation (2.6), and assume  for all
for all
 $a\in \mathcal {O}_K$
.
$a\in \mathcal {O}_K$
. -
(ii) For all field embeddings
 $\sigma \in \mathrm {Hom}( K,\mathbb {C})$
, we assume that there exists
$\sigma \in \mathrm {Hom}( K,\mathbb {C})$
, we assume that there exists
 $n_\sigma \in \mathbb {N}$
such that
$n_\sigma \in \mathbb {N}$
such that
 $\mathrm {PCO}_{n_\sigma }^{+}(\sigma (f))$
is contained in a hedgehog with at most
$\mathrm {PCO}_{n_\sigma }^{+}(\sigma (f))$
is contained in a hedgehog with at most
 $q_\sigma \ge 0$
quills.
$q_\sigma \ge 0$
quills.
Let
![]() $x\in \overline K$
be an algebraic integer. Then one of the following conclusions holds true:
$x\in \overline K$
be an algebraic integer. Then one of the following conclusions holds true:
-
(A) We have
(4.1) $$ \begin{align} \lambda^{\mathrm{max}}_{f}(x) \ge \frac{1}{[K:\mathbb{Q}]}\sum_{\sigma\in\mathrm{Hom}(K,\mathbb{C})} \frac{1}{p^{l+n_{\sigma}}}\left(\frac{\log 4}{q_\sigma+2[K(x):K]p^{-n_\sigma}}-{\log \mathsf{C}(\sigma(f))}\right). \end{align} $$
$$ \begin{align} \lambda^{\mathrm{max}}_{f}(x) \ge \frac{1}{[K:\mathbb{Q}]}\sum_{\sigma\in\mathrm{Hom}(K,\mathbb{C})} \frac{1}{p^{l+n_{\sigma}}}\left(\frac{\log 4}{q_\sigma+2[K(x):K]p^{-n_\sigma}}-{\log \mathsf{C}(\sigma(f))}\right). \end{align} $$
-
(B) We have
 $[K(f^{(k)}(x)):K]\le [K(x):K]/p$
.
$[K(f^{(k)}(x)):K]\le [K(x):K]/p$
. -
(C) The point x is f-preperiodic,
 $\mathrm {preper}(x) \le k$
, and
$\mathrm {preper}(x) \le k$
, and
 $\mathrm {per}(x) \le (l-k)[K(x):K]$
.
$\mathrm {per}(x) \le (l-k)[K(x):K]$
.
Proof. We begin by observing
![]() $c\in \mathcal {O}_K$
by Lemma 4.1(i). Let
$c\in \mathcal {O}_K$
by Lemma 4.1(i). Let
![]() $A\in K[X]$
be the K-minimal polynomial of x. Then
$A\in K[X]$
be the K-minimal polynomial of x. Then
![]() $A\in \mathcal {O}_K[X]$
has degree
$A\in \mathcal {O}_K[X]$
has degree
![]() $D=[K(x):K]$
$D=[K(x):K]$
We apply Proposition 2.5 to the ring
![]() $R=\mathcal {O}_K$
. There exists
$R=\mathcal {O}_K$
. There exists
![]() $\phi \in \mathcal {O}_K[[1/X]]$
with
$\phi \in \mathcal {O}_K[[1/X]]$
with
and
we recall Equation (2.10). Then
![]() $\sigma (\phi )^p = \sigma (A_l/A_k)^{p-1}$
for all
$\sigma (\phi )^p = \sigma (A_l/A_k)^{p-1}$
for all
![]() $\sigma \in \mathrm {Hom}(K,\mathbb {C})$
.
$\sigma \in \mathrm {Hom}(K,\mathbb {C})$
.
We split
![]() $\sigma (A) = (X-x_{\sigma ,1})\cdots (X-x_{\sigma ,D})$
, where
$\sigma (A) = (X-x_{\sigma ,1})\cdots (X-x_{\sigma ,D})$
, where
![]() $x_{\sigma ,1},\ldots ,x_{\sigma ,D}\in \mathbb {C}$
are conjugates of
$x_{\sigma ,1},\ldots ,x_{\sigma ,D}\in \mathbb {C}$
are conjugates of
![]() $\sigma (x)$
over
$\sigma (x)$
over
![]() $\sigma (K)\subseteq \mathbb {C}$
. Then
$\sigma (K)\subseteq \mathbb {C}$
. Then
 $$ \begin{align*} \sigma(\phi)^p =\prod_{j=1}^D \left(\frac{X-\sigma(f)^{(l)}(x_{\sigma,j})}{X-\sigma(f)^{(k)}(x_{\sigma,j})}\right)^{p-1}. \end{align*} $$
$$ \begin{align*} \sigma(\phi)^p =\prod_{j=1}^D \left(\frac{X-\sigma(f)^{(l)}(x_{\sigma,j})}{X-\sigma(f)^{(k)}(x_{\sigma,j})}\right)^{p-1}. \end{align*} $$
Recall the degree condition in Equation (4.3). The formal power series
![]() $\sigma (\phi ) \in \mathbb {C}[[1/X]]$
converges for all
$\sigma (\phi ) \in \mathbb {C}[[1/X]]$
converges for all
![]() $z\in \mathbb {C}$
for which
$z\in \mathbb {C}$
for which
![]() $|z|$
is sufficiently large. For these z, we have
$|z|$
is sufficiently large. For these z, we have
 $$ \begin{align} \sigma(\phi)(z)^p =\prod_{j=1}^D \left(\frac{1-\sigma(f)^{(l)}(x_{\sigma,j})/z}{1-\sigma(f)^{(k)}(x_{\sigma,j})/z}\right)^{p-1}. \end{align} $$
$$ \begin{align} \sigma(\phi)(z)^p =\prod_{j=1}^D \left(\frac{1-\sigma(f)^{(l)}(x_{\sigma,j})/z}{1-\sigma(f)^{(k)}(x_{\sigma,j})/z}\right)^{p-1}. \end{align} $$
We apply Proposition 3.4 to
![]() $\sigma (f) = T^p+\sigma (c)$
and
$\sigma (f) = T^p+\sigma (c)$
and
![]() $n_\sigma $
. By hypothesis,
$n_\sigma $
. By hypothesis,
![]() $\mathrm {PCO}_{n_\sigma }^{+}(\sigma (f))$
is contained in a hedgehog with at most
$\mathrm {PCO}_{n_\sigma }^{+}(\sigma (f))$
is contained in a hedgehog with at most
![]() $q_\sigma \ge 0$
quills. We take
$q_\sigma \ge 0$
quills. We take
![]() $m=2D$
and set
$m=2D$
and set
We obtain a simply connected domain
![]() $U_\sigma \subseteq \widehat {\mathbb {C}}$
with the two stated properties.
$U_\sigma \subseteq \widehat {\mathbb {C}}$
with the two stated properties.
The right-hand side of Equation (4.4) is well-defined and nonzero for all
![]() $z\in U_\sigma \smallsetminus \{\infty \}$
; indeed, none among
$z\in U_\sigma \smallsetminus \{\infty \}$
; indeed, none among
![]() $0$
and the Equation (4.5) lie in
$0$
and the Equation (4.5) lie in
![]() $U_\sigma $
by Proposition 3.4. So the right-hand side extends to a holomorphic function on
$U_\sigma $
by Proposition 3.4. So the right-hand side extends to a holomorphic function on
![]() $U_\sigma $
that never vanishes; the extension maps
$U_\sigma $
that never vanishes; the extension maps
![]() $\infty $
to
$\infty $
to
![]() $1$
. By the monodromy theorem from complex analysis and since
$1$
. By the monodromy theorem from complex analysis and since
![]() $U_\sigma $
is simply connected, we conclude that
$U_\sigma $
is simply connected, we conclude that
![]() $z\mapsto \sigma (\phi )(z)$
, defined a priori only if
$z\mapsto \sigma (\phi )(z)$
, defined a priori only if
![]() $|z|$
is large, extends to a holomorphic map
$|z|$
is large, extends to a holomorphic map
![]() $\sigma (\phi )\colon U_\sigma \rightarrow \mathbb {C}$
.
$\sigma (\phi )\colon U_\sigma \rightarrow \mathbb {C}$
.
We split up into two cases.
Case 1. First, suppose that
![]() $\phi $
is not a rational function.
$\phi $
is not a rational function.
Theorem 4.2 implies
Recall that
![]() $\lambda _{\sigma (f)}(0)=0$
as f is post-critically finite by hypothesis. This contribution can be omitted from the capacity bound from Proposition 3.4 since the local canonical height is nonnegative. So
$\lambda _{\sigma (f)}(0)=0$
as f is post-critically finite by hypothesis. This contribution can be omitted from the capacity bound from Proposition 3.4 since the local canonical height is nonnegative. So
![]() $k\le l$
implies
$k\le l$
implies
 $$ \begin{align} \sum_{\sigma\in\mathrm{Hom}(K,\mathbb{C})}\log \mathrm{cap}(\widehat{\mathbb{C}}\smallsetminus U_\sigma) \le \sum_{\sigma\in \mathrm{Hom}(K,\mathbb{C})} -\frac{\log 4}{q_\sigma p^{n_\sigma}+2D}+\frac{\log \mathsf{C}(\sigma(f))}{p^{n_\sigma}} +p^l \max_{1\le i\le D} \lambda_{\sigma(f)}(x_{\sigma,i}). \end{align} $$
$$ \begin{align} \sum_{\sigma\in\mathrm{Hom}(K,\mathbb{C})}\log \mathrm{cap}(\widehat{\mathbb{C}}\smallsetminus U_\sigma) \le \sum_{\sigma\in \mathrm{Hom}(K,\mathbb{C})} -\frac{\log 4}{q_\sigma p^{n_\sigma}+2D}+\frac{\log \mathsf{C}(\sigma(f))}{p^{n_\sigma}} +p^l \max_{1\le i\le D} \lambda_{\sigma(f)}(x_{\sigma,i}). \end{align} $$
We compare Equations (4.6) and (4.7) and rearrange to find
 $$ \begin{align*} \sum_{\sigma\in \mathrm{Hom}(K,\mathbb{C})} \max_{1\le i\le D} \lambda_{\sigma(f)}(x_{\sigma,i}) \ge \frac{1}{p^{l}}\sum_{\sigma\in\mathrm{Hom}(K,\mathbb{C})} \left(\frac{\log 4}{q_\sigma p^{n_\sigma}+2D} - \frac{\log \mathsf{C}(\sigma(f))}{p^{n_\sigma}}\right). \end{align*} $$
$$ \begin{align*} \sum_{\sigma\in \mathrm{Hom}(K,\mathbb{C})} \max_{1\le i\le D} \lambda_{\sigma(f)}(x_{\sigma,i}) \ge \frac{1}{p^{l}}\sum_{\sigma\in\mathrm{Hom}(K,\mathbb{C})} \left(\frac{\log 4}{q_\sigma p^{n_\sigma}+2D} - \frac{\log \mathsf{C}(\sigma(f))}{p^{n_\sigma}}\right). \end{align*} $$
The left-hand side is at most
![]() $[K:\mathbb {Q}]\lambda ^{\mathrm {max}}_f(x)$
. So conclusion (A) holds.
$[K:\mathbb {Q}]\lambda ^{\mathrm {max}}_f(x)$
. So conclusion (A) holds.
Case 2. Second, suppose that
![]() $\phi $
is a rational function.
$\phi $
is a rational function.
In particular,
![]() $\phi $
is meromorphic on
$\phi $
is meromorphic on
![]() $\mathbb {C}$
. It follows from Equation (4.2) that any root of
$\mathbb {C}$
. It follows from Equation (4.2) that any root of
![]() $A_l/A_k$
has vanishing order divisible by p. Let F be a splitting field of A. Then
$A_l/A_k$
has vanishing order divisible by p. Let F be a splitting field of A. Then
![]() $\{f^{(k)}(\tau (x)) : \tau \in \mathrm {Gal}(F/K) \}$
are the roots of
$\{f^{(k)}(\tau (x)) : \tau \in \mathrm {Gal}(F/K) \}$
are the roots of
![]() $A_k$
and
$A_k$
and
![]() $\{f^{(l)}(\tau (x)) : \tau \in \mathrm {Gal}(F/K) \}$
are the roots of
$\{f^{(l)}(\tau (x)) : \tau \in \mathrm {Gal}(F/K) \}$
are the roots of
![]() $A_l$
.
$A_l$
.
We split up into two subcases.
Subcase 2a. Suppose
![]() $\#\{f^{(k)}(\tau (x)) : \tau \in \mathrm {Gal}(F/K) \} \le D/p$
. This means
$\#\{f^{(k)}(\tau (x)) : \tau \in \mathrm {Gal}(F/K) \} \le D/p$
. This means
![]() $[K(f^{(k)}(x)):K]\le D/p$
, and we are in conclusion (B) because
$[K(f^{(k)}(x)):K]\le D/p$
, and we are in conclusion (B) because
![]() $D=[K(x):K]$
.
$D=[K(x):K]$
.
Subcase 2b. Suppose
![]() $\#\{f^{(k)}(\tau (x)) : \tau \in \mathrm {Gal}(F/K) \}> D/p$
. Recall
$\#\{f^{(k)}(\tau (x)) : \tau \in \mathrm {Gal}(F/K) \}> D/p$
. Recall
![]() $D=\deg A_k$
. Then there exists
$D=\deg A_k$
. Then there exists
![]() $\tau $
such that the vanishing order of
$\tau $
such that the vanishing order of
![]() $A_k$
at
$A_k$
at
![]() $f^{(k)}(\tau (x))$
is positive and strictly less than p. But then it must also be a zero of
$f^{(k)}(\tau (x))$
is positive and strictly less than p. But then it must also be a zero of
![]() $A_l$
. After replacing
$A_l$
. After replacing
![]() $\tau $
, we may assume
$\tau $
, we may assume
![]() $f^{(k)}(\tau (x))=f^{(l)}(x)$
. Recall
$f^{(k)}(\tau (x))=f^{(l)}(x)$
. Recall
![]() $k<l$
. A simple induction shows
$k<l$
. A simple induction shows
![]() $\tau ^e (f^{(k)}(x)) = f^{((l-k)e+k)}(x)$
for all
$\tau ^e (f^{(k)}(x)) = f^{((l-k)e+k)}(x)$
for all
![]() $e\in \mathbb {N}$
. Indeed, for
$e\in \mathbb {N}$
. Indeed, for
![]() $e\ge 2$
we have
$e\ge 2$
we have
as
![]() $f\in K[T]$
.
$f\in K[T]$
.
Take e to be
![]() $\#\mathrm {Gal}(F/K)$
. So
$\#\mathrm {Gal}(F/K)$
. So
![]() $\tau ^e(f^{(k)}(x)) = f^{(k)}(x)$
and thus
$\tau ^e(f^{(k)}(x)) = f^{(k)}(x)$
and thus
In particular, x is f-preperiodic and
![]() $f^{(k)}(x)$
is f-periodic. In other words,
$f^{(k)}(x)$
is f-periodic. In other words,
![]() $\mathrm {preper}(x)\le k$
. So the first two statements in conclusion (C) hold.
$\mathrm {preper}(x)\le k$
. So the first two statements in conclusion (C) hold.
By the pigeonhole principle, there are integers e and
![]() $e'$
with
$e'$
with
![]() $0\le e<e'\le [K(x):K]$
with
$0\le e<e'\le [K(x):K]$
with
![]() $\tau ^{e}(f^{(k)}(x)) = \tau ^{e'}(f^{(k)}(x))$
. So
$\tau ^{e}(f^{(k)}(x)) = \tau ^{e'}(f^{(k)}(x))$
. So
![]() $f^{((l-k)e+k)}(x)=f^{((l-k)e'+k)}(x)$
by Equation (4.8). Hence, x has minimal period at most
$f^{((l-k)e+k)}(x)=f^{((l-k)e'+k)}(x)$
by Equation (4.8). Hence, x has minimal period at most
![]() $(l-k)(e'-e) \le (l-k)[K(x):K]$
. Therefore, the final statement in conclusion (C) holds.
$(l-k)(e'-e) \le (l-k)[K(x):K]$
. Therefore, the final statement in conclusion (C) holds.
Theorem 4.4. Let p be a prime number, let K be a number field and let
![]() $f=T^p+c\in K[T]$
. Suppose further that there are
$f=T^p+c\in K[T]$
. Suppose further that there are
![]() $k,l\in \mathbb {N}$
with
$k,l\in \mathbb {N}$
with
![]() $k<l, f^{(k-1)}(0)=f^{(l-1)}(0),$
and the following properties.
$k<l, f^{(k-1)}(0)=f^{(l-1)}(0),$
and the following properties.
-
(i) Let
 $\delta $
be as in Equation (2.6), and assume
$\delta $
be as in Equation (2.6), and assume  for all
for all
 $a\in \mathcal {O}_K$
.
$a\in \mathcal {O}_K$
. -
(ii) We suppose hat f satisfies the quill hypothesis.
Then there exists a constant
![]() $\kappa>0$
depending on the data above with the following properties.
$\kappa>0$
depending on the data above with the following properties.
-
(i) Let
 $x\in \overline K$
be an algebraic integer and f-wandering. Then
$x\in \overline K$
be an algebraic integer and f-wandering. Then
 $\lambda _f^{\mathrm {max}} (x) \ge \kappa /[K(x):K]^k$
.
$\lambda _f^{\mathrm {max}} (x) \ge \kappa /[K(x):K]^k$
. -
(ii) Let
 $x\in \overline K$
be f-wandering. Then
$x\in \overline K$
be f-wandering. Then
 $\hat h_f (x) \ge \kappa /[K(x):K]^{k+1}$
.
$\hat h_f (x) \ge \kappa /[K(x):K]^{k+1}$
.
Proof. We remark that
![]() $c\in \mathcal {O}_K$
by Lemma 4.1(i). Let
$c\in \mathcal {O}_K$
by Lemma 4.1(i). Let
![]() $x\in \overline K$
be f-wandering.
$x\in \overline K$
be f-wandering.
Our proof of (i) is by induction on
![]() $[K(x):K]$
. Here, x is an algebraic integer. We will apply Proposition 4.3. Observe that an f-wandering point cannot lead to conclusion (C).
$[K(x):K]$
. Here, x is an algebraic integer. We will apply Proposition 4.3. Observe that an f-wandering point cannot lead to conclusion (C).
Let
![]() $\sigma _0\in \mathrm {Hom}(K,\mathbb {C})$
and
$\sigma _0\in \mathrm {Hom}(K,\mathbb {C})$
and
![]() $q\ge 0$
be as in the quill hypothesis. We introduce two parameters,
$q\ge 0$
be as in the quill hypothesis. We introduce two parameters,
![]() $\epsilon _0,\epsilon \in (0,1)$
both are sufficiently small and fixed in terms of f and the other given data such as q and
$\epsilon _0,\epsilon \in (0,1)$
both are sufficiently small and fixed in terms of f and the other given data such as q and
![]() $\sigma _0(f)$
, but independent of x. We will fix
$\sigma _0(f)$
, but independent of x. We will fix
![]() $\epsilon $
in function of
$\epsilon $
in function of
![]() $\epsilon _0$
.
$\epsilon _0$
.
Let
![]() $n_{\sigma _0}\ge 1$
be the unique integer with
$n_{\sigma _0}\ge 1$
be the unique integer with
![]() $p^{n_{\sigma _0}} \ge [K(x):K]/\epsilon _0> p^{n_{\sigma _0}-1}$
. For all
$p^{n_{\sigma _0}} \ge [K(x):K]/\epsilon _0> p^{n_{\sigma _0}-1}$
. For all
![]() $\sigma \in \mathrm {Hom}(K,\mathbb {C})$
with
$\sigma \in \mathrm {Hom}(K,\mathbb {C})$
with
![]() $\sigma \not =\sigma _0$
, we fix the unique
$\sigma \not =\sigma _0$
, we fix the unique
![]() $n_{\sigma }\in \mathbb {N}$
with
$n_{\sigma }\in \mathbb {N}$
with
![]() $p^{n_{\sigma }} \ge [K(x):K]/\epsilon> p^{n_{\sigma }-1}$
.
$p^{n_{\sigma }} \ge [K(x):K]/\epsilon> p^{n_{\sigma }-1}$
.
For any
![]() $\sigma $
, we set
$\sigma $
, we set
![]() $q_\sigma =\#\mathrm {PCO}^{+}(\sigma (f)) < \infty $
. Then
$q_\sigma =\#\mathrm {PCO}^{+}(\sigma (f)) < \infty $
. Then
![]() $\mathrm {PCO}^{+}(\sigma (f))$
is contained in a hedgehog with at most
$\mathrm {PCO}^{+}(\sigma (f))$
is contained in a hedgehog with at most
![]() $q_\sigma $
quills and therefore so is
$q_\sigma $
quills and therefore so is
![]() $\mathrm {PCO}^{+}_{n_{\sigma }}(\sigma (f)) \subseteq \mathrm {PCO}^{+}(\sigma (f))$
.
$\mathrm {PCO}^{+}_{n_{\sigma }}(\sigma (f)) \subseteq \mathrm {PCO}^{+}(\sigma (f))$
.
We have
 $$ \begin{align} Y&=\sum_{\sigma\in\mathrm{Hom}(K,\mathbb{C})} \frac{1}{p^{n_\sigma}}\left(\frac{\log 4}{q_\sigma + 2[K(x):K]p^{-n_\sigma}} -\log \mathsf{C}(\sigma(f))\right) \\ \nonumber &\ge \frac{1}{p^{n_{\sigma_0}}}\left( \frac{\log 4}{q + 2[K(x):K]p^{-n_{\sigma_0}}} -{\log \mathsf{C}(\sigma_0(f))}\right) - \sum_{\sigma\not=\sigma_0} \frac{\log \mathsf{C}(\sigma(f))}{p^{n_\sigma}} \\ \nonumber &\ge \frac{1}{p^{n_{\sigma_0}}}\left( \frac{\log 4}{q + 2\epsilon_0} -{\log \mathsf{C}(\sigma_0(f))}\right) - \frac{\epsilon}{[K(x):K]}\sum_{\sigma\not=\sigma_0} \log \mathsf{C}(\sigma(f)). \end{align} $$
$$ \begin{align} Y&=\sum_{\sigma\in\mathrm{Hom}(K,\mathbb{C})} \frac{1}{p^{n_\sigma}}\left(\frac{\log 4}{q_\sigma + 2[K(x):K]p^{-n_\sigma}} -\log \mathsf{C}(\sigma(f))\right) \\ \nonumber &\ge \frac{1}{p^{n_{\sigma_0}}}\left( \frac{\log 4}{q + 2[K(x):K]p^{-n_{\sigma_0}}} -{\log \mathsf{C}(\sigma_0(f))}\right) - \sum_{\sigma\not=\sigma_0} \frac{\log \mathsf{C}(\sigma(f))}{p^{n_\sigma}} \\ \nonumber &\ge \frac{1}{p^{n_{\sigma_0}}}\left( \frac{\log 4}{q + 2\epsilon_0} -{\log \mathsf{C}(\sigma_0(f))}\right) - \frac{\epsilon}{[K(x):K]}\sum_{\sigma\not=\sigma_0} \log \mathsf{C}(\sigma(f)). \end{align} $$
For
![]() $\epsilon _0$
small enough and fixed in function of f, the quill hypothesis (1.4) implies
$\epsilon _0$
small enough and fixed in function of f, the quill hypothesis (1.4) implies
![]() $(\log 4)/(q+2\epsilon _0) - \log \mathsf {C}(\sigma _0(f)) \ge \kappa _1$
where
$(\log 4)/(q+2\epsilon _0) - \log \mathsf {C}(\sigma _0(f)) \ge \kappa _1$
where
![]() $\kappa _1=\kappa _1(f)> 0$
depends only on f. So
$\kappa _1=\kappa _1(f)> 0$
depends only on f. So
 $$ \begin{align*} Y \ge \frac{\kappa_1}{p^{n_{\sigma_0}}} - \frac{\epsilon}{[K(x):K]}\sum_{\sigma\not=\sigma_0} \log \mathsf{C}(\sigma(f)) \ge \frac{1}{ [K(x):K]}\left(\frac{\kappa_1 \epsilon_0}{p} - {\epsilon}\sum_{\sigma\not=\sigma_0} \log \mathsf{C}(\sigma(f))\right). \end{align*} $$
$$ \begin{align*} Y \ge \frac{\kappa_1}{p^{n_{\sigma_0}}} - \frac{\epsilon}{[K(x):K]}\sum_{\sigma\not=\sigma_0} \log \mathsf{C}(\sigma(f)) \ge \frac{1}{ [K(x):K]}\left(\frac{\kappa_1 \epsilon_0}{p} - {\epsilon}\sum_{\sigma\not=\sigma_0} \log \mathsf{C}(\sigma(f))\right). \end{align*} $$
Now, we fix
![]() $\epsilon $
small in terms of
$\epsilon $
small in terms of
![]() $\epsilon _0$
and f to achieve
$\epsilon _0$
and f to achieve
![]() $\kappa _1\epsilon _0/(2p) \ge \epsilon \sum _{\sigma \not =\sigma _0} \log \mathsf {C}(\sigma (f))$
. So
$\kappa _1\epsilon _0/(2p) \ge \epsilon \sum _{\sigma \not =\sigma _0} \log \mathsf {C}(\sigma (f))$
. So
Suppose we are in conclusion (A) of Proposition 4.3. Then
![]() $\lambda _f^{\mathrm {max}}(x) \ge Y [K:\mathbb {Q}]^{-1}p^{-l} \ge \kappa _2p^{-l}/[K(x):\mathbb {Q}]$
. This is stronger than the claim as we may assume
$\lambda _f^{\mathrm {max}}(x) \ge Y [K:\mathbb {Q}]^{-1}p^{-l} \ge \kappa _2p^{-l}/[K(x):\mathbb {Q}]$
. This is stronger than the claim as we may assume
![]() $\kappa \le \kappa _2 [K:\mathbb {Q}]^{-1}p^{-l}$
.
$\kappa \le \kappa _2 [K:\mathbb {Q}]^{-1}p^{-l}$
.
Suppose we are in conclusion (B). Then we have
![]() $[K(f^{(k)}(x)):K] \le [K(x):K]/p<[K(x):K]$
. In particular, this rules out
$[K(f^{(k)}(x)):K] \le [K(x):K]/p<[K(x):K]$
. In particular, this rules out
![]() $x\in K$
, so the base case of the induction was handled by conclusion (A) above. Now,
$x\in K$
, so the base case of the induction was handled by conclusion (A) above. Now,
![]() $\lambda _f^{\mathrm {max}}(f^{(k)}(x)) = p^k \lambda _f^{\mathrm {max}}(x)$
. Induction on
$\lambda _f^{\mathrm {max}}(f^{(k)}(x)) = p^k \lambda _f^{\mathrm {max}}(x)$
. Induction on
![]() $[K(x):K]$
yields
$[K(x):K]$
yields
![]() $p^k \lambda _f^{\mathrm {max}}(x) \ge \kappa /[K(f^{(k)}(x)):K]^k \ge \kappa p^k/[K(x):K]^k$
. This completes the proof of (i) as conclusion (C) is impossible in the wandering case.
$p^k \lambda _f^{\mathrm {max}}(x) \ge \kappa /[K(f^{(k)}(x)):K]^k \ge \kappa p^k/[K(x):K]^k$
. This completes the proof of (i) as conclusion (C) is impossible in the wandering case.
For (ii), we observe that
![]() $\hat h_f(x)$
is a normalized sum of local canonical heights as in Equation (1.3). Moreover, every local canonical height takes nonnegative values. In particular,
$\hat h_f(x)$
is a normalized sum of local canonical heights as in Equation (1.3). Moreover, every local canonical height takes nonnegative values. In particular,
![]() $\hat h_f(x) \ge \lambda _{f}^{\mathrm {max}}(x)/[\mathbb {Q}(x):\mathbb {Q}]$
. If x is an algebraic integer, then part (i) implies the desired lower bound for
$\hat h_f(x) \ge \lambda _{f}^{\mathrm {max}}(x)/[\mathbb {Q}(x):\mathbb {Q}]$
. If x is an algebraic integer, then part (i) implies the desired lower bound for
![]() $\hat h_f(x)$
after adjusting
$\hat h_f(x)$
after adjusting
![]() $\kappa $
. So assume that x is not an algebraic integer. Let F be a number field containing x. There is a non-Archimedean
$\kappa $
. So assume that x is not an algebraic integer. Let F be a number field containing x. There is a non-Archimedean
![]() $v\in M_{\mathbb {Q}}$
, which we may identify with a prime number, and a field embedding
$v\in M_{\mathbb {Q}}$
, which we may identify with a prime number, and a field embedding
![]() $\sigma \in \mathrm {Hom}( F, \mathbb {C}_v)$
with
$\sigma \in \mathrm {Hom}( F, \mathbb {C}_v)$
with
![]() $|\sigma (x)|_v>1$
. By anticipating ramification, we find
$|\sigma (x)|_v>1$
. By anticipating ramification, we find
![]() $|\sigma (x)|_v \ge v^{1/[\mathbb {Q}(x):\mathbb {Q}]}$
. Thus,
$|\sigma (x)|_v \ge v^{1/[\mathbb {Q}(x):\mathbb {Q}]}$
. Thus,
![]() $|\sigma (x^p+c)|_v=|\sigma (x)|_v^p>1$
by the ultrametric triangle inequality and since
$|\sigma (x^p+c)|_v=|\sigma (x)|_v^p>1$
by the ultrametric triangle inequality and since
![]() $c\in \mathcal {O}_K$
. Furthermore,
$c\in \mathcal {O}_K$
. Furthermore,
![]() $|\sigma (f^{(n)}(x))|_v = |\sigma (x)|_v^{p^n}$
for all
$|\sigma (f^{(n)}(x))|_v = |\sigma (x)|_v^{p^n}$
for all
![]() $n\in \mathbb {N}$
. Therefore,
$n\in \mathbb {N}$
. Therefore,
![]() $\lambda _{\sigma (f),v}(\sigma (x)) = \log ^{+}|\sigma (x)|_v \ge (\log v)/[\mathbb {Q}(x):\mathbb {Q}]\ge (\log 2)/[\mathbb {Q}(x):\mathbb {Q}]$
. Again, we use that local canonical heights are nonnegative and conclude
$\lambda _{\sigma (f),v}(\sigma (x)) = \log ^{+}|\sigma (x)|_v \ge (\log v)/[\mathbb {Q}(x):\mathbb {Q}]\ge (\log 2)/[\mathbb {Q}(x):\mathbb {Q}]$
. Again, we use that local canonical heights are nonnegative and conclude
![]() $\hat h_f(x) \ge (\log 2)/[\mathbb {Q}(x):\mathbb {Q}]^2\ge (\log 2)/[K(x):\mathbb {Q}]^2 = [K:\mathbb {Q}]^{-2}(\log 2)/[K(x):K]^2$
. Thetheorem follows as we may assume
$\hat h_f(x) \ge (\log 2)/[\mathbb {Q}(x):\mathbb {Q}]^2\ge (\log 2)/[K(x):\mathbb {Q}]^2 = [K:\mathbb {Q}]^{-2}(\log 2)/[K(x):K]^2$
. Thetheorem follows as we may assume
![]() $\kappa \le [K:\mathbb {Q}]^{-2}\log 2$
.
$\kappa \le [K:\mathbb {Q}]^{-2}\log 2$
.
We consider an example before moving on. Let
![]() $c=-1.543689\ldots $
be the real root of
$c=-1.543689\ldots $
be the real root of
![]() $T^3+2T^2+2T+2$
. Then
$T^3+2T^2+2T+2$
. Then
![]() $[K:\mathbb {Q}]=3$
, where
$[K:\mathbb {Q}]=3$
, where
![]() $K=\mathbb {Q}(c)$
. Moreover,
$K=\mathbb {Q}(c)$
. Moreover,
![]() $f^{(3)}(0)=f^{(4)}(0)$
for
$f^{(3)}(0)=f^{(4)}(0)$
for
![]() $f=T^2+c$
and
$f=T^2+c$
and
![]() $\mathrm {PCO}^{+}(f)\subseteq \mathbb {R}$
is contained in a union of
$\mathrm {PCO}^{+}(f)\subseteq \mathbb {R}$
is contained in a union of
![]() $2$
quills. Let
$2$
quills. Let
![]() $\wp $
be a prime ideal of
$\wp $
be a prime ideal of
![]() $\mathcal {O}_K$
containing
$\mathcal {O}_K$
containing
![]() $2$
. Then
$2$
. Then
![]() $\wp ^3= 2\mathcal {O}_K$
follows from a pari/gp computation. We claim that
$\wp ^3= 2\mathcal {O}_K$
follows from a pari/gp computation. We claim that ![]() for all
for all
![]() $a\in \mathcal {O}_K$
. Indeed,
$a\in \mathcal {O}_K$
. Indeed,
![]() $a^4(a^4-1)\in 2\mathcal {O}_K$
if
$a^4(a^4-1)\in 2\mathcal {O}_K$
if
![]() $a\in \wp $
. If
$a\in \wp $
. If
![]() $a\not \in \wp $
, then a is a unit modulo
$a\not \in \wp $
, then a is a unit modulo
![]() $2\mathcal {O}_K$
. So
$2\mathcal {O}_K$
. So
![]() $a^4 -1 \in 2\mathcal {O}_K$
as the unit group
$a^4 -1 \in 2\mathcal {O}_K$
as the unit group
![]() $(\mathcal {O}_K/2\mathcal {O}_K)^\times $
has order
$(\mathcal {O}_K/2\mathcal {O}_K)^\times $
has order
![]() $4$
. So hypothesis (i) in Theorem 4.4 is satisfied with
$4$
. So hypothesis (i) in Theorem 4.4 is satisfied with
![]() $(k,l)=(4,5)$
; note
$(k,l)=(4,5)$
; note
![]() $\delta =1$
. The quill hypothesis is met since
$\delta =1$
. The quill hypothesis is met since
![]() $\mathsf {C}(f)<2$
by Lemma 3.7(ii).
$\mathsf {C}(f)<2$
by Lemma 3.7(ii).
Theorem 4.5. Let p be a prime number, let K be a number field and let
![]() $f=T^p+c\in K[T]$
. Suppose k and l are as in Theorem 4.4. Suppose furthermore that f satisfies the quill hypothesis. Let
$f=T^p+c\in K[T]$
. Suppose k and l are as in Theorem 4.4. Suppose furthermore that f satisfies the quill hypothesis. Let
![]() $x\in \overline K$
be f-preperiodic. Then
$x\in \overline K$
be f-preperiodic. Then
and
Proof. By hypothesis, the f-orbit of
![]() $0$
is finite and so is
$0$
is finite and so is
![]() $\mathrm {PCO}^{+}(f)$
. By Lemma 4.1(i), we see that c is an algebraic integer. So x, an f-preperiodic point, is also an algebraic integer. Moreover,
$\mathrm {PCO}^{+}(f)$
. By Lemma 4.1(i), we see that c is an algebraic integer. So x, an f-preperiodic point, is also an algebraic integer. Moreover,
![]() $\lambda _f^{\mathrm {max}}(x)=0$
.
$\lambda _f^{\mathrm {max}}(x)=0$
.
Let
![]() $\sigma _0\in \mathrm {Hom}(K,\mathbb {C})$
and
$\sigma _0\in \mathrm {Hom}(K,\mathbb {C})$
and
![]() $q\ge 0$
be as in the quill hypothesis. Let
$q\ge 0$
be as in the quill hypothesis. Let
![]() $\epsilon _0,\epsilon \in (0,1),n_{\sigma }\in \mathbb {N},$
and
$\epsilon _0,\epsilon \in (0,1),n_{\sigma }\in \mathbb {N},$
and
![]() $q_{\sigma }\in \mathbb {N}$
, for
$q_{\sigma }\in \mathbb {N}$
, for
![]() $\sigma \in \mathrm {Hom}(K,\mathbb {C})$
, be as in the proof of Theorem 4.4. Recall that
$\sigma \in \mathrm {Hom}(K,\mathbb {C})$
, be as in the proof of Theorem 4.4. Recall that
![]() $\epsilon ,\epsilon _0$
depend on
$\epsilon ,\epsilon _0$
depend on
![]() $f,q,$
and
$f,q,$
and
![]() $\sigma _0(f)$
, but they are independent of x. Moreover,
$\sigma _0(f)$
, but they are independent of x. Moreover,
![]() $\epsilon $
is small in terms of
$\epsilon $
is small in terms of
![]() $\epsilon _0$
. Arguing as in the said proof up to Equation (4.10), we find
$\epsilon _0$
. Arguing as in the said proof up to Equation (4.10), we find
![]() $Y>0$
with Y as in Equation (4.9). So the right-hand side of Equation (4.1) is strictly positive. Therefore, we can rule out conclusion (A) of Proposition 4.3.
$Y>0$
with Y as in Equation (4.9). So the right-hand side of Equation (4.1) is strictly positive. Therefore, we can rule out conclusion (A) of Proposition 4.3.
So we are either in conclusion (B) where
![]() $[K(f^{(k)}(x)):K]\le [K(x):K]/p$
or conclusion (C) where
$[K(f^{(k)}(x)):K]\le [K(x):K]/p$
or conclusion (C) where
![]() $\mathrm {preper}(x) \le k$
and
$\mathrm {preper}(x) \le k$
and
![]() $\mathrm {per}(x) \le (l-k)[K(x):K]$
.
$\mathrm {per}(x) \le (l-k)[K(x):K]$
.
Observe that we have
![]() $\mathrm {preper}(f(x)) = \max \{0,\mathrm {preper}(x)-1\}$
. Iterating gives
$\mathrm {preper}(f(x)) = \max \{0,\mathrm {preper}(x)-1\}$
. Iterating gives
![]() $\mathrm {preper}(f^{(m)}(x)) = \max \{0,\mathrm {preper}(x)-m\}$
for all integers
$\mathrm {preper}(f^{(m)}(x)) = \max \{0,\mathrm {preper}(x)-m\}$
for all integers
![]() $m\ge 0$
.
$m\ge 0$
.
We prove Equation (4.11) by induction on
![]() $\mathrm {preper}(x)$
. The claim is trivial if
$\mathrm {preper}(x)$
. The claim is trivial if
![]() $\mathrm {preper}(x)\le k$
. So let us assume
$\mathrm {preper}(x)\le k$
. So let us assume
![]() $\mathrm {preper}(x)>k$
. Then we are in conclusion (B) of Proposition 4.3. Hence,
$\mathrm {preper}(x)>k$
. Then we are in conclusion (B) of Proposition 4.3. Hence,
![]() $[K(f^{(k)}(x)):K]\le [K(x):K]/p$
and
$[K(f^{(k)}(x)):K]\le [K(x):K]/p$
and
![]() $\mathrm {preper}(f^{(k)}(x)) = \mathrm {preper}(x)-k < \mathrm {preper}(x)$
. By induction,
$\mathrm {preper}(f^{(k)}(x)) = \mathrm {preper}(x)-k < \mathrm {preper}(x)$
. By induction,
as desired.
The first inequality in Equation (4.12) is immediate. We prove the second inequality in the case where x is f-periodic first. Indeed, then
![]() $K(f(x))=K(x)$
and so we are again in conclusion (C). Hence,
$K(f(x))=K(x)$
and so we are again in conclusion (C). Hence,
![]() $[K(x):K]\ge \mathrm {per}(x)/(l-k)$
, as desired. If x is f-preperiodic, then Equation (4.12) is applicable to the f-periodic
$[K(x):K]\ge \mathrm {per}(x)/(l-k)$
, as desired. If x is f-preperiodic, then Equation (4.12) is applicable to the f-periodic
![]() $f^{(\mathrm {preper}(x))}(x)$
. We find
$f^{(\mathrm {preper}(x))}(x)$
. We find
![]() $[K(f^{(\mathrm {preper}(x))}(x)):K] \ge {\mathrm {per}(f^{(\mathrm {preper}(x))}(x))}/(l-k)$
. The theorem follows as
$[K(f^{(\mathrm {preper}(x))}(x)):K] \ge {\mathrm {per}(f^{(\mathrm {preper}(x))}(x))}/(l-k)$
. The theorem follows as
![]() $\mathrm {per}(f^{(m)}(x)) = \mathrm {per}(x)$
for all integers
$\mathrm {per}(f^{(m)}(x)) = \mathrm {per}(x)$
for all integers
![]() $m\ge 0$
.
$m\ge 0$
.
Proof of Theorem 1.1.
We suppose
![]() $f^{(l-1)}(0)=0$
with
$f^{(l-1)}(0)=0$
with
![]() $l\ge 2$
. We want to apply Theorem 4.4 to
$l\ge 2$
. We want to apply Theorem 4.4 to
![]() $\mathbb {Q}(c)$
. Indeed, it suffices to verify that hypothesis (i) holds true for
$\mathbb {Q}(c)$
. Indeed, it suffices to verify that hypothesis (i) holds true for
![]() $k=1$
after possibly adjusting l.
$k=1$
after possibly adjusting l.
By Lemma 4.1, the parameter c is an algebraic integer and
![]() $K/\mathbb {Q}$
is unramified above p.
$K/\mathbb {Q}$
is unramified above p.
We write m for the least common multiple of
![]() $l-1$
and all residue degrees of all prime ideals of
$l-1$
and all residue degrees of all prime ideals of
![]() $\mathcal {O}_K$
containing p. So
$\mathcal {O}_K$
containing p. So ![]() for all
for all
![]() $a\in \mathcal {O}_K$
. Moreover,
$a\in \mathcal {O}_K$
. Moreover,
![]() $f^{(l-1)}(0)=0$
implies
$f^{(l-1)}(0)=0$
implies
![]() $f^{(m)}(0)=0$
. Note that
$f^{(m)}(0)=0$
. Note that
![]() $[\mathbb {Q}(c,x):\mathbb {Q}(c)]\le [K(x):K][K:\mathbb {Q}]$
. Theorem 1.1 follows from Theorem 4.4 applied to
$[\mathbb {Q}(c,x):\mathbb {Q}(c)]\le [K(x):K][K:\mathbb {Q}]$
. Theorem 1.1 follows from Theorem 4.4 applied to
![]() $(k,l)=(1,m+1)$
; note
$(k,l)=(1,m+1)$
; note
![]() $\delta =0$
.
$\delta =0$
.
Proof of Corollary 1.3.
In cases (i) and (ii), the extension
![]() $K/\mathbb {Q}$
is unramified above p. As in the proof of Theorem 1.1, there exists
$K/\mathbb {Q}$
is unramified above p. As in the proof of Theorem 1.1, there exists
![]() $l\ge 2$
such that the pair
$l\ge 2$
such that the pair
![]() $(1,l)$
satisfies the hypothesis of Theorem 4.4.
$(1,l)$
satisfies the hypothesis of Theorem 4.4.
To prove (i), we assume that y is f-periodic. Let
![]() $x\in \overline K$
, and suppose
$x\in \overline K$
, and suppose
![]() $n\ge 0$
is minimal with
$n\ge 0$
is minimal with
![]() $f^{(n)}(x)=y$
. We may assume
$f^{(n)}(x)=y$
. We may assume
![]() $n\ge m=\mathrm {per}(y)$
. If
$n\ge m=\mathrm {per}(y)$
. If
![]() $\mathrm {preper}(x) \le n-m$
, then
$\mathrm {preper}(x) \le n-m$
, then
![]() $f^{(n-m)}(x)$
is f-periodic and one among
$f^{(n-m)}(x)$
is f-periodic and one among
![]() $f^{(n-m)}(x),\ldots ,f^{(n-1)}(x)$
must equal y. But this contradicts the minimality of n and so
$f^{(n-m)}(x),\ldots ,f^{(n-1)}(x)$
must equal y. But this contradicts the minimality of n and so
![]() $\mathrm {preper}(x) \ge n-m+1$
. Theorem 4.5 implies
$\mathrm {preper}(x) \ge n-m+1$
. Theorem 4.5 implies
![]() $[K(x):K]\ge p^{\mathrm {preper}(x)-1} \ge p^{n-m}$
. We conclude (i).
$[K(x):K]\ge p^{\mathrm {preper}(x)-1} \ge p^{n-m}$
. We conclude (i).
The proof of part (ii) is very similar. Let
![]() $n\in \mathbb {N}$
, and suppose
$n\in \mathbb {N}$
, and suppose
![]() $x\in \overline K$
satisfies
$x\in \overline K$
satisfies
![]() $f^{(n)}(x)=y$
. We use
$f^{(n)}(x)=y$
. We use
![]() $1\le \mathrm {preper}(y)=\mathrm {preper}(f^{(n)}(x)) = \max \{0,\mathrm {preper}(x)-n\}$
to infer
$1\le \mathrm {preper}(y)=\mathrm {preper}(f^{(n)}(x)) = \max \{0,\mathrm {preper}(x)-n\}$
to infer
![]() $\mathrm {preper}(x)=n+\mathrm {preper}(y)\ge n+1$
. Theorem 4.5 implies
$\mathrm {preper}(x)=n+\mathrm {preper}(y)\ge n+1$
. Theorem 4.5 implies
![]() $[K(x):K]\ge p^{\mathrm {preper}(x)-1} \ge p^n$
. But
$[K(x):K]\ge p^{\mathrm {preper}(x)-1} \ge p^n$
. But
![]() $[K(x):K]\le \deg (f^{(n)}-y)=p^n$
, so part (ii) follows.
$[K(x):K]\le \deg (f^{(n)}-y)=p^n$
, so part (ii) follows.
For part (iii), we no longer restrict the ramification of
![]() $K/\mathbb {Q}$
. But we assume that y is f-wandering. Note that c is an algebraic integer by Lemma 4.1(i). Let again
$K/\mathbb {Q}$
. But we assume that y is f-wandering. Note that c is an algebraic integer by Lemma 4.1(i). Let again
![]() $f^{(n)}(x)=y$
.
$f^{(n)}(x)=y$
.
We first suppose that y is an algebraic integer. Then x is also an algebraic integer. Then
![]() $\lambda _f^{\mathrm {max}}(x) \ge \kappa _1/[K(x):K]$
by Theorem 1.1(i). The functional equation of the local canonical height implies
$\lambda _f^{\mathrm {max}}(x) \ge \kappa _1/[K(x):K]$
by Theorem 1.1(i). The functional equation of the local canonical height implies
![]() $\lambda _f^{\mathrm {max}}(x) = \lambda _f^{\mathrm {max}}(y)/p^n$
. We combine and rearrange to find
$\lambda _f^{\mathrm {max}}(x) = \lambda _f^{\mathrm {max}}(y)/p^n$
. We combine and rearrange to find
![]() $[K(x):K]\lambda _f^{\mathrm {max}}(y) \ge \kappa _1p^n$
. So
$[K(x):K]\lambda _f^{\mathrm {max}}(y) \ge \kappa _1p^n$
. So
![]() $\lambda _f^{\mathrm {max}}(y)>0$
and
$\lambda _f^{\mathrm {max}}(y)>0$
and
![]() $[K(x):K]\ge \kappa p^n$
with
$[K(x):K]\ge \kappa p^n$
with
![]() $\kappa = \kappa _1/\lambda _f^{\mathrm {max}}(y)$
.
$\kappa = \kappa _1/\lambda _f^{\mathrm {max}}(y)$
.
Second, suppose that y is not an algebraic integer. Then there exists a prime number v and a field embedding
![]() $\sigma \in \mathrm {Hom}( K,\mathbb {C}_v)$
with
$\sigma \in \mathrm {Hom}( K,\mathbb {C}_v)$
with
![]() $|\sigma (y)|_v>1$
. The ultrametric triangle inequality implies
$|\sigma (y)|_v>1$
. The ultrametric triangle inequality implies
![]() $|\sigma (x)|_v>1$
and
$|\sigma (x)|_v>1$
and
![]() $|\sigma (y)|_v=|\sigma (f^{(n)}(x))|_v = |\sigma (x)|_v^{p^n}$
. So the ramification index of
$|\sigma (y)|_v=|\sigma (f^{(n)}(x))|_v = |\sigma (x)|_v^{p^n}$
. So the ramification index of
![]() $K(x)/K$
at some prime ideal above v grows like a positive multiple of
$K(x)/K$
at some prime ideal above v grows like a positive multiple of
![]() $p^n$
. In particular,
$p^n$
. In particular,
![]() $[K(x):K]\ge \kappa p^n$
for all
$[K(x):K]\ge \kappa p^n$
for all
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
![]() $\kappa>0$
is independent of n.
$\kappa>0$
is independent of n.
Proof of Corollary 1.4.
We will apply Proposition 4.3 to
![]() $p=2,K=\mathbb {Q},$
and
$p=2,K=\mathbb {Q},$
and
![]() $f=T^2-1$
.
$f=T^2-1$
.
Observe that
![]() $0=f^{(2)}(0)$
. As
$0=f^{(2)}(0)$
. As ![]() for all
for all
![]() $a\in \mathbb {Z}$
, we see that
$a\in \mathbb {Z}$
, we see that
![]() $(k,l)=(1,3)$
satisfies hypothesis (i) of Proposition 4.3; here,
$(k,l)=(1,3)$
satisfies hypothesis (i) of Proposition 4.3; here,
![]() $\delta =0$
. Note that
$\delta =0$
. Note that
![]() $\mathrm {PCO}^{+}(f) =\{-1,0\}$
. The single quill
$\mathrm {PCO}^{+}(f) =\{-1,0\}$
. The single quill
![]() $[-1,0]$
suffices to cover
$[-1,0]$
suffices to cover
![]() $\mathrm {PCO}_n^{+}(f)$
for all
$\mathrm {PCO}_n^{+}(f)$
for all
![]() $n\in \mathbb {N}$
. Moreover, the root r from Lemma 3.5 applied to
$n\in \mathbb {N}$
. Moreover, the root r from Lemma 3.5 applied to
![]() $d=2$
and
$d=2$
and
![]() $c=-1$
is the golden ratio
$c=-1$
is the golden ratio
![]() $(1+\sqrt 5)/2$
. So
$(1+\sqrt 5)/2$
. So
![]() $\mathsf {C}(T^2-1)\le (1+\sqrt 5)/2$
by Lemma 3.6.
$\mathsf {C}(T^2-1)\le (1+\sqrt 5)/2$
by Lemma 3.6.
Let x be as in (i). The proof of part (i) is by induction on
![]() $[\mathbb {Q}(x):\mathbb {Q}]$
. We fix
$[\mathbb {Q}(x):\mathbb {Q}]$
. We fix
![]() $n\in \mathbb {N}$
to be minimal with
$n\in \mathbb {N}$
to be minimal with
![]() $2^n \ge 3[\mathbb {Q}(x):\mathbb {Q}]$
, so
$2^n \ge 3[\mathbb {Q}(x):\mathbb {Q}]$
, so
![]() $2^{n-1}< 3[\mathbb {Q}(x):\mathbb {Q}]$
.
$2^{n-1}< 3[\mathbb {Q}(x):\mathbb {Q}]$
.
Observe that the f-wandering point x is in conclusion (A) or (B) of Proposition 4.3. If
![]() $x\in \mathbb {Q}$
, then we must be in conclusion (A).
$x\in \mathbb {Q}$
, then we must be in conclusion (A).
Conclusion (A) implies
 $$ \begin{align*} \lambda_f^{\mathrm{max}}(x) &\ge \frac{1}{2^{3+n}} \left(\frac{\log 4}{1+2[\mathbb{Q}(x):\mathbb{Q}]2^{-n}} - \log \frac{\sqrt 5+1}{2}\right) \ge \frac{1}{2^{3+n}}\log\left(\frac{4^{3/5}\cdot 2}{\sqrt 5+1}\right) \\ &\ge \frac{1}{48}\log\left(\frac{4^{3/5}\cdot 2}{\sqrt 5+1}\right)\frac{1}{[\mathbb{Q}(x):\mathbb{Q}]}. \end{align*} $$
$$ \begin{align*} \lambda_f^{\mathrm{max}}(x) &\ge \frac{1}{2^{3+n}} \left(\frac{\log 4}{1+2[\mathbb{Q}(x):\mathbb{Q}]2^{-n}} - \log \frac{\sqrt 5+1}{2}\right) \ge \frac{1}{2^{3+n}}\log\left(\frac{4^{3/5}\cdot 2}{\sqrt 5+1}\right) \\ &\ge \frac{1}{48}\log\left(\frac{4^{3/5}\cdot 2}{\sqrt 5+1}\right)\frac{1}{[\mathbb{Q}(x):\mathbb{Q}]}. \end{align*} $$
Part (i) follows in this case and in particular if
![]() $x\in \mathbb {Q}$
; which is the base case.
$x\in \mathbb {Q}$
; which is the base case.
In conclusion (B), we have
![]() $[\mathbb {Q}(f(x)):\mathbb {Q}]\le [\mathbb {Q}(x):\mathbb {Q}]/2$
. Part (i) follows by induction on
$[\mathbb {Q}(f(x)):\mathbb {Q}]\le [\mathbb {Q}(x):\mathbb {Q}]/2$
. Part (i) follows by induction on
![]() $[\mathbb {Q}(x):\mathbb {Q}]$
and since
$[\mathbb {Q}(x):\mathbb {Q}]$
and since
![]() $\lambda _f^{\mathrm {max}}(f(x))=2\lambda _f^{\mathrm {max}}(x)$
.
$\lambda _f^{\mathrm {max}}(f(x))=2\lambda _f^{\mathrm {max}}(x)$
.
The estimate in part (ii) follows from part (i) in the integral case. In the nonintegral case, we use the same argument as in the proof of Theorem 4.4(ii) and conclude using
![]() $\log 2> \log (4^{11/10}/(\sqrt 5+1))/48$
.
$\log 2> \log (4^{11/10}/(\sqrt 5+1))/48$
.
Proof of Corollary 1.5.
As in the proof of Corollary 1.4, we set
![]() $K=\mathbb {Q}$
and
$K=\mathbb {Q}$
and
![]() $(k,l)=(1,3)$
. The single quill
$(k,l)=(1,3)$
. The single quill
![]() $[-1,0]$
covers
$[-1,0]$
covers
![]() $\mathrm {PCO}^{+}(T^2-1)$
and we have
$\mathrm {PCO}^{+}(T^2-1)$
and we have
![]() $\mathsf {C}(T^2-1)\le (1+\sqrt {5})/2$
. The numerical condition in the quill hypothesis follows as
$\mathsf {C}(T^2-1)\le (1+\sqrt {5})/2$
. The numerical condition in the quill hypothesis follows as
![]() $(1+\sqrt 5)/2<4$
. The corollary follows from Theorem 4.5.
$(1+\sqrt 5)/2<4$
. The corollary follows from Theorem 4.5.
Acknowledgements
We thank Vesselin Dimitrov for suggesting to the second-named author to investigate the dynamical Schinzel–Zassenhaus for
![]() $f=T^2-1$
. The authors thank Holly Krieger for comments on a draft of this text and Tom Tucker for pointing out a mistake in an earlier version of Corollary 1.3.
$f=T^2-1$
. The authors thank Holly Krieger for comments on a draft of this text and Tom Tucker for pointing out a mistake in an earlier version of Corollary 1.3.
Competing interest
The authors have no competing interest to declare.
Financial support
The first-named author received funding from the Swiss National Science Foundation project n
![]() $^\circ $
200020_184623.
$^\circ $
200020_184623.