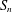Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-17T03:23:41.074Z Has data issue: false hasContentIssue false
  • English
  • Français

LOW-DEGREE BOOLEAN FUNCTIONS ON $S_{n}$, WITH AN APPLICATION TO ISOPERIMETRY

Part of: Extremal combinatorics

Published online by Cambridge University Press:  03 October 2017

DAVID ELLIS ,
YUVAL FILMUS  and
EHUD FRIEDGUT
DAVID ELLIS
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, Mile End Road, London E1 4NS, UK; [email protected]
YUVAL FILMUS
Affiliation:
Computer Science Department, Technion – Israel Institute of Technology, Technion City, Haifa 3200003, Israel; [email protected]
EHUD FRIEDGUT
Affiliation:
Faculty of Mathematics and Computer Science, Weizmann Institute of Science, Rehovot 76100, Israel; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that Boolean functions on 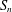$S_{n}$, whose Fourier transform is highly concentrated on irreducible representations indexed by partitions of $n$ whose largest part has size at least 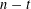$n-t$, are close to being unions of cosets of stabilizers of $t$-tuples. We also obtain an edge-isoperimetric inequality for the transposition graph on 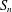$S_{n}$ which is asymptotically sharp for subsets of 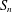$S_{n}$ of size 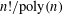$n!/\text{poly}(n)$, using eigenvalue techniques. We then combine these two results to obtain a sharp edge-isoperimetric inequality for subsets of 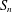$S_{n}$ of size 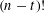$(n-t)!$, where $n$ is large compared to $t$, confirming a conjecture of Ben Efraim in these cases.

MSC classification

Primary: 05D05: Extremal set theory
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e23
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Alon, N. and Milman, V. D., ‘𝜆1 , isoperimetric inequalities for graphs, and superconcentrators’, J. Combin. Theory B 38 (1985), 73–88.Google Scholar
Ben Efraim, L., personal communication.Google Scholar
Bernstein, A. J., ‘Maximally connected arrays on the n-cube’, SIAM J. Appl. Math. 15 (1967), 1485–1489.Google Scholar
Bourgain, J., ‘On the distribution of the Fourier spectrum of Boolean functions’, Israel J. Math. 131 (2002), 269–276.Google Scholar
Cameron, P. J. and Ku, C. Y., ‘Intersecting families of permutations’, European J. Combin. 24 (2003), 881–890.CrossRefGoogle Scholar
Deza, M. and Frankl, P., ‘On the maximum number of permutations with given maximal or minimal distance’, J. Combin. Theory A 22 (1977), 352–360.Google Scholar
Diaconis, P. and Shahshahani, M., ‘Generating a random permutation with random transpositions’, Z. Wahrsch. Verw. Gebeite 57 (1981), 159–179.Google Scholar
Dinur, I., Knot, S., Kindler, G., Minzer, D. and Safra, M., On non-optimally expanding sets in Grassmann graphs, Electronic Colloquium on Computational Complexity (2017), Report No. 94. Preprint available at https://eccc.weizmann.ac.il/report/2017/094/.Google Scholar
Dodziuk, J., ‘Difference equations, isoperimetric inequality and transience of certain random walks’, Trans. Amer. Math. Soc. 284 (1984), 787–794.CrossRefGoogle Scholar
Ellis, D., ‘Stability for t-intersecting families of permutations’, J. Combin. Theory A 118 (2011), 208–227.Google Scholar
Ellis, D., ‘A proof of the Cameron–Ku conjecture’, J. Lond. Math. Soc. (2) 85 (2012), 165–190.Google Scholar
Ellis, D., Friedgut, E. and Filmus, Y., ‘A quasi-stability result for dictatorships in S n ’, Combinatorica 35 (2015), 573–618.Google Scholar
Ellis, D., Friedgut, E. and Filmus, Y., ‘A stability result for balanced dictatorships in S n ’, Random Structures Algorithms 46 (2015), 494–530.Google Scholar
Ellis, D., Friedgut, E. and Pilpel, H., ‘Intersecting families of permutations’, J. Amer. Math. Soc. 24 (2011), 649–682.Google Scholar
Filmus, Y., ‘A comment on ‘Intersecting families of permutations’, Preprint, 2017,arXiv:1706.10146.Google Scholar
Friedgut, E., Kalai, G. and Naor, A., ‘Boolean functions whose Fourier transform is concentrated on the first two levels’, Adv. Appl. Math. 29 (2002), 427–437.CrossRefGoogle Scholar
Friedgut, E., ‘Hypergraphs, entropy and inequalities’, Amer. Math. Monthly 111 (2004), 749–760.CrossRefGoogle Scholar
Harper, L. H., ‘Optimal assignments of numbers to vertices’, SIAM J. Appl. Math. 12 (1964), 131–135.CrossRefGoogle Scholar
Hart, S., ‘A note on the edges of the n-cube’, Discrete Math. 14 (1976), 157–163.Google Scholar
James, G. and Kerber, A., The Representation Theory of the Symmetric Group, Encyclopedia of Mathematics and its Applications, 16 (Cambridge University Press, Cambridge, 1985).Google Scholar
Kindler, G. and Safra, S., ‘Noise resistant Boolean functions are juntas’, Preprint, http://www.cs.huji.ac.il/∼gkindler/papers/noise-stable-r-juntas.ps.Google Scholar
Lindsey, J. H. II, ‘Assignment of numbers to vertices’, Amer. Math. Monthly 71 (1964), 508–516.CrossRefGoogle Scholar
Sagan, B. E., The Symmetric Group: Representations, Combinatorial Algorithms and Symmetric Functions (Springer, New York, 1991), 2nd revised printing, 2001.Google Scholar
Serre, J.-P., Linear Representations of Finite Groups, Graduate Texts in Mathematics, 42 (Springer, New York, 1977).Google Scholar
Tal, A., ‘Properties and applications of Boolean function composition’, inProceedings of the 4th Conference on Innovations in Theoretical Computer Science, ITCS 2013 (ACM, New York, 2013), 441–454.Google Scholar